УЗБЕКСКОЕ АГЕНТСТВО СВЯЗИ И ИНФОРМАТИЗАЦИИ
ТАШКЕНТСКИЙ УНИВЕРСИТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ
Кафедра АФУ
МЕТОДИЧЕСКОЕ РУКОВОДСТВО
К ЛАБОРАТОРНЫМ РАБОТАМ № 1,2
«ИССЛЕДОВАНИЕ РЕЖИМОВ РАБОТЫ ПРЯМОУГОЛЬНОГО
И КОАКСИАЛЬНОГО ВОЛНОВОДОВ»
по дисциплинам «Электромагнитные поля и волны»
и «Электродинамика и распространение радиоволн»
для студентов очного и заочного обучения
и направлений подготовки «Телевидение,
радиосвязь и радиовещание», «Радиотехника» и
«Телекоммуникации»
Ташкент 2004
1. ЦЕЛЬ РАБОТЫ
В результате выполнения лабораторной работы студенты должны приобрести знания особенностей распространения электромагнитных волн в прямоугольном и коаксиальном волноводах, устройства волноводных измерительных линий, умения в настройке линий передач в режиме бегущей волны, количественном определении степени согласования линии с нагрузкой и величины самой нагрузки, и настройке измерительной линии.
2. КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
2.1. Волны в направляющих системах
В дециметровом и сантиметровом диапазонах, в основном, используются линии передачи закрытого типа, в которых вся энергия сосредоточена в пространстве, экранированном от внешней среды металлической оболочкой.
Основными, широко используемыми линиями передачи закрытого типа, являются коаксиальный волновод (состоящий из соосных круглых провода и экрана), прямоугольный, круглый и эллиптический волноводы.
В направляющих системах могут распространяться волны класса Т (поперечные электромагнитные волны), волны класса Н (поперечно-электрические или магнитные волны), волны класса Е (поперечно-магнитные или электрические волны). Необходимо отметить, что волны класса Т могут распространяться только в тех направляющих системах, в которых имеются два изолированных друг от друга проводника, по которым возможна передача энергии постоянного тока.
В любой направляющей системе возможно существование большого числа типов волн (из классов Е и Н), количество которых зависит от выбора рабочей длины волны lр. Однако существует область длин волн, при которой распространение электромагнитных волн в волноводе невозможно (область отсечки), то есть когда рабочая длина волны lр больше или равна критической длине волны основного типа волны lкр (lр ³ lкр). Основным типом волны в волноводе называется волна, обладающая максимальной критической длиной волны. С учётом относительной диэлектрической проницаемости материала, заполняющего волновод, рабочая длина волны должна выбираться из условия
![]()
где l - длина волны генератора (длина волны в свободном пространстве).
В воздухе e = 1 и lр = l.
На рис.2.1 и 2.2 приведены картины мгновенного распределения электрического и магнитного полей (в продольном и поперечном сечениях) для основных типов волн Н10 и Н11 в прямоугольном и круглом волноводах, а на рис.2.3 – для волны класса Т в коаксиальном волноводе. Крестиками на этих рисунках показаны силовые линии, идущие «от нас», а кружочками – идущие «к нам».
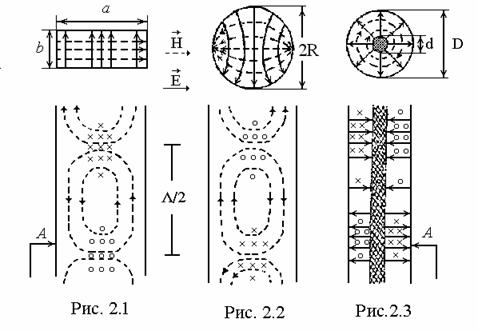
Значения волнового сопротивления Zв, фазовой vф и групповой vгр скоростей и длины волны L в волноводе в одноволновом режиме можно рассчитать по формулам:


где с – скорость света в вакууме;
a – внутренний размер широкой стенки прямоугольного волновода;
b – внутренний размер узкой стенки прямоугольного волновода;
D – диаметр оплётки коаксиального кабеля;
d – диаметр центральной жилы коаксиального кабеля.
То, что длина волны в прямоугольном волноводе L больше длины волны в свободном пространстве l, имеет простое физическое объяснение. Так как электромагнитные волны, распространяясь в волноводе, отражаются от его стенок (как показано на рис.2.4), то фронт волны, проходя расстояние lр вдоль направления распространения волны, одновременно пройдёт вдоль волновода расстояние, равное L.

2.2. Выбор рабочей длины волны (частоты) для создания одноволнового режима
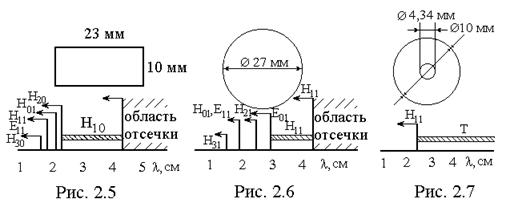
Для наглядности на рис.2.5…2.7 приведены распределения критических длин волн по шкале lр для прямоугольного, круглого и коаксиального волноводов. В случае одноволнового (одномодового) режима по волноводу распространяется основная волна. Как видно из рис.2.5, основной волной для прямоугольного волновода является волна Н10 с критической длиной волны lкрН10=2а. Первая волна высшего порядка в прямоугольном волноводе – волна Н20 с lкрН20=а. Следовательно, одноволновый режим будет наблюдаться при выполнении условия
a < l < 2a. (2.10)
Для круглого волновода (рис.2.6) основной волной является волна Н11 (lкрН11= 3,41R), а первой волной высшего порядка – Е01 (lкрЕ01=2,62R), таким образом, одноволновый режим будет выполняться при условии
2,62R<lр<3,41R. (2.11)
В коаксиальном волноводе (рис.2.7) основной волной является волна класса Т (lкрТ=¥), а первой волной высшего порядка – волна Н11 с lкрН11»p(D+d)/2, т.е. одноволновый режим будет выполняться при условии
p(D+d)/2< lр < ¥. (2.12)
На практике, обычно, из-за большого поглощения в области более длинных волн, т.е. близких к критической длине волны основного типа, значение рабочей длины волны выбирают на 20…30% ниже критической длины волны.
2.3. Виды амплитудных распределений в волноводе
Рассмотрим влияние характера нагрузки, установленной на конце волновода, на амплитудное распределение вдоль волновода. Вдоль оси волновода, с одноволновым режимом формируется распределение поля, аналогичное распределению поля в обычной двухпроводной линии, которая работает в режиме длинной линии.
Если на конце волновода установлена короткозамыкающая нагрузка, то возникает отраженная волна, сдвинутая по фазе на 180° относительно падающей волны. Амплитуда отраженной волны равна амплитуде падающей волны. В результате наложения этих двух волн возникает стоячая волна (режим стоячей волны). Амплитудное распределение в режиме стоячей волны показано на рис.2.8 сплошной линией. Расстояние между двумя соседними минимумами напряженности поля равно половине длины волны в волноводе. При замене короткозамыкающей нагрузки на согласованную, равную по величине характеристическому сопротивлению волновода, отражённой от нагрузки волны не будет и в волноводе установится режим бегущей волны, при котором амплитудное распределение будет характеризоваться постоянным значением амплитуды распределения поля (пунктирная линия на рис.2.8).

В тех случаях, когда от сопротивления нагрузки отражается часть падающей волны, в волноводе устанавливается смешанный режим, амплитудное распределение которого показано на рис.2.9. Амплитудное распределение в волноводе удобно характеризовать значением коэффициента бегущей волны КБВ=Еmin/Emax.

2.4. Конструкция волноводных измерительных линий
Для регистрации амплитудного распределения в волноводах используются волноводные измерительные линии. Конструкции этих линий, выполненные на отрезках прямоугольного и коаксиального волноводов, показаны на рис.2.10 и рис.2.11. Отличие измерительных линий состоит в разнице конструкций направляющих систем, вдоль которых перемещается измерительная головка с зондом, принцип действия которой и конструкция одинаковы для обеих измерительных линий.
Измерительная головка представляет собой объемный резонатор с короткозамыкающим поршнем, служащим для настройки объемного резонатора, с СВЧ диодом. Зонд располагается вдоль силовых линий электрического поля в волноводе. Электродвижущая сила (ЭДС), возникающая в зонде, пропорциональна напряженности поля в месте расположения зонда.
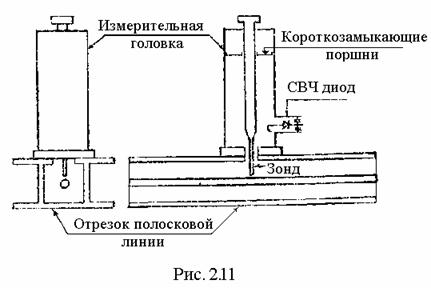
Эта ЭДС возбуждает объемный резонатор, создавая в нем электромагнитные колебания. Резонатор настраивается на частоту колебаний в направляющей системе, что приводит к максимальному усилению сигнала на выходе резонатора. С объемным резонатором связан кристаллический СВЧ диод, играющий роль преобразователя СВЧ колебаний в низкую частоту модуляции генератора. По принципу действия объемный резонатор схож с обычным колебательным контуром на более низких частотах.
Перемещая зонд вдоль волновода, можно найти распределение амплитуд напряженности поля и длину волны в волноводе. Регистрация амплитудного распределения производится при помощи микроамперметра, подключенного к СВЧ диоду. Ввиду того, что характеристика СВЧ диода квадратична, при определении значений КБВ, необходимо взять корень из показаний микроамперметра (amin и amax)

Иногда на практике используется коэффициент стоячей волны

Коэффициент бегущей волны связан с модулем коэффициента отражения |Г| соотношениями:

2.5. Виды нагрузочных сопротивлений
В настоящей лабораторной работе используются следующие виды нагрузок: согласованная нагрузка, короткозамыкающая нагрузка и реактивная нагрузка. Согласованная нагрузка представляет собой отрезок волновода, в котором находится вставка из смеси порошкового железа с полистиролом, поглощающая электромагнитную энергию волны. Реактивная нагрузка представляет собой отрезок волновода, вдоль которого перемещается короткозамыкаюший поршень. Амплитудное распределение, получаемое при реактивной нагрузке, сходно с амплитудным распределением при короткозамыкающей нагрузке, однако минимумы напряженности поля этих распределений смещены на величину Dz. Иногда на практике встречаются произвольные нагрузки, характеризуемые активным и реактивным сопротивлениями.
2.6. Расчет сопротивления нагрузки с помощью круговой
диаграммы полных сопротивлений (диаграммы Вольперта)
Круговая диаграмма полных сопротивлений устанавливает взаимную связь между составляющими полного сопротивления нагрузки, нормированных к волновому сопротивлению волновода (RH/Zв, XH/Zв), и модулем и фазой коэффициента отражения |ГН| и jН. Вместо значений |ГН| можно использовать значения коэффициента бегущей волны КБВ или коэффициента стоячей волны КСВ, т.к. они связаны между собой.
Приведенные вместе на одном рисунке, окружности RH/Zв=const (рис. 2.12) и окружности XH/Zв=const (рис. 2.13), образуют круговую диаграмму полных сопротивлений в полярной системе координат. Каждая точка этой круговой диаграммы соответствует нормированному комплексному сопротивлению.
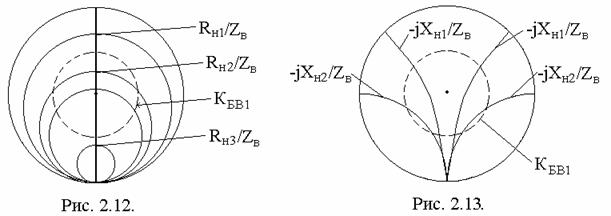
Центры окружностей постоянных значений активного нормированного сопротивления лежат на прямой, которая является осью симметрии круговой диаграммы. На этой оси нанесены значения активных нормированных сопротивлений от нуля до бесконечности. Значения КБВ совпадают на этой оси со значениями нормированного активного сопротивления от 0 до 1, а значения КСВ совпадают со значениями нормированного активного сопротивления на этой оси от 1 до бесконечности.
Центры окружностей постоянных значений нормированного реактивного сопротивления лежат на прямой, перпендикулярной оси симметрии круговой диаграммы и находятся вне диаграммы. Значения реактивных сопротивлений нанесены на внешней окружности, центр которой находится на оси диаграммы в точке RH/Zв=1. Две внешние окружности круговой диаграммы отградуированы в относительных сдвигах волн Dz/l=(zmin-zminКЗ)/l к генератору и к нагрузке (за точку отсчета берется координата узла zminКЗ при короткозамыкающей нагрузке).
Значения нормированных реактивных сопротивлений в правой части круговой диаграммы имеют индуктивный, а в левой части – емкостной характер. На круговой диаграмме может быть укреплена прозрачная линейка, вращающаяся относительно центра диаграммы. На линейке могут быть нанесены деления, соответствующие значениям КБВ, |Г| или КСВ.
Исходными данными для определения нормированного значения сопротивления нагрузки являются величина нормированного сдвига Dz/l, значение КБВ (КСВ или |ГН|). Сначала определяется величина нормированного сдвига Dz/l=(zmin-zminКЗ)/l, причем за положительное направление принимается такое, при котором координата минимума амплитудного распределения zmin ближе к генератору, чем координата узла при коротком замыкании.

Найдя значение нормированного сдвига волны Dz/l к генератору (к нагрузке), необходимо отложить это значение на внешней окружности круговой диаграммы и соединить эту точку воображаемой прямой линией (прозрачной линейкой) с центром диаграммы (RH/Zв=1). Далее необходимо провести окружность с радиусом, равным значению КБВ в волноводе. Центр этой окружности также находится в центре круговой диаграммы. Точка пересечения, проведенной прямой линии и окружности КБВ, обладает комплексным нормированным сопротивлением. Значение активной составляющий этого сопротивления определяется путем переноса этой точки по линиям окружности активного сопротивления (или параллельно ей) на ось симметрии круговой диаграммы, где отложены значения RH/ZB, а значение реактивного сопротивления – путем переноса точки пересечения по линии окружности реактивного сопротивления (или параллельно ей) на внутреннюю окружность круговой диаграммы (см. рис.2.14, 2.15).
Пример 1: Dz/l (к генератору)=0,112; КБВ=0,33; ZH/ZB=0,5+i0,7.
Пример 2: Dz/l (к нагрузке)=0,188; КБВ=0,33; ZH/ZB=1,4–il,4.
Полное комплексное сопротивление нагрузки определяется путем перемножения комплексного нормированного сопротивления на волновое сопротивление направляющей системы ZВ.
Значение ZB для коаксиального волновода равно 50 Ом, а для прямоугольного волновода ZB можно рассчитать по формуле (2.2).
Рис. 2.15. Круговая диаграмма полных сопротивлений
3. ЗАДАНИЕ К РАБОТЕ
3.1. Изучить устройство, принцип действия волноводной измерительной линии.
3.2. Рассчитать и установить одноволновый режим в волноводе.
3.3. Снять амплитудное распределение поля в волноводе при различных нагрузках. Определить значения длины волны и коэффициент бегущей волны (КБВ) в линии.
3.4. По экспериментальным данным определить характер и величину сопротивления нагрузки. Сравнить расчётные и полученные с помощью диаграммы Вольперта значения сопротивления нагрузки.
3.5. Рассчитать значения длин волн в прямоугольном волноводе при поочередном заполнении его различными видами диэлектриков.
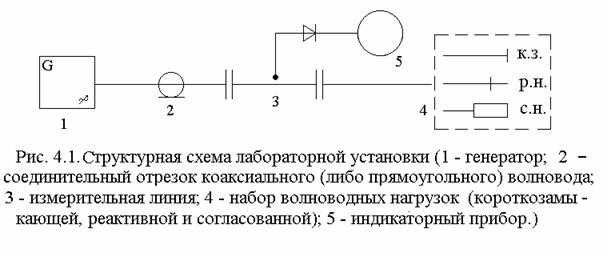
4. СТРУКТУРНАЯ СХЕМА ЛАБОРАТОРНОЙ УСТАНОВКИ
Установка позволяет определить вид амплитудного распределения поля вдоль волновода, длину волны в волноводе и комплексное сопротивление нагрузки. Структурная схема установки приведена на рис.4.1.
5. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
5.1. Расчётная часть к первому заданию
5.1.1. Рассчитать по размерам поперечного сечения волновода верхнюю lв и нижнюю lн границы одноволнового режима и соответствующие им частоты fв и fн.
5.1.2. Определить среднюю длину волны l=(lв+lн)/2 и частоту f=(fв+fн)/2 одноволнового режима.
5.1.3. Выбрать два значения частоты генератора f1, f2 (но не на краях диапазона) для создания одноволнового режима в волноводе.
5.1.4. Рассчитать значения длин волн в волноводе L1, L2 с воздушным заполнением, соответствующие частотам f1, f2.
5.2. Порядок проведения эксперимента на первом занятии
Построение амплитудных распределений при короткозамыкающей и согласованной нагрузках. Измерение длины волны в волноводе
5.2.1. Включить генератор и дать ему прогреться в течение 10…15 минут.
5.2.2. Установить в волноводе режим стоячей волны, для чего к выходу измерительной линии подключить короткозамыкающую нагрузку.
5.2.3. Настроить измерительную линию на частоту генератора при помощи перемещения короткозамыкающих поршней в измерительной головке линии, добиваясь максимального показания индикаторного прибора. При отсутствии показаний индикаторного прибора изменить местоположение головки на измерительной линии и настройку повторить.
5.2.4. Перемещая головку вдоль измерительной линии (изменяя координату z), снять амплитудное распределение поля в волноводе a=j(z), то есть зависимость показаний индикаторного прибора a от расстояния z.
5.2.5. Изменяя частоту генератора f1 на f2, повторить операции 5.2.3 и 5.2.4. Результаты измерений занести в таблицу типа табл. 5.1.
Таблица 5.1
Результаты экспериментального определения вида амплитудного распределения при ……………… нагрузке
|
|
|
min |
|
|
max |
|
|
min |
|
|
max |
|
|
|
a, мкА |
|
|
|
|
|
|
|
|
|
|
|
|
f1=… МГц |
|
z, мм |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a, мкА |
|
|
|
|
|
|
|
|
|
|
|
|
f2=… МГц |
|
z, мм |
|
|
|
|
|
|
|
|
|
|
|
|
5.2.6. По результатам измерений построить графики амплитудного распределения поля в волноводе a=j(z).
5.2.7. Определить экспериментально значения длин волн в волноводе L1, L2 и сравнить их с рассчитанными значениями.
5.2.8. Установить на выходе измерительной линии согласованную нагрузку вместо короткозамыкающей нагрузки и снять амплитудное распределение аналогично пункту 5.2.4. Результаты измерений занести в таблицу типа табл. 5.1 и построить график амплитудного распределения.
5.2.9. Сделать выводы.
5.3. Расчётная часть ко второму занятию
5.3.1. Рассчитать значение волнового сопротивления волновода с воздушным заполнением.
5.3.2. Для частоты, заданной преподавателем, рассчитать значения длин волн в прямоугольном волноводе с различным диэлектрическим заполнением. Значения относительных диэлектрических проницаемостей e применяемых диэлектриков приведены в табл. 5.2.
Таблица 5.2
Значения относительных диэлектрических проницаемостей диэлектриков
|
№ диэл. вставки |
Материал диэлектрической вставки |
e |
|
1 |
Полистирол |
2,56 |
|
2 |
Полиэтилен |
2,25 |
|
3 |
Фторопласт |
2,08 |
|
4 |
Плексиглас |
2,59 |
|
5 |
Бакелит |
3,68 |
|
6 |
Тефлон |
2,08 |
5.4. Порядок проведения эксперимента на втором занятии
Измерение и расчёт значений нормированного сдвига и коэффициента бегущей волны, необходимых для определения полного сопротивления нагрузки
5.4.1. Для частоты f2 определить координаты всех узлов амплитудного распределения в режиме стоячей волны. Данный пункт выполняется, если после выполнения пунктов 5.2.1…5.2.4 генератор выключался.
5.4.2. Определить длину волны L в волноводе.
5.4.3. Подключить к выходу измерительной линии реактивную нагрузку, предварительно отключив короткозамыкающую или согласованную нагрузку.
5.4.4. Определить координаты узлов zmin р.н. амплитудного распределения в волноводе для трёх положений L короткозамыкающего поршня.
5.4.5. Определить значения КБВ в волноводе при короткозамыкающей и реактивной нагрузках.
5.4.6. Определить величину и направление сдвига Dz – расстояния между ближайшим узлами амплитудных распределений при реактивной и короткозамыкающей нагрузках (для трёх положений короткозамыкающего поршня L). Направление сдвига определяется относительно координаты узла при коротком замыкании.
5.4.7. Отнормировать значения Dz к длине волны L в волноводе.
5.4.8. Результаты измерений и расчётов занести в таблицу типа табл. 5.3.
Таблица 5.3
Результаты экспериментального исследования
L |
10 (15) |
20 (25) |
30 (35) |
|
zmin КЗ |
|
|
|
|
zmin |
|
|
|
|
Dz |
|
|
|
|
Dz/L |
|
|
|
|
КБВ |
|
|
|
5.5 Определение полного сопротивления нагрузки
5.5.1. По известным значениям Dz/L и КБВ с помощью диаграммы полных сопротивлений (диаграммы Вольперта) определить нормированные значения составляющих комплексного сопротивления нагрузки. Методика определения приведена в разделе 2 описания настоящей лабораторной работы.
5.5.2. Определить значение комплексного сопротивления волноводной нагрузки.
5.5.3. Сделать выводы.
6. СОДЕРЖАНИЕ ОТЧЁТА
Отчёт должен содержать:
6.1. Структурную схему лабораторной установки.
6.2. Расчёт диапазона частот одноволнового режима.
6.3. Результаты расчёта длин волн в волноводе.
6.4. Амплитудные распределения поля в волноводе в виде таблиц и графиков.
6.5. Результаты определения комплексного сопротивления нагрузки.
7. КОНТРОЛЬНЫЕ ВОПРОСЫ
7.1. Нарисуйте коаксиальную линию, прямоугольный и круглый волноводы ([1] §13.1, [2] §3.1, §4.1, §5.1, [3] §19.1, §19.11, §19.19).
7.2. По какому признаку классифицируются направляемые электромагнитные волны? Какие направляемые электромагнитные волны называются поперечными (Т), какие – электрическими (Е), а какие – магнитными (Н)? ([1] §13.2, [2] §2.7, [3] §17.3).
7.3. Какие классы направляемых электромагнитных волн могут существовать в коаксиальной линии, а какие – в волноводах? ([1] §13.5, [3] §17.3).
7.4. Что называется длиной волны? ([1] §13.4, [3] §18.2).
7.5. Что называется критической частотой (или критической длиной волны) направляющей системы? При каком соотношении рабочей частоты (рабочей длины волны) и критической частоты (критической длины волны) волна определённого типа будет распространяться по волноводу? ([1] §13.4, [2] §2.4, §3.7, [3] §18.2).
7.6. Напишите выражение для длины волны в волноводе ([1] §13.4, [3] §18.2).
7.7. Какая волна называется основной (низшей) волной направляющей системы? ([1] §14.1, §14.2, §14.4, [2] §2.7, [3] §18.8)
7.8. Нарисуйте график распределения напряжённости электрического поля вдоль прямоугольного (коаксиального) волновода при следующих видах нагрузок: короткое замыкание; согласованная нагрузка; комплексная нагрузка ([1] §16.1, §16.2, [2] §7.1, [3] §21.2).
7.9. Объясните принцип действия измерительной линии ([2] §8.7).
7.10. Объясните смысл коэффициентов КБВ, КСВ. Как связаны между собой модуль коэффициента отражения, КБВ, КСВ? ([2] §7.1, [3] §21.2).
7.11. Разъясните понятие «критическая длина волны» волновода ([1] §13.4, [3] §18.2).
7.12. Каково условие одноволнового режима в прямоугольном (коаксиальном) волноводе? ([1] §14.4, §15.7, [2] §4.4).
7.13. В чём преимущества одноволнового режима? ([1] §14.4, §15.7, [2] §4.4).
7.14. Разъясните понятие «основная волна» волновода ([1] §14.1, §14.2, §14.4, [2] §2.7, [3] §18.8).
7.15. Нарисуйте структуру поля основной волны в прямоугольном волноводе ([1] §14.1, [2] §3.5, [3] §19.6).
7.16. Нарисуйте структуру поля основной волны в коаксиальном волноводе ([1] §14.4, §15.7, [2] §4.4).
7.17. Объясните, почему длина волны в прямоугольном волноводе больше, чем в свободном пространстве ([1] §14.4, §15.7, [2] §4.4).
7.18. Как изменится длина волны в волноводе при изменении его диэлектрического заполнения? ([1] §14.4, §15.7, [2] §4.4).
7.19. Нарисуйте и объясните зависимость фазовой и групповой скоростей от длины волны для основной волны в прямоугольном волноводе ([1] §14.4, §15.7, [2] §4.4).
7.20. Где на круговой диаграмме полных сопротивлений шкалы модуля коэффициента отражения, КБВ, КСВ? ([1] §16.4, [2] §7.3).
7.21. Приведите методику определения полного сопротивления нагрузки по круговой диаграмме полных сопротивлений (диаграмме Вольперта) ([1] §16.4, [2] §7.3).
7.22. Как можно определить значение КБВ по круговой диаграмме полных сопротивлений, если известно значение комплексного нормированного сопротивления нагрузки? ([1] §16.4, [2] §7.3).
ЛИТЕРАТУРА
1. Вольман В.И., Пименов Ю.В. Техническая электродинамика. – М.: Связь, 1971.
2. Лебедев И.В. Техника и приборы СВЧ. – М.: Высшая школа, 1970.
3. Фальковский О.И. Техническая электродинамика. – М.: Связь, 1978.
Методическое руководство к лабораторным работам № 1, 2 «ИССЛЕДОВАНИЕ РЕЖИМОВ РАБОТЫ ПРЯМОУГОЛЬНОГО И КОАКСИАЛЬНОГО ВОЛНОВОДОВ» по дисциплинам «Электромагнитные поля и волны» и «Электродинамика и распространение радиоволн» для студентов очного и заочного обучения и направлений образования «Телевидение, радиосвязь и радиовещание» и «Радиотехника» рассмотрено на заседании кафедры (протокол № 20 от 7.06.2004 г.) и рекомендовано к печати.
Отв. редактор доц. Ликонцев Д.Н.
Составители:
доц. Ликонцев Д.Н. (работы № 1,2,7)
доц. Габзалилов Г.Ф. (работа №6)
Редакционно-корректурная комиссия:
редактор доц. Романенко Б.А.
корректор ст. преп. Павлова С.И.
