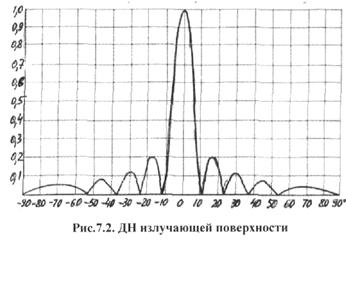
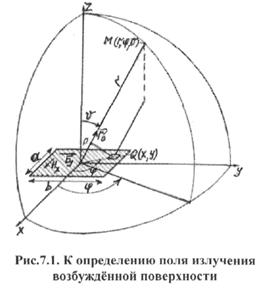
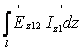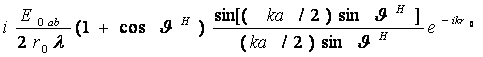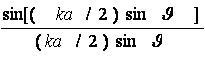УЗБЕКСКОЕ
АГЕНТСТВО СВЯЗИ И ИНФОРМАТИЗАЦИИ ТАШКЕНТСКИЙ
УНИВЕРСИТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ
КОНСПЕКТ ЛЕКЦИЙ
по разделу
«АНТЕННО-ФИДЕРНЫЕ
УСТРОЙСТВА. ЧАСТЬ 1»
дисциплин
«РАСПРОСТРАНЕНИЕ
РАДИОВОЛН и АНТЕННО-ФИДЕРНЫЕ УСТРОЙСТВА»,
«РАСПРОСТРАНЕНИЕ
РАДИОВОЛН и АНТЕННО-ФИДЕРНЫЕ УСТРОЙСТВА МОБИЛЬНЫХ СИСТЕМ СВЯЗИ»
по направлениям образования «Телевидение,
радиосвязь и
радиовещание», «Мобильные системы связи», и «Радиотехника»
Ташкент 2010
ПРЕДИСЛОВИЕ
Настоящий курс лекций
составлен в соответствии с действующей
типовой программой дисциплины для подготовки бакалавров по направлению по
направлениям образования
«Телевидение, радиосвязь и радиовещание», «Мобильные системы связи» и "Радиотехника". Отдельные разделы
пособия также используются при подготовке магистрантов по дисциплинам кафедры и будут полезны для слушателей
курсов повышения квалификации.
В первой части курса лекций
рассмотрены теоретические основы формирования полей линейных, апертурных
и других типов излучателей.
Во второй части курса лекций рассматриваются особенности конструкций и работы конкретных типов
антенн разных
диапазонов.
Приведенный объем материала в
первой и второй частях пособия
ориентирован на курс лекций в 34часа с учетом раздела "Распространение радиоволн" и выделения части материала для самообразования студентов.
ОГЛАВЛЕНИЕ
ЧАСТЬ 1
Стр.
1.ВВЕДЕНИЕ……................................................................................ ………………….5
1.1Краткий очерк развития теории и техники
антенных устройств ………5
1.1.Назначение антенн и
их классификация……………………......................10
1.2.Основные задачи теории антенн………………………….......................13
2.
ПАРАМЕТРЫ, ХАРАКТЕРИЗУЮЩИЕ
НАПРАВЛЕННЫЕ И ПОЛЯРИЗАЦИОННЫЕ
СВОЙСТВА
АНТЕНН............................................................................................................16
2.1. Характеристика
(диаграмма) направленности антенны ……………..16
2.2.
Коэффициент направленного действия (КНД), коэффициент
усиления антенны (КУ) и параметры,
связанные с КНД .......................20
2.3. Поляризационные
параметры антенн. Турникетный излучатель ...........22
3.
СИММЕТРИЧНЫЙ ЭЛЕКТРИЧЕСКИЙ ВИБРАТОР
В СВОБОДНОМ
ПРОСТРАНСТВЕ...........................................................26
3.1.Распределение тока и
заряда по вибратору……………….......................26
3.2.Направленные свойства
симметричного вибратора …………………..33
3.3.Мощность излучения, сопротивление
излучения и КНД симметрич-
ного
вибратора..............................................................................................33
3.4.Входное сопротивление симметричного
вибратора. Инженерный
расчет входного
сопротивления…….......................................................34
3.5.Основные результаты,
даваемые строгой теорией симметричного вибратора………………………………..……………………………........39
3.6.Симметричный щелевой
вибратор………………………………….......41
3.7.Способы расширения
рабочего диапазона вибраторных антенн……...45
4. ИЗЛУЧЕНЕНИЕ ДВУХ
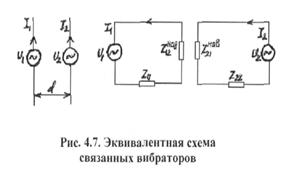
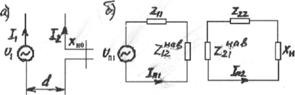
СВЯЗАННЫХ ВИБРАТОРОВ…………………………………………………………........47
4.1.Направленные
свойства системы из двух связанных вибраторов ........47
4.2.Расчет сопротивления
излучения и входного сопротивления
связанных вибраторов методом наведенных
ЭДС………………….......51
4.2.1.Сущность метода наведенных ЭДС
.......………………………………..51
4.2.2.Расчет взаимных и собственных
сопротивлений связанных вибраторов………………………………………………………………….….53
4.2.3.Расчет наведенного и полного сопротивлений
излучения .……........54
4.3.Расчет тока в пассивных вибраторах
.......................................................56
4.4.Методы получения
узких диаграмм направленности
.............................58
5. АНТЕННЫЕ РЕШЕТКИ С ПОПЕРЕЧНЫМ
ИЗЛУЧЕНИЕМ…………………………………………………………........61
5.1.Плоская антенная решетка. Равномерная
линейная антенная
решетка
……......…………………………………………………………..61
5.2
Синфазная
решетка
………………………………………………….........63
5.3
Управление диаграммой
направленности равномерной линейной
решетки........................................................................................................66
6. АНТЕННЫЕ РЕШЕТКИ С ОСЕВЫМ ИЗЛУЧЕНИЕМ (АНТЕННЫ БЕГУЩЕЙ ВОЛНЫ).......………………………………..69
6.1.
Излучение равномерного линейного ряда вибраторов,
перпендикулярных оси решетки…………………………………...…69
6.2.Излучение провода,
ток в котором изменяется по закону
бегущей волны…………………..………………………………………76
7. ИЗЛУЧЕНИЕ ВОЗБУЖДЕННЫХ
ПОВЕРХНОСТЕЙ……………………………………………………….78
7.1.Напряженность поля излучающей поверхности
в дальней зоне. Характеристики
направленности идеальной плоской антенны
.......78
7.2.Влияние
неравномерного амплитудного распределения поля на диаграмму направленности излучающей поверхности …………....82
7.3.КНД излучающей
поверхности…………………………………….....84
7.4.Влияние фазовых искажений
на направленные свойства излучающей поверхности…………………………………………………………….85
8. НЕКОТОРЫЕ ВОПРОСЫ ТЕОРИИ ПРИЕМНЫХ АНТЕНН…………………………………………………………………..92
8.1 Применение принципа взаимности
для изучения
приемных антенн ……...……………………………………………….92
8.2Мощность, выделяемая в нагрузке
приёмной антенны……………..96
8.3Влияние параметров приёмной антенны на
качество радиоприёма .…98
СПИСОК ЛИТЕРАТУРЫ
…………………………………….................10
1. ВВЕДЕНИЕ
1.1. Краткий очерк развития теории и техники
антенных устройств
Развитие
антенной техники на всем протяжении эволюции радио сопровождалось и было тесно связано с
развитием теории антенных устройств. Уже первая работа Генриха Герца по
экспериментальному доказательству существования электромагнитных волн была им
дополнена теоретическими изысканиями по излучению диполя. Одним из основных
элементов изобретения радио Александром Степановичем Поповым (1859...1906 гг.) явилась приемная антенна.
Именно соединение антенны с вибратором Герца и приемным контуром позволило
А.С. Попову увеличить протяженность линии радиосвязи, перешагнуть стены
лаборатории и тем самым положить начало радиотелеграфии и радиотехнике, как
новой области техники.
Техника
антенных устройств с момента открытия радио прошла большой и сложный путь.
Освоение новых диапазонов волн, новые применения радиотехники всегда вызывали
усовершенствования старых и появление принципиально новых антенных устройств.
Рассматривая
историю развития антенных устройств, можно разбить ее на отдельные периоды,
каждый из которых характеризуется некоторым основным направлением развития
радиотехники и в том числе антенной техники. Конечно, такая разбивка, а тем более
хронологические рамки каждого этапа, могут носить лишь сугубо ориентировочный
характер.
1 период
- подготовительный (XIX столетие).
Исследования в области электромагнетизма, предшествующие изобретению радио,
многим обязаны гениальным работам Майкла Фарадея (1791...1867 гг.), Джемса Кларка Максвелла (1851... 1879 гг.) и Генриха
Герца (1857...1894 гг.). Их мы вправе назвать основоположниками электродинамики,
одной из частей которой в настоящее время является теория и техника антенн.
Из работ
М. Фарадея, охватывающих различные области физики и химии, отметим открытие
закона электромагнитной индукции (1851 г.), введение "диэлектрической
проницаемости", открытие парамагнетизма и диамагнетизма, введение
представления об электрических и магнитных силовых линиях.
Знаменитый
"Трактат об электричестве и магнетизме" Д. Максвелла (1875 г.) вместе с
несколькими более ранними его работами позволили выразить картину силовых
линий Фарадея в математической форме и установили связь между оптикой и
электродинамикой. Уравнения Максвелла, в несколько преобразованной впоследствии форме,
до сих пор являются теоретической основой электродинамики.
Основное
направление научной деятельности Г. Герца - проверка теории Максвелла. В
работе "Силы электрических колебаний, рассматриваемые согласно теории
Максвелла" (1888 г.) применяется характерный метод решения, который в
настоящее время называют методом вектора Герца, и приводятся картины силовых
линий диполя Герца. Его экспериментальные работы по изучению электромагнитных
волн являются преддверием
открытия радио.
2 период - начало развития
радиотехники, развитие антенн для длинных и средних волн (1895... 1924 гг.). Как уже
указывалось, одним из элементов изобретения А.С. Попова явилась открытая
заземленная антенна, которая входила в схемы его первых приемных и передающих
устройств.
Если в опытах Герца
колебательный контур являлся одновременно излучателем электромагнитных волн, то в
схемах Попова антенна стала отдельным
элементом радиоустройства. Скачок от УКВ колебаний, генерируемых искровыми разрядниками, к весьма длинным
волнам, создаваемым машинными генераторами, поставил антенную технику в весьма
невыгодное положение, так как эффективность излучения на этих волнах была очень
низка. В первые годы применения радиотелеграфа было
обнаружено, что для повышения эффективности антенны следует, возможно, больше
увеличить ее высоту. Антенны в то время поднимали на высоких мачтах, иногда
подвешивали к змею или воздушному шару. Увеличение мощности передатчика
и, связанное с этим увеличение токов в
антенне и напряжения, приводящего к образованию короны, заставило заменить
одиночный провод системой параллельных или расходящихся проводов. Так,
например, антенна мощной радиостанции Маркони, которая дала в 1901 г. связь
через Атлантический океан, имела вид опрокинутой четырехгранной пирамиды,
составленной из веерообразно расходящихся проводов, поддерживаемых
четырьмя мачтами. Для увеличения
эффективности антенн и уменьшения числа вертикальных проводов к ним стали
добавлять горизонтальные провода, которые, не излучая сами, улучшали
распределение тока по вертикальной части антенны. Это позволило увеличить
мощность передающих устройств. К антеннам с горизонтальной частью относятся Т - и Г- образные,
а также зонтичная, сохранившиеся до
настоящего времени. В этот же период стала широко применяться рамочная
антенна, состоящая из многих витков, которая позволила осуществить направленный
прием.
Из-за малой
эффективности излучения (малого сопротивления излучения) длинноволновых антенн
мощность потерь в заземлении во много раз превышала мощность излучения, что приводило к
крайне низкому значению коэффициента полезного действия (КПД) антенного сооружения.
Поэтому, начиная с 20-х годов, велись интенсивные работы по уменьшению потерь в заземлении. Применение заземления, распределенного по большой площади, или широко развитого противовеса, расположенного над
землей, позволило уменьшить сопротивление потерь до единиц и долей Ома и
увеличить КПД антенныдо 10...30%. Значительное увеличение КПД дала антенна,
предложенная американским
радиоинженером Александерсеном и построенная в 1920
г. Она состоит из длинной горизонтальной части и нескольких вертикальных снижений, каждое из
которых имеет свое заземление. Взаимное влияние вертикальных частей
антенны приводит к увеличению общего
сопротивления излучения почти в 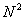 раз при
раз при 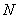 снижениях.
снижениях.
После А.С. Попова в
нашей стране теорией и конструированием антенн занимались Л.И. Мандельштам и Н.Д. Папалекси. Абрагам применил
теорию излучающего диполя к несимметричной антенне, заменив влияние хорошо
отражающей земли второй половиной вибратора. Формула для определения
сопротивления излучения антенны, короткой по сравнению с длиной волны, была
получена Рюденбергом. Ван-дер-Поль
нашел величину сопротивления излучения для антенны с произвольной нагрузкой на конце при
синусоидальном распределении тока в ней.
В СНГ бурное развитие
антенной техники, как и радиотехники в целом, началось только после 1917 года. В сентябре 1918 г. вышел первый номер научно-технического журнала "Телеграфия и телефония без
проводов", в котором печатались оригинальные статьи по теории и
расчету антенн.
Блестящим завершением
этого этапа развития антенн явилось создание в 1922...1924гг. М.В.Шулейкиным (1884...1939гг.) вузовского курса радиосетей,
как тогда назывались антенные сооружения. В этом курсе, задолго до зарубежных
ученых, были даны основные формулы и методика инженерного расчета антенн и
заземлений.
3 период - развитие
коротковолновых антенн (1925...1935 гг.). В середине 20-х годов выяснилось,
что короткие волны перекрывают большие расстояния лучше, чем длинные волны. Постройка
мощных коротковолновых радиостанций с направленными антеннами явилась
переворотом в радиосвязи, так как, помимо практически неограниченной дальности
действия на коротких волнах, можно получить значительную полосу частот,
обеспечивающую передачу нескольких каналов быстродействующей телеграфии. Короткие
волны открыли большие возможности и для антенной техники. Если
на длинных волнах высота антенн составляла только доли длины волны и антенны принадлежали к одному типу - несимметричный
вибратор с емкостной нагрузкой на
конце, то на коротких волнах стали вполне достижимыми сложные антенные системы
с размерами в несколько длин волн. Основным элементом KB
антенны стал полуволновый вибратор; из таких вибраторов строились большие
антенные полотна, обеспечивающие высокую направленность.
Вскоре была выявлена
периодичность в изменении состояния ионосферы и необходимость, в связи с этим, смены
волн на KB магистралях. Это дало толчок к конструированию
направленных антенн, работающих на нескольких частотах или перекрывающих
значительный диапазон; наибольшее распространение среди
последних получила ромбическая антенна.
Теоретической основой
для расчета сложных антенных систем, состоящих из многих вибраторов, явился метод
наведенных ЭДС. Этот метод был предложен в 1922 г. независимо друг от друга
Д.А. Рожанским и Л. Бриллуэном,
однако, свое практическое применение он получил, лишь начиная с 1928 г., после
работ И.Г. Кляцкина и А.А. Пистолькорса.
Этот метод, в сущности, позволил распространить хорошо известную теорию связанных
контуров и длинных линий на многовибраторные антенны.
К 1955 г. техника
коротковолновых антенн завершает первый цикл своего развития. Сложные
приемо-передающие антенны, используемые во всех странах мира, дают направленность,
близкую к предельно-допустимой.
Этот же период
характеризуется широким развитием радиовещания на средних волнах. Хотя
при построении вещательных антенн основные идеи были заимствованы в технике связных антенн
ДВ и СВ, здесь пришлось решить ряд специфичных задач,
связанных с увеличением мощности и полосы частот, а также приданием антенне
антифединговых свойств. Широкое распространение получили антенны в виде высоких
мачт и башен с электрической длиной, превышающей половину длины волны.
4 период - развитие антенн
ультракоротких волн (с 1935 г.). Внедрение в практику метровых волн для целей связи и
телевизионного вещания не вызвало вначале существенных изменений в технике
антенных устройств: применялись те же комбинации полуволновых диполей, что и на
коротких волнах. Однако специфические требования к диаграмме направленности и ши-рокополосности телевизионных антенн
привели к созданию специальных антенн, не имеющих аналогов на коротких волнах.
В предвоенные годы в
обстановке строгой секретности готовилось новое применение радиотехники -
радиолокация, потребовавшая совершенно новых антенных устройств и
способствовавшая быстрому освоению дециметрового и сантиметрового диапазонов волн. К
концу второй мировой войны техника сантиметровых волн оказалась уже широко
развитой. В этом диапазоне волн стали применяться полые волноводы, зеркальные, линзовые, рупорные и щелевые
антенны, принципы действия которых были заимствованы из оптики или
акустики.
Послевоенные годы
ознаменовались появлением нового вида связи -радиорелейных
линий. Они потребовали от антенны и волноводного тракта неискаженной передачи
широкополосного сигнала и остронаправленного излучения с низким уровнем лепестков.
Это привело к осуществлению ряда новых идей в конструкциях антенно-волноводного
тракта.
Новые виды связи,
использующие рассеяние радиоволн дециметрового и метрового диапазонов в
тропосфере и ионосфере, а также развитие радиоастрономии и возникновение
радиосвязи с космическими объектами, способствовали проникновению принципов
построения антенн сантиметровых волн в более длинноволновые диапазоны.
Освоение УКВ диапазона
потребовало коренного пересмотра теории антенн. До сих пор теория излучения сводилась
к нескольким каноническим формам, а определение параметров антенн производилось
приближенными методами с привлечением теории длинных линий, которая в принципе
исключает
возможность излучения.
С переходом к
метровым и дециметровым волнам, когда диаметр вибраторов стал
соизмерим с длиной волны, даже решение задачи о симметричном вибраторе
потребовало привлечения строгих методов электродинамики. Хотя в оптике
существуют прототипы многих антенн и волноводов УКВ, оптические методы не
могли быть непосредственно перенесены в теорию антенных устройств.
Дело в том, что в оптике размеры объектов считаются неизмеримо большими
длины волны. В антенно-волноводной технике эти величины соизмеримы, что
требует применения более строгих методов решения. Теория антенн стала к настоящему
времени чрезвычайно развитой областью электродинамики, оперирующей уравнениями
электромагнитного поля без внесения каких-либо приближений. Другой новой чертой
в современной теории антенн является переход от задач анализа характеристик
направленности
и других параметров антенны к синтезу антенн с оптимальными характеристиками. С
переходом к УКВ практически отпали ограничения в размерах антенн и в то же время стали
предъявляться более жесткие требования к ряду их параметров. Значительно
увеличилось и число типов антенных устройств с самыми разнообразными
характеристиками. Все это заставило, помимо анализа новых типов антенн, решать
задачи о построении антенных устройств, обладающих наилучшими из возможных характеристиками.
В настоящее время
стали все шире применяться антенны поверхностной волны стержневого и плоскостного
типа, использующие
явление "прилипания"
электромагнитной волны к среде или структуре, замедляющей ее скорость.
Существенную роль в
современной антенно-волноводной технике также играют высокочастотные магнитодиэлектрики - ферриты, которые позволили создать
антенны с электрическим управлением излучения и ряд новых элементов
волноводного тракта: вентили (пропускающие волну только одного направления), фазовращатели, вращатели
плоскости поляризации, циркуляторы и т.д.
Сложность явлений,
происходящих в современных антеннах поверхностного излучения, ферритовых
элементах и других устройствах антенно-волноводного тракта, способствовала
увеличению значения теории для дальнейшего развития антенной техники.
1.2. Назначение
антенн и их классификация
Антенной называется
радиотехническое устройство, предназначенное для излучения или приема
электромагнитных волн. Антенна является одним из важнейших элементов любой
радиотехнической системы, связанной с излучением или приемом радиоволн. К таким системам относят: системы радиосвязи, радиовещания, телевидения, радиоуправления, радиорелейной связи, радиолокации, радиоастрономии, радионавигации и
др.
В конструктивном
отношении антенна представляет собой провода, металлические поверхности,
диэлектрики, магнитодиэлектрики.
Электромагнитные
колебания высокой частоты, модулированные полезным сигналом, преобразуются передающей антенной в
электромагнитные волны, которые излучаются в
пространство. Обычно электромагнитные колебания подводят от передатчика к антенне не непосредственно, а с помощью фидера.
Приемная антенна улавливает распространяющиеся радиоволны преобразует их в
электромагнитные колебания, которые через фидер поступают на вход приёмного
устройства. В соответствии с принципам
обратимости антенн свойства антенны, работающей в режиме передачи не изменятся при работе этой
антенны в приемном режиме.
Преобразование
антенной одного вида электромагнитных волн в другой должно происходить с минимальными
потерями энергии, т.е. с максимально возможным КПД, определяемым в передающем режиме по
формуле 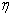 = P
= P / Р0, где
P
/ Р0, где
P -
мощность излучаемая антенной, Р0 - мощность подводимая к антенне.
-
мощность излучаемая антенной, Р0 - мощность подводимая к антенне.
Способность антенны излучать
электромагнитные волны с различной интенсивностью в разных направлениях
характеризуется её
направленными свойствами, т.е. диаграммой направленности (ДН).
Антенны, обладающие
узкой ДН, позволяют увеличивать напряженность поля в точке приёма без увеличения
мощности передатчика. В большинстве случаев это экономически более выгодно, чем
увеличения мощности передатчика. Кроме того, концентрация электромагнитных волн в требуемом
направлении приводит к уменьшению взаимных помех различных радиотехнических
систем. Наличие направленных приемных антенн ведёт к ослаблению приема
различных внешних помех, т.е. к повышению качества приёма и улучшению
помехозащищенности приемного устройства. Большими направленными свойствами
должны обладать антенны для космической радиосвязи, радиоастрономии, радиолокации,
радиорелейных линий.
В тоже время для
радио и телевидения передающие антенны должны иметь
одинаковое излучение в горизонтальной плоскости (за исключением отдельных
случаев - гор и т.д.).
Направленные свойства являются настолько важными, что принято говорить о двух функциях, выполняемых антенной:
- преобразование электромагнитных колебаний в свободные
электромагнитные волны;
- излучение этих волн в определенных направлениях.
Важную роль в работе
антенного устройства играет линия питания (фидерный тракт), которая передаёт (каналирует) электромагнитную энергию от генератора к
антенне (или от антенны к приёмнику). Фидер не должен излучать
электромагнитные волны и должен иметь минимальные потери. Его необходимо
согласовывать с выходной цепью
передатчика ( или с входной цепью приемника) и с входным
сопротивлением антенны, т.е. в фидере должен быть режим бегущей волны или
близкий к нему.
В зависимости от
диапазона радиоволн применяют различные типы фидеров: двухпроводные или многопроводные воздушные фидеры, несимметричные
экранированные (коаксиальные) линии, различные типы волноводов и др.
Классификацию антенн
можно, например проводить по способу формирования
излучаемого поля, выделяя следующие четыре класса антенн:
Излучатели небольших
размеров (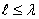 ,где
,где  - длина волны) для диапазона частот 10кГц...1ГГц. К
числу антенн этого класса относятся одиночные вибраторные и щелевые излучатели,
полосковые и микрополосковые антенны, рамочные
антенны, а также частотно-независимые излучатели.
- длина волны) для диапазона частот 10кГц...1ГГц. К
числу антенн этого класса относятся одиночные вибраторные и щелевые излучатели,
полосковые и микрополосковые антенны, рамочные
антенны, а также частотно-независимые излучатели.
Антенны бегущей волны размерами от  до 100
до 100 для диапазона частот 3МГц...10ГГц. Сюда относятся
спиральные, диэлектрические,директорные,
импедаксные антенны, а также антенны «вытекающей»
волны.
для диапазона частот 3МГц...10ГГц. Сюда относятся
спиральные, диэлектрические,директорные,
импедаксные антенны, а также антенны «вытекающей»
волны.
Антенные решетки размерами от до 100
до 100 и более для диапазона частот 3МГц...30ГГц. Это
антенны, состоящие из большого числа отдельных излучателей. Независимая регулировка
фаз (а иногда и амплитуд) возбуждения каждого элемента антенной решетки
обеспечивает возможность электрического управления диаграммой направленности.
Применяются линейные, плоские, кольцевые, выпуклые и конформные (совпадающие с
формой объекта установки) антенные решетки. На основе антенных решеток выполняют
антенные системы с обработкой сигнала, в том числе адаптивные к изменяющейся помеховой обстановке.
и более для диапазона частот 3МГц...30ГГц. Это
антенны, состоящие из большого числа отдельных излучателей. Независимая регулировка
фаз (а иногда и амплитуд) возбуждения каждого элемента антенной решетки
обеспечивает возможность электрического управления диаграммой направленности.
Применяются линейные, плоские, кольцевые, выпуклые и конформные (совпадающие с
формой объекта установки) антенные решетки. На основе антенных решеток выполняют
антенные системы с обработкой сигнала, в том числе адаптивные к изменяющейся помеховой обстановке.
Апертурные антенны размерами от  до 1000
до 1000 для диапазона частот 100МГц... 100ГГц и
выше. Наиболее распространены зеркальные, рупорные и линзовые апертурные антенны. К апертурным
антеннам примыкают, так называемые, «гибридные» антенны, представляющие
сочетание зеркал или линз с облучающей системой в виде антенной решетки. Апертурные антенны строятся по оптическим принципам и
обеспечивают наиболее высокую направленность излучения.
для диапазона частот 100МГц... 100ГГц и
выше. Наиболее распространены зеркальные, рупорные и линзовые апертурные антенны. К апертурным
антеннам примыкают, так называемые, «гибридные» антенны, представляющие
сочетание зеркал или линз с облучающей системой в виде антенной решетки. Апертурные антенны строятся по оптическим принципам и
обеспечивают наиболее высокую направленность излучения.
Свойства
направленности антенны описывают характеристикой (диаграммой) направленности.
Количественно эти свойства оцениваются с помощью таких параметров, как ширина ДН,
уровень боковых лепестков, коэффициент направленного действия (КНД) и других.
Важным параметром
является входное сопротивление антенны, характеризующее её как
нагрузку для генератора или фидера. Входным сопротивлением антенны называется
отношение напряжения между точками питания антенны (зажимы антенны) к току в этих
точках. Если антенна питается волноводом, то входное сопротивление определяется
отражениями, возникающими в волноводном тракте. В общем случае входное
сопротивление - величина комплексная Zвх= Rвх+ iXвх. Оно должно быть
согласовано с волновым сопротивлением фидерного тракта
(или с
выходным сопротивлением генератора) так, чтобы обеспечить в последнем режим,
близкий к режиму бегущей волны.
Мощность, излучаемая антенной РΣ, связана с током в
точках питания
антенны соотношением P = I02 R
= I02 R 0 / 2, где RΣ0 – сопротивление излучения антенны (при отсутствии потерь
в антенне это активная составляющая входного сопротивления антенны). Данное
определение относится к проволочным антеннам.
0 / 2, где RΣ0 – сопротивление излучения антенны (при отсутствии потерь
в антенне это активная составляющая входного сопротивления антенны). Данное
определение относится к проволочным антеннам.
Одним из основных
параметров антенны является ширина её рабочей полосы частот, в пределах
которой параметры антенны (характеристика направленности, входное сопротивление, КПД и
др.) удовлетворяют определенным техническим требованиям. Требования к
постоянству параметров антенны в пределах
рабочей полосы могут быть различными; они зависят от условий работы. Обычно
рабочая полоса частот определяется тем параметром, значение которого при
изменении частоты раньше других выходит из допустимых пределов. Очень часто
таким параметром является входное сопротивление антенны. Изменение его при
изменении частоты приводит к рассогласованию антенны с фидером. В ряде случаев
ширина рабочего диапазона определяется ухудшением одного из параметров,
характеризующих направленные свойства: изменением направления максимального излучения,
расширением ДН, уменьшением КНД и др. В зависимости от ширины рабочего
диапазона антенны условно разбивают на:
узкополосные
(настроенные), относительная рабочая полоса которых менее 10% номинальной
частоты;
широкополосные, с рабочей полосой
частот 10...50%;
диапазонные, коэффициент
перекрытия частот которых(fMAX/fMIN) составляет примерно 2...5;
частотно-независимые
(сверхширокополосные),
с коэффициентом перекрытия, теоретически не зависящим от частоты (практически fMAX/fMIN таких антенн >
5).
Еще одним параметром
является предельная мощность, которую можно подвести к антенне без опасности её
разрушения и не вызывая пробоя окружающей среды. Существуют также параметры,
характеризующие поляризационные свойства антенны.
В данном курсе
рассматриваются антенны следующих диапазонов: ми-риаметровые
или сверхдлинные волны ( = 10...100 км);
километровые или длинные волны (
= 10...100 км);
километровые или длинные волны ( = 1...10 км); гектометровые или средние волны (
= 1...10 км); гектометровые или средние волны ( = =100...1000
м); декаметровые или короткие волны (
= =100...1000
м); декаметровые или короткие волны ( = 10...100 м); метровые волны (
= 10...100 м); метровые волны ( = 1...10м); дециметровые волны (
= 1...10м); дециметровые волны ( = 10 см...1 м); сантиметровые волны (
= 10 см...1 м); сантиметровые волны ( = 1...10 см); миллиметровые волны (
= 1...10 см); миллиметровые волны ( = 1...10 мм). Последние четыре диапазона объединяются общим названием
"ультракороткие волны" (УКВ).
= 1...10 мм). Последние четыре диапазона объединяются общим названием
"ультракороткие волны" (УКВ).
1.3. Основные задачи
теории антенн
Основные задачи
теории антенн: задача анализа и задача синтеза. Задача анализа состоит
в определении электромагнитного поля в любой точке окружающего антенну пространства (в том
числе и на самой антенне). Источниками поля
являются токи и заряды, распределенные по антенне. Закон этого распределения (зависимость амплитуды и фазы
тока от координаты точки на
поверхности антенны) обычно неизвестен. Задача
анализа при заданной приложенной к антенне ЭДС (сторонняя ЭДС) может
быть решена строго исходя из следующих условий: искомое поле должно
удовлетворять уравнениям Максвелла; удовлетворять граничным условиям на
поверхности раздела при переходе из одной среды в другую (воздух - металл,
воздух -диэлектрик
и т.д.); должно выполняться условие излучения. Последнее означает, что на
большом расстоянии от антенны поле должно представлять бегущую волну, амплитуда которой с увеличением
расстояния r убывает как 1/r.
Строгое решение данной задачи встречает обычно большие математические
трудности: антенны, в основном, имеют сложные конфигурации; поверхности, на которых
заданы граничные условия, как правило, не совпадают с координатными
поверхностями каких-либо ортогональных систем координат. В связи с этим строгое
решение задачи анализа получено только для некоторых частных случаев.
Задачу анализа можно
упростить, разделив ее на две части: внутреннюю и внешнюю. Внутренняя задача
состоит в определении распределения возбуждающего тока по самой антенне или
распределения поля на произвольно выбранной замкнутой поверхности S,
ограничивающей объем V, в котором находятся
источники поля. Эта задача решается приближенными методами, выбираемыми в
зависимости от конкретных данных антенны. Например, часто задаются
синусоидальным распределением тока вдоль линейных вибраторов исходя из некоторой
аналогии между вибратором и разомкнутой на
конце длинной двухпроводной линией. В качестве примера антенны с синусоидальным распределением тока является
симметричный вибратор, используемый
в диапазонах декаметровых, метровых и дециметровых
волн. Эта антенна представляет собой
цилиндрический провод, длина которого соизмерима с длиной волны (часто длина
провода составляет половину длины волны). Между двумя половинами этого
провода ("плечами") включается источник ЭДС. Для проволочных антенн,
например, вибраторного типа, поле можно
рассчитать, мысленно разбивая антенну на ряд элементарных электрических вибраторов (ЭЭВ).
В тех случаях, когда распределение
тока по антенне либо неизвестно, либо является слишком сложным, внешнее поле
целесообразно находить заданием векторов Е
и Н на замкнутой поверхности S,
охватывающей источники (при
этом часто используют методы геометрической оптики). Этот способ широко применяется при анализе апертурных антенн ( рупорных, линзовых, параболических и др.). Если
известны тангенциальные составляющие векторов Е и Н на поверхности S, то эти составляющие на основании известного из электродинамики принципа
эквивалентности могут быть заменены
фиктивными эквивалентными поверхностными электрическими и магнитными токами. Разбивая поверхность S
на элементарные площадки dS и рассматривая каждую площадку как элемент
Гюйгенса, можно найти полное поле во внешней области Vs, суммируя поля, созданные отдельными элементами. Такой метод решения
внешней задачи называется приближением
Гюйгенса-Кирхгофа. Таким образом, излучающая система (пространство, заполненное токами, возбуждающими
электромагнитные волны) представляет собой не только реальные
электрические токи, текущие по металлическим
поверхностям, но и эквивалентные электрические и магнитные токи,
распределенные на замкнутых поверхностях, окружающих антенну, а также
поляризационные электрические и магнитные токи в объемах, занимаемых диэлектриками и магнитодиэлектриками.
Задача синтеза антенн состоит в
определении размеров и формы антенны и нахождении распределения источников
поля на ней по заданным требованиям к электрическим параметрам антенны (в
основном - по диаграмме
направленности). Эта задача возникает в связи с тем, что в ряде случаев параметры антенны, получающиеся при известном
распределении тока на ней, не отвечают предъявляемым требованиям.
Решение задач анализа
и синтеза, особенно в строгой постановке, требует, как правило, применения
ЭВМ. При этом ЭВМ используются не только в качестве расчетного инструмента для
быстрого получения характеристик исследуемых антенн, но и для ускорения и повышения качества
проектирования антенно-фидерных устройств,
что достигается применением системы автоматизированного проектирования
(САПР).
2. ПАРАМЕТРЫ, ХАРАКТЕРИЗУЮЩИЕ
НАПРАВЛЕННЫЕ И ПОЛЯРИЗАЦИОННЫЕ СВОЙСТВА АНТЕНН
2.1. Характеристика
(диаграмма) направленности антенны
При расчете
излученного антенной электромагнитного поля ее удобно рассматривать как
состоящую из бесконечного большого числа элементарных источников
(излучателей). Благодаря линейности уравнений Максвелла к полям элементарных
источников применим принцип суперпозиции, позволяющий найти поле
антенны в результате суммирования полей всех составляющих ее элементарных
излучателей с учетом амплитуд и фаз возбуждающих их токов. Суммирование полей сводится к их
интегрированию по источникам. Элементарными источниками являются: элементарные
электрические вибраторы ЭЭВ в случае
проволочных антенн; элементарные магнитные вибраторы в случае щелевых антенн;
бесконечно малые элементы волнового фронта или элементы Гюйгенса в случае апертурных антенн.
Формула для
комплексной амплитуды напряженности электрического поля Ė произвольной
реальной антенны в дальней зоне без учета векторного характера
электромагнитного поля имеет вид
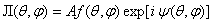 . (2.1)
. (2.1)
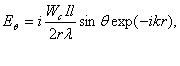 Здесь А - комплексный
множитель, не зависящий от направления на точку наблюдения (в него входит стандартный
множитель exp(-ikr)/r, где r
-расстояние от фазового
центра антенны до точки наблюдения;
Здесь А - комплексный
множитель, не зависящий от направления на точку наблюдения (в него входит стандартный
множитель exp(-ikr)/r, где r
-расстояние от фазового
центра антенны до точки наблюдения; 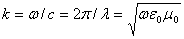 - коэффициент фазы или
волновое число в свободном пространстве); θ,φ - координаты точки наблюдения; |f(θ,φ)| - амплитудная
характеристика направленности; Ψ(θ,φ) - фазовая
характеристика направленности. Известно, что в случае элементарного
электрического вибратора
- коэффициент фазы или
волновое число в свободном пространстве); θ,φ - координаты точки наблюдения; |f(θ,φ)| - амплитудная
характеристика направленности; Ψ(θ,φ) - фазовая
характеристика направленности. Известно, что в случае элементарного
электрического вибратора
(2.2)
где I - амплитуда тока в
вибраторе; l - длина вибратора; 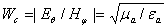 характеристическое сопротивление
волны; в свободном пространстве
характеристическое сопротивление
волны; в свободном пространстве 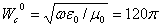 , Ом
, Ом
Амплитудной
характеристикой направленности антенны называется зависимость величины
(модуля) напряженности электрического поля, создаваемого антенной в точке наблюдения, от
направления на эту точку, характеризуемого
углами θ и φ сферической системы координат при постоянном
расстоянии (r = const) точки наблюдения от антенны. Фазовой характеристикой
направленности антенны Ψ (θ,φ) называется зависимость фазы поля, создаваемого антенной
в точке наблюдения, находящейся на поверхности сферы в дальней зоне, от направления
на эту точку, характеризуемого углами θ и φ. Множитель f(θ,φ) определяет не только
величину, но и фазу напря-
женности
поля, так как при переходе функции f(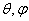 ) через нуль
меняется ее знак, что соответствует скачку фазы напряженности поля на 180°. Поэтому амплитудной характеристикой
направленности является модуль этой функции |f(
) через нуль
меняется ее знак, что соответствует скачку фазы напряженности поля на 180°. Поэтому амплитудной характеристикой
направленности является модуль этой функции |f(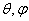 )|. В
дальнейшем для упрощения записи знак модуля опускаем.
В общем случае характеристика направленности является векторной и комплексной величиной. Выражение ƒ(
)|. В
дальнейшем для упрощения записи знак модуля опускаем.
В общем случае характеристика направленности является векторной и комплексной величиной. Выражение ƒ(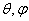 )=f(
)=f(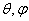 ) exp[i
) exp[i ] называется комплексной характеристикой направленности антенны. Она
полностью
определяет угловое распределение и фазовые свойства излучаемого электромагнитного поля в дальней зоне
антенны. Характеристика направленности
антенны определяется размерами и конфигурацией антенны, а также распределением
возбуждающего тока (как действительного, так и эквивалентного). Напомним, что дальняя
зона (зона излучения или зона Фраунгофе-ра) характеризуется
тем, что направления (лучи), проведенные из любой точки антенны на точку
наблюдения, находящуюся в этой зоне, считаются параллельными. При этом возникает ошибка в определении фаз полей, создаваемых
в точке наблюдения различными элементами антенны. Эта ошибка оказывается тем
меньше, чем больше расстояние от антенны до точки наблюдения по сравнению с
размерами антенны. Расстояние дальней зоны rизл
] называется комплексной характеристикой направленности антенны. Она
полностью
определяет угловое распределение и фазовые свойства излучаемого электромагнитного поля в дальней зоне
антенны. Характеристика направленности
антенны определяется размерами и конфигурацией антенны, а также распределением
возбуждающего тока (как действительного, так и эквивалентного). Напомним, что дальняя
зона (зона излучения или зона Фраунгофе-ра) характеризуется
тем, что направления (лучи), проведенные из любой точки антенны на точку
наблюдения, находящуюся в этой зоне, считаются параллельными. При этом возникает ошибка в определении фаз полей, создаваемых
в точке наблюдения различными элементами антенны. Эта ошибка оказывается тем
меньше, чем больше расстояние от антенны до точки наблюдения по сравнению с
размерами антенны. Расстояние дальней зоны rизл
определяется из условия rизл 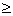 2R2/
2R2/ , где R - наибольший размер
излучающей системы. В этой зоне поле имеет поперечный характер (отсутствуют составляющие
векторов Е и Н в направлении распространения); в окрестности точки наблюдения поле имеет характер плоской
волны; амплитуды полей, излучаемых
элементами антенны, убывают обратно пропорционально расстоянию.
, где R - наибольший размер
излучающей системы. В этой зоне поле имеет поперечный характер (отсутствуют составляющие
векторов Е и Н в направлении распространения); в окрестности точки наблюдения поле имеет характер плоской
волны; амплитуды полей, излучаемых
элементами антенны, убывают обратно пропорционально расстоянию.
В антенной технике обычно интересуются
характером зависимости напряженности поля от направления на точку наблюдения,
а не абсолютной величиной напряженности
поля. Поэтому удобно пользоваться нормированной характеристикой
направленности F(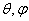 ), т.е. отношением напряженности поля, излучаемого антенной в
произвольном направлении, к значению напряженности поля в направлении
максимального излучения
), т.е. отношением напряженности поля, излучаемого антенной в
произвольном направлении, к значению напряженности поля в направлении
максимального излучения
F(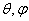 )= | E(
)= | E(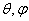 )| / | Emax(
)| / | Emax(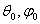 )| = f(
)| = f(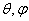 )/fmax(
)/fmax(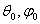 ).
).
Максимальная величина F(θ,φ) всегда равна единице.
Графическое изображение амплитудной
характеристики направленности называют диаграммой направленности (ДН)
антенны. Пространственная ДН изображается в виде поверхности f(θ,φ) или F(θ,φ), описываемой концом радиуса-вектора,
исходящего из начала координат, длина
которого в каждом направлении в определенном
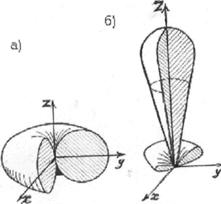
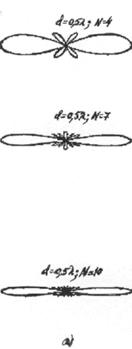
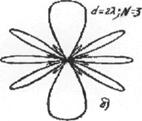
масштабе равна функции f(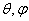 ). На рис.2.1.а изображена пространственная ДН элементарного вибратора (тороид),
на рис.2.1.б - ДН более сложной антенны (так
называемая игольчатая ДН). На практике обычно используют ДН, изображающие
характеристику направленности в каких-либо выбранных плоскостях. В качестве
таких плоскостей обычно выбирают две взаимно перпендикулярные
плоскости, проходящие
через направление
). На рис.2.1.а изображена пространственная ДН элементарного вибратора (тороид),
на рис.2.1.б - ДН более сложной антенны (так
называемая игольчатая ДН). На практике обычно используют ДН, изображающие
характеристику направленности в каких-либо выбранных плоскостях. В качестве
таких плоскостей обычно выбирают две взаимно перпендикулярные
плоскости, проходящие
через направление
максимального излучения
(главные плоскости). Для антенн, излучающих линейно поляризованное поле, главными
плоскостями называются плоскости, в которых лежит либо вектор Е (плоскость Е), либо вектор Н (плоскость Н).
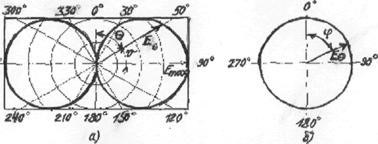
Диаграммы направленности изображают обычно либо в полярной (рис.2.2.а - ДН элементарного вибратора
в Е - плоскости; рис.2.2.б - ДН элементарного
вибратора в Н - плоскости), либо в декартовой
(прямоугольной) системе координат (рис.2.3. - ДН реальной антенны).
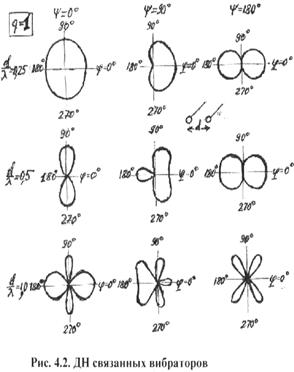
|
Рис. 2.1. Пространственная ДН (а-диполя Герца, б-игольчатая)
|
В некоторых случаях
применяется картографический метод изображения пространственных (трехмерных)
ДН. Он удобен для изображения многолепестковых (т.е. имеющих
много нулей и максимумов) ДН в широком диапазоне углов. Этот метод состоит в том, что
строится плоская сетка координат 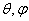 в какой-либо
координатной системе (прямоугольной, полярной и др.) подобно сетке меридианов и параллелей на
географической
карте. На этой сетке замкнутыми линиями изображаются одинаковые
в какой-либо
координатной системе (прямоугольной, полярной и др.) подобно сетке меридианов и параллелей на
географической
карте. На этой сетке замкнутыми линиями изображаются одинаковые
значения нормированной характеристики
направленности F(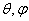 ) в том или ином масштабе. При изображении ДН часто используется логарифмический масштаб, вводимый соотношением в децибеллах
F(
) в том или ином масштабе. При изображении ДН часто используется логарифмический масштаб, вводимый соотношением в децибеллах
F(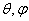 )=20
lgF(
)=20
lgF(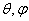 ).
).
|
Рис. 2,2. ДН диполя Герца (а-Е-плоскость, б-Н-плоскость)
|
В некоторых случаях пользуются понятием характеристики
(диаграммы) направленности по мощности F2(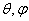 ). Функция F(
). Функция F(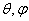 ) для
) для
различных углов 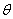 и
и  проходит через нуль и имеет несколько максимумов,
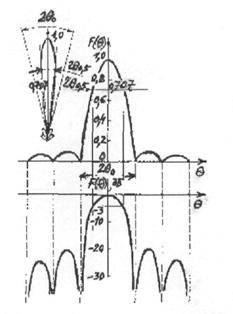
т.е. ДН имеет многолепестковый характер (см. рис.2.3). Диаграмму
направленности принято численно характеризовать шириной главного
лепестка (шириной луча) и относительным
уровнем боковых лепестков (УБЛ).
проходит через нуль и имеет несколько максимумов,
т.е. ДН имеет многолепестковый характер (см. рис.2.3). Диаграмму
направленности принято численно характеризовать шириной главного
лепестка (шириной луча) и относительным
уровнем боковых лепестков (УБЛ).
Шириной ДН (шириной
луча) называется угол между направлениями, вдоль которых напряженность поля
падает до определенного значения. Так, шириной ДН по
уровню нулевого излучения называют угол
2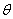 0
между нап-
0
между нап-
равлениями, вдоль которых
напряженность поля падает до нуля (см. рис.2.3). Шириной
ДН по половинной мощности называют угол 2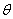 0,5 между направлениями, вдоль которых |Е| = |Emax|/
0,5 между направлениями, вдоль которых |Е| = |Emax|/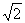 или соответственно среднее значение плотности потока мощности П=Пmaх/2. Наибольший лепесток, максимум которого
соответствует направлению максимального излучения, называют главным, меньшие лепестки - боковыми
(лепестки, находящиеся в задних квадрантах, т.е. в диапазоне углов 90°
или соответственно среднее значение плотности потока мощности П=Пmaх/2. Наибольший лепесток, максимум которого
соответствует направлению максимального излучения, называют главным, меньшие лепестки - боковыми
(лепестки, находящиеся в задних квадрантах, т.е. в диапазоне углов 90°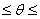 180° и 180°
180° и 180°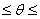 270°, часто называют задними).
270°, часто называют задними).
Относительный
УБЛ (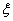 ) есть отношение напряженности поля в направлении максимума данного лепестка (ENmax) к напряженности поля
внаправлении главного максимума (Еmax), т.е.
) есть отношение напряженности поля в направлении максимума данного лепестка (ENmax) к напряженности поля
внаправлении главного максимума (Еmax), т.е.
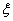 N=|ENmax|/|Еmax|=FN(
N=|ENmax|/|Еmax|=FN(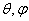 ), или в децибеллах
), или в децибеллах 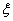 дБ = 20lg FN(
дБ = 20lg FN(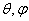 ), где N=1,2,3,...-номер бокового лепестка (для главного лепестка N=0).
), где N=1,2,3,...-номер бокового лепестка (для главного лепестка N=0).
|
Рис, 2.3, ДН реальной антенны
|
Обычно стремятся к
подавлению боковых лепестков, т.е. к тому, чтобы величина 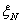 была мала. В большинстве случаев интересуются ам- плитудными характеристиками направленности
была мала. В большинстве случаев интересуются ам- плитудными характеристиками направленности
(слово "амплитудная" в дальнейшем не
используем). Фазовые характеристики направленности используют в радиолокации,
радионавигации и в некоторых других случаях.
Если
фаза, излучаемого антенной поля, не зависит от направления на точку наблюдения и
изменяется на обратную только при переходе функции f(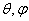 ) или F(
) или F(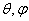 ) через нуль, т.е. при переходе от одного лепестка ДН к другому, то такая
антенна является источником сферических волн, о чем свидетельствует множитель
[ехр(-ikr)]/r. Эти волны исходят как бы из одной точки, называемой фазовым
центром антенны. Эта точка расположена в начале выбранной системы
координат, и поэтому, фазовая характеристика зависит от положения начала координат.
Однако не все реальные антенны обладают фазовым центром, т.е. излучают
сферические волны. Для них обычно можно подобрать сферу, наилучшим образом
аппроксимирующую фронт волны (обычно в пределах главного лепестка). Центр этой
сферы называют центром излучения антенны. Графическое изображение
фазовой характеристики называется фазовой ДН.
) через нуль, т.е. при переходе от одного лепестка ДН к другому, то такая
антенна является источником сферических волн, о чем свидетельствует множитель
[ехр(-ikr)]/r. Эти волны исходят как бы из одной точки, называемой фазовым
центром антенны. Эта точка расположена в начале выбранной системы
координат, и поэтому, фазовая характеристика зависит от положения начала координат.
Однако не все реальные антенны обладают фазовым центром, т.е. излучают
сферические волны. Для них обычно можно подобрать сферу, наилучшим образом
аппроксимирующую фронт волны (обычно в пределах главного лепестка). Центр этой
сферы называют центром излучения антенны. Графическое изображение
фазовой характеристики называется фазовой ДН.
2.2. Коэффициент направленного действия (КНД),
коэффициент усиления антенны (КУ) и
параметры, связанные с КНД
Коэффициент
направленного действия (КНД) характеризует способность антенны концентрировать
излученное электромагнитное поле в каком-либо определенном направлении. Это понятие
было введено в 1929 г. А.А.Пистолькорсом. Коэффициентом
направленного действия называется отношение среднего значения за период высокой
частоты плотности потока мощности (среднее значение вектора Пойнтинга),
излучаемого антенной в данном направлении 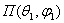 , к усредненному по всем направлениям значению плотности потока
мощности Пуср
, к усредненному по всем направлениям значению плотности потока
мощности Пуср
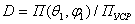 . (2.3)
. (2.3)
Здесь 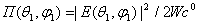 , где |
, где |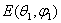 | - амплитудное значение напряженности электрического поля в
направлении, характеризуемом углами
| - амплитудное значение напряженности электрического поля в
направлении, характеризуемом углами 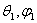 . Таким образом, при определении КНД данная антенна сравнивается с
воображаемой абсолютно ненаправленной (изотропной) антенной, излучающей ту же
мощность, что и данная. Очевидно, что
. Таким образом, при определении КНД данная антенна сравнивается с
воображаемой абсолютно ненаправленной (изотропной) антенной, излучающей ту же
мощность, что и данная. Очевидно, что
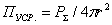 , (2.4)
, (2.4)
где 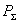 - мощность
излучения; r -
радиус воображаемой сферы, охватывающей антенну, причем величина r должна быть такой, чтобы поверхность сферы находилась в дальней зоне поля антенны.
- мощность
излучения; r -
радиус воображаемой сферы, охватывающей антенну, причем величина r должна быть такой, чтобы поверхность сферы находилась в дальней зоне поля антенны.
Коэффициент
направленного действия показывает во сколько раз следует уменьшить излучаемую
мощность при замене изотропной (ненаправленной) антенны на направленную, чтобы
среднее значение плотности потока мощности в точке наблюдения осталось
неизменным.
Учитывая, что 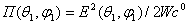 , и подставляя в (2.3) выражение (2.4), получаем формулу для КНД в другом
виде
, и подставляя в (2.3) выражение (2.4), получаем формулу для КНД в другом
виде 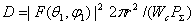 или для свободного
пространства (Wc°=120
или для свободного
пространства (Wc°=120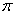 Ом) в направлении максимального излучения
Ом) в направлении максимального излучения
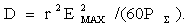 (2.5)
(2.5)
Если в эту формулу
подставить вместо 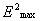 выражение (2.2) в квадрате (без фазовых множителей) и учесть, что
выражение (2.2) в квадрате (без фазовых множителей) и учесть, что 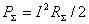 , где
, где 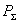 - сопротивление излучения элементарного электрического вибратора, то получим КНД элементарного вибратора D=1,5.
- сопротивление излучения элементарного электрического вибратора, то получим КНД элементарного вибратора D=1,5.
Коэффициент
направленного действия тем больше, чем уже главный лепесток пространственной
ДН и чем меньше УБЛ. Коэффициент направленного действия можно выразить с
помощью еще одного параметра, называемого действующей длиной или действующей
высотой антенны 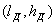 .Этот параметр иногда используют при
анализе приемных антенн, а также проволочных длинноволновых и средневолновых
антенн и антенн-мачт.
.Этот параметр иногда используют при
анализе приемных антенн, а также проволочных длинноволновых и средневолновых
антенн и антенн-мачт.
В случае линейной антенны ток по ее длине распределен
неравномерно. Однако реальную антенну можно
заменить воображаемым вибратором длиной lд (действующей длиной) с равномерным
распределением тока создающим в направлении максимального излучения поле, равное
полю данной антенны в главном направлении. При этом ток в точке питания
реальной антенны считается равным
току, текущему по воображаемому вибратору. По аналогии с (2.2) (вибратор с равномерным распределением тока)
напряженность поля реальной антенны в главном направлении можно представить в
виде
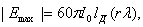 (2.6)
(2.6)
где I0 - амплитуда тока в
точках питания антенны; 60π = Wc°/2, где 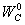 - волновое сопротивление среды. Напишем выражение для величины напряженности поля любой
вибраторной антенны в произвольном направлении
- волновое сопротивление среды. Напишем выражение для величины напряженности поля любой
вибраторной антенны в произвольном направлении
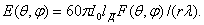 (2.7)
(2.7)
Подставляя в
(2.5) вместо 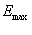 выражение (2.6)
и учитывая, что
выражение (2.6)
и учитывая, что
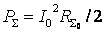 (
(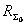 - сопротивление
излучения антенны, отнесенное к току в точках питания; I -ток в точках питания антенны), получаем
- сопротивление
излучения антенны, отнесенное к току в точках питания; I -ток в точках питания антенны), получаем
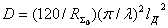 или
или 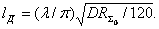 (2.8)
(2.8)
Формально параметром "действующая длина" можно пользоваться в случае любой антенны
(линейной, апертурной или какой-либо другой), так как этот параметр
выражается через КНД, а последний определяется только характеристикой направленности.
Коэффициент направленного действия не
учитывает потерь подводимой энергии в проводниках антенны, в изоляторах, в
окружающих антенну предметах
и в земле. В связи с этим вводится параметр, учитывающий эти потери, называемый коэффициентом усиления (КУ)
антенны, равный отношению среднего значения плотности потока мощности,
излучаемой антенной в данном направлении 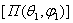 , к среднему значению плотности потока мощности,
создаваемого воображаемым абсолютно ненаправленным излучателем (Пн). При этом предполагается, что точка
наблюдения находится на одинаковом расстоянии от обеих антенн; мощности,
подводимые к той и другой антеннам, равны и КПД ненаправленной антенны равен
единице. Таким образом, КУ
, к среднему значению плотности потока мощности,
создаваемого воображаемым абсолютно ненаправленным излучателем (Пн). При этом предполагается, что точка
наблюдения находится на одинаковом расстоянии от обеих антенн; мощности,
подводимые к той и другой антеннам, равны и КПД ненаправленной антенны равен
единице. Таким образом, КУ
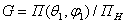 . (2.9)
. (2.9)
Коэффициент усиления показывает во сколько раз следует уменьшить мощность,
подводимую к направленной антенне, по сравнению с абсолютно ненаправленной
(изотропной) антенны, КПД которой считается равным единице, чтобы среднее
значение плотности потока мощности в точке наблюдения оставалось
неизменным.
Отличие КУ от КНД состоит в том, что при определении КУ исходят из равенства
мощностей, подводимых к исследуемой и эталонной
( ненаправленной) антеннам Р0, а не из равенства
мощностей излучения P , этих антенн. Умножим
и разделим правую
часть (2.9) на Пуср.
Тогда [П(
, этих антенн. Умножим
и разделим правую
часть (2.9) на Пуср.
Тогда [П(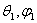 )/Пуср](Пуср/Пн),
где Пуср/Пн
=
)/Пуср](Пуср/Пн),
где Пуср/Пн
=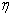 - КПД антенны.
- КПД антенны.
Параметры ( D,
G и 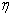 ) связаны соотношением
) связаны соотношением
G=D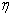 . (2.10)
. (2.10)
Учитывая, что D=G/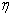 , можно написать
, можно написать
Emax=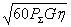 /r=
/r=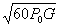 /r . (2.11)
/r . (2.11)
2.3. Поляризационные
параметры антенн. Турникетный излучатель
Направление векторов Е и Н излучаемого антенной поля определяется плоскостью поляризации,
т.е. плоскостью, проходящей через направление распространения волны
(вектор Пойнтинга) и вектор напряженности электрического поля. В
общем случае за один период высокой частоты плоскость поляризации делает
полный оборот вокруг направления распространения. Такое поле называют вращающимся.
За это время конец вектора Е
описывает
замкнутую кривую (эллипс), лежащую в плоскости, перпендикулярной направлению
распространения, и называемую поляризационным эллипсом. Это - эллиптическая
поляризация электромагнитного поля. Частными видами эллиптической
поляризации являются: линейная поляризация - конец вектора Е лежит на прямой линии; круговая
поляризация - конец вектора Е за один период высокой
частоты описывает окружность.
Существуют антенны,
рассчитанные на излучение (прием) поля круговой поляризации. Многие антенны
(симметричный вибратор и другие) излучают во всех направлениях линейно
поляризованные волны. Однако имеются антенны, которые либо из-за своих
конструктивных особенностей, либо из-за неточностей исполнения излучают волны чисто
линейной поляризации только в двух взаимно перпендикулярных плоскостях,
проходящих через направление максимального излучения (главные плоскости).
Поляризация поля в этих плоскостях называется главной или основной, В
других плоскостях имеется составляющая поля, поляризованная перпендикулярно
(ортогонально) основной поляризации (к таким антеннам относят, например, параболическую). Эта составляющая,
называемая поперечной или кроссполяризацион-ной, является вредной.
Ортогональность составляющих поля основной и кроссполяризации
(иногда ее называют паразитной) понимается как независимость переноса мощности
каждой из них. Мощность, соответствующая кроссполяризации, расходуется на
образование боковых лепестков, вследствие чего КНД антенны уменьшается. Кроме того,
возрастают помехи, создаваемые передающей антенной различным приемным антеннам,
работающим в том же или смежном диапазоне частот. Если поле передающей антенны имеет две
ортогональные составляющие, а приемная антенна рассчитана
на прием лишь линейно поляризованного поля, то часть излученной
мощности, соответствующая паразитной поляризации, не используется.
Эллиптическая поляризация может
рассматриваться либо как результат сложения двух линейно поляризованных взаимно
перпендикулярных составляющих поля, не
совпадающих по фазе, либо двух полей круговой поляризации с
противоположными направлениями вращения и разными амплитудами.
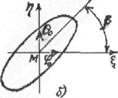
Отношение малой
полуоси эллипса к большой (рис.2.4.а) называется коэффициентом равномерности
(коэффициентом эллиптичности) поляризационного эллипса: t=b/a. В случае линейной
поляризации поля t = 0. Условием этой поляризации
является 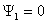 или
или 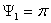 (
(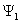 - сдвиг фаз между составляющими
- сдвиг фаз между составляющими 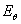 и
и 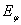 ). Линейная поляризация также имеет место,
если
). Линейная поляризация также имеет место,
если 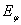 =0 или
=0 или 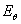 =0. При круговой поляризации поля (
=0. При круговой поляризации поля (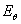 =
=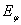 ;
;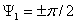 ) t=l.
Таким образом, коэффициент равномерности поляризационного эллипса может изменяться в пределах 0< t < 1. Зависимость коэффициента эллиптичности от
направления на точку наблюдения называется поляризационной
ДН.
) t=l.
Таким образом, коэффициент равномерности поляризационного эллипса может изменяться в пределах 0< t < 1. Зависимость коэффициента эллиптичности от
направления на точку наблюдения называется поляризационной
ДН.
Поляризационный
эллипс характеризуется также углом поляризации и направлением вращения вектора Е (направление вращения плоскости поляризации). Углом
поляризации 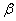 называется угол,
образованный большой осью поляризационного эллипса и направлением орта
называется угол,
образованный большой осью поляризационного эллипса и направлением орта 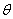 или
или  0 сферической системы координат (см. рис. 2.4.б).
Направление вращение вектора Е в
точке наблюдения определяется знаком угла
сдвига фаз между составляющими поля
0 сферической системы координат (см. рис. 2.4.б).
Направление вращение вектора Е в
точке наблюдения определяется знаком угла
сдвига фаз между составляющими поля
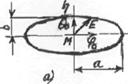
Рис. 2.4. К определению параметров эллиптической поляризации
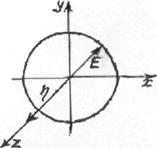
Рис. 2.5. К определению круговой поляризации поля
 и
и 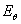 . Это направление
называется правым, если
наблюдатель, глядя навстречу волне,
видит вектор Е вращающимся против
часовой стрелки (рис. 2.5).
Противоположное направление вращения плоскости поляризации называется левым. Вектор Е всегда вращается в сторону составляющей поля, отстающей по фазе.
. Это направление
называется правым, если
наблюдатель, глядя навстречу волне,
видит вектор Е вращающимся против
часовой стрелки (рис. 2.5).
Противоположное направление вращения плоскости поляризации называется левым. Вектор Е всегда вращается в сторону составляющей поля, отстающей по фазе.
В соответствии с (2.3) под КНД антенны
с эллиптической поляризацией поля при полном поляризационном приеме будем
подразумевать величину 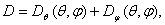 где
где 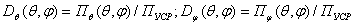 - парциальные КНД для каждой из ортогональных составляющих поля; Пуср — усредненное по всем направлениям значение
плотности потока мощности полного поля;
- парциальные КНД для каждой из ортогональных составляющих поля; Пуср — усредненное по всем направлениям значение
плотности потока мощности полного поля; 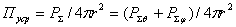 . Здесь
. Здесь 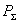 - полная мощность излучения;
- полная мощность излучения; 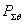 и
и 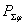 - мощности излучения, соответствующие ортогональным компонентам поля.
- мощности излучения, соответствующие ортогональным компонентам поля.
В соответствии с (2.3) под КНД антенны
с эллиптической поляризацией поля при полном поляризационном приеме будем
подразумевать величину 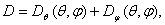 где
где 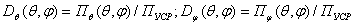 - парциальные КНД для каждой из ортогональных составляющих поля; Пуср — усредненное по всем направлениям значение
плотности потока мощности полного поля;
- парциальные КНД для каждой из ортогональных составляющих поля; Пуср — усредненное по всем направлениям значение
плотности потока мощности полного поля; 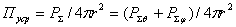 . Здесь
. Здесь 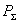 - полная мощность излучения;
- полная мощность излучения; 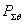 и
и 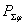 - мощности излучения, соответствующие ортогональным компонентам поля.
- мощности излучения, соответствующие ортогональным компонентам поля.
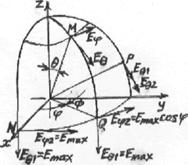
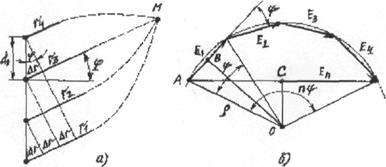
В качестве примера
простейшей антенны, создающей вращающееся поле рассмотрим два линейных
излучателя (для простоты считаем их элементарными), расположенных
крестообразно и питаемых токами равной амплитуды, но сдвинутых по фазе на 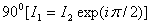 .Такой излучатель часто называют турникетным. В меридиональной по
отношению к обоим вибраторам плоскости yoz (см. рис.2.6) они создают поля одной поляризации, причем
векторы
.Такой излучатель часто называют турникетным. В меридиональной по
отношению к обоим вибраторам плоскости yoz (см. рис.2.6) они создают поля одной поляризации, причем
векторы 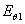 и
и 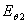 лежат на одной и той же линии. В
точке N, лежащей на нормали (ось х) к
плоскости расположения двух вибраторов, первый создаёт вектор напряжённости
электрического поля
лежат на одной и той же линии. В
точке N, лежащей на нормали (ось х) к
плоскости расположения двух вибраторов, первый создаёт вектор напряжённости
электрического поля 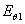 а второй -
а второй - 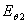 , находящиеся в плоскости, перпендикулярной оси х,
Эти векторы равны по амплитуде, сдвинуты по фазе друг относительно друга на 90° и
взаимно перпендикулярны. Таким образом в направлении
нормали плоскости вибраторов (yoz) имеет место
круговая поляризация поля.
, находящиеся в плоскости, перпендикулярной оси х,
Эти векторы равны по амплитуде, сдвинуты по фазе друг относительно друга на 90° и
взаимно перпендикулярны. Таким образом в направлении
нормали плоскости вибраторов (yoz) имеет место
круговая поляризация поля.
Рис.2.6. К получению круговой поляризации
поля
3. СИММЕТРИЧНЫЙ
ЭЛЕКТРИЧЕСКИЙ ВИБРАТОР В
СВОБОДНОМ ПРОСТРАНСТВЕ
3.1. Распределение тока и заряда по вибратору
Изучение
симметричного электрического вибратора представляет большой интерес, так
как, во-первых, этот вибратор применяется как самостоятельная антенна и,
во-вторых, он является составным элементом ряда сложных антенн. Симметричные вибраторы
начали широко применять в первой половине двадцатых годов в связи с возникновением
и развитием радиосвязи на коротких волнах. В настоящее время симметричный вибратор как самостоятельная
антенна применяется на коротких, метровых и дециметровых волнах. В этих же
диапазонах широко используются сложные антенны, состоящие из ряда симметричных
вибраторов. Симметричные вибраторы используются также в сантиметровом диапазоне волн в
качестве элементов сложных систем (например, облучатели зеркальных антенн).
Симметричный вибратор
состоит из двух одинаковых по размерам и форме проводников, между которыми
включается генератор высокой частоты (часто эти проводники называются
плечами). Рассмотрим симметричный вибратор, представляющий собой тонкий
цилиндрический проводник длиной 2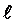 и радиусом а (рис.3.1), находящийся в свободном пространстве.
и радиусом а (рис.3.1), находящийся в свободном пространстве.
 Строгое решение
ос-
Строгое решение
ос-
новной задачи теории
антенн
для симметричного вибратора связано с большими
трудностями,
так как закон распределения тока по вибратору неизвестен.
Рис. 3.1. Симметричный
вибратор Существует
приближенный
метод расчета поля,
создаваемого симметричным
вибратором в дальней зоне. В основе этого метода лежит предположение о
синусоидальном распределении тока по вибратору, основанное на некоторой внешней аналогии
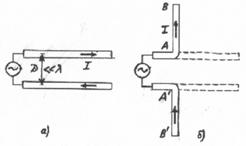
между симметричным вибратором и двухпроводной разомкнутой на конце линией без потерь. Действительно, от
двухпроводной линии (рис.3.2.а) можно перейти к симметричному вибратору, если
провода линии развернуть под углом 180° друг к другу (рис.3.2.б). Можно
полагать, что при переходе от двухпроводной линии к симметричному вибратору
закон распределения тока
не нарушается, т.е.
Iz = Iпsink(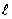 -
-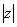 ) , где Iп - амплитуда тока в пучности тока
вибратора (в об-
) , где Iп - амплитуда тока в пучности тока
вибратора (в об-
щем случае, это величина комплексная) İп
= Iпexp(i );
); 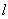 - длина одного плеча вибратора; z -
расстояние от начала вибратора (точки питания) до произвольной точки на
вибраторе (текущая координата); k = 2
- длина одного плеча вибратора; z -
расстояние от начала вибратора (точки питания) до произвольной точки на
вибраторе (текущая координата); k = 2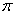 /
/ , - волновое число (коэффициент фазы тока в вибраторе).
, - волновое число (коэффициент фазы тока в вибраторе).
26
 Полагают, что длина
волны в вибраторе
Полагают, что длина
волны в вибраторе
λ, равна длине волны в свободном прост-
ранстве. В действительности
данная анна-
логия весьма приближённа.Обе системы-
линия и вибратор –
являются колебатель-
ными системами с распределенными па-
раметрами, однако
они существенно раз-
личаются. Во-первых, распределенные
параметры
Рис. 3.2. Преобразование двухпроводной
линии в симметричный вибратор
(а - линия, б - вибратор )
линии (Li,Ci) не изменяются по ее длине, распределенные параметры
вибратора непостоянны по его длине (рис.3.2.6). Во-вторых, линия служит для канализации
электромагнитных волн и является практически неизлучающей системой; вибратор же
излучает волны. В разомкнутой на конце линии ток изменяется по закону стоячей волны
только в том случае, если линия выполнена из идеального проводника, т.е. в ней
нет потерь энергии.
В вибраторе, выполненном даже из
идеального проводника, обязательно есть потери (полезные) на излучение.
Очевидно, поэтому ток в вибраторе, строго говоря, не может быть распределен по
закону стоячей волны. Однако расчет поля симметричного вибратора по формулам,
основанным на синусоидальном распределении тока, дает хорошее совпадение с
экспериментальными данными для дальней зоны и тонких вибраторов. Поэтому для инженерного
расчета это приближение в ряде случаев вполне допустимо. Строгая теория
симметричного вибратора подтверждает, что в тонких вибраторах ток распределен по
закону, весьма близкому к синусоидальному. Задавшись законом распределения
тока по вибратору, легко установить приближенный закон распределения заряда 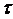 z=
z=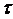 Пcosk(
Пcosk(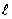 -
- 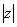 ), где
), где 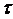 П амплитуда заряда в
его пучности.
Этот закон распределения заряда вдоль симметричного вибратора совпадает с
законом распределения потенциала (напряжения) в разомкнутой на конце длинной линии
без потерь. В теории антенн понятием напряжения следует пользоваться с большой
осторожностью, так как поле антенны не является потенциальным. Понятием напряжения
применительно к антенне можно пользоваться, если расстояние между точками
измерения мало по сравнению с длиной волны. Это справедливо при измерении
напряжения между зажимами антенны (точки присоединения генератора), а также для
длинноволновых антенн. На рис.3.3 приведены кривые распределения амплитуд тока
и заряда на вибраторах разной длины. По аналогии с волновым сопротивлением
длинной линии вводится понятие волнового сопротивления симметричного
вибратора. Как известно, из теории длинных линий, волновое сопротивление
двухпроводной линии без потерь определяется выражением W =
П амплитуда заряда в
его пучности.
Этот закон распределения заряда вдоль симметричного вибратора совпадает с
законом распределения потенциала (напряжения) в разомкнутой на конце длинной линии
без потерь. В теории антенн понятием напряжения следует пользоваться с большой
осторожностью, так как поле антенны не является потенциальным. Понятием напряжения
применительно к антенне можно пользоваться, если расстояние между точками
измерения мало по сравнению с длиной волны. Это справедливо при измерении
напряжения между зажимами антенны (точки присоединения генератора), а также для
длинноволновых антенн. На рис.3.3 приведены кривые распределения амплитуд тока
и заряда на вибраторах разной длины. По аналогии с волновым сопротивлением
длинной линии вводится понятие волнового сопротивления симметричного
вибратора. Как известно, из теории длинных линий, волновое сопротивление
двухпроводной линии без потерь определяется выражением W =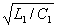 , где L1-распределенная
, где L1-распределенная
27
индуктивность
линии (индуктивность, приходящаяся на единицу длины линии), Г/м; C1 -, распределенная емкость линии, Ф/м. Так как 1/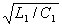 = с, где
= с, где
с - скорость света, м/с, то
W=l/cC1, Ом. (3.1)
Волновое
сопротивление двухпроводной линии связано с ее геометрическими размерами
соотношением
W=2761g (D/a), (3.2)
где D - расстояние между центрами проводов линии; а - радиус
провода.
|
Рис. 3.3. Распределение амплитуд тока и заряда на вибраторах разной длины
|
Волновое
сопротивление симметричного вибратора (а также других линейных антенн, т.е. антенн, длина которых
значительно превосходит размеры поперечного сечения) рассчитывают
по формуле (3.1).
Однако распределенная емкость по длине вибратора непостоянна. Поэтому в данном случае под C1 подразумевается усредненная величина, равная отношению полной статической емкости антенны (СА)
к ее длине (2l). Одним из наиболее распространенных
приближенных
методов расчета полной статической емкости является метод Хоу
или метод усредненных
потенциалов. Волновое сопротивление
симметричного вибратора из провода
цилиндрической формы, определенное
по методу Хоу,
WA=120(ln l/a-1), Oм, (3.3)
где l-длина плеча вибратора; а - радиус
провода.
Расчет волнового
сопротивления вибратора методом Хоу дает приемлемую точность
для вибраторов, коротких по сравнению с длиной волны. Точность этого метода снижается
по мере удлинения вибратора.
3.2. Направленные
свойства симметричного вибратора
Рассмотрим
симметричный вибратор произвольной длины (рис.3.4). Задаемся синусоидальным законом
распределения тока вдоль вибратора Iz = (I0/sinkl)sink(l -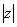 ), где I0 - ток в точках
питания вибратора (I0=Iпsinkl). Мысленно разобьем
вибратор на бесконечно большое число элементов dz. Так
как длина каждого элемента бесконечно мала, то можно полагать, что в пределах его ток не изменяется ни по
амплитуде, ни по фазе. Таким образом, весь
симметричный вибратор можно рассматривать как совокупность
), где I0 - ток в точках
питания вибратора (I0=Iпsinkl). Мысленно разобьем
вибратор на бесконечно большое число элементов dz. Так
как длина каждого элемента бесконечно мала, то можно полагать, что в пределах его ток не изменяется ни по
амплитуде, ни по фазе. Таким образом, весь
симметричный вибратор можно рассматривать как совокупность
28
элементарных электрических вибраторов dz и поле симметричного вибратора рассматривать
как результат сложения (интерференции) полей, излучаемых элементарными
вибраторами. Ввиду малости воздушного промежутка (зазора) между плечами
вибратора можно пренебречь влиянием электрического поля (магнитного тока), существующего в нем на
излучение, и считать, что электрический ток
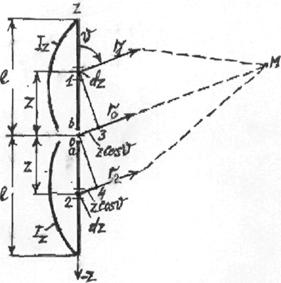
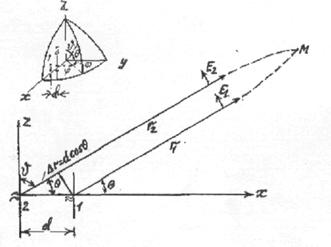
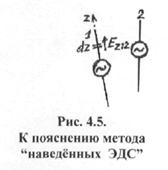
течет по сплошному проводнику длиной 2l. Выделим на вибраторе (рис.3.4) элементы 1 и 2, каждый длиной dz, симметричные относительно центра вибратора
0, и определим поле, создаваемое этими элементами в произвольной точке наблюдения М,
находящейся в зоне излучения.
Проведем от элементов 1 и 2 и от центра вибратора линии в точку наблюдения r1, r0, r2. Поскольку расстояние до точки наблюдения очень велико по сравнению с длиной
вибратора, то направления от всех точек вибратора на точку М можно считать параллельными.
Напряженность поля, излучаемого первым элементом в точке М
dE1 = i [60 Izdz/ (r1
Izdz/ (r1 )]sin
)]sin exp(-ikr1).
exp(-ikr1).
(3.4.a)
Напряженность поля, излучаемого вторым элементом в той же точке М dE2 = i [60 Izdz/(r2
Izdz/(r2 )] sin
)] sin exp(-ikr2).
exp(-ikr2).
(3.4.б)
Здесь Iz - амплитуда тока в
элементе,
находящемся на расстоянии z от центра вибратора;
r1 - расстояние от первого элемента до точки М;
г2
- расстояние от второго элемента до точки М;
|
Рис. 3.4. К определению
поля излучения симметричного вибратора
|
 - угол между осью
вибратора и направлением на точку наблюдения.
- угол между осью
вибратора и направлением на точку наблюдения.
Найдем суммарное поле, создаваемое в точке
наблюдения элементами 1 и 2. Так как
векторы напряженности полей, создаваемых всеми элементами вибратора в точке
наблюдения, направлены вдоль одной прямой (перпендикулярной направлению от данного элемента в точку наблюдения), то поля, создаваемые отдельными элементами, можно
складывать алгебраически. Поэтому
dE = dE1+dE2=i
(60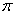 Izdz/
Izdz/ )sin
)sin [(exp(-ikr1)/r1+exp(-ikr2)/r2)]. (3.5)
[(exp(-ikr1)/r1+exp(-ikr2)/r2)]. (3.5)
Выразим расстояния r1 и r2 через расстояние r0. Для этого из точки 1 (рис.3.4)
опустим перпендикуляр на направление r0 и из точки 0 опустим перпендикуляр на направление r2. Из прямоугольных треугольников 1-0-3 и 2-0-4 находим, что разность расстояний от данных элементов и центра вибратора
до точки наблюдения равна  r =
r = 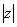 cos
cos .
.
29
Следовательно,
r1 = r0 - |z|cos и
r2 = r0 +
и
r2 = r0 + 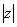 cos
cos . (3.6)
. (3.6)
Величину  r часто называют разностью
хода лучей. Так как точка наблюдения
находится в дальней зоне, то величина
r часто называют разностью
хода лучей. Так как точка наблюдения
находится в дальней зоне, то величина  r мала по сравнению с r0 и расстояния r1 и r2 мало отличаются друг от друга. Поэтому
можно считать, что амплитуды напряженности
полей, создаваемых элементами 1 и 2 в точке наблюдения М, одинаковы. Однако пренебрегать разностью хода в фазовых
множителях (exp(-ikr1) и exp(-ikr2)) ни в коем случае нельзя, так как пространственный сдвиг фаз между полями элементов 1 и 2 k
r мала по сравнению с r0 и расстояния r1 и r2 мало отличаются друг от друга. Поэтому
можно считать, что амплитуды напряженности
полей, создаваемых элементами 1 и 2 в точке наблюдения М, одинаковы. Однако пренебрегать разностью хода в фазовых
множителях (exp(-ikr1) и exp(-ikr2)) ни в коем случае нельзя, так как пространственный сдвиг фаз между полями элементов 1 и 2 k r = 2k|z|cosν = 4
r = 2k|z|cosν = 4 (|z|/
(|z|/ )cos
)cos определяется отношением разности хода лучей к длине волны. На
основании формул (3.6) получаем следующие выражения для фазовых множителей exp(-ikr1)= exp(-ikr0) * exp(ik|z|)cos
определяется отношением разности хода лучей к длине волны. На
основании формул (3.6) получаем следующие выражения для фазовых множителей exp(-ikr1)= exp(-ikr0) * exp(ik|z|)cos ;
;
exp (-ikr2) = exp (-ikro)
* exp (-ik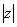 )cos
)cos .
.
Подставляя эти выражения в формулу (3.5), вынося за скобки общие множители и полагая, что в знаменателях r1 r2
r2  r0, получаем
r0, получаем
dE=i[60 I0sink(l-
I0sink(l-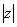 )dz/(r0
)dz/(r0  sinkl)]sin
sinkl)]sin exp(-ikr0)[(exp(ik
exp(-ikr0)[(exp(ik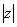 )cos
)cos +
+
+exp
(-ik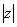 ) cos
) cos )].
)].
Воспользовавшись известной
формулой exp(i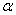 ) + exp(-i
) + exp(-i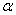 ) = 2cos
) = 2cos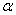 , получаем следующее
выражение
, получаем следующее
выражение
dE = i[120 I0/( r0
I0/( r0  sinkl)] sin
sinkl)] sin exp(-ikr0)sink(l-
exp(-ikr0)sink(l-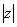 )cos(k
)cos(k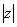 cos
cos )dz.
)dz.
Для определения напряженности поля, создаваемого в точке наблюде-
ния всем симметричным вибратором, необходимо это выражение проинтег-
рировать по длине одного плеча вибратора
Е=i[120 I0/(r0
I0/(r0  sinkl)] sin
sinkl)] sin exp(-ikr0)
exp(-ikr0) 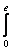 sink(l-
sink(l-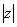 )cos(k
)cos(k cos
cos )dz.
)dz.
В результате
интегрирования получается формула для расчета напря-
женности поля симметричного
электрического вибратора
в дальней зоне
E=i [60I0/ (r0sinkl)] * [(cos(klcos ) - coskl) / sin
) - coskl) / sin ]exp(-ikr0). (3.7)
]exp(-ikr0). (3.7)
Как и в случае
элементарного электрического вибратора, эта формула состоит из трех множителей:
множителя, определяющего только величину напряженности поля и не зависящего от
направления в данную точку [60I0/(r0sinkl)], множителя, определяющего направленные
свойства (характеристика направленности).
f( )=[cos(klcos
)=[cos(klcos ) - coskl]/sin
) - coskl]/sin
и фазового множителя  = iexp(-ikr0) из выражения (3.7) видно, что симметричный
вибратор обладает направленными свойствами только в меридиональной плоскости (плоскость электрического
вектора). Напряженность
электрического поля симметричного вибратора в его экваториальной
= iexp(-ikr0) из выражения (3.7) видно, что симметричный
вибратор обладает направленными свойствами только в меридиональной плоскости (плоскость электрического
вектора). Напряженность
электрического поля симметричного вибратора в его экваториальной
30
плоскости ( плоскость магнитного вектора ν=  /2) - определяется выражением
/2) - определяется выражением
E = i [60I0/(r0sinkl)](l-coskl)exp(-ikro), (3.8)
т.е. не зависит от
азимутального угла  . Поэтому диаграмма направленности
. Поэтому диаграмма направленности
симметричного
вибратора в его экваториальной плоскости, как и в случае элементарного
вибратора, представляет в полярной системе координат ок-
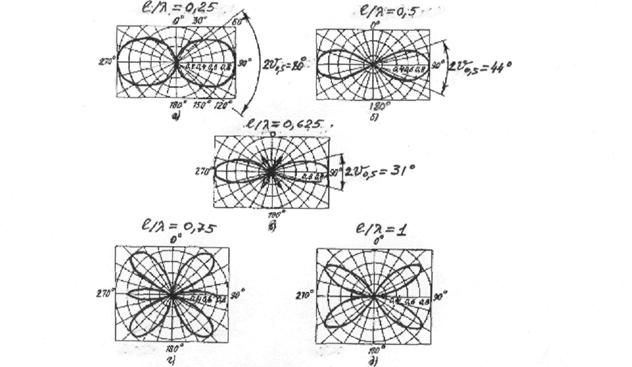
3.5.Диаграммы направленности симметричного вибратора
ружность. Как видно из формулы (3.7), направленные
свойства симметричного вибратора определяются только отношением длины плеча
вибратора к длине волны l/ .В случае полуволнового вибратора (l/
.В случае полуволнового вибратора (l/ =0,25) формула (3.7) принимает вид
=0,25) формула (3.7) принимает вид
Е= iA{cos[( /2)cos
/2)cos ]/(sin
]/(sin )}exp (-ikr0).
)}exp (-ikr0).
Амплитудные диаграммы направленности, рассчитанные по формуле (3.7),
для вибраторов с различной относительной длиной l/ показаны на
рис.3.5. Анализ формулы (3.7) и рассмотрение этих кривых показывают, что
при
любой величине отношения l/
показаны на
рис.3.5. Анализ формулы (3.7) и рассмотрение этих кривых показывают, что
при
любой величине отношения l/ симметричный вибратор
не излучает вдоль своей
оси. Если длина плеча симметричного вибратора l
симметричный вибратор
не излучает вдоль своей
оси. Если длина плеча симметричного вибратора l 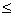 0,5
0,5 , то в направлении, перпендикулярном его оси (
, то в направлении, перпендикулярном его оси ( = 90°,
= 90°,  = 270°), т.е. в экваториальной
плоскости, поля всех элементарных вибраторов максимальны, синфазны и складываются арифметически. Поэтому поле в данном
направлении является максимальным. Диаграмма направленности
при l/
= 270°), т.е. в экваториальной
плоскости, поля всех элементарных вибраторов максимальны, синфазны и складываются арифметически. Поэтому поле в данном
направлении является максимальным. Диаграмма направленности
при l/
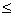 0,5 состоит из двух
(главных) лепестков (рис. 3.5.а, 3.5.б). Увеличение длины вибратора до l=0,5
0,5 состоит из двух
(главных) лепестков (рис. 3.5.а, 3.5.б). Увеличение длины вибратора до l=0,5 сопровождается ростом излучения в направлении, перпендикулярном
сопровождается ростом излучения в направлении, перпендикулярном
31
оси вибратора (главное направление излучения),за счет уменьшения
излучения в других направлениях. При этом диаграмма направленности становится
уже. При увеличении l/ до 0,625 излучение в главном направлении продолжает возрастать,
но характеристика направленности проходит через нуль не только при
до 0,625 излучение в главном направлении продолжает возрастать,
но характеристика направленности проходит через нуль не только при  =0° и
=0° и  =180°, но и при некоторых других значениях угла
=180°, но и при некоторых других значениях угла . Главные лепестки диаграммы становятся уже, но появляются
боковые лепестки (рис.3.5.в). При дальнейшем увеличении l/
. Главные лепестки диаграммы становятся уже, но появляются
боковые лепестки (рис.3.5.в). При дальнейшем увеличении l/ излучение в главном направлении уменьшается
и возрастают боковые лепестки. Уменьшение излучения в главном направлении
объясняется следующим. Результирующий сдвиг фаз полей, излучаемых элементарными
вибраторами в данном направлении, определяется пространственным сдвигом фаз и сдвигом фаз
токов, возбуждающих эти вибраторы. При l/
излучение в главном направлении уменьшается
и возрастают боковые лепестки. Уменьшение излучения в главном направлении
объясняется следующим. Результирующий сдвиг фаз полей, излучаемых элементарными
вибраторами в данном направлении, определяется пространственным сдвигом фаз и сдвигом фаз
токов, возбуждающих эти вибраторы. При l/ >0,5 на вибраторе появляются участки с
противофазными токами (рис.3.3), длина которых растет по мере увеличения l/
>0,5 на вибраторе появляются участки с
противофазными токами (рис.3.3), длина которых растет по мере увеличения l/ . Поэтому в данном случае, хотя в главном направлении
пространственные сдвиги фаз равны нулю, поля, излучаемые
отдельными элементами вибратора, складываются несинфазно, т.е. геометрически.
При l/
. Поэтому в данном случае, хотя в главном направлении
пространственные сдвиги фаз равны нулю, поля, излучаемые
отдельными элементами вибратора, складываются несинфазно, т.е. геометрически.
При l/ = 1 (или при l/
= 1 (или при l/ = п,
где п = 1, 2, ..,) излучение в главном
направлении отсутствует, так как противофазные участки вибратора имеют
одинаковую длину. Рост l/
= п,
где п = 1, 2, ..,) излучение в главном
направлении отсутствует, так как противофазные участки вибратора имеют
одинаковую длину. Рост l/ сопровождается также ростом боковых лепестков. Уже при
l/
сопровождается также ростом боковых лепестков. Уже при
l/ =0,75 напряженность поля в направлении максимума
бокового лепестка превосходит напряженность поля в главном направлении
(рис.3.3.г).
=0,75 напряженность поля в направлении максимума
бокового лепестка превосходит напряженность поля в главном направлении
(рис.3.3.г).
Нормированная характеристика направленности
симметричного вибратора, определяемая как F( ) = f(
) = f( )/f(90°), равна
)/f(90°), равна
F( ) = [cos(klcos
) = [cos(klcos ) - coskl]/[(l – coskl)sin
) - coskl]/[(l – coskl)sin ]. (3.9)
]. (3.9)
У Диполя Герца 2 0,5= 90°. Полуволновый
симметричный вибратор имеет ширину диаграммы направленности по половинной
мощности 2
0,5= 90°. Полуволновый
симметричный вибратор имеет ширину диаграммы направленности по половинной
мощности 2 0,5= 80°, волновой симметричный вибратор - 2
0,5= 80°, волновой симметричный вибратор - 2 0,5= 44°, симметричный вибратор, у которого
l/
0,5= 44°, симметричный вибратор, у которого
l/ =0,625, имеет 2
=0,625, имеет 2 0,5= 31°. Последний вибратор обладает наилучшими направленными свойствами, так как при дальнейшем увеличении l/
0,5= 31°. Последний вибратор обладает наилучшими направленными свойствами, так как при дальнейшем увеличении l/ , сильно возрастают боковые лепестки, хотя главный
лепесток диаграммы направленности становится
уже. На практике применяются
симметричные вибраторы, у которых l/
, сильно возрастают боковые лепестки, хотя главный
лепесток диаграммы направленности становится
уже. На практике применяются
симметричные вибраторы, у которых l/
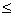 0,7. Фаза напряженности поля, создаваемого симметричным
вибратором в соответствии с выражением (3.7), в пределах одного лепестка
диаграммы направленности не зависит от координатного угла
0,7. Фаза напряженности поля, создаваемого симметричным
вибратором в соответствии с выражением (3.7), в пределах одного лепестка
диаграммы направленности не зависит от координатного угла  . Она изменяется скачком на обратную
при переходе напряжённости поля через нуль. Симметричный вибратор излучает
сферические волны, о чем свидетельствует множитель exp(-ikr)/r. Эти волны как бы
исходят из одной точки,
совпадающей с центром вибратора.
. Она изменяется скачком на обратную
при переходе напряжённости поля через нуль. Симметричный вибратор излучает
сферические волны, о чем свидетельствует множитель exp(-ikr)/r. Эти волны как бы
исходят из одной точки,
совпадающей с центром вибратора.
32
3.3. Мощность
излучения, сопротивление излучения и КНД симметричного вибратора
Мощность электромагнитной волны, излучаемой симметричным вибратором, можно
определить, как и для элементарного вибратора, методом вектора Пойнтинга. В соответствии с данным методом симметричный
вибратор окружается сферой, радиус которой r » , вследствие чего поверхность сферы находится в дальней зоне поля
вибратора. Центр вибратора совпадает с центром сферы, ось вибратора лежит на
оси z прямоугольной системы координат. На
поверхности сферы выделяется бесконечно малый элемент dS, площадь которого в сферической системе координат
dS = r2sinνd
, вследствие чего поверхность сферы находится в дальней зоне поля
вибратора. Центр вибратора совпадает с центром сферы, ось вибратора лежит на
оси z прямоугольной системы координат. На
поверхности сферы выделяется бесконечно малый элемент dS, площадь которого в сферической системе координат
dS = r2sinνd d
d .
Излучаемая
мощность, приходящаяся на данный элемент поверхности
.
Излучаемая
мощность, приходящаяся на данный элемент поверхности
dP = ПсрdS=(E2/2Wc)dS. (3.10)
= ПсрdS=(E2/2Wc)dS. (3.10)
Здесь Е - амплитуда (модуль) напряженности электрического поля в любой
точке элемента dS, определяемая выражением
E
= (60Iп/r)  [cos (kl cos
[cos (kl cos ) - cos kl] / sin
) - cos kl] / sin
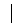 . (3.11)
. (3.11)
В общем виде выражение для сопротивления излучения имеет вид
R п = [r2Е2 макс/(
Wc Iп2 )]
п = [r2Е2 макс/(
Wc Iп2 )] 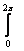
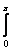 F2(
F2( ,
, )sin
)sin dνd
dνd . (3.12)
. (3.12)
P = Iп2R
= Iп2R п/2.
п/2.
Величина R п определяется
характером распределения электромагнитного поля в дальней зоне, т.е. диаграммой
направленности рассматриваемой антенны. Интегрирование дает следующую формулу, впервые
полученную Баллантайном в 1924 г.
п определяется
характером распределения электромагнитного поля в дальней зоне, т.е. диаграммой
направленности рассматриваемой антенны. Интегрирование дает следующую формулу, впервые
полученную Баллантайном в 1924 г.
R п
= 30 [2 (
п
= 30 [2 (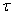 +ln2kl - Ci 2kl) + cos 2kl (
+ln2kl - Ci 2kl) + cos 2kl (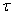 +lnkl+ Ci 4kl - 2Ci 2kl) +
+lnkl+ Ci 4kl - 2Ci 2kl) +
+sin2kl (Si
4kl- 2Si 2kl)]. (3.1)
Здесь 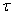 = 0,5772... - постоянная
Эйлера; Si x = (sin u/u)du – интегральный
= 0,5772... - постоянная
Эйлера; Si x = (sin u/u)du – интегральный
синус; Ci x =
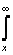 (cos u/u)du - интегральный косинус.
(cos u/u)du - интегральный косинус.
Как видно из формулы
(3.13), сопротивление излучения симметричного вибратора зависит только от величины
отношения l/ . Формула (3.13) является приближенной, поскольку при ее
выводе исходили из синусоидального распределения тока по вибратору, что
справедливо только для тонких вибраторов. Однако результаты расчетов по формуле (3.13)
хорошо совпадают с экспериментальными данными. Это объясняется тем, что сопротивление излучения
определяется полем в дальней зоне, которое мало зависит от толщины вибратора.
Следует также иметь в виду, что изложенный здесь метод расчета дает только
активную составляющую сопротивления излучения, так как учитывается только излученная
активная мощность.
. Формула (3.13) является приближенной, поскольку при ее
выводе исходили из синусоидального распределения тока по вибратору, что
справедливо только для тонких вибраторов. Однако результаты расчетов по формуле (3.13)
хорошо совпадают с экспериментальными данными. Это объясняется тем, что сопротивление излучения
определяется полем в дальней зоне, которое мало зависит от толщины вибратора.
Следует также иметь в виду, что изложенный здесь метод расчета дает только
активную составляющую сопротивления излучения, так как учитывается только излученная
активная мощность.
33
В литературе имеются таблицы и графики R п как функции отношения
(рис.3.6), рассчитанные по формуле (3.13). Осциллирующий характер зависимости объясняется
тем, что интерференционная картина поля в дальней зоне меняется при
изменении l/
п как функции отношения
(рис.3.6), рассчитанные по формуле (3.13). Осциллирующий характер зависимости объясняется
тем, что интерференционная картина поля в дальней зоне меняется при
изменении l/ .
.
Если
отношение l/ , не превышает
0,1, то формулу
(3.13) можно упростить R
, не превышает
0,1, то формулу
(3.13) можно упростить R п=20 (k l)4 .
п=20 (k l)4 .
КНД симметричного вибратора можно определить по формуле
D = (120 / R п
) (1 -coskl)2. (3.14)
п
) (1 -coskl)2. (3.14)
При l/ =0,25 R
=0,25 R п = 73,1 Ом и D=
1,64 ;
п = 73,1 Ом и D=
1,64 ;
l/ = 0,5 R
= 0,5 R п =199 Ом и D
= 2,4;
п =199 Ом и D
= 2,4;
l/ =0,625 R
=0,625 R п =110 Ом и D
= 3,l.
п =110 Ом и D
= 3,l.
Для сравнения КНД элементарного
электрического вибратора имеет
D = 1,5.
КНД любой вибраторной антенны можно рассчитать по формуле
D = (120/ R п) f2max (
п) f2max (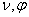 ). (3.15)
). (3.15)
В этой формуле R п - полное сопротивление излучения антенны. Действующая длина симметричного вибратора определяется по формуле
п - полное сопротивление излучения антенны. Действующая длина симметричного вибратора определяется по формуле
lд =  (1 - coskl) / (
(1 - coskl) / ( sinkl). (3.16)
sinkl). (3.16)
Рис 3.6. Зависимость R п От величины
l/
п От величины
l/
3.4. Входное сопротивление симметричного
вибратора. Инженерный метод расчета входного
сопротивления
Часть мощности, подводимой от генератора к
симметричному вибратору, излучается. Другая часть мощности теряется в самом
вибраторе (нагревание проводов), в изоляторах
и в окружающих вибратор предметах. Излученной мощности соответствует активное
сопротивление излучения. Мощности потерь
соответствует активное сопротивление потерь. Кроме излученного,
есть колеблющееся вблизи антенны
связанное с ней электромагнитное поле, которому соответствует реактивная
мощность. Эта мощность то отдается генератором,
34
переходя в ближнее
поле, то возвращается к нему обратно. Реактивной мощности в большинстве случаев
соответствует реактивное сопротивление антенны.
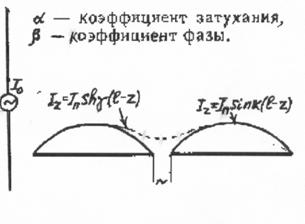 Таким образом, включенный
в антенну генератор нагружен на комплексное сопротивление, которое называется входным
сопротивлением антенны и равно отношению напряжения на зажимах вибратора (точки
питания) к току в точках питания ZBX=U0/I0=RBX+i XBX.
Таким образом, включенный
в антенну генератор нагружен на комплексное сопротивление, которое называется входным
сопротивлением антенны и равно отношению напряжения на зажимах вибратора (точки
питания) к току в точках питания ZBX=U0/I0=RBX+i XBX.
|
Рис. 3.7. Распределение тока по
"коротким" и "длинным" вибраторам
|
Величина и характер
входного сопротивления определяют режим работы включенного в антенну генератора. Обычно в
симметричных вибраторах потери малы, поэтому будем полагать, что RBX  R
R o, где R
o, где R o - сопротивление излучения вибратора, отнесенное к
току в точках питания. Для точного определения входного сопротивления
необходимо знать закон распределения тока вдоль вибратора. Часто с
достаточной для инже-
o - сопротивление излучения вибратора, отнесенное к
току в точках питания. Для точного определения входного сопротивления
необходимо знать закон распределения тока вдоль вибратора. Часто с
достаточной для инже-
нерных целей точностью
входное сопротивление рассчитывается, исходя из приближенных законов распределения
тока по вибратору. Рассмотрим такой приближенный (инженерный) метод расчета
входного сопротивления. Предположив, что ток вдоль вибратора распределен по закону
синуса, найдем входное сопротивление симметричного вибратора, у которого l/ =0,5 (рис.3.7). В этом случае ток в точках питания оказывается
равным нулю и очевидно, что ZBX = U0/I0=
=0,5 (рис.3.7). В этом случае ток в точках питания оказывается
равным нулю и очевидно, что ZBX = U0/I0= . В действительности же ток в точках питания никогда не бывает
равен нулю (его величина обязательно конечна), а следовательно,
входное сопротивление симметричного вибратора никогда не бывает бесконечно
велико. Физически это совершенно ясно. Ведь закон синуса (стоячая волна)
справедлив в линиях только при отсутствии потерь. Вибратор же в
принципе является системой с потерями на излучение. Следовательно, при расчете
входного сопротивления лучше проводить аналогию между симметричным вибратором и
разомкнутой на конце линией с потерями. Известно, что ток в такой линии
распределен по закону гиперболического синуса (рис.3.7) Iz = Iпsh
. В действительности же ток в точках питания никогда не бывает
равен нулю (его величина обязательно конечна), а следовательно,
входное сопротивление симметричного вибратора никогда не бывает бесконечно
велико. Физически это совершенно ясно. Ведь закон синуса (стоячая волна)
справедлив в линиях только при отсутствии потерь. Вибратор же в
принципе является системой с потерями на излучение. Следовательно, при расчете
входного сопротивления лучше проводить аналогию между симметричным вибратором и
разомкнутой на конце линией с потерями. Известно, что ток в такой линии
распределен по закону гиперболического синуса (рис.3.7) Iz = Iпsh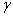 (z - l), где
(z - l), где 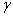 =
= 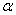 + i
+ i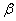 - коэффициент распространения,
- коэффициент распространения, 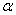 - коэффициент ослабления,
- коэффициент ослабления, 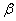 - коэффициент фазы.
- коэффициент фазы.
Из рис.3.7
видно, что существенная разница в распределении тока по законам кругового и
гиперболического синусов получается только на сравнительно близких расстояниях от
узла тока. Поэтому при расчете входных сопротивлений "коротких" вибраторов (l/ )
)  0,35...0,4;
(0,6...0,65)
0,35...0,4;
(0,6...0,65)  l/
l/
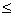 (0,85...0,9), т.е. таких, у которых узел тока
находится от точек питания вибратора не ближе, чем на расстоянии (0,1...0,15)
(0,85...0,9), т.е. таких, у которых узел тока
находится от точек питания вибратора не ближе, чем на расстоянии (0,1...0,15) , исходят из синусоидального распределения тока. При расчете входного сопротивления "длинных"
вибраторов (0,35
, исходят из синусоидального распределения тока. При расчете входного сопротивления "длинных"
вибраторов (0,35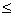 l/
l/
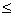 0,65) следует исходить из распределения тока по закону
гиперболического синуса. Найдем формулы
для расчета активной
0,65) следует исходить из распределения тока по закону
гиперболического синуса. Найдем формулы
для расчета активной
35
и реактивной
составляющих входного сопротивления "короткого" вибратора. Выразив мощность, излучаемую вибратором,
через амплитуды тока в пучности (IП) и в точках питания (Iо), получим:
P = (Iп2R
= (Iп2R п
)/2 и P
п
)/2 и P = (I02 R
= (I02 R 0)/2. (3.17)
0)/2. (3.17)
Так как левые части этих выражений
равны между собой, то I2п R п = I02 R
п = I02 R 0. Решая это равенство
относительно R
0. Решая это равенство
относительно R 0, получаем R
0, получаем R 0= R
0= R п (Iп2/ I02).
п (Iп2/ I02).
Подставляя вместо I0 выражение I0=Iпsinkl, получаем формулу
для расчета
активной составляющей входного сопротивления вибратора (без учета потерь в вибраторе)
R 0 = R
0 = R п /sin2kl. (3.18)
п /sin2kl. (3.18)
Величину R п для вибратора заданной длины легко найти из
таблиц или
графиков. При расчете реактивной составляющей входного сопротивления короткого симметричного вибратора
пользуются формулой входного сопротивления
разомкнутой на конце двухпроводной линии без потерь, заменяя в ней волновое
сопротивление линии волновым сопротивлением антенны
п для вибратора заданной длины легко найти из
таблиц или
графиков. При расчете реактивной составляющей входного сопротивления короткого симметричного вибратора
пользуются формулой входного сопротивления
разомкнутой на конце двухпроводной линии без потерь, заменяя в ней волновое
сопротивление линии волновым сопротивлением антенны
Xвх= -i WActg kl. (3.19)
Таким образом, полное
входное сопротивление короткого вибратора можно определить по формуле
Zвх= (R п/sin2kl) – i WActg kl. (3.20)
п/sin2kl) – i WActg kl. (3.20)
Точность расчетов по
формуле (3.20) повышается при уменьшении размеров поперечного сечения
вибратора. В случаях длинных вибраторов входное сопротивление рассчитывается
аналогично входному сопротивлению двухпроводной разомкнутой на конце линии, обладающей
потерями
Zвх = WA [(sh2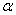 l- (
l- ( /
/ ) sin 2
) sin 2 l) / (ch2
l) / (ch2 l - cos 2
l - cos 2 l)] – i WA [(
l)] – i WA [( /
/ ) sh 2
) sh 2 l+
l+
+ sin 2 l) / (ch2
l) / (ch2 l - cos
2
l - cos
2 l)]. (3.21)
l)]. (3.21)
Здесь WA - волновое сопротивление вибратора; l- длина плеча вибратора;  - коэффициент фазы в вибраторе;
- коэффициент фазы в вибраторе;  - коэффициент затухания. По аналогии с длинными линиями, пренебрегая потерями в проводах вибратора коэффициент затухания можно рассчитать по формуле
- коэффициент затухания. По аналогии с длинными линиями, пренебрегая потерями в проводах вибратора коэффициент затухания можно рассчитать по формуле
 = R
= R 1 / WA, где R
1 / WA, где R 1 -активное сопротивление излучения, приходящееся на единицу
длины вибратора. Приближенно
полагая, что сопротивление излучения R
1 -активное сопротивление излучения, приходящееся на единицу
длины вибратора. Приближенно
полагая, что сопротивление излучения R п распределено равномерно по всей длине вибратора, для расчета R
п распределено равномерно по всей длине вибратора, для расчета R 1 получают формулу R
1 получают формулу R 1=
R
1=
R п/[l(l - (sin2kl/2kl)]. Данная формула позволяет, зная сопротивление излучения, отнесенное к пучности тока, найти
распределенное сопротивление
излучения. Следовательно, коэффициент ослабления
п/[l(l - (sin2kl/2kl)]. Данная формула позволяет, зная сопротивление излучения, отнесенное к пучности тока, найти
распределенное сопротивление
излучения. Следовательно, коэффициент ослабления
 = R
= R 1/
WA = R
1/
WA = R п/ [lWA (1- (sin2kl/2kl))].
п/ [lWA (1- (sin2kl/2kl))].
Коэффициент фазы  в формуле (3.21)
несколько отличается от
в формуле (3.21)
несколько отличается от
36
Рис. 3.8. Зависимость R вх от величины l/
коэффициента фазы в свобод-
ном
пространстве k, так как
фазовая скорость в линии с
потерями, а, следовательно, и в
вибраторе несколько меньше
скорости света. Поэтому =
=
 /
/ > k
=
> k
=  /с , где
/с , где  -фазовая
-фазовая
скорость
в вибраторе. Чем
меньше
волновое сопротивление вибратора (чем толще вибратор),
тем меньше фазовая
скорость.
Из формулы (3.21)
видно,
что как активная, так и
реактивная составляющие
входного сопротивления симметричного вибратора,
в общем
случае, зависят не только от длины вибратора, но и от его диаметра.
Зависимость входного сопротивления симметричного вибратора от величины отношения l/ и от волнового сопротивления WA показана на рис. 3.8 и 3.9.
и от волнового сопротивления WA показана на рис. 3.8 и 3.9.
Кривые рассчитаны по формуле (3.21). При расчете
полагалось, что 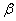 = k. Из кривых видно, что при увеличении l/
= k. Из кривых видно, что при увеличении l/ активная
составляющая входного сопротивления
постепенно растет и достигает при l/
активная
составляющая входного сопротивления
постепенно растет и достигает при l/ =0,5 максимума, величина которого тем больше, чем больше wa, т.е. чем тоньше вибратор. При
дальнейшем увеличении
l/
=0,5 максимума, величина которого тем больше, чем больше wa, т.е. чем тоньше вибратор. При
дальнейшем увеличении
l/ rbx постепенно
уменьшается и достигает минимума при
l/
rbx постепенно
уменьшается и достигает минимума при
l/ =0,75. Затем Rвх снова начинает увеличиваться и
достигает
=0,75. Затем Rвх снова начинает увеличиваться и
достигает
Рис. 3.9. Зависимость
X вх от величины l/
37
нового максимума при l= (на рисунке этот
максимум не показан). Вообще максимумы Rвх повторяются при всех отношениях l/
(на рисунке этот
максимум не показан). Вообще максимумы Rвх повторяются при всех отношениях l/ , кратных 0,5. Активная составляющая входного сопротивления
минимальна в тех случаях, когда относительная длина вибратора становится
равной нечетному числу
, кратных 0,5. Активная составляющая входного сопротивления
минимальна в тех случаях, когда относительная длина вибратора становится
равной нечетному числу  /4. В случае полуволнового вибратора минимум Rвх отсутствует. Реактивная
составляющая
входного сопротивления вибратора изменяется периодически, проходя через нуль
при l/
/4. В случае полуволнового вибратора минимум Rвх отсутствует. Реактивная
составляющая
входного сопротивления вибратора изменяется периодически, проходя через нуль
при l/ =0,25; 0,5;0,75; 1 и т.д.
При l/
=0,25; 0,5;0,75; 1 и т.д.
При l/ <0,25 Хвх имеет емкостный характер,
при 0,25< l/
<0,25 Хвх имеет емкостный характер,
при 0,25< l/ <0,5 - индуктивный. Можно сказать, что вблизи значений l/
<0,5 - индуктивный. Можно сказать, что вблизи значений l/ = (2n + 1)/4, где n=0,
1, 2..., симметричный вибратор ведет себя подобно последовательному колебательному
контуру (резонанс напряжения), а вблизи значений l/
= (2n + 1)/4, где n=0,
1, 2..., симметричный вибратор ведет себя подобно последовательному колебательному
контуру (резонанс напряжения), а вблизи значений l/ =n/2- подобно параллельному колебательному контуру
(резонанс токов). В первом случае вибратор питается в пучности тока, а во втором - в узле тока.
Наибольшую длину волны, при которой
вибратор оказывается настроенным в резонанс с питающим его генератором (Хвх=
0), называют собственной длиной волны антенны. Как видно из
формул (3.20) и (3.21), собственная длина волны симметричного вибратора
=n/2- подобно параллельному колебательному контуру
(резонанс токов). В первом случае вибратор питается в пучности тока, а во втором - в узле тока.
Наибольшую длину волны, при которой
вибратор оказывается настроенным в резонанс с питающим его генератором (Хвх=
0), называют собственной длиной волны антенны. Как видно из
формул (3.20) и (3.21), собственная длина волны симметричного вибратора  0=4l. В действительности
из-за того, что фазовая скорость распространения в вибраторе
несколько меньше скорости света (
0=4l. В действительности
из-за того, что фазовая скорость распространения в вибраторе
несколько меньше скорости света (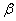 > k), резонансные длины вибраторов
оказываются несколько меньшими, чем получаемые по формулам (3.20) и
(3.21). При этом, чем толще вибратор, тем меньше
фазовая скорость
и тем короче его резонансная длина. В частности, при l/
> k), резонансные длины вибраторов
оказываются несколько меньшими, чем получаемые по формулам (3.20) и
(3.21). При этом, чем толще вибратор, тем меньше
фазовая скорость
и тем короче его резонансная длина. В частности, при l/ =0,25 и а
=0,25 и а 0 Хвх=i42,5
Ом. Обычно стремятся к нулевой реактивной составляющей входного сопротивления вибратора на
рабочей частоте. Поэтому длину плеча вибратора
делают несколько короче, чем
0 Хвх=i42,5
Ом. Обычно стремятся к нулевой реактивной составляющей входного сопротивления вибратора на
рабочей частоте. Поэтому длину плеча вибратора
делают несколько короче, чем  /4 или
/4 или  /2. Величина
укорочения тем больше, чем толще вибратор. Активная
составляющая входного сопротивления симметричного вибратора при питании
вибратора в пучности тока (последовательный
резонанс), как следует из формулы (3.20), равна Rвх=R
/2. Величина
укорочения тем больше, чем толще вибратор. Активная
составляющая входного сопротивления симметричного вибратора при питании
вибратора в пучности тока (последовательный
резонанс), как следует из формулы (3.20), равна Rвх=R 0=R
0=R п.. При определении входного сопротивления
симметричного вибратора, питаемого
вблизи узла тока, полагая, что
п.. При определении входного сопротивления
симметричного вибратора, питаемого
вблизи узла тока, полагая, что 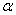 l<<1 (что соответствует действительности),
можно несколько преобразовать выражение (3.21) и получить следующие формулы:
l<<1 (что соответствует действительности),
можно несколько преобразовать выражение (3.21) и получить следующие формулы:
Rвх = R п / [sin2 kl+ (R
п / [sin2 kl+ (R п2/W2A)]; (3.22)
п2/W2A)]; (3.22)
Хвх = - i (WA/2) [sin2kl/ (sin2 kl + (R п2/W2A))] . (3.23)
п2/W2A))] . (3.23)
В случае параллельного резонанса (kl=180°) получаем
R 0 = WA2 / R
0 = WA2 / R п и
Хвх = 0. (3.24)
п и
Хвх = 0. (3.24)
Из формулы (3.24)
видно, что в случае параллельного резонанса R 0 весьма велико, так
как R
0 весьма велико, так
как R п
п 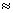 200 Ом, a WA составляет 300 ... 1000 Ом. Формулами (3.22) и
(3.23) можно пользоваться наряду с формулой (3.21) для расчета входного сопротивления
симметричного вибратора, если 0,35
200 Ом, a WA составляет 300 ... 1000 Ом. Формулами (3.22) и
(3.23) можно пользоваться наряду с формулой (3.21) для расчета входного сопротивления
симметричного вибратора, если 0,35 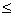 l/
l/
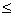 0,65. Отметим, что при
увеличении волнового сопротивления вибратора закон распределения тока по нему становится ближе к
синусоидальному.
0,65. Отметим, что при
увеличении волнового сопротивления вибратора закон распределения тока по нему становится ближе к
синусоидальному.
38
Поэтому в случае тонких вибраторов (WA=700...1000 Ом) пределы применимости формулы (3.20)
расширяются. Как видно из кривых рис. 3.8 и 3.9, при уменьшении волнового
сопротивления вибратора уменьшается зависимость его активного и реактивного
входного сопротивления от частоты (улучшаются диапазонные свойства). По аналогии с обычным
колебательным контуром можно сказать, что при уменьшении WA уменьшается
добротность вибратора, под которой понимается отношение связанной с вибратором
реактивной энергии к активной (излученной и теряемой) энергии. Добротность
вибратора определяется выражением
QA= A (WA/Rвх),
(3.25)
где А - коэффициент пропорциональности.
WA уменьшают, увеличивая размеры поперечного сечения
вибратора; при этом увеличивается распределенная емкость C1 вибратора.
Зависимость Rвх и Хвх
от относительной длины плеча вибраторов реальной толщины приведены на рис.3.10.
Рис. 3.10. Зависимость
Rвх и Xвх реальных
вибраторов от
величины l/
3.5. Основные
результаты, даваемые строгой теорией симметричного
вибратора
Задача об излучении
тонкого симметричного вибратора (электрический радиус вибратора ka < 0,1) в строгой
электродинамической постановке была решена Халленом и
независимо от него российскими учеными М.А.Леонтовичем и М.Л.Левиным методом
интегро-дифференциального уравнения. Как показали расчеты, даже в случае
сравнительно тонких вибраторов (ka 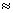 0,05) распределение
тока уже несколько отличается от синусоидального.
Таким образом, метод интегро-дифференциального уравнения подтверждает правильность
выбора приближенного (синусоидального) закона распределения тока и позволяет найти
точное распределение тока в
0,05) распределение
тока уже несколько отличается от синусоидального.
Таким образом, метод интегро-дифференциального уравнения подтверждает правильность
выбора приближенного (синусоидального) закона распределения тока и позволяет найти
точное распределение тока в
39
тонких вибраторах.
Однако он не позволяет найти закон распределения тока в вибраторах средней (ka= 0,1...0,5) и большой (ka > 0,5) толщины. Кроме
того, в рассмотренном методе не учитывается влияние ширины возбуждающего зазора на
распределение тока. Входное сопротивление полуволнового вибратора,
рассчитанное этим методом, при а 0 оказывается
комплексным и равным Zвх =
73,1 + i42,5 Ом. Как видно,
активная составляющая входного
сопротивления (R
0 оказывается
комплексным и равным Zвх =
73,1 + i42,5 Ом. Как видно,
активная составляющая входного
сопротивления (R 0) получается такой же, как и по методу
вектора Пойнтинга. Реактивная составляющая входного сопротивления
имеет индуктивный характер.
Укорочение
0) получается такой же, как и по методу
вектора Пойнтинга. Реактивная составляющая входного сопротивления
имеет индуктивный характер.
Укорочение  l, необходимое для того, чтобы сделать вибратор резонансным,
определяется по формуле
l, необходимое для того, чтобы сделать вибратор резонансным,
определяется по формуле
 l/l = - 0,225/ ln (l/a). (3.26)
l/l = - 0,225/ ln (l/a). (3.26)
Расчет входного
сопротивления полуволнового вибратора с учетом только первого приближения показал,
что даже в случае тонких вибраторов величина радиуса заметно, влияет на входное
сопротивление.
Задача об излучении
толстого вибратора (ka>0,5) в строгой постановке была решена Е. Н. Васильевым в 1958-1959 гг. В
отличие от методов Халлена или Леонтовича-Левина, где использовались
граничные условия для векторов
электрического поля на поверхности вибратора, в методе Васильева используется
граничное условие для векторов магнитного поля. Полученное из этого условия
интегральное уравнение относительно текущего по вибратору тока решается численно при помощи ЭВМ.
Решение тем более точно, чем толще
вибратор. В дальнейшем Е.Н. Васильевым и Г.Д. Малушковым был разработан
более общий метод решения задачи возбуждения осесимметричного
тела вращения, позволяющий рассчитать распределение тока на вибраторах среднего электрического радиуса (ka = 0,1...0,5),
что особенно важно для анализа работы
вибраторов, применяемых в метровом и особенно в дециметровом диапазонах волн. Проведенные расчеты показали, что распределение тока в вибраторах средней и большой толщины
значительно отличается от синусоидального. Ток на кромке торца имеет конечную
величину. В центре торца ток равен нулю. Расчеты
показали также, что: 1) с увеличением радиуса
цилиндра существенно уменьшается коэффициент отражения от его концов и
распределение тока по вибратору приобретает характер бегущей волны: амплитуда тока постепенно уменьшается по
мере удаления от точек питания
вибратора, фаза тока изменяется примерно по линейному закону; 2) ширина
зазора между плечами вибратора значительно влияет на распределение тока вблизи точек питания вибратора. Зависимость распределения тока от толщины вибратора влияет на диаграмму
направленности последнего. С
увеличением толщины вибратора направления нулевого излучения заменяются
направлениями минимального излучения. При этом чем
толще вибратор, тем менее глубоки минимумы.
Действительные
диаграммы направленности заметно отличаются от рассчитанных
приближенным методом при l/а, равном нескольким
десяткам.
40
3.6. Симметричный
щелевой вибратор
|
Рис.
3.11. Щелевой
вибратор (а) и его
аналог
(б)
|
В курсе «ЭМП и В» был рассмотрен элементарный щелевой излучатель,
представляющий собой узкую щель, прорезанную в безграничном идеально
проводящем плоском экране, длина которой во много раз меньше длины волны. На
практике широко применяются щелевые излучатели, длина которых соизмерима с длиной
волны. Излучающие щели обычно имеют прямолинейную форму (линейные щелевые
излучатели), но могут иметь и круглую форму (кольцевая щель). Излучающие щели
прорезают
в металлических поверхностях различных размеров и формы: в стенках прямоугольных и
круглых волноводов,
в оболочках коаксиальных кабелей, в плоских металлических экранах, в крыльях
самолетов и т.д. Иногда размеры металлической поверхности, в которой прорезана
щель, во много раз превышают длину волны, но практически обычно размеры этой
поверхности бывают соизмеримы с длиной волны. В
основном, щелевые антенны применяют в дециметровом, сантиметровом,
миллиметровом и редко в метровом (телевизионные
антенны) диапазонах волн. Кольцевые щелевые антенны можно применять в
диапазонах средних и даже длинных волн. Рассмотрим только идеализированный
случай - узкую щель, прорезанную в безграничном идеально проводящем экране. Под симметричной
щелью будем понимать узкую, прямоугольную
щель, питаемую в центре генератором высокой частоты (рис.3.11.а). ЭДС
генератора создает в щели электрическое поле, линии которого перпендикулярны ее краям. Под действием поля
в щели возникают электрические токи на металлической поверхности.
Электромагнитное поле в окружающем
пространстве определяется электрическим полем щели (магнитный ток) и электрическими токами, текущими по
металлической поверхности. На основании принципа двойственности по аналогии с
элементарной щелью, поле, создаваемое симметричной щелью, можно найти,
если известно поле, создаваемое симметричным
электрическим вибратором, имеющим одинаковую форму и размеры со щелью (рис.
3.11.б) и находящимся в свободном пространстве. Для этого в соответствии
с принципом двойственности надо в выражениях для составляющих поля
электрического вибратора произвести соответствующие замены. В случае очень
тонкого электрического вибратора ток в нем
распределен по закону синуса. По этому же закону
изменяется вдоль вибратора и тангенциальная составляющая напряженности магнитного поля. Следовательно,
вдоль узкого щелевого вибратора тангенциальная
составляющая напряженности электрического поля (а значит, и напряжение
-
42
магнитный ток) изменяется также по синусоидальному
закону,т.е. Uz= (U0/sinkl) (sink(l -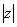 )), где U0 - амплитуда
напряжения в центре щели; l - длина половины щели.
)), где U0 - амплитуда
напряжения в центре щели; l - длина половины щели.
Я.Н.Фельд, решая задачу об
излучении узкой щели, по существу, аналогично методу интегро-дифференциального
уравнения для тонких электрических вибраторов, строго доказал, что вдоль такой
щели напряжение распределено
по закону синуса. В частности, в случае полуволновой щели напряжение распределено по закону синуса независимо
от точек включения генератора. Напряженность электрического поля, создаваемого
симметричным щелевым вибратором, в дальней зоне может быть определена
по формуле, получающейся из (3.7) путем
замены I0 на U0 и с учетом того, что
1А электрического тока
создает такое же электрическое поле как 60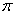 В напряжения в щели. Эта формула имеет вид
В напряжения в щели. Эта формула имеет вид
Е = i(U0/
= i(U0/ r0sinkl)[(cos(klcos
r0sinkl)[(cos(klcos )-coskl)/ sin
)-coskl)/ sin ] exp(-ikr0). (3.27)
] exp(-ikr0). (3.27)
Из принципа
двойственности и из данной формулы видно, что щелевой вибратор обладает
направленными свойствами в своей меридиональной плоскости. Диаграмма
направленности щелевого вибратора в этой плоскости зависит от
отношения l/ и совпадает с диаграммой направленности металлического
аналога щели в этой же плоскости. Вдоль своей оси щелевой вибратор не излучает. Максимум
излучения для отношения l/
и совпадает с диаграммой направленности металлического
аналога щели в этой же плоскости. Вдоль своей оси щелевой вибратор не излучает. Максимум
излучения для отношения l/ < 0,7
направлен вдоль нормали к оси щели (
< 0,7
направлен вдоль нормали к оси щели ( =90°). В экваториальной плоскости (плоскость вектора Е) щель не обладает направленными свойствами (в полярной системе
координат диаграмма направленности представляет собой окружность). Вектор Е поля щели перпендикулярен вектору Е ее металлического аналога.
Проводимость излучения симметричной щели можно рассчитать по формуле (3.28),
если в ней под
=90°). В экваториальной плоскости (плоскость вектора Е) щель не обладает направленными свойствами (в полярной системе
координат диаграмма направленности представляет собой окружность). Вектор Е поля щели перпендикулярен вектору Е ее металлического аналога.
Проводимость излучения симметричной щели можно рассчитать по формуле (3.28),
если в ней под  понимать
сопротивление излучения металлического аналога данной щели (симметричного вибратора).
понимать
сопротивление излучения металлического аналога данной щели (симметричного вибратора).
G щ = 4 R
щ = 4 R э / (120
э / (120 )2. (3.28)
)2. (3.28)
Входной проводимостью щели называется
отношение электрического
тока в точках ее питания к напряжению,
приложенному к этим точкам, т.е. Yвх = I0/U0. Как и входное сопротивление симметричного
электрического вибратора, входная проводимость щели в общем случае есть величина комплексная. Если
известно входное сопротивление металлического аналога данной щели, то входную
проводимость можно определить по формуле, аналогичной (3.28) и являющейся
обобщением ее на случай входной проводимости щели
Yвхщ=4Zвхэ/ (120 )2, (3.29)
)2, (3.29)
где Zэвх - входное сопротивление металлического аналога щели.
В большинстве случаев
известны входные сопротивления вибраторов, имеющих цилиндрическую форму. При
этом в формулу (3.29) можно подставить значение входного сопротивления
цилиндрического вибратора, радиус
которого в 4 раза меньше ширины щели.
Щель, как и
симметричный вибратор, обладает резонансными свойствами. Реактивная
проводимость щели обращается в нуль, если ее длина 2l приблизительно кратна  /2. Точнее, длина резонансной щели несколько меньше
/2. Точнее, длина резонансной щели несколько меньше  /2.
Необходимое укорочение тем больше, чем шире щель; приближенно оно может быть определено по формуле (3.26) для цилиндрического
вибратора, радиус которого равен 1/4
ширины щели. Обычно стремятся к тому, чтобы
щелевая антенна излучала только в одно полупространство, т.е. имела
однонаправленное излучение. Это можно, например, сделать, если со стороны
второго полупространства закрыть щель металлической полостью (коробом).
Высота короба h
выбирается так, чтобы он не шунтировал щель. Короб можно упрощенно представить в виде двухпроводной закороченной на конце
линии; такая линия при длине h=
/2.
Необходимое укорочение тем больше, чем шире щель; приближенно оно может быть определено по формуле (3.26) для цилиндрического
вибратора, радиус которого равен 1/4
ширины щели. Обычно стремятся к тому, чтобы
щелевая антенна излучала только в одно полупространство, т.е. имела
однонаправленное излучение. Это можно, например, сделать, если со стороны
второго полупространства закрыть щель металлической полостью (коробом).
Высота короба h
выбирается так, чтобы он не шунтировал щель. Короб можно упрощенно представить в виде двухпроводной закороченной на конце
линии; такая линия при длине h= /4 обладает
бесконечным входным сопротивлением.
Излучаемая мощность находится интегрированием вектора Пойнтинга по поверхности сферы большого радиуса, окружающей
щель. Однако в данном случае щель
излучает только в одно полупространство; во всех точках второго полупространства
напряженность поля равна нулю и, следовательно, интегрировать надо по
поверхности полусферы. Поэтому мощность излучения будет в 2 раза меньше, чем
при двусторонней щели.
/4 обладает
бесконечным входным сопротивлением.
Излучаемая мощность находится интегрированием вектора Пойнтинга по поверхности сферы большого радиуса, окружающей
щель. Однако в данном случае щель
излучает только в одно полупространство; во всех точках второго полупространства
напряженность поля равна нулю и, следовательно, интегрировать надо по
поверхности полусферы. Поэтому мощность излучения будет в 2 раза меньше, чем
при двусторонней щели.
Следовательно G одн= G
одн= G дв/2.
дв/2.
Таким образом,
проводимость излучения односторонней щели определяется по формуле
G одн = 2R
одн = 2R э/ (120
э/ (120 )2. (3.30)
)2. (3.30)
Входная проводимость односторонней щели
определяется по формуле
Y одн = 2Zвхэ/ (120
одн = 2Zвхэ/ (120 )2. (3.31)
)2. (3.31)
Строгий анализ
направленных свойств щели, прорезанной в металлической поверхности, размеры
которой соизмеримы с длиной волны, основан на решении задачи дифракции плоской
электромагнитной волны на данной поверхности. В результате такого анализа установлено, что на
диаграмму направленности щели в плоскости
вектора Е особенно сильно влияет
размер металлической поверхности,
параллельный этому вектору Е.
Диаграмма направленности щелевой антенны в плоскости вектора Н сравнительно слабо зависит от
размеров металлической поверхности и ориентировочно может определяться на
основании принципа двойственности.
3.7. Способы расширения рабочего
диапазона вибраторных антенн
Рабочий диапазон простых вибраторных антенн
(в том числе несимметричных) определяется частотной зависимостью входного
сопротивления антенны.
Уменьшить эту зависимость можно тремя
способами:
1)
как уже отмечалось - снижением волнового сопротивления вибратора; 2) плавным изменением его
поперечного сечения;
3)
коррекцией входного сопротивления вибратора.
Первый способ. Снижение волнового
сопротивления вибратора путем увеличения размеров поперечного сечения является одним из
основных методов расширения рабочего диапазона вибратора. По этому принципу построен симметричный
вибратор, предложенный в начале 30х годов С.И.Надененко, широко применяемый в диапазонах
коротких и метровых волн. Этот вибратор выполняется из ряда проводов,
натянутых по образующим цилиндра (рис.3.12), в результате чего волновое
сопротивление снижается до 250...400 Ом (вместо 600...1000 Ом у обычного
вибратора). Волновое сопротивление такого вибратора рассчитывается по формуле
WA = 120[ln (l/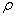 э-1], (3.32)
э-1], (3.32)
где 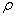 э - эквивалентный радиус вибратора.
э - эквивалентный радиус вибратора.
Рис. 3.12. Вибратор Надененко
Эквивалентным радиусом вибратора называется радиус
сплошного металлического цилиндра, волновое
сопротивление которого равно волновому сопротивлению данного цилиндра, выполненного из отдельных проводов
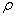 э =
э = 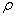
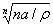 , (3.33)
, (3.33)
где  - радиус цилиндра,
образованного проводами;
- радиус цилиндра,
образованного проводами;
n - число проводов (обычно n
= 6...8)
а - радиус провода.
Диапазонные вибраторы
могут иметь различную форму поперечного сечения: круглую, прямоугольную, треугольную и т.д.
Второй способ. Этот способ основан
на том, что антенну можно рассматривать как переходное устройство между
фидерной линией, в которой су
45
ществует связанная плоская
волна, и свободным пространством,в котором существует пространственная волна. Если в качестве
фидера применяется двухпроводная
симметричная линия, то плавный переход от такой линии к свободному пространству
может быть осуществлён при помощи биконической
антенны (рис.3.13). Волновое сопротивление биконической антенны (l ) равно
) равно
WA=276lg [ctg ( /2)], (3.34)
/2)], (3.34)
где  - угол между осью конуса и его образующей. При 30° <
- угол между осью конуса и его образующей. При 30° <  < 60° входное сопротивление биконической антенны
в довольно широком диапазоне слабо зависит от частоты.
< 60° входное сопротивление биконической антенны
в довольно широком диапазоне слабо зависит от частоты.
Третий способ. Этот способ состоит в том, что антенна
выполняется из двух частей, реактивные составляющие
входных сопротивлений которых имеют
различные частотные зависимости (например, одно является индуктивным, а другое ёмкостным) и компенсируют друг друга в некоторой полосе частот. Примером может служить диапазонный шунтовой вибратор, предложенный Г.З.Айзенбергом.
4.
ИЗЛУЧЕНИЕ ДВУХ СВЯЗАННЫХ ВИБРАТОРОВ
4.1. Направленные свойства системы из двух связанных
вибраторов
Одиночные вибраторы
применяют только тогда, когда требуется ненаправленное или почти
ненаправленное излучение. В тех же случаях, когда необходимо получить
однонаправленное излучение или узкие диаграммы направленности применяют
антенны, состоящие из двух или нескольких вибраторов, расположенных на небольшом
расстоянии (меньше  ) друг от друга. Такие вибраторы заметно влияют друг на друга,
поэтому их называют связанными. Взаимодействие связанных вибраторов аналогично
взаимодействию связанных колебательных контуров с сосредоточенными
постоянными.
Поле одного вибратора наводит в другом вибраторе некоторую
ЭДС, что эквивалентно изменению сопротивления излучения или входного сопротивления
вибратора. Поле, создаваемое системой вибраторов, является результатом сложения полей,
- создаваемых отдельными вибраторами, с учетом фаз этих полей, определяемых как
разностью хода лучей, так и разностью фаз токов в излучателях. Ниже рассматривается
работа двух связанных симметричных вибраторов. Получаемые при этом результаты
нетрудно распространить на
случай нескольких связанных вибраторов. Выведем формулу для расчета характеристики направленности двух
параллельных вибраторов 1 и 2,
находящихся на расстоянии d друг от друга (рис.
4.1), питаемых токами
) друг от друга. Такие вибраторы заметно влияют друг на друга,
поэтому их называют связанными. Взаимодействие связанных вибраторов аналогично
взаимодействию связанных колебательных контуров с сосредоточенными
постоянными.
Поле одного вибратора наводит в другом вибраторе некоторую
ЭДС, что эквивалентно изменению сопротивления излучения или входного сопротивления
вибратора. Поле, создаваемое системой вибраторов, является результатом сложения полей,
- создаваемых отдельными вибраторами, с учетом фаз этих полей, определяемых как
разностью хода лучей, так и разностью фаз токов в излучателях. Ниже рассматривается
работа двух связанных симметричных вибраторов. Получаемые при этом результаты
нетрудно распространить на
случай нескольких связанных вибраторов. Выведем формулу для расчета характеристики направленности двух
параллельных вибраторов 1 и 2,
находящихся на расстоянии d друг от друга (рис.
4.1), питаемых токами
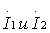 . Обозначим
. Обозначим
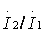 =q exp(i
=q exp(i ),
(4.1)
),
(4.1)
где q
- отношение модулей токов 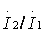 ;
; - сдвиг фазы тока I2 по отношению к току I1.
- сдвиг фазы тока I2 по отношению к току I1.
|
Рис. 4.1. К определению поля излучения связанных вибраторов
|
Рассмотрим поле в
меридиональной
плоскости вибраторов xoz. Так как расстояние между вибраторами d несоизмеримо мало по
сравнению с расстояниями до точки наблюдения (r1 и
r2), направления в точку М можно считать
параллельными. Опустив из центра первого вибратора перпендикуляр на
направление r2, найдем разность расстояний от
44 вибраторов до точки
47
наблюдения, равную  r = d cos
r = d cos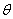 , где
, где 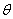 - угол между нормалью
к оси вибратора и направлением на точку наблюдения. Обозначим напряженность поля, создаваемого в точке наблюдения первым вибратором, через E1. Выразим
напряженность поля второго вибратора в точке наблюдения М через напряженность поля
первого вибратора, приняв ее фазу в точке наблюдения за
нулевую. Так как напряженность, создаваемого вибратором, поля пропорциональна току в вибраторе и влиянием
разности расстояний от вибратора до точки
наблюдения на амплитуду напряженности поля можно пренебречь,
то
- угол между нормалью
к оси вибратора и направлением на точку наблюдения. Обозначим напряженность поля, создаваемого в точке наблюдения первым вибратором, через E1. Выразим
напряженность поля второго вибратора в точке наблюдения М через напряженность поля
первого вибратора, приняв ее фазу в точке наблюдения за
нулевую. Так как напряженность, создаваемого вибратором, поля пропорциональна току в вибраторе и влиянием
разности расстояний от вибратора до точки
наблюдения на амплитуду напряженности поля можно пренебречь,
то 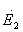 = E1q exp(-ikdcos
= E1q exp(-ikdcos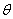 ) exp(i
) exp(i ), где kd cos
), где kd cos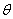 - сдвиг фаз полей из-за разности хода лучей
(пространственный сдвиг фаз). Найдем суммарное поле, создаваемое обоими
вибраторами в данной точке
- сдвиг фаз полей из-за разности хода лучей
(пространственный сдвиг фаз). Найдем суммарное поле, создаваемое обоими
вибраторами в данной точке
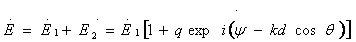 (4.2)
(4.2)
На основании формулы (3.7) и с учетом
того, что угол 0 является дополнительным по отношению к углу  , запишем
, запишем
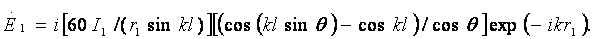
Обычно интересуются величиной
напряженности суммарного поля, а не ее фазой. Поэтому, переходя к модулю
выражения (4.2), получаем
Е =(60IП1 / r)[(cos(klsin ) - coskl) / cos
) - coskl) / cos ]
] 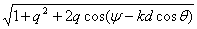 (4.3) или E= Af1(
(4.3) или E= Af1( )fc(
)fc( ).Как
видно из формулы (4.3), амплитудная характеристика направленности системы из
двух связанных вибраторов определяется двумя множителями. Первый множитель f1(
).Как
видно из формулы (4.3), амплитудная характеристика направленности системы из
двух связанных вибраторов определяется двумя множителями. Первый множитель f1( ) представляет
) представляет
48
собой
характеристику направленности симметричного
вибратора, находящегося в свободном пространстве. Второй множитель fc( ) учитывает наличие второго вибратора; он зависит от расстояния d
между вибраторами, от отношения амплитуд токов в вибраторах q и от сдвига фаз токов
в вибраторах
) учитывает наличие второго вибратора; он зависит от расстояния d
между вибраторами, от отношения амплитуд токов в вибраторах q и от сдвига фаз токов
в вибраторах  . Этот множительназывают множителем
системы. В экваториальной плоскости направленные свойства данной системы определяются только множителем системы, так как одиночный симметричный вибратор в этой плоскости (
. Этот множительназывают множителем
системы. В экваториальной плоскости направленные свойства данной системы определяются только множителем системы, так как одиночный симметричный вибратор в этой плоскости (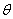 = 0°) не обладает направленными
свойствами. Напряженность суммарного поля в экваториальной плоскости определяется выражением
= 0°) не обладает направленными
свойствами. Напряженность суммарного поля в экваториальной плоскости определяется выражением
Е = А (1- coskl) 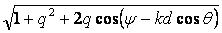 . (4.4)
. (4.4)
В зависимости от величин d/ , q и
, q и  диаграммы
направленности могут иметь различную форму (рис.4.2, 4.3), При увеличении
расстояния между вибраторами (начиная от d/
диаграммы
направленности могут иметь различную форму (рис.4.2, 4.3), При увеличении
расстояния между вибраторами (начиная от d/ = 0,5) диаграмма направленности приобретает многолепестковый характер; чем больше
d/
= 0,5) диаграмма направленности приобретает многолепестковый характер; чем больше
d/ , тем больше лепестков. Особенно важен случай однонаправленного излучения. Пусть
токи в вибраторах одинаковы по величине (q = 1). Тогда формулу
(4.4), воспользовавшись формулой для косинуса двойного угла, можно привести к
виду
, тем больше лепестков. Особенно важен случай однонаправленного излучения. Пусть
токи в вибраторах одинаковы по величине (q = 1). Тогда формулу
(4.4), воспользовавшись формулой для косинуса двойного угла, можно привести к
виду
Е = 2А (1 - cos kl) cos [ /2 - (kd/2)
cos
/2 - (kd/2)
cos ]
(4.5)
]
(4.5)
Положим теперь, что  =± 90° и расстояние между вибраторами d =
=± 90° и расстояние между вибраторами d = /4. При этом формула (4.5) принимает вид
/4. При этом формула (4.5) принимает вид
Е = 2А (1 - cos kl) cos (±45° - 45°cos ).
).
Множитель f( ) = cos(±45°- 45°cos
) = cos(±45°- 45°cos ) описывает кардиоиду. При
) описывает кардиоиду. При = + 90° и
= + 90° и  = 0° этот множитель обращается в единицу; при
= 0° этот множитель обращается в единицу; при  =180° он обращается в нуль. Таким образом, в
направлении
=180° он обращается в нуль. Таким образом, в
направлении  = 0° напряженность поля удваивается (по сравнению с полем одиночного вибратора, возбуждаемого
током, одинаковым с текущим по одному из связанных вибраторов). Это увеличение в одном
направлении происходит за счет уменьшения поля в других направлениях. При
= 0° напряженность поля удваивается (по сравнению с полем одиночного вибратора, возбуждаемого
током, одинаковым с текущим по одному из связанных вибраторов). Это увеличение в одном
направлении происходит за счет уменьшения поля в других направлениях. При  = - 90° напряженность поля
удваивается в обратном направлении (
= - 90° напряженность поля
удваивается в обратном направлении ( =180°); поле равно нулю в направлении
=180°); поле равно нулю в направлении  = 0°.
= 0°.
Поясним эти
результаты. Если ток во втором вибраторе пережает по
фазе ток в первом вибраторе, то в точке наблюдения, находящейся в направлении  = 0°, поля от обоих вибраторов складываются в фазе,
= 0°, поля от обоих вибраторов складываются в фазе,
49
так как сдвиг фаз за счет несинфазности возбуждающих токов ( = 90°) компенсируется пространственным сдвигом фаз (
= 90°) компенсируется пространственным сдвигом фаз ( р= kd = (2
р= kd = (2 /
/ )(
)( /4)= 90°). Этот сдвиг фаз берется со знаком
минус, так как второй вибратор находится дальше от точки наблюдения, чем
первый. В обратном направлении (
/4)= 90°). Этот сдвиг фаз берется со знаком
минус, так как второй вибратор находится дальше от точки наблюдения, чем
первый. В обратном направлении ( = 180°) множитель f(
= 180°) множитель f( ) обращается в нуль, потому что в этом направлении поля от первого и второго вибраторов
складываются в противофазе и компенсируют друг друга, так как
) обращается в нуль, потому что в этом направлении поля от первого и второго вибраторов
складываются в противофазе и компенсируют друг друга, так как  рез=
рез= +
+  р=180°. Если ток во втором вибраторе
отстает по фазе на 90° от тока в первом вибраторе (
р=180°. Если ток во втором вибраторе
отстает по фазе на 90° от тока в первом вибраторе ( = - 90°), то получается обратная картина. В первом случае (
= - 90°), то получается обратная картина. В первом случае ( = 90°) второй вибратор усиливает излучение в направлении на первый
вибратор. Во втором случае (
= 90°) второй вибратор усиливает излучение в направлении на первый
вибратор. Во втором случае ( = -90°) он усиливает излучение в обратном направлении и ослабляет
излучение в направлении первого вибратора. Вибратор,усиливающий излучение в
направлении на другой вибратор и ослабляющий излучение в обратном направлении,
называется рефлектором (отражателем). Чтобы рефлектирующее
действие вибратора было полным (в одном направлении поле увеличивается, а в
противоположном - равно нулю), в рассматриваемом случае (d =
= -90°) он усиливает излучение в обратном направлении и ослабляет
излучение в направлении первого вибратора. Вибратор,усиливающий излучение в
направлении на другой вибратор и ослабляющий излучение в обратном направлении,
называется рефлектором (отражателем). Чтобы рефлектирующее
действие вибратора было полным (в одном направлении поле увеличивается, а в
противоположном - равно нулю), в рассматриваемом случае (d = /4) токи в обоих вибраторах должны быть равны по величине (q
= 1), а ток в рефлекторе должен опережать ток во втором связанном вибраторе на
90° (рис.4.4.а). Вибратор, ослабляющий излучение в направлении на другой
вибратор и усиливающий излучение в противоположном направлении, называется директором
(направителем). В идеальном случае директор должен
работать в режиме (рис.4.4.б): q=l;
/4) токи в обоих вибраторах должны быть равны по величине (q
= 1), а ток в рефлекторе должен опережать ток во втором связанном вибраторе на
90° (рис.4.4.а). Вибратор, ослабляющий излучение в направлении на другой
вибратор и усиливающий излучение в противоположном направлении, называется директором
(направителем). В идеальном случае директор должен
работать в режиме (рис.4.4.б): q=l;
 = -
= - /2 (при d =
/2 (при d =  /4). Отметим, что в обоих случаях напряженность поля
увеличивается в направлении отставания фазы возбуждающего тока. Получить однонаправленное излучение
можно и при расстояниях между вибраторами, отличных от
/4). Отметим, что в обоих случаях напряженность поля
увеличивается в направлении отставания фазы возбуждающего тока. Получить однонаправленное излучение
можно и при расстояниях между вибраторами, отличных от  /4. Как видно из формулы (4.5), условие отсутствия излучения
в направлении
/4. Как видно из формулы (4.5), условие отсутствия излучения
в направлении
 = 180° можно записать
в виде
= 180° можно записать
в виде  +kd = 180°. Для выполнения этого условия при d
<
+kd = 180°. Для выполнения этого условия при d
<  /4 угол сдвига фаз у должен быть больше 90°. Хотя диаграмма направленности
при этом оказывается однонаправленной и максимум
излучения лежит в направлении
/4 угол сдвига фаз у должен быть больше 90°. Хотя диаграмма направленности
при этом оказывается однонаправленной и максимум
излучения лежит в направлении  = 0°, однако напряженность поля в этом направлении не
удваивается. Чем ближе друг к другу расположены вибраторы, тем меньшая
напряженность поля получается в направлении максимального излучения
(считая, что при изменении d величина тока в
вибраторах
постоянна).
= 0°, однако напряженность поля в этом направлении не
удваивается. Чем ближе друг к другу расположены вибраторы, тем меньшая
напряженность поля получается в направлении максимального излучения
(считая, что при изменении d величина тока в
вибраторах
постоянна).
Возбуждение каждого из
двух связанных вибраторов токами, сдвинутыми по фазе, усложняет систему питания. Поэтому
в большен-
стве случаев вибраторы, выполняющие
роль рефлекторов или
50
директоров, не содержат источников питания
(генераторов), т.е. являются пассивными. Они возбуждаются
электромагнитным полем активного (питаемого) вибратора. В случае
пассивных вибраторов не удается осуществить режим, обеспечивающий полное рефлекторное или директорное действие, так как не удается получить совместно q
= 1 и  = 90°. Поэтому не получается
полного удвоения поля в главном направлении и нуля поля - в обратном.
= 90°. Поэтому не получается
полного удвоения поля в главном направлении и нуля поля - в обратном.
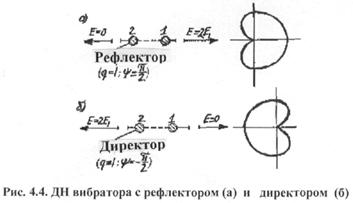
4.2. Расчет
сопротивления излучения и входного сопротивления связанных вибраторов
методом наведенных ЭДС
4.2.1. Сущность метода наведенных ЭДС
Полное сопротивление
излучения одного из связанных вибраторов Z 1 состоит из двух частей: собственного сопротивления Z
1 состоит из двух частей: собственного сопротивления Z 11, т.е. сопротивления, которым обладает данный
вибратор в свободном пространстве, и сопротивления, наведенного электромагнитным
полем второго вибратора Z
11, т.е. сопротивления, которым обладает данный
вибратор в свободном пространстве, и сопротивления, наведенного электромагнитным
полем второго вибратора Z 12нав. Таким образом, Z
12нав. Таким образом, Z 1= Z
1= Z 11 + Z
11 + Z 12нав и Z
12нав и Z 2= Z
2= Z 22 + Z
22 + Z 21нав.
21нав.
Полное сопротивление
излучения связанного вибратора можно найти методом наведенных
ЭДС. Идея этого метода была предложена независимо друг от друга в 1922 г. российским ученым Д.А.Рожанским и французом Бриллюэном.
Непосредственно к расчету антенн этот метод
применен И.Г.Кляцкиным, А.А.Пистолькорсом
и В.В.Татариновым.
Метод наведенных ЭДС позволяет находить наведенные
и собственные сопротивления вибраторов, а также амплитуды и фазы токов в пассивных вибраторах.
Сущность данного метода такова. Рассмотрим два связанных
51
произвольно ориентированных
друг относительно друга симметричных вибратора (рис.4.5). Поле второго вибратора
может создать у поверхности бесконечно малого элемента dz первого вибратора составляющую, параллельную оси этого вибратора (тангенциальную составляющую), Ez12,
вследствие чего в элементе dz возникает (наводится) ЭДС dЭ12 = Ez12dz.
Однако при этом
нарушаются граничные условия, согласно которым на поверхности идеального проводника
тангенциальная составляющая напряженности электрического поля равна нулю. Для
выполнения граничных условий в элементе dz должна появиться ЭДС –dЭ12,
компенсирующая ЭДС dЭ12. Вблизи поверхности
элемента dz появляется
тангенциальная составляющая
напряженности электрического поля -Ez12, равная по величине и противоположная
по фазе тангенциальной составляющей наведенного поля Ez12. Вследствие этого
тангенциальная составляющая напряженности суммарного электрического поля у поверхности
элемента dz обращается в нуль и граничное
условие выполняется. Появление тангенциальной составляющей напряженности поля
- Ez12 говорит о том, что
под влиянием поля второго вибратора происходит перераспределение поля первого
вибратора. ЭДС –dЭ12 создается генератором,
включенным в первый вибратор. Энергия, затрачиваемая генератором для создания этой
ЭДС в элементе dz, переходит в энергию
электромагнитного поля. Если известны ЭДС,возникающая на поверхности
элемента dz, и ток в этом
элементе Iz1 можно определить мощность dP 12, затрачиваемую генератором первого вибратора (под
действием поля второго вибратора), на создание поля, компенсирующего
тангенциальную составляющую напряженности электрического поля второго вибратора на
поверхности данного элемента. При этом ток в элементе dz и составляющая Ez12 на поверхности этого элемента могут иметь
различные
фазы. Считается, что закон распределения тока по одному из связанных вибраторов
в результате действия поля другого вибратора не изменяется и является
синусоидальным.
12, затрачиваемую генератором первого вибратора (под
действием поля второго вибратора), на создание поля, компенсирующего
тангенциальную составляющую напряженности электрического поля второго вибратора на
поверхности данного элемента. При этом ток в элементе dz и составляющая Ez12 на поверхности этого элемента могут иметь
различные
фазы. Считается, что закон распределения тока по одному из связанных вибраторов
в результате действия поля другого вибратора не изменяется и является
синусоидальным.
Полная мощность,
расходуемая генератором первого вибратора на создание в окружающем
пространстве электромагнитного поля, тангенциальная составляющая
напряженности электрического поля которого компенсирует на всей поверхности
вибратора тангенциальную составляющую напряженности электрического поля, создаваемого
током второго вибратора,
P 12 = - (1/2)
12 = - (1/2)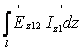 . (4.6)
. (4.6)
Итак, мощность,
отдаваемая генератором первого вибратора под
52
действием поля второго вибратора,
определяется током, текущим по первому вибратору, и тангенциальной составляющей
напряженности электрического поля, создаваемого вторым вибратором вблизи
первого. Ее активная часть представляет собой излученную мощность. Реактивная
часть характеризует электромагнитное поле, колеблющееся вблизи вибратора.
Выражение (4.6) математически формулирует метод наведенных ЭДС.
4.2.2. Расчет взаимных и собственных
сопротивлений связанных вибраторов
Для того чтобы
определить сопротивление, наведенное на первый вибратор вторым, нужно
знать закон распределения тока в первом вибраторе, его комплексную
амплитуду в пучности и тангенциальную составляющую напряженности
электрического поля, создаваемого вторым вибратором у поверхности первого. Активная
составляющая наведенного сопротивления R 12нав характеризует активную мощность,
излучаемую первым вибратором под действием поля второго. Реактивная составляющая
наведенного сопротивления X
12нав характеризует активную мощность,
излучаемую первым вибратором под действием поля второго. Реактивная составляющая
наведенного сопротивления X 12нав характеризует мощность электромагнитного
поля, связанного с вибратором, возникающего также под действием поля второго вибратора.
12нав характеризует мощность электромагнитного
поля, связанного с вибратором, возникающего также под действием поля второго вибратора.
Наведенное сопротивление рассчитать
значительно проще в частном случае, когда связанные вибраторы имеют одинаковую
длину, оси их параллельны и токи в них имеют одинаковую величину и фазу.
Очевидно, что в этом случае сопротивление, наведенное первым вибратором на второй, равно
сопротивлению,
наведенному вторым вибратором на первый.
|
Рис. 4.6. Графики взаимных сопротивлений
|
В этом частном случае
наведенное сопротивление называется взаимным (Z12). При известном взаимном сопротивлении двух вибраторов весьма просто
рассчитать
наведенное
сопротивление, если задано соотношение токов в вибраторах. Взаимное
сопротивление является функцией величин l/ , d/
, d/ и h/
и h/ , т.е. определяется исключительно геометрическими размерами
системы. Оно аналогично сопротивлению связи двух колебательных контуров c
сосредоточенными параметрами и определяется по таблицам и графикам. Таблицы для
определений активной со-составляющей (R12) взаимного сопротивления
, т.е. определяется исключительно геометрическими размерами
системы. Оно аналогично сопротивлению связи двух колебательных контуров c
сосредоточенными параметрами и определяется по таблицам и графикам. Таблицы для
определений активной со-составляющей (R12) взаимного сопротивления
53
полуволновых вибраторов рассчитаны А.А.Пистолькорсом в 1928 г., а для реактивной составляющей (Х12)
- В.В.Татариновым в 1936 г.
Графики, изображающие зависимости R12 = f(d/ ) и X12 = f (d/
) и X12 = f (d/ ) при h/
) при h/ = const, представлены на
рис.4.6. Имеются также графики, позволяющие определять взаимные сопротивления
вибраторов, длина которых отличается от полуволны. Как видно из рис.4.6, активная и реактивная составляющие взаимного сопротивления в
зависимости от относительного расстояния между вибраторами d/
= const, представлены на
рис.4.6. Имеются также графики, позволяющие определять взаимные сопротивления
вибраторов, длина которых отличается от полуволны. Как видно из рис.4.6, активная и реактивная составляющие взаимного сопротивления в
зависимости от относительного расстояния между вибраторами d/ принимают
как положительные, так и отрицательные значения
и при некоторых значениях d/
принимают
как положительные, так и отрицательные значения
и при некоторых значениях d/ проходят через нуль. Такой ход кривых взаимных сопротивлений объясняется
изменением фазы наведенной ЭДС при изменении расстояния между вибраторами. Если фаза наведенной ЭДС равна или противоположна фазе текущего по
вибратору тока, то взаимное сопротивление является
чисто активным.
Если фаза наведенной ЭДС отличается от фазы текущего по
вибратору тока на
проходят через нуль. Такой ход кривых взаимных сопротивлений объясняется
изменением фазы наведенной ЭДС при изменении расстояния между вибраторами. Если фаза наведенной ЭДС равна или противоположна фазе текущего по
вибратору тока, то взаимное сопротивление является
чисто активным.
Если фаза наведенной ЭДС отличается от фазы текущего по
вибратору тока на 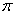 /2, то взаимное сопротивление является чисто реактивным. Активная составляющая взаимного сопротивления может быть
положительной или отрицательной; R12
отрицательно в тех случаях, когда под
действием поля второго вибратора мощность поля, излучаемого первым вибратором, уменьшается (при
неизменном токе в первом вибраторе).
/2, то взаимное сопротивление является чисто реактивным. Активная составляющая взаимного сопротивления может быть
положительной или отрицательной; R12
отрицательно в тех случаях, когда под
действием поля второго вибратора мощность поля, излучаемого первым вибратором, уменьшается (при
неизменном токе в первом вибраторе).
Метод
наведенных ЭДС может быть применен также для определения собственного
сопротивления излучения вибратора. Формула для расчета R 11 совпадает с формулой (3.13) для расчета R
11 совпадает с формулой (3.13) для расчета R п, полученной методом
вектора Пойнтинга, т.е. R
п, полученной методом
вектора Пойнтинга, т.е. R 11 = R
11 = R п .Это понятно, так
как при расчете сопротивления излучения
методом вектора Пойнтинга также, как и в данном
случае, исходят из синусоидального
распределения тока.
п .Это понятно, так
как при расчете сопротивления излучения
методом вектора Пойнтинга также, как и в данном
случае, исходят из синусоидального
распределения тока.
Формула для расчета X 11 имеет вид
11 имеет вид
X 11 = X
11 = X п = 30[2Si 2kl + sin 2kl (
п = 30[2Si 2kl + sin 2kl ( + lnkl +Ci
4kl - 2Ci 2kl -2ln (l/a)) +
+ lnkl +Ci
4kl - 2Ci 2kl -2ln (l/a)) +
+ cos 2kl (- Si 4kl + 2Si 2kl)].
(4.7)
Результаты,
полученные по методу наведенных ЭДС, тем более точны, чем тоньше вибратор.
4.2.3. Расчет
наведенного и полного сопротивлений излучения
Пусть имеются два
активных связанных вибратора, токи в которых не равны
ни по амплитуде, ни по фазе. Требуется найти полное сопротивление излучения каждого
вибратора. Заменим связанные вибраторы эквивалентной схемой, состоящей из
двух связанных колебательных контуров с сосредоточенными параметрами
(рис.4.7). Каждый контур содержит генератор высокой частоты, сопротивления Z11 или Z22, равные собственным сопротивлениям вибраторов, и наведенные сопротивления Z 12нав и Z
12нав и Z 21нав
которые неиз-
21нав
которые неиз-
54
вестны. Напряжение
генератора, включенного в связанный контур, компенсирует падение
напряжения на собственном сопротивлении контура и на сопротивлении связи.
Учитывая это, запишем уравнения Кирхгофа для данной эквивалентной схемы,
считая, что сопротивления связи (взаимные сопротивления) известны. Эти
уравнения имеют вид:
Uп1= Iп1Z 11 + Iп2Z12; (4.8)
11 + Iп2Z12; (4.8)
Uп2=Iп2 Z 22+Iп1Z21. (4.9)
22+Iп1Z21. (4.9)
Здесь Uп1 и Uп2 - напряжения первого и второго
генераторов, пересчитанные к точкам пучности тока в вибраторах. Данные
уравнения позволяют при заданных напряжениях Uп1 и Uп2 и известных собственных и взаимных сопротивлениях определить
токи в вибраторах. Полагая, что токи в вибраторах найдены, определим наведенные
сопротивления. Пусть Iп1 / Iп2 =qexp(i ). Перепишем
уравнения (4.8) и (4.9), вынося за скобки в уравнении (4.8) величину Iп1, а в уравнении (4.9) величину Iп2 и учитывая, что Z12 = Z21
). Перепишем
уравнения (4.8) и (4.9), вынося за скобки в уравнении (4.8) величину Iп1, а в уравнении (4.9) величину Iп2 и учитывая, что Z12 = Z21
Uп1= Iп1 [Z 11 + q exp (i
11 + q exp (i ) ZI2]; (4.10)
) ZI2]; (4.10)
Uп2= Iп2 [Z 22+ (l/ q) exp (-i
22+ (l/ q) exp (-i ) Z12]. (4.11)
) Z12]. (4.11)
Разделив уравнение
(4.10) на Iп1 а уравнение (4.11) на
Iп2, получим выражения для полных сопротивлений
контуров (вибраторов):
Uпl/ Iп1= Z 1 = R
1 = R 1 + i X
1 + i X 1= Z
1= Z 11+ q exp (i
11+ q exp (i ) Z12
; (4.12)
) Z12
; (4.12)
Uп2/ Iп2 = Z 2 = R
2 = R 2+ i
X
2+ i
X 2= Z
2= Z 22 + (1/q) exp (-i
22 + (1/q) exp (-i ) Z12. (4.13)
) Z12. (4.13)
Так как полное
сопротивление излучения вибратора равно сумме собственного и наведенного
сопротивлений излучения, то наведенные сопротивления вибраторов равны:
Z 12нав = R
12нав = R 12нав + i X
12нав + i X 12нав = q exp (i
12нав = q exp (i ) (R12 + i X12) ; (4.14)
) (R12 + i X12) ; (4.14)
Z 21нав = R
21нав = R 21нав + i X
21нав + i X 21нав = (1/q) exp (-i
21нав = (1/q) exp (-i ) (R12 + i X12). (4.15)
) (R12 + i X12). (4.15)
Таким образом,
еслизвестно взаимное сопротивление
вибраторов
(оно зависит только
от относительных
геометрических
размеров системы l/ , d/
, d/ , h/
, h/ ,
,
и
определяется по таблицам или по графикам) и известны отношения амплитуд токов q
и сдвиг фаз токов
в вибраторах Ψ, то наведенное
сопротивление
определяется весьма просто. Полная мощность,
55
излучаемая двумя связанными вибраторами,
равна 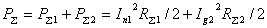 .
.
Входные сопротивления
связанных вибраторов могут быть рассчитаны по формулам, применяемым при инженерном
расчете входного сопротивления. В случае коротких вибраторов (расстояние от точек питания до узла тока не менее
0,15λ) входное сопротивление связанного вибратора можно определить по
формуле
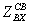 =
=  /sin2k/
или
/sin2k/
или  =
=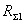 /sin2k l +i
/sin2k l +i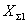 /sin2k l, (4.16) где
/sin2k l, (4.16) где 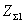 - полное сопротивление излучения связанного вибратора [формула (4.12)]. В случае
длинных вибраторов (расстояние от точек питания до минимума тока меньше
0,15λ) входное сопротивление связанного вибратора рассчитывается по
формуле, аналогичной (3.21)
- полное сопротивление излучения связанного вибратора [формула (4.12)]. В случае
длинных вибраторов (расстояние от точек питания до минимума тока меньше
0,15λ) входное сопротивление связанного вибратора рассчитывается по
формуле, аналогичной (3.21)
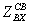 =
=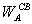 [(sh2
[(sh2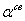 l - (
l - (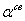 /k) sin2k l) / (ch2
/k) sin2k l) / (ch2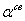 l - cos2k l)] -
l - cos2k l)] -
- i 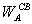 [((
[((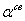 /k) sh2
/k) sh2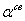 l + sin2kl) / ( ch2
l + sin2kl) / ( ch2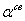 l - cos2kl)] . (4.17)
l - cos2kl)] . (4.17)
В данной формуле
учтено влияние одного вибратора на волновое сопротивление другого вибратора и
на его коэффициент затухания.
Здесь 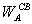 =
=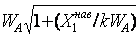 ,
, 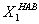 -реактивное
наведенное сопротивление, приходящееся на
единицу длины вибратора, определяемое по формуле
-реактивное
наведенное сопротивление, приходящееся на
единицу длины вибратора, определяемое по формуле
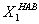 = 2
= 2 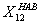 /[ l(1- (sin2kl / 2kl))];
/[ l(1- (sin2kl / 2kl))];
άсв= (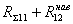 )/ [l
)/ [l 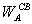 (1- (sin2k l / 2kl l))].
(1- (sin2k l / 2kl l))].
4.3. Расчет тока в пассивных вибраторах
Пассивные вибраторы
широко применяются для создания однонаправленного излучения в качестве
рефлекторов и директоров. Чтобы вибратор играл роль рефлектора или директора,
ток в нем должен иметь определенную величину и фазу по отношению к току в
активном вибраторе (в идеальном случае при расстоянии между вибраторами d=
λ/4 должны выполняться условия q = 1 и Ψ = ±90°).
Величины q и ψ для пассивного вибратора зависят от
расстояния между пассивным и активным вибраторами и от величин
активного и реактивного сопротивлений пассивного вибратора. Эти величины можно
регулировать, изменяя реактивное сопротивление пассивного
|
Рис. 4.8.
Эквивалентная схема связанных вибраторов, один из которых пассивный
|
вибратора. Рассчитаем величины q и Ψ. Заменим два
связанных
симметричных вибратора, из
которых
один пассивный с вклю-
ченным в его середину сопротив-
лением настройки Хн0 (рис.4.8.а),
эквивалентной
схемой (рис.4.8.б).
56
Уравнения Кирхгофа для этойсистемы имеют вид:
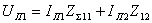 (4.18)
(4.18)
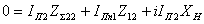 . (4.19)
. (4.19)
где 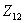 - взаимное
сопротивление вибраторов; Хн - реактивное
сопротивление настройки, включенное в пассивный вибратор и отнесенное к пучности тока. Можно считать
известными ток в активном вибраторе
- взаимное
сопротивление вибраторов; Хн - реактивное
сопротивление настройки, включенное в пассивный вибратор и отнесенное к пучности тока. Можно считать
известными ток в активном вибраторе 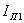 , а также собственные
, а также собственные
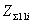 ,
, 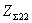 и взаимное
и взаимное 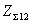 сопротивления,
поскольку относительная длина
вибраторов l/λ и относительное
расстояние между вибраторами d/λ заданы. Задано также сопротивление настройки. Таким образом, в уравнениях
(4.18) и (4.19) неизвестен только ток во втором вибраторе ( I2 ), который определяется из
уравнения (4.19) Iп2 = -IП1[(Z12/(
сопротивления,
поскольку относительная длина
вибраторов l/λ и относительное
расстояние между вибраторами d/λ заданы. Задано также сопротивление настройки. Таким образом, в уравнениях
(4.18) и (4.19) неизвестен только ток во втором вибраторе ( I2 ), который определяется из
уравнения (4.19) Iп2 = -IП1[(Z12/( 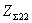 + iXH)).
+ iXH)).
Ранее было обозначено 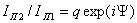 Поэтому
Поэтому
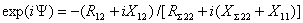 Отсюда модуль отношения токов
Отсюда модуль отношения токов
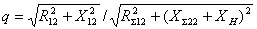 . (4.20)
. (4.20)
Относительная фаза
тока в пассивном вибраторе
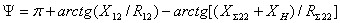 . (4.21)
. (4.21)
Входящие в формулы (4.20) и (4.21) сопротивления 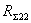 ,
, 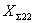 ,
, 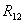 и
и
Х12
отнесены к пучности тока. Сопротивление 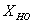 пересчитывается к
пересчитывается к
пучности тока в случае короткого вибратора
по формуле 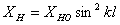
В случае длинного вибратора такой пересчет
можно сделать по формуле, учитывающей распределение тока по закону
гиперболического синуса 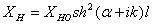 , где
, где  - коэффициент
затухания, без учета влияния активного вибратора.
- коэффициент
затухания, без учета влияния активного вибратора.
В случае пассивного
вибратора величины q и Ψ взаимозависимы. При изменении Хн
меняются одновременно обе эти величины. Поэтому добиться одновременно нужных значений q
и Ψ для пассивного вибратора невозможно. Пассивный вибратор обычно
настраивают так, чтобы получить максимальный коэффициент защитного действия.
Получаемые при этом величины q и Ψ отличаются
от соответствующих величин в идеальном случае (q
= 1, Ψ = 90°), и поэтому
максимальное защитное действие обычно получается не больше 10...20. Ток в
пассивном рефлекторе должен опережать
по фазе ток
в активном
вибраторе. Анализ формулы (4.21)
показывает, что пассивный вибратор будет играть роль рефлектора в том случае, когда
его полное реактивное сопротивление (собственное плюс сопротивление настройки) имеет
индуктивный характер. Этот вывод
справедлив, если 0,1
 d
d  0,25
0,25 .
.
57
Для получения оптимального рефлекторного
действия расстояние между рефлектором и активным вибратором следует брать
примерно (0,15...0,25) , а реактивное положительное сопротивление - приблизительно 10...50 Ом.
Ток в пассивном директоре должен отставать по фазе от тока в активном вибраторе. Из
анализа формулы (4.21)
следует, что для работы пассивного вибратора в режиме директора при 0,1
, а реактивное положительное сопротивление - приблизительно 10...50 Ом.
Ток в пассивном директоре должен отставать по фазе от тока в активном вибраторе. Из
анализа формулы (4.21)
следует, что для работы пассивного вибратора в режиме директора при 0,1
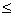 d
d 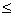 0,25
0,25 его полное реактивное сопротивление должно быть
отрицательным, т.е. должно иметь емкостный
характер. В коротковолновом диапазоне пассивные вибраторы обычно настраивают,
включая в середине вибратора
настроечное реактивное сопротивление в виде отрезка короткозамкнутой двухпроводной линии, длину которой можно
регулировать передвижным короткозамыкателем.
В диапазонах метровых и дециметровых волн настроечное сопротивление обычно не применяется. Пассивный вибратор настраивается
изменением его длины. Чтобы пассивный вибратор работал в качестве рефлектора, его полная длина должна быть несколько
больше
его полное реактивное сопротивление должно быть
отрицательным, т.е. должно иметь емкостный
характер. В коротковолновом диапазоне пассивные вибраторы обычно настраивают,
включая в середине вибратора
настроечное реактивное сопротивление в виде отрезка короткозамкнутой двухпроводной линии, длину которой можно
регулировать передвижным короткозамыкателем.
В диапазонах метровых и дециметровых волн настроечное сопротивление обычно не применяется. Пассивный вибратор настраивается
изменением его длины. Чтобы пассивный вибратор работал в качестве рефлектора, его полная длина должна быть несколько
больше  /2 (входное
сопротивление разомкнутой на конце двухпроводной линии, длина которой больше
/2 (входное
сопротивление разомкнутой на конце двухпроводной линии, длина которой больше
 /4, имеет индуктивный характер). Чтобы пассивный
вибратор работал в качестве директора, его
полная длина должна быть несколько меньше
/4, имеет индуктивный характер). Чтобы пассивный
вибратор работал в качестве директора, его
полная длина должна быть несколько меньше  /2. Величина
необходимого удлинения или укорочения определяется расстоянием между
вибраторами и их толщиной.
/2. Величина
необходимого удлинения или укорочения определяется расстоянием между
вибраторами и их толщиной.
4.4. Методы получения
узких диаграмм направленности вибраторных
антенн
В ряде случаев
необходимо, чтобы антенны концентрировали излучаемые ими
электромагнитные волны в узкие пучки, т.е. чтобы они обладали узкими диаграммами направленности,
большими КНД. Этого можно достичь при помощи
нескольких вибраторов, возбуждаемых так, что их поля в нужном
направлении складывались в фазе.
Пусть к симметричному вибратору подводится мощность P , которая полностью излучается. При этом в главном направлении
создается напряженность поля Е = A
, которая полностью излучается. При этом в главном направлении
создается напряженность поля Е = A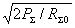 , где R
, где R o - входное сопротивление вибратора;
o - входное сопротивление вибратора;
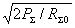 = I0 - ток в точках питания вибратора. Поместим
рядом точно такой же вибратор
(рис.4.9.а) и подведем к каждому из вибраторов мощность P'
= I0 - ток в точках питания вибратора. Поместим
рядом точно такой же вибратор
(рис.4.9.а) и подведем к каждому из вибраторов мощность P' = P
= P /2. Если считать, что входное сопротивление одного
/2. Если считать, что входное сопротивление одного
вибратора под действием
второго вибратора не изменяется, то
токи, текущие
в вибраторах, равны
58
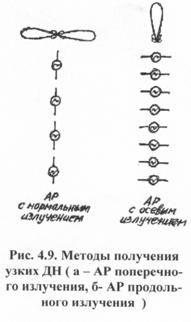 I1 = I2 =
I1 = I2 =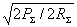 = I0/
= I0/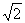 . Поскольку ток в каждом вибраторе уменьшился в
. Поскольку ток в каждом вибраторе уменьшился в 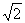 раз, то во столько же раз
уменьшается и напряженность поля, создаваемого одним вибратором в прежней
точке, т.е. Е1 = Е2 = Е/
раз, то во столько же раз
уменьшается и напряженность поля, создаваемого одним вибратором в прежней
точке, т.е. Е1 = Е2 = Е/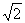 . Так как расстояние от обоих вибраторов до точки наблюдения одинаковы, то их
поля в этой точке синфаз-
. Так как расстояние от обоих вибраторов до точки наблюдения одинаковы, то их
поля в этой точке синфаз-
ны и
суммарное поле равно
Есум = Е1 +E2 = 2Е/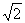 =
=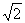 Е. Можно показать, что при излучении
Е. Можно показать, что при излучении
каждым из n
расположенных в ряд синфазно возбужденных вибраторов, мощности Р 1 = Р
1 = Р 2 = Р
2 = Р n= Р
n= Р /n и напряженность поля в главном направлении возрастает в
/n и напряженность поля в главном направлении возрастает в 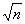 раз по сравнению
с одним вибратором,
излучающим мощность Р
раз по сравнению
с одним вибратором,
излучающим мощность Р .
.
Увеличить
напряженность поля в одном направлении за счет уменьшения ее в других направлениях
можно также, применив систему вибраторов, расположенных и возбужденных
таким образом, чтобы сдвиг фаз
полей от отдельных вибраторов в точке наблюдения из-за несинфазности
возбуждения компенсировался сдвигом фаз из-за разности расстояний (рис.4.9.б).
Сказанное справедливо, если расстояние между соседними вибраторами настолько велико,
что их взаимным влияниям можно пренебречь. При уменьшении расстояния между вибраторами
входное сопротивление каждого вибратора вследствие их взаимного влияния
возрастает. Поэтому при неизменной подводимой мощности токи в вибраторах уменьшаются и напряженность суммарного поля в главном
направлении увеличивается меньше, чем в 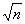 раз. Увеличение числа
вибраторов антенной системы при правильном выборе фаз токов, возбуждающих
вибраторы, и при правильном взаимном расположении вибраторов приводит к увеличению напряженности
поля в нужном направлении и к ослаблению ее в других направлениях, т.е. к
сужению диаграммы направленности антенны. Сужение диаграмм
направленности антенн, представляющих собой непрерывное распределение источников
(длинные провода, излучающие поверхности),
раз. Увеличение числа
вибраторов антенной системы при правильном выборе фаз токов, возбуждающих
вибраторы, и при правильном взаимном расположении вибраторов приводит к увеличению напряженности
поля в нужном направлении и к ослаблению ее в других направлениях, т.е. к
сужению диаграммы направленности антенны. Сужение диаграмм
направленности антенн, представляющих собой непрерывное распределение источников
(длинные провода, излучающие поверхности),
также происходит вследствие интерференции
полей отдельных элементов, на которые можно мысленно разбить антенну. Очевидно,
что получение узких диаграмм направленности путем синфазного
59
сложения полей от отдельных элементов
антенны в нужном направлении и создания резко несинфазных полей в других
направлениях требует увеличения габаритов антенны. Хотя изложенный здесь
способ получения узких диаграмм направленности путем синфазного или почти
синфазного сложения полей в данном направлении от отдельных элементов
антенны не является единственным и оптимальным, он по ряду причин в
настоящее время является основным.
5. АНТЕННЫЕ РЕШЕТКИ С ПОПЕРЕЧНЫМ
ИЗЛУЧЕНИЕМ
5.1. Плоская антенная
решетка. Равномерная линейная
антенная решетка
Пусть имеется ряд из n
симметричных вибраторов, одинаковым образом ориентированных в пространстве
(рис.4.9.а). Расстояние между центрами соседних вибраторов равно d1. Линейной решеткой
называется система идентичных излучателей, центры излучения которых
расположены на прямой, называемой осью решетки. Будем считать, что токи во всех элементах решетки имеют одинаковую величину (I1=I2=…In = I), фаза
же тока в каждом последующем вибраторе
данного ряда отстает от фазы тока в предыдущем на величину  . Таким образом, I2 = Iexp(-i
. Таким образом, I2 = Iexp(-i )...In = Iexp[-i(n-l)
)...In = Iexp[-i(n-l) ]. Следовательно, вдоль каждого ряда
вибраторов фаза возбуждающего тока изменяется по линейному закону.
]. Следовательно, вдоль каждого ряда
вибраторов фаза возбуждающего тока изменяется по линейному закону.
Рис. 5.1. К определению множителя
решётки поперечного излучения
Рассмотрим вначале
линейную систему из n ненаправленных излучателей, расположенных
на равных расстояниях друг от друга, возбужденных токами, равными по
амплитуде. Такая система вибраторов называется эквидистантной равноамплитудной
решеткой. Пусть фаза тока в каждом последующем вибраторе отстает на угол  по отношению к
току предыдущего. На большом удалении от
антенны в точке М, когда d1<<r,
лучи от отдельных вибраторов можно считать параллельными. Поле в точке М (рис.5.1.а), созданное
вибратором 1, обозначим через E1. В равноамплитудной
решетке амплитуды поля, созданные различными вибраторами на большом удалении, можно принять равными
амплитуде поля первого вибратора, но фазы этих полей будут различными. Поле Е2 вибратора 2 за счет разности хода лучей
по отношению к
току предыдущего. На большом удалении от
антенны в точке М, когда d1<<r,
лучи от отдельных вибраторов можно считать параллельными. Поле в точке М (рис.5.1.а), созданное
вибратором 1, обозначим через E1. В равноамплитудной
решетке амплитуды поля, созданные различными вибраторами на большом удалении, можно принять равными
амплитуде поля первого вибратора, но фазы этих полей будут различными. Поле Е2 вибратора 2 за счет разности хода лучей  r будет опережать поле вибратора 1 по фазе
на угол k
r будет опережать поле вибратора 1 по фазе
на угол k r = kd1sin
r = kd1sin и отставать на угол
и отставать на угол  за счет питания. Результирующий сдвиг по фазе
между полями, созданными
за счет питания. Результирующий сдвиг по фазе
между полями, созданными
61
вибраторами 1 и 2 равен Ф = kd1sin( -
- ). Этот сдвиг по фазе будет и для полей, созданных любыми соседними вибраторами. На рис.5.1.б
приведено графическое сложение полей отдельных вибраторов, сдвинутых по
фазе друг относительно друга на угол Ф.
). Этот сдвиг по фазе будет и для полей, созданных любыми соседними вибраторами. На рис.5.1.б
приведено графическое сложение полей отдельных вибраторов, сдвинутых по
фазе друг относительно друга на угол Ф.
Векторы полей образуют часть
правильного многоугольника, замыкающая сторона которого Еn равна результирующей напряженности поля,
созданной всеми
вибраторами в точке М. Перпендикуляры, восстановленные из середин сторон (векторов Е) правильного многоугольника,
пересекутся в одной точке 0, являющейся центром описанной окружности радиуса 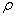 . Для треугольников ОАВ и ОАС можно записать
. Для треугольников ОАВ и ОАС можно записать
sin(Ф/2) = АВ/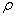 = Е1/2
= Е1/2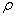 и sin(nФ/2)
= АС/
и sin(nФ/2)
= АС/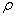 = Еn/2
= Еn/2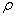 . Поделив одно уравнение
на другое, получим
. Поделив одно уравнение
на другое, получим
Еn/Е1= sin (0,5 nФ)/sin(0,5Ф) или Еn = Е1fс ( ), где Ф = kd1sin
), где Ф = kd1sin -
- ;
;
fc( ) = sin (0,5 nФ)/sin(0,5Ф) = sin[0,5 n(kd1sin
) = sin (0,5 nФ)/sin(0,5Ф) = sin[0,5 n(kd1sin -
- )]/ sin[0,5(kd1sin
)]/ sin[0,5(kd1sin -
- )] (5.1) -
множитель системы (решетки) излучателей.
)] (5.1) -
множитель системы (решетки) излучателей.
Здесь рассматривалась
решетка, состоящая из ненаправленных излучателей. Если линейную решетку
составить из направленных излучателей, например, симметричных вибраторов, то поле Е1 созданное каждым вибратором, определится его направленными свойствами
f1( ) и результирующая характеристика
направленности будет равна
) и результирующая характеристика
направленности будет равна
f( ) = f1(
) = f1( ) fc(
) fc( ). (5.2)
). (5.2)
На основании выражения
(5.2) может быть сформулирован общий принцип умножения характеристик
направленности: характеристика направленности системы (антенной решетки)
однотипных излучателей представляет собой произведение характеристики
направленности одного элемента данной системы на множитель системы.
При большом числе
вибраторов n множитель системы при изменении угла  изменяется,
значительно быстрее чем множитель f1(
изменяется,
значительно быстрее чем множитель f1( ). Это объясняется тем, что величина nkd1/2 значительно больше
величины kl. Поэтому характеристика направленности решетки, в
основном, определяется множителем системы. Поскольку множитель системы sin(nu)/sin(u)
является периодической функцией, то при изменении угла
). Это объясняется тем, что величина nkd1/2 значительно больше
величины kl. Поэтому характеристика направленности решетки, в
основном, определяется множителем системы. Поскольку множитель системы sin(nu)/sin(u)
является периодической функцией, то при изменении угла  этот множитель может
обращаться в нуль, затем он возрастает, достигая максимального значения, далее
уменьшается, снова становится равным нулю и т.д. Поэтому можно утверждать, что
диаграмма направленности решетки имеет многолепестковый
характер.
этот множитель может
обращаться в нуль, затем он возрастает, достигая максимального значения, далее
уменьшается, снова становится равным нулю и т.д. Поэтому можно утверждать, что
диаграмма направленности решетки имеет многолепестковый
характер.
62
5.2. Синфазная решетка
Широкое практическое
применение находят антенные решетки с одинаковыми по амплитуде и фазе токами в
вибраторах (равноамплитудные синфазные решетки). Полагая
в формуле (5.1)  =00, получим формулу для характеристики
направленности, такой решетки из т рядов в плоскости E
=00, получим формулу для характеристики
направленности, такой решетки из т рядов в плоскости E
E=
(m60Iп/r)[(cos(klsin ) -coskl)/ соs
) -coskl)/ соs ] *
] *
*sin [(n/2) (kd1sin )]/sin [(l/2) (kd1sin
)]/sin [(l/2) (kd1sin )]. (5.3)
)]. (5.3)
Напряженность,
излучаемого антенной, поля максимальна в направлении  =0° (главный максимум), т.е. в экваториальной плоскости
антенны. Каждый из вибраторов в этом
направлении излучает с максимальной интенсивностью, если l/
=0° (главный максимум), т.е. в экваториальной плоскости
антенны. Каждый из вибраторов в этом
направлении излучает с максимальной интенсивностью, если l/
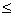 0,7; множитель f1(
0,7; множитель f1( ) в этом случае равен 1 - coskl. Поля от отдельных вибраторов в направлении
) в этом случае равен 1 - coskl. Поля от отдельных вибраторов в направлении  =00 синфазны и
складываются арифметически, так как в
направлении нормали к осям вибраторов разность расстояний до точки наблюдения равна нулю. Выражение множителя системы в этом случае представляет собой
неопределенность вида 0/0 , при раскрытии
которой по правилу Лопиталя оказывается, что
множитель системы максимален и равен n. Таким образом, в данном случае выражение
(5.3) принимает вид Еmах= nЕ1mах. Здесь n
- число симметричных вибраторов в решетке. Такой же вид принимает выражение (5.3) и
при
=00 синфазны и
складываются арифметически, так как в
направлении нормали к осям вибраторов разность расстояний до точки наблюдения равна нулю. Выражение множителя системы в этом случае представляет собой
неопределенность вида 0/0 , при раскрытии
которой по правилу Лопиталя оказывается, что
множитель системы максимален и равен n. Таким образом, в данном случае выражение
(5.3) принимает вид Еmах= nЕ1mах. Здесь n
- число симметричных вибраторов в решетке. Такой же вид принимает выражение (5.3) и
при  =1800. Как
следует из формулы (5.3), нормированная характеристика направленности
определяется выражением
=1800. Как
следует из формулы (5.3), нормированная характеристика направленности
определяется выражением
F ( ) = (Е/Емакс)
= [(cos (klsin
) = (Е/Емакс)
= [(cos (klsin ) - coskl) / соs
) - coskl) / соs (1- coskl)] *
(1- coskl)] *
*sin
[(n/2) (kd1sin )]/ {[nsin (l/2) kd1sin
)]/ {[nsin (l/2) kd1sin )]}. (5.4)
)]}. (5.4)
При некоторых
значениях угла  сдвиг фаз между полями соседних вибраторов, равный kd1sin
сдвиг фаз между полями соседних вибраторов, равный kd1sin , становится таким, что в
результате интерференции полей от
всех вибраторов суммарное поле обращается в нуль. Направления, в которых отсутствует излучение, определяются
из условия равенства нулю числителя
множителя системы, т.е. (nkd1/2)sin
, становится таким, что в
результате интерференции полей от
всех вибраторов суммарное поле обращается в нуль. Направления, в которых отсутствует излучение, определяются
из условия равенства нулю числителя
множителя системы, т.е. (nkd1/2)sin 0 = N, откуда sin
0 = N, откуда sin 0 = N
0 = N /(nd1), N = 1, 2, 3, ... .
Так как синус всегда меньше единицы, то чем больше знаменатель, тем больше
направлений нулевого излучения (N) имеет диаграмма
направленности. Следовательно, чем больше число вибраторов п (точнее, чем больше
относительный размер nd1/
/(nd1), N = 1, 2, 3, ... .
Так как синус всегда меньше единицы, то чем больше знаменатель, тем больше
направлений нулевого излучения (N) имеет диаграмма
направленности. Следовательно, чем больше число вибраторов п (точнее, чем больше
относительный размер nd1/ решетки), тем больше лепестков в
диаграмме направленности. Направления нулевого излучения рассчитываются по формуле
решетки), тем больше лепестков в
диаграмме направленности. Направления нулевого излучения рассчитываются по формуле
 0=arcsin [N
0=arcsin [N /(nd1)], где N=
1, 2, 3, ... (5.5)
/(nd1)], где N=
1, 2, 3, ... (5.5)
Направления максимумов
боковых лепестков приближенно можно найти из условия максимума числителя множителя
системы, так
63
как знаменатель этого множителя при kd1<<nkd1 (т.е. при большом числе вибраторов) с изменением угла  изменяется значительно медленнее числителя.
Это условие записывается в виде sin[(nkd1/2)sin
изменяется значительно медленнее числителя.
Это условие записывается в виде sin[(nkd1/2)sin max] = ±1, откуда nu=(nkd1/2)sin
max] = ±1, откуда nu=(nkd1/2)sin max = (2N+l)
max = (2N+l) /2, N=
1,2,3,...
/2, N=
1,2,3,...
Направления максимумов боковых лепестков
рассчитываются по формуле
 max = arcsin[(2N+l)
max = arcsin[(2N+l) /(2nd1)], где
N= 1,2,3, ... (5.6)
/(2nd1)], где
N= 1,2,3, ... (5.6)
На рис.5.2 приведены диаграммы направленности синфазной
решетки (в плоскости Е) для разного количества симметричных полуволновых вибраторов и
расстояния между ними. Ближайшее к главному максимуму направление
нулевого излучения определяют по формуле sin 0 =
0 =  /(nd1).
/(nd1).
Следовательно, главный
лепесток диаграммы направленности заключен в угле, равном 2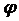 0. Как видно из формулы главный лепесток
диаграммы направленности тем уже, чем больше вибраторов в одном ряду, или чем
больше относительная длина антенны nd1/
0. Как видно из формулы главный лепесток
диаграммы направленности тем уже, чем больше вибраторов в одном ряду, или чем
больше относительная длина антенны nd1/ = L/
= L/ .
.
Рис. 5.2.
ДН синфазных антенных решёток
64
2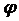 0 = 2(
0 = 2( /nd1), рад или 2
/nd1), рад или 2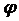 0
0 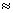 115°
115° /nd1. (5.7)
/nd1. (5.7)
В случае равномерной
синфазной решетки ширину диаграммы направленности по половинной мощности можно
определить по приближенной формуле
2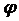 0,5
0,5  0,89(
0,89( /nd1), рад или 2
/nd1), рад или 2 0,5
0,5 510
510  /nd1. (5.8)
/nd1. (5.8)
Симметричный вибратор с относительной длиной l/ = 0,5 имеет ширину диаграммы направленности шириной по
половинной мощности 44°. Для того чтобы сузить диаграмму направленности до 6,4°, т.е. примерно в 7 раз,
надо применить 8 синфазных симметричных
вибраторов, т.е. увеличить размер антенны примерно в 8 раз.
= 0,5 имеет ширину диаграммы направленности шириной по
половинной мощности 44°. Для того чтобы сузить диаграмму направленности до 6,4°, т.е. примерно в 7 раз,
надо применить 8 синфазных симметричных
вибраторов, т.е. увеличить размер антенны примерно в 8 раз.
Направленные свойства
антенны характеризуются не только шириной главного лепестка диаграммы направленности,
но и уровнем боковых лепестков
 N= l/nsin{[(2N+l)/n)](
N= l/nsin{[(2N+l)/n)]( /2)}. (5.9)
/2)}. (5.9)
При большом значении n
(аргумент синуса мал) можно перейти к следующей приближенной формуле для расчета первых
двух боковых лепестков 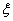 N= 2/[(2N+l)
N= 2/[(2N+l) ]. В этом случае уровень первого бокового лепестка
]. В этом случае уровень первого бокового лепестка 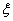 1=2/3
1=2/3
 0,21. Уровень второго
бокового лепестка составляет примерно 0,13. Уровень первого бокового лепестка в децибеллах составляет примерно -13,3 дБ. Отметим, что два главных максимума (при
0,21. Уровень второго
бокового лепестка составляет примерно 0,13. Уровень первого бокового лепестка в децибеллах составляет примерно -13,3 дБ. Отметим, что два главных максимума (при  =0° и
=0° и  =180°) или два главных
лепестка в диаграмме направленности получаются только при d1<
=180°) или два главных
лепестка в диаграмме направленности получаются только при d1< . При d1
. При d1 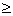
 возможно одновременное обращение в нуль
числителя и знаменателя множителя
системы при некоторых значениях углов
возможно одновременное обращение в нуль
числителя и знаменателя множителя
системы при некоторых значениях углов , не равных 0° и 180°. Это происходит при выполнении условия (kd1sin
, не равных 0° и 180°. Это происходит при выполнении условия (kd1sin )/2 = N
)/2 = N или kd1sin
или kd1sin = 2N
= 2N , т.е. в том случае, когда
сдвиг фаз между
полями соседних вибраторов равен или кратен
2
, т.е. в том случае, когда
сдвиг фаз между
полями соседних вибраторов равен или кратен
2 . При этом множитель системы, как и в случаях
. При этом множитель системы, как и в случаях  =0° и
=0° и  =180°, имеет наибольший
максимум, равный n. Это приводит к
появлению в
диаграмме направленности антенны, кроме боковых лепестков дополнительных
(вторичных) боковых лепестков. Уровень этих лепестков тем больше, чем шире
диаграмма направленности одного элемента решетки. Он равен единице, если
элементы не обладают направленными свойствами.
=180°, имеет наибольший
максимум, равный n. Это приводит к
появлению в
диаграмме направленности антенны, кроме боковых лепестков дополнительных
(вторичных) боковых лепестков. Уровень этих лепестков тем больше, чем шире
диаграмма направленности одного элемента решетки. Он равен единице, если
элементы не обладают направленными свойствами.
Так как симметричный
вибратор не обладает направленными свойствами в экваториальной плоскости, то
характеристика направленности синфазной решетки в плоскости H определяется только
множителем системы, который совершенно аналогичен этому множителю для плоскости
E. Ширину диаграммы направленности, направления максимумов боковых
лепестков и их уровень определяют по формулам, полученным для плоскости вектора Е решетки, заменяя в них угол  углом
углом  . Чем
больше рядов m в синфазной
решетке, тем уже ее диаграмма
. Чем
больше рядов m в синфазной
решетке, тем уже ее диаграмма
65
направленности в
плоскости H. КНД синфазной решетки в направлении максимального излучения может быть
рассчитан по формуле
D = (120/ R полн) (mn)2
(1-coskl)2, (5.10)
полн) (mn)2
(1-coskl)2, (5.10)
где R полн - полное
сопротивление излучения антенны. Заметим, что при
полн - полное
сопротивление излучения антенны. Заметим, что при
d1=>0, d2=>0, n=> , m=>
, m=> но при nd1= const = b и md2 = const = а, где а
и b –
но при nd1= const = b и md2 = const = а, где а
и b –
размеры излучающей системы в плоскостях Н и Е соответственно, с помощью
предельного перехода можно перейти от формул характеристик направленности антенных
решеток к формулам характеристик направленности систем с непрерывным
распределением возбуждающих источников (излучающих поверхностей). При а
>> , b >>
, b >> и небольших расстояниях между излучателями (d1 < 0,07
и небольших расстояниях между излучателями (d1 < 0,07 ) характеристики направленности обеих систем практически совпадают.
) характеристики направленности обеих систем практически совпадают.
5.3. Управление диаграммой направленности равномерной
линейной решетки
Выясним направленные свойства линейной
равномерной решетки. Как видно из выражений (5.1) и (5.4), множители системы равноамплитудной эквивалентной линейной и равноамплитудной эквидистантной синфазной решеток идентичны и отличаются
только аргументами синусов. Однако в случае равноамплитудной
эквидистантной линейной решетки множитель системы максимален и равен п при условии u
=  . При этом поля
от всех элементов антенны в точке наблюдения, характеризуются углом
. При этом поля
от всех элементов антенны в точке наблюдения, характеризуются углом  mах, имеют одинаковую
фазу, так как сдвиг фаз из-за несинфазности возбуждения Ψ компенсируется
пространственным сдвигом фаз Ψp = kd1 sin
mах, имеют одинаковую
фазу, так как сдвиг фаз из-за несинфазности возбуждения Ψ компенсируется
пространственным сдвигом фаз Ψp = kd1 sin . Из множителя
системы, получаем
. Из множителя
системы, получаем
sin maxuл =
maxuл =  λ / (2
λ / (2
 ). (5.11)
). (5.11)
Таким образом линейный закон изменения фазы возбуждающего поля приводит к изменению
направления максимального излучения. Это направление отклоняется от перпендикуляра к
оси решетки на угол φmaxгл. Так как излучение максимально
в том направлении, в котором происходит взаимная компенсация сдвигов фаз Ψ и
Ψр, то диаграмма направленности
поворачивается обязательно в сторону отставания фазы возбуждающего тока. Поворот
диаграммы направленности, т.е. управление ею путем изменения величины сдвига фаз Ψ, находит широкое
применение на практике.
Направление нулевых
излучений можно определить по формуле sin 0 = Nλ/(n
0 = Nλ/(n cosφmaxгл).
При узких диаграммах направленности значение
cosφmaxгл).
При узких диаграммах направленности значение
2φ0
равно
2φ0 = 2λ/(n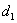 сщыφmaxгл).
сщыφmaxгл).
66
Таким образом
ширина диаграммы направленности растет по мере отклонения направления максимального излучения от перпендикуляра к оси решетки. Уровень боковых лепестков, близких к
главному, приближенно может быть найден тем же методом, что и в случае
синфазной решетки. Направления максимумов
боковых лепестков при этом определяются из формулы sin φmaxгл, = (2N+l)λ/(2nd1cos φmaxгл).
Так как при отклонении
направления максимального излучения от нормали к оси решетки диаграмма
направленности расширяется, а уровень боковых лепестков не изменяется, то казалось
бы, что КНД решетки должен уменьшаться.
Однако при этом пространственная диаграмма направленности приобретает коническую форму и телесный угол, в
пределах которого заключено
излученное поле (главный лепесток), уменьшается, что компенсирует расширение
диаграммы направленности в плоскости вектора Е. В результате
оказывается, что КНД линейной равномерной решетки не зависит от угла φmaxгл. КНД линейной
равномерной решетки, можно рассчитать по формуле D =
101,5/2φ0,5, где 2φ0,5 - ширина диаграммы
направленности по половинной мощности, рад. Рассмотренные антенные решетки излучают
с максимальной интенсивностью либо в
направлении нормали к своей оси (φ =  - синфазная решетка), либо под некоторым
углом к нормали (равномерная линейная
решетка). Вдоль оси решетки (ось у) излучение равно нулю, так как элементы
решетки в этом направлении не излучают, это - решетки с поперечным излучением.
- синфазная решетка), либо под некоторым
углом к нормали (равномерная линейная
решетка). Вдоль оси решетки (ось у) излучение равно нулю, так как элементы
решетки в этом направлении не излучают, это - решетки с поперечным излучением.
Вывод. Ширина ДН
синфазной решетки сужается с уменьшением длины волны, увеличением числа
вибраторов и увеличением расстоянии между ними. Если
в синфазной решетке уменьшить число вибраторов и увеличить расстояния между
ними так, чтобы сохранить неизменным произведение nd1, т.е. линейные
размеры антенны, то ширина главного лепестка останется неизменной,
но возрастут уровни боковых лепестков. При  < 0,5 λ, уровни боковых лепестков
практически остаются неизменными, но возрастает число вибраторов и усложняется
система питания. Поэтому расстояния
< 0,5 λ, уровни боковых лепестков
практически остаются неизменными, но возрастает число вибраторов и усложняется
система питания. Поэтому расстояния  между центрами
ненаправленных или полуволновых вибраторов обычно выбирают равными 0,5λ,
а одноволновых - λ. Для уменьшения уровня боковых
лепестков применяют эквидистантные решетки, в которых
центральные вибраторы имеют большие токи, а периферийные — меньшие или равноамплитудные решетки, в которых расстояния между
вибраторами по мере удаления от центра антенны увеличиваются. Подбирая закон распределения амплитуд
или размещения вибраторов, можно снижать уровни боковых лепестков до
необходимых значений.
между центрами
ненаправленных или полуволновых вибраторов обычно выбирают равными 0,5λ,
а одноволновых - λ. Для уменьшения уровня боковых
лепестков применяют эквидистантные решетки, в которых
центральные вибраторы имеют большие токи, а периферийные — меньшие или равноамплитудные решетки, в которых расстояния между
вибраторами по мере удаления от центра антенны увеличиваются. Подбирая закон распределения амплитуд
или размещения вибраторов, можно снижать уровни боковых лепестков до
необходимых значений.
67
При заданных линейных
размерах
антенны наибольшим КНД обладают равноамплитудные эквидистантные решетки. Следовательно, снижение уровня
боковых лепестков достигается уменьшением КНД или увеличением размеров
антенны.
Диаграмма
направленности системы ненаправленных (изотропных) синфазных
излучателей, расположенных вдоль прямой линии есть ДН линейной решетки, являющейся
фигурой вращения, ось которой совпадает с линией расположения
вибраторов в решетке. В плоскости, перпендикулярной линии расположения
вибраторов и проходящей через ее центр, синфазная линейная решетка имеет
круговую (ненаправленную) ДН. Для получения узких ДН в двух плоскостях,
например в горизонтальной и вертикальной, синфазная решетка должна быть двухмерной.
При линейном законе изменения фаз токов в
вибраторах ДН поворачивается в сторону отставания фаз.
Влияние амплитудного и фазовых распределений на ДН антенной решетки
поперечного излучения будет рассмотрено в лекции № 7.
6. АНТЕННЫЕ РЕШЕТКИ С
ОСЕВЫМ
ИЗЛУЧЕНИЕМ (АНТЕННЫ БЕГУЩЕЙ
ВОЛНЫ)
6.1. Излучение
равномерного линейного ряда вибраторов, перпендикулярных оси решетки
Рассмотрим равномерную линейную
решетку (рис.4.9.б), состоящую из ряда вибраторов, оси которых параллельны и
каждый вибратор излучает с максимальной интенсивностью вдоль оси решетки (оси х). Необходимый сдвиг фаз токов, в элементах антенны (ψ) можно создать с помощью соответствующих фазовращателей. Однако схема питания антенны при этом получается
весьма сложной. Проще последовательно возбуждать элементы антенны с помощью бегущей электромагнитной волны,
распространяющейся от начала антенны (первый вибратор) к ее концу с
определенной фазовой скоростью. При этом ток в последующем вибраторе
отстает по фазе от тока в предыдущем на
величину ψ = β где
где  - расстояние между вибраторами, β =
- расстояние между вибраторами, β =  /v = kc/v - коэффициент фазы, c/v - коэффициент
замедления. Таким образом, если считать, что токи в вибраторах равны по амплитуде,
то
/v = kc/v - коэффициент фазы, c/v - коэффициент
замедления. Таким образом, если считать, что токи в вибраторах равны по амплитуде,
то
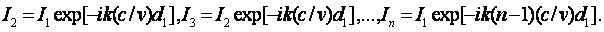
Так как последующий
вибратор возбуждается позже предыдущего, но находится ближе к точке наблюдения,
то сдвиг фаз между полями соседних вибраторов в этой точке (фаза поля первого
вибратора принимается за нулевую) равен
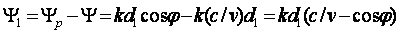 . (6.1)
. (6.1)
Сдвиг фаз между полями крайних вибраторов
Ψn = (n - l) k (cosφ
- c/v). (6.2)
(cosφ
- c/v). (6.2)
Учитывая сказанное, а
также то, что имеется только один ряд вибраторов (m=1),
можно от формулы (5.3) перейти к формуле (плоскость Е)
Е = (60Iп/ r) [(cos (klsinφ) - coskl) / cosφ ] *
* sin [(knd1/2) (c/v - cosφ)]/sin[(k /2)(c/v - cosφ)]. (6.3)
/2)(c/v - cosφ)]. (6.3)
Так как в плоскости Н элемент антенны не обладает
направленными свойствами ( ), то напряженность поля в этой плоскости определяется
по формуле
), то напряженность поля в этой плоскости определяется
по формуле
Е = (60Iп/r)(l- cosk ) sin[(kn
d1/2)(c/v - cosθ)]/sin[(k d1/2)(c/v - cosθ)]. (6.4)
) sin[(kn
d1/2)(c/v - cosθ)]/sin[(k d1/2)(c/v - cosθ)]. (6.4)
Как видно из формул
(6.3) и (6.4) характеристика направленности в плоскости Н определяется только множителем системы; в плоскости Е ха
69
рактеристика направленности
зависит также и от направленных свойств одного элемента решетки, но, в основном,
определяется также множителем системы Fс(φ) или Fc(θ). Поэтому
далее при анализе направленных свойств антенны бегущей волны (АБВ) будем рассматривать только этот
множитель.
Видно, что направленные свойства АБВ зависят от числа элементов решетки n, расстояния между
ними  и от фазовой скорости
питающей волны v. Определим направления нулевого излучения и
максимумов боковых лепестков. Для определения направлений
нулевого излучения приравняем числитель множителя системы
нулю или его аргумент (kn
и от фазовой скорости
питающей волны v. Определим направления нулевого излучения и
максимумов боковых лепестков. Для определения направлений
нулевого излучения приравняем числитель множителя системы
нулю или его аргумент (kn /2)(c/v - cosθ) = Nπ, где N =
1,2, ... . Отсюда
/2)(c/v - cosθ) = Nπ, где N =
1,2, ... . Отсюда
n (c/v - cosθ) = Nλ и
(c/v - cosθ) = Nλ и 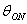 = arccos (c/v - Nλ / n
= arccos (c/v - Nλ / n ). (6.5)
). (6.5)
Для определения направлений максимумов боковых
лепестков приравняем числитель множителя системы единице или
его аргумент
(kn /2) > (c/v - cosθ) = (2N+1) (π/2), где N = 1,2,
.... Отсюда
/2) > (c/v - cosθ) = (2N+1) (π/2), где N = 1,2,
.... Отсюда
n (c/v - cosθ) = (2N+1)[
(c/v - cosθ) = (2N+1)[ /(2n
/(2n )]и θmaxN
= arcos{ c/v -(2N+1) (λ/(2n
)]и θmaxN
= arcos{ c/v -(2N+1) (λ/(2n )} (6.6)
)} (6.6)
Рассмотрим три режима работы антенны бегущей волны: 1) v = с; c/v = 1 (волна
свободного пространства); 2) v > с; c/v < 1 (быстрая волна) и 3) v < с; c/v >1 (медленная волна).
1) c/v=l. В этом случае при
 =0° множитель системы максимален и равен n. Нормированный множитель системы
=0° множитель системы максимален и равен n. Нормированный множитель системы
Fc (θ) = (1/n) sin [(kn /2)(l - cosθ)]/sin [(k
/2)(l - cosθ)]/sin [(k /2)(l - cosθ)]. (6.7)
/2)(l - cosθ)]. (6.7)
Результирующее поле максимально в направлении θ = 0° вследствие того, что поля от всех элементов антенны в точке наблюдения складываются
синфазно, так как сдвиг фаз из-за несинфазности
возбуждения Ψ полностью компенсируется пространственным сдвигом фаз Ψр.
При увеличении или уменьшении угла  (это же
относится и к углу θ) Ψ
(это же
относится и к углу θ) Ψ  Ψр . Вследствие этого напряженность
результирующего поля в точке наблюдения, характеризуемой
Ψр . Вследствие этого напряженность
результирующего поля в точке наблюдения, характеризуемой
|
Рис. 6.1. ДН АБВ при C/V = 1
|
некоторым углом θ 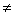 00, будет меньше, чем в точке, лежащей на продолжении оси антенны. Если cosθ отрицателен (90°<θ<270°), то фазовые сдвиги Ψ и Ψр при
00, будет меньше, чем в точке, лежащей на продолжении оси антенны. Если cosθ отрицателен (90°<θ<270°), то фазовые сдвиги Ψ и Ψр при  < λ/2 имеют одинаковые знаки. В этом случае вибратор, возбуждающийся раньше,
находится ближе к точке наблюдения, чем вибратор, возбуждающийся позже
< λ/2 имеют одинаковые знаки. В этом случае вибратор, возбуждающийся раньше,
находится ближе к точке наблюдения, чем вибратор, возбуждающийся позже
70
(пространственный
сдвиг фаз отрицателен). Сдвиг фаз 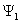 между полями соседних
вибраторов при малых
между полями соседних
вибраторов при малых  велик и результирующее поле в точке наблюдения мало. Следовательно, антенна бегущей волны обладает преимущественно однонаправленными свойствами и излучает с максимальной интенсивностью вдоль своей оси (антенна с осевым излучением) (рис.6.1). На
практике встречаются антенны бегущей волны, которые можно
рассматривать как непрерывное линейное распределение
слабонаправленных излучателей (например, диэлектрическая антенна). Без учета
затухания возбуждающего тока по длине антенны множитель системы может быть получен из
выражения (6.7)
велик и результирующее поле в точке наблюдения мало. Следовательно, антенна бегущей волны обладает преимущественно однонаправленными свойствами и излучает с максимальной интенсивностью вдоль своей оси (антенна с осевым излучением) (рис.6.1). На
практике встречаются антенны бегущей волны, которые можно
рассматривать как непрерывное линейное распределение
слабонаправленных излучателей (например, диэлектрическая антенна). Без учета
затухания возбуждающего тока по длине антенны множитель системы может быть получен из
выражения (6.7)
путем предельного перехода. Полагая n => , d=>0, n
, d=>0, n =>L, получаем
=>L, получаем
Fc(θ) = sin[(kL/2)(l- cosθ)]/[(kL/2)(l- cosθ)] . (6.8)
Уровень первого бокового лепестка ξ1 =F(θ1mах)=2/3π 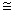 0,21 такой же,
как у синфазной
решетки вибраторов. Ширину диаграммы направленности по направлениям нулевого
излучения найдем из условия (kL/2)(l-cosφ0) = π. При
0,21 такой же,
как у синфазной
решетки вибраторов. Ширину диаграммы направленности по направлениям нулевого
излучения найдем из условия (kL/2)(l-cosφ0) = π. При
малых значениях λ/L (L - длина антенной решётки)
2θ0=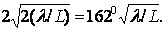 (6.9)
(6.9)
Ширина диаграммы
направленности по половинной мощности может быть определена по приближенной формуле
2θ 0,5  108°
108°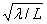 . (6.10)
. (6.10)
Сравнивая данную антенну
с равномерной синфазной решеткой, следует
отметить, что хотя диаграмма направленности АБВ получается шире, чем у синфазной решетки такой же длины, но зато один
ряд вибраторов, возбуждаемых бегущей волной тока, обладает направленными
свойствами в любой плоскости,
проходящей через ось антенны, в то время как один ряд синфазной решетки
обладает направленными свойствами только в одной плоскости. Если
элементы АБВ не обладают направленным действием или оно невелико, то диаграмму направленности антенны можно
считать осесимметричной. При этом КНД антенны бегущей волны можно определить
по общей формуле
D0= kL/ [Si2kL - (l - cos2kL)/(2kL)]. (6.11)
При 2kL » I
(практически при L/λ > 1) D0 4L /λ.
4L /λ.
2) c/v < I. На основании формулы
(6.4), имея в виду, что при условии
cosθ = c/v, множитель системы максимален и равен n (при этом условии
множитель системы обращается в неопределенность вида 0/0), и
используя
предельный переход ( =>0, n=>
=>0, n=> , n
, n >L), получаем нормированную характеристику
направленности
>L), получаем нормированную характеристику
направленности
71
F(θ) = sin[(kL/2)( c/v - cosθ)]/[(kL/2)( c/v - cosθ)]. (6.12)
Условие cosθ = c/v может выполняться при двух значениях угла θ = ±
θ mах, следовательно, имеются два направления максимального
излучения, не совпадающие с осью антенны. Данный режим работы является невыгодным,
так как направленные свойства антенны ухудшаются. Однако антенны быстрых волн
находят применение для создания диаграмм направленности специальной формы для
качания (сканирования) диаграммы направленности. Основой большинства антенн
быстрых волн являются волноводные структуры с неоднородностями (например,
волновод со щелями).
3) c/v > 1. Как видно из
выражений (6.1) и (6.2), в данном случае отсутствует направление, в котором поля
отдельных элементов антенны складываются синфазно, так как ни при каком
значении θ отношение c/v не
может стать равным cosθ и сдвиг фаз не
может обратиться в нуль.
Наименьший фазовый
сдвиг между полями отдельных вибраторов
Ψ1min = kd1(c/v - 1) получается в направлении θ = , т.е. вдоль оси антенны. Поля
отдельных вибраторов в точке наблюдения, лежащей в направлении θ =
, т.е. вдоль оси антенны. Поля
отдельных вибраторов в точке наблюдения, лежащей в направлении θ = , в данном случае
складываются геометрически, как показано на временной векторной диаграмме
(рис.6.2). Расчеты по формулам (6.4) и (6.12) показывают, что уменьшение
фазовой скорости, начиная от v = c, сопровождается постепенным сужением основного лепестка диаграммы направленности и
ростом боковых лепестков. Излучение в главном направлении θ =
, в данном случае
складываются геометрически, как показано на временной векторной диаграмме
(рис.6.2). Расчеты по формулам (6.4) и (6.12) показывают, что уменьшение
фазовой скорости, начиная от v = c, сопровождается постепенным сужением основного лепестка диаграммы направленности и
ростом боковых лепестков. Излучение в главном направлении θ = , сначала растет, достигая
максимума при некоторой определенной (для данного значения L =
, сначала растет, достигая
максимума при некоторой определенной (для данного значения L =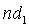 ) величине c/v,
а затем начинает уменьшаться и обращается в нуль при критической величине c/v
) величине c/v,
а затем начинает уменьшаться и обращается в нуль при критической величине c/v
(c/v)кр = 1+( /nd1). (6.13)
/nd1). (6.13)
Сужение главного
лепестка диаграммы направленности приводит к росту КНД антенны, а увеличение уровня
боковых лепестков - к его уменьшению. При увеличении c/v,
начиная от c/v =
1, сначала увеличивается КНД
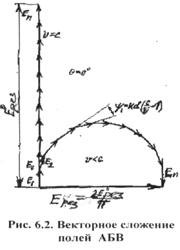 из-за сужения
диаграммы направленности. После достижения некоторой определенной величины c/v дальнейший
ее рост приводит к уменьшению КНД из-за увеличения уровня боковых лепестков.
Следовательно,
имеется оптимальная величина c/v (при заданной длине антенны L), при которой КНД достигает максимального значения. В случае ненаправленных элементов
антенны формула для КНД оказывается весьма громоздкой. Ее анализ показывает,
что КНД антенны бегущей
из-за сужения
диаграммы направленности. После достижения некоторой определенной величины c/v дальнейший
ее рост приводит к уменьшению КНД из-за увеличения уровня боковых лепестков.
Следовательно,
имеется оптимальная величина c/v (при заданной длине антенны L), при которой КНД достигает максимального значения. В случае ненаправленных элементов
антенны формула для КНД оказывается весьма громоздкой. Ее анализ показывает,
что КНД антенны бегущей
72
волны при заданной длине
антенны зависит от величины результирующего сдвига фаз между полями, создаваемыми
крайними (первым и последним) элементами антенны в точке наблюдения, лежащей на продолжении ее оси
(θ = 0°). КНД получается максимальным, если сдвиг фаз ψn, определяемый по формуле (6.2), равен 180°, т.е. если поля, создаваемые
крайними элементами антенны бегущей волны в точке, лежащей на продолжении оси
антенны, находятся в противофазе (см. рис.6.2). Таким
образом, на основании формулы (6.2) условием получения максимального КНД является
ψn опт. = kL(c/v
- 1) =  . (6.14)
. (6.14)
Воспользовавшись этой
формулой, можно определить оптимальную величину c/v при
заданной длине антенны L или определить оптимальную
длину
антенны
при заданной фазовой скорости. Очевидно, что:
(c/v)опт. 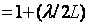 , (6.15)
, (6.15)
(L/ )опт. = 1/[2(c/v - 1)]. (6.16)
)опт. = 1/[2(c/v - 1)]. (6.16)
Как видно из формулы
(6.14), оптимальная длина антенны увеличивается при увеличении фазовой
скорости. В случае выполнения условия (6.14) КНД определяется по формуле
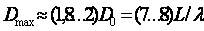 , (6.17)
, (6.17)
где D0 - КНД антенны бегущей
волны данной длины при с/v =1. На рис.6.3 приведены
графики зависимости отношения D/D0 от сдвига фаз между
полями крайних элементов антенны ψn, где D - КНД антенны определенной длины, работающей в режиме
замедления (v < с) или ускорения (v >c).
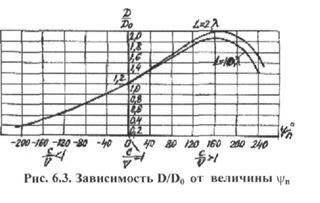 Как
видно из векторной временной диаграммы (рис.6.2), в оптимальном случае (ψn = 180°) вектор напряженности
результирующего поля в π/2 раз меньше, чем в случае АБВ, работающей в первом режиме
(приближенно можно считать, что вектор напряженности результирующего поля в оптимальном
случае равен
диаметру окружности, половина длины которой равна вектору напряженности
результирующего поля при c/v =
1).
Казалось бы, что КНД первой антенны должен быть меньше, чем второй. Увеличение
КНД антенны, работающей в режиме, близком к оптимальному, объясняется тем что при оптимальном и близких к нему
Как
видно из векторной временной диаграммы (рис.6.2), в оптимальном случае (ψn = 180°) вектор напряженности
результирующего поля в π/2 раз меньше, чем в случае АБВ, работающей в первом режиме
(приближенно можно считать, что вектор напряженности результирующего поля в оптимальном
случае равен
диаметру окружности, половина длины которой равна вектору напряженности
результирующего поля при c/v =
1).
Казалось бы, что КНД первой антенны должен быть меньше, чем второй. Увеличение
КНД антенны, работающей в режиме, близком к оптимальному, объясняется тем что при оптимальном и близких к нему
73
отношениях c/v токи
в элементах антенны из-за взаимного влияния возрастают. В частности, при
оптимальном отношении c/v ток
в элементах антенны увеличивается примерно в (π/2)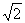 раз по сравнению с током в элементах антенны, работающей в
режиме c/v =
1 (при неизменной излучаемой мощности). Это приводит к увеличению напряженности поля, излучаемого каждым элементом
антенны. Приведенные здесь соотношения,
характеризующие оптимальный режим работы АБВ, справедливы только для
ненаправленных или слабонаправленных элементов антенны. При наличии у элементов антенны значительных направленных свойств эти
соотношения изменяются. Ширина диаграммы
направленности по нулевому излучению антенны,
работающей в оптимальном режиме, на основании формулы (6.12) находится из условия (kL/2)(c/v
- cos
раз по сравнению с током в элементах антенны, работающей в
режиме c/v =
1 (при неизменной излучаемой мощности). Это приводит к увеличению напряженности поля, излучаемого каждым элементом
антенны. Приведенные здесь соотношения,
характеризующие оптимальный режим работы АБВ, справедливы только для
ненаправленных или слабонаправленных элементов антенны. При наличии у элементов антенны значительных направленных свойств эти
соотношения изменяются. Ширина диаграммы
направленности по нулевому излучению антенны,
работающей в оптимальном режиме, на основании формулы (6.12) находится из условия (kL/2)(c/v
- cos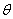 0)= π. Подставляя вместо c/v выражение
(6.15) и проводя рассуждения, аналогичные случаю c/v = 1, получаем sinθ0
=
0)= π. Подставляя вместо c/v выражение
(6.15) и проводя рассуждения, аналогичные случаю c/v = 1, получаем sinθ0
=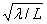 . При малых отношениях λ/L синус
можно заменить аргументом. Тогда
. При малых отношениях λ/L синус
можно заменить аргументом. Тогда
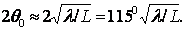 (6.18)
(6.18)
и, как видно из сравнения формул (6.9)
и (6.18), в этом случае АБВ с пониженной фазовой скоростью (оптимальной) имеет
диаграмму направленности в 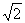 раз уже, чем антенна той же длины с c/v =
1. Ширина диаграммы направленности по половинной мощности может быть приближенно определена (для антенны, у которой L/λ
»1) по
раз уже, чем антенна той же длины с c/v =
1. Ширина диаграммы направленности по половинной мощности может быть приближенно определена (для антенны, у которой L/λ
»1) по
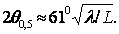 формуле:
формуле:
(6.19)
Диаграмма
направленности АБВ с пониженной фазовой скоростью, имеющей оптимальную
длину, изображена на рис.6.4. Сужение диаграммы направленности антенны оптимальной
длины по сравнению с диаграммой направленности антенны такой же длины, но
работающей в первом режиме (c/v =
1), объясняется тем, что при увеличении угла φ напряженность результирующего поля в
случае c/v >1 убывает
значительно быстрее, чем в случае c/v =
1. Это происходит потому, что в случае антенны оптимальной длины сдвиги фаз
между полями соседних вибраторов в точке наблюдения, определяемой углом
θ1 [при этом 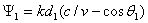 ], больше, чем в случае антенны с c/v =
1 [при этом
], больше, чем в случае антенны с c/v =
1 [при этом 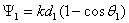 ].
].

74
Определим уровень первого бокового
лепестка диаграммы направленности
оптимальной антенны. Максимальная величина нормированной характеристики направленности оптимальной антенны,
определяемая по формуле (6.12), при θ =  и c/v
= 1+λ/2L равна 2π.
Значение F(θ) в направлении максимума первого
бокового лепестка можно определить, положив аргумент синуса в формуле
(6.12) равным 3π /2 и найдя из этого равенства cos θ1max. Подставляя в формулу (6.12) найденное значение cosθ1max и заменяя c/v его
выражением
(6.15), получаем F(θlmax) = 2π/3. Отсюда
уровень первого бокового лепестка
и c/v
= 1+λ/2L равна 2π.
Значение F(θ) в направлении максимума первого
бокового лепестка можно определить, положив аргумент синуса в формуле
(6.12) равным 3π /2 и найдя из этого равенства cos θ1max. Подставляя в формулу (6.12) найденное значение cosθ1max и заменяя c/v его
выражением
(6.15), получаем F(θlmax) = 2π/3. Отсюда
уровень первого бокового лепестка 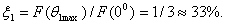
При увеличении длины
антенны по сравнению с оптимальной излучение в главном направлении уменьшается
и растут боковые лепестки. При L = 2LОПТ излучение в главном направлении совершенно исчезает. При уменьшении длины антенны по сравнению с
оптимальной главный лепесток диаграммы
направленности расширяется, уровень боковых лепестков уменьшается. Для того чтобы диаграмма
направленности становилась уже, надо увеличивать длину антенны. Вместе с
тем, чтобы при удлинении антенны бегущей
волны ее длина оставалась оптимальной, необходимо в соответствии с
соотношением (6.14) увеличивать фазовую скорость волны в антенне.
В антеннах бегущей
волны, применяющихся на практике, амплитуда возбуждающего тока уменьшается вдоль оси
решетки по экспоненциальному закону, т.е. I2 = . Это имеет место вследствие потерь энергии в антенне или
вследствие постепенного излучения энергии элементами антенны. Степень убывания
бывает разной и в некоторых случаях, при расчетах этим уменьшением
пренебрегают. Убывание амплитуды тока приводит к расширению основного лепестка
диаграммы направленности, к увеличению уровня боковых лепестков и к
исчезновению направлений нулевого излучения, которые заменяются направлениями
минимального излучения.
. Это имеет место вследствие потерь энергии в антенне или
вследствие постепенного излучения энергии элементами антенны. Степень убывания
бывает разной и в некоторых случаях, при расчетах этим уменьшением
пренебрегают. Убывание амплитуды тока приводит к расширению основного лепестка
диаграммы направленности, к увеличению уровня боковых лепестков и к
исчезновению направлений нулевого излучения, которые заменяются направлениями
минимального излучения.
Практическим примером
выполнения антенны бегущей волны в виде ряда вибраторов является директорная
антенна, широко применяемая в УКВ диапазоне (особенно на метровых и
дециметровых волнах). Эта антенна состоит из одного питаемого (активного) и
нескольких пассивных вибраторов, один из которых работает в режиме рефлектора, а остальные - в
режиме директора. Оси всех вибраторов
параллельны. Пассивные вибраторы возбуждаются электромагнитным полем активного вибратора. Длина активного вибратора (2 ) обычно берется несколько меньше λ/2 с тем, чтобы он
был резонансным. Для того чтобы пассивный вибратор работал в режиме
рефлектора, его входное сопротивление должно
иметь индуктивный характер, что достигается
) обычно берется несколько меньше λ/2 с тем, чтобы он
был резонансным. Для того чтобы пассивный вибратор работал в режиме
рефлектора, его входное сопротивление должно
иметь индуктивный характер, что достигается
75
некоторым удлинением этого вибратора по
сравнению с активным. Пассивный вибратор, работающий
в режиме директора, должен обладать реактивным сопротивлением емкостного
характера, для чего он должен быть несколько короче активного вибратора. Так как
рефлектор усиливает поле в направлении активного вибратора (вперед) и
ослабляет поле в обратном направлении, то применение нескольких рефлекторов не
имеет смысла, так как все рефлекторы, следующие за первым, будут очень слабо
возбуждаться. Первый директор усиливает поле в направлении следующего директора
и поэтому, если установить несколько директоров, то все они будут возбуждаться достаточно
интенсивно. Длины директоров и расстояния между ними подбирают так, чтобы в
каждом последующем вибраторе ток отставал по фазе от тока в предыдущем на
величину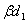 , несколько большую величины k
, несколько большую величины k Такую антенну можно рассматривать как АБВ с пониженной фазовойскоростью (c/v >
1). Максимум излучения совпадает с осью антенны (
Такую антенну можно рассматривать как АБВ с пониженной фазовойскоростью (c/v >
1). Максимум излучения совпадает с осью антенны ( ).
).
6.2. Излучение
провода, ток в котором изменяется по закону
бегущей волны
Рассмотрим провод
длиной L, ток в котором изменяется по закону бегущей волны. Пренебрегая затуханием, Iz =
I0exp[-ik(c/v)z], где
I0 - амплитуда
тока в начале провода; z - текущая координата.
Из формулы (6.12) известен множитель системы в случае непрерывного
распределения источников поля. На основании правила перемножения
характеристик направленности нормированная характеристика направленности провода
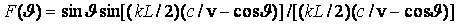
(6.20)
где sin - характеристика направленности элемента провода.
- характеристика направленности элемента провода.
Множитель системы
выражения (6.20) максимален при  =
=  (если v = c).
Однако результирующее поле провода в направлении его оси
(если v = c).
Однако результирующее поле провода в направлении его оси  =
= 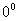 ) равно нулю, так
как sin
) равно нулю, так
как sin в формуле (6.20)
обращается в нуль. Физически это объясняется тем, что элементарный
вибратор не излучает вдоль своей оси. Так как множитель системы максимален в
направлении оси провода (это направление наиболее благоприятно для сложения
полей отдельных элементов провода), а характеристика направленности элемента
провода максимальна в направлении, перпендикулярном оси провода (
в формуле (6.20)
обращается в нуль. Физически это объясняется тем, что элементарный
вибратор не излучает вдоль своей оси. Так как множитель системы максимален в
направлении оси провода (это направление наиболее благоприятно для сложения
полей отдельных элементов провода), а характеристика направленности элемента
провода максимальна в направлении, перпендикулярном оси провода ( = 90°), то результирующее поле оказывается максимальным в некотором
промежуточном направлении, составляющем угол
= 90°), то результирующее поле оказывается максимальным в некотором
промежуточном направлении, составляющем угол 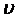 max (меньший 90°) с осью
провода. Очевидно, что таких направлений имеется два (в первом и в четвертом
квадрантах). При большой относительной
длине провода L/λ характеристика направленности приблизительно
max (меньший 90°) с осью
провода. Очевидно, что таких направлений имеется два (в первом и в четвертом
квадрантах). При большой относительной
длине провода L/λ характеристика направленности приблизительно
76
становится
максимальной, когда максимален числитель множителя системы (первый максимум). Поэтому угол
максимального излучения можно приближенно
найти из выражения
cos  max=(2L -
λ)/2L. (6.21)
max=(2L -
λ)/2L. (6.21)
Чем больше
относительная длина провода L/λ, тем меньше угол  тах, т.е. тем сильнее
излучаемое поле прижато к оси провода. Чем больше L/λ, тем уже главный лепесток
диаграммы направленности, но тем больше количество и уровень боковых
лепестков. Главные лепестки диаграммы направленности наклонены в сторону движения волны в
проводе (рис.6.5), т.е. пространственная диаграмма направленности имеет вид
конуса. Вследствие наличия двух направлений максимального излучения (в одной
плоскости) нецелесообразно применять одиночный провод с бегущей волной тока в
качестве антенны. Однако в антенной технике с успехом применяются различные комбинации из таких проводов,
обладающие достаточно хорошими направленными свойствами (например, ромбическая
антенна).
тах, т.е. тем сильнее
излучаемое поле прижато к оси провода. Чем больше L/λ, тем уже главный лепесток
диаграммы направленности, но тем больше количество и уровень боковых
лепестков. Главные лепестки диаграммы направленности наклонены в сторону движения волны в
проводе (рис.6.5), т.е. пространственная диаграмма направленности имеет вид
конуса. Вследствие наличия двух направлений максимального излучения (в одной
плоскости) нецелесообразно применять одиночный провод с бегущей волной тока в
качестве антенны. Однако в антенной технике с успехом применяются различные комбинации из таких проводов,
обладающие достаточно хорошими направленными свойствами (например, ромбическая
антенна).
7. ИЗЛУЧЕНИЕ
ВОЗБУЖДЕННЫХ ПОВЕРХНОСТЕЙ
7.1.
Напряженность поля излучающей поверхности
в дальней зоне. Характеристики
направленности идеальной плоской антенны.
Узкая диаграмма направленности может быть сформирована при помощи антенны, представляющей собой излучающую
поверхность, т.е. поверхность, на
которой распределены взаимно перпендикулярные составляющие векторов Е
и Н. Такую возбужденную поверхность рассматривают как совокупность элементарных источников Гюйгенса. Существующие на элементарной площадке dS значения векторов поля
Еу и Hх на основании принципа
эквивалентных токов можно представить как суперпозицию полей двух взаимно
перпендикулярных поверхностных токов - электрического Jэ и магнитного
Jм. Ввиду малости размеров площадки
совокупность указанных токов можно рассматривать как два взаимно
перпендикулярных элементарных диполя длиной dy и dx с токами Jэ и Jм. Излучение источника
Гюйгенса
направлено по нормали к элементарной площадке. Характеристика направленности в
плоскостях Е
и Н определяется по формуле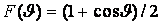 , а
ДН имеет форму кардиоиды. Антенны типа излучающей поверхности особенно широко применяются
в диапазоне сантиметровых волн (антенна в виде открытого конца волновода,
рупорные антенны, линзовые антенны, зеркальные антенны и др.).
, а
ДН имеет форму кардиоиды. Антенны типа излучающей поверхности особенно широко применяются
в диапазоне сантиметровых волн (антенна в виде открытого конца волновода,
рупорные антенны, линзовые антенны, зеркальные антенны и др.).
В общем случае как амплитуда, так и фаза
возбуждающего поля могут являться функциями координат точки излучающей поверхности,
т.е.
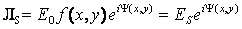
 , (7.1)
, (7.1)
где Es комплексная амплитуда
возбуждающего поля в данной точке прямоугольной возбужденной поверхности; E0 - амплитуда возбуждающего поля в центре антенны; f(x,у) - функция, характеризующая
зависимость амплитуды возбуждающего поля от координат (амплитудное распределение);
ψ(x,y) - функция, определяющая
зависимость фазы возбуждающего поля от
координат
точки излучающей поверхности (фазовое распределение). В ряде случаев
амплитудное или фазовое распределения бывают функциями только одной
координаты.
Найдем выражение для напряженности
электрического поля, создаваемого прямоугольной
излучающей поверхностью в
дальней зоне. Мысленно разобьем эту поверхность на элементарные площадки
со сторонами dx и dy, представляющие собой
источники Гюйгенса
78
(рис.7.1). Направления на точку наблюдения М,
характеризуемую
координатными углами  и φ,
от центрального элемента (x = y =
0) и от произвольного элемента с координатами х, у можно считать параллельными.
и φ,
от центрального элемента (x = y =
0) и от произвольного элемента с координатами х, у можно считать параллельными.
Рассмотрим наиболее
простой случай возбужденной поверхности идеальную излучающую поверхность (идеальную плоскую антенну).
Идеальной плоской
антенной называется плоская возбужденная поверхность, в каждой точке которой
тангенциальные составляющие векторов Е
и Н имеют одинаковые направления,
амплитуды и фазы, т.е. не зависят от координат. Т.к. f(x,y) = 1, ψ(х,у) = 0, φ= /2 получаем формулудля
расчета напряженности полного поля идеальной плоской антенны в плоскости Е (плоскости yoz)
/2 получаем формулудля
расчета напряженности полного поля идеальной плоской антенны в плоскости Е (плоскости yoz)
Ė=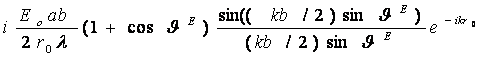 (7.2)
(7.2)
Выражение для напряженности результирующего
поля в плоскости Н (плоскость xoz), получаемое аналогичным путем
Ė=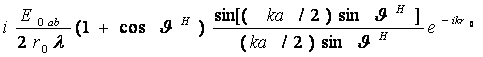 . (7.3)
. (7.3)
 Множитель вида
Множитель вида 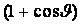 - характеристика направленности элемента излучающей
поверхности (элемента Гюйгенса) — определяет однонаправленные свойства этой
поверхности в плоскостях Е
и Н.
- характеристика направленности элемента излучающей
поверхности (элемента Гюйгенса) — определяет однонаправленные свойства этой
поверхности в плоскостях Е
и Н.
Множитель вида
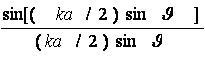 - множитель системы -
при изменении углов
- множитель системы -
при изменении углов 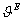 и
и 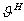 изменяется значительно быстрее, чем множитель (l + cos
изменяется значительно быстрее, чем множитель (l + cos ). Поэтому характеристика направленности идеальной плоской
антенны в одном
полупространстве, в основном, определяется множителем системы. Обозначая
). Поэтому характеристика направленности идеальной плоской
антенны в одном
полупространстве, в основном, определяется множителем системы. Обозначая 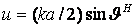 и
и 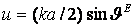 , множители системы можно записать в виде (sinu)/u и (sin
, множители системы можно записать в виде (sinu)/u и (sin )/
)/ . Функция вида (sinu)/u максимальна
при и = 0, и величина этого
максимума равна единице. Величины и и
. Функция вида (sinu)/u максимальна
при и = 0, и величина этого
максимума равна единице. Величины и и  могут быть равны нулю
только при равенстве нулю углов
могут быть равны нулю
только при равенстве нулю углов 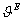 и
и 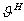 .
.
Так как источник Гюйгенса
излучает с максимальной интенсивностью в направлении
нормали к своей поверхности, то направления максимумов множителя системы и
характеристики направленности источника Гюйгенса совпадают. Поэтому
идеальная плоская антенна излучает с максимальной интенсивностью в направлении нормали (положительное направление оси z на рис.7.1 - направление движения возбуждающей
79
волны).
Из рис.7.2 видно, что диаграмма
направленности идеальной излучающей поверхности имеет многолепестковый
характер. Множитель системы
этой антенны незначительно отличается от аналогичного множителя синфазной равномерной антенной решетки. Таким
образом, характеристики направленности
этих антенн (при малом расстоянии между элементами решетки) по существу отличаются только множителями,
характеризующими направленные свойства одного элемента антенны.
Направления, в которых излучаемое поле обращается в нуль, находят
из условий: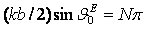 ,
,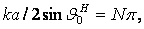 где N=1,2,3…,
где N=1,2,3…,
откуда 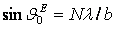 ,
,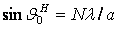 .
.
Первое направление
нулевого излучения определяют из формул:
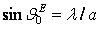 ;
; 
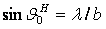 . (7.4); (7.5)
. (7.4); (7.5)
Направления нулевого излучения отсутствуют,
если λ
> а или λ > b Направлений нулевых
излучений, т.е. боковых лепестков, тем больше, чем больше относительная
ширина антенны (a/λ или b/λ). Формулы (7.4) и (7.5) совпадают с соответствующими формулами синфазной
решетки, если считать, что b = nd1 и a=md2.
При больших размерах
излучающих поверхностей [ (λ/а) «1
и(λ/b)«1] в формулах (7.4)
и (7.5) синусы можно заменить их аргументами,
и тогда
ширина диаграммы направленности идеальной плоской антенны
определяется по формулам:
в плоскости Е 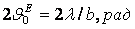 ;
; 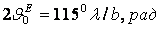 ; (7.6)
; (7.6)
в плоскости Н 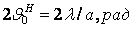 ;
; 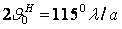 ; (7.7)
; (7.7)
Таким образом, диаграмма
направленности идеальной плоской антенны в данной плоскости тем уже, чем
больше размер антенны, параллельный этой плоскости. Ширина диаграммы
направленности в данной плоскости не зависит от размера антенны,
перпендикулярного этой плоскости.
Ширина диаграммы
направленности идеальной плоской антенны по половинной мощности определяется по формулам:
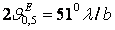 ;
; 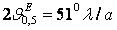 . (7.8); (7.9)
. (7.8); (7.9)
По таким же формулам определяется
ширина диаграммы направленности по половинной мощности синфазной решетки
вибраторов, если число вибраторов п
велико.
80
Уровень первого лепестка
в диаграмме направленности идеальной плоской антенны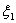 = 0,214.
= 0,214.
Анализ показывает, что
в пределах главного лепестка диаграммы направленности идеальной плоской
антенны сосредоточено около 82% излучаемой мощности; в боковых лепестках
сосредоточено приблизительно 18% излучаемой мощности. Расчет напряженности
поля, излученного круглой поверхностью, производится тем же методом, что и в случае прямоугольной
антенны. Однако при этом удобно использовать не прямоугольную, а полярную
систему координат. Круглая антенна расположена в плоскости хоу,
ρ и φ’ - полярные координаты элементарной площадки,
выделенной на этой антенне. Координаты
точки наблюдения -  (угол между нормалью к оси
антенны oz и направлением на точку наблюдения) и φ (азимутальный угол).
(угол между нормалью к оси
антенны oz и направлением на точку наблюдения) и φ (азимутальный угол).
В случае идеальной плоской круглой антенны, в результате
интегрирования для одной из главных
плоскостей ((φ = o
или φ =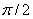 ) получаем
) получаем
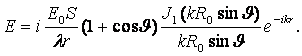
 (7.10)
(7.10)
Здесь 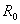 - радиус антенны, S =
- радиус антенны, S =  ~ площадь раскрыва антенны,
~ площадь раскрыва антенны,  - функция Бесселя нулевого порядка от
аргумента (kR0 sin
- функция Бесселя нулевого порядка от
аргумента (kR0 sin ).
).
Как и в случае идеальной прямоугольной
антенны, характеристика направленности
максимальна при  =
=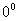 , т.е. в направлении нормали к излучающей поверхности.
, т.е. в направлении нормали к излучающей поверхности.
81
7.2. Влияние неравномерного
амплитудного распределения поля на диаграмму направленности излучающей
поверхности
Рассмотрим синфазную
прямоугольную излучающую поверхность с косинусоидальным амплитудным
распределением поля вдоль оси х (рис.7.3)
Es =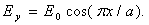 (7.11)
(7.11)
Приблизительно такое
распределение имеется на открытом конце прямоугольного волновода, возбуждаемого волной .Так как
распределение
возбуждающего поля вдоль оси у в данном случае такое же, как у идеальной
антенны (равномерное), то характеристика направленности рассматриваемой и
излучающей поверхности в плоскости вектора Е
(плоскости
yoz) не отличается от характеристики
направленности идеальной плоской антенны в этой плоскости. В случае, когда f(x,y) = f(x) =
.Так как
распределение
возбуждающего поля вдоль оси у в данном случае такое же, как у идеальной
антенны (равномерное), то характеристика направленности рассматриваемой и
излучающей поверхности в плоскости вектора Е
(плоскости
yoz) не отличается от характеристики
направленности идеальной плоской антенны в этой плоскости. В случае, когда f(x,y) = f(x) =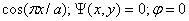 , получим выражение для характеристики
направленности антенны в плоскости вектора Н (плоскости xoz)
, получим выражение для характеристики
направленности антенны в плоскости вектора Н (плоскости xoz)
Ė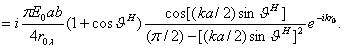 (7.12)
(7.12)
Нормированная характеристика
направленности излучающей поверхности с косинусоидальным распределением
возбуждающего поля в плоскости Н определяется выражением
F(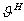 )
)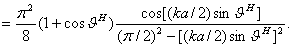 (7.13)
(7.13)
Таким образом
в данном случае, по сравнению с идеальной плоской антенной, изменился
вид множителя системы.
Ширина главного
лепестка определяется из условия равенства нулю числителя множителя системы. Однако
нельзя положить аргумент косинуса  равным π/2, так как при этом знаменатель множителя системы также обращается в
нуль и получается неопределенность вида 0/0. Раскрытие этой неопределенности дает
конечное значение множителя системы. Поэтому, чтобы множитель системы обратился в
нуль, следует положить
равным π/2, так как при этом знаменатель множителя системы также обращается в
нуль и получается неопределенность вида 0/0. Раскрытие этой неопределенности дает
конечное значение множителя системы. Поэтому, чтобы множитель системы обратился в
нуль, следует положить 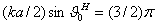 , откуда sin
, откуда sin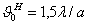 . При малых величинах λ/а эта
формула принимает вид
. При малых величинах λ/а эта
формула принимает вид 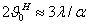 , рад, или
, рад, или
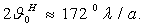 (7.14)
(7.14)
Ширина диаграммы направленности по половинной мощности в данном случае определяется по формуле
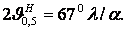 (7.15)
(7.15)
82
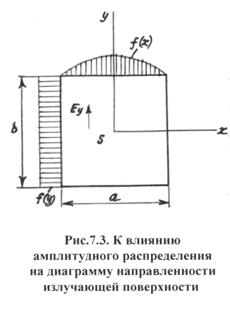 Таким образом при переходе от равномерного амплитудного распределения
к распределению, спадающему к краям излучающей поверхности по закону косинуса,
ширина диаграммы направленности в соответствующей плоскости увеличивается
примерно в 1,5 раза. Одновременно с расширением главного лепестка диаграммы
направленности уменьшается уровень боковых лепестков. Так, в рассмотренном случае
относительный уровень первого бокового лепестка
Таким образом при переходе от равномерного амплитудного распределения
к распределению, спадающему к краям излучающей поверхности по закону косинуса,
ширина диаграммы направленности в соответствующей плоскости увеличивается
примерно в 1,5 раза. Одновременно с расширением главного лепестка диаграммы
направленности уменьшается уровень боковых лепестков. Так, в рассмотренном случае
относительный уровень первого бокового лепестка 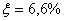 или -23 дБ
или -23 дБ
(вместо -13,2 дБ в случае идеальной плоской
антенны).
Расширение диаграммы направленности
объясняется тем, что
в соответствии с амплитудным распределением 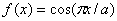 по мере удаления от центра антенны в направлении оси х возбуждение элементарных площадок становится слабее.
Очевидно, что поля, создаваемые близкими к краю поверхности площадками, из-за своей
малости почти не влияют на величину результирующего поля антенны. Следовательно,
уменьшение амплитуды возбуждающего
поля к краям антенны эквивалентно уменьшению соответствующего размера антенны с равномерным распределением амплитуды возбуждающего поля.
по мере удаления от центра антенны в направлении оси х возбуждение элементарных площадок становится слабее.
Очевидно, что поля, создаваемые близкими к краю поверхности площадками, из-за своей
малости почти не влияют на величину результирующего поля антенны. Следовательно,
уменьшение амплитуды возбуждающего
поля к краям антенны эквивалентно уменьшению соответствующего размера антенны с равномерным распределением амплитуды возбуждающего поля.
Обобщая полученные результаты и применяя их к
другим амплитудным распределениям, можно установить следующее: чем резче спадает амплитуда
возбуждающего поля к краям излучающей поверхности, тем шире главный лепесток
диаграммы направленности и тем меньше уровень боковых лепестков. Это же положение может
быть распространено и наантенные решетки. Данное
свойство излучающих поверхностей находит широкое практическое применение. Так,
в тех случаях, когда требуются диаграммы направленности с низким уровнем боковых лепестков добиваются резко спадающего к
краям антенны амплитудного распределения. Правда, при этом расширяется основной
лепесток диаграммы направленности.
83
7.3. КНД излучающей поверхности
В случае идеальной плоской антенны 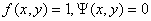 выражение для КНД принимает вид
выражение для КНД принимает вид
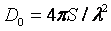 (7.16)
(7.16)
Таким образом, КНД идеальной плоской антенны
тем больше, чем больше площадь этой антенны и чем короче длина волны. КНД антенны обратно пропорционален
квадрату длины волны при постоянной площади антенны. Легко видеть, что с
укорочением длины волны облегчается построение антенн с высоким КНД. Так, для того
чтобы антенна, работающая на λ = 1 см, имела КНД D = 12,6 • 104, ее площадь должна составлять
всего 1 м2. В случае неравномерного амплитудного распределения по
аналогии с формулой (7.16)
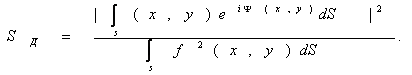
(7.17)
Величину 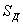 можно назвать действующей
(эффективной) площадью антенны.
Очевидно, что
можно назвать действующей
(эффективной) площадью антенны.
Очевидно, что
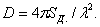 (7.18)
(7.18)
Выражая КНД излучающей поверхности с
произвольным распределением возбуждающего поля через КНД идеальной плоской
антенны с помощью выражений (7.16) и (7.18), получаем
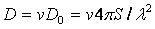 , (7.19)
, (7.19)
где 
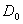 КНД
идеальной плоской антенны;
КНД
идеальной плоской антенны;
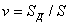 коэффициент
коэффициент
использования поверхности раскрыва
(КИП).
Величина КИП зависит от вида
амплитудного и фазового распределения возбуждающего поля.
КИП тем меньше,
чем резче амплитуда возбуждающего поля спадает к
краям антенны. Рассмотрим частный случай косинусоидальное амплитудное распределение: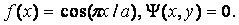
Тогда 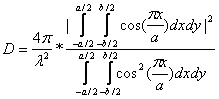
84
В результате интегрирования получаем
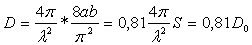 .
(7.20)
.
(7.20)
Уменьшение КНД
излучающей поверхности со спадающим к краям амплитудным распределением по
сравнению с идеальной излучающей поверхностью объясняется тем, что при
одинаковой излучаемой мощности напряженность поля первой антенны в главном
направлении будет меньше, чем напряженность поля второй антенны в этом направлении,
так как диаграмма
направленности первой антенны шире, чем второй.
В случае реальных излучающих поверхностей эффективная поверхность антенны  всегда меньше
ее геометрической площади S. Можно сказать, что действующей площадью
реальной антенны называется площадь такой идеальной плоской антенны, (излучающей
поверхности с равномерным амплитудным распределением и синфазным возбуждением)
КНД которой равен КНД данной реальной антенны. Как видно из формулы (7.19),
всегда меньше
ее геометрической площади S. Можно сказать, что действующей площадью
реальной антенны называется площадь такой идеальной плоской антенны, (излучающей
поверхности с равномерным амплитудным распределением и синфазным возбуждением)
КНД которой равен КНД данной реальной антенны. Как видно из формулы (7.19), 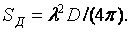
Влияние
реальных амплитудных распределений на
параметры, определяющие
направленные свойства апертурных антенн, видно из
табл. 7.1и
7.2.
7.4. Влияние фазовых искажений на направленные свойства
излучающей поверхности
Несинфазность излучающей
поверхности либо может быть присуща данной антенне
вследствие особенностей ее устройства, либо вызывается неточным выполнением антенны.
Фазовые искажения ухудшают
направленные свойства антенны. Однако в некоторых случаях на излучающей поверхности специально
устанавливают определенный закон
распределения фазы для получения диаграммы направленности специальной формы или управления диаграммой направленности (изменение положения диаграммы
направленности в пространстве).
В самом общем случае фазовое
распределение может являться функцией двух координат. Однако для упрощения исследования обычно
рассматривают зависимость фазы от каждой
координаты в отдельности.
Если начало прямоугольной системы
координат поместить в
центре прямоугольной излучающей поверхности, то распределение фазы
поля по
85
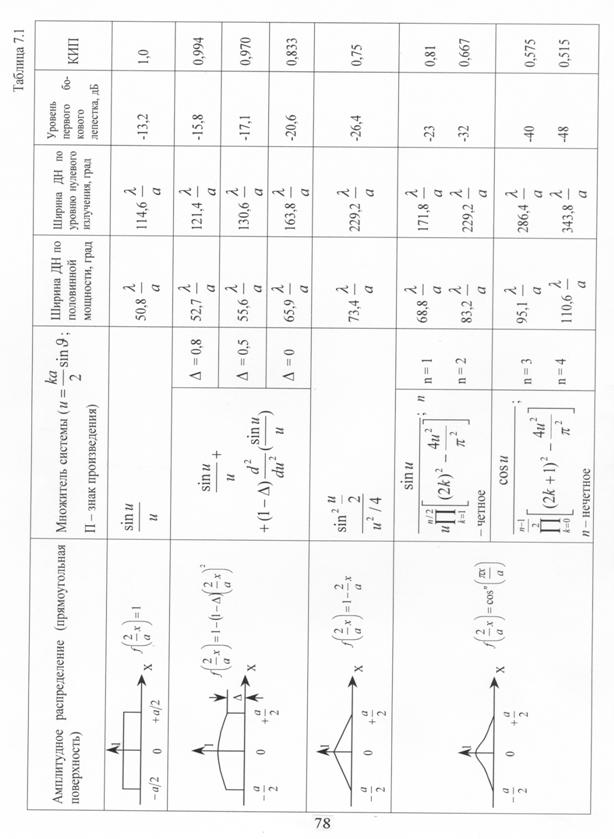
86
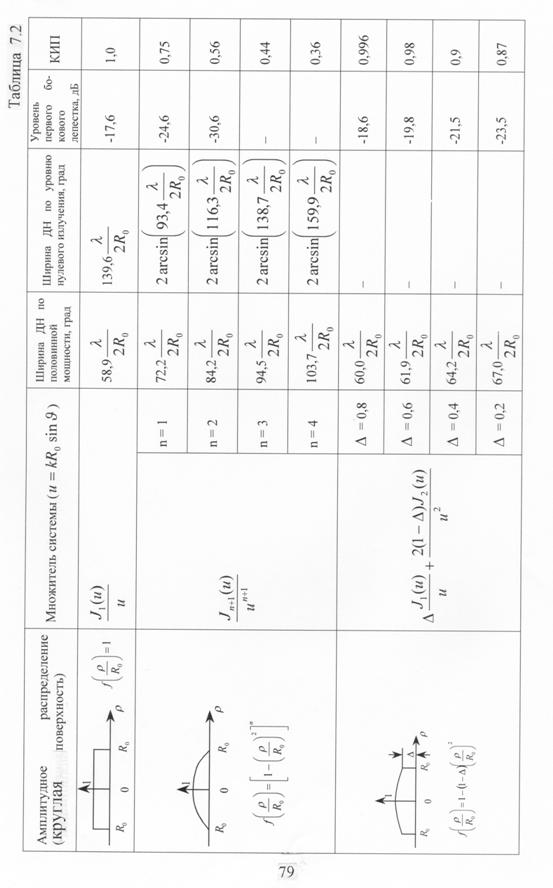
87
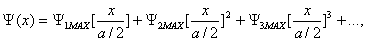 где
где 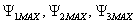 и т.д.
и т.д.
-максимальные фазовые сдвиги соответствующих составляющих фазового распределения, получающиеся
на краях излучающей поверхности (х = ±а/2).
Монотонные законы изменения фазы возбуждающего поля, как правило, могут быть с
достаточной точностью представлены тремя первыми членами данного ряда:
линейным, квадратичным и кубическим. В некоторых случаях фазовое распределение
антенны хорошо описывается одним членом ряда.
Выясним влияние на направленные свойства
антенны наиболее простых фазовых распределений: линейного, квадратичного и
кубического. При этом будем полагать, что амплитуда возбуждающего поля не зависит от координат.
При линейном распределении фазы
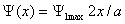 (рис.7.4.a)
напряженность
возбуждающего поля изменяется по закону
(рис.7.4.a)
напряженность
возбуждающего поля изменяется по закону
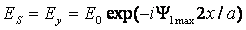 . Так как фаза возбуждающего поля изменяется только вдоль размера а антенны, то интересно исследовать
направленные свойства антенны только в плоскости xoz (рис.7.4.б). Для возбужденной поверхности с линейным
фазовым распределением имеем
. Так как фаза возбуждающего поля изменяется только вдоль размера а антенны, то интересно исследовать
направленные свойства антенны только в плоскости xoz (рис.7.4.б). Для возбужденной поверхности с линейным
фазовым распределением имеем
Ė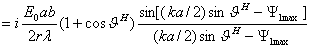 . (7.21)
. (7.21)
Излучение максимально при условии , откуда
, откуда
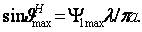 (7.22)
(7.22)
Все выводы, сделанные
в отношении поворота и расширения диаграммы
Направленности
равномерной линейной решетки и её КНД , остаются справедливыми и в данном случае. Пусть фаза возбуждающего
88
поля изменяется по
закону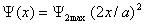 (рис.7.5). Напряженность возбуждающего поля определяется
выражением
(рис.7.5). Напряженность возбуждающего поля определяется
выражением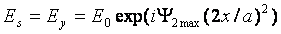 , тогда
, тогда
 É=
É=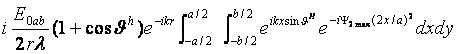 .
.
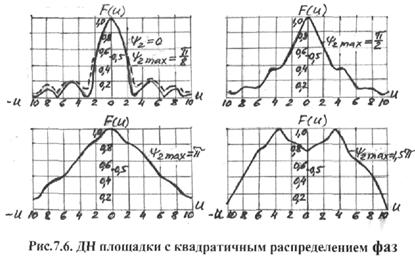 Формула для
характеристики направленности, получаемая в результате интегрирования этого
выражения, оказывается весьма громоздкой. Диаграммы направленности, рассчитанные по этой
формуле, приведены на рис.7.6. Как видно из этого рисунка, квадратичное фазовое
распределение не
Формула для
характеристики направленности, получаемая в результате интегрирования этого
выражения, оказывается весьма громоздкой. Диаграммы направленности, рассчитанные по этой
формуле, приведены на рис.7.6. Как видно из этого рисунка, квадратичное фазовое
распределение не
вызывает поворота
диаграммы
направленности. При всех значениях 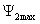 она остается
симметричной относительно нормали к поверхности. Этого и следовало ожидать, так как это распределение
симметрично относительно центра излучающей поверхности.
она остается
симметричной относительно нормали к поверхности. Этого и следовало ожидать, так как это распределение
симметрично относительно центра излучающей поверхности.
Влияние квадратичного изменения фазы на
направленные свойства излучающей поверхности сводится к следующему: исчезают
нули между лепестками диаграммы направленности; уровень боковых лепестков увеличивается:
главный лепесток диаграммы направленности расширяется и при больших значениях 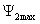 боковые лепестки
полностью поглощаются расширяющимся главным лепестком. При значениях сдвигов
фаз
боковые лепестки
полностью поглощаются расширяющимся главным лепестком. При значениях сдвигов
фаз 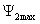
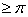 происходит раздвоение
главного лепестка: появляются два направления максимального излучения,
излучение в направлении нормали уменьшается. Следовательно, квадратичное фазовое
распределение приводит к искажению диаграммы направленности, к ухудшению направленных
свойств антенны. При максимальных сдвигах фаз, не превышающих 45°, диаграмма направленности как по
ширине основного лепестка по половинной мощности, так и по уровню
боковых лепестков почти не отличается от характеристики направленности
идеальной плоской антенны.
происходит раздвоение
главного лепестка: появляются два направления максимального излучения,
излучение в направлении нормали уменьшается. Следовательно, квадратичное фазовое
распределение приводит к искажению диаграммы направленности, к ухудшению направленных
свойств антенны. При максимальных сдвигах фаз, не превышающих 45°, диаграмма направленности как по
ширине основного лепестка по половинной мощности, так и по уровню
боковых лепестков почти не отличается от характеристики направленности
идеальной плоской антенны.
В
случае кубического закона изменения фазы напряженность возбуждающего поля
изменяется по
89
закону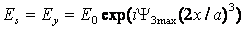 .
.
Фазовое распределение
имеет вид (рис.7.7) 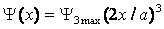 . Фаза распределена несимметрично относительно центра излучающей
поверхности.
. Фаза распределена несимметрично относительно центра излучающей
поверхности.
Формула характеристики направленности такой поверхности получается
чрезвычайно громоздкой. Характер влияния кубических фазовых искажений на диаграмму
направленности виден из рис.7.8. При кубическом
изменении фазы, как и при линейном, диаграмма направленности поворачивается
направление максимального излучения
отклоняется от нормали на угол  в сторону
отставания фазы. При этом
диаграмма направленности искажается, онастановится асимметричной
относительно направления максимального излучения, боковые лепестки по
одну сторону от главного лепестка уменьшаются, а по другую увеличиваются;
увеличение боковых лепестков происходит со стороны, совпадающей с
направлением отклонения главного лепестка. Угол, на который поворачивается
диаграмма направленности, вследствие наличия кубического фазового распределения
при небольших значениях
в сторону
отставания фазы. При этом
диаграмма направленности искажается, онастановится асимметричной
относительно направления максимального излучения, боковые лепестки по
одну сторону от главного лепестка уменьшаются, а по другую увеличиваются;
увеличение боковых лепестков происходит со стороны, совпадающей с
направлением отклонения главного лепестка. Угол, на который поворачивается
диаграмма направленности, вследствие наличия кубического фазового распределения
при небольших значениях 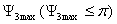 определяется по формуле
определяется по формуле
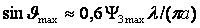 (7.23)
(7.23)
Из сравнения формул
(7.23) и (7.24) видно, что при 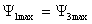
диаграмма
направленности при кубическом изменении фазы отклоняется на меньший угол, чем при линейном.
Все выводы
относительно влияния
различных
фазовых распределений
на
направленные свойства антенн
относятся к случаю равномерного распределения амплитуды возбуждающего поля (f(x)= 1). При
90
спадающем к
краям распределении
влияние изменения фазы на диаграмму направленности
уменьшается. Поскольку различные
законы изменения фазы связаны с ухудшением направленных свойств антенн, то, очевидно, что при наличии фазовых искажений
КИП уменьшается.
8. НЕКОТОРЫЕ ВОПРОСЫ
ТЕОРИИ ПРИЕМНЫХ
АНТЕНН
8.1. Применение принципа взаимности для
изучения приемных
антенн
Приемная антенна
должна принимать электромагнитные волны и преобразовывать их энергию в энергию токов высокой
частоты, поступающую
на вход приемного устройства. Основными вопросами при изучении приемных антенн
являются определение мощности, выделяемой в нагрузке антенны, т.е. в приемнике,
и определение направленных свойств антенны. Эти вопросы могут быть решены, если
известно распределение тока в приемной антенне. Под действием, излученного передающей
антенной, электромагнитного
поля в приемной антенне возникает ЭДС. В качестве приёмной антенны
возьмём симметричный вибратор, находящийся в поле действия плоской
электромагнитной волны, направление прихода которой (вектор Пойнтинга) образует с осью
вибратора угол υ (рис.8.1). Как видно из рисунка, вектор Е лежит в плоскости, проходящей через ось вибратора. Под действием
тангенциальной составляющей этого вектора 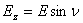 в каждой точке провода возникают ЭДС, фазы которых изменяются
вдоль провода, а амплитуды постоянны. Фазы ЭДС в двух точках провода, отстоящих на расстоянии z друг
от друга, отличаются на величину, равную kzcos
в каждой точке провода возникают ЭДС, фазы которых изменяются
вдоль провода, а амплитуды постоянны. Фазы ЭДС в двух точках провода, отстоящих на расстоянии z друг
от друга, отличаются на величину, равную kzcos . Таким образом, по всей длине провода действует распределенная
электродвижущая сила, под действием которой в вибраторе возникает ток. Этот ток
вызывает напряжение на
зажимах нагрузки ZH. Очевидно, что в общем случае закон распределения тока в приемной антенне должен отличаться от закона распределения
тока в такой же антенне при работе ее в качестве
передающей, так как ток в передающей антенне возникает под действием
сосредоточенной ЭДС. Обычно для определения
основных свойств приемных антенн пользуются принципом взаимности, который позволяет
определить свойства и параметры
приемной антенны, если известны свойства и параметры этой
. Таким образом, по всей длине провода действует распределенная
электродвижущая сила, под действием которой в вибраторе возникает ток. Этот ток
вызывает напряжение на
зажимах нагрузки ZH. Очевидно, что в общем случае закон распределения тока в приемной антенне должен отличаться от закона распределения
тока в такой же антенне при работе ее в качестве
передающей, так как ток в передающей антенне возникает под действием
сосредоточенной ЭДС. Обычно для определения
основных свойств приемных антенн пользуются принципом взаимности, который позволяет
определить свойства и параметры
приемной антенны, если известны свойства и параметры этой

же самой антенны при
работе ее в качестве передающей. Сущность
92
принципа взаимности состоит в
следующем. Если на входе линейного
пассивного четырехполюсника
(рис.8.2.а) действует ЭДС Э1 то на его выходе возникает ток 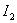 . Если теперь включить эту же самую ЭДС на выход четырехполюсника (рис.8.2.б), то на его входе
возникнет ток I1 равный току
. Если теперь включить эту же самую ЭДС на выход четырехполюсника (рис.8.2.б), то на его входе
возникнет ток I1 равный току 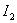 . Если при переключении
ЭДС со входа на выход увеличить ее в n
раз, то во столько же раз увеличится и ток
. Если при переключении
ЭДС со входа на выход увеличить ее в n
раз, то во столько же раз увеличится и ток 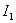 . Сказанное можно записать в виде соотношения,
выражающего аналитически принцип взаимности
. Сказанное можно записать в виде соотношения,
выражающего аналитически принцип взаимности
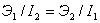 . (8.1)
. (8.1)
В 1927 г.
М.П.Свешникова доказала справедливость этого принципа применительно к
антеннам, показав, что радиоканал можно рассматривать как линейный пассивный
четырехполюсник (рис.8.3.а). М.С.Нейман в 1935г. впервые использовал этот
принцип для исследования приемной антенны. Применение принципа взаимности
требует, кроме линейности, также и изотропности
среды, в которой распространяются электромагнитные волны. Поэтому им нельзя
пользоваться при распространении радиоволн в ионосфере или какой-либо другой
анизотропной среде (например, в феррите).
Исследование свойств приемной антенны при помощи принципа взаимности проведем на
примере проволочной антенны, но его результаты можно распространить на антенны любого
типа. Рассмотрим две антенны -передающую 1 и приемную
2, которые могут быть совершенно различными (рис.8.3.а). К зажимам первой антенны
последовательно с генератором присоединено некоторое сопротивление ZH1 а к зажимам второй
антенны присоединено
сопротивление ZH2. Антенны находятся в
зоне излучения друг друга. Под действием ЭДС на зажимах первой антенны в этой
антенне возникает
ток. ЭДС, действующая на зажимах первой антенны,
определяется выражением
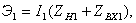 (8.2)
(8.2)
где 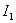 - ток в точках
питания первой антенны;
- ток в точках
питания первой антенны; 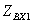 - входное сопротивление этой антенны.
- входное сопротивление этой антенны.
Благодаря току 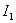 вблизи второй антенны появляется напряженность поля, которая может быть
определена по формуле
вблизи второй антенны появляется напряженность поля, которая может быть
определена по формуле
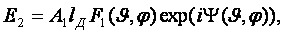 (8.3)
(8.3)
где 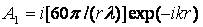 .
.
Из (8.3) получаем
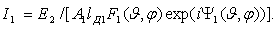 Подставим это
выражение в формулу (8.2), тогда
Подставим это
выражение в формулу (8.2), тогда
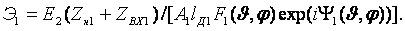 (8.4)
(8.4)
Теперь сделаем вторую антенну
передающей, а первую - приемной. Для этого генератор с ЭДС Э2
присоединим к зажимам второй антенны (рис.8.3.б). Проведя такие же рассуждения, что
и в
93
рассмотренном случае, получим выражение,
определяющее ЭДС Э2
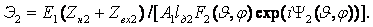 (8.5)
(8.5)
Воспользовавшись принципом взаимности,
запишем Э1/I2пр = Э2/ , где I2пр,
, где I2пр,  - токи в нагрузках первой и второй антенн, возникающие под действием ЭДС Э2
и Э1 соответственно. Предполагается, что взаимное расположение
антенн в первом и во втором случаях остается неизменным. Подставляя в данную
формулу вместо Э1 и Э2 их
значения из (8.4) и (8.5), группируя сомножители и
- токи в нагрузках первой и второй антенн, возникающие под действием ЭДС Э2
и Э1 соответственно. Предполагается, что взаимное расположение
антенн в первом и во втором случаях остается неизменным. Подставляя в данную
формулу вместо Э1 и Э2 их
значения из (8.4) и (8.5), группируя сомножители и
учитывая,чтоА1=А2,
получаем:
 (8.6)
(8.6)
В левой части равенства (8.6) находятся величины, относящиеся, к
первой
антенне, а в правой части - ко второй. Поскольку эти антенны
являются произвольными, то, очевидно, отношение величин, стоящих в
левой
или в правой частях равенства (8.6) является
постоянным, не
зависящим
от типа антенны. Таким образом, можно записать следующее
равенство, справедливое для любой антенны
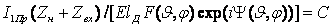 , где С - постоянная величина.
, где С - постоянная величина.
Ток, возникающий в
нагрузке любой приемной антенны, определяется по формуле
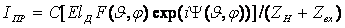 . (8.7.а)
. (8.7.а)
После ряда преобразований находим что С=1.
Таким образом, окончательное выражение для
определения тока в приемной антенне.
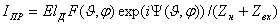 . (8.7.б)
. (8.7.б)
Величины 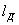 ,
, 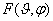 ,
, 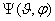 и Zвх являются характеристиками
и Zвх являются характеристиками
данной антенны при ее работе
в качестве передающей.
Характеристикой
направленности приемной
антенны называют зависимость
тока на входе
нагрузки антенны от
направления прихода волны.
Как видно из
выражения
(8.7.б), эта
зависимость определяется множителями  и
и
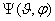 . Отсюда следует важный вывод, что направленные свойства антенны
. Отсюда следует важный вывод, что направленные свойства антенны
Рис.8.3.К использованию принципа взаимности
94
(амплитудная и
фазовая характеристики направленности, коэффициент направленного действия) при ее работе в качестве
передающей или в
качестве приемной
остаются одинаковыми (при условии,
что приемник и передатчик присоединяются к одним и тем же
точкам антенны). Этот вывод позволяет использовать при изучении приемных антенн
результаты, полученные при изучении передающих антенн, что в большинстве случаев значительно упрощает
дело. Таким образом, из принципа взаимности вытекает обратимость процессов приема и
передачи. Величину Эпр называют эквивалентной ЭДС
приемной антенны.
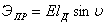
Величина Эпр будет
максимальной при приходе
волны с главного
направления. В этом случае 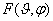 = 1 и
= 1 и 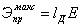 Е. Здесь lД - действующая длина данной антенны при ее
работе в режиме передачи. Действующей длиной приемной антенны называется коэффициент
пропорциональности, связывающий ЭДС, наводимую в
приемной антенне, с напряженностью поля, создаваемого вблизи антенны
электромагнитной волной, при ее приходе с главного направления
приема. При такой трактовке
действующая длина антенны равна
действующей длине той же антенны при ее работе в режиме передачи. Выражение,
связывающее ток в приемной антенне с КНД этой антенны и с ее сопротивлением излучения при работе
антенны в режиме передачи, справедливое для любой антенны имеет вид
Е. Здесь lД - действующая длина данной антенны при ее
работе в режиме передачи. Действующей длиной приемной антенны называется коэффициент
пропорциональности, связывающий ЭДС, наводимую в
приемной антенне, с напряженностью поля, создаваемого вблизи антенны
электромагнитной волной, при ее приходе с главного направления
приема. При такой трактовке
действующая длина антенны равна
действующей длине той же антенны при ее работе в режиме передачи. Выражение,
связывающее ток в приемной антенне с КНД этой антенны и с ее сопротивлением излучения при работе
антенны в режиме передачи, справедливое для любой антенны имеет вид
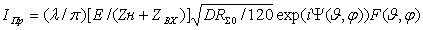 . (8.9)
. (8.9)
Данная формула (без
множителя exp(ψ(ν, φ)) была получена
М.С.Нейманом. А.Р.Вольперт показал, что при
определении тока в приемной антенне необходимо учитывать фазовую характеристику
антенны. Формула (8.9) получена
в предположении, что плоскости поляризации приемной антенны и приходящей волны совпадают. Заметим, что плоскостью
поляризации антенны называется
плоскость поляризации поля, которое антенна излучает в режиме передачи. ЭДС,
создаваемая в антенне приходящей волной, зависит от угла между плоскостями
поляризации антенны и приходящей волны (рис.8.5). Эта ЭДС
пропорциональна величине проекции вектора Е приходящей волны на плоскость
поляризации антенны, т.е. пропорциональна
косинусу угла χ. Если эти плоскости взаимно перпендикулярны, то Эпр
равна нулю. Следовательно, в
общем случае формула
(8.9) должна иметь вид
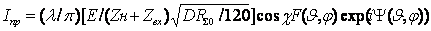 . (8.10)
. (8.10)
95
Мощность, выделяемая
в нагрузке приемной антенны
Формулу (8.7.б) можно кратко записать в виде
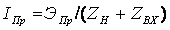 . (8.11)
. (8.11)
Эта формула позволяет
перейти к эквивалентной схеме приемной антенны (рис. 8.4). Здесь приемная антенна рассматривается по
отношению к нагрузке как генератор,
создающий ЭДС и обладающий внутренним сопротивлением,
равным входному сопротивлению данной антенны при ее работе в режиме передачи. Как известно, генератор
отдает в нагрузку максимальную
мощность в том случае, если сопротивление нагрузки и внутреннее сопротивление генератора являются
комплексно-сопряженными. В данном случае
условие отдачи в
нагрузку максимальной мощности
имеет
Вид  =
= 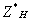 или
или 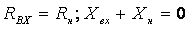 (условие
согласования нагрузки с антенной). Мощность, выделяемая в
нагрузке приемной антенны
(условие
согласования нагрузки с антенной). Мощность, выделяемая в
нагрузке приемной антенны
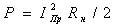 , (8.12)
, (8.12)
где Iпр - амплитуда тока в нагрузке приемной
антенны. Если выполняется условие отдачи
максимальной мощности, то в соответствии с формулами (8.12) и (8.11) мощность,
выделяемая в нагрузке, при приходе волны с направления максимального приема определяется выражением
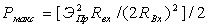 , (8.13)
, (8.13)
где 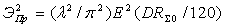 .
.
Подставляя это выражение в (8.13), получаем 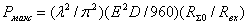 ,но
,но 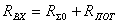 и
и 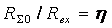 , где η - КПД антенны при ее работе в режиме передачи. Известно
также, что dη = G,
где G - коэффициент усиления антенны. Таким
образом, окончательно
, где η - КПД антенны при ее работе в режиме передачи. Известно
также, что dη = G,
где G - коэффициент усиления антенны. Таким
образом, окончательно
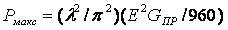 . (8.14)
. (8.14)
Максимальная мощность,
отдаваемая приемной антенной в нагрузку (при заданных напряженности поля и
длине волны), пропорциональна коэффициенту усиления антенны. Коэффициентом усиления
приемной антенны называется отношение мощности, выделяемой в нагрузке при приёме на данную
антенну, к мощности, выделяемой в нагрузке при приёме на ненаправленную
антенну (предполагается, что обе антенны имеют оптимальное
согласование с нагрузкой). Коэффициенты усиления антенны в режиме передачи и
приёма равны. Если нагрузка приемной антенны (приемник) соединена с антенной при помощи
питающей линии (фидера), имеющей потери, то максимальная мощность, выделяемая в
приемнике, определяется по
формуле
96
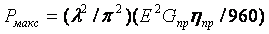 , (8.15)
, (8.15)
где 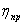 - КПД фидера приемной антенны.
- КПД фидера приемной антенны.
Если взять выражения
для напряженности поля, создаваемого передающей антенной в точке приема, при
распространении в среде без потерь, то
 ,(8.16)
,(8.16)
где 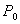 - мощность на входе фидера; Gnep - КУ передающей антенны;
- мощность на входе фидера; Gnep - КУ передающей антенны; 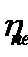 - КПД фидера передающей антенны.
- КПД фидера передающей антенны.
Отсюда следует, что мощность, выделяемая в нагрузке приемной антенны, пропорциональна произведению коэффициентов усиления приемной и передающей
антенны.
Рис. 8.4 Эквивалентная схема приемной антенны. В реальных схема условиях мощность
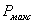 оказывается меньше получаемой по
формуле (8.16) вследствие наличияерь при
распространении радиоволн.
оказывается меньше получаемой по
формуле (8.16) вследствие наличияерь при
распространении радиоволн.
Полученная формула
для максимальноймощности (8.14) позволяет
ввести еще один параметр, характеризующийприемную антенну - действующую (эффективную) площадь 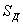 приемной
приемной
антенны. Представим себе, что вся мощность,
извлекаемая антенной из
пространства, проходит через некоторую воображаемую часть 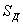 плоской
плоской
поверхности электромагнитной волны. Среднее
значение вектора Пойнтинга в любой точке поверхности 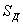
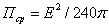 , а мощность электромагнитного поля, проходящего через эту поверхность
, а мощность электромагнитного поля, проходящего через эту поверхность
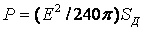 . (8.17)
. (8.17)
Положим теперь, что эта мощность выделяется в
нагрузке приемной антенны и что выполняется условие отдачи максимальной
мощности. Следовательно, левые части выражений (8.17) и (8.14) равны. Приравнивая
правые части этих выражений и, решая полученное равенство относительно SД, находим
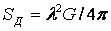 . (8.18)
. (8.18)
Если КПД антенны равен единице, то 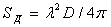 .
.
Понятие действующей
площади применимо к любой антенне. Так, в случае полуволнового симметричного вибратора
действующая площадь 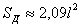 . Однако особенно удобно вводить этот параметр в случае антенн -излучающих
поверхностей. КНД антенны при помощи действующей площади определяется выражением
. Однако особенно удобно вводить этот параметр в случае антенн -излучающих
поверхностей. КНД антенны при помощи действующей площади определяется выражением
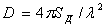 . (8.19)
. (8.19)
Выражая в (8.16) Gnep и Gnp через SД при помощи (8.18), получаем формулу, связывающую
максимальную мощность, выделяемую в нагрузке
97
приемной антенны, с действующими
площадями приемной и передающей антенн
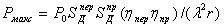 . (8.20)
. (8.20)
8.3. Влияние параметров приёмной антенны на качество радиоприёма
Качество радиоприема
определяется не абсолютной величиной полезного сигнала, принятого антенной, а
отношением напряжения, создаваемого на входе приемника полезным сигналом, к
напряжению, создаваемому различными помехами. Большую роль в увеличении этого отношения играют
направленные свойства приемной антенны. В связи с этим в ряде случаев к направленным свойствам приемных
антенн предъявляются более жесткие требования (снижение уровня боковых
лепестков), чем к передающим. Помехи при радиоприеме могут быть разделены на внешние и внутренние.
Внешние помехи складываются из: 1) атмосферных
помех,
вызываемых
электрическими разрядами в атмосфере; 2) промышленных,
вызываемых различными
электрическими аппаратами; 3) интерференционных,
вызываемых радиостанциями; 4) космических,
вызываемых радиоизлучением источников, находящихся за пределами земной атмосферы (солнца, звезд, отдаленных
галактик и т.д.); 5) помех (шумов),
вызываемых тепловым излучением
Земли и атмосферных газов, 6)
помех (шумов), обусловленных наличием осадков. Помехи первых трех видов встречаются, в
основном, в диапазонах средних, длинных и коротких волн. В диапазоне
ультракоротких волн, в основном, имеют место помехи, перечисленные в
пунктах с четвертого по шестой.
Внутренние помехи обусловливаются
тепловым движением электронов в различных элементах приемника (шумы флуктуационного
происхождения), а также в антенне и в элементах тракта питания.
Если
полезный и мешающий сигналы приходят с различных фиксированных направлений, то при
приеме на направленную антенну и при правильной ориентировке ее диаграммы
направленности можно значительно ослабить величину ЭДС, наводимую в антенне
мешающим сигналом, и увеличить отношение мощности полезного сигнала к мощности
помехи на входе
приемника, т.е. увеличить выигрыш, даваемый антенной. Если направления прихода
полезного сигнала и помехи совпадают или мало отличаются, то применение направленной
антенны не дает выигрыша. В случае направленных помех могут быть эффективны антенны с
регулируемой
диаграммой направленности, позволяющие совмещать направление нулевого
98
(минимального) приема с направлением
прихода помехи
и почти полностью ее устранять. В ряде случаев помехи не имеют направленного
характера или поступают из широкого сектора пространства. Эти помехи создаются,
так называемыми, протяженными источниками, например галактикой, Землей, атмосферой Земли
(источник называется протяженным, если область пространства, в пределах которой
концентрируется
его излучение, больше сечения диаграммы направленности приемной антенны).
Кроме того, помехи грозового характера, интерференционные помехи и другие часто
меняют направление своего прихода и могут приходить одновременно с разных
направлений. В этих случаях
условия работы приемной антенны близки к условиям, создающимся при приходе помех с произвольными амплитудами и
фазами одновременно со всех направлений
(ненаправленные помехи). Поэтому важно рассмотреть вопрос о том, будет ли давать выигрыш
направленная антенна по сравнению с
ненаправленной при приеме ненаправленных помех. При ненаправленных
помехах мешающие сигналы, приходящие с главного направления или с направлений,
близких к нему, усиливаются антенной, помехи
же, приходящие с направлений минимального приема, ослабляются. В результате
действие помех усредняется и эффект на входе приемника получается таким же, как при приеме на воображаемую
абсолютно ненаправленную антенну.
Применение направленных антенн в этом случае не уменьшает среднюю
мощность помех на входе приемника. Независимость величины средней мощности,
выделяемой на входе приемника при приеме ненаправленных
помех, от диаграммы направленности антенны можно доказать совершенно строго. Покажем, однако, что и в данном случае применение
направленных антенн весьма целесообразно, так как увеличивает отношение мощности, создаваемой полезным сигналом,
к мощности, создаваемой помехами.
Качество приема определяется отношением
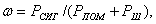 (8.21)
(8.21)
где Рсигн - мощность полезного
сигнала на входе приемника;
 - мощность внешних
помех на входе приемника;
- мощность внешних
помех на входе приемника;
Рш
-
мощность внутренних шумов
приемника (включая и шумы
самой антенны).
Различают три
режима приема: 1)
мощность внешних помех значительно превышает мощность внутренних
шумов, т.е.  ; 2) мощность внутренних
шумов значительно превышает мощность внешних помех, т.е.
; 2) мощность внутренних
шумов значительно превышает мощность внешних помех, т.е. 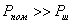 ; 3) величины Рпом и Рш
соизмеримы.
; 3) величины Рпом и Рш
соизмеримы.
Режим 1. Пренебрегая
величиной Рш по сравнению с  запишем формулу (8.21) в виде
запишем формулу (8.21) в виде  . Мощность, развиваемая
. Мощность, развиваемая
99
ненаправленными
помехами в нагрузке приемной антенны, может быть определена по формуле (8.15).
Так как в данном случае направленная антенна ведет себя как абсолютно
ненаправленная ( D =
1), то формула (8.15) принимает вид
 ,
,
где η - КПД антенны и тракта питания; 
 - напряженность поля помехи. Поскольку полезный сигнал приходит с
определенного направления, совмещаемого обычно с главным направлением приема,
то мощность, развиваемая в нагрузке приемной антенны полезным сигналом, равна
- напряженность поля помехи. Поскольку полезный сигнал приходит с
определенного направления, совмещаемого обычно с главным направлением приема,
то мощность, развиваемая в нагрузке приемной антенны полезным сигналом, равна
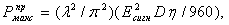 где D - КНД антенны в главном направлении;
где D - КНД антенны в главном направлении; 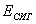 - напряженность поля полезного сигнала. Отсюда
- напряженность поля полезного сигнала. Отсюда 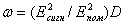 . Таким образом, при ненаправленных помехах в первом режиме приема величина
отношения мощности полезного сигнала к мощности помех на входе приемника пропорциональна КНД
антенны и не зависит от ее КПД. Заметим, что КНД приемной антенны характеризует
ее пространственную избирательность, определяющую возможность выделения
принимаемого сигнала на фоне помех, создаваемых радиосигналами, идущими с разных
направлений и порождаемых различными источниками. Первый режим работы характерен для средних и длинных
волн. Иногда этот режим имеет место на УКВ при наличии малошумящих приемных
устройств.
. Таким образом, при ненаправленных помехах в первом режиме приема величина
отношения мощности полезного сигнала к мощности помех на входе приемника пропорциональна КНД
антенны и не зависит от ее КПД. Заметим, что КНД приемной антенны характеризует
ее пространственную избирательность, определяющую возможность выделения
принимаемого сигнала на фоне помех, создаваемых радиосигналами, идущими с разных
направлений и порождаемых различными источниками. Первый режим работы характерен для средних и длинных
волн. Иногда этот режим имеет место на УКВ при наличии малошумящих приемных
устройств.
Режим 2. Пренебрегая
величиной Рпом по сравнению с Рш, получаем
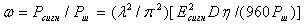 .
.
Так как Рш не зависит от
параметров антенны, то величина отношения мощности
полезного сигнала к мощности помех на входе приемника в данном случае пропорциональна произведению D на η, т. е. коэффициенту усиления антенны.
Таким образом, для большой величины ω в этом случае необходимо, чтобы
антенна обладала большим КНД и малыми потерями. Второй режим работы преобладает в
диапазоне УКВ в случае приемников обычных типов.
Режим 3. Он имеет место в
диапазоне коротких волн, а также в диапазоне УКВ при наличии малошумящих приемных устройств. Для увеличения ω в данном случае необходимо
выполнять те же условия, что и в случае второго режима.
Режим работы при
прочих равных условиях зависит от величины КУ антенны. При больших коэффициентах
усиления имеет место первый режим; при малых КУ - второй режим.
100
СПИСОК ЛИТЕРАТУРЫ
Основная литература:
1. Кочержевский Г.Н.
Антенно-фидерные устройства. - М.: Связь, 1972г.
2. Кочержевский Г.Н. Антенно-фидерные устройства. - М.: Связь,
1989г. 3.Ерохин
Г.А., Чернышев О.В., Козырев Н.Д., Кочержевский В.Г.
Антенно-фидерные
устройства и распространение радиоволн. - М.: Радио и связь, 1996г.
Дополнительная литература:
1.Ерохин Г.А., Чернышев О.В., Козырев
Н.Д., Кочержевский В.Г. Антенно-фидерные устройства
и распространение радиоволн. - М.: Радио и связь, 2004г.
2.Драбкин А.Л., Зузенко
В.Л., Кислов А.Г. Антенно-фидерные устройства. -М.:
Советское радио, 1974г.
3.Айзенберг Г.З., Ямпольский В.Г., Терёшин О.Н. Антенны УКВ. - М.: Связь, 1977г.
4.Айзенберг Г.З. и др.
Коротковолновые антенны. - М.: Радио и связь, 1985г. 5.Сазонов Д.М. Антенны и устройства СВЧ. -
М.: Высшая школа, 1988г. 6.Ликонцев Д.Н., Русинкевич
З.Э. Индивидуальные задания и методические указания
к их выполнению по дисциплинам: Распространение радиоволн и Антенно-фидерные
устройства. Ташкент, ТЭИС, 1997г. JohnD. Kraus. 7.Antennas. Second Edition. Singapore, 1988, Вузов А.Л., Казанский Л.С.,
и В Бузов др.
Антенно-фидерные устройства систем сухопутной
подвижной связи. - М: Радио и связь, 1997г.
АНТЕННО-ФИДЕРНЫЕ
УСТРОЙСТВА. Курс лекций (Часть 1) рассмотрен на заседании кафедры АФУ 10.04.2008 г. (протокол №5) и рекомендован к печати.
 Отв. редактор доц. Ликонцев Д.Н. Составитель
доц. Ликонцев Д.Н.
Отв. редактор доц. Ликонцев Д.Н. Составитель
доц. Ликонцев Д.Н.
 Редакционно-корректурная
группа:
Редакционно-корректурная
группа:
Редактор доц. Абдуазизов А.А.
Корректор ст.преп.
Павлова С.И
![]() раз при
раз при ![]() снижениях.
снижениях.![]() = P
= P![]() / Р0, где
P
/ Р0, где
P![]() -
мощность излучаемая антенной, Р0 - мощность подводимая к антенне.
-
мощность излучаемая антенной, Р0 - мощность подводимая к антенне.![]() ,где
,где ![]() - длина волны) для диапазона частот 10кГц...1ГГц. К
числу антенн этого класса относятся одиночные вибраторные и щелевые излучатели,
полосковые и микрополосковые антенны, рамочные
антенны, а также частотно-независимые излучатели.
- длина волны) для диапазона частот 10кГц...1ГГц. К
числу антенн этого класса относятся одиночные вибраторные и щелевые излучатели,
полосковые и микрополосковые антенны, рамочные
антенны, а также частотно-независимые излучатели.![]() до 100
до 100![]() для диапазона частот 3МГц...10ГГц. Сюда относятся
спиральные, диэлектрические,директорные,
импедаксные антенны, а также антенны «вытекающей»
волны.
для диапазона частот 3МГц...10ГГц. Сюда относятся
спиральные, диэлектрические,директорные,
импедаксные антенны, а также антенны «вытекающей»
волны.![]() до 100
до 100![]() и более для диапазона частот 3МГц...30ГГц. Это
антенны, состоящие из большого числа отдельных излучателей. Независимая регулировка
фаз (а иногда и амплитуд) возбуждения каждого элемента антенной решетки
обеспечивает возможность электрического управления диаграммой направленности.
Применяются линейные, плоские, кольцевые, выпуклые и конформные (совпадающие с
формой объекта установки) антенные решетки. На основе антенных решеток выполняют
антенные системы с обработкой сигнала, в том числе адаптивные к изменяющейся помеховой обстановке.
и более для диапазона частот 3МГц...30ГГц. Это
антенны, состоящие из большого числа отдельных излучателей. Независимая регулировка
фаз (а иногда и амплитуд) возбуждения каждого элемента антенной решетки
обеспечивает возможность электрического управления диаграммой направленности.
Применяются линейные, плоские, кольцевые, выпуклые и конформные (совпадающие с
формой объекта установки) антенные решетки. На основе антенных решеток выполняют
антенные системы с обработкой сигнала, в том числе адаптивные к изменяющейся помеховой обстановке.![]() до 1000
до 1000![]() для диапазона частот 100МГц... 100ГГц и
выше. Наиболее распространены зеркальные, рупорные и линзовые апертурные антенны. К апертурным
антеннам примыкают, так называемые, «гибридные» антенны, представляющие
сочетание зеркал или линз с облучающей системой в виде антенной решетки. Апертурные антенны строятся по оптическим принципам и
обеспечивают наиболее высокую направленность излучения.
для диапазона частот 100МГц... 100ГГц и
выше. Наиболее распространены зеркальные, рупорные и линзовые апертурные антенны. К апертурным
антеннам примыкают, так называемые, «гибридные» антенны, представляющие
сочетание зеркал или линз с облучающей системой в виде антенной решетки. Апертурные антенны строятся по оптическим принципам и
обеспечивают наиболее высокую направленность излучения.![]() = I02 R
= I02 R![]() 0 / 2, где RΣ0 – сопротивление излучения антенны (при отсутствии потерь
в антенне это активная составляющая входного сопротивления антенны). Данное
определение относится к проволочным антеннам.
0 / 2, где RΣ0 – сопротивление излучения антенны (при отсутствии потерь
в антенне это активная составляющая входного сопротивления антенны). Данное
определение относится к проволочным антеннам.![]() = 10...100 км);
километровые или длинные волны (
= 10...100 км);
километровые или длинные волны (![]() = 1...10 км); гектометровые или средние волны (
= 1...10 км); гектометровые или средние волны (![]() = =100...1000
м); декаметровые или короткие волны (
= =100...1000
м); декаметровые или короткие волны (![]() = 10...100 м); метровые волны (
= 10...100 м); метровые волны (![]() = 1...10м); дециметровые волны (
= 1...10м); дециметровые волны (![]() = 10 см...1 м); сантиметровые волны (
= 10 см...1 м); сантиметровые волны (![]() = 1...10 см); миллиметровые волны (
= 1...10 см); миллиметровые волны (![]() = 1...10 мм). Последние четыре диапазона объединяются общим названием
"ультракороткие волны" (УКВ).
= 1...10 мм). Последние четыре диапазона объединяются общим названием
"ультракороткие волны" (УКВ).![]() . (2.1)
. (2.1)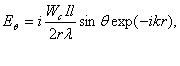 Здесь А - комплексный
множитель, не зависящий от направления на точку наблюдения (в него входит стандартный
множитель exp(-ikr)/r, где r
-расстояние от фазового
центра антенны до точки наблюдения;
Здесь А - комплексный
множитель, не зависящий от направления на точку наблюдения (в него входит стандартный
множитель exp(-ikr)/r, где r
-расстояние от фазового
центра антенны до точки наблюдения; ![]() - коэффициент фазы или
волновое число в свободном пространстве); θ,φ - координаты точки наблюдения; |f(θ,φ)| - амплитудная
характеристика направленности; Ψ(θ,φ) - фазовая
характеристика направленности. Известно, что в случае элементарного
электрического вибратора
- коэффициент фазы или
волновое число в свободном пространстве); θ,φ - координаты точки наблюдения; |f(θ,φ)| - амплитудная
характеристика направленности; Ψ(θ,φ) - фазовая
характеристика направленности. Известно, что в случае элементарного
электрического вибратора![]() характеристическое сопротивление
волны; в свободном пространстве
характеристическое сопротивление
волны; в свободном пространстве ![]() , Ом
, Ом![]() ) через нуль
меняется ее знак, что соответствует скачку фазы напряженности поля на 180°. Поэтому амплитудной характеристикой
направленности является модуль этой функции |f(
) через нуль
меняется ее знак, что соответствует скачку фазы напряженности поля на 180°. Поэтому амплитудной характеристикой
направленности является модуль этой функции |f(![]() )|. В
дальнейшем для упрощения записи знак модуля опускаем.
В общем случае характеристика направленности является векторной и комплексной величиной. Выражение ƒ(
)|. В
дальнейшем для упрощения записи знак модуля опускаем.
В общем случае характеристика направленности является векторной и комплексной величиной. Выражение ƒ(![]() )=f(
)=f(![]() ) exp[i
) exp[i![]() ] называется комплексной характеристикой направленности антенны. Она
полностью
определяет угловое распределение и фазовые свойства излучаемого электромагнитного поля в дальней зоне
антенны. Характеристика направленности
антенны определяется размерами и конфигурацией антенны, а также распределением
возбуждающего тока (как действительного, так и эквивалентного). Напомним, что дальняя
зона (зона излучения или зона Фраунгофе-ра) характеризуется
тем, что направления (лучи), проведенные из любой точки антенны на точку
наблюдения, находящуюся в этой зоне, считаются параллельными. При этом возникает ошибка в определении фаз полей, создаваемых
в точке наблюдения различными элементами антенны. Эта ошибка оказывается тем
меньше, чем больше расстояние от антенны до точки наблюдения по сравнению с
размерами антенны. Расстояние дальней зоны rизл
] называется комплексной характеристикой направленности антенны. Она
полностью
определяет угловое распределение и фазовые свойства излучаемого электромагнитного поля в дальней зоне
антенны. Характеристика направленности
антенны определяется размерами и конфигурацией антенны, а также распределением
возбуждающего тока (как действительного, так и эквивалентного). Напомним, что дальняя
зона (зона излучения или зона Фраунгофе-ра) характеризуется
тем, что направления (лучи), проведенные из любой точки антенны на точку
наблюдения, находящуюся в этой зоне, считаются параллельными. При этом возникает ошибка в определении фаз полей, создаваемых
в точке наблюдения различными элементами антенны. Эта ошибка оказывается тем
меньше, чем больше расстояние от антенны до точки наблюдения по сравнению с
размерами антенны. Расстояние дальней зоны rизл![]() 2R2/
2R2/![]() , где R - наибольший размер
излучающей системы. В этой зоне поле имеет поперечный характер (отсутствуют составляющие
векторов Е и Н в направлении распространения); в окрестности точки наблюдения поле имеет характер плоской
волны; амплитуды полей, излучаемых
элементами антенны, убывают обратно пропорционально расстоянию.
, где R - наибольший размер
излучающей системы. В этой зоне поле имеет поперечный характер (отсутствуют составляющие
векторов Е и Н в направлении распространения); в окрестности точки наблюдения поле имеет характер плоской
волны; амплитуды полей, излучаемых
элементами антенны, убывают обратно пропорционально расстоянию.![]() ), т.е. отношением напряженности поля, излучаемого антенной в
произвольном направлении, к значению напряженности поля в направлении
максимального излучения
), т.е. отношением напряженности поля, излучаемого антенной в
произвольном направлении, к значению напряженности поля в направлении
максимального излучения![]() )= | E(
)= | E(![]() )| / | Emax(
)| / | Emax(![]() )| = f(
)| = f(![]() )/fmax(
)/fmax(![]() ).
).![]() ). На рис.2.1.а изображена пространственная ДН элементарного вибратора (тороид),
на рис.2.1.б - ДН более сложной антенны (так
называемая игольчатая ДН). На практике обычно используют ДН, изображающие
характеристику направленности в каких-либо выбранных плоскостях. В качестве
таких плоскостей обычно выбирают две взаимно перпендикулярные
плоскости, проходящие
через направление
). На рис.2.1.а изображена пространственная ДН элементарного вибратора (тороид),
на рис.2.1.б - ДН более сложной антенны (так
называемая игольчатая ДН). На практике обычно используют ДН, изображающие
характеристику направленности в каких-либо выбранных плоскостях. В качестве
таких плоскостей обычно выбирают две взаимно перпендикулярные
плоскости, проходящие
через направление![]() в какой-либо
координатной системе (прямоугольной, полярной и др.) подобно сетке меридианов и параллелей на
географической
карте. На этой сетке замкнутыми линиями изображаются одинаковые
в какой-либо
координатной системе (прямоугольной, полярной и др.) подобно сетке меридианов и параллелей на
географической
карте. На этой сетке замкнутыми линиями изображаются одинаковые![]() ) в том или ином масштабе. При изображении ДН часто используется логарифмический масштаб, вводимый соотношением в децибеллах
F(
) в том или ином масштабе. При изображении ДН часто используется логарифмический масштаб, вводимый соотношением в децибеллах
F(![]() )=20
lgF(
)=20
lgF(![]() ).
).![]() ). Функция F(
). Функция F(![]() ) для
) для ![]() и
и ![]() проходит через нуль и имеет несколько максимумов,
т.е. ДН имеет многолепестковый характер (см. рис.2.3). Диаграмму
направленности принято численно характеризовать шириной главного
лепестка (шириной луча) и относительным
уровнем боковых лепестков (УБЛ).
проходит через нуль и имеет несколько максимумов,
т.е. ДН имеет многолепестковый характер (см. рис.2.3). Диаграмму
направленности принято численно характеризовать шириной главного
лепестка (шириной луча) и относительным
уровнем боковых лепестков (УБЛ).![]() 0
между нап-
0
между нап- ![]() 0,5 между направлениями, вдоль которых |Е| = |Emax|/
0,5 между направлениями, вдоль которых |Е| = |Emax|/![]() или соответственно среднее значение плотности потока мощности П=Пmaх/2. Наибольший лепесток, максимум которого
соответствует направлению максимального излучения, называют главным, меньшие лепестки - боковыми
(лепестки, находящиеся в задних квадрантах, т.е. в диапазоне углов 90°
или соответственно среднее значение плотности потока мощности П=Пmaх/2. Наибольший лепесток, максимум которого
соответствует направлению максимального излучения, называют главным, меньшие лепестки - боковыми
(лепестки, находящиеся в задних квадрантах, т.е. в диапазоне углов 90°![]() 180° и 180°
180° и 180°![]() 270°, часто называют задними).
270°, часто называют задними).![]() ) есть отношение напряженности поля в направлении максимума данного лепестка (ENmax) к напряженности поля
внаправлении главного максимума (Еmax), т.е.
) есть отношение напряженности поля в направлении максимума данного лепестка (ENmax) к напряженности поля
внаправлении главного максимума (Еmax), т.е.![]() N=|ENmax|/|Еmax|=FN(
N=|ENmax|/|Еmax|=FN(![]() ), или в децибеллах
), или в децибеллах ![]() дБ = 20lg FN(
дБ = 20lg FN(![]() ), где N=1,2,3,...-номер бокового лепестка (для главного лепестка N=0).
), где N=1,2,3,...-номер бокового лепестка (для главного лепестка N=0).![]() была мала. В большинстве случаев интересуются ам- плитудными характеристиками направленности
была мала. В большинстве случаев интересуются ам- плитудными характеристиками направленности![]() ) или F(
) или F(![]() ) через нуль, т.е. при переходе от одного лепестка ДН к другому, то такая
антенна является источником сферических волн, о чем свидетельствует множитель
[ехр(-ikr)]/r. Эти волны исходят как бы из одной точки, называемой фазовым
центром антенны. Эта точка расположена в начале выбранной системы
координат, и поэтому, фазовая характеристика зависит от положения начала координат.
Однако не все реальные антенны обладают фазовым центром, т.е. излучают
сферические волны. Для них обычно можно подобрать сферу, наилучшим образом
аппроксимирующую фронт волны (обычно в пределах главного лепестка). Центр этой
сферы называют центром излучения антенны. Графическое изображение
фазовой характеристики называется фазовой ДН.
) через нуль, т.е. при переходе от одного лепестка ДН к другому, то такая
антенна является источником сферических волн, о чем свидетельствует множитель
[ехр(-ikr)]/r. Эти волны исходят как бы из одной точки, называемой фазовым
центром антенны. Эта точка расположена в начале выбранной системы
координат, и поэтому, фазовая характеристика зависит от положения начала координат.
Однако не все реальные антенны обладают фазовым центром, т.е. излучают
сферические волны. Для них обычно можно подобрать сферу, наилучшим образом
аппроксимирующую фронт волны (обычно в пределах главного лепестка). Центр этой
сферы называют центром излучения антенны. Графическое изображение
фазовой характеристики называется фазовой ДН.![]() , к усредненному по всем направлениям значению плотности потока
мощности Пуср
, к усредненному по всем направлениям значению плотности потока
мощности Пуср![]() . (2.3)
. (2.3)![]() , где |
, где |![]() | - амплитудное значение напряженности электрического поля в
направлении, характеризуемом углами
| - амплитудное значение напряженности электрического поля в
направлении, характеризуемом углами ![]() . Таким образом, при определении КНД данная антенна сравнивается с
воображаемой абсолютно ненаправленной (изотропной) антенной, излучающей ту же
мощность, что и данная. Очевидно, что
. Таким образом, при определении КНД данная антенна сравнивается с
воображаемой абсолютно ненаправленной (изотропной) антенной, излучающей ту же
мощность, что и данная. Очевидно, что![]() , (2.4)
, (2.4)![]() - мощность
излучения; r -
радиус воображаемой сферы, охватывающей антенну, причем величина r должна быть такой, чтобы поверхность сферы находилась в дальней зоне поля антенны.
- мощность
излучения; r -
радиус воображаемой сферы, охватывающей антенну, причем величина r должна быть такой, чтобы поверхность сферы находилась в дальней зоне поля антенны.![]() , и подставляя в (2.3) выражение (2.4), получаем формулу для КНД в другом
виде
, и подставляя в (2.3) выражение (2.4), получаем формулу для КНД в другом
виде ![]() или для свободного
пространства (Wc°=120
или для свободного
пространства (Wc°=120![]() Ом) в направлении максимального излучения
Ом) в направлении максимального излучения![]() (2.5)
(2.5)![]() выражение (2.2) в квадрате (без фазовых множителей) и учесть, что
выражение (2.2) в квадрате (без фазовых множителей) и учесть, что ![]() , где
, где ![]() - сопротивление излучения элементарного электрического вибратора, то получим КНД элементарного вибратора D=1,5.
- сопротивление излучения элементарного электрического вибратора, то получим КНД элементарного вибратора D=1,5.![]() .Этот параметр иногда используют при
анализе приемных антенн, а также проволочных длинноволновых и средневолновых
антенн и антенн-мачт.
.Этот параметр иногда используют при
анализе приемных антенн, а также проволочных длинноволновых и средневолновых
антенн и антенн-мачт.![]() (2.6)
(2.6)![]() - волновое сопротивление среды. Напишем выражение для величины напряженности поля любой
вибраторной антенны в произвольном направлении
- волновое сопротивление среды. Напишем выражение для величины напряженности поля любой
вибраторной антенны в произвольном направлении![]() (2.7)
(2.7)![]() выражение (2.6)
и учитывая, что
выражение (2.6)
и учитывая, что![]() (
(![]() - сопротивление
излучения антенны, отнесенное к току в точках питания; I -ток в точках питания антенны), получаем
- сопротивление
излучения антенны, отнесенное к току в точках питания; I -ток в точках питания антенны), получаем![]() или
или ![]() (2.8)
(2.8)![]() , к среднему значению плотности потока мощности,
создаваемого воображаемым абсолютно ненаправленным излучателем (Пн). При этом предполагается, что точка
наблюдения находится на одинаковом расстоянии от обеих антенн; мощности,
подводимые к той и другой антеннам, равны и КПД ненаправленной антенны равен
единице. Таким образом, КУ
, к среднему значению плотности потока мощности,
создаваемого воображаемым абсолютно ненаправленным излучателем (Пн). При этом предполагается, что точка
наблюдения находится на одинаковом расстоянии от обеих антенн; мощности,
подводимые к той и другой антеннам, равны и КПД ненаправленной антенны равен
единице. Таким образом, КУ![]() . (2.9)
. (2.9)![]() , этих антенн. Умножим
и разделим правую
часть (2.9) на Пуср.
Тогда [П(
, этих антенн. Умножим
и разделим правую
часть (2.9) на Пуср.
Тогда [П(![]() )/Пуср](Пуср/Пн),
где Пуср/Пн
=
)/Пуср](Пуср/Пн),
где Пуср/Пн
=![]() - КПД антенны.
- КПД антенны. ![]() ) связаны соотношением
) связаны соотношением![]() . (2.10)
. (2.10)![]() , можно написать
, можно написать![]() /r=
/r=![]() /r . (2.11)
/r . (2.11)![]() или
или ![]() (
(![]() - сдвиг фаз между составляющими
- сдвиг фаз между составляющими ![]() и
и ![]() ). Линейная поляризация также имеет место,
если
). Линейная поляризация также имеет место,
если ![]() =0 или
=0 или ![]() =0. При круговой поляризации поля (
=0. При круговой поляризации поля (![]() =
=![]() ;
;![]() ) t=l.
Таким образом, коэффициент равномерности поляризационного эллипса может изменяться в пределах 0< t < 1. Зависимость коэффициента эллиптичности от
направления на точку наблюдения называется поляризационной
ДН.
) t=l.
Таким образом, коэффициент равномерности поляризационного эллипса может изменяться в пределах 0< t < 1. Зависимость коэффициента эллиптичности от
направления на точку наблюдения называется поляризационной
ДН.![]() называется угол,
образованный большой осью поляризационного эллипса и направлением орта
называется угол,
образованный большой осью поляризационного эллипса и направлением орта ![]() или
или ![]() 0 сферической системы координат (см. рис. 2.4.б).
Направление вращение вектора Е в
точке наблюдения определяется знаком угла
сдвига фаз между составляющими поля
0 сферической системы координат (см. рис. 2.4.б).
Направление вращение вектора Е в
точке наблюдения определяется знаком угла
сдвига фаз между составляющими поля