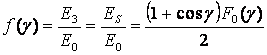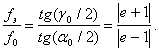ПРЕДИСЛОВИЕ
Настоящий курс лекций составлен в соответствии с действующей типовой программой дисциплины для
подготовки бакавлавров по направлению "Телевидение, радиосвязь и радиовещание". Он также
очень близок по содержанию к дисциплине "Антенны
и устройства СВЧ" для направления "Радиотехника". Отдельные
разделы пособия также используются при подготовке магистрантов по дисциплинам кафедры и будут полезны
для слушателей курсов повышения квалификации.
В первой части курса лекций рассмотрены теоретические основы формирования полей
линейных, апертурных и других типов излучателей. Во второй части курса лекций рассматриваются особенности конструкций и работы
конкретных типов антенн разных диапазонов.
Приведенный объем материала в первой и второй частях пособия ориентирован на курс лекций в 36 часов с
учетом раздела "Распространение
радиоволн" и выделения части материала для самообразования студентов.
ОГЛАВЛЕНИЕ
Стр.
ЛЕКЦИЯ 9. АПЕРТУРНЫЕ
АНТЕННЫ……………………………………………………………….5
9.1. Рупорные
антенны………………………………………………………………………………….5
9.1.1. Антенны в виде открытого конца
волновода………………………………………………5
9.1.2. Принцип действия,
основные свойства рупорных антенн………………………………..6
9.1.3. Рупорные антенны с
круговой поляризацией………………………………………………9
9.2. Зеркальные параболические
антенны………………………………………………………..11
9.2.1. Геометрические свойства и принцип действия
параболической антенны…………..12
9.2.2. Приближенные методы расчета ДН зеркальной
параболической антенны…………13
9.2.3. Коэффициенты усиления
и направленного действия параболической антенны….16
9.2.4. Влияние точности
выполнения зеркальной антенны на ее направленные
свойства…………………………………………………………………………………………………..18
9.2.5. Влияние
отражений от зеркала на входное сопротивление антенны
(реакция зеркала на облучатель)……………………………………………………………………19
9.2.6. Управление ДН параболической
антенны………………………………………………..20
9.3. Двухзеркальные
антенны………………………………………………………………………..21
9.4. Облучатели зеркальных
антенн………………………………………………………………..24
9.5. Цилиндро-параболическая антенна.
Уголковая антенна………………………………….. 25
9.6. Уголковая
антенна………………………………………………………………………………... 26
ЛЕКЦИЯ 10. ПРОСТЫЕ ВИБРАТОРНЫЕ АНТЕННЫ
УКВ ДИАПАЗОНА………………….28
10.1. Несимметричный вертикальный
заземленный вибратор…………………………………28
10.1.1. Направленные свойства несимметричного вертикального
заземленного вибратора……………….……………………………………………………………..28
10.1.2. Сопротивление излучения и входное
сопротивление несимметричного
вертикального заземленного вибратора………………………………………………………..29
10.2. Симметрирующие
устройства…………………………………………………………………30
10.3. Простейшие
вибраторные антенны…………………………………………………………...33
ЛЕКЦИЯ 11. АНТЕННЫ ПОПЕРЕЧНОГО И
ОСЕВОГО ИЗЛУЧЕНИЙ УКВ ДИАПОЗОНА………….36
11.1. Синфазные вибраторные
антенные решетки………………………………………………..36
11.2. Антенны в печатном исполнении……………………………………………………………..37
11.3. Многощелевые волноводные антенны………………………………………………………38
11.4. Директорные
антенны…………………………………………………………………………..43
11.5. Логопериодические вибраторные
антенны…………………………………………………45
11.6. Антенны вращающейся поляризации……………………………………………………….47
11.6.1. Турникетный
излучатель…………………..…………………………………………………47
11.6.2. Спиральные
антенны……………………..…………………………………………………..48
11.7. Антенны поверхностных волн
(АПВ)…………………………………………………………52
11.7.1. Диэлектрические стержневые
антенны…..………………………………………………..52
11.7.2. Плоские антенны поверхностных
волн…..………………………………………………54
11.7.3. Синтез плоских АПВ…………………..……….…………………………………………….55
ЛЕКЦИЯ 12. СКАНИРУЮЩИЕ АНТЕННЫЕ РЕШЕТКИ
И РЕШЕТКИ С ОБРАБОТКОЙ СИГНАЛОВ…………….58
12.1. Назначение и
методы сканирования…………………………………………………………58
12.2. Фазированные
антенные решетки……………………………………………………………59
12.2.1. Требования к шагу
решетки………………………………………………………………..59
12.2.2. Излучающие элементы ФАР………………………………………………………………..60
12.2.3. Схемы возбуждения
ФАР……………………………………………………………………61
12.2.4. Активные фазированные антенные
решетки (АФАР)……………………………………63
3
12.3. Многолучевые антенные
решетки………..………………………………………….64
12.4. Антенные решетки с обработкой
сигналов…………………………………………….66
12.4.1. Методы обработки сигналов…………..……..…………………………………………66
12.4.2. Адаптивные антенные решетки
(ААР)……..…….…………………………………..69
ЛЕКЦИЯ 13. ОСОБЕННОСТИ АНТЕНН ДЛЯ
ТЕЛЕВИДЕНИЯ, РАДИОРЕЛЕЙНЫХ ЛИНИЙ И КОСМИЧЕСКОЙ
РАДИОСВЯЗИ.…..72
13.1. Телевизионные
антенны………………..…..……………………………………………...72
13.1.1. Передающие телевизионные
антенн….………………………………………………72
13.1.2. Приемные телевизионные
антенны……………………………………………………75
13.2. Антенны радиорелейных
линий…………..………..………………………..…………79
13.2.1. Антенны
радиорелейных линий прямой видимости……………………………79
13.2.2. Пассивные ретрансляторы
РРЛ…………..……………………………………………84
13.2.3. Антенны
тропосферных РРЛ……………..……………………………………………86
13.3. Антенны для спутниковой и
космической радиосвязи…….………………………….87
13.4. Питание антенн радиорелейной,
спутниковой и космической радиосвязи…..……92
ЛЕКЦИЯ 14. ОСОБЕННОСТИ АНТЕНН ПОДВИЖНОЙ
РАДИОСВЯЗИ………………..97
14.1. Антенно -
фидерные устройства……………………….……..……………………….97
14.1.1. Одновходовые
приемно-передающие антенны…………………….………………97
14.1.2. Многовходовые
приемно-передающие антенны…………………………………...102
14.2. Основные электрические
характеристики антенн, размещаемых
на корпусе подвижного объекта
(автомобиля)………………………………………………105
14.2.1. Одночастотные
антенны……………………………………………………………...…106
14.2.2. Многочастотные
антенны…….…………………………………………………………107
14.3. Малогабаритные
антенны для ручных радиотелефонов……………………………108
14.3.1 Антенна в виде шлейфового симметричного
вибратора……………………….109
14.3.2 Спиральная антенна……………………………………………………………………..110
14.3.3 "Низкопрофильные"
антенны………………..…………………………………………112
14.3.4 Влияние абонента
на работу радиотелефона……………………………………….113
ЛЕКЦИЯ 15. АНТЕННЫ ДЕКАМЕТРОВОГО (КОРОТКОВОЛНОВОГО)
ДИАПАЗОНА………115
15.1.
Особенности
коротковолновых антенн. Учет влияния земли на диаграмму
направленности…………………………………………………………………………………..115
15.2. Простые KB антенны………………………………………………………………………117
15.3. Синфазные
горизонтальные диапазонные антенны (СГД)………………………….120
15.4. Ромбические
антенны……………………………………………………………………..122
15.5. Антенны бегущей
волны………………………………………………………………….125
15.6. Логопериодические антенны
(ЛПА)…………………………………………………….126
15.7. Вопросы питания коротковолновых
антенн…………………………………………...128
ЛЕКЦИЯ 16. АНТЕННЫ СРЕДНИХ, ДЛИННЫХ И
СВЕРХДЛИННЫХ ВОЛН…………131
16.1. Особенности
антенн……………………………………………………………………….131
16.2. Передающие средневолновые
антенны……………………………………………….132
16.3. Передающие антенны ДВ и СДВ
диапазонов………………………………………..136
16.4. Питание передающих антенн СВ, ДВ
и СДВ диапазонов…………………………...139
16.5. Приемные антенны
СВ, ДВ и СДВ диапазонов……………………………………….140
ЛЕКЦИЯ
17. ВОПРОСЫ ЭЛЕКТРОМАГНИТНОЙ СОВМЕСТИМОСТИ АНТЕНН…..144
17.1. Параметры антенн, определяющие
электромагнитную совместимость………….144
17.2. Методы
снижения бокового излучения апертурных антенн ………………………146
17.3. Активные методы борьбы с
помехами……………………………………….……153
СПИСОК ЛИТЕРАТУРЫ…………………………………………………………………………155
ЛЕКЦИЯ 9. АПЕРТУРНЫЕ АНТЕННЫ
9. 1.
Рупорные антенны
9. 1. 1. Антенны в виде открытого конца волновода
В качестве слабонаправленных антенн УКВ широко используются антенны в виде открытого конца
волноводов прямоугольного или круглого сечений.
Электромагнитная волна, распространяющаяся по волноводу, дойдя до его открытого конца, частично излучается и
частично отражается. Физическими
источниками излучения являются электрические токи, возбуждаемые главным образом, на внутренних
стенках волновода.
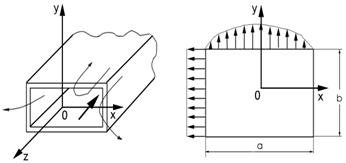
В инженерном решении приближенно полагают, что структура электромагнитного поля в плоскости открытого конца волновода такая же, как в поперечном сечении бесконечно длинного
волновода, т. е. пренебрегают волнами высших
типов, излучением токов, затекающих на наружные поверхности стенок волноводов, и не учитывают волны, отраженные от открытого конца волновода. В случае волновода
прямоугольного сечения (рис.9.1),
возбуждаемого основной волной Н10,
на его открытом
конце существуют взаимно
перпендикулярные тангенциальные составляющие поля Еy и Hх, зависимость которых от
координат известна.
Рис. 9. 1. Открытый конец
прямоугольного волновода
|
 Таким образом, характеристику
направленности открытого конца волновода прямоугольного сечения в плоскости Е,
параллельной размеру b поперечного сечения, можно представить в виде
произведения множителя системы плоского раскрыва на характеристику
направленности элемента Гюйгенса в этой плоскости.
Таким образом, характеристику
направленности открытого конца волновода прямоугольного сечения в плоскости Е,
параллельной размеру b поперечного сечения, можно представить в виде
произведения множителя системы плоского раскрыва на характеристику
направленности элемента Гюйгенса в этой плоскости.
В плоскости Н характеристика направленности открытого конца волновода прямоугольного сечения
представляет собой произведение множителя системы синфазного раскрыва с косинусоидальным
распределением амплитуды
возбуждающего поля на характеристику направленности элемента Гюйгенса в плоскости Н (см.
лекцию 7).
Поскольку
поперечные размеры прямоугольного волновода а и b невелики
и соизмеримы с длиной волны λ (обычно для
стандартных волноводов а = 0,7λ
, b = 0,35λ) и
поверхностные токи затекают на внешние стенки волновода, то ДН антенны в
виде открытого конца волновода имеет один широкий лепесток, т.е. антенна
является слабонаправленной.
Следует отметить, что точность расчетов по апертурным
формулам является удовлетворительной
только в переднем полупространстве.
Характеристики
направленности открытого конца волновода круглого сечения радиусом а в плоскостях Е и Н можно рассчитать по
приближенным формулам, полученным при тех же допущениях, что и для
прямоугольного волновода. При этом множитель системы выражается цилиндрическими
функциями.
Антенны в
виде открытого конца волновода применяются в сантиметровом диапазоне волн в тех
случаях, когда требуется широкая ДН. Их часто используют в качестве облучателей
зеркальных антенн.
Антенна в виде
открытого конца волновода оказывается плохо согласованной со свободным
пространством из-за резкого изменения условий распространения при переходе от
волновода к свободному пространству. Коэффициент отражения от открытого конца
прямоугольного волновода достигает значения 0,25...0,3, коэффициент отражения
от открытого конца круглого волновода несколько меньше и составляет 0,1...0,25.
Применяя
подстроечные элементы, можно значительно снизить коэффициент отражения от
открытого конца волновода.
9.1.2. Принцип действия,
основные свойства рупорных антенн

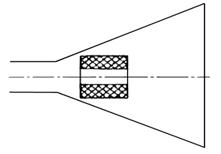
 Концентрация излучения в пределах более узкого
телесного угла достигается увеличением размеров синфазно возбужденной
поверхности. Если размеры сечения волновода выбираются таким образом, чтобы
обеспечить формирование необходимой структуры поля, то, плавно увеличивая
сечение волновода, эту структуру можно сохранить, а размеры излучаемой поверхности
увеличить. В месте перехода от волновода к рупору возникают высшие типы волн,
но при достаточно плавном расширении волновода (малый угол раствора рупора)
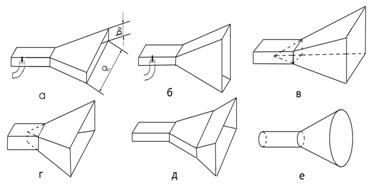
интенсивность этих волн невелика. Существуют различные типы рупоров. Рупор,
образованный увеличением размера а волновода, параллельного
вектор Н, называется секториальным Н- плоскостным (рис.9.2.а).
Рупор, образованный увеличением размера b волновода,
параллельного вектору Е, называется секториальным Е-плоскостным (рис.9.2.б).
Рупор, образованный одновременным увеличением размеров a u b поперечного сечения
волновода, называется пирамидальным (см. рис.9.2.в,г), а увеличением
поперечного сечения круглого волновода - коническим (рис.9.2.е). При плавном
переходе от волновода к рупору структура поля в последнем напоминает структуру
поля в волноводе.
Концентрация излучения в пределах более узкого
телесного угла достигается увеличением размеров синфазно возбужденной
поверхности. Если размеры сечения волновода выбираются таким образом, чтобы
обеспечить формирование необходимой структуры поля, то, плавно увеличивая
сечение волновода, эту структуру можно сохранить, а размеры излучаемой поверхности
увеличить. В месте перехода от волновода к рупору возникают высшие типы волн,
но при достаточно плавном расширении волновода (малый угол раствора рупора)
интенсивность этих волн невелика. Существуют различные типы рупоров. Рупор,
образованный увеличением размера а волновода, параллельного
вектор Н, называется секториальным Н- плоскостным (рис.9.2.а).
Рупор, образованный увеличением размера b волновода,
параллельного вектору Е, называется секториальным Е-плоскостным (рис.9.2.б).
Рупор, образованный одновременным увеличением размеров a u b поперечного сечения
волновода, называется пирамидальным (см. рис.9.2.в,г), а увеличением
поперечного сечения круглого волновода - коническим (рис.9.2.е). При плавном
переходе от волновода к рупору структура поля в последнем напоминает структуру
поля в волноводе.
Векторы
электромагнитного поля при переходе из волновода в рупор несколько изменяют
свою форму, чтобы обеспечить выполнение граничных условий на стенках рупора.
Направленные свойства
рупорной антенны приближенно можно анализировать, как и в случае открытого
конца волновода, пользуясь принципом эквивалентности. На излучающей поверхности
рупора действуют две взаимно перпендикулярные тангенциальные составляющие поля Еу
и Нх (прямоугольный раскрыв), амплитуды которых не зависят
от координаты у, а вдоль координаты х
они изменяются по закону косинуса.
Однако в отличие от поверхности открытого конца
волновода плоская излучающая поверхность рупора не может быть синфазной, так
как в раскрыве рупора имеются фазовые искажения. Найдем фазу возбуждающего поля
в произвольной точке М
излучающего
раскрыва H-плоскостного
рупора (рис.9.3). Дуга NOP окружности с центром в точке О
есть линия равных фаз. Предполагая для простоты, что
в рупоре β
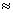 k
k 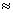
2π/
λ, получаем
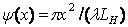 где Lh
- длина H-плоскостного рупора. Обычно LH>>x,поэтому можно ограничиться первым членом разложения. Тогда .
где Lh
- длина H-плоскостного рупора. Обычно LH>>x,поэтому можно ограничиться первым членом разложения. Тогда .
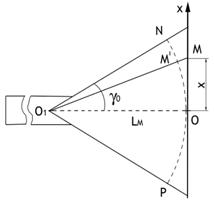 Следовательно, в раскрыве рупорной антенны имеется примерно
квадратичное фазовое распределение. Максимальный сдвиг фаз на краях раскрыва (х
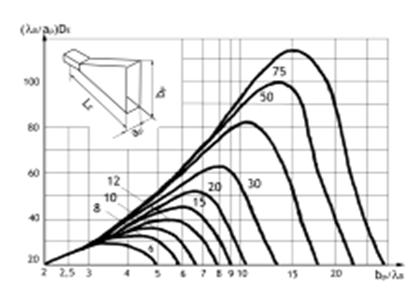
= ±ар /2), ψmах = πаp2 /(4λLH). При
достаточно больших значениях ψmах
(
Следовательно, в раскрыве рупорной антенны имеется примерно
квадратичное фазовое распределение. Максимальный сдвиг фаз на краях раскрыва (х
= ±ар /2), ψmах = πаp2 /(4λLH). При
достаточно больших значениях ψmах
(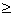 90°) ДН рупорной антенны заметно
отличается от ДН синфазной излучающей поверхности. При этом симметрия ДН
относительно нормали к возбужденной поверхности сохраняется.
90°) ДН рупорной антенны заметно
отличается от ДН синфазной излучающей поверхности. При этом симметрия ДН
относительно нормали к возбужденной поверхности сохраняется.
Рис.9.3. Фронт волны в Н-плоскостном
рупоре
|
Путем
аналогичных рассуждений получаем максимальный сдвиг фаз на краях Е-плоскостного рупора ψmах = πb2р
/( 4λLE), где LE - длина E-плоскостного рупора.
Максимальный сдвиг
фаз на краю раскрыва конического рупора
(радиус раскрыва ар,
длина рупора L) ψmах =π /(λL).
/(λL).
Поскольку в рупорной антенне практически невозможно
добиться полной синфазности излучающей поверхности, то обычно, задаваясь
некоторым допустимым сдвигом фаз, выбирают размеры раскрыва рупора и его длину.
Этот сдвиг
должен быть таким, чтобы ДН рупорной антенны мало отличалась от ДН синфазной
излучающей поверхности, размеры которой равны размерам раскрыва рупора.
Допустимый
максимальный сдвиг фаз определяется условием получения максимального КНД при
заданной относительной длине L/λ рупора. С увеличением
относительных размеров раскрыва рупора (ар/λ или bр /λ) при неизменной длине его
ДН сначала становится уже и КНД растет, так как увеличиваются размеры
излучающей поверхности, которая практически остается синфазной (сдвиг фаз ψтах мал). При
дальнейшем увеличении размеров заметно растут фазовые искажения, вследствие
чего ДН начинает расширяться и КНД уменьшается. На рис.9.4 по оси ординат
отложено произведение КНД Е-плоскостного
рупора на отношение λb/ар. Аналогичные
кривые существуют и для H-плоскостных рупоров. При
заданном отношении L/λ имеется определенное
оптимальное значение ар/λ или
bр/λ, при котором КНД антенны - максимально возможный.
Оптимальному значению ар/λ или bр/λ соответствует допустимый
сдвиг фаз. Рупор, размеры которого подобраны так, чтобы при заданной
длине L/λ получить максимальный КНД, называется
оптимальным.
 Из формул для ψmax видно,
что для того, чтобы при увеличении размеров раскрыва рупора максимальный сдвиг
фаз не изменялся, оставаясь равным допустимому, т.е. КНД возрастал,
относительная длина рупора L/λ должна увеличиваться
пропорционально квадрату относительных размеров раскрыва рупора.
Из формул для ψmax видно,
что для того, чтобы при увеличении размеров раскрыва рупора максимальный сдвиг
фаз не изменялся, оставаясь равным допустимому, т.е. КНД возрастал,
относительная длина рупора L/λ должна увеличиваться
пропорционально квадрату относительных размеров раскрыва рупора.
Рис.9.4. Зависимость КНД от длины и величины раскрыва рупора
|
Анализ
кривых, приведенных на рис.9.3, показывает, что в случае Е -плоскостного рупора максимальный КНД
получается при выполнении равенства 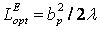 , тогда
допустимый максимальный сдвиг фаз для Е - плоскостного рупора
, тогда
допустимый максимальный сдвиг фаз для Е - плоскостного рупора  .
.
Рассмотрев аналогичные кривые DHλ /b = f(LH /λ,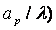 , можно найти допустимый сдвиг фаз
, можно найти допустимый сдвиг фаз 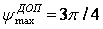 и оптимальную длину Н
-плоскостного рупора
и оптимальную длину Н
-плоскостного рупора  .
.
Увеличение допустимого сдвига
фаз в случае Н - плоскостного рупора по сравнению с E-плоскостным объясняется с паданием
амплитуды возбуждающего поля к краям раскрыва этого рупора в плоскости Н.
Коэффициент направленного действия оптимального Е- или Н-плоскостного рупора может быть
рассчитан по формуле D=va4πS/λ2, причем КИП рупора с учетом несинфазности и
неравномерности возбуждения составляет 0,64 (у пирамидального рупора va = 0,52).
Е
- плоскостной рупор
сужает ДН в плоскости Е, а Н - плоскостной рупор - в плоскости Н.
В
настоящее время находят применение рупоры, у которых сдвиги фаз поля в раскрыве значительно превосходят максимально
допустимые. При больших по сравнению
с λ раскрывах ар и bр и больших углах растворов рупора
γo ДН становится по форме близкой к
столообразной. Такие расфазированные рупоры обладают более широким рабочим диапазоном, чем
синфазные рупоры.
Их ДН при ψmax > 1,5π сравнительно мало зависят от
частоты.
9.1.3. Рупорные антенны с
круговой поляризацией
Для
получения круговой (или близкой к ней) поляризации, излучаемого рупором поля, применяются фазирующие секции, устанавливаемые
в волноводе, питающем рупор. В
фазирующей секции происходит разложение вектора линейно поляризованного электромагнитного поля на две взаимно
перпендикулярные составляющие, лежащие в плоскости, перпендикулярной
направлению распространения волны, и обеспечение между ними на выходе секции
сдвига фаз в 900.
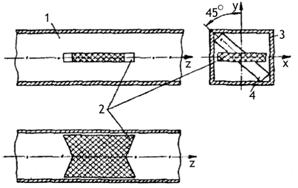 Существуют различные
Существуют различные
фазирующие секции. В качестве
фазирующей секции можно,
например, использовать отрезок
волновода с квадратным поперечным
сечением, возбуждаемый прямо-угольным
волноводом с волной H10.
Возбуждающий волновод
 соединяется с фазирующей
секцией плавным пирамидальным переходом. Поперечные сечения возбуждающего
волновода и фазирующей секции повернуты относительно друг друга на 45° (рис.9.5). В результате
вектор Е поля в фазирующей секции будет иметь составляющие Ех и Еу,
параллельные взаимно перпендикулярным
стенкам. Таким образом, поле в секции можно рассматривать как суперпозицию волн Н10 и H01.
соединяется с фазирующей
секцией плавным пирамидальным переходом. Поперечные сечения возбуждающего
волновода и фазирующей секции повернуты относительно друг друга на 45° (рис.9.5). В результате
вектор Е поля в фазирующей секции будет иметь составляющие Ех и Еу,
параллельные взаимно перпендикулярным
стенкам. Таким образом, поле в секции можно рассматривать как суперпозицию волн Н10 и H01.
Для создания необходимого сдвига фаз между составляющими Ех и Еу
в фазирующую секцию (1) устанавливают тонкую
диэлектрическую пластинку (2), причем так,
чтобы большой размер ее поперечного сечения был параллелен либо составляющей Ех, либо
Еу. Такая пластинка влияет, в основном, на фазовую скорость той
волны, линии вектора Е которой параллельны поверхности пластины. Толщина пластинки
выбирается достаточно
малой по сравнению с рабочей длиной волны. Тем самым она не оказывает заметного влияния на
фазовую скорость волны, вектор Е которой перпендикулярен поверхности пластины.
При квадратном раскрыве пирамидального рупора ширина
главного лепестка ДН в двух взаимно перпендикулярных плоскостях получается
неодинаковой из-за различных амплитудных распределений возбуждающего поля в Е- и Н-плоскостях. В H-плоскости ДН (по нулевому излучению) примерно в 1,5
раза шире, чем в E-плоскости. Между тем в ряде случаев желательно иметь одинаковые ДН в обеих плоскостях. Это особенно важно
при круговой поляризации излучаемого поля.
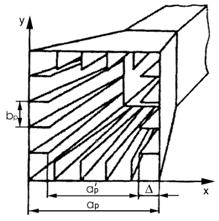 Один из способов получения одинаковых ДН состоит в
том, что в квадратном раскрыве устанавливаются металлические ребра высотой
Δ на расстоянии с < λ/2 друг от друга (рис.9.6). Если вектор Е
поляризован вдоль оси x, то такая
волна не может распространяться между пластинами, параллельными оси x, из-за
того, что размер с < λ/2. Для нее размер раскрыва ар как бы уменьшается и становится равным а – 2Δ. Если Δ= 0,17/ар, то размер апертуры
Один из способов получения одинаковых ДН состоит в
том, что в квадратном раскрыве устанавливаются металлические ребра высотой
Δ на расстоянии с < λ/2 друг от друга (рис.9.6). Если вектор Е
поляризован вдоль оси x, то такая
волна не может распространяться между пластинами, параллельными оси x, из-за
того, что размер с < λ/2. Для нее размер раскрыва ар как бы уменьшается и становится равным а – 2Δ. Если Δ= 0,17/ар, то размер апертуры 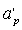 , параллельный оси х, в 1,5 раза будет меньше размера bр, параллельного
оси у. Так как на составляющую Еy данные
ребра не воздействуют, то ДН для обеих поляризаций поля в плоскости xoz будут примерно одинаковы. Аналогичным образом (с
помощью ребер, прикрепленных к другим стенкам рупора) можно выровнять ДН в
плоскости yoz.
, параллельный оси х, в 1,5 раза будет меньше размера bр, параллельного
оси у. Так как на составляющую Еy данные
ребра не воздействуют, то ДН для обеих поляризаций поля в плоскости xoz будут примерно одинаковы. Аналогичным образом (с
помощью ребер, прикрепленных к другим стенкам рупора) можно выровнять ДН в
плоскости yoz.
 Можно реализовать свойства
фазирующей секции и
без размещения диэлектрической пластины. Для этого вместо волноводной секции квадратного сечения следует
взять волновод, несколько
отличающийся от квадратного сечения.
Можно реализовать свойства
фазирующей секции и
без размещения диэлектрической пластины. Для этого вместо волноводной секции квадратного сечения следует
взять волновод, несколько
отличающийся от квадратного сечения.
Сдвиг фаз в 90° обеспечивается соотношением размеров
поперечного сечения а, b и длины
l такого волновода за счет различия коэффициентов
фазы 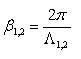 ;
; 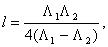 где
где 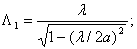
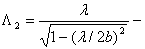 длины волн в
волноводе.
длины волн в
волноводе.
9.2.
Зеркальные параболические антенны
Зеркальная осесимметричная параболическая антенна состоит из отражающей
поверхности, выполненной в виде параболоида вращения, и небольшой
слабонаправленной антенны - облучателя, установленной в фокусе параболоида, и
облучающей внутреннюю поверхность последнего. На
базе такой классической зеркальной антенны разработаны различные модификации,
многообразие которых приводит к целесообразности сгруппировать их, т.е.
привести классификацию по основным отличительным признакам. Так, по числу
отражающих зеркал различают одно- и многозеркальные антенны. Последние, как
правило, содержат два зеркала. Часто эту группу называют двухзеркальными
антеннами.
По взаимной ориентации зеркал и облучателей антенны могут
быть симметричными и
осенесимметричными. В симметричных антеннах отражающее зеркало обладает осевой симметрией и поле,
отраженное от вершины
такого зеркала, попадает в облучатель. Если не принять специальных мер, то согласование
антенны будет невысоким. В осенесимметричных схемах антенн волны, отраженные от зеркала, проходят
мимо облучателя. Такие схемы называют еще антеннами с вынесенным облучателем (АВО). Их отличает
высокое согласование с трактом питания, но
в то же время они обладают повышенным уровнем кроссполяризации, что при одновременной работе на ортогональных
поляризациях является источником дополнительных помех.
По числу
основных лучей, создаваемых зеркальной антенной, различают одно- и многолучевые антенны. Число лучей определяется
числом облучателей. Многолучевые антенны могут создаваться как в
симметричном, так и в осенесимметричном
варианте. По типу кривизны основного зеркала используются параболические
и сферические отражающие зеркала, зеркала с классическим
и модифицированным профилями, обеспечивающими высокий результирующий КИП в условиях компромисса между
апертурным КИП и потерями за счет «перелива» энергии за края зеркала.
Это так называемые оптимизированные
антенны.
При фиксированном положении отражающего зеркала направление
максимального излучения (приема) может быть либо фиксированным, либо антенна может работать в режиме сканирования. Особое
место занимают зеркальные антенны с
пониженным УБЛ.
9.2.1.
Геометрические свойства и принцип действия параболической антенны
В прямоугольной системе координат (начало в вершине
параболоида) параболическая поверхность (рис.9.7) описывается уравением х2 + у2 = 4f0z, где f0 - фокусное расстояние.
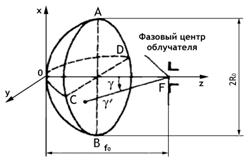
В сферической системе координат (начало в фокусе) эта
поверхность описывается
уравнением r'=2f0/(1+ cosγ), где r' - расстояние от фокуса до любой точки на внутренней
поверхности параболоида; γ - угол между направлением
на данную точку и фокальной осью зеркала (полярный угол).
В
случае параболоида вращения (рис.9.7) плоскость раскрыва (плоскость, проходящая через крайние точки поверхности зеркала
и перпендикулярная его фокальной оси)
имеет круглую форму; радиус этой плоскости называется радиусом раскрыва зеркала (R0). Радиус
раскрыва и угол раскрыва зеркала
(угол γ0 между
фокальной осью и прямой, проведенной из фокуса к кромке параболоида) связаны
соотношением R0=2f0tg(γo/2).
 Форма зеркала характеризуется
отношением R0/2f0
или углом раскрыва γ0. Зеркало называется длиннофокусным (мелким), если R0/2f0<1 либо 2γ0<π
или короткофокусным (глубоким), если R0/2f0>1 либо 2γ0 >π.
Форма зеркала характеризуется
отношением R0/2f0
или углом раскрыва γ0. Зеркало называется длиннофокусным (мелким), если R0/2f0<1 либо 2γ0<π
или короткофокусным (глубоким), если R0/2f0>1 либо 2γ0 >π.
 Принцип действия зеркальной антенны следующий. При падении, излучаемой облучателем,
электромагнитной волны на зеркало на последнем возникают электрические
поверхностные токи (вторичные источники
электромагнитного поля). Эти токи
существуют не только на внутренней,
обращенной к облучателю поверхности зеркала, но также из-за явления
дифракции электромагнитных волн и на его
внешней поверхности. Электромагнитное поле, создаваемое зеркальной антенной в любой точке окружающего пространства, есть результат сложения (интерференции) полей: вторичного,
создаваемого
Принцип действия зеркальной антенны следующий. При падении, излучаемой облучателем,
электромагнитной волны на зеркало на последнем возникают электрические
поверхностные токи (вторичные источники
электромагнитного поля). Эти токи
существуют не только на внутренней,
обращенной к облучателю поверхности зеркала, но также из-за явления
дифракции электромагнитных волн и на его
внешней поверхности. Электромагнитное поле, создаваемое зеркальной антенной в любой точке окружающего пространства, есть результат сложения (интерференции) полей: вторичного,
создаваемого
поверхностными токами,
и первичного, создаваемого
облучателем.
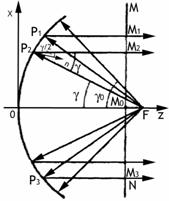
Рассмотрим
сечение параболоида в плоскости xoz (рис.9.8). Образованная
этим сечением парабола обладает тем свойством, что расстояния от ее
фокуса F до
любой точки,
лежащей на линии MN,
перпендикулярной
оси параболы и параллельной ее директрисе, по ломаным путям, (FP1M1, FP2M2 и др.) одинаковы. Следовательно,
получается плоский фронт волны. Установленный в точке F облучатель излучает волны,
близкие к сферическим. При этом расходящиеся лучи
совпадают с линиями FP1,
FP2
и т.д. Если бы
длина волны первичного источника была бесконечно мала, то лучи, падающие на внутреннюю поверхность параболоида,
отражались бы от нее по законам геометрической оптики. При этом, вследствие параболической формы зеркала, все
отраженные лучи были бы параллельны оси z и, таким образом, сферическая
волна преобразовывалась
бы параболоидом в плоскую. В действительности длина волны облучателя не бесконечно
мала, и поэтому отраженные лучи идут не параллельно, а несколько расходятся. Однако
расходимостью отраженных от зеркала лучей на небольшом участке пути от зеркала до
поверхности раскрыва
можно пренебречь, и эту поверхность можно считать синфазно возбужденной.
9.2.2.
Приближенные методы расчета ДН зеркальной параболической антенны
Имеется два приближенных метода определения направленных свойств параболической антенны:
апертурный и токовый.
Апертурный
метод состоит в
определении электромагнитного поля излучения по известному распределению возбуждающего поля на поверхности зеркала - на основе
принципа эквивалентности. Пренебрегая влиянием ряда факторов, считают, что излучающей поверхностью
зеркала является только поверхность его раскрыва.
Амплитудное
распределение в раскрыве зеркала и следовательно ДН антенны определяются ДН облучателя и формой
зеркала (отношением R0/f0). При расчете амплитудного
распределения полагают, что зеркало относительно облучателя находится в дальней зоне. Это
допустимо, так как обычно расстояние от фокуса до поверхности зеркала составляет десятки длин
волн. В этом случае относительная амплитуда напряженности поля, создаваемого облучателем в любой точке
поверхности зеркала (рис.9.9.а), могла быть найдена из следующих соображений. Поле облучателя,
являясь обычно сферической
волной, убывает обратно пропорционально пройденному расстоянию r'. С учетом
этого амплитуда напряженности поля в произвольной точке поверхности зеркала E3/E0=F0(γ)f/r'; F0(γ) -нормированная ДН облучателя; Е0 -
амплитуда напряженности поля у вершины зеркала. Пренебрегая затуханием поля при его распространении до
плоского раскрыва зеркала, принимаем,
что амплитуда напряженности поля в произвольной точке раскрыва ES = Е3. В нормированном
представлении
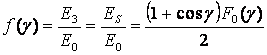 (9.1)
(9.1)
Отношение ЕS/Е0 - амплитудное
распределение поля в апертуре - удобно изображать в виде графика и
рассматривать как функцию относительного переменного радиуса раскрыва ρ/R0 (рис.9.9.б). Отметим, что представление амплитудного
распределения в виде точной аналитической функции f1(ρ/R0) либо
невозможно, либо приводит к громоздким вычислениям при расчете ДН.
В
случае осесимметричной ДН облучателя хорошие результаты дает аппроксимация функции f1(ρ/R0) степенным рядом
f(ρ/R0)
=1 + a2(ρ/R0)2
+ a4(ρ/R0)4
+…. (9.2)

При
этом для практических, расчетов можно ограничиться только первыми тремя членами ряда. Характеристика направленности
излучающего раскрыва
(без учета направленных свойств элемента Гюйгенса) будет иметь вид:
f(θ)=(1+а2+а4)Λ1(и)
- (а2/2+а4)Λ2(и) + (а4/3)Λ3(и),
(9.3)
где
и = kR0 sinθ; Λ1(u), Λ2(u), Λ3(u)-лямбда-функции.

 Для,
расчета ДН необходимо предварительно определить постоянные коэффициенты а2
и а4. Для этого по известной ДН облучателя строится график
амплитудного распределения f1(ρ/R0) (см. рис.9.9.б). Аппроксимирование этого амплитудного
распределения функций (9.2) сводится к такому подбору коэффициентов а2
и а4, чтобы аппроксимирующая функция f(ρ/R0)
совпадала с функцией (амплитудного
распределения f1(ρ/R0) в двух точках,
например, при ρ/R0=1 и ρ/R0=0,5 (в точке ρ/R0=0 совпадение функции f1(ρ/R0) с функцией (ρ/R0) выполняется
автоматически). Пусть при ρ/R0=1
f1(ρ/R0)=Δ1 и
при ρ/R0=0,5
f1(р/R0) = Δ2. Тогда
получаем
Для,
расчета ДН необходимо предварительно определить постоянные коэффициенты а2
и а4. Для этого по известной ДН облучателя строится график
амплитудного распределения f1(ρ/R0) (см. рис.9.9.б). Аппроксимирование этого амплитудного
распределения функций (9.2) сводится к такому подбору коэффициентов а2
и а4, чтобы аппроксимирующая функция f(ρ/R0)
совпадала с функцией (амплитудного
распределения f1(ρ/R0) в двух точках,
например, при ρ/R0=1 и ρ/R0=0,5 (в точке ρ/R0=0 совпадение функции f1(ρ/R0) с функцией (ρ/R0) выполняется
автоматически). Пусть при ρ/R0=1
f1(ρ/R0)=Δ1 и
при ρ/R0=0,5
f1(р/R0) = Δ2. Тогда
получаем
1 + a2+а4=Δ1; 1 + a2(0,5)2+а4(0,5)4=Δ2. (9.4) (9.4)
 В результате решения этих
уравнений определяются неизвестные коэффициенты а2
и а4.
В результате решения этих
уравнений определяются неизвестные коэффициенты а2
и а4.
Токовый
метод определения
направленных свойств параболической антенны базируется на известном распределении поверхностных токов на
внутренней поверхности зеркала. Полагая, что
эти токи существуют только на внутренней
поверхности зеркала, можно вектор плотности тока в данной точке поверхности зеркала определить с учетом
ориентации векторов Н в падающей и отраженной волнах по формуле Jэ = 2[пН1
], где п - единичный вектор внешней нормали к данной точке
поверхности зеркала; Н1 - вектор напряженности
магнитного поля, создаваемого падающей волной облучателя в данной точке на
поверхности зеркала.
На
рис.9.10 изображено распределение поверхностного тока, спроектированное на
плоскость хоу. Облучателем является
элементарный электрический вибратор (ось вибратора параллельна оси х) с контррефлектором, обеспечивающим однонаправленное
излучение в сторону зеркала. Зная закон распределения тока на
поверхности зеркала, можно рассчитать его ДН. Для этого необходимо
проинтегрировать по всей поверхности зеркала выражение для напряженности поля,
которое создает элемент поверхности зеркала, рассматриваемый как элементарный электрический
вибратор.
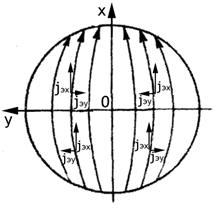
Как
видно из рис.9.10, поле в направлении оси z зеркала в случае
вертикальной поляризации создается только составляющими вектора Jэ, параллельными оси х, которые во всех квадрантах имеют одинаковые направления. Поля Ех,
излучаемые ими в направлении оси z, складываются синфазно,
т.е. это направление является направлением максимального излучения.
Составляющие плотности поверхностного тока Jэy в
различных квадрантах имеют взаимно противоположные направления; поля Еу,
обусловленные ими в направлении оси z,
попарно противофазны, следовательно, Jэy не
создают излучения в главном направлении. В других (боковых) направлениях из-за
появляющейся разности хода между полями от составляющих Jэу тока возникает
поле с поляризацией, перпендикулярной по отношению к основной составляющей Ех.
Составляющие
Jэz также не
создают излучения вдоль оси z
(вибратор вдоль своей
оси не излучает). Составляющие Jэу и Jэz не создают
излучения в обеих
главных плоскостях (плоскости xoz и yoz). Поляризация излучаемого поля в главных плоскостях является линейной (Ех). В других плоскостях, проходящих через ось z, имеет место также излучение за
счет составляющих Jэу
и Jэz, вследствие чего появляется
поперечная (относительно основной) поляризация поля. Суммарное поле оказывается эллиптически поляризованным. Поперечная поляризация (кроссполяризация) является
паразитной; она несколько уменьшает
КНД антенны. Уровень кроссполяризации
тем ниже, чем меньше отношение R0/f0, т.е. чем более длиннофокусным является
зеркало. Таким образом, токовый метод позволяет
учесть поляризационные эффекты в зеркальной
антенне.
Расчет ДН зеркальной антенны, основанный на приближенном определении токов на ее рабочей
поверхности, обеспечивает достаточно точные результаты в пределах главного лепестка и прилегающих
к нему одного -
трех боковых лепестков.
Оба метода (апертурный и токовый) тем более точны, чем
больше относительные размеры зеркала R0/λ и его радиус кривизны (т.е. чем меньше отношение R0/f0).
9.2.3. Коэффициенты
усиления и направленного действия параболической антенны
Как
было показано выше, коэффициент усиления G антенны связан с ее
коэффициентами направленного действия D и полезного действия η простым
соотношением G = Dη.
Коэффициент
полезного действия η зеркальной антенны учитывает тепловые потери энергии в облучателе, элементах
крепления облучателя, краске, покрывающей внутреннюю поверхность зеркала, и
т.д. Обычно принимают
η = 1. Поэтому рассмотрим подробно определение КНД.
Коэффициент
направленного действия зеркальной антенны можно рассчитать по формуле для КНД,
заменив в ней апертурный КИП (νa) множителем νрез
(результирующий или полный КИП), учитывающим
уменьшение КНД из-за действия ряда факторов: переливания части, излученной
облучателем, энергии через края зеркала, вызывающего увеличение УБЛ ДН
зеркальной антенны в задних квадрантах (дальние боковые лепестки); ошибки в
фазовом распределении на раскрыве; затенения части поверхности раскрыва
облучателем и элементами его крепления; кроссполяризации излучаемого поля и др.
Таким образом, D = v рез 4πS
/λ2, где S - πR02
- площадь раскрыва; νрез = νaν1ν2ν3ν4ν5... .
Здесь vа— апертурный КИП раскрыва зеркала; ν1 -
множитель, определяемый переливанием части энергии через края зеркала; ν2 - множитель, определяемый затенением; v3 -множитель, определяемый фазовыми ошибками; ν4 - множитель, учитывающий явление кроссполяризации; ν5 - множитель, учитывающий дифракцию поля на кромке
зеркала.
Множитель ν1, называемый коэффициентом перехвата, - есть
отношение мощности, излученной облучателем и перехватываемой зеркалом, к полной
мощности, излученной облучателем, при этом потери в зеркале не учитываются.
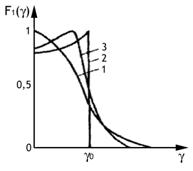
Если
при заданной форме зеркала (R0/f0=const) расширять ДН облучателя
(кривая 1 на рис. 9.11), то амплитудное распределение в раскрыве зеркала становится более равномерным (va растет). Однако вместе с тем увеличивается доля
энергии, проходящей мимо зеркала, приводящая к росту боковых лепестков (уменьшается v1). При сужении ДН
облучателя наоборот: уменьшается vа и увеличивается v1. Два противоположно действующих на результирующие КИП и КНД фактора при
постоянной величине отношения R0/f0 или угла раскрыва
зеркала γ0 и изменяемой
ширине ДН облучателя определяют
условие оптимального облучения зеркала с точки зрения получения максимального
КНД. Условие оптимального облучения примерно
обеспечивается при Δkр = Еkр/Е0
=0,316 (-10
дБ), где Еkр - напряженность поля на краю зеркала. При этом vav1 = 0,7...0,8.
С точки зрения получения максимального КНД при заданных
размерах зеркала
идеальной является ДН облучателя, изображенная на рис.9.11 (кривая 2). Она должна быть
осесимметричной и имеет два максимума в направлениях на края зеркала. Амплитудное
распределение раскрыва зеркала в данном случае получается близким к равномерному (с учетом
разных расстояний от
фокуса зеркала до его вершины и краев), т.е. va = 1; переливание энергии за края зеркала отсутствует (ДН имеет бесконечную крутизну ската), таким образом, v1=1.
Для обеспечения высокого значения vрез ДН облучателя должна иметь форму, по возможности приближающуюся к
идеальной (например, кривая 3 на рис.9.11). Близкие к ней ДН можно получить с помощью
расфазированных рупоров
и их модификаций. Кроме того, надо исключить или уменьшить влияние других факторов, снижающих
результирующий КИП антенны (устранить затенение раскрыва облучателем, снизить кроссполяризацию и т.д.).
 Реализация высоких значений νрез,
а следовательно, КНД антенн не является
единственно важной задачей в практическом приложении. В антенных системах ряда
радиослужб предъявляются высокие требования к УБЛ. Например, в системах спутниковой
связи, использующих геостационарную орбиту, от уровня первых боковых лепестков,
примыкающих к главному, во многом зависят помехозащищенность и
электромагнитная cовместимость, поэтому он должен быть ниже главного
минимум на 25...30 дБ. В ряде случаев, в частности, в радиорелейной связи,
важное значение имеет УБЛ в задних
квадрантах в направлениях,
близких к 180°. В
этих направлениях излучение (коэффициент защитного действия) должно составлять не более
-(60...70) дБ. Для параболических антенн с углами раскрыва 2γ0 =120...180° КЗД составляет - (50...60)
дБ.
Реализация высоких значений νрез,
а следовательно, КНД антенн не является
единственно важной задачей в практическом приложении. В антенных системах ряда
радиослужб предъявляются высокие требования к УБЛ. Например, в системах спутниковой
связи, использующих геостационарную орбиту, от уровня первых боковых лепестков,
примыкающих к главному, во многом зависят помехозащищенность и
электромагнитная cовместимость, поэтому он должен быть ниже главного
минимум на 25...30 дБ. В ряде случаев, в частности, в радиорелейной связи,
важное значение имеет УБЛ в задних
квадрантах в направлениях,
близких к 180°. В
этих направлениях излучение (коэффициент защитного действия) должно составлять не более
-(60...70) дБ. Для параболических антенн с углами раскрыва 2γ0 =120...180° КЗД составляет - (50...60)
дБ.
9.2.4.
Влияние точности выполнения зеркальной антенны на ее направленные свойства
Неточности,
неизбежные при создании конструкции антенны (например, при выполнении поверхности зеркала, установке облучателя), вызывают отклонение
распределения поля на излучающей поверхности от расчетного и соответствующие
искажения ДН.
Ошибки в распределении поля по раскрыву могут быть систематическими и случайными.
К систематическим
ошибкам относятся
такие, которые можно предусмотреть
при полном и точном расчете антенны. Причинами этих ошибок могут быть смещение
облучателя из фокуса, затенение раскрыва зеркала облучателем и элементами его крепления и др. Случайные ошибки обусловлены незакономерными и обычно небольшими
отклонениями параметров
антенны от их расчетных значений. Причинами таких ошибок являются недостаточная точность обработки поверхности
зеркала, случайные деформации поверхности
антенны вследствие изменения температуры или ветровых нагрузок и др.
Статистический анализ влияния случайных ошибок на
направленные свойства зеркальной
антенны позволяет сделать следующие выводы:
1.Случайные
ошибки в распределении возбуждающего поля в раскрыве антенны увеличивают УБЛ и уменьшают КНД.
2.Уровень
боковых лепестков параболической антенны пропорционален среднеквадратической
фазовой ошибке Δψ2 и квадрату интервала корреляции, измеренного в длинах волн.
3.Участки
зеркала, на которых реальная поверхность отклоняется от расчетной, должны быть
небольшими, т.е. при одном и том же допуске на точность обработки поверхности зеркало с меньшим
интервалом корреляции (более шероховатая поверхность) обеспечит более низкий
УБЛ.
4. При
повышении частоты увеличиваются как фазовые ошибки (Δρ2π/λ, где Δρ - неточность изготовления
зеркала), так и интервал корреляции, выраженный
в длинах волн. Поэтому КНД антенны с неизменной площадью раскрыва увеличивается
не пропорционально квадрату частоты, а медленнее. При данной точности выполнения поверхности зеркала и данном интервале корреляции существует предельный КНД, который
нельзя превзойти уменьшением λ, или увеличением диаметра зеркала.
5. Характер ДН в области боковых лепестков определяется в
большей степени точностью изготовления антенны, а не способом ее облучения.
9.2.5. Влияние отражений от зеркала на входное сопротивление
антенны (реакция зеркала на облучатель)
Часть,
отраженных от зеркала, лучей на пути которых находится облучатель,
перехватывается последним (реакция зеркала). По отношению к отраженным от
зеркала волнам облучатель ведет себя как приемная антенна. В основном, на
облучатель воздействуют волны, отраженные вблизи вершины зеркала. Очевидно, что
чем больше КНД облучателя, тем большую мощность он перехватывает. Перехваченная
мощность создает в линии питания волну, идущую от облучателя к генератору,
аналогичную по действию обычной отраженной волне, возникающей в линии
вследствие ее рассогласования с нагрузкой. Появление в тракте отраженной от
зеркала волны ухудшает согласование антенны, так как эквивалентно изменению
входного сопротивления антенны.
 Отраженную волну можно
скомпенсировать с помощью какого-либо согласующего устройства, устанавливаемого у
вершины зеркала (вспомогательное зеркало), либо в питающей линии вблизи
облучателя (ферритовый вентиль). Однако действие такого устройства будет
эффективным только на фиксированной частоте, поскольку с изменением частоты
(из-за изменения разности хода лучей) вновь появится отраженная волна.
Отраженную волну можно
скомпенсировать с помощью какого-либо согласующего устройства, устанавливаемого у
вершины зеркала (вспомогательное зеркало), либо в питающей линии вблизи
облучателя (ферритовый вентиль). Однако действие такого устройства будет
эффективным только на фиксированной частоте, поскольку с изменением частоты
(из-за изменения разности хода лучей) вновь появится отраженная волна.
 Если антенна излучает поле
вращающейся поляризации, то реакция зеркала на облучатель будет практически
отсутствовать. Дело в том, что при отражении от зеркала, излучаемой
облучателем, волны направление вращения плоскости поляризации изменяется на
обратное, вследствие чего она не принимается облучателем. Это антенна с
поляризационной развязкой.
Если антенна излучает поле
вращающейся поляризации, то реакция зеркала на облучатель будет практически
отсутствовать. Дело в том, что при отражении от зеркала, излучаемой
облучателем, волны направление вращения плоскости поляризации изменяется на
обратное, вследствие чего она не принимается облучателем. Это антенна с
поляризационной развязкой.
Удачным способом устранения
реакции зеркала на облучатель в широкой полосе частот является применение
невзаимных устройств, например ферритовых вентилей и циркуляторов. Они
устанавливаются в волноводном тракте перед облучателем и, внося сравнительно
малые потери для прямой волны, на 20...25 дБ ослабляют отраженную волну.
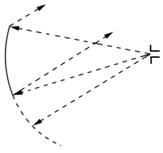
Наиболее радикальный способ уменьшения реакции зеркала состоит в выносе
облучателя из поля отраженных от зеркала лучей. Для этого облучатель
устанавливают в фокусе зеркала (разворачивают) так, чтобы направление его максимального
излучения составило некоторый угол с
фокальной осью зеркала
(рис.9.12). При этом облучается только часть зеркала, расположенная выше его
оси, и отраженные от нее лучи проходят мимо облучателя. Необлучаемая часть
зеркала удаляется (осенесимметричная антенна).
9.2.6. Управление ДН параболической
антенны

 Если фазовый центр облучателя
сместить из фокуса в направлении, перпендикулярном оси зеркала (рис.9.13.a), то поверхность раскрыва зеркала перестанет быть синфазной.
Лучи 1 и 1’,2 и 2’, отраженные от поверхности зеркала, достигают поверхности
раскрыва неодновременно. Можно показать, что при небольшом смещении облучателя Δx и
достаточно длиннофокусном зеркале фазовое распределение поверхности раскрыва
близко к линейному (3). Поэтому вынос облучателя из фокуса в направлении,
перпендикулярном оси зеркала, приводит к
повороту ДН в сторону, противоположную смещению облучателя. Угол поворота ДН θmах (рис.9.13.б) при малых смещениях
облучателя примерно равен углу смещения облучателя α1,
определяемому по формуле tgα1=Δx/f0. Синфазный фронт волны в раскрыве зеркала поворачивается на
угол α1. С увеличением Δх кроме линейного
изменения фазы появляются заметные фазовые ошибки более высоких порядков, из
которых наибольшую роль играют кубические (4). Знаки кубического и линейного
фазового распределений противоположны (рис.9.13.а). В этом случае ДН
поворачивается на угол, меньший, чем α1, главный лепесток становится несимметричным
относительно своего максимума и УБЛ со стороны, противоположной смещению ДН,
возрастает.
Если фазовый центр облучателя
сместить из фокуса в направлении, перпендикулярном оси зеркала (рис.9.13.a), то поверхность раскрыва зеркала перестанет быть синфазной.
Лучи 1 и 1’,2 и 2’, отраженные от поверхности зеркала, достигают поверхности
раскрыва неодновременно. Можно показать, что при небольшом смещении облучателя Δx и
достаточно длиннофокусном зеркале фазовое распределение поверхности раскрыва
близко к линейному (3). Поэтому вынос облучателя из фокуса в направлении,
перпендикулярном оси зеркала, приводит к
повороту ДН в сторону, противоположную смещению облучателя. Угол поворота ДН θmах (рис.9.13.б) при малых смещениях
облучателя примерно равен углу смещения облучателя α1,
определяемому по формуле tgα1=Δx/f0. Синфазный фронт волны в раскрыве зеркала поворачивается на
угол α1. С увеличением Δх кроме линейного
изменения фазы появляются заметные фазовые ошибки более высоких порядков, из
которых наибольшую роль играют кубические (4). Знаки кубического и линейного
фазового распределений противоположны (рис.9.13.а). В этом случае ДН
поворачивается на угол, меньший, чем α1, главный лепесток становится несимметричным
относительно своего максимума и УБЛ со стороны, противоположной смещению ДН,
возрастает.
Смещение облучателя из фокуса используется в антеннах систем
спутниковой связи и в радиолокации для сопровождения цели (ИСЗ, самолет и
т.д.). Во избежание значительных искажений ДН из-за появления кубической
фазовой ошибки угол поворота ДН должен быть невелик и обычно не может превышать
нескольких значений ширины главного лепестка ДН (по половинной мощности).
При смещении облучателя из фокуса вдоль оси зеркала
на поверхности раскрыва возникают квадратичные фазовые искажения, симметричные
относительно вершины зеркала, что расширяет главный лепесток и увеличивает УБЛ
ДН. При больших смещениях излучение в главном направлении уменьшается и главный
лепесток раздваивается. Чтобы фазовая ошибка из-за смещения облучателя не превышала допустимого значения π/4, должно выполняться условие Δzдon < λ /[8(1 - cos γ0)].
9.3.
Двухзеркальные антенны
Рассмотренные зеркальные параболические антенны по сравнению
с другими типами антенн обладают хорошими электрическими характеристиками,
технологичны в изготовлении и имеют сравнительно простую конструкцию. Наряду с
этими достоинствами они обладают недостатками, которые в ряде случаев не
позволяют удовлетворять комплексу требований, предъявляемых к современным
антеннам. Такими недостатками являются: большая длина фидерного тракта от
антенны до приемопередающей аппаратуры и его размещение в поле излучения
антенны; сложность обеспечения амплитудного распределения поля в раскрыве,
близкого к равномерному, с сохранением высокого значения результирующего КИП (vpeз); неприемлемые в ряде случаев
продольные габаритные размеры антенны и др. Поэтому наряду с однозеркальными
схемами антенн были разработаны, так называемые, двухзеркальные антенны, в
которых перечисленные недостатки проявляются в меньшей степени либо полностью
устраняются.
Среди многообразия типов двухзеркальных антенн есть две
классические: это двухзеркальные антенны Кассегрена (рис.9.14.а) и Грегори
(рис.9.14.б).
В этих антеннах используются две отражающие поверхности:
основная -большое
(обычно параболическое) зеркало и вспомогательная - малое зеркало, выполненное либо в виде части гиперболоида
вращения (рис.9.14.а), либо в виде части
эллипсоида вращения (рис.9.14.б).

 Пусть облучатель с фазовым
центром, находящимся в точке F2, излучает в направлении малого зеркала сферическую волну. В каждой
точке поверхности зеркала соблюдается правило: угол отражения равен углу
падения. При этом вследствие геометрических свойств гиперболы (или эллипса)
отражаемая малым зеркалом волна, снова оказываясь сферической, как бы исходит
из одной точки - фокуса гиперболы (или эллипса) F1, совмещенного с фокусом, большого зеркала - параболы. Эта
волна трансформируется большим зеркалом в плоскую. Второй фокус малого
зеркала F2 совмещается с фазовым центром
облучателя (обычно рупора).
Пусть облучатель с фазовым
центром, находящимся в точке F2, излучает в направлении малого зеркала сферическую волну. В каждой
точке поверхности зеркала соблюдается правило: угол отражения равен углу
падения. При этом вследствие геометрических свойств гиперболы (или эллипса)
отражаемая малым зеркалом волна, снова оказываясь сферической, как бы исходит
из одной точки - фокуса гиперболы (или эллипса) F1, совмещенного с фокусом, большого зеркала - параболы. Эта
волна трансформируется большим зеркалом в плоскую. Второй фокус малого
зеркала F2 совмещается с фазовым центром
облучателя (обычно рупора).
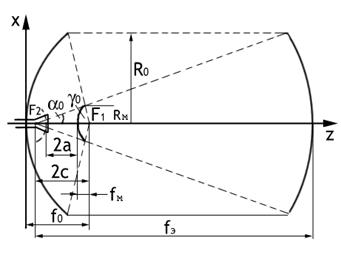
Геометрия двухзеркальной антенны определяется следующими
параметрами (рис.9.15): R0 и
Rм - соответственно радиусы раскрывов
большого и малого зеркал, обычно Rм=(0,1...0,2)R0; 2γ0 - угол раскрыва большого
параболоида; 2α0 - угол облучения источником
(облучателем) краев малого зеркала; f0 - фокусное расстояние большого
зеркала; fм - фокусное расстояние малого
зеркала; 2с - расстояние между фокусами малого
зеркала; е - эксцентриситет малого зеркала. Из
перечисленных параметров независимыми являются четыре параметра, остальные
могут быть определены через них. Обычно в качестве независимых переменных
берутся R0, Rм, γ0, α0.
 В антенне Кассегрена угол γ0 может быть больше 90o . В антенне Грегори угол γ0 может
быть взят лишь меньше 90° (если γ0>90°, то отраженные от одной
половины малого зеркала лучи на пути к большому встретят вторую половину малого
зеркала, т.е. будут им затенены). Поэтому антенны Грегори могут быть только длиннофокусными.
В антенне Кассегрена угол γ0 может быть больше 90o . В антенне Грегори угол γ0 может
быть взят лишь меньше 90° (если γ0>90°, то отраженные от одной
половины малого зеркала лучи на пути к большому встретят вторую половину малого
зеркала, т.е. будут им затенены). Поэтому антенны Грегори могут быть только длиннофокусными.
 Для расчета ДН двухзеркальной антенны необходимо
знать амплитудное распределение в раскрыве большого зеркала, которое можно
найти методом геометрической оптики. Для этого следует заменить двухзеркальную
систему эквивалентным параболоидом и найти амплитудное распределение в его
раскрыве.
Для расчета ДН двухзеркальной антенны необходимо
знать амплитудное распределение в раскрыве большого зеркала, которое можно
найти методом геометрической оптики. Для этого следует заменить двухзеркальную
систему эквивалентным параболоидом и найти амплитудное распределение в его
раскрыве.
Такой
прием позволяет при расчете амплитудного распределения исключить из
рассмотрения вспомогательное зеркало. Поверхность эквивалентного параболоида
представляет собой геометрическое место точек пересечения лучей, создаваемых
облучателем, находящимся в фокусе малого зеркала F2, с лучами, отраженными от основного зеркала (см. рис.9.15).
Двухзеркальная антенна по своим электрическим свойствам
эквивалентна однозеркальной антенне с параболическим зеркалом с фокусным
расстоянием fэ рассчитываемым по формулам,
полученным методом геометрической оптики: fэ = (е +1)f0/(е -1) (вспомогательное зеркало -
гиперболоид); fэ =(е + 1)f0/(1-е)(вспомогательное зеркало - эллипсоид); е - эксцентриситет малого зеркала.
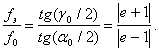 Радиус раскрыва
эквивалентного параболоида равен радиусу раскрыва большого зеркала двухзеркальнои
антенны R0. Величины f0 и
fэ связаны
cоотношением:
Радиус раскрыва
эквивалентного параболоида равен радиусу раскрыва большого зеркала двухзеркальнои
антенны R0. Величины f0 и
fэ связаны
cоотношением:
Амплитудные
распределения в раскрывах эквивалентного параболоида и основного зеркала одинаковы и рассчитываются также,
как в случае однозеркальной антенны. Для получения близкого к равномерному
амплитудного распределения (максимального КИП) ДН облучателя должна быть похожа
на идеализированную диаграмму, изображенную на рис.9.11 (кривая 2).
Фокусное
расстояние эквивалентного параболоида больше фокусного расстояния основного
зеркала. Следовательно, при данном облучателе амплитудное распределение в
раскрыве двухзеркальной антенны получается более равномерным, чем у
однозеркальной антенны с таким же отношением
R0/f0.
Двухзеркалъная антенна обладает
рядом преимуществ по сравнению с однозеркальной. Вспомогательное зеркало
облегчает подбор наиболее благоприятного амплитудного распределения в раскрыве
параболоида (подробный анализ показывает, что трансформация амплитуд поля
источника происходит только на малом зеркале; большое зеркало лишь выравнивает
фазовое распределение) и тем самым обеспечивает сравнительно высокий
результирующий КИП зеркала. Так как в двухзеркальной антенне облучатель можно
расположить близко к основному зеркалу, то упрощается подводка питания к
облучателю, укорачивается длина линии питания и облегчается крепление этой
линии и облучателя. Укорочение линии питания ведет к уменьшению потерь в ней и
снижению шумовой температуры тракта питания, что важно при использовании антенн
в спутниковой и космической радиосвязи.
Применяя в двухзеркальной системе поверхности, несколько
отличные от
правильных параболоидов, эллипсоидов и гиперболоидов (квазипараболические или
оптимизированные антенны), можно добиться более
равномерного амплитудного распределения поля в раскрыве основного зеркала при меньшем переливании энергии через его
края, чем это имеет место в обычной
двухзеркальной антенне. Более равномерное амплитудное распределение в раскрыве
большого зеркала при большом коэффициенте перехвата (v1) обеспечивается малым зеркалом благодаря модификации формы его поверхности. При этом
модифицированная форма поверхности большого зеркала восстанавливает синфазность возбуждения его
раскрыва.
Оптимизация двухзеркальной антенны состоит в подборе
профилей зеркал в
соответствии с заданной формой ДН облучателя. Основными требованиями, предъявляемыми к
форме ДН облучателя оптимизируемой антенны,
являются ее осевая симметрия и минимальная утечка энергии вне сектора облучения
малого зеркала (крутые скаты ДН).
Антенны Кассегрена маркируются АДГ (антенна двухзеркальная с
малым гиперболическим
зеркалом), а антенны Грегори - АДЭ (антенна двухзеркальная с малым эллиптическим зеркалом). Цифра
следующая за АДГ
или АДЭ обозначает диаметр зеркала в метрах.
9.4.
Облучатели зеркальных антенн
В
качестве облучателей зеркальных антенн применяют слабонаправленные антенны,
обладающие однонаправленным излучением (в сторону зеркала). Фазовый центр
облучателя совмещается с фокусом зеркала. Если облучатель не обладает
однозначно выраженным фазовым центром, как, например, пирамидальный рупор, то положение
такого облучателя относительно фокуса параболического зеркала подбирается
экспериментально.
Диаграмма направленности
облучателя должна обеспечивать требуемое амплитудное распределение в раскрыве
зеркала при малом переливании энергии через края зеркала, по возможности
обладать осевой симметрией и минимальным уровнем боковых и задних лепестков.
Диапазонные свойства параболической
антенны, в основном, зависят от облучателя и реакции зеркала на облучатель,
поэтому от него требуется широкая полоса пропускаемых частот, как по
направленным свойствам, так и по согласованию.
Вибраторные
облучатели, питаемые с помощью коаксиальных линий, применяют обычно в
дециметровом диапазоне и в длинноволновой части сантиметрового диапазона. Для
создания однонаправленного излучения используют контррефлекторы в виде
пассивных вибраторов или металлических дисков диаметром (0,7...0,8)λ.
Фазовый центр облучателя находится между вибратором и контррефлектором.
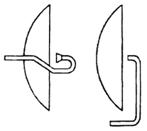
Вибраторы,
питаемые с помощью волноводов, - волноводно-вибраторные облучатели (рис.9.16) -
применяют на волнах короче 10 см. В середине выходного отверстия волновода
перпендикулярно линиям вектора Е устанавливается
тонкая металлическая пластина, к которой крепят два вибратора на расстоянии
примерно (0,3...0,25)λ друг от друга. Вибраторы возбуждаются полем,
выходящим из открытого конца волновода. Длины вибраторов подбираются так, чтобы
второй вибратор играл роль контррефлектора. Фазовый центр располагается между
вибраторами (ближе к первому из них).
Вибраторные
облучатели целесообразно использовать в случае довольно глубоких параболических
зеркал (при 2γ0 = 120...180°).
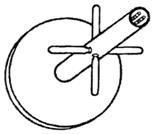
Для
создания круговой поляризации можно применять спиральный или турникетный
облучатель (рис.9.17). Облучатели этого типа используются также в зеркальных
антеннах, если передаваемые поля имеют взаимно перпендикулярную поляризацию. В
этом случае один из вибраторов предназначен для передачи, другой - для приема.
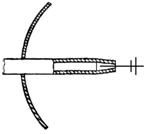
На сантиметровых и более
коротких волнах широко применяют волноводные (круглые и прямоугольные) и рупорные
облучатели (рис.9.18). Эти облучатели позволяют передавать большую мощность и
имеют лучшие диапазонные свойства, чем вибраторные. Рупорный облучатель с
фазирующей секцией позволяет получать волну с круговой поляризацией.
|
|
|
|
|
|
|
Рис.9.16.
Волноводно-вибраторный облучатель
|
|
|
Рис.9.17.
Турникетный облучатель
|
|
|
Рис.9.18.
Рупорный и волноводный облучатели
|
|
|

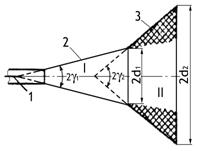



Облучатели,
предназначенные для двухзеркальных неоптимизированных и оптимизированных
антенн, должны иметь ДН с максимумами в направлении кромки малого зеркала и с
небольшой впадиной в направлении его вершины (см. рис.9.11, кривая 3, а лучше 2). Близкую к такой ДН имеют расфазированные
рупоры.
Среди
различных типов рупорных антенн, позволяющих получать требуемую форму ДН
облучателя двухзеркальных антенн, назовем расфазированные рупоры,
расфазированные рупоры с изломом конической образующей (рис.9.19), расфазированные
рупоры с диэлектрической втулкой (рис.9.20), рупор с импедансными структурами
(рис.9.21).
9.5.
Цилиндро-параболическая антенна
В ряде случаев необходимо в двух главных плоскостях иметь
ДН, значительно
отличающиеся по ширине. При этом пространственная ДН будет в форме веера. Для
получения веерной ДН размеры раскрыва антенны в двух взаимно перпендикулярных плоскостях должны быть различны.
Такую диаграмму легко получить с помощью антенны, состоящей
из металлического
зеркала, поверхность которого имеет форму параболического цилиндра, и линейного облучателя,
расположенного вдоль фокальной оси этого цилиндра (рис.9.22). Элементы
линейного излучателя возбуждаются синфазно. Сечение цилиндра плоскостью yoz представляет параболу, а плоскостью xoz - прямую линию. Длина облучателя равна примерно длине (высоте) цилиндра h.
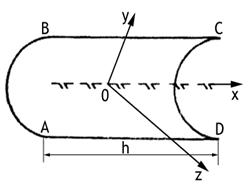 Если
на поверхность цилиндра падает
Если
на поверхность цилиндра падает
 волна, то благодаря геометрическим свойствам параболы эта волна, отражаясь по законам геометрической оптики, трансформируется в плоскости yoz в плоскую. В плоскости xoz
цилиндр не обладает трансформирующими свойствами. Поверхность раскрыва цилиндра ABCD имеет форму прямоугольника со сторонами 2R0=AB и h и возбуждается синфазно. Синфазность возбуждения вдоль
оси у обеспечивается трансформирующими свойствами параболического
цилиндра в плоскости yoz, а вдоль оси х - тем, что все элементы линейного облучателя возбуждаются синфазно и создают вдоль оси облучателя синфазное поле.
волна, то благодаря геометрическим свойствам параболы эта волна, отражаясь по законам геометрической оптики, трансформируется в плоскости yoz в плоскую. В плоскости xoz
цилиндр не обладает трансформирующими свойствами. Поверхность раскрыва цилиндра ABCD имеет форму прямоугольника со сторонами 2R0=AB и h и возбуждается синфазно. Синфазность возбуждения вдоль
оси у обеспечивается трансформирующими свойствами параболического
цилиндра в плоскости yoz, а вдоль оси х - тем, что все элементы линейного облучателя возбуждаются синфазно и создают вдоль оси облучателя синфазное поле.
В плоскости xoz
ДН параболического
цилиндра (см. рис.9.22) копирует ДН синфазного облучателя. Ее ширина определяется линейным
размером облучателя
и амплитудным распределением поля вдоль оси х.
Обычно результирующий КИП параболического
цилиндра не превышает 0,5...0,6.
Параболический цилиндр может облучаться с помощью синфазной многощелевой волноводной
антенны, волноводной многовибраторной антенны,
рупорной линейной решетки, сегментной параболической антенны, уголковой антенны
и т.д.
9.6.
Уголковая антенна
Уголковая
антенна (рис.9.23)
состоит из зеркала (рефлектора 1), образованного
двумя плоскими металлическими пластинами, и вибратора (2) или системы коллинеарных вибраторов, расположенных
в плоскости биссектрисы угла зеркала γ. Поле, излученное антенной, является суммой поля, излучаемого непосредственно
вибратором (облучателем), и поля, создаваемого вторичными токами, текущими по поверхности
зеркала. Подбором
угла γ и расстояния d от оси облучателя до вершины
зеркала максимальное
излучение получается в направлении биссектрисы γ. Угол γ обычно
берется равным 1800 /n, где п - целое число (1, 2, 3, ...).

Рис.9.23.уголковая аннтена (1-уголковое зеркало;
2-облучатель).
|
|
Установлено, что отношение d/λ, следует
выбирать в пределах: 0,25...0,75 при γ=90°; 0,35...0,8 при γ
= 60°; 0,5...1,1 при γ = 45°. Длину зеркала L следует выбирать: L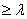 при γ =
90°;
при γ =
90°;  при
γ = 60° и L>2λ при γ = 45°. По высоте (Н) зеркало должно выступать за
пределы вибраторов на (0,1...0,2)λ.
при
γ = 60° и L>2λ при γ = 45°. По высоте (Н) зеркало должно выступать за
пределы вибраторов на (0,1...0,2)λ.
Уголковая антенна
отличается конструктивной простотой. Крепление вибраторов можно осуществлять с
помощью как диэлектрических, так и «металлических» изоляторов, что
предпочтительнее. Такая антенна при ее приемлемых размерах позволяет получать
ДН шириной примерно до 20° (по половинной мощности). По своим направленным
свойствам антенна близка к параболическому цилиндру с такими же размерами.
 Таким образом, характеристику
направленности открытого конца волновода прямоугольного сечения в плоскости Е,
параллельной размеру b поперечного сечения, можно представить в виде
произведения множителя системы плоского раскрыва на характеристику
направленности элемента Гюйгенса в этой плоскости.
Таким образом, характеристику
направленности открытого конца волновода прямоугольного сечения в плоскости Е,
параллельной размеру b поперечного сечения, можно представить в виде
произведения множителя системы плоского раскрыва на характеристику
направленности элемента Гюйгенса в этой плоскости.
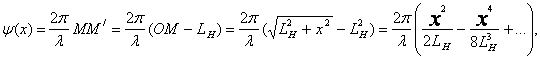






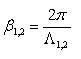 ;
;