ЛЕКЦИЯ 6. АНТЕННЫЕ РЕШЕТКИ С ОСЕВЫМ ИЗЛУЧЕНИЕМ (АНТЕННЫ БЕГУЩЕЙ ВОЛНЫ)
6.1. Излучение равномерного линейного ряда вибраторов, перпендикулярных оси решетки
Рассмотрим
равномерную линейную решетку (рис.4.9.б), состоящую из ряда вибраторов, оси которых
параллельны и каждый вибратор излучает с максимальной интенсивностью вдоль оси решетки
(оси х). Необходимый сдвиг фаз токов, в элементах антенны
(ψ) можно создать с помощью соответствующих фазовращателей. Однако
схема питания антенны при этом получается весьма сложной. Проще
последовательно возбуждать элементы антенны
с помощью бегущей электромагнитной волны, распространяющейся от начала
антенны (первый вибратор) к ее концу с определенной фазовой скоростью. При этом ток в последующем вибраторе отстает
по фазе от тока в предыдущем на величину ψ = β![]() где
где ![]() - расстояние между
вибраторами, β =
- расстояние между
вибраторами, β = ![]() /v
= kc/v - коэффициент фазы, c/v - коэффициент
замедления. Таким образом, если считать, что токи в вибраторах равны по амплитуде,
то
/v
= kc/v - коэффициент фазы, c/v - коэффициент
замедления. Таким образом, если считать, что токи в вибраторах равны по амплитуде,
то
![]()
Так как последующий вибратор возбуждается позже предыдущего, но находится ближе к точке наблюдения, то сдвиг фаз между полями соседних вибраторов в этой точке (фаза поля первого вибратора принимается за нулевую) равен
![]() .
(6.1)
.
(6.1)
Сдвиг фаз между полями крайних вибраторов
Ψn = (n - l) k![]() (cosφ - c/v).
(6.2)
(cosφ - c/v).
(6.2)
Учитывая сказанное, а также то, что имеется только один ряд вибраторов (m=1), можно от формулы (5.3) перейти к формуле (плоскость Е)
Е = (60Iп/ r) [(cos (klsinφ) -
coskl) / cosφ ] *
* sin [(knd1/2) (c/v - cosφ)]/sin[(k![]() /2)(c/v - cosφ)].
(6.3)
/2)(c/v - cosφ)].
(6.3)
Так как в плоскости Н элемент антенны не обладает направленными свойствами (![]() ),
то напряженность поля в этой плоскости определяется по формуле
),
то напряженность поля в этой плоскости определяется по формуле
Е = (60Iп/r)(l- cosk![]() ) sin[(kn
d1/2)(c/v - cosθ)]/sin[(k d1/2)(c/v -
cosθ)]. (6.4)
) sin[(kn
d1/2)(c/v - cosθ)]/sin[(k d1/2)(c/v -
cosθ)]. (6.4)
Как видно из формул (6.3) и (6.4) характеристика направленности в плоскости Н определяется только множителем системы; в плоскости Е характеристика направленности зависит также и от направленных свойств одного элемента решетки, но, в основном, определяется также множителем системы Fс(φ) или Fc(θ). Поэтому далее при анализе направленных свойств антенны бегущей волны (АБВ) будем рассматривать только этот множитель.
Видно, что направленные свойства АБВ зависят от числа элементов решетки n,
расстояния между ними ![]() и от фазовой скорости питающей
волны v. Определим направления нулевого излучения и
максимумов боковых лепестков. Для определения направлений нулевого излучения приравняем
числитель множителя
системы нулю или его аргумент (kn
и от фазовой скорости питающей
волны v. Определим направления нулевого излучения и
максимумов боковых лепестков. Для определения направлений нулевого излучения приравняем
числитель множителя
системы нулю или его аргумент (kn![]() /2)(c/v
- cosθ) = Nπ, где N = 1,2, ... . Отсюда
/2)(c/v
- cosθ) = Nπ, где N = 1,2, ... . Отсюда
n![]() (c/v
- cosθ) = Nλ и
(c/v
- cosθ) = Nλ и ![]() = arccos (c/v
- Nλ / n
= arccos (c/v
- Nλ / n![]() ). (6.5)
). (6.5)
Для определения направлений максимумов боковых лепестков приравняем числитель множителя системы единице или его аргумент
(kn![]() /2)
> (c/v - cosθ) =
(2N+1) (π/2), где N = 1,2, .... Отсюда
/2)
> (c/v - cosθ) =
(2N+1) (π/2), где N = 1,2, .... Отсюда
n![]() (c/v - cosθ) = (2N+1)[
(c/v - cosθ) = (2N+1)[![]() /(2n
/(2n![]() )]и θmaxN = arcos{ c/v -(2N+1) (λ/(2n
)]и θmaxN = arcos{ c/v -(2N+1) (λ/(2n![]() )} (6.6)
)} (6.6)
Рассмотрим три режима работы антенны бегущей волны: 1) v = с; c/v = 1 (волна свободного пространства); 2) v > с; c/v < 1 (быстрая волна) и 3) v < с; c/v >1 (медленная волна).
1) c/v=l.
В этом случае при ![]() =0° множитель системы максимален и равен n.
Нормированный множитель системы
=0° множитель системы максимален и равен n.
Нормированный множитель системы
Fc (θ) = (1/n) sin
[(kn![]() /2)(l - cosθ)]/sin [(k
/2)(l - cosθ)]/sin [(k![]() /2)(l - cosθ)]. (6.7)
/2)(l - cosθ)]. (6.7)
Результирующее поле максимально в направлении θ = 0° вследствие того, что поля от
всех элементов антенны в точке наблюдения складываются синфазно, так как сдвиг
фаз из-за несинфазности возбуждения Ψ полностью компенсируется
пространственным сдвигом фаз Ψр. При увеличении или уменьшении угла ![]() (это же относится и к
углу θ) Ψ
(это же относится и к
углу θ) Ψ ![]() Ψр . Вследствие
этого напряженность результирующего поля в
точке наблюдения, характеризуемой
Ψр . Вследствие
этого напряженность результирующего поля в
точке наблюдения, характеризуемой
|
|
|
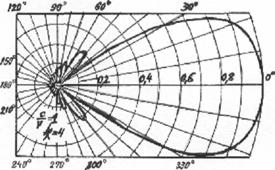
Рис. 6.1. ДН АБВ при C/V = 1 |
некоторым углом θ ![]() 00, будет меньше, чем в точке,
лежащей на продолжении оси антенны. Если cosθ отрицателен (90°<θ<270°), то фазовые сдвиги Ψ и Ψр при
00, будет меньше, чем в точке,
лежащей на продолжении оси антенны. Если cosθ отрицателен (90°<θ<270°), то фазовые сдвиги Ψ и Ψр при ![]() < λ/2 имеют
одинаковые знаки. В этом случае вибратор, возбуждающийся раньше, находится ближе к точке наблюдения,
чем вибратор, возбуждающийся позже (пространственный сдвиг фаз отрицателен). Сдвиг фаз
< λ/2 имеют
одинаковые знаки. В этом случае вибратор, возбуждающийся раньше, находится ближе к точке наблюдения,
чем вибратор, возбуждающийся позже (пространственный сдвиг фаз отрицателен). Сдвиг фаз ![]() между
полями соседних вибраторов при малых
между
полями соседних вибраторов при малых ![]() велик и результирующее
поле в точке наблюдения мало. Следовательно, антенна бегущей волны
обладает преимущественно однонаправленными свойствами и излучает с
максимальной интенсивностью вдоль своей оси (антенна с осевым излучением)
(рис.6.1). На практике встречаются антенны бегущей волны, которые можно
рассматривать как непрерывное линейное распределение слабонаправленных излучателей
(например, диэлектрическая антенна). Без учета затухания возбуждающего тока по
длине антенны множитель системы может быть получен из выражения (6.7)
велик и результирующее
поле в точке наблюдения мало. Следовательно, антенна бегущей волны
обладает преимущественно однонаправленными свойствами и излучает с
максимальной интенсивностью вдоль своей оси (антенна с осевым излучением)
(рис.6.1). На практике встречаются антенны бегущей волны, которые можно
рассматривать как непрерывное линейное распределение слабонаправленных излучателей
(например, диэлектрическая антенна). Без учета затухания возбуждающего тока по
длине антенны множитель системы может быть получен из выражения (6.7)
путем предельного перехода.
Полагая n =>![]() , d=>0, n
, d=>0, n![]() =>L,
получаем
=>L,
получаем
Fc(θ) = sin[(kL/2)(l- cosθ)]/[(kL/2)(l- cosθ)] . (6.8)
Уровень первого
бокового лепестка ξ1 =F(θ1mах)=2/3π ![]() 0,21
такой же, как у синфазной решетки вибраторов. Ширину диаграммы направленности по
направлениям нулевого излучения найдем из условия (kL/2)(l-cosφ0) = π. При малых значениях λ/L (L - длина антенной решётки)
0,21
такой же, как у синфазной решетки вибраторов. Ширину диаграммы направленности по
направлениям нулевого излучения найдем из условия (kL/2)(l-cosφ0) = π. При малых значениях λ/L (L - длина антенной решётки)
2θ0=![]() (6.9)
(6.9)
Ширина диаграммы направленности по половинной мощности может быть определена по приближенной формуле
2θ 0,5 ![]() 108°
108°![]() .
(6.10)
.
(6.10)
Сравнивая данную антенну с равномерной синфазной решеткой, следует отметить, что хотя диаграмма направленности АБВ получается шире, чем у синфазной решетки такой же длины, но зато один ряд вибраторов, возбуждаемых бегущей волной тока, обладает направленными свойствами в любой плоскости, проходящей через ось антенны, в то время как один ряд синфазной решетки обладает направленными свойствами только в одной плоскости. Если элементы АБВ не обладают направленным действием или оно невелико, то диаграмму направленности антенны можно считать осесимметричной. При этом КНД антенны бегущей волны можно определить по общей формуле
D0= kL/ [Si2kL - (l - cos2kL)/(2kL)]. (6.11)
При 2kL » I (практически при L/λ > 1) D0![]() 4L /λ.
4L /λ.
2) c/v < I. На основании формулы
(6.4), имея в виду, что при условии cosθ = c/v, множитель системы максимален и равен n (при этом условии множитель системы
обращается в неопределенность вида 0/0), и используя предельный переход (![]() =>0, n=>
=>0, n=>![]() , n
, n![]() >L),
получаем нормированную
характеристику направленности
>L),
получаем нормированную
характеристику направленности
F(θ) = sin[(kL/2)( c/v - cosθ)]/[(kL/2)( c/v - cosθ)]. (6.12)
Условие cosθ = c/v может выполняться при двух значениях угла θ = ± θ mах, следовательно, имеются два направления максимального излучения, не совпадающие с осью антенны. Данный режим работы является невыгодным, так как направленные свойства антенны ухудшаются. Однако антенны быстрых волн находят применение для создания диаграмм направленности специальной формы для качания (сканирования) диаграммы направленности. Основой большинства антенн быстрых волн являются волноводные структуры с неоднородностями (например, волновод со щелями).
3) c/v > 1. Как видно из выражений (6.1) и (6.2), в данном случае отсутствует направление, в котором поля отдельных элементов антенны складываются синфазно, так как ни при каком значении θ отношение c/v не может стать равным cosθ и сдвиг фаз не может обратиться в нуль.
Наименьший фазовый сдвиг между
полями отдельных вибраторов Ψ1min = kd1(c/v - 1) получается в направлении θ =![]() ,
т.е. вдоль оси антенны. Поля отдельных
вибраторов в точке наблюдения, лежащей в направлении θ =
,
т.е. вдоль оси антенны. Поля отдельных
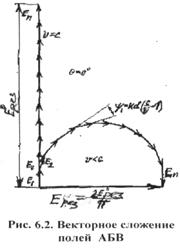
вибраторов в точке наблюдения, лежащей в направлении θ =![]() , в данном случае складываются геометрически, как
показано на временной векторной диаграмме (рис.6.2). Расчеты по формулам (6.4)
и (6.12) показывают, что уменьшение фазовой скорости, начиная от v = c, сопровождается постепенным
сужением основного лепестка диаграммы направленности и ростом боковых
лепестков. Излучение в главном направлении θ =
, в данном случае складываются геометрически, как
показано на временной векторной диаграмме (рис.6.2). Расчеты по формулам (6.4)
и (6.12) показывают, что уменьшение фазовой скорости, начиная от v = c, сопровождается постепенным
сужением основного лепестка диаграммы направленности и ростом боковых
лепестков. Излучение в главном направлении θ =![]() , сначала растет, достигая максимума при некоторой
определенной (для данного значения L =
, сначала растет, достигая максимума при некоторой
определенной (для данного значения L =![]() )
величине c/v,
а затем начинает уменьшаться и обращается в нуль при критической величине c/v
)
величине c/v,
а затем начинает уменьшаться и обращается в нуль при критической величине c/v
(c/v)кр = 1+(![]() /nd1).
(6.13)
/nd1).
(6.13)
Сужение главного лепестка диаграммы направленности приводит к росту КНД антенны, а увеличение уровня боковых лепестков - к его уменьшению. При увеличении c/v, начиная от c/v = 1, сначала увеличивается КНД
 из-за сужения
диаграммы направленности. После достижения некоторой определенной величины c/v дальнейший
ее рост приводит к уменьшению КНД из-за увеличения уровня боковых лепестков.
Следовательно,
имеется оптимальная величина c/v (при заданной длине антенны L), при которой КНД достигает максимального значения. В случае ненаправленных элементов
антенны формула для КНД оказывается весьма громоздкой. Ее
анализ показывает, что КНД антенны бегущей волны при заданной длине антенны зависит от величины результирующего
сдвига фаз между полями, создаваемыми крайними (первым и последним) элементами антенны в точке наблюдения, лежащей на продолжении ее оси (θ = 0°). КНД получается максимальным, если
сдвиг фаз ψn, определяемый по
формуле (6.2), равен 180°, т.е. если поля, создаваемые крайними элементами
антенны бегущей волны в точке, лежащей на продолжении оси антенны, находятся в
противофазе (см. рис.6.2). Таким образом, на основании формулы (6.2) условием
получения максимального КНД
является
из-за сужения
диаграммы направленности. После достижения некоторой определенной величины c/v дальнейший
ее рост приводит к уменьшению КНД из-за увеличения уровня боковых лепестков.
Следовательно,
имеется оптимальная величина c/v (при заданной длине антенны L), при которой КНД достигает максимального значения. В случае ненаправленных элементов
антенны формула для КНД оказывается весьма громоздкой. Ее
анализ показывает, что КНД антенны бегущей волны при заданной длине антенны зависит от величины результирующего
сдвига фаз между полями, создаваемыми крайними (первым и последним) элементами антенны в точке наблюдения, лежащей на продолжении ее оси (θ = 0°). КНД получается максимальным, если
сдвиг фаз ψn, определяемый по
формуле (6.2), равен 180°, т.е. если поля, создаваемые крайними элементами
антенны бегущей волны в точке, лежащей на продолжении оси антенны, находятся в
противофазе (см. рис.6.2). Таким образом, на основании формулы (6.2) условием
получения максимального КНД
является
ψn опт. = kL(c/v - 1) = ![]() .
(6.14)
.
(6.14)
Воспользовавшись этой формулой, можно определить оптимальную величину c/v при заданной длине антенны L или определить оптимальную длину антенны при заданной фазовой скорости. Очевидно, что:
(c/v)опт.
![]() ,
(6.15)
,
(6.15)
(L/![]() )опт. =
1/[2(c/v - 1)].
(6.16)
)опт. =
1/[2(c/v - 1)].
(6.16)
Как видно из формулы (6.14), оптимальная длина антенны увеличивается при увеличении фазовой скорости. В случае выполнения условия (6.14) КНД определяется по формуле
![]() ,
(6.17)
,
(6.17)
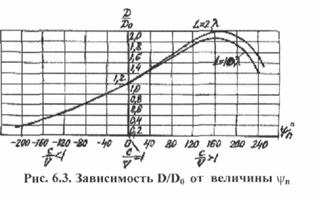
где D0 - КНД антенны бегущей волны данной длины при с/v =1. На рис.6.3 приведены графики зависимости отношения D/D0 от сдвига фаз между полями крайних элементов антенны ψn, где D - КНД антенны определенной длины, работающей в режиме замедления (v < с) или ускорения (v >c).
 Как
видно из векторной временной диаграммы (рис.6.2), в оптимальном случае (ψn = 180°) вектор напряженности результирующего поля
в π/2 раз меньше, чем в случае АБВ, работающей в первом режиме
(приближенно можно считать, что вектор напряженности результирующего поля в оптимальном
случае равен
диаметру окружности, половина длины которой равна вектору напряженности
результирующего поля при c/v =
1).
Казалось бы, что КНД первой антенны должен быть меньше, чем второй. Увеличение
КНД антенны, работающей в режиме, близком к оптимальному, объясняется тем что при оптимальном и близких к нему отношениях c/v токи
в элементах антенны из-за взаимного влияния возрастают. В частности, при
оптимальном отношении c/v ток
в элементах антенны увеличивается примерно в (π/2)
Как
видно из векторной временной диаграммы (рис.6.2), в оптимальном случае (ψn = 180°) вектор напряженности результирующего поля
в π/2 раз меньше, чем в случае АБВ, работающей в первом режиме
(приближенно можно считать, что вектор напряженности результирующего поля в оптимальном
случае равен
диаметру окружности, половина длины которой равна вектору напряженности
результирующего поля при c/v =
1).
Казалось бы, что КНД первой антенны должен быть меньше, чем второй. Увеличение
КНД антенны, работающей в режиме, близком к оптимальному, объясняется тем что при оптимальном и близких к нему отношениях c/v токи
в элементах антенны из-за взаимного влияния возрастают. В частности, при
оптимальном отношении c/v ток
в элементах антенны увеличивается примерно в (π/2)![]() раз по сравнению с током в элементах антенны, работающей в режиме c/v =
1 (при неизменной излучаемой мощности). Это приводит к увеличению напряженности поля, излучаемого каждым элементом
антенны. Приведенные здесь соотношения,
характеризующие оптимальный режим работы АБВ, справедливы только для
ненаправленных или слабонаправленных элементов антенны. При наличии у элементов антенны значительных направленных свойств эти
соотношения изменяются. Ширина диаграммы
направленности по нулевому излучению антенны,
работающей в оптимальном режиме, на основании формулы (6.12) находится из условия (kL/2)(c/v
- cos
раз по сравнению с током в элементах антенны, работающей в режиме c/v =
1 (при неизменной излучаемой мощности). Это приводит к увеличению напряженности поля, излучаемого каждым элементом
антенны. Приведенные здесь соотношения,
характеризующие оптимальный режим работы АБВ, справедливы только для
ненаправленных или слабонаправленных элементов антенны. При наличии у элементов антенны значительных направленных свойств эти
соотношения изменяются. Ширина диаграммы
направленности по нулевому излучению антенны,
работающей в оптимальном режиме, на основании формулы (6.12) находится из условия (kL/2)(c/v
- cos![]() 0)= π. Подставляя вместо c/v выражение
(6.15) и проводя рассуждения, аналогичные
случаю c/v = 1, получаем sinθ0
=
0)= π. Подставляя вместо c/v выражение
(6.15) и проводя рассуждения, аналогичные
случаю c/v = 1, получаем sinθ0
=![]() . При малых отношениях λ/L синус можно заменить аргументом. Тогда
. При малых отношениях λ/L синус можно заменить аргументом. Тогда
![]() (6.18)
(6.18)
и, как видно из
сравнения формул (6.9) и (6.18), в этом случае АБВ с пониженной фазовой
скоростью (оптимальной) имеет диаграмму направленности в ![]() раз уже,
чем антенна той же длины с c/v =
1. Ширина диаграммы направленности по половинной мощности может быть
приближенно определена (для антенны, у которой L/λ
»1) по
раз уже,
чем антенна той же длины с c/v =
1. Ширина диаграммы направленности по половинной мощности может быть
приближенно определена (для антенны, у которой L/λ
»1) по
![]() формуле:
формуле:
(6.19)
Диаграмма направленности АБВ с пониженной фазовой скоростью, имеющей оптимальную
длину, изображена на рис.6.4. Сужение диаграммы направленности антенны оптимальной
длины по сравнению с диаграммой направленности антенны такой же длины, но
работающей в первом режиме (c/v =
1), объясняется тем, что при увеличении угла φ напряженность результирующего поля в
случае c/v >1 убывает
значительно быстрее, чем в случае c/v =
1. Это происходит потому, что в случае антенны оптимальной длины сдвиги фаз
между полями соседних вибраторов в точке наблюдения, определяемой углом
θ1 [при этом ![]() ], больше, чем в случае антенны с c/v =
1 [при этом
], больше, чем в случае антенны с c/v =
1 [при этом ![]() ].
].

Определим уровень
первого бокового лепестка диаграммы направленности оптимальной антенны. Максимальная величина нормированной характеристики направленности оптимальной антенны,
определяемая по формуле (6.12), при θ = ![]() и
c/v = 1+λ/2L равна 2π.
Значение F(θ) в направлении максимума первого
бокового лепестка можно определить, положив аргумент синуса в формуле
(6.12) равным 3π /2 и найдя из этого равенства cos θ1max. Подставляя в формулу (6.12) найденное значение cosθ1max и заменяя c/v его
выражением
(6.15), получаем F(θlmax) = 2π/3. Отсюда уровень первого бокового лепестка
и
c/v = 1+λ/2L равна 2π.
Значение F(θ) в направлении максимума первого
бокового лепестка можно определить, положив аргумент синуса в формуле
(6.12) равным 3π /2 и найдя из этого равенства cos θ1max. Подставляя в формулу (6.12) найденное значение cosθ1max и заменяя c/v его
выражением
(6.15), получаем F(θlmax) = 2π/3. Отсюда уровень первого бокового лепестка ![]()
При увеличении длины антенны по сравнению с оптимальной излучение в главном направлении уменьшается и растут боковые лепестки. При L = 2LОПТ излучение в главном направлении совершенно исчезает. При уменьшении длины антенны по сравнению с оптимальной главный лепесток диаграммы направленности расширяется, уровень боковых лепестков уменьшается. Для того чтобы диаграмма направленности становилась уже, надо увеличивать длину антенны. Вместе с тем, чтобы при удлинении антенны бегущей волны ее длина оставалась оптимальной, необходимо в соответствии с соотношением (6.14) увеличивать фазовую скорость волны в антенне.
В антеннах бегущей волны, применяющихся на практике, амплитуда возбуждающего тока
уменьшается вдоль оси решетки по экспоненциальному закону, т.е. I2 =![]() . Это имеет место вследствие потерь энергии в антенне или
вследствие постепенного излучения энергии элементами антенны. Степень убывания
бывает разной и в некоторых случаях, при расчетах этим уменьшением
пренебрегают. Убывание амплитуды тока приводит к расширению основного лепестка
диаграммы направленности, к увеличению уровня боковых лепестков и к
исчезновению направлений нулевого излучения, которые заменяются направлениями
минимального
излучения.
. Это имеет место вследствие потерь энергии в антенне или
вследствие постепенного излучения энергии элементами антенны. Степень убывания
бывает разной и в некоторых случаях, при расчетах этим уменьшением
пренебрегают. Убывание амплитуды тока приводит к расширению основного лепестка
диаграммы направленности, к увеличению уровня боковых лепестков и к
исчезновению направлений нулевого излучения, которые заменяются направлениями
минимального
излучения.
Практическим примером выполнения антенны бегущей волны в виде ряда вибраторов является директорная
антенна, широко применяемая в УКВ диапазоне (особенно на метровых и
дециметровых волнах). Эта антенна состоит из одного питаемого (активного) и
нескольких пассивных вибраторов, один из которых работает в режиме рефлектора, а остальные - в
режиме директора. Оси всех вибраторов
параллельны. Пассивные вибраторы возбуждаются электромагнитным полем активного вибратора. Длина активного вибратора (2![]() ) обычно берется
несколько меньше λ/2 с тем, чтобы он был резонансным. Для того
чтобы пассивный вибратор работал в режиме рефлектора, его входное сопротивление должно иметь индуктивный характер, что
достигается некоторым удлинением этого вибратора по сравнению с активным. Пассивный вибратор, работающий в режиме
директора, должен обладать реактивным
сопротивлением емкостного характера, для чего он должен быть несколько короче активного вибратора. Так как
рефлектор усиливает поле в направлении
активного вибратора (вперед) и ослабляет поле в обратном направлении, то применение нескольких рефлекторов
не имеет смысла, так как все рефлекторы, следующие за первым, будут очень слабо
возбуждаться. Первый директор усиливает поле в направлении следующего директора
и поэтому, если установить несколько директоров, то все они будут возбуждаться достаточно интенсивно. Длины директоров и
расстояния между ними подбирают так, чтобы в каждом последующем вибраторе ток
отставал по фазе от тока в предыдущем на величину
) обычно берется
несколько меньше λ/2 с тем, чтобы он был резонансным. Для того
чтобы пассивный вибратор работал в режиме рефлектора, его входное сопротивление должно иметь индуктивный характер, что
достигается некоторым удлинением этого вибратора по сравнению с активным. Пассивный вибратор, работающий в режиме
директора, должен обладать реактивным
сопротивлением емкостного характера, для чего он должен быть несколько короче активного вибратора. Так как
рефлектор усиливает поле в направлении
активного вибратора (вперед) и ослабляет поле в обратном направлении, то применение нескольких рефлекторов
не имеет смысла, так как все рефлекторы, следующие за первым, будут очень слабо
возбуждаться. Первый директор усиливает поле в направлении следующего директора
и поэтому, если установить несколько директоров, то все они будут возбуждаться достаточно интенсивно. Длины директоров и
расстояния между ними подбирают так, чтобы в каждом последующем вибраторе ток
отставал по фазе от тока в предыдущем на величину![]() , несколько большую
величины k
, несколько большую
величины k![]() Такую антенну можно рассматривать как АБВ с
пониженной фазовойскоростью (c/v > 1). Максимум
излучения совпадает с осью антенны (
Такую антенну можно рассматривать как АБВ с
пониженной фазовойскоростью (c/v > 1). Максимум
излучения совпадает с осью антенны (![]() ).
).
6.2. Излучение провода, ток в котором изменяется по закону бегущей волны
Рассмотрим провод длиной L, ток в котором
изменяется по закону бегущей
волны. Пренебрегая затуханием, Iz = I0exp[-ik(c/v)z],
где I0 - амплитуда
тока в начале провода; z - текущая координата.
Из формулы (6.12) известен множитель системы в случае непрерывного
распределения источников поля. На основании правила перемножения
характеристик направленности нормированная характеристика направленности провода
![]()
(6.20)
где sin![]() - характеристика
направленности элемента провода.
- характеристика
направленности элемента провода.
Множитель системы выражения (6.20) максимален при
![]() =
= ![]() (если
v = c). Однако
результирующее поле провода в направлении его оси
(если
v = c). Однако
результирующее поле провода в направлении его оси ![]() =
= ![]() ) равно нулю, так как sin
) равно нулю, так как sin![]() в формуле (6.20) обращается в нуль. Физически это объясняется тем, что
элементарный вибратор не излучает вдоль своей оси. Так как множитель
системы максимален в направлении оси провода (это направление наиболее
благоприятно для сложения полей отдельных элементов провода), а характеристика
направленности элемента провода максимальна в направлении, перпендикулярном оси
провода (
в формуле (6.20) обращается в нуль. Физически это объясняется тем, что
элементарный вибратор не излучает вдоль своей оси. Так как множитель
системы максимален в направлении оси провода (это направление наиболее
благоприятно для сложения полей отдельных элементов провода), а характеристика
направленности элемента провода максимальна в направлении, перпендикулярном оси
провода (![]() = 90°), то
результирующее поле оказывается максимальным в некотором промежуточном направлении,
составляющем угол
= 90°), то
результирующее поле оказывается максимальным в некотором промежуточном направлении,
составляющем угол ![]() max (меньший 90°) с осью провода. Очевидно, что таких направлений имеется
два (в первом и в четвертом квадрантах). При большой относительной длине провода L/λ характеристика направленности приблизительно становится максимальной, когда максимален числитель множителя системы
(первый максимум). Поэтому угол максимального излучения можно приближенно найти из выражения
max (меньший 90°) с осью провода. Очевидно, что таких направлений имеется
два (в первом и в четвертом квадрантах). При большой относительной длине провода L/λ характеристика направленности приблизительно становится максимальной, когда максимален числитель множителя системы
(первый максимум). Поэтому угол максимального излучения можно приближенно найти из выражения
cos ![]() max=(2L - λ)/2L.
(6.21)
max=(2L - λ)/2L.
(6.21)
|
|
Чем больше относительная длина провода L/λ, тем меньше угол ![]() тах, т.е. тем сильнее излучаемое поле прижато к оси провода.
Чем больше L/λ, тем уже главный лепесток диаграммы
направленности, но тем больше количество и уровень боковых лепестков.
Главные лепестки диаграммы направленности наклонены в сторону движения волны в
проводе (рис.6.5), т.е. пространственная диаграмма направленности имеет вид
конуса. Вследствие наличия двух направлений максимального излучения (в одной
плоскости) нецелесообразно применять одиночный провод с бегущей волной тока в
качестве антенны. Однако в антенной технике с успехом применяются различные комбинации из таких проводов,
обладающие достаточно хорошими направленными свойствами (например, ромбическая
антенна).
тах, т.е. тем сильнее излучаемое поле прижато к оси провода.
Чем больше L/λ, тем уже главный лепесток диаграммы
направленности, но тем больше количество и уровень боковых лепестков.
Главные лепестки диаграммы направленности наклонены в сторону движения волны в
проводе (рис.6.5), т.е. пространственная диаграмма направленности имеет вид
конуса. Вследствие наличия двух направлений максимального излучения (в одной
плоскости) нецелесообразно применять одиночный провод с бегущей волной тока в
качестве антенны. Однако в антенной технике с успехом применяются различные комбинации из таких проводов,
обладающие достаточно хорошими направленными свойствами (например, ромбическая
антенна).