ЛЕКЦИЯ 5. АНТЕННЫЕ РЕШЕТКИ С ПОПЕРЕЧНЫМ ИЗЛУЧЕНИЕМ

5.1. Плоская антенная решетка. Равномерная линейная антенная решетка

Пусть имеется ряд из n симметричных вибраторов, одинаковым образом ориентированных в пространстве (рис.4.9.а). Расстояние между центрами соседних вибраторов равно d₁. Линейной решеткой называется система идентичных излучателей, центры излучения которых расположены на прямой, называемой осью решетки. Будем считать, что токи во всех элементах решетки имеют одинаковую величину (I₁=I₂=…I_n = I), фаза же тока в каждом последующем вибраторе данного ряда отстает от фазы тока в предыдущем на величину . Таким образом, I₂ = Iexp(-i)...I_n = Iexp[-i(n-l)]. Следовательно, вдоль каждого ряда вибраторов фаза возбуждающего тока изменяется по линейному закону.

Рис. 5.1. К определению множителя решётки поперечного излучения

Рассмотрим вначале линейную систему из n ненаправленных излучателей, расположенных на равных расстояниях друг от друга, возбужденных токами, равными по амплитуде. Такая система вибраторов называется эквидистантной равноамплитудной решеткой. Пусть фаза тока в каждом последующем вибраторе отстает на угол  по отношению к току предыдущего. На большом удалении от антенны в точке М, когда d₁<<r, лучи от отдельных вибраторов можно считать параллельными. Поле в точке М (рис.5.1.а), созданное вибратором 1, обозначим через E₁. В равноамплитудной решетке амплитуды поля, созданные различными вибраторами на большом удалении, можно принять равными амплитуде поля первого вибратора, но фазы этих полей будут различными. Поле Е₂ вибратора 2 за счет разности хода лучей r будет опережать поле вибратора 1 по фазе на угол kr = kd₁sin и отставать на угол  за счет питания. Результирующий сдвиг по фазе между полями, созданными вибраторами 1 и 2 равен Ф = kd₁sin(-). Этот сдвиг по фазе будет и для полей, созданных любыми соседними вибраторами. На рис.5.1.б приведено графическое сложение полей отдельных вибраторов, сдвинутых по фазе друг относительно друга на угол Ф.

Векторы полей образуют часть правильного многоугольника, замыкающая сторона которого Е_n равна результирующей напряженности поля, созданной всеми вибраторами в точке М. Перпендикуляры, восстановленные из середин сторон (векторов Е) правильного многоугольника, пересекутся в одной точке 0, являющейся центром описанной окружности радиуса . Для треугольников ОАВ и ОАС можно записать

sin(Ф/2) = АВ/ = Е₁/2 и sin(nФ/2) = АС/ = Е_n/2. Поделив одно уравнение на другое, получим

Е_n/Е₁= sin (0,5 nФ)/sin(0,5Ф) или Е_n = Е₁f_с (), где Ф = kd₁sin-;

f_c() = sin (0,5 nФ)/sin(0,5Ф) = sin[0,5 n(kd₁sin -)]/ sin[0,5(kd₁sin -)] (5.1) - множитель системы (решетки) излучателей.

Здесь рассматривалась решетка, состоящая из ненаправленных излучателей. Если линейную решетку составить из направленных излучателей, например, симметричных вибраторов, то поле Е₁ созданное каждым вибратором, определится его направленными свойствами f₁() и результирующая характеристика направленности будет равна

f() = f₁() f_c(). (5.2)

На основании выражения (5.2) может быть сформулирован общий принцип умножения характеристик направленности: характеристика направленности системы (антенной решетки) однотипных излучателей представляет собой произведение характеристики направленности одного элемента данной системы на множитель системы.

При большом числе вибраторов n множитель системы при изменении угла  изменяется, значительно быстрее чем множитель f₁(). Это объясняется тем, что величина nkd₁/2 значительно больше величины kl. Поэтому характеристика направленности решетки, в основном, определяется множителем системы. Поскольку множитель системы sin(nu)/sin(u) является периодической функцией, то при изменении угла этот множитель может обращаться в нуль, затем он возрастает, достигая максимального значения, далее уменьшается, снова становится равным нулю и т.д. Поэтому можно утверждать, что диаграмма направленности решетки имеет многолепестковый характер.

5.2. Синфазная решетка

Широкое практическое применение находят антенные решетки с одинаковыми по амплитуде и фазе токами в вибраторах (равноамплитудные синфазные решетки). Полагая в формуле (5.1) =0⁰, получим формулу для характеристики направленности, такой решетки из т рядов в плоскости E

E= (m60I_п/r)[(cos(klsin) -coskl)/ соs] *

*sin [(n/2) (kd₁sin)]/sin [(l/2) (kd₁sin)]. (5.3)

Напряженность, излучаемого антенной, поля максимальна в направлении =0° (главный максимум), т.е. в экваториальной плоскости антенны. Каждый из вибраторов в этом направлении излучает с максимальной интенсивностью, если l/0,7; множитель f₁() в этом случае равен 1 - coskl. Поля от отдельных вибраторов в направлении =0⁰ синфазны и складываются арифметически, так как в направлении нормали к осям вибраторов разность расстояний до точки наблюдения равна нулю. Выражение множителя системы в этом случае представляет собой неопределенность вида 0/0 , при раскрытии которой по правилу Лопиталя оказывается, что множитель системы максимален и равен n. Таким образом, в данном случае выражение (5.3) принимает вид Е_mах= nЕ_1mах. Здесь n - число симметричных вибраторов в решетке. Такой же вид принимает выражение (5.3) и при =180⁰. Как следует из формулы (5.3), нормированная характеристика направленности определяется выражением

F () = (Е/Е_макс) = [(cos (klsin) - coskl) / соs (1- coskl)] *
*sin [(n/2) (kd₁sin)]/ {[nsin (l/2) kd₁sin)]}.             (5.4)

При некоторых значениях угла  сдвиг фаз между полями соседних вибраторов, равный kd₁sin, становится таким, что в результате интерференции полей от всех вибраторов суммарное поле обращается в нуль. Направления, в которых отсутствует излучение, определяются из условия равенства нулю числителя множителя системы, т.е. (nkd₁/2)sin₀ = N, откуда sin₀ = N/(nd₁), N = 1, 2, 3, ... . Так как синус всегда меньше единицы, то чем больше знаменатель, тем больше направлений нулевого излучения (N) имеет диаграмма направленности. Следовательно, чем больше число вибраторов п (точнее, чем больше относительный размер nd₁/ решетки), тем больше лепестков в диаграмме направленности. Направления нулевого излучения рассчитываются по формуле

₀=arcsin [N/(nd₁)], где N= 1, 2, 3, ... (5.5)

Направления максимумов боковых лепестков приближенно можно найти из условия максимума числителя множителя системы, так как знаменатель этого множителя при kd₁<<nkd₁ (т.е. при большом числе вибраторов) с изменением угла  изменяется значительно медленнее числителя. Это условие записывается в виде sin[(nkd₁/2)sin_max] = ±1, откуда   nu=(nkd₁/2)sin_max = (2N+l)/2,   N= 1,2,3,...

Направления максимумов боковых лепестков рассчитываются по формуле

_max = arcsin[(2N+l)/(2nd₁)], где N= 1,2,3, ... (5.6)

На рис.5.2 приведены диаграммы направленности синфазной решетки (в плоскости Е) для разного количества симметричных полуволновых вибраторов и расстояния между ними. Ближайшее к главному максимуму направление нулевого излучения определяют по формуле sin₀ = /(nd₁).

Следовательно, главный лепесток диаграммы направленности заключен в угле, равном 2₀. Как видно из формулы главный лепесток диаграммы направленности тем уже, чем больше вибраторов в одном ряду, или чем больше относительная длина антенны nd₁/ = L/.

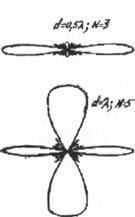
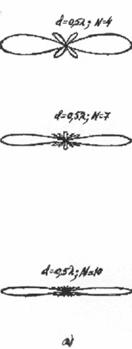
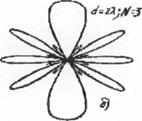
Рис. 5.2. ДН синфазных антенных решёток

2₀ = 2(/nd₁), рад или 2₀ 115°/nd₁. (5.7)

В случае равномерной синфазной решетки ширину диаграммы направленности по половинной мощности можно определить по приближенной формуле

2_0,5 0,89(/nd₁),    рад или 2_0,5 51⁰ /nd_1. (5.8)

Симметричный вибратор с относительной длиной l/ = 0,5 имеет ширину диаграммы направленности шириной по половинной мощности 44°. Для того чтобы сузить диаграмму направленности до 6,4°, т.е. примерно в 7 раз, надо применить 8 синфазных симметричных вибраторов, т.е. увеличить размер антенны примерно в 8 раз.

Направленные свойства антенны характеризуются не только шириной главного лепестка диаграммы направленности, но и уровнем боковых лепестков

_N= l/nsin{[(2N+l)/n)](/2)}. (5.9)

При большом значении n (аргумент синуса мал) можно перейти к следующей приближенной формуле для расчета первых двух боковых лепестков _N= 2/[(2N+l)]. В этом случае уровень первого бокового лепестка ₁=2/3  0,21. Уровень второго бокового лепестка составляет примерно 0,13. Уровень первого бокового лепестка в децибеллах составляет примерно -13,3 дБ. Отметим, что два главных максимума (при =0° и =180°) или два главных лепестка в диаграмме направленности получаются только при d₁<. При d₁  возможно одновременное обращение в нуль числителя и знаменателя множителя системы при некоторых значениях углов, не равных 0° и 180°. Это происходит при выполнении условия (kd₁sin)/2 = N или kd₁sin = 2N, т.е. в том случае, когда сдвиг фаз между полями соседних вибраторов равен или кратен 2. При этом множитель системы, как и в случаях =0° и =180°, имеет наибольший максимум, равный n. Это приводит к появлению в диаграмме направленности антенны, кроме боковых лепестков дополнительных (вторичных) боковых лепестков. Уровень этих лепестков тем больше, чем шире диаграмма направленности одного элемента решетки. Он равен единице, если элементы не обладают направленными свойствами.

Так как симметричный вибратор не обладает направленными свойствами в экваториальной плоскости, то характеристика направленности синфазной решетки в плоскости H определяется только множителем системы, который совершенно аналогичен этому множителю для плоскости E. Ширину диаграммы направленности, направления максимумов боковых лепестков и их уровень определяют по формулам, полученным для плоскости вектора Е решетки, заменяя в них угол   углом . Чем больше рядов m в синфазной решетке, тем уже ее диаграмма направленности в плоскости H. КНД синфазной решетки в направлении максимального излучения может быть рассчитан по формуле

D = (120/ R_полн) (mn)² (1-coskl)², (5.10)

где R_полн - полное сопротивление излучения антенны. Заметим, что при

d₁=>0, d₂=>0, n=>, m=> но при nd₁= const = b и md₂ = const = а, где а и b –

размеры излучающей системы в плоскостях Н и Е соответственно, с помощью предельного перехода можно перейти от формул характеристик направленности антенных решеток к формулам характеристик направленности систем с непрерывным распределением возбуждающих источников (излучающих поверхностей). При а >>, b >> и небольших расстояниях между излучателями (d₁ < 0,07) характеристики направленности обеих систем практически совпадают.

5.3. Управление диаграммой направленности равномерной

линейной  решетки

Выясним направленные свойства линейной равномерной решетки. Как видно из выражений (5.1) и (5.4), множители системы равноамплитудной эквивалентной линейной и равноамплитудной эквидистантной синфазной решеток идентичны и отличаются только аргументами синусов. Однако в случае равноамплитудной эквидистантной линейной решетки множитель системы максимален и равен п при условии u = . При этом поля от всех элементов антенны в точке наблюдения, характеризуются углом _mах, имеют одинаковую фазу, так как сдвиг фаз из-за несинфазности возбуждения Ψ компенсируется пространственным сдвигом фаз Ψ_p = kd₁ sin. Из множителя системы, получаем

sin _maxuл = λ / (2). (5.11)

Таким образом линейный закон изменения фазы возбуждающего поля приводит к изменению направления максимального излучения. Это направление отклоняется от перпендикуляра к оси решетки на угол φ_maxгл. Так как излучение максимально в том направлении, в котором происходит взаимная компенсация сдвигов фаз Ψ и Ψ_р, то диаграмма направленности поворачивается обязательно в сторону отставания фазы возбуждающего тока. Поворот диаграммы направленности, т.е. управление ею путем изменения величины сдвига фаз Ψ, находит широкое применение на практике.

Направление нулевых излучений можно определить по формуле    sin₀ = Nλ/(ncosφ_maxгл). При узких диаграммах направленности значение

                                  2φ₀ равно 2φ₀ = 2λ/(ncos φ_maxгл).

Таким образом ширина диаграммы направленности растет по мере отклонения направления максимального излучения от перпендикуляра к оси решетки. Уровень боковых лепестков, близких к главному, приближенно может быть найден тем же методом, что и в случае синфазной решетки. Направления максимумов боковых лепестков при этом определяются из формулы sin φ_maxгл, = (2N+l)λ/(2nd₁cos φ_maxгл).

Так как при отклонении направления максимального излучения от нормали к оси решетки диаграмма направленности расширяется, а уровень боковых лепестков не изменяется, то казалось бы, что КНД решетки должен уменьшаться. Однако при этом пространственная диаграмма направленности приобретает коническую форму и телесный угол, в пределах которого заключено излученное поле (главный лепесток), уменьшается, что компенсирует расширение диаграммы направленности в плоскости вектора Е. В результате оказывается, что КНД линейной равномерной решетки не зависит от угла φ_maxгл. КНД линейной равномерной решетки, можно рассчитать по формуле D = 101,5/2φ_0,5, где 2φ_0,5 - ширина диаграммы направленности по половинной мощности, рад. Рассмотренные антенные решетки излучают с максимальной интенсивностью либо в направлении нормали к своей оси (φ =  - синфазная решетка), либо под некоторым углом к нормали (равномерная линейная решетка). Вдоль оси решетки (ось у) излучение равно нулю, так как элементы решетки в этом направлении не излучают, это - решетки с поперечным излучением.

Вывод. Ширина ДН синфазной решетки сужается с уменьшением длины волны, увеличением числа вибраторов и увеличением расстоянии между ними. Если в синфазной решетке уменьшить число вибраторов и увеличить расстояния между ними так, чтобы сохранить неизменным произведение nd₁, т.е. линейные размеры антенны, то ширина главного лепестка останется неизменной, но возрастут уровни боковых лепестков. При < 0,5 λ, уровни боковых лепестков практически остаются неизменными, но возрастает число вибраторов и усложняется система питания. Поэтому расстояния между центрами ненаправленных или полуволновых вибраторов обычно выбирают равными 0,5λ, а одноволновых - λ. Для уменьшения уровня боковых лепестков применяют эквидистантные решетки, в которых центральные вибраторы имеют большие токи, а периферийные — меньшие или равноамплитудные решетки, в которых расстояния между вибраторами по мере удаления от центра антенны увеличиваются. Подбирая закон распределения амплитуд или размещения вибраторов, можно снижать уровни боковых лепестков до необходимых значений.

При заданных линейных размерах антенны наибольшим КНД обладают равноамплитудные эквидистантные решетки. Следовательно, снижение уровня боковых лепестков достигается уменьшением КНД или увеличением размеров антенны.

Диаграмма направленности системы ненаправленных (изотропных) синфазных излучателей, расположенных вдоль прямой линии есть ДН линейной решетки, являющейся фигурой вращения, ось которой совпадает с линией расположения вибраторов в решетке. В плоскости, перпендикулярной линии расположения вибраторов и проходящей через ее центр, синфазная линейная решетка имеет круговую (ненаправленную) ДН. Для получения узких ДН в двух плоскостях, например в горизонтальной и вертикальной, синфазная решетка должна быть двухмерной.

При линейном законе изменения фаз токов в вибраторах ДН поворачивается в сторону отставания фаз.

      Влияние амплитудного и фазовых распределений на ДН антенной решетки поперечного излучения будет рассмотрено в лекции № 7.