ЛЕКЦИЯ 4. ИЗЛУЧЕНИЕ ДВУХ СВЯЗАННЫХ ВИБРАТОРОВ

4.1. Направленные свойства системы из двух связанных вибраторов

Одиночные вибраторы применяют только тогда, когда требуется ненаправленное или почти ненаправленное излучение. В тех же случаях, когда необходимо получить однонаправленное излучение или узкие диаграммы направленности применяют антенны, состоящие из двух или нескольких вибраторов, расположенных на небольшом расстоянии (меньше ) друг от друга. Такие вибраторы заметно влияют друг на друга, поэтому их называют связанными. Взаимодействие связанных вибраторов аналогично взаимодействию связанных колебательных контуров с сосредоточенными постоянными. Поле одного вибратора наводит в другом вибраторе некоторую ЭДС, что эквивалентно изменению сопротивления излучения или входного сопротивления вибратора. Поле, создаваемое системой вибраторов, является результатом сложения полей, - создаваемых отдельными вибраторами, с учетом фаз этих полей, определяемых как разностью хода лучей, так и разностью фаз токов в излучателях. Ниже рассматривается работа двух связанных симметричных вибраторов. 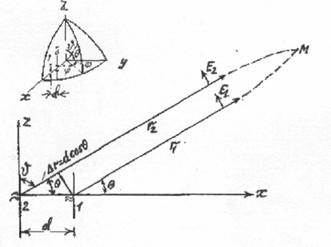Получаемые при этом результаты нетрудно распространить на случай нескольких связанных вибраторов. Выведем формулу для расчета характеристики направленности двух параллельных вибраторов 1 и 2, находящихся на расстоянии d друг от друга (рис. 4.1), питаемых токами

. Обозначим  =q exp(i),                                   (4.1)

где q - отношение модулей токов ; - сдвиг фазы тока I₂ по отношению к току I₁.

Рис. 4.1. К определению поля излучения связанных вибраторов

Рассмотрим поле в меридиональной плоскости вибраторов xoz. Так как расстояние между вибраторами d несоизмеримо мало по сравнению с расстояниями до точки наблюдения (r₁ и r₂), направления в точку М можно считать параллельными. Опустив из центра первого вибратора перпендикуляр на направление r₂, найдем разность расстояний от 44 вибраторов до точки

наблюдения, равную r = d cos, где - угол между нормалью к оси вибратора и направлением на точку наблюдения. Обозначим напряженность поля, создаваемого в точке наблюдения первым вибратором, через E₁. Выразим напряженность поля второго вибратора в точке наблюдения М через напряженность поля первого вибратора, приняв ее фазу в точке наблюдения за нулевую. Так как напряженность, создаваемого вибратором, поля пропорциональна току в вибраторе и влиянием разности расстояний от вибратора до точки наблюдения на амплитуду напряженности поля можно пренебречь, то = E₁q exp(-ikdcos) exp(i), где kd cos- сдвиг фаз полей из-за разности хода лучей (пространственный сдвиг фаз). Найдем суммарное поле, создаваемое обоими вибраторами в данной точке

(4.2)

На основании формулы (3.7) и с учетом того, что угол 0 является дополнительным по отношению к углу , запишем

Обычно интересуются величиной напряженности суммарного поля, а не ее фазой. Поэтому, переходя к модулю выражения (4.2), получаем

Е =(60I_П1 / r)[(cos(klsin) - coskl) / cos] (4.3) или E= Af₁()f_c().Как видно из формулы (4.3), амплитудная характеристика направленности системы из двух связанных вибраторов определяется двумя множителями. Первый множитель f₁() представляет собой характеристику направленности симметричного вибратора, находящегося в свободном пространстве. Второй множитель f_c() учитывает наличие второго вибратора; он зависит от расстояния d между вибраторами, от отношения амплитуд токов в вибраторах q и от сдвига фаз токов в вибраторах . Этот множительназывают множителем системы. В экваториальной плоскости направленные свойства данной системы определяются только множителем системы, так как одиночный симметричный вибратор в этой плоскости (= 0°) не обладает направленными свойствами. Напряженность суммарного поля в экваториальной плоскости определяется выражением

             Е = А (1- coskl) . (4.4)

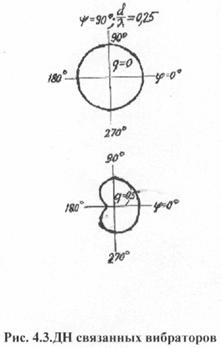
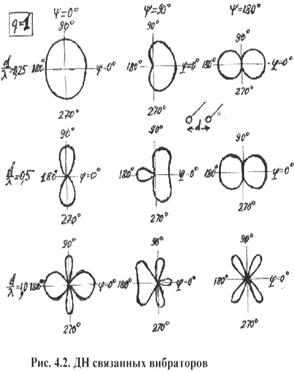
В зависимости от величин d/, q и  диаграммы направленности могут иметь различную форму (рис.4.2, 4.3), При увеличении расстояния между вибраторами (начиная от d/ = 0,5) диаграмма направленности приобретает многолепестковый характер; чем больше d/, тем больше лепестков. Особенно важен случай однонаправленного излучения. Пусть токи в вибраторах одинаковы по величине (q = 1). Тогда формулу (4.4), воспользовавшись формулой для косинуса двойного угла, можно привести к виду

Е = 2А (1 - cos kl) cos [/2 - (kd/2) cos]                         (4.5)

Положим теперь, что =± 90° и расстояние между вибраторами d =/4. При этом формула (4.5) принимает вид

Е = 2А (1 - cos kl) cos (±45° - 45°cos).

Множитель f() = cos(±45°- 45°cos) описывает кардиоиду.  При= + 90° и = 0° этот множитель обращается в единицу; при =180° он обращается в нуль. Таким образом, в направлении = 0° напряженность поля удваивается (по сравнению с полем одиночного вибратора, возбуждаемого током, одинаковым с текущим по одному из связанных вибраторов). Это увеличение в одном направлении происходит за счет уменьшения поля в других направлениях. При  = - 90° напряженность поля удваивается в обратном направлении (=180°); поле равно нулю в направлении = 0°.

Поясним эти результаты. Если ток во втором вибраторе пережает по фазе ток в первом вибраторе, то в точке наблюдения, находящейся в направлении = 0°, поля от обоих вибраторов складываются в фазе, так как сдвиг фаз за счет несинфазности возбуждающих токов (= 90°) компенсируется пространственным сдвигом фаз (_р= kd = (2/)(/4)= 90°). Этот сдвиг фаз берется со знаком минус, так как второй вибратор находится дальше от точки наблюдения, чем первый. В обратном направлении (= 180°) множитель f() обращается в нуль, потому что в этом направлении поля от первого и второго вибраторов складываются в противофазе и компенсируют друг друга, так как _рез=+ _р=180°. Если ток во втором вибраторе отстает по фазе на 90° от тока в первом вибраторе (= - 90°), то получается обратная картина. В первом случае ( = 90°) второй вибратор усиливает излучение в направлении на первый вибратор. Во втором случае ( = -90°) он усиливает излучение в обратном направлении и ослабляет излучение в направлении первого вибратора. Вибратор, усиливающий излучение в направлении на другой вибратор и ослабляющий излучение в обратном направлении, называется рефлектором (отражателем). 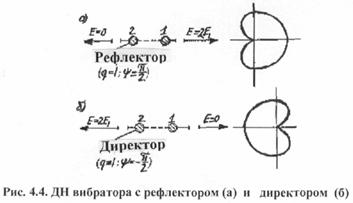Чтобы рефлектирующее действие вибратора было полным (в одном направлении поле увеличивается, а в противоположном - равно нулю), в рассматриваемом случае (d =/4) токи в обоих вибраторах должны быть равны по величине (q = 1), а ток в рефлекторе должен опережать ток во втором связанном вибраторе на 90° (рис.4.4.а). Вибратор, ослабляющий излучение в направлении на другой вибратор и усиливающий излучение в противоположном направлении, называется директором (направителем). В идеальном случае директор должен работать в режиме  (рис.4.4.б): q=l;  = -/2  (при d = /4). Отметим, что в обоих случаях напряженность поля увеличивается в направлении отставания фазы возбуждающего тока. Получить однонаправленное излучение можно и при расстояниях между вибраторами, отличных от /4. Как видно из формулы (4.5), условие отсутствия излучения в направлении  = 180° можно записать в виде  +kd = 180°. Для выполнения этого условия при d < /4 угол сдвига фаз у должен быть больше 90°. Хотя диаграмма направленности при этом оказывается однонаправленной и максимум излучения лежит в направлении  = 0°, однако напряженность поля в этом направлении не удваивается. Чем ближе друг к другу расположены вибраторы, тем меньшая напряженность поля получается в направлении максимального излучения (считая, что при изменении d величина тока в вибраторах постоянна).

Возбуждение каждого из двух связанных вибраторов токами, сдвинутыми по фазе, усложняет систему питания. Поэтому в большинстве случаев вибраторы, выполняющие роль рефлекторов или директоров, не содержат источников питания (генераторов), т.е. являются пассивными. Они возбуждаются электромагнитным полем активного (питаемого) вибратора. В случае пассивных вибраторов не удается осуществить режим, обеспечивающий полное рефлекторное или директорное действие, так как не удается получить совместно q = 1 и  = 90°. Поэтому не получается полного удвоения поля в главном направлении и нуля поля - в обратном.

4.2. Расчет сопротивления излучения и входного сопротивления связанных вибраторов методом наведенных ЭДС

                    4.2.1. Сущность метода наведенных ЭДС

Полное сопротивление излучения одного из связанных вибраторов Z₁ состоит из двух частей: собственного сопротивления Z₁₁, т.е. сопротивления, которым обладает данный вибратор в свободном пространстве, и сопротивления, наведенного электромагнитным полем второго вибратора Z₁₂^нав. Таким образом, Z₁= Z₁₁ + Z₁₂^нав и Z₂= Z₂₂ + Z₂₁^нав.

Полное сопротивление излучения связанного вибратора можно найти методом наведенных ЭДС. Идея этого метода была предложена независимо друг от друга в 1922 г. российским ученым Д.А.Рожанским и французом Бриллюэном. Непосредственно к расчету антенн этот метод

применен И.Г.Кляцкиным, А.А.Пистолькорсом и В.В.Татариновым.

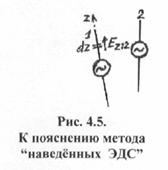
Метод наведенных ЭДС позволяет находить наведенные и собственные сопротивления вибраторов, а также амплитуды и фазы токов в пассивных вибраторах. Сущность данного метода такова. Рассмотрим два произвольно ориентированных друг относительно друга симметричных вибратора (рис.4.5). Поле второго вибратора может создать у поверхности бесконечно малого элемента dz первого вибратора составляющую, параллельную оси этого вибратора (тангенциальную составляющую), E_z12, вследствие чего в элементе dz возникает (наводится) ЭДС dЭ₁₂ = E_z12dz.

Однако при этом нарушаются граничные условия, согласно которым на поверхности идеального проводника тангенциальная составляющая напряженности электрического поля равна нулю. Для выполнения граничных условий в элементе dz должна появиться ЭДС –dЭ₁₂, компенсирующая ЭДС dЭ₁₂. Вблизи поверхности элемента dz появляется тангенциальная составляющая напряженности электрического поля -E_z12, равная по величине и противоположная по фазе тангенциальной составляющей наведенного поля E_z12. Вследствие этого тангенциальная составляющая напряженности суммарного электрического поля у поверхности элемента dz обращается в нуль и граничное условие выполняется. Появление тангенциальной составляющей напряженности поля - E_z12 говорит о том, что под влиянием поля второго вибратора происходит перераспределение поля первого вибратора. ЭДС –dЭ₁₂ создается генератором, включенным в первый вибратор. Энергия, затрачиваемая генератором для создания этой ЭДС в элементе dz, переходит в энергию электромагнитного поля. Если известны ЭДС,возникающая на поверхности элемента dz, и ток в этом элементе I_z1 можно определить мощность dP₁₂, затрачиваемую генератором первого вибратора (под действием поля второго вибратора), на создание поля, компенсирующего тангенциальную составляющую напряженности электрического поля второго вибратора на поверхности данного элемента. При этом ток в элементе dz и составляющая E_z12 на поверхности этого элемента могут иметь различные фазы. Считается, что закон распределения тока по одному из связанных вибраторов в результате действия поля другого вибратора не изменяется и является синусоидальным.

Полная мощность, расходуемая генератором первого вибратора на создание в окружающем пространстве электромагнитного поля, тангенциальная составляющая напряженности электрического поля которого компенсирует на всей поверхности вибратора тангенциальную составляющую напряженности электрического поля, создаваемого током второго вибратора,

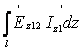P₁₂ = - (1/2). (4.6)

Итак, мощность, отдаваемая генератором первого вибратора под действием поля второго вибратора, определяется током, текущим по первому вибратору, и тангенциальной составляющей напряженности электрического поля, создаваемого вторым вибратором вблизи первого. Ее активная часть представляет собой излученную мощность. Реактивная часть характеризует электромагнитное поле, колеблющееся вблизи вибратора. Выражение (4.6) математически формулирует метод наведенных ЭДС.

4.2.2. Расчет взаимных и собственных сопротивлений связанных    вибраторов

Для того чтобы определить сопротивление, наведенное на первый вибратор вторым, нужно знать закон распределения тока в первом вибраторе, его комплексную амплитуду в пучности и тангенциальную составляющую напряженности электрического поля, создаваемого вторым вибратором у поверхности первого. Активная составляющая наведенного сопротивления R₁₂^нав характеризует активную мощность, излучаемую первым вибратором под действием поля второго. Реактивная составляющая наведенного сопротивления X₁₂^нав характеризует мощность электромагнитного поля, связанного с вибратором, возникающего также под действием поля второго вибратора.

Наведенное сопротивление рассчитать значительно проще в частном случае, когда связанные вибраторы имеют одинаковую длину, оси их параллельны и токи в них имеют одинаковую величину и фазу. Очевидно, что в этом случае сопротивление, наведенное первым вибратором на второй, равно сопротивлению, наведенному вторым вибратором на первый.

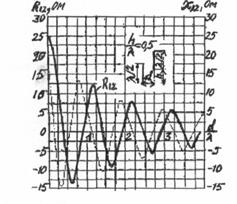
Рис. 4.6. Графики взаимных сопротивлений

В этом частном случае наведенное сопротивление называется взаимным (Z₁₂). При известном взаимном сопротивлении двух вибраторов весьма просто рассчитать наведенное сопротивление, если задано соотношение токов в вибраторах. Взаимное сопротивление является функцией величин l/, d/ и h/, т.е. определяется исключительно геометрическими размерами системы. Оно аналогично сопротивлению связи двух колебательных контуров c сосредоточенными параметрами и определяется по таблицам и графикам. Таблицы для определений активной со-составляющей (R₁₂) взаимного сопротивления полуволновых вибраторов рассчитаны А.А.Пистолькорсом в 1928 г., а для реактивной составляющей (Х₁₂) - В.В.Татариновым в 1936 г.

    Графики, изображающие зависимости R₁₂ = f(d/) и X₁₂ = f (d/) при       h/= const, представлены на рис.4.6. Имеются также графики, позволяющие определять взаимные сопротивления вибраторов, длина которых отличается от полуволны. Как видно из рис.4.6, активная и реактивная составляющие взаимного сопротивления в зависимости от относительного расстояния между вибраторами d/ принимают как положительные, так и отрицательные значения и при некоторых значениях d/ проходят через нуль. Такой ход кривых взаимных сопротивлений объясняется изменением фазы наведенной ЭДС при изменении расстояния между вибраторами. Если фаза наведенной ЭДС равна или противоположна фазе текущего по вибратору тока, то взаимное сопротивление является чисто активным. Если фаза наведенной ЭДС отличается от фазы текущего по вибратору тока на /2, то взаимное сопротивление является чисто реактивным. Активная составляющая взаимного сопротивления может быть положительной или отрицательной; R₁₂ отрицательно в тех случаях, когда под действием поля второго вибратора мощность поля, излучаемого первым вибратором, уменьшается (при неизменном токе в первом вибраторе).

Метод наведенных ЭДС может быть применен также для определения собственного сопротивления излучения вибратора. Формула для расчета R₁₁ совпадает с формулой (3.13) для расчета R_п, полученной методом вектора Пойнтинга, т.е. R₁₁ = R_п .Это понятно, так как при расчете сопротивления излучения методом вектора Пойнтинга также, как и в данном случае, исходят из синусоидального распределения тока.

Формула для расчета X₁₁ имеет вид

X₁₁ = X_п = 30[2Si 2kl + sin 2kl (+ lnkl +Ci 4kl - 2Ci 2kl -2ln (l/a)) +
+ cos 2kl (- Si 4kl + 2Si 2kl)].                                                   (4.7)

Результаты, полученные по методу наведенных ЭДС, тем более точны, чем тоньше вибратор.

4.2.3. Расчет наведенного и полного сопротивлений излучения

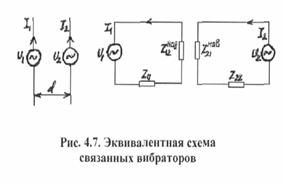
Пусть имеются два активных связанных вибратора, токи в которых не равны ни по амплитуде, ни по фазе. Требуется найти полное сопротивление излучения каждого вибратора. Заменим связанные вибраторы эквивалентной схемой, состоящей из двух связанных колебательных контуров с сосредоточенными параметрами (рис.4.7). Каждый контур содержит генератор высокой частоты, сопротивления Z₁₁ или Z₂₂, равные собственным сопротивлениям вибраторов, и наведенные сопротивления Z₁₂^нав и Z₂₁^нав  которые неизвестны. Напряжение генератора, включенного в связанный контур, компенсирует падение напряжения на собственном сопротивлении контура и на сопротивлении связи. Учитывая это, запишем уравнения Кирхгофа для данной эквивалентной схемы, считая, что сопротивления связи (взаимные сопротивления) известны. Эти уравнения имеют вид:

U_п1= I_п1Z₁₁ + I_п2Z₁₂; (4.8)

U_п2=I_п2 Z₂₂+I_п1Z₂₁. (4.9)

Здесь U_п1 и U_п2 - напряжения первого и второго генераторов, пересчитанные к точкам пучности тока в вибраторах. Данные уравнения позволяют при заданных напряжениях U_п1 и U_п2 и известных собственных и взаимных сопротивлениях определить токи в вибраторах. Полагая, что токи в вибраторах найдены, определим наведенные сопротивления. Пусть I_п1 / I_п2 =qexp(i). Перепишем уравнения (4.8) и (4.9), вынося за скобки в уравнении (4.8) величину I_п1, а в уравнении (4.9) величину I_п2 и учитывая, что Z₁₂ = Z₂₁

U_п1= I_п1 [Z₁₁ + q exp (i) Z_I2];                                                            (4.10)

U_п2= I_п2 [Z₂₂+ (l/ q) exp (-i) Z₁₂]. (4.11)

Разделив уравнение (4.10) на I_п1 а уравнение (4.11) на I_п2, получим выражения для полных сопротивлений контуров (вибраторов):

U_пl/ I_п1= Z₁ = R₁ + i X₁= Z₁₁+ q exp (i) Z₁₂ ; (4.12)

U_п2/ I_п2 = Z₂ = R₂+ i X₂= Z₂₂ + (1/q) exp (-i) Z₁₂. (4.13)

Так как полное сопротивление излучения вибратора равно сумме собственного и наведенного сопротивлений излучения, то наведенные сопротивления вибраторов равны:

Z₁₂^нав = R₁₂^нав + i X₁₂^нав = q exp (i) (R₁₂ + i X₁₂)  ; (4.14)

Z₂₁^нав  = R₂₁^нав + i X₂₁^нав = (1/q) exp (-i) (R₁₂ + i X₁₂).                            (4.15)

Таким образом, если известно взаимное сопротивление вибраторов (оно зависит только от относительных  геометрических размеров системы     l/,      d/,     h/, и определяется по  таблицам или по графикам) и известны    отношения амплитуд  токов q и сдвиг  фаз токов в вибраторах Ψ, то наведенное сопротивление определяется весьма просто. Полная мощность, излучаемая двумя связанными вибраторами, равна              .

Входные сопротивления связанных вибраторов могут быть рассчитаны по формулам, применяемым при инженерном расчете входного сопротивления. В случае коротких вибраторов (расстояние от точек питания до узла тока не менее 0,15λ) входное сопротивление связанного вибратора можно определить по формуле

 = /sin²k/ или =/sin²k l +i/sin²k l, (4.16) где - полное сопротивление излучения связанного вибратора [формула (4.12)]. В случае длинных вибраторов (расстояние от точек питания до минимума тока меньше 0,15λ) входное сопротивление связанного вибратора рассчитывается по формуле, аналогичной (3.21)

 = [(sh2 l - (/k) sin2k l) / (ch2 l - cos2k l)] -

- i  [((/k) sh2l + sin2kl) / ( ch2l - cos2kl)] .       (4.17)

В данной формуле учтено влияние одного вибратора на волновое сопротивление другого вибратора и на его коэффициент затухания.

Здесь ₌, -реактивное наведенное сопротивление, приходящееся на единицу длины вибратора, определяемое по формуле                   = 2 /[ l(1- (sin2kl / 2kl))];

ά^св= ()/ [l  (1- (sin2k l / 2kl l))].

4.3. Расчет тока в пассивных вибраторах

Пассивные вибраторы широко применяются для создания однонаправленного излучения в качестве рефлекторов и директоров. Чтобы вибратор играл роль рефлектора или директора, ток в нем должен иметь определенную величину и фазу по отношению к току в активном вибраторе (в идеальном случае при расстоянии между вибраторами d= λ/4 должны выполняться условия q = 1 и Ψ = ±90°). Величины q и ψ для пассивного вибратора зависят от расстояния между пассивным и активным вибраторами и от величин активного и реактивного сопротивлений пассивного вибратора. Эти величины можно регулировать, изменяя реактивное сопротивление пассивного

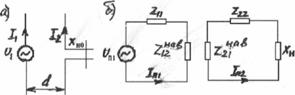
Рис. 4.8. Эквивалентная схема связанных вибраторов, один из которых пассивный

вибратора. Рассчитаем величины q и Ψ. Заменим два связанных     симметричных вибратора, из которых один пассивный с включенным в его середину сопротивлением настройки Х_н0 (рис.4.8.а), эквивалентной схемой (рис.4.8.б).

Уравнения Кирхгофа для этойсистемы имеют вид:

(4.18)

. (4.19)

где  - взаимное сопротивление вибраторов; Х_н - реактивное сопротивление настройки, включенное в пассивный вибратор и отнесенное к пучности тока. Можно считать известными ток в активном вибраторе , а также собственные ,  и взаимное сопротивления, поскольку относительная длина вибраторов l/λ и относительное расстояние между вибраторами d/λ заданы. Задано также сопротивление настройки. Таким образом, в уравнениях (4.18) и (4.19) неизвестен только ток во втором вибраторе ( I₂ ), который определяется из уравнения (4.19) I_п2 = -I_П1[(Z₁₂/(  + iX_H)).

Ранее было обозначено Поэтому

Отсюда модуль отношения токов

.                                                (4.20)

Относительная фаза тока в пассивном вибраторе

. (4.21)

Входящие в формулы (4.20) и (4.21) сопротивления , , и

Х₁₂ отнесены к пучности тока. Сопротивление  пересчитывается к

пучности тока в случае короткого вибратора по формуле

В случае длинного вибратора такой пересчет можно сделать по формуле, учитывающей распределение тока по закону гиперболического синуса , где - коэффициент затухания, без учета влияния активного вибратора.

В случае пассивного вибратора величины q и Ψ взаимозависимы. При изменении Х_н меняются одновременно обе эти величины. Поэтому добиться одновременно нужных значений q и Ψ для пассивного вибратора невозможно. Пассивный вибратор обычно настраивают так, чтобы получить максимальный коэффициент защитного действия. Получаемые при этом величины q и Ψ отличаются от соответствующих величин в идеальном случае (q = 1, Ψ = 90°), и поэтому максимальное защитное действие обычно получается не больше 10...20. Ток в пассивном рефлекторе должен опережать  по   фазе   ток   в   активном

вибраторе. Анализ формулы (4.21) показывает, что пассивный вибратор будет играть роль рефлектора в том случае, когда его полное реактивное сопротивление (собственное плюс сопротивление настройки)  имеет индуктивный характер. Этот вывод справедлив, если 0,1 d 0,25.

Для получения оптимального рефлекторного действия расстояние между рефлектором и активным вибратором следует брать примерно (0,15...0,25), а реактивное положительное сопротивление - приблизительно 10...50 Ом. Ток в пассивном директоре должен отставать по фазе от тока в активном вибраторе. Из анализа формулы (4.21) следует, что для работы пассивного вибратора в режиме директора при 0,1 d  0,25 его полное реактивное сопротивление должно быть отрицательным, т.е. должно иметь емкостный характер. В коротковолновом диапазоне пассивные вибраторы обычно настраивают, включая в середине вибратора настроечное реактивное сопротивление в виде отрезка короткозамкнутой двухпроводной линии, длину которой можно регулировать передвижным короткозамыкателем. В диапазонах метровых и дециметровых волн настроечное сопротивление обычно не применяется. Пассивный вибратор настраивается изменением его длины. Чтобы пассивный вибратор работал в качестве рефлектора, его полная длина должна быть несколько больше /2 (входное сопротивление разомкнутой на конце двухпроводной линии, длина которой больше /4, имеет индуктивный характер). Чтобы пассивный вибратор работал в качестве директора, его полная длина должна быть несколько меньше /2. Величина необходимого удлинения или укорочения определяется расстоянием между вибраторами и их толщиной.

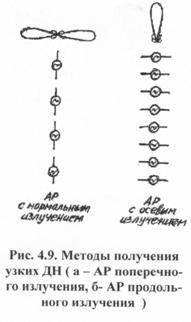
4.4. Методы получения узких диаграмм направленности вибраторных антенн                                  

В ряде случаев необходимо, чтобы антенны концентрировали излучаемые ими электромагнитные волны в узкие пучки, т.е. чтобы они обладали узкими диаграммами направленности, большими КНД. Этого можно достичь при помощи нескольких вибраторов, возбуждаемых так, что их поля в нужном направлении складывались в фазе.

Пусть к симметричному вибратору подводится мощность P, которая полностью излучается. При этом в главном направлении создается напряженность поля Е = A, где R_o - входное сопротивление вибратора;

= I₀ - ток в точках питания вибратора. Поместим рядом точно такой же вибратор (рис.4.9.а) и подведем к каждому из вибраторов мощность      P' = P/2. Если считать, что входное сопротивление одного

вибратора под действием второго вибратора    не    изменяется,    то   токи,    текущие  в    вибраторах,    равны

58

I₁ = I₂ == I₀/. Поскольку ток в каждом вибраторе уменьшился в  раз, то во столько же раз уменьшается и напряженность поля, создаваемого одним вибратором в прежней точке, т.е. Е₁ = Е₂ = Е/. Так как расстояние от обоих вибраторов до точки наблюдения одинаковы, то их поля в этой точке синфаз-

ны   и   суммарное   поле   равно   Е_сум   =   Е₁ +E₂  = 2Е/=Е. Можно показать, что при излучении

каждым из n расположенных в ряд синфазно возбужденных вибраторов, мощности Р₁ = Р₂ = Р_n= Р/n и напряженность поля в главном направлении возрастает в раз по сравнению с одним вибратором, излучающим мощность Р.

Увеличить напряженность поля в одном направлении за счет уменьшения ее в других направлениях можно также, применив систему вибраторов, расположенных и возбужденных

таким образом, чтобы сдвиг фаз полей от отдельных вибраторов в точке наблюдения из-за несинфазности возбуждения компенсировался сдвигом фаз из-за разности расстояний (рис.4.9.б). Сказанное справедливо, если расстояние между соседними вибраторами настолько велико, что их взаимным влияниям можно пренебречь. При уменьшении расстояния между вибраторами входное сопротивление каждого вибратора вследствие их взаимного влияния возрастает. Поэтому при неизменной подводимой мощности токи в вибраторах уменьшаются и напряженность суммарного поля в главном направлении увеличивается меньше, чем в раз. Увеличение числа вибраторов антенной системы при правильном выборе фаз токов, возбуждающих вибраторы, и при правильном взаимном расположении вибраторов приводит к увеличению напряженности поля в нужном направлении и к ослаблению ее в других направлениях, т.е. к сужению диаграммы направленности антенны. Сужение диаграмм направленности антенн, представляющих собой непрерывное распределение источников (длинные провода, излучающие поверхности), также происходит вследствие интерференции полей отдельных элементов, на которые можно мысленно разбить антенну. Очевидно, что получение узких диаграмм направленности путем синфазного сложения полей от отдельных элементов антенны в нужном направлении и создания резко несинфазных полей в других направлениях требует увеличения габаритов антенны. Хотя изложенный здесь способ получения узких диаграмм направленности путем синфазного или почти синфазного сложения полей в данном направлении от отдельных элементов антенны не является единственным и оптимальным, он по ряду причин в настоящее время является основным.