ЛЕКЦИЯ 3. СИММЕТРИЧНЫЙ ЭЛЕКТРИЧЕСКИЙ ВИБРАТОР В СВОБОДНОМ ПРОСТРАНСТВЕ
3.1. Распределение тока и заряда по вибратору
Изучение симметричного электрического вибратора представляет большой интерес, так как, во-первых, этот вибратор применяется как самостоятельная антенна и, во-вторых, он является составным элементом ряда сложных антенн. Симметричные вибраторы начали широко применять в первой половине двадцатых годов в связи с возникновением и развитием радиосвязи на коротких волнах. В настоящее время симметричный вибратор как самостоятельная антенна применяется на коротких, метровых и дециметровых волнах. В этих же диапазонах широко используются сложные антенны, состоящие из ряда симметричных вибраторов. Симметричные вибраторы используются также в сантиметровом диапазоне волн в качестве элементов сложных систем (например, облучатели зеркальных антенн).
Симметричный вибратор состоит из двух одинаковых по размерам и форме
проводников, между которыми включается генератор высокой частоты (часто эти
проводники называются плечами). Рассмотрим симметричный вибратор,
представляющий собой тонкий цилиндрический проводник длиной 2![]() и радиусом а (рис.3.1), находящийся в свободном пространстве.
и радиусом а (рис.3.1), находящийся в свободном пространстве.

Строгое решение основной задачи теории антенн для симметричного вибратора связано с большими трудностями, так как закон распределения тока по вибратору неизвестен.
Рис. 3.1. Симметричный вибратор
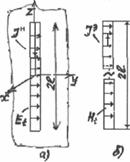
Существует приближенный метод расчета поля, создаваемого симметричным вибратором в дальней зоне. В основе этого метода лежит предположение о синусоидальном распределении тока по вибратору, основанное на некоторой внешней аналогии между симметричным вибратором и двухпроводной разомкнутой на конце линией без потерь. Действительно, от двухпроводной линии (рис.3.2.а) можно перейти к симметричному вибратору, если провода линии развернуть под углом 180° друг к другу (рис.3.2.б). Можно полагать, что при переходе от двухпроводной линии к симметричному вибратору закон распределения тока не нарушается, т.е.
Iz = Iпsink(![]() -
-![]() )
, где Iп - амплитуда тока в
пучности тока вибратора (в общем случае, это величина комплексная) İп = Iпexp(i
)
, где Iп - амплитуда тока в
пучности тока вибратора (в общем случае, это величина комплексная) İп = Iпexp(i![]() );
); ![]() - длина одного
плеча вибратора; z - расстояние от
начала вибратора (точки питания) до произвольной точки на вибраторе (текущая
координата); k = 2
- длина одного
плеча вибратора; z - расстояние от
начала вибратора (точки питания) до произвольной точки на вибраторе (текущая
координата); k = 2![]() /
/![]() ,
- волновое число (коэффициент фазы тока в вибраторе).
,
- волновое число (коэффициент фазы тока в вибраторе).
Полагают, что длина
волны в вибраторе λ, равна длине волны в свободном
пространстве. В действительности данная аналогия весьма
приближённа. Обе системы - линия и вибратор – являются колебательными системами с распределенными
параметрами, однако они существенно различаются. Во-первых,
распределенные параметры
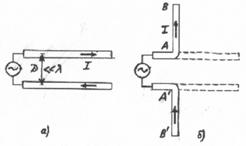
Рис. 3.2. Преобразование двухпроводной линии в симметричный вибратор (а - линия, б - вибратор )
линии (Li,Ci) не изменяются по ее длине, распределенные параметры вибратора непостоянны по его длине (рис.3.2.6). Во-вторых, линия служит для канализации электромагнитных волн и является практически неизлучающей системой; вибратор же излучает волны. В разомкнутой на конце линии ток изменяется по закону стоячей волны только в том случае, если линия выполнена из идеального проводника, т.е. в ней нет потерь энергии.
В
вибраторе, выполненном даже из идеального проводника, обязательно есть потери
(полезные) на излучение. Очевидно, поэтому ток в вибраторе, строго говоря, не
может быть распределен по закону стоячей волны. Однако расчет поля
симметричного вибратора по формулам, основанным на синусоидальном
распределении тока, дает хорошее совпадение с экспериментальными данными для
дальней зоны и тонких вибраторов. Поэтому для инженерного расчета это
приближение в ряде случаев вполне допустимо. Строгая теория симметричного
вибратора подтверждает, что в тонких вибраторах ток распределен по закону, весьма
близкому к синусоидальному. Задавшись законом распределения
тока по вибратору, легко установить приближенный закон распределения заряда ![]() z=
z=![]() Пcosk(
Пcosk(![]() -
- ![]() ),
где
),
где ![]() П
амплитуда заряда в его пучности. Этот закон распределения заряда вдоль
симметричного вибратора совпадает с законом распределения потенциала
(напряжения) в разомкнутой на конце длинной линии без потерь. В теории антенн
понятием напряжения следует пользоваться с большой осторожностью, так как
поле антенны не является потенциальным. Понятием напряжения применительно к антенне можно
пользоваться, если расстояние между точками измерения мало по сравнению с
длиной волны. Это справедливо при измерении напряжения между зажимами антенны
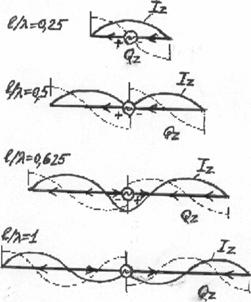
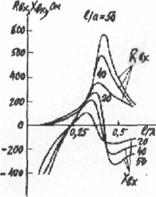
(точки присоединения генератора), а также для длинноволновых антенн. На рис.3.3
приведены кривые распределения амплитуд тока и заряда на вибраторах разной
длины. По аналогии с волновым сопротивлением длинной линии вводится понятие волнового
сопротивления симметричного вибратора. Как известно, из теории длинных
линий, волновое сопротивление двухпроводной линии без
потерь определяется выражением W =
П
амплитуда заряда в его пучности. Этот закон распределения заряда вдоль
симметричного вибратора совпадает с законом распределения потенциала
(напряжения) в разомкнутой на конце длинной линии без потерь. В теории антенн
понятием напряжения следует пользоваться с большой осторожностью, так как
поле антенны не является потенциальным. Понятием напряжения применительно к антенне можно
пользоваться, если расстояние между точками измерения мало по сравнению с
длиной волны. Это справедливо при измерении напряжения между зажимами антенны
(точки присоединения генератора), а также для длинноволновых антенн. На рис.3.3
приведены кривые распределения амплитуд тока и заряда на вибраторах разной
длины. По аналогии с волновым сопротивлением длинной линии вводится понятие волнового
сопротивления симметричного вибратора. Как известно, из теории длинных
линий, волновое сопротивление двухпроводной линии без
потерь определяется выражением W =![]() ,
где L1-распределенная
,
где L1-распределенная
индуктивность линии (индуктивность,
приходящаяся на единицу длины линии), Г/м; C1 -, распределенная
емкость линии, Ф/м. Так как 1/![]() = с,
где
= с,
где
с - скорость света, м/с, то
W=l/cC1, Ом. (3.1)
Волновое сопротивление двухпроводной линии связано с ее геометрическими размерами соотношением
W=2761g (D/a), (3.2)
|
|
где D
- расстояние между центрами проводов линии; а - радиус провода.
|
Рис. 3.3. Распределение амплитуд тока и заряда на вибраторах разной длины |
Волновое сопротивление симметричного вибратора (а также других линейных антенн, т.е. антенн, длина которых значительно превосходит размеры поперечного сечения) рассчитывают по формуле (3.1). Однако распределенная емкость по длине вибратора непостоянна. Поэтому в данном случае под C1 подразумевается усредненная величина, равная отношению полной статической емкости антенны (СА) к ее длине (2l). Одним из наиболее распространенных приближенных методов расчета полной статической емкости является метод Хоу или метод усредненных потенциалов. Волновое сопротивление симметричного вибратора из провода цилиндрической формы, определенное по методу Хоу,
WA=120(ln l/a-1), Oм, (3.3)
где l-длина плеча вибратора; а - радиус провода.
Расчет волнового сопротивления вибратора методом Хоу дает приемлемую точность для вибраторов, коротких по сравнению с длиной волны. Точность этого метода снижается по мере удлинения вибратора.
3.2. Направленные свойства симметричного вибратора
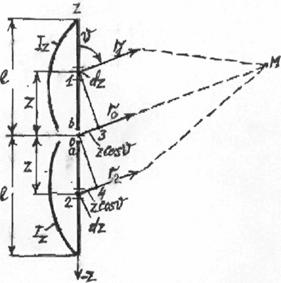
Рассмотрим симметричный вибратор произвольной длины (рис.3.4). Задаемся синусоидальным законом
распределения тока вдоль вибратора Iz = (I0/sinkl)sink(l -![]() ), где I0 - ток в точках питания вибратора (I0=Iпsinkl). Мысленно разобьем вибратор на бесконечно большое число
элементов dz. Так как длина каждого
элемента бесконечно мала, то можно полагать, что в пределах его ток не изменяется ни по
амплитуде, ни по фазе. Таким образом, весь
симметричный вибратор можно рассматривать как совокупность
), где I0 - ток в точках питания вибратора (I0=Iпsinkl). Мысленно разобьем вибратор на бесконечно большое число
элементов dz. Так как длина каждого
элемента бесконечно мала, то можно полагать, что в пределах его ток не изменяется ни по
амплитуде, ни по фазе. Таким образом, весь
симметричный вибратор можно рассматривать как совокупность
|
|
элементарных электрических вибраторов dz и поле симметричного вибратора рассматривать как результат сложения (интерференции) полей, излучаемых элементарными вибраторами. Ввиду малости воздушного промежутка (зазора) между плечами вибратора можно пренебречь влиянием электрического поля (магнитного тока), существующего в нем на излучение, и считать, что электрический ток течет по сплошному проводнику длиной 2l. Выделим на вибраторе (рис.3.4) элементы 1 и 2, каждый длиной dz, симметричные относительно центра вибратора 0, и определим поле, создаваемое этими элементами в произвольной точке наблюдения М, находящейся в зоне излучения. Проведем от элементов 1 и 2 и от центра вибратора линии в точку наблюдения r1, r0, r2. Поскольку расстояние до точки наблюдения очень велико по сравнению с длиной вибратора, то направления от всех точек вибратора на точку М можно считать параллельными. Напряженность поля, излучаемого первым элементом в точке М
dE1 = i [60![]() Izdz/ (r1
Izdz/ (r1![]() )]sin
)]sin![]() exp(-ikr1).
exp(-ikr1).
(3.4.a)
Напряженность
поля, излучаемого вторым элементом в той же точке М
dE2 = i [60![]() Izdz/(r2
Izdz/(r2![]() )] sin
)] sin![]() exp(-ikr2).
exp(-ikr2).
(3.4.б)
Здесь Iz - амплитуда тока в элементе, находящемся на расстоянии z от центра вибратора;
r1 - расстояние от первого элемента до точки М;
г2 - расстояние от второго элемента до точки М;
|
Рис. 3.4. К определению поля излучения симметричного вибратора |
![]() - угол между осью вибратора и направлением на
точку наблюдения.
- угол между осью вибратора и направлением на
точку наблюдения.
Найдем суммарное поле,
создаваемое в точке наблюдения элементами 1
и 2. Так как векторы напряженности полей, создаваемых всеми элементами
вибратора в точке наблюдения, направлены вдоль одной прямой (перпендикулярной направлению от данного элемента в
точку наблюдения), то поля,
создаваемые отдельными элементами, можно складывать алгебраически. Поэтому
dE = dE1+dE2=i
(60![]() Izdz/
Izdz/![]() )sin
)sin![]() [(exp(-ikr1)/r1+exp(-ikr2)/r2)].
(3.5)
[(exp(-ikr1)/r1+exp(-ikr2)/r2)].
(3.5)
Выразим расстояния r1 и r2 через расстояние r0. Для этого из точки
1 (рис.3.4) опустим
перпендикуляр на направление r0 и из точки
0 опустим перпендикуляр на направление r2. Из прямоугольных треугольников 1-0-3 и 2-0-4 находим, что разность расстояний от данных элементов и центра вибратора
до точки наблюдения равна ![]() r =
r = ![]() cos
cos![]() .
.
Следовательно,
r1 = r0 - |z|cos![]() и r2 = r0 +
и r2 = r0 + ![]() cos
cos![]() . (3.6)
. (3.6)
Величину ![]() r часто называют разностью хода лучей. Так как точка
наблюдения находится в дальней зоне, то
величина
r часто называют разностью хода лучей. Так как точка
наблюдения находится в дальней зоне, то
величина ![]() r мала по сравнению с r0 и расстояния r1 и r2 мало отличаются друг от друга. Поэтому
можно считать, что амплитуды напряженности
полей, создаваемых элементами 1 и 2 в точке наблюдения М, одинаковы. Однако пренебрегать разностью хода в фазовых
множителях (exp(-ikr1) и exp(-ikr2)) ни в коем случае нельзя, так как пространственный сдвиг фаз между полями элементов 1 и 2 k
r мала по сравнению с r0 и расстояния r1 и r2 мало отличаются друг от друга. Поэтому
можно считать, что амплитуды напряженности
полей, создаваемых элементами 1 и 2 в точке наблюдения М, одинаковы. Однако пренебрегать разностью хода в фазовых
множителях (exp(-ikr1) и exp(-ikr2)) ни в коем случае нельзя, так как пространственный сдвиг фаз между полями элементов 1 и 2 k![]() r = 2k|z|cosν = 4
r = 2k|z|cosν = 4![]() (|z|/
(|z|/![]() )cos
)cos![]() определяется отношением разности хода лучей к
длине волны. На основании формул (3.6) получаем следующие выражения для фазовых
множителей exp(-ikr1)= exp(-ikr0) * exp(ik|z|)cos
определяется отношением разности хода лучей к
длине волны. На основании формул (3.6) получаем следующие выражения для фазовых
множителей exp(-ikr1)= exp(-ikr0) * exp(ik|z|)cos![]() ;
;
exp (-ikr2) = exp (-ikro)
* exp (-ik![]() )cos
)cos![]() .
.
Подставляя эти выражения в формулу (3.5),
вынося за скобки общие множители и полагая,
что в знаменателях r1![]() r2
r2 ![]() r0, получаем
r0, получаем
dE=i[60![]() I0sink(l-
I0sink(l-![]() )dz/(r0
)dz/(r0 ![]() sinkl)]sin
sinkl)]sin![]() exp(-ikr0)[(exp(ik
exp(-ikr0)[(exp(ik![]() )cos
)cos![]() +
+
+exp (-ik![]() ) cos
) cos![]() )].
)].
Воспользовавшись известной формулой exp(i![]() ) + exp(-i
) + exp(-i![]() ) = 2cos
) = 2cos![]() , получаем следующее выражение
, получаем следующее выражение
dE = i[120![]() I0/( r0
I0/( r0 ![]() sinkl)] sin
sinkl)] sin![]() exp(-ikr0)sink(l-
exp(-ikr0)sink(l-![]() )cos(k
)cos(k![]() cos
cos![]() )dz.
)dz.
Для определения напряженности поля, создаваемого в точке наблюдения всем симметричным вибратором, необходимо это выражение проинтегрировать по длине одного плеча вибратора
Е=i[120![]() I0/(r0
I0/(r0 ![]() sinkl)] sin
sinkl)] sin![]() exp(-ikr0)
exp(-ikr0) ![]() sink(l-
sink(l-![]() )cos(k
)cos(k![]() cos
cos![]() )dz.
)dz.
В результате
интегрирования получается формула для расчета напряженности поля
симметричного электрического вибратора в
дальней зоне
E=i [60I0/ (r0sinkl)] * [(cos(klcos![]() ) - coskl) / sin
) - coskl) / sin![]() ]exp(-ikr0).
(3.7)
]exp(-ikr0).
(3.7)
Как и в случае элементарного электрического вибратора, эта формула состоит из трех множителей: множителя, определяющего только величину напряженности поля и не зависящего от направления в данную точку [60I0/(r0sinkl)], множителя, определяющего направленные свойства (характеристика направленности).
f(![]() )=[cos(klcos
)=[cos(klcos![]() ) - coskl]/sin
) - coskl]/sin![]()
и фазового множителя ![]() = iexp(-ikr0) из выражения (3.7) видно, что симметричный
вибратор обладает направленными свойствами только в меридиональной плоскости (плоскость электрического
вектора). Напряженность
электрического поля симметричного вибратора в его экваториальной
= iexp(-ikr0) из выражения (3.7) видно, что симметричный
вибратор обладает направленными свойствами только в меридиональной плоскости (плоскость электрического
вектора). Напряженность
электрического поля симметричного вибратора в его экваториальной
плоскости ( плоскость магнитного вектора ν=
![]() /2) - определяется выражением
/2) - определяется выражением
E = i
[60I0/(r0sinkl)](l-coskl)exp(-ikro),
(3.8)
т.е. не
зависит от азимутального угла ![]() . Поэтому
диаграмма направленности
. Поэтому
диаграмма направленности
симметричного вибратора в его экваториальной плоскости, как и в случае элементарного вибратора, представляет в полярной системе координат ок-
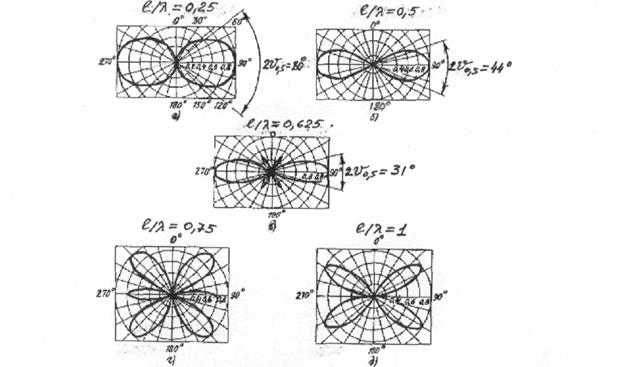
3.5.Диаграммы направленности симметричного вибратора
ружность. Как видно из формулы (3.7), направленные
свойства симметричного вибратора определяются только отношением длины плеча
вибратора к длине волны l/![]() .В случае полуволнового вибратора (l/
.В случае полуволнового вибратора (l/![]() =0,25) формула (3.7) принимает вид
=0,25) формула (3.7) принимает вид
Е= iA{cos[(![]() /2)cos
/2)cos![]() ]/(sin
]/(sin![]() )}exp (-ikr0).
)}exp (-ikr0).
Амплитудные диаграммы
направленности, рассчитанные по формуле (3.7), для вибраторов с различной
относительной длиной l/![]() показаны на
рис.3.5. Анализ формулы (3.7) и рассмотрение этих кривых показывают, что при любой величине
отношения l/
показаны на
рис.3.5. Анализ формулы (3.7) и рассмотрение этих кривых показывают, что при любой величине
отношения l/![]() симметричный
вибратор не излучает вдоль своей
оси. Если длина плеча симметричного вибратора l
симметричный
вибратор не излучает вдоль своей
оси. Если длина плеча симметричного вибратора l ![]() 0,5
0,5![]() , то в направлении, перпендикулярном
его оси (
, то в направлении, перпендикулярном
его оси (![]() = 90°,
= 90°, ![]() =
270°), т.е. в экваториальной плоскости, поля всех элементарных
вибраторов максимальны, синфазны и складываются арифметически. Поэтому
поле в данном направлении является максимальным. Диаграмма
направленности при l/
=
270°), т.е. в экваториальной плоскости, поля всех элементарных
вибраторов максимальны, синфазны и складываются арифметически. Поэтому
поле в данном направлении является максимальным. Диаграмма
направленности при l/![]()
![]() 0,5 состоит из
двух (главных) лепестков (рис. 3.5.а, 3.5.б). Увеличение длины
вибратора
до l=0,5
0,5 состоит из
двух (главных) лепестков (рис. 3.5.а, 3.5.б). Увеличение длины
вибратора
до l=0,5![]() сопровождается ростом
излучения в направлении, перпендикулярном оси вибратора (главное направление излучения),за счет уменьшения излучения в других направлениях.
При этом диаграмма направленности становится уже. При увеличении l/
сопровождается ростом
излучения в направлении, перпендикулярном оси вибратора (главное направление излучения),за счет уменьшения излучения в других направлениях.
При этом диаграмма направленности становится уже. При увеличении l/![]() до 0,625 излучение в главном направлении
продолжает возрастать, но характеристика направленности проходит
через нуль не только при
до 0,625 излучение в главном направлении
продолжает возрастать, но характеристика направленности проходит
через нуль не только при ![]() =0° и
=0° и ![]() =180°, но и при
некоторых других значениях угла
=180°, но и при
некоторых других значениях угла![]() . Главные лепестки диаграммы
становятся уже, но появляются боковые лепестки (рис.3.5.в). При дальнейшем увеличении l/
. Главные лепестки диаграммы
становятся уже, но появляются боковые лепестки (рис.3.5.в). При дальнейшем увеличении l/![]() излучение в главном направлении уменьшается и возрастают боковые лепестки.
Уменьшение излучения в главном направлении объясняется следующим.
Результирующий сдвиг фаз полей, излучаемых элементарными вибраторами в данном
направлении, определяется пространственным сдвигом фаз и сдвигом фаз
токов, возбуждающих эти вибраторы. При l/
излучение в главном направлении уменьшается и возрастают боковые лепестки.
Уменьшение излучения в главном направлении объясняется следующим.
Результирующий сдвиг фаз полей, излучаемых элементарными вибраторами в данном
направлении, определяется пространственным сдвигом фаз и сдвигом фаз
токов, возбуждающих эти вибраторы. При l/![]() >0,5 на
вибраторе появляются участки с противофазными токами (рис.3.3), длина которых растет
по мере увеличения l/
>0,5 на
вибраторе появляются участки с противофазными токами (рис.3.3), длина которых растет
по мере увеличения l/![]() . Поэтому в данном
случае, хотя в главном направлении пространственные сдвиги фаз равны нулю, поля, излучаемые
отдельными элементами вибратора, складываются несинфазно, т.е. геометрически.
При l/
. Поэтому в данном
случае, хотя в главном направлении пространственные сдвиги фаз равны нулю, поля, излучаемые
отдельными элементами вибратора, складываются несинфазно, т.е. геометрически.
При l/![]() = 1 (или при l/
= 1 (или при l/![]() = п, где п = 1, 2,
..,) излучение в главном направлении отсутствует, так как противофазные участки
вибратора имеют одинаковую длину. Рост l/
= п, где п = 1, 2,
..,) излучение в главном направлении отсутствует, так как противофазные участки
вибратора имеют одинаковую длину. Рост l/![]() сопровождается
также ростом боковых лепестков. Уже при l/
сопровождается
также ростом боковых лепестков. Уже при l/![]() =0,75
напряженность поля в направлении максимума бокового лепестка превосходит
напряженность поля в главном направлении (рис.3.3.г).
=0,75
напряженность поля в направлении максимума бокового лепестка превосходит
напряженность поля в главном направлении (рис.3.3.г).
Нормированная характеристика направленности симметричного вибратора, определяемая
как F(![]() ) = f(
) = f(![]() )/f(90°),
равна
)/f(90°),
равна
F(![]() ) = [cos(klcos
) = [cos(klcos![]() ) - coskl]/[(l
– coskl)sin
) - coskl]/[(l
– coskl)sin![]() ].
(3.9)
].
(3.9)
У Диполя Герца 2![]() 0,5= 90°. Полуволновый симметричный вибратор имеет
ширину диаграммы направленности по половинной мощности 2
0,5= 90°. Полуволновый симметричный вибратор имеет
ширину диаграммы направленности по половинной мощности 2![]() 0,5= 80°, волновой
симметричный вибратор - 2
0,5= 80°, волновой
симметричный вибратор - 2![]() 0,5= 44°,
симметричный вибратор, у которого l/
0,5= 44°,
симметричный вибратор, у которого l/![]() =0,625, имеет 2
=0,625, имеет 2![]() 0,5= 31°.
Последний вибратор обладает наилучшими
направленными свойствами, так как при дальнейшем увеличении l/
0,5= 31°.
Последний вибратор обладает наилучшими
направленными свойствами, так как при дальнейшем увеличении l/![]() , сильно возрастают боковые лепестки, хотя главный лепесток
диаграммы направленности становится уже. На практике
применяются симметричные вибраторы, у которых l/
, сильно возрастают боковые лепестки, хотя главный лепесток
диаграммы направленности становится уже. На практике
применяются симметричные вибраторы, у которых l/![]()
![]() 0,7. Фаза напряженности поля, создаваемого симметричным
вибратором в соответствии с выражением (3.7), в пределах одного лепестка
диаграммы направленности не зависит от координатного угла
0,7. Фаза напряженности поля, создаваемого симметричным
вибратором в соответствии с выражением (3.7), в пределах одного лепестка
диаграммы направленности не зависит от координатного угла ![]() .
Она изменяется скачком на обратную при переходе
напряжённости поля через нуль. Симметричный вибратор излучает сферические волны, о
чем
свидетельствует множитель
exp(-ikr)/r. Эти волны как бы
исходят из одной точки,
совпадающей с центром вибратора.
.
Она изменяется скачком на обратную при переходе
напряжённости поля через нуль. Симметричный вибратор излучает сферические волны, о
чем
свидетельствует множитель
exp(-ikr)/r. Эти волны как бы
исходят из одной точки,
совпадающей с центром вибратора.
3.3. Мощность излучения, сопротивление излучения и КНД симметричного вибратора
Мощность электромагнитной волны, излучаемой симметричным вибратором, можно
определить, как и для элементарного вибратора, методом вектора Пойнтинга. В соответствии с данным методом симметричный
вибратор окружается сферой, радиус которой r »![]() ,
вследствие чего поверхность сферы находится в дальней зоне поля вибратора. Центр
вибратора совпадает с центром сферы, ось вибратора лежит на оси z прямоугольной
системы координат. На поверхности сферы выделяется бесконечно малый элемент dS, площадь которого в сферической системе
координат dS = r2sinνd
,
вследствие чего поверхность сферы находится в дальней зоне поля вибратора. Центр
вибратора совпадает с центром сферы, ось вибратора лежит на оси z прямоугольной
системы координат. На поверхности сферы выделяется бесконечно малый элемент dS, площадь которого в сферической системе
координат dS = r2sinνd![]() d
d![]() .
Излучаемая
мощность, приходящаяся на данный элемент поверхности
.
Излучаемая
мощность, приходящаяся на данный элемент поверхности
dP![]() = ПсрdS=(E2/2Wc)dS.
(3.10)
= ПсрdS=(E2/2Wc)dS.
(3.10)
Здесь Е - амплитуда (модуль) напряженности электрического поля в любой
точке элемента dS, определяемая
выражением
E = (60Iп/r)
![]() [cos (kl cos
[cos (kl cos![]() ) - cos kl] / sin
) - cos kl] / sin![]()
![]() .
(3.11)
.
(3.11)
В общем виде выражение для сопротивления излучения имеет вид
R![]() п = [r2Е2 макс/(
Wc Iп2 )]
п = [r2Е2 макс/(
Wc Iп2 )] ![]()
![]() F2(
F2(![]() ,
,![]() )sin
)sin![]() dνd
dνd![]() .
(3.12)
.
(3.12)
P![]() = Iп2R
= Iп2R![]() п/2.
п/2.
Величина R![]() п определяется характером распределения
электромагнитного поля в дальней зоне, т.е. диаграммой направленности рассматриваемой
антенны.
Интегрирование дает следующую формулу, впервые полученную Баллантайном в
п определяется характером распределения
электромагнитного поля в дальней зоне, т.е. диаграммой направленности рассматриваемой
антенны.
Интегрирование дает следующую формулу, впервые полученную Баллантайном в
R![]() п = 30 [2 (
п = 30 [2 (![]() +ln2kl - Ci 2kl) + cos 2kl (
+ln2kl - Ci 2kl) + cos 2kl (![]() +lnkl+ Ci 4kl - 2Ci 2kl) +
+lnkl+ Ci 4kl - 2Ci 2kl) +
+sin2kl (Si 4kl- 2Si 2kl)].
(3.1)
|
|
|
|
|
|
Здесь ![]() = 0,5772... - постоянная
Эйлера; Si x =
(sin u/u)du – интегральный
= 0,5772... - постоянная
Эйлера; Si x =
(sin u/u)du – интегральный
синус; Ci x =
![]() (cos u/u)du - интегральный косинус.
(cos u/u)du - интегральный косинус.![]()
Как видно из формулы (3.13), сопротивление излучения симметричного вибратора зависит
только от величины отношения l/![]() . Формула
(3.13) является приближенной, поскольку при ее выводе исходили из
синусоидального распределения тока по вибратору, что справедливо только для
тонких вибраторов.
Однако результаты расчетов по формуле (3.13) хорошо совпадают с
экспериментальными данными. Это объясняется тем, что сопротивление излучения
определяется полем в дальней зоне, которое мало зависит от толщины вибратора.
Следует также иметь в виду, что изложенный здесь метод расчета дает только
активную составляющую сопротивления излучения, так как учитывается только излученная
активная мощность.
. Формула
(3.13) является приближенной, поскольку при ее выводе исходили из
синусоидального распределения тока по вибратору, что справедливо только для
тонких вибраторов.
Однако результаты расчетов по формуле (3.13) хорошо совпадают с
экспериментальными данными. Это объясняется тем, что сопротивление излучения
определяется полем в дальней зоне, которое мало зависит от толщины вибратора.
Следует также иметь в виду, что изложенный здесь метод расчета дает только
активную составляющую сопротивления излучения, так как учитывается только излученная
активная мощность.
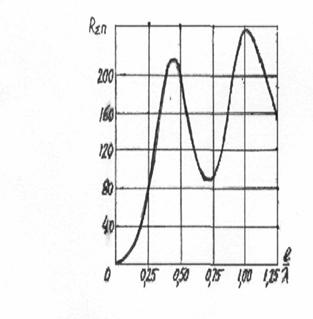
В литературе имеются
таблицы и графики R![]() п как функции отношения (рис.3.6), рассчитанные
по формуле (3.13). Осциллирующий характер зависимости объясняется тем, что
интерференционная картина поля в дальней зоне меняется при изменении l/
п как функции отношения (рис.3.6), рассчитанные
по формуле (3.13). Осциллирующий характер зависимости объясняется тем, что
интерференционная картина поля в дальней зоне меняется при изменении l/![]() .
.
Если
отношение l/![]() , не
превышает 0,1, то формулу (3.13)
можно упростить R
, не
превышает 0,1, то формулу (3.13)
можно упростить R![]() п=20 (k l)4 .
п=20 (k l)4 .
КНД симметричного вибратора можно определить по формуле
D = (120 / R![]() п
) (1 -coskl)2.
(3.14)
п
) (1 -coskl)2.
(3.14)
При l/![]() =0,25 R
=0,25 R![]() п = 73,1 Ом и D=
1,64 ;
п = 73,1 Ом и D=
1,64 ;
l/![]() = 0,5
R
= 0,5
R![]() п =199 Ом и D
= 2,4;
п =199 Ом и D
= 2,4;
l/![]() =0,625 R
=0,625 R![]() п =110 Ом и D = 3,l.
п =110 Ом и D = 3,l.
Для сравнения КНД элементарного электрического вибратора имеет
D = 1,5. КНД любой вибраторной антенны можно рассчитать по формуле
D = (120/ R![]() п) f2max (
п) f2max (![]() ).
(3.15)
).
(3.15)
В этой формуле R![]() п - полное
сопротивление излучения антенны. Действующая длина симметричного вибратора определяется по формуле
п - полное
сопротивление излучения антенны. Действующая длина симметричного вибратора определяется по формуле
|
|
lд = ![]() (1 - coskl) / (
(1 - coskl) / (![]() sinkl).
(3.16)
sinkl).
(3.16)
Рис 3.6. Зависимость R![]() п От величины l/
п От величины l/![]()
3.4. Входное сопротивление симметричного вибратора. Инженерный метод расчета входного сопротивления
Часть мощности, подводимой от генератора к
симметричному вибратору, излучается. Другая часть мощности теряется в самом
вибраторе (нагревание проводов), в
изоляторах и в окружающих вибратор предметах. Излученной мощности
соответствует активное сопротивление излучения. Мощности потерь соответствует активное сопротивление
потерь. Кроме излученного, есть колеблющееся вблизи антенны связанное с ней
электромагнитное поле, которому соответствует реактивная мощность. Эта мощность
то отдается генератором, переходя в ближнее поле, то возвращается к нему
обратно. Реактивной мощности в
большинстве случаев соответствует реактивное сопротивление антенны.
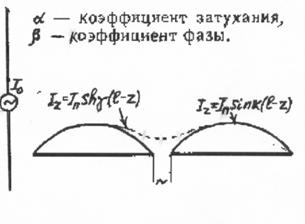
|
Рис. 3.7. Распределение тока по "коротким" и "длинным" вибраторам |
Таким образом, включенный в антенну
генератор нагружен на комплексное сопротивление, которое называется входным сопротивлением антенны и
равно отношению
напряжения на зажимах вибратора (точки питания) к току в точках питания ZBX=U0/I0=RBX+i XBX.
Величина
и характер входного сопротивления определяют режим работы включенного в
антенну генератора. Обычно в симметричных вибраторах потери малы, поэтому будем полагать, что RBX ![]() R
R![]() o, где R
o, где R![]() o - сопротивление излучения
вибратора, отнесенное к току в точках питания. Для точного определения входного сопротивления
необходимо знать закон распределения тока вдоль вибратора. Часто с
достаточной для инженерных целей точностью входное сопротивление рассчитывается,
исходя из приближенных
законов распределения тока по вибратору. Рассмотрим такой приближенный
(инженерный) метод расчета входного сопротивления. Предположив, что ток вдоль
вибратора распределен по закону синуса, найдем входное сопротивление симметричного
вибратора, у которого l/
o - сопротивление излучения
вибратора, отнесенное к току в точках питания. Для точного определения входного сопротивления
необходимо знать закон распределения тока вдоль вибратора. Часто с
достаточной для инженерных целей точностью входное сопротивление рассчитывается,
исходя из приближенных
законов распределения тока по вибратору. Рассмотрим такой приближенный
(инженерный) метод расчета входного сопротивления. Предположив, что ток вдоль
вибратора распределен по закону синуса, найдем входное сопротивление симметричного
вибратора, у которого l/![]() =0,5 (рис.3.7). В этом
случае ток в точках питания оказывается равным нулю и очевидно, что ZBX = U0/I0=
=0,5 (рис.3.7). В этом
случае ток в точках питания оказывается равным нулю и очевидно, что ZBX = U0/I0=![]() . В действительности же ток в точках
питания
никогда не бывает равен нулю (его величина обязательно конечна), а следовательно, входное сопротивление симметричного
вибратора никогда не бывает бесконечно велико. Физически это совершенно ясно.
Ведь закон синуса (стоячая волна) справедлив в линиях только при отсутствии
потерь. Вибратор
же в принципе является системой с потерями на излучение. Следовательно, при расчете
входного сопротивления лучше проводить аналогию между симметричным вибратором и
разомкнутой на конце линией с потерями. Известно, что ток в такой линии
распределен по закону гиперболического синуса (рис.3.7) Iz = Iпsh
. В действительности же ток в точках
питания
никогда не бывает равен нулю (его величина обязательно конечна), а следовательно, входное сопротивление симметричного
вибратора никогда не бывает бесконечно велико. Физически это совершенно ясно.
Ведь закон синуса (стоячая волна) справедлив в линиях только при отсутствии
потерь. Вибратор
же в принципе является системой с потерями на излучение. Следовательно, при расчете
входного сопротивления лучше проводить аналогию между симметричным вибратором и
разомкнутой на конце линией с потерями. Известно, что ток в такой линии
распределен по закону гиперболического синуса (рис.3.7) Iz = Iпsh![]() (z - l), где
(z - l), где ![]() =
= ![]() + i
+ i![]() - коэффициент распространения,
- коэффициент распространения, ![]() - коэффициент
затухания,
- коэффициент
затухания, ![]() - коэффициент
фазы.
- коэффициент
фазы.
Из рис.3.7 видно, что существенная разница в
распределении тока по законам кругового и гиперболического синусов получается
только на сравнительно
близких расстояниях от узла тока. Поэтому при расчете входных сопротивлений
"коротких" вибраторов (l/![]() )
) ![]() 0,35...0,4;
(0,6...0,65)
0,35...0,4;
(0,6...0,65) ![]() l/
l/![]()
![]() (0,85...0,9), т.е. таких, у которых узел тока
находится от точек питания вибратора не ближе, чем на расстоянии (0,1...0,15)
(0,85...0,9), т.е. таких, у которых узел тока
находится от точек питания вибратора не ближе, чем на расстоянии (0,1...0,15)![]() , исходят из синусоидального
распределения тока. При расчете входного сопротивления "длинных"
вибраторов (0,35
, исходят из синусоидального
распределения тока. При расчете входного сопротивления "длинных"
вибраторов (0,35![]() l/
l/![]()
![]() 0,65) следует
исходить из распределения тока по закону гиперболического синуса. Найдем формулы для
расчета активной
0,65) следует
исходить из распределения тока по закону гиперболического синуса. Найдем формулы для
расчета активной
и реактивной составляющих входного сопротивления "короткого" вибратора. Выразив мощность, излучаемую вибратором, через амплитуды тока в пучности (IП) и в точках питания (Iо), получим:
P![]() = (Iп2R
= (Iп2R![]() п )/2 и P
п )/2 и P![]() = (I02 R
= (I02 R![]() 0)/2.
(3.17)
0)/2.
(3.17)
Так как левые
части этих выражений равны между собой, то I2п R![]() п = I02 R
п = I02 R![]() 0. Решая
это равенство относительно R
0. Решая
это равенство относительно R![]() 0, получаем R
0, получаем R![]() 0= R
0= R![]() п (Iп2/ I02).
п (Iп2/ I02).
Подставляя вместо I0 выражение I0=Iпsinkl, получаем формулу для расчета активной составляющей входного сопротивления вибратора (без учета потерь в вибраторе)
R![]() 0 = R
0 = R![]() п /sin2kl.
(3.18)
п /sin2kl.
(3.18)
Величину R![]() п для вибратора заданной
длины легко найти из таблиц или графиков. При расчете реактивной составляющей
входного сопротивления
короткого симметричного вибратора пользуются формулой входного сопротивления разомкнутой на конце двухпроводной
линии без потерь, заменяя в ней волновое сопротивление линии волновым
сопротивлением антенны
п для вибратора заданной
длины легко найти из таблиц или графиков. При расчете реактивной составляющей
входного сопротивления
короткого симметричного вибратора пользуются формулой входного сопротивления разомкнутой на конце двухпроводной
линии без потерь, заменяя в ней волновое сопротивление линии волновым
сопротивлением антенны
Xвх= -i WActg kl. (3.19)
Таким образом, полное входное сопротивление короткого вибратора можно определить по формуле
Zвх= (R![]() п/sin2kl) – i WActg kl.
(3.20)
п/sin2kl) – i WActg kl.
(3.20)
Точность расчетов по формуле (3.20) повышается при уменьшении размеров поперечного сечения вибратора. В случаях длинных вибраторов входное сопротивление рассчитывается аналогично входному сопротивлению двухпроводной разомкнутой на конце линии, обладающей потерями
Zвх = WA [(sh2![]() l-
(
l-
(![]() /
/![]() ) sin 2
) sin 2![]() l)
/ (ch2
l)
/ (ch2![]() l - cos
2
l - cos
2![]() l)] – i
WA [(
l)] – i
WA [(![]() /
/![]() ) sh 2
) sh 2![]() l+
l+
+ sin 2![]() l)
/ (ch2
l)
/ (ch2![]() l - cos 2
l - cos 2![]() l)].
(3.21)
l)].
(3.21)
Здесь WA - волновое сопротивление вибратора; l- длина плеча вибратора; ![]() - коэффициент фазы
в вибраторе;
- коэффициент фазы
в вибраторе; ![]() - коэффициент затухания. По аналогии с длинными линиями, пренебрегая потерями
в проводах вибратора коэффициент
затухания можно рассчитать по формуле
- коэффициент затухания. По аналогии с длинными линиями, пренебрегая потерями
в проводах вибратора коэффициент
затухания можно рассчитать по формуле ![]() = R
= R![]() 1 / WA, где R
1 / WA, где R![]() 1 -активное сопротивление излучения,
приходящееся на единицу длины вибратора. Приближенно полагая, что сопротивление излучения R
1 -активное сопротивление излучения,
приходящееся на единицу длины вибратора. Приближенно полагая, что сопротивление излучения R![]() п распределено равномерно по всей длине вибратора, для расчета R
п распределено равномерно по всей длине вибратора, для расчета R![]() 1 получают формулу R
1 получают формулу R![]() 1= R
1= R![]() п/[l(l - (sin2kl/2kl)].
Данная формула позволяет, зная сопротивление излучения,
отнесенное к пучности тока, найти распределенное сопротивление излучения. Следовательно, коэффициент
затухания
п/[l(l - (sin2kl/2kl)].
Данная формула позволяет, зная сопротивление излучения,
отнесенное к пучности тока, найти распределенное сопротивление излучения. Следовательно, коэффициент
затухания
![]() = R
= R![]() 1/ WA = R
1/ WA = R![]() п/ [lWA (1- (sin2kl/2kl))].
п/ [lWA (1- (sin2kl/2kl))].
Коэффициент фазы ![]() в
формуле (3.21) несколько отличается от
в
формуле (3.21) несколько отличается от
Рис. 3.8. Зависимость R вх от
величины l/![]()
|
|
|
|
коэффициента фазы в
свободном
пространстве k, так как фазовая скорость в линии с потерями, а, следовательно, и в вибраторе несколько меньше скорости света. Поэтому![]() =
= ![]() /
/![]() > k
=
> k
= ![]() /с , где
/с , где ![]() -фазовая
скорость
в вибраторе. Чем меньше волновое сопротивление вибратора (чем толще вибратор), тем
меньше фазовая скорость. Из формулы (3.21) видно, что как активная, так и реактивная составляющие входного сопротивления симметричного
вибратора, в общем случае, зависят
не только от длины вибратора, но и от
его диаметра. Зависимость входного сопротивления симметричного вибратора от величины отношения l/
-фазовая
скорость
в вибраторе. Чем меньше волновое сопротивление вибратора (чем толще вибратор), тем
меньше фазовая скорость. Из формулы (3.21) видно, что как активная, так и реактивная составляющие входного сопротивления симметричного
вибратора, в общем случае, зависят
не только от длины вибратора, но и от
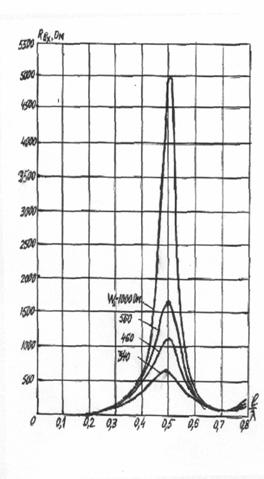
его диаметра. Зависимость входного сопротивления симметричного вибратора от величины отношения l/![]() и от волнового сопротивления
WA показана на рис. 3.8 и 3.9.
и от волнового сопротивления
WA показана на рис. 3.8 и 3.9.
Кривые рассчитаны по
формуле (3.21).
При расчете полагалось, что ![]() = k.
Из кривых видно, что при
увеличении l/
= k.
Из кривых видно, что при
увеличении l/![]() активная составляющая входного сопротивления постепенно растет и достигает при l/
активная составляющая входного сопротивления постепенно растет и достигает при l/![]() =0,5 максимума, величина
которого тем больше, чем больше wa, т.е. чем тоньше вибратор. При
дальнейшем увеличении
l/
=0,5 максимума, величина
которого тем больше, чем больше wa, т.е. чем тоньше вибратор. При
дальнейшем увеличении
l/![]() rbx постепенно
уменьшается и достигает минимума при
l/
rbx постепенно
уменьшается и достигает минимума при
l/![]() =0,75. Затем Rвх снова начинает увеличиваться и достигает
=0,75. Затем Rвх снова начинает увеличиваться и достигает
Рис. 3.9. Зависимость X вх от величины l/![]()
нового максимума при l=![]() (на рисунке этот
максимум не показан). Вообще максимумы Rвх повторяются
при всех отношениях l/
(на рисунке этот
максимум не показан). Вообще максимумы Rвх повторяются
при всех отношениях l/![]() , кратных
0,5. Активная составляющая входного сопротивления минимальна в тех случаях,
когда относительная
длина вибратора становится равной нечетному числу
, кратных
0,5. Активная составляющая входного сопротивления минимальна в тех случаях,
когда относительная
длина вибратора становится равной нечетному числу ![]() /4. В случае полуволнового
вибратора минимум Rвх отсутствует. Реактивная составляющая входного
сопротивления вибратора изменяется периодически, проходя через нуль
при l/
/4. В случае полуволнового
вибратора минимум Rвх отсутствует. Реактивная составляющая входного
сопротивления вибратора изменяется периодически, проходя через нуль
при l/![]() =0,25; 0,5;0,75; 1
и т.д. При l/
=0,25; 0,5;0,75; 1
и т.д. При l/![]() <0,25 Хвх имеет емкостный характер,
при 0,25<
l/
<0,25 Хвх имеет емкостный характер,
при 0,25<
l/![]() <0,5 - индуктивный.
Можно сказать, что вблизи значений l/
<0,5 - индуктивный.
Можно сказать, что вблизи значений l/![]() = (2n + 1)/4, где n=0,
1, 2..., симметричный вибратор ведет себя подобно последовательному колебательному
контуру (резонанс напряжения), а вблизи значений l/
= (2n + 1)/4, где n=0,
1, 2..., симметричный вибратор ведет себя подобно последовательному колебательному
контуру (резонанс напряжения), а вблизи значений l/![]() =n/2-
подобно параллельному колебательному контуру (резонанс токов). В первом случае
вибратор питается в пучности
тока, а во втором - в узле тока. Наибольшую длину волны, при которой вибратор оказывается настроенным в резонанс
с питающим его генератором (Хвх= 0), называют собственной длиной волны антенны.
Как видно из формул (3.20) и (3.21), собственная длина волны
симметричного вибратора
=n/2-
подобно параллельному колебательному контуру (резонанс токов). В первом случае
вибратор питается в пучности
тока, а во втором - в узле тока. Наибольшую длину волны, при которой вибратор оказывается настроенным в резонанс
с питающим его генератором (Хвх= 0), называют собственной длиной волны антенны.
Как видно из формул (3.20) и (3.21), собственная длина волны
симметричного вибратора ![]() 0=4l. В действительности из-за того, что фазовая скорость
распространения в вибраторе несколько меньше скорости света (
0=4l. В действительности из-за того, что фазовая скорость
распространения в вибраторе несколько меньше скорости света (![]() > k),
резонансные длины вибраторов оказываются несколько меньшими, чем получаемые по формулам (3.20) и
(3.21). При этом, чем толще вибратор, тем меньше
фазовая скорость
и тем короче его резонансная длина. В частности, при l/
> k),
резонансные длины вибраторов оказываются несколько меньшими, чем получаемые по формулам (3.20) и
(3.21). При этом, чем толще вибратор, тем меньше
фазовая скорость
и тем короче его резонансная длина. В частности, при l/![]() =0,25 и а
=0,25 и а![]() 0
Хвх=i42,5 Ом. Обычно стремятся к
нулевой реактивной составляющей входного сопротивления вибратора на рабочей частоте. Поэтому длину
плеча вибратора делают несколько короче, чем
0
Хвх=i42,5 Ом. Обычно стремятся к
нулевой реактивной составляющей входного сопротивления вибратора на рабочей частоте. Поэтому длину
плеча вибратора делают несколько короче, чем
![]() /4 или
/4 или ![]() /2. Величина
укорочения тем больше, чем толще вибратор. Активная
составляющая входного сопротивления симметричного вибратора при питании
вибратора в пучности тока (последовательный
резонанс), как следует из формулы (3.20), равна Rвх=R
/2. Величина
укорочения тем больше, чем толще вибратор. Активная
составляющая входного сопротивления симметричного вибратора при питании
вибратора в пучности тока (последовательный
резонанс), как следует из формулы (3.20), равна Rвх=R![]() 0=R
0=R![]() п..
При определении входного сопротивления симметричного вибратора, питаемого вблизи узла тока, полагая, что
п..
При определении входного сопротивления симметричного вибратора, питаемого вблизи узла тока, полагая, что
![]() l<<1 (что соответствует действительности),
можно несколько преобразовать выражение (3.21) и получить следующие формулы:
l<<1 (что соответствует действительности),
можно несколько преобразовать выражение (3.21) и получить следующие формулы:
Rвх = R![]() п / [sin2 kl+ (R
п / [sin2 kl+ (R![]() п2/W2A)];
(3.22)
п2/W2A)];
(3.22)
Хвх = - i (WA/2) [sin2kl/ (sin2
kl + (R![]() п2/W2A))] .
(3.23)
п2/W2A))] .
(3.23)
В случае параллельного резонанса (kl=180°) получаем
R![]() 0 = WA2 / R
0 = WA2 / R![]() п и Хвх = 0.
(3.24)
п и Хвх = 0.
(3.24)
Из формулы (3.24) видно, что в случае параллельного резонанса R![]() 0 весьма велико, так
как R
0 весьма велико, так
как R![]() п
п ![]() 200 Ом, a WA составляет 300 ... 1000 Ом. Формулами (3.22) и
(3.23) можно пользоваться наряду с формулой (3.21) для расчета входного сопротивления
симметричного вибратора, если 0,35
200 Ом, a WA составляет 300 ... 1000 Ом. Формулами (3.22) и
(3.23) можно пользоваться наряду с формулой (3.21) для расчета входного сопротивления
симметричного вибратора, если 0,35 ![]() l/
l/![]()
![]() 0,65.
Отметим, что при увеличении волнового сопротивления вибратора закон распределения тока по нему становится ближе к синусоидальному.
0,65.
Отметим, что при увеличении волнового сопротивления вибратора закон распределения тока по нему становится ближе к синусоидальному.
Поэтому в случае тонких вибраторов (WA=700...1000 Ом) пределы применимости формулы (3.20) расширяются. Как видно из кривых рис. 3.8 и 3.9, при уменьшении волнового сопротивления вибратора уменьшается зависимость его активного и реактивного входного сопротивления от частоты (улучшаются диапазонные свойства). По аналогии с обычным колебательным контуром можно сказать, что при уменьшении WA уменьшается добротность вибратора, под которой понимается отношение связанной с вибратором реактивной энергии к активной (излученной и теряемой) энергии. Добротность вибратора определяется выражением
QA= A (WA/Rвх), (3.25)
где
А - коэффициент пропорциональности.
|
|
WA уменьшают, увеличивая размеры поперечного сечения вибратора; при этом увеличивается распределенная емкость C1 вибратора.
Зависимость Rвх и Хвх от относительной длины плеча вибраторов реальной толщины приведены на рис.3.10.
Рис. 3.10. Зависимость Rвх и Xвх реальных вибраторов от величины l/![]()
3.5. Основные результаты, даваемые строгой теорией симметричного вибратора
Задача об излучении тонкого симметричного вибратора (электрический радиус вибратора
ka < 0,1) в строгой
электродинамической постановке была решена Халленом и
независимо от него российскими учеными М.А.Леонтовичем и М.Л.Левиным методом
интегро-дифференциального уравнения. Как показали расчеты, даже в случае
сравнительно тонких вибраторов (ka ![]() 0,05)
распределение тока уже несколько отличается от синусоидального.
Таким образом, метод интегро-дифференциального уравнения подтверждает
правильность выбора приближенного (синусоидального) закона распределения
тока и позволяет найти точное распределение тока в тонких вибраторах.
Однако он не позволяет найти закон распределения тока в вибраторах средней (ka= 0,1...0,5) и большой (ka > 0,5) толщины. Кроме
того, в рассмотренном методе не учитывается влияние ширины возбуждающего зазора на
распределение тока. Входное сопротивление полуволнового вибратора,
рассчитанное этим методом, при а
0,05)
распределение тока уже несколько отличается от синусоидального.
Таким образом, метод интегро-дифференциального уравнения подтверждает
правильность выбора приближенного (синусоидального) закона распределения
тока и позволяет найти точное распределение тока в тонких вибраторах.
Однако он не позволяет найти закон распределения тока в вибраторах средней (ka= 0,1...0,5) и большой (ka > 0,5) толщины. Кроме
того, в рассмотренном методе не учитывается влияние ширины возбуждающего зазора на
распределение тока. Входное сопротивление полуволнового вибратора,
рассчитанное этим методом, при а![]() 0 оказывается
комплексным и равным Zвх =
73,1 + i42,5 Ом. Как видно,
активная составляющая входного
сопротивления (R
0 оказывается
комплексным и равным Zвх =
73,1 + i42,5 Ом. Как видно,
активная составляющая входного
сопротивления (R![]() 0)
получается такой же, как и по методу вектора Пойнтинга. Реактивная составляющая входного сопротивления имеет индуктивный характер. Укорочение
0)
получается такой же, как и по методу вектора Пойнтинга. Реактивная составляющая входного сопротивления имеет индуктивный характер. Укорочение ![]() l, необходимое для того, чтобы сделать вибратор резонансным,
определяется по формуле
l, необходимое для того, чтобы сделать вибратор резонансным,
определяется по формуле
![]() l/l = - 0,225/ ln (l/a).
(3.26)
l/l = - 0,225/ ln (l/a).
(3.26)
Расчет входного сопротивления полуволнового вибратора с учетом только первого приближения показал, что даже в случае тонких вибраторов величина радиуса заметно, влияет на входное сопротивление.
Задача об излучении толстого вибратора (ka>0,5) в строгой постановке была решена Е. Н. Васильевым в 1958-1959 гг. В отличие от методов Халлена или Леонтовича-Левина, где использовались граничные условия для векторов электрического поля на поверхности вибратора, в методе Васильева используется граничное условие для векторов магнитного поля. Полученное из этого условия интегральное уравнение относительно текущего по вибратору тока решается численно при помощи ЭВМ. Решение тем более точно, чем толще вибратор. В дальнейшем Е.Н. Васильевым и Г.Д. Малушковым был разработан более общий метод решения задачи возбуждения осесимметричного тела вращения, позволяющий рассчитать распределение тока на вибраторах среднего электрического радиуса (ka = 0,1...0,5), что особенно важно для анализа работы вибраторов, применяемых в метровом и особенно в дециметровом диапазонах волн. Проведенные расчеты показали, что распределение тока в вибраторах средней и большой толщины значительно отличается от синусоидального. Ток на кромке торца имеет конечную величину. В центре торца ток равен нулю. Расчеты показали также, что: 1) с увеличением радиуса цилиндра существенно уменьшается коэффициент отражения от его концов и распределение тока по вибратору приобретает характер бегущей волны: амплитуда тока постепенно уменьшается по мере удаления от точек питания вибратора, фаза тока изменяется примерно по линейному закону; 2) ширина зазора между плечами вибратора значительно влияет на распределение тока вблизи точек питания вибратора. Зависимость распределения тока от толщины вибратора влияет на диаграмму направленности последнего. С увеличением толщины вибратора направления нулевого излучения заменяются направлениями минимального излучения. При этом чем толще вибратор, тем менее глубоки минимумы.
Действительные диаграммы направленности заметно отличаются от рассчитанных приближенным методом при l/а, равном нескольким десяткам.
3.6. Симметричный
щелевой вибратор
|
|
|
Рис. 3.11. Щелевой вибратор (а) и его аналог (б) |
В курсе «ЭМП и В» был рассмотрен элементарный щелевой излучатель,
представляющий собой узкую щель, прорезанную в безграничном идеально
проводящем плоском экране, длина которой во много раз меньше длины волны. На
практике широко применяются щелевые излучатели, длина которых соизмерима с длиной
волны. Излучающие щели обычно имеют прямолинейную форму (линейные щелевые
излучатели), но могут иметь и круглую форму (кольцевая щель). Излучающие щели
прорезают
в металлических поверхностях различных размеров и формы: в стенках прямоугольных и
круглых волноводов,
в оболочках коаксиальных кабелей, в плоских металлических экранах, в крыльях
самолетов и т.д. Иногда размеры металлической поверхности, в которой прорезана
щель, во много раз превышают длину волны, но практически обычно размеры этой
поверхности бывают соизмеримы с длиной волны. В
основном, щелевые антенны применяют в дециметровом, сантиметровом,
миллиметровом и редко в метровом (телевизионные
антенны) диапазонах волн. Кольцевые щелевые антенны можно применять в
диапазонах средних и даже длинных волн. Рассмотрим только идеализированный
случай - узкую щель, прорезанную в безграничном идеально проводящем экране. Под симметричной
щелью будем понимать узкую, прямоугольную
щель, питаемую в центре генератором высокой частоты (рис.3.11.а). ЭДС
генератора создает в щели электрическое поле, линии которого перпендикулярны ее краям. Под действием поля
в щели возникают электрические токи на металлической поверхности.
Электромагнитное поле в окружающем
пространстве определяется электрическим полем щели (магнитный ток) и электрическими токами, текущими по
металлической поверхности. На основании принципа двойственности по аналогии с
элементарной щелью, поле, создаваемое симметричной щелью, можно найти,
если известно поле, создаваемое симметричным
электрическим вибратором, имеющим одинаковую форму и размеры со щелью (рис.
3.11.б) и находящимся в свободном пространстве. Для этого в
соответствии с принципом двойственности надо в выражениях для составляющих поля
электрического вибратора произвести соответствующие замены. В случае очень
тонкого электрического вибратора ток в нем
распределен по закону синуса. По этому же закону изменяется вдоль вибратора и
тангенциальная составляющая напряженности магнитного поля. Следовательно, вдоль узкого щелевого вибратора тангенциальная составляющая напряженности электрического
поля (а значит, и напряжение - магнитный ток)
изменяется также по синусоидальному закону, т.е. Uz= (U0/sinkl) (sink(l -![]() )), где U0 - амплитуда напряжения в центре щели; l - длина половины щели.
)), где U0 - амплитуда напряжения в центре щели; l - длина половины щели.
Я.Н.Фельд, решая задачу об излучении узкой щели, по
существу, аналогично методу интегро-дифференциального уравнения для тонких электрических
вибраторов, строго доказал, что вдоль такой щели напряжение распределено по закону синуса. В частности, в
случае полуволновой щели напряжение
распределено по закону синуса независимо от точек включения генератора.
Напряженность электрического поля, создаваемого симметричным щелевым
вибратором, в дальней зоне может быть определена по формуле, получающейся из (3.7) путем замены I0 на U0 и с учетом того, что
1А электрического тока
создает такое же электрическое поле как 60![]() В
напряжения в щели. Эта формула имеет вид
В
напряжения в щели. Эта формула имеет вид
Е![]() = i(U0/
= i(U0/![]() r0sinkl)[(cos(klcos
r0sinkl)[(cos(klcos![]() )-coskl)/ sin
)-coskl)/ sin![]() ] exp(-ikr0).
(3.27)
] exp(-ikr0).
(3.27)
Из принципа двойственности и из данной формулы видно, что
щелевой вибратор обладает направленными свойствами в своей меридиональной плоскости. Диаграмма
направленности щелевого вибратора в этой плоскости зависит от
отношения l/![]() и
совпадает с диаграммой направленности металлического аналога щели в этой же
плоскости. Вдоль своей оси щелевой вибратор не излучает. Максимум излучения для отношения l/
и
совпадает с диаграммой направленности металлического аналога щели в этой же
плоскости. Вдоль своей оси щелевой вибратор не излучает. Максимум излучения для отношения l/![]() < 0,7 направлен вдоль
нормали к оси щели (
< 0,7 направлен вдоль
нормали к оси щели (![]() =90°). В экваториальной плоскости (плоскость вектора Е) щель не обладает направленными
свойствами (в полярной системе координат диаграмма направленности представляет
собой окружность). Вектор Е поля
щели перпендикулярен вектору Е ее металлического аналога. Проводимость
излучения симметричной щели можно рассчитать по формуле (3.28), если в ней под
=90°). В экваториальной плоскости (плоскость вектора Е) щель не обладает направленными
свойствами (в полярной системе координат диаграмма направленности представляет
собой окружность). Вектор Е поля
щели перпендикулярен вектору Е ее металлического аналога. Проводимость
излучения симметричной щели можно рассчитать по формуле (3.28), если в ней под ![]() понимать сопротивление
излучения
металлического аналога данной щели (симметричного вибратора).
понимать сопротивление
излучения
металлического аналога данной щели (симметричного вибратора).
G![]() щ = 4 R
щ = 4 R![]() э / (120
э / (120![]() )2.
(3.28)
)2.
(3.28)
Входной проводимостью щели называется отношение электрического
тока в точках ее питания к напряжению, приложенному к этим точкам, т.е. Yвх = I0/U0. Как и входное сопротивление симметричного электрического вибратора, входная проводимость щели в общем случае есть величина комплексная. Если известно входное сопротивление металлического аналога данной щели, то входную проводимость можно определить по формуле, аналогичной (3.28) и являющейся обобщением ее на случай входной проводимости щели
Yвхщ=4Zвхэ/ (120![]() )2,
(3.29)
)2,
(3.29)
где Zэвх - входное сопротивление металлического аналога щели.
В большинстве случаев известны входные сопротивления вибраторов, имеющих цилиндрическую форму. При этом в формулу (3.29) можно подставить значение входного сопротивления цилиндрического вибратора, радиус которого в 4 раза меньше ширины щели.
Щель, как
и симметричный вибратор, обладает резонансными свойствами. Реактивная проводимость
щели обращается в нуль, если ее длина 2l приблизительно кратна ![]() /2. Точнее, длина резонансной щели
несколько меньше
/2. Точнее, длина резонансной щели
несколько меньше ![]() /2. Необходимое укорочение тем больше, чем шире щель; приближенно оно может быть определено по формуле (3.26) для
цилиндрического вибратора, радиус
которого равен 1/4 ширины щели. Обычно стремятся к тому, чтобы щелевая антенна излучала только в одно полупространство,
т.е. имела однонаправленное излучение. Это можно, например, сделать, если со
стороны второго полупространства закрыть щель металлической полостью (коробом).
Высота короба h
выбирается так, чтобы он не шунтировал щель. Короб можно упрощенно представить в виде двухпроводной закороченной на конце
линии; такая линия при длине h=
/2. Необходимое укорочение тем больше, чем шире щель; приближенно оно может быть определено по формуле (3.26) для
цилиндрического вибратора, радиус
которого равен 1/4 ширины щели. Обычно стремятся к тому, чтобы щелевая антенна излучала только в одно полупространство,
т.е. имела однонаправленное излучение. Это можно, например, сделать, если со
стороны второго полупространства закрыть щель металлической полостью (коробом).
Высота короба h
выбирается так, чтобы он не шунтировал щель. Короб можно упрощенно представить в виде двухпроводной закороченной на конце
линии; такая линия при длине h=![]() /4 обладает бесконечным входным сопротивлением. Излучаемая мощность находится
интегрированием вектора Пойнтинга по
поверхности сферы большого радиуса, окружающей щель. Однако в данном случае щель излучает только в одно
полупространство; во всех точках второго полупространства напряженность поля
равна нулю и, следовательно, интегрировать надо по поверхности полусферы.
Поэтому мощность излучения будет в 2 раза меньше, чем при двусторонней щели.
/4 обладает бесконечным входным сопротивлением. Излучаемая мощность находится
интегрированием вектора Пойнтинга по
поверхности сферы большого радиуса, окружающей щель. Однако в данном случае щель излучает только в одно
полупространство; во всех точках второго полупространства напряженность поля
равна нулю и, следовательно, интегрировать надо по поверхности полусферы.
Поэтому мощность излучения будет в 2 раза меньше, чем при двусторонней щели.
Следовательно G![]() одн= G
одн= G![]() дв/2.
дв/2.
Таким образом, проводимость излучения односторонней щели определяется по формуле
G![]() одн = 2R
одн = 2R![]() э/ (120
э/ (120![]() )2.
(3.30)
)2.
(3.30)
Входная проводимость односторонней щели определяется по формуле
Y![]() одн = 2Zвхэ/ (120
одн = 2Zвхэ/ (120![]() )2.
(3.31)
)2.
(3.31)
Строгий анализ направленных свойств щели, прорезанной в металлической поверхности, размеры которой соизмеримы с длиной волны, основан на решении задачи дифракции плоской электромагнитной волны на данной поверхности. В результате такого анализа установлено, что на диаграмму направленности щели в плоскости вектора Е особенно сильно влияет размер металлической поверхности, параллельный этому вектору Е. Диаграмма направленности щелевой антенны в плоскости вектора Н сравнительно слабо зависит от размеров металлической поверхности и ориентировочно может определяться на основании принципа двойственности.
3.7. Способы расширения рабочего диапазона вибраторных антенн
Рабочий диапазон простых вибраторных антенн (в том числе несимметричных) определяется частотной зависимостью входного сопротивления антенны.
Уменьшить эту зависимость можно тремя способами:
1) как уже отмечалось - снижением волнового сопротивления вибратора; 2) плавным изменением его поперечного сечения;
3) коррекцией входного сопротивления вибратора.
Первый способ. Снижение волнового сопротивления вибратора путем увеличения размеров поперечного сечения является одним из основных методов расширения рабочего диапазона вибратора. По этому принципу построен симметричный вибратор, предложенный в начале 30х годов С.И.Надененко, широко применяемый в диапазонах коротких и метровых волн. Этот вибратор выполняется из ряда проводов, натянутых по образующим цилиндра (рис.3.12), в результате чего волновое сопротивление снижается до 250...400 Ом (вместо 600...1000 Ом у обычного вибратора). Волновое сопротивление такого вибратора рассчитывается по формуле
WA = 120[ln (l/![]() э-1],
(3.32)
э-1],
(3.32)
где ![]() э - эквивалентный радиус вибратора.
э - эквивалентный радиус вибратора.
|
|
|
|
|
|
Рис. 3.12. Вибратор Надененко
Эквивалентным радиусом вибратора называется радиус сплошного металлического цилиндра, волновое сопротивление которого равно волновому сопротивлению данного цилиндра, выполненного из отдельных проводов
![]() э =
э = ![]()
![]() ,
(3.33)
,
(3.33)
где ![]() - радиус цилиндра,
образованного проводами;
- радиус цилиндра,
образованного проводами;
n - число проводов (обычно n = 6...8)
а - радиус провода.
Диапазонные вибраторы могут иметь различную форму поперечного сечения: круглую, прямоугольную, треугольную и т.д.
Второй способ. Этот способ основан на том, что антенну можно рассматривать
как переходное устройство между фидерной линией, в которой существует
связанная плоская волна, и свободным пространством,в котором существует пространственная
волна. Если в качестве фидера применяется
двухпроводная симметричная линия, то плавный переход от такой линии к
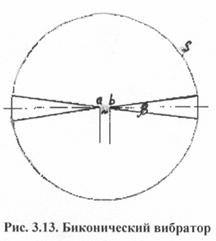
свободному пространству может быть осуществлён при помощи биконической антенны (рис.3.13). Волновое
сопротивление биконической антенны (l![]() ) равно
) равно
|
|
WA=276lg [ctg (![]() /2)],
(3.34)
/2)],
(3.34)
где ![]() -
угол между осью конуса и его образующей. При 30° <
-
угол между осью конуса и его образующей. При 30° < ![]() < 60°
входное сопротивление биконической антенны в довольно широком диапазоне слабо зависит
от частоты.
< 60°
входное сопротивление биконической антенны в довольно широком диапазоне слабо зависит
от частоты.
Третий способ. Этот способ состоит в том, что антенна выполняется из двух частей, реактивные составляющие входных сопротивлений которых имеют различные частотные зависимости (например, одно является индуктивным, а другое ёмкостным) и компенсируют друг друга в некоторой полосе частот. Примером может служить диапазонный шунтовой вибратор, предложенный Г.З.Айзенбергом.