ЛЕКЦИЯ 2. ПАРАМЕТРЫ, ХАРАКТЕРИЗУЮЩИЕ НАПРАВЛЕННЫЕ И ПОЛЯРИЗАЦИОННЫЕ СВОЙСТВА АНТЕНН
2.1. Характеристика (диаграмма) направленности антенны
При расчете излученного антенной электромагнитного поля ее удобно рассматривать как состоящую из бесконечного большого числа элементарных источников (излучателей). Благодаря линейности уравнений Максвелла к полям элементарных источников применим принцип суперпозиции, позволяющий найти поле антенны в результате суммирования полей всех составляющих ее элементарных излучателей с учетом амплитуд и фаз возбуждающих их токов. Суммирование полей сводится к их интегрированию по источникам. Элементарными источниками являются: элементарные электрические вибраторы ЭЭВ в случае проволочных антенн; элементарные магнитные вибраторы в случае щелевых антенн; бесконечно малые элементы волнового фронта или элементы Гюйгенса в случае апертурных антенн.
Формула для комплексной амплитуды напряженности электрического поля Ė произвольной реальной антенны в дальней зоне без учета векторного характера электромагнитного поля имеет вид
![]() . (2.1)
. (2.1)
Здесь А - комплексный множитель, не зависящий от направления на точку наблюдения (в
него входит стандартный множитель exp(-ikr)/r, где r -расстояние от фазового центра антенны до
точки наблюдения; ![]() - коэффициент фазы или волновое число в свободном
пространстве); θ,φ - координаты точки наблюдения; |f(θ,φ)| - амплитудная
характеристика направленности; Ψ(θ,φ) - фазовая характеристика
направленности. Известно, что в случае элементарного электрического вибратора
- коэффициент фазы или волновое число в свободном
пространстве); θ,φ - координаты точки наблюдения; |f(θ,φ)| - амплитудная
характеристика направленности; Ψ(θ,φ) - фазовая характеристика
направленности. Известно, что в случае элементарного электрического вибратора
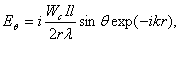 (2.2)
(2.2)
где I - амплитуда тока в
вибраторе; l - длина вибратора; ![]() характеристическое сопротивление волны; в
свободном пространстве
характеристическое сопротивление волны; в
свободном пространстве ![]() , Ом
, Ом
Амплитудной характеристикой направленности антенны называется зависимость величины (модуля) напряженности электрического поля, создаваемого антенной в точке наблюдения, от направления на эту точку, характеризуемого углами θ и φ сферической системы координат при постоянном расстоянии (r = const) точки наблюдения от антенны. Фазовой характеристикой направленности антенны Ψ (θ,φ) называется зависимость фазы поля, создаваемого антенной в точке наблюдения, находящейся на поверхности сферы в дальней зоне, от направления на эту точку, характеризуемого углами θ и φ. Множитель f(θ,φ) определяет не только величину, но и фазу напря-
женности поля, так
как при переходе функции f(![]() ) через нуль меняется ее знак, что соответствует
скачку фазы напряженности поля на 180°.
Поэтому амплитудной характеристикой направленности является модуль этой
функции |f(
) через нуль меняется ее знак, что соответствует
скачку фазы напряженности поля на 180°.
Поэтому амплитудной характеристикой направленности является модуль этой
функции |f(![]() )|. В дальнейшем для упрощения записи знак модуля опускаем. В общем случае характеристика
направленности является векторной и
комплексной величиной. Выражение ƒ(
)|. В дальнейшем для упрощения записи знак модуля опускаем. В общем случае характеристика
направленности является векторной и
комплексной величиной. Выражение ƒ(![]() )=f(
)=f(![]() ) exp[i
) exp[i![]() ] называется комплексной
характеристикой направленности антенны. Она полностью определяет угловое
распределение и фазовые свойства излучаемого электромагнитного поля в дальней зоне антенны.
Характеристика направленности антенны
определяется размерами и конфигурацией антенны, а также распределением
возбуждающего тока (как действительного, так и эквивалентного). Напомним, что дальняя
зона (зона излучения или зона Фраунгофе-ра) характеризуется
тем, что направления (лучи), проведенные из любой точки антенны на точку
наблюдения, находящуюся в этой зоне, считаются параллельными. При этом возникает ошибка в определении фаз полей, создаваемых
в точке наблюдения различными элементами антенны. Эта ошибка оказывается тем
меньше, чем больше расстояние от антенны до точки наблюдения по сравнению с
размерами антенны. Расстояние дальней зоны rизл
] называется комплексной
характеристикой направленности антенны. Она полностью определяет угловое
распределение и фазовые свойства излучаемого электромагнитного поля в дальней зоне антенны.
Характеристика направленности антенны
определяется размерами и конфигурацией антенны, а также распределением
возбуждающего тока (как действительного, так и эквивалентного). Напомним, что дальняя
зона (зона излучения или зона Фраунгофе-ра) характеризуется
тем, что направления (лучи), проведенные из любой точки антенны на точку
наблюдения, находящуюся в этой зоне, считаются параллельными. При этом возникает ошибка в определении фаз полей, создаваемых
в точке наблюдения различными элементами антенны. Эта ошибка оказывается тем
меньше, чем больше расстояние от антенны до точки наблюдения по сравнению с
размерами антенны. Расстояние дальней зоны rизл
определяется из
условия rизл ![]() 2R2 /
2R2 /![]() , где R - наибольший размер
излучающей системы. В этой зоне поле имеет поперечный характер (отсутствуют составляющие
векторов Е и Н в направлении распространения); в окрестности точки наблюдения поле имеет характер плоской
волны; амплитуды полей, излучаемых
элементами антенны, убывают обратно пропорционально расстоянию.
, где R - наибольший размер
излучающей системы. В этой зоне поле имеет поперечный характер (отсутствуют составляющие
векторов Е и Н в направлении распространения); в окрестности точки наблюдения поле имеет характер плоской
волны; амплитуды полей, излучаемых
элементами антенны, убывают обратно пропорционально расстоянию.
В антенной технике
обычно интересуются характером зависимости напряженности поля от направления
на точку наблюдения, а не абсолютной величиной
напряженности поля. Поэтому удобно пользоваться нормированной
характеристикой направленности F(![]() ), т.е. отношением
напряженности поля, излучаемого антенной в произвольном направлении, к значению
напряженности поля в направлении максимального излучения
), т.е. отношением
напряженности поля, излучаемого антенной в произвольном направлении, к значению
напряженности поля в направлении максимального излучения
F(![]() )= | E(
)= | E(![]() )| / | Emax(
)| / | Emax(![]() )| = f(
)| = f(![]() )/fmax(
)/fmax(![]() ).
).
Максимальная величина F(θ,φ) всегда равна единице. Графическое изображение амплитудной характеристики направленности называют диаграммой направленности (ДН) антенны. Пространственная ДН изображается в виде поверхности f(θ,φ) или F(θ,φ), описываемой концом 17
радиуса-вектора, исходящего из начала
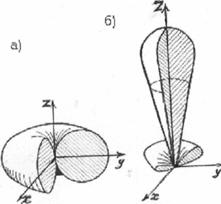
координат, длина которого в каждом направлении в определенном масштабе равна функции f(![]() ). На рис.2.1.а
изображена пространственная
ДН элементарного вибратора (тороид), на рис.2.1.б - ДН более сложной антенны (так называемая игольчатая ДН). На
практике обычно используют ДН, изображающие характеристику направленности в
каких-либо выбранных плоскостях. В качестве таких плоскостей обычно выбирают
две взаимно перпендикулярные плоскости, проходящие через направление
). На рис.2.1.а
изображена пространственная
ДН элементарного вибратора (тороид), на рис.2.1.б - ДН более сложной антенны (так называемая игольчатая ДН). На
практике обычно используют ДН, изображающие характеристику направленности в
каких-либо выбранных плоскостях. В качестве таких плоскостей обычно выбирают
две взаимно перпендикулярные плоскости, проходящие через направление
максимального излучения (главные плоскости). Для антенн, излучающих линейно поляризованное поле, главными плоскостями называются плоскости, в которых лежит либо вектор Е (плоскость Е), либо вектор Н (плоскость Н).
|
|
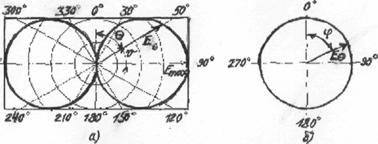
Диаграммы направленности изображают обычно либо в полярной (рис.2.2.а - ДН элементарного вибратора в Е - плоскости; рис.2.2.б - ДН элементарного вибратора в Н - плоскости), либо в декартовой (прямоугольной) системе координат (рис.2.3. - ДН реальной антенны).
|
Рис. 2.1. Пространственная ДН (а-диполя Герца, б-игольчатая) |
В некоторых случаях применяется картографический метод изображения пространственных
(трехмерных) ДН. Он удобен для изображения многолепестковых (т.е. имеющих много
нулей и максимумов) ДН в широком диапазоне углов. Этот метод состоит в том, что
строится плоская сетка координат ![]() в какой-либо координатной системе
(прямоугольной, полярной и др.) подобно сетке меридианов и параллелей на географической карте.
На этой сетке замкнутыми линиями изображаютсяодинаковые
в какой-либо координатной системе
(прямоугольной, полярной и др.) подобно сетке меридианов и параллелей на географической карте.
На этой сетке замкнутыми линиями изображаютсяодинаковые
значения
нормированной характеристики направленности F(![]() ) в том или ином масштабе. При
изображении ДН часто используется логарифмический масштаб, вводимый соотношением
в децибеллах F(
) в том или ином масштабе. При
изображении ДН часто используется логарифмический масштаб, вводимый соотношением
в децибеллах F(![]() )=20 lgF(
)=20 lgF(![]() ).
).
В некоторых случаях
пользуются понятием характеристики (диаграммы) направленности по мощности F2(![]() ). Функция F(
). Функция F(![]() ) для различных
) для различных
|
|
|
270 |
|
Рис. 2,2. ДН диполя Герца (а-Е-плоскость, б-Н-плоскость) |
углов ![]() и
и ![]() проходит через нуль и имеет несколько максимумов,
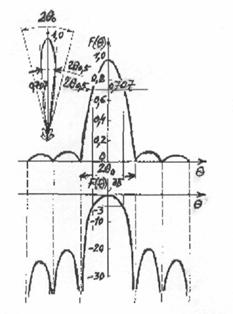
т.е. ДН имеет многолепестковый характер (см. рис.2.3). Диаграмму
направленности принято численно характеризовать шириной главного лепестка (шириной луча) и относительным
уровнем боковых лепестков (УБЛ).
проходит через нуль и имеет несколько максимумов,
т.е. ДН имеет многолепестковый характер (см. рис.2.3). Диаграмму
направленности принято численно характеризовать шириной главного лепестка (шириной луча) и относительным
уровнем боковых лепестков (УБЛ).
Шириной ДН (шириной луча) называется угол между направлениями, вдоль
которых напряженность поля падает до определенного значения. Так, шириной ДН по уровню
нулевого излучения называют угол 2![]() 0 между нап-
0 между нап-
|
|
равлениями, вдоль
которых напряженность поля падает до нуля (см. рис.2.3). Шириной ДН по половинной
мощности называют угол 2![]() 0,5 между направлениями, вдоль
которых |Е| = |Emax|/
0,5 между направлениями, вдоль
которых |Е| = |Emax|/![]() или соответственно среднее значение плотности
потока мощности П=Пmaх/2. Наибольший лепесток, максимум которого
соответствует направлению максимального излучения, называют главным, меньшие лепестки - боковыми
(лепестки, находящиеся в задних квадрантах, т.е. в диапазоне углов 90°
или соответственно среднее значение плотности
потока мощности П=Пmaх/2. Наибольший лепесток, максимум которого
соответствует направлению максимального излучения, называют главным, меньшие лепестки - боковыми
(лепестки, находящиеся в задних квадрантах, т.е. в диапазоне углов 90°![]() 180° и 180°
180° и 180°![]() 270°, часто называют задними).
270°, часто называют задними).
Относительный УБЛ (![]() ) есть отношение напряженности поля в
направлении максимума данного лепестка (ENmax) к напряженности поля
внаправлении
главного максимума (Еmax), т.е.
) есть отношение напряженности поля в
направлении максимума данного лепестка (ENmax) к напряженности поля
внаправлении
главного максимума (Еmax), т.е.
![]() N=|ENmax|/|Еmax|=FN(
N=|ENmax|/|Еmax|=FN(![]() ), или в децибеллах
), или в децибеллах ![]() дБ = 20lg FN(
дБ = 20lg FN(![]() ), где N=1,2,3,...-номер бокового лепестка (для главного
лепестка N=0).
), где N=1,2,3,...-номер бокового лепестка (для главного
лепестка N=0).
|
Рис, 2.3, ДН реальной антенны |
Обычно стремятся к подавлению боковых лепестков, т.е. к тому, чтобы величина ![]() была
мала. В большинстве случаев
интересуются амплитудными характеристиками направленности (слово
"амплитудная" в дальнейшем не используем). Фазовые характеристики направленности используют в радиолокации, радионавигации
и в некоторых других случаях.
была
мала. В большинстве случаев
интересуются амплитудными характеристиками направленности (слово
"амплитудная" в дальнейшем не используем). Фазовые характеристики направленности используют в радиолокации, радионавигации
и в некоторых других случаях.
Если фаза, излучаемого антенной поля, не зависит от направления на точку наблюдения и
изменяется на обратную только при переходе функции f(![]() ) или F(
) или F(![]() ) через нуль, т.е. при
переходе от одного лепестка ДН к другому, то такая антенна является источником
сферических волн, о чем свидетельствует множитель [ехр(-ikr)]/r. Эти волны исходят
как бы из одной точки, называемой фазовым центром антенны. Эта точка расположена
в начале выбранной системы координат, и поэтому, фазовая характеристика зависит от положения начала
координат. Однако не все реальные антенны обладают фазовым центром, т.е.
излучают сферические волны. Для них обычно можно подобрать сферу, наилучшим образом
аппроксимирующую фронт волны (обычно в пределах главного лепестка). Центр этой
сферы называют центром излучения антенны. Графическое изображение
фазовой характеристики называется фазовой ДН.
) через нуль, т.е. при
переходе от одного лепестка ДН к другому, то такая антенна является источником
сферических волн, о чем свидетельствует множитель [ехр(-ikr)]/r. Эти волны исходят
как бы из одной точки, называемой фазовым центром антенны. Эта точка расположена
в начале выбранной системы координат, и поэтому, фазовая характеристика зависит от положения начала
координат. Однако не все реальные антенны обладают фазовым центром, т.е.
излучают сферические волны. Для них обычно можно подобрать сферу, наилучшим образом
аппроксимирующую фронт волны (обычно в пределах главного лепестка). Центр этой
сферы называют центром излучения антенны. Графическое изображение
фазовой характеристики называется фазовой ДН.
2.2. Коэффициент направленного действия (КНД), коэффициент усиления антенны (КУ) и параметры, связанные с КНД
Коэффициент направленного действия (КНД) характеризует
способность
антенны концентрировать излученное электромагнитное поле в каком-либо определенном
направлении. Это понятие было введено в 1929 г. А.А.Пистолькорсом. Коэффициентом
направленного действия называется отношение среднего значения за период высокой
частоты плотности потока мощности (среднее значение вектора Пойнтинга),
излучаемого антенной в данном направлении ![]() ,
к усредненному по всем
направлениям значению
плотности потока мощности Пуср
,
к усредненному по всем
направлениям значению
плотности потока мощности Пуср
![]() . (2.3)
. (2.3)
Здесь ![]() , где |
, где |![]() | - амплитудное значение напряженности электрического поля в направлении, характеризуемом углами
| - амплитудное значение напряженности электрического поля в направлении, характеризуемом углами ![]() . Таким образом, при определении КНД
данная антенна сравнивается с воображаемой абсолютно ненаправленной
(изотропной) антенной, излучающей ту же мощность, что и данная. Очевидно, что
. Таким образом, при определении КНД
данная антенна сравнивается с воображаемой абсолютно ненаправленной
(изотропной) антенной, излучающей ту же мощность, что и данная. Очевидно, что
![]() , (2.4)
, (2.4)
где ![]() - мощность излучения; r - радиус воображаемой сферы, охватывающей антенну, причем
величина r должна быть такой, чтобы поверхность сферы находилась в дальней зоне поля антенны.
- мощность излучения; r - радиус воображаемой сферы, охватывающей антенну, причем
величина r должна быть такой, чтобы поверхность сферы находилась в дальней зоне поля антенны.
Коэффициент направленного действия показывает во сколько раз следует уменьшить излучаемую мощность при замене изотропной (ненаправленной) антенны на направленную, чтобы среднее значение плотности потока мощности в точке наблюдения осталось неизменным.
Учитывая, что ![]() , и подставляя в (2.3) выражение (2.4), получаем формулу для КНД в
другом виде
, и подставляя в (2.3) выражение (2.4), получаем формулу для КНД в
другом виде ![]() или для свободного пространства (Wc°=120
или для свободного пространства (Wc°=120![]() Ом) в направлении максимального излучения
Ом) в направлении максимального излучения
![]() (2.5)
(2.5)
Если в эту формулу подставить вместо ![]() выражение (2.2) в квадрате (без фазовых множителей) и учесть, что
выражение (2.2) в квадрате (без фазовых множителей) и учесть, что ![]() , где
, где ![]() -
сопротивление излучения элементарного
электрического вибратора, то получим КНД элементарного вибратора D=1,5.
-
сопротивление излучения элементарного
электрического вибратора, то получим КНД элементарного вибратора D=1,5.
Коэффициент направленного действия тем больше, чем уже главный лепесток
пространственной ДН и чем меньше УБЛ. Коэффициент направленного действия можно
выразить с помощью еще одного параметра, называемого действующей длиной или
действующей высотой антенны ![]() .Этот параметр иногда используют при
анализе приемных антенн, а также проволочных длинноволновых и средневолновых
антенн и антенн-мачт.
.Этот параметр иногда используют при
анализе приемных антенн, а также проволочных длинноволновых и средневолновых
антенн и антенн-мачт.
В случае линейной антенны ток по ее длине распределен неравномерно. Однако реальную антенну можно заменить воображаемым вибратором длиной lд (действующей длиной) с равномерным распределением тока создающим в направлении максимального излучения поле, равное полю данной антенны в главном направлении. При этом ток в точке питания реальной антенны считается равным току, текущему по воображаемому вибратору. По аналогии с (2.2) (вибратор с равномерным распределением тока) напряженность поля реальной антенны в главном направлении можно представить в виде
![]() (2.6)
(2.6)
где I0 - амплитуда тока в
точках питания антенны; 60π = Wc°/2, где ![]() - волновое
сопротивление среды. Напишем выражение для величины напряженности поля любой вибраторной антенны в
произвольном направлении
- волновое
сопротивление среды. Напишем выражение для величины напряженности поля любой вибраторной антенны в
произвольном направлении
![]() (2.7)
(2.7)
Подставляя в
(2.5) вместо ![]() выражение (2.6) и учитывая, что
выражение (2.6) и учитывая, что
![]() (
(![]() - сопротивление излучения антенны, отнесенное к току в
точках питания; I
-ток в точках питания
антенны), получаем
- сопротивление излучения антенны, отнесенное к току в
точках питания; I
-ток в точках питания
антенны), получаем
![]() или
или ![]() (2.8)
(2.8)
Формально параметром "действующая длина" можно пользоваться в 21
случае любой антенны (линейной, апертурной или какой-либо другой), так как этот параметр выражается через КНД, а последний определяется только характеристикой направленности.
Коэффициент
направленного действия не учитывает потерь подводимой энергии в
проводниках антенны, в изоляторах, в окружающих антенну предметах и в земле. В связи с этим
вводится параметр, учитывающий эти потери,
называемый коэффициентом усиления (КУ) антенны, равный отношению
среднего значения плотности потока мощности, излучаемой антенной в данном
направлении ![]() , к среднему значению плотности
потока мощности,
создаваемого воображаемым абсолютно ненаправленным излучателем (Пн). При этом предполагается,
что точка наблюдения находится на одинаковом расстоянии от обеих антенн; мощности, подводимые к той и
другой антеннам, равны и КПД ненаправленной антенны равен единице. Таким образом, КУ
, к среднему значению плотности
потока мощности,
создаваемого воображаемым абсолютно ненаправленным излучателем (Пн). При этом предполагается,
что точка наблюдения находится на одинаковом расстоянии от обеих антенн; мощности, подводимые к той и
другой антеннам, равны и КПД ненаправленной антенны равен единице. Таким образом, КУ
![]() . (2.9)
. (2.9)
Коэффициент усиления показывает во сколько раз следует уменьшить мощность, подводимую к направленной антенне, по сравнению с абсолютно ненаправленной (изотропной) антенны, КПД которой считается равным единице, чтобы среднее значение плотности потока мощности в точке наблюдения оставалось неизменным.
Отличие КУ от КНД состоит в том, что при определении КУ
исходят из
равенства мощностей, подводимых к исследуемой и эталонной ( ненаправленной)
антеннам Р0, а не из равенства мощностей излучения P![]() , этих антенн.
Умножим и разделим правую часть (2.9) на Пуср. Тогда [П(
, этих антенн.
Умножим и разделим правую часть (2.9) на Пуср. Тогда [П(![]() )/Пуср](Пуср/Пн),
где Пуср/Пн =
)/Пуср](Пуср/Пн),
где Пуср/Пн =![]() - КПД антенны.
- КПД антенны.
Параметры ( D, G и ![]() ) связаны соотношением
) связаны соотношением
G=D![]() . (2.10)
. (2.10)
Учитывая, что D=G/![]() , можно написать
, можно написать
Emax=![]() /r=
/r=![]() /r .
(2.11)
/r .
(2.11)
2.3. Поляризационные параметры антенн. Турникетный излучатель
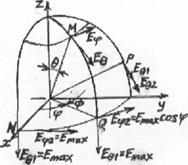
Направление векторов Е и Н излучаемого антенной поля определяется плоскостью поляризации, т.е. плоскостью, проходящей через направление распространения волны (вектор Пойнтинга) и вектор напряженности электрического поля. В общем случае за один период высокой частоты плоскость поляризации делает полный оборот вокруг направления распространения. Такое поле называют вращающимся. За это время конец вектора Е описывает замкнутую кривую (эллипс), лежащую в плоскости, перпендикулярной направлению распространения, и называемую поляризационным эллипсом. Это - эллиптическая поляризация электромагнитного поля. Частными видами эллиптической поляризации являются: линейная поляризация - конец вектора Е лежит на прямой линии; круговая поляризация - конец вектора Е за один период высокой частоты описывает окружность.
Существуют антенны, рассчитанные на излучение (прием) поля круговой поляризации. Многие антенны (симметричный вибратор и другие) излучают во всех направлениях линейно поляризованные волны. Однако имеются антенны, которые либо из-за своих конструктивных особенностей, либо из-за неточностей исполнения излучают волны чисто линейной поляризации только в двух взаимно перпендикулярных плоскостях, проходящих через направление максимального излучения (главные плоскости). Поляризация поля в этих плоскостях называется главной или основной, В других плоскостях имеется составляющая поля, поляризованная перпендикулярно (ортогонально) основной поляризации (к таким антеннам относят, например, параболическую). Эта составляющая, называемая поперечной или кроссполяризацион-ной, является вредной. Ортогональность составляющих поля основной и кроссполяризации (иногда ее называют паразитной) понимается как независимость переноса мощности каждой из них. Мощность, соответствующая кроссполяризации, расходуется на образование боковых лепестков, вследствие чего КНД антенны уменьшается. Кроме того, возрастают помехи, создаваемые передающей антенной различным приемным антеннам, работающим в том же или смежном диапазоне частот. Если поле передающей антенны имеет две ортогональные составляющие, а приемная антенна рассчитана на прием лишь линейно поляризованного поля, то часть излученной мощности, соответствующая паразитной поляризации, не используется.
Эллиптическая поляризация может рассматриваться либо как результат сложения двух линейно поляризованных взаимно перпендикулярных составляющих поля, не совпадающих по фазе, либо двух полей круговой поляризации с противоположными направлениями вращения и разными амплитудами.
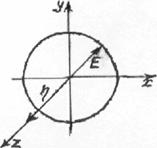
Отношение малой полуоси эллипса к большой (рис.2.4.а) называется коэффициентом
равномерности (коэффициентом эллиптичности) поляризационного эллипса: t=b/a. В случае линейной
поляризации поля t = 0. Условием этой поляризации является ![]() или
или ![]() (
(![]() - сдвиг фаз между составляющими
- сдвиг фаз между составляющими ![]() и
и ![]() ). Линейная поляризация также имеет место, если
). Линейная поляризация также имеет место, если ![]() =0 или
=0 или ![]() =0. При круговой поляризации поля (
=0. При круговой поляризации поля (![]() =
=![]() ;
;![]() ) t=l. Таким образом, коэффициент равномерности
поляризационного эллипса может изменяться в пределах 0< t < 1. Зависимость коэффициента
эллиптичности от направления на точку
наблюдения называется поляризационной ДН.
) t=l. Таким образом, коэффициент равномерности
поляризационного эллипса может изменяться в пределах 0< t < 1. Зависимость коэффициента
эллиптичности от направления на точку
наблюдения называется поляризационной ДН.
Поляризационный эллипс характеризуется также углом поляризации и направлением вращения
вектора Е (направление вращения плоскости поляризации). Углом
поляризации ![]() называется
угол, образованный большой осью поляризационного эллипса и направлением орта
называется
угол, образованный большой осью поляризационного эллипса и направлением орта ![]() или
или ![]() 0
сферической системы
координат (см. рис. 2.4.б). Направление вращение вектора Е в точке наблюдения определяется знаком угла сдвига фаз между
составляющими поля
0
сферической системы
координат (см. рис. 2.4.б). Направление вращение вектора Е в точке наблюдения определяется знаком угла сдвига фаз между
составляющими поля