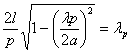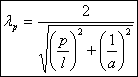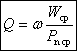УЗБЕКСКОЕ АГЕНТСТВО СВЯЗИ И
ИНФОРМАТИЗАЦИИ
ТАШКЕНТСКИЙ
УНИВЕРСИТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ
Факультет
Радиотехники, Радиосвязи и Телерадиовещания
Кафедра
Антенно-фидерных
устройств
Конспект лекций по дисциплине
“Устройства СВЧ и Антенны”
для
направления «Радиотехника»
Составитель
доц.
кафедры АФУ
Губенко
В.А.
ОГЛАВЛЕНИЕ
ТЕМА 1. Классификация и характеристики антенн
………………………………………………………………….3
ТЕМА 2. Теория симметричного вибратора
…………………………………………………………………………11
ТЕМА 3. Связанные вибраторы. Характеристики
вибраторных антенн …………………………………………..31
ТЕМА 4. Способы
увеличения рабочего диапазона волн вибраторных антенн.
Частотно–независимые
антенны
……………………………………………………………………………………...28
ТЕМА 5. Теория антенных решеток. Линейные и плоские
решетки……………………………………………….32
ТЕМА 6. Теория апертурных антенн. Устройство и
принцип действия рупорной и
зеркально-параболической антенн
……………………………………………………………………………………44
ТЕМА 7. Антенны поверхностных волн. Устройство и
принцип действия диэлектрической антенны. Коэффициент
замедления……………………………………………………………………………………………..61
Тема 8. Особенности построения антенн УВЧ и СВЧ
диапазонов. Синтез антенных систем и перспективы развития антенной
техники……………………………………………………………………………………………66
ТЕМА 9. Введение. Основные параметры и типы линий
передачи.
Классификация линий передачи. Основные режимы
работы…………………………………………………………………………………………………………76
ТЕМА 10.
Основные типы волн в волноводах. Возбуждение электромагнитных колебаний в
направляющих системах…………………………………………………………………………………………………………………80
ТЕМА 11. Элементы трактов СВЧ, их устройство,
параметры и характеристики………………………………..82
ТЕМА 12. Направленные
ответвители……………………………………………………………………………….94
ТЕМА 13. Фильтры и
согласующие цепи СВЧ………………………………………………………………………97
ТЕМА 14. Согласование линий
передач…………………………………………………………………………….. 98
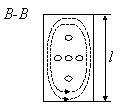
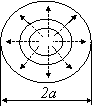
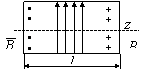
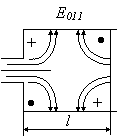
ТЕМА 15. Объемные
резонаторы СВЧ……………………………………………………………………………..100
ТЕМА 16. Управляющие
ферритовые устройства СВЧ…………………………………………………………..107
ТЕМА 17. Перспективы развития техники
СВЧ…………………………………………………………………..111
ТЕМА 1. Классификация и характеристики антенн
Антенной называется радиотехническое устройство, предназначенное для излучения или приема электромагнитных волн. Антенна является одним
из важнейших элементов любой радиотехнической системы, связанной с излучением
или приемом радиоволн. К таким системам относят: системы радиосвязи, радиовещания, телевидения, радиоуправления, радиорелейной связи, радиолокации, радиоастрономии, радионавигации и др.
В конструктивном отношении антенна представляет собой провода, металлические поверхности, диэлектрики, магнитодиэлектрики.
Электромагнитные колебания высокой частоты, модулированные полезным сигналом,
преобразуются передающей антенной в электромагнитные волны, которые излучаются в пространство. Обычно электромагнитные колебания подводят от передатчика к антенне не непосредственно,
а с помощью фидера.
Приемная антенна улавливает распространяющиеся радиоволны преобразует
их в электромагнитные колебания, которые через фидер поступают на вход
приёмного устройства. В соответствии с принципам обратимости антенн свойства антенны, работающей в режиме передачи не изменятся при работе этой антенны в приемном режиме.
Преобразование антенной одного вида электромагнитных волн в другой должно происходить с минимальными потерями энергии, т.е. с максимально возможным КПД, определяемым в передающем режиме по формуле 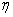 = P
= P / Р0, где
P
/ Р0, где
P - мощность излучаемая антенной, Р0 - мощность
подводимая к антенне.
- мощность излучаемая антенной, Р0 - мощность
подводимая к антенне.
Способность антенны излучать электромагнитные волны с различной интенсивностью
в разных направлениях характеризуется её
направленными свойствами, т.е.
диаграммой направленности (ДН).
Антенны, обладающие узкой ДН, позволяют увеличивать напряженность поля в точке приёма без увеличения мощности передатчика. В большинстве случаев это экономически более выгодно, чем увеличения мощности передатчика. Кроме того, концентрация электромагнитных волн в требуемом
направлении приводит к уменьшению взаимных помех различных радиотехнических систем.
Наличие направленных приемных антенн ведёт к ослаблению приема различных
внешних помех, т.е. к повышению качества приёма и улучшению помехозащищенности
приемного устройства. Большими направленными свойствами должны обладать
антенны для космической радиосвязи, радиоастрономии,
радиолокации, радиорелейных линий.
В тоже время для радио и телевидения передающие антенны должны иметь
одинаковое излучение в горизонтальной плоскости (за исключением отдельных
случаев - гор и т.д.).
Направленные свойства являются настолько
важными, что принято говорить о двух
функциях, выполняемых антенной:
- преобразование электромагнитных
колебаний в свободные
электромагнитные волны;
- излучение этих волн в определенных
направлениях.
Важную роль в работе антенного устройства играет линия питания (фидерный тракт), которая передаёт (каналирует) электромагнитную энергию
от генератора к антенне (или от антенны к приёмнику). Фидер не должен излучать электромагнитные волны и должен иметь минимальные потери. Его необходимо согласовывать с
выходной цепью передатчика
( или с
входной цепью приемника) и с входным сопротивлением антенны, т.е. в фидере
должен быть режим бегущей волны или близкий к нему.
В зависимости от диапазона радиоволн применяют различные типы фидеров: двухпроводные или многопроводные воздушные фидеры, несимметричные
экранированные (коаксиальные) линии, различные типы волноводов и др.
Классификацию антенн можно, например проводить по способу формирования
излучаемого поля, выделяя следующие четыре класса антенн:
Излучатели небольших размеров (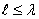 ,где
,где  - длина волны) для диапазона частот 10кГц...1ГГц. К числу
антенн этого класса относятся одиночные вибраторные и
щелевые излучатели, полосковые и микрополосковые антенны,
рамочные антенны, а также частотно-независимые излучатели.
- длина волны) для диапазона частот 10кГц...1ГГц. К числу
антенн этого класса относятся одиночные вибраторные и
щелевые излучатели, полосковые и микрополосковые антенны,
рамочные антенны, а также частотно-независимые излучатели.
Антенны бегущей волны размерами от  до 100
до 100 для диапазона частот 3МГц...10ГГц. Сюда
относятся спиральные, диэлектрические,директорные, импедаксные антенны, а также
антенны «вытекающей» волны.
для диапазона частот 3МГц...10ГГц. Сюда
относятся спиральные, диэлектрические,директорные, импедаксные антенны, а также
антенны «вытекающей» волны.
Антенные решетки размерами от до 100
до 100 и более для диапазона частот 3МГц...30ГГц. Это антенны, состоящие из большого числа отдельных излучателей. Независимая регулировка фаз (а иногда и амплитуд) возбуждения
каждого элемента антенной решетки обеспечивает возможность электрического управления диаграммой направленности. Применяются линейные, плоские, кольцевые, выпуклые и конформные (совпадающие с формой объекта установки) антенные решетки. На основе антенных решеток выполняют
антенные системы с обработкой сигнала, в том числе адаптивные к изменяющейся
помеховой обстановке.
и более для диапазона частот 3МГц...30ГГц. Это антенны, состоящие из большого числа отдельных излучателей. Независимая регулировка фаз (а иногда и амплитуд) возбуждения
каждого элемента антенной решетки обеспечивает возможность электрического управления диаграммой направленности. Применяются линейные, плоские, кольцевые, выпуклые и конформные (совпадающие с формой объекта установки) антенные решетки. На основе антенных решеток выполняют
антенные системы с обработкой сигнала, в том числе адаптивные к изменяющейся
помеховой обстановке.
Апертурные антенны размерами от  до 1000
до 1000 для диапазона частот 100МГц... 100ГГц и
выше. Наиболее распространены зеркальные, рупорные и линзовые апертурные
антенны. К апертурным антеннам примыкают, так называемые, «гибридные» антенны,
представляющие сочетание зеркал или линз с облучающей
системой в виде антенной решетки. Апертурные антенны строятся по оптическим принципам и обеспечивают наиболее высокую направленность излучения.
для диапазона частот 100МГц... 100ГГц и
выше. Наиболее распространены зеркальные, рупорные и линзовые апертурные
антенны. К апертурным антеннам примыкают, так называемые, «гибридные» антенны,
представляющие сочетание зеркал или линз с облучающей
системой в виде антенной решетки. Апертурные антенны строятся по оптическим принципам и обеспечивают наиболее высокую направленность излучения.
Свойства направленности антенны описывают характеристикой (диаграммой)
направленности. Количественно эти свойства оцениваются с помощью таких параметров, как ширина ДН, уровень боковых лепестков, коэффициент
направленного действия (КНД) и других.
Важным параметром является входное сопротивление антенны, характеризующее её как нагрузку для генератора или фидера. Входным сопротивлением
антенны называется отношение напряжения между точками питания антенны (зажимы антенны) к току в этих точках. Если антенна питается волноводом, то входное сопротивление определяется отражениями, возникающими в волноводном тракте. В общем случае входное сопротивление - величина комплексная Zвх= Rвх+ iXвх. Оно должно быть
согласовано с волновым сопротивлением фидерного тракта
(или с выходным сопротивлением генератора)
так, чтобы обеспечить в последнем режим, близкий к режиму
бегущей волны.
Мощность, излучаемая антенной РΣ, связана с током в точках питания
антенны
соотношением P = I02 R
= I02 R 0 / 2, где RΣ0 – сопротивление излучения антенны (при отсутствии потерь в антенне это
активная составляющая входного сопротивления антенны). Данное
определение относится к проволочным антеннам.
0 / 2, где RΣ0 – сопротивление излучения антенны (при отсутствии потерь в антенне это
активная составляющая входного сопротивления антенны). Данное
определение относится к проволочным антеннам.
Одним из основных параметров антенны является ширина её рабочей полосы
частот, в пределах которой параметры антенны (характеристика направленности, входное сопротивление, КПД и др.) удовлетворяют определенным техническим требованиям. Требования к постоянству параметров антенны в пределах рабочей полосы могут быть различными; они зависят от условий работы. Обычно рабочая полоса частот определяется тем параметром,
значение которого при изменении частоты раньше других выходит из допустимых
пределов. Очень часто таким параметром является входное сопротивление антенны.
Изменение его при изменении частоты приводит к рассогласованию антенны с
фидером. В ряде случаев ширина рабочего диапазона определяется ухудшением
одного из параметров, характеризующих направленные
свойства: изменением направления максимального излучения, расширением ДН,
уменьшением КНД и др. В зависимости от ширины рабочего диапазона антенны
условно разбивают на:
узкополосные (настроенные), относительная рабочая полоса которых менее 10% номинальной частоты;
широкополосные, с рабочей полосой
частот 10...50%;
диапазонные, коэффициент перекрытия частот которых(fMAX/fMIN) составляет примерно 2...5;
частотно-независимые (сверхширокополосные), с коэффициентом перекрытия, теоретически не зависящим от частоты (практически fMAX/fMIN таких антенн >
5).
Еще одним параметром является предельная мощность, которую можно подвести к антенне без опасности её разрушения и не вызывая пробоя окружающей
среды. Существуют также параметры, характеризующие поляризационные свойства
антенны.
В данном курсе рассматриваются антенны следующих диапазонов:
ми-риаметровые или сверхдлинные волны ( = 10...100 км);
километровые или длинные волны (
= 10...100 км);
километровые или длинные волны ( = 1...10 км); гектометровые или средние
волны (
= 1...10 км); гектометровые или средние
волны ( = =100...1000 м);
декаметровые или короткие волны (
= =100...1000 м);
декаметровые или короткие волны ( = 10...100 м); метровые волны (
= 10...100 м); метровые волны ( = 1...10м); дециметровые волны (
= 1...10м); дециметровые волны ( = 10 см...1 м); сантиметровые волны (
= 10 см...1 м); сантиметровые волны ( = 1...10 см); миллиметровые волны (
= 1...10 см); миллиметровые волны ( = 1...10 мм). Последние четыре диапазона объединяются общим названием "ультракороткие
волны" (УКВ).
= 1...10 мм). Последние четыре диапазона объединяются общим названием "ультракороткие
волны" (УКВ).
При расчете излученного антенной электромагнитного поля ее удобно рассматривать как состоящую из бесконечного большого числа элементарных
источников (излучателей). Благодаря линейности уравнений Максвелла к полям элементарных источников применим принцип суперпозиции, позволяющий найти поле антенны в результате суммирования полей всех составляющих
ее элементарных излучателей с учетом амплитуд и фаз возбуждающих их токов.
Суммирование полей сводится к их интегрированию по источникам. Элементарными
источниками являются: элементарные электрические вибраторы ЭЭВ в случае проволочных антенн; элементарные магнитные
вибраторы в случае щелевых антенн; бесконечно малые элементы волнового фронта
или элементы Гюйгенса в случае апертурных антенн.
Формула для комплексной амплитуды напряженности электрического поля Ė произвольной реальной антенны в дальней зоне без учета
векторного характера электромагнитного поля имеет вид
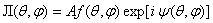 . (2.1)
. (2.1)
Здесь А - комплексный множитель, не зависящий от направления на точку наблюдения (в него входит стандартный множитель exp(-ikr)/r, где r -расстояние от
фазового центра антенны до точки наблюдения; 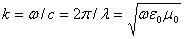 - коэффициент фазы или волновое число в свободном пространстве); θ,φ -
координаты точки наблюдения; |f(θ,φ)| - амплитудная характеристика направленности; Ψ(θ,φ) - фазовая характеристика
направленности. Известно, что в случае элементарного электрического вибратора
- коэффициент фазы или волновое число в свободном пространстве); θ,φ -
координаты точки наблюдения; |f(θ,φ)| - амплитудная характеристика направленности; Ψ(θ,φ) - фазовая характеристика
направленности. Известно, что в случае элементарного электрического вибратора
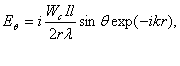 (2.2)
(2.2)
где I - амплитуда
тока в
вибраторе; l - длина вибратора; 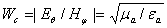 характеристическое сопротивление волны; в
свободном пространстве
характеристическое сопротивление волны; в
свободном пространстве 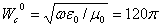 , Ом
, Ом
Амплитудной характеристикой направленности антенны называется зависимость величины (модуля) напряженности
электрического поля, создаваемого антенной в точке наблюдения, от направления на эту
точку, характеризуемого углами θ и
φ сферической системы координат при постоянном расстоянии (r = const) точки наблюдения от антенны. Фазовой характеристикой направленности
антенны Ψ (θ,φ) называется зависимость фазы поля, создаваемого
антенной в точке наблюдения, находящейся на поверхности сферы в дальней зоне, от направления на эту точку, характеризуемого
углами θ и φ. Множитель f(θ,φ)
определяет не только величину, но и
фазу напря-
женности поля, так как при переходе функции f(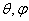 ) через нуль меняется ее знак, что соответствует скачку фазы
напряженности поля на 180°. Поэтому
амплитудной характеристикой направленности является модуль этой функции
|f(
) через нуль меняется ее знак, что соответствует скачку фазы
напряженности поля на 180°. Поэтому
амплитудной характеристикой направленности является модуль этой функции
|f(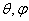 )|. В дальнейшем для упрощения записи знак модуля опускаем. В общем случае характеристика
направленности является векторной и
комплексной величиной. Выражение ƒ(
)|. В дальнейшем для упрощения записи знак модуля опускаем. В общем случае характеристика
направленности является векторной и
комплексной величиной. Выражение ƒ(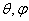 )=f(
)=f(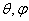 ) exp[i
) exp[i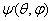 ] называется комплексной
характеристикой направленности антенны. Она полностью определяет угловое распределение и фазовые свойства излучаемого электромагнитного
поля в дальней зоне антенны. Характеристика направленности антенны определяется размерами и конфигурацией антенны, а также
распределением возбуждающего тока (как действительного, так и эквивалентного).
Напомним, что дальняя зона (зона излучения или зона Фраунгофе-ра)
характеризуется тем, что направления (лучи), проведенные из любой точки
антенны на точку наблюдения, находящуюся в этой зоне, считаются параллельными. При этом возникает ошибка в
определении фаз полей, создаваемых в точке наблюдения различными элементами
антенны. Эта ошибка оказывается тем меньше, чем больше расстояние от антенны до
точки наблюдения по сравнению с размерами антенны. Расстояние дальней зоны rизл
] называется комплексной
характеристикой направленности антенны. Она полностью определяет угловое распределение и фазовые свойства излучаемого электромагнитного
поля в дальней зоне антенны. Характеристика направленности антенны определяется размерами и конфигурацией антенны, а также
распределением возбуждающего тока (как действительного, так и эквивалентного).
Напомним, что дальняя зона (зона излучения или зона Фраунгофе-ра)
характеризуется тем, что направления (лучи), проведенные из любой точки
антенны на точку наблюдения, находящуюся в этой зоне, считаются параллельными. При этом возникает ошибка в
определении фаз полей, создаваемых в точке наблюдения различными элементами
антенны. Эта ошибка оказывается тем меньше, чем больше расстояние от антенны до
точки наблюдения по сравнению с размерами антенны. Расстояние дальней зоны rизл
определяется из
условия rизл 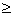 2R2/
2R2/ , где R - наибольший размер излучающей системы. В этой зоне поле имеет поперечный характер (отсутствуют составляющие
векторов Е и Н в направлении распространения); в окрестности точки наблюдения
поле имеет характер плоской волны; амплитуды полей, излучаемых элементами антенны, убывают обратно
пропорционально расстоянию.
, где R - наибольший размер излучающей системы. В этой зоне поле имеет поперечный характер (отсутствуют составляющие
векторов Е и Н в направлении распространения); в окрестности точки наблюдения
поле имеет характер плоской волны; амплитуды полей, излучаемых элементами антенны, убывают обратно
пропорционально расстоянию.
В антенной
технике обычно интересуются характером зависимости напряженности поля от
направления на точку наблюдения, а не абсолютной величиной напряженности поля. Поэтому удобно пользоваться нормированной
характеристикой направленности F(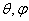 ), т.е. отношением напряженности поля,
излучаемого антенной в произвольном направлении, к значению напряженности поля
в направлении максимального излучения
), т.е. отношением напряженности поля,
излучаемого антенной в произвольном направлении, к значению напряженности поля
в направлении максимального излучения
F(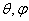 )= | E(
)= | E(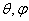 )| / |
Emax(
)| / |
Emax(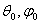 )| = f(
)| = f(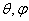 )/fmax(
)/fmax(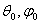 ).
).
Максимальная
величина F(θ,φ) всегда равна
единице. Графическое изображение амплитудной
характеристики направленности называют диаграммой направленности (ДН)
антенны. Пространственная ДН изображается в виде поверхности f(θ,φ) или F(θ,φ),
описываемой концом рдиуса-вектора, исходящего из начала координат, длина которого в
каждом направлении в определенном
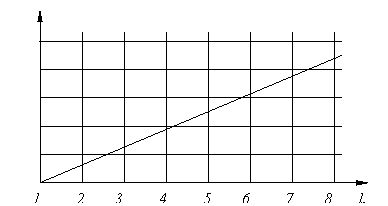
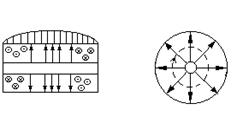
масштабе равна функции f(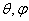 ). На рис.2.1.а изображена пространственная ДН
элементарного вибратора (тороид), на рис.2.1.б - ДН более сложной антенны (так называемая игольчатая ДН). На
практике обычно используют ДН, изображающие характеристику направленности в
каких-либо выбранных плоскостях. В качестве таких плоскостей обычно выбирают
две взаимно перпендикулярные плоскости,
проходящие через направление
). На рис.2.1.а изображена пространственная ДН
элементарного вибратора (тороид), на рис.2.1.б - ДН более сложной антенны (так называемая игольчатая ДН). На
практике обычно используют ДН, изображающие характеристику направленности в
каких-либо выбранных плоскостях. В качестве таких плоскостей обычно выбирают
две взаимно перпендикулярные плоскости,
проходящие через направление
максимального излучения (главные плоскости). Для антенн, излучающих линейно поляризованное поле, главными плоскостями называются плоскости, в которых лежит либо вектор Е (плоскость Е), либо вектор Н (плоскость Н).
Диаграммы направленности изображают обычно
либо в полярной (рис.2.2.а - ДН
элементарного вибратора в Е - плоскости; рис.2.2.б - ДН элементарного вибратора в Н -
плоскости), либо в декартовой (прямоугольной) системе координат
(рис.2.3. - ДН реальной антенны).
В некоторых случаях применяется картографический
метод изображения пространственных (трехмерных)
ДН. Он удобен для изображения многолепестковых (т.е.
имеющих много нулей и максимумов) ДН в широком диапазоне
углов. Этот метод состоит в том, что строится плоская сетка
координат 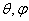 в какой-либо
координатной системе (прямоугольной, полярной и др.) подобно сетке меридианов и параллелей на географической
карте. На этой сетке замкнутыми линиями изображаются одинаковые
в какой-либо
координатной системе (прямоугольной, полярной и др.) подобно сетке меридианов и параллелей на географической
карте. На этой сетке замкнутыми линиями изображаются одинаковые
значения
нормированной характеристики направленности F(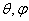 ) в том или ином масштабе. При изображении ДН часто
используется логарифмический масштаб, вводимый соотношением в децибеллах F(
) в том или ином масштабе. При изображении ДН часто
используется логарифмический масштаб, вводимый соотношением в децибеллах F(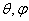 )=20 lgF(
)=20 lgF(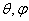 ).
).
В некоторых случаях пользуются понятием характеристики (диаграммы) направленности по мощности F2(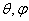 ). Функция F(
). Функция F(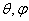 ) для
различных
) для
различных
|
Рис. 2,2. ДН диполя Герца
(а-Е-плоскость, б-Н-плоскость)
|
углов 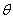 и
и  проходит через нуль и имеет несколько максимумов, т.е. ДН имеет
многолепестковый характер (см. рис.2.3).
Диаграмму направленности принято численно
характеризовать шириной главного
лепестка (шириной луча) и относительным
уровнем боковых лепестков (УБЛ).
проходит через нуль и имеет несколько максимумов, т.е. ДН имеет
многолепестковый характер (см. рис.2.3).
Диаграмму направленности принято численно
характеризовать шириной главного
лепестка (шириной луча) и относительным
уровнем боковых лепестков (УБЛ).
Шириной ДН (шириной луча) называется угол между направлениями, вдоль
которых напряженность поля падает до определенного значения. Так, шириной ДН по уровню нулевого излучения называют угол 2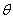 0
между направлениями вдоль которых напряженность поля падает до нуля (см. рис.2.3). Шириной ДН по половинной мощности называют угол 2
0
между направлениями вдоль которых напряженность поля падает до нуля (см. рис.2.3). Шириной ДН по половинной мощности называют угол 2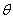 0,5 между направлениями,
вдоль которых |Е| = |Emax|/
0,5 между направлениями,
вдоль которых |Е| = |Emax|/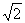 или соответственно среднее значение
плотности потока мощности П=Пmaх/2.
Наибольший лепесток, максимум которого соответствует
направлению максимального излучения, называют главным, меньшие лепестки - боковыми (лепестки, находящиеся в задних
квадрантах, т.е. в диапазоне углов 90°
или соответственно среднее значение
плотности потока мощности П=Пmaх/2.
Наибольший лепесток, максимум которого соответствует
направлению максимального излучения, называют главным, меньшие лепестки - боковыми (лепестки, находящиеся в задних
квадрантах, т.е. в диапазоне углов 90°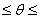 180° и 180°
180° и 180°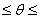 270°, часто называют задними).
270°, часто называют задними).
Относительный УБЛ (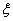 ) есть отношение апряженности поля в
направлении максимума данного лепестка (ENmax) к апряженности поля внаправлении главного максимума (Еmax), т.е.
) есть отношение апряженности поля в
направлении максимума данного лепестка (ENmax) к апряженности поля внаправлении главного максимума (Еmax), т.е.
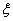 N=|ENmax|/|Еmax|=FN(
N=|ENmax|/|Еmax|=FN(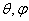 ), или в децибеллах
), или в децибеллах 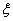 дБ = 20lg FN(
дБ = 20lg FN(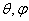 ), где N=1,2,3,...-номер бокового лепестка (для главного лепестка N=0).
), где N=1,2,3,...-номер бокового лепестка (для главного лепестка N=0).
Обычно стремятся к подавлению боковых лепестков, т.е. к тому, чтобы величина 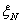 была мала.
была мала.
В большинстве
случаев интересуются амплитудными характеристиками направленности
(слово
"амплитудная" в дальнейшем не используем). Фазовые характеристики направленности используют в радиолокации, радионавигации и в некоторых других случаях.
Если фаза, излучаемого антенной поля, не зависит от направления на точку наблюдения и изменяется на обратную только при переходе функции f(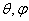 ) или F(
) или F(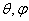 ) через нуль, т.е. при переходе от
одного лепестка ДН к другому, то такая антенна является
источником сферических волн, о чем свидетельствует
множитель [ехр(-ikr)]/r. Эти волны исходят как бы из одной точки, называемой фазовым
центром антенны. Эта точка расположена в начале выбранной системы
координат, и поэтому, фазовая характеристика зависит от
положения начала координат. Однако не все реальные антенны обладают фазовым
центром, т.е. излучают сферические волны. Для них обычно можно подобрать сферу, наилучшим образом аппроксимирующую фронт волны (обычно в пределах главного лепестка). Центр этой сферы называют центром
излучения антенны. Графическое изображение фазовой характеристики называется фазовой ДН.
) через нуль, т.е. при переходе от
одного лепестка ДН к другому, то такая антенна является
источником сферических волн, о чем свидетельствует
множитель [ехр(-ikr)]/r. Эти волны исходят как бы из одной точки, называемой фазовым
центром антенны. Эта точка расположена в начале выбранной системы
координат, и поэтому, фазовая характеристика зависит от
положения начала координат. Однако не все реальные антенны обладают фазовым
центром, т.е. излучают сферические волны. Для них обычно можно подобрать сферу, наилучшим образом аппроксимирующую фронт волны (обычно в пределах главного лепестка). Центр этой сферы называют центром
излучения антенны. Графическое изображение фазовой характеристики называется фазовой ДН.
Коэффициент
направленного действия (КНД), коэффициент усиления антенны (КУ) и параметры, связанные с КНД
Коэффициент направленного действия (КНД)
характеризует способность антенны концентрировать
излученное электромагнитное поле в каком-либо определенном
направлении. Это понятие было введено в 1929 г. А.А.Пистолькорсом. Коэффициентом
направленного действия называется отношение среднего значения за период высокой
частоты плотности потока мощности (среднее значение вектора
Пойнтинга), излучаемого антенной в данном направлении
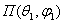 , к усредненному по всем направлениям
значению плотности потока мощности Пуср
, к усредненному по всем направлениям
значению плотности потока мощности Пуср
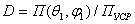 . (2.3)
. (2.3)
Здесь 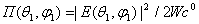 , где |
, где |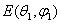 | - амплитудное значение напряженности электрического поля в направлении, характеризуемом углами
| - амплитудное значение напряженности электрического поля в направлении, характеризуемом углами 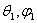 . Таким образом, при определении КНД данная
антенна сравнивается с воображаемой абсолютно ненаправленной (изотропной)
антенной, излучающей ту же мощность, что и данная. Очевидно, что
. Таким образом, при определении КНД данная
антенна сравнивается с воображаемой абсолютно ненаправленной (изотропной)
антенной, излучающей ту же мощность, что и данная. Очевидно, что
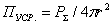 , (2.4)
, (2.4)
где 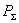 - мощность излучения; r - радиус
воображаемой сферы, охватывающей антенну, причем величина r должна быть такой, чтобы поверхность сферы находилась в дальней зоне поля антенны.
- мощность излучения; r - радиус
воображаемой сферы, охватывающей антенну, причем величина r должна быть такой, чтобы поверхность сферы находилась в дальней зоне поля антенны.
Коэффициент направленного действия показывает во сколько раз следует
уменьшить излучаемую мощность при замене изотропной (ненаправленной) антенны
на направленную, чтобы среднее значение плотности потока мощности в точке наблюдения осталось неизменным.
Учитывая, что 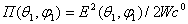 , и подставляя в (2.3) выражение (2.4), получаем формулу для КНД в другом виде
, и подставляя в (2.3) выражение (2.4), получаем формулу для КНД в другом виде 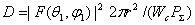 или для свободного пространства (Wc°=120
или для свободного пространства (Wc°=120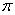 Ом) в направлении максимального излучения
Ом) в направлении максимального излучения
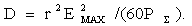 (2.5)
(2.5)
Если в эту формулу подставить вместо 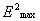 выражение (2.2) в квадрате (без фазовых
множителей) и учесть, что
выражение (2.2) в квадрате (без фазовых
множителей) и учесть, что 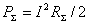 , где
, где 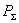 - сопротивление излучения элементарного электрического вибратора,
то получим КНД элементарного
вибратора D=1,5.
- сопротивление излучения элементарного электрического вибратора,
то получим КНД элементарного
вибратора D=1,5.
Коэффициент направленного действия тем больше, чем уже главный лепесток
пространственной ДН и чем меньше УБЛ. Коэффициент направленного действия можно
выразить с помощью еще одного параметра, называемого действующей длиной или
действующей высотой антенны 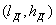 .Этот параметр иногда используют при
анализе приемных антенн, а также проволочных длинноволновых и средневолновых
антенн и антенн-мачт.
.Этот параметр иногда используют при
анализе приемных антенн, а также проволочных длинноволновых и средневолновых
антенн и антенн-мачт.
В случае линейной антенны ток по
ее длине распределен неравномерно. Однако
реальную антенну можно заменить воображаемым вибратором длиной lд (действующей длиной) с равномерным распределением тока
создающим в направлении максимального
излучения поле, равное полю данной антенны в главном направлении. При этом ток
в точке питания реальной антенны считается
равным току, текущему по воображаемому вибратору. По аналогии с (2.2) (вибратор с равномерным распределением тока)
напряженность поля реальной антенны в главном направлении можно представить в
виде
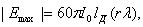 (2.6)
(2.6)
где I0 - амплитуда тока в точках питания антенны; 60π = Wc°/2, где 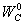 - волновое сопротивление
среды. Напишем выражение для величины напряженности поля
любой вибраторной антенны в произвольном направлении
- волновое сопротивление
среды. Напишем выражение для величины напряженности поля
любой вибраторной антенны в произвольном направлении
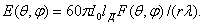 (2.7)
(2.7)
Подставляя в (2.5)
вместо 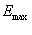 выражение
(2.6) и учитывая,
что
выражение
(2.6) и учитывая,
что
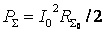 (
(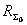 - сопротивление излучения антенны, отнесенное к току в точках
питания; I -ток в точках
питания антенны), получаем
- сопротивление излучения антенны, отнесенное к току в точках
питания; I -ток в точках
питания антенны), получаем
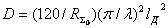 или
или 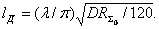 (2.8)
(2.8)
Формально параметром "действующая
длина" можно пользоваться в 21
случае любой антенны (линейной, апертурной или какой-либо другой), так как этот параметр выражается через КНД, а последний определяется только характеристикой
направленности.
Коэффициент
направленного действия не учитывает потерь подводимой энергии в проводниках антенны, в изоляторах, в окружающих антенну предметах и в
земле. В связи с этим вводится параметр, учитывающий эти потери, называемый коэффициентом усиления (КУ)
антенны, равный отношению среднего значения плотности потока мощности,
излучаемой антенной в данном направлении 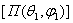 , к среднему значению плотности потока мощности, создаваемого воображаемым абсолютно ненаправленным излучателем
(Пн). При этом предполагается, что точка
наблюдения находится на одинаковом расстоянии от обеих
антенн; мощности, подводимые к той и другой антеннам, равны и КПД
ненаправленной антенны равен единице. Таким образом, КУ
, к среднему значению плотности потока мощности, создаваемого воображаемым абсолютно ненаправленным излучателем
(Пн). При этом предполагается, что точка
наблюдения находится на одинаковом расстоянии от обеих
антенн; мощности, подводимые к той и другой антеннам, равны и КПД
ненаправленной антенны равен единице. Таким образом, КУ
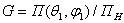 . (2.9)
. (2.9)
Коэффициент усиления показывает во сколько раз следует уменьшить мощность, подводимую к направленной антенне, по сравнению с абсолютно ненаправленной (изотропной) антенны, КПД которой считается равным
единице, чтобы среднее значение плотности потока мощности в точке наблюдения оставалось неизменным.
Отличие КУ от КНД состоит в том, что при
определении КУ исходят из равенства мощностей, подводимых к
исследуемой и эталонной ( ненаправленной) антеннам Р0, а не из равенства мощностей
излучения P , этих антенн.
Умножим и разделим
правую часть (2.9)
на Пуср. Тогда [П(
, этих антенн.
Умножим и разделим
правую часть (2.9)
на Пуср. Тогда [П(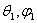 )/Пуср](Пуср/Пн), где Пуср/Пн
=
)/Пуср](Пуср/Пн), где Пуср/Пн
=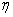 - КПД антенны.
- КПД антенны.
Параметры ( D, G и 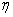 ) связаны соотношением
) связаны соотношением
G=D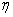 . (2.10)
. (2.10)
Учитывая, что D=G/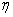 , можно написать
, можно написать
Emax=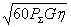 /r=
/r=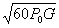 /r . (2.11)
/r . (2.11)
Поляризационные параметры антенн. Турникетный
излучатель
Направление векторов Е и Н излучаемого антенной поля
определяется плоскостью поляризации, т.е. плоскостью, проходящей через
направление распространения волны (вектор Пойнтинга) и
вектор напряженности электрического поля. В общем случае за
один период высокой частоты плоскость поляризации делает
полный оборот вокруг направления распространения. Такое поле называют вращающимся.
За это время конец вектора Е
описывает замкнутую кривую (эллипс), лежащую в
плоскости, перпендикулярной направлению распространения, и
называемую поляризационным эллипсом. Это - эллиптическая
поляризация электромагнитного поля. Частными видами эллиптической поляризации являются: линейная поляризация - конец
вектора Е лежит
на прямой линии; круговая поляризация - конец вектора Е за один период
высокой частоты описывает окружность.
Существуют антенны, рассчитанные на излучение (прием) поля круговой поляризации. Многие антенны (симметричный вибратор и другие) излучают во всех направлениях линейно поляризованные волны. Однако имеются
антенны, которые либо из-за своих конструктивных особенностей, либо из-за неточностей исполнения излучают волны чисто линейной поляризации только в двух взаимно перпендикулярных плоскостях, проходящих через направление максимального излучения (главные плоскости). Поляризация поля в
этих плоскостях называется главной или основной, В других
плоскостях имеется составляющая поля, поляризованная перпендикулярно
(ортогонально) основной поляризации (к таким антеннам относят, например,
параболическую). Эта составляющая, называемая поперечной
или кроссполяризацион-ной, является вредной. Ортогональность составляющих поля основной и кроссполяризации
(иногда ее называют паразитной) понимается как независимость переноса мощности
каждой из них. Мощность, соответствующая кроссполяризации,
расходуется на образование боковых лепестков, вследствие чего КНД антенны уменьшается. Кроме того, возрастают помехи, создаваемые передающей антенной различным приемным антеннам, работающим в том же или смежном диапазоне частот. Если поле передающей антенны имеет две ортогональные составляющие, а приемная антенна рассчитана
на прием лишь линейно поляризованного поля, то часть излученной
мощности, соответствующая паразитной поляризации, не используется.
Эллиптическая
поляризация может рассматриваться либо как результат сложения двух линейно
поляризованных взаимно перпендикулярных составляющих поля, не совпадающих по фазе, либо двух полей круговой поляризации
с противоположными направлениями вращения и разными амплитудами.
Отношение малой полуоси эллипса к большой (рис.2.4.а) называется коэффициентом
равномерности (коэффициентом эллиптичности) поляризационного эллипса: t=b/a. В случае линейной поляризации поля t = 0.
Условием этой поляризации является 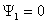 или
или 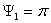 (
(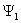 - сдвиг фаз между составляющими
- сдвиг фаз между составляющими 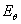 и
и 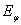 ). Линейная
поляризация также имеет место, если
). Линейная
поляризация также имеет место, если 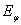 =0 или
=0 или 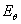 =0. При круговой
поляризации поля (
=0. При круговой
поляризации поля (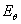 =
=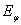 ;
;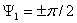 ) t=l. Таким образом, коэффициент равномерности поляризационного эллипса может изменяться в пределах 0< t < 1. Зависимость коэффициента эллиптичности от
направления на точку наблюдения называется поляризационной
ДН.
) t=l. Таким образом, коэффициент равномерности поляризационного эллипса может изменяться в пределах 0< t < 1. Зависимость коэффициента эллиптичности от
направления на точку наблюдения называется поляризационной
ДН.
Поляризационный эллипс характеризуется также углом поляризации и направлением вращения вектора Е
(направление вращения плоскости поляризации). Углом
поляризации 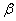 называется угол,
образованный большой осью поляризационного эллипса и
направлением орта
называется угол,
образованный большой осью поляризационного эллипса и
направлением орта 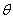 или
или  0 сферической системы координат (см. рис. 2.4.б).
Направление вращение вектора Е в
точке наблюдения определяется знаком угла
сдвига фаз между составляющими поля.
0 сферической системы координат (см. рис. 2.4.б).
Направление вращение вектора Е в
точке наблюдения определяется знаком угла
сдвига фаз между составляющими поля. 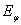 и
и 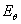 . Это направление называется правым, если наблюдатель, глядя навстречу волне, видит вектор Е вращающимся против часовой стрелки (рис. 2.5). Противоположное
направление вращения плоскости поляризации называется левым. Вектор Е
всегда вращается в сторону составляющей поля, отстающей по фазе.
. Это направление называется правым, если наблюдатель, глядя навстречу волне, видит вектор Е вращающимся против часовой стрелки (рис. 2.5). Противоположное
направление вращения плоскости поляризации называется левым. Вектор Е
всегда вращается в сторону составляющей поля, отстающей по фазе.
В соответствии
с (2.3) под КНД антенны с эллиптической поляризацией поля при полном поляризационном приеме будем подразумевать величину 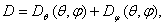 где
где 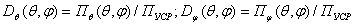 - парциальные КНД для
каждой из ортогональных составляющих поля; Пуср — усредненное по всем направлениям значение плотности потока мощности полного поля;
- парциальные КНД для
каждой из ортогональных составляющих поля; Пуср — усредненное по всем направлениям значение плотности потока мощности полного поля; 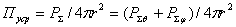 . Здесь
. Здесь 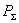 -
полная мощность излучения;
-
полная мощность излучения; 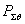 и
и 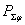 - мощности излучения, соответствующие ортогональным
компонентам поля. В соответствии с (2.3)
под КНД антенны с эллиптической поляризацией поля при полном
поляризационном приеме будем подразумевать величину
- мощности излучения, соответствующие ортогональным
компонентам поля. В соответствии с (2.3)
под КНД антенны с эллиптической поляризацией поля при полном
поляризационном приеме будем подразумевать величину 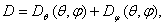 где
где 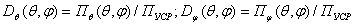 - парциальные КНД для
каждой из ортогональных составляющих поля; Пуср — усредненное по всем направлениям значение плотности потока мощности полного поля;
- парциальные КНД для
каждой из ортогональных составляющих поля; Пуср — усредненное по всем направлениям значение плотности потока мощности полного поля; 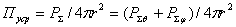 . Здесь
. Здесь 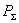 -
полная мощность излучения;
-
полная мощность излучения; 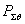 и
и 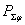 - мощности излучения, соответствующие
ортогональным компонентам поля.
- мощности излучения, соответствующие
ортогональным компонентам поля.
В качестве
примера простейшей антенны, создающей вращающееся поле рассмотрим два линейных
излучателя (для простоты считаем их элементарными), расположенных
крестообразно и питаемых токами равной амплитуды, но
сдвинутых по фазе на 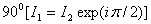 .Такой излучатель часто называют турникетным. В меридиональной по отношению к обоим вибраторам
плоскости yoz (см. рис.2.6) они создают поля одной поляризации, причем векторы
.Такой излучатель часто называют турникетным. В меридиональной по отношению к обоим вибраторам
плоскости yoz (см. рис.2.6) они создают поля одной поляризации, причем векторы 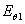 и
и 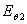 лежат
на одной и той же линии. В точке N, лежащей на нормали (ось х) к плоскости
расположения двух вибраторов, первый создаёт вектор
напряжённости электрического поля
лежат
на одной и той же линии. В точке N, лежащей на нормали (ось х) к плоскости
расположения двух вибраторов, первый создаёт вектор
напряжённости электрического поля 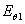 а второй -
а второй - 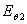 , находящиеся в плоскости, перпендикулярной
оси х, Эти векторы равны по амплитуде, сдвинуты по фазе друг
относительно друга на 90° и взаимно
перпендикулярны. Таким образом в направлении нормали плоскости вибраторов (yoz) имеет место круговая поляризация поля.
, находящиеся в плоскости, перпендикулярной
оси х, Эти векторы равны по амплитуде, сдвинуты по фазе друг
относительно друга на 90° и взаимно
перпендикулярны. Таким образом в направлении нормали плоскости вибраторов (yoz) имеет место круговая поляризация поля.
ТЕМА 2. Теория симметричного вибратора
Изучение симметричного электрического вибратора представляет большой интерес, так как, во-первых, этот вибратор применяется как самостоятельная
антенна и, во-вторых, он является составным элементом ряда сложных антенн. Симметричные вибраторы начали широко применять в первой половине двадцатых годов в связи с возникновением и развитием радиосвязи на коротких волнах. В настоящее время симметричный вибратор как самостоятельная антенна применяется на коротких, метровых и дециметровых
волнах. В этих же диапазонах широко используются сложные антенны, состоящие из
ряда симметричных вибраторов. Симметричные вибраторы
используются также в сантиметровом диапазоне волн в качестве элементов сложных систем (например, облучатели зеркальных антенн).
 Симметричный вибратор состоит из двух одинаковых по размерам и форме
проводников, между которыми включается генератор высокой частоты (часто эти
проводники называются плечами). Рассмотрим симметричный вибратор, представляющий собой тонкий цилиндрический проводник длиной 2
Симметричный вибратор состоит из двух одинаковых по размерам и форме
проводников, между которыми включается генератор высокой частоты (часто эти
проводники называются плечами). Рассмотрим симметричный вибратор, представляющий собой тонкий цилиндрический проводник длиной 2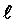 и радиусом а (рис.3.1), находящийся в
свободном пространстве. Строгое решение
основной
задачи теории антенн
и радиусом а (рис.3.1), находящийся в
свободном пространстве. Строгое решение
основной
задачи теории антенн
для симметричного
вибратора связано с большими трудностями, так как закон распределения тока по вибратору
неизвестен.
Существует приближенный метод расчета поля,
создаваемого симметричным вибратором в
дальней зоне. В основе этого метода лежит предположение о синусоидальном
распределении тока по вибратору, основанное на некоторой внешней
аналогии между симметричным вибратором и двухпроводной разомкнутой
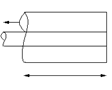
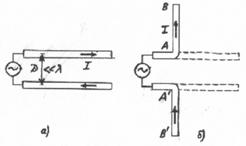
на конце линией без потерь. Действительно, от
двухпроводной линии (рис.3.2.а) можно перейти к симметричному вибратору, если
провода линии развернуть под углом 180° друг к другу (рис.3.2.б). Можно
полагать, что при переходе от двухпроводной линии к симметричному вибратору
закон распределения тока
не нарушается, т.е.
Iz = Iпsink(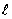 -
-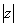 ) , где Iп - амплитуда тока в пучности тока вибратора (в
об-
) , где Iп - амплитуда тока в пучности тока вибратора (в
об-
щем случае, это величина
комплексная) İп = Iпexp(i );
); 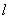 - длина одного плеча вибратора; z - расстояние от
начала вибратора (точки питания) до произвольной точки на
вибраторе (текущая координата); k = 2
- длина одного плеча вибратора; z - расстояние от
начала вибратора (точки питания) до произвольной точки на
вибраторе (текущая координата); k = 2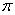 /
/ , - волновое число (коэффициент фазы тока в
вибраторе).
, - волновое число (коэффициент фазы тока в
вибраторе).
 Полагают, что длина волны в вибраторе
Полагают, что длина волны в вибраторе
λ, равна длине волны в свободном прост-
ранстве. В действительности данная анна-
логия весьма приближённа.Обе системы-
линия и вибратор – являются колебатель-
ными системами с распределенными па-
раметрами, однако они существенно раз-
личаются. Во-первых, распределенные
параметры
линии (Li,Ci) не изменяются по ее длине, распределенные параметры вибратора
непостоянны по его длине (рис.3.2.6). Во-вторых, линия служит для канализации электромагнитных волн и является практически неизлучающей
системой; вибратор же излучает волны. В разомкнутой на конце линии ток изменяется по закону стоячей волны только в том случае, если линия выполнена
из идеального проводника, т.е. в ней нет потерь энергии.
В вибраторе,
выполненном даже из идеального проводника, обязательно есть потери (полезные) на излучение. Очевидно, поэтому ток в
вибраторе, строго говоря, не может быть распределен по
закону стоячей волны. Однако расчет поля симметричного вибратора по
формулам, основанным на синусоидальном распределении тока, дает хорошее
совпадение с экспериментальными данными для дальней зоны и
тонких вибраторов. Поэтому для инженерного расчета это приближение в ряде
случаев вполне допустимо. Строгая теория симметричного вибратора подтверждает,
что в тонких вибраторах ток распределен по закону, весьма
близкому к синусоидальному. Задавшись законом
распределения тока по вибратору, легко установить приближенный закон распределения заряда 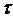 z=
z=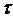 Пcosk(
Пcosk(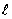 -
- 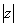 ), где
), где 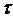 П амплитуда заряда в его пучности. Этот закон распределения заряда вдоль симметричного вибратора
совпадает с законом распределения потенциала (напряжения) в разомкнутой на конце длинной линии без потерь. В теории антенн понятием напряжения следует пользоваться с большой осторожностью, так как поле антенны не является потенциальным. Понятием напряжения применительно к антенне можно
пользоваться, если расстояние между точками измерения мало по сравнению с
длиной волны. Это справедливо при измерении напряжения между зажимами антенны
(точки присоединения генератора), а также для длинноволновых антенн. На рис.3.3
приведены кривые распределения амплитуд тока и заряда на вибраторах разной
длины. По аналогии с волновым сопротивлением длинной линии вводится
понятие волнового сопротивления симметричного вибратора. Как известно,
из теории длинных линий, волновое сопротивление двухпроводной линии
без потерь определяется выражением W =
П амплитуда заряда в его пучности. Этот закон распределения заряда вдоль симметричного вибратора
совпадает с законом распределения потенциала (напряжения) в разомкнутой на конце длинной линии без потерь. В теории антенн понятием напряжения следует пользоваться с большой осторожностью, так как поле антенны не является потенциальным. Понятием напряжения применительно к антенне можно
пользоваться, если расстояние между точками измерения мало по сравнению с
длиной волны. Это справедливо при измерении напряжения между зажимами антенны
(точки присоединения генератора), а также для длинноволновых антенн. На рис.3.3
приведены кривые распределения амплитуд тока и заряда на вибраторах разной
длины. По аналогии с волновым сопротивлением длинной линии вводится
понятие волнового сопротивления симметричного вибратора. Как известно,
из теории длинных линий, волновое сопротивление двухпроводной линии
без потерь определяется выражением W =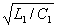 , где L1-распределенная индуктивность линии (индуктивность, приходящаяся на единицу длины линии), Г/м; C1 -, распределенная емкость линии, Ф/м. Так как
1/
, где L1-распределенная индуктивность линии (индуктивность, приходящаяся на единицу длины линии), Г/м; C1 -, распределенная емкость линии, Ф/м. Так как
1/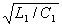 = с, где
= с, где
с - скорость света, м/с, то
W=l/cC1, Ом. (3.1)
Волновое сопротивление двухпроводной линии связано с ее геометрическими
размерами соотношением
W=2761g (D/a), (3.2)
где D - расстояние между
центрами проводов линии; а - радиус провода.
Волновое сопротивление симметричного
вибратора (а также других линейных
антенн, т.е. антенн, длина которых значительно
превосходит размеры поперечного
сечения) рассчитывают по формуле (3.1).
Однако распределенная емкость по длине вибратора непостоянна. Поэтому в данном случае под C1 подразумевается
усредненная величина, равная отношению полной статической емкости антенны (СА) к ее длине (2l). Одним из наиболее
распространенных приближенных методов расчета полной статической емкости является метод Хоу или метод усредненных
потенциалов. Волновое сопротивление симметричного
вибратора из провода цилиндрической формы, определенное по
методу Хоу,
WA=120(ln l/a-1), Oм, (3.3)
где l-длина плеча
вибратора; а - радиус провода.
Расчет волнового сопротивления вибратора методом Хоу дает приемлемую точность для вибраторов, коротких по сравнению с длиной волны. Точность этого метода снижается по мере удлинения вибратора.
Направленные свойства симметричного вибратора
Рассмотрим симметричный вибратор произвольной длины (рис.3.4). Задаемся
синусоидальным законом распределения тока вдоль вибратора Iz = (I0/sinkl)sink(l -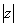 ), где I0 - ток в точках
питания вибратора (I0=Iпsinkl). Мысленно разобьем вибратор на бесконечно
большое число элементов dz. Так как длина
каждого элемента бесконечно мала, то можно полагать, что в пределах его ток
не изменяется ни по амплитуде, ни по фазе. Таким образом, весь симметричный вибратор можно рассматривать как
совокупность
), где I0 - ток в точках
питания вибратора (I0=Iпsinkl). Мысленно разобьем вибратор на бесконечно
большое число элементов dz. Так как длина
каждого элемента бесконечно мала, то можно полагать, что в пределах его ток
не изменяется ни по амплитуде, ни по фазе. Таким образом, весь симметричный вибратор можно рассматривать как
совокупность
элементарных
электрических вибраторов dz и поле симметричного вибратора рассматривать
как результат сложения (интерференции) полей, излучаемых элементарными вибраторами. Ввиду малости воздушного промежутка
(зазора) между плечами вибратора можно пренебречь влиянием электрического поля
(магнитного тока), существующего в нем на излучение, и считать, что электрический ток течет по сплошному
проводнику длиной 2l. Выделим на
вибраторе (рис.3.4) элементы 1 и 2, каждый длиной dz, симметричные
относительно центра вибратора 0, и определим поле, создаваемое этими элементами в произвольной точке наблюдения М, находящейся в зоне излучения. Проведем от
элементов 1 и 2 и от центра вибратора линии в точку наблюдения r1, r0, r2. Поскольку
расстояние до точки наблюдения очень велико по сравнению с
длиной вибратора, то направления от всех точек вибратора на точку М можно
считать параллельными. Напряженность поля, излучаемого первым элементом в
точке М
dE1 = i [60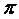 Izdz/ (r1
Izdz/ (r1 )]sin
)]sin exp(-ikr1).
exp(-ikr1).
(3.4.a)
Напряженность поля,
излучаемого вторым элементом в той же точке М dE2 = i [60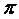 Izdz/(r2
Izdz/(r2 )] sin
)] sin exp(-ikr2).
exp(-ikr2).
(3.4.б)
Здесь Iz - амплитуда тока в элементе, находящемся
на расстоянии z от центра вибратора;
r1 - расстояние от первого элемента до точки М;
г2 - расстояние от второго элемента до
точки М;
 - угол между осью
вибратора и
направлением на точку наблюдения.
- угол между осью
вибратора и
направлением на точку наблюдения.
Найдем суммарное
поле, создаваемое в точке наблюдения элементами
1 и 2. Так как векторы напряженности полей, создаваемых всеми элементами
вибратора в точке наблюдения, направлены вдоль одной прямой (перпендикулярной направлению от данного элемента в
точку наблюдения), то поля,
создаваемые отдельными элементами, можно складывать алгебраически. Поэтому
dE = dE1+dE2=i
(60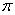 Izdz/
Izdz/ )sin
)sin [(exp(-ikr1)/r1+exp(-ikr2)/r2)]. (3.5)
[(exp(-ikr1)/r1+exp(-ikr2)/r2)]. (3.5)
Выразим расстояния r1 и r2 через расстояние r0. Для этого из точки 1 (рис.3.4) опустим перпендикуляр на направление r0 и из точки 0 опустим перпендикуляр на направление r2. Из прямоугольных треугольников 1-0-3 и 2-0-4 находим, что разность расстояний от данных
элементов и центра вибратора до точки наблюдения равна  r =
r = 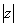 cos
cos .
.
Следовательно,
r1 = r0 - |z|cos и r2 = r0 +
и r2 = r0 + 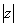 cos
cos . (3.6)
. (3.6)
Величину  r часто называют разностью хода
лучей. Так как точка наблюдения
находится в дальней зоне, то величина
r часто называют разностью хода
лучей. Так как точка наблюдения
находится в дальней зоне, то величина  r мала по
сравнению с r0 и расстояния r1 и r2 мало отличаются друг от друга. Поэтому можно считать, что амплитуды напряженности полей, создаваемых
элементами 1 и 2 в точке наблюдения М,
одинаковы. Однако пренебрегать разностью хода в фазовых множителях (exp(-ikr1) и exp(-ikr2)) ни в коем
случае нельзя, так как пространственный
сдвиг фаз между полями элементов 1 и 2 k
r мала по
сравнению с r0 и расстояния r1 и r2 мало отличаются друг от друга. Поэтому можно считать, что амплитуды напряженности полей, создаваемых
элементами 1 и 2 в точке наблюдения М,
одинаковы. Однако пренебрегать разностью хода в фазовых множителях (exp(-ikr1) и exp(-ikr2)) ни в коем
случае нельзя, так как пространственный
сдвиг фаз между полями элементов 1 и 2 k r = 2k|z|cosν = 4
r = 2k|z|cosν = 4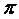 (|z|/
(|z|/ )cos
)cos определяется отношением разности хода лучей к длине волны. На
основании формул (3.6) получаем следующие выражения для фазовых множителей exp(-ikr1)= exp(-ikr0) * exp(ik|z|)cos
определяется отношением разности хода лучей к длине волны. На
основании формул (3.6) получаем следующие выражения для фазовых множителей exp(-ikr1)= exp(-ikr0) * exp(ik|z|)cos ;
;
exp (-ikr2) = exp (-ikro) * exp (-ik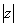 )cos
)cos .
.
Подставляя эти выражения в
формулу (3.5), вынося за скобки общие множители
и полагая, что в знаменателях r1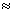 r2
r2 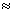 r0, получаем
r0, получаем
dE=i[60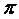 I0sink(l-
I0sink(l-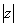 )dz/(r0
)dz/(r0  sinkl)]sin
sinkl)]sin exp(-ikr0)[(exp(ik
exp(-ikr0)[(exp(ik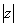 )cos
)cos +
+
+exp (-ik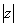 ) cos
) cos )].
)].
Воспользовавшись известной формулой exp(i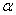 ) + exp(-i
) + exp(-i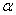 ) = 2cos
) = 2cos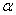 , получаем следующее выражение
, получаем следующее выражение
dE = i[120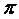 I0/( r0
I0/( r0  sinkl)] sin
sinkl)] sin exp(-ikr0)sink(l-
exp(-ikr0)sink(l-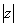 )cos(k
)cos(k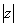 cos
cos )dz.
)dz.
Для определения напряженности поля,
создаваемого в точке наблюде-
ния всем симметричным вибратором, необходимо это
выражение проинтег-
рировать по длине одного плеча вибратора
Е=i[120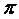 I0/(r0
I0/(r0  sinkl)] sin
sinkl)] sin exp(-ikr0)
exp(-ikr0) 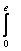 sink(l-
sink(l-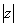 )cos(k
)cos(k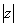 cos
cos )dz.
)dz.
В результате интегрирования получается формула для расчета напря-
женности поля симметричного электрического вибратора
в дальней зоне
E=i [60I0/ (r0sinkl)] * [(cos(klcos ) - coskl) / sin
) - coskl) / sin ]exp(-ikr0). (3.7)
]exp(-ikr0). (3.7)
Как и в случае элементарного электрического вибратора, эта формула
состоит из трех множителей: множителя, определяющего только величину напряженности поля и не зависящего от направления в данную точку [60I0/(r0sinkl)], множителя, определяющего направленные свойства (характеристика
направленности).
f( )=[cos(klcos
)=[cos(klcos ) - coskl]/sin
) - coskl]/sin
и фазового множителя 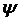 = iexp(-ikr0) из выражения
(3.7) видно, что симметричный вибратор
обладает направленными свойствами только в меридиональной плоскости (плоскость электрического вектора). Напряженность электрического поля симметричного вибратора
в его экваториальной
= iexp(-ikr0) из выражения
(3.7) видно, что симметричный вибратор
обладает направленными свойствами только в меридиональной плоскости (плоскость электрического вектора). Напряженность электрического поля симметричного вибратора
в его экваториальной
плоскости ( плоскость магнитного
вектора ν= 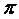 /2) - определяется выражением
/2) - определяется выражением
E = i [60I0/(r0sinkl)](l-coskl)exp(-ikro), (3.8)
т.е. не зависит от азимутального угла 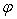 . Поэтому
диаграмма направленности
. Поэтому
диаграмма направленности
симметричного вибратора в его экваториальной плоскости, как и в случае элементарного вибратора,
представляет в полярной
системе координат ок-
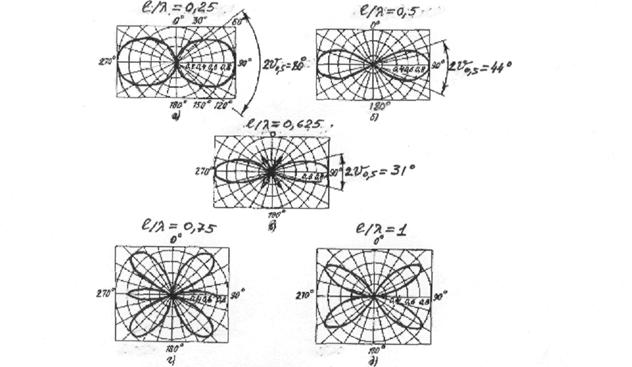
Диаграммы направленности симметричного
вибратора
ружность. Как видно из формулы (3.7),
направленные свойства симметричного вибратора определяются только отношением
длины плеча вибратора к длине волны l/ .В случае полуволнового вибратора (l/
.В случае полуволнового вибратора (l/ =0,25) формула (3.7) принимает вид
=0,25) формула (3.7) принимает вид
Е= iA{cos[(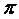 /2)cos
/2)cos ]/(sin
]/(sin )}exp (-ikr0).
)}exp (-ikr0).
Амплитудные диаграммы направленности,
рассчитанные по формуле (3.7), для вибраторов с различной относительной длиной
l/ показаны
на рис.3.5. Анализ формулы (3.7) и
рассмотрение этих кривых показывают, что при любой величине
отношения l/
показаны
на рис.3.5. Анализ формулы (3.7) и
рассмотрение этих кривых показывают, что при любой величине
отношения l/ симметричный вибратор
не излучает вдоль своей оси. Если длина плеча симметричного
вибратора l
симметричный вибратор
не излучает вдоль своей оси. Если длина плеча симметричного
вибратора l 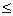 0,5
0,5 ,
то в направлении, перпендикулярном его
оси (
,
то в направлении, перпендикулярном его
оси ( = 90°,
= 90°,  = 270°), т.е. в экваториальной
плоскости, поля всех элементарных вибраторов
максимальны, синфазны и
складываются арифметически. Поэтому
поле в данном
направлении является
максимальным. Диаграмма направленности при l/
= 270°), т.е. в экваториальной
плоскости, поля всех элементарных вибраторов
максимальны, синфазны и
складываются арифметически. Поэтому
поле в данном
направлении является
максимальным. Диаграмма направленности при l/
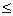 0,5 состоит из двух
(главных) лепестков (рис. 3.5.а, 3.5.б).
Увеличение длины вибратора до l=0,5
0,5 состоит из двух
(главных) лепестков (рис. 3.5.а, 3.5.б).
Увеличение длины вибратора до l=0,5 сопровождается ростом
излучения в направлении,
перпендикулярном оси вибратора
(главное направление излучения),за
счет уменьшения излучения в других направлениях. При этом диаграмма
направленности становится уже. При увеличении l/
сопровождается ростом
излучения в направлении,
перпендикулярном оси вибратора
(главное направление излучения),за
счет уменьшения излучения в других направлениях. При этом диаграмма
направленности становится уже. При увеличении l/ до 0,625 излучение в главном
направлении продолжает возрастать, но характеристика направленности проходит через нуль не только при
до 0,625 излучение в главном
направлении продолжает возрастать, но характеристика направленности проходит через нуль не только при  =0° и
=0° и  =180°, но и при некоторых других
значениях угла
=180°, но и при некоторых других
значениях угла . Главные лепестки диаграммы становятся уже, но появляются боковые лепестки (рис.3.5.в). При дальнейшем увеличении l/
. Главные лепестки диаграммы становятся уже, но появляются боковые лепестки (рис.3.5.в). При дальнейшем увеличении l/ излучение в главном направлении
уменьшается и возрастают боковые лепестки.
Уменьшение излучения в главном направлении объясняется следующим.
Результирующий сдвиг фаз полей, излучаемых элементарными вибраторами в данном
направлении, определяется пространственным сдвигом фаз и сдвигом фаз токов, возбуждающих эти вибраторы. При l/
излучение в главном направлении
уменьшается и возрастают боковые лепестки.
Уменьшение излучения в главном направлении объясняется следующим.
Результирующий сдвиг фаз полей, излучаемых элементарными вибраторами в данном
направлении, определяется пространственным сдвигом фаз и сдвигом фаз токов, возбуждающих эти вибраторы. При l/ >0,5 на вибраторе появляются
участки с противофазными токами (рис.3.3), длина которых растет по мере увеличения l/
>0,5 на вибраторе появляются
участки с противофазными токами (рис.3.3), длина которых растет по мере увеличения l/ . Поэтому в данном случае, хотя в
главном направлении пространственные сдвиги фаз равны нулю, поля, излучаемые отдельными элементами вибратора, складываются несинфазно, т.е. геометрически. При l/
. Поэтому в данном случае, хотя в
главном направлении пространственные сдвиги фаз равны нулю, поля, излучаемые отдельными элементами вибратора, складываются несинфазно, т.е. геометрически. При l/ = 1 (или при l/
= 1 (или при l/ = п, где п = 1, 2, ..,) излучение в главном направлении отсутствует, так как противофазные участки
вибратора имеют одинаковую длину. Рост l/
= п, где п = 1, 2, ..,) излучение в главном направлении отсутствует, так как противофазные участки
вибратора имеют одинаковую длину. Рост l/ сопровождается также ростом боковых
лепестков. Уже при l/
сопровождается также ростом боковых
лепестков. Уже при l/ =0,75 напряженность поля в направлении максимума бокового лепестка превосходит напряженность поля в главном направлении (рис.3.3.г).
=0,75 напряженность поля в направлении максимума бокового лепестка превосходит напряженность поля в главном направлении (рис.3.3.г).
Нормированная характеристика
направленности симметричного вибратора,
определяемая как F( ) = f(
) = f( )/f(90°), равна
)/f(90°), равна
F( ) = [cos(klcos
) = [cos(klcos ) - coskl]/[(l –
coskl)sin
) - coskl]/[(l –
coskl)sin ]. (3.9)
]. (3.9)
У Диполя Герца 2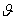 0,5= 90°. Полуволновый симметричный вибратор имеет
ширину диаграммы направленности по половинной мощности 2
0,5= 90°. Полуволновый симметричный вибратор имеет
ширину диаграммы направленности по половинной мощности 2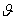 0,5= 80°, волновой
симметричный вибратор - 2
0,5= 80°, волновой
симметричный вибратор - 2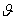 0,5= 44°,
симметричный вибратор, у которого l/
0,5= 44°,
симметричный вибратор, у которого l/ =0,625, имеет 2
=0,625, имеет 2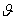 0,5= 31°.
Последний вибратор обладает наилучшими
направленными свойствами, так как при дальнейшем увеличении l/
0,5= 31°.
Последний вибратор обладает наилучшими
направленными свойствами, так как при дальнейшем увеличении l/ , сильно возрастают боковые лепестки, хотя главный лепесток
диаграммы направленности становится уже. На
практике применяются симметричные вибраторы,
у которых l/
, сильно возрастают боковые лепестки, хотя главный лепесток
диаграммы направленности становится уже. На
практике применяются симметричные вибраторы,
у которых l/
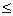 0,7. Фаза напряженности поля,
создаваемого симметричным вибратором в соответствии с
выражением (3.7), в пределах одного лепестка диаграммы направленности
не зависит от координатного угла
0,7. Фаза напряженности поля,
создаваемого симметричным вибратором в соответствии с
выражением (3.7), в пределах одного лепестка диаграммы направленности
не зависит от координатного угла  . Она изменяется скачком на обратную при переходе
напряжённости поля через нуль. Симметричный вибратор
излучает сферические волны, о чем свидетельствует множитель exp(-ikr)/r. Эти волны как бы исходят из одной точки,
совпадающей с центром вибратора.
. Она изменяется скачком на обратную при переходе
напряжённости поля через нуль. Симметричный вибратор
излучает сферические волны, о чем свидетельствует множитель exp(-ikr)/r. Эти волны как бы исходят из одной точки,
совпадающей с центром вибратора.
Мощность излучения, сопротивление излучения и КНД симметричного вибратора
Мощность электромагнитной волны,
излучаемой симметричным вибратором, можно определить, как и для
элементарного вибратора, методом вектора Пойнтинга.
В соответствии с данным методом симметричный вибратор окружается сферой,
радиус которой r » , вследствие чего поверхность сферы
находится в дальней зоне поля вибратора. Центр вибратора совпадает с центром
сферы, ось вибратора лежит на оси z прямоугольной системы координат. На
поверхности сферы выделяется бесконечно малый элемент dS, площадь которого в сферической системе координат dS = r2sinνd
, вследствие чего поверхность сферы
находится в дальней зоне поля вибратора. Центр вибратора совпадает с центром
сферы, ось вибратора лежит на оси z прямоугольной системы координат. На
поверхности сферы выделяется бесконечно малый элемент dS, площадь которого в сферической системе координат dS = r2sinνd d
d .
Излучаемая мощность, приходящаяся на данный
элемент поверхности
.
Излучаемая мощность, приходящаяся на данный
элемент поверхности
dP = ПсрdS=(E2/2Wc)dS. (3.10)
= ПсрdS=(E2/2Wc)dS. (3.10)
Здесь Е - амплитуда (модуль) напряженности
электрического поля в
любой
точке элемента dS, определяемая выражением
E = (60Iп/r) 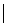 [cos (kl cos
[cos (kl cos ) - cos kl] / sin
) - cos kl] / sin
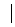 . (3.11)
. (3.11)
В общем виде выражение для сопротивления
излучения имеет вид
R п = [r2Е2 макс/( Wc Iп2 )]
п = [r2Е2 макс/( Wc Iп2 )] 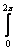
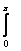 F2(
F2( ,
, )sin
)sin dνd
dνd . (3.12)
. (3.12)
P = Iп2R
= Iп2R п/2.
п/2.
Величина R п определяется
характером распределения электромагнитного поля в дальней
зоне, т.е. диаграммой направленности рассматриваемой антенны. Интегрирование дает следующую формулу, впервые полученную Баллантайном в 1924 г.
п определяется
характером распределения электромагнитного поля в дальней
зоне, т.е. диаграммой направленности рассматриваемой антенны. Интегрирование дает следующую формулу, впервые полученную Баллантайном в 1924 г.
R п = 30 [2 (
п = 30 [2 (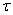 +ln2kl - Ci 2kl) + cos 2kl (
+ln2kl - Ci 2kl) + cos 2kl (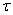 +lnkl+ Ci 4kl - 2Ci 2kl) +
+lnkl+ Ci 4kl - 2Ci 2kl) +
+sin2kl (Si 4kl- 2Si 2kl)]. (3.1)
Здесь 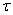 =
0,5772... - постоянная Эйлера; Si x = (sin u/u)du –
интегральный
=
0,5772... - постоянная Эйлера; Si x = (sin u/u)du –
интегральный
синус; Ci x = 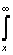 (cos u/u)du - интегральный косинус.
(cos u/u)du - интегральный косинус.
Как видно из формулы (3.13), сопротивление излучения симметричного вибратора зависит только от величины отношения l/ . Формула (3.13) является приближенной,
поскольку при ее выводе исходили из синусоидального распределения тока по
вибратору, что справедливо только для тонких вибраторов.
Однако результаты расчетов по формуле (3.13) хорошо совпадают с экспериментальными данными. Это объясняется тем, что сопротивление излучения определяется полем в дальней зоне, которое мало зависит от толщины вибратора. Следует также иметь в виду, что изложенный здесь
метод расчета дает только активную составляющую сопротивления излучения, так как учитывается только излученная активная мощность.
. Формула (3.13) является приближенной,
поскольку при ее выводе исходили из синусоидального распределения тока по
вибратору, что справедливо только для тонких вибраторов.
Однако результаты расчетов по формуле (3.13) хорошо совпадают с экспериментальными данными. Это объясняется тем, что сопротивление излучения определяется полем в дальней зоне, которое мало зависит от толщины вибратора. Следует также иметь в виду, что изложенный здесь
метод расчета дает только активную составляющую сопротивления излучения, так как учитывается только излученная активная мощность.
В литературе
имеются таблицы и графики R п как функции
отношения (рис.3.6), рассчитанные по формуле (3.13). Осциллирующий характер
зависимости объясняется тем, что интерференционная картина
поля в дальней зоне меняется при изменении l/
п как функции
отношения (рис.3.6), рассчитанные по формуле (3.13). Осциллирующий характер
зависимости объясняется тем, что интерференционная картина
поля в дальней зоне меняется при изменении l/ .
.
Если отношение
l/ ,
не превышает 0,1,
то формулу (3.13)
можно упростить R
,
не превышает 0,1,
то формулу (3.13)
можно упростить R п=20 (k l)4 .
п=20 (k l)4 .
КНД симметричного вибратора можно
определить по формуле
D = (120 / R п ) (1 -coskl)2. (3.14)
п ) (1 -coskl)2. (3.14)
При l/ =0,25
R
=0,25
R п = 73,1 Ом и
D= 1,64 ;
п = 73,1 Ом и
D= 1,64 ;
l/ = 0,5 R
= 0,5 R п =199 Ом и D = 2,4;
п =199 Ом и D = 2,4;
l/ =0,625 R
=0,625 R п =110 Ом и D = 3,l.
п =110 Ом и D = 3,l.
Для сравнения КНД
элементарного электрического вибратора имеет
D = 1,5. КНД
любой вибраторной антенны можно рассчитать по формуле
D = (120/ R п) f2max (
п) f2max (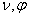 ). (3.15)
). (3.15)
В этой формуле R п - полное сопротивление излучения антенны.
Действующая
длина симметричного вибратора
определяется по формуле lд =
п - полное сопротивление излучения антенны.
Действующая
длина симметричного вибратора
определяется по формуле lд =  (1 - coskl) / (
(1 - coskl) / (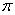 sinkl).
sinkl).
Зависимость R п От величины l/
п От величины l/
Входное
сопротивление симметричного вибратора. Инженерный
метод расчета входного сопротивления
Часть мощности,
подводимой от генератора к симметричному вибратору, излучается. Другая часть
мощности теряется в самом вибраторе (нагревание
проводов), в изоляторах и в окружающих вибратор предметах. Излученной мощности
соответствует активное сопротивление излучения. Мощности потерь соответствует активное сопротивление
потерь. Кроме излученного, есть
колеблющееся вблизи антенны связанное с ней электромагнитное поле, которому
соответствует реактивная мощность. Эта мощность то отдается генератором,
переходя в ближнее поле, то возвращается к нему обратно. Реактивной мощности в большинстве случаев соответствует
реактивное сопротивление антенны.
 Таким образом, включенный в антенну генератор нагружен на комплексное сопротивление, которое называется входным сопротивлением антенны и
равно отношению напряжения на зажимах вибратора (точки
питания) к току в точках питания ZBX=U0/I0=RBX+i XBX.
Таким образом, включенный в антенну генератор нагружен на комплексное сопротивление, которое называется входным сопротивлением антенны и
равно отношению напряжения на зажимах вибратора (точки
питания) к току в точках питания ZBX=U0/I0=RBX+i XBX.
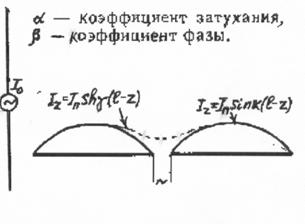
|
Рис. 3.7. Распределение тока по "коротким" и "длинным" вибраторам
|
Величина и характер входного сопротивления определяют режим работы включенного в антенну генератора. Обычно в
симметричных вибраторах потери малы, поэтому будем полагать, что RBX 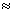 R
R o, где R
o, где R o - сопротивление
излучения вибратора, отнесенное к току в точках питания. Для точного определения входного сопротивления
необходимо знать закон распределения тока вдоль вибратора. Часто с достаточной для инже-
o - сопротивление
излучения вибратора, отнесенное к току в точках питания. Для точного определения входного сопротивления
необходимо знать закон распределения тока вдоль вибратора. Часто с достаточной для инже-
нерных целей
точностью входное сопротивление рассчитывается, исходя из приближенных законов распределения тока по вибратору. Рассмотрим такой
приближенный (инженерный) метод расчета входного сопротивления. Предположив, что ток вдоль вибратора распределен по закону синуса, найдем входное сопротивление симметричного вибратора, у которого l/ =0,5 (рис.3.7). В этом случае ток в точках
питания оказывается равным нулю и очевидно, что ZBX = U0/I0=
=0,5 (рис.3.7). В этом случае ток в точках
питания оказывается равным нулю и очевидно, что ZBX = U0/I0=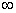 . В действительности же ток в точках питания никогда не бывает равен нулю (его величина обязательно конечна), а следовательно, входное сопротивление симметричного вибратора никогда не бывает бесконечно велико. Физически это совершенно ясно. Ведь закон синуса
(стоячая волна) справедлив в линиях только при отсутствии потерь. Вибратор же в принципе является системой с потерями на излучение. Следовательно, при расчете входного сопротивления лучше проводить аналогию между симметричным вибратором и разомкнутой на конце линией с потерями. Известно, что ток в такой линии распределен по закону гиперболического
синуса (рис.3.7) Iz = Iпsh
. В действительности же ток в точках питания никогда не бывает равен нулю (его величина обязательно конечна), а следовательно, входное сопротивление симметричного вибратора никогда не бывает бесконечно велико. Физически это совершенно ясно. Ведь закон синуса
(стоячая волна) справедлив в линиях только при отсутствии потерь. Вибратор же в принципе является системой с потерями на излучение. Следовательно, при расчете входного сопротивления лучше проводить аналогию между симметричным вибратором и разомкнутой на конце линией с потерями. Известно, что ток в такой линии распределен по закону гиперболического
синуса (рис.3.7) Iz = Iпsh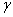 (z - l), где
(z - l), где 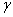 =
= 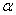 + i
+ i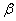 - коэффициент распространения,
- коэффициент распространения, 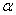 -
коэффициент ослабления,
-
коэффициент ослабления, 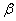 -
коэффициент фазы.
-
коэффициент фазы.
Из рис.3.7 видно, что существенная разница в распределении тока по законам кругового и гиперболического синусов получается только на сравнительно близких расстояниях от узла тока. Поэтому при расчете входных сопротивлений "коротких" вибраторов (l/ )
) 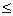 0,35...0,4; (0,6...0,65)
0,35...0,4; (0,6...0,65) 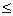 l/
l/
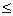 (0,85...0,9), т.е. таких, у которых узел тока
находится от точек питания вибратора не ближе, чем на расстоянии
(0,1...0,15)
(0,85...0,9), т.е. таких, у которых узел тока
находится от точек питания вибратора не ближе, чем на расстоянии
(0,1...0,15) , исходят из синусоидального
распределения тока. При расчете входного сопротивления "длинных" вибраторов (0,35
, исходят из синусоидального
распределения тока. При расчете входного сопротивления "длинных" вибраторов (0,35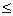 l/
l/
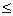 0,65) следует исходить из распределения тока по закону гиперболического синуса. Найдем формулы для расчета активной
0,65) следует исходить из распределения тока по закону гиперболического синуса. Найдем формулы для расчета активной
35
и реактивной
составляющих входного сопротивления "короткого" вибратора. Выразив
мощность, излучаемую вибратором, через амплитуды тока в пучности (IП) и в точках питания (Iо), получим:
P = (Iп2R
= (Iп2R п )/2 и P
п )/2 и P = (I02 R
= (I02 R 0)/2. (3.17)
0)/2. (3.17)
Так как левые части этих выражений равны между
собой, то I2п R п = I02 R
п = I02 R 0. Решая это равенство относительно R
0. Решая это равенство относительно R 0, получаем R
0, получаем R 0= R
0= R п (Iп2/ I02).
п (Iп2/ I02).
Подставляя вместо I0 выражение I0=Iпsinkl, получаем формулу для расчета активной
составляющей входного сопротивления вибратора (без учета потерь в
вибраторе)
R 0 = R
0 = R п /sin2kl. (3.18)
п /sin2kl. (3.18)
Величину R п
для вибратора заданной длины легко найти из
таблиц или графиков. При расчете реактивной
составляющей входного сопротивления короткого симметричного вибратора
пользуются формулой входного сопротивления
разомкнутой на конце двухпроводной линии без потерь, заменяя в ней волновое
сопротивление линии волновым сопротивлением антенны
п
для вибратора заданной длины легко найти из
таблиц или графиков. При расчете реактивной
составляющей входного сопротивления короткого симметричного вибратора
пользуются формулой входного сопротивления
разомкнутой на конце двухпроводной линии без потерь, заменяя в ней волновое
сопротивление линии волновым сопротивлением антенны
Xвх= -i WActg kl. (3.19)
Таким образом, полное входное сопротивление короткого вибратора можно определить
по формуле
Zвх= (R п/sin2kl) – i WActg kl. (3.20)
п/sin2kl) – i WActg kl. (3.20)
Точность расчетов по формуле (3.20) повышается при уменьшении размеров
поперечного сечения вибратора. В случаях длинных вибраторов входное сопротивление рассчитывается аналогично входному сопротивлению двухпроводной разомкнутой на конце линии, обладающей потерями
Zвх = WA [(sh2 l- (
l- (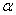 /
/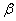 ) sin 2
) sin 2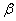 l) / (ch2
l) / (ch2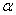 l - cos 2
l - cos 2 l)] – i WA [(
l)] – i WA [( /
/ ) sh 2
) sh 2 l+
l+
+ sin 2 l) / (ch2
l) / (ch2 l - cos 2
l - cos 2 l)]. (3.21)
l)]. (3.21)
Здесь WA - волновое сопротивление вибратора; l- длина плеча
вибратора;  - коэффициент фазы в вибраторе;
- коэффициент фазы в вибраторе;  - коэффициент затухания. По аналогии с длинными линиями, пренебрегая потерями в проводах вибратора коэффициент затухания можно рассчитать по формуле
- коэффициент затухания. По аналогии с длинными линиями, пренебрегая потерями в проводах вибратора коэффициент затухания можно рассчитать по формуле
 = R
= R 1 / WA, где R
1 / WA, где R 1 -активное сопротивление излучения, приходящееся на единицу длины вибратора.
Приближенно полагая, что сопротивление излучения R
1 -активное сопротивление излучения, приходящееся на единицу длины вибратора.
Приближенно полагая, что сопротивление излучения R п распределено равномерно по всей длине вибратора, для расчета R
п распределено равномерно по всей длине вибратора, для расчета R 1 получают
формулу R
1 получают
формулу R 1= R
1= R п/[l(l - (sin2kl/2kl)]. Данная
формула позволяет, зная сопротивление излучения,
отнесенное к пучности тока, найти распределенное сопротивление излучения. Следовательно, коэффициент
ослабления
п/[l(l - (sin2kl/2kl)]. Данная
формула позволяет, зная сопротивление излучения,
отнесенное к пучности тока, найти распределенное сопротивление излучения. Следовательно, коэффициент
ослабления
 = R
= R 1/ WA = R
1/ WA = R п/ [lWA (1- (sin2kl/2kl))].
п/ [lWA (1- (sin2kl/2kl))].
Коэффициент фазы 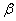 в формуле (3.21)
несколько отличается от
в формуле (3.21)
несколько отличается от
Зависимость R вх
от величины
l/
коэффициента фазы в
свобод-
ном пространстве k, так как
фазовая
скорость в линии с потерями, а,
следовательно, и в
вибраторе несколько меньше
скорости света. Поэтому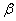 =
=
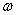 /
/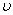 > k =
> k = 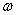 /с , где
/с , где 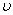 -фазовая
-фазовая
скорость в вибраторе. Чем
меньше волновое сопротивление вибратора (чем толще вибратор),
тем меньше фазовая
скорость. Из формулы (3.21)
видно, что как активная, так и
реактивная составляющие
входного
сопротивления симметричного вибратора, в общем случае, зависят не только от длины вибратора,
но и от его диаметра. Зависимость входного сопротивления симметричного
вибратора от величины отношения l/ и от волнового сопротивления WA показана на рис. 3.8 и 3.9.
и от волнового сопротивления WA показана на рис. 3.8 и 3.9.
Кривые рассчитаны
по формуле (3.21). При расчете полагалось, что 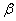 = k. Из кривых видно, что при увеличении l/
= k. Из кривых видно, что при увеличении l/ активная составляющая
входного сопротивления постепенно растет и достигает при l/
активная составляющая
входного сопротивления постепенно растет и достигает при l/ =0,5 максимума, величина которого тем больше, чем больше
wa, т.е. чем тоньше вибратор. При дальнейшем увеличении l/
=0,5 максимума, величина которого тем больше, чем больше
wa, т.е. чем тоньше вибратор. При дальнейшем увеличении l/ rbx постепенно уменьшается и достигает минимума при l/
rbx постепенно уменьшается и достигает минимума при l/ =0,75. Затем Rвх снова начинает увеличиваться и достигает
=0,75. Затем Rвх снова начинает увеличиваться и достигает
Рис. 3.9.
Зависимость X вх от величины
l/
нового максимума
при l= (на рисунке этот максимум не показан). Вообще максимумы Rвх повторяются при всех отношениях l/
(на рисунке этот максимум не показан). Вообще максимумы Rвх повторяются при всех отношениях l/ , кратных 0,5. Активная составляющая входного сопротивления
минимальна в тех случаях, когда относительная
длина вибратора становится равной нечетному числу
, кратных 0,5. Активная составляющая входного сопротивления
минимальна в тех случаях, когда относительная
длина вибратора становится равной нечетному числу  /4. В случае полуволнового вибратора
минимум Rвх отсутствует. Реактивная составляющая входного сопротивления вибратора изменяется периодически, проходя через нуль при l/
/4. В случае полуволнового вибратора
минимум Rвх отсутствует. Реактивная составляющая входного сопротивления вибратора изменяется периодически, проходя через нуль при l/ =0,25; 0,5;0,75; 1 и т.д. При l/
=0,25; 0,5;0,75; 1 и т.д. При l/ <0,25 Хвх имеет емкостный характер, при 0,25< l/
<0,25 Хвх имеет емкостный характер, при 0,25< l/ <0,5 - индуктивный. Можно сказать, что вблизи значений l/
<0,5 - индуктивный. Можно сказать, что вблизи значений l/ = (2n + 1)/4, где n=0, 1, 2...,
симметричный вибратор ведет себя подобно последовательному
колебательному контуру (резонанс напряжения), а
вблизи значений l/
= (2n + 1)/4, где n=0, 1, 2...,
симметричный вибратор ведет себя подобно последовательному
колебательному контуру (резонанс напряжения), а
вблизи значений l/ =n/2- подобно параллельному колебательному контуру
(резонанс токов). В первом случае вибратор питается в пучности тока, а
во втором - в узле тока. Наибольшую длину волны, при которой вибратор оказывается настроенным в резонанс с питающим его генератором (Хвх= 0), называют собственной
длиной волны антенны. Как видно из формул (3.20) и (3.21), собственная
длина волны симметричного вибратора
=n/2- подобно параллельному колебательному контуру
(резонанс токов). В первом случае вибратор питается в пучности тока, а
во втором - в узле тока. Наибольшую длину волны, при которой вибратор оказывается настроенным в резонанс с питающим его генератором (Хвх= 0), называют собственной
длиной волны антенны. Как видно из формул (3.20) и (3.21), собственная
длина волны симметричного вибратора  0=4l. В действительности из-за того, что
фазовая скорость распространения в вибраторе
несколько меньше скорости света (
0=4l. В действительности из-за того, что
фазовая скорость распространения в вибраторе
несколько меньше скорости света (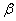 > k), резонансные длины вибраторов оказываются несколько меньшими, чем получаемые по формулам (3.20) и (3.21). При этом, чем
толще вибратор, тем меньше фазовая скорость и тем
короче его резонансная длина. В частности, при l/
> k), резонансные длины вибраторов оказываются несколько меньшими, чем получаемые по формулам (3.20) и (3.21). При этом, чем
толще вибратор, тем меньше фазовая скорость и тем
короче его резонансная длина. В частности, при l/ =0,25 и а
=0,25 и а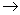 0
Хвх=i42,5 Ом. Обычно стремятся к нулевой
реактивной составляющей входного сопротивления вибратора на рабочей частоте.
Поэтому длину плеча вибратора делают
несколько короче, чем
0
Хвх=i42,5 Ом. Обычно стремятся к нулевой
реактивной составляющей входного сопротивления вибратора на рабочей частоте.
Поэтому длину плеча вибратора делают
несколько короче, чем  /4 или
/4 или  /2. Величина
укорочения тем больше, чем толще вибратор. Активная составляющая входного сопротивления
симметричного вибратора при питании вибратора в пучности тока (последовательный резонанс), как следует из
формулы (3.20), равна Rвх=R
/2. Величина
укорочения тем больше, чем толще вибратор. Активная составляющая входного сопротивления
симметричного вибратора при питании вибратора в пучности тока (последовательный резонанс), как следует из
формулы (3.20), равна Rвх=R 0=R
0=R п.. При определении входного сопротивления симметричного вибратора, питаемого вблизи узла тока, полагая, что
п.. При определении входного сопротивления симметричного вибратора, питаемого вблизи узла тока, полагая, что  l<<1 (что соответствует действительности), можно несколько преобразовать выражение (3.21) и получить следующие формулы:
l<<1 (что соответствует действительности), можно несколько преобразовать выражение (3.21) и получить следующие формулы:
Rвх = R п / [sin2 kl+ (R
п / [sin2 kl+ (R п2/W2A)]; (3.22)
п2/W2A)]; (3.22)
Хвх = - i (WA/2) [sin2kl/
(sin2 kl + (R п2/W2A))] . (3.23)
п2/W2A))] . (3.23)
В случае параллельного резонанса (kl=180°) получаем
R 0 = WA2 / R
0 = WA2 / R п и
Хвх = 0. (3.24)
п и
Хвх = 0. (3.24)
Из формулы (3.24) видно, что в случае параллельного резонанса R 0
весьма велико, так как R
0
весьма велико, так как R п
п 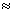 200 Ом, a WA составляет 300 ... 1000 Ом. Формулами (3.22) и (3.23)
можно пользоваться наряду с формулой (3.21) для расчета входного сопротивления
симметричного вибратора, если 0,35
200 Ом, a WA составляет 300 ... 1000 Ом. Формулами (3.22) и (3.23)
можно пользоваться наряду с формулой (3.21) для расчета входного сопротивления
симметричного вибратора, если 0,35 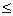 l/
l/
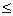 0,65. Отметим, что при
увеличении волнового сопротивления вибратора закон распределения тока по нему становится ближе к синусоидальному.
0,65. Отметим, что при
увеличении волнового сопротивления вибратора закон распределения тока по нему становится ближе к синусоидальному.
Поэтому в случае тонких вибраторов (WA=700...1000 Ом) пределы применимости формулы
(3.20) расширяются. Как видно из кривых рис. 3.8 и 3.9, при уменьшении волнового сопротивления вибратора уменьшается зависимость
его активного и реактивного входного сопротивления от частоты (улучшаются
диапазонные свойства). По аналогии с обычным колебательным контуром можно сказать, что при уменьшении WA уменьшается добротность
вибратора, под которой понимается отношение связанной с вибратором
реактивной энергии к активной (излученной и теряемой) энергии. Добротность
вибратора определяется выражением
QA= A (WA/Rвх), (3.25)
где А - коэффициент
пропорциональности.
WA уменьшают,
увеличивая размеры поперечного сечения вибратора; при этом
увеличивается распределенная емкость C1 вибратора.
Зависимость Rвх и Хвх от относительной длины плеча вибраторов реальной толщины приведены
на рис.3.10.
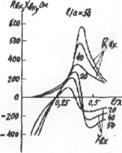 Зависимость Rвх и
Xвх реальных
Зависимость Rвх и
Xвх реальных
вибраторов от
величины l/
Основные результаты, даваемые строгой теорией симметричного вибратора
Задача об излучении тонкого симметричного вибратора (электрический радиус вибратора ka < 0,1) в строгой электродинамической постановке была решена Халленом и независимо от него российскими учеными М.А.Леонтовичем и М.Л.Левиным методом интегро-дифференциального
уравнения. Как показали расчеты, даже в случае сравнительно тонких вибраторов (ka  0,05) распределение тока уже несколько
отличается от синусоидального. Таким образом, метод интегро-дифференциального
уравнения подтверждает правильность выбора
приближенного (синусоидального) закона распределения
тока и позволяет найти точное распределение тока в тонких вибраторах. Однако он не позволяет найти закон распределения тока
в вибраторах средней (ka= 0,1...0,5) и большой (ka > 0,5) толщины. Кроме того, в рассмотренном методе
не учитывается влияние ширины возбуждающего зазора на
распределение тока. Входное сопротивление полуволнового вибратора, рассчитанное этим методом, при а
0,05) распределение тока уже несколько
отличается от синусоидального. Таким образом, метод интегро-дифференциального
уравнения подтверждает правильность выбора
приближенного (синусоидального) закона распределения
тока и позволяет найти точное распределение тока в тонких вибраторах. Однако он не позволяет найти закон распределения тока
в вибраторах средней (ka= 0,1...0,5) и большой (ka > 0,5) толщины. Кроме того, в рассмотренном методе
не учитывается влияние ширины возбуждающего зазора на
распределение тока. Входное сопротивление полуволнового вибратора, рассчитанное этим методом, при а 0 оказывается
комплексным и равным Zвх = 73,1 + i42,5 Ом. Как видно,
активная составляющая входного сопротивления (R
0 оказывается
комплексным и равным Zвх = 73,1 + i42,5 Ом. Как видно,
активная составляющая входного сопротивления (R 0) получается такой же, как и по методу вектора Пойнтинга. Реактивная составляющая входного
сопротивления имеет индуктивный
характер. Укорочение
0) получается такой же, как и по методу вектора Пойнтинга. Реактивная составляющая входного
сопротивления имеет индуктивный
характер. Укорочение  l, необходимое для того, чтобы сделать вибратор резонансным, определяется по формуле
l, необходимое для того, чтобы сделать вибратор резонансным, определяется по формуле
 l/l = - 0,225/ ln (l/a). (3.26)
l/l = - 0,225/ ln (l/a). (3.26)
Расчет входного сопротивления полуволнового вибратора с учетом только первого приближения показал, что даже в случае тонких вибраторов
величина радиуса заметно, влияет на входное сопротивление.
Задача об излучении толстого вибратора (ka>0,5) в строгой постановке была решена Е. Н.
Васильевым в 1958-1959 гг. В отличие от методов Халлена или
Леонтовича-Левина, где использовались граничные условия для векторов электрического поля на поверхности
вибратора, в методе Васильева используется граничное условие для векторов
магнитного поля. Полученное из этого условия интегральное уравнение
относительно текущего по вибратору
тока решается численно при помощи ЭВМ. Решение тем более точно, чем толще вибратор. В дальнейшем Е.Н. Васильевым
и Г.Д. Малушковым был разработан
более общий метод решения задачи возбуждения осесимметричного тела вращения,
позволяющий рассчитать распределение тока на вибраторах среднего электрического радиуса (ka = 0,1...0,5), что особенно важно для анализа работы вибраторов, применяемых в метровом и особенно в дециметровом диапазонах волн. Проведенные расчеты показали, что распределение тока в вибраторах средней и большой толщины значительно отличается от синусоидального. Ток на кромке торца имеет конечную величину. В центре торца ток
равен нулю. Расчеты показали также, что: 1) с увеличением радиуса цилиндра существенно уменьшается
коэффициент отражения от его концов и распределение тока по вибратору
приобретает характер бегущей волны:
амплитуда тока постепенно уменьшается по мере удаления от точек питания вибратора, фаза тока изменяется примерно по
линейному закону; 2) ширина зазора между плечами вибратора значительно
влияет на распределение тока вблизи точек
питания вибратора. Зависимость распределения тока от толщины вибратора влияет на диаграмму направленности последнего. С увеличением толщины вибратора направления
нулевого излучения заменяются направлениями минимального излучения. При
этом чем толще вибратор, тем менее глубоки минимумы.
Действительные диаграммы направленности заметно отличаются от
рассчитанных приближенным методом при l/а, равном нескольким
десяткам.
ТЕМА 3. Связанные вибраторы. Характеристики вибраторных
антенн
Одиночные вибраторы применяют только тогда, когда требуется ненаправленное
или почти ненаправленное излучение. В тех же случаях, когда необходимо получить
однонаправленное излучение или узкие диаграммы направленности применяют
антенны, состоящие из двух или нескольких вибраторов,
расположенных на небольшом расстоянии (меньше  ) друг от друга. Такие вибраторы заметно влияют
друг на друга, поэтому их называют связанными. Взаимодействие связанных вибраторов аналогично взаимодействию связанных
колебательных контуров с сосредоточенными постоянными. Поле одного вибратора наводит в другом вибраторе некоторую ЭДС, что
эквивалентно изменению сопротивления излучения или входного сопротивления
вибратора. Поле, создаваемое системой вибраторов, является результатом сложения полей, - создаваемых отдельными вибраторами, с учетом фаз этих полей, определяемых как разностью хода лучей, так и разностью фаз токов в излучателях. Ниже рассматривается работа двух связанных симметричных
вибраторов. Получаемые при этом результаты нетрудно распространить на
случай нескольких связанных вибраторов. Выведем формулу для расчета характеристики направленности двух
параллельных вибраторов 1 и 2,
находящихся на расстоянии d друг от друга (рис. 4.1), питаемых токами
) друг от друга. Такие вибраторы заметно влияют
друг на друга, поэтому их называют связанными. Взаимодействие связанных вибраторов аналогично взаимодействию связанных
колебательных контуров с сосредоточенными постоянными. Поле одного вибратора наводит в другом вибраторе некоторую ЭДС, что
эквивалентно изменению сопротивления излучения или входного сопротивления
вибратора. Поле, создаваемое системой вибраторов, является результатом сложения полей, - создаваемых отдельными вибраторами, с учетом фаз этих полей, определяемых как разностью хода лучей, так и разностью фаз токов в излучателях. Ниже рассматривается работа двух связанных симметричных
вибраторов. Получаемые при этом результаты нетрудно распространить на
случай нескольких связанных вибраторов. Выведем формулу для расчета характеристики направленности двух
параллельных вибраторов 1 и 2,
находящихся на расстоянии d друг от друга (рис. 4.1), питаемых токами
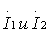 . Обозначим
. Обозначим
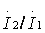 =q exp(i
=q exp(i ), (4.1)
), (4.1)
где q - отношение модулей токов 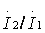 ;
; - сдвиг фазы тока I2 по отношению к току I1.
- сдвиг фазы тока I2 по отношению к току I1.
|
Рис. 4.1. К определению поля
излучения связанных вибраторов
|
Рассмотрим поле в меридиональной плоскости вибраторов xoz. Так как
расстояние между вибраторами d несоизмеримо мало по сравнению с
расстояниями до точки наблюдения (r1 и r2), направления в точку М
можно считать параллельными. Опустив из центра первого вибратора перпендикуляр на направление r2, найдем разность расстояний от 44 вибраторов до точки
47
наблюдения, равную  r = d cos
r = d cos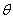 , где
, где 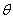 - угол между нормалью к оси вибратора и направлением на точку
наблюдения. Обозначим напряженность поля,
создаваемого в точке наблюдения первым вибратором,
через E1. Выразим напряженность поля второго вибратора в точке наблюдения М через напряженность поля первого вибратора, приняв ее фазу в точке наблюдения за нулевую. Так как напряженность, создаваемого вибратором,
поля пропорциональна току в вибраторе и влиянием разности расстояний от вибратора до точки наблюдения на амплитуду
напряженности поля можно пренебречь, то
- угол между нормалью к оси вибратора и направлением на точку
наблюдения. Обозначим напряженность поля,
создаваемого в точке наблюдения первым вибратором,
через E1. Выразим напряженность поля второго вибратора в точке наблюдения М через напряженность поля первого вибратора, приняв ее фазу в точке наблюдения за нулевую. Так как напряженность, создаваемого вибратором,
поля пропорциональна току в вибраторе и влиянием разности расстояний от вибратора до точки наблюдения на амплитуду
напряженности поля можно пренебречь, то 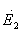 = E1q exp(-ikdcos
= E1q exp(-ikdcos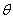 ) exp(i
) exp(i ), где kd cos
), где kd cos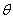 - сдвиг фаз полей из-за
разности хода лучей (пространственный сдвиг фаз). Найдем суммарное поле,
создаваемое обоими вибраторами в данной точке
- сдвиг фаз полей из-за
разности хода лучей (пространственный сдвиг фаз). Найдем суммарное поле,
создаваемое обоими вибраторами в данной точке
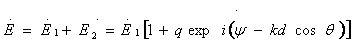 (4.2)
(4.2)
На основании
формулы (3.7) и с учетом того, что угол 0 является дополнительным по отношению
к углу  , запишем
, запишем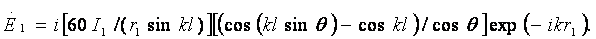
Обычно
интересуются величиной напряженности суммарного поля, а не ее фазой. Поэтому, переходя к модулю выражения (4.2), получаем
Е =(60IП1 / r)[(cos(klsin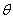 ) - coskl) / cos
) - coskl) / cos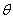 ]
] 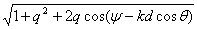 (4.3) или E= Af1(
(4.3) или E= Af1( )fc(
)fc( ).Как видно из
формулы (4.3), амплитудная характеристика направленности системы из двух
связанных вибраторов определяется двумя множителями. Первый множитель
f1(
).Как видно из
формулы (4.3), амплитудная характеристика направленности системы из двух
связанных вибраторов определяется двумя множителями. Первый множитель
f1( ) представляет собой характеристику направленности симметричного вибратора, находящегося в свободном
пространстве. Второй множитель fc(
) представляет собой характеристику направленности симметричного вибратора, находящегося в свободном
пространстве. Второй множитель fc( ) учитывает наличие второго вибратора; он зависит от расстояния d между вибраторами, от отношения амплитуд токов в вибраторах q и от сдвига фаз токов в вибраторах
) учитывает наличие второго вибратора; он зависит от расстояния d между вибраторами, от отношения амплитуд токов в вибраторах q и от сдвига фаз токов в вибраторах  . Этот множительназывают
множителем системы. В экваториальной плоскости направленные свойства данной системы определяются только
множителем системы, так как одиночный
симметричный вибратор в этой плоскости (
. Этот множительназывают
множителем системы. В экваториальной плоскости направленные свойства данной системы определяются только
множителем системы, так как одиночный
симметричный вибратор в этой плоскости (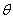 = 0°) не обладает направленными
свойствами. Напряженность суммарного поля в экваториальной плоскости определяется выражением
= 0°) не обладает направленными
свойствами. Напряженность суммарного поля в экваториальной плоскости определяется выражением
Е = А (1- coskl) 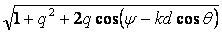 . (4.4)
. (4.4)
В зависимости от величин d/ , q и
, q и  диаграммы
направленности могут иметь различную форму (рис.4.2, 4.3),
При увеличении расстояния между вибраторами
(начиная от d/
диаграммы
направленности могут иметь различную форму (рис.4.2, 4.3),
При увеличении расстояния между вибраторами
(начиная от d/ = 0,5) диаграмма направленности приобретает многолепестковый характер; чем больше d/
= 0,5) диаграмма направленности приобретает многолепестковый характер; чем больше d/ , тем больше лепестков. Особенно важен случай однонаправленного излучения. Пусть токи в
вибраторах одинаковы по величине (q = 1). Тогда формулу (4.4), воспользовавшись
формулой для косинуса двойного угла, можно привести к виду
, тем больше лепестков. Особенно важен случай однонаправленного излучения. Пусть токи в
вибраторах одинаковы по величине (q = 1). Тогда формулу (4.4), воспользовавшись
формулой для косинуса двойного угла, можно привести к виду
Е = 2А (1 - cos kl) cos [ /2 - (kd/2)
cos
/2 - (kd/2)
cos ] (4.5)
] (4.5)
Положим теперь, что  =± 90° и расстояние между вибраторами d =
=± 90° и расстояние между вибраторами d = /4. При этом формула (4.5) принимает вид
/4. При этом формула (4.5) принимает вид
Е = 2А (1 - cos kl) cos (±45° - 45°cos ).
).
Множитель f( ) = cos(±45°- 45°cos
) = cos(±45°- 45°cos ) описывает кардиоиду. При
) описывает кардиоиду. При = + 90° и
= + 90° и  = 0° этот множитель обращается в единицу; при
= 0° этот множитель обращается в единицу; при  =180° он обращается в нуль. Таким образом, в
направлении
=180° он обращается в нуль. Таким образом, в
направлении  = 0° напряженность поля удваивается (по сравнению с полем одиночного вибратора, возбуждаемого током, одинаковым с текущим по одному из связанных вибраторов). Это увеличение в одном направлении происходит за счет уменьшения поля в других направлениях. При
= 0° напряженность поля удваивается (по сравнению с полем одиночного вибратора, возбуждаемого током, одинаковым с текущим по одному из связанных вибраторов). Это увеличение в одном направлении происходит за счет уменьшения поля в других направлениях. При  = -
90° напряженность поля удваивается в обратном направлении (
= -
90° напряженность поля удваивается в обратном направлении ( =180°); поле равно нулю в направлении
=180°); поле равно нулю в направлении  = 0°.
= 0°.
Поясним эти результаты. Если ток во втором вибраторе пережает по фазе ток
в первом вибраторе, то в точке наблюдения, находящейся в направлении  = 0°, поля от обоих вибраторов
складываются в фазе, так как сдвиг фаз за счет
несинфазности возбуждающих токов (
= 0°, поля от обоих вибраторов
складываются в фазе, так как сдвиг фаз за счет
несинфазности возбуждающих токов ( = 90°) компенсируется пространственным сдвигом фаз (
= 90°) компенсируется пространственным сдвигом фаз ( р= kd = (2
р= kd = (2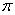 /
/ )(
)( /4)= 90°). Этот сдвиг фаз берется со знаком минус, так как второй вибратор находится дальше от точки
наблюдения, чем первый. В обратном направлении (
/4)= 90°). Этот сдвиг фаз берется со знаком минус, так как второй вибратор находится дальше от точки
наблюдения, чем первый. В обратном направлении ( = 180°) множитель f(
= 180°) множитель f( ) обращается в нуль, потому что в этом
направлении поля от первого и второго вибраторов складываются в
противофазе и компенсируют друг друга, так как
) обращается в нуль, потому что в этом
направлении поля от первого и второго вибраторов складываются в
противофазе и компенсируют друг друга, так как  рез=
рез= +
+  р=180°. Если
ток во втором вибраторе отстает по фазе на 90° от тока в
первом вибраторе (
р=180°. Если
ток во втором вибраторе отстает по фазе на 90° от тока в
первом вибраторе ( = - 90°), то получается обратная картина. В первом случае (
= - 90°), то получается обратная картина. В первом случае ( = 90°) второй вибратор усиливает излучение в
направлении на первый вибратор. Во втором случае (
= 90°) второй вибратор усиливает излучение в
направлении на первый вибратор. Во втором случае ( = -90°) он усиливает излучение в обратном направлении и ослабляет излучение в направлении первого вибратора. Вибратор,усиливающий
излучение в направлении на другой вибратор и ослабляющий излучение в обратном направлении, называется рефлектором (отражателем). Чтобы рефлектирующее действие вибратора было
полным (в одном направлении поле увеличивается, а в противоположном - равно
нулю), в рассматриваемом случае (d =
= -90°) он усиливает излучение в обратном направлении и ослабляет излучение в направлении первого вибратора. Вибратор,усиливающий
излучение в направлении на другой вибратор и ослабляющий излучение в обратном направлении, называется рефлектором (отражателем). Чтобы рефлектирующее действие вибратора было
полным (в одном направлении поле увеличивается, а в противоположном - равно
нулю), в рассматриваемом случае (d = /4) токи в обоих вибраторах должны быть равны по величине (q = 1), а ток в рефлекторе должен опережать ток во втором связанном
вибраторе на 90° (рис.4.4.а). Вибратор, ослабляющий излучение в направлении на другой вибратор и усиливающий излучение в противоположном направлении, называется директором (направителем). В
идеальном случае директор должен работать в режиме (рис.4.4.б): q=l;
/4) токи в обоих вибраторах должны быть равны по величине (q = 1), а ток в рефлекторе должен опережать ток во втором связанном
вибраторе на 90° (рис.4.4.а). Вибратор, ослабляющий излучение в направлении на другой вибратор и усиливающий излучение в противоположном направлении, называется директором (направителем). В
идеальном случае директор должен работать в режиме (рис.4.4.б): q=l;  = -
= -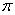 /2 (при d =
/2 (при d =  /4). Отметим, что в обоих случаях
напряженность поля увеличивается в направлении
отставания фазы возбуждающего тока. Получить однонаправленное излучение можно и при расстояниях между вибраторами, отличных от
/4). Отметим, что в обоих случаях
напряженность поля увеличивается в направлении
отставания фазы возбуждающего тока. Получить однонаправленное излучение можно и при расстояниях между вибраторами, отличных от  /4. Как видно из формулы (4.5), условие
отсутствия излучения в направлении
/4. Как видно из формулы (4.5), условие
отсутствия излучения в направлении  = 180° можно записать
в виде
= 180° можно записать
в виде  +kd = 180°. Для
выполнения этого условия при d <
+kd = 180°. Для
выполнения этого условия при d <  /4 угол сдвига фаз у должен быть больше 90°. Хотя диаграмма направленности при этом оказывается однонаправленной и максимум
излучения лежит в направлении
/4 угол сдвига фаз у должен быть больше 90°. Хотя диаграмма направленности при этом оказывается однонаправленной и максимум
излучения лежит в направлении  = 0°,
однако напряженность поля в этом направлении не удваивается. Чем
ближе друг к другу расположены вибраторы, тем меньшая напряженность поля
получается в направлении максимального излучения (считая, что при
изменении d величина тока в вибраторах постоянна).
= 0°,
однако напряженность поля в этом направлении не удваивается. Чем
ближе друг к другу расположены вибраторы, тем меньшая напряженность поля
получается в направлении максимального излучения (считая, что при
изменении d величина тока в вибраторах постоянна).
Возбуждение каждого из двух связанных вибраторов токами, сдвинутыми по фазе, усложняет систему питания. Поэтому в большен-
стве случаев вибраторы, выполняющие роль рефлекторов или директоров, не содержат
источников питания (генераторов), т.е. являются пассивными. Они возбуждаются электромагнитным полем активного (питаемого) вибратора. В
случае пассивных вибраторов не удается осуществить режим, обеспечивающий полное рефлекторное или директорное действие, так как не удается получить совместно q = 1 и  = 90°. Поэтому не получается полного удвоения поля в главном направлении и нуля поля - в обратном.
= 90°. Поэтому не получается полного удвоения поля в главном направлении и нуля поля - в обратном.
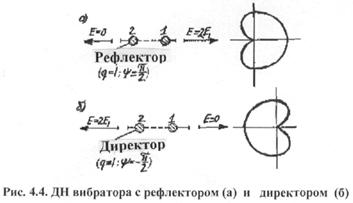
ТЕМА 4. Способы увеличения
рабочего диапазона волн вибраторных антенн.
Частотно–независимые антенны
Рабочий диапазон простых вибраторных антенн (в том числе несимметричных)
определяется частотной зависимостью входного сопротивления антенны.
Уменьшить эту
зависимость можно тремя способами:
1) как уже отмечалось - снижением волнового
сопротивления вибратора; 2) плавным изменением его поперечного
сечения;
3) коррекцией входного сопротивления
вибратора.
Первый способ. Снижение
волнового сопротивления вибратора путем увеличения размеров
поперечного сечения является одним из основных методов расширения рабочего диапазона вибратора. По этому принципу построен симметричный вибратор, предложенный в начале 30х годов С.И.Надененко, широко применяемый в диапазонах коротких и метровых волн. Этот вибратор выполняется из ряда проводов, натянутых по образующим
цилиндра (рис.3.12), в результате чего волновое сопротивление снижается до 250...400 Ом (вместо 600...1000 Ом у обычного вибратора). Волновое сопротивление такого вибратора рассчитывается по формуле
WA = 120[ln (l/ э-1], (3.32)
э-1], (3.32)
где  э - эквивалентный радиус вибратора.
э - эквивалентный радиус вибратора.
Вибратор Надененко
Эквивалентным радиусом вибратора
называется радиус сплошного металлического
цилиндра, волновое сопротивление которого равно волновому сопротивлению данного цилиндра, выполненного из
отдельных проводов
 э =
э = 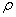
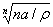 , (3.33)
, (3.33)
где 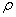 - радиус цилиндра,
образованного проводами;
- радиус цилиндра,
образованного проводами;
n - число проводов (обычно n = 6...8)
а - радиус провода.
Диапазонные вибраторы могут иметь различную форму поперечного сечения: круглую,
прямоугольную, треугольную и т.д.
Второй способ. Этот способ основан на том, что
антенну можно рассматривать как переходное устройство между фидерной линией, в
которой существует связанная плоская волна, и свободным пространством,в котором
существует пространственная волна. Если в качестве фидера применяется двухпроводная симметричная линия, то
плавный переход от такой линии к свободному пространству может быть осуществлён
при помощи биконической антенны
(рис.3.13). Волновое сопротивление биконической антенны (l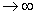 ) равно
) равно
WA=276lg [ctg (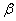 /2)], (3.34)
/2)], (3.34)
где 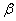 - угол между осью конуса и его образующей. При 30° <
- угол между осью конуса и его образующей. При 30° < 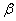 < 60° входное сопротивление биконической антенны в довольно широком диапазоне слабо зависит от частоты.
< 60° входное сопротивление биконической антенны в довольно широком диапазоне слабо зависит от частоты.
Третий способ. Этот способ
состоит в том, что антенна выполняется из двух частей, реактивные составляющие входных сопротивлений которых имеют различные частотные зависимости (например,
одно является индуктивным, а другое
ёмкостным) и компенсируют друг друга
в некоторой
полосе частот. Примером может служить
диапазонный шунтовой вибратор, предложенный Г.З.Айзенбергом.
Логопериодические антенны (ЛПА) относятся к классу
сверхширокополосных антенн, сохраняющих
при изменении частоты как ДН, так и величину входного сопротивления. Работа
антенны основана на принципе электродинамического подобия, согласно которому
при изменении размеров антенны в определенное количество раз и изменении длины
волны во столько же раз характеристики антенны останутся без изменения.
Существует большое число различных модификации ЛПА. Рассмотрим вариант
вибраторной ЛПА, приведенной на рис.11.10. Антенна состоит из линейных
вибраторов, присоединенных к двухпроводной линии. Возбуждение осуществляется с
помощью коаксиальной линии, которая
проложена внутри одного из проводов двухпроводной линии, имеющей форму трубки.
Подобный переход от коаксиальной к двухпроводной линии не требует
симметрирующего устройства.
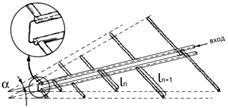
Длины вибраторов удовлетворяют соотношению
ln /ln+1
=τ,
где
τ -
период структуры, независимо от номера n (n = 1, 2, ...). Линии, соединяющие концы вибраторов,
образуют угол α.
По принципу действия подобная ЛПА напоминает директорную
антенну. На частоте f0 резонирует, т.е. возбуждается наиболее
интенсивно вибратор, длина плеча которого близка к λ0/4 (λ0 =c/f0 ), поскольку входное
сопротивление этого вибратора можно считать активным. Другие вибраторы
возбуждаются значительно слабее, так как входное сопротивление их велико из-за
большой реактивной составляющей. Активная область антенны, формирующая
излученное поле, включает обычно
три - пять вибраторов, в том числе
резонансный и прилегающие к нему с двух сторон. Фазовые соотношения токов в
вибраторах активной области определяются
длиной вибраторов,
взаимным влиянием и поочередным подключением их к разным проводникам питающей
линии. При этом оказывается, что токи в более коротких вибраторах отстают, а в
более длинных - опережают по фазе ток в резонансном вибраторе. Соответственно
более короткие вибраторы работают в режиме директоров, а более длинные
выполняют функцию рефлектора. Максимум излучения направлен в сторону вершины
антенны.
Если частота генератора уменьшится и станет равной τf0, то начнет
резонировать следующий, более длинный вибратор, соответственно активная область
переместится в сторону более длинных вибраторов. Напротив, при увеличении
частоты активная область сместится к вершине антенны. На всех частотах fn =τn-1f1, где n - номер вибратора; fn - резонансная
частота n-го вибратора,
свойства антенны остаются неизменными. В интервалах между резонансными частотами
свойства антенны меняются, но незначительно. Прологарифмировав, получим lnfn =(n-1)lnτ + lnf1. В
логарифмическом масштабе резонансные частоты повторяются через интервалы,
равные lпτ, что и
определило название антенны этого класса.
Из изложенного ясно, что ширина рабочей полосы частот ЛПА с
нижней стороны ограничивается допустимыми размерами самых длинных вибраторов (λmах ≈ 4lmах ), а с верхней
стороны - возможной точностью выполнения вибраторов вблизи точек питания (λmin ≈4lmin). Практически можно получить примерно в десятикратном
диапазоне волн (fmax/fmin =10) почти неизменную ДН. В этом же диапазоне КБВ в фидере
не падает ниже 0,6... 0,7. Следует учитывать, что вследствие перемещения
активной области по длине антенны с изменением частоты меняется также положение
фазового центра антенны. Последнее обстоятельство не имеет значения, например,
при приеме телевизионных программ, но принципиально при использовании ЛПА в
качестве облучателя параболических антенн (см. лк.9), а также при работе с
широкополосными сигналами.
Расчет токов в вибраторах ЛПА требует учета их взаимного
влияния не только по свободному пространству, но и по проводам питающей линии.
В связи с тем, что в излучении на данной частоте участвует
только несколько вибраторов, ДН получается довольно широкой, причем в Е-плоскости (плоскость, в которой расположены
вибраторы) получается уже, чем в H-плоскости. Увеличение τ при неизменном α сужает ДН, так как увеличивается число вибраторов, входящих
в активную область. Уменьшение угла α
при неизменном τ также сужает ДН, поскольку при этом увеличивается
расстояние между соседними вибраторами, т.е. активная область расширяется.
Сказанное справедливо только до некоторых критических значений τmах≈0,95
и αmin≈10°.
Если провода линии, питающей ЛПА,
разместить под углом друг к другу, то получится пространственная ЛПА (рис.11.11).
Диаграмма направленности такой
антенны в H-плоскости получается 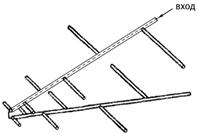 значительно
уже, чем у плоской ЛПА, за счет влияния множителя системы, образованной
разнесением в H-плоскости
активных областей каждого из полотен. В E-плоскости вид ДН остается
практически прежним. Провода питающей линии в подобной конструкции вызывают
излучение с паразитной поляризацией,
однако оно, как правило, невелико.
значительно
уже, чем у плоской ЛПА, за счет влияния множителя системы, образованной
разнесением в H-плоскости
активных областей каждого из полотен. В E-плоскости вид ДН остается
практически прежним. Провода питающей линии в подобной конструкции вызывают
излучение с паразитной поляризацией,
однако оно, как правило, невелико.
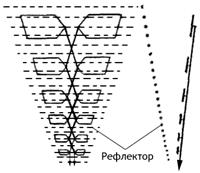
 В диапазоне УКВ логопериодические антенны применяются в
качестве широкополосных
В диапазоне УКВ логопериодические антенны применяются в
качестве широкополосных
облучателей параболических и линзовых антенн,
приемных телевизионных антенн и т.д.
На практике используются также вертикальные
синфазные ЛПА (рис.11.12), максимум излучения
которых перпендикулярен плоскости полотна
антенны. Вибраторы такой антенны питаются
двухпроводной линией. Сужение ДН в горизонтальной плоскости достигается
применением двух или трех секций, питаемых синфазно. Такие ЛПА с рефлектором
используются в секторных антеннах, применяемых в сотовой радиосвязи. В
частности, антенна, состоящая
из двух полотен
по 6 вибраторов имеет коэффициент
усиления порядка 13 дБ.
ТЕМА 5. Теория антенных решеток. Линейные и плоские решетки
Пусть имеется ряд из n симметричных вибраторов, одинаковым образом
ориентированных в пространстве (рис.4.9.а). Расстояние между центрами соседних
вибраторов равно d1. Линейной решеткой называется система идентичных излучателей, центры излучения которых расположены на прямой, называемой осью решетки. Будем считать, что токи во всех элементах решетки имеют
одинаковую величину (I1=I2=…In = I), фаза же тока в каждом
последующем вибраторе данного ряда отстает от фазы тока в предыдущем на величину  . Таким образом, I2 = Iexp(-i
. Таким образом, I2 = Iexp(-i )...In =
Iexp[-i(n-l)
)...In =
Iexp[-i(n-l) ]. Следовательно, вдоль каждого ряда вибраторов фаза
возбуждающего тока изменяется по линейному закону.
]. Следовательно, вдоль каждого ряда вибраторов фаза
возбуждающего тока изменяется по линейному закону.
Рис. 5.1. К
определению множителя решётки поперечного
излучения
Рассмотрим вначале линейную систему из n ненаправленных
излучателей, расположенных на равных расстояниях
друг от друга, возбужденных токами, равными по амплитуде. Такая
система вибраторов называется эквидистантной
равноамплитудной решеткой. Пусть фаза тока в каждом последующем вибраторе
отстает на угол  по отношению к
току предыдущего. На большом удалении от
антенны в точке М, когда d1<<r, лучи от
отдельных вибраторов можно считать параллельными. Поле
в точке М (рис.5.1.а), созданное вибратором 1, обозначим через E1. В равноамплитудной решетке амплитуды поля, созданные различными
вибраторами на большом удалении, можно принять
равными амплитуде поля первого вибратора, но фазы этих полей будут различными. Поле Е2 вибратора 2 за счет разности
хода лучей
по отношению к
току предыдущего. На большом удалении от
антенны в точке М, когда d1<<r, лучи от
отдельных вибраторов можно считать параллельными. Поле
в точке М (рис.5.1.а), созданное вибратором 1, обозначим через E1. В равноамплитудной решетке амплитуды поля, созданные различными
вибраторами на большом удалении, можно принять
равными амплитуде поля первого вибратора, но фазы этих полей будут различными. Поле Е2 вибратора 2 за счет разности
хода лучей  r будет опережать поле вибратора 1 по фазе на угол k
r будет опережать поле вибратора 1 по фазе на угол k r = kd1sin
r = kd1sin и отставать на угол
и отставать на угол  за счет питания. Результирующий сдвиг по фазе
между полями, созданными вибраторами 1 и 2 равен Ф = kd1sin(
за счет питания. Результирующий сдвиг по фазе
между полями, созданными вибраторами 1 и 2 равен Ф = kd1sin( -
- ). Этот сдвиг по фазе будет и для полей, созданных любыми соседними вибраторами. На рис.5.1.б
приведено графическое сложение полей отдельных вибраторов, сдвинутых по
фазе друг относительно друга на угол Ф.
). Этот сдвиг по фазе будет и для полей, созданных любыми соседними вибраторами. На рис.5.1.б
приведено графическое сложение полей отдельных вибраторов, сдвинутых по
фазе друг относительно друга на угол Ф.
Векторы полей
образуют часть правильного многоугольника, замыкающая сторона которого Еn равна
результирующей напряженности поля, созданной всеми
вибраторами в точке М. Перпендикуляры, восстановленные из середин сторон (векторов Е) правильного
многоугольника, пересекутся в одной точке 0, являющейся центром описанной
окружности радиуса 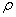 . Для треугольников ОАВ и ОАС можно записать
. Для треугольников ОАВ и ОАС можно записать
sin(Ф/2) = АВ/ = Е1/2
= Е1/2 и sin(nФ/2) = АС/
и sin(nФ/2) = АС/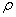 = Еn/2
= Еn/2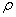 . Поделив одно уравнение
на другое, получим
. Поделив одно уравнение
на другое, получим
Еn/Е1= sin (0,5 nФ)/sin(0,5Ф) или Еn = Е1fс ( ), где Ф = kd1sin
), где Ф = kd1sin -
- ;
;
fc( ) = sin (0,5 nФ)/sin(0,5Ф) = sin[0,5 n(kd1sin
) = sin (0,5 nФ)/sin(0,5Ф) = sin[0,5 n(kd1sin -
- )]/ sin[0,5(kd1sin
)]/ sin[0,5(kd1sin -
- )] (5.1) - множитель системы (решетки) излучателей.
)] (5.1) - множитель системы (решетки) излучателей.
Здесь рассматривалась решетка, состоящая из ненаправленных излучателей.
Если линейную решетку составить из направленных излучателей, например, симметричных вибраторов, то поле Е1 созданное каждым
вибратором, определится его направленными свойствами f1( ) и результирующая характеристика
направленности будет равна
) и результирующая характеристика
направленности будет равна
f( ) = f1(
) = f1( ) fc(
) fc( ). (5.2)
). (5.2)
На основании выражения (5.2) может быть сформулирован общий принцип умножения характеристик направленности: характеристика направленности
системы (антенной решетки) однотипных излучателей представляет собой произведение характеристики направленности одного элемента данной системы на множитель системы.
При большом числе вибраторов n множитель системы при изменении угла  изменяется,
значительно быстрее чем множитель f1(
изменяется,
значительно быстрее чем множитель f1( ). Это объясняется тем, что величина nkd1/2 значительно больше величины kl. Поэтому характеристика
направленности решетки, в основном, определяется множителем системы. Поскольку множитель системы sin(nu)/sin(u) является
периодической функцией, то при изменении угла
). Это объясняется тем, что величина nkd1/2 значительно больше величины kl. Поэтому характеристика
направленности решетки, в основном, определяется множителем системы. Поскольку множитель системы sin(nu)/sin(u) является
периодической функцией, то при изменении угла  этот множитель может обращаться в нуль, затем он возрастает, достигая
максимального значения, далее уменьшается, снова становится равным нулю и т.д.
Поэтому можно утверждать, что диаграмма направленности решетки имеет
многолепестковый характер.
этот множитель может обращаться в нуль, затем он возрастает, достигая
максимального значения, далее уменьшается, снова становится равным нулю и т.д.
Поэтому можно утверждать, что диаграмма направленности решетки имеет
многолепестковый характер.
Синфазная решетка
Широкое практическое применение находят антенные решетки с одинаковыми
по амплитуде и фазе токами в вибраторах (равноамплитудные синфазные решетки). Полагая в формуле (5.1)  =00, получим формулу для характеристики направленности, такой решетки из т рядов в плоскости E
=00, получим формулу для характеристики направленности, такой решетки из т рядов в плоскости E
E= (m60Iп/r)[(cos(klsin ) -coskl)/ соs
) -coskl)/ соs ] *
] *
*sin [(n/2) (kd1sin )]/sin [(l/2)
(kd1sin
)]/sin [(l/2)
(kd1sin )]. (5.3)
)]. (5.3)
Напряженность, излучаемого антенной, поля максимальна в направлении  =0° (главный максимум), т.е. в экваториальной плоскости
антенны. Каждый из вибраторов в этом
направлении излучает с максимальной интенсивностью, если l/
=0° (главный максимум), т.е. в экваториальной плоскости
антенны. Каждый из вибраторов в этом
направлении излучает с максимальной интенсивностью, если l/
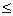 0,7; множитель f1(
0,7; множитель f1( ) в этом случае равен 1 - coskl. Поля от
отдельных вибраторов в направлении
) в этом случае равен 1 - coskl. Поля от
отдельных вибраторов в направлении  =00 синфазны и складываются арифметически, так как в направлении нормали к осям
вибраторов разность расстояний до
точки наблюдения равна нулю. Выражение множителя системы в этом случае представляет собой
неопределенность вида 0/0 , при раскрытии
которой по правилу Лопиталя оказывается, что множитель системы максимален
и равен n. Таким образом, в данном случае
выражение (5.3) принимает вид Еmах= nЕ1mах. Здесь n - число симметричных вибраторов в решетке. Такой же
вид принимает выражение (5.3) и при
=00 синфазны и складываются арифметически, так как в направлении нормали к осям
вибраторов разность расстояний до
точки наблюдения равна нулю. Выражение множителя системы в этом случае представляет собой
неопределенность вида 0/0 , при раскрытии
которой по правилу Лопиталя оказывается, что множитель системы максимален
и равен n. Таким образом, в данном случае
выражение (5.3) принимает вид Еmах= nЕ1mах. Здесь n - число симметричных вибраторов в решетке. Такой же
вид принимает выражение (5.3) и при  =1800. Как
следует из формулы (5.3), нормированная характеристика направленности
определяется выражением
=1800. Как
следует из формулы (5.3), нормированная характеристика направленности
определяется выражением
F ( ) = (Е/Емакс) =
[(cos (klsin
) = (Е/Емакс) =
[(cos (klsin ) - coskl) / соs
) - coskl) / соs (1- coskl)] *
(1- coskl)] *
*sin [(n/2) (kd1sin )]/ {[nsin (l/2) kd1sin
)]/ {[nsin (l/2) kd1sin )]}. (5.4)
)]}. (5.4)
При некоторых значениях угла  сдвиг фаз между полями соседних вибраторов, равный kd1sin
сдвиг фаз между полями соседних вибраторов, равный kd1sin , становится таким, что в
результате интерференции полей от
всех вибраторов суммарное поле обращается в нуль. Направления, в которых отсутствует излучение, определяются
из условия равенства нулю числителя
множителя системы, т.е. (nkd1/2)sin
, становится таким, что в
результате интерференции полей от
всех вибраторов суммарное поле обращается в нуль. Направления, в которых отсутствует излучение, определяются
из условия равенства нулю числителя
множителя системы, т.е. (nkd1/2)sin 0 = N, откуда sin
0 = N, откуда sin 0 = N
0 = N /(nd1), N = 1, 2, 3, ...
. Так как синус всегда меньше единицы, то чем больше
знаменатель, тем больше направлений нулевого излучения (N) имеет
диаграмма направленности. Следовательно, чем больше число вибраторов п (точнее, чем больше относительный размер nd1/
/(nd1), N = 1, 2, 3, ...
. Так как синус всегда меньше единицы, то чем больше
знаменатель, тем больше направлений нулевого излучения (N) имеет
диаграмма направленности. Следовательно, чем больше число вибраторов п (точнее, чем больше относительный размер nd1/ решетки), тем больше лепестков в диаграмме направленности. Направления нулевого излучения рассчитываются по формуле
решетки), тем больше лепестков в диаграмме направленности. Направления нулевого излучения рассчитываются по формуле
 0=arcsin [N
0=arcsin [N /(nd1)], где N= 1, 2, 3,
... (5.5)
/(nd1)], где N= 1, 2, 3,
... (5.5)
Направления максимумов боковых лепестков приближенно можно найти из условия максимума числителя множителя системы, так как знаменатель этого множителя при kd1<<nkd1 (т.е. при большом числе вибраторов) с изменением угла  изменяется значительно медленнее числителя.
Это условие записывается в виде sin[(nkd1/2)sin
изменяется значительно медленнее числителя.
Это условие записывается в виде sin[(nkd1/2)sin max] = ±1, откуда nu=(nkd1/2)sin
max] = ±1, откуда nu=(nkd1/2)sin max = (2N+l)
max = (2N+l)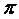 /2, N= 1,2,3,...
/2, N= 1,2,3,...
Направления
максимумов боковых лепестков рассчитываются по формуле
 max =
arcsin[(2N+l)
max =
arcsin[(2N+l) /(2nd1)],
где N= 1,2,3, ... (5.6)
/(2nd1)],
где N= 1,2,3, ... (5.6)
На рис.5.2 приведены диаграммы
направленности синфазной решетки (в
плоскости Е) для разного количества
симметричных полуволновых вибраторов и расстояния между ними. Ближайшее к
главному максимуму направление нулевого излучения определяют по формуле sin 0 =
0 =  /(nd1).
/(nd1).
Следовательно, главный лепесток диаграммы направленности заключен в угле, равном 2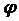 0. Как видно из формулы главный лепесток
диаграммы направленности тем уже, чем больше вибраторов в одном ряду, или чем
больше относительная длина антенны nd1/
0. Как видно из формулы главный лепесток
диаграммы направленности тем уже, чем больше вибраторов в одном ряду, или чем
больше относительная длина антенны nd1/ = L/
= L/ .
.
2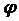 0 = 2(
0 = 2( /nd1), рад или 2
/nd1), рад или 2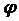 0
0 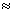 115°
115° /nd1. (5.7)
/nd1. (5.7)
В случае равномерной синфазной решетки ширину диаграммы направленности по половинной мощности можно определить по приближенной формуле
2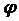 0,5
0,5 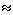 0,89(
0,89( /nd1),
рад или 2
/nd1),
рад или 2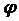 0,5
0,5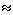 510
510  /nd1. (5.8)
/nd1. (5.8)
Симметричный
вибратор с относительной длиной l/ = 0,5 имеет ширину диаграммы направленности шириной по
половинной мощности 44°. Для того чтобы сузить диаграмму направленности до 6,4°,
т.е. примерно в 7 раз, надо применить 8
синфазных симметричных вибраторов, т.е. увеличить размер антенны примерно в 8 раз.
= 0,5 имеет ширину диаграммы направленности шириной по
половинной мощности 44°. Для того чтобы сузить диаграмму направленности до 6,4°,
т.е. примерно в 7 раз, надо применить 8
синфазных симметричных вибраторов, т.е. увеличить размер антенны примерно в 8 раз.
Направленные свойства антенны характеризуются не только шириной главного лепестка диаграммы направленности, но и уровнем боковых лепестков
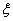 N= l/nsin{[(2N+l)/n)](
N= l/nsin{[(2N+l)/n)](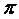 /2)}. (5.9)
/2)}. (5.9)
При большом значении n (аргумент синуса мал) можно перейти к следующей приближенной формуле для расчета первых двух боковых лепестков  N= 2/[(2N+l)
N= 2/[(2N+l)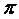 ]. В этом случае уровень первого бокового лепестка
]. В этом случае уровень первого бокового лепестка  1=2/3
1=2/3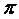
 0,21. Уровень второго
бокового лепестка составляет примерно 0,13. Уровень
первого бокового лепестка в децибеллах составляет примерно -13,3 дБ. Отметим, что два главных максимума (при
0,21. Уровень второго
бокового лепестка составляет примерно 0,13. Уровень
первого бокового лепестка в децибеллах составляет примерно -13,3 дБ. Отметим, что два главных максимума (при  =0° и
=0° и  =180°) или два главных
лепестка в диаграмме направленности получаются только при d1<
=180°) или два главных
лепестка в диаграмме направленности получаются только при d1< . При d1
. При d1 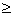
 возможно одновременное
обращение в нуль числителя и знаменателя
множителя системы при некоторых значениях углов
возможно одновременное
обращение в нуль числителя и знаменателя
множителя системы при некоторых значениях углов , не равных 0° и 180°. Это происходит при выполнении условия (kd1sin
, не равных 0° и 180°. Это происходит при выполнении условия (kd1sin )/2 = N
)/2 = N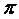 или kd1sin
или kd1sin = 2N
= 2N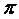 , т.е. в том случае, когда сдвиг фаз между полями соседних
вибраторов равен или кратен 2
, т.е. в том случае, когда сдвиг фаз между полями соседних
вибраторов равен или кратен 2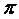 . При этом множитель системы, как и в случаях
. При этом множитель системы, как и в случаях  =0° и
=0° и  =180°, имеет наибольший
максимум, равный n. Это приводит к появлению в диаграмме направленности антенны, кроме боковых лепестков дополнительных
(вторичных) боковых лепестков. Уровень этих лепестков тем больше, чем шире диаграмма направленности одного элемента решетки. Он равен единице, если элементы не обладают направленными свойствами.
=180°, имеет наибольший
максимум, равный n. Это приводит к появлению в диаграмме направленности антенны, кроме боковых лепестков дополнительных
(вторичных) боковых лепестков. Уровень этих лепестков тем больше, чем шире диаграмма направленности одного элемента решетки. Он равен единице, если элементы не обладают направленными свойствами.
Так как симметричный вибратор не обладает направленными свойствами в экваториальной плоскости, то характеристика направленности синфазной
решетки в плоскости H определяется только множителем системы, который совершенно аналогичен
этому множителю для плоскости E. Ширину диаграммы направленности, направления максимумов боковых
лепестков и их уровень определяют по формулам, полученным для плоскости вектора Е решетки, заменяя в них угол  углом
углом 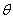 . Чем больше рядов m в синфазной
решетке, тем уже ее диаграмма направленности
в плоскости H. КНД синфазной решетки в направлении максимального излучения может быть
рассчитан по формуле
. Чем больше рядов m в синфазной
решетке, тем уже ее диаграмма направленности
в плоскости H. КНД синфазной решетки в направлении максимального излучения может быть
рассчитан по формуле
D = (120/ R полн) (mn)2 (1-coskl)2, (5.10)
полн) (mn)2 (1-coskl)2, (5.10)
где R полн - полное сопротивление излучения антенны. Заметим, что при
полн - полное сопротивление излучения антенны. Заметим, что при
d1=>0, d2=>0, n=>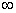 , m=>
, m=>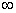 но при nd1= const = b и md2 = const = а, где а и b –
но при nd1= const = b и md2 = const = а, где а и b –
размеры излучающей системы в плоскостях Н
и Е соответственно, с помощью
предельного перехода можно перейти от формул характеристик направленности антенных решеток к формулам характеристик направленности систем с непрерывным распределением возбуждающих источников (излучающих поверхностей). При а >> , b >>
, b >> и небольших расстояниях между излучателями (d1 < 0,07
и небольших расстояниях между излучателями (d1 < 0,07 ) характеристики направленности обеих систем практически совпадают. Выясним направленные свойства линейной равномерной решетки.
Как видно из выражений (5.1) и (5.4), множители системы равноамплитудной
эквивалентной линейной и равноамплитудной
эквидистантной синфазной решеток идентичны и отличаются только аргументами
синусов. Однако в случае равноамплитудной эквидистантной линейной решетки
множитель системы максимален и равен
п при условии u =
) характеристики направленности обеих систем практически совпадают. Выясним направленные свойства линейной равномерной решетки.
Как видно из выражений (5.1) и (5.4), множители системы равноамплитудной
эквивалентной линейной и равноамплитудной
эквидистантной синфазной решеток идентичны и отличаются только аргументами
синусов. Однако в случае равноамплитудной эквидистантной линейной решетки
множитель системы максимален и равен
п при условии u =  . При этом поля от всех элементов антенны в точке наблюдения,
характеризуются углом
. При этом поля от всех элементов антенны в точке наблюдения,
характеризуются углом  mах, имеют
одинаковую фазу, так как сдвиг фаз из-за несинфазности возбуждения Ψ компенсируется пространственным сдвигом фаз Ψp = kd1 sin
mах, имеют
одинаковую фазу, так как сдвиг фаз из-за несинфазности возбуждения Ψ компенсируется пространственным сдвигом фаз Ψp = kd1 sin . Из множителя системы, получаем
. Из множителя системы, получаем
sin maxuл =
maxuл =  λ / (2
λ / (2
 ). (5.11)
). (5.11)
Таким образом линейный закон изменения фазы возбуждающего поля приводит к изменению направления максимального излучения. Это направление отклоняется от перпендикуляра к оси решетки на угол φmaxгл. Так как излучение
максимально в том направлении, в котором происходит взаимная компенсация сдвигов фаз Ψ и Ψр, то диаграмма
направленности поворачивается обязательно в сторону отставания
фазы возбуждающего тока. Поворот диаграммы направленности, т.е. управление ею
путем изменения величины сдвига фаз Ψ, находит широкое применение на практике.
Направление нулевых излучений можно определить по формуле sin 0 = Nλ/(n
0 = Nλ/(n cosφmaxгл). При узких диаграммах направленности значение
cosφmaxгл). При узких диаграммах направленности значение
2φ0 равно 2φ0 = 2λ/(n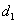 сщыφmaxгл).
сщыφmaxгл).
Таким образом
ширина диаграммы направленности растет по мере отклонения направления максимального излучения от перпендикуляра к оси решетки. Уровень боковых лепестков, близких к
главному, приближенно может быть найден тем же методом, что и в случае
синфазной решетки. Направления максимумов
боковых лепестков при этом определяются из формулы sin φmaxгл, = (2N+l)λ/(2nd1cos φmaxгл).
Так как при отклонении направления максимального излучения от нормали к оси решетки диаграмма направленности расширяется, а уровень боковых лепестков не изменяется, то казалось бы, что КНД решетки должен уменьшаться. Однако
при этом пространственная диаграмма направленности приобретает коническую форму и телесный угол, в пределах которого заключено излученное поле (главный лепесток),
уменьшается, что компенсирует расширение диаграммы направленности в плоскости
вектора Е. В результате оказывается, что КНД линейной равномерной
решетки не зависит от угла φmaxгл. КНД линейной равномерной решетки, можно рассчитать по формуле D = 101,5/2φ0,5, где 2φ0,5 - ширина диаграммы направленности по половинной
мощности, рад. Рассмотренные антенные решетки излучают
с максимальной
интенсивностью либо в направлении нормали к своей оси (φ = 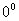 - синфазная решетка),
либо под некоторым углом к нормали (равномерная
линейная решетка). Вдоль оси решетки (ось у) излучение равно нулю, так как
элементы решетки в этом направлении не излучают, это - решетки с поперечным излучением.
- синфазная решетка),
либо под некоторым углом к нормали (равномерная
линейная решетка). Вдоль оси решетки (ось у) излучение равно нулю, так как
элементы решетки в этом направлении не излучают, это - решетки с поперечным излучением.
Вывод. Ширина ДН синфазной решетки сужается с уменьшением длины волны, увеличением числа вибраторов и увеличением расстоянии между
ними. Если в синфазной решетке уменьшить число вибраторов и увеличить расстояния между ними так, чтобы сохранить неизменным произведение nd1, т.е. линейные размеры антенны, то
ширина главного лепестка останется
неизменной, но возрастут уровни боковых лепестков. При  < 0,5 λ, уровни боковых лепестков
практически остаются неизменными, но возрастает число
вибраторов и усложняется система питания. Поэтому расстояния
< 0,5 λ, уровни боковых лепестков
практически остаются неизменными, но возрастает число
вибраторов и усложняется система питания. Поэтому расстояния  между центрами ненаправленных или полуволновых вибраторов обычно выбирают равными 0,5λ, а одноволновых - λ. Для уменьшения уровня боковых
лепестков применяют эквидистантные решетки, в которых центральные вибраторы
имеют большие токи, а периферийные — меньшие или равноамплитудные решетки, в которых расстояния между вибраторами по
мере удаления от центра антенны увеличиваются. Подбирая закон распределения амплитуд или размещения вибраторов, можно снижать уровни боковых лепестков до необходимых значений.
между центрами ненаправленных или полуволновых вибраторов обычно выбирают равными 0,5λ, а одноволновых - λ. Для уменьшения уровня боковых
лепестков применяют эквидистантные решетки, в которых центральные вибраторы
имеют большие токи, а периферийные — меньшие или равноамплитудные решетки, в которых расстояния между вибраторами по
мере удаления от центра антенны увеличиваются. Подбирая закон распределения амплитуд или размещения вибраторов, можно снижать уровни боковых лепестков до необходимых значений.
При заданных линейных размерах антенны
наибольшим КНД обладают равноамплитудные эквидистантные решетки.
Следовательно, снижение уровня боковых лепестков достигается уменьшением КНД или увеличением размеров антенны.
Диаграмма направленности системы ненаправленных (изотропных) синфазных излучателей, расположенных вдоль прямой линии есть ДН линейной решетки, являющейся фигурой вращения, ось которой совпадает с линией расположения вибраторов в решетке. В плоскости, перпендикулярной линии расположения вибраторов и проходящей через ее центр, синфазная линейная решетка имеет круговую (ненаправленную) ДН. Для получения узких
ДН в двух плоскостях, например в горизонтальной и вертикальной, синфазная решетка
должна быть двухмерной.
При линейном
законе изменения фаз токов в вибраторах ДН поворачивается в сторону отставания
фаз.
Рассмотрим равномерную линейную решетку
(рис.4.9.б), состоящую из ряда вибраторов, оси которых параллельны и каждый
вибратор излучает с максимальной интенсивностью вдоль оси
решетки (оси х). Необходимый сдвиг фаз токов, в элементах антенны (ψ)
можно создать с помощью соответствующих фазовращателей. Однако схема питания
антенны при этом получается весьма сложной. Проще последовательно возбуждать
элементы антенны с помощью бегущей электромагнитной
волны, распространяющейся от начала антенны (первый вибратор) к
ее концу с определенной фазовой скоростью. При этом ток в последующем
вибраторе отстает по фазе от тока в предыдущем
на величину ψ = β где
где  - расстояние между вибраторами, β =
- расстояние между вибраторами, β =  /v = kc/v - коэффициент фазы, c/v - коэффициент замедления. Таким образом, если считать, что токи в вибраторах равны по амплитуде,
то
/v = kc/v - коэффициент фазы, c/v - коэффициент замедления. Таким образом, если считать, что токи в вибраторах равны по амплитуде,
то
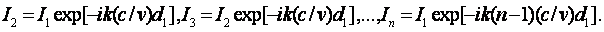
Так как последующий вибратор возбуждается позже предыдущего, но
находится ближе к точке наблюдения, то сдвиг фаз между полями соседних
вибраторов в этой точке (фаза поля первого вибратора принимается за нулевую) равен
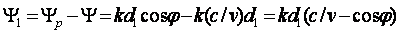 . (6.1)
. (6.1)
Сдвиг фаз между полями крайних
вибраторов
Ψn = (n - l) k (cosφ -
c/v). (6.2)
(cosφ -
c/v). (6.2)
Учитывая сказанное, а также то, что имеется только один ряд вибраторов (m=1), можно от формулы (5.3) перейти к формуле (плоскость Е)
Е = (60Iп/ r) [(cos (klsinφ) - coskl) /
cosφ ] *
* sin [(knd1/2) (c/v - cosφ)]/sin[(k /2)(c/v -
cosφ)]. (6.3)
/2)(c/v -
cosφ)]. (6.3)
Так как в плоскости Н элемент
антенны не обладает направленными свойствами (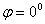 ), то напряженность поля в этой плоскости определяется по формуле
), то напряженность поля в этой плоскости определяется по формуле
Е = (60Iп/r)(l- cosk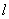 ) sin[(kn d1/2)(c/v - cosθ)]/sin[(k d1/2)(c/v - cosθ)]. (6.4)
) sin[(kn d1/2)(c/v - cosθ)]/sin[(k d1/2)(c/v - cosθ)]. (6.4)
Как видно из формул (6.3) и (6.4) характеристика направленности в плоскости Н определяется
только множителем системы; в плоскости Е
характеристика направленности зависит также и от направленных свойств одного элемента решетки, но, в основном, определяется также множителем системы Fс(φ) или Fc(θ).
Поэтому далее при анализе направленных свойств антенны бегущей волны (АБВ) будем
рассматривать только этот множитель.
Видно, что направленные свойства АБВ зависят от
числа элементов решетки n, расстояния между ними  и от фазовой скорости
питающей волны v. Определим направления нулевого излучения и
максимумов боковых лепестков. Для
определения направлений нулевого излучения приравняем числитель множителя системы нулю или его аргумент (kn
и от фазовой скорости
питающей волны v. Определим направления нулевого излучения и
максимумов боковых лепестков. Для
определения направлений нулевого излучения приравняем числитель множителя системы нулю или его аргумент (kn /2)(c/v - cosθ) = Nπ, где N =
1,2, ... . Отсюда
/2)(c/v - cosθ) = Nπ, где N =
1,2, ... . Отсюда
n (c/v - cosθ) = Nλ
и
(c/v - cosθ) = Nλ
и 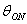 = arccos (c/v - Nλ / n
= arccos (c/v - Nλ / n ). (6.5)
). (6.5)
Для определения направлений
максимумов боковых лепестков приравняем числитель множителя системы единице или его аргумент
(kn /2) >
(c/v - cosθ) = (2N+1) (π/2), где N = 1,2,
.... Отсюда
/2) >
(c/v - cosθ) = (2N+1) (π/2), где N = 1,2,
.... Отсюда
n (c/v - cosθ) = (2N+1)[
(c/v - cosθ) = (2N+1)[ /(2n
/(2n )]и θmaxN
= arcos{ c/v -(2N+1) (λ/(2n
)]и θmaxN
= arcos{ c/v -(2N+1) (λ/(2n )} (6.6)
)} (6.6)
Рассмотрим три режима работы антенны бегущей
волны: 1) v = с; c/v = 1 (волна свободного пространства); 2) v > с; c/v < 1 (быстрая волна) и 3) v < с; c/v >1 (медленная волна).
1) c/v=l. В этом случае при  =0° множитель системы максимален и равен n. Нормированный множитель системы
=0° множитель системы максимален и равен n. Нормированный множитель системы
Fc (θ) = (1/n) sin [(kn /2)(l - cosθ)]/sin [(k
/2)(l - cosθ)]/sin [(k /2)(l - cosθ)]. (6.7)
/2)(l - cosθ)]. (6.7)
Результирующее поле максимально в направлении θ = 0° вследствие того, что поля от всех элементов антенны в точке наблюдения складываются
синфазно, так как сдвиг фаз из-за несинфазности возбуждения Ψ полностью компенсируется
пространственным сдвигом фаз Ψр. При увеличении или уменьшении угла  (это же
относится и к углу θ) Ψ
(это же
относится и к углу θ) Ψ 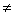 Ψр . Вследствие этого напряженность
результирующего поля в точке наблюдения, характеризуемой
Ψр . Вследствие этого напряженность
результирующего поля в точке наблюдения, характеризуемой
|
Рис.
6.1. ДН АБВ при C/V = 1
|
некоторым углом θ 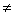 00, будет меньше, чем в точке, лежащей на продолжении оси антенны. Если cosθ отрицателен (90°<θ<270°), то фазовые сдвиги Ψ и Ψр при
00, будет меньше, чем в точке, лежащей на продолжении оси антенны. Если cosθ отрицателен (90°<θ<270°), то фазовые сдвиги Ψ и Ψр при  < λ/2
имеют одинаковые знаки. В этом
случае вибратор, возбуждающийся
раньше, находится ближе к точке
наблюдения, чем вибратор, возбуждающийся
позже (пространственный сдвиг фаз отрицателен). Сдвиг фаз
< λ/2
имеют одинаковые знаки. В этом
случае вибратор, возбуждающийся
раньше, находится ближе к точке
наблюдения, чем вибратор, возбуждающийся
позже (пространственный сдвиг фаз отрицателен). Сдвиг фаз 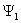 между полями соседних
вибраторов при малых
между полями соседних
вибраторов при малых  велик и результирующее поле в точке наблюдения мало. Следовательно, антенна бегущей волны обладает преимущественно
однонаправленными свойствами и излучает с максимальной интенсивностью вдоль своей оси (антенна с осевым излучением) (рис.6.1). На практике встречаются антенны бегущей волны, которые можно рассматривать как
непрерывное линейное распределение
слабонаправленных излучателей (например, диэлектрическая антенна). Без учета
затухания возбуждающего тока по длине антенны множитель
системы может быть получен из
выражения (6.7)
велик и результирующее поле в точке наблюдения мало. Следовательно, антенна бегущей волны обладает преимущественно
однонаправленными свойствами и излучает с максимальной интенсивностью вдоль своей оси (антенна с осевым излучением) (рис.6.1). На практике встречаются антенны бегущей волны, которые можно рассматривать как
непрерывное линейное распределение
слабонаправленных излучателей (например, диэлектрическая антенна). Без учета
затухания возбуждающего тока по длине антенны множитель
системы может быть получен из
выражения (6.7)
путем предельного перехода. Полагая n => , d=>0, n
, d=>0, n =>L, получаем
=>L, получаем
Fc(θ) = sin[(kL/2)(l- cosθ)]/[(kL/2)(l-
cosθ)] . (6.8)
Уровень первого
бокового лепестка ξ1 =F(θ1mах)=2/3π 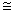 0,21 такой же,
как у синфазной решетки вибраторов. Ширину
диаграммы направленности по направлениям нулевого излучения найдем из условия (kL/2)(l-cosφ0) = π. При
0,21 такой же,
как у синфазной решетки вибраторов. Ширину
диаграммы направленности по направлениям нулевого излучения найдем из условия (kL/2)(l-cosφ0) = π. При
малых значениях λ/L (L - длина антенной решётки)
2θ0=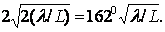 (6.9)
(6.9)
Ширина диаграммы направленности по половинной мощности может быть определена по приближенной формуле
2θ 0,5 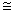 108°
108°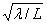 . (6.10)
. (6.10)
Сравнивая данную
антенну с равномерной синфазной решеткой, следует отметить, что хотя диаграмма направленности АБВ получается шире, чем у синфазной решетки такой же длины, но зато один
ряд вибраторов, возбуждаемых бегущей волной тока, обладает направленными
свойствами в любой плоскости,
проходящей через ось антенны, в то время как один ряд синфазной решетки
обладает направленными свойствами только в одной плоскости. Если элементы АБВ не обладают направленным
действием или оно невелико, то
диаграмму направленности антенны можно считать осесимметричной. При этом КНД антенны бегущей волны можно определить
по общей формуле
D0= kL/ [Si2kL - (l - cos2kL)/(2kL)]. (6.11)
При 2kL » I (практически
при L/λ > 1) D0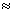 4L /λ.
4L /λ.
2) c/v < I. На основании формулы (6.4), имея в виду, что при условии
cosθ = c/v, множитель системы максимален и
равен n (при этом условии
множитель системы обращается в неопределенность вида 0/0), и используя
предельный переход ( =>0, n=>
=>0, n=>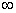 , n
, n >L), получаем нормированную характеристику
направленности
>L), получаем нормированную характеристику
направленности
F(θ) = sin[(kL/2)( c/v - cosθ)]/[(kL/2)( c/v - cosθ)]. (6.12)
Условие cosθ = c/v может
выполняться при двух значениях угла θ = ± θ mах, следовательно, имеются два
направления максимального излучения, не совпадающие с осью антенны. Данный
режим работы является невыгодным, так как направленные свойства антенны
ухудшаются. Однако антенны быстрых волн находят применение для создания
диаграмм направленности специальной формы для качания (сканирования) диаграммы
направленности. Основой большинства антенн быстрых волн являются волноводные
структуры с неоднородностями (например, волновод со щелями).
3) c/v > 1. Как видно из выражений (6.1) и (6.2), в данном случае отсутствует направление, в котором поля отдельных элементов антенны складываются
синфазно, так как ни при каком значении θ отношение c/v не может стать равным cosθ и сдвиг фаз не может обратиться в нуль.
Наименьший фазовый сдвиг
между полями отдельных
вибраторов Ψ1min = kd1(c/v - 1) получается в направлении θ =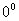 , т.е. вдоль оси антенны. Поля
отдельных вибраторов в точке наблюдения, лежащей в направлении θ =
, т.е. вдоль оси антенны. Поля
отдельных вибраторов в точке наблюдения, лежащей в направлении θ =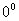 , в данном случае
складываются геометрически, как показано на временной векторной диаграмме
(рис.6.2). Расчеты по формулам (6.4) и (6.12) показывают, что уменьшение
фазовой скорости, начиная от v = c, сопровождается
постепенным сужением основного лепестка диаграммы направленности и ростом
боковых лепестков. Излучение в главном направлении θ =
, в данном случае
складываются геометрически, как показано на временной векторной диаграмме
(рис.6.2). Расчеты по формулам (6.4) и (6.12) показывают, что уменьшение
фазовой скорости, начиная от v = c, сопровождается
постепенным сужением основного лепестка диаграммы направленности и ростом
боковых лепестков. Излучение в главном направлении θ =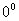 , сначала растет, достигая
максимума при некоторой определенной (для данного значения L =
, сначала растет, достигая
максимума при некоторой определенной (для данного значения L =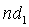 ) величине c/v, а затем начинает уменьшаться и обращается в нуль при критической величине c/v
) величине c/v, а затем начинает уменьшаться и обращается в нуль при критической величине c/v
(c/v)кр =
1+( /nd1). (6.13)
/nd1). (6.13)
Сужение главного лепестка диаграммы направленности приводит к росту КНД антенны, а увеличение уровня боковых лепестков - к его уменьшению. При увеличении c/v, начиная от c/v = 1,
сначала увеличивается КНД
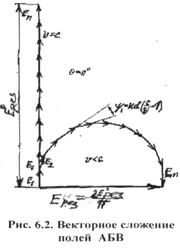 из-за сужения диаграммы направленности. После достижения некоторой
определенной величины c/v дальнейший ее рост приводит к уменьшению КНД из-за увеличения уровня боковых лепестков. Следовательно, имеется оптимальная величина c/v (при заданной длине антенны L), при которой КНД достигает максимального значения. В случае ненаправленных элементов антенны формула для КНД
оказывается весьма громоздкой. Ее анализ показывает, что КНД антенны бегущей
волны при заданной длине антенны зависит от величины результирующего сдвига фаз между полями, создаваемыми крайними (первым и
последним) элементами антенны в точке наблюдения, лежащей на продолжении ее оси (θ = 0°). КНД получается максимальным, если сдвиг фаз ψn, определяемый по
формуле (6.2), равен 180°, т.е. если поля, создаваемые
крайними элементами антенны бегущей волны в точке,
лежащей на продолжении оси антенны, находятся в противофазе (см. рис.6.2). Таким
образом, на основании формулы (6.2) условием получения максимального КНД
является
из-за сужения диаграммы направленности. После достижения некоторой
определенной величины c/v дальнейший ее рост приводит к уменьшению КНД из-за увеличения уровня боковых лепестков. Следовательно, имеется оптимальная величина c/v (при заданной длине антенны L), при которой КНД достигает максимального значения. В случае ненаправленных элементов антенны формула для КНД
оказывается весьма громоздкой. Ее анализ показывает, что КНД антенны бегущей
волны при заданной длине антенны зависит от величины результирующего сдвига фаз между полями, создаваемыми крайними (первым и
последним) элементами антенны в точке наблюдения, лежащей на продолжении ее оси (θ = 0°). КНД получается максимальным, если сдвиг фаз ψn, определяемый по
формуле (6.2), равен 180°, т.е. если поля, создаваемые
крайними элементами антенны бегущей волны в точке,
лежащей на продолжении оси антенны, находятся в противофазе (см. рис.6.2). Таким
образом, на основании формулы (6.2) условием получения максимального КНД
является
ψn опт. = kL(c/v - 1) = 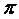 . (6.14)
. (6.14)
Воспользовавшись этой формулой, можно определить оптимальную величину c/v при заданной длине антенны L или определить оптимальную длину антенны при заданной фазовой скорости.
Очевидно, что:
(c/v)опт. 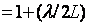 , (6.15)
, (6.15)
(L/ )опт. = 1/[2(c/v - 1)]. (6.16)
)опт. = 1/[2(c/v - 1)]. (6.16)
Как видно из формулы (6.14), оптимальная длина антенны увеличивается при
увеличении фазовой скорости. В случае выполнения условия
(6.14) КНД определяется по формуле
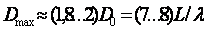 , (6.17)
, (6.17)
где D0 - КНД антенны бегущей волны данной длины при с/v =1. На рис.6.3
приведены графики зависимости отношения D/D0 от сдвига фаз между полями
крайних элементов антенны ψn, где D - КНД антенны определенной длины, работающей в режиме
замедления (v < с) или ускорения (v >c).
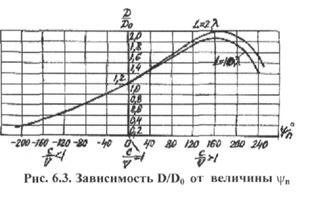 Как видно из векторной временной диаграммы (рис.6.2), в оптимальном случае (ψn = 180°) вектор напряженности результирующего поля в π/2 раз меньше, чем в
случае АБВ, работающей в первом режиме (приближенно можно считать, что вектор напряженности результирующего поля в оптимальном случае равен диаметру
окружности, половина длины которой равна вектору напряженности результирующего
поля при c/v = 1). Казалось бы, что КНД первой антенны должен быть меньше, чем
второй. Увеличение КНД антенны, работающей в режиме, близком к оптимальному,
объясняется тем что при оптимальном и близких к нему отношениях c/v токи в
элементах антенны из-за взаимного влияния возрастают. В
частности, при оптимальном отношении c/v ток в элементах антенны увеличивается
примерно в (π/2)
Как видно из векторной временной диаграммы (рис.6.2), в оптимальном случае (ψn = 180°) вектор напряженности результирующего поля в π/2 раз меньше, чем в
случае АБВ, работающей в первом режиме (приближенно можно считать, что вектор напряженности результирующего поля в оптимальном случае равен диаметру
окружности, половина длины которой равна вектору напряженности результирующего
поля при c/v = 1). Казалось бы, что КНД первой антенны должен быть меньше, чем
второй. Увеличение КНД антенны, работающей в режиме, близком к оптимальному,
объясняется тем что при оптимальном и близких к нему отношениях c/v токи в
элементах антенны из-за взаимного влияния возрастают. В
частности, при оптимальном отношении c/v ток в элементах антенны увеличивается
примерно в (π/2)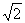 раз по сравнению с током в элементах антенны, работающей в
режиме c/v = 1 (при неизменной излучаемой мощности). Это приводит к увеличению
напряженности поля, излучаемого каждым элементом антенны. Приведенные здесь
соотношения, характеризующие оптимальный
режим работы АБВ, справедливы только для ненаправленных или слабонаправленных
элементов антенны. При наличии у элементов антенны значительных
направленных свойств эти соотношения
изменяются. Ширина диаграммы направленности по нулевому излучению антенны, работающей в оптимальном режиме, на
основании формулы (6.12) находится из
условия (kL/2)(c/v - cos
раз по сравнению с током в элементах антенны, работающей в
режиме c/v = 1 (при неизменной излучаемой мощности). Это приводит к увеличению
напряженности поля, излучаемого каждым элементом антенны. Приведенные здесь
соотношения, характеризующие оптимальный
режим работы АБВ, справедливы только для ненаправленных или слабонаправленных
элементов антенны. При наличии у элементов антенны значительных
направленных свойств эти соотношения
изменяются. Ширина диаграммы направленности по нулевому излучению антенны, работающей в оптимальном режиме, на
основании формулы (6.12) находится из
условия (kL/2)(c/v - cos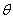 0)= π. Подставляя вместо c/v выражение (6.15) и проводя рассуждения, аналогичные случаю c/v = 1, получаем sinθ0
=
0)= π. Подставляя вместо c/v выражение (6.15) и проводя рассуждения, аналогичные случаю c/v = 1, получаем sinθ0
=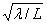 . При малых отношениях λ/L синус можно
заменить аргументом. Тогда
. При малых отношениях λ/L синус можно
заменить аргументом. Тогда
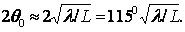 (6.18)
(6.18)
и, как видно
из сравнения формул (6.9) и (6.18), в этом случае АБВ с пониженной фазовой скоростью (оптимальной) имеет диаграмму направленности в 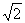 раз уже, чем антенна той же длины с c/v = 1. Ширина диаграммы направленности по
половинной мощности может быть приближенно определена
(для антенны, у которой L/λ »1) по
раз уже, чем антенна той же длины с c/v = 1. Ширина диаграммы направленности по
половинной мощности может быть приближенно определена
(для антенны, у которой L/λ »1) по
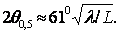 формуле:
формуле:
(6.19)
Диаграмма направленности АБВ с пониженной фазовой скоростью, имеющей оптимальную длину, изображена на рис.6.4. Сужение диаграммы направленности антенны оптимальной длины по сравнению с диаграммой
направленности антенны такой же длины, но работающей в первом режиме (c/v = 1), объясняется тем, что при увеличении угла φ напряженность результирующего поля в случае c/v >1 убывает значительно быстрее, чем в
случае c/v = 1. Это происходит потому, что в случае антенны оптимальной длины сдвиги фаз между полями соседних вибраторов в точке наблюдения, определяемой углом θ1 [при этом 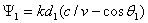 ], больше, чем в случае антенны с c/v = 1 [при этом
], больше, чем в случае антенны с c/v = 1 [при этом 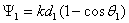 ].
].

74
Определим
уровень первого бокового лепестка диаграммы направленности оптимальной антенны. Максимальная величина нормированной характеристики направленности оптимальной антенны,
определяемая по формуле (6.12), при θ = 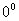 и c/v = 1+λ/2L равна 2π. Значение F(θ) в направлении максимума первого бокового лепестка можно определить, положив аргумент синуса в формуле (6.12) равным 3π /2 и найдя из этого равенства cos θ1max. Подставляя в формулу (6.12) найденное значение cosθ1max и заменяя c/v его выражением (6.15), получаем F(θlmax) = 2π/3. Отсюда уровень первого бокового лепестка
и c/v = 1+λ/2L равна 2π. Значение F(θ) в направлении максимума первого бокового лепестка можно определить, положив аргумент синуса в формуле (6.12) равным 3π /2 и найдя из этого равенства cos θ1max. Подставляя в формулу (6.12) найденное значение cosθ1max и заменяя c/v его выражением (6.15), получаем F(θlmax) = 2π/3. Отсюда уровень первого бокового лепестка 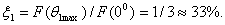
При увеличении длины антенны по сравнению с оптимальной излучение в главном направлении уменьшается и растут боковые лепестки. При L = 2LОПТ излучение в главном направлении совершенно
исчезает. При уменьшении длины антенны по сравнению с оптимальной главный
лепесток диаграммы направленности
расширяется, уровень боковых лепестков уменьшается.
Для того чтобы диаграмма направленности становилась уже, надо
увеличивать длину антенны. Вместе с тем, чтобы при удлинении антенны бегущей волны ее длина оставалась оптимальной,
необходимо в соответствии с соотношением (6.14) увеличивать фазовую
скорость волны в антенне.
В антеннах бегущей волны, применяющихся на практике, амплитуда возбуждающего тока уменьшается вдоль оси решетки по экспоненциальному закону, т.е. I2 =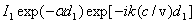 . Это имеет место вследствие потерь энергии в антенне или вследствие постепенного излучения энергии элементами
антенны. Степень убывания бывает разной и в некоторых случаях, при расчетах
этим уменьшением пренебрегают. Убывание амплитуды тока приводит к расширению
основного лепестка диаграммы направленности, к увеличению уровня боковых
лепестков и к исчезновению направлений нулевого излучения, которые заменяются
направлениями минимального излучения.
. Это имеет место вследствие потерь энергии в антенне или вследствие постепенного излучения энергии элементами
антенны. Степень убывания бывает разной и в некоторых случаях, при расчетах
этим уменьшением пренебрегают. Убывание амплитуды тока приводит к расширению
основного лепестка диаграммы направленности, к увеличению уровня боковых
лепестков и к исчезновению направлений нулевого излучения, которые заменяются
направлениями минимального излучения.
Практическим примером выполнения антенны бегущей волны в виде ряда вибраторов является директорная антенна, широко применяемая в УКВ
диапазоне (особенно на метровых и дециметровых волнах). Эта антенна состоит из
одного питаемого (активного) и нескольких пассивных вибраторов, один из которых
работает в режиме рефлектора, а остальные - в режиме директора. Оси всех вибраторов параллельны. Пассивные вибраторы возбуждаются электромагнитным полем активного вибратора.
Длина активного вибратора (2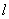 ) обычно берется несколько меньше λ/2 с тем, чтобы он
был резонансным. Для того чтобы пассивный вибратор работал в режиме
рефлектора, его входное сопротивление должно
иметь индуктивный характер, что достигается некоторым удлинением этого вибратора
по сравнению с активным. Пассивный вибратор, работающий в режиме директора,
должен обладать реактивным
сопротивлением емкостного характера, для чего он должен быть несколько короче активного вибратора. Так как
рефлектор усиливает поле в направлении
активного вибратора (вперед) и ослабляет поле в обратном направлении, то применение нескольких
рефлекторов не имеет смысла, так как все рефлекторы, следующие за первым, будут
очень слабо возбуждаться. Первый директор усиливает поле в направлении
следующего директора и поэтому, если установить несколько директоров, то все
они будут возбуждаться достаточно
интенсивно. Длины директоров и расстояния между ними подбирают так, чтобы в
каждом последующем вибраторе ток отставал по фазе от тока в предыдущем на величину
) обычно берется несколько меньше λ/2 с тем, чтобы он
был резонансным. Для того чтобы пассивный вибратор работал в режиме
рефлектора, его входное сопротивление должно
иметь индуктивный характер, что достигается некоторым удлинением этого вибратора
по сравнению с активным. Пассивный вибратор, работающий в режиме директора,
должен обладать реактивным
сопротивлением емкостного характера, для чего он должен быть несколько короче активного вибратора. Так как
рефлектор усиливает поле в направлении
активного вибратора (вперед) и ослабляет поле в обратном направлении, то применение нескольких
рефлекторов не имеет смысла, так как все рефлекторы, следующие за первым, будут
очень слабо возбуждаться. Первый директор усиливает поле в направлении
следующего директора и поэтому, если установить несколько директоров, то все
они будут возбуждаться достаточно
интенсивно. Длины директоров и расстояния между ними подбирают так, чтобы в
каждом последующем вибраторе ток отставал по фазе от тока в предыдущем на величину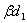 , несколько большую величины k
, несколько большую величины k Такую антенну можно рассматривать как АБВ с пониженной
фазовойскоростью (c/v > 1). Максимум излучения совпадает
с осью антенны (
Такую антенну можно рассматривать как АБВ с пониженной
фазовойскоростью (c/v > 1). Максимум излучения совпадает
с осью антенны (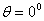 ).
).
Рассмотрим провод длиной L, ток в котором изменяется по закону бегущей волны.
Пренебрегая затуханием, Iz = I0exp[-ik(c/v)z], где I0 - амплитуда тока в
начале провода; z - текущая координата. Из формулы (6.12)
известен множитель системы в случае непрерывного распределения источников поля. На основании правила перемножения характеристик направленности нормированная характеристика направленности провода
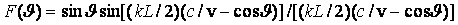
где sin - характеристика направленности элемента
провода.
- характеристика направленности элемента
провода.
Множитель системы выражения (6.20) максимален при  =
= 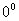 (если v = c). Однако результирующее поле провода в
направлении его оси
(если v = c). Однако результирующее поле провода в
направлении его оси  =
= 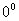 ) равно нулю, так как
sin
) равно нулю, так как
sin в формуле (6.20) обращается в нуль.
Физически это объясняется тем, что элементарный вибратор не
излучает вдоль своей оси. Так как множитель системы максимален в
направлении оси провода (это направление наиболее
благоприятно для сложения полей отдельных элементов провода), а характеристика
направленности элемента провода максимальна в направлении,
перпендикулярном оси провода (
в формуле (6.20) обращается в нуль.
Физически это объясняется тем, что элементарный вибратор не
излучает вдоль своей оси. Так как множитель системы максимален в
направлении оси провода (это направление наиболее
благоприятно для сложения полей отдельных элементов провода), а характеристика
направленности элемента провода максимальна в направлении,
перпендикулярном оси провода ( = 90°), то результирующее поле оказывается максимальным в некотором промежуточном направлении,
составляющем угол
= 90°), то результирующее поле оказывается максимальным в некотором промежуточном направлении,
составляющем угол 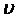 max (меньший 90°) с осью провода. Очевидно, что
таких направлений имеется два (в первом и в четвертом квадрантах). При большой относительной
длине провода L/λ характеристика направленности приблизительно становится максимальной, когда максимален числитель множителя системы
(первый максимум). Поэтому угол максимального излучения можно приближенно найти из выражения
max (меньший 90°) с осью провода. Очевидно, что
таких направлений имеется два (в первом и в четвертом квадрантах). При большой относительной
длине провода L/λ характеристика направленности приблизительно становится максимальной, когда максимален числитель множителя системы
(первый максимум). Поэтому угол максимального излучения можно приближенно найти из выражения
cos  max=(2L - λ)/2L. (6.21)
max=(2L - λ)/2L. (6.21)
Чем больше относительная длина провода L/λ, тем меньше
угол  тах, т.е. тем сильнее излучаемое поле прижато к оси
провода. Чем больше L/λ,
тем уже главный лепесток диаграммы направленности,
но тем больше количество и уровень боковых
лепестков. Главные лепестки диаграммы направленности
наклонены в сторону движения волны в проводе (рис.6.5),
т.е. пространственная диаграмма направленности имеет вид конуса. Вследствие наличия двух направлений максимального излучения (в одной плоскости) нецелесообразно применять одиночный провод с бегущей волной тока в качестве антенны. Однако в антенной технике с успехом применяются различные комбинации из таких проводов, обладающие достаточно хорошими направленными свойствами
(например, ромбическая антенна).
тах, т.е. тем сильнее излучаемое поле прижато к оси
провода. Чем больше L/λ,
тем уже главный лепесток диаграммы направленности,
но тем больше количество и уровень боковых
лепестков. Главные лепестки диаграммы направленности
наклонены в сторону движения волны в проводе (рис.6.5),
т.е. пространственная диаграмма направленности имеет вид конуса. Вследствие наличия двух направлений максимального излучения (в одной плоскости) нецелесообразно применять одиночный провод с бегущей волной тока в качестве антенны. Однако в антенной технике с успехом применяются различные комбинации из таких проводов, обладающие достаточно хорошими направленными свойствами
(например, ромбическая антенна).
ТЕМА 6. Теория апертурных
антенн. Устройство и принцип действия рупорной и
зеркально-параболической антенн
Рассмотрим синфазную прямоугольную излучающую поверхность с косинусоидальным амплитудным распределением поля вдоль оси х (рис.7.3)
Es =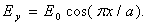 (7.11)
(7.11)
Приблизительно
такое распределение имеется на открытом конце прямоугольного
волновода, возбуждаемого волной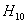 .Так как
распределение возбуждающего поля вдоль оси у в
данном случае такое же, как у идеальной антенны
(равномерное), то характеристика направленности рассматриваемой
и излучающей поверхности в плоскости вектора Е (плоскости yoz) не отличается от характеристики
направленности идеальной плоской антенны в этой плоскости. В случае, когда f(x,y) = f(x) =
.Так как
распределение возбуждающего поля вдоль оси у в
данном случае такое же, как у идеальной антенны
(равномерное), то характеристика направленности рассматриваемой
и излучающей поверхности в плоскости вектора Е (плоскости yoz) не отличается от характеристики
направленности идеальной плоской антенны в этой плоскости. В случае, когда f(x,y) = f(x) =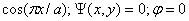 , получим выражение для характеристики
направленности антенны в плоскости вектора Н (плоскости xoz)
, получим выражение для характеристики
направленности антенны в плоскости вектора Н (плоскости xoz)
Ė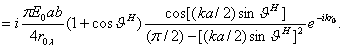 (7.12)
(7.12)
Нормированная
характеристика направленности излучающей поверхности с косинусоидальным распределением возбуждающего поля в плоскости Н определяется выражением
F( )
)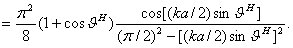 (7.13)
(7.13)
Таким образом
в данном случае, по сравнению с идеальной плоской антенной, изменился вид множителя системы.
Ширина главного лепестка определяется из условия равенства нулю числителя множителя системы. Однако нельзя положить аргумент косинуса 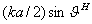 равным π/2, так как при этом знаменатель
множителя системы также обращается в нуль и получается
неопределенность вида 0/0. Раскрытие этой неопределенности дает
конечное значение множителя системы. Поэтому, чтобы множитель
системы обратился в нуль, следует положить
равным π/2, так как при этом знаменатель
множителя системы также обращается в нуль и получается
неопределенность вида 0/0. Раскрытие этой неопределенности дает
конечное значение множителя системы. Поэтому, чтобы множитель
системы обратился в нуль, следует положить 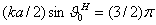 , откуда sin
, откуда sin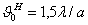 . При малых величинах λ/а эта
формула принимает вид
. При малых величинах λ/а эта
формула принимает вид 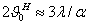 , рад, или
, рад, или
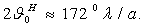 (7.14)
(7.14)
Ширина диаграммы направленности по
половинной мощности в данном случае определяется по формуле
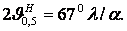 (7.15)
(7.15)
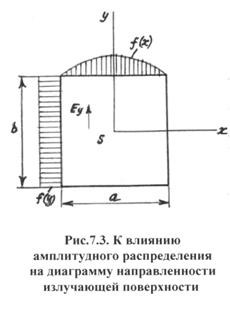 Таким образом при переходе от равномерного амплитудного распределения к
распределению, спадающему к краям излучающей
поверхности по закону косинуса, ширина диаграммы
направленности в соответствующей плоскости увеличивается примерно в 1,5 раза. Одновременно с расширением главного лепестка диаграммы направленности уменьшается уровень боковых лепестков. Так, в рассмотренном
случае относительный уровень первого бокового
лепестка
Таким образом при переходе от равномерного амплитудного распределения к
распределению, спадающему к краям излучающей
поверхности по закону косинуса, ширина диаграммы
направленности в соответствующей плоскости увеличивается примерно в 1,5 раза. Одновременно с расширением главного лепестка диаграммы направленности уменьшается уровень боковых лепестков. Так, в рассмотренном
случае относительный уровень первого бокового
лепестка 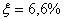 или -23 дБ
или -23 дБ
(вместо -13,2 дБ в случае идеальной плоской
антенны).
Расширение диаграммы направленности объясняется тем, что в соответствии с амплитудным распределением 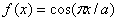 по мере удаления от центра антенны в направлении оси х возбуждение элементарных площадок становится слабее. Очевидно, что поля, создаваемые
близкими к краю поверхности
площадками, из-за своей малости почти не влияют на величину результирующего поля антенны. Следовательно,
уменьшение амплитуды возбуждающего поля к краям антенны эквивалентно
уменьшению соответствующего размера антенны
с равномерным распределением амплитуды возбуждающего
поля.
по мере удаления от центра антенны в направлении оси х возбуждение элементарных площадок становится слабее. Очевидно, что поля, создаваемые
близкими к краю поверхности
площадками, из-за своей малости почти не влияют на величину результирующего поля антенны. Следовательно,
уменьшение амплитуды возбуждающего поля к краям антенны эквивалентно
уменьшению соответствующего размера антенны
с равномерным распределением амплитуды возбуждающего
поля.
Обобщая полученные
результаты и применяя их к другим амплитудным распределениям,
можно установить следующее: чем резче спадает амплитуда возбуждающего поля к краям излучающей поверхности, тем шире главный лепесток диаграммы направленности и тем меньше уровень боковых лепестков. Это же положение может быть
распространено и наантенные решетки. Данное свойство излучающих
поверхностей находит широкое практическое применение. Так, в тех случаях, когда
требуются диаграммы направленности с низким уровнем
боковых лепестков добиваются резко спадающего к краям антенны
амплитудного распределения. Правда, при этом расширяется
основной лепесток диаграммы направленности.
КНД излучающей поверхности
В случае идеальной плоской
антенны 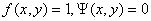 выражение для КНД принимает
вид
выражение для КНД принимает
вид
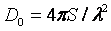 (7.16)
(7.16)
Таким образом, КНД
идеальной плоской антенны тем больше, чем больше площадь этой антенны и чем короче длина волны. КНД антенны обратно пропорционален квадрату длины волны при
постоянной площади антенны. Легко видеть, что с
укорочением длины волны облегчается построение антенн с
высоким КНД. Так, для того чтобы антенна, работающая на λ = 1 см, имела КНД D = 12,6 • 104,
ее площадь должна составлять всего 1 м2. В случае
неравномерного амплитудного распределения по
аналогии с формулой (7.16)
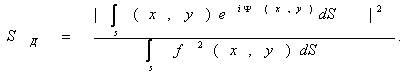
(7.17)
Величину 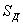 можно
назвать действующей (эффективной) площадью антенны. Очевидно, что
можно
назвать действующей (эффективной) площадью антенны. Очевидно, что
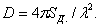 (7.18)
(7.18)
Выражая КНД
излучающей поверхности с произвольным распределением возбуждающего поля через
КНД идеальной плоской антенны с помощью выражений (7.16) и
(7.18), получаем
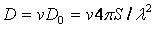 , (7.19)
, (7.19)
где 
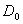 КНД идеальной
плоской антенны;
КНД идеальной
плоской антенны; 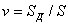 коэффициент
коэффициент
использования
поверхности раскрыва (КИП).
Величина КИП зависит от вида
амплитудного и фазового распределения возбуждающего поля.
КИП тем меньше,
чем резче амплитуда возбуждающего поля спадает к
краям антенны. Рассмотрим частный случай косинусоидальное
амплитудное распределение: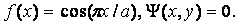
Тогда 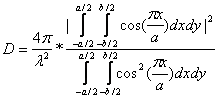
84
В результате
интегрирования получаем
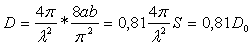 .
(7.20)
.
(7.20)
Уменьшение КНД излучающей
поверхности со спадающим к краям амплитудным распределением по сравнению с
идеальной излучающей поверхностью объясняется тем, что при одинаковой
излучаемой мощности напряженность поля первой антенны в главном направлении
будет меньше, чем напряженность поля второй антенны в этом
направлении, так как диаграмма направленности первой
антенны шире, чем второй.
В случае реальных излучающих поверхностей
эффективная поверхность антенны 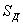 всегда меньше
ее геометрической площади S. Можно сказать, что
действующей площадью реальной антенны называется площадь
такой идеальной плоской антенны, (излучающей
поверхности с равномерным амплитудным распределением и синфазным возбуждением)
КНД которой равен КНД данной реальной антенны. Как видно из формулы (7.19),
всегда меньше
ее геометрической площади S. Можно сказать, что
действующей площадью реальной антенны называется площадь
такой идеальной плоской антенны, (излучающей
поверхности с равномерным амплитудным распределением и синфазным возбуждением)
КНД которой равен КНД данной реальной антенны. Как видно из формулы (7.19), 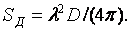
Влияние реальных амплитудных распределений на
параметры, определяющие направленные свойства апертурных антенн, видно из
табл. 7.1и
7.2.
Влияние фазовых искажений на направленные свойства излучающей
поверхности
Несинфазность
излучающей поверхности либо может быть присуща данной
антенне вследствие особенностей ее устройства, либо вызывается неточным
выполнением антенны.
Фазовые искажения
ухудшают направленные свойства антенны. Однако в некоторых случаях на излучающей
поверхности специально устанавливают определенный
закон распределения фазы для получения диаграммы направленности специальной формы или управления диаграммой направленности (изменение положения диаграммы
направленности в пространстве).
В самом общем
случае фазовое распределение может являться функцией двух координат.
Однако для упрощения исследования обычно рассматривают зависимость фазы от каждой координаты в отдельности.
Если
начало прямоугольной системы
координат поместить в
центре прямоугольной
излучающей поверхности, то
распределение фазы поля
по
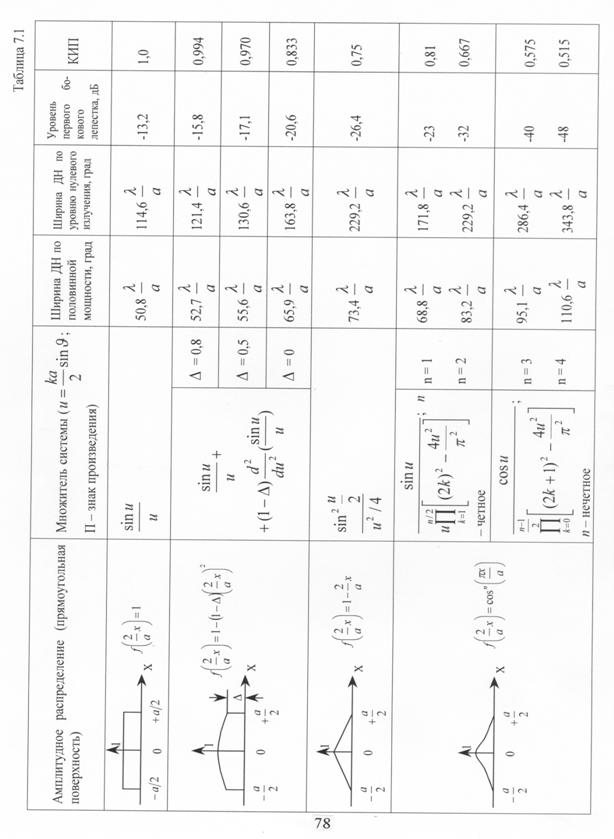
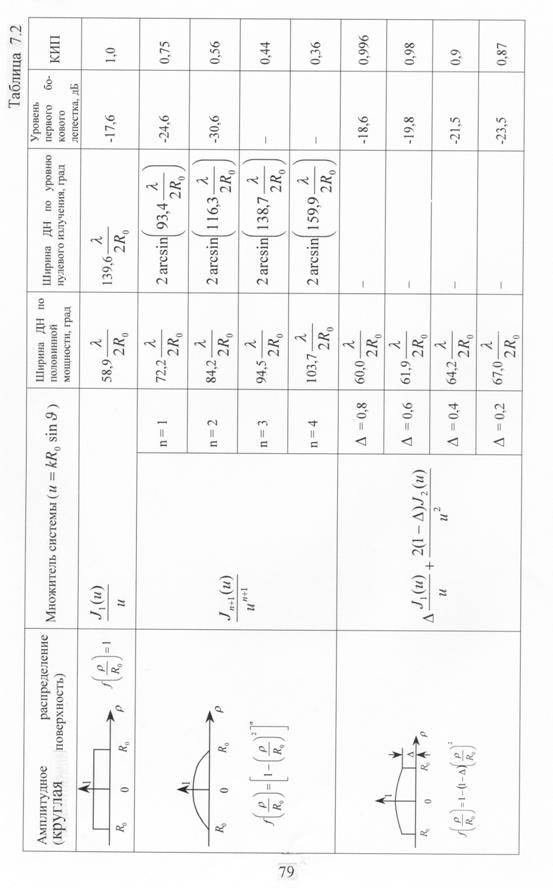
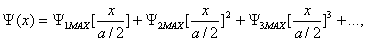 где
где 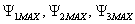 и т.д.
и т.д.
-максимальные фазовые сдвиги соответствующих составляющих
фазового распределения, получающиеся на краях
излучающей поверхности (х = ±а/2).
Монотонные законы изменения фазы возбуждающего
поля, как правило, могут быть с достаточной точностью
представлены тремя первыми членами данного ряда:
линейным, квадратичным и кубическим. В некоторых случаях фазовое распределение
антенны хорошо описывается одним членом ряда.
Выясним влияние на направленные свойства
антенны наиболее простых фазовых распределений: линейного, квадратичного и
кубического. При этом будем полагать, что амплитуда
возбуждающего поля не зависит от координат.
При линейном распределении фазы
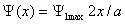 (рис.7.4.a)
напряженность
возбуждающего поля изменяется по
закону
(рис.7.4.a)
напряженность
возбуждающего поля изменяется по
закону
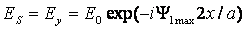 .
Так как фаза возбуждающего поля изменяется только вдоль
размера а антенны, то интересно исследовать
направленные свойства антенны только в плоскости xoz (рис.7.4.б). Для возбужденной
поверхности с линейным фазовым распределением имеем
.
Так как фаза возбуждающего поля изменяется только вдоль
размера а антенны, то интересно исследовать
направленные свойства антенны только в плоскости xoz (рис.7.4.б). Для возбужденной
поверхности с линейным фазовым распределением имеем
Ė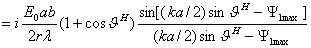 . (7.21)
. (7.21)
Излучение
максимально при условии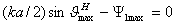 , откуда
, откуда
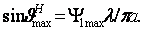 (7.22)
(7.22)
Все выводы, сделанные в отношении поворота и расширения диаграммы
Направленности равномерной линейной
решетки и её КНД , остаются справедливыми и в данном случае. Пусть фаза возбуждающегополя изменяется по закону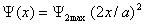 (рис.7.5).
Напряженность возбуждающего поля определяется
выражением
(рис.7.5).
Напряженность возбуждающего поля определяется
выражением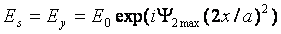 , тогда
, тогда
 É=
É=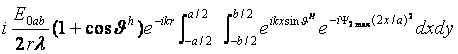 .
.
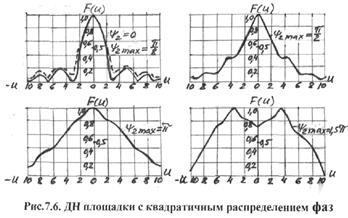 Формула для характеристики направленности, получаемая в результате интегрирования этого выражения, оказывается весьма громоздкой. Диаграммы направленности, рассчитанные по этой формуле, приведены на
рис.7.6. Как видно из этого рисунка, квадратичное фазовое распределение не
Формула для характеристики направленности, получаемая в результате интегрирования этого выражения, оказывается весьма громоздкой. Диаграммы направленности, рассчитанные по этой формуле, приведены на
рис.7.6. Как видно из этого рисунка, квадратичное фазовое распределение не
вызывает поворота
диаграммы
направленности.
При всех значениях 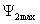 она остается симметричной относительно нормали
к поверхности. Этого и следовало ожидать,
так как это распределение симметрично относительно центра излучающей поверхности.
она остается симметричной относительно нормали
к поверхности. Этого и следовало ожидать,
так как это распределение симметрично относительно центра излучающей поверхности.
Влияние
квадратичного изменения фазы на направленные свойства излучающей поверхности сводится к следующему: исчезают нули между лепестками диаграммы направленности; уровень боковых лепестков
увеличивается: главный лепесток диаграммы направленности расширяется и при
больших значениях 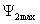 боковые лепестки полностью поглощаются расширяющимся главным лепестком. При значениях сдвигов фаз
боковые лепестки полностью поглощаются расширяющимся главным лепестком. При значениях сдвигов фаз 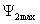
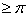 происходит раздвоение главного лепестка: появляются два направления
максимального излучения, излучение в направлении нормали уменьшается. Следовательно, квадратичное фазовое распределение приводит к искажению диаграммы направленности, к ухудшению направленных свойств антенны. При максимальных сдвигах фаз, не превышающих 45°, диаграмма направленности как по ширине основного лепестка по половинной мощности, так и по уровню боковых лепестков почти не отличается от характеристики
направленности идеальной плоской антенны.
происходит раздвоение главного лепестка: появляются два направления
максимального излучения, излучение в направлении нормали уменьшается. Следовательно, квадратичное фазовое распределение приводит к искажению диаграммы направленности, к ухудшению направленных свойств антенны. При максимальных сдвигах фаз, не превышающих 45°, диаграмма направленности как по ширине основного лепестка по половинной мощности, так и по уровню боковых лепестков почти не отличается от характеристики
направленности идеальной плоской антенны.
В случае кубического закона изменения фазы
напряженность возбуждающего поля изменяется по закону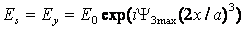 .
.
Фазовое распределение имеет вид (рис.7.7) 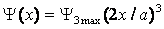 . Фаза распределена несимметрично относительно
центра излучающей поверхности.
. Фаза распределена несимметрично относительно
центра излучающей поверхности.
Формула
характеристики направленности такой поверхности
получается чрезвычайно громоздкой. Характер влияния
кубических фазовых искажений на диаграмму
направленности виден из рис.7.8. При кубическом изменении фазы, как и при
линейном, диаграмма направленности поворачивается направление максимального излучения отклоняется от нормали на угол 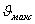 в сторону
отставания фазы. При этом
диаграмма направленности искажается, онастановится
асимметричной относительно направления максимального
излучения, боковые лепестки по одну сторону от главного
лепестка уменьшаются, а по другую увеличиваются;
увеличение боковых лепестков происходит со
стороны, совпадающей с направлением отклонения главного лепестка. Угол, на который поворачивается
диаграмма направленности, вследствие наличия кубического фазового распределения
при небольших значениях
в сторону
отставания фазы. При этом
диаграмма направленности искажается, онастановится
асимметричной относительно направления максимального
излучения, боковые лепестки по одну сторону от главного
лепестка уменьшаются, а по другую увеличиваются;
увеличение боковых лепестков происходит со
стороны, совпадающей с направлением отклонения главного лепестка. Угол, на который поворачивается
диаграмма направленности, вследствие наличия кубического фазового распределения
при небольших значениях 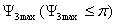 определяется по формуле
определяется по формуле
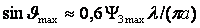
Из сравнения формул (7.23) и (7.24) видно, что при 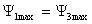
диаграмма
направленности при кубическом изменении фазы отклоняется на меньший угол, чем при линейном.
Все выводы относительно влияния
различных фазовых распределений
на направленные свойства антенн
относятся к случаю равномерного распределения амплитуды возбуждающего поля
(f(x)= 1). При 90 спадающем к
краям распределении влияние изменения фазы на
диаграмму направленности
уменьшается. Поскольку различные
законы изменения фазы связаны с ухудшением направленных свойств антенн, то,
очевидно, что при наличии фазовых искажений КИП уменьшается.
Принцип
действия, основные свойства рупорных антенн

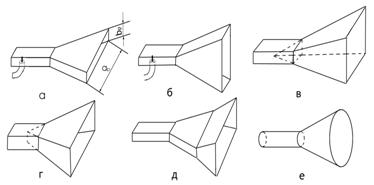 Концентрация
излучения в пределах более узкого телесного угла достигается увеличением
размеров синфазно возбужденной поверхности. Если размеры сечения волновода
выбираются таким образом, чтобы обеспечить формирование необходимой структуры
поля, то, плавно увеличивая сечение волновода, эту структуру можно сохранить, а
размеры излучаемой поверхности увеличить. В месте перехода от волновода к
рупору возникают высшие типы волн, но при достаточно плавном расширении
волновода (малый угол
раствора рупора) интенсивность
этих волн невелика. Существуют различные типы
рупоров. Рупор, образованный
увеличением размера а волновода, параллельного вектор Н,
называется секториальным Н- плоскостным (рис.9.2.а). Рупор,
образованный увеличением размера b волновода, параллельного
вектору Е, называется секториальным
Е-плоскостным (рис.9.2.б). Рупор, образованный
одновременным увеличением размеров
a u b поперечного сечения волновода, называется пирамидальным
(см. рис.9.2.в,г), а увеличением поперечного сечения круглого волновода -
коническим (рис.9.2.е). При плавном переходе от волновода к рупору структура
поля в последнем напоминает структуру поля в волноводе.
Концентрация
излучения в пределах более узкого телесного угла достигается увеличением
размеров синфазно возбужденной поверхности. Если размеры сечения волновода
выбираются таким образом, чтобы обеспечить формирование необходимой структуры
поля, то, плавно увеличивая сечение волновода, эту структуру можно сохранить, а
размеры излучаемой поверхности увеличить. В месте перехода от волновода к
рупору возникают высшие типы волн, но при достаточно плавном расширении
волновода (малый угол
раствора рупора) интенсивность
этих волн невелика. Существуют различные типы
рупоров. Рупор, образованный
увеличением размера а волновода, параллельного вектор Н,
называется секториальным Н- плоскостным (рис.9.2.а). Рупор,
образованный увеличением размера b волновода, параллельного
вектору Е, называется секториальным
Е-плоскостным (рис.9.2.б). Рупор, образованный
одновременным увеличением размеров
a u b поперечного сечения волновода, называется пирамидальным
(см. рис.9.2.в,г), а увеличением поперечного сечения круглого волновода -
коническим (рис.9.2.е). При плавном переходе от волновода к рупору структура
поля в последнем напоминает структуру поля в волноводе.
Векторы электромагнитного поля при переходе из волновода в рупор
несколько изменяют свою форму, чтобы обеспечить выполнение граничных условий на
стенках рупора.
Направленные
свойства рупорной антенны приближенно можно анализировать, как и в случае
открытого конца волновода, пользуясь принципом эквивалентности. На излучающей
поверхности рупора действуют две взаимно перпендикулярные тангенциальные
составляющие поля Еу и Нх (прямоугольный раскрыв), амплитуды которых
не зависят от координаты у, а вдоль
координаты х они изменяются по закону
косинуса.
Однако в отличие от поверхности открытого конца волновода плоская
излучающая поверхность рупора не может быть синфазной, так как в раскрыве
рупора имеются фазовые искажения. Найдем фазу возбуждающего поля в произвольной
точке М излучающего раскрыва H-плоскостного рупора (рис.9.3). Дуга NOP окружности с центром в точке О есть линия равных фаз. Предполагая для простоты, что в рупоре β
 k
k  2π/λ, получаем
2π/λ, получаем
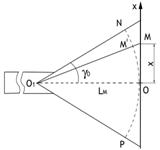
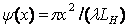 где Lh - длина H-плоскостного
рупора. Обычно LH>>x,поэтому
можно ограничиться первым членом
разложения. Тогда .
где Lh - длина H-плоскостного
рупора. Обычно LH>>x,поэтому
можно ограничиться первым членом
разложения. Тогда .
Следовательно, в раскрыве рупорной антенны имеется примерно
квадратичное фазовое распределение. Максимальный сдвиг фаз на краях раскрыва (х = ±ар /2), ψmах = πаp2 /(4λLH). При достаточно больших
значениях ψmах (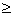 90°) ДН рупорной антенны заметно отличается от ДН синфазной
излучающей поверхности. При этом симметрия ДН относительно нормали к
возбужденной поверхности сохраняется.
90°) ДН рупорной антенны заметно отличается от ДН синфазной
излучающей поверхности. При этом симметрия ДН относительно нормали к
возбужденной поверхности сохраняется.
Путем аналогичных рассуждений получаем максимальный сдвиг фаз на краях Е-плоскостного рупора ψmах = πb2р /( 4λLE), где LE - длина E-плоскостного
рупора.
Максимальный сдвиг
фаз на краю раскрыва конического рупора (радиус раскрыва ар,
длина рупора L) ψmах =π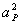 /(λL).
/(λL).
Поскольку в рупорной антенне практически невозможно
добиться полной синфазности излучающей поверхности, то обычно, задаваясь
некоторым допустимым сдвигом фаз, выбирают размеры раскрыва рупора и его длину.
Этот сдвиг должен быть таким, чтобы ДН рупорной антенны мало отличалась
от ДН синфазной излучающей поверхности, размеры которой равны размерам раскрыва
рупора.
Допустимый
максимальный сдвиг фаз определяется условием получения максимального КНД при
заданной относительной длине L/λ рупора. С увеличением относительных размеров раскрыва рупора (ар/λ или
bр /λ) при неизменной длине его ДН сначала становится уже и КНД растет, так
как увеличиваются размеры излучающей поверхности, которая практически остается
синфазной (сдвиг фаз ψтах мал). При дальнейшем увеличении размеров заметно растут фазовые искажения,
вследствие чего ДН начинает расширяться и КНД уменьшается. На рис.9.4 по оси
ординат отложено произведение КНД Е-плоскостного
рупора на отношение λb/ар. Аналогичные
кривые существуют и для H-плоскостных рупоров. При заданном отношении L/λ имеется определенное оптимальное значение ар/λ или bр/λ, при котором КНД антенны - максимально возможный. Оптимальному
значению ар/λ или bр/λ соответствует допустимый сдвиг фаз. Рупор, размеры которого подобраны так, чтобы
при заданной длине L/λ получить максимальный КНД, называется оптимальным.
Из формул для ψmax видно, что для
того, чтобы при увеличении размеров раскрыва рупора максимальный сдвиг фаз не
изменялся, оставаясь равным допустимому, т.е. КНД возрастал, относительная
длина рупора L/λ должна увеличиваться пропорционально квадрату относительных размеров
раскрыва рупора.
|
Рис.9.4.
Зависимость КНД от длины и величины раскрыва рупора
|
Анализ кривых, приведенных на
рис.9.3, показывает, что в случае Е -плоскостного рупора
максимальный КНД получается при выполнении равенства
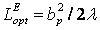 , тогда допустимый
максимальный сдвиг фаз для Е - плоскостного рупора
, тогда допустимый
максимальный сдвиг фаз для Е - плоскостного рупора
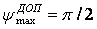 .
.
Рассмотрев
аналогичные кривые DHλ
/b = f(LH /λ,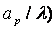 , можно найти допустимый сдвиг фаз
, можно найти допустимый сдвиг фаз 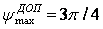 и
оптимальную длину Н -плоскостного
рупора
и
оптимальную длину Н -плоскостного
рупора 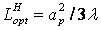 .
.
Увеличение
допустимого сдвига фаз в случае Н - плоскостного
рупора по
сравнению с
E-плоскостным
объясняется с паданием амплитуды возбуждающего поля к краям
раскрыва этого рупора в плоскости Н.
Коэффициент
направленного действия оптимального Е- или Н-плоскостного рупора может быть рассчитан по формуле D=va4πS/λ2,
причем КИП рупора с учетом несинфазности и неравномерности
возбуждения составляет 0,64
(у пирамидального рупора va = 0,52).
Е - плоскостной рупор сужает ДН в плоскости Е, а
Н - плоскостной рупор - в плоскости Н.
В настоящее время находят применение рупоры, у которых сдвиги фаз поля
в раскрыве значительно превосходят
максимально допустимые. При больших по
сравнению с λ
раскрывах ар и bр и больших углах растворов рупора γo ДН становится
по форме близкой к столообразной. Такие расфазированные рупоры обладают более широким рабочим диапазоном,
чем синфазные рупоры.
Их ДН при ψmax > 1,5π
сравнительно мало зависят от
частоты.
фазы 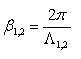 ;
; 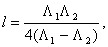 где
где
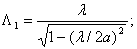
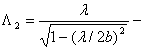 длины волн в волноводе.
длины волн в волноводе.
Зеркальные параболические антенны
Зеркальная осесимметричная параболическая антенна состоит из
отражающей поверхности, выполненной в виде параболоида вращения, и небольшой
слабонаправленной антенны - облучателя, установленной в фокусе параболоида, и
облучающей внутреннюю поверхность последнего. На базе такой классической зеркальной антенны разработаны различные
модификации, многообразие которых приводит к целесообразности сгруппировать их,
т.е. привести классификацию по основным отличительным признакам. Так, по числу
отражающих зеркал различают одно- и многозеркальные антенны. Последние, как
правило, содержат два зеркала. Часто эту группу называют двухзеркальными
антеннами.
По взаимной ориентации зеркал и облучателей антенны
могут быть симметричными
и осенесимметричными. В симметричных антеннах отражающее зеркало обладает осевой симметрией и поле, отраженное от вершины такого зеркала, попадает в облучатель.
Если не принять специальных
мер, то согласование антенны будет невысоким. В осенесимметричных схемах антенн волны, отраженные от зеркала, проходят
мимо облучателя. Такие схемы называют еще антеннами с вынесенным облучателем (АВО). Их отличает высокое
согласование с трактом питания, но в то же время они
обладают повышенным уровнем кроссполяризации, что при одновременной работе на ортогональных поляризациях является источником
дополнительных помех.
По числу основных лучей, создаваемых зеркальной антенной, различают одно- и многолучевые антенны. Число лучей
определяется числом облучателей. Многолучевые антенны могут создаваться
как в симметричном, так и в осенесимметричном
варианте. По типу кривизны основного зеркала используются параболические
и сферические отражающие зеркала, зеркала с классическим
и модифицированным профилями, обеспечивающими высокий результирующий КИП в условиях компромисса между
апертурным КИП и потерями за счет «перелива» энергии за края зеркала.
Это так называемые оптимизированные
антенны.
При фиксированном положении отражающего зеркала
направление максимального излучения (приема) может быть либо фиксированным,
либо антенна может работать в режиме сканирования. Особое место занимают зеркальные антенны с пониженным УБЛ В прямоугольной системе координат (начало в вершине
параболоида) параболическая поверхность (рис.9.7) описывается уравением
х2 + у2 =
4f0z, где f0 -
фокусное расстояние.
В сферической системе координат (начало в фокусе)
эта поверхность описывается уравнением r'=2f0/(1+ cosγ), где r' - расстояние от фокуса до любой точки на внутренней поверхности параболоида; γ - угол между направлением
на данную точку и фокальной осью зеркала (полярный угол).
В
случае параболоида вращения (рис.9.7) плоскость раскрыва (плоскость, проходящая через крайние точки поверхности зеркала
и перпендикулярная его фокальной оси)
имеет круглую форму; радиус этой плоскости называется радиусом раскрыва зеркала (R0). Радиус раскрыва и угол раскрыва зеркала
(угол γ0 между фокальной осью и прямой, проведенной из фокуса к кромке параболоида)
связаны соотношением R0=2f0tg(γo/2).
Форма зеркала характеризуется
отношением R0/2f0 или углом раскрыва γ0. Зеркало называется длиннофокусным (мелким), если R0/2f0<1 либо 2γ0<π или
короткофокусным (глубоким), если R0/2f0>1 либо 2γ0 >π.
Принцип
действия зеркальной антенны следующий. При падении, излучаемой облучателем,
электромагнитной волны на зеркало на последнем возникают электрические
поверхностные токи (вторичные источники
электромагнитного поля). Эти токи
существуют не только на внутренней, обращенной
к облучателю поверхности зеркала, но также из-за явления дифракции
электромагнитных волн и на его внешней
поверхности. Электромагнитное поле, создаваемое зеркальной антенной в любой точке окружающего пространства,
есть результат сложения (интерференции) полей:
вторичного, создаваемого
поверхностными токами, и
первичного, создаваемого облучателем.
Рассмотрим сечение параболоида в плоскости xoz (рис.9.8). Образованная этим
сечением парабола обладает тем
свойством, что расстояния от ее
фокуса F до любой
точки, лежащей
на линии MN, перпендикулярной оси параболы и параллельной ее директрисе, по ломаным путям, (FP1M1, FP2M2 и др.) одинаковы. Следовательно, получается плоский фронт волны. Установленный в точке F облучатель
излучает волны, близкие к сферическим. При этом расходящиеся лучи совпадают с линиями FP1, FP2 и т.д. Если бы длина волны первичного источника была бесконечно мала, то лучи, падающие
на внутреннюю поверхность
параболоида, отражались бы от нее по законам геометрической оптики. При этом, вследствие параболической формы зеркала, все
отраженные лучи были бы параллельны оси z и, таким образом, сферическая волна преобразовывалась бы параболоидом в плоскую. В
действительности длина волны
облучателя не бесконечно мала, и поэтому отраженные лучи идут не параллельно, а несколько расходятся. Однако
расходимостью отраженных от зеркала
лучей на небольшом участке пути от зеркала до поверхности раскрыва можно пренебречь, и эту поверхность можно
считать синфазно возбужденной.
Коэффициенты
усиления и направленного действия параболической антенны
Как было показано выше, коэффициент усиления G антенны связан с ее коэффициентами направленного
действия D и полезного действия η
простым соотношением G = Dη.
Коэффициент полезного
действия η зеркальной антенны учитывает тепловые потери энергии в облучателе, элементах
крепления облучателя, краске, покрывающей внутреннюю поверхность зеркала, и
т.д. Обычно принимают
η = 1. Поэтому рассмотрим подробно определение
КНД.
Коэффициент направленного действия зеркальной антенны можно рассчитать
по формуле для КНД, заменив в ней апертурный КИП (νa) множителем νрез
(результирующий или полный КИП), учитывающим
уменьшение КНД из-за действия ряда факторов: переливания части, излученной
облучателем, энергии через края зеркала, вызывающего увеличение УБЛ ДН
зеркальной антенны в задних квадрантах (дальние боковые лепестки); ошибки в
фазовом распределении на раскрыве; затенения части поверхности раскрыва
облучателем и элементами его крепления; кроссполяризации излучаемого поля и др.
Таким образом, D = v рез 4πS /λ2, где S - πR02 - площадь раскрыва; νрез
= νaν1ν2ν3ν4ν5... . Здесь vа— апертурный КИП раскрыва зеркала; ν1 - множитель,
определяемый переливанием части энергии через края зеркала; ν2 - множитель, определяемый затенением; v3
-множитель, определяемый фазовыми ошибками; ν4
- множитель, учитывающий явление кроссполяризации; ν5
- множитель, учитывающий дифракцию поля на кромке зеркала.
Множитель
ν1,
называемый коэффициентом перехвата, - есть отношение мощности, излученной
облучателем и перехватываемой зеркалом, к полной мощности, излученной
облучателем, при этом потери в зеркале не учитываются.
Если
при заданной форме зеркала (R0/f0=const) расширять ДН облучателя
(кривая 1 на рис. 9.11), то амплитудное распределение в раскрыве зеркала
становится более равномерным (va
растет). Однако вместе с тем увеличивается доля энергии, проходящей мимо
зеркала, приводящая к росту боковых лепестков (уменьшается v1). При
сужении ДН облучателя наоборот: уменьшается vа и увеличивается v1. Два
противоположно действующих на результирующие КИП и КНД фактора при
постоянной величине отношения R0/f0 или угла раскрыва зеркала γ0 и изменяемой ширине ДН облучателя
определяют условие оптимального облучения зеркала с точки зрения получения
максимального КНД. Условие оптимального облучения примерно
обеспечивается при Δkр = Еkр/Е0
=0,316 (-10 дБ), где Еkр -
напряженность поля на краю зеркала. При этом vav1 = 0,7...0,8.
С точки зрения получения максимального КНД при
заданных размерах зеркала
идеальной является ДН облучателя, изображенная на рис.9.11 (кривая 2). Она должна быть осесимметричной и
имеет два максимума в направлениях
на края зеркала. Амплитудное распределение раскрыва зеркала в данном случае получается близким к равномерному
(с учетом разных расстояний
от фокуса зеркала до его вершины и краев), т.е. va = 1; переливание энергии за края зеркала отсутствует (ДН имеет бесконечную крутизну ската), таким образом, v1=1.
Для обеспечения высокого значения vрез ДН облучателя должна иметь форму, по возможности приближающуюся к идеальной (например,
кривая 3 на рис.9.11). Близкие к ней ДН можно получить с
помощью расфазированных рупоров
и их модификаций. Кроме того, надо исключить или уменьшить влияние других факторов, снижающих результирующий
КИП антенны (устранить
затенение раскрыва облучателем, снизить кроссполяризацию и т.д.).
Реализация
высоких значений νрез, а следовательно,
КНД антенн не является единственно важной задачей в практическом приложении. В
антенных системах ряда радиослужб предъявляются высокие требования к УБЛ.
Например, в системах спутниковой связи, использующих геостационарную орбиту,
от уровня первых боковых лепестков, примыкающих к главному, во многом зависят
помехозащищенность и электромагнитная cовместимость, поэтому он
должен быть ниже главного минимум на 25...30 дБ. В
ряде случаев, в
частности, в радиорелейной связи,
важное значение имеет УБЛ
в задних
квадрантах в направлениях, близких к 180°. В этих направлениях излучение (коэффициент защитного действия) должно составлять не более -(60...70) дБ. Для
параболических антенн с углами
раскрыва 2γ0 =120...180° КЗД составляет - (50...60) дБ.
Влияние
точности выполнения зеркальной антенны на ее направленные свойства
Неточности, неизбежные при создании конструкции антенны (например, при выполнении поверхности зеркала, установке
облучателя), вызывают отклонение распределения поля на излучающей
поверхности от расчетного и соответствующие искажения ДН.
Ошибки в распределении поля по раскрыву могут быть
систематическими и случайными.
К систематическим ошибкам относятся такие, которые можно предусмотреть при полном и точном расчете антенны.
Причинами этих ошибок
могут быть смещение облучателя из фокуса, затенение раскрыва зеркала облучателем и элементами его крепления и
др. Случайные ошибки обусловлены незакономерными и обычно небольшими отклонениями параметров антенны от их расчетных значений.
Причинами таких ошибок являются недостаточная
точность обработки поверхности зеркала, случайные деформации поверхности антенны вследствие изменения температуры или ветровых нагрузок и др.
Статистический анализ влияния случайных ошибок на
направленные свойства зеркальной
антенны позволяет сделать следующие выводы:
1.Случайные ошибки в распределении возбуждающего
поля в раскрыве антенны увеличивают УБЛ и
уменьшают КНД.
2.Уровень боковых лепестков параболической антенны
пропорционален среднеквадратической фазовой
ошибке Δψ2 и квадрату
интервала корреляции, измеренного в
длинах волн.
3.Участки
зеркала, на которых
реальная поверхность отклоняется
от расчетной,
должны быть небольшими, т.е. при одном и том же допуске на точность обработки поверхности зеркало с меньшим
интервалом корреляции (более шероховатая поверхность) обеспечит более низкий
УБЛ.
4. При повышении частоты увеличиваются как фазовые
ошибки (Δρ2π/λ, где Δρ -
неточность изготовления зеркала), так и интервал корреляции, выраженный в длинах волн. Поэтому КНД антенны с неизменной площадью
раскрыва увеличивается не пропорционально квадрату частоты, а медленнее. При данной точности выполнения поверхности зеркала
и данном интервале корреляции
существует предельный КНД, который нельзя превзойти уменьшением λ, или
увеличением диаметра зеркала.
5. Характер ДН в области боковых лепестков
определяется в большей степени точностью изготовления антенны, а не способом ее
облучения.
Влияние
отражений от зеркала на входное сопротивление антенны (реакция зеркала на
облучатель)
Часть, отраженных от зеркала, лучей на пути которых
находится облучатель, перехватывается последним (реакция зеркала). По отношению
к отраженным от зеркала волнам облучатель ведет себя как приемная антенна. В
основном, на облучатель воздействуют волны, отраженные вблизи вершины зеркала.
Очевидно, что чем больше КНД облучателя, тем большую мощность он перехватывает.
Перехваченная мощность создает в линии питания волну, идущую от облучателя к
генератору, аналогичную по действию обычной отраженной волне, возникающей в
линии вследствие ее рассогласования с нагрузкой. Появление в тракте отраженной от зеркала волны ухудшает согласование
антенны, так как эквивалентно изменению входного сопротивления антенны.
 Отраженную волну можно скомпенсировать с помощью какого-либо согласующего устройства, устанавливаемого у вершины зеркала (вспомогательное зеркало), либо в питающей
линии вблизи облучателя (ферритовый вентиль). Однако действие такого устройства
будет эффективным только на фиксированной частоте, поскольку с изменением
частоты (из-за изменения разности хода лучей) вновь появится отраженная волна.
Отраженную волну можно скомпенсировать с помощью какого-либо согласующего устройства, устанавливаемого у вершины зеркала (вспомогательное зеркало), либо в питающей
линии вблизи облучателя (ферритовый вентиль). Однако действие такого устройства
будет эффективным только на фиксированной частоте, поскольку с изменением
частоты (из-за изменения разности хода лучей) вновь появится отраженная волна.
 Если
антенна излучает поле вращающейся поляризации, то реакция зеркала на облучатель
будет практически отсутствовать. Дело в том, что при отражении от зеркала,
излучаемой облучателем, волны направление вращения плоскости поляризации
изменяется на обратное, вследствие чего она не принимается облучателем. Это
антенна с поляризационной развязкой.
Если
антенна излучает поле вращающейся поляризации, то реакция зеркала на облучатель
будет практически отсутствовать. Дело в том, что при отражении от зеркала,
излучаемой облучателем, волны направление вращения плоскости поляризации
изменяется на обратное, вследствие чего она не принимается облучателем. Это
антенна с поляризационной развязкой.
Удачным способом устранения реакции зеркала на
облучатель в широкой
полосе частот является применение невзаимных
устройств, например ферритовых
вентилей и циркуляторов. Они устанавливаются в волноводном тракте перед облучателем и, внося сравнительно
малые потери для прямой волны, на 20...25 дБ ослабляют отраженную волну.
Наиболее радикальный способ уменьшения реакции зеркала состоит в выносе
облучателя из поля отраженных от зеркала лучей. Для этого облучатель
устанавливают в фокусе зеркала (разворачивают) так, чтобы направление его
максимального излучения составило
некоторый угол с фокальной осью зеркала (рис.9.12). При
этом облучается только часть зеркала, расположенная выше его оси, и отраженные
от нее лучи проходят мимо облучателя. Необлучаемая часть зеркала удаляется
(осенесимметричная антенна).
Управление
ДН параболической антенны
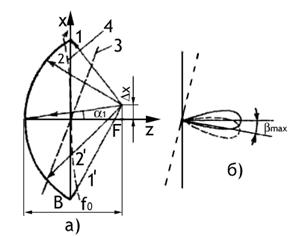 Если фазовый центр облучателя сместить из фокуса в направлении,
перпендикулярном оси зеркала (рис.9.13.a), то поверхность раскрыва зеркала перестанет
быть синфазной. Лучи 1 и 1’,2 и 2’, отраженные от поверхности зеркала,
достигают поверхности раскрыва неодновременно. Можно показать, что при
небольшом смещении облучателя Δx и
достаточно длиннофокусном зеркале фазовое распределение поверхности раскрыва
близко к линейному (3). Поэтому вынос облучателя из фокуса в направлении,
перпендикулярном оси зеркала, приводит
к повороту ДН в сторону, противоположную смещению облучателя. Угол поворота ДН θmах (рис.9.13.б) при малых смещениях облучателя
примерно равен углу смещения облучателя α1, определяемому по
формуле tgα1=Δx/f0. Синфазный фронт волны в раскрыве зеркала
поворачивается на угол α1. С увеличением Δх кроме
линейного изменения фазы появляются заметные фазовые ошибки более высоких
порядков, из которых наибольшую роль играют кубические (4). Знаки кубического и
линейного фазового распределений противоположны (рис.9.13.а). В этом случае ДН
поворачивается на угол, меньший, чем α1,
главный лепесток становится несимметричным относительно своего максимума и УБЛ
со стороны, противоположной смещению ДН, возрастает.
Если фазовый центр облучателя сместить из фокуса в направлении,
перпендикулярном оси зеркала (рис.9.13.a), то поверхность раскрыва зеркала перестанет
быть синфазной. Лучи 1 и 1’,2 и 2’, отраженные от поверхности зеркала,
достигают поверхности раскрыва неодновременно. Можно показать, что при
небольшом смещении облучателя Δx и
достаточно длиннофокусном зеркале фазовое распределение поверхности раскрыва
близко к линейному (3). Поэтому вынос облучателя из фокуса в направлении,
перпендикулярном оси зеркала, приводит
к повороту ДН в сторону, противоположную смещению облучателя. Угол поворота ДН θmах (рис.9.13.б) при малых смещениях облучателя
примерно равен углу смещения облучателя α1, определяемому по
формуле tgα1=Δx/f0. Синфазный фронт волны в раскрыве зеркала
поворачивается на угол α1. С увеличением Δх кроме
линейного изменения фазы появляются заметные фазовые ошибки более высоких
порядков, из которых наибольшую роль играют кубические (4). Знаки кубического и
линейного фазового распределений противоположны (рис.9.13.а). В этом случае ДН
поворачивается на угол, меньший, чем α1,
главный лепесток становится несимметричным относительно своего максимума и УБЛ
со стороны, противоположной смещению ДН, возрастает.
Смещение облучателя из фокуса используется в
антеннах систем спутниковой связи и в радиолокации для сопровождения цели (ИСЗ,
самолет и т.д.). Во избежание значительных искажений ДН из-за появления
кубической фазовой ошибки угол поворота ДН должен быть невелик и обычно не
может превышать нескольких значений ширины главного лепестка ДН (по половинной
мощности).
При смещении облучателя из
фокуса вдоль оси зеркала на поверхности раскрыва возникают квадратичные фазовые
искажения, симметричные относительно вершины зеркала, что расширяет главный
лепесток и увеличивает УБЛ ДН. При больших смещениях излучение в главном
направлении уменьшается и главный лепесток раздваивается. Чтобы фазовая ошибка
из-за смещения облучателя не превышала допустимого значения π/4, должно выполняться условие Δzдon < λ /[8(1 - cos γ0)].
ТЕМА 7. Антенны поверхностных волн. Устройство и принцип
действия диэлектрической антенны. Коэффициент замедления
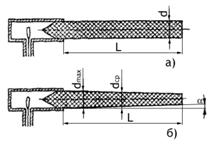 Диэлектрические
стержневые антенны,
Диэлектрические
стержневые антенны,
относящиеся к антеннам осевого излучения,
наиболее широко применяются в диапазоне
сантиметровых волн. Антенны представляют
собой диэлектрический стержень, выполненный
из высокочастотного диэлектрика с малыми
потерями (полистирол, тефлон и др.). Возбуждение обычно осуществляется отрезком
волновода прямоугольного или круглого
сечения (рис. 11.18). Структура поля в волноводе
соответствует волне основного типа - H10 (прямоугольный волновод) или H11 (круглый волновод).
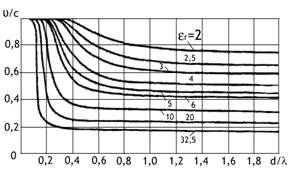 При бесконечной длине стержня указанный способ возбуждения приводит к возникновению в стержне как
в диэлектрическом волноводе бегущей волны гибридного типа НЕ11, имеющей продольные составляющие как магнитного, так и электрического поля. Структура поля этой
волны изображена на рис. 11.19.
При бесконечной длине стержня указанный способ возбуждения приводит к возникновению в стержне как
в диэлектрическом волноводе бегущей волны гибридного типа НЕ11, имеющей продольные составляющие как магнитного, так и электрического поля. Структура поля этой
волны изображена на рис. 11.19.
 Волна НЕ11 относится
к, так
Волна НЕ11 относится
к, так
называемым, поверхностным волнам,
поле которых при удалении от
поверхности стержня в радиальном
направлении убывает по закону,
близкому к экспоненциальному. Физически возникновение поверхностной волны объясняется эффектом полного
внутреннего отражения на границе раздела диэлектрик - воздух. Фазовая скорость волны υ зависит
от материала стержня. Чем больше диаметр стержня, тем ближе υ к скорости света в неограниченном
диэлектрике, т.е. к величине 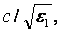 где ε1 - относительная
диэлектрическая проницаемость материала стержня. С уменьшением d величина
υ
где ε1 - относительная
диэлектрическая проницаемость материала стержня. С уменьшением d величина
υ  с, при этом волна слабо связана со стержнем.
Зависимость υ/c от ε1 и отношения d/λ приведена на рис.11.20. Особенностью волны НЕ11 в диэлектрическом волноводе
является отсутствие критической длины волны
с, при этом волна слабо связана со стержнем.
Зависимость υ/c от ε1 и отношения d/λ приведена на рис.11.20. Особенностью волны НЕ11 в диэлектрическом волноводе
является отсутствие критической длины волны
(λkp=∞),
т.е. волна может распространяться в стержне при любом его диаметре. Однако при
большом диаметре в стержне могут возбудиться волны высших типов, что нежелательно,
т.к. они искажают ДН.
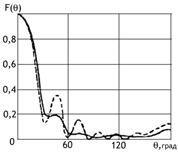 Отметим, что поверхностной волной НЕ11 передается только часть мощности (P1),
подведенной к возбуждающему волноводу. Остальная часть мощности (Р2)
непосредственно излучается возбудителем в окружающее пространство. Соотношение
между этими мощностями определяет эффективность возбудителя β = Р1
/(Р1 + Р2) .
Отметим, что поверхностной волной НЕ11 передается только часть мощности (P1),
подведенной к возбуждающему волноводу. Остальная часть мощности (Р2)
непосредственно излучается возбудителем в окружающее пространство. Соотношение
между этими мощностями определяет эффективность возбудителя β = Р1
/(Р1 + Р2) .
При конечной длине диэлектрического стержня можно
приближенно
полагать, что структура поля остается такой же, как в бесконечном
волноводе, однако обрыв стержня приводит к возникновению излучения.
Результирующая ДН антенны определяется взаимодействием излучения,
формируемого за счет конечности стержня, и непосредственного излучения
возбудителя. Сложный характер формирования ДН затрудняет оценку точного
положения фазового центра. В первом приближении считают, что он находится в
средней точке по длине стержня.
Приближенно можно
считать, что по направленным свойствам диэлектрическая антенна соответствует
непрерывной системе излучателей, возбуждаемых с равной амплитудой и линейным изменением фазы, характерным для
антенны бегущей волны. Роль излучателей
играют, так называемые, токи поляризации, плотность
которых определяется разностью диэлектрической проницаемости стержня и диэлектрической
проницаемости окружающей среды.
Как видно из рис.11.19, токи поляризации, соответствующие
волне НЕ11, имеют преимущественное направление, параллельное
оси х, и формируют линейно поляризованное поле излучения. Направленные
свойства каждого элементарного излучателя могут не учитываться в
приближенных расчетах основного лепестка результирующей ДН. Однако в области
первых боковых лепестков ДН излучающего элемента может оказать сильное влияние.
Отраженная
волна от конца стержня приводит к появлению в ДН дополнительных боковых
лепестков, соответствующих излучению антенны в обратную сторону. Коэффициент
отражения зависит от скорости υ волны в стержне. Для уменьшения отраженной волны стержню
придают коническую форму (рис 11.18.б); что приводит к постепенному росту
фазовой скорости υ и приближению ее к
скорости света с у конца стержня.
Уровень боковых лепестков у конической антенны получается меньше. На рис.11.21
приведены результаты точного расчета ДН двух антенн длиной L =
3,Зλ:
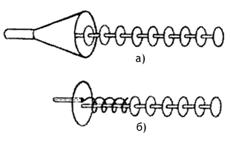 конического
стержня с максимальным диаметром dmax = 0,627λ и
углом α = 4° (сплошная линия) и цилиндрического
стержня с диаметром, равным среднему диаметру конического стержня (штриховая
линия). Диэлектрическая проницаемость в обоих случаях εr =2,5.
конического
стержня с максимальным диаметром dmax = 0,627λ и
углом α = 4° (сплошная линия) и цилиндрического
стержня с диаметром, равным среднему диаметру конического стержня (штриховая
линия). Диэлектрическая проницаемость в обоих случаях εr =2,5.
Диэлектрические антенны являются сравнительно широкополосными. Диапазон рабочих частот определяется, в
основном, свойствами возбуждающего волновода. Ширина ДН по уровню половинной
мощности одиночной диэлектрической антенны составляет обычно не менее 20...25°.
Применяются диэлектрические антенны как самостоятельные излучатели, облучатели
зеркал и элементы различных антенных решеток поперечного излучения.
Используются также ребристо-стержневые антенны, аналогичные
по своим свойствам диэлектрическим стержневым антеннам. Для получения
вращающейся поляризации возбуждение ребристо-стержневых антенн осуществляется
спиральным излучателем.
Рассмотрим три режима работы антенны бегущей
волны: 1) v = с; c/v = 1 (волна свободного пространства); 2) v > с; c/v < 1 (быстрая волна) и 3) v < с; c/v >1 (медленная волна).
1) c/v=l. В этом случае при  =0° множитель системы максимален и равен n. Нормированный множитель системы
=0° множитель системы максимален и равен n. Нормированный множитель системы
Fc (θ) = (1/n) sin [(kn /2)(l - cosθ)]/sin [(k
/2)(l - cosθ)]/sin [(k /2)(l - cosθ)]. (6.7)
/2)(l - cosθ)]. (6.7)
Результирующее поле максимально в направлении θ = 0° вследствие того, что поля от всех элементов антенны в точке наблюдения складываются
синфазно, так как сдвиг фаз из-за несинфазности возбуждения Ψ полностью
компенсируется пространственным сдвигом фаз Ψр. При увеличении
или уменьшении угла  (это же
относится и к углу θ) Ψ
(это же
относится и к углу θ) Ψ 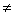 Ψр . Вследствие этого напряженность
результирующего поля в точке наблюдения, характеризуемой
Ψр . Вследствие этого напряженность
результирующего поля в точке наблюдения, характеризуемой
|
Рис.
6.1. ДН АБВ при C/V = 1
|
некоторым углом θ 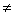 00, будет меньше, чем в точке, лежащей на продолжении оси антенны. Если cosθ отрицателен (90°<θ<270°), то фазовые сдвиги Ψ и Ψр при
00, будет меньше, чем в точке, лежащей на продолжении оси антенны. Если cosθ отрицателен (90°<θ<270°), то фазовые сдвиги Ψ и Ψр при  < λ/2
имеют одинаковые знаки. В этом
случае вибратор, возбуждающийся раньше,
находится ближе к точке наблюдения,
чем вибратор, возбуждающийся
позже
< λ/2
имеют одинаковые знаки. В этом
случае вибратор, возбуждающийся раньше,
находится ближе к точке наблюдения,
чем вибратор, возбуждающийся
позже
70
(пространственный сдвиг фаз отрицателен). Сдвиг фаз 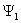 между полями соседних
вибраторов при малых
между полями соседних
вибраторов при малых  велик и результирующее поле в точке наблюдения мало. Следовательно, антенна бегущей волны обладает преимущественно
однонаправленными свойствами и излучает с максимальной интенсивностью вдоль своей оси (антенна с осевым излучением) (рис.6.1). На практике встречаются антенны бегущей волны, которые можно рассматривать как
непрерывное линейное распределение
слабонаправленных излучателей (например, диэлектрическая антенна). Без учета
затухания возбуждающего тока по длине антенны множитель
системы может быть получен из
выражения (6.7)
велик и результирующее поле в точке наблюдения мало. Следовательно, антенна бегущей волны обладает преимущественно
однонаправленными свойствами и излучает с максимальной интенсивностью вдоль своей оси (антенна с осевым излучением) (рис.6.1). На практике встречаются антенны бегущей волны, которые можно рассматривать как
непрерывное линейное распределение
слабонаправленных излучателей (например, диэлектрическая антенна). Без учета
затухания возбуждающего тока по длине антенны множитель
системы может быть получен из
выражения (6.7)
путем предельного перехода. Полагая n =>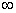 , d=>0, n
, d=>0, n =>L, получаем
=>L, получаем
Fc(θ) = sin[(kL/2)(l- cosθ)]/[(kL/2)(l-
cosθ)] . (6.8)
Уровень первого
бокового лепестка ξ1 =F(θ1mах)=2/3π 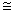 0,21 такой же,
как у синфазной решетки вибраторов. Ширину
диаграммы направленности по направлениям нулевого излучения найдем из условия (kL/2)(l-cosφ0) = π. При
0,21 такой же,
как у синфазной решетки вибраторов. Ширину
диаграммы направленности по направлениям нулевого излучения найдем из условия (kL/2)(l-cosφ0) = π. При
малых значениях λ/L (L - длина антенной решётки)
2θ0=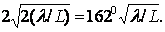 (6.9)
(6.9)
Ширина диаграммы направленности по половинной мощности может быть определена по приближенной формуле
2θ 0,5 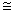 108°
108° . (6.10)
. (6.10)
Сравнивая данную
антенну с равномерной синфазной решеткой, следует отметить, что хотя диаграмма направленности АБВ получается шире, чем у синфазной решетки такой же длины, но зато один
ряд вибраторов, возбуждаемых бегущей волной тока, обладает направленными
свойствами в любой плоскости,
проходящей через ось антенны, в то время как один ряд синфазной решетки
обладает направленными свойствами только в одной плоскости. Если элементы АБВ не обладают направленным
действием или оно невелико, то
диаграмму направленности антенны можно считать осесимметричной. При этом КНД антенны бегущей волны можно определить
по общей формуле
D0= kL/ [Si2kL - (l - cos2kL)/(2kL)]. (6.11)
При 2kL » I (практически
при L/λ > 1) D0 4L /λ.
4L /λ.
2) c/v < I. На основании формулы (6.4), имея в виду, что при условии
cosθ = c/v, множитель системы максимален и
равен n (при этом условии
множитель системы обращается в неопределенность вида 0/0), и используя
предельный переход ( =>0, n=>
=>0, n=> , n
, n >L), получаем нормированную характеристику
направленности
>L), получаем нормированную характеристику
направленности
71
F(θ) = sin[(kL/2)( c/v - cosθ)]/[(kL/2)( c/v - cosθ)]. (6.12)
Условие cosθ = c/v может
выполняться при двух значениях угла θ = ± θ mах, следовательно, имеются два
направления максимального излучения, не совпадающие с осью антенны. Данный
режим работы является невыгодным, так как направленные свойства антенны
ухудшаются. Однако антенны быстрых волн находят применение для создания
диаграмм направленности специальной формы для качания (сканирования) диаграммы
направленности. Основой большинства антенн быстрых волн являются волноводные
структуры с неоднородностями (например, волновод со щелями).
3) c/v > 1. Как видно из выражений (6.1) и (6.2), в данном случае отсутствует направление, в котором поля отдельных элементов антенны складываются
синфазно, так как ни при каком значении θ отношение c/v не может стать равным cosθ и сдвиг фаз не может обратиться в нуль.
Наименьший фазовый сдвиг
между полями отдельных
вибраторов Ψ1min = kd1(c/v - 1) получается в направлении θ =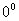 , т.е. вдоль оси антенны. Поля
отдельных вибраторов в точке наблюдения, лежащей в направлении θ =
, т.е. вдоль оси антенны. Поля
отдельных вибраторов в точке наблюдения, лежащей в направлении θ =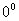 , в данном случае
складываются геометрически, как показано на временной векторной диаграмме
(рис.6.2). Расчеты по формулам (6.4) и (6.12) показывают, что уменьшение
фазовой скорости, начиная от v = c, сопровождается
постепенным сужением основного лепестка диаграммы направленности и ростом
боковых лепестков. Излучение в главном направлении θ =
, в данном случае
складываются геометрически, как показано на временной векторной диаграмме
(рис.6.2). Расчеты по формулам (6.4) и (6.12) показывают, что уменьшение
фазовой скорости, начиная от v = c, сопровождается
постепенным сужением основного лепестка диаграммы направленности и ростом
боковых лепестков. Излучение в главном направлении θ =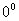 , сначала растет, достигая
максимума при некоторой определенной (для данного значения L =
, сначала растет, достигая
максимума при некоторой определенной (для данного значения L =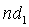 ) величине c/v, а затем начинает уменьшаться и обращается в нуль при критической величине c/v
) величине c/v, а затем начинает уменьшаться и обращается в нуль при критической величине c/v
(c/v)кр =
1+( /nd1). (6.13)
/nd1). (6.13)
Сужение главного лепестка диаграммы направленности приводит к росту КНД антенны, а увеличение уровня боковых лепестков - к его уменьшению. При увеличении c/v, начиная от c/v = 1,
сначала увеличивается КНД
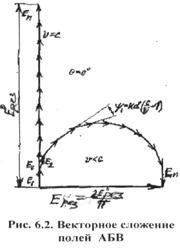 из-за сужения диаграммы направленности. После достижения некоторой
определенной величины c/v дальнейший ее рост приводит к уменьшению КНД из-за увеличения уровня боковых лепестков. Следовательно, имеется оптимальная величина c/v (при заданной длине антенны L), при которой КНД достигает максимального значения. В случае ненаправленных элементов антенны формула для КНД
оказывается весьма громоздкой. Ее анализ показывает, что КНД антенны бегущей
волны при заданной длине антенны зависит от величины результирующего сдвига фаз между полями, создаваемыми крайними (первым и
последним) элементами антенны в точке наблюдения, лежащей на продолжении ее оси (θ = 0°). КНД получается максимальным, если сдвиг фаз ψn, определяемый по
формуле (6.2), равен 180°, т.е. если поля, создаваемые
крайними элементами антенны бегущей волны в точке,
лежащей на продолжении оси антенны, находятся в противофазе (см. рис.6.2).
Таким образом, на основании формулы (6.2) условием получения
максимального КНД является
из-за сужения диаграммы направленности. После достижения некоторой
определенной величины c/v дальнейший ее рост приводит к уменьшению КНД из-за увеличения уровня боковых лепестков. Следовательно, имеется оптимальная величина c/v (при заданной длине антенны L), при которой КНД достигает максимального значения. В случае ненаправленных элементов антенны формула для КНД
оказывается весьма громоздкой. Ее анализ показывает, что КНД антенны бегущей
волны при заданной длине антенны зависит от величины результирующего сдвига фаз между полями, создаваемыми крайними (первым и
последним) элементами антенны в точке наблюдения, лежащей на продолжении ее оси (θ = 0°). КНД получается максимальным, если сдвиг фаз ψn, определяемый по
формуле (6.2), равен 180°, т.е. если поля, создаваемые
крайними элементами антенны бегущей волны в точке,
лежащей на продолжении оси антенны, находятся в противофазе (см. рис.6.2).
Таким образом, на основании формулы (6.2) условием получения
максимального КНД является
ψn опт. = kL(c/v - 1) = 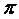 . (6.14)
. (6.14)
Воспользовавшись этой формулой, можно определить оптимальную величину c/v при заданной длине антенны L или определить оптимальную длину антенны при заданной фазовой скорости.
Очевидно, что:
(c/v)опт. 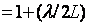 , (6.15)
, (6.15)
(L/ )опт. = 1/[2(c/v - 1)]. (6.16)
)опт. = 1/[2(c/v - 1)]. (6.16)
Как видно из формулы (6.14), оптимальная длина антенны увеличивается при
увеличении фазовой скорости. В случае выполнения условия
(6.14) КНД определяется по формуле
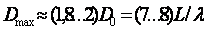 , (6.17)
, (6.17)
где D0 - КНД антенны бегущей волны данной длины при с/v =1. На рис.6.3
приведены графики зависимости отношения D/D0 от сдвига фаз между полями
крайних элементов антенны ψn, где D - КНД антенны определенной длины, работающей в режиме
замедления (v < с) или ускорения (v >c).
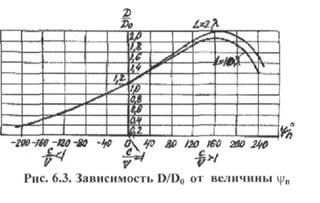 Как видно из векторной временной диаграммы (рис.6.2), в оптимальном случае (ψn = 180°) вектор напряженности результирующего поля в π/2 раз меньше, чем в
случае АБВ, работающей в первом режиме (приближенно можно считать, что вектор напряженности результирующего поля в оптимальном случае равен диаметру
окружности, половина длины которой равна вектору напряженности результирующего
поля при c/v = 1). Казалось бы, что КНД первой антенны должен быть меньше, чем
второй. Увеличение КНД антенны, работающей в режиме, близком к оптимальному,
объясняется тем что при оптимальном и близких к нему
Как видно из векторной временной диаграммы (рис.6.2), в оптимальном случае (ψn = 180°) вектор напряженности результирующего поля в π/2 раз меньше, чем в
случае АБВ, работающей в первом режиме (приближенно можно считать, что вектор напряженности результирующего поля в оптимальном случае равен диаметру
окружности, половина длины которой равна вектору напряженности результирующего
поля при c/v = 1). Казалось бы, что КНД первой антенны должен быть меньше, чем
второй. Увеличение КНД антенны, работающей в режиме, близком к оптимальному,
объясняется тем что при оптимальном и близких к нему
73
отношениях c/v токи в
элементах антенны из-за взаимного влияния возрастают. В
частности, при оптимальном отношении c/v ток в элементах антенны увеличивается
примерно в (π/2)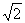 раз по сравнению с током в элементах антенны, работающей в
режиме c/v = 1 (при неизменной излучаемой мощности). Это приводит к увеличению
напряженности поля, излучаемого каждым элементом антенны. Приведенные здесь
соотношения, характеризующие оптимальный
режим работы АБВ, справедливы только для ненаправленных или слабонаправленных
элементов антенны. При наличии у элементов антенны значительных
направленных свойств эти соотношения
изменяются. Ширина диаграммы направленности по нулевому излучению антенны, работающей в оптимальном режиме, на
основании формулы (6.12) находится из
условия (kL/2)(c/v - cos
раз по сравнению с током в элементах антенны, работающей в
режиме c/v = 1 (при неизменной излучаемой мощности). Это приводит к увеличению
напряженности поля, излучаемого каждым элементом антенны. Приведенные здесь
соотношения, характеризующие оптимальный
режим работы АБВ, справедливы только для ненаправленных или слабонаправленных
элементов антенны. При наличии у элементов антенны значительных
направленных свойств эти соотношения
изменяются. Ширина диаграммы направленности по нулевому излучению антенны, работающей в оптимальном режиме, на
основании формулы (6.12) находится из
условия (kL/2)(c/v - cos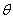 0)= π. Подставляя вместо c/v выражение (6.15) и проводя рассуждения, аналогичные случаю c/v = 1, получаем sinθ0
=
0)= π. Подставляя вместо c/v выражение (6.15) и проводя рассуждения, аналогичные случаю c/v = 1, получаем sinθ0
=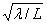 . При малых отношениях λ/L синус можно
заменить аргументом. Тогда
. При малых отношениях λ/L синус можно
заменить аргументом. Тогда
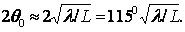 (6.18)
(6.18)
и, как видно
из сравнения формул (6.9) и (6.18), в этом случае АБВ с пониженной фазовой скоростью (оптимальной) имеет диаграмму направленности в 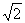 раз уже, чем антенна той же длины с c/v = 1. Ширина диаграммы направленности
по половинной мощности может быть приближенно определена
(для антенны, у которой L/λ »1) по
раз уже, чем антенна той же длины с c/v = 1. Ширина диаграммы направленности
по половинной мощности может быть приближенно определена
(для антенны, у которой L/λ »1) по
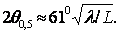 формуле:
формуле:
(6.19)
Сужение диаграммы направленности антенны оптимальной
длины по сравнению с диаграммой направленности антенны такой же длины, но
работающей в первом режиме (c/v = 1),
объясняется тем, что при увеличении угла φ напряженность результирующего поля в случае c/v >1 убывает значительно быстрее, чем в
случае c/v = 1. Это происходит потому, что в случае антенны оптимальной длины сдвиги фаз между полями соседних вибраторов в точке наблюдения, определяемой углом θ1 [при этом 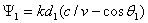 ], больше, чем в случае антенны с c/v = 1 [при
этом
], больше, чем в случае антенны с c/v = 1 [при
этом 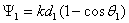 ].
].
Тема 8. Особенности построения антенн УВЧ и СВЧ
диапазонов. Синтез антенных систем и перспективы развития антенной техники
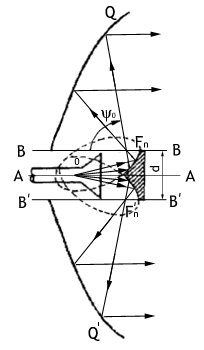 На
рис. изображена двухзеркальная симметричная антенна со смещенной фокальной осью
(АДЭ - антенна двухзеркальная со смещенной фокальной осью и с эллиптической
образующей малого зеркала), в которой эффект затенения отсутствует. В схеме
такой антенны фокальная ось параболы, являющаяся образующей основного зеркала,
не совпадает с осью симметрии. Фазовый центр 0 рупора, излучающего сферическую
волну, расположен на оси симметрии антенны АА. Фокальная ось ВВ параболы BQ с фокусом в точке Fn смещена параллельно оси АА на
расстояние d/2. Симметричная парабола B'Q' с фокусом в
точке F'n также смещена от оси симметрии на d/2. В пространстве фокусы параболы располагаются на фокальном кольце с
диаметром d. Фокус параболы Fn и фазовый центр рупора 0
выбираются в качестве фокусов эллипса. Вращением отрезка этого эллипса вокруг
оси симметрии АА образована поверхность малого зеркала. Рассмотрим ход лучей в
антенне. Лучи рупора, являющегося источником сферической волны, падая на
поверхность малого зеркала, собираются в фокусах Fn и F'n. Эти точки могут быть представлены как точечные источники (в плоскости
рисунка), облучающие параболы BQ и B'Q'. Следовательно, в раскрыве большого зеркала образуется синфазный
волновой фронт с направлением распространения, совпадающим с осью симметрии.
Чтобы исключить возврат части лучей в рупор после их отражения от малого
зеркала, размер его раскрыва следует ограничить диаметром d. В этом случае параболоид полностью освещается полем, отраженным от
малого зеркала, от начального значения угла ψ = 0 ° до
предельного угла раскрыва ψ = ψ0. Данная антенна по сравнению с обычными двухзеркальными антеннами
обладает рядом преимуществ:
На
рис. изображена двухзеркальная симметричная антенна со смещенной фокальной осью
(АДЭ - антенна двухзеркальная со смещенной фокальной осью и с эллиптической
образующей малого зеркала), в которой эффект затенения отсутствует. В схеме
такой антенны фокальная ось параболы, являющаяся образующей основного зеркала,
не совпадает с осью симметрии. Фазовый центр 0 рупора, излучающего сферическую
волну, расположен на оси симметрии антенны АА. Фокальная ось ВВ параболы BQ с фокусом в точке Fn смещена параллельно оси АА на
расстояние d/2. Симметричная парабола B'Q' с фокусом в
точке F'n также смещена от оси симметрии на d/2. В пространстве фокусы параболы располагаются на фокальном кольце с
диаметром d. Фокус параболы Fn и фазовый центр рупора 0
выбираются в качестве фокусов эллипса. Вращением отрезка этого эллипса вокруг
оси симметрии АА образована поверхность малого зеркала. Рассмотрим ход лучей в
антенне. Лучи рупора, являющегося источником сферической волны, падая на
поверхность малого зеркала, собираются в фокусах Fn и F'n. Эти точки могут быть представлены как точечные источники (в плоскости
рисунка), облучающие параболы BQ и B'Q'. Следовательно, в раскрыве большого зеркала образуется синфазный
волновой фронт с направлением распространения, совпадающим с осью симметрии.
Чтобы исключить возврат части лучей в рупор после их отражения от малого
зеркала, размер его раскрыва следует ограничить диаметром d. В этом случае параболоид полностью освещается полем, отраженным от
малого зеркала, от начального значения угла ψ = 0 ° до
предельного угла раскрыва ψ = ψ0. Данная антенна по сравнению с обычными двухзеркальными антеннами
обладает рядом преимуществ:
1)
наличие конического острия на
малом зеркале значительно ослабляет реакцию зеркала на облучатель и улучшает
согласование антенны;
2)
появляется возможность
существенно сократить расстояние между
облучателем и малым зеркалом и тем самым уменьшить утечку энергии за
это зеркало и упростить его крепление;
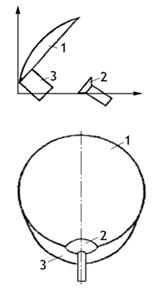 3) вследствие того, что
лучи, идущие через область центра раскрыва облучателя (которым соответствует
наибольшая плотность энергии), переизлучаются малым зеркалом на периферию
параболоида, а лучи, отраженные от точек, находящихся вблизи краев
вспомогательного зеркала (им соответствует меньшая плотность энергии),
попадают на участки поверхности параболоида, близкие к его вершине,
обеспечивается большая равномерность амплитудного распределения поля в
раскрыве антенны (более высокий апертурный КИП).
3) вследствие того, что
лучи, идущие через область центра раскрыва облучателя (которым соответствует
наибольшая плотность энергии), переизлучаются малым зеркалом на периферию
параболоида, а лучи, отраженные от точек, находящихся вблизи краев
вспомогательного зеркала (им соответствует меньшая плотность энергии),
попадают на участки поверхности параболоида, близкие к его вершине,
обеспечивается большая равномерность амплитудного распределения поля в
раскрыве антенны (более высокий апертурный КИП).
В последнее
время значительно повысился интерес к антеннам с вынесенным облучателем (АВО).
Однозеркальная АВО (рис.13.9) содержит: отражающее зеркало 1, представляющее
собой вырезку из параболоида вращения цилиндром, ось которого смещена на
некоторое расстояние относительно фокальной оси исходного параболоида;
облучатель 2, в качестве которого используется расфазированный рупор с изломом
образующей, поворотом оси и косым срезом раскрыва (РРИП) (рис.13.10); экран 3,
увеличивающий ее КЗД. Оси малого 1 и основного 2 элементов рупора (см.
рис.13.10) развернуты на некоторый угол γ. Так как при этом углы α1 и α2 оказываются различными, то вершина главного лепестка ДН рупора становится
неосесимметричной. В перпендикулярной плоскости углы, аналогичные углам α1 и α2, остаются равными, а ДН симметричной. Срезав раскрыв основного рупора,
не перпендикулярного его оси, можно устранить различную расфазировку поля в
точках В и В', лежащих на границах раскрыва. Облучатель типа РРИП обеспечивает
симметричное по главным осям возбуждение апертуры неосесимметричной антенны
при очень малом УБЛ. Среди существующих антенн наименьшим боковым излучением
(наилучшей помехозащищенностью) обладают рупорно-параболические антенны (РПА).
Такая антенна состоит из питаемого волноводом
пирамидального или конического рупора и непосредственно присоединенного к нему
зеркала, являющегося частью параболоида вращения (рис.13.11.а). Фокус
параболоида F совпадает с фазовым центром рупора, находящимся у вершины последнего.
Электромагнитные волны, исходя из рупора, отражаются от параболического
зеркала (рис.13.11.б). Фронт отраженной от зеркала волны близок к плоскому, и
поверхность раскрыва зеркала (поверхность АВ) является синфазной. В такой
системе почти вся электромагнитная энергия облучателя попадает на зеркало, что
резко уменьшает задние лепестки ДН. Облучатель (рупор) не затеняет поверхность
зеркала, что приводит к уменьшению УБЛ. Так как отраженная от зеркала энергия
не попадает в рупор, то отсутствует реакция зеркала на облучатель. При
использовании достаточно длинных рупоров, присоединяемых к волноводу с помощью
плавных переходов, высокое согласование рупора и волновода обеспечивается в
двухкратном диапазоне частот. В этом диапазоне может быть получен КБВ, равный,
примерно 0,98. Коэффициент защитного действия РПА равен примерно -(65...70) дБ,
КИП - около 0,65...0,75, коэффициент поперечной поляризации поля антенны в
главном направлении составляет -(36...42) дБ. Обычно углы раствора рупора в
плоскостях Е и Н выбираются в пределах 30...50°, а площадь раскрыва несимметричного
параболоида (площадь апертуры антенны) составляет 5...15м2. Антенна
может быть использована одновременно для приема и передачи радиоволн с взаимно
перпендикулярной поляризацией, а также для излучения и приема радиоволн с
круговой поляризацией (при соответствующих схемах возбуждения и приема).
Недостатками РПА являются значительные габаритные размеры (вертикальный
размер) и соответственно большая масса. Однако существует ряд модификаций РПА
с уменьшенными габаритными размерами конструкции. Это, например, РПА с
инверсированным рупорным облучателем, трижды сложенная РПА и другие.
На РРЛ применяются также перископические антенные системы (рис.13.12),
особенностью которых является отсутствие длинного фидера (в описанных ниже
схемах длина фидера достигает 100 м). В перископической антенной системе
энергия передается с помощью беспроводной линии передачи, состоящей из нижнего
зеркала с облучателем (излучателя), установленного у основания мачты, и
верхнего зеркала (переизлучателя). Излучателями могут
быть несимметричные, выполненные по схеме АВО, или эллипсоидальные
зеркальные антенны. В перископической антенне, выполненной по так называемой
трехэлементной схеме (см. рис.13.12), облучатель нижнего зеркала (например,
рупор с изломом) устанавливается непосредственно в техническом здании. В
качестве переизлучателя обычно применяется плоское зеркало. Излучатель и
переизлучатель так ориентируются относительно друг друга, что волны, излученные
нижним зеркалом, «перехватываются» верхним и переизлучаются в направлении на
соседний ретрансляционный пункт. Фокусирующее действие нижнего зеркала сужает
поток энергии, распространяющийся от него к верхнему зеркалу. Это приводит к
увеличению КПД передачи энергии от нижнего зеркала к верхнему (отношение мощности,
принятой переизлучателем, к мощности, излученной нижним зеркалом). Однако
часть энергии все же переливается через края верхнего зеркала. Выгоднее
использовать верхний плоский переизлучатель не с прямоугольным, а с
эллиптическим контуром обреза, имеющим в плоскости, перпендикулярной
распространению волны, круглую поверхность раскрыва, так как при этом
увеличивается КПД беспроводной линии передачи и уменьшается УБЛ ДН верхнего
зеркала.
Антенно-фидерные устройства базовых станций мобильной связи
Штыревые антенны, вследствие
относительно небольшого усиления, целесообразно
применять на временных или передвижных базовых станциях, благодаря небольшим габаритам и весу. В качестве
примера приведём приёмопередающую
штыревую антенну для передвижных базовых станций и центральных ретрансляторов транкинговых сетей.
Конструкция такой антенны показана на рис.14.1. Она содержит несимметричный
вибратор (штырь), противовес, выполненный из четырех равномерно ориентированных
по азимуту проводников, шунт, совмещённый с одним из проводников противовеса, и опору, внутри которой проходит, возбуждающий
антенну, коаксиальный фидер. В
верхней точке опоры центральный проводник фидера подключается к вибратору, а его экран к опоре. Проводники
противовеса электрически соединены с опорой в верхней её точке и
имитируют "землю" для вибратора.
Токи в проводниках текут радиально в разных направлениях (допустим к
вибратору), и при горизонтальном их расположении противовес практически не
излучает, определяя главным образом, ближнее поле и входной импеданс антенны.
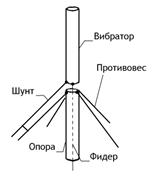 При наклонном положении проводников противовеса, как показано
на рис. 14.1, горизонтальные составляющие текущих в них токов по-прежнему направлены в противоположные
стороны, т.е. паразитное излучение горизонтально поляризованной волны отсутствует. Между тем, вертикальные
составляющие токов сонаправлены, вследствие чего противовес излучает
вертикально поляризованную волну, что несколько увеличивает КНД антенны.
При наклонном положении проводников противовеса, как показано
на рис. 14.1, горизонтальные составляющие текущих в них токов по-прежнему направлены в противоположные
стороны, т.е. паразитное излучение горизонтально поляризованной волны отсутствует. Между тем, вертикальные
составляющие токов сонаправлены, вследствие чего противовес излучает
вертикально поляризованную волну, что несколько увеличивает КНД антенны.
Шунт представляет собой
проводник, расположенный параллельно одному из проводников противовеса на
небольшом расстоянии от
него (малом по сравнению с длиной волны). В верхней точке шунт электрически соединён
с вибратором (вблизи его точки питания), в нижней - с проводником противовеса.
При этом шунт совместно с последним образует короткозамкнутый шлейф,
подключенный параллельно вибратору. Такой шлейф служит для двухдиапазонного
согласования. Вибратор без шлейфа целесообразно настраивать на частотах
передачи, обеспечивая шлейфом вторую полосу согласования на частотах приёма.
Кроме того шлейф обеспечивает грозозащиту антенны.
Удлинённый дросселем штырь (рис.14.2)
имеет большее усиление. Дроссель в основании штыря служит для согласования. Вместе с ним
входное сопротивление антенны получается около 50 Ом, что удобно для согласования с кабелем. Для своей установки
антенна требует плоскую металлическую поверхность или систему противовесов. Антенна относительно
узкополосная.
Дискоконусная антенна (см. лекцию
10) применяется, когда требуется весьма широкая
полоса. У антенн для дециметрового диапазона диск и конус выполняются сплошными, для метрового диапазона -
из стержней, расположенных по
радиусам у диска и по образующим у конуса.
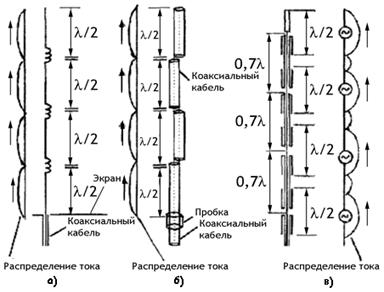
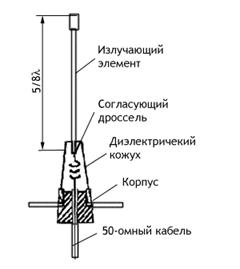 Коллинеарная антенна. Одним из эффективных путей реализации
антенны вертикальной поляризации с высокой направленностью состоит в том, чтобы
формировать линейную антенную решетку,
в которой
Коллинеарная антенна. Одним из эффективных путей реализации
антенны вертикальной поляризации с высокой направленностью состоит в том, чтобы
формировать линейную антенную решетку,
в которой
комбинируется несколько синфазных коллинеарных излучающих элементов.
На рис. 14.3 изображены типичные конструкции коллинеарных антенн с графическими
пояснениями их работы. В антенне на рис.14.3.а между полуволновыми излучающими элементами для обеспечения синфазного питания
включены катушки индуктивности. Этот тип
антенны называется нагруженной антенной и часто используется как автомобильная
антенна. Антенны, показанные на рис.14.3.б,в,
обычно известны как коаксиальные коллинеарные антенны. Эти антенны
используются как автомобильные антенны, так и как антенны базовых станций.
Синфазность питания антенн, показанных на рис.14.3.б,в, зависит от длины
излучающих элементов и расстояния между ними, поэтому эти антенны узкополосные.
На рис.14.4 показаны варианты реализации антенны Маркони
- Франклина. Катушки на рис.14.4.а и
участки линий на рис.14.4.б имеют электрическую
длину в полволны; в этих катушках и участках токи имеют противоположное
направление, но они не излучают. На остальных излучающих участках антенны токи синфазны.
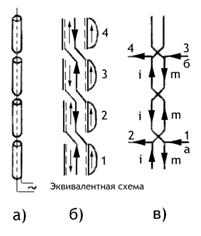
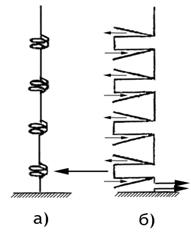
Рис.14.5 поясняет конструкцию и
принцип работы антенны из отрезков коаксиальной
линии с перекрещиванием. Внешние и внутренние проводники полуволновых отрезков соединены перекрестно.
Внутренний проводник и внутренняя поверхность трубы служат линией питания, к
которой в точках а и б подключаются
излучающие вибраторы в виде внешних поверхностей трубы 1 и 2 или 3 и 4. У основания эта
антенна должна питаться симметрично, иначе половина вибраторов получит потенциал земли, и не будет излучать. На рис.14.6 показан вариант
такой антенны, отличающийся большой технологичностью в производстве. Как и все
современные антенны, эта антенна заключена в диэлектрический (обычно стеклопластиковый) корпус, защищающий от климатических
воздействий и являющийся опорной
конструкцией.
На рис.14.3.в был
представлен еще один вариант коллинеарной антенны. Источниками питания симметричных
вибраторов здесь являются щели во внешнем проводнике коаксиала. Препятствием
проникновения токов на внешнюю поверхность внешнего проводника коаксиала
являются четвертьволновые стаканы, из которых состоят вибраторы -
сопротивление этих стаканов на открытом конце весьма велико и ток не попадает
внутрь стакана.
У антенн, запитываемых с одного конца, каковыми являются
все рассмотренные выше коллинеарные антенны,
ток по мере приближения к другому концу антенны, спадает из-за затухания,
обусловленного излучением, особенно у антенн с относительно большими
поперечными сечениями.
Ниже приведены типичные характеристики
современных коллинеарных антенн: полоса рабочих частот по уровню КСВ =1,5 для приёмной антенны 820...855 МГц, для передающей 860...895 МГц, коэффициент
усиления относительно
полуволнового вибратора 9 дБ, ширина ДН в вертикальной плоскости по уровню половинной мощности - 7°,
поляризация вертикальная, входная мощность до 0,5 кВт, вес 9 кг, высота
3470 мм, диаметр 71...58 мм (сужается к верхнему концу). Другой пример: антенна
450...470 МГц, входная мощность 0,5
кВт, усиление 4 дБ, ширина ДН 18°, масса 8 кг, высота 2430 мм, диаметр 73 мм. На рис.14.7 приведена ДН такой
антенны.
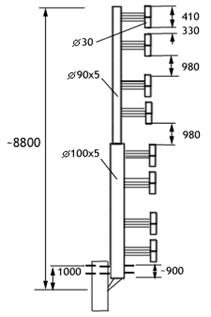
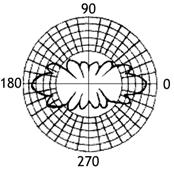 По своим электрическим характеристикам коллинеарные антенны во многом
уступают многовходовым ан-тенным системам с кольцевыми решетками.
По своим электрическим характеристикам коллинеарные антенны во многом
уступают многовходовым ан-тенным системам с кольцевыми решетками.
В качестве антенн
базовых станций
применяются линейные
антенные решетки

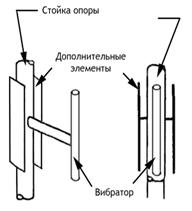 поперечного излучения с параллельным питанием вибраторов. Диапазон, изображённой на рисунке 14.8, антенны -
300 МГц.
Построить антенну указанной длины на основе несущего диэлектрического кожуха не
удалось бы. Вместе с тем металлическая стойка влияет на ДН антенны в горизонтальной плоскости
(неравномерности ДН около 6дБ). Улучшить равномерность
ДН можно введением удлиненных (длина несколько меньше половины длины волны)
металлических элементов, размещаемых симметрично по объему сторонами стойки
опоры. На рис.14.9 изображен один этаж такой антенны.
поперечного излучения с параллельным питанием вибраторов. Диапазон, изображённой на рисунке 14.8, антенны -
300 МГц.
Построить антенну указанной длины на основе несущего диэлектрического кожуха не
удалось бы. Вместе с тем металлическая стойка влияет на ДН антенны в горизонтальной плоскости
(неравномерности ДН около 6дБ). Улучшить равномерность
ДН можно введением удлиненных (длина несколько меньше половины длины волны)
металлических элементов, размещаемых симметрично по объему сторонами стойки
опоры. На рис.14.9 изображен один этаж такой антенны.
В современных сотовых системах связи применяются,
в основном, секторные антенны из-за преимуществ при
повторении частот. Получить секторную ДН в горизонтальной
плоскости можно, например, используя симметричный
полуволновый вибратор с уголковым рефлектором (см. лекцию 9).
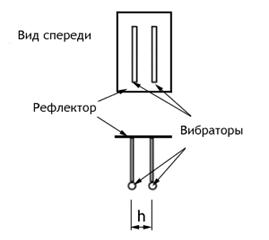 Другой пример получения секторных ДН использование антенной решетки из параллельных вибраторов в каждом этаже. При этом, чем больше горизонтальный размер решётки, тем уже ДН в горизонтальной плоскости. Так, у антенны на рис.14.10 ДН будет тем уже, чем
больше размер h. В разных типах секторных антенн применяются и тот и другой способы, а также некоторые другие, например, используя
рефлектор в виде параболического цилиндра. Для увеличения КУ (сужения ДН в
вертикальной плоскости) увеличивается число этажей.
Другой пример получения секторных ДН использование антенной решетки из параллельных вибраторов в каждом этаже. При этом, чем больше горизонтальный размер решётки, тем уже ДН в горизонтальной плоскости. Так, у антенны на рис.14.10 ДН будет тем уже, чем
больше размер h. В разных типах секторных антенн применяются и тот и другой способы, а также некоторые другие, например, используя
рефлектор в виде параболического цилиндра. Для увеличения КУ (сужения ДН в
вертикальной плоскости) увеличивается число этажей.
Для наклона ДН, требующегося для уменьшения помех другим сотам
создаётся необходимое распределение фазы между этажами за счёт разности длин распределённых фидеров (электрический способ), или наклоняется сама антенна (механический способ).
В качестве секторных антенн также
используется плоская синфазная ЛПА с рефлектором (см. лекцию 11).
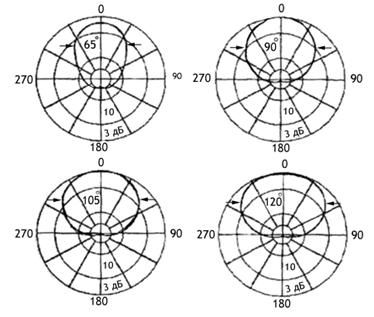
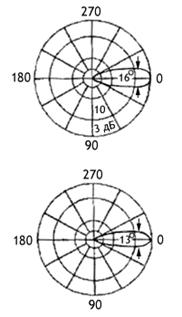 В качестве примера приведём характеристики
некоторых из антенн, применяемых для системы GSM: диапазон 870...960 МГц, входная мощность до 800 Вт, КСВ не более
1,3, поляризация вертикальная. ДН в вертикальной плоскости для различных
вариантов исполнения антенны приведены на рис.14.11, а в горизонтальной плоскости на рис.14.12. Размеры
антенн 1074
В качестве примера приведём характеристики
некоторых из антенн, применяемых для системы GSM: диапазон 870...960 МГц, входная мощность до 800 Вт, КСВ не более
1,3, поляризация вертикальная. ДН в вертикальной плоскости для различных
вариантов исполнения антенны приведены на рис.14.11, а в горизонтальной плоскости на рис.14.12. Размеры
антенн 1074 279
279 113 мм и
113 мм и
1290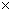 279
279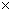 113 мм, масса 8 и 9,3 кг. Усиление относительно изотропного излучателя 15; 13,8;
13,2; 12,8; 16; 14,7; 14; 13,7 дБ; КЗД от 30 до 20 дБ. Антенны защищены от климатических
воздействий диэлектрическим кожухом.
113 мм, масса 8 и 9,3 кг. Усиление относительно изотропного излучателя 15; 13,8;
13,2; 12,8; 16; 14,7; 14; 13,7 дБ; КЗД от 30 до 20 дБ. Антенны защищены от климатических
воздействий диэлектрическим кожухом.
Другой пример - характеристики одной
из антенн для системы AMPS: полоса частот 790…960 МГц, входная мощность до 500 Вт,
КСВ в полосе не хуже 1,5,
коэффициент усиления 16,1 дБ, ширина ДН по уровню половинной мощности в горизонтальной плоскости 60°, в
вертикальной плоскости - 14°. Габариты 300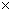 130
130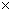 1250 мм, масса 6,5 кг. Антенна защищена кожухом из
стеклопластика. Конструкция крепления антенны обеспечивает наклон в вертикальной плоскости 0°... 10°.
1250 мм, масса 6,5 кг. Антенна защищена кожухом из
стеклопластика. Конструкция крепления антенны обеспечивает наклон в вертикальной плоскости 0°... 10°.
Многовходовые приёмно-передающие антенны
Базовые станции систем радиосвязи с
подвижными объектами должны обеспечивать одновременную работу большого числа
каналов, причём канальная ёмкость
системы является одной из основных её характеристик. При этом возникает задача обеспечения независимой
одновременной работы нескольких
приёмников и передатчиков. В зависимости от способа объединения приёмников и передатчиков в составе базовых
станций используются либо
одновходовые антенны, либо многовходовые
(антенные решетки).
Одновременная независимая работа N приёмников достаточно просто
обеспечивается применением специальных (2N +2) - полюсных устройств -разветвителей
сигнала. Такое устройство имеет один вход и N развязанных выходов
(развязка необходима для обеспечения независимой работы) и часто конструктивно совмещается с антенным усилителем,
компенсирующим ослабление сигнала вследствие его разделения. Понятно,
что при таком способе объединения может
использоваться одновходовая антенна.
Обеспечение одновременной независимой работы, нескольких
пере-датчиков представляет собой более сложную проблему. Применяются следующие
основные способы сложения сигналов передатчиков с обеспечением развязки между
ними: пространственное; с частотным разделением (частотное уплотнение); схемное
(мостовое) и схемно-пространственное.
Пространственное
сложение обеспечивается применением
антенной решетки - многовходовой системы
слабо связанных излучателей, каждый из которых
возбуждается одним определенным передатчиком. Передатчики считаются
работающими независимо, однако в реальной решетке вследствие электромагнитной
связи между излучателями, во-первых, возникают существенные ограничения на
реализуемую развязку, во-вторых, в той или иной степени искажается ДН. Место и
способ размещения решетки при всенаправленном
излучении (что, как правило, требуется в подвижной связи) должны
исключать затенение излучателей местными предметами и элементами конструкции.
Все это существенно ограничивает возможности применения пространственного сложения в системах связи с подвижными объектами.
Частотное
уплотнение тракта посредством сложения
некогерентных сигналов в общем фидере
(одновходовая антенна) с помощью частотно-избирательных устройств целесообразно применять при относительно больших разносах складываемых (разделяемых) сигналов,
например при сложении сигналов
различных диапазонов, а также разделения сигналов приёма и передачи (для
обеспечения дуплексной связи). При малых разносах частот вследствие
необходимости обеспечения высокой избирательности фильтров резко ухудшаются их массогабаритные и стоимостные
показатели. По этой причине, а также
из-за необходимости закрепления передатчиков за определенными частотными полосами сложение сигналов на
основе частотного разделения в
пределах одного диапазона применяется крайне редко.
Схемный способ сложения сигналов
также позволяет использовать одновходовую антенну и предполагает сложение
нескольких некогерентных сигналов в общем фидере с помощью мостовых устройств.
КПД мостового сложения некогерентных сигналов весьма низок.
Схемно-пространственный способ объединения
передатчиков (схемно-пространственная мультиплексия) представляет собой
сочетание методов пространственного и схемного сложения. Сигналы передатчиков поступают на многополюсное распределяющее
устройство - диаграммообразующую схему (ДОС), которое возбуждает многовходовую
антенную решетку. На входы антенны подаются аддитивные смеси сигналов передатчиков, а окончательное объединение сигналов
происходит в пространстве.
Схемный и схемно-пространственный способы сложения сигналов
свободны от серьёзных недостатков,
свойственных остальным способам: ограничений по размещению антенны
(пространственные сложение); ограничений по частотному разносу и
закреплению частотных полос за передатчиком (частотное
уплотнение). Это обусловило их широкое применение в подвижной связи. Следует
отметить, что эти способы сложения могут сочетаться.
Неизбежность весьма больших потерь в
балластных нагрузках является серьёзным недостатком мостового сложения по
сравнению со схемно-пространственным. Весьма широкое его применение в
зарубежных разработках,
по-видимому, обусловлено возможностью использования простых одновходовых антенн. Схемно-пространственный способ
сложения сочетает достоинства
мостового (отсутствие сколько-нибудь значительных ограничений по условиям размещения
антенны) и пространственного (относительно малые потери) способов и поэтому является наиболее перспективным (в частности,
- основным при совместном использовании с мостовым). Поскольку в подвижной связи требуется, как правило,
всенаправленное излучение (приём) в горизонтальной плоскости, наибольшее
применение в качестве многовходовых антенн, обеспечивающих
схемно-пространственное сложение, нашли кольцевые антенные решётки (КАР). КАР
представляет собой систему излучателей,
расположенных по окружности (рис.14.13).
Такая система может
дать как остро
направленную, так и
воронкообразную ДН. Для решёток с равномерно размещенными
по кольцу и возбуждаемыми с одинаковой амплитудой
излучателями имеем In=I0exp(iψn). Тогда характеристика направленности
f(θ,φ)=exp[ika sinθ cos(φ - φn) - iψn] (14.1)
где In и ψn-ток и
фаза питания n-ого излучателя соответственно; φn - его
азимут; а - радиус кольца.
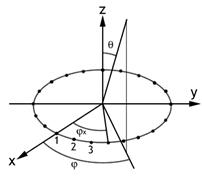 Для того, чтобы в направлении θгл, φгл поля от всех элементов складывались в фазе,
необходимо
выполнить условие
Для того, чтобы в направлении θгл, φгл поля от всех элементов складывались в фазе,
необходимо
выполнить условие
ψn= k a sin θ гл соs( φ гл -
φ ).
Это выражение показывает, что для получения
направленного излучения распределение фаз по кольцу должно быть симметрично относительно диаметра φ=φгл и антисимметрично относительно диаметра φ=φгл + π/2. В таком виде кольцевая решетка эквивалентна линейной, расположенной по диаметру φ = φгл и обладающей линейным фазовым
распределением. Максимальная разность фаз (между токами крайних элементов) для
заданного угла θ гл определяется
Δφ max = 2ka sin θ гл.
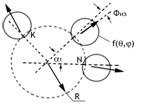 КАР
(рис.14.14) представляет собой систему N излучателей,
обладающих симметрией поворота. Если известна
ДН излучателя f(θ,φ), определенная относительно
его условного центра в присутствии остальных излучателей, то КАР с точки зрения
ДН в горизонтальной плоскости полностью характеризуется радиусом rkap и ориентирующим азимутом излучателя Физ - углом поворота
максимума ДН излучателя относительно
радиального (нормального) направления, как показано на
рис.14.14 (азимут центра - k-гo излучателя αk= 2πk/N). Неравномерность
ДН КАР в горизонтальной
плоскости, в основном, обусловлена интерференцией в дальней зоне полей
отдельных излучателей. Можно показать, что в этом
смысле наилучшей является ориентация
при Физ=±π/2 (тангенциальная ориентация), наихудшей - при Физ = 0° (нормальная ориентация).
КАР
(рис.14.14) представляет собой систему N излучателей,
обладающих симметрией поворота. Если известна
ДН излучателя f(θ,φ), определенная относительно
его условного центра в присутствии остальных излучателей, то КАР с точки зрения
ДН в горизонтальной плоскости полностью характеризуется радиусом rkap и ориентирующим азимутом излучателя Физ - углом поворота
максимума ДН излучателя относительно
радиального (нормального) направления, как показано на
рис.14.14 (азимут центра - k-гo излучателя αk= 2πk/N). Неравномерность
ДН КАР в горизонтальной
плоскости, в основном, обусловлена интерференцией в дальней зоне полей
отдельных излучателей. Можно показать, что в этом
смысле наилучшей является ориентация
при Физ=±π/2 (тангенциальная ориентация), наихудшей - при Физ = 0° (нормальная ориентация).
Тангенциальная ориентация позволяет увеличить расстояние между излучателями и за счёт ослабления связи между
ними, снизить потери на отражение.
Однако практическая реализация КАР данного типа встречает ряд серьёзных
трудностей, обусловленных, прежде всего взаимным затенением излучателей.
Практика показывает, что КАР с тангенциальной ориентацией могут применяться при числе излучателей не более
четырёх.
На рис. схематично показана четырехэлементная
КАР с тангенциальной ориентацией. Излучатели панельные, представляющие собой
вертикальные вибраторы (1\), снабженные плоскими рефлекторами (2\).
Питание такой КАР должно
быть квадратурным (фазы напряжений на входах соседних излучателей отличаются на ±π/2), что может быть обеспечено, например, матрицей Батлера 4x4 или аналогичной,
схема которой показана на рис.14.16. Данная
матрица выполнена на основе направленных ответвителей (НО) с переходным ослаблением, в общем случае
отличным от 3 дБ, соединённых отрезками кабеля равной длины. Основные её
достоинства - равнозначность входов, создающих амплитудно-фазовые распределения на входах КАР, совпадающие с
точностью до угла поворота ДН, кратного ± π/2, и возможность
оптимизации амплитудного распределения. Кроме того, вследствие равенства длин кабелей она более широкополосна.
направленных ответвителей (НО) с переходным ослаблением, в общем случае
отличным от 3 дБ, соединённых отрезками кабеля равной длины. Основные её
достоинства - равнозначность входов, создающих амплитудно-фазовые распределения на входах КАР, совпадающие с
точностью до угла поворота ДН, кратного ± π/2, и возможность
оптимизации амплитудного распределения. Кроме того, вследствие равенства длин кабелей она более широкополосна.
КАР с нормальной ориентацией весьма просто
реализуется на примере 16-элементной
решетки, в виде системы вертикальных вибраторов, расположенных ТЕМА 9. Введение. Основные
параметры и типы линий передачи.
Классификация линий передачи. Основные режимы работы
Когда линия замкнута на
сопротивление, равное волновому, в ней возникает бегущая волна. При этом
входное сопротивление линии (определяемое отношением напряжения в начале линии
к току) равно волновому сопротивлению линии независимо от ее длины.
Если же сопротивление нагрузки не
равно волновому, то в конце линии происходит отражение энергии и возникает
волна, бегущая в обратном направления — от конца линии к ее началу. При этом в
линии происходит суммирование прямой и обратной бегущих волн.
В результате
наложения (интерференции) прямой и отраженной бегущих волн в линии, разомкнутой
на конце, образуются стоячие волны тока и напряжения (рис. 1.1).
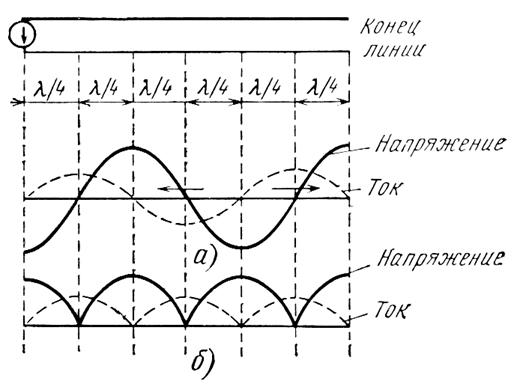
Стоячие волны тока и напряжения в разомкнутой на конце линии
На рис. 1.1,а изображены кривые
распределения тока в одном из проводов линии (штриховая линия) и напряжения
между проводами (сплошная линия) на участке длиной 1,5λ для некоторого момента времени. Для любого поперечного
сечения линии токи в обоих проводах направлены в противоположные стороны.
На рис. 1.1,б показаны кривые,
которые можно получить при измерении тока вдоль линии с включенным амперметром
в одном из ее проводов или при измерении напряжения с включенным вольтметром
между проводами линии. Эти кривые уже не учитывают изменения фазы тока и
напряжения в линии.
Следует иметь в виду, что ток и
напряжение в каждой точке изменяются во времени от нуля до максимального
значения по синусоидальному закону. Ток и напряжение сдвинуты между собой по
фазе на угол 90°, что свидетельствует об отсутствии расхода энергии в самой
линии и на ее конце.
Если фидерную линию замкнуть
накоротко на конце, в ней также возникнут стоячие волны, но, в отличие от
разомкнутой линии, на конце ее вместо пучности будет узел напряжения, а вместо
узла тока — его пучность. Кривые распределения тока и напряжения как бы
сдвинутся на четверть волны.
В соответствии с изменением тока
и напряжения при изменении длины линии будет изменяться и ее входное
сопротивление.
Разомкнутая па конце линия длиной
менее чем четверть волны имеет емкостное сопротивление; при длине разомкнутой
линии в четверть волны ее входное сопротивление равно нулю. При наличии
небольших потерь в четвертьволновой линии входное сопротивление ее не было бы
равным нулю, а имело бы некоторое малое значение и активный характер. В этом
отношении четвертьволновая разомкнутая линия эквивалентна последовательному
контуру, настроенному в резонанс.
Если линию нагрузить на конце
сопротивлением, не равным волновому, то в линии возникнут бегущие и стоячие
волны, накладывающиеся одна на другую (такой режим иногда называют режимом
смешанных волн). Часть энергии будет поглощаться в нагрузке, а часть —
отражаться от конца линии. В качестве примера на рис. 1.2,а показана линия с волновым сопротивлением ZB=500 Ом, нагруженная на конце
сопротивлением R=2000 Ом.
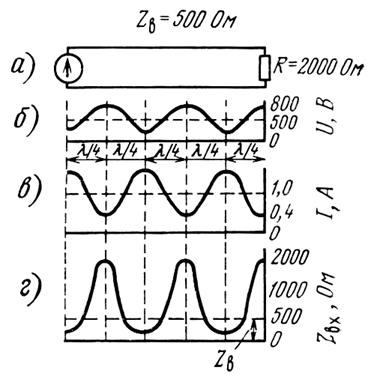
Распределение тока и напряжения вдоль линии, а
также изменение входного сопротивления в зависимости от длины линии, нагруженной
активным сопротивлением
На рис. 1.2,б
изображена кривая изменения действующих значений напряжения U, а на рис. 1.2,в —
кривая действующих значений силы тока I вдоль линии. Эти кривые характеризуются
максимумами и минимумами, но последние уже не достигают нулевых значений.
Штриховые горизонтальные прямые соответствуют значениям действующих напряжения
и тока, которые имели бы место в линии, если бы она была нагружена
сопротивлением, равным волновому сопротивлению линии. На рис. 1.2,г показана кривая изменения модуля
входного сопротивления линии Zвх построенная на
основании данных, полученных делением напряжения на ток, значения которых взяты
по кривым рис. 1.2,б и в. Входное сопротивление линии, длина
которой равна целому числу полуволн, равно сопротивлению нагрузки на конце.
При длине линии, равной нечетному числу четверти волны, ее
входное сопротивление при активном сопротивлении нагрузки
Zвх=Zв2/R. (1.1)
Изменение напряжения вдоль линии
обычно характеризуется отношением напряжения в минимуме Uмин к напряжению в
максимуме Uмакc. Это отношение
обозначается буквой Кбв и называется коэффициентом бегущей волны (КБВ):
Кбв=Uмин/Uмакс. (1.2)
Коэффициент бегущей волны Кбв определяет, насколько
близко режим в линии приближается к режиму бегущей волны. При Кбв=1, т. е. когда нет
минимумов и максимумов напряжения и оно во всех точках линии одинаково, имеет
место режим бегущей волны в линии. Наоборот, Кбв=0 характеризует режим чисто стоячих волн в линии.
Наряду с понятием КБВ используется термин коэффициент
стоячей волны (КСВ), равный
Ксв=1/Кбв=Uмакс/Uмин. (1.3)
Если линию с потерями нагрузить
на конце активным сопротивлением, равным ее волновому сопротивлению, то в ней,
так же как и в линии без потерь, установится чисто бегущая волна. Отличие от
линии без потерь будет состоять лишь в том, что амплитуда тока или напряжения
при бегущей волне в линии с потерями уже не будет оставаться неизменной, а
будет постепенно убывать в направлении от генератора к нагрузке вследствие
потерь в линии. Входное сопротивление линии с потерями при бегущей волне, т. е.
сопротивление в точках присоединения к генератору, равно волновому
сопротивлению линии независимо от ее длины.
В том случае
если сопротивление нагрузки на конце линии отлично от волнового сопротивления,
то от конца линии произойдет отражение и возникнет волна, бегущая в обратном
направлении — от конца линии к ее началу. Отраженная волна, распространяясь от
нагрузки к генератору, будет также иметь амплитуду, убывающую вдоль линии в
сторону к генератору.
В тех точках, где для разомкнутой
линии без потерь должны были быть нулевые значения, будут лишь некоторые
минимумы. Пучности тока или напряжения не будут одинаковыми через каждую
половину волны, а будут постепенно уменьшаться от начала линии к ее концу.
Входное сопротивление линии с
потерями, разомкнутой на конце, уже не будет чисто реактивным. Наряду с
реактивной составляющей появится и активная составляющая сопротивления.
Активная и реактивная составляющие входного сопротивления разомкнутой линии с
потерями в зависимости от длины линии l.
Коэффициент полезного действия
(КПД) линии с потерями, определяемый отношением мощности в конце линии (т. е. в
нагрузке) к мощности в начале линии, максимален в случае бегущей волны в ней
ηмакс = e-2al (1.4)
где a — коэффициент затухания; l — длина линии. Для линии с малыми
потерями (al<<1)
ηмакс≈1-2al. (1.5)
Линии
передачи разных типов
При использовании фидерных линий
для передачи электромагнитной энергии от передатчика к антенне или от антенны к
приемнику к ним предъявляются следующие требования общего характера.
Потери электромагнитной энергии,
передаваемой по фидеру, должны быть минимальными.
Линии должны обладать достаточной
электрической прочностью, т. е. должны быть рассчитаны на передачу требуемой
мощности без опасности возникновения электрического пробоя.
Фидерные линии не должны обладать
антенным эффектом, т. е. не должны излучать или принимать электромагнитные
волны; излучение электромагнитных волн фидерной линией нежелательно из-за
возрастания потерь в линии (потерь на излучение) и вследствие искажения
диаграммы направленности антенны.
Степень важности каждого из
указанных требований зависит от характера работы радиостанции. Так, например,
для приемных антенн вопрос о перенапряжениях, естественно, отпадает, в то время
как роль антенного эффекта для них возрастает. Действительно, антенный эффект
приемного фидера может свести на нет все достоинства направленной антенны и
дать резкое увеличение уровня внешних помех на входе приемника. Для приемных
антенн длинных и средних волн, когда внешние помехи значительны, потери в
линиях не играют существенной роли; в диапазоне же УКВ, особенно на СВЧ, когда
мощность внутренних шумов приемных устройств может превосходить мощность
внешних помех, КПД линий необходимо по возможности увеличивать.
На коротких, метровых и
отчасти дециметровых волнах применяются воздушные двухпроводные (реже
четырехпроводные) фидерные линии и радиочастотные кабели. При переходе к
сантиметровым и более коротким волнам указанные линии передачи становятся
непригодными. Открытые линии непригодны из-за того, что расстояние между
проводами становится соизмеримым с длиной волны и линии начинают заметно
излучать. Экранированные же линии не имеют излучения.
Воздушные и экранированные линии.
Для
питания проволочных антенн применяются два типа фидерных линий: воздушные и
экранированные.
Из
воздушных наиболее распространенными являются двухпроводные линии (рис. 1.3).
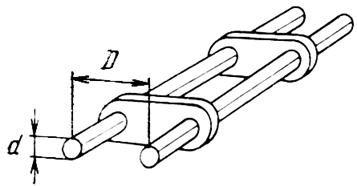
Рис. 1.3. Воздушная двухпроводная
(неэкранированная) линия
Отсутствие
антенного эффекта достигается уменьшением расстояния между проводами линии, так
как при малом (по сравнению с волной) расстоянии электромагнитное поле,
создаваемое вне линии током одного провода, уравновешивается полем (обратного
знака) второго провода, в котором ток протекает в противоположном направлении.
Но располагать провода очень близко друг от друга нельзя из-за возможности их
соприкосновения, а также из-за уменьшения электрической прочности линии.
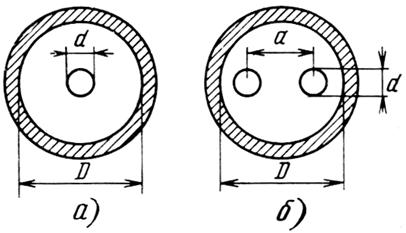
Рис.
1.4. Экранированные линии (поперечное сечение)
На
рис. 1.4 показаны экранированные линии: концентрическая (или коаксиальная) и
двухпроводная. Конструктивно такие линии выполняются жесткими или гибкими.
Жесткий
концентрический фидер (рис. 1.4,а)
изготовляется из медных или латунных трубок, помещенных одна внутри другой. При
малых диаметрах вместо внутренней трубки применяется сплошной цилиндрический
стержень. По центральному проводу протекает ток одного направления, а по экрану
— другого. Центральный провод отделяется от наружного шайбами из диэлектрика.
В
гибком высокочастотном коаксиальном кабеле внутренний провод представляет собой
медную жилу, сплошную или из тонких проводников. Наружный проводник состоит из
медной оплетки в виде сетки или тонкой ленты. Пространство между внутренним
проводом и экранирующей оболочкой заполняется пластической массой из
фторопласта или полиэтилена. Снаружи кабель покрывается защитной изоляционной
оболочкой.
Двухпроводный
кабель (рис. 1.4,б) состоит из двух
проводов, разделенных изоляцией и окруженных экранирующей оболочкой. Он
применяется главным образом для симметричных антенн.
По
сравнению с воздушными линиями преимущество экранированных линий в том, что они
не имеют антенного эффекта, более удобны при монтаже, в частности могут быть
зарыты в землю, лучше защищены от влияния атмосферных условий. С другой стороны,
экранированные линии более сложны по конструкции, чем воздушные, и поэтому
более дорогие. В экранированных линиях труднее обнаруживать повреждения и
устранять их.
Волновое
сопротивление линии определяется конфигурацией, геометрическими размерами и
материалом, заполняющим пространство между проводами. На рис. 1.5 представлены
графики для определения волнового сопротивления двухпроводной воздушной линии
(см. рис. 1.3,а).
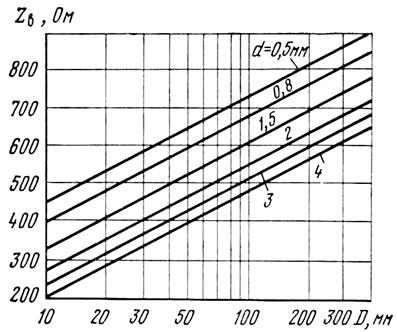
Рис.
1.5. Графики для расчета волновых сопротивлений двухпроводных (симметричных) воздушных
линий
На рис. 1.6 приведен график для определения волнового
сопротивления Zв коаксиальных линий с воздушным
диэлектриком. Для определения Zв таких линий,
заполненных диэлектриком с er>1, надо значение, определенное по
графику, разделить на sqrt(er) (Некоторые справочные данные о
радиочастотных линиях передачи приведены в приложении П.1.)
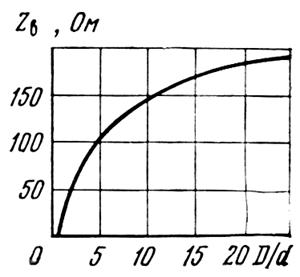
ТЕМА 10. Основные типы волн в
волноводах. Возбуждение электромагнитных колебаний в направляющих системах
В аппаратуре сантиметровых и миллиметровых волн в качестве
линий передачи наибольшее применение находят волноводы, представляющие собой
полые металлические трубы из хорошо проводящего металла. Наиболее
распространенными являются волноводы прямоугольного и круглого поперечного
сечения. Толщина стенок волновода выбирается из условий механической прочности,
а внутренняя поверхность для уменьшения потерь иногда покрывается тонким слоем
серебра или золота.
В связи с отсутствием внутренних изоляторов и
центрального провода относительно малого сечения волноводы обеспечивают
передачу энергии с меньшими потерями, чем в коаксиальных линиях.
Для передачи электромагнитных волн по волноводу нет
необходимости во втором проводнике (как в случае коаксиального кабеля), так как
направляемые волны образуются вследствие многократного отражения от его стенок.
В волноводе возможны различные структуры (типы)
электромагнитного поля. На рис. 1.7 для
примера показана структура поля для некоторого момента в наиболее широко
применяемом прямоугольном волноводе при распространении в нем волны типа H10.
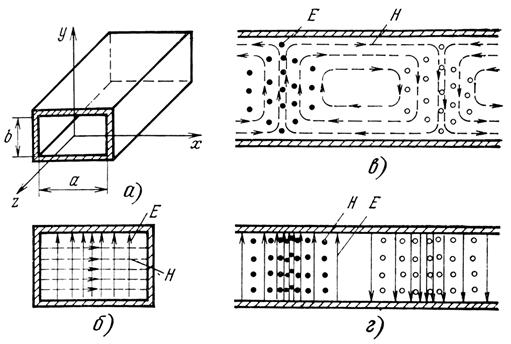
Рис. 1.7. Прямоугольный волновод (а) и структура поля в нем при волне типа
Н10: в плоскостях xoy (б); xoz (в); yoz (г)
Особенностью волновода является то, что по волноводу
заданных поперечных размеров нельзя передавать колебания, длина волны которых
больше некоторой критической волны lкр. Для упомянутой выше волны типа Н10 (при воздушном заполнении)
lкр = 2а, (1.6)
где а — размер широкой стенки
волновода.
l/2 < а < l; b < l/2.
где l — длина волны в воздухе.
Для колебаний других типов в прямоугольном волноводе
критическая длина волны будет несколько меньшей, чем для колебаний волны Н10, и определяется более
сложной формулой.
Длина волны в волноводе (определяемая фазовой скоростью
волн) получается большей, чем в свободном пространстве (вакууме), и равна (для
волновода с воздушным заполнением)
lв=l/sqrt((1-l/lкр)2). (1.7)
В волноводе бесконечной длины или ограниченных размеров,
но с согласованной на конце нагрузкой, так же как и в двухпроводной линии,
устанавливается режим бегущих волн, характеризующийся наибольшим КПД передачи
электромагнитной энергии по волноводу и отсутствием перенапряжений, возникающих
в пучностях в режиме стоячих волн.
Для возбуждения волн внутрь волновода обычно помещается
небольшой проводник — «штырек», располагаемый перпендикулярно широкой стенке
волновода.
Для того чтобы электромагнитные волны внутри волновода
распространялись в одном направлении, конец волновода, вблизи которого
располагается источник, закрывается стенкой или поршнем. Расстояние от стенки
до источника берется равным приблизительно четверти длины волны в волноводе.
Полосковые линии.
Широко применяются в качестве фидерных линий и элементов
различных узлов в диапазоне СВЧ так называемые полосковые линии передачи. Они
составляют серьезную конкуренцию элементам из отрезков волноводных и
коаксиальных линий из-за простоты конструкции и малых габаритных размеров, а
также вследствие того, что в ряде случаев могут включаться в печатные
микросхемы.
Симметричная линия
выполнена в виде узкой металлической полоски, расположенной
между двумя экранирующими пластинами и изолированной от них диэлектриком. Несимметричная линия выполнена в виде
металлической полоски, расположенной над экранирующей пластиной и изолированной
от нее диэлектриком.
В симметричной полосковой линии ток одного направления
проходит по центральной полоске, а обратно — по внутренней поверхности
экранирующих пластинок, соединенных параллельно в начале линии. Картина поля в
такой линии напоминает картину поля в линии провода с прямоугольным (замкнутым)
экраном, и по ней распространяются поперечные электромагнитные волны типа Т.
Картина поля в несимметричной полосковой линии
напоминает поле соответствующего проводника над бесконечным плоским экраном или
поле в полупространстве соответствующей двухпроводной симметричной линии с
расстоянием между проводниками, равным двойному расстоянию от провода до
экрана. В указанной полосковой линии распространяются волны, близкие к волнам
типа Т. При малом расстоянии (по
сравнению с длиной волны) между металлической полоской и экранирующей пластиной
вся энергия распространяющейся волны сосредоточена в непосредственной близости
от проводящей полоски. равномерно
вокруг цилиндрического экрана.
ТЕМА 11. Элементы трактов
СВЧ, их устройство, параметры и характеристики
Одним из наиболее распространенных элементов трактов
являются согласованные нагрузки, предназначенные
для поглощения передаваемой по линии СВЧ - мощности. Согласованные нагрузки
применяют также в качестве эквивалентов
антенн при настройке передающей аппаратуры и в виде меры сопротивления в
измерительных СВЧ - устройствах (например, в установках для измерения матриц
рассеяния многополюсников).
Основной электрической характеристикой согласованной
нагрузки является величина модуля ее коэффициента отражения 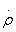 (или соответствующие
величины КБВ или КСВ) в заданной полосе частот. На практике возможно создание нагрузок с |
(или соответствующие
величины КБВ или КСВ) в заданной полосе частот. На практике возможно создание нагрузок с |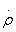 |£0,01 в относительной полосе
частот Df c/fo=20-30 % и более. Ввиду малости
|
|£0,01 в относительной полосе
частот Df c/fo=20-30 % и более. Ввиду малости
|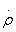 | требования к фазе коэффициента отражения от нагрузки не
предъявляются, и эта фаза может иметь любую величину в интервале от 0 до 2 p.
| требования к фазе коэффициента отражения от нагрузки не
предъявляются, и эта фаза может иметь любую величину в интервале от 0 до 2 p.
Важной характеристикой нагрузки является величина
допустимой поглощаемой мощности. Существуют нагрузки для низкого уровня мощности
(£1 Вт) и нагрузки,
предназначенные для высокого уровня мощности.
Конструктивное выполнение нагрузок зависит от типа
линии передачи, диапазона частот и уровня мощности. Различают сосредоточенные
и распределенные нагрузки, причем последние путем увеличения размеров и массы
могут быть выполнены на большую мощность.
В коаксиальном тракте простейшей
нагрузкой является сосредоточенный резистор с сопротивлением, равным волновому
сопротивлению линии передачи. Однако на сантиметровых волнах размеры резистора
соизмеримы с длиной волны, входное сопротивление становится частотно-зависимым
и качество согласования заметно ухудшается. Для снижения коэффициента отражения
и расширения рабочей полосы частот коаксиальные нагрузки сантиметрового
диапазона волн часто выполняют в виде отрезков нерегулярной линии передачи с
потерями. Поглощающие элементы в таких
нагрузках могут быть объемными или в
виде тонких поглощающих пленок.
Коаксиальная нагрузка с объемным
поглощающим элементом в виде конуса показана на рис.1, а. Хорошее
качество согласования в этой конструкции достигается при длине поглощающего
элемента 1³l.
Более распространены коаксиальные нагрузки
с поглощающими элементами в виде керамических цилиндров, покрытых
металлооксидными или углеродистыми проводящими пленками. Толщину пленки
выбирают малой по сравнению с глубиной погружения тока, поэтому поверхностное
сопротивление пленки почти не зависит от частоты. Чтобы входные сопротивления
коаксиальных нагрузок с цилиндрическими поглощающими элементами были чисто
активными и почти не менялись в значительном интервале частот, такие нагрузки
снабжают нерегулярными металлическими экранами со специально подобранными
профилями и размерами.
На рис.1, б показана коаксиальная нагрузка
с экраном ступенчатой формы. Найдено, что оптимальное качество согласования
при l³.61получается при
выборе уменьшенного диаметра экрана в соответствии с соотношением: 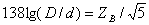 , где ZB — волновое сопротивление основного коаксиального волновода.
Длина уступа внешнего проводника должна быть несколько меньше длины пленочного
поглощающего элемента.
, где ZB — волновое сопротивление основного коаксиального волновода.
Длина уступа внешнего проводника должна быть несколько меньше длины пленочного
поглощающего элемента.
Наиболее широкополосные коаксиальные
нагрузки имеют внешний экран воронкообразной формы (рис.1, в). Например, при
выборе формы экрана в соответствии с уравнением r(г)=аеАг
(где
а — диаметр внутреннего проводника коаксиального волновода; А — константа) нагрузка оказывается
работоспособной при А>l. Существуют и более широкополосные коаксиальные нагрузки,
экран которых имеет профиль в виде специальной кривой — трактрисы.
Согласованные нагрузки для полосковых
линий передачи представляют собой тонкопленочные полоски из резистивных материалов,
нанесенные на полосковую плату и закороченные с одного конца на экран
полосковой линии. Толщину полоски подбирают в несколько раз меньше глубины
проникновения тока, а длина полоски может быть малой по сравнению с длиной
волны. Однако из-за небольшой площади теплоотвода такие сосредоточенные нагрузки
выдерживают лишь небольшую мощность. Для увеличения рассеиваемой мощности
нагрузки выполняют в виде протяженных (l~l) отрезков
регулярных или нерегулярных линий передаче с
потерями.
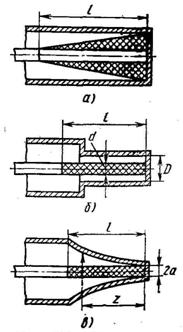
Рис. 1 Коаксиальные согласованные
нагрузки
При этом необходим специальный подбор формы поглощающей поверхности. В полосковых узлах СВЧ применяют также навесные
нагрузки в виде керамических пластинок
или стержней с нанесенным пленочным поглощающим покрытием. На полосковых платах
при выполнении нагрузок и в других случаях части возникают трудности с
осуществлением короткого замыкания полосковых проводников на экраны полосковых
линий. При узкой полосе частот Df c/fo=5-8% эти трудности
преодолевают применением четвертьволновых разомкнутых шлейфов, обладающих
близким к нулю входным сопротивлением.
Волноводные
согласованные нагрузки выполняют в виде поглощающих вставок переменного профиля в отрезке
короткозамкнутого волновода. В маломощных нагрузках вставки имеют вид тонких
диэлектрических пластин, покрытых графитовыми или металлическими пленками
(рис.2, а). Объемные поглощающие
вставки (рис.2, б, в, г) с большой
мощностью рассеивания выполняют из композитных материалов на основе порошков
графита, карбонильного железа или карбида кремния.
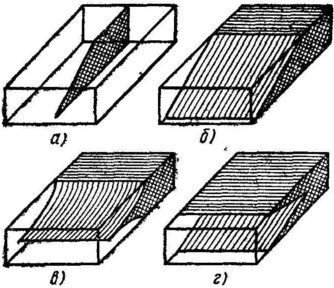
Рис. 2 Волноводные согласованные
нагрузки
Для уменьшения отражений поглощающим вставкам
придают вид клиньев или пирамид. Наименьшие отражения в широкой полосе частот
обеспечиваются от вставок, входная часть которых имеет форму экспоненциального
клина в плоскости вектора Е. Для устранения отражения от
короткозамыкателя вставка должна вносить ослабление 20—25 дБ. Для улучшения
теплоотвода площадь соприкосновения вставки со стенками волновода делают
максимальной, а внешнюю поверхность волновода снабжают радиатором.
Реактивные нагрузки, применяемые в качестве мер при
измерениях на СВЧ, а также в согласующих и управляющих устройствах СВЧ,
должны обладать стабильным нормированным входным сопротивлением, величина
которого может быть строго рассчитана по геометрическим размерам. В качестве
реактивных двухполюсников обычно используют короткозамкнутые отрезки закрытых
линий передачи, иначе говоря короткозамкнутые шлейфы. Реактивное
сопротивление короткозамкнутого шлейфа определяют по формуле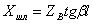 , где ZВ — нормированное волновое
сопротивление; b - коэффициент фазы, l - длина шлейфа. Основным
параметром, характеризующим качество
реального шлейфа, является величина входного КСВ, которая должна быть
как можно более высокой. В нерегулируемых
коаксиальных или волноводных шлейфах с неподвижным запаянным поршнем КСВ может достигать. 500 и более. В
регулируемых шлейфах с подвижными поршнями значения КСВ из-за
дополнительных потерь в контактах получаются ниже, однако, как правило, превышают 100. Холостой ход в шлейфах, т.е. размыкание выхода, может
быть реализован только в закрытых многопроводных
линиях передачи, когда устранено излучение.
, где ZВ — нормированное волновое
сопротивление; b - коэффициент фазы, l - длина шлейфа. Основным
параметром, характеризующим качество
реального шлейфа, является величина входного КСВ, которая должна быть
как можно более высокой. В нерегулируемых
коаксиальных или волноводных шлейфах с неподвижным запаянным поршнем КСВ может достигать. 500 и более. В
регулируемых шлейфах с подвижными поршнями значения КСВ из-за
дополнительных потерь в контактах получаются ниже, однако, как правило, превышают 100. Холостой ход в шлейфах, т.е. размыкание выхода, может
быть реализован только в закрытых многопроводных
линиях передачи, когда устранено излучение.
Возможные конструктивные решения
подвижных короткозамыкающих поршней для прямоугольных волноводов показаны
на рис. 3 для продольных
сечений, параллельных узкой
стенке волновода. В первой конструкции
(рис. 3, а) разрезные пружинные контакты А вынесены от
закорачивающей стенки В внутрь
волновода на расстояние lв/4. Поэтому контакты оказываются в сечении волновода с нулевыми значениями
продольного тока на стенках волновода, и неидеальность контактов не приводит к
потерям мощности.
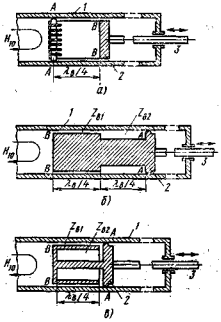
Рис. 3 Волноводные короткозамыкающие
поршни:
1 — волновод; 2 — поршень;
3 — тяга
Во второй конструкции поршня (рис. 3,б) механические
контакты А включены в волновод через два трансформирующих отрезка линии передачи с низкими значениями
нормированного волнового сопротивления ZВ1 и ZВ2. Предполагая, что активное
сопротивление контактов в точке А равно rа, и применяя дважды формулу
пересчета сопротивления через четвертьволновый трансформатор,
находим входное сопротивление в точках В: rB= =rA(ZВ1/ZВ2)2.
При выборе ZВ1<<ZВ2 удается
существенно уменьшить эквивалентное сопротивление контакта rA и увеличить КСВ поршня.
В третьей конструкции поршня
(рис. 3, в) точки механического контакта помещены в середину свернутого
короткозамкнутого полуволнового отрезка линии передачи, состоящего из двух
каскадно включенных четвертьволновых отрезков с волновыми сопротивлениями
ZВ1 и
ZВ2. К активному сопротивлению контакта rA добавляется бесконечное
реактивное сопротивление короткозамкнутого
четвертьволнового шлейфа с волновым сопротивлением ZВ2, и сумма
сопротивлений контакта и шлейфа трансформируется четвертьволновым
отрезком с волновым сопротивлением ZВ1 в практически нулевое
сопротивление в точке В (т. е. в
точке В создается виртуальное короткое замыкание для токов СВЧ).
Рассмотренные принципы выполнения
волноводных поршня непосредственно применимы и в коаксиальных поршнях для диапазона коротких сантиметровых волн. На
дециметровых и более длинных волнах применяются коаксиальные поршни с
обычными пружинными контактами в точках
короткого замыкания линии передачи,
так как четвертьволновые трансформирующие отрезки оказываются слишком громоздкими.
Диафрагмами называют тонкие металлические
перегородки, частично перекрывающие поперечное сечение волновода. В прямоугольном волноводе наиболее употребительны
симметричная индуктивная, симметричная емкостная и резонансная диафрагмы, показанные на рис. 4.
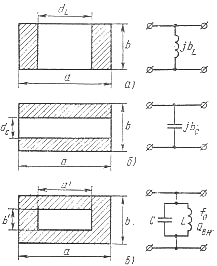
Рис. 4 Диафрагмы в прямоугольном
волноводе
В индуктивной диафрагме (рис.
4,а) поперечные токи на широких стенках волновода частично замыкаются через пластины, соединяющие эти стенки. В магнитном поле токов,
текущих по пластинкам диафрагмы,
запасается магнитная энергия. Схема замещения индуктивной диафрагмы представляет собой индуктивность, включенную параллельно в линию передачи.
Нормированную реактивную проводимость индуктивной диафрагмы bL определяют по приближенной формуле
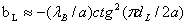 (2.2.1)
(2.2.1)
где 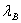 — длина волны в
волноводе; а – размер широкой стенки волновода;
dL — ширина зазора диафрагмы.
— длина волны в
волноводе; а – размер широкой стенки волновода;
dL — ширина зазора диафрагмы.
Емкостная
диафрагма (рис.
4, б) уменьшает зазор между широкими стенками волновода, между кромками
диафрагмы концентрируется поле Е и создается некоторый запас
электрической энергия. Поэтому схемой замещения емкостной диафрагмы является
емкость, включенная параллельно в
линию передачи. Нормированная реактивная
проводимость емкостной диафрагмы bс определяется по приближенной
формуле
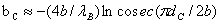 (2.2.2.)
(2.2.2.)
где b — размер узкой стенки
волновода; dc — ширина
зазора диафрагмы. Емкостная диафрагма сильно снижает электрическую прочность
волновода.
Резонансная
диафрагма (резонансное
окно) - металлическая пластинка с отверстием прямоугольной или овальной формы (рис. 4, в), содержащая в себе элементы индуктивной
и емкостной диафрагм. Размеры
отверстия резонансной диафрагмы могут быть
выбраны так, чтобы на заданной резонансной частоте диафрагма не оказывала влияния на распространение
волны H10 в
волноводе, т. е. имела нулевую проводимость. Схема замещения резонансной
диафрагмы имеет вид параллельного резонансного контура, включенного в
линию передачи параллельно. Приближенно резонансную частоту
резонансной диафрагмы определяют из условия равенства волновых
сопротивлений линии передачи, эквивалентной волноводу, и отверстия диафрагмы на
основании формулы (2.2.3):
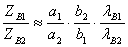 (2.2.3)
(2.2.3)
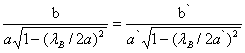 (2.2.4)
(2.2.4)
Можно убедиться, что выбранной резонансной длине
волны l0 в формуле (2.2.4)
соответствует множество диафрагм с отверстиями различных размеров, начиная с
узкой щели длиной l0/2 и кончая полным
поперечным сечением волновода. Эти резонансные диафрагмы обладают разной
внешней добротностью, т. е. добротностью эквивалентного колебательного LC-контура 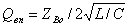 с учетом
влияния согласованной с
двух концов линии передачи, в которую
включен этот контур.
с учетом
влияния согласованной с
двух концов линии передачи, в которую
включен этот контур.
Индуктивный штырь,
показанный вместе со
схемой замещения на рис.5, а, представляет
собой проводник круглого сечения,
установленный в поперечном сечении прямоугольного волновода по направлению силовых линий поля Е, и
соединенный с двух концов с широкими
стенками волновода.
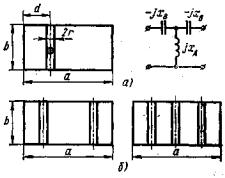
Рис. 5 Индуктивный штырь в
прямоугольном волноводе
Схема замещения индуктивного штыря содержит
параллельно включенную индуктивность и два
последовательных емкостных сопротивления,
учитывающих конечную толщину штыря.
Номиналы элементов определяются по формулам и
графикам, имеющимся в справочной
литературе. Индуктивные штыри не снижают электрической прочности волновода и просты в изготовлении. Когда необходимы
низкие значения параллельного сопротивления ха, применяют решетки
из нескольких индуктивных штырей, располагаемых в поперечном сечении волновода, как показано на рис. 5, б.
Емкостный штырь (рис. 6) представляет собой
круглый проводник,
установленный по направлению силовых
линий поля Е и соединенный одним концом с широкой стенкой волновода.
Схема замещения емкостного штыря содержит последовательный LC-контур, включенный
параллельно в линию передачи. Емкость этого контура связана с концентрацией
поля E в области разомкнутого конца штыря, а
индуктивность обусловлена прохождением токов по штырю. При некоторой длине штыря,
близкой к l0/4, проводимость
последовательного контура обращается в бесконечность, и волновод закорачивается.
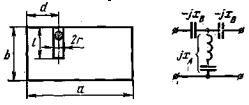
Рис. 6 Емкостной штырь в
прямоугольном волноводе
Более короткие штыри имеют емкостную проводимость: при длинах штыря,
больших резонансной, проводимость носит
индуктивный характер. Последовательные емкостные сопротивления в схеме
замещения учитывают конечность толщины штыря. При малых диаметрах штыря
эти сопротивления малы, и их влиянием можно пренебречь. Емкостные штыри в основном применяют в качестве
регулируемых реактивных элементов,
вводимых внутрь волновода с помощью резьбовых отверстий на широкой стенке. Однако емкостные штыри заметно снижают электропрочность волноводов, и
поэтому в мощных трактах они не находят применения.
Для осуществления сборки и разборки трактов
отдельные узлы и устройства СВЧ оснащают специальными разъемами, которые должны
обеспечивать надежный электрический контакт в местах соединения проводников
между собой. Основные требования к разъемам
состоят в сохранении согласования и электрической прочности тракта при
минимальном ослаблении мощности и отсутствии:
паразитного излучения.
В высококачественных соединителях для гибких
коаксиальных кабелей контакты обеспечивают с помощью пружинных цанг и штекеров
(рис. 7, а), удерживаемых в
соединении посредством внешних резьбовых соединений или иных фиксирующих
приспособлений. Соотношение диаметров проводников на любом участке внутри
коаксиальных высокочастотных соединителей подбирают таким образом, чтобы с
учетом параметров диэлектрика обеспечивалось постоянство волнового
сопротивления линии. Согласование в высокочастотных коаксиальных соединителях в
сильной степени зависит от заделки кабеля и при аккуратном выполнении
характеризуется среднеквадратическим значением КСВ порядка 1,05—1,15.
Высокочастотное соединители для жестких
коаксиальных, волноводов на повышенный уровень мощности выполняют без опорных
диэлектрических шайб. Эскиз возможной
конструкции коаксиального соединителя для жесткой коаксиальной линии
показан на рис. 7, б. Во многих
случаях высокочастотные соединители для жестких коаксиальных волноводов должны
быть герметичными как для защиты внутренних
рабочих поверхностей проводника от внешних воздействий, так и для
повышения электрической прочности тракта путем создания внутри тракта избыточного давления.
РАЗЪЕМЫ
Соединение отрезков прямоугольных волноводов
осуществляют с помощью фланцев двух типов:
контактных и дроссельных.
Контактные притертые фланцы требуют тщательной обработки и строгой параллельности
соприкасающихся поверхностей и могут обеспечивать
высокое качество сочленения, которое, однако, быстро ухудшается при многократных
пересборках тракта.
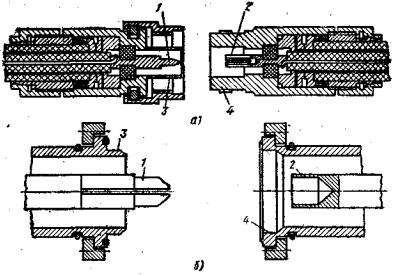
Рис. 7
Высокочастотные коаксиальные соединители:
1 — штыревой контакт 2 —
гнездовой контакт; 3 — штыревая
втулка; 4 — гнездовая втулка
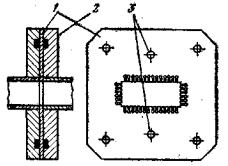
Рис. 8 Контактный волноводный фланец:
1 — контактная прокладка; 2 —
канавки с уплотнителем; 3 — отверстия
для фиксирующих
штифтов
Для улучшения качества контакта между фланцами на штифтах помещают бронзовую прокладку,
имеющую ряд разведенных пружинящих лепестков, прилегающих к внутреннему периметру поперечного сечения соединяемых волноводов (рис. 8). Защита сочленения от пыли и влаги осуществляется
резиновыми уплотнительными кольцами, уложенными в канавках на фланцах по обе стороны от контактной прокладки.
В дроссельном фланце (рис. 9) контакт между волноводами осуществляется через
последовательный короткозамкнутый шлейф длиной
lВ/2,
выполненный в форме канавок и углубления внутри фланца.
Четвертьволновой участок между
точкой короткого замыкания А и
точкой механического контакта В является
коаксиальным волноводом с волной типа Н11, а второй
четвертьволновый участок между точкой механического контакта В и точкой включения шлейфа в волновод С является отрезком радиальной линии
передачи. Точка механического контакта попадает в узел распределения
поверхностного тока J и поэтому на сопротивлении контакта rк не происходит заметного выделения мощности. Виртуальное
короткое замыкание между сочленяемыми волноводами в точке С обеспечивается тем, что суммарная длина дроссельных канавок от точки А
до точки С составляет lв/2. Для защиты полости тракта от внешних воздействий применяют уплотнительную прокладку,
укладываемую в добавочную концентрическую канавку.
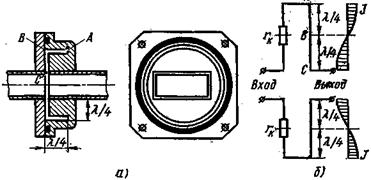
Рис. 9 Дроссельный
волноводный фланец: a — эскиз;
б — схема замещения
Дроссельные фланцы
не критичны к качеству механического контакта и небольшим
перекосам в сочленении, не снижают электрической прочности тракта. Их
недостатками являются зависимость качества
согласования от частоты и сложность конструкции.
Повороты и изгибы линий
передачи относятся к числу нерегулярностей, снижающих качество согласования и
электропрочность трактов СВЧ. В уголковых
изгибах любых линий передачи в той или
иной мере возбуждаются поля нераспространяющихся волн высших типов,
которым соответствует определенный запас
электромагнитной энергии.
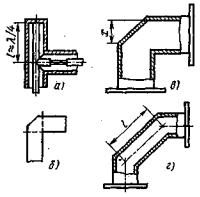
Рис. 10 Поворот линий передачи с
компенсацией отражений
Для минимизации возникающих из-за этого отражений конструкции изгибов дополняют различными согласующими элементами. Например, изгиб на 90°
коаксиального тракта сочетают с
четвертьволновым изолятором и дополняют небольшой проточной на
внутреннем проводнике линии (рис. 10,а). Подбор расположения размеров проточки, а также правильный выбор длины четвертьволнового изолятора позволяют сохранить хорошее согласование
в тракте в широкой полосе частот.
Повороты в полосковой линии
передачи согласовывают с помощью «подрезания» внешних углов примерно на одну
треть диагонали,
соединяющей внутренний и внешний углы поворота (рис. 10, б). Однако такие
компенсированные повороты вносят небольшое добавочное запаздывание в линию
передачи, которое должно учитываться
при расчете электрических длин резонансных отрезков. Подрезание углов оказывается эффективным способом
уменьшения отражений также в прямоугольных и круглых волноводах, причем
оптимальный размер скоса (рис.10, в) находят
с помощью графиков, имеющихся в справочной литературе. Концентрация силовых
линий поля Е в области резких изгибов
снижает электрическую прочность тракта. Этот недостаток в значительной мере
устраняется в двойных поворотах и в плавных изгибах. В двойных поворотах (рис.
10, г) две нерегулярности разносят на
расстояние l, примерно равное lВ/4. Улучшение согласования происходит
как из-за уменьшения отражений от каждой нерегулярности, так и из-за взаимной
компенсации отражений от них.
Плавные изгибы
тракта
могут быть охарактеризованы схемой замещения в виде отрезка линии передачи с
несколько измененным волновым сопротивлением. Для улучшения согласования следует
увеличивать радиус изгиба или выбирать длину изгиба, кратной lВ/2.
Очень распространенными узлами СВЧ - трактов
являются переходы с одной линии передачи на другую, которые также называют
возбудителями волны заданного типа. По схеме замещения переходы являются
взаимными реактивными четырехполюсниками, и в их проектировании основное внимание уделяется достижению Хорошего качества согласования входов в полосе
частот при обеспечении необходимой электрической прочности. Рассмотрим ряд характерных конструкций переходов.
Возбуждение прямоугольного волновода с волной типа H10 от коаксиального волновода с Т-волной производится с
помощью коаксиально-волноводных
переходов (рис.11).
Основным элементом таких
переходов являются обтекаемые электрическим током штыри, размещаемые в
короткозамкнутом с одной стороны волноводе
параллельно силовым линиям поля Е.
В зондовом
переходе (рис.11, а) согласование входов обеспечивается изменением длины
зонда l3, а также подбором расстояний
l и х, определяющих, положение зонда. Для расширения полосы частот согласования желательно увеличивать
диаметр зонда d. При тщательном выполнении зондовый переход обеспечивает
полосу частот согласования 15—20 % относительно расчетной частоты при КБВ³О,95.
Недостатком зондового перехода является снижение электропрочности из-за концентрации
силовых линий поля Е на конце зонда. В определенной мере этот недостаток преодолевается в коаксиально-волноводном переходе с последовательным шлейфом (рис. 11, б), однако даже при самом тщательном подборе расстояний l и lш рабочая
относительная полоса частот составляет ~7%.
Лучшие результаты по
согласованию и электропрочности имеет переход с поперечным стержнем (рис. 11, в), дополненный согласующей индуктивной диафрагмой. В такой конструкции достижима
относительная полоса частот согласования
~15%.
Максимальных широкополосности (~20%
при КБВ³0,95) и электропрочности достигают в коаксиально-волноводных
переходах так называемого «пуговичного» типа (рис. 11, г),
требующих, однако, тщательного
экспериментального подбора формы проводников в сочетании с дополнительной настройкой
качества согласования с помощью индуктивной диафрагмы. 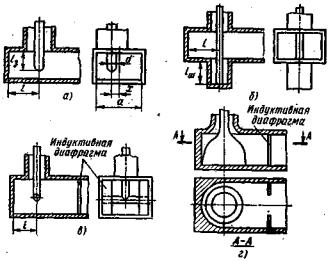
Рис. 11 Коаксиально-волноводные
переходы:
а — зондовый; б — с коаксиальным шлейфом;
в — с поперечным
стержнем;
г—пуговичный
Применение коаксиально-волноводных переходов для
возбуждения волны Е10 в круглом волноводе показано на рис. 12 на
примере вращающёгося сочленения.
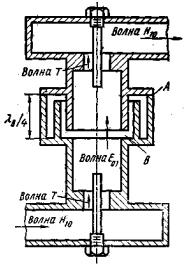
Рис. 12 Волноводное
вращающееся сочленение с волной типа Е01
Короткие отрезки коаксиального
волновода с Т-волной обеспечивают фильтрацию волн высших типов и устраняют возможность
возбуждения в круглом волноводе паразитной аксиально-несимметричной волны Н11 (эта волна более низкого типа, чем волна E01). Соединение вращающихся частей круглого волновода осуществляют с помощью коаксиального дросселя длиной lо/2, аналогичного дросселям
вращающегося коаксиального сочленения на рис. 7.10.
Возбуждение волны низшего типа Н11 в круглом волноводе возможно с помощью плавного перехода от
прямоугольного волновода с постепенной
деформацией формы поперечного сечения от прямоугольной к круглой (рис.
13, а).
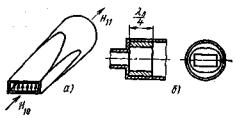
Рис. 13 Соосные переходы от прямоугольного
волновода с волной Н01 к
круглому волноводу с волной Н11
Если длина такого перехода превышает длину волны,
то отражения в широкой полосе частот
оказываются незначительными. В более компактном узкополосном переходе,
показанном на рис. 13, б, сочленение
соосных прямоугольного и круглого волноводов
осуществляется через согласующую
четвертьволновую вставку с овальной формой поперечного сечения.
Возбуждение волны Н11 в
круглом волноводе может также производиться через отверстие в его боковой стенке от
прямоугольного волновода. Если широкие
стенки прямоугольного волновода ориентированы
параллельно оси круглого волновода (рис. 14, а),то в круглом волноводе возбуждаются волны Н11, распространяющиеся в обе
стороны от ответвления с одинаковыми фазами. При поперечном расположении возбуждающей щели в круглом волноводе (рис. 14, 6) волны, возбуждающиеся справа и слева от нее, противофазны. Если требуется обеспечить передачу волны Н11 в одном направлении, то один из концов круглого
волновода закорачивают, причем в случае разветвления, показанного на
рис. 14, а, расстояние между центром щели и короткозамыкателем должно быть
близким к lв/4,
а в случае, показанном на рис. 14, б,—
близким к lо/2.
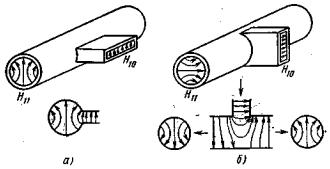
Рис. 14 Тройниковые разветвления
прямоугольного и круглого волноводов
Рассмотрим теперь некоторые компактные способы
возбуждения осесимметричной волны Е01 в круглом волноводе от
прямоугольного волновода с волной Н10,
не использующие промежуточных коаксиально-волноводных переходов.
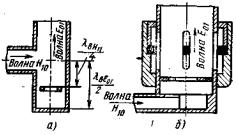
Рис. 15 Способы
возбуждения волны Е01 в круглом волноводе
В устройстве, показанном на рис. 15, а, прямоугольный волновод соединяется с
круглым через поперечное отверстие. Для лучшего возбуждения волны Е01 круглый волновод с одной стороны закорачивается на расстоянии lвЕ01/2 от возбуждающего отверстия. Для
подавления паразитной волны низшего типа Н11, которая
также возбуждается отверстием, в
короткозамкнутом отрезке круглого
волновода располагают тонкое
металлическое кольцо. Периметр
кольца выбирают близким
к lо, чтобы волна Н11 возбуждала в нем
резонансные колебания с одной вариацией тока
по периметру. Это
резонансное кольцо действует
на волну Н11 подобно короткозамыкателю. Располагая
кольцо на расстоянии lвН11/4 от центра
щели, удается эффективно
подавить колебания волны Н11
в круглом волноводе. На волну типа Е01,
силовые линии поля Е которой перпендикулярны
проводнику кольца, резонансное кольцо практически не влияет;
Другой возбудитель волны Е01 в круглом
волноводе с высокой степенью подавления паразитной волны Н11 показан на рис. 15,б.
Прямоугольный волновод сочленяется с круглым так же, как в предыдущей
конструкции с коротким замыканием одной половины круглого волновода
непосредственно у места сочленения. Кроме того, в круглом волноводе помещено
резонансное кольцо, закорачивающее его для волны Н11. Волна Н11,
просочившаяся через резонансное кольцо, испытывает поглощение, возбуждая через продольные щели в стенках круглого волновода
коаксиальный резонатор с колебаниями типа Н01.
В пучности поля Е этого резонатора помещено кольцо из поглотителя, в котором и происходит выделение
энергии волны Н11. Волна Е01
не имеет поперечных токов на стенках круглого волновода и поэтому не возбуждает
продольные щели и резонатор с поглотителем.
Особенно трудной задачей является конструирование
возбудителей волны Н01 в круглом волноводе. Здесь главное
требование состоит в обеспечении высокой степени чистоты возбуждения волны Н01 при
глубоком подавлении целого ряда низших и высших типов волн, способных к
распространению в круглом волноводе большого диаметра.
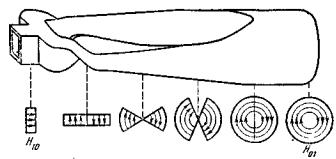
Рис. 16 Плавный переход для
возбуждения волны Н01 в круглом волноводе
На рис. 16 показана одна из возможных конструкций
перехода от прямоугольного волновода с волной Н10 к круглому
волноводу с волной Н01 основанная на принципе плавной деформации
формы поперечного сечения волновода и структуры электрического поля.
Волноводный Е - тройник и две продольные
скрутки на углы в 90° в противоположных направлениях образуют систему двух
прямоугольных волноводов, соединенных узкими стенками и содержащих поля равной
амплитуды с противоположными фазами. Затем эта система плавно преобразуется к
двум секторным волноводам с общим ребром. Постепенное увеличение угла раскрыва
секторных волноводов образует круглый волновод с продольной металлической
перегородкой. Обрыв этой перегородки не изменяет структуры электромагнитного
поля, и на выходе перехода получается круглый волновод с волной H01. Для обеспечения надлежащей
чистоты возбуждения волны H01 этот переход должен иметь
достаточно большую длину.
Определенные трудности, связанные
с достижением хорошего качества согласования в широкой полосе частот, возникают также при выполнении переходов от полосковых линий передачи к коаксиальным и прямоугольным волноводам.
Коаксиально-полосковые
переходы в зависимости
от взаимного расположения соединяемых проводников могут быть соосными или перпендикулярными (рис.
17).
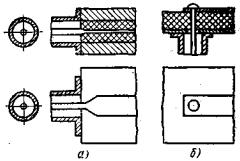
Рис. 17 Коаксиально-полосковые переходы
Для
уменьшения иррегулярности в области
сочленения диаметр внешнего проводника коаксиального волновода должен
быть близким к расстоянию между внешними пластинами симметричной полосковой линии или к удвоенной толщине основания несимметричной полосковой линии. Для улучшения согласования в
соосном переходе делают скосы на конце полоскового
проводника (рис. 17, а). Согласование
перпендикулярного коаксиально-полоскового перехода (рис. 17, б) осуществляют подбором диаметра соединительного штыря, проходящего через диэлектрическое
основание, а также подбором размеров
коаксиальной диафрагмы на выходе из коаксиального
волновода и короткого разомкнутого шлейфа из отрезка полоскового проводника.
Часто коаксиально-полосковые переходы совмещают с коаксиальными соединителями.
Устройства для возбуждения
полосковой линии передачи от прямоугольного волновода с волной Н10 называются
волноводно-полосковыми
переходами. Соединение полосковой линии с прямоугольным волноводом может быть
выполнено через плавный или ступенчатый
переход на П-образном волноводе (рис. 18, а).
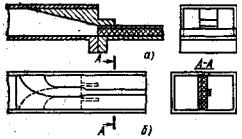
Рис. 18 Волноводно-полосковые
переходы
В такой конструкции перехода
обеспечивается широкополосное
согласование прямоугольного волновода с полосковой линией передачи я устраняется паразитное
излучение из открытого конца волновода.
Волноводно-полосковый переход другого типа, в
котором используется часть волновода в качестве корпуса для полоскового узла,
показан на рис. 18, б. Этот переход выполнен на диэлектрической пластине,
установленной продольно в средней плоскости прямоугольного волновода,
параллельно силовым линиям поля Е. С
двух сторон диэлектрической пластины напечатаны проводники, имеющие контакт
один с верхней, а другой с нижней стенками волновода, и образующие плавный
переход к симметричной полосковой линии. Далее на той же диэлектрической пластине
располагается несимметричная полосковая линия, возбуждаемая от ленточной линии
через симметрирующее устройство в виде двух четвертьволновых щелей в экране.
Экран несимметричной полосковой линии замыкает широкие стенки прямоугольного
волновода, что препятствует проникновению волны Н10 в область
волновода с полосковым узлом.
ТЕМА 12. Направленные
ответвители
К несимметричной антенне несимметричный фидер
можно подключить непосредственно:
центральный проводник к вибратору, а внешний к заземлению, противовесу или корпусу, если входное сопротивление антенны равно волновому сопротивлению фидера. В противном случае
между антенной и фидером ставят
согласующий трансформатор.
Непосредственное подключение коаксиального
фидера к симметричному вибратору, как это показано на рис, без направленного
ответтвителя вызывает появление различий между амплитудами токов в плечах
вибратора и приводит к возникновению токов на поверхности внешнего проводника фидера. Асимметрия токов в плечах вибратора
вызвана тем, что между плечом,
подключенным к центральному проводнику коаксиального фидера, и внешним его проводником образуются токи
смещения. Второе плечо вибратора имеет потенциал внешнего проводника фидера,
разности потенциалов здесь
нет и токов смещения не образуется. Асимметрия токов в вибраторе несколько искажает его ДН. Более
существенное влияние оказывают токи на внешнем
проводнике коаксиального фидера. Результатом их
действия является антенный эффект фидера. Эти токи при работе горизонтального
вибратора на передачу создают паразитное поле излучения с вертикальной
поляризацией. В случае горизонтальных приемных антенн за счет асимметрии происходит прием вертикально поляризованного
поля помех.
Рассмотрим некоторые симметрирующие устройства, устраняющие указанный нежелательный эффект.
Симметрирующая приставка. Она выполняется
в виде двухпроводной симметричной линии из металлических трубок длиной 0,25λ или 0,75λ (рис. 10.2.б).
С одного конца линия замкнута накоротко, а с
другого нагружается симметричной антенной (например, полуволновым вибратором) или симметричной линией. В
точках подключения антенны
сопротивление приставки при пренебрежении потерями в ней на резонансной частоте очень велико (Z = i W tgkl =¥), и ее шунтирующим действием можно
пренебречь. В приставке устанавливается стоячая волна с узлом напряжения и пучностью тока в месте короткого замыкания (точке 0). Коаксиальную линию
вводят в одну из трубок приставки в
точке нулевого потенциала и присоединяют к приставке со стороны подключения к ней антенны: внешний
проводник к трубке приставки, в
которой он происходит, а центральный - ко второй трубке. Этим исключается антенный эффект фидера. Для
согласованного режима работы необходимо,
чтобы Ra=WФ. За счет симметрирующей приставки несколько расширяется полоса пропускания вибратора,
поскольку реактивные составляющие
входных сопротивлений полуволнового вибратора и приставки вблизи резонанса с изменением частоты имеют разные знаки и частично компенсируются.
Симметрирующее U-колено. Симметричную антенну с входным сопротивлением Ra можно представить в виде двух
последовательно соединенных
сопротивлений 0,5Rа с нулевым потенциалом между ними. Для симметричного возбуждения антенны фазы питающего напряжения на ее зажимах а и б (рис.10.2.в) должны отличаться на π. Такой сдвиг фаз можно получить, соединив зажимы антенны а и б отрезком линии длиной 0,5λк.
Нагруженная линия длиной 0,5λk. имеет входное сопротивление, равное сопротивлению нагрузки на ее
конце. В соответствии с рис.10.2.в коаксиальная линия с волновым сопротивлением
Wф, оказывается нагруженной на два
параллельно соединенных сопротивления, каждое из
которых равно по величине 0,5Ra, или на результирующее
сопротивление,
равное 0,25Rа. При симметрировании посредством U-колена для выполнения
согласования необходимо, чтобы Ra = 4Wф. Для фидера с Wф = 75 Ом входное сопротивление антенны должно быть равно 300 Ом.
Таким сопротивлением обладает петлевой вибратор.
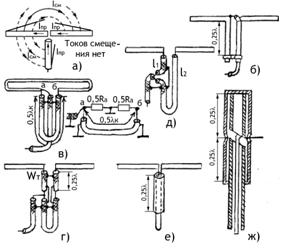 В
случае полуволнового вибратора с Ra = 73,1 Ом между симметрирующим
устройством и вибратором необходимо установить четвертьволновый трансформатор
(рис.10.5.г) с волновым сопротивлением WTP=
В
случае полуволнового вибратора с Ra = 73,1 Ом между симметрирующим
устройством и вибратором необходимо установить четвертьволновый трансформатор
(рис.10.5.г) с волновым сопротивлением WTP=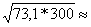 150 Ом. Трансформатор выполняется из
двух отрезков кабеля с волновым сопротивлением 75 Ом и совмещается с
симметрирующим устройством (рис.10.2.д). Длины отрезков: l1=λk/4=λ/4
150 Ом. Трансформатор выполняется из
двух отрезков кабеля с волновым сопротивлением 75 Ом и совмещается с
симметрирующим устройством (рис.10.2.д). Длины отрезков: l1=λk/4=λ/4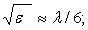
Симметрирующий
стакан.Коаксиальная линия длиной0,25λ, замкнутая на одном конце, образует резонатор и имеет очень большое
входное сопротивление.
В
симметрирующем устройстве такой
резонатор образуется наружным проводником коаксиального фидера и одетой на него
металлической трубкой (рис.10.2.е).
На одном (нижнем) конце трубка подключена (припаяна) к внешнему
проводнику фидера. Одно плечо симметричного вибратора подключается к внешнему,
а другое - к внутреннему проводникам фидера. Наведенная на внешнем проводнике
фидера ЭДС за пределами симметрирующего устройства не вызовет тока в фидере, поскольку
последовательно оказывается включенным
резонатор симметрирующего
устройства с
большим сопротивлением. При работе на частоте, отличной от резонансной,
симметрирующее устройство начинает шунтировать одно плечо вибратора реактивным
сопротивлением конечной величины и симметрия питания плеч вибратора нарушается.
Более широкополосным является симметрирующее устройство, состоящее из двух
резонаторов (рис.10.2.ж). Плечи вибратора здесь подключаются симметрично к
данному симметрирующему устройству и при любой частоте шунтируются одинаково.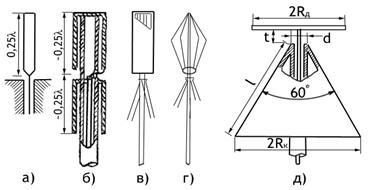 В
диапазонах дециметровых и метровых волн в качестве простейших антенн
применяются различные симметричные и несимметричные вибраторы. На подвижных
объектах желательно иметь антенну с наименьшей длиной. Этим требованиям
удовлетворяет вертикальный несимметричный штыревой вибратор (рис.10.3.а),
питаемый коаксиальным фидером. Центральный проводник фидера подключается к
четвертьволновому вибратору, а внешний к противовесу или корпусу. Входное
сопротивление такого резонансного вибратора приблизительно равно 36 Ом.
Непосредственное подключение фидера с волновым сопротивлением 50 Ом или 75 Ом
обеспечивает КБВ соответственно 0,7 или 0,5. При желании получить больший КБВ
между фидером и вибратором ставят четвертьволновый трансформатор с волновым
сопротивлением 40...50 Ом.
В
диапазонах дециметровых и метровых волн в качестве простейших антенн
применяются различные симметричные и несимметричные вибраторы. На подвижных
объектах желательно иметь антенну с наименьшей длиной. Этим требованиям
удовлетворяет вертикальный несимметричный штыревой вибратор (рис.10.3.а),
питаемый коаксиальным фидером. Центральный проводник фидера подключается к
четвертьволновому вибратору, а внешний к противовесу или корпусу. Входное
сопротивление такого резонансного вибратора приблизительно равно 36 Ом.
Непосредственное подключение фидера с волновым сопротивлением 50 Ом или 75 Ом
обеспечивает КБВ соответственно 0,7 или 0,5. При желании получить больший КБВ
между фидером и вибратором ставят четвертьволновый трансформатор с волновым
сопротивлением 40...50 Ом.
При установке
антенн на мачтe для лучшей грозозащиты ее вибраторы
должны заземляться. На рис.
10.3.б показан коаксиальный симметричный полуволновый вибратор, плечи которого
непосредственно соединены металлической
мачтой, заземленной в своем основании. Внутри мачты диаметром (0,007...0,008)λ располагают коаксиальный фидер. Вибраторы выполняют из трубок
диаметром примерно 0,02λ.
На
рис.10.3.в изображен вибратор, у которого нижнее плечо выполнено из металлических
трубок или стержней. На рис.10.3.г приведена конструкция несимметричного
вибратора, у которого оба плеча выполнены из трубок или
стержней. Такие вибраторы обладают пониженным волновым
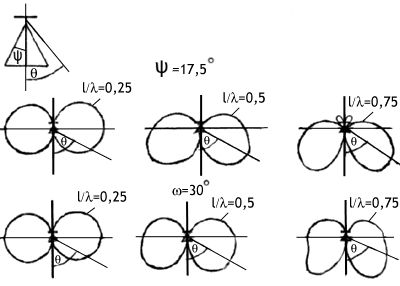
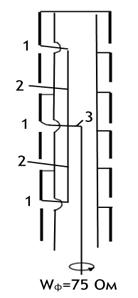 сопротивлением,
более
сопротивлением,
более
широкой полосой пропускания. и
относительно небольшой парусностью.
Большими диапазонными свойствами λmax /λmax =4…5 при Кб.в>
0,5 обладает диско-конусная антенна
(рис.10.3.д), питаемая
фидером с волновым
сопротивлением 50 Ом.
Размеры антенны определяются максимальной длиной волны и выбираются из условий l=(0,25...0,28)λmax; 2Rk=(0,18...0,2)λmax. Размеры узла возбуждения должны удовлетворять соотношению t ≈ 0,3d, где d - диаметр оплетки кабеля. Для уменьшения парусности в метровом диапазоне
волн антенна выполняется из стержней или трубок, расположенных по радиусам
диска и образующим конуса. Внешние концы трубок диска и конуса для увеличения
жесткости присоединяются к металлическим кольцам, при этом Rд=0,7Rk.
Экспериментальные ДН антенны приведены на рис. 10.4. Направленные в
вертикальной и ненаправленные в горизонтальной плоскостях ДН позволяют получить
коллинеарные синфазные антенны (рис.10.5), составленные из коаксиальных
вибраторов. В коллинеарной антенне из трех полуволновых симметричных вибраторов с учетом взаимного
влияния сопротивления излучения крайних
вибраторов оказываются равными 95 Ом, а среднего 126 Ом. При параллельном
соединении всех вибраторов входное сопротивление антенны равно 35 Ом. Для
работы с горизонтально поляризованными волнами антенны выполняют симметричными.
Петлевой вибратор. Предложенный А. А. Пистолькорсом петлевой вибратор
(рис.10.6.а) можно рассматривать как два полуволновых синфазных вибратора,
расположенных на малом расстоянии (D<<λ) друг от
друга, соединенных по концам.
Относительно точек питания ае
вибратор является симметричной системой.
В наиболее
удаленной от точек питания точке о система оказывается короткозамкнутой, и
здесь устанавливается пучность тока. По мере продвижения от точки о ко входу антенны
амплитуды тока уменьшаются и в точках b u d, отстоящих от точки о на расстоянии, равном 0,25λ, образуются
узлы тока. Далее за точками b и d токи меняют
свое направление на обратное, а их амплитуды по мере приближения к точкам а и е
возрастают. Отрезки вибратора bа и de
соответственно в точках b и d относительно
верхнего отрезка bоd развернуты навстречу друг другу, следовательно, токи в обоих
вибраторах 1 и 2 имеют одно направление. Расположение в точке о пучности тока и
узла напряжения позволяет крепить вибратор в этой точке к металлической стреле
или мачте непосредственно без изоляторов, обеспечивая надежную грозозащиту.
ТЕМЫ 13.
Фильтры и согласующие цепи СВЧ
Основное назначение радиотехнических линий передачи - это соединение
антенны с передатчиком или приемником.
Отрезки линии с дополнительными элементами в диапазоне коротких и
особенно ультракоротких волн часто используются в качестве элементов
согласования; для соединения неподвижных участков линий с подвижными (в
частности, в качестве вращающихся сочленений); как симметрирующие устройства
(для перехода от несимметричной (коаксиальной) линии к симметричной антенне);
как развязывающие устройства (аттенюаторы, направленные ответвители,
циркуляторы); как переключающие устройства (коммутаторы); как фазовращатели
(для изменения фазы передаваемых колебаний); для защиты узла от перенапряжений;
в качестве металлических изоляторов, резонансных колебательных контуров и для
других целей.
Ниже кратко рассматриваются наиболее важные применения отрезков линий и
некоторые специальные узлы линий передачи.
Согласование линии передачи с
нагрузкой. В технике антенно-фидерных устройств
большую роль играет согласование антенны с линией передачи, т. е. меры,
принимаемые для устранения волн, отраженных от нагрузки, в результате чего в
линии устанавливается бегущая волна.
Режим бегущей волны обладает рядом преимуществ. Можно доказать, что при
одной и той же мощности, передаваемой по линии без потерь (или практически с
малыми потерями), отношение максимального напряжения Uмакс в
рассогласованной линии к напряжению U в согласованной
линии определяется формулой
Uмакс/U=1/sqrt(Кбв).
При достаточно высоком Кбв в линии ее входное сопротивление,
являющееся нагрузкой для генератора, имеет значительную активную составляющую и
мало зависит от длины линии. Это обеспечивает нормальную работу генератора.
Кроме того, как указывалось в § 2.1, КПД в линии с потерями получается
максимальным в случае бегущей волны, что делает возможным передачу максимальной
мощности в нагрузку. На рис. 2.8 показана принципиальная схема получения
бегущей волны в линии, нагруженной на конце сопротивлением Za, не равным волновому сопротивлению линии Zв.

Рис. 2.8. Принципиальная схема получения бегущей волны в линии
Между нагрузкой и линией включается переходное устройство, которое может
обеспечивать согласование по одному из следующих методов: согласование по
методу В. В. Татаринова с помощью реактивного сопротивления; методу ступенчатых
и плавных переходов; методу поглощения отраженной волны.
Наиболее простой и удобный метод согласования на одной частоте (или в
узкой полосе частот) разработал в 1931 г. проф. В. В. Татаринов. По этому
методу на некотором определенном расстоянии от конца линии (от нагрузки), где
активная составляющая проводимости линии равна волновой, включается параллельно
линии, реактивное сопротивление, компенсирующее реактивную составляющую
проводимости линии.
Нетрудно убедиться, что в линии между генератором и точками подключения
реактивного сопротивления при этом установится бегущая волна. В качестве
реактивного сопротивления используется отрезок вспомогательной линии
(реактивный шлейф, индуктивный мостик), длина которой изменяется с помощью
короткозамыкающей перемычки. Для коаксиальных экранированных линий и
волноводов, когда трудно подбирать место подключения реактивного шлейфа,
применяются два или три настраиваемых шлейфа, включаемые недалеко от нагрузки
на расстоянии четверти волны друг от друга.
Когда нагрузка линии (антенна) имеет чисто активное сопротивление Ra, не равное
волновому сопротивлению линии Zв, согласование на
фиксированной волне можно осуществить с помощью так называемого
четвертьволнового трансформатора. В этом случае переходное устройство (см. рис.
2.8) представляет собой отрезок линии длиной в четверть волны, включаемый между
нагрузкой и основной линией передачи, имеющей волновое сопротивление
Zт = sqrt(Ra Zв)
а сопротивление со
стороны входных зажимов переходного устройства будет равно Zв и в линии
установится бегущая волна.
Для широкополосного согласования линий с разными волновыми
сопротивлениями можно применять отрезок линии с плавно изменяющимся волновым
сопротивлением, включаемый между согласуемыми линиями. Эскиз такого плавного
перехода для коаксиальных линий с воздушным диэлектриком и наружным экраном
неизмененного диаметра показан на рис. 2.9.
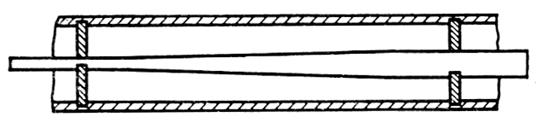
Эскиз плавного перехода для
согласования двух коаксиальных линий с разными волновыми сопротивлениями
ТЕМЫ 14 Согласование линий передач
Внутренний проводник перехода имеет форму усеченного конуса. Длина
перехода должна быть не меньше половины длины максимальной волны диапазона, в
котором осуществляется согласование.
Плавный переход при согласовании линий можно заменить многоступенчатым с
постепенным изменением волнового сопротивления от ступени к ступени.
Симметрирующие устройства. Непосредственное присоединение коаксиального
несимметричного кабеля к симметричной двухпроводной линии (или антенне)
нарушает симметрию токов в последней и приводит к появлению тока на наружной
поверхности экрана коаксиала, что недопустимо, так как приводит к излучению
фидерной линии.
Поэтому для соединения коаксиального фидера с симметричной линией (или
антенной) применяются специальные переходные устройства, называемые
симметрирующими. К ним предъявляют следующие требования: ток на внешней оболочке
(экране) коаксиального кабеля должен отсутствовать; токи на двухпроводной
системе должны оставаться равными по амплитуде и противоположными по
направлению; напряжения по отношению к плоскости симметрии должны быть на обоих
проводах двухпроводной системы одинаковыми.
Симметрирующее устройство может быть разных типов: трансформаторное,
фазоинверторное, в виде симметрирующей щели, дроссельное и др.
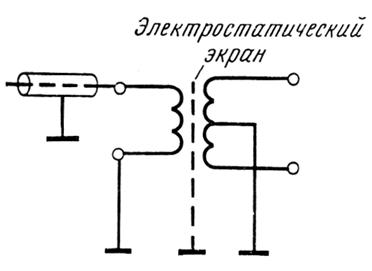
На рис. 2.10 показано подобное устройство в виде трансформатора,
первичная обмотка которого одним концом соединена с оболочкой (экраном)
коаксиального кабеля, а вторым — с центральным проводом коаксиала; середина
вторичной обмотки соединяется с экраном, а концы ее — с проводами симметричной
системы (линии). Между обмотками устанавливается электро-статический экран.
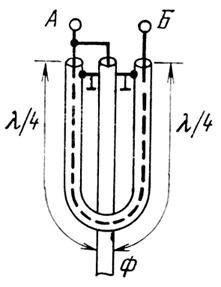
На рис. 2.11 показана схема фазоинверторного симметрирующего устройства,
называемого также устройством типа «U-колено». В нем центральный провод коаксиального фидера присоединяется к
одному зажиму (А) симметричной линии, а от этой точки напряжение к другому
зажиму (Б) симметричной линии подается через участок кабеля длиной le/2, где le — длина волны в кабеле. Фаза
напряжения на участке длиной le/2 изменяет свой знак на обратный.
Поэтому к зажимам АБ подводится требуемое противофазное напряжение и к этим
точкам можно присоединять симметричную линию. Оболочки всех отрезков кабелей
соединены между собой и заземлены. Отметим, что U-колено является трансформатором сопротивления: входное сопротивление
нагрузки фидера Ф между точками AЗ в 4 раза меньше, чем сопротивление
нагрузки на зажимах АБ (З — точка заземления).
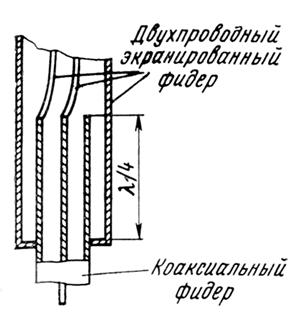
Симметрирующее устройство дроссельного типа показано на рис. 2.12. Его
называют также «четвертьволновый стакан». Здесь металлический цилиндр
(«стакан») длиной в четверть волны охватывает внешнюю оболочку коаксиального
кабеля и припаян к ней с нижней стороны. Внешняя часть цилиндра соединяется с
экраном двухпроводной экранированной линии.
Сопротивление нагрузки для коаксиальной линии при точной настройке
«стакана» остается примерно равным входному сопротивлению симметричной пинии в
точках присоединения к коаксиальной линии.
Рассмотренное переходное устройство так же, как и «U-колено», является узкополосным.
ТЕМА 15. Объемные резонаторы
СВЧ
Самым распространённым элементом радиотехнических
схем, является колебательный контур, образованный параллельным соединением
индуктивности и ёмкости.
Характерная особенность колебательных
контуров, заключается в том, что размеры L и C, много меньше реальной
длины волны.
Рис.1 Рис.2 Рис.3
(1)
Недостаток контура низкая добротность, связанная с уменьшением энергии
электромагнитного поля в такой системе с увеличением активных потерь
обусловленных поверхностным эффектом и с потерями на излучение.
(2)
Возрастает запасенная энергия, уменьшаются потери. В таких объемных
резонаторах сохранены конструктивные особенности присущие системам с
сосредоточенными параметрами (можно выделить L и C).
С ростом частоты, L
и C уменьшаются, и в пределе получают контур как на
Рис.2. Он вырождается в утилитарную конструкцию, в которой роль ёмкости играют
две металлические пластины, а роль индуктивности – проводник соединяющий их.
Это характерное преобразование для волн сантиметрового диапазона. Добротность
таких контуров достаточно низка. Причина этого в следующем, малая величина LC элементов, приводит к
снижению энергии, запасённой в таком контуре.
Вследствие
поверхностного эффекта, увеличиваются потери в проводниках. 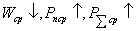 . Сильно возрастают потери на излучении. Возможен следующий
путь увеличения добротности на ВЧ. Как показано на Рис.2, вследствие
параллельного соединения элементов, увеличивается резонансная частота.
. Сильно возрастают потери на излучении. Возможен следующий
путь увеличения добротности на ВЧ. Как показано на Рис.2, вследствие
параллельного соединения элементов, увеличивается резонансная частота.
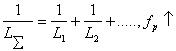
Отсюда мы получим
конструкцию как на Рис.3.
Получим локальный объём, ограниченный
локальными стенками.
Колебательная система, ограничивающая себя
проводящими, локальными стенками называют объёмным резонатором.
Этот
подход обладает недостатками, которые присущи колебательным системам с
сосредоточенными параметрами.
С
ростом частоты, объём колебательной системы уменьшается 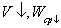 , снижается добротность. Сростом частоты возрастают
технологические трудности реализации подобных систем.
, снижается добротность. Сростом частоты возрастают
технологические трудности реализации подобных систем.
Рассмотрим более прогрессивный способ
реализации подобных систем, с использованием структур с распределёнными
параметрами. Рассмотрим реализацию колебательной системы из отрезков линии
передач.
Рассмотрим КЗ двухпроводную линию.
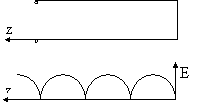
В
такой линии режим КЗ.
Режим
КЗ, будет повторятся в точках,
которым
удовлетворяют следующие
соотношения.

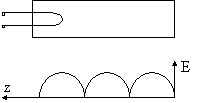
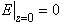 ,
, 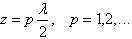
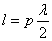
В частности, если взять линию КЗ с двух
сторон, то как показано в курсе ОТЦ, в ней будет колебательный процесс. Причём,
его частные параметры:
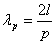
Характерная особенность таких
колебательных систем, что они могут резанировать на множестве частот. Вдоль
такой колебательной системы, должно укладываться целое число полуволн.
Мы
рассмотрели колебательную систему на примере отрезка двухпроводной линии.
Также, подобные системы могут быть реализованы на любых линиях передач, в том
числе и на волноводах.
Характерные особенности, будут заключатся, в следующем:
Стоячая волна может возникать по всем трём
координатам, внутри резонатора. Подобные резонаторы будут резонировать на
кратных частотах, вследствие явления дисперсии.
1. частотная дисперсия
2. стоячие волны 3-м
координатам
Объемный резонатор из отрезка прямоугольного волновода
Берём стандартный, прямоугольный
волновод, с волной 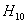 .
.
Рассмотрим
прямоугольный волновод сечением 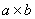 .
.
Определим структуру поля и параметры
электромагнитных колебаний, возникающих в таком резонаторе.
z=0, z=l
 H10
H10
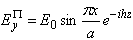
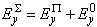
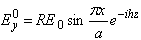
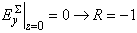
При наличии КЗ, в стенке
появится отражённая волна.
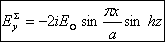
По определению, продольно-волновое число 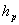 . Для его определения воспользуемся граничной задачей.
. Для его определения воспользуемся граничной задачей.
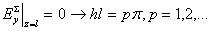
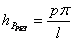 ,
, 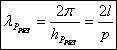
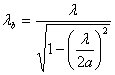 ; учитывая это, можно
написать:
; учитывая это, можно
написать: 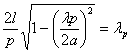
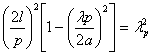
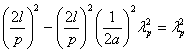
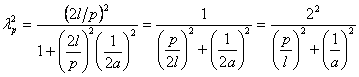
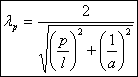 - длина волны
резонансная, в свободном пространстве.
- длина волны
резонансная, в свободном пространстве.
Индекс “p”, имеет простой физический
смысл. Он показывает, число стоячих полуволн, вдоль оси резонатора.
Рассматриваемый тип колебаний, имеет
следующую абривеатуру 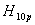 .
.
До
образования резонатора, в волноводе, существовала волна 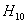 .
.
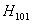 - в таком резонаторе
одна полуволна.
- в таком резонаторе
одна полуволна.
Тип колебаний: H10p Структура поля: H101
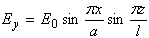 - так обозначим “y”
компоненту.
- так обозначим “y”
компоненту. 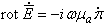
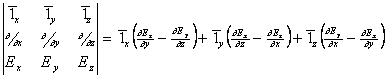
имеется только 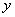 составляющая.
составляющая.







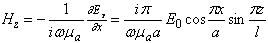 ]
]
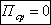 Поверхностные
токи:
Поверхностные
токи:
Из выражения для
составляющих поля следует, что E и H
отличаются на 900, что свидетельствует о нулевом значении среднего
за период вектора Пойнтинга и существование в резонаторе колебательного
процесса.
В
ходе этого процесса, дважды за период, энергия
электрического поля преобразуется в магнитное и наоборот.
Общая задача о колебаниях в прямоугольном резонаторе. Классификация
типов волн.
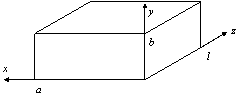 Eши
Eши
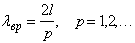
Определить совокупность резонансных частот всех возможных типов
колебаний, существующих в прямоугольном резонаторе с размерами 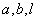 . Введём декартову систему координат, при этом пусть размер
. Введём декартову систему координат, при этом пусть размер 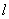 совпадает с осью
совпадает с осью 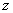 .
.
Пусть в поперечном сечении с размерами 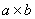 структура поля
совпадает со структурой поля волны
структура поля
совпадает со структурой поля волны 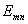 . Резонансная длина волны, связана с длиной волны в волноводе
с размерами
. Резонансная длина волны, связана с длиной волны в волноводе
с размерами 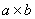 дисперсионным
уравнением.
дисперсионным
уравнением.
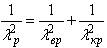
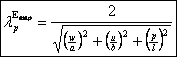
Пологая если структура колебания в
поперечном сечении резонатора, с размерами 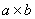 совпадает с поперечной
структурой волны Hmn в прямоугольном волноводе, то мы получим
уравнение.
совпадает с поперечной
структурой волны Hmn в прямоугольном волноводе, то мы получим
уравнение.
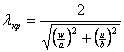
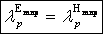
Из рассмотренных в предыдущих параграфах
следует, что случай H в прямоугольном волноводе по крайней мере 1-н может
принимать.
Из h
следует, что индексы mn входят в это соотношение
совершенно равноправно. Рассмотрим возможность при которой индекс p
соответствует нулевому значению.
p=0®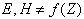

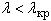
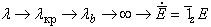
E110
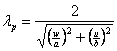
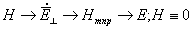
Если мы поставим две металлические плоскости на
расстоянии l, ненулевые индексы m и n на этих плоскостях будут
удовлетворяться механически. Структура поля остается неизменной (какой была в
отсутствии плоскостей).
В случае Hmn один из индексов может быть
не равен нулю. В случае Н-волн имеется только поперечная составляющая эл. поля.
Устремив длину волны к критической получим наличие продольной составляющей
магнитного поля, относительно поперечных пластин эти составляющие ориентированы
перпендикулярно, а поперечные составляющие эл. поля тангенциально.
Колебание Emn0 возможно, при этом
резонансные явления наблюдаются в поперечной плоскости. В продольном
направлении резонансные явления отсутствуют.
Колебания Hmn0 – невозможны.
Классификация типов колебаний
Классификация неоднозначно
зависит от выбора продольного размера резонатора и осуществляется следующим
образом.
- Один из размеров
полагается продольным .
- Определяем поперечную
структуру и тип волны, порождающей колебания в эквивалентном прямоугольном
волноводе с размерами
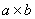 .
. 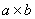 отсюда следует Emn.
отсюда следует Emn.
- Определяем индекс p,
и на основании этого имеем Emnp
Алгоритм классификации неоднозначно зависит
от первоначального выбора объемного размера
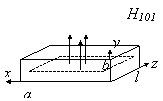
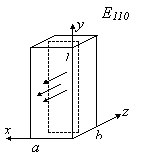
1. l
–продольный размер
2. 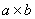 следует определить
структуру
следует определить
структуру
3. Определим индекс p.
Индекс p =1, отсюда H101.
Определим число стоячих
полуволн E110, отсюда число стоячих полуволн равно нулю. 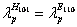
Цилиндрический объемный резонатор.
Определить совокупность резонансных
частот в всевозможных типов колебаний цилиндрического резонатора длиной l и
диаметром 2а. Размер l считаем продольным,
поперечное сечение соответствует Emn в волноводе.
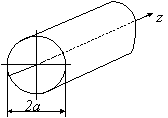
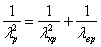
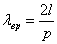 ;
; 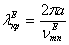 ;
; 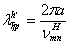

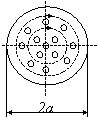
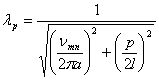
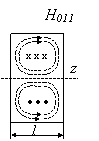
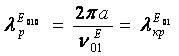
Точно
такими же рассуждениями, как в предыдущем параграфе показывается, что Emn0
– может существовать, и Hmn0 – не может. Приведем
структурные схемы некоторых характерных типов колебаний.
Способы возбуждения объемных резонаторов.
На практике резонаторы включают в
качестве радиотехнической схемы. Представляют интерес элементы связи в
резонаторе с внешними цепями. Различают электрического и магнитного типа
возбуждающие устройства.
Для возбуждения колебаний в
резонаторах используют возбуждающие устройства:
1) Эл. типа (элементарные
электрические излучатели)
2) Магнитные возбуждающие
устройства( элементарные магнитные излучатели).
Для наиболее интенсивного
возбуждения заданного типа колебаний с помощью эл. колебательного устройства,
которое представляет собой линейный проводник с током, он должен быть
ориентирован параллельно линиям эл. поля и находиться в максимуме его
интенсивности.
Возбуждающее устройство
магнитного типа выполнено в виде петлевого проводника с переменным током, петля
перпендикулярна линиям напряженности магнитного поля и находиться в максимуме
его интенсивности.
Покажем некоторые способы
возбуждения.
Существует два характерных способа включения
резонаторов в общую радиотехническую схему.
Абсорбционный способ включения
(параллельный)
Один элемент связи
Проходной способ
включения
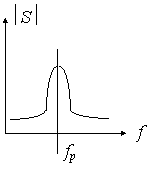 Два элемента связи
Два элемента связи
Чем выше коэффициент связи, тем ниже добротность,
следовательно, нужно достичь наименьшего коэффициента связи.
Электрический излучатель, представляет из себя,
металлический, электрический проводник (штырь) с переменным электрическим
током. Этот проводник должен находиться в максимуме электрического поля и
должен быть параллелен силовым линиям вектора E.
Магнитный
элемент связи – одна из разновидностей это петлевой элемент связи. Он должен
находиться в максимуме напряженности магнитного поля, возбуждения типа
колебаний и поверхность петли должна быть перпендикулярна силовым линиям
вектора H.
Добротность объемных резонаторов.
В разделе теоремы Пойнтинга
рассматривалась задача об изолированной системе. Для нее энергетические
отношения выглядели следующим образом.
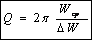
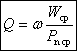
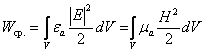
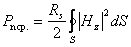
Мощность потерь
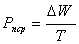
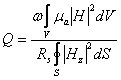
V - изолированная система
Для расчета конкретных значений добротности легко
могут быть получены следующие соотношения.
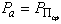
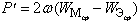
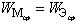
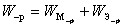
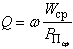
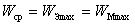
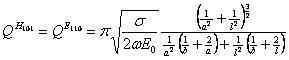
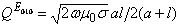
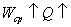
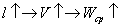 быстрее
быстрее
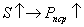
Все приведенные рассуждения касались
собственной системы резонаторов, когда резонатор рассматривался как
изолированная система, реально он связан с внешней схемой, которая вносит в
резонатор внешние потери. Она оказывает шунтирующее действие. Чем сильнее связь
с внешними цепями, тем меньше добротность. Добротность с учитываемыми внешними
цепями называют нагруженной добротностью, в отличие от собственной добротности.
Другие типы объемных
резонаторов
Коаксиальный резонатор
Учитывая, что в коаксиале с основным типом волн резонанс
не существует, то для обозначение колебаний в резонаторе из коаксиальных линий
используют следующие абривиатуры: Т001...
Характерная особенность резонатора на коаксиальной
линии , то что он резонирует на кратных частотах.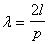 , р=1,2…
, р=1,2… 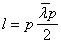 Используют такие
резонаторы в качестве волномера. По сравнению с цилиндрическим резонатором (из
отрезка кругового волновода) коаксиальный резонатор имеет меньшую добротность
из-за большей площади
Используют такие
резонаторы в качестве волномера. По сравнению с цилиндрическим резонатором (из
отрезка кругового волновода) коаксиальный резонатор имеет меньшую добротность
из-за большей площади
(рис.2) поверхности внутри и меньшего объема.
Очень распространены
диэлектрические резонаторы(рис.2)
Возбуждаясь за счет эффекта ПВО, диэлектрические
резонаторы не требуют специального возбуждения.
Как правило, диэлектрические резонаторы выполняют из
искусственных материалов с большим коэффициентом диэлектрической проницаемости.
Существуют полуоткрытые резонаторы, образованные
параболическими поверхностями.
Такие структуры используют для активных сред (плазмы), для которых
непосредственный контакт невозможен.
Основной недостаток: существуют потери на излучение.
Раздел 19. Распространение электромагнитных волн в
анизотропных средах
ТЕМА 16. Управляющие
ферритовые устройства СВЧ
Анизотропия в ферритах связана с особенностью их внутренней
структуры. Ферриты имеют области
самопроизвольной намагниченности (так называемые домены).Это достаточно объемные образования. Магнитные моменты отдельных атомов
ориентированны параллельно, так что даже в отсутствии внешнего поля домен
намагничен до насыщения, суммарный магнитный момент соответствует отдельным
доменам. В отсутствии внешнего магнитного поля домены ориентированы хаотично и
результирующее магнитное поле равно нулю.
Теория
ферритов достаточно сложна и выходит за рамки классической электродинамики, но
существует теория, рассматривающая поведение электрона в магнитном поле, выводы
которой на качественном уровне достаточно хорошо совпадают с практическими
результатами.
Все
особенности, характеризующие электрон в магнитном поле, обусловлены наличием у него спина. Спин - это, упрощенно, вращение электрона
относительно собственной оси.
Электрон
обладает массой, вращается относительно собственной оси.Он обладает
механическим моментом, кроме того, электрон обладает зарядом, то есть он обладает
механическим моментом. Кроме того, электрон обладает зарядом, и его можно
уподобить элементарной рамке с током. С одной стороны, электрон подобен
гироскопу, с другой - некоторому элементарному магниту при его внесении в
постоянное магнитное поле. Так как он подобен
элементарному магниту, то на него действует пара сил, старающихся ориентировать
его параллельно линиям магнитного поля;
но, т.к. он обладает еще и
свойствами гироскопа, то вместо того, чтобы ориентироваться по направлению
внешнего поля, конец вектора магнитного момента начинает описывать окружность,
лежащую в плоскости ûë b, это так называемая, прецессия
электромагнитного поля. Эта прецессия продолжается сколь угодно долго, но из-за
наличия потерь она является затухающей.
Время прецессии составляет
0,01 мкс.
Прецессия осуществляется с частотой wo=½g½Ho ,
где g - некоторая отрицательная
константа, связанная со свойствами феррита.
Пусть кроме постоянного
магнитного поля действует еще и переменное
магнитное поле, с частотой 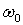 и направлением вдоль 1х. При этом электрон возобновляет
прецессию, причем прецессия становится незатухающей. Конец вектора магнитного момента описывает
замкнутые кривые. Известно, что эти замкнутые
кривые –эллипсы Частота прецессии
совпадает с частотой высокочастотного поля. Здесь усматривается аналогия с
колебательным контуром. При наличии
постоянного поля, физический эффект напоминает собственные колебания, а при
наличии дополнительно и ВЧ поля, процесс схож с вынужденными колебаниями в
контуре.
и направлением вдоль 1х. При этом электрон возобновляет
прецессию, причем прецессия становится незатухающей. Конец вектора магнитного момента описывает
замкнутые кривые. Известно, что эти замкнутые
кривые –эллипсы Частота прецессии
совпадает с частотой высокочастотного поля. Здесь усматривается аналогия с
колебательным контуром. При наличии
постоянного поля, физический эффект напоминает собственные колебания, а при
наличии дополнительно и ВЧ поля, процесс схож с вынужденными колебаниями в
контуре.
Управляющие устройства, предназначенные для изменения фазы, называются фазовращателями.
Особенно большую роль играют фазовращатели в фазированных антенных
решетках, где применяется большое число антенных элементов, соотношение фаз
между которыми должно либо сохраняться неизменным, либо в процессе работы
изменяться по определенному закону.
Имеются фазовращатели различных типов: механические, полупроводниковые,
ферритовые.
В механических фазовращателях для изменения фазы колебаний между двумя
неподвижными сечениями линии передачи последовательно включается секция,
например, «тромбонного» типа (подковообразной формы), длина которой механически
изменяется с помощью скользящих контактов.
В другом варианте механического фазовращателя для волновода изменение
фазы достигается, например, механическим погружением диэлектрической пластины
параллельно силовым линиям электрического поля Е в прямоугольный волновод через неизлучающую щель в середине
широкой стенки. Это приводит к замедлению электромагнитной волны и увеличению
запаздывания на выходе фазовращателя. Недостатком механических фазовращателей
являетется невозможность изменения фазы с большой скоростью.
В фазовращателях на полупроводниковых диодах этот недостаток отсутствует.
К их достоинствам относятся малые габаритные размеры и масса большая скорость и
простота управления. Полупроводниковые фазовращатели изготавливают в
волноводном, полосковом и микрополосковом исполнении.
В полупроводниковых фазовращателях СВЧ используются главным образом
коммутационные p-i-n диоды. Кроме них в управляющих
устройствах CBЧ применяются также коммутационные р-п
диоды, в том числе и варикапы Однако p-i-n диоды по сравнению с р-п диодами
позволяют пропускать значительно большие мощности СВЧ, вплоть до сотен киловатт
в импульсе (или среднюю мощность в сотни ватт).
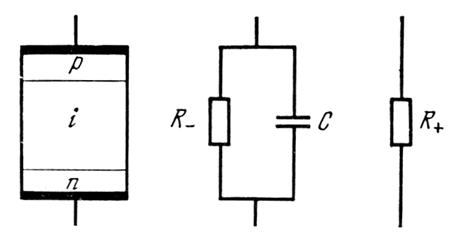
Рис. 2.13. Диод типа p-i-n и его эквивалентные схемы
Диоды p-i-n (в отличие от диодов р-п) кроме слоев p и n содержат высокоомную область i, расположенную между слоями р и п (рис. 2.13,а). Область i называют базой диода. Торцевые поверхности
диода (диаметром около 1 мм) прилегающие к слоям р и п, металлизируют и
используют в качестве выводов При отрицательном напряжении на диоде он
оказывается запертым и его эквивалентная схема (рис. 2.13,б) имеет вид большого активного сопротивле ния R_ (несколько
килоом), шунтированного малой емкостью С диода
(десятые доли пикофарады). При подаче на диод положительного управляющего
напряжения (порядка 1 ... 2 В) его сопротивление резко уменьшается (в сотни
раз) и может быть эквивалентно представлено малым активным сопротивлением R+ (рис. 2.13,в).
Возможная схема изменения фазы высокочастотного колебания на выхода линии
передачи показана на рис. 2.14. Здесь в основную линию передачи с волновым
сопротивлением Zв последовательно
включен отрезок линии передачи с электрической длиной bl и волновым сопротивлением Zт; по концам линии включены шунтирующие
проводимости G1 и G2. Подбором значений G1, G2, bl и Zт можно обеспечить требуемое изменение фазы
высокочастотного колебания на выходе линии и согласование промежуточного
отрезка линии с основной линией передачи.
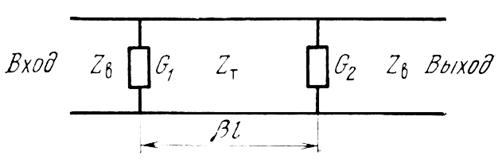
Рис. 2.14. Схема линии передачи с проходными фазовращателями
В качестве изменяющихся проводимостей G1 и G2 можно использовать отражательные
фазовращатели. Такой фазовращатель (рис. 2.15) представляет собой отрезок линии
передачи, шунтированный в ряде сечений коммутационными элементами, например, в
виде описанных выше p-i-n диодов. При подаче
на один из диодов напряжения питания можно уменьшить его сопротивление до малой
величины и замкнуть накоротко линию в данном сечении. Остальные коммутационные
элементы имеют (при отсутствии питания) высокие сопротивления и не оказывают
заметного влияния на линию. При переключении коммутационных элементов
изменяется положение плоскости короткого замыкания в линии передачи и
соответственно ее входная G1 или G2.
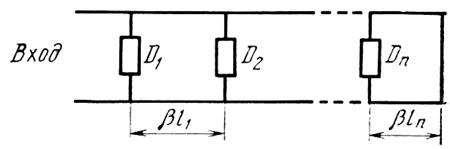
Отражательный фазовращатель в виде
отрезка линии передачи, шунтированного в ряде сечений коммутационными
элементами
В технике СВЧ широко применяются ферритовые фазовращатели. Феррит
представляет собой химическое соединение окиси железа (Fe2O3) с окисью таких металлов, как никель,
марганец и др. По своему внешнему виду ферритовые стержни напоминают керамику,
а по электрическим свойствам являются полупроводниками, приближающимися к
диэлектрикам. Большое удельное сопротивление ферритов (106... 108
Ом·см), в отличие от других ферромагнитных материалов, обусловило
возможность применения их в диапазоне СВЧ. Диэлектрическая проницаемость
ферритов на СВЧ колеблется в пределах 5...15, а магнитная при отсутствии
подмагничивания близка к единице.
Особо интересные свойства приобретает феррит под воздействием постоянного
магнитного поля и высокочастотных колебаний. В этих условиях магнитная
проницаемость феррита начинает зависеть сложным образом от постоянного
магнитного поля, причем эта зависимость для высокочастотных полей круговой
поляризации разного направления вращения получается различной.
Эти особые свойства ферритов позволяют конструировать в диапазоне СВЧ ряд
технических устройств. К ним относятся волноводные циркуляторы, т. е.
устройства в виде ряда каналов, характеризующиеся тем, что электромагнитные
волны распространяются из одного канала в другой только в определенной
последовательности. В частности, циркулятор может быть превращен в вентиль,
служащий, например, для развязки генератора от нагрузки. Ограничимся описанием
лишь ферритовых фазовращателей.
Ферритовый фазовращатель в
прямоугольном волноводе с продольным намагничиванием. По оси волновода расположен ферритовый стержень, круглого или
прямоугольного сечения. Управляющее магнитное поле направлено продольно и
создается соленоидом, намотанным снаружи непосредственно на волноводе.
Изменением управляющего магнитного поля можно менять магнитную проницаемость
феррита и соответственно скорость распространения и длину волны высокочастотных
колебаний внутри волновода, а следовательно, и фазу поля за ферритовым
стержнем. Достоинством такого фазовращателя является его простота и возможность
регулировки фазы в широких пределах (0...3600) при небольшом
ослаблении мощности колебаний СВЧ (0,5... 1,0 дБ).
Ферритовый фазовращатель в
прямоугольном волноводе с поперечным полем подмагничивания. Ферритовая пластина прямоугольного поперечного сечения размещается
параллельно узкой стенке между ней и серединой волновода (приблизительно на
расстоянии а/4 от узкой стенки, где а •— размер широкой стороны волновода).
Полюса магнита N и S устанавливаются по обе стороны пластины. В
таком фазовращателе для увеличения фазового сдвига и уменьшения общей длины
обычно используются две ферритовые пластины, располагаемые по обе стороны от
средней плоскости волновода и соответственно намагничиваемые.
Возможен коаксиальный вариант фазовращателя, в котором феррит заполняет
часть пространства между центральным проводом и экранирующим цилиндром, а
поперечное магнитное поле создается магнитом, устанавливаемым снаружи отрезка
коаксиальной линии.
Ферритовые
фазовращатели СВЧ успешно конкурируют с фазовращателями на p-i-n диодах и позволяют управлять более высокими
мощностями, но обладают несколько меньшим быстродействием.
ТЕМА 17. Перспективы
развития техники СВЧ
Бурное развитие радиотехнических систем
различного назначения сопровождается, как освоением
новых диапазонов частот, так и предоставлением
одной полосы частот нескольким радиослужбам. В результате основные спектры,
излучаемые и принимаемые отдельными радиосредствами, оказываются частично или
полностью перекрывающимися, что приводит к увеличению числа мешающих сигналов (неумышленные помехи) и снижению отношения сигнал/шум. Вопросы, связанные с изучением
причин возникновения и способов снижения неумышленных радиопомех,
относятся к проблеме электромагнитной
совместимости (ЭМС) радиосредств. Среди возможных причин появления неумышленных
помех следует различать помехи, проникающие в радиотехническую систему
через антенну, и помехи, возникающие помимо
антенны и обусловленные, в основном, электромагнитными связями между
различными узлами данной системы или между элементами двух или более систем, размещенных близко друг от друга.
Существенным фактором появления помех являются паразитные электромагнитные
связи в антенно-фидерных линиях. Они
существуют в системах, расположенных как на одном объекте, так и на далеко стоящих друг от друга. В
современных радиосистемах основной причиной появления помех является прием
антенной нежелательных мешающих сигналов. Пространственная и частотная
избирательности, присущие антенным системам, позволяют существенно улучшить
электромагнитную обстановку.
Насколько велика роль антенн в обеспечении ЭМС, можно судить по тому факту, что из 30 основных параметров
радиоэлектронного оборудования, влияющих на ЭМС, 12 параметров определяются
антенной системой. Совокупность характеристик антенны, существенных для
обеспечения ЭМС, будем называть помехозащищенностью антенны. В ряде случаев
требования к помехозащищенности разрабатываемых антенн оказываются столь
жесткими, что их выполнение сопровождается некоторым снижением КУ, ухудшением согласования, сужением рабочего диапазона частот и т.д. Проблему ЭМС в рамках конкретной
радиотехнической системы решают
двумя путями:
1)
разрабатывают более
помехозащищенные радиотехнические системы;
2)
проводят их
оптимальное проектирование с точки зрения уменьшения
создаваемых ими помех.
В последние годы разрабатывается новый класс антенн - так называемые
адаптивные антенные системы, позволяющие производить подстройку под данную
помеховую обстановку таким образом, чтобы свести влияние помех к минимуму.
Основными характеристиками антенн, расположенных на большом
расстоянии друг от друга
(в зоне излучения) и способных влиять на ЭМС, являются: направленные свойства в рабочем
диапазоне (ширина главного
лепестка ДН, КНД, КУ, УБЛ и др.); внеполосное излучение антенны (излучение в полосах частот, примыкающих к рабочей полосе,
- результат модуляции); направленные
свойства на частотах побочных излучений (излучения на гармониках,
паразитные, комбинационные и интермодуляционные); поляризационные характеристики; искажение направленных свойств из-за влияния посторонних объектов; стабильность
характеристик во времени и др. Что касается внеполосных излучений, то
антенная система совместно с линией питания
является в какой-то мере фильтром этих излучений. Например, в волноводной линии
антенны подавляются все частоты, являющиеся запредельными для данного
сечения волновода. Для обеспечения ЭМС различных радиосистем ДН, как передающих, так и приемных антенн этих систем, должны обладать малым боковым и задним
излучениями. Это объясняется тем, что
нежелательные сигналы часто попадают на вход приемника через боковые и
задние лепестки ДН антенны и оказывают на качество работы системы большое влияние. Такая ситуация создается в
системах, работающих в условиях слабых полезных сигналов или при высоком уровне
помех. Поэтому снижение УБЛ во многом решило бы проблему ЭМС. Однако,
как известно, в данном случае должен быть
соблюден определенный компромисс, связанный со снижением апертурного КИП
антенны. При работе антенны в реальных условиях возникают дополнительные
причины, искажающие ее направленные свойства. Эти причины обусловлены влиянием
размеров и формы конструкции, на которой расположена антенна, а также рядом
расположенных других антенн и т.д. При оценке влияния направленных свойств антенны
на уровень ЭМС необходимо учитывать все указанные факторы. Многие из них могут быть установлены только
экспериментальным путем. Рассмотрим влияние помехозащищенности в конкретном
случае на примере собственных помех РРЛ, когда недостаточная пространственная
избирательность антенн приводит к ухудшению характеристик РРЛ. На
рис.17.1 схематически показан участок РРЛ, включающий три ретрансляционных
пункта А, В, С. Антенна В1 станции
В принимает кроме полезного сигнала от антенны А2 станции А два мешающих сигнала от антенн A1 и С1. При двухчастотном плане распределения частот передача на каждой станции РРЛ в оба направления идет на одинаковых частотах, а частоты передатчиков повторяются через станцию. Поэтому все три сигнала, принимаемые антенной В1, имеют
одинаковые частоты и
ослабление помех от антенн A1 и C1 может быть обеспечено только направленными свойствами антенн. Чтобы указанные помехи не оказывали заметного влияния на качественные показатели линии,
необходимо, чтобы КЗД антенн РРЛ, т.е.
уровень излучения антенн в направлении θ = 180°, по
отношению к излучению в направлении θ = 0° не превышал -(65...70) дБ.
В ряде случаев для улучшения ЭМС применяется развязка антенн по поляризации
электромагнитного поля. При этом две антенны работают с полями, поляризованными взаимно перпендикулярно, либо, если антенны с вращающейся поляризацией поля, направления вращения векторов электромагнитного поля у обеих антенн
противоположны. Иногда антенны
располагаются на небольшом расстоянии друг от друга (в зоне ближнего поля). Это имеет место на KB, CB и ДВ радиоцентрах, при установке антенн ретрансляционных пунктов РРЛ на одних и тех же мачтах, а также при размещении антенн на ограниченной
площади космического корабля или спутника. Из-за пространственной
электромагнитной связи изменяются направленные свойства и входные
сопротивления антенн, поэтому необходимо принимать специальные
меры для увеличения переходного затухания
между антеннами. К ним относятся рациональное размещение антенн относительно
друг друга (например, взаимное влияние двух параболических антенн РРЛ
уменьшается, если их установить не рядом, а «спина к спине»), включение в
антенны реактивных развязывающих элементов и др. Совместное использование одних и тех же полос частот
различными спутниковыми и наземными
радиослужбами, что допускается международными соглашениями (см., например,
Регламент радиосвязи), усложняет электромагнитную обстановку. Таким образом,
возникает сложная проблема электромагнитной совместимости. Эта проблема
касается обеспечения совместимости между спутниковыми системами и спутниковых
систем с наземными службами. С целью соблюдения необходимых условий ЭМС в
настоящее время принято сопоставлять ДН антенн спутниковой связи с так
называемыми справочными ДН. Последние
представляют собой графическое изображение огибающей рекомендуемой МККР ДН
относительно изотропного излучателя (в децибелах). Следует отметить,
что международные рекомендации периодически пересматриваются. Это подтверждает тенденцию ужесточения требований к ДН антенн спутниковой связи с целью более полного
удовлетворения требованиям ЭМС. Остановимся более подробно на вопросах ЭМС
апертурных антенн.
![]() = P
= P![]() / Р0, где
P
/ Р0, где
P![]() - мощность излучаемая антенной, Р0 - мощность
подводимая к антенне.
- мощность излучаемая антенной, Р0 - мощность
подводимая к антенне.![]() ,где
,где ![]() - длина волны) для диапазона частот 10кГц...1ГГц. К числу
антенн этого класса относятся одиночные вибраторные и
щелевые излучатели, полосковые и микрополосковые антенны,
рамочные антенны, а также частотно-независимые излучатели.
- длина волны) для диапазона частот 10кГц...1ГГц. К числу
антенн этого класса относятся одиночные вибраторные и
щелевые излучатели, полосковые и микрополосковые антенны,
рамочные антенны, а также частотно-независимые излучатели.![]() до 100
до 100![]() для диапазона частот 3МГц...10ГГц. Сюда
относятся спиральные, диэлектрические,директорные, импедаксные антенны, а также
антенны «вытекающей» волны.
для диапазона частот 3МГц...10ГГц. Сюда
относятся спиральные, диэлектрические,директорные, импедаксные антенны, а также
антенны «вытекающей» волны.![]() до 100
до 100![]() и более для диапазона частот 3МГц...30ГГц. Это антенны, состоящие из большого числа отдельных излучателей. Независимая регулировка фаз (а иногда и амплитуд) возбуждения
каждого элемента антенной решетки обеспечивает возможность электрического управления диаграммой направленности. Применяются линейные, плоские, кольцевые, выпуклые и конформные (совпадающие с формой объекта установки) антенные решетки. На основе антенных решеток выполняют
антенные системы с обработкой сигнала, в том числе адаптивные к изменяющейся
помеховой обстановке.
и более для диапазона частот 3МГц...30ГГц. Это антенны, состоящие из большого числа отдельных излучателей. Независимая регулировка фаз (а иногда и амплитуд) возбуждения
каждого элемента антенной решетки обеспечивает возможность электрического управления диаграммой направленности. Применяются линейные, плоские, кольцевые, выпуклые и конформные (совпадающие с формой объекта установки) антенные решетки. На основе антенных решеток выполняют
антенные системы с обработкой сигнала, в том числе адаптивные к изменяющейся
помеховой обстановке.![]() до 1000
до 1000![]() для диапазона частот 100МГц... 100ГГц и
выше. Наиболее распространены зеркальные, рупорные и линзовые апертурные
антенны. К апертурным антеннам примыкают, так называемые, «гибридные» антенны,
представляющие сочетание зеркал или линз с облучающей
системой в виде антенной решетки. Апертурные антенны строятся по оптическим принципам и обеспечивают наиболее высокую направленность излучения.
для диапазона частот 100МГц... 100ГГц и
выше. Наиболее распространены зеркальные, рупорные и линзовые апертурные
антенны. К апертурным антеннам примыкают, так называемые, «гибридные» антенны,
представляющие сочетание зеркал или линз с облучающей
системой в виде антенной решетки. Апертурные антенны строятся по оптическим принципам и обеспечивают наиболее высокую направленность излучения.![]() = I02 R
= I02 R![]() 0 / 2, где RΣ0 – сопротивление излучения антенны (при отсутствии потерь в антенне это
активная составляющая входного сопротивления антенны). Данное
определение относится к проволочным антеннам.
0 / 2, где RΣ0 – сопротивление излучения антенны (при отсутствии потерь в антенне это
активная составляющая входного сопротивления антенны). Данное
определение относится к проволочным антеннам.![]() = 10...100 км);
километровые или длинные волны (
= 10...100 км);
километровые или длинные волны (![]() = 1...10 км); гектометровые или средние
волны (
= 1...10 км); гектометровые или средние
волны (![]() = =100...1000 м);
декаметровые или короткие волны (
= =100...1000 м);
декаметровые или короткие волны (![]() = 10...100 м); метровые волны (
= 10...100 м); метровые волны (![]() = 1...10м); дециметровые волны (
= 1...10м); дециметровые волны (![]() = 10 см...1 м); сантиметровые волны (
= 10 см...1 м); сантиметровые волны (![]() = 1...10 см); миллиметровые волны (
= 1...10 см); миллиметровые волны (![]() = 1...10 мм). Последние четыре диапазона объединяются общим названием "ультракороткие
волны" (УКВ).
= 1...10 мм). Последние четыре диапазона объединяются общим названием "ультракороткие
волны" (УКВ).![]() . (2.1)
. (2.1)![]() - коэффициент фазы или волновое число в свободном пространстве); θ,φ -
координаты точки наблюдения; |f(θ,φ)| - амплитудная характеристика направленности; Ψ(θ,φ) - фазовая характеристика
направленности. Известно, что в случае элементарного электрического вибратора
- коэффициент фазы или волновое число в свободном пространстве); θ,φ -
координаты точки наблюдения; |f(θ,φ)| - амплитудная характеристика направленности; Ψ(θ,φ) - фазовая характеристика
направленности. Известно, что в случае элементарного электрического вибратора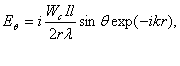 (2.2)
(2.2)![]() характеристическое сопротивление волны; в
свободном пространстве
характеристическое сопротивление волны; в
свободном пространстве ![]() , Ом
, Ом![]() ) через нуль меняется ее знак, что соответствует скачку фазы
напряженности поля на 180°. Поэтому
амплитудной характеристикой направленности является модуль этой функции
|f(
) через нуль меняется ее знак, что соответствует скачку фазы
напряженности поля на 180°. Поэтому
амплитудной характеристикой направленности является модуль этой функции
|f(![]() )|. В дальнейшем для упрощения записи знак модуля опускаем. В общем случае характеристика
направленности является векторной и
комплексной величиной. Выражение ƒ(
)|. В дальнейшем для упрощения записи знак модуля опускаем. В общем случае характеристика
направленности является векторной и
комплексной величиной. Выражение ƒ(![]() )=f(
)=f(![]() ) exp[i
) exp[i![]() ] называется комплексной
характеристикой направленности антенны. Она полностью определяет угловое распределение и фазовые свойства излучаемого электромагнитного
поля в дальней зоне антенны. Характеристика направленности антенны определяется размерами и конфигурацией антенны, а также
распределением возбуждающего тока (как действительного, так и эквивалентного).
Напомним, что дальняя зона (зона излучения или зона Фраунгофе-ра)
характеризуется тем, что направления (лучи), проведенные из любой точки
антенны на точку наблюдения, находящуюся в этой зоне, считаются параллельными. При этом возникает ошибка в
определении фаз полей, создаваемых в точке наблюдения различными элементами
антенны. Эта ошибка оказывается тем меньше, чем больше расстояние от антенны до
точки наблюдения по сравнению с размерами антенны. Расстояние дальней зоны rизл
] называется комплексной
характеристикой направленности антенны. Она полностью определяет угловое распределение и фазовые свойства излучаемого электромагнитного
поля в дальней зоне антенны. Характеристика направленности антенны определяется размерами и конфигурацией антенны, а также
распределением возбуждающего тока (как действительного, так и эквивалентного).
Напомним, что дальняя зона (зона излучения или зона Фраунгофе-ра)
характеризуется тем, что направления (лучи), проведенные из любой точки
антенны на точку наблюдения, находящуюся в этой зоне, считаются параллельными. При этом возникает ошибка в
определении фаз полей, создаваемых в точке наблюдения различными элементами
антенны. Эта ошибка оказывается тем меньше, чем больше расстояние от антенны до
точки наблюдения по сравнению с размерами антенны. Расстояние дальней зоны rизл![]() 2R2/
2R2/![]() , где R - наибольший размер излучающей системы. В этой зоне поле имеет поперечный характер (отсутствуют составляющие
векторов Е и Н в направлении распространения); в окрестности точки наблюдения
поле имеет характер плоской волны; амплитуды полей, излучаемых элементами антенны, убывают обратно
пропорционально расстоянию.
, где R - наибольший размер излучающей системы. В этой зоне поле имеет поперечный характер (отсутствуют составляющие
векторов Е и Н в направлении распространения); в окрестности точки наблюдения
поле имеет характер плоской волны; амплитуды полей, излучаемых элементами антенны, убывают обратно
пропорционально расстоянию.![]() ), т.е. отношением напряженности поля,
излучаемого антенной в произвольном направлении, к значению напряженности поля
в направлении максимального излучения
), т.е. отношением напряженности поля,
излучаемого антенной в произвольном направлении, к значению напряженности поля
в направлении максимального излучения![]() )= | E(
)= | E(![]() )| / |
Emax(
)| / |
Emax(![]() )| = f(
)| = f(![]() )/fmax(
)/fmax(![]() ).
).![]() ). На рис.2.1.а изображена пространственная ДН
элементарного вибратора (тороид), на рис.2.1.б - ДН более сложной антенны (так называемая игольчатая ДН). На
практике обычно используют ДН, изображающие характеристику направленности в
каких-либо выбранных плоскостях. В качестве таких плоскостей обычно выбирают
две взаимно перпендикулярные плоскости,
проходящие через направление
). На рис.2.1.а изображена пространственная ДН
элементарного вибратора (тороид), на рис.2.1.б - ДН более сложной антенны (так называемая игольчатая ДН). На
практике обычно используют ДН, изображающие характеристику направленности в
каких-либо выбранных плоскостях. В качестве таких плоскостей обычно выбирают
две взаимно перпендикулярные плоскости,
проходящие через направление![]() в какой-либо
координатной системе (прямоугольной, полярной и др.) подобно сетке меридианов и параллелей на географической
карте. На этой сетке замкнутыми линиями изображаются одинаковые
в какой-либо
координатной системе (прямоугольной, полярной и др.) подобно сетке меридианов и параллелей на географической
карте. На этой сетке замкнутыми линиями изображаются одинаковые![]() ) в том или ином масштабе. При изображении ДН часто
используется логарифмический масштаб, вводимый соотношением в децибеллах F(
) в том или ином масштабе. При изображении ДН часто
используется логарифмический масштаб, вводимый соотношением в децибеллах F(![]() )=20 lgF(
)=20 lgF(![]() ).
).![]() ). Функция F(
). Функция F(![]() ) для
различных
) для
различных ![]() и
и ![]() проходит через нуль и имеет несколько максимумов, т.е. ДН имеет
многолепестковый характер (см. рис.2.3).
Диаграмму направленности принято численно
характеризовать шириной главного
лепестка (шириной луча) и относительным
уровнем боковых лепестков (УБЛ).
проходит через нуль и имеет несколько максимумов, т.е. ДН имеет
многолепестковый характер (см. рис.2.3).
Диаграмму направленности принято численно
характеризовать шириной главного
лепестка (шириной луча) и относительным
уровнем боковых лепестков (УБЛ).![]() 0
между направлениями вдоль которых напряженность поля падает до нуля (см. рис.2.3). Шириной ДН по половинной мощности называют угол 2
0
между направлениями вдоль которых напряженность поля падает до нуля (см. рис.2.3). Шириной ДН по половинной мощности называют угол 2![]() 0,5 между направлениями,
вдоль которых |Е| = |Emax|/
0,5 между направлениями,
вдоль которых |Е| = |Emax|/![]() или соответственно среднее значение
плотности потока мощности П=Пmaх/2.
Наибольший лепесток, максимум которого соответствует
направлению максимального излучения, называют главным, меньшие лепестки - боковыми (лепестки, находящиеся в задних
квадрантах, т.е. в диапазоне углов 90°
или соответственно среднее значение
плотности потока мощности П=Пmaх/2.
Наибольший лепесток, максимум которого соответствует
направлению максимального излучения, называют главным, меньшие лепестки - боковыми (лепестки, находящиеся в задних
квадрантах, т.е. в диапазоне углов 90°![]() 180° и 180°
180° и 180°![]() 270°, часто называют задними).
270°, часто называют задними).![]() ) есть отношение апряженности поля в
направлении максимума данного лепестка (ENmax) к апряженности поля внаправлении главного максимума (Еmax), т.е.
) есть отношение апряженности поля в
направлении максимума данного лепестка (ENmax) к апряженности поля внаправлении главного максимума (Еmax), т.е.![]() N=|ENmax|/|Еmax|=FN(
N=|ENmax|/|Еmax|=FN(![]() ), или в децибеллах
), или в децибеллах ![]() дБ = 20lg FN(
дБ = 20lg FN(![]() ), где N=1,2,3,...-номер бокового лепестка (для главного лепестка N=0).
), где N=1,2,3,...-номер бокового лепестка (для главного лепестка N=0).![]() была мала.
была мала. ![]() ) или F(
) или F(![]() ) через нуль, т.е. при переходе от
одного лепестка ДН к другому, то такая антенна является
источником сферических волн, о чем свидетельствует
множитель [ехр(-ikr)]/r. Эти волны исходят как бы из одной точки, называемой фазовым
центром антенны. Эта точка расположена в начале выбранной системы
координат, и поэтому, фазовая характеристика зависит от
положения начала координат. Однако не все реальные антенны обладают фазовым
центром, т.е. излучают сферические волны. Для них обычно можно подобрать сферу, наилучшим образом аппроксимирующую фронт волны (обычно в пределах главного лепестка). Центр этой сферы называют центром
излучения антенны. Графическое изображение фазовой характеристики называется фазовой ДН.
) через нуль, т.е. при переходе от
одного лепестка ДН к другому, то такая антенна является
источником сферических волн, о чем свидетельствует
множитель [ехр(-ikr)]/r. Эти волны исходят как бы из одной точки, называемой фазовым
центром антенны. Эта точка расположена в начале выбранной системы
координат, и поэтому, фазовая характеристика зависит от
положения начала координат. Однако не все реальные антенны обладают фазовым
центром, т.е. излучают сферические волны. Для них обычно можно подобрать сферу, наилучшим образом аппроксимирующую фронт волны (обычно в пределах главного лепестка). Центр этой сферы называют центром
излучения антенны. Графическое изображение фазовой характеристики называется фазовой ДН.![]() , к усредненному по всем направлениям
значению плотности потока мощности Пуср
, к усредненному по всем направлениям
значению плотности потока мощности Пуср![]() . (2.3)
. (2.3)![]() , где |
, где |![]() | - амплитудное значение напряженности электрического поля в направлении, характеризуемом углами
| - амплитудное значение напряженности электрического поля в направлении, характеризуемом углами ![]() . Таким образом, при определении КНД данная
антенна сравнивается с воображаемой абсолютно ненаправленной (изотропной)
антенной, излучающей ту же мощность, что и данная. Очевидно, что
. Таким образом, при определении КНД данная
антенна сравнивается с воображаемой абсолютно ненаправленной (изотропной)
антенной, излучающей ту же мощность, что и данная. Очевидно, что![]() , (2.4)
, (2.4)![]() - мощность излучения; r - радиус
воображаемой сферы, охватывающей антенну, причем величина r должна быть такой, чтобы поверхность сферы находилась в дальней зоне поля антенны.
- мощность излучения; r - радиус
воображаемой сферы, охватывающей антенну, причем величина r должна быть такой, чтобы поверхность сферы находилась в дальней зоне поля антенны.![]() , и подставляя в (2.3) выражение (2.4), получаем формулу для КНД в другом виде
, и подставляя в (2.3) выражение (2.4), получаем формулу для КНД в другом виде ![]() или для свободного пространства (Wc°=120
или для свободного пространства (Wc°=120![]() Ом) в направлении максимального излучения
Ом) в направлении максимального излучения![]() (2.5)
(2.5)![]() выражение (2.2) в квадрате (без фазовых
множителей) и учесть, что
выражение (2.2) в квадрате (без фазовых
множителей) и учесть, что ![]() , где
, где ![]() - сопротивление излучения элементарного электрического вибратора,
то получим КНД элементарного
вибратора D=1,5.
- сопротивление излучения элементарного электрического вибратора,
то получим КНД элементарного
вибратора D=1,5.![]() .Этот параметр иногда используют при
анализе приемных антенн, а также проволочных длинноволновых и средневолновых
антенн и антенн-мачт.
.Этот параметр иногда используют при
анализе приемных антенн, а также проволочных длинноволновых и средневолновых
антенн и антенн-мачт.![]() (2.6)
(2.6)![]() - волновое сопротивление
среды. Напишем выражение для величины напряженности поля
любой вибраторной антенны в произвольном направлении
- волновое сопротивление
среды. Напишем выражение для величины напряженности поля
любой вибраторной антенны в произвольном направлении![]() (2.7)
(2.7)![]() выражение
(2.6) и учитывая,
что
выражение
(2.6) и учитывая,
что![]() (
(![]() - сопротивление излучения антенны, отнесенное к току в точках
питания; I -ток в точках
питания антенны), получаем
- сопротивление излучения антенны, отнесенное к току в точках
питания; I -ток в точках
питания антенны), получаем![]() или
или ![]() (2.8)
(2.8)![]() , к среднему значению плотности потока мощности, создаваемого воображаемым абсолютно ненаправленным излучателем
(Пн). При этом предполагается, что точка
наблюдения находится на одинаковом расстоянии от обеих
антенн; мощности, подводимые к той и другой антеннам, равны и КПД
ненаправленной антенны равен единице. Таким образом, КУ
, к среднему значению плотности потока мощности, создаваемого воображаемым абсолютно ненаправленным излучателем
(Пн). При этом предполагается, что точка
наблюдения находится на одинаковом расстоянии от обеих
антенн; мощности, подводимые к той и другой антеннам, равны и КПД
ненаправленной антенны равен единице. Таким образом, КУ![]() . (2.9)
. (2.9)![]() , этих антенн.
Умножим и разделим
правую часть (2.9)
на Пуср. Тогда [П(
, этих антенн.
Умножим и разделим
правую часть (2.9)
на Пуср. Тогда [П(![]() )/Пуср](Пуср/Пн), где Пуср/Пн
=
)/Пуср](Пуср/Пн), где Пуср/Пн
=![]() - КПД антенны.
- КПД антенны. ![]() ) связаны соотношением
) связаны соотношением![]() . (2.10)
. (2.10)![]() , можно написать
, можно написать![]() /r=
/r=![]() /r . (2.11)
/r . (2.11)![]() или
или ![]() (
(![]() - сдвиг фаз между составляющими
- сдвиг фаз между составляющими ![]() и
и ![]() ). Линейная
поляризация также имеет место, если
). Линейная
поляризация также имеет место, если ![]() =0 или
=0 или ![]() =0. При круговой
поляризации поля (
=0. При круговой
поляризации поля (![]() =
=![]() ;
;![]() ) t=l. Таким образом, коэффициент равномерности поляризационного эллипса может изменяться в пределах 0< t < 1. Зависимость коэффициента эллиптичности от
направления на точку наблюдения называется поляризационной
ДН.
) t=l. Таким образом, коэффициент равномерности поляризационного эллипса может изменяться в пределах 0< t < 1. Зависимость коэффициента эллиптичности от
направления на точку наблюдения называется поляризационной
ДН.![]() называется угол,
образованный большой осью поляризационного эллипса и
направлением орта
называется угол,
образованный большой осью поляризационного эллипса и
направлением орта ![]() или
или ![]() 0 сферической системы координат (см. рис. 2.4.б).
Направление вращение вектора Е в
точке наблюдения определяется знаком угла
сдвига фаз между составляющими поля.
0 сферической системы координат (см. рис. 2.4.б).
Направление вращение вектора Е в
точке наблюдения определяется знаком угла
сдвига фаз между составляющими поля. ![]() и
и ![]() . Это направление называется правым, если наблюдатель, глядя навстречу волне, видит вектор Е вращающимся против часовой стрелки (рис. 2.5). Противоположное
направление вращения плоскости поляризации называется левым. Вектор Е
всегда вращается в сторону составляющей поля, отстающей по фазе.
. Это направление называется правым, если наблюдатель, глядя навстречу волне, видит вектор Е вращающимся против часовой стрелки (рис. 2.5). Противоположное
направление вращения плоскости поляризации называется левым. Вектор Е
всегда вращается в сторону составляющей поля, отстающей по фазе.![]() где
где ![]() - парциальные КНД для
каждой из ортогональных составляющих поля; Пуср — усредненное по всем направлениям значение плотности потока мощности полного поля;
- парциальные КНД для
каждой из ортогональных составляющих поля; Пуср — усредненное по всем направлениям значение плотности потока мощности полного поля; ![]() . Здесь
. Здесь ![]() -
полная мощность излучения;
-
полная мощность излучения; ![]() и
и ![]() - мощности излучения, соответствующие ортогональным
компонентам поля. В соответствии с (2.3)
под КНД антенны с эллиптической поляризацией поля при полном
поляризационном приеме будем подразумевать величину
- мощности излучения, соответствующие ортогональным
компонентам поля. В соответствии с (2.3)
под КНД антенны с эллиптической поляризацией поля при полном
поляризационном приеме будем подразумевать величину ![]() где
где ![]() - парциальные КНД для
каждой из ортогональных составляющих поля; Пуср — усредненное по всем направлениям значение плотности потока мощности полного поля;
- парциальные КНД для
каждой из ортогональных составляющих поля; Пуср — усредненное по всем направлениям значение плотности потока мощности полного поля; ![]() . Здесь
. Здесь ![]() -
полная мощность излучения;
-
полная мощность излучения; ![]() и
и ![]() - мощности излучения, соответствующие
ортогональным компонентам поля.
- мощности излучения, соответствующие
ортогональным компонентам поля.![]() .Такой излучатель часто называют турникетным. В меридиональной по отношению к обоим вибраторам
плоскости yoz (см. рис.2.6) они создают поля одной поляризации, причем векторы
.Такой излучатель часто называют турникетным. В меридиональной по отношению к обоим вибраторам
плоскости yoz (см. рис.2.6) они создают поля одной поляризации, причем векторы ![]() и
и ![]() лежат
на одной и той же линии. В точке N, лежащей на нормали (ось х) к плоскости
расположения двух вибраторов, первый создаёт вектор
напряжённости электрического поля
лежат
на одной и той же линии. В точке N, лежащей на нормали (ось х) к плоскости
расположения двух вибраторов, первый создаёт вектор
напряжённости электрического поля ![]() а второй -
а второй - ![]() , находящиеся в плоскости, перпендикулярной
оси х, Эти векторы равны по амплитуде, сдвинуты по фазе друг
относительно друга на 90° и взаимно
перпендикулярны. Таким образом в направлении нормали плоскости вибраторов (yoz) имеет место круговая поляризация поля.
, находящиеся в плоскости, перпендикулярной
оси х, Эти векторы равны по амплитуде, сдвинуты по фазе друг
относительно друга на 90° и взаимно
перпендикулярны. Таким образом в направлении нормали плоскости вибраторов (yoz) имеет место круговая поляризация поля. Симметричный вибратор состоит из двух одинаковых по размерам и форме
проводников, между которыми включается генератор высокой частоты (часто эти
проводники называются плечами). Рассмотрим симметричный вибратор, представляющий собой тонкий цилиндрический проводник длиной 2
Симметричный вибратор состоит из двух одинаковых по размерам и форме
проводников, между которыми включается генератор высокой частоты (часто эти
проводники называются плечами). Рассмотрим симметричный вибратор, представляющий собой тонкий цилиндрический проводник длиной 2![]() и радиусом а (рис.3.1), находящийся в
свободном пространстве. Строгое решение
основной
задачи теории антенн
и радиусом а (рис.3.1), находящийся в
свободном пространстве. Строгое решение
основной
задачи теории антенн![]() -
-![]() ) , где Iп - амплитуда тока в пучности тока вибратора (в
об-
) , где Iп - амплитуда тока в пучности тока вибратора (в
об-![]() );
); ![]() - длина одного плеча вибратора; z - расстояние от
начала вибратора (точки питания) до произвольной точки на
вибраторе (текущая координата); k = 2
- длина одного плеча вибратора; z - расстояние от
начала вибратора (точки питания) до произвольной точки на
вибраторе (текущая координата); k = 2![]() /
/![]() , - волновое число (коэффициент фазы тока в
вибраторе).
, - волновое число (коэффициент фазы тока в
вибраторе). Полагают, что длина волны в вибраторе
Полагают, что длина волны в вибраторе![]() z=
z=![]() Пcosk(
Пcosk(![]() -
- ![]() ), где
), где ![]() П амплитуда заряда в его пучности. Этот закон распределения заряда вдоль симметричного вибратора
совпадает с законом распределения потенциала (напряжения) в разомкнутой на конце длинной линии без потерь. В теории антенн понятием напряжения следует пользоваться с большой осторожностью, так как поле антенны не является потенциальным. Понятием напряжения применительно к антенне можно
пользоваться, если расстояние между точками измерения мало по сравнению с
длиной волны. Это справедливо при измерении напряжения между зажимами антенны
(точки присоединения генератора), а также для длинноволновых антенн. На рис.3.3
приведены кривые распределения амплитуд тока и заряда на вибраторах разной
длины. По аналогии с волновым сопротивлением длинной линии вводится
понятие волнового сопротивления симметричного вибратора. Как известно,
из теории длинных линий, волновое сопротивление двухпроводной линии
без потерь определяется выражением W =
П амплитуда заряда в его пучности. Этот закон распределения заряда вдоль симметричного вибратора
совпадает с законом распределения потенциала (напряжения) в разомкнутой на конце длинной линии без потерь. В теории антенн понятием напряжения следует пользоваться с большой осторожностью, так как поле антенны не является потенциальным. Понятием напряжения применительно к антенне можно
пользоваться, если расстояние между точками измерения мало по сравнению с
длиной волны. Это справедливо при измерении напряжения между зажимами антенны
(точки присоединения генератора), а также для длинноволновых антенн. На рис.3.3
приведены кривые распределения амплитуд тока и заряда на вибраторах разной
длины. По аналогии с волновым сопротивлением длинной линии вводится
понятие волнового сопротивления симметричного вибратора. Как известно,
из теории длинных линий, волновое сопротивление двухпроводной линии
без потерь определяется выражением W =![]() , где L1-распределенная индуктивность линии (индуктивность, приходящаяся на единицу длины линии), Г/м; C1 -, распределенная емкость линии, Ф/м. Так как
1/
, где L1-распределенная индуктивность линии (индуктивность, приходящаяся на единицу длины линии), Г/м; C1 -, распределенная емкость линии, Ф/м. Так как
1/![]() = с, где
= с, где![]() ), где I0 - ток в точках
питания вибратора (I0=Iпsinkl). Мысленно разобьем вибратор на бесконечно
большое число элементов dz. Так как длина
каждого элемента бесконечно мала, то можно полагать, что в пределах его ток
не изменяется ни по амплитуде, ни по фазе. Таким образом, весь симметричный вибратор можно рассматривать как
совокупность
), где I0 - ток в точках
питания вибратора (I0=Iпsinkl). Мысленно разобьем вибратор на бесконечно
большое число элементов dz. Так как длина
каждого элемента бесконечно мала, то можно полагать, что в пределах его ток
не изменяется ни по амплитуде, ни по фазе. Таким образом, весь симметричный вибратор можно рассматривать как
совокупность![]() Izdz/ (r1
Izdz/ (r1![]() )]sin
)]sin![]() exp(-ikr1).
exp(-ikr1).![]() Izdz/(r2
Izdz/(r2![]() )] sin
)] sin![]() exp(-ikr2).
exp(-ikr2).![]() - угол между осью
вибратора и
направлением на точку наблюдения.
- угол между осью
вибратора и
направлением на точку наблюдения.![]() Izdz/
Izdz/![]() )sin
)sin![]() [(exp(-ikr1)/r1+exp(-ikr2)/r2)]. (3.5)
[(exp(-ikr1)/r1+exp(-ikr2)/r2)]. (3.5)![]() r =
r = ![]() cos
cos![]() .
.![]() и r2 = r0 +
и r2 = r0 + ![]() cos
cos![]() . (3.6)
. (3.6)![]() r часто называют разностью хода
лучей. Так как точка наблюдения
находится в дальней зоне, то величина
r часто называют разностью хода
лучей. Так как точка наблюдения
находится в дальней зоне, то величина ![]() r мала по
сравнению с r0 и расстояния r1 и r2 мало отличаются друг от друга. Поэтому можно считать, что амплитуды напряженности полей, создаваемых
элементами 1 и 2 в точке наблюдения М,
одинаковы. Однако пренебрегать разностью хода в фазовых множителях (exp(-ikr1) и exp(-ikr2)) ни в коем
случае нельзя, так как пространственный
сдвиг фаз между полями элементов 1 и 2 k
r мала по
сравнению с r0 и расстояния r1 и r2 мало отличаются друг от друга. Поэтому можно считать, что амплитуды напряженности полей, создаваемых
элементами 1 и 2 в точке наблюдения М,
одинаковы. Однако пренебрегать разностью хода в фазовых множителях (exp(-ikr1) и exp(-ikr2)) ни в коем
случае нельзя, так как пространственный
сдвиг фаз между полями элементов 1 и 2 k![]() r = 2k|z|cosν = 4
r = 2k|z|cosν = 4![]() (|z|/
(|z|/![]() )cos
)cos![]() определяется отношением разности хода лучей к длине волны. На
основании формул (3.6) получаем следующие выражения для фазовых множителей exp(-ikr1)= exp(-ikr0) * exp(ik|z|)cos
определяется отношением разности хода лучей к длине волны. На
основании формул (3.6) получаем следующие выражения для фазовых множителей exp(-ikr1)= exp(-ikr0) * exp(ik|z|)cos![]() ;
;![]() )cos
)cos![]() .
.![]() r2
r2 ![]() r0, получаем
r0, получаем![]() I0sink(l-
I0sink(l-![]() )dz/(r0
)dz/(r0 ![]() sinkl)]sin
sinkl)]sin![]() exp(-ikr0)[(exp(ik
exp(-ikr0)[(exp(ik![]() )cos
)cos![]() +
+![]() ) cos
) cos![]() )].
)].![]() ) + exp(-i
) + exp(-i![]() ) = 2cos
) = 2cos![]() , получаем следующее выражение
, получаем следующее выражение![]() I0/( r0
I0/( r0 ![]() sinkl)] sin
sinkl)] sin![]() exp(-ikr0)sink(l-
exp(-ikr0)sink(l-![]() )cos(k
)cos(k![]() cos
cos![]() )dz.
)dz.![]() I0/(r0
I0/(r0 ![]() sinkl)] sin
sinkl)] sin![]() exp(-ikr0)
exp(-ikr0) ![]() sink(l-
sink(l-![]() )cos(k
)cos(k![]() cos
cos![]() )dz.
)dz.![]() ) - coskl) / sin
) - coskl) / sin![]() ]exp(-ikr0). (3.7)
]exp(-ikr0). (3.7)![]() )=[cos(klcos
)=[cos(klcos![]() ) - coskl]/sin
) - coskl]/sin![]()
![]() = iexp(-ikr0) из выражения
(3.7) видно, что симметричный вибратор
обладает направленными свойствами только в меридиональной плоскости (плоскость электрического вектора). Напряженность электрического поля симметричного вибратора
в его экваториальной
= iexp(-ikr0) из выражения
(3.7) видно, что симметричный вибратор
обладает направленными свойствами только в меридиональной плоскости (плоскость электрического вектора). Напряженность электрического поля симметричного вибратора
в его экваториальной![]() /2) - определяется выражением
/2) - определяется выражением![]() . Поэтому
диаграмма направленности
. Поэтому
диаграмма направленности
![]() .В случае полуволнового вибратора (l/
.В случае полуволнового вибратора (l/![]() =0,25) формула (3.7) принимает вид
=0,25) формула (3.7) принимает вид![]() /2)cos
/2)cos![]() ]/(sin
]/(sin![]() )}exp (-ikr0).
)}exp (-ikr0). ![]() показаны
на рис.3.5. Анализ формулы (3.7) и
рассмотрение этих кривых показывают, что при любой величине
отношения l/
показаны
на рис.3.5. Анализ формулы (3.7) и
рассмотрение этих кривых показывают, что при любой величине
отношения l/![]() симметричный вибратор
не излучает вдоль своей оси. Если длина плеча симметричного
вибратора l
симметричный вибратор
не излучает вдоль своей оси. Если длина плеча симметричного
вибратора l ![]() 0,5
0,5![]() ,
то в направлении, перпендикулярном его
оси (
,
то в направлении, перпендикулярном его
оси (![]() = 90°,
= 90°, ![]() = 270°), т.е. в экваториальной
плоскости, поля всех элементарных вибраторов
максимальны, синфазны и
складываются арифметически. Поэтому
поле в данном
направлении является
максимальным. Диаграмма направленности при l/
= 270°), т.е. в экваториальной
плоскости, поля всех элементарных вибраторов
максимальны, синфазны и
складываются арифметически. Поэтому
поле в данном
направлении является
максимальным. Диаграмма направленности при l/![]()
![]() 0,5 состоит из двух
(главных) лепестков (рис. 3.5.а, 3.5.б).
Увеличение длины вибратора до l=0,5
0,5 состоит из двух
(главных) лепестков (рис. 3.5.а, 3.5.б).
Увеличение длины вибратора до l=0,5![]() сопровождается ростом
излучения в направлении,
перпендикулярном оси вибратора
(главное направление излучения),за
счет уменьшения излучения в других направлениях. При этом диаграмма
направленности становится уже. При увеличении l/
сопровождается ростом
излучения в направлении,
перпендикулярном оси вибратора
(главное направление излучения),за
счет уменьшения излучения в других направлениях. При этом диаграмма
направленности становится уже. При увеличении l/![]() до 0,625 излучение в главном
направлении продолжает возрастать, но характеристика направленности проходит через нуль не только при
до 0,625 излучение в главном
направлении продолжает возрастать, но характеристика направленности проходит через нуль не только при ![]() =0° и
=0° и ![]() =180°, но и при некоторых других
значениях угла
=180°, но и при некоторых других
значениях угла![]() . Главные лепестки диаграммы становятся уже, но появляются боковые лепестки (рис.3.5.в). При дальнейшем увеличении l/
. Главные лепестки диаграммы становятся уже, но появляются боковые лепестки (рис.3.5.в). При дальнейшем увеличении l/![]() излучение в главном направлении
уменьшается и возрастают боковые лепестки.
Уменьшение излучения в главном направлении объясняется следующим.
Результирующий сдвиг фаз полей, излучаемых элементарными вибраторами в данном
направлении, определяется пространственным сдвигом фаз и сдвигом фаз токов, возбуждающих эти вибраторы. При l/
излучение в главном направлении
уменьшается и возрастают боковые лепестки.
Уменьшение излучения в главном направлении объясняется следующим.
Результирующий сдвиг фаз полей, излучаемых элементарными вибраторами в данном
направлении, определяется пространственным сдвигом фаз и сдвигом фаз токов, возбуждающих эти вибраторы. При l/![]() >0,5 на вибраторе появляются
участки с противофазными токами (рис.3.3), длина которых растет по мере увеличения l/
>0,5 на вибраторе появляются
участки с противофазными токами (рис.3.3), длина которых растет по мере увеличения l/![]() . Поэтому в данном случае, хотя в
главном направлении пространственные сдвиги фаз равны нулю, поля, излучаемые отдельными элементами вибратора, складываются несинфазно, т.е. геометрически. При l/
. Поэтому в данном случае, хотя в
главном направлении пространственные сдвиги фаз равны нулю, поля, излучаемые отдельными элементами вибратора, складываются несинфазно, т.е. геометрически. При l/![]() = 1 (или при l/
= 1 (или при l/![]() = п, где п = 1, 2, ..,) излучение в главном направлении отсутствует, так как противофазные участки
вибратора имеют одинаковую длину. Рост l/
= п, где п = 1, 2, ..,) излучение в главном направлении отсутствует, так как противофазные участки
вибратора имеют одинаковую длину. Рост l/![]() сопровождается также ростом боковых
лепестков. Уже при l/
сопровождается также ростом боковых
лепестков. Уже при l/![]() =0,75 напряженность поля в направлении максимума бокового лепестка превосходит напряженность поля в главном направлении (рис.3.3.г).
=0,75 напряженность поля в направлении максимума бокового лепестка превосходит напряженность поля в главном направлении (рис.3.3.г).![]() ) = f(
) = f(![]() )/f(90°), равна
)/f(90°), равна![]() ) = [cos(klcos
) = [cos(klcos![]() ) - coskl]/[(l –
coskl)sin
) - coskl]/[(l –
coskl)sin![]() ]. (3.9)
]. (3.9)![]() 0,5= 90°. Полуволновый симметричный вибратор имеет
ширину диаграммы направленности по половинной мощности 2
0,5= 90°. Полуволновый симметричный вибратор имеет
ширину диаграммы направленности по половинной мощности 2![]() 0,5= 80°, волновой
симметричный вибратор - 2
0,5= 80°, волновой
симметричный вибратор - 2![]() 0,5= 44°,
симметричный вибратор, у которого l/
0,5= 44°,
симметричный вибратор, у которого l/![]() =0,625, имеет 2
=0,625, имеет 2![]() 0,5= 31°.
Последний вибратор обладает наилучшими
направленными свойствами, так как при дальнейшем увеличении l/
0,5= 31°.
Последний вибратор обладает наилучшими
направленными свойствами, так как при дальнейшем увеличении l/![]() , сильно возрастают боковые лепестки, хотя главный лепесток
диаграммы направленности становится уже. На
практике применяются симметричные вибраторы,
у которых l/
, сильно возрастают боковые лепестки, хотя главный лепесток
диаграммы направленности становится уже. На
практике применяются симметричные вибраторы,
у которых l/![]()
![]() 0,7. Фаза напряженности поля,
создаваемого симметричным вибратором в соответствии с
выражением (3.7), в пределах одного лепестка диаграммы направленности
не зависит от координатного угла
0,7. Фаза напряженности поля,
создаваемого симметричным вибратором в соответствии с
выражением (3.7), в пределах одного лепестка диаграммы направленности
не зависит от координатного угла ![]() . Она изменяется скачком на обратную при переходе
напряжённости поля через нуль. Симметричный вибратор
излучает сферические волны, о чем свидетельствует множитель exp(-ikr)/r. Эти волны как бы исходят из одной точки,
совпадающей с центром вибратора.
. Она изменяется скачком на обратную при переходе
напряжённости поля через нуль. Симметричный вибратор
излучает сферические волны, о чем свидетельствует множитель exp(-ikr)/r. Эти волны как бы исходят из одной точки,
совпадающей с центром вибратора.![]() , вследствие чего поверхность сферы
находится в дальней зоне поля вибратора. Центр вибратора совпадает с центром
сферы, ось вибратора лежит на оси z прямоугольной системы координат. На
поверхности сферы выделяется бесконечно малый элемент dS, площадь которого в сферической системе координат dS = r2sinνd
, вследствие чего поверхность сферы
находится в дальней зоне поля вибратора. Центр вибратора совпадает с центром
сферы, ось вибратора лежит на оси z прямоугольной системы координат. На
поверхности сферы выделяется бесконечно малый элемент dS, площадь которого в сферической системе координат dS = r2sinνd![]() d
d![]() .
Излучаемая мощность, приходящаяся на данный
элемент поверхности
.
Излучаемая мощность, приходящаяся на данный
элемент поверхности![]() = ПсрdS=(E2/2Wc)dS. (3.10)
= ПсрdS=(E2/2Wc)dS. (3.10)![]() [cos (kl cos
[cos (kl cos![]() ) - cos kl] / sin
) - cos kl] / sin![]()
![]() . (3.11)
. (3.11)![]() п = [r2Е2 макс/( Wc Iп2 )]
п = [r2Е2 макс/( Wc Iп2 )] ![]()
![]() F2(
F2(![]() ,
,![]() )sin
)sin![]() dνd
dνd![]() . (3.12)
. (3.12)![]() = Iп2R
= Iп2R![]() п/2.
п/2.![]() п определяется
характером распределения электромагнитного поля в дальней
зоне, т.е. диаграммой направленности рассматриваемой антенны. Интегрирование дает следующую формулу, впервые полученную Баллантайном в 1924 г.
п определяется
характером распределения электромагнитного поля в дальней
зоне, т.е. диаграммой направленности рассматриваемой антенны. Интегрирование дает следующую формулу, впервые полученную Баллантайном в 1924 г.![]() п = 30 [2 (
п = 30 [2 (![]() +ln2kl - Ci 2kl) + cos 2kl (
+ln2kl - Ci 2kl) + cos 2kl (![]() +lnkl+ Ci 4kl - 2Ci 2kl) +
+lnkl+ Ci 4kl - 2Ci 2kl) +![]()
![]() =
0,5772... - постоянная Эйлера; Si x = (sin u/u)du –
интегральный
=
0,5772... - постоянная Эйлера; Si x = (sin u/u)du –
интегральный![]() (cos u/u)du - интегральный косинус.
(cos u/u)du - интегральный косинус.![]()
![]() . Формула (3.13) является приближенной,
поскольку при ее выводе исходили из синусоидального распределения тока по
вибратору, что справедливо только для тонких вибраторов.
Однако результаты расчетов по формуле (3.13) хорошо совпадают с экспериментальными данными. Это объясняется тем, что сопротивление излучения определяется полем в дальней зоне, которое мало зависит от толщины вибратора. Следует также иметь в виду, что изложенный здесь
метод расчета дает только активную составляющую сопротивления излучения, так как учитывается только излученная активная мощность.
. Формула (3.13) является приближенной,
поскольку при ее выводе исходили из синусоидального распределения тока по
вибратору, что справедливо только для тонких вибраторов.
Однако результаты расчетов по формуле (3.13) хорошо совпадают с экспериментальными данными. Это объясняется тем, что сопротивление излучения определяется полем в дальней зоне, которое мало зависит от толщины вибратора. Следует также иметь в виду, что изложенный здесь
метод расчета дает только активную составляющую сопротивления излучения, так как учитывается только излученная активная мощность.![]() п как функции
отношения (рис.3.6), рассчитанные по формуле (3.13). Осциллирующий характер
зависимости объясняется тем, что интерференционная картина
поля в дальней зоне меняется при изменении l/
п как функции
отношения (рис.3.6), рассчитанные по формуле (3.13). Осциллирующий характер
зависимости объясняется тем, что интерференционная картина
поля в дальней зоне меняется при изменении l/![]() .
.![]() ,
не превышает 0,1,
то формулу (3.13)
можно упростить R
,
не превышает 0,1,
то формулу (3.13)
можно упростить R![]() п=20 (k l)4 .
п=20 (k l)4 .![]() п ) (1 -coskl)2. (3.14)
п ) (1 -coskl)2. (3.14)![]() =0,25
R
=0,25
R![]() п = 73,1 Ом и
D= 1,64 ;
п = 73,1 Ом и
D= 1,64 ;![]() = 0,5 R
= 0,5 R![]() п =199 Ом и D = 2,4;
п =199 Ом и D = 2,4;![]() =0,625 R
=0,625 R![]() п =110 Ом и D = 3,l.
п =110 Ом и D = 3,l.![]() п) f2max (
п) f2max (![]() ). (3.15)
). (3.15)![]() п - полное сопротивление излучения антенны.
Действующая
длина симметричного вибратора
определяется по формуле lд =
п - полное сопротивление излучения антенны.
Действующая
длина симметричного вибратора
определяется по формуле lд = ![]() (1 - coskl) / (
(1 - coskl) / (![]() sinkl).
sinkl).![]() п От величины l/
п От величины l/![]()
 Таким образом, включенный в антенну генератор нагружен на комплексное сопротивление, которое называется входным сопротивлением антенны и
равно отношению напряжения на зажимах вибратора (точки
питания) к току в точках питания ZBX=U0/I0=RBX+i XBX.
Таким образом, включенный в антенну генератор нагружен на комплексное сопротивление, которое называется входным сопротивлением антенны и
равно отношению напряжения на зажимах вибратора (точки
питания) к току в точках питания ZBX=U0/I0=RBX+i XBX.![]() R
R![]() o, где R
o, где R![]() o - сопротивление
излучения вибратора, отнесенное к току в точках питания. Для точного определения входного сопротивления
необходимо знать закон распределения тока вдоль вибратора. Часто с достаточной для инже-
o - сопротивление
излучения вибратора, отнесенное к току в точках питания. Для точного определения входного сопротивления
необходимо знать закон распределения тока вдоль вибратора. Часто с достаточной для инже-![]() =0,5 (рис.3.7). В этом случае ток в точках
питания оказывается равным нулю и очевидно, что ZBX = U0/I0=
=0,5 (рис.3.7). В этом случае ток в точках
питания оказывается равным нулю и очевидно, что ZBX = U0/I0=![]() . В действительности же ток в точках питания никогда не бывает равен нулю (его величина обязательно конечна), а следовательно, входное сопротивление симметричного вибратора никогда не бывает бесконечно велико. Физически это совершенно ясно. Ведь закон синуса
(стоячая волна) справедлив в линиях только при отсутствии потерь. Вибратор же в принципе является системой с потерями на излучение. Следовательно, при расчете входного сопротивления лучше проводить аналогию между симметричным вибратором и разомкнутой на конце линией с потерями. Известно, что ток в такой линии распределен по закону гиперболического
синуса (рис.3.7) Iz = Iпsh
. В действительности же ток в точках питания никогда не бывает равен нулю (его величина обязательно конечна), а следовательно, входное сопротивление симметричного вибратора никогда не бывает бесконечно велико. Физически это совершенно ясно. Ведь закон синуса
(стоячая волна) справедлив в линиях только при отсутствии потерь. Вибратор же в принципе является системой с потерями на излучение. Следовательно, при расчете входного сопротивления лучше проводить аналогию между симметричным вибратором и разомкнутой на конце линией с потерями. Известно, что ток в такой линии распределен по закону гиперболического
синуса (рис.3.7) Iz = Iпsh![]() (z - l), где
(z - l), где ![]() =
= ![]() + i
+ i![]() - коэффициент распространения,
- коэффициент распространения, ![]() -
коэффициент ослабления,
-
коэффициент ослабления, ![]() -
коэффициент фазы.
-
коэффициент фазы.![]() )
) ![]() 0,35...0,4; (0,6...0,65)
0,35...0,4; (0,6...0,65) ![]() l/
l/![]()
![]() (0,85...0,9), т.е. таких, у которых узел тока
находится от точек питания вибратора не ближе, чем на расстоянии
(0,1...0,15)
(0,85...0,9), т.е. таких, у которых узел тока
находится от точек питания вибратора не ближе, чем на расстоянии
(0,1...0,15)![]() , исходят из синусоидального
распределения тока. При расчете входного сопротивления "длинных" вибраторов (0,35
, исходят из синусоидального
распределения тока. При расчете входного сопротивления "длинных" вибраторов (0,35![]() l/
l/![]()
![]() 0,65) следует исходить из распределения тока по закону гиперболического синуса. Найдем формулы для расчета активной
0,65) следует исходить из распределения тока по закону гиперболического синуса. Найдем формулы для расчета активной![]() = (Iп2R
= (Iп2R![]() п )/2 и P
п )/2 и P![]() = (I02 R
= (I02 R![]() 0)/2. (3.17)
0)/2. (3.17)![]() п = I02 R
п = I02 R![]() 0. Решая это равенство относительно R
0. Решая это равенство относительно R![]() 0, получаем R
0, получаем R![]() 0= R
0= R![]() п (Iп2/ I02).
п (Iп2/ I02).![]() 0 = R
0 = R![]() п /sin2kl. (3.18)
п /sin2kl. (3.18)![]() п
для вибратора заданной длины легко найти из
таблиц или графиков. При расчете реактивной
составляющей входного сопротивления короткого симметричного вибратора
пользуются формулой входного сопротивления
разомкнутой на конце двухпроводной линии без потерь, заменяя в ней волновое
сопротивление линии волновым сопротивлением антенны
п
для вибратора заданной длины легко найти из
таблиц или графиков. При расчете реактивной
составляющей входного сопротивления короткого симметричного вибратора
пользуются формулой входного сопротивления
разомкнутой на конце двухпроводной линии без потерь, заменяя в ней волновое
сопротивление линии волновым сопротивлением антенны![]() п/sin2kl) – i WActg kl. (3.20)
п/sin2kl) – i WActg kl. (3.20)![]() l- (
l- (![]() /
/![]() ) sin 2
) sin 2![]() l) / (ch2
l) / (ch2![]() l - cos 2
l - cos 2![]() l)] – i WA [(
l)] – i WA [(![]() /
/![]() ) sh 2
) sh 2![]() l+
l+![]() l) / (ch2
l) / (ch2![]() l - cos 2
l - cos 2![]() l)]. (3.21)
l)]. (3.21)![]() - коэффициент фазы в вибраторе;
- коэффициент фазы в вибраторе; ![]() - коэффициент затухания. По аналогии с длинными линиями, пренебрегая потерями в проводах вибратора коэффициент затухания можно рассчитать по формуле
- коэффициент затухания. По аналогии с длинными линиями, пренебрегая потерями в проводах вибратора коэффициент затухания можно рассчитать по формуле
![]() = R
= R![]() 1 / WA, где R
1 / WA, где R![]() 1 -активное сопротивление излучения, приходящееся на единицу длины вибратора.
Приближенно полагая, что сопротивление излучения R
1 -активное сопротивление излучения, приходящееся на единицу длины вибратора.
Приближенно полагая, что сопротивление излучения R![]() п распределено равномерно по всей длине вибратора, для расчета R
п распределено равномерно по всей длине вибратора, для расчета R![]() 1 получают
формулу R
1 получают
формулу R![]() 1= R
1= R![]() п/[l(l - (sin2kl/2kl)]. Данная
формула позволяет, зная сопротивление излучения,
отнесенное к пучности тока, найти распределенное сопротивление излучения. Следовательно, коэффициент
ослабления
п/[l(l - (sin2kl/2kl)]. Данная
формула позволяет, зная сопротивление излучения,
отнесенное к пучности тока, найти распределенное сопротивление излучения. Следовательно, коэффициент
ослабления![]() = R
= R![]() 1/ WA = R
1/ WA = R![]() п/ [lWA (1- (sin2kl/2kl))].
п/ [lWA (1- (sin2kl/2kl))].![]() в формуле (3.21)
несколько отличается от
в формуле (3.21)
несколько отличается от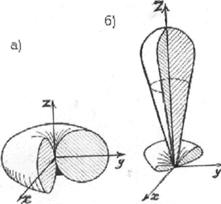
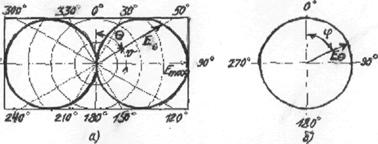
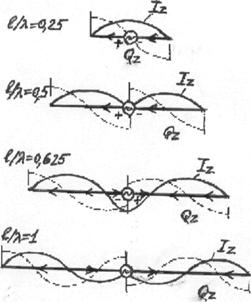
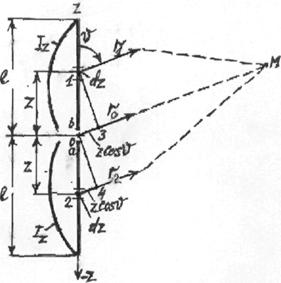
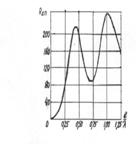
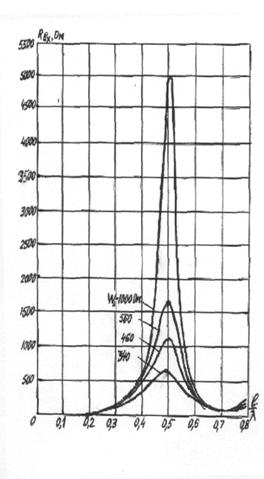
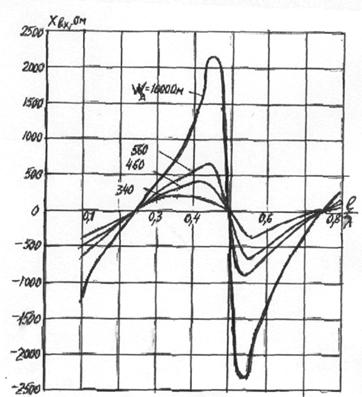

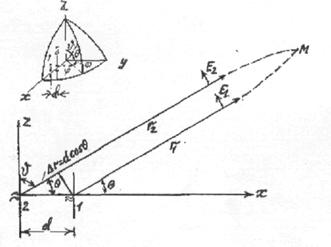
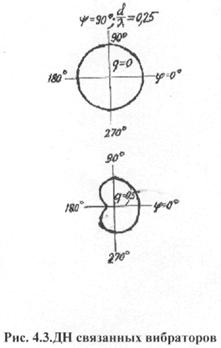
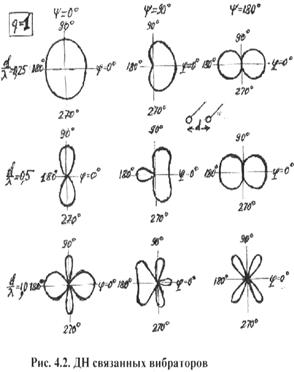


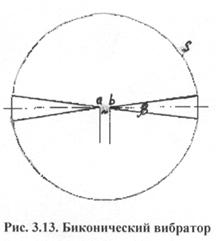



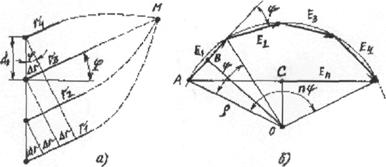
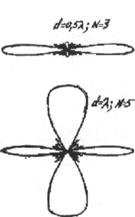
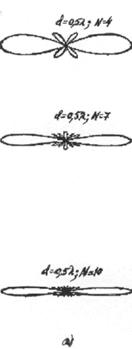
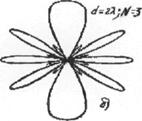
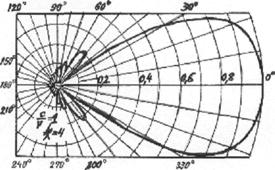





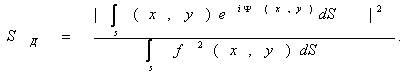
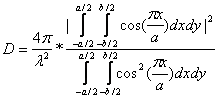


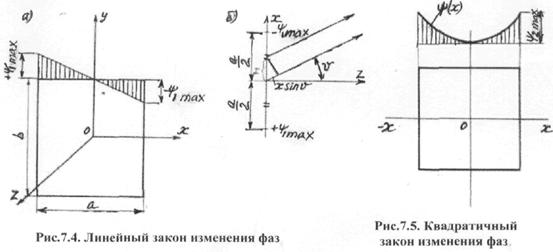
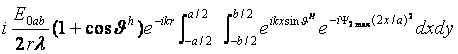

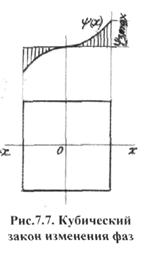
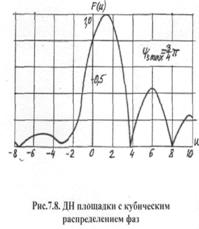

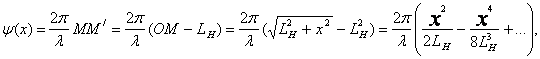

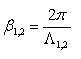 ;
;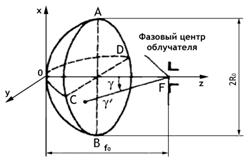
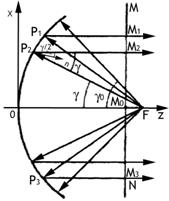
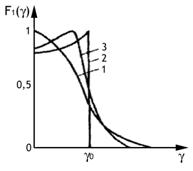




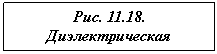




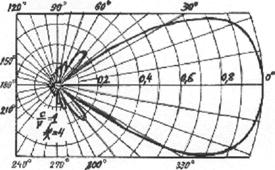









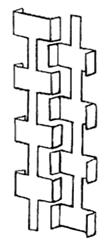









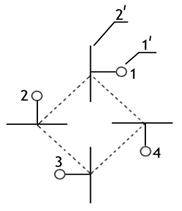
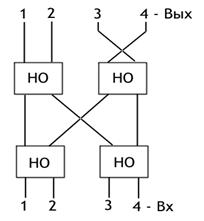












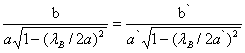
























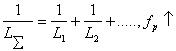



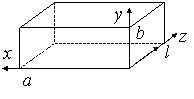
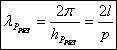
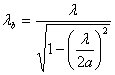 ;
;