УЗБЕКСКОЕ АГЕНТСТВО СВЯЗИ И ИНФОРМАТИЗАЦИИ
ТАШКЕНТСКИЙ УНИВЕРСИТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ
Факультет
Радиотехники, Радиосвязи и Телерадиовещания
Кафедра
Антенно-Фидерных
Устройств
Методическое пособие
“Теория электромагнитного
поля. Часть
по дисциплинам: “Электромагнитные
поля и волны” и “Электродинамика и
распространение радиоволн”
Ташкент 2007
Аннотация
Данное методическое пособие предназначено
для студентов, изучающих курсы “Электромагнитные поля и волны” и “Электродинамика и распространение радиоволн”
по направлениям образования: “Телевидение,
радиосвязь и радиовещание” и “Радиотехника”.
В пособии приводятся основные понятия
теории электромагнетизма, дается раскрытие физического смысла фундаментальных
законов электродинамики – системы уравнений Максвелла в их классической
интегральной и дифференциальной формах.
СОДЕРЖАНИЕ:
1.
Электростатика.
1.1.
Электрический заряд.
1.2.
Напряженность электростатического поля.
1.3. Безвихревой
характер электростатического поля.
1.4.
Электрический потенциал.
1.5. Графическое
изображение электростатического поля.
1.6. Поляризованность
диэлектрика и электрическая индукция.
1.7. Теорема
Гаусса.
1.8. Проводники в
электростатическом поле.
1.9. Граничные
условия в электростатическом поле.
1.10
Энергия электростатического поля.
2.
Ток и плотность
тока проводимости.
3.
Дивергенция
плотности тока проводимости.
4.
Закон Ома в
дифференциальной форме.
5.
Полный
электрический ток.
6.
Магнитное поле.
6.1. Основные величины, характеризующие
магнитное поле.
6.2. Магнитный поток и его непрерывность.
6.3. Скалярный потенциал магнитного поля.
6.4. Векторный потенциал магнитного поля.
6.5. Граничные условия в магнитном поле.
6.6. Энергия магнитного поля.
6.7. Методы расчетов магнитных
полей.
7.
Система уравнений
Максвелла.
7.1. Первое
уравнение Максвелла.
7.2. Второе
уравнение Максвелла.
7.3. Третье
уравнение Максвелла.
7.4. Четвёртое
уравнение Максвелла.
8.
Полная система
уравнений электромагнитного поля.
1. ЭЛЕКТРОСТАТИКА
1.1 Электрический заряд
Электрический заряд можно считать бесконечно делимым и пользоваться понятием плотности заряда. Если заряд “q” распределен в пространстве, то объемная плотность заряда
 .
.
Соответственно заряд
![]() .
.
Если заряд “q” распределен по поверхности “S”, то поверхностная плотность заряда
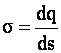
и суммарный заряд определяется как
![]() .
.
Линейная плотность заряда
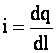 ,
,
где dl - элемент линии, вдоль которой распределен заряд.
Тогда
![]() .
.
Два точечных заряда одного знака, находящиеся друг от друга на расстоянии R, отталкиваются друг от друга. Сила отталкивания “F” в вакууме определяется законом Кулона

где q1 и q2 - точечные заряды, к - коэффициент пропорциональности, определяемый как
 ,
,
где
e0 -
электрическая постоянная, равная 8,85 .10
-12 ф/м.
Если заряженные тела находятся в однородной изотропной среде, то

где e - относительная диэлектрическая проницаемость среды.
Сила, действующая на заряд q, в векторной форме записывается как

1.2 Напряженность электростатического поля
Предел отношения силы F, действующей на пробный заряд, к величине этого заряда q, когда он стремится к нулю, называют напряженностью электрического поля
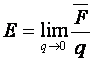 .
.
Напряженность электрического поля точечного заряда
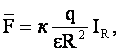
в системе СИ [E] = [в/м].
Сила взаимодействия двух точечных зарядов
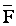 = E × q .
= E × q .
Если в поле отсутствует пробный заряд q, механическая сила взаимодействия равна нулю, но напряженность Е в каждой точке отлична от нуля.
Электрическим смещением или электрической индукцией называют величину D, которая в однородных и изотропных средах пропорциональна напряженности электрического поля:
D = ee0Е - в вакууме,
D= e0Е - в системе СИ [D] = [кл/м2] .
Если поле создается несколькими зарядами, то общая напряженность Е в любой точке равна геометрической сумме
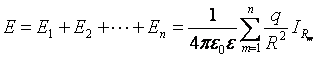 .
.
В общем случае электростатическое поле могут возбудить неподвижные объемные, поверхностные и линейные заряды. Разбив объемы V, поверхности S и линии l на элементы dV, dS, dl можно записать:
dq1 = rdV
dq2 = sdS
dq3 = t dl ,
где r - объемная, s - поверхностная, t - линейная плотности зарядов.
Тогда:
 ,
,
 ,
,
 .
.
Суммируя геометрически вектора dE 1 по V , dE2 по S, dE3 по l получим
Е = Е1 + Е2 + Е3.
Это уравнение позволяет вычислить Е, если известно распределение зарядов в пространстве.
Вычисление сводится к определению проекций вектора Е в такой системе координат, в которой расчеты получаются наиболее простыми.
1.3 Безвихревой характер электростатического поля
Работа, совершенная силами поля при перемещении заряда q из точки 1 в точку 2 определяется как
 .
.
Работа сил поля вдоль замкнутой кривой равна нулю. Для этого необходимо доказать, что циркуляция вектора Е равна нулю
![]() .
.
В случае точечного заряда

Так как ![]() а
а  то
то ![]() .
.
Пользуясь
теоремой Стокса
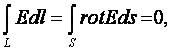
Получаем
![]()
Это соотношение выражает основное свойство электростатического поля - оно безвихревое.
1.4 Электрический потенциал
Так как электрическое поле безвихревое (rotE = 0), то можно найти скалярную функцию j, градиент которой, взятый со знаком “+” или “-”, равен вектору напряженности Е
grad j = ± E.
В теории поля выбирают знак “-”, который указывает на то, что напряженность направлена в сторону убывания j. Скалярная функция j называется потенциальной функцией или просто потенциалом.
Потенциал любой точки
j = - ò E dl + const,
L
где постоянная интегрирования определяется заданием точки с нулевым потенциалом. В системе СИ [j] = [в].
Разность потенциалов
![]()
 .
.
Разность потенциалов не зависит от формы пути интегрирования.
Потенциал поля точечного заряда
 .
.
Потенциал поля неподвижных объемных, поверхностных и линейных зарядов
j = ò rdV_____ + ò sdS ___+ ò ___t dl __ .
V 4pe0eR S 4pe0eR L 4pe0eR
Зная потенциал, можно найти напряженность Е
Е = - grad j.
В поле объемных зарядов вектор Е везде конечен и непрерывен. В поле поверхностных зарядов Е конечен всюду, но претерпевает разрыв на поверхности S, по которой распределен заряд. В поле линейных зарядов вектор Е обращается в бесконечность на линии L, вдоль которой распределен заряд.
1.5 Графическое изображение электростатического поля
Электростатическое поле графически изображается с помощью эквипотенциальных поверхностей и линий вектора поля. Эквипотенциальные поверхности определяются уравнением j = const. Задавая различные значения постоянной, получают семейство поверхностей. Эквипотенциальные поверхности наносятся так, чтобы разность потенциалов двух соседних поверхностей отличалась на одну и ту же величину:
j2 = j1 + Dj
j3 = j2 + Dj = j1 + 2 Dj
jn+1 = jn + Dj = j1 + n Dj
Там, где эквипотенциальные поверхности располагаются ближе, напряженность поля больше. Эквипотенциальные поверхности не пересекаются, так как потенциал - функция однозначная. Линии напряженности совпадают с касательной и пересекаются с эквипотенциальными поверхностями под прямым углом. Дифференциальное уравнение линий вектора
[E dl] = 0 .
В декартовой системе:
Ey dz -
Ez dy = 0 Ez
dx - Ex dz = 0 Ex
dy - Ey dx = 0 .
Одна из эквипотенциальных поверхностей разбивается на прямоугольные площадки. Размер площадок подбирается таким образом, чтобы поток вектора поля сквозь них имел одну и ту же величину. На чертеж наносится по одной линии вектора на каждую площадку, причем так, чтобы эта линия проходила через центр площадки. В тех областях поля, в которых напряженность больше, линии вектора сгущаются. В электростатическом поле линии вектора Е разомкнутые кривые, они начинаются у положительных зарядов и заканчиваются у отрицательных.
1.6 Поляризованность диэлектрика и электрическая индукция
Изменение напряженности электрического поля в диэлектрике в “e“ раз вызывается поляризацией диэлектрика. При наличии внешнего поля диэлектрик перестает быть нейтральным, он поляризуется. Заряды, выявившиеся при поляризации, называются свободными. Связанные заряды создают поле, напряженность которого будет направлена противоположно напряженности внешнего поля. Поэтому Е уменьшается. Степень поляризации диэлектрика характеризуется вектором поляризованности P
P = e0 КЭЕ,
где КЭ - диэлектрическая восприимчивость.
Поляризованность Р показывает, на сколько электрическая индукция в данной среде отличается от электрической индукции в вакууме
Р = D - e0 Е = e0 ( e - 1)Е.
В системе СИ [Р] = [кл/м2]
1.7 Теорема Гаусса
Поток вектора электрической индукции D сквозь произвольную замкнутую поверхность S равен алгебраической сумме свободных зарядов q, расположенных в объеме, ограниченном этой поверхностью.
 .
.
Теорема Гаусса в интегральной форме
Преобразуем поток вектора электрической индукции по теореме Остроградского
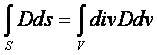 .
.
В случае объемного распределения заряда
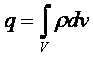 .
.
По теореме Гаусса:
 ,
,

Дифференциальная форма теоремы Гаусса
Объем V был выбран произвольно и равенство справедливо для всех его значений. При таком условии
div D = r,
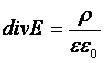 .
.
Из чего следует, что источники электрического поля находятся только в тех местах, в которых имеются электрические заряды.
1.8 Проводники в электростатическом поле
Если проводнику сообщить заряд, то под действием сил отталкивания элементы этого заряда будут перемещаться по проводнику и сосредотачиваться на его поверхности в слое, который можно считать бесконечно тонким. Напряженность Е внутри проводника равна нулю. Все точки проводника должны иметь один и тот же потенциал, то есть поверхность проводника представляет собой эквипотенциальную поверхность.
Под действием внешнего поля свободные электроны перемещаются по проводнику. На одной части сосредоточатся отрицательные заряды, на противоположной - положительные. Напряженность поля внутри проводника равна нулю. Поверхность проводника будет границей электростатического поля, которое локализовано в диэлектрике, окружающем проводник. Это используется в технике при электростатическом экранировании радиоаппаратуры.
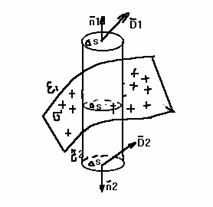
1.9 Граничные условия в электростатическом поле
Рассмотрим границу двух непроводящих сред, диэлектрические проницаемости которых e1 и e2.
|
|
Пусть на границе имеется заряд с поверхностной плотностью.
Проведем замкнутую цилиндрическую поверхность S так, чтобы одна ее половина была расположена в первом диэлектрике, другая - во втором.
По теореме Гаусса
ò D ds= s DS .
s
Представим поток вектора D в виде суммы трех потоков
ò D ds = ò D1 ds
+ ò D2 ds
+ ò D ds .
S DS D
Если площадка DS невелика, то можно считать, что во всех точках этой площадки вектор D имеет одну и ту же величину, тогда:
ò D1 ds = D1n DS,
DS
ò D2 ds =
- D2n DS.
DS
Если высоту цилиндра уменьшать так, чтобы площадки DS стремились к границе между диэлектриками, то поток через боковую поверхность будет стремиться к нулю, тогда:
D1nDS - D2nDS = s DS,
D1n - D2n
= s,
или
e0 e1Е1n - e0 e2Е2n =
s .
Нормальная составляющая вектора электрической индукции на границе двух непроводящих сред претерпевает скачок, равный поверхностной плотности свободных зарядов, распределенных на границе.
Если s = 0, то
D1n = D2n
e0 e1Е1n = e0 e2Е2n .
Нормальная составляющая вектора D на границе непрерывна. Для получения второго граничного условия проведем замкнутую линию L так, чтобы одна ее часть находилась в первом диэлектрике, другая - во втором.
Если отрезки 2-3 и 4-1 постепенно уменьшать так, чтобы в пределе они стали равными нулю, а отрезки Dl совпали с граничной поверхностью, то
Е1tDl - Е2tDl = 0,
Е1t = Е2t или D1t / e1 = D2t / e2.
На границе двух непроводящих сред касательные составляющие вектора напряженности электрического поля равны.
На
поверхности раздела двух сред потенциал непрерывен
j1 = j2.
Если одна из сред проводящая, то граничные условия изменятся.
Пусть первая среда - диэлектрик с проницаемостью e, вторая - проводник, тогда граничные условия запишутся:
Е2 = 0, D2 = 0, j2 = const,
D1n = D1 = s, или e0e Е1 = s,
Е1t = 0, D1t = 0.
1.10 Энергия электростатического поля
В общем случае энергия электростатического поля определяется как
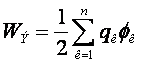 .
.
Эта формула учитывает только энергию взаимодействия. Собственная энергия точечного заряда формально равна бесконечности, так как, для того, чтобы сосредоточить заряд конечной величины в точке, надо было бы затратить бесконечно большую работу.
Этой формулой можно пользоваться, когда заряды отстоят друг от друга на расстояниях значительно больших, чем размеры тел, несущих эти заряды.
Энергия электростатического поля может быть записана
 .
.
Из курса векторного анализа получаем
div (jD) = j divD + Dgradj .
Используя это выражение, можно записать
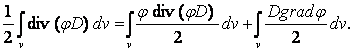
Так
как divD =r, gradj = - E,
ò div (jD) dV = ò jD dS,
V S
то
 , но
, но
DdS = -DdS = - sdS.
Тогда

и энергия электрического поля

В однородных и изотропных средах
D = e0e Е , то
. 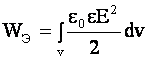 .
.
Физический смысл этого уравнения заключается в том, что носителем энергии является электрическое поле, причем энергия распределена во всем пространстве с объемной плотностью
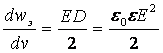
Там, где напряженность Е отлична от нуля, силы поля могут совершать работу за счет энергии поля.
2. Ток и плотность тока проводимости
Мерой тока служит предел отношения заряда Dq, проходящего сквозь заданную поверхность в течение некоторого времени Dt, когда Dt®0
 .
.
Ток - величина скалярная [i]=[A].
Плотностью тока называют векторную величину J, численное значение которой равно пределу отношения тока, протекающего через некоторую площадку, расположенную нормально к направлению движения зарядов, к величине площади этой площадки, когда она стремится к нулю, как к пределу
 .
.
Направление вектора J выбирается таким образом, чтобы оно совпадало с направлением движения положительных зарядов.
Ток и плотность тока связаны соотношением
 .
.
Плотность тока в системе СИ [J] = [А¤м2]
Иногда рассматривают поверхностные токи, которые протекают только по поверхности проводника
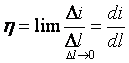 .
.
В системе СИ [h] = [А¤м].
3. Дивергенция плотности тока проводимости
Постоянные
токи могут быть только в замкнутых цепях. Линии вектора ![]() непрерывны и div
непрерывны и div![]() = 0. Постоянный ток через произвольную замкнутую поверхность
всегда равен нулю.
= 0. Постоянный ток через произвольную замкнутую поверхность
всегда равен нулю.
Переменные
токи могут иметь место и в незамкнутых цепях. Следовательно, в переменных полях цепи с токами проводимости могут быть
незамкнутыми. Там, где заканчиваются линии вектора плотности тока проводимости ![]() , могут накапливаться заряды: поток вектора плотности тока
проводимости через замкнутую поверхность может не равняться нулю.
, могут накапливаться заряды: поток вектора плотности тока
проводимости через замкнутую поверхность может не равняться нулю.
Пусть в объёме V, ограниченном поверхностью S, имеется заряд q, объёмная плотность которого равна r. Если через поверхность S выходит ток проводимости i, то заряд q станет уменьшаться и ток
 .
.
Выразим ток через плотность. Получим

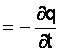 , но
, но
![]() .
.
Преобразовав
поток вектора ![]() по теореме
Остроградского
по теореме
Остроградского
![]()
получим
 или
или
![]() .
.
Дивергенция плотности тока проводимости равна скорости
убывания плотности объёмных зарядов. Плотность тока проводимости может иметь
источники и стоки в виде изменяющихся во времени объёмных зарядов.
4. Закон Ома в дифференциальной форме
В однородном изотропном проводнике плотность тока проводимости d пропорциональна напряженности электрического поля Е
![]() .
.
Это выражение носит название закон Ома в дифференциальной форме. Для того, чтобы в проводнике длительно проходил ток, необходимо наличие электрического поля, силы которого перемещают заряды. Такое поле может быть создано и будет поддерживаться процессами неэлектростатического происхождения (химическими, термоэлектрическими и др.), и носит название стороннего электрического поля.
Напряженность стороннего электрического поля
 .
.
Напряженность результирующего поля
![]() .
.
В тех областях проводника, в
которых имеются сторонние силы, закон Ома записывается в виде:
![]() ,
,
где d- удельная проводимость.
В системе СИ [d]=[см/м]
5. Полный электрический ток
Электрический ток в проводящей среде представляет собой направленное движение электрических зарядов под действием сил поля. Такой ток называется током проводимости.
Согласно закону Ома:
![]() .
.
Если заряженное тело или частицы движутся в непроводящей среде или в вакууме со скоростью V, то они образуют ток переноса:
![]() .
.
В молекулах диэлектрика, который вносится во внешнее электрическое поле, под воздействием сил поля связанные заряды будут смещаться и образуют ток поляризации:
 ,
,
где ![]() – вектор
поляризованности.
– вектор
поляризованности.
Для сред, в
которых ![]() =e0kэ
=e0kэ![]()
![]() .
.
Все три перечисленные виды тока представляют собой перемещение электрических зарядов. Каждый из этих токов сопровождается магнитным полем.
Максвелл предложил назвать электрическим током изменение во времени электрического тока в вакууме
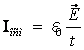 .
.
Отличие тока смещения в вакууме от других видов токов заключается в том, что он не вызывает тепловых потерь.
Полным электрическим током называется совокупность всех явлений, при которых образуется магнитное поле
Iполн=I + Iпер + Iполяр + Iосн .
Сумму тока
поляризации и тока смещения в вакууме называют током смещения в диэлектрике
Iсм=Iполяр+
Плотность тока в
этом случае
Iполн = I + Iсм= dE +![]() .
.
Ток переноса рассматривать не будем. В хорошо проводящей среде I>>Iсм, в диэлектрике с малыми потерями Iсм >>I. В проводящей среде токи проводимости и токи смещения соизмеримы.
6. Магнитное поле
6.1 Основные величины, характеризующие магнитное поле
Основным свойством магнитного поля является силовое
воздействие его как на движущие в нём заряженные тела, так и на неподвижные
проводники с электрическим током. Величиной, характеризующей магнитное поле,
является вектор магнитной индукции ![]() . Зная значение и направление вектора
. Зная значение и направление вектора ![]() , можно установить свойства магнитного поля и вызываемых им
явлений. Вектор
, можно установить свойства магнитного поля и вызываемых им
явлений. Вектор ![]() можно определить по силе, с которой поле действует на контур
с током.
можно определить по силе, с которой поле действует на контур
с током.
Сила, действующая на линейный элемент тока, может быть определена по формуле
![]() .
.
В системе
СИ ![]() измеряется в Тл.
измеряется в Тл.
Связь между током и возбужденной им в пустоте индукции в дифференциальной форме определяется как
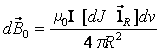 ,
,
где J – плотность тока,
dV – элементарный объём,
R – расстояние от dV до точки, в которой
определяется ![]() ,
,
m0 – магнитная постоянная m0=4p×10-7 Гн/м.
Если размеры поперечного сечения проводника малы по сравнению с длиной проводника и расстоянием до точки наблюдения ( проводник линейный ), можно положить
[![]() ]dv=[
]dv=[![]() ]
] ![]() =[(
=[(![]() )
)![]() ]=I[
]=I[![]() ].
].
Проинтегрировав данное выражение, определим
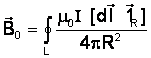 .
.
Если контур с
током находится в каком-либо веществе, то величина магнитной индукции будет
отличаться от ![]() 0 в m раз
0 в m раз
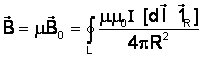 ,
,
где m – относительная магнитная проницаемость среды.
Напряженность магнитного поля
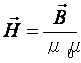 .
.
Напряжённость магнитного поля не зависит от свойств среды.
Для линейного проводника с током
 .
.
Это уравнение получило название закон Био-Савара Лапласа.
Собственное
макроскопическое поле вещества можно характеризовать вектором М, который
называется вектором намагниченности. Этот вектор определяет, насколько
магнитная индукция в данной среде ![]() =mm0
=mm0![]() отличается от
магнитной индукции в вакууме
отличается от
магнитной индукции в вакууме ![]() =m0
=m0![]() при одной и той же напряжённости магнитного поля:
при одной и той же напряжённости магнитного поля:
![]() -
-![]() 0=m0М,
0=m0М,
М=km![]() ,
,
где km – магнитная восприимчивость.
![]() =m0М+m0
=m0М+m0![]() =m0(1+ km)
=m0(1+ km)![]() = mm0
= mm0![]() ,
,
следовательно, m=1+ km.
В системе СИ [![]() ]=[А/м], [М]=[А/м].
]=[А/м], [М]=[А/м].
6.2 Магнитный поток и его непрерывность
Поток вектора магнитной индукции записывается как
Ф=![]() .
.
В системе СИ [Ф]=[Вб].
Магнитный поток сквозь замкнутую поверхность всегда равен нулю
![]() .
.
Пользуясь теоремой Остроградского, можно записать:
![]() .
.
Это равенство справедливо для любого объёма. Следовательно,
div![]() =0.
=0.
Это
соотношение - дифференциальная форма принципа непрерывности магнитного потока.
В любой точке магнитного поля нет ни истока, ни стока линий вектора магнитной
индукции. Линии ![]() нигде не прерываются, они представляют собой замкнутые сами
на себя линии.
нигде не прерываются, они представляют собой замкнутые сами
на себя линии.
Количественная
связь между циркуляцией вектора ![]() по замкнутому контуру
и током внутри контура определяется законом полного тока
по замкнутому контуру
и током внутри контура определяется законом полного тока
![]() I.
I.
Выделим в
какой-либо среде небольшой контур и составим циркуляцию вектора ![]() :
:
![]() dп
D
dп
D![]() d
d
![]()
![]()
![]()




 Di =J, D
Di =J, D![]() =Jп D
=Jп D![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
![]()
![]() Разделим
обе части на D
Разделим
обе части на D![]() и устремим D
и устремим D![]() ®0:
®0:
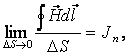
rotп![]() =Jп,
=Jп,
rot![]() =J.
=J.
rot![]() =J -
закон полного тока в дифференциальной форме.
=J -
закон полного тока в дифференциальной форме.
Вектор может быть определён как функция, характеризующая поле в рассматриваемой точке в отношении способности к образованию вихрей.
6.3 Скалярный потенциал магнитного поля
Вихревыми
принято называть поля, ротор которых отличен от нуля. Так как для магнитного
поля постоянного тока rot![]() =J,
где J¹0,
поле вектора
=J,
где J¹0,
поле вектора ![]() является полем
вихревым. Где J=0, rot
является полем
вихревым. Где J=0, rot![]() =0 и магнитное поле можно рассматривать как потенциальное.
=0 и магнитное поле можно рассматривать как потенциальное.
Для таких областей:
![]() =-gradjM, т.к.
=-gradjM, т.к.
div![]() =divmm0
=divmm0![]() =0,
=0,
div![]() =0,
=0,
div gradjM=0,
или Ñ2jМ=0 – уравнение Лапласа для областей не занятых током.
Разность скалярных магнитных потенциалов между точками 1 и 2 называют падением магнитного напряжения между точками 1 и 2
UM12=jM1-jM2=![]() .
.
Следует различать понятия «падение магнитного напряжения» и
«магнитное напряжение». Первое определяется только линейным интегралом от ![]() на
на ![]() по выбранному пути. Второе -
не только этим интегралом, но и ЭДС, имеющейся на пути.
по выбранному пути. Второе -
не только этим интегралом, но и ЭДС, имеющейся на пути.
6.4 Векторный потенциал магнитного поля
Для расчёта магнитного поля используется векторный потенциал
![]() =rot
=rot![]() .
.
Основанием для представления индукции в виде ротора от вектора потенциала служит то, что дивергенция любого ротора тождественно равна нулю:
div![]() =0, тогда div rot
=0, тогда div rot![]() =0.
=0.
Векторный потенциал применяется для определения магнитной индукции для определения магнитного потока, пронизывающий какой-либо контур.
6.5 Граничные условия в магнитном поле
Для магнитного
поля Н1t=Н2t. Это равенство
выводится путём составления линейного интеграла ![]() по плоскому контуру
mnpq. Стороны np и mq ничтожно малы по сравнению
по плоскому контуру
mnpq. Стороны np и mq ничтожно малы по сравнению
|
|
со сторонами mn и pq . Длину стороны mn и pq обозначим dl. Тогда :
H1sina1dl - H2sina2dl = 0 ,
H1sina1 = H1t , H2sina2 = H2t .
Следовательно, H1t=H2t. Это условие не выполняется, если на поверхности раздела двух сред протекает так называемый поверхностный ток. В этом случае:
H1sina1dl - H2sina2dl = sdl ,
H1t-H2t=s.
При наличии поверхностного тока с плотностью s тангенциальная составляющая напряжённости поля терпит разрыв.
Для магнитного поля
В1п=В2п .
Это вытекает из принципа магнитного потока
![]() =0 .
=0 .
|
|
Выделим на
границе раздела небольшой плоский параллелепипед и подсчитаем потоки
вектора ![]() через нижнюю грань – В1п DS и верхнюю грань – В2п DS:
через нижнюю грань – В1п DS и верхнюю грань – В2п DS:
-В1п DS+ В2п DS=0,
В1п= В2п,
 .
.
6.6 Энергия магнитного поля
Магнитный поток сквозь элементарную площадку dl равен: dФ=![]() d
d![]() .
.
Весь поток
Ф=![]() .
.
Построим в контуре, ограничивающем площадку d![]() , силовые трубки. Так как в магнитном поле линии вектора
, силовые трубки. Так как в магнитном поле линии вектора ![]() всегда замкнуты, то
силовые трубки получаются замкнутыми. Они заполняют весь объём V, занятый магнитным полем. Если обозначить ось трубки L, то
всегда замкнуты, то
силовые трубки получаются замкнутыми. Они заполняют весь объём V, занятый магнитным полем. Если обозначить ось трубки L, то
![]() .
.
Энергия 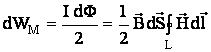 ,
или
,
или
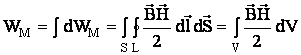 , то
, то
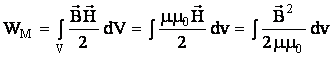 .
.
Так как
![]() =rot
=rot![]() , то
, то
 , но
, но
div[![]()
![]() ]=
]=![]() rot
rot![]() -
- ![]() rot
rot![]() .
.
Тогда можно записать
 .
.
По теореме Остроградского:
![]() .
.
Так как
магнитное поле занимает неограниченный объём, то S можно представить себе как шаровую
поверхность бесконечно большого радиуса R. Вектор [![]()
![]() ] убывает в функции расстояния не медленнее
] убывает в функции расстояния не медленнее ![]() , тогда как поверхность растёт не быстрее R2,следовательно, при R® ¥
, тогда как поверхность растёт не быстрее R2,следовательно, при R® ¥
![]() .
.
Тогда по первому
уравнению Максвелла rot![]() =
=![]() получим
получим
 .
.
6.7 Методы расчетов магнитных полей
Расчет
магнитных полей чаще всего сводится к определению вектора ![]() . Величины токов и положение проводников, по которым эти токи
протекают, должны быть заданы. Если
рассматривается поле в неферромагнитной среде, mm0»m0=4p10-7
Гн/м .
. Величины токов и положение проводников, по которым эти токи
протекают, должны быть заданы. Если
рассматривается поле в неферромагнитной среде, mm0»m0=4p10-7
Гн/м .
Если
непосредственное определение ![]() связано с большими
математическими трудностями, удобно вводить векторный потенциал. Определив векторный потенциал, можно найти
напряжённость поля. При расчёте магнитных полей могут быть применены следующие
методы: применение закона полного тока в интегральной форме; применение первого
уравнения Максвелла; применение уравнений Пуассона и Лапласа для векторного
потенциала; метод зеркальных изображений; метод конформных преобразований,
графический метод расчёта.
связано с большими
математическими трудностями, удобно вводить векторный потенциал. Определив векторный потенциал, можно найти
напряжённость поля. При расчёте магнитных полей могут быть применены следующие
методы: применение закона полного тока в интегральной форме; применение первого
уравнения Максвелла; применение уравнений Пуассона и Лапласа для векторного
потенциала; метод зеркальных изображений; метод конформных преобразований,
графический метод расчёта.
7. Система
уравнений Максвелла
7.1 Первое уравнение Максвелла
Из закона полного тока следует

![]()
Преобразовав по теореме Стокса:

тогда получим
или

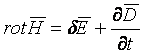
Физический смысл этого уравнения заключается в утверждении, что вихревое
магнитное поле возбуждается как токами проводимости, так и изменяющимся во
времени электрическим полем:
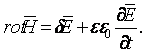
Для идеальных диэлектриков d=0.
1-ое уравнение Максвелла устанавливает зависимость между изменением во времени напряжённости электрического поля и изменением в пространстве напряженности магнитного поля, и указывает на то, что электромагнитное поле всегда находится в движении.
7.2 Второе уравнение Максвелла
Оно представляет дифференциальную форму закона электромагнитной индукции,
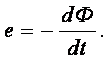
наведенной в контуре
Будем считать, что поверхность S и контур L неподвижны и не деформируются, тогда
по теореме Стокса
![]()
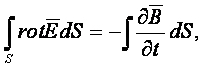
Следовательно

или
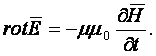
Физический смысл уравнения заключается в утверждении, что изменяющееся во
времени магнитное поле возбуждает вихревое электрическое поле. Так как rotE¹0 , то линии E могут быть замкнутыми,
причём они должны обхватывать линии вектора В. Для сред с m=const
2-е уравнение Максвелла устанавливает зависимость между изменением во времени Н и изменением в пространстве Е.
7.3. Третье уравнение
Максвелла
Третье уравнение Максвелла является обобщением закона Гаусса на случай переменных процессов. Закон Гаусса связывает поток вектора электрического смещения через произвольную замкнутую поверхность S с зарядом Q, сосредоточенным внутри этой поверхности
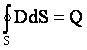 .
.
где![]() ; n0 — орт внешней нормали к поверхности S.
; n0 — орт внешней нормали к поверхности S.
До
Максвелла это уравнение рассматривалось только в применении к постоянным
полям. Максвелл предположил, что его можно использовать и в случае переменных
полей.
Заряд Q может быть произвольно распределен внутри поверхности S. Поэтому в общем случае

где V — объем, заключенный внутри
поверхности S;
ρ
— объемная плотность заряда, которая определяется как предел отношения заряда
ΔQ, сосредоточенного внутри объема ΔV, к объему ΔV при неограниченном уменьшении
ΔV
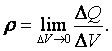
С учетом этого окончательно получаем

Это
уравнение обычно называют третьим
уравнением Максвелла в интегральной форме.
7.4. Четвертое уравнение Максвелла
Четвертое уравнение Максвелла в интегральной форме совпадает
с законом Гаусса для магнитного поля, который можно сформулировать
следующим образом. Поток вектора В через любую замкнутую
поверхность S равен нулю
![]() .
.
Это означает, что не существует линий вектора В, которые
только входят в замкнутую поверхность S (или, наоборот, только выходят из поверхности S) - они всегда пронизывают ее.
Это уравнение называют четвертым уравнением Максвелла в
интегральной форме. К дифференциальной форме можно перейти с помощью
теоремы Остроградского—Гаусса так же, как это было сделано в случае третьего уравнения
Максвелла. В результате получим
div B = 0.
Уравнение представляет собой четвертое уравнение
Максвелла. Оно показывает, что в природе отсутствуют магнитные заряды. Из
этого уравнения также следует, что линии вектора В (силовые линии магнитного
поля) являются непрерывными.
8. Полная система уравнений электромагнитного поля
Электромагнитное поле характеризуется четырьмя векторами Е,D,В,Н. Для сред с постоянной проницаемостью электромагнитное поле характеризуется четырьмя векторами `Е,`D,`В,`Н. Для сред с постоянной проницаемостью
D=ee0E, B=m0mH.
Поэтому при расчёте достаточно определить только два вектора. Обычно определяют `Е и Н из уравнения Максвелла.
Для однозначности определения `Е и Н этих уравнений недостаточно. Поэтому надо знать ещё и дивергенцию `Е и `Н.

По теореме Гаусса в дифференциальной
форме div`D=r.
При постоянном значении e
Основное свойство магнитного поля – его соленоидальность (div`B=0) позволит определить дивергенцию вектора `Н. При постоянном m div`H=0.
При решении конкретных задач должны быть учтены начальные граничные условия.

На границе раздела двух сред значения e, m и g меняются скачком,
следовательно, на поверхности раздела будет иметь место разрыв непрерывности
векторов поля, причём граничные условия, полученные для постоянных во времени
полей сохраняют силу и для мгновенных значений проекций векторов электромагнитного поля:
Если на поверхности раздела нет свободных зарядов, s=0 и тока JS=0.
Физический смысл основных уравнений электромагнитного поля заключается в том, что магнитное поле всегда вихревое и возбуждается оно как движущимися зарядами, так и изменяющимся во времени электрическим полем.
Электрические и магнитные поля связаны непрерывным взаимным превращением и представляют собой различные проявления единого электромагнитного поля, которое находится в движении и несёт с собой запас энергии.
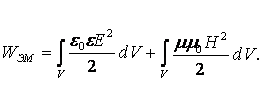
Для
постоянных во времени процессов уравнения поля распадаются на две независимые
системы:
для электрического поля - rot`E = 0, dive0eE = r,
для магнитостатического поля - rotH = d, divm0mH = 0.
ЛИТЕРАТУРА
1.
Вольман В.И., Пименов Ю.В. Техническая электродинамика. – М.: Связь, 2002.
2. Лебедев И.В. Техника и приборы СВЧ. – М.: Высшая школа, 1970.
3. Фальковский О.И. Техническая электродинамика. – М.: Связь, 1978.
Методическое пособие “Теория электромагнитного
поля. Часть
по дисциплинам “Электромагнитные поля и волны” и
“Электродинамика и распространение радиоволн” рассмотрено на
заседании кафедры АФУ (протокол № 26 от 28.03.2006) и рекомендовано к печати.
Отв. редактор доц. Ликонцев Д.Н.
Составитель и.о.доц. Губенко В.А.
Редакционно-корректурная комиссия:
редактор доц. Абдуазизов А.А.
корректор асс. Васильева Т.В.