УЗБЕКСКОЕ АГЕНТСТВО СВЯЗИ И
ИНФОРМАТИЗАЦИИ
ТАШКЕНТСКИЙ
УНИВЕРСИТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ
Факультет
Радиотехники, Радиосвязи и Телерадиовещания
Кафедра
Антенно-фидерных
устройств
Конспект лекций по дисциплине
“РРВ и антенны мобильной связи”
для
направления «Мобильная связь»
Ташкент 2010
ОГЛАВЛЕНИЕ
Тема
1. Введение. Классификация радиоволн по способу распространения.
Тема
2. Распространение радиоволн в свободном пространстве.
Тема
3. Распространение земных радиоволн УКВ диапазона.
Тема
4. Распространение тропосферных радиоволн.
Тема 5.
Распространение ионосферных радиоволн.
Тема 6. Распространение радиоволн в условиях крупного
города.
Тема 7.
Классификация и характеристики антенн.
Тема 8.
Теория симметричного вибратора.
Тема 9.
Характеристики вибраторных антенн.
Тема 10. Способы увеличения рабочего диапазона волн вибраторных антенн. Частотно–независимые антенны.
Тема 11.
Теория антенных решеток. Линейные и плоские решетки.
Тема 12.
Теория апертурных антенн. Устройство и принцип действия рупорной и
зеркально-параболической антенн.
Тема 13.
Обзор основных типов антенн мобильной связи
ТЕМА 1. Введение. Классификация
радиоволн по способу распространения
Радиоволнами называют
электромагнитные волны (ЭМВ), лежащие в диапазоне от 103 до 1012
Гц.
В системах связи и вещания
широко используется свободное распространение радиоволн. При этом линией
передачи является естественная среда, заполняющая пространство, в котором
распространяются радиоволны от передающей антенны к приемной. На наземных
линиях типа Земля-Земля такая среда включает атмосферу и поверхностные толщи
Земли. На космических линиях типа Земля- космический аппарат путь
распространения проходит через атмосферу Земли и космическое пространство.
Земная атмосфера и
поверхностные толщи земли являются поглощающими электрически неоднородными
средами. Их диэлектрическая проницаемость и проводимость не остаются
постоянными в пространстве и во времени и изменяются в зависимости от частоты
распространяющейся волны.
Резко выраженная частотная
зависимость законов распространения приводит к необходимости разграничения
диапазона радиоволн по поддиапазонам, в которых условия распространения
радиоволн (РРВ) примерно одинаковы. Ниже, в табл.1.1, приведены частотные
границы диапазонов и их названия.
Таблица 1.1
Частотные границы диапазонов и их названия
|
N |
Частота |
Длина волны |
Диапазон |
Название по Регламенту радиосвязи |
|
4 |
3кГц...30 кГц |
100 км-10 км |
СДВ |
Мириаметровые |
|
5 |
30 кГц...300 кГц |
10 км...1 км |
ДВ |
Километровые |
|
6 |
300 кГц...3000 кГц |
1 км...100 м |
СВ |
Гектометровые |
|
7 |
3 МГц...30 МГц |
100 м...10 м |
КВ |
Декаметровые |
|
8 |
30 МГц...300 МГц |
10 м...1м |
УКВ |
Метровые |
|
9 |
300 МГц...3000 МГц |
1 м... 10 см |
УКВ |
Дециметровые |
|
10 |
3 ГГц...30 ГГц |
10 см....1 см |
УКВ |
Сантиметровые |
|
11 |
30 ГГц...300 ГГц |
1 см....1 мм |
УКВ |
Миллиметровые |
|
12 |
300 ГГц...3000 ГГц |
1 мм...0,1 мм |
УКВ |
Децимилли-метровые |
Так, например, мы можем
передать информацию на большие
расстояния в декаметровом и сантиметровом диапазонах волн, но в декаметровом
диапазоне мы сразу можем обеспечить дальность радиосвязи на тысячи и десятки
тысяч км с шириной полосы сигнала в несколько кГц, а в сантиметровом диапазоне
- с шириной полосы сигнала в несколько МГц, но через ретрансляторы,
установленные в пределах прямой видимости.
Общую задачу о
распространении радиоволн в реальной атмосфере вдоль реальной земной
поверхности обычно разделяют на несколько отдельных задач, каждая из которых
исследует свой механизм распространения, обусловленный частными свойствами тракта
распространения.
К первому регулярному
механизму относится РРВ вдоль границы раздела воздух - земная поверхность
(рис.1.1.а). Этот механизм подчиняется законам дифракции (дифракция - процесс
огибания препятствия при длине волны l больше размеров препятствия).
Радиоволны, распространяющиеся в непосредственной близости от поверхности Земли
и частично огибающие выпуклость земного шара вследствие явления дифракции
получили название земных или поверхностных волн.
Интенсивная плавная
электрическая неоднородность верхних ионизированных слоев атмосферы является
причиной второго регулярного механизма РРВ с частотой до 30...40 МГц путем
последовательного многократного отражения от ионизированных слоев атмосферы и
поверхности Земли (рис.1.1.б). Радиоволны, распространяющиеся на большие
расстояния и огибающие земной шар в результате однократного или многократного
отражения от ионосферы (l ³ 10м), а также волны,
рассеивающиеся на неоднородностях ионосферы, получили название ионосферных или пространственных волн.
За счет слабых электрических
неоднородностей локального характера в тропосфере происходит рассеивание
радиоволн (рис.1.1.в). Механизм рассеивания используют для передачи информации
на частотах выше 300 МГц на наземных радиолиниях. Радиоволны, распространяющиеся
на значительные расстояния до 1000 км за счет рассеивания в тропосфере и
направляющего действия тропосферы, получили название тропосферных волн.
Связь между земным пунктом и
космической станцией может осуществляться только за счет так называемой прямой
волны, которая распространяется через всю толщу атмосферы и космическое
пространство (рис.1.1.г). Радиоволны, распространяющиеся в однородной или слабо
неоднородной среде по прямолинейным или близким к ним траекториям, получили
название свободно распространяющихся или прямых волн.
Изучение частных механизмов
распространения позволяет при проектировании линий связи выбирать основные
параметры систем с учетом свойств тракта распространения.
Тема 2. Распространение радиоволн в свободном пространстве
Свободное пространство представляет собой однородную
непоглощающую среду для которой
относительная диэлектрическая и магнитная проницаемости равны единице, а
удельная проводимость равна нулю (e= l; m= l; s= 0), т.е.
среда имеет параметры eо = 8,85 10-12,Ф/м; mо = 4p10-7 Гн/м.
Примеры : воздух, космическое пространство.
Все антенны в волновой
зоне (дальней зоне) излучают сферические волны. Распространение
такой волны сопровождается сферической
расходимостью ее фронта и
соответственно сферической расходимостью потока электромагнитной энергии по
мере удаления от источника. В практике работы радиолиний в свободном
пространстве ослабление напряженности поля из-за уменьшения плотности потока
энергии во многих случаях определяет требование к энергетическим показателям
аппаратуры.
Поместим в свободном пространстве антенну излучающую
равномерно по всем направлениям (изотропный излучатель). Вокруг источника
электромагнитных волн проведем воображаемую сферу радиуса r. Если к излучателю подведена мощность Р1 и
она равномерно распределится по поверхности сферы с площадью 4pr2, то средняя за период плотность потока мощности
(мощность приходящаяся на единицу поверхности) равна Поср = Р1/4pr2 . Из курса “ Электромагнитные поля и волны” мы знаем,
что Пср связано с действующими значениями напряженности
электрического и магнитного полей соотношением Пср = ЕдНд.
Значения Ед и Нд связаны через волновое сопротивление
среды Zс = 120p. Отсюда Нд
= Ед/120p и Поср
=Ед2/120 p. Из
сравнения двух выражений для Поср получим формулу для расчета Ед:
Ед = Ö30Р1/r - действующего
значения напряженности электрического поля в свободном пространстве для
ненаправленного излучателя.
Правило написания формул: если мы пишем формулу и не
указываем в виде индексов наименование единиц, то это означает, что применяются
для всех величин основные единицы.
Амплитудное значение напряженности поля будет в Ö2 раз больше, т.е. ЕM=Ö60P1/r.
На практике обычно
рассчитывается и измеряется действующее значение напряженности электрического
поля. Реально изотропные антенны не существуют (существуют квазиизотропные) и
антенны обладают направленностью. Направленные свойства антенн характеризуются
формой диаграммы направленности, коэффициентом усиления G или
коэффициентом направленного действия D. Диаграмма направленности
показывает зависимость напряженности поля от пространственных координат.
Коэффициент направленного действия (КНД) показывает во сколько раз надо
уменьшить излучаемую мощность, если ненаправленную (изотропную) антенну
заменить направленной для получения одинаковых значений напряженности поля в
точке приема. Коэффициент усиления (КУ) показывает во сколько раз надо
уменьшить подводимую мощность, если ненаправленную (изотропную) антенну
заменить направленной для получения одинаковых значений напряженности поля в
точке приема; при этом КПД изотропной антенны принимается равным единице. Таким
образом
Eм=Ö30 P1G1/r,
Произведение
P1G1=P1экв называют
эквивалентной мощностью излучения, которую надо подвести к ненаправленной
антенне, чтобы получить в точке приема такую же напряженность поля, как от
направленной антенны с коэффициентом усиления G1, к которой подведена мощность Р1.
Из
формулы следует, что даже в свободном пространстве, среде без потерь,
напряженность поля в точке приема убывает обратно пропорционально первой
степени расстояния, что обусловлено уменьшением плотности мощности (среднего за
период колебаний значения вектора Пойнтинга) при удалении от источника.
Для
удобства расчетов формулу несколько видоизменим для подстановки значений Р1
в кВт, r в км и чтобы результат расчета
получился в мВ/м, тогда
Ед=173ÖР1(кВт)G1/r(км),мВ/м.
При расчете и проектировании
радиолиний, особенно в диапазонах сантиметровых и дециметровых волн, необходимо
знать мощность сигнала на входе приемника. Эта мощность определяется различно
для радиолиний двух типов. На радиолинии I типа передача информации ведется
непосредственно из пункта передачи в пункт приема (рис. 2.1). На радиолиниях II
типа принимаются сигналы, испытавшие пассивную ретрансляцию на пути от передатчика
к приемнику (рис.2.2). На этих линиях непосредственная передача энергии волны
от источника до точки приема по каким-либо причинам невозможна (например, этот
путь перекрыт препятствием). На наземных радиолиниях с пассивной ретрансляцией
на пути распространения имеется специальное пассивное антенное устройство (или
другой объект), которое облучается первичным полем и переизлучает его в виде
вторичного поля, предназначенного для приема. По такому же принципу работают
системы пассивной радиолокации, где первичное поле облучает обнаруживаемую
цель, а поле, переизлученное целью, принимается локатором.
На любой радиолинии мощность
на входе приемного устройства Р2 связана с плотностью потока
мощности в месте приема П2 соотношением
Р2=П2Sдh2,
где h2— КПД фидера приемной антенны; Sд= G2l2/4p — действующая площадь
приемной антенны .
На радиолинии первого типа в
условиях свободного пространства плотность потока мощности в месте приема равна
П2=Р1h1G1/(4pr2),
где P1 - мощность на выходе
передающего устройства, h1 - КПД передающего фидера, G1 - коэффициент усиления передающей антенны. Для
радиолинии первого типа мощность на входе приемника в условиях свободного
пространства равна P12=P1h1G1G2h2l2/(4pr2).
На радиолинии второго типа
значение П2 зависит от тех же параметров, что и на линии первого
типа, и, кроме того, от переизлучающих свойств ретранслятора. Если какое-либо
тело облучается полем, то его способность переизлучать это поле оценивается
эффективной площадью рассеяния dэф (ЭПР). Величина ЭПР зависит
от формы, размеров, электрических свойств материала из которого выполнен
переизлучатель, а также от его ориентации относительно направления
распространения первичного поля и направления на прием.
Если около переизлучающего
тела плотность потока мощности первичного поля Роп= P1h1G1/(4pr12), то переизлученная
мощность Роп=Попdэф ,
а плотность потока мощности
вторичного поля вблизи приемной антенны в условиях свободного пространства П2=Роп/(4pr22).
Тогда мощность на входе
приемного устройства для радиолинии второго типа PII2=P1h1G1G2h2dэфl2/[(4p)3r12r22] .
В
тех случаях, когда r1=r2=r, PII2=P1h1G1G2h2dэф l2/[(4p
)3r4] и
получается уравнение радиолокации.
Из формул видно, что в свободном пространстве при
отсутствии пассивного ретранслятора на линии мощность на входе приемника
уменьшается обратно пропорционально квадрату расстояния, а при работе с
ретранслятором — обратно пропорционально четвертой степени. Такое быстрое
убывание поля на линиях второго типа объясняется тем, что поле дважды
испытывает расходимость сферического фронта волны: первичное поле — на пути от
источника (передающей антенны) до пассивного ретранслятора и вторичное поле —
на пути от ретранслятора до пункта приема.
При проектировании систем
радиосвязи, радиовещания, радиолокации и т.д. необходимо знать величину потерь
при передаче электромагнитной энергии. Потерями передачи L
называют отношение мощности Р1', подводимой к передающей антенне, к
мощности Р2' на входе приемной антенны L=P1’/P2'=Plh1h2/P2.
Для радиолинии первого типа
в условиях свободного пространства
потери передачи равны L1=(4pr/l)2/G1G2.
Расчеты упрощаются, если в
формуле выделить составляющую Lo, которая называется
основными потерями передачи и характеризует только потери, обусловленные
сферической расходимостью фронта волны (при G1=G2=l ) Lo=(4pr/l)2.
Полные потери передачи
обычно выражают через L. Можно записать
L1=Lo/G1G2.
Для радиолинии второго типа
в условиях свободного пространства при r1=r2=r потери передачи равны L11=[(4p)3r4/l2][1/G1G2sэф]
или L11=L02[(1/G1G2sэф)(l2/4p)] .
В случае реальных сред,
отличных по своим свойствам от свободного пространства, вводят так называемый
множитель ослабления F=E/Eo=Fexp(-ijv),
где F — модуль множителя
ослабления, который оценивает дополнительное ослабление амплитуды напряженности
поля по сравнению с ее ослаблением в условиях свободного пространства; jv— фаза множителя ослабления,
которая оценивает дополнительное изменение фазы волны. Отсюда следует, что E=E0 F.
Тема 3. Распространение земных радиоволн
УКВ диапазона
Определение поля излучателя, расположенного в атмосфере вблизи земной
поверхности, с учетом реальных свойств Земли и атмосферы представляет собой
чрезвычайно сложную задачу. Для облегчения ее решения вводят некоторые
упрощения. Поверхность Земли считают электрически однородной, сферической и
идеально гладкой. Электрические параметры атмосферы (воздуха) принимают такими
же, как и параметры свободного пространства.
Поле земной волны можно
считать результатом суперпозиции полей, созданных вторичными источниками,
которые возбуждены первичным полем в воздухе и земле. Полупроводящие свойства
Земли приводят к оттоку энергии волны из воздуха в почву. Сферическая земная
поверхность является препятствием, которое земная волна огибает при
распространении за линию горизонта. Процесс огибания - процесс дифракции
радиоволн вдоль сферического препятствия приводит к дополнительным потерям по
сравнению со случаем распространения радиоволн над плоской поверхностью.
Полное решение задачи
дифракции радиоволн для сферической идеально гладкой Земли с однородными электрическими
параметрами и однородной атмосферы получено В. А. Фоком в 1945 г. Эта формула
представляет собой бесконечный ряд из специальных функций Эйри и расчеты по ней
весьма громоздки. В ряде случаев, встречающихся на практике, общую
дифракционную формулу Фока можно упростить или вместо нее использовать другие,
более простые методы расчета поля.
Для практических расчетов
общее решение дифракционной задачи можно разделить на несколько частных.
Критерием для применения частных решений служат высота подъема антенн над
поверхностью Земли и длина радиотрассы (расстояния от пункта передачи до пункта
приема). Оба параметра определяют степень затенения земной поверхностью
пространственных зон Френеля, а следовательно, и закон ослабления поля в
процессе дифракции.
В зависимости от высот
расположения антенн различают два класса задач. К первому классу относят
задачи, в которых высота подвеса антенн h >> l и которые питаются неизлучающим фидером. Это так называемые поднятые антенны, что на практике характерно
при работе в диапазоне УКВ и с некоторыми ограничениями в диапазоне КВ. Второй
класс задач рассматривает процесс дифракции радиоволн при низко расположенных
антеннах, когда h<<l.
Этот случай характерен для работы в диапазонах СДВ, ДВ СВ и частично КВ.
Вдоль пути распространения
земной волны в зависимости от степени освещенности точки приема излучением
передающей антенны выделяют три области (зоны): освещенности (I), полутени
(II) и тени (III), как показано на рис.6.1. Термин “Зона освещенности” имеет
смысл только при поднятых антеннах. При низко расположенных антеннах область,
прилегающую к передающей антенне, называют зоной “приближения плоской Земли”,
поскольку в пределах этой зоны поверхность Земли можно приближенно считать
плоской.
В зонах полутени и тени расчет напряженности
поля как для поднятых, так и для низко расположенных антенн ведется по общим
дифракционным формулам Фока.
Рассматривая среды,
параметры которых указаны в табл.6.1, видим, что для морской воды равенство
плотности токов проводимости и токов смещения наступает при длине волны l, равной 0,33 м. Поэтому для радиоволн,
имеющих длину волны сантиметрового диапазона, морская вода может
рассматриваться как диэлектрик.
Таблица 6.1
Параметры сред
|
Вид земного покрова |
e |
s,См.м |
|
Морская вода |
80 |
1...6 |
|
Пресная вода рек и озер |
80 |
10-3...10-2 |
|
Влажная почва |
10...30 |
3.10-3...3.10-2 |
|
Сухая почва |
3...6 |
1.10-5...5.10-3 |
|
Мерзлая почва |
3...6 |
10-3...10-2 |
|
Лед (t= -100С) |
4...5 |
10-2...10-1 |
|
Снег (t= -100C) |
1 |
10-6 |
Для влажной почвы это условие выполняется на длине волны l, равной 17 м. Влажная почва может
рассматриваться как диэлектрик для метровых и более коротких волн. Таким
образом, для волн сантиметрового диапазона все виды земной поверхности имеют свойства, близкие к
свойствам идеального диэлектрика.
Отметим также, что при
оценке условий распространения земной волны в случае h >> l сравнивают длину радиолинии r с
расстоянием прямой видимости rо (рис.6.2). Высоты подвеса
приемных и передающих антенн h1, h2<<aз, где aз=6370 км - радиус Земли,
поэтому величина rо, отсчитываемая по дуге большого круга, приближенно
равна прямой АВ. Из рис.6.2 видно,
что rпр=АС+СВ,
где AC=Öaз+hl)2—aз2»Ö2aзh1; CB»Ö2aзмh2, откуда rо=Ö2азм(Öh1+Öh2). Если rо выразить в километрах, h1 и h2 - в метрах, то после
подстановки численного значения аз
и отсутствии рефракции получим ro=3,57 (Öh1+Öh2). При обычных высотах поднятия антенн (порядка
нескольких десятков метров) предельное расстояние прямой видимости составляет
несколько десятков километров (как правило, не более 50...60 км). Таким
образом, в случае h >> l деление трассы
распространения земной волны на зоны производят следующим образом: r < rо -
зона освещенности; 0,8ro < r <
1,2rо —
зона полутени; r >
1,2rо —
зона тени.
Распространение радиоволн при поднятых передающей и приемной антеннах
Изучение распространения земных
радиоволн естественно надо начать с этого наиболее простого случая. При
небольших расстояниях между передающей и приемной антеннами кривизной
поверхности Земли можно пренебречь. Будем считать поверхность Земли гладкой и
однородной на протяжении всей трассы. Задача формулируется так: заданы
геометрические параметры: расстояние между передающей и приемной антеннами, высоты
подвеса передающей h1 и приемной h2 антенн и электрические
параметры: подводимая к передающей антенне мощность Р1, коэффициенты
усиления передающей и приемной антенн G1 и G2, длина волны l, вид поляризации волны, относительная
диэлектрическая проницаемость почвы e и ее удельная проводимость s. Требуется определить множитель ослабления F и
напряженность поля по формуле
![]() .
.
Как впервые было показано
еще в 1922 году академиком Б.А.Введенским электрическое поле радиоволны в месте
расположения приемной антенны можно рассматривать как результат интерференции
прямого луча 1 и луча 2, отраженного в точке С от поверхности Земли (рис.6.3).
При решении задачи РРВ вдоль границы воздух - Земля
существенное значение имеет абсолютная величина комплексной диэлектрической
проницаемости почвы
![]()
![]() .
.
Обычно она не бывает меньше 10, правда для сухого
песка в дециметровом диапазоне eк = 2...5. Способность земной
поверхности отражать радиоволны тоже связана с относительной комплексной
диэлектрической проницаемостью. Значения модулей коэффициентов отражения для
вертикальной поляризации Rв и горизонтальной
поляризации Rг можно определить по формулам:
![]() ,
,
![]() ,
,
где g - угол скольжения, который
определяется по формуле
![]() .
.
Земная волна,
распространяясь вдоль границы раздела воздух-почва, возбуждает в воздухе и
почве токи, которые являются источниками вторичного поля. В соответствии с
принципом Гюйгенса-Кирхгофа поле земной волны можно считать результатом
суперпозиции полей, наведенных воображаемыми вторичными источниками, которые
возбуждаются первичным полем в воздухе и почве. В почве интенсивность вторичных
источников ослаблена по сравнению со свободным пространством, за счет тепловых
потерь, которые появляются из-за конечных значений проводимости s. Почва экранирует проникновение поля в
глубокие области Земли (явление скин эффекта), что препятствует оттоку энергии
в нижнюю полусферу. Сферическая земная
поверхность является препятствием, которое волна огибает при распространении за
линию горизонта. Процесс огибания - процесс дифракции радиоволн вдоль
сферического неидеального экрана с радиусом 6370 км сопровождается большими
потерями.
Запишем
мгновенные значения для напряженности электрического поля лучей 1 и 2
![]() ;
;![]() .
.
Обозначим b = q+2pDr/l; Считая, что r(км) + Dr(км)» r(км), т.к. Dr<<r можно записать
![]() , так как
, так как
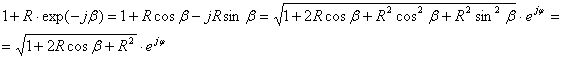
![]() , то
, то
![]() и
и
![]() ,мВ/м.
,мВ/м.
Так как Dr »2h1h2/r, то можно записать
![]() ,
мВ/м.
,
мВ/м.
Полученная формула показывает, что в месте
расположения приемной антенны поле действительно имеет интерференционную
структуру. По мере удаления от передающей антенны будем наблюдать такую картину
(рис.6.4). При изменении r косинус аргумента будет
меняться. Когда косинус равен единице поле максимально. При ![]()
![]() где
N=0,1,2,…
где
N=0,1,2,… ![]() .
.
Когда косинус равен минус единице поле минимально.
При![]() ,
,![]() где
N=0,1,2,..
где
N=0,1,2,.. ![]() .
.
Отсчет максимумов и минимумов ведется от конца
радиотрассы. При r £ 4h1h2/l наблюдаются максимумы и
минимумы напряженности поля, а при r > 4h1h2/l наблюдается плавное уменьшение напряженности
поля с увеличением расстояния.
Дальнейшее
упрощение интерференционных формул. С увеличением расстояния значение R
стремится к 1, а q - к 180о, тогда
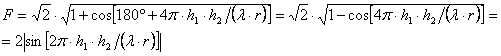
![]() или
или
![]() .
.
При дальнейшем увеличении расстояния когда![]() , то синус аргумента можно заменить его аргументом
, то синус аргумента можно заменить его аргументом ![]() , при
, при ![]()
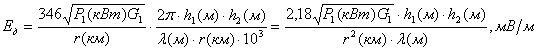 .
.
Напряженность поля на расстояниях r ³ 18 h1h2/l убывает с квадратом расстояния. Надо твердо
помнить, что в условиях применимости формулы Введенского, луч отраженный от
поверхности Земли является вредным, т.к. он стремится скомпенсировать поле
прямого луча. Векторная диаграмма сложения полей (структура поля в точке приема) приведена на рис.6.5. Многие
изобретатели старались скомпенсировать вредный отраженный луч (рассыпали уголь
в месте отражения, ставили стенку на пути отраженного луча). Но они не учли
того, что как луч занимает часть пространства, так и волна отражается не в
одной точке, а от площади описываемой эллипсоидом с горизонтальными размерами
2аn и 2bn (рис.6.6), которые при одинаковых высотах
подвеса антенн можно рассчитать по формулам ![]() ;
; ![]() .
.
Многолучевая структура. Диаграмма направленности в вертикальной
плоскости. Будем
строить зеркальное изображение антенны (рис.6.7). Из треугольника Dr = 2hsing, тогда
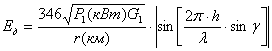 ,мВ/м.
,мВ/м.
Угол g меняется в пределах от 0 до
p/2 (0о - пологий луч, 90о
- направлено в зенит).Тогда (2phsing)/l будет меняться от нуля до 2ph/l. Для примера возьмем Ташкентский РТПЦ h1 = 350м, l = 7м, Dr =2hsing . Если вертолет будет
облетать (по вертикали) ТашРТПЦ, то будет обнаружено 100 максимумов (n=2h/l).
Учет сферичности земной
поверхности при расчете напряженности поля. Сферичность земной волны влияет на амплитуду
за счет рассеивания от выпуклой поверхности Земли и фазу отраженной волны, т.к.
выпуклость земной поверхности изменяет длину пути отраженной волны. Если в
точке отражения радиоволны от поверхности Земли (рис.6.8) провести плоскость MN,
касательную к поверхности Земли и отсчитывать высоты подвеса антенн не от
поверхности Земли, а от указанной плоскости, то подставляя в интерференционные
формулы вместо действительных высот h1 и h2 «приведенные высоты» h1¢и h2¢, получим правильное
значение напряженности поля в месте приема, ибо угол скольжения луча
относительно выпуклой поверхности Земли тот же, что и угол скольжения над
касательной плоскостью. Учет кривизны Земли при пользовании интерференционными
формулами сводится к нахождению приведенных высот h¢1 и h¢2 по известным значениям r, h1, h2.
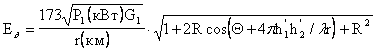 , мВ/м;
, мВ/м;
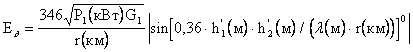 , мВ/м;
, мВ/м;
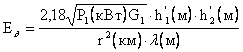 , мВ/м.
, мВ/м.
Расчет напряженности поля в зоне
полутени и тени. В.А.Фок получил выражение
для функции ослабления пригодное для любых удалений от передатчика. На
небольших расстояниях от передатчика оно переходило в интерференционную
формулу. Наоборот при больших расстояниях, решение превращалось в одночленную
дифракционную формулу. Фок ввел понятия о ²масштабе расстояний² L и о ²масштабе высот² Н. Это позволяет длину трассы r и высоты подвеса антенн h1 и h2 выразить в безразмерных
единицах: относительное расстояние х=r/L, относительные высоты подвеса антенн y1=h1/H, y2=h2/H.
Выражение для множителя
ослабления одночленной дифракционной формулы (для расчета уровня поля в зоне
тени) может быть представлено в виде произведения трех сомножителей F=U(x)V(y1)V(y2), первый из которых зависит
от расстояния, второй и третий от высот подвеса передающей и приемной антенн.
Расчет напряженности поля в области тени в диапазонах СДВ, ДВ, СВ и большей
части КВ значительно проще, т.к. F=U(x). Для расчета значения
множителя ослабления в зоне тени используются графики (рис.6.9 и 6.10) для
определения значений U(x),V(y1),V(y2) в дБ, тогда F=U(x)+V(y1)+V(y2), дБ. Из дБ в разы значение
множителя ослабления можно пересчитать по формуле F=10FдБ/20. Значение напряженности поля рассчитывается по формуле Е=ЕоF, где Ео
- напряженность поля в свободном пространстве.
В
зоне полутени для приближенной оценки уровня напряженности поля известную
пользу приносит способ определения множителя ослабления на границе прямой
видимости, т.е. на таком расстоянии, где интерференционные формулы показывают
уже нулевые значения поля. Метод разработан для горизонтально поляризованного
излучения. При вертикальной поляризации он дает менее точные результаты и
используется для l < 50 см. Множитель ослабления на границе
прямой видимости рассчитывается по формуле F = (ro/L)F(y1,y2).Значение функции F(y1,y2) получено из многочленной
дифракционной формулы и определяется графически из рис.6.11 в дБ. Это значение
пересчитывается в разы по формуле F=10F(y1,y2)дБ/20. Напряженность поля
рассчитывается по формуле Е = ЕоF.
Тема 4. Распространение тропосферных
радиоволн
Электрические свойства
атмосферы, как и любой среды, характеризуются диэлектрической проницаемостью,
магнитной проницаемостью и удельной проводимостью. Магнитная проницаемость
атмосферы с достаточно высокой степенью точности принимается величиной
постоянной и равной магнитной проницаемости вакуума. Остальные два параметра
испытывают значительные изменения в зависимости от положения точки наблюдения,
времени, солнечной активности, частоты распространяющейся волны и т. д.
Согласно представлениям
макроскопической электродинамики диэлектрическая проницаемость и проводимость
определяются совокупностью токов, возникающих в среде под действием внешнего
поля. В неионизированных областях атмосферы (тропосфере и стратосфере)
плотность полного тока, наводимого внешним полем, имеет две составляющие j = jсмо+jпол . Здесь jсмо —плотность тока смещения в
свободном пространстве jсмо=iweE=i2pfeoE ,
jпол—плотность тока поляризации jпол=eоcгdE/dt=iweocгЕ,
где cг —относительная
диэлектрическая восприимчивость вещества, зависящая от электрической и
магнитной структур молекул и атомов, термодинамических условий, а также от
частоты воздействующего поля.
В общем случае cг — комплексная величина,
однако на частотах ниже 15...20ГГц, когда потери в тропосфере и стратосфере
малы , cг можно считать
действительной величиной.
Относительная
диэлектрическая проницаемость тропосферы
eт=[(1+1,552.10-4)/T](р+4810e/T),
где р - давление газа, мБар ; е - абсолютная
влажность воздуха, т. е. давление водяных паров, мБар; Т - температура, К.
Из формул видно, что чем
больше р и е, тем больше eг. Это связано с тем, что при
возрастании р и е увеличивается число молекул в единице объема и,
следовательно, ток поляризации. При увеличении Т возрастает скорость
хаотического теплового движения молекул, препятствующего упорядоченному
смещению связанных зарядов, т. е. ток поляризации уменьшается.
Относительная
диэлектрическая проницаемость тропосферы связана с коэффициентом преломления
тропосферы nт выражением
nт=Öeт=[1+(0,776.10-4 /T)](p+4810e/T).
Сильное влияние на
коэффициент преломления оказывают водяные пары. Так как nт (как и eт) весьма мало отличаются от
единицы у поверхности Земли и лежат в
пределах 1,00025... 1,00046. Оперировать такими значениями не всегда удобно,
поэтому для удобства был введен индекс коэффициента преломления тропосферы,
показывающий насколько миллионных долей коэффициент преломления отличается от
единицы.
Nт = (nт-1)106 =
77,6(р+4810e/T)/T.
Численные значения индекса коэффициента преломления
называются N - единицами. У поверхности
Земли Nт
меняется от 260 до 460 N -
единиц. Зависимость величины Nт от высоты h
оценивается градиентом индекса коэффициента преломления тропосферы dNт/dh.
Аналогичная
зависимость для eт(h) имеет вид
eт(h)=1+5,78.10-4exp(-1,36.10-4h).
На распространение радиоволн
сильное влияние оказывают локальные неоднородности диэлектрической проницаемости
тропосферы.
Слоистые неоднородности представляют собой образования, горизонтальные
размеры которых заметно превышают вертикальные. Одной из основных причин их
возникновения является температурная инверсия , а также наличие облачности.
Интенсивность неоднородностей слоистого типа,
оцениваемая как отличие диэлектрической проницаемости в пределах слоя от
диэлектрической проницаемости окружающей среды колеблется от 10-6 до
(5...10) 10-5. Число и интенсивность слоев с увеличением высоты над
земной поверхностью уменьшаются. Размеры слоистых неоднородностей изменяются в
широких пределах. Толщина слоев характеризуется величинами от десятых долей
метра до нескольких сотен метров, а их горизонтальные размеры изменяются от
десятков метров до десятков километров и более.
Неоднородности турбулентного характера имеют соизмеримые размеры
во всех направлениях. Из-за малых сил вязкости движение атмосферного газа
практически всегда турбулентное, так что неоднородности такого типа всегда
существуют в тропосфере, при любых метеоусловиях.
Размеры неоднородностей
турбулентного происхождения определяются размерами (масштабами) элементарных
вихрей и ограничиваются размерами от нескольких миллиметров до нескольких
десятков метров.
Земная атмосфера
представляет собой пространственно-неоднородную поглощающую среду, а верхняя ее
часть - ионосферная плазма - обладает еще дисперсными и анизотропными
свойствами. Распространение радиоволн в такой среде сопровождается следующими
физическими процессами:
а) преломлением волн, обусловленным пространственной
неоднородностью атмосферы; процесс преломления осложняется двойным
лучепреломлением в анизотропной ионосфере;
б) рассеянием поля на локальных неоднородностях
атмосферы;
в) ослаблением напряженности поля в газах
тропосферы, в осадках типа дождя, тумана и др.;
г) поглощением, обусловленным конечной проводимостью
ионосферы;
д) изменением поляризации волны в анизотропной
ионосфере и деполяризацией в осадках;
е) регулярными и случайными флуктуациями
напряженности поля, связанными с изменениями электрических параметров
атмосферы;
ж) искажениями передаваемой информации из-за
многолучевой структуры принимаемого поля и дисперсии.
Рассмотрение количественных характеристик этих
процессов, имеющих резко выраженную частотную зависимость в пределах радиодиапазона,
приводится ниже.
Преломление радиоволн
Общие соображения. Диэлектрическая проницаемость атмосферы плавно
меняется по высоте. Распространение радиоволн в такой среде сопровождается
плавным искривлением траектории распространения - явлением рефракции.
При наличии рефракции
траектория представляет кривую, к которой касателен вектор, характеризующий
скорость распространения энергии волны. Известно, что при распространении
сигнала, энергия которого сконцентрирована в пределах полосы частот - таким
вектором в среде без дисперсии (тропосфера, стратосфера) является вектор
фазовой скорости, в среде с дисперсией (ионосфера) - вектор групповой скорости.
Выражения сф и сгр показывают,
что в атмосфере скорость распространения волны различна на различных высотах.
Поэтому элементы фронта волны, распределенные в пространстве, перемещаются с
разными скоростями, что и является причиной поворота фронта в процессе
распространения, т. е. причиной рефракции.
При определении траектории радиоволн в атмосфере
используют метод приближения
геометрической оптики. Этот метод рассматривает непрерывный волновой
процесс, распределенный в неоднородной среде, как совокупность множества
дискретных лучей. При этом каждая точка среды является источником преломленного
и отраженного лучей. Лучевое представление справедливо для неоднородных сред с
настолько медленным изменением коэффициента преломления, что на отрезке пути,
соизмеримом с длиной волны в среде, можно принять n(h) = const. При этом в первом приближении можно пренебречь отраженным
лучом и свести процесс распространения к наличию только преломленного. В
атмосфере приближение геометрической оптики справедливо для всех волн
радиодиапазона, за исключением диапазонов СДВ и ДВ (l>1000 м).
Влияние
тропосферы на распространение земных радиоволн.
Явление атмосферной рефракции
Влияние неоднородности
тропосферы на условия распространения земных волн теснейшим образом связано с
явлением атмосферной рефракции, известным ещё с глубокой древности (2 век до н. э.). Явление атмосферной рефракции,
как известно, заключается в преломлении световых лучей (а следовательно, и
радиоволн), распространяющихся в земной
атмосфере. Выведем выражение для радиуса кривизны траектории радиоволны,
распространяющейся в тропосфере. Для простоты пренебрежём влиянием кривизны
Земли и будем считать, что поверхности одинаковых значений показателя преломления n представляют собой плоскости параллельные плоской
поверхности Земли. Рассмотрим две из таких поверхностей отстоящих друг от друга
на расстоянии dh (рис.4.1). Луч,
падающий на нижнюю поверхность под углом j и испытывающий преломление
на участке dh, падает на верхнюю
поверхность под углом j+dj. Искомый радиус кривизны R
определяется выражением R=ab/d. Из треугольника abc находим ab=dh/cos(j+dj)=dh/cosj отсюда R=dh/cosjdj
В средах с плавно меняющимся
значением коэффициента преломления закон преломления (закон синусов) должен
выполняться во всех точках траектории. Следовательно, он должен выполняться
также в точках а и b . На основании этого можем
написать nsinj =(n+dn)sin(j+dj )
nsinj = nsinj +sinjdn+ncosjdj+cosjdjdn
.Предположим, что cosjdj =1, sindj=dj . Отсюда cosj dj= - (dn/n)sinj R=dh/cosjdj R=n/[sinj (-dn/dh)]
n » 1. Когда луч пологий sinj Þ1. Отсюда R=106/(-dN/dh).
Знак минус у производной
означает, что радиус кривизны будет положительным, т.е. траектория волны будет
обращена выпуклостью вверх, только в том случае, если коэффициент преломления
уменьшается с высотой.
Это выражение показывает,
что радиус кривизны луча в нижних слоях тропосферы определяется не абсолютным
значением показателя преломления, а быстротой изменения показателя преломления
с высотой. Знак минус у производной означает, что радиус кривизны будет
положительным, т. е. траектория будет обращена выпуклостью вверх только в том
случае, если показатель преломления уменьшается с высотой.
При распространении в
нормальной тропосфере, которая характеризуется постоянством градиента — во всей
толще тропосферы, траектории радиоволн получают форму дуг окружности радиуса R = 2500 км.
Следует отметить, что
радиоволны испытывают в нормальной тропосфере несколько большее преломление,
чем световые лучи. Объясняется это тем, что обладающие постоянным дипольным
моментом молекулы воды вследствие конечной массы не успевают под действием электромагнитного
поля весьма высоких частот, свойственных
видимому свету (4 1014 Гц - 7,5 1014 Гц), менять свою ориентировку. Наоборот, в
диапазоне радиоволн (f<3.1011 МГц)
полярные молекулы в полной мере участвуют в колебательном движении и вносят
свои изменения в значение показателя
преломления. Для световых лучей. R » 50000 км. Атмосферная рефракция, имеющая место в
нормальной тропосфере, получила название нормальной
рефракции.
Учёт атмосферной рефракции при распространении
радиоволн в пределах прямой видимости. Понятие об эквивалентном радиусе Земного
шара
Рассмотрим учёт влияния
атмосферной рефракции на распространение радиоволн при поднятых передающей и
приёмной антеннах в условиях применимости интерференционных формул. Как
известно, подобные условия встречаются только в диапазоне ультракоротких волн.
Необходимость такого учёта именно в диапазоне ультракоротких волн обусловлена
тем, что в условиях применимости интерференционных формул результирующее поле в
месте приёма зависит от геометрической разности хода прямого и отражённого от
земли лучей. Вывод интерференционных формул основывался на предположении, что
волны распространяются по прямым, тогда как в действительности радиоволны
распространяются по криволинейным траекториям, т. е. проходят более длинные
пути, что несомненно влияет на геометрическую разность хода лучей. Кроме того,
изменение электрической проницаемости с высотой влияет на скорость
распространения радиоволн, а следовательно, и на «оптическую разность хода
лучей», как принято называть разность хода, вычисленную с учётом скорости
распространения волн. На рис.4.2
пунктирными линиями показаны
прямолинейные траектории прямого и отражённого от земли лучей при распространении
в однородной атмосфере. В нормальной тропосфере радиоволны распространяются по
криволинейным траекториям, точнее, по дугам
окружностей, показанных на рисунке сплошными линиями. Замена
прямолинейных траекторий дугами окружностей изменит конечные значения разности
хода лучей. В 1933 г. Скиллинг, Берроуз и Феррелл предложили упрощённый способ учёта влияния
атмосферной рефракции, заключающийся в том, что оба луча, как и прежде,
распространяются по прямолинейным траекториям, однако не над поверхностью земли
радиуса а, а над воображаемой
поверхностью с эквивалентным радиусом аэ Значение эквивалентного
радиуса определяется из условия сохранения постоянства относительной кривизны
между лучом и поверхностью Земли в действительных условиях и в эквивалентной
схеме распространения (табл.4.1). Относительной кривизной в аналитической
геометрии называют разность 1/a -
1/R. Отсюда 1/a - 1/R = 1/aэ - 1/¥ Из этого выражения получаем
формулу для эквивалентного радиуса Земли
аэ=а/(1-a/R)
aэ = a/[1+a(dN/dh)10-6]. При нормальной тропосферной рефракции aэ = 8500 км.
Представление об эквивалентном радиусе земного шара позволяет
распространить все ранее полученные формулы на неоднородную атмосферу путём
замены в них действительного радиуса Земли а
его эквивалентным значением. Прежде всего это можно сделать по отношению к
формуле для определения расстояния прямой видимости. При учёте влияния
атмосферной рефракции эта формула принимает вид ro=Ö2aэ (Öh1+Öh2)
Принцип, положенный в основу
представления об эквивалентном радиусе земного шара, показывает, что таким
методом можно пользоваться в тех случаях, когда выполняемые исследования или
расчёты основаны на сохранении неизменной относительной кривизны траектории. С
этой точки зрения вовсе не очевидно, можно ли допустить применение концепции об
эквивалентном радиусе земного шара к расчётам, производимым по
интерференционным формулам. Действительно, при пользовании интерференционными
формулами напряжённость поля в месте приёма в значительной степени определяется
разностью фаз между прямым и отражённым от земли лучами.
Пока атмосферная рефракция во внимание не
принималась, разность фаз в месте приёма определялась геометрической разностью
хода прямого и отражённого от земли лучей в предположении, что оба луча
распространяются прямолинейно. При учёте атмосферной рефракции необходимо
принимать во внимание одновременно два фактора. Во-первых, искривление
траектории и, во-вторых, зависимость скорости распространения волн от
меняющегося по высоте значения показателя преломления.
Простые рассуждения
показывают, что в условиях нормальной атмосферной рефракции учёт только первого
фактора приводит к уменьшению разности хода лучей, так как при этом длина
прямого луча увеличивается в большей степени, чем общая длина отражённого от
земли луча. Наоборот, учёт только второго фактора приводит к увеличению
оптической разности хода лучей, т. е. к увеличению разности фаз, обусловленной
разностью хода лучей. Оптическая длина пути отражённого луча, который
распространяется в более низких, в более плотных слоях атмосферы, увеличивается
в большей степени, -чем оптическая длина прямого луча. Численные расчёты
показывают, что решающее влияние оказывает второй фактор; таким образом, при
учёте обоих факторов оптическая разность хода лучей возрастает. Выполненное Б.
А. Введенским и М. И. Пономаревым исследование
показывает допустимость применения концепции об эквивалентном радиусе
земного шара для достаточно пологих лучей. Основываясь на этом, считают
возможным при пользовании интерференционными формулами и, в частности, формулой
Введенского учитывать влияние атмосферной рефракции путём замены для определения приведённых высот
действительного радиуса Земли его эквивалентным значением. В табл.4.1 приведены
значения эквивалентного радиуса Земли, реальные и эквивалентные траектории для
различных видов тропосферной рефракции. В тех случаях, когда кривизна земли во
внимание не принимается, что возможно при расчётах напряжённости поля на
небольших удалениях от передатчика, можно не принимать во внимание и
атмосферную рефракцию.
Тема 5. Распространение ионосферных
радиоволн
В ионосфере полный ток,
наводимый внешним полем, равен сумме трех токов: тока смещения свободного
пространства и конвекционного тока,
обусловленного движением свободных зарядов под действием поля, т.е. j=jсмо+jк=iweоЕ+еNеuе , где uе - средняя скорость
упорядоченного движения электронов, которая определяется из уравнения движения
электрона.
jк=eNeue=-ie2NewE/[me(g2эф+w2)]+e2NegэфЕ/[me(g2эф+w2)],
где е - заряд электрона, mе - масса электрона.
Формула показывает, что конвекционный ток,
возбужденный полем волны, имеет две составляющие: реактивную и активную.
Реактивная составляющая за счет инерции электронов отстает по фазе от поля на
90°. Активная составляющая, синфазная с полем, представляет собой ток
проводимости (jnp = sЕ)
и обусловливает необратимые тепловые потери. Плотность полного тока в ионосфере
равна
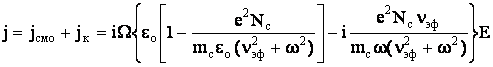
Напомним, что в среде с потерями плотность полного
тока j =iw(eоe-is/w). Сравнивая это выражение с
предыдущим, находим относительную диэлектрическую проницаемость и проводимость
ионосферы
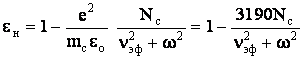
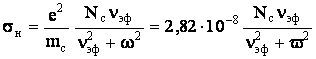
На достаточно высоких частотах, когда w2>>g2эф, т.е. в диапазонах КВ и УКВ
выражения для eи и sи упрощаются:
eи = 1-80,8 Nc / f2; sи = 7.17 10-10 Ncnэф/f2 , См/м.
Рассмотрим основные свойства
ионосферы, вытекающие из полученных формул для eи и sи формул. Формулы для eи показывают, что
диэлектрическая проницаемость ионосферы:
- меньше диэлектрической
проницаемости свободного пространства (eи<1) за счет наличия
конвекционного тока. Свободные электроны движутся против поля, а jсм совпадает по направлению с Е. Поэтому конвекционный ток, вычитаясь
из тока смещения, уменьшает суммарный реактивный ток, наводимый в ионосфере, по
сравнению с током в свободном пространстве;
- зависит от электронной
концентрации и частоты столкновений, которые претерпевают пространственные и
временные изменения; следовательно, ионосфера является электрически
неоднородной средой. На рис. 3.3 показано качественное изменение eи ионосферного слоя по высоте
h. Видно, что диэлектрическая проницаемость сначала уменьшается, а затем, выше
максимума ионизации слоя, возрастает с высотой;
- диэлектрическая
проницаемость зависит от частоты, т. е. ионосфера является диспергирующей
средой. Это обусловлено тем, что электроны, обладая конечной массой, проявляют
инерционные свойства. С повышением частоты упорядоченная скорость движения
электронов, а следовательно и конвекционный ток уменьшаются и свойства
ионосферы приближаются к свойствам свободного пространства. Практически
основное влияние ионосферы на условия распространения радиоволн наблюдается на
частотах f < 100 МГц (l >3м);
- диэлектрическая
проницаемость может принимать нулевые значения, если частота приложенного поля w будет равна так называемой собственной
частоте ионосферной плазмы wе.
На частотах w<wе диэлектрическая проницаемость
ионосферы eи<0. На рис. 3.3 показан
случай, когда для некоторой частоты f3 на высотах от h1
до h2
eи<0. Распространение волны
с частотой f3 в указанной области ионосферы невозможно. Это
обстоятельство имеет важное значение для отражения радиоволн от ионосферы.
Полученные формулы для
удельной проводимости позволяют сделать следующие выводы:
1. Проводимость ионосферы на
разных высотах различна, так как зависит от электронной плотности и частоты
соударений, которые в свою очередь зависят от высоты. На рис. 3.4 показан
пример зависимостей Ne, nэф, а также их произведения Nеnэф от высоты h. Из рисунка
видно, что хотя электронная концентрация Ne уменьшается на один -
два порядка ниже уровня 100 км, тем не менее это полностью компенсируется более
резким возрастанием nэф, и таким образом
произведение Nеnэф оказывается максимальным на
высотах слоя D и нижней части слоя Е ионосферы. В результате
удельная проводимость sи, зависящая от произведения Nеnэф, максимальна на тех же
высотах. Учитывая, что слой D существует только в дневное время, можно сделать
еще один вывод - проводимость, а следовательно, и поглощение в ионосфере в
дневное время больше, чем в ночное.
2. Удельная проводимость,
характеризующая поглощение в ионосфере, тем меньше, чем выше частота (при w>>nэф). Это происходит потому,
что с увеличением частоты из-за инерции электронов их средняя колебательная
скорость уменьшается и, следовательно, уменьшается энергия, которую электроны
отдают тяжелым частицам при столкновении. Практически поглощение в ионосфере мало
на частотах f > 100 МГц.
Магнитное поле Земли
значительно усложняет характер движения зарядов в ионосфере и приводит к
изменениям ее диэлектрической проницаемости и проводимости . На движущийся
электрон со стороны магнитного поля Земли действует сила Лоренца, которая
закручивает электрон вокруг силовых линий магнитного поля, превращая траекторию
его движения в спиральную линию. Частота вращения электронов вокруг магнитных
силовых линий (в отсутствие других полей) называется электронной гиромагнитной частотой
wн=еmоНз/m и fн=еmоНз/(2pm), где е и m —
заряд и масса электрона соответственно; Нзм — напряженность
магнитного поля Земли. Учитывая, что в средних широтах Нзм»40 А/м, гиромагнитная частота равна 1,4 МГц,
т. е. лежит в диапазоне средних волн (l = 214 м). На этой частоте
работать нельзя так как будет наблюдаться повышенное поглощение. Сила Лоренца
зависит от угла между направлением распространения волны и вектором Нзм.
Это приводит к тому, что волны, движущиеся в разных направлениях относительно Нзм,
наводят разные токи и, следовательно, диэлектрическая проницаемость и
проводимость ионосферы оказываются зависящими от направления распространения.
Таким образом, ионосфера представляет собой анизотропную среду. Отметим , что под влиянием магнитного поля Земли
в ионосфере возникают некоторые специфические явления, характерные для
анизотропных сред. Например, возникает явление двойного лучепреломления, когда
электромагнитная волна расщепляется на две волны — обыкновенную и
необыкновенную, распространяющиеся по различным траекториям с различными
скоростями и испытывающие различное поглощение.
Локальные неоднородности в ионосфере и ионосферные бури. Существенное влияние на
работу радиолиний оказывают отклонения электронной концентрации от регулярных
средних значений. Различают два вида .отклонений: флуктуации около средних
значений и длительные аномальные изменения самих средних значений. Флуктуации
наблюдаются всегда, аномальные изменения — только в периоды так называемых
ионосферных возмущений. Флуктуации электронной концентрации обусловливают
неоднородную быстро меняющуюся микроструктуру ионосферы. Ионосфера
представляется как скопление локальных образований, изменяющихся во времени и
подвижных в пространстве. В пределах неоднородностей электронная концентрация
отличается от среднего значения в данной области ионосферы.
Мелкомасштабные неоднородности с горизонтальными размерами в несколько сотен
метров образуются в результате процессов турбулентности и диффузии.
Интенсивность неоднородностей определяется среднеквадратическим значением
отношения перепада электронной концентрации на неоднородности к среднему
значению. В области высот 80... 400 км интенсивность мелкомасштабных
неоднородностей оценивается величиной порядка 10-2.
Крупномасштабные неоднородности с горизонтальными размерами в десятки и сотни
километров образуются в результате колебательных процессов в ионосфере и
представляют образования эллипсоидальной формы с преимущественной ориентацией
вдоль силовых линий магнитного поля Земли.
Длительные аномальные
изменения средних значений электронной концентрации, наблюдаемые в течение 1 ч
и более, называются ионосферными
возмущениями или бурями.
Наиболее важные для работы радиолиний ионосферные возмущения имеют
корпускулярную природу. Напомним, что корпускулы производят ударную ионизацию
атмосферного газа. Возмущения появляются, когда атмосфера Земли попадает в
корпускулярные потоки, излученные из активных областей возмущенного Солнца.
Корпускулы, достигая области действия магнитного поля Земли как заряженные
частицы, начинают двигаться по спиралям вокруг магнитных силовых линий и
направляются к полярным областям. Корпускулярные потоки вызывают не только
ионосферные, но и магнитные бури, поэтому часто говорят о магнитно-ионосферных
возмущениях. Возмущения протекают по разному в зависимости от широты точки
наблюдения.
Возмущения корпускулярного
происхождения в средних и низких широтах характеризуются аномальным изменением
в основном области F. Лишь в периоды очень сильных бурь возмущения достигают
нижних слоев ионосферы.
Для средних широт характерны
так называемые отрицательные возмущения, при которых электронная концентрация
слоя понижается на 30...40%. Во
время бури на плавное изменение электронной концентрации слоя F2 налагаются
интенсивные неоднородности.
Возмущения корпускулярного
происхождения в полярных широтах характеризуются изменением ионизации всей
толщи ионосферы, включая слой D. При аномальном повышении ионизации этого слоя
увеличивается удельная проводимость ионосферы и, следовательно, поглощение
радиоволн. В кольцевой зоне полярных сияний одновременно с изменением состояния
слоя D наблюдается возмущенность слоя F2, проявляющаяся в освещенной части зоны
в виде значительного понижения Ne max, а в затененной — в
виде значительного повышения Ne
max за счет спорадических образований.
Возмущения волнового
происхождения проявляются в виде резкого возрастания ионизации слоя D в
результате мощного рентгеновского излучения, источником которого является
хромосферная вспышка на Солнце. Возмущения этого типа, сопровождаемые резким
увеличением поглощения (эффект Делинжера), наступают внезапно и длятся от
нескольких минут до 1...2 часов. Обычно они охватывают всю освещенную часть
земного шара, распределяясь с разной интенсивностью в зависимости от широты.
Условия отражения
от ионизированного слоя. До сих
пор рассматривались различные случаи распространения радиоволн в однородном
ионизированном газе. Реальная ионосфера представляет собой неоднородный
ионизированный газ. Влияние неоднородности ионосферы проявляется прежде всего в
том, что радиоволны в таких условиях будут распространяться не по прямолинейным
траекториям (как то имело место во всех рассмотренных выше случаях), а по
криволинейным. В известных условиях радиоволны, испытывая полное отражение от
ионосферы, возвращаются на Землю.
Рассмотрим
сначала случай распространения радиоволн в «плоской ионосфере», т. е. в таком
ионизированном газе, у которого поверхности одинаковых значений электронной
концентрации представляют параллельные друг другу плоскости (рис.4.2). Кроме
того, на первых порах будем считать ионосферу состоящей из ряда плоских слоев
весьма малой толщины, в пределах каждого из которых электронная концентрация
имеет постоянное значение. Обозначим через N1 электронную концентрацию внутри первого слоя, через N2 -электронную концентрацию внутри второго слоя и т. д.,
причём будем считать, что выполняется неравенство, N1 < N2 <N3 < ...
<Nn, .
Предположим далее, что на самый нижний слой из неионизированного воздуха падает
луч частоты f под углом падения jо (рис.4.2).
Основываясь на выражении для показателя
преломления 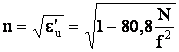
можно
написать 1>n1>n2>n3>...>nn>nn+1. Применяя к каждой границе
закон синусов, получим ![]() ,
, ![]()
![]() . После достаточного числа преломлений угол падения у n-го
слоя может сколь угодно близко подойти к 900. Полагая jn » 900 и сохраняя в равенстве
крайние члены, получим sinj0 = n или
. После достаточного числа преломлений угол падения у n-го
слоя может сколь угодно близко подойти к 900. Полагая jn » 900 и сохраняя в равенстве
крайние члены, получим sinj0 = n или
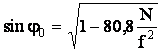
![]()
![]()
![]()
![]() закон секанса.
закон секанса.
Физической
причиной поворота волны в вершине траектории следует считать полное внутреннее
отражение. Напомним , что полное отражение происходит в том случае, когда при
переходе из оптически более плотной в оптически менее плотную среду (т. е.
среду с меньшим значением показателя преломления) угол падения превышает
некоторое критическое значение, определяемое (в наших условиях) формулой
jn > arcsin[1 - (Dn/nn)]
Дополнительными условиями являются: 1 -
радиус кривизны траектории радиоволны должен быть меньше аз+hотр. 2 - в точке поворота
радиоволны dN/dh должно превышать некоторое
критическое значение Численные расчёты показывают, что последнее условие почти
всегда выполняется автоматически и решающим является условие ( ), которое в силу этого можно практически
считать единственным условием поворота волны.
Практическое значение дополнительного условия заключается в
следующем: в точке отражения электронная концентрация обязательно должна
возрастать, а отражение не может происходить в области максимума электронной
концентрации и тем более в области уменьшения электронной концентрации с
высотой.
Наибольшая
частота, при которой радиоволны отражаются от данного ионосферного слоя при
вертикально направленном луче, получила название критической частоты. Условие
поворота радиоволны может быть выполнено только и только в том случае, если
частота волны не превосходит fmax. Волны, не
удовлетворяющие этому условию, от ионосферы не отражаются, а пронизывают её
насквозь.
Отражение от ионосферы вертикально
направленных лучей. При нормальном падении радиоволны на ионосферу от неё
будут отражаться только те радиоволны, частота которых не превосходит
критического значения. Действительно, положив в расчетной формуле jо = 0,
находим n=0 или, что то же, eи =0. Таким
образом, вертикально направленный луч отражается от той области ионосферы, в
которой электрическая проницаемость обращается в нуль. Предположив, что на
больших высотах электронная концентрация продолжает возрастать приходим к
выводу, что на этих высотах электрическая проницаемость делается отрицательной,
а показатель преломления мнимым. Существенно заметить, что при учёте
столкновений показатель преломления не обращается в нуль даже при отрицательных
значениях электрической проницаемости.
Тема 6.
Распространение радиоволн в условиях крупного города
Условия приема сигналов в
диапазоне УКВ существенно зависят от расположения приемной антенны относительно
окружающих ее предметов. В городских условиях такими предметами являются
здания, деревья, заводские трубы, мачты и т. п. Близко расположенные здания
могут в зависимости от их расположения оказаться затеняющими препятствиями или
источниками местных отраженных волн. Затеняющее действие отдельного препятствия
приводит к тому что поле за препятствием появляется в результате двух
процессов: дифракции и проникновения через препятствие. Дифракция в
рассматриваемом диапазоне волн протекает с большими потерями. Проникновение
сквозь препятствия типа стен зданий также сопровождается большими потерями за
счет поглощения. Измерения показывают, что напряженность поля за отдельно
стоящим кирпичным зданием на 20...30дБ ниже, чем перед ним, а за железобетонным
строением уровень сигнала падает на 30...40 дБ. В. целом внутри городской
застройки имеются многочисленные теневые зоны, где сигнал значительно ослаблен.
Действие окружающих зданий как источников отраженных волн проявляется, как в
виде неравномерного распределения амплитуды поля в пространстве из-за
интерференции многочисленных отраженных волн, так и в своеобразном
подсвечивании теневых зон. В случае вертикальной поляризации первичного поля
отражения наиболее интенсивны от предметов, протяженных по вертикали (стены
зданий, деревья). Большое влияние местных предметов на условия приема
вертикально-поляризованного поля является одной из причин преимущественного
применения горизонтальной поляризации в системах телевизионного вещания.
Сложность условий
распространения УКВ в городе определяет статистический характер, как
теоретических, так и экспериментальных исследований. По условиям приема сигнала
можно выделить три наиболее типичных ситуации: передающая и приемная антенны
находятся над уровнем городской застройки и между ними имеется прямая
видимость; связь между подвижным объектом и базовой станцией; связь между двумя
подвижными объектами. В первом случае, характерном для приема сигналов
телевизионного вещания, расчет напряженности поля можно вести по формуле
Введенского, умножая результат расчета на поправочный коэффициент (обычно
0,4...0,6). Во втором и третьем случаях между пунктами передачи и приема, как
правило, нет прямой видимости и основной вклад в формирование многолучевого
поля вносят отражения от зданий в окрестности подвижного пункта.
Рассмотрим закономерности
изменения напряженности поля в точке приема в городских условиях в зависимости
от расстояния, частоты волны и высот установки антенн. На рис.10.5 приведены
зависимости среднего (медианного) значения мощности сигнала Рс от расстояния r при различных высотах
подвеса антенны базовой станции h1,
измеренные на частоте 922 МГц. Высота подвеса антенны на подвижном объекте h2 = Зм. Штриховой линией
показана зависимость Рс от расстояния для условий свободного
пространства. Уровень 0 дБ соответствует полю в свободном пространстве на
расстоянии 1 км от базовой станции. Анализ приведенных зависимостей показывает,
что при увеличении расстояния до 15 км мощность сигнала убывает как r-3.
Последующее увеличение r приводит к еще более
быстрому уменьшению уровня сигнала. Ослабление сигнала в городе возрастает с
увеличением его частоты. Если эту зависимость представить в виде Pc=Af-n, где A -
коэффициент пропорциональности. C увеличением частоты от 100
до 2000 МГц значение коэффициента n изменяется от 0,2 до 1 .
При r =1...10 км зависимость уровня поля от частоты слабая, но при
дальнейшем увеличении расстояния значение коэффициента n начинает зависеть от него и
растет значительно быстрее. Изменение медианного значения множителя ослабления
от частоты, при h1=200 м и h2=3 м для расстояний 1, 5, 20
и 40 км, показано на рис.10.6. Зависимость среднего уровня поля от высоты
расположения антенны базовой станции можно проследить по рис.10.7. Высота
подвеса антенны сильно не влияет на скорость уменьшения уровня сигнала с
расстоянием. Однако подъем антенны базовой станции приводит к увеличению
абсолютного значения поля примерно пропорционально квадрату высоты
(6дБ/октаву). На поле в точке приема влияют не только рассмотренные факторы, но
и многие другие. В частности, установлено, что уровень сигнала существенно
зависит от расположения улиц в городе, которые оказывают канализирующее
действие на распространяющиеся волны. Вдоль радиально расположенных улиц
(относительно антенн базовой станции) уровень сигнала на 10...20 дБ выше, чем в
перпендикулярных направлениях.
Условие приема на метровых и более коротких волнах зависит от
расположения приемной антенны относительно окружающих ее предметов и местных
неровностей рельефа. Близко расположенные здания, мачты, растительность, склоны
оврагов, небольшие возвышенности могут в зависимости от их расположения
оказаться затеняющими препятствиями или источниками местных отраженных волн.
Затеняющее действие отдельного препятствия приводит к тому, что поле за
препятствием появляется в результате двух процессов: дифракции и проникновения
сквозь препятствие. Дифракция в рассматриваемых диапазонах волн протекает с
большими потерями. Проникновение сквозь препятствия типа стен зданий, группы
деревьев и других сопровождается также большими потерями за счет поглощения.
«Непрозрачными» препятствиями считают возвышенности земной поверхности и
железобетонные строения. За такими препятствиями поле появляется только в
результате дифракции. К «полупрозрачным» препятствиям относят кирпичные и
деревянные строения, растительность. При распространении в лесу с подлеском
погонное ослабление оценивается
единицами и десятками дБ/км, увеличиваясь с частотой и изменяясь в
зависимости от густоты лиственного покрова и влажности. Действие окружающих
предметов как источников отраженных волн может проявиться в виде двух явлений:
неравномерного распределения амплитуды поля в пространстве из-за интерференции
отраженных волн или запаздывающих сигналов, если предмет достаточно удален от
приемной антенны.
Спецификой условий работы вещательной сети является
прием излучения одного передатчика одновременно множеством приемных пунктов,
случайно распределенных на некоторой территории. В зависимости от характера
рельефа условия приема в пределах этой территории могут быть различными. Кроме
того, принимаемое поле подвержено быстрым и медленным флуктуациям, и его
среднее значение изменяется в зависимости от климатических условий. В
результате в сети вещания принято оценивать напряженность поля вероятностными
характеристиками, основанными на измерениях. Необходимо отметить, что при
оценке условий приема вещания учитывают только медленные флуктуации, принимая,
что мгновенные значения поля подчиняются нормально-логарифмическому распределению
с дисперсией, зависящей от климатических
условий. Быстрые замирания порядка долей секунд и секунд не оказывают
влияния на качество приема телевизионного и звукового вещания из-за инерции
слухового и зрительного аппаратов человека. Параметрами для статистических
характеристик поля служат: диапазон частот, климатический район, средние
условия рельефа, процент времени наблюдений, процент приемных пунктов, в
которых может наблюдаться данная
напряженность поля. Напряженность поля
определяют с помощью кривых, рекомендуемых МККР. В качестве примера на рис.10.4 приведены три кривые,
справедливые для ОВЧ
(40...250 МГц) в условиях среднепересеченной местности и умеренного
климата, характерных для Европы и Северной Америки. Величина напряженности поля,
определяемая из этих кривых, превышается в 50% приемных пунктов в течение 50%,
10 % и 1% времени. Кривые построены для эквивалентной излучаемой мощности 1 кВт, когда высота подвеса передающей
антенны h1 =300м,
высота подвеса приемной антенны h2 = 10 м. Напряженность поля
выражена в децибелах относительно 1 мкВ/м. Кривые справедливы для вертикально-
и горизонтально поляризованных волн. В указанной рекомендации имеются серии
аналогичных кривых для диапазона УВЧ (450...1000 МГц). Для каждого диапазона
даются поправочные коэффициенты, учитывающие степень неровности рельефа и
высоту передающей и приемной антенн.
Тема
7. Классификация и характеристики антенн
Антенной называется радиотехническое устройство, предназначенное для излучения или приема электромагнитных волн. Антенна является одним
из важнейших элементов любой радиотехнической системы, связанной с излучением
или приемом радиоволн. К таким системам относят: системы радиосвязи, радиовещания, телевидения, радиоуправления, радиорелейной связи, радиолокации, радиоастрономии, радионавигации и др.
В конструктивном отношении антенна представляет собой провода, металлические поверхности, диэлектрики, магнитодиэлектрики.
Электромагнитные колебания высокой частоты, модулированные полезным сигналом,
преобразуются передающей антенной в электромагнитные волны, которые излучаются в пространство. Обычно электромагнитные колебания подводят от передатчика к антенне не
непосредственно, а с помощью
фидера.
Приемная антенна улавливает распространяющиеся радиоволны преобразует
их в электромагнитные колебания, которые через фидер поступают на вход
приёмного устройства. В соответствии с принципам обратимости антенн свойства антенны, работающей в режиме передачи не изменятся при работе этой антенны в приемном режиме.
Преобразование антенной одного вида электромагнитных волн в другой должно происходить с минимальными потерями энергии, т.е. с максимально возможным КПД, определяемым в передающем режиме по формуле ![]() = P
= P![]() / Р0, где
P
/ Р0, где
P![]() - мощность излучаемая антенной, Р0 - мощность
подводимая к антенне.
- мощность излучаемая антенной, Р0 - мощность
подводимая к антенне.
Способность антенны излучать электромагнитные волны с различной
интенсивностью в разных направлениях характеризуется её
направленными свойствами, т.е.
диаграммой направленности (ДН).
Антенны, обладающие узкой ДН, позволяют увеличивать напряженность поля в точке приёма без увеличения мощности передатчика. В большинстве случаев это экономически более выгодно, чем увеличения мощности передатчика. Кроме того, концентрация электромагнитных волн в требуемом
направлении приводит к уменьшению взаимных помех различных радиотехнических
систем. Наличие направленных приемных антенн ведёт к ослаблению приема
различных внешних помех, т.е. к повышению качества приёма и улучшению
помехозащищенности приемного устройства. Большими направленными свойствами
должны обладать антенны для космической радиосвязи,
радиоастрономии, радиолокации, радиорелейных линий.
В тоже время для радио и телевидения передающие антенны должны иметь
одинаковое излучение в горизонтальной плоскости (за исключением отдельных
случаев - гор и т.д.).
Направленные свойства являются настолько
важными, что принято говорить о двух
функциях, выполняемых антенной:
- преобразование электромагнитных
колебаний в свободные
электромагнитные волны;
- излучение этих волн в определенных
направлениях.
Важную роль в работе антенного устройства играет линия питания (фидерный тракт), которая передаёт (каналирует) электромагнитную энергию
от генератора к антенне (или от антенны к приёмнику). Фидер не должен излучать электромагнитные волны и должен иметь минимальные потери. Его необходимо согласовывать с
выходной цепью передатчика
( или с
входной цепью приемника) и с входным сопротивлением антенны, т.е. в фидере
должен быть режим бегущей волны или близкий к нему.
В зависимости от диапазона радиоволн применяют различные типы фидеров: двухпроводные или многопроводные воздушные фидеры, несимметричные
экранированные (коаксиальные) линии, различные типы волноводов и др.
Классификацию антенн можно, например проводить по способу формирования
излучаемого поля, выделяя следующие четыре класса антенн:
Излучатели небольших размеров (![]() ,где
,где ![]() - длина волны) для диапазона частот 10кГц...1ГГц. К числу
антенн этого класса относятся одиночные вибраторные и
щелевые излучатели, полосковые и микрополосковые антенны,
рамочные антенны, а также частотно-независимые излучатели.
- длина волны) для диапазона частот 10кГц...1ГГц. К числу
антенн этого класса относятся одиночные вибраторные и
щелевые излучатели, полосковые и микрополосковые антенны,
рамочные антенны, а также частотно-независимые излучатели.
Антенны бегущей волны размерами от ![]() до 100
до 100![]() для диапазона частот 3МГц...10ГГц. Сюда
относятся спиральные, диэлектрические,директорные, импедаксные антенны, а также
антенны «вытекающей» волны.
для диапазона частот 3МГц...10ГГц. Сюда
относятся спиральные, диэлектрические,директорные, импедаксные антенны, а также
антенны «вытекающей» волны.
Антенные решетки размерами от![]() до 100
до 100![]() и более для диапазона частот 3МГц...30ГГц. Это антенны, состоящие из большого числа отдельных излучателей. Независимая регулировка фаз (а иногда и амплитуд) возбуждения
каждого элемента антенной решетки обеспечивает возможность электрического управления диаграммой направленности. Применяются линейные, плоские, кольцевые, выпуклые и конформные (совпадающие с формой объекта установки) антенные решетки. На основе антенных решеток выполняют
антенные системы с обработкой сигнала, в том числе адаптивные к изменяющейся
помеховой обстановке.
и более для диапазона частот 3МГц...30ГГц. Это антенны, состоящие из большого числа отдельных излучателей. Независимая регулировка фаз (а иногда и амплитуд) возбуждения
каждого элемента антенной решетки обеспечивает возможность электрического управления диаграммой направленности. Применяются линейные, плоские, кольцевые, выпуклые и конформные (совпадающие с формой объекта установки) антенные решетки. На основе антенных решеток выполняют
антенные системы с обработкой сигнала, в том числе адаптивные к изменяющейся
помеховой обстановке.
Апертурные антенны размерами от ![]() до 1000
до 1000![]() для диапазона частот 100МГц... 100ГГц и
выше. Наиболее распространены зеркальные, рупорные и линзовые апертурные
антенны. К апертурным антеннам примыкают, так называемые, «гибридные» антенны,
представляющие сочетание зеркал или линз с облучающей
системой в виде антенной решетки. Апертурные антенны строятся по оптическим принципам и обеспечивают наиболее высокую направленность излучения.
для диапазона частот 100МГц... 100ГГц и
выше. Наиболее распространены зеркальные, рупорные и линзовые апертурные
антенны. К апертурным антеннам примыкают, так называемые, «гибридные» антенны,
представляющие сочетание зеркал или линз с облучающей
системой в виде антенной решетки. Апертурные антенны строятся по оптическим принципам и обеспечивают наиболее высокую направленность излучения.
Свойства направленности антенны описывают характеристикой (диаграммой)
направленности. Количественно эти свойства оцениваются с помощью таких параметров, как ширина ДН, уровень боковых лепестков, коэффициент
направленного действия (КНД) и других.
Важным параметром является входное сопротивление антенны, характеризующее её как нагрузку для генератора или фидера. Входным сопротивлением
антенны называется отношение напряжения между точками питания антенны (зажимы антенны) к току в этих точках. Если антенна питается волноводом, то входное сопротивление определяется отражениями, возникающими в волноводном тракте. В общем случае входное сопротивление - величина комплексная Zвх= Rвх+ iXвх. Оно должно быть
согласовано с волновым сопротивлением фидерного тракта
(или с выходным сопротивлением генератора)
так, чтобы обеспечить в последнем режим, близкий к режиму
бегущей волны.
Мощность, излучаемая антенной РΣ, связана с током в точках питания
антенны
соотношением P![]() = I02 R
= I02 R![]() 0 / 2, где RΣ0 – сопротивление излучения антенны (при отсутствии потерь в антенне это
активная составляющая входного сопротивления антенны). Данное
определение относится к проволочным антеннам.
0 / 2, где RΣ0 – сопротивление излучения антенны (при отсутствии потерь в антенне это
активная составляющая входного сопротивления антенны). Данное
определение относится к проволочным антеннам.
Одним из основных параметров антенны является ширина её рабочей полосы
частот, в пределах которой параметры антенны (характеристика направленности, входное сопротивление, КПД и др.) удовлетворяют определенным техническим требованиям. Требования к постоянству параметров антенны в пределах рабочей полосы могут быть различными; они зависят от условий работы. Обычно рабочая полоса частот определяется тем параметром,
значение которого при изменении частоты раньше других выходит из допустимых
пределов. Очень часто таким параметром является входное сопротивление антенны.
Изменение его при изменении частоты приводит к рассогласованию антенны с
фидером. В ряде случаев ширина рабочего диапазона определяется ухудшением
одного из параметров, характеризующих направленные
свойства: изменением направления максимального излучения, расширением ДН,
уменьшением КНД и др. В зависимости от ширины рабочего диапазона антенны
условно разбивают на:
узкополосные (настроенные), относительная рабочая полоса которых менее 10% номинальной частоты;
широкополосные, с рабочей полосой
частот 10...50%;
диапазонные, коэффициент перекрытия частот которых(fMAX/fMIN) составляет примерно 2...5;
частотно-независимые (сверхширокополосные), с коэффициентом перекрытия, теоретически не зависящим от частоты (практически fMAX/fMIN таких антенн >
5).
Еще одним параметром является предельная мощность, которую можно подвести к антенне без опасности её разрушения и не вызывая пробоя окружающей
среды. Существуют также параметры, характеризующие поляризационные свойства
антенны.
В данном курсе рассматриваются антенны следующих диапазонов:
ми-риаметровые или сверхдлинные волны (![]() = 10...100 км); километровые
или длинные волны (
= 10...100 км); километровые
или длинные волны (![]() = 1...10 км); гектометровые или средние
волны (
= 1...10 км); гектометровые или средние
волны (![]() = =100...1000 м);
декаметровые или короткие волны (
= =100...1000 м);
декаметровые или короткие волны (![]() = 10...100 м); метровые волны (
= 10...100 м); метровые волны (![]() = 1...10м); дециметровые волны (
= 1...10м); дециметровые волны (![]() = 10 см...1 м); сантиметровые волны (
= 10 см...1 м); сантиметровые волны (![]() = 1...10 см); миллиметровые волны (
= 1...10 см); миллиметровые волны (![]() = 1...10 мм). Последние четыре диапазона объединяются общим названием "ультракороткие
волны" (УКВ).
= 1...10 мм). Последние четыре диапазона объединяются общим названием "ультракороткие
волны" (УКВ).
При расчете излученного антенной электромагнитного поля ее удобно рассматривать как состоящую из бесконечного большого числа элементарных
источников (излучателей). Благодаря линейности уравнений Максвелла к полям элементарных источников применим принцип суперпозиции, позволяющий найти поле антенны в результате суммирования полей всех составляющих
ее элементарных излучателей с учетом амплитуд и фаз возбуждающих их токов.
Суммирование полей сводится к их интегрированию по источникам. Элементарными
источниками являются: элементарные электрические вибраторы ЭЭВ в случае проволочных антенн; элементарные магнитные
вибраторы в случае щелевых антенн; бесконечно малые элементы волнового фронта
или элементы Гюйгенса в случае апертурных антенн.
Формула для комплексной амплитуды напряженности электрического поля Ė произвольной реальной антенны в дальней зоне без учета
векторного характера электромагнитного поля имеет вид
![]() . (2.1)
. (2.1)
Здесь А - комплексный множитель, не зависящий от направления на точку наблюдения (в него входит стандартный множитель exp(-ikr)/r, где r -расстояние от
фазового центра антенны до точки наблюдения; ![]() - коэффициент фазы или волновое число в свободном пространстве); θ,φ -
координаты точки наблюдения; |f(θ,φ)| - амплитудная характеристика направленности; Ψ(θ,φ) - фазовая характеристика
направленности. Известно, что в случае элементарного электрического вибратора
- коэффициент фазы или волновое число в свободном пространстве); θ,φ -
координаты точки наблюдения; |f(θ,φ)| - амплитудная характеристика направленности; Ψ(θ,φ) - фазовая характеристика
направленности. Известно, что в случае элементарного электрического вибратора
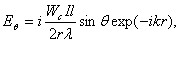 (2.2)
(2.2)
где I - амплитуда
тока в
вибраторе; l - длина вибратора; ![]() характеристическое сопротивление волны; в
свободном пространстве
характеристическое сопротивление волны; в
свободном пространстве ![]() , Ом
, Ом
Амплитудной характеристикой направленности антенны называется зависимость величины (модуля)
напряженности электрического поля, создаваемого антенной в точке наблюдения, от
направления на эту точку, характеризуемого
углами θ и φ сферической системы координат при постоянном
расстоянии (r = const) точки наблюдения от антенны. Фазовой характеристикой
направленности антенны Ψ (θ,φ) называется зависимость фазы поля, создаваемого
антенной в точке наблюдения, находящейся на поверхности сферы в дальней зоне, от направления на эту точку, характеризуемого
углами θ и φ. Множитель f(θ,φ)
определяет не только величину, но и
фазу напря-
женности поля, так как при переходе функции f(![]() ) через нуль меняется ее знак, что соответствует скачку фазы
напряженности поля на 180°. Поэтому
амплитудной характеристикой направленности является модуль этой функции
|f(
) через нуль меняется ее знак, что соответствует скачку фазы
напряженности поля на 180°. Поэтому
амплитудной характеристикой направленности является модуль этой функции
|f(![]() )|. В дальнейшем для упрощения записи знак модуля опускаем. В общем случае характеристика
направленности является векторной и
комплексной величиной. Выражение ƒ(
)|. В дальнейшем для упрощения записи знак модуля опускаем. В общем случае характеристика
направленности является векторной и
комплексной величиной. Выражение ƒ(![]() )=f(
)=f(![]() ) exp[i
) exp[i![]() ] называется комплексной
характеристикой направленности антенны. Она полностью определяет угловое распределение и фазовые свойства излучаемого электромагнитного
поля в дальней зоне антенны. Характеристика направленности антенны определяется размерами и конфигурацией антенны, а также
распределением возбуждающего тока (как действительного, так и эквивалентного).
Напомним, что дальняя зона (зона излучения или зона Фраунгофе-ра)
характеризуется тем, что направления (лучи), проведенные из любой точки
антенны на точку наблюдения, находящуюся в этой зоне, считаются параллельными. При этом возникает ошибка в
определении фаз полей, создаваемых в точке наблюдения различными элементами
антенны. Эта ошибка оказывается тем меньше, чем больше расстояние от антенны до
точки наблюдения по сравнению с размерами антенны. Расстояние дальней зоны rизл
] называется комплексной
характеристикой направленности антенны. Она полностью определяет угловое распределение и фазовые свойства излучаемого электромагнитного
поля в дальней зоне антенны. Характеристика направленности антенны определяется размерами и конфигурацией антенны, а также
распределением возбуждающего тока (как действительного, так и эквивалентного).
Напомним, что дальняя зона (зона излучения или зона Фраунгофе-ра)
характеризуется тем, что направления (лучи), проведенные из любой точки
антенны на точку наблюдения, находящуюся в этой зоне, считаются параллельными. При этом возникает ошибка в
определении фаз полей, создаваемых в точке наблюдения различными элементами
антенны. Эта ошибка оказывается тем меньше, чем больше расстояние от антенны до
точки наблюдения по сравнению с размерами антенны. Расстояние дальней зоны rизл
определяется из
условия rизл ![]() 2R2/
2R2/![]() , где R - наибольший размер излучающей системы. В этой зоне поле имеет поперечный характер (отсутствуют составляющие
векторов Е и Н в направлении распространения); в окрестности точки наблюдения
поле имеет характер плоской волны; амплитуды полей, излучаемых элементами антенны, убывают обратно
пропорционально расстоянию.
, где R - наибольший размер излучающей системы. В этой зоне поле имеет поперечный характер (отсутствуют составляющие
векторов Е и Н в направлении распространения); в окрестности точки наблюдения
поле имеет характер плоской волны; амплитуды полей, излучаемых элементами антенны, убывают обратно
пропорционально расстоянию.
В антенной
технике обычно интересуются характером зависимости напряженности поля от
направления на точку наблюдения, а не абсолютной величиной напряженности поля. Поэтому удобно пользоваться нормированной
характеристикой направленности F(![]() ), т.е. отношением напряженности поля,
излучаемого антенной в произвольном направлении, к значению напряженности поля
в направлении максимального излучения
), т.е. отношением напряженности поля,
излучаемого антенной в произвольном направлении, к значению напряженности поля
в направлении максимального излучения
F(![]() )= | E(
)= | E(![]() )| / |
Emax(
)| / |
Emax(![]() )| = f(
)| = f(![]() )/fmax(
)/fmax(![]() ).
).
Максимальная
величина F(θ,φ) всегда равна
единице. Графическое изображение амплитудной
характеристики направленности называют диаграммой направленности (ДН)
антенны. Пространственная ДН изображается в виде поверхности f(θ,φ) или F(θ,φ),
описываемой концом рдиуса-вектора, исходящего из начала координат, длина которого в
каждом направлении в определенном
масштабе равна функции f(![]() ). На рис.2.1.а изображена пространственная ДН
элементарного вибратора (тороид), на рис.2.1.б - ДН более сложной антенны (так называемая игольчатая ДН). На
практике обычно используют ДН, изображающие характеристику направленности в
каких-либо выбранных плоскостях. В качестве таких плоскостей обычно выбирают
две взаимно перпендикулярные плоскости,
проходящие через направление
). На рис.2.1.а изображена пространственная ДН
элементарного вибратора (тороид), на рис.2.1.б - ДН более сложной антенны (так называемая игольчатая ДН). На
практике обычно используют ДН, изображающие характеристику направленности в
каких-либо выбранных плоскостях. В качестве таких плоскостей обычно выбирают
две взаимно перпендикулярные плоскости,
проходящие через направление
максимального излучения (главные плоскости). Для антенн, излучающих линейно поляризованное поле, главными плоскостями называются плоскости, в которых лежит либо вектор Е (плоскость Е), либо вектор Н (плоскость Н).
|
|
Диаграммы направленности изображают обычно
либо в полярной (рис.2.2.а - ДН
элементарного вибратора в Е - плоскости; рис.2.2.б - ДН элементарного вибратора в Н -
плоскости), либо в декартовой (прямоугольной) системе координат
(рис.2.3. - ДН реальной антенны).
В некоторых случаях применяется картографический
метод изображения пространственных (трехмерных)
ДН. Он удобен для изображения многолепестковых (т.е.
имеющих много нулей и максимумов) ДН в широком диапазоне углов.
Этот метод состоит в том, что строится плоская сетка координат ![]() в какой-либо
координатной системе (прямоугольной, полярной и др.) подобно сетке меридианов и параллелей на географической
карте. На этой сетке замкнутыми линиями изображаются одинаковые
в какой-либо
координатной системе (прямоугольной, полярной и др.) подобно сетке меридианов и параллелей на географической
карте. На этой сетке замкнутыми линиями изображаются одинаковые
значения
нормированной характеристики направленности F(![]() ) в том или ином масштабе. При изображении ДН часто
используется логарифмический масштаб, вводимый соотношением в децибеллах F(
) в том или ином масштабе. При изображении ДН часто
используется логарифмический масштаб, вводимый соотношением в децибеллах F(![]() )=20 lgF(
)=20 lgF(![]() ).
).
В некоторых случаях пользуются понятием характеристики (диаграммы) направленности по мощности F2(![]() ). Функция F(
). Функция F(![]() )
для различных
)
для различных
|
|
|
270 |
|
Рис. 2,2. ДН диполя Герца
(а-Е-плоскость, б-Н-плоскость) |
углов ![]() и
и ![]() проходит через нуль и имеет несколько максимумов, т.е. ДН имеет
многолепестковый характер (см. рис.2.3).
Диаграмму направленности принято численно характеризовать шириной главного лепестка (шириной луча) и
относительным уровнем боковых лепестков (УБЛ).
проходит через нуль и имеет несколько максимумов, т.е. ДН имеет
многолепестковый характер (см. рис.2.3).
Диаграмму направленности принято численно характеризовать шириной главного лепестка (шириной луча) и
относительным уровнем боковых лепестков (УБЛ).
Шириной ДН (шириной луча) называется угол между направлениями, вдоль
которых напряженность поля падает до определенного значения. Так, шириной ДН по уровню нулевого излучения называют угол 2![]() 0
между направлениями вдоль которых напряженность поля падает до нуля (см. рис.2.3). Шириной ДН по половинной мощности называют угол 2
0
между направлениями вдоль которых напряженность поля падает до нуля (см. рис.2.3). Шириной ДН по половинной мощности называют угол 2![]() 0,5 между направлениями,
вдоль которых |Е| = |Emax|/
0,5 между направлениями,
вдоль которых |Е| = |Emax|/![]() или соответственно среднее значение
плотности потока мощности П=Пmaх/2.
Наибольший лепесток, максимум которого соответствует
направлению максимального излучения, называют главным, меньшие лепестки - боковыми (лепестки, находящиеся в задних
квадрантах, т.е. в диапазоне углов 90°
или соответственно среднее значение
плотности потока мощности П=Пmaх/2.
Наибольший лепесток, максимум которого соответствует
направлению максимального излучения, называют главным, меньшие лепестки - боковыми (лепестки, находящиеся в задних
квадрантах, т.е. в диапазоне углов 90°![]() 180° и 180°
180° и 180°![]() 270°, часто называют задними).
270°, часто называют задними).
Относительный УБЛ (![]() ) есть отношение апряженности поля в
направлении максимума данного лепестка (ENmax) к апряженности поля внаправлении главного максимума (Еmax), т.е.
) есть отношение апряженности поля в
направлении максимума данного лепестка (ENmax) к апряженности поля внаправлении главного максимума (Еmax), т.е.
![]() N=|ENmax|/|Еmax|=FN(
N=|ENmax|/|Еmax|=FN(![]() ), или в децибеллах
), или в децибеллах ![]() дБ = 20lg FN(
дБ = 20lg FN(![]() ), где N=1,2,3,...-номер бокового лепестка (для главного лепестка N=0).
), где N=1,2,3,...-номер бокового лепестка (для главного лепестка N=0).
Обычно стремятся к подавлению боковых лепестков, т.е. к тому, чтобы величина ![]() была мала.
была мала.
В большинстве
случаев интересуются амплитудными
характеристиками направленности
(слово "амплитудная"
в дальнейшем не используем). Фазовые характеристики направленности используют в радиолокации, радионавигации и в некоторых других случаях.
Если фаза, излучаемого антенной поля, не зависит от направления на точку наблюдения и изменяется на обратную только при переходе функции f(![]() ) или F(
) или F(![]() ) через нуль, т.е. при переходе от
одного лепестка ДН к другому, то такая антенна является
источником сферических волн, о чем свидетельствует
множитель [ехр(-ikr)]/r. Эти волны исходят как бы из одной точки, называемой фазовым
центром антенны. Эта точка расположена в начале выбранной системы
координат, и поэтому, фазовая характеристика зависит от
положения начала координат. Однако не все реальные антенны обладают фазовым
центром, т.е. излучают сферические волны. Для них обычно можно подобрать сферу, наилучшим образом аппроксимирующую фронт волны (обычно в пределах главного лепестка). Центр этой сферы называют центром
излучения антенны. Графическое изображение фазовой характеристики называется фазовой ДН.
) через нуль, т.е. при переходе от
одного лепестка ДН к другому, то такая антенна является
источником сферических волн, о чем свидетельствует
множитель [ехр(-ikr)]/r. Эти волны исходят как бы из одной точки, называемой фазовым
центром антенны. Эта точка расположена в начале выбранной системы
координат, и поэтому, фазовая характеристика зависит от
положения начала координат. Однако не все реальные антенны обладают фазовым
центром, т.е. излучают сферические волны. Для них обычно можно подобрать сферу, наилучшим образом аппроксимирующую фронт волны (обычно в пределах главного лепестка). Центр этой сферы называют центром
излучения антенны. Графическое изображение фазовой характеристики называется фазовой ДН.
Коэффициент
направленного действия (КНД), коэффициент усиления антенны (КУ) и параметры, связанные с КНД
Коэффициент направленного действия (КНД)
характеризует способность антенны концентрировать
излученное электромагнитное поле в каком-либо определенном
направлении. Это понятие было введено в 1929 г. А.А.Пистолькорсом. Коэффициентом
направленного действия называется отношение среднего значения за период высокой
частоты плотности потока мощности (среднее значение вектора
Пойнтинга), излучаемого антенной в данном направлении
![]() , к усредненному по всем направлениям
значению плотности потока мощности Пуср
, к усредненному по всем направлениям
значению плотности потока мощности Пуср
![]() . (2.3)
. (2.3)
Здесь ![]() , где |
, где |![]() | - амплитудное значение напряженности электрического поля в направлении, характеризуемом углами
| - амплитудное значение напряженности электрического поля в направлении, характеризуемом углами ![]() . Таким образом, при определении КНД данная
антенна сравнивается с воображаемой абсолютно ненаправленной (изотропной)
антенной, излучающей ту же мощность, что и данная. Очевидно, что
. Таким образом, при определении КНД данная
антенна сравнивается с воображаемой абсолютно ненаправленной (изотропной)
антенной, излучающей ту же мощность, что и данная. Очевидно, что
![]() , (2.4)
, (2.4)
где ![]() - мощность излучения; r - радиус
воображаемой сферы, охватывающей антенну, причем величина r должна быть такой, чтобы поверхность сферы находилась в дальней зоне поля антенны.
- мощность излучения; r - радиус
воображаемой сферы, охватывающей антенну, причем величина r должна быть такой, чтобы поверхность сферы находилась в дальней зоне поля антенны.
Коэффициент направленного действия показывает во сколько раз следует
уменьшить излучаемую мощность при замене изотропной (ненаправленной) антенны
на направленную, чтобы среднее значение плотности потока мощности в точке наблюдения осталось неизменным.
Учитывая, что ![]() , и подставляя в (2.3) выражение (2.4), получаем формулу для КНД в другом виде
, и подставляя в (2.3) выражение (2.4), получаем формулу для КНД в другом виде ![]() или для свободного пространства (Wc°=120
или для свободного пространства (Wc°=120![]() Ом) в направлении максимального излучения
Ом) в направлении максимального излучения
![]() (2.5)
(2.5)
Если в эту формулу подставить вместо ![]() выражение (2.2) в квадрате (без фазовых
множителей) и учесть, что
выражение (2.2) в квадрате (без фазовых
множителей) и учесть, что ![]() , где
, где ![]() - сопротивление излучения элементарного электрического вибратора,
то получим КНД элементарного
вибратора D=1,5.
- сопротивление излучения элементарного электрического вибратора,
то получим КНД элементарного
вибратора D=1,5.
Коэффициент направленного действия тем больше, чем уже главный лепесток
пространственной ДН и чем меньше УБЛ. Коэффициент направленного действия можно
выразить с помощью еще одного параметра, называемого действующей длиной или
действующей высотой антенны ![]() .Этот параметр иногда используют при
анализе приемных антенн, а также проволочных длинноволновых и средневолновых
антенн и антенн-мачт.
.Этот параметр иногда используют при
анализе приемных антенн, а также проволочных длинноволновых и средневолновых
антенн и антенн-мачт.
В случае линейной антенны ток по
ее длине распределен неравномерно. Однако
реальную антенну можно заменить воображаемым вибратором длиной lд (действующей длиной) с равномерным распределением тока
создающим в направлении максимального
излучения поле, равное полю данной антенны в главном направлении. При этом ток
в точке питания реальной антенны считается
равным току, текущему по воображаемому вибратору. По аналогии с (2.2) (вибратор с равномерным распределением тока)
напряженность поля реальной антенны в главном направлении можно представить в
виде
![]() (2.6)
(2.6)
где I0 - амплитуда тока в точках питания антенны; 60π = Wc°/2, где ![]() - волновое сопротивление
среды. Напишем выражение для величины напряженности поля
любой вибраторной антенны в произвольном направлении
- волновое сопротивление
среды. Напишем выражение для величины напряженности поля
любой вибраторной антенны в произвольном направлении
![]() (2.7)
(2.7)
Подставляя в (2.5)
вместо ![]() выражение
(2.6) и учитывая,
что
выражение
(2.6) и учитывая,
что
![]() (
(![]() - сопротивление излучения антенны, отнесенное к току в точках
питания; I -ток в точках
питания антенны), получаем
- сопротивление излучения антенны, отнесенное к току в точках
питания; I -ток в точках
питания антенны), получаем
![]() или
или ![]() (2.8)
(2.8)
Формально параметром "действующая
длина" можно пользоваться в 21
случае любой антенны (линейной, апертурной или какой-либо другой), так как этот параметр выражается через КНД, а последний определяется только характеристикой
направленности.
Коэффициент
направленного действия не учитывает потерь подводимой энергии в проводниках антенны, в изоляторах, в окружающих антенну предметах и в
земле. В связи с этим вводится параметр, учитывающий эти потери, называемый коэффициентом усиления (КУ)
антенны, равный отношению среднего значения плотности потока мощности,
излучаемой антенной в данном направлении ![]() , к среднему значению плотности потока мощности, создаваемого воображаемым абсолютно ненаправленным излучателем
(Пн). При этом предполагается, что точка
наблюдения находится на одинаковом расстоянии от обеих
антенн; мощности, подводимые к той и другой антеннам, равны и КПД
ненаправленной антенны равен единице. Таким образом, КУ
, к среднему значению плотности потока мощности, создаваемого воображаемым абсолютно ненаправленным излучателем
(Пн). При этом предполагается, что точка
наблюдения находится на одинаковом расстоянии от обеих
антенн; мощности, подводимые к той и другой антеннам, равны и КПД
ненаправленной антенны равен единице. Таким образом, КУ
![]() . (2.9)
. (2.9)
Коэффициент усиления показывает во сколько раз следует уменьшить мощность, подводимую к направленной антенне, по сравнению с абсолютно ненаправленной (изотропной) антенны, КПД которой считается равным
единице, чтобы среднее значение плотности потока мощности в точке наблюдения оставалось неизменным.
Отличие КУ от КНД состоит в том, что при
определении КУ исходят из равенства мощностей, подводимых к исследуемой
и эталонной ( ненаправленной) антеннам Р0, а не из равенства мощностей
излучения P![]() , этих антенн.
Умножим и разделим
правую часть (2.9)
на Пуср. Тогда [П(
, этих антенн.
Умножим и разделим
правую часть (2.9)
на Пуср. Тогда [П(![]() )/Пуср](Пуср/Пн), где Пуср/Пн
=
)/Пуср](Пуср/Пн), где Пуср/Пн
=![]() - КПД антенны.
- КПД антенны.
Параметры ( D, G и ![]() ) связаны соотношением
) связаны соотношением
G=D![]() . (2.10)
. (2.10)
Учитывая, что D=G/![]() , можно написать
, можно написать
Emax=![]() /r=
/r=![]() /r .
(2.11)
/r .
(2.11)
Поляризационные параметры антенн. Турникетный
излучатель
Направление векторов Е и Н излучаемого антенной поля
определяется плоскостью поляризации, т.е. плоскостью, проходящей через
направление распространения волны (вектор Пойнтинга) и
вектор напряженности электрического поля. В общем случае за
один период высокой частоты плоскость поляризации делает
полный оборот вокруг направления распространения. Такое поле называют вращающимся.
За это время конец вектора Е
описывает замкнутую кривую (эллипс), лежащую в
плоскости, перпендикулярной направлению распространения, и
называемую поляризационным эллипсом. Это - эллиптическая
поляризация электромагнитного поля. Частными видами эллиптической поляризации являются: линейная поляризация - конец
вектора Е лежит
на прямой линии; круговая поляризация - конец вектора Е за один период
высокой частоты описывает окружность.
Существуют антенны, рассчитанные на излучение (прием) поля круговой поляризации. Многие антенны (симметричный вибратор и другие) излучают во всех направлениях линейно поляризованные волны. Однако имеются
антенны, которые либо из-за своих конструктивных особенностей, либо из-за неточностей исполнения излучают волны чисто линейной поляризации только в двух взаимно перпендикулярных плоскостях, проходящих через направление максимального излучения (главные плоскости). Поляризация поля в
этих плоскостях называется главной или основной, В других
плоскостях имеется составляющая поля, поляризованная перпендикулярно
(ортогонально) основной поляризации (к таким антеннам относят, например,
параболическую). Эта составляющая, называемая поперечной
или кроссполяризацион-ной, является вредной. Ортогональность составляющих поля основной и
кроссполяризации (иногда ее называют паразитной) понимается как независимость
переноса мощности каждой из них. Мощность, соответствующая кроссполяризации, расходуется на образование боковых лепестков, вследствие чего КНД антенны уменьшается. Кроме того, возрастают помехи, создаваемые передающей антенной различным приемным антеннам, работающим в том же или смежном диапазоне частот. Если поле передающей антенны имеет две ортогональные составляющие, а приемная антенна рассчитана
на прием лишь линейно поляризованного поля, то часть излученной мощности,
соответствующая паразитной поляризации, не используется.
Эллиптическая
поляризация может рассматриваться либо как результат сложения двух линейно
поляризованных взаимно перпендикулярных составляющих поля, не совпадающих по фазе, либо двух полей круговой поляризации
с противоположными направлениями вращения и разными амплитудами.
Отношение малой полуоси эллипса к большой (рис.2.4.а) называется коэффициентом
равномерности (коэффициентом эллиптичности) поляризационного эллипса: t=b/a. В случае линейной поляризации поля t = 0.
Условием этой поляризации является ![]() или
или ![]() (
(![]() - сдвиг фаз между составляющими
- сдвиг фаз между составляющими ![]() и
и ![]() ). Линейная
поляризация также имеет место, если
). Линейная
поляризация также имеет место, если ![]() =0 или
=0 или ![]() =0. При круговой
поляризации поля (
=0. При круговой
поляризации поля (![]() =
=![]() ;
;![]() ) t=l. Таким образом, коэффициент равномерности поляризационного эллипса может изменяться в пределах 0< t < 1. Зависимость коэффициента эллиптичности от
направления на точку наблюдения называется поляризационной
ДН.
) t=l. Таким образом, коэффициент равномерности поляризационного эллипса может изменяться в пределах 0< t < 1. Зависимость коэффициента эллиптичности от
направления на точку наблюдения называется поляризационной
ДН.
Поляризационный эллипс характеризуется также углом поляризации и направлением вращения вектора Е
(направление вращения плоскости поляризации). Углом
поляризации ![]() называется угол,
образованный большой осью поляризационного эллипса и
направлением орта
называется угол,
образованный большой осью поляризационного эллипса и
направлением орта ![]() или
или ![]() 0 сферической системы координат (см. рис. 2.4.б).
Направление вращение вектора Е в
точке наблюдения определяется знаком угла
сдвига фаз между составляющими поля.
0 сферической системы координат (см. рис. 2.4.б).
Направление вращение вектора Е в
точке наблюдения определяется знаком угла
сдвига фаз между составляющими поля. ![]() и
и ![]() . Это направление называется правым, если наблюдатель, глядя навстречу волне, видит вектор Е вращающимся против часовой стрелки (рис. 2.5). Противоположное
направление вращения плоскости поляризации называется левым. Вектор Е
всегда вращается в сторону составляющей поля, отстающей по фазе.
. Это направление называется правым, если наблюдатель, глядя навстречу волне, видит вектор Е вращающимся против часовой стрелки (рис. 2.5). Противоположное
направление вращения плоскости поляризации называется левым. Вектор Е
всегда вращается в сторону составляющей поля, отстающей по фазе.
В
соответствии с (2.3) под КНД антенны с эллиптической поляризацией поля при полном поляризационном приеме будем подразумевать величину ![]() где
где ![]() - парциальные КНД для
каждой из ортогональных составляющих поля; Пуср — усредненное по всем направлениям значение плотности потока мощности полного поля;
- парциальные КНД для
каждой из ортогональных составляющих поля; Пуср — усредненное по всем направлениям значение плотности потока мощности полного поля; ![]() . Здесь
. Здесь ![]() -
полная мощность излучения;
-
полная мощность излучения; ![]() и
и ![]() - мощности излучения, соответствующие
ортогональным компонентам поля. В соответствии с (2.3) под КНД антенны с эллиптической поляризацией поля при полном поляризационном приеме будем подразумевать величину
- мощности излучения, соответствующие
ортогональным компонентам поля. В соответствии с (2.3) под КНД антенны с эллиптической поляризацией поля при полном поляризационном приеме будем подразумевать величину ![]() где
где ![]() - парциальные КНД для
каждой из ортогональных составляющих поля; Пуср — усредненное по всем направлениям значение плотности потока мощности полного поля;
- парциальные КНД для
каждой из ортогональных составляющих поля; Пуср — усредненное по всем направлениям значение плотности потока мощности полного поля; ![]() . Здесь
. Здесь ![]() -
полная мощность излучения;
-
полная мощность излучения; ![]() и
и ![]() - мощности излучения, соответствующие ортогональным
компонентам поля.
- мощности излучения, соответствующие ортогональным
компонентам поля.
В качестве
примера простейшей антенны, создающей вращающееся поле рассмотрим два линейных
излучателя (для простоты считаем их элементарными), расположенных
крестообразно и питаемых токами равной амплитуды, но
сдвинутых по фазе на ![]() .Такой излучатель часто называют турникетным. В меридиональной по отношению к обоим вибраторам
плоскости yoz (см. рис.2.6) они создают поля одной поляризации, причем векторы
.Такой излучатель часто называют турникетным. В меридиональной по отношению к обоим вибраторам
плоскости yoz (см. рис.2.6) они создают поля одной поляризации, причем векторы ![]() и
и ![]() лежат
на одной и той же линии. В точке N, лежащей на нормали (ось х) к плоскости
расположения двух вибраторов, первый создаёт вектор
напряжённости электрического поля
лежат
на одной и той же линии. В точке N, лежащей на нормали (ось х) к плоскости
расположения двух вибраторов, первый создаёт вектор
напряжённости электрического поля ![]() а второй -
а второй - ![]() , находящиеся в плоскости, перпендикулярной
оси х, Эти векторы равны по амплитуде, сдвинуты по фазе друг
относительно друга на 90° и взаимно
перпендикулярны. Таким образом в направлении нормали плоскости вибраторов (yoz) имеет место круговая поляризация поля.
, находящиеся в плоскости, перпендикулярной
оси х, Эти векторы равны по амплитуде, сдвинуты по фазе друг
относительно друга на 90° и взаимно
перпендикулярны. Таким образом в направлении нормали плоскости вибраторов (yoz) имеет место круговая поляризация поля.
Тема 8. Теория симметричного вибратора
Изучение симметричного электрического вибратора представляет большой интерес, так как, во-первых, этот вибратор применяется как самостоятельная
антенна и, во-вторых, он является составным элементом ряда сложных антенн. Симметричные вибраторы начали широко применять в первой половине двадцатых годов в связи с возникновением и развитием радиосвязи на коротких волнах. В настоящее время симметричный вибратор как самостоятельная антенна применяется на коротких, метровых и дециметровых
волнах. В этих же диапазонах широко используются сложные антенны, состоящие из
ряда симметричных вибраторов. Симметричные вибраторы
используются также в сантиметровом диапазоне волн в качестве элементов сложных систем (например, облучатели зеркальных антенн).
 Симметричный вибратор состоит из двух одинаковых по размерам и форме
проводников, между которыми включается генератор высокой частоты (часто эти
проводники называются плечами). Рассмотрим симметричный вибратор, представляющий собой тонкий цилиндрический проводник длиной 2
Симметричный вибратор состоит из двух одинаковых по размерам и форме
проводников, между которыми включается генератор высокой частоты (часто эти
проводники называются плечами). Рассмотрим симметричный вибратор, представляющий собой тонкий цилиндрический проводник длиной 2![]() и радиусом а (рис.3.1), находящийся в
свободном пространстве. Строгое решение
основной
задачи теории антенн
и радиусом а (рис.3.1), находящийся в
свободном пространстве. Строгое решение
основной
задачи теории антенн
для симметричного
вибратора связано с большими трудностями, так как закон распределения тока по вибратору
неизвестен.
Существует приближенный метод расчета поля,
создаваемого симметричным вибратором в
дальней зоне. В основе этого метода лежит предположение о синусоидальном
распределении тока по вибратору, основанное на некоторой внешней
аналогии между симметричным вибратором и двухпроводной разомкнутой
на конце линией без потерь. Действительно, от
двухпроводной линии (рис.3.2.а) можно перейти к симметричному вибратору, если
провода линии развернуть под углом 180° друг к другу (рис.3.2.б). Можно
полагать, что при переходе от двухпроводной линии к симметричному вибратору
закон распределения тока
не нарушается, т.е.
Iz = Iпsink(![]() -
-![]() ) , где Iп - амплитуда тока в пучности тока вибратора (в
об-
) , где Iп - амплитуда тока в пучности тока вибратора (в
об-
щем случае, это величина
комплексная) İп = Iпexp(i![]() );
); ![]() - длина одного плеча вибратора; z - расстояние от
начала вибратора (точки питания) до произвольной точки на
вибраторе (текущая координата); k = 2
- длина одного плеча вибратора; z - расстояние от
начала вибратора (точки питания) до произвольной точки на
вибраторе (текущая координата); k = 2![]() /
/![]() , - волновое число (коэффициент фазы тока в
вибраторе).
, - волновое число (коэффициент фазы тока в
вибраторе).
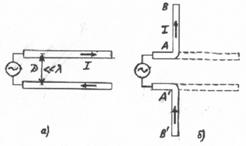 Полагают, что длина волны в вибраторе
Полагают, что длина волны в вибраторе
λ, равна длине волны в свободном прост-
ранстве. В действительности данная анна-
логия весьма приближённа.Обе системы-
линия и вибратор – являются колебатель-
ными системами с распределенными па-
раметрами, однако они существенно раз-
личаются. Во-первых, распределенные
параметры
линии (Li,Ci) не изменяются по ее длине, распределенные параметры вибратора
непостоянны по его длине (рис.3.2.6). Во-вторых, линия служит для канализации электромагнитных волн и является практически неизлучающей
системой; вибратор же излучает волны. В разомкнутой на конце линии ток изменяется по закону стоячей волны только в том случае, если линия выполнена
из идеального проводника, т.е. в ней нет потерь энергии.
В вибраторе,
выполненном даже из идеального проводника, обязательно есть потери (полезные) на излучение. Очевидно, поэтому ток в
вибраторе, строго говоря, не может быть распределен по
закону стоячей волны. Однако расчет поля симметричного вибратора по
формулам, основанным на синусоидальном распределении тока, дает хорошее
совпадение с экспериментальными данными для дальней зоны и
тонких вибраторов. Поэтому для инженерного расчета это приближение в ряде
случаев вполне допустимо. Строгая теория симметричного вибратора подтверждает,
что в тонких вибраторах ток распределен по закону, весьма
близкому к синусоидальному. Задавшись законом распределения
тока по вибратору, легко установить приближенный закон
распределения заряда ![]() z=
z=![]() Пcosk(
Пcosk(![]() -
- ![]() ), где
), где ![]() П амплитуда заряда в его пучности. Этот закон распределения заряда вдоль симметричного вибратора
совпадает с законом распределения потенциала (напряжения) в разомкнутой на конце длинной линии без потерь. В теории антенн понятием напряжения следует пользоваться с большой осторожностью, так как поле антенны не является потенциальным. Понятием напряжения применительно к антенне можно
пользоваться, если расстояние между точками измерения мало по сравнению с
длиной волны. Это справедливо при измерении напряжения между зажимами антенны
(точки присоединения генератора), а также для длинноволновых антенн. На рис.3.3
приведены кривые распределения амплитуд тока и заряда на вибраторах разной
длины. По аналогии с волновым сопротивлением длинной линии вводится
понятие волнового сопротивления симметричного вибратора. Как известно,
из теории длинных линий, волновое сопротивление двухпроводной линии
без потерь определяется выражением W =
П амплитуда заряда в его пучности. Этот закон распределения заряда вдоль симметричного вибратора
совпадает с законом распределения потенциала (напряжения) в разомкнутой на конце длинной линии без потерь. В теории антенн понятием напряжения следует пользоваться с большой осторожностью, так как поле антенны не является потенциальным. Понятием напряжения применительно к антенне можно
пользоваться, если расстояние между точками измерения мало по сравнению с
длиной волны. Это справедливо при измерении напряжения между зажимами антенны
(точки присоединения генератора), а также для длинноволновых антенн. На рис.3.3
приведены кривые распределения амплитуд тока и заряда на вибраторах разной
длины. По аналогии с волновым сопротивлением длинной линии вводится
понятие волнового сопротивления симметричного вибратора. Как известно,
из теории длинных линий, волновое сопротивление двухпроводной линии
без потерь определяется выражением W =![]() , где L1-распределенная индуктивность линии (индуктивность, приходящаяся на единицу длины линии), Г/м; C1 -, распределенная емкость линии, Ф/м. Так как
1/
, где L1-распределенная индуктивность линии (индуктивность, приходящаяся на единицу длины линии), Г/м; C1 -, распределенная емкость линии, Ф/м. Так как
1/![]() = с, где
= с, где
с - скорость света, м/с, то
W=l/cC1, Ом. (3.1)
Волновое сопротивление двухпроводной линии связано с ее геометрическими
размерами соотношением
W=2761g (D/a), (3.2)
|
|
где D - расстояние между
центрами проводов линии; а - радиус провода.
Волновое сопротивление симметричного
вибратора (а также других линейных
антенн, т.е. антенн, длина которых значительно
превосходит размеры поперечного
сечения) рассчитывают по формуле (3.1).
Однако распределенная емкость по длине вибратора непостоянна. Поэтому в данном случае под C1 подразумевается
усредненная величина, равная отношению полной статической емкости антенны (СА) к ее длине (2l). Одним из наиболее распространенных
приближенных методов расчета полной статической емкости является метод Хоу или метод усредненных
потенциалов. Волновое сопротивление симметричного
вибратора из провода цилиндрической формы, определенное по
методу Хоу,
WA=120(ln l/a-1), Oм, (3.3)
где l-длина плеча
вибратора; а - радиус провода.
Расчет волнового сопротивления вибратора методом Хоу дает приемлемую точность для вибраторов, коротких по сравнению с длиной волны. Точность этого метода снижается по мере удлинения вибратора.
Направленные свойства симметричного вибратора
Рассмотрим симметричный вибратор произвольной длины (рис.3.4). Задаемся
синусоидальным законом распределения тока вдоль вибратора Iz = (I0/sinkl)sink(l -![]() ), где I0 - ток в точках
питания вибратора (I0=Iпsinkl). Мысленно разобьем вибратор на бесконечно
большое число элементов dz. Так как длина
каждого элемента бесконечно мала, то можно полагать, что в пределах его ток
не изменяется ни по амплитуде, ни по фазе. Таким образом, весь симметричный вибратор можно рассматривать как
совокупность
), где I0 - ток в точках
питания вибратора (I0=Iпsinkl). Мысленно разобьем вибратор на бесконечно
большое число элементов dz. Так как длина
каждого элемента бесконечно мала, то можно полагать, что в пределах его ток
не изменяется ни по амплитуде, ни по фазе. Таким образом, весь симметричный вибратор можно рассматривать как
совокупность
|
|
элементарных
электрических вибраторов dz и поле симметричного вибратора рассматривать
как результат сложения (интерференции) полей, излучаемых элементарными вибраторами. Ввиду малости воздушного промежутка (зазора)
между плечами вибратора можно пренебречь влиянием электрического поля
(магнитного тока), существующего в нем на излучение, и считать, что электрический ток течет по сплошному
проводнику длиной 2l. Выделим на
вибраторе (рис.3.4) элементы 1 и 2, каждый длиной dz, симметричные
относительно центра вибратора 0, и определим поле, создаваемое этими элементами в произвольной точке наблюдения М, находящейся в зоне излучения. Проведем от
элементов 1 и 2 и от центра вибратора линии в точку наблюдения r1, r0, r2. Поскольку
расстояние до точки наблюдения очень велико по сравнению с
длиной вибратора, то направления от всех точек вибратора на точку М можно
считать параллельными. Напряженность поля, излучаемого первым элементом в
точке М
dE1 = i [60![]() Izdz/ (r1
Izdz/ (r1![]() )]sin
)]sin![]() exp(-ikr1).
exp(-ikr1).
(3.4.a)
Напряженность поля,
излучаемого вторым элементом в той же точке М dE2 = i [60![]() Izdz/(r2
Izdz/(r2![]() )] sin
)] sin![]() exp(-ikr2).
exp(-ikr2).
(3.4.б)
Здесь Iz - амплитуда тока в элементе, находящемся
на расстоянии z от центра вибратора;
r1 - расстояние от первого элемента до точки М;
г2 - расстояние от второго элемента до
точки М;
![]() - угол между осью вибратора и направлением на
точку наблюдения.
- угол между осью вибратора и направлением на
точку наблюдения.
Найдем суммарное
поле, создаваемое в точке наблюдения элементами
1 и 2. Так как векторы напряженности полей, создаваемых всеми элементами
вибратора в точке наблюдения, направлены вдоль одной прямой (перпендикулярной направлению от данного элемента в
точку наблюдения), то поля,
создаваемые отдельными элементами, можно складывать алгебраически. Поэтому
dE = dE1+dE2=i
(60![]() Izdz/
Izdz/![]() )sin
)sin![]() [(exp(-ikr1)/r1+exp(-ikr2)/r2)]. (3.5)
[(exp(-ikr1)/r1+exp(-ikr2)/r2)]. (3.5)
Выразим расстояния r1 и r2 через расстояние r0. Для этого из точки 1 (рис.3.4) опустим перпендикуляр на направление r0 и из точки 0 опустим перпендикуляр на направление r2. Из прямоугольных треугольников 1-0-3 и 2-0-4 находим, что разность расстояний от данных
элементов и центра вибратора до точки наблюдения равна ![]() r =
r = ![]() cos
cos![]() .
.
Следовательно,
r1 = r0 - |z|cos![]() и r2 = r0 +
и r2 = r0 + ![]() cos
cos![]() . (3.6)
. (3.6)
Величину ![]() r часто называют разностью хода
лучей. Так как точка наблюдения
находится в дальней зоне, то величина
r часто называют разностью хода
лучей. Так как точка наблюдения
находится в дальней зоне, то величина ![]() r мала по
сравнению с r0 и расстояния r1 и r2 мало отличаются друг от друга. Поэтому можно считать, что амплитуды напряженности полей, создаваемых
элементами 1 и 2 в точке наблюдения М,
одинаковы. Однако пренебрегать разностью хода в фазовых множителях (exp(-ikr1) и exp(-ikr2)) ни в коем
случае нельзя, так как пространственный
сдвиг фаз между полями элементов 1 и 2 k
r мала по
сравнению с r0 и расстояния r1 и r2 мало отличаются друг от друга. Поэтому можно считать, что амплитуды напряженности полей, создаваемых
элементами 1 и 2 в точке наблюдения М,
одинаковы. Однако пренебрегать разностью хода в фазовых множителях (exp(-ikr1) и exp(-ikr2)) ни в коем
случае нельзя, так как пространственный
сдвиг фаз между полями элементов 1 и 2 k![]() r = 2k|z|cosν = 4
r = 2k|z|cosν = 4![]() (|z|/
(|z|/![]() )cos
)cos![]() определяется отношением разности хода лучей к длине волны. На
основании формул (3.6) получаем следующие выражения для фазовых множителей exp(-ikr1)= exp(-ikr0) * exp(ik|z|)cos
определяется отношением разности хода лучей к длине волны. На
основании формул (3.6) получаем следующие выражения для фазовых множителей exp(-ikr1)= exp(-ikr0) * exp(ik|z|)cos![]() ;
;
exp (-ikr2) = exp (-ikro) * exp (-ik![]() )cos
)cos![]() .
.
Подставляя эти выражения в
формулу (3.5), вынося за скобки общие множители
и полагая, что в знаменателях r1![]() r2
r2 ![]() r0, получаем
r0, получаем
dE=i[60![]() I0sink(l-
I0sink(l-![]() )dz/(r0
)dz/(r0 ![]() sinkl)]sin
sinkl)]sin![]() exp(-ikr0)[(exp(ik
exp(-ikr0)[(exp(ik![]() )cos
)cos![]() +
+
+exp (-ik![]() ) cos
) cos![]() )].
)].
Воспользовавшись известной формулой exp(i![]() ) + exp(-i
) + exp(-i![]() ) = 2cos
) = 2cos![]() , получаем следующее выражение
, получаем следующее выражение
dE = i[120![]() I0/( r0
I0/( r0 ![]() sinkl)] sin
sinkl)] sin![]() exp(-ikr0)sink(l-
exp(-ikr0)sink(l-![]() )cos(k
)cos(k![]() cos
cos![]() )dz.
)dz.
Для определения напряженности поля,
создаваемого в точке наблюде-
ния всем симметричным вибратором, необходимо это
выражение проинтег-
рировать по длине одного плеча вибратора
Е=i[120![]() I0/(r0
I0/(r0 ![]() sinkl)] sin
sinkl)] sin![]() exp(-ikr0)
exp(-ikr0) ![]() sink(l-
sink(l-![]() )cos(k
)cos(k![]() cos
cos![]() )dz.
)dz.
В результате интегрирования получается формула для расчета напря-
женности поля симметричного электрического вибратора
в дальней зоне
E=i [60I0/ (r0sinkl)] * [(cos(klcos![]() ) - coskl) / sin
) - coskl) / sin![]() ]exp(-ikr0). (3.7)
]exp(-ikr0). (3.7)
Как и в случае элементарного электрического вибратора, эта формула
состоит из трех множителей: множителя, определяющего только величину напряженности поля и не зависящего от направления в данную точку [60I0/(r0sinkl)], множителя, определяющего направленные свойства (характеристика
направленности).
f(![]() )=[cos(klcos
)=[cos(klcos![]() ) - coskl]/sin
) - coskl]/sin![]()
и фазового множителя ![]() = iexp(-ikr0) из выражения
(3.7) видно, что симметричный вибратор
обладает направленными свойствами только в меридиональной плоскости (плоскость электрического вектора). Напряженность электрического поля симметричного вибратора
в его экваториальной
= iexp(-ikr0) из выражения
(3.7) видно, что симметричный вибратор
обладает направленными свойствами только в меридиональной плоскости (плоскость электрического вектора). Напряженность электрического поля симметричного вибратора
в его экваториальной
плоскости ( плоскость магнитного
вектора ν= ![]() /2) - определяется выражением
/2) - определяется выражением
E = i [60I0/(r0sinkl)](l-coskl)exp(-ikro), (3.8)
т.е. не зависит от азимутального угла ![]() . Поэтому
диаграмма направленности
. Поэтому
диаграмма направленности
симметричного вибратора в его экваториальной плоскости, как и в случае элементарного вибратора,
представляет в полярной
системе координат ок-
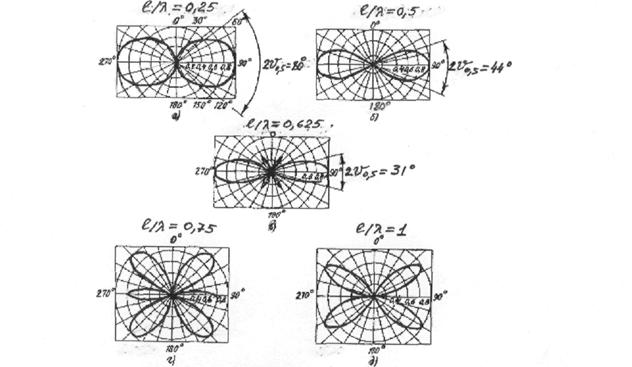
Диаграммы направленности симметричного
вибратора
ружность. Как видно из формулы (3.7),
направленные свойства симметричного вибратора определяются только отношением
длины плеча вибратора к длине волны l/![]() .В случае полуволнового вибратора (l/
.В случае полуволнового вибратора (l/![]() =0,25) формула (3.7) принимает вид
=0,25) формула (3.7) принимает вид
Е= iA{cos[(![]() /2)cos
/2)cos![]() ]/(sin
]/(sin![]() )}exp (-ikr0).
)}exp (-ikr0).
Амплитудные диаграммы направленности,
рассчитанные по формуле (3.7), для вибраторов с различной относительной длиной
l/![]() показаны
на рис.3.5. Анализ формулы (3.7) и
рассмотрение этих кривых показывают, что при любой величине
отношения l/
показаны
на рис.3.5. Анализ формулы (3.7) и
рассмотрение этих кривых показывают, что при любой величине
отношения l/![]() симметричный вибратор
не излучает вдоль своей оси. Если длина плеча симметричного
вибратора l
симметричный вибратор
не излучает вдоль своей оси. Если длина плеча симметричного
вибратора l ![]() 0,5
0,5![]() ,
то в направлении, перпендикулярном его
оси (
,
то в направлении, перпендикулярном его
оси (![]() = 90°,
= 90°, ![]() = 270°), т.е. в
экваториальной плоскости, поля
всех элементарных вибраторов
максимальны, синфазны и
складываются арифметически. Поэтому
поле в данном
направлении является
максимальным. Диаграмма направленности при l/
= 270°), т.е. в
экваториальной плоскости, поля
всех элементарных вибраторов
максимальны, синфазны и
складываются арифметически. Поэтому
поле в данном
направлении является
максимальным. Диаграмма направленности при l/![]()
![]() 0,5 состоит из двух
(главных) лепестков (рис. 3.5.а, 3.5.б).
Увеличение длины вибратора до l=0,5
0,5 состоит из двух
(главных) лепестков (рис. 3.5.а, 3.5.б).
Увеличение длины вибратора до l=0,5![]() сопровождается ростом
излучения в направлении,
перпендикулярном оси вибратора
(главное направление излучения),за
счет уменьшения излучения в других направлениях. При этом диаграмма
направленности становится уже. При увеличении l/
сопровождается ростом
излучения в направлении,
перпендикулярном оси вибратора
(главное направление излучения),за
счет уменьшения излучения в других направлениях. При этом диаграмма
направленности становится уже. При увеличении l/![]() до 0,625 излучение в главном
направлении продолжает возрастать, но характеристика направленности проходит через нуль не только при
до 0,625 излучение в главном
направлении продолжает возрастать, но характеристика направленности проходит через нуль не только при ![]() =0° и
=0° и ![]() =180°, но и при некоторых других
значениях угла
=180°, но и при некоторых других
значениях угла![]() . Главные лепестки диаграммы становятся уже, но появляются боковые лепестки (рис.3.5.в). При дальнейшем увеличении l/
. Главные лепестки диаграммы становятся уже, но появляются боковые лепестки (рис.3.5.в). При дальнейшем увеличении l/![]() излучение в главном направлении
уменьшается и возрастают боковые лепестки.
Уменьшение излучения в главном направлении объясняется следующим.
Результирующий сдвиг фаз полей, излучаемых элементарными вибраторами в данном
направлении, определяется пространственным сдвигом фаз и сдвигом фаз токов, возбуждающих эти вибраторы. При l/
излучение в главном направлении
уменьшается и возрастают боковые лепестки.
Уменьшение излучения в главном направлении объясняется следующим.
Результирующий сдвиг фаз полей, излучаемых элементарными вибраторами в данном
направлении, определяется пространственным сдвигом фаз и сдвигом фаз токов, возбуждающих эти вибраторы. При l/![]() >0,5 на вибраторе появляются
участки с противофазными токами (рис.3.3), длина которых растет по мере увеличения l/
>0,5 на вибраторе появляются
участки с противофазными токами (рис.3.3), длина которых растет по мере увеличения l/![]() . Поэтому в данном случае, хотя в
главном направлении пространственные сдвиги фаз равны нулю, поля, излучаемые отдельными элементами вибратора, складываются несинфазно, т.е. геометрически. При l/
. Поэтому в данном случае, хотя в
главном направлении пространственные сдвиги фаз равны нулю, поля, излучаемые отдельными элементами вибратора, складываются несинфазно, т.е. геометрически. При l/![]() = 1 (или при l/
= 1 (или при l/![]() = п, где п = 1, 2, ..,) излучение в главном направлении отсутствует, так как противофазные участки
вибратора имеют одинаковую длину. Рост l/
= п, где п = 1, 2, ..,) излучение в главном направлении отсутствует, так как противофазные участки
вибратора имеют одинаковую длину. Рост l/![]() сопровождается также ростом боковых
лепестков. Уже при l/
сопровождается также ростом боковых
лепестков. Уже при l/![]() =0,75 напряженность поля в направлении максимума бокового лепестка превосходит напряженность поля в главном направлении (рис.3.3.г).
=0,75 напряженность поля в направлении максимума бокового лепестка превосходит напряженность поля в главном направлении (рис.3.3.г).
Нормированная характеристика
направленности симметричного вибратора,
определяемая как F(![]() ) = f(
) = f(![]() )/f(90°), равна
)/f(90°), равна
F(![]() ) = [cos(klcos
) = [cos(klcos![]() ) - coskl]/[(l –
coskl)sin
) - coskl]/[(l –
coskl)sin![]() ]. (3.9)
]. (3.9)
У Диполя Герца 2![]() 0,5= 90°. Полуволновый симметричный вибратор имеет
ширину диаграммы направленности по половинной мощности 2
0,5= 90°. Полуволновый симметричный вибратор имеет
ширину диаграммы направленности по половинной мощности 2![]() 0,5= 80°, волновой
симметричный вибратор - 2
0,5= 80°, волновой
симметричный вибратор - 2![]() 0,5= 44°,
симметричный вибратор, у которого l/
0,5= 44°,
симметричный вибратор, у которого l/![]() =0,625, имеет 2
=0,625, имеет 2![]() 0,5= 31°.
Последний вибратор обладает наилучшими
направленными свойствами, так как при дальнейшем увеличении l/
0,5= 31°.
Последний вибратор обладает наилучшими
направленными свойствами, так как при дальнейшем увеличении l/![]() , сильно возрастают боковые лепестки, хотя главный лепесток
диаграммы направленности становится уже. На
практике применяются симметричные вибраторы,
у которых l/
, сильно возрастают боковые лепестки, хотя главный лепесток
диаграммы направленности становится уже. На
практике применяются симметричные вибраторы,
у которых l/![]()
![]() 0,7. Фаза напряженности поля,
создаваемого симметричным вибратором в соответствии с
выражением (3.7), в пределах одного лепестка диаграммы
направленности не зависит от координатного угла
0,7. Фаза напряженности поля,
создаваемого симметричным вибратором в соответствии с
выражением (3.7), в пределах одного лепестка диаграммы
направленности не зависит от координатного угла ![]() . Она изменяется скачком на обратную при переходе
напряжённости поля через нуль. Симметричный вибратор
излучает сферические волны, о чем свидетельствует множитель exp(-ikr)/r. Эти волны как бы исходят из одной точки,
совпадающей с центром вибратора.
. Она изменяется скачком на обратную при переходе
напряжённости поля через нуль. Симметричный вибратор
излучает сферические волны, о чем свидетельствует множитель exp(-ikr)/r. Эти волны как бы исходят из одной точки,
совпадающей с центром вибратора.
Мощность излучения, сопротивление излучения и КНД симметричного вибратора
Мощность электромагнитной волны,
излучаемой симметричным вибратором, можно определить, как и для элементарного
вибратора, методом вектора Пойнтинга. В соответствии с
данным методом симметричный вибратор окружается сферой, радиус которой r »![]() , вследствие чего поверхность сферы
находится в дальней зоне поля вибратора. Центр вибратора совпадает с центром
сферы, ось вибратора лежит на оси z прямоугольной системы координат. На
поверхности сферы выделяется бесконечно малый элемент dS, площадь которого в сферической системе координат dS = r2sinνd
, вследствие чего поверхность сферы
находится в дальней зоне поля вибратора. Центр вибратора совпадает с центром
сферы, ось вибратора лежит на оси z прямоугольной системы координат. На
поверхности сферы выделяется бесконечно малый элемент dS, площадь которого в сферической системе координат dS = r2sinνd![]() d
d![]() .
Излучаемая мощность, приходящаяся на данный
элемент поверхности
.
Излучаемая мощность, приходящаяся на данный
элемент поверхности
dP![]() = ПсрdS=(E2/2Wc)dS. (3.10)
= ПсрdS=(E2/2Wc)dS. (3.10)
Здесь Е - амплитуда (модуль) напряженности
электрического поля в
любой
точке элемента dS, определяемая выражением
E = (60Iп/r) ![]() [cos (kl cos
[cos (kl cos![]() ) - cos kl] / sin
) - cos kl] / sin![]()
![]() . (3.11)
. (3.11)
В общем виде выражение для сопротивления
излучения имеет вид
R![]() п = [r2Е2 макс/( Wc Iп2 )]
п = [r2Е2 макс/( Wc Iп2 )] ![]()
![]() F2(
F2(![]() ,
,![]() )sin
)sin![]() dνd
dνd![]() . (3.12)
. (3.12)
P![]() = Iп2R
= Iп2R![]() п/2.
п/2.
Величина R![]() п определяется
характером распределения электромагнитного поля в дальней
зоне, т.е. диаграммой направленности рассматриваемой антенны. Интегрирование дает следующую формулу, впервые полученную Баллантайном в 1924 г.
п определяется
характером распределения электромагнитного поля в дальней
зоне, т.е. диаграммой направленности рассматриваемой антенны. Интегрирование дает следующую формулу, впервые полученную Баллантайном в 1924 г.
R![]() п = 30 [2 (
п = 30 [2 (![]() +ln2kl - Ci 2kl) + cos 2kl (
+ln2kl - Ci 2kl) + cos 2kl (![]() +lnkl+ Ci 4kl - 2Ci 2kl) +
+lnkl+ Ci 4kl - 2Ci 2kl) +
+sin2kl (Si 4kl- 2Si 2kl)]. (3.1)
![]()
Здесь ![]() =
0,5772... - постоянная Эйлера; Si x = (sin u/u)du –
интегральный
=
0,5772... - постоянная Эйлера; Si x = (sin u/u)du –
интегральный
синус; Ci x = ![]() (cos u/u)du - интегральный косинус.
(cos u/u)du - интегральный косинус.![]()
Как видно из формулы (3.13), сопротивление излучения симметричного вибратора зависит только от величины отношения l/![]() . Формула (3.13) является приближенной,
поскольку при ее выводе исходили из синусоидального распределения тока по
вибратору, что справедливо только для тонких вибраторов.
Однако результаты расчетов по формуле (3.13) хорошо совпадают с экспериментальными данными. Это объясняется тем, что сопротивление излучения определяется полем в дальней зоне, которое мало зависит от толщины вибратора. Следует также иметь в виду, что изложенный здесь
метод расчета дает только активную составляющую сопротивления излучения, так как учитывается только излученная активная мощность.
. Формула (3.13) является приближенной,
поскольку при ее выводе исходили из синусоидального распределения тока по
вибратору, что справедливо только для тонких вибраторов.
Однако результаты расчетов по формуле (3.13) хорошо совпадают с экспериментальными данными. Это объясняется тем, что сопротивление излучения определяется полем в дальней зоне, которое мало зависит от толщины вибратора. Следует также иметь в виду, что изложенный здесь
метод расчета дает только активную составляющую сопротивления излучения, так как учитывается только излученная активная мощность.
В литературе
имеются таблицы и графики R![]() п как функции
отношения (рис.3.6), рассчитанные по формуле (3.13). Осциллирующий характер
зависимости объясняется тем, что интерференционная картина
поля в дальней зоне меняется при изменении l/
п как функции
отношения (рис.3.6), рассчитанные по формуле (3.13). Осциллирующий характер
зависимости объясняется тем, что интерференционная картина
поля в дальней зоне меняется при изменении l/![]() .
.
Если отношение
l/![]() ,
не превышает 0,1,
то формулу (3.13)
можно упростить R
,
не превышает 0,1,
то формулу (3.13)
можно упростить R![]() п=20 (k l)4 .
п=20 (k l)4 .
КНД симметричного вибратора можно
определить по формуле
D = (120 / R![]() п ) (1 -coskl)2. (3.14)
п ) (1 -coskl)2. (3.14)
При l/![]() =0,25
R
=0,25
R![]() п = 73,1 Ом и
D= 1,64 ;
п = 73,1 Ом и
D= 1,64 ;
l/![]() = 0,5 R
= 0,5 R![]() п =199 Ом и D = 2,4;
п =199 Ом и D = 2,4;
l/![]() =0,625 R
=0,625 R![]() п =110 Ом и D = 3,l.
п =110 Ом и D = 3,l.
Для сравнения КНД
элементарного электрического вибратора имеет
D = 1,5. КНД
любой вибраторной антенны можно рассчитать по формуле
D = (120/ R![]() п) f2max (
п) f2max (![]() ). (3.15)
). (3.15)
|
|
В этой формуле R![]() п - полное сопротивление излучения антенны.
Действующая
длина симметричного вибратора
определяется по формуле lд =
п - полное сопротивление излучения антенны.
Действующая
длина симметричного вибратора
определяется по формуле lд = ![]() (1 - coskl) / (
(1 - coskl) / (![]() sinkl).
sinkl).
Зависимость R![]() п От величины l/
п От величины l/![]()
|
|
Входное
сопротивление симметричного вибратора. Инженерный
метод расчета входного сопротивления
Часть мощности,
подводимой от генератора к симметричному вибратору, излучается. Другая часть
мощности теряется в самом вибраторе (нагревание
проводов), в изоляторах и в окружающих вибратор предметах. Излученной мощности
соответствует активное сопротивление излучения. Мощности потерь соответствует активное сопротивление
потерь. Кроме излученного, есть
колеблющееся вблизи антенны связанное с ней электромагнитное поле, которому
соответствует реактивная мощность. Эта мощность то отдается генератором, переходя
в ближнее поле, то возвращается к нему обратно. Реактивной мощности в большинстве случаев соответствует
реактивное сопротивление антенны.
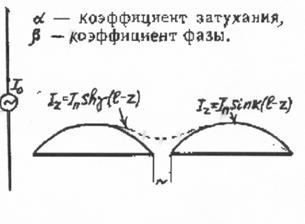 Таким образом, включенный в антенну генератор нагружен на комплексное сопротивление, которое называется входным сопротивлением антенны и
равно отношению напряжения на зажимах вибратора (точки
питания) к току в точках питания ZBX=U0/I0=RBX+i XBX.
Таким образом, включенный в антенну генератор нагружен на комплексное сопротивление, которое называется входным сопротивлением антенны и
равно отношению напряжения на зажимах вибратора (точки
питания) к току в точках питания ZBX=U0/I0=RBX+i XBX.
|
Рис. 3.7. Распределение тока по "коротким" и "длинным" вибраторам |
Величина и характер входного сопротивления определяют режим работы
включенного в антенну генератора. Обычно в
симметричных вибраторах потери малы, поэтому будем полагать, что RBX ![]() R
R![]() o, где R
o, где R![]() o - сопротивление
излучения вибратора, отнесенное к току в точках питания. Для точного определения входного сопротивления
необходимо знать закон распределения тока вдоль вибратора. Часто с достаточной для инже-
o - сопротивление
излучения вибратора, отнесенное к току в точках питания. Для точного определения входного сопротивления
необходимо знать закон распределения тока вдоль вибратора. Часто с достаточной для инже-
нерных целей
точностью входное сопротивление рассчитывается, исходя из приближенных законов распределения тока по вибратору. Рассмотрим такой
приближенный (инженерный) метод расчета входного сопротивления. Предположив, что ток вдоль вибратора распределен по закону синуса, найдем входное сопротивление симметричного вибратора, у которого l/![]() =0,5 (рис.3.7). В этом случае ток в точках
питания оказывается равным нулю и очевидно, что ZBX = U0/I0=
=0,5 (рис.3.7). В этом случае ток в точках
питания оказывается равным нулю и очевидно, что ZBX = U0/I0=![]() . В действительности же ток в точках питания никогда не бывает равен нулю (его величина обязательно конечна), а следовательно, входное сопротивление симметричного вибратора никогда не бывает бесконечно велико. Физически это совершенно ясно. Ведь закон синуса
(стоячая волна) справедлив в линиях только при отсутствии потерь. Вибратор же в принципе является системой с потерями на излучение. Следовательно, при расчете входного сопротивления лучше проводить аналогию между симметричным вибратором и разомкнутой на конце линией с потерями. Известно, что ток в такой линии распределен по закону гиперболического
синуса (рис.3.7) Iz = Iпsh
. В действительности же ток в точках питания никогда не бывает равен нулю (его величина обязательно конечна), а следовательно, входное сопротивление симметричного вибратора никогда не бывает бесконечно велико. Физически это совершенно ясно. Ведь закон синуса
(стоячая волна) справедлив в линиях только при отсутствии потерь. Вибратор же в принципе является системой с потерями на излучение. Следовательно, при расчете входного сопротивления лучше проводить аналогию между симметричным вибратором и разомкнутой на конце линией с потерями. Известно, что ток в такой линии распределен по закону гиперболического
синуса (рис.3.7) Iz = Iпsh![]() (z - l), где
(z - l), где ![]() =
= ![]() + i
+ i![]() - коэффициент распространения,
- коэффициент распространения, ![]() -
коэффициент ослабления,
-
коэффициент ослабления, ![]() -
коэффициент фазы.
-
коэффициент фазы.
Из рис.3.7 видно, что существенная разница в распределении тока по законам кругового и гиперболического синусов получается только на сравнительно близких расстояниях от узла тока. Поэтому при расчете входных сопротивлений "коротких" вибраторов (l/![]() )
) ![]() 0,35...0,4; (0,6...0,65)
0,35...0,4; (0,6...0,65) ![]() l/
l/![]()
![]() (0,85...0,9), т.е. таких, у которых узел тока
находится от точек питания вибратора не ближе, чем на расстоянии
(0,1...0,15)
(0,85...0,9), т.е. таких, у которых узел тока
находится от точек питания вибратора не ближе, чем на расстоянии
(0,1...0,15)![]() , исходят из синусоидального
распределения тока. При расчете входного сопротивления "длинных" вибраторов (0,35
, исходят из синусоидального
распределения тока. При расчете входного сопротивления "длинных" вибраторов (0,35![]() l/
l/![]()
![]() 0,65) следует исходить из распределения тока по закону гиперболического синуса. Найдем формулы для расчета активной
0,65) следует исходить из распределения тока по закону гиперболического синуса. Найдем формулы для расчета активной
35
и реактивной
составляющих входного сопротивления "короткого" вибратора. Выразив
мощность, излучаемую вибратором, через амплитуды тока в пучности (IП) и в точках питания (Iо), получим:
P![]() = (Iп2R
= (Iп2R![]() п )/2 и P
п )/2 и P![]() = (I02 R
= (I02 R![]() 0)/2. (3.17)
0)/2. (3.17)
Так как левые части этих выражений равны между
собой, то I2п R![]() п = I02 R
п = I02 R![]() 0. Решая это равенство относительно R
0. Решая это равенство относительно R![]() 0, получаем R
0, получаем R![]() 0= R
0= R![]() п (Iп2/ I02).
п (Iп2/ I02).
Подставляя вместо I0 выражение I0=Iпsinkl, получаем формулу для расчета активной
составляющей входного сопротивления вибратора (без учета потерь в
вибраторе)
R![]() 0 = R
0 = R![]() п /sin2kl. (3.18)
п /sin2kl. (3.18)
Величину R![]() п
для вибратора заданной длины легко найти из
таблиц или графиков. При расчете реактивной
составляющей входного сопротивления короткого симметричного вибратора
пользуются формулой входного сопротивления
разомкнутой на конце двухпроводной линии без потерь, заменяя в ней волновое
сопротивление линии волновым сопротивлением антенны
п
для вибратора заданной длины легко найти из
таблиц или графиков. При расчете реактивной
составляющей входного сопротивления короткого симметричного вибратора
пользуются формулой входного сопротивления
разомкнутой на конце двухпроводной линии без потерь, заменяя в ней волновое
сопротивление линии волновым сопротивлением антенны
Xвх= -i WActg kl. (3.19)
Таким образом, полное входное сопротивление короткого вибратора можно определить
по формуле
Zвх= (R![]() п/sin2kl) – i WActg kl. (3.20)
п/sin2kl) – i WActg kl. (3.20)
Точность расчетов по формуле (3.20) повышается при уменьшении размеров
поперечного сечения вибратора. В случаях длинных вибраторов входное сопротивление рассчитывается аналогично входному сопротивлению двухпроводной разомкнутой на конце линии, обладающей потерями
Zвх = WA [(sh2![]() l- (
l- (![]() /
/![]() ) sin 2
) sin 2![]() l) / (ch2
l) / (ch2![]() l - cos 2
l - cos 2![]() l)] – i WA [(
l)] – i WA [(![]() /
/![]() ) sh 2
) sh 2![]() l+
l+
+ sin 2![]() l) / (ch2
l) / (ch2![]() l - cos 2
l - cos 2![]() l)]. (3.21)
l)]. (3.21)
Здесь WA - волновое сопротивление вибратора; l- длина плеча
вибратора; ![]() - коэффициент фазы в вибраторе;
- коэффициент фазы в вибраторе; ![]() - коэффициент затухания. По аналогии с длинными линиями, пренебрегая потерями в проводах вибратора коэффициент затухания можно рассчитать по формуле
- коэффициент затухания. По аналогии с длинными линиями, пренебрегая потерями в проводах вибратора коэффициент затухания можно рассчитать по формуле
![]() = R
= R![]() 1 / WA, где R
1 / WA, где R![]() 1 -активное сопротивление излучения, приходящееся на единицу длины вибратора.
Приближенно полагая, что сопротивление излучения R
1 -активное сопротивление излучения, приходящееся на единицу длины вибратора.
Приближенно полагая, что сопротивление излучения R![]() п распределено равномерно по всей длине вибратора, для расчета R
п распределено равномерно по всей длине вибратора, для расчета R![]() 1 получают
формулу R
1 получают
формулу R![]() 1= R
1= R![]() п/[l(l - (sin2kl/2kl)]. Данная
формула позволяет, зная сопротивление излучения,
отнесенное к пучности тока, найти распределенное сопротивление излучения. Следовательно, коэффициент
ослабления
п/[l(l - (sin2kl/2kl)]. Данная
формула позволяет, зная сопротивление излучения,
отнесенное к пучности тока, найти распределенное сопротивление излучения. Следовательно, коэффициент
ослабления
![]() = R
= R![]() 1/ WA = R
1/ WA = R![]() п/ [lWA (1- (sin2kl/2kl))].
п/ [lWA (1- (sin2kl/2kl))].
Коэффициент фазы ![]() в формуле (3.21)
несколько отличается от
в формуле (3.21)
несколько отличается от
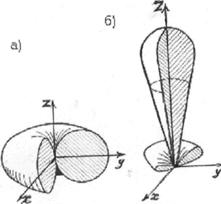
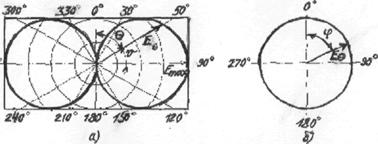
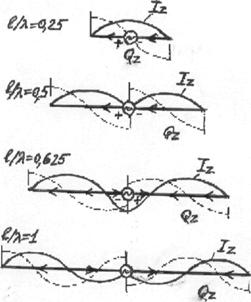
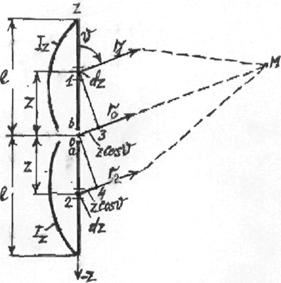
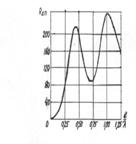
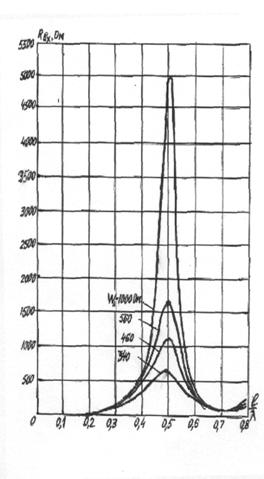
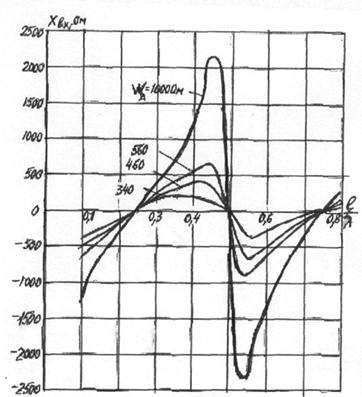
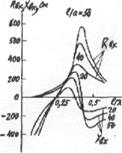
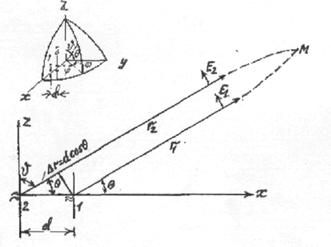
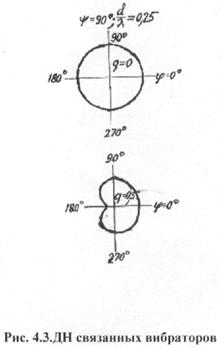
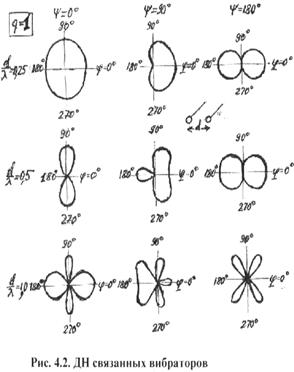
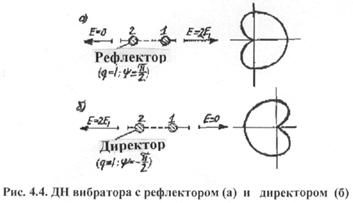

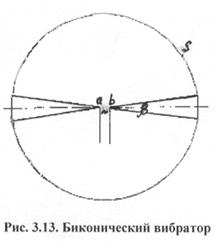
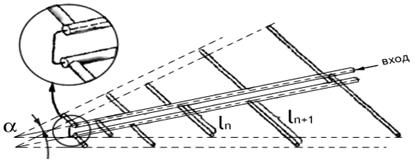
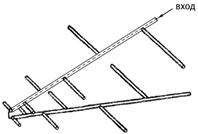
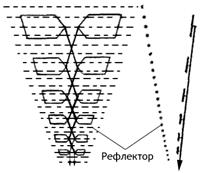
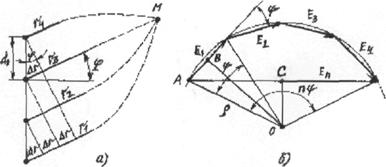
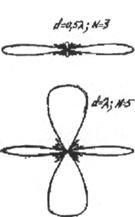
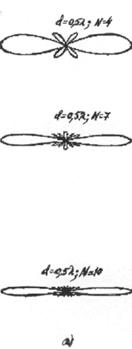
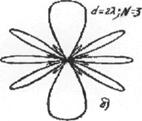
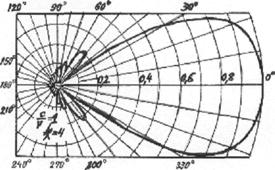
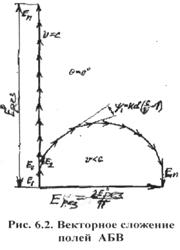
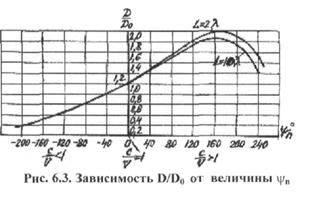


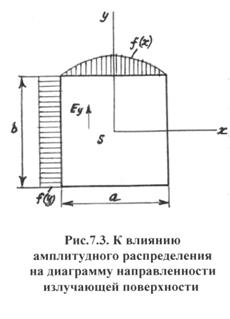
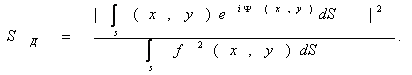
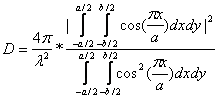
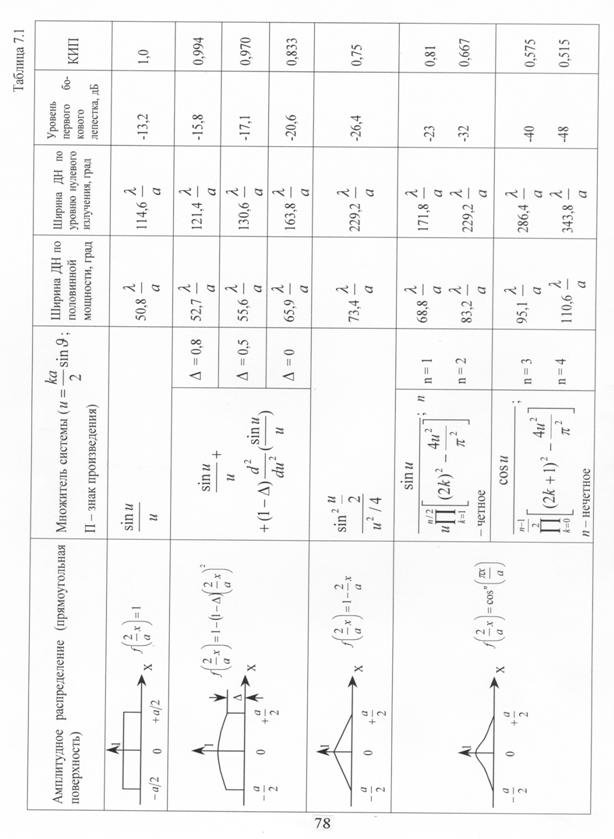
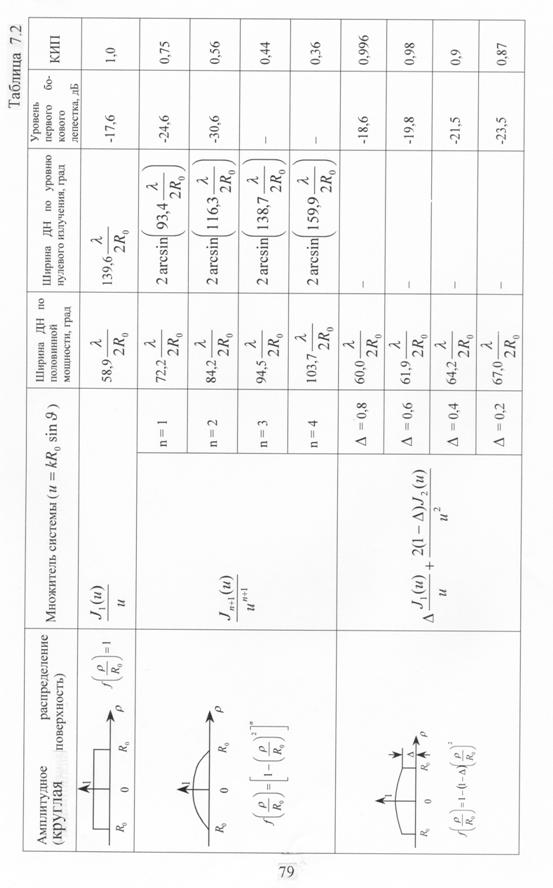
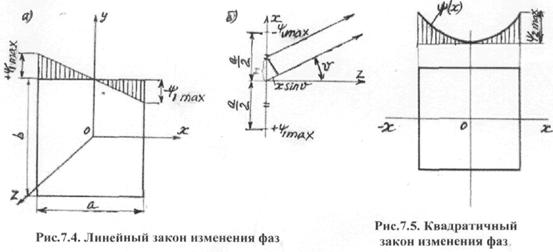
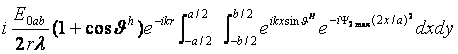
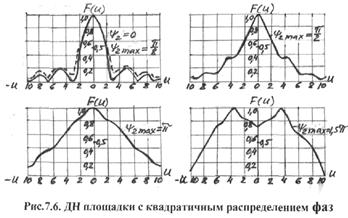
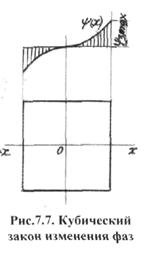
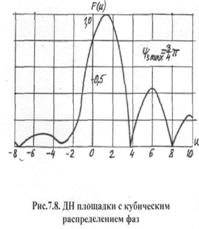
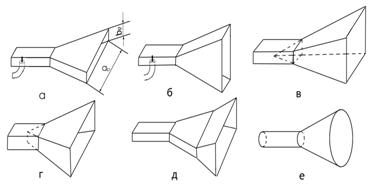
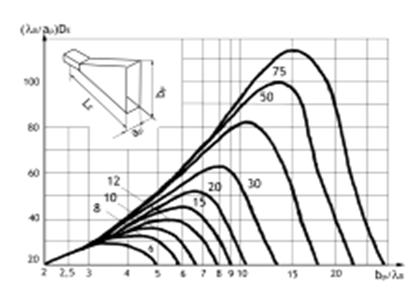
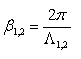 ;
;