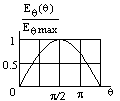УЗБЕКСКОЕ АГЕНТСТВО
СВЯЗИ И ИНФОРМАТИЗАЦИИ
ТАШКЕНТСКИЙ УНИВЕРСИТЕТ
ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ
Факультет Радиотехники,
Радиосвязи и Телерадиовещания
Кафедра
Антенно-фидерных
устройств
Конспект лекций по дисциплине
ЭЛЕКТРОМАГНИТНЫЕ ПОЛЯ И
ВОЛНЫ
для направления «Радиотехника»
Составитель
доц. кафедры АФУ
Губенко В.А.
Ташкент 2010
СОДЕРЖАНИЕ:
РАЗДЕЛ 1.
ЭЛЕКТРОДИНАМИКА
ТЕМА 1. Электромагнитное
поле (ЭМП), векторы ЭМП, операторы теории
поля……………………………………………………………………………………………………………………..3
ТЕМА 2. Электродинамические
параметры сред, классификация сред, материальные уравнения
электродинамики………………………………………………………………………………………………………6
ТЕМА 3. Система
уравнений Максвелла для электрического и магнитного полей, уравнение непрерывности полного
тока……………………………………………………………………………………………………………9
ТЕМА 4. Монохроматическое
ЭМП, его уравнения, комплексные векторы, комплексная диэлектрическая
проницаемость………………………………………………………………………………………………………..14
ТЕМА
5. Граничные условия для векторов
поля…………………………………………………………………..19
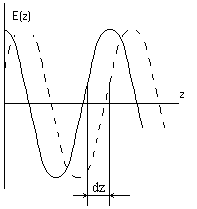
ТЕМА 6. Плоская
однородная волна, поляризация волн………………………………………………………….23
ТЕМА 7. Элементарный
электрический и магнитный излучатели……………………………………………….35
ТЕМА 8. Электромагнитная
волна на границе раздела сред, законы Снеллиуса, коэффициенты Френеля, полное
прохождение волны через границу сред…………………………………………………………………………….37
ТЕМА 9. Направляющие
системы: полые волноводы, коаксиальные волноводы. Основные типы волн в
волноводах, рабочие частоты, критические длины волн. Особенности применения
волноводов, их основные параметры………………………………………………………………………………………………………………46
РАЗДЕЛ 2. РАСПРОСТРАНЕНИЕ РАДИОВОЛН
ТЕМА 10. Распространение
радиоволн в свободном пространстве……………………………………………….52
ТЕМА 11. Распространение
земных радиоволн УКВ диапазона…………………………………………………..54
ТЕМА 12. Особенности
распространения радиоволн в тропосфере, дальнее тропосферное
распространение..58
ТЕМА 13. Особенности
распространения ионосферных радиоволн, свойства ионосферы……………………..62
ТЕМА 14. Особенности
распространения коротких, средних и длинных волн…………………………………..65
ТЕМА 15. Распространение
радиоволн в городских условиях…………………………………………………….76
ТЕМА 1.
Электромагнитное поле (ЭМП), векторы ЭМП,
операторы теории поля
1.1. Понятие
электромагнитного поля
Под электромагнитным полем
(ЭМП) понимают вид материи, характеризующийся совокупностью взаимно связанных и
взаимно обусловливающих друг друга электрического и магнитного полей. Важнейшей
отличительной особенностью внешнего ЭМП является его способность оказывать
силовое воздействие на заряженную частицу, которое зависит от величины
электрического заряда частицы и скорости ее движения. В телекоммуникации
используются переменные во времени поля. В таких полях электрическая часть
неотделима от магнитной и наоборот. Однако теория ЭМП использует исторически
накопленный опыт изучения электрических и магнитных явлений в природе, начиная
с постоянных во времени (стационарных) процессов. Постоянные электрическое и
магнитное поля могут существовать раздельно, независимо друг от друга, но они
не могут быть использованы для передачи информации. В современной теории
переменного ЭМП – электродинамике продолжается использование понятий
электрического и магнитного полей, как двух форм проявления единого ЭМП.
ЭМП объективно существует в
природе, поэтому является видом материи, отличающимся от другой формы материи -
вещества. Различные поля, накладываясь друг на друга, могут существовать в
одном объеме, а частицы вещества взаимно непроницаемы. Частицы вещества имеют
массу покоя m0 и скорость v. Частицы ЭМП - фотоны массы покоя не
имеют, так как существуют только в движении со скоростью с » 3× 108 м/с в вакууме.
Вещество никогда не может
достигнуть этой скорости, т.к. его масса ![]() при
этом обратилась бы в бесконечность.
при
этом обратилась бы в бесконечность.
В движении ЭМП в виде
электромагнитной волны, также как вещество, имеет инертную массу. Она была
обнаружена в уникально тонких опытах П. Н.Лебедева по измерению светового давления,
а как доказал Д. К. Максвелл, свет тоже является электромагнитным процессом.
Позже А. Эйнштейн установил взаимосвязь массы m со скоростью перемещения с и энергией материи W=mc2.
Отсюда следует, что антенна
радиостанции мощностью 1000 кВт и течение одного часа излучает ЭМП массой 0,04
мг. Высокая скорость распространения столь малой массы создает значительную
энергию.
Вещество и ЭМП, как виды
материи, обладают одинаковыми характеристиками: энергией, массой и количеством
движения. ЭМП поэтому, может быть использовано как переносчик энергии сигнала
телекоммуникации. Волновые электромагнитные процессы используются не только для
передачи в свободном пространстве и по линиям передачи, но и в различных
электродинамических устройствах техники радиосвязи и радиовещания.
Используемые в инженерной
практике явления обычно не требуют знания подробностей сложных электромагнитных
процессов, происходящих в микроскопических, атомных масштабах. В большинстве
технических задач интерес представляют процессы, протекающие в макроскопическом
масштабе, т.е. усредненные во времени и пространстве. Усреднение мысленно
проводится на расстояниях значительно больше размеров атомов и молекул вещества
(но гораздо меньше длины используемой
электромагнитной волны). Интервал усреднения во времени значительно больше
периода орбитального и спинового вращения элементарных частиц, но значительно
меньше периода колебания векторов внешнего ЭМП. Рассматриваемая нами теория ЭМП
не учитывает квантовые эффекты в веществе, она называется макроскопической (или
классической) электродинамикой.
1.2. Векторы
ЭМП
В ЭМП на заряды и токи
действуют силы, которые, совершая работу
по их перемещению, уменьшают энергию поля. В качестве пробного тела, при помощи
которого можно не только обнаружить, но и изменить поле, рассматривают
достаточно малое заряженное тело - точечный заряд. На него в ЭМП действует сила
Лоренца:
F = q (E
+ [υ,B ]),
где q, ![]() –
электрический заряд и скорость его движения; E (r, t) - вектор напряженности электрического поля; B(r, t) - вектор магнитной индукции; r – радиус-вектор точки пространства, в
которой находится заряд; t — время. В
случае неподвижного заряда (υ
=0) сила Fэ = qE, т.е.
–
электрический заряд и скорость его движения; E (r, t) - вектор напряженности электрического поля; B(r, t) - вектор магнитной индукции; r – радиус-вектор точки пространства, в
которой находится заряд; t — время. В
случае неподвижного заряда (υ
=0) сила Fэ = qE, т.е. ![]() - это сила, с которой ЭМП действует на
единичный положительный неподвижный заряд. Размерность вектора
- это сила, с которой ЭМП действует на
единичный положительный неподвижный заряд. Размерность вектора ![]() :
Н/Кл = В/м.
:
Н/Кл = В/м.
Магнитное поле действует
только на движущие заряды (токи):
Fм = q [ υ, B ].
Сила воздействия
максимальна, если υ
перпендикулярен ![]() ,
и отсутствует, если векторы υ и B совпадают по направлению. Таким
образом, вектор
,
и отсутствует, если векторы υ и B совпадают по направлению. Таким
образом, вектор ![]() определяется по силовому воздействию ЭМП на
движущиеся заряды. Размерность вектора B:
Н×с/(Кл×м) = В×с/м2 = Вб/м2
= Т.
определяется по силовому воздействию ЭМП на
движущиеся заряды. Размерность вектора B:
Н×с/(Кл×м) = В×с/м2 = Вб/м2
= Т.
Содержание рассмотренных
векторов E и B связано с воздействием внешнего поля на очень малые заряды и
элементарные токи. Малость зарядов необходима, чтобы они не искажали измеряемое
поле. Но ведь электрический заряд и элемент тока имеют собственное
электрическое и магнитное поле. Вокруг заряда всегда существует электрическое
поле, линии которого исходят из него самого. Провода (элементы проводов) с
током создают собственное магнитное поле, линии которого окружают его.
Элементарные связанные заряды в молекулах диэлектриков и элементарные магнитные
поля в магнитных материалах могут значительно изменить проникающие в материал
ЭМП. Тогда для описания явлений требуется введение дополнительной пары
векторов:
D (r, t) - электрическая индукция,
H (r, t) -напряженность магнитного поля.
D-называют также вектором
электрического смещения. Размерность векторов, как видно из дальнейших
уравнений равна [D] = Кл/м2 и [![]() ] = А/м. Так как эти вектора D (и H)
характеризуют связь заряда (и тока) с собственным электрическим (и магнитным)
полем, их называют функциями источников.
] = А/м. Так как эти вектора D (и H)
характеризуют связь заряда (и тока) с собственным электрическим (и магнитным)
полем, их называют функциями источников.
Считают, что поле
определено, если в каждой точке пространства в любой момент времени известны
величины и направления четырех векторов E,
D, B и H. Так как вектор определяется своими
компонентами, то каждый из векторов (например, вектор E (x,y,z)) представляет
собой три математические пространственно-временные функции от x,y,z и t. В формальном
(математическом) подходе к
понятию «поле», его можно рассматривать как физическую величину (силу), которая
в разных точках пространства принимает различные значения.
Теория ЭМП сложилась в
результате накопления и обобщения экспериментальных фактов, а также развития
математического аппарата, который опирается на векторный анализ. В основных
уравнениях ЭМП векторы E, D, B ,H
связаны с помощью операторов «дивергенция» и «ротор» с другими величинами р и J
.
Электрический заряд в каждой
точке пространства характеризуется объёмной плотностью
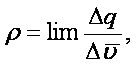
Кл/м3 (1.1)
где
q – суммарный заряд в объеме.
Упорядоченное движение
зарядов через каждую точку поля характеризуется вектором плотности
электрического тока проводимости
Jnp = p×![]() , А/м2 (1.2)
, А/м2 (1.2)
Суммарный электрический ток,
протекающий через некоторую поверхность S
является скалярной величиной и связан с ![]() пр интегральным соотношением
пр интегральным соотношением
![]()
, A
(1.3)
где dS -
представляет вектор элементарной площадки. Интеграл вида (1.3) называют потоком
вектора J через поверхность S. Следовательно, электрический ток
можно рассматривать как поток плотности тока через заданную поверхность.
1.3. Операторы
теории поля
Основными операторами,
используемыми при анализе электромагнитных явлений, являются: поток вектора
через поверхность, циркуляция вектора по замкнутому контуру, дивергенция и
ротор вектора.
Примеры интегральных операторов:
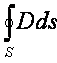
- поток
вектора D через замкнутую поверхность
S;
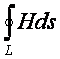
-
циркуляция вектора H по
замкнутому контуру L
Интегральные операторы,
усредняющие в пространстве поток и циркуляцию векторов по поверхности или
контуру, могут быть приведены в дифференциальную форму, т.е. превращены в
характеристики поля в точке пространства. Операции поток и дивергенция связаны
между собой равенством:
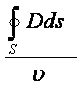
![]()
![]()
=
(1.4)
т.е. поток вектора через поверхность, окружающую
точку в пространстве отображает его дивергенцию.
Так как скалярное
произведение Dd![]() = Dd
= Dd![]() ×cosa может дать как
положительный, так и отрицательный результат, то поток и дивергенция тоже
представляют собой положительные либо отрицательные величины. Если угол между
векторами D и d
×cosa может дать как
положительный, так и отрицательный результат, то поток и дивергенция тоже
представляют собой положительные либо отрицательные величины. Если угол между
векторами D и d![]() (направлен по внешней нормали к поверхности) менее 900 (силовая линия D выходит из поверхности), то divD > 0. Если силовая линия
направлена во внутрь поверхности, то угол
a >900, cosa > 0 и divD
< 0. Следовательно, в точке поля, где
собираются силовые линии, дивергенция отрицательна, а в точке, откуда
наблюдается исток линий - дивергенция положительна.
(направлен по внешней нормали к поверхности) менее 900 (силовая линия D выходит из поверхности), то divD > 0. Если силовая линия
направлена во внутрь поверхности, то угол
a >900, cosa > 0 и divD
< 0. Следовательно, в точке поля, где
собираются силовые линии, дивергенция отрицательна, а в точке, откуда
наблюдается исток линий - дивергенция положительна.
Определение (1.4) можно
представить в разных системах координат через частные пространственные
производные проекций вектора. В прямоугольной системе координат дивергенция
представляется суммой частых производных проекций вектора по своим направлениям
![]()
![]() . (1.5)
. (1.5)
В отличие от дивергенции
операция ротор дает векторную величину. Нормальная к поверхности контура
циркуляции составляющая ротора связана операцией взятия предела
![]()
![]()
![]()
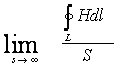 , (1.6)
, (1.6)
где S -
площадь, заключенная внутри контура L,
окружающая в пределе точку в пространстве.
В прямоугольной системе
координат операция взятия ротора представляет следующую комбинацию частых
производных проекций вектора
![]()
![]()
![]()
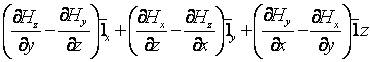 , (1.7)
, (1.7)
где ![]() - представляют единичные векторы (орты) осевых
направлений.
- представляют единичные векторы (орты) осевых
направлений.
Если результат операции
(1.7) равен нулю, то поле называют «безвихревое». Неизменное во времени
электрическое поле во всех точках пространства rotE = 0, т.е. электрическое
поле является безвихревым.
ТЕМА 2.
Электродинамические параметры сред, классификация сред, материальные уравнения
электродинамики
Внутри любого вещества могут
существовать электрические заряды, которые под воздействием внешнего
электрического поля могут перемещаться от одной молекулы к другой, т.е. они
свободные заряды или смещаться в пределах одной молекулы, т.е. оставаться
связанными. В первом случае мы имеем пример поведения электронов и ионов в
металлах, электролитах и ионизированных газах. В диэлектрических средах мы
имеем дело со связанными зарядами. Смещение связанных зарядов в атомах и
молекулах создает явление, которое называют «поляризацией среды». Поляризация
приводит к созданию внутреннего электрического поля, направленного против
внешнего поля Е0 . Поэтому
внутри диэлектрика проникающее внешнее поле ослабляется. Степень ослабления
выражают через параметр εа
- абсолютную диэлектрическую
проницаемость. Этот параметр связывает два электрических вектора ЭМП
![]()
![]()
![]() ,
(2.1)
,
(2.1)
которое называют первым материальным уравнением
электродинамики.
Насыщенность вещества
свободными электронами определяет свойство вещества создавать ток проводимости.
Это свойство характеризуется параметром s - удельной электрической
проводимостью. Параметр s связывает вектора Jnp и Е равенством
Jпр = s E,
(2.2)
которое тоже относится к материальным уравнениям
электродинамики. Известный из теории цепей закон Ома для участка цепи является
следствием уравнения (2.2), поэтому его называют также законом Ома в
дифференциальной форме.
Внутри любого вещества
существует также источники магнитного поля замкнутые элементарные электрические
токи, которые являются результатом орбитального движения и спинового вращения
электронов. Эти элементарные токи обладают магнитными моментами,
ориентирующимися под воздействием внешнего ЭМП. Суммарный магнитный момент в
данном объеме определяет процесс намагничивания среды. Количественно
намагничивание оценивается параметром mа - абсолютной магнитной
проницаемостью, который связывает два магнитных вектора ЭМП
B = mа H. (2.3)
Это уравнение является
третьим материальным уравнением электродинамики.
Параметры εа, mа, s, зависят от физико-химических особенностей
(структуры) данного вещества, температуры, частоты, давления и воздействующих
полей. Их определением занимается квантовая электродинамика. В изучаемой нами
классической электродинамике среда представляется сплошной, а величины,
характеризующие ЭМП, – непрерывно распределенными в пространстве, т.е. в
макроскопическом виде. В макроскопической электродинамике пользуются указанными
параметрами как заданными.
Материальные уравнения (2.1)
- (2.3) записаны так, что параметры εа,
mа, s, являются скалярными
величинами. Такие среды являются изотропными. В них направления векторов D и
E, B и H, J и E совпадают, а свойства среды не зависят от направления векторов
(т.е. и направления распространения поля).
В технике СВЧ находят
применение два особых материала: сегнетоэлектрики и ферриты которые меняют свои
свойства под воздействием внешних условий. Эти явления невозможно описать через
скалярные параметры εа, mа.
Приходится использовать матрицу (тензор) параметров:
![]()
![]() mхх mхy mхz
mхх mхy mхz
mа = myх myy myz (2.4)
mzх myz mzz
и при этом, например, одна из составляющих вектора B
запишется в виде
![]() ,
,
т.е. каждая проекция вектора зависит от всех
составляющих вектора H. Это говорит о
том, в этой среде векторы B и H не совпадают по направлению, т.е.
свойства среды зависят от направления прохождения ЭМП в виде волны. Такая среда
называется анизотропной по магнитным свойствам. В анизотропной среде
электродинамический параметр подставляется не скалярным коэффициентом, а
тензорным. Сегнетоэлектрики анизотропны по электрическому полю, т.е. по
параметру εа.
Говорят, что среда однородна
в области, если параметры εа, mа, s, (скаляры или тензоры)
постоянны в объеме V. Если же их
следует рассматривать как функцию координат, то среда неоднородна. Наконец,
параметры среды в большинстве случаев можно считать независящим от векторов
поля. Материальные уравнения (2.1) - (2.3) при этом линейны. Линейными,
называют и соответствующие среды. Нелинейность большинства сред проявляется
только в очень сильных полях. В нашем курсе лекций рассматриваются линейные,
однородные и изотропные среды. Анизотропным средам посвящена последняя лекция.
Примеры сред. Наиболее
широко в современной технике СВЧ применяются такие диэлектрики, как полиэтилен,
полистирол и фторопласт, обладающие малыми диэлектрическими потерями,
достаточно высокой электрической прочностью и легкообрабатываемые. Применяются
так же различные типы высокочастотной керамики, стекло, конструкционные
пластмассы и др. Диэлектрические материалы характеризуются параметром εа. В принятой системе единиц СИ
его можно представить в виде:
εа = ε0 × ε,
где ε0
= (1/36p)10-9, Ф/м -
электрическая постоянная. Относительная диэлектрическая проницаемость ε - множитель не имеющий
размерности упрощает табулирование материалов по этому параметру, т.к. не содержит
иррационального числа p для всех диэлектриков ε > l. Диэлектрики полиэтилен, полистирол и фторопласт
имеют близкие по значению ε в диапазоне 2,0 ... 2,6. Для брокерита
(керамика) ε = 6,6, а для стекла
ε = 4,0. Воздух очень близок к
вакууму: ε = 1; εа = ε0. Для сухой земли ε = 3...6; для воды ε
» 80.
Проводниковые материалы в
конструкциях СВЧ устройств должны иметь высокое значение электрической
проводимости s. На сверхвысоких значениях
частоты токи в волноводах протекают лишь по поверхности металла обращенной к
ЭМП. Тонкий поверхностный слой вносит потери передачи энергии, увеличивающиеся
с ростом частоты и параметра mа и уменьшением величины s. Поэтому абсолютная
магнитная проницаемость применяемых металлов
mа = m0 × m
должна быть близка к магнитной постоянной m0 = 4p×10-7 Гн/м, т.е.
относительная магнитная проницаемость должна быть ближе к единице. Равенство m = 1 говорит о том, что
данный материал, так же как и вакуум и воздух не намагничивается. Диамагнетик
медь имеет m = 0,99999044 (m <1), а парамагнетик
алюминий - m = 1,0000222 (m >1), т.е. и тот и другой
металл по магнитным свойствам очень близок к вакууму.
По электропроводности
металлы расположены по убыванию значений параметра s в следующем порядке: серебро — 6,17×107 См/м; медь –
5,8×107 См/м; золото
– 4,1×107 Cм/м;
алюминий - 3,72·107 См/м. Серебро, как правило, используется для
нанесения покрытий, обладающих высокой электропроводностью. Однако, на влажном
воздухе серебро (и медь) легко окисляются, покрываясь слоем, имеющим большое удельное сопротивление и вносящим
тепловые потери передачи мощности ЭМП. Слой золота толщиной всего в несколько
микрон, нанесенный на поверхность легкоокисляющихся металлов, становится
практически непроницаемым для кислорода.
ТЕМА 3. СИСТЕМА УРАВНЕНИЙ МАКСВЕЛЛА ДЛЯ ЭЛЕКТРИЧЕСКОГО И МАГНИТНОГО ПОЛЕЙ, УРАВНЕНИЕ НЕПРЕРЫВНОСТИ ПОЛНОГО ТОКА
3.1. Третье и четвертое уравнения Максвелла
Максвелл обобщил теорию
электромагнетизма и экспериментальную электродинамику своего времени (1864 год)
в ряде уравнений. Позже установили, что только четыре его уравнения являются
базисными и независимыми. Уравнения Максвелла являются основой современной
классической электродинамики. Они универсальны, с их помощью совместно с
материальными уравнениями можно решить теоретически любую электродинамическую
задачу.
Ниже рассмотрено
содержание уравнений Максвелла, записанных в современной системе единиц СИ и
математических операции векторного анализа. Рассмотрение изложено по принципу
«от более простых к более сложным».
Третье уравнение Максвелла
является обобщением для переменных во времени электрических зарядов, известной
теоремы Гаусса из электростатики
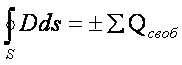
, (3.1)
где Qсвоб алгебраическая сумма свободных
электрических зарядов, расположенных в объёме, ограниченном поверхностью S. Если заряд в объеме распределен
непрерывно, то
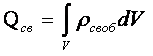
, (3.2)
где rсвоб - функция распределения объемной плотности зарядов.
Если применить к (3.1)
с учетом (3.2), операцию (1.4), то получим
divD = rсвоб. . (3.3)
Следовательно, в каждой
точке поля дивергенция вектоpa D численно равна объемной плотности
свободных зарядов в этой же точке. Если заряд положителен div D>0, силовые линии D
исходят из точки. А в точках, где r < 0 силовые линии сходятся, наблюдается их
сток.
Уравнения (3.1) и (3.3) носят название третьего уравнения
Максвелла соответственно в интегральной и дифференциальной формах. Если подставить в них первое материальное
уравнение (2.1), то это уравнение Максвелла для
случая однородной диэлектрической среды приобретает вид
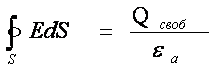
, (3.4)
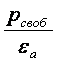 либо
либо
divE = . (3.5)
В равенствах (3.4) и (3.5) присутствуют как свободные электрические заряды, так и
связанные, действие которых отображается параметром eа . Переход в записи уравнения к вектору
D (см (3.3)) исключает из расчетов явление поляризации диэлектрика,
т.е. параметр eа. Это говорит о том, что при расчете
вектора D не учитывается характер диэлектрика
(его атомно-молекулярное строение) и поля, обусловленные одними и теми же
свободными зарядами, характеризуются в любых веществах и вакууме одними и теми же значениями вектора D. Поэтому можно утверждать, что вектор D обусловлен только свободными зарядами,
а вектор E - как
свободными, так и связанными зарядами. Введение вектора D
для описания электрических полей в веществе очень упрощает задачу. В
абсолютной системе единиц (СГС) вектор D
численно равен напряженности электрического E поля
от заданного заряда в вакууме.
Четвертое уравнение
Максвелла фактически является утверждением того, что силовые линии магнитного
поля непрерывны - не имеют ни начала ни конца.
Вследствие этого магнитный поток через любую замкнутую поверхность всегда
равен нулю - входящий в объем (отрицательный) поток равен выходящему
(положительному).
Магнитные заряды в природе
не обнаружены, поэтому нет точек в пространстве, где бы они могли прерваться.
Эти утверждения выражаются с помощью операторов в следующем виде:
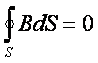
, (3.6)
divB= 0. (3.7)
Равенство нулю дивергенции
вектора поля показывает на то, что линии вектора либо начинаются и
заканчиваются в бесконечности, либо имеют замкнутый вид кольца. Такие поля
называются также соленоидальными.
3.2. Второе уравнение Максвелла
М. Фарадей экспериментальным путем
открыл закон электромагнитной индукции который утверждает, что в проводящем
контуре L возникает ЭДС, величина которой Э
равна скорости изменения магнитного потока
Фм во времени, т.е.
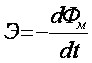
. (3.8)
Знак «минус» означает, что
возникающая ЭДС создает в контуре ток такого направления, который создает
вторичный поток, направленный против первичного внешнего магнитного потока. ЭДС
в замкнутом контуре определяется циркуляцией
вектора ![]() вдоль этого контура
вдоль этого контура
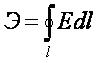 .
.
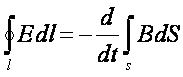 С учетом
математического определения оператора
«поток» формула (3.8) запишется в виде
С учетом
математического определения оператора
«поток» формула (3.8) запишется в виде
, (3.9)
где S
– площадь, охваченная контуром L.
Это и есть закон
электромагнитной индукции Фарадея, обобщенный Максвеллом на случай любого
воображаемого контура (не только Фарадеевского проводящего). Производная во времени может быть внесена под
знак интеграла, т.е.
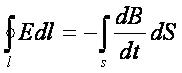
![]() . (3.10)
. (3.10)
Уравнения (3.9) и (3.10)
равнозначны, отличаются только тем, что в них изменен порядок математических
операций - в формуле (3.10)
сначала дифференцируется функция вектора
В, затем берётся
интеграл, а в формуле (3.9) наоборот. Эти уравнения представляют второе
уравнение Максвелла в интегральной форме в современной нумерации и фоpмe
записи.
Применив к обеим частям
операцию взятия ротора (подобно (1.6)), получим дифференциальную форму
уравнения
![]()
rotE= . (3.11)
Это уравнение утверждает,
что вычисленный ротор вектора Е в любой точке поля совпадает по величине и
направлению (помните, ротор является векторной величиной) с вектором скорости
изменения вектора B взятого с обратным знаком.
Следовательно, если в этой точке есть переменное магнитное поле (dB/dt ¹ 0), то вокруг этой точки всегда
существует вихревое электрическое поле (rotE ¹ 0). Переменные во времени электрические и магнитные поля
неразрывно связаны друг с другом.
Электрическое поле создаётся не только электрическими зарядами, но и переменным
во времени магнитным полем.
Уравнение (3.11) в скалярной форме в прямоугольной системе координат
имеет вид
![]()
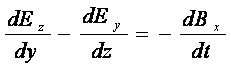
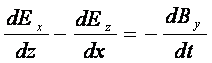 (3.12)
(3.12)
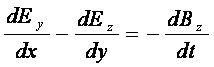
3.3. Первое уравнение
Максвелла
Экспериментальные
исследования магнитного поля постоянного тока в воздушной среде показали, что
существует связь между циркуляцией вектора B по контуру L окружающему провода с алгебраической
суммой их постоянных токов I в виде
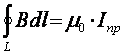
, (3.13)
Здесь m0 - магнитная постоянная вакуума. В
системе единиц СИ m0 = 4p × 10-7 Г/м, а в системе
единиц СГС равна 1.
В любой материальной среде
кроме тока проводимости I существуют также внутримолекулярные
упорядоченные элементарные токи, охватывающие контур интегрирования. Как было
указано в п.3.3, характер ориентации элементарных токов под воздействием
внешнего магнитного поля определяется параметром mа. Поэтому подставив в формулу (3.13) mа
вместо m0
для однородной изотропной среды получим
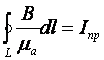 , (3.14)
, (3.14)
или применив материальное уравнение
(2.3), имеем
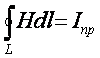 . (3.15)
. (3.15)
Таким образом,
рассматривавшая математическая связь между постоянными токами и создаваемыми
ими магнитными полями может быть выражена, как через вектор B, так и вектор H. Сравнение формул (3.14) и (3.15) показывает, что
при проведении расчетов поля через H магнитные свойства среды исключаются из учета. Введение H очень упрощает описание магнитных
полей в веществе - напряженность магнитного поля H имеет одно и тоже значение в любых
средах (в одной и той же точке, от одного и того же источника). Уравнение (3.14) показывает, вектор B
обусловлен как макроскопическими токами Iпр так и элементарными
токами (отображенными параметром mа). При проведении расчета поля через H, внутримолекулярные токи не участвуют
напрямую в расчетах.
По аналогии с
электрическим смещением (индукции) D (см.п.3.1) вектор H
в силу сходности рассуждений следовало бы назвать вектором магнитного смещения
(индукции), а B - вектором
напряженности магнитного поля. К сожалению, установившуюся терминологию
изменить невозможно.
Максвелл выявил
способность переменных электрического и магнитного полей возбуждать друг друга.
Возбуждение вихревого электрического поля переменным магнитным полем
показывает (см.п.1.3) уравнение
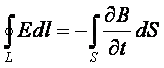
,
а переменное электрическое поле (т.е. ¶D/dt ¹ 0 или ¶Е/dt ¹ 0) должно бы создавать вихревое магнитное поле, т.е.
описание полей должно
быть симметричным:
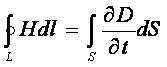
![]() .
.
Дальнейшие теоретические исследования показали, что в переменном поле
уравнение (3.15) приобретает вид
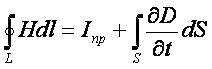
, (3.16)
Максвелл ввел новые понятия
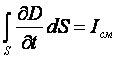
- ток смещения,
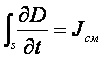
- плотность тока смещения,
а вектор D второе название - вектор
электрического смещения.
Формула (3.16) выражает обобщенный
закон полного тока и является первым уравнением Максвелла в интегральной форме.
Оно утверждает, что циркуляция вектора Н по любому замкнутому контуру в
электромагнитном поле численно равна алгебраической сумме токов проводимости и
смещения, пронизывающих поверхность внутри контура. С учетом формул (1.3),
(2.1), (2.2) уравнение (3.16) записывают также
в видах:
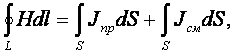
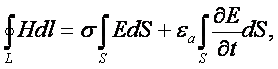 (3.17)
(3.17)
взятие операции вида (1.6) с обеих
частей уравнений (3.17) переводит их в дифференциальную форму
![]() ,
,
либо 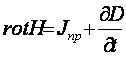 ,
,
либо 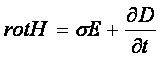 . (3.18)
. (3.18)
Дифференциальная
форма 1-го уравнения Максвелла утверждает, что ![]() в любой точке ЭМП
равен алгебраической сумме плотностей токов проводимости и смещения,
протекающих через точку. Так как ротор представляет векторную величину, то
равенство соблюдается по всем одноименным проекциям векторов в правой и левой
частях уравнения.
в любой точке ЭМП
равен алгебраической сумме плотностей токов проводимости и смещения,
протекающих через точку. Так как ротор представляет векторную величину, то
равенство соблюдается по всем одноименным проекциям векторов в правой и левой
частях уравнения.
Если рассмотреть идеально
диэлектрическую среду — вакуум или
близкий к нему чистый сухой воздух, то в (3.18) следует принять s = 0.
Тогда уравнение (3.18) приобретает вид
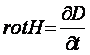
. (3.19)
Отсюда следует, что если в
данной точке пространства присутствует переменное электрическое поле (т.е. ¶D/dt ¹ 0), то оно создает вокруг точки
вихревое магнитное поле. Иначе говоря, магнитное поле создается не только
токами проводимости, но и переменным электрическим полем. Переменные
электрическое и магнитное поля неразрывны и представляют единое ЭМП.
Скорость изменения электрического
поля
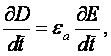
как было указано выше, представляет
плотность тока смещения. Ток смещения в реальных диэлектриках создается, в
основном, за счет колебательного движения связанных зарядов под взаимодействием
переменного электрического поля, т.е. является поляризованным током. Однако он
существует и в вакууме, где нет связанных зарядов. В этом легко убедиться
опытным путем, подключив последовательно в цепь источника переменного
напряжения вакуумный (либо воздушный) конденсатор. Амперметр показывает наличие
тока в цепи с участком из вакуума, который для постоянного напряжения
представляет разрыв цепи.
3.4. Уравнение непрерывности полного тока
Это уравнение получается
из первого уравнения Максвелла, т.е. является его следствием. Возьмем операцию
дивергенция с обеих частях, т.е.
div (rot H) = div (Jnp +
Jcм).
Из векторного анализ известно, что
дивергенция от ротора тождественно равна нулю. Тогда
div (Jпр + Jсм) = 0
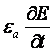 или
или
div (Jпр + ) = 0
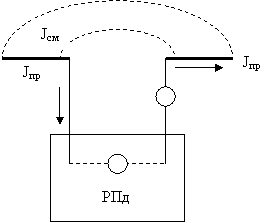
 Равенство нулю дивергенции вектора означает, что
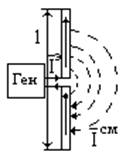
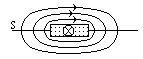
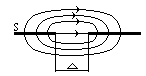
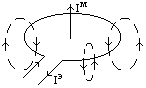
линии вектора замкнуты (см.п.3.1, формула (3.7)). Следовательно линии полного тока неразрывны. Это объясняет тот факт,
почему протекает ток через антенны, представляющие незамкнутые отрезки
проводов. На рис.3.1 приведена схема радиопередатчика (РПдУ) с антенной типа
«симметричный вибратор». Хотя концы проводов антенны разомкнуты, индикатор
выходного каскада показывает наличие
тока в антенне. Линии тока проводимости замыкаются через воздушное пространство
токами смещения.
Равенство нулю дивергенции вектора означает, что
линии вектора замкнуты (см.п.3.1, формула (3.7)). Следовательно линии полного тока неразрывны. Это объясняет тот факт,
почему протекает ток через антенны, представляющие незамкнутые отрезки
проводов. На рис.3.1 приведена схема радиопередатчика (РПдУ) с антенной типа
«симметричный вибратор». Хотя концы проводов антенны разомкнуты, индикатор
выходного каскада показывает наличие
тока в антенне. Линии тока проводимости замыкаются через воздушное пространство
токами смещения.
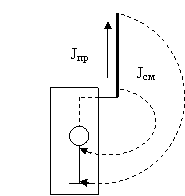
Рис.3.1. Непрерывность линий полного тока
ТЕМА 4. Монохроматическое ЭМП, его
уравнения, комплексные векторы, комплексная диэлектрическая проницаемость
4.1. Комплексные вектора, уравнения ЭМП в комплексной форме
Уравнения, рассмотренные выше, записаны
для мгновенных значений векторов поля, т.е. справедливы для их произвольного
характера изменения во времени. Если вектора изменяются во времени
синусоидально с постоянным периодом, то такое поле называют монохроматическим.
Для такого поля можно вводить комплексные векторы, т.е. воспользоваться методом
комплексных амплитуд (МКА). В этом методе вместо мгновенного значения,
например, H = Hmsin(wt+jн) ставят формальную комплексную величину Hmejwt. Видно, что
H
= Im[Hmejwt],
где Im
указывает на мнимую
часть комплексной величины.
В большинстве книг по
теории ЭМП монохроматическим считают
поле, косинусоидально
изменяющееся во времени. Тогда Н = Re [Hmejwt], т.е. применяют вещественную часть комплексной величины. Переход
от мгновенных значений
значительно упрощает математическое рассмотрение гармонических физических явлений, т.к. исчезают
операции дифференцирования
и интегрирования во времени, они заменяются на операции умножения и деления на множитель (jw), где w - частота рассматриваемой гармоники. Плотность тока смещения
заменяют соответствующей величиной
вида
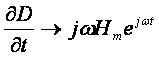 .
.
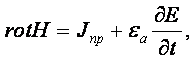 Вместо уравнения
Вместо уравнения
(3.1)
используют ![]() ,
,
![]() а
сократив на общий множитель получают вид
а
сократив на общий множитель получают вид
. (3.2)
Первое уравнение Максвелла (3.1) в
отличии от комплексного вида (3.2) записано для реально существющих полей.
Уравнение (3.2) скорее является математическим образом (3.1), и оно справедливо
только для гармонического поля, т.е. для одной спектральной составляющей
сигнала, а сигнал связи, как известно, состоит из набора спектральных
составляющих. Следует помнить, что при использовании уравнений ЭМП в
комплексной форме расчеты проводятся для гармонического характера изменения
векторов поля, т.е. для частного случая.
Остальные уравнения Максвелла в
комплексной дифференциальной форме имеет вид
rot E = - jwmа![]() ,
,
divD = rсвоб,
divB = 0.
В интегральной форме уравнений, дополнительно появляются
только точки над векторами. Из ответов, полученных из решения комплексных
уравнений, для получения истинного ответа выделяют вещественную часть комплексного вектора
4.2. Комплексная диэлектрическая проницаемость. Угол потерь
Подставим в (3.2) третье
материальное уравнение (1.5) и получим
rоt H = (s+jwea) E.
Преобразуем
множитель правой части уравнения
rot H = jwea (1-j![]() ) E.
) E.
![]() Математическая запись анализа процессов
значительно сокращается если ввести новый коэффициент - комплексную
диэлектрическую проницаемость
Математическая запись анализа процессов
значительно сокращается если ввести новый коэффициент - комплексную
диэлектрическую проницаемость
ea = ea (1- j
) , (3.3)
Тогда уравнение
приобретает вид
rot H = jwea E.
Формулу (3.3)
можно записать в алгебраической и показательной формах комплексного числа
ea = ea - j , (3.3.a)
![]()
![]() ea = . (3.3.б)
ea = . (3.3.б)
Тождественность (3.3а) и (3.3б)
показывает изображение числа (3.3а) на комплексной плоскости (см. рис.3.1)
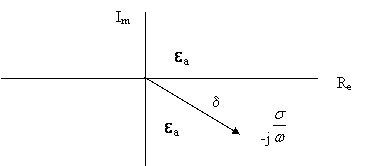
Рис.3.1.Комплексная
диэлектрическая проницаемость
Полученная из (3.3.б) с помощью формулы Эйлера
тригонометрическая форма комплексной проницаемости
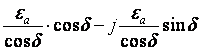 eа =
eа =
приводит к еще одной необходимой форме
![]() , (3.4)
, (3.4)
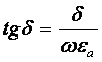 где , (3.5)
где , (3.5)
называют тангенсом угла диэлектрических потерь tgd. Потери электрического поля вызываются токами
проводимости и токами смещения в среде. Параметр tgd указывает на потери от тока
смещения, т.е. от трения заряженных частиц при смещении их в молекулах под
воздействием внешнего электрического поля.
Модуль
комплексной плотности тока проводимости равен
![]() ,
,
а тока смещения
![]() ,
,
Их отношение равно
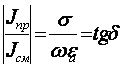 . (3.6)
. (3.6)
Следовательно, параметр tgd показывает на сколько в данной среде токи
проводимости превышают токи смещения, и является критерием деления сред на
проводники и диэлектрики.
Если tgd >10 (tg d » 10), то эту среду считают средой с большими потерями
или проводником.
Если tgd <0,l, то эта среда с малыми потерями, т.е. является
диэлектриком.
Если 0,1<tgd <l0 , то в этой среде с потерями токи проводимости и смещения
отличаются несильно, среду условно
называют полупроводящей.
Сухой чистый воздух можно считать очень близким к вакууму, т.е. средой без потерь - tgd = 0).
Для
реальных качественных диэлектриков
в радиодиапазоне (до f = 30 ГГц) tgd = 10-2…10-4.
4.3. Система уравнений монохроматического поля с учетом стороннего источника
В уравнениях (3.1) и (3.2) отсутствуют
токи Jпр и Jсм , созданные в этой среде присутствующим полем. Эти токи
не являются источниками поля, а возникли под его воздействием. В тоже время ЭМП
само создается каким-то источником за счет энергии, получаемой извне. Таким
источником чаще всего является антенна, ток по которой создает мощный выходной
каскад радиопередатчика (см. рис.2.1). Ток антенны определяется мощностью
внешних ресурсов (трансформаторной подстанцией) и не является функцией векторов
рассматриваемого поля в среде. Источник
электромагнитного поля принято называть сторонней силой, Сторонняя сила,
это заданная функция, которая является исходной величиной при расчете ЭМП. Эту
силу чаще выражают через плотность тока
Jст, она присутствует в правой чести
первого уравнения Максвелла
rot![]() =
=![]() .
.
Так как ![]() = jweа, то первое
уравнение в комплексной форме имеет вид
= jweа, то первое
уравнение в комплексной форме имеет вид
rot ![]() = jweа
= jweа ![]() , (3.7)
, (3.7)
а
остальные уравнения:
rot ![]() = jwmа
= jwmа![]() , (3.8)
, (3.8)
div ![]() = r
своб . (3.9)
= r
своб . (3.9)
В уравнении (3.8) присутствует
комплексная магнитная проницаемость применяемая для учета потерь в магнитных
материалах от трения доменов при перемагничивании. Однако в технике СВЧ получил применение лишь
один тип магнитного материала - намагниченный феррит обладающий уникальными
свойствами. Другие материалы, применяемые в радиотехнике являются немагнитными,
не имеют магнитных потерь, поэтому в уравнении (3.8) вместо m
будем в дальнейшем писать mа.
Присутствие стороннего источника в
правой части уравнения (3.7) делает его неоднородным, т.е. уравнения без
сторонних источников
![]() rot
rot ![]() - jweа
- jweа ![]() = 0 (3.10)
= 0 (3.10)
rot![]() + jwmа
+ jwmа ![]() =0
=0
являются однородными.
Нетрудно заметить, что первое уравнение
получается из второго, а второе из первого, если заменитьH на
E , а eа на
mа . Это свойство уравнений Максвелла называют принципом
двойственности. Его применяют для получения решения некоторых задач путем
замены символов в ответах соответствующих уже решенных двойственных задач.
Некоторые задачи электродинамики
значительно упрощаются также, если ввести в систему уравнений сторонние
магнитные токи Jстм . Так как реально существующих магнитных
зарядов нет в природе, поэтому с физическом точки зрения Jстм является
фиктивной величиной.
Тогда симметричными по форме становятся и неоднородные уравнения
Максвелла:
![]() rot H -
jweа E = Jстм (3.11)
rot H -
jweа E = Jстм (3.11)
rotE
+ jwmа H = -J стм
С помощью симметричных однородных и
неоднородных уравнений Максвелла (3.10) и (3.11) путем перестановки векторов и
параметров получают решения рада задач, используя известные расчетные соотношения двойственных задач.
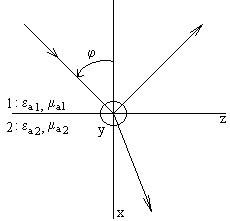
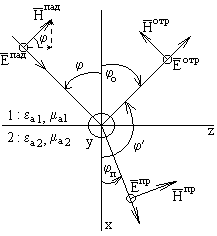
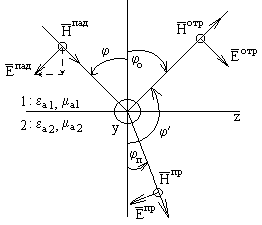
ТЕМА 5. Граничные условия для векторов поля
Граничными называют условия, которым
подчиняется поле на границах раздела
сред, отличающихся по
одной или нескольким парам электродинамических параметров.
Рассмотрим, например, одну из проекций
1-го уравнения Максвелла в среде без потерь (s = 0; Jпр = 0):
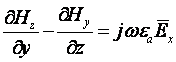 .
.
Это дифференциальное уравнение в
частных производных относительно составляющих вектора Hz и Hy связывает их с заданной величиной Еx
в одной из двух сред.
Подобного вида уравнения имеют
бесчисленное множество решений. Чтобы найти единственное решение следует найти
постоянные интегрирования. Их определяют исходя из граничных условий. В теории
электрических цепей такими являются начальные условия, известные по законам
коммутации. В теории ЭМП, в отличии от
Теории Электрических Цепей существует
много условий, т.к. каждый вектор поля имеет две проекции, для которых
граничные условия могут быть различными.
5.1. Составляющие векторов на границе раздела сред
Между материальными средами 1 и 2
находится поверхность - граница, по обе
стороны которой различные
электродинамические параметры,
одна пара - e1 и e2 или
m1 и m2. Среды могут различаться по
диэлектрическому параметру e, магнитному
m,
электропроводности s либо по
всем параметрам одновременно.
При переходе
ЭМП через границу проекции некоторых векторов поля скачкообразно, либо не
изменяются. Составляющими векторов
являются их проекции на касательную 1![]() и нормаль 1
и нормаль 1![]() к поверхности в точках над и под границей. Эти точки
очень близки к поверхности. На рис. 4.1 указаны составляющие вектора E в первый и во второй средах в этих точках 1 и 2. E1n и E2п — называются нормальными, а E1t и E2t
-касательными (тангенциальными) составляющими вектора E.
к поверхности в точках над и под границей. Эти точки
очень близки к поверхности. На рис. 4.1 указаны составляющие вектора E в первый и во второй средах в этих точках 1 и 2. E1n и E2п — называются нормальными, а E1t и E2t
-касательными (тангенциальными) составляющими вектора E.
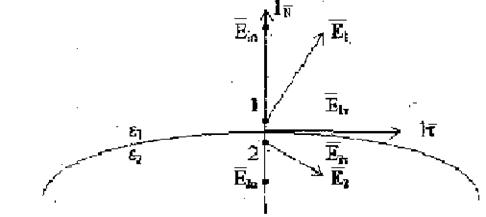
Рис. 4.1. Составляющие вектора E на границе разделе диэлектриков
5.2. Основные граничные условия
Характер границы определяет содержание
граничных условий. В общем случае по
граничной поверхности могут скапливаться сторонние электрические заряды
(например, на металлической поверхности в постоянном электрическом поле) или
протекать сторонний электрический ток. Поверхностные токи и заряды считают
сосредоточенными в бесконечно тонком слое, т.е. объемная плотность заряда r с
размерностью Кл/м3 превращается в rs с размерностью Кл/м2, а
плотность тока J
(А/м2) - в Js (A/k),
Js
отлична от нуля только в переменном электромагнитном поле на поверхностях с
очень высокой проводимостью.
1. Условие для нормальных составляющих вектора D на границе раздела с поверхностными
зарядами имеет вид
D1n-E1n= rs , (4.1)
т.е. при переходе поля из одной среды в другую, изменяется скачкообразно на величину rs. Если же нет поверхностных зарядов (например, на границе
диэлектрических сред), тo rs=0, а
D1n = D2n , (4.2)
Следовательно, в этом случае Dn поля не изменяется, т.е., она ocтается
непрерывной величиной.
2. Условие
для касательных составляющих вектора H.
На границе с
поверхностными токами наблюдается условие
H1t - H2t =JS, (4.3)
а если
нет поверхностных токов, (например, по поверхности проводов с постоянным
током), то
H1t = H2t . (4.4)
3. Условие
для нормальных составляющих вектора B. На границах
любого типа при переходе поля из одной среды в другую, Вn не может
измениться скачком, т.е.
В1n – В1n, (4.5)
4. Условие
для касательных соcтавляющих вектора E. Как показано на рис.4.1. при переходе ЭМП через границу векторы E1 и E2 в непосредственной близости над и под
границей отличаются как по длине и направлению, но у них неизменная проекция на
касательную к поверхности, т.е.
E1t = Е 2t (4.6)
Это граничное условие
справедливо для любых
границ, оно
показывает,
что на границе раздела сред Еt непрерывна.
Остальные
граничные условия получаются
из рассмотренных
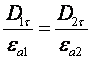 Используя материальные уравнения электродинамики.
Например, из (4.6) и (1.4) получим:
Используя материальные уравнения электродинамики.
Например, из (4.6) и (1.4) получим:
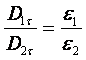 или
(4.7)
или
(4.7)
т.е. касательная составляющая
вектора электрической индукции при переходе ноля через границу сред изменяется
скачкообразно на величину отношения диэлектрических проницаемостей.
Таким
же образом из (4.2) получим;
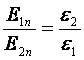 (4.8)
(4.8)
5.3. Условия на границе с идеальным проводником
В технике СВЧ наиболее распространенным
видом является граница в виде поверхности очень хорошего проводника - меде, серебра и др. металлов. При рассмотрении электромагнитных явлений
вблизи таких поверхностей, их можно считать идеально проводящими, т.е. с
параметром s бесконечно большим. Такое приближение
ведет к незначительной погрешности при определении поля в 1-ой диэлектрической
среде над поверхностью хорошего проводника (2-ой среды). В тоже время внутри идеального проводника ЭМП
не существует. В этом можно убедиться рассмотрев третье материальное уравнение ![]() пр2 = s E2 , где s=¥
превращает ток проводимости в бесконечность, что противоречит физике явлений.
Даже при очень больших значениях s;
пр2 = s E2 , где s=¥
превращает ток проводимости в бесконечность, что противоречит физике явлений.
Даже при очень больших значениях s;![]() пр остается конечной величиной, т.е. ¥ × E2 ¹ ¥.
Это возможно только при Е2
= 0, т.к. произведение ¥ × 0 неопределенная, т.е.
любая величина Равенство E2 = ¥.
отвечает также , E2t = E2n = 0.
пр остается конечной величиной, т.е. ¥ × E2 ¹ ¥.
Это возможно только при Е2
= 0, т.к. произведение ¥ × 0 неопределенная, т.е.
любая величина Равенство E2 = ¥.
отвечает также , E2t = E2n = 0.
Таким образом, внутри идеального
проводника электрического поля не бывает. Если учесть это (E2 = 0), то из уравнения rot Е2=-¶В2/¶t
следует, что в этом случае либо В2 = 0, либо В2
постоянная величина. В телекоммуникации применяют лишь переменные во времени
поля, поэтому внутри идеального проводника В2t=В2n=0, нет магнитного поля. Подставив эти
утверждения в равенства (4.3), (4.5) и (4.6) получим основные граничные условия на поверхности идеального проводника:
В1n = 0,
(4.9)
H1t = Js,
(4.10)
E1t
= 0. (4.11)
Равенство
(4.10) может быть записано в векторной форме
Js = [1N´H1t] (4.10.a)
Эти
условии графически изображены на рис. 4.1 и 4.2.
![]()
Е1
= Е1n
В1 = 1tВ1t
![]()
![]()
Рис. 4. 1. Расположение силовых линий поля вблизи идеально проводящей поверхности
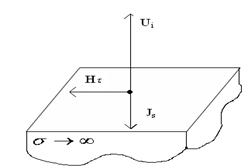
Рис. 4.2. Связь линии магнитного поля над
идеальным проводником с линиями поверхностного тока
Из
рисунков 4.1 , 4.2 следует, что
над поверхностью идеального проводника электрические силовые линии E всегда перпендикулярны, а магнитные -
параллельны ей. Плотность электрического тока на поверхности проводника равна
по величине и перпендикулярна по направлению касательной составляющей
напряженности магнитного поля у
поверхности. Этот вывод широко применяется при исследовании волн разных типов в
полых металлических волноводах
Можно также показать [Семенов],
структура поля в 1 среде такова, что касательная составляющая магнитного поля
достигает у плоской границы идеального проводника экстремального значения (в
направлении нормали к границе), т.е.
 .
(4.11)
.
(4.11)
Условие (4.11) также применяют в
частности при исследовании полей в металлических волноводах.
ТЕМА
6. Плоская однородная волна, поляризация волн
Под
волнами подразумевают колебательные движения непрерывных сред. Принципиальные
отличия в математическом описании волновых процессов и колебаний токов и
напряжений в радиотехнических цепях состоит в том, что для полного описания
любой системы достаточно знать конечное число токов и напряжений на различных
участках схем. Для полного описания волнового процесса необходимо знать его
характеристики в бесконечно большом числе точек в рассматриваемом пространстве.
Природа волновых процессов весьма разнообразна: электромагнитные волны,
акустические, гравитационные и т. д. Физики полагают, что при распространении любых
волн среда постепенно вовлекается в некоторый физический процесс, в результате
которого происходит распространение энергии в пространстве.
6.1. Плоские электромагнитные
волны в однородной изотропной в среде без потерь
Будем
рассматривать свободные (существующие без сторонних источников) гармонические
колебания электромагнитного поля в однородной изотропной среде без потерь. В
этом случае удобно воспользоваться однородными уравнениями Гельмгольца
относительно векторов электромагнитного поля.
![]() 1,
1,
![]() 2 ,
2 ,
![]() .
.
Векторные уравнения (1) и (2) можно записать в виде
системы из трех скалярных уравнений:
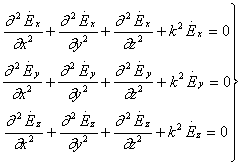 3,
3,
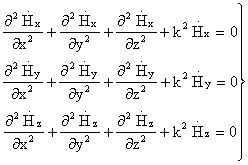 4.
4.
Наиболее просто уравнения (3) и (4) и их решения
выглядят в случае рассмотрения плоских электромагнитных волн. Под плоскими
подразумевают электромагнитные волны, распространяющиеся вдоль линейной
координаты, в каждый фиксированный момент времени неизменные в плоскости,
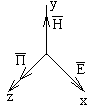
перпендикулярной направлению распространения. Будем полагать, что волна
распространяется вдоль оси Z, т.е. вектор Пойнтинга:
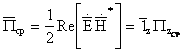 5.
5.
Из соотношения (5) видно, что вектор Пойнтинга
определяется компонентами электромагнитного поля, находящимися в плоскости xOy.
В данном случае отсутствуют составляющие поля вдоль оси z. Таким образом,
должно выполняться условие: поскольку по определению поле должно быть неизменно
в плоскости распространения волны, то
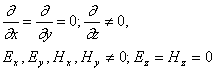 6.
6.
Используя соотношение (6), выражения (3) и (4) можно
переписать следующим образом
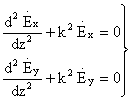 7,
7,
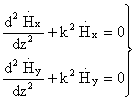 8.
8.
Решение каждого из уравнений ![]() 9 ,
9 ,
![]() 10.
10.
Для того, чтобы не увеличивать количество постоянных
интегрирования, компоненты поля ![]() найдем, используя решения (9), (10) и уравнения Максвелла.
найдем, используя решения (9), (10) и уравнения Максвелла.
![]() ,
,
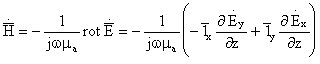 11,
11,
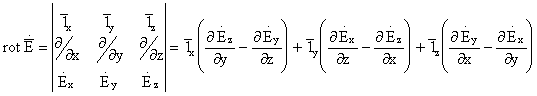 .
.
Используя соотношение (11), получим:
![]() 12,
12,
![]() 13.
13.
Вынося jk за скобки, получим: 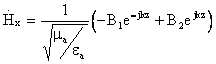 14,
14,
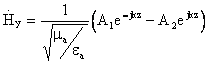 15.
15.
В итоге получим систему решений: ![]() 16,
16,
![]() 17,
17,
![]() 18,
18,
![]() 19.
19.
где 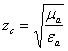 , [Ом] — характеристическое сопротивление среды,
определяющееся свойствами среды.
, [Ом] — характеристическое сопротивление среды,
определяющееся свойствами среды.
Пары (16)-(17) и (18)-(19)
образуют вектор Пойнтинга, ориентированный по оси z. Полученные нами решения
представляют собой сумму двух слагаемых (так как решалось дифференциальное
уравнение). Уточним физический смысл каждого слагаемого. Для этого в уравнении
(16) перейдем от комплексных амплитуд к мгновенным значениям.
![]() ,
,
![]() 20.
20.
Аргумент первого слагаемого — ![]() 21 ,
21 ,
Аргумент второго слагаемого — ![]() .
.
Рассмотрим аргументы и слагаемые для t=t1,
z=z1, т.е. ![]() . Дадим приращение времени
. Дадим приращение времени ![]() и определим смещение
точек
и определим смещение
точек ![]() этого волнового процесса
с постоянными фазами
этого волнового процесса
с постоянными фазами ![]() .
.
|
|
Для того, чтобы оценить это смещение, рассмотрим
следующие равенства:
![]() 22,
22,
![]() 23.
23.
Приводя подобные члены в соотношениях (22) и (23),
получим:
![]() 24,
24,
![]() 25.
25.
Выражая ![]() в первом и втором
случаях, получаем:
в первом и втором
случаях, получаем:
![]() 26,
26,
![]() 27.
27.
Соотношение (26) определяет перемещения фиксированной
фазы ![]() , а соотношение (27) —
, а соотношение (27) — ![]() , т.е. соотношения (26) и (27) определяют фазовую скорость.
Соотношение (26) определяет положительную фазовую скорость. Следовательно,
компоненты
, т.е. соотношения (26) и (27) определяют фазовую скорость.
Соотношение (26) определяет положительную фазовую скорость. Следовательно,
компоненты ![]() и
и ![]() соответствуют плоской волне,
распространяющейся в положительном направлении оси z. Аналогично и в
соотношении (27).
соответствуют плоской волне,
распространяющейся в положительном направлении оси z. Аналогично и в
соотношении (27).
Итак,
в полученном нами решении (16) первое слагаемое - для плоской волны в
положительном направлении, второе слагаемое - в отрицательном.
Уточним физический
смысл волнового числа k. Волновое число k показывает изменение фазы волны в
радианах при прохождении волной пути в 1 метр. Минимальное расстояние на
котором фаза волны изменяется на 2p называется длинной волны (пространственным периодом).
![]() 28,
28,
![]() 29.
29.
Проанализируем полученные
решения на примере ![]() ,
, ![]() .
.
![]() ,
,
![]() .
.
В этих общих
решениях выделим слагаемые, которые соответствуют волне, распространяющейся в
положительном направлении оси z:
![]() 30,
30,
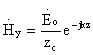 31.
31.
Перейдем
к мгновенным значениям:
![]() 32,
32,
![]() 33.
33.
Из приведенных соотношений следует:
- z = const — это поверхность
равных фаз представляет собой плоскость
- Поверхность равных амплитуд
совпадает с поверхностью равных фаз (плоская однородная волна)
- В направлении
распространения отсутствуют составляющие поля (плоская, однородная, поперечная)
- Компоненты поля плоской
волны взаимноортогональны и перпендикулярны направлению распространения волны.
Между составляющими поля плоской волны
существует взаимосвязь.
|
|
![]() ,
,
![]() .
.
Определим энергетические
характеристики:
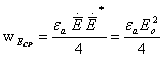 — объемная плотность
электрической энергии,
— объемная плотность
электрической энергии,
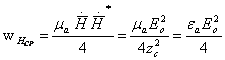 — объемная плотность
магнитной энергии.
— объемная плотность
магнитной энергии.
Так
как среда однородная, изотропная и без потерь,
 .
.
Определим скорость распространения энергии:
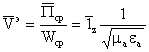 .
.
Уравнение для фазовой скорости: ![]() , где
, где ![]() .
.
Тогда в случае среды без потерь: ![]() .
.
Различные
комбинации полного решения для плоской электромагнитной волны фактически
соответствуют одной и той же плоской волне при различных ее ориентациях
относительно выбранной системы координат.
6.2. Плоские волны в однородной изотропной среде с проводимостью, отличной от нуля
В среде с проводимостью, отличной от нуля, энергия
электромагнитной волны частично расходуется на возбуждение и поддержание токов
проводимости. В общем случае в среде могут присутствовать также диэлектрические
и магнитные потери. Тогда:
![]() 1,
1,
![]() 2,
2,
![]() 3.
3.
В этом случае решения по
форме совпадают с полученными в предыдущем параграфе.
![]() 4,
4,
![]() 5,
5,
![]() 6.
6.
Перейдем для уяснения
физического смысла к мгновенным значениям:
![]() ,
,
![]() .
.
В некоторый фиксированный
момент времени изобразим ![]() .
.
Отметим физический смысл: g — комплексная постоянная распределения;
b — ее действительная часть, смысл тот же, что
и у k, т.е. показывает изменение фазы волны в радианах при прохождении волной
пути в 1 метр (фазовая постоянная); a — мнимая часть g. Показывает, во сколько раз уменьшается
амплитуда волны на пути в 1 метр (постоянная затухания).
Уменьшение амплитуды волны в
процессе распространения характеризуют величиной затухания:
 , [Нп]
7,
, [Нп]
7,
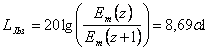 , [дБ].
, [дБ].
Будем рассматривать случай, когда потери в среде
вызваны конечной проводимостью (только Джоулевы потери):
![]() и
и ![]() ,
,
![]() 8,
8,
Чтобы
получить выражения для b и a, возведем в квадрат и
получим:
![]() , Ñ.
, Ñ.
![]()
Выразим во втором уравнении мнимую часть и подставим
в первое.
![]() ,
,
 .
.
Решаем квадратное уравнение:
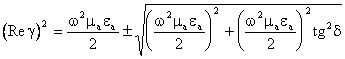 ,
,
![]() .
.
Так как в левой части стоит
возведение в квадрат, то в этом соотношении учитывается только знак
"+". Тогда: ![]() ,
,
откуда получаем: ![]() 9.
9.
Воспользуемся соотношением (Ñ), из которого следует, что
мнимая часть
![]() .
.
Подставим (9) в (Ñ).
![]() ,
,
![]() .
.
Так как левая часть
возведена в квадрат, то правая часть не может быть отрицательной. Получаем:
![]() ,
,
![]() 10.
10.
Проанализируем экспоненциальный множитель ![]() . Подстановкой можно получить:
. Подстановкой можно получить: ![]() . Физически реальными являются первое и последнее произведения.
Первое из них соответствует затухающей волне, распространяющейся в
положительном направлении оси z, а последнее — в отрицательном направлении оси
z. Таким образом поле плоской волны, распространяющейся в среде с потерями,
может быть представлено следующими соотношениями:
. Физически реальными являются первое и последнее произведения.
Первое из них соответствует затухающей волне, распространяющейся в
положительном направлении оси z, а последнее — в отрицательном направлении оси
z. Таким образом поле плоской волны, распространяющейся в среде с потерями,
может быть представлено следующими соотношениями:
![]() 11,
11,
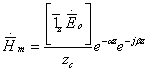 12.
12.
В данном случае
характеристическое сопротивление среды является комплексной величиной.

![]() .
.
Это можно преобразовать следующим образом:
![]() ,
,
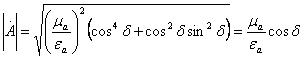 ,
,
![]() ,
,
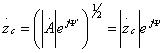 ,
,
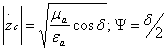 13.
13.
![]() .
.
Рассмотрим, как меняются
фаза и характеристическое сопротивление при изменении s = 0...¥.
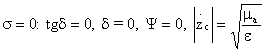 ,
,
![]() .
.
С ростом проводимости
характеристическое сопротивление по модулю убывает.
Вывод:
По определению ![]() . В среде с отличной от нуля проводимостью при постоянной
напряженности электрического поля
. В среде с отличной от нуля проводимостью при постоянной
напряженности электрического поля ![]() с ростом проводимости увеличивается амплитуда магнитной
компоненты
с ростом проводимости увеличивается амплитуда магнитной
компоненты ![]() .
.
Физически это можно
объяснить так:
в среде с проводимостью,
равной нулю, присутствуют только токи смещения ![]() . Если проводимость равна нулю, то в среде дополнительно
появляются токи проводимости. Причем при неизменной напряженности
электрического поля и диэлектрической проницаемости среды плотность тока
остается неизменной.
. Если проводимость равна нулю, то в среде дополнительно
появляются токи проводимости. Причем при неизменной напряженности
электрического поля и диэлектрической проницаемости среды плотность тока
остается неизменной.
Проанализируем полученный результат. Пусть ![]() имеет только иксовую
составляющую, тогда вектор
имеет только иксовую
составляющую, тогда вектор ![]() будет иметь одну
составляющую, ориентированную по оси y, если волна распространяется вдоль оси
z. Будем предполагать, что амплитуда
будет иметь одну
составляющую, ориентированную по оси y, если волна распространяется вдоль оси
z. Будем предполагать, что амплитуда ![]() является действительной величиной.
является действительной величиной.
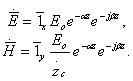
Перейдем к мгновенным
значениям: ![]() ,
,
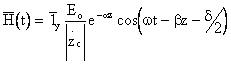
Проанализируем. Поверхность
равных фаз определяется уравнением z =const. Поверхность равных амплитуд
совпадает с поверхностью равных фаз, т.е. рассмотренный процесс является
плоской однородной волной.
Имеются составляющие поля, взаимноортогональные и
перпендикулярные направлению распространения волны, т.е. она является и
поперечной. Амплитуда волны экспоненциально убывает в процессе ее
распространения. В данном случае магнитная составляющая поля отстает от
электрической на угол ![]() .
.
Проанализируем основные характеристики электромагнитной
волны. Фазовая скорость равна:
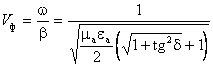 .
.
Из этого уравнения следует,
что так как b>k, то фазовая скорость в
среде с потерями меньше фазовой скорости в среде без потерь, так как ![]() .
.
В данном случае фазовая
скорость является функцией частоты. С ростом частоты tgd убывает и фазовая скорость возрастает.
Фазовая скорость зависит от проводимости среды. С ростом проводимости tgd увеличивается и фазовая скорость убывает.
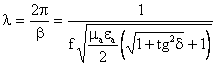 .
.
Из соотношения видно, что l в среде с потерями меньше l в среде без потерь. С ростом проводимости tgd увеличивается и l убывает. Распространение волны
сопровождается переносом энергии. Вектор Пойнтинга:
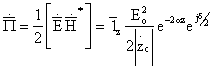 .
.
Среднее за период
значение: 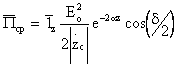 .
.
Вычислим скорость
распространения энергии:
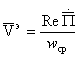 .
.
После подстановки получим,
что ![]() .
.

В результате можно отметить, что характеристики
плоских волн в среде с потерями и без потерь существенно отличаются. Главное
принципиальное отличие состоит в том, что Vф , VЭ , zс
в среде без потерь неизменны на любых частотах и определяются только
электродинамическими параметрами среды. В среде с потерями эти же параметры
являются функциями частоты. Явление зависимости параметров электромагнитной
волны от частоты называется дисперсией, а соответствующие среды
называются диспергирующими. Дисперсия возможна и в средах без потерь,
если хотя бы один из электродинамических параметров является функцией частоты.
Рассмотрим
два характерных случая распространения электромагнитных волн в реальных средах,
т.е. определим параметры плоской волны в реальных диэлектриках и металлах.
6.3. Распространение волн в
реальных диэлектриках
Для реальных диэлектриков ![]() .
. ![]() .
.
Используя неравенство,
скобку можно представить в виде ряда Маклорена:
![]() ,
,
![]() .
.
Ограничиваясь тремя
элементами разложения, пренебрегая всеми остальными, получаем:
![]() .
.
Приравнивая реальную и
мнимую части, получим:
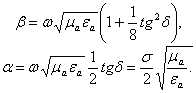
Используя выражение для b, получим:
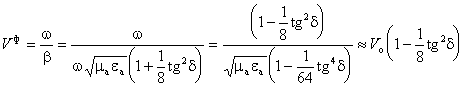 ,
,
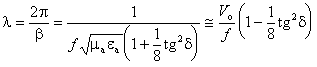 ,
,
где Vо
— скорость света в среде.
Из результатов следует, что параметры плоской волны в
реальных диэлектриках мало отличаются от параметров в среде без потерь.
Постоянная затухания l в реальных диэлектриках
является очень малой величиной и в первом приближении не зависит от частоты.
6.4. Распространение волн в
реальных металлах
В проводящих средах ![]() . Общее выражение:
. Общее выражение:
![]() ,
,
![]() .
.
Пренебрегая единицей, получим:
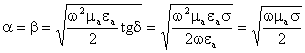 .
.
b и a нелинейно зависят от w, следовательно, с изменением w они будут существенно изменяться.
Получим выражение для фазовой скорости 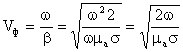
и
для длины волны
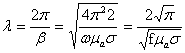 .
.
Характеристическое сопротивление:
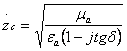 ,
,
пренебрегая единицей, получим
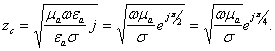
Представим ![]() в виде реальной и
мнимой частей:
в виде реальной и
мнимой частей:
![]() .
.
|
медь Vф=VЭ=421
м/сек l=4,21*10-6 м zс=3,74*10-4
Ом |
|
вакуум Vф=VЭ=3*108
м/с l=300 м zc=120p=377 Ом |
Сравним параметры плоских волн в
вакууме и меди при частоте f =1МГц В
реальных проводниках электромагнитные волны
испытывают сильное поглощение. Так в меди с f = 1МГц на пути в 1 мм затухание составит
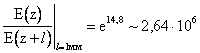
Металлы следует использовать
при экранировании переменного
электромагнитного
поля.
6.5.
Характерные параметры проводящих сред
Расстояние, на котором амплитуда волны уменьшается в
е раз, называется
глубиной проникновения d, т.е.
![]() ;
; ![]() .
.
В
общем случае: 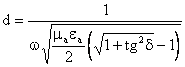 ,
,
или для проводящих сред:
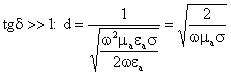 .
.
Отсюда следует, что w®d¯
6.6. Поляризация волн
Для описания ориентации волн в пространстве вводят
понятие поляризации. Под плоскостью
поляризации подразумевают плоскость, проходящую через направление
распространения волны параллельно
вектору ![]() .
.
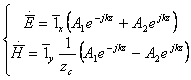 1,
1,
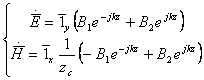 2.
2.
Для того, чтобы проанализировать возможные случаи
поляризации, рассмотрим следующие решения. Пусть плоская волна представляет
собой композицию решений из (1) и (2), которые также являются решением
уравнения Гельмгольца.
|
|
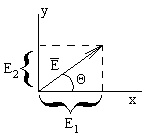
![]() 3.
3.
1.
Пусть слагаемые в соотношении (3) синфазные, т.е. ![]() ;
; ![]() ;
;
![]() .
.
Тогда результирующий вектор ![]() , а стало быть и плоскость поляризации оказываются
повернутыми на угол Q относительно оси x, причем
положение плоскости поляризации в процессе распространения волны остается
неизменным.
, а стало быть и плоскость поляризации оказываются
повернутыми на угол Q относительно оси x, причем
положение плоскости поляризации в процессе распространения волны остается
неизменным.
2.
Пусть слагаемые равны по амплитуде, а по фазе отличаются на 90°:
![]() ,
, ![]() ,
,
тогда
получим:
![]() .
.
Определим положение угла Q:
![]()
В этом случае положение плоскости поляризации
изменяется во времени и пространстве. Если зафиксируем некоторую плоскость, то
вектор ![]() будет вращаться со скоростью V, и его конец будет описывать окружность. Если зафиксируем время,
то вектор будет описывать спираль вдоль оси z. Этот случай поляризации
называется круговой, т.е. в процессе распространения плоскость поляризации
вращается. Это случай левой поляризации. Для получения правой поляризации
необходимо, чтобы
будет вращаться со скоростью V, и его конец будет описывать окружность. Если зафиксируем время,
то вектор будет описывать спираль вдоль оси z. Этот случай поляризации
называется круговой, т.е. в процессе распространения плоскость поляризации
вращается. Это случай левой поляризации. Для получения правой поляризации
необходимо, чтобы
![]() ,
, ![]() .
.
Условием круговой поляризации волны
является временная и пространственная квадратура составляющих в соотношении
(3). Компоненты должны быть взаимно ортогональны и должны отличаться по фазе на
90°, также необходимо выполнение условия
равенства амплитуд. В том случае, когда одно из условий не выполняется, имеем
эллиптическую поляризацию. В любой фиксированной плоскости вектор Е движется по
эллиптической замкнутой кривой. Степень поляризации характеризуют отношением
большой оси к малой.
ТЕМА 7.
Элементарный электрический и магнитный излучатели
|
|
|
|
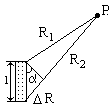
Под ЭЭИ подразумевают линейный проводник с переменным электрическим током, длина которого <<l (диаметр << длины). ЭЭИ предназначен для возбуждения электромагнитного поля в свободном пространстве.
Учитывая, что длина ЭЭИ << l, его можно рассматривать как гипотетический изотропный излучатель.
Для вычисления поля в точке Р, вдали от ЭЭИ, можно воспользоваться принципом суперпозиции. Для этого ЭЭИ можно разбить на элементарные излучатели, каждый из которых можно рассматривать как точечный излучатель.
Поле, возбуждаемое в каждом из фрагментов, будет отличаться по
фазе вследствие геометрической разности хода. Эта разность будет максимальна
для фрагментов, расположенных на краях ЭЭИ. Из рисунка видно, что максимальная
разность хода будет: ![]() ,
,
максимальная разность фаз ![]() .
.
По определению ![]() . Таким образом видно, что Dj будет мало при любом угле
a.
То есть это свойство, которое является основным свойством точечного излучателя,
позволяет ЭЭИ также рассматривать в качестве точечного.
. Таким образом видно, что Dj будет мало при любом угле
a.
То есть это свойство, которое является основным свойством точечного излучателя,
позволяет ЭЭИ также рассматривать в качестве точечного.
7.3. Ближняя и дальняя зоны ЭЭИ
В связи с тем, что поле при ![]() и при
и при ![]() существенно
отличается, вводят понятия ближней и дальней зоны ЭЭИ.
существенно
отличается, вводят понятия ближней и дальней зоны ЭЭИ.
Ближнюю
зону (БЗ) определяют правилом gr<<1 1.
Дальняя
зона (ДЗ)
gr>>1 2.
Точной границы между ними не существует.
Рассмотрим свойства электромагнитного поля в ближней и дальней зонах.
В БЗ поле имеет преимущественно реактивный характер. Говорят, что в БЗ поле является квазистатическим, т.е. в БЗ поле сохраняется даже частота возбуждающего тока стремится к 0. В БЗ существуют все 3 компоненты Е q, Еr, Нj. Амплитуда поля в БЗ быстро затухает с удалением от ЭЭИ.
В ДЗ (зона излучения) компоненты поля синфазны, что свидетельствует об активном характере электромагнитного поля. Еr пренебрежимо мала по сравнению с Е q. Вектор П чисто активен и параллелен радиальной координате, т. е. активная мощность переносится в радиальном направлении. Поле в ДЗ имеет характер бегущей волны, уносящей энергию на бесконечность.
Ввиду особой важности поля рассмотрения в ДЗ приведем предельные соотношения для составляющих поля в ДЗ:
![]() 3,
3,
![]() 4,
4,
![]() 5.
5.
Компоненты поля взаимно перпендикулярны и перпендикулярны направлению распространения волны (одно из свойств плоской волны). Из соотношений видно, что фазовый фронт имеет форму сферической волны.
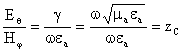 .
.
(Одно из свойств плоской волны). На достаточно большом удалении от ЭЭИ локальный фрагмент фазового фронта обладает свойствами локально плоской волны (компоненты поля взаимно перпендикулярны и перпендикулярны направлению распространения).
7.4. Диаграмма направленности ЭЭИ
Из соотношений (3), (4) предыдущего параграфа видно, что амплитуда поля в различных направлениях существенно различна, т. е. ЭЭИ обладает направленными свойствами. Для описания направленных свойств излучателей вводят диаграмму направленности. Под ней подразумевают зависимость амплитуды поля в ДЗ от угловых координат. Из (3), (4) видно, что диаграмма направленности описывается sinq. При анализе характеристик антенн пользуются понятием нормированной диаграммы направленности. Под нормированной подразумевают диаграмму направленности пронормированную к максимальному значению
|
|
![]() .
.
|
|
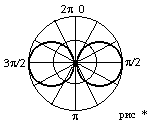
Очень наглядным является изображение диаграммы направленности в полярной системе координат. В полярной системе координат для наглядности q измеряют не от 0 до p, а от 0 до 2p с тем, чтобы показать пространственную симметрию ЭЭИ.
|
|
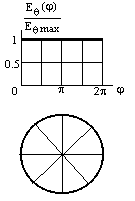
В меридианальной плоскости (проходящей через ось ЭЭИ) диаграмма направленности имеет, показанный вид рис . В плоскости перпендикулярной оси излучателя (экваториальная плоскость) ДН приведена на рис.**.
Рис.**
7.5.
Вычисление излучаемой мощности.
Сопротивление излучения
Так как излучение в форме бегущей волны существует в ДЗ, то данный анализ должен относится исключительно к ДЗ. В ДЗ составляющие поля имеют вид:
![]() 1,
1,
![]() 2.
2.
Вычислим Пср,
а затем, т. к. ЭЭИ является единственным, найдем ![]() . Замкнутая поверхность должна охватывать ЭЭИ и находится в
ДЗ. Форма ее может быть произвольная. Наиболее просто интегрирование
осуществляется для сферической поверхности.
. Замкнутая поверхность должна охватывать ЭЭИ и находится в
ДЗ. Форма ее может быть произвольная. Наиболее просто интегрирование
осуществляется для сферической поверхности.
Вычислим Пср: 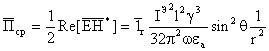 .
.
Осуществим
интегрирование в сферической системе координат. Учтем, что ![]() .
.
Получим 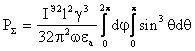 .
.
Учитывая, что 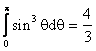 (табличный) получим:
(табличный) получим: ![]() 3.
3.
Из соотношения (3)
следует, что мощность излучения пропорциональна квадрату амплитуды тока в ЭЭИ.
Возникают ассоциации с обычным электротехническим определением: ![]() 4.
4.
В связи с этим RS называют сопротивлением излучения
![]() .
.
Преобразуем: ![]() ,
, ![]() ,
, 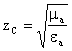 ,
,
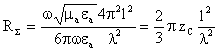 5.
5.
Если речь идет о
воздушном пространстве или вакууме, для которого ![]() Ом получим:
Ом получим:
![]() 6,
6,
из выражения для мощности излучения следует, что при постоянном токе с ростом сопротивления излучения мощность также возрастает. Поэтому, когда анализируют излучение, отмечают, что сопротивление излучения характеризует излучательную способность антенны, подчеркивая тем самым приведенную логическую связь:
![]() .
.
Поэтому с точки зрения антенных свойств (антенна предназначена для наиболее полного излучения мощности, подводимой к ее входу) ЭЭИ является плохой антенной (низкое сопротивление, мощность при постоянном токе).
7.6. Понятие о магнитном токе
|
|
Пусть имеется бесконечно тонкая пластина, по которой протекает электрический ток. В близости он нее магнитные линии повторяют контуры проводника. При удалении от пластины они постепенно стремятся к окружности.
В силу полной симметрии задачи на поверхности S тангенциальная компонента магнитного поля равна 0.
![]() (на поверхности S)
вне проводника,
(на поверхности S)
вне проводника, ![]() на проводнике.
на проводнике.
|
|
Рассмотрим две полубесконечных разнополярных металлических пластины, расположенные в плоскости S. Толщина исчезающе мала (бесконечно тонкие пластины). Между ними имеется зазор D. Силовые линии также превращаются в окружности.
![]() вне зазора;
вне зазора; ![]() в зазоре.
в зазоре.
Из сопоставления двух рисунков видно, что с точностью до направления силовых линий рисунки совпадают. Из этого совпадения следует заключение, что в зазоре параллельно его кромкам протекает магнитный ток, который и возбуждает подобное электрическое поле. В природе в настоящее время магнитных зарядов и токов не обнаружено, но введение подобным образом магнитных токов существенно упрощает решение многих задач.
Недостатки щелевых излучателей:
|
|
для излучения большой мощности напряжение щели должно быть велико, в свою очередь напряжение ограничено величиной пробоя в среде при заданных условиях.
Щелевой
излучатель является неединственным вариантом ЭМИ. В качестве ЭМИ могут
рассматриваться элементарные рамки с электрическим током (периметр рамки должен
быть << l). В этом случае можно полагать, что перпендикулярно поверхности рамки
протекает магнитный ток.
ТЕМА 8. Электромагнитная волна на границе раздела сред, законы
Снеллиуса, коэффициенты Френеля, полное прохождение волны через границу сред
8.1. Плоские
волны произвольной ориентации
В предыдущих параграфах мы рассматривали плоские волны, распространяющиеся вдоль осей декартовой системы.
|
|
Предполагаем, что среда без потерь.
![]() ,
,
![]() ,
,
![]() ,
,
где 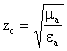 ,
, ![]() 1.
1.
Косинусы углов, определяющих направление волны, называются направляющими.
Уравнение фазовой плоскости (![]() =const):
=const):
![]() ,
,
где ![]() 2.
2.
Тогда скалярное произведение
![]() 3,
3,
 4.
4.
Мы
предполагали, что среда без потерь. В случае среды с потерями соотношения не
меняются, только вместо k подставляется g =b — ja. Перед началом рассмотрения
волновых явлений дадим ряд определений.
Плоскость,
проходящая через нормаль к границе раздела параллельно направлению
распространения волны, называется плоскостью
падения. Вектор ![]() перпендикулярен
направлению распространения волны, а относительно плоскости падения волны он
ориентирован произвольным образом.
перпендикулярен
направлению распространения волны, а относительно плоскости падения волны он
ориентирован произвольным образом.
Не
теряя обобщенности рассуждений, достаточно рассмотреть два случая ориентации ![]() .
.
1.) ![]() перпендикулярен
плоскости падения (нормальная поляризация)
перпендикулярен
плоскости падения (нормальная поляризация)
2.) ![]() параллелен плоскости
падения (параллельная поляризация)
параллелен плоскости
падения (параллельная поляризация)
При
произвольной ориентации вектора ![]() , он может быть представлен как суперпозиция двух этих
случаев.
, он может быть представлен как суперпозиция двух этих
случаев.
8.2. Падение плоской волны на
границу раздела двух диэлектриков
|
|
Вводное замечание
Рассмотрим падение плоской волны на плоскую границу раздела сред. Предположим, что потери в средах отсутствуют. Будем считать, что плоскость падения совпадает с плоскостью xOy декартовой системы координат. Угол между направлением распространения и осью x называется углом падения. Граница раздела сред совпадает с плоскостью yOz. Направляющие косинусы будут определяться следующим соотношением:
![]() ,
,
т.е. фазовый множитель:
![]() , где
, где
![]() .
.
8.3. Нормальная поляризация
В общем случае:
![]() 1,
1,
![]() 2.
2.
В данном случае вектор ![]() направлен так же, как
ось у.
направлен так же, как
ось у.
![]()
|
|
Фазовый множитель — ![]() ;
;
![]() ;
; 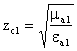 .
.
Можно записать уравнение падающей волны. Подставляя предыдущие замечания в уравнения (1) и (2), получим:
![]() 3,
3,
![]() 4.
4.
В общем случае в результате падения волны на границу падающая волна полностью или частично отражается или преломляется.
Естественно предположить, что отраженная и преломленная волны являются также плоскими, линейно поляризованными. Полагаем, что направление распространения падающей, отраженной и преломленной волн находится в плоскости xOz. Кроме того, отраженная и преломленная волны, так же как и падающая, являются нормально поляризованными. Тогда для отраженной и преломленной волн можно записать:
![]() 5,
5,
![]() 6,
6,
![]() 7,
7,
![]() 8,
8,
где ![]() ;
; 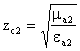 .
.
В данном
случае являются известными характеристики падающей волны j, ![]() . Искомыми являются j¢, jn,
. Искомыми являются j¢, jn,
![]() ,
, ![]() . Если в результате решения задачи нам удастся получить
решение, которое удовлетворяет следующим граничным условиям:
. Если в результате решения задачи нам удастся получить
решение, которое удовлетворяет следующим граничным условиям:
![]() ;
; ![]() 9,
9,
то,
в соответствии с теоремой единственности, найденное решение будет верным и
единственно возможным. Соотношения (9) должны выполняться во всех точках
границы раздела, которая совпадает с осью z, т.е. при любых z граничные условия
(9) должны выполняться. Это возможно, если падающая, отраженная и преломленная
волны имеют одинаковую зависимость по z.
![]() 10,
10,
![]() 11.
11.
Учитывая, что
угол j¢
имеет пределы ![]() , а угол j имеет пределы
, а угол j имеет пределы ![]() , мы делаем заключение, что:
, мы делаем заключение, что:
![]() 12.
12.
При анализе подобных задач обычно предпочитают пользоваться не углом j¢, а дополняющим углом jо — углом отражения:
![]() 13.
13.
Подставляя
соотношение (13) в (12), получим: ![]() 14
14
— первый закон Снелиуса.
Воспользуемся соотношением (11) из которого следует, что:
![]() 15,
15,
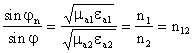 16.
16.
Соотношение
(15), записанное в форме (16), называется вторым
законом Снелиуса.
Отношение синуса угла отражения к синусу угла падения равно относительному коэффициенту преломления. Граничное условие (9) записывается следующим образом:
![]() , x = 0 17,
, x = 0 17,
![]() , x = 0 18,
, x = 0 18,
где
учтено, что тангенциальные компоненты в первой среде образуются падающей и
отраженной волнами, а тангенциальные компоненты во второй среде образуются
преломленными волнами. Подставляя в соотношения (17), (18) соответствующие
компоненты из соотношений (3) — (8), получим:
![]() 19,
19,
![]() 20.
20.
Учитывая одинаковую зависимость
по z, отметим, что все фазовые множители одинаковые, и их можно сократить.
Кроме того, ![]() , получим:
, получим:
![]() 21,
21,
![]() 22.
22.
Амплитуда
отраженной и преломленной волн пропорциональна ![]() , т.е.
, т.е.
![]()
где ![]() — коэффициент
отражения,
— коэффициент
отражения, ![]() — коэффициент
преломления.
— коэффициент
преломления.
![]() ,
,
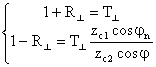 23.
23.
Решая эту систему, получим:
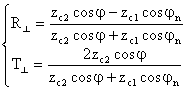 24.
24.
Коэффициенты отражения и преломления часто называют коэффициентами Френеля.
В соотношении (24) угол преломления можно исключить, используя закон Снелиуса.
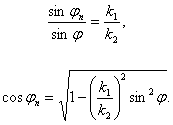
Теперь можем
записать результирующее поле в первой и второй средах, где учтено, что ![]() и
и ![]() :
:

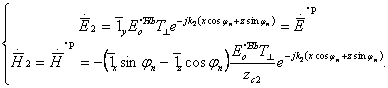
8.4. Параллельная поляризация
Рассмотрим
плоскую линейную поляризованную волну. Вектор ![]() находится в плоскости
падения ( так же, как и в первом случае).
находится в плоскости
падения ( так же, как и в первом случае).
Выражения для падающей, отраженной и преломленной волн:
![]() х £
0 1,
х £
0 1,
![]() , х £
0 2.
, х £
0 2.
Аналогично для отраженной и преломленной волн:
![]() , х £
0 3,
, х £
0 3,
![]() , х £ 0 4,
, х £ 0 4,
![]() , х ³ 0
5,
, х ³ 0
5,
![]() , х ³ 0 6.
, х ³ 0 6.
Неизвестными являются j¢,
jn,
![]() ,
, ![]() . Они могут быть найдены в результате решения граничной
задачи:
. Они могут быть найдены в результате решения граничной
задачи:
: ![]() ;
; ![]() 7.
7.
В данном случае соотношение (7) записывается следующим образом:
![]() , х = 0
8,
, х = 0
8,
|
|
![]() , х = 0
9.
, х = 0
9.
Соотношения (7), (8), (9) должны выполняться во всех точках границы раздела, т.е. при любых значениях координаты z. Это возможно, если составляющие поля отраженной, падающей и преломленной волн имеют одинаковую зависимость от z,
т.е.
![]() 10,
10,
![]() 11.
11.
Из соотношений (10), (11) следуют
законы Снелиуса: 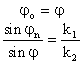 ,
,
т.е. законы Снелиуса инвариантны (безразличны) к поляризации падающей волны.
Подставим соотношения (8), (9) в соответствующие выражения для проекций поля:
![]() 12,
12,
![]() 13,
13,
Из соотношений (10), (11) следует, что все экспоненты равны. Сокращаем их и получаем:
![]() 14,
14,
![]() 15,
15,
![]() .
.
Тогда
соотношения (14), (15) можно переписать:
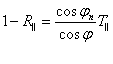 16,
16,
![]() 17.
17.
Решая систему, получим:
![]() 18,
18,
![]() 19.
19.
— коэффициенты Френеля для параллельной поляризации.
Косинус j можно исключить 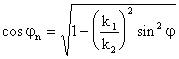
Если сравнить коэффициенты Френеля для нормальной и параллельной поляризации, то можно отметить, что для разных поляризаций коэффициенты Френеля различны.
Получим выражения для результирующего поля в первой и второй средах для параллельной поляризации:
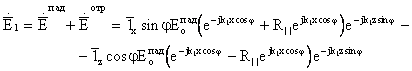 х £
0 20,
х £
0 20,
![]() х £
0 21,
х £
0 21,
![]() х ³
0 22,
х ³
0 22,
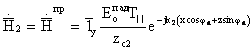 х ³
0 23.
х ³
0 23.
В том случае, если плоская волна падает по нормали к плоскости раздела, понятие плоскости падения теряет смысл. В этом случае углы падающий, отраженный и преломленный равны нулю, и выражения для коэффициентов Френеля упрощаются:
![]() ,
,
![]() .
.
8.5. Условия полного
прохождения волны во вторую среду.
Угол Брюстера
В случае эффекта полного преломления волна в первую среду не отражается и коэффициент отражения равен нулю.
Рассмотрим
случай параллельной поляризации:
![]() 1,
1,
![]() 2.
2.
Выражая косинусы угла падения через синусы, и возводя правую и левую части в квадрат, получим:
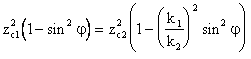 ,
,
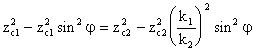 ,
,
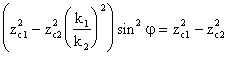 ,
,
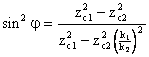 ,
,

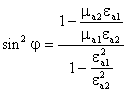 3,
3,
![]() .
.
Для
реальных диэлектрических сред выполняется равенство:
![]() 4.
4.
Тогда: 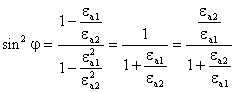 5.
5.
Вспоминая известное
тригонометрическое тождество: ![]() , получаем:
, получаем:
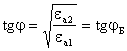 6.
6.
Угол ![]() называется углом
Брюстера.
называется углом
Брюстера.
В том случае, если в диэлектрических средах магнитные проницаемости не совпадают, то условие существования угла Брюстера определяется следующим неравенством:
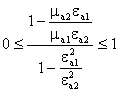 .
.
Рассмотрим
случай нормальной поляризации: ![]() ,
, ![]() .
.
Выражая ![]() и
и ![]() через
через ![]() и возводя в квадрат,
получим:
и возводя в квадрат,
получим:
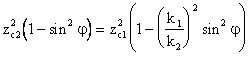 ,
,
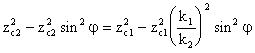 .
.
Выражая ![]() , получим:
, получим: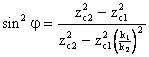 .
.
Вынося ![]() из числителя и
знаменателя и раскрывая ее через параметры среды, получим:
из числителя и
знаменателя и раскрывая ее через параметры среды, получим:
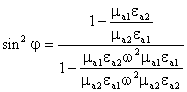 ,
,
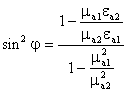 7.
7.
Из
соотношения (7) следует, что в этом случае существование полного преломления
возможно, если ![]() 8.
8.
Будем полагать, что ![]() 9.
9.
Получим: 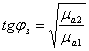 10.
10.
Если же в этой среде ![]() , то существование угла Брюстера определяется следующим
неравенством:
, то существование угла Брюстера определяется следующим
неравенством:
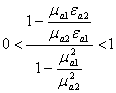 .
.
Полное
внутреннее преломление на границе диэлектрических сред с соотношениями ![]() и
и ![]() возможно только в
случае параллельной поляризации. Волны, нормально поляризованные, от границы
раздела двух диэлектриков отражаются при любых условиях.
возможно только в
случае параллельной поляризации. Волны, нормально поляризованные, от границы
раздела двух диэлектриков отражаются при любых условиях.
ТЕМА 9. Направляющие системы: полые волноводы, коаксиальные волноводы. Основные типы волн в волноводах, рабочие частоты, критические длины волн. Особенности применения волноводов, их основные параметры
Направляемые волны, в отличие от свободно распространяющихся в пространстве, могут существовать только при наличии направляющих элементов. Совокупность направляющих элементов образуют направляющую систему. Направляющие системы называют также линиями передачи энергии .
![]()
![]()
![]()
![]() Все
линии передачи можно разделить на два больших класса: линии передачи открытого
типа и линии передачи закрытого типа. В линиях передачи закрытого типа вся
энергия сосредоточена в пространстве, экранированном от внешнего металлической оболочкой. В линиях передачи
открытого типа ЭМП, строго говоря, распределено во всем пространстве,
окружающем линию. Однако открытые линии выполнены обычно т.о., что подавляющая
часть энергии ЭМП сосредотачивается в непосредственной близости от линии.
Все
линии передачи можно разделить на два больших класса: линии передачи открытого
типа и линии передачи закрытого типа. В линиях передачи закрытого типа вся
энергия сосредоточена в пространстве, экранированном от внешнего металлической оболочкой. В линиях передачи
открытого типа ЭМП, строго говоря, распределено во всем пространстве,
окружающем линию. Однако открытые линии выполнены обычно т.о., что подавляющая
часть энергии ЭМП сосредотачивается в непосредственной близости от линии.
Классификация направляемых волн
Направляемые
волны делятся: на поперечные, электрические, магнитные и смешанные. Поперечными или волнами типа Т называются волны, у которых в продольном направлении /в
направлении распространения энергии/ отсутствуют составляющие векторов
напряженностей электрического и магнитного полей. Векторы ![]() и
и ![]() лежат в плоскости,
перпендикулярной направлению распространения. Электрическими или
волнами типа Е называются волны, у которых вектор
электрического поля помимо поперечных составляющих, имеет продольную
составляющую. Продольная составляющая вектора магнитного поля равна нулю. Магнитными или
волнами типа Н называются волны, у которых вектор магнитного
поля, помимо поперечных составляющих, имеет продольную составляющую. Продольная
составляющая вектора электрического поля равна нулю. Смешанными (гибридными) называются волны, у которых векторы
электрического и магнитного полей имеют как продольную, так и поперечную
составляющую.
лежат в плоскости,
перпендикулярной направлению распространения. Электрическими или
волнами типа Е называются волны, у которых вектор
электрического поля помимо поперечных составляющих, имеет продольную
составляющую. Продольная составляющая вектора магнитного поля равна нулю. Магнитными или
волнами типа Н называются волны, у которых вектор магнитного
поля, помимо поперечных составляющих, имеет продольную составляющую. Продольная
составляющая вектора электрического поля равна нулю. Смешанными (гибридными) называются волны, у которых векторы
электрического и магнитного полей имеют как продольную, так и поперечную
составляющую.
Критическая частота. Критическая длина волны
![]()
h, является вещественной величиной, если
![]() 1,
1,
и мнимой
величиной, если ![]() 2,
2,
В первом случае фаза изменяется вдоль оси Z по линейному закону, что является признаком распространения волны с постоянной фазовой скоростью вдоль этой оси . Во втором случае вдоль оси Z фаза остается постоянной , а амплитуда убывает по экспоненте , что является признаком отсутствия переноса энергии вдоль направляющей системы .
Частота определяется
из условия ![]() 3,
3,
называется
критической . ![]() 4,
4,
Соответствующая этой частоте критическая длина волны равна:
![]() 5,
5,
Тогда ![]() 6,
6,
где ![]() - волновое число,
- волновое число,
а ![]() - длина волны в среде
с параметрами
- длина волны в среде
с параметрами ![]() и
и ![]() .
.
Согласно (1) свободное распространение волны по
направляющей системе имеет место лишь на частотах, превышающих критическую ![]() .
.
Назовем длиной волны ![]() в направляющей системе
минимальное расстояние между поперечными сечениями, соответствующими различным
значениям координаты Z
, в которых колебания сдвинуты по фазе на
2p. Так
как зависимость составляющих поля от координаты
Z описывается выражением:
в направляющей системе
минимальное расстояние между поперечными сечениями, соответствующими различным
значениям координаты Z
, в которых колебания сдвинуты по фазе на
2p. Так
как зависимость составляющих поля от координаты
Z описывается выражением: ![]() , то
, то
![]() 7.
7.
Направляющие системы
Прямоугольный волновод
Электрические волны (![]() и
и ![]() ) тип волны Е
) тип волны Е ![]()
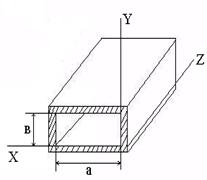
![]()
![]() (12.3. 14) имеет в декартовой системе координат вид :
(12.3. 14) имеет в декартовой системе координат вид : ![]() 1,
1,
Решение (1)
: ![]() 2,
2,
где Х(Х) - функция только Х , Y(y) - функция только Y .
(2)® (1) Þ ![]() 3,
3,
Выполнение (3) при произвольных значениях Х и Y возможно, если
![]() 4,
4,
где
![]() 5,
5,
![]() 6,
6,
Решение (6) имеет вид:
![]() 7,
7,
(7)® (2) Þ
![]() (*).
(*).
Так как стенки
волновода предполагаются идеально проводящими, то, применяя граничное условие ![]() :
: ![]() при х=0, х=a и при y=0, y=b
при х=0, х=a и при y=0, y=b
![]()
![]()
это
возможно, если: ![]() ,
,
для этого
необходимо : 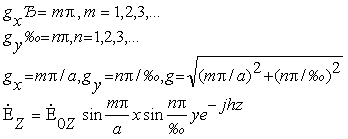 8,
8,
где ![]() и имеет смысл
амплитуды продольной составляющей
и имеет смысл
амплитуды продольной составляющей ![]() .
.
(1)и (2) в декартовой системе координат имеют вид:
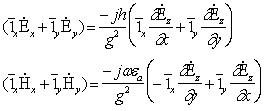
Подставляя (8) получим :
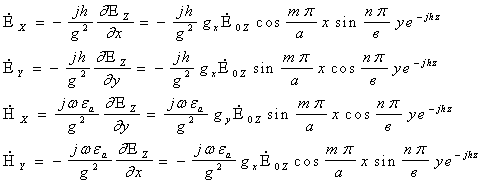 9.
9.
Как
следует из (8) , (9) структура поля волн типа Е в
плоскости поперечного сечения соответствуют структуре стоячих волн, причем m равно числу полуволн ,
укладывающихся вдоль стенки длиной а , и
n - число
полуволн , укладывающихся вдоль стенки длиной
b. Каждой паре
чисел m и n
соответствует определенная структура ЭМП , обозначаемая Еmnа .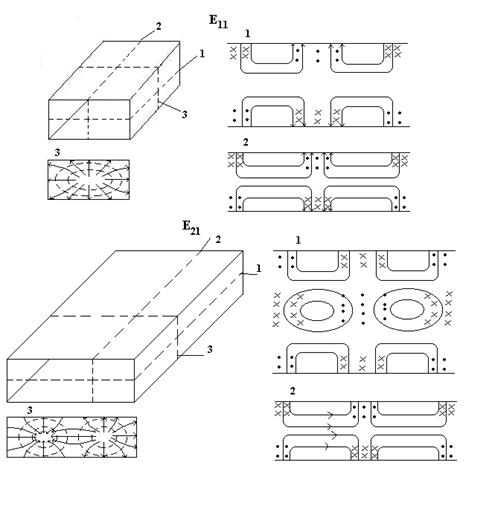
Отметим, что структуру волны Еz1 можно получить повторением структуры волны Е11 вдоль соответствующей координаты .
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() .
.
Низшим типом среди волн Еmn , обладающей наибольшей lкр, является волна Е11. Волны Еmn с различной структурой поля, которым соответствуют одинаковые значения g, имеющие равные коэффициенты распространения, фазовые скорости и скорости распространения энергии, называются вырожденными.
Магнитные волны (![]() и
и ![]() )
)
![]()
![]()
![]() (12.3.15) имеет в
декартовой системе координат вид:
(12.3.15) имеет в
декартовой системе координат вид: ![]() 10,
10,
![]() 11,
11,
На поверхности
идеально проводящих стенок волновода должно
выполнятся граничное условие: ![]() .
.
![]() 12,
12,
![]() 13,
13,
Подставляя (12), (13) в (11), приходим к соотношениям
![]() 14,
14,
Как следует из (14), у волн Н, как и у волн Е,
![]() ,
,
т.е. волны Н и Е с равными индексами являются вырожденными.
Подставляя в (11)
(14) и значения ![]() , получим:
, получим:
![]() 15,
15,
где Н0Z - =АС - амплитуда продольной составляющей магнитного поля.
Соотношения (8.7.1) , (8.7.2) в декартовой системе координат имеет вид:
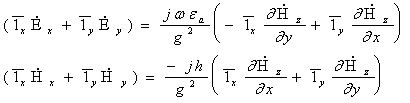
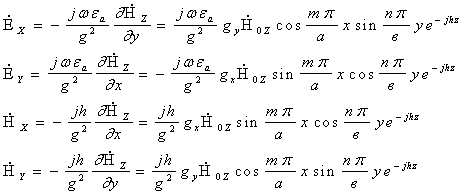 16
16
Как следует из (15), (16), у волн типа Н, как и у волн типа Е , структура поля в плоскости поперечного сечения соответствует структуре стоячих волн .
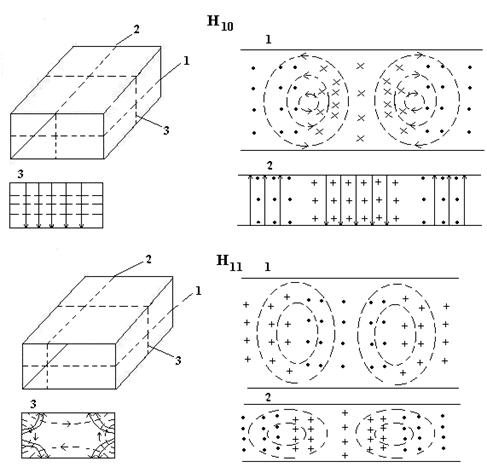
Как следует из равенств (15), (16), у волн Н, в отличие от волн Е, обращение в нуль одного из индексов (m или n) не влечет за собой обращения в нуль всех составляющих поля. Поэтому, если полагать а>b, то низшим типом волн Н является волна Н10.
![]() ,
,
![]()
Поскольку ![]() , то волна Н10
является низшим типом волны не только среди волн Н , но и среди всех
возможных типов волн в прямоугольном волноводе. Это означает, что при l>2а
передача энергии по прямоугольному волноводу невозможна.
, то волна Н10
является низшим типом волны не только среди волн Н , но и среди всех
возможных типов волн в прямоугольном волноводе. Это означает, что при l>2а
передача энергии по прямоугольному волноводу невозможна. ![]() ,
,
![]() ,
,
![]() .
.
Волна Н10
Волна Н10
имеет наибольшую критическую длину волны. Поэтому на заданной частоте
размеры поперечного сечения волновода, при которых возможна передача энергии по
волноводу, наименьшие для этой волны.
Полагая в (15), (16) m=1 и n=0 , получим:
![]() 17,
17,
![]() 18,
18,
![]() 19,
19,
![]() 20
20
Остановимся на картине распространения поля волны Н в плоскостях параллельных широкой стенке волновода .
В ЭМП волны Н10, магнитные силовые линии охватывают токи смещения, текущие между широкими стенками параллельно оси у.
Максимальная плотность тока смещения находится в центре
замкнутых магнитных силовых линий, где напряженность электрического поля равна
нулю
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]()
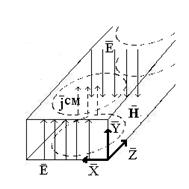
Диаграмма типов волн прямоугольного
волновода
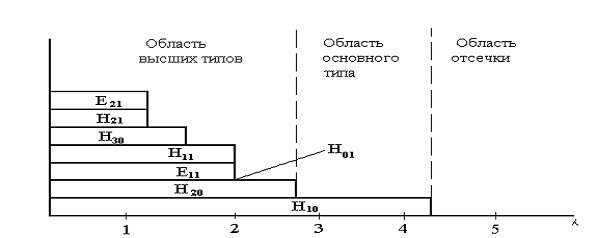
Раздел «Распространение радиоволн»
ТЕМА 10. Распространение радиоволн в свободном пространстве
Свободное пространство представляет собой однородную
непоглощающую среду для которой
относительная диэлектрическая и магнитная проницаемости равны единице, а
удельная проводимость равна нулю (e= l; m= l; s= 0), т.е.
среда имеет параметры eо = 8,85 10-12,Ф/м; mо = 4p10-7 Гн/м.
Примеры : воздух, космическое пространство.
Все антенны в волновой
зоне (дальней зоне) излучают сферические волны. Распространение
такой волны сопровождается сферической
расходимостью ее фронта и
соответственно сферической расходимостью потока электромагнитной энергии по
мере удаления от источника. В практике работы радиолиний в свободном
пространстве ослабление напряженности поля из-за уменьшения плотности потока
энергии во многих случаях определяет требование к энергетическим показателям
аппаратуры.
Поместим в свободном пространстве антенну излучающую
равномерно по всем направлениям (изотропный излучатель). Вокруг источника
электромагнитных волн проведем воображаемую сферу радиуса r. Если к излучателю подведена мощность Р1 и
она равномерно распределится по поверхности сферы с площадью 4pr2, то средняя за период плотность потока мощности
(мощность приходящаяся на единицу поверхности) равна Поср = Р1/4pr2 . Из курса “ Электромагнитные поля и волны” мы знаем,
что Пср связано с действующими значениями напряженности электрического
и магнитного полей соотношением Пср = ЕдНд.
Значения Ед и Нд связаны через волновое сопротивление
среды Zс = 120p. Отсюда Нд
= Ед/120p и Поср
=Ед2/120 p. Из
сравнения двух выражений для Поср получим формулу для расчета Ед:
Ед = Ö30Р1/r - действующего
значения напряженности электрического поля в свободном пространстве для
ненаправленного излучателя.
Правило написания формул: если мы пишем формулу и не указываем в виде
индексов наименование единиц, то это означает, что применяются для всех величин
основные единицы.
Амплитудное значение напряженности поля будет в Ö2 раз больше, т.е. ЕM=Ö60P1/r.
На практике обычно
рассчитывается и измеряется действующее значение напряженности электрического
поля. Реально изотропные антенны не существуют (существуют квазиизотропные) и
антенны обладают направленностью. Направленные свойства антенн характеризуются
формой диаграммы направленности, коэффициентом усиления G или
коэффициентом направленного действия D. Диаграмма направленности показывает зависимость напряженности поля от
пространственных координат. Коэффициент направленного действия (КНД) показывает
во сколько раз надо уменьшить излучаемую мощность, если ненаправленную
(изотропную) антенну заменить направленной для получения одинаковых значений
напряженности поля в точке приема. Коэффициент усиления (КУ) показывает во
сколько раз надо уменьшить подводимую мощность, если ненаправленную
(изотропную) антенну заменить направленной для получения одинаковых значений
напряженности поля в точке приема; при этом КПД изотропной антенны принимается
равным единице. Таким образом
Eм=Ö30 P1G1/r,
Произведение
P1G1=P1экв называют эквивалентной мощностью излучения, которую надо подвести к
ненаправленной антенне, чтобы получить в точке приема такую же напряженность
поля, как от направленной антенны с коэффициентом усиления G1, к которой подведена мощность Р1.
Из
формулы следует, что даже в свободном пространстве, среде без потерь,
напряженность поля в точке приема убывает обратно пропорционально первой
степени расстояния, что обусловлено уменьшением плотности мощности (среднего за
период колебаний значения вектора Пойнтинга) при удалении от источника.
Для
удобства расчетов формулу несколько видоизменим для подстановки значений Р1
в кВт, r в км и чтобы результат расчета
получился в мВ/м, тогда
Ед=173ÖР1(кВт)G1/r(км),мВ/м.
При расчете и проектировании
радиолиний, особенно в диапазонах сантиметровых и дециметровых волн, необходимо
знать мощность сигнала на входе приемника. Эта мощность определяется различно
для радиолиний двух типов. На радиолинии I типа передача информации ведется
непосредственно из пункта передачи в пункт приема (рис. 2.1). На радиолиниях II
типа принимаются сигналы, испытавшие пассивную ретрансляцию на пути от
передатчика к приемнику (рис.2.2). На этих линиях непосредственная передача
энергии волны от источника до точки приема по каким-либо причинам невозможна
(например, этот путь перекрыт препятствием). На наземных радиолиниях с
пассивной ретрансляцией на пути распространения имеется специальное пассивное
антенное устройство (или другой объект), которое облучается первичным полем и
переизлучает его в виде вторичного поля, предназначенного для приема. По такому
же принципу работают системы пассивной радиолокации, где первичное поле
облучает обнаруживаемую цель, а поле, переизлученное целью, принимается
локатором.
На любой радиолинии мощность
на входе приемного устройства Р2 связана с плотностью потока
мощности в месте приема П2 соотношением
Р2=П2Sдh2,
где h2— КПД фидера приемной антенны; Sд= G2l2/4p —
действующая площадь приемной антенны .
На радиолинии первого типа в
условиях свободного пространства плотность потока мощности в месте приема равна
П2=Р1h1G1/(4pr2),
где P1 - мощность на выходе
передающего устройства, h1 - КПД передающего фидера, G1 - коэффициент усиления передающей антенны. Для
радиолинии первого типа мощность на входе приемника в условиях свободного
пространства равна P12=P1h1G1G2h2l2/(4pr2).
На радиолинии второго типа
значение П2 зависит от тех же параметров, что и на линии первого
типа, и, кроме того, от переизлучающих свойств ретранслятора. Если какое-либо
тело облучается полем, то его способность переизлучать это поле оценивается
эффективной площадью рассеяния dэф (ЭПР). Величина ЭПР зависит
от формы, размеров, электрических свойств материала из которого выполнен
переизлучатель, а также от его ориентации относительно направления
распространения первичного поля и направления на прием.
Если около переизлучающего
тела плотность потока мощности первичного поля Роп= P1h1G1/(4pr12), то переизлученная
мощность Роп=Попdэф ,
а плотность потока мощности
вторичного поля вблизи приемной антенны в условиях свободного пространства П2=Роп/(4pr22).
Тогда мощность на входе
приемного устройства для радиолинии второго типа PII2=P1h1G1G2h2dэфl2/[(4p)3r12r22] .
В
тех случаях, когда r1=r2=r, PII2=P1h1G1G2h2dэф l2/[(4p
)3r4] и
получается уравнение радиолокации.
Из формул видно, что в свободном пространстве при
отсутствии пассивного ретранслятора на линии мощность на входе приемника
уменьшается обратно пропорционально квадрату расстояния, а при работе с
ретранслятором — обратно пропорционально четвертой степени. Такое быстрое
убывание поля на линиях второго типа объясняется тем, что поле дважды
испытывает расходимость сферического фронта волны: первичное поле — на пути от
источника (передающей антенны) до пассивного ретранслятора и вторичное поле — на
пути от ретранслятора до пункта приема.
При проектировании систем
радиосвязи, радиовещания, радиолокации и т.д. необходимо знать величину потерь
при передаче электромагнитной энергии. Потерями
передачи L называют отношение мощности
Р1', подводимой к передающей
антенне, к мощности Р2' на входе приемной антенны L=P1’/P2'=Plh1h2/P2.
Для радиолинии первого типа
в условиях свободного пространства
потери передачи равны L1=(4pr/l)2/G1G2.
Расчеты упрощаются, если в
формуле выделить составляющую Lo, которая называется
основными потерями передачи и характеризует только потери, обусловленные
сферической расходимостью фронта волны (при G1=G2=l ) Lo=(4pr/l)2.
Полные потери передачи
обычно выражают через L. Можно записать
L1=Lo/G1G2.
Для радиолинии второго типа
в условиях свободного пространства при r1=r2=r потери передачи равны L11=[(4p)3r4/l2][1/G1G2sэф]
или L11=L02[(1/G1G2sэф)(l2/4p)] .
В случае реальных сред, отличных
по своим свойствам от свободного пространства, вводят так называемый множитель ослабления F=E/Eo=Fexp(-ijv),
где F —
модуль множителя ослабления, который оценивает дополнительное ослабление
амплитуды напряженности поля по сравнению с ее ослаблением в условиях
свободного пространства; jv—
фаза множителя ослабления, которая оценивает дополнительное изменение фазы
волны. Отсюда следует, что E=E0 F.
ТЕМА 11.
Распространение земных радиоволн УКВ диапазона
Определение поля излучателя, расположенного в атмосфере вблизи земной поверхности, с учетом реальных свойств Земли и атмосферы представляет собой чрезвычайно сложную задачу. Для облегчения ее решения вводят некоторые упрощения. Поверхность Земли считают электрически однородной, сферической и идеально гладкой. Электрические параметры атмосферы (воздуха) принимают такими же, как и параметры свободного пространства.
Поле земной волны можно
считать результатом суперпозиции полей, созданных вторичными источниками,
которые возбуждены первичным полем в воздухе и земле. Полупроводящие свойства
Земли приводят к оттоку энергии волны из воздуха в почву. Сферическая земная
поверхность является препятствием, которое земная волна огибает при
распространении за линию горизонта. Процесс огибания - процесс дифракции
радиоволн вдоль сферического препятствия приводит к дополнительным потерям по
сравнению со случаем распространения радиоволн над плоской поверхностью.
Полное решение задачи
дифракции радиоволн для сферической идеально гладкой Земли с однородными электрическими
параметрами и однородной атмосферы получено В. А. Фоком в 1945 г. Эта формула
представляет собой бесконечный ряд из специальных функций Эйри и расчеты по ней
весьма громоздки. В ряде случаев, встречающихся на практике, общую
дифракционную формулу Фока можно упростить или вместо нее использовать другие,
более простые методы расчета поля.
Для практических расчетов
общее решение дифракционной задачи можно разделить на несколько частных.
Критерием для применения частных решений служат высота подъема антенн над
поверхностью Земли и длина радиотрассы (расстояния от пункта передачи до пункта
приема). Оба параметра определяют степень затенения земной поверхностью
пространственных зон Френеля, а следовательно, и закон ослабления поля в
процессе дифракции.
В зависимости от высот
расположения антенн различают два класса задач. К первому классу относят
задачи, в которых высота подвеса антенн h >> l и которые питаются неизлучающим фидером. Это так называемые поднятые антенны, что на практике характерно
при работе в диапазоне УКВ и с некоторыми ограничениями в диапазоне КВ. Второй
класс задач рассматривает процесс дифракции радиоволн при низко расположенных
антеннах, когда h<<l.
Этот случай характерен для работы в диапазонах СДВ, ДВ СВ и частично КВ.
Вдоль пути распространения
земной волны в зависимости от степени освещенности точки приема излучением
передающей антенны выделяют три области (зоны): освещенности (I), полутени
(II) и тени (III), как показано на рис.6.1. Термин “Зона освещенности” имеет
смысл только при поднятых антеннах. При низко расположенных антеннах область,
прилегающую к передающей антенне, называют зоной “приближения плоской Земли”,
поскольку в пределах этой зоны поверхность Земли можно приближенно считать
плоской.
В зонах полутени и тени расчет напряженности
поля как для поднятых, так и для низко расположенных антенн ведется по общим
дифракционным формулам Фока.
Рассматривая среды,
параметры которых указаны в табл.6.1, видим, что для морской воды равенство
плотности токов проводимости и токов смещения наступает при длине волны l, равной 0,33 м. Поэтому для радиоволн,
имеющих длину волны сантиметрового диапазона, морская вода может
рассматриваться как диэлектрик.
Таблица 6.1
Параметры
сред
|
Вид земного покрова |
e |
s,См.м |
|
Морская вода |
80 |
1...6 |
|
Пресная вода рек и озер |
80 |
10-3...10-2 |
|
Влажная почва |
10...30 |
3.10-3...3.10-2 |
|
Сухая почва |
3...6 |
1.10-5...5.10-3 |
|
Мерзлая почва |
3...6 |
10-3...10-2 |
|
Лед (t= -100С) |
4...5 |
10-2...10-1 |
|
Снег (t= -100C) |
1 |
10-6 |
Для влажной почвы это условие выполняется на длине волны l, равной 17 м. Влажная почва может
рассматриваться как диэлектрик для метровых и более коротких волн. Таким
образом, для волн сантиметрового диапазона все виды земной поверхности имеют свойства, близкие к
свойствам идеального диэлектрика.
Отметим также, что при
оценке условий распространения земной волны в случае h >> l сравнивают длину радиолинии r с
расстоянием прямой видимости rо (рис.6.2). Высоты подвеса приемных
и передающих антенн h1, h2<<aз, где aз=6370 км - радиус Земли,
поэтому величина rо, отсчитываемая по дуге большого круга, приближенно
равна прямой АВ. Из рис.6.2 видно,
что rпр=АС+СВ,
где AC=Öaз+hl)2—aз2»Ö2aзh1; CB»Ö2aзмh2, откуда rо=Ö2азм(Öh1+Öh2). Если rо выразить в километрах, h1 и h2 - в метрах, то после
подстановки численного значения аз
и отсутствии рефракции получим ro=3,57 (Öh1+Öh2). При обычных высотах поднятия антенн (порядка
нескольких десятков метров) предельное расстояние прямой видимости составляет
несколько десятков километров (как правило, не более 50...60 км). Таким
образом, в случае h >> l деление трассы
распространения земной волны на зоны производят следующим образом: r < rо -
зона освещенности; 0,8ro < r <
1,2rо —
зона полутени; r >
1,2rо —
зона тени.
Распространение радиоволн при поднятых передающей и приемной антеннах
Изучение распространения земных
радиоволн естественно надо начать с этого наиболее простого случая. При
небольших расстояниях между передающей и приемной антеннами кривизной
поверхности Земли можно пренебречь. Будем считать поверхность Земли гладкой и
однородной на протяжении всей трассы. Задача формулируется так: заданы
геометрические параметры: расстояние между передающей и приемной антеннами, высоты
подвеса передающей h1 и приемной h2 антенн и электрические
параметры: подводимая к передающей антенне мощность Р1, коэффициенты
усиления передающей и приемной антенн G1 и G2, длина волны l, вид поляризации волны, относительная
диэлектрическая проницаемость почвы e и ее удельная проводимость s. Требуется определить множитель ослабления F и
напряженность поля по формуле
![]() .
.
Как впервые было показано
еще в 1922 году академиком Б.А.Введенским электрическое поле радиоволны в месте
расположения приемной антенны можно рассматривать как результат интерференции
прямого луча 1 и луча 2, отраженного в точке С от поверхности Земли (рис.6.3).
При решении задачи РРВ вдоль границы воздух - Земля
существенное значение имеет абсолютная величина комплексной диэлектрической
проницаемости почвы
![]()
![]() .
.
Обычно она не бывает меньше 10, правда для сухого
песка в дециметровом диапазоне eк = 2...5. Способность земной
поверхности отражать радиоволны тоже связана с относительной комплексной
диэлектрической проницаемостью. Значения модулей коэффициентов отражения для
вертикальной поляризации Rв и горизонтальной
поляризации Rг можно определить по формулам:
![]() ,
,
![]() ,
,
где g - угол скольжения, который
определяется по формуле
![]() .
.
Земная волна,
распространяясь вдоль границы раздела воздух-почва, возбуждает в воздухе и
почве токи, которые являются источниками вторичного поля. В соответствии с
принципом Гюйгенса-Кирхгофа поле земной волны можно считать результатом
суперпозиции полей, наведенных воображаемыми вторичными источниками, которые
возбуждаются первичным полем в воздухе и почве. В почве интенсивность вторичных
источников ослаблена по сравнению со свободным пространством, за счет тепловых
потерь, которые появляются из-за конечных значений проводимости s. Почва экранирует проникновение поля в
глубокие области Земли (явление скин эффекта), что препятствует оттоку энергии
в нижнюю полусферу. Сферическая земная
поверхность является препятствием, которое волна огибает при распространении за
линию горизонта. Процесс огибания - процесс дифракции радиоволн вдоль
сферического неидеального экрана с радиусом 6370 км сопровождается большими
потерями.
Запишем
мгновенные значения для напряженности электрического поля лучей 1 и 2
![]() ;
;![]() .
.
Обозначим b = q+2pDr/l; Считая, что r(км) + Dr(км)» r(км), т.к. Dr<<r можно записать
![]() , так как
, так как
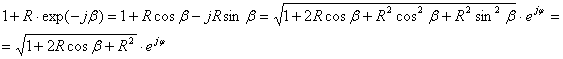
![]() , то
, то
![]() и
и
![]() ,мВ/м.
,мВ/м.
Так как Dr »2h1h2/r, то можно записать
![]() ,
мВ/м.
,
мВ/м.
Полученная формула показывает, что в месте
расположения приемной антенны поле действительно имеет интерференционную
структуру. По мере удаления от передающей антенны будем наблюдать такую картину
(рис.6.4). При изменении r косинус аргумента будет
меняться. Когда косинус равен единице поле максимально. При ![]()
![]() где
N=0,1,2,…
где
N=0,1,2,… ![]() .
.
Когда косинус равен минус единице поле минимально.
При![]() ,
,![]() где
N=0,1,2,..
где
N=0,1,2,.. ![]() .
.
Отсчет максимумов и минимумов ведется от конца
радиотрассы. При r £ 4h1h2/l наблюдаются максимумы и
минимумы напряженности поля, а при r > 4h1h2/l наблюдается плавное уменьшение напряженности
поля с увеличением расстояния.
Дальнейшее
упрощение интерференционных формул. С увеличением расстояния значение R
стремится к 1, а q - к 180о, тогда
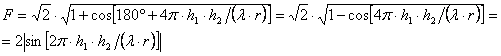
![]() или
или
![]() .
.
При дальнейшем увеличении расстояния когда![]() , то синус аргумента можно заменить его аргументом
, то синус аргумента можно заменить его аргументом ![]() , при
, при ![]()
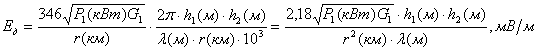 .
.
Напряженность поля на расстояниях r ³ 18 h1h2/l убывает с квадратом расстояния. Надо твердо
помнить, что в условиях применимости формулы Введенского, луч отраженный от
поверхности Земли является вредным, т.к. он стремится скомпенсировать поле
прямого луча. Векторная диаграмма сложения полей (структура поля в точке приема) приведена на рис.6.5. Многие
изобретатели старались скомпенсировать вредный отраженный луч (рассыпали уголь
в месте отражения, ставили стенку на пути отраженного луча). Но они не учли
того, что как луч занимает часть пространства, так и волна отражается не в
одной точке, а от площади описываемой эллипсоидом с горизонтальными размерами
2аn и 2bn (рис.6.6), которые при одинаковых высотах
подвеса антенн можно рассчитать по формулам ![]() ;
; ![]() .
.
Многолучевая структура. Диаграмма направленности в вертикальной
плоскости. Будем
строить зеркальное изображение антенны (рис.6.7). Из треугольника Dr = 2hsing, тогда
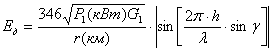 ,мВ/м.
,мВ/м.
Угол g меняется в пределах от 0 до
p/2 (0о - пологий луч, 90о
- направлено в зенит).Тогда (2phsing)/l будет меняться от нуля до 2ph/l. Для примера возьмем Ташкентский РТПЦ h1 = 350м, l = 7м, Dr =2hsing . Если вертолет будет
облетать (по вертикали) ТашРТПЦ, то будет обнаружено 100 максимумов (n=2h/l).
Учет сферичности земной
поверхности при расчете напряженности поля. Сферичность земной волны влияет на амплитуду
за счет рассеивания от выпуклой поверхности Земли и фазу отраженной волны, т.к.
выпуклость земной поверхности изменяет длину пути отраженной волны. Если в
точке отражения радиоволны от поверхности Земли (рис.6.8) провести плоскость MN,
касательную к поверхности Земли и отсчитывать высоты подвеса антенн не от
поверхности Земли, а от указанной плоскости, то подставляя в интерференционные
формулы вместо действительных высот h1 и h2 «приведенные высоты» h1¢и h2¢, получим правильное
значение напряженности поля в месте приема, ибо угол скольжения луча
относительно выпуклой поверхности Земли тот же, что и угол скольжения над
касательной плоскостью. Учет кривизны Земли при пользовании интерференционными
формулами сводится к нахождению приведенных высот h¢1 и h¢2 по известным значениям r, h1, h2.
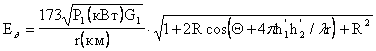 , мВ/м;
, мВ/м;
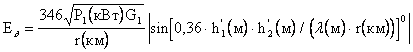 , мВ/м;
, мВ/м;
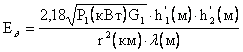 , мВ/м.
, мВ/м.
Расчет напряженности поля в зоне
полутени и тени. В.А.Фок получил выражение
для функции ослабления пригодное для любых удалений от передатчика. На
небольших расстояниях от передатчика оно переходило в интерференционную
формулу. Наоборот при больших расстояниях, решение превращалось в одночленную
дифракционную формулу. Фок ввел понятия о ²масштабе расстояний² L и о ²масштабе высот² Н. Это позволяет длину трассы r и высоты подвеса антенн h1 и h2 выразить в безразмерных
единицах: относительное расстояние х=r/L, относительные высоты подвеса антенн y1=h1/H, y2=h2/H.
Выражение для множителя
ослабления одночленной дифракционной формулы (для расчета уровня поля в зоне
тени) может быть представлено в виде произведения трех сомножителей F=U(x)V(y1)V(y2), первый из которых зависит
от расстояния, второй и третий от высот подвеса передающей и приемной антенн.
Расчет напряженности поля в области тени в диапазонах СДВ, ДВ, СВ и большей
части КВ значительно проще, т.к. F=U(x). Для расчета значения
множителя ослабления в зоне тени используются графики (рис.6.9 и 6.10) для
определения значений U(x),V(y1),V(y2) в дБ, тогда F=U(x)+V(y1)+V(y2), дБ. Из дБ в разы значение
множителя ослабления можно пересчитать по формуле F=10FдБ/20. Значение напряженности поля рассчитывается по формуле Е=ЕоF, где Ео
- напряженность поля в свободном пространстве.
В
зоне полутени для приближенной оценки уровня напряженности поля известную
пользу приносит способ определения множителя ослабления на границе прямой
видимости, т.е. на таком расстоянии, где интерференционные формулы показывают
уже нулевые значения поля. Метод разработан для горизонтально поляризованного
излучения. При вертикальной поляризации он дает менее точные результаты и
используется для l < 50 см. Множитель ослабления на границе
прямой видимости рассчитывается по формуле F = (ro/L)F(y1,y2).Значение функции F(y1,y2) получено из многочленной
дифракционной формулы и определяется графически из рис.6.11 в дБ. Это значение
пересчитывается в разы по формуле F=10F(y1,y2)дБ/20. Напряженность поля
рассчитывается по формуле Е = ЕоF.
ТЕМА 12.
Особенности распространения радиоволн в тропосфере, дальнее тропосферное
распространение
Электрические свойства
атмосферы, как и любой среды, характеризуются диэлектрической проницаемостью,
магнитной проницаемостью и удельной проводимостью. Магнитная проницаемость
атмосферы с достаточно высокой степенью точности принимается величиной
постоянной и равной магнитной проницаемости вакуума. Остальные два параметра
испытывают значительные изменения в зависимости от положения точки наблюдения,
времени, солнечной активности, частоты распространяющейся волны и т. д.
Согласно представлениям
макроскопической электродинамики диэлектрическая проницаемость и проводимость
определяются совокупностью токов, возникающих в среде под действием внешнего
поля. В неионизированных областях атмосферы (тропосфере и стратосфере)
плотность полного тока, наводимого внешним полем, имеет две составляющие j = jсмо+jпол . Здесь jсмо —плотность тока смещения в
свободном пространстве jсмо=iweE=i2pfeoE ,
jпол—плотность тока поляризации jпол=eоcгdE/dt=iweocгЕ,
где cг —относительная
диэлектрическая восприимчивость вещества, зависящая от электрической и
магнитной структур молекул и атомов, термодинамических условий, а также от
частоты воздействующего поля.
В общем случае cг — комплексная величина,
однако на частотах ниже 15...20ГГц, когда потери в тропосфере и стратосфере
малы , cг можно считать
действительной величиной.
Относительная
диэлектрическая проницаемость тропосферы
eт=[(1+1,552.10-4)/T](р+4810e/T),
где р - давление газа, мБар ; е - абсолютная
влажность воздуха, т. е. давление водяных паров, мБар; Т - температура, К.
Из формул видно, что чем
больше р и е, тем больше eг. Это связано с тем, что при
возрастании р и е увеличивается число молекул в единице объема и,
следовательно, ток поляризации. При увеличении Т возрастает скорость
хаотического теплового движения молекул, препятствующего упорядоченному
смещению связанных зарядов, т. е. ток поляризации уменьшается.
Относительная
диэлектрическая проницаемость тропосферы связана с коэффициентом преломления
тропосферы nт выражением
nт=Öeт=[1+(0,776.10-4 /T)](p+4810e/T).
Сильное влияние на
коэффициент преломления оказывают водяные пары. Так как nт (как и eт) весьма мало отличаются от
единицы у поверхности Земли и лежат в
пределах 1,00025... 1,00046. Оперировать такими значениями не всегда удобно,
поэтому для удобства был введен индекс коэффициента преломления тропосферы, показывающий
насколько миллионных долей коэффициент преломления отличается от единицы.
Nт = (nт-1)106 =
77,6(р+4810e/T)/T.
Численные значения индекса коэффициента преломления
называются N - единицами. У поверхности
Земли Nт
меняется от 260 до 460 N -
единиц. Зависимость величины Nт от высоты h
оценивается градиентом индекса коэффициента преломления тропосферы dNт/dh.
Аналогичная
зависимость для eт(h) имеет вид
eт(h)=1+5,78.10-4exp(-1,36.10-4h).
На распространение радиоволн
сильное влияние оказывают локальные неоднородности диэлектрической
проницаемости тропосферы.
Слоистые неоднородности представляют собой образования, горизонтальные
размеры которых заметно превышают вертикальные. Одной из основных причин их
возникновения является температурная инверсия , а также наличие облачности.
Интенсивность неоднородностей слоистого типа,
оцениваемая как отличие диэлектрической проницаемости в пределах слоя от
диэлектрической проницаемости окружающей среды колеблется от 10-6 до
(5...10) 10-5. Число и интенсивность слоев с увеличением высоты над
земной поверхностью уменьшаются. Размеры слоистых неоднородностей изменяются в
широких пределах. Толщина слоев характеризуется величинами от десятых долей метра
до нескольких сотен метров, а их горизонтальные размеры изменяются от десятков
метров до десятков километров и более.
Неоднородности турбулентного характера имеют соизмеримые размеры
во всех направлениях. Из-за малых сил вязкости движение атмосферного газа
практически всегда турбулентное, так что неоднородности такого типа всегда
существуют в тропосфере, при любых метеоусловиях.
Размеры неоднородностей
турбулентного происхождения определяются размерами (масштабами) элементарных
вихрей и ограничиваются размерами от нескольких миллиметров до нескольких
десятков метров.
Земная атмосфера
представляет собой пространственно-неоднородную поглощающую среду, а верхняя ее
часть - ионосферная плазма - обладает еще дисперсными и анизотропными
свойствами. Распространение радиоволн в такой среде сопровождается следующими
физическими процессами:
а) преломлением волн, обусловленным пространственной
неоднородностью атмосферы; процесс преломления осложняется двойным
лучепреломлением в анизотропной ионосфере;
б) рассеянием поля на локальных неоднородностях
атмосферы;
в) ослаблением напряженности поля в газах
тропосферы, в осадках типа дождя, тумана и др.;
г) поглощением, обусловленным конечной проводимостью
ионосферы;
д) изменением поляризации волны в анизотропной
ионосфере и деполяризацией в осадках;
е) регулярными и случайными флуктуациями
напряженности поля, связанными с изменениями электрических параметров
атмосферы;
ж) искажениями передаваемой информации из-за
многолучевой структуры принимаемого поля и дисперсии.
Рассмотрение количественных характеристик этих
процессов, имеющих резко выраженную частотную зависимость в пределах
радиодиапазона, приводится ниже.
Преломление радиоволн
Общие соображения. Диэлектрическая проницаемость атмосферы плавно
меняется по высоте. Распространение радиоволн в такой среде сопровождается
плавным искривлением траектории распространения - явлением рефракции.
При наличии рефракции
траектория представляет кривую, к которой касателен вектор, характеризующий
скорость распространения энергии волны. Известно, что при распространении
сигнала, энергия которого сконцентрирована в пределах полосы частот - таким
вектором в среде без дисперсии (тропосфера, стратосфера) является вектор
фазовой скорости, в среде с дисперсией (ионосфера) - вектор групповой скорости.
Выражения сф и сгр показывают,
что в атмосфере скорость распространения волны различна на различных высотах.
Поэтому элементы фронта волны, распределенные в пространстве, перемещаются с
разными скоростями, что и является причиной поворота фронта в процессе
распространения, т. е. причиной рефракции.
При определении траектории радиоволн в атмосфере
используют метод приближения
геометрической оптики. Этот метод рассматривает непрерывный волновой
процесс, распределенный в неоднородной среде, как совокупность множества
дискретных лучей. При этом каждая точка среды является источником преломленного
и отраженного лучей. Лучевое представление справедливо для неоднородных сред с
настолько медленным изменением коэффициента преломления, что на отрезке пути,
соизмеримом с длиной волны в среде, можно принять n(h) = const. При этом в первом приближении можно пренебречь
отраженным лучом и свести процесс распространения к наличию только
преломленного. В атмосфере приближение геометрической оптики справедливо для
всех волн радиодиапазона, за исключением диапазонов СДВ и ДВ (l>1000 м).
Влияние
тропосферы на распространение земных радиоволн.
Явление атмосферной рефракции
Влияние неоднородности
тропосферы на условия распространения земных волн теснейшим образом связано с
явлением атмосферной рефракции, известным ещё с глубокой древности (2 век до н. э.). Явление атмосферной
рефракции, как известно, заключается в преломлении световых лучей (а
следовательно, и радиоволн),
распространяющихся в земной атмосфере. Выведем выражение для радиуса
кривизны траектории радиоволны, распространяющейся в тропосфере. Для простоты
пренебрежём влиянием кривизны Земли и будем считать, что поверхности одинаковых
значений показателя преломления n представляют собой плоскости параллельные плоской
поверхности Земли. Рассмотрим две из таких поверхностей отстоящих друг от друга
на расстоянии dh (рис.4.1). Луч,
падающий на нижнюю поверхность под углом j и испытывающий преломление
на участке dh, падает на верхнюю
поверхность под углом j+dj. Искомый радиус кривизны R
определяется выражением R=ab/d. Из треугольника abc находим ab=dh/cos(j+dj)=dh/cosj отсюда R=dh/cosjdj
В средах с плавно меняющимся
значением коэффициента преломления закон преломления (закон синусов) должен
выполняться во всех точках траектории. Следовательно, он должен выполняться
также в точках а и b . На основании этого можем
написать nsinj =(n+dn)sin(j+dj )
nsinj = nsinj +sinjdn+ncosjdj+cosjdjdn
.Предположим, что cosjdj =1, sindj=dj . Отсюда cosj dj= - (dn/n)sinj R=dh/cosjdj R=n/[sinj (-dn/dh)]
n » 1. Когда луч пологий sinj Þ1. Отсюда R=106/(-dN/dh).
Знак минус у производной
означает, что радиус кривизны будет положительным, т.е. траектория волны будет
обращена выпуклостью вверх, только в том случае, если коэффициент преломления
уменьшается с высотой.
Это выражение показывает,
что радиус кривизны луча в нижних слоях тропосферы определяется не абсолютным
значением показателя преломления, а быстротой изменения показателя преломления
с высотой. Знак минус у производной означает, что радиус кривизны будет
положительным, т. е. траектория будет обращена выпуклостью вверх только в том
случае, если показатель преломления уменьшается с высотой.
При распространении в
нормальной тропосфере, которая характеризуется постоянством градиента — во всей
толще тропосферы, траектории радиоволн получают форму дуг окружности радиуса R = 2500 км.
Следует отметить, что
радиоволны испытывают в нормальной тропосфере несколько большее преломление,
чем световые лучи. Объясняется это тем, что обладающие постоянным дипольным
моментом молекулы воды вследствие конечной массы не успевают под действием
электромагнитного поля весьма высоких частот, свойственных видимому свету (4 1014 Гц - 7,5 1014
Гц), менять свою ориентировку.
Наоборот, в диапазоне радиоволн (f<3.1011 МГц)
полярные молекулы в полной мере участвуют в колебательном движении и вносят
свои изменения в значение показателя
преломления. Для световых лучей. R » 50000 км. Атмосферная рефракция, имеющая место в
нормальной тропосфере, получила название нормальной
рефракции.
Учёт атмосферной рефракции при распространении
радиоволн в пределах прямой видимости. Понятие об эквивалентном радиусе Земного
шара
Рассмотрим учёт влияния
атмосферной рефракции на распространение радиоволн при поднятых передающей и
приёмной антеннах в условиях применимости интерференционных формул. Как
известно, подобные условия встречаются только в диапазоне ультракоротких волн.
Необходимость такого учёта именно в диапазоне ультракоротких волн обусловлена
тем, что в условиях применимости интерференционных формул результирующее поле в
месте приёма зависит от геометрической разности хода прямого и отражённого от
земли лучей. Вывод интерференционных формул основывался на предположении, что
волны распространяются по прямым, тогда как в действительности радиоволны
распространяются по криволинейным траекториям, т. е. проходят более длинные
пути, что несомненно влияет на геометрическую разность хода лучей. Кроме того,
изменение электрической проницаемости с высотой влияет на скорость
распространения радиоволн, а следовательно, и на «оптическую разность хода
лучей», как принято называть разность хода, вычисленную с учётом скорости
распространения волн. На рис.4.2
пунктирными линиями показаны
прямолинейные траектории прямого и отражённого от земли лучей при
распространении в однородной атмосфере. В нормальной тропосфере радиоволны
распространяются по криволинейным траекториям, точнее, по дугам окружностей, показанных на рисунке сплошными
линиями. Замена прямолинейных траекторий дугами окружностей изменит конечные
значения разности хода лучей. В 1933 г. Скиллинг, Берроуз и Феррелл предложили упрощённый способ учёта влияния
атмосферной рефракции, заключающийся в том, что оба луча, как и прежде,
распространяются по прямолинейным траекториям, однако не над поверхностью земли
радиуса а, а над воображаемой
поверхностью с эквивалентным радиусом аэ Значение эквивалентного
радиуса определяется из условия сохранения постоянства относительной кривизны
между лучом и поверхностью Земли в действительных условиях и в эквивалентной
схеме распространения (табл.4.1). Относительной кривизной в аналитической
геометрии называют разность 1/a -
1/R. Отсюда 1/a - 1/R = 1/aэ - 1/¥ Из этого выражения получаем
формулу для эквивалентного радиуса Земли
аэ=а/(1-a/R)
aэ = a/[1+a(dN/dh)10-6]. При нормальной тропосферной рефракции aэ = 8500 км.
Представление об эквивалентном радиусе земного шара позволяет
распространить все ранее полученные формулы на неоднородную атмосферу путём
замены в них действительного радиуса Земли а
его эквивалентным значением. Прежде всего это можно сделать по отношению к
формуле для определения расстояния прямой видимости. При учёте влияния
атмосферной рефракции эта формула принимает вид ro=Ö2aэ (Öh1+Öh2)
Принцип, положенный в основу
представления об эквивалентном радиусе земного шара, показывает, что таким
методом можно пользоваться в тех случаях, когда выполняемые исследования или
расчёты основаны на сохранении неизменной относительной кривизны траектории. С
этой точки зрения вовсе не очевидно, можно ли допустить применение концепции об
эквивалентном радиусе земного шара к расчётам, производимым по
интерференционным формулам. Действительно, при пользовании интерференционными
формулами напряжённость поля в месте приёма в значительной степени определяется
разностью фаз между прямым и отражённым от земли лучами.
Пока атмосферная рефракция во внимание не
принималась, разность фаз в месте приёма определялась геометрической разностью
хода прямого и отражённого от земли лучей в предположении, что оба луча
распространяются прямолинейно. При учёте атмосферной рефракции необходимо
принимать во внимание одновременно два фактора. Во-первых, искривление
траектории и, во-вторых, зависимость скорости распространения волн от
меняющегося по высоте значения показателя преломления.
Простые рассуждения
показывают, что в условиях нормальной атмосферной рефракции учёт только первого
фактора приводит к уменьшению разности хода лучей, так как при этом длина
прямого луча увеличивается в большей степени, чем общая длина отражённого от
земли луча. Наоборот, учёт только второго фактора приводит к увеличению
оптической разности хода лучей, т. е. к увеличению разности фаз, обусловленной
разностью хода лучей. Оптическая длина пути отражённого луча, который распространяется
в более низких, в более плотных слоях атмосферы, увеличивается в большей
степени, -чем оптическая длина прямого луча. Численные расчёты показывают, что
решающее влияние оказывает второй фактор; таким образом, при учёте обоих
факторов оптическая разность хода лучей возрастает. Выполненное Б. А.
Введенским и М. И. Пономаревым исследование
показывает допустимость применения концепции об эквивалентном радиусе
земного шара для достаточно пологих лучей. Основываясь на этом, считают
возможным при пользовании интерференционными формулами и, в частности, формулой
Введенского учитывать влияние атмосферной рефракции путём замены для определения приведённых высот
действительного радиуса Земли его эквивалентным значением. В табл.4.1 приведены
значения эквивалентного радиуса Земли, реальные и эквивалентные траектории для
различных видов тропосферной рефракции. В тех случаях, когда кривизна земли во
внимание не принимается, что возможно при расчётах напряжённости поля на
небольших удалениях от передатчика, можно не принимать во внимание и
атмосферную рефракцию.
Дальнее тропосферное распространение
Атмосфера представляет собой
среду, в которой наблюдается медленное изменение по высоте диэлектрической
проницаемости er(h) и одновременно существуют,
подвижные локальные объемы с диэлектрической проницаемостью, отличающейся на
небольшую величину Der от диэлектрической
проницаемости окружающего пространства. Как плавная неоднородность, так и
локальные объемы являются источниками рассеяния радиоволн Процессом рассеяния называют процесс переизлучения
электромагнитного поля в неоднородной среде по направлениям, отличным от
направления распространения первичного поля. Структуру рассеянного поля
представляют как многолучевую. Элементарные составляющие этой структуры появляются
в результате рассеяния первичного поля в разных участках неоднородной среды. В
зависимости от свойств рассеивателей различают два вида рассеяния:
некогерентное и когерентное.
Некогерентное рассеяние есть результат переизлучения первичного поля
подвижными локальными неоднородностями диэлектрической проницаемости,
хаотически двигающимися в пространстве. В этом случае фазы элементарных полей,
рассеянных отдельными неоднородностями, меняются во времени по случайным
независимым законам.
Когерентное рассеяние есть результат сложения элементарных полей, фазы
которых изменяются по детерминированному (неслучайному) закону.
Свойства неоднородностей изменяются в пределах толщи
атмосферы. Различают рассеяние радиоволн в тропосфере и ионосфере. Первый
механизм называется дальним тропосферным
распространением (ДТР), второй — ионосферным
рассеянием (ИР). Наиболее применим в системах связи механизм ДТР. Характеристики рассеянного поля будем
рассматривать применительно к параметрам тропосферы и геометрии трасс
ДТР(рис.4.3). При оценке условий рассеяния необходимо знать ту область
тропосферы, которая эффективно участвует в формировании рассеянного поля на
данной радиолинии. Эта область называется эффективным
рассеивающим объемом или просто рассеивающим
объемом Vpac. На линиях ДТР, где пункты приема всегда
располагаются за линией горизонта, прием осуществляется за счет
неоднородностей, существующих в области тропосферы, нижняя граница которой
ограничивается плоскостями, касательными к Земле в точках расположения
передатчика и приемника (рис.4.3). Нижняя граница рассеивающего объема
располагается на высоте hmin » r2/(8aэ).
В условиях средней рефракции
для трасс протяженностью
r =200...600 км hmin=0,6... 5 км. При работе с
направленными антеннами размер рассеивающего объема ограничен областью
пересечения телесных углов главных лепестков диаграмм направленности передающей
и приемной антенн. Линейные размеры Vpac пропорциональны ширине диаграмм направленности Dq, а объем Vpac пропорционален
Dqо3 Vpac=r3 Dq3/(4qpac); qрaс » r/aэ,
где qрас—угол рассеяния,
образованный пересечением направлений максимального излучения передающей
антенны и максимального приема приемной антенны . На трассах
протяженностью 200...600 км qрас » 1,3...4°, т. е. объем рассеяния сильно
вытянут вдоль трассы. В соответствии с высотой расположения рассеивающего
объема в тропосфере, а также с учетом его размеров считают, что в пределах
этого объема существуют неоднородности трех видов: локальные неоднородности
турбулентного происхождения, инверсионные слои и плавная неоднородность erт(h). Неоднородности первого
вида являются источниками некогерентно-рассеянного поля, два других —
источниками когерентных составляющих поля.
Теоретические исследования
показывают, что интенсивность некогеретно-рассеянного поля имеет резко
выраженный максимум при qрас=0, т. е. в направлении
распространения первичного поля. Такой вид рассеяния называется рассеянием вперед, и его источниками
являются слабые неоднородности, через которые основная часть энергии первичного
поля проходит «вперед» и только малая часть рассеивается по боковым
направлениям, что действительно наблюдается при ДТР. Интенсивность рассеянного
поля этого вида быстро уменьшается по мере увеличения длины радиолинии, так как
угол рассеяния qрас пропорционален r. С целью уменьшения угла qрас и тем самым увеличения
напряженности поля в точке приема диаграммы направленности антенн на передаче и
приеме стараются по возможности «прижать» к поверхности Земли.
Реальное поле ДТР,
формируемое в результате некогерентного и когерентного рассеянии, подвержено
быстрым и медленным флуктуациям во времени и в пространстве. Распределение
амплитуд поля носит характер сложного нестационарного случайного процесса.
Инженерные расчеты линий ДТР базируются в основном на статистически обобщенных
результатах измерений.
ТЕМА 13.
Особенности распространения ионосферных радиоволн, свойства ионосферы
В ионосфере полный ток,
наводимый внешним полем, равен сумме трех токов: тока смещения свободного
пространства и конвекционного тока,
обусловленного движением свободных зарядов под действием поля, т.е. j=jсмо+jк=iweоЕ+еNеuе , где uе - средняя скорость
упорядоченного движения электронов, которая определяется из уравнения движения
электрона.
jк=eNeue=-ie2NewE/[me(g2эф+w2)]+e2NegэфЕ/[me(g2эф+w2)],
где е - заряд электрона, mе - масса электрона.
Формула показывает, что конвекционный ток,
возбужденный полем волны, имеет две составляющие: реактивную и активную.
Реактивная составляющая за счет инерции электронов отстает по фазе от поля на
90°. Активная составляющая, синфазная с полем, представляет собой ток
проводимости (jnp = sЕ)
и обусловливает необратимые тепловые потери. Плотность полного тока в ионосфере
равна
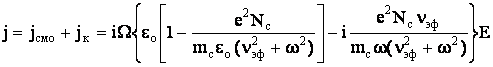
Напомним, что в среде с потерями плотность полного
тока j =iw(eоe-is/w). Сравнивая это выражение с
предыдущим, находим относительную диэлектрическую проницаемость и проводимость
ионосферы
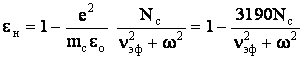
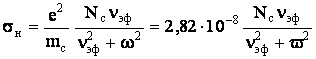
На достаточно высоких частотах, когда w2>>g2эф, т.е. в диапазонах КВ и УКВ
выражения для eи и sи упрощаются:
eи = 1-80,8 Nc / f2; sи = 7.17 10-10 Ncnэф/f2 , См/м.
Рассмотрим основные свойства
ионосферы, вытекающие из полученных формул для eи и sи формул. Формулы для eи показывают, что
диэлектрическая проницаемость ионосферы:
- меньше диэлектрической
проницаемости свободного пространства (eи<1) за счет наличия
конвекционного тока. Свободные электроны движутся против поля, а jсм совпадает по направлению с Е. Поэтому конвекционный ток, вычитаясь
из тока смещения, уменьшает суммарный реактивный ток, наводимый в ионосфере, по
сравнению с током в свободном пространстве;
- зависит от электронной
концентрации и частоты столкновений, которые претерпевают пространственные и
временные изменения; следовательно, ионосфера является электрически
неоднородной средой. На рис. 3.3 показано качественное изменение eи ионосферного слоя по высоте
h. Видно, что диэлектрическая проницаемость сначала уменьшается, а затем, выше
максимума ионизации слоя, возрастает с высотой;
- диэлектрическая
проницаемость зависит от частоты, т. е. ионосфера является диспергирующей
средой. Это обусловлено тем, что электроны, обладая конечной массой, проявляют
инерционные свойства. С повышением частоты упорядоченная скорость движения
электронов, а следовательно и конвекционный ток уменьшаются и свойства
ионосферы приближаются к свойствам свободного пространства. Практически
основное влияние ионосферы на условия распространения радиоволн наблюдается на
частотах f < 100 МГц (l >3м);
- диэлектрическая
проницаемость может принимать нулевые значения, если частота приложенного поля w будет равна так называемой собственной
частоте ионосферной плазмы wе.
На частотах w<wе диэлектрическая
проницаемость ионосферы eи<0. На рис. 3.3 показан
случай, когда для некоторой частоты f3 на высотах от h1
до h2
eи<0. Распространение волны
с частотой f3 в указанной области ионосферы невозможно. Это
обстоятельство имеет важное значение для отражения радиоволн от ионосферы.
Полученные формулы для
удельной проводимости позволяют сделать следующие выводы:
1. Проводимость ионосферы на
разных высотах различна, так как зависит от электронной плотности и частоты
соударений, которые в свою очередь зависят от высоты. На рис. 3.4 показан
пример зависимостей Ne, nэф, а также их произведения Nеnэф от высоты h. Из рисунка
видно, что хотя электронная концентрация Ne уменьшается на один -
два порядка ниже уровня 100 км, тем не менее это полностью компенсируется более
резким возрастанием nэф, и таким образом
произведение Nеnэф оказывается максимальным на
высотах слоя D и нижней части слоя Е ионосферы. В результате
удельная проводимость sи, зависящая от произведения Nеnэф, максимальна на тех же
высотах. Учитывая, что слой D существует только в дневное время, можно сделать
еще один вывод - проводимость, а следовательно, и поглощение в ионосфере в
дневное время больше, чем в ночное.
2. Удельная проводимость,
характеризующая поглощение в ионосфере, тем меньше, чем выше частота (при w>>nэф). Это происходит потому,
что с увеличением частоты из-за инерции электронов их средняя колебательная
скорость уменьшается и, следовательно, уменьшается энергия, которую электроны
отдают тяжелым частицам при столкновении. Практически поглощение в ионосфере
мало на частотах f > 100 МГц.
Магнитное поле Земли
значительно усложняет характер движения зарядов в ионосфере и приводит к
изменениям ее диэлектрической проницаемости и проводимости . На движущийся
электрон со стороны магнитного поля Земли действует сила Лоренца, которая
закручивает электрон вокруг силовых линий магнитного поля, превращая траекторию
его движения в спиральную линию. Частота вращения электронов вокруг магнитных
силовых линий (в отсутствие других полей) называется электронной гиромагнитной
частотой wн=еmоНз/m и fн=еmоНз/(2pm), где е и m —
заряд и масса электрона соответственно; Нзм — напряженность
магнитного поля Земли. Учитывая, что в средних широтах Нзм»40 А/м, гиромагнитная частота равна 1,4 МГц,
т. е. лежит в диапазоне средних волн (l = 214 м). На этой частоте
работать нельзя так как будет наблюдаться повышенное поглощение. Сила Лоренца
зависит от угла между направлением распространения волны и вектором Нзм.
Это приводит к тому, что волны, движущиеся в разных направлениях относительно Нзм,
наводят разные токи и, следовательно, диэлектрическая проницаемость и
проводимость ионосферы оказываются зависящими от направления распространения.
Таким образом, ионосфера представляет собой анизотропную среду. Отметим , что под влиянием магнитного поля
Земли в ионосфере возникают некоторые специфические явления, характерные для
анизотропных сред. Например, возникает явление двойного лучепреломления, когда
электромагнитная волна расщепляется на две волны — обыкновенную и
необыкновенную, распространяющиеся по различным траекториям с различными
скоростями и испытывающие различное поглощение.
Локальные неоднородности в ионосфере и ионосферные бури. Существенное влияние на
работу радиолиний оказывают отклонения электронной концентрации от регулярных
средних значений. Различают два вида .отклонений: флуктуации около средних
значений и длительные аномальные изменения самих средних значений. Флуктуации
наблюдаются всегда, аномальные изменения — только в периоды так называемых
ионосферных возмущений. Флуктуации электронной концентрации обусловливают
неоднородную быстро меняющуюся микроструктуру ионосферы. Ионосфера
представляется как скопление локальных образований, изменяющихся во времени и
подвижных в пространстве. В пределах неоднородностей электронная концентрация
отличается от среднего значения в данной области ионосферы.
Мелкомасштабные неоднородности с горизонтальными размерами в несколько сотен
метров образуются в результате процессов турбулентности и диффузии.
Интенсивность неоднородностей определяется среднеквадратическим значением
отношения перепада электронной концентрации на неоднородности к среднему
значению. В области высот 80... 400 км интенсивность мелкомасштабных
неоднородностей оценивается величиной порядка 10-2.
Крупномасштабные неоднородности с горизонтальными размерами в десятки и сотни
километров образуются в результате колебательных процессов в ионосфере и
представляют образования эллипсоидальной формы с преимущественной ориентацией
вдоль силовых линий магнитного поля Земли.
Длительные аномальные
изменения средних значений электронной концентрации, наблюдаемые в течение 1 ч
и более, называются ионосферными
возмущениями или бурями. Наиболее
важные для работы радиолиний ионосферные возмущения имеют корпускулярную
природу. Напомним, что корпускулы производят ударную ионизацию атмосферного
газа. Возмущения появляются, когда атмосфера Земли попадает в корпускулярные
потоки, излученные из активных областей возмущенного Солнца. Корпускулы,
достигая области действия магнитного поля Земли как заряженные частицы,
начинают двигаться по спиралям вокруг магнитных силовых линий и направляются к
полярным областям. Корпускулярные потоки вызывают не только ионосферные, но и
магнитные бури, поэтому часто говорят о магнитно-ионосферных возмущениях.
Возмущения протекают по разному в зависимости от широты точки наблюдения.
Возмущения корпускулярного
происхождения в средних и низких широтах характеризуются аномальным изменением
в основном области F. Лишь в периоды очень сильных бурь возмущения достигают
нижних слоев ионосферы.
Для средних широт характерны
так называемые отрицательные возмущения, при которых электронная концентрация
слоя понижается на 30...40%. Во
время бури на плавное изменение электронной концентрации слоя F2 налагаются
интенсивные неоднородности.
Возмущения корпускулярного
происхождения в полярных широтах характеризуются изменением ионизации всей
толщи ионосферы, включая слой D. При аномальном повышении ионизации этого слоя
увеличивается удельная проводимость ионосферы и, следовательно, поглощение
радиоволн. В кольцевой зоне полярных сияний одновременно с изменением состояния
слоя D наблюдается возмущенность слоя F2, проявляющаяся в освещенной части зоны
в виде значительного понижения Ne max, а в затененной — в
виде значительного повышения Ne
max за счет спорадических образований.
Возмущения волнового
происхождения проявляются в виде резкого возрастания ионизации слоя D в
результате мощного рентгеновского излучения, источником которого является
хромосферная вспышка на Солнце. Возмущения этого типа, сопровождаемые резким
увеличением поглощения (эффект Делинжера), наступают внезапно и длятся от
нескольких минут до 1...2 часов. Обычно они охватывают всю освещенную часть
земного шара, распределяясь с разной интенсивностью в зависимости от широты.
Условия отражения
от ионизированного слоя. До сих
пор рассматривались различные случаи распространения радиоволн в однородном
ионизированном газе. Реальная ионосфера представляет собой неоднородный
ионизированный газ. Влияние неоднородности ионосферы проявляется прежде всего в
том, что радиоволны в таких условиях будут распространяться не по прямолинейным
траекториям (как то имело место во всех рассмотренных выше случаях), а по
криволинейным. В известных условиях радиоволны, испытывая полное отражение от
ионосферы, возвращаются на Землю.
Рассмотрим
сначала случай распространения радиоволн в «плоской ионосфере», т. е. в таком
ионизированном газе, у которого поверхности одинаковых значений электронной
концентрации представляют параллельные друг другу плоскости (рис.4.2). Кроме
того, на первых порах будем считать ионосферу состоящей из ряда плоских слоев
весьма малой толщины, в пределах каждого из которых электронная концентрация
имеет постоянное значение. Обозначим через N1 электронную концентрацию внутри первого слоя, через N2 -электронную концентрацию внутри второго слоя и т. д.,
причём будем считать, что выполняется неравенство, N1 < N2 <N3 < ...
<Nn, .
Предположим далее, что на самый нижний слой из неионизированного воздуха падает
луч частоты f под углом падения jо (рис.4.2).
Основываясь на выражении для показателя
преломления 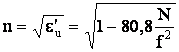
можно
написать 1>n1>n2>n3>...>nn>nn+1. Применяя к каждой границе
закон синусов, получим ![]() ,
, ![]()
![]() . После достаточного числа преломлений угол падения у n-го
слоя может сколь угодно близко подойти к 900. Полагая jn » 900 и сохраняя в равенстве
крайние члены, получим sinj0 = n или
. После достаточного числа преломлений угол падения у n-го
слоя может сколь угодно близко подойти к 900. Полагая jn » 900 и сохраняя в равенстве
крайние члены, получим sinj0 = n или
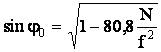
![]()
![]()
![]()
![]() закон секанса.
закон секанса.
Физической
причиной поворота волны в вершине траектории следует считать полное внутреннее
отражение. Напомним , что полное отражение происходит в том случае, когда при
переходе из оптически более плотной в оптически менее плотную среду (т. е.
среду с меньшим значением показателя преломления) угол падения превышает некоторое
критическое значение, определяемое (в наших условиях) формулой
jn > arcsin[1 - (Dn/nn)]
Дополнительными условиями являются: 1 - радиус
кривизны траектории радиоволны должен быть меньше аз+hотр. 2 - в точке поворота
радиоволны dN/dh должно превышать некоторое
критическое значение Численные расчёты показывают, что последнее условие почти
всегда выполняется автоматически и решающим является условие ( ), которое в силу этого можно практически
считать единственным условием поворота волны.
Практическое значение дополнительного условия заключается в
следующем: в точке отражения электронная концентрация обязательно должна
возрастать, а отражение не может происходить в области максимума электронной
концентрации и тем более в области уменьшения электронной концентрации с
высотой.
Наибольшая
частота, при которой радиоволны отражаются от данного ионосферного слоя при
вертикально направленном луче, получила название критической частоты. Условие
поворота радиоволны может быть выполнено только и только в том случае, если
частота волны не превосходит fmax. Волны, не
удовлетворяющие этому условию, от ионосферы не отражаются, а пронизывают её
насквозь.
Отражение от ионосферы вертикально
направленных лучей. При нормальном падении радиоволны на ионосферу от неё
будут отражаться только те радиоволны, частота которых не превосходит
критического значения. Действительно, положив в расчетной формуле jо = 0,
находим n=0 или, что то же, eи =0. Таким
образом, вертикально направленный луч отражается от той области ионосферы, в
которой электрическая проницаемость обращается в нуль. Предположив, что на
больших высотах электронная концентрация продолжает возрастать приходим к
выводу, что на этих высотах электрическая проницаемость делается отрицательной,
а показатель преломления мнимым. Существенно заметить, что при учёте
столкновений показатель преломления не обращается в нуль даже при отрицательных
значениях электрической проницаемости.
ТЕМА 14.
Особенности распространения коротких, средних и длинных волн
Основной механизм распространения коротких волн. К диапазону КВ (декаметровые
волны) относят радиоволны с длиной волны от 100 до 10м. В отличие от более
коротких волн, которые распространяются земной волной, декаметровые волны
распространяются в основном путем отражения от ионосферы. Радиус действия
земной волны в диапазоне коротких волн сравнительно невелик и при обычно
используемых мощностях передатчиков не превышает нескольких десятков
километров. Это обусловлено потерями в полупроводящей поверхности Земли и
большими потерями в процессе дифракции вдоль Земли.
Но короткие волны могут
распространяться на многие тысячи километров путем многократных
последовательных отражений от ионосферы и Земли (рис. 9.1), и для этого не
требуются передатчики большой мощности. Это уникальное свойство диапазона КВ и
используется для построения систем дальней связи. Кроме радиосвязи декаметровые
волны широко используются для радиовещания, дальней (загоризонтной)
радиолокации, исследования ионосферы и др. Однако ряд неблагоприятных
особенностей распространения снижает эффективность использования этого
диапазона. К таким особенностям следует отнести: многолучевость,
сопровождающуюся глубокими замираниями; ограниченность неискаженной полосы
передачи и скорости телеграфирования; подверженность влиянию ионосферных
возмущений и др.
Рабочие частоты. Одной из основных особенностей КВ радиолиний является ограничение
рабочих частот как со стороны высоких, так и низких значений, причем обе
границы зависят от изменчивой структуры
ионосферы. В результате на КВ линиях, в отличие от линий других диапазонов,
возникает необходимость периодической смены рабочих частот в соответствии с
изменяющимся состоянием ионосферы. Верхняя граница рабочих частот определяется
тем, что декаметровые волны, особенно коротковолновая часть этого диапазона (l £ 30 м), весьма критичны по
условиям отражения от ионосферы . Максимальная частота, при которой отраженная
от ионосферы волна может быть принята в заданном пункте приема, называется
максимальной применимой частотой (МПЧ). МПЧ определяется как максимум
произведения эквивалентной частоты вертикального падения fкр на
секанс угла падения волны на слой ионосферы seсjо . МПЧ =(fкрsecjо)mах.
В общем случае МПЧ зависит
от длины трассы, высоты отражения, закона распределения электронной концентрации
по высоте, критической частоты слоя. По условиям отражения от ионосферы рабочая
частота fp на коротковолновых радиолиниях не должна превышать МПЧ,
т. е. fр
£ МПЧ. Нижняя граница рабочих
частот определяется тем, что с уменьшением частоты увеличивается поглощение в
ионосфере (в освещенное время суток), и, как следствие этого, уменьшается
напряженность поля. Кроме того, увеличивается число лучей, приходящих в пункт
приема. Все это ведет к снижению устойчивости работы линии. Наименьшая частота,
при которой устойчивость работы снижается до минимально допустимого уровня,
называется наименьшей применимой частотой (НПЧ). Значение НПЧ зависит от
поглощения, уровня помех, мощности излучения, требуемой устойчивости работы и
т. д. Расчет НПЧ сводится к определению методом последовательных приближений
частоты, на которой устойчивость работы уменьшается до минимально допустимого
уровня при заданных параметрах приемопередающей аппаратуры. Рабочая частота fp
выбирается так, чтобы удовлетворялось неравенство НПЧ £ fp £ МПЧ. При изменении
состояния ионосферы НПЧ и МПЧ изменяются. Для обеспечения непрерывного действия
КВ радиолиний необходима периодическая смена рабочих частот. Рабочая частота в
значительной мере определяет структуру поля в точке приема. В частности, от
степени близости рабочей частоты к МПЧ зависит соотношение между зеркально
отраженной волной и волной, рассеянной на неоднородностях ионосферы. На
частотах fp<(0,8...0,9) МПЧ в структуре поля преобладает
зеркальный компонент, в то время как по мере приближения рабочей частоты к МПЧ
возрастает роль рассеянного компонента.
Модели распространения. Радиолинии КВ диапазона характеризуются большим
разнообразием условий распространения и весьма сложной и изменчивой структурой
поля. Это обусловлено тем, что при непрерывно изменяющемся состоянии ионосферы
рабочая частота некоторое время остается неизменной. В результате соотношение
между fp и МПЧ, которое определяет условия распространения,
непрерывно меняется. Короткие волны могут приходить в точку приема по разным
траекториям, испытывая разное число отражений от того или иного слоя ионосферы.
Для различных типов траекторий вводят условные обозначения: 1Е, 2Е, IF, 2F и т.
д., в которых цифра перед названием слоя указывает на число отражений от него.
Например, в случае, показанном на
рис.9.2 и характерном для трасс протяженностью около 3000 км, в точке
приема наблюдается три траектории: 2Е, 1F, 2F. Каждой траектории в зависимости
от угла наклона и критических частот слоев ионосферы соответствует определенное
значение максимальной применимой частоты: МПЧ2Е, МПЧ1F,
МПЧ2F. Наибольшее значение определяет МПЧ для всей
трассы. Та или иная траектория наблюдается в точке приема, если для нее
выполняется условие отражения, что возможно в том случае, когда рабочая частота
не превышает соответствующей этой траектории МПЧ. При увеличении частоты и
приближении ее к МПЧ трассы условия отражения становятся все более критичными,
число наблюдаемых траекторий (лучей) уменьшается и при fp » МПЧ имеет место однолучевой прием.
Необходимо также учитывать, что по мере приближения fp к МПЧ
возрастает роль рассеянного компонента поля. Из многообразия возможных условий
распространения коротких волн можно выделить некоторые типовые условия,
называемые моделями распространения. Каждой модели соответствует определенная
структура поля в точке приема, характеризуемая типом и числом траекторий,
соотношением амплитуд сигналов, достигающих точки приема по разным траекториям,
соотношением между уровнями зеркального и рассеянного компонентов поля. Особое
значение придается многолучевости, поскольку большое время запаздывания,
характерное для КВ линий, существенно снижает показатели работы. В качестве
примера рассмотрим модели распространения на среднеширотной трассе
протяженностью 2000...3000 км (рис.9.3).
Модели 1 и 2 не содержат
запаздывающих сигналов, но в модели 1, где fр/МПЧ<0,9, преобладает
зеркальный компонент 1F, а в модели 2, где fр/МПЧ>0,9, преобладает
рассеянный компонент той же траектории 1F. В модели 3, наблюдаемой при работе
на более низкой частоте (fр/МПЧ2F£1), в точке приема
присутствуют два луча: 1F и 2F, но с несоизмеримыми амплитудами (U2F³3U1F),
поэтому запаздывающие сигналы практически отсутствуют. Модель 3 отличается от
модели I тем, что преобладающим является поле второго луча 2F. Модели 4 и 5,
наблюдаемые, когда fp далека от МПЧ трассы, характеризуются наличием
запаздывающих сигналов с соизмеримыми амплитудами. Для модели 4 характерно
одновременное существование траекторий 1F и 2F, а для модели 5 - 2Е и 2F. .
Модель 6 не содержит запаздывающих сигналов, так как наблюдаемые траектории 2Е
и 2F имеют несоизмеримые амплитуды (U2Е ³ 3U2F).
В точке приема доминирует волна, отраженная только от слоя Е ионосферы.
Качественные признаки описанных моделей распространения сохраняются для трасс
любой протяженности. В зависимости от длины трассы изменяются только типы
траекторий, формирующих ту или иную модель. С точки зрения устойчивости связи
наиболее неблагоприятными являются модели 4 и 5 с запаздывающими сигналами.
Ясно, что существование той или иной модели зависит от рабочей частоты fp
и состояния ионосферы на данной трассе. При изменении fp или
параметров ионосферных слоев происходит смена моделей распространения.
Поскольку состояние ионосферы подвержено не только регулярным, но и случайным
изменениям, вероятность существования каждой из моделей можно определить только
статистически. В табл.9.1 приведены данные о проценте времени существования
однотипных моделей распространения на среднеширотных трассах различной
протяженности. Они получены за интервал времени наблюдений в один год при
среднем уровне солнечной активности (W=80). Рабочие частоты выбирались согласно
волновому расписанию на каждой радиолинии.
Таблица 9.1
Процент времени существования однотипных моделей
|
Длина трассы,км |
Процент времени существования однотипных моделей
распространения |
|||||
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1500 |
7 |
0 |
0 |
5 |
64 |
24 |
|
3000 |
50 |
9 |
14 |
9 |
6 |
12 |
|
4000 |
38 |
18 |
0 |
7 |
29 |
8 |
Из данных табл.9.1 следует, что относительное время
существования однотипных моделей в значительной мере зависит от длины трассы,
причем наиболее неблагоприятные модели 4 и 5 с запаздывающими сигналами гораздо
чаще наблюдаются на трассах протяженностью, отличной от 3000 км. Вероятность
появления каждой из моделей зависит не только от длины трассы, но и уровня
солнечной активности, что позволяет на основе прогноза относительного числа
солнечных пятен прогнозировать процент времени существования той или иной
модели распространения .
Замирания и разнесенный прием. В диапазоне КВ, как и в других диапазонах, прием
всегда сопровождается непрерывным изменением уровня сигнала во времени, т. е.
замираниями . Замирания на КВ линиях имеют интерференционное и поляризационное
происхождение, а также связаны с изменением поглощения в ионосфере и
фокусировкой и дефокусировкой волн на ионосферных неоднородностях. Основными
причинами интерференционных замираний являются: интерференция нескольких волн,
претерпевших различное число отражений от ионосферы (рис.9.4,а); интерференция
рассеянных компонент волны (рис.9.4,б); интерференция обыкновенной («о»)
и необыкновенной («н») составляющих
волны (рис.9.4,в) . Поляризационные замирания наблюдаются как при приеме
одного луча, так и при многолучевой структуре поля .В диапазоне КВ
интерференционные и поляризационные замирания обычно протекают как быстрые;
медленные замирания приписывают процессам медленных изменений поглощения;
замирания за счет изменения условий фокусировки лучей не имеют регулярного
среднего периода. На КВ радиолиниях основные характеристики быстрых замираний
(частота и глубина замираний, масштабы пространственной и частотной корреляций
и др.) существенно изменяются даже в течение относительно коротких интервалов
времени, т. е. быстрые флуктуации сигнала представляют нестационарный процесс.
Это обусловлено сменой моделей распространения, от которых зависят
статистические характеристики принимаемого сигнала. Так, при моделях 4 и 5
интерферируют сигналы, соизмеримые по амплитуде. При однолучевой модели 1
замирания вызываются интерференцией магнитоионных составляющих, из которых одна
(«х»-я) обычно сильно ослаблена. Во время существования модели 2, для которой
характерен прием рассеянного поля, замирания обусловлены интерференцией
большого числа элементарных рассеянных волн со случайным распределением
фаз. На трассах разной протяженности
преобладают модели разных типов, соответственно изменяются и типовые
статистические характеристики замираний. Различные виды статистического
распределения мгновенных значений уровня сигнала обусловливают существенно
различное качество работы радиолиний.
Для примера на рис.9.5 показаны зависимости вероятности ошибок р при
приеме дискретной информации от наблюдаемого отношения сигнал-помеха Uc/Uп. Из рисунка видно, что в
предположении отсутствия замираний для работы с вероятностью ошибок не более,
например, 10-3 достаточно обеспечить превышение уровня сигнала над
уровнем помех всего на 6 дБ. В случае замираний, описываемых законом Рэлея,
необходимое отношение сигнал-помеха возрастает до 30 дБ. При интерференции
нескольких зеркально отраженных волн, когда вероятность низких значений поля
увеличивается по сравнению с распределением Рэлея, заданное качество работы не
может быть обеспечено даже при Uс/Uп=50 дБ.
Разнесенный прием. Для повышения устойчивости
работы КВ линий связи при наличии замираний обычно используют прием на
разнесенные антенны и в некоторых случаях разнесение по поляризации . В
диапазоне декаметровых волн в направлении, перпендикулярном трассе, масштаб
пространственной корреляции замираний составляет (10...25)l. Из-за ограниченности площади антенных полей
расстояний между двумя приемными антеннами обычно выбирают около 10l. Выигрыш в устойчивости работы, получаемый за
счет применения разнесенного приема, существенно зависит от статистической
структуры поля. Для примера на рис.6.6 показана зависимость эффективности
разнесенного приема Q от допустимой вероятности ошибок р при передаче дискретной информации для двух моделей
распространения. Значение Q показывает, во сколько раз (на сколько децибел)
необходимо увеличить мощность передатчика при одинарном приеме, чтобы получить
то же качество работы р, что и при разнесенном приеме. Из рис.9.6 видно, что
эффективность разнесенного приема при интерференционной структуре поля (модели
4 и 5 с запаздывающими сигналами) значительно больше, чем при рассеянной, и
может достигать 36 дБ. В этом случае использование разнесенного приема
эквивалентно увеличению мощности передатчика в 4000 раз.
Пространственно- или
поляризационно-разнесенный прием не может быть использован для борьбы с
медленными замираниями, поскольку этим замираниям не свойственны
пространственная и поляризационная избирательности. При расчете коротковолновых
линий медленные замирания необходимо учитывать независимо от системы приема.
Кроме случайных изменений амплитуды поля на коротковолновых радиолиниях всегда
имеют место частотно-селективные замирания, при которых нарушается
статистическая связь между флуктуациями амплитуд отдельных составляющих спектра
сигнала, т. е. возникают искажения амплитудно-частотной характеристики (АЧХ) в
пределах передаваемой полосы частот. В зависимости от структуры поля в точке
приема (моделей распространения) и требований к равномерности АЧХ сигнала
неискаженная полоса передачи характеризуется значениями от 100 Гц до 2...3 кГц.
По сравнению с диапазоном УКВ коротковолновый тракт распространения значительно
более узкополосный.
Время запаздывания. Магистральные линии связи в диапазоне декаметровых
волн используются в основном для передачи информации в дискретной форме
(дискретный телефон, телеграф, фототелеграф, передача данных), т. е. работа
ведется импульсными посылками определенной длительности. В результате влияния
тракта распространения длительность импульса в точке приема отличается от
исходной, т. е. имеют место временные искажения. Временные искажения импульсных
посылок наиболее существенны в тех случаях, когда в точку приема приходит
несколько волн с соизмеримыми амплитудами и значительным временем запаздывания
(модели распространения 4 и 5).
Время запаздывания Dtmax для этих
моделей изменяется в широких пределах зависимости от длины трассы, соотношения
между рабочей частотой и МПЧ, времени суток, сезона, уровня солнечной
активности. Расчеты показывают, что максимальные значения Dtmax на трассах протяженностью
1500, 3000 и 4000 км могут достигать соответственно 2,8; 1,5; 2 мс. Если
принять, что исправляющая способность аппаратуры равна 40%, то минимально
допустимые длительности импульсов должны быть в 2,5 раза больше указанных
значений Dtmax, т. е.
составлять 7; 3,75 и. 5 мс. Следовательно, скорость передачи дискретной
информации на КВ линиях связи протяженностью 1500, 3000 и 4000 км ограничены
соответственно значениями 143, 267 и 200 бит/с. Отметим, что такие ограничения
получаются при максимально возможных значениях времени запаздывания Dtmax. При этом общая скорость работы достигает 1200
бит/с на трассах протяженностью около 3000 км и 600 бит/с на трассах длиной
1000...2000 и 3000...5000 км.
Влияние ионосферных возмущений. Существенное влияние на
работу КВ радиолиний оказывают ионосферные возмущения. В средних широтах
наиболее опасными являются отрицательные возмущения , когда критические частоты
слоя F2 понижаются более чем на 20%. Это понижение fкрF2 сужает
применимый диапазон рабочих частот, поскольку значения МПЧ приближаются к НПЧ.
Кроме того, диффузность слоя F2 повышает глубину и скорость замираний сигнала
за счет увеличения рассеяния. Непрохождение волн на среднеширотных радиолиниях
при ионосферных возмущениях наблюдается обычно в тех случаях, которые и в
отсутствие возмущений являются наиболее неблагоприятными для связи: ночные
часы, часы вечерней и особенно утренней полутени, большая долготная
протяженность трассы и др.
Основными мероприятиями по
улучшению работы среднеширотных радиолиний в периоды ионосферных возмущений
являются оперативная смена рабочих частот; повышение эффективности технических
средств, в частности увеличение мощности передатчика до нескольких десятков киловатт
вместо мощности в несколько ватт, необходимой для работы в отсутствие
возмущений; применение на радиолиниях большой протяжённости ретрансляции через
пункты, расположенные в более южных широтах, где критические частоты, как
правило, имеют меньшие отрицательные возмущения и длительность возмущенных
периодов также меньше. Перечисленные выше мероприятия непригодны для борьбы с
«вспышками» поглощения , так как они сопровождаются столь резким увеличением
поглощения, что работа КВ радиолинии оказывается вообще невозможной. На
радиолиниях, проходящих в высоких широтах, в периоды сильного поглощения
(зональное поглощение и поглощение: в полярной шапке) прямая радиосвязь в
диапазоне декаметровых волн не может быть обеспечена даже при применении
высокоэффективных технических средств. Для поддержания связи в этих случаях
рекомендуют применять ретрансляцию через пункты, расположенные в средних и
южных широтах, а также резервирование с помощью механизмов распространения, не
подверженных влиянию ионосферных возмущений: тропосферного или ионосферного
рассеяния.
Расчет КВ радиотрассы. Углы наклона траектории D и максимальные применимые частоты на
коротковолновых радиолиниях можно рассчитать, выбирая за основу
экспериментальные данные вертикального зондирования ионосферы . Пересчет этих
данных на наклонное падение достаточно сложен и обычно проводится с
использованием ряда приближений. В простейшем случае, когда пренебрегают
сферичностью ионосферы и влиянием магнитного поля Земли, для пересчета
используют закон секанса. На частотах,
обычно применяемых на среднеширотных радиолиниях, такие значения hд для действующих высот
отражения слоя F2 могут быть приняты следующими: зима, день—250 км; зима, ночь
— 350 км; лето, день — 400 км; лето, ночь — 250 км. Максимальные применимые
частоты рассчитывают для каждого слоя ионосферы, и наибольшее значение из них
определяет МПЧ трассы. На протяженных радиолиниях, когда волна приходит в точку
приема за счет нескольких отражений от ионосферы, МПЧ определяют для каждой
области отражения и наименьшая из этих частот является МПЧ всей трассы в целом.
Расчет напряженности поля. Ослабление поля на KB
радиолиниях вызвано расходимостью волны, поглощением в ионосфере, отражением от
поверхности Земли и другими причинами. Одним из основных методов расчета
напряженности поля является метод, предложенный А. Н. Казанцевым. Наибольшую
точность этот метод обеспечивает при расчете трасс, проходящих в средних
широтах. В соответствии с указанным методом действующее значение напряженности
поля в точке приема
Ед=
Поясним структуру этой формулы.
Первый множитель соответствует полю в свободном
пространстве. Здесь Р1 - мощность, подводимая к передающей антенне; G1(D)—коэффициент усиления передающей антенны
относительно изотропного излучателя с учетом влияния Земли, т. е. G1(D)=G1maxF2(D), где F(D) - нормированная ДН
передающей антенны в вертикальной плоскости с учетом влияния Земли;
D—угол возвышения траектории
волны; rв—путь,
проходимый волной от точки передачи до точки приема. Второй множитель (1/2)
соответствует, уменьшению поля (или мощности) на 6дБ. Из них З дБ А. Н.
Казанцев относит за счет того, что приемная антенна имеет линейную поляризацию,
а волна в процессе отражения от ионосферы приобретает эллиптическую (а иногда и
круговую) поляризацию. Другие З дБ обусловлены тем, что волна в ионосфере
расщепляется на обыкновенную и необыкновенную; необыкновенная составляющая
сильно поглощается, а для приема оказывается полезной только половина
излученной мощности. Третий множитель (1+R)/2 учитывает влияние
отраженной от Земли волны в месте расположения приемной антенны. Если бы
приемная антенна находилась на оптимальной высоте h2 над земной поверхностью, то
волны 1 и 2 имели бы одинаковую фазу в точке приема и результирующее поле (при
горизонтальной поляризации) имело бы значение (1+R)Eo,
где Eo - поле прямой волны 1. В реальных условиях
вследствие колебаний высоты отражающего слоя обеспечить оптимальное сложение
волн 1 и 2 не удается, и А. Н. Казанцев берет среднее значение коэффициента,
учитывающего влияние отраженной от Земли волны, а именно (1+R)/2.
Обычно выбирают среднее значение R порядка 0,8. Четвертый
множитель Rn-1 учитывает дополнительные
потери при отражении от поверхности Земли в промежуточных точках в случае
многоскачкового распространения. Здесь n - число отражений от
ионосферы. На односкачковых линиях (с одним отражением от ионосферы) n = 1 и Rn-1=
1. Наконец, пятый множитель ехр(-Ги) учитывает поглощение в
ионосфере. Полный интегральный коэффициент поглощения Ги определяется как сумма
поглощения в тех слоях ионосферы, которые волна проходит (неотклоняющее
поглощение), и поглощения в отражающем слое ионосферы (отклоняющее поглощение).
В случае, когда в ионосфере существуют все регулярные слои и отражение
происходит от слоя F2, полный
коэффициент поглощения Ги=АS/(fp+FL)2 + BF2fp2
Первое слагаемое определяет неотклоняющее
поглощение. Здесь AS - коэффициент, зависящий от критической частоты
слоя E ионосферы (как мера электронной плотности во всех слоях) и длины
трассы (рис.9.7); рабочая частота fр и частота продольного
гиромагнитного резонанса fL.
выражены в мегаГерцах. Чем больше степень ионизации ионосферы (fкрЕ), тем больше ее удельная
проводимость и больше поглощение. Чем
больше длина трассы, тем больший путь проходит волна в неотклоняющих слоях и
тем больше поглощение. Из формулы следует, что с уменьшением fр возрастают потери, так как
растет проводимость ионосферы. Второе слагаемое в формуле оценивает отклоняющее
поглощение при отражении волны от слоя F2. Коэффициент BF2 зависит от протяженности
трассы и действующей высоты отражения волны (рис.9.8). Из рисунка видно, что
при увеличении r значения BF2 уменьшаются, т. е.
уменьшается поглощение. Это можно объяснить тем, что на более длинных трассах
используются волны с более пологими траекториями, .которые меньше проникают
вглубь отражающего слоя и меньше поглощаются.
Влияние условий распространения на работу радиовещания. Декаметровые волны имеют ограниченное применение для
вещания из-за большой загруженности этого диапазона, высокого уровня помех
станций и относительно низкого качества приема. Наиболее типично применение KB
диапазона для вещания на труднодоступные удаленные районы, когда системы,
работающие на более коротких (УКВ) или более длинных (СВ, ДВ) волнах, оказываются
непригодными из-за ограниченного радиуса действия. Вещание на декаметровых
волнах предусматривает обслуживание заданной территории с помощью ионосферных
волн. Волновое расписание для вещания составляется с учетом условий
распространения в течение целого сезона. В результате во многих случаях работа
ведется на частотах, далеких от ОРЧ, что снижает уровень сигнала и. качество
приема. Зона обслуживания вещательного передатчика имеет границы, которые при
учете помех только природного происхождения определяются минимально-допустимой
напряженностью поля Еmin.
Для диапазона KB
характерно наличие мертвой зоны, в пределах которой регулярный прием
невозможен, так как радиус действия земной волны обычно меньше, нем наименьшее
расстояние, перекрываемое по Земле ионосферной волной. Внутренний радиус этой
зоны (рис.9.9) устанавливают путем расчета напряженности поля земной волны.
Рассчитывая напряженность поля на разных .расстояниях от. передающей антенны,
определяют .то расстояние, при котором уровень поля равен минимально
допустимому значению. Внешний радиус устанавливается по критическому углу
падения волны на ионосферу. Если в первом приближении отражающий слой ионосферы
считать достаточно тонким, то внешний радиус мертвой зоны можно оценить по
приближенной формуле
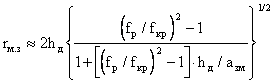
Из формулы видно, что .на частоте fр = fкр внешний радиус мертвой
.зоны равен нулю. С возрастанием частоты радиус rмз увеличивается, достигая
максимального значения на частоте fp,
равной МПЧ.
Волновое расписание. Количественная оценка
крайних частот рабочего диапазона МПЧ и НПЧ) обычно производится на основе
проектных материалов .Верхняя граница рабочего диапазона определяется с помощью
часовых медианных значений МПЧ. Однако, работая на частоте, равной месячной
медианной МПЧ данного часа суток, можно в этот час получить отражение волны от
ионосферы примерно лишь в 50% дней данного месяца из-за флуктуаций критических
частот и высот слоев от дня ко дню. Частота, обеспечивающая связь по условиям
отражения в течение 90% времени за месяц, называется оптимальной рабочей
частотой (ОРЧ) и является верхним пределом рабочего диапазона частот при
составлении волнового расписания. Статистическая обработка наблюдений показала,
что при спокойном состоянии ионосферы ОРЧ должна быть ниже месячной медианной
МПЧ слоя F2 на 10...20%. Однако флуктуации слоя F2 не всегда одинаковы: они
изменяются от дня к ночи и зависят от географического положения точки
наблюдения. Поэтому более точно расчет ОРЧ ведут по данным о флуктуациях МПЧ и
специальным номограммам, приводимым в месячном прогнозе распространения
радиоволн. Такие уточнения наиболее важны для радиолиний, проходящих в полярных
областях, где флуктуации особенно велики и ОРЧ может быть ниже МПЧ на 40%.
Для каждой радиолинии
согласно международным правилам выделяется ряд фиксированных частот. Для
протяженных магистральных линий число таких частот достигает не более
четырех...пяти, а для менее ответственных линий - двух...трех.
На каждый месяц составляется
волновое расписание, которое устанавливает, на каких из выделенных частот
следует работать в различные часы суток. Для этого по данным прогноза
рассчитываются и строятся зависимости ОРЧ и НПЧ от времени суток (рис.9.10). В
каждый данный период времени работа может
вестись на любой частоте не выше ОРЧ и не ниже НПЧ. Из закрепленного
набора частот для разных периодов суток выбираются частоты ближе к ОРЧ, так как
при этом выше устойчивость работы. Наиболее трудно составить волновое
расписание на протяженных линиях, ориентированных примерно вдоль параллелей в
часы частичной освещенности трассы, так как состояние ионосферы на западном и
восточном участках трассы различно. На неосвещенном участке предутренний
минимум электронной концентрации слоя F2 обусловливает низкие значения ОРЧ для
всей линии. В то же время на освещенной части происходит большое поглощение,
поэтому НПЧ оказываются высокими. На наиболее трудных линиях НПЧ бывают выше
ОРЧ. В таких случаях прямая связь оказывается невозможной и используют
ретрансляцию через пункт расположенный примерно в середине трассы.
Углы возвышения и требования к диаграммам направленности антенн. В диапазоне коротких волн при работе на частотах, близких к
оптимальным, в точке приема поле обычно формируется несколькими волнами,
претерпевшими различное число, отражений от ионосферы. В разные сезоны и
периоды суток соотношение между уровнями напряженности поля отдельных волн
меняется. Поэтому для поддержания устойчивой работы антенны на передаче и
приеме должны обеспечить интенсивное излучение и прием в направлении спектра
углов, соответствующих волнам с наибольшими амплитудами. Выбор наклона и ширины
диаграмм направленности антенн в вертикальной плоскости рекомендуется
производить с учетом как средних значений углов наклона траектории Dср, так и возможных флуктуаций
относительно Dср. Средние значения углов Dср рассчитываются исходя из регулярных суточных и сезонных
изменений действующих высот отражения. Верхняя граница углов Dср определяется максимально
возможным наблюдаемым числом отражений от слоя F2 на данной трассе в периоды,
когда высота этого слоя максимальна. Нижняя граница Dср для всей линий обычно
принимается около 2...3°. Траектории с более низкими углами малоэффективны
из-за сильного ослабления в ионосфере и влияния Земли. Для трасс протяженностью
более 2000...3000 км нижняя и верхняя границы углов Dср, рассчитанных с учетом
реально наблюдаемых траекторий, приведены в табл. 9.2.
Таблица 9.2
|
Длина трассы,км |
Domin |
Domax |
Виды траекторий |
|
2000...3000 |
2...3 |
20 |
1F,
2F |
|
3000...4000 |
2...3 |
15...18 |
1F,
2F |
|
5000...7000 |
2...3 |
10...12 |
2F,
3F |
|
7000...10000 |
2...3 |
10...12 |
3F,
4F, 5F |
Флуктуации углов наклона
траекторий относительно средних значений во многих случаях весьма существенны. Они
обусловлены различными причинами, одна из которых состоит в непрерывном
случайном изменении высоты расположения отражающего слоя, другая - в том, что
отражающая область ионосферы, имеющая горизонтальные размеры в несколько сотен
километров часто не является сферически- слоистой. Поэтому в формировании
принимаемого сигнала участвует попеременно или одновременно несколько областей
ионосферы. Такой характер распределения даже при приеме одного луча приводит к
распределению энергии волны в широком секторе углов, т. е. к флуктуациям углов
наклона траекторий. При многолучевом приеме флуктуации углов наклона присущи
каждой из траекторий и секторы углов, в которых распределена энергия волны,
могут частично или полностью перекрывать друг друга. Для расчета и проектирования
коротковолновых линий связи и вещания необходимо располагать количественными
данными о возможных флуктуациях углов D на различных трассах в
различные периоды времени. Такие данные, полученные .в результате измерений на
среднеширотных радиолиниях, приведены в табл.9.3. Они характерны для модели 1
распространения , когда в точке приема наблюдается однолучевой прием волны,
отраженной
от слоя F2 ионосферы.
Таблица 9.3
Флуктуации углов наклона
траекторий в градусах за период
|
Длина трассы, км |
Лето |
Зима |
||
|
|
День |
Ночь |
День |
Ночь |
|
1000...3000 |
±2 |
±6 |
±4 |
0...24 |
|
3000...5000 |
±3 |
±8 |
±6 |
0...30 |
Из данных табл.9.3 видно, что сравнительно малые
флуктуации углов наклона траекторий относительно средних значений имеют место
только в летнее дневное время. Для ночных периодов характерны флуктуации на
значительную величину, особенно в зимнее время, когда энергия волны
распределяется в очень широком секторе углов как на коротких, так и на длинных
трассах. Приведенные величины могут использоваться для оценки флуктуаций D при всех возможных уровнях солнечной
активности.
В горизонтальной плоскости на ширину диаграмм направленности антенн оказывает влияние так называемая девиация лучей, т. е. отклонение направления распространения волны от дуги большого круга. Основными причинами девиации лучей являются наклоны отражающих слоев ионосферы в направлении, перпендикулярном трассе, а также боковое рассеяние на ионосферных неоднородностях. Можно ориентировочно полагать, что в горизонтальной плоскости антенны должны обеспечивать интенсивное излучение и прием в диапазоне углов ± (3...5°) относительно дуги большого круга, соединяющей пункты передачи и приема. В высоких широтах из-за большей неоднородности ионосферы углы девиации лучей более значительны.
Устойчивость работы. Магистральные линии связи в
диапазоне коротких волн используются в основном для передачи дискретной
информации, поэтому устойчивость определяется как вероятность обеспечения
допустимого числа ошибочно принятых посылок в течение определенного времени.
Обычно при работе дискретного телефона требуется обеспечить относительное число
ошибок не более 10-2 в течение 70% времени за сутки, магистрального
телеграфа—не более 10-3 в течение 90% времени и при передаче
цифровых данных—не более 10-4 в течение 98% времени за сутки.
Устойчивость работы зависит от наблюдаемого отношения сигнал-помеха на входе
приемника, которое подвержено регулярным и нерегулярным изменениям за счет непрерывных
изменений уровней сигнала и помехи. При снижении скорости передачи информации и
увеличении допустимой вероятности ошибок при том же отношении сигнал-помеха
устойчивость работы линии связи возрастает.
Влияние условий распространения на работу радиовещания. Короткие волны имеют
ограниченное применение для вещания из-за большой загруженности этого
диапазона, высокого уровня помех станций и относительно низкого качества
приема. Наиболее типично применение КВ диапазона для вещания на труднодоступные
удаленные районы, когда системы, работающие на более коротких или более длинных
волнах, оказываются непригодными из-за ограниченного радиуса действия. Вещание
на коротких волнах предусматривает обслуживание заданной территории с помощью
ионосферных волн. Волновое расписание
для вещания составляется с учетом условий распространения в течение
целого сезона, поскольку частая смена рабочих волн неудобна для массы
слушателей. В результате во многих случаях работа ведется на частотах, далеких
от ОРЧ, что снижает уровень сигнала и качество приема. Для диапазона коротких
волн характерно наличие мертвой зоны , в пределах которой регулярный прием
невозможен, так как радиус действия земной волны обычно меньше, чем наименьшее
расстояние, перекрываемое по Земле ионосферной волной.
Зона обслуживания
вещательного передатчика имеет границы, которые при учете помех только
естественного природного происхождения определяются минимально допустимой
напряженностью поля Emin , которая в диапазоне КВ принимается равной
50 дБ по отношению к 1 мкВ/м.
Диапазон средних длин волн (l = 1000...100 м).Тропосфера не влияет. Волны
этого диапазона полосы характеризуются примерно одинаковыми условиями
распространения, основной особенностью которых является прием днем только
земной волны, а ночью - и земной, и пространственной. В дневное время радиус действия станций
обычно составляет несколько сотен километров, увеличиваясь ночью до 2000...3000
км и более. Такие условия наиболее типичны для среднего участка рассматриваемой
полосы частот. При приближении к верхнему краю усиливается роль
пространственных волн, при приближении к нижнему краю происходит постепенный
переход к волноводному распространению. Наиболее применимы эти частоты в службе
вещания, для которой Комитетом частот МККР выделена полоса 1,6 МГц...150 кГц (l = 187...2000 м). Кроме того, эти частоты
используются для целей морской связи. На морских линиях условия распространения
земной волны наиболее благоприятны из-за малой утечки энергии в подстилающую
среду — морскую воду, которая обладает высокой проводимостью.
Условия распространения земной волны вдоль электрически- однородной гладкой
земной поверхности хорошо соответствуют теории дифракции. Однако в
рассматриваемом диапазоне на поле земной волны оказывают влияние два свойства,
характерные для реальной земной поверхности: электрическая неоднородность почвы
вдоль трассы и по глубине почвенного покрова, а также неровности рельефа.
Неоднородность электрических параметров по глубине можно учесть, если оценивать
условия распространения с помощью эффективной проводимости земной поверхности sзм.эфф, которая определяется путем
измерений электропроводимости почвы в пределах той ее толщи, которая активно
участвует в процессе распространения волны. Согласно экспериментальным
данным такой толще, соответствует
участок, ограниченный глубиной проникновения волны в почву. Глубина
проникновения изменяется в зависимости от проводимости почвы и длины
распространяющейся волны и в данном диапазоне составляет в среднем 10...20 м.
Измерения показывают, что распределение sзм.эфф носит ярко выраженный
случайный характер, даже если измерения производятся на небольших по размерам
площадях. Это объясняется сложными и многообразными условиями образования почв,
различием в расположении слоев осадочных пород, уровней грунтовых вод и др.
Часть результаты многочисленных измерений sзм.эфф, проведенных в странах
СНГ можно найти в табл. 8.1.
Таблица 8.1
|
Вид земной поверхности |
eзмк |
sзмк, См/м |
|
Море |
81 |
1...4,6 |
|
Реки, озера |
80 |
0,001 |
|
Пастбища, небольшие холмы, жирные земли |
14...20 |
0,01...0,03 |
|
Пастбища, холмы средней величины, леса |
13 |
0,006 |
|
Пастбища, холмы средней величины и леса, тяжелая
глинистая земля |
13 |
0,004 |
|
Скалистая почва, крутые холмы |
14 |
0,002 |
|
Песчаная, сухая, плоская местность |
10 |
0,002 |
|
Города |
3...5 |
0,0001...0,001 |
Заметное влияние на
напряженность поля в диапазоне средних волн оказывает рельеф местности. Для
диапазонов ДВ и СВ волн большинство видов земной поверхности, за исключением
высоких горных хребтов, относится к классу шероховатых поверхностей, в пределах
которых множество небольших неровностей (h < l) распределены статистически
равномерно. Для волн диапазона 100...2000 м такими шероховатыми поверхностями
являются обычная холмистая местность (класс длинных пологих неровностей),
сильно взволнованная поверхность моря (класс коротких пологих неровностей),
шероховатая поверхность в виде рельефа большого города (класс мелких крутых
неровностей) и др. Влияние шероховатой поверхности сводится к рассеянию
энергии, в результате чего происходит ослабление плотности потока энергии в
заданном направлении. Расчет среднего значения напряженности рассеянного поля в
случае скользящего распространения земной волны можно выполнить статистическими
методами и свести ослабление плотности потока энергии к изменению электрических
параметров земной поверхности. Расчет напряженности поля в этом случае ведут с
учетом так называемых кажущихся значений диэлектрической проницаемости eзмк и проводимости sзмк, которые зависят не только
от электрических свойств подстилающей поверхности, но и от характера рельефа.
Кажущаяся удельная проводимость для холмистой местности определяется из
соотношения 1/Ösзмк=1/Ösзмэфф+1/Ösзмр, где sзмэфф - эффективная удельная проводимость,
учитывающая только электрические свойства почвы, sзмр = 10-5l3o/h4o
- составляющая кажущейся проводимости, учитывающая влияние рельефа в виде
пологих холмов, для которых lo >>l, ho/lo<<1, lo и ho - средние горизонтальные и
вертикальные размеры неровности . Например , при lo=2,5км, ho=50м sзмр» 20 10-3 См/м. Значения кажущихся eзмк и sзмк часто определяют по
результатам измерений напряженности поля, поскольку ослабление поля на трассе
можно свести к влиянию соответствующих электрических параметров среды.
Измерения показали, что для равнинной местности sзмк отличается от sзмэфф в 1,5...2 раза, а для
холмистой .местности это различие доходит до 5...7 раз. При расчете напряженности поля земной волны
желательно пользоваться кажущимися значениями параметров земной поверхности .
Значение напряженности поля
земной волны зависит от растительного покрова. Распространяющаяся над лесом
волна поглощается за счет токов, наводимых ею в стволах деревьев. Проводимость
древесины зависит от температуры и влажности, увеличиваясь с их повышением,
поэтому летом ослабление за счет деревьев больше, чем зимой. Расчеты возможных
сезонных изменений уровня сигнала, связанные с сезонными изменениями поглощения
в деревьях, дают удовлетворительное совпадение. Зимой напряженность поля земной
волны на 20...50% выше, чем летом.
Расчет напряженности поля земной волны. В реальных условиях
среднепересеченной местности и относительно однородных электрических параметров
почвы вдоль трассы напряженность поля земной волны удовлетворительно
оценивается дифракционными формулами, справедливыми для низко расположенных
антенн . При этом расчет поля необходимо вести с учетом кажущихся электрических
параметров почвы eзмк и sзмк . В табл. 8.1 приведены
типичные значения этих величин. В инженерной практике для определения поля
земной волны широко применяются графики МККР, которые рекомендованы Х Пленарной
Ассамблеей МККР (Женева, 1963 г.) и представляют результат расчета
напряженности поля по дифракционным формулам для разных проводимостей подстилающей
поверхности.
В качестве примера на рис.
8.1 и 8.2 приведены такие графики для моря и почвы с проводимостью sзм=10-3 См/м.
Значения напряженности поля, приведенные на графиках (мкВ/м—правая шкала и
децибелы относительно 1 мкВ/м—левая шкала), соответствуют излученной мощности,
равной 1 кВт, и короткой вертикальной
передающей антенне (элементарному вибратору), стоящей на поверхности
идеальной Земли. Коэффициент усиления такой антенны G"=1, поскольку она принимается
за эталонную в этом диапазоне частот. Если эквивалентная излучаемая мощность Р1э
отлична от 1 кВт, то напряженность поля, определенную из графика, следует
умножить на ÖР1э=ÖР1G1¢¢
где P'1 — мощность, подводимая к
передающей антенне; кВт;
G1¢¢ - коэффициент усиления
передающей антенны в направлении вдоль Земли, вычисленный по отношению к
элементарному электрическому вибратору, расположенному над идеальной Землей.
Напряженность поля,
рассчитанная по графикам МККР, соответствует наблюдаемому дневному полю на
расстояниях г £ 2000 км для частот около
150 кГц...2 МГц, когда поле пространственной волны пренебрежимо мало по
сравнению с полем земной волны.
Распространение ионосферной волной. Когда вся трасса распространения оказывается
в зоне полной темноты, то в точке приема кроме земной появляется
пространственная волна, отраженная от ионосферы. Для радиоволн в диапазоне
100...2000 м условия отражения волн от ионосферы выполняются в течение суток, в
основном в слое Е. Однако в дневные часы ионосферная волна испытывает настолько
сильное поглощение в слое D, что ее прием оказывается невозможным при обычно
применяемых мощностях передатчиков. С наступлением темноты, когда слой D
пропадает, напряженность поля пространственной волны резко возрастает, и на
расстояниях, превышающих 100...200 км, эта волна становится доминирующей.
Напряженность поля пространственной волны изменяется в зависимости от
геомагнитной широты трассы, поскольку магнитное поле Земли оказывает
существенное влияние на распространение радиоволн в ионосфере ,особенно сильно
это влияние оказывается на частотах, близких к гиромагнитной , которая в
средних геомагнитных широтах равна примерно 1,4 МГц.
Случайные флуктуации напряженности поля. На расстояниях, где в
течение суток доминирует поле земной волны, уровень сигнала устойчив. Эта область
расстояний называется зоной уверенного приема. Далее расположена зона ближних
замираний, где с наступлением темноты принимаемое поле есть результат
интерференции соизмеримых по амплитуде земной и пространственной волн.
Вследствие нерегулярных флуктуаций электронной плотности в ионосфере фаза
пространственной волны непрерывно изменяется, поэтому в ближней зоне прием
сопровождается глубокими быстрыми замираниями интерференционного происхождения.
Кроме того, вследствие изменения ориентации и отношения осей эллипса
поляризации принимаемого поля имеют
место замирания поляризационного происхождения. Замирания в ближней зоне носят
частотно-селективный характер и без
принятия специальных мер прием в этой зоне неустойчив. Особенно резко
селективные замирания выражены в наиболее коротковолновой части средневолнового
диапазона.
За зоной ближних замираний
расположена зона дальнего приема, или так называемая зона дальних замираний. В
этой зоне прием осуществляется за счет пространственных волн, n-кратно
отраженных от ионосферы. Амплитуды многократно отраженных волн в два и большее
число раз меньше амплитуды однократно отраженной волны, поэтому в этой зоне
замирания менее глубоки, чем в зоне ближних замираний, и их селективные
свойства выражены слабо. В условиях массового приема вещания общие замирания
удается компенсировать автоматической регулировкой усиления приемника. Борьба с
селективными замираниями значительно сложнее. Для увеличения радиуса зоны
уверенного приема,т.е. увеличения напряженности поля земной волны и уменьшения
напряженности поля пространственных волн применяют так называемые
«антифединговые» антенны, которые имеют диаграммы направленности, «прижатые» к
поверхности Земли (рис. 8.3). Наилучшей с точки зрения антифединговых свойств
являются вертикальные антенны больших размеров с относительной длиной h/l=0,53. Излучение этих антенн под углами D > 45...50° ничтожно мало. Такие антенны
позволяют в 2...2,5 раза увеличить зону уверенного приема по сравнению с
короткой антенной, имеющей h/l = 0,25.
Перекрестная модуляция в ионосфере. В ночное время в зоне приема ионосферных
волн может наблюдаться явление перекрестной модуляции. Это явление проявляется
в следующем: при настройке приемника на частоту f, которая принадлежит
передатчику относительно малой мощности, может прослушиваться передача мощного
передатчика (Pi > 50 кВт), при этом несущая частота мешающего
передатчика fм находится вне полосы пропускания приемника. Такое
явление возможно, если поле маломощного передатчика оказывается
промодулированным сигналом мощной станции. Модуляция происходит в ионосфере за
счет ее нелинейных свойств, коэффициент поглощения dи пропорционален sи. Если напряженность поля
мощной (мешающей) станции промодулирована низкой частотой W то sи, а следовательно, и dи изменяются в такт с этой
частотой. Необходимо выбирать мощности передатчиков и их взаимное расположение,
а также диаграммы направленности антенн с учетом эффекта перекрестной
модуляции.
Расчет напряженности поля ионосферной волны. В ночное время необходимо
учитывать, кроме земной волны наличие волны, отраженной от ионосферы.
Результирующая напряженность поля E=ÖE2зм+E2и.
Расчет составляющей, Ези рассмотрен в
предыдущем параграфе. Напряженность поля ионосферной волны Еи
рекомендуют определять, используя результаты статистической обработки
измерений, проведенных на Европейском континенте в течение более чем 45000 ч.
Напряженность поля пространственной волны на частоте f в заданный час t темного
времени суток на расстояниях более 300 км для Тн % ночей работы в
течение года определяется по формуле Eи(r,t,Tн) = Р1+DА+Fo(r,f)+Dj+Dн(Тн)-0,02Wс.
где P'1 — мощность, подводимая к
передающей антенне,дБ;
DА(h/l, r) — коэффициент, учитывающий
влияние диаграммы направленности передающей антенны высотой h (рис.8.4);
Fo(r,
f) —коэффициент, зависящий от длины радиолинии r и частоты f (рис.8.5);
DJ—поправка, определяемая по
рис.8.6 и учитывающая магнитное наклонение j в средней точке трассы ;
D(Тн)—коэффициент, зависящий от
времени t в средней точке трассы, когда задан процент времени
работы Tн
% в течение года (рис.8.7);
Wс—среднегодовое
число солнечных пятен.
Все величины, входящие в формулу и определяемые по
графикам рис. 8.4...8.7,
рекомендуются для расчета напряженности поля лишь на Европейском континенте,
где были получены исходные данные. В низких широтах северного полушария и южном
полушарии напряжённость поля обычно значительно выше, чем в Европейской зоне.
Зона обслуживания. Независимо от полосы частот, в которой работает вещательный передатчик,
принцип определения зоны обслуживания одинаков . В зависимости от частоты
изменяются вид и интенсивность помех и соответственно нормы на минимально
допустимый уровень напряженности поля Еmin и защитные отношения А.
Напомним, что величина Еmin лимитирует размеры зоны
обслуживания, если учитывать только внешние помехи природного происхождения, а
также промышленные и внутренние шумы приемника. Защитное отношение S
ограничивает зону обслуживания по уровню помех, создаваемых радиостанциями. Для
диапазонов ДВ и СВ расчет радиуса зоны обслуживания по заданной величине Еmin
проводится по следующей схеме. В
табл.8.2 приведены значения минимально допустимой напряженности поля на границе
зоны обслуживания, установленные в
соответствии с рекомендациями МККР.
Таблица 8.2
|
Частота, МГц |
0,2 |
0,5 |
1,0 |
1,5 |
|
Еmin, дБ/мкВ/м. |
73 |
66 |
60 |
57 |
Величина Еmin для диапазонов средних и
длинных волн и ДВ диапазонов определяется в основном атмосферными помехами,
поскольку граница зоны обычно проходит в сельской местности. Приведенные
значения Еmin справедливы для полосы
приема Df=6 кГц
и предусматривают отношение сигнал/шум = 40 дБ. В дневное время радиус зоны обслуживания
rзо
в предположении примерно однородных электрических параметров почвы в пределах
зоны определяется из условия Езм = Еmin, где Езм
- напряженность поля земной волны при
эквивалентной излучаемой мощности P1э. Для определения rзо удобно равенство записать относительно Езм(rзо), т. е. напряженности поля
на границе зоны при Р1э = 1кВт. Поскольку Езм(rзo) = Eзмl (rзо)ÖР1э, то получаем Езм1(rзо) = Еmin/Р1э Величины Еmin и P1э задаются.
Вычислив Eзм1(rзо) по кривым МККР, определяют
радиус rзо.
В ночное время на разных удалениях от передатчика изменяется соотношение между
полем земной и пространственной волн. Ориентировочно принимают, что на
расстояниях меньше 100 км преобладает поле земной волны Езм, если г ³ 300 км, то преобладает поле
ионосферной волны Еи; если r » 100...300 км —
результирующее поле Е = ÖЕ2зм+Е2и.
Граница зоны обслуживания в темное время суток проходит обычно в области
действия ионосферной волны, для которой характерны флуктуации часовых медианных
значений поля от дня ко дню. Поэтому при вычислении радиуса зоны пользуются
вероятностными характеристиками. Радиус зоны по ионосферной волне определяется
из равенства Eи(rзо,t,Tн)=Emin,
где Еи(rзо, t, Ти) — напряженность, поля
ионосферной волны на расстоянии rзо в заданный час t
темного времени суток для Tн % ночей работы в течение
года. Величина Еи является сложной функцией расстояния, поэтому
радиус rзо
можно определить только после построения зависимости Еи(г) для
данного часа t, принимая в соответствии с нормами качественного вещания Tн=90%. Радиус rзо есть то расстояние, на
котором Еи=Еmin. Определение границы зоны
обслуживания с учетом мешающего действия станции достаточно громоздко,
поскольку учитывает флуктуации полей как полезной, так и мешающей станций .
Диапазон ДВ - участок радиодиапазона 10 км...1км (30...300 кГц).
Тропосфера не влияет. Диапазон электромагнитных волн, создаваемых с помощью
различных радиоустройств, ограничен длинами волн около 20...30 км
(15...10 кГц). Мощные поля более длинных волн возбуждаются только
естественным природным источником — молниевыми разрядами, которые излучают
непрерывный спектр волн, особенно
интенсивных на частотах от 30...50
кГц до нескольких сотен Герц и меньше.
Область применения диапазона
СДВ и ДВ определяется особенностями их распространения. Относительно малое
затухание поля в тракте распространения и устойчивость по отношению к
ионосферным возмущениям позволяет использовать эти диапазоны для связи на
дальние расстояния, простирающиеся до антипода. Однако малая частотная емкость
этих диапазонов позволяет применять только телеграфные системы с малыми
скоростями телеграфирования (например, работа ключом). Большое применение эти
частоты находят в системах дальней навигации и передачи сигналов точного
времени, что объясняется большой стабильностью амплитудных и фазовых
характеристик поля. Наилучшее объяснение наблюдаемых закономерностей изменения
поля в пространстве и во времени дает теория волноводного распространения.
Современные теории принимают, что ионосферные сверхдлинные и длинные волны распространяются в сферическом волноводе,
нижней стенкой которого является поверхность Земли, а верхней — днем слой D,
ночью — слой Е. Сложность физических процессов при распространении радиоволн в
таком волноводе, обусловлена следующими основными причинами: сферичностью Земли
и ионосферы, размытостью и конечной проводимостью нижней границы ионосферы, ее
анизотропными свойствами за счет влияния магнитного поля Земли, конечной
проводимостью и сложным рельефом земной поверхности. Нахождение поля в
сферическом волноводе Земля - нижняя граница ионосферы сводится к решению
уравнений Максвелла с учетом граничных условий, в которых отражены форма и
электрические характеристики стенок волновода. Несмотря на трудности, теория
волноводного распространения достаточно хорошо разработана. Однако на
сегодняшний день еще не создан метод, удобный для практических расчетов поля.
Волноводная
теория показывает, что, как и в идеальном волноводе, поле в точке приема
представляет результат интерференции множества волн, претерпевших n-кратные
отражения от стенок волновода. Каждая n-составляющая, называемая
парциальной волной, распространяется по наклонной по отношению к оси волновода
траектории с фазовой скоростью, равной скорости света в данной среде. Каждой парциальной
волне соответствует свой угол падения jn
на стенки волновода. От этого угла зависят коэффициент отражения от стенок, а
следовательно, и закон затухания волны. Из курса “ Электромагнитные поля и
волны” известно, что в волноводе с идеальными стенками парциальные волны
формируют дискретный набор поперечных магнитных волн ТН и поперечных
электрических волн ТЕ, распространяющихся вдоль оси волновода с фазовой
скоростью, которая всегда превышает скорость света в среде. В сферическом
волноводе Земля — нижняя граница ионосферы поле представляет также результат
суперпозиции множества дискретных волн, но квазипоперечного типа —
квазипоперечных магнитных ТН волн и квазипоперечных электрических ТЕ волн. Эти
волны называются квазипоперечными, поскольку содержат слабые продольные
составляющие: волна квази-ТН — составляющую Н, волна квази-ТЕ — составляющую Е.
Появление этих составляющих обусловлено преобразованием в анизотропной
ионосфере линейно-поляризованного поля в
поле с эллиптической поляризацией.
Квазипоперечные
волны различают по номерам m и называют модами или
«нормальными волнами». Существует набор мод
квази- ТНm, где m==0, 1,
2,..., и квази-ТЕm, где m =1, 2,
3, ... Номер m определяет характер распределения поля по высоте
волновода. Каждый мод формируется
двумя или более парциальными волнами, различающимися по углам падения.
Поскольку от угла падения зависит, коэффициент отражения от стенок волновода,
то каждому моду соответствует свой коэффициент затухания. Расчеты показывают,
что с увеличением номера мода коэффициент затухания увеличивается. Сильно
ослабленными оказываются моды,
формирующиеся парциальными волнами с углами падения, близкими к углам Брюстера,
для которых характерно почти полное прохождение энергии падающей волны через
отражающую область. Быстрое затухание мод с высокими номерами приводит к тому,
что с увеличением расстояния все меньшее число мод оказывается существенным при
формировании поля. На больших расстояниях число мод, формирующих поле, зависит
также от часов суток. Ночью в формировании поля участвует большее число мод,
чем днем, поскольку в темное время суток слой D пропадает и затухание всех мод
уменьшается.
Различают по расстоянию три области
формирования поля — ближнюю, промежуточную и дальнюю.
В ближней области (r < 1000 км) справедлива
лучевая трактовка распространения, когда поле представляется в виде суммы полей
земной волны и волн, n-кратно отраженных от
ионосферы. Сравнение расчетов и эксперимента показывает, что погрешность
расчета порядка 5% может быть получена при учете набора волн до пятикратно
отраженных от ионосферы.
В
промежуточной области (r =
1000...2000 км) справедлива только волноводная схема распространения и поле
формируется как основными модами квази-TH1 и квази-ТН2,
так и модами с более высокими номерами.
В дальней области (r >
2000 км) также справедлива
волноводная схема, но поле формируется только основными модами, При
расчете с погрешностью до 10% дневное поле в этой области определяется волной
квази-TH1, а ночью — тремя волнами: квази-TH1, квази-ТН2
и квази-TE1. Изменение структуры поля в течение суток приводит
к разным суточным закономерностям изменения поля на разных расстояниях в
дальней области. Днем, когда доминирует одна волна, поле плавно уменьшается по
мере увеличения расстояния; ночью эта зависимость носит немонотонный характер
за счет интерференции трех основных мод. Необходимо отметить еще одну
особенность распределения поля с расстоянием, наблюдаемую только в диапазоне
СДВ, которая сводится к так называемому эффекту “антипода”. Измерения
показывают, что на расстоянии около 20000 км от излучателя (точка антипода)
напряженность поля возрастает (рис. 7.1). В антиподе амплитуда поля превышает
ее значения на экваторе в 6...7 раз. Теория волноводного распространения
подтверждает существование такого эффекта в сферическом волноводе. Чисто
качественно его можно объяснить как результат «стекания» в эту область волн,
приходящих с разных направлений, т. е. лучи, огибающие Землю, у антипода
сходятся как в фокус оптической системы.
Изменения напряженности поля в течение суток. Регулярные изменения во
времени напряженности поля длинных и сверхдлинных волн связаны с регулярными изменениями состояния
ионосферы — высоты ее основания и степени ионизации отражающей области. Сложная
интерференционная структура ночного поля, зависящая от расстояния, делает
суточный ход неоднозначным. Нормальным суточным ходом считается повышение поля
от дня к ночи , что объясняется уменьшением поглощения ионосферных волн при
пропадании слоя D в темное время суток. Несмотря на то, что ночью возрастает
обычно не только поле полезного сигнала, но и поле помех, отношение
сигнал/помеха оказывается в большинстве случаев более выгодным ночью, чем днем.
На некоторых линиях во время восхода и захода Солнца появляются глубокие
минимумы поля. Это явление называется сумеречным эффектом.
Сезонные изменения напряженности поля в промежуточной и дальней зонах выражены
слабо и не всегда однозначно. Обычно в летние месяцы значения Е ниже, чем зимой
.
Влияние цикла солнечной активности. Многочисленные наблюдения показали, что с
увеличением активности Солнца напряженность поля волн НЧ и ОНЧ возрастает , что
объясняется ростом градиента электронной плотности у основания ионосферы при
повышенной солнечной активности.
Нерегулярные изменения напряженности поля обусловлены неоднородной
структурой ионосферы, меняющейся во
времени. Случайные колебания поля в диапазонах СДВ и
ДВ незначительны по глубине и происходят настолько медленно, что не
прослушиваются при слуховом приеме. Их можно обнаружить только при записи
напряженности поля на самописец. Колебания имеют интерференционное
происхождение и обусловлены изменением сдвига фаз между интерферирующими
составляющими. Значительные изменения фазовых сдвигов на волнах километровой
длины возможны при случайных отклонениях длин траекторий на единицы
километров (Dr =l/2). Такие отклонения не
могут произойти за короткий промежуток времени. Поэтому случайные неглубокие
изменения уровня сигнала имеют плавный характер и протекают в течение десятков
минут и даже часов. Отсутствие быстрых замираний является характерной
особенностью условий приема волн СДВ и ДВ.К нерегулярным изменениям уровня
сигнала следует отнести некоторое ослабление поля в начале ионосферных
возмущений корпускулярного происхождения и увеличение в дни, следующие за
возмущением. Внезапные возмущения типа «вспышки» поглощения всегда приводят к
увеличению напряженности поля на время «вспышки» - возрастает ионизация слоя D
и уменьшается проникновение волн СДВ и ДВ диапазона в поглощающую область
ионосферы. С укорочением длины волны эта тенденция ослабевает.
ТЕМА 15.
Распространение радиоволн в городских условиях
Условия приема сигналов в
диапазоне УКВ существенно зависят от расположения приемной антенны относительно
окружающих ее предметов. В городских условиях такими предметами являются
здания, деревья, заводские трубы, мачты и т. п. Близко расположенные здания
могут в зависимости от их расположения оказаться затеняющими препятствиями или
источниками местных отраженных волн. Затеняющее действие отдельного препятствия
приводит к тому что поле за препятствием появляется в результате двух
процессов: дифракции и проникновения через препятствие. Дифракция в
рассматриваемом диапазоне волн протекает с большими потерями. Проникновение сквозь
препятствия типа стен зданий также сопровождается большими потерями за счет
поглощения. Измерения показывают, что напряженность поля за отдельно стоящим
кирпичным зданием на 20...30дБ ниже, чем перед ним, а за железобетонным
строением уровень сигнала падает на 30...40 дБ. В. целом внутри городской
застройки имеются многочисленные теневые зоны, где сигнал значительно ослаблен.
Действие окружающих зданий как источников отраженных волн проявляется, как в
виде неравномерного распределения амплитуды поля в пространстве из-за
интерференции многочисленных отраженных волн, так и в своеобразном
подсвечивании теневых зон. В случае вертикальной поляризации первичного поля
отражения наиболее интенсивны от предметов, протяженных по вертикали (стены
зданий, деревья). Большое влияние местных предметов на условия приема
вертикально-поляризованного поля является одной из причин преимущественного
применения горизонтальной поляризации в системах телевизионного вещания.
Сложность условий
распространения УКВ в городе определяет статистический характер, как
теоретических, так и экспериментальных исследований. По условиям приема сигнала
можно выделить три наиболее типичных ситуации: передающая и приемная антенны
находятся над уровнем городской застройки и между ними имеется прямая
видимость; связь между подвижным объектом и базовой станцией; связь между двумя
подвижными объектами. В первом случае, характерном для приема сигналов
телевизионного вещания, расчет напряженности поля можно вести по формуле
Введенского, умножая результат расчета на поправочный коэффициент (обычно
0,4...0,6). Во втором и третьем случаях между пунктами передачи и приема, как
правило, нет прямой видимости и основной вклад в формирование многолучевого
поля вносят отражения от зданий в окрестности подвижного пункта.
Рассмотрим закономерности
изменения напряженности поля в точке приема в городских условиях в зависимости
от расстояния, частоты волны и высот установки антенн. На рис.10.5 приведены
зависимости среднего (медианного) значения мощности сигнала Рс от расстояния r при различных высотах
подвеса антенны базовой станции h1,
измеренные на частоте 922 МГц. Высота подвеса антенны на подвижном объекте h2 = Зм. Штриховой линией
показана зависимость Рс от расстояния для условий свободного
пространства. Уровень 0 дБ соответствует полю в свободном пространстве на
расстоянии 1 км от базовой станции. Анализ приведенных зависимостей показывает,
что при увеличении расстояния до 15 км мощность сигнала убывает как r-3.
Последующее увеличение r приводит к еще более
быстрому уменьшению уровня сигнала. Ослабление сигнала в городе возрастает с
увеличением его частоты. Если эту зависимость представить в виде Pc=Af-n, где A -
коэффициент пропорциональности. C увеличением частоты от 100
до 2000 МГц значение коэффициента n изменяется от 0,2 до 1 .
При r =1...10 км зависимость уровня поля от частоты слабая, но при
дальнейшем увеличении расстояния значение коэффициента n начинает зависеть от него и
растет значительно быстрее. Изменение медианного значения множителя ослабления
от частоты, при h1=200 м и h2=3 м для расстояний 1, 5, 20
и 40 км, показано на рис.10.6. Зависимость среднего уровня поля от высоты
расположения антенны базовой станции можно проследить по рис.10.7. Высота
подвеса антенны сильно не влияет на скорость уменьшения уровня сигнала с
расстоянием. Однако подъем антенны базовой станции приводит к увеличению
абсолютного значения поля примерно пропорционально квадрату высоты
(6дБ/октаву). На поле в точке приема влияют не только рассмотренные факторы, но
и многие другие. В частности, установлено, что уровень сигнала существенно
зависит от расположения улиц в городе, которые оказывают канализирующее
действие на распространяющиеся волны. Вдоль радиально расположенных улиц
(относительно антенн базовой станции) уровень сигнала на 10...20 дБ выше, чем в
перпендикулярных направлениях.
Условие приема на метровых и более коротких волнах зависит от расположения приемной антенны относительно окружающих ее предметов и местных неровностей рельефа. Близко расположенные здания, мачты, растительность, склоны оврагов, небольшие возвышенности могут в зависимости от их расположения оказаться затеняющими препятствиями или источниками местных отраженных волн. Затеняющее действие отдельного препятствия приводит к тому, что поле за препятствием появляется в результате двух процессов: дифракции и проникновения сквозь препятствие. Дифракция в рассматриваемых диапазонах волн протекает с большими потерями. Проникновение сквозь препятствия типа стен зданий, группы деревьев и других сопровождается также большими потерями за счет поглощения. «Непрозрачными» препятствиями считают возвышенности земной поверхности и железобетонные строения. За такими препятствиями поле появляется только в результате дифракции. К «полупрозрачным» препятствиям относят кирпичные и деревянные строения, растительность. При распространении в лесу с подлеском погонное ослабление оценивается единицами и десятками дБ/км, увеличиваясь с частотой и изменяясь в зависимости от густоты лиственного покрова и влажности. Действие окружающих предметов как источников отраженных волн может проявиться в виде двух явлений: неравномерного распределения амплитуды поля в пространстве из-за интерференции отраженных волн или запаздывающих сигналов, если предмет достаточно удален от приемной антенны.
Спецификой условий работы вещательной сети является
прием излучения одного передатчика одновременно множеством приемных пунктов,
случайно распределенных на некоторой территории. В зависимости от характера
рельефа условия приема в пределах этой территории могут быть различными. Кроме
того, принимаемое поле подвержено быстрым и медленным флуктуациям, и его
среднее значение изменяется в зависимости от климатических условий. В
результате в сети вещания принято оценивать напряженность поля вероятностными
характеристиками, основанными на измерениях. Необходимо отметить, что при
оценке условий приема вещания учитывают только медленные флуктуации, принимая,
что мгновенные значения поля подчиняются нормально-логарифмическому
распределению с дисперсией, зависящей от климатических условий. Быстрые замирания порядка долей
секунд и секунд не оказывают влияния на качество приема телевизионного и
звукового вещания из-за инерции слухового и зрительного аппаратов человека.
Параметрами для статистических характеристик поля служат: диапазон частот,
климатический район, средние условия рельефа, процент времени наблюдений,
процент приемных пунктов, в которых
может наблюдаться данная напряженность поля. Напряженность поля определяют с помощью
кривых, рекомендуемых МККР. В качестве примера на рис.10.4 приведены три кривые,
справедливые для ОВЧ
(40...250 МГц) в условиях среднепересеченной местности и умеренного
климата, характерных для Европы и Северной Америки. Величина напряженности
поля, определяемая из этих кривых, превышается в 50% приемных пунктов в течение
50%, 10 % и 1% времени. Кривые
построены для эквивалентной излучаемой
мощности 1 кВт, когда высота
подвеса передающей антенны h1 =300м, высота подвеса приемной антенны h2 = 10 м. Напряженность поля
выражена в децибелах относительно 1 мкВ/м. Кривые справедливы для вертикально-
и горизонтально поляризованных волн. В указанной рекомендации имеются серии
аналогичных кривых для диапазона УВЧ (450...1000 МГц). Для каждого диапазона
даются поправочные коэффициенты, учитывающие степень неровности рельефа и
высоту передающей и приемной антенн.