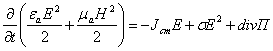УЗБЕКСКОЕ АГЕНСТВО СВЯЗИ И ИНФОРМАТИЗАЦИИ

ТАШКЕНТСКИЙ УНИВЕРСИТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ

Кафедра

Антенно-фидерных

устройств

Г.Ф. Габзалилов, В.С. Кан

Конспект лекций по дисциплине

ЭЛЕКТРОМАГНИТНЫЕ ПОЛЯ И ВОЛНЫ

Часть 1. Основные принципы электродинамики

Ташкент 2007

ВВЕДЕНИЕ

Доля радиотехнических систем в современной телекоммуникации все более увеличивается. При этом наблюдается смещение рабочего диапазона используемых несущих колебаний в более высокую область спектра частот. Например, исчерпав возможности диапазона 4…6 ГГЦ спутниковое телевидение заняло следующий интервал 11…14 ГГЦ готовится к освоению третье поколение телевещания через космические ретрансляторы в диапазоне 20…30 ГГц. Увеличение частоты несущей сигнала позволяет размещение большего числа каналов, т.е. способствует увеличению емкости используемого диапазона. С этой точки зрения возможности оптического диапазона частоты выше 3×10¹² Гц чрезвычайно высоки. Именно поэтому в современной телекоммуникации волоконно-оптические линии связи (ВОЛС) занимают ведущее место. Основной частью ВОЛС является кварцевая нить, соединяющая стационарные приемные и предающие устройства. Однако для связи с подвижными объектами ВОЛС на может выступать в качестве главного вида связи - для перемещающегося корреспондента удобнее использование свободных радиоволн. Сотовая связь с подвижными объектами широко использует, например, диапазон около частоты 900 МГц.

Приведенные примеры современных систем телекоммуникации показывают, что использование спектра высоких частот очень перспективное направление. Теоретическая база техники сверх-высокочастотной (в том числе и оптической) телекоммуникации основана на уравнениях Максвелла и использует элементы векторной алгебры и векторного анализа. Изучение волновых явлений в устройствах СВЧ, или пространственной структуры поля в свободном пространстве и линиях передачи не требует рассмотрения вопросов на уровне квантовой физики, достаточно их представление через непрерывные в пространстве поля. Такое рассмотрение называют макроскопическим, а теорию использующую такое «усреднение» называют классической электродинамической.

Настоящая первая часть конспекта лекций содержит теоретические основы электродинамики и служит базой для изучения последующих разделов дисциплины ЭМП и В.

1.ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ

1.1. Понятие электромагнитного поля

Под электромагнитным полем (ЭМП) понимают вид материи, характеризующийся совокупностью взаимно связанных и взаимно обусловливающих друг друга электрического и магнитного полей. Важнейшей отличительной особенностью внешнего ЭМП является его способность оказывать силовое воздействие на заряженную частицу, которое зависит от величины электрического заряда частицы и скорости ее движения. В телекоммуникации используются переменные во времени поля. В таких полях электрическая часть неотделима от магнитной и наоборот. Однако теория ЭМП использует исторически накопленный опыт изучения электрических и магнитных явлений в природе, начиная с постоянных во времени (стационарных) процессов. Постоянные электрическое и магнитное поля могут существовать раздельно, независимо друг от друга, но они не могут быть использованы для передачи информации. В современной теории переменного ЭМП – электродинамике продолжается использование понятий электрического и магнитного полей, как двух форм проявления единого ЭМП

ЭМП объективно существует в природе, поэтому является видом материи, отличающимся от другой формы материи - вещества. Различные поля, накладываясь друг на друга могут существовать в одном объеме, а частицы вещества взаимно непроницаемы. Частицы вещества имеют массу покоя m₀ и скорость v. Частицы ЭМП - фотоны массы покоя не имеют, так как существуют только в движении со скоростью с » 3× 10⁸ м/с в вакууме. Вещество никогда не может достигнуть этой скорости, т.к. его масса при этом обратилась бы в бесконечность.

В движении ЭМП в виде электромагнитной волны, также как вещество, имеет инертную массу. Она была обнаружена в уникально тонких опытах П.Н.Лебедева по измерению светового давления, а как доказал Д.К. Максвелл свет тоже является электромагнитным процессом. Позже А. Эйнштейн установил взаимосвязь массы m со скоростью перемещения с и энергией материи W=mc².

Отсюда следует, что антенна радиостанции мощностью 1000 кВт и течение одного часа излучает ЭМП массой 0,04 мг. Высокая скорость распространения столь малой массы создает значительную энергию.

Вещество и ЭМП, как виды материи, обладают одинаковыми характеристиками: энергией, массой и количеством движения. ЭМП поэтому, может быть использовано как переносчик энергии сигнала телекоммуникации. Волновые электромагнитные процессы используются не только для передачи в свободном пространстве и по линиям передачи, но и в различных электродинамических устройствах техники радиосвязи и радиовещания.

Используемые в инженерной практике явления обычно не требуют знания подробностей сложных электромагнитных процессов, происходящих в микроскопических, атомных масштабах. В большинстве технических задач интерес представляют процессы, протекающие в макроскопическом масштабе, т.е. усредненные во времени и пространстве. Усреднение мысленно проводится на расстояниях значительно больше размеров атомов и молекул вещества (но гораздо меньше длины используемой электромагнитной волны). Интервал усреднения во времени значительно больше периода орбитального и спинового вращения элементарных частиц, но значительно меньше периода колебания векторов внешнего ЭМП. Рассматриваемая нами теория ЭМП не учитывает квантовые эффекты в веществе, она называется макроскопической (или классической) электродинамикой.

1.2. Векторы ЭМП

В ЭМП на заряды и токи действуют силы, которые совершая работу по их перемещению уменьшают энергию поля. В качестве пробного тела, при помощи которого можно не только обнаружить, но и изменить поле, рассматривают достаточно малое заряженное тело - точечный заряд. На него в ЭМП действует сила Лоренца

F=q(E+[V,B])

где q, V – электрический заряд и скорость его движения; Е (r, t) - вектор напряженности электрического поля; В (r, t) - вектор магнитной индукции; r – радиус-вектор точки пространства, в которой находится заряд; t — время. В случае неподвижного заряда (V =0) сила

F_э = qE

т.е. Е - это сила, с которой ЭМП действует на единичный положительный неподвижный заряд. Размерность вектора Е Н/Кл=В/м.

Магнитное поле действует только на движущие заряды (токи)

F_м = q [V,B]

Сила воздействия максимальна, если V перпендикулярна B, и отсутствует, если векторы V и В совпадают по направлению. Таким образом, вектор В определяется по силовому воздействию ЭМП на движущиеся заряды. Размерность вектора В Н×с/(Кл×м) = В×с/м² = Вб/м² = Т.

Содержание рассмотренных векторов Е и В связано с воздействием внешнего поля на очень малые заряды и короткие токи. Малость зарядов необходима чтобы они не искажали измеряемое поле. Но ведь электрический заряд и элемент тока имеют собственное электрическое и магнитное поле. Вокруг заряда всегда существует электрическое поле, линии которого исходят из него самого. Провода (элементы проводов) с током создают собственное магнитное поле, линии которого окружают его. Элементарные связанные заряды в молекулах диэлектриков и элементарные магнитные поля в магнитных материалах могут значительно изменить проникающие в материал ЭМП. Тогда для описания явлений требуется введение дополнительной пары векторов:

D (r, t) - электрическая индукция,

Н (r, t) – напряженность магнитного поля.

D - называют также вектором электрического смещения. Размерность векторов, как видно из дальнейших уравнений равна [D] = Кл/м² и [Н] = А/м. Так как эти вектора D (и Н) характеризуют связь заряда (и тока) с собственным электрическим (и магнитным) полем, их называют функциями источников.

Считают, что поле определено, если в каждой точке пространства в любой момент времени известны величины и направления четырех векторов Е, D, В и Н. Так как вектор определяется своими компонентами, то каждый из векторов (например, вектор Е (x,y,z)) представляет собой три математические пространственно-временные функции от x,y,z и t. В формальном (математическом) подходе к понятию «поле», его можно рассматривать как физическую величину (силу), которая в разных точках пространства принимает различные значения.

Теория ЭМП сложилась в результате накопления и обобщения экспериментальных фактов, а также развития математического аппарата, который опирается на векторный анализ. В основных уравнениях ЭМП векторы Е, D, Н, В связаны с помощью операторов «дивергенция» и «ротор» с другими величинами р и J .

Электрический заряд в каждой точке пространства характеризуется объёмной плотностью

(1.1)

где q –суммарный заряд в объеме.

Упорядоченное движение зарядов через каждую точку поля характеризуется вектором плотности электрического тока проводимости

J_np=p×V, (1.2)

Суммарный электрический ток, протекающий через некоторую поверхность S является скалярной величиной и связан с J_пр интегральным соотношением:

I = ∫ J× dS, A (1.3)

где dS - представляет вектор элементарной площадки. Интеграл вида (1.3) называют потоком вектора J через поверхность S. Следовательно, электрический ток можно рассматривать как поток плотности тока через заданную поверхность.

1.3. Электродинамические параметры сред. Классификация сред

Внутри любого вещества могут существовать электрические заряды, которые под воздействием внешнего электрического поля могут перемещаться от одной молекулы к другой, т.е. они свободные заряды или смещаться в пределах одной молекулы, т.е. оставаться связанными. В первом случае мы имеем пример поведения электронов и ионов в металлах, электролитах и ионизированных газах. В диэлектрических средах мы имеем дело со связанными зарядами. Смещение связанных зарядов в атомах и молекулах создает явление, которое называют «поляризацией среды». Поляризация приводит к созданию внутреннего электрического поля, направленного против внешнего поля Е₀ . Поэтому внутри диэлектрика проникающее внешнее поле ослабляется. Степень ослабления выражают через параметр ε_а - абсолютную диэлектрическую проницаемость. Этот параметр связывает два электрических вектора ЭМП

D = ε_а × E (1.4)

которое называют первым материальным уравнением электродинамики.

Насыщенность вещества свободными электронами определяет свойство вещества создавать ток проводимости. Это свойство характеризуется параметром s - удельной электрической проводимостью. Параметр s связывает вектора J_np и Е равенством:

J_np=s ×E, (1.5)

которое тоже относится к материальным уравнениям электродинамики. Известный из теории цепей закон Ома для участка цепи является следствием уравнения (1.5), поэтому его называют также законом Ома в дифференциальной форме.

Внутри любого вещества существует также источники магнитного поля замкнутые элементарные электрические токи, которые являются результатом орбитального движения и спинового вращения электронов. Эти элементарные токи обладают магнитными моментами, ориентирующимися под воздействием внешнего ЭМП. Суммарный магнитный момент в данном объеме определяет процесс намагничивания среды Количественно намагничивание оценивается параметром m_а - абсолютной магнитной проницаемостыо, который связывает два магнитных вектора ЭМП

В=m_а × Н (1.6)

Это уравнение является третьим материальным уравнением электродинамики.

Параметры ε_а, m_а, s, а зависят от физико-химических особенностей (структуры) данного вещества, температуры, частоты, давления и воздействующих полей. Их определением занимается квантовая электродинамика. В изучаемой нами классической электродинамике среда представляется сплошной, а величины, характеризующие ЭМП, непрерывно распределенными в пространстве., т.е. в макроскопическом виде. В макроскопической электродинамике пользуются указанными параметрами как заданными

Материальные уравнения (1.4) - (1.6) записаны так, что параметры ε_а, m_а, s, являются скалярными величинами. Такие среды являются изотропными. В них направления векторов D и Е, В и Н, J и Е совпадают, а свойства среды не зависят от направления векторов (т.е. и направления распространения поля)

В технике СВЧ находят применение два особых материала: сегнетоэлекгрики и ферриты которые меняют свой свойства под воздействием внешних условий. Эти явления невозможно описать через скалярные параметры ε_а, m_а. Приходится использовать матрицу (тензор) параметров

m_хх m_хy m_хz

m_а = m_yх m_yy m_yz (1.7)

m_zх m_yz m_zz

и при этом, например, одна из составляющих вектора В запишется в виде:

В_х = m _ххН_х + m_yхН_y +m_zх Н_z,

т.е. каждая проекция вектора зависит от всех составляющих вектора Н. Это говорит о том, в этой среде векторы В и Н не совпадают по направлению, т.е. свойства среды зависят от направления прохождения ЭМП в виде волны Такая среда называется анизотропной по магнитным свойствам. В анизотропной среде электродинамический параметр подставляется не скалярным коэффициентом, а тензорным. Сегнетоэлектрики анизотропны по электрическому полю т.е. по параметру ε_а.

Говорят, что среда однородна в области, если параметры ε_а, m_а, s, (скаляры или тензоры) постоянны в V. Если же их следует рассматривать как функцию

координат, то среда неоднородна. Наконец, параметры среды в большинстве случаев можно считать независящим от векторов поля. Материальные уравнения (1.4)-(1.б) при этом линейны. Линейными, называют и соответствующие среды. Нелинейность большинства сред проявляется только в очень сильных полях. В нашем курсе лекций рассматриваются линейные, однородные и изотропные среды. Анизотропным средам посвящена последняя лекция.

Примеры сред. Наиболее широко в современной технике СВЧ применяются такие диэлектрики, как полиэтилен, полистирол и фторопласт, обладающие малыми диэлектрическими потерями, достаточно высокой электрической прочностью и легкообрабатываемые. Применяются так же различные типы высокочастотной керамики, стекло, конструкционные пластмассы и др. Диэлектрические материалы характеризуются параметром ε_а. В принятой системе единиц СИ его можно представить в виде

ε_{а =} ε₀×ε

где ε₀ = (1/36p)10^-9 Ф/м - электрическая постоянная. Относительная диэлектрическая проницаемость ε - множитель не имеющий размерности упрощает табулирование материалов по этому параметру , т.к. не содержит иррационального числа p для всех диэлектриков ε >l. Диэлектрики полиэтилен, полистирол и фторопласт имеют близкие по значению ε в диапазоне 2,0 ... 2,6. Для брокерита 9 (керамика) ε = 6,6, а для стекла ε = 4,0. Воздух очень близок к вакууму : ε = 1; ε_{а =} ε₀ . Для сухой земли ε = 3...6; для воды ε » 80.

Проводниковые материалы в конструкциях СВЧ устройств должны

иметь высокое значение электрической проводимости s. На сверхвысоких значениях частоты токи в волноводах протекают лишь по поверхности металла обращенной к ЭМП. Тонкий поверхностный слой вносит потери передачи энергии, увеличивающейся с ростом частоты и параметра m_а и уменьшением s. Поэтому абсолютная магнитная проницаемость применяемых металлов

m_а =m₀ × m

должна быть близка к магнитной постоянной m₀ = 4p×10⁷ Гн/м, т.е. относительная магнитная проницаемость должна быть ближе к единице. Равенство m = 1 говорит о том, что данный материал так же как и вакуум и воздух не намагничивается. Диамагнетик медь имеет m = 0,99999044 m <1), а парамагнетик алюминий - m = 1,0000222 (m >1), т.е. и тот и другой металл по магнитным свойствам очень близок к вакууму.

По электропроводности металлы расположены по убыванию параметра s в следующем ряде: серебро — 6,17×10⁷ См/м; медь – 5,8×10⁷ См/м; золото – 4,1×10⁷ Cм/м; алюминий - 3,72× 10⁷ См/м. Серебро, как правило, используется для нанесения покрытий, обладающих высокой электропроводностью. Однако, на влажном воздухе серебро (и медь) легко окисляются покрываясь слоем, имеющим большое удельное сопротивление и вносящим тепловые потери передачи мощности ЭМП. Слой золота толщиной всего в несколько микрон, нанесенный на поверхность легкоокисляющихся металлов, становится практически непроницаемым для кислорода.

2. Уравнения ЭМП

2.1. Операторы векторов поля

Основными операторами, используемыми при анализе электромагнитных явлений являются: поток вектора через поверхность, циркуляция вектора по замкнутому контуру, дивергенция и ротор вектора.

Примеры интегральных операторов:

- поток вектора D через замкнутую поверхность S;

- циркуляция вектора Н по замкнутому контуру

Интегральные операторы, усредняющие в пространстве поток и циркуляцию векторов по поверхности или контуру могут быть приведены в дифференциальную форму, т.е. превращены в характеристики поля в точке пространства. Операции поток и дивергенция связаны между собой равенством

lim_V®0 = divD, (2.1)

т.е. поток вектора через поверхность, окружающую точку в пространстве отображает его дивергенцию.

Так как скалярное произведение Dds=Dds×cosa может дать как положительный, так и отрицательный результат, то поток и дивергенция тоже представляют положительные либо отрицательные величины. Если угол между векторами D и ds (направлен по внешней нормали к поверхности) менее 90⁰ (силовая линия D выходит из поверхности), то div D >0. Если силовая линия направлена во внутрь поверхности, то a >90⁰, cosa>0 и div D <0. Следовательно, в точке пола, где собираются силовые линии, дивергенция отрицательна., а в точке, откуда наблюдается исток линий - дивергенция положительна

Определение (2.1) можно в разных системах координат через частные пространственные производные проекций вектора В прямоугольной системе координат дивергенция представляется суммой частых производных проекций вектора по своим направлениям:

div D = (2.2)

В отличие от дивергенции операция ротор дает векторную величину. Нормальная к поверхности контура циркуляции составляющая ротора связана операцией взятия предела:

rot_nH = lim_S®0 (2.3)

где S - площадь, заключенная внутри контура L, окружающая в пределе точку в пространстве.

В прямоугольной системе координат операция взятия ротора представляет следующую комбинацию частых производных проекций вектора:

rot H = 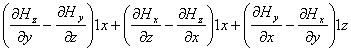(2.4)

где 1_х, 1_y, 1_z - представляют единичные векторы (орты) осевых направлений,

Если результат операции (2.4) равен нулю, то поле называют «безвихревое». Неизменное во времени электрическое поле во всех точках пространства rot Е = О, т.е. электрическое поле является безвихревым.

2.2. Третье и четвертое уравнение Максвелла

Максвелл обобщил теорию электромагнетизма и экспериментальную электродинамику своего времени (1864 год) в ряде уравнений. Позже установили, что только четыре его уравнения являются базисными и независимыми. Уравнения Максвелла являются основой современной классической электродинамики. Они универсальны, с их помощью совместно с материальными уравнениями можно решить теоретически любую электродинамическую задачу.

Ниже рассмотрено содержание уравнений Максвелла, записанных в современной системе единиц СИ и математических операции векторного анализа. Рассмотрение изложено по принципу «от более простых к более сложным».

Третье уравнение Максвелла является обобщением для переменных во времени электрических зарядов, известной теоремы Гаусса из электростатики:

(2.5)

где Q_своб алгебраическая сумма свободных электрических зарядов, расположенных в объёме, ограниченном поверхностью S. Если заряд в объеме распределен непрерывно, то

(2.6)

где r_своб - функция распределения объемной плотности зарядов.

Если применить к (2.5) с учетом (2.6), операцию (2.1), то получим:

divD = r_своб (2.7)

Следовательно, в каждой точке поля дивергенция вектоpa D численно равны объемной плотности свободных зарядов в этой же точке. Если заряд положителен div D>0, силовые линии D исходят из точки. А в точках, где r<0 силовые линии сходятся, наблюдается их сток.

Уравнения (2.5) и (2,7) носят название третьего уравнения Максвелла соответственно в интегральной и дифференциальной формах. Если подставить в них первое материальное уравнение (1...), то это уравнение Максвелла для случая однородной диэлектрической среды приобретает вид:

(2.8)

либо

div E = (2.9)

В равенствах (2.8) и (29) присутствуют как свободные электрические заряды, так и связанные, действие которых отображается параметром e_а Переход в записи уравнения к вектору D (см (2.7)) исключает из расчетов явление поляризации диэлектрика т.е. параметр e_а . Это говорит о том, что при расчете вектора D не учитывается характер диэлектрика (его атомно-молекулярное строение) и поля, обусловленные одними и теми же свободными зарядами, характеризуются в любых веществах и вакууме одними и теми же значениями вектора D. Поэтому можно утверждать, что вектор D обусловлен только свободными зарядами, а вектор Е - как свободными, так и связанными зарядами. Введение вектора D для описания электрических полей в веществе очень упрощает задачу. В абсолютной системе единиц (СГС) вектор D численно равен напряженности электрического поля Е от заданного заряда в вакууме.

Четвертое уравнение Максвелла фактически является утверждением того, что силовые линии магнитного поля непрерывны - не имеют ни начала ни конца. Вследствие этого магнитный поток через любую замкнутую поверхность всегда равен нулю — входящий в объем (отрицательный) поток равен выходящему (положительному).

Магнитные заряды в природе не обнаружены, поэтому нет точек в пространстве, где бы они могли прерваться. Эти утверждения выражаются с помощью операторов в следующем виде:

(2.10)

divB = 0 (2.11)

Равенство нулю дивергенции вектора поля показывает на то, что линии вектора либо начинаются и заканчиваются в бесконечности, либо имеют замкнутый вид кольца. Такие поля называются также соленоидальными.

2.3. Второе уравнение Максвелла

М. Фарадей экспериментальным путем открыл закон

электромагнитной индукции который утверждает, что в проводящем контуре L возникает ЭДС , величина которой Э равна скорости изменения магнитного потока Фм во времени, т.е.

(2.12)

Знак «минус» означает, что возникающая ЭДС создает в контуре ток такого направления, который создает вторичный поток, направленный против первичного внешнего магнитного потока ЭДС в замкнутом контуре определяется циркуляцией вектора Е вдоль этого контура;

С учетом математического определения оператора «поток» формула (2. 12) запишется в виде:

(2.13)

где S – площадь, охваченная контуром L

Это и есть закон электромагнитной индукции Фарадея, обобщенный Максвеллом на случай любого воображаемого контуре (не только фарадеевского проводящего). Производная во времени может быть внесена под знак интеграла, т.е.

(2.14)

Уравнения (2. 13) и (2. 14) равнозначны, отличаются только тем, что в них изменен порядок математических операций - в формуле (2.14) сначала дифференцируется функция вектора В, затем берётся интеграл, а в формуле (2.13) наоборот. Эти уравнения представляют второе уравнение Максвелла в интегральной форме в современной нумерации и фоpмe записи.

Применив к обеим частям операцию взятия ротора (подобно (2.3)), получим дифференциальную форму уравнения

rotE = (2.15)

Это уравнение утверждает, что вычисленный ротор вектора Е в любой точке поля совпадает по величине и направлению (помните, ротор является векторной величиной) с вектором скорости изменения вектора В взятого с обратным знаком. Следовательно, если в этой точке есть переменное магнитное поле (dB/dt ¹ 0), то вокруг этой точки всегда существует вихревое электрическое поле (rotE ¹ O). Переменные во времени электрические и магнитные поля неразрывно связаны друг с другом. Электрическое поле создаётся не только электрическими зарядами, но и переменным во времени магнитным полем.

Уравнение (2. 15) в скалярной форме в прямоугольной системе координат имеет вид:

(2.16)

2.4. Первое уравнение Максвелла

Экспериментальны исследования магнитного поля постоянного тока в воздушной среде показали, что существует связь между циркуляцией вектора В по контуру L окружающему провода с алгебраической суммой их постоянных токов I в виде

(2. 17)

Здесь m₀ - магнитная постоянная вакуума. В системе единиц СИ m₀ = 4p × 10⁷ Г/м, а в системе единиц СГС равна 1.

В любой материальной среде кроме тока проводимости I существуют также внутримолекулярные упорядоченные элементарные токи, охватывающие контур интегрирования. Как было указано в п.1.3, характер ориентации элементарных токов под воздействием внешнего магнитного поля определяется параметром m_а. Поэтому подставив в формулу (2.17) m_а вместо m₀ для однородной изотропной среды получим:

(2.18)

или применив материальное уравнение (1.6), имеем

(2.19)

Таким образом, рассматривавшая математическая связь между постоянными токами и создаваемыми ими магнитными полями может быть выражена, как через вектор В, так и вектор Н. Сравнение формул (2. 18) и (2. 19) показывает, что при проведении расчетов поля через Н магнитные свойства среды исключаются из учета. Введение Н очень упрощает описание магнитных полей в веществе - напряженность магнитного поля Н имеет одно и тоже значение в любых средах (в одной и той же точке, от одного и того же источника). Уравнение (2.18) показывает, вектор В обусловлен как макроскопическими токами I_пр так и элементарными токами (отображенными параметром m_а). При проведении расчета поля через Н, внутримолекулярные токи не участвуют напрямую в расчетах.

По аналогии с электрическим смещением (индукции) D (см.п.2.2) вектор В, Н в силу сходности рассуждений следовало бы назвать вектором магнитного смещения (индукции), а В - вектором напряженности магнитного поля. К сожалению, установившуюся терминологию изменить невозможно,

Максвелл выявил способность переменных электрического и магнитного полей возбуждать друг друга. Возбуждение вихревого электрического поля переменным магнитным полем показывает (см.п. 2.3) уравнение

а переменное электрическое поле (т.е. ¶D/dt ¹ 0 или ¶Е/dt ¹ 0) должно бы создавать вихревое магнитное поле, т.е. описание полей должно быть симметричным:

Дальнейшие теоретические исследования показали, что в переменном поле уравнение (2.19) приобретает вид

(2.20)

Максвелл ввел новые понятия

- ток смещения,

- плотность тока смещения,

а вектор D втрое наименование - вектор электрического смещения.

Формула (2.20) выражает обобщенный закон полного тока и является первым уравнением Максвелла в интегральной форме. Оно утверждает, что циркуляция вектора Н по любому замкнутому контуру в электромагнитном поле численно равна алгебраической сумме токов проводимости и смещения, пронизывающих поверхность внутри контура. С учетом формул (1.3) - (1.5) уравнение (2.20) записывают также в видах:

(2.21)

взятие операции вида (2...) с обеих частей уравнений (2.21) переводит их в дифференциальную форму

либо

либо (2.22)

Дифференциальная форма 1-го уравнения Максвелла утверждает, что Н в любой точке ЭМП равен алгебраической сумме плотностей токов проводимости и смещения, протекающих через точку. Так как ротор представляет векторную величину, то равенство соблюдается по всем одноименным проекциям векторов в правой и левой частях уравнения.

Если рассмотреть идеально диэлектрическую среду — вакуум или близкий к нему чистый сухой воздух, то в (2.22) следует принять s =0. Тогда уравнение (2.22)приобретает вид:

(2.23)

Отсюда следует, что если в данной точке пространства присутствует переменное электрическое поле (т.е. ¶D/dt ¹ 0), то оно создает вокруг точки вихревое магнитное поле. Иначе говоря, магнитное поле создается не только токами проводимости, но и переменным электрическим полем. Переменные электрическое и магнитное поля неразрывны и представляют единое ЭМП.

Скорость изменения электрического поля

как было указано выше, представляет плотность тока смещения. Ток смещения в реальных диэлектриках создается, в основном, за счет колебательного движения связанных зарядов под взаимодействием переменного электрического поля, т.е. является поляризованным током. Однако он существует и в вакууме, где нет связанных зарядов. В этом легко убедиться опытным путем, подключив последовательно в цепь источника переменного напряжения вакуумный (либо воздушный) конденсатор. Амперметр показывает наличие тока в цепи с участком из вакуума, который для постоянного напряжения представляет разрыв цепи.

2.5. Уравнение непрерывности полного тока

Это уравнение получается из первого уравнения Максвелла, т.е. является его следствием. Возьмем операцию дивергенция с обеих частях, т.е.

div (rot H) = div (J_np + J_cм).

Из векторного анализ известно, что дивергенция от ротора тождественно равна нулю. Тогда

div (J_пр + J_см) = 0

или

div (J_пр + ) = 0

Равенство нулю дивергенции вектора означает, что линии вектора замкнуты (см.п.2.2). Следовательно линии полного тока неразрывны. Это объясняет тот факт, почему протекает ток через антенны, представляющие незамкнутые отрезки проводов. На рис.2.1 приведена схема радиопередатчика РПдУ с антенной типа «симметричный вибратор». Хотя концы проводов антенны разомкнуты, индикатор выходного каскада А показывает наличие тока в антенне. Линии тока проводимости замыкаются через воздушное пространство токами смещения. Такое же явление наблюдается в переносных радиостанциях со штыревой антенной (сотовых радиотелефонах).

Рис.2.1. Непрерывность линий полного тока

3, Уравнения ЭМИ для монохроматического поля

3.1. Комплексные вектора, уравнения ЭМП в комплексной форме

Уравнения, рассмотренные выше, записаны для мгновенных значений векторов поля, т.е. справедливы для их произвольного характера изменения во времени. Если вектора изменяются во времени синусоидально с постоянным периодом, то такое поле называют монохроматическим. Для такого поля можно вводить комплексные векторы, т.е. воспользоваться методом комплексных амплитуд (МКА). В этом методе вместо мгновенного значения, например, Н = H_msin(wt+j_н) ставят формальную комплексную величину Н_me^jwt. Видно, что

Н = I_m[H_me^jwt]

где I_m указывает на мнимую часть комплексной величины. В большинстве книг по теории ЭМП монохроматическим считают поле, косинусоидально изменяющееся во времени. Тогда Н = Re [H_me^jwt], т.е. применяют вещественную часть комплексной величины. Переход от мгновенных значений значительно упрощает математическое рассмотрение гармонических физических явлений, т.к. исчезают операции дифференцирования и интегрирования во времени, они заменяются на операции умножения и деления на множитель (jw), где w - частота рассматриваемой гармоники. Плотность тока смещения заменяют соответствующей величиной вида

Вместо уравнения

(3.1)

используют

а сократив на общий множитель получают вид

(3.2)

Первое уравнение Максвелла (3. 1) в отличии от комплексного вида (3.2) записано для реально существющих полей. Уравнение (3.2) скорее является математическим образом (3. 1), и оно справедливо только для гармонического поля, т.е. для одной спектральной составляющей сигнала, а сигнал связи, как известно, состоит из набора спектральных составляющих. Следует помнить, что при использовании уравнений ЭМП в комплексной форме расчеты проводятся для гармонического характера изменения векторов поля, т.е. для частного случая.

Остальные уравнения Максвелла в комплексной дифференциальной форме имеет вид

rot Е = - jwm_аН,

div D = r_своб ,

div B = 0

В интегральной форме уравнений, дополнительно появляются только точки над векторами. Из ответов, полученных из решения комплексных уравнений, для получения истинного ответа выделяют вещественную часть комплексного вектора

3.2. Комплексная диэлектрическая проницаемость. Угол потерь.

Подставим в (3.2) третье материальное уравнение (1.5) и получим

rоt Н = (s+jwe_a)Е.

Преобразуем множитель правой части уравнения

rot H = jwe_a (1-j)E

Математическая запись анализа процессов значительно сокращается если ввести новый коэффициент - комплексную диэлектрическую проницаемость:

e_a = e_a (1- j) (3.3)

Тогда уравнение приобретает вид

rot H = jwe_a E

Формулу (3.3) можно записать в алгебраической и показательной формах комплексного числа

e_a = e_a - j (3.3a)

e_a = (3.3б)

Тождественность (3.3а) и (3.3б) показывает изображение числа (3.3а) на комплексной плоскости (см. рис.3.1)

		ea
	ea

R_e

-j

d

Рис. 1 Комплексная диэлектрическая проницаемость

Полученная из (3.3б) с помощью формулы Эйлера тригонометрическая форма комплексной проницаемости

e_а =

приводит к еще одной необходимой форме

(3.4)

где (3.5)

называют тангенсом угла диэлектричесих потерь d. Потери электрического поля называются токами проводимости и токами смещения в среде. Параметр tgd указывает на потери от тока смещения, т.е. от трения заряженных частиц при смещении их в молекулах под воздействием внешнего электрического поля.

Модули комплексной плотностей тока проводимости равен

а тока смещения

Их отношение равно

(3.6)

Следовательно, параметр tgd показывает на сколько в данной среде токи проводимости превышают токи смещения, и является критерием деления сред на проводники и диэлектрики.

Если tgd >10 (tg d » 10), то эту среду считают средой с большими потерями или полупроводниками.

Если tgd <0.l, то эта среда с малыми потерями, т.е. является диэлектриком.

Если 0.1<tgd <l0 , то в этой среде с потерями токи проводимости и смещения отличаются не сильно, среду условно называют полупроводящей.

Сухой чистый воздух можно считать очень близким к вакууму, т.е. средой без потерь - tgd = 0).

Для реальных качественных диэлектриков в радио диапазоне (до f = 30 ГГц) tgd = 10^-2…10^-4

3.3. Система уравнений монохроматического поля с учетом стороннего источника

В уравнениях (3.1) и (3.2) отсутствуют токи J_пр и J_см созданные в этой среде присутствующим полем. Эти токи не являются источниками поля, а возникли под его воздействием. В тоже время ЭМП само создается каким-то источником за счет энергии, получаемой извне. Таким источником чаще всего является антенна, по которой создает ток мощный выходной каскад радиопередатчика (см. рис. 2.1). Ток антенны определяется мощностью внешних ресурсов (трансформаторной подстанцией) и не является функцией векторов рассматриваемого поля в среде. Источник электромагнитного поля принято называть сторонней силой, Сторонняя сила, это заданная функция, которая является исходной величиной при расчете ЭМП. Эту силу чаще выражают через плотность тока J_ст, она присутствует в правой чести первого уравнения Максвелла:

rot H = J_пр + J_см + J_ст .

Так как J_пр + J_см = jwe_а , то первое уравнение в комплексной форме имеет вид:

rot H = jwe_а Е + J_ст, (3.7)

а остальные уравнения;

rot Е = jwm_а Н (3.8)

div D = r _своб (3.9)

В уравнении (3.8) присутствует комплексная магнитная проницаемость применяемая для учета потерь в магнитных материалах от трения доменов при перемагничивании. Однако в технике СВЧ получил применение лишь один тип магнитного материала - намагниченный феррит обладающий уникальными свойствами. Другие материалы, применяемые в радиотехнике являются немагнитными, не имеют магнитных потерь, поэтому в уравнении (3.8) вместо m будем в дальнейшем писать m.

Присутствие стороннего источника в правой части уравнения (3.7) делает его неоднородным, т.е. уравнения без сторонних источников

rot H - jwe_а Е = 0 (3.10)

rot Е + jwm_а Н = 0

являются однородными.

Нетрудно заметить, что первое уравнение получается из второго, а второе из первого, если заменить Н на Е, а e_а на m_а . Это свойство уравнений Максвелла называют принципом двойственности. Его применяют для получения решения некоторых задач путем замены символов в ответах соответствующих уже решенных двойственных задач.

Некоторые задами электродинамики значительно упрощается также, если ввести в систему уравнений сторонние магнитные токи J_стм . Так как реально существующих магнитных зарядов нет в природе, поэтому с физическом точки зрения J_стм является фиктивной величиной.

Тогда симметричными по форме становятся и неоднородные уравнения Максвелла:

rot H - jwe_а Е = J_стм (3.11)

rot Е + jwm_а Н = - J_стм

С помощью симметричных однородных и неоднородных уравнений Максвелла (3.10) и (3.11) путем перестановки векторов и параметров получают решения рада задач, используя известные расчетные соотношения двойственных задач.

4 Граничные условия 4.1. Необходимость граничных условий

Граничными называют условия, которым подчиняется поле на границах раздела сред, отличающихся по одной или нескольким парам электродинамических параметров.

Рассмотрим, например, одну из проекций 1-го уравнения Максвелла в среде без потерь (s = 0; J_пр = 0):

Это дифференциальное уравнение в частных производных относительно составляющих вектора Н_z и Н_y обязывает их с заданной величиной Е_x в одной из двух сред.

Подобного вида уравнения имеют бесчисленное множество решений. Чтобы найти единственное решение следует найти постоянные интегрирования. Их определяют исходя из граничных условий. В теории электрических цепей такими являются начальные условия, известные по законам коммутации. В теории ЭМП, в отличии от ТЭЦ существует много условии, т.к. каждый вектор поля имеет две проекции, для которых граничные условия могут быть различными.

4.2. Составляющие векторов на границе раздела сред

Между материальными средами 1 и 2 находится поверхность - граница, по обе стороны которой различные электродинамические параметры, одна пара - e₁ и e₂ или m₁ и m₂. Среды могут различаться по диэлектрическому параметру e, магнитному m, электропроводности s либо по всем параметрам одновременно.

При переходе ЭМП через границу проекции некоторых векторов поля скачкообразно, либо не изменяются. Составляющими векторов
являются их проекции на касательную 1t и нормаль 1N к поверхности в точках над и под границей. Эти точки очень близки к поверхности. На рис. 4.1 указаны составляющие вектора Е в первый и во второй средах в этих точках 1 и 2. Е_1n и Е_2п — называются нормальными, а Е_1t и Е_2t — касательными (тангенсиальными) составляющими вектора.

Рис. 4.1. Составляющие вектора Е на границе разделе диэлектриков

4.3. Основные граничные условия

Характер границы определяет содержание граничных условий. В общем случае по граничной поверхности могут скапливаться сторонние электрические заряды (например, на металлической поверхности в постоянном электрическом поле) или протекать сторонний электрический ток. Поверхностные токи и заряды считают сосредоточенными в бесконечно тонком слое, т,е. объемная плотность заряда r с размерностью Кл/м³ превращается в r_s с размерностью Кл/м², а плотность тока J (А/ м²) - J_s (A/k), J_s отлична от нуля только в переменном электромагнитном поле на поверхностях с очень высокой проводимостью,

1. Условие для нормальных составляющих вектора D на границе раздела с поверхностными зарядами имеет вид:

D_1n-E_1n= r_s , (4.1)

т.е. при переходе поля из одной среды в другую , изменяется скачкообразно на величину r_s. Если же нет поверхностных зарядов (например, на границе диэлектрических сред), тo r_s=0, а

D_1n = D_2n , (4.2)

Следовательно, в этом случае D_n поля не изменяется, т.е., она ocтается непрерывной величиной.

2. Условие для касательных составляющих вектора Н. На границе с
поверхностными токами наблюдается условие:

H_1t - H_2t =J_S, (4.3)

а если нет поверхностных токов, (например, по поверхности проводов с постоянным током), то

H_1t = H_2t . (4.4)

3. Условие для нормальных составляющих вектора В. На границах
любого типа при переходе поля из одной среды в другую, В_n не может
измениться скачком, т.е.

В_1n – В_1n, (4.5)

4. Условие для касательных соcтавляющих вектора Е. Как показано на рис.4.1. при переходе ЭМП через границу векторы Е₁ и Е₂ в непосредственной близости над и под границей отличаются как по длине и направлению, но у них неизменная проекция на касательную к поверхности, т.е.

E_1t = Е _2t (4.6)

Это граничное условие справедливо для любых границ, оно

показывает, что на границе раздели сред Е_t непрерывна.

Остальные граничные условия получаются из рассмотренных

Используя материальные уравнения электродинамики. Например, из (4.6) и (1.4) получим:

или (4.7)

т.е. касательная составляющая вектора электрической индукции при переходе ноля через границу сред изменяется скачкообразно на величину отношения диэлектрических проницаемостей.

Таким же образом из (4.2) получим;

(4.8)

4.4. Условия на границе с идеальным проводником

В технике СВЧ наиболее распространенным видом является граница в виде поверхности очень хорошего проводника - меде, серебра и др. металлов. При рассмотрении электромагнитных явлений вблизи таких поверхностей, их можно считать идеально проводящими, т.е. с параметром s бесконечно большим. Такое приближение ведет к незначительной погрешности при определении поля в 1-ой диэлекрической среде над поверхностью хорошего проводника (2-ой среды). В тоже время внутри идеального проводника ЭМП не существует. В этом можно убедиться рассмотрев третье материальное уравнение, Jnp2 = s E2 , где s=¥ превращает ток проводимости в бесконечность, что противоречит физике явлений. Даже при очень больших значениях s; Jnp остается конечной величиной, т.е. ¥ × Е2 ¹ ¥. Это возможно только при Е2 = 0, т.к. произведение ¥ × 0 неопределенная, т.е. любая величина Равенство Е2 = ¥. отвечает также , Е2t = Е2n = 0.

Таким образом, внутри идеального проводника электрического поля не бывает. Если учесть это (Е₂ = 0), то из уравнения rot Е₂=-¶В₂/¶t следует, что в этом случае либо В₂ = 0, либо В₂ постоянная величина. В телекоммуникации применяют лишь переменные во времени поля, поэтому внутри идеального проводника В_2t=В_2n=0, нет магнитного поля. Подставив эти утверждения в равенства (4.3), (4.5) и (4.6) получим основные граничные условия на поверхности идеального проводника:

В_1n = 0 (4.9)

H_1t = Js (4.10)

E_1t = 0 (4.11)

Равенство (4.10) может быть записано в векторной форме

J_s = [1_N´H_1t] (4.10a)

Эти условии графически изображены на рис. 4.1 и 4.2.

Е₁ = Е_1n

В₁ = 1tВ₁t

Рис. 4. 1. Расположение силовых линий поля вблизи идеально проводящей поверхности

Рис. 4.2. Связь линии магнитного поля над идеальным проводником с линиями поверхностного тока

Из рисунков следует, что над поверхностью идеального проводника электрические силовые линии Е всегда перпендикулярны, а магнитные - параллельны ей. Плотность электрического тока на поверхности проводника равна по величине и перпендикулярна по направлению касательной (составляющей напряженности магнитного поля у поверхности. Этот вывод широко применяется при исследовании волн разных типов в полых металлических волноводах

Можно также показать [Семенов], структура поля в 1 среде такова, что касательная составляющая магнитного поля достигает у плоской границы идеального проводника экстремального значения (в направлении нормали к границе), т.е.

(4.11)

Условие (4.11) также применяют в частности при исследовании полей в металлических волноводах.

5. Энергия и мощность ЭМП

5.1. Основные гипотезы.

ЭМП как один из видов материи способно совершить работу - например, перемещать заряженные частицы. Следовательно, оно обладает энергией. При рассмотрении энергетических явлений в макроскопической теории поля используют следующие два предположения, устанавливающие связь между векторами поля и его энергетическими характеристиками.

1. Электромагнитная энергия распределена в пространстве с объемной плотностью:

w = wэ + wм = ½ (E×D + H×B), Дж/м3,

где wэ = E×D/2 и wм = H×B/2 – объемные плотности энергии электрического и магнитного полей.

2. Плотность потока электромагнитной энергии равна векторному произведению напряженностей электрического и магнитного полей:

П = [Е,Н], Вт/ м2,

где П - вектор Пойнтинга, указывающий направление движения энергии и равный по величине плотности её потока. Размерность вектора указывает также, что он равен плотности мощности - т.е. мощности волны, проходящей через перпендикулярную к направлению движения и размером 1м² площадку.

5.2. Баланс энергии.

ЭМП как вид материй подчиняется закону сохранения энергии. Поэтому в любом объеме V, ограниченном поверхностью S соблюдается равенство поступающей в объем и расходуемой энергии. В данный момент времени энергия в объеме может быть вычислена интегрированием:

W= (5.1).

С течением времени энергия изменяется по ряду причин:

- переходит в другие виды энергии. Тепловое движение электронов во входной цепи радиоприемного устройства под воздействием ЭМП приводит потерям энергии в объеме (полезным для потребителя). Скорость отдачи энергии полем называется мощностью его потерь

- пополняется энергией сторонних источников, например, излучаемый из антенны энергии, находящейся в данном объеме. Скорость увеличения энергии равна мощность сторонних сил Р_ст;

- излучается из объема или пополняется энергией источников, находящихся вне объема. Поток электромагнитных волн из объема называют излучением. Мощность излучения определяется оператором «поток»:

P_S= Вт (5.2).

Вспомним, что вектор электромагнитной площадки ds направлен по внешней нормали к окружающей объем поверхности. Если направление векторов П и ds противоположное, (т.е. поток мощности направлен во внутрь объема), то имеем отрицательное значение (см.п.2.1). Тогда величину Р_S можно было бы назвать не мощностью излучения, а мощностью поступления. Но такой термин не используется, а только подразумевается.

Мы рассмотрели все возможные причины изменения энергии во времени dW/dt в данном объеме. Следовательно:

= Р_ст – Р_п - Р_S , (5.3).

Выражение (5.3) является общим физическим уравнением баланса мощностей ЭМП в заданном объеме.

5.3. Теорема Пойнтинга для мгновенных значений векторов ЭМП.

Подставить в уравнение (5.3) выражения (5 .2) и (5.1)

Р_ст – Р_п - (5.4)

Раскроем содержание величин Р_ст и Р _п.

Потери энергии ЭМП связаны с движением зарядов под воздействием поля. При этом неподвижные заряды не могут вызвать потерь. Движение зарядов осуществляет электрическое поле, магнитная компонента не совершает работу, т.к. сила её воздействия (см. п. 1.2)

F_м = Q[V,B]

перпендикулярна к вектору скорости движения V, а мощность потерь представляет собой скалярное произведение

P_n = F_э × V = QE × V (5.5)

справедливость которого подтверждается размерностью полученной величины [(Кл×В/м) ×м/с] = [(А×с×В/м) ×м/с] = А×В = Вт.

Для рассмотрения баланса энергии в каждой точке объема и вводят понятия объемных плотностей мощности потерь и сторонних сил

Из формулы (5.5) получим объемную плотность потерь

p_n = r × E × V,

где r × V представляет собой вектор плотности электрического тока (см. формулу (1.2)).

Поэтому потери характеризуются величиной

p_n = J × E = J × E cosa (5.6)

Применяя к (5.6) равенство (1.5) получим другую расчетную

формулу

p_n = s E²= (5.7)

Соотношение (5.7) представляет собой закон Джоуля-Ленца в дифференциальной форме.

Так как скалярное произведение (5.6) может быть положительной и отрицательной величиной, то случаю р_п > 0 соответствует отдача энергии поля на создание движения зарядов. В случае, когда J и Е направлены противоположно ЭМП приобретает энергию от сторонних источников. Поэтому

Р_cт = — J_ст × Е (5.8)

Тогда из формулы (5.4) получим закон сохранения энергии ЭМП в
интегральной форме:

(5.9)

Путем предельного перехода объема в точку в пространстве получим дифференциальную форму закона

(5.10)

где раскрыты произведения ED = e_а Е² , НВ = m_а Н² и использована теорема Остроградского-Гаусса

.

Теорема Пойнтинга доказывает, мощность ЭМП, накопленная в объеме состоит из алгебраической суммы мощностей, приобретенной от сторонних источников, доставленной из вне в виде потока и потерь на совершение полезной работы.

Уравнение баланса мощностей имеет большое значение в теории ЭМП. В частности, это уравнение является универсальным аппаратом проверки правильности решений электродинамических задач. Уравнения (5.9) и (5.10) записаны для мгновенных значений векторов, поэтому они справедливы для любых переменных полей. Для гармонических полей они имеют более простой вид.

5.4. Теорема Пойнтинга для комплексных векторов ЭМП.

Физическую сущность гармонических процессов позволяют выявить средние за период значения энергетических характеристик. Подобно тому как в цепи переменного тока для вычисления полной комплексной мощности S = UI = Р + jQ в теории ЭМП вводится в употребления комплексные мощности потерь и излучения. При этом, учитывается что характер мощности зависит от размерности фаз колебаний, а не от суммы фаз, второй множитель в скалярных произведениях берется комплексно сопряженной величиной. Например,

Е × Н = Е × Не^j(y_E^{+ y}_H⁾

Е × Н = Е × Не^j(y_E^{- y}_H⁾

Поэтому средняя плотность электрической и магнитной энергий ЭМП соответственно равны:

Средняя объемная плотность мощности потерь:

p _cpn = J × E = sE × E =sE²

Cредняя плотность мощности сторонних cил

где р_ст - комплексная объемная плотность мощности сторонних

сил.

Комплексный вектор Пойнтинга определяется как произведение вида:

П = ëЕ´Нû (5.11)

Поток комплексного вектора содержит активную и мнимую

части.

Среднее за период значение плотности потока энергии равно вещественной части комплексного вектора, т.е.

П_ср = RеП (5.12)

Мощность излучения из объема пространства, ограниченного поверхностью S определяется как интеграл вида:

Р_S = (5.13)

В большинстве учебников по теории ЭМП в формуле (5.11) подразумеваются амплитудные значения векторов Е и Н, тогда равенство (5.12) пишут в виде

П_ср =

Е_Д = Е_m/Ö2, Н_Д = /Ö2, а ЕН = Е_m Н_m /2

Таким образом, для гармонического (монохроматического) поля вещественная часть уравнения баланса энергий (5.9) приобретает вид:

(5.14)

а уравнение (5.10):

div П _cр + р_{ср n} = p_{cр ст} (5.15)

Уравнение (5.15) записано для вещественной части комплексного уравнения

divП + j2w(w_cpм +w_срэ) + Р_прn = Р_срст +jr_ст

Полученного из (5 .10) путем подстановки комплексных значений параметров. Уравнения баланса для мнимой части записывается раздельно подобно уравнению (5 . 1 5).

Литература

1. Витевский В.Б., Павловская Э.А. Электромагнитные волны в технике связи. - М: Радио и связь, 1995.-121с.

2. Витевский В.Б., Маслов О.Н., Павловская Э.А. Сборник упражнений и задач по электродинамическим дисциплинам. - М.: Радио и связь, 1996.

3. Фальковский О.И. Техническая электродинамика..— М.: Связь, 1978. - 430с.

4. Вольман В.И., Пименов Ю.В. Техническая электродинамика. - М.: Связь, 1971.-487с.

5. Семенов Н.А. Техническая электродинамика. — М: Связь, 1973. - 420с.

6. Никольский В.В-, Никольская Т.Н. Электродинамика и распространение радиоволн. - М.: Наука, 1989. - 554с.