ЎЗБЕКИСТОН РЕСПУБЛИКАСИ ОЛИЙ ВА ЎРТА МАХСУС ТАЪЛИМ ВАЗИРЛИГИ

ТОШКЕНТ АХБОРОТ ТЕХНОЛОГИЯЛАРИ УНИВЕРСИТЕТИ

А.Ш. ШАХОБИДДИНОВ, В.А. ГУБЕНКО

ЭЛЕКТРОДИНАМИКА

(ЭЛЕКТРОМАГНИТ МАЙДОНЛАР ВА ТЎЛҚИНЛАР)

ФАНИ БЎЙИЧА МАЪРУЗАЛАР МАТНИ

Тошкент 2007

МУНДАРИЖА

бет

КИРИШ

МАВЗУ № 1. ЭЛЕКТРОСТАТИКА

1.1. Электр заряди................................................................................................3

1.2. Электростатик майдон кучланганлиги.......................................................4

1.3. Электростатик майдоннинг уюрмасиз тавсифи........................................6

1.4. Электр потенциали.......................................................................................7

1.5. Электростатик майдоннинг график тасвири.............................................8

1.6. Диэлектрикнинг қутбланиши ва электр индукцияси...............................8

1.7. Гаусс теоремаси............................................................................................9

1.8. Электростатик майдонда ўтказгичлар......................................................10

1.9. Электростатик майдонда чегаравий шартлар..........................................10

1.10. Электростатик майдон энергияси.............................................................12

МАВЗУ № 2. ЭЛЕКТРОМАГНИТ МАЙДОНДА ЭЛЕКТР ТОКИ

2.1. Ток ва ўтказувчанлик токи зичлиги..........................................................14

2.2. Ўтказувчанлик токи зичлигининг дивергенцияси...................................14

2.3. Дифференциал шаклдаги Ом қонуни........................................................15

2.4. Тўлиқ электр токи.......................................................................................16

МАВЗУ № 3. МАГНИТ МАЙДОНИ

3.1. Магнит майдонни тавсифловчи асосий катталиклар...............................18

3.2. Магнит оқими ва унинг узлуксизлиги.......................................................19

3.3. Магнит майдонининг скаляр потенциали.................................................21

3.4. Магнит майдонининг вектор потенциали................................................21

3.5. Магнит майдонидаги чегаравий шартлар.................................................21

3.6. Магнит майдони энергияси........................................................................22

3.7. Магнит майдоннинг ҳисоблаш усуллари..................................................23

МАВЗУ № 4. МАКСВЕЛЛ ТЕНГЛАМАЛАРИ ТИЗИМИ

4.1. Максвелнинг биринчи тенгламаси............................................................25

4.2. Максвелнинг иккинчи тенгламаси.............................................................25

4.3. Максвеллнинг учинчи тенгламаси.............................................................26

4.4. Максвеллнинг тўртинчи тенгламаси.........................................................27

4.5. Электромагнит майдоннинг тўлиқ тенгламалар тизими.........................27

4.6. Тўлиқ токнинг узлуксизлиги тенгламаси.................................................29

МАВЗУ № 5. МОНОХРОМАТИК МАЙДОН УЧУН МАКСВЕЛЛ

ТЕНГЛАМАЛАРИ

5.1. Комплекс векторлар. Максвелл тенгламаларининг комплекс

Шакллари………….......................................................................30

5.2. Комплекс диэлектрик сингдирувчанлик. Йўқотишлар бурчаги.............31

5.3. Монохроматик майдон учун четки манбаъларни хисобга олувчи

тенгламалар тизими………………….…………………………………...32

МАВЗУ № 6. ЭЛЕКТРОМАГНИТ МАЙДОН ЭНЕРГИЯСИ ВА ҚУВВАТИ

6.1. Асосий гипотеза…………………………………………………………..35

6.2. Энерия баланси…………………………………………………………...35

6.3. Электромагнит майдон векторларининг оний қийматлари учун

Пойтинг теоремаси…..................................................................................36

6.4. Электромагнит майдоннинг комплекс векторлари учун Пойнтинг

теоремаси……................................................................……………….…38

МАВЗУ № 7. ЭЛЕКТРОМАГНИТ ТЎЛҚИНЛАРНИНГ НУРЛАНИШИ

7.1. Элементар электр тебратгич......................................................................40

7.2. Элементар электр тебратгич майдони тузилишининг тахлили..............41

МАВЗУ № 8. ЯССИ ЭЛЕКТРОМАГНИТ ТЎЛҚИНЛАР

8.1. Ясси электромагнит тўлқин параметрлари...............................................47

8.2. Электромагнит тўлқиннинг қутбланиши..................................................49

МАВЗУ № 9. МУХИТЛАР ЧЕГАРАСИДАГИ ТЎЛҚИНЛИ ЖАРАЁНЛАР

9.1. Электромагнит тўлқиннинг мухитлар чегарасидан ўтиши ва

аксланиши....................................................................................................53

9.2. Ясси электромагнит тўлқиннинг иккинчи мухитга тўлиқ ўтиши.

Брюстер бурчаги..........................................................................................57

МАВЗУ № 10. ЮЗА ЭФФЕКТИ

10.1. Юза эффекти ходисаси...............................................................................59

10.2. Ўтказгичнинг юза қаршилиги ва ундаги энергия йўқотишлари.............60

МАВЗУ № 11. ЙЎНАЛТИРУВЧИ ТИЗИМЛАР

11.1. Йўналтирувчи тизимларнинг синфланиши...............................................61

11.2. Бир тўлқинли режимни ҳосил қилиш учун тўлқиннинг ишчи

узунлигини танлаш.....................................................................................64

11.3. Тўлқинўтказгичдаги амплитудавий тақсимотнинг турлари...................65

АДАБИЁТЛАР......................................................................................................67

МУНДАРИЖА

КИРИШ

Электромагнетизм назарияси асосида электромагнит майдони тушунчаси ётади. Электромагнит майдон эса материянинг алохида, мухим кўриниши бўлиб, бир-бирини шартли равишда тўлдирувчи ва доимо бирга мавжуд бўлувчи электр ва магнит майдонларининг йиғиндиси хисобланади.

Замонавий телекоммуникация соҳасида радиотехник тизимларнинг ҳиссаси тобора юксалмоқда. Шу билан биргаликда, фойдаланилаётган радиочастота спектрининг юқорироқ тебранишлар сохасига силжиши кузатилмоқда. Масалан, сунъий йўлдошли алоқа тизимлари 4...6 ГГц диапазонининг имкониятларида тўла фойдаланиб, энди 11...14 ГГц частота диапазонига кўчиб ўтган. Коинот станциялари эса 20...30 ГГц диапазонида фаолият юритиш учун катта амалий салохиятга эга.

Сигналларни ташувчи частоталарнинг ошиб бориши унинг ёрдамида кўпсонли каналларни узатиш имконини беради, яъни, фойдаланилаётган диапазон ҳажмини кенгайтиришга таъсир кўрсатади. Шу нуқтаи назардан ҳам 3000 ГГц частотали оптик диапазонининг имкониятлари жуда ҳам юқоридир. Замонавий телекоммуникация соҳасида оптик толали алоқа тизимларининг асосий ўринни эгаллаб бориши хам ана шу омил билан боғлиқ. ОТАТ нинг асосий элементи сифатида қурилмаларни боғловчи кварц толасини эътироф этиш лозим. Аммо, ҳаракатдаги объектлар билан алоқа ўрнатишда ОТАТ асосий алоқа тури сифатида намоён бўла олмайди. Чунки, харакатдаги объект учун эркин тарқалувчи радиотўлқинлардан фойдаланиш қулайроқ. Масалан, уяли алоқа тизимларида 450, 800, 900, 1800, 1900 МГц частота спектрларидан кенг фойдаланилади.

Замонавий телекоммуникация тизимларидан келтирилган мисоллар шуни кўрсатадики, юқори частотали спектрлардан фойдаланиш ривожланувчан йўналишдир. Ўта юқори частотали (шунингдек оптик) техниканинг назарий захираси Максвелл тенгламаларига асосланган ва унда векторли алгебра, векторлар таҳлили элементларидан фойдаланилади.

Эркин фазодаги, ЎЮЧ қурилмаларидаги, хамда узатиш линияларидаги тўлқинли жараёнларни квант физикаси даражасида ўрганиш талаб этилмайди. Уларни чексиз фазодаги узлуксиз майдонлар кўринишида тахлил қилиш етарли. Бундай кузатувни макроскопик кузатув дейилади. Бу каби енгиллаштирилган назарияни эса классик электродинамика дейилади.

Ушбу маърузалар матнининг 1-қисми электродинамиканинг назарий асосларини қамраб олган ва техник электродинамика соҳасининг бошқа қисмларини ўрганишда назарий захира вазифасини бажаради.

МАВЗУ 1. ЭЛЕКТРОСТАТИКА

1.1. Электр заряди

Электр зарядини чексиз бўлинувчан деб ҳисоблаш мумкин ва «заряд зичлиги» тушунчаси орқали ифодаланади. Агар «q» заряд фазода тақсимланган бўлса, унда заряднинг хажмий зичлиги

, (1.1)

заряд эса қуйидагича аниқланади

. (1.2)

Агар «q» заряд «S» юзада тақсимланган бўлса, унда юзадаги заряд зичлиги

, (1.3)

у ҳолда умумий заряд

, (1.4)

ифода ёрдамида аниқланади.

Заряднинг чизиқли зичлиги

, (1.5)

бу ерда dl – заряд тақсимланган чизиқнинг бир қисми.

Шунга кўра заряд

. (1.6)

Бир ҳил ишорали иккита нуқтавий заряд бир-бирини итаради. Итариш кучи вакумда Кулон қонуни асосида аниқланади.

(1.7)

бу ерда

q₁ ва q₂ - нуқтавий заряд

к - пропорционаллик коэффициенти.

, (1.8)

бу ерда e₀ - электр доимийси

. (1.9)

Агар зарядланган жисмлар биржинсли изотроп муҳитда жойлашган бўлса,

(1.10)

бу ерда e - муҳитнинг нисбий диэлектрик сингдирувчанлиги.

q зарядга таъсир этувчи куч вектор кўринишида қуйидагича ёзилади

(1.11)

1.2. Электростатик майдон кучланганлиги

Электр майдон кучланганлиги бу синов заряди q нолга интилган ҳолда унга таъсир этаётган куч ва заряд ўртасидаги муносабат орқали аниқланадиган тушунчадир.

. (1.12)

Нуқтавий заряднинг электр майдон кучланганлиги

(1.13)

Нуқтавий заряднинг СИ тизимидаги электр майдон кучланганлиги ўлчов бирлиги.

Иккита нуқтавий заряднининг ўзаро таъсир кучи

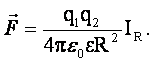(1.14)

Агар майдонда синов заряди q мавжуд бўлмаса, у ҳолда механик таъсир кучи нолга тенг, аммо ҳар бир нуқтадаги майдон кучланганлиги Е нолдан фарқ килади.

Электр силжиши ёки электр индукцияси D деб биржинсли ва изотроп муҳитларда электр майдон кучланганлигига пропорционал бўлган катталикка айтилади.

- вакуумда

- мухитда

СИ тизимида [] = [Кл/м² ]

Агарда майдон бир неча зарядлар томонидан юзага келтирилаётган бўлса, унда фазонинг исталган нуқтасидаги умумий кучланганлик қуйидаги геометрик йиғиндига тенг

. (1.15)

Умуман, электростатик майдонни ҳаракатсиз ҳажмий, юза ва чизиқли зарядлар хосил қила олади.

V ҳажм, S юза ва l чизиқларни dv,ds,dl ларга бўлиб, қуйидагини ёзиш мумкин

(1.16)

Бу ерда q – ҳажмий заряд зичлиги, σ –юза заряди зичлиги, τ- чизиқли заряд зичлиги.

Шунда

,

, (1.17)

,

Геометрик векторлар ни V хажм бўйича, ни S юза бўйича, ни эса l чизиқ бўйича қўшиб қуйидагига эга бўламиз

. (1.18)

Келтирилган тенглама, зарядларнинг фазодаги тақсимоти аниқ бўлганда, электр майдон кучланганлиги векторини хисоблаш имконини беради. Хисоблашлар, векторнинг проекцияларини осонроқ хисоблаб олиш мумкин бўлган тизимни аниқлашга қаратилган бўлиши лозим.

1.3. Электростатик майдоннинг уюрмасиз тавсифи

Майдон кучи билан q зарядни бир нуқтадан иккинчи нуқтага силжитилганда бажариладиган иш қуйидаги ифода орқали аниқланади

. (1.19)

Майдон кучининг ёпиқ эгри чизиқ бўйича бажарган иши нолга тенг. Бунинг учун векторининг циркуляцияси нолга тенглигини исботлаш керак.

, (1.20)

Нуқтавий заряд ҳолатида

(1.21)

Мадомики, қуйидаги ифодалар ўринли экан

демак, келтирилган (1.20) ифода, чиндан хам ўринли.

Стокс теоремасидан фойдаланиб қуйидаги тенгламани хосил қиламиз

(1.22)

Бу тенглама электростатик майдоннинг уюрмасиз эканлигини ифодалайди.

1.4. Электр потенциали

Электр майдони уюрмасиз бўлганлиги учун (), скаляр функция j ни топиш мумкин. Бунда функциянинг «+» ёки «-» ишора билан олинган градиенти электр майдон кучланганлиги векторига тенг.

grad j = ± E. (1.23)

Майдонлар назариясида «-» ишора танланади ва бу майдон кучланганлиги j нинг сўниши томонига йўналганлигини кўрсатади. Скаляр функция j ни потенциал функция ёки шунчаки потенциал дейилади.

Исталган нуқтадаги потенциал қуйидагича аниқланиши мумкин

. (1.24)

Бунда интеграллаш доимийси ноль потенциалли нуқтани бериш орқали аниқланади. СИ тизимида [φ]=[В].

Потенциаллар фарқи эса

. (1.25)

Нуқтавий заряд потенциаллар фарқи интеграллаш усулига боғлиқ эмас. Нуқтавий заряд майдонининг потенциали

. (1.26)

Харакатсиз ҳажмий, юза ва чизиқли зарядларнинг майдон потенциаллари

. (1.27)

Потенциални аниқлагандан сўнг электр майдон кучланганлиги «Е» ни хисоблаб олса бўлади. Бунинг учун қуйидаги ифодадан фойдаланиш лозим

Е = - grad j. (1.28)

Ҳажмий зарядлар майдонида «Е» вектори доимо узлуксиз ва тугалланган. Юза зарядлари майдонида «Е» доимо тугалланган, бироқ «S» юзада узилишларга дуч келади. Чизиқли зарядлар майдонида эса, «Е» вектори зарядлар тақсималанган l чизиқда чексизликка айланади.

1.5. Электростатик майдоннинг график тасвири

Электростатик майдон эквипотенциал юза ва майдон вектори чизиқлари орқали тасвирланади. Эквипотенциал юзалар j = const тенгламаси ёрдамида аниқланади. Доимий қийматни ўзгартириш орқали эквипотенциал юзалар гурухини хосил қилиш мумкин. Тасвирлашда эквипотенциал юзалар шундай жойлаштириладики, бунда ёнма-ён жойлашган қўшни юзалар потенциаллар фарқи бир ҳил қийматга эга бўлиши лозим.

j₂=j₁ + Dj :

j₃ =j₂ + Dj =j₁ + 2 Dj: (1.29)

j_n+1 =j_n + Dj =j₁ + n Dj.

Эквипотенциал юзалар яқин жойлашган жойда майдон кучланганлиги юқори бўлади ва улар ўзаро кесишмайди..Электр майдон куч чизиқлари эквипотенциал юзанинг урунматашкил этувчиси билан мос келади ва тўғри бурчак остида кесишади. Вектор чизиқларининг дифференциал тенгламаси

[E dl] = 0. (1.30)

Декарт координатлар тизимида

E_y dz - E_z dy = 0 : E_z dx - E_x dz = 0: E_x dy - E_y dx = 0. (1.31)

Эквипотенциал юзаларнинг биттаси тўғри бурчакли бўлакларга бўлинади. Бўлакларнинг ўлчамини шундай танлаш лозимки, бунда майдон векторининг барча бўлаклар орқали оқими бир хил қийматга эга бўлсин. Чизмада хар бир бўлакка биттадан вектор чизиғи ўтказилади ва бу чизиқ хар бир бўлакнинг марказидан ўтиши керак. Майдоннинг кучланганлик юқори бўлган ҳудудларида вектор чизиқлари сони кўпаяди, яъни зичроқ жойлаштирилади. Электростатик майдонда Е векторининг чизиқлари туташмаган, эгри, хамда улар мусбат заряддан манфий заряд томонга йўналган бўлади. Бунда мусбат ва манфий зарядлар куч чизиқларининг бошланиш ва тугаш нуқталари сифатида намоён бўлади.

1.6. Диэлектрикнинг қутбланиши ва электр индукцияси

Диэлектрикда электр майдон кучланганлигининг «ε» марта ўзгариши диэлектрикнинг қутбланиши натижасида юз беради. Ташқи майдон таъсири остида диэлектрик ўзининг нейтраллик ҳусусиятини йўқотади ва қутбланади. Кутбланиш пайтида намоён бўлган зарядлар эркин зарядлар деб аталади. Боғланган зарядлар ташқи майдон йўналишига тескари бўлган майдон хосил қилади. Шунинг учун хам «Е» нинг қиймати камаяди. Диэлектрикнинг қутбланиш даражаси кутбланиш вектори Р орқали тавсифланади.

, (1.32)

бунда К_Э – диэлектрик таъсирчанлик.

Қутбланганлик ҳавода электр индукцияси вакуумдагига нисбатан қанчага фарқ қилишини кўрсатади.

. (1.33)

СИ тизимида [Р] = [Кл/м²].

1.7. Гаусс теоремаси

Электр индукцияси вектори D нинг чегараланган ихтиёрий S юза орқали оқими, шу юза билан чегараланган ҳажмда жойлашган q эркин зарядларнинг алгебраик йиғиндисига тенг

. (1.34)

Интеграл шаклдаги Гаусс теоремаси. Электр индукция вектори оқимини Остраградский теоремасига кўра алмаштириб, қуйидаги ифодани хосил қиламиз

. (1.35)

Заряд ҳажмий таксимотга эга бўлганда

. (1.36)

Гаусс теоремасига кўра

,

. (1.37)

Дифференциал шаклдаги Гаусс теоремаси. V – ҳажм иҳтиёрий равишда танланган эди ва тенглик унинг барча кийматларида хам ўринли бўлади. Бу ҳолда:

div D = r

. (1.38)

Келтирилган тенгликларга кўра, электр майдон манбаалари фақатгина электр зарядлари таъсир этаётган жойдагина мавжуд бўлишини айтиш мумкин.

1.8. Электростатик майдонда ўтказгичлар

Агар ўтказгичга заряд киритсак, юзага келадиган итарилиш кучлари таъсири остида заряд ўтказгич бўйлаб харакатлана бошлайди. Харакатланиш ўтказгичнинг устки чексиз юпқа қатламида амалга ошади ва барча зарядлар айнан шу қатламда жамланади. Ўтказгичнинг ичида эса электр майдон кучланганлиги Е нолга тенг бўлади. Ўтказгичнинг юзасидаги барча нцқталарда токлар бир хил потенциалга эга бўлиши керак, яъни ўтказгич юзаси эквипотенциал сиртни ҳосил қилади.

Ташқи майдон таъсирида эркин электронлар ўтказгич бўйлаб харакатланади. Бунда ўтказгичнинг бир қисмида «-» зарядлар, иккинчи қисмида эса «+» зарядлар тўпланади. Ўтказгич ичида майдон мавжуд эмас. Атрофи диэлектрик билан қопланган ўтказгичнинг юзаси электростатик майдон чегараси бўлиб хизмат қилади. Бу техникада радиоапаратурани электростатик экранлаш (ташқи таъсирлардан сақлаш) мақсадида ишлатилади.

1.9. Электростатик майдонда чегаравий шартлар

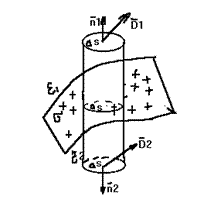
Диэлектрик ўтказувчанлик ε₁ ва ε₂ бўлган икки муҳитлар чегарасини кўриб чиқамиз. Айтайлик, мухитлар чегарасида қандайдир қийматга эга бўлган юза заряди мавжуд бўлсин. Ёпиқ цилиндрсимон S юзани тенгма-тенг равишда икки мухитда жойлаштирамиз. Гаусс теоремасига кўра

. (1.39)

D векторининг оқимини учта векторлар оқими йиғиндиси орқали ифодалаймиз

. (1.40)

Агар юзани кичик ўлчамли деб қабул қилсак, у ҳолда бу майдоннинг барча нуқтасида D вектори бир хил қийматга эга дейишимиз мумкин, яъни

ò D₁ ds = D_1n DS,

^DS

ò D₂ ds = - D_2n DS.

^DS

Агар цилиндрнинг баландлигини нолга интилтириб, юзаларни диэлектриклар чегарасига келтирсак, цилиндрнинг ён томони бўйича юзага келадиган вектор оқими нолга тенг бўлади, у ҳолда

ёки

. (1.41)

Электр индукциясининг нормал ташкил этувчилари икки ўтказмайдиган муҳитлар чегарасида сакрашга учрайди. Бу сакраш қиймати чегара бўйлаб тақсимланган эркин юза зарядлари зичлигига тенг. Агар s = 0 бўлса,

,

e₀ e₁Е_1n = e₀ e₂Е_2n. (1.42)

D векторнинг нормал ташкил этувчиси мухитлар чегарасида узлуксиз. Иккинчи чегаравий шартни хосил қилиш учун эса ёпиқ L чизиқни икки мухитларда тенг қийматларда жойлаштиришимиз керак бўлади.

Агар 2-3 ва 1-4 кесмаларни камайтириб, пировардида уларни нолга тенгласак, Dl кесмасини эса чегара юзасида жойлаштирсак

Е₁tDl - Е₂tDl = 0,

Е₁t = Е₂t

ёки

D₁t / e₁ = D₂t / e₂.

Ўтказгич бўлмаган икки мухитлар чегарасида электр майдони кучланганлиги векторининг урунма ташкил этувчилари ўзаро тенг. Агар Икки муҳитлар чегарасида потенциаллар узлуксиз

j₁ = j_2.

Агар муҳитлардан бири ўтказгич бўлса, у ҳолда чегаравий шартлар ўзгаради.

Агар биринчи муҳит диэлектрик, иккинчи мухит эсак ўтказгич бўлса, чегаравий шартлар қуйидагича ёзилади

Е₂ = 0 D₂ = 0 j₂ = const

D_1n = D₁ = s ёки e₀e Е₁ = s

Е₁t = 0 D₁t = 0.

1.10. Электростатик майдон энергияси

Умумий холда, электростатик майдон энергияси қуйидагича аниқланади

. (1.43)

Бу ифода фақат таъсирлашиш энергиясини хисобга олади. Нуқтавий заряднинг хусусий энергияси расман чексизга тенг. Чунки, чекланган миқдорли бу зарядни бир нуқтага жамлаш учун чексиз катта ишни бажариш талаб этилади. Бу формуладан фойдаланиш учун, зарядлар орасидаги масофа уларни ташувчи жисмлар ўлчамидан анча катта бўлган масофада жойлашган бўлиши лозим.

Электростатик майдон энергиясини қуйидаги ифода ёрдамида ёзиш мумкин

. (1.44)

Векторлар тахлили курсидан қуйидаги маълум

div (jD) = j div D + Dgrad j. (1.45)

Юқоридаги формуладан фойдаланиб, қуйидагини ёзиш мумкин

, (1.46)

Мадомики , қуйидаги ифодалар ўринли экан,

divD =r, gradj = - E,

ò div (jD) dV = ò jD dS,

^{V S}

демак,

, (1.47)

DdS = -DdS = - sdS.

У ҳолда

, (1.48)

ва электр майдон энергияси

. (1.49)

Биржинсли ва изотроп муҳитларда

D = e₀e Е , (1.50)

демак,

, (1.51)

Бу тенгламанинг физик маъноси қуйидагича, электр майдони энергия ташувчиси бўлиб хизмат қилади ва энергия бутун фазода хажмий зичлик билан тақсимланган.

. (1.52)

Электр майдон кучланганлиги нолдан фарқли бўлган холларда майдон кучлари майдон энергияси хисобига иш бажариши мумкин.

МАВЗУ 2. ЭЛЕКТРОМАГНИТ МАЙДОНДА ЭЛЕКТР ТОКИ

2.1. Ток ва ўтказувчанлик токи зичлиги

Dq заряднинг берилган юза орқали маълум бир Dt вақт ичида оқиб ўтиш нисбати ток ўлчови сифатида ҳизмат қилади. Бунда Dt®0 га интилади.

. (2.1)

Ток скаляр катталикдир [i]=[A].

Ток зичлиги – бу вектор катталик J бўлиб, зарядлар ҳаракат йўналишига перпендикуляр жойлаштирилган юзадан оқиб ўтувчи токнинг шу юза ўлчамига нисбатига айтилади. Бунда юзанинг майдони нолга интилтирилади.

. (2.2)

J векторининг йўналиши мусбат зарядларнинг ҳаракати йўналиши билан бир хилда танланади.

Ток ва ток зичлиги қуйидаги муносабат билан боғланган

. (2.3)

Ток зичлиги СИ тизимида [ J ] = [А¤м²].

Айрим ҳолларда, ўтказувчининг фақат юза қисмидан оқиб ўтувчи юза токлари кўриб чиқилади

. (2.4)

СИ тизимида [h] = [А¤м].

2.2. Ўтказувчанлик токи зичлигининг дивергенцияси

Ўзгармас токлар фақатгина ёпиқ занжирларда мавжуд бўлади. J векторининг куч чизиқлари узлуксиз ва div J=0. Ихтиёрий ёпиқ юза бўйича ўзгармас токнинг оқими доимо нолга тенг.

Ўзгарувчан токлар ёпиқ бўлмаган занжирларда хам мавжуд бўла олади. Демак, ўзгарувчан майдонларда ўтказувчанлик токи оқадиган занжирлар туташмаган бўлиши хам мумкин. Ўтказувчанлик токи зичлиги вектори J нинг куч чизиқлари тугалланадиган жойда зарядлар тўпланади. Шу векторнинг ёпиқ юза бўйича оқими нолдан фарқли бўла олади.

Айтайлик, S юза билан чегараланган V хажмда q заряд жойлаштирилган бўлсин. Унинг хажмий зичлиги r орқали берилган. Агар ўтказувчанлик токи i юзадан чиқса, унда q заряд камаяди.

Токни унинг зичлиги, зарядни эса хажмий зичлик орқали ифодалайлик

,

.

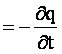Остраградский теоремаси асосида J векторининг оқимини алмаштириб

қуйидагини хосил қиламиз

,

ёки

.

Ўтказувчанлик токи зичлигининг дивергенцияси зарядлар хажмий зичлигининг камайиш тезлигига тенг. Ўтказувчанлик токининг зичлиги ўз манбасига эга бўлиши мумкин. Унинг оқиб кириш чизиқлари (стоклари) вақт бўйича ўзгарувчан хажмий зарядлар кўринишида бўлади.

2.3. Дифференциал шаклдаги Ом қонуни

Биржинсли изотроп ўтказгичдаги ўтказувчанлик токи зичлиги J электр майдони кучланганлиги Е га тўғри пропорционал.

(2.5)

Бу тенглама дифференциал кўринишидаги Ом қонуни номи билан юритилади.

Ўтказгичдан ток узлуксиз равишда оқиб туриши учун зарядларни ҳаракатга келтирувчи электр майдон бўлиш шарт. Бундай майдонни юзага келтириш мумкин ва у ноэлектростатик жараёнлар (кимёвий ва термоэлектростатик) томонидан қўллаб қувватланади. Бу жараёнда иштирок этаётган майдон четки электр майдон деб аталади. Четки электр майдоннинг кучланганлиги

. (2.6)

Натижавий майдон кучланганлиги

. (2.7)

Ўтказгичнинг четки кучлар мавжуд бўлган ҳудудларида Ом қонуни куйидагича ёзилади

. (2.8)

Бунда σ – солиштирма ўтказувчанлик.

СИ тизимида [s]=[См/м].

2.4. Тўлиқ электр токи

Ўтказгич мухитдаги электр токи майдон кучлари таъсири остида юзага келадиган эркин электр зарядларининг тартибли харакатидир. Бу ток ўтказувчанлик токи деб аталади.

Ом қонунига кўра

Агар зарядланган жисм ёки зарралар ўтказгич бўлмаган мухит ёки вакуумда V тезлик билан харакатлансалар, улар кўчиш токини юзага келтиради.

Четки электр майдони таъсирига киритилган диэлектрикнинг молекулалари харкатланиб, қутбланиш токини юзага келтиради.

бу ерда - қутбланиш вектори.

Баъзи бир мухитларда =e₀k_э тенглик ўринли. Бу холда

Юқорида айтиб ўтилган уччала ток турлари хам электр зарядларининг силжишини ифодалайди. Хар бир ток ўзининг магнит майдонига эга.

Максвелл электр токи деб токнинг вакуумдаги вақт бўйича ўзгаришини айтишни таклиф этган

Силжиш токининг бошқа турдаги токлардан фарқи шундаги, бу ток иссиқлик йўқотишларини (қизиш хисобига юзага келадиган энергия йўқотишлари) юзага келтирмайди.

Тўлиқ электр токи деб – магнит майдонини юзага келишида қатнашадиган ьарча турдаги токларнинг йиғиндисига айтилади

I_тўл=I + I_кўч + I_қутб + I_0сил.

Вакуумдаги қутбланиш ва силжиш токлари йиғиндисини диэлектрикдаги силжиш токи деб аталади.

Бу холатда ток зичлиги

J_тўлиқ = J_ўтк + J_сил= sE +.

Кўчиш токини кўриб чиқиш шарт эмас. Яхши ўтказувчанликка эга бўлган мухитда I >> I_сил, кам йўқотишли диэлектрикда эса I_сил >> I. Яримўтказгич мухитларда иккала токлар хам ўзаро тенг қийматларга эга бўлади.

МАВЗУ 3. МАГНИТ МАЙДОНИ

3.1. Магнит майдонни тавсифловчи асосий катталиклар

Магнит майдонни тавсифловчи асосий катталиклар шундан иборатки улар ўз таъсири остидаги ҳаракатланаётган зарядланган жисмга ва ток оқаётган ҳаракатсиз ўтказгичга куч билан таъсир килади. Магнит майдонни магнит индукцияси вектори орқали тавсифланади. векторининг йўналиши ва қийматини билган холда, у томонидан ҳосил килиниши мумкин бўлган ҳодисаларни аниқлаш мумкин. векторини ток оқаётган контурга таъсир этаётган куч орқали аниқлаш мумкин. Токнинг чизиқли қисмига таъсир кўрсатувчи кучни қуйидаги формула билан аниқлаш мумкин.

. (3.1)

СИ тизимида []= [Тл].

Ток ва у томонидан бўшлиқда қўзғатилган индукция орасидаги боҳлиқликнинг дифферциал кўриниши қуйидагича

, (3.2)

бу ерда J – ток зичлиги

dV – элементар ҳажм

R – вектор аниқланадиган нуқтагача бўлган масофа

m₀ – магнит доимийси m₀=4p×10^-7 Гн/м.

Агар ўтказгичнинг кўндаланг кесими ўтказгич узунлиги ва кузатиш нуқтасигача бўлган масофадан кичик бўлса (бу ерда ўтказгич чизиқли)

[ ]dv=[ ] =[()]=I[]. (3.3)

Тенгламани интеграллаб қуйидаги ифодани хосил қиламиз

. (3.4)

Агар, токли контур бирор муҳитда жойлашган бўлса, унда магнит индукциясининг қиймати ₀ дан m марта фарқ қилади

(3.5)

m - нисбий магнит сингдирувчанлик.

Магнит майдон кучланганлиги қуйидагича аниқланади

. (3.6)

Магнит майдон кучланганлиги муҳит хоссаларига боғлик эмас. Токли ўтказгич учун Био-Савар-Лаплас қонуни қуйидагича

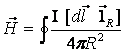. (3.7)

Муҳитнинг хусусий макроскопик майдонини M вектори билан тавсифлаш мумкин. У магнитланиш вектори деб аталлади. Бу вектор бир хил кучланганликка эга бўлган магнит майдони таъсир этаётган мухитда ва вакуумда магнит индукцияси векторлари ўзаро қанчага фарқ қилишини (=mm₀ муҳитдаги магнит индукцияси, =m₀ вакуумдаги магнит индукцияси) кўрсатади.

-₀=m₀, (3.8)

M=k_m. (3.9)

бу ерда k_m –магнит таъсирчанлик

=m₀M+m₀=m₀(1+ k_m)= mm₀. (3.10)

Юқоридагиларга кўра, m=1+ k_m

СИ бирликлар тизимида []=[А/м], [M]=[А/м].

3.2. Магнит оқими ва унинг узлуксизлиги

Магнит индукцияси векторининг оқими қуйидагича ёзилади

Ф=. (3.11)

СИ тизимида [Ф] = [Вб].

Ёпиқ юза орқали магнит оқими доимо нолга тенг.

. (3.12)

Остраградский теоремасидан фойдаланиб қуйидаги ифодани ёзиш мумкин

. (3.13)

Бу тенглама исталган ҳажм учун ўринли ва шунга асосан

div=0. (3.14)

Келтирилган тенглама магнит оқимининг узлуксизлик принципи бўлиб, дифференциал шаклда ёзилган. Бу магнит майдонининг исталган нуқтасида хам келувчи (сток) ва кетувчи (исток) магнит индукция куч чизиқларининг мавжуд эмаслигини ифоджалайди. Магнит индукцияси чизиқлари ҳеч қачон узилмайди ва улар доимо ўз-ўзига туташган.

векторининг ёпиқ контур бўйича циркуляцияси ва контурдаги ток билан миқдорий алоқаси тўлиқ ток қонуни орқали аниқланади.

I . (3.15)

Бирон-бир мухитда унча катта бўлмаган контур оламиз ва унда векторини циркуляциясини кўриб чиқамиз.

J_ўтк D J

Di =J D=J_ўтк D

Ифоданинг иккала томонини D га бўлиб, юзанинг майдонини нолга интилтирамиз D®0.

,

rot_п =J_ўтк,

rot =J.

rot =J тенглама тўлиқ ток қонунининг дифференциал шакли хисобланади.

H вектори кузатилаётган нуқтада майдонга уюрмали кўриниш бера оладиган функция сифатида кўриб чиқилиши мумкин.

3.3. Магнит майдонининг скаляр потенциали

Ротори нолдан фарқ қилувчи майдонни уюрмали майдон дейилади. Ўзгармас ток юзага келтираётган майдонда rot =J бўлганлиги, ва бу ерда J¹0 тенглик бажарилганлиги учун векторининг майдони уюрмали бўлади. Агар J=0 ва rot=0 бўлса, магнит майдонни потенциал майдон сифатида қўриб чиқиш лозим.

Бундай холларда

=-grad j_M,

чунки

div=divmm₀=0,

div=0,

div gradj_M=0. (3.16)

ёки Ѳj_М=0 – токсиз тармоқлар учун Лаплас тенгламаси.

Биринчи ва иккиинчи нуқталардаги скаляр магнит потенциаллари фарқини шу нуқталар орасидаги магнит кучланишининг тушуши деб аталади.

U_M12=j_M1-j_M2=. (3.17)

“Магнит кучланишнинг тушиши” ва “магнит кучланиш” орасидаги фарқни тушуниб олиш керак. Биринчиси фақат дан бўйича танланган йўл орқали чизиқли интегралаш билан, иккинчиси эса нафақат шу интеграл билан, балки, шу йўлда мавжуд бўлган ЭЮК билан хам аниқланади.

3.4. Магнит майдонининг вектор потенциали

Магнит майдонини ҳисоблаш учун вектор потенциалидан фойдаланилади

=rot .

Магнит индукциясини вектор потенциалидан олинган ротор сифатида тасвирлаш учун ихтиёрий роторнинг дивергенцияси нолга тенг эканлиги хақидаги айният асос бўлиб хизмат қилади

div =0 экан, демак div rot =0.

Ихтиёрий контурни ёриб ўтаётган магнит оқими ва магнит индукциясини топиш учун вектор потенциалидан фойдаланиш маъқул.

3.5. Магнит майдонидаги чегаравий шартлар

Магнит майдони учун Н_1t=Н_2t шарт ўринли. Бу шарт mnpq ясси контури бўйлаб чизиқли интегрални тузиш орқали келтириб чиқарилган. Контурнинг np ва mq томонлар mn ва pq томонларга нисбатан жуда хам кичик. Контурнинг mn ва pq томонларини dl деб белгилаб қуйидагини хосил қиламиз

H₁sina₁dl-H₂sina₂dl=0, (3.18)

H₁sina₁=H_1t H₂sina₂=H_2t

Демак, H_1t=H_2t шарт чиндан хам ўринли. Агар икки мухитлар чегарасида юза токлари оқаётган бўлса, бу шарт бажарилмайди. Бундай холларда

H₁sina₁dl - H₂sina₂dl = J_sdl ,

H_1t - H_2t = J_s.

J_s зичликка эга бўлган юза токи мавжуд бўлганда майдоннинг урунма ташкил этувчиси мухитлар чегарасида узилишга учрайди, яъни сакраб ўзгаради.

Магнит майдони учун

В_1п=В_2п

Бу ифода магнит оқими принципидан келиб чиқади

=0

Икки муҳитлар чегарасида унча катта бўлмаган ясси паралипипед хосил қилайликда, ундаги оқимларни хисоблайлик. Хисоб-китобларни паралеллепипеднинг қуйи В_1п DS ва юқори В_2п DS чеккалари учун амалга оширмиз. Натижада қуйидаги тенгликлар хосил бўлади

-В_1п DS+ В_2п DS=0,

В_1п= В_2п,

. (3.19)

3.6. Магнит майдони энергияси

dl элементар майдонни кесиб ўтаётган магнит оқими dФ=d га тенг. Тўла оқим эса

Ф=. (3.20)

d юзани чегараловчи контурда куч найчаларини чизамиз. векторининг магнит майдондаги чизиқлари доимо ўзаро туташган бўлганлиги учун, куч найчалари хам ёпиқ (туташган) бўлади. Улар магнит майдони билан банд бўлган V ҳажмни тўлдиради. Агар най ўқини L билан белгиласак, у ҳолда

Майдон энергияси эса

,

ёки

,

у ҳолда

. (3.21)

Агар =rot эканлигини ҳисобга олсак

,

бироқ,

div[]=rot- rot.

Шундай экан,

тенгламани ёзиш мумкин.

Остроградский теоремасига кўра

. (3.22)

Магнит майдони чексиз ҳажмни эгаллаганлиги учун S ни чексиз катта R радиусли шарнинг юзаси деб қараш мумкин. [] вектор масофа функцияси сифатида дан тезроқ, юза эса R² дан секинроқ ўсиб боради. Ўундай экан, R®¥ холатида

.

У холда, Максвеллнинг (rot=J) биринчи тенгламасига кўра

(3.23)

тенгламани ҳосил қиламиз.

3.7. Магнит майдоннинг ҳисоблаш усуллари

Магнит майдонини ҳисоблаш кўпинча Н векторни аниқлашга тақалади.

Бунда, ток ыийматлари ва ток оқаётган ўтказгичларнинг жойлашуви берилиши шарт. Агар майдон ферромагнитсиз муҳитда таъсир этаётган бўлса,

mm₀»m₀=4p10^-7 Гн/м . (3.24)

Агар Н ни ҳисоблаш катта математик қийинчиликлар туғдирса, у ҳолда вектор потенциал тушунчасини киритиш қулай. Вектор потенциалини аниқлаш орқали майдон кучланганлигини топиш мумкин. Магнит майдонини ҳисоблашда қуйидаги усуллардан фойдаланиш мумкин:

· Интеграл кўринишдаги тўлиқ ток қонуни қўллаш;

· Максвелнинг биринчи тенгламасини қўллаш;

· Вектор потенциали учун Пуассон – Лаплас тенгламасини қўллаш;

· Кўзгули тасвир усули;

· Конформ ўзгаришлар усули;

· график хисоблаш усулини.

МАВЗУ 4. МАКСВЕЛЛ ТЕНГЛАМАЛАРИ ТИЗИМИ

4.1. Максвелнинг биринчи тенгламаси

Тўлиқ ток қонунига асосан

. (4.1)

Бу тенглама Стокс теоремаси асосида ўзгартирилгач, қуйидаги кўринишга келади

. (4.2)

Натижада

ёки

Ушбу тенгламанинг физик маъноси шундаки, уюрмали магнит майдони хам ўтказувчанлик токлари туфайли, хам вақт мобайнида ўзгарувчан электр майдонлари туфайли юзага келади.

Идеал диэлектриклар учун солиштирма электр ўтказувчанлик s = 0 га тенг.

у ҳолда тўлиқ диэлектрик сингдирувчанлик муҳити e=const учун Максвелнинг биринчи тенгламасини вақт давомида ўзгарувчан электр майдони ва магнит майдони кучланганлигининг фазода ўзгариши ўртасидаги боғлиқликни ўрнатади ва электромагнит майдон доимо харакатда эканлигини исботлайди.

4.2. Максвелнинг иккинчи тенгламаси

Бу тенглама контурда хосил қилинган электромагнит индукция қонунининг дифференциал кўриниши бўлиб, қуйидагича аниқланади

. (4.3)

S юза ҳамда L контур кўзғалмас ва шаклан ўзгармас деб тасаввур қилацлик. У холда, Стокс теоремасига кўра

, (4.4)

Шундай экан,

(4.5)

ёки

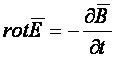. (4.6)

Бу тенгламанинг физик маъноси шундан иборатки, уюрмали электр майдони ўзгарувчан магнит майдонини қўзғатади. rotE¹0 бўлганлиги учун, Е векторининг куч чизиқлари ёпиқ бўлиши мумкин ва улар В вектори чизиқларини қамраб олиши керак.

Магнит сингдирувчанлик m=const бўлган муҳитлар учун эса

. (4.7)

Шундай қилиб, Максвелнинг иккинчи тенгламаси Н векторининг вақт бўйича ўзгариши билан Е векторининг фазода ўзгариши ўртасидаги боғлиқликни ўрнатади.

4.3. Максвеллнинг учинчи тенгламаси

Максвеллнинг учинчи тенгламаси Гаусс қонунининг ўзгарувчан жараёнлар холати учун умумлаштирилган кўриниши хисобланади. Гаусс қонуни ихтиёрий ёпиқ S юза орқали электр силжиши вектори оқимининг шу юзада жамланган Q заряд билан боғлайди

, (4.8)

Максвеллгача бу тенглама фақатгина ўзгармас майдонларга нисбатан қўлланилар эди. Максвелл эса бу тенгламани ўзгарувчан майдонларда хам қўллаш мумкин деган фикр билан чиқди. Q заряд S юзада ихтиёрий тақсимланган бўлиши мумкин. шунинг учун, умумий холда

бу ерда V- S юзада жойлашган хажм;

ρ – заряднинг хажмий зичлиги.

Заряднинг хажмий зичлиги эса

_{Юқоридагиларни хисобга олган холда, қуйидаги тенгламани хосил қиламиз}

_(4.9)

Бу тенгламани Максвеллнинг интеграл шаклдаги учинчи тенгламаси деб аташади. Остраградский теоремасига асосан бу тенгламани дифференциал шакли қуйидагича

(4.10)

Максвеллнинг учинчи тенгламасидан қуйидаги физик маъно келиб чиқади; Электр силжиш векторининг ёпиқ юза бўйича оқими шу юзада тақсимланган зарядларнинг хажмий зичлигига тенг ва электр майдони куч чизиқлари мусбат зарядлардан манфий зарядлар томонга йўналган бўлади.

4.4. Максвеллнинг тўртинчи тенгламаси

Максвеллнинг интеграл шаклдаги тўртинчи тенгламаси магнит майдони учун Гаусс қонуни билан мос келади. Унга кўра, B векторининг ихтиёрий S юза орқали оқими нолга тенг

. (4.11)

Бу эса, В векторининг фақатгина юзага кирувчи ёки юзадан чиқувчи куч чизиқлари мавжуд эмас, улар доимо юзани ёриб ўтишини ифодалайди.

Ушбу тенглама Максвеллнинг интеграл шаклдаги тўртинчи тенгламаси номи билан юритилади. Унинг дифференциал шаклига Максвеллнинг учинчи тенгламасидаги каби, Остраградский-Гаусс теоремасини қўллаган холда ўтиш мумкин. Натижада

div B = 0. (4.12)

Бу тенглама эса Максвеллнинг тўртинчи тенгламасини дифференциал шакли. Унга кўра, табиатда магнит зарядлари мавжуд эмас ва В векторининг (магнит майдонининг) куч чизиқлари доимо ўзига-ўзи туташган.

4.5. Электромагнит майдоннинг тўлиқ тенгламалар тизими

Электромагнит майдонни тўртта D,E,B,H вектор катталиклар билан тавсифланади. Доимий сингдирувчанликка эга бўлган муҳитлар учун

D=ee₀E, B=m₀mH (4.13)

Шунинг учун хам, ҳисоблашларда икки векторни аниқлаш кифоя қилади. Одатда,`Е ва `Н векторлари Максвел тенгламаларидан аниқланади

`Е ва`Н ни аниқлаш учун юқоридаги тенгламаларнинг ўзи етарли эмас. Шунинг учун, векторларнинг дивергенцияларини ҳам аниқлаш керак. Гаусснинг дифференциал шаклдаги теоремасига кўра div`D=r.

e доимий қийматга эга бўлганда

(4.14)

Магнит майдоннинг асосий ҳусусияти бу унинг соленоидаллиги (div`B=0). Агар m доимий бўлса, div`H=0.

Аниқ масалаларни ечишда бошланғич чегаравий шартлари инобатга олиш лозим.

Икки муҳитлар чегарасида e, m ва s нинг қийматлари сакраб, кескин ўзгаради. Демакки, чегара юзасида магнит майдон вектори узлуксизлигининг узилиши ўрин тутади. Вақт бўйича доимий майдон учун олинган чегаравий шартлар электромагнит майдон векторларининг оний қийматлари учун ҳам ахамиятини йўқотмайди.

(4.15)

Электромагнит майдоннинг асосий тенгламаларидан қуйидаги физик маъно келиб чиқади:

- магнит майдони доимо уюрмалидир ва у ҳаракатланаётган зарядлар билан хам, вақт бўйича ўзгарувчан электр майдони билан хам қўзғалади.

Электр ва магнит майдонлари доимий ўзаро бир-бири билан алмашиб турувчи жараён бўлиб, ягона электромагнит майдонинг икки томони сифатида намоён бўлади. Электромагнит майдон доимо харакатда ва ўзи билан энергия заҳирасини олиб юради.

(4.16)

Вақт бўйича доимий жараёнларда майдон тенгламаси икки бир-биридан мустақил тизимларга ажралади

электр майдон учун rotE=0, dive₀eE=r

магнитостатистик майдон учун rotH=J, divm₀m`H=0.

4.6. Тўлиқ токнинг узлуксизлиги тенгламаси

Бу тенглама Максвеллнинг биринчи тенгламасидан хосил қилинади. Бунинг учун тенгламанинг иккалал томонига нисбатан дивергенция амалини қўллаш лозим, яъни

(4.17)

векторлар тахлилига кўра, ротордан олинган дивергенция нолга тенг деган айният мавжуд. Шунинг учун

(4.18)

вектор дивергенциясининг нолга тенглиги, унинг куч чизиқлари ёпиқ эканлигини англатади. Шундай экан, тўлиқ токнинг куч чизиқлари узлуксиз. Бу холат алохида икки ёки ундан кўп симлардан ташкил топган антенналарда нима учун ток оқиб ўтиши ва ёпиқ занжир хосил бўлишини тушунтиради. Бундай тизимда, ўтказувчанлик токининг куч чизиқлари фазо орқали силжиш токининг куч чизиқлари ёрдамида туташади ва антеннада ток оқиши учун шароит яратади. Худди шундай ходиса мобиль ва радиотелефонларда хам кузатилади.

МАВЗУ 5. МОНОХРОМАТИК МАЙДОН УЧУН ЭММ ТЕНГЛАМАЛАРИ

5.1. Комплекс векторлар. ЭММ тенгламаларининг комплекс шакллари

Юқорида ёзилган тенгламалар майдон векторларининг оний қийматлари учун ёзилган, яъни, улар майдоннинг вақт бўйича ихтиёрий ўзгариши учун ўринли. Агар векторлар вақт бўйича доимий даврли синусоидал қонун бўйича ўзгарса, бундай майдонлар монохроматик деб аталади. Бундай майдонлар учун комплекс векторларни керитиш, яъни, комплекс амплитудалар усулини қўллаш ўринли. Бу усулда оний қийматлар ўрнига формал катталикларни қўлланилади. Масалан, Н = H_msin(wt+j_н) ўрнига Н_me^jwt кўринишдаги комплекс катталик ёзилади.

Қуйидаги тенгламага кўра, I_m комплекс миқдорнинг мавхум қисмини кўрсатади

ЭММ бўйича кўп адабиётларда, вақт бўйича косинусоидал қонун бўйича ўзгарадиган майдонларни монохроматик майдон деб аталади. У холда,

яъни, комплекс миқдорнинг моддий қисми қўлланилади.

Оний қийматлардан комплекс қийматларга ўтиш гармоник физик жарёнларни математик усулда кўриб чиқишни осонлаштиради. Бунда дифференциаллаш ва интеграллаш амаллари уларни (jw) кўпайтувчисига кўпайтириш ёки бўлиш амаллари билан алмаштирилади. Бу ерда w - кўриб чиқилаётган частота гармоникаси.

Масалан, силжиш токининг зичлигини қуйидагича алмаштириш мумкин

Қуйидаги тенглама ўрнига

(5.1)

мана бу тенгламадан фойдаланилади

.

Уни умумий кўпайтувчисига қисқартириб қуйдаги кўринишга эга бўламиз

(5.2)

(5.1) даги Максвеллнинг биринчи тенгламаси реал мавжуд бўлган майдонлар учун ёзилган. (5.2) тенглама эса (5.1) нинг математик шакли хисобланади ва фақатгина гармоник майдон учун, яъни, сигналнинг битта спектрал ташкил этувчиси учун ёзилган. Шуни ёдда тутиш керакки, ЭММ тенгламаларининг комплекс шакллари майдон векторларининг гармоник ўзгаришлари учун, хусусий холат сифатида намоён бўлади. Максвеллнинг қолган тенгламалари комплекс шаклда қуйидаги кўринишга эга бўлади

Векторларнинг комплекс шакллари уларнинг устида нуқта белгиси киритилганлиги билан фарқланади. Комплекс шаклдаги тенгламалардан хосил бўлган жавобларнинг реал қисми тўғри жавоб сифатида қабул қилинади.

5.2. Комплекс диэлектрик сингдирувчанлик. Йўқотишлар бурчаги

(5.2) га электродинамиканинг учинчи моддий тенгламасини қўйиб, қуйидагини хосил қиламиз

Тенгламанинг ўнг томонини математик ўзгартириб

(5.4)

тенгламага эга бўламиз.

Электромагнит жараёнларни тахлил қилишда янги коэффициент – комплекс диэлектрик сингдирувчанликнинг киритилиши тенгламаларни соддалаштириш имконини беради.

(5.5)

Шундай экан, тенглама қуйидаги кўринишга келади

формулани алгебраик ва кўрсатмали шаклларда ёзиш мумкин

(5.5.а)

(5.5.б)

Эйлер формуласи асосида ўзгартиришлар бажарилганидан сўнг, яна бир асосий тенгламага эга бўламиз

(5.6)

(5.6) ни диэлектрик йўқотишлар бурчагининг тангенси деб атайдилар. Электр майдонининг энергия йўқотишлари ўтказувчанлик токлари ва мухитдаги силжиш токлари хисобига юзага келадилар. tgd параметри силжиш токи хисобига хосил бўладиган йўқотишларни, яъни, ташқи электр майдони таъсири остида юзага келадиган харакат туфайли пайдо бўладиган йўқотишларни кўрсатади.

Комплекс ўтказувчанлик токининг зичлиги модули қуйидагига тенг

Силжиш токи зичлигининг модули эса

Уларнинг нисбати бизга йўқотишлар бурчаги тангенсини беради

Шунга кўра, бу параметр мухитда ўтказувчанлик токи силжиш токидан қанча катта қийматга эга эканлигини кўрсатади ва мухитларни ўтказгич ва диэлектрикларга бўлиш мезони бўлиб хизмат қилади.

Агар tgd >10 (tg d » 1) бўлса, бундай мухитни катта йўқотишли мухит ёки ўтказгич мухит деб атайдилар.

Агар tgd <0,l (tg d « 1) бўлса, бундай мухитни кичик йўқотишли мухит деб атайдилар, яъни бу мухит диэлектрикка хос.

Агарда бу параметр қиймати 0,1<tgd <l0 (tg d ≈ 1) оралиқда жойлашган бўлса, бундай мухитни йўқотишли ёки яримўтказгич мухит деб атайдилар. Тоза ва қуруқ хавони вакуумга яқин деб хисоблаш мумкин ва у йўқотишларни юзага келтирмайди (tgd = 0). Амалда қўлланиладиган сифатли диэлектриклар радиочастота диапазонида (f = 30 ГГц гача) tgd = 10^-2…10^-4 қийматга эгадирлар.

5.3. Монохроматик майдон учун четки манбаъларни хисобга олувчи тенгламалар тизими

(5.1) ва (5.2) тенгламаларида қатнашувчи майдон орқали шу муҳитда вужудга келтирилган ва токлари йўқ. Бу токлар майдоннинг манбаълари бўлиб ҳисобланмайди, балки улар унинг таъсири остида пайдо бўлган. Шу вақтнинг ўзида ЭММ четдан олинадиган энергия ҳисобига қандайдир майдон томонидан вужудга келади. Бундай манба сифатида кўпинча радиоузатгичнинг кувватли чиқиш каскади ёрдамида антеннада юзага келадиган ток ҳисобланади. Антеннанинг токи четки ресурс (трансформаторли ёрдамчи станция) нинг қуввати орқали аниқланади ва муҳитда кўрилаётган майдон векторлари функцияси ҳисобланмайди. Электромагнит майдон манбасини четки куч деб аташ қабул қилинган. Четки куч - бу ЭММ ни ҳисоблашда бошланғич миқдор ҳисобланадиган функциядир. Бу куч кўпинча J_силж токининг зичлиги орқали ифодаланади. У Максвеллнинг 1-тенгламасини ўнг тарафида қатнашади.

(5.7)

бўлганлиги сабабли, биринчи тенглама комплекс шаклда қуйидаги кўринишга эга

Қолган тенгламалар эса

(5.8)

(5.9)

(5.8) тенгламада қайта магнитланишда юзага келадиган йўқотишларни ҳисобга олишда қўлланиладиган комплекс магнит ўтказувчанлик қатнашади. Аммо ЎЮЧ техникасида фақатгина бир магнит модда — ноёб хусусиятларга эга магнитланган ферритгина қўлланилади. Радиотехникада қўлланиладиган бошқа модалар магнит хоссасига эга эмас ва магнит йўқотишларини юзага келтирмайди. Шунинг учун (5.8) тенгламасида бундан кейин m ўрнига m_а ни ёзамиз.

(5.7) тенгламасида четки мабаларнинг мавжудлиги уни бир жинсли эмас қилиб қўяди. Четки манбаларсиз тенглама эса бир жинсли ҳисобланади.

(5.10)

Шуни пайқаш қийин эмаски, аган ни га, e_а ни эса m_а га алмаштирсак 1-тенглама 2-тенгламадан, 2-тенглама эса 1-тенгламадан хосил қилиниши мумкин. Максвелл тенгламаларининг бу хуссусияти икки тарафламалик принципи деб аталади. Унинг ёрдамида, ечилган икки тарафламали масалалар жавобларининг мос келувчи символларини алмаштириш йўли билан баъзи бир тенгламаларнинг ечилишини олиш учун қўлланилади.

Электродинамиканинг баъзи бир масалалари, шунингдек агар тенгламалар тизимиига четки магнит токи J_четм киргизилса ҳам соддалашади. Табиатда реал мавжуд магнит зарядлар йўқлиги сабабли, физик нуқтаи назардан сохта миқдор ҳисобланади. У ҳолда Максвеллнинг бир жинсли бўлмаган тенгламалари ҳам шакл жиҳатдан симметрик бўлади

(5.11)

Максвеллнинг симметрик бир жинсли ва бир жинсли бўлмаган (5.10) ва (5.11) тенгламалари ёрдамида, векторлар ва параметрлар ўрнини алмаштириш йўли билан, икки тарафламали масалаларнинг амалларидан фойдаланиб бир қатор масалаларнинг ечими олинади.

МАВЗУ 6. ЭЛЕКТРОМАГНИТ МАЙДОН ЭНЕРГИЯСИ ВА ҚУВВАТИ

6.1. Асосий гипотеза

ЭММ - материянинг ўзига хос тури сифатида иш бажаришга қодир. Масалан, у зарядланган зарядларни харакатга келтира олади. Макроскопик майдондаги энергетик нисбатларни кўриб чиқилаётганда, уларнинг орасида алоқа ўрнатувчи қуйидаги икки тахминдан фойдаланилади.

1. Электромагнит энергия фазода ҳажий зичлик билан тақсимланган

w=w_э+w_м=1/2 (Е*D+H*B), Дж/м³

бу ерда w_э=(E*D)/2 ва w_м=(Н*В)/2 — электр ва магнит майдон энергияларининг ҳажмий зичликлари.

2. Электромагнит энергия оқимининг зичлиги электр ва магнит майдон кучланганликларининг вектор кўпайтмасига тенг

П=[EхH], Bт/м²

Бу ерда П — энергия ҳаракатининг йўналишини кўрсатувчи ва миқдори бўйича унинг оқими зичлигига тенг бўлган Пойнтинг вектори. Векторнинг ўлчов бирлиги унинг қувват зичлигига тенглигини, яъни ҳаракат йўналишига перпендикуляр жойлашган 1 м² майдондан ўтувчи тўлқин қувватини кўрсатади.

6.2. Энерия баланси

ЭММ энергиянинг сақланиш қонунига бўйсунади. Шунинг учун S юза билан чегараланган ҳар қандай V ҳажмда келаётган ва ундан чиқаётган энергиялар тенглиги шарти бажарилади. Берилган вақт лахзасида ҳажмдаги энергия қийматини қуйидаги тенгламани интеграллаш орқали аниқлаш мумкин

Вақт ўтиши билан энергия қиймати бир қатор сабабларга кўра ўзгаради:

— энергия бошқа турларга айланади. Радиотўлқинларни қабул қилувчи қурилманинг кириш занжирида электронларнинг ЭММ таъсири остида иссиқлик ҳаракати ҳажмдаги (истеъмолчи учун фойдали) энергия йўқотишларига олиб келади. Энергиянинг сарфланиш тезлиги унинг йўқотишлар қуввати деб аталади;

— четки (бегона) манбаъларнинг энергияси ҳисобига тўлиб боради. Масалан, берилган ҳажмда жойлашган антеннанинг нурлаши хисобига майдон энергияси кўпаяди. Бунда, энергия кўпайишининг тезлиги четки кучлар қуввати Р_чет га тенг;

— хажмдан нурланади ёки ҳажм ташқарисидаги манбаълар энергияси ҳисобига тўлади. Ҳажмдан чиқувчи электромагнит оқимини нурланиш деб атаймиз. Нурланиш қуввати “оқим” оператори орқали аниқланади:

(6.2)

Ёдингизда бўлса, электромагнит майдон вектори dS шу юзани ўраб турувчи ҳажмга ташқи нормал бўйича йўналган. Агар П ва dS векторларининг йўналишлари қарама –қарши (яъни қувват оқими ҳажм ичига йўналган) бўлса, у ҳолда қувватнинг манфий қийматига эга бўламиз. Унда Р_S миқдорни нурланиш қуввати деб эмас, балки кириш қуввати деб аташ лозим бўлади. Лекин, бундай атама электродинамикада ишлатилмайди, балки фақат назарда тутилади.

Биз берилган ҳажмдаги энергиянинг вақт бўйича ўзгариш (dW/dt) сабабларининг барчасини қўриб чиқдик. Демак

бу ерда P_четки – четки манбаъ қуввати,

Р_й – йўқотишлар қуввати (истеъмол қилинган),

Р_Σ – нурланиш қуввати.

(6.3) ифода берилган ҳажмдаги ЭММ қуввати балансининг умумий физик тенгламаси ҳисобланади.

6.3. Электромагнит майдон векторларининг оний қийматлари учун Пойтинг теоремаси

(6.3) тенгламага (6.2) ва (6.1) ифодаларни қўйсак қуйидаги тенгламани хосил қиламиз

P_четки билан Р_й нинг таркибини тахлил қилайлик. ЭММ нинг энергия йўқотишлари зарядларнинг майдон таъсири остидаги ҳаракатига боғлиқ. Шу билан бирга, қўзғалмас зарядлар йўқотишларга олиб келмайди. Зарядларнинг ҳаракатини электромагнит майдон рўёбга чиқаради, яъни магнит майдони бу харакатга таъсир кўрсатмайди. Чунки, унинг таъсир этиш кучи

харакатнинг тезлиги вектори V га перпендикуляр, йўқотишлар қуввати эса скаляр кўпайтма хисобланади

Бу тенгликнинг тўғрилиги олинган миқдорнинг ўлчов бирлиги ([(Кл*В/м)*м/с]=[(А*с*В/м)*м/с]=А*В=Вт) билан хам тасдиқланади. Ҳажмнинг ҳар бир нуқтасидаги энергия балансини кўриб чиқиш учун ҳам йўқотишлар қувватининг ҳажмий зичлиги ва четки кучлар тушунчалари киритилади

(6.5) формулада йўқотишларнинг ҳажмий зичлигини хосил қилинади

Бу ерда r*V электр токининг зичлиги векторини ифодалайди. Шунинг учун йўқотишлар қуйидаги миқдор билан таърифланади

(6.6) тенгламани қуйидаги кўринишга хам келтириш мумкин

(6.7) тенглама Жоуль-Ленц қонунининг диференциал шакли хисобланади.

(6.6) скаляр кўпайтма мусбат ҳамда манфий миқдор бўлиши мумкинлиги сабабли, Р_й>0 ҳолати майдон энергиясининг зарядлар ҳаракатини ҳосил қилишига сарфланишини ифодалайди. J вa Е қарама-қарши йўналган бўлса, ЭММ четки манбаълардан энергия олади. Шунинг учун

Унда (6.4) ифодадан интеграл шаклдаги ЭММ энергиясининг сақланиш қонуни хосил қилиш мумкин

(6.9)

Ҳажмнинг камайтирилиши, яъни фазодаги нуқтачалик кичик ўлчамга ўтказилиши йўли билан қонуннинг дифференциал шаклини хосил қилинади

(6.10)

Бунда ED=, НВ= кўпайтмалари очиб берилган ва Остраградский – Гаусс теоремаси қўлланилган.

=

Пойтинг теоремаси шуни исботлайдики, ҳажмда тўпланган ЭММ қуввати фойдали иш бажариш учун сарфланган хамда ташқаридан оқим кўринишида олинган четки манбалар қувватларнинг алгебраик йиғиндисига тенг. Қувват баланси тенгламаси ЭММ назариясида катта аҳамиятга эга. Хусусан, бу тенглама электродинамик масалалар жавобларининг тўғрилигини текширувчи универсал аппарат ҳисобланади. (6.9) ва (6.10) тенгламалари векторларининг оний қийматлари учун ёзилган. Шунинг учун хам улар ҳар қандай ўзгарувчи майдон учун ўринли. Гармоник майдонлар учун эса улар анча соддароқ кўринишга эга.

6.4. Электромагнит майдоннинг комплекс векторлари учун Пойнтинг теоремаси

Гармоник жараёнларнинг физик моҳияти давр давомидаги ўртача энергетик характеристикаларни аниқлаш имконини беради. Ўзгаруви ток занжирида тенглик қўлланилгани каби, ЭММ назариясида комплекс йўқотишлар ва нурланиш қувватлари тушунчалари киритилади. Шу билан бирга, шуни ҳам назарда тутиш керакки, қувватнинг характери фазалар йиғиндисига эмас, балки тебранишлар фазасининг ўлчов бирлигига боғлиқ. Скаляр кўпайтмадаги иккинчи кўпайтма комплекс холда боғланган миқдор сифатида олинади

Шунинг учун, ЭММ электр ва магнит энергияларининг ўртача зичлиги мос равишда қуйидагиларга тенг

Йўқотишлар қувватининг ўртача хажмиий зичлиги эса

Четки кучлар қувватининг ўртача зичлиги

Бунда — четки кучлар қувватининг коплекс ҳажмий зичлиги.

Комплекс Пойнтинг вектори қуйидаги кўринишдаги кўпайтма сифатида аниқланади

Комплекс вектор оқими актив ва мавхум қисмларни ўз ичига олади.

Энергия оқими зичлигининг бир даврдаги ўртача қиймати комплекс векторнинг моддий қисмига тенг, яъни

Чекланган S юзали фазонинг ҳажмидан чиқувчи нурланиш қувввати қуйидаги интеграл кўринишида аниқланади

ЭММ назарияси бўйича ўқув қўлланмаларида, (6.11) ифодадаги Е ва Н лар остида векторларнинг амплитуда қийматлари фаҳмланади. У ҳолда (6.12) тенглама қуйидаги кўринишда ёзилади

Шундай қилиб гармоник (монохроматик) майдон учун энергия баланси тенгламаси (5.9) нинг моддий қисми қуйидаги кўринишга эга бўлади

(6.10) тенгламаси эса

(6.15) тенгламаси (6.10) га параметрларнинг комплекс қийматларини қўйиш йўли комплекс тенгламанинг моддий қисми учун ёзилган

Энергия баланси тенгламаси қувватнинг мавхум қисми учун айрим ҳолларда (6.15) тенгламасига ўхшаб ёзилади.

МАВЗУ № 7. ЭЛЕКТРОМАГНИТ ТЎЛҚИНЛАРНИНГ НУРЛАНИШИ

7.1. Элементар электр тебратгич

Элементар электр тебратгич деб – бутун узунлиги бўйлаб доимий амплитуда ва фазага эга бўлган ва ўлчамлари ишчи тўлқин узунлигидан анча кичик бўлган сим бўлагига айтилади.

Бу тебратгич, нурлатувчи тизимларни тахлил қилишда катта қулайликлар яратадиган идеаллаштирилган тизим ҳисобланади. Идеаллаштирилган дейилишига сабаб эса, бутун узунлиги бўйича ўзгармас тўлқин амплитудаси ва фазасига эга бўлган тебратгични яратиш мумкин бўлмаганлигидир.

Элементар электр тебратгични ўрганиш, антеннанинг тўлқин нурлатиш жараёнини тушуниш учун жудда хам мухим. Ток оқаётган ҳар қандай ўтказгични элементар электр тебратгичлардан ташкил топган нурлантирувчи тизим деб хисоблаш мумкин. Бунда, токлар орқали хосил қилинадиган майдони аниқлашда суперпозиция усулларидан фойдаланиш, яъни антеннани элементар тебратгичларнинг йиғиндиси сифатида кўриб чиқиш мумкин.

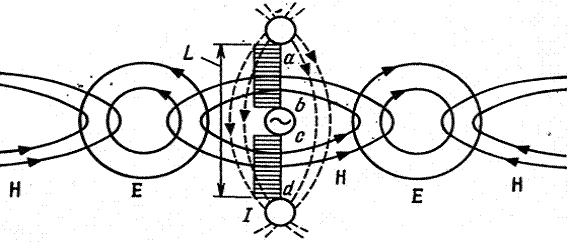
7.1-расм. Герц диполи ёрдамида электромагнит тўлқинларнинг хосил қилиниши

параметрлари билан тавсифланувчи, чексиз бир жинсли изотроп ўтказмас мухитда жойлашган элементар электр тебратгичнинг майдонини тахлил қиламиз. Тебратгичдаги токни маълум қонун бўйича ўзгарувчи четки ток деб хисоблаймиз. Тебратгичлар томонидан хосил қилинувчи майдон комплекс амплитудалар усули билан кўриб чиқилаётгани сабабли I_чет токининг ўрнига комплекс катталик киргизамиз.

Шундай қилиб, масалан берилган ток тақсимланиш майдонини топишга айланади. Биринчи вектор потенциали ни топамиз. Бунинг учун сферик координаталар тизими (r, φ, θ) дан фойдаланамиз. Унинг қутб ўқи (о х z) тебратгичнинг ўқи билан мос келади, координаталар боши эса унинг марказида туради.

(7.1)

бунда

вектори вектори потенциали билан нисбати билан боғланган.

векторини формуласи орқали топиш мумкин, аммо магнит майдон кучланганлигини топиб векторини Максвеллнинг биринчи тенгламасидан топиш осонроқ

. (7.2)

7.2. Элементар электр тебратгич майдони тузилишининг тахлили

Тебратгичнинг ЭММ тузилишини тахлил қилишда унинг атрофидаги фазо 3 зонага бўлинади

1) узоқ ёки тўлқинли зона (kr»1);

2) яқин зона (kr«1);

3) оралиқ зона (kr ≈ 1).

7.2-расм. Элементар тебратгичнинг майдон ташкил этувчиларини аниқлаш

Узоқ зона кўрсатиб ўтилганидек 2πr » λ шарти билан характерланади. Формулаларни солиштиришдан ифодаларида k=2π/λ ва эканлигини ҳисобга олган холда қуйидагига эга бўламиз

(7.3)

(7.4)

Шундай қилиб, узоқ зонада электр майдон кучланганлиги фақат ташкил этувчисига, магнит майдон кучланганлиги эса ташкил этувчисига ва ва векторлари бир хил фазага эга. Майдон векторлари фазаси вибраторнинг марказидан улар хисобланадиган нуқтагача бўлган r масофа билан аниқланади. Тенг фазалар юзалари маркази координаталар бошида жойлашган концентрик сфераларни хосил қилади. Тенг фазалар юзаларидан ҳоҳлаган биттасини танлаб оламиз ва вақт ўтиши билан унга нима бўлишини кузатиб турамиз. Майдон фазаси r₀ координатали нуқтада t₀ вақт лахзасида га тенг. t₁=t₀+ лахзада ҳудди ўша r₀ нуқтада у φ₀ дан ўзгача бўлади. r₁=r₀+ координатали нуқтада t₁ лахзада фаза учун математик ифодани ёзиб, шу ифодани φ₀ га қайта тенглаштириб га эга бўламиз. Шунга мувофиқ, да тенг фазалар юзаси оралиққа силжийди, t₁ лахзада эса r+ радиусга эга сферани ифодалайди. Тенг фазалар юзасининг силжиш тезлиги

. (7.5)

Шундай қилиб, элементар электр тебратгич узоқ зонада сферасимон тўлқин тарқатувчи хисобланади. Тўлқиннинг харакатланиш тезлиги шу мухитдаги ёруғлик тезлигига тенг. Майдон ташкил этувчиларининг нисбатлари доимий катталикка тенг

. (7.6)

Бу нисбат қаршилик ўлчамлигига эга ва муҳитнинг тўлқинли қаршилиги деб аталади. Вакуум ҳолатида муҳитнинг тўлқинли қаршилиги Ом га тенг.

Яқин зона. Яқин зонада 2πr « λ. Аммо тебратгич майдони учун хисоб формулалари r » l тахминдан келиб чиққан холда ёзилган. Шунинг учун хам яқин зона l « r « λ / 2 π тенгсизликлар билан ҳарактерланади.

Яқин зона учун майдон қуйидаги ташкил этувчиларга эга

(7.7)

(7.8)

(7.9)

векторининг оний қийматларига ўтиб, қуйидагиларга эга бўламиз

(7.10)

Яқин зонадаги тебратгичнинг электр майдони тахлилига ўтамиз. Тебратгичдаги токнинг ўзгариши унинг охирларидаги зарядлар катталикларининг ўзгаришига олиб келади. Яқин зонада тебратгич майдони қуйидаги ташкил этувчилар орқалигина аниқланади

(7.11)

Яқин зонадаги ташкил этувчиларни тахлилидан келиб чиққан холда шуни айтишм мумкинки, бу ерда майдон кўпроқ реактив характерга эга, яъни, тебратгичга боғлиқ бўлган, нурланмайдиган энергия катта қийматга эришади.

Оралиқ зона яқин зонадан узоқ зонага ўтиш зонаси ҳисобланади. Шунга мувофиқ, оралиқ зонада тўлқин тарқалишини тахлил қилишда, юқоридаги ташкил этувчиларнинг хар бирини хисобга олишимиз лозим. Бу холатда нурланиш майдони ва реактив (тебратгичда қолиб кетадиган) майдон бир хил тартибга (даражага) эга бўлади.

Хар бир нурлантирувчи тизим электромагнит майдон энергиясини бирон бир йўналишда жамлаш хусусиятига эга. Элементар электр тебратгич хам ўзи нурлатаётган майдонни маълум қонуният асосида бирон йўналишда нурлатади. Бу хусусият нурлатгичнинг йўналганлик тавсифи орқали ифодаланади. Йўналганлик тавсифи деб вектори комплекс амплитудаларининг θ ва φ бурчак координаталарига боғлиқлигига айтилади. Йўналганлик тавсифининг график кўринишиги ифодаси йўналганлик диаграммаси деб аталади. Элементар электр тебратгичгичнинг йўналганлик тавсифи қуйидагича аниқланади

(7.12)

Турли тизимларнинг йўналганлик тавсифларини ва диаграммаларини ягона масштабда тасвирлаш ва уларни солиштириш учун қийматларни меъёрлаштириш амалга оширилади. Бундай меъёрлаштириш қуйидаги ифода ёрдамида амалга оширилади

(7.13)

Гармоник тебранишнинг амплитудаси фақат мусбат қийматларга эга. Шунинг учун (7.13) формулада нинг модуль қиймати ишлатилган. Йўналганлик тавсифи қутбли ёки тўғри бурчакли координаталар тизимида тасвирланади. Меъёрланган қийматли йўналганлик диаграммасининг тасвири қуйидаги кўринишга эга.

7.3-расм. Элементар электр тебратгичнинг қутбий координаталар тизимида тасвирланган Е-текисликдаги йўналганлик диаграммаси

7.4-расм. Элементар электр тебратгичнинг тўғрибурчакли координаталар тизимида тасвирланган Е-текисликдаги йўналганлик диаграммаси

(7.13) формуладан кўриниб турибдики, азимутал амплитуда φ бурчакка боғлиқ эмас, яъни нурлатгич φ бурчак оралиғида бир хил нурлатади (7.5-расм).

7.5-расм. Элементар электр тебратгичнинг қутбий координаталар тизимида тасвирланган H- текисликдаги йўналганлик диаграммаси

7.6-расм. Элементар электр тебратгичнинг тўғрибурчакли координаталар тизимида тасвирланган H-текисликдаги йўналганлик диаграммаси

Гармоник токларнинг нурлатиш қуввати қуйидаги формула орқали аниқланади

(7.14)

Шундай қилиб, антенна, сиртида қувват оқими зичлигининг тақсимланган ўртача қийматига эга бўлган сфера билан ўралган. У холда қувват, (3.6) формула ўзгартирилгандан сўнг қуйидагича ифодаланади

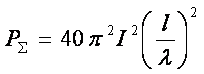(7.15)

Демак, нурлатиш қуввати нурлатгичнинг узунлиги ва тўлқин узунлиги орасидаги муносабатга боғлиқ. Жоул-Ленц қонунига асосан, электр схемасида сарфланаётган қувватни қуйидагича хам ифодалаш мумкин

, (7.16)

бу ерда

. (7.17)

R_Σ Ом бирлигида ўлчанадиган катталик бўлиб, тебратгичнинг нурланиш қаршилиги деб аталади. Эркин фазода уни хисоблаш ифодаси қуйидагича

(7.18)

Нурлатиш қуввати ва нурлатиш қаршилиги ифодаларини тахлил қилиб, шуни англаш мумкинки, элементар электр нурлатгичнинг нурлатиш қувватини ошириш учун қўшимча энергия сарфлаш ўрнига унинг нурлатиш қаршилишигини оширишнинг ўзи кифоя бўлади. Бу тебратгич модели идеаллаштирилган бўлганлиги сабабли хам, унда тебратгич узунлиги l нинг тўлқин узунлиги λ га нисбати оширилганда хам фаза ва амплитуданинг бир хилда қолиши таъминланади. Аммо, реал шароитда, буни амалга ошириш мумкин эмас. Шунинг учун хам, антенналарнинг ўлчамлари тўлқин узунлигига узвий боғлиқ.

МАВЗУ № 8. ЯССИ ЭЛЕКТРОМАГНИТ ТЎЛҚИНЛАР

8.1. Ясси электромагнит тўлқин параметрлари

Амалиётда, электромагнит майдонларни хисоблаш талаб этилганда, бирон бир математик моделдан фойдаланиш катта ахамиятга эга. Чунки, айнан шу модель ёрдамида электромагнит тўлқинларнинг реал шароитда тарқалишини ифодалаб бериш мумкин. Ана шулардан бири ясси электромагнит тўлқин модели бўлиб, унинг ёрдамида кўпгина тўлқинли жараёнларни хисоблаш мумкин. Келинг, аввал ясси электромагнит тўлқин хақида бироз тушунчага эга бўлайлик. Бунда, авваламбор, тўлқин фронти ёки тўлқинли юза тушунчасини билиб олиш лозим. Тўлқин фронти деб шундай сиртга айтиладики, бунда, унинг хар бир нуқтасида майдон кучланганлиги векторларининг фазалари бир хил қийматга эга бўлади. Майдонни хосил қилаётган нурлантирувчининг шаклига кўра, тўлқин фронти цилиндрсимон, сферасимон ёки бошқа шаклга эга бўлиши мумкин. Шуни хам таъкидлаш лозимки, ихтиёрий нурлантирувчи тизим томонидан хосил қилинган тўлқин фронти, ундан жуда хам катта масофада сверасимон шаклга эга бўлади. Ана шу холатга чуқурроқ назар ташлайдиган бўлсак, қуйидагини англашимиз мумкин. Радиоалоқа линияларида, деярли барча холларда, қабул қилувчи антенна катта масофада жойлашган бўлади. Бунда, майдоннинг тўлқин узунлиги ана шу масофадан ўн марта кичик бўлса, бу холатни узоққа тарқалиш деб хисоблаш мумкин. Амалда эса бу шарт деярли хар доим бажарилади. Агар тўлқин фронтининг сферик тарқалишини хисобга оладиган бўлсак, қабул қилувчи антенна бу фронтнинг ўзининг ўлчамига тенг бўлган жуда хам кичик бўлагини қабул қилади. Сферанинг жуда кичик бўлагини эса, биз доимо ясси деб қабул қилишимиз мумкин. Шу сабабдан хам, ясси электромагнит тўлқин моделининг ўрни ахамиятли. Векторлар хосил қиладиган монохроматик майдоннинг тўлқинли юзаси ўзаро параллел жойлашган, ёки улар бир текисликда ётувчи тўлқинни ясси тўлқин деб атайдилар. Тўлқин фронтининг барча нуқталарида майдон векторларининг қийматлари бир хил бўлган ясси тўлқинни биржинсли ясси тўлқин деб атайдилар.

Чексиз биржинсли мухитда тарқалаётган ясси гармоник электромагнит тўлқин қуйидаги тенглама ёрдамида ифодаланиши мумкин

(8.1)

Майдон векторининг оний қийматлари учун ифодаси қуйидаги кўринишга эга

(8.2)

Ясси электромагнит тўлқиннинг эркин фазода тарқалиш холатида еттита параметрлари билан тавсифланади. Бу параметрлар тўлқиннинг ўтказгич, яримўтказгич ва диэлектрик хоссасига эга бўлган мухитларда тарқалиш холатлари учун алохида ёзилади. Аввалги параграфларда айтиб ўтилганидек, мухитнинг ўтказувчанлик хоссалари бўйича синфланиши tg  параметри орқали амалга оширилади

.

Қуйида келтирилган формулалар ясси электромагнит тўлқин параметрларининг ифодаларидир.

1. γ – тўлқин тарқалишининг комплекс қоэффициенти. Бу математик параметр ифодаларни соддалаштириш ва ўзгартириш учун қўлланилади

(8.3)

2. α – сусайиш коэффициенти. Бу параметр тўлқиннинг 1 м масофа босиб ўтганда юзага келадиган энергиянинг сўнишини кўрсатади.

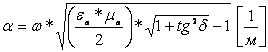(8.4)

3. β – фаза коэффициенти. Бу катталик тўлқиннинг 1 м масофа босиб ўтганида ўз фазасини қанча бурчакка ўзгартиришини ифодалайди.

(8.5)

4. v_ф – фаза тезлиги. Бу параметр тўлқли юзанинг харакатланиш тезлигини ифодалайди, бошқача қилиб айтганда, майдон векторининг тебраниш тезлигини кўрсатади.

(8.6)

5. v_г – гурухий тезлик. Бу параметр энергиянинг тарқалиш тезлигини кўрсатади

(8.7)

6. λ – тўлқин узунлиги. Бу параметр бир тўлиқ давр мобайнида тўлқин томонидан босиб ўтилган масофани кўрсатади

(8.8)

7. Z_c – мухитнинг тавсифий қаршилиги. Бу параметр майдон векторларининг комплекс амплитудалари нисбати орқали аниқланади

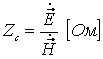(8.9)

Вакуум холатида мухитнинг тавсифий қаршилиги 120π Омга тенг бўлади. Реал мухитлар учун эса у комплекс характерга эга бўлиб, қуйидагича аниқланиши мумкин

(8.10)

(8.11)

Юқорида келтирилганлардан шуни англаш мумкинки, ясси электромагнит тўлқинни фақатгина фазонинг чекланган қисмидагина хосил қилиш мумкин. Бироқ, кўпгина амалий масалаларни ечишда, ташқи майдонни фазонинг барча нуқталарида хам тўлалигича ясси деб қабул қилинади. Бу эса электродинамик масалаларнинг ечимини осонлаштиради.

8.2. Электромагнит тўлқиннинг қутбланиши

Тарқалиш муҳити параметри tg δ диэлектрик йўқотишларнинг тангенс бурчаги деб аталади

.

Бу бурчак қиймати берилган материалдаги эркин зарядларнинг ҳаракати ва модданинг қутбланиши оқибатида электромагнит майдон энергиясининг йўқотишлар даражасини ҳисоблаш учун ишлатилади. σ қанча катта бўлса, tg δ ҳам шунча катта бўлади, йўқотишлар ҳам катта бўлади. Агар майдон частотаси ω ортса, tg δ камаяди, йўқотишлар ҳам камаяди, муҳит диэлектрикка яқинроқдир. Агар частота камайса, tg δ ортади, йўқотишлар ҳам ортади, муҳит ўтказгичга яқинроқдир. Йўқотишларнинг қиймати майдоннинг тебраниш частотасига боғлиқ, бир муҳит турли частоталарда диэлектрик ёки ўтказгич бўлиши мумкин.

Тўлқин ёки тўлқин тарқалиш жараёни электромагнит тўлқиннинг тарқалиши натижасида фазода энергия узатилишининг ҳосил бўлишидан иборатдир. Агар E ва H векторларнинг амплитудаси кўндаланг координатага боғлиқ бўлмаса, тўлқин бир жинсли деб аталади.

Фазода c (с – ёруғлик тезлиги, 3*10⁸ м/с га тенг) тезлик билан ҳаракатланувчи гармоник майдон югурма тўлқин деб аталади. Тарқалиш ўқи бўйлаб фазанинг

y = wt - kz (8.12)

кўринишдаги чизиқли ўзгариши югурма тўлқинга хосдир,

бунда - тўлқин сони ёки чексиз муҳитда тўлқин тарқалиш доимийси; – циклик частота.

Тўлқин тарқалишининг яна бир тури турғун тўлқин ҳисобланади, у қарама–қарши тарқалаётган икки тўлқиннинг устма-уст,

яъни y₁ = wt - kz ва y₂ = wt + kz фазалар фарқи билан тушишидан ҳосил бўлади.

Бу тўлқинларнинг майдонлари йиғиндиси

E = E₁ + E₂ = E₀₁ cos (wt – kz -j₁) + E₀₂ cos (wt + kz - j₂) (8.13)

Агар E₀₁ = E₀₂ = E₀ ва j₁ = j₂= j бўлса, у холда

E = E₀ cos kz cos (wt + j). (8.14)

(2.4) формула орқали ифодаланган майдон вақтнинг ҳар онида ва фазонинг исталган нуқтасида гармоник тақсимотнинг ўзгармас қолиши билан тавсифланади ва бу жараён турғун тўлқин деб аталади.

Қутбланиш деганда фазонинг берилган нуқтасида E ёки H векторнинг узунлиги ва йўналиши ўзгариши тушунилади. Қутбланиш жараёни қутбланиш текислиги тушунчаси билан боғлиқдир. E векторининг тарыалиш йўналиши бўйлаб хосил қиладиган текислиги қутбланиш текислиги деб аталади.

8.1-расм. Қутбланиш текислигининг шаклланиши

Қутбланиш - электромагнит тўлқинни тавсифловчи жуда хам мухим катталик хисобланади. Электромагнит тўлқиннинг эркин фазода тарқалиш вақтида уч турдаги қутбланиш турлари эътироф этилади. Қутбланиш турларини (2.3) ва (2.4) формулалар орқали ифодаланган майдонлар мисолида кўриб чиқиш қулайдир.

1. Чизиқли қутбланган тўлқин деб фазонинг исталган нуқтасида вақт ўтиши билан E ёки H векторларининг тебранишлар йўналиши ўзгармас бўлиб қолишига айтилади.

8.2-расм. Чизиқли қутбланишнинг график тасвири

2. Айлана бўйича қутбланган тўлқин деб фазонинг исталган нуқтасида E ёки H векторининг бир текис айланишига айтилади, яъни вектор бир T давр вақт мобайнида ўз учи билан айлана ҳосил қилади.

8.3-расм. Айланали қутбланишнинг график тасвири

3. Эллипссимон қутбланган тўлқин деб фазонинг исталган нуқтасида E ёки H векторининг айланишига айтилади, яъни вектор бир T давр вақт мобайнида ўз учи билан эллипс ҳосил қилади. Эллипссимон қутбланишда ортогонал ташкил этувчи векторларнинг фазалар фарқи j 0, p, p/2, -p/2 қийматлардан ташқари исталган қийматни олиши мумкин. Эллипснинг ўлчамлари ва ўқлари йўналишлари j катталикка боғлиқдир.

8.4-расм. Эллипссимон қутбланиш турининг график тасвири

Бундан ташқари, векторнинг айланиш йўналиши қутбланишнинг турини аниқлайди ва чапга (LZ) айланадиган ёки ўнгга (RZ) айланадиган айланали қутбланиш турлари юзага келади. Айланиш йўналиши узатувчи антеннадан қабул қилувчи антенна томон йўналишида аниқланади. Бунда соат миллари йўналиши бўйича харакатланувчи вектор ўнг томонли айланали қутбланишни юзага келтиради.

Эллипссимон қутбланиш (ЭҚ) атайин юзага келтирилмайди, чунки ЭҚ да сигнал қабул қилиш қуввати айланасимон қутбланишдаги (АҚ) сигнал қабул қилиш қувватидан камроқ. Шуни эсда тутиш керакки, АҚ ли антенна (нурлатгич) майдоннинг шу турли қутбланишини фақатгина нурлатгич ўқи йўналишида ишлаб чиқаради. Бошқа йўналишларда бу майдон эллипссимон қутбланиш сифатида қабул қилинади. Яна шуни эсда тутиш керакки, бир турдаги қутбланишга эга бўлган антенна идеал холатда бошқа турдаги қутбланиш сигналини қабул қилмаслиги лозим. Реал шароитда эса бу қутбланишлар сусайган холда қабул қилинади.

АҚ ли тўлқинлар радиотехника ва алоқада кенг қўлланилади. АҚ ли тўлқинларни вужудга келтиришда шуни назарда тутиш керакки, бундай тўлқин E (H) векторнинг фазода ортогонал бўлган, бир хил амплитудали ва тебранишниг фаза силжиши 90⁰ ни ташкил қилган икки чизиқли қутбланган тўлқинларнинг қўшилиши натижасидир.

Ўз навбатида, чизиқли қутбланган тўлқинни ҳаракатнинг қарама-қарши йўналишига ва E (H) векторнинг бир хил амплитудаларига эга бўлган, айланасимон қутбланишли икки тўлқиннинг суперпозицияси сифатида тасвирлашимиз мумкин.

Шахар шароитида тарқатиладиган электромагнит тўлқинлар учун жойнинг қурилишини хисобга олган холда қутбланиш тури танланади. Масалан, телевизион сигналларнинг шахар шароитида вертикал электр устунлари, кўп қаватли биноларнинг арматурали каркаслари томонидан қўшимча сусайишларини олдини олиш мақсадида, горизонтал қутбланиш туридан фойдаланилади. Буни антеннани ер сиртига нисбатан горизонтал жойлаштириш орвали хосил қилинади. Юқорида айтиб ўтилганидек, антеннанинг чиқишидаги қутбланиш тури унинг ўқи бўйлабгина ўз холатини сақлайди. Шахар шароитида сигналлар кўпгина тўсиқлар ва биноларнинг деворларидан аксланиши хисобига, қабул нуқтасига маълум бурчак остида, дастлабки холатидан оғган холда келиши мумкин. Бунда сигнални қабул қилишда унинг энергияси тўлиқ истеъмол қилина олмайди. Шунинг учун хам антеннанинг ер сиртига нисбатан жойлашувини ўзгартириб, сигнал сатхининг максимал қийматига кўра уни созлаш яхши натижа беради.

МАВЗУ № 9. МУХИТЛАР ЧЕГАРАСИДАГИ ТЎЛҚИНЛИ ЖАРАЁНЛАР

9.1. Электромагнит тўлқиннинг мухитлар чегарасидан ўтиши ва аксланиши

Ясси электромагнит тўлқин e_а1 ва m_а1 параметрли муҳитдан параметрлари e_а2 ва m_а2 (бу ерда e_а ва m_а - муҳитнинг абсолют диэлектрик ва магнит сингдирувчанликлари) бўлган ясси чегарага тушганда қисман бу чегарадан қайтади ва қисман эса тарқалиш йўналишини ўзгартирган ҳолда иккинчи муҳитга ўтади. хоу текислигини иккита муҳит чегараси деб қабул қиламиз.

9.1-расм. Тўлқиннинг муҳитлар чегарасидан қайтиши ва ўтишининг геометрик тасвири

Муҳитлар чегарасига нормал ўқ (Z ўқи) орқали ўтаётган XOZ текислиги ҳамда тушаётган тўлқинининг тарқалиш йўналиши тушиш текислиги деб аталади.

Қайтган ва ўтган (синган) тўлқинлар ҳам ясси бўлади, ҳамда уларнинг тарқалиш йўналишлари ва ҳам тушиш текислигида жойлашади.

Тушаётган тўлқиннинг тарқалиш йўналиши ҳамда муҳитлар чегараси нормали ўртасидаги φ бурчаги (бурчак Z ўқининг мусбат йўналишидан бошлаб ҳисобланади) тушиш бурчаги деб аталади.

Қайтувчи (аксланган) тўлқиннинг тарқалиш йўналиши ва нормал ўртасидаги бўлиниш чегараси томон йўналган j' бурчаги қайтиш бурчаги дейилади. Аммо, геометрик оптикада қайтиш бурчаги j₁ деб, j' бурчакни 180⁰ гача тўлдирадиган бурчакка айтилади.

Ўтувчи (синувчи) тўлқиннинг тарқалиш йўналиши билан нормал ўртасидаги бўлиниш чегараси томон йўналган q бурчаги синиш бурчаги дейилади.

j, j' ва q бурчакларнинг қийматлари ўртасидаги боғлиқлик Снеллиус қонунлари орқали ифодаланади:

j¢ = p - j , (9.1)

(9.2)

Тушувчи тўлқиннинг электр майдони кучланганлиги вектори тарқалиш йўналишига перпендикуляр бўлади, ва умумий ҳолда тушиш текислигига нисбатан турлича жойлашиши мумкин. Бироқ у доимо иккита ўзаро перпендикуляр векторлар йиғиндиси кўринишида тасвирланиши мумкинлиги сабабли, иккита ҳолатни, яъни вектори тушиш текислигида жойлашган ва тушиш текислигига перпендикуляр жойлашган ҳолатларни кўриб чиқиш кифоя.

Биринчи ҳолда тўлқиннинг қутбланиши паралел деб аталади. Бунда вектори координаталар ўқида иккита проекцияга ( ва ), эса фақат проекцияга эга бўлади (9.2.б-расм).

Қайтган ва синган и тўлқинлар ҳам тушиш текислигида жойлашади. Иккинчи ҳолда, тўлқиннинг қутбланиши нормал қутбланиш деб аталади. Бунда вектори битта проекцияга, эса иккита ва проекцияларга эга бўлади. Қайтган ва синган тўлқинлар ҳам тушиш текислигига перпендикуляр ҳолда жойлашган бўлади.

Қайтган ва тушувчи тўлқинлар комплекс амплитудаларининг нисбати қайтиш коэффициенти R деб аталади, яъни

. (9.3)

9.2-расм. Нормал ва параллел қутбланишда

векторларнинг проекциялари

Синган ва тушувчи тўлқинлар комплекс амплитудаларининг нисбатлари ўтиш коэффициенти χ деб аталади, яъни

. (9.4)

Бу ўринда R ва c умумий ҳолатда комплекс қийматлар эканини таъкидлаб ўтишимиз лозим. Уларнинг модуллари тегишли тўлқинлар амплитудаларининг муносабатларини тавсифлайди, аргументлари эса муҳитлар чегарасида ушбу майдонлар ўртасидаги фазалар силжишини билдиради.

Параллел қутбланиш ҳолатида

, (9.5)

, (9.6)

Нормал қутбланиш ҳолатида эса

, (9.7)

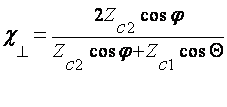, (9.8)

Бу ерда Z_c1=, Z_c2= - биринчи ва иккинчи муҳитларнинг тўлқин қаршиликларидир. (9.5)…(9.8) ифодаларни кўпинча Френель формулалари деб атайдилар.

Ясси электромагнит тўлқин ясси ўтказгич юзасига тушганда ундан қайтади. Бу холатда эса, ўтказгичлардаги тўлқин қаршилигини қуйидагича аниқланади

бу ерда w = 2p f -циклик частота, s -муҳитнинг ўтказувчанлиги.

Идеал ўтказгич учун (s=¥) тўлқин қаршилиги нолга тенг. Шунинг учун ясси тўлқин диэлектрикдан идеал ўтказгич юзига тушганда, тушиш бурчагидан қатъий назар, (9.5)....(9.8) формулаларидан қуйидаги тенглик келиб чиқади

R_|| = 1, R_^ = -1, c_|| = c_^ = 0 (9.9)

Демак, тўлқин тўлиқ қайтади ва идеал ўтказгич ичида майдон бўлмайди.

Реал металлар чекли ўтказувчанликка эга. Бироқ металларнинг ўтказувчанлиги катта (таҳминан 10⁶–10⁷ См/м) бўлгани сабабли, металларнинг тўлқин қаршилиги барча радиодиапазонларда нолга яқин бўлади. Демак, ҳар қандай тушиш бурчакларида ҳам қайтиш коэффицентининг модули кичик томонга 1 дан кўп ҳам фарқ қилмайди.

9.2. Ясси электромагнит тўлқиннинг иккинчи мухитга тўлиқ ўтиши. Брюстер бурчаги

Ясси электромагнит тўлқин ҳавода жойлашган d қалинликли ясси диэлектрик қатламига тушганда (9.3-расм), тушган тўлқин қисман қайтади ва қисман иккинчи қатламга ўтади. Қатламнинг пастки чегарасига етгач, тўлқин яна қисман қайтади, қисман эса қатламдан чиқади. Қатламнинг пастки чегарасидан қайтган тўлқин устки чегарага келиб тушади, бу ерда у яна қисман қайтади, қисман эса қатламдан чиқади ва ҳ.к. Шундай қилиб, қатламдан қайтган тўлқин бир хил йўналишда (Z-ўқига нисбатан j’ бурчакда) тарқалаётган ҳисобсиз тўлқинларнинг устма-уст тахланишини билдиради. Бу тўлқинлар қатлам ичидаги тўлқиннинг қайтиш сонига боғлиқ бўлган амплитудалари ва фазалари билан бир-биридан фарқ қилади.

Қатламдан ўтган тўлқин ҳақида ҳам худди шундай хулоса чиқариш мумкин.

9.3-расм. Ясси электромагнит тўлқиннинг диэлектрик

қатламига тушиши

Шуни ҳам таъкидлашимиз керакки, қатламдан ўтган тўлқиннинг тарқалиш йўналиши тушаётган тўлқин йўналишига мос келади. Қайтган тўлқинни ташкил қилувчи барча тўлқинларнинг комплекс амплитудаларини жамласак, тўлқиннинг қатламдан қайтиш коэффициенти R ва ўтиш коэффициентлари c учун қуйидаги ифодаларга эга бўламиз

R = ,

c = ,

бу ерда R₁₂ - тўлқиннинг ҳаводан қатлам чегарасига тушаётгандаги қайтиш коэффициенти бўлиб, у параллел қутбланишда (9.5) формула ёрдамида, нормал қутбланишда эса (9.7) формула ёрдамида аниқланади.

k₂ = , бурчак эса Снеллиуснинг (9.2) да келтирилган иккинчи қонунидан аниқланади.

Қайтиш ва ўтиш коэффициентларининг модуллари қуйидаги ифодалар ёрдамида аниқланади

, (9.10)

. (9.11)

Агар иккала муҳит ҳам диэлектрик бўлиб, m_а1=m_а2=m₀ бўлса, унда нормал қутбланган тўлқиннинг қайтиш коэффициенти, тушиш бурчаги j қандай бўлишидан қатъий назар, нолга тенг бўлмайди. Параллел қутбланишда эса Брюстер бурчаги деб аталувчи

(9.12)

бурчак мавжуд бўлиб, бунда қайтиш коэффициенти нолга тенг ва тўлқин иккинчи муҳитга тўлиқ ўтади.

Демак, параллел қутбланган ясси электромагнит тўлқин диэлектрик қатламига Брюстер бурчаги остида тушганда, унинг қатламдан тўлиқ ўтиши кузатилади. Буни (9.10), (9.11) ифодалардан кўришимиз мумкин. Бу шароитларда R₁₂ қайтиш коэффициенти нолга тенг бўлгани учун, қатламдан қайтиш ва ўтиш коэффициентлари мос ҳолда 0 ва 1 га тенг.

МАВЗУ № 10. ЮЗА ЭФФЕКТИ

10.1. Юза эффекти ходисаси

Аввалги бўлимларда айтиб ўтилганидек, ўзгарувчан электромагнит майдоннинг кучланганлиги, демак, унинг ток зичлиги хам металл ичида экспоненциал қонун бўйича камайиб боради. Ўта юқори частоталарда барча ток, ўтказгичнинг сирти яқинида жамланади. Бу ходисани юза эффекти ёки скин эффект деб аталади.

Юза эффекти натижасида ўтказгичнинг кўндаланг кесими камаяди, яъни, самарали фойдаланилаётган кесим геометрик кесимдан кам бўлиб қолади. Бу эса ўтказгичнинг актив қаршилигини ошишига олиб келади. Юқори частоталарда бу қаршилик симнинг доимий ток холатидаги қаршилигидан жуда кўп марта катта бўлиши мумкин. Бундан ташқари, юза эффекти ўтказгичнинг ичида жамланган магнит энергиясини, ва бунинг натижаси ўлароқ, симнинг ички индуктивлигини камайтиради. Бундан кўринадики, агар симнинг диаметри қанчалик катта бўлса, юза эффекти шунчалик камроқ намоён бўлади. Юза эффектининг таъсири остида симнинг марказий қисмидан фойдаланилмас экан, буни ўтказгичларни тайёрлашда хисобга олиш лозим. Шунинг учун хам, юқори частоталарда, металлни иқтисод қилиш учун тўла симлар ичи бўш (найсимон) симлар билан алмаштирилади.

Юза эффекти ходисаси кўпгина радиотехник қурилмалар ва элементларни ташқи майдон таъсиридан мухофазалаш имконини беради. Бунинг учун металл экранлардан фойдаланилади. Агар химояловчи экран қурилмани тўлиқ ўраб турган бўлса ва унинг қалинлиги етарлича бўлса, ташқи майдоннинг таъсирини деярли йўқотиш мумкин. Агар экран қурилмани тўла қопламаган бўлса, ёки унинг қалинлиги етарлича бўлмаса, ташқи электромагнит майдон дифракция ходисаси туфайли қобиқдан кириши мумкин. Шуни хам таъкидлаш лозимки, доимий ва паст частотали майдон холларида металл экранлар қурилмани электр майдонидан сақлаши мумкин. Бироқ, агар экран парамагнит ёки диамагнит материалдан тайёрланган бўлса, у магнит майдони учун тўсиқ бўла олмайди.

Металлдан тайёрланадиган экран электромагнит таъсирлардан тўлиқ химоялаши учун, экран листининг қалинлиги маълум қийматдан кичик бўлмаслиги керак. Бунда, майдоннинг металлга сингиш чуқурлиги параметридан фойдаланилади. Майдоннинг металлга сингиш чуқурлиги деб шундай масофага айтиладики, бунда майдон кучланганлиги е марта камаяди. Сингиш чуқурлиги майдоннинг сусайиш коэффициентига тескари катталик хисобланади ва уни қуйидагича хисоблаш мумкин

(10.1)

Бу ерда α – тўлқин амплитудасининг 1 м масофа босиб ўтгандаги сусайиши.

Ўта юқори частота диапазонида бу параметр жуда хам кичик қийматларга эришади.

10.2. Ўтказгичнинг юза қаршилиги ва ундаги энергия йўқотишлари

Юза эффектини кўриб чиқиш вақтида, албатта, юза қаршилиги параметрини хам хисобга олиш зарур. Чунки, бу ходиса туфайли, самарали фойдаланилаётган юза камаяди ва унинг тўлқинга бўлган қаршилиги ортади. Ўтказгич сиртида электр майлонининг урунма ташкил этувчиси ва эквивалент юза токи зичликлари бир хил йўналган. Демак, улар орасида қуйидаги боғлиқлик мавжуд

Пропорционаллик коэффициенти Z_s ни ўтказгичнинг юза қаршилиги деб атайдилар. Чегаравий шартларга кўра, Z_s учун қуйидаги ифодани ёзиш мумкин

(10.2)

Юза қаршилигининг актив ташкил этувчиси эса

(10.3)

Бу ифодадан шуни англаш мумкинки, фазони тўлдириб турувчи ўтказгичнинг юза эффекти таъсири остида эришган қаршилиги юза эффекти мавжуд бўлмаган Δ⁰ қалинликка эга бўлган металл билан бир хил қийматга эга бўлади.

Шуни хам таъкидлаш керакки, электромагнит тўлқиннинг металлда тарқалиши вақтида юзага келадиган энергия йўқотишлари комплекс қувват орқали ифодаланади. Комплекс йўқотишлар қувватини эса эквивалент юза токи ва юза қаршилиги ёрдамида ифодалаш мумкин

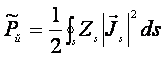. (10.4)

Идеал ўтказгич сиртидаги чегаравий шартлардан келиб чиққан холда (), комплекс қувватни хисоблаш учун магнит майдон векторининг урунма ташкил этувчиси қийматини билишнинг ўзи кифоя. Аввал айтилганидек, металлнинг сиртидаги майдон тузилиши идеал ўтказгич сиртидаги майдон тузилишига жуда хам ўхшаш. Шунинг учун, йўқотишлар қувватини хисобланилаётганда шарт бажарилади деб қабул қилинади. Бу тахмин хисоблашлар хажмини камайтиргани холида, мухандислик амалиёти учун етарлича аниқликдаги натижаларни бера олади.

МАВЗУ №11. ЙЎНАЛТИРУВЧИ ТИЗИМЛАР

11.1. Йўналтирувчи тизимларнинг синфланиши

Электромагнит тебранишларнинг тарқалиш ҳудудини чегараловчи ва оқимни берилган йўналишга йўналтирувчи қурилма узатиш линияси деб аталади. Бу линиялар энергияни манбадан қабул қилгичга узатиш учун қўлланилади, масалан узаткичдан антеннага, антеннадан қабул қилгич киришига ва ҳоказо. Соддалаштириш учун, йўналтирувчи тизим идеал ўтказувчи сиртга эга деб хисобланса, шу сирт орқали тўлқинларнинг йўналиш жараёнини ўтказгичдаги ток ва зарядлар орасидаги боғлиқлик орқали тушунтирса бўлади.

Узатиш линияларини икки гуруҳга ажратиш мумкин: очиқ узатиш линиялари ва ёпиқ узатиш линиялари (тўлқинўтказгичлар). Тўлқинўтказгич бир ёки бир неча туташтирилган ўтказувчи контур кўринишидаги кўндаланг кесимли ўтказувчи сиртлардан иборат узатиш линиясидир. Тўлқинўтказгич майдони ташқи қобиқ билан экранланади.

Бўш тўлқинўтказгичлардаги тўлқинларни тадқиқ қилиш қуйидаги шартлар билан бажарилади:

1) тўлқинўтказгичнинг ички юзаси идеал ўтказувчи (σ = ∞);

2) тўлқинўтказгичнинг ичи вакуумдир.

Бу чекловлар масаланинг моҳиятини ўзгартирмаган холда майдон тахлилини осонлаштиради, чунки тўлқин ўтказгичлар юқори солиштирма электр ўтказувчанликка эга бўлган металлдан тайёрланади, тўлқин ўтказгич ҳавоси эса ўзининг параметрлари бўйича вакуумга ўхшашдир.

Дециметрли ва сантиметрли диапазонларда асосан ёпиқ турдаги узатиш тармоқлари қўлланилади. Бу тармоқларда бутун энергия ташқи муҳитдан темир қобиқ билан ажратилган майдонда жамланган бўлади.

Коаксиал тўлқин ўтказгич, тўғри бурчакли, айланали ва эллипссимон тўлқин ўтказгичлар асосий, кенг қўлланиладиган ёпиқ турдаги узатиш тармоқларидир.

Йўналтирувчи тизимларда Т туркумли тўлқинлар (кўндаланг электромагнит тўлқинлар), Н туркумли тўлқинлар (кўндаланг электр ёки бўйлама магнитли тўлқинлар), Е туркумли тўлқинлар (кўндаланг магнитли ёки бўйлама электр тўлқинлар) тарқатилиши мумкин. Шуни қайд этиб ўтиш керакки, Т туркумли тўлқинлар фақат бир-биридан ажратилган (ўзгармас ток энергиясини узатса бўладиган) иккита ва ундан кўп ўтказгичга эга йўналтирувчи тизимларда тарқатилиши мумкин.

Ҳар қандай йўналтирувчи тизимоларда (Е ва Н туркумларига мансуб) тўлқинларнинг жуда кўп турлари мавжуд бўлиши мумкин. Уларнинг миқдори l_и тўлқининг ишчи узунлигининг танланишига боғлиқ бўлади. Аммо тўлқинлар узунликларининг шундай бир соҳаси мавжудки, унда, яъни l_и тўлқинининг ишчи узунлиги асосий турга мансуб тўлқинининг l_кр критик узунлигидан катта ёки унга тенг (l_и ³ l_кр) бўлган тўлқин ўтказгичда электромагнит тўлқинларнинг тарқалиши мумкин эмас (ажратилган соҳа). Максимал критик узунликка эга бўлган тўлқин шу тўлқин ўтказгичдаги асосий тўлқин деб аталади. Тўлқинўтказгични тўлдирувчи материалнинг нисбий диэлектрик сингдирувчанлигидан келиб чиқиб, тўлқиннинг ишчи узунлиги қуйидаги шартдан келтириб чиқарилиши лозим

бу ерда l - генератор тўлқинининг узунлиги (эркин фазодаги тўлқин узунлиги).

Ҳавода e = 1 ва l_и = l шарт бажарилади.

11.1 ва 11.2-расмларда тўғри бурчакли ва айланали тўлқин ўтказгичларда Н₁₀ ва Н₁₁ турига мансуб асосий тўлқинлар учун, 11.3-расмда эса – коаксиал тўлқин ўтказгичда Т туркумли тўлқинлар учун электр ва магнит майдонларининг оний тарқалиш манзаралари келтирилган. Бу расмларда «биздан» кетган кучланиш чизиқлари крестчалар билан, «бизга» қараб келувчи чизиқлар эса – доирачалар билан кўрсатилган.

Бир тўлқинли режимда тўлқин ўтказгичдаги тўлқин қаршилиги Z_т, фаза v_ф ва гуруҳий v_гур тезликлар ҳамда йўналтирувчи тизимдаги тўлқин узунлиги L миқдорларини қуйидаги формулалар бўйича ҳисоблаш мумкин:

бу ерда с – вакуумдаги ёруғлик тезлиги;

a – тўғри бурчакли тўлқин ўтказгич кенг деворининг ички ҳажми;

b – тўғри бурчакли тўлқин ўтказгич тор деворининг ички ҳажми;

D – коаксиал кабель тўқимасининг (экран қобиғининг) ички диаметри;

d – коаксиал кабель марказий симининг ташқи диаметри.

Тўғри бурчакли тўлқин ўтказгичдаги тўлқин узунлиги L эркин фазодаги тўлқин узунлиги l дан катталиги қуйидаги оддий физик ҳолат билан изоҳланади. Электромагнит тўлқинлар тўлқин ўтказгичда унинг деворларига урилиб қайтиши натижасида тарқалади (11.4-расмга қаранг). Бунда, тўлқин фронти тўлқиннинг тарқалиш йўналиши бўйлаб l_и масофани босиб ўтиб, айни вақтда тўлқин ўтказгич бўйлаб L га тенг бўлган масофани босиб ўтади.

11.2. Бир тўлқинли режимни ҳосил қилиш учун тўлқиннинг ишчи узунлигини танлаш

11.5…11.7-расмларда тўғри бурчакли, айланали ва коаксиал тўлқинўтказгичлар учун l_и шкаласи бўйича тўлқинлар критик узунликларининг тақсимланиши келтирилган. Биртўлқинли режим ҳолатида тўлқинўтказгич бўйлаб асосий тўлқин тарқалади. 11.5-расмдан кўриниб турганидек, тўлқинининг критик узунлиги l_кр^Н10=2а бўлган Н₁₀ тўлқини тўғри бурчакли тўлқинўтказгич учун асосий тўлқин ҳисобланади. Тўғрибурчакли тўлқинўтказгичда олий тартибдаги биринчи тўлқин – критик узунлиги l_кр^Н20=а бўлган Н₂₀ тўлқинидир. Бинобарин, биртўлқинли режим қуйидаги шарт бажарилган ҳолда кузатилади

a < l < 2a. (11.10)

Айланали тўлқинўтказгич (11.6-расм) учун Н₁₁ тўлқини асосий тўлқин (l_кр^Н11=3,41R), Е₀₁ тўлқини эса – олий тартибдаги биринчи тўлқин (l_кр^Е01=2,62R) ҳисобланади. Шундай қилиб, бир тўлқинли режим қуйидаги шарт бажарилган ҳолда кузатилади

2,62R<l_р<3,41R. (11.11)

Коаксиал тўлқинўтказгичда (11.7-расм) Т туркумига мансуб тўлқин асосий тўлқин (l_кр^Т=¥), критик узунлиги l_кр^Н11»p(D+d)/2 бўлган Н₁₁ тўлқини эса – олий тартибдаги биринчи тўлқин ҳисобланади, яъни бир тўлқинли режим қуйидаги шарт бажарилган ҳолда кузатилади

p(D+d)/2< l_р < ¥. (11.12)

Амалда, нисбатан узун тўлқинлар, яъни асосий турга мансуб тўлқиннинг критик узунлигига яқин соҳада энергия сусайиши кўп бўлганлиги учун, тўлқиннинг ишчи узунлиги миқдори тўлқиннинг критик узунлигидан 20...30% кам олинади.

11.3. Тўлқинўтказгичдаги амплитудавий тақсимотнинг турлари

Тўлқинўтказгич бўйлаб амплитудавий тақсимотга тўлқинўтказгичнинг чиқишида ўрнатилган юклама хусусиятининг таъсирини кўриб чиқамиз. Тўлқинўтказгич ўқи бўйлаб биртўлқинли режим билан бирга майдоннинг тақсимланиши шаклланади. Бу тақсимот узун чизиқ (линия) режимида ишлайдиган одатдаги иккисимли тармоқда майдоннинг тақсимоти билан бир хил бўлади.

Агар тўлқинўтказгич учига қисқатуташувчи юклама ўрнатилган бўлса, тушувчи тўлқинга нисбатан фаза бўйлаб 180° га сурилган қайтган (аксланган) тўлқин юзага келади. Аксланган тўлқин амплитудаси тушувчи тўлқин амплитудасига тенгдир. Бу икки тўлқиннинг туташиши натижасида турғун тўлқин (турғун тўлқин режими) юзага келади. Турғун тўлқин режимидаги амплитудавий тақсимот 11.8-расмда узлуксиз чизиқ билан кўрсатилган. Майдон жадаллигининг икки қўшни минимумлари ўртасидаги масофаси тўлқинўтказгичдаги тўлқин узунлигининг ярмига тенг. Қисқатуташувчи юклама қаршилиги тўлқинўтказгичнинг тавсифий қаршилигига тенг бўлган мослашган (мувофиқлаштирилган) юкламага алмаштирилганида, юкламадан аксланган тўлқин бўлмайди ва тўлқинўтказгичда югурувчи тўлқин режими қарор топади. Бунда амплитудавий тақсимот майдоннинг тўлқинўтказгич бўйлаб амплитуда миқдорининг ўзгармаслиги билан тавсифланади (11.8-расмдаги пунктир чизиқ).

Юкламадан тушувчи тўлқиннинг бир қисми аксланган ҳолларда тўлқин ўтказгичда аралаш режим қарор топади. Бу режимнинг амплитудавий тақсимоти 11.9-расмда кўрсатилган. Тўлқинўтказгичдаги амплитудавий тақсимотни югурувчи тўлқин коэффициенти миқдори ЮТК=Е_min/E_max билан тавсифлаш қулайдир. Амалда қўлланиладиган мослаштирилган юкламаларнинг ЮТК си 0,65-0,85 оралиқларда бўлади. Бунда, кўрсаткичнинг 1 га яқинлашишига интилинади.

АДАБИЁТЛАР

1. Вольман В.И., Пименов Ю.В, Техническая электродинамика, - М: Радио и Связь, 2002 г.

2. Витевский В.И., Павловская Э.А. Электромагнитные волны в технике связи. - М.: Радио и связь, 1995.

3. Никольский В.В., Никольская Т.И. Электродинамика и распространение радиоволн. – М.: Наука, 1989.

4. Федоров Н.Н. Основы электродинамики. – М.: Высшая школа, 1980.

5. Гольштейн Л.Д., Зернов Н.В. Электромагнитные поля и волны. – М.: Сов. радио, 1971.

6. Сборник задач по курсу "Электродинамика и распространение радиоволн" / Под ред. С.И. Баскакова. - М: Высшая школа, 1981.