ЎЗБЕКИСТОН АЛОҚА ВА АХБОРОТЛАШТИРИШ АГЕНТЛИГИ

ТОШКЕНТ ИНФОРМАЦИОН ТЕХНОЛОГИЯЛАРИ УНИВЕРСИТЕТИ

ТВ ва РЭ кафедраси

ЭЛЕКТРОМАГНИТ МАЙДОНЛАР ВА ТЎЛҚИНЛАР

ўқув қўлланма

II қисм

5522100 - Телевидение, радиоалоқа, радиоэшиттириш

5524400 - Телекоммуникация

5522000 - Радиотехника

йўналишида таълим олувчи талабалар учун

Тошкент 2010

МУНДАРИЖА

1.ГАРМОНИК МАЙДОННИНГ ЭЛЕКТРОДИНАМИК ПОТЕНЦИАЛЛАРИ………………………………………………………….......5

1.1. Гельмгольц тенгламаси………………………………………………….......5

1.2. Гельмгольцнинг биржинсли бўлмаган тенгламаларининг ечими………..6

2. ЯССИ ЭЛЕКТРОМАГНИТ ТЎЛҚИНЛАР…………………………………..8

2.1. Умумий маълумотлар………………………………………………………..8

2.2. Йўқотишларсиз биржинсли изотроп муҳитда ясси электромагнит тўлқинлар…………………………………………………………………………8

2.3. Ўтказувчанлиги нолдан фарқ қилувчи биржинсли изотроп муҳитдаги ясси тўлқинлар…………………………………………………………………..11

2.4. Реал диэлектрикларда тўлқинларнинг тарқалиши…………………….....15

2.5. Реал металларда тўлқинларнинг тарқалиши……………………………...15

2.6. Тўлқинларнинг қутбланиши…………………………………………….....16

3. ИККИТА МУҲИТ ЧЕГАРАСИДА ТЎЛҚИНЛИ ҲОДИСАЛАР………...20

3.1. Эркин ориентацияли ясси тўлқинлар……………………………………..20

3.2. Ясси тўлқиннинг икки диэлектрик чегарасига оғиши…………………...21

3.3. Нормал қутбланиш………………………………………………………....20

3.4. Параллел қутбланиш……………………………………………………….21

3.5. Тўлқиннинг иккинчи муҳитга тўлиқ ўтиши шартлари. Брюстер бурчаги…………………………………………………………………………...27

3.6. Икки муҳитнинга чегараларидан тўлиқ акс этиш Икки диэлектрик муҳитлар…………………………………………………………………………28

3.7. Тўлиқ ички акс этишнинг ҳосил бўлиш шартлари……………………….28

4. СИРТИЙ ЭФФЕКТ…………………………………………………………...35

4.1. Сиртий эффект ходисаси ………………………………………………….35

4.2. Электр ўтказгичларида энергиянинг йўқолиши………………………….35

_{4.3. Сиртий қаршиликлар……………………………………………………….37}

5. ЭЛЕКТРОМАГНИТ ТЎЛҚИНЛАР НУРЛАНИШИ..……………………...39

5.1. Умумий тушунчалар……………………………………………………….39

5.2. ЭЭН нурланиш майдони…………………………………………………...39

5.3. ЭЭН йўналиши диаграммаси………………………………………………42

6. ЙЎНАЛТИРУВЧИ ВА ЮЗАКИ ТЎЛҚИНЛАР…………………………….44

6.1. Тўлиқ ички қайтарилиш…………………………………………………...44

6.2. Нормал майдонлашда биринчи оралиқдаги майдон……………………..45

6.3. Нормал майдонлашда иккинчи оралиқдаги майдон……………………..45

7. МЕТАЛЛИ ТЕКИСЛИКГА ТЕКИС ТЎЛҚИН ТУШИШИДАГИ ВУЖУДГА КЕЛАДИГАН МАЙДОНДАГИ ТАСВИРИ………………….....47

7.1 Е вектор тушиш векторида ётади. Электр тўлқинлар………………….....47

7.2. Е вектор тушиш текислигига перпендикуляр. Магнит типли тўлқинлар………………………………………………………………………...50

7.3 Икки текисликли тўлқинўтказгич …………………………………………50

8. ЙУНАЛТИРУВЧИ СИСТЕМАЛАР ВА ЙУНАЛТИРИЛГАН ЭЛЕКТРОМАГНИТ ТЎЛҚИНЛАР……………………………………………53

8.1 Йўналтирувчи системалар………………………………………………….53

8.2. Йўналтирувчи тўлқинларнинг синфланиши………………………….......53

8.3. Йўналтирилган оралиқдаги, ёндошиш ва кесмали тўлдирувчиларнинг ўзаро алоқаси……………………………………………………………………53

8.4. Критик частота. Критик тўлқин узунлиги……………………………….55

9. КЎНДАЛАНГ ЭЛЕКТРОМАГНИТ ТЎЛҚИНЛАР………………………..57

9.1. (Е_z =0 , Н_z =0) критик тўлқин узунлиги…………………………………...57

9.2. Йуналтириш доимийси. Тўлқиннинг фазали тезлиги………………........57

9.3. Кўрсатилган қаршилик…………………………………………………....58

10.1 ЭЛЕКТР ТЎЛҚИНЛАР……………………………………………….......60

10.1 Майдон тўлдирувчилар орасидаги алоқа (и )……………...60

10.2. Тавсифий қаршилик……………………………………………………....60

10.3. Фаза тезлиги. Дисперсия………………………………………………....60

11. ЙЎНАЛТИРУВЧИ СИСТЕМАЛАР……………………………………….62

11.1. Тўғрибурчакли тўлқин берувчи. ( и ) Электр тўлқинлари………………………………………………………………………62

11.2 ( и ) магнит тўлқинлар…………………………………..65

11.4 Айлана шаклли тўлқин тарқатувчи……………………………………...69

11.5 Электр тўлқинлар………………………………………………………….69

11.6. (, ) магнит тўлқинлар…………………………………..72

11.7. Т тўлқини. Коаксисиал чизиқнинг тўлқинли қаршилиги…………….74

_{11.8 Электр ва магнит тўлқинлар………………………………………………76}

11.9. Коаксиал чизиқлардаги тўлқинлар тури диаграммаси………………...77

12. СВЧ ТЕБРАНИШ ҚУРИЛМАЛАРИ. ҲАЖМЛИ РЕЗОНАТОРЛАР…..80

12.1 Электромагнит ва тебраниш қурилмалари ривожи……………………80

12.2. Тўғри бурчак кесмасидаги ҳажмли резонатор ( ярими масала)……….80

12.3 H_10p тебраниш тури. H₁₀₁ тузилиш майдони………………………...81

_{12.4. Тўғри бурчакли резонаторда умумий масала. Тўлқин турлари синфланиши……………………………………………………………………...82}

12.5. Тебранишлар турларининг синфланиши………………………………..83

_{12.6. Цилиндрли ҳажмли резонатор……………………………………………84}

12.7. Ҳажмли резонаторлар кучлантириш усуллари………………………...85

12.8. Ҳажмли резонаторлар фойдалиги ………………………………………87

12.9 Ҳажмли резонаторнинг бошқа турлари. Коаксиал резонатор………....88

13. АНИЗАТРОП ОРАЛИҚЛАРДА ЭЛЕКТРОМАГНИТ ТЎЛҚИНЛАР ТАРҚАЛИШИ…………………………………………………………………..90

13.1. Умумий тушунчалар……………………………………………………...90

13.2. Магнитланган оралиқдаги чизиқли полярлашган тўлқинлар…………90

_{13.3. Фарадей эффекти………………………………………………………….91}

_{13.4. Тўғри бурчакли кесмали, магнитланган ферритли, тўлқин тарқатувчида силжиш эффекти………………………………………………...92}

14. ЮЗАКИ ТЎЛҚИННИНГ УЗАТИШ ЧИЗИҚЛАРИ…………………….95

14.1. Бир симли ўтказиш чизиғи………………………………………………95

14.2. Диэлектрли тўлқин тарқатувчи………………………………………….96

14.3 Толали нурўтказгич……………………………………………………….98

АДАБИЁТЛАР…………………………………………………………………103

1. ГАРМОНИК МАЙДОННИНГ ЭЛЕКТРОДИНАМИК ПОТЕНЦИАЛЛАРИ

1.1. Гельмгольц тенгламаси

Электродинамиканинг барча масалалари амалий жиҳатдан 2 турга бўлинади:

- тўғри масала - берилган четки манбаларнинг тақсимоти асосида мос келувчи электромагнит майдон тақсимотини аниқлашдан иборат;

- тескари масала - берилган электромагнит майдон тақсимоти асосида мос келувчи четки манбаларнинг тақсимотини аниқлашдан иборат.

Ушбу бобда электродинамиканинг тўғри масалаларини ечиш усуллари кўриб чиқилади.

Майдон векторларининг оний қийматларга тегишли бўлган масалалар мураккаблиги туфайли кам ҳолларда ечилади. Одатда, масалаларни гармоник майдонлар учун комплек амплитуда усули ёрдамида ечилади. Электродинамиканиг ихтиёрий масаласини ечишда бевосита Максвелл тенгламаларидан ҳам фойдаланилади. Бунда Максвелл тенгламаларини маълум бўлган дифференциал кўринишга келтиришга ҳаракат қилинади.

Электромагнит гармоник жараённи кўриб чиқамиз. Максвелл тенгламаларини комплек амплитудалар учун ёзамиз:

(1.1)

(1.2)

(1.1) тенгламанинг ўнг ва чап тарафларига ротор амалини қўллаган холда қуйидагиг ифода эришамиз

(1.3)

Маълум айниятдан фойдаланиб,

_{Максвелнинг 4- тенгламасига кўра,}

(1.4)

Тенглама (1.4) ва (1.2) ларни (1.3) га қўямиз ва _{ёки (1.5)}

_{эга бўламиз. Бунда,}

к=.

Ўтказилган ўзгартиришлар натижасида биз биржинсли бўлмаган дифференциал тенгламани ҳосил қилдик. Бу формула математик физикада Гельмгольцнинг биржинсли бўлмаган тенгламаси деб аталади. Ушбу тенглама тўлқин жараёнларини ифодалайди.

1.2. Гельмгольцнинг биржинсли бўлмаган тенгламаларининг ечими

Гельмгольцнинг биржинсли бўлмаган тенгламаларини ечиш учун вектор функцияси _{киритилади. Бунда -} векторли электр потенциал деб номланади.

Қуйидаги векторли айниятлар мавжуд

_ва (1.6)

Гельмгольцнинг биржинсли бўлмаган тенгламасини оламиз

_(1.7)

_{(1.6) тенгламани (1.7) куйиб куйдагига эга буламиз:}

_{Расм.1.1. ни кўриб чиқамиз. Унда белгиланган V хажмдан ташқарида жойлашган Р нуқтадаги майдон характеристикасини ифодалаш талаб этилган бўлиб, соха ичидаги ихтиёрий нуқтадан Р гача булган масофа белгиланган хажмнинг улчамларидан ката.}

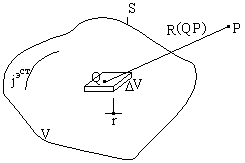
_{Расм 1.1. Майдон характеристикасини ифодалаш учун}

_{Берилган хажмнинг ички сохасида Q нуқтани белгилаймиз ва унинг атрофида элементар майдон V ни хосил киламиз. Бунда, R – Q ва Р нуқталари орасидаги масофа. Биз Р нуқтада четки токлар билан кўзғатилган АЭ майдоннинг интенсивлигини қидирамиз. Ушбу интенсивлик}

_{га пропорционал бўлиб, бунда - ток хажмий зичлигининг баъзи бир ўртача қийматлари. Хажм V нинг ўлчамлари масофа R дан анча кичик бўлганлиги сабабли V ни ундан оқиб ўтувчи четки токлар билан биргаликда нуқтавий манба деб қараш мумкин.}

_{Нуқтавий манба ёрдамида кўзғатиладиган майдон амплитудаси фақат r га боғлиқ бўлган содда холат билан чекланамиз}

_{( 1.9)}

_{йукотишларсиз манбада учун га тенг. ,}

_(1.10)

_{Бунда r – радиал координата. Охирги муносабат сферик тўлқинларни хосил қилади. Шундай килиб, юкоридаги токлар билан кузгатилувчи майдон V хажмда}

_(1.11)

2. ЯССИ ЭЛЕКТРОМАГНИТ ТЎЛҚИНЛАР

2.1. Умумий маълумотлар

Узлуксиз муҳитларнинг тебранма ҳаракатлари тўлқин дейилади. Радиотехник занжирларда тўлқинли жараёнлар, ток тебранишлари ва кучланишларининг математик тасвиридаги принципиал фарқлар шундан иборатки, унда исталган тизимни тўлиқ тасвирлаш учун схеманинг турли жойларида ток ва кучланишларнинг охирги сонини билиш етарли. Тўлқинли жараённи тўлиқ тасвирлаш учун кўриб чиқилаётган муҳитда чексиз кўп нуқталарда унинг характеристикасини билиш керак.Тўлқинли жараёнлар табиати турлича: электромагнит, акустик, гравитацион ва ҳ.з. тўлқинлар. Физикларнинг фикрига кўра исталган тўлқинларнинг тарқалишида муҳит секин-аста муайян физик жараёнга жалб этилади ва натижада энергиянинг атрофга тарқалиши рўй беради.

2.2. Йўқотишларсиз биржинсли изотроп муҳитда ясси электромагнит тўлқинлар

Йўқотишларсиз бир турдаги изотроп муҳитда электромагнит майдоннинг эркин гармоник тебранишларини кўриб чиқамиз. Бу ҳолатда Гельмгольцнинг электромагнит майдон векторларига тегишли бир турли тенгламаларидан фойдаланиш қулай

(2.1)

(2.2)

(2.1) вектор тенгламаларини учта скаляр тенгламалардан иборат тизим кўринишида ёзиш мумкин:

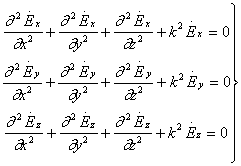(2.3)

(2.3) тенгламаcи ва унинг ечими ясси электромагнит тўлқинларни кўриб чиқаётганда соддароқ кўринади. Чизиқли координаталар бўйлаб тарқалувчи, ҳар бир қайд этилган лаҳзада тарқалиш йўналишига перпендикуляр бўлган яссилиги ўзгармайдиган электромагнит тўлқинлар ясси тўлқинлар дейилади. Тасаввур қилайлик, тўлқин Z ўқи бўйлаб тарқаляпти, яъни Пойнтинг вектори

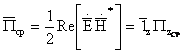(2.4)

(2.4) нисбатидан кўриниб турганидек, Пойнтинг вектори хОу яссилигида жойлашган электромагнит майдон компонентлари билан аниқланади. Бу ҳолатда Z ўқи бўйлаб майдон таркибий қисмлари йўқ. Шундай қилиб, қуйидаги шарт бажарилиши керак: қоида бўйича майдон тўлқининг тарқалиш яссилигида бўлиши кераклиги учун

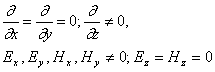(2.5)

(2.5) нисбатидан фойдаланиб (2.3) ифодани қуйидагича ёзиш мумкин

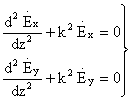(2.6)

Ҳар бир тенглама ечими

(2.7)

(2.8)

Мунтазам интеграцияланиши сонини оширмаслик учун (2.7), (2.8) ечимлари ва Максвелл тенгламаларидан фойдаланиб Н майдони компонентларини топамиз

,

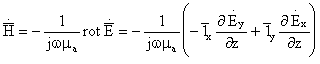(2.9)

Ушбу тенглама ечими қатор ўзгаришлардан сўнг қуйидаги кўринишга эга бўлади

(2.10)

(2.11)

(2.12)

где 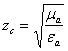, [Ом] — муҳит хусусиятлари билан аниқланувчи муҳитнинг характерли қаршилиги.

(2.10) ва (2.11)-(2.12) формулалари Z ўқи бўйлаб йўналтирилган Пойнтинг векторини ҳосил қилади. Қўлга киритилган ечимлар икки қўшилувчининг йиғиндисидир. Ҳар бир қўшилувчининг физик маъносини аниқлаймиз.

Демак, (2.12) нинг ечимида биринчи қўшилувчи- ясси тўлқин учун мусбат йўналишда, иккинчи қўшилувчи- манфий йўналишда.

К тўлқин сонининг физик маъносини аниқлаймиз. К тўлқин сони тўлқин фазасининг тўлқиннинг 1 метрлик йўлни босиб ўтишида радианларда ўзгаришини кўрсатади. Тўлқин фазаси 2p га ўзгарадиган минимал масофа тўлқин узунлиги деб аталади.

(2.13)

(2.14)

Олинган ечимларни , (2.7)-(2.11) мисолларда таҳлил қиламиз.

,

Ушбу умумий ечимларда Z ўқининг мусбат йўналишида тарқалувчи тўлқинга тўғри келувчи қўшилувчиларни ажратамиз:

(2.16)

Лаҳзалик қийматларга ўтамиз:

(2.17)

Келтирилган нисбатлардан қуйидагилар келиб чиқади:

- z = const — тенг фазаларнинг ушбу юзаси яссиликни келтириб чиқаради

- Тенг амплитудалар юзаси тенг фазалар юзасига тўғри келади

- Тарқалиш йўналишида майдон таркибий қисмлари бўлмайди

- Ясси тўлқин майдонининг компонентлари ўзаро ортогонал ва тўлқиннинг тарқалиш йўналишига перпендикуляр.

Шундай қилиб бир турдаги, изотроп ва йўқотишларсиз муҳит

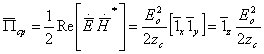. (2.18)

Энергиянинг тарқалиш тезлигини аниқлаймиз

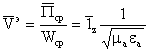. (2.19)

Фазавий тезлик учун тенглама: ,

Бу ерда . (2.20)

Унда йўқотишларсиз муҳит ҳолати учун

(2.21)

Ясси электромагнит тўлқин учун тўлиқ ечимнинг турли комбинациялари битта тўлқиннинг танланган координаталар тизимига нисбатан ориентацияларига мос келади.

2.3. Ўтказувчанлиги нолдан фарқ қилувчи биржинсли изотроп муҳитдаги ясси тўлқинлар

Нолдан фарқли ўтказувчанли муҳитда электромагнит энергияси қисман қўзғалишга ва ўтказувчанлик токларини қўллаб-қувватлашга сарфланади. Умумий ҳолатларда диэлектрик ва магнит йўқотишлар ҳам бўлиши мумкин. Унда:

(2.22)

(2.23)

Бу ҳолатда шакл бўйича ечим олдинги параграфда олинган ечимга тўғри келади.

(2.24)

(2.25)

Физик мазмунни аниқлаш учун лаҳзалик қийматларга ўтамиз:

, (2.26)

. (2.27)

Айрим қайд этилган лаҳзада _{ни тасвирлаймиз.}

Физик мазмунни аниқлаймиз g - тақсимлашнинг комплекс доимийлиги.

b — унинг ҳақиқий қисми,мазмуни худди К никидек, яъни тўлқин 1 метр йўлни ўтганда тўлқин фазасининг радианларда ўзгаришини кўрсатадиа (фазавий доимийлик) a g нинг тахминий қисми, 1 метр йўлда тўлқин амплитудаси қанчага кичрайишини кўрсатади.

Муҳитда йўқотишлар охирги ўтказувчанлик туфайли рўй берган ҳолатни кўриб чиқамиз:

и ,

(2.28)

b ва a учун ифодаларни ҳосил қилиш учун уларнинг квадратини чиқариб қуйидагини ҳосил қиламиз:

, (*)

_(2.29)

Иккинчи тенгламадаги тахминий қисмни ифодалаб, биринчи тенгламага қўямиз

,

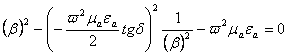. _(2.30)

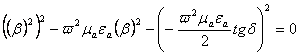_(2.31)

Квадратли тенгламани ечамиз:

,

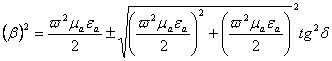. (2.32)

Чап қисмда квадрат чиқарилган, бу нисбатда фақат “+” белгиси ҳисобга олинади. Унда:

,

(2.33)

(Ñ) нисбатдан фойдаланиб тахминий қисмни ҳосил қиламиз:

. _(2.34)

(2.38) ни (Ñ) га қўяямиз.

,

. _(2.35)

Чап қисм квадратга ўтказилганлиги учун, ўнг қисм манфий бўлмайди. Ҳосил қиламиз:

,

,

_(2.36)

_{экспоненциал кўпайтувчини таҳлил қиламиз. Ўрнига қўйиш йўли билан қуйидагиларни ҳосил қиламиз:} . Биринчи ва охирги кўпайтма физик реал ҳисобланади. Улардан бири z ўқининг мусбат йўналишида тарқалувчи сўнувчи тўлқинга мос келади, охиргиси эса z ўқининг манфий йўналишига тарқалади.

Шундай қилиб, йўқотишли муҳитда тарқалаётган ясси тўлқин майдони қуйидаги нисбатлар билан ифодаланиши мумкин:

_(2.37)

Ушбу ҳолатда муҳитнинг характеристик қаршилиги комплекс катталий ҳисобланади.

_(2.38)

Буни қуйидагича ўзгартириш мумкин:

,

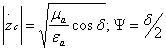_(2.39)

бу ерда - диэлектрик йўқотишлар бурчагининг тангенси.

Лаҳзали қийматларга ўтамиз:

,

Тенг фазалар юзаси z =const тенгламаси билан аниқланади. Тенг амплитудалар юзаси тенг фазалар юзасига мос келади, яъни кўриб чиқилган жараён ясс и бир турдаги тўлқин ҳисобланади.

Майдоннинг тўлқин тарқалиши йўналишига ўзаро ортогонал ва перпендикуляр таркибий қисмлари бор. Тўлқин амплитудаси унинг тарқалиш жараёнида экспоненциал камаяди. Ушбу ҳолатда майдоннинг магнит таркибий қисми электр таркибий қисмидан бурчакка орқада қолади.

Электромагнит тўлқиннинг асосий характеристикаларини кўриб чиқамиз. Фазавий тезлик қуйидагига тенг

Фазавий тезлик қуйидагига тенг:

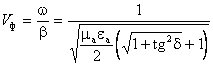_(2.40)

Демак b>k бўлганлиги сабабли йўқотишли муҳитда фазавий тезлик йўқотишларсиз муҳитда фазавий тезликдан кичик бўлади, чунки .

Ушбу ҳолатда фазавий тезлик частота функцияси ҳисобланади. Частота ўсиши билан tgd камаяди ва фазавий тезлик ошади. Фазавий тезлик муҳит ўтказувчанлигига боғлиқ. Ўтказувчанлик ўсиши билан tgd катталашади ва фазавий тезлик камаяди.

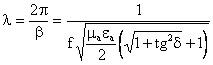_(2.41)

Нисбатдан кўриниб турганидек, йўқотишли муҳитдаги l, йўқотишларсиз муҳитдаги l дан кам. Ўтказувчанлик ўсиши билан tgd катталашади ва l камаяди. Тўлқиннинг тарқалиши энергиянинг ўтиши билан кузатилади. убывает. Пойнтинг вектори

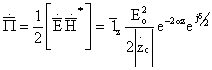_(2.42)

Энергиянинг тарқалиш тезлигини ҳисоблаб чиқарамиз

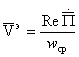_(2.43)

Асосий принципиал тафовут шундаки, йўқотишларсиз муҳитда V_ф , V_Э , z_с исталган частотатларда ўзгармайди ва фақат муҳитнинг электродинамик параметрлари билан аниқланади. Йўқотишли муҳитда худди шу параметрлар частота функцияси ҳисобланади. Электромагнит тўлқин параметрларининг частотага боғлиқлиги дисперсия дейилади, тегишли муҳитлар эса дисперланувчи деб аталади. Агар электродинамик параметрларнинг ҳеч бўлмаганда биттаси частота функцияси бўлса, йўқотишларсиз муҳитда ҳам дисперсия бўлиши мумкин.

Реал муҳитда электромагнит тўлқинларнинг тарқалишининг иккита характерли ҳолатини кўриб чиқамиз, яъни реал диэлектрик ва металларда ясси тўлқин параметрларини аниқлаймиз.

2.4. Реал диэлектрикларда тўлқинларнинг тарқалиши

Реал диэлектриклар учун . .

Тенгсизликдан фойдаланиб, қавсни Маклорен қатори кўринишида бериш мумкин:

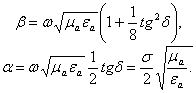_(2.44)

b учун ифодадан фойдаланиб, қуйидагини ҳосил қиламиз:

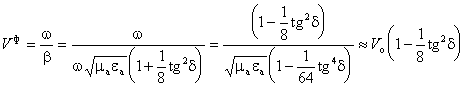, (2.45)

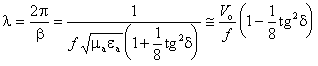, (2.46)

бу ерда V_о — муҳитда ёруғлик тезлиги.

Натижалардан реал диэлектрикларда ясси тўлқин параметрлари йўқотишларсиз муҳитдаги параметрлардан унча фарқ қилмаслигини кўриш мумкин. Реал диэлектрикларда l сўниш доимийси жуда кичик катталик ҳисобланади ва биринчи яқинлашишда частотага боғлиқ эмас.

2.5. Реал металларда тўлқинларнинг тарқалиши

Ўтказувчи муҳитларда . Умумий ифода:

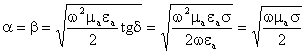. (2.47)

b ва a w га ночизиқ боғлиқ, w нинг ўзгариши билан улар ҳам ўзгаради.

Фазавий тезлик учун қуйидаги ифодани ҳосил қиламиз:

_(2.48)

Тўлқин узунлиги учун қуйидаги ифодани ҳосил қиламиз:

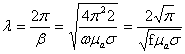. (2.49)

Характерли қаршилик:

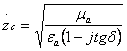, (2.50)

Бирга эътибор бермай қуйидагини ҳосил қиламиз:

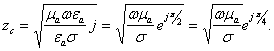_(2.51)

ни реал ва эҳтимолий қисмлар кўринишда ифодалаймиз:

. (2.52)

Ясси тўлқинлар параметрларини вакуум ва мисда f =1МГц частотада таққослаймиз.

мис

V_ф=V_Э=421 м/сек

l=4,21*10^{-6 м}

z_с=3,74*10^-4 Ом

вакуум

V_ф=V_Э=3*10⁸ м/с

l=300 м

z_c=120p=377 Ом

Реал ўтказувчиларда электромагнит тўлқинлар кучли ютилишга дуч келади. Масалан, мисда f = 1МГц бўлганда 1 мм йўлда сўниш қуйидагича бўлади:

_(2.53)

Металлардан ўзгарувчи электромагнит майдонни экранлаштиришда фойдаланиш мумкин.

2.6. Тўлқинларнинг қутбланиши

Қутбланиш Е электр майдони кучланиш векторининг ўрин-вақт ориентациясини характерлайди. Е вектор орқали ўтадиган юза ва тўлқиннинг тарқалиш йўналиши қутбланиш яссилиги дейилади.

Z ўқининг мусбат йўналишида тарқалувчи ясси тўлқинни кўриб чиқамиз.

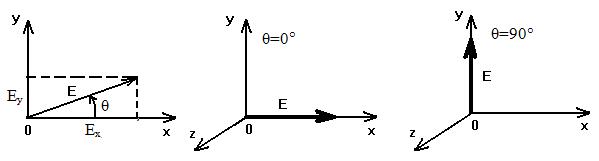
Рис.2.1 Рис. 2.2 Рис 2.3

Оғиш яссилигидагиЕ Горизонтал Вертикал

вектор қутбланиш қутбланиш

Бундай тўлқиннинг Е вектори х0у яссилигида ётади ва умумий ҳолатда фаза бўйлаб φ катталикка силжиган иккита проекцияга эга бўлиши мумкин

E=x°Ј_0xcos (ωt—kz)-у°Eо_y.cos(ωt-kz-φ) (2.54)

Е векторининг фазодаги ориентациясини қуйидаги бурчакда Е вектори ва xoz яссилиги ўртасида бериш қулай.

(2.55)

E_0X, Е_0Y қийматлари ва 2.54 даги φ га қараб тўлқин қутбланишининг бир неча турларини ажратиш мумкин:

1. φ=0 и Е_0x ≠Е_0y бўлсин. 2.54 ва 2.55га биноан θ=arctg(E_0y/E_0x). Бунда Е вектор горизонтал яссиликка θ бурчак остида оғган яссиликда ётади (2.1.-расм). Қутбланиш ясси ва чизиқли бўлиши мумкин.

Айрим ҳолатларда, θ=0 (расм. 2.2) ёки θ=90° (расм. 2.3) бўлганда чизиқли қутбланиш горизонтал ёки вертикал деб аталиши мумкин.

2. φ=90° и Е_0х=Еоу=Е₀ бўлсин. Бунда:

(2.56)

Θ бурчак вақт ва фазода ўзгаради, қутбланиш яссилиги эса айланади. z=const бўлганда Е вектори φ бурчакли частота билан айланади, унинг катталиги эса ўзгаришсиз ва тенг бўлиб қолади.

Е векторининг учи z=const яссиликда айланани ҳосил қилади (2.4,а,б-расм), фазода эса-айланма спирални ҳосил қилади. Қутбланиш айланали деб аталади. Айланали қутбланишнинг икки тури мавжуд. Е векторнинг тўлқин тарқалиши йўналишига нисбатан соат йўналиши бўйича айланиши билан характерланувчи ўнг қутбланиш (2.4,а-расм)., ва Е вектор соат йўналишига тескари айланувчи чап қутбланиш (2.4,б-расм). Одатда ўнг қутбланишли тўлқинни Е+ орқали, чап қутбланишли тўлқинни эса Е- орқали белгиланади. Ўнг айланиш φ = 90° бўлганда, чап айланиш эса φ = —90° бўлганда рўй беради.

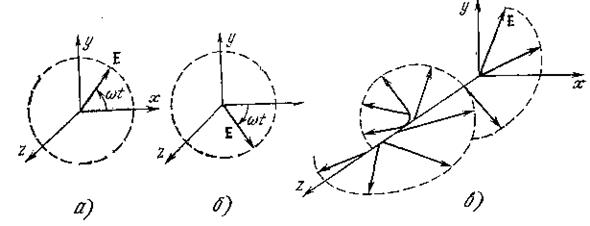
Рис.2.4 Айланма қутбланиш, чап ва ўнг айланишлар

3. Агар φ=±90° ва Еох≠Е бўлса, Е вектор z=const яссиликда айланади, бироқ унинг узунлиги бунда ўзгаради. Натижада Е вектор учи эллипсни чизади, қутбланиш эса эллиптик деб аталади (2.5-расм). Фазаларнинг эркин силжишида тўлқин шунингдек эллиптик қутбланади, бироқ эллипс ўқи х ўқига нисбатан γ бурчакка бурилган, ва у қуйидаги формула бўйича топилади

(2.57)

Айланма қутбланиш тўлқинлари радиотехника ва алоқада кенг қўлланилади. Айланма қутбланиш тўлқинларини қўзғатиш учун бундай тўлқин Е векторлари фазода ортогонал, амплитуда бўйича тенг ва 90° фазада силжиган иккита чизиқли қутбланган тўлқинларини қўшиш натижаси ҳисобланади.

2.5-расм. Эллиптик қутбланиш 2.6-расм Эллипснинг х ўқига нисбатан

γ бурчакка қутбланиши

Ўз навбатида, чизиқли қутбланган тўлқинни қарама-қарши йўналишли ва Е векторнинг амплитудали айланма қутбланишнинг икки тўлқиннинг суперпозицияси сифатида тасаввур қилиш мумкин. 2.7-расмдаги тўлқин тарқалиши ўқида турли вазиятларга тўғри келувчи векторли диаграммалар келтирилган.

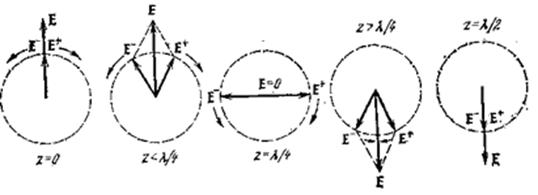
2.7-расм. Векторли диаграммалар

3. ИККИТА МУҲИТ ЧЕГАРАСИДА ТЎЛҚИНЛИ ҲОДИСАЛАР

3.1. Эркин ориентацияли ясси тўлқинлар

Олдинги параграфларда биз декарт тизим ўқлари бўйлаб тарқалувчи ясси тўлқинларни кўриб чиқдик. Тасаввур қилайлик, муҳит йўқотишларсиз.

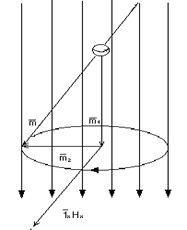
3.1-расм. Цилиндрик тизимда ясси тўлқин, бу ерда

3.1.-расмни кўриб чиқамиз.

,

,

,

(3.1)

Тўлқин йўналишини аниқловчи бурчаклар косинуси йўналтирувчи косинуслар деб аталади.

₍=const) фазавий яссилиги тенгламаси:

,

(3.2)

Унда скаляр кўпайтма:

(3.3)

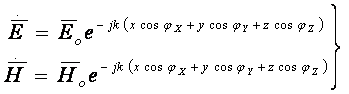(3.4)

Биз муҳитни йўқотишларсиз деб олган эдик. Йўқотишли муҳит ҳолатида нисбат ўзгармайди, фақат k ўрнига g =b — ja берилади. Тўлқинли ҳодисаларни кўриб чиқишдан олдин қатор таърифларни берамиз. Тўлқиннинг тарқалиш йўналишига параллел, чегарага нормал ўтувчи яссилик оғиш яссилиги дейилади. _{вектор тўлқиннинг тарқалиш йўналишига перпендикуляр, тўлқиннинг оғиш яссилигига нисбатан эса у эркин тарзда йўналган.}

Мулоҳазалар умумийлигини йўқотмаган ҳолда, _{ориентациянинг икки ҳолатини кўриб чиқиш етарли.}

1) оғиш яссилигига перпендикуляр (нормал қутбланиш)

2) оғиш яссилигига параллел (параллел қутбланиш)

_{векторининг эркин ориентациясида у бу икки ҳолатнинг суперпозицияси сифатида тақдим этилиши мумкин.}

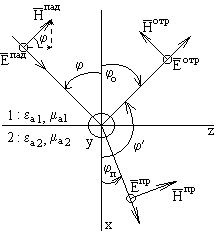
3.2. Ясси тўлқиннинг икки диэлектрик чегарасига оғиши

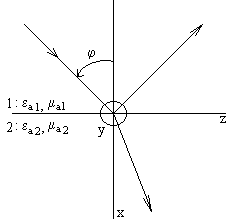
3.2-расм

Ясси тўлқиннинг а муҳитнинг ясси чегарасига оғишини 3.2-расмда кўриб чиқамиз. Тасаввур қилайлик, муҳитларда йўқотишлар йўқ. Оғиш яссилиги координатларнинг декарт тизими xoy яссилигига мос келади, деб ҳисоблаймиз. Тарқалиш йўналиши ва x ўқи орасидаги бурчак оғиш дейилади. А муҳитлар чегараси yoz яссилигига мос келади. Йўналтирувчи косинуслар қуйидаги нисбат билан аниқланади.

,

яъни фазавий кўпайтувчи:

,

бу ерда .

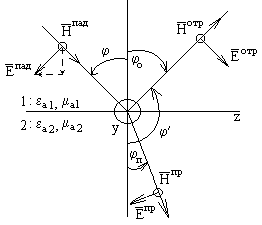
3.3. Нормал қутбланиш

Умумий ҳолатда

(3.5)

Ушбу ҳолатда _вектор у ўқи сингари йўналган.

3.3-расм. Нормал қутбланишя

Фазавий кўпайтувчи — ;

Оғувчи тўлқин тенгламасини ёзиш мумкин. Олдинги қайдларни (3.5) га қўйиб қуйидагини ҳосил қиламиз:

(3.6)

Тўлқиннинг чегарага оғиши натижасида оғувчи тўлқин тўлиқ ёки қисман акс этади ёки синади.

Акс этган ва синган тўлқинларни ясси, чизиқли қутбланган деб тахмин қилиш табиий. Оғувчи, акс этган ва синган тўлқинларнинг тарқалиш йўналиши xoz яссиликда жойлашган деб қабул қиламиз. Бундан ташқари, акс этган ва синган тўлқинлар, оғувчи тўлқинлар сингари нормал қутбланган ҳисобланади. Унда акс этган ва синган тўлқинлар учун қуйидагиларни ёзиш мумкин:

(3.7)

(3.8)

бу ерда ; .

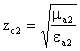Ушбу ҳолатда j, оғувчи тўлқиннинг характеристикалари машҳур j¢, j_n, , _{лар изланади. Агар масалани ечиш натижасида қуйидаги шартларни қондирувчи ечимни ҳосил қилсак}

; (3.9)

унда бирлик теоремасига биноан топилган ечим тўғри ва ягона бўлади. (3.9) нисбати а чегаранинг z ўққа мос келувчи барча нуқталарида бажарилиши керак, яъни исталган z да чегара шартлари (3.9) бажарилиши керак. Бу агар оғувчи, акс этувчи ва синган тўлқинлар z бўйича бир ҳил тобеликка эга бўлсагина мумкин

(3.10)

(3.11)

j¢ бурчаги _{чегарага} j бурчак эса чегарага эга эканлигини ҳисобга олиб қуйидаги хулосани ясаймиз

(3.12)

Бундай масалаларни таҳлил қилишда j¢ бурчакдан эмас, қўшимча j_{о бурчак-} акс этувчи бурчакадан фойдаланилади

(3.13)

(3.12) ва (3.13) га қўйиб қуйидагини ҳосил қиламиз

(3.14)

—Снелиуснинг биринчи қонунига қўра оғиш бурчаги акс этиш бурчагига тенг.

(3.11) нисбатидан фойдаланиб ва бундан қуйидаги келиб чиқади:

(3.15)

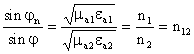(3.16)

(3.16) кўринишида ёзилган (3.15) нисбати Снелиуснинг иккинчи қонуни дейилади ва унга кўра оғиш бурчаги синусининг синиш бурчаги синусига муносабати биринчи ва иккинчи муҳит синиш коэффициентлари муносабатига тенг.

Акс этиш бурчаги синусининг оғиш бурчаги синусига муносабати синиш нисбий коэффициентига тенг. (3.9) чегаравий шарт қуйидагича ёзилади:

, x = 0 (3.17)

бу ерда биринчи муҳитдаги тангенциал компонентлар иккинчи муҳитда синган тўлқинлар билан ҳосил қилинади. (3.17), (3.18) нисбатларга (3.3)-(3.8) нисбатлардан тегишли компонентларни қўйиб, қуйидагини ҳосил қиламиз:

(3.18)

(3.19)

Z га бир ҳил боғлиқликни ҳисобга олиб, барча фазавий кўпайтувчилар бир ҳил эканлиги ва уларни қисқартириш мумкинлигини қайд этамиз. Бундан ташқари, _{бўлганда, қуйидагини ҳосил қиламиз}:

(3.20)

(3.21)

Акс этган ва синган тўлқинлар амплитудаси га пропорционал, яъни:

Бу ерда — акс этиш коэффициенти, — синиш коэффициенти

,

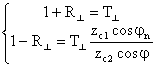(3.22)

Ушбу тизимни ечиб, қуйидагини ҳосил қиламиз:

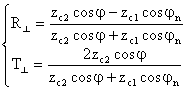(3.23)

Акс этиш ва синиш коэффициентини кўпинча Френель коэффициенти деб аталади.

3.4. Параллел қутбланиш

Ясси чизиқли қутбланган тўлқинни кўриб чиқамиз. вектори оғиш яссилигида жойлашган.

Оғувчи, акс этган ва синган тўлқинлар учун ифодалар қуйидагича:

х £ 0 (3.24)

Акс этган ва синган тўлқинлар учун ифода қуйидагича:

, х £ 0 (3.25)

, х ³ 0 (3.26)

j¢, j_n, , лар номаълум. Уларни чегаравий масалани ечиш натижасида топиш мумкин:

(3.27)

Ушбу ҳолатда (3.27) нисбати қуйидагича ёзилади:

, х = 0 (3.28)

3.4-расм. Параллел қутбланиш

(3.27), (3.28) нисбатлар а чегаранинг барча нуқталарида, яъни z координатанинг исталган қийматларида бажарилиши керак. Агар акс этган, оғувчи ва синган тўлқинларнинг таркибий қисмлари z га бир хил боғлиқ бўлсалар, буни амалга ошириш мумкин.

яъни

(3.29)

(3.30)

(3.29) ва (3.30) нисбатлардан Снелиус қонунлари келиб чиқади: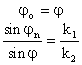

Яъни Снелиус қонунлари оғувчи тўлқин қутбланишига инвариантли.

(3.28) нисбатини майдон проекцияси учун тегишли ифодаларга қўямиз:

(3.31)

(3.32)

(3.29), (3.30) нисбатлардан барча экспонентлар тенг эканлиги келиб чиқади. Уларни қисқартириб, қуйидагиларни ҳосил қиламиз:

(3.33)

.

(3.33), нисбатни қуйидагича ёзиш мумкин:

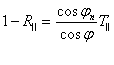(3.34)

(3.35)

Тизимни ечиб, қуйидагини ҳосил қиламиз:

(3.36)

(3.37)

— параллел қутбланиш учун Френель коэффициентлари.

j косинусини олиб ташлаш мумкин

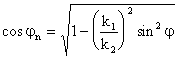
Нормал ва параллел қутбланиш учун Френель коэффициентини таққосласак, турли қутбланишлар учун Френель коэффициенти ҳар хил бўлади.

Ясси тўлқин нормал бўйича а яссиликка оғиши ҳолатида, оғиш яссилиги тушунчаси ўз моҳиятини йўқотади. Бунда оғувчи, акс этувчи ва синган бурчаклар нолга тенг ва Френель коэффициентлари учун ифодалан соддалашади:

,

. (3.38)

3.5. Тўлқиннинг иккинчи муҳитга тўлиқ ўтиши шартлари. Брюстер бурчаги

Тўлиқ синиш эффекти ҳолатида тўлқин биринчи муҳитда акс этмайди ва акс этиш коэффициенти нолга тенг.

Параллел қутбланиш ҳолатини кўриб чиқамиз:

_(3.39)

. (3.40)

Оғиш бурчаги косинусларини синуслар орқали ифода этиб, ўнг ва чап қисмларнинг квадратини чиқариб, қуйидагини ҳосил қиламиз

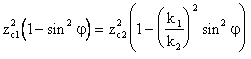, (3.41)

ни нисбатан ечиб қуйидагини оламиз:

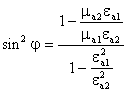(3.42)

.

Реал диэлектрик муҳитлар учун қуйидаги тенглама бажарилади:

(*)

(3.43)

Маълум тригонометрик ўхшашликни эслаб, қуйидагини ҳосил қиламиз: ,

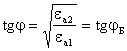(3.44)

бурчаги тўлиқ қутбланиш деб ҳам аталувчи Брюстер бурчаги деб аталади.

3.6. Икки муҳитнинга чегараларидан тўлиқ акс этиш

Икки диэлектрик муҳитлар

А муҳитлар чегарасида синган тўлқин бўлмайдиган, яъни тўлиқ ички акс этиш эффекти рўй берадиган шартларни аниқлаймиз. Синиш бурчаги 90° тенг бўлган оғиш бурчагининг қиймати критик бурчак дейилади.

(3.45)

(3.46)

, бўлганда оғиш бурчаги катталашганда, оғувчи тўлқиннинг қутбланишида акс этиш коэффициенти бирга тенг бўлиши мумкин:

. (3.47)

Унда бўлганда қуйидаги тенгсизликка амал қилиниши керак

(3.48)

бурчакнинг реал қийматларида ушбу тенгсизлик бўлиши мумкин эмас. Шунинг учун бирдан катта бўлиши учун, айтайлик комплекс катталик бўлсин. Унда:

(3.49)

(3.50)

,

.

Бу хусусиятдан фойдаланамиз. (3.51) нисбатни бажариш учун:

, ,

, (3.51)

т.е. , бўлиши керак.

3.7. Тўлиқ ички акс этишнинг ҳосил бўлиш шартлари

1 шарт , чунки sinj<1, унда k₂<k₁

иккинчи муҳитнинг зичлиги биринчига нисбатан камроқ бўлиши керак.

2 шарт . _{бўлганда биринчи муҳитда натижавий тўлқин майдони тузилиши учун ифодани ҳосил қиламиз}

, ; (3.52)

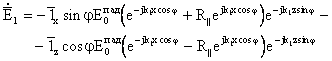, ; (3.53)

Бизнинг ҳолатда коэффициентлар ,

Нисбатларни жамлаш учун _{кўпайтувчини айлана қавсдан чиқариш керак.}

Амалга оширилган ўзгартиришларни ҳисобга олиб:

, ; (3.54)

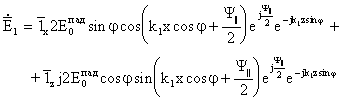, ; (3.55)

Олинган нисбатлардан қуйидагилар келиб чиқади:

1. Улар ясси электромагнит тўлқинни тасвирлайди.

2. Турли фазалар юзаси z ўқига перпендикуляр яссиликлар оиласини ҳосил қилади, яъни Z=const тенгламаси билан аниқланади.

3. Ясси тўлқинлар амплитудаси j оғиш бурчаги ва Х координатасига боғлиқ бўлади.

4. Тенг амплитудалар юзаси X=const тенгламаси билан аниқланади.

5. Тенг амплитудалар юзаси тенг фазалар юзасига мос келмайди.

6. Ясси тўлқинлар бир хил эмас;

7. Биринчи муҳитда ясси тўлқинлар Z ўқи бўйлаб, яъни а чегара бўйлаб тарқалади ва бундай тўлқинлар йўналтирилган тўлқинлар дейилади.

Перпендикуляр ва параллел қутбланиш ҳолатида ясси тўлқинлар тарқалиш йўналишида майдон таркибий қисмларига эга, яъни олинган ечимлар ясси бир турдаги бўлмаган, кўндаланг бўлмаган тўлқин демакдир. Фазавий тезликни анқлаймиз.

Умумий ифода . (3.56)

Бизнинг ҳолатда . (3.57)

Таҳлил қиламиз ,

; ,

, ,

(3.58)

(3.58) дан кўриниб турганидек, йўналтирилган тўлқин эркин фазада ясси тўлқиннинг биринчи муҳит параметрларига эга фазавий тезлигидан ошиқ. Бироқ эркин фазада иккинчи муҳит параметрларига эга фазавий тезлигидан кам фазавий тезлик билан тарқалиши кўриниб турибди.

Тўлқиннинг тарқалиш узунлигини аниқлаймиз , ёки ушбу ҳолатда

(3.59)

нисбатидан а чегарага перпендикуляр йўналишда майдон фазавий муддатли ёки узун тўлқинли турувчи тўлқин характерига эга.

.

Рис. 3.5

Ушбу нисбатларга қараб, шуни қайд этиш мумкинки, майдоннинг тарқалиш йўналишига нисбатан кўндаланг компонентлари() — синфазали. Энергетик параметрларини аниқлаймиз.

Пойнтинг комплекс векторини аниқлаймиз.

(3.59)

( 3.59) ифодада "+" белгиси нормал қутбланишга, "-" белгиси эса параллел қутбланишга тўғри келади. (3.59) ифодадан Пойнтинг вектори реал ва тахминий қисмларга эга эканлиги келиб чиқади.

Муддат ичида Пойнтинг векторининг ўртача қиймати Z ўқи бўйлаб йўналган.

(3.60)

Яъни, муддат ичида ўртача энергия Z ўқи бўйлаб ўтади. А чегарага перпендикуляр йўналишда қувватнинг реактив оқими мажуд. (*) дан х ўқига перпендикуляр яссиликларнинг чексиз сони мавжудлиги кўриниб туради ва уларда Е_t и Н_n нолга айланади. Ушбу яссиликларнинг Х ўқи билан кесишиш нуқтасини қуйидаги нисбатлардан аниқлаш мумкин.

.

Қутбланиш ҳолатида, параллел чегарада Е_z компонентаси бор. Юқоридаги нисбатдан қуйидаги келиб чиқади.

(3.61)

Бу ерда n=1, 2, 3, … .

Келтирилган мулоҳазалардан иш келиб чиқадики, а чегарага параллел бўлган (3.61) ифодада таърифланган яссиликларда (Е_t=0, Н_n=0) идеал ўтказувчи юзасидаги шартларга мос келувчи чегаравий шартлар қониқтирилади.

Агар биз бу яссиликлардан бирини идеал ўтказувчи (Х_n) билан алмаштирсак, бўлганда (яъни биринчи муҳитдаги яссилик устида) майдон ўзгаришсиз қолади.

3.6 расм.

Ушбу (3.61) яссиликларнинг яна бир характерли хусусияти шундаки, ушбу юзалар орқали энергия оқими нолга тенг.

Муддат ичида тезликнинг ўртача қийматини аниқлаймиз.

Энергиянинг биринчи муҳитда тарқалиши.

Биринчи муҳитда _, бўлганда энергетик трубкани, яъни ён юзалари орқали энергиянинг ўтиши бўлмаган фазонинг бир қисмини ажратамиз, яъни

Энергетик трубка сифатида (3.61) ифода билан аниқланувчи қўшни юзалар билан чекланган фазонинг бир қисмини олий қулай. Масалан, X_n , X_n+1.

Майдон таркибий қисми Х координатага боғлиқлигини ҳисобга олиб энергиянинг тарқалиш тезлиги учун ифода интеграллашни ўз ичига олади. Тегишли комоненталарни қўйиб ва интеграллашни амалга ошириб қуйидагини ҳосил қиламиз:

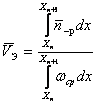(3.62)

(3.63)

(3.63) дан кўриниб турганидек, биринчи муҳитда энергиянинг тарқалиш тезлиги биринчи муҳитда ёруғлик тезлигидан кам.

Фазавий тезлик учун ифода .

Иккинчи муҳитда майдонни кўриб чиқамиз.

ошланғич нисбат:

, (3.64)

, (3.65)

бўлганда техминий катталик.

Қуйидаги ифодани киритиш қулай

(3.66)

бу ерда, a бўлганда ҳақиқий катталик ҳисобланади:

Снелиус қонунидан қуйидаги келиб чиқади: , ,

, , .

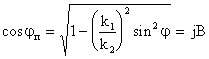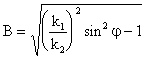(3.66)даги минус физик қарашлардан келиб чиққан.

(3.66) ни (3.62) - (3.65) га қўйиб, ни ҳисобга олиб қуйидагиларни ҳосил қиламиз

, (3.67)

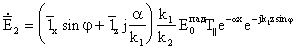, (3.68)

(3.67) - (3.68) дан кўриниб турганидек, бўлганда иккинчи муҳитдаги майдон а чегараси бўйлаб тарқалувчи ясси тўлқин характерига эга. Тенг амплитудалар юзаси тенг фазалар юзасига перпендикуляр, яъни ясси тўлқин бир турли эмас Z ўқи бўйлаб тарқалиш йўналишида майдон таркибий қисмлари мавжуд, яъни ясси бир турли бўлмаган тўлқин кўндаланг эмас. Тўлқиннинг фазавий тезлиги ва тўлқин узунлиги биринчи муҳит тўлқинни учун каби нисбатлар билан аниқланади.

, ,

, .

Характерли фарқ: ясси тўлқин амплитудаси а чегарадан экспонциал камаяди, яъни майдон айрим чегарадан қатламда мавжуд бўлади. Амплитудалари а чегарадан узоқлашганда экспонциал камаювчи йўналтирилган тўлқинлар юзаки тўлқинлар деб аталади. А чегарага перпендикуляр йўналишда тўлқин амплитудасининг камайишини характерловчи a -коэффициент қандай чегараларда ўзгаришини тахлил қилиб кўрамиз.

бўлганда a ҳақиқий коэффициент бўлади. Ўзгарганда эса

3.7-расм.

a қуйидагича ўзгаради: .

Энергиянинг тарқалиш тезлигини ҳисоблаш учун энергетик трубка сифатида фазонинг до гача чўзиладиган қисмини олиш керак.

Биринчи муҳитда Пойнтинг вектори:

Х₀ координата қуйидаги нисбатдан аниқланади:

, .

Ушбу ҳолатда интеграллаш майдон бўйича эмас, Х координата амалга оширилади.

, .

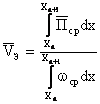Иккинчи муҳитда энергиянинг тарқалиш тезлиги, биринчи муҳитдагидек нисбат билан аниқланади.

4. СИРТИЙ ЭФФЕКТ

4.1. Сиртий эффект ходисаси

Олдинги мавзуларда келтирилганидек, ўзгарувчан электромагнит майдони содда қилиб айтганда ток отказиш ҳажми, ўтказиладиган жойларда а (). чегарадан узоқлашиши билан камаяди, бевосита катта частатоларда майдон ва ток кичик оралиқда иҳчамлашган бўлади. Бу жараён юзаки ёки скин-эффекти деб ном олган.

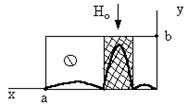
4.1-расм

Юзаки эффект давомида, симнинг кесмаси унинг геометрик кесмасидан сезирарли даражада анча кам бўлади, бу асосий қаршиликнинг кучайшига олиб келади. Иккинчи тарафдан юзаки эффект сақланадиган металли экранлар ҳосил қилади ва бошқа электромагнит майдонлардан радиотехник қурилмани сақлайди.

Шуни айтиб ўтиш керакки, доимий ёки камчастотали электромагнит майдон ҳосил бўлса, экранлар диомагнит ёки парамагнит материаллардан ишланади. Бу электр майдонининг сақланишига ва магнит майдонининг экранлашмаслигига олиб келади.

4.2. Электр ўтказгичларида энергиянинг йўқолиши

Реал электр ўтказгичлар юзасида Еτ 0. Бу энергия оқимини борлигига сабаб, ўтказиш жойининг ичига қаратилган бўлади. Йўқотилиш қувватиниг тақсимини оламиз.

Электр ўтказувчи жисм ва минимал радиуснинг ўлчами >> d деб хисоблаймиз ( кириш чуқурлиги). Бу усул Шукин-Леонтович усулига ўхшаш. Бу ҳолда энергия оқими , ўтказиш жойнинг ичига қаратилган, джоулли йўқотишларни аниқлайди. Масалан, S юзада Н τ компонента берилган бўлсин.

Еτ ни Шукин-Леонтович чегара усули билан аниқлаш мумкин.

Е ва Н га миқдор қўйиб унинг ўтказиш жойнинг ичига қаратилган энергия оқими қувватини хисоблаймиз.

(4.1)

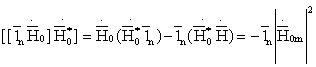(4.2)

4.2-расм. Электр ўтказгичлар чегарасидаги юзаки ток

Шундай қилиб 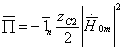_(4.3)

Бу ерда манфий чунки энергия оқими унинг ўтқазиш жойнинг ичига қаратилган, нормал эса сиртига қаратилган булиши керак.

Агар нарса ўлчамлари кириш чуқурлигидан >> d , энергия оқими нарсадан ўтадиган булса, унда П векторини S юзада интеграллаш йўли билан комплекс ёқотиш қувватини ҳисоблаш мумкин:

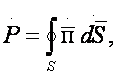
Юза векторли элементи , ҳисобга олсак , биз қуйидаги формулани оламиз:

(4.4)

.

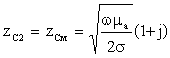
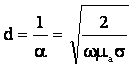
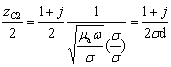Шундай қилиб _(4.5)

Йўқотишларнинг ўртача умумий тенглиги:

_(4.6)

_{4.3. Сиртий қаршиликлар}

_{Ўтказувчанлик қаватининг юзасида тангенциал қўшимча Е ва юзаки}

_{токнинг қувват вектори бир хил йўналишга эга. Шунинг учун қуйидаги}

_{ечимни ёзиш мумкин:}

_(4.7)

Бу ерда Z_S юзаки қаршилик. Юзаки ток

(4.8)

Ва - Шукин- Леонтович чегара қонунлари. (4.9)

(4.7) – (4.9) формулаларидан келиб чиққан ҳолда

(4.10)

(4.11)

Юзаки қаршиликнинг бутун қисмини ажратамиз

(4.12)

(4.12) дан, юзаки эффект жараёнида ўтказувчанлик яримқавати шундай аниқ қаршиликга эга эканлиги келиб чиқади, d қалинлиги билан ўтказувчанлик қаватига мос .

Кириталган юзаки қаршилигининг янги тушунчасини қуйидаги комплекс йўқотиш қувватида ёзиш мумкин

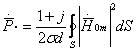
_(4.13)

_Демак

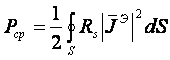_(4.

5. ЭЛЕКТРОМАГНИТ ТЎЛҚИНЛАР НУРЛАНИШИ

5.1. Умумий тушунчалар

Нурланиш деганда электромагнит майдон энергиясининг ёритгичдан силжиши тушинилади. Электромагнит майдоннинг силжиши энергия сақланиши қонунидан келиб чиққан ҳолда, унинг асосий вазифаларидан бири саналади. Электромагнит энергиясининг ёритгичдан узилиши унинг силжиш токининг борлигига, ва унинг диэлектрикда ва вакуумда мавжуд бўлиши мумкиндир. Шунинг учун ҳар қандай жойда силжиш токини, ҳосил қиладиган ёритгич, электромагнит тўлқинлар нурлантирувчиси деб аталади.

Нурлантириш масаласи шундан иборатки у нурланган электромагнит майдон векторларини, бошқа токлардан тақсимланиши , топиш ва элементар нурлантирувчиларга ечилади. Элементар нурлантирувчилар идеаллашган моделлар бўлиб, теретик тақсимланиш учун жуда қулай .

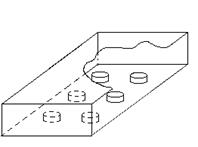
Элементар электр нурлантирувчи (ЭЭН) деб тўлқинга қараганда кичик, ўзгарувчан токнинг элементи , бу кесмадан (5.1. расм. а) ўтадиган ток: амплитуда тақсимланиши ва нурланиш фазаси ноаниқ деб киритилади.

Элементар магнит нурлантирувчи (ЭМН) деб тўлқинга қараганда кичик, ўзгарувчан токли доирани айтади. (5.1. расм. б)

Элементар dS фронтли тўлқинларни тарқатиш жойни Гюйгенс элементи деб атайди. (5.1. расм. в).

5.2. ЭЭН нурланиш майдони

ЭЭН нурланишининг текширувини сферик координаталар йигимида ўрганиш қулай, маркази нурлантирувчи жойлашган (5.2. расм. ). Электромагнит майдон векторлари уч кўринишга эга:

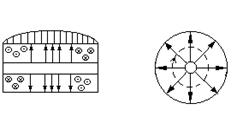
5.1. Расм. Элементар электр нурлантирувчи

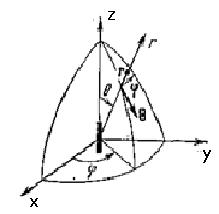
5.2. Сферик координаталар йигимидаги элементар электр

нурлантирувчи.

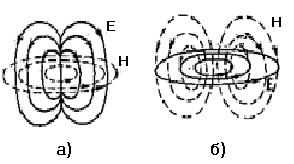
5.3. Элементар электр нурлантирувчи майдонинг тузилиши.

(5.1)

(5.2)

(5.3)

(5.4)

(5.1-5.4) формулалар гармоник электромагнит, радиал йўналиш ва мураккаб таркибга эга, тўлқинларни ифодалайди.

Майдоннинг алоҳида қўшимчалари r масофадан ҳар хил муштоқликларга эга бўлгани сабаб, масалани майдонини енгиллаштириш учун уч қисмга бўлинади:

1) яқинидагисини, kr<<1 масофасига мос равишда;

2) оралиғдагисини — kr ≠1;

3) узоқдагисини — kr>>1;

(5.1-5.4) формулаларни ишлатиб, яқин ва узоқ жойлардаги, яқинлашган ечимларини олса бўлади.

Яқинилашган масофадаги kr<<1 майдон қуйидаги формулалар билан ечилади:

(5.5)

(5.6)

(5.7)

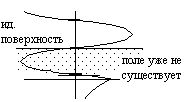
Буларни текшируви шунга олиб келадики, яқин орадаги майдон тўлқинга эга эмас( электр ва магнит майдон фазаси координаталарга боғлиқ эмас). ва векторлари 90° фаза буйлаб силжинган . Бундан келиб чиқадики, энергия оқимининг қуввати:

=

Реактив характерга эга, энергия оқими ўртачаси умуман йўқ, чунки . Бу яқин майдон оралигидаги, энергиянинг сақланиши, нурлантирувчи майдонлардан устун, бундан 5.1-5.4 дан 5.5-5.7 ларда фойдалангандик. Яқин оралиқ, реактив яқин майдоннинг жойи деб саналади.

Ўртадаги оралиқ, 5.1-5.4 формулаларда киритилганидек, нурланиш яқин майдоннинг жойи ёқи Френел дифракцияси оралиги деб аталади. Узоқдаги майдон қуйидаги кўринишга эга бўлади :

(5.8)

(5.9)

5.8-5.9 ларда Е_r≈0, чунки бу Е векторнинг қошимчаси, узоқдаги оралиқда Е_θ анча кам.

5.8-5.9 майдон бу сферик тўлқин, чунки унинг фронти r = const сферасидир. ЭЭН нурланиши куч чизиқларининг узоқ оралиги 5.3.а. расмда ифодаланган. 5.8-5.9 ни узоқ оралиғидаги текшируви ЭЭНнинг қуйидаги тақсимотларини беради:

· Е ва Н векторлар ўзаро перпендикуляр, чунки Е = θЕ_θ ,

· Е ва Н векторлар тўлқинлар йўналишига нисбатан ортаганал, чунки тўлқинлар радиал йўналиш бўйлаб жўналган, векторлар эса радиал қўшимчаларга эга эмас (Е_r= H_r = 0);

· Е ва Н векторлар синфазли;

· Е ва Н векторлар амплитудалари тақсимоти оралиқдан тегишли

Z_c параметри чегараланмаган оралигда тўлқин қаршилиги деб номланади. Вакуум ва бўш оралиққа :

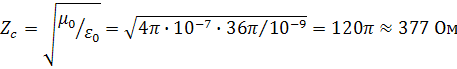
ЭМН узоқдаги оралиқда E_φ ва H_θ қўшимчаларга эга, ва ЭЭН дан фарқланади. (5.3.б.расм).

5.3. ЭЭН йўналиши диаграммаси

5.8,5.9 формулалардан келиб чиқадики Е_т и Н_т амплитудалари θ и r координаталарига боғлиқ.

.

θ = 0 E_m = H_m = 0,да θ = 90° E_m ва Н_т ларда максимал ечимга эга. Бундан келиб чиқадики , ЭЭН нурланиши майдони йўналишга эга, бунинг тақсимоти учун йўналиш диаграммаси (ЙД) киритилади.

Ҳар қандай ёритгичнинг йўналиш диаграммаси – бу Е_т ёқи Н_т амплитудаларнинг, ўлчанган масофада (r = const), график тақсимотидир. Сферик координаталар йиғиндисида (5.2. расм) куриш йўнаилшига иктта (θ ва φ) бурчакли координаталар билан берилади. Одатда нормаллаштирилган, максимал амплитудага оборилган ЙД ни ишлатади.

F(θ,φ) =Е_т (θ, φ)/Е_т max = Sin θ функцияси

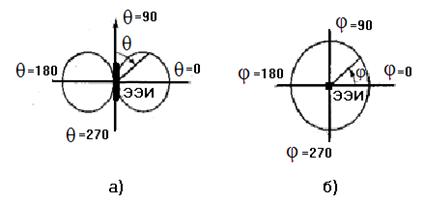
5.4. ЭЭН йўналиш диаграммаси.

нормаллаштирилган йуналиш тақсимоти деб аталади. Олинган формуладан кўринадики ЭЭН майдон меридионал бурчакка θ га боғлиқ ва азимуталли бурчак φ га боғлиқмас. F (θ, φ) графиклари, меридионал (φ = const) ва ва азимутал (θ = const) юзаларда 5.4 расмда кўрсатилган. ЙД қуришда,марказида ЭЭН жойлашган, поляр координаталар йигиндисида ишлатилган.

6. ЙЎНАЛТИРУВЧИ ВА ЮЗАКИ ТЎЛҚИНЛАР

6.1. Тўлиқ ички қайтарилиш

Амалиётда электромагнит тўлқинларнинг, икки диэлектрик чегарасида ёки идеал ўтқазувчан юзада, тўлиқ қайтарилиши кенг ишлатилади, чунки бундай чегаралар электромагнит энергияни йўналтиришга эга. Тўлиқ қайтарилиш кузатиладиган жараённи яратамиз ва бу тўлқинлар жараёнини ўрганиб чиқамиз.

Тўлиқ қайтарилиш, эгри тўлқиннинг йўқолиши билан боғлиқ. 3.4 расмда эгри бурчак, 0 дан 90° гача ўзгариб турганлиги кўриниб турибди, θ = 90° охири. Тушиш бурчаги θ = 90° , чегарали ёқи критик деб номланади (φ_Кр). Снеллиуснинг 2-чи қонунидан келиб чиққан ҳолда sinφ_кр = n₁/n₂ . sinφ_Kp<1 бўлгани сабаб келиб чиққан тенглик аниқ, икки диэлектрик n₂<n₁ тенгламага мос бўлса, агар иккинчи қават оптик жиҳатдан қуввати кам бўлса биринчисига қараганда. Агар φ>φ_кр, θ = (n₁/n₂) sinφ қиймати бирдан кўп бўлса, геометрик бурчак функцияси мақсади йўқолади ва жараённинг параметри бўлиб кўриб чиқилади. Френел формуласи билан коэфицентини топиш учун биз

(6.1)

соддалик билан ноаниқ жавоб оламиз. 3.21 ва 3.22 формулалари билан шуни таққослаб, биз қуйидаги формулаларни оламиз:

.

Махражида комплекс тақсимланган ўлчам ёзилганлиги сабаб, уларнинг модули тенг, а чегарадан қайтарилган тўлқин , , тўлиқ қайтарилади.

Шундай қилиб электромагнит майдоннинг икки диелектрикнинг чегараларидан тўлиқ қайтарилиши мумкин. Қуйидаги вазиятларда, биринчидан тушиш бурчаги φ_кр, дан ошган бўлса, иккинчидан, иккинчи оралик оптик жиҳадан куватсизроқ бўлса биринчисидан.

Тўлқин идеал симнинг чегарасидан хам тўлиқ қайтарилиш олади. Бу 3.22.323 да кузатилган, чунки инобатли қаршилик σ₂=∞ :

Амаладаги қизиқиш нафақат тўлиқ қаётарилишни кўрсатади балки келиб чиққан тўлқинлар жараёнини хам ўз ичига олади. Шу жараённи тақсимлаймиз. Шу вазифа билан биринчи ва иккинчи оралиқдаги майдонни текширамиз, нормал полярлаш билан тақсимланиб. Параллел майдонлашда майдон ўзгармас бўлади.

6.2. Нормал майдонлашда биринчи оралиқдаги майдон

Биринчи оралиқдаги майдон Е1 , тушаётган ва қайтарилган тўлқинларнинг суперпозицияси деб ҳисобланади. Чунки

ва ва қўйдаги формулани инобатга олиб

E^пад_m=y⁰E₀e^{-ik1(cosφ+zsinφ)}

И E^қай₀= y⁰E₀e^{-ik1(-xcosφ+zsinφ)} биринчи оралиқда майдон қуйидагича ёзилади:

ва ларни қовус ичига олиб ва Эйлер формуласини қоллаган ҳолда қўйдаги формулани оламиз:

Қўйдаги формулани қўллаб биз биринчи оралиқда, майдон ясси тўлқин эканлигини кўрамиз, z –ўқига қараб жўнатилган, муайян а чегарасига қараб, тўлқинлар сони билан .

амплитуда майдони текисликда (х ўқига қараб) тўлқиннинг туриш қонуни билан ва тўлқинлар сони билан аниқланади.

Майдоннинг амплитудалар координаталарига боғлиқлиги бирликмас тўлқин эканлиги билдиради.

Шундай қилиб, биринчи оралиқда, а чегара яқинида ясси тўлқин вужудга кедади. Бу тўлқин йўналтирилган деб номланади.

6.3. Нормал майдонлашда иккинчи оралиқдаги майдон

Иккинчи оралиқдаги майдонни кўриб чиқамиз. Бу ерда мана шу тенглик ишлатган ҳолда:

E^пр_m= y⁰E^прe^{-ik2(-xcosθ+zsinθ)}

Бу ерда уни:

деб ифодалаймиз.

6.1. га қараб уни физик жинсни аниқлаб уни деб ифодалаймиз. Снеллиуснинг иккинчи қонунидан келиб чиққан ҳолда:

Шуни инобатга олиб бу ерда:

ёқи бўлади.

Охирги тенглама ясси тўлқиннинг майдонини ифодалайди, β тўлқин сони билан а чегара бўйлаб иккинчи оралиқда ўтаётган ҳолатини. Бу тўлқиннинг асосий вазифаларидан бири бу майдоннинг амплитудасини сўниши ҳисобаланади. Бу майдоннинг иккинчи оралиқнинг ичига кирмаслигадан ва а юза олдида иҳчамлашганлигини кўрсатади. Шундай тўлқинлар юзаки деб аталади. Тўлқинли β сонлар ва тўлқинлар юзаларининг тенглиги фазали тезликнинг тенглигини кўрсатади.

Юзаки тўлқиннинг тақсимланишини ∆° масофа билан ифодалайди, бунда зайфлашган тўлқинлар А = 1 Нп га тенг (майдон е марттадан кийн ўчади),чунки , то ∆°=1/α. Идеал симдан тўлиқ қайтарилишда юзаки тўлқин бўлмайди.

7. МЕТАЛЛИ ТЕКИСЛИКГА ЯССИ ТЎЛҚИН ТУШИШИДАГИ ВУЖУДГА КЕЛАДИГАН МАЙДОНДАГИ ТАСВИРИ

7.1 Е вектор тушиш векторида ётади. Электр тўлқинлар

Пойтинг вектори П дан фойдаланилган ҳолда, унда бир хил фазали текислик кузатилаётган, тушаётган тўлқиннинг фронти, П вектрои нормаллашган бўлади. Текислик изларини қалин чизиқлар билан белгилаймиз. (7.1 расм.)

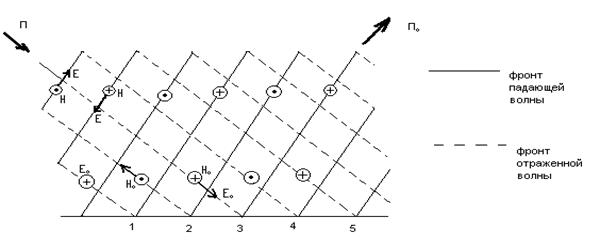
7.1. Расм. Тушиш текслигидаги Е векторнинг жойлашиши.

Ҳар бир қалин чизиқ, олдидагисига нисбатан маълум бир тўлқин узунлигининг тенг яримига масофага силжиган бўлсин. Шу чизиқлар оралиғида Е вектор ўлчами ва йўналиши ўзгартирилмаган бўлсин. Қўшни қизиқларда Е вектори ўлчамлари бир ва йуналиши тескари бўлади. Е векторини киритиб бир фротни қизиғига киритиб, ва П векторнинг йўналишини билиб, Н векторнинг жинсини аниқлаш мумкин. Тушаётган тўлқин, металли текисликга етгач, Пойтинг векторининг П қайтарилиш тўлқинини йўналишига қаратилиб, қайтарилиш тўлқинини вужудга келтиради. Қайтарилган тўлқинларнинг фронтларидан векторнинг йўналишини аниқлаганда, Е майдоннинг умумий тангенциал векторлар йигиндиси нолга тенг бўлган, идеал металли текислик чегара қонунларини инобатга олиш керак. векторнинг йўналиши векторнинг йўналиши ва Пойтинг векторининг қайтарилган тўлқинлар жинси билан аниқланади.

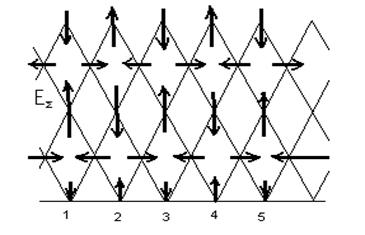
7.2. Электр майдоннинг кучланиш чизиқлари.

7.2 Расмда тушаётган фронт тугуни ва қайтарилган тўлқинларнинг умумий векторлари йўналишлари кўрсатилган . вектор чизиқлари битилган тугунларни ифодалайди. 7.3. расмда тушаётган фронт тугуни ва қайтарилган тўлқинларнинг, текисликга нормал мослашган, йўналиши кўрсатилган.

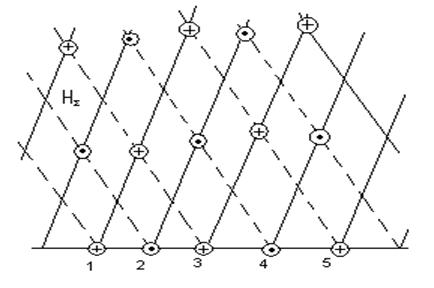
7.3. Магнит майдон кучланиш чизиқлари

7.4-расмда 7.2 ва 7.3 расмларга қараб қилинган кучланиш чизиқларининг электр ва магнит майдонларининг умумий тарқалиши ифодаланган. Кўрсатилган расмлар белгиланган вақтда ифодаланган. Улар металл тексилик бўйлаб, чапдан ўнгга силжийди. Олинган расмларнинг масшатаби ва ва уларнинг силжиш тезлигини аниқлаймиз.

7.4. Электр ва магнит майдоннинг умумий тасвири

7.5. расмда иккита қайтарилган тўлқин фронти ва иккита тушиш тўлқинининг қўшилиши кўрсатилган. Расмдан қуйидагидар келиб чиқади:

, . (7.1.)

Шундай қилиб расмлар масштаби тўлқин узунлиги ва металли тексиликга ясси тўлқин тушиш бурчаги билан аниқланади.

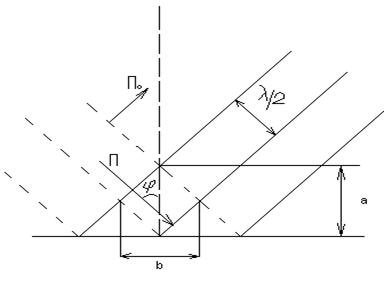
7.5 расм. Иккита фронтли қайтарилиш тўлқини билан тушиш тўлқини.

7.4. расмдан кўриниб турибдики, а чегара бўйлаб силжиётган майдон, силжиш йўналишига қараганда фақат кесмадаги магнит майдонга Н эга. Е электр майдон кесмали тўлдирувчидан ташқари, йуналиши ва фаза векторининг тезлиги билан мос, ионлашган тўлдирувчига ҳам эга.

Бундай тўлқинларни электр типли тўлқинлар деб атайди ва Е деб белгиланади. Шундай қилиб Е типли тўлқинлар деб Шундай тўлқинларни айтишадики, бунда ионлашган тўлдирувчининг вектор қуввати электр майдони ва ионлашган тўлдирувчининг вектор қуввати магнит майдони бўлади.

7.2. Е вектор тушиш текислигига перпендикуляр

Магнит типли тўлқинлар

Иккинчи ҳолатда ҳам ҳудди биринчи ҳолатдагидек йўл тутилган. Фарқ шундаки Е чизиқдаги тугуни Н чизиғи тунунлари билан алмашади.

Майдон расмининг масштаблари ва фаза тезлигининг ечимлари хам бир бирига ўхшаш. Биринчи ҳолатда Е типли тўлқин вужудга келади, иккинчи ҳолатда Е майдон, фаза тезлиги вектори билан мос келадиган, йёндошиш тўлдирувчиларга эга эмас ва ва йуналишга перпендикуляр текисликда жойлашган.

Н майдон йонлашиш тўлдирувчисига эга. Бундай тўлқинларни магнит типли тўлқинлар деб атайди ва Н деб белгилайди. Ўтказилган текширув бизга электромагнит майдоннинг, металли текисликнинг, бир тарафига йўналтириш қисқартирилиши кўрсатади. Электромагнит майдонни икки томонини ҳам, иккинчи текисликни биринчисига параллел, килиб қисқартирамиз.

7.3 Икки текисликли тўлқинўтказгич

Идеал металлнинг иккинчи чексиз текислигини биринчи текисликнинг тепасидан, майдон расмларини бузмасликка харакат қилиб, қўйямиз. Бунинг учун иккинчи текисликни масофага қўйиш керак, n=1,2,3,… - бу сонлар қатори. Бунда е майдон металли текисликларда нормал жойлашади, Н майдони эса тангенциал. Чегара ўлчамлари инобатга олинади ва икки текислик оралигидаги майдон расми бир текисликдадек бўлади.

7.6 расмда n=1 да Е типли тўлқин расми кўрсатилган. Бундай тўлқинлар битта вариация йўналишидан иборат бўлиб, текисликларга перпендикуляр бўлади ва E₁ деб типли тўлқин деб номланади. n=2 да H₂ типли тўлқин:

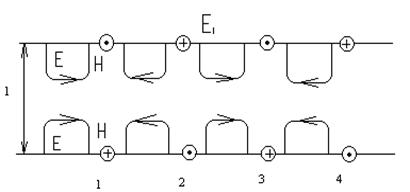
7.6. расм Е типли майдон расми.

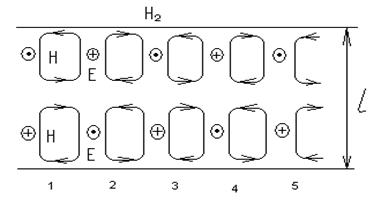
7.7.Расм. H типли майдон расми.

7.1. формуласини инобатга олиб текислик орасидаги масофа:

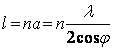(7.2)

масофа φ тушиш бурчагига боғлиқ. Агар катта типли тўлқин керак бўлса 2n, унда масофани икки мартага кўпайтириш керак. n=1 да тўлқин вужудга келишинг минимал масофаси:

n=2 да минимал тўлқин вужудга келиши минимал масофаси:

да (7.3)

Бу n=1 да ягоналигини кўрсатади. Катта индексли тўлқинлар икки тексилик орасида бўлади.

_{масофада} n=2 ли тўлқин вужудга келади ва n=3 да тўлқин бўлмайди. Лекин бир вақтда n=1 ли тўлқин бор бўлади. Шундай қилиб тексилик орасидаги масофани танлаш йўли билан, асосий типли тўлқинлар ягоналиги берилиши ва олий типли тўлқинлар ягоналиги берилмаслиги кўзда тутилади. Иккинчи текисликнинг киритилиши бизга электромагнит майдонни янада чеклашга олиб келиди. Икки чексиз текислик йигиндиси физик жиҳатдан нореал. Кийнчалик реал канализарлаш йигиндилари кўриб чиқилади- тўлқин берувчилар.

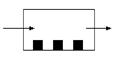
7.2 формулага қараб икки текисликли тўлқин тўлдирувчида , ечим бўича Е ёқи Н типли тўлқинлар бўлмайди. Лекин электр майдоннинг қучланиш чизиқлари текисликга тангенциал йуналтирилган бўлса электр майдоннинг кучланиш чизиқлари уларга перпендикуляр бўлса, 7.8 расмда кўрсатилганидек , унда Пойтинг векторида тўлқин берувчи ўқига мос тўлқин вужудга келади. Бундай тўлқинлар электр ва магнит майдон йўналтириш тўлдирувчисига эга бўлмайди ва Т типли тўлқин деб номланади. Шу Пойтинг вектори, бундай тўлқинда йўшналиш ўқи билан мос келгани сабаб, Т типли тўлқин фазали тезлиги, тўлқин берувчи оралиқда, ёруғлик тезлигига тенг. Бу тўлқиннинг тушиш бурчаги φ , 90° тенг бўлиши керак.

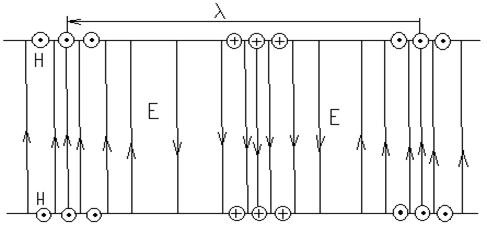
7.8-расм. Е ва Н векторларнинг бир бири билан жойлашиши

8. ЙУНАЛТИРУВЧИ СИСТЕМАЛАР ВА ЙУНАЛТИРИЛГАН ЭЛЕКТРОМАГНИТ ТЎЛҚИНЛАР

8.1 Йўналтирувчи системалар

Оралиқдаги эркин йўналтирилган тўлқинлар, йўналтирилган тўлқинлардан қараганда фақат йўналтирилган элементлар қўшилиб бор бўлади. Йўналтирилагн элементлар бирлашмаси, йўналтирилиш системасини ҳосил қилади. Йўналтирувчи системаларни яна энергия ўтқазиш чизиқлари деб аталади.

Барча ўтказиш чизиқларини икки турга ажратиш мумкин: очиқ турдаги ўтқазиш чизиқлари ва ёпиқ турдаги уьқазиш чизиқларига. Ёпиқ тупда ҳамма энергия хажми металли оралиқда экранлашган жойда еҳчамлашган. ЭМЎ нинг очиқ турида, энергия, ҳамма оралиқда жойлашган . Очиқ турда энергия оддийлаштирилган, чунки ЭМЎ чизиқ олдида еҳчамланади.

8.2. Йўналтирувчи тўлқинларнинг синфланиши

Йўналтирилган тўлқинлар: кесмали, электрли, магнит ва аралаш тўлқинларга бўлинади. Кесмали, Т типли тўлқинлар деб, энергия йўналишига мос, электр ва магнит майдон вектор тўлдирувчилари бўлмаган тўлқинлар айтилади. ва векторлар, йўналишга перпендикуляр текисликда ётади. Электрли ёки Е типли тўлқинлар деб, электр майдони вектори кесмали тўлдирувчи нисбатан, ёндошиш тўлдирувчисига эга тўлқинлар аталади. Магнит майдоннинг вектор ёндошиш тўлдирувчиси нолга тенг. Магнит ёқи Н типли тўлқинлар деб, магнит майдони вектори кесмали тўлдирувчига нисбатан, ёндошиш тўлдирувчисига эга. Электр майдоннинг вектор ёндошиш тўлдирувчиси нолга тенг. Аралаш (гибрид) типли тўлқинлар деб, электр ва магнит майдон векторлари, ёндошиш ва кесмали тўлдирувчига эга.

8.3. Йўналтирилган оралиқдаги, ёндошиш ва кесмали тўлдирувчиларнинг ўзаро алоқаси

Чексиз узун, Z ўқи бўйлаб, йўналтирилган системани кўриб чиқамиз. Йўналтирилган система йўқотиш бермайди ва ягонали деб ҳисоблаймиз,

n Кесма охиридаги хил Z ўқи координатасига боғлиқ эмас.

n ЭМЎ йўналтирилган, оралигдаги ўлчам , Z ўқи координатасига боғлиқ эмас.

берувчидан алоҳида Гельмгольц тенгламаларини цониқтириш керак:

ва нинг Z ўқига боғлиқлиги кўпайтмаси ёердамида ёзилади.

(8.1)

оламиз (8.2)

Бу ерда g – тўлқин сони.

(8.1) тенгламаcи учта, битта ёндошиш ва икта юзма-юз тўлдирувчидан иборат, скаляр тенглама эквивалент. Юзма-юз тўлдирувчиларни ёндошиш алоқасини, Максвелл дифференциал тенгламалари, ёрдамида ифодалаш мумкин.

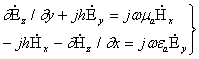(8.3)

8.3 системани билан, ечганда қуйидагини оламиз:

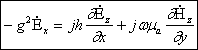(8.4)

(8.4) келиб чиққан ҳолда:

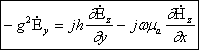(8.5)

(8.4)-(8.5) системаси тенгламалари, юзма-юз ва ёндашган тўлдирувчилар майдонини декарт координаталар системасида бирлаштиради. Бу бирлашмани эркин координатаси системадасида ифодалаш учун вектор тенглама турига ўтамиз.

.

ни киритиб

Ва ҳисобга олиб

Қуйидагиги олмаиз:

(8.6)

Бундан қуйидаги тенглама келиб чиқади.

Тўлиқ майдоннинг тузилишини топиш учун қуйидаги иккта диференчиал тенгламани ечиш керак:

(8.7)

8.6 тенгламалардан фойдаланиб, юзмаюз тўлдирувчиларни аниқлашда.

8.4. Критик частота. Критик тўлқин узунлиги

(8.8)

бўлса h – нарса йиғиндиси бўлади.

Агар (8.9)

ноаниқ ўлчам бўлса .

Биринчи ҳолатда фаза Z ўқи бўйлаб чизиқлиқ конуни билан, ўзгаради, тўлқиннинг йуналиши доимий фазали тезлик билан шу ўқ бўйлаб ўзгаради. Иккинчи ҳолатда Z ўқи бўйлаб фаза доимий бўлиб қолади. Амплитуда эса экспонента бўйлаб камаяди, йўналиш системаси бўйлаб, бу энергиянинг ўтқазилиши асоратидир.

Частота қуйидаги формуладан ҳисобланади

(8.10)

ва критик деб номаланади.

(8.11)

Шу частотага мос критик тўлқин узунлиги,

(8.12)

Унда (8.13)

Бу ерда - тўлқин сони.

- эса ва параметрли, тўлқин узунлиги.

8.9. га биноан тўлқиннинг эркин йуналиши фақат критик дан катта бўлган жойларда мавжуд.

деб тўлқин узунлигини , тебранишлар 2p фаза буйлаб силжиган, Z ўқининг харқандай ўлсамига тенг, масофани айтамиз. Чунки Z ўкдаги майдон тўлдирувчилари бўлади ,

Унда (8.14)

9. КЎНДАЛАНГ ЭЛЕКТРОМАГНИТ ТЎЛҚИНЛАР

9.1. (Е_z =0 , Н_z =0) критик тўлқин узунлиги

8.7 ва 8.8 Е_z = Н_z =0 дан фойдаланиб

, (9.1)

ва қониқтиради,

Агар (9.2)

8.11. 8.12 биноан бу g улчамларига, и тўғри. Демак Т тўлқинлари йуналадиган, учта йуналтирувчи системада, бу тўлқинлар ҳар хил частотада мавжуд.

9.2. Йуналтириш доимийси. Тўлқиннинг фазали тезлиги

, Þ (9.3)

(9.4)

Майдоннинг потенчиал характери.

Тенгламаларда ни хисобга олиб ,

Е_z = Н_z =0

Биз (9.5)

ни оламиз.

9.5. да Лаплас иккитали тенгламаларини ифодалайди. Лаплас тенгламаларига мос келадиган майдон потенциал бўлади. Бу 9.5 тенгламани ечишда қаисидир градиент тенгламаларни қўллаш тўҳри келади. Масалан:

(9.6)

бу ерда - Лаплас тенгламасини қониқтрадиган, скаляр потенциали.

.

ва векторлар бир бири билан ифодаланади. 8.6 да Е_z = Н_z =0 , инобатга олиб,

Қуйидаги тенгликни оламиз:

,

Буларни битта векторли тенглама сифатида ёзиш мумкин:

(9.7)

Бундан ва тўлқинлар ўзаро перпендикуляр эканлиги кўринади.

9.3. Кўрсатилган қаршилик

9.3 ни 9.6 қоийб биз қўйдаги формулани оламиз:

(9.8)

Бу ерда - Т тўлқиннинг қўрсатилган қаршилиги.

9.8 даги тенгламада частота чиқмайди. Бундан шундай ҳулоса қилиш мумкинки, Т тўлқиннинг тузилиши частотага боғлиқ эмас. Юзма-юз кесмадаги Т тўлқиннинг электр майдонининг тақсимланиши шу системадаги статистик электр майдоннинг тақсимланиша мос келади. Бунадай ўхшашлик магнит майдонлар тақсимотида ҳам мавжуд. Бу расмда икки электрўтказшичли ли ва коаксиал чизиқларнинг кесмасидаги электр ва магнит майдонлар тузилиши келтирилган.

Т тўлқин ҳам худди шу тузилишга эга бўлади . Т тўлқин фақат доимий ток энергияси ўтказиладиган оралиқда мавжуд бўлади.

9.1. Расм. Иккисимли ва коаксиал чизиқдаги электр ва магнит майдон тузилиши.

Бундай йуналтирилган системалар икки ажралган симлардан иборат бўлиш керак. Юзма-юз текисликдаги Т тўлқин ёнида, вақт бўйча ўзгармас, чунки статистик ҳолатда, амплитудасини эса синус қонуни бўйча доим ўзгартиради, Z координатасига боғлиқ.

Симларнинг идеал ўтказувчанлигида ЭМЎ металлдан ўтади. Шукин- Леонтович чегара қонунларига биноан, Z ўқига параллел , нолдан фарқли электр майдон тўлдирувчиси ҳосил бўлади, бу Т тўлқиннинг ҳосил бўлишини олдини олади. Лекин металлнинг тез ўтқазувчанлигида тўлқин тузилиши Т майдон тузилишидан кам фарқ қилади бу фарқликдан кўп ҳолатда фойдаланса бўлади.

10.1 ЭЛЕКТР ТЎЛҚИНЛАР

10.1 Майдон тўлдирувчилар орасидаги алоқа (и )

,

,

, ни инобатга олиб , биз қуйидаги формулани оламиз:

, (10.1)

, (10.2)

. (10.3)

Е тўлқиннинг ва векторлари ўзаро перпендикуляр.

10.2. Тавсифий қаршилик

. (*)

10.3 га мувофиқ кўрсатилган қаршиликни қуйидагича ёзиш мумкин:

, (10.4)

.

l > lкр ®- ноаниқ ўлчам. Бу электр ва магнит майдон кесмали вектор тўлдирувчилари, фаза буйлаб 90 градусга силжиган. Дарҳақиқат, Пойтинг вектори ноаниқ ўлчамга эга, ва ЛП буйлаб энергия ўтқазилиши йўқ. Шунинг учун майдонларнинг экспоненциал амплитудаларининг камайши йуналиш системасидаги камайш эмас балки балки ЭМП нинг чизиқдаги реактив характери деб номланади.

10.3. Фаза тезлиги. Дисперсия

(8.5) , V_ф > V₀ ; l = l_кр ® V_ф = µ.

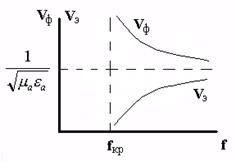
Фазали тезликни (V)_ф частотага боғликлиги, дисперсия деб аталади, дисперсия жой оладиган тўлқинлар эса дисперсиалашган деб номланди.

11. ЙЎНАЛТИРУВЧИ СИСТЕМАЛАР

11.1. Тўғрибурчакли тўлқин берувчи. ( и ) Электр тўлқинлари.

11.1 Расм. Тўгри бурчакли тўлқин берувчи.

_,

_{декарт координаталар системасида қуйидаги кўринишга эга бўлади:}

, (11.1)

11.1 ечими . (11.2)

Бу ерда Х(Х) – фақат Х-нинг, Y(y) - фақат Н-нинг функцияси.

(11.2)® (11.1) Þ (11.3)

11.3 Х ва Y нинг эркин ўлчамлари фақат қўйдаги формулага биноан ёзилади:

, (11.4)

Бу ерда

, (11.5)

. (11.6)

11.6 қуйидаги кўринишга эга:

(11.7)

(11.7)® (11.2) Þ (11.8).

Тўлқин узатувчининг ёнлари идеал ўтқазувчан бугани сабаб, чегара ўонуни қўллаб, : х=0, х=a да ва y=0, y=b

_{Бунинг бўлиши мумкин, агар:}

Бунинг учун 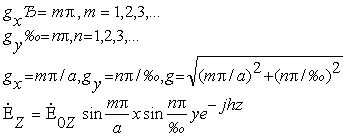_(11.9)

Бу ерда _{амплитуда масаласи.}

_{11.1 ва 11.2 декарт координаталар системасида қуйидаги кўринишга эга.}

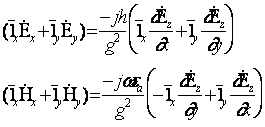
11.9 ни қойиб қуйидагини оламиз:

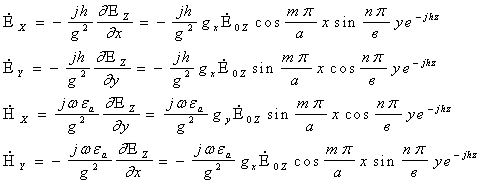(11.10)

11.9 ва 11.10 Е типли майдон тузилиши юзма-юз текислигидаги кесмаси турган тўлқинлар қонунига мувофиқ, m эса яримтўлқинлар сонига тенг, а узунлигда b ёни буйлаб жойлашадиган. Ҳар m ва n сонлар жуфтига, Еmnа деб белгиланадиган, ЭМЎ нинг аниқ тузилмаси мос бўлади.

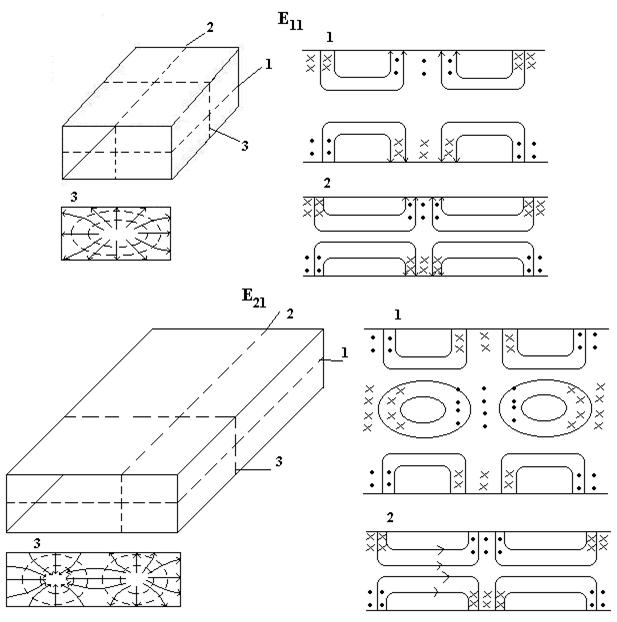
11.2. Расм . Е₁₁ ва Н₂₁ тўлқиннинг тузилиш майдони.

Е_z1 тузилилмаси , Е₁₁ нинг қайтарилиши билан, мос координата буйлаб, аниқланади:

,

,

,

.

Е_mn нинг пастки типи, енг катта l_кр эга бўлган, Е₁₁ тўлқин бўлади. Е_mn нинг тўлқинлари, майдоннинг хар хаил тузилмасига эга, буларга g нинг бирхил ўлчамлари, хархил йуналиш коэфиқентига эга, фазали тезликлар ва энергиянинг тарқалиш тезлиги тўғма деб номланади.

11.2 ( и ) магнит тўлқинлар

,

.

_{Декарт координаталари системасида қуйидаги кўринишга эга:}

, (11.11)

. (11.12)

Тўлқин тарқативчининг идеал ўткзиш ёнлари юзасида, қуйидаги масала ечилиши керак: .

, (11.12)

. (11.13)

11.13 ва 11.14 ни 11.12 га қойиб қуйидаги ечимга келамиз,

(11.15)

11.15 келиб чиққан ҳолда Н тўлқинларда ҳудди е тўлқинлардагидек.

_{Бир хил индексли Н ва Е тўлқинлари тугма бўлади.}

_{(11.12 ) (11.15) га ни қўйиб қуйидагини оламиз:}

. (11.16)

_{Бу ерда-} Н0Z - =АС - _{магнит майдон амплитуда тўлдирувчиси.}

_{11.1 ва 11.2 декарт системаси координатасида қуйидаги кўринишга эга:}

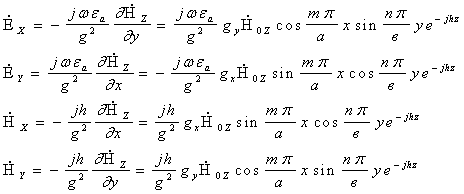(11.17)

11.16 11.17 дан кўриниб тургандек, Н типли тўлқинларда, Е тўлқинлардан фарқли равишда , бир индексларидан (m ёқи n) нолга алоқаси озини ортига ҳаммани нолга алоқадор қилмайди. Шунинг учун а>b бўлганда Н тўлқинларнинг пастки типи, бу Н₁₀ тўлқин.

,

Н₁₀ тўлқин, нафақат Н тўлкинлар ичида пастки тўлқинлар типи бўлади, балки ҳамма мавжуд тўғрибурчакли тўлқин берувчилардан ҳам. Бу l>2а бўйича энергия оқими бўлмаслигини айтади.

,

,

.

Н₁₀ Тўлқини энг катта критик тўлқин узунлигига тенг. Шунинг учун берилган частотада тўлқин узатувчиниинг юзма-юз кесмаси ўлчамлари, энергиянинг узатилиши мумкин булган ҳолатда, бунга нисбатан жуда кичик.

(11.16), (11.17) қараб қуйидагини оламиз.

, (11.18)

, (11.19)

, (11.20)

. (11.21)

Н тўлқиннинг тарқалиш майдони, текисликларда тўлқин тарқатувчининг қалин ёнларига параллел бўлган, расмида тўхталиб ўтамиз.

ЭМЎ да Н10 тўлқинлар, магнит кучланиш чизиқлари, у ўқи ёни бўйлаб силжиаётган, силжиш токини қамраб олади.

Силжиш токининг максимал қуввати, электр майдоннинг улчами нолга тенг, битилган магнит чизиқлари марказида жойлашади.

,

,

,

,

_.

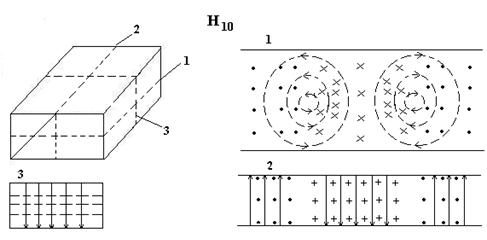
11.3. Н₁₀ тўлқин

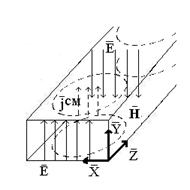
11.4 Расм. Н₁₀ тўлқиннинг тузилиш структураси.

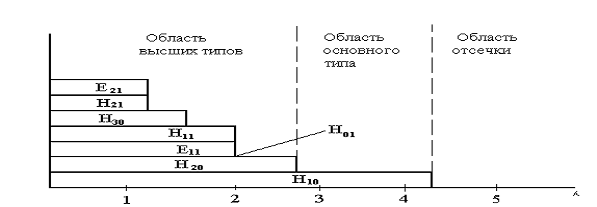
11.5 расм. Тўгри бурчакли тўлқин тарқатувчи типларининг диаграммаси.

11.4 Айлана шаклли тўлқин тарқатувчи

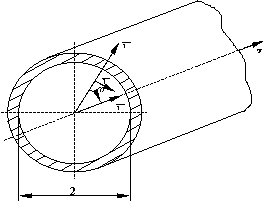
11.6 Айлана шаклли тўлқин тарқатувчи

Айлана шаклли тўлқин тарқатувчида E ва H тўлқинлари мавжуд бўлиб Т тўлқинлар тарқалиши мукин эмас.

11.5 Электр тўлқинлар

Текширувни ўқни тўлқин тарқатувчи ўқи билан мос равишда целиндрли координаталар системасидан фойдаоанган ҳолда хисоблаймиз. _{тенгламаси поляр координаталдар системасида} қуй даги кўринишга эга:

(11.22)

11.22 ечими _. (11.23)

11.23 ни 11.22 га қойиб иккила томонини r² кўпайтириб, ва дифференциаллаштириб, ва олинган қийматни га , қуйидагини оламиз,

(11.24)

11.24 нинг чап қисми фақат r га боғлиқ, ўн тарафи эса фақат j га . r ва j - ўзгарувчилар мустақил. Демак 11.24. – бу икки мустақил функчия тенгламасидир. Бунинг булиш эҳтимоли бор агар функциянинг ҳар бири доимий бўлса, доимийни m² деб ифодалаб, икктта диференциал тенгламага ўтамиз.

, (11.25)

(11.26)

(11.27)

_(11.28)

11.25 тенгламанинг ечими қуйидагича бўлади:

,

Бу ерда А ва В - еркин доимийлар. 11.28 тенгламаси агар m=0,1,2...

Бўлса ишланади.

11.26 Бессел тенгламаси бўлади. Унинг ечимини қуйидагича ифодаласа бўлади:

_. (11.29)

Бу ерда ва - Бессел функчиясининг -чи биринчи ва иккинчи жинчсли, тартиби , - эса эркин доимийлар.

_, (11.30)

_.

11.30 да иккинчи жинсли ли Бессел функцияси ¥ интилади. Чунки , электр тарқатувчининг , майдон электр қуввати хар бир нуқтасида чекланган бўлиши керак, шунинг учун . Ни талаб қилиш кетак. Унда :

_. (11.31)

Бу ерда - ёндошиш вектори тўлдирувчиси амплитудаси.

: ни ҳисобга олиб,

(11.32)

Бу ерда штрих диференциалашни англатади.

Чегара қонунига биноан :

. (11.33)

11.31 ни 11.33 қоийб қуйидагини олмаиз:

(11.34)

Бессел тенгламаси нолга тенг ҳолат хали кўп ҳолатларда кўзатилган. Бу ўлчамлар Бессел функчиясининг илдизлари деб номланади. Бессел функциясининг n-чи илдизини m-чи (11.35)

Е тўлқинларнинг рақамланиши, бир-биридан майдони тузилиши жиҳатдан фарқ қилувчи ва текислик кесмаси тенглама илдизига мос рақам билан ўзгаради(11.4). Шу билан m индекси, тўлқин узатувчинининг айланаси ёнида ихчамлашган, турган тўлқинлар тўлиқ сонига тенг, n индекси эса радиус буйлаб ихчамлашган, турган тўлқинлар сонига тенг.

_{Бессел функциясининг тенгламасининг бир нечта биринчи илдизлари, шунга мос критик тўлқин узунлиги, қуйидаги жадвалда келтирилган:}

Тип волны	E01	E11	E21	E	E	E	E	E
	2.405	3.832	5.135	5.520	6.379	7.016	7.586	8.407
	2.613	1.640	1.223	1.138	0.985	0.895	0.828	0.746

Е тўлқинларнинг пастки типи, айлана шаклли тўлқин узатувчида, бу E₀₁ тўлқинидир.

,

,

,
,

_.

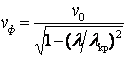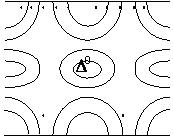
11.7. Расм. Е₀₁ тўлқин тузилиш майдони.

11.6. (, ) магнит тўлқинлар

Электр тўлқинларга ўхшаб ҳисоблаймиз:

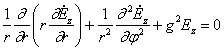
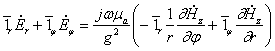
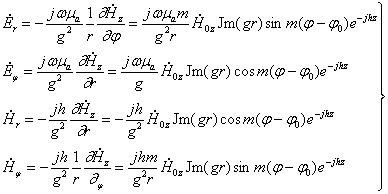(11.37)

J_m(ga)=0 ни ечганда бўйча:

(11.38)

_{Бессел функциясининг тенгламасининг бир нечта биринчи илдизлари, шунга мос критик тўлқин узунлиги, қуйидаги жадвалда келтирилган:}

Тип волны	H11	H21	H01	H31	H41	H12	H51	H21	H02
	1.84	3.05	3.83	4.20	5.32	5.33	6.42	6.71	7.02
	3.41	2.06	1.64	1.50	1.182	1.178	0.979	0.934	0.838

Нафақат Е тўлқинларнинг пастки типи, балки ҳамма тўлқинларнинг айлана шаклли тўлқин узатувчида, бу H₁₁ тўлқинидир.

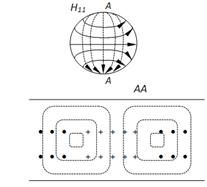
Расм. 11.8. Е₁₁ тўлқинлар тузилиш майдони.

Расм.11.9. Айлана шаклли тўлқин тарқатувчи диаграммаси.

11.7. Т тўлқини. Коаксисиал чизиқнинг тўлқинли қаршилиги

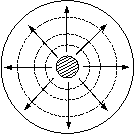
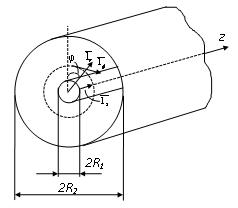
Рис. .1 Коаксиал тўлқин тарқатувчининг тузилиши.

Коаксиал чизиқларда T, E ва H тўлқинлар ҳосил бўлиши мумкин.

T тўлқин коаксиал тўлқинлар ичида энг пастки типи саналади.

(*)

Лаплас тенгламаси () поляр координаталар системасида қуйидаги кўринишга эга.

_(11.39)

Тенглама икки турдаги ҳисобланишга эга:

_(11.40)

, (11.41)

Бу ерда m - бутун сон.

Идеал ўтказувчи деб айтилаётган, ички симнинг юзасида, сиртқи симнинг ички юзасида, тегишли электр майдони нолга айланиши керак.

(11.42)

11.40 ечим да 11.42 тенгламани қониқтирмайди ва уни четлатиш керак. Иккинчи ечим учун:

,

11.42 тенгламаси D константанинг эркин ўлчамида ва Y₂ функциянинг ечими ҳисобланади.

(*) ва () ни Y₂ функцияга қўйиб қуйидагини оламиз.

, (11.43)

(11.44)

Бу ерда , E₀ – бу ички симнинг юзаки электр майдон қуввати .

11.43 11.44 тузилилмаси 11.8 расмда кўрсатилган.

_{Марказдаги ва ташқи симларнинг потенциаллар тақсимоти қуйидагига тенг:}

_(11.45)

_{Марказ симнинг юзасида ўтаётган ва ички симнинг юзасида ўтаётган ток қуйидагига тенг.}

(11.46)

u нинг I токка тақсимоти тўлқиннинг коаксиал чизиқнинг қаршилиги деб номланади.

(11.47)

_{11.8 Электр ва магнит тўлқинлар}

_{Е тўлқиннин ёндошиши тўлдирувчиси} E_{z 11.39 тенгламанинг ечими ҳисобланади, 11.47 билан мос равишда қуйидаги кўринишга эга.}

(11.48)

E_{z ички ва ташқи симнинг юзасидаги нолга айлангани сабаб,}

(11.49)

11.49 трансцендент тенглама бўлиб ундан ўлчам олинади. Магнит майдонлардахам ўлчам трансцендент тенглама илдизи саналади.

(11.50)

_{11.49 ва 11.50 тенгламалар текшуруви курсатадики коаксиал чизиқ биринчи оллий типли тўлқини бу} H_{11 тўлқинидир.}

_{Агар бўлса} R₁ = 0 коаксиал чизиқ аилана шаклли тўлқин тарқатувчига айланади, унинг пастки типи бу H11 _{тўлқиннидир. Юпқа металли буюмни айлана шаклли тўлқин тарқатувчи буйлаб киритиш} H_{11 тўлқин тарқалишига кам қаршилик курсатади, унда ёндошиш Е тўлдирувчилари йўқлиги сабаб. Шунинг учун} R₁

(11.51)

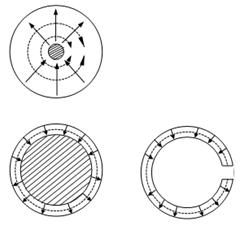
11.9 Расм. H₁₁ Ўтказиш чизиқларида майдон тузилиши.

Бошқа усулни кўриб чиқамиз. Тўғри бурчакли тўлқин тарқатувчида Н тўлқин тузилмаси тўғри бурчакли тўлқин тарқатувчининг

энига тенг. Унинг узунлигини эгри тўлқин тарқатувчида _{деб ҳисобласа бўлади. Демак да :}

(11.52)

_{11.52 формула бўлса унда оламиз. Бу дан 10% фарқ қилади, 11.51 формулага биноан.}

_{Шундай қилиб 11.52 формуладан,} R₁ ваR₂ эркин қийматларида бемалол фойдаланса бўлади.

11.9. Коаксиал чизиқлардаги тўлқинлар тури диаграммаси

11.10 Коаксиал чизиқлардаги тўлқинлар тури диаграммаси.

12. СВЧ ТЕБРАНИШ ҚУРИЛМАЛАРИ. ҲАЖМЛИ РЕЗОНАТОРЛАР

12.1 Электромагнит ва тебраниш қурилмалари ривожи

Радиотехник қурилмаларнинг энг ривожланган элементи бу тебраниш контури ҳисобланади, индуктивлик ва ҳажмнинг паралелл уланганидан ташкил топган.

Тебраниш контурининг асосий афзаллиги бу L ва C ўлчамларининг реал тўлқин узунлигидан анча камлиги ҳисобланади.

12.1.Расм 12.2 расм. 12.3 расм.

Тебраниш контури Локал хажим локал

ёнлари билан чегараланган.

Контурнинг заифлиги бу кам ихчамликдир, электромагнит майдон камайши сабаб бўлган актив ёўқотишлар кўпайши, юзаки эффект ва нурланишга кетган йўқотишлар сабаб.

Сақланган энергия кўпаяди, йўқотишлар камаяди. Бундай хажмли резонаторларда эхчамлашган параметрли йигиндилирга мос афзалликлар сақланган (L ва C ни ажратса бўлади).

Частота ошиши билан, L ва C камаяди, 12.2 дагидек контур ҳосил бўлади. У конструкчиядан иборат, икта металли пластина ва индуктивлик урани улаётган сим бўлади. Унинг сантиметрли диапазон тўлқинлари қайта ишлаши бўлади. Бундай контурларнинг фойдалиги жудуям кам . Бунинг сабабаи қуйидагича, L ва C элементларнинг кам ўлчами, бу контурда сақланган , энергиянинг камайишига олиб келади,.

Юзаки эффект жараёнида симларда йўқотишлар кўпаяди.

_{Нурланишда йўқотишлар анча кўпаяди. ВЧ да фойдасини кўпайтириш учун қуйидаги йул тўтиш мумкин: 12.2 расмда кўрсатилганидек, элементларнинг параллел уланишида резонанс частотаси кўпаяди,}

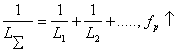
Бу ердан биз 12.3 дагидек расм тузилмасини оламиз.

Локал ёнлар билан чегараланган, локал ҳажмни оламиз.

Ўзини ўтқазиш локал ёнлари билан чегаралайдиган тебраниш контур – ҳажмли резонатор деб аталади.

Бу келишув, тебраниш контурларига мос, камчиликлардан иборат.

Частота ўсиши билан тебраниш контурининг, яхшилигини камайтириб, ҳажми камаяди

_{Частота ўсиши билан бунуқа қурилмалар, ҳосил қилиниши қийнлашади.}

_{Бундай кқрилмаларнинг реал ҳолатини кўриб чиқамиз. Тебраниш контурининг реалланишини энергия ўтқазиш чизиқларида кўриб чиқамиз.}

КЗ иккисимли чизиқни кўриб чиқамиз.

Шу чизиқда КЗ ҳолати.

КЗ ҳолати қуйидаги нуқталарда қаитарилади.

12.4 Расм. КЗ иккисимли чизиқ ҳолати. ,

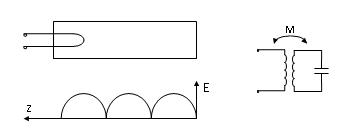
12.5 расм. Тебраниш контуридаги КЗ ҳолати.

Агар КЗ чизиқни иккти томонлама бўғласак ОТЦ курсида кўрсида кўрсатилгантдек, бунда тебраниш харакати мавжуд бўлади. Кийн унинг ўлчамлари:

Бу тебраниш контурларининг асосий афзалликларидан бири бу уларнинг кўп частоталарда резонланиши мумкинлигидир. Бундай тебраниш контури бўйлаб тўлиқ яримтўлқинларнинг сони ҳосил бўлиш керак.

Биз кесмадаги тебраниш контурини кўриб чиқдиқ. Бундай йигиндалар ҳар хил зтқазиш чизиқларида мавжуд бўлиши мумкин.

Бунинг афзалликлари қуйидагилар бўлади:

Тўрган тўлқин резонатор ичидаги, ҳамма уч координата мавжуд бўлиши мумкин. Қуйидаги резонаторлар, дисперсия туфайли, кисқа частоталарда резонлашади.

12.2. Тўғри бурчак кесмасидаги ҳажмли резонатор

( ярими масала)

Стандарт, тўлқинли, тўғрибурчакли тўлқин тарқатувчини оламиз.

_{кесмали тўғри бурчакли тўлқин тарқатувчини кўриб чиқамиз.}

12.6 расм. Тўғри бурчакли тўлқин тарқатувчи.

Бу резонаторда келиб чиққан, майдон тузилиши ва электромагнит қурилмалар тебранишини кўриб чиқамиз.

z=0, z=l

H₁₀

_{КЗ нинг мавжудлигида ёнида қайтарилган тўлқин мавжуд бўлади,}

ёндошиш тўлқин сони . бунинг учун чегарали масаладан фойдаланамиз.

,

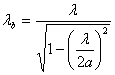_{ни хисобга олиб буни қуйидагича ёзса бўлади:}

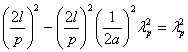
_{Бу ерда}

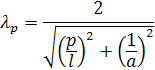
Резонансли тўлқин узунлиги.

“р” индекси оддий физик ахамиятга эга. У ,ўқи бўйлаб турган яримтўлқинлар сонини кўрсатади. Қўриб чиқилган тебранишлар тури қуйидаги аббревиатурага эга :

Резонаторнинг ҳосил бўлишидан олдин. Тўлқин тарқатувчида

_{- Тўлқин мавжуд бўлган.}

_{- да эса битта яримтўлқин.}

12.3 H_10p тебраниш тури. H₁₀₁ тузилиш майдони

_{буни у компонента деб белгилаймиз:}

_{Фақат у тўлдирувчига эга.}

_{12.7 расм. Н101 майдон тузилиши.}

_{Юзаки токлар:}

_{Е ва Н 90 градусга фарқ қилиниш кўриниб турибди, Пойтинг вектори ва тебраниш контуринг мавжудлигига, бу нолли ахамиятга эгалиги кўрсатади. Шу жараён давомида электр магнит энергияси икки марта магнитлига ўзгаради ва аксинча.}

_{12.4. Тўғри бурчакли резонаторда умумий масала.}

_{Тўлқин турлари синфланиши}

E_ши

12.8 расм. Тўғри бурчакли резонаторю

Тўғри бурчакли резонаторда мавжуд бўладиган, ўлчамли, ҳамма турдаги тебранишларни кўриб чиқамиз. Декарт координаталар системасини киритьамиз бунда нинг учами _{ўқи биоан мос келсин}.

Юзмаюз кесмада тузилиш майдон тузилиши билан мос келсин. Резонансли тўлқин узунлиги тўлқин тарқатувчи узунлиги билан мос келсин.

Агар тебраниш тузилмаси юзмаюз кесмадаги резонаторда , H_mn тўлқиннинг ўлчами билан мос келса, биз қуйидаги тенгламани олмаиз:

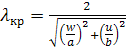
Қуриб чиқилган мавзуларда Н ҳолат Тўғри бурчакли тўлқин тарқатувсида, камида битта қабул қилади.

h дан келиб чиққан ҳолда, mn индекслари тақсимотга тўғридан-тўғри киради. р индекс нолга тенг ҳолатни кўриб чиқамиз.

p=0®

E₁₁₀

12.9 Расм. Е₁₁₀ В хажмли резонаторда даги майдон тузилиши

Агар биз икки металли текисликни l масофага қўйсак , m ва n нолли индекслари бунда, механик жиҳатдан қониқтирилади. Майдон тузилиши ўзгармас бўлиб қолади.

H_mn ҳолатда индекслардан биттаси нолга тенг бўлмаслиги мумкин, Н ҳолатда, фақат юзма-юз тўлдирувчисига эга. Тўлқин узунлигини критиклаб, магнит майдон ёндошиш тўлдирувчисига эга бўламиз, юзма-юз пластиналардан алоҳида, бу пластиналар перпендикуляр жойлашган, электр майдоннинг юзма-юз тўлдирувчилари эса тангенциал.

H_mn0 – тебранишлар бўлиши мумкин эмас.

12.5. Тебранишлар турларининг синфланиши

Синфлаш резонаторнинг ёндошишига боғлиқ ва қуйидагича ифодаланади:

1. Ўлчамлардан биттаси ёндошган бўлиб ҳисобланади.

2. Тўлқиннинг юзмаюз тузилиши ва турини аниқлаймиз, _{ўлчамли тебранишлар ҳосил қилувчи, эквивалент тўғри бурчакли тўлқин тарқатгичда.}

_{3. р индексини аниқлаймиз, ва} E_{mnp га эга бўламиз}

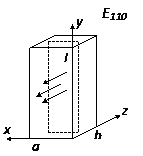_{Синфлаш алгоритми биринчи бўлиб, ҳажм ўлчамини танлашига боғлиқ,}

Рис.12.10. Н₁₀₁ и Е₁₁₀ Тўлқинлар майдон тузилиши

1. Ёндошиш ўлчами.

2. тузилмасини топиш кетак.

3. р индексини аниқлаймиз. p =1 индекси бу ерда H_101.

Е₁₁₀ Тўлқинлар сонини топамиз, бу ердан тўлқинлар сони нолга тенг.

_{12.6. Цилиндрли ҳажмли резонатор}

_{Резонанс частоталарнинг, ҳамма турдаги тебранишларнинг, узунлиги 1 ва диаметри 2а ли цилиндрли резонаторнинг тақсимотини топинг. 1 узунликни ёндошган деб ҳисоблаймиз, кесмаси тўлқин тарқатувчида .}

; ;

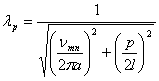
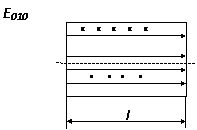
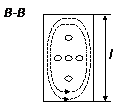
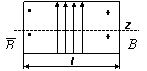
Рис.13.11. Н₀₁₁ и Е₀₁₀ Тўлқинлар майдон тузилиши.

Олдинги мавзуда исботлангандек, E_mn0 – ҳосил бўлиши мумкин. Бирнечта тебраниш турларининг тузилиш схемасини кўрсатамиз.

12.7. Ҳажмли резонаторлар кучлантириш усуллари

Амалиётда резонаторларни радиотехник схемалар сифатида ёқади. Ташқи занжирли алоқа элементлари қизиктириш уйғотади. Электр ва магнит типли кучлантириш ускуналари кузатилади. Резонаторларда тебранишларни кучлантириш учун қуйидаги ускуналардан фойдаланилади:

1) Электр типли (элементар электр узатувчилар).

2) Магнитли кучлантириш ускуналари ( элементар магнит нурлантирувчилар)

_{Электр тебраниш қурилмадан, эҳчамлашган, кучланишни олиш учун, ўзини чизиқли симли ток бўлган, у электр майдоннинг чизиқларига параллел ва унинг эҳчамланишидан максимумда жойлашган бўлиши керак.}

_{Магнит типли кучлантириш қурилмаси, тугунли симга мос равишда ўзгарувчи ток билан, тугун магнит майдонинг электр қувватига перпендикуляр жойлашган.}

_{Кучланишнинг бир нечта усулини кўрсатамиз.}

_{12.12. расм.} Е₀₁₁ и Е_{010 Тўлқинлар кучланиши.}

_{Радиотехник схемага резонатор йёқтриш учун икта усул мавжуд.}

_{Абсорбциоб ёқиш усули}

_{(параллел)}

_{Бир элемент алоқаси}

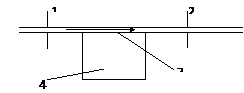
Рис.12.13 параллел ёқиш усули.

Ўтқазиш усули.

Икки алоқа элементи

12.14 расм. Ўтказиш усули.

Алоқа коэфиценти қанча катта бўлса, фойдалик ҳам камаяди, шунинг учун жудаям кам алоқа коэфицентига эга бўлиш керак.

Электр нурлантирувчи , ўзидан, металли электрли, ўзгарувчан электр токли симни ташкил қилади. Бу сим электр майдондан максимумда жойлашган бўлиши керак ва Е векторнинг кучланиш чизиқларига параллел бўлиш керак.

Магнитли алоқа элементи - бу тугунли алоқа элементининг бир хили. У магнит майдоннинг максимуда жойлашиши керак, тугуннинг юзаси Н вектор кучланиш чизиқларига перпендикуляр бўлиш керак.

12.8. Ҳажмли резонаторлар фойдалиги

Пойнтингнинг е теоремасида чегараланган система кўриб чиқилган эди. Бунга энергия тақсимотлари қуйидагича эди:

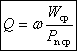
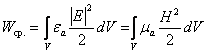
Йўқотиш қуввати

_{V- қэгараланган система.}

_{Фойдаликнинг конкрет ўлчамларини ҳисоблаш учун, қуйидаги} тақсимотлар олиниши мумкин:

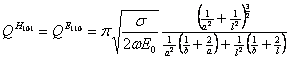
быстрее

_{Ҳамма келтирилган ўлчамлар, оезонаторлар системасига тегишли эди, Резонатор чегараланган система шаклида олинган эди, у резонаторга йуқотиш олиб келадиган у реал ташқи система билан боғлиқ. У шунтирлаш усулигп эга, ташқи занжирлар билан алоқа қанча катта бўлса, фойдалик шунчага кам. Фойдаликни ташқи занжирлар билан хисобга олинган ҳолда ўзининг фойдалигидан қараганда , юкланган фойдалик ҳисобланади,}

12.9 Ҳажмли резонаторнинг бошқа турлари.

Коаксиал резонатор

Коаксиал тўлқин тарқатувчида, асосий тўлқин турларида резонанс бўлмагани сабаб, бу тебранишларни ифодалаш учун қуйидаги аббревиатуралар ишлатилади: Т001...

12.15 расм. Коаксиал ҳажмли резонатор.

Коаксиал системадаги резонаторнинг асосий афзаллиги бу унинг ., р=1,2… частоталарда резонланиши.

12.16. расм. Диэлектрли резонатор.

Бундай резонаторларни тўлқин ўлчагич сифатида ўлчанади. Цилиндрли резонатор билан фарқли коаксиал резонатор кам фойдаликга эга катта юза ва кам ҳажм бўлгани сабаб.

Диэлектрли резонаторлар жудаям ривожланган. 12.16 расм.

ПВО эфекти сифатида кучланиб, диэлектрли резонаторлар махсус кучланишга муштоқ эмас.

Диэлектрли резонаторларни, катта коэфицентли диэлектр ўтқазувчанли сунъий маҳсулотлардан ишланади.

12.17. расм. Диэлектрли резонатор.

Ярим очиқ, параболик юзалардан иборат, резонаторлар мавжуд.

12.18 расм. Диэлектрли резонатор.

Бундай тузилмаларни актив оралиқларда(плазмаларда) ишлатадади, булар учун тегишиш бўлмайди. Асосий камчилиги бу нурланишга ёўқотишлар мавжуд.

13. АНИЗАТРОП ОРАЛИҚЛАРДА ЭЛЕКТРОМАГНИТ ТЎЛҚИНЛАР ТАРҚАЛИШИ

13.1. Умумий тушунчалар

Олдинги мавзуларда анизатроп оралиқлар мавжудлигини айтиб ўтган эдик. Радиотехникада анизатропларнинг кўп учрайдиган тури – ферритлар катта ривож топган.

Ферритлар - бу керамикага ухшаш, темир суюқлигининг ва иккинчи валентли металлар (Zn, Mg, Mn…) катта температурали қайнатилишида, сунний йўл билан ҳосил бўлган, каттиқ жисмлардир.

Ферритларнинг анизатропияси уларга доимий магнит майдон тегишидан ҳосил бўлади. Бундай оралиқлар гиромагнит ҳисобланади. Ферритлар ажойиб материал ҳисобланади: бир тарафдан улар ферромагнетик ( темирга ўхшаш) бўлади, ва магнит ўтувчанлиги қалин оралиқларда ўзгаради ва <1 ўлчамга( сантиметрли диапазонда) эга бўлиши мумкин ва бир неча мингга етиши мумкин ( кичик частоталарда).

Бошқа тарафдан, ферритлар оддий диэлектрикларга ўхшаш бўлади. Уларнинг ҳажмли қаршилиги Ом/см га тенг. Шунинг учун, оддий диэлектриклардагидек, уларда электромагнит тўлқинлар тарқалиши мумкин.

Диэлектрли ўтқазувчанлиги 10 30 га тенг.

13.2. Магнитланган оралиқдаги чизиқли полярлашган тўлқинлар

Ферритлардаг анизатропия уларнинг тузилишига боғлиқ. Ферритлар эркин магнитлашган тузилишга эга (доменлар). Бу жуда катта ҳажмли тузилмалар. Алохида атомлар магнит вақтлари параллел ифодаланган, ташқи майдон бўлмаса ҳам домен етарлича магнитланган, умумий момент ҳар бир моментларга тенг. Ташқи магнит майдон йўқлигида домен хаотик ифодаланган ва кўрсатма магнит айдон нолга тенг.

Ферритлар теорияси жудаям мурракаб ва классик электродинамикадан ташқарига чиққан, лекин электроннинг, амалиет билан мос келадиган ҳолда магнит майдондаги харакатини ифодаловчи теория мавжуд.

Ҳамма электроннинг магнит майдонда афзалликлари унинг орқаси спини борлигидир. СПИН ғ бу оддийлик билан электроннинг ўз уўқида айланишидир.

Электрон вазнга эга ва ўз ўқи атрофида айланади. У механик моментга эга. Бундан ташқари электрон зарядга эга ва уни элементар рамкада ифодалаш мумкин. Бир тарафдан электрон гироскопга ўхшаш, иккинчисидан уни магнит майдонга киритганда қанақадир элементар магнитга ўхшаш, унга икта куқ таъсир қилади уни магнит майдон чизиқларига параллел жойлаштириш учун, у гироскопга ўхшагани боис у ûë b текисликда айлана шакилни ифодалайди. Бу электромагнит майдоннинг прецессиясидир. Бу жараён кўп марта такрорланади, лекин ёуқитишлар сабаб у сўнувчи саналади.

Прецессия вақти 0,01 мкс ни ташқил қилади.

Прецессия w_o=½g½H_o частота билан ташқилланади.

g - бу феррит билан боғлиқ, манфий константа.

Доимий магнит майдондан ташқари яна, частотали, 1х йуналишга эга, ўзгаручан магнит майдонҳам бўлсин. Электрон прецесияни қайта ишлайди ва прецессия сўнувчи бўлмайди. Магнит майдоннинг охирини битилган егрилар ташқи қилади. Бу битилган эгрилар - эллипслардир. Прецессия частотаси юқори частотали майдон частотаси билан мос келади. Бу ерда тебраниш контурли аналогия кузатилади. Доймий майдон т туфайли физик эффект ўзининг тебранишларни кўрсатади. Кўшимча ВЧ майдон бўлса жараён мажбур тебранишларга ўхшаш.

13.1расм.Магнитлашган ферритли оралиқдаги чизиқли полярлашган тўлқин,

_{13.3. Фарадей эффекти}

_{Гиромагнит оралиқдаги чизиқли поялрлашган тўлқин, тарқалишга қайтамиз. Физика ва математикадан келиб чиққан ҳолда чизиқли полярлашган тўлқинни икки, айлана полярлашган ярим полярлашган чизиқнинг ва икки томонлама айланадиган, тўлқинлар суперпозицияси деб ифодаласа бўлади. 14.3 расмда кўрсатилган.}

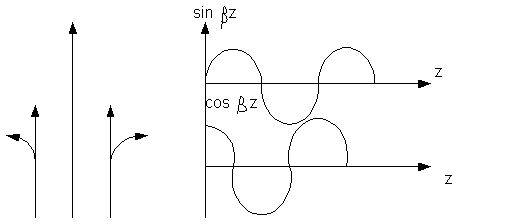
_{14.3расм. Амплитудали ва айланиш полярлашиш чизиқли тўлқин.}

_{Тўлқин учун бўлади , ва қуйидаги муносабат кузатилади:}

q=bZ ,

Бу ерда

_{Гиромагнит оралиқлардаги текислик айланиш эффекти Фарадей эффекти деб аталади.}

_{13.4 расм. Фарадей эффектини олиниши.}

_{13.4. Тўғри бурчакли кесмали, магнитланган ферритли, тўлқин тарқатувчида силжиш эффекти}

13.5. Электр майдон векторлари амплитудаси.

zox ,

.

х_о ва - текисликларда, вектор амплитудалари тенг бўлади( расмда кўрсатилган.

,

; ,

, .

х_о кесмада ферритли пластина коямиз ва уни доимий майдон билан магнитлаштирмиз.

Ферритли пластинадаги тўлқин тарқалиш ҳолати гиротроп оралиқдагига ўхшаш.

Z йуналиши бўйлаб жунатилган тўлқин учун, магнитлашган оралиқда магнитлашган майдон чап полярланишга эга бўлади, бунда магнитлашган магнит ва электр ўтқазувчанликга эга феррит, хавода бу ўлчамлардан катта.

Шунинг учун майдон феррит ёнида тақсимланади.

13.5. расм. Магнитлашган оралиқда Н тўлқинларнинг Z йуналишга тарқалиши.

13.3 расм. Феррит майдонининг ЭМЎ си.

Z ўқи бўйлаб, манфий йуналиш буйлаб тарқалаётган айлана полярланиш, х_о кесмасида, ўн томон айланишига эга бўлади ва шунга мос равишда манфий магнит ўтқазувчанликга эга бўлади. Бунда тарқалиш доимийси ноаниқ ўлчам бўлади, оддийлик билан феррита тўлқин ҳосил бўлмайди. Майдон ферритдан чиқади.14.7.

Бу эффект электрониканинг ВЧсида кенг ишлатилади, (бу тўртполюсли сигнал ўтказувчи). Бунинг учун тўлқин максимуда ёқи тескарисида қабулловчи керак. Ферритда қабулқилувчини конструктивли чизиш қулай. Бунда ферритда тарқалаётган тўлқин сезирарли суниш кузатилади. Вентилларнинг бошқа реаллаш усули бор, ферромагнит резонанснинг ишлатилишида ҳосил бўлган. Бунинг вазиваси қуйидагидар: доимий магнитлашган майдоннинг ўлчамини Шундай оладики бунда ўнғполярлашган тўлқинда ферромагнит ҳолати кузатилсин. Бунда ферритда ўн полярланишга эга, қабулланган тўлқинлар резонанс йўқотишлар сифатида етказилади. Келтирилган гаплардан қуйидаги афзалликлар тури мавжуд:

1) Уларнинг реалланиши учун катта қувватли магнит система керак.

2) Улар тарангполюсли бўлади.

14. ЮЗАКИ ТЎЛҚИННИНГ УЗАТИШ ЧИЗИҚЛАРИ

14.1. Бир симли ўтказиш чизиғи

Бир симли ўтказиш чизиғи ёқи юзаки тўлқин чизиғи(ЮТЧ) ўзидан, юққа диэлектрик билан ўралган, ягона металли сини ташқил қилади.14.1.расм. базида диэлектрик орнидаметалл юзасида ҳосил бўладиган ва кам ўтқазувчанликга эга, юққа оқимли юза(пленка) ишлатилади.

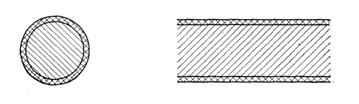
14.1 Юзаки тўлқин чизиғи(ЮТЧ)

ЮТЧ нинг ишлаш принципи , “диэлектрик- ҳаво” , симнинг юзасидан, тўлиқ қайтарилишга асосланган. Бунда диэлектрли оралиқда йуналтирувчи тўлқин ҳосил бўлади, ҳавода эса юзаки тўлқин. Бу чизиқларда асосан икта, λкр = ∞ эга, тўлқин саналади: Е00 ва НЕ11. Е00 тўлқин, кам заифланиш коэфицентига эга, қатиқ қизиқувчанлиқ ўйғотади. 14.2 расмда бу тўлкиннинг тузилиши ва унинг коаксиал тўлқин тарқатувчи ёрдамида, кучланиши кўрсатилган. ЮТЧ нинг афзалликларига унинг кенг чизиқлиги, катта электр қуввати, конструкчиянинг оддийлиги ва тежамкорлиги киради . Чизиқ очиқ бўлгани боиз у қуйидаги камчиликларга эга: ташқи майдон борлиги боийз, кам қаршиликкабардошлик, индукцион йўқотишларнинг борлиги , тўлиқ қайтарилишнинг ҳолатини бузилиши, атмосфера ўқимлари бойз нурланиш.

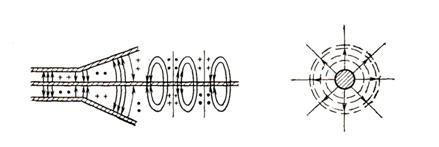
14.2. Коаксиал тўлқин тарқатувчининг кононик рупорга ўтиши.

Сантиметрли тўлқинлар диапазонида ЮТЧ лар фидер сифатида ишлатилади. Ва метрли тўлқинларда телеқизион программаларни ўзатилишда қ 50 дан 100 км гача, узилиш мажбуриятида, магистрал кабел ёқи радиорелейли алоқа чизиқларидан. Бунда чизиқлар изоляторлар ёрдамида симли алоқа столбаларида осилади. Улурни дицеметрли тўлқинларда ишлатиш мақсадга мувофиқ. Бундай чизиқнинг тез қўилиши унинг ҳар хил силжиш системаларида ишлатилишини самарали қилади.

14.2. Диэлектрли тўлқин тарқатувчи

Бундай тўлқин тарқатувчи 14.3 расмда цилиндрли r,φ,z координаталар системасида қўрсатилган.

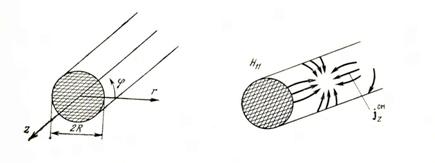
14.3 расм. Цилиндрли координаталар

системасида диэлектрли силжиш расми.

Тўлқин тарқатувчининг ишлаш принципи тўлқиннинг тўлиқ қайтарилишига асосланган “ диэлектрик-ҳаво”. Диэлектрикнинг ε₁ диэлектрли ўтқазувчанлиги ва ҳавонинг — ε_2. Энергиянинг қайтариш чегараси буйлаб ўзатилиши, ики тўлқин билан амалга оширилади: диэлектрли стержен ичида тарқаладиган, йуналтирувчи билан ва юзаки хавода тарқаладиган. Етп ва Нтп тўлқинлар айланали ва диэлектрли тўлқин узатучида мавжуд бўлади. Лекин улар орасидаги фарқ, диэлектрли тўлқин тарқатувчида тўлқинлар майдон (Е0п ва Н0п) тузилишига симметрик тўлқинлар, алохидла мавжуд бўлиши мумкин. Симметр бўлмаган Етп ва Нтп (m ≥ 1) тўлқинлар, аралаш ва гибрид тўлқинларни НЕтп ёқи ЕНтп. ҳосил қилади, тўлқин НЕтп деб белгиланади агар Еz>Нz —ЕНтп бўлса.

Гибрид тўлқинларнинг физик жиҳатдан юқрлигини қуйидаги метталли тўлқин тарқатувчи, аналогияни ишлатган ҳолда ифодалаш мумкин. Тўлиқ метталли тўлқин тарқатувчида кесмали ва ёндошиш тўлдирувчиларини ташқил қилади. Масалан H₁₁ тўлқиннинг js тузилмаси , 2.19.б. расмда кўрсатилган. H₁₁ тўлқиннниг диэлектрли тўлқин тарқатувчи кучланишида қуйидаги токлар мавжуд бўлади. 15.4 расм.

Ёндошиш тўлдирувчисининг силжиш токи :

нинг борлиги Еz≠0 дан H₁₁ кучлантиришини кўрсатади, гибрид тўлқининг ҳосил бўлишида. НЕ11 тўлқин асосий бшлади, чунки . Унинг тузилиши 14.5 расмда кўрсатилган. Бир тўлқинли ўтказувчи қуйидаги кўринишга эга.

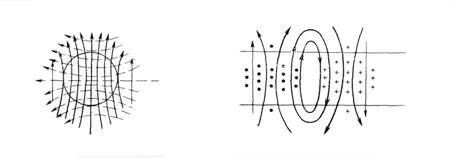
14.5. расм. НЕ₁₁ тўлқин тузилиши.

Диэлектрли тўлқин тарқатувчи ишлаш режими fkp/f тақсимотига боглиқ. f=fкр да қайтарилиш вазиваси бузилади, йуналтирилган тўлқин йўқолади ва унинг энергияси эса радиал йуналиш буйча тарқалади. f>fкр частоталарда , лекин fкр га яқин частоталарда, энергиянинг асосий қисми юзаки тўлқин хавода υ≈3∙ 108 м/с тезлик билан ташилади. НЕ11 тўлқин майдон тузилиши ва Т тўлқин майдон тузилишига яқин. Сўниши жуда кам. f»fкр частоталарда ҳамма энергия стержен ичида конқентралашади. Тарқалиш ҳолати бунда текис ягонали тўлқинлар тарқалишига яқин бўлади, (υ≈с/) тўлқин тарқатувчи ишланган материалдан.

Диэлектрли тўлқин тарқатувчи: афзалликлари:

1) Конструкчия оддийлиги, ишлатиш технологиясининг арзонлиги, металли тўлқин тарқатувчилардан фарқли, ўлчамларга кам талаблик.

2) Юқори сифатли диэлектрикларни ишлатилишида, (полистерол, полиэтилен, фторопласт ва ҳ.к.), сантиметрли тўлқинларда суниш коефиценти металли тўлқин тарқатувчи билан тенглашади, миллиметрли тўлқинларда, тўлқин анча кам бўлади, суниш камдир.

3) Юқори электрли қувват.

Диэлектрли тўлқин тарқатувчиларни милиметрли ва ундан кам тўлқинлар, диапазонларда ишлатиш мақсадга мувофиқ.

Диэлектрли тўлқин камчиликларига қўйдагилар киради.

1) Очиқ ташқи, йўшқотишларга сабаб бўлган, майдон мавжудлиги, тўлқин тарқатувчининг бурчакларидаги нурланишга, бундай нурланишларнинг йўқолиши учун (10..20) λ ли радиус ҳосил қилиш керак.

2) Диэлектрли стерженнинг жойлаштирилиши қийнлиги,

Диэлектрли тўлқин тарқатувчинининг Н11 тўлқинини одатда металли тўлқин тарқатувчи билан кучлантиради.

Кучлантириш тузилмаси 14.6 расмда кўрсатилган. (1- меьалли тўлқин тарқатувчи, 2- диэлектрли тўлқин тарқатувчи)

Диэлектрли тўлқин тарқатувчилар фидер сифатида яқин масофали диапазонда ишлатилади. Дилектрли тўлқин тарқатувилар оптик диапазонда кенг ривож топган. Бундай тўлқинлар нурўтказгич номини олган.

14.3 Толали нурўтказгич

λ= 0,3... 30 мкм диапазонли, f= 1013... 1015 Гц частоталарга мос, тўлқин оптик саналади. Волокон нурўтказгич ўзидан, тўлқин тарқатувчи, айлана шакилли диэлектрик кесмани ташқил этади.

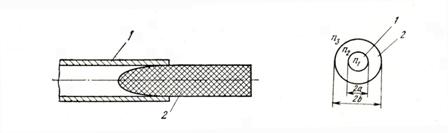
14.6. расм. Диэлектрли тўлқин тарқатувчи. 14.7 Толали нурўтказгич

Лекин амалиётда икки оралиқли нурўтказгичлар ишлатилади, сердцевина(1) ва кичик букиш ўлчамли материалдан ишланган п1>п2>п3 пўстлоғ(2). Сердқевина-пўстлоғ чегарасида тўлқинларнинг тўлиқ қайтарилиши кузвтилвди. Пўстлоғнинг борлиги оптик усул билан волокноларни бошқаларидан сақлашга имкон беради, чунки пўстлоғдаги юзаки тўлқин чегарага ҳаво билан орқали бормайди.

Толали нурўтказгичда алохида оссиметрик тузилашга эга, E0n, H0n тўлқинлар(модалар) мавжуд бўлиши мумкин, симметр эмас модалар (m≥1) гибрид саналади НЕтп ва ЕНmn.

Тўлқиннинг критик узунлиги формула бўйча аниқланади. 14.1.

νmn —бу Бессел функцияси илдизлари, унинг ўлчамлари 14.2 жадвалда келтирилган.

(14.1) ва νmn ўлчамлари текшируви , НЕ11 – толали нурўтказгичнинг асосий тўлқини эканлигини кўрамиз, чунки у λкр = ∞ га эга ва у коаксиал системадаги, Т тўлқинга ўхшаб ҳар хил частоталарда ва радиусларда тарқалиши мумкин.

Е0п ва H0n симметрик тўлқинларни мавжудлигидан холос бўлиш осон, агар бўлса. НЕ21 гибрид оралиқлар орасида енг яқини ҳисобланади. Чунки бир тўлқинли ўлчами қўйдаги тенглама орқали ҳисобланади:

(14.2)

(14.2) тақсимотидан келиб чиқадиқи сердқевина радиуси n1/n2 га боғлик. Қанча бирга яқин бўлса , шунча катта радиусда, биртўлқинли ўзатилиш сақланади.

Тип волны	m	п
		1	2	3
Е,Н	0	2,405	5,520	8,654
НЕ	1	0	3,832	7,016
ЕН	1	3,832	7,016	10,173
НЕ	2	2,455	5,538	8,665
ЕН	2	5,136	8,417	11,620

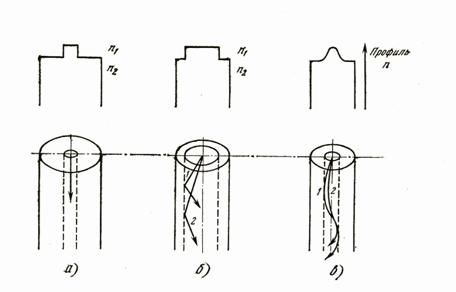
14.8-расм. Бирмодали, кўпмодали нурўтказгич.

Оптик волокнонинг қурилиш қийнликлари унинг радиуси камаиши билан ошади. Шунинг учун волокноларни (n1-n2)/ n1 тақсимотли ва 10-2... 10-3 навбатли материаллардан ишланади.

Биртўлқинли режим кўзатилган нурўтказгич – бир модали деб номланади.

Толали нурўтказгич турлари. Хозирги вақтда толали нурўтказгичларнинг бирнечта тури кенг ишлатилади.

Бирмодали нурўтказгич (14.8-расм) минимал дисперсияга эга ва чизиқли ўтқазувчанлик кенг чизиғига эга. Аммо оптик волокналар арзон ўтқазувчан оралиқ бўлгани сабаб, улар таранг чизиқлар оралигидахам қизиқтириш га эга. Бу кўп модли нурўтказгичларнинг ишлатилишига олиб келади. 14.8.б. расмда кўп модли нурўтказгич кўрсатилган. Бунқа нурўтказгич бўйлаб, кўп модлар тарқалиши мумкин. 14.8 расмда. Икки моднинг траекторияси кўрсатилган. Алоҳида модларнинг гурухли тезликлардаги фарқи бунда сигналларнинг бузилиши ва нурўтказгич ўтқазувчанлигини камаитиради. Барибир кўп модли нурўтказгич бирмодли нурўтказгичга қараганда кўп афзалликларга эга. Агар бир модли нурўтказгич диаметри 2.. 8 мкм , буни иўлаб чиқариш жуда қийн бўлса, кўпмодли нурўтказгичлар диаметри 50 мкмга тенг. Нурўтказгичнинг катта радиусда ишланиши уни арзонлаштиради ва когеренмас қурилмалар билан ишлашга вазият тўғдиради ва нурўтказгичларни улашга кам талабчанлик талаб қилади.

Модали дисперсияга градиент нурўтказгич эга. Кийшайиш ўлчамини перефирия марказидан 14.8.в. расм. кўрсатмасини ўзгартирувчи асосини. Градиент нурўтказгич кўп модли нурўтказгич саналади. Лекин қийш нинг асосий профили гуруҳ тақсимотини минималлаштиради . Бу нурўтказгич нурлар кишайган траектория буйлаб (14.8 расмдаги 1 ва 2 нурлар), нурўтказгич ўқидан яқин тарқалаётган нур биринчи нурдан қараганда, кам йул ўтади ва катта тезликга эга бўлиши керак. Лекин у катта қишаиш шўлчами билан тарқалади,тезлик тақсимотини тўлдиради. Градиент кўпмодли нурўтказгичлар, кўпмодли қадам профилли нурўтказгичларга қараганда, кенгчизиқли бўлади, аммо уларнинг ишлаб чиқариш технологияси қийинроқ ва кимматроқ.

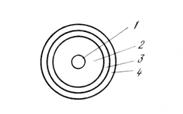
14.9-расм. Толали нурўтказгичнинг тузилиши.

Толали нурўтказгичнинг амалий конструкчияси 14.9 расмда кўрсатилган.

1 сердцевина ва 2 пўстлоғ қабуллардан қочиш учун, катта тозаликли шишадан ишланади. Пўстлоғ қалинлиги деярли 10 мартага сердқевина радиусидан ушиши керак. Ташқи оралиқ 3 кам тозали ва пўстлоғ кишаиш ўлчамига эга бўлиши керак. Унинг вазифаси, у билан ишлаш осон бўлиш учун, сетовод диаметрини катталаштиришдир.

Кўпмодли нурўтказгичлар, қадамли профил кишаиш ўлчами бўйча, оддийроқ конструкцияга эга бўлса бўлади:

Ташқи оралиқ талаб қимидиган, пластик пўслоғли нурўтказгич. Полимерли нурўтказгич, унинг ишлашида, махсус эхтиёткорлик талаб қилмайдиган шунинг учун ташқи оралиқсиз ва сақлаш пўстлоҳисиз 4.

Бундай нурўтказгичлар тарангчизиқли лекин жудаям тежамкор.

Волоконли нурўтказгичлар қуйидаги нарсаларда ишлатилади.

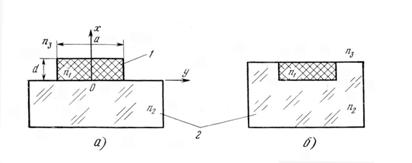
14.10-расм. Ясси нурўтказгичлар конструкцияси

Ясси нурўтказгичлар Ясси нурўтказгич ўзидан диэлекторли тўғри бурчакли кесмали тўлқин тарқатувчини ҳосил филади. Ясси нурўтказгичларнинг икки хилини ажратади: планар ёқи пленли. 14.10. а. Расм. каналли 14.10. б. расм.

Бу нурўтказгичларинг ишлаш принципи бир хил. 1 пленка ва 2 подлжка оптик кўринадиган, хархил кийшаиш ўлчамлари билан п1>п2>п3 диэлектриклардан ишланади, одатда а»d (14.10 расм.) шунинг учун Оу ўқи буйдаги майдон, деярди биттлаи, ва тўлқинлар бундай нурўтказгичларда Ет0, Нт0 деб белгиланади. (т– тўлиқ , х ўқи бўйлаб турган, ярим тўлқинлар сони). Металли тўлқин тарқатувчилардан фарқли пленка чегарасидаги майдон (х=0 ва x=d) нолга тенг эмас.Е00 дэган нурўтказгичлар мавжуд бўлиши мумкин.

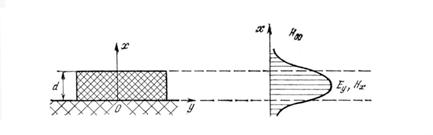
14.11-расм. Н00 тўлқин тарқалишининг эпюраси

Н00 тўлқин тарқалишининг эпюраси 14.11 расмда кўрсатилган. “Думлар” – пленка ташқарисига майдон тарқалиши (х<0, x>d) , юзаки тўлқинга мос.

Иш режимининг ифодаланиши учун, λкр улчамига мос, критик қалинлиқ dkp киритилади. Еm0 ва Нm0 тўлқинларга

,

,

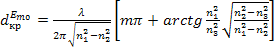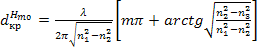Тўлқинлар тури сони (модлар) . Ясси нурўтказгичларда > бўлади. Максимал λкр га ва минимал dkр эга тўлқин асосий ҳисобланади.

Ўлчўвлар кўрсатадики бирмодли режим пленканинг жуда кам қалинлигида ифодаланади, буни технологик жихатдан реаллаштириш жуда мураккаб. Бу мурракабликни қуйидаги усул билан чеетлаб ўтиш мумкин . Т индексни кўпайтирган сари, dkр ўлчамга ошади ва бундан Δd кўпаяди. Одатда кийш ўлчами 10-2... 10-3 қаторли тақсимот материаллари ишлатилади. Бунда Н10,Е10, Н20 ва ҳ.қ. тўлқинларни филтирлаш мумкин Е00 тўлқинни олиб ташлаш учун пленка юзасини металлаштиради. Металли пленка Е00 тўлқинни заифлаштиради. Бу ҳамма уринишлар кўп модли нурўтказгичда, асосий тўлқин тарқалиши учун қилинади. Ясси нурўтказгичлар ҳамма интеграл оптика қурилмаларининг боши саналади: модуляторлар, ёндурувчилар, филтрлар, йуналтирилган узувчилар, уловчилардан, волоконли нурўтказгичларни нурловчилар(лазерлар) билан боғловчи қурилмалар, ёруғлик тўлқинларини қабулловчилар(фотодиодлар), ясси констукцияга эга қурилмалар.

АДАБИЁТЛАР

1. Пименов Ю.В, Вольман В.И. , Техническая электродинамика, - М: Радио и Связь, 2002 г.

2. Витевский В. И., Павловская Э. А. Электромагнитные волны в технике
связи, - М: Радио и связь, 1995-125с.

3. Фальковский О.И, Техническая электродинамика, - М.; Связь, 1978.

4. Вольман В.И., Пименов Ю.В, Техническая электродинамика, - М: Связь, 1971

5. Никольский В. В., Никольская Т. И. Электродинамика и распространение радиоволн. - М.: Наука, 1989.

6. Лебедев И.В. Техника и приборы сверх высоких частот в 2-х т., т. 1. - М.: Госэнергоиздат, 1970.

7. Федоров Н.Н. Основы электродинамики. – М.: Высшая школа, 1980.

8. Павловская Э.Л. Направляющие системы . КЭИС1977.

9. Семенов Н. А. Техническая электродинамика, - М: Связь, 1973

10.

5522100 – «Радиоалоқа, радиоэшиттириш ва телевидение», 5522000 - «Радиотехника», 5524400 – «Мобил алоқа тизимлари», 5522200 – «Телекоммуникация» йўналишлари учун «Электромагнит майдонлар ва тўлқинлар» фанидан ўқув қўлланмаси ТВ ва РЭ кафедраси мажлисида кўриб чиқилган ва нашрга тавсия этилган. («__»__ 20 й даги № - баённома).

ТАТУ ИУК мажлисининг «__» __ 20 й. даги № - баённомаси асосида нашрга тавсия этилган.

Муаллиф: катта ўқит. Кан В.С.

Масъул мухаррир: катта ўқит. Шахобиддинов А.Ш.

Тахририй-мусаххихлик хайъати:

Муҳаррир: доц. Абдуазизов А.А.

Мусаххих: катта ўқит. Абдуллаева С.Х.