узбекское агентство почты и телекоммуникации

таШкентский электротехнический институт связи

 

 

 

 

Абдурахманова М.Ф.

Ходжаев Н.С.

 

 

Кафедра ТС и СК

 

 

 

 

 

 

ТЕОРИЯ телетрафики

 

 

 

Конспект лекций для бакалавров по направлению

 

Б522300 - Телекоммуникация

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ТАШКЕНТ - 2000

В соответствии с рабочим учебным планом, утверждённым 30.09.1999г. (протокол № 2(479) по направлению: В522300 – Телекоммуникация (Телекоммуникационные сети и системы коммутации)). Читается курс лекции по дисциплине «Теория Телетрафики».

 

Лекция 1

 

Тема: Предмет и задачи теории телетрафика.

 

          Появления и широкое распространение в последней четверти XIX в. ручные телефонные станции, а затем в начале XX в. авто­матические, привели к зарождению новой научной дисциплины ТРИ. Предметом изучения стали процессы обслуживания системами распределения информации поступающих потоков сообщений и их количественных характеристик. К системам распределения информации относятся станция, КУ, сеть связь, а также их отдельные части обслуживающие телефонные, телеграфные и другие виды сообщений.

          Основы теорий ТРИ были заложены в трудах (1828-1929 г.г.) датского математика, сотрудника копенгагенской телефонной компании А.К. Эрланга. Сформулированный им принцип статистического равновесия и получение на его основе формулы для расчёта полнодоступного и идеально-симметричного неполнодоступного включения и сегодня является базовыми в теории распределения информации и отделившейся от неё впоследствии теории массового обслуживания. Три является одним из классов теории массового обслуживания. Родилась теория массового обслуживания в первой четверти ХХ века вследствие возникновения потребностей разработки тематических методов для оценки качества функционирования телефонных систем.

          Математическая модель процесса обслуживания, исследуемая в теории распределения информации, включает четыре основных элемента:

поток поступающих сообщений, систему распределения информации, характеристика качества и дисциплину обслуживания.

Понятие потока сообщений включает информацию о модели потока вызовов / требуемые на соединение, законе распределения длительности обслуживания сообщений, множестве адресов источников и приёмников сообщений, а так же тип занимаемого для передачи сообщений канала и способ передачи (аналогов и дискрет).

Система обслуживания – зависит от типа используемого оборудования. Под дисциплиной обслуживания понимают: способ обслуживания (с явным потерями, с ожиданием, повторными вызовами); порядок обслуживания (в порядке очерёдности, случайном порядке или приоритетом); режим искания выходов КС (свободный, групповой).

          К характеристикам качества обслуживания поступающих сообщений относятся вероятность явной или условной потери сообщений, среднее время задержки сообщения, вероятность потери поступившего вызова, интенсивность обслуженной нагрузки и другое.

          Исторически первыми в ТРИ возникли и заняли доминирующее положение задачи анализа – определение характеристик качества обслуживания в зависимости от параметров и свойств входящего потока сообщений, параметров и структуры системы обслуживания и дисциплины обслуживания.

          Первые средства коммутации обладали относительно простой структурой – использовались полнодоступные и реже неполнодоступные схемы включений и решение задач анализа в основном удовлетворяло потребности практики. Так для ручной АТС необходимо было знать число Ш пар и число телефонисток в зависимости от заданного времени ожидания соединения. Для АТС рассчитывалось число приборов по ступеням искания с учётом вероятности потери вызовов. Однако уже тогда была сформулирована задача нового типа – оптимизации параметров и способа построения схемы. Из всех возможных вариантов схем НПД включения следовало выбрать оптимальный, обеспечивающий при прочих равных условия наименьшие потери вызовов.

          С появлением квазиэлектронных и электронных АТС на передний план выдвигаются задачи синтеза структуры коммутационной системы с оптимизацией её параметров. Для станции или узла определённой ёмкости требуется построить схему коммутационного поля таким образом, чтобы при заданных потоках, дисциплине и качестве обслуживания его стоимость была минимальной либо были минимальными потери вызовов при заданных потоках.

          Задача оптимизации схемы КП электронных АТС тесно увязана с разработкой оптимальных алгоритмов поиска путей. Для снижения нагрузки на процессор время поиска свободного выхода и пути к нему в КП должно быть минимальными. При неудачном алгоритме за счёт ограниченного времени поиска потери вызовов могут быть выше по сравнению с потенциальной возможностью КЕ. Таким образом, при исследовании пропускной способности программно – управляемой АТС в математической модели появляются новые компоненты – время и алгоритм поиска пути.

          В связи с усложнением сети связи возникает необходимость анализа сети до её построения (нагрузка, количество абонентов, взаимное тяготение).

          Нормирование и оптимальное распределение по участкам сети показателей качества обслуживания – ещё один круг задач, решаемых в теории распределении информации. Математический аппарат ТРИ базируется в основном на теории вероятностей, математической статистике. А так же используется – линейная алгебра, теория графов, системный анализ.

          А так же значительные результаты ТРИ получены благодаря сформулированному А.К.Эрлангом понятию статистического равновесия. Вероятностный процесс находится в состоянии статистического равновесия, если его вероятностные характеристики не зависят от времени.

 

          Основы ТРИ были заложены в работах Эрланга (1909-1918г.г.) по исследованию пропускной способности ПД пучка линий, при обслуживании ППВ с потерями и с ожиданием, он рассматривал входящий поток вызовов от бесконечного числа источников при показательном и постоянном времени обслуживания.

          В 1918 г. – Энгсет обобщил результаты Эрланга на случай обслуживания ПД пучка вызовов от конечного числа источника нагрузки.

          В 1927 г. – О’Делла опубликовал результаты исследования по НПД ступенчатым схемам.

          В этом же году Э.Молина – написал работу по теории группообразования.

          В 1928 г. Фрай написал первую книгу по теории вероятностей и в ней раздел теории теле трафика.

          В 1933 г. появились первые работы Хингина по исследованию систем с ожиданием.

          В 1943 г. шведский учёный Пальм обобщил результаты Эрланга на случай обслуживания потока с ограниченным последействием.

          С появлением координатных АТС возникло необходимость разработки методов расчёта многозвенных схем. Первое большое исследование в этом направлении было сделано в 1950 г. Якобееусом который основывался на опорных  распределений вероятностей состояний системы. Другой метод это метод вероятностных графов был предложен в 1955 г. ЛИ.

          С появлением автоматических МТС возникал необходимость расчёта пропускной способности по обходимым направлениям, которым занялся Вилкинсон в 1956 г.

          В 1953 году Клоз опубликовал первую работу по многозвенным не блокирующим коммутационным схемам, а вначале 60-ч годов серию работ по анализу и синтезу много звеньевых схем выполнил В.Беняш.

          В настоящее время широкое применение нашло метод статистического моделирования, которым занимаются башарин в Москве, Лившиц в Ленинграде, Шнапс в Риге.

 

 

Лекция 2.

 

Тема: Потоки вызовов.

 

          Потоком вызовов или событий называется последовательность вызовов, поступающих через какие-либо интервалы или какие-либо моменты времени. В теории массового обслуживания под потоком вызовов принято понимать не только последовательность вызовов, поступающих от группы абонентов или группы устройств телефонной сети, поток телеграмм, писем, поток неисправностей в станках и так далее.            

Потоки подразделяются на детерминированный и случайный потоки вызовов.

          Детерминированный поток вызовов – последовательность вызовов, в которой вызовы поступают в определенные, строго фиксированные неслучайные моменты или через определенные, строго фиксированные, неслучайные промежутки времени.

Случайный поток вызовов отличается от детерминированного тем и только тем, что моменты поступления вызовов и промежутки времени между вызовами являются не строго фиксированными, а случайными величинами. Детерминированные потоки являются частным случаем случайных потоков и на практике редко встречаются.

          Поток вызовов может быть определён тремя эквивалентными способами:

1.     последовательностью вызывающих моментов (t1,t2 …tn);

2.     последовательностью промежутков времени между вызывающими моментами (Z1,Z2 … Zn);

3.     последовательностью чисел, определяющих количество вызовов, поступающих в течении заданных отрезков времени R1, R2, …Rn (t0, t1) (t0, t1) (t0, tn).

При этом под вызывающим моментом понимается момент одновременного поступления одного, двух и более вызовов.

     Для задания случайных потоков вызовов, как и любых других случайных величин и процессов, используется функции распределения.

     Функция распределения вероятностей некоторой случайной величины Х называется функция:

 

                                  F (x)=P{X<x}

 

определяющая  вероятность того, что Х<х, где х – определённая, заданная величина. В связи с этим для случайного потока.

          1) совместный закон распределения n случайных вызывающих моментов:

          P{Ti<ti , i = 1,2 … n} = P{T1<t1 , T2 < t2 … Tn<tn}

 

где  Тi-i –й вызывающий момент; n – момент принимать любые значения.

          2) совместный закон распределения n случайных промежутков времени между вызывающими моментами:

 

          P{Zi<Zi , i = 1,2 … n} = P{Z1<Z1 , Z2<Z2 … Zn<Zn}

 

где  - Zi – промежуток времени между (i-1) и i-м вызывающими моментами.

          3) совместный закон распределения числа вызовов К на n отрезках времени. [t0,t1] , [t0,t2] , [t0,tn]

 

          P{K(t0,t1) = Ri, i=1,2 … n} = p{K(t0,t1) = R1K(t0,t2)}

 

где n может принимать любые значения.

 

          Потоки вызовов подразделяются на неоднородные и однородные. В неоднородном потоке вызовов каждый вызов имеет две и более характеристики. Например, вызовы, поступающие от абонентов телефонной сети, определяются моментами их поступления, направлением установления соединений, длительностью их обслуживания.

          Однородный поток вызовов характеризуется последовательностью, определяющий только закономерность поступления вызовов, то есть последовательностью моментов поступления вызовов является неоднородными, но для исследований целесообразно изучить последовательность моментов поступления вызовов, поэтому в дальнейшем под потоком вызовов будем понимать однородный поток вызовов.

          Математическое ожидание числа вызовов, поступающих в интервале времени [0,t] называется ведущей         функцией потока     (0,t) – эта функция неотрицательна неубывающая и в практических задачах принимает конечное значение.

          Поток вызовов классифицируются с точки зрения стационарности, ординарности и последствия.

          Стационарность потока.

          Поток вызовов являются стационарным, если при любом n совместный закон распределения числа вызовов за промежутки времени [t0,t1] [t0,t2] … [t0,tn]

                                      P{K(t0,ti); i=1,2 … n}

зависит только от длины промежутков времени и не зависит от момента t0.

          Это значит, что для стационарного потока вероятность поступления некоторого числа вызовов за какой-то промежуток времени зависит от длины этого промежутка и не зависит от его начала. В противном случае поток является нестационарным. Интенсивность потоков вызовов на телефонных сетях резко колеблются в зависимости в зависимости от времени в суток: количество вызовов за единицу времени в дневные и вечерние часы достигает max величины, а к ночные часы уменьшается. Это значит что поток вызовов, поступающий в течении суток являются нестационарным. Значит, что внутри ограниченного отрезка суток, например часа, не стационарность телефонного потока вызовов малоощутима, что позволяет для практических задач полагать стационарным.

          Ординарность потока – поток вызовов называется ординарным, когда вероятность одновременного поступления двух и более вызовов в любой момент времени невозможен. Примером ординарного потока является поток вызовов, поступающий на АТС от абонентской группы любой ёмкости. Потоки телефонных вызовов к абонентам диспетчерской или конференц-связи, потоки телеграмм в несколько адресов являются неординарными.

          Последействие потока. Поток вызовов являются потоками без последействия, если вероятность поступления K(t0,ti) вызовов за промежутки [t0,ti], i=1,2 … n

 

                   P{K(0,ti) – K(0,t0) = K(t0,ti) i=1,2 … n}

 

не зависит от вероятностного процесса поступления вызовов до момента t0. Иными словами, отсутствие последействия потока означает независимость течения случайного потока вызовов после какого-либо момента времени от его течения до этого момента.

Примером потока без последствия может служить поток телефонных вызовов, поступающих от большой группы источников. Действительно, лишь небольшая часть абонентской группы одновременно участвует в телефонных соединениях. Поэтому вероятность поступления, какого – либо числа вызовов  от большой группы источников на любом отрезке времени практически не зависит от процесса поступления вызовов до начала данного отрезка.

          Поток вызовов являются с потоком с последствием, если вероятность поступления того или иного числа вызовов за некоторый промежуток времени зависит от процесса поступления вызовов до начала этого промежутка.

                   Характеристики потоков вызовов.

          К основным характеристикам потока вызовов следует отнести ведущую функцию потока, его параметр и интенсивность.

          Под параметром потока  l (t) в момент времени t понимается предел отношения вероятности поступления хотя бы одного вызова за время [t,t*t] к длине этого отрезка времени  tпри t ®0

t®0
 

П(t,t+t)
 

=
 
                            

t
 
lim                            l (t)                   (1)

 

то есть параметр потока есть интенсивность вероятности наступления вызывающего момента в момент t.

          Исходя из [1], находим вероятность поступления одного и долее вызовов за время [t,t+t]

 

                   П1(t,t+t) = l(t) t + 0 (t),t®0.

 

          Согласно определению стационарного потока, вероятность поступления определённого числа вызовов за некоторый промежуток времени одна и та же не зависит от месторасположения на оси времени этого промежутка. Следовательно, и плотность вероятности поступления вызовов стационарного потока, то есть его параметр l(t) есть величина постоянная, не зависящая от момента t, то есть l(t) = l . Отсюда для стационарного потока

 

                   П1(t,t + t) = lt + 0(t),t®0.

 

          Параметр потока l(t) характеризует не поток вызовов, а поток вызывающих моментов, и эта характеристика относится не ко всему отрезку [0,t], а лишь к фиксированному моменту t.

          Интенсивность стационарного потока       называется математическое ожидание числа вызовов, поступающих в единицу времени. Единица времени может быть произвольно, однако в теории теле трафика в качестве такой единицы большей частью принимают среднюю длительность одного занятия. Для стационарного потока ведущая функция за промежуток времени [0,t] равна Л(0,t) =     t.

          Для нестационарных потоков используется понятия средней и мгновенной интенсивности.

          Средняя интенсивность потока на отрезке времени [t1,t2] есть

 

t2 – t1
 

[Л(0,t2) – Л(0,t1)]
 
                 m (t1,t2) =                                    (2)

 

мгновенная интенсивность

 

                 m         (t) = lim                                          (3)

t
 

Л(0,t + t) – Л(0,t)
 

t®0
 
         

 

          Так же как и параметр потока l(t), мгновенная интенсивность потока m (t) относится не к отрезку времени поступления вызовов, а только к моменту t. В то же время в отличие от параметра потока, характеризующего потока вызывающих моментов, мгновенная интенсивность потока характеризует поток поступления вызовов.

          Для любых потоков вызовов   (t) ³ l(t), при чет для ординарных потоков m (t) = l(t). Для стационарных потоков интенсивность и параметр постоянны: m (t) = m , l(t) = l следовательно, для любых стационарных потоков m ³l, а стационарных ординарных m =l.

Лекция 3

 

Тема: Простейший поток вызовов (ППВ)

 

 

Потоки вызовов можно рассматривать в виде следующего графа.

 

 

 

 

 

 

 

 

 

 


     ССРИ – структура системы распределения информации

      ДО – дисциплина обслуживания (с ожиданием и с потерями)

      ХКО – характеристика качества обслуживания формула сини то-

                   пилади.

 

                          ХКО = f (ПВ, ДО, ССРИ).

t
 
 


 

                          t1             t2    

                                 

    Z = t 2  -  t 1 , z 1 , z 2 – интервал  между вызовами.

 

Т1 , Т2 – тушаётган чакирикларнинг интервал сони.

F(x) – функция распределения.

 

1.     Ведомая функция l(0,t)

2.     Параметр потока l(t)

3.     Интенсивность m (t) – (бу вакт биринчи ичида канча вызов тушишини курсатади)

 

l(t) = m (t)

 

Простейший поток вызовов – это стационарный, ординарный поток, без последствия.

          Для задания ППВ используются вероятность Рк(t0,t0 + t) – это вероятность показывает, что с момента t0 до t поступит точно к вызовов.

 

 


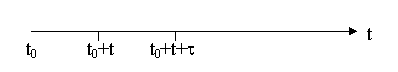
          Если рассмотрим отрезок времени [t0,t0 + t + t) который можно представить в виде двух отрезков [t0,t0 + t + t] = [t0,t0 + t) + (t+t).

t + t
 
          Для того, чтобы в течении отрезка [t0,t0 + t + t] поступило точно R вызовов, необходимо чтобы за первый промежуток времени поступило R, R-1 … R-i, и соответственно за второй промежуток 0,1,i или R вызовов.  

 

 

 

 

 


1.       К                     0

2.       К – 1               1

3.       К – 2                2                       

                                                        Рi ( t 0, t 0 + t )

                                                                   Рj ( t 0 + t 1 * t 0 +t + t )

 

0                     К

      t                      t

 

 

O – t  - интервалда тушган чакириклар сони

К - t    - интервалдан тушган вызов сони

РК (t 0,t 0  + t  + t )  - это вероятность поступления точно  R вызовов за отрезок времени  (t 0,t 0 + t + t )

PК - 1 (t 0,t 0 + t ) – за первый отрезок времени (t 0,t +t)

Рi (t 0,t +t)  - за второй отрезок времени.

Согласно определению простейший поток является стационарными отсюда вероятность поступления того или иного числа вызовов за отрезки времени  (t 0,t 0 + t + t) или (t 0,t 0 + t) не зависят от момента отчета, а зависит только от длины отрезка времени. Упростим выражения.

 

                               РК (t 0,t 0 + t  + t) = РК  (t +t)

                               Рi (t 0,t0  + t) = Рi (t)

                               Рj – i (t 0 + t,t 0 + t + t) = Рj (t)

 

Простейший поток является потоком без последствия. Поэтому независимыми является событие, заключающиеся в поступлении какого – либо числа вызовов за первый и второй промежутки времени и вероятность поступления точно R вызовов за время (t+t) при i=0,1,R.

 

 Pk(t + t) = Pk(t) * P0(t,t + t) + Pk-1 (t) * P1(t,t + t) + … + P0(t)*Pk(t,t + t);                         

                K

Pk(t+t) = å Pi(t) Pk-1 (t)            (1)

               i=0

 

Выражение [1] представляет собой систему, состоящую из бесконечного числа уравнений, поэтому устремим отрезок времени t®0. В следствии ординарности потока П2(t,t + t) = 0(t), t®0.

П2(t) – интервал поступления двух и более вызовов, отсюда 1 выражение примет вид:

 

          Pk(t + t) = PR(t) * P0(t) + Pk-1(t) * P1(t) + 0 (t)

 

определяется вероятность P0(t) и Р1(t).

 

Р1(t) = П1(t) – П2(t)

П1(t) = Р1(t) + Р2(t)

П2(t) = Р2(t) + Р3(t)

Р1(t) = П1(t) – П2(t) = lt + 0 (t)

 

где 0 (t) = ординарность потока

 

П1(t,t +t)
 

t
 

П2(t,t +t)
 
                   lim                           = 0           П2(t,t+t) = 0 (t)

                   t®0                                            

 


t
 
          l(t) = lim                            = lim               ;

                   t®0                                                   t®0

 

          П1(t) = l(t)t + 0(t)

П1(t) = l t + 0(t)

P1(t) = l t + 0(t)

P0(t) = П0(t) – П1(t)

P0(t) = 1 – П1(t) = 1 - l t + 0(t)

 

Рк (t + t) = Pk (t) [lt + 0(t)] + Pk-1 (t) * lt + 0 (t);

 

 


                             = l Pk(t) + l Pk-1 (t) +              ;

 

 


lim                            = - l Pk(t) + l Pk-1 (t).

 

 

 

 

 

 

 

 


                            

t + t
 

P’k(t) = - l Pk(t) + l Pk-1(t) , k = 0,1,2 …

Получим систему ДМФ уравнений первого порядка.

Решение этих систем даёт.

K!
 

(lt)k
 
Pk(t) =                       e -lt          - эта формула называется формулой

                                                 Пуассона

 

Пример: l = 180 выз/час

                t = 8 мин

               К = 5

(180 * 8/60)5
 
              Рк(t) = ?

5!
 
Pk(t) = P5(8 мин) =                                      е –180*8/ 60 = 0,3

 

Определяем вероятность поступления более чем i вызовов.

¥
 

K=i+1
 
Pi > i(t) = å Pk(t)

 

 

i
 

¥
 

K=0
 
å Pk(t) = 1

K=0
 

K=i+1
 

¥
 
P>i (t) = å Pk(t) = 1 - å Pk(t)

l = 180 выз/час

t = 8 мин

i = 6

Р > i (t) = ?

P > i (t) = P6 (8 мин) = 1 – (Р0(8 мин) + … Р6(8 мин))

i
 
Вероятность поступления не более i вызовов определяется по формуле.

K=0
 
P £ i(t) = å Pk(t)

Определяем рекуретную формулу для расчёта вероятности

(lt/K!)k * e -lt
 
 


(lt)k-1/(k-1) * e -lt
 

Pk-1(t)
 

Pk(t)
 
Pk(t).                           =                                    =                    

 


Pk(t) =              Pk-1(t)

Лекция 4.

Тема: Нестационарный и неординарный поток Пуассона.

          Нестационарный поток Пуассона называется ординарный поток без последействия, то есть это ординарный поток без последействия, для которого в любой момент времени t существует конечный параметр l(t), зависящий от момента t. Для этого потока вероятность поступления К вызовов с момента t0 до момента t определяется по следующей формуле:

[    l(4) du]k
 
 


K
 
Pk(t0,t) =                                   e -     l(4)du.

допустим (t0,t) = t, тогда l(4) = l    l(4)du = l (t-t0) = lt

Стационарный неординарный поток без последействия называется ординарным потоком Пуассона.

Для неординарного потока Пуассона вероятность того, что за время t будет n вызывающих моментов определяется по формуле Пуассона.

n!
 

(lt)n
 
                   Pn(t) =               e -lt

          Различают два типа неординарных потока: это поток вызывающих моментов и поток вызовов. Поток вызывающих моментов характеризуется вероятностью появления точно i вызывающих моментов в промежутке времени t. Эта вероятность определяется формулой Пуассрна, отсюда число вызовов поступающий в каждый вызывающий момент является постоянной величиной и равна е – называется неординарности потока.

          В этом случае Pk(t) определяется по формуле

Pk = n/e       n = k/e

 

(k/e)!
 

(lt)k/e
 
Pk/e(t) =              = e -lt

 

Для других неординарных потоков характеристика неординарности является случайной величиной.

 

 

 

Тема: Поток с простым последствием.

          Для потоков с простым последействием основным отличительным признаком является зависимость параметра этого потока от состоянии коммутационной системы. Под состоянием коммутационной системы понимается число занятых входов, выходов, промежуточных линий и так далее.

Отсюда под потоком с простым последейтсвием понимается ординарный поток для которого в любой момент времени t существует конечный параметр потока в состоянии S(t), зависящий только от состояния S(t)Ке в момент t.

 
 
lS(t) – параметр потока с простым последействием.

 

t®0
 

t
 

П1(t0,t + r) S(t)
 
lS(t) = lim                           

 

 

 

Среди потоков с простым последействием важное место занимает симметричный поток. Симметричным потоком называется такой поток, параметры которого зависят от числа i – свободных источников. Поэтому параметр X i , i = 0, 1, 2 … n.

Частным случаем симметричного потока является примитивный поток ( поток от ограниченного числа источников).

Примитивный поток – это такой поток, параметр которого прямо пропорционально количеству свободных источников.

                   li = (n – i) * a

   n – общее число источников

   i – число занятых источников.

 

 

 

 

 

 


     Потоки с повторными вызовами так же являются потоком с простым последействием.

Поток с повторными вызовами состоит из двух потоков:

1.     Потока первичных вызовов

2.     Потока повторных вызовов.

Параметр потока определяется

lå = lпер + lпов

 

 

 

Тема : Поток с ограниченным последействием.

     Потоком с ограниченным последействием называется такой поток для которого промежутки между вызовами являются взаимно независимо случайными величинами.

                             Fk(t) = P {Zk £ t, k=1,2}

Частным случаем потока с ограниченным последействием является рекуретный поток, для рекуретного потока имеет место

F1 (t) = F 2 (t) =  F3 (t) … F (t)

 

Простейший поток вызовов является частным случаем рекуретного потока.

                                   F (t) = P { z £ t } = 1 – e - l t

    К потокам с ограниченным последействием относится также поток Эрланга.

ППВ
 
Поток Эрланга m – го порядка получают следующим образом. Из простейшего Потока ударяется m  вызовов и остаётся m + 1.

t
 

t
 

t
 

Поток Эрланга второго порядка.
 
                   х х х х х х х х х х

ПЭ2
 
                   х        х        х

m + 1
 

l
 

lm =
 
                      х         х         х

Тема: Поток освобождений.

          Потоком освобождений называется последовательность моментов окончания обслуживания вызовов. Пусть в момент времени t в занятом состоянии находится  линий, найдём вероятность того, что за время t освобождаётся точно i линий.

i
 

R
 
 


t
 

t+l
 

t
 

t
 
                                     

 

          Pi (R, t) = Cki Pi (1 - P)

где Р-вероятность того, что за время t освобождается только одна линия.

Если время обслуживания абонента подчиняется экспотенциальному закону, то

                             F(t) = 1 –e -bt

          b = 1 / t  интенсивность обслуживания, где Р = 1 – е bt

          t  - среднее время обслуживания

Pi {R, t} = Cki Pi (1 – P)k-i = Cki (1 – e -bt)i e -b(k-i)t

P0 (k, t) = e -kbt - это вероятность того, что за время t не будет освобождаться ни одна линия. Определяем вероятность хотя бы одной линии за время t.

j=0
 

¥
 

j !
 

(Kbt)j
 
          П1(t) = 1 – P0 (R, t) = 1 – e -kbt = 1 -å (-1)j *                          =

(Kbt)2
 

0(t)
 

3 !
 

2 !
 

(Kbt)3
 
          = Kbt -           +             = Kbt + 0(t)

 

 

0(t)
 

t
 

t®0
 
g (t) = lim (Rb +                ) = Rb

 

 

Из этого видно что поток освобождений обладает свойством ординарности.

1.     Определяем среднее число поступающих вызовов для ППВ за время t.

При объединении n независимых простейших потоков с l1 … ln образется общий простейший поток А вероятность поступ точно К вызовов за отрезок времени t определяется формулой Пуассо.
 
 


n1 n2 … nm

¥
 
P1 P2 … Pm

 

(lt)K-1
 

(R-1)!
 

R!
 

(lt)R
 

¥
 

¥
 

¥
 

k=0
 

R=0
 

R=0
 
M [k] = å k PR (t) = å k                          e -lt = lt * e -lt * å                 = lt

 

M(k) = lt

 

2.     Дисперсия числа поступающего вызова равна

 

m
 

å * ni
 
Д[k] = lt                             M[k] =                 

1
 
 


m-1
 
Д[k] =                å (ni – M(k))2

Определяем распределения интервала между вызовами

Согласно определению функции F(Z) равна вероятности того, что промежуток времени между вызовами Z будет меньше заданного промежутка t, что равносильно вероятности П1(Z) того, что за промежуток t поступит один и более вызовов.
 
     F(t) = P{Z £ t}

Z – интервал между вызовами

 

 

 

F(t) = P{Z  £ t} = П1(t) =  П0(t) – P0(t) = 1 – e -lt  при t ³0.

Таким образом распределение промежутков времени между вызовами простейшего потока показательному закону (отрицательному экспотенциальному). Функция F(Z) зависит от параметра потока l.

          Функция распределения интервала между вызовами.

Пример:

l = 180 выз/час

t = 3 мин

F(t) = ?                           F(t) = 1 – е180*3 = 0,7

 

 

Лекция 5.

Тема: Понятие о телефонной нагрузке. Колебание нагрузки.

          Суммарное время обслуживания вызовов принято называть нагрузкой. Следует различать нагрузки: поступающую, обслуженную и потерянную. I0 = это нагрузка которая была обслужена КЕ за рассматриваемый промежуток времени. За единицу измерений нагрузки принято одно часо-занятия. Одно-часо-занятия – это такая нагрузка, которая может быть обслужена одним выходом в течение часа при непрерывном занятии этого выхода.

Под интенсивностью нагрузки понимается нагрузка за единицу времени, обычно за 1 ч.

          Интенсивность обслуженной нагрузки, выраженная в эрлангах, количественно равна среднему числу одновременно занятых выходов, обслуживающих эту нагрузку. Под поступающей на КЕ за промежуток времени [t1, t2] нагрузкой I[t1, t2] понимается такая нагрузка, которая была бы обслужена коммутационной системой за рассматриваемый промежуток времени, если бы каждому поступающему вызову тотчас было предоставлено соединение со свободным выходом.

          За единицу измерения поступающей нагрузки принято одночасо-занятие, интенсивности поступающей нагрузки – один эрланг. Для количественной оценки интенсивности поступающей нагрузки, создаваемой простейшим потоком вызовов, количественно равна тематическому ожидание числа вызовов, поступающих за время, равное средней длительности одного занятия.

          Потерянная КЕ в течении промежутка времени [t1, t2] нагрузка Iп (t1t2) представляет собой разность между поступающей и обслуженной нагрузками за рассматриваемый промежуток времени. Так как ТРИ в большинстве случаев рассматривается обслуживание случайных потоков вызовов.

При этом поступающая, обслуженная и потерянная нагрузки являются случайными величинами.

Интенсивность нагрузки вступающая в разные часы суток различна или в одни и те же часы суток, но в разные дни тоже различна. Наблюдениями установлено, что наряду со случайными колебаниями интенсивности нагрузки по часам суток, дням недели и месяцам года существуют и периодические, относительно регулярные колебания, которое необходимо учитывать при прогнозировании нагрузки.

          Из значительной степени они зависят от распорядка жизни в городе и структурного состава абонента включённых в АТС.

 

 

 

 

 

 

 


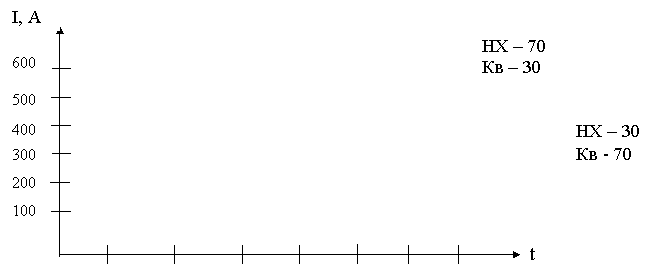
9        11         13           15        17        19        21      23

Для удовлетворительного качества обслуживания абонентов в любое время суток расчёт объёма оборудования необходимо выполнять исходя из значения интенсивности нагрузки в тот час когда она является наибольшей. Этот час называется часом наибольшей нагрузки и сокращенно обозначается ЧНН. Час наибольшей нагрузки – это непрерывный интервал времени в 60 мин, в течение которого средняя интенсивность нагрузки является наибольшей. Измерения проводятся обычно в рабочие дни двух последовательных недель 2 раза в год в месяцы наибольшей нагрузки. Результаты исследования записываются в таблицу, из чего определяется величина интенсивности нагрузки в ЧНН.

Степень концентрации нагрузки в ЧНН оценивается коэффициентом концентрации нагрузки:

Усут
 

УЧНН
 
                             RЧНН =                 

Величина коэффициента концетрации в основном зависит от струк­турного состава абонентов АТС и лежит в пределах 0,09 – 0,15. Чтобы объём оборудования был минимальным и загрузка его равномерной, величина коэффициента концентрации должна его равномерной, величина коэффициента концентрации должна быть минимальной. Наблюдениями установленно, что нагрузка в ЧНН в разные дни недели одинакова, причём кроме случайных колебаний имеют место и регулярные колебания нагрузки по дням недели. В субботу и воскресенье нагрузка значительно ниже, чем в рабочие дни недели. Регулярные колебания нагрузки наблюдаются и по месяцам года (декабре, январе, феврале, марте, ноябре).

 

t    9 – 915    9­­­15 – 930    930 – 945    945 – 10     1000 – 1015    1015 - 1030

 

 

 

 

 

 

 


                                                                  

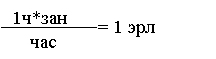
å Vi
 
Интенсивность обслуженной нагрузки равна среднему числу занятых линий

n – число источников нагрузки
 

n
 
                           У =                          

 


Лекция 6.

Тема: Параметры и расчёт интенсивности телефонной нагрузки.

Основными параметрами телефонной нагрузки является:

1.     Число источников нагрузки – n.

2.     Среднее число вызовов поступающее от одного источника в ЧНН-с.

3.     Среднее время обслуживания одного вызова – t.

 

У = n * c * t

Учитывая активность источников нагрузки для расчёта интенсивности нагрузки все источники делятся на определённые категории.

1.     nки           3. nнх

2.     nкк           4. nтф.          5. nсл – соединительные линии от УАТС

 

n = nки + nкк + nнх + nтф + nсл

 

Эта величина составляет ёмкость АТС.
 

 

1)    

6¸10
 

6¸10
 

1,9¸3,4
 
Ски , Скк , Снх , Стф , Ссл.

1)     0,7 ¸ 1 выз/час

2)     1 ¸ 1,3

 


nки + nкк + nнх + nтф + nсл

 
 

nки Ски + nккСкк + nнхСнх + nтфСтф + nслСсл

 
 
С =                                                                                                                                                                                          

 

Средняя длительность занятия коммутационной системы при обслуживании одного вызова – t.

Под длительностью одного занятия понимается промежуток времени с момента снятия абонентом микротелефона до момента возвращения приборов станции, занятых в обслуживании вызова, в исходное состояние.

Величина t  зависит от того каким исходом завершается поступивший вызов. 

Возможно следующие исходы :

1.     Вызов завершается разговором – при этом среднее время занятия

tр

2.     Вызов не завершается разговором по следующим причинам:

а) занятость вызываемого абонента – tзн.

б) не ответ вызываемого абонента – tно.

в) по техническим причинам

     (занятость линии и приборов),

     занятии неисправных приборов – tтех.

г) Из-за ошибки вызывающего

     абонента                                     - tош.

Вызов поступающий на АТС, в зависимости от состояния КС, линии может либо окончиться разговором или не окончиться разговором это явление обозначает через:

     Рр – доля вызовов которые завершились разговором

     Рзн – не завершились разговором из-за занятости вызываемого     

   абонента

          Рно – не ответ абонента

          Ртех – по техническим причинам

          Рош – из-за ошибки при наборе номера вызывающего абонента.

                   Рр + Рзн + Рно + Ртех + Рош = 1

          Рр = 0,5 ¸ 0,6 , Рзн = 0,2 ¸ 0,3 , Рно = 0,08 ¸ 0,12

          Ртех = 0,03 ¸ 0,05 , Рош = 0,04 ¸ 0,01

1.     Разговор состоялся. Средняя длительность этого вида занятия может быть рассчитана по формуле:

Tp = tco + tc + tпв + T + t0

                             tco = 3 сек.

 

tyc =  m * tнн = tнн - время набора одной цифры, m – число знаков.

tyc =  1,5 * m, АТСДШ

tyc = 1,5 * m, с АТСК – время установления соединения.

tпв = 7 ¸ 8 с

Тр – зависит от категории источника

Тки ¸ 130 ¸ 140 сек.

Ткк = 120 ¸ 130 сек.       при дневном ЧНН

Тсл = 100 ¸ 110 сек.

Тки = 220 ¸ 230 с            Тнх = 125 ¸ 130 с            вечерний ЧНН

Ткк = 205 ¸ 210 с            Тт = 160 ¸ 165с              Тсл = 125 ¸ 130

 


å ni ciTiPpi
 

å ni ciTiPpi
 
                   Тр =                                    - средняя продолжительность

                                                                 разговора по АТС в целом.

2.     Разговор не состоялся из-за занятости вызываемого абонета.

tзн = tco + tyc + tсзн + to

          tcз = 4 ¸ 5 с    если ДШАТС

          tсз = 0            если АТСК

3.     Не ответ абонента.

tно =  tсо + tус + tсно + tо

          tсно – время посылки вызова при не ответе абонента.

          tсно = 30 сек., tтех = 10 ¸ 15 сек., tош = 18 ¸ 20 сек.

4. Разговор не состоялся из-за ошибки вызывающего абонента                          

    tош =18 ¸ 20 с.

5.Разговор не состоялся по техническим причинам.

                   tтех = 10 ¸ 15 с

          Средняя длительность одного занятия на АТС в целом может быть рассчитана.

t = tрРр + tзнРзн + tноРно + tошРош + tтехРтех =

Pзнtзн + tноРно + tошРош + tтехРтех
 

Ррtр
 
= Ррtр [1 +                                                  ] = lPptp

 

 

У = n * c * t = l * n * c * tpPp  - интенсивность перегрузки.

 

l - это коэффициент показывающий увеличение интенсивности нагрузки за счёт технических вызовов которые не закончились разговором.

l - определяется исходя из величин Рр; Тр.

l = ¦ (Рр; Тр)

 

 

 

 

Лекция 7.

 

Тема: Расчёт и распределение телефонной нагрузки.

 

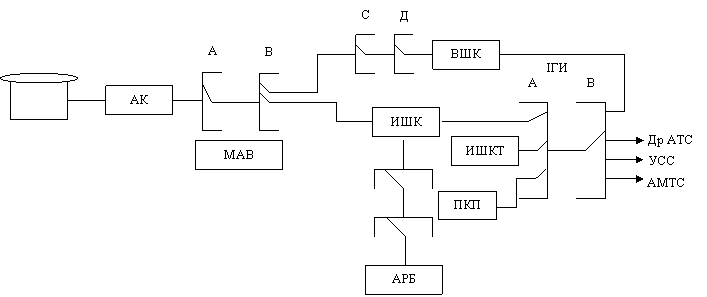          Расчёт телефонной нагрузки рассмотрим на примере АТСКУ и ДШАТС.

1)     на АТСК

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1.     Определим общию интенсивность возникающий нагрузки I от каждой категории абонентов.

У = n * c * tpPpl

2.     Определяем нагрузки на входе I ГИ.

 

 

 

 

 

 

 

 

 

 


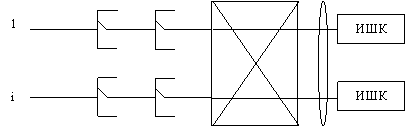
                   УИШК = У / N – число тысячных групп

                   УвхIГИ = å УИШКi + УИШКт + У ПКП

                   УвыхIГИ = УвхIГИ * (1 – РIГИ) * tвых IГИ / tвх IГИ

          tвых IГИ = tвх IГИ + tсо + tнн * m

 

                             Увн

Увых IГИ
 
                             УАМТС

                                          Умеж.стан.

                             УУСС

 

МКБ
 

КБ
 
Определяем нагрузку поступающего на маркеры.

 

                             Укб = Скб * tкб

                             Ум = См * tм     См = Скб

tм
 
                            

tкб
 
Ум = Укб *                     

 

 

 

          Нагрузка поступающая на регистр определяется по формуле.

         

Урег = Угришк * tрег / tвх I ГИ

 

Тема: Расчёт межстанционных потоков.

 

          Обычно телефонная сеть содержит несколько АТС поэтому необходимо определить нагрузку между станциями. По величине этой нагрузки рассчитываются необходимое число линий между этими АТС. Обозначим через Уij – нагрузку от АТС i к АТС j величина этих нагрузок можно задавать следующей матрицей.

 

 


                                      У11   У12   …   У1m

                   Уij      =      У21   У22   …   У2m

                                      Уm1   Уm2  …   Уmm

 

 

Исходящей нагрузкой этих станций является:

 

 

m
 

j=1
 
                   Уисх i = å Уij

 

 

          Уисх i = Увых  I ГИ – УАМТС – У­УСС

 

Межстанционная нагрузка может определяется при двух предположениях:

1)     Равномерное распределение нагрузки.

2)     Распределение нагрузки с учётом коэффициента тяготения.

Если имеет место 1 предположение, то межстанционная нагрузка определяется по формуле:

 


                             Уij = Уисх i *                                      

 

Эта формула не учитывает расположение станции и расстояние между станциями и поэтому обычно не используется для расчёта межстанционной нагрузки. Межстанционная нагрузка рассчитывается с учётом коффициента тяготения.

 

 

nij Уисх i
 

å ni k Уисх к

 
          Уij = Уисх i                      

 

nij – нормированный коэффициент тяготения.

 

nij
 
          nij = ¦(lij)               lij = АТСi до АТСj

 

 

 

 

 

 

 


Тама: Распределение нагрузки по ступеням искания.

 

          Общая нагрузка, поступающая на входы I ГИ, может быть определена по формуле:

 

                   Увх ГИ = Унх + Укк + Ут

 


                   Увых ГИ = Увх I ГИ                       = Увх ГИ * 0,95

 

Увх I ГИ
 
 


å Ni Ci
 
                   Увх ГИ =                ;

 

 

                   Увых ГИ = tвх ГИ – (0,6 + tc 0 + ntn);

 

0,6 – среднее время установления соединения через ступень I ГИ.

n – число цифр станционного кода, ДШАТС числу цифр набираемого номера АТСК.

 

tвых I ГИ
 
 


tвх I ГИ
 
                   Увых I ГИ = Увх I ГИ *                       ( (1 – PI  ГИ) = 0,003

 

                   УАМТС = 0,05 * Увых I ГИ ; УУСС = 0,03 * Увых I ГИ

 

                   Уисх = (Увых I ГИ – УАМТС  - УУСС)

 

Уисх j * nij
 
 


å Уисх j * nij
 
                   Уij = Уисх i                                      

 

Увх II ГИ
 

n
 

i
 
                   Увх II ГИ = å Уij

 


                   Увых II ГИ = Увых II ГИ                             =   (1 - PII ГИ) = 0,98

 


2
 
                   Увх III ГИ =             

n
 
                   Увых III ГИ = 0,98 * Увх III ГИ; Увх ли =                 .

 

 

 

 

 

Лекция 8.

 

Тема: Характеристика качества обслуживания вызовов и дисциплина обслуживания вызовов.

 

          Качество обслуживания поступающих вызовов характеризуется возможностью соединений или длительностью ожидания предоставления соединений.

          Применяется следующая дисциплина обслуживания вызовов:

1.        Дисциплина обслуживания без потерь – называется такая дисциплина, когда любому поступающему вызову немедленно продостовляется свободная линия или прибор АТС. Это дисциплина обслуживания не применяется по экономическим соображениям, так как требует большие затраты на организации сетей

2.        Дисциплина обслуживания с потерями. При этом часть вызовов обслуживаются немедленно, а другая часть вызовов получает отказ в обслуживании или обслуживается с некоторым ожиданием.

В свою очередь дисциплина обслуживания с потерями делятся:

а) дисциплина обслуживания с явными потерями;

б) дисциплина обслуживания с условными потерями.

Дисциплина обслуживания с явными потерями эта такая дисциплина, когда вызовов поступающий в момент занятости всех доступных линий получает отказ и полностью покидает систему обслуживания. Дисциплина обслуживания с условными потерями называется такая дисциплина, когда вызов поступающий в момент занятости всех приборов и линий обслуживаются после некоторой задержки или ожидания.

          Это дисциплина реализуется двумя способами:

1)     С организацией ожидания (система с ожиданием);

2)     Повторным поступающем вызовов (система с повторными вызовами)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


Каждая ДО имеет свою характеристику качества обслуживания. Для ДО с явными потерями качества обслуживания по вызову характеризуется:

1)     Вероятность потерь по вызовам.

 

Cпот (t1, t2)
 
 


C (t1, t2)
 
Pв =                      

 

где Спот (t1, t2) – число потерянных вызовов с момента t1 до момента t2.

С (t1, t2) = число поступающих вызовов с момента t1 до мо­мента t2.

 

2)     Вероятность потерь по нагрузке.

 

 


Pн (t1, t2) =                               

 

Ун (t1, t2)
 

где                 потерянная нагрузка с момента t1 до момента t2.

-        

У (t1, t2)
 
поступающая нагрузка с момента t1 до момента t2.

 

 

3)     Вероятность потерь по времени.

 

å ti
 
 


t2 – t1
 
Рt =                               

 

 

где å ti – суммарное время в течении которого все линии были в за­нятом состоянии.

          Потери по времени за отрезок времени [t1, t2) – это доля времени, в течение которого все соединительные пути, доступные группе источников, заняты.

          Дисциплиной обслуживания с условными потерями называется такая, при которой поступающий на КС в момент отсутствия соединительных путей вызовов не теряется, а обслуживается с ожиданием.

Если используется ДО с ожиданием, то характеристика качества обслуживания вызова является:

1.     вероятность ожидания.

 

P[g>0] g - время ожидания всегда должно быть больше нуля.

 

P[g>0] = М(С3)/М(С)

 

где М(С3) – количество задержанных вызовов или ожидающий вызов.

М(С) – математическое ожидание числа поступающих    вызовов.

 

2.     Функция распределения времени ожидания.

 

P[g>t] = C(g>t)/C

 

С(g>t) – число вызовов ожидающих больше чем t.

С – общее число поступающих вызовов.

 

3.     Среднее время ожидания.

 

g

 

4.     r – среднее число вызовов находящийся в очереди.

 

Если вызовов обслуживается после многократных повторений попыток установить соединение, то имеет место дисциплина обслуживания с повторением.

Если имеет место ДО с повторными вызовами, то в качестве показателей используется:

1.     Вероятность потерь первичного вызова.

2.     Вероятность потерь повторных вызовов.

3.     Вероятность потерь произвольного вызова.

Для количественной оценки качества обслуживания с повторением вызовов рассчитываются:

          а) среднее число повторных вызовов на один первичный вызов – С0;

          б) вероятность потери поступившего первичного вызова - Р.

          в) вероятность потери поступившего повторного вызова - РП;

          г) вероятность потери любого поступившего вызова - РВ;

          д) вероятность потерь по времени - Рt;

          ж) вероятность потерь по нагрузке – Рн.

На практике кроме дисциплины ОБС с явными и условными потерями встречаются разные их комбинации.

Дисциплина обслуживания с комбинациями потерями называется такая, при которой часть поступающих вызовов обслуживания с явными потерями, а другая часть с условными или все вызовы обслуживания с условными потерями ограниченными по каким либо признакам. Например ограничив число вызовов находящей на ожидании, или абонент получивший отказ в соединении повторяет попытки установления соединений. После нескольких попыток установления соединения абонент отказывается от дальнейших попыток. Для оценки качества обслуживания с комбинированными потерями используются характеристики дисциплин обслуживания с явными и условными потерями.

Дисциплина обслуживания с потерями бывают без приоритетов и с приоритетами.

Дисциплина обслуживания с приоритетами называется такая при которой поступающие вызовы делятся на категории и вызовы более высокой категории при обслуживании имеют какие-либо преимущества перед вызовами более низкой категории, и без приоритетов, если ни один из поступающих вызовов не имеет каких либо преимуществ в обслуживании перед другими, пример обслуживания с приоритетом может служить установления местных и междугородних соединений.

 

Лекция 9

 

Тема: Методы расчёта одно-звеньевых коммутационных систем.

 

Расчёт однозвенных полнодоступных схем.

 

Обслуживание вызовов простейшего потока.

 

Подпись: КС включено полно¬дос¬туп¬но V линий. Вызов об-служивается по дисципли-не с явными потерями. Каждый вызов занимает для своего обслуживания свободной линии на слу-чайное время распреде-лённая по экпонициальному закону с пареметром b.

          Пусть имеется однозвенная полнодоступная КС на вход этой КС поступают вызовы простейшего потока с параметром l.На входе

 

                   F(t) = 1 – e-bt

 

          Требуется определить характеристики качества обслуживания вызовов. Для определения характеристик качества обслуживания вызовов необходимо найти вероятностные состояние системы.

          Pi(t) – вероятность того, что в момент вемени t система находиться в состоянии i.

          Различают микросостояние системы и макросостояние системы. Если V=2, то полнодоступноый пучок имеет следующие микросостояние:

                             0 0 – буш – буш

                             0 1 – свобод – свобод

                             1 0 – занят – свобод

                             1 1 – занят

Это же система имеет следующее макро состояние:

                             0 (0 0)

                             1 (10, 01)

                             2 (1 1)

Таким образом пучок из V линий имеет 2V микросостоянии, или V+1 макро состоянии. Причём V+1£2V.

 

 

 

Для определения характеристик качества обслуживания вызовов достаточно рассматривать макро состояние ПД пучка. Таким образом необходимо определить

t
 

t + t
 

t
 
                   Pi(t)             i=0,1 … V.

 

 

 

 

 

 

 

 

                   0                 i

                   1                 i-1

 

 

                  

                   i-1               1

                   i                  0

                   i+1              -1

                   i+2              -2

¥
 

Pi (t + t) = å Pj (t) * Pji (t)

j=0
 

Так как простейший поток является ординарным потоком кроме того поток освобождений является так же ординарным потоком. Поэтому вероятность поступления за время t два и более вызовов иметь очень малое значение. Так же вероятность освобождений два или более линий так же очень мало.

 

0 (t) = Pi-1 (t) * Pi-1 (t) + Pi (t) Pi,i (t) + Pi+1 (t) Pi+1,i (t) + Pi-1,i (t) =  = l t + 0 (t)

         

          Pi+1,i (t) = (i + 1) b t + 0 (t)

 

          Pi,i (t) = [(1 - lt) + 0 (t)] [1-ibt + 0 (t)] = 1 – (l + ib)t + 0 (t)

 

Pi (t + t) = lt * Pi-1 (t) + (1 – (l + ib)t) * Pi (t) + (i + 1) bt * Pi+1 (t) *0(t)

 

 


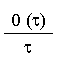
                         = l Pi-1 (t) – (l + ib) Pi (t) + (i + 1)b Pi+1 +         

 

 


t ® 0
 
lim                            = Pi (t) = lPi-1 (t) – (l + ib) Pi (t) + (i + 1)b * Pi+1 (t)

 

 

          Эрланг показал и сформулировал теорему согласно которому при t ® ¥ величина Pi (t) не будет зависеть от t и поэтому Pi (t) = Pi.

Такой режим называется установившемся режимом.

Таким образом, для установившегося режима имеем:

 

          lPi-1 – (l + ib)Pi + (i + 1)b Pi+1 = 0              i = 0, V

          -l P0 + bP1 = 0

          l P0 – (t + b) P1 + 2bP2 = 0

 

 

 

 


          l PV-1 - Vb PV = 0

 

Решения этой системы уравнения возможно с учётом условия нормировки.

V
 

i=0
 
          å Pi = 1

 

l
 

(l/b)­­­­­2
 

2!
 

b
 
          Pi =           P0         P2 =           P0

 

 

 


i!
 
                             Pi =           P0

 

 

          å            P0 = P0 å              = 1

 

 

1
 
 


å (l/b)i / i!
 
          P0 =                                         b = 1 / t       l/b = lt = y

 

(l/b)i / i!
 

y1 / i!
 
 

 


å yj / j!
 

å (l/b)j / j!
 
Pi =                        =                -> эта формула называется распределением

    Эрланга

 

 

 

(l/b)i / i! = 1         Pi = ¦ (y, V, i)

 

 

Значения вероятности Pi можно было бы определить, используя методику теории Марковского процесса.

Марковский процесс – это такой процесс, когда будущее определяется настоящим и не зависит от предыстории.

Кроме того рассматриваемый процесс является частным случаем Марковского процесса, который называется процессом рождения и гибели.

При этом поступлении нового вызова считается процессом рождения, освобождения линии процессом гибели.

Процесс рождения и гибели – это такой процесс, когда из состояния i возможно переход только на соседнее состояние  (i + 1 и i – 1), либо система остаётся в состоянии i. При этом вероятность того, что за время t ® 0 произойдёт более одного изменения состояния, равно 0(t).

При использовании процесса рождения и гибели значения вероятности Pi­ определяется в следующем порядке:

1. Составляется диаграмма переходов.

 

 

 

 

 

 

 

 


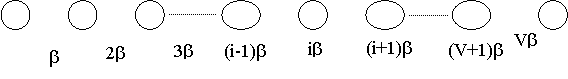
2. Анализируя каждую вершину диаграммы переходов составляется уравнения для вероятностного состояния.

 

-lP0 + bP1 = 0

lP0 – (l + b)P1 + 2bP2 = 0

 

 

 


lPV-1 - VbPV­ = 0

 

1.     В момент t пучок находится в состоянии (i – 1) Pi-1 (t) и за время t на обслуживание поступит точно один вызов Pi(t). Тогда вероятность перехода пучка за промежуток времени (t, t + t) из состояния i – 1 в состояния i составляет Pi-1, i (t) = Pi-1 (t) Pi (t). При этом вероятность Pi (t) является условной. Она определяется с учётом того, что в момент t пучок находился в состоянии i – 1.

2.     В момент t пучок находится в состоянии i + 1 Pi+1 (t) и за время t освободится точно одна из i + 1 занятых линий Pi+1 (t). Вероятность перехода пучка за промежуток времени [t, t + t) из состояния i + 1 в состояние i составляет Pi+1,i (t) = Pi+1 (t) Pi+1 (t).

3.     В момент t пучок находится в состоянии i Pi (t). За время t пучок не изменяет своего состояния, он остаётся в состоянии i, т.е. на пучок не поступает вызов и в нём не освобождается ни одна из занятых линий, вероятность этого события (1 Pi (t) – Pос i (t)]. Вероятность перехода пучка из состояния i в состояние i:

 

Pii­ (t) = Pi (t) [(1 – Pi (t) – Poci (t)]

 

4. За время [t, t+t] в пучке происходят два и более переходов в результате поступления двух и более вызовов, либо освобождение двух и более линий, либо поступления одного и более вызовов и одновременно освобождение одной и более линий. Вероятность таких событий составляет 0 (t).

 

Рассмотрим пример расчёта:

 

У %!
 

1
 

1
 
 


1+У + (У2/2!) + (У3/3!)
 

å Уj / j!
 
У = 2 Эрл                      Po =                      =                                        =

V = 3

                                     

1 + 2 + 2 + 8/6
 
Pi = ?                              =                             » 0,35

 

 

У
 
 


å Уi / j!
 
P1 =                      = 0,25                             P2 = … 0,25

 

 

Для расчёта Pi целесообразно использовать рекуретную формулу.

 

 

 

Pi+1
 

У
 
 

 


Уi +1
 

Уi / i!
 

Pi
 
                   =                                                       =

 

 

 

 


Pi = У / i * Pi-1

 

 

i
 

У
 
 

 

 


Определяем среднее число занятых линий.

 

 

 


M (i) = å i Pi = å i                      = У                                         =                                  

 

 


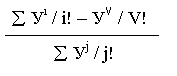
=                                   = У (1 – PV)

 

 

 

Определяем характеристики качества обслуживаний вызовов.

Вероятность потери по времени равно численно вероятности занятости всех V линий.

 

 

УV / V!
 
 


å Уj / j
 
                   Pt = PV =

 

 

 

Определяем вероятность потерь по вызовам.

 

Pb = MП / М – интенсивность потерь потока вызовов

m = lРV       - интенсивность поступившего потока вызовов

МП = å lPi = l

РВ = МП / М = lРV / l = PV

 

Определяем вероятность потерь по нагрузке.

 

                   PH = УП  / У =             =                  = PV

 

 

 

У0 = М(i) = У (1 – РV)

РВ = РН = Рt = РV

 

 

УV / V!
 
 


å Уj / j!
 
                   P =                       - первая формула Эрланга

 

 

Для облегчения практических расчётов формула Эрланга табулирована. Эта таблица называется таблицей Пальма. Очень часто используется символическая запись распределения Эрланга и первой формулы Эрланга.

 

 


          Pi = EV,i (У) =

 

 

 


          P = EVV (У) =

 

 

 

Произведём логический анализ первой формулы Эрланга.

При этом учтём, что

1.    

Из графика видно, что пр 

y = const, чем больше допустимые потери Р, тем меньше требуется линий в пучке для обслуживания поступающей нагрузке, если Р3>P2>P1, то V3<V2<V1.
 
Если P = Ey (V) при у = const .

P
 
 

 

 

 

 

 

 

 

 

 

 

 

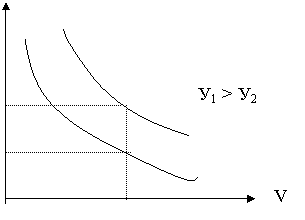
å (Уj/j!) – (УV/V!)
 

У
 
 


å Уj / j!
 

V
 
 =                                                      = У/V [1 – EV (У)]

 

 

EV (У) [1 + (У/V) * EV-1 (У)] = У/V EV-1 (У)

 

У/V EV-1 (У)
 
 


1 + (У/V) EV-1 (У)
 
EV (У) =                                   -  рекуретная формула Эрланга

 

 

Рассмотрим пример расчёта.

4
 

j=0
 
1) У = 3 Эрл                            P = EV (У) = У4 (3) = (3/4) / å 34/4! = 0,35

    V = 4

                                     

      P = ?

 

2) V = 15 лин                 Р = EV (У)   0,005 = E15 (У)

    Р = 5 %

 


    У = ?                          У = 8 Эрл

 

 

 

Лекция 10.

 

Тема: Обслуживания вызовов примитивным потоком.

 

Симметричным потоком называется поток с простым последействием, параметр которого ls(t) в любой момент времени t зависит только от числа i обслуживаемых в этот момент вызовов и не зависит от других характеристик, определяющих состояние S(t) коммуникационной системы.

          Примитивным называется такой симметричный поток, параметр которого li прямо пропорционален числу свободных в данных момент источников:

 

                                      li = (n – i)a

 

где n – общее число источников вызова;

i – число занятых источников, a - параметр потока источника в              свободном состоянии.

 

n
 

i=0
 
                                      l = å li Pi

 

 

Pi – вероятность того, что в системе занято i источников. Заметим, что в обслуживающей примитивный поток КС не требуется соединительных устройств более n, так как занятый источник не может производить вызовы.

          Пусть имеется однозвенная КС. На вход этой КС поступает вызов от примитивного потока с параметром li.

 

 

 

 

 

 

 

 

 

 

 


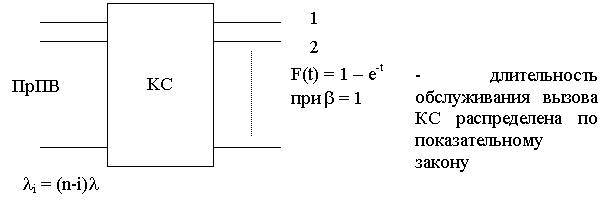
          На входе КС полнодоступно включено V линий. Вызовы обслуживаются по дисциплине обслуживания вызова с явными потерями. Время обслуживания вызова является случайной величиной распределённой по экспоненциальному закону с параметром b. Требуется определить характеристику обслуживания вызовов.

          Рассмотрим возможное состояние системы. Под состоянием системы будем понимать число занятых линий и составляем диаграмму переходов.

 

 

 

 

 

 

 


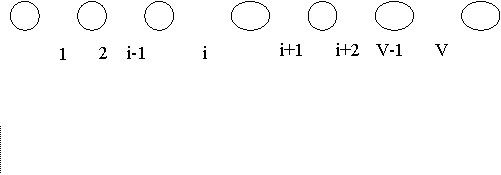
- l0 P0 + P1 = 0

 

 


li-1 Pi-1 – (li + i)Pi + (i + 1) Pi+1 = 0

 

 

l V-i PV-1 – VPV = 0

 

П lк
 
 


Pi =                         * P0   -> вероятность того, что этот пучок находится в

     состоянии i.

 

 

 


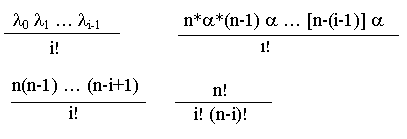
Pi =                          * P0 =                                              * P0 = Cin ai – P0                             

 

Cin =                               =

 

 

 


C210 =                             = 45

 

i=0
 
С учётом условия нормировки å Рi = 1 имеем å Сin ai P0 = 1

 

 


V
 
          P0 =                                         Pi =

 

 

 

Эта формула называется распределением Энгсета.

         

 

Необходимо отметить что, простейший поток можно рассматривать как предельный частный случай примитивного потока, отсюда формула Энгсета является более общей, чем формула Эрланга, и формулу Эрланга можно получить из формулы Энгсета. Для этого         и одновременно l-0 параметр одного свободного источника. При этом l вызовов всех свободных источников сохраняем const.

 

 

n(n-1) … (n-i+1)
 
 


n®¥
 

n®¥
 

n®¥
 

i!
 
lim Cin ai = lim                              ai = lim ni*ai / i! = li / i!

 

 


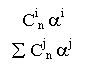
n®¥
 

n®¥
 
                   lim Pi = lim                    =

 

 

          Для практических расчётов целесообразно использовать не параметр потока от данного источника a, а нагрузку поступающую от одного источника.

         Нагрузка поступающая от одного источника обозначим через а.

 

0 £ a £ 1

 

Для определения величины а рассмотрим систему содержащую один источник и одну линию.

n = V = 1, т.е. систему в которой число линий равно числу источников.

 

P0  = 1 / (1 + a)              P1 =  a / (a + 1)             P1 = a = a / (1 + a)

 

 

a = a / (1 – a)

 

 

 

a = a / (1+a);       a = a / (1-a)

 

Установим соотношение между параметром потока вызовов, поступающих от одного источника в системе без потерь, и параметром потока a одного свободного источника. Согласно определению параметр потока есть

 


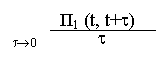
                   lim

         

 

Вероятность П1 (t, t+t) того, что за промежуток времени  t®0 от рассматриваемого источника поступит один и более вызовов. Определяется произведением вероятности Р0 того, что в момент t источник свободен, на сумму состоящую из вероятности того, что за промежуток времени [t, t+t] от свободного источника поступит точно один вызов – эта вероятность равна l t + 0(t) и вызова ®0(t).

Поэтому П1 (t, t+t) = P0 (at + 0(t))  и параметр потока вызовов одного источника равна:

 

 


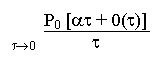
                   lim                        = P0 a = a / (1+a)

 

Cin (a / (1-a))j
 

Cin ai (1-a)n-i
 
 


1
 

å Cjn (a / (1-a))j
 
Pi =                             =

 

 

 

å Cjn aj (1-a)n-j = (a + 1 – an) = 1- согласно биному Ньютону

 

 

Определяем характеристику качества обслуживания вызова.

 

1)      Вероятность потерь по времени численно равны вероятности занятости всех V линий пучка.

 

CVn (a / (1-a))V
 

CVn aV (1-a)n-V
 
 


å Cjn aj (1-a)n-j
 

å Cjn (a / (1-a))j
 
                             Pt = PV =                          =

 

 

2)      Определяем вероятность потерь по вызовам.

 

 

 


nl å Cjn-1 aj
 

j!
 

n(n-1) … (n-j)
 

å
 
Pb = CVn-1 lV / å Cjn-1 lj =                                              =

 

 

CVn-1 aV (1-a)n-1-V
 
 


å Cjn-1 aj (1-a)n-1-j
 
PB = mn / m = lV PV / å lj Pj = Pb = CVn-1 lV / å Cjn-1 lj  =

 

 

 

          Pt = (n, V, a) = Pb (n-1, a, V)

 

 

3)      Определяем вероятность потерь по нагрузке

 

 

PH = УП / У = (У-У0) / У = (1 – (V/n))Pt      У = n*a

V
 
                                                                  

i=0
 
У0 = å i*Pi

 

 

Pt > Pb > PH

 

 

          Для расчёта вероятности потерь можно воспользоваться таблицей. Эта таблица называется таблицей Энгсета. При чём для каждого значения а имеется отдельная таблица, которая имеет вид.

 

                   а = а*

 

V       n

n*

n*+1

 

 

Pt (n*,a*,V*)

V*

PB (n*,a*,V*)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

8. Идеально симметрично неполнодоступная схема.

 

          Идеально симметричной НПД схемой называют такую схему которая при числе линий V, доступности d, имеет число нагрузочных групп:

-         в случае упорядочного искания g = Cdv

-         в случае случайного искания

 

g = d! Cdv

 

Если число линий равно трём V = 3, d = 2, то имеем:

 

3!
 
 


2! (3-2)!
 
          G = Cdv = C23 =                        = 3

 

          Идеально симметричная НПД схема отличается обычно, тем, что для которых в настоящее время получена точная формула расчёта. А для обычных НПД схем используется приближённые методы расчёта формула Эрланга для идеально-симметричных НПД схем. Пусть имеется идеальная симметричная НПД схема с V линиями. На вход этой системы поступает вызов ПП, время обслуживания вызова случайная величина распределённая по экспоненциальному закону. Требуется определить характеристики качества обслуживания вызовов.

 

 

 

 

 

 

 

 


Составляем диаграмму переходов для рассматриваемых систем. Для идеально-симметричных НПД схем достаточно рассмотреть макро состояние систем.

 

 

 

 

 


Если число занятых линий меньше d, то ни одна нагрузочная группа не будет блокироваться, поэтому:

 

l0 = l1 = … ld-1 = l

lk = l(1 - -gk         k ³ d                     l = å lk

Идеально-симметричная НС отличается от обычной тем, что для каждого из возможных сочетаний по d линий предусматривается отдельная нагрузочная группа.

 

 


g = CdV = C23

 

 

          g = C34 = 4

 

 

 

 

 

Из этих схем видно, что каждая нагрузочная группа пользуется своим набором выходов, отличающимся от других наборов, по крайне мере, одним выходом.

gк – условная вероятность потери вызова при К занятых линий.

 

 

                                                nk = K*b

 

Составим систему уравнения и режим этого уравнения, из которой получим формулу:

 

 


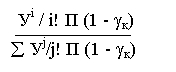
Pi =   

 

 

вероятность потерь определяется по формуле:

V
 
 


i=d
 
                                      P = å gi Pi

 

Для практических расчётов необходимо определить значение gi:

 

gi = gdi / g     -> количество нагрузочных групп блокируемых при занятости

                        i линий.

 

gi = gdi / g = Cdi / CdV

 

 

 

 

 

Окончательно получим:

 

 

å Cdi / CdV * Уi / i! П (1-( Cdi / CdV))
 
 

 


å Уj / j! П (1- ( Cdi / CdV))
 
P =

 

 

Эта формула называется третьей формулой Эрланга.

 

8. Нагрузка обслуживаемая одной линий ПД пучка.

          Обслуживания потока Пальма.

На входе КС поступает У система обслуживания ПД пучком. Искание свободных линий в пучке – упорядоченное. Каждый поступающий вызов обслуживается свободной линий с наименьшим номером и теряется если в момент поступлением вызова заняты все линии пучка.

          пучки ёмкостью i и i – 1.

 

У0 (i) = У (1 – Ei (У); У0 (i-1) = У (1 – Ei-1­ (У)]

 

Разность этих нагрузок определяет h01 – нагрузка обслуживаемая i- й линий пучка любой ёмкости.

 

h0i = У0 (i) – У (i – 1) = У (Ei-1 (У) – Ei (У)]

 

h0i = У0 (i) - У (i – 1) = У [1 – Ei (У)] – У [1 - Ei-1 (У)] = У [Ei-1 (У) – Ei (У)]

 

Необходимо отметить на высокое использование первой линии пучка при обслуживании им даже небольшой по величине нагрузки.

 

          h01 = У[Е0 (У) – Е1 (У) согласно формуле Эрланга.

 

Е0 (У) можно получить и не пользуясь формулой Эрланга.

При V=0 ни один из поступивших вызовов не обслуживается, вся поступа-ющая нагрузка теряется и потери равны 1.
 
h01 = У [E0 (У) – E1 (У)]          Согласно формуле Эрланга

Е0 (У) = 1   Е1 (У) = У / (1+У)

h01 = У / (1+У)

h02 = У [E2 / У – E1 (У)] =

= У [ (У2/2) / 1+У+(У2/2) -

- У/ (1+У)

 

 

 

 

 

 

1
 

h01
 

h02 < h01
 
При У=200,100,50 пропуская способность h01=0,99, 0,98 и 0,91 средняя интенсивность нагрузки, обслуживания одной линией h=У0/V, тем больше чем больше ёмкость пучка. Высокое качество обслуживания малая величина потерь - приводит к небольшому использованию последних линий пучка.

Этот факт объясняется тем, что если первый выход поступает ППВ, то на последующий выход поступает избыточный поток (поток Пальма) этот поток характеризуется большой неравномерностью промежутков между вызовами. Поэтому при упорядоченном искании в случае поступления на разные линии полнодоступного пучка потоков Пальма с одинаковой интенсивностью, линия с большим номером обладает меньшей пропускной способностью по сравнению с линией, имеющей меньший номер.

 

 

 

 

Лекция 11.

 

Тема: Неполнодоступное включение.

 

Понятия о неполнодоступном включении.

 

          Неполнодоступным включением называется такое включение линий, когда любому входу доступны не все выходы, а только часть выходов КС. Совокупность выходов имеющий доступ к одним и тем же выходам называется нагрузочной группой.

 

 

 

 

 

 

 

 

 


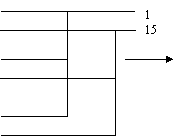
Число выходов d – доступных каждому входу одной нагрузочной группе называется доступностью неполнодоступной схемы, при d³V полнодступный d£V неполнодоступный.

Применяется следующий тип неполнодоступных схем.

1.     Ступенчатая неполнодоступная схема.

2.     Равномерная неполнодоступная схема.

 

Ступенчатая неполнодоступная схема это такая схема, когда количество объединяемых выходов монотонно возрастатет помере номера ШИ.

 

 

 

 

 

 


          V £ 5                              не ПД     V > 5

 

 

 

 

 

 

 

ступенчатая схема может быть включена с перехватом.

          Равномерная схема это такая схема, когда для включения каждой линии запаралеливаются одинаковые число выходов или допускается различие не более чем на единицу.

 

                                                         

 

 

 

 

Неполнодоступные схемы характеризуются следующими параметрами:

1.     Число нагрузочных групп – д.

2.     Доступность – Д.

3.     Коэффициент уплотнения или кроссировочный коэффициент.

Для характеристики схем НПД включения используют коэффициент уплотнения.

 

g = gd / d

 

          Значения g лежит в пределах 1<g<д. При g=д НПД схем превращается в ПД схему, а при g=1 НПД схем распадается на д изолированных ПД схем. Таким образом НС не распадалось на д отдельных ПС должно соблюдаться неравенство g>1.

          Для уточнения величины g можно привлечь следующие соображения. При проведении предварительного запараллеливания надо получить такое число групп, чтобы телефонная нагрузка создаваемая каждой группой была меньше нагрузки, которую могут обслужить d линий ПД пучка при заданных потерях.

          Если при заданных потерях Р интенсивность нагрузки, обслуживаемой всеми V линиями НПД пучка равна Уопс(P,V,d).

 

 

Уопс (P, V, d) = V hhc (P, V, d) средняя нагрузка пропускаемая каждой

         линией НПД пучка, состоящего из V линий.

 

          При равномерном распределении нагрузки между группами, нагрузка каждой группы будет равна:

 

 

Уонс (PVd) / g = V hhc (P, V, d) / g

 

 

Интенсивность нагрузки Уопс(P,V=d) g = gd / V > hhc (P,V,d) / hпс (P, V=d)

из выражения видно, что нижняя граница g зависит от величины потерь P,V,d.

 

                   g = 2 ¸ 4 отсюда число групп д = (2 ¸ 4) V/d

 

          Кроссировочный коэффициент показывает то, что в среднем сколько выходов запараллеливаются для схемы одной линии.

 

                                      g = д*d / V

 

При выборе значения g необходимо учитывать следующее:

1.          Чем больше величина g, тем больше пропускная способность НЕПД схемы.

2.          Чем больше , тем больше требуется монтажных работ из-за траты станционного кабеля. Поэтому на практике используют  g = 2 ¸ 4.

3.          Матрица связанности. Для каждой НЕПД схемы можно составить матрицу связанности. Эта матрица показывает сколько общих линий имеет i-тая нагрузочная группа с j- ти нагрузочной группой.

 

1  2              g                 g = 4    d = 3

 


     1   2   3   4

1   3   2   1   1

2   2   3   1   1

3   1   1   3   2

4   1   1   2   3
 
1        d  r12            r1g

2        r21  d            r2g

 

 

 


g        rg1                d

 

 

 


d   9   6   6

                                                          9   d   6   6

                                                          6   6   d   9

          6   6   9   d

 

 

 

 

 

 

 

 

 

 

 

Тема: Выбор оптимальной структуры ступенчатой НEПД схемы.

 

          При заданных значениях V и d можно строить несколько вариантов ступенчатой НЕПД схемы. Эти схемы отличаются друг от друга пропускной способностью и сложностью реализации. Поэтому среди этих схем необходимо определить наилучшую схему. Это производиться в следующем порядке.

1.     Определяется рациональное число нагрузочных групп.

 

g = gd / V = 2 ¸ 4

g = (2 ¸ 4) * V / d

VIГИ =  28    d = 18                   g = (2 ¸ 4) * 28/10 = 6 ¸ 12      g = 8

 

          2. Определяется возможные варианты запараллеливания

                   1,2,4,8

 

          Пусть Ri – это число шагов искания, где производится запараллеливания выходов.

                   R1, R2, R4, R8

          3. Определяется значение Ri.

å Ri = d                                            R1 + R2 + R4 + R8  = 10

                                                          8R1 + 4R2 + 2R4 + R8 = 28

å g/i = V                                           7R1 + 3R2 + R4 = 18

 

 

Среди этих вариантов необходимо определить наилучший вариант. Вариант считается наилучшим если при данном варианте достигается min следующей формулы
 

Ri

 

1

 

2

 

3

 

4

R1

R2

R3

R4

2

1

1

6

2

0

4

4

1

3

2

4

1

2

5

2

S

6

4

5

7

 

 

 

 

 

 

 

S = å (R, Ri-1)

 

 

 

 

Тема: Выбор оптимальной структуры равномерной неполнодоступной схеме.

 

          При выборе оптимальной структуры равномерной неполнодоступной схемы необходимо учитывать следующее:

1.        Каждая линия должна быть доступна одинаковому числу нагрузочных групп (производится запараллеливание одинакового числа выходов) или число нагрузочных групп отличающихся не более чем на единицу.

2.        Каждая нагрузочная группа должна иметь одинаковое число связей с любой другой нагрузочной группой (матрица связанности должна быть равномерной).

3.        Каждая линия должна объединять выхода принадлежащее к соседним шагам искания (схема должна быть со сдвигом).

 

Рассмотрим порядок построения равномерной неполнодоступной схемы:

1.     Определяется число нагрузочных групп по формуле:

 

g = (2 ¸ 4) * V/d

 

2. Определяется количество запараллеливаемых выхода для включения одной линии. На основании  первого принципа число запараллеливаеиых выхода может быть r, r+1.

 

                   R = g*d / V = g

         

3.Определяется число линий V1, V2 соответственно получаемые путём объединения r+1 выхода или r выхода.

 

                   V1 = g*d - rV

                   V2 = (r+1)V - gd

 

4. После выполнения пунктов 1,3 необходимо обеспечения второго и третьего принципа.

 

Выполнения этих принципов обеспечиваются путём составления общей неполнодоступной схемы из отдельных цилиндров.

Цилиндр эта равномерная элементарная схема, построенная R шагах искания с одинаковым сдвигом между соседними шагами искания.

1. Рассмотрим двух шаговый цилиндр (R=2).

 

                                                g=5

                                                R=1 шаг сдвига равно1

 

                                                [2]

 

Если для двух шагового цилиндра число нагрузочных групп равно д, а шаг сдвига равно i, то первая нагрузочная группа будет иметь связь со следующими нагрузочными группами.

 

          i + 1   z + 1   Z = g – i

          1   2   3   4   5

   1     2   1   0   0   1                 показывает связи групп

   2     1   2   1   0   0

          1   2   3   4   5

          2   0   1   1   0

 

2.     Рассмотрим трёх шаговый цилиндр – характеризуется шагом сдвига i и j и шаг сдвига между первым и вторым шагом исканя, j между вторым и третьим искания.

В данном случае первая нагрузочная группа будет иметь связь со следующими нагрузоч-

ными группами.
 
 


[1,2]

 

 

          i+1, j+1, z+1

          i+j+1, i+z+1, j+z+1         z=g-i-j

          1 2 3 4 5

     1   3 1 2 2 1

 

3.     Четырёх – шаговый цилиндр.

 

                                                [i, j, l]          i+1,j+1,l+1,z+1

                                                [1, 1, 1]       i+j+1,i+l+1,i+z+1

                                                                   i+l+1,j+z+1,l+z+1

                                                i+j+l+1        i+j+z+1,j+l+z+1,i+l+z+1

                                                z= g – i – j - l

 

 

 

 

 

 

 

 

 


d = 20, V = 88

1) g = (2¸4) 88/g = (2¸4) 40/10 = 8 ¸ 16       g=10

 

2) g1 r = [g*d/V] = [2,5] = 2

    g2 r +1 = 3

   V1 = g*d – r*V = 10*20 – 2*88 = 24         l1 = (g2*V-dg) / g

   V2 = (r+1)V – g*d = 3*88 – 10*90 = 64    l2 = (gd-g1V) /g

 

          3) Определяем число 3х шаговых и 2х шаговых цилиндра.

 

 

          n3x V1 / g  = 24/10 = 2,4

          n2x V2 / g = 64/10 = 6,4

 

          Производим анализ схемы.

                                                Анализ характеристики.

 

1 Ci = 1,9

1 2 3 4 5 6 7 8 9

1 1 1 -  -  - 1 1 1

1 – 1 1 -  1 1 -  1

2 1 2 1 -  1 2 1 2

1 1 1 2 2 2 1 1 1

3 2 3 3 2 3 3 2 3
 
2 Ci = 2,8

3 Ci = 3,7

4 Ci = 4,6

5 Ci = 5,5                                                   

6 Ci = 6,4

1 Ci = 127    3,9,8

2 Ci = 163    7,9,4

 

Составляем матрицу связанности.

 

1

20

3

2

3

3

2

3

3

2

3

 

20

3

2

3

5

2

3

3

4

3

2

3

Х

3

2

3

3

2

3

3

2

3

Х

3

2

3

5

2

3

3

4

3

2

3

Х

3

2

3

3

2

3

3

2

3

Х

3

2

3

5

2

3

3

4

3

2

3

Х

3

2

3

3

2

3

3

2

3

Х

3

2

3

5

2

3

5

3

3

2

3

Х

3

2

3

3

2

5

3

2

3

Х

3

2

3

5

2

6

2

3

3

2

3

Х

3

2

3

3

2

5

3

2

3

Х

3

2

3

5

7

3

2

3

3

2

3

Х

3

2

3

3

2

5

3

2

3

Х

3

2

3

8

3

3

2

3

3

2

3

Х

3

2

3

3

2

5

3

2

3

Х

3

2

9

2

3

3

2

3

3

2

3

Х

3

4

3

3

2

5

3

2

3

Х

3

10

3

2

3

3

2

3

3

2

3

Х

3

4

3

3

2

5

3

2

3

х

 

 

 

 

В некоторых случаях общая равномерная схема не может  быть составлена полностью из отдельных цилиндров. В этом случае поступают следующим образом: 1. При заданных параметрах д,V,d смотрят максимально возможное число r, r+1 шаговых цилиндров, и получают число линий V’ оставшиеся линии включаются на оставшиеся шаги искания, таким образом чтобы соблюдались выше изложенные три принципа.

Пример построения оптимальной ступенчатой схемы для ступени I ГИ.

Дано: V = 79 d = 15

Для построения оптимальной ступенчатой схемы для ступени I ГИ определим нагрузочную группу.

g = (2¸4) V/d = (2¸4) 79/15 = 10,53 ¸ 21,06

 

 

 

 

отсюда выбираем д=10, тогда кроссировочные коэффициенты К1, К2, К5, К10.

Составим уравнения:

10K1 +5K2 + 2K5 + 1K10 = 79

K1 + K2 + K5 + K10  = 15

9K1 + 4K2 + K5 = 64 лин

Находим кроссировочные коэффициенты и занесём эти коэффициенты в таблицу 3.

                   9К1 + 4К2 + 2К5 = 64

пусть К1 = 7 отсюда К5 = 1

          К2 = 0                       К10 = 7

                   9*7 + 4*0 + К5 = 64

                   63 + К5 = 64    К5 = 1

 

1

2

3

4

5

6

7

8

9

10

   К1

7

6

6

5

5

4

4

3

2

 

К2

0

2

1

4

3

7

6

9

14

 

К5

1

2

6

3

7

0

4

1

2

 

К10

7

4

2

3

0

4

1

2

1

 

Si

14

6

14

2

13

14

7

15

19

 

          Si = |К1 – К2| + |К2 – К5| + |К5 – К10) = min

Выбираем 4 вариант, где К1=5, К2=4, К5=3, К10=3

строим оптимальную ступенчатую схему.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

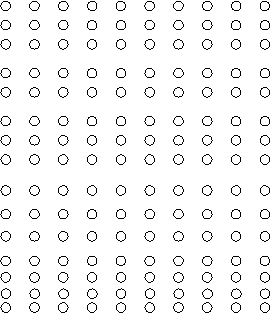
Рис1. Схема оптимальной ступенчатой схемы.
 
 

 

 

 

 

 

 


Лекция 12.

 

Тема: Приближённые методы расчёта потерь в НПД схемах.

 

          Для НПД схем в настоящее время не разработано точная методика расчёта. Это объясняется тем, что вероятность потерь зависит от числа занятых линий, но и от того какие линии заняты. Поэтому для расчёта вероятности потерь необходимо рассматривать микросостояние системы, а это очень сложно производить. Поэтому для практических расчётов используется приближённые методы расчёта. К ним относятся:

1.     Упрощённая формула Эрланга.

Этот метод предполагает, что вероятность занятости линий равно удельной обслуженной нагрузке эти линии и считают что поступающий вызов с любой нагрузочной группы будет потерян если занято d фиксированных линий. Поэтому вероятность потерь Р равно вероятности занятости Hd фиксированных линий. Если общая обслуженная нагрузка в НПД схеме У0, а ёмкость пучка V, то вероятность занятости каждой линий будет равно У0/V. А вероятность занятости:

 

 

Hd = У0 / V * У0 / V … У0 / V = (У0 / V)d

 

                                      P = Hd = (У0 / V)d

 

 

V = У0 /   Р           У0 = V *   P          PПД = ¦ (У, V)

                                                          PНПД  = ¦(У, V, d)

 

У = 80 Эрл

V = 95

d = 10                             P = (80/95)10

 


P =

 

 

 

 

 

2.     Метод Лотца-Бабицкого.

 

При использовании данного метода предполагают что, число занятых линий НПД схем имеет распределения Эрланга.

 

В этом случае вероятность занятия i фиксированных соединительных устройств в ПД пучке при тех же значениях числа приборов и нагрузке будет равно.
 

 


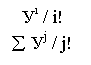
Ei,V (У) =                            ;

 

 

 

Hi,V (У) = EVV (У) / EV-i,V-i (У) = EV (У) / EV-i (У)

 

тогда, считая, что вероятность потерь в НПД пучке равно вероятности занятия d определённых устройств получим.

 

P = Hd = EV (У) / EV-d (У)

 

Эта формула называется формулой Лотца-Бабицкого. Чем меньше вероятность потерь, тем больше точность данного момента. Для использования данной формулы и при больших значениях потерь используется формула которая называется модификационной формулой Пальма-Якобеуса.

 

P = EV (Уф) / EV-d (Уф)              Уф = У0 (1 – EV (Уф)]

 

Пример:

 

У = 30 Эрл

d = 10

Р = 5 %                          0,005 = EV (30) / EV-10 (30)

 


V = ?

 

Пусть V = 45        E45 (30) / E35 (30) … = 0,007

          V = 47

 

3.     Метод О’Делла.

 

При использовании данного метода предполагается, что общая обслуженная нагрузка У0 НПД схемы определяется как сумма нагрузок обслуженных d линиями ПД пучка и V-d линиями НПД пучка.

 

У0 = Уd + УV-d

 

При чём каждая линия ПД го пучка обслуживает минимальную нагрузку равное:

 

Уmin = Уd / d

 

Относительно второго пучка предполагается что каждая из   V-d его линий пропустит нагрузку лежащую между Уmin и Уmax.

 

                             Уmax =    Р

 

отсюда

 

                             У = Уd / d + К (    Р   - (Уd / d))

 

                             У0 = Уd + (V – d) [(Уd / d) + K (   P   - (Уd / d))]

 

где К – это коэффициент учитывающий характер поступающего потока при чём К=1 когда поступает выровненная нагрузка, т.е.   / У < 1. Если     / У = 1 следует принимать значение R = 1, то

 

                                                                             К = 0,53

 

                   У0 = Уd + (V – d)    P

 

(У0 – Уd)
 
 


Р
 
                   V = d +                                    Р = [(У0 – У) / (V – d)]d

 

 

Этой формулой можно пользоваться на всех ступенях искания кроме IГИ.

 

 

На IГИ ступени можно использовать

 

 


                   V = d +

 

 

 

                   У0 = У (1 – Р)                Уd = Уd=V (1 – P)

 

 

4.     Инженерный метод расчёта.

 

Р = Еd (Уd)

 

Сущность инженерного метода заключается в использовании готовых таблиц для расчёта числа линий.

 

 

1
 
 

 


(Уd / d) + K (   P – (Уd / d))
 
V = d -                                               +                                          * (1-P)У                            

 

V = aУ + b

 

V
 
a,b = ¦(P, d)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


Лекция 13.

 1    2       n
 
 


Тема: Звеньевые коммутационные системы. Двухзвенная ПД схема.

На данной схеме поступивший вызов теряется в следующих случаях:

1.     Если занято m промежуточных линий коммутатора.

2.     При занятости всех выходов рассматриваемого направления.

3.     При не удачном сочетании свободных выходов и промежуточных линий.
 
 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


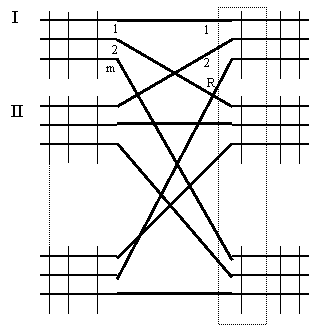
Hi                     Hj
 

          Таким образом в многозвенных схемах вероятность потерь зависит не только от состоянии выходов (сколько и какие выходы заняты), но и от состояний промежуточных линий. Поэтому число микросостояний звеньевых схем горазда больше, чем число микросостояний НПД схем. Поэтому точные методы звеньевых схем в настоящее время отсутствуют. В основном используются приближённые методы:

1.     Комбинаторный метод.

2.     Метод эффективной доступности.

3.     Метод вероятностных графов.

 

Тема: Комбинаторный метод. ПДВ выходов.

 

Рассмотрим на примере одно-связанную двух звеньевую схему. Если считать, что рассматриваемый вызов поступил на отмеченный вход первого коммутатора в момент, когда i промежуточных линий из m, подключённых к выходам данного коммутатора, заняты, то для подключения входа к одному из выходов требуемого направления могут быть использованы только оставшиеся m-i промежуточных линий. Если же выходы требуемого направления, соответствующие этим m-i линиям, заняты, то наступят потери. Это утверждение справедливо для любого i лежащего в пределах 0 £ i £ m и охватывает  два случая занятости: всех промежуточных линий (i=m) и всех выходов в направлении (i=0).

Допустим поступивший вызов требует свободный выход, определённом направлении где q=1. Требуется определить вероятность потерь в этом направлении. Обозначим через Wi вероятность занятости промежуточных линий из общего числа m, а через Hm-i вероятность занятости m-i фиксированных выходов. В этом случае вероятность потерь можно определить по формуле:

m
 

i=0
 
          P = W0Hm + W1Hm-1 + W2Hm-2 + … + WmH0 = S WiHm-i

 

Данная формула имеет место в следующих предположениях:

1.     Значение Wi и Hm-i взаимнонезависимы.

2.     Занятие промежуточных линий и выходов производится случайным образом.

Комбинаторный метод предполагает  использование двух распределений:

1.     Распределение Эрланга.

2.     Распределение Бернулли.

При использовании распределения Эрланга вероятность занятия i-любых соединительных устройств в пучке из m таких устройств при интенсивности нагрузки УЭРЛ на пучок принимается равной

 

 

 


                                      Ei,m(У) = Wi =                      ,

 

 

 

 

а вероятность занятия m-i фиксированных соединительных устройств в пучке из m устройств

 

                   Hm-i, m(У) = Hm-i = Em (У) / Ei (У)

 

Тема: Расчёт двухзвенных схем при отсутствии сжатия и расширения.

 

          При отсутствии сжатия и расширения число входов в каждый коммутатор первого звена n равно  число выходов m в каждом из этих коммутаторов. В данном случае для промежуточных линий можно принять Бернулли, так как число входов (число источников нагрузки) равно числу соединительных устройств. Если для выходов двух схем можно так же принять распределение Бернулли, что может быть справедливо при небольшом числе коммутаторов первого звена, тогда Wi и Hm-i будет иметь следующие выражения:

 

 

учитывая формулу бинома Нютона получаем

 
 
 


          P = S WiHm-i = S Cmi bi (1-b)m-i Cm-i = (b+c-b*c)m ->

 

 

где  Wi = Cmi bi (1-b)m-i – для промежуточных линий

где Сim – число сочетаний из m и i, b средняя интенсивность нагрузки обслуженная одной промежуточной линией, о для Hm-i  = отнесённая к выходам = Cm-i, С – средняя интенсивность нагрузки, обслуженной одним выходом рассматриваемого направления. Если b¹1, q¹1

 

                   P = (b¦ + Cq - b¦ Cq)       (Б-Б)

 

          Если число коммутаторов k  в первом звене велико, тогда для выходов рассматриваемого направления целесообразно принять распределение Эрланга.

Где выражение Еm(У) – это потери в ПД пучке из m соединительных устройств при интенсивности нагрузки УЭРЛ на пучок,

 

 

 

 


                                                Em (У) =                                  

 

 

 

 

Ei (У) – потери при той же интенсивности нагрузки в пучке из i-соединительных устройств.

 

 

 


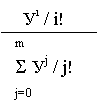
                                      Е2 =                               

 

 

 

Распределение Бернулли используется при ограниченном числе источников, т.е. вероятность Wi занятия i любых соединительных устройств в пучке из m-устройств при интенсивности нагрузки УЭРЛ на пучок принимается равной:

 

 

                   Wi = Cim hi (i - h)m-i

 

где Сim – число сочетаний из m по i; h - средняя нагрузка, ослуженная одним соединительным устройством в пучке.

 

 

Вероятность Hm-i занятия m-i фиксированных соединительных устройств при тех же условиях принимается равной

 

                   Hm-i, m (У) = Hm-i = hm-i

 

При расчёте двухзвенных схем для промежуточных линий всегда используется распределение Бернулли. Распределение Эрланга рекомендуют принимать при определении вероятности занятия тех соединительных устройств, для которых число источников нагрузки больше числа соединительных устройств.

Относя Wi к направлению, Hm-i к промежуточным линиям.

 

 

 


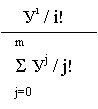
                   Wi =                               Hm-i = bm-i

 

 

 

 

 

         

                   P =                       bm-i

 

 

 

 

Выносим затем не суммирующиеся множители за знак суммы.

 

 

 

Уj / b!
 

m
 

i!
 

i=0
 

i=0
 
                   P =                       S                

 

 

 

 

 


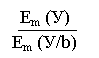
                   P =                      

 

 

если q=1, ¦=1.

 

Emq (У)
 
 


Emq (У/b¦ )
 
          P =                       [Б-Э] m=n

 

Пример:      40 х 40 х 100

                   Увх = 20 Эрл

                   Унап = 7 Эрл

                   V = Д = 10

                   P = ?

                                                          МКС = 10 х 10 х 6

 

 

m = 10

n = 10                             b = Увх / Vпл = Увх / R*m = 20 / 4*10 = 0,5 Эрл

R = 4

¦ = 1                     С = Унап / V = 7 / 10 = 0,7 Эрл

q = 1

 

 

 

 

 


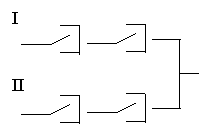
                                      P = (b          ¦ + Cq - b¦ Cq)m = (0,5 + 0,7 – 0,5*0,7) =0,007

 

 

                                      b = Увх / Vпл = 80 / 400 = 0,2 Эрл

 

 


                                      Р =                  =   0,01

 

 

 

Тема: Схема со сжатием.

 

При этом имеем n>m.

 

                                      В этом случае поступающий вызов может теряться

                                      в следующих случаях.

 

1.     При занятости ПЛ рассматриваемого коммутатора звена А.

2.     При занятости всех выходов рассматриваемого направления.

3.     При неудачном сочетании свободных выходов и промежуточных линий.

4.     При поступлении на коммутатор звена А более m вызовов.

Если при q ³ 1 и распределение Бернули для промежуточных линией и выходов Wi отнести, к промежуточным линиям, а H(m-i)q – к выходом рассматриваемого направление, то можно записать:

 

                   Wi = Cin ai (1 – a)n-i                   H(m-i)q = C(m-i)q

где а – средняя интенсивность нагрузки, обслуженной одним входом коммутатора первого звена.

          Поэтому потери можно определить по формуле:

n
 

n
 

m
 

m
 

i>m+1
 

i<m+1
 

i=0
 

i=0
 
P = S Wi H(m-i)q + å Wi = å Cin ai (1-a)n-i C(m-i)q + å Cin ai (1-a)n-i

 

 

 

          В этом выражении первое слагаемое учитывает потери из-за неудачных сочетаний при занятиях промежуточных линий и выходов, а второе – потери за счёт поступления более m вызовов в один коммутатор первого звена. Если искание свободных выходов в схемах с q>1 производить в два этапа, т.е. таким образом, чтобы в первую очередь занимались все выходы от 1 до q-1 во всех коммутатора звена В. Если среди этих выходов нет свободных, то производится поиск свободного выхода среди остальных выходов.

          В этом случае имеем формулу:

 

P = bm¦ + (b¦ + Cq -b¦Cq)mq       (Б-Б)

 

Если занятия свободного выхода производится случайным образом (одно этапный поиск), то используется формула:

 

P = b (b¦ + Cq -b¦Cq)m

 

где b – нагрузка обслуженная одной ПЛ b = (n/m)a.

      С – нагрузка обслуженная одним выходом рассматриваемого

  направления.

 

Если для первого звена сохранить распределение Бернулли, а для второго звена принять распределение Эрланга, то для двух этапного поиска получим:

 

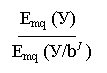
                             P = bm +                        

 

Для одноэтапного поиска ипользуется формула:

 

                             Р =                      

 

У – поступающая нагрузка на рассматриваемое направление.

 

 

 

Рассмотрим пример.

 

Блок 100 х 60 х 20

ПВ ПВ.

 

                   Увх = 5 Эрл                    МКС 10 х 10

                   Уисх = 10 Эрл                           n = 10                   m = 6          q = 3,33

                                                                   R =10                   ¦ = 1

                   Рисх = ?

 

60
 

15
 

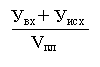
          b =                  =         = 0,25 Эрл

 

 

 

          С = Уисх / Vисх = 10 / 20 = 0,5 Эрл

 

          Р = 0,256 + (0,2 + 0,53,33 – 0,25 * 0,53,33)5 * 3,33 =

 

100 х 60 х 20

 

 

 

 

 

 

 

 


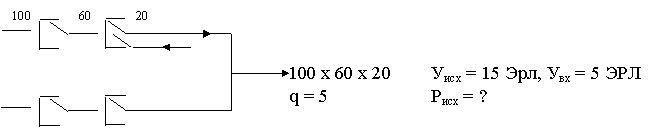
15
 

Уисх + Увх
 

(60*q) = 60*5
 

Vпл
 
          b =                  =                         = 0,05 Эрл

 

 


Е10 (10)
 

Е10 (10/0,05)
 
          Р = 0,056 +                     ;

 

 

 

Тема: Двухзвенная схема с расширением.

 

          В схемах с расширением числа выходов n в каждом коммутаторе первого звена меньше числа выходов m из коммутатора. В такой схеме число одновременных вызовов не превышает n, а следовательно, меньше m, поэтому потери могут быть по следующим причинам:

1)     занятости всех выходов;

2)     неудачное сочетания свободных выходов и промежуточных линий.

Поэтому имеем n<m          q³1.

Для ПЛ и выходов справедливо распределении Бернулли

Wi = Cin ai (1-a)n-i для ПЛ

H(m-i)q = C(m-i)q

 

n
 

m
 

n
 

i=0
 

i=0
 

i=0
 
P = S Wi Hm-i = å Cin ai (1-a)n-i C(m-i)q = å Cin ai (1-a)n-i (Cq)m-n

 

 

P = C(m-n)q (a + Cq – aC)n          (Б-Б)

 

Если имеет места распределение (Б-Э), то имеем:

 

Р + Еmq (У) / Еnq (У/а¦)

 

          а – нагрузка поступающая на один вход.

          У – нагрузка поступающая на направление.

 

Пример: 60 х 30 х 400.            ВПВП.

 

Увх = 50 Эрл                  МКС 10 х 20

Унапр = 25 Эрл                         m = 20         ¦ = 1

Д = mq = 40                                      R = 4           RB = m = 20

                                                n =15

 

 

          а = 50 / 60 = 0,8 Эрл      С = 25 / 40 = 0,6 Эрл

 

          Р = 0,6(20-15)*2 (0,8 + 0,62 – 0,8*0,62)15 = 0,078

 

60 х 80 х 400

g = 5

Увх = 150 Эрл                 a = 150 / 300 = 0,5 Эрл

Унапр = 25 Эрл

Д = mq = 40                             Р = Е40 (25) / Е30 (25/0,5) =

 


P = ?

 

Лекция 14.

 

Тема: Двух звеньевые НПД схемы.

 

60
 

100
 

100
 
Рассмотрим двух звеньевую схему на основе ступени АИ.

1

 

 

 

x
 

1

 

 

 

2

 

 

 

 

k

 

 

 

g
 

V
 

20
 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


Данная схема содержит g – двух звеньевых схем. Если число выходов из каждого блока равно mq, а число таких блоков g, то из общего числа выходов всех блоков равно gmq, путём запараллеливания получаем число выходов V, необходимых для включения приборов следующей ступени искания.

При этом справедливо следующее неравенство: mq < V < gmq. Из V выходов последующей ступени искания любому входу в любой блок искания доступны только mq выходов.

Для расчёта таких схем применяется два метода.

1.     Комбинаторный метод Якобеуса (основанный на идеи О’Делла).

2.     Метод эффективной доступности.

 

1.     Комбинаторный метод Якобеуса.

 

Этот метод использует идею О’Делла. Как известно при использовании метода О’Делла число линий определяется по формуле:

У0 - Уd
 

У0 - Уd
 
 


P
 
V = d +

 

 

из этой формулы известно, что средняя интенсивность нагрузки, обслуживаемая каждым соединительным устройством при НПД однозвенном включённом пучке из V таких устройств обслуживающих интенсивность поступающей нагрузки У при доступности d с потерями Р, принимается лежащей в промежутке между минимальными значениям У d/d, где Уd определяется Р = Ed (Уd), и максимальными значением Р = У’ отсюда формула примет вид:

 

Cmax
 

Уmax
 
V = d +

 

 

Для двух схем 1) d = mq или же V = d в данном случае неполнодоступное при потерях P нагрузку которую можно принять равной Уd и определить из I формулы Эрланга Уd = Уmq.

 

У – Уmq
 
2.Уmax = Сmax – это максимальная пропускная способность выхода. Поэтому для двух звеньевых НПД схемы

 

                   V = mq +                       

                            

 

Значение Уmq определяется по соответствующей формуле полученной для случая ПД двух звеньевых схем для случая отсутствия сжатия и расширения (n=m) распределения Бернулли для промежуточных линий

 

распределения Эрланга для выходов в связи с этим Уmq определяется:

Emq (Уmq)
 

 

Emq (Уmq/b¦ )
 
                   Р =                                

 

 

Выходы двух НПД достигнут максимального значения средней пропускной способности в том случае, когда число выходов V будет велико. В этом случае при расчёте схемы следует принимать распределение Бернулли и для промежуточных линий и для выходов. Тогда Сmax определяется из следующего соотношения:

 

                                       P = (b¦ + Cqmax - b¦ * Cqmax)m

 

Следовательно, в соответствии с идеей О’Делла средняя интенсивность нагрузки, обслуживаемой каждым из mq выходов в двух НПД схем, имеющий V выходов, будет равно Уmq / mq. Остальные V-mq выходов пропустят каждый в среднем Сmax нагрузки отсюда:

 


                             V = mq +                       

 

 

Данная формула может быть применена для случая в схемах со сжатым и при одноэтапного искания.

У – Уmq
 
Если n>m, двух этапное искания.

 


Сmax
 
                   V = mq +                       

 

         

Emq (Уmq)
 
 


Emq (Уmq / b¦ )
 
P = bm +                                   Для Уmq

 

 

P = bm + (b¦ + Cqmax - b¦ Cqmax )mq

 

Р – bm  - b¦
 
 


1 - b¦
 
Cmax =

 

если n<m

 

У – Уmq
 
 


Cmax
 
          V = mq +                                

 

 

 

          P = Emq (Уmq) / Enq (Уnq / a¦ ) -> Уmq

 

 

          P = C(m-n)qmax (a¦ + Cqmax - a¦ Cqmax)n -> Cmax

 

Пример: схема со сжатием

100 х 60 х 20

Уисх + Увх
 
 


Vпл
 
g = 10                                       b =                        = 110 / 60*10 = 0,2 Эрл

Уисх = 60 Эрл       

Увх = 50 Эрл

Р = 3 %                          0,003 = 0,26 + Е20 (Уmq) / Е20 (Уmq / 0,2)

                                     

Vишк = ?                          Уmq = 13,2 Эрл

 

0,003 – 0,26  - 0,2

 
 


1 – 0,2
 
                   Сmax =                                      = 0,65 Эрл

 

 

У - Уmq
 

60 – 13,2
 
 


0,65
 

Сmax
 
                   V = mq +                    = 20 +                       = 83

 

 

Пример 40 х 40 х 200 схема без расширения и сжатия.

 

g = 5

Уисх = 100 Эрл                0.005 = Е20 (Уmq) / E20 (Уmq / 0,5)   Уmq = 11,2 Эрл

Р  - b
 

0,005   - 0,5
 
Унап = 30 Эрл

1 - b
 

1 – 0,5
 
Д = 20                            Сmax =                   = 0,56 Эрл         Сmax = 

Р = 5 %

b = 0,5

                                      V = 20 + (30 – 11,2) / 0,56 = 45 мин

V = ?

 

 

 

 

 

 

 

Схема с расширением.

 

60 х 80 х 400

 

g = 5

Увх = 150 Эрл                 0.005 = Е40 (Уmq) / E30 (Уmq / 0,5)   Уmq = 23 Эрл

Унап = 80 Эрл

Д = 40                            0,005 = С5*2max (0,5 + С2max – 0,5*С2max)15

Р = 5 %                         

                                       Cmax = 0,6 Эрл

V = ?                   

V = 40 + (90 – 23) / 0,6 = 115 мин    

 

 

 

 

Тема: Метод эффективной доступности.

 

          Данный метод может использоваться для расчёта двух звеньевых ДП и НПД схем. При этом, учитывается то, что доступность двух схем изменяется от минимального до максимального зависимости от обслуживаемых вызовов. Если в рассматриваемой схеме каждому входу доступен любой выход требуемого направления только тогда, когда нет занятых соединительных путей. В этом случае доступность выходов данного направления будет максимальной и при q=1 будет равна m. В общем случае dmax = mq. Если занята одна промежуточная линия, то для всех входов в том коммутаторе, из которого она выходит, доступность выходов в указанном направлении уменьшится на единицу для случая q=1 и на q в общем случае, так как занятая промежуточная линия заблокирует выходы рассматриваемого напрваления, к которым можно подключиться с её помощью.

          При наличии i  занятых ПЛ для всех входов в этот коммутатор, в котором имеются занятые i линий доступность уменьшается на iq и составит величину:

 

di = (m – i)q

 

          Минимальная доступность выходов рассматриваемого направления для случая сжатия (n>m) равна нулю. Для схем с расширением или без расширения и сжатия (n<m)

 

dmin = (m – n + 1)q

 

так, как к моменту поступления последнего вызова (n-1)-я промежуточная линия занята и следовательно, доступность уменьшилась на величину      (n-1)q. Таким образом, в процессе работы двух схем в режиме группового искания доступность di выходов меняется в пределах между наибольшим и наименьшим значениями.

 

dmin £ di £ dmax

 

Каждое из значений доступности di появляются с вероятностью Wi, где    Wi-вероятность занятия i ПЛ из m линий, принадлежащих одному коммутатору первого звена.

          Таким образом dmin £ di £ dmax – это показывает, что любая двух схема показывает, что любая двух схема может быть эквивалентно заменена на однозвенную НПД схему с доступностью dэфф. Эта доступность называется эффективной доступностью двух схемы.

 

 

 

Расчёт эффективной доступности производится в следующем порядке.

1.     Определяется min доступность.

 

dmin = (m – n + 1)q

 

2.     Определяется средняя доступность.

m
 

m
 

i=0
 

i=0
 
d = å Wi (m-i)q = [m - å i W0]*q = [m – Уm)q

 

 

W0  mq        где Уm = b*m – обслуженная нагрузка

W1 (m-1)q       m промежуточных линий или одним коммутатором звена А.

W2 (m-2)q

 


                             d = (m – Уm)q

 

3.     Эффективная доступность.

 

dэфф  = dmin + q (d – dmin)

 

где q - коэффициент 0,65 ¸ 0,75, определяемый зависимостью потерь от доступности и распределением Wi.

После определения Дэф для расчётов используется формула полученная для однозвенной НПД схемы.( О’Делла, инженерный метод).

 

V = ay + b

 

Пример:

 

80 х 120 х 400

g = 5                     m = 20                  dmin = (20 – 13,3 + 1)*1 = 7,7

Увх = 200 Эрл       R = 6                    d = (20 – 6,3)*1 = 13,7

Унап = 70 Эрл        n = 13,3                Уm = Увх / R*q = 6,6

d = 20                             ¦ = 1                     dэ = dmin + q (d – dmin)

Р = 5 %                q = 1                     dэ  = 7,7 + 0,6 (13,7 - 7,7) = 11

                                       0,005 = EV (70) / EV-11 (70)

V = ?                              V = 97

 

 

 

 

 

 

 

Тема: Система с повторными вызовами.

 

          Если рассмотрим КС с потерями, то поступивший вызов в момент занятости всех линий в пучке теряется, но в реальных условиях источник получив отказ, не отказывается от обслуживания, а осуществляет повторные вызовы с целью добиться требуемого обслуживания. В модели системы с повторными вызовами различаются два этапа обслуживания вызова.

Первый этап обслуживания характеризуется занятием коммутационной системы, процессом установления соединения и его разъединения независимо от того, чем завершается это соединения разговором, занятостью линий вызываемого абонента, не ответом вызываемого абонента.

Второй этап обслуживания характеризуется разговорным состоянием соединения. Вызов считается обслуженным, если он завершился вторым этапом – разговором. Вызов считается не обслуженным, если обслуживание его завершается первым этапом. Источник такого вызова с заданной вероятностью осуществляет повторный вызов.

Пусть задан ПП ёмкостью V линий поступают первичные вызовы, образующие ППВ с параметром l. Вызов, поступивший в момент отсутствия в пучке свободных линий, не обслуживается. Если в пучке имеется хотя бы одна свободная линия, то происходит первый этап обслуживания источника, осуществившего этот вызов. После окончания первого этапа обслуживания либо по этой линии происходит второй этап обслуживания либо линия освобождается и вызов остаётся не обслуженным. Вероятность того, что вызов остаётся не обслуженным, обозначим j, а вероятность того, что вызов будет полностью обслужен,

 

                             - Y = 1 - j

 

Длительность занятия линии первым и вторым этапами обслуживания вызова распределена по показательному закону с параметрами соответственно l и b и следовательно, среднее значение времени обслуживания первым и вторыми этапами равны

 

                             tl = 1/l , tb = 1/b

 

Абоненты, вызовы которых не обслуживаются по причине отсутствия свободных линий в пучке или завершилось только первым этапом обслуживания, является источником повторных вызовов. От каждого такого источника поступают повторные вызовы, образующие простейший поток с параметром r. А если в течении заданного времени источник не производит повторного вызова, то вызов теряется. Это время примем распределённым по показательному закону с параметром g. Таким образом, время в течении которого источник принимает решение произвести повторный вызов или окончательно отказаться от обслуживания неудачно сделанного им вызова, распределено по показательному закону с параметром r + g. Отсюда среднее время существования источника повторных вызовов, равной среднему времени между двумя соседними попытками источника добиться обслуживания своего вызова, составляем

 

                                      Z = 1 /  r + g

 

При этом вероятность повторных вызовов

 

                                      Р = r /  r + g

 

а вероятность окончательно отказа от обслуживания.

 

                                      1 – Н = g / r + g

 

Вероятность Н определяет меру настойчивости источника добиться полного обслуживания вызова.

Для того чтобы не создавалось неограниченного количества необслуженных первичных и вторичных вызовов, введём некоторые ограничения.

 

                                      Н = (У / V) < 1 Эрл

 

                   Н определяет из соотношения.

 

                                      Н = (С / V) t

 

t  - средняя суммарная длительность занятия линий пучка полным обслуживанием одного вызова с учётом того, что для его обслуживания источник может производить и повторные вызовы.

С- интенсивность потока первичных вызовов в течение 1 ч.

Первичные и повторные вызовы, поступающие в момент занятости всех V линий пучка, не занимают линии пучка. Поэтому на величину t влияют только вызовы ,попадающие на первый этап обслуживания. При первом этапе обслуживания одного вызова среднее время занятости линии пучка равно tl,а втором этапе обслуживания с вероятностью Y - tb.Среднее время занятости линии для обслуживания каждой такой попытки составляет         

Если обозначим через L среднее число попыток на первом этапе обслуживания с целью полного обслуживания одного вызова, то величина t составит

                                      t = L (tl + Ytb)

 

Определим величину L ,которая зависит от  меры настойчивости источника H = 1, g = 0

 


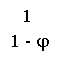
                                      L =           = 1 / Y

 

Вызов первый раз поступает на первый этап обслуживания. С вероятностью  данный вызов не попадает на второй этап обслуживания. При этом вероятность того ,что источник указанного вызова осуществляет повторный вызов, равна Н. Следовательно с вероятностью jН поступает повторный вызов. Снова с вероятностью   этот повторный вызов не поступает на второй этап и с вероятностью Н источник производит повторный вызов и т. д.

1
 
                        

(1-jH)

 
 
          L=1+jH+(jH) 2+…=                   = (r + g) / ( yr + g).

 

Из этого сдует, что среднее число   на первом этапе обслуживания, которое производит источник до полного обслуживания вызова, зависит только от вероятности y м и не зависит от характера r потока повторных вызовов.

 

 


1 - jH
 
                             Н =                                  < 1 Эрл H<1        

 

 

V
 

C
 

Y
 
                             n =          (          + tb ) < 1 H = 1

 

 


Принимая за единицу времени, среднее суммарное время занятии линии пучка полным обслуживанием одного вызова   находим ,что интенсивность потока за такую единицу времени  m = Ct , отсюда l = m для ППВ, отсюда

 

                                                H = (l / V) <1

 

 

 

 

 

 

 

 

 

 

                                       Список литературы

 

1.Корнышев Ю.А . Потоки  вызовов  и нагрузка, ОЭИС 1975.

 

2.Ливщиц Б.С. Фидлин Я.В. Теория телетрафика М.связь 1979

 

3.Башарин.Г.Г. Таблица вероятностей и средних квадратических отклонений потерь в ПП линий. М.АН СССР 1962

 

4.Корнышев Ю.Н  К.Л.Фан Ген Ли. Теория распределения информации. М. “Радио и связь” 1985

 

Оглавление:

 

1

Предметы и задачи теории телетрафика

3

2

Потоки вызовов.

6

3

Простейший поток вызовов.

10

4

Нестационарный и неординарный поток Пуассона.

15

5

Понятие о телефонной нагрузке. Колебание нагрузки.

21

6

Параметры и расчёт интенсивности телефонной нагрузки.

24

7

Расчёт и распределение телефонной нагрузки.

28

8

Характеристика качества обслуживания вызовов и дисциплина обслуживания вызовов.

 

32

9

Методы расчёта однозвенных коммутационных систем. Расчёт однозвенных полнодоступных схем. Обслуживание вызовов простейшего потока.

 

36

10

Обслуживание вызовов примитивным потоком.

44

11

Неполнодоступное включения. Понятия о неполнодоступном включении.

 

54