УЗБЕКСКОЕ АГЕНТСТВО СВЯЗИ И ИНФОРМАТИЗАЦИИ

ТАШКЕНТСКИЙ УНИВЕРСИТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ

Кафедра ТС и СК

ОСНОВЫ НАУЧНЫХ ИССЛЕДОВАНИЙ

Учебное пособие для магистрантов специальности:

5А522202 – Сети, узлы связи и распределение информации

Ташкент 2008

Оглавление

	Введение ...................................................................	3
1.	Методологические основы научного познания и творчества………………………………………….	4
2.	Исследование операций. Линейное программирование..................................	8
3.	Динамическое программирование. ………………	15
4.	Марковский случайный процесс………………….	19
5.	1. Основы теории случайных ошибок .......................	25
6.	Статистическое моделирование случайных процессов (метод Монте-Карло).............................	31
7.	Системы коммутации с запоминанием..................	36
8.	Теория поиска...........................................................	41
	Литература ...............................................................	46

Введение

На сегодня широкое развитие информационно-коммуникационных технологий является глобальной тенденцией в научных исследованиях индустриально развитых государствах, ибо они играют важную роль в политическом и экономическом развитии этих стран.

Развитие коммутационной техники, сопровождаемое созданием в этих странах разнообразных систем телекоммуникаций нового поколения, требует переосмысления методов описания коммутационных сетей, систем коммутации, разнообразных способов предоставления услуг пользователям. Если в классические книги в качестве существенной части материала входили описания принципов действия конкретных систем, то сейчас такой подход практически невозможен. Развитие элементной базы, применение новых принципов управления и расширение функций систем коммутации требуют сосредоточить внимание преподавателей и магистрантов на более общих принципах и закономерностях построения систем коммутации, интегральных сетей, сетей NGN, используя материал, относящийся к конкретным системам, лишь для иллюстрации.

Отсюда следует, что в процессе учебы в университете необходимо обратить внимание магистрантов на вопросы методологи: постановки задач, выбору математических моделей, осмысление результатов расчета. В ходе учебного процесса и период разработки магистерской диссертации возникают проблемы оценки точности и надежности измерений при данном количестве замеров, гарантирующие требуемую (заданную) точность и надежность измерений. Наряду с этим возникает необходимость исключить грубые ошибки ряда, определить достоверность полученных данных и др.

Решение этих проблем будет свидетельствовать о том, что магистрант научился самостоятельно вести научный поиск, видеть профессиональные проблемы средств и сетей телекоммуникации и знает общие методы и приемы их решения.

Данное пособие по дисциплине «Основы научных исследований» позволит магистрантам специальности 5А522202 – “Сети, узлы связи и распределение информации” изучить вопросы методологии научного творчества; проведения исследовательской работы; моделирования в техническом творчестве; рассмотрения теории поиска минимакса при исследовании заданных функций и т.д.

1.Методологические основы научного познания и творчества.

1.1.Понятие научного знания

Знание - воспроизведение в языковой форме представлений о закономерных связях объективного мира.

Процесс движения человеческой мысли от незнания к знанию называют познанием. В основе познания лежит отражение объективной действительности в сознании человека в процессе его производственной и научной деятельности на практике.

Практика является основой и движущей силой развития познания, его целью. Познание включает в себя два уровня:

1. чувственный;

2. рациональный

Чувственное познание формирует эмпирическое познание, а рациональное - теоретическое. Элементами чувственного познания являются: ощущения, восприятие, представление и воображение.

Рациональное познание опережает и дополняет чувственное, способствует осознанию сущности процессов, раскрывает закономерности развития. Формой рационального познания является абстрактное мышление.

Мышление - опосредованное и обоснованное содержание в мозгу человека существенных свойств, причинных отношений и закономерных связей между объектами и явлениями.

Опосредованный характер мышления заключается в том, что человек через доступные органам чувств свойства, связи, отношения предметов проникает в скрытые свойства, связи, отношения. Действительность познается не только в результате приобретения своего личного опыта, но в большинстве случаев косвенным путем в процессе обучения преподавателем. Мышление непосредственно связано с языком и не осуществимо вне его.

Основной (элемент) инструмент мышления – логические рассуждения человека. Структурными элементами логического рассуждения являются понятие, суждение и умозаключение.

Понятие – это мысль, отражающая существенные и необходимые признаки предмета или явления. Раскрытие содержания понятия называют его определением. Определение характеризуется двумя признаками:

а) определение должно указывать на ближайшее родовое понятие;

б) определение должно указывать на то, чем данное понятие отличается от других понятий.

Пример.

Понятие «квадрат». Определяя понятие «квадрат» нужно указать на то, что

а) квадрат относится к роду прямоугольников

б) отличается (выделяется) среди прямоугольников признаками равенства своих сторон.

При научных исследованиях определением завершается процесс исследования, им закрепляют результата, к которым пришел исследователь. Без определения понятий не возможно логическое толкование мыслей автора исследования. Определение понятия возможно только в том случае, когда мы знаем к какому роду оно относится и какие у него видовые признаки т.е. чем отличается данный предмет, теория, устройство от подобных.

Установление отличительных или важных свойств осуществляется при помощи деление понятия. Делением понятия называется раскрытие всех видов (отличительных признаков), входящих в состав данного понятия. Деление отличительных признаков подчиняется следующим правилам:

а) члены деления должны исчерпывать объём данного понятия;

б) деление должно производиться с точки зрения определенного основания;

в) члены деления должны исключать друг друга.

Суждение - это мысль, в которой посредством связи понятий утверждается или отрицается что-либо. В речи суждение выражается в виде предложения. Суждение - это сопоставление понятий, устанавливемое по их признакам или cоответствий между предметами и классом предметов. Суждение делится по признакам: качеству, количеству, отношению, модульности.

· По количеству - на общее, частное и единичное.

· По отношению - на категорические.

· По модульности - на проблематические и ассерторические. В проблематических суждениях предполагается наличие связи понятий с некоторой степенью вероятности, а в ассерторических суждениях предполагается наличие действительно существующей связи понятий.

К суждению о предмете или явлении человек может прийти или путем непосредственного наблюдения какого-либо факта или опосредованным путем с помощью умозаключения.

Умозаключение - процесс мышления, составляющий последовательность двух или нескольких суждений, в результате которых выводится новое суждение. Часто умозаключение называют выводом, через который становится возможным переход от мысли к действию, практике. Умозаключение делится на две категории:

1. Дедуктивное умозаключение - выведение частичного случая из какого-нибудь общего положения.

2. Индуктивное умозаключение - на основании частичного случая приходят к общему положению.

1.2. Этапы научного исследования.

Процесс научного исследования может состоять из этапов:

а) возникновение идеи;

б) формирование понятий;

в) суждение;

г) выдвижение гипотез;

д) обобщение научных фактов;

е) доказательство правильности гипотез и идей.

1. Научная идея - интуитивное объяснение явлений без промежуточной аргументации, на основании которой делается вывод. Свою материализацию идея находит в гипотезе.

2. Гипотеза - это предположение о причине, которая вызывает данное следствие. Если гипотеза согласуется с фактами, то в науке её называют теорией или законом. По мере уточнения и исправления гипотеза превращается в закон.

3. Закон - внутренняя существенная связь явлений, обуславливающая их необходимое закономерное развитие. Закон выражает определенную связь между явлениями или свойствами материальных объектов.

4. Теория - система обобщенного знания. Теория возникает в результате обобщения познавательной деятельности и практики. Это обобщенный опыт в сознании людей. Исходные положения научной теории называют аксиомой.

5. Аксиома – это положения, которые берутся в качестве исходных, недоказуемых в данной теории, и из которых выводятся все остальные предположения и выводы теории по заранее фиксированным правилам.

1.3. Методы теоретических и эмпирических исследований.

Метод - это способ достижения цели. Метод - программа построения и практического применения теории. Одновременно метод субъективен, он является продуктом мышления исследователя.

К общенаучным методам относятся:

а) наблюдение;

б) сравнение;

в) счет;

г) эксперимент;

д) обобщение;

е) абстрагирование;

ж) формализация;

з) анализ и синтез;

и) индукция и дедукция;

к) аналогия;

л) моделирование;

м) идеализация.

· наблюдение - метод основан на непосредственном наблюдении без вмешательства со стороны исследователя;

· сравнение - установление различий между объектами, предметами при помощи органов чувств, так и при помощи специального оборудования;

· измерение - физический процесс определения человеком значения некоторых величин путем сравнения с эталоном;

· эксперимент - сфера практической деятельности исследователя, в которой подвергается проверке истинность выдвигаемых гипотез;

· обобщение - определение общего понятия, характеризующего объекты данного класса;

· формализация-отображение объекта или явления в знаковой форме какого-либо искусственного языка (математического, физического или химического) по формализованным соотношениям;

· анализ - метод познания при помощи разложения предмета исследования на составные части.

· синтез - соотнесение отдельных сторон предмета в единое целое.

Анализ-синтез взаимосвязаны, они представляют собой единство противоположностей.

1.4. Ситемный анализ.

В основе системного анализа лежит понятие системы. Под системой понимают множество объектов, обладающих заранее определенными свойствами с фиксированными между ними соотношениями.

Системный анализ складывается из 4 этапов:

1. Постановка задачи - определение объекта, цели и задачи исследования, а также критерии для изучения и управления объектами.

2. Определение границы изучаемой системы. Различают замкнутые и открытые системы. При изучении замкнутых систем влиянием внешних факторов на поведение системы пренебрегается. Выделены отдельные составляющие части системы - её элементы, устанавливаются взаимодействие между ними и внешние связи.

3. Составление математической модели исследуемой системы.

4. Анализ полученной математической модели с целью формирования выводов.

2. Исследование операций (ИО)

2.1. Общие понятия.

ИО - применение математических, количественных методов для обоснования решений в конкретной области, например в телекоммуникационных технологиях.

Обоснование решений - это какой-то выбор вариантов решений, имеющихся у исследователя.

ИО начинается тогда, когда для обоснования решений применяется тот или другой математический аппарат.

Например, чтобы решить как одеться выходя на улицу, где перейти улицу математика не нужна. А для принятия решения - как проектировать городскую телекоммуникационную сеть нужна математика: как построить ГТС, как разместить узловые АТС, расчет нагрузки для отдельных участков и т.д.

В любой задаче исследования операций имеются элементы решения, условия и т.д., которые образуют множество возможных решений.

Обозначим это множество буквой Х, а решение х, принадлежащее этому множеству (элемент х входит в множество Х). Если получаются разные решения , чтобы сравнить их между собой нужно иметь количественный критерий-показатель эффективности или целевая функция – W. Выбирая решение, предпочитают такое решение, которое обращает показатель W в максимум или минимум.

Например. Доход предприятия в максимум, затраты на оборудование в минимум.

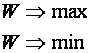
Пример

План пропускной способности нагрузки коммутационной системы.

2.2. Линейное программирование.

Пусть задана телекоммуникационная сеть () с 5 станциями А1, А2, А3, А4, А5 . Куда поступили пакеты А1=30, А2=48, А3=20, А4=30, А5=0 по исходящей связи. Эти пакеты предназначены станциям В1=18, В2=27, В3=42, В4=15, В5=26.

Транспортная задача линейного программирования ставится следующим образом: имеются m АТС, куда поступают заявки (пакеты) , пакеты поступающие на эти станции соответственно . Имеются n АТС, куда назначаются пакеты информации. Приемные АТС . Назначение пакетов соответственно .

- число станций передачи, - число станций приема.

Сумма всех заявок равна сумме пакетов. Условием, когда все вызовы в системе будут обслужены, будет условие 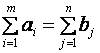(1):

(1)

Для характеристики эффективности решения транспортной задачи вводят понятие стоимости маршрута - от каждой предающей станции к каждой приемной. Обычно стоимость отдельных маршрутов объединяют в виде матрицы или таблицы стоимости передачи информации (2).

- стоимость маршрута ij

(2)

Требуется составить план передачи пакетов (откуда, куда и сколько пакетов надо передать), чтобы все пакеты были переданы, а общая стоимость всех передач была минимальной.

Чтобы решить задачу методом линейного программирования, обозначим -количество пакетов информации, отправляемых из АТС к . Значения переменных можно записать в виде матрицы:

(3)

Совокупность чисел составляет план передачи, а сами величины - пакетами передачи. Эти переменные должны удовлетворять следующим условиям (4) и (5):

(4)

(5)

2)-суммарное количество пакетов, доставляемых в каждый пункт назначения из всех АТС группы .

2.3. Основная задача линейного программирования

Суммарная стоимость передачи, т.е. сумма величин умноженных на соответствующие стоимости должна быть минимальной.

Необходимо найти целевую функцию L по формуле:

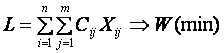(6)

В данном случае целевой функцией будет функция стоимости передачи от станции А к В и очевидно, она должна быть минимальной.

Число линейно независимых параметров равно m+n , а m+n-1 – число базисных уравнений, общее число переменных равно m*n.

Тогда число свободных переменных:

Пусть дано число станций передачи =5. Число станций приема =5. Сеть построена по принципу «каждая с каждой». План распределения нагрузки считается допустимым, если он удовлетворяет условиям (4) и (5) - т.е. все заявки удовлетворены.

Допустимой будем считать схему распределения, если в ней отличны от нуля не более m+n-1 базисных передач заявок, а остальные пути передачи равны нулю. План будем считать оптимальным, если он, среди всех допустимых планов приводит к минимальной суммарной стоимости передачи информации т.е.

Пример

Транспортная таблица состоит из m строк и n столбцов.

Таблица 1

						По
	13	7	14	7	5	30
	14	8	12	6	8	48
	6	10	10	8	11	20
	14	8	10	10	15	30
	-	-	-	-	-	-
Пн	18	27	42	15	26	128

По - пункт отправления

Пн - пункт назначения

В таблице 1 приведены стоимости передачи информации для различных пунктов приема и передачи.

План организации передачи не оптимален. Если произвести «циклическую перестановку» передачи между циклом передачи, скажем А2В3 со стоимость 12 , и увеличить передачу в дешевом цикле А2В4 со стоимостью 6, то улучшится план передачи . Чтобы план оставался оптимальным, мы должны при этом определить определенный цикл как базовый, а один из циклов свободным.

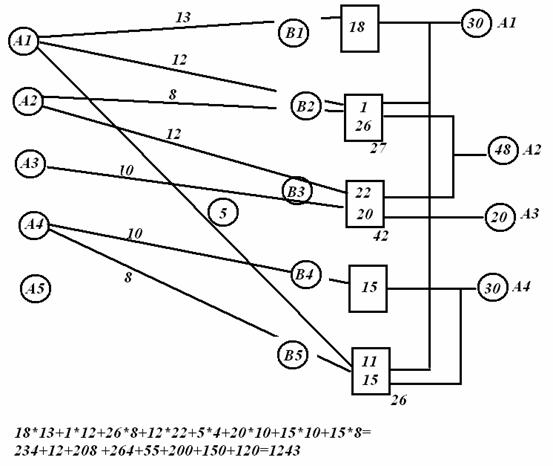
Составим таблицу 2 и расчитаем стоимость передачи:

L1=18*13+12*7+15*8+33*12+9*10+11*8+4*10+26*15=1442 у.е.

Вариант распределения заявок (пакетов) L=1442 Таблица 2

						По
	18	12				30
		15	33			48
			9	11		20
				4	26	30
	-	-	-	-	-	-
Пн	18	27	42	15	26	128

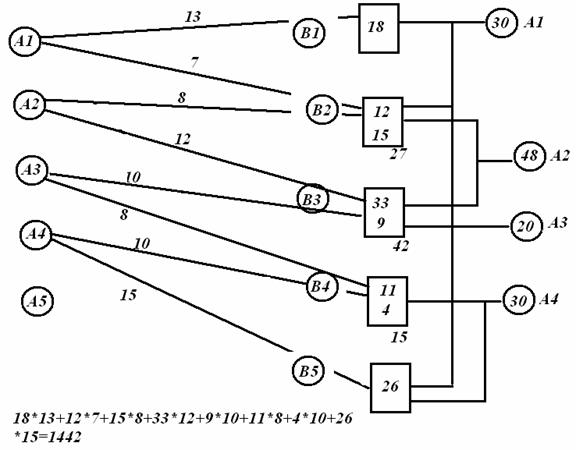
1 шаг минимизации L2=1398 Таблица 3

						По
	18	12				30
		15	22	11		48
			20			20
				4	26	30
	-	-	-	-	-	-
Пн	18	27	42	15	26	128

Анализ транспортной таблицы стоимости показывает, что если из ячейки А2В3-33 единицы информации, можно перенести информацию со стоимостью 12 у.е. в ячейку А2В2, то стоимость 23 передачи уменьшится и получится равной L2=1398 у.е.

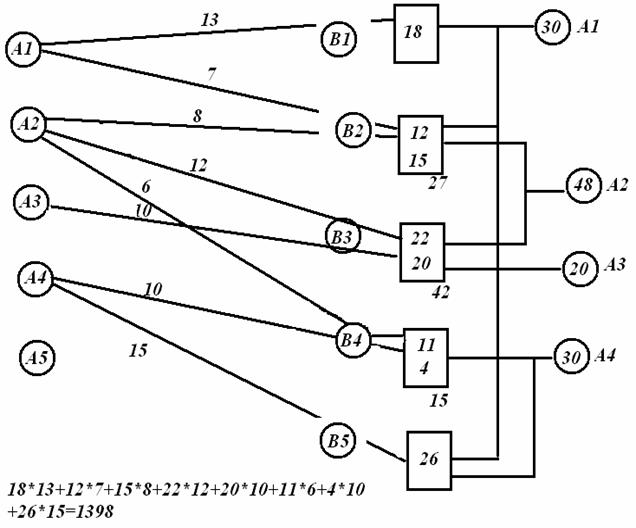
Для решения оптимизации необходимо найти циклы передачи. Возьмем (вершины) тракты передачи

(2,4)→(3,4)→(3,3)→(2,3)↔(А2В4)(А3В4)(А3В3)(А2В3)

Для дальнейшего уменьшения стоимости передачи построим новый цикл передачи: (A1B2)(A1B5)(А4В4)(А2В4)(А2В2) тогда стоимость передачи станет L3=1243

Таблица 4

L3=1243

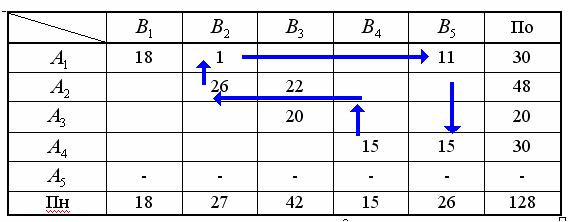
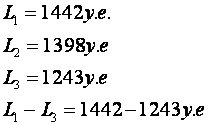
Т.о. эффективность передачи увеличивается с 1442 до 1243, т.е. на 199 единиц. На следущих рисунках приведены различные варианты расчетов стоимости передачи.

3. Динамическое программирование

3.1. Метод динамического программирования (ДП)

Имеется некоторая операция (О), распадающаяся на ряд последовательных шагов, например сеть связи.

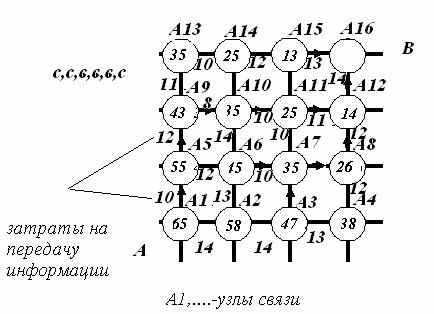
Рис. 1 Сеть связи.

Необходимо найти оптимальный вариант установления соединения. Пусть эффективность операции установления соединения характеризуется показателем -W (целевой функцией). Предположим, что функция W за всю операцию установления соединения складывается из эффективных шагов установления соединения:

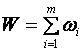(1)

-эффективность в условных единицах на i-ом шаге.

Если целевая функция обладает свойством (1) ,то такая функция называется аддитивным критерием.

Операция О - установление соединения - управляемый процесс, т.е. мы можем выбрать варианты ,влияющие на ход процесса и на его исход. Причем на каждом шаге выбираются какие-то решения : при установления соединения от А к В – устанавливать соединение А1-А5 или А1-А2.

Совокупность всех шаговых управлений представляет собой управление операцией установления соединения в целом.

Обозначим эту совокупность как, а шаговые управления до получения решения .

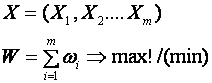(2)

Буквы в общем случае – это не числа, ими могут быть обозначены векторы ,функции и т.д.

Необходимо найти такое управление Х при котором целевая функция обращается в максимум. То управление Х* при котором W достигает максимума, называется оптимальным управлением. Оно состоит из совокупности оптимальных шаговых управлений:

(3)

При этом максимальная /минимальная целевая функция будет:

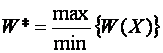(4)

Задача оптимального управления решается пошаговой оптимизацией, которая лежит в основе динамического программирования.

Продемонстрируем это решение на примере установления соединения от АТС А1 до АТС А16(В) (рис 1).

Как видно, эти АТС отстоят друг от друга в восточном направлении и северном направлении из 3-х частей. Тогда любой путь от А1 до А14 состоит из 6 соединительных линий. На каждом отрезке проставлена в условных единицах стоимость услуги.

Требуется выбрать такой путь установления соединения от А1 до А14 для которого целевая функция W-была бы минимальной.

Будем рассматривать устанавливаемый путь как управляющую систему S(A1A16).

Состояние этой системы перед началом каждого шага будет характеризоваться двумя координатами: восточной (Х) и северной (У). Обе координаты целочисленные .

Для каждого из состояний системы (узловых АТС –Ai) мы должны найти условное оптимальное управление: идти из этой точки на север (С) или на восток (В).

Будем выбирать это управление так, чтобы стоимость управления оставшихся до конца этапов (включая данный) была бы минимальной.

Процедуру оптимизации будем развивать в обратном направлении от конца к началу. Движение либо на юг, либо на запад.

Произведем условную оптимизацию последнего 6–го шага. Рассмотрим отдельно правый верхний угол (рис 1, рис.2).

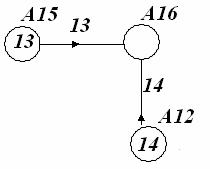6 шаг

Рис. 2

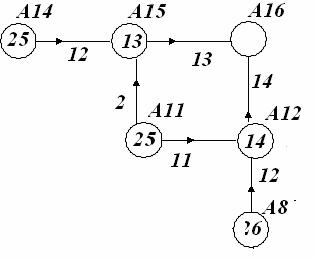5 шаг

Рис. 3

Где мы можем находиться после 6 шага. Только оттуда за один шаг можно попасть в А16 (из А15 или А12).Если мы находимся в А15, то выбора нет, мы идем на восток (В). Затраты в этом случае 13 у.е. Для узла А12 – направление на север и стоимость пути - 14 у.е. (Эти значения записаны в кружочки).

Теперь найдем оптимальное управление для 5-го шага. Для А14 управление для пути на восток и обойдется это направление в до конца в 25 у.е. Для узла А11 – мы можем идти как на восток (В), так и на север (С). В первом случае затраты на данном шаге 11 у.е. и от А12 до А16-14 у.е. и всего 25 у.е. Если пойдем на север, также затраты составят 25 у.е.

Для точки А8 направление выбирается на север (С), затраты составят до конца пути 26 у.е. и ставим стрелку на север , значение 26 записываем в кружок А8.

Далее ход решения аналогичный.

Минимальные затраты на решение задачи-65 единиц. Оптимальный тракт-С, С, В, В, В, С (В- восток, С-север).

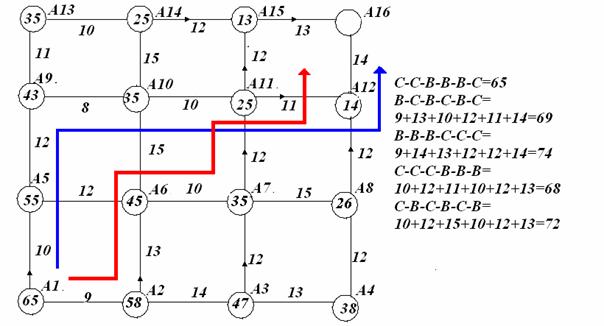
Рис. 4.

На рисунке 4 показонны варианты решения задачи по установлению соеденения. Оптимальным трактом установления соединения между узлами является тракт, прозодязий узлы: А1-А5-А9-А10-А11-А12-А16. При этом минимальная целевая функция W* равна 65 у.е. А все остальные пути потребуют больших затрат.

4. Марковский случайный процесс (МСП)

4.1. Общие понятия.

При анализе многих случайных дискретных процессов используется Марковский случайный процесс. Случайный процесс называется марковским, если для любого момента Если для любого момента времени вероятностные характеристики процесса в будущем зависят только от его состояния в данный момент времени и не зависят от того, когда и как система пришла в это состояние.

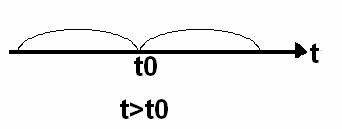
МСП характеризуется дискретным состоянием и непрерывным временем.

1) Дискретное состояние – при этом есть возможные состояния S1,S2…, которые можно заранее перечислить и переход системы из одного состояния в другое происходит «скачком».

2) Процесс является непрерывным по времени, если моменты возможных переходов из состояний S_i в S_j не зафиксированы заранее. Переход может осуществиться в любой момент времени.

Исходя из этих свойств, процессы в телекоммуникации рассматриваются как потоки событий и среди них можно выделить простейший поток (обладающий свойством ординарности, стационарности и не влекущий за собой последствий).

Характеристиками потока являются интенсивность – среднее число событий, приходящихся на единицу времени. Таким свойством обладает Пуассоновский поток. В таких потоках вероятность появления числа событий х=1,2,… в единицу времени определяется формулой:

(1)

Эта формула используется в системе массового обслуживания (СМО). СМО определяет условия наибольшей эффективности работы системы «требование-обслуживание».

СМО состоит из:

а) числа входящего потока требований

б) обслуживающего прибора (автомата)

в) выходящего потока

В зависимости от условий функционирования системы, СМО (число требований) создает очередь на обслуживание.

Основными характерными особенностями системы СМО являются:

а) интенсивность заявок на обслуживание ;

б) интенсивность обслуживания - пропускная способность аппарата обслуживания -;

в) коэффициент обслуживания ;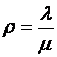

г) время ожидания в очереди до обслуживания ;

д) длительность обслуживания в системе ;

е) число требований в очереди ;

ж) математическое ожидание числа требований в системе ;

Между этими величинами имеются соотношения

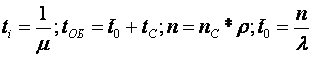
4.2 Формула Литтла.

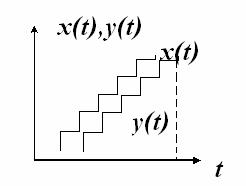
Рис. 1.

-число заявок, прибывающих в СМО

-число заявок покидающих СМО

Для предельного стационарного режима

- число заявок, поступающих в систему, равно среднему числу заявокЮ покидающих её, оба потока заявок имееют одну и ту же интенсивность λ. Среднее число заявок находящихся в СМО

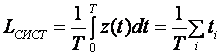
Среднее число заявок, пришедших за время Т равна .

-среднее время пребывания заявки в системе.

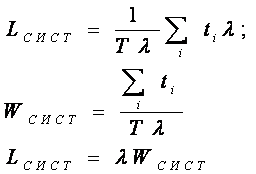
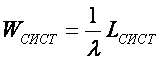, формула Литтла

Среднее время пребывания заявки в системе равно среднему числу заявок в системе, деленному на интенсивность потока заявок.

Рассмотрим:

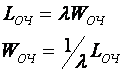
n - канальная СМО с отказом (задача Эрланга)

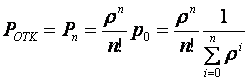
Относительная пропускная способность – вероятность того ,что вызов будет обслужен:

Абсолютная пропускная способность:

Среднее число занятых каналов:

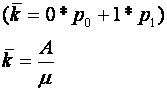
Пример

Пусть имеется коммутатор с n=3 каналами, =1,5 заявки в минуту. А=0.981,Q=0.654, =0.346,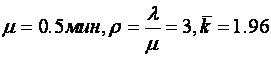

4.3. Одноканальная система СМО с очередью

Поступает поток вызовов с интенсивностью , интенсивность обслуживания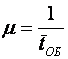. Требуется найти вероятности состояний СМО, а также характеристики её эффективности.

-среднее число заявок в системе

-среднее время пребывания заявки в системе

-среднее число вызовов в очереди

-среднее время пребывания вызова в очереди

-вероятность того, что канал занят.

-все вызовы рано или поздно будут обслужены.

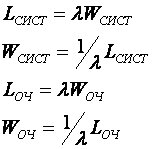
Среднее число заявок в СМО:

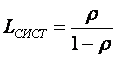
Среднее время пребывания в системе:

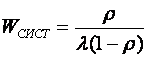
Среднее число заявок с очередью:

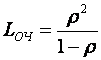(1*)

5.Среднее время пребывания заявки в очереди:

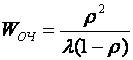(2*)

Если имеется n – канальная система массового обслуживания:

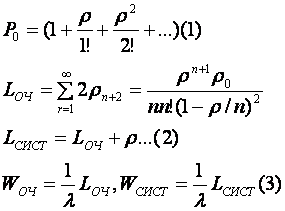
ЗАДАЧА

Университетская касса выдачи стипендии с двумя окошками представляет собой 2-х канальную СМО с очередью.

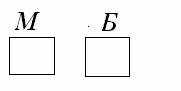
Интенсивность потока студентов для М и Б одинаковы в минуту. В сумме получается общий поток . Касса тратит на обслуживание студента в среднем 2 минуты. У кассы скапливается очередь. Студенты жалуются на медленное обслуживание. Один магистрант предложил рационалистическое предложение - вместо единых касс, выдающих стипендии, установить специализированные кассы, т.е. в кассе М будут выдавать стипендию магистрантам, а в Б - бакалаврам. По данному предложению возникают споры о его рациональности. Требуется проверить правильность предложения расчетом. Все потоки студентов простейшие.

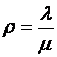Вариант 1 (существующий). На двухканальную СМО поступает поток заявок с интенсивностью =0,9,интенсивность обслуживания потока =1/2=0,5 =1,8.

По формуле (1) =0,0525,по формуле (2)=7,68.

Среднее время, проведенное студентами в очереди по формуле (3). Среднее время пребывания в очереди:

=8,54 мин

Вариант 2. Рассматриваются 2 одноканальные СМО (2 специализированных окошка), на которые поступает поток заявок (студентов) ,,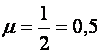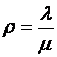=0,9.По формуле (1*)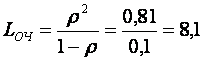

Т.е. длина очереди выросла. Среднее время ожидания в очереди по формуле (2*)

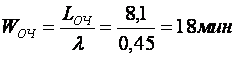
Т.е. данное предложение не эффективно - длина очереди и время ожидания увеличиваются.

5. Основы теории случайных ошибок.

5.1. Основы теории случайных ошибок и методов оценки случайных погрешностей в измерениях.

Анализ случайных погрешностей основывается на теории случайных ошибок, дающей возможность с определенной гарантией вычислить действительное значение измеренной величины и оценить возможные ошибки. Основу теории случайных ошибок составляют предположения о том,

- что при большом числе измерений случайные погрешности одинаковой величины, но разного знака встречаются одинаково часто;

- что большие погрешности встречаются реже, чем малые;

- что при большом числе измерений истинное значение измеряемой величины равно среднеарифметическому значению всех результатов измерений;

- что появление того или иного результата измерения как случайного события описывается нормальным законом распределения.

Различают генеральную и выборочную совокупность измерений.

· Генеральная совокупность – это все множество значений измерений X_i.

· Выборочная совокупность – ограниченное число изменений n. Обычно считают, что если n>30, то среднее значение данной совокупности измерений достаточно близко приближается к его истинному значению (бросание монет).

Теория случайных ошибок позволяет оценить точность и надежность измерения при данном количестве замеров, гарантирующее заданную (требуемую) точность и надежность измерений.

5.2. Интервальная оценка с помощью доверительной вероятности.

Для нормального закона распределения общей оценкой является дисперсия D и коэффициент вариации К_в

F(x) =^- ,

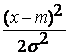где m=M[x]; D[x]=²; - среднеквадратическое отклонение.

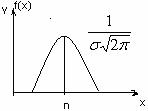
Рис. 1

Для большой выборки и нормального закона распределения общей оценочной характеристикой является дисперсия D и коэффициент вариации К_в.

D=²=; (1)

К_в=_.

Доверительная вероятность (достоверность) измерения – это вероятность того, что истинное значение измеряемой величины попадает в данный доверительный интервал, т.е. в зону ax_дb. Эта величина определяется в долях единицы или процентах. Доверительная вероятность определяется:

P_д=P [ax_дb] = (2),

где (t) – интегральная функция Лапласа

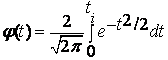(3),

где t= - гарантийный коэффициент

; (4),

Если в качестве P_д=0,95, то устанавливается точность измерений (достоверный интервал 2) на основе соотношения P_д =(). Тогда половина доверительного интервала равна:

=arg(P_д)=t (5),

где arg(P_д) – аргумент функции Лапласа, а при n<3 – функции Стьюдента (табл. П.2).

Доверительный интервал характеризует точность измерения данной величины данной выборки. Доверительная вероятность – достоверность измерения.

Пример 1.

Пусть выполнено 30 измерений нагрузки Е=170 Эрл и вычисленном значении =3,1 Эрл , D=²=9.

Требуемую точность измерений можно определить для разных уровней доверительной вероятности (P_д=0,9;0,95;0,99), приняв значения t по таблице интегральной функции Лапласа. В этом случае соответственно

=3,1*1,65=5,1 (Эрл); =3,1*2,0=6,2 (Эрл); =3,1*3,0=9,3 (Эрл).

Следовательно, для данного средства и метода доверительный интервал возрастает примерно в 2 раза, если увеличить P_д только на 10%.

Доверительный интервал. Таблица 1

t	1,65	1,70	1,75	1,80	1,85	1,90	1,95	2,00	2,25	2,50	3,0
Pд	0,90	0,91	0,92	0,93	0,94	0,94	0,945	0,995	0,97	0,98	0,99

Следовательно для данного средства и метода доверительный интервал возрастает примерно в два раза, если увеличить P_д только на 10%.

5.3. Определение достоверности измерения.

Для установления доверительного интервала =7 Эрл по формуле (4) t==7/3.1=2,26. По таблице П.1 для t=2,26 определяем P_д=0,97. Это означает, что в заданный доверительный интервал из 100 измерений не попадает только 3.

Значение (1- P_д) называется уровнем значимости. Из него следует, что при нормальном законе распределения погрешность, превышающая доверительный интервал, будет встречаться один раз из n_и измерений:

n_и= P_д / (1- P_д) (6)

5.4. Определение количества измерений в опыте.

По формуле (6) при P_д=0,9; n_и= 0,9 / (1- 0,9)=9 (измерений);

При P_д=0,95 и 0,99 – соответственно 19 и 367 измерений.

5.5. Определение минимального количества измерений.

Задача сводится к установлению минимального объема выборки (числа измерений) N_min при заданных значениях доверительного интервала 2 и доверительной достоверности. При выполнении измерений необходимо знать

их точность

(7),

где - среднеарифметическое значение и равно

(8)

называют средней ошибкой. Доверительный интервал ошибки измерения определяется как

(9)

Тогда доверительная вероятность ошибки измерения определяется по таблице П.1. Если требуется определить минимальное количество измерений, гарантирующих требуемые значения и P_д, то их можно определить по формулам

(10)

При N_min=n получаем:

(11),

где - коэффициент вариации (изменчивости), % ;

- точность измерения, %.

5.6. Определение N_min .

Для определения N_min применяется следующий порядок вычисления:

1. Определяют n=2050.

2. Определяют среднеквадратическое отклонение по формуле:

3. Устанавливается требуемая точность измерений .

4. Устанавливается нормированное отклонение t (задается).

5. По формуле (11) определяют N_min.

Пример. Пусть N_min=25 измерений, = 0,1 Эрл, предварительно вычисленное значение =0,4 Эрл. Гарантийный коэффициент:

t =.

По таблице П.1 находим при t=1,25 P_д = 0,79. Погрешность, превышающая доверительный интервал 2=0,2 Эрл согласно формуле (6) будет встречаться один раз из 4-ех измерений:

n_и= P_д / (1- P_д)=0,79/(1-0,79)=3,374

Это недопустимо. В связи с этим необходимо вычислить минимальное количество измерений с доверительной вероятностью P_д , равной P_д=0,9 и P_д=0,95. По формуле (11)

N_min = 0,4² * 1,65²/0,1²=43 измерения,

и 64 измерения при P_д=0,95, что значительно превышает установленные 25 измерений.

5.7. Кривые распределения Стьюдента.

Метод Стьюдента для нахождения границы доверительного интервала. Метод применяется при малых значениях n<30.

Для малой выборки доверительный интервал определяется:

_ст= (12)

- коэффициент Стьюдента - табулирован в зависимости от значений доверительной вероятности P_д, принимается по табл.2.

Коэффициент Стьюдента Таблица 2

n	Pд
	0,80	0,90	0,95	0,99	0,995	0,999
2	3,080	6,31	12,71	63,70	127,30	637,20
4	1,638	2,35	3,188	5,84	7,50	12,94
8	1,415	1,90	2,36	3,50	4,03	5,40
10	1,383	1,83	2,26	3,25	3,69	4,78
12	1,368	1,80	2,20	3,11	3,50	4,49
14	1,35	1,77	2,16	3,01	3,37	4,22
18	1,33	1,74	2,11	2,90	3,22	3,96
20	1,32	1,73	2,09	2,86	3,17	3,88
30	1,31	1,70	2,04	2,75	3,15	3,65

Зная _ст можно вычислить действительное значение изучаемой величины для малой выборки.

х_д=_ст (13).

Можно и решать задачу следующим образом. По n известным измерениям малой выборки необходимо определить доверительную вероятность P_д при условии, что погрешность среднего значения не выйдет за пределы _ст.

Задача решается последовательно:

1) вычисляется - среднее значение;

2) =/ ;

3) =_ст/;

4) с помощью величин , известного n и табл.2 определяют P_д.

Пример.

1) = 74,83; n=18;

2) =6,58;

3) =6,58 * = 6,58 * 4,2=27,9;

Для P_д=0,9 _ст==27,9 * 1,74=48,5; t==48,5/6,5=7,46;

Для P_д=0,8 _ст==27,9 * 1,33=37,10; t==37,1/6,5=5,7;

Для P_д=0,95 _ст==27,9 * 2,11=58,8; t==58,8/6,5=9,0;

Для P_д=0,99_ст==27,9 * 2,9=80,91; t==80,91/6,5=12,4.

Половина доверительного интервала равна =t, т.о.

1) =6,58 * 5,7=37,5; 2) =6,58 * 7,46=49.

6. СТАТИСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ СЛУЧАЙНЫХ ПРОЦЕССОВ (МЕТОД МОНТЕ-КАРЛО)

6.1. Общие сведения.

Идея метода состоит в следующем: производится «розыгрыш» случайного явления с помощью специально организованной процедуры, включающей в себя случайность и дающей следующий результат.

В действительности конкретное осуществление (реализация) случайного процесса складывается каждый раз по-иному; так же как и в результате статистического моделирования («розыгрыша») мы получаем каждый раз новую, отличную от других реализацию исследуемого процесса. При моделировании случайных явлений методом Монте - Карло мы пользуемся самой случайностью как аппаратом исследования.

Например, работает многоканальная СМО с очередью. Требуется определить характеристики СМО: вероятности состояний как функции времени, среднюю длину очереди, среднее время пребывания в системе и т.д.

Эту задачу можно решить двумя методами: аналитическим и методом статистического моделирования.

Только при аналитическом методе требуется допущения, что процесс «марковский» (т.е. чтобы поток заявок был простейшим). Если процесс не «марковский», то задачу можно решить только методом статистического моделирования (промежутки между заявками имеют непоказательское распределения, время обслуживания - тоже).

6.2. Единичный жребий и формы его организации.

Основным элементом, из совокупности которых складывается статистическая модель, является одна случайная реализация моделируемого явления, например, одна заявка в СМО. Из таких заявок состоит поток вызовов.

Реализация – это как бы один «экземпляр» случайного явления со всеми присущими ему случайностями. Сами реализации отличаются друг от друга за счет этих случайностей. Отдельная реализация разыгрывается с помощью специально разработанной процедуры (алгоритма), в которой важную роль играет «бросание жребия».

«Единичным жребием» называют любой опыт со случайным исходом, который отвечает на один из следующих вопросов:

1. произошло или нет событие А?;

2. какое значение приняла случайная величина Х?;

3. какое из событий А₁, А₂,…, А_к произошло.

Для «единичного жребия» может быть использован механизм розыгрыша - умение получить случайное число R, все значения которого от 0 до 1 равновероятны, т.е. R – это случайное число от 0 до 1. С помощью такого числа можно разыгрывать любой «единичный жребий».

Произошло или нет событие А? Чтобы ответить на этот вопрос, надо знать вероятность р события А. Разыгрывается случайное число R от 0 до 1, и если оно оказалось меньше p, как показано на рис. 1 то событие А произошло.

Рис. 1

6.3. Какое из нескольких событий появилось?

События А₁, А₂,…, А_к несовместимы и образуют полную группу. Тогда сумма их вероятностей P₁, P₂,…, P_к равна единице.

Разделим интервал (0,1) на к участков длиной P₁, P₂,…, P_к . На какой из участков попало число R, то событие и произошло.

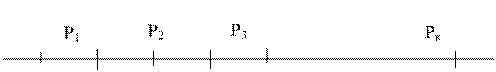
0 R 1

Рис. 2

Метод статистического моделирования сводится к розыгрышу (одно- или многократному) случайного числа R от 0 до 1.

Как разыграть число R? Один из способов – воспользоваться таблицей случайных чисел.

Таблица случайных чисел. 16 случайных цифр

Таблица 1.

86515	90795	66155	66434	56558	12332	94377	57802
69186 . . .	03393	42502	99224	88955	53758	91641	18867

Задача. Разыгрывание дискретной случайной величины.

Допустим, что нам нужно получить значение случайной величины с распределением

Рассмотрим интервал 0<y<1 и разобьем его на n интервалов, длины которых равны P₁, P₂,…, P_к . Координатами точек деления будут: R= P₁, R= P₁+ P₂, и т.д.

R= P₁ +P₂ +…+P_n .

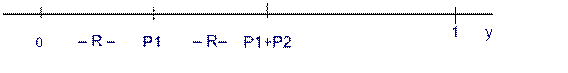
Рис. 3

На этом приготовление к розыгрышу заканчивается. Каждый раз, когда нам надо будет «поставить опыт» и разыгрывать значения , мы будем выбирать значения R и строить точку y=R. Если эта точка попадет в интервал c номером i, то будем считать, что =x_i (в этом опыте).

Пример 1. Разыгрывается 10 значений случайной величины с распределением

=

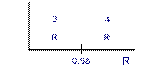
Рис. 4

В качестве значений γ выбираем пары цифр из таблицы случайных цифр, умножаем на 0,01.

Итак γ =0,86; 0,51; 0,59; 0,07; 0,95; 0,66; 0,15; 0,56; 0,64; 0,34.

Очевидно, по нашей схеме значениям γ, меньше 0,58, относят значение =3, а γ 0,58 – значение =4. Следовательно, мы получим значения:

=4; 3; 4; 3; 4; 4; 3; 3; 4; 3.

Пример 2.

Пример 2 моделируется методом Монте-Карло работе одноканальной системы массового обслуживания СМО с очередью. В качестве СМО возьмем работу кассы для выдачи зарплаты. Число мест в очереди ограничено двумя. Сотрудник пришедший в кассу, когда оба места заняты, покидает ее без зарплаты. Время от времени касса может простаивать (кассир занят разговором по телефону). Если кассир занят другшими делами, находящиеся у кассы сотрудники ждут нначало работы кассира. Требуется определить возможное состояние СМО кассы. Состояние кассы определяется следующим статистическим рядом

Где S-состояние системы, n-число сотрудников, p-вероятность их состояния.

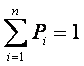; N=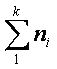; K=1..8

Граф состояний СМО(кассы) выглядит как показано на рис.1

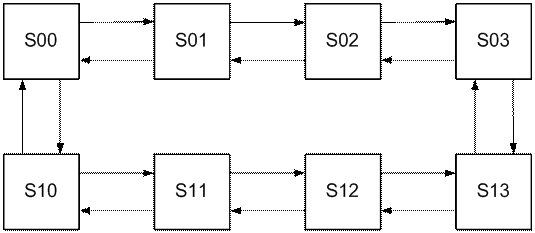
Рис.5 Граф состояний СМО

где,

S0i – кассир в состоянии выдавать зарплату, в кассе i сотрудников.

S1i – кассир отвлекается от процесса выдачи зарплаты, в кассе i сотрудников.

Требуется определить характеристики жффективности работы СМО-кассы:

1. Pисп – вероятность того, что кассир готов исполнять работу по выплате зарплаты сотрудникам;

2. Pотк – вероятность того, что сотрудник уйдет из кассы без зарплаты;

3. А – абсолютная пропускная способность кассы;

4. Lсист – среднее количество сотрудников в кассе;

5. Lоч – среднее число сотрудников пребывающих в очереди;

6. Wсист – среденее время пребывания сотрудника в кассе;

7. Wоч – среднее пребывание сотрудникав очереди.

Для составления алгортма “бросания жребий” – R выбираем пары цифр из таблицы случайных цифр, умножаем на 0,003, тогда получим R:

R=0,26; 0,153; 0,177; 0,021; 0,285; 0,198; 0,045; 0,168;

На основе R разыграем события Q:

Q = ( 32; 19; 24; 1; 32; 24; 4; 19; 24 и т.д.)

Определим вероятностно-временные характеристики работы СМО кассы:

1. Вероятность того, что сотрудник уйдет из кассы без зарплаты. Возможно если у кассы уже пребывает 3 человека, т.е.:

Pотк = Р03 + Р13 = 0,14 + 0,008 = 0,148

2. Абсолютная пропускная способность кассы за час равна:

А = λ (1-Ротк)=32(1-0,148)=27,3 человека,

если поток сотрудников в кассу 32 чел/час

3. Вероятность того, что кассир готов исполнять работу по выплате зарплаты сотрудникам равна:

Рисп = Р00 + Р01 + Р02 + Р03 = 0,27 + 0,20 + 0,16 + 0,14 = 0,77

4. Среднее количество сотрудников в СМО (в кассе) равно:

Lсист = 1*(Р01 + Р11) + 2(Р02 + Р12) + 3(Р03 + Р13) =

1*0,26 + 2*0,194 + 3*0,148 = 1,1 чел

5. Среднее число сотрудников пребывающих в очереди равно числено вероятности того, что кассир занят:

Lоч = [1 – (Р00 + Р10)] = 1 – (0,27 - 0,2) = 0,53

6. C среденее время пребывания сотрудника в кассе равно:

Wсист = Lсист/λ = 1,1/32 = 0,035 часа (или 2,1 минуты)

7. Cреднее пребывание сотрудникав очереди

Wоч = Lоч/ λ = 0,53/32 = 0,017 часа (или ≈ 1минуту)

7. Система коммутации с запоминаниями

7.1. Общие сведения.

Сети передачи данных делятся на системы с коммутацией каналов и с адресным разделением. Известны два вида коммутации с запоминаниями:

1. коммутация сообщений

2. пакетная коммутация - пакеты могут передаваться раздельно, а затем на приемном конце объединяются в исходное сообщение.

Существует два метода обработки информационных пакетов в сети с пакетной коммутацией:

1. виртуальный вызов

2. датаграмма

Рис. 1 Сеть передачи данных.

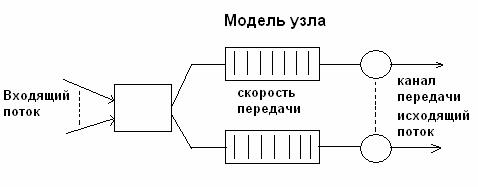
Рис. 2. Модель узла.

Модель узла, в которой имеется процессор, обрабатывающий адрес, содержащийся в заголовке пакета, и распределяющий эти пакеты в соответствии с этим адресом на канал передачи. Основными параметрами сетей с коммутацией пакетов являются:

Среднее время прохождения информационного блока в сети. Для обеспечения диалогового режима в сетях с коммутацией пакетов необходимо обеспечить уменьшение времени прохождения блока. Поэтому методы расчета сводятся к решению проблемы манипуляции среднего времени прохождения. Цель заключается в определении скоростей передачи на участках тракта. Если заданы параметры телетрафика:

1. средняя частота поступления пакетов в сеть,

2. средняя длин пакета,

3. вероятность выбора направления по которому информационные пакеты проходят по сети

Задача. Пусть имеется сеть с Nk коммутационными узлами, NL участками передачи между узлами

К узлу поступает нагрузка со средней частотой обращения Yk. Эта нагрузка распределяется по трактам передачи.

Пусть средняя интенсивность поступления информации по матрице интенсивности обмена линии i будет равна λi

Все интервалы между поступающими пакетами распределены экспоненциально.

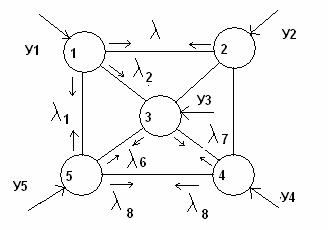
Рис. 3 Модель сети.

Длина информационных пакетов также имеет экспоненциальное распределение со средним значением 1/μ=L

Требуется минимизировать среднее значение времени tf прохождения блока по сети с учетом того, что для этой сети заданы общие затраты D

Таблица 1

Матрица интенсивности обмена

i	Yij пакетов в сек, при j равном
	1	2	3	4	5
1	-	40	10	20	20
2	40	-	30	20	30
3	10	30	-	20	10
4	20	20	20	-	10
5	30	10	10	10	-
∑	100	100	70	70	60

Среднее время прохождения ti линии i сети составляет

(1)

где Ci - скорость передачи двоичных сигналов по линии i

Зависимость затрат от скорости передачи выражается формулой

(2)

d_i - стоимостный коэффициент, α стремится 0 ≤ α ≤ 1.

Рассмотрим функцию:

(3)

по методу Лагранжа берем частную производную по Ci и равняем к нулю, получим

d Ф / d Ci = 0

i = 1 получим: после преобразования (α = 1, di = 1, У = 1)

Ci = λi/μ + √ λi/Уμ (4)

Время прохождения пакета по линии i определятся как:

√ √ (5)

(6)

Среднее время прохождения пакетов в сети:

(7)

Если

(8)

где – среднее число путей передачи на одно соединение.

Если зададим параметр Т – как дополнительной условие – как среднее время прохождения пакета, постоянное значение

(9)

средняя скорость передачи двоичных сигналов

(10)

Индивидуальное время прохождения ti становится равным

(11)

В таблице 2 приведены значения интенсивности обмена для сети по отдельным направлениям Таблица 2

i	1	2	3	4	5	6	7	8
λi пак/с	40	30	50	30	20	40	30	10

Средняя длина пакета составляет 1000 бит. Из таблицы 1 – матрицы интенсивности обмена. Управление (процессор) обмена выбирает кратчайшие пути. Обмен между узлом 1 и 5 проходит через 3. Также обмен между узлами 2 и 4 проходит через узел 3. Таблица 2 показывает интенсивность обмена в сети.

Интенсивность пакетов У, попадающих в сеть составляет 200 пак/сек, а обмен λ, проходящий по сети составляет 250 пак/сек. Для упрощения задачи примем α = 1, di = 1 и зададим среднее время прохождения Т = 1 сек, то можно по формулам (4) и (10) рассчитать скорости передачи двоичных сигналов, и индивидуальное время прохождения сигналов по формулам (5) и (11) В таблице 3 приведены скорости передачи двоичной информации и соответствующее им индивидуальное время прохождения пакета.

Скорости передачи двоичной информации и соответствующее им индивидуальное время прохождения пакета. Таблица 3

i	λi пак/с	Ci бит/с	ti с	Ci бит/с	ti с
1	40	40019		41250	0.8
2	30	30012		31250	0.8
3	50	50015		21250	0.8
4	30	30012		31250	0.8
5	20	20010		21250	0.8
6	40	40014		41250	0.8
7	30	30012		31250	0.8
8	10	10007		11250	0.8
По формуле (4)	250	По формуле (4)	По формуле (5)	По формуле (10)	По формуле (11)

Из формулы (10) Ci = λi/μ + n /μ T n / T = 1,25

_

Из формулы (11) ti = T / n = 0,8

Ci = 50 / μ + √50/200μ = 50000+√50000/200 = 50015 …..

Общие расходы D согласно формуле (2)

а) равны по формуле (4) – 250096

б) равны по формуле (10) – 260000

Стандартное отклонение индивидуального времени прохождения ti от среднего времени прохождения Т (0,8-1)^2=0.04 D=√0.04=0.2

D*=96 (формула 6)

ti = 2,5

8. Теория поиска и числа Фибоначчи

8.1. Теория поиска.

Пусть о функции f(x) известно, что она от заданного до некоторого неизвестного убывает, а от этого до заданного возрастает (рис.1).

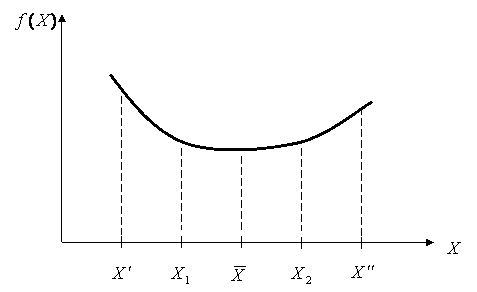
Рис.1

В точке функция f(x) принимает свое наименьшее значение которое называется её «минимальным» значением, т.е. функция достигает минимум или «минимизирующей» точкой функции.

План поисков на отрезке от до точки , минимизирующей функцию f(x) принимает следующий вид (если в конце пункта не указывается, к какому пункту следует переходить, то нужно переходить к следующему пункту).

8.2. Алгоритм определения 7

Сравнить 1 и n, где (n – шаговый план поиска точки минимизирующей значение f(x) на отрезке длины L за n-шагов, обладающий следующими свойствами:

1) на каждом шаге рассматривается некоторый отрезок .

2) на первом шаге вычисляется значение функции f(x) в одной из точек:

3) к началу каждого из последующих шагов с номером k известно значение f(x) в одной из следующих точек:

(7)

4) На каждом k- м шаге вычисляется значения в другой из точек (*).

5) на k-м ( шаге производится сравнение чисел при этом, если окажется, что ), то на (k+1) шаге рассматривается отрезок , а если то отрезок .

1. Вычислить .

2. Вычислить на этом процессе заканчивается.

3. Вычислить

.

5. Вычислить .

6. Сравнить 2 и n:

а) если n=2, то перейти к п.7;

б) если n >2, то перейти к п.10.

7. Сравнить

а) если то перейти к п.8;

б) если то перейти к п.9.

8. Положить и закончить процесс вычисления.

9. Положить и закончить процесс вычисления.

10. Сравнить

а) если то перейти к п. ;

б) если то перейти к п.14.

11. Переобозначить

12. Вычислить

13. Вычислить и перейти к п.6.

14. Преобразовать

15. Вычислить

16. Вычислить и перейти к п.6.

8.3. Блок-схема вычислительного процесса

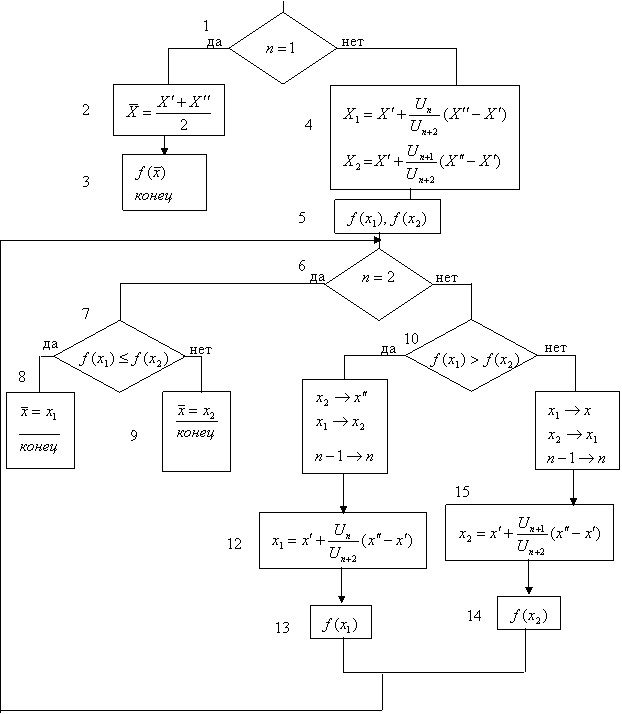
Рис.2

8.4. Пример вычислительного процесса

Пример для нахождения с помощью пяти вычислений на отрезке от до точки , минимизирующую функцию

(**)

Замечание: величины U_n+1, U_n+2 ……… суть числа

Фибоначчи: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377.

1. Сравнить n=5 и 1. Сравнение показывает, что поэтому нужно переходить к п.4.

4. Вычислить:

4. Вычислить:

5. Сравнить n=5 и 2. Сравнение дает, что , поэтому переходим к п.10.

10. Сравнить f(x₁) = 1, 89892 и f(x₂) = 1, 89003. Сравнение дает, что ; поэтому переходим к п.14.

n=4

15. Вычислить:

16. Вычислить:

Переходим к п.6.

6. Сравнить n=4 и 2. Поскольку , переходить к п.10.

10. Сравнить f(x₁) = 1, 89003 и f(x₂) = 1, 89534: поскольку

то необходимо переходить к п.11.

11. Переобозначить:

12. Вычислить:

13. Вычислить:

и переходить к п.6

6. Сравнить Поскольку , то необходимо переходить к п.10.

10. Сравнить то необходимо переходить к п.14.

14. Переобозначить:

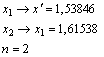
15. Вычислить:

16. Вычислить:

и переходить к п.6.

6. Сравнить Сравнение показывает, что ; поэтому необходимо переходить к п.7.

7. Сравнить: Сравнение показывает: поэтому необходимо переходить к п.8.

8. Полагая, что найденное значение может отличаться от истинного положения минимизирующей точки не более на Тогда, наименьшее значение функции

Литература

1. Саати Т. Математические методы исследования операций. Воен.издат, М, 1968

2. Шнепс М.А. Системы распределения информации. Методы расчета. М. «Связь», 1979

3. Основы научных исследований под редакцией проф. В.И. Крутова. М. «Высшая школа», 1989

4. Безир Х. и др. Цифровая коммутация. М. «Радио и связь», 1984

5. Венцель Е.С. Исследование операций. М. «Наука», 1980