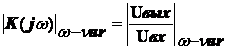УЗБЕКСКОЕ АГЕНСТВО СВЯЗИ И ИНФОРМАТИЗАЦИ

ТАШКЕНТСКИЙ УНИВЕРСИТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ

 

 

 

 

КАФЕДРА

ТЕЛЕКОММУНИКАЦИОННЫЕ

 СИСТЕМЫ ПЕРЕДАЧИ

 

 

 

КОНСПЕКТ ЛЕКЦИЙ

ПО ДИСЦИПЛИНЕ ЭЛКТРОРАДИОИЗМЕРЕНИЯ

 

 

 

           

 

 

Автор

 старший преподаватель кафедры ТСП

Н.А.Полетаева

 

 

 

 

 

 

 

Лекция 1. ИЗМЕРЕНИЯ ФИЗИЧЕСКИХ ВЕЛИЧИН

 

Все объекты окружающего мира характеризуются своими свойствами.                                   Свойство объекта (явления, процесса) обуславливает  его различие или общность с другими объектами и обнаруживается в его отношении к ним.

Физическая величина – свойство физических объектов, общее в качественном отношении для многих объектов, но в количественном отношении индивидуальное для каждого из них.

 Размер физической величины – количественное содержание в данном объекте свойства, соответствующего понятию величина.

          Единица физической величины – это физическая величина фиксированного размера, которой по определению условно присвоено стандартное числовое значение, равное единице.

          Значение физической величины – это оценка её размера в виде некоторого числа принятых для неё единиц измерения.

         Числовое значение физической величины – это отвлеченное число, выражающее отношение значения величины к соответствующей единице данной физической величины.

          

         Единицы физических  величин делят на основные и производные и объединяют в системы единиц физических величин. Основные единицы выбираются обоснованно, но произвольным образом. Производные единицы выражают через основные на основе известных уравнений связи между ними.

         Совокупность основных и производных единиц физических величин, образованная в соответствии с принятыми принципами называется системой                   

единиц физических величин. Единица основной физической величины является основной единицей системы.

          Международная система единиц SI (СИ) была принята ХI Генеральной конференцией по мерам и весам (ГКМВ) в 1960 г. И уточнена на последующих ГКМВ.    В основу системы СИ положены семь основных физических единиц: метр, килограмм, секунда, ампер, кельвин, моль и кандела.

          Системная единица – единица физической величины, входящая в одну из принятых систем. Все основные и производные, а также кратные и дольные единицы являются системными.

          Образование кратных и дольных единиц от единиц СИ допускается только по принципу десятичной кратности, т. е. умножением размера исходной единицы СИ на 10n, где n – целое положительное или отрицательное число.

           Внесистемная единица – единица физической величины, не входящая в принятые системы единиц. Внесистемные единицы делят на: допускаемые наравне с единицами СИ; допускаемые к применению в специальных областях; временно допускаемые и устаревшие.

     

Контрольные вопросы

1.     Дайте определение физической величины.

2.  Дайте определение системы физических величин.

3.  Какие единицы величин системы единиц называют основными?

     4.  Перечислите основные единицы системы СИ.

 

Лекция 2. КЛАССИФИКАЦИЯ ИЗМЕРЕНИЙ

 

2.1. Виды и методы измерений

По общим приемам   получения    результатов  измерения делятся на прямые, косвенные, совместные и совокупные измерения.

        Прямым называется измерение, когда искомое значение физической величины А находят непосредственно из опытных данных.  

Косвенным называется измерение, при котором искомое значение величины находят на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям.  

Совокупными  называются проводимые одновременно измерения нескольких одноименных величин, при которых их значения находят решением системы уравнений, получаемых при прямых или косвенных измерениях различных сочетаний этих величин.

Совместными называют проводимые одновременно измерения двух или  нескольких  неодноименных   величин   для  установления   зависимости

между ними.

Современные методы измерений принято делить на методы непосредственной оценки и методы сравнения.

Метод непосредственной оценки – это метод измерений, при котором значение физической величины определяют непосредственно по показанию измерительного прибора.

Метод сравнения – это метод измерения, при котором измеряемую величину сравнивают с величиной, воспроизводимой мерой.

 

2.2. Средства измерений

Средство измерений – техническое средство, используемое для измерений и имеющее нормированные метрологические свойства.

Мера – средство измерений, предназначенное для воспроизведения физической величины заданного размера.

Измерительный преобразователь – средство измерений, предназначенное для выработки сигнала измерительной информации в форме, удобной для передачи, преобразования, обработки и хранения, но не поддающейся непосредственному восприятию наблюдателем.

Измерительным прибором называется средство измерения, предназначенное  для   выработки   сигнала   измерительной   информации   в

форме, доступной для непосредственного восприятия наблюдателем.

Измерительная система – совокупность средств измерений и вспомогательных устройств, соединенных между собой каналами связи, предназначенная для выработки сигналов измерительной информации в удобной для автоматической обработки форме, ее передачи и использования в различных системах управления.

 

Контрольные вопросы

1.           Дайте определения прямых, косвенных, совокупных и совместных измерений.

2.           Какие методы измерений вам известны?

3.           Что представляет собой средство измерений?

4.           Как классифицируют средства измерений?

 

Лекция 3. ОСНОВЫ ТЕОРИИ ПОГРЕШНОСТЕЙ

 

3.1.Погрешности измерений и их классификация

Погрешностью результата измерения называется отклонение найденного значения от истинного (действительного) значения измеряемой физической величины.  По форме количественного выражения погрешности делятся на абсолютные, относительные и приведенные.

Абсолютной погрешностью  называют отклонение результата измерения  от истинного значения измеряемой величины :

                                                                                                     (3.1)

Относительной погрешностью  называют отношение абсолютной погрешности измерения к истинному значению измеряемой величины:

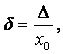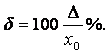                                          или                                     (3.2)

         Приведенной погрешностью  называют отношение  абсолютной погрешности  к некоторому нормирующему значению :

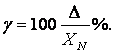                                                                                               (3.3)

По характеру (закономерности) проявления погрешности делят на систематические, случайные и грубые (промахи).

Систематические погрешности  – это составляющие погрешности измерения, которые остаются постоянными или закономерно изменяются при повторных измерениях одной и той же величины в одних и тех же условиях.

Случайные погрешности  – составляющие погрешности, изменяющиеся случайным образом по значению и знаку при повторных измерениях одной и той же физической величины в одних и тех же условиях.

Грубые погрешности – погрешности, существенно превышающие ожидаемые при данных условиях измерения.

 

3.2. Систематические погрешности и методы их уменьшения

Отличительным признаком систематических погрешностей является то, что они могут быть предсказаны и обнаружены. По характеру изменения во времени систематические погрешности разделяют на постоянные и переменные.

Постоянными называют такие систематические погрешности, которые остаются неизменными  в течение всей серии измерений.

Переменными называют погрешности, изменяющиеся в процессе измерений.  

Систематическую погрешность можно исключить путем устранения источников погрешности до начала измерений (профилактика погрешности).

Если происхождение систематической погрешности и ее значение  может быть достаточно точно определено, то в таких случаях вводят поправку или поправочный множитель. Систематическую погрешность можно существенно уменьшить, используя специальные методы измерения, например, замещения и компенсации погрешности по знаку.

 

Контрольные вопросы

1.Что такое «погрешность измерения»?

          2. Назовите признаки, по которым классифицируют погрешности.

3. На какие виды делят погрешности по характеру проявления?

4. Какие используют методы исключения или уменьшения систематических погрешностей?

 

Лекция 4. ОСНОВЫ ТЕОРИИ ПОГРЕШНОСТЕЙ

 

4.1. Характеристики случайных погрешностей и их оценки.

Случайные погрешности можно представить случайными величинами и для их количественного анализа использовать аппарат теории вероятностей и математической статистики.

Самой исчерпывающей характеристикой любой случайной величины является дифференциальный или интегральный закон ее распределения.

В метрологии при анализе случайных погрешностей чаще всего применяют нормальный (Гаусса), равномерный, треугольный законы, а также закон распределения Стьюдента.

В качестве основного закона распределения в теории погрешностей принят нормальный закон.

Нормальный закон распределения описывается плотностью вероятности:

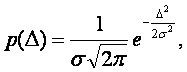                                                                                   (4.1)

где  – случайная погрешность;  –  среднеквадратическое отклонение.

Целью количественного расчета случайных погрешностей является установление зоны неопределенности  для каждого средства измерений. Вероятность нахождения погрешности в интервале от  до  определяется выражением:

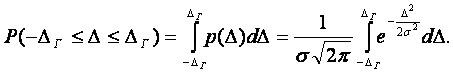                            (4.2)

Для проведения  практических расчетов применяют  нормированное нормальное распределение, при котором вводят нормированную безразмерную величину . Тогда с учетом симметричного интервала предел интегрирования заменяют на , а выражение (4.2) преобразуется в известный, табулированный интеграл , называемый интегралом вероятностей:

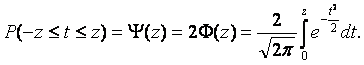                                     (4.3)

                                                       

4.2. Суммирование погрешностей

Достижимая точность измерения ограничивается наличием погрешностей, как систематических, так и случайных. При суммировании погрешностей руководствуются следующим:

1. Систематические погрешности , если они известны или достаточно точно определены, суммируют алгебраически (с учетом собственных знаков)

                                                                                                (4.4)

 

2. Случайные погрешности (средние квадратические оценки) суммируются с учетом их взаимных корреляционных связей. Из теории вероятности известно, что дисперсия суммы двух случайных величин

                                                                         (4.5)

где  и  – дисперсии случайных величин,  – коэффициент корреляции между ними.

Отсюда суммарная средняя квадратическая погрешность

                                                                  (4.6)

 

Контрольные вопросы

1. Приведите характеристики и оценки случайных погрешностей.

2.  Назовите основные законы распределения случайных погрешностей.

3. Каким образом суммируют случайные и систематические погрешности?

Лекция 5. КЛАССЫ ТОЧНОСТИ СРЕДСТ ИЗМЕРЕНИЙ

 

Класс точности средств измерений – обобщенная характеристика данного типа средств измерений, отражающая уровень их точности, определяемая пределами допускаемых основной и дополнительных погрешностей, а также другими характеристиками, влияющими на точность.

Пределы допускаемых основной и дополнительных погрешностей выражаются в форме приведенных, относительных или абсолютных погрешностей.

Пределы допускаемой абсолютной основной погрешности устанавливают по одной из формул:

                                                                                                            (5.1)

                                                                                                (5.2)

где  – значение измеряемой величины;  – положительные числа, независящие от .

Предел допускаемой приведенной основной погрешности, в процентах выражают формулой:

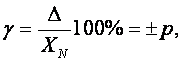                                                                                    (5.3)

Предел допускаемой относительной основной погрешности устанавливают по формуле:

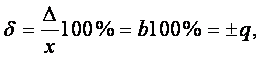                                                                             (5.5)

Если абсолютная погрешность задается формулой (5.2), то предел допускаемой относительной основной погрешности устанавливают по формуле:

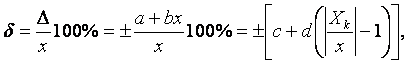                                    (5.6)

          С использованием чисел определенного ряда (5.4) разработаны условные обозначения классов точности средств измерений, наносимые на них и указываемые в технической документации.

 

Контрольные вопросы

1.     Перечислите основные принципы, лежащие в основе выбора нормируемых метрологических характеристик средств измерений?

2. Дайте определение понятию «класс точности средств измерений».

3. Как выражают пределы допускаемых основной и дополнительной       погрешностей?

     4. Поясните различия между аддитивными и мультипликативными погрешностями.

    

     Лекция 6. МАТЕМАТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

 

6.1. Прямые однократные измерения.

 Большинство технических измерений являются прямыми однократными. Прямые однократные измерения проводят в случаях, если: отсутствует возможность повторных измерений, при измерениях может произойти разрушение объекта измерения, имеет место экономическая целесообразность.

При прямых однократных измерениях используют единственное значение отсчета показаний прибора. Являясь случайным, однократный отсчет x включает в себя инструментальную, методическую и личную составляющие погрешности измерения, в каждой из которых могут быть выделены систематические и случайные составляющие. Поэтому до измерения должна быть определена априорная оценка составляющих погрешности  с использованием всех доступных данных. При определении доверительных границ погрешности результата измерений доверительная вероятность принимается, как правило, равной 0,95. Стандартом регламентирована следующая форма записи результата прямого однократного измерения величины .

 

6.2. Многократные равноточные измерения

Необходимость в многократных наблюдениях некоторой физической величины возникает при наличии в процессе измерений значительных случайных погрешностей.

   Методика статистической обработки результатов наблюдений состоит из следующих операций:

1. Проводят  наблюдений и фиксируют  результатов наблюдений одного и того же значения физической величины : ;

2. Исключают известные систематические погрешности;

3. Находят среднее арифметическое значение исправленных результатов наблюдений:

                                                                                                        (6.1)

4. Вычисляют оценку среднего квадратического отклонения результатов наблюдений:

                                                                                    (6.2)

5. Вычисляют  оценку среднего квадратического отклонения результата измерения :

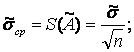                                                                                              (6.3)

6. Вычисляют доверительные границы случайной составляющей погрешности измерений, которая без учета знака определяется по формуле:

                                                                                                 (6.4)

где  – коэффициент Стьюдента.

Для симметричных доверительных границ погрешности результат измерения величины   представляется в форме:

                                                                                                (6.5)

 

Контрольные вопросы

1.  В каких случаях проводят многократные измерения?

2.Перечислите алгоритмы обработки результатов многократных наблюдений.    3. Какие критерии используют для обнаружения грубых погрешностей?

 

Лекция 7. ИЗМЕРЕНИЕ НАПРЯЖЕНИЯ И СИЛЫ ТОКА

   

     7.1. Параметры напряжений переменного тока.

Воздействие переменного напряжения на электрическую цепь можно определить по амплитудному, среднему квадратическому, среднему (постоянной составляющей) или средневыпрямленному значениям.

         Мгновенное значение напряжения  - это значение напряжения в определенный момент времени.

Амплитуда (пиковое значение)  - это наибольшее мгновенное значение напряжения (относительно оси времени) за период.

Среднее квадратическое значение напряжения – это корень квадратный из среднего квадрата его мгновенного значения за  период:

         

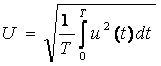                                           .                                               (7.1)

Среднее значение (постоянная составляющая) напряжения – это среднее арифметическое всех его мгновенных значений за время измерения 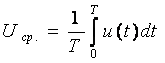                                                                                                                                                                                                                           (7.2)

Средневыпрямленное значение напряжения – это среднее арифметическое его абсолютных мгновенных значений за время измерения :

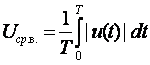                                                                                             (7.3)

 

 

 

7.2. Электромеханические  приборы

Классификация электромеханических приборов производится на основании типа измерительного механизма. Наиболее распространенными  й являются следующие системы: магнитоэлектрическая, электромагнитная, электродинамическая, электростатическая.

Магнитоэлектрическая система. В этой системе измерительный механизм состоит из проволочной рамки с протекающим в ней током, помещенной в поле постоянного магнита (магнитопровода). Поле в зазоре, где находится рамка, равномерно за счет особой конфигурации магнитопровода. Под воздействием тока I рамка вращается в магнитном поле, угол поворота α ограничивают специальной пружиной, поэтому передаточная функция (часто называемая уравнением шкалы) линейна:

                                       α  = I Ψо / W ,                                                     (7.4)

где Ψо – удельное потокосцепление, определяемое параметрами рамки и магнитной индукцией; W – удельный противодействующий момент, создаваемый специальной пружиной.

Измерительные приборы магнитоэлектрической системы имеют достаточно высокую точность, сравнительно малое потребление энергии из измерительной цепи, высокую чувствительность, но работают лишь на постоянном токе.

Электромагнитная система. Принцип действия электромагнитной системы  основан на взаимодействии катушки с ферромагнитным сердечником. Ферромагнитный сердечник втягивается в катушку при любой полярности протекающего по ней тока. Следовательно, прибор электромагнитной системы может работать на переменном токе. Достоинствами приборов электромагнитной системы являются простота конструкции, способность выдерживать значительные перегрузки, возможность градуировки приборов, предназначенных для измерения в цепях переменного тока, на постоянном токе. К недостаткам приборов этой системы можно отнести большое собственное потребление энергии, невысокую точность, малую чувствительность и сильное влияние магнитных полей.

 

7.3. Аналоговые электронные вольтметры.

Электронные вольтметры представляют собой сочетание электронного преобразователя и измерительного прибора. Классифицируют электронные вольтметры по ряду признаков:

по назначению – вольтметры постоянного, переменного и импульсного напряжений; универсальные, фазочувствительные, селективные;

по способу измерения – приборы непосредственной оценки и приборы сравнения;

по характеру измеряемого значения напряжения – амплитудные, среднего квадратического значения, средневыпрямленного значения;

по частотному диапазону – низкочастотные, высокочастотные, сверхвысокочастотные.

При создании аналоговых вольтметров важную роль играют преобразователи переменного напряжения в постоянное (детекторы).

 

Контрольные вопросы

1. Что называется амплитудным, средним, средневыпрямленным и средним квадратическим значениями напряжения или силы тока?

2.  Перечислите основные системы электромеханических приборов и дайте сравнительные характеристики по параметрам.

          3. По каким признакам классифицируют  электронные вольтметры?

 

Лекция 8. ИЗМЕРЕНИЕ НАПРЯЖЕНИЯ И СИЛЫ ТОКА

 

Детекторные измерительные преобразователи

Детекторы можно классифицировать по функции преобразования входного напряжения в выходное: амплитудные (пиковые), среднего квадратического и средневыпрямленного значений.

Амплитудный детектор – это измерительный преобразователь, напряжение, на выходе которого соответствует максимальному (амплитудному) значению измеряемого напряжения. Амплитудный детектор должен обязательно содержать элемент, запоминающий амплитудное значение напряжения. Таким элементом обычно является конденсатор, заряжаемый через диод до максимального значения входного напряжения

         Детектор среднего квадратического значения – преобразователь переменного напряжения в постоянное, пропорциональное корню квадратному  из  среднего  квадрата мгновенного  значения напряжения. 

Это значит, что измерение среднего квадратического значения напряжения связано с выполнением трех последовательных операций: возведение в квадрат мгновенного значения сигнала, усреднение и извлечение корня из результата усреднения. Возведение в квадрат осуществляется полупроводниковой ячейкой, используя квадратичный участок ее характеристики; иногда этот участок аппроксимируют искусственно.

             Детектор средневыпрямленного значения – это устройство, преобразующее переменное напряжение в постоянный ток, пропорциональный средневыпрямленному значению напряжения. Детектор средневыпрямленного значения должен выполнять операцию нахождения модуля измеряемого сигнала  с последующим интегрированием в соответствии с определением средневыпрямленного значения: 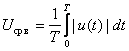. Вольтамперная характеристика такого детектора должна иметь линейный участок в пределах диапазона входных напряжений. Таким  преобразователем может служить двухполупериодный выпрямитель с магнитоэлектрическим усредняющим прибором.

                                                                                                                                                   

8.2. Цифровые вольтметры

Принцип работы цифровых измерительных приборов основан на дискретном и цифровом представлении непрерывных измеряемых величин. В общем случае цифровой вольтметр состоит из входного устройства, аналого-цифрового преобразователя (АЦП), цифрового отсчетного устройства и управляющего устройства.

По типу АЦП цифровых вольтметров могут быть разделены на четыре основные группы: кодоимпульсные; времяимпульсные; частотно-импульсные; пространственного кодирования. В настоящее время цифровые вольтметры строятся чаще на основе  время импульсного преобразования.

В основе принципа действия вольтметра времяимпульсного (временного) типа лежит преобразование с помощью АЦП измеряемого напряжения в пропорциональный интервал времени, который заполняется счетными импульсами, следующими с известной частотой следования.

 

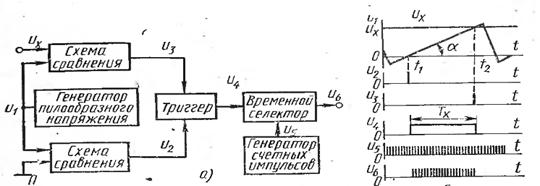
Рис.8.4. Цифровой вольтметр с времяимпульсным преобразованием:

а – структурная схема; б- временные диаграммы

 

В результате такого преобразования дискретный сигнал измерительной информации на выходе преобразователя имеет вид пачки счетных импульсов, число которых пропорционально уровню измеряемого напряжения.     

Контрольные вопросы

1. Что используется в качестве индикаторного устройства в аналоговых вольтметрах, содержащих детекторные преобразователи?

2. Как функционируют детекторные преобразователи амплитудного, средневыпрямленного и среднего квадратического значений?

  3. На каком принципе строят вольтметры времяимпульсного типа?

  

Лекция 9. ИЗМЕРИТЕЛЬНЫЕ ГЕНЕРАТОРЫ

                

9.1. Общие сведения

Измерительные генераторы сигналов (автогенераторы) —  источники элек­трических колебаний различных форм и частот, предназначенные для работы с электронными схемами. В зависимости от формы выходных сигналов различают измерительные генераторы гармонических и релаксационных (импульсных) колебаний.

По частотному диапазону генераторы делятся на: инфранизкочастотные (0,01. ..20 Гц), низкочастотные, или генераторы звукового диапазона (20...300000 Гц), генераторы высоких частот (0,3...300 МГц), и сверхвысокочастотные (СВЧ, свыше 300 МГц).

Независимо от назначения,  принципа действия и схемотехнического выполнения генератор любых перечисленных колебаний состоит из нелинейного усилителя, цепи положительной обратной связи и источника питания постоянного тока. Форма и частота выходных колебаний определяются только параметрами самого генератора. Генератор гармонических колебаний должен содержать в своем составе узкополосную колебательную систему. Принцип действия релаксационных генераторов основан на зарядно-разрядных или на­копительно-поглощающих явлениях, протекающих в широкополосных энергоемких цепях положительной обратной связи.

9.2. Измерительные генераторы гармонических колебаний

Рассмотрим условия самовозбуждения генератора гармонических колебаний. Для возбуждения и генерации колебаний часть их мощно­сти с выхода усилителя (точнее, с колебательной системы) подают на его вход по специально введенной цепи положительной обратной свя­зи (ОС). Говоря иначе, подобное устройство «возбуждает само себя» и поэтому называется генератором с самовозбуждением.

Генератор гармонических колебаний можно представить обобщен­ной структурной схемой (рис. 9.1), состоящей из нелинейного резо­нансного усилителя с комплекс­ным коэффициентом усиления  К = K(j ω) и цепи по­ложительной ОС с комплексным коэффициентом передачи по напряжению β=β(jω). В схеме этого генератора отмечены комплексные амплитуды следующих напряжений: входного — Uвх = Uвх(jω); выходного — Uвых = Uвых(jω)  и обратной связи — Uoc = Uос(jω).

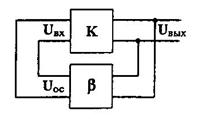
Рис. 9.1. Обобщенная структурная схема генератора

Выражение для напряжения обратной связи на любой частоте генерации ω запишем в виде

                                                     Uoc = Uвх = βUвых  .                                         (9.1)

 

Тогда выходное напряжение определяют как Uвых = KUвх, или с учетом формулы (9.1) Uвых = КβUвых. Отсюда следует, что генератор будет работать в стационарном режиме при условии, когда

                                                          Кβ = 1.                                                (9.2)                                                                                                                                                                                                                                            

Если Кβ > 1, то амплитуда выходных колебаний нарастает, что оп­ределяет необходимое условие самовозбуждения генератора.

Представим формулу (9.2) следующим образом:

 

                                                 (9.3)

 

Контрольные вопросы

1.     Как различают измерительные генераторы в зависимости от формы выходного сигнала?

2.     Как подразделяются генераторы по частотным характеристикам?

3.     Каковы условия самовозбуждения генератора гармонических колебаний? Какими методами они реализуются?

 

 

Лекция 10.     ИССЛЕДОВАНИЕ ФОРМЫ   СИГНАЛОВ    

      

10.1. Универсальные  осциллографы

Основным и наиболее широко применяемым прибором для исследования формы напряжения служит электронный осциллограф – прибор для визуального наблюдения электрических сигналов, а также измерения их параметров с использованием средства отображения формы сигналов. Обобщенная структурная схема универсального осциллографа представлена на рис. 10.1. В осциллографе можно выделить следующие функциональные блоки: канал вертикального отклонения (Y), канал горизонтального отклонения (X), канал управления яркостью (Z), средства измерения параметров сигналов (калибраторы), электронно-лучевую трубку (ЭЛТ).

 

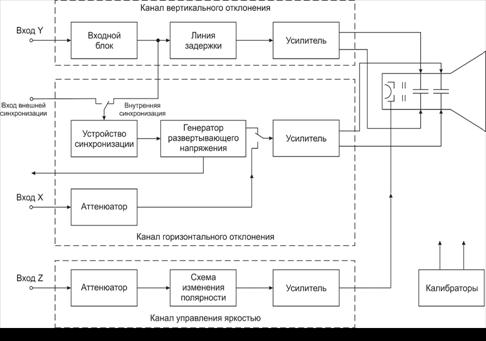
Рис. 10.1. Структурная схема универсального осциллографа

 

10.2. Виды разверток в универсальном осциллографе

Одним из основных блоков осциллографа является ЭЛТ,  выходные элементы которой -  две пары пластин, отклоняющие луч горизон­тально и вертикально. Если развертывающее напряжение приложено к одной паре отклоняющих пластин (обычно к пластинам X), то раз­вертку называют по форме развертывающего напряжения (например, линейной или синусоидальной). Если развертывающие напряжения приложены к отклоняющим пластинам X и Y трубки одновременно, то название развертке дают по ее форме (например, круговая или эллиптическая).

Наиболее широко используется линейная развертка, соз­даваемая пилообразным напряжением Up генератора развертки.  В зависимости от режима работы генератора развертки различают автоколебатель­ную, ждущую и однократную развертки.

 

Контрольные вопросы

 

1.     Для каких целей применяют осциллографы?

2. Какие блоки входят в состав структурной схемы универсального осциллографа? Их назначение?

3. Для чего применяется синхронизация разверток осциллографа? 

4.  Перечислите основные виды разверток?

 

Лекция 11.  ИЗМЕРЕНИЯ ЧАСТОТНО-ВРЕМЕННЫХ ПАРАМЕТРОВ СИГНАЛОВ

              

11.1. Общие сведения

Частота f или период Т  относятся к основным параметрам любого гармонического или периодиче­ского процесса. В общем случае под частотой понимают  число идентичных событий, происходящих за единицу времени. Единица циклической частоты  f  – герц (Гц) – соответствует одному колебанию за 1 с.   Гармонический сигнал записыва­ется в следующем виде: u(t) = Um cos (ωt+φ0) = Um cos φ(t),   где  Um – амплитуда;  ω – угловая  (круговая)  частота;  φ0 – начальная  фаза; φ(t) = ωt+ φ0 – полная (текущая, мгновенная) фаза.

         Периодом Т называют интервал времени, через который регуляр­но повторяются мгновенные значения гармонического или периоди­ческого сигнала u(t). Из определения следует, что u(t) = u(t + nT), где п = 1, 2, 3, ... .

 

11.2. Осциллографические методы измерения

 амплитуды и временных интервалов

В универсальных осциллографах амплитуду сигналов измеряют с помощью масштабной сетки, помещенной на экране ЭЛТ. Цену деле­ния сетки устанавливают с по­мощью калибраторов. Метод измерения параметров пе­риодического сигнала показан на рис. 11.1. Параметры импульсов определяются следующим обра­зом: размах (амплитуда импульса) U p= Су1У ;

|Су| — цена деления сет­ки по вертикали, В/дел; Т= СХLХ — период следования импульсов; τи = СХ lХ — длительность им­пульса; |СХ|— цена деления сет­ки по горизонтали, с/дел; ly> Lx, lx — выражены в делениях сетки.

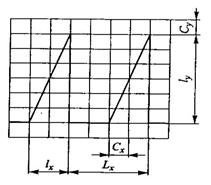
Рис. 11.1. Определение параметров сигнала   с помощью масштабной сетки                       

 

 Погрешность измерения амплитуды сигнала составляет 3...5 %.

 

11.3. Осциллографические методы измерения частоты

Измерение частоты на основе сравнения – по фигурам Лиссажу

Способ измерения частоты по интерференционным фигурам, называемым фигурами Лиссажу, основан на сравнении неизвестной частоты fизм с известной частотой fобр, воспроизводимой мерой. С этой целью напряжение неизвестной частоты подаётся на вход вертикального (Y) или горизонтального (Х) отклонения, а напряжение образцовой частоты соответственно на вход горизонтального или вертикального отклонения. Генератор развертки осциллографа выключается. Частоту образцового генератора fобр подстраивают так, чтобы на экране осциллографа наблюдалась простейшая устойчивая фигура. Форма фигур Лиссажу зависит от отношения частот и начальных фаз сравниваемых колебаний. Полученную фигуру нужно мысленно пересечь вертикальной и горизонтальной линиями (не проходящими через узлы) и сосчитать число пересечений ими ветвей фигуры по вертикали nв  и по горизонтали nг.

Значение измеряемой частоты определяется из соотношения  f · n = = f· nг.      

Точность этого метода определения частоты  ко­лебания оказывается  высокой и определяется стабильно­стью образцового генератора, од­нако получение и наблюдение таких фигур — достаточно сложная из­мерительная задача.

                                                         

Контрольные вопросы

1.           Что понимают под частотой периодического сигнала?

2.           Как осуществляется измерение амплитуды и временных интервалов с помощью осциллографа?

3.           Каким образом можно провести измерение частоты сигнала методом фигур Лиссажу?

 

 

Лекция 12. ИЗМЕРЕНИЯ ЧАСТОТЫ И ИНТЕРВАЛОВ ВРЕМЕНИ

 

12.1. Цифровой метод измерения частоты.

Принцип действия цифрового час­тотомера основан на измерении частоты в соответствии с ее опреде­лением, т. е. на счете числа импульсов за интервал времен            fx= N /∆t0.              

На рис. 12.1 приведена структурная схема цифро­вого частотомера, работающего в режиме измерения частоты.    Исследуемый сигнал поступает на входное устройство, где осуществляется усиление (ослабление) и фильтрация сигнала. Формирующее устройство преобразует исследуемый сигнал в последовательность импульсов UФУ, частота которых равна частоте исследуемого сигнала.

 

 

Рис. 12.1. Схема  цифрового частотомера в режиме измерения частоты

 

        Селектор представляет собой управляемый электронный ключ, который пропускает на электронный счетчик сформированные импульсы неизвестной частоты только при наличии на управляющем входе стробирующего импульса Uуу , длительность которого определяет время измерения Δt0.

       Стробирующий импульс вырабатывается устройством управления с помощью делителей частоты из сигнала опорного высокостабильного генератора, и его длительность выбирается кратной 10 k с, где k – целое число.  Число импульсов N отсчитанное электрическим счетчиком  на выходе селектора и фиксируемое цифровым отсчетным устройством пропорционально частоте входного сигнала.

       

11.2. Резонансный и гетеродинный методы измерения частоты

Принцип действия резонансного метода основан на сравнении измеряемой частоты fx c собственной резонансной частотой fр градуированного колебательного  контура или резонатора. Измерительные приборы, рабо­тающие на основе этого метода, называются резонансными часто­томерами.

Перестраиваемая колебательная система возбуждается сигналом измеряемой частоты и(fх). Интенсивность колебаний в колебательной системе резко увеличивается в момент ре­зонанса, т. е. при fх =fР. Данный момент фиксируется с помощью индикатора резо­нанса, связанного с колебательной системой, и значение измеряемой частоты fх считывается с градуированной шкалы механизма настройки. Относительная погрешно­стью 10־3 – 10־4.                          

Гетеродинный метод является одной из разновидностей методов сравнения измеряемой частоты fх с частотой эталонного генератора — гетеродина. Этот метод использует принцип построения измеритель­ных схем с нулевыми биениями. Упрощенная структурная схема гете­родинного частотомера представлена на рис. 12.3.

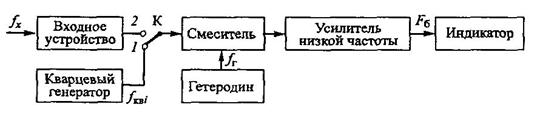
Рис.12.3. Упрощенная структурная схема гетеродинного частотомера

 

Гетеродинные частотомеры являются достаточно точными изме­рительными приборами. Их относительная погрешность измерения лежит в пределах 10-3 - 10-5.

 

Контрольные вопросы

1. Поясните, какой основной принцип используется для реализации цифровых приборов?

2. Приведите структурные схемы цифрового частотомера для разных режимов работы.

3.  Поясните сущность резонансного метода измерения частоты.

4. В чем заключается принцип работы гетеродинного частотомера?

 

Лекция 13. ИЗМЕРЕНИЕ ФАЗОВОГО СДВИГА

        

13.1. Общие сведения

Понятие «фаза» характеризует гармоническое (синусоидальное) колебание в любой конкретный момент времени. Для гармонического колебания u1(t) = Um1sin (ωt + φ1) с амплитудой Um1 и круговой частотой ω текущая (мгновенная) фаза в любой момент времени t равна φ(t) = ωt + φ1, где φ1 – начальная фаза.

Фазовым сдвигом Δφ двух гармонических колебаний одинаковой частоты u1(t) = Um1sin (ωt + φ1) и u2(t) = Um2sin (ωt + φ2) называется модуль разности их начальных фаз:

                                          Δφ‌ = ‌|φ1 – φ2|.                                                (13.1)

Величина φ1 – φ2 называется разностью фаз сигналов.

Чтобы измерить фазовый сдвиг, применяют различные методы и приемы измерений: осциллографические, компенсационный, преобразования фазового сдвига во временной интервал, цифровой (дискретного счета), по геометрической сумму и разности напряжений, а также с преобразованием частоты.

 

Осциллографические методы измерения фазовых сдвигов.

При осциллографических измерениях сдвиг фаз измеряют методом эллипса (способ синусоидальной развертки) или по осциллограммам исследуемых напряжений (способ линейной развертки).

          В первом случае напряжения исследуемых сигналов U и U (например, входное и выходное напряжения четырехполюсника) подаются в каналы вертикального и горизонтального отклонения; генератор развертки выключен;  усиления по Y и Х регулируются так, чтобы выполнялось равенство полных отклонений луча по осям Ym и Хm.

Тогда на экране будет получено изображение эллипса, по размерам Х и Хm (рис.13.1)  которого можно определить :

                   sin= X / Xm     или           = arcsin X / Xm    .                           (13.3)

При измерении фазового сдвига способом линейной развёртки используется двухлучевой или двухканальный осциллограф. Напряжения исследуемых сигналов  U и U подают в каналы вертикального отклонения; генератор развёртки осциллографа включён. После уравнивания амплитуд обоих напряжений осциллограмма будет иметь вид, представленный на рис.13.2.

Y

 

 

 


Х
 

Ym
 

 


Х

 

 

 


 


Рис.13.1. Измерение фазового сдвига методом эллипса

 

 

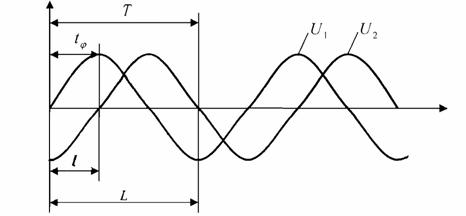
Рис. 13.2. Измерение фазового сдвига по осциллограммам напряжений

Если измерить в одинаковых единицах длины  l и L, соответствующие в временам tи Т, то фазовый сдвиг φx можно определить из пропорции:

                      φx / 360˚ = tφ / T = l / L,        φx = 360l / L .                          (13.4)

   

Контрольные вопросы

1. Какой смысл вложен в понятие «фаза» сигнала?

2. Что называется фазовым сдвигом двух сигналов?

3. В чем состоит метод линейной развертки измерения фазового сдвига?

4. Как измерить фазовый сдвиг методом эллипса?

 

Лекция 14. ИЗМЕРЕНИЕ ФАЗОВОГО СДВИГА

     Метод  преобразования фазового сдвига во временной интервал.

Сущность метода, основанного на преобразовании фазового сдвига во временной интервал, состоит в преобразовании исследуемых синусоидальных напряжений U и U, фазовый сдвиг которых требуется измерить, в периодические последовательности коротких импульсов, формируемых в моменты перехода этих напряжений через нуль с производными одинакового знака. Интервалы времени ∆Т между ближайшими импульсами пропорциональны измеряемой разности фаз.                     

Фазометр  (рис.14.1) содержит входные цепи и формирующие устройства. Исследуемые напряжения преобразуются в серию коротких импульсов с крутыми фронтами. Из соседних пар импульсов с помощью триггера формируются прямоугольные импульсы, длительность которых равна интервалу времени ∆Т. Период повторения этих импульсов равен периоду исследуемых напряжений. Магнитоэлектрический измерительный прибор, включенный на выходе триггера, показывает среднее за период значение напряжения: Uср= Um∆Т / Т,   j=360 Uср / Um.

Из уравнения видно, что зависимость между величинами j  и U линейная. Шкалу индикаторного прибора можно проградуировать непосредственно в градусах (для данного прибора U=const).

1
 
 
 
 
 

 
 

 
 
 

 

 

 

 

 

 

 

 

 

 


Рис. 14.1. Фазометр с преобразованием фазового сдвига во временной интервал

 

14.2. Цифровые фазометры

Цифровой фазометр с время – импульсным преобразованием.

 


Цифровой способ измерения фазового сдвига включает две основные операции: 1) преобразование фазового сдвига в интервал времени;

        2) измерение интервала времени методом дискретного счета.

При использовании принципа измерения за один период формирующее устройство (рис.14.3) вырабатывает напряжение Uфув виде последовательности  импульсов  с длительностью  ∆tф  и периодом Т. Триггер формирует импульс с длительностью, равной периоду Т. Этот импульс управляет   временным селектором, через который на счетчик проходят импульсы от генератора импульсов.

Арифметическое устройство осуществляет считывание общего числа импульсов N, прошедших в счетчик в течение периода Т, а также промежуточного числа NΔt, соответствующего интервалу времени ∆tф. Запись этих чисел в арифметическое устройство осуществляется по окончании срезов импульсов Uфу, Ump. В арифметическом устройстве производится вычисление отношения kNΔt/ NT = k∆tф/ T=φ.                                      

                 

Арифметическое устройство
 

Цифровое

отсчетное устройство
 

Генератор

импульсов
 

Временной

селектор
 

Счетчик
 
 


                                     

Формирующее

устройство
 
                                                                    

 

 


Триггер
 
    U 

 


    U2

 

 


Рис. 14.3. Цифровой фазометр с время-импульсным преобразованием

 

 

       Контрольные вопросы

1. Поясните принцип действия  фазометра с преобразованием фазового сдвига в интервал времени? Приведите структурную схему и временные осциллограммы.

2. Укажите основные источники погрешностей в фазометре с преобразованием фазового сдвига во временной интервал.

3. Поясните принцип действия цифрового фазометра.

 

Лекция 15. АНАЛИЗ СПЕКТРА СИГНАЛОВ

15.1. Общие сведения

Чтобы провести анализ прохождения сигнала через электрические цепи, необходимо его представить в удобной математической форме (временной или спектральной). При временном способе анализа значения сигналов рассматриваются как функции времени. Спектральный способ основан на представлении (аппроксимации) сигнала в виде суммы гармонических составляющих разных, обычно кратных друг другу частот.

Для спектрального анализа непериодических сигналов (функций) используют аппарат интегрального преобразования Фурье. При этом применяется известная формула прямого преобразования Фурье, характеризующая спектральную плотность непериодического (импульсного) сигнала:

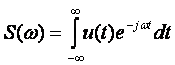                                                                            (15.1)

где ω = 2πf – угловая частота.

В реальных условиях функция S(ω)  измеряется на конечном интервале времени, т.е. фактически определяется так называемый текущий спектр:

                                     .                                     (15.2)

Автоматическое представление спектра сигналов осуществляется специальными приборами – анализаторами спектра.

 

15.2. Параллельный анализ спектра

Анализаторы параллельного типа применяют в основном для анализа спектров одиночных импульсных сигналов. Параллельный анализ осуществляется с помощью совокупности узкополосных фильтров (высокодобротных резонаторов) с идентичными амплитудно-частотными характеристиками, каждый из которых настроен на определенную частоту. При одновременном воздействии исследуемого сигнала на все фильтры (резонаторы), каждый из них выделяет соответствующую его настройке составляющую спектра.

Выходные напряжения фильтров поступают на детекторы, которые преобразуют гармонические напряжения в постоянные напряжения, пропорциональные амплитудам соответствующих гармоник. Далее напряжения спектральных составляющих поступают на регистрирующие устройства.

 

                           15.3.Последовательный анализ спектра.

При исследовании спектров повторяющихся процессов чаще всего применяют последовательный анализ. Метод последовательного частотного анализа реализуется за счет плавной перестройки резонансной частоты узкополосного фильтра. При этом резонансная частота последовательно совпадает с частотами гармонических составляющих анализируемого сигнала, которые поочередно возбуждают сигналы на выходе фильтра. В устройствах последовательного частотного анализа достаточно иметь один перестраиваемый фильтр и один детектор, что существенно упрощает прибор. Однако перестройка фильтра в широком диапазоне частот при сохранении высокой избирательности является сложной задачей. Главная причина ограничения скорости анализа при последовательном способе заключается в продолжительности переходных процессов, возникающих в фильтре при его возбуждении. Чем уже полоса пропускания фильтра, тем медленнее устанавливаются процессы в нем.

 

Контрольные вопросы

1. Для каких целей используется спектральный анализ сигналов?

2. Какой физический смысл лежит в основе прямого и обратного преобразования Фурье?

3. На чем основан параллельный и последовательный анализ спектра исследуемых сигналов?

 

Лекция 16. ИЗМЕРЕНИЕ АМПЛИТУДНО-ЧАСТОТНЫХ ХАРАКТЕРИСТИК

 

Амплитудно-частотная характеристика (АЧХ) радиотехнических устройств является важнейшим параметром, характеризующим качественные характеристики, и представляет собой зависимость модуля коэффициента передачи от частоты, т.е.

.

(16.1)

         Простейшая схема анализа зависимости  приведена на рис. 16.1. Исследования по схеме рис. 16.1, когда генератор оператором перестраивается на ряд дискретных частот, представляют собой трудоемкий процесс и обычно выполняются для анализа АЧХ относительно широкополосных устройств.

Структурная схема панорамного анализатора формы АЧХ четырехполюсника в упрощенном варианте приведена на рис. 16.2.

 

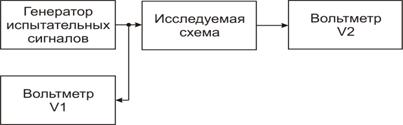
Рис. 16.1. Структурная схема анализа АЧХ

На рис. 16.2 генератор качающейся частоты (ГКЧ) является источником синусоидального колебания с линейно-изменяющейся частотой и стабильной амплитудой. Выходное напряжение ГКЧ является частотно-модулированным, при этом перестройка частоты (частотная модуляция) осуществляется с помощью пилообразного управляющего напряжения, поступающего с генератора развертки электронного луча осциллографа.

         

 

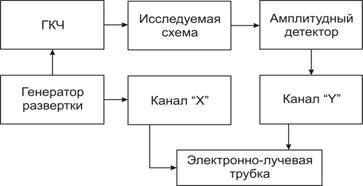
Рис.16.2. Упрощенная структурная схема панорамного прибора для исследования АЧХ

 

Амплитудные значения частотно-модулированного колебания, поданного на вход исследуемой схемы, претерпевают изменения. При достаточно медленном процессе перестройки частоты амплитуда выходного напряжения пропорциональна коэффициенту передачи исследуемого четырехполюсника на данных частотах, следовательно, ЧМ-колебания преобразуются в амплитудно-частотно-модулированное колебание. Таким образом, огибающая ЧМ-колебания несет информацию о форме частотной характеристики исследуемой схемы.

 

Контрольные вопросы

1.     Что называется амплитудно-частотной характеристикой?

2.     Приведите структурную схему измерителя амплитудно-частотных характеристик и  поясните его принцип действия.

 

 

Лекция 17. ИЗМЕРЕНИЕ ПАРАМЕТРОВ ЦЕПЕЙ

 

17.1. Мостовые методы измерения параметров двухполюсников

Для измерения параметров элементов электрических цепей широко применяют  мосты. Мостовые схемы обладают высокой чувствительностью, большой точностью, широким диапазоном измеряемых значений параметров элементов. На основе мостовых методов строятся средства измерения, предназначенные как для измерения какой-либо одной величины, так и универсальные аналоговые и цифровые приборы.

Классическая схема измерительного моста переменного тока состоит из четырех комплексных сопротивлений Z1, Z2, Z3, Z4, соединенных в виде кольца (рис. 17.1). Элементы Z1 … Z4 – называют плечами моста. Цепь А-В, к которой подводится напряжение источника питания, называется диагональю питания, а цепь С-D – измерительной диагональю.


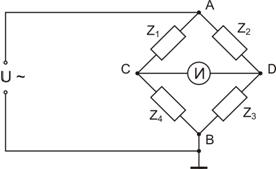
Рис. 17.1. Схема четырехплечего измерительного моста

Процесс измерения с помощью мостовых схем основан на соблюдении определенного соотношения между сопротивлениями плеч, называемого условием равновесия или баланса, которое характеризуется отсутствием напряжения и тока в диагонали индикатора между точками С и D при наличии напряжения питания в точках А-В.

Уравнение баланса четырехплечих мостов переменного тока имеет вид:

Z1 · Z3 = Z2 · Z4.

(17.1)

Если представить комплексные сопротивления Zi в показательной форме Zi = | Zi | · e jφi, где | Zi | – модули полных сопротивлений плеч, а φi – фазовые сдвиги между током и напряжением в соответствующих плечах, то уравнение ( 17.1) примет вид:

| Z1 | · | Z3 | · e j( φ1 + φ3 ) = | Z2 | · | Z4 | · e j( φ2 + φ4 ).                      

 

(17.2)

Для соблюдения этого равенства требуется, чтобы

 

            | Z1 | · | Z3 | = | Z2 | · | Z4 |;   φ1 + φ3 = φ2 + φ4,             

  

(17.3)

 

 

 

т.е. произведение модулей сопротивлений и сумма величин фазовых сдвигов противоположных плеч были равны.

Погрешность измерений моста переменного тока определяется погрешностями значений элементов образующих мост, переходных сопротивлений контактов, чувствительностью схемы и индикатора. Уравновешенные мосты переменного тока обеспечивают погрешность измерения от 0,5 до 5 %.

 

17.2. Цифровые методы измерения параметров двухполюсников

При построении цифровых средств измерения параметров элементов электрических цепей, чаще всего используют сочетание аналогового преобразователя, преобразующего определяемый параметр элемента в активную величину, и соответствующего цифрового прибора для измерения этой величины.

Одним из методов измерения сопротивления, индуктивности и емкости является метод прямого преобразования их значений в пропорциональный интервал времени и измерение этого интервала путем заполнения его счетными импульсами. Этот метод измерения называют методом дискретного счета.

При методе дискретного счета используются закономерности апериодического процесса, возникающего при подключении заряженного конденсатора или катушки индуктивности с протекающим в ней током к образцовому резистору. При измерении активного сопротивления применяют процесс разряда образцового конденсатора через измеряемый резистор.

Измеряемый интервал времени оказывается функционально связанным с преобразуемым параметром. Данные преобразователи отличаются высокой точностью, быстродействием, линейностью функции преобразования, удобным для преобразования в цифровой код видом выходного сигнала.

Если цепочку RС (или LR)  использовать как интегрирующее звено и подключить к источнику постоянного напряжения Uвх, тогда выходное напряжение Uвых будет изменяться во времени согласно уравнения:

                                  Uвых (t) = Uвх (1 - е–t/τ).                                         (17.4)

В момент, когда текущее время t = τ, напряжение на выходе будет точно равно значению:

                                Uвых  = Uвх (1 - е–1)  = 0,632 Uвх.                            (17.5)

Из уравнения (17.5) следует, что необходимо зафиксировать момент переходного процесса, когда t = τ. Если использовать образцовый источник                                  Uо  = Uвх, схему сравнения (компаратор) с опорным напряжением, равным 0,632 Uо и один из образцовых элементов Rо,  Со,  и  Lо, тогда достаточно измерить время   t = τ и по известным соотношениям τ = RС; τ = L/ R, рассчитать один из параметров Rх,  Сх,  и  Lх.

Погрешность измерений цифровым методом составляет 0,1...0,2 % и зависит от нестабильности сопротивлений образцовых элементов, нестабильности частоты генератора счетных импульсов, а также неточности  срабатывания устройства сравнения.

 

Контрольные вопросы

1. Перечислите основные методы измерения параметров элементов электрических цепей.

2. Какой из известных методов измерений реализуется в мостовых схемах? Что называют балансом мостовой цепи?

3.  Приведите схемы мостов для измерения параметров L, C, R.

4. Поясните принцип действия цифрового  измерителя параметров двухполюсников. Назовите источники погрешностей.