УЗБЕКСКОЕ АГЕНТСТВО СВЯЗИ И ИНФОРМАТИЗАЦИИ
ТАШКЕНТСКИЙ УНИВЕРСИТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ
Кафедра Теория передачи
сигналов
КОНСПЕКТ ЛЕКЦИЙ
по курсу
ОСНОВЫ РАДИОЛОКАЦИИ
Ташкент 2002
ВВЕДЕНИЕ
Рождение радиолокационной техники и у нас в стране, и за рубежом было связано с решением задачи заблаговременного обнаружения самолётов. Радиолокационные станции позволили решить эту задачу значительно лучше (на большей дальности, с более высокой точностью, с большим быстродействием, при любых метеорологических условиях), чем все известные ранее средства обнаружения (звуковые и оптические).
Работы по созданию радиолокационных станций велись в СССР отдельными группами учёных с начала 30-х годов. В 1941 году советские учёные Ю.Б. Козырев, П.А. Погорелко и Н.Я. Чернецов за разработку первых серийных отечественных станций для обнаружения самолётов были удостоены Государственной премии. Приблизительно к этому же времени относится появление первых радиолокационных устройств аналогичного назначения за рубежом.
С тех пор радиолокация развивалась быстрыми темпами и в настоящее время превратилась в самостоятельную отрасль науки и техники, имеющую чрезвычайно большое значение и для военных целей, и для народного хозяйства.
В пособии изложены принцип радиолокации, методы измерения координат и обзора пространства, рассмотрены вопросы измерения их параметров и разрешения. Данное пособие предназначается для студентов специального факультета. Однако авторы стремились создать пособие, которое было бы полезным не только впервые изучающим студентам, но и всем, кто заинтересован данным предметом в той или иной степени.
ГЛАВА 1. ОБЩИЕ СВЕДЕНИЯ О РАДИОЛОКАЦИИ
1.1. Задачи и применение радиолокации
Радиолокацией называется область радиотехники, использующая явления отражения и излучения электромагнитных волн различными объектами для обнаружения и измерения координат этих объектов. Радиотехнические устройства, предназначенные для решения указанных задач, называются радиолокационными станциями (РЛС).
С помощью радиолокационных средств решаются самые разнообразные задачи навигации, управления полётом и посадкой летательных аппаратов, проводкой кораблей, прогнозирования погоды, перехвата объектов противника и прицеливания при стрельбе по ним. Радиолокационные устройства начинают использоваться при исследовании свойств объектов наблюдения, для определения их физических и кинематических характеристик.
При решении различных задач радиолокационные станции обеспечивают:
ü обнаружение объектов;
ü определение их государственной принадлежности (опознавание);
ü измерение координат объектов и определение их положения;
ü определение параметров движения объектов, выявление их траекторий и предсказание их последующих положений;
ü определение некоторых физических свойств и характеристик объектов.
Измерение координат объектов радиолокационными средствами осуществляется либо в сферической, либо в цилиндрической системах. За центр системы принимается место расположения РЛС (точка О на рис.1.1).
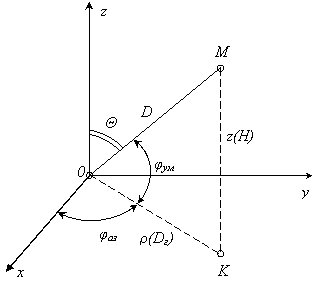 |
Рис.1.1. Система координат, принятая в радиолокации.
Сферическими координатами объекта наблюдения (точка М на рис.1.1) будут: D – радиус – вектор (дальность), jаз – долгота (азимут), jум – угол места, дополняющий полярное расстояние q до 900 (jум = 900 - q). В цилиндрической системе положение объекта определяется аппликатой z (высота Н) и полярными координатами jаз и r (горизонтальная дальность Dг) проекции точки М на плоскость хОy.
Объектом радиолокационного наблюдения или, как чаще говорят, целью может быть любое тело или группа тел с электрическими или магнитными свойствами, отличными от свойств среды, в которой распространяются радиоволны; целью может быть также и тело, характеризующееся собственным излучением радиоволн. Радиолокационными целями являются самолёт, корабль, человек, грозовое облако, участок поверхности земли, специальный радиомаяк и т.п.
1.2. Физические основы обнаружения целей и
определения их координат и скорости
При радиолокационном наблюдении информация о целях переносится радиолокационными сигналами. Радиолокационными сигналами называются электромагнитные колебания, параметры которых определенным образом связаны с целью.
Известно несколько методов получения радиолокационных сигналов:
1.Метод активной радиолокации является наиболее распространённым и основан на облучении цели электромагнитной энергией и приёме отражённых (рассеянных) целью радиоволн приёмным устройством РЛС.
2.Метод активного ответа – при этом при облучении цели электромагнитной энергией срабатывает установленный на цели ретранслятор (ответчик), который посылает вполне определённые радиосигналы; эти сигналы принимаются приёмником РЛС.
3.Метод пассивной радиолокации заключается в приёме сигналов собственного радиоизлучения целей (радиотепловое излучение тел, излучение собственных радиотехнических устройств и др.)
Обнаружение целей состоит в фиксации поступающих на вход приёмного устройства РЛС радиолокационных сигналов.
Измерение координат обнаруженных целей основано на определении значений параметров радиолокационных сигналов, несущих информацию об этих целях. При этом используются следующие физические свойства радиоволн:
Ø скорость распространения радиоволн в свободном пространстве (с) имеет конечное и приблизительно постоянное значение;
Ø траектории распространения радиоволн можно считать прямыми линиями;
Ø Частота принимаемых электромагнитных колебаний отличается от частоты излучённых колебаний в том случае, если цель перемещается относительно РЛС (эффект Доплера).
Время распространения радиоволн от РЛС до цели и обратно tD:
![]() .
.
Тогда дальность цели по методу активной радиолокации:
|
|
(1.1) |
Обычно величину tD называют временем запаздывания отражённого сигнала.
Радиальная составляющая скорости движения цели:
|
|
(1.2) |
где ![]() - доплеровское смещение
частоты отражённых от целей радиолокационных сигналов;
- доплеровское смещение
частоты отражённых от целей радиолокационных сигналов;
Vр - основано на использовании эффекта Доплера, который проявляется дважды:
во – первых, частота электромагнитных колебаний, переизлучаемых движущейся целью fотр, отличается от частоты излучённых колебаний fизл:
![]() .
.
и, во – вторых, частота колебаний, принятых отражённых сигналов:
![]() .
.
Тогда
![]() .
.
Принимаем, что ![]() .
.
Знак “+” соответствует сближению РЛС и цели, знак “-” – их удалению.
1.3. Тактические данные и
технические характеристики РЛС
При проектировании новых РЛС необходимо учитывать следующие тактические данные аппаратуры:
ü размеры области пространства, в пределах которой осуществляется наблюдение целей, - зону обзора;
ü время, требующееся для осмотра заданной области, или период обзора Тобз;
ü измеряемые координаты;
ü точность измерения координат и скорости целей;
ü разрешающую способность;
ü эксплуатационную надёжность;
ü помехозащищённость.
Зона обзора ограничивается максимальной (Dмакс) и минимальной (Dмин) дальностью действия и секторами обзора в горизонтальной (Фаз) и вертикальной (Фум) плоскостях (рис.1.2).
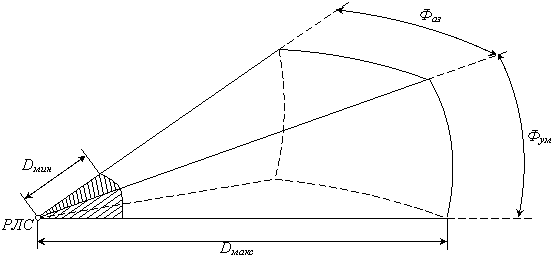 |
Рис.1.2. Зона обзора РЛС.
Разрешающая способность РЛС характеризует возможность раздельного наблюдения целей, которые отличаются либо значением одной из координат, либо скоростью движения.
Разрешающая способность по дальности d(D) определяется минимальным расстоянием между двумя целями, имеющими одинаковые угловые координаты и скорости, при котором эти цели наблюдаются раздельно. Если расстояние между целями станет меньше d(D), то РЛС будет воспринимать их как одну цель.
Разрешающая способность по угловой координате d(j) определяется минимальным углом между направлениями на две цели, характеризующиеся одинаковыми дальностями и скоростями движения, при котором возможно раздельное наблюдение целей.
Разрешающая способность по скорости d(Vр) определяется минимальным различием скоростей двух целей, наблюдаемых раздельно, при условии равенства их дальностей и угловых координат.
Эксплуатационной надёжностью РЛС называется её свойство выполнять заданные функции в течение определённого времени в допускаемых при эксплуатации условиях. Обычно эксплуатационную надёжность характеризуют вероятностью безотказной работы станции в течение заданного промежутка времени.
Помехозащищённостью называется способность радиолокационного устройства сохранять свои основные тактические показатели при воздействии помех того или иного вида.
Тактические данные РЛС определяются её техническими характеристиками:
ü принцип построения РЛС (метод получения радиолокационных сигналов, вид излучаемых колебаний, способ обработки сигналов в приёмнике);
ü несущая частота излучаемых колебаний f или длина волны l;
ü закон модуляции излучаемых колебаний;
ü средняя Рср и пиковая Ри мощности излучения;
ü форма и ширина диаграммы направленности антенны qаз, qум;
ü чувствительность приёмного устройства по мощности (Рпр мин) или энергией (Епр мин);
ü тип выходного устройства.
ГЛАВА 2. МЕТОДЫ ИЗМЕРЕНИЯ КООРДИНАТ И
СКОРОСТИ ДВИЖЕНИЯ ЦЕЛЕЙ
2.1. Методы измерения дальности
Известны различные подходы к классификации методов измерения дальности. В соответствии с параметрами сигналов существуют амплитудный, фазовый или частотный методы измерения.
1. Амплитудный метод
При амплитудном методе измерения определяется время запаздывания характерного изменения амплитуды принимаемого радиолокационного сигнала. Из различных видов модуляции излучаемых колебаний наиболее употребительной является импульсная.
Рассмотрим устройство импульсной дальномерной РЛС (рис. 2.1 и 2.2). Передатчик станции генерирует радиоимпульсы длительностью tи с периодом повторения Ти (напряжение u2 на рис.2.2). Антенный переключатель (АП) подсоединяет антенну к передатчику на время генерации (tи) и к приёмнику на всё остальное время. Отражённые импульсные сигналы запаздывают на время tD; на вход приёмника поступают и колебания передатчика и отражённые сигналы (u3).
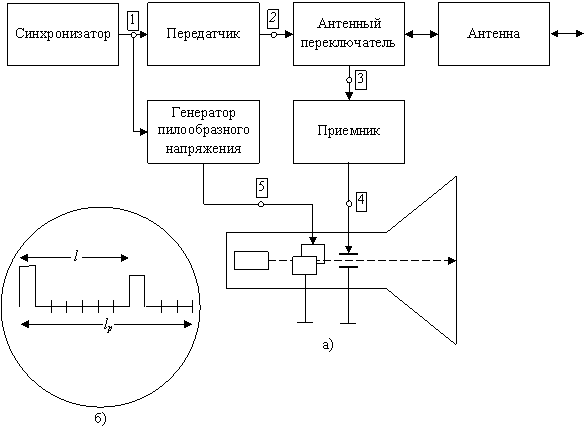
Рис.2.1. Функциональная схема импульсного измерителя дальности (а) изображение сигналов на экране электроннолучевого индикатора (б)
Время запаздывания отражённых сигналов мало (оно составляет тысячные или даже миллионные доли секунды), и обычные часовые механизмы для его измерения непригодны. Одним из наиболее употребительных приборов для измерения времени запаздывания является электроннолучевая трубка. На рис.2.1, а показана трубка с электростатическим управлением. К вертикально отклоняющим пластинам трубки подводятся импульсы напряжения с выхода приёмника u4; к горизонтально отклоняющим пластинам от специальной схемы подводится пилообразное напряжение u5 (рис.2.2). Передатчик и схема создания пилообразного напряжения запускаются одновременно импульсами синхронизирующего устройства, поэтому одновременно с излучением импульса передатчика начинается горизонтальное перемещение пятна по экрану трубки.
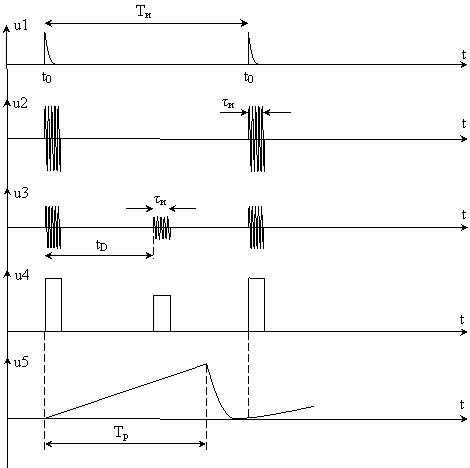

Рис.2.2. Эпюры напряжений в точках 1-5 схемы импульсного дальномера (рис.2.1, а).
Картина, наблюдаемая на индикаторе, иллюстрируется рис.2.1,б, пятно воспроизводит огибающие излучённого и отражённого импульсов, расстояние между которыми l пропорционально дальности обнаруженной цели:
|
|
(2.1) |
где VП – скорость движения пятна по экрану индикатора, откуда
|
|
(2.2) |
Достоинства импульсных дальномеров:
ü возможность построения РЛС с одной антенной;
ü простота индикаторного устройства;
ü удобство одновременного измерения дальности многих целей;
ü простота разделения излучаемых импульсов, длящихся очень малое время tи, и принимаемых сигналов.
Недостатки импульсного метода:
ü необходимость использования больших импульсных мощностей передатчиков;
ü невозможность измерения малых дальностей;
ü большая минимальная дальность станции (определяющаяся длительностью излучаемых импульсов и временем протекания переходных процессов в антенном переключателе), которая составляет сотни или даже тысячи метров.
2. Частотный метод
Частотный метод определения дальности основан на использовании частотной модуляции излучаемых непрерывных колебаний; время запаздывания определяется путём измерения разности частот излучённых колебаний и отражённого сигнала. Функциональная схема РЛС с частотной модуляцией изображена на рис.2.3.
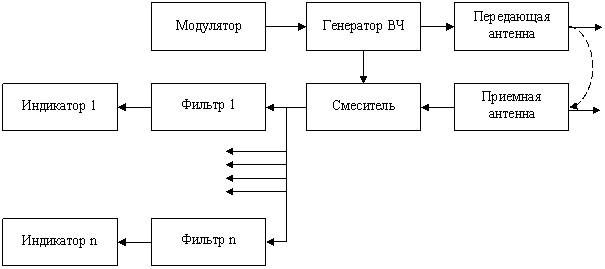
Рис.2.3. Функциональная схема измерителя дальности с частотной модуляцией.
Генератор высокой частоты, управляемый модулятором, вырабатывает колебания с частотой, изменяющейся по периодическому закону (рис.2.4, сплошная линия). Частота сигнала, отражённого от неподвижной цели, будет изменяться по такому закону, но только со сдвигом по временной оси на время запаздывания tD.
На рис. 2.4, а частота отражённых колебаний показана штриховой линией. Отражённые сигналы и колебания генератора подводятся к смесителю. Образующаяся на выходе смесителя разностная частота (рис.2.4, б) (частота биений) пропорциональна дальности цели. Если круговая частота излучения
![]() ,
,
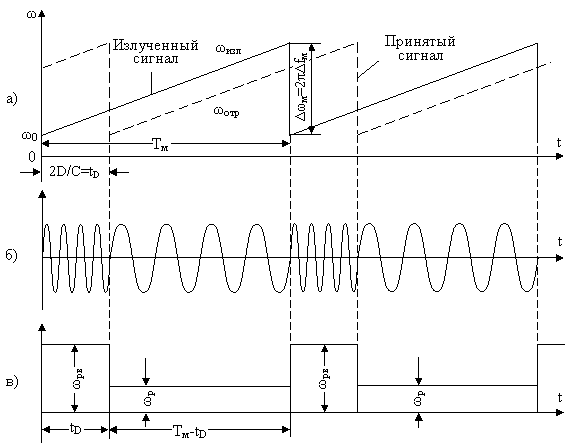

Рис. 2.4. Изменение частоты излучаемых и принимаемых колебаний:
а) - частоты излучённого и принятого сигнала;
б) - преобразованный сигнал (биения);
в) - изменение частоты преобразованного сигнала.
где Dwм – девиация частоты передатчика, то частота сигнала, отражённого от неподвижной цели, будет равна
![]() .
.
Разностная частота, выделяемая на выходе смесителя,
|
|
(2.3) |
Откуда
|
|
(2.4) |
Формулы (2.3) и (2.4) поясняют зависимость между дальностью цели и разностной частотой и позволяют понять сущность метода.
Для измерения разностных частот используются фильтры и счётчики импульсов. При использовании фильтров возможны два варианта: применяется группа фильтров, настроенных на фиксированные частоты, или один фильтр с переменной настройкой. Попадание сигнала разностной частоты в тот или иной фильтр (на что укажет соответствующий индикатор, например неоновая лампочка) позволит определить дальность цели.
Дальномеры данного типа позволяют определять очень малые дальности и использовать передатчики с малой мощностью излучения.
Недостатки дальномеров с частотной модуляцией:
ü необходимость использования либо двух антенн, либо сложного устройства для разделения излучаемых и принимаемых сигналов;
ü ухудшение чувствительности приёмника вследствие просачивания в приёмный тракт через антенну излучения передатчика, подверженного случайным изменениям;
ü высокие требования к линейности изменения частоты.
3. Фазовые методы
Фазовые методы основаны на измерении разности фаз излучённых синусоидальных колебаний и принятых радиосигналов. Функциональная схема простейшего фазового дальномера изображена на рис.2.5.
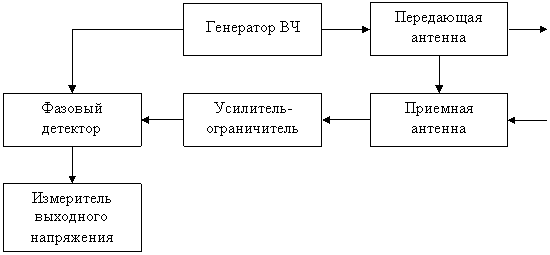

Рис.2.5. Функциональная схема простейшего фазового
измерителя дальности.
Генератор создаёт незатухающие колебания частоты w0, излучаемые в пространство. Фаза излучённых колебаний
![]() ,
,
где y1 – начальное значение фазы.
Фаза принимаемого сигнала
![]() .
.
Здесь yотр – фазовый сдвиг, связанный с отражением радиоволны от цели;
yРЛС – фазовый сдвиг в цепях РЛС, который можно считать известным, так как он поддаётся измерению и может быть учтён.
Принятые колебания сравниваются с колебаниями высокочастотного генератора; разность фаз пропорциональна дальности цели
|
|
(2.5) |
или
|
|
(2.6) |
Данный метод измерения практически не используют по
двум обстоятельствам. Во–первых, очень мал диапазон однозначного измерения и,
во–вторых, в формулу (2.6) входит неизвестная величина yотр.
Неоднозначность измерений определяется тем, что фазометрическое устройство
позволяет определять фазовые сдвиги только в пределах от 0 до 2p. Допустив, что Dy£2p, из формулы
(2.6) получим, что диапазон однозначного измерения дальности не превышает
половины длины волны: ![]() .
.
В радиолокации используются ультракороткие волны и, следовательно, диапазон однозначно измеряемой дальности не превышает единиц метров. Что касается фазового сдвига yотр, образующегося при отражении высокочастотных колебаний от цели, то, поскольку он весьма сложным образом зависит от конфигурации цели, её размеров и расположения относительно РЛС, то заранее знать нельзя и поэтому нельзя корректировать показания измерителя.
Указанные недостатки простейшего фазового дальномера устраняются при использовании более сложных схем, в которых применяется не менее двух частот.
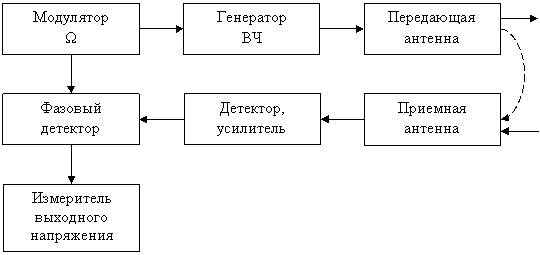

Рис.2.6. Функциональная схема фазового измерителя
дальности с модулятором.
На рис.2.6 изображена функциональная схема фазового дальномера с использованием низкой частоты W, на которой осуществляется измерение фазового сдвига, и высокой w0, играющей роль переносчика информации.
Модулятор создаёт синусоидальное напряжение ![]() , модулирующее
по амплитуде колебания генератора высокой частоты:
, модулирующее
по амплитуде колебания генератора высокой частоты:
![]() ,
,
где m - коэффициент модуляции.
Модулированные колебания излучаются в пространство. Принятые сигналы после усиления детектируются, и выделяется их огибающая, фаза которой сравнивается с фазой колебаний модулятора. Фаза огибающей принятых сигналов зависит от дальности цели
|
|
(2.7) |
В формулу (2.7) не включён фазовый сдвиг огибающей колебаний при отражении yотр, который пренебрежимо мал.
Фазовый сдвиг в цепях РЛС yРЛС может быть измерен и учтён при градуировке
фазометрического устройства. Разность фаз низкочастотных колебаний ![]() позволяет
определить дальность цели
позволяет
определить дальность цели
|
|
(2.8) |
Частота может быть выбрана достаточно низкой, что обеспечит большой диапазон однозначно измеряемых дальностей.
Данное дальномерное устройство характеризуется рядом достоинств:
ü требуется малая мощность излучения, так как генерируются незатухающие колебания;
ü точность измерения дальности практически не зависит от доплеровского сдвига частоты отражённого сигнала;
ü просто само измерительное устройство.
Недостатки:
ü - отсутствует разрешение по дальности, так как при наличии одновременно двух целей их сигналы раздельно наблюдать нельзя;
ü - чувствительность приёмника ухудшается вследствие просачивания излучения передатчика;
ü - необходимы две антенны или система развязки излучаемых и принимаемых колебаний.
Известен другой вариант двухчастотного фазового дальномера (рис.2.7).
РЛС включает два генератора высокочастотных колебаний и два приёмника, работающих соответственно на частотах w1 и w2. Колебания обоих генераторов подводятся к передающей антенне, а также к первому смесителю; с выхода приёмников два сигнала воздействуют на второй смеситель.
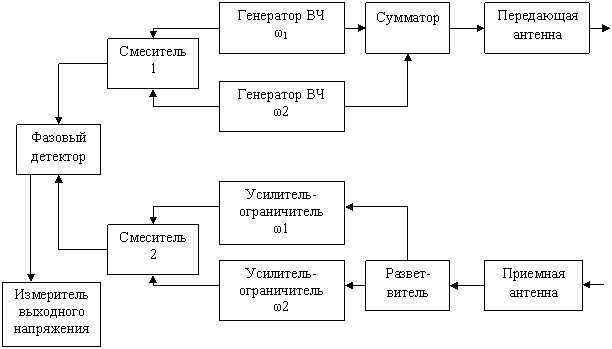

Рис.2.7.Функциональная схема двух частотного фазового
измерителя дальности.
Пусть напряжение генераторов:
![]()
и
![]() .
.
На выходе первого смесителя получим колебания первой разностной частоты
![]() .
.
Если не учитывать фазовых сдвигов в цепях РЛС, то оба принятых сигнала могут быть записаны как
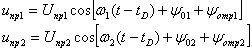
и напряжение второй разностной частоты на выходе второго смесителя
![]() .
.
При условии, что излучаемые частоты мало отличаются
друг от друга 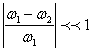 , фазовые сдвиги при
отражении от цели на обеих частотах можно считать одинаковыми, т. е. yотр1»yотр2.
, фазовые сдвиги при
отражении от цели на обеих частотах можно считать одинаковыми, т. е. yотр1»yотр2.
Измерение фазового сдвига Dy позволяет определить дальность цели
|
|
(2.9) |
Анализ формулы (2.9) показывает, что в рассмотренном дальномере может быть обеспечен большой диапазон однозначного измерения дальности [разность (w1-w2) является малой величиной], а также исключается влияние на результат измерений фазового сдвига yотр. Такому дальномеру присущи перечисленные выше достоинства и недостатки, свойственные всем РЛС с непрерывным излучением.
2.2. Методы измерения угловых координат
Для определения угловых координат целей используются угломерные или пеленгационные радиолокационные устройства.
Угломерное устройство включает антенну (антенную систему), приёмник для обработки принятых радиолокационных сигналов и измерительное устройство. Одной из основных характеристик угломерного устройства является его пеленгационная характеристика, представляющая собой зависимость выходного напряжения приёмника от направления прихода радиоволны Uвых(j). В зависимости от того, какой параметр сигнала – амплитуда, частота или фаза – оказывает основное влияние на формирование пеленгационной характеристики, методы измерения угловых координат можно подразделять на амплитудные, частотные и фазовые.
1. Амплитудные методы
В настоящее время известны и широко используются несколько амплитудных методов: максимума, минимума, сравнения, равносигнальный.
При пеленгации по методу максимума плавно изменяется угловое положение антенны, и она в течение некоторого времени принимает сигналы цели; отсчёт угловой координаты цели производится в тот момент, когда амплитуда сигнала на выходе приёмника достигает наибольшего значения. Функциональная схема соответствующего угломерного устройства показана на рис.2.8.


Рис.2.8. Функциональная схема угломерного устройства с отсчётом по максимуму.
Механизм поворота вращает антенну; одновременно приводится в действие указатель поворота, по шкале которого отсчитывается направление оси антенны. Когда цель окажется в пределах диаграммы направленности антенны F(j), в приёмник начнут поступать сигналы. Амплитуда сигналов зависит от углового положения антенны по отношению к цели. При вращении антенны выходное напряжение приёмника Uвых повторяет форму диаграммы направленности антенны (рис.2.9).


Рис.2.9. Пеленгационная характеристика при пеленгации по максимуму.
Это и будет пеленгационная характеристика угломерного устройства
|
|
(2.10) |
где k - коэффициент пропорциональности.
Когда ось антенны совпадает с направлением на цель, выходное напряжение приёмника достигнет максимума; в этот момент указатель поворота антенны покажет пеленг цели jц.
Достоинства метода:
ü простота его технической реализации;
ü получение наибольшей (при прочих равных условиях) амплитуды принимаемого сигнала в момент точного пеленга.
Недостатком метода является относительно низкая точность измерений угловой координаты.
Точность измерения угла характеризуется пеленгационной чувствительностью, представляющей собой крутизну пеленгационной характеристики вблизи направления на цель:
|
|
(2.11) |
Если измерительное устройство позволяет заметить минимальное изменение выходного напряжения, равное DUмин, то эта величина связана с соответствующей угловой ошибкой Dj:
|
|
(2.12) |
Следовательно, чем больше пеленгационная чувствительность, тем выше точность измерения угловой координаты.
При пеленгации по методу максимума для диаграмм
направленности любого типа пеленгационная чувствительность очень мала (при
точном пеленге ![]() ), поэтому и точность
измерения координат относительно низка.
), поэтому и точность
измерения координат относительно низка.
Метод пеленгации по минимуму отличатся тем, что отсчёт угловой координаты производится в момент уменьшения до минимума выходного напряжения приёмника. Диаграмма направленности антенны пеленгатора имеет в средней части провал до нуля. Этого можно добиться, например, используя две антенны, повёрнутые в пространстве одна относительно другой на угол, равный ширине диаграммы направленности по нулевому уровню (рис.2.10, а).
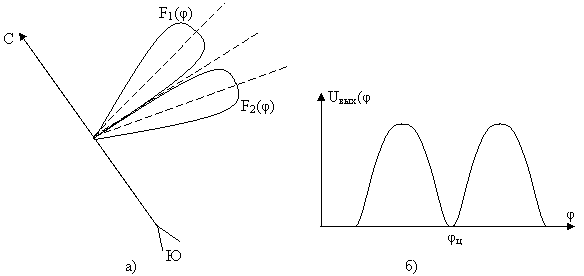
Рис.2.10. Диаграмма направленности антенного устройства (а) и пеленгационная характеристика при пеленгации по минимум (б).
Функциональная схема пеленгационного устройства такая
же, как и при пеленгации по максимуму (рис.2.8). Изменения амплитуды
сигнала на выходе приёмника при повороте антенны характеризуются графиком рис.2.10,б;
аналогичный вид имеет и пеленгационная характеристика ![]() , где
функция F(j)–результирующая диаграмма направленности.
, где
функция F(j)–результирующая диаграмма направленности.
При пеленгации по минимуму может быть получена высокая точность измерения угловой координаты, так как пеленгационная чувствительность велика. Но амплитуда сигнала вблизи направления пеленга мала; при точном пеленге она становится равной нулю.
Практически по методу минимума можно пеленговать только источники мощного собственного излучения. Поэтому метод пеленгации по минимуму в радиолокации не используется.
Метод сравнения характеризуется тем, что пеленг цели определяется по соотношению амплитуд сигналов, принятых одновременно двумя антеннами. Функциональная схема пеленгационного устройства, в котором использован метод сравнения, приведена на рис.2.11; графики рис.2.12 характеризуют пространственное расположение диаграмм направленности антенного устройства.
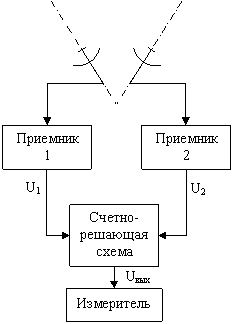

Рис.2.11. Функциональная схема пеленгатора, в котором
используется метод сравнения.
Амплитуды сигналов на выходе приёмников
пропорциональны модулям векторов ![]() и
и ![]() (рис 2.11):
(рис 2.11):
![]() и
и ![]() .
.
В счетно-решающей схеме осуществляется сравнение амплитуд сигналов. Технически наиболее просто осуществить вычитание одного сигнала из другого, т.е.
|
|
(2.13) |
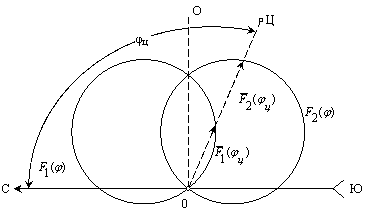

Рис.2.12. Пространственное расположение диаграмм направленности
при использовании метода сравнения.
При этом выходное напряжение зависит от абсолютных значений амплитуд сигналов и, следовательно, будет изменяться в зависимости от расстояния между РЛС и целью, отражающих свойств цели, поглощения в среде и т.д. Исключить влияние изменения амплитуд сигналов на результат измерений можно либо с помощью системы АРУ, управляющей усилением обоих приёмников, либо осуществляя деление одного сигнала на другой:
|
|
(2.14) |
Вид пеленгационной характеристики иллюстрирует рис.2.13.
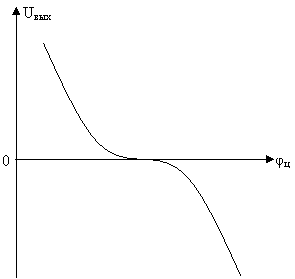 |
Рис.2.13. Пеленгационная характеристика при использовании
метода сравнения.
Основное достоинство метода сравнения – возможность мгновенного определения направления на цель в пределах относительно широкого сектора при неподвижной антенной системе. Наиболее существенным недостатком является относительно низкая точность измерения, существенно меняющаяся в зависимости от вида и взаимного расположения диаграмм направленности антенн, а также от направления прихода волны.
Частным случаем метода сравнения является равносигнальный метод пеленгации. Он также основан на сравнении амплитуд сигналов, принимаемых двумя антеннами, но для отсчёта углового положения добиваются равенства сигналов. При пеленгации цели по равносигнальному методу антенное устройство поворачивают до тех пор, пока выходное напряжение не станет равным нулю. В этот момент угловая координата цели определяется по положению антенны.
Равносигнальный метод характеризуется высокой точностью, так как при измерении используется небольшой участок диаграмм направленности (вблизи равносигнального направления ОО, рис.2.12) с относительно большой крутизной. Этот метод часто используют для автоматического слежения за целью по угловым координатам. При этом выходное напряжение Uвых подводят к системе управления механизмом поворота антенны. В зависимости от знака рассогласования между равносигнальным направлением ОО и направлением на цель механизм будет поворачивать антенну в ту или иную сторону, чтобы свести напряжение Uвых к нулю; при этом равносигнальное направление антенны всё время будет оставаться направленным на цель.
Равносигнальный метод можно реализовать при использовании одной антенны, диаграмма направленности которой периодически изменяет своё положение в пространстве. В этом случае сравнению подлежат сигналы, принятые в различные моменты времени при разных положениях диаграммы направленности.
2. Фазовые методы
Фазовые методы основаны на измерении разности фаз электромагнитных колебаний, принимаемых различными антеннами. Пусть в точках 1 и 2 расположены две приёмные антенны (рис.2.14), расстояние между которыми (база) равно d.
Принятые антеннами сигналы подводятся к фазовому детектору. Выходное напряжение фазового детектора будет определяться только разностью фаз колебаний (можно считать амплитуды обоих колебаний на входе детектора одинаковыми)
![]() .
.
Если направление прихода радиоволны составляет угол j с перпендикуляром к базе, то фазовый сдвиг высокочастотных колебаний в антеннах равен
![]() ,
,

Рис.2.14. Функциональная схема фазового измерителя
угловых координат.
а при малых значениях j, когда приближенно можно считать ![]() ,
,
|
|
(2.15) |
С учётом (2.15) пеленгационная характеристика будет
|
|
(2.16) |
(кривая 1 на рис.2.15).
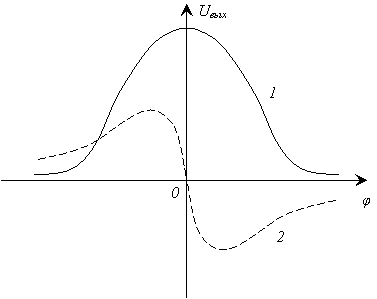

Рис.2.15. Пеленгационные характеристики фазового пеленгатора
Измеряя Uвых, можно определить направление прихода радиоволны при неподвижном антенном устройстве.
Из формулы (2.16) можно видеть, что точность измерения угловой координаты вблизи значения j=0 низка. Кроме того, нельзя определить направление смещения цели от перпендикуляра к базе. Оба недостатка могут быть устранены, если ввести искусственный фазовый сдвиг сигнала на 900 в одном из усилителей. На рис.2.14 такой фазосдвигающий элемент изображён пунктиром в верхнем усилительном канале.
При введении дополнительного фазового сдвига получим
|
|
(2.17) |
(кривая 2 на рис.2.15).
Метод характеризуется относительно высокой точностью измерения; он может быть использован для автоматического слежения за целями по угловым координатам.
Недостатками метода являются:
ü неоднозначность отсчёта;
ü отсутствие разрешения целей.
Если диапазон однозначного измерения фазы принять равным 2p, то пределы однозначного измерения угла могут быть определены с помощью формулы (2.15)
![]() .
.
Неоднозначность измерения угловых координат фазовым методом может быть устранена, если в пеленгаторе используются антенны с достаточно узкими диаграммами направленности qА<Djодн, где qА - ширина диаграммы направленности антенны.
2.3. Методы измерения радиальной скорости
Измерения радиальной скорости основано на определении допплеровского сдвига частоты отраженного сигнала. Схема простейшей станции, обеспечивающей измерение допплеровской частоты сигналов, приведена на рис.2.16.

Рис.2.16. Функциональная схема измерителя доплеровской частоты.
Генератор высокой частоты (f0) создаёт незатухающие колебания, излучаемые в пространство. Частота сигнала, отражённого от движущейся цели, будет отличаться от f0 на доплеровский сдвиг FД; отражённый сигнал можно записано в таком виде:
![]() .
.
Принятые колебания смешиваются с колебаниями
генератора ![]() . На выходе смесителя
образуются колебания с частотой Допплера. Огибающая высокочастотных колебаний
(частота биений) выделяется с помощью амплитудного детектора. Далее колебания
на частоте FД
усиливаются и подводятся к измерителю частоты. Шкала измерителя градуируется
прямо в единицах радиальной скорости цели
. На выходе смесителя
образуются колебания с частотой Допплера. Огибающая высокочастотных колебаний
(частота биений) выделяется с помощью амплитудного детектора. Далее колебания
на частоте FД
усиливаются и подводятся к измерителю частоты. Шкала измерителя градуируется
прямо в единицах радиальной скорости цели
|
|
(2.18) |
Достоинства метода:
ü простота устройства станции;
ü нечувствительность к медленным уходам частоты генератора.
Недостатки метода:
ü высокие требования к кратковременной стабильности частоты генератора (за время распространения радиоволн до цели и обратно);
ü влияние любой паразитной модуляции колебаний генератора на работоспособность устройства;
ü возникновение помех работы станции при наличии нескольких целей (на выходе детектора будут образовываться комбинации допплеровских частот и их гармоник [kFДi±mFДj]).
ГЛАВА 3. ХАРАКТЕРИСТИКИ РАДИОЛОКАЦИОННЫХ ЦЕЛЕЙ
3.1. Основные свойства и классификация
Основные характеристики объектов, рассматриваемых в качестве радиолокационных целей:
ü отражающая способность, определяющая свойство цели переизлучать большую или меньшую долю падающей на неё электромагнитной энергии;
ü закон распределения и спектр флуктуаций фазового фронта отражённого сигнала;
ü закон распределения и спектр флуктуаций амплитуды (мощности) отражённого сигнала;
ü особенности траектории движения.
Отражающие свойства цели наряду с данными РЛС определяют её дальность действия. Отражающие свойства зависят от размеров цели, материала, из которого она выполнена, конфигурации, от длины волны РЛС и направления облучения. Практическая невозможность точного учёта всех перечисленных факторов привела к необходимости введения специальной расчётной величины – эффективной отражающей площади цели. Эффективная отражающая площадь цели определяется следующим образом (рис.3.1).


Рис.3.1. К определению эффективной отражающей площади цели.
Пусть РЛС создаёт у цели, находящейся на расстоянии D, плотность потока мощности rмц. Цель частично поглощает падающую на неё энергию, переизлучая остальную часть в пространство. Переизлучение происходит во многих случаях неравномерно. Чтобы не иметь дела с коэффициентом отражения и характеристиками переизлучения цели, в расчёт вводят некоторую фиктивную поверхность, имеющую площадь Sэфф. Эта поверхность не обладает поглощением и переизлучает всю падающую на неё электромагнитную энергию во все стороны с одинаковой интенсивностью. При этом величина Sэфф выбирается из условия, чтобы у приёмной антенны РЛС создавалась такая же плотность потока мощности rРЛС, как и от реальной цели. Таким образом, если цель с эффективной отражающей площадью Sэфф воспринимает мощность
![]() ,
,
то у антенны станции при принятых условиях будет создана плотность потока мощности, равная
![]() .
.
Отсюда
|
|
(3.1) |
Учитывая, что мощность пропорциональна квадрату напряжённости электромагнитного поля, получим другой вид формулы (3.1)
|
|
(3.2) |
где xРЛС и xц - напряженности поля вблизи РЛС и цели соответственно.
Эффективная отражающая площадь цели – это такая фиксированная поверхность, являющаяся изотропным и не поглощающим энергию переизлучателем, которая, будучи помещена в точку цели, создаёт у антенны РЛС такую же плотность потока мощности отражённого сигнала, как и реальная цель. Эффективная отражающая поверхность является одной из важнейших характеристик радиолокационной цели, необходимой для расчёта дальности действия РЛС.
При неравномерной диаграмме переизлучения реальных целей сложной конфигурации всякое случайное или регулярное изменение ракурса их облучения со стороны РЛС приводит к флуктуациям мощности отражённого сигнала у антенны станции. Поэтому эффективная отражающая площадь таких флуктуирующих целей будет случайной величиной и может быть определена лишь статистически – законом распределения и его числовыми характеристиками. Обычно в расчётах используется среднее значение эффективной отражающей площади Sэфф0, приводимое в таблицах.
Кроме закона распределения Sэфф необходимо знать также спектр её флуктуаций, чтобы правильно выбрать постоянную времени АРУ приёмника, частоту сканирования антенны при коническом обзоре и полосу пропускания следящей системы РЛС.
Случайные относительные перемещения цели и РЛС приводят также к флуктуациям фазового фронта отражённого сигнала.
Фазовым фронтом называется поверхность, в любой точке которой отражённый сигнал имеет одну и ту же фазу.
Эффективная отражающая площадь и закон распределения, спектр её флуктуаций и спектр флуктуаций фазового фронта тесно связаны с относительным движением цели.
Радиолокационные цели удобно классифицировать по методу определения их эффективной отражающей площади. С этой точки зрения все цели можно разделить на элементарные и сложные. Эффективная отражающая площадь элементарных целей может быть определена аналитически по формулам (3.1) и (3.2). Такой расчёт возможен лишь для ограниченного числа объектов простейшей формы, выполненных из однородного идеально отражающего материала. Примерами элементарных целей могут служить металлические шар, лист, вибратор, уголковые отражатели.
Эффективная отражающая площадь сложных целей может быть определена только экспериментальным путём и описана статистически вследствие сложности их конфигурации и случайных перемещений относительно РЛС. К сложным целям относится подавляющее большинство реальных целей.
Сложные цели, в свою очередь, могут быть разделены на точечные и распределённые.
Точечные цели – это цели, линейные и угловые размеры которых значительно меньше элементов разрешения РЛСМ по дальности и угловым координатам, а разность радиальных скоростей их крайних точек много меньше элемента разрешения по скорости. Эффективная отражающая площадь точечных целей определяется экспериментально. Примерами точечной цели могут служить самолёты корабли на больших удалениях от РЛС, искусственные спутники.
Распределёнными целями называют, для которых указанные выше соотношения не выполняются. Распределённые цели могут быть поверхностными (земная поверхность) и объёмными (облако пассивных отражателей, гидрометеоры). Для распределённых целей экспериментально определяется средняя удельная эффективная отражающая площадь Sэфф у. Эта величина характеризует отражающие свойства единицы площади или объёма. Полная величина Sэфф о находится из соотношений:
для поверхностных целей:
|
|
(3.3) |
для объёмных целей:
|
|
(3.4) |
где d(S) и d(V) – размеры элементов разрешения РЛС соответственно по площади и по объёму.
3.2. Элементарные цели
Элементарные цели находят практическое применение в качестве пассивных ответчиков при испытании радиолокационной аппаратуры, маскирующих отражателей при создании пассивных помех, средств имитации целей для отвлечения сил противника от действительных объектов. К элементарным целям могут быть также отнесены воздушные шары, шары – пилоты, ИСЗ простейшей геометрической конфигурации и т. д. Основными характеристиками элементарных целей являются величина их эффективной отражающей площади и ширина диаграммы переизлучения.
Рассчитаем в качестве примера эффективную отражающую площадь элементарной цели в виде полуволнового вибратора. Отражатели этого типа широко применяются в массовых количествах для создания пассивных помех радиолокационным станциям.
Э.д.с., наводимая в вибраторе, равна
![]() ,
,
где ![]() - действующая высота
полуволнового вибратора;
- действующая высота
полуволнового вибратора;
j - угол между осью вибратора и направлением на РЛС. Ток, наводимый этой э.д.с. в вибраторе (без учёта потерь),
![]() ,
,
где RS - сопротивление излучения полуволнового вибратора, равное 73,3 Ом.
Напряжённость поля, создаваемая вибратором в точке расположения РЛС, находящейся на расстоянии D, равна
|
|
(3.5) |
Подставляя (3.5) в (3.2), получим
|
|
(3.6) |
Полученное выражение указывает на большую зависимость эффективной отражающей площади вибратора от его ориентации относительно РЛС и от длины волны.
В таблице 3.1 приведены для сравнения значения эффективной отражающей площади различных типов отражателей, имеющих одинаковые характерные размеры а, м, при длине волны облучающих колебаний l = 3 см.
Таблица3.1
|
Тип отражателя |
Расчётная формула |
Значение Sэфф, м2 |
|
Полуволновой отражатель длиной l=l/2=а |
|
3,44а2 |
|
Металлический лист площадью S=а2, где а – сторона квадрата |
|
14×103а4 |
|
Металлический шар диаметром dш=а (причём а>4l) |
|
0,78а2 |
|
Уголковый отражатель с треугольными гранями и длиной ребра lр=а |
|
4,7×103а4 |
|
Уголковый отражатель с квадратными гранями и длиной ребра lр=а |
|
42×103а4 |
3.3. Точечные цели
1. Условия, при которых цели являются точечными.
Цели являются точечными, если имеют место неравенства:
|
|
(3.7)
|
где lц – наибольшей размер цели; d(D), d(jаз), d(jум), d(Vр) – разрешающие способности РЛС соответственно по дальности, угловым координатам и скорости; d(j)D = d(l) – линейная разрешающая способность по угловой координате.
Таким образом, точечные цели – это такие цели, которые практически не увеличивают длительности отражённого сигнала и не изменяют его спектр по сравнению с сигналом, отражённым от цели – геометрической точки. Эти неравенства показывают также, что понятие точечной цели не является абсолютным: самолёт, например, будет точечной целью для большинства РЛС на больших расстояниях, несколько сотен метров, указанные неравенства уже не выполняются.
2. Особенности траекторий целей и
их влияние на параметры РЛС.
Траектория – это кривая, описываемая центром массы цели при её движении. Форма траектории может быть закономерной и случайной. Закономерными траекториями обладают баллистические ракеты, искусственные спутники. Закономерная траектория может быть однозначно определена, если измерено необходимое количество её параметров.
Закономерный характер движения цели обусловливает и закономерность изменения параметров принимаемых отражённых сигналов. Это обстоятельство является весьма важным, так как оно допускает длительное накопление энергии принимаемых сигналов. Такое накопление энергии большого количества отражённых сигналов, каждый из которых несёт малую энергию, позволяет при прочих равных условиях обеспечить очень большую дальность обнаружения и высокую точность измерения параметров траектории движущихся целей.
Однако при обнаружении целей, имеющих случайные траектории, нельзя использовать длительное накопление энергии принимаемых сигналов для увеличения дальности обнаружения, так как изменение их параметров не имеет закономерного характера на больших интервалах времени. Эффективное накопление в таких случаях может быть осуществлено лишь за время облучения цели сканирующим лучом антенны.
Случайность траекторий маневрирующих целей требует определение характеристик обзора пространства радиолокационной станцией. Чем быстрее маневрирует цель, тем чаще должно производиться её облучение и измерение координат, для того чтобы можно было точно воспроизвести траекторию её движения. Траектория представляет непрерывную пространственно – временную функцию S(t) (рис.3.2), которая может быть задана совокупностью зависимостей D(t), jаз(t) и jум(t), выражающих полярные координаты цели как функции времени. За интервал наблюдения Тн каждая из этих функций может быть описана конечным числом дискретных отсчётов. Число этих отсчётов может быть определено по теореме Котельникова:
![]() ,
,
где FВ – наивысшая частота спектра воспроизводимой функции.
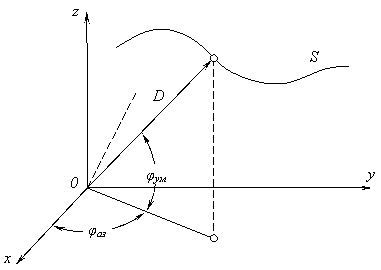

Рис.3.2. Траектория маневрирующей цели.
Следовательно, конкретная траектория цели может быть воспроизведена, если период обзора РЛС будет удовлетворять неравенству
![]() ,
,
причём FВ – это наиболее высокая частота из определённых по спектрам функций D(t), jаз(t) и jум(t).
Так как различных траекторий может быть бесчисленное множество, а обзор проще осуществлять с постоянной скоростью, то при выборе периода обзора следует ориентироваться на самую неблагоприятную траекторию, для которой спектры функций D(t), jаз(t) и jум(t) наиболее широкие.
3.Особенности движения целей вокруг центра массы и их влияние на характер отражённого сигнала.
Случайные колебания цели относительно центра массы происходят вследствие возмущений в окружающей среде и в системе управления полётом. Баллистические ракеты и искусственные спутники в полёте испытывают случайные колебания и вращения вокруг осей, случайно меняющих своё направление («кувыркаются») с «периодом» от нескольких минут до нескольких десятков минут. Случайные рыскания, продольные и поперечные крены самолётов по результатам многочисленных экспериментальных исследований имеют среднее значение амплитуды колебаний около 1-20 и средний «период» в несколько секунд. Однако для различных типов самолётов эти данные могут значительно расходиться и, кроме того, на них в сильно степени влияет состояние атмосферы. Поэтому приведённые величины следует рассматривать как весьма ориентировочные.
В первом приближении моделью сложной цели, такой, как самолёт, может служить цель, состоящая из двух стабильно отражающих точек 1и 2, расположенных на расстоянии lц, равном размеру самолёта (рис.3.3).


Рис.3.3. Модель цели, состоящая из двух точек.
Оценим характер переизлучения такой цели. Для этого надо сначала определить напряженность поля результирующего сигнала в отдалённой точке В, находящейся на расстоянии D от центра О цели (D³lц). Сигнал, пришедший от точки 1, имеет вид
|
|
(3.8) |
Сигнал, пришедший от точки 2:
|
|
(3.9) |
Если бы существовал только один изотропный источник излучения в точке О, то сигнал от него в точке В имел бы вид
|
|
(3.10) |
Таким образом, сигнал, пришедший от точки 1, отстаёт по фазе на угол
|
|
(3.11) |
от сигнала е0, а сигнал от точки 2 опережает его на такой же угол (рис.3.4).
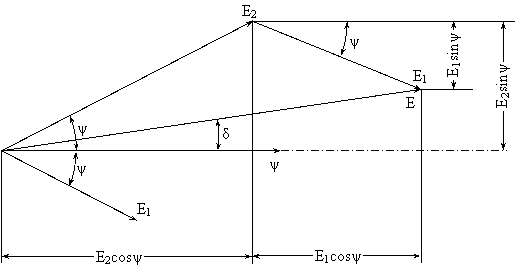

Рис.3.4. Векторная диаграмма сигналов, отражённых от точек 1 и 2 цели рис. 3.3.
Нетрудно видеть, что амплитуда результирующего сигнала
|
|
(3.12) |
а фазовый сдвиг по отношению к сигналу е0 равен
|
|
(3.13) |
Таким образом, результирующий сигнал, принятый от точек 1 и 2, имеет вид:
|
|
(3.14) |
Выражение (3.12) показывает, что при Е1=Е2=Е0
амплитуда результирующего сигнала при измени направления облучения может
изменяться от нуля (при ![]() ) до 2Е0 (при
) до 2Е0 (при ![]() ). Ширина
«лепестка» диаграммы переизлучения по «нулям» может быть найдена из условия
). Ширина
«лепестка» диаграммы переизлучения по «нулям» может быть найдена из условия
|
|
(3.15) |
или
|
|
(3.16) |
Считая приближённо sinj»j, получим ширину «лепестка» равной
|
|
(3.17) |
Принимая l=3см, lц=10м, находим
|
|
(3.18) |
При l=10см ![]() . Таким образом, диаграмма
переизлучения рассмотренной цели является весьма «изрезанной», состоящей из
множества узких лепестков.
. Таким образом, диаграмма
переизлучения рассмотренной цели является весьма «изрезанной», состоящей из
множества узких лепестков.
В реальных условиях при случайных движениях цели относительно центра массы и при её манёврах амплитуда отражённого сигнала будет случайной функцией времени с резкими изменениями, доходящими до нескольких десятков децибел.
Закон распределения амплитуд сигналов, отражённых от различных сложных целей (самолёта, корабля, облака искусственных отражателей), по результатам различных экспериментов хорошо совпадает с распределением Релея:
|
|
(3.19) |
где s2и – дисперсия амплитуды сигналов.
4. Эффективная отражающая площадь.
Определим эффективную отражающую площадь двухточечной цели (рис.3.3).
Мощность отражённого сигнала на входе приёмника:
|
|
(3.20) |
где SА – эффективная площадь раскрыва антенны РЛС;
rмРЛС – плотность потока мощности.
Таким образом, при k=const мощность отражённого сигнала будет прямо пропорциональна эффективной отражающей площади цели.
Мощность отражённого сигнала, в свою очередь, пропорциональна квадрату напряженности поля. Полагая, что амплитуды напряжённости поля, переизлучаемого точками 1 и 2, одинаковы и равны Е0, будем иметь
|
|
|
Отсюда мощность отражённого сигнала
|
|
(3.21) |
и
|
|
(3.22) |
где Sэфф1 – эффективная отражающая площадь каждого излучателя.
Следовательно, при изменении угла y величина Sэфф может колебаться в пределах (0¸4)Sэфф1. Считая все значения y равновероятными в интервале 0¸2p, получим среднее значение эффективной отражающей площади двухточечной цели:
|
|
(3.23) |
Перейдём теперь к определению закона распределения эффективной отражающей площади сложной цели.
Мощность и амплитуда отражённого сигнала на входе приёмника связаны соотношением
|
|
|
где Rвх – входное сопротивление приёмника.
Принимая для простоты Rвх=1, получим
|
|
|
Считая, что распределение амплитуды отражённого сигнала подчиняется закону распределения Релея (3.19), найдем закон распределения мощности, а, следовательно, и эффективной отражающей площади. Используем для этого формулу функционального преобразования законов распределения:
|
|
(3.24) |
Учитывая, что ![]() и дисперсия амплитуды есть
средняя мощность флюктуирующего отражённого сигнала
и дисперсия амплитуды есть
средняя мощность флюктуирующего отражённого сигнала ![]() , получим
, получим
|
|
(3.25) |
Учитывая также, что
|
|
(3.26) |
и подставляя (3.25) и (3.26) в (3.24), будем иметь
|
|
(3.27) |
Переходя от мощности к пропорциональной ей величине отражающей эффективной отражающей поверхности, получим окончательное выражение для плотности распределения
|
|
(3.28) |
Обычно интересуются вероятностью того, что случайное значение будет не меньше выбранной расчётной величины Sэфф р. Интегрируя (3.28) в пределах от Sэфф р до ¥, получим
|
|
(3.29) |
Отметим, что среднему значению эффективной отражающей площади соответствует вероятность W(Sэфф ³ Sэфф0)=0,37. Именно это значение Sэфф0 и используется в расчётах дальности действия РЛС.
5. Спектр флюктуаций амплитуды.
Ширина спектра амплитудных флюктуаций цели в основном
определяется степенью изрезанности диаграммы переизлучения и скоростью
изменения ракурса облучения. Чем уже лепестки диаграммы и чем больше указанная
скорость, тем выше частота флюктуаций. Ширина лепестков q0
достигает в сантиметровом диапазоне (0,1 – 0,05)0 . Скорость
изменения ракурса при маневрах самолётов может иметь величину w = 10¸20 град/сек.
Таким образом, при грубой оценке антенна РЛС за одну секунду примет ![]() «периодов»
колебаний сигнала, что и определяет наивысшую частоту спектра флюктуаций Fфл1 =100¸400 Гц.
«периодов»
колебаний сигнала, что и определяет наивысшую частоту спектра флюктуаций Fфл1 =100¸400 Гц.
При рысканиях и случайных кренах самолёта скорость изменения ракурса составляет 1-2 град/сек, и частота флюктуаций, соответствующая этим движениям цели, лежит в пределах
|
|
(3.30) |
Эта оценка хорошо согласуется с экспериментальными данными. На рис.3.5, а показан типичный спектр амплитудных флюктуаций сигнала, отражённого от неманеврирующего самолёта, на рис.3.5,б– соответствующая этому спектру корреляционная функция. Видно, что флюктуации наиболее интенсивны в области частот 0-10 Гц, а время корреляции составляет 0,05 сек.
Следует заметить, что при малых дальностях в сантиметровом диапазоне волн флюктуации могут создаваться также вследствие биений сигналов, отражённых от различных точек цели, имеющих по отношению к РЛС различные радиальные скорости, а, следовательно, отражающих сигналы с различными доплеровскими смещениями частоты.
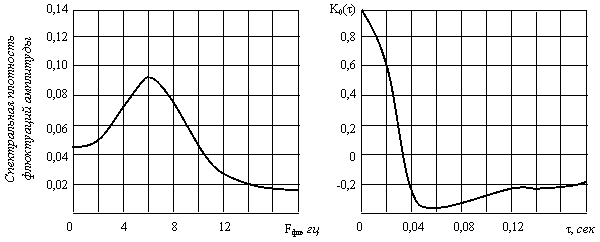
а) б)
Рис.3.5.Спектр флюктуаций амплитуды и корреляционная функция сигнала, отражённого от самолёта.
Флюктуации амплитуды отражённого сигнала являются одним из основных источников ошибок в РЛС с автоматическим измерением угловых координат путём последовательно сравнения амплитуд (конический обзор). В такой системе автосопровождения для выделения сигнала ошибки используется узкополосный фильтр с резонансной частотой равной частоте сканирования. Поэтому частоту сканирования выбирают в области меньших интенсивностей флюктуаций – от 40 Гц и выше. Радикальным методом борьбы с ошибками, вызываемыми флюктуациями амплитуды сигнала, является применение моноимпульсных пеленгаторов, в которых осуществляется одновременное сравнение амплитуд, исключающее указанные ошибки. Характер изменения интенсивности амплитудных флюктуаций по частоте учитывается также при выборе постоянной времени АРУ в системах автосопровождения цели.
6. Флюктуации фазового фронта отражённого сигнала.
Было замечено, что с уменьшением расстояния до сложной цели ошибки сопровождения по угловым координатам растут. Причиной этого являются флюктуации фазового фронта отражённого сигнала. Для точечного изотропного излучателя фазовой фронт представляет сферу. Поэтому пеленгация точечного изотропного излучателя при прочих идеальных условиях всегда будет осуществляться без ошибки. При пеленгации сложной цели пеленгатор при тех же условиях будет в каждый момент указывать положение нормали к фазовому фронту, не проходящей в общем случае через центр цели. При случайных перемещениях цели относительно РЛС положение нормали будет также случайным образом меняться и цель в этих условиях может быть заменена точкой, блуждающей в некотором объёме, размеры которого могут превосходить размеры цели. Эту блуждающую точку называют эффективным центром отражения цели. Таким образом, пеленгатор в некоторых случаях может указывать направление, выходящее за пределы контура цели.
Обратимся снова к простейшей модели реальной цели в виде двух изотропных переизлучателей с базой lц (рис.3.3) и найдём для неё уравнение эквифазной поверхности и ошибку пеленгации. Уравнение эквифазной поверхности можно получить, если поставить условие, чтобы фаза для фиксированного момента времени оставалась постоянной:
|
|
(3.31) |
Из этого уравнения могут быть найдены пары значений j и D, определяющие каждую точку эквифазной поверхности в зависимости от соотношения амплитуд сигналов.
Выражение для ошибки пеленга при фиксированном значение угла j (рис.3.3) может быть найдено следующим образом. Производная dD/dj в какой-либо точке (j, D) поверхности определяет искривление фазового фронта двухточечной цели по сравнению со сферой, проходящей через эту же точку.
Угол Dj между нормалью к поверхности в точке (j, D) и радиус-вектором D, проходящим через эту же точку, и является ошибкой пеленгации. Тангенс этого угла, как это видно из рис.3.3, равен
|
|
(3.32) |
Выражение (3.32) показывает, что ошибка пеленгации Dj уменьшается с увеличением расстояния до цели. Это ясно и из физических соображений; если приближённо принять наибольшую амплитуду блужданий эффективного центра отражения равной размеру цели lц, то угловая ошибка при этом будет обратно пропорциональна дальности цели
|
|
(3.33) |
При движении реальной цели угол j случайным образом меняется и ошибка флюктуирует. Это проявляется в виде случайных изменений сигнала ошибки измерения угла цели на выходе приёмника, что дало основание назвать флюктуации фазового фронта угловыми шумами цели.
7.Флюктуации времени запаздывания отражённого сигнала (флюктуации дальности)
Блуждание эффективного центра отражения происходит в пределах некоторого объёма, заключающего реальную цель.
Поэтому кроме флюктуаций по угловым координатам возникают также флюктуации времени прихода сигнала. Соответствующие им отклонения по дальности обычно не превышают геометрических размеров цели в направлении облучения. Спектр этих флюктуаций и плотность распределения их амплитуд весьма близко совпадают с соответствующими характеристиками угловых шумов. Величина среднеквадратического отклонения от среднего значения дальности составляет около 0,8 размера цели.
3.4 Свойства сигналов, отражённых от распределённых целей
1.Общие сведения
Как уже отмечалось, распределённые цели представляют собой сочетание большого количества отражающих объектов, расположенных или на поверхности земли или в некотором объёме пространства. Отражения от таких целей чаще всего относятся к мешающим сигналам, которые затрудняют распознавание полезных радиолокационных целей. Однако отражения от распределённых целей иногда являются и полезными, например, в случае, когда ведётся наблюдение земной поверхности с воздуха. Положение отражающих объектов на поверхности характеризует или особенности растительного покрова или вид рельефа.
Оценим эффективную отражающую площадь распределённой цели. Сигналы, приходящие от распределённой цели, создаются за счёт отражений от всех элементов цели, которые попадают в разрешаемый объём. Разрешаемый объём зависит от вида сигнала, характеристики направленности антенны и является в общем случае также и функцией расстояния до цели. Если принять, что в разрешаемом объёме находится N равномерно расположенных элементарных отражателей, то результирующий сигнал можно представить в виде суммы сигналов, отражённых от этих элементарных отражателей. Почти во всех случаях отражённые сигналы можно считать не зависящими друг от друга, они имеют случайные фазы и амплитуды. Мощность суммарного сигнала равна сумме мощностей сигналов, отражённых от отдельных рассеивателей, входящих в разрешаемый объём РЛС
|
|
(3.34) |
Мощность сигнала, отражённого от отдельного элементарного отражателя, пропорциональна, как известно, эффективной отражающей площади Sэффi этого отражателя:
|
|
(3.35) |
Из соотношений (3.34) и (3.35) следует, что
|
|
(3.36) |
Сигнал, отражённый от распределённой цели, также можно представить в виде:
|
|
(3.37) |
Используя формулы (3.36) и (3.37), получаем, что эффективная площадь распределённой цели равна сумме эффективных площадей отдельных отражателей:
|
|
(3.38) |
Если разрешаемый объём РЛС не слишком мал, то для характеристики отражающих свойств распределённой цели вводят удельную эффективную площадь отражения Sэфф у. Удельная эффективная площадь не зависит ни от вида сигнала (от длительности импульса в импульсной РЛС), ни от ширины луча антенны. Полную эффективную площадь поверхностной цели в этом случае можно найти путём умножения удельной эффективной площади на геометрическую площадь Sп участка поверхностной цели, попавшей в разрешаемый объём:
|
|
(3.39) |
Аналогично для объёмной цели Sэфф об эффективная площадь отражения равна произведению
|
|
(3.40) |
где Vоб – геометрический объём цели, который равен разрешаемому объёму РЛС.
2.Флюктуации сигналов, отражённых от сложных целей
Отражённые сигналы от распределённых целей непрерывно, случайным образом изменяются во времени, флюктуируют.
Флюктуации сигналов зависят от целого ряда причин. Существенную роль, в частности, играют собственные хаотические перемещения отдельных отражателей, входящих в состав цели. К таким перемещениям относятся, например, колебания ветвей деревьев или травы при ветре, падение капель дождя, движение волн на морской поверхности.
Флюктуации возникают также при изменении частоты облучения и количества отражателей, попадающих в разрешаемый объём при движении РЛС или при вращении антенны РЛС во время обзора пространства.
Случайные колебания амплитуды результирующего сигнала характеризуются некоторыми распределениями плотностей вероятности. Известно, что одномерное распределение плотности вероятностей амплитуд, как и для случая сложной цели, подчинено закону Релея. Однако одномерные распределения вероятностей не позволяют судить о характере флюктуаций сигналов во времени, не дают представления о спектре частот отражённого сигнала. В большинстве случаев для этого достаточно знать двумерный закон распределения плотности вероятностей амплитуд. С высокой степенью точности можно считать, что двумерное распределение плотностей вероятностей сигнала, отражённого от распределённой цели, является нормальным.
Совместное распределение амплитуд и фаз сигналов имеет вид:
|
|
(3.41)
где Uм1, Uм2 – амплитуды результирующего сигнала, отражённого от распределённой цели, соответственно в моменты времени t1 и t2;
y1 и y2 – фазы сигналов также в моменты времени t1 и t2;
Рср – средняя мощность отражённого сигнала;
К0(t) – нормированная корреляционная функция флюктуаций отражённого сигнала;
t– разность времени: t= t1 - t2.
В общем случае, когда имеется много независимых причин, вызывающих флюктуации Кi(t), корреляционная функция может быть представлена в виде произведения частных корреляционных функций, каждая из которых учитывает какаю-то одну причину:
|
|
(3.42) |
где М – общее количество различных факторов, вызывающих флюктуации отражённого сигнала.
Такое представление корреляционной функции (3.42) удобно тем, что позволяет находить вид корреляционной функции экспериментальных или теоретических исследований каждого из факторов отдельно.
Флюктуации отраженного сигнала можно характеризовать спектром мощности сигнала. Как известно, спектр мощности можно найти, применяя преобразование Фурье корреляционной функции (соотношение Хинчина-Винера). Из свойств преобразования Фурье следует, что чем шире корреляционная функция, тем уже спектр мощности флюктуаций. Ширина спектра увеличивается, например, при увеличении скорости ветра, при уменьшении длины волны. Ширина спектра мощности флюктуации обычно находиться в пределах от десятка до нескольких сотен герц.
Если обозначить tк – время корреляции, соответствующее значению корреляционной функции К0(t) на уровне 1/е, то можно найти ширину спектра мощности флюктуации Dfфл также на уровне 1/е по формуле
|
|
(3.43) |
При гауссовской форме корреляционной функции соотношение для времени корреляции имеет вид
|
|
(3.44) |
а формула для ширины спектра мощности флюктуаций имеет вид
|
|
(3.45) |
При приёме сигналов в самолётных условиях нужно учитывать большое количество факторов, влияющих на характер флюктуаций. Часто само движение самолёта является причиной значительного расширения спектра флюктуаций до нескольких сотен герц и больше.
3.5. Эффективная отражающая площадь поверхностных целей
1.Импульсные сигналы
Для вычисления эффективной отражающей площади поверхностных целей необходимо найти площадь Sп поверхности земли в пределах разрешаемого объема.
Облучаемая импульсным сигналом площадь в общем случае зависит от длины разрешаемого объёма по дальности, ширины диаграммы направленности антенны в горизонтальной и вертикальной плоскостях.
Для обычных импульсных сигналов длина разрешаемого объёма по дальности равна сtИ/2. При малых углах визирования цели b (рис.3.6) разрешаемая площадь равна
|
|
(3.46) |
Так как обычно угол b мал, то
|
|
(3.47) |
Другой предельный случай получается при больших углах наклона b и узкой диаграмме направленности. Разрешаемая площадь при этом не зависит от длительности импульса и равна
|
|
(3.48) |
При расчётах необходимо выбирать меньшую из величин, определяемых по формулам (3.46) и (3.48).
В случае применения в РЛС других более сложных сигналов вычисление Sп выполняется аналогичным образом. Находится в каждом случае длина разрешаемого объёма как функция параметров сигнала.
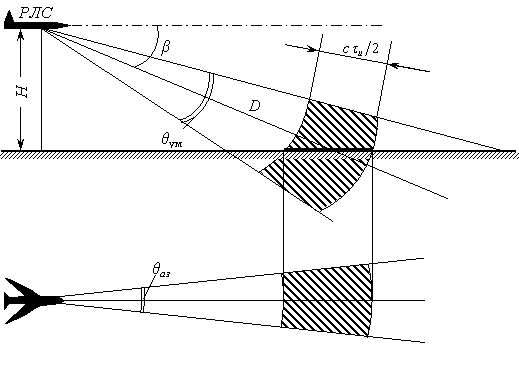

Рис.3.6. Определение эффективной отражающей площади поверхностной цели при малых углах наклона луча b.
2.Непрерывное излучение
Рассмотрим в качестве примера вычисление площади Sп для РЛС непрерывного излучения с доплеровской селекцией сигналов. На рис.3.7 показан участок поверхности земли, облучаемый лучом антенны. В пределах этого участка различные точки создают отражённые сигналы с различными доплеровскими частотами. Так как в РЛС обычно применяется фильтр с полосой Dfф для выделения сигналов, то через фильтр проёдут только доплеровские частоты в пределах от FД1 до FД1+Dfф. Следовательно, в РЛС применяются только сигналы, отражённые от узкой полоски земли, которая на рис.3.7 заштрихована. Определим размеры этой полоски.
Доплеровская частота сигнала, отражённого от ближнего к РЛС участка полоски, равна
|
|
(3.49) |
где Vc – скорость полёта.
Соответственно для дальнего участка полоски имеем
|
|
(3.50) |
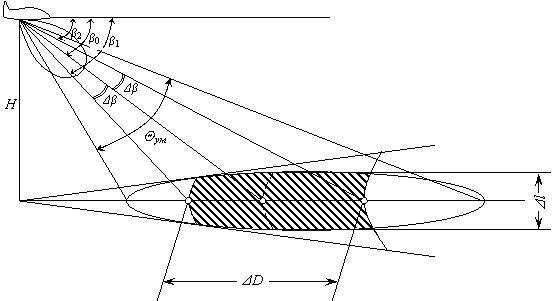

Рис.3.7. К определению эффективной отражающей площади поверхностной цели для РЛС с доплеровской селекцией сигналов.
Разность частот Доплера тогда равна
|
|
(3.51) |
Из рис.3.7 видно, что
|
|
(3.52) |
Левая часть формулы (3.51) равна Dfф. Правую часть преобразуем с учётом соотношений (3.52). В результате формула (3.51) принимает вид
|
|
(3.53) |
Определим ширину полоски DD. Как следует на рис.3.7, она равна
|
|
(3.54) |
Подставляя произведение синусов из (3.53), получаем для ширины отражающей полоски равенство
|
|
(3.55) |
Азимутальный размер полоски Dl равен
|
|
(3.56) |
Окончательно площадь отражающей полоски находим в виде
|
|
(3.57) |
Из формулы (3.57) следует, что площадь полоски зависит от ширины полосы пропускания применяемого в РЛС фильтра доплеровских частот Dfф, от угла b0 и наклонной дальности D.
3.Удельная эффективная площадь
Рассмотрим, каким образом удельная эффективная площадь зависит от отражающих свойств т структуры поверхности земли.
Поверхность земли. Основные факторы, которые влияют на величину отражения сигнала: неровности рельефа, значение угла падения, комплексная диэлектрическая постоянная отражающей поверхности и несущая частота.
Неровность поверхности является одним из основных факторов. Гладкими или зеркальными можно считать поверхности, у которых среднеквадратичное значение колебаний высоты неровностей рельефа значительно меньше длины волны. Для сантиметровых волн, например, гладкими являются поверхности асфальта или бетона. Для гладких поверхностей так же, как и для световых волн, справедлив закон равенства угла падения волны углу отражения. Зеркальное отражение характерно для спокойных водных поверхностей.
Оценить степень неровности поверхности, при которой поверхность считается ещё гладкой, можно используя критерий Релея. Согласно этому критерию поверхность является гладкой, если разность фаз двух лучей, отражённых от гребня и впадины неровности, меньше p/2. Из рис.3.8 видно, что разность хода лучей Dl, отражённых от вершины неровности (А¢ О¢ В¢) и от впадины (АОВ) находится как
|
|
|
По критерию Релея должно быть
|
|
|
Это приводит к соотношению
|
|
(3.58) |
Из этой формулы следует, что допустимая высота неровности зависит не только от длины волны, но и от угла падения b. Поверхность может внешне казаться, при большом h, неровной, но если угол b мал, то отражение от неё будет скорее зеркальным, чем рассеянным, и такую поверхность можно считать гладкой.
В тех случаях, когда имеются значительные неровности и не выполняется условие (3.58), поверхности называют шероховатыми. Они дают рассеянное (диффузное) отражение. Сигнал, отражённый от такой поверхности, почти не зависит от поляризации падающей волны, а отношение удельной эффективной площади отражения Sэфф у к sinb постоянно и не зависит от угла b (закон Ламберта).
Поверхности, покрытые растительностью, имеют изотропное рассеяние, при котором удельная эффективная площадь почти не зависит от угла падения b.


Рис.3.8. Влияние неровностей поверхностей на путь
прохождения лучей.
Морская поверхность. Отражения от морской поверхности также носят очень сложный характер. Удельная эффективная площадь зависит от угла падения, состояния моря, поляризации, частоты сигнала.
1. Имеется сильная зависимость Sэфф у от угла наклона луча b. Как правило, величина Sэфф у возрастает с увеличением угла наклона.
Эмпирически получена формула, которая характеризует отражающие свойства поверхности моря и хорошо согласуется с экспериментальными результатами:
|
|
(3.59) |
Данная формула применима для больших значений углов b.
2. Изменения величины Sэфф у в зависимости от частоты сигнала исследованы ещё недостаточно. Всё же можно отметить, что при спокойном море удельная эффективная площадь возрастает с увеличением частоты приблизительно пропорционально f4. Многие экспериментальные данные говорят о линейной зависимости от 3 – 30 см.
3. Изменения величины Sэфф у в зависимости от вида поляризации связаны с частотой излучения и состоянием моря. При спокойном море отражённый сигнал при вертикальной поляризации примерно на 20 – 30 дб больше, чем при горизонтальной поляризации. Если море неспокойно, разница между сигналами при различных поляризациях уменьшается.
При умеренном волнении (волны от 1 до 2 м) отражённые сигналы при обоих видах поляризации примерно одинаковы.
4. Удельная эффективная площадь зависит от направления и скорости ветра. При больших углах b (более 700) величина Sэфф у уменьшается при увеличении ветра, а при углах b меньше 700 увеличивается. Эффективная удельная площадь при одинаковом ветре на 5-6дб возрастает, когда луч антенны направлен навстречу ветру.
5. Удельная эффективная площадь Sэфф у зависит от волнения моря. В общем случае интенсивность отражённого сигнала возрастает при усилении волнения. Однако было установлено, что увеличивается с ростом высоты волн только до некоторого предела. При высоте волн больше 60 см удельная эффективная площадь для различных волн практически одинаковая. Для волн ниже 60 см можно отметить быстрый рост Sэфф у с высотой волн.
3.6. Эффективная отражающая площадь объёмных целей
1.Импульсные сигналы
Для вычисления эффективной отражающей площади объёмной цели необходимо знать величину разрешаемого объёма Vоб и удельную эффективную отражающую площадь Sэфф у.
При применении импульсных сигналов разрешаемый объём равен произведению протяжённости разрешаемого участка по дальности lр и площади поперечного сечения луча антенны Sл:
|
|
(3.60) |
где
|
|
(3.61) |
Площадь Sл определяется шириной луча по азимуту θаз и углу места θум (рис.3.9). Если луч имеет эллиптическое сечение, то
|
|
(3.62) |
Следовательно, эффективная площадь распределённой объёмной цели при импульсном сигнале равна
|
|
(3.63) |
Удельная эффективная площадь зависит от вида отражателей, составляющих объёмную цель. Если объёмная цель представляет собой совокупность однородных отражателей: капель дождя, снежинок, диполей, то удельная эффективная площадь отражений определяется плотностью таких отражателей в пространстве и эффективной площадью каждой из частиц.
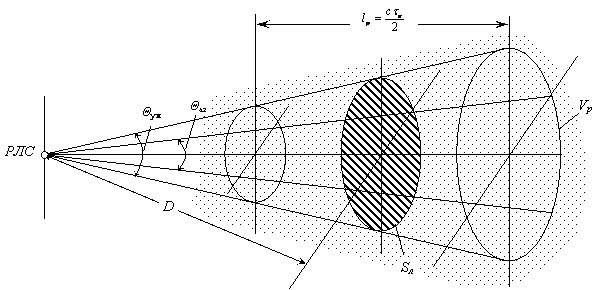 |

Рис.3.9. К определению эффективной отражающей площади объёмной цели для импульсной РЛС.
2.Удельная эффективная площадь
В случае, когда объёмная цель представляет собой область тумана или облака, отражающими частицами являются капли воды, сферические по форме с радиусом r. Можно показать, что если длина волны велика по сравнению с окружностью рассеивающей капли (область рассеяния Релея), то её эффективная площадь отражения равна
|
|
(3.64) |
Удельная эффективная площадь дождя зависит от его интенсивности и длины волны РЛС.
Объёмной целью являются и искусственные образования, которые применяются для маскировки объектов от радиолокационного наблюдения (пассивные помехи). Обычно «облака пассивных помех» состоят из совокупности полуволновых вибраторов (дипольных отражателей), которые представляют собой, например, полоски алюминиевой фольги.
Так как эффективная площадь отдельного дипольного отражателя равна Sэффi=0,86λ2, то с укорочением длины волны необходимо увеличивать количество отражателей для того, чтобы «облако» помех было бы эквивалентно по эффективной отражающей площади маскируемой цели. Для создания «облака», эквивалентного крупному самолёту (Sэффi=50м2), необходимо выбросить 50 – 60 диполей при длине волны 1,5 м и около 13000 диполей при длине волны 10 см.
ГЛАВА 4. РАДИОЛОКАЦИОННЫЙ ОБЗОР
4.1. Основные положения
Радиолокационный обзор заключается в периодическом облучении всех точек обзора и приеме сигналов тех целей, которые находятся в этой зоне. Обзор называется одновременным, если необходимые координаты целей (а если нужно и производные координат) определяются одновременно в пределах всей зоны обзора. На практике из-за существенных трудностей реализации одновременный обзор используют редко. В качестве примера можно указать на английские РЛС измерения высоты самолетов в районе аэродрома, которые обеспечивают одновременный обзор большой зоны: 1200 по азимуту и 300 по углу места. Антенная система такой станции включает более 1000 рупорных приемных антенн, позволяющих одновременно и независимо определять координаты целей в пределах всей зоны.
Если измерение координат различных целей разнесено во времени и осуществляется постепенно путем перехода от одних целей к другим, обзор называется последовательным. С принципиальной точки зрения обзор всегда является последовательным, так как время запаздывания отраженных сигналов зависит от дальности целей и, следовательно, сигналы от ближних целей приходят раньше, чем от дальних. Но большей частью с этим обстоятельством можно не считаться, так как время облучения цели Тобл (время, в течение которого принимаются сигналы от точечной цели при однократном проходе зоны обзора лучом РЛС) гораздо больше максимального времени запаздывания
|
|
(4.1) |
Иногда преднамеренно используют последовательный обзор о дальности. При этом приемник РЛС отпирается только на время прихода сигналов с интервала дальности ∆D, много меньшего максимальной дальности действия станции, и последовательно просматриваются сначала малые дальности потом большие или наоборот. Время наблюдения сигналов от каждого участка дальности ∆D остается равным Тобл..
Наиболее часто обзор оказывается последовательным потому, что ширина диаграммы направленности антенны РЛС много меньше угловых размеров зоны обзора и узкий луч по определенному закону перемещается в пределах зоны обзора с одного направления на другое.
4.2. Период последовательного обзора
При последовательном обзоре по угловым координатам луч РЛС непрерывно движется в пределах зоны обзора, периодически повторяя заданную траекторию. Периодом обзора (Тобз) называется отрезок времени, необходимый для однократного перемещения луча по всей зоне обзора. Иногда в период обзора включают и то время, которое требуется для перемещения луча по всей зоне обзора и его возврата в некоторое начальное положение.
Период обзора является важной тактической характеристикой РЛС. Имея в виду практическое применение радиолокационных станций, следует выбирать период обзора как можно меньшим. Этот период составляет интервал между двумя последовательными измерениями координат цели. За Тобз цель, движущаяся со скоростью υц, перемещается на расстояние Тобз∙ υц. Чем меньше Тобз, тем меньше скачки отметки цели по экрану индикатора РЛС и выше точность измерения координат цели. При уменьшении Тобз повышается точность воспроизведения траектории цели. Исходя из назначения станции и условий её применения, можно довольно точно указать максимально допустимое значение её периода обзора.
С другой стороны, необходимость накапливать энергию отраженных сигналов для улучшения условий их наблюдения при наличии помех заставляет увеличивать период обзора: чем больше Тобз, тем больше достоверность обнаружения сигналов при прочих равных условиях.
1. Минимально допустимый период обзора
Рассмотрим соотношения, определяющие минимально допустимый период обзора, при котором каждое облучение цели позволяет накапливать определённую энергию отражённых сигналов. Пусть имеется точечная цель, время облучения которой (время накапливания энергии отражённых сигналов) равно Тобл. Допустим, что Тобл много больше максимального значения времени запаздывания отражённых сигналов. Пусть обзор зоны, ограниченной максимальной дальностью Dмакс и секторами обзора Фаз и Фум , осуществляется идеализированным лучом, имеющим вид пирамиды с угловыми размерами θаз и θум (рис.4.1). Луч движется с постоянной угловой скоростью. Дойдя до конца строки 1, луч мгновенно перемещается на строку 2 и движется в обратном направлении с той же скоростью и т. д.
В данном случае период обзора определяется
|
|
(4.2) |
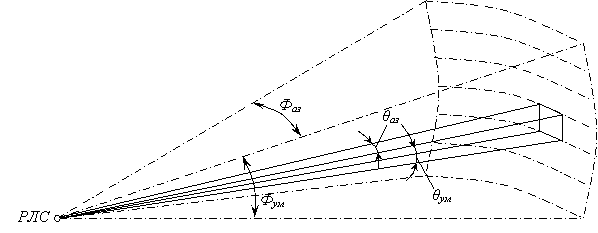

Рис.4.1. Размеры зоны обзора и траектория движения
идеализированной диаграммы направленности.
Формула (4.2) определяет минимально допустимое значение периода обзора, необходимое для требуемого накопления энергии сигналов. Если в РЛС, для которой заданы значения Тобл, Фаз и Фум, θаз и θум, реальное значение периода обзора окажется меньше рассчитанного по формуле (4.2), то действительное время облучения цели будет меньше заданного.
Если осуществляется последовательный обзор и по углам и по дальности, т.е. в каждый данный момент просматривается только отрезок δD из всей протяженности зоны обзора Dмакс, то требуемое значение минимально допустимого периода обзора возрастает и становится равным
|
|
(4.3) |
Следовательно, уменьшение периода обзора РЛС может быть достигнуто тремя путями:
ü уменьшением времени облучения цели, которое может быть скомпенсировано увеличением мощности или длительности излучаемых колебаний или повышением чувствительности приемника;
ü расширением луча диаграммы направленности антенны РЛС, что ухудшает точность измерения угловых координат, снижает разрешающую способность по угловым координатам, а также, и мощность принимаемых сигналов;
ü уменьшением размеров зоны обзора.
2. Относительный период обзора
В реальных станциях время облучения целей не остаётся постоянным: в зависимости от положения цели в зоне обзора она облучается большее или меньшее время. Так как необходимое накопление энергии сигналов должно осуществляться в наихудших условиях, т.е. при минимальном времени облучения цели, то увеличение времени облучения по сравнению с минимальным (Тобл мин) приведет к ненужному увеличению периода обзора. Непостоянство времени облучения связано с изменением скорости движения луча (на краях зоны обзора луч должен останавливаться и изменять направления движения), а также с изменением угла, в пределах которого облучается точечная цель. На рис.4.2 показаны сечения луча РЛС на соседних строках (1 и 2) его траектории. Из рисунка видно, что цель А облучается во время поворота луча на угол θаз, а цель Б выйдет из луча при повороте последнего на значительно меньший угол θБ.
 |
Рис.4.2.Перекрытие сечений РЛС на соседних строках
его траектории.
Чтобы не пропустить цель при обзоре, шаг траектории ψ (угловое перемещение луча при переходе от одной строки траектории к другой) должен быть меньше ширины луча (рис.4.2). При этом некоторые цели (например, цель Б на рис.4.2) будут облучаться дважды, что также приводит к ненужным потерям времени при обзоре. В ряде случаев реальные размеры зоны обзора могут отличаться от заданных.
Рассмотренные обстоятельства приводят к существенному увеличению минимального значения периода обзора в реальной системе по сравнению с идеализированной. Это различие характеризуют относительным периодом обзора Кобз:
|
|
(4.4) |
Значения относительного периода обзора лежат в пределах от 1 до 3 в зависимости от вида обзора.
При последовательном обзоре по угловым координатам период обзора равен
|
|
(4.5) |
при введении ещё и последовательного обзора по дальности
|
|
(4.6) |
4.3. Виды последовательного обзора
1. Обзор плоским лучом
Плоским называется луч, у которого угол раствора в одной плоскости много меньше, чем в другой. На рис.4.3 в качестве примера изображен веерный луч, у которого θаз « θум. Простейшим видом обзора плоским лучом является круговой обзор: луч непрерывно вращается с постоянной угловой скоростью вокруг вертикальной оси. Сектор обзора по азимуту получается при этом равным 3600. При круговом обзоре непроизводительные потери времени очень малы и Кобз≈1. Если луч вращается с угловой скоростью Ω град/сек и число оборотов в минуту равно n, то период кругового обзора равен
|
|
(4.7) |
а время облучения точечной цели
|
|
(4.8) |

Рис.4.3.Круговой обзор плоским лучом.
Круговой обзор позволяет получить плоскую картину расположения целей в пространстве: измеряются дальность и азимут, а по углу места разрешение отсутствует.
Если плоский луч перемещают в секторе, меньшем 3600, то обзор называется секторным. При секторном обзоре луч обычно совершает колебательное движение, останавливаясь в крайних положениях. Совершенно очевидно, что при секторном обзоре угловая скорость луча Ω(φ) не постоянна. В общем виде период обзора и время облучения определяются соотношениями
|
|
(4.9) |
здесь φ – текущее значение угловой координаты.
Задаваясь средним значением угловой скорости луча, получаем
|
|
(4.10) |
Из-за реверсирования луча при секторном обзоре возникают потери времени, приводящие к увеличению относительного периода обзора (Кобз=1,3÷1,5).
2. Обзор иглообразным лучом
Лучи РЛС, симметричные относительно направления максимального излучения, для которых справедливо соотношение θаз≈θум=θ, называются иглообразными. Ширина таких лучей изменяется от 1-20 до 25-300. Основными видами обзоров иглообразным лучом являются: винтовой, зигзагообразный, спиральный и поступательно-конический.
При винтовом обзоре луч быстро вращается в горизонтальной
плоскости и относительно медленно изменяет своё положение в вертикальной. За
каждый оборот в горизонтальной плоскости луч смещается по вертикали на угол ψ.
Естественно, что ψ должен быть меньше ширины луча: ψ=(0,7÷0,8)θ.
Если требуемое значение сектора обзора в вертикальной плоскости равно Фум,
то угловое перемещение луча по вертикали должно быть Фум –
θ. Число строк по вертикали будет![]() , и при угловой скорости
горизонтального перемещения луча Ωгор период винтового
обзора и время облучения цели можно определить по формулам
, и при угловой скорости
горизонтального перемещения луча Ωгор период винтового
обзора и время облучения цели можно определить по формулам
|
|
(4.11) |
Основными достоинствами винтового обзора является: возможность обзора на 3600 в горизонтальной плоскости; простота изменения сектора обзора в вертикальной плоскости; относительно малые потери времени (Кобз=1,1÷1,3), определяющиеся, главным образом, перекрытием сечений луча на соседних строках.
Если сектор обзора в горизонтальной плоскости должен быть равен 1800 или 1200, то винтовой обзор с одним лучом использовать нецелесообразно. Удобно применить антенное устройство, создающее два или три луча, которые смещены друг относительно друга на 1800 или 1200 в горизонтальной плоскости и на ψ – в вертикальной. При вращательном движении антенного устройства каждый луч будет использоваться в течение ½ или 1/3 длительности оборота антенны.
При зигзагообразном (телевизионном) обзоре луч совершает относительно быстрое возвратно-поступательное движение по одной угловой координате и медленно изменяет своё положение по другой (рис.4.4). Если угловая скорость и сектор обзора при быстром перемещении равны Ωб(φ) и Фб, а шаг траектории и сектор обзора в направлении медленного перемещения ψм и Фм, то период обзора и время облучения будут равны
|
|
(4.12) |
Для среднего значения угловой скорости быстрого перемещения луча Ωб=Ωср получим
|
|
|
и
|
|
(4.13) |
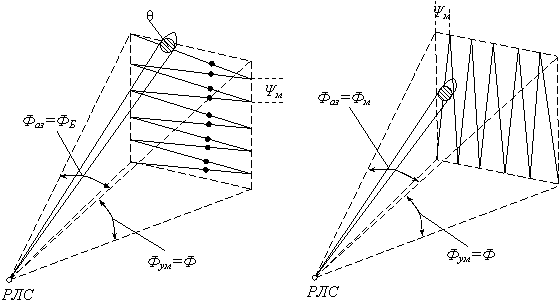 |
а) б)
Рис.4.4.Зигзагообразный, или телевизионный, обзор.
Если луч перемещается плавно по азимуту, то по углу места он движется скачками, и наоборот. Скачкообразное перемещение луча приводит к дополнительным ошибкам измерения угловой координаты. Поэтому при горизонтальном расположении строк (рис.4.4,а) точнее измеряется азимут целей, а при вертикальном (рис.4.4,б) – угол места.
Иногда зигзагообразный обзор осуществляется несколько иначе. Например, после перемещения по горизонтальной строке луч смещается на шаг по вертикали и т.д. (рис.4.5). Основным достоинством зигзагообразного обзора является простота независимого изменения секторов обзора в обеих плоскостях. Недостаток этого обзора состоит в относительно больших потерях времени из-за реверса движения луча и наложения сечений луча на соседних участках траектории (Кобз≈2 ).
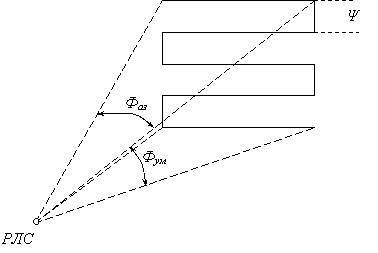 |
Рис.4.5.Разновидность зигзагообразного обзора.
Спиральный обзор
создаётся путем быстрого вращения луча вокруг оси ОО' (рис.4.6)
и медленного изменения угла α между осью луча и осью вращения. Если
предположить, что длительность одного оборота луча при вращательном движении Твр
остаётся постоянной независимо от значения угла α (0< α
< αмакс), а число оборотов, необходимое для просмотра
всей зоны, равно ![]() , то период спирального
обзора
, то период спирального
обзора
|
|
(4.14) |
Угловая скорость вращения луча при спиральном обзоре является величиной переменной. Угловое перемещение луча за один оборот вращательного движения вокруг оси ОО' составляет β=360 sinα град. Так как было принято, что Твр=const, то
|
|
(4.15) |
т.е. угловая скорость луча изменяется при изменении угла α. С учётом (4.15) время облучения цели при спиральном обзоре
|
|
(4.16) |
Основное преимущество спирального обзора: простота перехода к коническому сканированию, используемому при автоматическом сопровождении целей по угловым координатам.
Главный недостаток: очень большие потери времени (Кобз≈2 ÷2,5).


Рис. 4.6.Спиральный обзор.
При поступательно-коническом обзоре луч совершает быстрое коническое вращение и медленно смещается по горизонтали. Угловое перемещение луча за один оборот по конусу составит 360 sinФум град. Если период конического вращения равен Твр, то угловая скорость луча будет
|
|
(4.17) |
Приняв шаг траектории равным ψ, получим
|
|
(4.18) |
Поступательно-конический обзор применяется в тех случаях, когда зона обзора РЛС должна иметь существенно разные угловые размеры (Фаз>>Фум) и после обнаружения цели желательно использовать коническое сканирование для автоматического сопровождения по угловым координатам. Основной недостаток метода: значительные потери времени, которые вызываются повторными облучениями целей и большим перекрытием сечений луча на соседних витках траектории (Кобз≈2).
4.4. Программированный обзор
До сих пор предполагалось, что в процессе обзора луч РЛС движется по заданному закону с определё1нной скоростью и, следовательно, время облучения целей вполне определенно. Можно создать системы обзора, в которых время облучения данного направления изменяется по некоторой программе. Такие системы называются системами с программированным обзором. Цель программирования – уменьшить среднее значение периода обзора.
Схема на рис.4.7 позволяет уяснить основную идею программированного обзора. В РЛС имеется антенное устройство с электронно-управляемым лучом. Траектория движения луча задается системой управления, а время облучения данного направления изменяется под воздействием анализатора выходного напряжения приёмника. С помощью анализатора оценивается вероятность существования сигнала на входе приёмника в данный момент времени. Если эта вероятность мала, то луч быстро переводится с одного направления на другое. Но как только вероятность наличия сигнала увеличивается, луч замедляет движение и облучает данное направление до тех пор, пока не будет принято решение о том, есть цель или цели нет, а имеются одни помехи. После принятия решения луч возобновляет быстрое движение по заданной траектории.
Следовательно, луч задерживается только на тех направлениях, где возрастает вероятность появления сигнала. При отсутствии в РЛС специального анализатора следовало бы задерживать луч в каждом положении одинаково долго, ожидая появления цели с любого направления. Таким образом, в среднем период обзора при программировании уменьшается.
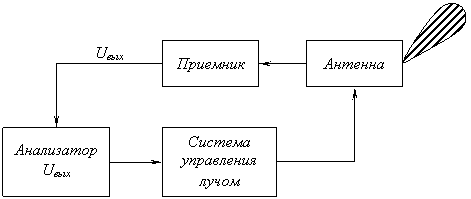


Рис. 4.7.Схема управления лучом при программированном обзоре.
Программированный обзор позволяет реализовать выигрыш во времени обзора лишь в таких РЛС, где не определяются дальность и скорость целей.
ГЛАВА 5. ОБНАРУЖЕНИЕ РАДИОЛОКАЦИОННЫХ СИГНАЛОВ
5.1. Основные положения
Обнаружением радиолокационных сигналов называется процесс принятия решения об их наличии или отсутствии путём анализа выходного напряжения приёмника РЛС. Проблема обнаружения возникает в тех случаях, когда сигналы принимаются в присутствии значительных помех. Если помех нет или они малы по сравнению с сигналом, то решение о наличии или отсутствии сигнала не вызывает на выходе приёмника, значит есть и сигнал; выходное напряжение мало или равно нулю – сигнала нет.
Трудности возникают тогда, когда амплитуда сигнала сравнима или существенно меньше средней амплитуды помехи. В этих условиях при наличии сигнала он может быть замаскирован или подавлен помехой, а при отсутствии сигнала помеха (шумы приёмного устройства) может быть принята за сигнал.
В принципе в любой ситуации допустимы только два решения: сигнал есть или сигнала нет. Всякие уклончивые решения исключается. Если сигнал действительно есть, то решение о его наличии называется правильным обнаружением и характеризуется вероятностью правильного обнаружения (Wпо); решение об отсутствии сигнала в этом случае называется пропуском сигнала и характеризуется вероятностью пропуска (Wпр). Пропуск является ошибкой РЛС при обнаружении сигнала, возникающей вследствие мешающего действия шума. Так как правильное обнаружение и пропуск при наличии сигнала составляют полную группу несовместных событий, то сумма вероятностей этих событий равна единице:
|
|
(5.1) |
Если сигнала на выходе приёмника нет, то решение о его отсутствии называется правильным необнаружением и ему соответствует вероятность Wпно; решение о наличии сигнала в этом случае называется ложной тревогой (соответственно существует вероятность ложной тревоги Wлт). Ложная тревога также является ошибкой, вызываемой наличием шума. Правильное необнаружение и ложная тревога составляют полную группу несовместных событий, поэтому
|
|
(5.2) |
Как можно видеть, при обнаружении сигналов возможно четыре независимых события, характеризуемых четырьмя вероятностями: Wпр, Wпо, Wпно, Wлт.
Основным показателем, определяющим значения вероятностных характеристик при обнаружении, являются отношение сигнал/шум по энергии:
|
|
(5.3) |
здесь Ес – энергия сигнала на входе приёмника, равная
|
|
|
при условии, что входное сопротивление Rвх=1 Ом; uc(t) - мгновенное значение напряжения сигнала на входе приёмника; τс – длительность сигнала; N0 – спектральная плотность мощности шума, имеющая размерность энергии и равная N0 = Pш/Δfш (Рш – мощность шума в полосе Δfш).
Критерий качества приёмного устройства РЛС при обнаружении должен быть связан со значениями вероятностей правильных решений и ошибок. Наиболее употребительными являются критерии идеального наблюдателя и Неймана-Пирсона. В соответствии с критерием идеального наблюдателя оптимальный (наилучший) приёмник должен минимизировать полную вероятность ошибки Wош при обнаружении, т.е.
|
|
(5.4) |
W(uc)иW(0) представляют собой безусловные вероятности наличия и отсутствия сигнала на входе приёмника (так называемые априорные вероятности). Вероятности Wпо и Wлт являются условными, так как характеризуют события, возникающие при условии, что сигнал есть или нет его. Любой другой приёмник, неоптимальный по критерию идеального наблюдателя, при заданном отношении сигнал/ шум q0 и прочих равных условиях будет характеризоваться большей вероятностью ошибки.
В соответствии с критерием Неймана-Пирсона оптимальный приёмник должен обеспечивать получение наибольшей вероятности правильного обнаружения при заданных значениях вероятности ложной тревоги отношения сигнал/шум; при использовании любого приёмника, неоптимального по критерию Неймана-Пирсона, для тех же значений Wлт и q0 вероятность правильного обнаружения будет меньше.
В оптимальном приёмнике независимо от выбранного критерия должны выполняться следующие операции, имеющие принципиальное значение: а) входное напряжение приёмника uвх(t) нужно перемножить с опорным напряжением uоп(t), представляющим собой копию излученных передатчиком РЛС колебаний; б) результат перемножения следует интегрировать за время существования сигнала τс; в) выходное напряжение интегратора необходимо сравнивать с некоторым постоянным напряжением, именуемым пороговым или просто порогом Uпор.
Математическая запись указанных операций такова:
а)
образуется интеграл вида 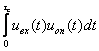 , где
, где ![]() - сумма напряжений
сигнала и шума при наличии сигнала на входе приёмника (если сигнала нет, то uвх(t)=uш(t));
- сумма напряжений
сигнала и шума при наличии сигнала на входе приёмника (если сигнала нет, то uвх(t)=uш(t)); ![]() ;
;
б)
выходное напряжение интегратора 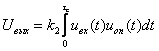 сравнивается с пороговым
напряжением Uпор:
если Uвых>Uпор, то принимается
решение о наличии сигнала, и с вероятностью Wпо это будет соответствовать действительности; при Uвых<Uпор считают, что
сигнала нет и это соответствует действительному положению с вероятностью Wпно. Схема на рис.5.1
сугубо упрощенно иллюстрирует устройство оптимального приёмника.
сравнивается с пороговым
напряжением Uпор:
если Uвых>Uпор, то принимается
решение о наличии сигнала, и с вероятностью Wпо это будет соответствовать действительности; при Uвых<Uпор считают, что
сигнала нет и это соответствует действительному положению с вероятностью Wпно. Схема на рис.5.1
сугубо упрощенно иллюстрирует устройство оптимального приёмника.
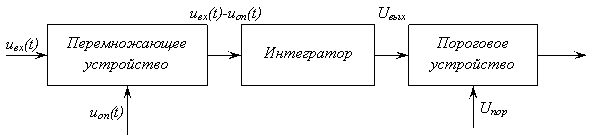

Рис.5.1.Упрощенная функциональная схема оптимального приёмника.
5.2. Характеристики обнаружения радиолокационных сигналов с полностью известными параметрами
Полностью известным называется радиолокационный сигнал, значение которого, если он имеется на входе приёмника, может быть заранее точно указано для любого момента времени. Пусть, например, используется сигнал длительностью τс
|
|
(5.5) |
где А≠0 лишь в интервале времени t1<t<t1+τс.
Для полного знания такого сигнала необходимо заранее точно определить значения параметров А, ω и ψ0. Единственное, что предполагается заранее неизвестным, это сам факт наличия сигнала: сигнал может существовать, а может и отсутствовать в данное время. Задача приёмника – облегчить принятие правильного решения.
В реальных условиях обычно неизвестны значения всех перечисленных параметров обнаруживаемого сигнала.
Если требуется построить приёмник, оптимальный в соответствии с критерием идеального наблюдателя, то он должен обеспечивать определение апостериорных (т.е. получаемых после обработки входного напряжения) вероятностей наличия и отсутствия входного сигнала и сравнение их между собой. Решение следует принимать в соответствии с тем, какая из вероятностей окажется больше. При этом вероятность ошибки будет минимально возможной, что и требуется по выбранному критерию оптимальности.
Нетрудно убедиться в том, что подобный приёмник будет оптимальным и в соответствии с критерием Неймана-Пирсона, когда Wлт считается заданной и требуется обеспечить максимум Wпо. Если Wлт=const, а W(uc) и W(0) известны до опыта, то минимуму вероятности полной ошибки соответствует минимум вероятности пропуска сигнала. Но так как Wпр=1- Wпо, то, добиваясь получения минимальной вероятности полной ошибки, одновременно обеспечивается максимум вероятности правильного обнаружения.
Для выявления структуры оптимального приёмника следует проанализировать выражения, определяющие указанные апостериорные вероятности. Сначала обратимся к плотностям апостериорных распределений, предполагая, что полностью известных сигналов может быть бесконечное множество, кодирование сигналов производится по амплитуде, амплитуды сигналов лежат в пределах от Амакс до нуля, а различие амплитуд двух соседних сигналов бесконечно мало. Все параметры каждого сигнала заранее известны. Неизвестно, какой из сигналов имеется в данное время. Отсутствие сигналов соответствует при данной постановке задачи наличию сигнала с нулевой амплитудой.
Из теоремы Байеса следует, что плотность апостериорной вероятности наличия различных сигналов во входном напряжении равна
|
|
(5.6) |
где К – нормирующий множитель, определяемый из условия, что интеграл от плотности апостериорной вероятности сигналов по всей области этих сигналов должен быть равен единице:
|
|
|
ω(uc) –
плотность априорной вероятности присутствия различных сигналов uc; ![]() плотность условной
вероятности образования входного напряжения uвх при наличии на входе сигнала uc.
плотность условной
вероятности образования входного напряжения uвх при наличии на входе сигнала uc.
Так как К – постоянная величина, априорное
распределение сигналов ω(uc) должно
быть известно до опыта, то для определения апостериорного распределения нужно
найти функцию![]() , называемую функцией
правдоподобия. Эта функция позволяет определить, какому сигналу
правдоподобнее всего соответствует имеющееся входное напряжение.
, называемую функцией
правдоподобия. Эта функция позволяет определить, какому сигналу
правдоподобнее всего соответствует имеющееся входное напряжение.
Во входном напряжении случайной величиной является только шум. Пусть шум имеет равномерный спектр в области частот, значительно превышающий полосу пропускания приёмника РЛС Δfпр. Мгновенные значения шумового напряжения подчинены нормальному распределению
|
|
(5.7) |
где σш – среднее квадратическое или эффективное значение напряжения шума;
σш2 – дисперсия шума, равная мощности шума Рш, выделяемой на сопротивлении 1 Ом.
Анализируя входное напряжение приёмника в течение времени существования сигнала τс, необходимо представить шумовое напряжение k его независимыми дискретными значениями (согласно теореме Котельникова)
|
|
|
где fв – наивысшая частота полосы пропускания приёмника.
Многомерная плотность распределения шума выражается:
|
|
(5.8) |
Так как сигнал является закономерно изменяющейся величиной, а случайным изменениям подвержен только шум, то распределение входного напряжения определяется распределением шума. Поэтому для определения функции правдоподобия вместо напряжения шума нужно использовать равную ему разность входного напряжения и напряжения сигнала
|
|
|
и
|
|
(5.9) |
И тогда плотность апостериорной вероятности равна:
|
|
(5.10) |
Здесь интеграл 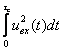 характеризует энергию
входного воздействия. В дальнейшем можно объединить экспоненциальный множитель
характеризует энергию
входного воздействия. В дальнейшем можно объединить экспоненциальный множитель 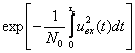 , К
и
, К
и ![]() и
обозначить это произведение символом К1 :
и
обозначить это произведение символом К1 :
|
|
|
Интеграл 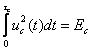 определяет энергию
принимаемого сигнала – величину, известную до опыта, но он не несет новой
информации о сигнале.
определяет энергию
принимаемого сигнала – величину, известную до опыта, но он не несет новой
информации о сигнале.
Интеграл 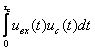 позволяет получить
дополнительную (к ранее известной, априорной) информацию о присутствии сигнала.
Тогда плотность апостериорной вероятности можно представить в виде:
позволяет получить
дополнительную (к ранее известной, априорной) информацию о присутствии сигнала.
Тогда плотность апостериорной вероятности можно представить в виде:
|
|
(5.11) |
Используя (5.11), обратимся к решению задачи
обнаружения одного единственного полностью известного сигнала. Вместо плотности
распределения апостериорной вероятности множества сигналов теперь будет лишь
две вероятности двух возможных событий: апостериорная вероятность наличия
сигнала ![]() и апостериорная вероятность
его отсутствия
и апостериорная вероятность
его отсутствия ![]() . Выражение, определяющее
. Выражение, определяющее ![]() , получим
из (), подставив в него вместо априорного распределения сигналов априорную
вероятность появления одного возможного сигнала
, получим
из (), подставив в него вместо априорного распределения сигналов априорную
вероятность появления одного возможного сигнала ![]() , т.е.
, т.е.
|
|
(5.12) |
Для определения апостериорной вероятности отсутствия сигнала необходимо в (5.11) подставить априорную вероятность того, что сигнала нет W(0) и приравнять к нулю энергию сигнала (Ес=0), тогда
|
|
(5.13) |
В оптимальном приёмнике следовало бы выполнить операции (5.12) и (5.13) и сравнить полученные результаты между собой; в зависимости от того, что будет больше, принимается решение о наличии сигнала.
Но можно существенно упростить решаемую техническую задачу. С принципиальной точки зрения безразлично, что сравнивать - значения самих апостериорных вероятностей или значения монотонных функций этих величин. Если использовать логарифмы апостериорных вероятностей, то устройство оптимального приёмника сильно упрощается:
|
|
(5.14а) |
|
|
(5.14б) |
Значит, в приёмнике нужно воссоздать величины, соответствующие функциям (5.14а) и (5.14б), и определить, какая из них больше. Но это равнозначно сравнению величин
|
|
|
Таким образом, в приёмнике, оптимальном по критерию идеального наблюдателя (а значит и по критерию Неймана-Пирсона), при обнаружении полностью известного сигнала, достаточно образовать интеграл вида
|
|
(5.15а) |
и сравнить результат интегрирования (после умножения на постоянный множитель 2/N0) с величиной, называемой порогом:
|
|
(5.15б) |
Если порог превышен, то принимается решение о наличии сигнала; если порог не превышен, то считают, что сигнала нет. Практически в приёмнике сравниваются не сами указанные величины, а пропорциональные им напряжения: напряжение на выходе схемы интегрирования
|
|
|
и пороговое напряжение
|
|
|
здесь а – одинаковый для обеих схем коэффициент пропорциональности. При математическом анализе процессов будем считать коэффициент а равным единице.
Приёмник, в котором выполняются указанные операции, называется достаточным. На рис.5.2 изображена функциональная схема достаточного приёмника для обнаружения полностью известного сигнала. В связи с тем, что схемы умножения и интегрирования в приёмнике производят операции, с точностью до постоянного множителя совпадающие с корреляционной функцией входного и опорного напряжений, такой приёмник называют корреляционным.
Входной сигнал и опорное напряжение всегда находятся в фазе, поэтому при отсутствии шума выходное напряжение коррелятора (Uвых) линейно нарастало бы в течение всей длительности сигнала. Выходное напряжение достигает максимума в момент t0, соответствующий концу сигнала. После этого должно быть обеспечено спадание выходного напряжения до нуля для того, чтобы подготовить приёмник к обнаружению других сигналов.



Рис.5.2.Функциональная схема корреляционного приёмника.
Если бы на входе приёмника был бы один шум, имеющий случайные амплитуду и фазу колебаний, то в результате перемножения опорного напряжения с входным образовалось бы случайное по амплитуде и знаку напряжение.
Когда на входе приёмника имеются и сигнал, и шум, напряжение на выходе схемы перемножения будет алгебраической суммой того, что мы получили бы при воздействии только сигнала и только шума; схему перемножения можно считать линейным радиотехническим устройством. Выходное напряжение коррелятора при одновременном воздействии сигнала и шума будет случайной величиной. Предсказать значения выходного напряжения коррелятора нельзя. Но известно, что составляющая напряжения от сигнала будет достигать своего максимума в момент и именно в этот момент отношение напряжения сигнала к среднему квадратическому значению напряжения шума на выходе коррелятора достигает максимума. В момент t0 следует производить сравнение выходного напряжения коррелятора с порогом. При этом вероятность правильного суждения о наличии или отсутствии сигнала будет наибольшей.
Рассмотрим зависимости, позволяющие определить вероятности правильного обнаружения и ложной тревоги в оптимальной системе обработки входного напряжения. Образующийся в приёмнике после интегрирования сигнал можно разложить на две составляющие, принимая во внимание, что входное напряжение состоит из сигнала и шума:
|
|
|
Первая составляющая, содержащая произведение сигнала и опорного напряжения, равна
|
|
(5.16) |
Так как опорное напряжение точно совпадает с напряжением сигнала, то значение величины S вполне определенно:
|
|
(5.17а) |
В общем случае, когда рассматривается обнаружение сигнала с неизвестными заранее параметрами, величина S становится функцией временного сдвига S(t) и её называют сигнальной функцией.
Вторая составляющая содержит произведение шума с опорным напряжением и называется шумовой функцией:
|
|
(5.17б) |
Если сигнала нет, то на выходе коррелятора имеется только шумовая функцией; превышение ею порога составляет ложную тревогу. Шумовая функция является случайной величиной с нормальным законом распределения (так как сам шум распределен по нормальному закону, а uоп(t) – детерминированная величина) со средним значением, равным нулю, и дисперсией
|
|
|
здесь Еоп – энергия опорного напряжения за длительность сигнала.
Так как Еоп=Ес, то дисперсия шумовой функции равна удвоенному отношению энергии сигнала и спектральной плотности шума
|
|
|
Среднее квадратическое значение шумовой функции
|
|
(5.17в) |
Таким образом, максимальное отношение сигнал/шум по напряжению на выходе коррелятора (так же как и на выходе согласованного с сигналом фильтра) составляет
|
|
(5.18) |
т.е. оно зависит только от соотношения энергии сигнала и спектральной плотности шума на входе приёмника.
С учётом сказанного плотность распределения шумовой функции равна
|
|
(5.19) |
Вероятность ложной тревоги представляет собой вероятность того, что шумовая функция превысит порог β, т.е.
|
|
(5.20) |
Используя функцию Лапласа
|
|
|
формулу (5.20) можно преобразовать
|
|
(5.21) |
При наличии сигнала следует учитывать и шумовую и
сигнальную функцию. Выходное напряжение коррелятора будет характеризоваться
суммой шумовой функции и постоянной величины 2Ес/N0. Плотность распределения
этой суммы подчиняется нормальному закону со средним значением, равным ![]() , и
дисперсией
, и
дисперсией ![]()
|
|
|
Вероятность правильного обнаружения представляет собой вероятность того, что α превысит порог, т.е.
|
|
(5.22) |
Используя функцию Лапласа, получим
|
|
(5.23) |
Формулы (5.21) и (5.23) устанавливают взаимосвязь между вероятностями правильного обнаружения и ложной тревоги, с одной стороны, и пороговым уровнем и энергетическим отношением сигнал/шум на входе приёмника, с другой. Задавшись значениями β и q0, можно вычислить Wпо и Wлт.
5.3. Характеристики обнаружения радиолокационных
сигналов с неизвестной начальной фазой
Допущение о незнании начальной фазы сигнала является первым шагом на пути от гипотетического сигнала с полностью известными параметрами к реальному сигналу, поступающему на вход приёмника. Пусть амплитуда и частота сигнала известны, но положение сигнала на временной оси известно с точностью до периода высокой частоты, т.е. значение начальной фазы случайно и заранее неизвестно. Будем считать распределение фазы равновероятным в пределах от 0 до 2π:
|
|
|
В принципе схема оптимального приёмника должна остаться той же: нужно перемножать входное напряжение с опорным и результат суммирования подводить к пороговому устройству. Но должны появиться какие-то особенности. Так как фаза сигнала заранее неизвестна, то нельзя сфазировать опорное напряжение с сигналом и на выходе схемы умножения амплитуда напряжения Uумн будет пропорциональна косинусу разности фаз ψразн сигнала и опорного напряжения:
|
|
|
Следовательно, результат перемножения сигнала с опорным напряжением является случайной величиной. Чтобы устранить случайность изменения выходного напряжения, применяют два параллельных канала, опорные напряжения в которых сдвинуты по фазе на 900 (рис.5.3). В таком устройстве на выходе первой схемы умножения получим амплитуду напряжения
|
|
|
а на выходе второй, при их симметричности,
|
|
|
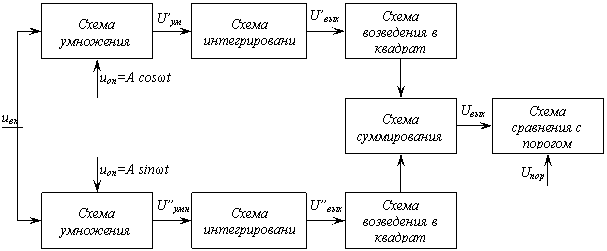

Рис.5.3.Функциональная схема приёмника, оптимального для обнаружения сигналов с неизвестной начальной фазой.
Максимальные напряжения на выходе схем интегрирования будут пропорциональны амплитудам напряжения, поступающего от схем перемножения, поэтому
|
|
|
где а – соответствующий коэффициент пропорциональности.
Если теперь результаты интегрирования возвести в квадрат и сложить, то на выходе системы обработки получим от сигнала напряжение, максимум которого является постоянной величиной, на зависящей от фазы принятого сигнала:
|
|
|
Можно построить оптимальный приёмник и по значительно более простой схеме, в которой используется согласованный фильтр. Под воздействием сигнала в фильтре будут нарастать колебания. Амплитуда колебаний достигнет максимумам в некоторый момент времени t0, зависящий от начальной фазы сигнала. При обнаружении полностью известного сигнала было точно известно положение момента t0 на временной оси. Не зная начальной фазы сигнала можно определить положение момента t0 только с точностью до периода высокой частоты Т0. Но такой точности отсчёта совершенно не достаточно, так как за период высокочастотных колебаний выходное напряжение фильтра изменяется от максимального положительного значения до максимального отрицательного, отсчёт в произвольный момент не даст нужного эффекта. Для того чтобы обеспечить однозначность отсчёта напряжения, нужно после фильтра поставить амплитудный детектор, выделяющий огибающую колебаний Uдет. Тогда можно считать, что практически в любой момент времени в пределах периода Т0 выходное напряжение системы обработки будет одинаково и равно максимальному значению. Следовательно, и в этом устройстве, схема которого изображена на рис.5.4, устранена случайность выбора выходного напряжения, вызванная незнанием начальной фазы сигнала.



Рис.5.4. Функциональная схема фильтрового варианта оптимального приёмника обнаружения сигнала
с неизвестной начальной фазой.
Рассмотрим рабочие характеристики приёмника, оптимального для обнаружения сигнала с неизвестной начальной фазой. Предположим, что используется приёмник с согласованным фильтром (рис.5.4). Это предположение не снижает общности результатов, которые не зависят от используемого варианта построения приёмника, но существенно упрощает математическую сторону задачи.
Огибающая нормального шума Uш на выходе линейного узкополосного фильтра подчинена закону Релея:
|
|
|
Следовательно, вероятность ложной тревоги будет равна
|
|
(5.24) |
Заменой переменного ![]() приводим интеграл в (5.24) к
табличному
приводим интеграл в (5.24) к
табличному
|
|
|
при Uш=β![]() , поэтому
, поэтому
|
|
|
Но так как ![]() , получим
, получим
|
|
(5.25) |
Из этой формулы можно видеть, что при заданном соотношении сигнал/шум вероятность ложной тревоги определяется только значением выбранного порога. При β=0 вероятность ложной тревоги достигает единицы (любой шумовой выброс принимается за сигнал), а при β=∞ Wлт=0 – ни один шумовой выброс не может превысить порог.
Если на фильтр воздействуют и сигнал, и шум, то распределение огибающей результирующего напряжения Uс+ш на выходе согласованного фильтра подчинено обобщенному закону Релея
|
|
(5.26) |
здесь I0 – функция Бесселя нулевого порядка от мнимого аргумента;
Uс – максимальная амплитуда сигнала на выходе фильтра, которая является известной величиной.
Заменив величины Uс и σш через q0, придем к следующему выражению плотности распределения:
|
|
(5.27) |
и вероятность правильного обнаружения
|
|
(5.28) |
Формулы (5.25) и (5.28) могут быть использованы для вычисления вероятностей правильного обнаружения и ложной тревоги и построения характеристик приёмника; для определения Wпо нужно приметь численное интегрирование.
Значительно удобнее пользоваться при расчётах приближенной формулой, связывающей Wпо, Wлт и q0:
|
|
(5.29) |
Погрешность вычислений по формуле (5.29) не превышает 15% при Wлт ≤0,1 и Wпо≥0,9.
5.4.Характеристики обнаружения радиолокационных сигналов с неизвестной начальной фазой и флюктуирующей амплитудой
Следующим приближенным к реальному сигналу является допущение о том, что заранее неизвестна и амплитуда сигнала.
Пусть сигнал характеризуется неизвестными заранее амплитудой А и начальной фазой ψ0. При неизвестной начальной фазе апостериорная вероятность появления сигнала равна
|
|
|
где М – мгновенное значение огибающей напряжения на выходе согласованного фильтра при наличии и сигнала и шума;
W(uc) – априорная вероятность появления одного возможного сигнала с известным параметрами.
Если амплитуда подвержена случайным изменениям, то необходимо учитывать априорные сведения не только о самом сигнале в целом, но и отдельно о его амплитуде. Примем предположение о релеевском распределении амплитуд сигнала и допустим, что в течение времени обнаружения амплитуда сигнала (или группы сигналов) не меняется. Следовательно,
|
|
|
где А0 – среднее значение амплитуды сигнала.
Энергия одиночного сигнала равна
|
|
|
и для среднего значения амплитуды
|
|
|
Разумно допустить предположение о независимости априорных вероятностей появления сигнала и нахождения его амплитуды в некотором интервале dA. Будем считать, что априорная вероятность появления сигнала с амплитудой, лежащей в интервале А1÷(А1+dА), равна произведению априорной вероятности появления (и отсутствия) сигнала и априорной вероятности попадания амплитуды в указанный интервал
|
|
|
При этом апостериорная вероятность сигнала с амплитудой А будет равна
|
|
(5.30) |
Для исключения из формулы (5.30) случайно изменяющегося параметра и получения выражений, определяющих структуру приёмника, проинтегрируем (5.30) по амплитуде в пределах от 0 до ∞
|
|
|
Записанный интеграл является табличным вида
|
|
|
где
![]() ;
;
![]() ;
;
![]() .
.
Следовательно, апостериорная вероятность существования сигнал равна
|
|
|
соответственно апостериорная вероятность отсутствия сигнала
|
|
|
В достаточном приёмнике следует сравнивать логарифмы обеих апостериорных вероятностей, т.е. сопоставлять
|
|
|
Единственными принципиальными операциями в оптимальном приёмнике являются: во-первых, образование огибающей (М) выходного напряжения на выходе согласованного фильтра (рис.5.4) или квадрата этой величины (М2) в двухканальном устройстве обработки (рис.5.3) и, во-вторых, сравнение полученной величины с порогом.
Учёт случайных изменений амплитуды сигнала не приводит к изменению схемы оптимального приёмника. Изменяется лишь значение порога, при котором достигается минимум вероятности ошибки или максимум вероятности правильного ответа, если с порогом сравнивается величина М; если образуется М2, то её нужно сравнивать с β2опт:
|
|
|
Величины Wпо, Wлт и q0ср (среднее значение отношения сигнал/шум на входе приёмника) при обнаружении сигнала с неизвестными амплитудами и фазой связаны простым соотношением
|
|
(5.31) |
5.5. Характеристики обнаружения радиолокационных сигналов с неизвестными значениями начальной фазы,
амплитуды и частоты
В реальных условиях и частота сигнала никогда не бывает заранее точно известна. Несовпадение частоты принимаемых сигналов с частотой излучённых колебаний возникает вследствие эффекта Доплера. Скорость цели по отношению РЛС – величина случайная, поэтому и частотный сдвиг сигнала заранее известен быть не может. Если различие частоты отраженного сигнала и номинального значения частоты настройки приёмного тракта невелико (не превышает, например, половины ширины спектра сигнала), то схема оптимального приёмника остаётся прежней (см.рис.5.3 и 5.4).
Но при прочих равных условиях случайные изменения частоты сигнала приводят к ухудшению соотношения сигнала и шума перед пороговым устройством, а, следовательно, к ухудшению вероятностных характеристик при обнаружении. Ухудшение отношения сигнал/шум может быть названо потерями из-за расстройки сигнала, характеризуемыми коэффициентом потерь αр.
Физическое объяснение возникновения потерь из-за расстройки сигнала состоит в следующем. При различии частоты сигнала и опорного напряжения (в корреляторе) или резонансной частоты(в согласованном фильтре) максимальное значение сигнальной составляющей уменьшается; шумовая же составляющая остаётся неизменной. Если Uc(0) - наибольшее значение сигнальной составляющей при отсутствии расстройки, а Uc(Δfp) – значение той же величины при наличии расстройки, то ухудшение отношения сигнал/шум перед пороговым устройством составит
|
|
|
Для компенсации этого ухудшения нужно увеличить энергетическое отношение сигнал/шум на входе приёмника. Так как максимальное значение сигнальной составляющей пропорционально энергии входного сигнала, то входное отношение сигнал/шум должно быть увеличено ровно настолько, насколько уменьшается амплитуда сигнальной составляющей из-за расстройки. Следовательно, коэффициент потерь расстройки будет равен
|
|
(5.32) |
Если расстройка велика (превышает половину ширины спектра сигнала) сигнала, то схема оптимального приёмника меняется. Большая расстройка сигнала из-за доплеровского эффекта возможна в реальных условиях. В оптимальном приёмнике должен быть обеспечен приём любого сигнала и, если диапазон частот сигналов превышает полосу пропускания системы обработки, то необходимо применить несколько параллельно работающих схем обработки (каналов), настроенных на разные частоты.
5.6. Характеристики обнаружения сигнала в одном
из его возможных положений
В реальных условиях на вход приёмника может поступать одновременно несколько сигналов от нескольких целей. Время прихода и частота сигналов могут изменяться в весьма широких пределах.
Угловые координаты, дальность и скорость движения цели являются непрерывными функциями времени, и сигнал может занимать бесконечное множество положений на соответствующих координатных осях. Анализ обнаружения сигнала с непрерывным распределением возможных положений является задачей очень сложной и не имеющей особого практического значения. Вполне удовлетворительные результаты по точности решения даёт анализ более простой задачи: исследование возможностей обнаружения сигналов, которые могут занимать одно из m дискретных неперекрывающихся положений. Все цели, которые находятся в пределах одного элемента разрешения, воспринимаются станцией как одна цель. Для раздельного наблюдения двух целей необходимо, чтобы различие их координат или скорости превышало разрешающую способность РЛС. Допусти, например, что зона обзора РЛС разбита на прилегающие друг к другу элементы разрешения, общее число которых равно m. Это m определяет максимальное число разрешаемых целей, одновременно находящихся в зоне обзора. Если допустить, что при перемещении цели занимают дискретные положения, соответствующие центрам элементов разрешения, то возможных положений не может быть больше m. Следовательно, можно сделать предположение о том, что сигнал одиночной цели может занимать m дискретных неперекрывающихся положений. В том случае, когда в РЛС кроме трёх координат целей (дальность, азимут и угол места) измеряется ещё и их скорость, число возможных положений сигнала будет больше m. Если же измерению подлежат только две координаты, например дальность и азимут, то число возможных положений уменьшится по сравнению с m.
Предыдущий анализ позволил выявить схему приёмника, оптимального при обнаружении сигнала, положение которого приблизительно известно. Допустив, что отдельный сигнал может занимать m дискретных неперекрывающихся положений и одновременно может существовать несколько сигналов, приходим к выводу о том, что в пригодном для практических целей оптимальном приёмнике нужно использовать m независимых схем обработки сигналов; приёмник становится многоканальным. Каждая из схем должна включать коррелятор (или согласованный фильтр с детектором), а в случае необходимости – накопительное устройство и схему сравнения с порогом. Каждая из схем предназначается для обнаружения сигнала в одном из его возможных положений. Входное напряжение одновременно воздействует на все схемы обработки.
Будем называть вероятностью правильного обнаружения сигнала в его i-м положении (Wпоi) вероятность превышения порога в i-й схеме в том случае, если такой сигнал в действительности есть на входе приёмника. Вероятностью ложной тревоги для i-й схемы обработки назовем вероятностью превышения порога в данной схеме при отсутствии сигнала на входе приёмника. Так как на каждую схему обработки может воздействовать только вполне определенный сигнал (сигнал, занимающий i-е положение), то значение вероятностей Wпоi и Wлтi не изменяются от того, что работает не одна схема, а m параллельных схем. То, что входное напряжение uвх(t) поступает одновременно к нескольким схемам обработки и мощность сигнала на входе отдельной схемы уменьшается в m раз, не имеет значения, так как и мощность шума, определяемого параметрами входных цепей, на входе каждой из схем уменьшается во столько же раз, а соотношение сигнала и шума на входе приёмника и на входе отдельной схемы остаётся одним и тем же. Поэтому полученные ранее зависимости между Wпо, Wлт и q0 полностью применимы к Wпоi и Wлтi.
Для оценки рабочих характеристик рассматриваемого многоканального приёмника необходимо найти зависимость вероятностных характеристик всей системы от вероятностей Wпоi и Wлтi отдельной схемы обработки. В силу идентичности схем обработки и независимости действующих в них шумов (смещение по времени моментов работы различных схем превышает время корреляции шума вероятности правильного обнаружения в различных схемах, так же как и вероятности ложной тревоги, можно считать одинаковыми) Wлтi= Wлтj и Wпоi= Wпоj при i≠j.
Вероятность правильного необнаружения сигнала системой связана с вероятностью правильного необнаружения отдельной схемой соотношением
|
|
|
вытекающим из того, что необнаружением различными схемами являются независимыми событиями. Так как вероятность ложной тревоги в системе (вероятность того, что хотя бы в одной из схем порог будет превышен при наличии на входе только шума) однозначно зависит от вероятности правильного необнаружения системы
|
|
|
то
|
|
(5.33) |
При Wлтi «1 можно воспользоваться формулой
|
|
(5.34) |
Формула (5.34) показывает, что вероятность ложной тревоги в системе в m раз больше вероятности ложной тревоги в отдельной схеме обработки.
Вероятность пропуска сигнала в системе равна произведению вероятности пропуска в соответствующей схеме (Wпрi) и вероятности непревышения шумовым напряжением порога во всех остальных схемах [(1- Wлтi)m-1]
|
|
(5.35) |
Для [(m-1) Wлтi] «1 второй сомножитель можно принять равным единице:
|
|
|
Принимая во внимание, что вероятности пропуска и правильного обнаружения однозначно определяют друг друга
|
|
|
из (5.35) получим
|
|
|
или
|
|
(5.36) |
т.е. вероятность правильного обнаружения в системе приблизительно равна вероятности правильного обнаружения в отдельной схеме обработки.
В многоканальном приёмнике могут иметь место искажения информации, состоящие в том, что при наличии i-го сигнала порог будет превышен в j-й схеме и создастся впечатление, что присутствует j-й сигнал. Вероятности искажения (Wиск) и правильного указания сигнала (Wпус) однозначно определяют друг друга:
|
|
|
Вероятность правильного указания сигнала равна произведению вероятности правильного обнаружения этого сигнала соответствующей схемой обработки (Wпоi) и вероятности непревышения порога во всех остальных схемах [(1- Wлтi)m-1]:
|
|
(5.37) |
В (5.37) при Wлтi«1 можно допустить, что для m»1 (1- Wлтi)m-1≈1- mWлтi, и тогда
|
|
(5.38) |
Можно выразить вероятность искажений через вероятностные характеристики всей системы:
|
|
(5.39) |
Для полностью известного сигнала, который может занимать одно из m возможных положений:
|
|
(5.40) |
Для сигнала с неизвестной начальной фазой такую же подстановку нужно сделать в формуле (5.29), после чего получим
|
|
(5.41) |
Для сигнала с неизвестной начальной фазой и флюктуирующей амплитудой, занимающего одно из m возможных положений, вместо (5.31) получим
|
|
(5.42) |
Формулы (5.40), (5.41) и (5.42) связывают отношение сигнал/шум на входе приёмника с вероятностями правильного обнаружения и ложной тревоги системы обработки, оптимальной при приёме одного или нескольких сигналов, которые могут занимать m возможных положений.
5.7. Коэффициент различимости при обнаружении
радиолокационных сигналов
Коэффициентом различимости называется то значение отношения энергии сигнала к спектральной плотности шума на входе приёмника, при котором сигнал обнаруживается с заданными значениями вероятностей Wпо и Wлт реальным приёмным устройством:
|
|
|
Исходным моментом при расчёте коэффициента
различимости является определение значения q0, которое вычисляется по одной из выше приведенных
формул. Если обнаружение ведётся по одному сигналу, то вычисляется значение
величины q0/2; при обнаружении по пачке из сигналов Nc нужно
определить q0/2Nc. После
этого нужно учесть многочисленные потери (уменьшение отношения сигнал/шум в
реальной РЛС). В силу целого ряда причин действительное соотношение сигнала и
шума перед пороговым устройством оказывается значительно меньше того, которое
можно было бы получить в теоретически мыслимой модели РЛС при прочих равных
условиях. Для того чтобы и в реальных условиях обеспечить требуемые значения
вероятностей Wпо и Wлт,, приходится
увеличивать отношение сигнал/шум на входе приёмника по сравнению с его
теоретически необходимым значением q0. Если влияние элемента i–го РЛС приводит к ухудшению отношения сигнал/шум в αi раз, а всего в РЛС имеется n
элементов, влияющих на это отношение,
то общие потери составят ![]() или
или ![]() , где αj выражено в
децибелах, и для их компенсации входное отношение сигнал/шум должно быть
увеличено во столько же раз.
, где αj выражено в
децибелах, и для их компенсации входное отношение сигнал/шум должно быть
увеличено во столько же раз.
Тогда соотношение, связывающее коэффициент различимости и величину q0:
|
|
(5.43) |
если производится обнаружение одиночного сигнала,
|
|
(5.44) |
при обнаружении пачки из Nc сигналов.
ГЛАВА 6. ДАЛЬНОСТЬ ДЕЙСТВИЯ РАДИОЛОКАЦИОННЫХ СТАНЦИЙ
6.1. Дальность действия в свободном пространстве
Дальностью действия радиолокационной станции называется наибольшее расстояние между станцией и целью, на котором обнаружение цели производится с заданными вероятностями правильного обнаружения и ложной тревоги.
Дальность действия зависит от технических параметров станции, характеристик цели, условий распространения радиоволн, наличия и уровня различного рода помех и ряда других факторов, большинство из которых изменяется во времени случайным образом. Их количественные значения, необходимые для расчёта дальности, могут определяться лишь с какой-то вероятностью, определяющей в итоге и вероятность полученного значения дальности действия. График на рис.6.1 иллюстрирует характер зависимости относительного изменения дальности обнаружения от значения вероятности правильного обнаружения Wпо при заданной ложной тревоге Wлт.
Рассмотрим дальность действия РЛС без учёта влияния земной поверхности и атмосферы на распространение радиоволн, т.е. РЛС и цель находятся в «свободном» пространстве.
При облучении потоком электромагнитной энергии одиночной цели, находящейся в свободном пространстве, небольшая часть рассеиваемой целью энергии направляется в сторону приёмной антенны РЛС. Обычно приёмная антенна располагается в одном пункте с передающей или (при импульсной работе) является одновременно и передающей.
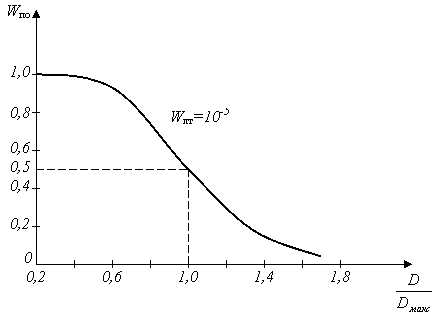


Рис.6.1. Зависимость относительного изменения дальности обнаружения от значения вероятности правильного обнаружения.
Если передающее устройство РЛС вырабатывает энергию излучения Еизл, максимальное значение коэффициента усиления передающей антенны по мощности равно Gопрд и цель находится на расстоянии D от радиолокационной станции, то плотность потока энергии у цели
|
|
|
где 4πD2 – поверхность сферы радиусом D;
|
|
|
Ризл – мощность излучения;
τс – время непрерывного облучения цели (при импульсной работе - длительность одного импульса).
Количество энергии, переизлучаемое целью, определяется средним значением эффективной отражающей площади цели Sэфф0
|
|
|
Плотность потока энергии у приёмной антенны
|
|
|
Энергия радиолокационного сигнала, поступающего из антенны в согласованный с ней приёмник, равна
|
|
(6.1) |
где Sа прм – эффективная площадь приёмной антенны, связанная с геометрической площадью раскрыва антенны соотношением
|
|
(6.2) |
На максимальной дальности обнаружения энергии принимаемого сигнала равна пороговому значению, т.е. минимально необходимому для обнаружения с заданными вероятностями Wпо и Wлт.
Величина порогового значения энергии определяется чувствительность приёмника РЛС Епрм мин. Таки образом, для максимального значения дальности Dмакс имеем.
|
|
(6.3) |
где коэффициент различимости равен:
|
|
|
Спектральная плотность мощности шума приёмника:
|
|
|
kш – коэффициент шума приёмника;
k – постоянная Больцмана, равная 1,38·10-23 вт·сек/град;
Т0 – абсолютная температура, при которой определяется величина kш (обычно 2900 К).
Из формулы (6.1) с учётом (6.3) получаем следующее выражение для максимальной дальности действия:
|
|
(6.4) |
Это выражение может быть также представлено в других эквивалентных видах, если использовать известную зависимость между коэффициентом усиления и раскрывом антенны:
|
|
|
Заменяя в (6.4) Gопрд и в соответствии с приведёнными выше формулами, получим
|
|
(6.5) |
Использование одного из трёх приведённых выражений для расчёта Dмакс зависит от заданных (известных) параметров передающей и приёмной антенн.
Если в РЛС для излучения и приёма используется одна и та же антенна, то в формулу (6.5) вместо произведений Sа прд Sа прм и Gопрд Gопрм следует подставить величины Sа2 и Gо2 соответственно
|
|
(6.6) |
Анализируя выражения для Dмакс можно сделать следующие выводы:
1. Дальность действия РЛС определяется энергией излучаемых сигналов и не зависит от их формы (при прочих заданных параметрах станции).
2. Увеличение энергии излучения, так же как и улучшение чувствительности приёмника (уменьшение kш), не очень существенно влияет на величину Dмакс, так как
|
|
(6.7) |
С точки зрения экономии потребляемой РЛС энергии выгоднее для увеличения Dмакс улучшать чувствительность приёмника (уменьшать величину Епрм мин), но из соображений повышения помехозащищённости станции целесообразно увеличивать Еизл.
Обычно при конструировании станций стремятся увеличить как за счёт увеличения чувствительности приёмника, так и путём выбора максимально возможной для конкретных условий энергии излучения.
3. Существенное увеличение дальности действия может быть достигнуто за счёт увеличения размеров антенны. При использовании одной антенны для излучения и приёма
|
|
|
где dа – диаметр рефлектора (линейный размер) антенны.
4. При заданных размерах антенн, т.е. при Sа прд=const и
Sа прм=const:
|
|
|
т.е. укорочение волны при неизменных размерах антенн вызывает увеличение Dмакс. Это объясняется тем, что в этом случае уменьшение λ приводить к увеличению коэффициента усиления антенн.
5. Если фиксировать значение Gо, то:
|
|
|
Такая зависимость появляется в связи с тем, что при увеличении длины волны для сохранения прежних значений коэффициентов усиления антенн, необходимо увеличивать Sа прд и Sа прм.
В РЛС, где размеры антенн ограничиваются определёнными габаритами, для повышения дальности действия целесообразно уменьшать длину волны. Если же требования к размерам антенн не являются жесткими, можно повышать Dмакс, увеличивая длину волны с одновременным увеличением размеров антенны так, чтобы величина Gо=const.
6. Небольшое изменение эффективной отражающей площади цели не очень существенно влияют на величину Dмакс, так как
|
|
|
В ряде случаев удобнее пользоваться формулами, в которых отношение энергии излучения и порогового значения энергии сигнала заменяется отношением соответствующих мощностей. Такая замена возможна при условии согласования полосы пропускания приёмника Δf с длительностью сигнала τс. Так как в общем случае Δf τс=ξ, то отношение
|
|
|
При согласовании полосы пропускания приёмника Δf
с длительностью сигнала τс коэффициент ξ=1 и
отношение ![]() . Если ξ≠1,
указанная замена может производиться лишь при учёте значения ξ.
. Если ξ≠1,
указанная замена может производиться лишь при учёте значения ξ.
Для получения необходимой величины kp при обнаружении цели, находящейся на максимальной дальности, значение энергии излучения передатчика определяется при прочих заданных параметрах станции выражением:
|
|
(6.8) |
Если обеспечить получение необходимой величины Еизл за время τс по каким-либо причинам невозможно, то производят несколько облучений цели и накопление отражённых сигналов.
Иногда передающая и приёмная антенны оказываются разнесёнными на значительное расстояние друг от друга. Тогда количество энергии, переизлучаемой целью в направлении приёмной антенны, равно
|
|
|
где Dпрд – расстояние от РЛС до цели.
Значение энергии отраженного сигнала на входе приёмника:
|
|
|
где Dпрм – расстояние от цели до приёмной антенны.
Для порогового значения сигнала получим
|
|
(6.9) |
Последнее выражение показывает, что при малом расстоянии между целью и приёмным устройством облучение цели может производиться с большого расстояния, и наоборот, но обязательно должно выполняться условие:
|
|
|
6.2.Дальность действия при активном ответе
Для решения некоторых тактических задач и повышения тактических возможностей РЛС (например, для опознавания целей, увеличения дальности обнаружения, повышения точности измерения координат и т.д.) на объектах, подлежащих радиолокационному наблюдению, устанавливают ответчики (ретрансляторы). На приёмную антенну ответчика поступает прямой (запросный) сигнал передатчика РЛС. После соответствующих преобразований этот сигнал поступает на запуск передатчика ответчика, вырабатывающего ответный сигнал. Ответный сигнал, значительно превышающий по энергии сигнал, отражённый от цели, принимается антенной РЛС (рис.6.2). При заданных параметрах РЛС (запросчика): Еизл з, Gопрд з, Sа прм з, и ответчика: Еизл от, Gопрд от, Sа прм от, энергия запросного сигнала на входе приёмника ответчика, находящегося на расстоянии D от РЛС, равна
|
|
|



Рис.6.2.РЛС с активным ответом
Максимальной дальности запроса Dмаксз соответствует пороговое значение энергии запросного сигнала на входе приёмника ответчика, равное чувствительности приёмника, Епрм мин от=kрот kшот kT0.
Таким образом,
|
|
(6.10) |
Энергия ответного сигнала на входе приёмника РЛС равна
|
|
|
а максимальная дальность ответа Dмакс от определится чувствительностью приёмника запросчика Епрм мин з=kрз kшз kT0
|
|
(6.11) |
Для радиолокационной системы с активным ответом параметры системы целесообразно выбирать таким образом, чтобы Dмакс з=Dмакс от, так как в противном случае дальность действия системы будет определяться наименьшим значением Dмакс по одному из каналов (запроса или ответа), а возможности другого канала не будут полностью реализованы.
Считая Dмакс з=Dмакс от получим выражение для дальности действия системы с активным ответом
где λз – длина волны запросчика;
λот – длина волны ответчика.
Энергетические параметры системы должны при этом выбираться исходя из равенства выражений (6.10) и (6.11):
|
|
(6.12) |
Если запрос и ответ иногда осуществляется на одной частоте и для передачи и приёма у запросчика, так же как и у ответчика, используется одна и та же антенна, то
|
|
(6.13) |
Полученное соотношение иногда называют уравнением сбалансированной системы с активным ответом.
Выражение (6.11) будет справедливо при пассивной радиолокации, когда цель излучает энергию Ец=Еизл от, энергия запросного сигнала на, а направленность излучения характеризуется коэффициентом Gц=Gопрд от.
6.3. Влияние отражений от земной поверхности
на дальность действия РЛС
Если в наземных (корабельных) РЛС применены антенны с широкой диаграммой направленности, радиоволны достигают цели и возвращаются обратно к РЛС как прямым путем, так и отражаясь предварительно от земной поверхности.
Земля в районе точки отражения является достаточно «»гладкой и идеально отражающей поверхностью, цель наблюдается в пределах угла места φум≤100, амплитудные различия слагаемых сигнала несущественны.
Амплитуда напряженности поля излучения с учётом влияния земли при таких условиях равна
|
|
(6.14) |
где ζm – амплитуда напряженности поля для случая свободного пространства;
h – высота расположения антенны РЛС;
φум – угол места цели.
Диаграмма направленности антенны из-за влияния земли
приобретает лепестковый характер с максимумом ![]() в точках, где
в точках, где 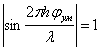 , и
минимальными значениями
, и
минимальными значениями ![]() при
при 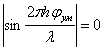 .
.
Число лепестков диаграммы направленности nл и их ширина θум зависят от высоты подъема антенны h и длины волны
|
|
|
Угол места максимума нижнего лепестка равен приблизительно λ/4h.
При подъеме антенны РЛС число лепестков будет увеличиваться при одновременном их сужении, а нижний лепесток будет располагаться ближе к земной поверхности.
Максимальное значение коэффициента направленного действия антенны по мощности с учетом влияния земли, которое принимаем практически равным соответствующему значению коэффициента усиления антенны, обозначим через G0зм. Так как
|
|
|
то
|
|
(6.15) |
Считая, что в РЛС используются для передачи и приёма одинаковые антенны, расположенные на одинаковой высоте h, или одна и та же антенна, получим формулу для максимальной дальности с учётом влияния земли:
|
|
(6.16) |
где Dмакс – максимальная дальность в свободном пространстве.
При обнаружении низколетящих целей, когда направление на цель антенной системы лежит ниже максимума первого лепестка,
|
|
|
и
|
|
|
выражение (6.15) примет следующий вид:
|
|
|
При подстановке этого выражения в (6.6) получим формулу максимальной дальности обнаружения низколетящих целей с учётом влияния земли:
|
|
(6.17) |
Зависимость дальности обнаружения низколетящих целей от энергии излучения и чувствительности приёмника ещё слабее, чем для свободного пространства. Более существенно дальность обнаружения зависит от высоты полета цели H и высоты антенны радиолокационной станции h. Наиболее целесообразным способом увеличения дальности в этом случае является увеличение высоты подъема антенны радиолокационной станции.
6.4. Влияние на дальность действия РЛС ослабления энергии радиоволн в атмосфере
Распространяясь в атмосфере, радиоволны ослабляются из-за потери части электромагнитной энергии, которая поглощается и рассеивается молекулами кислорода и водяного пара, атмосферными осадками, частицами пыли и другими неоднородностями атмосферы.
Ослабление энергии радиоволн осадками происходит как за счёт её поглощения частицами влаги (в основном при малых размерах капель, например при тумане), так и вследствие её рассеяния (при крупных каплях).
Ослабление энергии зависит от длины волны, температуры, влажности, атмосферного давления и параметров частиц, вызывающих поглощение и рассеивание электромагнитной энергии.
Снег и град при одинаковой с дождем интенсивности значительно меньше влияют на величину ослабления энергии, поэтому их можно не принимать во внимание.
Следует иметь в виду, что затухание радиоволн уменьшается более чем в три раза при повышении температуры от 0 до 400 С. Поглощение в кислороде пропорционально квадрату давления и, следовательно, уменьшается с подъемом на высоту. Поглощение в парах воды пропорционально влажности.
При прохождении радиоволн в прямом и обратном направлении через участок атмосферы длиной l км, на котором затухание характеризуется величиной δп дБ/км, общее ослабление энергии будет равно 2lδп дБ. Выражая в децибелах отношение энергий сигналов на входе приёмника без учёта и с учётом ослабления, получим:
|
|
|
Переходя к натуральным логарифмам, находим
|
|
|
т.е. затухание энергии в атмосфере имеет экспоненциальный характер.
При отсутствии ослабления энергии принимаемого сигнала
![]() ,
а при его учёте
,
а при его учёте![]() , где kD– величина, определяемая остальными параметрами,
входящими в выражении для дальности. Из-за наличия ослабления одному и тому же
пороговому значению сигналов (Епрммин) будут соответствовать
различные дальности.
, где kD– величина, определяемая остальными параметрами,
входящими в выражении для дальности. Из-за наличия ослабления одному и тому же
пороговому значению сигналов (Епрммин) будут соответствовать
различные дальности.
В первом случае D=Dmax, а во втором случае, когда требуется компенсировать потери энергии, меньшая дальность: D=Dmax п. Таким образом, для пороговых условий получим
|
|
|
Отсюда находим выражение для максимальной дальности обнаружения с учётом ослабления энергии в атмосфере
|
|
(6.18) |
6.5. Влияние кривизны земной поверхности и атмосферной рефракции на дальность действия
В реальных условиях следует учитывать кривизну земной поверхности, так как способность радиоволн диапазона УКВ к огибанию выпуклых поверхностей выражена очень слабо и дальность действия будет ограничиваться предельным значением Dпред.
При прямолинейном распространении радиоволн предельная дальность, называемая «дальностью прямой видимости», будет равна (рис.6.3)
|
|
|
где Rз=6370 км – радиус Земли.
Так как ![]() и
и ![]() , то
, то
|
|
(6.19) |
При обнаружении высоколетящих космических объектов, например спутников связи, когда величины Rз и Н соизмеримы,
|
|
(6.20) |



Рис.6.3.Предельная дальность действия РЛС при прямолинейном распространении радиоволн.
Неоднородность тропосферных слоев атмосферы по высоте приводит к искривлению траектории радиоволн (рефракции) в вертикальной плоскости. Величина и характер рефракции зависят от скорости изменения коэффициента преломления n при изменении высоты. Величина n определяется формулой
|
|
(6.21) |
где Т0 – абсолютная температура воздуха;
рв – барометрическое давление воздуха, мбар (1 мм рт.ст.=1,3332 мбар);
е – парциальное давление водяного пара (абсолютная влажность), мбар
Учёт влияния рефракции при расчётах распространения радиоволн обычно состоит в замене радиуса Земли Rз его эффективным значением Rз эфф; атмосфера при этом считается однородной (радиоволны распространяются прямолинейно).
Значение эффективного радиуса Земли определяется из уравнения
|
|
|
Для стандартной атмосферы ![]() , и выражение для
предельной дальности с учётом рефракции:
, и выражение для
предельной дальности с учётом рефракции:
|
|
(6.22) |
ГЛАВА 7. ТОЧНОСТЬ ИЗМЕРЕНИЯ КООРДИНАТ И РАДИАЛЬНОЙ СКОРОСТИ ЦЕЛЕЙ
Важнейшим показателем РЛС как измерительного устройства является точность измерения, характеризуемая ошибкой измерения. Общая ошибка измерения по величине и знаку является случайной, так как она вызывается случайными помехами, всегда сопровождающими любое измерение. Случайные ошибки имеют нормальный закон распределения. Для оценки точности используют среднеквадратическую ошибку σ(α), иногда же применяют вероятную (срединную) ошибку или так называемые квазимаксимальные ошибки с указанием соответствующей им вероятности (0,9; 0,95; 0,99). Для нормального закона распределения справедливо соотношение между величинами ошибок различной категории:
|
|
(7.1) |
где Δ(α) – общее обозначение ошибки измерения параметра α.
При оценке точности работы уже существующего радиоустройства наиболее надежным является экспериментальный метод. При этом методе производятся многократные измерения параметра сигнала, отраженного от эталонной цели, координаты (скорость) которой известны с большой точностью.
При каждом измерении вычисляется ошибка
|
|
|
где α0 – истинное значение параметра; αi - его значение при i–м измерении.
Среднеквадратическая ошибка при этом может быть вычислена по формуле:
|
|
(7.2) |
где n – общее количество измерений.
Систематическая ошибка определяется из соотношения
|
|
(7.3) |
где αср – среднее значение параметра, вычисленное по результатам измерений
|
|
(7.4) |
Важнейшими факторами, влияющими на величину общей ошибки, являются: отношение энергий принимаемого сигнала и шумов, форма сигнала, степень согласования характеристик приёмного тракта с характеристиками сигнала, степень совершенства выполнения отдельных узлов, метод отсчёта и допускаемое время, отводимое на измерение, отклонение траекторий распространения радиоволн от расчетных.
Составляющая общей ошибки, определяемая отношением энергий сигнал/шум и формой сигнала, называется потенциальной. Она характеризует предельно достижимую точность работы устройства при прочих идеальных условиях.
7.1. Потенциальная точность измерения одного параметра сигнала
Значение параметра измеряется со случайной ошибкой,
т.е. является случайной величиной. Конечной целью при измерении параметра является
нахождение его среднего значения. Для характеристики точности измерений
необходимо найти также дисперсию или среднеквадратическое значение ошибки.
Наилучшим будет метод, дающий оценку α0 параметра α,
которая при усреднении по множеству измерений совпадает с истинным значением
параметра α0, т.е. ![]() . Такая оценка называется несмещенной.
. Такая оценка называется несмещенной.
Дисперсия оценок дальности и скорости и среднеквадратические ошибки их измерений для входного сигнала в виде одиночного импульса с гауссовой огибающей и линейной частотной модуляцией.
Дисперсия оценки времени прихода сигнала:
|
|
(7.5) |
где q0 – отношение сигнал/шум;
kсж – коэффициент сжатия.
Дисперсия оценки дальности равна:
|
|
(7.6) |
Потенциальная среднеквадратическая ошибка измерения дальности:
|
|
(7.7) |
Формулы (7.6) и (7.7) показывают, что потенциальную точность измерений дальности можно повысить, увеличивая отношение энергий сигнал/шум, уменьшая длительность сигнала и увеличивая девиацию частоты. При отсутствии частотной модуляции (b=0; kсж=1)
|
|
(7.8) |
Таким образом, применение частотной модуляции увеличивает точность измерений дальности по сравнению с немодулированными сигналами.
Для немодулированных сигналов дисперсия оценки скорости равна:
|
|
(7.9) |
Потенциальная среднеквадратическая ошибка измерения дальности:
|
|
(7.10) |
Формула показывает, что точность измерения скорости повышает при увеличении отношения энергии сигнал/шум и длительности сигнала.
7.2. Потенциальная точность одновременного измерения двух параметров
Пусть выходное напряжение является функцией двух параметров α, β и может быть представлено в виде:
|
|
(7.11) |
где
|
|
(7.12) |
и
|
|
(7.13) |
Дисперсии оценок дальности и скорости определяются формулами:
|
|
(7.14) |
|
|
(7.15) |
Потенциальные средние квадратические ошибки измерения дальности и скорости соответственно равны:
|
|
(7.16) |
|
|
(7.17) |
При одновременном измерении времени и частоты точность измерения времени может быть улучшена только лишь одним путем – уменьшением длительности импульса. Но это приводит к ухудшению точности измерения частоты. Применение модуляции не помогает. И наоборот, при одновременном измерении применение модуляции в kсж раз ухудшает точность измерения частоты по сравнению с немодулированным сигналом.
Приходим к выводу, что при одновременном измерении дальности и скорости применение сигналов в виде одиночных импульсов нецелесообразно, так как не позволяет разрешить противоречие между необходимостью уменьшать длительность импульсов при измерении дальности и увеличивать её при измерении скорости. Выход может быть найден только лишь при переходе к другим видам сигналов, например, к «пачке» когерентных импульсов. При таком сигнале точность измерения дальности определяется также выражением (7.16), но точность измерения частоты улучшается примерно в NTи/τи раз.
7.3. Реальная точность измерения параметров сигналов
Реальная точность измерений может быть в некоторых случаях значительно меньше потенциальной. Причинами уменьшения точности являются дополнительные ошибки, связанные с условиями распространения радиоволн, с уменьшением отношения энергий сигнал/шум в различных узлах приёмного тракта из-за несогласованности их характеристик с характеристиками сигнала, с несовершенством отсчётных устройств. Результирующая ошибка измерения параметра α с учётом этих факторов быть представлена в виде
|
|
(7.18) |
где Δ(α)пот – потенциальная ошибка измерения;
Δ(α)распр – ошибка, связанная с условиями распространения;
Δ(α)i – ошибка, возникающая в i–м узле аппаратуры из-за несовершенства его выполнения. Коэффициент ухудшения точности измерения параметра α.
|
|
(7.19) |
Ошибки, связанные с условиями распространения, возникают, главным образом, из-за искривления траекторий распространения, вызываемого непостоянством коэффициента преломления по высоте. Величина коэффициента преломления зависит от концентрации электронов N и несущей частоты
|
|
(7.20) |
Ошибка в измерении дальности для слоистой тропосферы может быть рассчитана по формуле:
|
|
(7.21) |
где τDi – время запаздывания при распространении в i –м слое.
Так как
|
|
|
и
|
|
|
то формула (7.21) может быть представлена в виде:
|
|
(7.22) |
Ошибки измерения дальности также увеличиваются с
уменьшением угла места и увеличением влажности и имеют в неблагоприятных
случаях существенную для точных измерений величину. Ещё больше эти ошибки при
распространении в ионосфере. Множитель ошибки ![]() представляет квадрат
отношения несущей частоты сигнала к среднему значению плазменной частоты.
Плазменная частота может быть определена по формуле
представляет квадрат
отношения несущей частоты сигнала к среднему значению плазменной частоты.
Плазменная частота может быть определена по формуле
|
|
|
где N – число электронов в 1м3.
Ошибка в определении радиальной скорости цели равна
|
|
|
Так как
|
|
|
то при Δφ«φ
|
|
(7.23) |
Угол Δφ зависит от отношения показателей преломления в месте расположения РЛС и у цели и не зависит от коэффициентов преломления промежуточных слоев. Поэтому ошибка измерения радиальной скорости не накапливается по пути распространения.
Ошибки в определении угла места цели, дальности и скорости, вызванные искривлением траекторий, по сути дела являются систематическими. Но практическая невозможность точного их расчёта на всем пути распространения заставляет рассматривать их как случайные. Возможен следующий подход к определению величины ошибки распространения. Пусть, например, требуется учесть ошибку в определении угла места в тропосфере. Предполагая равновероятное появление цели на любом угле места в пределах сектора обзора РЛС, можно определить среднюю ошибку как
|
|
(7.24) |
Считая эту ошибку систематической, следует её компенсировать. При этом среднеквадратическая ошибка будет равна
|
|
(7.25) |
Кроме систематических ошибок имеются истинно случайные ошибки в измерении указанных параметров, вызываемые случайно появляющимися неоднородностями атмосферы. Однако эти ошибки относительно малы.
Анализ ошибок, возникающих в узлах аппаратуры из-за их несовершенства, может быть произведен только лишь для конкретного типа РЛС при подробном рассмотрении её схемы и конструкции. Как правило, решающее влияние на точность измерения выбор выходного устройства измерителя. Наибольшие ошибки возникают при использовании индикаторных устройств с визуальным отсчётом, наименьшие – в случае непрерывного слежения за измеряемым параметром с помощью автоматических выходных устройств непрерывного действия (дальномеров, угломеров, частотомеров). Однако эти устройства могут следить за сигналами только одного объекта.
Когда в качестве выходных устройств применены цифровые вычислительные машины дискретного действия, можно автоматически следить за сигналами многих объектов, причем аппаратурная ошибка может быть сделана сравнимой с потенциальной. Однако эти преимущества достигаются за счёт усложнения выходного устройства.
7.4. Точность измерения положения цели
Если панорамная радиолокационная станция измеряет дальность и азимут наземной (надводной) цели с ошибками Δ(D) и Δ(φаз), то требуется найти ошибку Δl (рис.7.1), определить закон её распределения и числовые характеристики этого закона.



Рис.7.1. К вычислению ошибки определения места цели.
Пусть ошибки Δ(D) и Δ(φаз) взаимонезависимы и имеют нормальные законы распределения со средними значениями, равными нулю. Тогда эти ошибки в прямоугольной системе координат с центром в точке расположения цели:
|
|
|
Эти величины в отдельности также будут иметь нормальные законы распределения, а плотность вероятности величин выражаться формулой
|
|
(7.26) |
Здесь
|
|
|
Ошибка в определении места цели Δl равна
|
|
(7.27) |
И тогда дисперсию линейной ошибки Δl
|
|
|
Переходя к полярным координатам l и θ, получим
|
|
|
Тогда закон распределения Δl:
|
|
(7.28) |
Вероятность того, что ошибка Δl не превысит величины Δl0, равна
|
|
(7.29) |
В общем случае этот интеграл выражается через гипергеометри ческую функцию. В частном случае, когда
|
|
|
выражение () переходит в закон распределения Релея:
|
|
(7.30) |
и
|
|
(7.31) |
При σx=σy=σz=σ имеет следующий вид и описывает распределение Максвелла:
|
|
(7.32) |
ЛИТЕРАТУРА
1. Васин В.В., Власов О.В., Григорин-Рябов В.В., Дудник П.И., Степанов Б.М. Радиолокационные устройства. Изд-во "Советское радио", 1970.
2. Дулевич В.Е. и др. Теоретические основы радиолокации. Изд-во "Советское радио", 1964.
3. Фалькович С.Е. Приём радиолокационных сигналов на фоне флуктуационных помех. Изд-во "Советское радио", 1961.
4. Бакулев П.А. Радиолокация движущихся целей. Изд-во "Советское радио", 1964.
5. Вентцель Е.С. Теория вероятностей. Изд-во "Наука", 1969.
6.Гуткин Л.С. Теория оптимальных методов радиоприёма при флуктуационных помехах. Госэнергоиздат, 1961.
7.Левин Б.Р. Теория случайных процессов и её применение в радиотехнике. Изд-во "Советское радио", 1960.
8.Хелстром К. Статистическая теория обнаружения сигналов. Изд-во иностранной литературы, 1963.
СОДЕРЖАНИЕ
|
ВВЕДЕНИЕ………………………………………………………….…….. |
2 |
|
|
ГЛАВА 1. ОБЩИЕ СВЕДЕНИЯ О РАДИОЛОКАЦИИ……………….. |
3 |
|
|
1.1. |
Задачи и применение радиолокации…………………………….. ... |
3 |
|
1.2. |
Физические основы обнаружения целей и определения их координат и скорости……………………………………………….. |
4 |
|
1.3. |
Тактические данные и технические характеристики РЛС…….…. |
6 |
|
ГЛАВА 2. МЕТОДЫ ИЗМЕРЕНИЯ КООРДИНАТ И СКОРОСТИ ДВИЖЕНИЯ ЦЕЛЕЙ……………………………………………………... |
7 |
|
|
2.1. |
Методы измерения дальности……………………………………… |
7 |
|
2.2. |
Методы измерения угловых координат……………………………. |
16 |
|
2.3. |
Методы измерения радиальной скорости…………………………. |
23 |
|
ГЛАВА 3. ХАРАКТЕРИСТИКИ РАДИОЛОКАЦИОННЫХ ЦЕЛЕЙ… |
24 |
|
|
3.1. |
Основные свойства и классификация……………………………… |
24 |
|
3.2. |
Элементарные цели…………………………………………………. |
27 |
|
3.3. |
Точечные цели………………………………………………………. |
28 |
|
3.4. |
Свойства сигналов, отражённых от распределённых целей……... |
37 |
|
3.5. |
Эффективная отражающая площадь поверхностных целей……... |
40 |
|
3.6. |
Эффективная отражающая площадь объёмных целей……………. |
45 |
|
ГЛАВА 4. РАДИОЛОКАЦИОННЫЙ ОБЗОР…………………………... |
47 |
|
|
4.1. |
Основные положения……………………………………………….. |
47 |
|
4.2. |
Период последовательного обзора…………………………………. |
48 |
|
4.3. |
Виды последовательного обзора…………………………………… |
51 |
|
4.4. |
Программированный обзор………………………………………… |
56 |
|
ГЛАВА 5. ОБНАРУЖЕНИЕ РАДИОЛОКАЦИОННЫХ СИГНАЛОВ.. |
57 |
|
|
5.1. |
Основные положения……………………………………………….. |
57 |
|
5.2. |
Характеристики обнаружения радиолокационных сигналов с полностью известными параметрами……………………………… |
59 |
|
5.3. |
Характеристики обнаружения радиолокационных сигналов с неизвестной начальной фазой……………………………………… |
66 |
|
5.4. |
Характеристики обнаружения радиолокационных сигналов с неизвестной начальной фазой и флюктуирующей амплитудой…. |
70 |
|
5.5. |
Характеристики обнаружения радиолокационных сигналов с неизвестными значениями начальной фазы, амплитуды и частоты………………………………………………………………. |
72 |
|
5.6. |
Характеристики обнаружения сигнала в одном из его возможных положений……………………………………………… |
73 |
|
5.7. |
Коэффициент различимости при обнаружении радиолокационных сигналов……………………………………….. |
76 |
|
ГЛАВА 6. ДАЛЬНОСТЬ ДЕЙСТВИЯ РАДИОЛОКАЦИОННЫХ СТАНЦИЙ…………………………………………………………………. |
77 |
|
|
6.1. |
Дальность действия в свободном пространстве……………….….. |
77 |
|
6.2. |
Дальность действия при активном ответе…………………………. |
82 |
|
6.3. |
Влияние отражений от земной поверхности на дальность действия РЛС………………………………………………………... |
83 |
|
6.4. |
Влияние на дальность действия РЛС ослабления энергии радиоволн в атмосфере……………………………………………... |
85 |
|
6.5. |
Влияние кривизны земной поверхности и атмосферной рефракции на дальность действия…………………………………. |
86 |
|
ГЛАВА 7. ТОЧНОСТЬ ИЗМЕРЕНИЯ КООРДИНАТ И РАДИАЛЬНОЙ СКОРОСТИ ЦЕЛЕЙ……………………………………. |
88 |
|
|
7.1. |
Потенциальная точность измерения одного параметра сигнала… |
89 |
|
7.2. |
Потенциальная точность одновременного измерения двух параметров…………………………………………………………… |
90 |
|
7.3. |
Реальная точность измерения параметров сигналов……………… |
91 |
|
7.4. |
Точность измерения положения цели……………………………… |
93 |
|
|
ЛИТЕРАТУРА………………………………………………………. |
95 |
Конспект лекций по курсу
"Основы радиолокации" для студентов,
обучающихся на специальном факультете
Рассмотрено на заседании кафедры
ТПС (протокол № )
и рекомендовано к печати
Составители:
Абдуазизов А.А.
Маненков В.И.
Нефедова Н.В.
Ответственный редактор Абдуазизов А.А.
Редакционно-корректурная комиссия:
Редактор___________
Корректор__________
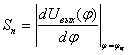 .
.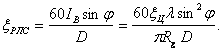
 .
. ,
,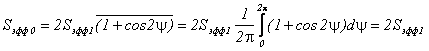 .
.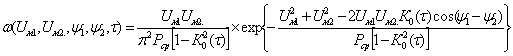
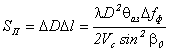
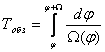 и
и 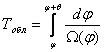 ;
;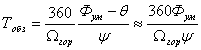 и
и 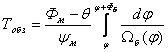 и
и 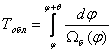 .
.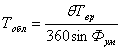 .
.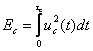 .
.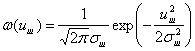 ,
,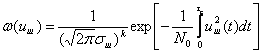
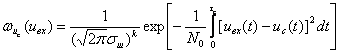
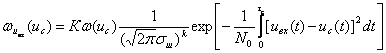
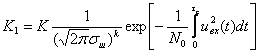
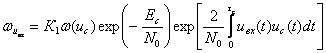
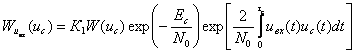
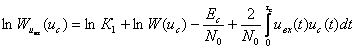 ,
,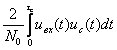 и
и 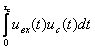 .
.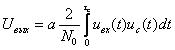
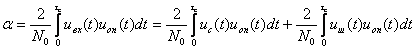
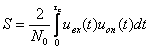 .
. 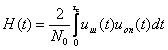 .
. 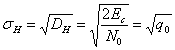 .
.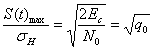 ,
,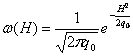 .
.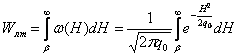 .
. ,
,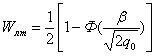 .
.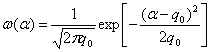 .
. .
.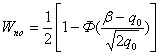 .
.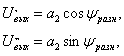 .
.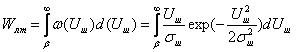 .
.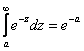 .
.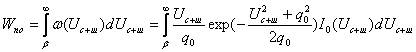 .
.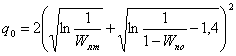 .
. ,
,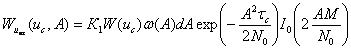 .
.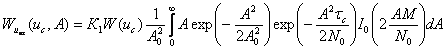 .
.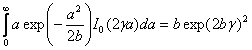 ,
,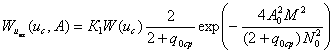 ,
,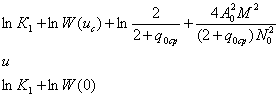
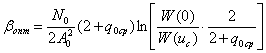 .
.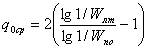 .
.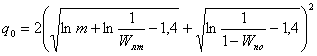 .
.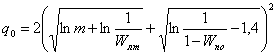 .
.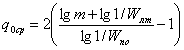 .
.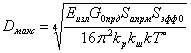
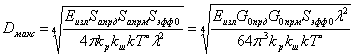 .
.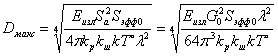 .
.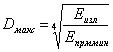 .
.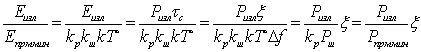 .
.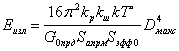
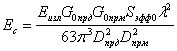 ,
,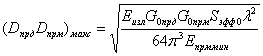 .
.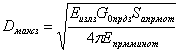 .
.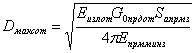 .
.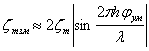 ,
,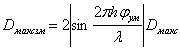 .
.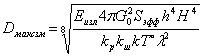 .
.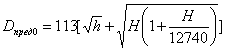 км.
км. 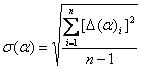 ,
, 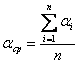 .
. 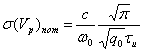 .
. 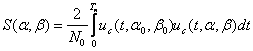
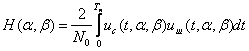
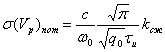 .
. 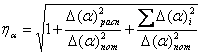 .
. 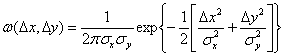 .
.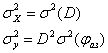 .
.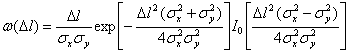 .
.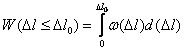 .
.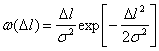
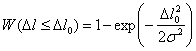 .
.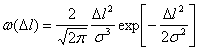 .
.