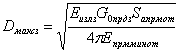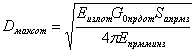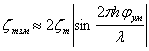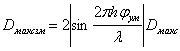УЗБЕКСКОЕ АГЕНТСТВО СВЯЗИ И ИНФОРМАТИЗАЦИИ

ТАШКЕНТСКИЙ УНИВЕРСИТЕТ

ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ

Кафедра Теории

передачи сигналов

ОСНОВЫ ТЕОРИИ РАДИОТЕХНИЧЕСКИХ СИСТЕМ

конспект лекций

Ташкент 2002

ВВЕДЕНИЕ

Дисциплина "Основы теории радиотехнических систем" является одной из дисциплин для подготовки бакалавра в области разработки и исследования РТС различного назначения. Основная задача дисциплины состоит в том, чтобы на базе знаний и умений, полученных в предшествующих и смежных курсах, вооружить будущего бакалавра современными методами статистического анализа и синтеза оптимальных и квазиоптимальных устройств РТС; научить по заданным тактико-техническим характеристикам системы рационально выбрать принцип и структуру построения системы, технические параметры и структуру входящих в систему устройств, произвести оценку выбранных технических решений. Изучение дисциплины должно привить студентам системный подход к проектированию радиотехнических устройств, входящих в состав систем.

          В результате изучения дисциплины студенты должны:

- знать основные понятия о сигналах, характеристики и модели сигналов и помех;

- знать критерии оптимальности обнаружения, принцип работы цифровых обнаружителей и различителей сигналов; различение детерменированных сигналов на фоне белого гауссовского шума;

- уметь оценить неизвестные параметры сигнала с помощью различных методов; иметь понятие об аномальных ошибках измерения и о фильтрации меняющихся параметров сигналов;

- иметь представление об основах построения радиолокационных систем; методы и устройства измерения дальности; методы и устройства измерения угловых координат;

- знать основы теории передачи информации; основные задачи теории информации; пропускную способность дискретных и непрерывных каналов;

- уметь применять теорему кодирования для канала с помехами; знать принципы построения корректирующих кодов, их классификацию, основные характеристики и корректирующие свойства.

ГЛАВА 1. ОСНОВНЫЕ ПОНЯТИ О СИГНАЛАХ

1.1.Сигналы и помехи – переносчики информации. Характеристики и

 модели сигналов и помех

          Информация, передаваемая по каналу связи или извлекаемая в результате измерения, заключена в сигнале. Для оценки информационной емкости сигнала должна быть установлена связь между параметрами сигнала и количеством информации, которое можно передать с помощью данного сигнала.

Прирост количества информации равен:

                                          (1.1)      

где Р₁ – априорная вероятность события, Р₂ – апостериорная вероятность.

При условии, что канал связи является идеальным, т.е. в нем полностью отсутствуют помехи, а также искажения сигналов, событие после приема сообщения о нем становится достоверным, вероятность Р₂ обращается в единицу:

                                                    (1.2)

Количество информации зависит от вероятности Р₁ события до приема сообщения. Чем меньше эта вероятность, т.е. чем больше неопределенность исхода, тем большая информация о нем получается при приеме сообщения.

Сигналы. Сигналом назовем изменяющуюся физическую величину, отображающую сообщение. Известно, что реальные сигналы всегда являются действительными функциями времени. Произвольный сигнал запишется в виде

                                              (1.3)

огибающая А(t) и фаза θ(t) определяются с помощью соотношений

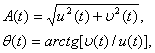                                        (1.4)     

где υ(t) – сигнал, комплексно-сопряженный с u(t).

          Фаза сигнала связана с его мгновенной частотой ω(t) и может быть записана

                                           (1.5)

где ω₀- несущая частота, φ(t)- в общем случае нелинейное слагаемое, β- начальная фаза.

Таким образом, произвольный сигнал

                                   (1.6)

Помехи. Помехи, искажающие сигнал, подразделяют на аддитивные и мультипликативные (модулирующие). Аддитивной помехой n(t) называется такая помеха, которая входит в смесь сигнала с помехой в качестве слагаемого

                                                    (1.7)

Для неаддитивных помех смесь сигнала с шумом запишется

                                                    (1.8)

где ν(t)- мультипликативная помеха.

Наиболее важной из аддитивных помех является собственный шум радиоприемного устройства, всегда присутствующий на его входе. Шум является случайной функцией времени и его можно считать стационарным случайным процессом. Собственный шум обладает равномерным энергетическим спектром во всем диапазоне частот от 0 до бесконечности. Такой шум называют белым.

          Наличие шума, уменьшает достоверность приема сообщений, количество информации уменьшается (информация разрушается). Разрушение информации может быть следствием действия еще различного рода помех: естественных, взаимных и намеренных. Естественные помехи – входные тепловые и дробовые шумы приемника, отражения радиосигналов от природных образований (суши, моря и т.п.), излучения Солнца или иных внеземных источников. Взаимные – мешающие сигналы, возникающие на входе приемного устройства из-за излучения других радиотехнических устройств, также производящие полезную передачу или извлечение информации. Намеренные – создаются сознательно с целью воспрепятствовать получению противником полезной для него информации.

Модели радиосигналов. В теории обнаружения и оценки параметров пользуются определенными моделями сигналов. Модель должна, с одной стороны, удовлетворять требованию близости ее к реальному сигналу и, с другой – позволять достаточно просто проводить теоретический анализ, результаты которого можно распространить на более общие случаи.

Простейшей моделью является сигнал с полностью известными параметрами:   

                                          (1.9)

Более сложной моделью является сигнал с неизвестной начальной фазой:

                                     (1.10)

Модель сигнала со случайными амплитудой и начальной фазой запишется так: 

                               (1.11)

где В – случайная величина, распределение которой можно считать релеевским

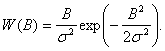                                            (1.12)

Модель в виде нефлюктуирущей по амплитуде пачки со случайными начальными фазами отдельных импульсов, причем β_k – случайные независимые величины:

                       (1.13)

Эта модель соответствует некогерентной пачке импульсов.

Если все начальные фазы  β_k равны β, то имеем когерентную пачку радиоимпульсов. Для модели такого сигнала можно записать:

                             (1.14)

Для модели сигнала, соответствующей пачке радиоимпульсов с флюктуирующей огибающей и со случайными начальными фазами отдельных радиоимпульсов можно записать так:

                  (1.15)

1.2. Корреляционные функции сигналов

          В практике часто возникает необходимость в характеристике, которая давала бы общее представление об  изменении сигнала во времени без разложения его на гармонические составляющие. Подобная «временная» характеристика особенно важна для анализа случайных сигналов и шумов, а также для обнаружения сигналов в шумах, когда решение о наличии сигнала принимается после сличения смеси сигнал + шум с заранее известной копией принимаемого сигнала.

          В качестве такой временной характеристики широко используется автокорреляционная функция сигнала.

          Для детерминированного сигнала s(t) конечной длительности автокорреляционная функция определяется следующим выражением:

                                         (1.16)

где t - величина временного сдвига сигнала.

          Для оценки степени связи между двумя различными сигналами s₁(t) и s₂(t) используется взаимная корреляционная функция, которая определяется выражениями:

                  (1.17)

          Корреляционная функция стационарного процесса при τ = 0 определяется:

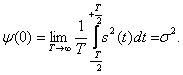                                     (1.18)

Отсюда видно, что Y(0) совпадает с дисперсией (средней мощностью) процесса.

          Установление связи между спектральной и корреляционной характеристиками имеет особенно важное значение для сигналов и шумов типа стационарных случайных процессов.

          Существует теорема Винера-Хинчина, утверждающая, что автокорреляционная функция и энергетический спектр стационарного случайного процесса связаны между собой интегральными преобразованиями Фурье:

                                    (1.19)

Здесь W₁(w) – энергетический спектр, определяемый на всей оси частот -∞<w<+∞. Если определять энергетический спектр только на положительной оси частот, имеет место соотношение:  При этом

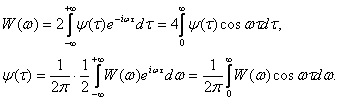               (1.20)

Из этого выражения вытекает:

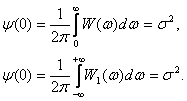                                    (1.21)

На основании всех этих выражений можно сделать заключение: чем шире энергетический спектр случайного процесса, тем меньше время корреляции и, соответственно, чем больше время корреляции, тем уже спектр процесса.

1.3. Функция неопределенности

                   Квадрат модуля двумерной функции корреляции │R(τ,Ω)│² называют функцией неопределенности. Эта функция есть уравнение поверхности, расположенной над плоскостью Ω, τ. Абсолютное максимальное значение эта функция имеет при τ = 0 и Ω= 0:  

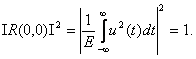                                (1.22)

Площадь, представляющая собой основание цилиндра с высотой, равной главному максимуму, и объемом, равным объему, ограниченному всей поверхностью , называется эквивалентной площадью неопределенности:

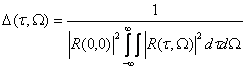                           (1.23)

Объем под поверхностью функции не зависит от формы сигнала и равен:

                                      (1.24)

при этом,                                      (1.25)

Из соотношения (1.25) следует, что имеется предел совместимой разрешающей способности по дальности и скорости. Сжатие функции по одной оси в плоскости τ, Ω, приводит к расширению ее по другой оси так, что объем остается постоянным. Это явление известно как «принцип неопределенности» в радиолокации.

                   Функция неопределенности (форма ее поверхности, область сильной корреляции) определяется выбором зондирующего сигнала. Отсюда выбор тонкой структуры сигнала определяет, в первую очередь, разрешающую способность по дальности и скорости.

ГЛАВА 2. ОБНАРУЖЕНИЕ И РАЗЛИЧЕНИЕ СИГНАЛОВ

          В литературе задача оценки сообщения, принадлежащего дискретному конечному ансамблю, называется обычно «задачей различения m сигналов». Дискретная модель хорошо подходит для описания сообщений в цифровых системах передачи информации, таких, как цифровая телеметрическая система или система передачи дискретных сообщений. Объем ансамбля определяется выбранным методом приема (посимвольным, пословным и т.д.). Число m при пословном приеме равно числу кодовых комбинаций (команд); при посимвольном приеме – основанию кода. В частности, при посимвольном приеме двоичного кода m=2.

Практически работа любой радиосистемы начинается с обнаружения сигнала, при этом по наблюдаемой реализации смеси требуется определить, имеется ли в смеси сигнал или он отсутствует. Если случай отсутствия сигнала можно отождествить с одним значением сообщения х₀, а наличия – с другим х₁, то задача обнаружения сведется к задаче различения двух значений сообщения и принципиально ничем не будет отличаться от задачи посимвольного приема двоичной информации. Может встретиться ситуация, например, в системе передачи дискретных сообщений, когда на заданном интервале времени может или передаваться сигнал, соответствующий одному из возможных значений сообщения, или ничего не передаваться. Система обработки в этом случае должна вынести решение о том, имеется ли в наблюдаемой смеси сигнал, и если да, то какой именно. В литературе эта задача называется задачей различения m сигналов с обнаружением. Ясно, что и эта задача приводится к общей задачи различения m + 1 сигналов, если в ансамбль сообщений ввести дополнительный («нулевой») сигнал, соответствующий отсутствию сигнала в смеси.

          Таким образом, одной из наиболее важных проблем радиообнаружения является отыскание оптимальных способов выделения сигналов при наличии помех. Оптимальными методами обнаружения называются такие, которые обеспечивают наилучшее выделение сигналов из смеси сигнала с помехой.

          В результате  процесса обнаружения должно быть выдано решение о наличии или отсутствии сигнала в смеси, действующей на входе обнаружителя.

2.1. Обнаружение сигналов как статистическая задача

          Пусть на вход обнаружителя поступает сумма сигнала u(t) и шума n(t), представляющая собой непрерывный случайный процесс, x(t) = au(t) + n(t); u(t) – полностью известный сигнал, т.е. такой сигнал, единственным неизвестным параметром которого является сообщение а. В простейшем случае при обнаружении сообщения а может принимать два значения: а = а₀ = 0 или а = а₁ = 1.

          Когда а₀ = 0, сигнал на входе обнаружителя отсутствует, когда  а₁ = 1, сигнал на входе обнаружителя присутствует. Априорные вероятности присутствия и отсутствия сигнала на входе обнаружителя равны Р(а₁) и Р(а₀) соответственно.

Обнаружитель анализирует колебание x(t) в течение заранее выбранного (конечного) интервала времени Т и должен на основании анализа воспроизвести сообщение а. Функцию x(t), ограниченную во времени Т, будем называть реализацией колебания.

В настоящее время для решения подобных задач широко применяются методы математической статистики. Основной задачей ее является установление законов распределения случайных величин на основе результатов наблюдения над этими величинами.

В случае обнаружения сигналов реализация колебания x(t) является непрерывной функцией времени (при непрерывном или дискретном сигнале u(t) в смеси) с ограниченным спектром.

Представим x(t) выборочными значениями(x₁, …,x_n), взятыми в соответствии с теоремой Котельникова с интервалом Δt = 1/F, где F – ширина спектра колебания x(t). При этом, объем выборки определится соотношением:

n = T/ΔT = TF                                               (2.1)

На основании анализа выборки x₁, …,x_n обнаружитель должен оценить параметр а. Очевидно точность оценки зависит от объема выборки при неограниченном времени наблюдения Т. Однако на практике Т ограниченно, а с увеличением объема выборки при Т = const погрешность оценки не устремляется к нулю. Выборка, у которой n → ∞ при Т = const, называется непрерывной.

Поскольку в задачах обнаружения оценка дискретная (а=0 или1), при конечном объеме выборки можно лишь с некоторыми вероятностями высказать статистические гипотезы. Следовательно, решение задачи обнаружения сводится к проверке двух альтернативных (противоположных) статистических гипотез. Гипотеза H₁- сигнал во входной смеси есть и гипотеза H₀- сигнала нет.

Решение статистической задачи обнаружения сигнала в шуме имеет следующую последовательность:

¨ Выбор и обоснование критериев оптимальности.

¨ Нахождение математического правила решения задачи оптимального обнаружения.

¨ Реализация правила решения с помощью радиотехнических средств (нахождение структурной схемы обнаружителя).

¨ Исследование характеристик оптимального обнаружителя.

¨ Сравнение оптимального и реального обнаружителей.

2.2. Критерии оптимальности обнаружения. Отношение правдоподобия

Критерием оптимальности называется правило, по которому из всех

возможных обнаружителей можно выбрать наилучший.

          Пусть сообщение принимает два значения: а₀ = 0 и а₁ = 1 с априорными вероятностями Р(а₀) и Р(а₁) соответственно.

          В результате наблюдения выборки x₁, …,x_n должно быть получено одно из двух взаимоисключающих решений: А₁ – сигнал есть, А₀ - сигнала нет. Каждая возможная выборка представляется в многомерном пространстве одной точкой. Оптимальный обнаружитель должен разделить пространство выборок на два подпространства Х₁ и Х₀ (соприкасающихся, но непересекающихся) (рис. 2.1.). Если точка М, соответствующая

k-й выборке  (x₁, …,x_n), попадет в подпространство Х₁, - принимается решение А₁, в противном случае принимается решение А₀.

          При решении задачи возможны ошибки двух видов – ложные тревоги (с вероятностью Р_л) и пропуски сигналов (с вероятностью Р_п). Ложные тревоги имеют место в случае, когда в отсутствии сигнала выборка попадает в пространство Х₁. Пропуски сигналов имеют место, если при наличии сигнала на входе обнаружителя выборка попадает в Х₀.

Из рис. 2.1. следует, что если подпространство Х₁ выбрать равным нулю, то Р_л = 0, Р_п = 1. Если же выбрать равным нулю подпространство Х₀,  то Р_л = 1, Р_п = 0. Таким образом, путем изменения границ подпространств Х₁ и Х₀ можно получить любое соотношение между вероятностями Р_л и Р_п. Уменьшая Р_л, мы тем самым увеличиваем Р_п, и наоборот.

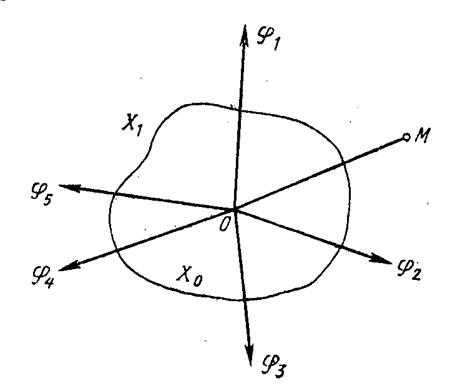
Рис. 2.1. Пространство выборок

Оптимальный обнаружитель должен наилучшим образом по определенному критерию разделить пространство выборок Х на два подпространства: Х₁ и Х₀. Наиболее распространенными критериями оптимальности обнаружения являются следующие:

1. Критерий минимума среднего риска

                                 (2.2) 

где r_л и r_п – «весовые» коэффициенты, выбираемые, исходя из значимости каждой ошибки.

Величина называется средним риском.

2. Критерий минимальной «взвешенной» вероятности ошибки

                                             (2.3)

где a и b – весовые коэффициенты.

3. Критерий минимума вероятности полной ошибки (или критерий

идеального наблюдателя, или критерий Зигерта-Котельникова)

                               (2.4)

4. Критерий Неймана – Пирсона

                                         (2.5)

Величиной Р_л задаются, исходя из физической постановки задачи. При этом Р_п минимизируют.

Если априорные вероятности Р(а₀) и Р(а₁) неизвестны, что имеет место во многих случаях, то критерием пользоваться невозможно. В радиолокации чаще пользуются критерием Неймана – Пирсона.

Рассмотрим подробнее критерий минимальной «взвешенной»

вероятности ошибки.

Обозначим отношение тогда

                                                (2.6)

где                                                                    (2.7)

                     (2.8)

          Если при наличии сигнала выборка (х₁,…,х_n) попадет в область Х₁, то имеет место правильное обнаружение. Вероятность правильного обнаружения

              (2.9)

откуда

                    (2.10)

Из (2.6), (2.8) и (2.9)

           (2.11)

Следовательно, оптимальный обнаружитель должен обеспечивать максимум интеграла в (2.11)

         (2.12)

Это возможно при положительной подынтегральной разности

> 0;                          (2.13)

т.е.                        > .                            (2.14)

Таким образом, оптимальный обнаружитель должен вычислять величину

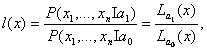                                   (2.15)

определяемую отношением функций правдоподобия и и называемую отношением правдоподобия. Если сравнить с некоторым порогом , то

при   > - сигнал есть,

при   < - сигнала нет.

Все критерии дают оптимальное решение задачи обнаружения, основанное на вычислении отношения правдоподобия и сравнения его с порогом. Отличаются критерии лишь выбором порога.

Для критерия минимума среднего риска

                                         (2.16)

Для критерия минимума взвешенной вероятности ошибки

                                                (2.17)

Для критерия Неймана – Пирсона  задается и минимизируется значение Р_п.

2.3. Бинарное обнаружение полностью известного сигнала

Положим, что сигнал u(t) известен точно. Сообщение а принимает два значения: а=а₀=0 и а=а₁=1, с априорными вероятностями Р(а₀) и Р(а₁) соответственно.

          Колебание на входе обнаружителя x(t)=au(t)+n(t), n(t) – нормальный белый шум.

          На основании теоремы Котельникова представим колебание x(t) выборкой (х₁, …х_n) и найдем функцию правдоподобия для выборки в отсутствие сигнала

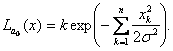                              (2.18)

          Функция правдоподобия для выборки в присутствии сигнала

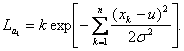                           (2.19)

          В выражениях (2.18) и (2.19) дисперсии равны в силу физической симметрии и определяются соотношением

                              (2.20)

где N₀ – спектральная мощность шума; F=1/Dt.

          Подставим значения s² в выражения (2.18) и (2.19) и перейдем от суммы к интегралу, устремив при Т=const. Тогда

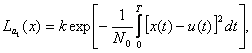                 (2.21)

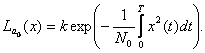                           (2.22)

Отношение правдоподобия

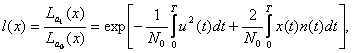        (2.23)

где 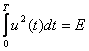- энергия входного сигнала; 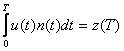- корреляционный интеграл.

Отношение правдоподобия для полностью известного сигнала имеет следующий вид:

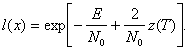                            (2.24)

Для вынесения решения необходимо сравнить с порогом ограничения .

Если > - сигнал есть, 

Если <  - сигнала нет.

Реализовать правило решения (2.24) радиотехническими методами, т.е. построить обнаружитель, который вычислял бы  и затем сравнивал с порогом, сложно. Желательно отыскать более простое правило решения.

Поскольку при Е=const зависит только от корреляционного интеграла z(T) и эта зависимость монотонная, то вместо  можно установить более простое правило z(T) и сравнивать с порогом z₀.

Если z(T) > z₀ – сигнал есть,

Если z(T) < z₀  - сигнала нет.

Схема оптимального обнаружителя представлена на рис. 2.2 и состоит  из перемножителя, интегратора и порогового устройства (ПУ).

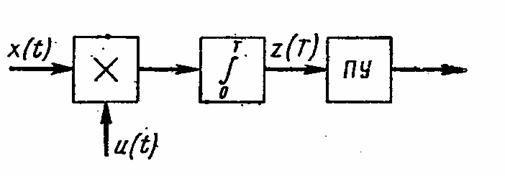
Рис. 2.2. Схема оптимального обнаружителя

          При вычислении корреляционного интеграла z(T) осуществляются переход от многомерного распределения n выборочных значений напряжения на входе обнаружителя к одномерному распределению напряжения z(T) на его выходе в момент времени Т в результате накопления (суммирования) n выборочных значений в течение длительности выборки Т.

          Если входная выборка представляет собой шум n, то z_n(T) определяет напряжение шума на выходе коррелятора. Если выборка – смесь сигнала с шумом, то z_nc(T) можно рассматривать на выходе как аддитивную смесь, поскольку операции суммирования и интегрирования линейные.

          Переход от суммы выборочных значений при n→∞ и Т=const к интегралу осуществляется на основании теоремы Котельникова. Напряжение шума на выходе коррелятора

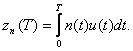                                      (2.25)

Напряжение смеси

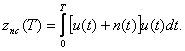                           (2.26)

Эти напряжения есть максимальные значения отклика коррелятора на шум и смесь соответственно. Превышение порога z₀ величиной z_nc(T) есть правильное обнаружение и вероятность превышения и называется вероятностью правильного обнаружения Р₀, а превышение порога z₀ величиной z_n(T) с вероятностью Р_л называется ложной тревогой.

Основными показателями обнаружителя являются рабочие характеристики. Каждая характеристика определяет зависимость Р₀, Р_л и q²(q²-отношение сигнал/шум). На рис. 2.3 даны качественные характеристики.

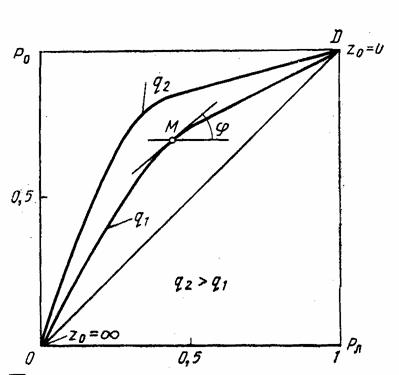
Рис. 2.3. Качественные характеристики обнаружителя.

 Из анализа этих характеристик следует:

¨ вероятность правильного обнаружения Р₀=0 при вероятности ложной тревоги Р_л=0.

¨ чем больше отношение сигнал/шум при заданной вероятности ложной тревоги Р_л, тем больше вероятность правильного обнаружения Р₀.

¨ Если изменять порог z₀ от 0 до ∞, то Р₀ и Р_л будут изменяться от 1 до 0.

По характеристикам можно определить пороговое отношение

сигнал/шум, которое удовлетворяет заданным вероятностям Р₀ и Р_л. Найденному значению  и заданной вероятности Р_л соответствует точка М. Тангенс угла наклона касательной к рабочей характеристике в точке М определяет необходимую величину порога.

.                                                (2.27)

Для расчета и построения характеристик обнаружения необходимо знать закон распределения отклика коррелятора z(T).

          В отсутствии сигнала отклик определяется шумами на входе обнаружителя и может дать ложную тревогу. Величина отклика сравнивается с порогом z₀ и вероятностью того, что z_n(T) превысит порог z₀, называется вероятностью ложной тревоги.

          Закон распределения  z_n(T) будет нормальным с нулевым средним значением. Дисперсия, которая определяет мощность шума на выходе коррелятора:

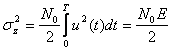.                                 (2.28)

Сренеквадратичное напряжение шума на выходе коррелятора  Закон распределения отклика коррелятора z_n(T) на шум n(t)

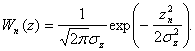                            (2.29)

С увеличением порога ограничения z₀ вероятность Р_л уменьшается. Аналитически вероятность ложной тревоги определяется выражением

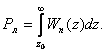                                           (2.30)

В присутствии на входе обнаружителя отклик коррелятора на смесь сигнала с шумом

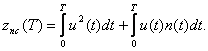                        (2.31)

Первый интеграл выражения (2.31) равен Е и определяет амплитуду напряжения на входе коррелятора, которое численно равно энергии входного сигнала и, следовательно, является максимально возможной величиной. Второй интеграл определяет флюктуацию с нулевым средним значением отклика (напряжение шумов) коррелятора.

Случайная величина z_nс(T) распределена по нормальному закону

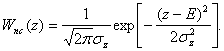                   (2.32)

Распределения W_n(z) и W_nc(z) отличаются средними значениями, дисперсии откликов одинаковы.

Вероятность правильного обнаружения вычисляется по формуле

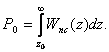                                       (2.33)

После преобразований вероятность правильного обнаружения

                               (2.34)

Порог ограничения вычисляется в соответствии с выбранным критерием оптимальности.

Зависимость Р₀ от q² при Р_л=const называется характеристикой обнаружения. Для различных значений Р_л можно построить семейство характеристик обнаружения. Характеристики обнаружения для полностью известного сигнала изображены на рис. 2.4

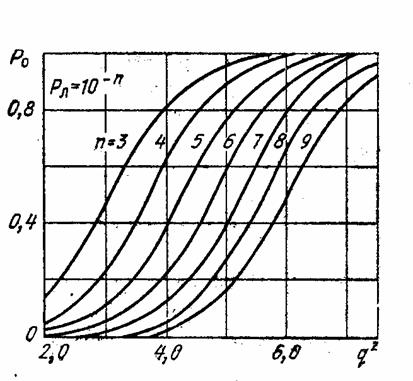
Рис. 2.4. Характеристики обнаружения для полностью известного сигнала

2.4. Обнаружение сигнала со случайной начальной фазой

          Рассмотрим задачу обнаружения сигнала, у которой фаза высокочастотного колебания изменяется по случайному закону. Плотность распределения фазы равномерна в пределах 0….2π. Отношение правдоподобия в этом случае будет еще и функцией фазы β. Энергия сигнала мало зависит от β, поэтому считаем ее постоянной.

Выражение для корреляционного интеграла через огибающую и фазу запишется в виде:

                (2.35)

где

.

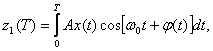
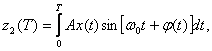
Отношение правдоподобия для полностью известного сигнала равно:

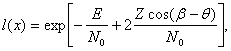                            (2.36)

которое является случайной функцией β.

Отношение правдоподобия для сигнала со случайной фазой:

                           (2.37)

Показатель экспоненты является постоянной величиной, - монотонной функцией Z(T), поэтому оптимальным правилом решения задачи обнаружения сигнала является вычисление корреляционного интеграла Z(T). Затем Z(T) сравнивается с порогом Z₀.

Если Z(T) > Z₀ – сигнал есть, если Z(T) < Z₀ – сигнала нет.

Структурная схема обнаружителя, включающая два квадратурных канала, представлена на рис. 2.5  В каждом канале вычисляется корреляционный интеграл z₁ (T) и z₂(T) соответственно. В квадратичном детекторе (Кв.Д.) осуществляется операция возведения в квадрат; после вычисления величины  производится сравнение с порогом Z_0, который устанавливается в соответствии с выбранным критерием оптимальности.

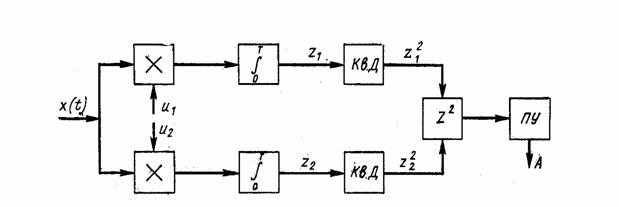
Рис. 2.5. Структурная схема обнаружителя

В качестве опорных напряжений на умножителях используются сдвинутые по фазе на π/2 колебания высокой или промежуточной частоты  и В результате отклик Z² не зависит от случайной фазы сигнала, так как

Вероятность правильного обнаружения равна:

                           (2.38)

где - относительный порог ограничения.

2.5. Бинарное обнаружение сигнала со случайными амплитудой и начальной фазой

Для сигнала  среднеквадритичное значение амплитуды принять равным единице, то выражение для отношения правдоподобия запишется в следующем виде:

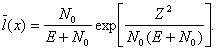                         (2.39)

Схема оптимального обнаружителя сигнала со случайными амплитудой и начальной фазой не отличается от схемы оптимального обнаружителя сигнала со случайной фазой. По-прежнему оптимальной является квадратурная схема обработки. Изменяется только оптимальный порог, который вычисляется по формуле

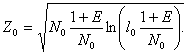                              (2.40)

По этой зависимости можно построить характеристики обнаружения

.                                             (2.41)

Особенность характеристик обнаружителя со случайными амплитудой и начальной фазой состоит в том, что с ростом q² вероятность обнаружения увеличивается сначала быстро, после достижения значений q²=0,5…0,6 это увеличение замедляется, а затем становится очень медленным.

Таким образом, характеристики обнаружения для сигнала со случайной начальной фазой сдвигаются в сторону увеличения отношения сигнал/шум, т.е. для обнаружения сигнала требуется   большое напряжение его на входе, чем для полностью известного сигнала. Для сигнала со случайной амплитудой и начальной фазой отклик является случайной функцией амплитуды и фазы, поэтому необходимо усреднить отношение правдоподобия и по амплитуде, и по фазе. Характеристики обнаружения сдвигаются еще правее, за исключением участка, где отношение сигнал/шум меньше единицы. Флюктуации амплитуды при q² < 1 несколько увеличивают вероятность обнаружения.

2.6. Обнаружение сигнала в виде пачки радиоимпульсов

В радиолокации часто применяют сигналы, представляющие собой последовательность из N импульсов, которую для краткости называют пачкой импульсов.

Каждый импульс u_i(t) такой пачки полностью характеризуется амплитудой a_i, частотой f_i, начальной фазой φ_i, длительностью τ_i, моментом возникновения t_i.

Если зависимость между всеми параметрами импульсов пачки в месте приема полностью известна, то такие импульсы и такая пачка называются когерентными. В противном случае пачка называется некогерентной.

2.6.1. Когерентная пачка импульсов с полностью известными параметрами

Пачка с полностью известными параметрами является частным случаем, полностью известного сигнала и для нее справедливы все расчетные формулы для известного случая. Энергия сигнала u(t): 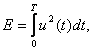 поэтому для пачки энергия:  где Е_i – энергия i-го импульса.

Следовательно, все приведенные выше формулы для вероятностей ошибок будут справедливы и для пачки импульсов, если в них понимать под Е энергию всех импульсов пачки, равную сумме энергий всех N импульсов пачки. Если суммарная энергия пачки импульсов такая же, как и у одиночного импульсного сигнала, ошибки обнаружения не изменяются.

Структурная схема обнаружителя для пачки подобна изображенной на рис. 2.2.  Однако в этом случае на перемножитель нужно подавать «копию» сигнала в виде пачки радиоимпульсов. Максимальное значение отклика коррелятора будет в момент окончания пачки.

2.6.2. Некогерентная пачка радиоимпульсов с независимыми флюктуациями амплитуды

Сигнал в этом случае запишется так:  Оптимальное правило решения будем искать на основании критерия максимума отношения правдоподобия. Для k-го импульса отношение правдоподобия :

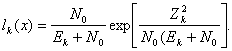                     (2.42)

При независимых флюктуациях амплитуды импульсов отношение правдоподобия для всего сигнала можно представить в виде произведения отношений правдоподобия для импульсов, тогда:

                                         (2.43)

После выполнения операции умножения в показателе экспоненты будет сумма откликов на каждый импульс пачки. Поскольку  монотонно изменяется с изменением этой суммы, то в этом случае нужно вычислять

                                        (2.44)

Так же, как и для одиночного импульса, отклик Z(T) будет пропорционален энергии входного сигнала, т.е. энергии пачки импульсов. Результат сравнивают с порогом Z₀, выбранным на основании критерия оптимальности. Схема обнаружителя аналогична данной на рис. 2.5.  Разница будет состоять в том, что копии сигналов, подаваемых на перемножители, в данном случае представляют собой пачки радиоимпульсов.

2.7. Различение детерминированных сигналов на фоне белого гауссовского шума

                   Корреляционная функция белого шума со спектральной плотностью N₀ равна  После соответствующих преобразований получаем оптимальный аналоговый алгоритм различения сигналов на фоне аддитивного белого гауссовского шума: принимается решение о том, что передан сигнал S_k(t), если

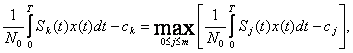(2.45)

где с_j определяется по формуле   в которой параметр 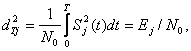 т.е. равен отношению энергии Е_j сигнала S_j(t) на интервале наблюдения к спектральной плотности белого шума.

Для ортогональных сигналов :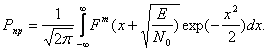

2.8. Принцип работы цифровых обнаружителей и различителей сигналов

          Оптимальные алгоритмы обнаружения и различения сигналов, как известно, заключаются в накоплении сигнала за длительность входной реализации, сравнении с порогом и измерении параметров сигнала. Реализация алгоритмов в аналоговой форме имеет существенные недостатки:

¨ Аналоговым накопителям свойственно насыщение, в результате которого уменьшается отношение сигнал/шум при накоплении сигналов.

¨ Результаты накопления изменяются в процессе эксплуатации за счет нестабильности элементов динамической памяти.

¨ Нет возможности полной автоматизации процесса обработки сигналов.

¨ Оценка параметров сигналов в процессе обзора сопровождается ошибками, существенно превышающими потенциальные.

Цифровые алгоритмы квазиоптимальны за счет потерь в отношении сигнал/шум при квантовании смеси по амплитуде и дискретизации по времени. Кроме того, реализация алгоритмов в цифровой форме осуществляется на стандартных элементах вычислительной техники, что упрощает конструкции, снижает вес и габариты, увеличивает надежность.

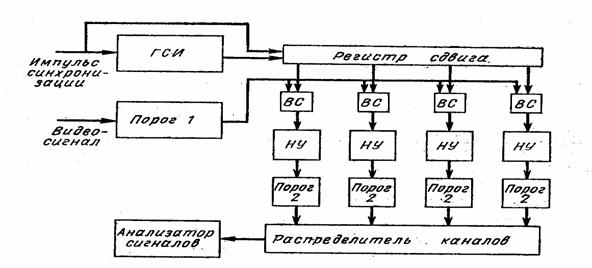
Рис. 2.6. Цифровая схема обнаружения

На рис. 2.6 дана простейшая схема цифровой схемы обнаружения сигналов. Схема включает квантователь по уровню смеси сигнала с шумом (пороговое устройство 1), дискретизатор по времени, выполненный в виде генератора стандартных импульсов (ГСИ), многоканальную схему измерения дальности, включающую регистр сдвига, вентили совпадений (ВС) и накопители сигналов (НУ), распределитель каналов (коммутатор) и анализатор сигналов.

2.9. Дискретизация и квантование непрерывных сигналов

                   Длительность и период дискретизации выбирают так, чтобы последовательность дискретных значений непрерывного сигнала в течение времени наблюдения позволила восстановить исходный сигнал с заданной точностью.

Вероятность обнаружения смеси Z(t):

                       (2.46)

Из этого выражения следует, что с увеличением μ увеличивается вероятность обнаружения сигнала и тем больше, чем меньше исходная вероятность Р₀₁.

                   Следовательно, увеличение периода квантования приводит к увеличению вероятности обнаружения сигнала, но при этом уменьшается разрешающая способность и точность измерения дальности. Поэтому период квантования Т₀ выбирается из условий получения заданной точности измерения при ограниченной сложности измерительного устройства.

                   Квантование амплитуд сигналов на два уровня означает определение наличия или отсутствия сигнала в дискретном по времени выборочном значении сигнала. На выходе бинарного квантователя появляются 1 и 0 в присутствии сигнала с вероятностью правильного обнаружения

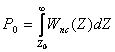     (2.47)

и пропуска сигнала Р_п = 1 – Р₀, а в отсутствие сигнала с вероятностью ложной тревоги

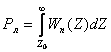(2.48)

и правильного необнаружения  Р_н = 1 – Р_л. Функции W_nc(Z) и W_n(Z) – распределение смеси сигнала с шумом и шума на выходе детектора огибающей.

После логарифмирования отношения правдоподобия ) получаем условие оптимального обнаружения квантованной пачки в виде:

ГЛАВА 3.  ОЦЕНКА НЕИЗВЕСТНЫХ ПАРАМЕТРОВ СИГНАЛА

          Определим элементарный сеанс связи как совокупность следующих операций:

¨ выбор источником одного сообщения из множества возможных и отправление его получателю;

¨ преобразование посланного сигнала под действием помех в реализацию смеси, которая наблюдается получателем;

¨ принятие получателем по наблюдению реализации смеси решения о том, какое сообщение выбрал в данном случае источник, т.е. оценка сообщений. 

          Применение некоторого правила принятия решения (оценивания) – это установление соответствия между наблюдаемой получателем реализацией смеси и одной из возможных оценок.

          Функция двух переменных r(x_i, x_j^*), значение которой (в некотором масштабе) равно стоимости решения x_j^* при условии, что передавалось сообщение x_i , называется функцией потерь (риска, штрафа и т.д.) Если оценка ошибочна, т.е. при истинном передаваемом сообщении x_i принято решение  x_j^*≠ x_i , то неправильные действия получателя повлекут за собой некоторые потери r, которых бы не было, будь оценка безошибочной.

3.1. Байесовские оценки при различных функциях потерь

          Измерение координат и параметров сигналов является задачей статической в силу флюктуационной природы помех в смеси х(t) и в силу случайного (непредсказуемого) изменения параметров сигнала. Задачи оценки параметров сигнала и обнаружения сигнала имеют общую статистическую модель.

          Поскольку потери   r(x_i, x_j^*) в каждом элементарном сеансе случайны из-за случайности x_i, и x_j^* , построение критерия после задания функции потерь требует определения статистически устойчивого параметра, характеризующего качество системы на множестве сеансов. Чаще всего применяется подход, основанный на использовании математического ожидания потерь, при котором гарантируется минимум суммарных потерь. Математическое ожидание потерь:

 (3.1)

называется средним риском, а система, минимизирующая средний риск (при условии, что функция потерь не зависит от правила решения), называется оптимальной байесовой системой.

    (3.2)

где - совместное распределение вероятностей сообщения и оценки.

   (3.3)

        (3.4)

          Функцию p_z называют условным средним риском при данной реализации смеси, а р_х – условным средним риском при данном истинном сообщении. Условный средний риск при данном сообщении р_х может служить характеристикой качества системы, а условный средний риск при данной реализации смеси р_z используется для определения структуры оптимальной байесовой системы.

3.2. Неравенство Рао – Крамера

          Существует неравенство, с помощью которого можно определить нижнюю границу среднеквадратических ошибок при использовании любых оценок параметра. Предположим, что границы области действительной оси, где плотность распределения  отлична от нуля, не зависит от . Это условие выполняется, например, если на всей действительной оси и для х ≥ 0. Предположим, кроме того, что функция  дифференцируема по параметру .

          Введем новое обозначение

   (3.5)

чтобы подчеркнуть зависимость функции правдоподобия от неизвестного параметра .

          Неотрицательная величина

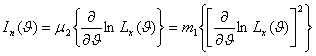 (3.6)

называется информацией по Фишеру о параметре , содержащейся в выборке х.

          Найдем искомую нижнюю границу дисперсии оценок (неравенство

Рао - Крамера)

  (3.7)

          Правая часть неравенства является также нижней границей среднеквадратических отклонений оценок от оцениваемого параметра.

          Для несмещенных оценок

(3.8)

3.3. Оценки максимального правдоподобия, их свойства и связь с байесовскими

          Рассмотрим оценку векторного параметра , оптимальную по критерию максимального правдоподобия. Так как логарифм – монотонная функция, то экстремумы функций L_x() и ln L() достигаются при одинаковых аргументах . Поэтому критерий максимального правдоподобия можно представить в виде:

(3.9)

Функцию правдоподобия можно заменить статистикой отношения правдоподобия

(3.10)

где  - фиксированный вектор.

Система уравнений максимального правдоподобия

    (3.11)

          Оценку , удовлетворяющую системе уравнений, называют оценкой максимального правдоподобия векторного параметра   или совместной оценкой максимального правдоподобия компонента этого векторного параметра. Оценки максимального правдоподобия состоятельные и асимптотически совместно эффективные.

          Рассмотрим связь байесовых оценок с оценкой максимального правдоподобия на примере нормального распределения амплитуды сигнала.

Байесовская оценка амплитуды а квазидетерминированного сигнала

   (3.12)

где - оценка максимального правдоподобия,

- отношение дисперсии априорного распределения амплитуды к дисперсии ее оценки максимального правдоподобия.

          Из (3.11) следует, что байесовская оценка представляет среднее взвешенное двух величин: оценки максимального правдоподобия и априорного среднего а₀, причем отношение веса, приписываемого первой величине, к весу второй равно Ясно, что в рассматриваемом случае байесовская оценка распределенной по нормальному закону амплитуды сигнала, совпадает с оценкой максимальной апостериорной плотности

          Если отношение неограниченно возрастает, т.е. дисперсия оценки максимального правдоподобия много меньше дисперсии априорного распределения, то  ~, т.е. байесовская оценка приближается к оценке максимального правдоподобия. Если дисперсия априорного распределения много меньше дисперсии оценки максимального правдоподобия, то  ~, т.е. наблюдаемая реализация не влияет на оценку, которая принимается равной априорному среднему оцениваемого параметра.

3.4. Функционал отношения правдоподобия гауссовского процесса

          Оптимальный по любому из критериев качества аналоговый алгоритм проверки гипотезы Н₀ против альтернативы Н₁ предписывает сравнение с порогом логарифма функционала отношения правдоподобия. Поэтому для синтеза оптимального аналогового алгоритма обнаружения сигнала на фоне гауссовской помехи необходимо определить логарифм функционала отношения правдоподобия гауссовского случайного процесса с указанием ограничений, при которых этот функционал существует.

          Гипотеза Н₀ состоит в том, что наблюдаемая реализация принадлежит гауссовскому процессу с корреляционной функцией В(t,y) и средним значением s₀(t), а альтернатива Н₁ – в том, что реализация принадлежит гауссовскому процессу с той же корреляционной функцией и средним значением s₁(t). Для рассматриваемой здесь задачи обнаружения  s₀(t) ≡ 0 и s₁(t) ≡ s(t).

          Запишем логарифм отношения правдоподобия для дискретной выборки х=(х₁,…,х_n), полученной отбором на интервале (0,Т) через равные промежутки времени из реализации х(t) гауссовского случайного процесса

  (3.13)

где Х – вектор с компонентами s_1, s₀ – векторы с компонентами  - корреляционная матрица (положительно определенная) размером nxn.

Введем вектор V=K^-1(s₁-s₀).

Тогда s₁-s₀ = KV.

          После преобразований логарифм функционала отношения правдоподобия равен

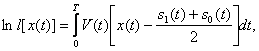 (3.14)

где V(t) – решение интегрального уравнения:

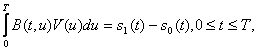  (3.15)

тогда среднее значение логарифма функционала отношения правдоподобия при гипотезе и при альтернативе равен:

(3.16)

где .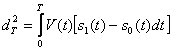

3.5. Оценка амплитуды детерминированного сигнала

          Рассмотрим оценку максимального правдоподобия неизвестной амплитуды а детерминированного сигнала as(t) на фоне аддитивной гауссовской помехи. Эта оценка является частным случаем оценки при m=1 и =a. Для рассматриваемого скалярного случая следует

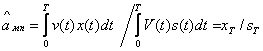(3.17)

V(t) – решение линейного интегрального уравнения

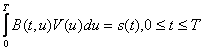  (3.18)

          Из анализа оценки максимального правдоподобия векторного параметра линейной модели сигнала следует, что оценка амплитуды сигнала несмещенная и эффективная, т.е.

          Доверительный интервал для неизвестной амплитуды сигнала может быть представлен неравенствами

(3.19)

где - процентная точка нормального распределения, определяемая по заданному коэффициенту доверия γ.

          Для реализации оптимального аналогового алгоритма оценивания амплитуды сигнала на фоне аддитивной гауссовской помехи необходимо вычислить нормированный корреляционный интеграл. Эту операцию можно осуществить при помощи аналогового коррелометра или физически реализуемого линейного фильтра с импульсной характеристикой

      (3.20)

          Оптимальная оценка амплитуды получается в конце наблюдения на выходе фильтра, если только импульсная характеристика фильтра нормируется величиной s_T (или умножается на дисперсию оценки).

3.6. Оценки амплитуды и фазы гармонического сигнала

          Сигнал s(t;) – гармонический с известной частотой ω₀ и неизвестными амплитудой  а и фазой φ:

(3.21)

    (3.22)

   (3.23)

          Решая систему двух линейных относительно ₁ и ₂ уравнений, получаем оценки максимального правдоподобия этих параметров:

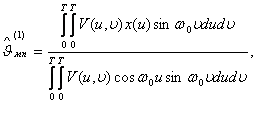 (3.24)

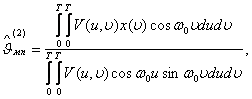  (3.25)

где

          Полагая ω₀Т = 2πk, где k – целое число, находим оценки максимального правдоподобия:

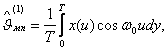 (3.26)

   (3.27)

          Эти оценки максимального правдоподобия можно использовать для получения оценок амплитуды и фазы сигнала на фоне аддитивного белого гауссовского шума:

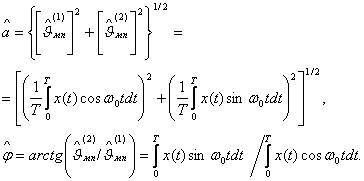
3.7. Совместная оценка частоты и фазы гармонического сигнала при аддитивном белом шуме

          Рассмотрим пример совместной оценки двух неэнергетических параметров – частоты ω и фазы φ гармонического сигнала, наблюдаемого в аддитивной смеси с белым шумом. Поскольку частота неизвестна, следует условиться, на какой момент времени приходится оценка фазы. Будем считать, что оценивается фаза, приходящаяся на середину интервала наблюдения, а наблюдение проводится, начиная с момента – Т/2 до момента Т/2.

          Уравнение, определяющее оценку частоты, запишется так:

          Приведенное уравнение не имеет аналитического решения, но можно показать, что оно имеет множество корней. Воспользуемся линеаризацией этой формулы, предположив, что известно опорное значение ω, близкое к искомому решению ω^* = ω + Δω^*, причем  Δω^*Т<< π/2. Тогда, считая,  что cos Δω^*(t₁ – t₂) ≈ 1 и sin Δω^*(t₁ – t₂) ≈ Δω^*(t₁ – t₂), получаем

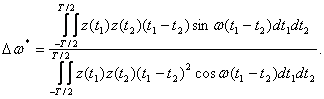(3.28)

          Если частота находится в диапазоне шириной Ω = ω_max - ω_min, то для определения опорного значения частоты ω_i требуется число каналов

 (3.29)

3.8. Понятие об аномальных ошибках измерения

          Ошибки системы, определяющей параметры радиосигнала, обычно принято делить на два вида: малые (нормальные) и большие (аномальные). Такое разделение ошибок имеет смысл потому, что каждый из видов удобнее оценивать различными критериями. При оценке аномальных ошибок величина среднеквадратической ошибки и максимальной ошибки чаще всего не важны, ибо само появление аномальной ошибки означает нарушение работы системы, невыполнение поставленной задачи. Аномальные ошибки наиболее удобно характеризовать вероятностью их появления, и при проектировании следует создавать условия, при которых эта вероятность пренебрежимо мала.

          Если речь идет о начальном этапе проектирования, когда система еще не определена и выбирается только радиосигнал, можно считать аномальными все ошибки, лежащие вне главного экстремума функции различия ε (Δх). Область нормальных ошибок обычно располагается симметрично около нуля на оси Δх (или около х_и на оси х). Обозначим соответствующие граничные точки х_н1 и х_н2 (рис. 3.1). Эти точки лежат внутри области априорной неопределенности, границы которой обозначены х_а1 и х_а2.

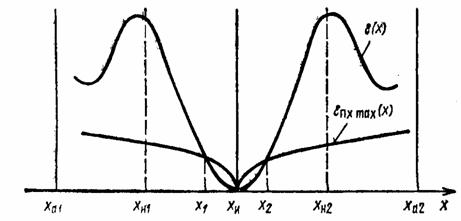
Рис. 3.1. К определению аномальных ошибок

          Допустим, что причиной является действие аддитивной помехи. Тогда, учитывая, что оценка параметра определяется наименьшим значением измеренной функцией различия, получаем достаточное условие отсутствия аномальных ошибок в виде

  (3.30)

          Это условие можно записать в виде

  (3.31)

или, отбросив одинаковые члены в обеих частях неравенства, получим достаточное условие в виде

  (3.32)

причем это условие должно выполняться для всех х, лежащих вне области х_н1 – х_н2.

3.9. Понятие об оценке (фильтрации) меняющихся параметров сигналов

          Задача оценки сообщения сводится к задаче оценки совокупности параметров (при оценке в целом) или одного параметра (при фильтрации).

          Предположим, что на интервале наблюдения (0,Т) получена реализация х(t) аддитивной смеси сигнала ξ(t) и помехи η(t), которые представляют центрированные случайные процессы с известными корреляционными функциями В_ξ(u,υ) и В_η(u,υ), причем и сигнал, и помеха необязательно гауссовские. Необходимо синтезировать оценку стохастического сигнала по наблюдаемой реализации х(τ), 0≤ τ ≤ T.

          Определение оценки как функционала от х(τ) при t=T называется задачей фильтрации сигнала.

          Располагая реализацией аддитивной смеси сигнала и помехи, иногда необходимо определить также оценку некоторого стохастического сигнала , представляющего требуемую операцию над сигналом ξ(t). Это может быть линейная операция (сдвиг, однократные или многократные дифференцирование и интегрирование) или даже нелинейная.

3.10. Линейная и нелинейная фильтрация

Линейная фильтрация. Рассмотрим задачу оптимальной линейной фильтрации сигнала на фоне аддитивной помехи, которая формируется следующим образом. В качестве оценки сигнала принимается линейный функционал

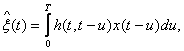(3.33)

т.е. значение процесса на выходе линейного фильтра с импульсной характеристикой h(t,τ), когда на вход действует наблюдаемая реализация смеси сигнала с помехой. Необходимо в классе этих линейных фильтров определить фильтр, оптимальный по критерию минимума среднего квадрата ошибки оценивания

(3.34)

где

          Так как по предложению сигнал и помеха – центрированные случайные процессы, то средний квадрат ошибки совпадает с ее дисперсией. Поэтому критерий минимума среднего квадрата ошибки оценивания будем называть критерием минимума дисперсии ошибки. Для определения импульсной характеристики h^* (t,τ) такого оптимального фильтра достаточно располагать указанными априорными данными о сигнале и помехе.

          Если реализация х(τ) аддитивной смеси сигнала и помехи определена для всех действительных значений τ, тогда линейную оценку сигнала можно представить в виде

(3.35)

Дисперсия ошибки оценивания

(3.36)

         Из этой формулы видно, что дисперсия линейной оценки зависит только от корреляционных функций сигнала и помехи и не зависит от распределения вероятностей этих случайных процессов.

         Обозначим через h^* (t,τ) импульсную характеристику оптимального линейного фильтра, а через ε^*(t) ошибку оценивания сигнала при оптимальной линейной фильтрации. Тогда

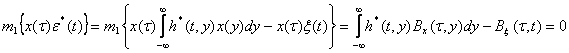 (3.37)

Это соотношение выражает так называемый принцип ортогонального проецирования, который является достаточным условием минимума дисперсии ошибок оценивания сигнала.

         Положительными свойствами линейных методов являются их простота по сравнению с нелинейными методами и для синтеза оптимального линейного фильтра требуются ограниченные статистические данные о сообщениях и смесях, что весьма важно с точки зрения практики.  

Нелинейная фильтрация. Если отказаться от условия линейности алгоритма обработки наблюдаемой реализации, то в более широком классе допускаемых оценок можно получить оценки, которые по заданному критерию минимума среднего квадрата ошибки будут лучше линейных оценок. В общем случае оптимальной по критерию минимума среднего квадрата ошибки, оценкой сигнала  по наблюдаемой реализации х(τ) аддитивной смеси сигнала с помехой η(t), является условное среднее

 (3.38)

         За исключением гауссовских процессов и η(t) вычисление нелинейного функционала встречает значительные трудности, связанные, прежде всего с определением апостериорной плотности вероятности. Один из подходов к решению задачи оптимальной нелинейной фильтрации состоит в ограничении класса исследуемых нелинейных процессов марковскими или их компонентами. При таком ограничении удается преодолеть трудности, связанные с вычислением апостериорной плотности оцениваемого процесса. После этого можно получить оценку по критерию минимума среднего квадрата ошибки. Мы рассмотрим другой подход, основанный на аппроксимации нелинейного функционала  рядом Вольтерра:

 (3.39)

         Если K_m≡0 для всех m>1, то получаем линейный функционал и K₁(u) можно трактовать как импульсную характеристику линейного фильтра. Добавление членов ряда при m>1 означает введение нелинейности. Совокупность функций K_m(u₁,…u_m), m=характеризует нелинейный фильтр n-го порядка. Ограничение  суммы ряда первыми n членами позволяет аппроксимировать функционал F[x(τ)] процессом на выходе фильтра n –го порядка при входной воздействии x(τ).

         Если n=2, то для формирования оценки использована простейшая нелинейная система – фильтр второго порядка. Задача состоит в том, чтобы определить характеристику K₂(u₁,u₂) нелинейности так, чтобы средний квадрат ошибки

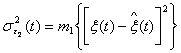 (3.40)

был минимальным.

После преобразований получим минимальное значение дисперсии ошибки

 (3.41)

или

   (3.42)

где

    (3.43)

- минимальная дисперсия ошибки линейной оценки.

Таким образом, использование оптимального нелинейного корректирующего звена в фильтре второго порядка позволяет дополнительно уменьшить дисперсию ошибки на

    (3.44)

3.11. Фильтры Винера и Калмана

         Задача фильтрации (на фоне стационарного шума) сообщения, представляющего собой стационарный случайный процесс, при условии, что наблюдение длится бесконечно долго, называют обычно винеровской фильтрацией, а фильтры, структура которых находится при такой постановке задачи, называются винеровскими.

         Если и сигнал, и помеха стационарны, а фильтр представляет линейную систему с постоянными во  времени параметрами, то при t→∞ импульсная характеристика h^*(t) оптимального фильтра определяется решением интегрального уравнения

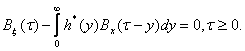       (3.45)

       При этом минимальное значение дисперсии ошибки

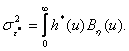 (3.46)

После преобразований следует

  (3.47)

Из этого условия находим передаточную функцию оптимального физически реализуемого фильтра

 (3.48)

Обратным преобразованием Фурье из последней формулы находим импульсную характеристику h^*(t) оптимального физически реализуемого фильтра (решение уравнения Винера-Хопфа). Таким образом, определение оптимального физически реализуемого фильтра сводится к факторизации спектра аддитивной смеси сигнала и помехи, и разложению функции на сумму сопряженных функций. Указанная факторизация может быть всегда выполнена, если выполняется условие Винера-Пэли

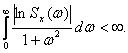  (3.49)

Фильтр Калмана. Если спектр сигнала представляет рациональную функцию переменной ω², то сигнал ξ(t) со спектром получаем на выходе формирующего фильтра, структура которого определяется дифференциальным уравнением первого порядка где - белый шум со спектральной интенсивностью S_0. Предположим, что помеха η(t) также представляет белый шум с интенсивностью N₀, причем  η(t) и  некоррелированы. Используя линейную оценку сигнала, получим

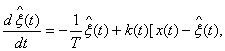   (3.50)

где

                   Выражение (3.50) представляет собой оптимальный по критерию минимума дисперсии ошибки алгоритм фильтрации сигнала со спектром на фоне аддитивного белого шума. Соответствующая этому алгоритму структурная схема оптимального фильтра (фильтра Калмана) изображена на рис. 3.2, где, кроме того, показана структурная схема формирующего фильтра, на выходе которого получаем сигнал со спектром. Здесь осталась неизвестной функция k(t), которую называют коэффициентом усиления. Она равна

(3.51)

т.е. коэффициент усиления полностью определяется минимальным значением дисперсии ошибки при линейной фильтрации сигнала.

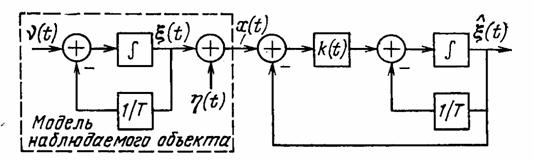
Рис. 3.2. Схема фильтра Калмана

ГЛАВА 4. РАЗРЕШЕНИЕ СИГНАЛОВ

                   Возможны случаи, когда полезный сигнал и помеха одинаковы по своей структуре и отличаются только параметром, несущим сообщение. При этом, в общем говоря, имеется возможность разрешить сигналы, т.е. обнаружить присутствие второго сигнала (помехи) и, если нужно, раздельно определить параметры обоих сигналов. При малых различиях между параметрами разрешение становится ненадежным из-за ошибок измерения. Наименьшая разность параметров, при которой еще возможно надежное разрешение сигналов, характеризует качество сигналов, которое называется разрешающей способностью.

4.1. Разрешающая способность по дальности и скорости

                   Различить сигналы многих целей можно по параметрам эхо-сигналов. Разрешающая способность включает в себя понятие о разделении. Она означает способность определять, имеется ли одна или более целей в поле зрения РЛС. Рассмотрим отдельно разрешающую способности по дальности (времени задержки) и по скорости (доплеровскому смещению частоты).

Разрешающая способность по дальности. Допустим, принимаются два сигнала, отраженных от целей, находящихся на одном направлении, но на разных дальностях. Задержки сигналов u(t) и u(t-τ) отличаются друг от друга на величину τ. Для простоты полагаем, что энергия сигналов одинакова и равна Ею Необходимо оценить, при каких значениях τ их можно раздельно наблюдать. В методе различимости двух сигналов, предложенным Вудвордом, определяется средний квадрат отклонения u(t) и u(t-τ):

(4.1)

После вычислений: , где нормированная автокорреляционная функция равна:

Таким образом, мерой разрешающей способности сигналов во времени является автокорреляционная функция сигнала. Для того чтобы различие сигналов было большим, нужно форму сигнала u(t) выбирать такой, чтобы │R(τ)│ было как можно ближе к нулю всюду, за исключением окрестности точки τ=0.

                   Разрешающая способность по времени тем выше, чем меньше длительность отклика СФ. При обнаружении сигнала со случайной начальной фазой ее влияние на отклик СФ исключают с помощью детектора, включенного после фильтра.

Если цель перемещается, то разрешающая способность  по дальности согласно:

.           (4.2)

Разрешающая способность по скорости. При движении цели частота отраженного от нее сигнала будет отличаться на величину доплеровского смещения F_д или Ώ = 2π F_д.

          Допустим, принимается два сигнала, спектр одного , спектр другого . Для различения двух целей, находящихся на одной дальности и одном направлении, но имеющих разные радиальные составляющие скорости движения, можно взять, как и в предыдущем случае, интеграл от квадрата разности спектров в качестве меры разрешающей способности по частоте

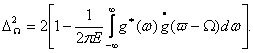
  (4.3)

Величину необходимо максимизировать для всех априорных значений допплеровских смещений, исключая область, близкую к Ω = 0.

Обозначим    - это выражение комплексной функции частотной корреляции. Можно определить постоянную разрешения Ω_э (интервал неопределенности) по допплеровской частоте как эквивалентную ширину функции

 (4.4)

Постоянная разрешения по скорости определяется соотношением:

(4.5)

4.2. Классы зондирующих сигналов

                   Все существующие виды сигналов можно разделить на простые и сложные. Простыми сигналами будем называть сигналы, для которых произведение эффективной длительности Т сигнала на эффективную ширину спектра F равно единице: FT = 1.

К простым сигналам относятся одиночные радиоимпульсы с огибающими, описываемыми простыми функциями времени и частоты.

Сложный сигнал можно получить из простого импульсного сигнала путем дополнительной внутриимпульсной модуляции ВЧ колебаний по частоте или фазе. Тогда при той же длительности простого сигнала получается более широкий спектр за счет дополнительной внутриимпульсной модуляции, и произведение длительности сигнала на ширину спектра будет на много больше единицы. Сложный сигнал характеризуется соотношением    F T >> 1. Сложные сигналы описываются сложными функциями времени и частоты.

4.3. Сжатие сложного сигнала по времени и частоте

                   Для оптимальной обработки сигнала в обнаружителях применяют либо корреляторы, либо  согласованные фильтры. Коррелятор является фильтром с переменными параметрами, его называют активным фильтром. Согласованный фильтр имеет постоянные параметры и его называют пассивным фильтром. Максимальное значение откликов коррелятора и СФ пропорционально энергии входного сигнала, однако форма откликов коррелятора и СФ на сложный сигнал различна.

Отклик СФ через спектр входного сигнала:

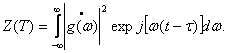(4.6)

Из этого выражения видно, что фазовый спектр сигнала компенсируется обратной фазовой характеристикой СФ. В результате длительность отклика определяется энергетическим спектром сигнала  Чем шире энергетический спектр входного сигнала, тем короче отклик СФ. В результате длительность сигнала на выходе СФ равна

     (4.7)

Произведение            

(4.8)

Коэффициент сжатия сложного сигнала по длительности определяется отношением

    (4.9)

Величину FT называют базой сигнала. Таким образом, сигнал по длительности сжимается на величину, равную базе сигнала.

                   Рассмотрим отклик коррелятора на сложный сигнал. Для обработки такого сигнала коррелятором необходимо на перемножитель подать синхронно и синфазно копию сигнала. Тем самым внутриимпульсная модуляция снимается, и спектр полностью будет определяться только огибающей сигнала Если длительность входного сигнала Т, то ширина спектра огибающей отклика коррелятора 1/Т. Таким образом, коррелятор производит сжатие по спектру.

                   В той же мере, в какой сжатие по длительности повышает разрешающую способность по дальности, сжатие по спектру повышает разрешающую способность по скорости. Применяя смешанный корреляционно-фильтровой метод обработки сложного сигнала, можно производить сжатие сложного сигнала по длительности и частоте. Это свойство сложных сигналов привлекло специалистов тем, что появилась возможность увеличить энергию сигнала не за счет повышения импульсной мощности, а за счет увеличения длительности сигналов, не ухудшая при этом разрешающей способности по дальности. Увеличение энергии сигнала путем повышения импульсной мощности зондирующего сигнала ограничивается энергоспособностью электронных приборов и электрической прочностью антенно-фидерных трактов.

Другой причиной, по которой сложные сигналы стали использоваться, является повышение помехоустойчивости радиосистем относительно некоторых классов помех. 

4.4. Сложные сигналы с линейно-частотной модуляцией

                   Несущая частота такого сигнала изменяется в пределах длительности импульса Т линейно со скоростью Δω/Т, если девиация частоты Δω. Мгновенное значение частоты сигнала определяется выражением

    при    (4.10)

где ω₀ – средняя частота сигнала.

Фаза сигнала есть интеграл от изменения частоты

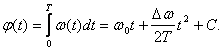(4.11)

Положив φ = 0, при t = 0 получим С = 0. Тогда мгновенное напряжение сигнала

  при    (4.12)

Спектр сложного ЛЧМ сигнала найдем с помощью преобразования Фурье

  (4.13)

После преобразований получим амплитудный и фазовый спектры огибающей ЛЧМ сигнала

 (4.14)

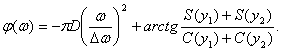     (4.15)

где FT = D,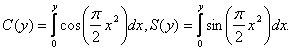

Амплитудный и фазовый спектры ЛЧМ сигнала будут лишь смещены на частоту ω₀ – несущую частоту сигнала. Для них можно записать

(4.16)

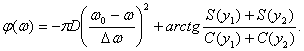      (4.17)

При больших D амплитудный спектр в пределах полосы от ω₀-Δω/2   до ω₀+Δω/2 становится более равномерным и на границах полосы резко спадает, поскольку С(у) и S(y) при больших у стремятся к значению 0,5. Поэтому при больших значениях D, спектр сложного ЛЧМ сигнала близок к прямоугольному.

Корреляционная функция ЛЧМ сигнала равна

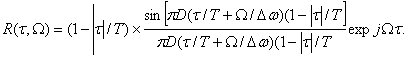   (4.18)

Квадрат модуля корреляционной функции │R(τ,Ω│² огибающей будет функцией неопределенности ЛЧМ сигнала. (рис. 4.1)

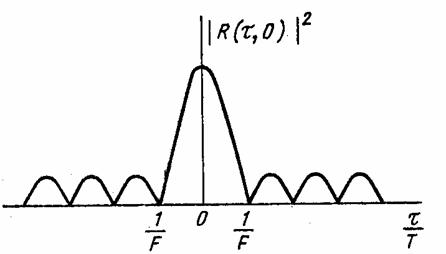
Рис. 4.1. Функция неопределенности ЛЧМ сигнала

Максимум этой функции будет при τ=0 и Ω=0. Длительность корреляционной функции будет определяться 2Т, поскольку │R(τ,Ω│=0 при │τ│=Т. Внутри интервала от τ=-Т до τ=Т корреляционная функция комплексной огибающей будет колебательной. Нули и максимумы ее будут определяться функцией sin x/x. Первый нуль будет определяться значением τ_и=1/F или 2π/Δω. Ширина главного лепестка корреляционной функции комплексной огибающей по нулевым значениям будет равна 2F=4π/ω.

Для сложного ЛЧМ сигнала с большим D сечение функции неопределенности по оси Ω близко к прямоугольной форме,  а по оси τ определяется функцией sin x/x.        

4.5. Сложные фазоманипулированные сигналы

          Фазоманипулированным сигналом (ФМ) называют последовательность радиоимпульсов длительностью τ_и одинаковой формы, следующих друг за другом с интервалом τ_и и отличающиеся фазами ВЧ колебаний. Амплитуды импульсов чаще одинаковые, но могут быть и разными.

Фаза спектра ФМ сигнала

  (4.19)

является нечетной функцией частоты ψ(-ω)= - ψ(ω). Символы могут быть найдены из выражения

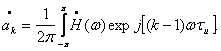 (4.20)

Спектр комплексной огибающей в общем виде записывается так:

  (4.21)

Корреляционная функция комплексной огибающей ФМ сигнала  определяет энергию единичного импульса. Корреляционная функция сигнала с прямоугольной огибающей описывается функцией

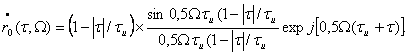 (4.22)

Максимальное значение  Область сильной корреляции по оси времени равно τ_и, а по оси частот 2π/τ_и. Тогда корреляционная функция комплексной огибающей ФМ сигнала

 (4.23)

Число слагаемых этой функции (в двойной сумме) равно 2N. Максимум функции расположен при значениях τ=(n-k)τ_и и Ω=0. Максимальные значения по оси τ следуют через интервалы τ_и и образуют решетчатую функцию. Методика вычисления может быть сведена к составлению квадратной матрицы, элементы которой равны произведению . Сумма элементов главной диагонали дает значение максимума главного лепестка корреляционной функции. Соединение с главной боковые диагонали образуют два первых боковых лепестка. Сумма их дает максимум первых лепестков справа и слева от главного и т.д.

ГЛАВА 5. ОСНОВНЫЕ ПРИНЦИПЫ ПОСТРОЕНИЯ РАДИОЛОКАЦИОННЫХ СИСТЕМ

5.1. Задачи и применение радиолокации

Радиолокацией называется область радиотехники, использующая явления отражения и излучения электромагнитных волн различными объектами для обнаружения и измерения координат этих объектов. Радиотехнические устройства, предназначенные для решения указанных задач, называются радиолокационными станциями (РЛС).

С помощью радиолокационных средств решаются самые разнообразные задачи навигации, управления полётом и посадкой летательных аппаратов, проводкой кораблей, прогнозирования погоды, перехвата объектов противника и прицеливания при стрельбе по ним. Радиолокационные устройства начинают использоваться при исследовании свойств объектов наблюдения, для определения их физических и кинематических характеристик.

При решении различных задач радиолокационные станции обеспечивают:

¨ обнаружение объектов;

¨ определение их государственной принадлежности (опознавание);

¨ измерение координат объектов и определение их положения;

¨ определение параметров движения объектов, выявление их траекторий и предсказание их последующих положений;

¨ определение некоторых физических свойств и характеристик объектов.

Измерение координат объектов радиолокационными средствами осуществляется либо в сферической, либо в цилиндрической системах. За центр системы принимается место расположения РЛС (точка О на рис.5.1).

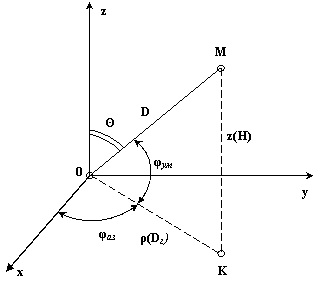Рис.5.1. Система координат, принятая в радиолокации.

Сферическими координатами объекта наблюдения (точка М на рис.5.1) будут: D – радиус – вектор (дальность), j_аз – долгота (азимут), j_ум – угол места, дополняющий полярное расстояние q до 90⁰ (j_ум = 90⁰ - q). В цилиндрической системе положение объекта определяется аппликатой z (высота Н) и полярными координатами j_аз и r (горизонтальная дальность D_г) проекции точки М на плоскость хОy.

Объектом радиолокационного наблюдения или, как чаще говорят, целью может быть любое тело или группа тел с электрическими или магнитными свойствами, отличными от свойств среды, в которой распространяются радиоволны; целью может быть также и тело, характеризующееся собственным излучением радиоволн. Радиолокационными целями являются самолёт, корабль, человек, грозовое облако, участок поверхности земли, специальный радиомаяк и т.п.   

5.2. Физические основы обнаружения целей и

определения их координат и скорости

При радиолокационном наблюдении информация о целях переносится радиолокационными сигналами. Радиолокационными сигналами называются электромагнитные колебания, параметры которых определенным образом связаны с целью.

Известно несколько методов получения радиолокационных сигналов:

1.Метод активной радиолокации является наиболее распространённым и основан на облучении цели электромагнитной энергией и приёме отражённых (рассеянных) целью радиоволн приёмным устройством РЛС.

2.Метод активного ответа – при этом при облучении цели электромагнитной энергией срабатывает установленный на цели ретранслятор (ответчик), который посылает вполне определённые радиосигналы;  эти сигналы принимаются приёмником РЛС.

3.Метод пассивной радиолокации заключается в приёме сигналов собственного радиоизлучения целей (радиотепловое излучение тел, излучение собственных радиотехнических устройств и др.)

Обнаружение целей состоит в фиксации поступающих на вход приёмного устройства РЛС радиолокационных сигналов.

Измерение координат обнаруженных целей основано на определении значений параметров радиолокационных сигналов, несущих информацию об этих целях. При этом используются следующие физические свойства радиоволн:

¨ скорость распространения радиоволн в свободном пространстве (с) имеет конечное и приблизительно постоянное значение;

¨ траектории распространения радиоволн можно считать прямыми линиями;

¨ частота принимаемых электромагнитных колебаний отличается от частоты излучённых колебаний в том случае, если цель перемещается относительно РЛС (эффект Доплера).

Время распространения радиоволн от РЛС до цели и обратно t_D:

.

Тогда дальность цели по методу активной радиолокации:

.

(5.1)

Обычно величину t_D  называют временем запаздывания отражённого сигнала.

Радиальная составляющая скорости движения цели:

,

(5.2)

где   - доплеровское смещение частоты отражённых от целей радиолокационных сигналов;

V_р - основано на использовании эффекта Доплера, который проявляется дважды:

во – первых, частота электромагнитных колебаний, переизлучаемых движущейся целью f_отр, отличается от частоты излучённых колебаний f_изл:

.

и, во – вторых, частота колебаний, принятых отражённых сигналов:

.

Тогда

.

Принимаем, что .

Знак “+” соответствует сближению РЛС и цели, знак “-” – их удалению.

5.3. Дальность действия в свободном пространстве

Дальностью действия радиолокационной станции называется наибольшее расстояние между станцией и целью, на котором обнаружение цели производится с заданными вероятностями правильного обнаружения и ложной тревоги.

Дальность действия зависит от технических параметров станции, характеристик цели, условий распространения радиоволн, наличия и уровня различного рода помех и ряда других факторов, большинство из которых изменяется во времени случайным образом. Их количественные значения, необходимые для расчёта дальности, могут определяться лишь с какой-то вероятностью, определяющей в итоге и вероятность полученного значения дальности действия. График на рис.5.2 иллюстрирует характер зависимости относительного изменения дальности обнаружения от значения вероятности правильного обнаружения W_по при заданной ложной тревоге W_лт.

Рассмотрим дальность действия РЛС без учёта влияния земной поверхности и атмосферы на распространение радиоволн, т.е. РЛС и цель находятся в «свободном» пространстве.

При облучении потоком электромагнитной энергии одиночной цели, находящейся в свободном пространстве, небольшая часть рассеиваемой целью энергии направляется в сторону приёмной антенны РЛС. Обычно приёмная антенна располагается в одном пункте с передающей или (при импульсной работе) является одновременно и передающей.

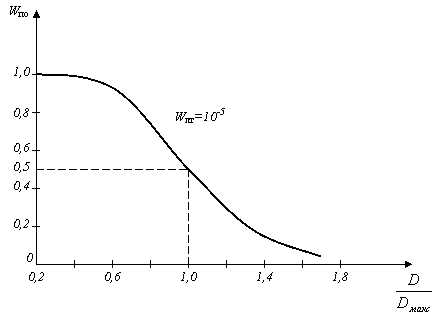
Рис.5.2. Зависимость относительного изменения дальности обнаружения от значения вероятности правильного обнаружения.

Если передающее устройство РЛС вырабатывает энергию излучения Е_изл, максимальное значение коэффициента усиления передающей антенны по мощности равно G_опрд и цель находится на расстоянии D от радиолокационной станции, то плотность потока энергии у цели

.

где 4πD² – поверхность сферы радиусом D;

;

Р_изл – мощность излучения;

τ_с – время непрерывного облучения цели (при импульсной работе - длительность одного импульса).

Количество энергии, переизлучаемое целью, определяется средним значением эффективной отражающей площади цели S_эфф0

.

Плотность потока энергии у приёмной антенны

.

Энергия радиолокационного сигнала, поступающего из антенны в согласованный с ней приёмник, равна

,

(5.3)

где S_{а прм} – эффективная площадь приёмной антенны, связанная с геометрической площадью раскрыва антенны соотношением

.

(5.4)

На максимальной дальности обнаружения энергии принимаемого сигнала равна пороговому значению, т.е. минимально необходимому для обнаружения с заданными вероятностями W_по и W_лт.

Величина порогового значения энергии определяется чувствительностью приёмника РЛС Е_{прм мин}. Таки образом, для максимального значения дальности D_макс имеем.

,

(5.5)

где коэффициент различимости равен

.

Спектральная плотность мощности шума приёмника

k_ш – коэффициент шума приёмника;

k – постоянная Больцмана, равная 1,38·10^-23 вт·сек/град;

Т⁰ – абсолютная температура, при которой определяется величина k_ш (обычно 290⁰ К).

Получим следующее выражение для максимальной дальности действия

(5.6)

Это выражение может быть также представлено в других эквивалентных видах, если использовать известную зависимость между коэффициентом усиления и раскрывом антенны

 или .

Заменяя в (5.6) G_опрд и в соответствии с приведёнными выше формулами, получим

.

(5.7)

Использование одного из трёх приведённых выражений для расчёта D_макс зависит от заданных (известных) параметров передающей и приёмной антенн.

Если в РЛС для излучения и приёма используется одна и та же антенна, то в формулу (5.7) вместо произведений S_{а прд} S_{а прм} и G_опрд G_опрм,  следует подставить величины S_а² и G_о² соответственно

.

(5.8)

Анализируя выражения для D_макс можно, сделать следующие выводы:

1. Дальность действия РЛС определяется энергией излучаемых сигналов и не зависит от их формы (при прочих заданных параметрах станции).

2. Увеличение энергии излучения, так же как и улучшение чувствительности приёмника (уменьшение k_ш), не очень существенно влияет на величину D_макс, так как

.

(5.9)

С точки зрения экономии потребляемой РЛС энергии выгоднее для увеличения D_макс улучшать чувствительность приёмника (уменьшать величину Е_{прм мин}), но из соображений повышения помехозащищённости станции целесообразно увеличивать Е_изл.

Обычно при конструировании станций стремятся увеличить как за счёт увеличения чувствительности приёмника, так и путём выбора максимально возможной для конкретных условий энергии излучения.

3. Существенное увеличение дальности действия может быть достигнуто за счёт увеличения размеров антенны. При использовании одной антенны для излучения и приёма

,

где d_а – диаметр рефлектора (линейный размер) антенны.

4. При заданных размерах антенн, т.е. при S_{а прд}=const и

S_{а прм}=const:

,

т.е. укорочение волны при неизменных размерах антенн вызывает увеличение D_макс. Это объясняется тем, что в этом случае уменьшение λ приводить к увеличению коэффициента усиления антенн.

5. Если фиксировать значение G_о, то

.

Такая зависимость появляется в связи с тем, что при увеличении длины волны для сохранения прежних значений коэффициентов усиления антенн, необходимо увеличивать S_{а прд} и S_{а прм}.

В РЛС, где размеры антенн ограничиваются определёнными габаритами, для повышения дальности действия целесообразно уменьшать длину волны. Если же требования к размерам антенн не являются жесткими, можно повышать D_макс, увеличивая длину волны с одновременным увеличением размеров антенны так, чтобы величина G_о=const.

6. Небольшое изменение эффективной отражающей площади цели не очень существенно влияют на величину D_макс, так как

.

В ряде случаев удобнее пользоваться формулами, в которых отношение энергии излучения и порогового значения энергии сигнала заменяется отношением соответствующих мощностей. Такая замена возможна при условии согласования полосы пропускания приёмника Δf с длительностью сигнала τ_с. Так как в общем случае Δf τ_с=ξ, то отношение

.

При согласовании полосы пропускания приёмника Δf с длительностью сигнала τ_с коэффициент ξ=1 и отношение . Если ξ≠1, указанная замена может производиться лишь при учёте значения ξ.

Для получения необходимой величины k_p при обнаружении цели, находящейся на максимальной дальности, значение энергии излучения передатчика определяется при прочих заданных параметрах станции выражением

.

(5.10)

Если обеспечить получение необходимой величины Е_изл за время  τ_с по каким-либо причинам невозможно, то производят несколько облучений цели и накопление отражённых сигналов.

Иногда передающая и приёмная антенны оказываются разнесёнными на значительное расстояние друг от друга. Тогда количество энергии, переизлучаемой целью в направлении приёмной антенны, равно

,

где D_прд – расстояние от РЛС до цели.

Значение энергии отраженного сигнала на входе приёмника

,

где D_прм – расстояние от цели до приёмной антенны.

Для порогового значения сигнала получим

.

(5.11)

Последнее выражение показывает, что при малом расстоянии между целью и приёмным устройством облучение цели может производиться с большого расстояния, и наоборот, но обязательно должно выполняться условие

.

5.4. Дальность действия при активном ответе

Для решения некоторых тактических задач и повышения тактических возможностей РЛС (например, для опознавания целей, увеличения дальности обнаружения, повышения точности измерения координат и т.д.) на объектах, подлежащих радиолокационному наблюдению, устанавливают ответчики (ретрансляторы). На приёмную антенну ответчика поступает прямой (запросный) сигнал передатчика РЛС. После соответствующих преобразований этот сигнал поступает на запуск передатчика ответчика, вырабатывающего ответный сигнал. Ответный сигнал, значительно превышающий по энергии сигнал, отражённый от цели, принимается антенной РЛС (рис.5.3). При заданных параметрах РЛС (запросчика): Е_{изл з}, G_{опрд з}, S_{а прм з}, и ответчика: Е_{изл от}, G_{опрд от}, S_{а прм от}, энергия запросного сигнала на входе приёмника ответчика, находящегося на расстоянии D от РЛС, равна

.

Рис.5.3. РЛС с активным ответом

Максимальной дальности запроса D_максз соответствует пороговое значение энергии запросного сигнала на входе приёмника ответчика, равное чувствительности приёмника, Е_{прм мин от}=k_рот k_шот kT⁰.

Таким образом,

.

(5.12)

Энергия ответного сигнала на входе приёмника РЛС равна

,

а максимальная дальность ответа D_{макс от} определится чувствительностью приёмника запросчика Е_{прм мин з}=k_рз k_шз kT⁰

.

(5.13)

Для радиолокационной системы с активным ответом параметры системы целесообразно выбирать таким образом, чтобы D_{макс з}=D_{макс от}, так как в противном случае дальность действия системы будет определяться наименьшим значением D_макс по одному из каналов (запроса или ответа), а возможности другого канала не будут полностью реализованы.

Считая D_{макс з}=D_{макс от}, получим выражение для дальности действия системы с активным ответом

,

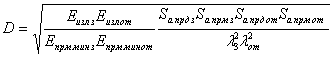где λ_з – длина волны запросчика;

      λ_от – длина волны ответчика.

Энергетические параметры системы должны при этом выбираться исходя из равенства выражений (5.12) и (5.13):

.

(5.14)

Если запрос и ответ иногда осуществляется на одной частоте и для передачи и приёма у запросчика, так же как и у ответчика, используется одна и та же антенна, то

.

(5.15)

Полученное соотношение иногда называют уравнением сбалансированной системы с активным ответом.

Выражение (5.13) будет справедливо при пассивной радиолокации, когда цель излучает энергию Е_ц=Е_{изл от}, энергия запросного сигнала на, а направленность излучения характеризуется коэффициентом G_ц=G_{опрд от}.

5.5. Влияние отражений от земной поверхности

на дальность действия РЛС

Если в наземных (корабельных) РЛС применены антенны с широкой диаграммой направленности, радиоволны достигают цели и возвращаются обратно к РЛС как прямым путем, так и отражаясь предварительно от земной поверхности.

Земля в районе точки отражения является достаточно «»гладкой и идеально отражающей поверхностью, цель наблюдается в пределах угла места φ_ум≤10⁰, амплитудные различия слагаемых сигнала несущественны.

Амплитуда напряженности поля излучения с учётом влияния земли при таких условиях равна

,

(5.16)

где ζ_m – амплитуда напряженности поля для случая свободного пространства;

         h – высота расположения антенны РЛС;

         φ_ум – угол места цели.

Диаграмма направленности антенны из-за влияния земли приобретает лепестковый характер с максимумом  в точках, где 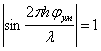, и минимальными значениями  при .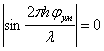

Число лепестков диаграммы направленности n_л и их ширина θ_ум зависят от высоты подъема антенны h и длины волны

, .

Угол места максимума нижнего лепестка равен приблизительно  λ/4h.

При подъеме антенны РЛС число лепестков будет увеличиваться при одновременном их сужении, а нижний лепесток будет располагаться ближе к земной поверхности.

Максимальное значение коэффициента направленного действия антенны по мощности с учетом влияния земли, которое принимаем практически равным соответствующему значению коэффициента усиления антенны, обозначим через G_0зм. Так как

,

то

.

(5.17)

Считая, что в РЛС используются для передачи и приёма одинаковые антенны, расположенные на одинаковой высоте h, или одна и та же антенна, получим формулу для максимальной дальности с учётом влияния земли:

.

(5.18)

где D_макс – максимальная дальность в свободном пространстве.

При обнаружении низколетящих целей, когда направление на цель антенной системы лежит ниже максимума первого лепестка,

,

и

,

выражение (5.17) примет следующий вид

.

При подстановке этого выражения в (5.8), получим формулу максимальной дальности обнаружения низколетящих целей с учётом влияния земли

.

(5.19)

Зависимость дальности обнаружения низколетящих целей от энергии излучения и чувствительности приёмника ещё слабее, чем для свободного пространства. Более существенно дальность обнаружения зависит от высоты полета цели H и высоты антенны радиолокационной станции h. Наиболее целесообразным способом увеличения дальности в этом случае является увеличение высоты подъема антенны радиолокационной станции.

5.6. Влияние на дальность действия РЛС ослабления энергии радиоволн в атмосфере

Распространяясь в атмосфере, радиоволны ослабляются из-за потери части электромагнитной энергии, которая поглощается и рассеивается молекулами кислорода и водяного пара, атмосферными осадками, частицами пыли и другими неоднородностями атмосферы.

Ослабление энергии радиоволн осадками происходит как за счёт её поглощения частицами влаги (в основном при малых размерах капель, например, при тумане), так  и вследствие её рассеяния (при крупных каплях).

Ослабление энергии зависит от длины волны, температуры, влажности, атмосферного давления и параметров частиц, вызывающих поглощение и рассеивание электромагнитной энергии.

Снег и град при одинаковой с дождем интенсивности значительно меньше влияют на величину ослабления энергии, поэтому их можно не принимать во внимание.

Следует иметь в виду, что затухание радиоволн уменьшается более чем в три раза при повышении температуры от 0 до 40⁰ С. Поглощение в кислороде пропорционально квадрату давления и, следовательно, уменьшается с подъемом на высоту. Поглощение в парах воды пропорционально влажности.

При прохождении радиоволн в прямом и обратном направлении через участок атмосферы длиной l км, на котором затухание характеризуется величиной δ_п дБ/км, общее ослабление энергии будет равно 2lδ_п дБ. Выражая в децибелах отношение энергий сигналов на входе приёмника без учёта и с учётом ослабления, получим

.

Переходя к натуральным логарифмам, находим

и ,

т.е. затухание энергии в атмосфере имеет экспоненциальный характер.

При отсутствии ослабления энергии принимаемого сигнала , а при его учёте, где k_D– величина, определяемая остальными параметрами, входящими в выражении для дальности. Из-за наличия ослабления одному и тому же пороговому значению сигналов (Е_прммин) будут соответствовать различные дальности.

В первом случае D=D_max, а во втором случае, когда требуется компенсировать потери энергии, меньшая дальность: D=D_{max п}. Таким образом, для пороговых условий получим

.   

Отсюда находим выражение для максимальной дальности обнаружения с учётом ослабления энергии в атмосфере

.

(5.20)

5.7.  Влияние кривизны земной поверхности и атмосферной рефракции на дальность действия

В реальных условиях следует учитывать кривизну земной поверхности, так как способность радиоволн диапазона УКВ к огибанию выпуклых поверхностей выражена очень слабо и дальность действия будет ограничиваться предельным значением D_пред.

При прямолинейном распространении радиоволн предельная дальность, называемая «дальностью прямой видимости», будет равна (рис.5.4)

,   

где R_з=6370 км – радиус Земли.

Так как и , то

км.

(5.21)

При обнаружении высоколетящих космических объектов, например спутников связи, когда величины R_з и Н соизмеримы,

км.

(5.22)

Рис.5.4. Предельная дальность действия РЛС при прямолинейном распространении радиоволн.

Неоднородность тропосферных слоев атмосферы по высоте приводит к искривлению траектории радиоволн (рефракции) в вертикальной плоскости. Величина и характер рефракции зависят от скорости изменения коэффициента преломления n при изменении высоты. Величина n определяется формулой

,

(5.23)

где Т⁰ – абсолютная температура воздуха;

р_в – барометрическое давление воздуха, мбар (1 мм рт.ст.=1,3332 мбар);

е – парциальное давление водяного пара (абсолютная влажность), мбар

Учёт влияния рефракции при расчётах распространения радиоволн обычно состоит в замене радиуса Земли R_з его эффективным значением

R_{з эфф}; атмосфера при этом считается однородной (радиоволны распространяются прямолинейно).

Значение эффективного радиуса Земли определяется из уравнения

,

Для стандартной атмосферы , и выражение для предельной дальности с учётом рефракции:

км.

(5.24)

ГЛАВА 6. МЕТОДЫ И УСТРОЙСТВА ИЗМЕРЕНИЯ ДАЛЬНОСТИ

6.1. Методы измерения дальности

Известны различные  подходы к классификации методов измерения дальности. В соответствии с параметрами сигналов существуют амплитудный, фазовый или частотный методы измерения.

1. Амплитудный метод

При амплитудном методе измерения определяется время запаздывания характерного изменения амплитуды принимаемого радиолокационного сигнала. Из различных видов модуляции излучаемых колебаний наиболее употребительной является импульсная.

Рассмотрим устройство импульсной дальномерной РЛС (рис. 6.1 и 6.2). Передатчик станции генерирует радиоимпульсы длительностью t_и с периодом повторения Т_и (напряжение u₂ на рис.6.2). Антенный переключатель (АП) подсоединяет антенну к передатчику на время генерации (t_и) и к приёмнику на всё остальное время. Отражённые импульсные сигналы запаздывают на время t_D; на вход приёмника поступают и колебания передатчика и отражённые сигналы (u₃).

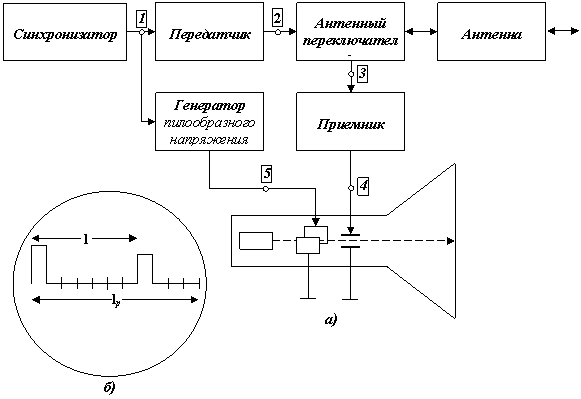Рис.6.1. Функциональная схема импульсного измерителя дальности (а) изображение сигналов на экране электроннолучевого индикатора (б)

Время запаздывания отражённых сигналов мало (оно составляет тысячные или даже миллионные доли секунды), и обычные часовые механизмы для его измерения непригодны. Одним из наиболее употребительных приборов для измерения времени запаздывания является электроннолучевая трубка. На рис.6.1, а показана трубка с электростатическим управлением. К вертикально отклоняющим пластинам трубки подводятся импульсы напряжения с выхода приёмника  u₄; к горизонтально отклоняющим пластинам от специальной схемы подводится пилообразное напряжение u₅ (рис.6.2). Передатчик и схема создания пилообразного напряжения запускаются одновременно импульсами синхронизирующего устройства, поэтому одновременно с излучением импульса передатчика начинается горизонтальное перемещение пятна по экрану трубки.

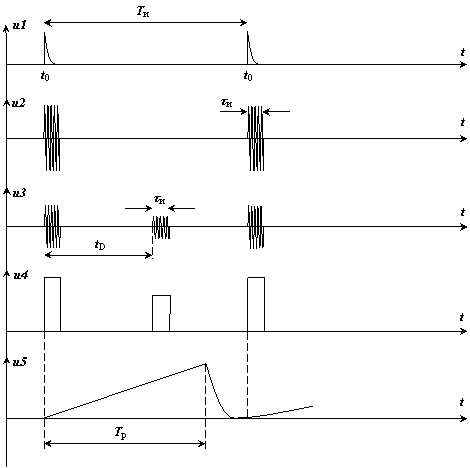
Рис.6.2. Эпюры напряжений в точках 1-5 схемы импульсного дальномера (рис.6.1, а).

Картина, наблюдаемая на индикаторе, иллюстрируется рис.6.1,б, пятно воспроизводит огибающие излучённого и отражённого импульсов, расстояние между которыми l пропорционально дальности обнаруженной цели          

,

(6.1)

где V_П – скорость движения пятна по экрану индикатора, откуда                     

.

(6.2)

Достоинства импульсных дальномеров:

¨ возможность построения РЛС с одной антенной;

¨ простота индикаторного устройства;

¨ удобство одновременного измерения дальности многих целей;

¨ простота разделения излучаемых импульсов, длящихся очень малое время t_и, и принимаемых сигналов.

Недостатки импульсного метода:

¨ необходимость использования больших импульсных мощностей передатчиков;

¨ невозможность измерения малых дальностей;

¨ большая минимальная дальность станции (определяющаяся длительностью излучаемых импульсов и временем протекания переходных процессов в антенном переключателе), которая составляет сотни или даже тысячи метров.

2. Частотный метод

Частотный метод определения дальности основан на использовании частотной модуляции излучаемых непрерывных колебаний; время запаздывания определяется путём измерения разности частот излучённых колебаний и отражённого сигнала. Функциональная схема РЛС с частотной модуляцией изображена на рис.6.3.

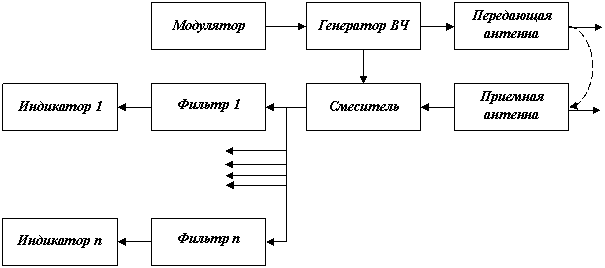
Рис.6.3. Функциональная схема измерителя дальности с частотной модуляцией.

Генератор высокой частоты, управляемый модулятором, вырабатывает колебания с частотой, изменяющейся по периодическому закону (рис.6.4, сплошная линия). Частота сигнала, отражённого от неподвижной цели, будет изменяться по такому закону, но только со сдвигом по временной оси на время запаздывания t_D.

На рис.6.4, а частота отражённых колебаний показана штриховой линией. Отражённые сигналы и колебания генератора подводятся к смесителю. Образующаяся на выходе смесителя разностная частота (рис.6.4, б) (частота биений) пропорциональна дальности цели. Если круговая частота излучения

,

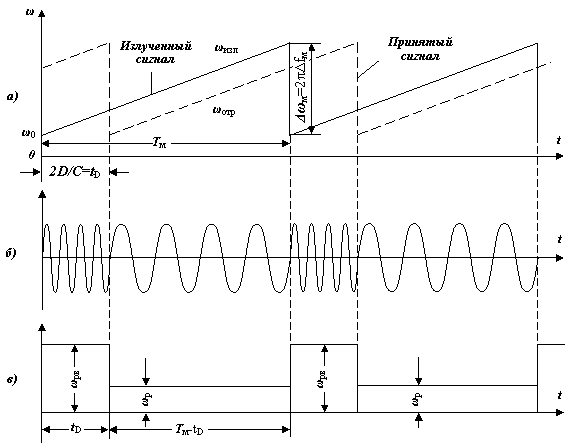
Рис. 6.4. Изменение частоты излучаемых и принимаемых колебаний:

а) - частоты излучённого и принятого сигнала;

б) - преобразованный сигнал (биения);

в) - изменение частоты преобразованного сигнала.

где Dw_м – девиация частоты передатчика, то частота сигнала, отражённого от неподвижной цели, будет равна

.

Разностная частота, выделяемая на выходе смесителя,                 

.

(6.3)

Откуда                                                 

.

(6.4)

Формулы (6.3) и (6.4) поясняют зависимость между дальностью цели и разностной частотой и позволяют понять сущность метода.

Для измерения разностных частот используются фильтры  и счётчики импульсов. При использовании фильтров возможны два варианта: применяется группа фильтров, настроенных на фиксированные частоты, или один фильтр с переменной настройкой. Попадание сигнала  разностной частоты в тот или иной фильтр (на что укажет соответствующий индикатор, например неоновая лампочка) позволит определить дальность цели.

Дальномеры данного типа позволяют определять очень малые дальности и использовать передатчики с малой мощностью излучения.

Недостатки дальномеров с частотной модуляцией:

¨ необходимость использования либо двух антенн, либо сложного устройства для разделения излучаемых и принимаемых сигналов;

¨ ухудшение чувствительности приёмника вследствие просачивания в приёмный тракт через антенну излучения передатчика, подверженного случайным изменениям;

¨ высокие требования к линейности изменения частоты.

3. Фазовые методы

Фазовые методы основаны на измерении разности фаз излучённых синусоидальных колебаний и принятых радиосигналов. Функциональная схема простейшего фазового дальномера изображена на рис.6.5.

Генератор создаёт незатухающие колебания частоты w₀, излучаемые в пространство. Фаза излучённых колебаний

,

где y₁ – начальное значение фазы.

Фаза принимаемого сигнала

.

Здесь y_отр – фазовый сдвиг, связанный с отражением радиоволны от цели;

y_РЛС – фазовый сдвиг в цепях РЛС, который можно считать известным, так как он поддаётся измерению и может быть учтён.

Принятые колебания сравниваются с колебаниями высокочастотного генератора; разность фаз пропорциональна  дальности цели         

(6.5)

или                         

.

(6.6)

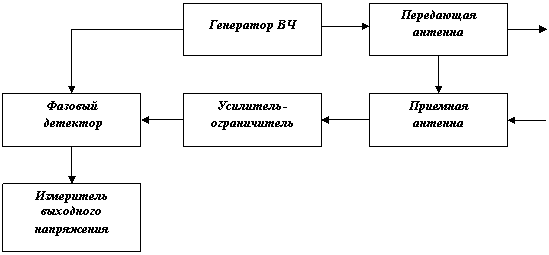Рис.6.5. Функциональная схема простейшего фазового

измерителя дальности.

Данный метод измерения практически не используют по двум обстоятельствам. Во–первых, очень мал диапазон однозначного измерения и, во–вторых, в формулу (6.6) входит неизвестная величина y_отр. Неоднозначность измерений определяется тем, что фазометрическое устройство позволяет определять фазовые сдвиги только в пределах от 0 до 2p. Допустив, что Dy£2p, из формулы (6.6) получим, что диапазон однозначного измерения дальности не превышает половины длины волны: .

В радиолокации используются ультракороткие волны и, следовательно, диапазон однозначно измеряемой дальности не превышает единиц метров. Что касается фазового сдвига y_отр, образующегося при отражении высокочастотных колебаний от цели, то, поскольку он весьма сложным образом зависит от конфигурации цели, её размеров и расположения относительно РЛС, то заранее знать нельзя и поэтому нельзя корректировать показания измерителя.

Указанные недостатки простейшего фазового дальномера устраняются при использовании более сложных схем, в которых применяется не менее двух частот.

На рис.6.6 изображена функциональная схема фазового дальномера с использованием низкой частоты W, на которой осуществляется измерение фазового сдвига, и высокой w₀, играющей роль переносчика информации.

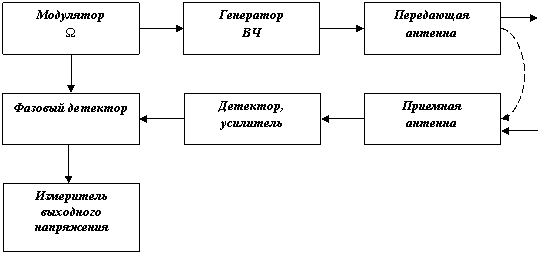Рис.6.6. Функциональная схема фазового измерителя

 дальности с модулятором.

Модулятор создаёт синусоидальное напряжение , модулирующее по амплитуде колебания генератора высокой частоты

,

где m - коэффициент модуляции.

Модулированные колебания излучаются в пространство. Принятые сигналы после усиления детектируются, и выделяется их огибающая, фаза которой сравнивается с фазой колебаний модулятора. Фаза огибающей принятых сигналов зависит от дальности цели

.

(6.7)

В формулу (6.7) не включён фазовый сдвиг огибающей колебаний при отражении y_отр, который пренебрежимо мал.

Фазовый сдвиг в цепях РЛС y_РЛС может быть измерен и учтён при градуировке фазометрического устройства. Разность фаз низкочастотных колебаний  позволяет определить дальность цели

.

(6.8)

Частота может быть выбрана достаточно низкой, что обеспечит большой диапазон однозначно измеряемых дальностей.

Данное дальномерное устройство характеризуется рядом достоинств:

¨ требуется малая мощность излучения, так как генерируются незатухающие колебания;

¨ точность измерения дальности практически не зависит от доплеровского сдвига частоты отражённого сигнала;

¨ просто само измерительное устройство.

Недостатки:

¨ отсутствует разрешение по дальности, так как при наличии одновременно двух целей их сигналы раздельно наблюдать нельзя;

¨ чувствительность приёмника ухудшается вследствие просачивания излучения передатчика;

¨ необходимы две антенны или система развязки излучаемых и принимаемых колебаний.

          Известен другой вариант двухчастотного фазового дальномера (рис.6.7).

РЛС включает два генератора высокочастотных колебаний и два приёмника, работающих соответственно на частотах w₁ и w₂. Колебания обоих генераторов подводятся к передающей антенне, а также к первому смесителю; с выхода приёмников два сигнала воздействуют на второй смеситель.

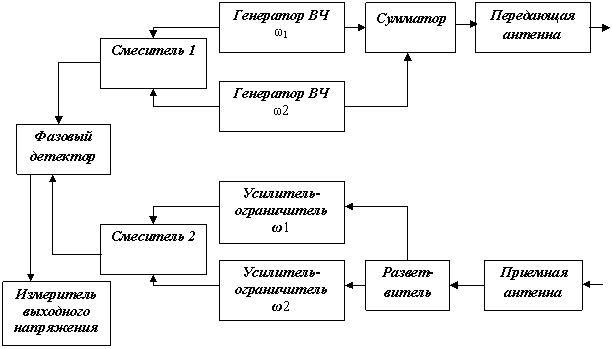
Рис.6.7.Функциональная схема двух частотного фазового

измерителя дальности.

Пусть напряжение генераторов:

и

.

На выходе первого смесителя получим колебания первой разностной частоты

 .

Если не учитывать фазовых сдвигов в цепях РЛС, то оба принятых сигнала могут быть записаны как

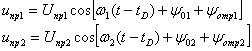
и напряжение второй разностной частоты на выходе второго смесителя

 .

При условии, что излучаемые частоты мало отличаются друг от друга 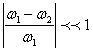, фазовые сдвиги при отражении от цели на обеих частотах можно считать одинаковыми, т. е. y_отр1»y_отр2.

Измерение фазового сдвига Dy позволяет определить дальность цели   

.

(6.9)

Анализ формулы (6.9) показывает, что в рассмотренном дальномере может быть обеспечен большой диапазон однозначного измерения дальности [разность (w₁-w₂) является малой величиной], а также исключается влияние на результат измерений фазового сдвига y_отр. Такому дальномеру присущи перечисленные выше достоинства и недостатки, свойственные всем РЛС с непрерывным излучением.

ГЛАВА 7.  МЕТОДЫ И УСТРОЙСТВА ИЗМЕРЕНИЯ УГЛОВЫХ КООРДИНАТ

Для определения угловых координат целей используются угломерные или пеленгационные радиолокационные устройства.

Угломерное устройство включает антенну (антенную систему), приёмник для обработки принятых радиолокационных сигналов и измерительное устройство. Одной из основных характеристик угломерного устройства является его пеленгационная характеристика, представляющая собой зависимость выходного напряжения приёмника от направления прихода радиоволны U_вых(j). В зависимости от того, какой параметр сигнала – амплитуда, частота или фаза – оказывает основное влияние на формирование пеленгационной характеристики, методы измерения угловых координат можно подразделять на амплитудные, частотные и фазовые.

1. Амплитудные методы

В настоящее время известны и широко используются несколько амплитудных методов: максимума, минимума, сравнения, равносигнальный.

При пеленгации по методу максимума плавно изменяется угловое положение антенны, и она в течение некоторого времени принимает сигналы цели; отсчёт угловой координаты цели производится в тот момент, когда амплитуда сигнала на выходе приёмника достигает наибольшего значения. Функциональная схема соответствующего угломерного устройства показана на рис.7.1.

Рис.7.1. Функциональная схема угломерного устройства с отсчётом по максимуму.

Механизм поворота вращает антенну; одновременно приводится в действие указатель поворота, по шкале которого отсчитывается направление  оси антенны. Когда цель окажется в пределах диаграммы направленности антенны F(j), в приёмник начнут поступать сигналы. Амплитуда сигналов зависит от углового положения антенны по отношению к цели. При вращении антенны выходное напряжение приёмника U_вых повторяет форму диаграммы направленности антенны (рис.7.2).

Рис.7.2. Пеленгационная характеристика при пеленгации по максимуму.

Это и будет пеленгационная характеристика угломерного устройства

,

(7.1)

где k - коэффициент пропорциональности.

Когда ось антенны совпадает с направлением на цель, выходное напряжение приёмника достигнет максимума; в этот момент указатель поворота антенны покажет пеленг цели j_ц.

Достоинства метода:

¨ простота его технической реализации;

¨ получение наибольшей (при прочих равных условиях) амплитуды принимаемого сигнала в момент точного пеленга.

Недостатком метода является относительно низкая точность измерений угловой координаты.

Точность измерения угла характеризуется пеленгационной чувствительностью, представляющей собой крутизну пеленгационной характеристики вблизи направления на цель:

.

(7.2)

Если измерительное устройство позволяет заметить минимальное изменение выходного напряжения, равное DU_мин, то эта величина связана с соответствующей угловой ошибкой Dj:

.

(7.3)

Следовательно, чем больше пеленгационная чувствительность, тем выше точность измерения угловой координаты.

При пеленгации по методу максимума для диаграмм направленности любого типа пеленгационная чувствительность очень мала (при точном пеленге ), поэтому и точность измерения координат относительно низка.

Метод пеленгации по минимуму отличатся тем, что отсчёт угловой координаты производится в момент уменьшения до минимума выходного напряжения приёмника. Диаграмма направленности антенны пеленгатора имеет в средней части провал до нуля. Этого можно добиться, например, используя две антенны, повёрнутые в пространстве одна относительно другой на угол, равный ширине диаграммы направленности по нулевому уровню (рис.7.3, а).

Функциональная схема пеленгационного устройства такая же, как и при пеленгации по максимуму (рис.7.1). Изменения амплитуды сигнала на выходе приёмника при повороте антенны характеризуются графиком рис.7.3,б; аналогичный вид имеет и пеленгационная характеристика , где функция F(j)–результирующая диаграмма направленности.

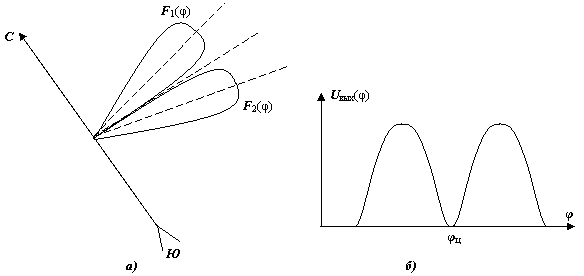
Рис.7.3. Диаграмма направленности антенного устройства (а) и пеленгационная характеристика при пеленгации по минимум (б).

При пеленгации по минимуму может быть получена высокая точность измерения угловой координаты, так как пеленгационная чувствительность велика. Но амплитуда сигнала вблизи направления пеленга мала; при точном пеленге она становится равной нулю.

Практически по методу минимума можно пеленговать только источники мощного собственного излучения. Поэтому метод пеленгации по минимуму в радиолокации не используется.

Метод сравнения характеризуется тем, что пеленг цели определяется по соотношению амплитуд сигналов, принятых одновременно двумя антеннами. Функциональная схема пеленгационного устройства, в котором использован метод сравнения, приведена на рис.7.4; графики рис.7.5 характеризуют пространственное расположение диаграмм направленности антенного устройства.

Амплитуды сигналов на выходе приёмников пропорциональны модулям векторов  и  (рис 7.4):

 и  .

В счетно-решающей схеме осуществляется сравнение амплитуд сигналов. Технически наиболее просто осуществить вычитание одного сигнала из другого, т.е.   

.

(7.4)

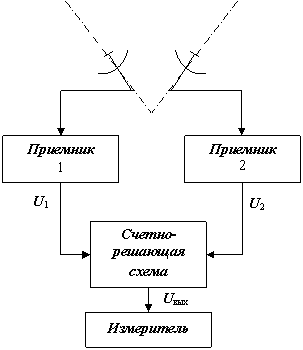
Рис.7.4. Функциональная схема пеленгатора, в котором

 используется метод сравнения.

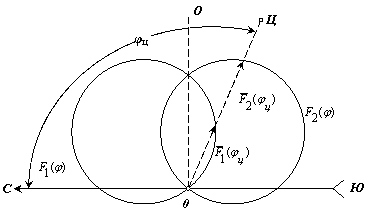
Рис.7.5. Пространственное расположение диаграмм направленности

при использовании метода сравнения.

При этом выходное напряжение зависит от абсолютных значений амплитуд сигналов и, следовательно, будет изменяться в зависимости от расстояния между РЛС и целью, отражающих свойств цели, поглощения в среде и т.д. Исключить влияние изменения амплитуд сигналов на результат измерений можно либо с помощью системы АРУ, управляющей усилением обоих приёмников, либо осуществляя деление одного сигнала на другой:

.

(7.5)

Вид пеленгационной характеристики иллюстрирует рис.7.6.

Рис.7.6. Пеленгационная характеристика при использовании

метода сравнения.

Основное достоинство метода сравнения – возможность мгновенного определения направления на цель в пределах относительно широкого сектора при неподвижной антенной системе. Наиболее существенным недостатком является относительно низкая точность измерения, существенно меняющаяся в зависимости от вида и взаимного расположения диаграмм направленности антенн, а также от направления прихода волны.

Частным случаем метода сравнения является равносигнальный метод пеленгации. Он также основан на сравнении амплитуд сигналов, принимаемых двумя антеннами, но для отсчёта углового положения добиваются равенства сигналов. При пеленгации цели по равносигнальному методу антенное устройство поворачивают до тех пор, пока выходное напряжение не станет равным нулю. В этот момент угловая координата цели определяется по положению антенны.

Равносигнальный метод характеризуется высокой точностью, так как при измерении используется небольшой участок диаграмм направленности (вблизи равносигнального направления ОО, рис.7.5) с относительно большой крутизной. Этот метод часто используют для автоматического слежения за целью по угловым координатам. При этом выходное напряжение U_вых подводят к системе управления механизмом поворота антенны. В зависимости от знака рассогласования между равносигнальным направлением ОО и направлением на цель механизм будет поворачивать антенну в ту или иную сторону, чтобы свести напряжение U_вых к нулю; при этом равносигнальное направление антенны всё время будет оставаться направленным на цель.

Равносигнальный метод можно реализовать при использовании одной антенны, диаграмма направленности которой периодически изменяет своё положение в пространстве. В этом случае сравнению подлежат сигналы, принятые в различные моменты времени при разных положениях диаграммы направленности.

2. Фазовые методы

Фазовые методы основаны на измерении разности фаз электромагнитных колебаний, принимаемых различными антеннами. Пусть в точках 1 и 2 расположены две приёмные антенны (рис.7.7), расстояние между которыми (база) равно d.

Принятые антеннами сигналы подводятся к фазовому детектору. Выходное напряжение фазового детектора будет определяться только разностью фаз колебаний (можно считать амплитуды обоих колебаний на входе детектора одинаковыми)

.

Если направление прихода радиоволны составляет угол j с перпендикуляром к базе, то фазовый сдвиг высокочастотных колебаний в антеннах равен

,

а при малых значениях j, когда приближенно можно считать ,

Рис.7.7. Функциональная схема фазового измерителя

угловых координат.

.

(7.6)

С учётом (7.6) пеленгационная характеристика будет

(7.7)

 (кривая 1 на рис.7.8).

Рис.7.8. Пеленгационные характеристики фазового пеленгатора

Измеряя U_вых, можно определить направление прихода радиоволны при неподвижном антенном устройстве.

Из формулы (7.7) можно видеть, что точность измерения угловой координаты вблизи значения j=0 низка. Кроме того, нельзя определить направление смещения цели от перпендикуляра к базе. Оба недостатка могут быть устранены, если ввести искусственный фазовый сдвиг сигнала на 90⁰ в одном из усилителей. На рис.7.7 такой фазосдвигающий элемент изображён пунктиром в верхнем усилительном канале.

При введении дополнительного фазового сдвига, получим

(7.8)

(кривая 2 на рис.7.8).

Метод характеризуется относительно высокой точностью измерения; он может быть использован для автоматического слежения за целями по угловым координатам.

Недостатками метода являются:

¨ неоднозначность отсчёта;

¨ отсутствие разрешения целей.

Если диапазон однозначного измерения фазы принять равным 2p, то пределы однозначного измерения угла могут быть определены с помощью формулы (7.6)

.

Неоднозначность измерения угловых координат фазовым методом может быть устранена, если в пеленгаторе используются антенны с достаточно узкими диаграммами направленности q_А<Dj_одн, где q_А  - ширина диаграммы направленности антенны.

ГЛАВА 8. ОСНОВЫ ТЕОРИИ ПЕРЕДАЧИ ИНФОРМАЦИИ

8.1. Информация, сообщение, сигнал

          Под информацией понимают совокупность сведений о каком - либо событии, объекте. Для хранения, обработки и преобразования информации используют условные символы ( буквы, математические знаки, рисунки, формы колебаний, слова), позволяющие представить информацию в той или иной форме. Информация, выраженная в определенной форме, предназначенная для передачи, называется сообщением. Так, при телеграфной передачи информация представляется в виде букв и цифр. Соответственно сообщением является текст телеграммы, представляющий последовательность этих знаков. В телефонных системах сообщением является речь (непрерывное изменение звукового давления). На практике часто информация представляется в двоичной форме, т.е. только двумя условными символами, например 1 и 0. Соответственно сообщением служит последовательность конечного числа двоичных символов.

          Одни сообщения (речь, температура, давление) являются функциями времени, другие (текст телеграммы) - нет. Природа сообщений может быть как электрической, так и неэлектрической.

          Для передачи сообщений от источника и получателю используют физические процессы, например, звуковые и электромагнитные волны, ток. Физический процесс, отображающий сообщение, называется сигналом. По своей природе сигналы могут быть электрическими, световыми, звуковыми и т.п. В РСПИ используются электрические сигналы. Поэтому при передаче сообщения неэлектрической природы предварительно преобразуются в электрические колебания с помощью преобразователей: микрофонов, передающие телевизионных трубок, датчиков температуры, давления и т.п. Эти электрические колебания обычно называют первичными сигналами.

          Любой первичный сигнал является функцией времени х(t). В зависимости от области определения и области возможных значений этой функции различают следующие виды сигналов:

¨ непрерывные по уровню и по времени (рис. 8.1,а);

¨ непрерывные по уровню и дискретные по времени (рис. 8.1,б);

¨ дискретные (квантованные) по уровню и непрерывные по времени (рис.8.1,в);

¨ дискретные по уровню и по времени (рис.8.1,г).

          Сигналы первого вида, называемые непрерывными, задаются на конечном или бесконечном временном интервале и могут принимать любые значения в некотором диапазоне. Примером таких сигналов являются сигналы на выходах микрофона, датчиков температуры, давления, положения и т.п. Являясь электрическими модулями физических величин, такие сигналы часто называются аналоговыми.

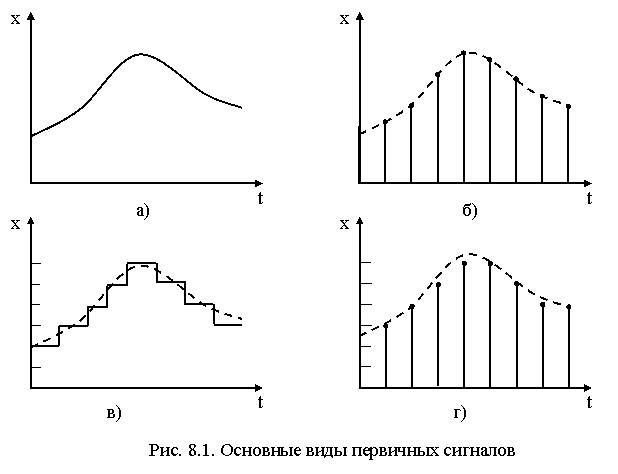
          Сигналы второго вида задаются в определенные дискретные моменты времени и могут принимать любые значения из некоторого диапазона. Их можно получить из непрерывных сигналов путем взятия отсчетов в определенные моменты. Это преобразование называется дискретизацией во времени. Шаг дискретизации T_д (промежуток времени между двумя соседними отсчетами) может быть как постоянным, так и переменным. Обычно его значение выбирают, исходя из допустимой погрешности при восстановление непрерывного сигнала по конечному числу его отсчетов.

          Сигналы третьего вида, называемые квантованными по уровню, задаются на некотором временном интервале и характеризуются тем, что принимают только вполне определенные дискретные значения. Их можно получить из непрерывных сигналов, применяя к ним операцию квантования по уровню. В результате этой операции непрерывный сигнал заменяется ступенчатой функцией. Шаг квантования ∆х (расстояние между двумя соседними разрешенными уровнями) может быть как постоянным, так и переменным. Его обычно выбирают из условия обеспечения требуемой точности восстановления непрерывного сигнала из квантованного.

          Сигналы четвертого вида, называемые дискретными, задаются в определенные дискретные моменты и принимают определенные дискретные значения. Их можно получить, например, из непрерывных сигналов, осуществляя операции дискретизации по времени и квантования по уровню. Такие сигналы легко представить в цифровой форме, т.е. в виде чисел с конечным числом разрядов. По этой причине их часто называют цифровыми.

          Аналогичная классификация возможна и для сообщений.

          Сообщения, подлежащие передаче, являются или случайной величиной, или случайной функцией. Детерминированные (заранее известные) сообщения не содержат информации, и нет смысла их передавать. Соответственно сигнал также следует рассматривать как случайный процесс. Детерминированные сигналы не несут информацию. В технике связи они используются для изучения свойств различных радиотехнических цепей.

          Множество возможных сообщений (сигналов) с заданным на нем распределением вероятностей называется ансамблем сообщений (сигналов).

8.2.Обобщенная структурная схема, основные подсистемы

          Под системой связи (рис.8.2.) понимают совокупность технических средств, предназначенных для передачи информации, включая источник сообщений и получателя сообщений.

Источник сообщений- это устройство, осуществляющее выбор сообщений из ансамбля сообщений. Им может быть датчик, ЭВМ и т.п.  В зависимости от типа сообщений различают дискретные и непрерывные источники.

Учитывая, что первичные сигналы часто отождествляют с передаваемыми сообщениями, в дальнейшем под источником сообщений будем понимать источник первичных сообщений разной природы и преобразователь неэлектрической величины в электрическую.

Передающее устройство предназначено для преобразования сообщения x(t)  в сигнал S(t) , который может распространяться по линии связи. В общем случае оно выполняет операции кодирования и модуляции (рис.8.3.). При передаче непрерывных сообщений цифровыми методами передающее устройство осуществляет операции дискретизации по времени и квантования по уровню.

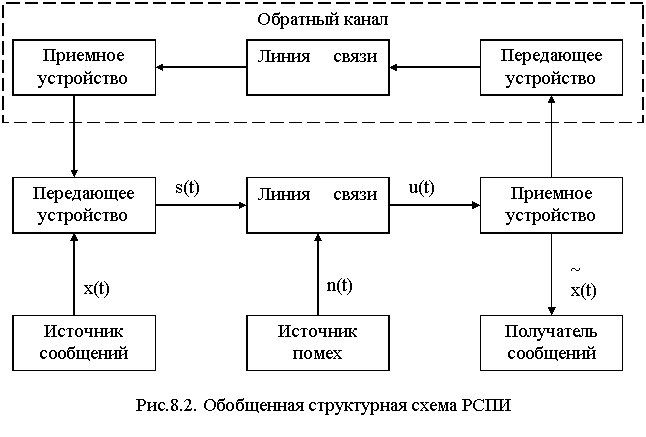
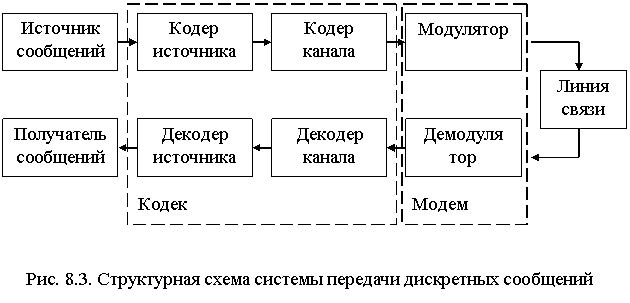
В узком смысле кодирование представляет собой преобразование дискретного сообщения в последовательность кодовых символов, осуществляемое по определенному правилу. Множество всех кодовых последовательностей (кодовых комбинаций), возможных при данном правиле кодирования, образует код. Совокупность символов, из которых составляются кодовые последовательности, называют кодовым алфавитом, а их число (объем кодового алфавита)- основанием кода. Число символов в кодовой комбинации может быть одинаковым или разным. Соответственно различают равномерные и неравномерные коды. Число символов в кодовой комбинации равномерного кода называется длиной кода.

          Кодирование позволяет повышать достоверность передачи информации. Предварительно отметим, что все коды делятся на простые и помехоустойчивые. Простые коды состоят из всех возможных кодовых комбинаций. Поэтому превращение одного символа кодовой комбинации в другой из-за действия помех приводит к новой кодовой комбинации, т.е. к появлению необнаруживаемой ошибки. В помехоустойчивых кодах используется лишь некоторая часть из общего числа возможных кодовых комбинаций. Благодаря этому появляется возможность обнаруживать и исправлять ошибки в принятых комбинациях, что и способствует повышению достоверности передачи информации.

          В соответствии с задачами кодирования различают кодирующее устройство (кодер) для источника и кодирующее устройство для канала (рис.8.3). Задачей первого является экономное (в смысле минимума среднего числа символов) представление достоверной передачи сообщений.

          Первичные сигналы, как правило, низкочастотные. Их можно передавать лишь по проводным линиям связи. Для передачи сообщений по радиолиниям используют специальные колебания, называемые переносчиками. Они должны хорошо распространяться по линии связи. В РСПИ в качестве переносчиков используются высококачественные колебания.

          Сами переносчики не содержат информации о передаваемом сообщении. Для того чтобы заложить в них эту информацию, применяют операцию модуляции, которая заключается в изменении одного или нескольких параметров переносчика по закону передаваемого сообщения. Устройство, осуществляющее эту операцию, называется модулятором.

          Приемное устройство. Основной задачей приемного устройства является выделение передаваемого сообщения из принятого сигнала u (t). В общем случае это достигается выполнением над принятым сигналом операций демодуляции и декодирования. Устройства, выполняющие эти операции, называются соответственно демодулятором и декодером.

          Операция демодуляции заключается в преобразовании принятого модулированного сигнала, искаженного помехами, в модулирующий сигнал. В системах передачи непрерывных сообщений при аналоговой модуляции сигнал на выходе демодулятора совпадает с первичным сигналом, отображающим сообщение. Поэтому он без дальнейших преобразований поступает к получателю. 

8.3. Классификация систем передачи информации

          Современные РСПИ характеризуются большим разнообразием видов передаваемых сообщений, способов модуляции, принципов построения, режимов работы и т.п. Соответственно они могут быть классифицированы по многим признакам.

          По числу каналов различают одноканальные и многоканальные системы. По наличию обратного канала различают системы без обратной связи и с обратной связью.

          По режиму использования канала различают системы односторонней связи, симплексные и системы двусторонней связи. В первых передача осуществляется в одном направлении, в последних возможна одновременная передача в обоих направлениях. В симплексной системе возможна двусторонняя связь, но передача и прием ведутся поочередно.

          По виду передаваемых сообщений различают системы передачи дискретных и непрерывных сообщений.

          По назначению передаваемых сообщений различают следующие типы систем: телефонные, предназначенные для передачи речи; телеграфные, предназначенные для передачи текста; фототелеграфные, предназначенные для передачи неподвижных изображений; телевизионные, предназначенные для передачи изображений; телеметрические, предназначенные для передачи измерительной информации; системы телеуправления, предназначенные для передачи команд управления; системы передачи данных, предназначенные для обслуживания автоматизированных систем управления.

          В зависимости от механизма распространения радиоволн, используемых для передачи сообщений, различают ионосферные, тропосферные, метеорные и космические системы.

Непрерывные каналы. Искажения сигналов и помехи в реальных каналах связи весьма разнообразны. Тем не менее математическая модель канала должна по возможности точно описывать основные особенности реального канала и в то же время быть достаточно простой для получения конечных результатов при анализе и синтезе систем передачи.

Идеальный канал без помех вносит детерминированные искажения, связанные с изменением амплитуды и временного положения сигнала. Переданный сигнал может быть полностью восстановлен на приемной стороне в новом временном отсчете. Эта модель используется для описания каналов с закрытым распространением малой протяженности (кабель, провод, волновод, световод и т.д.).

Канал с гауссовским белым шумом представляет собой идеальный канал, в котором на сигнал накладывается помеха

.

Коэффициент передачи  и запаздывание  постоянны и известны в точке приема. Такая модель, например, соответствует радиоканалам, работающим в пределах прямой видимости.

Гауссовский канал с неопределенной фазой сигнала отличается от предыдущего тем, что фаза несущего колебания в точке приема предполагается случайной с плотностью распределения  в интервале. Эта неопределенность вызвана двумя причинами: отсутствием устройств оценки и предсказания фазы либо ошибками в оценке фазы при их работе. Важно знать скорость флуктуаций фазы. В дискретных системах различают каналы с быстрыми флуктуациями, когда интервал их корреляции меньше длительности посылки, и с медленными, когда это условие не выполняется. При медленных фруктуациях фаза несущего колебания за длительность посылки практически не изменяется.

Гауссовский канал с неопределенной амплитудой и фазой сигнала вносит в сигнал наряду с флуктуациями фазы и флуктуации амплитуды, которые связаны с изменением во времени по случайному закону коэффициента передачи . Как и в предыдущем случае, флуктуации могут быть быстрыми и медленными. Для определения модели канала необходимо задать плотность распределения  и корреляционную функцию флуктуаций .

          В гауссовском канале с линейными искажениями форма сигнала изменяется из-за наличия избирательных цепей. В общем случае линейные искажения носят случайный характер. Частотная характеристика канала неравномерна в полосе частот сигнала  и изменяется во времени, а импульсная характеристика  имеет длительность  (время памяти канала), превышающую величину . Такая модель полезна при анализе систем, использующих, например, каналы с рассеянием сигнала. Сигнал на выходе канала с линейными искажениями

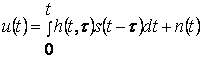                             (8.1)

          В радиосистемах передачи дискретной информации, когда время памяти канала  соизмеримо с длительностью посылки  (а тем более превышает ее), имеет место межсимвольная интерференция (МСИ), которая проявляется в наложении друг на друга соседних посылок. Одной из причин возникновения МСИ является увеличение скорости передачи при ограниченной полосе пропускания канала.

          В гауссовском канале с нелинейными искажениями сигнала, как и в предыдущем случае, аддитивная помеха предполагается в виде гауссовского белого шума, однако смесь сигнала и помехи, проходя по каналу, претерпевает нелинейные искажения так, что на входе приемника

, где  - амплитудная характеристика нелинейного звена канала.

Линейный канал со сложной аддитивной помехой характеризуется тем, что на сигнал могут воздействовать помехи любого вида: сосредоточенные по спектру, по времени, гауссовские, негауссовские и т.д. Модель помех можно определить, указав способ вычисления многомерной плотности распределения вероятностей. Эта модель наиболее полно отображает реальный шум в каналах связи, однако редко используется из-за сложности. Наиболее просто задать модель сложных аддитивных помех в виде небелого гауссовского шума с изменяющейся во времени и по частоте спектральной плотностью , характеризуемой как случайный процесс плотностью распределения  и корреляционными функциями во временной  и частотной областях.

Дискретно - непрерывные каналы.  Дискретно-непрерывный канал имеет дискретный вход и непрерывный выход. Примером такого канала является канал, образованный совокупностью технических средств между выходом кодера канала и входом демодулятора. Для его описания необходимо знать алфавит входных символов α_r, r=1,…., m, вероятности появления символов алфавита ρ(α_r), r=1, ….,  m , полосу пропускания непрерывного канала F_Κ, входящего в рассматриваемый канал, и плотности вероятности ω[u|α_r] появления сигнала u(t) на выходе канала при условии, что передавался символ α_r.

          Зная вероятности ρ(α_r) и плотности распределения вероятностей ω[u|α_r], можно найти апостериорные вероятности

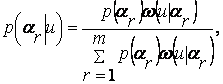
                 (8.2)

на основе которых, как правило, и принимается решение о переданном символе.

          Ширина спектра сигнала u(t) не может превышать значения F_κ. Поэтому в соответствии с теоремой Котельникова его можно представить совокупностью Μ=2F_кТ_с отсчетов, где Т_с - длительность сигнала. Соответственно условные плотности вероятности ω(u|α_r), r =1,…, m, можно задать как Μ- мерные плотности вероятности совокупности Μ отсчетов сигнала u(t).

В тез случаях, когда сигнал u(t) является аддитивной смесью полезного сигнала s_r(t) с известными параметрами, несущего информацию о символе [u1] α_r, и шума n(t), Μ-мерная плотность вероятности ω_м(u₁, u₂,…., u_м |α_r) будет плотностью вероятности шума, т.е.

,

(8.3)

где  и  - отсчеты сигналов  и шума  в момент .

          При независимых отсчетах шума

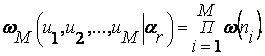                          (8.4)

          Если плотность вероятности  для любого сочетания  и  не зависит от времени, то канал называется стационарным.

          Если выполняется условие

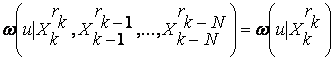,                  (8.5)

где  - последовательность передаваемых импульсов, то такой канал называется каналом без памяти.

          Реальные каналы являются обычно нестационарными и обладают памятью. Тем не менее модель дискретно-непрерывного стационарного канала с памятью часто применяется благодаря ее простоте.

Дискретные каналы. Дискретный канал имеет дискретный вход и дискретный выход. Примером такого канала является канал, образованный совокупностью технических средств между выходом кодера канала и выходом демодулятора. Для описания дискретного канала необходимо знать алфавит входных символов , их вероятность появления , скорость передачи символов , и значения переходных вероятностей, появления символа  при условии передачи символа .

          Первые две характеристики определяются свойствами источника сообщений, скорость - полосой пропускания непрерывного канала, входящего в состав дискретного канала, объем алфавита входных символов - алгоритмом работы решающей схемы, переходные вероятности  - характеристиками непрерывного канала.

          Заметим, что в общем случае в дискретном канале объемы входных и выходных символов не совпадают. Примером может быть канал со стиранием. Алфавит на его выходе содержит один добавочный символ по сравнению с алфавитом на входе. Этот добавочный символ (символ стирания) появляется на выходе тогда, когда анализируемый сигнал нельзя с большой вероятностью отождествить ни с одним из передаваемых символов. Стирание символов при применении соответствующего помехоустойчивого кода позволяет существенно повышать помехоустойчивость.

          Зная вероятности   и можно вычислить апостериорные вероятности

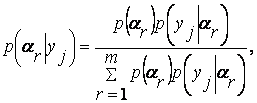                        (8.6)

того, что при принятом символе  был передан символ . Вероятности  и  позволяют определить полную вероятность ошибки в канале (или полную вероятность правильного приема) и информационные характеристики дискретного канала.

          Дискретный канал называется стационарным, если переходные вероятности  не зависят от времени. Дискретный канал называется без памяти, если переходные характеристики  не зависят от того, какие символы передавались и принимались ранее.

          Если в стационарном дискретном канале алфавиты на входе и выходе совпадают и

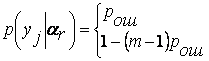
                              (8.7)

то такой канал называется симметричным.

          Математическая модель канала должна обеспечивать возможность нахождения основных характеристик потока ошибок. К ним относятся: вероятность ошибки в приеме символа р_ош; распределение вероятностей Р_n(r) появления ошибок r в блоке длины n; распределение длин интервалов между соседними ошибками; распределение длин серий ошибок и т.п.

          Модель должна быть простой и удобной для проведения расчетов. В то же время она должна достаточно точно описывать реальный канал, т.е. находиться в хорошем соответствии с экспериментальными данными. Наиболее простой является модель стационарного симметричного канала без памяти. В таком канале ошибки возникают независимо друг от друга, т.е. между ошибками отсутствуют статистические связи. вероятность ошибки р_ош при передаче любого символа одинакова и не меняется во времени. Стационарный симметричный канал без памяти полностью описывается вероятностью р_ош. Распределение ошибок в нем подчиняется биномиальному закону

(8.8)

где n - число символов в блоке, r - число ошибочных символов.

          Зная вероятность ошибки р_ош и используя выражение (8.8), можно найти все необходимые характеристики. В частности вероятность правильного приема блока из n символов  вероятность приема блока,  содержащего хотя бы одну ошибку,  вероятность появления в блоке и более ошибок

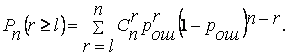                     (8.9)

          Большинство реальных каналов имеют "память", которая проявляется в том, что вероятность ошибки в символе зависит от того, какие символы передавались до него и как они были приняты. Первый факт обусловлен межсимвольными искажениями, являющимися результатом рассеяния сигнала в канале, а второй - изменением отношения сигнал-шум в канале или характера помех.

          При рассеянии сигнала приходящая на вход посылка является суммой некоторого числа предыдущих посылок с соответствующими весовыми коэффициентами. Поэтому вероятность ошибки в последующем символе будет зависеть от характера передаваемой информации за время рассеяния сигнала. Например, при чередовании посылок разных частот ошибка будет больше, чем внутри последовательности, состоящей из посылок одной частоты. Если менять длительность отдельных мешающих воздействий, например, в результате общих замираний сигнала или изменения уровня помех, то ошибки будут группироваться в пачки. Вероятность ошибки при приеме символа в этом случае зависит от того, была ошибка в предыдущем символе или нет. Простой моделью двоичного симметричного канала с памятью является канал, который может находиться в одном из двух состояний: d=0 и d=1. В обоих состояниях возможны независимые ошибки с вероятностями р₀ и р₁, где нижние индексы указывают на состояние канала.

          Одним из распространенных методов описания дискретного канала с памятью, связанной с межсимвольными искажениями, является использование аппарата цепей Маркова (посимвольное описание). В этом случае последовательность состояний двоичного канала рассматривается как N-связная двоичная цепь Маркова, а значения символов на каждой позиции - как состояние цепи, где N - число символов, на которое распространяется память канала.

8.4.Основные характеристики

          Любая система характеризуется рядом показателей, которые можно разделить на информационно-технические (достоверность, помехоустойчивость, скорость передачи информации, задержка, диапазон частот и т.п.) и конструктивно-эксплуатационные (объем и масса аппаратуры, энергетический КПД, мобильность, гибкость, эксплуатационная надежность, стоимость).

Достоверность передачи информации характеризует степень соответствия принятых сообщений переданным. Она зависит от параметров самой системы, степени ее технического совершенства и условий работы. Последние определяются типом и состоянием линии связи, видом и интенсивностью помех, а также организационными мероприятиями по соблюдению правил радиообмена и эксплуатации аппаратуры.

          Для различных РСПИ критерии соответствия принятого сигнала переданному могут существенно отличаться. При передаче дискретных сообщений действие помех проявляется в том, что вместо переданного символа принимается другой. В этом случае достоверность передачи сообщений целесообразно характеризовать или вероятностью правильного приема , или вероятностью ошибки .

          Под помехоустойчивостью СПИ понимается способность системы противостоять вредному действию помех на передачу сообщений. Она зависит от способа кодирования, модуляции, метода приема и т.п. Количественно помехоустойчивость систем передачи дискретных сообщений можно характеризовать вероятностью ошибки  при заданном отношении средних мощностей сигнала и помехи в полосе частот, занимаемой сигналом, или требуемым отношением средних мощностей сигнала и помехи на входе приемника системы, при котором обеспечивается заданная вероятность ошибки . Помехоустойчивость систем передачи непрерывных сообщений удобно оценивать отношением средних мощностей сигнала и помехи на входе приемника системы, обеспечивающим заданные значения этих показателей. При сравнительной оценке систем часто пользуются "обобщенным выигрышем системы"

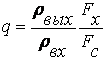,                                        (8.10)

где -отношение мощностей сообщения x(t) и шума на выходе приемника; -отношение мощностей сигнала и шума на входе приемника; - ширина спектра сообщения; - ширина спектра сигнала, используемого для передачи сообщения.

          При передаче дискретных сообщений для характеристики быстродействия аппаратуры формирования информационных символов пользуются понятием техническая скорость. Она определяется числом символов дискретного сообщения, передаваемых в единицу времени, и измеряется в бодах.

          Одной из важных характеристик системы передачи информации является задержка, под которой понимается промежуток времени между подачей сообщения от источника на вход передающего устройства и выдачей восстановленного сообщения получателю приемным устройством. Она зависит от протяженности линии связи и времени обработки сигнала в передающем и приемном устройствах.

          Пусть  T_C  - среднее время передачи одного символа. Тогда величина

R=I^′(А;Y)=(1/ T_C ) I(A;Y) характеризует среднее количество информации, передаваемое в единицу времени. Ее называют скоростью передачи информации.  I(A;Y)   - как среднее количество информации, получаемой приходом каждого символа.

ГЛАВА 9. ОСНОВНЫЕ ЗАДАЧИ ТЕОРИИ ИНФОРМАЦИИ

          Теория информации - область, в которой изучаются основные количественные закономерности, связанные с получением, хранением, передачей и обработкой информации.

          Теория информации позволяет сравнивать различные системы связи. Решение указанных задач стало возможным лишь с введением в ней таких понятий как энтропия и количество информации, которые позволили получить количественное описание процессов передачи информации и установить их общие закономерности.

          Особенностью теории информации является то, что она изучает предельные возможности статистического и помехоустойчивого кодирования, которые понимаются в том смысле, что допускается любая, в пределе бесконечно большая, продолжительность операций кодирования и декодирования, а также любая сложность кодеров и декодеров.

9.1. Количество информации в дискретных сообщениях. Энтропия источника дискретных сообщений.

Для сравнения различных систем связи необходимо ввести некоторую количественную меру, позволяющую оценивать объем информации, содержащейся в сообщении, и объем передаваемой информации.

          Рассмотрим сначала основные положения теории информации для дискретных систем связи. Обозначим возможные различные символы на входе некоторого блока СПИ через α_i, i = 1,…, m, а выходные символы через y_j, j = 1,…,n. Под символом α_i можно подразумевать символы источника, информационные последовательности, сигналы на входе линии связи, а под символами y_j - символы закодированных сообщений, кодовые последовательности, сигналы на выходе линии связи.

          Рассмотрим простейший случай, когда α_i, i = 1,…, m, взаимно независимые. При этом источник А полностью описывается априорными вероятностями  которые и характеризуют первоначальное незнание (первоначальную неопределенность) о появлении конкретного символа α_i на входе блока.

          При наличии помех между символами α_i и y_j нет однозначного соответствия, т.е. символ α_i может перейти в любой символ y_j с некоторой условной вероятностью которую можно вычислить, если известен механизм такого перехода. Зная вероятности  и  нетрудно найти вероятности  появления на входе блока символов α_i, i = 1,…, m, при условии, что на выходе блока наблюдался символ y_j. Эти вероятности, называемые апостериорными, характеризуют оставшееся незнание (оставшуюся неопределенность) о появлении на входе символов α_i, i = 1,…, m, при наблюдении символа y_j на выходе блока.

          Таким образом, полученная информация о символе α_i при наблюдении символа y_j приводит к изменению вероятности появления символа α_i от ее априорного значения  к ее апостериорному значению . При этом представляется обоснованным взять за количество информации о символе α_i, содержащейся в символе y_j, некоторую функцию только вероятностей  и :

                        (9.1)

Такое определение количества информации, несвязанное с физической природой сообщения, позволяет строить довольно общую теорию, в частности, сравнивать различные системы связи по эффективности.

          В качестве функции  удобно использовать логарифм отношения апостериорной  вероятности к априорной , т.е. определить  как

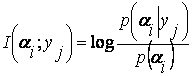(9.2)

При таком задании, в частности, количество информации обладает свойством аддитивности: количество информации о символе α_i(в дальнейшем для общности рассуждения - событии α_i), доставляемой двумя независимыми символами (событиями) y_j и z_k:

(9.3)

Это свойство хорошо согласуется с "интуитивным" понятием информации.

          Основание логарифма может быть любым. От него зависит единица измерения количества информации. В технических приложениях обычно используют основание 2. При этом количество информации I измеряется в двоичных единицах или битах. При проведении математических выкладок зачастую удобно пользоваться натуральными логарифмами. Соответственно информация измеряется в натуральных единицах или натах.

          Введенная величина  обладает важным свойством симметрии по отношению к α_i и y_j:

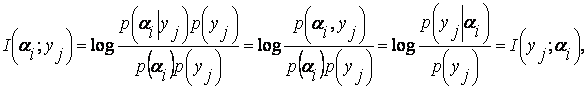
(9.4)

т.е. информация, доставляемая событием y_j о событии α_i равна информации, доставляемой событием α_i о событии y_j. По этой причине  называется взаимной информацией двух случайных событий относительно друг друга.

          Из (9.4) следует, что если события α_i и y_j статистически независимы, то , т.е. независимые события не несут друг о друге никакой информации.

          Взаимная информация при фиксированной вероятности принимает максимальное значение, когда апостериорная вероятность , т.е. когда наблюдаемое событие y_j однозначно определяет событие α_i. При этом

(9.5)

          Величина называется собственной информацией события α_i. Ее можно интерпретировать как количество информации, которое доставляет событие α_i или любое другое, однозначно связанное с ним. Собственная информация всегда является неотрицательной величиной, причем чем менее вероятно событие, тем она больше. Взаимная информация может быть как положительной, так и отрицательной величиной.

          Пусть α_i, y_j, z_k - статистически зависимых события. Предположим, что событие z_k известно. Количество информации о событии α_i, доставляемое событием y_j при условии, что z_k известно, называется условной взаимной информацией. Она определяется так же, как и взаимная информация, однако априорная и апостериорная вероятности должны быть взяты при условии z_k, т.е.

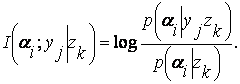                        (9.6)

Отсюда следует, что условная взаимная информация при фиксированной вероятности  принимает максимальное значение, когда . При этом

                  (9.7)

Величина  называется условной собственной информацией. Ее можно интерпретировать как количество информации, доставляемое событием α_i при известном событии z_k, или как количество информации, которое должно доставляться некоторым другим событием для однозначного определения события при известном z_k.

          Покажем, что взаимная информация удовлетворяет свойству аддитивности. Пусть α_i, y_j и z_k - три статистически зависимых события. Тогда количество информации о событии α_i, которое доставляют события y_j и z_k

(9.8)

          Таким образом, количество информации о событии α_i, которое доставляют события y_j и z_k, равно сумме информации, доставляемой z_k при известном событии y_j.

          Аналогично можно показать, что

                     (9.9)

          Используя соотношения (9.2), (9.4), (9.5) и (9.7), можно взаимную информацию записать в одной из следующих форм:

                        (9.10)

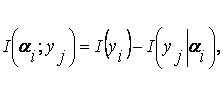                          (9.11)

                     (9.12)

где  - собственная информация сложного события α_iy_j.

          Соотношение (9.10) можно интерпретировать следующим образом. Взаимная информация  равна разности между количеством информации, требуемой для определения α_i до и после того, как становится известным y_j. Нетрудно пояснить и соотношения (9.11) и (9.12), а количество информации о множестве А передаваемых символов, которое в среднем содержится в множестве Y принимаемых символов.

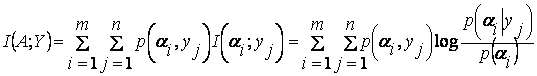.   (9.13)

Величина I(A;Y) называется средней взаимной информацией.

          Нетрудно показать, что

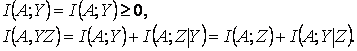         (9.14)

          На практике также вызывает интерес не собственная информация, а средняя собственная информация.

(9.15)

Она характеризует количество информации, которое в среднем необходимо для определения любого символа из множества А возможных передаваемых символов.

          Выражение (9.15) идентично выражению для энтропии системы в статистической механике. Поэтому величину I(A) называют энтропией дискретного источника А и обозначают через Н(А). Чем больше Н(А), тем более неопределенным является ожидаемый символ. Поэтому энтропию можно рассматривать как меру неопределенности символа до того, как он был принят.

          Из (9.15) следует, что Н(А)≥0, т.е. энтропия является неотрицательной величиной. Она обращается в нуль, когда одна из вероятностей р(α_i) равна единице, а остальные нулю. Этот результат хорошо согласуется с физическим смыслом. Действительно, такая ситуация возникает, например, когда передается только один символ. Поскольку он заранее известен, то неопределенность источника равна нулю и с появлением символа мы не получаем никакой информации.

          Энтропия удовлетворяет неравенству

(9.16)

причем знак неравенства имеет место, когда где m - число возможных событий α_i (число различных символов, сообщений и т.п.). Это свойство можно доказать, используя неравенство

                                             (9.17)

Рассмотрим разность

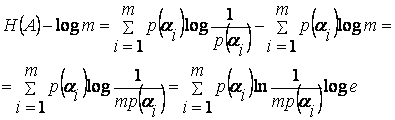       (9.18)

Учитывая (9.17), находим

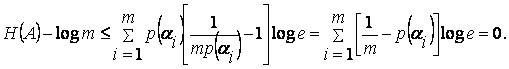   (9.19)

Знак равенства имеет место, когда 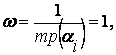так как только при  неравенство (9.17) превращается в равенство. При этом энтропия принимает максимальное значение .

          Из (9.16) вытекает следующий важный вывод: при заданном алфавите символов количество информации, которое в среднем может содержаться в одном символе, достигает максимума, когда все символы используются с равной вероятностью. При этом величину  называют информационной емкостью алфавита.

          Для алфавита, состоящего из двух символов,

где р - вероятность появления одного из символов. При р = 1/2 (рис.9.1.) энтропия принимает максимальное значение дв.ед. Таким образом, двоичная единица информации, или бит, - количество информации, которое содержится в одном двоичном символе, появляющемся с вероятностью р=0,5.

Подобно тому, как было введено понятие средней собственной информации, можно ввести понятие условной собственной информации:

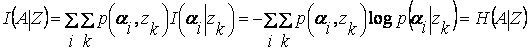   (9.20)

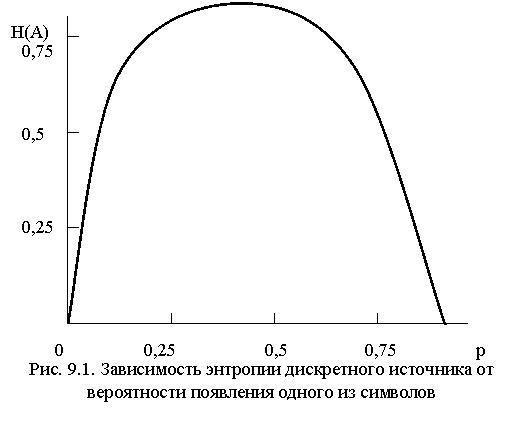
          Величина  характеризует количество информации, которое в среднем необходимо для определения любого символа из алфавита А при известном множестве событий Z, т.е. характеризует неопределенность символа алфавита А до того, как он был принят, при условии, что множество событий Z известно. Она называется условной энтропией и обозначается через .

          Используя неравенство (9.17), нетрудно показать, что

                                    (9.21)

причем знак равенства имеет место, когда события α_i и z_k статистически независимы ( для всех индексов i и k).

          Соотношение (9.21) играет важную роль в теории кодирования. На его основе можно сделать следующий вывод: для того, чтобы каждый символ кодовой комбинации доставлял как можно больше информации, необходимо обеспечивать статистическую независимость каждого символа кодовой комбинации от предыдущих символов.

          Можно ввести понятие энтропии множества совместных событий A и Z:

(9.22)

Подставляя вместо вероятности  под знаком логарифма произведение , выражение (9.22) можно привести к виду

(9.23)

Если события α_i и z_k статистически независимы, то формулу (9.23) можно переписать в виде

 (9.24)

          Соотношения (9.23) и (9.24) есть не что иное, как свойство аддитивности энтропии.

          Среднюю взаимную информацию можно представить как

(9.25)

(9.26)

(9.27)

          Выражение (9.25) имеет простую физическую интерпретацию, когда  α_i- переданный символ, а  y_j - принятый. При этом Н(А) можно рассматривать как среднее количество передаваемой информации, H(A│Y) - как среднее количество информации, теряемой в канале связи (величину H(A│Y) обычно называют надежностью), I(A;Y) - как среднее количество информации, получаемой с приходом каждого символа. Нетрудно дать соответствующие интерпретации соотношениям (9.26) и (9.27).

          Энтропия H(Y│A)  определяется только помехой в канале связи и называется шумовой.

          Пусть  T_C  - среднее время передачи одного символа. Тогда величина R=I^′(А;Y)=(1/ T_C ) I(A;Y) характеризует среднее количество информации, передаваемое в единицу времени. Ее называют скоростью передачи информации.

          Величина H`(A)=(1/T_c)H(A) характеризует среднее количество информации, выдаваемое источником. Ее называют производительностью источника.

          Найдем среднее количество информации, передаваемое по двоичному симметричному каналу (рис.9.2)

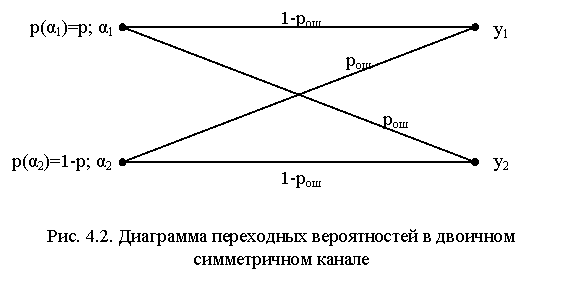
Пусть на вход канала поступают двоичные символы α₁ и α₂ с вероятностями р и (1-р) соответственно. На выходе канала появляются двоичные символы y₁ и y₂. Вероятность ошибки при передаче любого символа равна р_ош. Таким образом,

          Воспользуемся формулой (9.26). Энтропия

.

С учетом рассматриваемой модели канала

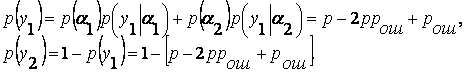
Нетрудно убедиться, что H(Y) принимает максимальное значение, равное 1, при р = 1/2.

          Условная энтропия

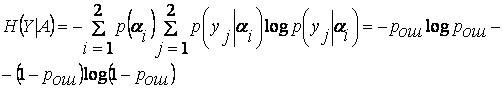
Заметим, что для рассматриваемого случая H(Y│A) не зависит от вероятности р.

          Подставляя выражения для H(Y) и H(Y│A) в (4.21), находим I(A;Y). В частности, при р = 1/2

 (9.28)

Таким образом, среднее количество информации, передаваемое каждым символом по двоичному симметричному каналу, при р = 1/2 зависит только от вероятности ошибочного приема символа (рис. 9.3)

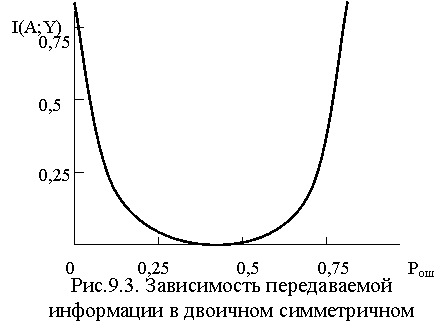
В отсутствие помех (р_ош=0) I(A;Y)=1 дв.ед., при р_ош=1/2 I(A;Y)=0, т.е. никакой информации не передается; при р_ош=1 I(A;Y)=1 дв.ед. В последнем случае, хотя все принятые символы ошибочные, однако передаваемые сообщения можно легко восстановить, поставив в соответствие сигналу  y₁ символ α₂, а сигналу y₂ символ α₁.

9.2. Избыточность сообщений

          Рассмотрим ансамбль A, состоящий из m различных символов . Энтропия такого дискретного источника достигает максимального значения , когда символы статистически независимы и появляются на его выходе с одинаковой вероятностью, равной 1/ m. На практике часто символы неравновероятны и зависимы. Поэтому энтропия источника . Соответственно количество информации, доставляемое такими символами, меньше возможного в  раз.

          Пусть сообщение состоит из n символов. Очевидно, что количество информации в нем . При использовании алфавита с максимальной энтропией для передачи такого же объема информации потребовалось бы число символов. Очевидно, что количество информации в нем I=nH(A). При использовании алфавита с максимальной энтропией для передачи такого же объема информации потребовалось бы число символов

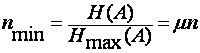
где, 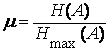- коэффициент, характеризующий допустимую степень сжатия сообщений.

          Величина называется избыточностью источника.

9.3. Пропускная способность дискретных каналов с шумом

Среднее количество информации, передаваемое по дискретному каналу в расчете на один символ, определяется как

где А и Y -множества символов на входе и выходе канала. Энтропия Н(А) определяется только источником входных символов. Энтропии H(A│Y), H(A) и H(Y│A) в общем случае зависят как от источника входных символов, так и от свойств канала. Поэтому скорость передачи информации зависит не только от канала, но и от источника сообщений. Максимальное количество переданной информации в единицу времени, взятое по всевозможным источникам входных символов (по всем многомерным распределениям вероятности Р(А), характеризующим эти источники),

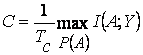                                   (9.29)

называется пропускной способностью канала.

          Пропускную способность канала можно определить и в расчете на символ:

                               (9.30)

9.4. Пропускная способность непрерывных каналов с

аддитивным шумом

Пусть сигнал y(t) на выходе канала представляет собой сумму полезного сигнала x(t) и шума n(t), т.е.

y(t) = x(t) + n(t), 0≤t≤T, (9.31)

причем сигнал x(t) и шум n(t) статистически независимы. Допустим, что канал имеет ограниченную полосу пропускания шириной F_к. Тогда в соответствии с теоремой Котельникова функции y(t) , x(t) и n(t) можно представить совокупностями отсчетов y_i, x_i и n_i, i=1,…,M, где М = 2F_кТ. При этом статистические свойства сигнала x(t) можно описать многомерной плотностью вероятности  а статистические свойства шума - плотностью вероятности   где x и n - векторы с координатами  и  соответственно.

          Пропускная способность непрерывного канала

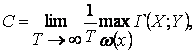
где - количество информации о какой-либо реализации сигнала x(t) длительности Т, которое в среднем содержит реализация сигнала y(t) той же длительности Т, максимум ищется по всем возможным распределениям ω(x).

          Среднюю взаимную информацию можно определить как

где

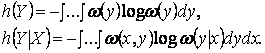
Заметим, что с учетом (9.31) условная плотность вероятности  и

          Таким образом, пропускная способность непрерывного канала с аддитивным шумом

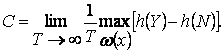(9.32)

          Вычислим пропускную способность непрерывного канала без памяти с аддитивным белым гауссовским шумом, имеющим одностороннюю спектральную плотность N₀, для случая, когда средняя мощность полезного сигнала равна P_c. При этом отсчеты шума оказываются статистически независимыми и дифференциальная энтропия

(9.33)

где  - дисперсия шума n(t).

          Определим максимально возможное значение дифференциальной энтропии h(Y). Прежде всего отметим, что

т.е. средний квадрат отсчета Y_i фиксирован. При этом дифференциальная энтропия h(Y_i) принимает максимальное значение, когда случайная величина Y_i  является гауссовской с нулевым математическим ожиданием. Это имеет место, если случайная величина X_i гауссовская с нулевым математическим ожиданием.

          Дифференциальная энтропия h(Y) совокупности из n отсчетов будет максимальна, если отсчеты будут статистически независимы. Это имеет место, если спектральная плотность мощности процесса X(t) равномерна в полосе частот F_k.

          При выполнении указанных требований к сигналу

(9.34)

          Подставляя (9.33) и (9.34) в (9.32), находим

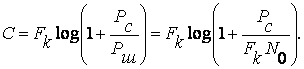(9.35)

          Формулу (9.35) часто называют формулой Шеннона. Подчеркнем, что она справедлива для следующей идеализированной модели канала связи. Выходное колебание y(t) представляет собой сумму входного сигнала x(t) и шума n(t), причем сигнал и шум являются статистически независимыми гауссовскими случайными процессами с нулевыми математическими ожиданиями и имеют равномерные спектральные плотности мощности в полосе частот .

          Формула (9.35) очень важна для системы связи, так как она устанавливает связь между пропускной способностью непрерывного канала с ограниченной полосой частот и техническими характеристиками системы: шириной полосы пропускания канала и отношением сигнал/шум. Из нее следует, что одну и ту же пропускную способность можно получить при различных соотношениях F_k и P_c/P_ш. Другими словами, формула (9.35) указывает на возможность обмена полосы пропускания на мощность сигнала и наоборот. С учетом зависимостей С от F_k и С от P_c/P_ш очевидна целесообразность обмена мощности сигнала на полосу.

          Из (9.35) нетрудно видеть, что пропускная способность канала растет с увеличением полосы частот F_k (рис.9.4.) и при  стремится к предельному значению

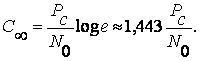
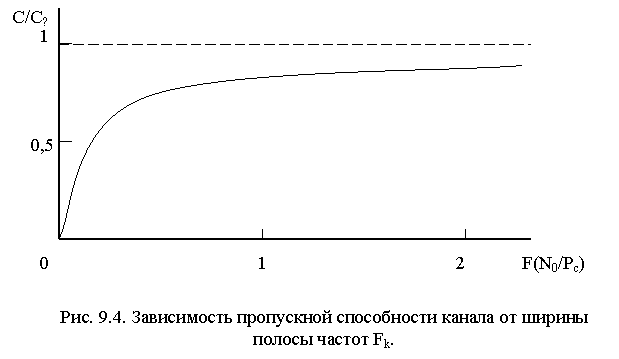
Заметим, что пропускная способность непрерывного канала, в котором действует шум, отличный от белого гауссовского, больше, чем дает формула (9.35)

9.5. Теорема кодирования для канала с помехами

          Пропускная способность дискретного и непрерывного каналов характеризуют их предельные возможности как средств передачи информации. Они раскрываются в фундаментальной теореме теории информации, которая известна как основная теорема кодирования К.Шеннона. Применительно к дискретному источнику она гласит: если производительность источника сообщений H^{`</sup>(A)  меньше пропускной способности канала С, то существует по крайней мере одна процедура кодирования и декодирования, и ненадежность H(A│Y) могут быть сколь угодно малы. Если H<sup>`}(A)>C, то такой процедуры не существует.

          Результат основной теоремы кодирования для канала с шумом в определенной степени неожидан. В самом деле, на первый взгляд кажется, что уменьшение вероятности ошибок в передаче сообщений требует соответствующего уменьшения скорости передачи и, что последняя должна стремиться к нулю вместе с вероятностью ошибок. Такой вывод, в частности, вытекает из рассмотрения многократной повторной передачи символов источника по каналу как способа уменьшения вероятности ошибок в передаче сообщений. В этом случае при наличии помех в канале связи обеспечить стремление к нулю вероятности ошибки в передаче сообщения можно только при стремлении скорости передачи к нулю.

          Однако теорема кодирования показывает, что в принципе можно вести передачу со скоростью, сколь угодно близкой к С, достигая при этом сколь угодно малой вероятности ошибки. К сожалению, теорема, указывая на принципиальное существование помехоустойчивого кода, не дает рецепта его нахождения. Можно лишь отметить, что для этого необходимо применять коды большой длины. При этом по мере приближения скорости передачи к пропускной способности и уменьшения вероятности ошибки код усложняется вследствие увеличения длины блоков, что приводит к резкому усложнению кодирующего и декодирующего устройств и запаздыванию при декодировании. Применяемые в настоящее время способы кодирования не реализуют потенциальных возможностей систем связи. О степени совершенства системы связи можно судить по отношению .

          Для канала с пропускной способностью С, на входе которого включен источник непрерывных сообщений, К.Шеннон доказал следующую теорему: если при заданном критерии эквивалентности сообщений источника  его эпсилон-энтропия  меньше пропускной способности канала С, то существует способ кодирования и декодирования, при котором погрешность воспроизведения сколь угодно близка к . При  такого способа не существует.

ГЛАВА 10. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ, КОДЕКИ ДИСКРЕТНОГО КАНАЛА

10.1. Принципы построения корректирующих кодов

          Повышение требований к скорости и достоверности передачи информации, увеличение протяженности линий связи приводит к необходимости применения специальных мер, уменьшающих вероятность появления ошибок. В настоящее время найден ряд возможностей для решения указанной задачи. Одной из них является применение помехоустойчивого кодирования.

          Под помехоустойчивыми понимаются коды, позволяющие обнаруживать и исправлять ошибки, возникающие при передаче из-за действия помех. Идея их построения заключается в том, что из N₀ возможных комбинаций длиной n применяется лишь некоторая часть. Пусть их число равно N. Используемые при передаче кодовые комбинации обычно называются разрешенными, а остальные, число которых N₀-N, - запрещенными.

          Поясним способность кода исправлять ошибки. Разобьем множество кодовых комбинаций на N подмножеств M_i, i=1,2,…,N, и каждому подмножеству поставим в соответствие разрешенную кодовую комбинацию B_i. Зададимся следующим правилом приема: если принятая кодовая комбинация попадает в подмножество M_i, то принимается решение в пользу кодовой комбинации B_i. Очевидно, что при таком правиле приема будут исправляться все те ошибки, которые не выводят передаваемую кодовую комбинацию за пределы принадлежащего ей подмножества.

          При построении кода, работающего в режиме декодирования с исправлением ошибок, основной сложностью является разбиение множества запрещенных кодовых комбинаций на N подмножеств и сопоставление их разрешенным кодовым комбинациям. Очевидно, что для уменьшения вероятности ошибочного декодирования в подмножество M_i следует включать те запрещенные кодовые комбинации  , для которых

где P(B_i) - априорная вероятность передачи кодовой комбинации B_i,  - условная вероятность принятия кодовой комбинации  при передаче кодовой комбинации B_i. Таким образом, в подмножество M_i должны входить кодовые комбинации , при приеме которых наиболее вероятной переданной комбинацией является B_i.

          При декодировании по максимуму правдоподобия решение принимается в пользу кодовой комбинации B_i, если вероятность  максимальна. Для симметричного двоичного канала без памяти

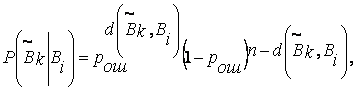(10.1)

Где р_ош - вероятность искажения символа, 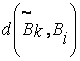 - число разрядов, в которых комбинации  и B_i отличаются друг от друга (расстояние Хэмминга между B_k и B_i). Из (10.1) следует, что при р_ош<1/2 вероятность  монотонно убывает с возрастанием расстояния 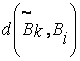, принимая максимальное значение для кодовой комбинации B_i, которая отличается от принятой комбинации  в меньшем числе символов. Таким образом, сформулированное правило декодирования соответствует критерию максимума правдоподобия.

10.2. Классификация кодов

Известно большое число помехоустойчивых кодов, которые классифицируются по различным признакам. Прежде всего помехоустойчивые коды можно разделить на два больших класса: блочные и непрерывные. При блочном кодировании последовательность элементарных сообщений источника разбивается на отрезки и каждому отрезку ставится в соответствие определенная последовательность (блок) кодовых символов, называемая обычно кодовой комбинацией. Множество всех кодовых комбинаций, возможных при данном способе блочного кодирования, и есть блочный код.

          Длина блока может быть как постоянной, так и переменной. Соответственно различают равномерные и неравномерные блочные коды. Помехоустойчивые коды являются, как правило, равномерными. Поэтому неравномерные коды в дальнейшем не рассматриваются.

          Блочные коды бывают разделимыми и неразделимыми. К разделимым относятся коды, в которых символы по их назначению могут быть разделены на информационные (символы, несущие информацию о сообщениях) и проверочные. Такие коды обозначаются как (n, k), где n - длина кода, k - число информационных символов. Число комбинаций в коде не превышает 2^k. К неразделимым относятся коды, символы которых нельзя разделить по их назначению на информационные и проверочные. К ним относятся, например, коды с постоянным весом и коды на основе матриц Адамара.

          Среди разделимых кодов различают линейные и нелинейные. К линейным относятся коды, в которых поразрядная сумма по модулю 2 любых двух кодовых слов также является кодовым словом. Линейный код называется систематическим, если первые k символов его любой кодовой комбинации являются информационными, остальные (n-k) символов - проверочными.

          Среди линейных систематических кодов наиболее простым является код (n, n-k), содержащий один проверочный символ, который равен сумме по модулю 2 всех информационных символов. Этот код, называемый кодом с проверкой на четность, позволяет обнаружить все сочетания ошибок нечетной кратности. Вероятность необнаруженной ошибки в первом приближении можно определить как вероятность искажения двух символов:

          Подклассом линейных кодов являются циклические коды. Они характеризуются тем, что все наборы, образованные циклической перестановкой любой кодовой комбинации, являются также кодовыми комбинациями. Это свойство позволяет в значительной степени упростить кодирующее и декодирующее устройства, особенно при обнаружении ошибок и исправлении одиночной ошибки. Примерами циклических кодов являются коды Хэмминга, коды Боуза - Чоудхури - Хоквингема (БЧХ - коды) и др.

          Непрерывные коды характеризуются тем, что операции кодирования и декодирования производятся над непрерывной последовательностью символов без разбиения ее на блоки. Среди непрерывных наиболее применимы сверточные коды.

10.3. Основные характеристики и корректирующие свойства

 блочных кодов

К числу основных характеристик кода относятся длина кода n, его основание m, мощность N (число разрешенных кодовых комбинаций), полное число кодовых комбинаций N₀, число информационных символов k, число проверочных символов r = n - k, вес кодовой комбинации (число единиц в комбинации), избыточность кода, кодовое расстояние. Из перечисленных характеристик лишь две последние нуждаются в пояснении.

Избыточность кода в общем случае определяется выражением

или для двоичного кода (m=2) при N=2^k

где величина k/n называется относительной скоростью кода.

          Введем понятие кодового расстояния. Предварительно отметим, что для оценки отличия одной кодовой комбинации от другой можно использовать расстояние Хэмминга d(B_i, B_j), определяемое числом разрядов, в которых одна кодовая комбинация отличается от другой. Для двоичного кода

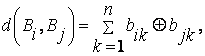
где b_ik и b_jk -  символы кодовых комбинаций B_i и B_j соответственно, ⊕ - символ суммирования по модулю 2. Наименьшее расстояние Хэмминга для данного кода называется кодовым расстоянием. В дальнейшем его будем обозначать через d.

          Если существует блочный линейный код (n, k), то для него справедливо неравенство

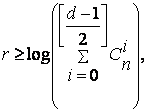(10.2)

называемое верхней границей Хэмминга, где 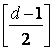 означает целую часть числа  .

          Граница Хэмминга (10.2) близка к оптимальной для кодов с большими значениями k/n. Для кодов с малыми значениями k/n более точной является верхняя граница Плоткина:

(10.3)

          Можно также показать, что существует блочный линейный код (n, k) с кодовым расстоянием d, для которого справедливо неравенство

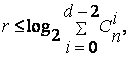(10.4)

называемое нижней границей Варшамова - Гильберта.

          Таким образом, границы Хэмминга и Плоткина являются необходимыми условиями существования кода, а граница Варшамова - Гильберта - достаточным.

          Приведенные границы (10.2), (10.3) и (10.4) можно обобщить на недвоичные коды, а границу (10.3) - и на нелинейные.

          Равенство в (10.2) справедливо только для так называемых совершенных кодов. Они исправляют все ошибки кратности [(d-1)/2] и не менее и не исправляют ни одной ошибки кратности  где  - целая часть числа . Следует отметить, что число совершенных кодов невелико. Примером таких кодов являются коды Хэмминга.

          Равенство в (10.3) справедливо только для эквидистантных кодов, в которых расстояние Хэмминга между любыми двумя различными кодовыми комбинациями одно и то же. К ним относятся, например, коды, построенные на основе матриц Адамара.

10.4. Блочные коды. Построение кодеков

10.4.1. Линейные коды

          Из определения следует, что любой линейный код (n, k) можно получить из k  линейно независимых кодовых комбинаций путем их посимвольного суммирования по модулю 2 в различных сочетаниях. Исходные линейно - независимые кодовые комбинации называются базисными.

          Представим базисные кодовые комбинации в виде матрицы

(10.5)

          В теории кодирования она называется порождающей. Тогда процесс кодирования заключается в выполнении операции B=AG, где А - вектор размерностью k, соответствующий сообщению, B - вектор размерностью n, соответствующий кодовой комбинации.

          Таким образом, порождающая матрица (10.5) содержит всю необходимую для кодирования информацию. Она должна храниться в памяти кодирующего устройства. Для двоичного кода объем памяти равен двоичных символов. При табличном задании кодирующее устройство должно запомнить  двоичных символов.

          Две порождающие матрицы, которые отличаются друг от друга только порядком расположения столбцов, задают коды, которые имеют одинаковое расстояние Хэмминга между соответствующими кодовыми комбинациями, а следовательно, одинаковые корректирующие способности. Такие коды называются эквивалентными.

          Линейный (n, k) код может быть задан так называемой проверочной матрицей Н размерности . При этом комбинация В принадлежит коду только в том случае, если вектор В ортогонален всем строкам матрицы Н, т.е. если выполняется равенство

(10.6)

где Т - символ транспонирования матрицы.

          Так как (10.6) справедливо для любой кодовой комбинации, то

          Каноническая форма матрицы Н имеет вид

(10.7)

где Р^Т - подматрица, столбцами которой служат строки подматрицы Р (10.5),   I - единичная  подматрица.

          Подставляя (10.7) в (10.6), можно получить n-k уравнений вида

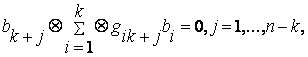(10.8)

которые называются уравнениями проверки.

          С помощью проверочной матрицы сравнительно легко можно построить с заданным кодовым расстоянием. Это построение основано на следующей теореме: кодовое расстояние линейного (n, k) кода равно d тогда и только тогда, когда любые d-1 столбцов проверочной матрицы этого кода линейно независимы, но некоторые d столбцов проверочной матрицы линейно зависимы.        Заметим, что строки проверочной матрицы линейно независимые. Поэтому проверочную матрицу можно использовать в качестве порождающей для некоторого другого линейного кода (n, n-k), называемого двойственным.

          Кодирующее устройство для линейного кода (n, k) (рис. 10.1) состоит из k- разрядного сдвигающего регистра и r = n - k блоков сумматоров по модулю 2. Информационные символы одновременно поступают на вход регистра и на выход кодирующего устройства через коммутатор К. С поступлением k-го информационного символа на выходах блоков сумматоров в соответствии с уравнениями (10.8) формируются проверочные символы, которые затем поступают на выход кодера.

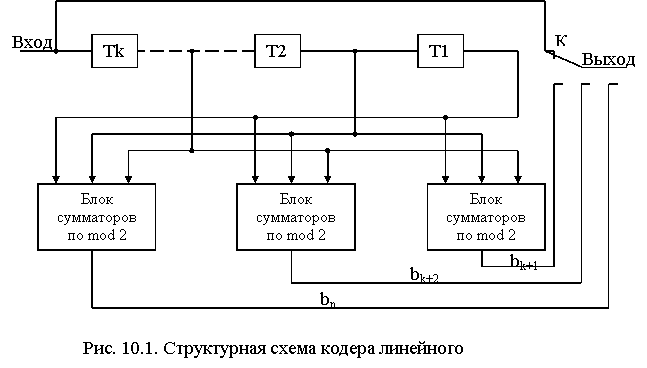
          Процесс декодирования сводится к выполнению операции

где S - вектор размерностью (n-k), называемый синдромом,  - вектор принятой кодовой комбинации.

          Если принятая кодовая комбинация  совпадает с одной из разрешенных В (это имеет место тогда, когда - либо ошибки в принятых символах отсутствуют, либо из-за действия помех одна разрешенная комбинация переходит в другую), то

В противном случае , причем вид синдрома зависит только от вектора ошибок е. Действительно

где В - вектор, соответствующий передаваемой кодовой комбинации. При S=0 декодер принимает решение об отсутствии ошибок, а при  - о наличии ошибок. Число различных синдромов, соответствующих различным сочетаниям ошибок, равно 2^n-k-1. По конкретному виду синдрома можно в пределах корректирующей способности кода указать на ошибочные символы и их исправить.

          Декодер линейного кода (рис. 10.2) состоит из k-разрядного сдвигающего регистра, n-k блоков сумматоров по модулю 2, схемы сравнения, анализатора ошибок и корректора. Регистр служит для запоминания информационных символов принятой кодовой последовательности, из которых в блоках сумматоров формируются проверочные символы. Анализатор ошибок по конкретному виду синдрома, получаемого в результате сравнения формируемых на приемной стороне и принятых проверочных символов, определяет места ошибочных символов. Исправление информационных символов производится в корректоре.

Заметим, что в общем случае при декодировании линейного кода с исправлением ошибок в памяти декодера должна храниться таблица соответствий между синдромами и векторами ошибок, содержащая 2^n-k строк. С приходом каждой кодовой комбинации декодер должен перебрать всю таблицу. При небольших значениях n-k эта операция не вызывает затруднений. Однако для высокоэффективных кодов длиной n, равной нескольким десяткам, разность n-k принимает такие значения, что перебор таблицы из 2^n-k строк оказывается практически невозможным. Например, для кода, имеющего кодовое расстояние d = 5, таблица состоит из 2¹² = 4096 строк.

При заданных значениях n и k существует 2^k(n-k) линейных кодов. Задача заключается в выборе наилучшего (с позиции того или иного критерия) кода.

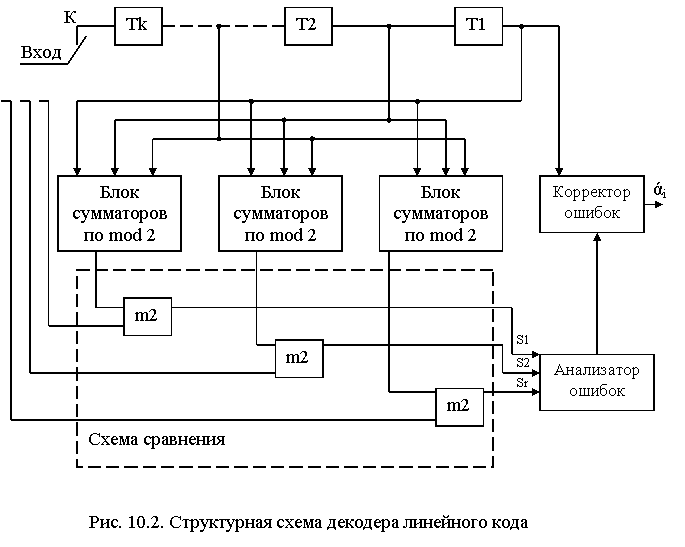
10.4.2. Циклические коды

Циклические коды относятся к классу линейных систематических. Поэтому для их построения в принципе достаточно знать порождающую матрицу.

Можно указать другой способ построения циклических кодов, основанный на представлении кодовых комбинаций многочленами b(x) вида

где b_n-1 b_n-2 … b₀ -кодовая комбинация. Над данными многочленами можно производить все алгебраические действия с учетом того, что сложение здесь осуществляется по модулю 2.

          Каждый циклический код (n, k) характеризуется так называемым порождающим многочленом. Им может быть любой многочлен р(х) степени n-k, который делит без остатка двучлен . Циклические коды характеризуются тем, что многочлены b(х) кодовых комбинаций делятся без остатка на р(х). Поэтому процесс кодирования сводится к отысканию многочлена b(х) по известным многочленам а(х) и р(х), делящегося на р(х), где а(х) - многочлен степени k-1, соответствующий информационной последовательности символов.

          Очевидно, что в качестве многочлена b(х) можно использовать произведение а(х)р(х). Однако при этом информационные и проверочные символы оказываются перемешанными, что затрудняет процесс декодирования. Поэтому на практике в основном применяется следующий метод нахождения многочлена b(x).

          Умножим многочлен а(х) на х^n-k и полученное произведение разделим на р(х). Пусть

(10.9)

где m(х) - частное, а с(х) - остаток. Так как операции суммирования и вычитания по модулю 2 совпадают, то выражение (10.9) перепишем в виде

(10.10)

Из (10.10) следует, что многочлен  делится на р(х) и, следовательно, является искомым.

          Многочлен a(x)x^n-k имеет следующую структуру: первые n-k членов низшего порядка равны нулю, а коэффициенты остальных совпадают с соответствующими коэффициентами информационного многочлена а(х). Многочлен с(х) имеет степень меньше n-k. Таким образом, в найденном многочлене b(x) коэффициенты при х в степени n-k и выше совпадают с информационными символами, а коэффициенты при остальных членах, определяемых многочленом с(х), совпадают с проверочными символами.

          В соответствии с (10.10) процесс кодирования заключается в умножении многочлена а(х) на x^n-k и нахождении остатка от деления

а(х)х^n-k на р(х) с последующим его сложением по модулю 2 с многочленом

а(х)х^n-k.

          На рис. 10.3. в качестве примера приведена схема кодера для кода (7, 4) с порождающим многочленом . В исходном состоянии ключи К1 и К2 находятся в положении 1. Информационные символы поступают одновременно на вход канала и на выход ячейки х³ сдвигающего регистра (это соответствует умножению многочлена а(х) на х³). В течение четырех тактов происходит деление многочлена а(х)х³ на многочлен . В результате в регистре записывается остаток, представляющий собой проверочные символы. Ключи К1 и К2 перебрасываются в положение 2, и в течение трех последующих тактов содержащиеся в регистре символы поступают в канал.

          Циклический код может быть задан проверочным многочленом h(x): кодовая комбинация В принадлежит данному циклическому коду, если . Проверочный многочлен связан с порождающим отношением

          Задание кода проверочным многочленом эквивалентно заданию кода системой проверочных уравнений (10.8). Характерной особенностью циклического кода является то, что все проверочные уравнения можно получить из одного путем циклического сдвига индексов символов, входящих в исходное уравнение. Так, для кода (7, 4) с порождающим многочленом  проверочный многочлен имеет вид . Проверочные уравнения получаются из условия

          Осуществив умножение и приравняв коэффициенты при х⁴, х⁵ и х⁶ нулю, получим следующие уравнения

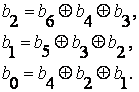(10.11)

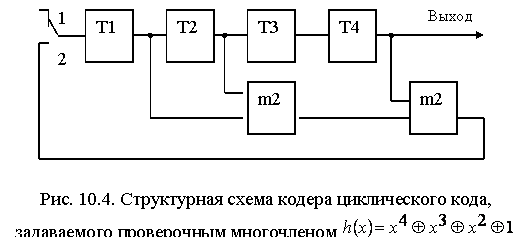
В качестве примера на рис.10.4 показана схема кодера циклического кода (7, 4), задаваемого проверочным многочленом  или, что то же самое, проверочными соотношениями (10.11). в исходном состоянии ключ находится в положении 1. В течение четырех тактов импульсы поступают в регистр, после чего ключ переводится в положение 2. При этом обратная связь замыкается. Начиная с пятого такта, формируются проверочные символы в соответствии с (10.11). После седьмого такта все проверочные символы оказываются сформированными, ключ вновь переключается в положение 1. Кодер готов к приему очередного сообщения. Символы кодовой комбинации поступают в канал, начиная с пятого такта.

          Корректирующая способность кода зависит от порождающего многочлена р(х). Поэтому его выбор очень важен при построении циклического кода. Необходимо помнить, что степень порождающего многочлена должна быть равна числу проверочных символов. Кроме того, многочлен р(х) должен делить двучлен .

          Обнаружение ошибок при использовании таких кодов заключается в делении многочлена , соответствующего принятой комбинации , на р(х). Если остаток s(х) оказывается равным нулю, то считается, что ошибки нет, в противном случае фиксируется ошибка.

          Один из алгоритмов исправления ошибок основан на следующих свойствах циклического кода. Пусть имеется циклический код с кодовым расстоянием d, исправляющий все ошибки до кратности 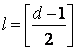 включительно, где   - целая часть числа . Тогда можно показать, что

¨ если исправляемый вектор ошибок искажает только проверочные символы, то вес синдрома будет меньше или равен , а сам синдром будет совпадать с вектором ошибок;

¨ если вектор ошибки искажает хотя бы один информационный символ, то вес синдрома будет больше ;

¨ если s(х) - остаток от деления многочлена b(х) на р(х), то остатком от деления многочлена b(x)xⁱ на р(х) является многочлен s(x)xⁱmodp(x), другими словами, синдром некоторого циклического сдвига многочлена b(х) является соответствующим циклическим сдвигом синдрома исходного многочлена, взятого по модулю р(х).

          Существуют и другие, более универсальные алгоритмы декодирования.

          К циклическим кодам относятся коды Хэмминга, которые являются примерами немногих известных совершенных кодов. Они имеют кодовое расстояние d=3 и исправляют все одиночные ошибки. Длина кода выбирается из условия 2^n-k-1 = n, которое имеет простой смысл: число различных ненулевых синдромов равно числу символов в кодовой последовательности. Так существуют коды Хэмминга (2^r-1, 2^r-r-1), в частности коды (7,4), (15,11), (31,26), (63,57) и т.д.

          Заметим, что ранее использованный многочлен  является порождающим для кода Хэмминга (7,4).

          Среди циклических кодов широкое применение нашли коды Боуза-Чоудхури-Хоквингема (БЧХ). Можно показать, что для любых целых положительных чисел m и  существует двоичный код БЧХ длины        n = 2^m-1 с кодовым расстоянием , причем число проверочных символов .

          Для кодов БЧХ умеренной длины и ФМ при передаче символов можно добиться значительного выигрыша (4 дБ и более). Он достигается при скоростях . При очень высоких и очень низких скоростях выигрыш от кодирования существенно уменьшается.

10.4.3. Мажоритарные циклические коды

          Иногда целесообразно использовать коды с несколько худшей корректирующей способностью по сравнению с лучшими известными кодами, но простые в реализации. К ним относятся коды, допускающие мажоритарное декодирование. Оно основано на возможности для некоторых циклических кодов выразить каждый информационный символ с помощью Q различных линейных соотношений. Решение о значении символа принимается по большинству значений, даваемых каждым отдельным соотношением. Для исправления всех ошибок до кратности  включительно необходимо иметь  независимых соотношений.

          В некоторой области значений параметров мажоритарные коды имеют корректирующую способность незначительно уступающую корректирующей способности кодов БЧХ. В то же время их реализация сравнительно проста.

          Проиллюстрируем принцип мажоритарного декодирования на примере кода (7.3) с проверочной матрицей

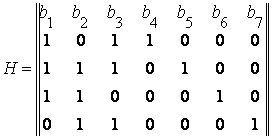(10.12)

          Рассматриваемый код является циклическим с порождающим многочленом . Он имеет кодовое расстояние d = 4.

          Используя матрицу (10.12), можно записать следующие соотношения для символа b₁:

(10.13)

          С учетом (10.13) в декодере имеется возможность четырьмя разными способами вычислить первый информационный символ:

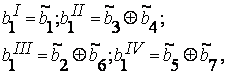(10.14)

где  - принятая кодовая комбинация.

          При отсутствии ошибок , т.е. все проверочные соотношения (10.14) дают один и тот же результат. При наличии одного ошибочного символа три проверочных соотношения дают правильное значение, а соотношение, в котором участвует ошибочный символ, дает неверный результат. Принимая решение по большинству, декодер выдает правильный символ b₁.

          Пусть ошибочно приняты два символа. Если они входят в различные проверочные соотношения, то две проверки дадут значение 1, а две проверки - значение 0. В этом случае декодер выдает сигнал отказа от декодирования. Если оба искаженных символа входят в одно проверочное соотношение, то все четыре проверки выдают один и тот же результат. Декодер выдает правильный символ b₁.

          Аналогично определяются остальные информационные символы. Проверочные соотношения для символов  и  получаются из (10.14) циклической перестановкой:

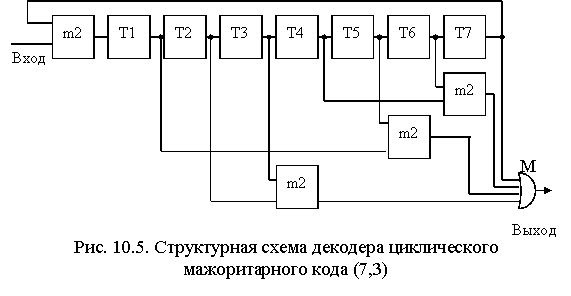
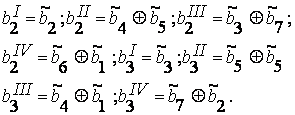
          Схема декодера (рис.10.5) состоит из сдвигающего регистра, сумматоров по модулю 2 и мажоритарного элемента М. Простота ее обусловлена тем, что в данном случае каждый символ кодовой комбинации участвует в одном проверочном соотношении. Код, для которого выполняется это условие, называется кодом с разделенными проверками.

          Мажоритарное декодирование возможно и тогда, когда один и тот же символ участвует в нескольких проверочных соотношениях. Однако алгоритм декодирования усложняется.

10.5. Свёрточные коды

10.5.1. Методы задания сверточных кодов

          Сверточный код - это линейный рекуррентный код. В общем случае он образуется следующим образом. В каждый i-й тактовый момент времени на вход корректирующего устройства поступает k₀ символ сообщения: a_i1a_i2…a_ik0. Выходные символы b_i1b_i2…b_in0 формируются с помощью рекуррентного соотношения из К символов сообщения, поступивших в данный и в предшествующие тактовые моменты времени:

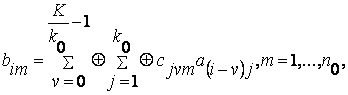(10.15)

где  - коэффициенты, принимающие значения 0 или 1.

          Символы сообщения, из которых формируются выходные символы, хранятся в памяти кодирующего устройства. Величина К называется длиной кодового ограничения. Она показывает, на какое максимальное число выходных символов влияет данный информационный символ, и играет ту же роль, что и длина блочного кода. Сверточный код имеет избыточность  и обозначается как ().

Типичные параметры сверточного кода: k₀, n₀ = 1, 2,…, 8; k₀/n₀ = 1/4…7/8; K = 3…10.

          Сверточный код получается систематическим, если в каждый тактовый момент k₀ выходных символов совпадают с символами сообщения. На практике обычно используются несистематические сверточные коды.

          Различают прозрачные и непрозрачные сверточные коды. Первые характеризуются свойством инвариантности по отношению к операции инвертирования кода, которое заключается в следующем: если значения символов на входе кодера поменять на противоположные, то выходная последовательность символов также инвертируется. Соответственно декодированная последовательность символов будет иметь такую же неопределенность в знаке, что и принятая последовательность символов, а следовательно, неопределенность знака последовательности можно устранить после декодирования сверточного кода. Указанное свойство прозрачных кодов особенно важно для СПИ, использующих противоположные фазоманипулированные сигналы, которым свойственно явление обратной работы.

          Для непрозрачного кода неопределенность знака последовательности символов приходится устранять до сверточного декодирования, что приводит к увеличению вероятности ошибок. Нетрудно показать, что сверточный код будет прозрачным, если каждый его порождающий многочлен содержит нечетное число членов.

          Помимо рассмотренного способа задания сверточного кода, возможны и другие. В частности, выходные символы можно рассматривать как свертку импульсной характеристики кодера с информационной последовательностью (отсюда происходит название кода).

10.5.2. Методы декодирования сверточных кодов

          Сверточные коды можно декодировать различными методами. Различают декодирование с вычислением и без вычисления проверочной последовательности.

          Декодирование с вычислением проверочной последовательности применяется только для систематических кодов. По своей сущности оно ничем не отличается от соответствующего метода декодирования блочных кодов. На приемной стороне из принятых информационных символов формируют проверочные символы по тому закону, что и на передающей стороне, которые затем сравнивают с принимаемыми проверочными символами. В результате сравнения формируется проверочная последовательность, которая при отсутствии ошибок состоит из одних нулей. При наличии ошибок на определенных позициях последовательности появляются единичные символы. Закон формирования проверочных символов выбирается таким образом, чтобы по структуре проверочной последовательности можно было определить искаженные символы.

          К числу методов декодирования без вычисления проверочной последовательности относятся декодирование по принципу максимума правдоподобия и последовательное декодирование.

          Декодирование по принципу максимума правдоподобия сводится к задаче отождествления принятой последовательности с одной из 2^N возможных, где N - длина информационной последовательности. Решение принимается в пользу той кодовой последовательности, которая в меньшем числе позиций отличается от принятой. Метод применим для любого сверточного кода. Однако при больших значениях N, он практически нереализуем из-за необходимости перебора 2^N возможных кодовых последовательностей. Существенное упрощение процедуры декодирования по максимуму правдоподобия предложил Витерби. Характерной особенностью его метода является то, что на каждом шаге декодирования запоминается только 2^К-1 наиболее правдоподобных путей.

          Алгоритм Витерби обладает рядом преимуществ. При небольших значениях длины кодового ограничения декодирующее устройство оказывается достаточно простым, реализуя в то же время высокую помехоустойчивость. Так, исследования показывают, что применение сверточных кодов с К = 3, 5 и 7 при фиксированной вероятности ошибки р_ош=10^-5 позволяет получить энергетический выигрыш 4…6 дБ по сравнению с системой, использующей ФМ сигналы без кодирования. Важным преимуществом по сравнению с методом последовательного декодирования является фиксация числа вычислительных операций на один декодированный символ. Декодирование по методу Витерби особенно перспективно в каналах с независимыми ошибками.

10.5.3. Реализация алгоритма Витерби

          Декодер Витерби (рис.10.6) состоит из синхронизатора, устройства управления и тактирования, устройства для вычисления метрики ветвей, устройства для обновления и хранения метрик ветвей, устройства для обновления и хранения гипотетических информационных последовательностей и решающего устройства.

	Рис. 10.6. Структурная схема декодера, реализующего алгоритм Витерби

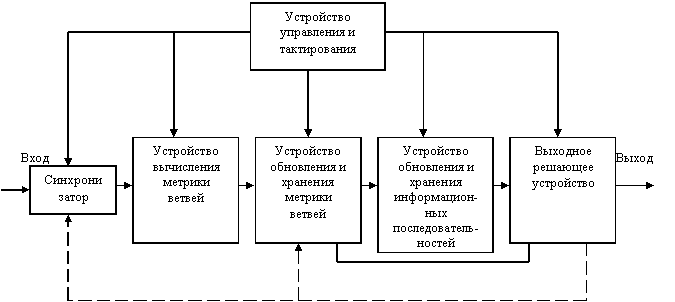
Устройство хранения и обновления метрик путей осуществляет сложение метрик ветвей с хранящимися метриками путей, проделывает необходимые сравнение и запоминает новые метрики путей.

          Устройство хранения и обновления гипотетических информационных последовательностей может быть выполнено на сдвигающих регистрах, в каждом из которых хранится полная информационная последовательность символов, соответствующая одному из "выживших" путей. Их число равно числу узлов. После обработки новой ветви регистры обмениваются содержимым в соответствии с тем, какие последовательности "выживают" при сравнении. В последнюю ячейку каждого регистра поступает новый информационный символ, а самый старый символ каждого регистра поступает в выходное решающее устройство.

          Выходное решающее устройство принимает решение о переданных информационных символах. Наилучшие результаты получаются, когда в качестве переданного информационного символа берется наиболее старый символ в последовательности с наименьшей метрикой. Иногда используют мажоритарный принцип: за переданный информационный символ выбирается чаще всего встречающийся символ из самых старых символов всех последовательностей.

          Устройство управления и тактирования задает необходимый ритм работы декодера.

10.6. Использование кодов в системах с обратной связью

          Во многих системах кроме основного (прямого) канала, с помощью которого сообщение передается от источника кпотребителю, имеется обратный канал для вспомогательных сообщений, которые позволяют улучшить качество передачи сообщений по прямому каналу.

          Наиболее распространены системы с обратной связью, в которых для обнаружения ошибок применяют избыточные коды. Такие системы называются системами с решающей обратной связью, или системами с переспросом. В качестве кодов часто используют коды с проверкой на четность, простейшие интерактивные коды, циклические коды и др. Они позволяют хорошо обнаруживать ошибки при сравнительно небольшой избыточности и простой аппаратурной реализации.

          Передаваемое сообщение кодируется избыточным кодом. Полученная комбинация передается потребителю и одновременно запоминается в накопителе-повторителе. Принятая последовательность символов декодируется с обнаружением ошибок. Если при этом ошибки не обнаружены, то сообщение поступает потребителю. В противном случае сообщение бракуется и по обратному каналу передается специальный сигнал переспроса. По этому сигналу производится повторная передача забракованной кодовой комбинации, которая извлекается из накопителя-повторителя.

          Можно показать, что если в обратом канале ошибки отсутствуют, то остаточная вероятность ошибочного приема кодовой комбинации

,

где Р_н.о - вероятность необнаруженной ошибки (вероятность того, что переданная кодовая комбинация перешла в другую разрешенную), Р_о.о - вероятность обнаружения ошибки (вероятность того, что вместо переданной кодовой комбинации принята какая-либо запрещенная кодовая комбинация). Вероятности  и  можно найти, если известны свойства канала и задан код.

          Соответственно эквивалентная вероятность ошибки определяется как

,

где k - число информационных символов в кодовой комбинации.

          Среднее число передач одного сообщения

          Хотя обратный канал можно сделать весьма помехоустойчивым (обычно скорость передачи информации в обратном канале значительно меньше, чем в прямом), тем не менее существует конечная вероятность того, что сигнал переспроса будет принят как сигнал подтверждения, и наоборот. В первом случае сообщение не поступает к потребителю, а во втором случае оно поступает дважды.

          Одним из средств борьбы с ошибками в обратном канале, приводящими к потере сообщения, является использование несимметричного правила декодирования, при котором вероятность ошибки приема сигнала переспроса существенно меньше вероятности ошибочного приема сигнала подтверждения. Например, сигнал переспроса передается кодовой комбинацией из n единичных символов, а сигнал подтверждения - комбинацией из n нулей. При приеме кодовой комбинации, содержащей хотя бы одну единицу, решение принимается в пользу сигнала переспроса. Очевидно, что в этом вероятность ошибочного приема сигнала переспроса может быть сделана ничтожно малой.

          Для того чтобы к потребителю не поступали лишние сообщения из-за ошибочного приема сигнала подтверждения, передаваемые кодовые комбинации либо снабжаются номерами, либо дополняются опознавательными символами, по которым можно узнать, передается ли кодовая комбинация в первый раз или она повторяется. При этом принятая повторная комбинация при отсутствии сигнала переспроса стирается и не поступает потребителю. Возможны и другие способы борьбы с такого рода ошибками.

          Системы с решающей обратной связью весьма эффективны в случае каналов с замираниями. При ухудшении состояния канала увеличивается частота переспроса (уменьшается скорость передачи информации), но вероятность ошибочных сообщений, поступающих потребителю, практически не увеличивается. При улучшении состояния канала частота переспроса уменьшается. Таким образом, система как бы автоматически приспосабливается к состоянию канала связи, используя все его возможности в отношении передачи информации.

          Следует заметить, что применение решающей обратной связи, конечно, не увеличивает пропускной способности прямого канала, но позволяет простыми средствами по сравнению с длинными кодами приблизить скорость передачи информации к пропускной способности канала.

10.7. Сигнально-кодовые комбинации

          Как известно, многопозиционные сигналы, такие, как сигналы многократной ФМ, сигналы АФМ, обеспечивают высокую удельную скорость передачи информации (высокую частотную эффективность) при уменьшении энергетической эффективности, а помехоустойчивые коды позволяют повышать энергетическую эффективность при снижении удельной скорости передачи. Сочетание методов многопозиционной модуляции и помехоустойчивого кодирования дает возможность повысить либо энергетическую эффективность без уменьшения частотной, либо частотную эффективность без уменьшения энергетической, а в ряде случаев - оба параметра. Задача заключается в формировании сигнальных последовательностей, которые можно достаточно плотно разместить в многомерном пространстве (для обеспечения высокой частотной эффективности) и в то же время разнести на достаточно большие расстояния (для обеспечения высокой энергетической эффективности). Такие последовательности, построенные на базе помехоустойчивых кодов и многопозиционных сигналов с плотной упаковкой, называют сигнально-кодовыми конструкциями.

          В качестве помехоустойчивого кода обычно используют каскадные, интерактивные и сверточные коды, а в качестве многопозиционных сигналов - сигналы многократной ФМ и сигналы АФМ.

          Для согласования кодека двоичного помехоустойчивого кода и модема многопозиционных сигналов используется манипуляционный код, при котором большему расстоянию по Хэммингу между кодовыми комбинациями соответствует большее расстояние между соответствующими им сигналами. Этому требованию частично удовлетворяет код Грея. Возможны и другие способы такого преобразования.

10.8. Прием кодированных сигналов в целом

          До сих пор предполагалось, что кодовые комбинации принимаются посимвольно, т.е. на приемной стороне вначале выносится решение о каждом символе кодовой комбинации, а затем по совокупности n принятых символов принимается решение о том, какая кодовая комбинация была передана.

          При избыточных кодах такая двухэтапная процедура принятия решения оказывается неоптимальной. Объясняется это тем, что процесс демодуляции является необратимой операцией и может сопровождаться потерей информации. Действительно, после принятия решения о символе ни соответствующий элемент сигнала, ни фактическое значение результата обработки этого символа (значение апостериорной вероятности или функции правдоподобия) в дальнейшем процессе приема (при декодировании) не принимаются во внимание. В то же время их учет мог бы привести к уменьшению вероятности ошибочного декодирования кодовой комбинации.

          Вся информация, содержащаяся в принимаемом сигнале, будет наиболее полно использована, если отказаться от посимвольного приема и демодулировать кодовую комбинацию в целом.

          Можно показать, что при использовании кода с избыточностью помехоустойчивость приема в целом выше помехоустойчивости поэлементного приема с исправлением ошибок, однако уступает помехоустойчивости поэлементного приема с обнаружением ошибок и переспросом по обратному каналу. При использовании кода без избыточности прием в целом не имеет преимуществ по сравнению с поэлементным приемом.

          В общем случае вычислить вероятность ошибочного приема кодовой комбинации трудно. Однако иногда, например, при использовании ортогональных, биортогональных и симплексных кодов, эту вероятность можно вычислить через интегралы, которые можно определить численными методами.

          Недостатком приема в целом является то, что он требует значительно более сложной аппаратуры по сравнению с поэлементным приемом. В частности, для его реализации требуется 2^k корреляторов. Очевидно, что при достаточно эффективном коде (такой код является длинным) прием в целом технически не реализуем. Так, если используется код (n, k) c k=10, то демодулятор, реализующий прием в целом, будет состоять из 1024 корреляторов или согласованных фильтров.

          В связи с трудностями построения оптимального демодулятора для приема в целом большое внимание уделяется алгоритмам приема, которые не используют всю информацию о принятом сигнале, но допускают меньшие потери по сравнению с поэлементным приемом. Такие алгоритмы являются двухэтапными, как и при поэлементном приеме. Однако на первом этапе решение о переданном символе не принимается, а запоминаются значения напряжений на выходах корреляторов или согласованных фильтров, предназначенных для приема различных символов, из которых составляются кодовые комбинации. Такой вид решения  называется "мягким". Как известно, эти напряжения пропорциональны логарифму функций правдоподобия и несут информацию о степени соответствия принятого сигнала тому или иному символу. Их использование при дальнейшей обработке (декодировании) и позволяет получить лучшие результаты по сравнению с поэлементным приемом.

          В реальных системах выходные напряжения обычно квантуются и представляются числами, т.е. вместо оптимального аналогового декодирования по максимуму правдоподобия используют цифровое декодирование. Цифровое декодирование уже при восьми уровнях квантования практически дает те же результаты, что и аналоговое декодирование. В то же время оно значительно проще в реализации.

          Существуют и другие методы приема, занимающие промежуточное положение между поэлементным приемом и приемом в целом, например, прием по наиболее надежным символам. В его основу положен тот факт, что при применении кода с кодовым расстоянием d любую его комбинацию можно декодировать, если "стереть" d-1 символов. Устройство приема состоит из двух решающих схем. Первая из них вычисляет апостериорные вероятности и принимает предварительно решение о переданном символе. Полученная последовательность символов подается на вторую решающую схему, куда также поступает  информация об апостериорных вероятностях. Декодирование выполняется по n-d+1 наиболее надежным (имеющим большие значения апостериорной вероятности) символам.

          Описанный метод дает лучшие результаты, чем поэлементный прием, так как в нем частично используется информация об апостериорных вероятностях, но уступает приему в целом, так как информация о d-1 менее надежных символах не используется.

ЛИТЕРАТУРА

1. Зюко А.Г., Кловский Д.Д. Теория передачи сигналов - М.: Радио и связь, 1986.

2. Борисов В.А., Калмыков В.В., Ковальчук Я.М. Радиотехнические системы передачи информации. Изд-во "Радио и связь", 1990.

3. Васин В.В., Власов О.В., Григорин-Рябов В.В., Дудник П.И., Степанов Б.М. Радиолокационные устройства. Изд-во "Советское радио", 1970.

4. Дулевич В.Е. и др. Теоретические основы радиолокации. Изд-во "Советское радио", 1964.

5. Фалькович С.Е. Приём радиолокационных сигналов на фоне флуктуационных помех. Изд-во "Советское радио", 1961.

6. Бакулев П.А. Радиолокация движущихся целей. Изд-во "Советское радио", 1964.

7. Вентцель Е.С. Теория вероятностей. Изд-во "Наука", 1969.

8. Гуткин Л.С. Теория оптимальных методов радиоприёма при флуктуационных помехах. Госэнергоиздат, 1961.

9. Левин Б.Р. Теория случайных процессов и её применение в радиотехнике. Изд-во "Советское радио", 1960.

10. Хелстром К. Статистическая теория обнаружения сигналов. Изд-во иностранной литературы, 1963.

СОДЕРЖАНИЕ

ВВЕДЕНИЕ………………………………………………………….……..			2
ГЛАВА 1. ОСНОВНЫЕ ПОНЯТИЯ О СИГНАЛАХ…..………………..			3
1.1.		Сигналы и поля - переносчики информации. Характеристики и модели сигналов и помех…………..…………………………….. ...	3
1.2.		Корреляционные функции сигналов………………………………..	5
1.3.		Функция неопределенности………………………………..…….….	6
ГЛАВА 2. ОБНАРУЖЕНИЕ И РАЗЛИЧЕНИЕ СИГНАЛОВ……….….			7
2.1.		Обнаружение сигналов как статистическая задача………………..	8
2.2.		Критерии оптимальности обнаружения. Отношение правдоподобия……………………………………………………….	9
2.3.		Бинарное обнаружение полностью известного сигнала.………….	12
2.4.	Обнаружение сигнала со случайной начальной фазой…………….		16
2.5.		Бинарное обнаружение сигнала со случайными амплитудой и начальной фазой……………………..………………………………	18
2.6.		Обнаружение сигнала в виде пачки радиоимпульсов…………….	18
2.7.		Различение детерминированных сигналов на фоне белого гауссовского шума………………………………………………….	20
2.8.		Принцип работы цифровых обнаружителей и различителей сигналов……………………………………………….	20
2.9.		Дискретизация и квантование непрерывных сигналов…………....	21
ГЛАВА 3. ОЦЕНКА НЕИЗВЕСТНЫХ ПАРАМЕТРОВ СИГНАЛА…..			22
3.1.		Байсовские оценки при различных функциях потерь……………..	23
3.2.		Неравенство Рао-Крамера………..………………………………….	23
3.3.		Оценки максимального правдоподобия, их свойства и связь с байесовскими………………………………………………………	24
3.4.		Функционал отношения правдоподобия гауссовского процесса...	25
3.5.		Оценка амплитуды детерминированного сигнала………………..	26
3.6.		Оценки амплитуды и фазы гармонического сигнала..……………	27
3.7.		Совместная оценка частоты и фазы гармонического сигнала при аддитивном белом шуме……..……………………………………...	28
3.8.		Понятие об аномальных ошибках измерения………………….…..	29
3.9.		Понятие об оценке (фильтрации) меняющихся параметров сигналов………………………………………………………………	30
3.10.		Линейная и нелинейная фильтрация……………………………….	30
3.11.		Фильтры Винера и Калмана………………………………………...	33
ГЛАВА 4. РАЗРЕШЕНИЕ СИГНАЛОВ………………………………….			34
4.1.		Разрешающая способность по дальности и скорости……….…….	34
4.2.		Классы зондирующих сигналов…………………………………….	36
4.3.		Сжатие сложного сигнала по времени и частоте……………….…	36
4.4.		Сложные сигналы с линейно-частотной модуляцией…..………....	37
4.5.		Сложные фазоманипулированные сигналы………………………..	39
ГЛАВА 5. ОСНОВНЫЕ ПРИНЦИПЫ ПОСТРОЕНИЯ РАДИОЛОКАЦИОННЫХ СИСТЕМ…………………………………….			40
5.1.		Задачи и применение радиолокации……………………………..…	40
5.2.		Физические основы обнаружения целей и определения их координат и скорости..………………………………………………	40
5.3.		Дальность действия в свободном пространстве…………………...	43
5.4.		Дальность действия при активном ответе………………………….	48
5.5.		Влияние отражений от земной поверхности на дальность действия РЛС………………………………………………………...	50
5.6.		Влияние на дальность действия РЛС ослабления энергии радиоволн в атмосфере……………………………………………...	51
5.7.		Влияние кривизны земной поверхности и атмосферной рефракции на дальность действия…………………………………	52
ГЛАВА 6. МЕТОДЫ И УСТРОЙСТВА ИЗМЕРЕНИЯ ДАЛЬНОСТИ...			54
6.1.		Амплитудный метод………….……………………………………	54
6.2.		Частотный метод……………………………………………………..	56
6.3.		Фазовые методы……………………………………………………..	58
ГЛАВА 7. МЕТОДЫ И УСТРОЙСТВА ИЗМЕРЕНИЯ УГЛОВЫХ КООРДИНАТ………………………………………………………………			62
7.1.		Амлитудные методы…………………………………………………	62
7.2.		Фазовые методы……………………………………………………...	68
ГЛАВА 8. ОСНОВЫ ТЕОРИИ ПЕРЕДАЧИ ИНФОРМАЦИИ…………			70
8.1.		Информация, сообщение, сигнал…………………………………...	70
ГЛАВА 9. ОСНОВНЫЕ ЗАДАЧИ ТЕОРИИ ИНФОРМАЦИИ………...			82
9.1.		Количество информации в дискретных сообщениях. Энтропия источника дискретных сообщений…………………………………	82
9.2.		Избыточность сообщений…………………………………………...	91
9.3.		Пропускная способность дискретных кагналов с шумом………...	91
9.4.		Пропускная способность непрерынвых каналов с аддитивным шумом………………………………………………………………...	92
9.5.		Теорема кодирования для канала с помехами……………………..	94
ГЛАВА 10. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ, КОДЕКИ ДИСКРЕТНОГО КАНАЛА………………………………………………..			96
10.1.		Принципы построения корректирующих кодов…………………...	96
10.2.		Классификация кодов………………………………………………..	97
10.3.		Основные характеристики и корректирующие свойства блочных кодов………………………………………………………………….	98
10.4.		Блочные коды. Построение кодеков………………………………..	100
10.5.		Сверточные коды…………………………………………………….	109
10.6.		Использование кодов в системах с обратной связью……………...	112
10.7.		Сигнально-кодовые комбинации…………………………………...	114
10.8.		Приём кодированных сигналов в целом…………………………...	115
ЛИТЕРАТУРА……………………………………………………………...			117

Конспект лекций по курсу

"Основы теории радиотехнических систем"

 для студентов,

обучающихся на

Рассмотрено на заседании кафедры

 ТПС        (протокол №  )

и рекомендовано к печати

Составители:

Абдуазизов А.А.

Фазилжонов И.Р.

Маненков В.И.

Нефедова Н.В.

Косьяненко И.В.

Шаюсупова Х.Х.

Ответственный редактор               Абдуазизов А.А.

Редакционно-корректурная комиссия:

Редактор___________

Корректор__________

---

[u1]ени