Узбекистон почта ва телекоммуникациялари агентлиги
ТОШКЕНТ ЭЛЕКТРОТЕХНИКА АЛОКА ИНСТИТУТИ
Сигналларни узатиш
назарияси кафедраси
ЭЛЕКТР АЛОКАСИ НАЗАРИЯСИ
КУРСИ БУЙИЧА
М АЪ Р У З А Л А Р
КОНСПЕКТИ
Тошкент 2000
Маъруза-1 КИРИШ
СИГНАЛЛАР ВА АЛОКА ТИЗИМЛАРИ ХАКИДА УМУМИЙ ТУШУНЧАЛАР. ЭЛЕКТР АЛОКА ТИЗИМИНИ ФУНКЦИОНАЛ СХЕМАСИ. ЭАН КУРСИНИ ВАЗИФАСИ.
Информация – бу хар хил физик жараёнлар, тарихий ходисалар, кундалик вокеалар туºрисидаги маълумотлардир. Информацияни узатиш учун уни маълум бир шаклга келтириш лозим (текст, жадвал, график, формула, тасвир куринишига). Бу шаклланиш натижисида информация хабарга айланади. Хабарни бир жойдан иккинчи жойга узатиш учун уни маълум бир жараёнга юклатишимиз яъни уни сигналга айлантиришимиз лозим.
Сигнал деб, бирор бир физик жараённинг бир ёки бир нечта параметрини хабарга мос равишда узгаришига айтилади.
Электр сигнали деб, электр жараённинг бир ёки бир нечта параметрини хабарга мос равишда узгаришига айтилади.
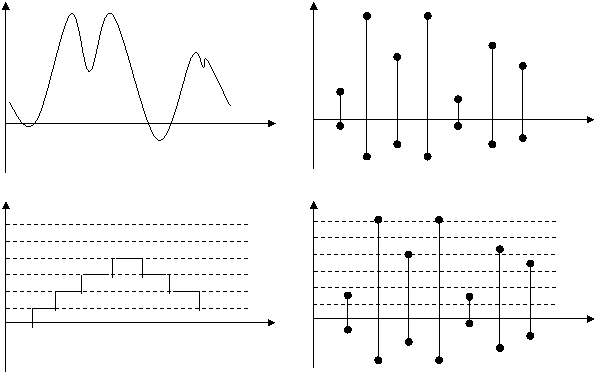
Электр сигналларининг куйидаги турлари мавжуд:
 S(t) S(t)
S(t) S(t)
t t
а) б)
S(t) S(t)
t t
в) г)
 |
S(t)
t
д)
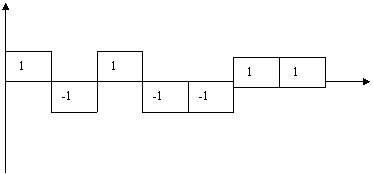
1 расм: а) узлуксиз сигнал; б) сатх буйча узлуксиз, вакт буйича узлукли (дискрет) сигнал; в) сатх буйча узлукли (дискрет), вакт буйича узлуксиз сигнал; г) хам вакт, хам сатх буйича узлукли (дикрет) сигнал; д) икки
асосли ракамли сигнал.
Сигналлар учун куйидаги умумий параметрлар мавжуд:
1. Тс – сигналнинг давомийлиги ёки сигнални мавжудлик интервали;
2. Дс – сигналнинг динамик диапазони:
Dcк10 Lg Pmax/Pmin , [dб];
1) Fс – сигналнинг спектр кенглиги;
4.Vc – сигналнинг хажми:
Vc кТc * F c*Dc.
Сигналнинг хажми – сигналнинг хабар узата олиш кобилиятини курсатади.
Сигнални ёки хабарни хосил булган жойдан истеътемолчига етказиш учун керак булган техник курилмалар ва воситалар тупламига алока тизими дейилади.
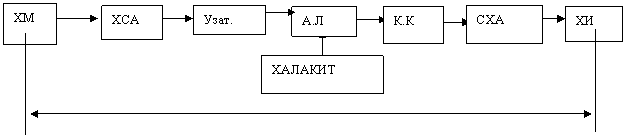
Умумий куринишдаги алока тизимини структуравий схемаси 2-чи расмда берилган.
а(t) в(t)
S(t) Z(t)![]() в˜(t)
a˜(t)
в˜(t)
a˜(t)
n(t)
АТ
2 расм. Умумий куринишдаги алока тизимини структуравий схемаси. Бу ерда: ХМ – хабар манбаи; ХСА – хабарни сигналга айлантиргич; У – узатгич;
АЧ – алока чизиºи; Х – халакит; КК – кабул килгич; СХА – сигнални хабарга айлантиргич; ХИ – хабар истеъмолчиси; АТ – алока тизими; а(t) – хабар,
в(t) – бирламчи электр сигнали, S(t) – алока чизиºи буйича узатилишга мослашган сигнал, Z(t) – кабул килиш томонидаги кабул килинаётган сигнал, n(t) – халакит.
Алока чизиги буйича узатилаётган S(t) сигналга n(t) – халакитлар таъсир килади. Агар сигнал халакит билан кушилса бундай халакит аддитив халакит дейилади.
z(t)кs(t)Кn(t)
Агар сигнал халакит билан купайтирилса у мультипликатив халакит дейилади.
Алока канали деб хабар манбаси ва истеъмолчиси хохлаган иккита нукта орасидаги техник курилмалар тупламига айтилади.
Алока каналлари кириши ва чикишидаги сигналлар турига караб, алока каналлари узлуксиз ва дискрет булиши мумкин.
Алока тизимининг тури хам ишлатилаётган канал турига мос келади.
Алока тизимлари узатилаётган хабар турига караб маьлум турларга булинади:
нутк узатиш (телефония), харакатдаги тасвир (телевидение), текст узатиш (телеграфия),ахборот узатиш ва хаказо.
Алока канали параметрлари:
1) Тк - сигнални каналдан утиш вакти (сек)
2) Fк - алока канали спектр кенглиги (Гц).
3) D к – алока каналини динамик диапозони.
Dкк10 Lg Pc/Pш [dб]
4) Vк кТк * F к*Dк – канал хажми.
Сигналларни алока каналларидан йукотишларсиз узатиш учун куйидаги шарт бажарилиши лозим.
Vк> Vс
Маъруза-2 1-булим. СИГНАЛЛАРНИНГ МАТЕМАТИК МОДЕЛИ.
НОЧИЗИКЛИ ВА ПАРАМЕТРИК ЭЛЕМЕНТЛАР ВА УЛАРНИНГ ТАВСИФЛАРИ.
1.1 СИГНАЛЛАРНИНГ МАТЕМАТИК МОДЕЛИ.
Сигналлар мураккаб жараён булганлиги учун уларни туºридан – туºри тадбик килиш жуда кийин. Шунинг учун сигналларни тахлил килишда, уларни оддий ташкил этувчилрга ажратиб, уларни хусусиятларини аниклаб, умумлаштириб сигнал хакида маълумт олиш мумкин.
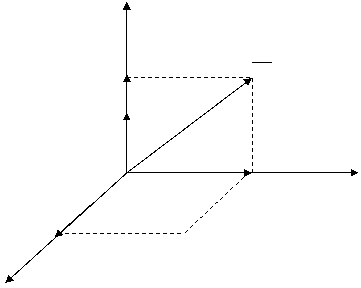
Юкорида айтиб утилганларни амалга ошириш учун n улчовли фазадаги вектор деб караш мумкин. Бу векторнинг хар бир координата укидаги проекциялар унинг ташкил этувчилари булади. Уч улчовли фазадаги векторни куриб чикайлик.
z
Az A
K
Ay
y
Ax
x
Ā к iAxК jAy К kAz (1)
A – вектор учта Ax,Ay ,Az векторларнинг йиºиндисидан иборат.
![]() (2)
(2)
dA – А векторнинг нормаси ёки узунлиги дейилади.
Реал сигналлар учун улчов бирлиги катта булганлиги учун (2) формулани куйидагича ёзиш мумкин.
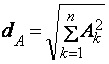
Агар уч улчовли фазада иккита А ва В векторлар берилган булса, бу иккита вектор орасидаги масофа куйидаги формула буйича топилади.

Ортаганал фаза деб, фаза уклари узаро перпендикуляр булган фазага айтилади.
Сигнални тахлил килишда умумий куринишдаги Фурье катори жуда кул келади.
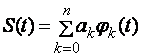
ак – Фурье катори коэффициенти.
φк(t) – Фурье каторининг базис функцияси.
Агар φк(t) базис функция вактга боглик булса, бундай фаза функционал фаза дейилади.Агар 2 чи формулада n → ∞ десак , у холда сигнални нормаси ёки сигнални узунлиги куйидаги формула ёрдамида топилади.
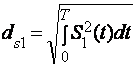
Е
к 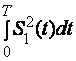 (7)
– сигнални энергияси.
(7)
– сигнални энергияси.
Агар S1 ва S2 сигналлар берилган булса улар орасидаги масофа куйидагича топилади.
 (8)
(8)
Базис функциялар ортоганал булиши учун улар орасидаги бурчак 900С булиши керак.
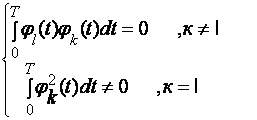 (9)
(9)
Умумий куринишда Фурье каторини куйидагича ёзиш мумкин:
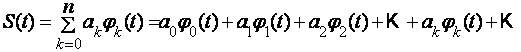 (10)
(10)
ак – коэффициентини куйидаги формула оркали топилади.
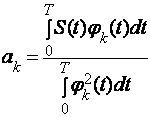 (11)
(11)
Базис функциялар сифатида куп холларда Sin kΩt, Cos kΩt
,![]() ва
ва ![]() куринишдаги функциялар ишлатилади.
куринишдаги функциялар ишлатилади.
Маъруза-3 1.2 НОЧИЗИКЛИ ВА ПАРАМЕТРИК ЭЛЕМЕНТЛАР ВА УЛАРНИНГ ТАВСИФЛАРИ .
![]() x(t)
У(t)кf [x(t)].
x(t)
У(t)кf [x(t)].
ЭЭ- электр элементи
![]() Ночизикли элементлар деб, суперпозиция принципини кулланиб
булмайдиган элементларга айтилади,яьни куйидаги шартлар бажарилмаса.
Ночизикли элементлар деб, суперпозиция принципини кулланиб
булмайдиган элементларга айтилади,яьни куйидаги шартлар бажарилмаса.
f(x1Кx2)к f(x1)Кf(x2); f(ax)кa f(x)
Ночизикли элементларнинг параметрлари узгарувчан булиб улар электр режимга боºлик булади. Ночизикли элементлар инерцион ва ноинерцион ночизикли элементларга (НЭ) булинади.
Агар НЭ нинг киришига электр жараёни таьсир этганда унинг чикишида шу ондаёк жавоб реакцияси хосил булса, бундай НЭ ноинерцион акс холда, инерцион дейилади.
Ночизикли элементлар ночизикли резисторлар ва ночизикли реактив элементларга булинади.
Ночизикли резисторлар бошкариладиган ва бошкарилмайдиган ночизикли резисторларга булинади.
Бошкарилмайдиган резисторларга варистор, ярим утказгичли ва вакумли диодлар, газаразрядли лампа ва терморезисторлар кирадилар.
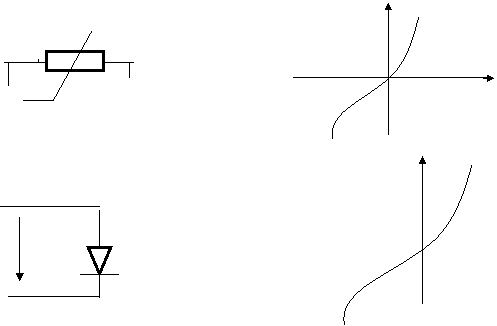 i
i
u
UкR(i)*i iк auk
Яримутказгичли диод.
u
![]() u
u
Вакуумли диод.
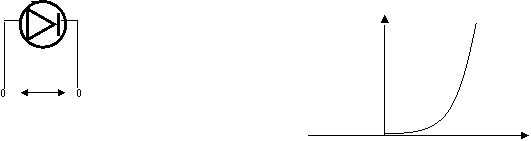 ia
ia
ua
Ночизикли реактив элементлар сифатида ночизикли конденсатор ва ночизикли индуктивликлар ишлатилади.
Ночизикли конденсатор сифатида сигимли диодлар-варикаплар ва варикондлар ишлатилади.
С
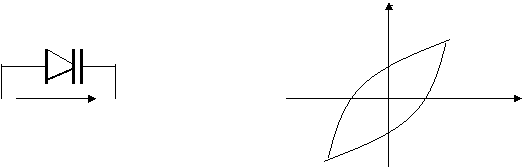
u u
Варикапнинг Волт-Фарада тавсифи.
Варикап бу р-n утишини сиºими унга берилган тескари кучланишни кийматига боºлик булган ярим утказгичли диоддир.
Вариконд- пластикалари орасида сегнетоэлектрик тулдирилган –диэлектрик утказувчанлиги кучланишга боºлик конденсатор.
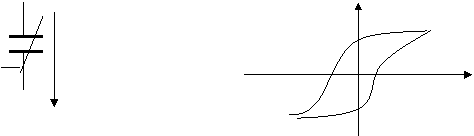
С
u
Вариконднинг Волт-Фарада тавсифи.
Ночизикли индуктивликлар сифатида феррит узакли ºалтак ишлатилади.
 Ф
Ф
i
ФкL(i)*i
Ф-магнит окими
Ночизикли элементли занжирларни НЭ ни тавсифлари ёрдамида урганишда график ва аналитик методлар кулланилади. График методлар оддий НЗ ларгаэлементар оддий таьсирлар таьсир этганда ишлатилади ва бу методнинг хисоблаш аниклиги кичик булади.
Аналитик методлар мураккаб таьсирлар учун ишлатилади ва хисоблаш аниклиги катта булади.
График сифатида берилган тавсифлар учун уларга якин булган формулаларни топишга аппроксимация дейилади.
Куйидаги аппроксимацияловчи функциялар мавжуд:
1)Даражали купхадлар. 2)Экспоненциал купхадлар. 3) Транцендент функциялар. 4)Булакли туºри чизиклар ёрдамида.
1) n-даражали купадлар.
iка0 Ка1u Ка2u2……….аnun
2) Экспоненциал купхадлар.
iкA1ea1u К A2ea2u К……..Aneanu
3) Трацендент функциялар.
iкA(1Кth au)-гиперболик тангенс.
Булакли – туºри чизикли аппроксимация.
![]() 0, агар U<U0
0, агар U<U0
iк S(U-U0) ,агар U0<U<UТ
iТ ,агар U>UТ
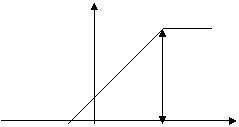 i
i
iТ
u
U0 UТ
S – хар. киялиги.
IТ - туйиниш токи.
UТ – туйиниш кучланиши.
Uo – ёпиш ёки кесим кучланиши.
Бу метод факат кириш сигналари катта амплитудали булган холларда ишлатилади.
Маъруза-4 2-булим. СИГНАЛЛАРНИ ФОРМАСИНИ ВА СПЕКТРИНИ
УЗГАРТИРИШ.
2.1.НОЧИЗИКЛИ ЗАНЖИРЛАРДА ТЕБРАНИШЛАРНИ СПЕКТРАЛ АНАЛИЗ МЕТОДЛАРИ.
Сигналлар устида хар хил функционал амаллар бажарганда ночизикли занжарлар чикишидаги тебранишларни спекторини аниклаш масаласи жуда куп учрайди. Шунинг учун спектр анализ методларини урганиш керак булади.
Спектрал анализ методларини куйидаги турлари мавжуд:
1. Тригонометрик формулаларга асосланган метод; полномли аппроксимацияда ишлатилади.
2. Кесиш бучаги методи, булакли туºри чизикли аппроксимацияда ишлатилади.
3. Уч ва беш ордината методи.
4. Маълум аргументли Бессель функцияларига асосланган метод.
Ночизикли занжирларда тебранишларни спектрал тахлил килганда тригонометрик формулалар кулланилади.
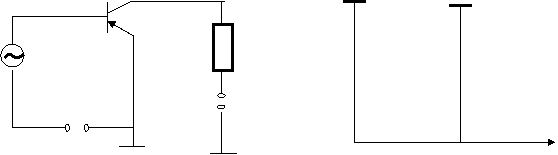 E0 U
E0 U
U1 R
Ek
Ec
0 ω0 ω
iкa0Кa1uКa2U2; uTкU Cos ω0t; uкир к E0 КU Cos ω t
ik к I0КIω0 Cos ω0t К I2ω0Cos 2ω0t; I0кa0Кa1E0Кa2E20Кa2U2/2
Iωкa1UК2a2E0U; ![]()
I0
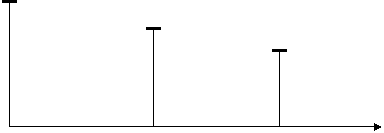 Iω
Iω
I2ω
0 ω0 2ω0 ω
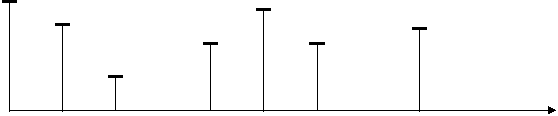
Таъсир сигнали бигармоник булса, яъни:
uкиркU1Cos ω1t К U2Cos ω2t
iк a1u К a2u2
булса,у холда спектр ташкил этувчилари куйидагилардан иборат булади.
I0 к
![]() , Iω1кa1U1 , Iω2кa1U2 ,
, Iω1кa1U1 , Iω2кa1U2 , 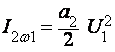
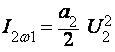 ,
I ω2 - ω1кa2U1U2, I ω2 К ω1кa2U1U2
,
I ω2 - ω1кa2U1U2, I ω2 К ω1кa2U1U2
 I0
I0
Iω1 Iω1 Iω1
0
ω1 ω2 ω1- ω1 ω2 ω1К ω2 2ω2 ω
Маъруза-5 КЕСМА БУРЧАГИ УСУЛИ.
Кесма бурчаги усули НЭ характеристикаси булакли туºри чизикли аппроксимация килинганда ишлатилади.
НЭ тавсифи куйидаги ифода билан берилган булсин:
![]() 0, агар U<U0
0, агар U<U0
i к S(U-U0) , агар U>U0 (1)
U0- кесиш кучланиши.
НЭ кришига куйидаги кучланиш берилган булсин:
Uк ЕсКUm cos ωt (2)
иш нуктаси шундай олинганки Um>IU0-ЕI
Ес-силжиш кучланиши.

i i
![]()
I΄0
u ωt
2θ
u
θ U0
i
токнинг утиш даврини ярмига кесма бурчаги дейилади.
S(U-U0) , 0<ωt< θ
iк 0, θ < ω t<2 π – θ (3)
S(U-U0), 2 π - θ < ω t<2 π К θ
iк0 хол учун (3) формулага (2) куйиб куйидагини хосил киламиз:
S к ЕmКSUmcos ω t-SU0 (4)
Расмда куриниб турибдики ωtк θ булганда iк0 яьни
0 к SЕmКSUm cos θ -SU0 (5)
Бу формуладан cos θ ни аниклаймиз.
cos θ к -Em-U0/Um (6)
(4) дан (5) ни айирамиз.
i к SUm(cos ω t-cos θ) (7)
ω t к 0 булганда iкimax
imax к SUm(1-cos θ) (8)
НЭ чикишидаги i токимиз даврий ва жуфт функциядир.Шунинг учун бу функцияни Фурье каторига ёйилмаси факат косинус гармоникаларидан иборат.
iкI0КI1cos ω tКI2 cos 2 ω tК……In cos n ω t К….. (9)
Бу катордаги гармоникаларни амплитудаси куйидаги формула ёрдамида топилади:
Inк SUm 2[Sin nθCos θ – nCos nθ Sin θ]/π (10)
Гармоникаларнинг амплитудасини imax га нисбатини оламиз,яъни
αn(θ)к In / imax ни аниклаймиз.
αn(θ)к 2[Sin nθCos θ – nCos nθ Sin θ]/[πn(n2-1)(1- Cos θ)] (11)
Бу формуладан куриниб турибдики бу нисбат факат кесиш бурчагига боºлик.
In гармоникаларнинг амплитудалари маьлум бир кесиш бурчакларда максимум кийматларга эга булади. Бу оптимал кесиш бурчаклари куйидаги формула ёрдамида аникланади.
θ к1200/n
УЧ ВА БЕШ ОРДИНАТА МЕТОДЛАРИ.
Бу метод тебранишларни гармоник анализларда тахлилий график аналитик методи булиб, мухандислик амалиётида кучайтиргич, модулятор ва бошка курилмада ночизикли бузилишларни аниклашда ишлатилади.
Беш ордината методи ёрдамида жуда осон ва тез равишда токнинг узгармас кисми ва 4- та гармоникаларини амплитудасини аниклаш мумкин.
![]() iк I0 К I1Cos ωt
К I2Cos 2ω1t К I3Cos 3ωt К I4Cos
4ωt (1)
iк I0 К I1Cos ωt
К I2Cos 2ω1t К I3Cos 3ωt К I4Cos
4ωt (1)
imaxк I0 К I1 К I2 К I3 К I4 ωt к 0
i1к I0 К ½ I1 К ½ I2 К ½ I3 К ½ I4 ωt к π/3
i0к I0 - I2 К I4 ωt к π/2 (2)
i2к I0 - ½I1 - ½ I2 К ½I3 -½ I4 ωt к 2π/3
iminк I0 - I1 К I2- I3 К I4 ωt к π
Токларни амплитудаси куйидаги формулалар ёрдамида аниклаймиз:
![]() ;
; ![]()
![]() ;
; ![]()
![]() ;
; ![]()
Уч ордината методини куриб чикайлик.Бу методда учта нукта олиниб, ωtк0, π/2, π imax,i0 ,imin – ток кийматлари топилади.
![]() ;
; ![]() ;
; ![]()
Беш ордината методининг аниклиги уч ордината методининг аниклигидан юкорирок булади.
Маъруза-6 2.2.СИГНАЛЛАРНИ СПЕКТРИНИ УЗГАРТИРИШ МАСАЛАСИ ВА УНИ НОЧИЗИКЛИ, ПАРАМЕТРИК ЗАНЖИРЛАР ¨РДАМИДА ЕЧИШ.
ЧЕГАРАГИЧЛАР.
Чегарагичларни икки хили мавжуд: оний киймат чегарагичлари ва амплитуда чегарагичлари.
Кучланиш ёки токнинг оний кийматларини чегараланиши деб, шундай ночизикли амалга айтиладики, бу холда кучланиш ёки токнинг оний кийматлари берилган маьлум кийматлар –чегарасидан ошмайди ёки камаймайди.
Амалда уч хил оний киймат чегарагичлари кулланилади:
1) Юкоридан ёки максимум буйича чегараланиш.
2) Пастдан ёки минимум буйича чегараланиш.
3) Икки томонлама чегаралагичлар.
Кучланиш чегаралагичларини асосий тавсифлари бу уларни чикиш кучланиши U2 ни кириш кучланиши U1 га боºликлигидир.Уч хил чегараланиш жараёнини куриб чикайлик.
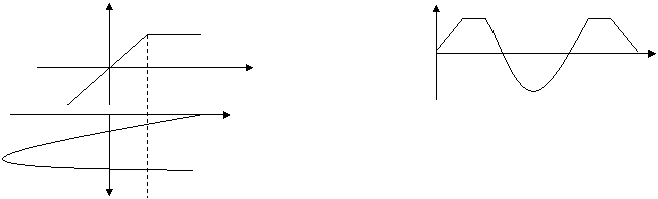 U2 U2
U2 U2
U1
U1
t
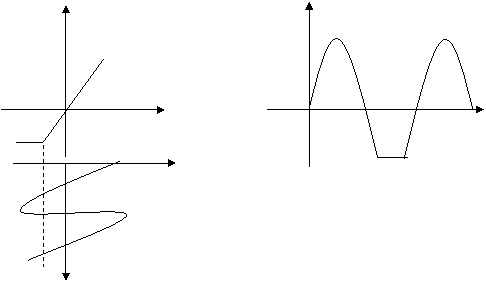 |
Пастдан чегаралаш.
U2 U2
U1 t
U1
t
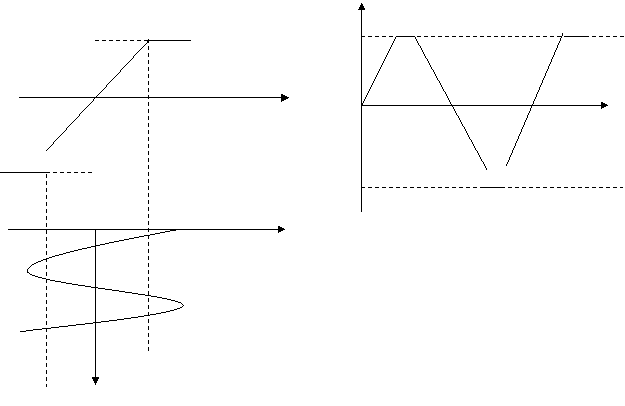 U2
U2
U2
U2
E1
U1 t
E2
U1
t
Диодли чегарагичларни ишлаш принципини куриб чикайлик. Диодли чегарагичларни схемаларини икки хил тури мавжуд: кетма – кет ва паралел схемалар (диодни уланинишига караб).
Диодли чегарагичлар диод ва резистордан иборат. Диодли чегаралагичлар учун куйидаги шартлар бажарилиши лозим.
R>>rд оч ,R<<rд ёп
 |
D
U2
R
U1 U2
К E1
- E1
U1
D
 U2
U2
R
U1 U2
- E2
К
E2 U1
R
U2
E1
D1 D2
К E1 - E2 U1
- К
E2
Транзисторли юкламали чегаралагич схемаси.
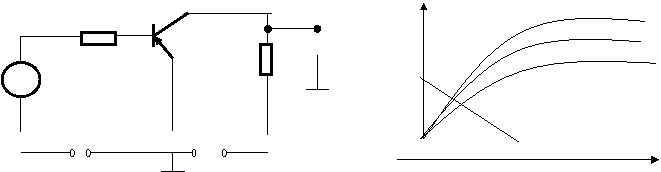
Rб Ik
Uкэ
Rю
- К К -
Еб Ек IUкэI IЕкI Ukэ
Чегаралагич туºри ишлаши учун Rб>>Rочтр шарт бажарилиши керак. Транзисторнинг юклама тавсифи ётикрок булиши учун Rн катта булиши лозим. ек0 булганда база токи iб тенг. е<0 булганда эммитор утиши купрок очилиб iб токи олинади.iб>tб учун чикиш характеристикалари билан юкланиш характеристикасини кесишган нуктаси А га туºри келган IUкэImin узгармас булиб нолга якин.IUкэImin киймати биринчи чегарани курсатади. Мусбат е ни бериб эммитор утишини ёпиб иккинчи чегара UкэкЕк хосил киламиз.
Маъруза-7 СПЕКТРНИНГ ФОЙДАЛИ ТАШКИЛ ЭТУВЧИ
ТЕБРАНИШЛАРИНИ АЖРАТИБ ОЛИШ.
Ночизикли элемент киришига сигнал таьсир килганда унинг чикишида фойдали тебранишлардан ташкари фойдасиз булган тебранишлар хам хосил булади. Улар фойдали тебранишларга салбий таьсир этиб, сигнални ночизкли бузилишларга олиб келади. Фойдали тебранишларни ажратиб олиш учун асосан филтрлаш усули ишлатилади.
Юкори частотали тебранишларни ажратиб олиш учун LC паралел тебраниш контури , паст частотали ва узгармас ташкил этувчини ажратиб олиш учун эса RC –паралел занжир ишлатилади.
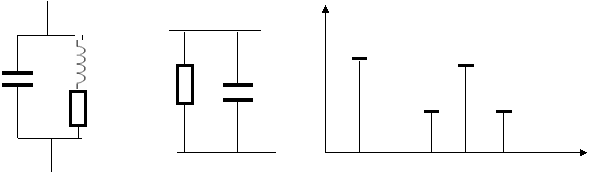 |
In
L
С R C
R
0 Ω ω0- Ω ω0 ω0К Ω ω
ω0 -частотага созланган паралел LC-тебраниш контурининг каршилигини модули куйидагича аникланади.
Zэ(ω)кRэ
/![]() , (1)
, (1)
бу ерда, RэкL/rC – контурнинг актив эквивалент каршилиги ;
Qк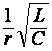 - контур
асиллиги;
- контур
асиллиги;  -
частотани ω0
резонанс частотадан четланиши. ωк ω0 булганда Zэ(ω)кRэ
га тенг булади.
-
частотани ω0
резонанс частотадан четланиши. ωк ω0 булганда Zэ(ω)кRэ
га тенг булади.
![]() Z(ω)
Z(ω)
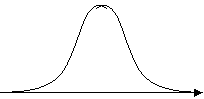
ω0 ω
RС - занжирни каршилиги куйидаги формула ёрдамида топилади.
Z(ω)кR/![]() (2)
(2)
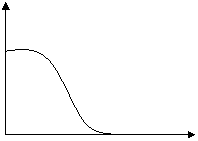
ω0 к0 булганда Z(ω)кR га тенг булади
 Z(ω)
Z(ω)
R
ω
Z(ω) нинг камайиш тезлиги RC ни купайтмасига боºлик.
ЧАСТОТАНИ КУПАЙТИРИШ
Частотани купайтирилганда ночизикли узгартирувчи курилма киришига ω0 частотали тебраниш берилганда унинг чикишида nω0 частотали тебраниш хосил булади.Бу ерда n-мусбат бутун сон.
Демак частота купайтиргични киришига
S1 (t)к A Cos(ω 0К φ) (1) - тебраниш берилганда унинг чикишида
S2(t) к BCos(n ω 0tК φ) (2) - тебраниш хосил киламиз.
Транзисторли частота купайтиргични ишлаш принципини куриб чикайлик.
 VT1
VT1
C L Uчик
U -
К - К Ек
Ес
Кириш кучланиши UкиркU Cos ω0t булганда чикиш занжиридаги ток нокосинусоидал булиб, ω0 частотадан ташкари унинг гармоникалари хам мавжуд.
Частота купайтиргични киришига амплитудаси катта булган тебраниш берилгани учун транзисторни ВАТ и булакли туºри чизикли аппроксимация килинади.
Токнинг керакли булган амплитудаси куйидаги маьлум булган ифода ёрдамида топилади.
Inкαn(θ)imax (3)
Берилган imax да керакли булган гармоникани In ни амплитудасини максимал кийматини олиш учун θопт – оптимал кесиш бурчагини олиш керак.
θопт к120/n
Берилган θопт ва imax караб Ес ва U кириш кучланишини аниклаш мумкин.
Ес к U0 - U Cosθ (4)
Uкimaх / S(1- Cosθ) (5)
n-нинг усиши билан αn(θ) коэффициентларининг кийматини тез камайиши сабабли , In хам тез камаяди . Шунинг учун бундай схема ёрдамида частотани факат икки ёки уч марта купайтириш мумкин.
Тебранишларни куп марта купайтириш учун бошка усул кулланилади.
Ночизикли курилма ёрдамида даври Тк 2π/ω0 булган гармоник тебраниш кенглиги τ<<Т булган киска туºри бурчакли импульслар кетма-кетлигига айтилади. τ/Т нисбат канчалик кичик булса, n усиши билан гармоникаларни амплитудаси секинрок камайиб боради. Бу усул билан частотани купайтириш куйидаги структуравий схема ёрдамида амалга оширилади.
S1(t) к A Cos(ω 0К φ) S2(t) к BCos(n ω 0tК φ)
![]() δ(t)
δ(t)
Схемада: ИХК – юкори частотали гармоник тебранишдан импульслар кетма – кетлигини хосил килувчи курилма; Ф – керакли булган гармоникани ажратиб олувчи фильтр; δ(t) – кенглиги киска булган ипульслар кетма – кетлиги.
Киришига U к UCosω0t тебраниш таьсир килганда чикишида ягона iк кInCos n ω0t тебраниш хосил буладиган частота купайтиргичларга идеал частота купайтиргичлар дейилади. Бундай купайтиргичларда фильтрлар ишлатилмайди.
Маъруза-8 3.булим. МОДУЛЯЦИЯ ˉАКИДА ТУШИНЧА. МОДУЛЯЦИЯЛАНГАН СИГНАЛЛАРНИ
ˉОСИЛ КИЛИШ ВА ДЕТЕКТОРЛАШ.
Паст частотали бирламчи сигналлар:
1) Телефон сигналлари:300-3400 Гц
2) Мусика сигналлари : 20Гц- 18000Гц.
3) Телеграф сигналлари: 0- 100 Гц
Паст частотали бирламчи сигналларни куввати камлиги учун уларни узок масофаларга узатиб булмайди. Узатиш томонидан кабул килиш жойигача масофа ортган сари бирламчи сигналлар тезрок суна боради. Шунинг учун паст частотали сигналларни узок масофаларга узатиш учун алока каналлари оркали узатишга мослашган юкори частотали сигналлардан фойдаланилади. Бундай сигналларга ташувчи юкори частотали сигналлар дейилади. Ташувчи сигналлар сифатида юкори частотали гармоник тебранишлар ёки туºри бурчакли импульслар кетма- кетлиги кулланилади.
Бизга юкори частотали гармоник тебраниш берилган булсин.
U(t)к Acos(ω0tК φ)
Агар ПЧС энг юкори частотаси Ωmаx булса ва куйидаги шарт бажарилса.
ω0 >> Ωmаx
Юкори частотали гармоник тебранишнинг бирон бир параметрини (А, ω, φ) бирламчи паст частотали сигналнинг узгариш конунига, мос равишда узгаришига модуляция дейилади.
Узлуксиз модуляциянинг уч хили мавжуд: АМ,ЧМ,ФМ.
Модуляцияланган сигналларни умумий куринишдаги ифодасини куйидагича ёзиш мумкин:
Uм(t)к U(t)Cos ψ(t); ψ(t)к ω(t)К φ(t)
1)Агар U(t)к U0Кk x(t) φ(t)к φ0 ва ω(t)к ω0 булса АМ ни хосил киламиз.
2) Агар ω(t)к ω0Ка x(t) φ(t)к φ0 ва U(t)к U0 булса ЧМ ни хосил киламиз.
3) Агар φ(t)к φ0Кв(t) U(t)к U0 ва ω(t)к ω0 булса ФМ ни хосил киламиз.
АМПЛИТУДА МОДУЛЯЦИЯСИ.
Юкори частотали гармоник ташувчи сигнал берилган булсин.
U(t)к U0Cos( ω0(t)К φ0)
Амплитуда модуляцияси деб, юкори частотали ташувчи сигналнинг амплитудасини бирламчи ПЧС нинг узгариш конунига караб узгаришига айтилади. Демак куйидаги конун билан узгарар экан.
Uамк U0К Uамк U0Кk x(t)
бу ерда к- коэффициент, x(t)-бирламчи ПЧС.
У холда амплитуда буйича модуляциланган сигнал куйидаги куринишда булади.
Uамк 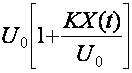 Cos
Cos![]() (ω0(t)К φ0)
(ω0(t)К φ0)
Энг оддий холда ПЧС бирламчи сигнал гармоник тебраниш булсин.
![]()
![]()
![]()
![]() булсин.
булсин.
У холда ![]() ;
; ![]()
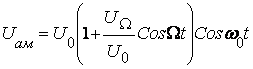 ;
; 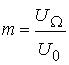 ;
;
![]()
m-модуляция
коэффициенти.![]()
![]() модуляция чукурлиги.
модуляция чукурлиги.
![]()
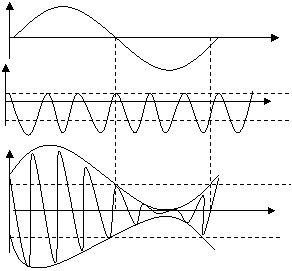 Амплитудаси буйича модуляцияланган сигналларни вакт
диаграммасини куриб чикамиз.
Амплитудаси буйича модуляцияланган сигналларни вакт
диаграммасини куриб чикамиз.
UΩ
t
Uω
t
Uам
t
АМ сигналларни спектрини аниклаймиз.
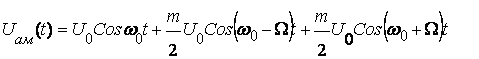
Кириш синалигини спектри
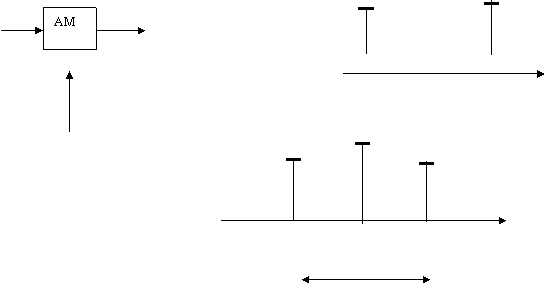 UΩ Uω
UΩ Uω
ω
![]()
![]()
Чикиш спектри.
![]()
ω0-Ω ω0 ω0КΩ
![]()
2Δω- АМ сигнални спектр кенглиги.
Бирлмачи сигналимиз мураккаб булсин, масалан хар хил частотали гармоник тебранишлар йиºиндиси булсин.
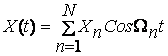
У холда АМ сигналнинг амплитудаси:
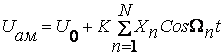
АМ сигналнинг аналитик ифодаси куйидагича куринишда булади.
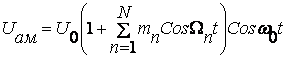
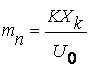 - парциал модуляция
коэффициентлари.
- парциал модуляция
коэффициентлари.
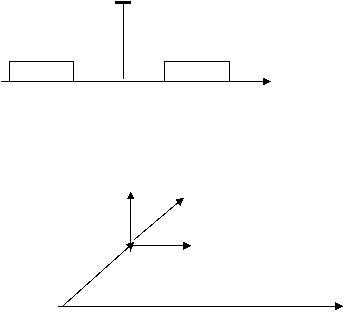 |
ω0-Ωn ω-Ω1 ω0 ω0КΩ1 ω0КΩn ω
АМ сигнални вектор диаграммасини куриб чикайлик.
Uам
Uω
UΩ
t
Uю ва Uп лар карама карши йуналишларда Ω бурчакли тезликда айланади. Учта вектор йиºиндиси булган Uам , U0 ни йуналиши билан туºри келади. АМ сигнални оний киймати t вакт укига пропорцияси сифатида топилади.
Маъруза-9 ГАРМОНИК АМ СИГНАЛЛАРДА ЭНЕРГЕТИК
МУНОСАБАТЛАР.
Гармоник АМ сигналлардаги энергиянинг шу АМ сигнални ташкил килувчи тебранишлардаги энергияни таксимланишини куриб чикамиз.
АМ сигнални амплитудаси:
![]()
- юкори
частотали тебраниш даври 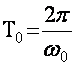 оралиºида
секин узгаради.Шунинг учун 1 Ом каршиликда Т0 давирда уртача
кувват куйидагича аникланади.
оралиºида
секин узгаради.Шунинг учун 1 Ом каршиликда Т0 давирда уртача
кувват куйидагича аникланади.
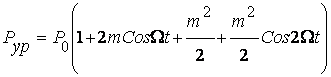
Бу ерда 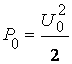 -ташувчи тебранишнинг куввати.
-ташувчи тебранишнинг куввати. ![]()

![]() булгангда эса.
булгангда эса. ![]()
mк1 булганда
![]()
![]() шунинг
учун
шунинг
учун ![]()
Энди паст частота даври 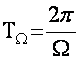 оралиºида Рурт
ни аниклаймиз.
оралиºида Рурт
ни аниклаймиз.
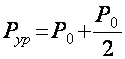
АМ СИГНАЛЛАРНИ ТУРЛАРИ.
Амплитудаси буйича модуляция килинган сигналларни куйидаги турлари мавжуд:
1) Икки минтакали ташувчиси мавжуд АМ сигнал:
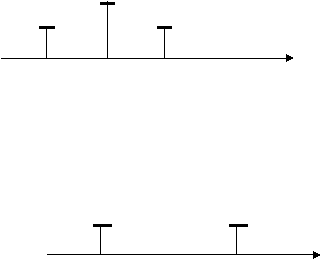 |
ω0-Ω ω0 ω0КΩ ω
2) Икки минтакали ва ташувчиси йукотилган АМ сигнал.
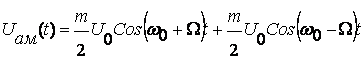
ω ω0-Ω ω0КΩ
3) а) Ташувчиси мавжуд битта минтакали АМ сигнал.

![]()
ω
ω0 ω0КΩ
б) ![]()
ω0-Ω ω0 ω
4) Битта минтакали ташувчиси йуколган АМ сигнал.
 а)
а) 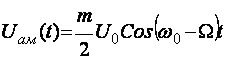 ω
ω
ω0-Ω
![]() б)
б) 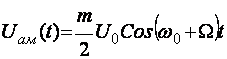
![]() ω
ω
ω0КΩ
Маъруза-10 ДИОДЛИ АМПЛИТУДА МОДУЛЯТОРИ.
НЭ сифатида ярим утказгич диод берилган булсин.Унинг ВАХ иккинчи даражали полином билан аппроксимация килинган.
iкa0Кa1UКa2U2
D
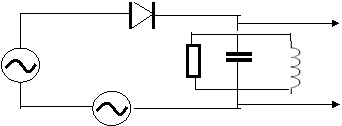 |
U2 Rэ C L
U1
UкиркU1КU2кUω0Cos ω0tКUΩCosΩt
![]() iкa0Кa1(Uω0КCos ω0tКUΩCosΩt )Кa2(Uω0Cos ω0tКUΩCosΩt )2
iкa0Кa1(Uω0КCos ω0tКUΩCosΩt )Кa2(Uω0Cos ω0tКUΩCosΩt )2
 Контурдаги каршилик
Контурдаги каршилик 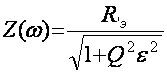
![]()
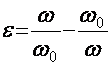
ω0 ω
i ω0кa1 Uω0Cos ω0tК2 a2UΩ Uω0 CosΩt Cos ω0t
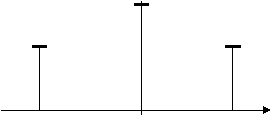 Агар ω0, ω0-Ω, ω0КΩ частоталар
учун контур каршилиги:
Агар ω0, ω0-Ω, ω0КΩ частоталар
учун контур каршилиги: ![]() ва бошка тебранишлар учун
ва бошка тебранишлар учун ![]() булса:uчиккUчик(1КmCosΩt)Cos ω0t;
Uчиккa1,Rэ,
Uω0
булса:uчиккUчик(1КmCosΩt)Cos ω0t;
Uчиккa1,Rэ,
Uω0 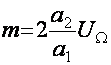
Uчик
m/2 Uчик m/2 Uчик
ω0-Ω ω0 ω0КΩ
Маъруза-11 БАЗА МОДУЛЯЦИЯЛИ ТРАНЗИСТОРЛИ
АМПЛИТУДА МОДУЛЯТОРИ.
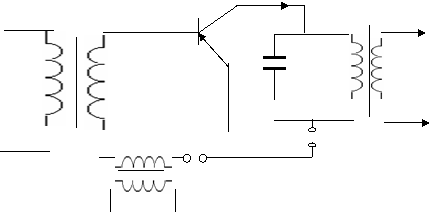 |
VT
C Uам
U2
U1
Транзисторнинг ВАХ учинчи даражали полином ёрдамида аппроксимация килинган булсин.
ikкa0Кa1UбэКa2U2бэКа3 U3бэ; UкиркЕКU1КU2
U1кUΩCosΩt , U2к UωCosωt ωрк ω0
iω0кI ω0Cos ω0tКIω0КΩCos(ω0КΩ)tК Iω0-ΩCos(ω0-Ω)tК Iω0К2ΩCos(ω0К2Ω)tК
Iω0-2ΩCos(ω0-2Ω)t;
I ω0ка1U0К2a2E U0К3a3E
2U0К
Iω0-Ωк2a2UΩU0К3a3E UΩU0; Iω0КΩк2a2UΩU0К3a3E UΩU0
![]() Iω0-2Ωк
Iω0-2Ωк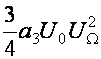 ;
Iω0К2Ωк
;
Iω0К2Ωк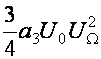
Модуляция коэффициенти:
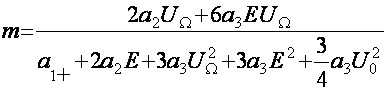 ;
;

Амплитуда модуляторининг туºри ишлаш режимини танлаш учун унинг статик модуляцион характеристикаси олинади.
Амплитуда модуляторининг статик модуляцион характеристикаси деб- U0кconst . UΩк0 ,булганда коллектор токининг биринчи гармоникасини силжиш кучланиши Е га боºликлигига айтилади.
Ik1кƒ(E)
Ik1к а1U0К2a2E Uω0К3a3E 2U0К
 Ik1
Ik1
I0
Е E0
Маъруза-12 БАЛАНСЛИ МОДУЛЯТОР.
Балансли модулятор ёрдамида ташувчиси булмаган икки
минтакали АМ сигнал хосил килинади.Бу модулятор ёрдамида АМ сигнални бузувчи ω0![]() 2Ω
комбинацион частоталардан кутулиш мумкин.
2Ω
комбинацион частоталардан кутулиш мумкин.
 D1
D1
R1
R2
D2
u1кU0Cosω0t R1кR2; u 2кUΩCosΩt L1кL2
uд1к u1К u2; uд2к u1- u2; iкa0Кa1UКa2U2Кa3U3
i1кa0Кa1(u1К u1)Кa2(u1К u1)2Кa3U3
i2кa0Кa1(u1- u1)Кa2(u1- u1)2Кa3(u1К u1)3
iчикк i1- i2
iчикк 2 a1 u2 К4 a2 u1 u 2К6 a3 u21u2К2a3 u32
uчикк iчикRк 2 a1 u2 RК4 a2 u1 u 2RК6 a3 u21u2RК2a3 u32R
Бу формуладан куриниб турибдики чикиш кучланишини
спектрида ω0 ва АМ сигнални бузувчи ![]() частоталари
йук.
частоталари
йук.
 |
ω
Ω 3 Ω ω0- Ω ω0К Ω 2ω0- Ω 2ω0К Ω
Чикиш кучланишини спектрида факат ![]() тебранишларни
колдириш учун схемада фильтр ишлатиш лозим.
тебранишларни
колдириш учун схемада фильтр ишлатиш лозим.
 D1
D1
C
D2
Бу балансли модулятор чикишида хосил булган кучланишни спектри куйидаги куринишда булади.
 |
ω0-Ω ω0 ω0КΩ ω
Маъруза-13 ХАЛКАЛИ МОДУЛЯТОР
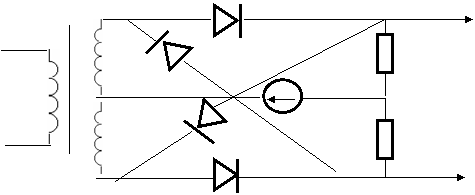
Балансли модулятордаги хосил булувчи керакмас Ω,3Ω, 2ω0-Ω ва 2ω0КΩ, ва фильтрдан кутилиш учун бу схемага иккита диод кушиб халкали модуляторни хосил килиш мумкин.
D1
D3
R1
U0
UΩ
D4 R2
D2
R1кR2кR , L1кL2 , ВАХ1 к ВАХ2 к ВАХ3 к ВАХ4
u2кUΩCosΩt , u1кU0Cosω0t
uд1к u1К u1 uд3к- u1-u1; uд2к u1- u1 uд4к -u1К u1
iчикк( i1- i2)К ( i3- i4)к iчик1К iчик2
i1 ва i2 токлар балансли модулятордаги каби топилади ва худди шундай куринишга эга булади i1- i2 токлар айирмаси хам худди шундай булади.
iчик1к 2 a1 u2 К4 a2 u1 u 2К6 a3 u21u2К2a3 u32
i3 - i4 токлар айирмаси
iчик2к -2 a1 u2 К4 a2 u1 u 2-6 a3 u21u2-2a3 u32; iчикк iчик1К iчик2к8 a2 u1 u 2
uчиккRiчикк8a2 Ru1u2кiчикк8a2RUΩCosΩtU0Cosω0tк4a2RUΩU0Cos(ω0-Ω)t
К 4 a2 RUΩ U0Cos(ω0КΩ)t
 |
ω0- Ω ω0К Ω ω
Шундай килиб хар бир диодларда ва кириш сигналларини амплитудаси кичик булганда диодларнинг ВАХ лари учинчи даражали полином билан аппроксимация килинганда халкали модулятор икки сигнални идеал купайтиргич сифатида ишлайди ва унинг чикиш спектрида ω0КΩ ва ω0-Ω тебранишлар хосил булади.
Ташувчиси булмаган икки ён томонли АМ сигналнинг вакт диаграммаси куйидаги куринишда булади.
 Uам
Uам
t
Маъруза-14 АМПЛИТУДАСИ БУЙИЧА МОДУЛЯЦИЯЛАНГАН
СИГНАЛЛАРНИ ДЕТЕКТОРЛАШ.
Детекторлаш модуляцияга нисбатан тескари жараёндир. Амплитуда модуляциясида юкори частотали ташувчи тебранишнинг амплитудаси бошкарувчи паст частотали сигналнинг узгаришига пропорционалдир. АМ сигнални детекторлашда эса модуляция килинган сигналлардан бошкарувчи паст частотали сигнал кайта тикланади.
Умумлаштирилган холда АМ детекторини схемасини куриб чикамиз.

Детектор НЭ ёки ПЭ ва паст частотали фильтр ПЧФ дан ташкил топган.
НЭ нинг киришига гармоник uкирк UCos(ωtКφ) таьсир килганда унинг чикишида узгармас ташкил этувчи I10 ва U10 кучланиш хосил булади.ПЧФ эса детекторнинг чикишига юкори частотали ташкил килувчиларни утишига тускинлик килади.Амлитуда детектори учун I10 киймати детектор киришига берилаётган U кучланишни амплитудага боºлик булиши лозим. Агар шу шарт бажарилса АМ детекторни киришига АМ сигнал берилса унинг чикишидаги I10 ток бошкарувчи паст частотали сигнални узгариш конуни буйича узгаради, яъни детекторлаш жараёни амалга ошади.
НЭ сифатида диод берилган булса унинг киришига АМ сигнал таъсир килсин.
u кирк U(1КmCosΩt ) Cosω0t (1)
Диод ярим утказгич булганлиги учун ундан окиб утувчи токнинг амплитудаси АМ сигналнинг амплитудасига мос равишда узгарувчи импульслар кетма-кетлигидан иборат булади.ˉосил булган импульслар кетма-кетлигида Ω частотали тебраниш хам мавжуд. Бу i токнинг паст частотали сигнал ёрдамида модуляция килинган импульслар кетма-кетлигини Фурье катори куринишида ифодалаш мумкин.
iк(1КmCosΩt)(I0КI1 Cosω0t К I2Cos2ω0tК I3 Cos3ω0tК…..) (2)
 Шундай килиб бу ифодага биноан ток ПЧС билан модуляция килинган узгармас ω0 ва унинг гармоникаларидан иборат
Шундай килиб бу ифодага биноан ток ПЧС билан модуляция килинган узгармас ω0 ва унинг гармоникаларидан иборат
i i
u t
uкир uчик1
t
t
uчик2
t
Бу формулага ва расмга биноан I10 ни ифодасини куйидагича ёзиш мумкин.
I10 к(1КmCosΩt)I0
Детекторни чикишига юкори частотали ташкил этувчиларини утказмаслик учун ПЧФ куйилади. Бунинг натижасида диодли детекторнинг схемасини хосил киламиз.

D С1
i
R1
С
ω-Ω ω ωКΩ ω
I
Ω ω-Ω ω ωКΩ 2ω-Ω 2ω 2ωКΩ ω
0 Ω ω
Юкори частотали тебранишлар детектор чикишига утмаслиги учун R >> 1/ ω0C ва ПЧ тебранишлар детектор чикишида кучланиш хосил килиши учун ПЧ учун
R << 1/ΏC
Бу иккала шартни бирлаштириб куйидаги тенгсизликни хосил киламиз:
1/ω0C << R << 1/ ΏC ( 4 )
Детектор чикишидаги Uчик дан холис булиш учун детектор чикишига С1 ва R1 сиºим ва каршиликлар уланади.
R каршилик шунчалик катта олинадики уни i токга таьсирини инобатга олишимиз лозим. Детектор киришига uкиркUcosω0t гармоник тебраниш таьсир килсин.Бу холда диодга куйидаги кучланиш таьсир килади. u к uкирКU0
бу ерда U0 к -I01R - узгармас силжиш кучланиши.
Шуни инобатга олиб, диоддан окиб утувчи i токни куриб чикайлик.
 i
i
i
i
I΄0
u ωt
θ 2θ
u
U0
ωt
Катта кийматли R учун кичик кесим бурчак режимида ишлайди, яъни кийматли диоддан даврнинг кичик кисми давомидагина ток окиб утади.Очик диоднинг кашилиги кичик булганлиги учун бу вакт ичида сиºим тезда зарядланиб ундаги кучланиш uс ортади. uкир uс булиши биланок, диод ёпилиб, С сиºим катта кийматли R каршилик оркали разрядланади.
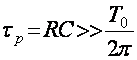 ёки τ>>T0
ёки τ>>T0
Шунинг учун T0 даврнинг конденсаторнинг разрядланиш вактида ундаги uс кучланиш кам камаяди.
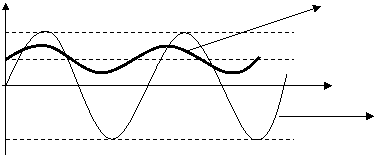 uс
Uc к Uчик к U0
uс
Uc к Uчик к U0
t
Uкир
Амплитуда детектори икки хил режимда ишлаш мумкин:
1) Квадратик режимда;
2) Чизикли режимда;
Квадратик детекторнинг ишлаш режимини куриб чикамиз.
Агар кириш сигналининг амплитудаси 0,2—0,3В>U кичик булса амплитуда детектори квадратик детектор дейилади ва унинг ВАХ и иккинчи даражали полином ёрдамида берилади:
i к a0 К a1u К a2u2 (5); Uкирк Ucos ω0t (6)
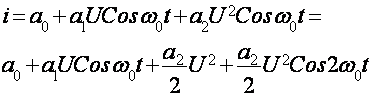
Бу ифодада токнинг узгармас кисми  (7)
(7)
бу ток I0кa0 ишчи нуктасидаги куйидаги кийматга фарк килади:
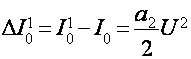 (8)
(8)
(8) - ифодага амплитуда детекторнинг детокторлаш характеристикаси дейилади.
 Iд
Iд
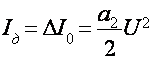 (9)
(9)
0 U
Бу ифодадан куриниб турибдики квадратик детокторни детекторлаш характеристикаси квадрат функция куринишида.
Бу детекторни киришига АМ сигнал таъсир килсин.
uкиркU(t)Cosω0t (10);
U(t)кU(1КmCosΩt) iкa0Кa1U(t)Cosω0tКa2 U2(t)Cos2ω0t у холда
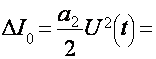
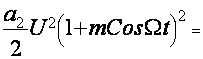

Бу формуладан куриниб турибдики кавдратик детекторнинг спектрида
Iузк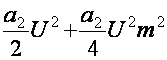 тебранишлари
мавжуд.
тебранишлари
мавжуд.
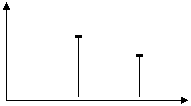 |
![]() ва I2Ωк
ва I2Ωк 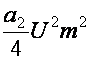
0 Ω 2Ω ω
I2Ω -паст частотали бирамличи сигралга салбий таъсир этади.Бу таъсирни бахолаш учун ночизикли бузилиш коэффициенти аникланади.
 m -100% булганда
m -100% булганда 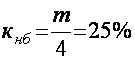
Агар деткторни киришига 0,5—1В катта амплитудали сигнал берилса детектор чизикли режимда ишлаб унинг ВАХ булакли чизикли аппроксимацияланади.
![]() U, u
U, u![]() i
i
iк
Su, ![]()
U
Детекторга куйидаги кучланиш таъсир килсин uкиркUcosω0t
У холда диоддаги кучланиш uдкUcosω0tКU0
Бу ерда U0к-I10R
I10-токнинг узгармас кисми, агар Uк0 булса U0к0 I10к0
кириш сигналини амплитудаси купайиши U0 силжиш кучланиши ошишига олиб келади.
θ-кесим бурчагини аниклаймиз.
ω0tк
θ булганда uкUcos θ КU0к0 бу формулада cos
θк-![]() ; cos θк-
; cos θк-![]()
Маълумки кесим бурчаги методига асаосланиб
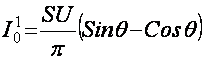
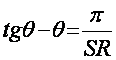
Бу тенгламани ечиб θ ни аниклаш мумкин.
Агар θк900 булса
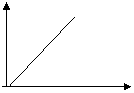 Id
Id
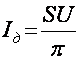
U
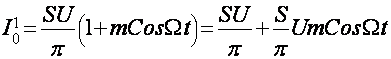 ;
;
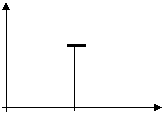 i
i

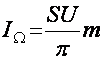
0 Ώ ω
Маъруза-15 СИНХРОН ДЕТЕКТОРЛАШ
Модуляция килинган сигналларни детекторлашда параметрик элементлардан фойдаланилса, бундай детекторларни синхрон детекторлар дейилади.
Параметрлари вактга боºлик булган элементлар параметрик элементлардейилади.
Синхрон детекторни ишлашини куриб чикайлик:

R(t)
C R
Параметрик элементни каршилиги куйидаги конун буйича узгарсин

Синхрон детектор киришига АМ сигнал берилган булсин:
uамкU(1КmCosΩt)Cosω0t; iк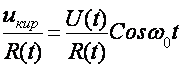
Бу токнинг узгармас кисмини ПЧФ ёрдамида ажратиб оламиз.
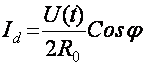
Бу формуладан куриниб турибдики ![]() токи U(t) пропорционал булиб, СД ни детекторлаш
характеристикаси чизиклидир.
токи U(t) пропорционал булиб, СД ни детекторлаш
характеристикаси чизиклидир.
 СД чикишидаги сигнал спектрини куриб чикамиз.
СД чикишидаги сигнал спектрини куриб чикамиз. 
0 Ω ωt
Маъруза-16 ЧАСТОТА МОДУЛЯЦИЯСИ
Частота модуляцияси деб, юкори частотали гармоник тебранишнинг частотасини паст частотали бошланºич сигналнинг узгариш конунига мос равишда узгаришига айтилади.
Юкори частотали тебраниш берилган булсин. uг к U cos (ω0t К φ0) (1)
Бу тебранишнинг оний ёки тулик фазаси Ψ(t) к ω0t К φ0 (2)
у холда uг к U cos Ψ(t) (3)
Частота модуляциясида Ψ(t) - оний ёки тулик фазани узгариши ундаги частотани ПЧ S(t) - сигнални узгариш конунига мос равишда узгаришига боºлик булади. ω к ω0 К KS(t) (4)
Агар S(t)- гармоник тебраниш S(t) к UΩ cosΩt (5)
у холда ω к ω0 К K UΩ cosΩt (6)
Частотани максимал узгаришига частота девиацияси дейилади. Δ ω к K UΩ
ω к ω0 К Δ ω cosΩt (7)
Маълумки частота фазани узгариш тезлигидир. Шунинг учун фазани топиш учун (7) формуладан интеграл оламиз.
Ψ(t) к∫ ωdt к ω0 t К Δ ω/Ω sinΩtКφ0 (8)
φ0 к 0 тенг деб олсак u к U cos (ω0 t К Δ ω/Ω sinΩt) (9)
M к Δ ω/Ω; uчм к U cos (ω0 t К Mч sinΩt) (10)
ЧМ сигнални вакт диаграммасини куриб чикайлик.
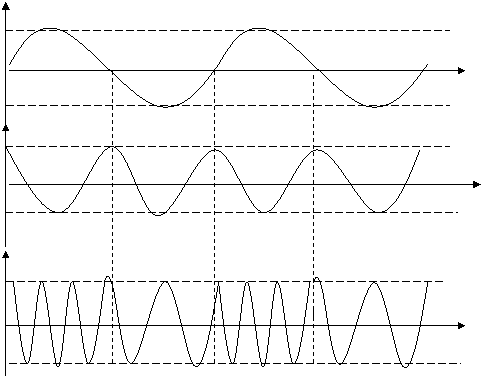
UΩcosΩt
t
Uωcosωt
t
Uчм
t
Гармоник ЧМ сигнални спектрини аниклаймиз.
uчм к U cos (ω0 t К Mч sinΩt)к |cos (λ К β) к cos λ cos β – sin λ sin β| к U cos (Mч sinΩt) * cos ω0 t – U sin (Mч sinΩt) * sin ω0 t (11)
Mч<<1 булсин,у холда
cos (Mч sinΩt) ≈ 1
(12)
sin (Mч sinΩt) ≈ Mч sinΩt
uчм к U cos ω0 t - UMч sinΩt * sin ω0 t к U cos ω0 t – Mч/2 U cos (ω0 - Ω)t К Mч/2 U cos (ω0 К Ω)t (13)
(13) ифодадан куриниб турибдики ЧМ сигнални спектри АМ сигнални спектрига ухшаб кетади. ЧМ даги паст ён томон частотасини фазаси 1800 булишида
 U0
U0
![]()
ω0 - Ω ω
ω0 ω0 К Ω
-![]()
Кенг спектрли ЧМ да (12) ифода хакли эмасдир.
Бессель функциялари назариясида бу функциялар Фурье каторига ёйилиши исбот килинган.
cos (Mч sinΩt) к I0 (Mч) К 2I2 (Mч) * cos 2Ωt К 2 I4 (Mч) * cos 4Ωt ….. sin (Mч sinΩt) к 2I1 (Mч) sinΩt К 2I3 (Mч) sin3Ωt К2I5 (Mч) sin5Ωt К …… (14)
n-чи даражали Бессель функцияси:
uчм к U [I0 (Mч) cos ω0 t К I1 cos (ω0 К Ω)t - I1 (Mч) cos (ω0 - Ω)t К I2 (Mч) cos (ω0 К 2Ω)t К I2 (Mч) cos (ω0 - 2Ω)t К I3 (Mч) cos (ω0 К3Ω)t – I3 (Mч) cos (ω0 - 3Ω)t К К……….…] (15)
Бу ифодадан куриниб турибдики гармоник ЧМ сигналнинг спектри дискрет, ω0 - частоттага нисбатан симметрик ва чексизта ω0 К nΩ ён томон частоталаридан иборат.
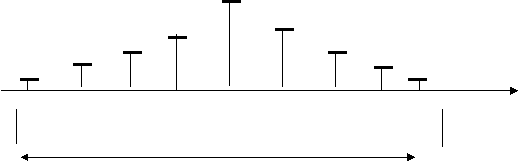 |
ω
Δчм
Δчмк2 Δ ωк2М Ω
Маъруза-17 ЧМ СИГНАЛЛАРНИ ХОСИЛ
КИЛИШ.
Юкори частотали uг к Ucos (ω0 tКφ0) гармоник тебранишни ишлаб чикувчи автогенератор берилган булсин.
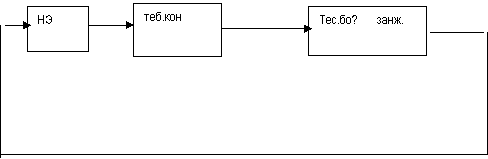
![]()
Маълумки тебраниш контуридаги Lkкconst ва Ckкcosnt булса автогенератор ишлаб чикарилган тебраниш частотаси хам ω0 к const узгармас булади.
Резонанс частотаси ω0к
ωрк
Автогенератор ишлаб чикарувчи тебранишларни частотасини узгартириш учун Lk ёки Ck ни узгартириш лозим.
Агар Lkкƒ1(UΩ) ва Ckк ƒ2(UΩ) булса, яъни тебраниш контуридаги индуктивлик ёки сиºимни параметрлари паст частотали бирламчи сигнални узгариш конуни буйича узгарса автогенератор ишлаб чикарувчи тебранишнинг частотаси хам шу конун буйича узгаради: ωк φ(UΩ)
Шундай килиб бу усул ёрдамида частота буйича модуляцияланган сигналларни хосил килиш мумкин.
Частота модуляторлари автогенераторлар асосида курилиб ЮЧ тебранишни частотасини ПЧС узгариш конунига мос равишда узгартириш учун уларни тебраниш контурларига паралелл равишда бошкарувчи реактив элементлар уланади.
ВАРИКАПЛИ ЧМ МОДУЛЯТОРИ.
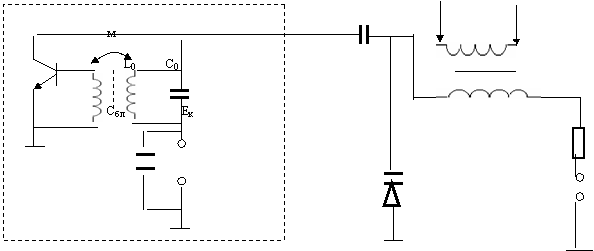 |
Ср uΩ(t)
Rдоб
B
Ес
Варикап – ярим утказгичли диод булиб унинг р-n утишни барьер сиºимини киймати унга берилган тескари кучланишни кийматига боºлик булади.
Агар ПЧ бирламчи сигналимиз соs конуни буйича узгарса варикапни сиºми хам соs конуни буйича узгариб транзисторни коллектор занжиридаги умумий сиºимни хам соs конуни буйича узгаришига олиб келади.
Натижада автогенератор частотаси соs конуни буйича узгарувчи тебранишларни ишлаб чикаради,яъни ЧМ модуляция хосил булади.
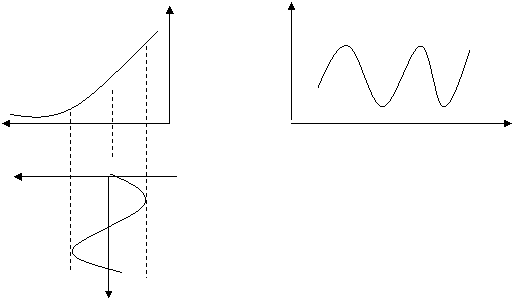 |
C C(t)
-u t
u
t
C(t)к
CgК∆ C(t); C∑(t)кC0К ∆C(t); 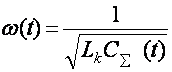
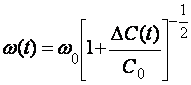 ;
;
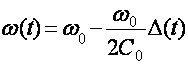
Маъруза-18 ФАЗА МОДУЛЯЦИЯСИ.
Фаза модуляцияси деб, юкори частотали ташувчи тебранишнинг фазасини паст частотали бирламчи сигналнинг узгариш конунига мос равишда узгаришига айтилади.
ФМ сигналнинг ифодасини умумий куринишда куйидагича ёзиш мумкин.
uк Ucos (ω0tКφ(t)) бу ерда φ(t) кφ0КKS(t)
ПЧС бирпамчи сигнал сифатида гармоник сигнал берилган булсин.
![]() S(t)к
UΩSinΩt у
холда φ(t) кφ0КK UΩSinΩt
S(t)к
UΩSinΩt у
холда φ(t) кφ0КK UΩSinΩt
Δ φк K UΩ- фаза девиацияси. Мфкк K UΩ-модуляция индекси.
Агар φ0к0 булса φ(t) к МфSinΩt uфмк Ucos (ω0tК МфSinΩt)
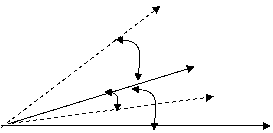
ФМ сигналнинг вектр диаграммаси куйидаги куринишда булади.
 U'
U'
Δ φmax
U0
U'
φ0 Δ φ
ω0
ФМ сигнал учун оний частота ωкdψ(t)/ dt
ψ(t) к ω0tК МфSinΩt ωкω0-МфSinΩt ΔωкМΩ-ФМ учун частота девиацияси.
Гармоник бошкарувчи сигнал учун ФМ ва ЧМ сигнални ифодалари бир-бирига ухшаб кетади.Лекин уларни табиати хар хил бу фарк бирламчи сигнал мураккаб булганда куринади.
М ва ЧМ сигналларни спектрлари буйича таккослаб курайлик.ЧМ сигналлар учун модуляция индекси бирламчи сигналнинг хам амплитудасига хам частотасига боºлик.
Mч к Δω/Ω к КUΩ/Ω
ФМ сигналларда эса модуляция индекси факат бирламчи сигнални амплитудасига боºликдир. Mф к КUΩ
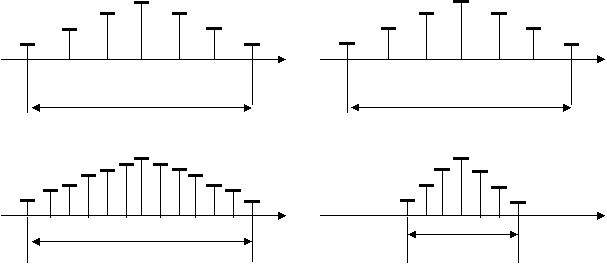
Модуляция индексини киймати эса уз навбатида ФМ ва ЧМ сигнал-ларини спектр кенглигига таъсир килади.
ω0 к ω0фм к ω0 Ωчм к Ωфм к Ω Мф к Мч Δωчм к Δωфм
ω0 ω0
Δчмк2 Δω Δфмк2Δω
Δчмк2 Δω ΔфмкΔω/2
Маъруза-19 ФМ СИГНАЛЛАРНИ ˉОСИЛ КИЛИШ.
ФМ сигналлрни хосил килиш учун купайтиргич схемасидан фойдаланилади.Купайтиргичнинг параллел тебраниш контурига параллел равишда реактив бошкарувчи каршилик уланади.Бу каршиликни киймати бирламчи паст частотали сигналнинг узгаришига пропорционал узгаради.
Коллектор токининг биринчи гармоникаси iк1 ва кириш кучланишлари синфаздирлар.Паст частотали сигналга мос равишда бошкарувчи реактив элемент ёрдамида контурнинг резонанс частотасини узгариши контурдаги кучланишни фазасини хам амплитудасини узгаришига олиб келади. Уларнинг кийматлари берилган iк1 коллектор токини кийматида частота ва фаза характеристикалари ёрдамида аникланади.Стационар режимда тебраниш контурини хар кандай созлаганда хам бу контурдаги табранишларнинг частотаси кириш тебранишини ω0 частотасига тенг булади.
 Cp
Cp
ik1
Xy(t)
Uкир Ck Lk
Уч хил частота учун контурнинг частота ва фаза характеристикаларини куриб чикайлик.
Z, φ
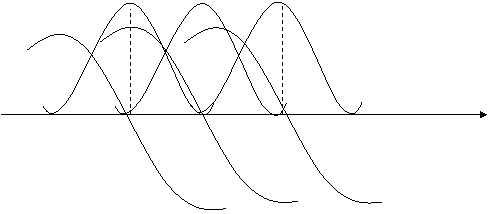 |
Z1 Z2 Z3
ω φ1 φ2 φ3
Шу уч хол учун вектор диаграммаларини куриб чикайлик.
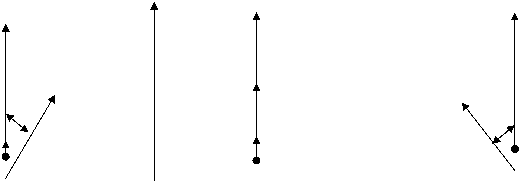 |
Ik1 Uk Ik1
Uk Ik1 Uk
φ1 φ2
Uкир Uкир
Агар контурни резонанс частотаси модуляцияловчи паст частотали сигнал таъсирида секин ω0 , дан ω02 га узгарганда контурдаги чикиш кучланишни фазаси хам φ1 ва φ2 орасида узгаради яъни фаза модуляцияси амалга оширилади.Бундан ташкари бу схемада паразит АМ модуляция хам хосил булади.Бу усул билан модуляция индекси кичик 2О0 – 3О0 булганда ишлатилади.
ФМ сигналларни хосил килиш учун АМ сигнални ФМ сигналга айлантириш усулини хам ишлатиш мумкин.
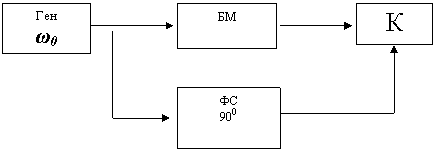 |
ФС – фаза сургичда фаза сурилмаганда ташувчиси мавжуд булган АМ сигнални хосил килинади.
Uам

Uю Uпч
Ташувчиси 9О0 сурилгандан кейин эса куйидаги ФМ сигнални хосил киламиз.
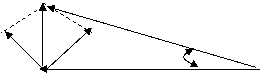 Uам
Uам
U
Uю Uпч φ
Бу схемада хам паразит АМ сигнални хосил килмаслик учун модуляция индекси кичик булиши лозим.
Частота модулятори ёрдамида хам ФМ хосил килиш мумкин.Бирламчи ПЧС булиши у холда ФМ сигнал ифодаси: uфмкU Cos (ω0КKS(t))
Бирламчи сигнал y(t) булганда ЧМ сигнал ифодаси uчмкU Cos (ω0tКK ∫ y(t)dt
Маълумки частота фазани узгариш тезлигидир.Демак агар S(t) дан хосила олсак
y(t)кdS(t)/dt
ва y(t) ни бошкарувчи сигнал сифатида ЧМ модуляторга берсак у холда S(t) сигналга нисбатан биз ФМ сигнални хосил киламиз. Бу усул билан катта модуляция индекси ФМ сигналларни хосил килиш мумкин.
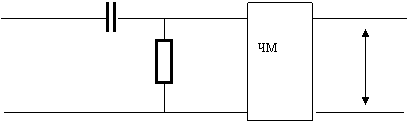 С
С
S(t) R Uфм
Маъруза-20 ЧМ СИГНАЛЛАРНИ ДЕТЕКТОРЛАШ.
ЧМ сигналларни туºридан туºри детекторлаб булмайди.ЧМ сигоналларни детекторлаш учун уларни бошка турдаги модуляцияланган сигналларга айлантирилиб керакли булган детектор ёрдамида детекторланади.ЧМ сигналларни бундай детекторлашни уч хил тури мавжуд..
1) ЧМ сигналлар АМ сигналларга айлантирилиб амплитуда детектори ёрдамида детекторланади.
2) ЧМ сигналлар импульсли модуляцияланган сигналларга айлантирилиб импульсли детекторлар ёрдамида детекторланади.
3) ЧМ сигналлар ФМ сигналларга айлантирилиб фаза детектори ёрдамида детекторланади.
Амалиётда 1 чи усул энг куп кулланилади.ЧМ сигналларни АМ сигналларга айлантириш учун созланмаган контурлардан фойдаланилади.1 та созланмаган контурли ЧМ детектор схемасини куриб чикайлик.
D
 |
Ck Lk Cн Rн UΩ
Агар тебраниш контурининг резонанс частотаси юкори частотали ташувчи тебраниншнинг частотасига тенг булмаса бундай контур созланмаган контур дейилади.
Контурда iчм токи окиб утиши контурнинг эквивалент Zэ каршилиги хар хил частоталар учун хар хил кийматга эга. Шунинг учун контурга келаётган тебраниншнинг частотаси узгариши билан контурдаги Uk кучланишнинг киймати хам узгаради. Uk(ω)кI* Zэ(ω)
Kонтур ёрдамида ЧМ сигнални АМ сигналга айланиши жараёнини куриб чикайлик.
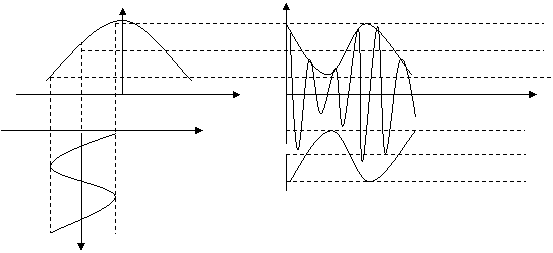 Zэ
Uk
Zэ
Uk
ω t
ωp ω(t)
t
ЧМ сигнални частотаси cos конуни буйича узгарсин. ω(t)кω0КΔωCosΩt
Uk(ω) ни характеристикасини чизикли участкаси куйидаги ифода ёрдамида берилган булсин.
Uk(ω)кU0Кk ω(t); mкKΔω/U0КKω0; Ukк uчик кu1-u2
Контур чикишида хосил булган хам амплитуда хам частота буйича модуляцияланагн сигнални детекторлаш учун оддий чизикни амплитуда детектори ишлатилади.
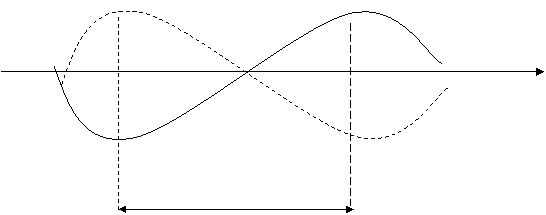
Бу схеманинг асосий камчилиги частота характеристикасини ночизиклиги булиб у бирламчи сигнални бузилишига олиб келади.Шунинг учун бу схема частота девиацияси кичик булган ЧМ сигналларни детекторлашда ишлатилади.Частота девиацияси катта булган ЧМ сигналларни детекторлаш учун 2 та созланмаган контурли ЧМ детекторлар ишлатилади.
 |
D1
L1 C1 Cн1 Rн1
L2 C2 Cн2 Rн2
D2
uчик кu1-u2; ω0к ωр1К ωр2/2
![]() Zэ(ω)
Zэ(ω)
ω
2Δω
Маъруза-21 ФМ СИГНАЛЛАРНИ ДЕТЕКТОРЛАШ.
Фаза детекторларини чикишидаги узгармас кучланиш унинг киришидаги бир хил частотали тебранишларнинг фазалари фаркига боºлик булиши керак.Бундай детекторга мисол булиб иккита киришли оддий диодли детектор мисол була олади.
 D
D
U2 Rн Cн
U1
Бундай детекторнинг киришига бир вактнинг узида u2кU2cos(ω0tКφ) детекторланувчи кучланиши ва u1 к U1cos ω0t - этолонли кучланиш берилади. У холда кириш кучланиши uкир кu1Кu2 Кириш кучланишининг вектор диаграммасини куриб чикайлик.
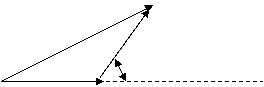 Uкир
Uкир
U2
U1
Вектор диаграммаларидан куриниб турибдики, кириш кучланишинг амплитудаси куйидаги ифода ёрдамида аникланади:
![]()
Чизикли детектор чикишидаги кучланиш ифодаси куйидаги куринишда булади:
UчиккK![]()
К – φ фазага боºлик булган детекторнинг узатиш коэффициенти .
ФМ тебранишини яъни U2 кучланишнинг фазаси секин узгарганда детектор чикишидаги кучланишнинг амплитудаси хам узгаради.
Фаза детекторини детекторлаш характеристикаси бу унинг чикишидаги кучланишнинг амплитудаси детекторланувчи тебранишнинг фазасига боºлик характеристикасидир. Uчиккƒ(φ)
Юкоридаги схема учун детекторлаш характеристикаси ночизикли булганлиги учун бундай схема катта ночизикли бузилишларни вужудга келади.Шунинг учун амалиётда икки тактли балансли фаза детектори ишлатилади.
D1
 |
![]()
R C
R C
D2
Диодлардаги кучланишларни комплекс амплитудалари
![]()
![]() Úд1к
Ú1К Ú2/2
Úд1к
Ú1К Ú2/2
(3) Úд2к Ú1 - Ú2/2
Бу кучланишлар учун вектор диаграмма:
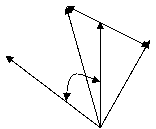 ½Ú1
½Ú1
- ½ Ú1
Úд2 Ú1
φ
Ú2 Úд2
Хар бир детектор чикишидаги кучланишлар
Uчик1кK![]()
Uчик2кK![]()
Умумий чикиш кучланиши Uчикк Uчик1- Uчик2кK(Uд1- Uд2)
Бундай балансли детектор учун детекторлаш характеристикаси куйидаги куринишга эга:
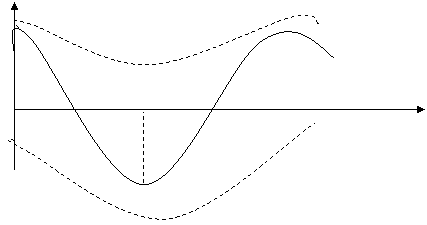 Uчик
Uчик
φ
900 1800 2700
φ к 900 ва 2700 атрофида детекторлаш характеристикаси чизикли куринишга эга.Шунинг учун бу участкаларда бузилмаган детекторлашнинг амалга ошириш мумкин.
Маъруза-22 ДИСКРЕТ МОДУЛЯЦИЯ ТУРЛАРИ
Агар бирламчи сигналлар дискрет кийматларга эга булса (м-н: телеграф сигнали), у холда гармоник юкори частотали тебранишлар модуляция килинганда уларнинг параметрлари (амплитудаси, частотаси ёки фазаси) сакраб узгаради. Бундай сигналларга дискрет модуляцияланган яъни монипуляцияланган сигналлар дейилади. Дискрет модуляциянинг куйидаги турлари мавжуд:
1) АМ, 2) ЧМ, 3) ФМ, 4) НФМ (ОФМ)
 |
1
-1
Uам
t
Uчм
t
Uфм
t
Uнфм
t
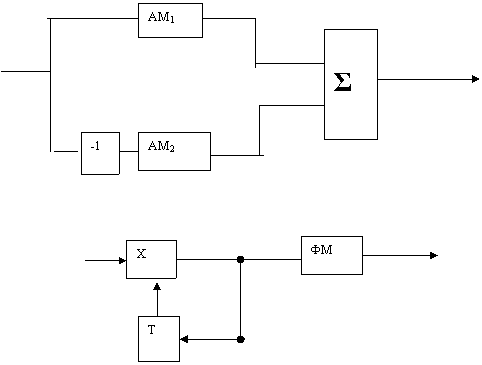 |
X(t)
Sчм
Sфм(t) кSам1(t)КSам2(t)
 Хк(t) Sофм
Хк(t) Sофм
Yk(t) к -Y k-1(t)*Xk(t)
Маъруза-23 ДИСКРЕТ МОДУЛЯЦИЯЛАНГАН СИГНАЛЛАРНИ
СПЕКТРИ
Дискрет модуляцияланган сигналлар учун модуляцияловчи бошкарувчи сигнал сифатида куйидаги х (t) сигнал берилган булсин.
![]() 1,0<t<T/2
1,0<t<T/2
x(t) к -1, -T/2<t,0
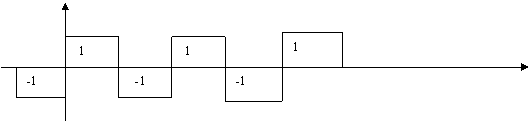 |
Бу
бошкарувчи сигнални спектрини аниклаймиз: 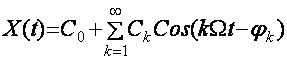
х (t)- функция ток функция булганлиги учун 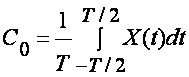
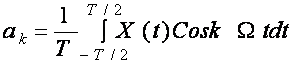
Шундай килиб бу сигнал факат синус гармоникалардан иборат.
![]() ; Ckк
bkк 2/кπ[1-CosKπ]
; Ckк
bkк 2/кπ[1-CosKπ]
Sам(t) к 0.5Sinω0tК
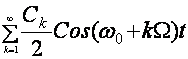
Sфм (t) к К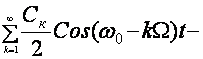
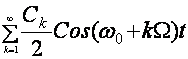
Маълумки НФМ учун нисбийлик киритувчи курилма чикишидаги сигналнинг частотаси Ω2 к Ω1/2 (олдинги утилган маъруза каралсин)
Шунинг учун НФМ сигналнинг спектри ФМ сигнални спектрига ухшаш булади.Лекин Ω2 Ω1 га нисбатан 2 марта кичик булганлиги учун НФМ спектр кенглиги ФМ га караганда 2 баробар тор булади.
Маъруза- 24.
4- булим. УЗЛУКСИЗ СИГНАЛЛАРНИ РАКАМЛИ УЗАТИШ НАЗАРИЯСИ. УЗЛУКСИЗ СИГНАЛЛАРНИ ДИСКРЕТЛАШ.
КОТЕЛЬНИКОВ ТЕОРЕМАСИ.
Узлуксиз сигнал берилган улсин
 U
U
t
Умумий холда узлуксиз сигналлар вактнинг хар бир моментида узлуксиз узатилади.
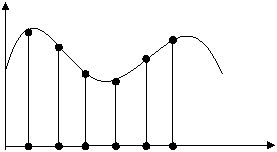
Хар кандай S(t) узлуксиз сигнални Т интервалдан аник кабул килиш (тиклаш) учун, унинг Т интервалдаги хамма вакт нукталаридаги оний кийматларини билиш лозимдир.Лекин маълум шартлар бажарилганда узлуксиз сигнални Δt ораликда олинган оний кийматлари туплами бу узлуксиз сигнални тулик ифодалаши мумкин.
 S(t)
S(t)
t
Маълум шартлар бажарилиб КΔt вакт моментларида олинган сигналнинг оний кийматларида вакт буйича дискретланган сигнал дейилади.Бундай дискретланган сигналлардан узлуксиз сигналларни кайта тиклаш мумкин.
Бу оний кийматлар узлуксиз сигнални керакли аниклик билан ифодалаши (характерлаши) учун бу сигналнинг оний кийматлари тенг Δt ораликларида керакли частота (тезлик) билан олиниши лозим.
Δt оралик кандай олиниши керак деган саволга Котельников теоремаси жавоб беради.
Котельников теоремаси:
Спектри чегараланган (Fm, Fmax) кандай узлуксиз сигналларни уларнинг S(КΔt) санокли оний кийматлари оркали тулик кайта тиклаш мумкин,агар Δt дискретлаш интервали куйидагича аникланса (олинса): Δ t ≤ 1/2Fm
Fm - узлуксиз сигнал спектрининг энг юкори частотаси.
ƒД к 1/Δt к 2 Fm - дискретлаш частотаси.
Бу теорема асосида узлуксиз сигналларни Котельников катори куринишда ифодалаш мумкин:
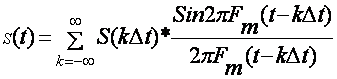
S (КΔ t) –Котельников катори коэффициентлари ёки КΔt вакт нукталаридаги узлуксиз сигналнинг оний кийматлари.
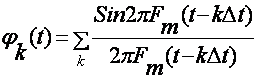
![]() Котельников каторининг
базис функциялари
Котельников каторининг
базис функциялари
агар tкk Δt булса φk(kΔt)
tкn Δt булиб n≠k булса φk (kΔt)к0
 φк
(t)
φк
(t)
1
t
Δ t
φк(t) – функциялар бир-бирига нисбатан Δ t ораликка сурилган.
Узлуксиз сигнални Котельников катори билан ифодалаб курайлик.
S(t)
 |
![]() t
t
Sд(t)
t
S(t)
![]() t
t
Вакт буйича дискретланган сигналларни хосил килиш учун электрон калитдан фойдаланилади:
бошкарувчи импульсларнинг кайтарилиш даври ƒД к 2 Fm
Вакт буйича дискретланган сигналларнинг спектри.
ЭК ни бошкарувчи импульслар кетма-кетлигини дельта
импульслар кетма-кетлиги деб караш мумкин. y(t)к![]() δ(t-kΔt)
δ(t-kΔt)
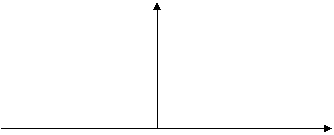
Дельта импульс деб амплитудаси чексизга интилган импульс кенглиги 0 га интилган, юзаси эса 1 га тенг математик импульс га айтилади.
![]()
∞, tк t0 δ(t)
δ(t0) к
0, t≠ t0
t0 t
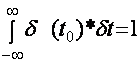 ;
; 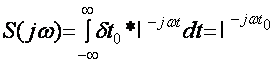
S(jω) кS(ω)*ejφω
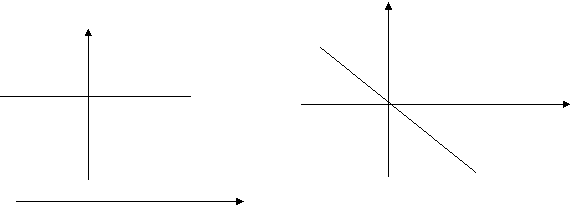 |
S(ω)
1
ω
ω
Sq(t) кS(t)* y(t)кS(t)*![]() δ(t-kΔt)
δ(t-kΔt)
Узлуксиз S(t) сигнални Sq(јω)спектр зичлиги маълум булсин.
Вакт буйича дискретланган спектр зичлиги куйидаги Фурье
алмаштириш ёрдамида топилади. 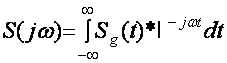
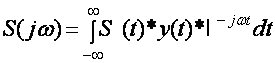 ;
; 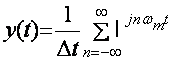
 ;
; 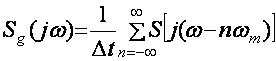
Бу формуладан куриниб турибдики Sq(јω) вакт буйича дискретланган сигналнинг спектри узлуксиз сигналнинг спектрининг чексизта копияларини йиºиндисидан иборат экан.Бу копиялар частота уки буйича бир – биридан бир хил 2 ωм ораликка сурилган.
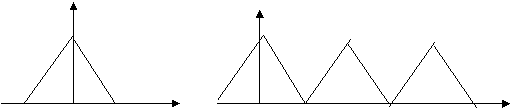 |
Sq(јω) Sq(јω)
ω ω
Маъруза -25. ВАКТ БУЙИЧА ДИСКРЕТЛАНГАН СИГНАЛЛАРДАН УЗЛУКСИЗ СИГНАЛЛАРНИ ТИКЛАШ.
Узлуксиз сигналларни вакт бйича дискретланган сигналлардан кайта тиклаш учун уларни идеал ПЧФ дан утказиш керак.
Идеал ПЧФ узатиш коэффициенти ёки АЧХ си:
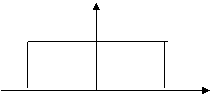 K(jω)
K(jω)
![]() K0,
-ωm < ω< ωm
K0,
-ωm < ω< ωm
K(jω)к
0, ω< ωm ; ω> ωm
ω
РТК импульс характеристикаси деб – унинг киришига дельта импульс берилганда унинг чикишидаги хосил булган жавоб сигналига айтилади.
 |
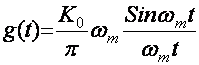 ;
; 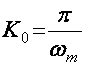 ;
;
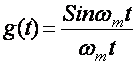
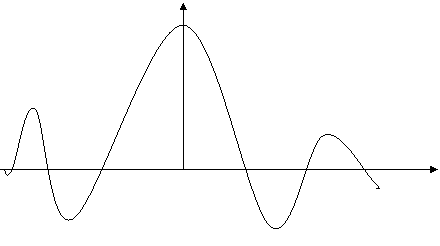 g(t)
g(t)
t
ПЧФ чикишидаги сигнални топиш учун Дюамель интегралидан фойдаланамиз.:
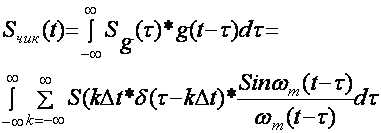
Дельта импульсни фильтрлаш хоссасига асосланиб
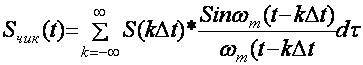
Охирги формуладан куриниб турибдики идеал ПЧФ ёрдамида вакт буйича дискретланган сигналлардан узлуксиз сигналларнитиклаш мумкин экан.
Котельников теоремасининг ахамияти:
1) Сигнал / шовкин нисбати оширилади.
2) Берилган Т вакт оралигида сигналнинг хамма кийматлари узатилмаганлиги сабабли узлуксиз сигналнинг оний кийматлари орасида бошка сигналларнинг оний кийматларини узатиш мумкин. Бу холда сигнални вакт буйича ажратиш асосида куп каналли алокани хосил килиш мумкин.
3) Модуляциянинг импульсли турларидан фойдаланиш мумкин.
4) Узлуксиз сигналларни ракамли холда узатиш мумкин.
Маъруза-26 5-булим УЗЛУКСИЗ СИГНАЛЛАРНИ РАКАМЛИ
ХОЛДА УЗАТИШ.
Узлуксиз сигналларни узатиш учун дискрет алока каналларидан фойдаланиш мумкин. Бунинг учун узлуксиз сигналларни ракамли сигналга айлантириш лозим.
Ракамли модуляциянинг куйидаги турлари мавжуд:
1) Импульс кодли модуляция-ИКМ.
2) Дельта модуляция – ДМ
3) Дифференциал импульс кодли модуляция – ДИКМ.
4) Адаптив дельта модуляция – АДМ.
Ракамли узатиш методлари узлуксиз узатиш методларига караганда куйидаги афзалликларгага.
1) Ракамли узатиш методларида узлуксиз узатиш методларига караганда хабарларни узатиш аниклиги юкоридир,
2) Ракамли узатиш сифати алока линиясини узунлигига боºлик эмасдир, чунки шовкинлар алока линияси буйлаб тупланмайди.
3) Хамма турдаги информация сигналлари – телефон, ахборот узатиш, телевизион, видиотелефон сигналлари бир хил ракамли формага эга, шунинг учун бу сигналларни узатишда умумий узатиш ва коммутация килиш воситалари ишлатилади. Бу эса алока тармокларини иктисодий самарадорлигини оширади.
4) Ракамли техника ва хисоблаш техникаси элементлари кенг кулланилади.
5) Ретрпанслция вактида сигналларни формасини регенерация (тиклаш) мумкин.
ИМПУЛЬС КОДЛИ МОДУЛЯЦИЯ
ИКМ узатиш системасини структуравий схемаси.
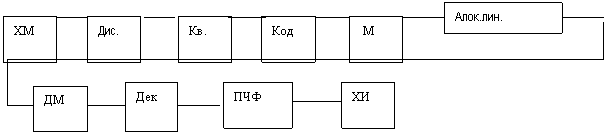
ИКМ сигнални хосил килиш учун узлуксиз сигналлар устида учта амал бажарилади.
1) Вакт буйича дискретлаш.
2) Квантлаш.
3) Кодлаш.
ИКМ сигнални хосил килиш учун дискретизатор, кодер, квантловчи курилма керак булади. Хабар манбаидан келувчи узлуксиз сигнал дискретизаторга берилади.Котельников теоремасига асосланиб узлуксиз сигналдан хар ∆t ораликда унинг S(∆t) оний кийматлари, яъни узлуксиз сигнал вакт буйича дискретланади.Квантловчи курилмада вакт буйича дискретланган сигналнинг оний кийматлари дискрет кийматлар сатхлар билан алмаштирилади.Кодерда сигнанинг хар бир квантланган сатхи икки асосли код билан кодланади. Шундай килиб кодер кишида ИКМ сигнал хосил булади.
ИКМ сигналнинг вакт диаграммасини куриб чикайлик.
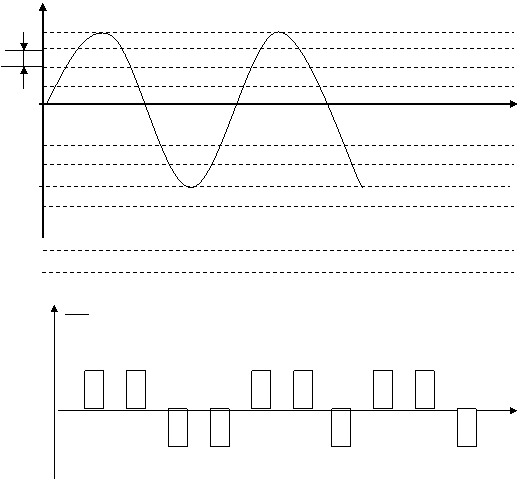 |
Δb
0 t
b(t)
t
Квантлаш хатолигини аниклаш учун ночизикли квантлаш кулланилади. Бу холда катта амплитудали сигнал катта кадам билан кичик амплитудали сигналлар кичик кадам билан квантланади.
Ночизикли квантлаш курилмасининг характеристикаси.
 Uчик
Uчик
Uкир
Ночизикли квантлашнинг энг куп таркалган тури, бу сигнани компандерлаб квантлашдир.
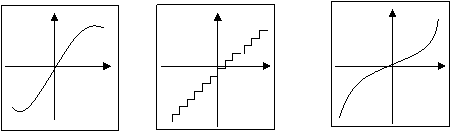 |
Бу усулда компрессор ёрдамида сигналнинг динамик диапозони сикилади кейин бу сигнал чизикли квантланади, кабул килишдан олдин эса экспондер ёрдамида сигналнинг динамик диапозони олдинги холатга кайтарилади.
ДЕЛЬТА МОДУЛЯЦИЯ
Дельта модуляция алока системасининг структура схемаси куйидаги куринишга эга.
 |
Айирувчи курилма киришига к∆t вакт моментида келган S(∆t) оний кийматдан Sкв(∆t)((к-1)(∆t)) олдинги квантланган оний киймати айрилиб
e(t)к S(к∆t) - Sкв((к-1)(∆t))
хатолик фарк сигналини хосил килинади.
Бу фарк сигналини ишораси квантловчи курилмада – 1 ки К1 билан квантланиб (кодланади) дельта модуляцияланган сигнал хосил килиниб алока чизиºига узатилади.
К1, e(t)>0
γ(k)к
-1, e(t)<0
Айирувчи курилмага берилган Sкв((к-1)(∆t)) сигнални хосил килиш учун интегратор ишлатилади. Итеграторнинг киришига келган хар хил ишорали ±1 импульслар арифметик кушилиб зинапояли куринишдаги Sкв сигнал хосил килинади.
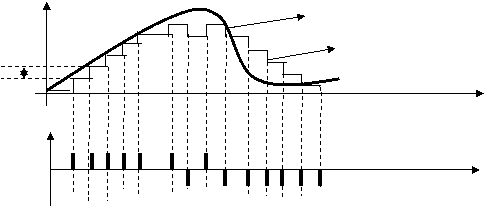 |
S
S(t)
Sкв(k)
t
j(k)
t
Кабул килиш томонидаги интегратор хам зинапояли Sкв(к∆t) квантланган сигнални хосил килади.Бу сигнал эса ПЧФ ёрдамида узлуксиз S(t) сигналга тикланади.Тикланган S(t) узатилган S(t) сигналга купрок ухшашлиги учун дискретлаш частотасини ошириш ва ∆t кадамини камайтириш лозим.Квантлаш кадамини камайтириш худди шунча марта дискретлаш частотасини купайтиришга олиб келади. Булмаса узатилган ва кабул килинган сигналлар ухшамайди. Лекин квантлаш кадамини жуда хам кичик килиб танлаб булмайди. Бу холда киялик хатолиги хосил булади.
Шунинг учун дельта модуляция дискретлаш частотасини fg Котельников теоремаси асосида эмас, балки тикланган сигналнинг берилган амплитуда тиклаш шарти асосидаолинади, яъни fgк20Fm
Аммо узатиш тезлиги ИКМ ва ДМ сигналларда тахминан бир хил чунки ДМ да бир разрядли код ИКМ да эса n разрядли код ишлатилади.
Uикм к n fgк n*2Fmк16* Fm; UДмк20Fm
Агар ИКМ ва ДМ сигналларни таккосласак куйидаги фарклар келиб чикади:
1) Сигнални квантлаш хатолиги нисбатини узатиш тезлигига боºлик характеристикаси буйича ИКМ ДМ дан афзалрокдир.
2) Алока чизиºида шовкиларга нисбатан ДМ ИКМ га нисбатан шовкин бардошлидир.
3) ИКМ учун такт ва цикл буйича синхранизация ДМ учун факат такт буйича синхронизация амалга оширилади.
4) Якка канал учун ДМ ни хосил килиш курилмаси ИКМ никига караганда оддийрокдир. Лекин куп каналли алока системаларида дельта модуляциясини ИКМ га нисбатан мураккаб булиши мумкин.
5) ИКМ сигналларга караганда ёлºон импульслар шовкиннинг таъсири ДМ сигналлар учун зарари камрок.
АДАБИЁТЛАР
1. Зюко А.Г., Коржик К.И., Назаров М.В., Кловский Д.Д. Теория электрической связи. М.: Радио и связь, 1998.
2. Баскаков С.И. Радиотехнические цепи и сигналы М.: Высшая школа, 1998 или 1983.
3. Гоноровский И.С. Радиотехнические цепи и сигналы М.: Радио и связь,1986.
4. Андреев В.А. Теория нелинейных электрических цепей М.: Радио и связь,1982.
5. Кушнир В.Ф., Ферсман Б.А. Теория нелинейных электрических цепей М.: Связь, 1974.
6. Баскаков С.И. Радиотехнические цепи и сигналы М.: Высшая школа, 1987.
7. Кловский Д.Д., Шилкин В.А. Теория передачи сигналов в задачах М.: Связь, 1978.
8. Статистическая радиотехника, примеры и задачи (под редакцией В.И. Тихонова)- М.: Советское радио,1981.
9. Заездный А.М. Основы расчетов по статистической радиотехники М.: Связь, 1969.