УЗБЕКСКОЕ АГЕНТСТВО СВЯЗИ И ИНФОРМАТИЗАЦИИ

ТАШКЕНТСКИЙ УНИВЕРСИТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ

Кафедра Теория

передачи сигналов

ПРОЕКТИРОВАНИЕ, ТЕХНОЛОГИЯ РАДИОЭЛЕКТРОННЫХ СРЕДСТВ

КОНСПЕКТ ЛЕКЦИЙ

Ташкент. 2003

ПРЕДИСЛОВИЕ

Дисциплина "ПРОЕКТИРОВАНИЕ, ТЕХНОЛОГИЯ РАДИОЭЛЕКТРОННЫХ СРЕДСТВ" – одна из дисциплин для подготовки бакалавра в области разработки и исследования РЭС различного назначения. Основная задача дисциплины: на базе знаний и умений, полученных в предшествующих и смежных курсах, вооружить бакалавра современными методами разработки, проектирования и технологии устройств электронной техники; научить по заданным тактико-техническим характеристикам системы рационально выбрать принцип и структуру построения системы, технические параметры и структуру входящих в систему устройств, произвести оценку выбранных технических решений. Изучение дисциплины должно привить студентам системный подход к проектированию радиоэлектронных устройств, входящих в состав систем.

         В результате изучения дисциплины студенты должны:

- знать основные понятия о сигналах, характеристики и модели сигналов и помех;

- знать критерии оптимальности обнаружения, принцип работы цифровых обнаружителей и различителей сигналов; различение детерминированных сигналов на фоне белого гауссовского шума;

- уметь оценить неизвестные параметры сигнала с помощью различных методов; иметь понятие об аномальных ошибках измерения и о фильтрации меняющихся параметров сигналов;

- иметь представление об основах построения радиолокационных систем; методы и устройства измерения дальности; методы и устройства измерения угловых координат;

- знать основы теории передачи информации; основные задачи теории информации; пропускную способность дискретных и непрерывных каналов;

- уметь применять теорему кодирования для канала с помехами; знать принципы построения корректирующих кодов, их классификацию, основные характеристики и корректирующие свойства.

Лекция 1. Введение

Проектирование сложных систем вызвало развитие теоретических дисциплин: теория систем, теория больших систем, системный анализ, теория радиосистем. Развиваются инженерные методики расчета и анализа отдельных звеньев радиотехнического тракта. Теория радиосистем опирается на теорию сигналов и цепей, теорию информации, теорию автоматического регулирования, теорию решений.

         В системе важную роль играет структура, обеспечивающая связь и совместное функционирование элементов структуры. При создании системы возникают проблемы постановки технической задачи и выбора теоретического аппарата исследования системы.

         Для выработки общих подходов и методов решения задач проектирования, для упорядочивания создания и исследования радиосистем они классифицируются по некоторым признакам. Часто используется классификация по назначению: связные, командные, телеметрические, радиолокационные, траекторные, системы радиоуправления и др.

Независимо от назначения систем часть проблем общая. Большинство радиотехнических систем предназначено для установления информационной связи наблюдателя с наблюдаемым объектом. Сообщения, в которые облекается информация, отображаются сигналами – физическими процессами. Помехи – мешающие физические процессы.

         При проектировании радиосистем широко используется классификация информационных радиосистем, которая разбивает их на три класса.

         Первый класс – радиосистемы передачи информации. Подлежащие передаче сообщения поступают от внешних источников и радиосистемы этого класса передают их получателю. Радиосистемы этого класса преобразуют сообщения в сигналы, которые могут распространяться в заданных линиях связи. На выходе линии связи сигналы преобразуются к виду, удобному для восприятия наблюдателем. К этому классу относятся связные, командные, телеметрические, вещательные, телевизионные и фототелеграфные радиосистемы.

Второй класс – радиосистемы извлечения информации. Сообщения здесь характеризуют параметры среды распространения радиоволн. Информацию несут параметры направления, протяженности линии связи, скорость изменения этих параметров. По значениям этих параметров можно определять положение и характеристики движения излучающих или отражающих объектов (радиолокационные системы, системы траекторных измерений). Сообщением могут быть параметры среды распространения – показатели поглощения и преломления (радиометеорологические системы). Информация может содержаться в структуре радиосигнала (радиоастрономия или разведка).

Третий класс – радиосистемы разрушения информации – организация радиопомех.

Основная часть любой радиосистемы – радиолиния, в состав которой входят тракты формирования радиосигнала (передающая часть), тракты приема, антенные сооружения и среда распространения радиоволн. В некоторых  системах передающая часть отсутствует, в измерительных запросных радиосистемах можно рассматривать либо единую радиолинию с переизлучением (ретрансляцией) сигнала, либо отдельно «запросную» и «ответную» радиолинии.

Тип радиолинии определяет характер радиосистемы, проектирование радиосистемы сводится к проектированию радиолинии. В состав радиосистемы может входить несколько радиолиний. Основная задача системы выполняется главной радиолинией. Вспомогательные радиолинии доставляют информацию, необходимую для работы главной (передача сигналов единого времени, сигналов синхронизации, связь и т.д.). В состав радиосистемы входят вспомогательные подсистемы, предназначенные для отображения, хранения и обработки информации. Ряд подсистем обеспечивают работу радиолинии (системы питания, управления, диагностики и т.д.).

Радиолинии могут классифицироваться, как и радиосистемы, по месту возникновения информации: радиолинии передачи или извлечения информации. Эти классы радиолиний различаются местом и способом модуляции. Радиолинии извлечения информации называются радиолиниями с внешней модуляцией – сообщение модулирует сигнал вне аппаратуры радиолинии.

При классификации радиолиний по различным признакам обращается внимание на отличие разных классов, а также на то, что в них общее.

Лекция 2. ОБЩИЕ ВОПРОСЫ ПРОЕКТИРОВАНИЯ РАДИОСИСТЕМ

2.1. Методология проектирования радиосистем

Термин «проектирование радиосистемы» – достаточно широкий. Проектирование включает определение принципа действия системы, обоснование и выбор вида сигналов, методов их формирования и обработки, конструирование отдельных составляющих системы (устройств, блоков), разработку технологии производства, методов контроля, испытаний и т.д. При разработке приходится разбивать сложную систему на отдельные подсистемы — это может рассматриваться как самостоятельная задача проектирования. В дальнейшем основное внимание будет уделяться принципам функционирования создаваемой системы, а вопросы, относящиеся к конструированию аппаратуры и технологии ее производства, не будут затрагиваться. Излагаемый материал в основном относится к начальным этапам проектирования, таким, как разработка технического задания, технические предложения, эскизное проектирование.

Поэтапная организация работы необходима для упорядочения процесса проектирования во времени и полезна с точки зрения лучшего использования коллективов людей, участвующих в создании системы. С другой стороны, такая организация проектирования наилучшим образом соответствует структурным особенностям сложных систем, в частности, их иерархичности. Иерархичность систем проявляется при изучении их функционирования, когда приходится учитывать, что ряд систем низшего ранга оказывается подчиненным системе высшего ранга. С этим необходимо считаться и при проектировании, поскольку требования к системам низшего ранга обусловливаются параметрами систем высшего ранга.

Все, что обсуждается ниже о методологии проектирования, может быть отнесено к системам, находящимся на любом уровне иерархии. Можно сказать, что для каждой конкретной системы внешнее проектирование является частью внутреннего проектирования системы более высокого ранга и, соответственно в процессе внутреннего проектирования данной системы решаются задачи, касающиеся внешнего проектирования систем более низкого ранга. Не следует думать, однако, что на практике процесс проектирования разворачивается постепенно от высших (по рангу) систем к низшим. Фактически после проработки систем определенного уровня сложности приходится возвращаться назад, на более высокий уровень и производить коррекцию результатов расчета. Таким образом, при проектировании сложной системы характерным является использование метода последовательных приближений, когда решение уточняется на каждом следующем шаге. По-видимому, именно этот процесс и обеспечивает переход от «незнания» к «знанию», в результате которого создается новая система, отличная от существующих систем.

         Потребность в создании новой системы возникает при решении задачи, которая не может быть решена с помощью уже существующих систем. Начиная проектирование, очень важно выяснить, почему же именно непригодны существующие системы.

    При этом обычно оказывается,  что значительная часть принципов, использованных в них, остается пригодной. Таким образом, при проектировании наиболее важным является нахождение главного фактора, который определяет новое качество создаваемой системы. Следовательно, на первых этапах проектирование системы может сводиться к исследованию этого определяющего фактора. Этим фактором может быть выбор сигнала новой структуры, применение нового принципа обработки, использование новой элементной базы и т.д. Разумеется, изменение одного решения, скорее всего, повлечет за собой необходимость изменения многих других частей системы, что и будет являться предметом проектирования на следующих этапах. Естественно, новое качество системы может быть достигнуто разными техническими способами, следовательно, в качестве главного может выступать различное решение при одинаковом исходном варианте. Так, например, повышение дальности действия радиолинии может быть обеспечено в результате изменения принципа обработки сигнала в приемнике или увеличения мощности передатчика. В общем, проектирование всегда может быть сведено к выбору одного из вариантов достижения цели из множества возможных. Ясно, что если имеется лишь один возможный вариант, один способ действия, одна структура системы, то сама задача проектирования исчезает. Для того чтобы она могла быть поставлена, необходимо, во-первых, иметь либо перечень возможных  вариантов, либо метод его получения и, во-вторых, необходимо располагать правилом предпочтения одного варианта перед другим (или иметь возможность производить сравнение их между собой). При выборе, конечно, предпочтение отдается в некотором смысле лучшему, оптимальному варианту. Таким образом, в постановке задачи проектирования неявно содержится требование оптимизации.

         В простейшем случае (при конечном числе вариантов) правило предпочтения может представлять собой список, в котором указывается качество каждого варианта. В этом случае не возникает никаких дополнительных проблем — «надо выбрать вариант с наилучшим качеством». В инженерной практике с такой ситуацией можно столкнуться, если для оценки качества вариантов системы использовать готовые данные из литературы, технических отчетов, протоколов испытаний и т. д. Указанная ситуация в чистом виде практически встречается довольно редко. Во-первых, может случиться, что таких списков окажется несколько, причем они будут противоречить друг другу, во-вторых, основным недостатком такого правила является то, что оно заранее ограничено определенным числом заданных вариантов. Никакой новый, не включенный в список вариант здесь не может быть рассмотрен.

Общий подход определяет некоторый признак – показатель качества, характеризующий данный вариант, и правило, по которому системе с заданным значением показателя качества отдается предпочтение перед другой системой. В совокупности задание показателя качества и правила предпочтения образует критерий выбора системы. Например, при показателе качества — дальности действия  критерием является максимум дальности действия, при показателе качества — стоимости  критерием является минимум стоимости и т. д.

Выработка критерия – первый шаг в процессе проектирования – производится на основе анализа поставленной задачи. Выбранный показатель качества должен численно характеризовать степень приближения к цели, сформулированной при постановке задачи, для достижения которой создается система. Для лучшей системы показатель качества должен быть наибольшим (или наименьшим). После введения критерия задача оптимизации сводится к поиску экстремума показателя качества.

Вообще говоря, критерий для данной системы может быть получен в результате исследования системы более высокого ранга. При этом можно установить, как и какие показатели данной системы влияют на эффективность системы, стоящей на более высокой ступени иерархии. Мысленно этот процесс можно продолжать до бесконечности, однако практически он очень скоро прерывается, в большинстве случаев на следующем же шаге. Поэтому вопрос о формальном построении критерия не может быть не решен окончательно. Рано или поздно критерий придется выбрать на основе субъективных оценок проектировщика, основанных на его интуиции, опыте и, наконец, просто привычке. Здесь можно посоветовать не пользоваться без необходимости какими-то особыми критериями, а применить по возможности известные, общепринятые критерии, чтобы результаты были сравнимы с имеющимися в литературе. Конечно, система, оптимизированная по субъективно выбранному критерию, будет субъективно оптимальной. Однако при этом субъективный момент оказывается четко локализованным, что позволяет избавиться от неопределенности или двусмысленности при сравнении результатов.

В различных случаях показатель, положенный в основу критерия системы, может иметь разную физическую природу. Иногда необходимо увеличить его значения, а иногда – уменьшить. В качестве обобщения различных ситуаций можно принять, что в одном случае показатель определяет некоторый выигрыш, а в другом — проигрыш (или плату). Это эквивалентно тому, что выбранному показателю ставится в соответствие некоторая  цена (в условных единицах).

В тех случаях, когда выбор производится из множества уже созданных и действующих систем, показатель качества может быть определен в результате испытания. Если же прямые испытания невозможны или речь идет о системах, еще не созданных — проектируемых, то нужно создать расчетную модель исследуемой системы.

Понятие модели системы можно определить как приближенное, упрощенное, идеализированное представление некоторой конкретной ситуации и действия определенной системы в этой ситуации. При этом подразумевается отражение основных закономерностей функционирования системы и существенных связей между отдельными подсистемами, составляющими ее, в форме, пригодной для исследования математическими методами.

Построение математической модели обязательно в любой отрасли знания, применяющей количественные методы исследования. Действительно, исследованию поддается не само по себе некоторое явление (или процесс), а его упрощенное отображение, в котором отражены существенные (при данном рассмотрении) стороны явления. Во многих сравнительно простых задачах, решаемых в рамках хорошо разработанной теории, например, в задаче исследования некоторой электрической схемы, модель которой — это соединение сосредоточенных индуктивностей, сопротивлений и т. д., процесс построения модели в достаточной мере формализован, и обычно используется стандартная модель. При проектировании сложной системы построение математической модели всегда представляет собой самостоятельный этап, сопряженный с преодолением значительных трудностей, тем больших, чем выше ранг проектируемой системы. Суть этих трудностей, так же, как и при выборе критерия, заключается в том, что процесс создания модели практически не поддается формализации и требует творческого подхода от проектировщика.

При выборе модели необходимо найти компромисс между сложностью реального явления и простотой его описания. Иначе говоря, модель должна быть достаточно простой, чтобы поддаваться исследованию, но в то же время отражать сущность задачи, чтобы полученные с ее помощью результаты имели практическую ценность. Выбор критерия и построение модели тесно взаимосвязаны и определяются поставленной целью. Трудно сказать заранее, какие из свойств системы существенные, и какие допущения необходимо принять при построении модели в каждом конкретном случае. Основное требование к модели выглядит почти тривиально, но достаточно сложная по сути: модель должна обеспечивать возможность расчета показателя качества, иначе говоря, она должна устанавливать связь между характеристиками системы, параметрами внешних воздействий и величинами, входящими в математическое выражение показателя качества.

Степень сложности модели зависит, во-первых, от количества априорных сведений, которыми мы располагаем, и, во-вторых, оттого, что именно требуется получить от исследования данной модели, какую точность результатов нам необходимо обеспечить.

При проектировании систем характерно поэтапное усложнение модели. Модели так же, как и критерии, образуют иерархию. По мере того, как прорабатываются системы низшего ранга, модель системы в целом становится все более подробной.

По способу математического описания системы (по используемому математическому аппарату) модели могут быть разбиты на два типа — жесткие или детерминированные и вероятностные или статистические.

Модель второго типа предполагает задание вероятностной связи между свойствами систем и поведением ее в данной ситуации. Детерминированная модель поведение системы однозначно связана с ее характеристиками и заданными внешними условиями.

Построив модель и выбрав критерий, можно приступить к решению задачи оптимизации. Здесь в распоряжении проектировщика два основных подхода: анализ и синтез. При анализе известными считаются модели внешних воздействий и модель оптимизируемой системы. В результате анализа определяется значение показателя качества, а возможность оптимизации основана на том, что часть параметров модели системы можно варьировать. Разумеется, значение показателя качества окажется функцией этих варьируемых параметров. Тогда, решая задачу о поиске экстремума этой функции, получаем систему, оптимальную по заданному критерию в классе систем, соответствующих всем возможным значениям параметров. С помощью анализа может быть проведена оптимизация и в случае, когда класс систем, среди которых ищется оптимальная, представляет собой конечное множество. Тогда для каждой модели определяется значение показателя качества, и выбирается та из них, для которой он имеет экстремальное значение.

В задаче синтеза модель оптимизируемой системы не задается. Однако в этом случае проектировщик располагает некоторыми соотношениями (уравнениями), непосредственно определяющими оператор оптимальной системы для заданных моделей внешних воздействий и выбранного критерия. Решая уравнения, проектировщик находит этот оператор, который, в свою очередь, определяет структуру оптимальной системы.

Синтез позволяет, отказавшись от слепого поиска наилучшего варианта, существенно сократить время проектирования, и главное, гарантировать то, что найденная система действительно наилучшая из возможных моделей. При использовании анализа (перебора вариантов) этого принципиально нельзя сделать, ибо проектировщик не может быть уверен, что рассмотрел все возможные варианты.

Указанные преимущества синтеза не дают, однако, основания переоценивать его значение для проектирования радиотехнических систем. Синтез оптимальной системы является лишь одним из многих вариантов, хотя и мощных, методов, используемых при проектировании. Получение практически значимых результатов здесь возможно лишь при существенном упрощении модели сигналов и помех, действующих в радиосистеме. Чем более простой выбрана модель, тем больше оснований надеяться, что решение задачи синтеза удастся довести до конца. В лучшем случае полученное решение будет представлять собой алгоритм, который практически можно реализовать лишь с какой-то степенью точности. При реализации этого алгоритма проектировщик неизбежно сталкивается с дополнительными воздействиями и ограничениями, не учтенными им при построении модели. Это заставляет проектировщика отходить от оптимального алгоритма, заменять одни операции другими, вводить новые операции, не следующие прямо из решения задачи оптимизации. Таким образом, оптимальное решение: в лучшем случае может лишь указать путь к созданию реальной системы, но не может полностью определить ее структуру.

Таким образом, проектировщик в равной степени должен владеть методами анализа и синтеза, используя их там, где это необходимо. Следует отметить, что во всех случаях возможность получения окончательного решения существенно определяется тем, насколько удачно построена модель и выбран критерий. Ясно, что упрощение модели облегчает решение задачи, но уводит проектировщика от сложности реальной действительности. Практическое применение результатов решения задачи оптимизации при этом наталкивается на существенные трудности. Здесь от проектировщика требуются интуиция, практический опыт и изрядная доля здравого смысла.

2.2. Формулировка задач оптимизации. Критерии качества систем

Определение критерия в терминах минимума потерь или максимума выигрыша позволяет условно разбить процедуру его построения на два этапа (рис. 1.2.1): выделение некоторой характеристики, определяющей качество системы, и назначение платы за эту характеристику.

Информация о месте системы в комплексе	Рис. 1.2.1.
	Процедура построения критерия системы

Выше отмечалось, что выбор критерия принципиально не поддается формализации и, следовательно, невозможно предложить набор правил, руководствуясь которыми можно было бы легко выбрать критерий для каждой конкретной задачи. Тем не менее, можно сформулировать некоторые рекомендации по методологии выбора критерия и предварительным преобразованиям его для облегчения решения задачи оптимизации.

Поскольку все, что касается выбора критерия, предшествует решению задачи оптимизации, приведенные соображения остаются справедливыми независимо от того, используется ли при решении метод перебора вариантов, метод параметрической оптимизации или метод синтеза.

Монотонное преобразование функции стоимости. Пусть определена (назначена) некоторая функция платы r = f(h). Задача оптимизации состоит в поиске системы, обеспечивающей экстремальное значение r. Ясно, что результат не изменится, если в качестве функции платы выбрать любую другую функцию, монотонно связанную, с r:

R = F(r) = F[f(h)].

При возрастающей функции F(x) (если существует производная, то дF/дх > 0) характер экстремума не меняется. При убывающей F(х) (если производная существует, дF/дх < 0) максимуму r соответствует минимум R, и наоборот. Простейшим преобразованием, приводящим критерий максимума выигрыша  r_в к критерию минимизации потерь r_в может быть следующее F(r_в) = const – r_в = r_в. Исходя из этого, без нарушения общности везде, где это удобно в дальнейшем, будем говорить только о критерии минимума «потерь» (штрафов).

Построение критерия при наличии случайных факторов.

Статистический характер модели проектируемой системы обусловлен либо наличием случайных внешних воздействий, либо случайным законом функционирования самой системы.

r Рис.2.2. Построение критерия при случайной модели

В подавляющем большинстве радиотехнических задач используются вероятностные модели. При этом значение h в каждой отдельной операции (в каждом испытании) случайно и, следовательно, сравнивать системы по значению r невозможно. Процесс построения критерия нужно дополнить вычислением некоторой устойчивой характеристики величины r (в дальнейшем обозначаемой символом р) которая и служит мерой качества системы (рис. 2.2). Разумеется, этот этап также не свободен от элемента субъективизма и столь же труден для проектировщика, как и этап назначения платы.

При дальнейшем обсуждении будем считать, что сравниваются две системы S₁ и S ₂. Это, конечно, не нарушает общности, ибо выбор из любого числа вариантов при одном показателе качества принципиально может быть сведен к последовательности попарных сравнений и выборов. Для начала, положим, что нам известны плотности вероятностей (распределения) w_1h (h) и w_2h(h) соответствующие системам S ₁ S ₂.

Поскольку плата r функционально связана с характеристикой h, то можно считать, что известны w_1r (r) и w_2r (r) Следовательно, сравнение систем при случайном показателе качества сводится к сравнению соответствующих распределений

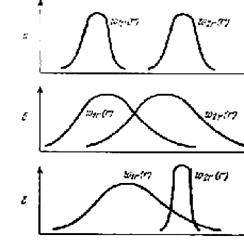         Рассмотрим случай, при котором плотности распределения w_1r и w_2r не перекрываются, так что r₁ всегда  меньше, чем r₂  (рис.1.2.3.а). Очевидно, что система S _1, которой соответствует, w_1r(r), лучше системы S₂, которой соответствует, w_2r (r), и, следовательно, случайный характер величин h (или r) не даёт ни чего нового по сравнению с детерминированным анализом.

         Нетривиальное содержание в задаче появляется тогда, когда распределения перекрываются так, что в одних случаях система S₁ лучше, чем S₂, (r₁ < r₂), а в других – хуже  (r₁ > r₂), рис. 1.2.3, б).

Рис.1.2.3. Распределение вероятностей

платы для двух систем

Теперь для сравнения надо выбрать тот или иной параметр распределения и отдать предпочтение той или иной системе в зависимости от назначения этого параметра. Один из наиболее распространённых подходов состоит в том, сравнение систем проводится по средним потерям, т. е. скажем, S₁ считается лучшей, если выполняется условие:

r₁=r₁=òf(h)w_1h(h)dh <r₂ = r₂ =ò r w_2r (r) dr =ò f(h)w_2h (h)dh.

   Метод оптимизации по критерию средних потерь достаточно хорошо разработан (именно на нём базируется байесов подход к построению оптимальных по помехоустойчивости систем),  но, он конечно, не является единственно возможным разумным методом формирования критерия в статистических задачах. Например, критерий оптимальности можно определить как минимум вероятности того, что потери превышают некоторую фиксированную величину r₀ .Тогда система S₁  предпочитается S₂ если выполняется соотношение:

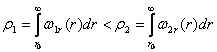(1.2.2)

Отметим одно важное обстоятельство. Различные подходы, связанные с определением величины r, становятся эквивалентными, если соответствующим образом изменить функцию платы. Такое преобразование может быть полезным при решении задачи оптимизации. Например, соотношение (1.2.2) может быть приведено к (1.2.1), если в качестве функции платы выбрать:

.                                                               (1.2.3)

Если показатель h имеет два значения, одно из которых соответствует успеху при функционировании системы S, а другое – неудаче, то часто в качестве показателя качества используется вероятность неудачи. Такой критерий может рассматриваться как частный случай критерия среднего (1.2.1), если положить, что плата r(h) равна единице при неудачном исходе и нулю – при удачном.

Выбирая в качестве критерия r иные параметры распределений, можно продолжить этот ряд.

Для критериев (1.2.1), (1.2.2) и подобных характерно, что показатель качества для каждой системы вычисляется независимо от всех остальных систем. Пример иного рода дает критерий, согласно которому наилучшей считается та система, для которой вероятность того, что потери в ней меньше, чем в других системах, максимальна. Для двух систем S₁ и S₂ предпочтение отдается системе S₁ если выполняется неравенство:

                 (1.2.4)                

(здесь предполагается, что случайные величины r₁ и r₂ статистически независимы). В частном случае, если r₁ и r₂ нормальны, то решение, принятое в соответствии с (1.2.4), совпадает с решением, вытекающим из условия (1.2.1) Критерий вида (1.2.4) определяет лишь «относительное» качество системы.

   Пока все приведенные соотношения носят чисто формальный характер. Попытка физически интерпретировать их (или, точнее, попытка определить физические предпосылки для выбора того или иного критерия) требует рассмотрения достаточно большого множества однотипных операций (испытаний), в которых действует система. Строго говоря, на практике мы не имеем дела ни с вероятностями, ни с моментами, а лишь с относительными частотами появления тех или иных событий или выборочными средними. В определенном смысле близость этих понятий гарантируется предельными теоремами теории вероятностей. Как отмечают авторы: «Познавательная ценность теории вероятностей раскрывается только предельными теоремами».

Так, теоремой Чебышева-Маркова гарантируется сходимость (по вероятности) среднего арифметического множества выборочных значений случайной величины к ее математическому ожиданию, а теоремой Бернулли – сходимость относительной частоты появления события к его вероятности. Учитывая это, можно сказать, что логическое обоснование критерия средних потерь (1.2.1) состоит в том, что его применение обеспечивает минимальные суммарные потери (при проведении достаточно большого количества однотипных операций). Аналогично соотношение (1.2.2) гарантирует (при тех же условиях) наименьшее количество операций, в которых потери превышают заданный уровень.

Грубо говоря, (1.2.1) следует использовать при ограниченности «стратегических» резервов (здесь минимизируется суммарная плата), а (1.2.2) — при ограниченности «тактических» возможностей, когда ограничивается единичная плата в каждой операции.

Легко заметить, что вышеприведенные рассуждения не вполне строгие, и причина этого лежит в том, что сходимость соответствующих статистических характеристик (моментов, вероятностей) к наблюдаемым (выборочным) характеристикам (средним, частотам) обеспечивается лишь в вероятностном смысле. Теорема Чебышева, например, может быть записана в виде:

.

Рассматривать случай бесконечного п не имеет смысла, ибо, во-первых, при этом суммарные потери бесконечны и сравнивать их нельзя, а во-вторых, любая реальная система существует конечное время и число испытаний ограничено. При любом же конечном п остается конечная вероятность достаточно больших отклонений среднего арифметического от математического ожидания. Таким образом, для интерпретации предельной теоремы при большом, но конечном п мы должны располагать уже совокупностью (достаточно большой) множеств испытаний. Поскольку и здесь мы можем иметь дело лишь с относительными частотами, а не с вероятностями, то надо перейти к совокупности совокупностей и т. д.

До сих пор предполагалось, что случайный характер потерь обусловлен случайными факторами, действующими в самой модели системы (r получалось как результат заданного функционального преобразования случайной величины h). Это предположение эквивалентно тому, что эффективность комплекса в целом однозначно определяется конкретным значением h. В действительности, для достаточно сложных комплексов логичнее считать, что при каждой h потери будут случайными, так что величина h определяет не потери, а лишь условное распределение потерь w (rôh). Например, для системы радиоуправления снарядом параметр h можно отождествить с ошибкой наведения. Тогда потери, связанные с не поражением цели, будут случайными при каждом h.

Если воспользоваться критерием минимума средних потерь (1.2.1), то показатель качества для некоторой системы S_i может быть записан в виде

.                                    (1.2.5)

 Замечаем, что внутренний интеграл есть не что иное, как условное среднее потерь r_n, при фиксированном значении h. Тогда предыдущее соотношение может быть записано в виде:

.                                  (1.2.6)

Сравнивая (1.2.1) и (1.2.6), замечаем, что ситуация со случайными потерями эквивалентна рассмотренной выше, если функцию платы выбрать равной условному среднему значению потерь:

Все изложенные подходы к построению критерия используют для сравнения систем некоторые средние характеристики потерь и соответственно требуют знания распределения потерь, построить которое практически иногда бывает невозможно. При этом приходится отказываться от статистического подхода и сравнивать системы по результатам, характерным для крайних случаев.

Пусть для каждой системы потери ограничены пределами r_imin < r_i < r_imax (это практически всегда выполняется). Тогда лучшей может считаться система, для которой максимальное значение потерь минимально. Такой подход называется минимаксным. Система S₁ предпочитается другой системе S₂, если:

r_{1 max} < r_{2 max}                                   (1.2.7)                   

Минимаксный подход часто называется «пессимистичным», ибо здесь расчет ведется исходя из наихудшей ситуации, когда потери достигают максимума. Противоположным в этом смысле является минимальный критерий, когда наилучшей считается система, обеспечивающая минимум потерь в наилучшем случае. Система S₁ предпочитается S₂, если:

r_{1 min} < r_{2 min}                                   (1.2.8)              

Промежуточным является критерий Гурвица, где минимизируется среднее взвешенное значение потерь:

r = c r_{i min} +(1-c) r_{i max}                                      (1.2.9)                                       

Коэффициент c выбирается в пределах от нуля до единицы. При c = 1 имеем (1.2.8), а при c = 0 — (1.2.7).

Переход к критериям (1.2.7) — (1.2.9) оправдан и в том случае, когда распределение потерь известно, но число операций, в которых участвует система (или множество аналогичных систем), невелико, так что предельные свойства функций от выборочных значений не могут проявиться.

Ограничения в задаче оптимизации. До сих пор основное внимание уделялось формированию критерия, а относительно множества систем, среди которых производится поиск оптимальной, не делалось никаких предположений. В то же время ясно, что любая практическая задача проектирования обязательно содержит какие-либо ограничения этого множества.

Если оптимизация производится путем перебора конечного числа заданных вариантов, то ограничения сводятся лишь к уменьшению их общего числа, так что никаких принципиальных затруднений здесь не возникает. Иное дело, если оптимизация проводится путем расчета модели (безразлично, методом вариации параметров или методом прямого синтеза). Прежде всего, отметим, что само по себе использование модели предполагает наличие ограничений, ибо в модели находит отражение лишь конечное число свойств и характеристик реального явления. Однако после того как модель построена, эти ограничения ничем себя не проявляют и возникают вновь лишь после решения задачи оптимизации — на этапе практической интерпретации полученных результатов. Этими ограничениями сейчас заниматься не будем. Рассмотрим ограничения, накладываемые на решение задачи оптимизации уже в рамках построенной модели. Все они, по сути, сводятся к уменьшению разнообразия вариантов, среди которых может производиться выбор. Для того чтобы конкретизировать последующие рассуждения, будем предполагать, что оптимизация производится методом вариации конечного числа параметров.

Итак, при параметрической оптимизации задача состоит в том, чтобы найти такие значения параметров a, b,..., при которых потери r (a,b, ...) или средние потери r(a, b, ...), (в статистической ситуации) минимальны. Вид зависимости r(a, b, ...) или r (a, b,…) определяется классом систем, среди которых ищется оптимальная. Разумеется, эти зависимости включают в себя некоторые постоянные, не варьируемые в данной задаче параметры, которые задаются обычно исходя из модели системы, стоящей в иерархической структуре выше, чем оптимизируемая. Ограничения могут быть наложены на значение показателя качества, на варьируемые параметры и на параметры, непосредственно не определяющие критерий. Наконец, ограничения могут возникать из-за использования тех или иных математических методов решения задачи оптимизации. Ограничения первого вида могут быть заданы в форме:

 r _опт < r _о .                                             (1.2.10)                     

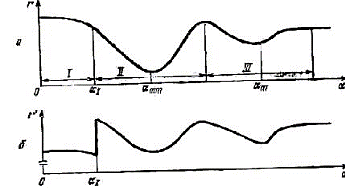
Рис. 1.2.4. Зависимость показателя качества от варьируемого связи и его длительности

С этими ограничениями приходится считаться в том случае, когда оптимальное значение r_опт не удовлетворяет неравенству (1.2.10). При этом приходится пересматривать техническое задание (менять r_о) или изменять первоначально введенную модель, корректируя значение дополнительных (не варьируемых) параметров, определяющих критерий, или, наконец, менять класс систем, в котором проводится оптимизация, т. е, изменять вид зависимости потери r (a, b, ...).

Ограничения второго вида формализуются заданием соотношений типа:

g_i (a,b,…) ³ 0,                       i = 1, 2,…, m                                  (1.2.11)

В простейшем случае они сводятся к заданию пределов изменения варьируемых параметров:

a_Min < a < a _max, b_min < b <b_max.                                  1.2.12)

Часто неравенства (1.2.12) бывают односторонними, когда варьируемые переменные ограничиваются либо только по максимуму, либо только по минимуму.

Физически ограничения типа (1.2.12) могут быть вызваны                                                                                                                     различными причинами:

Общие технические ограничения связанны с предельными на момент проектирования техническими характеристиками элементов систем (максимальные мощности генераторов, минимальные шумовые температуры усилителей, максимальное быстродействие импульсных элементов).

Тактические ограничения, характерные для данной задачи:

ограничения массы, габаритов, энергопотребления, времени проведения сеанса.

Частные технические ограничения,  обусловленные взаимодействием оптимизируемой системы с другими системами в составе комплекса: ограничения, наложенные на выбор используемых частот исходя из требований электромагнитной совместимости, ограничения на полосы пропускания тех или иных трактов и т. д.

Наличие ограничений может в общем случае существенно изменить вид решения задачи оптимизации. Для примера на рис. 1.2.4, а) изображена возможная зависимость показателя качества типа потерь от одного из варьируемых параметров (а). Если ограничения отсутствуют, то, очевидно, решением задачи будет a_mm, обеспечивающее абсолютный (глобальный) минимум. Если теперь ограничить диапазон значений параметра a, то решение может соответствовать либо глобальному минимуму a_mm допустимой является область II, либо локальному минимуму (a_m), если допустимой является область III, либо, наконец, граничной точке a_i, если допустимой является область I.

Введение ограничений не только изменяет вид решения, но и, как правило, приводит к существенному усложнению процесса решения.

Минимизация заданной функции r (a, b, ...) при наличии ограничений вида (1.2.11) сводится к задаче нелинейного рограммирования. При решении задачи оптимизации с ограничениями часто бывает удобно сначала привести ее к эквивалентной задаче без ограничений. Один из возможных приемов состоит в том, что исходная функция стоимости соответствующим образом преобразуется. Вернемся к рис. 1.2.4, а. Пусть требуется найти минимум величины r при условии, что a лежит в области 1. Введем новую функцию стоимости

                                                              r’ = r + f (a),

где      f(a)=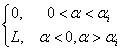                                                                    (1.2.13)                                                                                       

Величина L выбирается достаточно большой, по крайней мере

L > r(a _mm).

График функции r’ приведен на рис. 1.2.4,6. Видно, что теперь a₁ является точкой, обеспечивающей безусловный (глобальный) минимум функции r'. Значит, нахождение минимума функции r при наличии ограничений эквивалентно минимизации функции r' без ограничений.

Рассмотрим ограничения, наложенные на параметры g, d, ..., не определяющие непосредственно показатель качества, но связанные с варьируемыми параметрами a, b ... Первый (не формальный) шаг в решении этой задачи состоит в том, чтобы сначала логически обосновать связь этих дополнительных параметров с варьируемыми параметрами задачи, а затем построить дополнительную модель, отображающую зависимость варьируемых параметров a, b, … от g, d, ... В простейшем случае эта зависимость будет иметь вид

a = f₁ ( d,g,…), b= f₂ (d, g,…),                          (1.2.14)

После построения этой дополнительной модели задача оптимизации сводится к предыдущей.

Наконец, обратимся к ограничениям, связанным с использованием приближенных методов решения задачи оптимизации. Эти ограничения возникают уже после того, как задача сформулирована, и большей частью касаются интерпретации полученных результатов. Обычно они формулируются в виде некоторых условий относительно характеристик искомой оптимальной системы, так что после получения решения необходимо проверить, выполняются ли исходные предположения. Если нет, то следует либо рассмотреть следующее приближение, либо вообще изменить первоначальную модель. Часто в качестве такого дополнительного условия выступает предположение о высокой точности оптимизируемой системы (в том случае, когда оптимизация проводится по точностным критериям).

Оптимизация при наличии векторного показателя качества

До сих пор для простоты предполагалось, что качество системы полностью определяется единственным параметром h, значениям которого приписывается соответствующая стоимость. Практически дело обстоит сложнее. На качество системы влияет множество показателей, так что система определяется целой совокупностью выходных параметров

h {h_1,...h₂}

Действительно, проектировщик хочет построить не только точную, но и достаточно дешевую систему — систему, обладающую высокой надежностью и в то же время имеющую небольшие массу, габариты и энергопотребление. Список таких требований можно легко продолжить, но уже из перечисленных примеров видна основная трудность, возникающая при проектировании системы с учетом нескольких показателей: требования к системе противоречивы, так что в общем случае нельзя найти систему, наилучшую по всем показателям одновременно. Значит, нужно от совокупности показателей качества перейти к одному показателю. После этого задача сводится к предыдущей задаче.

Итак, пусть система характеризуется вектором параметров h {h_1,...h _m}. Для определенности будем считать, что т = 2 (все последующие рассуждения без труда обобщаются на случай большего числа составляющих). Значению каждого из показателей может быть поставлена в соответствие некоторая цена, так что показателями качества системы будут r₁(h₁) и  r₂(h₂)   При необходимости нужно перейти к определенным статистическим характеристикам потерь, заменив r_i; на r_i. Допустим, что имеется множество систем, обладающих различными сочетаниями значений r₁ и  r₂.

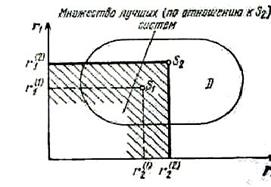
В координатах r₁ и r₂ каждая система будет однозначно определяться некоторой точкой, а совокупность систем образует некоторую область D. Поскольку практически r₁ и r₂ всегда ограничены, путем эквивалентных преобразований функций платы эта область может быть целиком помещена в первый квадрант. Для простоты предположим, что эта область одно связна (рис. 1.2.5) и включает в себя границу. Пусть r₁ и r₂ означают потери, которые необходимо минимизировать. Прежде всего, отметим, что не все системы, принадлежащие множеству D, необходимо рассматривать в задаче оптимизации, часть из них можно отбросить сразу. Действительно, рассмотрим некоторые системы  и S₂,(r₁⁽²⁾ , r₂⁽²⁾) и S₁,(r₁⁽¹⁾ , r₂⁽¹⁾) такие, что выполняется одно из двух условий

r₁⁽¹⁾ £ r₂⁽²⁾)   r₂⁽¹⁾ < r₂⁽²⁾)                                                             (1.2.15)

или

                                r₁⁽¹⁾ < r₁⁽²⁾)                    r₂⁽¹⁾ £ r₂⁽²⁾).                         (1.2.16)                                                                

Ясно, что какой бы не выбрали окончательный критерий предпочтения, система S₂ окажется безусловно хуже, чем система S₁, поскольку потери для нее не меньше по первому показателю r₁ и больше по второму r₂ (1.2.15) или больше по первому показателю r₁ и не меньше по второму r₂ (1.2.16). Система S₁ может быть при этом названа лучшей по отношению к S₂ или наоборот, S₂—худшей по отношению к S₁.

Ясно, таким образом, что в задаче оптимизации следует рассматривать только те системы, для которых нет лучших. Множество таких систем, будем называть множеством не худших систем. Иначе говоря, не худшей системой можно назвать такую, для которой множество лучших систем не содержит ни одной точки (т. е. пусто).

Рис. 1.2.5. Графическая интерпретация множества систем

Точки, отображающие лучшие системы по отношению к некоторой заданной системе S₂, лежат левее и ниже точки S₂ (см. рис. 1.2.5). Следовательно, множество точек, отображающих не худшие системы, образует левую нижнюю границу множества D.

Если уравнение левой нижней границы имеет вид r₁=F (r₂) то из очевидных соображений F (r₂) — монотонно убывающая функция {дF/дr < 0, если производная существует).

Нижняя граница множества отображает системы, для которых r₁= r_{1 min} некотором значении r_2,а левая граница — системы, для которых r₂= r_{2 min} при фиксированном r₁ Для нахождения множества наихудших систем следует построить одну из зависимостей

r_{1 min} = f (r₂)                         (1.2.17a)                                                                      

или

                                                      r_{2 min} = φ (r₁),                                    (1.2.17б)

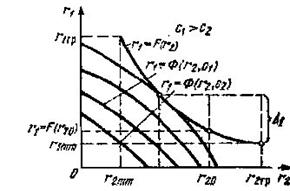
а затем выделить из (1.2.17а) или (1.2.17б) монотонно убывающий участок. Если функции f (r₂) и φ (r₁) немонотонны, так что при некоторых r_2ГР и r_1ГР функции f (r₂) и φ (r₁) имеют абсолютные минимумы r_1mm = f(r_2ГР) и r_2mm= φ(r_1ГР) то кривая не худших систем ограничена точками r_1mm, r_2ГР  и r_2mm r_1ГР

Если зависимости f (r₂) и φ (r₁) монотонны, то кривая не худших систем определена для всех значений r₂ и r₁ Впрочем и здесь, исходя из тех или иных практических соображений, ее можно ограничить и по оси абсцисс, и по оси ординат. Для кривой не худших систем характерно то, что, «двигаясь» по ней, мы улучшаем значение одного из показателей качества, ухудшая значение другого, иными словами, производим «обмен» одного показателя на другой. В связи с этим кривые не худших систем часто называются диаграммами, обмена. Трудно переоценить роль диаграмм обмена в практике проектирования. В любой реальной задаче наличие нескольких показателей качества почти обязательно. Выявление обменных параметров позволяет правильно поставить задачу оптимизации. Решение этой задачи отображается точкой на диаграмме обмена.

Важную роль играют диаграммы обмена, носящие общий характер и применяемые к широкому классу систем. В таких диаграммах отражаются либо фундаментальные результаты теории, либо обобщение результатов большого числа частных разработок. Сюда относятся такие результаты, как обмен между динамической и флюктуационной ошибками в следящих системах, обмен мощности и полосы канала связи, основанный на использовании формул Шеннона, диаграммы типа «стоимость—эффективность».

До сих пор полагалось, что каждая система (из множества допустимых) характеризуется значениями переменных r₂ и r₁ Если оптимизация производится методом вариации параметров, то фактически система задается значениями этих варьируемых параметров a,b, .... а стоимости r₂ и (r₁)  выражаются как их явные функции. Пусть есть всего один варьируемый параметр, а функции стоимостей имеют вид:

r₂ = q₂(a) и r₁ = q₁(a).                                               (1.2.18)

Система уравнений (1.2.18) в параметрической форме задает некоторую функцию r₁ = p(r₂), и множество возможных систем в координатах r_1, r₂ собой линию, соответствующую этой функции. Очевидно, диаграмма обмена будет соответствовать монотонно убывающему участку этой линии. Если на пределы изменения параметра a наложены дополнительные ограничения, их следует учесть, уточнив область определения и область существования диаграммы обмена — функции r₁ = F (r₂).

Для того чтобы множество возможных систем соответствовало некоторой области в координатах r₁,r₂ нужно, чтобы число варьируемых параметров было не меньше двух. Пусть варьируются параметры a, b, а функции стоимости имеют вид:

r₁ =g₁ (a,b), r₂ = g₂ (a,b).                                                               (1.2.19)

При каждом фиксированном b (1.2.19) определяет некоторую кривую в координатах r₁,r₂ а при непрерывном изменении b получается область D (рис. 1.2.5). Теперь для определения области не худших систем требуется найти левую нижнюю границу D. Нижняя граница определяется соотношениями

r₁ = g (a, b) = r_1min при r₂ = g (a,b) = const.                        (1.2.20)

Последнее соотношение соответствует задаче поиска условного экстремума функции двух переменных a, b. Решая эту задачу (например, методом неопределенных множителей Лагранжа),  получаем зависимость r_1min= f (r₂) После этого нужно выделить монотонно убывающий участок f (r₂).

Рассмотрим теперь конкретные способы приведения векторного критерия к скалярному. Еще раз подчеркнем, что во всех случаях оптимальной системе будет соответствовать одна из точек на диаграмме обмена и для решения задачи достаточно оперировать лишь на худшими системами.

Метод ограничений. Из двух показателей r₂ и r₁ выбирается наиболее важный с точки зрения проектировщика, пусть для определенности это будет r₁,. Система оптимизируется в смысле минимума r₁, а на величину r₂ накладываются ограничения вида r₂ <r₂₀. Из рис. 1.2.6 видно, что если r₂₀ < r_2rp то оптимальной будет система, обеспечивающая

r₂, = r₂₀, r₁ = F (r₂₀).

Метод уступок. Первый шаг здесь тот же, что и в методе ограничений: показатели r₁,r₂ располагаются по степени важности (пусть более важным опять будет r₁). Дальше задача решается в два этапа — сначала находится система, оптимальная по критерию r₁ (при произвольном r₂), после чего производится вариация показателя r₂ (с целью его уменьшения), но так, чтобы ухудшение по показателю r₁ не превышало заданной величины ∆₁ (∆₁ называется «уступкой» по показателю r₁). Обращаясь к рис. 1.2.6, видим, что на первом этапе должна быть выбрана система с показателями r₁ = r_1mm , r₂ = r_2гр втором (окончательном) этапе выбирается система с показателями r₁ = r_1mm + ∆₁, r₂ = F - (r₁ = r_1mm +∆₁) , где F‘ — функция, обратная F.

Метод обобщенного критерия. При использовании этого метода сначала задается некоторая функция двух показателей качества R = h (r₁, r₂), после чего R рассматривается как новый скалярный показатель качества, значение которого для оптимальной системы должно быть минимальным. Ясно, что R не может быть произвольной функцией аргументов r₁ и r₂. Поскольку выгодно уменьшение r₁ и r₂, то R не должно возрастать при уменьшении значений своих аргументов. Частные производные R по r₁ и r₂ (если они существуют) должны быть неотрицательными:

¶R/¶r₁ ³0, дR/дr₂ ³0.                                                       (1.2.21)

Рассмотрим в координатах r₁ r₂ кривую, соответствующую уравнению (заданному в неявном виде):

                                              R = R (r₁, r₂) = с = const.                             (1.2.22)

           Для простоты будем считать, что (1.2.22) разрешимо относительно r₁ так что уравнение этой кривой имеет вид:

                                                                 r₁= Ф (r_2,с).                               (1.2.23)

При изменении константы с (1.2.23) порождает параметрическое семейство кривых в координатах r₁ r₂. Заметим, что при каждом фиксированном с функция r₁ = Ф (r₂, с) — не возрастающая, а при изменении величины с кривая r₁ = Ф (r₂, с₁) лежит всегда выше (правее) кривой r₁ = Ф (r₂, c₂), если только с₁ > c₂.

Эти утверждения становятся очевидными, если обратиться к неявному заданию r₁ = Ф (r₂, с) в виде (1.2.22). Действительно, при постоянном с увеличение r₂, должно не уменьшать R, значит для того, чтобы R осталось неизменным, нужно изменить значение r₁ по крайней мере не увеличивая его. Если увеличить с (при постоянном значении r₁), то для увеличения R потребуется увеличить r₁.

Не возрастающая функция (1.2.23) в координатах r₁ r₂ называется кривой безразличия, поскольку любые системы, отображаемые точками, лежащими на этой кривой (если такие точки вообще найдутся), имеют одинаковое значение показателя качества R и в этом смысле не различимы для проектировщика. Ясно, что оптимальное решение должно соответствовать той точке, лежащей на диаграмме обмена r₁ = F (r₂), которая принадлежит кривой r₁ = Ф (r₂, c) с наименьшим значением константы c. Иначе говоря, оптимальные значения параметров r₁, r₂ могут быть найдены как результат решения системы уравнений

                                           r₁ = F(r₂),           r₁ = Ф(r₂, c)                     (1.2.24)

для наименьшего значения параметра c, при котором решение (1.2.24) еще существует.

Разумеется, на практике не обязательно буквально следовать атому указанию. Другие способы могут быстрее привести к цели. Например, можно, подставив первое из соотношений (1.2.24) в выражение для R, искать безусловный минимум функции R [F (r₂), r₂]по аргументу r₂. Если множество не худших систем задано неявной функцией F (r₁, r₂) = 0, то для поиска условного экстремума R (r_1, r₂) можно воспользоваться, например, методом множителей Лагранжа.

Для конкретных функций R (r₁, r₂) решение может существенно упрощаться. Рассмотрим, например, часто используемую в практике функцию

                                                       R = r₁ + q r₂. (1.2.25)

Коэффициент q (0 £ q£ ¥) учитывает относительный вес потерь r₁ и r₂, сам критерий минимизации величины R называется критерием минимума суммарных взвешенных потерь. Видно, что при функции стоимости (1.2.25) точка, определяющая оптимальную систему, будет точкой касания кривой «обмена» и кривой «безразличия» r₁ + q r₂ = с. Следовательно, угловой коэффициент касательной к кривой, отображающей диаграмму обмена в точке, соответствующей оптимальной системе, должен быть равен угловому коэффициенту прямой (1.2.25). Таким образом, для определения оптимальных значений r₁^*, r₂^* имеем соотношения

                                         dF (r₂*)/dr₂* = –q,     r₁^*₌ F(r₂*).                (1.2.26)

Если в пределах r_2mm— r_2rp (1.2.26) не имеет решения, то оптимальной будет либо одна из граничных точек диаграммы обмена, либо одна из точек излома.

В качестве второго примера рассмотрим не дифференцируемую функцию

                                              R = max (r₁, r₂).                                 (1.2.27)

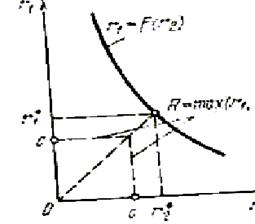
Такую функцию целесообразно выбрать, например, в том случае, когда r₁ и r₂, представляют собой плату за время работы каких-то двух устройств, решающих общую задачу. При этом полагается, что задача полностью решена, когда заканчивает работу функционирующее дольше устройство. Минимизация R в этом случае означает минимизацию времени решения задачи. Функция безразличия для критерия (1.2.27) R = c приведена на рис. 1,2.7, из которого видно, что оптимальная точка на кривой обмена будет соответствовать соотношению r₁ = r₂. Таким образом, уравнения для оптимальных значений r₁, r₂ в этом случае будут иметь вид

                                                 F(r₂^*)= r₂^*,   r₁^*=F(r₂^*).                              (1.2.28)

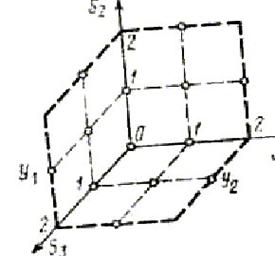Рис. 1.2.8. Графическая интерпретация возможных упорядочений для трех систем

Рис. 1.2.7. К выбору оптимальной системы при обобщенном критерии вида

R = max (r₁, r₂)

Уже неоднократно указывалось на трудности, возникающие перед проектировщиком на этапе формирования критерия. При работе с векторным критерием возникает дополнительная трудность, связанная с переходом к скалярному показателю качества. Ясно, что этот переход тоже не может быть формализован и, следовательно, результату задачи оптимизации свойствен элемент субъективизма. «Степень субъективизма» при использовании каждого из рассмотренных выше трех методов сведения векторного показателя качества к скалярному, грубо говоря, одна и та же. Это следует из того, что при соответствующем выборе начальных условий задачи все три метода (ограничений, уступок и обобщенного показателя качества) могут быть сделаны эквивалентными в том смысле, что будут приводить к одному и тому же решению r₁^*, r₂^*.

Последнее обстоятельство очень удобно для практики, ибо сначала можно воспользоваться тем методом, который проще обосновать логически, а затем искать решение для того метода, который более прост с аналитической (или вычислительной) точки зрения.

Лекция 3. ОБЩИЕ ПРИНЦИПЫ АНАЛИЗА РАДИОСИСТЕМ

3.1. Задачи анализа и математические модели сообщений, сигналов и помех

К анализу приходится обращаться при проектировании любой радиосистемы. В некоторых практических случаях методы анализа оказываются главными. При анализе взятая по каким-либо соображениям (аналогии, эвристики и т. д.) структура системы рассчитывается с целью получения тех или иных ее показателей. Результаты расчетов могут быть использованы для оптимизации системы по заданному критерию (методом вариации параметров). Как уже говорилось, на первых этапах проектирования анализ радиосистем сводится к анализу главной радиолинии.

Анализ радиолинии состоит из исследования характеристик сигнала и радиотехнических трактов. Очевидно, что анализ тракта нельзя начинать, не имея представления, хотя бы приблизительного, о структуре сигнала и основных его свойствах. Поэтому чаще всего анализ начинается именно с сигнала. Не следует думать, однако, что к анализу тракта можно приступить лишь после того, как сигнал полностью изучен. Как и обычно при проектировании, эти этапы в значительной мере развиваются параллельно и получаемые промежуточные результаты используются для последующего уточнения и углубления исследования. В анализе может быть выделено три основных момента: первый, не формализуемый — выбор расчетного показателя и построение модели, второй, формальный — расчет этого показателя теми или иными математическими методами и, наконец, третий — обсуждение и трактовка полученных результатов и установление границ их применимости на практике.

В этой лекции рассматриваются модели сигналов. Эти модели могут иметь относительно самостоятельное значение, ибо некоторые свойства сигналов интересны независимо от того, в какой системе они используются. В других случаях модели сигналов входят Уставной частью в общую модель анализируемой радиолинии. При этом сигнал часто рассматривается как внешнее воздействие. Кроме того, при анализе тракта могут потребоваться модели других внешних воздействий — сообщений и помех. Вопрос, является ли отдельно взятый временной процесс сигналом или помехой, решается в зависимости от того, что требуется получателю, так что при создании математической модели общие методы остаются одинаковыми, идет ли речь о сообщении, сигнале или помехе. Поэтому в дальнейшем везде, где это будет удобно, будем употреблять единый термин «сигнал».

В теории связи полагается то, что сигнал несет информацию, а помеха мешает приему информации. И сигнал, и помеха должны рассматриваться как случайные процессы или явления. Определение случайного явления подразумевает задание некоторого множества, из которого производится случайный выбор (в дальнейшем такое множество мы будем называть ансамблем или выборочным пространством), и вероятностных характеристик на этом множестве, показывающих, грубо говоря, как часто выбирается тот или иной его элемент. Выбранный из случайного множества элемент будем называть реализацией. После того как реализация выбрана, она становится неслучайной. В задачах анализа полезные сообщения и сигналы обычно рассматриваются как детерминированные, а помехи — как случайные процессы, а в задачах синтеза и сообщения и помехи, как правило, считаются случайными.

Математические модели детерминированных сигналов. Смысл задания детерминированных сигналов состоит в том, чтобы использовать их для исследования искажений, возникающих в радиосистеме. Такие исследования могут производиться теоретически или экспериментально. В последнем случае в систему вводятся калибровочные сигналы с точно известной структурой. Сравнивая сигнал, заданный на входе, с тем, который получается на выходе, оценивают искажения, по которым можно судить о качестве системы.

В результате экспериментов с реальными радиосистемами получают временное описание сигналов в виде цифровых таблиц (по точкам) либо графиков, если применяются осциллографы. Часто от такого описания требуется перейти к аналитической записи. Так возникает задача аппроксимации, которая решается путем подбора функции, наилучшим образом согласующейся с результатами эксперимента. Если функция, описывающая сигнал, должна быть использована для теоретического исследования, необходимо стремиться не только к точности описания, но и учитывать выполнимость и простоту дальнейших преобразований. Часто удобно записывать сигнал с помощью комбинаций простых функций или в виде различных функций на разных отрезках времени.

Все реальные сигналы ограничены во времени и имеют ограниченную мощность и энергию. Однако во многих случаях целесообразно использовать для описания сигнала функции, не ограниченные во времени (например, импульс с экспоненциальным затуханием), или функции f(t), не интегрируемые с квадратом (т. е. такие, для которых расходится интеграл 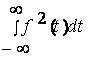). Сигнал, описываемый такой функцией, имел бы бесконечную энергию, но в ряде случаев это не мешает исследованию. Наиболее характерным примером такого рода является использование периодических функций для исследования установившихся процессов. В некоторых случаях допустимо использовать даже функции, соответствующие сигналам с бесконечной мощностью, например, описывая короткие импульсы сигнала с помощью δ-функций. Естественно, что все подобные допущения ограничивают область применимости результатов, и соответствующие границы необходимо также определять при исследованиях.

В частном случае полагается, что сигнал отличен от нуля в определенных временных интервалах и равен нулю при всех других значениях времени (такие сигналы обычно называются импульсными). Возможен и другой случай, когда сигнал задан только на ограниченном интервале времени, а вид его вне этого интервала безразличен для результатов исследования. Иногда в таких случаях удобно доопределить сигнал вне заданного интервала так, чтобы. упростить вычисления. Например, можно положить, что вне заданного интервала сигнал повторяется периодически или тождественно равен нулю и т. д.

Среди других следует специально отметить представление радиосигнала в виде суммы:

,                                (3.1.1)

где совокупность функций φ_k(t) при разных k обычно является линейно-независимой, в частности, ортогональной системой. Если исходное представление (2.1.1)  не ортогонально, а при исследовании удобно пользоваться ортогональным разложением, то всегда можно провести ортогонализацию. Во многих случаях запись сигнала в форме (2.1.1) позволяет упростить вычисления, поскольку оказывается достаточным ограничиться изучением преобразования отдельных слагаемых. Форма (2.1.1) является разложением u(t) в ряд по заданной системе базисных функций. При конечном числе членов суммы равенство (3.1.1) надо рассматривать как приближенное. Для получения правильных результатов стремятся обеспечить наилучшее согласование суммы (3.1.1) с заданной функцией u(t).

При использовании представления (3.1.1) прежде всего, возникает задача рационального выбора системы функций φ_k(t). Решение этой задачи определяется целями исследования. Целесообразно выбирать такие функции, преобразование которых в элементах рассматриваемого радиоканала достаточно просто или хорошо известно (стандартизовано). В других случаях удобнее работать с суммой, содержащей малое число членов. При этом φ_k(t) выгодно выбирать так, чтобы ряд быстро сходился. Такой результат будет получен, например, тогда, когда в качестве первого члена суммы взята удобная для преобразований функция φ₀(t), в общих чертах похожая на сигнал  u(t), а остальные члены дают малые поправки, позволяя представить сигнал с нужной точностью.

Если сигнал в форме (3.1.1) должен быть воспроизведен при эксперименте, то значительную роль играет простота и удобство генерирования функций φ_k(t). Наконец, надо учитывать и форму задания сигнала. Так, если функция u(t) задана на всей оси времени, то для представления (3.1.1), вообще говоря, подойдут функции, ортогональные на бесконечном интервале. Сигнал, заданный на конечном отрезке Т, может быть представлен любой полной системой ортогональных функций, в частности системой, ортогональной на Т.  При этом сумма должна близко совпадать с сигналом на отрезке Т, а вне его она может определять сигнал произвольно. Важное значение имеет случай периодического сигнала. Если для его разложения использовать систему периодических функций с интервалом ортогональности, равным периоду сигнала, то представление в форме (3.1.1) оказывается справедливым не только на интервале ортогональности, но и на всей оси времени.

При разложении сигнала в ряд (3.1.1) необходимо выбрать начало отсчета и масштаб разложения, так как обычно системы базисных функций бывают заданы в виде функций φ_k(z) безразмерного аргумента z с интервалом ортогональности от z₁ до z₂ Сигнал же известен как функция времени u(t), где t берется, например, в секундах. Для того чтобы представление в форме (3.1.1) было справедливым, его следует записать, заменив   переменную z на (t – t₀)/T₀:

,                                (3.1.2)

а коэффициенты разложения (при ортогональном базисе) определять по формуле.

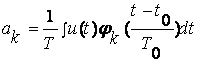.                                     (3.1.3)

При ограниченном интервале определения сигнала (-Т/2≤ t ≤ T/2 параметры t₀ и Т₀, входящие в (3.1.3), должны подбираться так, чтобы интервал ортогональности был согласован с интервалом определения сигнала (например, при изменении t от –Т/2 до Т/2 переменная должна меняться от z₁ до z₂). Это условие дает:

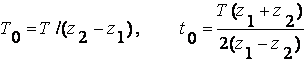.               (3.1.4)

Если применяются ортогональные функции с бесконечным интервалом ортогональности, то интеграл (3.1.3) берется в пределах от –∞ до ∞, а параметры Т₀ и t₀ могут выбираться, вообще говоря, произвольно. Однако их разумный выбор существенно ускоряет сходимость ряда (3.1.2). Общая рекомендация здесь может заключаться в том, чтобы подбирать Т₀ и t₀ такими, при которых член ряда φ₀[(t-t₀)/T₀] как можно лучше соответствовал сигналу u(t).

На практике используются различные системы базисных ортогональных функций: тригонометрические, функции отсчетов (Котельникова), различные ортогональные полиномы, функции Уолша, функции Бесселя и др. Из не ортогональных базисов наиболее широко применяются степенные функции (ряд Тейлора). Эти системы называются полными. Кроме того, могут использоваться и неполные системы функций, которые хотя и не обеспечивают точного (в математическом смысле) представления, но являются вполне приемлемыми на практике. Среди таких базисных функций отметим систему, состоящую из не перекрывающихся импульсов прямоугольной формы.

Представление u(t) в виде (3.1.1) допускает весьма наглядную геометрическую интерпретацию сигнала. При заданной системе базисных функций сигнал полностью характеризуется набором n коэффициентов разложения a_k. Совокупность n чисел можно рассматривать как координаты вектора в пространстве n измерений. Таким образом, каждому сигналу u(t)  можно поставить в соответствие точку (вектор) в «n-мерном пространстве, которое будем называть сигнальным пространством. Координатами этого вектора являются коэффициенты разложения a_k. Преобразования сигнала в тракте радиосистемы можно интерпретировать как геометрические преобразования соответствующего вектора.

Математические модели случайных сигналов. Рассмотрим основные модели ансамблей случайных сигналов, используемые при исследовании радиосистем.

Ансамбли дискретных сигналов представляют собой множества символов (чисел), каждый из которых имеет для получателя определенный смысл. Появление того или иного символа можно рассматривать как некоторое случайное событие. Для передачи и приема дискретных сигналов существенно знать их основные характеристики: общее количество символов в множестве N, время существования одного символа τ_c, статистику появления того или иного символа в источнике сообщения. Исчерпывающей статистической характеристикой дискретного ансамбля является многомерное распределение вероятностей. В наиболее простой модели предполагается статистическая независимость отдельных символов. При этом Достаточно знать лишь вероятность р_i, появления i-го символа. Более совершенной (и сложной) является модель марковской односвязной цепи. Здесь кроме p_i нужно задать еще матрицу вероятностей переходов {p_ij}.

Ансамбль непрерывных сигналов представляет множество функций времени, заданных на некотором интервале. Такой ансамбль при условии, что в каждый момент времени значение функции является случайным, приводит к определению случайного процесса. На практике широко используется два класса моделей случайных процессов: «квазидетерминированные» и «чисто случайные».

Квазидетерминированным процессом будем называть такой, который представляет собой полностью известную функцию времени t и некоторых параметров α₁…, α_n:

u(t)=f(t,α₁…, α_n)              (3.1.5)

при условии, что параметры α₁…, α_n — случайные величины. Ясно, что исчерпывающей статистической характеристикой такого процесса является многомерная плотность вероятности w_n(α₁…, α_n). Зависимость (3.1.5) часто конкретизируется в виде рядов Тейлора или Фурье, причем случайными полагаются коэффициенты разложений.

Частным случаем является представление сигнала в виде случайной постоянной величины. Такая модель оказывается удобной для описания реальных сигналов (сообщений), которые «мало», и «медленно» изменяются на интервале наблюдения. Для такой модели исчерпывающей статистической характеристикой является одномерная плотность вероятности w(x). Если некоторые из значений, принимаемых случайной величиной, имеют конечную вероятность появления, то имеем дело с дискретно-непрерывной случайной величиной. В выражение для плотности вероятности

такой величины входят δ-функции.

Под чисто случайным процессом мы будем понимать такой, в котором согласно «случайность рождается в каждый момент времени». В качестве характеристики такого процесса используется многомерная плотность распределения вероятностей значений процесса (вектора) х{х₁, ..., х_n} в моменты времени t₁,…t_n: w (x) =w(x₁, t₁, …, x_n, t_n).

Чем больше мерность плотности вероятности, тем полнее она описывает случайный процесс х (t). Если известна n-мерная плотность, можно определить и все плотности с мерностью, меньшей n, путем интегрирования по ненужным переменным. Однако в общем случае знания n-мерной плотности недостаточно для определения совместной плотности величин, число которых больше n. Поэтому n - мерная плотность при любом конечном n в общем случае не может служить исчерпывающей характеристикой процесса, хотя в частных случаях она является вполне достаточной. Если моменты отсчетов t₁, ..., t_n равномерно расположены через Δt, в интервале [0, T], на котором задан случайный процесс, то n-мерная плотность при большом n приблизительно может рассматриваться как плотность вероятности для реализации случайного процесса.

Если информация заключена в нескольких сигналах (сообщениях), то для их обобщенного обозначения используют понятие случайного вектора.    

Попытка получить выражение для плотности вероятности непрерывного процесса (функционала плотности вероятности) путем предельного перехода при n → ∞ (Δt → 0) приводит к соотношению, которое нельзя физически интерпретировать. Например, появляются коэффициенты, стремящиеся к бесконечности. Отсутствие функционала вероятности препятствует формулировке некоторых задач, связанных с оценкой случайного процесса. Однако в ряде других задач встречается только отношение функционалов, которое уже конечно. Поэтому в промежуточных выкладках понятие функционала иногда используется.

Не следует думать, что во всех случаях, когда исследуется случайный процесс в радиотехнической системе, приходится обращаться к многомерной плотности вероятности. Для многих практических задач оказывается достаточным знание одно или двумерной плотности. Если же для исследования системы необходима многомерная плотность распределения, то наиболее часто в качестве моделей для описания сигналов и помех используются случайные процессы, у которых многомерная плотность полностью определяется одно- или двумерной плотностью вероятности. Простейшим примером такого рода является процесс, значения которого в любые различные моменты времени t₁, t₂, …, t_n независимы. В этом случае n-мерная плотность вероятности выражается через произведение одномерных, т. е.

w_n(x₁,t₁,…x_n,t_n)=w₁(x₁,t₁) w₁(x₂,t₂),… w₁(x_nt_n)

 Именно таким свойством обладает «белый шум».

Нормальный случайный процесс. Двумерная плотность вероятности является исчерпывающей характеристикой для процесса с нормальным (или гауссовым) распределением вероятностей. Действительно, n-мерная нормальная плотность вероятностей записывается с помощью следующих соотношений:

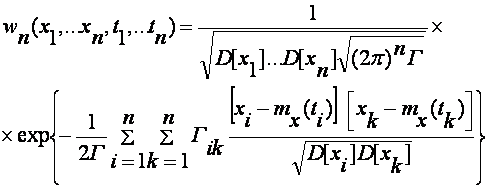      (3.1.6)

где

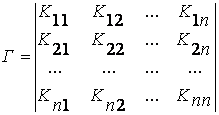
Г_ik—алгебраическое дополнение в определителе Г элемента;

Таким образом, n-мерная плотность будет определена, если заданы математическое ожидание m_x (t) и автокорреляционная функция К_х (t, t'). Но эти параметры, в свою очередь, могут быть найдены, если известна двумерная плотность вероятности w₂(x, х'; t, t'), которая, следовательно, является исчерпывающей характеристикой процесса.

Марковский случайный процесс. Во многих случаям весьма удобные и простые модели строятся на основе так называемых случайных процессов без последействия, или процессов Маркова [55]. Случайный процесс х(t) называется марковским (первого порядка), если условная плотность вероятности значения процесса х_n в момент t_n по всем предыдущим значениям x_n-1,x_n-2,…,x₁ зависит  только от x_n-1, т. е.

w(x_n|x_n-1,…,x₁) = w(x_n|x_n-1)                   (3.1.7)

Условная плотность w (x_i, t_i | x_l, t_l,) = p (x_i|x_l) играет фундаментальную роль в теории марковских процессов и называется плотностью вероятности перехода. Если задана двумерная плотность, w (x_i, x_l, ) то плотность вероятности перехода находится из соотношения

p( x_i|x_l)= w (x_i, x_l)/w(x_l) (2.1.8)

где  — одномерная плотность вероятности. С учетом (2.1.7), (2.1.8) многомерная плотность вероятности марковского процесса может быть записана в виде

  (3.1.9)

Плотности вероятности переходов для трех значений х₁, х₂, x₃, соответствующих трем последовательным моментам времени t₁,t₂,t₃, связаны интегральным соотношением, носящим название уравнения Смолуховского (Чепмена—Колмогорова):

(3.1.10)

Это соотношение легко получить, если воспользоваться выражением (3.1.9) для совместных плотностей w (х₁, х₃), w (х₁, х₂, x₃) и вспомнить, что эти плотности связаны между собой условием

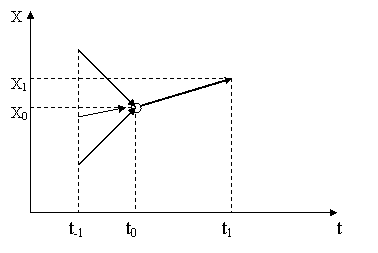
Рассмотрим физическую модель, порождающую марковский процесс (рис. 2.1.1). Пусть в момент t₀ процесс имеет значение x₀=x(t₀). Если производная х(t) процесса является случайной, то, конечно, значение х₁= х(t₁) тоже будет случайным, причем это значение (статистически) будет зависеть от того, каково было значение процесса в момент t₀. Независимость х₁ от предшествующих значений, например какого-то x_-1=x(t_-1), означает по сути независимость от пути, по которому процесс пришел в x₀. Это значит, что скорость процесса должна принимать независимые значения в два любых (сколь угодно близких) момента времени, иначе говоря, производная марковского процесса должна содержать белый шум. Действительно, строгая теория показывает, что марковский процесс удовлетворяет дифференциальному уравнению

                                               (3.1.11)

где — производная процесса х; F — некоторая нелинейная функция от х; n(t) — белый шум (со спектральной плотностью G_o). Соотношение (3.1.11) носит название стохастического (флюктуационного) уравнения.

Пользуясь представлением (2.1.11), можно получить дифференциальное уравнение в частных производных относительно функции распределения w(х, t) следующего вида:

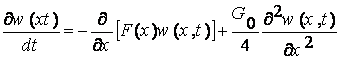             3.1.12

Это уравнение в литературе известно как уравнение Фоккера—Планка (Колмогорова).

Рис.3.1.1. К  модели марковского процесса

Стохастическое уравнение (3.1.11) возникает при исследовании нелинейных замкнутых систем (первого порядка), на которые воздействует шум. Решение уравнения (3.1.12) (при соответствующих начальных и граничных условиях) позволяет найти нестационарное распределение интересующего выходного параметра. Для стационарных систем и стационарных входных воздействий значительно проще определяется стационарная плотность распределения w(х), которая соответствует установившемуся режиму работы. При этом производная по времени в (3.1.12) полагается равной нулю.

Как неоднократно отмечалось ранее, построение модели в любом случае связано с введением ограничений. Поэтому при практической интерпретации результатов, полученных с помощью той или иной модели, следует четко представлять, когда они являются справедливыми. Так, например, используя гауссов закон распределения, нельзя забывать о том, что реальный шум всегда ограничен по максимальному значению, что противоречит соотношению (3.1.6). Если это не учитывать, то можно допустить грубые ошибки в таких задачах, где приходится иметь дело с «хвостами» нормального распределения, скажем, при вычислении «малых» вероятностей превышения «больших» пороговых значений. В связи со сказанным следует весьма осторожно относиться к результатам, касающимся вероятностей ошибок порядка 10^–8 и меньше.

Вопрос о соответствии марковской модели и реального процесса довольно подробно изложен в литературе. В частности, отмечается, что марковская модель хорошо описывает «крупномасштабные» флюктуации реального процесса и существенно отличается от последнего в «тонкой» структуре. Это связано с тем, что марковский процесс имеет бесконечную дисперсию производной, что, очевидно, не соответствует реальности.

Каноническое разложение. Между двумя формами представления случайного процесса — квазидетерминированной и чисто случайной нет непреодолимого противоречия.   В ряде случаев чисто случайный процесс бывает полезно представить в виде (3.1.1), где координатные (базисные) функции заданы, а коэффициенты разложения являются случайными. Введя в рассмотрение центрированный случайный процесс

u₀(t) = u(t) – m_u(t),

где m_u(t) — математическое ожидание процесса u(t), представляющее по определению известную неслучайную функцию времени, запишем для u₀(t) представление (3.1.1) в виде

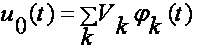.                                  (3.1.13)

Если коэффициенты V_k подобраны так, что  = 0 и  = 0 при k ¹ q, то представление случайного процесса в форме (2.1.13) называется каноническим разложением.

Каноническое разложение для чисто случайного процесса позволяет представить его реализацию в виде точки (вектора) в сигнальном пространстве, аналогично тому, как это делалось для детерминированного сигнала . Очевидно, что это же может быть сделано и для реализации квази-детерминированного процесса. Тогда множество реализации, образующих процесс, может быть представлено множеством точек («облаком»), плотность которого зависит от распределения вероятностей процесса.

Случайные стационарные и нестационарные процессы. Очень часто при рассмотрении установившихся режимов в качестве моделей используют случайные стационарные процессы. Стационарный процесс ведет себя однородно во времени, что выражается в независимости его законов распределения вероятности от начала отсчета времени. Одномерная плотность вероятностей w₁(x) у такого процесса от времени не зависит, а двумерная w (x, x', τ) зависит только от разности двух моментов времени τ=t — t'. Большинство случайных стационарных процессов обладает очень важным с практической точки зрения свойством — одна достаточно продолжительная реализация процесса содержит все сведения о его характеристиках. Это свойство называется эргодичностью. Не все стационарные процессы являются эргодическими. Достаточное условие эргодичности состоит в том, чтобы автокорреляционная функция процесса затухала на бесконечности, т. е.

В ряде задач (анализ переходных режимов, рассмотрение взаимодействия сигналов и помех) приходится сталкиваться со случайными нестационарными процессами. Однако, поскольку исследование преобразований случайного нестационарного процесса обычно оказывается сложным, на практике стремятся упростить задачу путем замены нестационарного процесса стационарным. Здесь имеется две возможности. Первая используется в случае так называемой медленной нестационарности. При этом весь процесс разбивается по времени на отдельные интервалы, на каждом из которых он считается стационарным. В частном случае процесс считается стационарным на всем заданном интервале и для расчета берутся средние или наихудшие значения его параметров.

Вторая возможность связана с представлением сигнала в виде случайного процесса, приводимого к стационарному процессу. Простейший вид процесса, приводимого к стационарному процессу, записывается как

x(t) = f₁(t) + у(t),                                    (3.1.14)

где у(t) — случайный стационарный процесс, a f₁(t) — детерминированная функция времени.                                                       __

Не нарушая общности, можно считать, что у(t) = 0, а f₁(t) = m_x(t)  — математическое ожидание процесса x(t). Выражение (2.1.14) представляет собой весьма распространенную модель аддитивной смеси детерминированного сигнала со стационарным шумом. Нетрудно видеть, что у этого процесса постоянная дисперсия, а автокорреляционная функция зависит только от временного сдвига τ.

В более сложном варианте случайный процесс представляется виде

x(t)=f₁(t) + f₂(t) + f₃(t)z(t)             (3.1.15)

где f₁(t), f₂(t),f₃(t) — детерминированные функции; x(t), z(t) — случайные стационарные процессы.

В таком виде часто представляются модулированные случайным процессом радиосигналы или процессы на выходе линейных систем с переменными параметрами. Статистические характеристики процесса х(t), записанного в виде (3.1.15), могут быть найдены через заданные характеристики у (t) и z(t).

Представление (3.1.15) может быть использовано и для стационарного процесса. Так, для случайного узкополосного стационарного процесса х (t), спектр которого сосредоточен вблизи высокой частоты ω₀, справедливо соотношение

х (t) = A (f) cos ω₀t + B (t) sin cos ω₀t = E(t) cos [ω₀t+φ(t)],  (3.1.16)

где A(t)  и  В(t) — ортогональные компоненты процесса, представляющие собой случайные стационарные процессы, спектры которых лежат вблизи нулевой частоты; Е (t) и φ(t) — огибающая и фаза случайного процесса, соответственно связанные с A(t) и В(t) соотношениями перехода от декартовой к полярной системе координат.

Упрощенные характеристики случайных процессов. При решении

а можно ограничиться только основными числовыми характеристиками, из которых чаще всего используются математическое ожидание (первый начальный момент) , дисперсия (второй центральный момент)  и автокорреляционная функция

Прямая черта сверху означает усреднение по ансамблю (статистическое усреднение).

Иногда корреляционную функцию К(t, t') удобно представить в виде

                                                 (3.1.17)

Такое представление может быть получено, например, путем разложения функции К (t, t') при фиксированном t по ортогональному базису φ_i(t^’). При этом коэффициенты разложения оказываются зависящими от t.

У стационарных процессов математическое ожидание и дисперсия постоянны, и корреляционные функции зависят только от разности моментов отсчета.

У эргодических процессов усреднение по множеству реализации для одного момента времени совпадает с усреднением по времени. Это означает, что математическое ожидание может находиться как среднее по времени

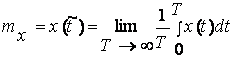                                                    (3.1.18)

(волнистая черта сверху означает операцию усреднения по времени). Соответственно дисперсию можно определять как

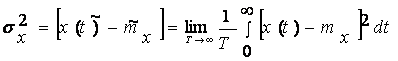                    (3.1.19)

а автокорреляционную функцию как

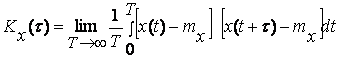.                                 (3.1.20)

Практически для пользования этими формулами достаточно, чтобы время усреднения T было достаточно велико. Свойство эргодичности открывает путь для простого экспериментального определения характеристик по одной реализации. Так, если х(t) является напряжением или током, его математическое ожидание согласно (3.1.18) является постоянной составляющей и может быть измерено прибором постоянного тока, а дисперсия соответствует мощности (при m_x== 0, на сопротивлении 1 Ом) и для ее измерения можно использовать, например, тепловой прибор.

Для процессов, приводимых к стационарным [вида (3.1.15)], математическое ожидание находится в результате усреднения по множеству как

m_x(t)=m_yf₁(t) + m_zf₂(t)                                                    (3.1.21)

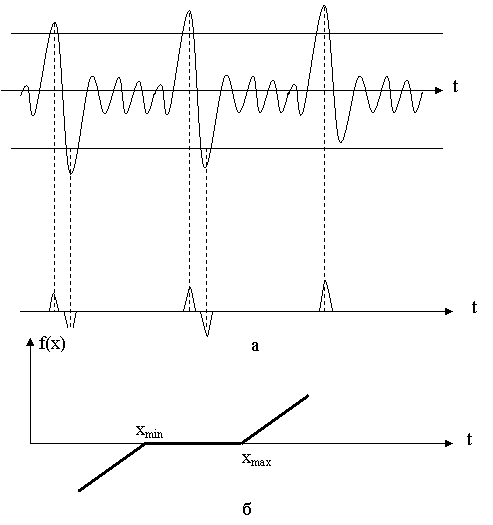где

Рис. 3.1.2. Определение сигнала ошибки при выборе динамического диапазона

Чтобы найти автокорреляционную функцию  недостаточно знать характеристики у (t) и z (t), а необходимо определить их взаимосвязь. Для этого используются взаимно-корреляционные функции двух процессов

.                          (3.1.22)

Если функция K_yz(t, t') зависит только от разности  — t' = τ, то процессы у(t) и z(t) называются стационарно-связанными. В частном случае, когда у(t) и z(t) не коррелированны:

;                       

;                  (3.1.23)

.                                (3.1.24)

В ряде случаев бывает полезно определить динамический диапазон сигнала. Динамический диапазон [х_min, x_mах] может быть найден, если известна одномерная плотность вероятности w (х). Если принятая модель такова, что х может изменяться в бесконечных пределах, для определения динамического диапазона, прежде всего, следует задаться каким-либо критерием. Весьма часто в качестве такого критерия используют вероятность p_Т выхода величины х за пределы  [х_min, x_mах] (p_Т должна быть мала). Тогда динамический диапазон определяется из равенства

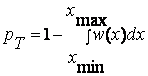.                                             (3.1.25)

Если х(t) — стационарный процесс, то р_T одновременно определяет и относительное время, в течение которого нарушается соотношение   

x_min ≤ x ≤ x_max.

Другой критерий — энергетический — основан на вычислении мощности сигнала ошибки, который появится, если сигнал х (t) ограничить пределами х_min – x_mах (рис. 2.1.2, а). Динамический диапазон в этом случае следует определить как пределы х_min – x_mах, при которых мощность   сигнала ошибки мала по сравнению с мощностью процесса х(t). Величину можно найти с помощью следующего преобразования:

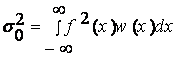,                                   (3.1.26)

где

Вид функции f(x) показан на рис. 3.1,2, б. Зависимости (3.1.25) и (3.1.26) для случая, когда w (х) соответствует нормальному закону с нулевым средним, а

х_min – x_mах = Δ,        Δ = β₀ σ_x

приведены на графиках рис. 2.2.3. Если динамический диапазон ограничен только с одной стороны  – x_mах = ∞, х_min = – Δ, то ординаты на графике рис. 3.1.3 уменьшатся на три децибела. Естественно, что, задавая динамический диапазон, следует указать и критерий, по которому он определен.

В некоторых задачах пределы изменения сигнала, т. е. динамический диапазон, заданы физическими свойствами системы, в которой действует случайный процесс. В то же время для математического описания процесса может оказаться удобным использование плотности вероятности, определенной в бесконечных пределах (например, гауссовой плотности). При подборе параметров этой плотности также можно использовать приведенные соотношения (3.1.25) или (3.1.26).

Автокорреляционная функция К_x(τ) и энергетический спектр G_x(ω) характеризуют быстроту изменения случайного процесса. Чем быстрее меняется сигнал, тем шире его спектр и тем быстрее затухает автокорреляционная функция. Иногда вместо полной зависимости G_x(ω) бывает достаточно задать некоторые числовые характеристики спектра. Обобщенной характеристикой быстроты процесса, зависящей как от ширины спектра, так и от положения спектра на оси частот, является среднеквадратическая частота ω₁, определяемая выражением

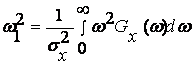.                         (3.1.27)

Удобный параметр – эффективная полоса сигнала Δω_х – определяется как полоса прямоугольного спектра, совпадающего с G_x (ω) в какой-либо характерной точке (при ω) имеющего ту же площадь (рис. 3.1.4):

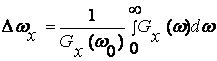.                               (3.1.28)

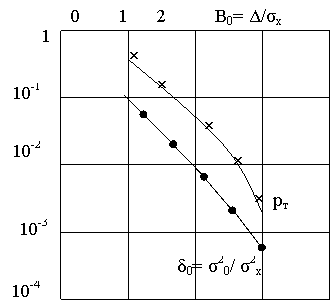Рис. 3.1.3. К определению динамического   диапазона нормального процесса

Рис. 3.1.4. К определению характерных параметров спектра

За ω₀ обычно берут частоту, соответствующую максимальному значению спектра или его оси симметрии. Иногда удобно выбирать ω₀= 0.

Диапазон занимаемых частот (Δω_m) определяется как полоса, в пределах которой находится основная часть мощности процесса х(t). Такой параметр удобен при оценке необходимой полосы пропускания систем, фильтрующих сигнал. Для определения Δω_m требуется также задать, какой частью γ полной мощности допустимо пренебречь. Так, например, если диапазон занимаемых частот примыкает к ω = 0 (рис. 3.1.4), то Δω_m определяется из равенства

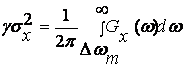,                                (3.1.29)

где γ — коэффициент (γ << 1), показывающий относительную мощность сигнала ошибки, возникающего, если процесс х(t) ограничить по спектру пределами от 0 до Δω_m

Знание полной автокорреляционной функции сигнала К_х(τ) также иногда может быть не обязательно, если известны ее характерные параметры. Важнейшим из них является время корреляции τ_x, определяемое как интервал времени, на котором два значения х(t) становятся практически некоррелированными. Время корреляции можно определить по-разному. Одно из определений задает его как такой временной сдвиг, при котором автокорреляционная функция уменьшается до величины, малой по сравнению со своим начальным значением [К_х(0)=σ²_x ]

К_х(τ_x)=qσ²_x ,        при q « 1.                                 (3.1.30)

Другое определение задает Тд, исходя из площади, ограниченной кривой [К_х(τ_x)]

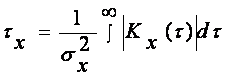.                             (3.1.31)

В некоторых случаях удобно определение

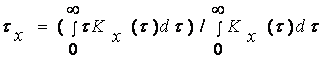.                  (3.1.32)

Наконец, K_x может определяться как наименьшее значение интервала, при котором справедливо равенство

K_x(τ) = 0.                                            (3.1.33)

Между диапазоном занимаемых частот и временем корреляции существует связь, которую можно выразить следующим соотношением:

Δω_m τ_x = d,                                      (3.1.34)

где d – постоянная величина, зависящая от формы спектра и способа определения величин Δω_m и τ_x. В большинстве практических случаев полагают, что величина d порядка единицы.

Вместо среднеквадратической частоты ω₁ можно применять эквивалентную ей величину — начальную кривизну автокорреляционной функции

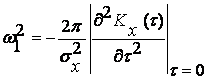.                       (3.1.35)

Лекция 4. ХАРАКТЕРИСТИКИ РАДИОСИГНАЛА

4.1. Функция различия, сигнальная функция и функция определенности

Передача информации с помощью различных видов радиосигналов всегда основана на том, что сообщение заложено в каком-либо параметре сигнала. На приемном конце радиолинии этот параметр измеряется и таким образом определяется переданное сообщение. Поскольку в радиолинии всегда имеют место всякого рода помехи, измерения вносится ошибка, искажающая сообщение. В зависимости от того, как сообщение заложено в сигнале, оно будет по-разному искажаться от помех. В связи с этим при проектировании радиосистем передачи информации возникает вопрос о наиболее целесообразном методе модуляции сигнала. В радиосистемах с внешней модуляцией необходимо выбрать форму излучаемого (зондирующего) сигнала.

Рассмотрим математический аппарат, позволяющий сравнивать различные радиосигналы по устойчивости передаваемых ими сообщений к искажениям из-за помех.

Пусть принимается сигнал s (t, х_и), где х_и — постоянный во времени параметр, несущий сообщение. Задачей приема является измерение этого параметра.

Один путь для решения такой задачи состоит в том, чтобы сделать приемное устройство в виде преобразователя сигнала, на выходе которого получается величина  пропорциональная х_и (рис. 4.1.1). Эту величину следует измерить, т.е. сравнить с эталонными образцами , образующими измерительную шкалу, и выбрать один образец, совпадающий с . Этот образец и дает оценку параметра х*.

Возможен, однако, и иной метод приема, при котором не требуется выделения . Поскольку структура сигнала считается полностью известной (за исключением величины x_и), можно построить измерительную шкалу из образцов сигнала s {t, х_i) или частично преобразованного сигнала s_п (t, x_i) и сравнивать с ней соответствующий принятый сигнал (на рис. 4.1.1 разные способы построения приемного устройства соответствуют замыканию ключей В1, В2 или ВЗ). В результате сравнения следует выбрать образец сигнала, совпадающий с принятым, что также обеспечивает получение оценки х*. Следует отметить, что если прием происходит без помех и искажений, а параметр х имеет дискретное множество значений то принятый сигнал обязательно совпадает с одним из образцов. Если же х изменяется непрерывно, то точного совпадения может не быть, но ошибка дискретности в принципе может быть сделана как угодно малой, если соответственно увеличить число образцов (уточнить шкалу).

Действие помехи изменяет форму сигнала. Поэтому даже при дискретном х может не быть совпадения принятого процесса ни с одним из образцов. В этом случае для выбора надо задаться каким-либо количественным критерием различия (или сходства)

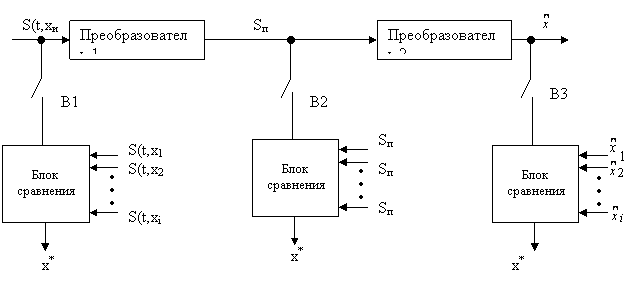Рис. 4.1.1. Модель измерения параметра х

принятого искаженного сигнала s_иск (t,x_и) с образцом. Можно использовать среднеквадратический критерий, задаваемый соотношением

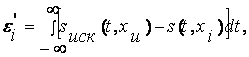                                            (4.1.1)

выбирая тот из образцов, для которого окажется минимальным.

Ясно, что при таком способе выбора возможность перепутать значения сообщения будет тем меньше, чем сильнее отличаются образцы друг от друга. Поэтому один из возможных критериев оценки качества сигнала как переносчика сообщения может быть основан на определении величины ε, называемой мерой различия:

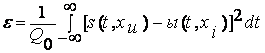                                (4.1.2)

где

                                            (4.1.3)

— энергия сигнала при некотором фиксированном значении х₀ параметра х. Если сигнал ограничен во времени, то пределы в интеграле (4.1.2) распространяются на время существования сигнала.

Меру различия, определенную согласно (4.1.2), можно рассматривать как функцию х_i или разности Δх = х_и—х_i. Функция различия ε (Δх) всегда положительна, проходит через нуль при Δх = 0 (т. е. в точке х_i = х_и и возрастает с увеличением абсолютного значения аргумента Δх хотя и не обязательно монотонно. ^н0 По виду функции различия ε (Δх) можно судить о качестве исследуемого сигнала как переносчика сообщения. Быстрое возрастание ε (Δх) от нуля с увеличением Δх свидетельствует о том, что даже малое изменение параметра в образце сигнала приводит к резкому увеличению меры различия в. Следовательно, это различие легко обнаружить и труднее замаскировать помехой. Значит сигналы с быстро нарастающей функцией различия ε (Δх) могут обеспечить передачу сообщений с меньшими искажениями. Выражение (4.1.2) может быть преобразовано к виду

ε (Δх) = Q/Q₀ + Q_i/Q₀ - 2q (Δх).           (4.1.4)

где Q и Q_i — энергии сигналов при значениях параметра х_и и х_i, которые определяются выражениями, аналогичными (4.1.3);

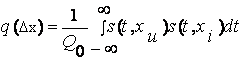      (4.1.5)

Зависимость q (Δх) носит название сигнальной функции.

Все существующие методы модуляции можно разбить на две группы. К первой (неэнергетической} относятся те методы, при которых не происходит изменения энергии сигнала из-за изменения модулируемого параметра. Эта группа включает в себя большую часть практически применяемых радиосигналов. Сюда относятся все методы модуляции, в которых на последней ступени не используется AM, и многие сигналы с AM на последней ступени, например: ВИМ-АМ, ШИМ-ЧМ-АМ. Ко второй группе (энергетической) относятся методы модуляции, при которых энергия сигнала меняется. Сюда относятся сигналы AM, АИМ-АМ, ШИМ-АМ и др.

Для всех неэнергетических методов модуляции зависимость (4.1.4) преобразуется к виду

ε(Δх) = 2[1 —q (Δх)]               (4.1.6)

Следовательно, качество сигнала полностью определяется видом сигнальной функции q (Δх). Как следует из (4.1.6), сигнальная функция должна убывать с ростом аргумента Δх и чем круче будет спадать q (Δх) с увеличением | Δх |, тем точнее измеряется параметр. Максимальное значение q (0) = 1. Из определения (4.1.5) видно, что по своей структуре сигнальная функция аналогична автокорреляционной функции сигнала, а когда модулируемым параметром является временная задержка, эти две функции становятся тождественными.

Среднеквадратический критерий (4.1.1) и вытекающие из него меры различия (или сходства) двух сигналов (ε, q) допускают весьма наглядное геометрическое изображение. Как отмечалось в §2.1 каждому сигналу s (t) можно поставить в соответствие вектор в n - мерном пространстве, причем координатами или проекциями этого вектора являются коэффициенты разложения а_k функции s (t) в ортогональный ряд. Длина вектора в n - мерном евклидовом пространстве определяется через его координаты как

                                             (4.1.7)

но на основании равенства Парсеваля для разложения в ортогональный ряд сигнала длительностью T имеем

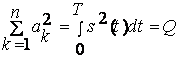                              (4.1.8)

Следовательно, длина вектора, изображающего сигнал, равна квадратному корню из его энергии.

Предположим теперь, что в сигнале изменился параметр х, несущий сообщение. Новый сигнал также может быть представлен вектором в той же системе координат и отличается от первого своими проекциями. Если мы имеем дело с неэнергетическим методом модуляции, то при изменении х энергия сигнала не изменится, а следовательно, вектор повернется, не меняя своей длины. Таким образом, при неэнергетических методах модуляции конец вектора сигнала всегда лежит на поверхности n - мерной сферы радиуса √Q. Если параметр х меняется непрерывно, то конец вектора сигнала прочерчивает на этой сфере некоторую непрерывную линию, называемую линией сигналов. При энергетической модуляции вектор сигнала изменяет свою длину, так что линия сигналов не лежит на сфере постоянного радиуса. Дискретному изменению х соответствует конечное множество изолированных точек.

Определим теперь расстояние в евклидовом пространстве между двумя точками, находящимися на концах векторов, изображающих сигналы s (t, х) и s (t, х + Δx). Если первый сигнал имеет координаты a_k, а второй b_k, то расстояние d_э определяется формулой

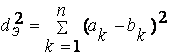                               (4.1.9)

Заметим, что вектор dg имеет координаты с_к = а_k — b_k и, следовательно, изображает сигнал s_p (t) == s (t, х) — s (t, х + Δх). Поэтому согласно теореме Парсеваля

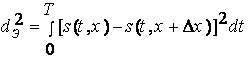                (4.1.10)

Сравнивая это выражение с (4.1.2), видим, что расстояние меду векторами сигналов в евклидовом пространстве пропорционально мере различия ε при среднеквадратическом критерии, которой использовался ранее. Если модуляция неэнергетическая, то

                                       (4.1.11)

где Q — энергия сигнала, a q (Δх) — сигнальная функция, определяемая (4.1.5). Быстрое спадание функции q (Δх) с увеличением Δх можно трактовать как большой поворот сигнального вектора, в результате чего из-за изменения параметра х резко увеличивается расстояние между сигналами d_э. Следовательно, приращение вектора сигнала из-за добавления к нему вектора помехи приведет соответственно к меньшей ошибке в оценке параметра х. Если функция q (Δх) уменьшается немонотонно и имеет выбросы, сравнимые с единицей, это означает, что линия сигналов на n- мерной сфере извивается так, что ее отдельные точки сближаются в пространстве. Такая картина указывает на опасность появления «больших» (аномальных) ошибок при действии даже сравнительно малой помехи. Таким образом, векторное представление сигнала в евклидовом пространстве также показывает, что сигнальная функция (иди функция различия) может служить мерой качества радиосигнала как переносчика сообщений.

Анализ радиосигналов с помощью сигнальных функций можно обобщить на случай, когда в принимаемом сигнале неизвестно несколько (m) параметров. (В этом случае в сигнальном пространстве при изменении сообщения образуется не линия, а сигнальная поверхность.) При этом образцы сигнала должны охватывать все возможные сочетания разных значений неизвестных параметров. Сигнальная функция измеряется для каждого образца, чтобы выбрать тот, для которого она будет наибольшей. Таким образом, сигнальная функция будет многомерной величиной, зависящей от 2m аргументов, а количество образцов становится равным

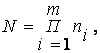                                                       (4.1.12)

где n_i — количество измеряемых градаций i-ro параметра.

Используя многомерную сигнальную функцию, можно обобщить исследование свойств радиосигнала и на те случаи, когда какие-то из неизвестных параметров изменяются за время измерения. 1акие переменные параметры следует представить в виде квазидетерминированной функции (§ 2.1). Ее коэффициенты рассматриваются как новые неизвестные параметры. Таким образом, изменение параметра во времени можно учесть соответствующим повышением мерности сигнальной функции.

Когда неизвестных параметров два (х, γ), сигнальная функция будет, вообще говоря, зависеть от четырех переменных (х_и, х_i,γ_и γ_i) и

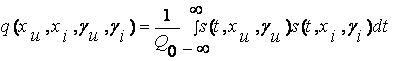    (4.1.13)

Часто, однако, число переменных уменьшается до двух: Δх: = х_и — х_i и Δγ = γ_и -  γ_i, и сигнальная функция становится двумерной.

Измерение задержки и частоты. Функция неопределенности. Рассмотрим один важный частный случай анализа радиосигнала, предназначенного для совместного измерения временной задержки и частотного сдвига. Важность этого случая определяется тем, что на практике часто используются системы, определяющие дальность и скорость какого-либо объекта путем совместного измерения времени задержки и доплеровского смещения приходящего от него радиосигнала. Сигналы, применяемые в таких системах, как правило, узкополосные и их удобно представлять в виде

u(t) = a(t)cos[ω₀t + φ(t) + φ₀],           (4.1.14)

где а (t), φ (t) — сравнительно медленные функции времени по сравнению с cosω₀t.

Образец сигнала u_i(t) будет, вообще говоря, сдвинут по времени на Δτ и по частоте на Ω. Поэтому двумерная сигнальная функция согласно (4.1.13) должна быть записана как

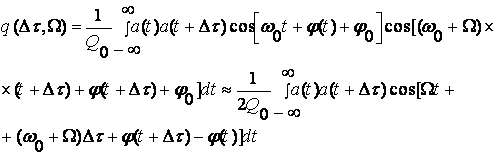(4.1.15)

Сделанное приближение возможно при медленных функциях а(t), φ(t), вследствие чего интеграл от второго члена при разложении произведения косинусов оказывается значительно меньше первого. Полученная сигнальная функция представляет собой некоторую поверхность (в координатах Δτ, Ω), которая вдоль оси Δτ имеет характер частых затухающих колебаний с периодом 2π/ω₀.

Выражение (4.1.15) можно получить и несколько иным способом, если для записи сигналов использовать комплексное представление;

 (4.1.16)

Определим комплексный корреляционный интеграл

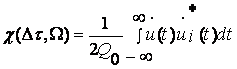                                            (4.1.17)

где  — функция, комплексно-сопряженная с . Нетрудно показать, что найденная в (4.1.15) сигнальная функция представляет собой действительную часть комплексной величины, определенной (4.1.17), т. е.

q (Δτ,Ω) = Re [χ (Δτ, Ω)].                                         (4.1.18)

Следовательно, функцию

Q(Δτ,Ω) =|χ(Δτ,Ω)|                                              (4.1.19)

можно рассматривать как огибающую сигнальной функции. Во многих случаях огибающая сигнальной функции достаточно полно характеризует качество радиосигнала, и поэтому она широко используется при анализе радиосистем. Функцию Q (Δτ, Ω) в литературе часто называют функцией неопределенности [24]. Это название связано с одним замечательным свойством данной функции, которое может быть записано в виде следующих равенств:

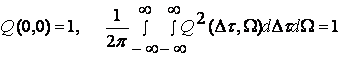                           (4.1.20)

Первое равенство получено в результате нормирования, а второе определяется тем, что величины Δτ и Ω являются связанными переменными при преобразовании Фурье (доказательство (4.1.20) приведено, например, в 1241). Для получения высокой точности измерения задержки и частоты радиосигнал должен иметь функцию неопределенности, как можно более круто спадающую от начала координат. Однако условие (4.1.20) означает, что объем, ограниченный поверхностью Q²(Δτ, Ω), равен 2π, следовательно, произвольно сжимать функцию Q(Δτ, Ω) нельзя.

4.2. Сравнение радиосигналов с помощью функций различия и сигнальных функций

Анализ функций различия и сигнальных функций позволяет оценивать качество различных радиосигналов. В результате оказывается возможным отобрать наиболее перспективные для дальнейшего изучения радиосигналы, с помощью которых можно доиться наилучшей точности или достоверности передачи сообщений. Анализ сигнальных функций оказывается также необходимым для определения такого важного параметра системы извлечения информации, как разрешающая способность [24], или для оценки предельного уровня между канальных помех [19].

Естественно, что если не заданы конкретный вид и значения помех, нельзя дать и количественную оценку искажений сообщения. Однако, сравнивая сигнальные функции двух различных радиосигналов (при неэнергетических методах модуляции), можно сказать, какой из них может обеспечить меньшие искажения при весьма общих предположениях о характере помех. Иногда полезно сравнивать сигнальные функции преобразованного   сигнала s_п (t, х) (рис. 4.1.1), исключая из рассмотрения способ демодуляции несущей.

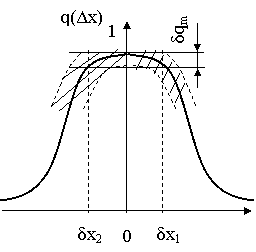
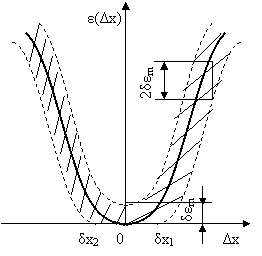Рис. 4.2.1. К определению ошибки измерения параметра, x.

В этом параграфе сравнение проводится лишь качественно. Оно необходимо только для того, чтобы иметь возможность обсудить конкретные виды сигнальных функций, получаемых в последующих параграфах этой главы. Количественные соотношения, нужные для окончательного выбора сигнала при проектировании, получены в гл. 10.

Пусть прием сообщения осуществляется сравнением принятого сигнала с образцами. Тогда определение х сводится к измерению множества значений ε_i' (4.1.1) (для разных образцов) и выбору среди них наименьшего. При отсутствии помех (искажений) ε_i' совпадает с мерой различия (4.1.2). Если же искажения есть, то ε' будет отличаться от ε на некоторую величину — ошибку δε, которая и приводит к тому, что выбирается другой образец сигнала, а следовательно, параметр х определяется с ошибкой. Предположим, что образцов сигнала может быть сколь угодно много и дискретность   измерения (x_i+1-x_i) весьма мала. Тогда функция ε (Δχ) определяет точность измерения параметра х, если задана точность измерения меры различия ε. Это иллюстрируется рис. 4.2.1, a где вдоль кривой ε (Δχ) показана полоса возможных ошибок шириной ± δε_m. Определяя х по минимальному значению ε', мы ошибемгя на величину, которая лежит в пределах от δχ₁ до δχ₂. Очевидно, оем круче нарастают обе ветви функции ε (Δχ)), тем меньше будут пределы ошибок (δχ₂ — δχ₁).

Сигнальная функция q (Δχ) при неэнергетической модуляции связана с мерой различия простым соотношением (4.1.6), т. е. вместо измерения ε' можно говорить об измерении q' с ошибкой δq_m и определять точность оценки параметра х по графику сигнальной функции, как показано на рис. 4.2.1, б.

Сравнивая сигнальные функции для двух случаев (1 и 2) на рис. 4.2.2, а, можно утверждать, что сигнал, которому соответствует сигнальная функция 2, обеспечивает при равных ошибках bqm лучшую точность передачи сообщения, чем сигнал, которому соответствует функция 1. Несколько сложнее обстоит дело, когда приходится сравнивать сигнальные функции 1 и 2, представленные на рис. 4.2.2, б. При высокой точности измерения, когда ошибки измерения параметра значительно меньше величин δx₁ и δx₂, сигнал с сигнальной функцией 2 лучше, чем сигнал с функцией 1. При более грубых измерениях это уже не обязательно, и, если ошибки, большие δχ₁ и δχ₂ встречаются достаточно часто, сигнал с функцией 1 может оказаться предпочтительнее.

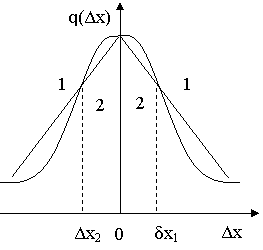
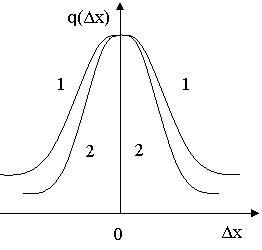
Рис. 4.2.2. К сравнению двух сигнальных функций.

Возможен и другой подход к анализу такой сигнальной функции. Допустим, что ошибки измерения bq большей частью малы, но существует и некоторая вероятность (малая) появления больших ошибок. Тогда можно считать, что точность оценки параметра х определяется начальным участком сигнальной функции, но могут иметь место и аномальные большие ошибки. Вероятность отсутствия аномальных ошибок характеризует надежность измерения. При таком подходе сигнальные функции следует сравнивать по двум показателям: точности и надежности. Чем меньше уровень боковых максимумов в сигнальной функции, тем выше надежность измерения.

В некоторых случаях параметр х, несущий информацию, может принимать только ряд дискретных фиксированных значений и задача   измерения сводится к определению номера значения х в радиосигнале. Такой случай характерен, например, для цифровых методов передачи информации. Сигнальная функция для такого сигнала также будет дискретной. Ошибка при измерении сигнальной функции может привести к тому, что вместо истинного значения параметра х_и будет принято другое фиксированное значение х_j. Качество измерения при этом удобно характеризовать вероятностью ошибки, а сигнал будет тем лучше, чем больше отличаются от единицы значения сигнальной функции.

Анализируя двумерную сигнальную функцию, необходимо различать следующие два случая.

1. Оба неизвестных параметра несут сообщения, которые должны быть измерены на приемном конце радиолинии. С таким случаем мы сталкиваемся, например, в измерительных радиосистемах, где по одному сигналу измеряются расстояние и скорость. Возможно также применение совмещенных радиосистем, где сигнал, модулированный сообщением в передатчике, одновременно используется для определения расстояния или скорости. Двумерная сигнальная функция q(Δx, Δγ) представляет собой некоторую поверхность, причем в начале координат q(0, 0) = 1. Чем быстрее спадает эта поверхность при отклонении в любом направлении от начала координат, тем точнее будут оценки параметров для заданной ошибки измерения bq. Наличие у поверхности q(Δx, Δγ) нескольких максимумов может быть причиной неоднозначного определения параметров. Поэтому желательно, чтобы все дополнительные максимумы были значительно меньше основного или отстояли достаточно далеко от него.

2. Только один параметр х несет сообщение. Второй неизвестный параметр γ не дает полезной информации для решения задачи, т. е. является паразитным случайным параметром. Несмотря на то, что измерять γ не требуется, образцы сигнала должны также варьироваться и по γ, хотя количество и величина градаций по каждому параметру могут сильно различаться. Пусть, например, полезным параметром является задержка т, а паразитным — смещение частоты Ω. Если образцы сигнала будут различаться между собой только по задержке τ то вполне возможно, что ни один из них не даст хорошего сходства с принятым сигналом из-за различия по частоте, в том числе и тот, у которого будет τ_i = τ_и. Значит, в случае, когда один из двух параметров паразитный, сигнальную функцию следует также рассматривать как функцию двух переменных. Однако требования к виду сигнальной функции теперь будут другие. Быстрый спад поверхности q (Δx, Δγ) необходим только вдоль оси Δx. По оси Δγ он должен быть как можно более пологим, это позволит уменьшить чувствительность радиосистемы к изменениям паразитного параметра.

Лекция 5.

ВЫБОР СТРУКТУРЫ

И ОЦЕНКА ТОЧНОСТИ РАДИОСИСТЕМ

ОБОБЩЕННАЯ МОДЕЛЬ ПРИЕМА И ЗАДАЧА ОПТИМИЗАЦИИ

5.1. Постановка задачи оптимизации радиоприема

Теория оптимальных методов радиоприема (теория оптимального обнаружения  и выделения сигнала, теория оптимального оценивания, теория синтеза оптимальных систем) – важнейшая область современной радиотехники. В соответствии с требованиями практики теория оптимальных методов радиоприема существенно развита на основе аппарата математической статистики и теории статистических решений. Эта теория представляет собой достаточно мощный инструмент исследования, позволяет решать широкий круг практических задач, возникающих при проектировании радиосистем.

Использование теории оптимального приема дает возможность, отказавшись от поиска наилучшего варианта путем перебора, сразу (по определенному правилу) найти структуру оптимальной системы. Это позволяет существенно сократить время проектирования и, главное, гарантировать то, что найденная система действительно является наилучшей.

Даже если полученную оптимальную структуру невозможно физически реализовать, само исследование этой структуры может подсказать проектировщику направление, которому надо следовать при построении реальной системы и тем самым способствовать развитию инженерной интуиции проектировщика. Не менее важным для практики результатом, полученным с помощью методов теории оптимальных систем, является нахождение предельных (потенциальных — по определению Котельникова) характеристик качества радиосистем. Эти характеристики могут использоваться для того, чтобы судить, насколько та или иная реальная система близка к идеалу. Такое сравнение позволяет достаточно объективно решить вопрос о необходимости усовершенствования данной системы (или разработки новой).

Все сказанное не дает, однако, основания переоценивать значение теории оптимального приема для проектирования реальных радиотехнических систем. Прежде всего, это связано с тем, что оптимальность систем в рамках этой теории рассматривается лишь с точки зрения улучшения помехоустойчивости, которая является хотя и важным, но не единственным требованием, предъявляемым к проектируемой радиосистеме. Наличие дополнительных требований и ограничений (технического, технологического и эксплуатационного характера) заставляет проектировщика отходить от оптимального алгоритма обработки, заменять одни операции над сигналом другими, вводить новые операции, непосредственно не следующие из решения задачи оптимизации.

Получение практически значимых результатов оказывается возможным лишь при существенном упрощении модели сигналов и помех, действующих в радиосистеме. При этом в лучшем случае может быть получен алгоритм обработки в виде совокупности математических операций над сигналом. Отличие свойств реальных сигналов и помех от принятых в модели, конечная точность реализации необходимых математических операций также ограничивают возможности практического применения теории. Таким образом, теория оптимальных методов радиоприема должна применяться лишь в сочетании с другими методами расчета.

Задача оптимизации структуры обработки сигнала в радиосистеме подчинена задаче оптимизации комплекса. Учитывая ограниченность (с точки зрения полной оптимизации) этой задачи желательно сформулировать ее так, чтобы полученные результаты относились, по возможности, к широкому классу радиосистем. Для этого первоначальная модель должна быть достаточно общей. Исходным пунктом для построения модели здесь может служить целевое назначение радиосистемы, которое состоит в доставлении получателю информации, необходимой для функционирования комплекса.

Обобщенная модель приема сообщения, элементарный сеанс

Главным при построении модели является то, что с помощью радиосистемы получатель приобретает дополнительную информацию, проще говоря, после приема радиосигнала он узнает нечто новое об интересующем его сообщении. Конкретный физический смысл сообщений, способ модуляции, а также то, где происходит модуляция — на трассе распространения или в передатчике, — здесь несущественно. Поэтому модель будет одинаково хорошо применима к системам извлечения и передачи информации.

При описании модели удобнее пользоваться терминологией, которая чаще применяется для описания систем передачи, а не систем извлечения информации. Например, термин «сообщение, передаваемое получателю» применительно к системам извлечения информации следует понимать, как одно из возможных пространственно-временных положений объекта, а термин  «источник сообщений» – как пространственно-временную область, в которой может находиться объект.

 С точки зрения приема радиосигнала извлечение информации можно рассматривать как передачу от некоторого эквивалентного источника.

Элементарный сеанс связи определим как совокупность операций:

— выбор источником одного сообщения из множества возможных вариантов и (после преобразования в сигнал) отправление его получателю;

— преобразование посланного сигнала под действием помех в реализацию смеси, которая наблюдается получателем (приемником);

— принятие получателем по наблюдению реализации смеси решения о том, какое сообщение выбрал в данном случае источник, т. е. оценка сообщения. При этом множество возможных оценок совпадает с множеством исходных сообщений.

Термин «оценка» имеет два значения: 1) оценка как сам процесс принятия решения (иногда здесь употребляется термин «оценивание»); 2) оценка как получаемый результат. Соответственно, например, «произвести оценку» — выполнить определенные операции в процессе решения; «характеристики оценки» — характеристики полученного результата. Поскольку из контекста всегда ясно, о каком значении идет речь, этот термин в дальнейшем будет употребляться в обоих возможных значениях без дополнительных оговорок.

Применение некоторого правила принятия решения (оценивания) или оператора A — это установление соответствия между наблюдаемой получателем реализацией смеси и одной из возможных оценок. Оптимизация обработки — выбор среди возможных правил наилучшего (по определенному критерию).

Таким образом, элементарный сеанс задается множествами (ансамблями) исходных сообщений и оценок. Физический смысл, конкретное содержание сообщения, длительность передачи и т.д. в этой первоначальной модели не играют никакой роли. Каждый реальный сеанс приема сообщений может представляться либо одним элементарным сеансом, либо последовательностью элементарных сеансов в зависимости от того, какова совокупность возможных решений. Так, например, если в системе цифровой передачи информации применяется посимвольный прием, то элементарный сеанс соответствует приему одного символа, а прием слова — последовательности элементарных сеансов. При приеме в целом (пословном) элементарный сеанс соответствует приему слова, а прием последовательности слов образует совокупность элементарных сеансов. Вопрос о том, из каких соображений определяется элементарный сеанс при решении конкретных задач оптимизации, будет неоднократно затрагиваться при рассмотрении различных моделей сообщений и ограничений, накладываемых на решение.

Пока предполагается, что отдельные элементарные сеансы независимы, так что информация, полученная в одном сеансе, не используется при проведении последующих сеансах. Иногда, например, в задачах последовательного анализа, приходится учитывать зависимость следующих друг за другом элементарных сеансов.

С целью упрощения анализа положим для начала, что множество возможных сообщений (и соответственно множество решений — оценок), а также множество всех реализации смесей, наблюдаемых получателем, дискретные и конечные. На практике встречаются случаи, когда ситуация точно соответствует такой модели, например в системе передачи дискретных сообщений при обработке дискретной и квантованной по уровню выборки из наблюдаемой смеси.

В тех случаях, когда множества сообщений и смесей не дискретные, основой для использования дискретной модели служит теорема отсчетов. Любая величина, принимающая непрерывное множество значений, с достаточной степенью точности (с учетом конечной разрешающей способности (апертуры) любых реальных устройств) может быть представлена дискретными значениями, отстоящими на величину апертуры. С учетом ограничения динамического диапазона (всегда выполняющегося на практике) количество таких дискретных значений получается конечным.

Это же рассуждение может быть распространено на сообщения или смеси, представляющие собой совокупность нескольких величин, т. е. векторы. Поскольку практически функция времени с любой заданной точностью может быть представлена вектором в n-мерном пространстве, все сказанное можно отнести к случаю, когда сообщение или смесь – функция времени.

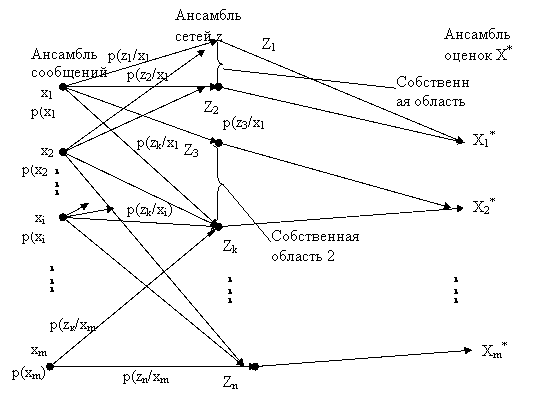Рис. 5.1.1.  Модель приёма сообщений.

С формальной точки зрения для перехода от дискретных ансамблей к непрерывным в приведенных далее выражениях необходимо заменить распределения вероятностей плотностями вероятностей, а суммы — интегралами соответствующих размерностей; там, где необходимо, это будет делаться без дополнительных оговорок.

Для дискретных ансамблей удобно воспользоваться графическим представлением модели приема сообщений – рис. 5.1.1. Каждая точка представляет собой один из элементов соответствующего множества сообщений X, смесей Z или оценок X^*. Стрелки, соединяющие элементы множества X и Z, отображают переход истинного сообщения,   выбранного источником, в одну из реализации смеси. Из-за случайного характера помех одно и то же сообщение может (с той или иной вероятностью) переходить в различные реализации смеси и в одну и ту же реализацию смеси могут переходить разные сообщения. Статистические свойства помех удобно задать вероятностью перехода 1-го сообщения в k-ю смесь, т. е. условной вероятностью р(z_k|x_i).

Стрелки,   соединяющие реализации смеси с элементами множества оценок, отображают правило (или оператор системы),   по   которому  каждой  принятой реализации смеси ставится в соответствие одно из множества возможных значений сообщений. Можно сказать иначе: каждое правило соответствует разбиению всего множества смесей Z на ряд непересекающихся (т. е. не имеющих общих элементов) подмножеств — областей. Число областей равно числу сообщений (или числу решений), каждая такая область называется собственной областью одного из решений. При попадании реализации в j-ю собственную область выбирается решение х^*_j. Кажется очевидным, что (за исключением вырожденных случаев) общее число элементов множества смесей п должно быть не меньше числа возможных сообщений m. Обычно выполняется условие п > m. Если сообщения и смеси допускают векторное представление, то это может означать, что размерность пространства смесей больше размерности пространства сообщений.

На рис. 5.1.1 не выделена явно операция преобразования сообщения в сигнал, поскольку при заданном виде этого преобразования (т. е. при заданном методе модуляции) соответствие между сигналом и сообщением взаимнооднозначное и не вносит ничего нового в структуру рассматриваемой модели. Однако конкретные значения переходных вероятностей р(z_k|x_i) и сама структура множества Z обязательно зависят от вида сигнала и помех, действующих в радиолинии.

Каждому элементарному сеансу на рис. 5.1.1 соответствует какая-то одна цепочка переходов x_i ® z_k ® х^*_j. Если x_i совпадает с х^*_j (i = j), сообщение принято правильно, если нет, то произошла ошибка при приеме.

Апостериорное распределение. Что может знать получатель о сообщении до и после каждого элементарного сеанса? До сеанса ему может быть известно лишь множество возможных сообщений, но не известно, какое именно сообщение выберет источник в данном сеансе. Будем полагать также, что получателю известно распределение вероятностей р(x_i) на множестве X, т.е. получатель знает, как часто в среднем выбирает источник то или иное сообщение. В дальнейшем р(x_i) называется априорным распределением.

В течение сеанса наблюдается одна из возможных реализации смеси. Если помехи отсутствуют, все условные вероятности р(z_k|x_i) равны нулю, кроме одной, равной единице. При этом получатель может дать точный ответ на вопрос о том, какое сообщение передавалось. В присутствии помех дать такой однозначный ответ невозможно, так как в одну и ту же реализацию смеси могли перейти различные сообщения. Следовательно, и после приема z_k сведения получателя о передаваемом сообщении имеют вероятностный характер. Полученная реализация смеси определяет не конкретное сообщение, а некоторое новое распределение вероятностей на множестве сообщений, называемое апостериорным распределением. Отличие апостериорного распределения от априорного – перераспределение вероятностей отдельных значений сообщения – содержит всю дополнительную информацию для получателя после приема реализации смеси.

Апостериорное распределение р(x_i|z_k) представляет собой условное распределение выбранного источником сообщения при заданной реализации смеси z_k. Функция р(x_i|z_k) явно зависит от принятой в сеансе реализации смеси z_k. Уточнение сведений о переданном сообщении после приема получателем реализации смеси связано с тем, что апостериорное распределение оказывается «ýже» априорного, причем если помехи отсутствуют, то

,

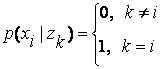и получатель достоверно (с вероятностью, равной единице) опознает сообщение. Если же р(z_k|x_i) не зависит от x_i (физически это означает, что сигнал в смеси отсутствует), апостериорное распределение совпадает с априорным и никакой дополнительной информации получатель из смеси не извлекает – рис. 5.1.2.

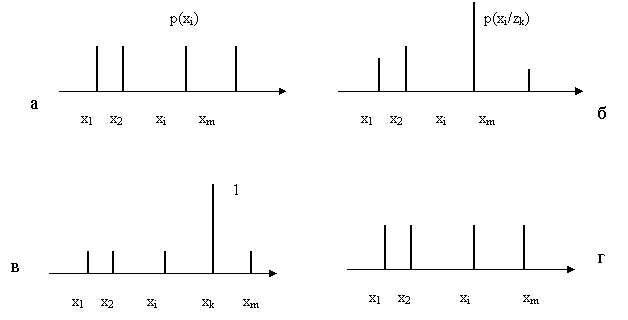Рис. 5.1.2. Априорное распределение сообщения (а) и апостериорные распределения при k-й принятой реализации (общий случай) (б), при отсутствии помех (в) и при отсутствии сигнала (г).

Постановка задачи синтеза оптимальной системы

Для корректной постановки задачи синтеза оптимальной приемной структуры (оптимальной совокупности операций над реализацией смеси)  необходимо определить:

— ансамбль сообщений – задать «элементарный сеанс»;

— вид помех, действующих в радиолинии;

— критерий оптимальности;                     

— ограничения, которые накладываются на правило оценки, т.е. класс систем, среди которых ищется оптимальная система.

Следует помнить, что не существует систем, оптимальных вообще, а может существовать система, оптимальная в заданном классе, при данном виде помех, для заданного ансамбля сообщений и, наконец, в смысле заданного критерия. Надо отметить, что сравнивать системы, построенные для разных исходных предположений, имеет смысл в тех случаях, когда возможность изменения условий, соответствующих этим предположениям, находится в распоряжении проектировщика. Можно говорить, что система, оптимальная по заданному критерию в некотором заданном классе, лучше (или хуже) системы, оптимальной потому же критерию в другом классе. Однако при решении вопроса о практическом предпочтении той или иной системы необходимо привлечь дополнительные критерии, учитывающие различия классов, например по сложности, стоимости и т. д.

Критерии оптимизации системы. Очевидно, что лучшей следует считать ту систему, которая обеспечивает наименьшие искажения передаваемого сообщения. Точный смысл этому утверждению можно придать, основываясь на общем подходе, подробно обсуждавшемся в гл. 1, а именно, когда качество воспроизведения сообщения связывается с некоторыми потерями (платой), и синтезируется система, обеспечивающая наименьшие потери. Функция двух переменных r(x_i, x^*_j), значение которой (в некотором масштабе) равно стоимости решения x^*_j при условии, что передавалось сообщение х_i, называется функцией потерь (риска, штрафа и т.д.). При выборе функции потерь исходным пунктом служит соображение, что радиосистема является подсистемой комплекса, который использует поступающую от нее информацию. Если оценка ошибочна, т. е. при истинном передаваемом сообщении х_i принято решение x^*_j ¹ x_i, то неправильные действия получателя (в составе комплекса) повлекут за собой некоторые потери r, которых бы не было, будь оценка безошибочной. Потери в общем случае, конечно, зависят от того, какое именно x^*_j принято вместо x_i.

Предположение о том, что действия получателя однозначно определяются значением оценки x^*_j эквивалентно тому, что потери полностью определяются парой значений x_i, x^*_j и не зависят от используемого правила решения от того, какой путь соединяет точки x_i и x^*_j – рис. 5.1.1. Именно такие функции потерь и рассматриваются в дальнейшем.

Поскольку потери r (x_i, x^*_j) в каждом элементарном сеансе случайны из-за случайности x_i и x^*_j построение критерия после задания функции потерь требует определения статистически устойчивого параметра, характеризующего качество системы на множестве сеансов. Чаще всего применяется подход, основанный на использовании математического ожидания потерь, при котором гарантируется минимум суммарных потерь. Математическое ожидание потерь

                                           (5.1.1)

называется средним риском, а система, минимизирующая средний риск (при условии, что функция потерь не зависит от правила решения), называется оптимальной байесовой системой.

Потери в каждом элементарном сеансе по предположению не зависят от структуры оператора обработки А, но средний риск явно зависит от оператора Л, так как последний определяет совместное распределение p(x_i, x^*_j), иначе говоря, от вида оператора зависит, сколь часто встречается то или иное сочетание x_i, x^*_j.

Таким образом, оптимальный оператор А* определяется условием

,                              (5.1.2)

где – любой оператор, принадлежащий заданному классу A.

Выражение (5.1.1) может быть переписано в следующем виде:

,

где р(x_i, x^*_j) — совместное распределение вероятностей сообщения и оценки.

Каждой реализации смеси z_k ставится в соответствие определенное x^*_j – результат применения к z_k оператора A, т.е.

х^* = х^*(z_k) = A {z_k},

поэтому последнее выражение можно представить в виде

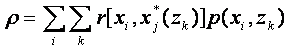.                  (5.1.3)

Здесь  р(x_i, z_k) = р(x_i)р(z_k|x_i) = р(z_k)р(x_i|z_k) — совместное распределение вероятностей z_k и x_i. Выражение (5.1.3) можно еще раз переписать в виде

                        (5.1.4)

или

.                     (5.1.5)

Рассмотрим выражения

;                               (5.1.6)

.                            (5.1.7)

Функцию r_z называют условным средним риском при данной реализации смеси, а r_x — условным средним риском при данном истинном сообщении. Эти понятия являются весьма важными для дальнейшего рассмотрения. В частности, условный средний риск при данном сообщении r_х может служить характеристикой качества системы, а условный средний риск при данной реализации смеси r_z используется для определения структуры оптимальной байесовой системы.

5.2. Ограничения в задаче оптимизации

Любое решение проектировщика можно назвать ограниченным из-за того, что при построении модели учитывается конечное число явлений бесконечно сложной действительности. В рассматриваемой задаче эти ограничения обусловлены заданием ансамблей сообщений и наблюдаемых смесей. Ясно, что проектировщик обладает довольно большой свободой выбора первого из названных ансамблей.

Обычно чем «проще» ансамбль сообщений, тем проще структура оптимального оператора. Правда, может оказаться, что качество оценок будет хуже, чем в случае более сложных ансамблей. Поясним это примером. Рассмотрим прием дискретных сообщений в системе передачи информации с двоичной КИМ. Реальный сеанс связи длится время T, в течение которого передается n слов. Используя весь массив полученной информации, получатель принимает некоторое практическое решение. Для данной задачи можно определить элементарный сеанс или как прием одного символа — при этом ансамбль сообщений (и оценок) содержит два элемента, или как прием слова — ансамбль сообщений состоит из m элементов (m — количество уровней квантования), или как прием блока, состоящего из k слов — ансамбль сообщений включает m^k возможных комбинаций. В принципе возможен случай, когда число k равно n, при этом элементарный сеанс соответствовует реальному сеансу, а множество сообщений имеет mⁿ элементов.

Реально используется посимвольный прием и реже прием в целом отдельных слов, который оказывается сложнее, хотя и обеспечивает более высокую помехоустойчивость. Применение блочного приема наталкивается на существенные трудности при реализации, связанные с быстрым ростом числа возможных исходных сообщений и оценок. Однако в принципе блочный прием может обеспечить еще более высокое качество оценок.

Разумеется, сравнивать оценки, соответствующие разным моделям исходного сообщения, не имеет смысла – они принадлежат разным множествам. Сказанное выше о различном качестве оценок следует понимать так, что если, например, в первом из перечисленных способов приема по отдельным символам восстановить слова, а затем и всю совокупность слов, то оценка этой совокупности может оказаться хуже, чем для последнего случая.

Вид оптимального оператора существенно зависит и от множества наблюдаемых реализаций смеси. Под термином смесь в данной модели вовсе не обязательно подразумевается процесс на входе приемника. Исходя из технических возможностей реальных систем обработки, стремления снизить сложность синтезируемой системы и, наконец, из имеющегося опыта и здравого смысла, проектировщик обычно задает ряд предварительных преобразований сигнала в приемном тракте и лишь после этого ставит задачу нахождения оптимального оператора. Наличие этих предварительных преобразователей принципиально не изменяет исходной модели приема сообщений (рис. 6.1.1), а соответствующим образом определяет условные вероятности p(z_k|x_i). Такая постановка приводит к задаче синтеза в частично заданной структуре. Часто наблюдаемые смеси рассматриваются на выходе УПЧ, но могут встречаться и другие случаи, например синтез системы последетекторной обработки. В отдельных случаях смесь может подвергаться предварительной обработке специального вида. Например, если оптимизируемая система должна быть реализована на ЭВМ, требуется дискретизация процесса во времени и квантование по уровню и т. д.

Иногда задача оптимизации приема может разбиваться на ряд подзадач в частично заданных структурах. При этом оценки, получаемые в предыдущей системе, являются исходными для формирования модели ансамбля смесей для последующей системы обработки. Так, задачу приема корректирующего кода можно разбить на две:

— прием отдельного символа (ансамбль сообщений – «0» и «1», ансамбль смесей – реализации случайного процесса на интервале времени, равном длительности символа);

— прием комбинации символов – слов (ансамбль сообщений – множество разрешенных слов, ансамбль реализации – последовательности нулей и единиц заданной длины).

Рассмотренные ограничения, связанные с заданием ансамблей сообщений и смесей, появляются на этапе построения модели и, можно сказать, не являются ограничениями в формальном (математическом) смысле, ибо после того, как модель построена, т. е. задача формализована, они никак себя не проявляют. Учитывать их приходится при практической интерпретации полученного решения.

Сосредоточим внимание на ограничениях другого рода, которые появляются после построения модели и состоят в том, что не все возможные операторы обработки сигнала считаются разрешенными. Иными словами, поиск оптимального оператора производится среди операторов некоторого класса, обладающего определенными свойствами. Пока рассматриваются нерандомизированные операторы, т. е. те, которые при данном значении z_k однозначно определяют некоторое значение х*_j. Вновь обратимся к модели, введенной в начале первого параграфа – рис. 5.1.1. Здесь оператор может быть задан или таблицей, где каждому z_k ставится в соответствие некоторая х*_j или совокупностью стрелок (ребер графа), соединяющих точки множества Z сточками множества X*.

Рассмотрим сначала случай отсутствия ограничений. Это означает, что возможны любые сочетания наблюдаемых смесей и оценок, так, что если какому-то z_k поставлено в соответствие некоторое х_i, то любому другому z_i может быть поставлено в соответствие любое х*_m (в частности, может быть х*_m = х*_j). После того как задано соответствие (отображение) z_k ®  x*_j, может быть вычислен условный средний риск

         (5.2.1)

причем его значение, как легко видеть, зависит только от данного соответствия z_k ®  x*_j и не зависит ни от каких других z_i ®  x*_m. Отображение z_k ®  x*_j, может быть выбрано так, чтобы р_z было минимально (на множестве х*_j). Поскольку ограничения отсутствуют, для любого другого z_l, может быть сделано то же самое. Тогда полученный оператор (совокупность всех z_k ®  x*_j) будет обеспечивать минимум условного среднего риска r_z при каждой реализации смеси z_k. Но в таком случае этот оператор будет обеспечивать и минимум полного среднего риска. Действительно, если оператор А* системы таков, что условный риск

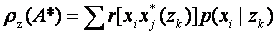
меньше, чем для любой другой системы с оператором , то и полный средний риск в такой системе

будет минимальным. Это следует из того, что все p(z_k) неотрицательны. Следовательно, А* – оптимальный байесов оператор.

Таким образом, минимум условного (при данном z_k) среднего риска – достаточным условием для минимума полного среднего риска, а поскольку при отсутствии ограничений оператор, минимизирующий условный риск, всегда существует, то это условие одновременно и необходимым.

Следовательно, для нахождения оптимального оператора при отсутствии ограничений проектировщик располагает двумя эквивалентными условиями: условием минимума среднего риска (5.1.2) и условием минимума условного среднего риска

.                                      (5.2.2)

Из двух подходов, соответствующих условиям (5.1.2) и (5.2.2), последний – более простой по применяемому математическому аппарату. Выражение условного среднего риска r_z представляет собой просто функцию х* (если оценка является векторной, то это функция нескольких переменных). Реализация смеси может рассматриваться как параметр функции r_z (если z — реализация случайного процесса, то в r_z входит некоторый функционал от реализации). Задача, таким образом, сводится к определению значений аргумента х*, обеспечивающего минимум функции r_z. При этом могут использоваться все известные математические методы отыскания экстремума. Найденное значение х* будет, конечно, зависеть от параметра функции, т. е. от z_k. Эта зависимость и будет выражением для искомого оптимального оператора.

Итак, для нахождения оптимального оператора достаточно располагать апостериорным распределением, которое может быть найдено через априорное распределение смеси при заданном сообщении по формуле Байеса

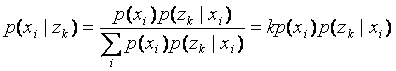.                 (5.2.3)

Аналогично для непрерывного ансамбля сообщений

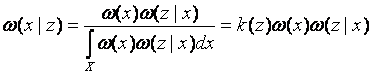.              (5.2.4)

Подразумевается, что х и z могут быть случайными векторами, тогда соответствующие плотности и интегралы следует понимать как многомерные.

Когда z — реализация непрерывного процесса, структура формулы (5.2.4) сохраняется, но выражение w (х | z), рассматриваемое как функция z, уже не является условной плотностью вероятности реализации. Сомножители p(z_k|x_i) и w(х|z), рассматриваемые при фиксированном z как функции сообщения х, называются функциями правдоподобия, и обозначаются в дальнейшем L(х). Множитель k обеспечивает нормировку w(х|z) и, поскольку он не зависит от х, может опускаться при нахождении оптимального оператора из условия (5.2.2).

Таким образом, получение оценки в байесовой системе (без ограничений) всегда принципиально можно свести к следующей последовательности операций:

— вычисление апостериорного распределения сообщения при принятой реализации смеси; для этого необходимо располагать знанием вида априорного распределения и условного распределения смесей при данном сообщении; полученное апостериорное распределение является функцией сообщения;

— вычисление условного (при данной реализации смеси) среднего риска r_z; для этого нужно задаваться видом функции потерь r(x_i, x*_j) исходя из опасности (стоимости) ошибок в воспроизведении сообщения; условный средний риск является функцией оценки х*;

— нахождение значения оценки х^*₀, минимизирующей условный средний риск.

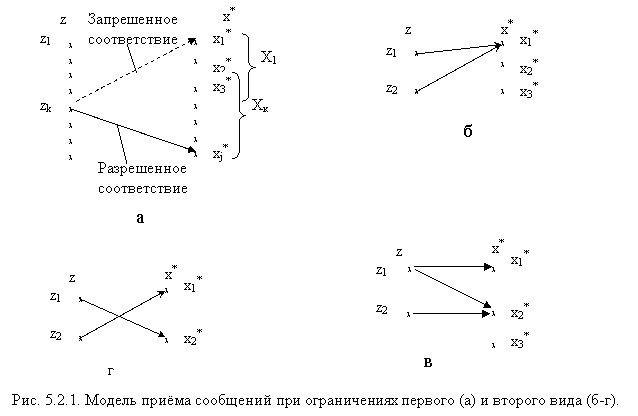Решая задачу оптимизации в численном виде, можно прямо реализовать эту последовательность операций, однако практически делать так нецелесообразно. Если удается найти аналитическую зависимость оптимальной оценки от наблюдаемой смеси, то эту зависимость и нужно реализовать в алгоритме обработки. Если же полного аналитического решения найти не удается, то, как правило, оказывается возможным свести указанные выше операции к эквивалентным, но более простым с точки зрения практического выполнения.

Теперь предположим, что на класс операторов наложены ограничения. Для нашей модели это означает, что лишь часть соответствий z_k ® x*_j является разрешенной, другие же соответствия запрещены. Иными словами, не все возможные таблицы соответствий (или комбинации стрелок на рис. (5.1.1) могут рассматриваться в задаче оптимизации. Разумеется, чтобы задача выбора оптимального оператора имела смысл, число разрешенных таблиц (комбинаций стрелок) должно быть больше единицы. При наличии ограничений следует рассмотреть две ситуации, приводящие к различию в нахождении решения: 1) отображение z_k ® x*_j может быть не любым, но, тем не менее, может выбираться независимо от того, как выбраны другие z_l ® x*_m ; 2) выбор конкретного соответствия z_k ® x*_j  зависит от того, как выбраны другие соответствия z_i ® x*_m.

Пользуясь наглядным представлением задачи (рис. 5.1.1), приведем примеры ограничений первого и второго вида, не заботясь пока о физической интерпретации, которая будет дана ниже.

Примером ограничения первого вида является случай, когда некоторому z_k может быть поставлено в соответствие х*_i, принадлежащее некоторому подмножеству X*_k множества X* (X*_k Ì X*). Подмножества X*_k, X*_i могут пересекаться –  рис. 6.2.1, а.

Построение примера ограничений второго вида поясняется рис. 5.2.1, б—г. Положим, что запрещенные комбинации приводят к пересечению стрелок, тогда рис. 5.2.1, б, в  соответствуют разрешенным комбинациям, а рис. 5.2.1, г – запрещенной. Видно, что в этом случае возможность выбрать соответствие

z₂ ®x*₁ зависит от того, как выбрано соответствие z₁ ®  x*_j, и наоборот.

При ограничении первого вида каждое соответствие z_k®x*_j и, следовательно, оператор в целом можно выбрать так, чтобы обеспечивался условный (при условии, что z_k ®  x*_j разрешено) минимум условного (при данном z_k) среднего риска r_z. Повторяя предыдущие рассуждения, можно утверждать, что этот оператор обеспечит минимум полного риска в заданном классе операторов. Следовательно, задача опять-таки может быть сведена к нахождению оператора, минимизирующего условный средний риск (при данном z_k), но при минимизации необходимо дополнительно учесть ограничения. Полученная оптимальная система в общем случае будет хуже, чем система, оптимизированная при отсутствии ограничений; из-за того, что абсолютный минимум  может не совпадать с условным (при наложенных ограничениях) минимумом.

Совсем иная картина будет при ограничении второго вида. Допустим, что минимизация условного среднего риска начинается с z₁. Тогда в разрешенном классе соответствий может быть определено z₁ ® x*_p, при котором условный риск r_z = r^’₁ минимален. Переходя к z₂, мы оказываемся связанными дополнительными ограничениями, и минимум условного риска r_z = r’₂ будет зависеть от вида преобразования z₁®x*_p. Рассуждение можно легко продолжить для остальных z_k (k = 3, 4, ..., п). Тогда получится последовательность условно (из-за наличия ограничений) минимальных значений риска.

Если же начать минимизацию с какого-либо другого z, например с z₂, то получится другая последовательность: . При этом может оказаться, что некоторые , а другие . Полный средний риск r будет теперь зависеть от конкретных значений вероятностей р(z_k), и, следовательно, условная минимизация (при наличии ограничений) условного среднего риска r_z не дает решения задачи поиска байесовой системы. Точнее говоря, каждая процедура минимизации r_z определяет одну из нехудших систем, среди которых нужно искать оптимальную в смысле минимума взвешенной суммы r_z. Таким образом, при наличии ограничений второго вида для нахождения оптимального оператора можно использовать лишь условие (5.1.2).

Теперь приведенным иллюстративным примерам можно придать физический смысл. Пусть проводится синтез в частично заданной структуре, так что оценка получается из наблюдаемой смеси путем преобразования заданным оператора , определяемого с точностью до некоторых параметров (a, b, g). Задача оптимизации сводится к выбору оптимальных параметров a, b, g.  Предположим, что параметры преобразования a, b, g могут выбираться различными для разных реализации z_k. Тогда имеют место ограничения первого вида. Условный средний риск (при данной реализации) определяется выражением   

                             (5.2.5)

после чего остается выбрать a = a (z_k), b = b (z_k), g = g(z_k) так, чтобы (5.2.5) обращалось в минимум. Очевидно, что при этом будет одновременно достигаться и минимум безусловного среднего риска (5.1.2).

Если при той же исходной постановке задачи потребовать, чтобы a, b, g были одинаковы для всех z_k, то возникнут ограничения второго вида. Выбор постоянной времени фильтра в §5.3 можно рассматривать как простейший пример такой задачи. Можно, скажем, минимизировать (5.2.5) при z₁, но для всех остальных z_k (k ¹ 1) условные риски окажутся фиксированными. Следовательно, для оптимизации необходимо пользоваться требованием минимума полного (безусловного) риска (5.1.2). Именно такого рода ограничения возникают в задаче оптимальной линейной фильтрации, где оценка связана с наблюдаемой реализацией линейным преобразованием, заданным с точностью до весовой функции, которую и нужно определить.

При определении оптимального оператора в ограниченном классе может оказаться, что для решения задачи требуется меньше статистических данных об ансамблях сообщений и помех. Так, при синтезе в классе линейных систем оказывается достаточным знание не полного апостериорного распределения, а лишь вторых моментов сообщений и смесей. Последнее обстоятельство также играет существенную роль при выборе ограничений на класс оператора: если знания статистики ансамблей ограничены, нет смысла ставить задачу оптимизации в классе всех систем.

Рандомизированные правила. Заметим теперь, что операторы, которые по заданному правилу ставят в соответствие каждому z_k определенную оценку x^*_j, не исчерпывают всех возможных операторов.

Поскольку принятая реализация определяет не конкретное сообщение, а лишь распределение вероятностей, получатель может для нахождения оценки применить механизм случайного выбора. При этом после получения реализации смеси включается генератор случайных чисел, генерирующий выборку оценок x^* с некоторым распределением w (x^*|z), параметры которого определяются принятой реализацией. Выпавшее случайное значение x^* принимается в качестве оценки. Такие правила оценки называются рандомизированными (случайными) в отличие от нерандомизированных. Модель для рандомизированного правила аналогична рис. 5.1.1. Но в отличие от него каждая z_k, должна быть соединена не с одной x^*_j, а со всеми, причем переход определяется условной вероятностью р(x^*_j|z_k). Возникает вопрос, не может ли рандомизированный оператор обеспечить меньший средний риск, чем нерандомизированный. Оказывается, нет. Действительно, при каждом z_k случайный выбор того или иного x^*_j эквивалентен случайному выбору одного из возможных правил решения (при отсутствии ограничений). Тогда условный (при данном значении z_k,) средний риск для рандомизированного оператора

,

где r⁽ⁱ⁾_z – условный риск, соответствующий i-му правилу; р_i – вероятность выбора этого правила.

Поскольку среднее всегда не меньше, чем минимальная из усредняемых величин (которая обеспечивается именно байесовой системой), то r_zранд ³ r_zб. Значит, в рамках рассматриваемой модели использование рандомизированных правил не приводит к лучшим результатам. Необходимость в таких правилах может возникнуть в случае активного противодействия противника при условии, что противник знает о наших действиях и может использовать это зна-ние для нанесения дополнительного ущерба. Это так называемые игры с полной информацией при отсутствии седловой точки. В игровых задачах рандомизированные правила носят название смешанных стратегий.

Затраты на наблюдение реализации смеси. Последовательные правила принятия решения. До сих пор работа радиосистемы в комплексе оценивалась лишь с точки зрения качества информации, доставляемой получателю. Однако уже сам подход, использованный нами, при котором ошибке в приеме сообщения приписывается определенная стоимость и выбором оператора минимизируются суммарные затраты, содержит в себе элемент ограниченности, и более широкий взгляд на задачу заставляет усложнять первоначально введенную модель.

Действительно, раз система строится исходя из требования наименьших затрат в комплексе, то естественно учесть не только потери, вызванные неправильным приемом сообщения, но и средства, затраченные на создание самой радиосистемы, а также стоимость проведения сеанса связи (извлечения информации). Разумеется, проблема отсутствовала бы, если бы оптимальность достигалась по всем критериям одновременно. Очевидно, однако, что сформулированные требования являются противоречивыми: высокоточная система будет дороже низкоточной.

Основные результаты, расширяющие исходную модель приема сообщения, достигнуты при решении задачи, в которой учитывается, что время, затраченное на наблюдение выборки смеси, имеет определенную стоимость. Разумность такой постановки задачи очевидна — чем дольше наблюдается смесь, тем большую энергию расходует передатчик (затраты на само излучение и обслуживание), дольше работает приемник (затраты, связанные с его функционированием). Наконец, для повышения эффективности всего комплекса часто важно получить оценку сообщения как можно раньше, например, чем раньше обнаружена цель противника, тем легче ее поразить.

Очевидно, что при прочих равных условиях, при более длительном наблюдении можно обеспечить лучшие характеристики оценки. Для того чтобы учесть в постановке задачи стоимость времени наблюдения, следует несколько изменить модель, введенную в начале этого параграфа, в частности придать иной смысл понятию элементарного сеанса. Ранее предполагалось, что задание элементарного сеанса на интервалах времени разной длительности соответствует переходу к другому ансамблю сообщений.

Теперь будем предполагать, что при изменении времени наблюдения реализации смеси сообщение, содержащееся в сигнале, принадлежит одному и тому же ансамблю и сохраняет неизменное значение, так что по желанию получателя элементарный сеанс при сохранении ансамбля сообщений может быть задан на произвольном интервале времени. Например, в системе передачи информации передатчик может передавать одно и то же слово до тех пор, пока получатель информации по обратному каналу не передаст команду на переход к передаче следующего слова (радиолиния с решающей обратной связью). В системе измерения дальности (до неподвижного объекта) получатель имеет возможность выбрать сеанс наблюдения произвольно. Вместо дальности можно наблюдать любой другой неизменный параметр: скорость, интенсивность излучения и т. д.

При такой постановке задачи у получателя появляется дополнительная свобода действий — получить оценку раньше, но плохую или позже, но хорошую. Для того чтобы выбрать способ действия, необходимо построить критерий, учитывающий как стоимость ошибки, так и стоимость времени наблюдения, ибо если время ничего не стоит, то получатель, конечно, не откажется наблюдать так долго, как это возможно.

Случаи, когда возможное время наблюдения не ограничено, называются «неурезанными процедурами», при ограничении времени — «урезанными». С формальной точки зрения оперировать не урезанными процедурами проще. Однако практически возможный интервал наблюдения всегда ограничен, в частности, ограничения появляются в связи с невозможностью обосновать неизменность сообщения на большом интервале времени. Результаты для урезанной и не урезанной процедур различаются мало, если максимально возможное время наблюдения настолько велико, что практически все наблюдения заканчиваются раньше.

Задав определенную стоимость времени наблюдения (здесь те же проблемы, что и при выборе функции потерь), можно по-разному подойти к построению критерия эффективности системы. Например, задавшись максимально допустимой стоимостью одного из факторов, минимизировать стоимость другого. Обобщенный критерий эффективности может быть построен на основе требования минимума суммы потерь из-за обеих причин. Минимизация здесь понимается в среднем. Разумеется, возможны и минимаксные подходы, но, насколько известно, таких результатов пока нет.

Необходимо обратить внимание на то, что сформулированные задачи могут решаться при двух различных предположениях об ансамбле наблюдаемых реализации или, что то же самое, при разных предположениях относительно класса операторов.

При первом предположении каждому оператору приписывается определенный фиксированный интервал наблюдения, так что для любого данного оператора все сеансы будут иметь одинаковую длительность. Выбрав среди всех таких операторов наилучший (по заданному критерию), мы тем самым одновременно определяем оптимальную длительность сеансов, и наилучший способ обработки реализации смеси такой длительности.

При втором предположении интервал наблюдения для каждого оператора заранее не фиксируется, а является случайным и определяется в зависимости от результатов текущей обработки поступающей на вход реализации. Здесь в каждый момент времени принимается решение — сформировать ли оценку или продолжить наблюдение. Такие правила формирования оценки называются последовательными.

Нетрудно заметить, что рассмотренные в предыдущих разделах байесовые системы оптимальные по критерию минимума потерь из-за ошибок при заданных затратах на наблюдение.

Первый подход может рассматриваться как частный случай второго, если потребовать, чтобы формирование оценки происходило в один и тот же момент времени. Синтез в соответствии с первым подходом, следовательно, можно рассматривать как синтез с наложением ограничений. На основе общих соображений можно предположить, что второй подход (т. е. синтез без ограничений) позволяет достичь большей эффективности. При постоянном объеме выборки условный риск из-за ошибок в сообщении неодинаков для разных реализаций. Поэтому реализации, которым уже в начале сеанса соответствует довольно малое значение риска, целесообразно усечь, что и делается при последовательном анализе. При этом получается выигрыш в смысле среднего времени наблюдения, хотя отдельные сеансы могут быть весьма длительными. К сожалению, нахождение последовательных оптимальных операторов встречает серьезные трудности математического характера. В частности, достаточно трудно в общем случае обосновать саму возможность последовательного принятия решения. Полученные результаты относятся в основном к случаям обнаружения и посимвольного приема двоичной информации.

При оптимизации на основе первого предположения решение задачи не представляет труда. Здесь полностью пригодны методы, используемые при байесовом подходе. Действительно, для каждой фиксированной длительности сеанса можно найти оптимальный байесов оператор и вычислить средний риск как функцию времени наблюдения Т. После этого, минимизируя суммарный риск по времени наблюдения, можно определить его оптимальное значение.  

Лекция 6. Модели сообщений

6.1. Общие соображения по выбору модели сообщения в задаче синтеза

Для того чтобы задача построения оптимального оператора могла быть приведена к математической формулировке в виде (5.1.2), (5.2.2), исходя из анализа реально существующей ситуации, необходимо построить модели ансамблей сообщений, сигналов, помех, обоснованно выбрать функцию потерь, найти апостериорное распределение, задать ограничения на класс операторов. Далее рассматриваются вопросы построения ансамбля сообщений (оценок) и выбора функции потерь. Для некоторых функций потерь проводится минимизация (5.2.2) и получается оптимальное байесово правило (оператор) формирования оценки. Сама оценка при этом выражается через те или иные параметры апостериорного распределения, которое предполагается известным. Таким образом, результаты следующих параграфов применимы во всех случаях, когда апостериорное распределение может быть найдено.

Задание ансамбля оценок (сообщений) – первый шаг в постановке задачи синтеза системы. Важность этого шага обусловливается самой природой статистических выводов. Любое решение, принимаемое в условиях неопределенности, т. е. при наличии помех, является статистическим выводом. Суть статистических выводов прекрасно выражена Налимовым В.В. [Теория эксперимента. –М., «Наука», 1971]: «Нельзя предложить набор алгоритмов, которые выводили бы новые закономерности из результатов новых наблюдений. Сначала исследователь должен выдвинуть несколько гипотез, а затем, пользуясь статистическими методами, выбрать одну из них». Статистическая оценка не может быть получена иначе как в результате выбора из некоторого заранее (до наблюдения) обусловленного множества. Это положение и является главным в той модели приема сообщения, которая обсуждалась ранее. В дальнейшем будет рассматриваться возможность уточнения ансамбля сообщений в процессе наблюдения реализации смеси. Однако и в этом случае суть дела не меняется, по-прежнему на основе наблюдений отдается предпочтение одной из принятых заранее гипотез.

Если при проектировании системы обработки принято предположение о том, что сообщение принадлежит некоторому конкретному ансамблю, то оценка, получаемая в такой системе, будет принадлежать именно этому ансамблю независимо оттого, что представляет собой реальное сообщение.

Неправильное задание ансамбля неизбежно приведет к непригодному для практического использования решению, даже если это решение будет «оптимальным» по принятому критерию. Так, например, предположив, что дальность до цели постоянна (хотя реально она меняется), мы сможем получить по результатам наблюдений «оптимальную» оценку параметра — дальности. Однако ясно, что если воспользоваться этой оценкой для управления стрельбой, то к попаданию это не приведет. Здесь, как обычно, окончательное суждение о том, насколько хороши были исходные предположения, может быть вынесено только после проведения эксперимента.

При проектировании конкретной системы трудности в построении модели ансамбля сообщений будут проявляться в разной степени в зависимости от того, какой предварительной информацией располагает проектировщик. Для систем передачи информации множество сообщений обычно бывает известно. Хуже обстоит дело для систем извлечения информации, где сообщение представляет собой совокупность параметров траектории (дальность, скорость и т. д.) и определяется характером движения цели, который может быть плохо известен проектировщику. В этом случае все равно приходится задаваться моделью сообщения в первом приближении, считая, что ошибки будут исправлены впоследствии по мере получения новых сведений. Незнание ансамбля сообщений можно рассматривать как предельный случай незнания априорного распределения сообщения, когда не известны не только относительные частоты появления тех или иных сообщений, но и то, какие сообщения вообще появляются.

Рассматривая применимость моделей сообщений к конкретным ситуациям, подчеркнем еще раз, что в задачах синтеза могут использоваться только вероятностные, недетерминированные модели.

После того как ансамбль сообщений определен, можно приступить к выбору функции потерь. Очевидно, что функция потерь, определяющая критерий качества радиосистемы (т. е. частный критерий с точки зрения построения комплекса), должна выбираться исходя из общего критерия эффективности. Общую тенденцию здесь уловить нетрудно — стоимость ошибки должна возрастать с ростом ошибки, однако в большинстве случаев достаточно трудно установить количественную связь ошибки с эффективностью большой системы. Иногда затруднительно даже определить более или менее четко структуру этой большой системы или охарактеризовать ее эффективность.

Два примера поясняют сказанное.

Пример 1. Рассмотрим определяющий координаты цели радиолокатор в комплексе радиоуправления снарядом. Цепочка соотношений, связывающих ошибку измерения с эффективностью комплекса, выглядит так: ошибка измерения — точность наведения — промах — вероятность поражения — наносимый (предотвращенный) ущерб — эффективность. В этом случае возможно, по крайней мере, в принципе, установить цену ошибки радиолокатора исходя из соответствующего уменьшения эффективности из-за наличия ошибок.

Пример 2. Радиолокатор, предназначенный для исследования планет солнечной системы. Полученные этим локатором результаты, прежде всего, вносят дополнения и изменения в систему знаний о вселенной. Ввести понятие эффективности такой системы и оценить, к чему приведут ошибки измерения, представляется почти невозможным.

Как будет показано, в практически важном случае высокоточных оценок конкретный вид функций потерь мало влияет на структуру оптимальной системы. Это позволяет ограничиться при проектировании сравнительно небольшим набором стандартных функций потерь, которые и будут рассмотрены. Это полезно еще и потому, что многие практически применимые критерии оказываются байесовыми при специальных функциях потерь. Это позволяет установить связь между различными подходами и использовать результаты, базирующиеся на общей байесовой теории, что в ряде случаев облегчает синтез оптимальных алгоритмов. Поскольку оптимальная байесова система минимизирует среднее значение функции потерь (средний риск), то, очевидно, что функция потерь может определяться с точностью до произвольного постоянного слагаемого и постоянного множителя. Это, в частности, позволяет всегда считать, что правильному воспроизведению сообщений (при отсутствии ошибки) соответствуют нулевые потери.

6.2. Дискретная модель сообщения

Задача оценки сообщения, принадлежащего дискретному конечному ансамблю, называется обычно «задачей различения m сигналов». Дискретная модель хорошо подходит для описания сообщений в цифровых системах передачи информации, таких, как цифровая телеметрическая система или система передачи дискретных команд. Объем ансамбля определяется выбранным методом приема (посимвольным, пословным и т.д.). Число m при пословном приеме равно числу кодовых комбинаций (команд); при посимвольном приеме — основанию кода. В частности, при посимвольном приеме двоичного кода m = 2.

Очевидно, что элементарный сеанс по времени должен совпадать с интервалом, на котором существует только одно из возможных сообщений (слово, символ). Следовательно, использование дискретной модели сообщения обязательно предполагает установление синхронизации соответствующего вида (посимвольной, пословной), причем ошибки системы синхронизации должны быть пренебрежимо малыми по сравнению с длительностью элементарного сеанса. На установление синхронизации требуется некоторое время, в течение которого информация не принимается. Таким образом, получаемые алгоритмы можно считать лишь условно оптимальными. Это положение достаточно общее.

Практически работа любой радиосистемы начинается с обнаружения сигнала, при этом по наблюдаемой реализации смеси требуется определить, имеется ли в смеси сигнал или он отсутствует. Если случай отсутствия сигнала отождествить с одним значением сообщения x₀, а наличия — с другим x₁, то задача обнаружения сводится к задаче различения двух значений сообщения и принципиально ничем не отличается от задачи посимвольного приема двоичной информации. Может встретиться ситуация, например, в системе передачи дискретных команд, когда на заданном интервале времени может или передаваться сигнал, соответствующий одному из возможных значений сообщения, или ничего не передаваться. Система обработки в этом случае должна вынести решение о том, имеется ли в наблюдаемой смеси сигнал, и если да, то какой именно. В литературе эта задача называется задачей различения т сигналов с обнаружением. Ясно, что и эта задача приводится к общей задаче различения m + 1 сигналов, если в ансамбль сообщений ввести дополнительный («нулевой») сигнал, соответствующий отсутствию сигнала в смеси.

Функция потерь для дискретного ансамбля будет функцией номеров истинного сообщения и оценки. Поэтому удобнее всего ее записать в виде матрицы

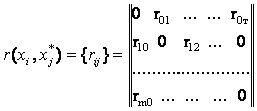                                                          (6.2.1)

Элемент r_ij стоящий на пересечении i-й строки и j-ro столбца, равен потерям, которые несет получатель, при истинном сообщении x_i и оценке х*_j. Нули в главной диагонали матрицы соответствуют отсутствию потерь при правильном решении.

При конечном ансамбле сообщений число возможных решений (для каждой реализации смеси) конечное и оптимальное правило может быть всегда найдено с помощью перебора. Величина условного (при данном z) среднего риска, соответствующая решению х*_j, равна взвешенной сумме элементов j-го столбца матрицы (6.2.1), причем весовыми коэффициентами являются апостериорные вероятности

                                                          (6.2.2)

В качестве решения выбирается та оценка х*_i, для которой условный средний риск минимален. Таким образом, система различения m сигналов должна в общем случае включать в себя блок формирования апостериорных вероятностей р (x_i|z_k), которые вырабатываются на основе анализа смеси z, блок линейного преобразования (6.2.2) и блок выбора минимума.

Широко используется так называемая простая функция потерь, задаваемая соотношением

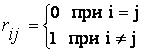
Функция вида (6.4.3) соответствует предположению об одинаковости потерь при любой возможной ошибке.

Полный средний риск для функции (6.2.3)

r  = 0 * р_прав + 1 * р_ош = р_ош

где р_прав — вероятность правильного решения, т. е. того, что при истинном x_i принята оценка x*_i; р_ош = 1 — р_прав — вероятность ошибки.

Таким образом, система, оптимальная в смысле критерия минимума вероятности ошибки, оказывается частным случаем байесовой системы при простой функции потерь.

Нетрудно найти и правило решения, соответствующее простой функции потерь. Согласно (6.2.2) имеем

                                                  (6.2.4)

Очевидно, что минимум (6.2.4) достигается, когда в качестве оценки берется то значение сообщения, которому соответствует максимум апостериорной вероятности. Структура системы оценки при этом сводится к сравнению значений апостериорных вероятностей. Конечно, можно сравнивать не сами апостериорные вероятности, а любые монотонные функции от них, в частности их логарифмы. Как будет видно из дальнейшего, часто это оказывается удобным. Правило, согласно которому принимается то значение сообщения, апостериорная вероятность которого максимальна, является вполне логичным и вне связи с общей теорией. Именно это правило было исходным при построении оптимальных приемников в работе [157]. Как видно из приведенного рассмотрения, это правило является байесовым в предположении о равной опасности (стоимости) любых возможных ошибок.

Использование простой функции потерь логически оправдано, например, при проектировании командной радиолинии, где отдельное сообщение отождествляется с какой-то функциональной командой, так что принятие любого значения сообщения, отличного от истинного, является одинаково опасным. Наоборот, в том случае, когда отдельное дискретное сообщение соответствует определенному значению некоторого параметра (как в цифровой телеметрической системе), естественно считать, что более опасны те ошибки в опознавании сообщения, которые приводят к большим ошибкам воспроизводимого параметра. При этом простая функция потерь непригодна. Пусть, например, по радиолинии передаются три команды, каждая из которых вызывает отклонение руля снаряда на –1, 0, +1° соответственно. При этом можно принять, что перепутывание этих команд одинаково опасно. Если же три сообщения в телеметрической системе соответствуют значениям температуры в каком-то отсеке 10, 20, 30°, то искажение, приводящее к замене первого сообщения третьим, более опасно, чем те, при которых первое заменяется вторым, или второе — первым. В матрице потерь это должно быть учтено выбором r₁₃ > r₂₃, r₁₃ > r₁₂.

В задаче различения с обнаружением отдельно необходимо задать потери, соответствующие ложной тревоге (когда вырабатывается оценка какого-то сообщения при отсутствии сигнала) и пропуску (когда выносится решение об отсутствии сигнала при наличии последнего).

Может встретиться случай, когда требуется оценить, присутствует ли в наблюдаемой смеси сигнал (безразлично какой) или его нет. Такая задача может возникнуть при проектировании контрольной или разведывательной системы, которая должна устанавливать лишь сам факт работы радиолинии. В литературе эта задача называется задачей обнаружения без различения или задачей сложного обнаружения. Соответствующим выбором функции потерь в рамках общей теории может быть учтен и этот случай. Действительно, отсутствие необходимости различать сигналы равносильно тому, что ошибки, которые приводят к замене одного значения сообщения другим (за исключением нулевого сообщения, соответствующего отсутствию сигнала), не приносят дополнительных потерь. Плата за пропуск или ложную тревогу для любого из сигналов здесь одинакова, обозначим их r_п и r_лт соответственно. Тогда матрица потерь будет иметь вид

верхняя строка соответствует «нулевому» сигналу, а первый столбец — «нулевому» решению.

Согласно (6.2.2) условный средний риск для такой матрицы потерь

Видно, что решение будет тем же, если переформулировать задачу и различать всего два сообщения х₀ и х*₁, причем х*₁ считать сложным случайным событием, состоящим в появлении любого из x_i. Поскольку никакие х_i, x_j не могут появляться одновременно, апостериорная вероятность

Рассмотрим более подробно случай двух сообщений. Матрица потерь состоит всего из четырех элементов

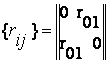                                                                                 (6.2.5)

и при воспроизведении сообщения возможны ошибки только двух видов: можно принять х*₁ при истинном x₀ и, наоборот, х*₀ при истинном x₁. В задаче обнаружения, когда , r₀₁ — плата за ложную тревогу, r₁₀ — плата за пропуск сигнала. Если обозначить априорную вероятность наличия сигнала р, а вероятность его отсутствия b = 1 — р, то полный средний риск

                                                                  (6.2.6)

где р_п , р_лт — вероятности пропуска и ложной тревоги соответственно.

Условный риск (при данном z) определяется соотношением

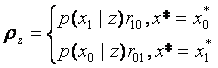                                                          (6.2.7)

Отсюда следует, что оптимальным правилом является следующее:

в качестве оценки выбирается х*₁, если

                                                               (6.4.8)

и x*₀ при выполнении противоположного неравенства или в случае равенства правой и левой частей (6.2.8). Условие (6.2.8) можно переписать в виде

                                                               (6.2.9)

Таким образом, алгоритм оптимального различения двух сигналов (обнаружения) сводится к сравнению отношения апостериорных вероятностей сообщений с порогом r₀₁ / r₁₀.

Обычно последнее выражение приводится к эквивалентному виду, где с порогом сравнивается отношение функций правдоподобия

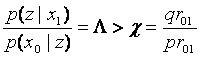.                                                                 (6.2.10)

Отношение функций правдоподобия L, стоящее в левой части (6.2.10), называется коэффициентом правдоподобия. Можно сравнить с порогом не сам коэффициент правдоподобия, а любую монотонную функцию от него. Так, наиболее часто используется соотношение

lnL>lnc.                                                                                             (6.2.11)

Многие распространенные критерии обнаружения являются частными случаями байесова при соответствующих функциях потерь. Так, простая функция потерь (r₁₀ = r₀₁ = 1) приводит к так называемому критерию идеального наблюдателя (критерию Зигерта—Котельникова), минимизирующего полную вероятность ошибки.

В задаче обнаружения часто используется критерий Неймана— Пирсона, согласно которому требуется минимизировать вероятность пропуска сигнала при заданной вероятности ложной тревоги:

р_п®min                                                                                       (6.2.12 a)

р_лт =a                                                                   (6.2.12 6)

Покажем, что и этот критерий частный случай байесова. Действительно, соотношение (6.2.12) можно рассматривать как требование условного минимума, которое, используя метод Лагранжа, можно заменить требованием безусловного минимума функции:

р_п+l(р_лт – a),                                                                           (6.2.13)

где l — неопределенный множитель Лагранжа.

Поскольку в (6.2.13) от оценки зависят только р_п и р_лт, то условием для выбора оценки будет

р_п+lр_лт®min.                                                                            (6.2.14)

Видно, что (6.4.14) соответствует общему выражению (6.2.6) минимума среднего риска, если в последнем положить

r₁₀=1/p,                 r₀₁=l/q                                                            (6.2.15)

Следовательно, порог, с которым надо сравнивать коэффициент правдоподобия, равен c=l. Неопределенный коэффициент l легко получить из условия (6.2.126). Надо вычислить вероятность ложной тревоги как функцию l (это всегда принципиально возможно, поскольку алгоритм оценки определен) и затем найти l из условия р_лт (l) =a.

Видно, что при использовании критерия Неймана—Пирсона нет необходимости знать априорные вероятности наличия и отсутствия сигнала, однако потери, которые приписываются ошибкам того и другого рода, не определены и считаются обратно пропорциональными соответствующим априорным вероятностям р и q.

6.3. Непрерывная одномерная модель сообщения

Перейдем к случаю, когда сообщение в каждом элементарном сеансе считается случайной величиной, принимающей любые значения в некотором интервале. Практически это означает, что принимаемый сигнал содержит неизвестный информационный параметр, который остается постоянным на интервале времени, соответствующем элементарному сеансу. В гл. 2, где обсуждались свойства такой модели, указывалось, что она может быть использована, когда изменения сообщения в течение сеанса связи достаточно малы.

Для того чтобы получить количественное (хотя бы приближенное) соотношение, определяющее, какие именно изменения параметра можно считать малыми на выбранном интервале, следует i сравнить ошибку оптимальной оценки, полученной в предположении о постоянстве параметра, с диапазоном ожидаемых изменений параметра. Если изменения меньше ошибки оценки, то модель достаточно хорошо соответствует реальной ситуации.

Модель сообщения в виде случайной постоянной величины хорошо подходит для таких задач, как оценка координат медленно движущейся цели в радиолокационной станции с круговым обзором на интервале времени, равном периоду обзора, оценка значения телеметрического сообщения за время одного кадра, оценка навигационного параметра траектории космического аппарата в течение нескольких минут. В последнем случае следует считать оцениваемым сообщением не само значение параметра, который может сильно меняться на интервале наблюдения, а отличие его от прогнозируемого

Вообще говоря, любой процесс может рассматриваться как постоянная величина на интервале времени, существенно меньшем эффективного времени корреляции. Однако, поскольку имеет смысл рассматривать лишь высокоточные оценки, а точность оценки падает при уменьшении времени наблюдения, возможности использования такой модели часто ограничены.

Вопрос о правомерности использования модели сообщения в виде постоянной величины является частным по отношению к более общей проблеме выбора модели при оценке сообщения, заданного как функция времени. Эта проблема будет обсуждаться более подробно Для рассматриваемой модели функция потерь в общем случае должна задаваться как функция двух переменных x и х^*, однако чаще используются функции потерь, значения которых полностью определяются ошибкой х^* – x. Это предположение является логичным для большинства задач, но, разумеется, не обязательным. Вполне можно, например, допустить, что цена потерь зависит от относительной ошибки (х^* – х)/ х так, что функция потерь не будет функцией одной ошибки.

Обычно принимается, что потери зависят от значения ошибки и не зависят от ее знака. Примером такой функции потерь является

r (х, х*) = |x*-x|^k                          (6.3.1)

Наибольшее распространение в практике получили функции вида (6.3.1) при k = 1, 2, особенно при k = 2 (квадратичная функция потерь). Байесова система при квадратичной функции потерь обеспечивает наименьшее среднеквадратическое уклонение оценки от истинного значения.

Легко найти алгоритм получения такой оценки. Условный средний риск

                (6.3.2)

Для нахождения оптимальной оценки достаточно продифференцировать (6.3.2) по х* и приравнять производную нулю. Стационарная точка здесь единственная, она и дает искомое решение

.

Учитывая условие нормировки для w(х|z), получаем

.                                       (6.3.3)

Таким образом, оценка, обладающая минимальным среднеквадратическим уклонением, является апостериорным средним. Аналогично легко показать, что оптимальная оценка, соответствующая функции потерь r (х, х*) = |х—х*|, равна медиане апостериорного распределения.

Использование функций потерь типа (6.3.1) не всегда бывает оправданным. Часто есть основания считать, что при слишком больших ошибках оценка, полученная в системе, вообще становится непригодной для дальнейшего использования и, следовательно, увеличение ошибки не приведет к увеличению потерь. При этом целесообразно выбрать функцию потерь, значения которой ограничены при увеличении ошибки. Примером такой функции может служить

.                                           (6.3.4)

Заметим, что в том случае, когда апостериорная плотность существенно уже, чем эффективная ширина D функции вида (6.3.4), и ограниченные и неограниченные функции потерь будут приводить практически к одинаковым оценкам. Как предельную форму ограниченных функций потерь можно рассматривать

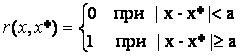   .                                          (6.3.5)

При использовании функции вида (6.5.5) полагается, что оценки, получаемые в системе, одинаково хороши, если ошибка не превышает по модулю величины а (потери равны нулю), и одинаково плохи, если ошибка по модулю больше а. Применение такой функции потерь оправдано, например, для измерителя координат в системе радиоуправления, если поражение цели происходит при любом прямом попадании и не происходит при промахе. В этом случае а, определяется размерами цели.

Вычислим средний риск для функции (6.3.5)

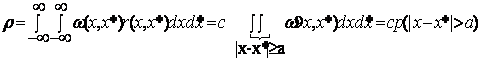    (6.3.6)

             Таким образом, критерий минимума вероятности того, что модуль ошибки превысит заданное значение, является частным случаем байесова критерия с функцией потерь вида (6.3.5) (при с =1)

Для того чтобы найти правило решения, запишем условный средний риск в виде

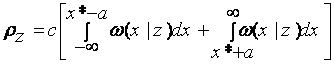.                    (6.3.7)

Дифференцируя по х^* и приравнивая нулю производную, находим условие, определяющее оценку:

.                                                 (6.3.8)

Следовательно, оценку надо выбирать так, чтобы значения апостериорной плотности в точках х^* + а и х^* – а были равны. Если апостериорная плотность симметрична относительно некоторого значения , то оценка совпадает с центром симметрии .

При уменьшении величины а до нуля (одновременно нужно увеличивать величину «скачка» с, чтобы интегрирование имело смысл) из (6.3.5) получается функция потерь

r (х, х*) = –d (х – x*).              (6.3.9)

Используя фильтрующее свойство d-функции, находим, что условный риск

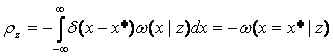,                                (6.3.10)

откуда следует, что оптимальной байесовой оценкой с функцией потерь (6.3.9) будет х^* = х_м, где х_м — значение параметра, при котором апостериорная плотность вероятности максимальна. Здесь, как и в дискретном случае (при использовании простейшей функции потерь), оценка, соответствующая правилу максимума апостериорной вероятности, является частным случаем байесовой оценки.

Функция потерь (6.3.9) не поддается физической интерпретации, и ее использование оправдано тем, что соответствующая оценка, с одной стороны, достаточно удобная при аппаратурном построении алгоритма, а с другой — дает хорошее приближение (в случае высокой точности) к оценкам, соответствующим другим, физически обоснованным функциям потерь. Остановимся на этом более подробно. Из только что полученных примеров решений для функций потерь (6.3.1), (6.3.5), (6.3.9) видно, что если апостериорное распределение является одномодальным и симметричным относительно точки максимума, то оценки для всех функций потерь совпадают. Этот результат можно обобщить следующим образом.

Если функция потерь является неубывающей функцией модуля разности сообщения и оценки r(х, х^*) = r(х – х^*) = r(х^* – х) = r(|х – х^*|), а апостериорное распределение таково, что при некотором x_м =y (z) оно имеет единственный максимум и симметрично спадает относительно точки х_m, то байесовой оценкой является x_m независимо от конкретного вида апостериорного распределения. Это достаточно очевидно: для того чтобы интеграл

был минимальным, нужно минимум первого сомножителя подынтегрального выражения r(|х – х^*|) совместить с максимумом второго w(x|z).

Из приведенной теоремы вытекает полезный для практики вывод: при сформулированных ограничениях на апостериорное распределение и функцию потерь оптимальное решение инвариантно к виду последней. Это позволяет выбрать функцию потерь так, чтобы аналитические трудности, связанные с нахождением оптимальной оценки, были минимальными, или привести задачу к уже решенной в литературе. Поскольку практически удается осуществить устройства, лишь приближенно реализующие оптимальные алгоритмы, имеет смысл искать условия, при которых результат, подобный сформулированному, приближенно выполняется при более слабых ограничениях (при этом удается охватить большое число практически интересных случаев).

Постановка задачи синтеза оптимальной системы практически имеет смысл только в том случае, когда апостериорная плотность распределения существенно уже априорной. В противном случае никакая система обработки не сможет существенно уточнить сообщение после проведения сеанса связи. Оценки, соответствующие узким апостериорным плотностям, будем называть высокоточными. Предположение о высокой точности оценок приводит к ряду существенных упрощений и позволяет доводить до конца задачи, не решаемые в общем виде. Если оценки высокоточные, то по мере уменьшения уровня помех, т.е. по мере сужения апостериорного распределения, все менее существенной становится форма функции потерь и форма самого апостериорного распределения (надо только положить, что правильному решению соответствуют минимальные потери). При отсутствии помех для любой функции потерь решение соответствует значению сообщения, при котором апостериорное распределение отлично от нуля. Эти интуитивные рассуждения формально можно обосновать с помощью следующих элементарных выкладок: если апостериорное распределение имеет максимум при х = х_м и существенно отлично от нуля в малой области ±e около х_m, а функция потерь является «медленной» функцией х, то условный средний риск приближенно может быть определен выражением

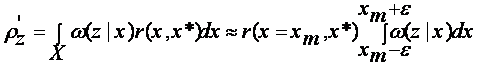      (6.3.11)

Поскольку второй сомножитель (6.3.11) не зависит от х^*, а функция потерь минимальна при х^* = х_m, то, очевидно, оптимальным решением в этом случае будет х^* = х_m. С чисто формальной точки зрения тот же результат получается, если положить, что функция потерь узка по сравнению с функцией правдоподобия (см. 6.3.10).

Это оправдывает практическое использование функции потерь вида (6.3.9). Таким образом, снова приходим к предыдущему результату – в качестве оценки следует выбирать значение сообщения, при котором апостериорное распределение достигает максимума.

Предположение о «медленности» функции потерь кажется естественным в свете следующих рассуждений. От всякой теории требуется, чтобы получаемые результаты, которые предполагается использовать в практике, мало менялись при малом изменении входных данных. Это свойство называют «грубостью» системы (или получаемых решений). Важность выполнения этого условия совершенно очевидна. По аналогии с известным требованием физической возможности оно может быть названо требованием технической реализуемости, так как на практике характеристики входных воздействий и компонентов систем известны всегда с конечной точностью. Так что, если потери резко растут при вариации оценки вблизи оптимального значения, практическое осуществление системы становится невозможным. Функция потерь должна задаваться так, чтобы ощущалась разница в значениях риска при использовании априорного распределения, т. е. при отсутствии радиосистемы и при использовании апостериорного распределения, когда принимается и обрабатывается сигнал, но она не должна сильно изменяться при малых ошибках, определяемых апостериорным распределением.

Только что изложенные результаты нельзя рассматривать как догму. Они действительно часто оказываются справедливыми, но обоснования для их применения каждый раз должны рассматриваться особо. Так, например, если функция апостериорной вероятности имеет вид нескольких узких всплесков, разнесенных на интервалы, существенно большие их ширины, то оценка может существенно зависеть от вида функции потерь.

Пока все рассмотренные функции потерь были четными. Это, конечно, не обязательно. Если, исходя из условий конкретной задачи, есть основание полагать, что ошибки разного знака (одинаковые по модулю) приводят к различным потерям, то функцию потерь нужно выбирать несимметричной.

Найденные выше правила решения связывают оценку с тем или иным параметром распределения (медианой, математическим ожиданием, модой и т.д.). Эти параметры, в свою очередь, определенным образом выражаются через наблюдаемую реализацию z. B тех случаях, когда эту зависимость найти не удается (или когда вообще не удается выразить оценку через параметры распределения), приходится прибегать к моделированию, т. е. строить зависимость r_z(х^*) и затем производить поиск значения х^*, обеспечивающего минимум риска. Аппаратурное построение функции r_z(х^*) подразумевает дискретизацию оцениваемого параметра с некоторым шагом Dx. При этом, по сути, непрерывное сообщение, реально присутствующее в наблюдаемой смеси, заменяется дискретным. Для каждого из дискретных значений в соответствующем канале вычисляется условный средний риск. Алгоритм оценки сводится к сравнению каналов и выбору одного из них. Число каналов  п = (x_max  -x_min)/ Dx: выбирается так, чтобы ошибка квантования Dх/2 была существенно меньше ошибки оптимальной оценки.

Затронем еще один вопрос, касающийся методов реализации оптимальных алгоритмов. Оценка, полученная по результатам наблюдения смеси на некотором интервале Т, будет, очевидно, зависеть от величины этого интервала. Практически оценка параметра на интервале [0, T] может строиться двояким образом. В одном случае предварительно (до наблюдения) задаваясь продолжительностью элементарного сеанса Т, можно ввести эту величину Т как константу в алгоритм вычисления. При этом оценка получается только в момент времени Т (если пренебречь временем вычислений), а значения, которые могут получаться на выходе оценивающей схемы раньше (в моменты времени t < T), вообще не имеют смысла и не используются.

Во втором случае интервал Т заранее не фиксируется и вычисление осуществляется на текущем интервале [0, t] (при этом параметры устройства, реализующего алгоритм, меняются в течение сеанса). В каждый момент времени получается оптимальная оценка, соответствующая длительности элементарного сеанса [0, t]. Такая оценка называется последовательной, или текущей. Точность текущей оценки возрастает по мере увеличения времени наблюдения, Если текущая оценка, соответствующая интервалу [0, t+Dt], является функцией только оценки, полученной на предыдущем интервале [0, t], и смеси, наблюдаемой на интервале Dt, то такая оценка называется рекуррентной. Построение последовательных (в частности, рекуррентных) алгоритмов позволяет получать оценки в случае, если сеанс прекращается раньше намеченного времени, или использовать дополнительное время (сверх расчетного) для уточнения оценки.

6.4. Векторная модель сообщения

Вводить векторную модель приходится в двух случаях. Во-первых, когда несколько различных параметров сигнала, заключенного в принимаемой смеси, несут информацию, нужную получателю. Для систем передачи информации это соответствует наличию нескольких каналов. В системах извлечения информации различные параметры сигнала несут информацию о разных параметрах траектории объекта, например, запаздывание сигнала, определяет дальность, а частота — мгновенную скорость объекта. Во-вторых, когда сообщение, подлежащее оценке, является функцией времени, определяемой совокупностью постоянных коэффициентов, и оценка сообщения сводится к оценке этих коэффициентов.

Как и раньше, в основном, будем рассматривать функции потерь, зависящие только от ошибки, которая в данном случае представляет разность векторов (х— х^*) = D{x₁ – х^*₁, ..., x_m – х^*_m}. Довольно часто оправданным является предположение о том, что вес ошибки определяется только модулем вектора D и не зависит от направления последнего в m-мерном пространстве сообщений. Если расстояние определяется в евклидовом пространстве, т. е,

        (6.4.1)

то по аналогии с (6.5.1) может быть введена функция потерь

r (x,x*) = d^k                                                                              (6.4.2)

Пока полагаем, что все x_i, х^*_i безразмерны. В частном случае оценки двух параметров х₁ и х₂ функции потерь (6.4.2) при k = 1, 2 описывают соответственно конус и параболоид вращения с центрами в точке х^*.

Запишем выражение для условного среднего риска с квадратичной функцией потерь

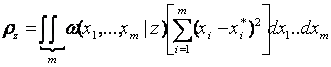
Дифференцируя по х^*_i приравнивая нулю частные производные, получаем систему уравнений

откуда, учитывая, что

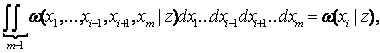
имеем

Таким образом, при квадратичной функции потерь каждая из составляющих х^*_i вектора оценки х^* равна апостериорному среднему соответствующей составляющей x_i вектора сообщения х. Вообще, можно сделать следующее, полезное для практики замечание: если функция потерь имеет вид суммы

r (х, х^*) = Sj₁(x_i – х^*_i),

то составляющие вектора оценки  совпадают х^*_i с оценками скалярных параметров, полученными при функциях потерь j (x_i — х^*_i).

По аналогии с одномерными функциями потерь (6.3.4), (6.3.5), (6.3.9) из тех же соображений могут быть введены многомерные функции вида

         (6.4.3)

или

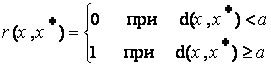
(6.4.4)

и, наконец,

(6.4.5)

Такой функции потерь соответствует оценка х^* = x_m, где x_m — точка, в которой w (x₁, ..., x_m|z) достигает максимума.

Использование функций вида (6.6.2)—(6.6.5) равносильно предположению о том, что равные ошибки различных составляющих вектора сообщения одинаково опасны. Если есть основания считать, что потери, связанные с равными ошибками по разным координатам вектора х, различны, то это может быть учтено введением весовых (масштабных) множителей. При этом линии равных потерь будут вытянуты вдоль той из координат, ошибки которой менее опасны (в многомерном пространстве следует говорить о гиперповерхностях равных потерь).

Так, с учетом различной стоимости ошибок отдельных составляющих (6.6.2) при k =2 преобразуем к виду

.                             (6.4.6)

Аналогично это может быть сделано и для функций вида (6.4.3)—(6.4.5). Если вес ошибки по какой-то координате устремить к нулю, то в пределе функция потерь перестает зависеть от этой координаты, при этом поверхность, отображающая функцию потерь, превратится в цилиндрическую. Выражение для условного среднего риска, определяющее алгоритм оценки, преобразуется следующим образом:

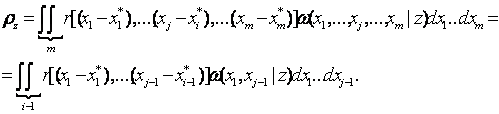    (6.4.7)

Здесь считается, что нулевой «вес» имеют ошибки по координатам с j-й по     m-ю. Иначе говоря, в рассматриваемом случае можно считать сообщением, подлежащим оценке, вектор меньшей размерности х {x₁, ..., x_j-i}, построить для него апостериорную плотность распределения w {x₁, ..., x_j-i|z} и привести задачу к предыдущей.

Остальные составляющие вектора х (от j- до m-й) можно назвать «паразитными» параметрами и рассматривать как помехи, модулирующие полезный сигнал. Действительно, если значение ошибки по какому-то параметру неважно, то это означает, что знание самого этого параметра не нужно получателю и, следовательно, неизвестное приращение этого параметра является помехой. Здесь интересно то, что удается проследить постепенный переход от понятия «полезное сообщение» к понятию «помеха». Все сказанное, разумеется, относится к «медленным» помехам, не меняющимся на интервале наблюдения.

Фактически ряд неизвестных (паразитных) параметров, таких, как амплитуда, начальная фаза и частота несущей, всегда содержится в принимаемом сигнале. Таким образом, задача оценки единственного информационного параметра в предположении, что все остальные известны (задача оценки параметра полностью известного сигнала), рассмотренная в § 6.5, имеет практический смысл только тогда, когда предполагается, что в приемном устройстве идеально действуют системы автоподстройки (АРУ, АПЧ, ФАП и др.). Эти системы должны осуществлять захват сигнала до начала работы системы оценки полезного параметра, для чего должно быть отведено определенное время, и в процессе работы обеспечивать «малые» ошибки по отслеживаемому параметру. Использование систем автоподстройки позволяет исключить из рассмотрения паразитные параметры и тем самым упростить структуру системы для оптимальной оценки информационного параметра, но требует дополнительного времени для захвата.

Вопрос о том, как сформулировать задачу синтеза оптимальной системы — с учетом или без учета паразитных параметров, — решается по-разному в зависимости от конкретной ситуации. Например, в радиолокационной задаче оценки дальности импульсным методом в режиме кругового обзора число импульсов, отраженных от цели, невелико и применять автоподстройку нецелесообразно. Следовательно, приходится ставить задачу оценки задержки пачки импульсов при наличии паразитных параметров: амплитуды, начальной фазы и т. д. Другой пример: в телеметрической системе ВИМ-АМ практически всегда можно затратить определенное время на захват сигнала системами автоподстроек, следовательно, задача может быть приведена к оценке параметра—задержки импульса полностью известного сигнала. Подчеркнем, что хотя в каждом из приведенных примеров модуляция сигнала полезным (информационным) параметром одинакова (ВИМ-АМ), но постановка задачи и решение ее различны из-за различия дополнительных условий, наложенных на каждую из них.

Функция потерь для векторного сообщения есть не что иное, как обобщенный показатель качества для системы, оптимизируемой по нескольким параметрам. Трудности, возникающие здесь, являются частным проявлением тех трудностей, которые присущи этапу построения обобщенного критерия. В частности, здесь приходится решать вопрос об установлении относительной «ценности» отдельных составляющих вектора сообщений.

Задача облегчается, когда отдельные составляющие вектора оценки комбинируются в виде некоторого обобщенного параметра для определения критерия качества комплекса.

Рассмотрим гипотетический пример, когда по совместной оценке дальности и скорости D*₀, V*_o (в момент t_o) прогнозируется значение дальности объекта D*₁ = D*₀ + TV*_o в момент t₁ = t₀ + Т.

Если требуется обеспечить минимальное квадратичное уклонение оценки прогноза, то, очевидно, функцию потерь для оценки вектора  следует взять в виде

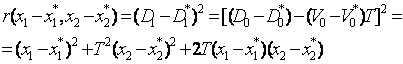.        (6.4.8)

В координатах (x₁ – х^*₁), (x₂ – х^*₂) выражение (6.4.8) описывает параболический цилиндр, касающийся координатной плоскости вдоль прямой:

(x₁ – х^*₁) = –T(x₂ – х^*₂).                            (6.4.9)

Физически это означает, что ошибки в определении дальности и скорости, связанные соотношением (6.6.9), не приводят к ошибке в определении D*₁ и, следовательно, не дают дополнительных потерь.

Рассмотрим теперь другой пример, когда интервал прогнозирования Т – случайная величина, независимая от оценок V^*₀ и D^*₀, со средним значением  и дисперсией . Тогда для определения среднего риска функцию потерь придется усреднять не только по оценкам, но и по интервалу Т. Последнее можно сделать сразу и вместо (6.4.8) получить функцию потерь в виде

.    (6.4.10)

Выражение (6.4.10) в координатах (x₁ – х^*₁), (x₂ – х^*₂) описывает эллиптический параболоид, касающийся _координатной плоскости  в начале координат, поскольку . Большая полуось эллипса в сечении r = с наклонена к координатной оси (x₁ – х^*₁). В этом случае компенсации ошибок по скорости и дальности не происходит, и функция потерь обращается в нуль только при нулевых ошибках по каждой из составляющих V₀ и D₀.

Выражения (6.4.8), (6.4.10) в отличие от (6.4.2), (6.4.6) несимметричны относительно координатных осей. Это является следствием того, что потери зависят не только от значений ошибок по отдельным составляющим вектора, но и от их знаков. Обобщением (6.4.6) на этот случай является функция потерь вида

,                         (6.4.11)

где матрица коэффициентов {К_ij} положительно определенная. Аналогичные обобщения допускают и функции потерь (6.4.3), (6.4.4).

Отметим интересную особенность функции (6.4.11). Оптимальное байесово решение, соответствующее ей, совпадает с решением, соответствующим (6.4.2) при k = 2, в чем нетрудно убедиться, продифференцировав (6.6.11) по всем х^*_i и приравняв нулю полученные частные производные. Это обстоятельство позволяет избежать трудностей, связанных с выбором коэффициентов K_ij.

Если отдельные составляющие вектора оценки используются совершенно независимо, и нет необходимости считать потери функцией вектора оценок, то можно по очереди рассматривать каждую составляющую как отдельное сообщение, полагая все остальные бесполезными. При этом оптимальная система разбивается на m параллельных подсистем, в каждой из которых оценивается только один параметр (по одной и той же реализации смеси). Разумеется, те операции, которые одинаковы для всех подсистем, нет необходимости повторять m раз.

Если расстояние между векторами х и х^* определить в ином (не евклидовом) смысле, можно получить такие, например, функции потерь:

.         (6.4.12)

Рассмотренные выше функции потерь (6.4.11), (6.4.6) также можно рассматривать, как функции неевклидова расстояния.

Все сказанное по существу остается справедливым и тогда, когда одни составляющие вектора дискретны, а другие — непрерывны. Такая модель возникает, например, при оценке задержки сигнала одновременно с его обнаружением или при различении символа в системе передачи информации с одновременной оценкой амплитуды для контроля условий связи. Пусть для простоты имеется одна непрерывная x_н и одна дискретная x_д составляющая сообщения, Дискретная составляющая принимает l значений x_д1, ..., x_д2.

Если в такой задаче непрерывный параметр дискретизировать, то придем к рассмотренной выше задаче различения m сигналов. При этом m = lk, где k — число уровней квантования непрерывного параметра. Полагая, что k®µ , нетрудно записать функцию потерь в виде матрицы {r_ij}, где i — номер значения дискретной составляющей; j- номер оценки этой составляющей, а сама r_ij – функция непрерывной составляющей сообщения и ее оценки r_ij=r_ij(x_н , х^*_н). Условный средний риск как функция оценок х^*_дj и х^*_н имеет вид

,                   (6.4.13)

где w(x_н, x_li|z)dx_н — совместная апостериорная вероятность того, что непрерывная составляющая сообщения лежит в интервале dx_н около x_н, а дискретная имеет значение x_дj. Определение оптимальной оценки х^*_н, х^*_дj сводится к минимизации каждой из ρ_zj по непрерывной компоненте и последующему перебору по x_дj , для нахождения минимума миниморума условного риска. Если каждый элемент матрицы r_ij представляет собой сумму, в которой отдельные слагаемые соответствуют потерям по одной из компонент сообщения, то, как и в общем случае, рассмотренном раньше, система совместной оценки разбивается на независимые системы оценки каждой компоненты.

Приведем пример такой функции потерь. Пусть дискретная составляющая имеет два возможных значения: x_д1, x_д2 . Положим, что потери из-за любых ошибок по этой составляющей одинаковы. Потери, связанные с ошибкой по непрерывной составляющей, квадратичны, и общие потери равны сумме потерь из-за ошибок по каждой из составляющих. Тогда матрица потерь выглядит так:

.

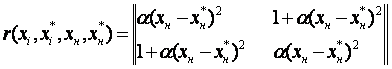Здесь α — весовой множитель, учитывающий относительную цену ошибок по дискретной и непрерывной компоненте.

Отметим некоторые особенности, присущие функции потерь в задаче одновременного обнаружения сигнала и оценки его параметра. Если выносится решение об отсутствии сигнала, то, естественно, не должна формироваться оценка параметра х^*_н. С другой стороны, в случае ложной тревоги сформированной оценке параметра х^*_н не соответствует никакое истинное значение сообщения x_н. С учетом сказанного функция потерь должна иметь вид

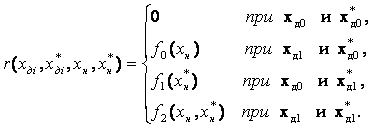                             (6.4.14)

Здесь x_д0 соответствует случаю отсутствия сигнала, а x_д1 — случаю наличия сигнала; f_o (x_н) — цена пропуска сигнала с параметром x_н, а f_i (x_н^*) — цена ложно сформированной оценки x_н^*. Если обозначить апостериорную вероятность отсутствия сигнала р(x_д0|z), апостериорная вероятность непрерывного параметра x_н имеет вид

[1 — р(x_д0|z)] w_y(x_н|z),

где w_y(x_н|z) — условная апостериорная плотность при условии, что сигнал присутствует в наблюдаемой смеси.

Условный средний риск может быть записан в виде

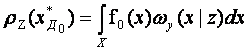                           (6.4.15)

при принятии решения об отсутствии сигнала,

       (6.4.16)

при принятии решения о наличии сигнала. Для нахождения оптимального решения необходимо минимизировать (6.4.16) по х*_н, после чего сравнить полученное минимальное значение с (6.4.15).

Если (6.4.15) окажется меньше, то выносится решение об отсутствии сигнала, если же больше, то выносится решение о наличии последнего со значением параметра х^*_н, минимизирующим (6.4.16).

6.5. Модель сообщения в виде функции времени

Обратимся к случаю, когда сообщение существенно изменяется на интервале наблюдения и, следовательно, должно рассматриваться как некоторая функция времени х = х(t). Задача оценки такого сообщения важная для практики и наиболее сложная теоретически среди других задач оптимального синтеза. Возможность ее решения в значительной мере определяется тем, насколько удачно выбрана модель для описания оцениваемого процесса, какими приближениями можно воспользоваться в том или ином конкретном случае, чтобы довести решение до конца. При выборе модели надо стремиться к тому, чтобы, используя ограничения, вытекающие из физики задачи, «сузить» класс функций, в котором можно достаточно хорошо описать поведение реального процесса.

Рассмотрим сначала задачу оценки выборочных значений функции. Разобьем интервал наблюдения T на n интервалов длительностью Dt каждый, и будем оценивать значение сообщения х(t_i), t_i = iDt, i = 0, 1, …, n  считая, что наблюдаемая смесь представляет выборку из непрерывного процесса в те же моменты времени. Такая модель, являющаяся приближением к модели непрерывного процесса, имеет самостоятельный интерес, если обработка проводится с помощью цифровых установок.

Видно, что в такой постановке задача не представляет ничего нового и сводится к предыдущей задаче оценки вектора. Значение сообщения х(t_i) можно рассматривать как i-ю составляющую вектора сообщения. После этого применимы все изложенные методы. Здесь возможны два подхода:

— наблюдение ведется на полном интервале времени Т, т. е. наблюдается полная выборка z {z(t₁), ..., z(t_n)}, после этого оценивается совокупность х(t_i); каждая оценка х^*(t_i) в общем случае является функцией всех значений наблюдаемой смеси z₁, .... z_i;

— в конце интервала длительностью t_i т. е. после наблюдения выборки z₁, .... z_i, оценивается только х(t_i). Все остальные значения сообщения х(t₁), ..., x(t_i-1) при этом рассматриваются как паразитные параметры.

Параметры х(t₁), ..., х(t_i–1) рассматриваются как паразитные в том смысле, что значение их не нужно получателю именно в момент t_i. Конечно, при наличии статистических связей между выборочными значениями процесса х(t) в предыдущих   значениях х(t₁), ..., х(t_i–1) содержится информация относительно х(t_i), но этот факт автоматически учитывается при интегрировании апостериорной плотности по бесполезным параметрам:

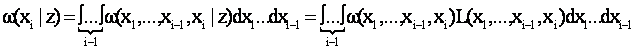 где L (x₁,…, x_i) — функция правдоподобия, a w (x₁,…, x_i-1, …,x_i) – априорное распределение параметров x₁,…, x_i.

Изменение характера статистической связи, т. е. изменение вида априорного распределения, в общем случае приведет к изменению априорной плотности вероятности w (x_i | z).

Здесь  как  бы  образуется  совокупность  сеансов с длительностями t_i (i = 0, 1, 2, ...); оценка х^*(t_i) зависит в общем случае от всех прошедших значений смеси z_j (j < i), но не зависит от последующих z_j(j > i). Способ оценки, соответствующий второму подходу, называется фильтрацией. Термин «фильтрация» в современной литературе имеет очень много значений. Иногда он употребляется для обозначения любой обработки сигнала на фоне шума.

Первый способ в отличие от фильтрации назовем «оценкой в целом».

Практически фильтрация необходима в тех случаях, когда полученное значение оценки немедленно используется в комплексе. Кроме того, часто оказывается, что процесс фильтрации может строиться как рекуррентный, когда для получения следующей оценки х(t_i) нужно только одно значение наблюдаемой смеси Zi и значения оценок х(t_i) (j < i). Наблюдение смеси и формирование оценки на интервале Dt может рассматриваться как отдельный элементарный сеанс, для которого априорные вероятности определяются не только тем, что было известно получателю до начала сеанса связи, но и тем, какие оценки х^*(t_i), ..., х^*(t_i-1) были получены на предыдущих элементарных сеансах.

При фильтрации точность оценки х^*(t_i) будет хуже, хотя, может быть, незначительно, чем при оценке в целом, поскольку не используется информация об х(t_i), содержащаяся в последующих уборочных значениях смеси. Это, конечно, не означает, что существуют оценки лучше, чем оптимальная. Дело здесь в том, что оценка в целом соответствует другому элементарному сеансу, на котором оценка, получаемая фильтрацией, уже не оптимальная. Таким образом, задача фильтрации сводится к оценке не вектора, а единственного параметра х(t_i), и все рассмотренные методы применимы здесь; единственное, что нужно сделать — это определить

w (x_i | z_{1, … ,} z_i).

В изложенной постановке [т.е. при дискретном представлении х(t)] задача оценки сообщения — функции времени — выглядит совершенно тривиальной (с принципиальной, а не с вычислительной точки зрения). Кажется, что для получения решения при непрерывном времени нужно лишь потребовать, чтобы  и соответственно . Однако переход к непрерывному времени при  в задаче оценки функции времени в целом невозможен из-за того, что «функционала плотности вероятности» не существует. Именно этими формальными трудностями и вызваны замечания к формуле (5.2.4) для случая, когда наблюдаемая реализация – случайный непрерывный процесс.

Относительно получения «оценки в целом» заметим, что, учитывая конечную разрешающую способность всех реальных приборов и их конечное быстродействие, можно считать, что все реализации процесса, заключенные в конечную «трубку», ширина которой меньше разрешающей способности прибора, не различимы для получателя.

Поэтому практически оценить функцию в конечном числе достаточно близко отстоящих точек t_i, (Dt < t_кор) все равно, что оценить всю функцию.

При реализации системы обработки сигнала в виде цифрового вычислительного устройства (или в виде программы для ЭВМ) дискретная оценка полностью исчерпывает ситуацию, так что вообще не имеет смысла говорить о «функционале вероятности».

Иной подход к оценке изменяющегося на интервале наблюдения сообщения состоит в том, что в качестве модели сообщения выбирается квазидетерминированная функция времени, т. е. заданная функция времени t и ряда неизвестных получателю параметров a, b, g, ...  :   x(t) = (t, a, b, g, ...).

Оценить сообщение х(t) в этом случае - то же, что оценить совокупность коэффициентов a, b, g, ... функцию потерь для оценки вектора a, b, g, ... нужно выбирать так, чтобы она согласовывалась с требованиями, предъявляемыми к воспроизводимому сообщению х(t). Пусть производится «оценка в целом». При этом функция потерь всегда является функционалом двух функций: истинного сообщения х(t) и оценки x*(t). В качестве меры близости сообщения и оценки можно взять, например, энергию их разности

                                                    (6.5.1)

Выражение (6.5.1) является непрерывным аналогом функции потерь (6.4.2) при k = 2. Поскольку х(t) = f (t, a, b, g, ...), a    х*(t) =f(t, a*, b*, g*,  ...), то (6.5.1) перепишем в виде

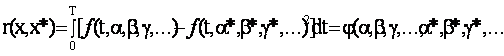,        (6.5.2)

здесь φ – функция потерь для оценки вектора a, b, g, ...

В некоторых случаях функции х(t) по своей природе являются квазидетерминированными; таковы, например, параметры движения (скорость, дальность и т. д.) космического аппарата на участке свободного полета. Однако и в тех случаях, когда сообщение, строго говоря, не является квазидетерминированным, можно приближенно представить его таковым. Действительно, каждая произвольная функция при некоторых ограничениях, которые практически всегда выполняются, может быть с нужной степенью точности представлена в виде конечного ряда по какой-то системе базисных функций

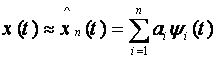.                                 (6.5.3)

Таким образом, каждая реализация сообщения х(t) может быть представлена в виде (6.5.3), т. е. в виде квазидетерминированной функции после чего становятся применимы изложенные рассуждения. Выбор базисной системы Y_i определяется классом функций, к которому принадлежит х(t). Надо выбрать базис так, чтобы сходимость была наиболее быстрой.

Статистические характеристики совокупности коэффициентов разложения определяются (при заданном базисе) статистическими. Характеристиками процесса х(t).

Пусть базис — ортогональный и нормированный, тогда

.

Если х(t) — нормальный процесс, то совокупность коэффициентов разложения — нормальный случайный вектор, полностью определяемый строкой математических ожиданий:

и корреляционной матрицей

,

где  и К._x (t₁ и t₂) — математическое ожидание и корреляционная функция процесса х(t).

Наиболее просто дело обстоит в том случае, когда представление (6.5.3) является некоторым каноническим разложением. При этом коэффициенты разложения а, не коррелированны, а если они нормальны, то и независимы.

При выбранном базисе разложения возникает вопрос о том, каким числом членов ряда п ограничиться. Рассмотрение, касающееся обоснованности выбора в качестве модели сообщения постоянной величины, является частным случаем, когда n = 1, y₁ = const. С одной стороны, увеличение числа членов ряда увеличивает точность представления истинной функции х(t) разложением х^{^}(t), но, с другой стороны, при этом ухудшается точность оценки х^*(t), так как из-за присутствия помех каждый коэффициент разложения будет оцениваться с ошибкой и результирующая погрешность будет тем больше, чем больше число членов. Часто бывает, что точность оценки каждого коэффициента разложения падает при увеличении числа n, так что ухудшение результирующей точности будет происходить еще быстрее. Физическое содержание задачи здесь то же, что и при выборе полосы некоторого фильтра: сужение полосы приводит к уменьшению шумовой составляющей ошибки, но увеличивает динамическую ошибку, расширение полосы приводит к обратному эффекту.

Более или менее строго задача об определении необходимого числа членов разложения может быть поставлена следующим образом. Пусть разложение ортогональное, а критерий близости функций х(t) и х^{^}_n(t) среднеквадратический. При этом всегда (по крайней мере, в принципе) можно получить зависимость ошибки погрешности представления функции х(t) разложением x^_n(t):

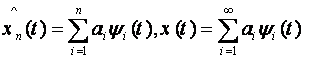                             (6.5.4)

Усреднение проводится по ансамблю функций х (t) или, что то же самое, по ансамблю коэффициентов а_i.

Построив оптимальную систему для оценки совокупности коэффициентов а_i , можно найти погрешность оценки

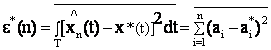                               (6.5.5)

Здесь  — средний квадрат отклонения оценки а_i* от истинного значения а_i. Усреднение проводится по ансамблю реализации смеси при данном х(t).

Полагая, что помеха, искажающая принимаемый сигнал, и само передаваемое сообщение статистически независимы, запишем выражение для энергии суммарной ошибки оценки х^*(t) относительно истинной х(t):

.                                        (6.5.6)

Первое слагаемое e*, связанное с действием помехи, возрастает при увеличении n, второе е, возникающее из-за ограниченности разложения (6.5.3), уменьшается. Приблизительный характер изменения е* и е в зависимости от n показан на рис. 6.5.1. Видно, что имеется некоторое n_опт котором обеспечивается наилучшая точность оценки сообщения, характеризует точность оптимальных (по возможным операторам при данном n) оценок в зависимости от n, т.е. оптимальных оценок, соответствующих разным моделям сообщения.

В практической деятельности инженеру нет необходимости проводить детальное исследование вопроса о наилучшем числе членов ряда на основе строгой постановки задачи. Задаваясь высокой окончательной точностью оценок, можно выбрать число членов разложения так, чтобы ошибка приближения х^(t) к х(t) была достаточно малой. Если после расчета точности оценки х^*(t) окажется, что ошибка оценки х*(t) относительно х^(t) того же порядка что и ошибка приближения, то на этом можно остановиться; если ошибка оценки значительно больше, число членов ряда следует уменьшить, если наоборот, то увеличить.

Следует отметить, что хотя формально всегда можно выбрать такое число членов разложения, при котором обеспечивается минимальная суммарная ошибка оценки, однако практически имеет смысл рассматривать только те случаи, когда суммарная ошибка мала, т.е. оценка точная. Для представления сообщения в виде квазидетерминированной функции вовсе не обязательно пользоваться только разложениями типа (6.5.3), где х(t) линейно связана с неизвестными параметрами.   В ряде случаев более быстрая сходимость может быть обеспечена нелинейным представлением х(t) относительно неизвестных параметров.

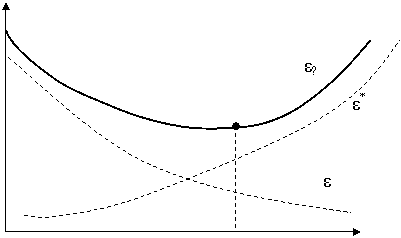Рис. 6.5.1. Зависимость ошибок воспроизведения сообщения

от числа членов разложения

При выборе базиса, кроме вопросов чисто математических (быстрота сходимости, погрешность представления и т. д.), необходимо учитывать, что разные системы базисных функций будут более или менее удобны с точки зрения реализации системы обработки.

Это последнее обстоятельство в ряде случаев может оказаться решающим. Поэтому часто достаточно сложные квазидетерминированные функции представляются тем или иным приближенным разложением по более простому базису. Так обычно поступают при оценке навигационных параметров траектории космического аппарата. Зависимость от времени измеряемого (навигационного) параметра в топоцентрической системе координат описывается достаточно громоздким выражением, нелинейным относительно времени и начальных параметров траектории.

Практически, вместо того чтобы пользоваться этим громоздким выражением, полагают, что изменения измеряемого параметра, точнее приращения этого параметра относительно прогнозируемого, описываются несколькими первыми членами ряда Тейлора. Обработка сводится к оценке коэффициентов этого ряда, которые затем уже используются для определения начальных параметров орбиты.

Лекция 7.

7.1. Количество информации в дискретных сообщениях. Энтропия источника дискретных сообщений.

Для сравнения различных систем связи необходимо ввести некоторую количественную меру, позволяющую оценивать объем информации, содержащейся в сообщении, и объем передаваемой информации.

         Рассмотрим сначала основные положения теории информации для дискретных систем связи. Обозначим возможные различные символы на входе некоторого блока СПИ через α_i, i = 1,…, m, а выходные символы через y_j, j = 1,…,n. Под символом α_i можно подразумевать символы источника, информационные последовательности, сигналы на входе линии связи, а под символами y_j - символы закодированных сообщений, кодовые последовательности, сигналы на выходе линии связи.

         Рассмотрим простейший случай, когда α_i, i = 1,…, m, взаимно независимые. При этом источник А полностью описывается априорными вероятностями  которые и характеризуют первоначальное незнание (первоначальную неопределенность) о появлении конкретного символа α_i на входе блока.

         При наличии помех между символами α_i и y_j нет однозначного соответствия, т.е. символ α_i может перейти в любой символ y_j с некоторой условной вероятностью которую можно вычислить, если известен механизм такого перехода. Зная вероятности  и  нетрудно найти вероятности  появления на входе блока символов α_i, i = 1,…, m, при условии, что на выходе блока наблюдался символ y_j. Эти вероятности, называемые апостериорными, характеризуют оставшееся незнание (оставшуюся неопределенность) о появлении на входе символов α_i, i = 1,…, m, при наблюдении символа y_j на выходе блока.

         Таким образом, полученная информация о символе α_i при наблюдении символа y_j приводит к изменению вероятности появления символа α_i от ее априорного значения  к ее апостериорному значению . При этом представляется обоснованным взять за количество информации о символе α_i, содержащейся в символе y_j, некоторую функцию только вероятностей  и :

                        (7.1.1)

Такое определение количества информации, не связанное с физической природой сообщения, позволяет строить довольно общую теорию, в частности, сравнивать различные системы связи по эффективности.

         В качестве функции  удобно использовать логарифм отношения апостериорной  вероятности к априорной , т.е. определить  как

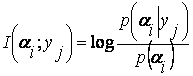                              (7.1.2)

При таком задании, в частности, количество информации обладает свойством аддитивности: количество информации о символе α_i(в дальнейшем для общности рассуждения - событии α_i), доставляемой двумя независимыми символами (событиями) y_j и z_k:

                    (7.1.3)

Это свойство хорошо согласуется с "интуитивным" понятием информации.

         Основание логарифма может быть любым. От него зависит единица измерения количества информации. В технических приложениях обычно используют основание 2. При этом количество информации I измеряется в двоичных единицах, или битах. При проведении математических выкладок зачастую удобно пользоваться натуральными логарифмами. Соответственно информация измеряется в натуральных единицах, или натах.

         Введенная величина  обладает важным свойством симметрии по отношению к α_i и y_j:

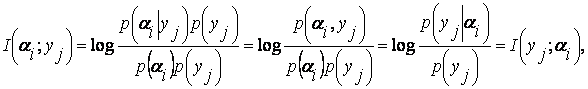
(7.1.4)

т.е. информация, доставляемая событием y_j о событии α_i равна информации, доставляемой событием α_i о событии y_j. По этой причине  называется взаимной информацией двух случайных событий относительно друг друга.

         Из (9.4) следует, что если события α_i и y_j статистически независимы, то , т.е. независимые события не несут друг о друге никакой информации.

         Взаимная информация при фиксированной вероятности принимает максимальное значение, когда апостериорная вероятность , т.е. когда наблюдаемое событие y_j однозначно определяет событие α_i. При этом

                            (7.1.5)

         Величина  называется собственной информацией события α_i. Ее можно интерпретировать как количество информации, которое доставляет событие α_i или любое другое, однозначно связанное с ним. Собственная информация всегда является неотрицательной величиной, причем чем менее вероятно событие, тем она больше. Взаимная информация может быть как положительной, так и отрицательной величиной.

         Пусть α_i, y_j, z_k - статистически зависимых события. Предположим, что событие z_k известно. Количество информации о событии α_i, доставляемое событием y_j при условии, что z_k известно, называется условной взаимной информацией. Она определяется так же, как и взаимная информация, однако априорная и апостериорная вероятности должны быть взяты при условии z_k, т.е.

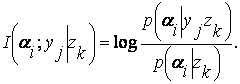                        (7.1.6)

Отсюда следует, что условная взаимная информация при фиксированной вероятности  принимает максимальное значение, когда . При этом

                  (7.1.7)

Величина  называется условной собственной информацией. Ее можно интерпретировать как количество информации, доставляемое событием α_i при известном событии z_k, или как количество информации, которое должно доставляться некоторым другим событием для однозначного определения события при известном z_k.

         Покажем, что взаимная информация удовлетворяет свойству аддитивности. Пусть α_i, y_j и z_k - три статистически зависимых события. Тогда количество информации о событии α_i, которое доставляют события y_j и z_k

(7.1.8)

         Таким образом, количество информации о событии α_i, которое доставляют события y_j и z_k, равно сумме информации, доставляемой z_k при известном событии y_j.

         Аналогично можно показать, что

                     (7.1.9)

         Используя соотношения (9.2), (9.4), (9.5) и (9.7), можно взаимную информацию записать в одной из следующих форм:

                        (7.1.10)

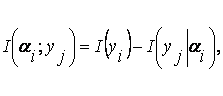                                                                     (7.1.11)

                     (7.1.12)

где  - собственная информация сложного события α_iy_j.

         Соотношение (9.10) можно интерпретировать следующим образом. Взаимная информация  равна разности между количеством информации, требуемой для определения α_i до и после того, как становится известным y_j. Нетрудно пояснить и соотношения (7.1.11) и (7.1.12), а количество информации о множестве А передаваемых символов, которое в среднем содержится в множестве Y принимаемых символов.

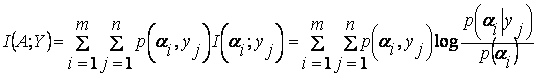.   (7.1.13)

Величина I(A;Y) называется средней взаимной информацией.

Нетрудно показать, что

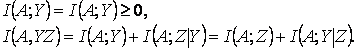         (7.1.14)

         На практике также вызывает интерес не собственная информация, а средняя собственная информация.

         (7.1.15)

Она характеризует количество информации, которое в среднем необходимо для определения любого символа из множества А возможных передаваемых символов.

         Выражение (7.1.15) идентично выражению для энтропии системы в статистической механике. Поэтому величину I(A) называют энтропией дискретного источника А и обозначают через Н(А). Чем больше Н(А), тем более неопределенным является ожидаемый символ. Поэтому энтропию можно рассматривать как меру неопределенности символа до того, как он был принят.

         Из (7.1.15) следует, что Н(А)≥0, т.е. энтропия является неотрицательной величиной. Она обращается в нуль, когда одна из вероятностей р(α_i) равна единице, а остальные нулю. Этот результат хорошо согласуется с физическим смыслом. Действительно, такая ситуация возникает, например, когда передается только один символ. Поскольку он заранее известен, то неопределенность источника равна нулю и с появлением символа мы не получаем никакой информации.

         Энтропия удовлетворяет неравенству

                                           (7.1.16)

причем знак неравенства имеет место, когда где m - число возможных событий α_i (число различных символов, сообщений и т.п.). Это свойство можно доказать, используя неравенство

                                             (7.1.17)

Рассмотрим разность

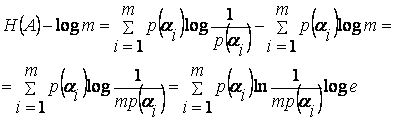       (7.1.18)

Учитывая (7.1.17), находим

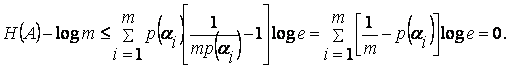   (7.1.19)

Знак равенства имеет место, когда 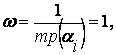так как только при  неравенство (7.1.17) превращается в равенство. При этом энтропия принимает максимальное значение .

         Из (7.1.16) вытекает следующий важный вывод: при заданном алфавите символов количество информации, которое в среднем может содержаться в одном символе, достигает максимума, когда все символы используются с равной вероятностью. При этом величину  называют информационной емкостью алфавита.

         Для алфавита, состоящего из двух символов,

где р - вероятность появления одного из символов. При р = 1/2 (рис.7.1.1) энтропия принимает максимальное значение дв.ед. Таким образом, двоичная единица информации, или бит, - количество информации, которое содержится в одном двоичном символе, появляющемся с вероятностью р=0,5.

Подобно тому, как было введено понятие средней собственной информации, можно ввести понятие условной собственной информации:

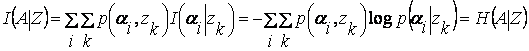   (7.1.20)

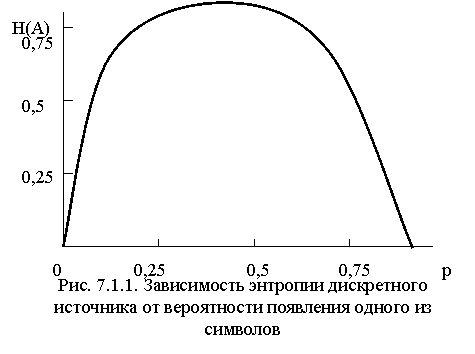         Величина  характеризует количество информации, которое в среднем необходимо для определения любого символа из алфавита А при известном множестве событий Z, т.е. характеризует неопределенность символа алфавита А до того, как он был принят, при условии, что множество событий Z известно. Она называется условной энтропией и обозначается через .

         Используя неравенство (7.1.17), нетрудно показать, что

                                    (7.1.21)

причем знак равенства имеет место, когда события α_i и z_k статистически независимы ( для всех индексов i и k).

         Соотношение (9.21) играет важную роль в теории кодирования. На его основе можно сделать следующий вывод: для того, чтобы каждый символ кодовой комбинации доставлял как можно больше информации, необходимо обеспечивать статистическую независимость каждого символа кодовой комбинации от предыдущих символов.

         Можно ввести понятие энтропии множества совместных событий A и Z:

    (7.1.22)

Подставляя вместо вероятности  под знаком логарифма произведение , выражение (7.1.22) можно привести к виду

                            (7.1.23)

Если события α_i и z_k статистически независимы, то формулу (7.1.23) можно переписать в виде

                              (7.1.24)

         Соотношения (7.1.23) и (7.1.24) есть не что иное, как свойство аддитивности энтропии.

         Среднюю взаимную информацию можно представить как

                            (7.1.25)

                             (7.1.26)

                  (7.1.27)

         Выражение (7.1.25) имеет простую физическую интерпретацию, когда  α_i- переданный символ, а  y_j - принятый. При этом Н(А) можно рассматривать как среднее количество передаваемой информации, H(A│Y) - как среднее количество информации, теряемой в канале связи (величину H(A│Y) обычно называют надежностью), I(A;Y) - как среднее количество информации, получаемой с приходом каждого символа. Нетрудно дать соответствующие интерпретации соотношениям (7.1.26) и (7.1.27).

         Энтропия H(Y│A)  определяется только помехой в канале связи и называется шумовой.

         Пусть  T_C  - среднее время передачи одного символа. Тогда величина R=I^′(А;Y)=(1/ T_C ) I(A;Y) характеризует среднее количество информации, передаваемое в единицу времени. Ее называют скоростью передачи информации.

         Величина H`(A)=(1/T_c)H(A) характеризует среднее количество информации, выдаваемое источником. Ее называют производительностью источника.

         Найдем среднее количество информации, передаваемое по двоичному симметричному каналу (рис.7.1.2)

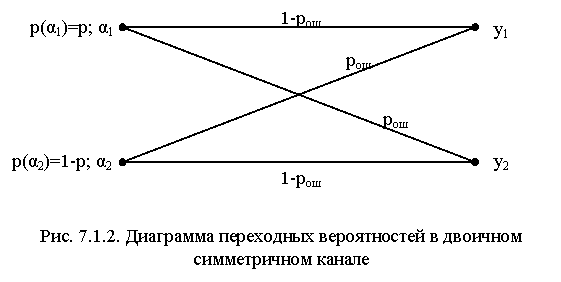
Пусть на вход канала поступают двоичные символы α₁ и α₂ с вероятностями р и (1-р) соответственно. На выходе канала появляются двоичные символы y₁ и y₂. Вероятность ошибки при передаче любого символа равна р_ош. Таким образом,

         Воспользуемся формулой (9.26). Энтропия

.

С учетом рассматриваемой модели канала

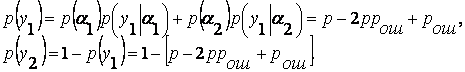
Нетрудно убедиться, что H(Y) принимает максимальное значение, равное 1, при р = 1/2.

         Условная энтропия

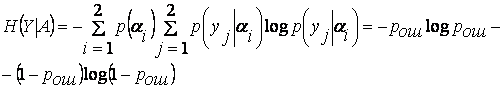
Заметим, что для рассматриваемого случая H(Y│A) не зависит от вероятности р.

         Подставляя выражения для H(Y) и H(Y│A) в (4.21), находим I(A;Y). В частности, при р = 1/2

       (7.1.28)

Таким образом, среднее количество информации, передаваемое каждым символом по двоичному симметричному каналу, при р = 1/2 зависит только от вероятности ошибочного приема символа (рис. 7.1.3)

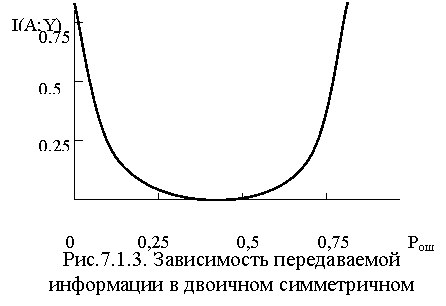В отсутствие помех (р_ош=0) I(A;Y)=1 дв.ед., при р_ош=1/2 I(A;Y)=0, т.е. никакой информации не передается; при р_ош=1 I(A;Y)=1 дв.ед. В последнем случае хотя все принятые символы ошибочные, однако передаваемые сообщения можно легко восстановить, поставив в соответствие сигналу  y₁ символ α₂, а сигналу y₂ символ α₁.

7.2. Избыточность сообщений

         Рассмотрим ансамбль A, состоящий из m различных символов . Энтропия такого дискретного источника достигает максимального значения , когда символы статистически независимы и появляются на его выходе с одинаковой вероятностью, равной 1/ m. На практике часто символы неравновероятны и зависимы. Поэтому энтропия источника . Соответственно количество информации, доставляемое такими символами, меньше возможного в  раз.

         Пусть сообщение состоит из n символов. Очевидно, что количество информации в нем . При использовании алфавита с максимальной энтропией для передачи такого же объема информации потребовалось бы число символов. Очевидно, что количество информации в нем I=nH(A). При использовании алфавита с максимальной энтропией для передачи такого же объема информации потребовалось бы число символов

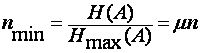
где, 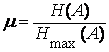- коэффициент, характеризующий допустимую степень сжатия сообщений.

         Величина  называется избыточностью источника.

7.3. Пропускная способность дискретных каналов с шумом

Среднее количество информации, передаваемое по дискретному каналу в расчете на один символ, определяется как

где А и Y -множества символов на входе и выходе канала. Энтропия Н(А) определяется только источником входных символов. Энтропии H(A│Y), H(A) и H(Y│A) в общем случае зависят как от источника входных символов, так и от свойств канала. Поэтому скорость передачи информации зависит не только от канала, но и от источника сообщений. Максимальное количество переданной информации в единицу времени, взятое по всевозможным источникам входных символов (по всем многомерным распределениям вероятности Р(А), характеризующим эти источники),

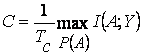                                   (7.3.1)

называется пропускной способностью канала.

         Пропускную способность канала можно определить и в расчете на символ:

                               (7.3.2)

7.4. Пропускная способность непрерывных каналов с

аддитивным шумом

Пусть сигнал y(t) на выходе канала представляет собой сумму полезного сигнала x(t) и шума n(t), т.е.

y(t) = x(t) + n(t), 0≤t≤T,                           (7.4.1)

причем сигнал x(t) и шум n(t) статистически независимы. Допустим, что канал имеет ограниченную полосу пропускания шириной F_к. Тогда в соответствии с теоремой Котельникова функции y(t) , x(t) и n(t) можно представить совокупностями отсчетов y_i, x_i и n_i, i=1,…,M, где М = 2F_кТ. При этом статистические свойства сигнала x(t) можно описать многомерной плотностью вероятности  а статистические свойства шума - плотностью вероятности   где x и n - векторы с координатами  и  соответственно.

         Пропускная способность непрерывного канала

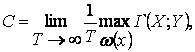
где - количество информации о какой-либо реализации сигнала x(t) длительности Т, которое в среднем содержит реализация сигнала y(t) той же длительности Т, максимум ищется по всем возможным распределениям ω(x).

         Среднюю взаимную информацию можно определить как

где

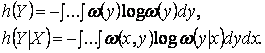
Заметим, что с учетом (7.4.1) условная плотность вероятности  и

         Таким образом, пропускная способность непрерывного канала с аддитивным шумом

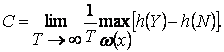                          (7.4.2)

         Вычислим пропускную способность непрерывного канала без памяти с аддитивным белым гауссовским шумом, имеющим одностороннюю спектральную плотность N₀, для случая, когда средняя мощность полезного сигнала равна P_c. При этом отсчеты шума оказываются статистически независимыми и дифференциальная энтропия

  (7.4.3)

где  - дисперсия шума n(t).

         Определим максимально возможное значение дифференциальной энтропии h(Y). Прежде всего отметим, что

т.е. средний квадрат отсчета Y_i фиксирован. При этом дифференциальная энтропия h(Y_i) принимает максимальное значение, когда случайная величина Y_i  является гауссовской с нулевым математическим ожиданием. Это имеет место, если случайная величина X_i гауссовская с нулевым математическим ожиданием.

         Дифференциальная энтропия h(Y) совокупности из n отсчетов будет максимальна, если отсчеты будут статистически независимы. Это имеет место, если спектральная плотность мощности процесса X(t) равномерна в полосе частот F_k.

         При выполнении указанных требований к сигналу

                          (7.4.4)

         Подставляя (7.4.3) и (7.4.4) в (7.4.2), находим

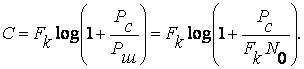                    (7.4.5)

         Формулу (7.4.5) часто называют формулой Шеннона. Подчеркнем, что она справедлива для следующей идеализированной модели канала связи. Выходное колебание y(t) представляет собой сумму входного сигнала x(t) и шума n(t), причем сигнал и шум являются статистически независимыми гауссовскими случайными процессами с нулевыми математическими ожиданиями и имеют равномерные спектральные плотности мощности в полосе частот .

         Формула (9.35) очень важна для системы связи, так как она устанавливает связь между пропускной способностью непрерывного канала с ограниченной полосой частот и техническими характеристиками системы: шириной полосы пропускания канала и отношением сигнал-шум. Из нее следует, что одну и ту же пропускную способность можно получить при различных соотношениях F_k и P_c/P_ш. Другими словами, формула (7.4.5) указывает на возможность обмена полосы пропускания на мощность сигнала и наоборот. С учетом зависимостей С от F_k и С от P_c/P_ш очевидна целесообразность обмена мощности сигнала на полосу.

         Из (7.4.5) нетрудно видеть, что пропускная способность канала растет с увеличением полосы частот F_k (рис.7.4.4.) и при  стремится к предельному значению

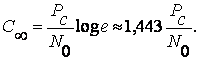
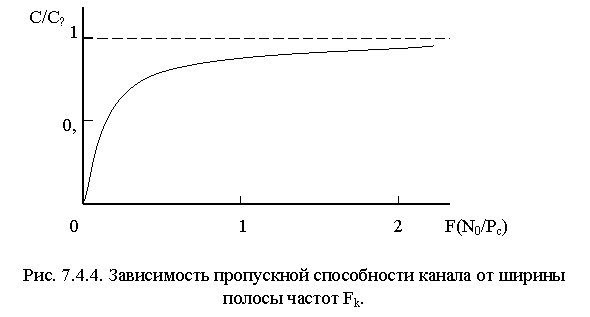Заметим, что пропускная способность непрерывного канала, в котором действует шум, отличный от белого гауссовского, больше, чем дает формула (7.4.5)

7.5. Теорема кодирования для канала с помехами

         Пропускная способность дискретного и непрерывного каналов характеризуют их предельные возможности как средств передачи информации. Они раскрываются в фундаментальной теореме теории информации, которая известна как основная теорема кодирования К.Шеннона. Применительно к дискретному источнику она гласит: если производительность источника сообщений H^{`</sup>(A)  меньше пропускной способности канала С, то существует по крайней мере одна процедура кодирования и декодирования и ненадежность H(A│Y) могут быть сколь угодно малы. Если H<sup>`}(A)>C, то такой процедуры не существует.

         Результат основной теоремы кодирования для канала с шумом в определенной степени неожидан. В самом деле, на первый взгляд кажется, что уменьшение вероятности ошибок в передаче сообщений требует соответствующего уменьшения скорости передачи и что последняя должна стремиться к нулю вместе с вероятностью ошибок. Такой вывод, в частности, вытекает из рассмотрения многократной повторной передачи символов источника по каналу как способа уменьшения вероятности ошибок в передаче сообщений. В этом случае при наличии помех в канале связи обеспечить стремление к нулю вероятности ошибки в передаче сообщения можно только при стремлении скорости передачи к нулю.

         Однако теорема кодирования показывает, что в принципе можно вести передачу со скоростью, сколь угодно близкой к С, достигая при этом сколь угодно малой вероятности ошибки. К сожалению, теорема, указывая на принципиальное существование помехоустойчивого кода, не дает рецепта его нахождения. Можно лишь отметить, что для этого необходимо применять коды большой длины. При этом по мере приближения скорости передачи к пропускной способности и уменьшения вероятности ошибки код усложняется вследствие увеличения длины блоков, что приводит к резкому усложнению кодирующего и декодирующего устройств и запаздыванию при декодировании. Применяемые в настоящее время способы кодирования не реализуют потенциальных возможностей систем связи. О степени совершенства системы связи можно судить по отношению .

         Для канала с пропускной способностью С, на входе которого включен источник непрерывных сообщений, К.Шеннон доказал следующую теорему: если при заданном критерии эквивалентности сообщений источника  его эпсилон-энтропия  меньше пропускной способности канала С, то существует способ кодирования и декодирования, при котором погрешность воспроизведения сколь угодно близка к . При  такого способа не существует.

Лекция 8. ОСНОВНЫЕ ПОНЯТИЯ НАДЕЖНОСТИ

Надежность есть свойство системы сохранять величины выходных параметров в пределах установленных норм при заданных условиях (обеспечивать нормальную работу системы).

Под «заданными условиями» подразумеваются различные факторы, которые могут влиять на выходные параметры системы и выводить их за пределы установленных норм.

Положим, что рассматриваемой системой является латунная серебреная пластина с хорошо отполированной поверхностью. На нее возлагается рабочая функция — отражение светового луча с минимальными потерями. Известно, что полированная серебреная поверхность обладает максимальным коэффициентом отражения 0,98.

Вначале (сразу после полирования) серебрённая поверхность имеет максимальный коэффициент отражения. С течением времени, вследствие влияния кислорода воздуха, на серебрённой поверхности образуются молекулы окислов серебра, ухудшающие отражательную способность поверхности. Если в окружающей среде имеется небольшое количество сероводорода (в обычных помещениях оно всегда существует), то на поверхности серебреной пластины появляются молекулы сернистого серебра, которые приводят к заметному ее потемнению. Другие сернистые газы (в очень незначительных количествах) в окружающей атмосфере также уменьшают отражательную способность пластины. Наличие влаги в воздухе способствует развитию этих процессов.

Через некоторый промежуток времени отражательная способность может заметно ухудшиться (с 0,98 до 0,4 и ниже). Если бы величина коэффициента отражения была установлена не менее 0,9, то через сравнительно короткий отрезок времени эта пластина перестала бы удовлетворять необходимым требованиям, так как ее выходной параметр вышел бы за установленные нормы.

В качестве другого примера рассмотрим изоляционную деталь, находящуюся под действием электрического поля. В начальный момент времени электрическая прочность этой детали такова, что электрическое поле ее не пробивает. С течением времен вследствие химических и физических процессов, постепенно изменяющихся под воздействием окружающей атмосферы и электрического поля, электрическая прочность материала данной детали уменьшается в некоторый момент времени, когда она становится меньше напряжение, которое к ней приложено, деталь пробивается.

Итак, в приведенных примерах первым заданным условием является время, в течение которого протекают процессы, приводящие к выходу параметров за установленные нормы, вторым — окружающая среда, которая воздействует на систему, изменяя ее состояние и выводя выходные параметры за пределы установленных норм.

Могут быть также условия, при которых параметры стабилизируются или улучшаются. Например, литые детали с течением времени в результате внутренней рекристаллизации упрочняются. Однако значительно больше систем, у которых надежность со временем уменьшается. Например, свойства всех органических изоляционных материалов в результате непрекращающихся внутренних процессов и внешних воздействий окружающей среды через некоторое время ухудшаются.

Свойства металлических деталей, находящихся под действием внутренних процессов, внешних механических нагрузок и химико-физического воздействия внешней среды, также ухудшаются. Даже у литых деталей, которые упрочняются с течением времени, под действием механических нагрузок и внешних воздействий окружающей среды ухудшаются механические свойства.

В сложных системах с большим количеством конструктивных элементов, выполненных из различных материалов и находящихся под рабочими и внешними воздействиями многочисленных факторов, как правило, происходят физические изменения, ухудшающие их первоначальные свойства.

Из всего сказанного следует, что надежность, прежде всего является функцией времени. В какой-то момент времени может наступить событие, после появления которого выходные параметры (или один из них) выйдут за пределы установленных норм.

О т к а з о м называют событие, после которого система не выполняет своих функций в установленном объеме (не обеспечивает нормальной работы).

Например, отказ непроволочного резистора бывает из-за выхода его величины за установленные нормы (за допуск) или обрыва проводящего слоя или вывода.

Отказ конденсатора, работающего в колебательном контуре, может быть в результате выхода величины емкости и диэлектрических потерь за установленные нормы, а также пробоя электрическим полем диэлектрика конденсатора.

Норма выходного параметра полупроводникового диода или триода не является универсальной и зависит от условий их использования. Например, некоторая максимально допустимая величина обратного тока в одном случае для диода не будет играть никакой роли, а в другом случае она может оказаться чрезмерно большой.

Бывают случаи, когда отказ системы на некоторое время не оказывает  влияния на конечный результат.

Допустим, что по радиолинии, которая в любой момент времени готова к передаче и приему телеграмм, используется часть общего времени ее действия. Отказ линии и перерыве между приемом и Передачей не отразится  своевременном и правильном ее действии в требуемый момент.

Понятие отказа относится к выходным параметрам системы. Говорить об  как о ситуации, после появления которой выходные характеристики системы оказываются за допустимыми пределами, недостаточно. Необходимо указывать при этом на состояние системы при выполнении ею заданных функций.

Отказы элементов системы можно разделить на следующие группы: отказы элементов, не влияющие на отказ системы; отказы элементом, выбывающие частичный отказ системы; отказы элементов, вызывающие полный отказ системы.

Без учета степени связи между параметрами элементов системы и ее выходными параметрами нельзя сделать правильных выводов о надежности системы при заданных уровнях надежности ее элементов.

Отказы бывают полные или перемежающиеся,

II о л н ы й   отказ характеризуется тем, что параметры системы выходят за установленные нормы и пока он не будет устранен, использование системы невозможно.

Для многих простейших систем полный отказ является невосстанавливаемым: пробой конденсатора с твердым диэлектриком (для большинства чипов конденсаторов); перегорание непроволочного резистора.

Перемежающиеся отказы возникают на короткий промежуток времени, после которого система вновь восстанавливает свои свойства. К простейшим системам с возможными перемежающимися отказами можно отнести, например, металлобумажный конденсатор, который после кратковременного пробоя быстро восстанавливает свою электрическую прочность.

Радиотехническая система, работающая на коротких волнах, и результате изменения свойств верхних слоев атмосферы также может иметь перемежающиеся отказы при передаче сигналов.

Отказы могут быть предсказываемые или случайные. Для предсказываемых отказов можно с некоторой сравнительно высокой точностью установит время их появления. Такие отказы иногда называют закономерными. Они не представляют особого интереса, поскольку легко предотвращаются. Гораздо больший интерес представляют отказы случайные.

Случайный характер отказов является результатом большого количества факторов и сложных процессов, определяющих выходные, параметры системы.

Во многих случаях бывают точно известны причины, вызывающие отказ, но никогда не удается точно предсказать время отказа. Например, после пробоя конденсатора иногда можно установить причину, но нельзя объяснить, почему именно в данный момент появились псе неблагоприятные факторы. Не всегда можно установить и причину, вызывающую отказ; например, причину перегорания нити накала электронной лампы, если напряжение на ней не превышало допустимых значений.

Полезный выход конструкции (ее заданная величина) обеспечивается строго определенными количественными соотношениями взаимосвязанных сил (энергий), действующих в системе. Нарушение этих соотношений может привести к недопустимой величине выхода, т. е, к отказу. Изменения какого-либо первичного параметра конструкции, вызывающие недопустимые изменения выходного параметра, могут происходить с большей или меньшей скоростью.

В зависимости от характера изменения выходного параметра конструкции отказы разделяют на две основные группы: постепенные, и внезапные.

Внезапным отказом назовем мгновенно (скачкообразно) насту пившее событие, после которого система не обеспечивает нормальной работы.

Постепенным отказом будем называть событие, наступившее и результате медленного изменения выходных параметров системы, после которого она не обеспечивает нормальной работы.

Поскольку время, в течение которого выходной параметр переходит границы допустимых значений, не регламентировано, трудно установить, является ли тот или иной отказ результатом внезапных или постепенных изменений первичных параметров. В этом и состоит их условность.

В РЭА встречаются как внезапные, так и постепенные отказы.

Нередко внезапный отказ конструкции обусловлен постепенным накоплением небольших изменений физических состояний элементов или их взаимосвязей. Постепенный отказ, в свою очередь, может быть следствием накопления небольших изменений, вызываемых внезапными отказами, происходящими на более низком уровне связей в элементах конструкции.

Например, в процессе эксплуатации радиоэлектронный аппарат может находиться под действием механических вибраций или ударов, вследствие чего у перемененoго или построечного конденсатора скачками (внезапно) может перемещаться его ротор. Через определенное время от многократных скачкообразных перемещений ротора конденсатора частота настройки колебательного контура может измениться на недопустимую величину и вызвать постепенный отказ. Из-за постепенного уменьшения напряжения на коллекторе транзистора, работающего и качестве генератора, его выходное напряжение заданной частоты, уменьшаясь, может перейти уровень допустимого значения и возникнет oтказ (постепенный). Но при уменьшении напряжения на коллекторе генерация может прекратиться раньше, чем выходное напряжение достигнет своего придельного значения. В этом случае произойдет внезапный отказ. Постепенные отказы являются результатом монотонных изменений первичных параметров от различных причин. Этими причинами могут быть, например, изменение напряжения питания, стабилизация параметров физических тел или любое их изменение в результате мате внутренних процессов, временное изменение внешних воздействий (тепла, холода, влаги, вибраций, ударов и т. п.).

Постепенные отказы могут быть следствием необратимых процессов, происходящих со временем в материалах элементов конструкции, или механического износа.

С течением времени заметно ухудшают свои характеристики многие электровакуумные изделия, элементы различных механизмов, работающие при сравнительно больших нагрузках, и некоторые другие части конструкций РЭА. Однако, кап показывает практика, отказы РЭА, вызываемые старением и износом, встречаются значительно реже, чем происходящие от других причин, особенно блоков РЭА, выполненных на транзисторах и других полупроводниковых изделиях.

Большинство отказов элементов РЭА взаимозависимо. Изменение параметров одного или одновременно нескольких элементов конструкции РЭА вызывает изменение состояния других элементов, а следовательно, и их склонность к отказам. Сложный характер различных отказов, которые наблюдаются в РЭА, в значительной мере затрудняют их анализ и расчет надежности конструкций.

Долговечность — это продолжительность работы системы элемент от начала эксплуатации до ее технической непригодности. Долговечность характеризуется либо временем, либо числом циклов, либо объемом произведенной работы.

В ряде случаев применяют термин ресурс, под которым понимают время, в течение которого система при необходимом техническом обслуживании может выполнять возложенные на нее функции, а после истечения этого времени эксплуатация системы становится невозможной или экономически нецелесообразной.

Системы могут быть обслуживаемые и необслуживаемые.

О б с: л ужи в а е м ы е системы предполагают в процессе эксплуатации возможность контроля ее выходных параметров, а к ряде случаев их регулирование. В таких системах обычно возможно проведение профилактических ремонтов и предотвращение енхшожных внезапных отказов, что позволяет, в известной мере, поддерживать определенный уровень надежности.

Необслуживаемые системы исключают возможность контроля регулирования и ремонта в процессе эксплуатации. Поэтому надежность такой системы не может поддерживаться на желаемом уровне и определяется только теми свойствами,, которые были нее «заложены» в процессе проектирования, конструировании и изготовления.

Различают системы невосстанавливаемые и восстанавливаемые.

Невосстанавливаемые системы после необратимого отказа становятся непригодными к дальнейшему использованию. Для некоторых систем невосстанавливаемость определяется условиями их использования, при которых нельзя устранить возникший отказ. Например, отказ радиоэлектронной системы ракеты не может быть восстановлен в процессе ее полета. Надежность таких систем определяется вероятностью исправной работы до первого отказа.

Восстанавливаемые системы после возникновения отказа могут быть исправлены и вновь приведены в годное для работы состояние. Такие системы характеризуются наработкой на отказ (средней продолжительностью работы системы между отказами) и временем восстановления. Обе характеристики являются случайными и зависят от различных факторов: характера отказов, ремонтопригодности, квалификации обслуживающего персонала и т. п.

Вероятность восстановления, среднее время восстановления и интенсивности, восстановления, являющиеся также характеристикой рассматриваемой системы, могут быть выражены в аналитической форме. Однако в реальных условиях определение этих характеристик при проектировании систем крайне затруднено.

Кроме того, существуют эксплуатационные коэффициенты надежности: коэффициент использования, коэффициент готовности, коэффициент простоя и т. п., которые находят по статистическим данным эксплуатации; как правило, они не могут быть рассчитаны в процессе проектирования систем.

8.1.  КОЛИЧЕСТВЕННАЯ ОЦЕНКА НАДЕЖНОСТИ

Надежность системы характеризуется степенью ее безотказности во времени. Поскольку отказ является случайной функцией времени, то надежность характеризуется случайной функцией времени. Следовательно, вероятность безотказной р а б о т ы  с и с т е м ы адекватна вероятности надежной р а б о т ы  систем ы.

Если задано, что система должна работать в течение времени t, то вероятность того, что она надежно (безотказно) будет работать в течение времени Т, можно выразить уравнением

P(t)=P(T>t)                                                                             (8.1.1)

Поскольку любая система состоит из элементов, ее надежность зависит от надежности элементов. Зная надежность элементов, нетрудно определить надежность системы.

Вероятное, надежной работы элементов будем обозначать через p(t). Дли вероятности надежной работы элементов уравнение (8.1.1) можно переписать в виде

р(t)=P(T>t)                                                                         (8.1.2)

Событие, противоположное надежности, есть ненадежность. Вероятность ненадежной работы элементов определяется уравнением

q(t)=P(T≥t)                                                                 (8.1.3)

Так как

то

подставим чту величину в (8.1.4), получим

(8.1.4)

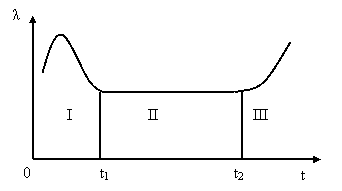Рис. 8.1.1. Зависимость интенсивности отказов от времени.

Итак, из (8.1.4) следует, что скорость отказов элементов  отнесения к оставшемуся количеству не отказавших (исправных) элементов [N₀ – n(t)], равна относительной скорости изменения надежности элементов. Знак минус в (8.1.4) указывает на «падение» скорости отказов элементов во времени.

Левая часть (8.1.4) есть относительное изменение скорости отказов, или интенсивность отказов λ;

Интегрируя (8.1.5), получим

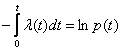
или

Уравнение (8.1.6) устанавливает связь между вероятностью надежной работы элемента и его интенсивностью отказов. Расчетным путем найти величину λ(t) для элемента нельзя. Поэтому пользуются экспериментальными данными, полученными в результате испытаний большого количества элементов и при длительном времени испытаний.

Наиболее часто встречающаяся зависимость интенсивности отказов элемента от времени представлена на рис. 8.1.1.

На рис. 4.11 кривая имеет три характерных участка. Первый период I — время приработки (t₀ — t₁), когда после включения в работу N₀ элементов явно ненадежные (а чаще просто с грубыми дефектами) начинают быстро выходить из строя. Затем количество выходящих из строя элементов из-за грубых дефектов уменьшается и наступает II период (t₁-t₂) когда действует большое количество случайных факторов, определяющих отказы. В этот период, когда интенсивность отказов почти постоянна, уравнение (8.1.4) будет иметь вид

                                      (8.1.5)

Далее, нIII времени после t₂ наступает процесс старения элементов и количество отказов быстро увеличивается со временем.

Если сравнить кривую рис. 8.1.1 со статистической зависимостью смертности людей (рис. 8.1.2), то нетрудно

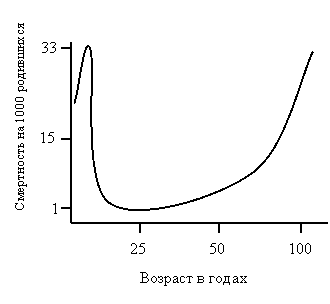Рис. 8.1.2. Стилистическая зависимость смертности людей

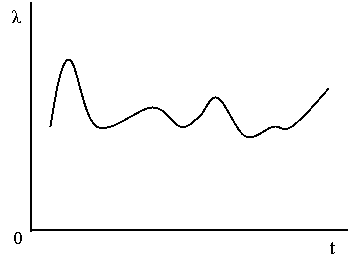Рис. 8.1.3. Практическая кривая интенсивности отказов

заметить их сходство. По - видимому сложные системы, независимо от их природы, обладают одинаковыми свойствами ненадежности.

В различных системах всегда могут оказаться доминирующие факторы, и наибольшей степени влияющие на надежность. Поэтому и зависимость интенсивности отказов от времени у таких систем может существенно отличаться от представленной на рис. 8.1.1. Практически зависимость интенсивности отказов от времени показана на рис. 8.1.3.

Если имеется возможность экспериментальным путем найти постоянную величину интенсивности отказов, то необходимо во время испытаний поддерживать постоянное число элементов путем немедленной замены отказавших элементов новыми, т. е. всегда должно соблюдаться первоначальное значение N₀. Но λ = const будет только в том случае, если число отказавших элементов п в процессе испытаний будет увеличиваться пропорционально времени, т. е. по линейному закону (конечно, в среднем). Следовательно, если за время t отказало п элементов, то в среднем за единицу времени число отказавших элементов . Скорость изменения отказавших элементов  можно заменить на ,  на  (поскольку вышедшие из строи элементы заменяются). Тогда

Итак, λ может быть найдена экспериментальным путем как отношение числа отказавших элементов к произведению первоначального элементов на время.

Размерность

От N₀t зависит возможность и точность определения λ. В самом деле, допустим, что истинная (искомая) величина . Чтобы в эксперименте получилось значение 10-^в, необходим по крайней мере один отказ при N₀t — 10⁵. Только тогда.

Если иметь в виду, что испытания относятся к вероятностной категории, то вероятность получения одного отказа при N₀t невелика; достоверность экспериментально определяемой λ увеличивается с увеличением N₀t.

Когда имеется возможность воспользоваться большим количеством элементов, уменьшается время испытаний. В противном случае требуется увеличение времени,

Не зная порядка ожидаемой величины λ (при малых значениях N₀t), можно ошибиться в определении ее истинной величины, так как в силу закона вероятностного распределения отказов во времени даже через малый промежуток времени элемент может отказать. Вероятность такого события не равна нулю. Очевидно, для правильной оценки У. и величина п не должна быть малой. Все предыдущие рассуждения относились к экспериментальному нахождению λ = - const, т. е. к рабочему участку кривой рис. 8.1.1.

Возвращаясь к (8.1.3), следует заметить, что — p'(t) указывает на скорость изменения вероятности безотказной работы элемента в момент времени t. Она отрицательна и свидетельствует о падении надежности во времени. Графически это показано на рис. 8.1.4. На основании (8.1.4) можно записать

                                                                    (8.1.6)

где  — частота, с: которой в любой момент времени происходят отказы при испытаниях без замены отказавших элементов.

Зависимость от времени представляет собой распределение

отказов всех первоначальных N. элементов.

Следовательно, функция (4.20), которая является отношением скорости изменения числа отказавших элементов к общему числу первоначальных элементов, есть функция плотности вероятности отказов

                                                             (8.1.7)

Как для всякой нормированной функции вероятностей, общая площадь, ограниченная кривой f(t), равна единице (рис. 8.1.).

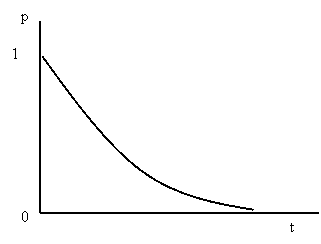Рис. 8.1.4.  Зависимость вероятности безотказной работы от времени

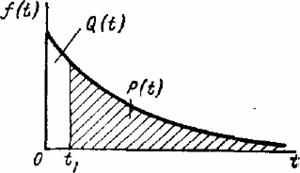
Рис. 8.1.5. Экспоненциальная функция плотности вероятности безотказной работы.  

Из (8.1.6) с учетом (4.21) можно записать

                               (8.1.8)

Из (8.1.8) видно, что λ(t) равна f(f), деленной на вероятность безотказной работы элементов для того же значения t. Уравнение (8.1.8) справедливо для любого закона распределения времени безотказной работы элемента.

Для частного случая, когда λ= const, с учетом (8.1.8) получим

(8.1.9)

Пользуясь (4.10) и (4.21), можно записать

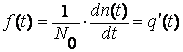(8.1.10)

Интегрируя (4.24), получим

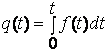                                                 (8.1.11)

Лекция 9. ОСНОВЫ РАСЧЕТА НАДЁЖНОСТИ

9. 1. УЧЕТ РАЗЛИЧНЫХ ФАКТОРОВ

Для получения более или менее достоверных расчетных данных о надежности разрабатываемого изделия необходимо располагать аналитическими зависимостями, в наилучшей степени характеризующими взаимосвязи параметров элементов с выходными параметрами изделия, степенью влияния параметров элементов на выходные параметры изделия, т. е. свес» каждого элемента в общей надежности изделия. Нужно знать поведение параметров элементов от действующих на них нагрузок, определяющихся режимом их использования и внешними воздействиями. Кроме того, необходимо иметь сведения о вероятностях появления возможных уровней режимов и внешних воздействий, а тают степень взаимосвязей и взаимозависимостей элементов.

Поскольку элементы в общем случае могут находиться в рабочей режиме различное время, отличающееся от рабочего времени изделия, это также должно учитываться при расчете надежности.

Располагать всеми данными, требующимися для расчета надежности вновь разрабатываемого изделия, в реальных условиях не всегда удается. Чем сложнее изделие, чем больше в нем элементов и чем многочисленнее и многообразнее связи между ними, тем труднее рассчитать его надежность. Но даже в наиболее благоприятных случаях, когда имеются все необходимые данные о надежности элементов и их взаимосвязях, полученная расчетная величина надежности нового изделия может существенно отличаться от обнаруживаемой в эксплуатации. Это является следствием существенного влияния производящей и эксплуатационной системы на надежность изделия. Причем данными этих систем, как правило, нельм воспользоваться для корректировки расчета.

Далее речь будет идти в большей мере о методике подход к расчету надежности изделия, чем о самом расчете, поскольку для каждого конкретного типа изделия порядок расчета может быть как таковой целесообразный только для него.

Ориентировочная оценка порядка уровней надежности может быть произведена по известным средним значениям интенсивностей отказов, входящих в изделие элементов. Целесообразна следующая последовательность расчета:

         1) все элементы изделия разбивают на группы с примерно одинаковыми значениями интенсивности отказов;

2) находят произведение числа элементов каждой группы на интенсивность отказов N_tK_t\

3) рассчитывают интенсивность отказов изделия как сумму

произведений N_iλ_i

4) определяют среднее время до первого отказа

5) пользуясь уравнением

для заданного времени t находят искомое значение Р (t). Определение величины Р (t) по заданным значениям t и T_ср._с упрощается если воспользоваться номограммой.

Допустим, что известно Т_Ср._с = 46 ч и требуется определить Р (t), когда t= 12 ч. Для этого из точки Т_cp.c = 46 ч на оси абсцисс проводят вертикальную линию до пересечения с линией (параллельной этой оси), соответствующей величине P(t)= 0,37 (получающейся при t = Т_ср.с). Из точки пересечения этих линий проводят прямую к точке P(t) = 1. Затем из точки оси абсцисс, соответствующей заданному значению t= 12 ч, проводят вертикальную прямую до ее пересечения с ранее полученной наклонной прямой. От полученной точки пересечения проводят линию, параллельную оси абсцисс. Ее пересечение с осью ординат и даст искомую величину Р(t) = 0,75.

Если известно Т_ср._с = 138 ч и задана величина Р (t)=0,9, то нетрудно найти время работы изделия, при котором будет обеспечиваться заданная величина безотказной работы изделия. В данном примере это время t =14 ч.

Третий вид задачи, которая может решаться с помощью номограммы, сводится к определению T_cp.c по заданным значениям P(t) и t.

Учет несовпадения времени работы элемента с временем работы изделия производится следующим образом.

Если интенсивность отказов элемента за 1 ч его работы λ₁, а время его работы в изделии в 10 раз меньше времени работы изделия, то вероятность безотказной работы его

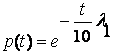
В общем случае, когда время работы элемента t₀, интенсивность отказов его п масштабе времени работы изделия

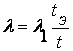
Следовательно, при определении надежности изделия для элементов с t_э < t величины их интенсивности отказов должны находиться по приведенной формуле.

Однако в рассмотренном случае предполагалось, что в нерабочем состоянии элемент имеет нулевую интенсивность отказов. В действительности этого не бывает.

Если в нерабочем состоянии интенсивность отказов элемента равна λ.₂ и он в течение времени t₁ находится в рабочем состоянии, а в течение времени t₂ = t — t₁. — в нерабочем состоянии, то его интенсивность отказов в масштабе времени работы изделия

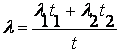
Различное время работы элементов обычно связано с условиями использования изделия. Например, в нем могут в определенное время включаться или выключаться отдельные части (каскады и отдельные элементы — электровакуумные или полупроводниковые изделия). Интенсивность отказов элементов, как правило, зависит от числа циклов включения и выключения.

Если интенсивность отказов элемента за один рабочий цикл λ_ц и если он совершает с операций за t ч работы изделия, то его интенсивность отказов

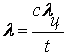
Общее значение интенсивности отказов элемента в масштабе

времени работы изделия

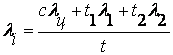
При практических расчетах следует учитывать соотношение величин λ_д, λ₁ и λ₂. Если одно (или два) из них существенно меньше других, то им целесообразно пренебречь. Например, в большинстве случаев λ₂<< λ₁, тогда величиной λ_ц можно пренебречь. Для переключающих устройств λ почти полностью определяется величиной λ_ц, тогда значением λ₁ можно пренебречь. Интенсивность отказов электронных и индикаторных ламп, а также в известной степени полупроводниковых изделий значительно зависит как от λ_ц, так и от λ₁.

Учет уровня нагрузок на элементы при расчете надежности изделия может быть произведен, если для них известны зависимости интенсивности отказов от нагрузок. Не для всех элементов такие зависимости бывают известны, а некоторые опубликованные данные о них являются общими, относящимися к типам элементов, а не к конкретным образцам. Различие между типовыми данными об интенсивности отказов элементов (в зависимости от уровней нагрузок) и реально существующими интенсивностями отказов используемых образцов данной партии изделий часто бывает настолько большими, что ошибки расчета величины Λ достигают одного, а иногда и двух порядков.

Вместе с тем анализ многих типовых элементов показывает, что существенное увеличение их интенсивности отказов наблюдается при таких уровнях нагрузок, которые в практике разработки радиотехнических изделий не используются. Это обстоятельство в известной мере уменьшает возможные ошибки расчета.

В общем случае интенсивность отказов элементов является функцией уровня нагрузок:

λ_i=f(z).

где z — уровень нагрузки.

Обычно задается величина λ_0i соответствующая интенсивности отказов некоторой номинальной нагрузки. Увеличение этой нагрузки определяется коэффициентом

где     z — уровень действующей нагрузки;   z_ном — уровень номинальной нагрузки.

Если известен К_ном, то по специальным графикам (обычно составляемым поставщиком) находят соответствукяцее ему значение λ_i. Например,   для   непроволочных   углеродистых  резисторов

При К_ном= 1,5, λ_i=1,2 λ_0i

а при К_ном=0,5                    λ_i=0,3 λ_0i

Кроме нагрузки, связанной с условиями использования элементов (механическая, тепловая, электрическая и т. п.), необходимо учитывать влияние внешних посторонних воздействий, снижающих уровень надежности элементов. Для этого нужно знать зависимости интенсивности отказов элементов от уровня внешних воздействий, например, от степени влажности, вибраций и т. п.

Многочисленные факторы, определяющие условия работы элементов, действуют в различных сочетаниях и в различные отрезки времени. Если зависимость интенсивности отказов элементов от комбинированного воздействия нескольких факторов известно и время, в течение которого они работают, также определено, то в общую расчетную формулу надежности подставляют величины λ_i с учетом: времени работы каждого элемента. Однако подобный идеализированный случай в практике встречается крайне редко. Чаще необходимые зависимости неизвестны, а время действия различных внешних факторов подчиняется случайным закономерностям, распределение вероятности которых также не бывает известно. Поэтому при расчете надежности делают некоторые допущения, основанные на анализе возможных условий использования элементов в изделии и условий эксплуатации. При этом стремятся коэффициенты нагрузок брать с величинами, близкими к их верхнему (возможному в данных условиях) пределу.

Итак, чтобы найти величину интенсивности отказов элемента с учетом всех условий его использования, нужно, кроме ранее определенных факторов, знать степень увеличения λ_i от действия внешних факторов (их наиболее неблагоприятного сочетания). Последние будут оказывать влияние на интенсивность отказов элементов!: в рабочем, нерабочем и циклическом режиме (λ₁, λ₁, λ_ц)

Это влияние может быть учтено с помощью соответствующих коэффициентов — z_1, z₂, z_ц.

Таким образом, для расчета надежности изделия в качестве вв-личины интенсивности отказов элементов нужно брать

Тогда надежность изделия в простейшем случае может быть найдена из уравнения

P(t)=e^-Λt

Трудности расчета надежности изделия, как это видно из приведенных соотношений, связаны с необходимостью большого количества данных о каждом элементе.

Если величины λ₁, λ₁, λ_ц и с в ряде случаев бывают известны, то z_1, z₂, z_ц как правило, неизвестны. Например, для некоторых типов реле известны величины λ_ц, а z_ц, зависящие от степени влияния влажности, тепла, загрязнения атмосферы активными газами, обычно неизвестны.

Величина λ₁ может быть найдена по данным некоторых типовых изделий (резисторы, конденсаторы, электронные лампы и т. п.), а величина z₂ для них, зависящая от воздействия совокупности внешних факторов, также обычно неизвестна. Поэтому выбор величины λ_i производят па основании далеко несовершенных статистических данных эксплуатации изделий, аналогичных вновь разрабатываемым. В этом состоит еще одна трудность получения достоверных расчетных величин надежности вновь разрабатываемых изделий.

9. 2. РАСЧЕТ НАДЕЖНОСТИ, ОБУСЛОВЛЕННОЙ

ПОСТЕПЕННЫМИ ОТКАЗАМИ.

Расчет надежности, обусловленный постепенными отказами, сводится к определению вероятности перехода выходного параметра (или нескольких выходных параметров) за пределы установленных для него норм.

Для этого нужно знать функциональные связи между первичными и выходными параметрами изделия и плотности вероятностей дли величин первичных параметров.

В процессе работы изделия обычно происходят постепенные изменением первичных параметров. Причем скорость этого изменения меняется во времени. Поэтому для расчета нужно знать зависимость средних значений первичных параметров и их дисперсией от времени. При этом задача будет заключаться в отыскании параметров нестационарного случайного процесса. Решение такой задачи в общем виде очень сложно. Поэтому делают ряд допущений.

Но и в этом случае расчет оказывается достаточно трудоемким. Некоторое облегчение по его выполнению достигается за счет использования ЭЦВМ. Однако результаты расчета на ЭЦВМ определяются главным образом точностью используемых исходных данных. В реальных условиях, как правило, для большинства первичных параметров радиотехнических изделии неизвестны зависимости их средних значений и дисперсией от времени.

Поэтому и здесь необходимы известные допущения.

ЛЕКЦИЯ 10. ЭЛЕМЕНТЫ ИНЖЕНЕРНОЙ ПСИХОЛОГИИ

10.1. ЗВУКОВЫЕ И ТАКТИЛЬНЫЕ ВОСПРИЯТИЯ

Слух здорового человека воспринимает звуковые частоты в диапазоне 16—20 000 Гц. У различных людей этот диапазон различен и зависит от уровня громкости и условий восприятия. Звуки с частотой ниже 16 Гц называют инфразвуками с частотой выше 20 000 Гц — ультразвуками.

При увеличении частоты вдвое высота тона всегда повышается на одну и ту же величину, называемую октавой.

Весь диапазон слышимых звуков содержит примерно 10 октав. Звуки отличаются по частоте и силе. Кроме простых звуков, в виде отдельных тонов существуют сложные, состоящие из большого количества составляющих частот, т. е. обладающие широким частотным спектром. Число различных по частоте и силе тонов, воспринимаемых ухом, приблизительно 540 000. Минимальное изменение частоты, которое может воспринять человеческий слух (при частоте 400 Гц), составляет 0,3% исходной частоты. На более низких частотах это значение в 2—3 раза больше (до 1%).

ТАБЛИЦА 10.1

Уровень звука, дБ	Сила звука, вт/см^2	Звуковое давление, бар	Субъективная оценка действия шума на человека
0 80 90 100 110 120 130	10^-16 10^-8 10^-7 10^-6 10^-5 10^-4 10^-3	2·10^-4 2 6.3 20 63 200 630	Порог слышимости Шум заметен Шум беспокоит: Разговор требует повышенного голоса Шум мешает Разговор невозможна Шум подавляет и раздражает Болевые ощущения

Восприятие интенсивности звука зависит от звукового давления.

Порог слышимости — это минимальная величина звукового давления, необходимого для того, чтобы звук был слышен. Он зависит от частоты и в диапазоне 800—2000 Гц составляет примерно 2-10^-4 бар (2-10^-10аm). Для других частот (больших и меньших упомянутого диапазона) уровень порога растет, т. е. чувствительность уха уменьшается постепенно на 6—7 порядков у граничных частот слышимого диапазона.

Ухо способно воспринимать большой динамический диапазон громкостей (до 60 дб) без ущерба для слухового аппарата. При больших громкостях (например, при давлениях в несколько сотен бар) в ухе начинает возникать болевое ощущение, а при дальнейшем повышении звукового давления может произойти повреждение слухового аппарата.

Уровень силы звука обычно оценивают по величине превышения порога слышимости и выражают в децибелах. Уровень звуков, с которыми приходится встречаться конструкторам радиоэлектронных устройств, достигает 125—128 дб (шумы в танках и летательных аппаратах). Некоторое представление о субъективной оценке действия шума на человека можно получить из табл. 10.1.

Зависимость громкости от частоты обычно представляют в виде кривых равной громкости (рис. 10.3). До уровня 90 дб заметна зависимость громкости от частоты, выше этого уровня зависимость практически исчезает. В пределах 700—4000 Гц громкость достигает максимума. Область слухового восприятия в зависимости от частоты – рис. 10.1.

Рис. 10.1. Область звуков, вызывающих слуховые ощущения

Рис. 10.2. Зависимость уровня громкости, интенсивности и частоты колебаний звука

Продолжительность воздействия звука влияет на восприятие его громкости. Максимальная громкость, достигнутая обычно за 0,5 сек, при увеличении этого времени может несколько уменьшиться за счет адаптации уха на звук. Для звуков очень малой продолжительности убывание громкости обычно выражено более резко. Критическая продолжительность, ниже которой громкость резко падает, равна 0,15-0,2 сек, хотя и зависит в некоторой степени: от частоты; так, при низкой частоте громкость снижается больше, чем при высокой при одинаковой длительности. На рис. 10.4 приведена диаграмма зависимости уровня громкости, интенсивности и частоты колебании звука.

Различимость уровней громкости зависит как от абсолютной ее величины, так и от характера звука. Чистые тона при средней громкости различаются по уровню в пределах ± 1 дб (а в некоторых случаях и меньше). При восприятии сложных звуков различимость находится в пределах +2 ¸ 3 дб, а надежная различимость. — в прадедах ± 6 дб.

Ориентировка с помощью слуха, т. е. точность определения направления источника звука, не зависит от удаленности источника звука. При восприятии звука обоими ушами она значительно выше. При слушании обоими ушами звуки, идущие справа и слева, никогда не смешиваются, а направления на звук вперед и назад, вверх и вниз смешиваются довольно часто. Одновременно могут восприниматься направления разных звуков. Шумы обычно воспринимаются лучше, чем простые звуки.

Тактильная чувствительность человека — это способность воспринимать механические раздражения кожи. При легком касании к предмету появляется чувство прикосновения, а при более сильном — давления. Тактильной чувствительностью обладает вся кожа человека, но наибольший интерес представляют руки, которые обладают хорошей чувствительностью, так как число тактильных точек ладоней и кончиков пальцев большое.

Как и другие чувствительные органы человека, тактильная чувствительность зависит от ряда факторов. В частности она повышается при нагревании кожи и уменьшается при охлаждении. Длительные механические раздражения, как правило, снижают возбудимость тактильных точек.

10.2. Требования к зрительным индикаторам

К числу зрительных индикаторов относятся: предметные и световые индикаторы.

Предметные индикаторы и сигнализаторы выполняют в виде шкал, цифр, надписей, семафоров, фигур и т. п.

Информация, даваемая предметными индикаторами, определяется числом их различных состояний; количеством делений шкалы, числом цифр, количеством и содержанием надписей числом положений семафоров (флажков), числом различных фигур.

Световые индикаторы и сигнализаторы представляют собой сигнальные лампы, светящиеся надписи и фигуры и др.

Требования, предъявляемые к любым зрительным индикаторам, сводятся к следующему:

1) число различных индикаторов должно быть минимальным;

2) индикаторы должны допускать быстрое их восприятие оператором;

3) точность показаний должна находиться в установленных
нормах;

4) индикаторы должны обеспечивать высокую надежность показаний в заданных условиях наблюдения.

Одним из важных условий обеспечения этих требований является высокая степень различения отдельных показаний зрительных индикаторов. Оценка индикаторов производится по различным критериям.

1. По скорости передачи информации.

2. По функции поступающей информации в процессе управления (командная или осведомительная).

3.  По способу использования индикатора (в отношении чтения
его показаний):

а) для проверочного (контрольного) чтения. Воспринимая их
показания, оператор решает простую альтернативную задачу по
типу «да» или «нет»;

б) для качественного чтения. Они дают информацию о направлении изменений управляемых параметров аппарата (например, возрастает или уменьшается данная величина);

в) для количественного чтения. Они передают информацию в виде численных значений управляемых величин.

Такое деление является условным, так как в большинстве индикаторов совмещаются возможности всех трех групп чтения.

4. По форме сигнала, т. е. по отношению его свойств к свойствам объекта.

При оценке изображений главную роль играет их полнота (степень схематизации, детализации, количество воспринимаемых свойств). Если же речь идет о символах, то прежде всего оценивается способ кодирования. Поскольку сообщения об одном и том же событии могут быть переданы с помощью разных кодов, а один и тот же код использован для передачи сообщений о разных событиях, вопрос о выборе оптимального способа кодирования приобретает особое значение.

5. По масштабу, т, е. по количественному отношению величин
изменения сигнала (будет ли это интенсивность свечения лампы или
путь движения стрелки) к величине изменения управляемого пара
метра.

Лекция 11. КОНТРАСТ, РАЗЛИЧЕНИЕ СВЕТОВЫХ СИГНАЛОВ И ЦВЕТОВОЕ КОДИРОВАНИЕ

Яркость, освещенность и  контраст  в значительной мере определяют характеристики видимости. Отношение разности яркости объекта и фона (или наоборот — яркости фона и объекта) к яркости фона называют яркостным контрастом, являющимся самой важной характеристикой условий видимости.

Различают два вида контраста — прямой и обратный. Если объект темнее контраст называют прямым, если объект ярче фона — обратным.

Значение яркостного контраста рассчитывают по формулам

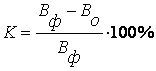
при условии, что В_Ф>В₀ (прямой контраст), и

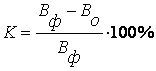
при условии, что В_ф<В₀ (обратный контраст), где В_ф — яркость фона; В₀ —  яркость объекта.

Обычно уровни контрастов разделяют на следующие группы:

малый контраст K =20%;

средний контраст K = (20 ¸ 50)%;

высокий контраст K>50%.

Рекомендуемая, зона величины контраста находится в пределах от 65 до 96%, при этом оптимальным является контраст, равный 85—90%.

Контраст выше 90% можно использовать в тех случаях, когда требуется наибольшая четкость изображения, а общее время работы небольшое. При более длительной работе предпочтение следует отдавать контрасту величиной 85—90%.

Видимость зависит не только от самой величины контраста, но и от того, как контраст воспринимается в конкретных условиях, поскольку он зависит от порогового контраста рассматриваемых

Поэтому видимость по контрасту V определяется отношением контраста объекта с фоном К к пороговому контрасту K_пор:

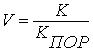
Для получения хорошей видимости величина V должна быть равна 15 - 30. Пороговую величину контраста находят по кривым зависимости контраста, освещенности и угловых размеров (рис. 10.19).

Из опыта известно, что изображения с прямым контрастом создают лучшие условия для восприятия глазом наблюдаемых объектов, чем изображения с обратным контрастом.

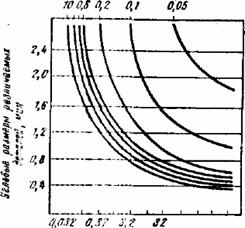
Рис. 11.1. Разрешающая способность глаза в зависимости  от яркости  при

Различение световых сигналов на экране электроннолучевых трубок, радиолокационных индикаторов имеет свои характерные особенности, связанные со световыми контрастами, формами фигур и скоростями их изменения, с шумами, уменьшающими различимость слабых сигналов.

Изучение зависимости «порога обнаруживаемости» сигнала от частоты импульсов и скорости вращения радиолокационной антенны показало, что с увеличением частоты вероятность обнаружения, по которой определяется этот порог, возрастает, но только до тех пор, пока фон экрана не станет однообразным.

Поскольку оператору приходится не только обнаруживать сигналы, но и следить за их перемещением, важным оказывается порог зрительного восприятия скорости и ускорений.

Найдено, что нижний порог зрительного восприятия движения равен примерно 1—2 угл. мин/сек. Эта величина действительна в тех случаях, когда человек оценивает движение точки относительно покоящегося объекта. Если же таких объектов нет, то порог возрастает до 15—30 улг. мин.сек.

Порог различения изменения скорости прямолинейного движения точки является величиной переменной, зависящей от исходной скорости. Чем выше скорость движения светящегося пятна, тем выше порог остроты зрения. Детали объектов (символов на экране электроннолучевой трубки) лучше различают при перемещении справа налево и снизу вверх, чем при перемещении в противоположных направлениях.

Рис. 11.2.  Зависимость временного порога восприятия (1) и опознания   контура  знака   (2) от углового размера

В настоящее время широкое применение находят совмещенные индикаторы, объединяющие радиолокационное изображение со знаковой индикацией. В таких индикаторах изображается положение объекта в горизонтальной плоскости, а вертикальная координата (высота) обозначается цифрой.¹ Кроме того, цифрами, буквами,

геометрическими символами и пиктографическими маркерами обозначают целый ряд других параметров управляемого объекта. Использование совмещенных индикаторов в системах управления летающими объектами значительно повышает их пропускную способность. Однако необходимость декодирования цифровых символов (перевод их в пространственные представления) снижает эффективность таких индикаторов.

Цветовое кодирование используют для обозначения принадлежности объектов к той или иной категории, для отметок критических точек на шкалах приборов, для передачи информации о режиме работы аппарата (например, включен, выключен, дежурный режим и т. п.). Наиболее широко цветовое кодирование применяют для передачи сигналов об опасности.

Целесообразно, например, использование изменения насыщенности цветового сигнала для передачи информации о направлении изменений регулируемых процессов. Иногда цвет можно применять не только в качестве кода, но и как средство изображения некоторых свойств объектов,

При разработке цветового кода необходимо учитывать закономерности цветового зрения и те условия, в которых оно осуществляется.

В добавлении к уже упомянутым особенностям цветового восприятии отметим, что видимый цвет предметов зависит от их освещения. Натуральный цвет обнаруживается только при белом (дневном) освещении, но он изменяется, если освещение хроматическое (табл. 10.6). Как уже указывалось, различимость цветов зависят от интенсивности освещения. При слабом освещении тепловые тона сдвигаются в сторону красных, холодные — в сторону зелено-голубых. В условиях сумерек цвет перестает быть видимым (за исключением голубого).

При восприятии предметов под малым углом зрения (10—20) наблюдается «стягивание» цветов к двум точкам: теплых — к красному, холодных — к голубому.

Точность различения цвета зависит от величины окрашенной поверхности: чем больше поверхность, тем точнее распознается цвет. На малых поверхностях лучше различаются чистые, особенно теплые топа.

Известно, что цвет оказывает влияние на восприятие величины объекта. Пользуясь цветом, можно изменять впечатление видимой величины, т. е. «уменьшать» или «увеличивать» предметы.

Следует иметь в виду, что цвета под влиянием контраста изменяются в сторону цвета, дополнительного к цвету фона.

Холодные тона дают более заметный контраст, чем теплые.

Несмотря на большое разнообразие цветов и их оттенков для цветового кодирования, пока используют малое количество цветов. Объясняется это рядом причин: недостаточностью изучения возможностей цветового кодирования, неосведомленностью конструкторов и некоторым несовершенством красок, которые под воздействием внешней среды (особенно ультрафиолетового излучения) могут менять свои оттенки.

Известны определенные комбинации цветов, применяющиеся для некоторых видов кодирования. Например, по Международному стандарту сигналами опасности являются теплые тона безопасности — холодные. При этом степень опасности обозначается разными цветами.

Принято состояние включения аппарата индицировать горением красной лампы; расцветку шкал, как отмечалось, производить черной краской на белом фоне, выделять отдельные шкалы красной краской. Поля поверхностей шкал в много шкальных конструкциях разделять на такие цвета, как красный, синий, желтый и т. п.

Цвет проводов рекомендуется следующий: для цепей с повышенным потенциалом — красный, для низкочастотных цепей — синий или черный.

11.2. СРАВНИТЕЛЬНЫЕ ОСОБЕННОСТИ РАЗЛИЧНЫХ ГРУПП ЗРИТЕЛЬНЫХ ИНДИКАТОРОВ

Сопоставление различных зрительных знаков и выяснение их относительной приемлемости для передачи одной и той же информации дало бы возможность правильно выбрать наиболее подходящие знаки для конкретных объектов. Однако точных данных о такой оценке пока еще нет, хотя. имеющиеся результаты экспериментальных исследований могут иногда оказать помощь в выборе зрительных знаков. В известных исследованиях сравнивались пять абстрактных способов кодирования: в качестве алфавита использовались цифры, буквы, геометрические фигуры, конфигурации и цвета (рис, 11.2).

ЦИФРЫ	1    2    3    4    5    6   7    8
БУКВА	A   B    C   D   E    F   G   H
ГЕОМЕТРИЧЕСКИЕ ФОРМЫ
Бор. Оранж Зел. Зел. Жел. Кор Чер. син Крас.. Чер. ЦВЕТА

Рис. 11.2. Пять абстрактных способов кодирования

Осуществлялось опознание сигналов и их счета, нахождение места, сравнение и проверка данных. Наилучшие результаты были получены при использовании цифрового и цветового кодов, наихудшие — при использовании конфигурации. Но, как выяснилось, шкала оценок разных кодов не является абсолютной; она зависит от характера конкретной выполняемой деятельности. Например, при опознании наиболее эффективным (по точности) оказался цифровой код; цветовой занял лишь четвертое место; при определении местоположения объектов наилучшие результаты были получены при использовании цветового кода.

Эффективность кодирования определяется задачей, которую должен решать оператор. Процесс приема информации включает в себя следующие элементарные гностические процессы и действия: 1) поиск (и обнаружение), 2) различение, 3) идентификацию, 4) декодирование (интерпретацию).

Попе к. Время поиска (и обнаружения) тем, короче, чем больше вновь появляющийся сигнал отличается от фона и других окружающих сигналов.

Цвет, если он «броский» и хорошо выделяет сигнал из фона, обеспечивает его сравнительно быстрое обнаружение. Легко обнаруживаются визуальные сигналы, если их появление сопровождается мельканием, частота которого ниже критической.

Поиск визуального сигнала среди других по размеру или форме включает сложную систему гностических и измерительных действий, что, естественно, требует дополнительного времени и снижает общую Эффективность обнаружения.

Скорость и точность обнаружения зависят от числа сходных сигналов. Эксперимента со зрительными сигналами показали, что критическим числом является 5 - 6 сигналов. Новый сигнал легко обнаруживается на фоле 2 - 3 подобных, без большого труда он обнаруживается также на фоне 4 - б сигналов.

Различение играет большую роль в процессе обнаружения сигнала. Человек обладает способностью различать большое количество градаций теговых сигналов. Однако число состояний сигнала, при различении которых обеспечивается максимальная скорость приема информации, существенно меньше количества градаций, которое человек способен различать. Существует так называемый порог оптимального различения, который и снижает возможности обнаружения различных сигналов.

Здесь следует учитывать и степень влияния различных помех. Например, и одних условиях могут оказаться большие помехи при приеме цифровой, а в других — цветовой информации.

Установлено, что существует определенная последовательность различия разных признаков. При зрительном восприятии прежде всего различается положение сигнала в поле зрения, а затем его цветовой тон и яркость и лишь впоследствии форма.

Идентификация — это опознание данного стимула как
данного. Число точно идентифицируемых градаций одномерного
сигнала сравнительно невелико. Оно равно примерно 7±2. При
увеличении количества признаков это число возрастает. 

Решающую роль в идентификации играет сравнение воспринимаемых сигналов с некоторыми эталонами, хранящимися в памяти
в форме представлений и образующими субъективную шкалу,
по которой оцениваются воспринимаемые сигналы. Эффективность
идентификация определяется четкостью и организованностью системы эталонов. Преимущество цифрового кода при опознании объясняется, по-видимому, тем, что соответствующая система эталонов,
сформированная и непрерывно используемая в опыте человека, является высокоорганизованной.

Декодирование сводится к тому, что оператор должен оценить состояние управляемого объекта, т. е. соотнести сигнал с объектом. Основным моментом процесса декодирования является перевод образа сигнала в образ управляемого объекта. Скорость, точность и надежность перешифровки, очевидно, определяется структурой той системы ассоциаций, которая формируется у оператора в процессе обучения и накопления опыта работы.

Таким образом, выбор той или иной системы зрительных сигналов оказывается достаточно сложным и не всегда однозначным. Выбор должен основываться на характеристиках процессов обнаружения, различения, идентификации и декодирования. Именно эти характеристики определяют длину алфавита сигналов и «насыщение» каждого из них информацией.

В настоящее время еще недостаточно изучены все эти процессы, Поэтому выбор зрительных сигналов целесообразно производить прежде всею с учетом отмеченных особенностей приема информации и всегда стремиться к обеспечен максимальной различимости их различимости на заданном фоне и с учетом посторонних сигналов (предметов) и возможных случайных помех. Однако некоторые общие рекомендации о восприятии различной информации и характере ее переработка можно дать по 134].

Восприятие количественной информации лучше всего осуществляется человеком при чтении счетчика. Однако это справедливо только в том случае, когда показания меняются не очень быстро,

Контрольное считывание используется, когда оператор не нуждается в точных количественных показателях и важным является знание того, нормален или ненормален режим системы или ее части. Для этих целей лучшим считают прибор с движущейся стрелкой. Положение стрелки определяют легко, и она очень удобна для контрольного чтения: оператор скоро привыкает к тому, что при определенном положении стрелки аппарат работает нормально, и всегда быстро реагирует на уменьшение или увеличение измеряемого параметра. Движущаяся шкала и счетчик для контрольного считывания подходят меньше, так как они не позволяют оператору судить о направлении и величине отклонения без предварительного восприятия числа или показаний шкалы, для чего требуется дополнительное время.

Передача информации от человека к аппарату с помощью зрительных индикаторов лучше всего может быть произведена при использовании движущейся стрелки или счетчика. Обычно предпочитав движущуюся стрелку. Прибор с движущейся стрелкой дает возможность установить простые и прямые связи между движениями стрелки и органа управления. Кроме того, положение стрелки помогает оператору следить за изменениями, которые происходят при перемещении органа управления.

Счетчик позволяет с большой точностью следить за пер еде чей информации человеком аппарату. Однако иногда отношение между движением органа управления и движением счетных шкал двойственны. Другой недостаток счетчика состоит в том, что при быстрых движениях он становится практически нечитаем.

      Слежение при использовании зрительных сигналов лучше всего производить при прямой связи между движением стрелки и воздействующим на нее органом управления. Счетчик не подходит для слежения, поскольку трудно наблюдать за изменением его показаний. Связь между движением цифр на счетчике и органе управления неоднозначна; счетчик, как уже отмечалось, плохо читается при быстрых изменениях показаний.

Лекция 12. ОРГАНЫ УПРАВЛЕНИЯ

Получив информацию, оператор ее перерабатывает и при определенных условиях использует для осуществления рабочих функций. К последним в частности относится управление, с помощью которого оператор изменяет состояние системы (аппарата), его выходные параметры.

Управление возможно различными видами сигналов: световыми, звуковыми, электрическими (биотоками), механическими.

Наиболее известным и хорошо изученным является механическое управление с помощью непосредственного контакта оператора с элементами управления аппарата. Все процессы механического управления связаны со способностью оператора передавать информацию объекту, т. е. с характеристиками его моторного «выхода», что обусловливает определенные требования к конструкции органов управления.

Исследованию упомянутых характеристик посвящено много работ. Некоторые данные этих характеристик приводятся далее по [33].

Диапазон скоростей движения руки от 0,01 (движение пальцев при тонкой регулировке) до 8000 см/сек. Наиболее часто встречающиеся скорости от 5 до 800 см/сек.

Считают, что движение рук в направлении «к телу» быстрее, чем в направлении «от тела». Однако последние отличаются более высокой точностью. Скорость движения в вертикальной плоскости больше, чем в горизонтальной. Наибольшей скоростью обладают движения «сверху — вниз», наименьшей — «снизу — вверх». Движения в направлении «вперед — назад» в горизонтальной плоскости быстрее, чем латеральные (боковые; отдаленные от середины). Скорость движения «слева — направо» (для правой руки) несколько больше, чем скорость движений в обратном направлении. Скорость движений в направлениях под углом к вертикальной и горизонтальной осям тела меньше, чем в направлениях по этим осям.

Вращательные движения совершаются в полтора раза быстрее, чем поступательные.

Более экономичными (с точки зрения усилий) являются движения, производимые с максимальными начальными скоростями, которые постепенно уменьшаются (движения «толчками»).

Данные о величинах движений органов правой половины тела приведены в табл. 10.7.

Эти данные позволяют оценить возможности различных частей моторного аппарата при условии их изолированного движения (при неподвижности всех остальных). В реальных условиях обычно действуют не отдельные части моторного аппарата, а кинематические цепи, что позволяет увеличивать объем производимых движений. Следует иметь в виду, что на предельных положениях конечностей требуется большая затрата времени и энергии, работа при этом быстро утомляет оператора.

Максимальная и нормальная рабочие зоны для обеих рук представлены на рис. 12.1.1.

Рис. 12.1.1. Максимальная  и нормальная рабочие зоны в горизонтальной плоскости

На рис. 12.1.2 показано максимальное пространство при работе руками.

Число степеней свободы рук достаточно большое. Кисть по отношению к плечевому поясу имеет семь степеней свободы (за счет плечевого сустава, локтевого совместно с лучелоктевым, лучезапястного). Кончик пальца по отношению к грудной клетке имеет 16 степеней свободы, а по отношению к опоре (стопам) — около 30.

Наличие большого числа степеней свободы является предпосылкой универсальности исполнительных функций руки.

Из всех возможных движений рук в реальных условиях оказываются более выгодными и экономичными плавные эллиптические и круговые движения, поскольку они полнее, чем иные, отвечают 'радиальной форме перемещения звеньев тела в пространстве.

Силы, с которыми человек может производить движения, определяют требования к моментам органов управления. Они также связаны со скоростью и точностью двигательных реакций.

Сила, которая может быть развита при выполнении элементарных движений руки, изменяется в зависимости от их направления. В   табл. 10.8   представлены   результаты   измерений   силы руки   при   выполнении   движений   в   разных направлениях.

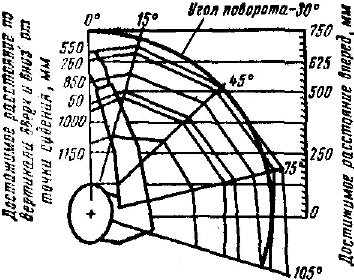
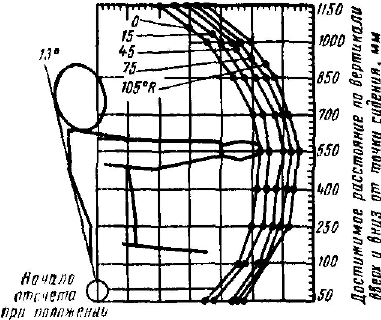
Рис. 12.1.2. Максимальная зона при работе руками: а — вид сверху; б —вид сбоку

Максимальное усилие, развиваемое человеком при манипулировании рукоятками управления, зависит от их формы и длины.

Результаты некоторых исследований показывают, что лучшими являются рукоятки Т-образной формы по отношению к Образной. Очевидно, большая длина подобных рукояток всегда лучше коротких.

Физическая сила человека для разных возрастов и индивидуальных особенностей

может различаться в 2—3 раза.

Регуляция рабочих движений связана с точностью и скоростью двигательных реакций. Поэтому знание особенностей регуляций движений позволит выбрать правильные расположения управляющих элементов и других их характеристик. Воспользуемся некоторыми исследованиями по этому вопросу, рассмотренными в [33].

Установлено, что пространственно двигательная ориентировка точнее для уровня ниже груди. Короткие движения руки, как правило, переоцениваются, длинные — недооцениваются. "Нейтральная точка", разделяющая короткие и длинные движения, по данным различных авторов, находится в пределах от 8 до 16 ем. Только движения, направленные сверху вниз, всегда переоцениваются. С увеличением амплитуды возрастает и абсолютная ошибка. Наиболее точно оцениваются движения правой руки, совершаемые в направлении из центра направо.

В процессе контакта человека с объектом немалое значение имеют так называемые гностические действия, направленные на познание объекта и условий (ощупывающие или осязательные движения), и приспособительное движения, с помощью которых исправляются ошибки, возникающие в процессе выполнения действия.

Интересно отметить, что при манипуляциях элементами ручного управления аппарата (тумблеры, выключатели, рукоятки, рычаги и т. п.) разные пальцы выполняют различные функции. Например, большой, указательный, а иногда и средний производят рабочие движения; средний и безымянный выполняют гностические движении, в то же время безымянный — приспособительные. Однако каждый тип движения не связан однозначно с определенным пальцем. В процессе манипулирования происходит смена функций пальцев и «передача» движений от одного к другому. Самый процесс манипулирования состоит из ряда микродвижений каждого пальца, совершаемых как в контакте, так и вне контакта с органом управления.

Повторяющиеся движения, с помощью которых осуществляют операции кодирования и передачи информации, а также точной нацеленной установки могут быть вращательными, нажимными или ударными.

Установлено, что темп вращения для ведущей руки 4,83 об/сек, для неведущей — 4 об/сек.

Как оказалось, наибольший темп приходится на рукоятки с диаметром G см. При увеличении диаметра темп уменьшается, с уменьшением диаметра темп также уменьшается, но менее заметно, чем при увеличении.

Темп зависит от момента вращения. Увеличение требуемого момента уменьшает темп. Это особенно заметно на рукоятках с диаметром менее 6см, но оно почти незаметно при использовании рукояток с диаметром более 16 см,

Максимальный темп нажимных движений при величине усилия 25 г для ведущей руки составляет 6,68 нажимов/сек, для неведущей --- 5,3 нажимов/сек. При увеличении усилия до 400 г эти различия уменьшаются (6,14 — для ведущей; 5,59— для неведущей).

Точность регулирования усилий наилучшей получается при 5 нажимах/ сек,

Максимальный темп ударных движений пальцами находится в пределах от 5 до 14 ударов/сек. При этом наблюдаются различия между пальцами (например, мизинец правой руки 56, а указательный — 70).

Время реагирования, в течение которого человек может полученный сигнал реализовать в виде ударного движения, по некоторым литературным данным должно быть не менее 0,5 сек.

Если сигнал для второго движения подается через более короткий промежуток времени, то реакция на него задерживается: она не начинается раньше завершения реакции на первый сигнал. По известным данным задержка происходит лишь при интервалах, меньших 0,25 сек. При высоком темпе сигналов задержки аккумулируются и возникает «психологическая блокировка», выражающаяся в пропуске сигналов и появлении реакции с большими латентными периодами.

Настройка аппаратуры требует дозированных движений по их силовым, пространственным и временным параметрам в соответствии с некоторой заданной мерой. Основным фактором, определяющим их динамику, является требование точности дозированных реакций.

Латентный период и время выполнения самого движения зависят от направления поворота. Движение правой руки вправо (изнутри - наружу) начинается позже, но совершается быстрее, чем движение в обратном направлении (снаружи — внутрь).

Точность установки рукояток лучше всего получается на положениях 0; 90 и 180˚. Установка рукоятки в пределах 0 и 90˚ дает наибольшие положительные постоянные ошибки, а в пределах 90— 180˚ — отрицательные.

В диапазоне 0—90˚ большая точность достигается в действиях правой руки, в диапазоне 90-180˚ — левой. Аналогичная картина наблюдается и при оценке установленного положения.

Точность установки, кроме прочих причин, определяется дробностью дозирования движения руки. Известно, что в процессе поворота рукоятки управления пальцами свершается более 100 микродвижений. Манипуляция с переключателями сопровождается с микродвижениями
в два раза меньшими. Ведущая роль в манипуляциях с рукоятками принадлежит большому, указательному и среднему пальцам; остальные выполняют преимущественно функцию уравновешивания.

Рис. 12.1.3. Зависимость рабочих и

коррегирующих движений руки от

передаточного   числа:

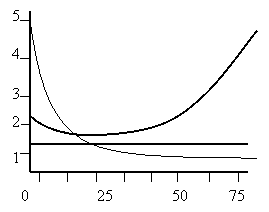
Корригирующие      движения (исправляющие ошибки), как и  рабочие, требуют определенного  времени, которое зависит от отношения между величиной поворота рукоятки и вызываемым им  перемещением указателя  (рис. 12.1.3). С увеличением передаточного  числа время рабочих движений сокращается, а коррегирующих возрастает. Оптимальным является такое отношение, при котором полный поворот рукоятки дает перемещение указателя на 2,5—5 см.

Соответствие     направления движения и направления сигнала, поступающего на сенсорный «вход» оператора, оказывает заметное влияние на условия регулирования движения.

Наиболее быстрыми и точными оказываются те движения, направление которых совпадает с направлением сигнала. Например, у круглой шкалы указатель должен двигаться в направлении увеличения данных (рис. 12.4); при наличии нулевых отсчетов вправо (положительные) и влево (отрицательные) (см. рис. 12.1.4). Для прямоугольных шкал направление движения должно быть вверх или вправо. Небольшое увеличение сопротивления приводит к заметному увеличению точности. Форма рукояток управления, предназначающихся для разных целей, должна быть различной. Это в значительной степени улучшит процесс их опознания;

скорость и точность оператора при этом будет повышена. Однако при большом разнообразии форм (и большом количестве рукояток) опознание их затрудняется. Поэтому, когда число рукояток управления большое, целесообразно их делать различными по форме, размерам и цвету.

Рис. 12.4. Легко различимые формы рукояток

В литературе приводятся формы рукояток, легко различимые на ощупь (рис. 12.4), Однако не следует забывать, что они определены только по одному критерию тактильному опознанию, поэтому не отвечают ряду других важных требований. По-видимому, более целесообразно пользоваться формами рукояток, например, появлении на рис. 12.1.5.

Рис.  12.1.5. Рекомендуемые формы рукояток вращающихся селекторных переключателей

ЭКОНОМИЧЕСКИЕ ОСНОВЫ   КОНСТРУИРОВАНИЯ РЭА

12.2. КОМПЛЕКСНАЯ ОЦЕНКА КАЧЕСТВА РЭА

Качество РЭА оценивают рядом показателей: выходными параметрами, надежностью, ресурсом, ремонтопригодностью, художественным оформлением, технологичностью, экономичностью и т. п.

Не все показатели могут быть выражены количественными мерами, а многие из них находятся в противоречивой взаимосвязи. Например, производственные показатели (технологичность, себестоимость и др.) находятся в противоречии с техническим уровнем РЭА; уровень надежности — с затратами на разработку и производство. Удобство и эстетические особенности РЭА также не могут быть выражены с помощью количественных мер.

Часто о качестве РЭА судят не по абсолютным, а по относительным показателям. Например, вновь разработанный РЭА сравнивают с существующим прототипом или с каким-либо образцом, принятым за эталон.

Несовершенство такой оценки очевидно, поскольку, во-первых, она производится в сравнении со «старым» РЭА, а, во-вторых, при такой оценке понятия «лучше» или «хуже» не являются количественными мерами.

Сложность оценки заключается еще в том, что многочисленные показатели изменяются не в одинаковой мере.

Например, чувствительность одного радиовещательного приемника может быть увеличена и 5 раз, а полоса частот расширена на 10%, в то время как у другого приемника полоса частот может быть расширена в два раза, а чувствительность увеличена только в 3 раза. При этом другие показатели могут быть улучшены тоже в разной степени и не всегда легко определить величину изменения качества при сравнении комплекса различных показателей.

Количественные оценки качества РЭА в свою очередь могут приводить к большим ошибкам. Так оценка заказчиком новых РЭА часто бывает субъективной.

Все сказанное, относится не только к РЭА, ко к большинству других изделий. Поэтому в последнее время проводятся многочисленные работы по выработке комплексного критерия качества изделий. Один для таких критериев рассматривается  в [35].

В этой работе под оптимальным уровнем качества изделия (РЭА) понимается такое сочетание его различных свойств (технических, экономических, эстетических), которое обеспечивает определенные потребности с минимально возможными издержками на их создание и использование.

Качество изделия (РЭА) считается тем выше, чем полнее удовлетворяются определенные потребности при минимально возможных затратах общественного труда.

Критерий оценки качества изделий (РЭА) должен быть комплексным, т. е.:

а) учитывать характер и объем потребности, для которой создается или используется данное изделие (РЭА);

б) оценивать эффективность изделия по производительности общественного труда;

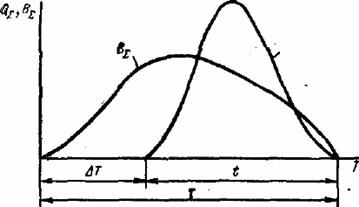
Рис.12.2.1. Распределение во времени полной целевой отдачи и затрат:

t - время на достижение целевой отдачи;   τ—период  времени расходования средств; ΔТ —время на проектирование   серийное  производство и подготовку к применению изделия

в)           учитывать влияние фактора врем времени (изменение эксплуатационной
эффективности во времени, распределение затрат и потребности во времени),
разновременность затрат и эффекта;

г) давать количественную оценку.

В связи с этим комплексный критерий качества изделия (РЭА) можно представить в следующем виде:

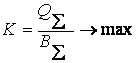
где q_Σ — полная целевая отдача всей совокупности изделий (РЭА) за период их эксплуатации;

В_Σ — сумма издержек народного хозяйства на достижение полной щелевой отдачи.

Большое значение для оценки уровня качества изделий (РЭА) имеет распределение полного целевой отдачи и суммы издержек во времени (рис. 11.1).

Полная целевая отдача зависит от многих технических и организационных факторов: от подготовки парка изделий (РЭА), условий их эксплуатации, форм и методов ее организации, квалификации обслуживающего персонала и др. И все это изменяется во времени. Например, по мере освоения эксплуатации новых надели и (РЭА) растет их эффективность использования, по мере освоения серийного производства увеличивается надежность и уменьшается себестоимость.

СПИСОК ЛИТЕРАТУРЫ

1. Березин Л.В. и Вейцель В.А. Теория и проектирование радиосистем. Под ред. В.Н.Типугина. Учебное пособие для вузов. М., "Сов радио", 1977.

2. Фролов А.Д. Теоретические основы конструирования и надежности радиоэлектронной аппаратуры. М., "Высшая школа", 1970.

3. Космические траекторные измерения. Под. Ред.П.А.Агажанова, В.Е.Дулиевича, А.А.Коростелева. М., "Сов.радио", 1969. Авт.: П.А.Агажанова,Н.М.Барабанов, Н.И.Буренин и др.

4. Астафьев Г.П., Шебшаевич В.С., Юрков Ю.А. Радиотехнические средства навигации летательных аппаратов.М., "Сов.радио",1962.

5. Основы радиоуправления. Под.ред. В.А. Вейцель, В.Н.Типугина., М., "Сов.радио", 1973. Авт.: Л.В.Березин, В.А.Вейцель, С.А.Волковский и др.

6. Налимов В.В. Теория эксперимента. М., "Наука", 1971.

7. Типугин В.Н., Вейцель В.А. Радиоуправления. М., "Сов. радио", 1962.

8. Основы теоретического проектирования систем связи через ИСЗ. Под.ред.А.Д.Фортушенко.М.,"Связь", 1970. Авт.:А.Д.Фортушенко,Г.Б.Аскинази, В.Л. Быков и др.

9. Гуткин Л.С. Оптимизация радиоэлектронныхустройтв. М., "Сов.радио",1975.

СОДЕРЖАНИЕ ПРЕДИСЛОВИЯ …………………………………………………………. ЛЕКЦИЯ 1. Введение. …………………………………………………… ЛЕКЦИЯ 2. Общие вопросы проектирования радиосистем ……….….   2.1. Методология проектирования радиосистем……………….        2.2. Формулировка задач оптимизации. Критерии качества                           систем…………………………………………………………… ЛЕКЦИЯ 3. Общие принципы анализа радиосистем……………………        3.1. Задачи анализа и математические модели сообщений, сигналов и помех …………………………………………………………. ЛЕКЦИЯ 4. Характеристика радиосигнала ….………………………….         4.1. Функция различия, сигнальная функция и функция определенности ………………………………………….………………..         4.2. Сравнение радиосигналов с помощью функций различия и сигнальных функций……………………………………………………… ЛЕКЦИЯ 5. Выбор структуры и оценка точности радиосистем. Обобщенная модель приема и задача оптимизации………….………….…………………………………………          5.1. Постановка задачи оптимизации радиоприема ………………          5.2. Ограничения в задаче оптимизации …………………………. ЛЕКЦИЯ 6. Модели сообщений ………………………………………...          6.1. Общие соображения по выбору модели сообщения в задаче синтеза ……………………………………………………………………...          6.2. Дискретная модель сообщения …………………….…………..          6.3. Непрерывная одномерная модель сообщения …..…………....          6.4. Векторная модель сообщения ..………………………………...          6.5. Модель сообщения в виде функции времени………………… ЛЕКЦИЯ 7. Основы информации ………………………………………..          7.1. Количество информации в дискретных сообщениях. Энтропия источника дискретных сообщений …………..……………...          7.2. Избыточность сообщений……………………………….…….          7.3. Пропускная способность дискретных каналов с шумом…....          7.4. Пропускная способность непрерывных каналов с аддитивным шумом.………………………………………………………          7.5. Теорема кодирования для канала с помехами ………………. ЛЕКЦИЯ 8. Основные понятия надежности ……………………………          8.1. Количественная оценка надежности ………………………….  ЛЕКЦИЯ 9. Основы расчета надежности ………………………………. 9.1. Учет различных факторов ………………………………….. 9.2. Расчет надежности, обусловленной постепенными отказами………………………………………………………. ЛЕКЦИЯ 10. Элементы инженерной психологии……………………….          10.1. Звуковые и тактильные воспитания ………………………….          10.2. Требования к зрительным индикаторам …………………….. СПИСОК  ЛИТЕРАТУРЫ………………………………………………

2 3 5 5 10 26 26 43 43 49 53 53 61 71 71 73 78 84 91 97 97 105 106 106 109 110 116 121 121 126 127 127 130

ЛЕКЦИЯ 11.Контраст, различение световых сигналов и цветовое кодирование ……………………………………………………………….            11.2. Сравнительные особенности различных групп зрительных индикаторов ……….……….…………………………………………….. ЛЕКЦИЯ 12. 12.1 Органы управления …………………………………            12.2. Комплексная оценка качества РЭА ……………………….. СПИСОК  ЛИТЕРАТУРЫ………………………………………………

131 135 138 145 148

" Проектирование, технология

радиоэлектронных средств"

конспект лекций

для курсантов Специального факультета

Рассмотрено на заседании кафедры

 ТПС        (протокол № 17)

и рекомендовано к печати

Составители:

Абдуазизов А.А.

Маненков В.И.

Собирова У.Ш.

Ответственный редактор               Абдуазизов А.А.

Редакционно-корректурная комиссия:

Редактор_______Ибраимов Р.Р.

Корректор  _____  Абдуллаева С.Х.