Узбекское агентство почты и телекоммуникации

Ташкентский электротехнический институт связи

 

 

 

Кафедра

Теории электрических цепей

 

 

 

 

ТЕОРИЯ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

 

Конспекты лекций

 

для студентов заочного факультета

 

 

Ташкент 2002

 

 

 

Белова Л.Н.  «Теория электрических цепей» Конспекты лекций для студентов заочного факультета, обучающихся по направлениям образования: 5222000:<Радиотехника>, 5222100: <Радиосвязь, радиовещание, телевидение>, 5222200: <Телекоммуникации> Ташкент: ТЭИС. 2002.-94 с.

 

В пособии приведены лекции, составленные в соответствии с рабочей программой курса ТЭЦ и предназначенные для облегчения самостоятельной работы студентов заочного факультета. Приведены вопросы для самоконтроля усвоения материала и список рекомендуемой литературы.

Пособие предназначено для студентов заочного факультета, обучающихся по направлению  <Телекоммуникации>, <Радиотехника>, <Радиосвязь, радиовещание, телевидение>.

 

 

 

Введение

 

Дисциплина «Теория электрических цепей» (ТЭЦ) предназначена для общетеоретической подготовки студентов к изучению специальных дисциплин. ТЭЦ закладывает основы знаний и умений анализа и расчёта электротехнических и радиотехнических устройств. Она вводит в мир профессиональных понятий, определений, терминов и методов расчёта электрических цепей.

В свою очередь, дисциплина ТЭЦ опирается на знания предшествующих курсов высшей математики и тесно переплетена с одновременно изучаемыми курсами электронных и квантовых приборов и теории электрической связи.

Дисциплина ТЭЦ изучается в 4,5 семестрах. В обоих семестрах студенты должны выполнить цикл лабораторных работ и сдать итоговый контроль. В сессионный период студентам читаются лекции, на которых преподаватель объясняет наиболее трудные разделы дисциплины, в объеме – 10 часов (5 лекций) в четвертом семестре и 10 часов (5 лекций) в пятом семестре.

Цель настоящего пособия оказать помощь студентам заочного факультета в их самостоятельной работе по изучению курса ТЭЦ при отсутствии единого учебника.

Самостоятельно изучать дисциплину целесообразно в следующем порядке:

1. Ознакомиться с содержанием конспекта лекций 1÷5 лекций в четвертом семестре и 5÷9 - в пятом семестре.

2. Ответить на вопросы, предложенные по материалу каждой лекции. Если ответы на вопросы будут вызывать затруднения, студенты могут воспользоваться учебными пособиями из рекомендуемого списка литературы.

3. После изучения теории (или хотя бы внимательного прочтения конспекта лекций) целесообразно приступить к решению задач.

При возникновении вопросов или затруднений при изучении курса ТЭЦ можно обратиться на кафедру по телефону 35-07-44.

 

 

 

 

Лекция 1. ОСНОВНЫЕ ЭЛЕМЕНТЫ, ПОНЯТИЯ И ЗАКОНЫ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

 

1.1.     Определение электрических цепей. Понятие тока, напряжения и ЭДС

 

Электрической цепью (ЭЦ) называется совокупность электропроводящих устройств, электромагнитные процессы в которых описываются с помощью понятий напряжения и тока.

Электрический ток – это упорядоченное движение электрических зарядов. Сила тока i – количество электричества, прошедшее через поперечное сечение проводника в единицу времени.

	dq

 

dt

i(t) = i =         [A]                                          (1.1)

 

Принято считать значение тока i положительным, если движение положительно заряженных частиц совпадает с заранее выбранным направлением отсчета тока и отрицательным в противном случае. Выбор направления отсчета тока произволен и показывается стрелкой (рис. 1.1, а).

 

 

 

 

 

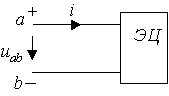      а)                                                             б)

Рис. 1.1

 

Электрическое напряжение между двумя точками определяется количеством энергии, затрачиваемой на перемещение единичного заряда из одной точки в другую

	dw

 

dt

u(t) = u=         [B]                                      (1.2)                                     

 

В потенциальном электрическом поле напряжение между двумя точками определяется  разностью потенциалов между ними (рис. 1.1, б).

 

u_ab = j_a - j_b                                                (1.3)

 

Положительное направление напряжения выбирается произвольно. Чаще всего его выбирают совпадающим с положительным направлением тока и указывают стрелкой или знаком «+» или «-».

Электродвижущей силой (ЭДС) e(t) называется работа сторонних сил по перемещению единичного заряда внутри источника энергии. ЭДС измеряется в вольтах [B].

 

1.2.     Элементы электрических цепей и их свойства

 

Элементом ЭЦ называют идеализированное устройство, отображающее какое-либо из свойств реальной ЭЦ.

Электрические цепи, в которых параметры всех элементов не зависят от величины и направлений токов и напряжений, т.е. графики вольт-амперных характеристик (ВАХ) элементов являются прямыми линиями, называются линейными. Соответственно такие элементы называются линейными.

Когда параметры элементов ЭЦ существенно зависят от тока или напряжения, т.е. графики ВАХ этих элементов имеют криволинейный характер, то такие элементы называют нелинейными. Если ЭЦ содержит хотя бы один нелинейный элемент, то она является нелинейной электрической цепью.

В теории электрических цепей различают активные и пассивные  элементы. Первые вносят энергию в электрическую цепь, а вторые ее потребляют.

1.2.1.       Пассивные элементы

 

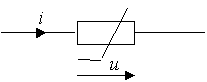
Резистивным сопротивлением называется идеализированный элемент ЭЦ, обладающий свойством необратимого рассеивания энергии.

 

 

 

 

 

 

 

 

 

 

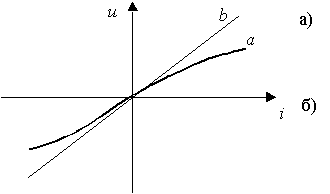
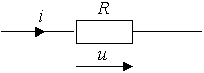
Рис. 1.2.

 

Графическое изображение этого элемента и его  вольт-амперная характеристика показана на рис. 1.2 (а - нелинейное сопротивление, б -линейное сопротивление).

Напряжение и ток на резистивном сопротивлении связаны между собой зависимостями:

u = iR,               i = Gu.                                       (1.4)

Коэффициенты пропорциональности R и G в формулах (1.4) называются соответственно сопротивлением и проводимостью и измеряются в омах [Ом] и сименсах [См].

	1

 

G

R  =         .                                                     (1.5)

 

Индуктивным элементом называется идеализированный элемент ЭЦ, обладающий свойством накопления им энергии магнитного поля.

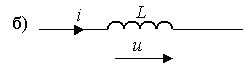
Графическое изображение этого элемента показано на рис. 1.3 (а -нелинейного, б - линейного).

 

 

 

 

 

 

 

 

 

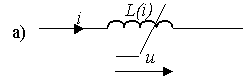Рис. 1.3.

 

Линейная индуктивность характеризуется линейной зависимостью между потокосцеплением y и током i, называемой вебер-амперной характеристикой  y  = Li. 

dy

Напряжение и ток связаны соотношением

	di

 

dt

u =          = L         .                                         (1.6)

dt

 

Коэффициент пропорциональности L в формуле (1.6) и называется индуктивностью и измеряется в генри (Гн).

Емкостным элементом (емкостью) называется идеализированный элемент ЭЦ, обладающий свойством накапливания энергии электрического поля.

Графическое изображение этого элемента показано на рис. 1.4. (а-нелинейного, б-линейного).

 

			a)

 

 

 

 

 

 

 

 

 

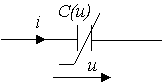
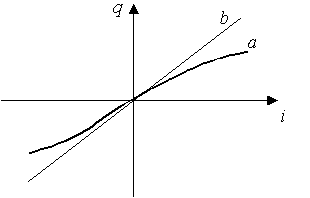
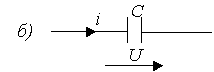
Рис. 1.4.

 

Линейная емкость характеризуется линейной зависимостью между зарядом и напряжением, называемой  кулон-вольтовой характеристикой

 

q = Cu                                                  (1.7)

 

Напряжение и ток емкости связаны соотношениями

	du

 

dt

dt

i =         =C        .                                       (1.8)

 

1.2.2.      

dq

Активные элементы

 

Активными называются элементы цепи, которые отдают энергию в цепь, т.е. источники энергии. Существуют независимые и зависимые источники. Независимые источники: источник напряжения и источник тока.

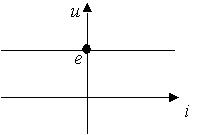
Источник напряжения - идеализированный элемент ЭЦ, напряжение на зажимах которого не зависит от протекающего через него тока (рис. 1.5).

 

 

 

 

 

 

 

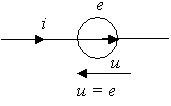Рис. 1.5.

 

Внутреннее сопротивление идеального источника напряжения равно нулю.

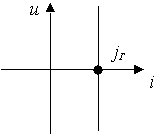
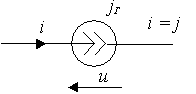
Источник тока – это идеализированный элемент ЭЦ, ток которого не зависит от напряжения на его зажимах.

 

 

 

 

 

 

Рис. 1.6.

 

Внутреннее сопротивление идеального источника тока равно бесконечности

Источники напряжения (тока) называются зависимыми (управляемыми), если величина напряжения (тока) источника зависит от напряжения или тока другого участка цепи. Зависимыми источниками моделируются электронные лампы, транзисторы, усилители, работающие в линейном режиме. Различают четыре типа зависимых источников.

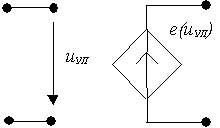
1. ИНУН – источник напряжения, управляемый напряжением:

 

 

 

 

 

 

а) нелинейный                                        б) линейный

                          m – коэффициент усиления напряжения

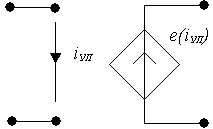2. ИНУТ - источник напряжения, управляемый током:

 

 

 

 

 

 

 

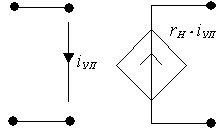а) нелинейный                                           б) линейный

r_Н – передаточное сопротивление

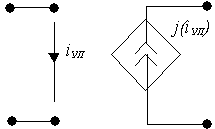
3. ИТУТ – источник тока, управляемый током:

 

 

 

 

 

 

а) нелинейный                                       б) линейный

b - коэффициент усиления тока

 

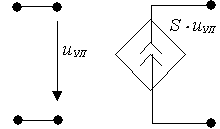
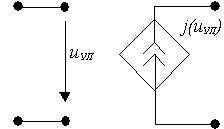4. ИТУН – источник тока, управляемый напряжением:

 

 

 

 

 

 

а) нелинейный                                                б) линейный

S - крутизна(передаточная проводимость)

 

1.2.3.   Схемы замещения реальных элементов ЭЦ

 

Реальные элементы ЭЦ можно представить моделью (эквивалентной схемой) из нескольких идеализированных элементов, причем только один из них отражает полезное качество. Остальные элементы являются паразитными.

Качество реальных элементов, т.е. их степень близости к идеализированным, оценивается с помощью коэффициента Q, называемого  добротностью.

1.Резистор

 

 

2. Катушка индуктивности

 

 

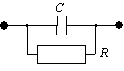3. Конденсатор

 

 

4. Реальный источник напряжения

 

 

 

 

 

5. Реальный источник тока

 

 

 

 

 

 

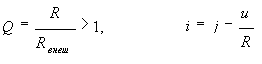6. Трехполюсный усилитель (лампа, транзистор)

 

 

 

 

 

 

 

 

 

 

 

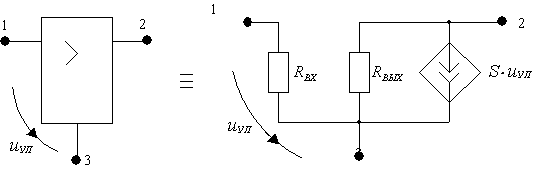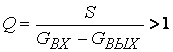
1.3.     Электрическая схема и ее элементы

 

Схемой называется графическое изображение ЭЦ. Ее элементами являются узлы, ветви, контуры.

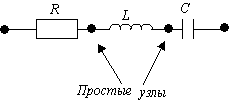
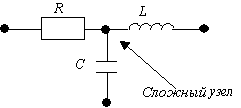Простым узлом называют место соединения зажимов двух элементов (рис. 1.7, а), а сложным - место соединения зажимов трех и более элементов

 

 

 

 

 

а)                                                             б)

 

 

 

 

 

 

в)

 

 

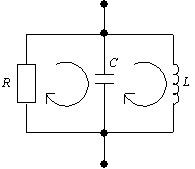
Рис. 1.7.

 

Ветвью - называют участок цепи, включаемой между двумя узлами, через который течет один и тот же электрический ток.

Контур - любой замкнутый путь, проходящий  по нескольким узлам (рис. 1.7, в).

Главные (независимые) контуры, это контуры, отличающиеся друг от друга хотя бы одной ветвью.

 

 

 

 

 

 

 

 

 

 

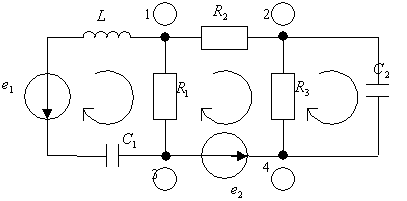Рис. 1.8.

 

Например, схема рис. 1.8 содержит узлов N_У = 4, ветвей N_В = 6, независимых контуров N_Н.К = 3.

 

Число независимых контуров можно рассчитать по формуле:

 

1.4.     Виды соединений элементов ЭЦ

 

Последовательным соединением элементов называется такое, при котором через все элементы проходит один и тот же ток i (рис. 1.9, а)

 

 

 

а)                                                                                          б)

Рис. 1.9.

 

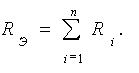При последовательном соединении эквивалентное сопротивление определяется по формуле:

 

 

 

Параллельным соединением элементов называется такое, при котором ко всем элементам приложено одно и то же напряжение u (рис. 1.10, а)

 

 

 

 

 

 

 

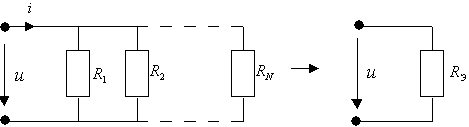
а)                                                                         б)

Рис. 1.10.

 

При параллельном соединении

 

 

 

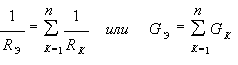Последовательно-параллельные цепи с одним источником можно рассчитывать путем эквивалентных преобразований, когда вся цепь, кроме  источника , преобразуется в одно эквивалентное сопротивление.

 

1.5.     Законы Кирхгофа

 

В основе всех методов анализа и расчета ЭЦ лежат законы Кирхгофа, установленные опытным путем в 1845 году. Распределение токов и напряжений в электрических цепях подчиняется этим законам.

Первый закон Кирхгофа: алгебраическая сумма токов в любом узле электрической цепи равна нулю, т.е. в любой момент времени

 

 

 

 

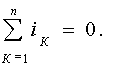Правило знаков: со знаком «-» берут токи, направленнные от узла и со знаком «+»- к узлу или наоборот.

 

 

 

 

 

 

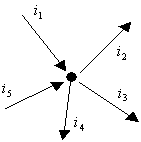Если ЭЦ содержит N_У узлов, то по первому закону Кирхгофа необходимо составить N₁ = N_У – 1 линейно-независимых уравнений.

 

Второй закон Кирхгофа: алгебраическая сумма падений напряжений на элементах любого замкнутого контура ЭЦ равна алгебраической сумме ЭДС в любой момент времени:

 

 

 

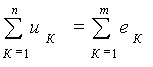Правило знаков: со знаком «+» берут те напряжения и ЭДС, направления которых совпадают с произвольно выбранным направлением обхода контура, в противном случае берут знак «-».

В общем случае для ЭЦ, содержащей N_В ветвей и N_И.Т. источников тока, по второму закону Кирхгофа необходимо составить

 

N₂ = N_В – N_У + 1 – N_И.Т.

 

линейно независимых уравнений).

Общее число линейно-независимых уравнений по законам Кирхгофа

 

N = N₁ + N₂

 

Замечание: Перед тем как составлять уравнения по законам Кирхгофа необходимо:

Произвольно выбрать положительные направления токов в ветвях и обозначить их на схеме  стрелками;

Выбрать положительные направления обходов независимых контуров и указать их стрелками;

Пример: Составить уравнения по законам Кирхгофа для схемы рис. 1.11.

 

 

 

 

 

 

 

 

 

 

Рис. 1.11.

 

+ i₁ -  i₂ – i₃ = 0

+ u₁ + u₂ + u₃ = e₁

– u₂ + u₄ + u₃ = – e₂

 

1.6.     Закон Ома

 

Этот закон менее универсален, чем законы Кирхгофа. С помощью этого закона можно рассчитать простые цепи, содержащие только один источник, или определить токи на участках цепи. Известны три формы закона Ома:

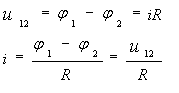 - для пассивного участка цепи;

 

 

 

 

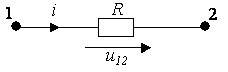- для активного участка цепи;

 

 

 

 

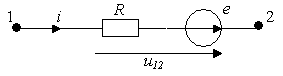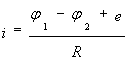- для замкнутого контура.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вопросы для самоконтроля к лекции 1

 

1.     Дайте определение электрической цепи. Какая цепь называется линейной?

2.     Перечислите известные Вам идеальные элементы электрической цепи. Напишите компоненты уравнения пассивных элементов.

3.     Приведите схемы замещения операционного усилителя.

4.     Какое соединение элементов называется последовательным?

5.     Какое соединение элементов называется параллельным?

6.     Сформулируйте первый и второй закон Кирхгофа. Как определяется число независимых уравнений, составленных по этим законам?

7.     Укажите порядок расчета электрической цепи методом контурных токов. Как выполняется расчет токов ветвей этим методом?

8.     Укажите порядок расчета цепи методом узловых напряжений

9.     Как определяется токи ветвей по известным узловым напряжениям?

10. Разберите решение задач 1.1, 1.15, 1.26, 1.38, 1.41 из [4].

11. Решите задачи 1.3, 1.27, 1.40, 1.43 из [4], 2.2, 2.3, 2.16, 3.15, 3.9 из [7].

 

Литература: [1] c.11- 40; [2] c.7-24; [3] c.9-27; [4] c.5-9; [5] c.40-61.

 

 

Лекция 2. МЕТОДЫ РАСЧЕТА ЦЕПЕЙ ПОСТОЯННОГО ТОКА

 

2.1. Определение и порядок расчета цепей постоянного тока

 

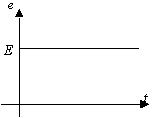
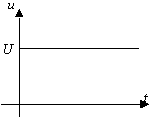
ЭДС, напряжения и токи, не изменяющиеся  во времени, называются постоянными (рис. 2.1)

В цепях постоянного тока приняты обозначения E, U, I.

 

 

 

 

 

 

 

 

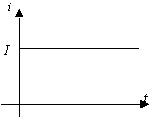Рис. 2.1. Зависимости от времени постоянных ЭДС (а), напряжения (б), тока (в).

 

Для цепи рис. 2.2 составим уравнения по второму закону Кирхгофа

 

 

 

 

 

 

 

 

Рис. 2.2.

 

 

 

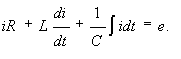При воздействии постоянной ЭДС получим:

e=E=const; i=I=const; u=U=const;

 

 

 

 

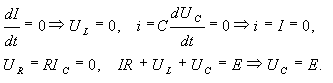Из (2.2) можно сделать выводы:

1.     Постоянный ток не протекает через емкость и она может быть представлена разрывом цепи.

 

 

 

 

 

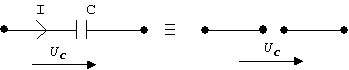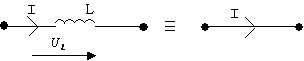
2.     Постоянный ток не создает напряжение на индуктивности, т.е для режима постоянного тока индуктивность может быть представлена короткозамкнутым элементом.

 

 

 

 

 

Порядок расчета ЛЭЦ при воздействии постоянной ЭДС

 

1.     Разомкнуть все ветви, содержащие емкость

2.     Закоротить все участки, содержащие индуктивности

3.     Рассчитать для режима постоянного тока оставшуюся часть цепи

 

Пример: Для цепи рис. 2.3 определить токи и напряжения на всех элементах

 

 

 

 

 

 

 

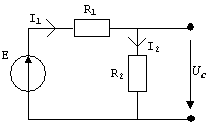а)                                                        б)

 

Рис. 2.3 Заданная а) и эквивалентная б) схема цепи постоянного тока

 

Решение:

 

По закону Ома находим

 

 

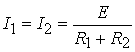
Напряжение на элементах равны:

 

 

2.2. Расчет резистивных ЛЭЦ

 

Резистивными называются цепи, содержащие источники энергии и сопротивления

2.2.1. Расчет одноконтурных цепей выполняется на основании закона Ома

 

 

 

 

 

 

 

 

Рис. 2.4

По закону Ома, ток контура бедет равен

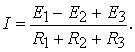2.2.2. Расчет разветвленных цепей с одним источником энергии выполняется методом эквивалентного преобразования схемы. Последовательность расчета.

 

 

 

 

 

 

 

 

 

 

 

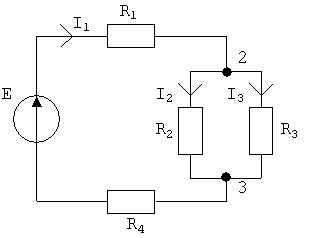Рис. 2.5.

 

 

 

 

 

 

 

 

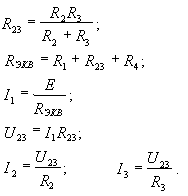2.2.3. Расчет разветвленных цепей с несколькими источниками выполняется методом уравнений Кирхгофа

 

 

 

 

 

 

 

 

 

 

 

 

 

 

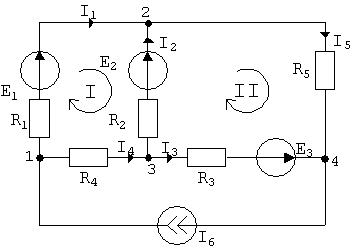Рис. 2.6.

 

Схема рис. 2.6 имеет 4 узла 6  ветвей, 1 источник тока.

N₁ = N_У –1 = 3

N₂ = N₆ – N_У + 1 – N_И.Т = 2

Следовательно, для определения 5 неизвестных токов необходимо составить 3 уравнения по первому закону Кирхгофа и 2 уравнения по второму закону Кирхгофа.

для

узла

I

I

I

для

узла

I

I

I

для

узла

I

I

I

-

-

+

=

+

-

=

-

-

+

=

1

4

6

1

2

5

2

3

4

(

1

)

:

0

;

(

2

)

:

0

;

(

3

)

:

0

1 закон Кирхгофа:

	;

 

 

 

 

-

-

-

=

-

-

+

-

=

-

для

го

контура

I

R

I

R

I

R

E

E

для

го

контура

I

R

I

R

I

R

E

E

1

1

2

2

4

4

1

2

2

2

5

5

3

3

2

3

(

1

)

:

;

(

2

)

:

2 Закон Кирхгофа:

	.

 

 

 

Для определения 5 неизвестных токов  необходимо решить систему уравнений, составленных по первому и второму законам Кирхгофа.

 

2.3. Метод контурных токов

 

Метод контурных токов (МКТ) является одним из основных методов расчета ЭЦ, которым широко пользуются на практике. При расчете цепи этим методом полагают, что в каждом независимом контуре протекает свой контурный ток, направление которого выбирается произвольно. Уравнения составляют относительно контурных токов. После их нахождения их определяют токи ветвей через контурные токи.

Для цепи, содержащей  N_Н.К = N_B – N_У +1 – N_И.Т. независимых контуров, каноническая система контурных уравнений имеет вид:

 

R₁₁I_K1 + R₁₂I_K2 + … + R_1NI_KN = E₁₁;

R₂₁I_K1 + R₂₂I_K2 + … + R_2NI_KN = E₂₂;

…………………………………………………                                        (2.3)

R_N1I_K1 + R_N2I_K2 + … +R_NNI_KN = E_NN,

 

где R₁₁, R₂₂, … , R_NN  - собственные сопротивления 1 – го, 2 – го, …,

N–го контура (сумма сопротивлений всех ветвей, входящих в контур);

R_KN, R_LM = R_ML – взаимные (общие) сопротивления L – го и M – го контуров;

E₁₁, E₂₂, …, E_NN  - алгебраическая сумма ЭДС, входящих в 1 – ий,

2 – ой, … N – ый контур.

 

Правила составления уравнений по МКТ

Уравнения составляются для независимых контуров. Направление обхода контуров совпадают с выбранными произвольно направлениями контурных токов.

Если контурные токи, протекающие через общее сопротивление для двух контуров, направлены встречно то падение напряжения на нем записывается со знаком «-», если согласно – со знаком «+».

Если направление ЭДС в контуре совпадает с направлением контурного тока, то эта ЭДС записывается в уравнение со знаком «+», если не совпадает – со знаком «-».

Ток в любой ветви определяется как алгебраическая сумма контурных токов, протекающих по этой ветви. Со знаком «+» берется контурный ток, совпадающий по направлению с током ветви и со знаком «-» - направленный противоположно.

 

Если цепь содержит Nт источников тока, то кроме независимых контуров, необходимо выбрать контура, в которые входили бы источники тока. Контурные токи в них будут известны и равны токам источникам тока.

Порядок расчета по МКТ

 

1.     Определяется число уравнений;

2.     Выбираются независимые контуры;

3.     Произвольно выбираются направления токов ветвей и контурных токов;

4.     Составляется и решается система контурных уравнений;

5.     Определяются токи ветвей.

 

Пример: Для цепи рис. 2.7 определить токи ветвей с помощью МКТ.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

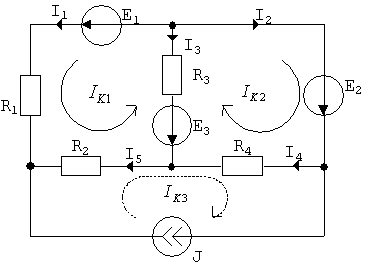Рис. 2.7.

Решение:

N_B = 6;    N_У = 4;   N_T = 1;

N_Н.К. = 6 – 4 + 1 – 1 = 2;

I_K1(R₁ + R₂ + R₃) + I_K2R₃ + I_K3R₂ = E₁ – E₃

I_K1R₃ + I_K2(R₃ + R₄) – I_K3R₄ = E₂ – E₃

I_K3 = J

Токи ветвей равны:

I₁ = I_K1;     I₂ = I_K2;   I₃ = - I_K1 – I_K2;

I₄ = I_K2 – J;     I₅ =  – I_K1 – J.

 

2.4. Метод узловых напряжений

 

       Методом узловых напряжений (МУН) можно определить значения токов и напряжений в электрической цепи, если найти потенциалы узлов, отсчитанные относительно некоторого одного узла, называемого базисным или опорным. Потенциал базисного узла принимается равным нулю. Напряжения в узлах цепи, отсчитанные относительно опорного, называются узловыми напряжениями.

       Для цепи, имеющей  независимых узлов, каноническая система узловых уравнений имеет вид:

1

1

G₁₁U₁ – G₁₂U₂ – … – G_1NU_N = SEG + SJ

2

2

– G₁₁U₁ + G₂₂U₂ – … – G_2NU_N = SEG + SJ

…………………………………………………                                (2.4)

N

N

– G_N1U₁ – G_N2U₂ – … – G_NNU_N = SEG + SJ

 

 

где G₁₁, G₂₂ … G_NN – собственные проводимости 1 – го, 2 – го …

N – го узлов, равные сумме проводимостей ветвей, сходящихся в 1 – м,

2 – м … N – м узле;

G_KM = G_MK – взаимные (общие) проводимости между узлами К и М, равные сумме проводимостей ветвей, содержащие эти узлы;

1

2

SEG, SEG … SEG – алгебраическая сумма произведений ЭДС ветвей,

примыкающих к 1 – му, 2 – му … N – му узлу, на их проводимости;

N

N

1

2

SJ, SJ …SJ – алгебраическия сумма токов источников тока,

 присоединенных к соответствующему узлу.

 

Правила составления уравнений по МУН

Со знаком «+» в уравнение по МУН записывается узловое напряжение того узла, относительно которого составляется уравнение, все остальные – со знаком «-».

Задающие токи источников ЭДС и тока берутся со знаком «+», если направление источников ориентированно к узлу, относительно которого составляется уравнение, и со знаком «-» - если от узла.

При наличии в схеме ветви с идеальным источником ЭДС необходимо принять за опорный узел один из узлов к которому присоединена данная ветвь. Тогда узловое напряжение другого узла будет равным величине ЭДС.

Порядок расчета по МУН

1.     Определяется число уравнений;

2.     Выбирается опорный узел;

3.     Составляется и решается система уравнений по МУН;

4.     По закону Ома определяются токи ветвей.

 

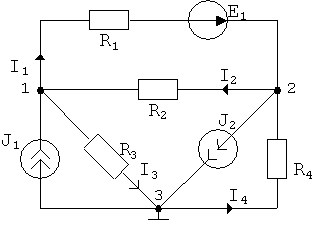Пример: Для цепи рис 2.8 составить уравнения по МУН и определить токи ветвей.

 

 

 

 

 

 

 

 

 

 

Рис. 2.8

Решение:

Примем U₃ = 0;

 

 

 

 

 

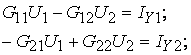
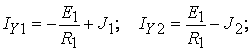
Токи ветвей определяются по закону Ома через найденные значения узловых напряжений:

 

 

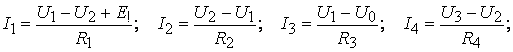
2.5. Вопросы для самоконтроля к лекции 2

 

1.     Какие напряжения и токи называются постоянными?

2.     Каков порядок расчета цепи постоянного тока?

3.     Какими методами можно рассчитать резистивную цепь?

4.     Укажите порядок расчета электрической цепи методом контурных токов. Как выполняется расчет токов ветвей этим методом?

5.     Укажите порядок расчета электрической цепи методом узловых напряжений

6.     Как определяются токи ветвей по известным узловым напряжениям?

7.     Разберите решения задач 1.38, 1.39, 1.41, 1.42,1.44 из [4]

8.     Решите задачи 1.40, 1.45 из [4].

 

Литература: [1] с. 63-72; [2] c. 26-31; [3] c. 82-88; [4] c. 8-12; [5] c. 71-75.

 

Лекция 3. ЛЭЦ ПРИ ГАРМОНИЧЕСКОМ ВОЗДЕЙСТВИИ

 

3.1. Гармонические колебания и их описание

 

Электромагнитный процесс в ЭЦ, при котором мгновенные значения напряжения и токов повторяются через равные промежутки времени, называются периодическим.

Периодический процесс называется гармоническим, если функция f(t) (напряжение, ЭДС, ток) изменяется по закону синуса

 

f(t) = A_m sin(wt +j);                                       (3.1)

u = U_m sin(wt +j_U);    e = E_m sin(wt + j_e);    i = Im sin(wt = j_i)

 

Значения u, e, i, в любой момент времени называются мгновенными значениями.

Наибольшее по абсолютному значению отклонение колеблющейся величины называется ее амплитудой  .

Наименьшее значение времени, после которого процесс полностью повторяется, называется периодом колебания Т.

Число циклов колебаний в единицу времени называется циклической частотой  .

Число циклов колебаний в интервале времени равному 2p единицам, называется угловой частотой .

Величина  называется фазой колебания. Она характеризует состояние колебания в любой момент времени t.

Значение фазы колебания в момент времени t=0 называется начальной фазой  . Начальная фаза является алгебраической величиной. При начало синусоиды сдвинуто влево, а при  - вправо от начала координат.

 

 

 

 

 

 

 

 

 

 

 

Рис. 3.1.

 

3.2. Действующее значение периодической функции

 

Действующим значением любой периодической функции называют ее среднеквадратичное значение за период.

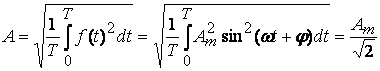.                      (3.2)

Действующее значение синусоидального тока или напряжения в  раз меньше его амплитуды

                        (3.3)

Действующее значение периодического синусоидального тока равно по величине такому постоянному току, который, проходя через сопротивление R за интервал времени Т, выделит такое же количество тепла, что  и данный периодический ток

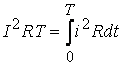                                              (3.4)

Большинство измерительных приборов показывают действующее значение тока и напряжения.

 

3.3. Представление гармонических колебаний векторами

 

Для непосредственного сложения синусоидальных функций необходимо производить достаточно громоздкие операции. Существенное упрощение достигается, если синусоидальную функцию изобразить в виде вращающегося вектора.

Векторное изображение синусоиды строится следующим образом (см. рис. 3.2).

 

 

 

 

 

 

 

 

Рис. 3.2.

 

На плоскости из начала координат под углом , равному начальной фазе синусоиды, проводится прямая и на ней откладывается в масштабе отрезок, равный амплитуде колебания. Угол  откладывается против часовой стрелки от горизонтальной оси, если ; и по часовой стрелке, если . Если угол откладывать от горизонтальной оси, то проекция вектора на вертикальную ось равна (в выбранном масштабе) мгновенному значению синусоидальной функции.

Построим векторное изображение суммы двух функций (рис. 3.3):

 

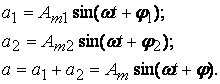                               (3.5)

 

Очевидно, что вместо сложения синусоид удобно геометрически складывать их векторные изображения. Таким образом, получили простейшую векторную диаграмму.

 

 

 

 

 

 

 

 

 

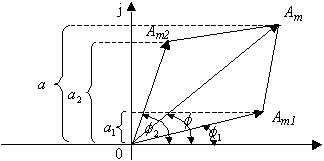Рис. 3.3.

 

Векторная диаграмма представляет собой совокупность векторов, изображающих синусоидальные функции одинаковой частоты, построенных с соблюдением масштаба и правильной ориентации их друг относительно друга по фазе.

Условились: вместо амплитуд на векторных диаграммах откладывать действующее значение функции.

 

3.4. Связь между мгновенными значениями напряжения и тока на элементах цепи

 

1. Активное сопротивление

 

 

 

 

 

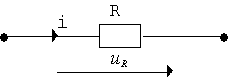По закону Ома имеем:

 

u

 

Временная и векторная диаграммы представлены на рис. 3.4.

 

 

 

 

 

 

 

 

Рис. 3.4.

 

Углом сдвига фаз межу током и напряжением  называется разность начальных фаз напряжения и тока

 

.

 

Выводы:

-               напряжение на участке с активным сопротивлением при синусоидальном токе будет также синусоидальным, при этом напряжение и ток совпадают по фазе, амплитуда напряжения равна ;

-     закон Ома для участка с активным сопротивлением одинаково справедлив и для мгновенных значений, и для амплитуд, и для действующих значений.

Мгновенная мощность P_R = u_Ri содержит две составляющие: постоянную и переменную, которая изменяется по закону косинуса с частотой

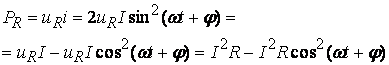                  (3.8)

Среднее за период значение мгновенной мощности (называется активной мощностью) равно:

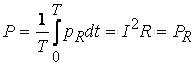                                   (3.9)

 

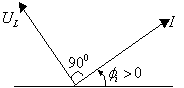
2. Индуктивность

 

 

 

Напряжение на индуктивности определяется по закону электромагнитной индукции

 

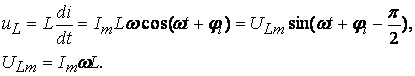          (3.10)

 

Обозначим , тогда U_Lm = I_mX_L   или  u_L = IX_L

Выводы:

–       если ток на индуктивности изменяется по синусоидальному закону, то и напряжение также изменяется синусоидальному закону, однако начальные фазы этих  синусоид не совпадают – они сдвинуты на (рис. 3.5), кривая напряжения опережает кривую тока на , т.е. ;

–       если величину  называть индуктивным сопротивлением, то амплитуда напряжения на индуктивности будет равна произведению амплитуды тока и индуктивного сопротивления. Следовательно, получается формула, аналогичная закону Ома.  Точно также связаны действующие значения напряжения и тока. Мгновенные значения закону Ома не подчиняются.

 

 

 

 

 

 

 

 

 

 

а) временные диаграммы                             б)векторная диаграмма

 

Рис. 3.5.

 

 

Мгновенная мощность  будет равна

 

.

 

Средняя (активная) мощность на участке с индуктивностью равна нулю, но энергия на этом участке пульсирует. Когда ток возрастает от нуля до максимума по абсолютной величине, мощность (положительна), энергия поступает от источника в индуктивность и там накапливается в виде энергии магнитного поля W_m = Li²/2. Когда ток уменьшается от max до 0 , энергия переходит из магнитного поля обратно в источник, мощность .

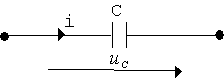
3.Емкость

 

 

 

 

Напряжение u_C определяется по формуле:

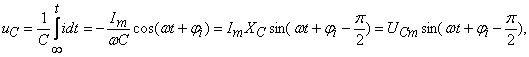 (3.12)

 

где  или .

Обозначим  - емкостное сопротивление.

 

 

 

 

 

 

 

 

 

а) временные диаграммы                          б) векторная диаграмма

 

Рис. 3.6.

 

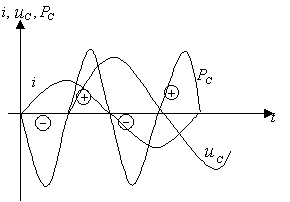
Мгновенная мощность  равна

 

    (3.13)

 

Средняя мощность P_C = 0, т.е. на участке с емкостью в среднем энергия не расходуется – она пульсирует. Когда напряжение u_C возрастает от 0 до max>0, энергия переходит из источника  в электрическое поле конденсатора и там накапливаются. Когда напряжение u_C уменьшается по абсолютной величине, мощность энергия возвращается обратно в источник.

 

3.5. Последовательное соединение элементов R, L, C

 

 

 

 

 

 

 

 

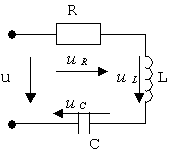Рис. 3.7.

 

По цепи протекает ток

На основании второго закона Кирхгофа u_R+u_L+u_C = u, или

 

                                      (3.14)

 

Подставляя значения тока i, получим

 

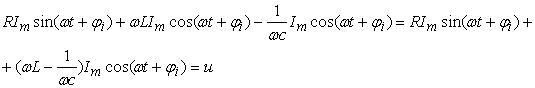 (3.15)

 

Так как , то j_i + f = j_U   и   u = Um sin(wt + yi + j).

Величины  называется реактивным сопротивлением цепи. Если , то реактивное сопротивление X>0 - имеет  индуктивный  характер; если  то X<0 – емкостной характер.

Для определения  и  воспользуемся  тригонометрическими соотношениями:

                 

Получим

(3.17)

(3.16)

Величина  называется полным сопротивлением цепи.

 

Выводы:

-     если по участку цепи с последовательным соединением RLC -  элементов протекает синусоидальный ток, то напряжение на этом участке также будет синусоидальным, но фаза напряжения будет отличаться  от фазы тока на величину , т.е. синусоиды тока и напряжения будут сдвинуты друг относительно друга на угол ;

-     если >0, x>0, то напряжение u опрежает ток i (см.рис.3.8.а), если <0, x<0 – напряжение u отстает по фазе от тока i.(рис.3.8,б);

-     ток совпадает по фазе с напряжением при =0, т.е. когда  (рис.3.8, в). Такой режим работы электрической цепи называется  резонансным, напряжение на индуктивности и емкости компенсируют друг друга, и в цепи имеет место резонанс напряжений.

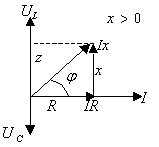
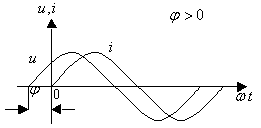Временные и векторные диаграммы цепи RLC для трех случаев приведены на рис. 3.8.

а)

 

 

 

 

 

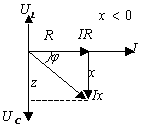
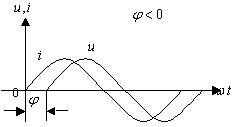б)

 

 

 

 

 

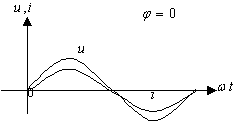в)

 

 

 

 

 

 

 

Рис. 3.8.

3.6. Вопросы для самоконтроля к лекции 3

 

1.     Какие напряжения (токи) называют гармоническими?

2.     Как связаны частота f и период Т гармонических сигналов?

3.     Что называют фазой и начальной фазой гармонического напряжения (тока)? Нарисуйте кривые гармонических сигналов, сдвинутые относительно друг друга по фазе. Объясните, какие кривые являются опережающими и какие отстающими.

4.     Как строят векторные диаграммы гармонических напряжений (токов)?

5.     Для каких значений гармонических напряжений и токов выполняются законы Ома?

6.     Чем объясняется наличие фазового сдвига между напряжением и током  в индуктивности и емкости?

7.     Объясните изменение мгновенной мощности  на элементах цепи.

8.     Разберите решения задач 2.1-2.3, 2.6, 2.10 из [4].

9.     Решите задачи 2.5, 2.8 из [4].

 

Литература: [1] с.98-114; [2] с.37-46; [3] с. 28-46; [5] с. 151-157.

 

 

Лекция 4. СИМВОЛИЧЕСКИЙ МЕТОД РАСЧЕТА ЦЕПЕЙ ГАРМОНИЧЕСКОГО ТОКА

 

Метод, основанный на символическом изображении синусоидальных функций времени комплексными величинами, называют символическим (комплексным) методом или методом комплексных амплитуд.

 

4.1. Символическое изображение синусоидальных функций комплексными величинами

 

Любую гармоническую функцию можно изобразить в виде вектора (рис. 4.1, а), а каждому вектору можно поставить в соответствие комплексное число (рис. 4.1, б).

a)                                                                                                                                                        
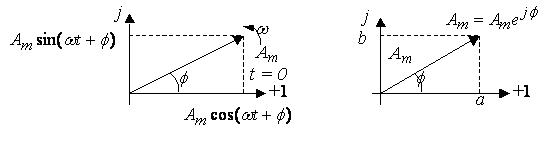б)

Рис. 4.1.

 

Существуют три формы записи комплексного числа

1. - показательная (А - модуль комплексного числа, j - его аргумент);

2. - тригонометрическая;

3. - алгебраическая (а - вещественная часть, б - мнимая

часть).

Переход от одной формы записи к другой можно осуществить с помощью формул:

 

; ;                                                                   (4.1)

;     .

 

Необходимо запомнить:

 

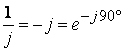;    ;    ;    .                           (4.2)

 

Комплексной амплитудой  называется комплексная величина, модуль которой равен амплитуде синусоидального тока, а аргумент - начальной фазе.

В раз меньшую величину называют комплексным действующим

значением - комплексным током.

 

 

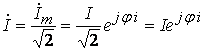
Аналогично

- комплексная амплитуда напряжения;

- комплексное напряжение.

 

Составим новое комплексное число

	(4.4)

(4.3)

 

которое называется вращающимся вектором тока.

Разложим по формуле Эйлера:

 

             (4.5)

 

Следовательно, синусоидальный ток является мнимой частью вращающегося вектора, т.е.

,

где j - знак мнимой части.

Часто величины i, u, называют оригиналами, а  – их комплексными изображениями. Примеры:

 

1)     ;

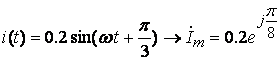2)     ;

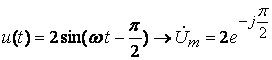3) .

4.2. Изображение производной и интеграла от синусоидальной функции

Пусть , где  знак соответствия,

Тогда

, т.е.

 

Операция    дифференцирования    синусоидальной    функции соответствует умножению на   ее комплексного изображения.

Пример: С производной мы встречаемся при определении напряжения на индуктивности

При  - для вращающихся векторов получим:

 

,

откуда имеем .

 

При этом получаем комплексное сопротивление индуктивности , как чисто мнимое число.

 

При ,                         (4.7)

 

т.е. 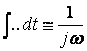- операция интегрирования синусоидальной функции

соответствует делению на jw ее комплексного изображения.

Пример: С интегралом мы встречаемся при определении напряжения

на емкости

.

 

Для вращающихся векторов получим

,

 

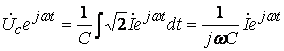откуда имеем,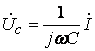

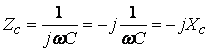 - комплексное cопротивление емкости    (4.8)

 

Пример: Рассмотрим цепь RLC (рис.4.2.).

 

 

 

 

 

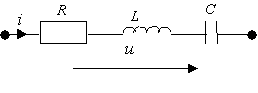Рис. 4.2.

Уравнение цепи для мгновенных значении напряжений имеет вид:

 

При  для комплексных зображений получим

.

 

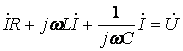4.3. Комплексные сопротивления и проводимость

 

Комплексным сопротивлением называется отношение комплексного напряжения к комплексному току :

 

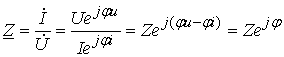                        (4.9)

 

Используя формулу Эйлера, получим

 

                     (4.10)

 

где  - модуль комплексного сопротивления, равный полному сопротивлению цепи;

 - аргумент комплексного сопротивления;

R и Х - активное и реактивное сопротивление цепи.

 

Комплексной проводимостью называется величина, обратная комплексному сопротивлению

 

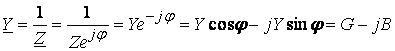;                          (4.11)

;     ;

 

Y, G, В - полная , активная, реактивная проводимость.

Очевидна следующая связь , используя которую можно установить зависимость между эквивалентными сопротивлениями и проводимостями ЭЦ. При заданном комплексном сопротивлении некоторого участка цепи можно определить комплексную проводимость того же участка:

 

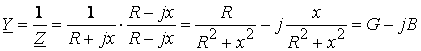                     (4.12)

 

Если задана комплексная проводимость некоторого участка ЭЦ, то комплексное сопротивление того же участка равно

 

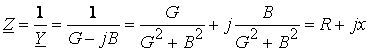.                                 (4.13)

 

4.4. Законы Ома и Кирхгофа в комплексной форме

 

Выражения закона Ома в комплексной форме имеют вид

 

                                            (4.14)

 

Первый закон Кирхгофа для мгновенных значений токов, имеющий вид

,

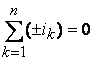в комплексной форме записываются в виде

 

,

 

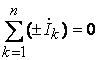т.е. алгебраическая сумма комплексных токов ветвей в любом узле ЭЦ равна нулю.

Второй закон Кирхгофа для .комплексных значений напряжений и ЭДС имеет вид

 

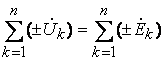,                                         (4.16)

 

т.е. алгебраическая сумма комплексных напряжений в любом замкнутом контуре ЭЦ равна алгебраической сумме комплексных ЭДС в том же контуре.

Вывод: законы Ома и Кирхгофа, записанные в комплексной форме, имеют такой же вид, что и для цепей постоянного тока. Поэтому для расчета цепей синусоидального тока символическим методом применимы все методы расчета резистивных цепей, если в них произвести замены

 

 

Расчет ЭЦ символическим методом производится в следующем порядке:

1)         от заданных гармонических воздействий переходят к комплексным изображениям;

2)         с помощью любого известного метода расчета определяют комплексные токи и напряжения (реакция цепи);

3)         от комплексных изображений токов и напряжений переходят к их мгновенным значениям.

 

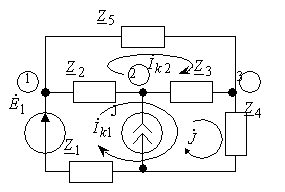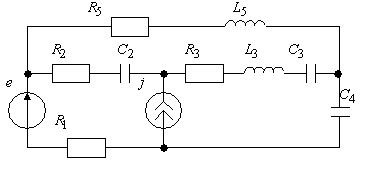
Пример: Составить уравнения по МКТ и МУН для схемы рис. 4.3.

 

Рис 4.3.

 

 ;

;

 

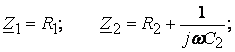
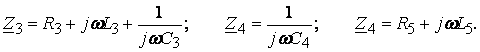
Метод контурных токов (МКТ)

I.                  

II.               

 

 

Метод узловых напряжений (МУН)

1)     ;

2)     ;

3)     .

 

 

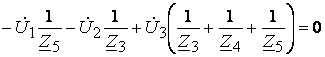4.5. Выражение мощности в комплексной форме. Баланс мощностей

Под комплексной мощностью понимается величина, определяемая по формуле  

 

        (4.17)

 

где - комплексное действующее значение напряжения;

 - сопряженный комплексный ток.

Вещественная часть комплексной мощности равна активной мощности  (измеряется в Вт), мнимая часть - реактивной мощности  (измеряется в ВАр). Модуль комплексной мощности равен полной мощности  (измеряется в ВА).

Связь между активной, реактивной и полной мощностями

 

                                               (4.18)

 

Из закона сохранения энергии следует, что в любой ЭЦ соблюдается   баланс как мгновенных, так и активных мощностей:

Сумма отдаваемых источниками мгновенных (активных) мощностей равна сумме потребляемых цепью мгновенных (активных) мощностей. Баланс выполняется также для реактивных и для комплексных мощностей,

 

т.е.    ;     ;         (4.19)

 

Комплексная мощность, отдаваемая источником ЭДС определяется по формуле: , а источником тока 

 

 

 

 

 

 - комплексная      мощность,  потребляемая всеми сопротивлениями (приемниками) цепи, где

 

 

4.6. Условие передачи максимальной мощности от источника в нагрузку

 

В системах передачи сигналов часто требуется получить максимальное значение активной мощности в нагрузке. Режим, при котором обеспечивается передача максимальной мощности, называется режимом согласования (режим согласования нагрузки).

Рассмотрим, при каких условиях от генератора с внутренним сопротивлением  в нагрузку  передается максимальная активная мощность (рис. 4.4)

 

 

 

 

Рис. 4.4.

 

Активная мощность, выделяемая в нагрузке, равна

 

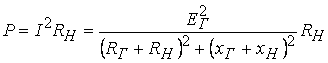                                         (4.20)                

Для получения максимума этой мощности необходимо: чтобы , при этом мощность Р будет равна

 

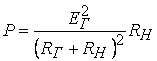                                       (4.21)

 

Максимум мощности Р получается при , так как

 

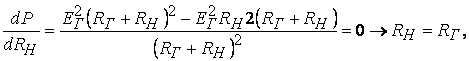 тогда

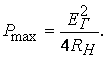                                                  (4.22)

 

Вывод: для передачи максимальной мощности в нагрузку необходимо, чтобы , т.е. сопротивление нагрузки должно быть равно сопряженному внутреннему сопротивлению генератора.

 

4.7. Вопросы для самоконтроля к лекции 4

 

1. Чем отличается комплексные значения величины от ее модуля?

2. Как записать уравнение мгновенных значений напряжений (токов) по их комплексной форме записи?

3. Запишите комплексное  число    в  алгебраической  и тригонометрической форме.

4. Что такое комплексное сопротивление, полное сопротивление и аргумент комплексного сопротивления?

5. Что такое комплексная проводимость и полная проводимость?

6. Запишите выражения комплексных напряжений на R, L, C элементах.

7. Сформулируйте закон Ома и законы Кирхгофа в комплексной форме.

8. Для произвольно выбранной цепи составьте уравнение по методам контурных токов и узловых напряжений в символической форме.

9. Как определяется комплексная мощность в цепи?

10. При каких условиях от источника в нагрузку передается максимальная активная мощность?

11.Разберите решения задач: 2.21, 2.23, 2.34, из [4] или 6.12, 6.14, 6.34,

6.52 из [7]. 12.Решите задачи: 2.30, 2.55 из [4] или 5.1, 5.2, 5.10, 6.2, 6.18, 6.35,

6.61 из [7].

Литература: [1] с.115-134; [2] с.46-54; [З] с.48-58; [5] с.157-174.

 

 

Лекция 5. ПРОСТЕЙШИЕ ЧАСТОТНО-ИЗБИРАТЕЛЬНЫЕ ЦЕПИ

 

5.1. Комплексная передаточная функция

 

Любая ЭЦ может быть представлена в виде пассивного четырехполюсника

 

 

 

 

 

 

 

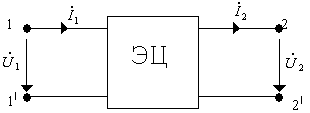Рис. 5.1.

 

При анализе ЛЭЦ вместо расчетов токов и напряжений часто требуется находить лишь их отношение в определенных точках, рассматривая так называемые характеристики передачи цепи. Для нахождения таких характеристик в схеме выделяются точки, называемые входом и выходом.

Напряжение и ток, действующие на входе цепи называются воздействием, а на выходе – реакцией (откликом) ЭЦ.

Комплексной передаточной функцией (КПФ) называется отношение реакции к воздействию.

 

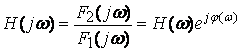.                                    (5.1)

 

В зависимости от того, что рассматривается под воздействием и реакцией - ток или напряжение, комплексная передаточная функция может быть либо безразмерной, либо иметь размерность проводимости или сопротивления.

 

 - КПФ по напряжению.

 

 - КПФ по току.

 

 - передаточное сопротивление.

 - передаточная проводимость.

 

Амплитудно-частотной характеристикой (АЧХ) называется частотная зависимость модуля КПФ .

Фазочастотной характеристикой (ФЧХ) называется частотная зависимость аргумента КПФ .

АЧХ и ФЧХ не зависят от значений амплитуд и начальных фаз воздействий, а определяется числом, характером, значениями и видом соединения друг с другом ее элементов.

Частотные характеристики линейных электрических цепей имеют важное значение, т.к. позволяют наглядно судить о том, колебания каких частот пропускаются цепью, а какие «подавляются».

Пример. Найти КПФ RC (рис. 5.1.a). Построите графики АЧХ и ФЧХ.

 

 

 

 

 

 

 

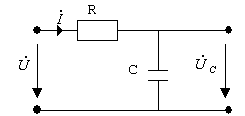Рис. 5.1.а

Решение:

 

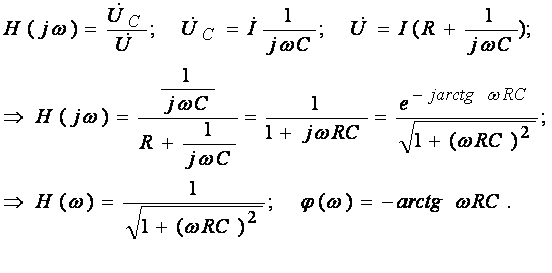
График АЧХ и ФЧХ цепи RC показаны на рис. 5.2.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

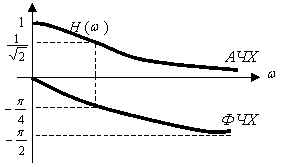Рис.5.2.

 

5.2. Явление резонанса и его значение в радиотехнике и электросвязи

 

Явление значительного возрастания амплитуды гармонической реакции цепи по мере приближения частоты внешнего гармонического воздействия к частоте собственных колебаний цепи называется резонансом. Резонанс представляет собой такой режим ЭЦ, содержащей индуктивности и емкости, при которых реактивное сопротивление и реактивная проводимость цепи равны нулю, а входное напряжение и ток совпадают по фазе. Различают резонанс напряжений и резонанс токов.

Резонанс напряжений наблюдается в ЭЦ с последовательным соединением элементов R,L,C. Такую цепь называют последовательным колебательным контуром.

Резонанс токов наблюдается в ЭЦ с параллельным колебательным контуром.

Явление резонанса и колебательные контуры широко используются в технике связи. Резонансные цепи применяются в электросвязи и являются неотъемлемой частью любого радиотехнического устройства. Многие устройства, предназначенные для формирования и обработки сигналов, содержат колебательные контуры или их электронные аналоги.

При решении различных инженерных задач, связанных с передачей сигналов, требуются цепи, способные выделять из спектра воздействия колебания отдельных группы частот. Такие цепи называются селективными и избирательными. Частотные характеристики (ЧХ) таких цепей имеют немонотонный характер. Такие ЧХ можно получить с помощью резонансных контуров.

 

 

 

 

 

5.3. Последовательный колебательный контур.

 

 

 

 

 

 

 

Рис. 5.3.

 

Комплексное сопротивление контура зависит от частоты:

 

 

Резонанс напряжений наступает при частоте , когда

 

 

 

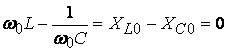
и (условие резонанса напряжения) (5.2)

 

Из равенств (5.2) определяется резонансная частота контура

 

 или                                  (5.3)

 

Сопротивление контура на резонансной частоте

 

 - чисто активное

 

Ток контура при резонансе достигает наибольшего значения, равного

 

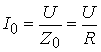                                                (5.4)

 

Сопротивление индуктивности и емкости на резонансной частоте называют характеристическими (волновыми) сопротивлением контура и обозначают

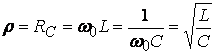                                    (5.5)

 

Напряжения на индуктивности и емкости при резонансе равны друг другу

                                 (5.6)

 

отношение ,                                       (5.7)

 

называют добротностью контура. Добротностью Q определяет усилительные свойства контура.

Величина, обратная добротности контура, называется затуханием и обозначается

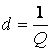                                               (5.8)

 

5.4. Виды расстроек контура

 

Абсолютной расстройкой  называют разность между данной частотой и резонансной:

 

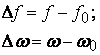                                                  (5.9)

Относительной расстройкой называется отношение  или

=.                                              (5.10)

 

Обобщенной расстройкой называется отношение реактивного сопротивления контура к активному

 

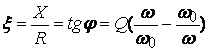.                                    (5.11)

 

При резонансе все расстройки равны нулю, при  - отрицательны, при  - положительны.

Если частота генератора, подключенного к контуру, равна резонансной частоте этого контура, то говорят, контур построен на частоту источника, а если частота генератора отличается от резонансной частоты, то расстроен. Настроить контур в резонансе можно:

1)     путем изменения частоты генератора;

2)     путем изменения индуктивности или емкости контура.

 

5.5. Частотные характеристики последовательного колебательного контура

 

Входное сопротивление контура равно:

 

 

 - частотная характеристика модуля входного сопротивления

 - ФЧХ контура.

При построении ЧХ удобно пользоваться относительными единицами, т.к. при этом сокращается число параметров, и становится возможным пользоваться стандартными кривыми. Так

 

,                           (5.13)

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

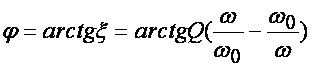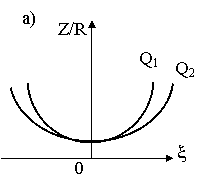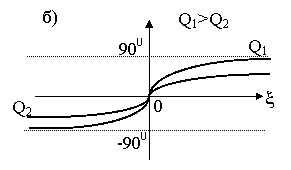Рис. 5.4. Частотная зависимость относительного сопротивления контура а) и его ФЧХ б).

 

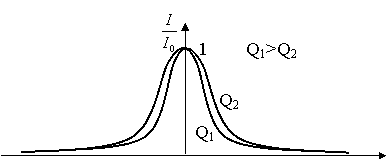
Частотная зависимость действующего значения тока называется резонансной кривой тока или его АЧХ (рис. 5.5)

 

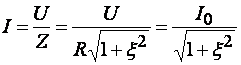  или    (5.14)

 

 

			x

 

 

 

 

 

 

 

 

 

Рис. 5.5. АЧХ последовательного контура.

 

Как видно из 5.13 и 5.14 с увеличением добротности увеличивается крутизна характеристик (рис. 5.4, 5.5).

 

5.6. Полоса пропускания

 

Полосой пропускания называется диапазон частот, на границах которого ток уменьшается в  раз относительно резонансного значения I₀ (рис. 5.6)

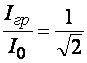.                                                 (5.15)

 

Полосу пропускания  ещё характеризуют как полосу частот, границы которой соответствуют половине мощности, расходуемой при резонансе.

 

 

 

 

 

 

 

 

 

 

 

 

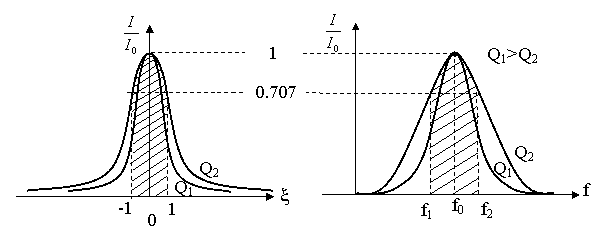Рис. 5.6.

 

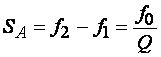 - абсолютная ПП                     (5.16)

 

С увеличением добротности контура (5.16) происходит сужение ПП и увеличение избирательности контура. На границах ПП контур обладает следующими свойствами: j_гр=±45⁰, x=±1, R=|X|.

 

5.7. Вопросы для самоконтроля к лекции 5

 

1.     Дайте определение комплексной передаточной функции электрической цеп.

2.     Как определяются амплитудно-частотная и фазочастотная характеристики цепи?

3.     Как можно определить реакцию цепи, если известны воздействия и комплексная передаточная функция?

4.     Какие электрические цепи называются колебательными?

5.     Какие виды резонансов Вы знаете?

6.     Укажите условие резонанса напряжений

7.     Почему на резонансной частоте сопротивление колебательного контура резистивное?

8.     Что такое абсолютная, относительная и обобщенная расстройки?

9.     Что называется полосой пропускания колебательного контура?

10.  Как изменится полоса пропускания контура, если уменьшить в 2 раза:

а) индуктивность L;

б) ёмкость C;

в) сопротивление R?

11.  Разберите решение задачи 5.7, 5.12, 5.41 из [3]

12.  Решите задачи 5.15, 5.19, 5.42 из [3].

 

Литература: [1] с. 148-170; [2] с. 54-62; [3] с. 122-131; [4] с. 126-128; [5] с. 191-205; 211-226.

 

 

Лекция 6. ПереходнЫе процессы в ЛЭЦ

 

6.1. Понятие о переходном процессе

 

Переходным процессом называется процесс перехода от одного режима работы ЭЦ к другому, возникающий в результате коммутации в цепи.

Коммутацией называется процесс замыкания или размыкания рубильников, выключателей, в результате которого происходит изменение параметров цепи, её конфигурации, подключение или отключение источников. Будем считать, что коммутация производится мгновенно в момент t=0.

Изучение переходных процессов даёт возможность установить, как деформируются по форме и амплитуде сигналы при прохождении их через усилители, фильтры и другие устройства, позволяет выявить возможные превышения напряжения и токов на отдельных участках цепи, которые могут в десятки раз превышать их установившиеся значения.

 

6.2. Законы коммутации

 

Первый закон. В начальный момент времени после коммутации ток в индуктивности остаётся таким же, каким он был непосредственно перед коммутацией, а затем плавно изменяется.

 

                                     (6.1)

 

Невозможность скачкообразного изменения тока следует из того, что в противном случае на индуктивности появилось бы бесконечно большое напряжение 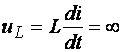, что лишено физического смысла.

Второй закон. В начальный момент времени после коммутации напряжение на ёмкости остаётся таким же, каким было до коммутации, а затем плавно изменяется.

 

                             (6.2)

 

Невозможность скачкообразного изменения напряжения на ёмкости следует из того, что в противном случае через ёмкость проходил бы бесконечно большой ток 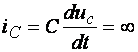, что также лишено физического смысла.

 

Следует отметить, что скачкообразно могут изменяться:

1)     токи в сопротивлениях и емкостях;

2)     напряжения на сопротивлениях и индуктивностях.

 

Значения токов в индуктивности и напряжение на ёмкости в момент коммутации называют независимыми начальными условиями.

 

6.3. Классический метод расчёта переходных процессов

 

Классический метод расчёта основан на решении неоднородных дифференциальных уравнений, выражающих законы Кирхгофа для мгновенных значений токов и напряжений.

Например, переходной процесс в цепи, состоящей из последовательно соединённых R,L,С элементов при включении в неё источника ЭДС е(t) описывается уравнением:

 

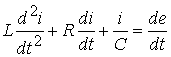 или                             (6.3)

 

Решение уравнения (6.3) ищется в виде

,

где  - частное решение неоднородного уравнения

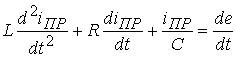,                                (6.4)

 

 - общее решение однородного дифференциального уравнения

 

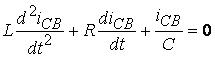.                                 (6.5)

 

Функция  зависит от вида воздействия и называется принужденной составляющей реакции цепи. Она может быть найдена любым методом расчёта установившегося процесса.

Функция  не зависит от внешнего воздействия, определяется характером цепи, её начальными условиями и называется свободной составляющей реакции цепи (свободная составляющая тока).

В зависимости от параметров элементов цепи  и соответственно вида корней характеристического уравнения, общее решение однородного дифференциального уравнения, приведенного в примере, ищется в виде:

1)     корни характеристического уравнения действительные

 

,                                (6.6)

 

где А₁, А₂- постоянные интегрирования, определяемые из начальных условий; p₁, p₂ – корни характеристического уравнения.

В этом случае  изменяется по экспоненциальному закону (рис. 6.1а)

 

 

 

 

 

 

 

 

 

 

 

 

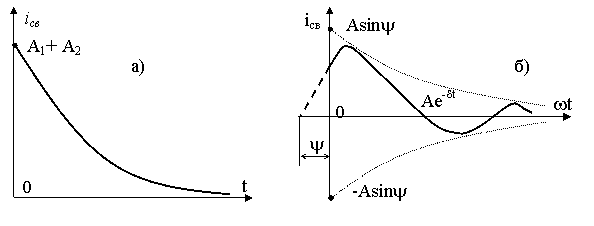Рис. 6.1. Временная зависимость свободной составляющей тока в случае

а) действительных корней характеристического уравнения б) комплексно-сопряженных корней.

 

2)     Корни характеристического уравнения комплексно-сопряженные p_1,2=d±jw

 

Свободная составляющая изменяется по гармоническому закону с частотой w и начальной фазой y, с амплитудой уменьшающейся по экспоненциальному закону (рис. 6.1, б)

 

6.4. Способы составления характеристического уравнения

 

Существует два способа составления уравнений:

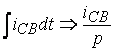1. В однородных дифференциальных уравнениях, составленных для мгновенных значений токов и напряжении по законам Кирхгофа, произвести замену  или  ,  или  .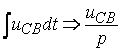

Найти главный определитель полученной после замены системы уравнений и приравнять его к нулю. D=0. Полученное уравнение является характеристическим.

2. Записать комплексное входное сопротивление цепи относительно любой из её ветвей. Произвести замену jw на р и полученное выражение приравнять к нулю.

 

Z(p)=Z(jw)|_jw=p=0.

 

6.5. Порядок расчёта переходных процессов классическим методом

 

1.     Определяются независимые начальные условия.

2.     Составляются уравнения по законам Кирхгофа для цепи после коммутации.

3.     Определяются принужденные составляющие токов и напряжений.

4.     Составляется и решается характеристическое уравнение.

5.     Определяются постоянные интегрирования.

6.     Определяются переходные токи и напряжения.

 

6.6. Включение цепи RL на постоянное напряжение

 

В момент t=0 цепь рис. 6.2 включается на постоянное напряжение. Рассчитаем переходной ток в цепи

 

 

 

 

 

 

 

Рис. 6.2. Включение цепи RL  на постоянное напряжение.

 

До коммутации цепь не была подключена к источнику, поэтому i(-0)=0

Дифференциальное уравнение, составленное по второму закону Кирхгофа для цепи после коммутации, имеет вид . Решение этого уравнения ищется в виде .

Принужденная составляющая равна , т.к. в установившемся режиме в цепи будет протекать постоянный ток, а сопротивление индуктивности в этом случае равно нулю.

Однородное дифференциальное уравнение имеет вид  . Перейдём к характеристическому уравнению:

.

Свободная составляющая тока равна .

 

.

При t=0 имеем

.

 

По первому закону коммутации i(0)=i(-0)=0, тогда

 

.

 

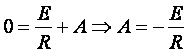Окончательно имеем

 

.

 

 

 

 

 

 

 

 

 

 

 

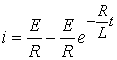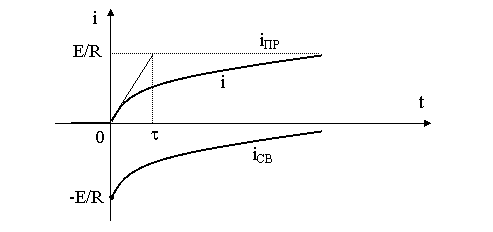Рис. 6.3. Временная зависимость переходного тока.

 

Мерой длительности переходного процесса является постоянная времени .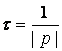

 

Постоянная времени равна промежутку времени, в течение которого свободная составляющая тока убывает в е раз.

Графически постоянная времени определяется длинной подкасательной к кривой тока при любом значении t.

Теоретически переходной процесс длится бесконечно долго, практически он заканчивается за время t=(4¸5)t

 

6.7. Включение цепи RC на постоянное напряжение

 

 

 

Определим переходное напряжение на ёмкости при подключении цепи RC в момент t=0 к источнику постоянного напряжения (рис. 6.4).

Расчёт будем вести в соответствии с вышеизложенным порядком расчёта (см. 6.5, 6.6).

 

1.     U_C(-0)=0

2.     Ri+u_C=E Þ

u_C=u_Спр +u_Ccв

 

3.     u_Cпр=E

 

4.      

5.           

 

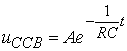
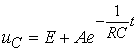
При t=0  u_C(0)=E+A. По второму закону коммутации u_C(-0)=u_C(0)=0,

 0=E+A Þ A=-E.

6.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

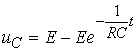
Рис. 6.5. Временная зависимость переходного напряжения на ёмкости.

 

6.8. Вопросы для самоконтроля к лекции 6

 

1.     Какой процесс в ЭЦ называется переходным?

2.     Сформулируйте законы коммутации и поясните их физический смысл

3.     Какова сущность классического метода анализа переходных процессов?

4.     Какой физический смысл имеет свободный режим?

5.     Какой физический смысл имеет принужденный режим?

6.     Как рассчитываются токи и напряжения ЭЦ в свободном и установившемся режимах?

7.     Какова последовательность расчёта переходного процесса классическим методом?

8.     Разберите решение задач 8.4,8.9,8.18,8.26 из [4].

9.     Решите задачи 8.7, 8.16 из [4].

 

Литература: [1] с. 185-198; [2] с. 103-112; [3] с. 199-209; [5] с. 344-363.

 

Лекция 7. Операторный метод расчёта переходных процессов

 

7.1. Преобразования Лапласа

 

Расчёт переходных процессов классическим методом сводится к решению дифференциальных уравнений. При этом основные трудности решения заключаются в определении постоянных интегрирования. По мере усложнения ЭЦ и соответственно повышения порядка дифференциальных уравнений эти трудности увеличиваются.

Более удобным является метод решения линейных дифференциальных уравнений, при котором заданные начальные условия включаются в исходные уравнения и не требуется определять постоянные интегрирования. Таким методом является операторный метод.

В основе операторного метода лежит преобразование Лапласа, которое позволяет перенести решение из области функций действительного переменного t в область функции комплексного переменного р=с+jw, где операции принимают более простой вид: вместо интегродифференциальных уравнений получаются алгебраические уравнения (7.1) (7.2)

Различают прямое и обратное преобразование Лапласа. Функция f(t) определена при t³0  и при t<0 f(t)=0

 

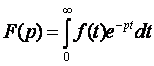                                  (7.1)

 

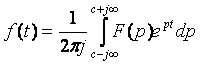                            (7.2)

 

Функция f(t) называется оригиналом, F(p)- её изображением. Фразу «оригинал f(t) имеет своим изображением F(p)» будем заменять символически с помощью знака соответствия Û

 

f(t) Û F(p)  или  F(p) Ûf(t).

 

7.2. Некоторые свойства преобразования Лапласа

 

1.     Изображение постоянной величины

 

.                                    (7.3)

Пример:

,

2.     Свойство линейности

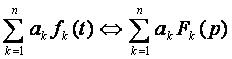                      (7.4)

Пример:

i₁ÛI₁(p); i₂ÛI₂(p); i₁R₁+i₂R₂ ÛI₁(p)R₁+I₂(p)R₂

 

3.     Дифференцирование оригинала f(t)

 

f’(t)Û pF(p) - f(0) - при ненулевых начальных условиях         (7.5)

 

f’(t)Û pF(p) - при нулевых начальных условиях

 

Пример: iÛ I(p)

.

4.     Интегрирование оригинала

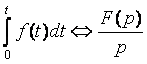                               (7.6)

Пример: iÛ I(p)

.

 

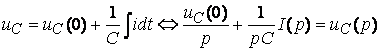7.3. Законы Ома и Кирхгофа в операторной форме

 

Благодаря линейности преобразования Лапласа, законы Ома и Кирхгофа можно написать для изображений токов и напряжений

 

Закон Ома: 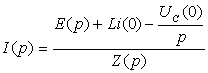                                                (7.7)

где

Z(p)=R+Z_L(p)+Z_C(p) - операторное сопротивление цепи;

 

Z_L(p)=pL                   -операторное сопротивление индуктивности;

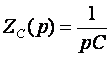           -операторное сопротивление ёмкости;

E(p)                            -изображение ЭДС;

Li(0) и 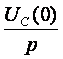       - расчётные напряжения, характеризующие запасенную энергию в индуктивности и ёмкости к моменту коммутации.

 

Первый закон Кирхгофа: 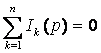                                           (7.8)

 

Второй закон Кирхгофа: 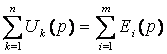                             (7.9)

 

Т.к. для изображений справедливы законы Кирхгофа, то для нахождения изображений токов и напряжений и цепи можно использовать все методы расчёта ЭЦ. При этом удобно пользоваться эквивалентными операторными схемами (рис. 7.1), составленными на основании (7.3-7.6)

 

 

 

 

 

 

 

 

 

 

 

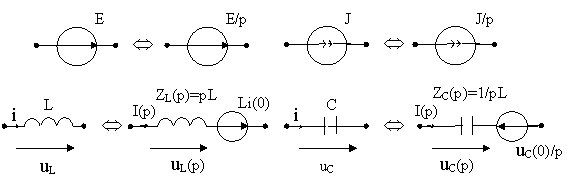Рис. 7.1. Операторные схемы замещения элементов ЭЦ.

 

7.4. Определение оригинала функции по его изображению

 

Существуют три способа определения оригинала искомой функции по его изображению:

1)                      с помощью обратного преобразования Лапласа;

2)                      с помощью таблиц;

3)                      по теореме разложения.

 

Если изображение F(p) получено в виде рациональной дроби 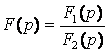 , то оригинал определяется по теореме разложения. В зависимости от вида корней уравнения F₂(p)=0, существуют следующие виды записи теоремы разложения:

1)     корни вещественны и различны

 

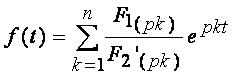, где р_к – корни функции                       (7.10)

 

F₂(p)=0; n -число корней;

 

.

 

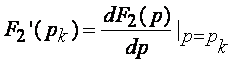2)     при наличии нулевого корня

 

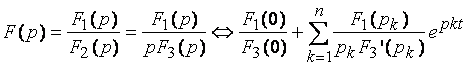     (7.11)

Пример: Определить оригинал функции .

;       

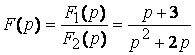p₁= -2; p₂=0

 

F₁(0)=3; F₃(0)=2; F₁(p1)=-2+3=1; F₃’(p1)=2

 

.

 

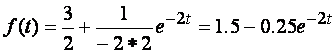7.5. Порядок расчёта переходных процессов операторным методом

 

Расчёт производится  в следующем порядке:

 

1.     Определение независимых начальных  условий

2.     Составление эквивалентной операторной схемы цепи после коммутации

3.     С помощью любого из методов расчёта определить изображение искомых величин

4.     По полученному изображению определить оригинал искомой функции

 

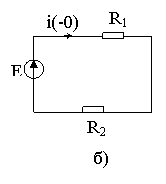
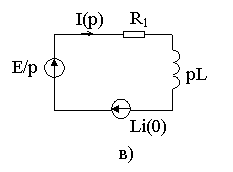
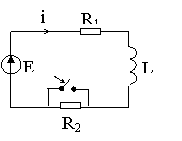
Пример: Определить переходной ток в цепи рис. 7.2а операторным методом.

		a)

 

 

 

 

 

 

 

 

 

Рис. 7.2.

 

Независимые начальные условия определяются по схеме рис. 7.2б.

.

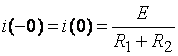Эквивалентная операторная схема приведена на рис. 7.2в

 

По закону Ома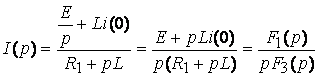            

 

Определим оригинал тока:

1 способ - с помощью таблицы «оригинал-изображение»

 

 

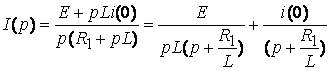
По таблице  ;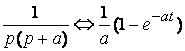       

 

 

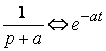
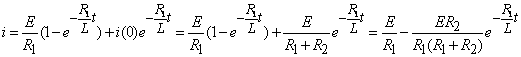
2 способ - по теореме разложения (7.11)

 

;

F₁(0)=E; F₃(0)=R1; F₃’(p)=L;

 

,

 

.

 

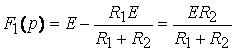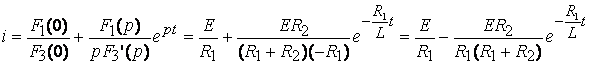7.6. Операторная передаточная функция

 

Важную роль в методах анализа и синтеза ЭЦ играет операторная передаточная функция H(p), равная отношению изображения реакции цепи и изображению воздействия при нулевых начальных условиях. Различают следующие виды передаточных функций:

 

;    ;   ;   .

 

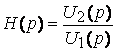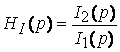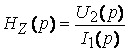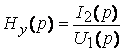Операторная передаточная функция представляет собой дробно-рациональную функцию с вещественными коэффициентами

 

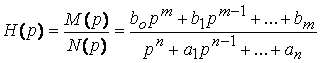.                            (7.12)

 

Степени полиномов числителя и знаменателя зависят от числа реактивных элементов цепи и её схемы.

Устойчивыми называются ЭЦ, у которых при произвольных начальных условиях свободные колебания стремятся к нулю с неограниченным ростом времени, т.е. переходные процессы будут затухающими.

Цепь будет устойчивой, если все полюсы передаточной функции (корни уравнения N(p)=0) располагаются в левой полуплоскости комплексной переменной р. Они могут быть вещественными или комплексно- сопряженными. Для этого необходимо, чтобы полином N(p) содержал вещественные коэффициенты, т.е. являлся полиномом Гурвица.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

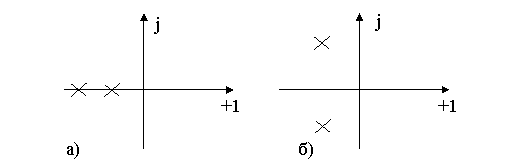Рис. 7.3. Расположение полюсов устойчивой цепи в случае

а) действительных корней; б) комплексно- сопряженных корней.

 

Зная операторную передаточную функцию, можно найти изображение реакции, а по нему и реакцию цепи на заданное воздействие.

Пример: Определить u₂(t) цепи рис. 7.4а

 

 

 

 

 

 

 

 

 

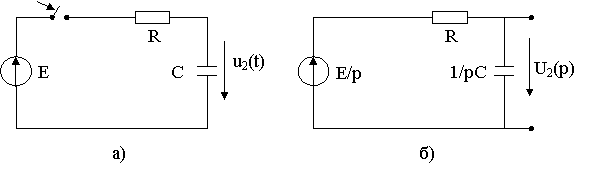
Рис. 7.4. Исходная схема а) и её операторная схема замещения б).

 

;

 

 

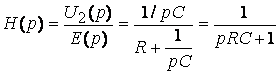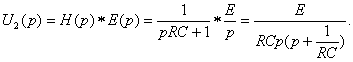
По таблице определим оригинал u₂(t)

 

 

 

 

 

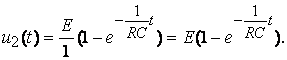
7.7. Вопросы для самоконтроля к лекции 7

 

1.     Какова сущность операторного метода расчёта переходных процессов?

2.     Что такое оригинал функции?

3.     Что такое изображение функции?

4.     Разберите основные свойства преобразования Лапласа.

5.     Как составляются эквивалентные операторные схемы?

6.     Как можно найти оригинал функции по известному изображению?

7.     Какова последовательность расчёта электрической цепи операторным методом?

8.     Дайте определение операторной передаточной функции. Каковы её свойства?

9.     Разберите решения задач 9.1, 9.4 из [4]

10.  Решите задачи 9.2, 9.3 из [4].

 

Литература: [1] с. 218-248; [2] с. 121-127; [3] с. 219-237; [4] с. 251-257; [5] с. 381-391.

 

Лекция 8. Анализ ЛЭЦ при импульсных воздействиях

 

8.1. Единичная и импульсная функции

 

Единичной ступенчатой функцией 1(t) называется скачкообразное изменение напряжения от 0 до 1 (рис. 8.1б). Физически подключение цепи к источнику постоянного напряжения 1 В есть воздействие в виде единичной функции 1(t) (рис. 8.1а)

 

            1(t)=      0   при t<0                                                                            (8.1)

                          1   при t³0

 

Единичной импульсной функцией d(t) (дельта - функцией) называется бесконечно большой импульс бесконечно малой продолжительности, площадь которого равна 1 (рис. 8.1, в)

 

    d(t)=     0     при  t<0  и  t>0

                 ¥    при  t=0                                                                          (8.2)

 

 

 

 

 

 

 

 

 

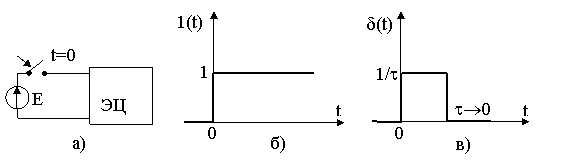Рис. 8.1.

 

Эти функции представляют собой идеализации, облегчающие приближенное математическое описание реальных сигналов. Они связаны между собой соотношением:

d(t)=                                            (8.3)

 

8.2. Переходная и импульсная характеристики

 

Переходной характеристикой h(t) называется реакция цепи на воздействие в форме единичной ступенчатой функции 1(t).

Импульсной характеристикой g(t) называется реакция цепи в форме единичной импульсной функции d (t).

Операторная передаточная функция и переходная и импульсная характеристики связаны между собой:

 

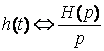; g(t)Û H(p)                                      (8.4)

 

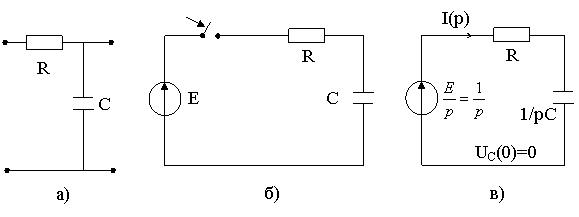
Пример: Определить переходную и импульсную характеристики цепи (рис. 8.2а)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

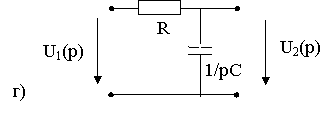Рис. 8.2.

 

Расчёт можно произвести тремя методами:

1.     Классический метод расчёта (рис. 8.2, б)

u_C(0)=0; u_C(t)=u_Cпр+u_Cсв; u_Cпр=Е;

 

;

 

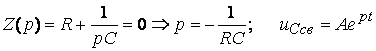; при t=0 u_C(0)=E+A=0ÞA=-E;

;

.

 

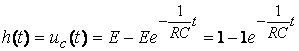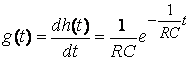2.      Операторный метод расчёта.

Эквивалентная операторная схема приведена на рис. 8.2, в

 

;

;

 

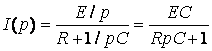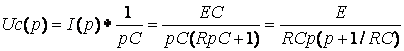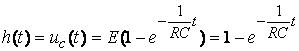
3.     С помощью операторной передаточной функции (рис. 8.2г)

 

;

 

.

 

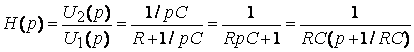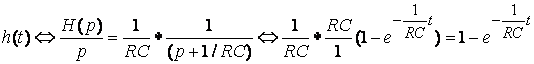8.3. Временной метод анализа ЛЭЦ

 

Временной метод анализа применяется для определения реакции цепи на сложное воздействие при нулевых начальных условиях. Использование понятий переходной и импульсной характеристик позволяет свести расчёт реакции цепи на сложное воздействие к определению реакции на простейшее воздействие типа единичной 1(t) или импульсной функции d(t), с помощью которых аппроксимируется исходное воздействие. При этом результирующая реакция находится как сумма реакций цепи на элементарные воздействия.

Если известна переходная характеристика цепи, то сложное воздействие f₁(t) аппроксимируется ступенчатыми функциями, возникающими через равные промежутки времени Dt (рис. 8.3)

 

 

 

 

 

 

 

 

 

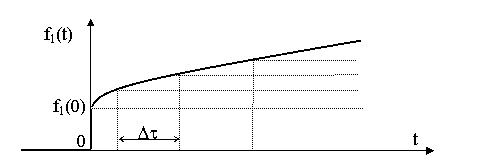Рис. 8.3 Представление сложной функции ступенчатой функцией.

 

В этом случае реакция цепи определяется при помощи интеграла Дюамеля.

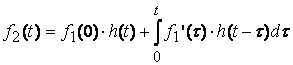                     (8.5)

 

Если известна  или легко определяется импульсная характеристика цепи, то сложное воздействие f₁(t) аппроксимируется последовательностью прямоугольных импульсов (рис. 8.4)

 

 

 

 

 

 

 

 

 

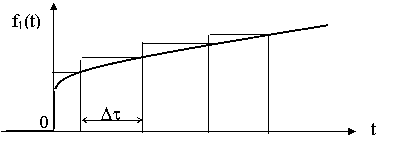Рис. 8.4. Представление сложной функции последовательностью прямоугольных импульсов.

 

В этом случае реакция цепи f₂(t) определяется при помощи интеграла наложения.

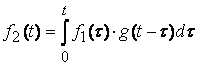.                                  (8.6)

 

Расчёт ЭЦ временным методом производится в следующем порядке:

1.     Определение переходной h(t) или импульсной g(t) характеристики цепи.

2.     Определение переходной h(t-t) или импульсной g(t-t) характеристики путём замены t на t-t.

3.     Определение производной от входного напряжения u₁(t) по времени.

4.     Определение реакции с помощью интеграла Дюамеля или наложения.

Пример: Определить u₂(t) цепи рис. 8.5.

 

 

 

 

 

 

 

 

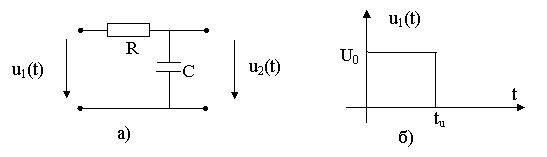Рис. 8.5. Исходная схема а) и вид воздействия б).

;

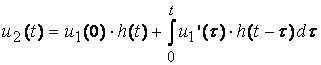u₁(0)=U; ; u₁’(t)=U₀’=0;

При  0£ t £ t_U

.

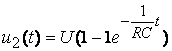При t ³ t_U

            .

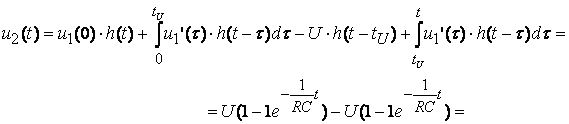
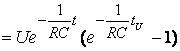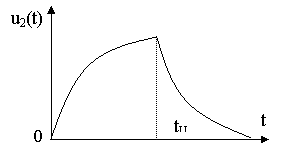Рис. 8.6. Временная зависимость выходного напряжения.

 

8.4. Частотный метод анализа ЛЭЦ

 

При передаче информации по каналам связи в процессе преобразования сигналов в различных устройствах используют периодические несинусоидальные и непериодические (импульсные) воздействия.

Методы анализа цепей, находящихся под воздействием таких сигналов, базируются на спектральном ( частотном) представлении этих сигналов.

Спектральное представление воздействий – это разложение воздействий на сумму гармонических составляющих с различными частотами.

Периодические несинусоидальные воздействия представляются в виде ряда Фурье

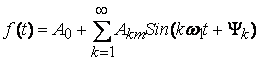.                             (8.7)

 

Слагаемые ряда Фурье представляют собой гармонические колебания с частотами kw₁(k=1,2…). Поэтому периодическое несинусоидальное воздействие – это результат наложения бесконечно большого числа гармонических колебаний с частотами w₁, 2w₁, 3w₁, … с амплитудами А_1m, А_2m, А_3m, … и начальными фазами  y₁, y₂, y₃  

Совокупность частотных параметров А_km образует амплитудный спектр АЧС (рис. 8.7, а), y_k - фазовый спектр ФЧС (рис. 8.7, б). Спектры периодических несинусоидальных воздействий – дискретные (линейчатые).

 

 

 

 

 

 

 

 

 

 

 

 

 

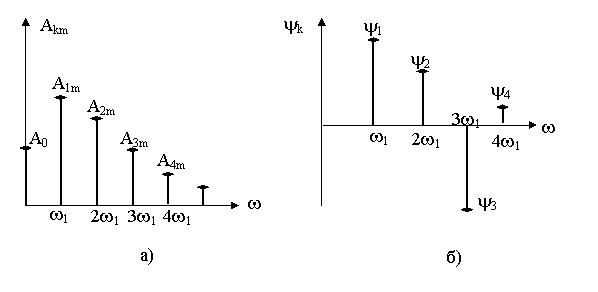Рис. 8.7. Амплитудный а) и фазовый б) спектры периодических несинусоидальных сигналов.

 

Непериодические воздействия могут быть представлены в виде наложения гармонических составляющих с помощью интеграла Фурье

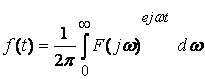,                           (8.8)

где                                   .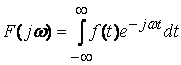

 

С помощью интеграла Фурье непериодические воздействия представляются как результат наложения бесконечно большого числа бесконечно близких по частоте гармонических колебаний с бесконечно малыми амплитудами.

Функцию F(jw)=F(w)e^jj(w) называют спектром непериодического воздействия, F(w) - спектральной плотностью амплитуд (амплитудный спектр) (рис. 8.8а), j(w) - спектром фаз (рис. 8.8б)

 

 

 

 

 

 

 

 

 

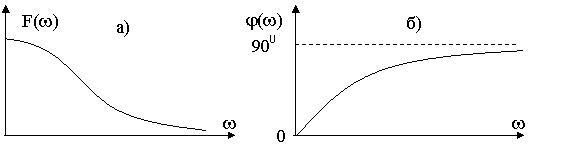Рис. 8.8. Пример амплитудного а) и фазового б, спектров непериодического сигнала.

 

Представление периодических несинусоидальных и непериодических воздействий в виде суммы гармонических колебаний позволяет применять к спектрам все методы расчёта установившихся синусоидальных процессов в ЛЭЦ.

В основе частотного метода анализа ЛЭЦ лежит использование свойств комплексного коэффициента передачи цепи. Расчёт ведётся в следующем порядке:

1.     Определяем спектр воздействия

2.     Определяется комплексная передаточная функция цепи H(jw)

3.     Определяется спектр реакции

4.     По найденному спектру определяется оригинал реакции.

 

Пример: Определить u₂(t) цепи рис. 8.9, а частотным методом

 

 

 

 

 

 

 

 

 

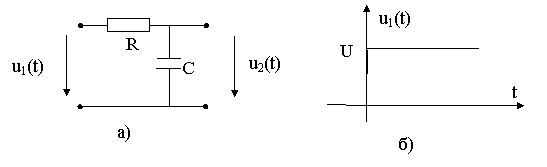Рис. 8.9. Исходная схема а) и вид воздействия б).

 

;

 

;

 

.

 

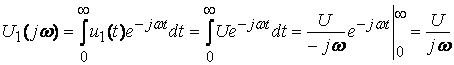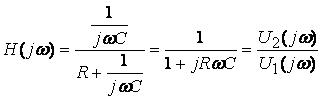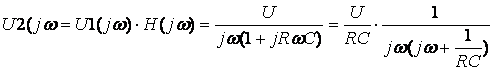По таблице «оригинал- изображение» при p=jw находим

 

;

 

.

 

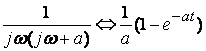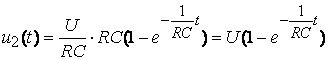8.5. Вопросы для самоконтроля к лекции 8

 

1.     Что такое единичная ступенчатая и единичная импульсная функции?

2.     Объясните физический смысл переходной и импульсной характеристик

3.     Какова связь между  переходной и импульсной характеристиками?

4.     Какова последовательность расчёта ЭЦ временным методом?

5.     Что понимается под спектром периодического несинусоидального воздействия?

6.     Как определяются спектральные характеристики непериодического воздействия?

7.     Как определить спектр на выходе цепи?

8.     Разберите решение задач 8.33, 8.44, 8.53, 8.58, 7.2, 7.7, 10.10, 10.11 из [4]

9.     Решите задачи  8.39, 8.42, 8.45, 8.56 из [4].

 

Литература: [1] с. 254-302; [3] с. 238-241, 245-277; [4] с. 257-258, 215-219, 274-277; [5] с. 391-397.

 

Лекция 9. Электрические фильтры

 

9.1. Назначение и классификация электрических фильтров

 

Электрическим фильтром (ЭФ) называется четырёхполюсник, пропускающий без ослабления  колебания одних частот и пропускающий колебания других частот с большим ослаблением.

Полоса частот, при которых ослабление мало, называется полосой пропускания (ПП), а остальная область частот называется полосой задерживания (ПЗ). По взаимному расположению ПП и ПЗ различают 4 типа фильтров (рис. 9.1):

а) фильтры нижних частот (ФНЧ) (рис. 9.1, а);

б) фильтры верхних частот (ФВЧ) (рис. 9.1, б);

в) полосовые фильтры (ПФ) (рис. 9.1, в);

г) режекторные фильтры (РФ) (рис. 9.1, г);

 

 

 

 

 

 

 

 

 

 

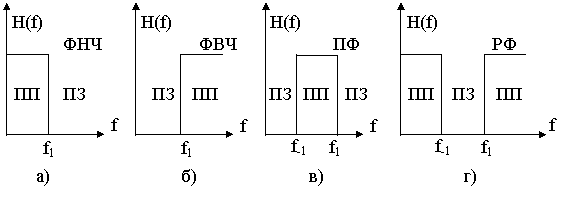Рис. 9.1. Амплитудно-частотные передаточные характеристики идеальных фильтров.

 

9.2. Рабочие характеристики электрических фильтров

 

АЧХ передаточной функции идеального ФНЧ определяется выражением

 

               |H(jw)|² =     1      0< w < w_C

                        0            w>w_C                                                                                   (9.1)

 

Ослабление фильтра равно

 

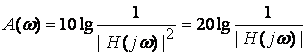                              (9.2)

 

 

 

 

 

 

 

 

 

 

	б)

 

 

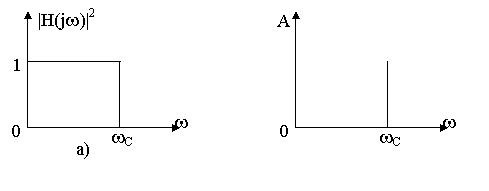Рис. 9.2.

 

Реальные фильтры имеют АЧХ отличные от идеальных. Требования к характеристикам фильтров задаются в виде допустимых пределов их изменения:

DА - максимально допустимое ослабление в ПП;

А_S - минимально допустимое ослабление в ПЗ;

f₁ - граничная частота ПП (для ПФ и РФ задаются f_-1 и f₁);

f_S – граничная частота ПЗ ( для ПФ и РФ задаются f_S1 b f_S2 ).

 

Требования по ослаблению для всех типов фильтров показаны на рис. 9.3. Между ПП и ПЗ расположена переходная область (ПО).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

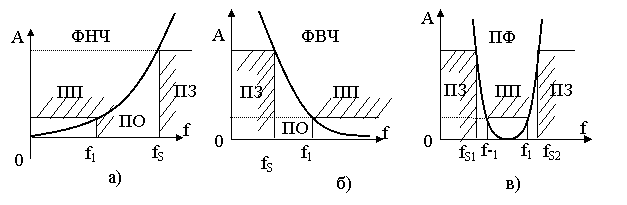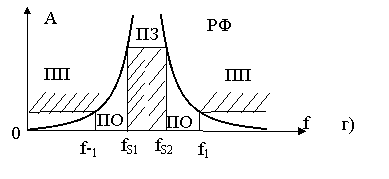Рис. 9.3. Частотные характеристики ослабления фильтров.

 

 

9.3 . Полиномиальные фильтры

 

Идеальные частотные характеристики фильтра (рис. 9.2) заведомо нереализуемы физической цепью с конечным числом элементов. АЧХ реальных фильтров (рис. 9.3) могут лишь приближаться к ним с той или иной степенью точности в зависимости от сложности схемы фильтра. Поэтому необходимо решить задачу аппроксимации, т.е. найти такую функцию, достаточно точно воспроизводящую требуемую характеристику.

На практике эта задача решается с помощью:

1.     полиномов Баттерворта – получают фильтры с максимально плоскими характеристиками ослабления (фильтры Баттерворта);

2.     полиномов Чебышева – получают фильтры с равноволновыми характеристиками ослабления в ПП (фильтры Чебышева).

Фильтром Баттерворта (ФБ) называется фильтр, у которого ослабление монотонно возрастает и на границах ПП DA=3дБ. Передаточная функция ФБ определяется выражением

 

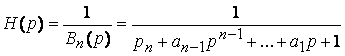,                     (9.3)

 

где B_n (p) -полином Баттерворта порядка n;

a_n,…, a_n-1 - положительные вещественные числа.

 

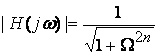, где

 

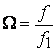
.                                        (9.4)

 

 

 

 

 

 

 

 

 

 

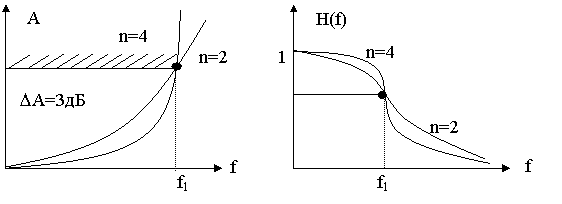           а)                                                          б)

Рис. 9.4. Амплитудно-частотные характеристики ФНЧ Баттерворта

 

Крутизна частотных характеристик ФБ зависит от степени n (порядка фильтра). Чем выше порядок фильтра, определяемый числом реактивных элементов, тем круче идёт характеристика в ПЗ и тем меньше ослабление в ПП.

Фильтром Чебышева (ФЧ) называется фильтр, у которого ослабление в ПП имеет колебательный характер с амплитудой, не превышающей DА=0,01¸2 дБ, а в ПЗ монотонно возрастает с крутизной, большей чем у ФБ такого же порядка.

Передаточная функция ФЧ определяется выражением

 

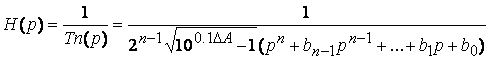          (9.5)

 

где T_n(p) - полином Чебышева порядка n

 

|H(jw)|²=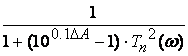                              (9.6)

 

 

 

 

 

 

 

 

 

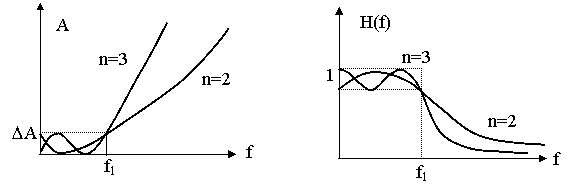а)                                                                  б)

Рис. 9.5. Амплитудно-частотные характеристики ФНЧ Чебышева:

а) ослабления, б) модуля передаточной функции.

 

Число экстремальных точек в ПП у ФЧ равно порядку фильтра.

Схемы ФБ и ФЧ порядка n одинаковы, но различаются значениями элементов.

 

 

 

 

 

 

 

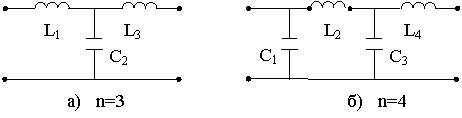Рис. 9.6. Схемы ФНЧ Баттерворта и Чебышева а) с Т-образным входом б) с П-образным входом.

9.4 . Расчёт полиномиальных фильтров

 

Полиномиальные фильтры в зависимости от особенностей их применения могут быть реализованы в виде пассивных LC – фильтров или активных RC - фильтров. Рассмотрим расчёт пассивных LC - фильтров.

При расчёте фильтров по рабочим параметрам применяется нормирование элементов рассчитываемой схемы. Нормирование осуществляется относительно сопротивления нагрузки и граничной частоты ПП, т.е. 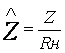 и .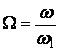

В настоящее время общепризнанной является методика расчёта фильтров заключающаяся в том, что требования к заданному фильтру преобразуются в требования к нормированному ФНЧ - прототипу.

ФНЧ – прототипом называется ФНЧ с нормированными значениями сопротивления и частоты, равными единице. Расчёт фильтров можно выполнить аналитическим и табличным методами.

Для сложных фильтров большого порядка расчёт аналитическим методом очень трудоёмок. Для наиболее часто используемых фильтров составлены подробные таблицы, упрощающие расчёт. В них приведены схемы и значения элементов для ФНЧ – прототипа n=3¸10.

 

9.5. Табличный метод расчёта фильтров

 

Рассмотрим порядок расчёта фильтров табличным методом:

1.     Нахождение нормирующей частоты фильтра

 

 

2.     Нахождение нормированной граничной частоты полосы задерживания

 

3.     Нахождение порядка ФНЧ – прототипа

 

Тип фильтра	Фильтр Баттерворта	Фильтр Чебышева
n³

Порядок n можно также определить по справочнику [5], исходя из требований: на частоте W_S  A³A_S, а DA£ DA _{заданного при W=1}

 

4. Нахождение по таблицам [5] нормированных значений элементов ФНЧ - прототипа и его схемы. Порядок фильтра совпадает с числом реактивных элементов.

 

 

 

 

 

 

 

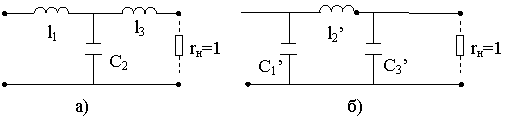Рис. 9.7. Схемы ФНЧ- прототипа а) с Т-образным входом б) с П-образным входом.

 

5.     Нахождение коэффициентов денормирования по формулам

 

; .

 

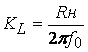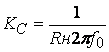6.     Переход от схемы ФНЧ - прототипа к схеме заданного фильтра и определение значений его элементов.

Подробные примеры расчёта фильтров приведены в [8].

 

ФНЧ- прототип	ФНЧ	ФВЧ	ПФ	РФ

 

9.6. Вопросы для самоконтроля к лекции 9

 

1.     Дайте определение электрического фильтра

2.     Приведите классификацию фильтров по диапазону пропускаемых частот

3.     Что называется порядком фильтра?

4.     Что означает нормирование по частоте, по сопротивлению? Как оно используется при расчёте фильтров?

5.     Дайте определение полиномиального фильтра, приведите примеры их схем

6.     Как влияет увеличение порядка фильтра на его частотную характеристику ослабления?

7.     Сравните частотные характеристики ослабления фильтров Баттерворта и Чебышева. Каковы их достоинства и недостатки

8.     Как перейти от ФНЧ - прототипа к ФВЧ, ПФ, РФ?

9.     Разберите решение задач 15.1, 15.5, 15.7, 15.9, 15.10, 15.12 из [4]

10.  Решите задачи 15.2,15.11,15.13 из [4].

 

Литература: [1] с. 444-463; [2] с. 208-231; [4] с. 413-425; [5] с. 414-430; [8].

 

 

 

 

 

 

 

Литература

 

1.     Белецкий А.Ф. Теория линейных электрических цепей: Учебник для вузов. – М.: Радио и Связь, 1986. - 544 с.

2.     Бакалов В.П., Игнатов А.Н., Круг Б.И. Основы теории электрических цепей и электроники: Учебник для вузов. – М.: Радио и Связь, 1989. - 525 с.

3.     Шебес М.Р., Каблукова М.В. Задачник по теории линейных электрических цепей. – М.: Высшая школа, 1990. - 544 с.

4.     Добротворский И.Н. Теория электрических цепей: Учебник для техникумов. – М.: Радио и Связь, 1990. - 472с.

5.     Ханзел Г. Справочник по расчёту фильтров. - М.: Советское радио, 1974. - 288 с.

6.     Воробиенко П.П. Теория линейных электрических цепей. Сборник задач и упражнений. Учебное пособие для вузов. – М.: Радио и Связь, 1989. - 328 с.

7.     Дмитриев В.Н., Зелинский М.М. Теория электрических цепей. Конспект лекций. Часть 1. Ташкент: ТЭИС. 2000. - 83 с. Часть 2. Ташкент: ТЭИС. 2000. - 91 с.

8.     Белова Л.Н., Дмитриев В.Н., Теория электрических цепей. Задания и методические указания к выполнению курсовой работы по теме “Расчет электрических фильтров”. Для студентов заочного факультета, обучающихся по направлению В522300 - <Телекоммуникации>. Ташкент: ТЭИС.-2000.- 84 с.

 

 

 

 

 

 

 

 

 

 

 

 

 

Содержание

 

Введение ……………………………………………………………………..……….…. 3

Лекция 1. ОСНОВНЫЕ ЭЛЕМЕНТЫ, ПОНЯТИЯ И ЗАКОНЫ

ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ………………………………..….………………………. 4

1.1. Определение электрических цепей. Понятие тока, напряжения и ЭДС …. 4

1.2. Элементы электрических цепей и их свойства …………….………………. 5

1.3. Электрическая схема и ее элементы ……………………………………..…. 9

1.4. Виды соединений элементов ЭЦ ………………………………………...… 11

1.5. Законы Кирхгофа …………………………………………………………… 12

1.6. Закон Ома ……………………………………………………..…………….. 14

1.7. Вопросы для самоконтроля к лекции 1 ……………………………………… 15

Лекция 2. МЕТОДЫ РАСЧЕТА ЦЕПЕЙ ПОСТОЯННОГО ТОКА …………….…. 16

2.1. Определение и порядок расчета цепей постоянного тока ………………... 16

2.2. Расчет резистивных ЛЭЦ …………………………………………………… 18

2.3. Метод контурных токов ………………………………….…………………. 19

2.4. Метод узловых напряжений …………..………………..….……………….. 21

2.5. Вопросы для самоконтроля к лекции 2 ……………………………………. 23

Лекция 3. ЛЭЦ ПРИ ГАРМОНИЧЕСКОМ ВОЗДЕЙСТВИИ ………………....…... 24

3.1. Гармонические колебания и их описание ………………………….……… 24

3.2. Действующее значение периодической функции ……………………...…. 25

3.3. Представление гармонических колебаний векторами ….……………….... 25

3.4. Связь между мгновенными значениями напряжения и тока

на элементах цепи …………………………………..………………….……….... 26

3.5. Последовательное соединение элементов R, L, C ……………….…………30

3.6. Вопросы для самоконтроля к лекции 3 ………………………………....…. 32

Лекция 4. СИМВОЛИЧЕСКИЙ МЕТОД РАСЧЕТА ЦЕПЕЙ

ГАРМОНИЧЕСКОГО ТОКА …………………………………………..………………33

4.1. Символическое изображение синусоидальных функций

комплексными величинами ……………………………………….…………….. 33

4.2. Изображение производной и интеграла от синусоидальной функции …... 35

4.3. Комплексные сопротивления и проводимость …………………………..... 36

4.4. Законы Ома и Кирхгофа в комплексной форме ………………………..…. 37

4.5. Выражение мощности в комплексной форме. Баланс мощностей ……..... 39

4.6. Условие передачи максимальной мощности от источника в нагрузку ….. 40

4.7. Вопросы для самоконтроля к лекции 4 ………………….…………….…... 41

Лекция 5. ПРОСТЕЙШИЕ ЧАСТОТНО-ИЗБИРАТЕЛЬНЫЕ ЦЕПИ ………….….. 43

5.1. Комплексная передаточная функция ……………………….…………….... 43

5.2. Явление резонанса и его значение в радиотехнике и электросвязи ……... 45

5.3. Последовательный колебательный контур ……………….…………….…. 46

5.4. Виды расстроек контура ……………………………………………..….….. 47

5.5. Частотные характеристики последовательного колебательного контура . 48

5.6. Полоса пропускания ……………………………………………………....… 49

5.7. Вопросы для самоконтроля к лекции 5 ……………………………………. 50

 

Лекция 6. ПереходнЫе процессы в ЛЭЦ ……………………………………. 51

6.1. Понятие о переходном процессе …………………………………………… 51

6.2. Законы коммутации …………………………………………………………. 51

6.3. Классический метод расчёта переходных процессов …………………….. 52

6.4. Способы составления характеристического уравнения ……………….….. 53

6.5. Порядок расчёта переходных процессов классическим методом ………... 54

6.6. Включение цепи RL на постоянное напряжение …………………………. 54

6.7. Включение цепи RC на постоянное напряжение …………………………. 56

6.8. Вопросы для самоконтроля к лекции 6 ……………………………………. 57

Лекция 7. Операторный метод расчёта переходных процессов .. 58

7.1. Преобразования Лапласа …………………………………………………… 58

7.2. Некоторые свойства преобразования Лапласа ……………………………. 58

7.3. Законы Ома и Кирхгофа в операторной форме …………………………… 59

7.4. Определение оригинала функции по его изображению ………………….. 60

7.5. Порядок расчёта переходных процессов операторным методом ………... 61

7.6. Операторная передаточная функция ………………………………………. 63

7.7. Вопросы для самоконтроля к лекции 7 ………………………………….… 65

Лекция 8. Анализ ЛЭЦ при импульсных воздействиях ………..….… 66

8.1. Единичная и импульсная функции ………………………………………… 66

8.2. Переходная и импульсная характеристики ………………………………... 66

8.3. Временной метод анализа ЛЭЦ ……………………………………….……. 68

8.4. Частотный метод анализа ЛЭЦ …………………………………………….. 70

8.5. Вопросы для самоконтроля к лекции 8 ……………………………………. 73

Лекция 9. Электрические фильтры ………………………………………...… 74

9.1. Назначение и классификация электрических фильтров ………………….. 74

9.2. Рабочие характеристики электрических фильтров ………………………... 74

9.3. Полиномиальные фильтры ……………………………………………….… 76

9.4. Расчёт полиномиальных фильтров ……………………………………….… 78

9.5. Вопросы для самоконтроля к лекции 9 ……………………………………. 80

Литература …………………………………………………………………………….. 81

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Белова Л.Н.  «Теория электрических цепей» Конспекты лекций для студентов заочного факультета, обучающихся по направлениям образования: 5222000:<Радиотехника>, 5222100: <Радиосвязь, радиовещание, телевидение>, 5222200: <Телекоммуникации> Ташкент: ТЭИС. 2002.-94 с.

 

Печатается по решению научно-методического совета ТЭИС в соответствии с планом издания учебно-методических документов в 2001/2002 учебном году.

 

Ответственный редактор: доцент М.М. Зелинский

 

Рецензент: проф. Соколов В.К.

Корректор: Халимова Р.С.