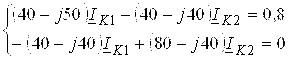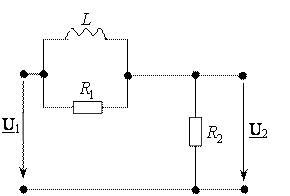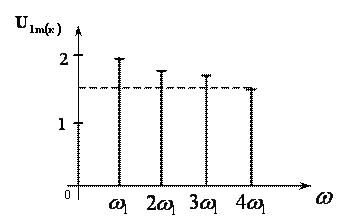УЗБЕКСКОЕ АГЕНТСТВО СВЯЗИ И ИНФОРМАТИЗАЦИИ
ТАШКЕНТСКИЙ УНИВЕРСИТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ
ТАШКЕНТСКИЙ УНИВЕРСИТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ
Кафедра ТЭЦ
Индивидуальная работа
по теории электрических цепей,
часть 1
Ташкент 2006
ЗАДАНИЕ №1
РАСЧЁТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
С НЕЗАВИСИМЫМИ ИСТОЧНИКАМИ
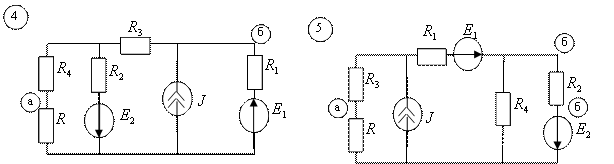
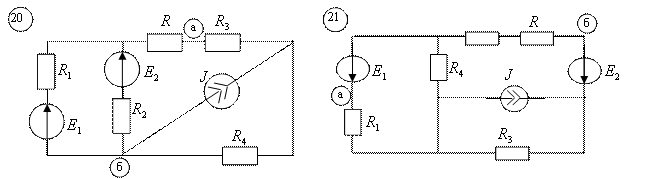
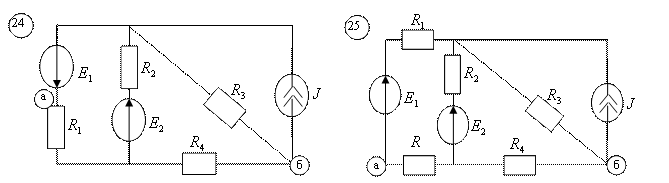
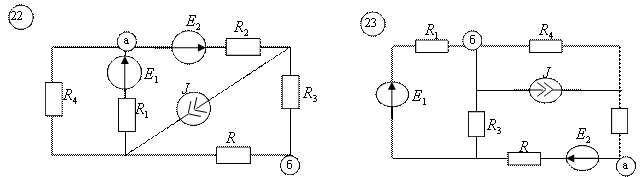
1.1. В соответствии с номером варианта (N – порядковый номер под которым записана фамилия в групповом журнале), выбрать схему и рассчитать параметры её элементов
; 
,
где М – две последние цифры номера группы.
Например: для группы 337 Тр имеем М = 37.
1.1.1. Составить системы уравнений в алгебраической форме для расчёта электрических цепей по законам Кирхгофа, методом контурных токов (МКТ) и методом узловых напряжений (МУН). Привести в алгебраической форме выражения токов всех ветвей через контурные токи и узловые напряжения.
1.1.2. Рассчитать токи во всех ветвях и падения напряжения на всех элементах цепи оптимальным из рассмотренных методов.
1.1.3. Проверить правильность расчёта, используя уравнение баланса мощностей.
Дополнительное задание.
Определить напряжение между точками а и б, указанных на схеме, и эквивалентное сопротивление цепи относительно этих точек.
Указание:
при определении эквивалентного сопротивления исключите из схемы источники ЭДС 
и
источник тока 
.
Пример выполнения задания №1
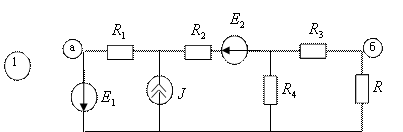
Исходные данные Е1=1 В; Е2=6 В; Е3=10 В; J=1,4 A;
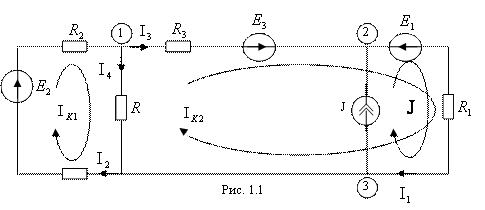R1=8 Ом; R2=12 Ом; R3=10 Ом; R4=5 Ом; R=3 Ом.
1.2. Составление уравнений для расчёта схемы.
1.2.1. Уравнения по законам Кирхгофа.
В данной схеме три узла 
, пять ветвей 
.
Количество уравнений, составляемых по законам Кирхгофа, определим по
формулам 
;
.
Уравнения по законам Кирхгофа имеют вид
(1.1)
1.3.2. Уравнения по методу контурных токов.
Количество уравнений, составляемых по МКТ равно
.
Токи ветвей: 
1.3.3. Уравнения по методу узловых напряжений.
Количество уравнений, составляемых по МУН равно 
.
Примем узловое напряжение третьего узла равным нулю, т.е. 
тогда
уравнения для первого и второго узлов запишутся следующим образом
Запишем выражения для токов ветвей через узловые напряжения U1, U2 по закону Ома
1.3.4. Из п. 1.2. видно, что для решения задачи по
МКТ и МУН необходимо решить одинаковое количество уравнений – два, т.е. по
объёму расчётов они примерно равнозначны, а по законам Кирхгофа – четыре.
Выберем для дальнейшего решения задачи МКТ.
После подстановки в систему уравнений (1.2) числовых значений параметров элементов получим систему уравнений
(3+12+5)Iк1-3Iк2=6;
-3Iк1+(8+10+3)Iк2=-1,4
8-1+10.
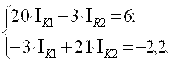
Решим
систему уравнений 
с помощью определителей
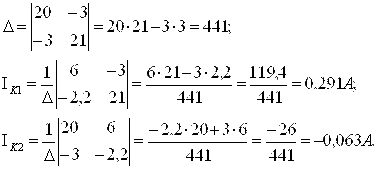
Систему
уравнений 
удобно решить на ПЭВМ с
помощью математической программы MathCAD 2001 (см. приложение П1). Токи в ветвях цепи
определяем через контурные токи (рис. 1.1).
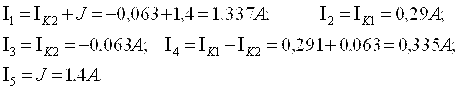
1.4. Проверка баланса мощностей.
Мощность, отдаваемая источниками энергии, равна
,
где
,
Мощность, потребляемая сопротивлениями равна
Баланс мощностей выполняется, т.е. 
; 
.
Примечание: баланс мощностей считается выполненным, если
расхождение между мощностью отдаваемой источниками и мощностью потребляемой
приёмниками (сопротивлениями) не превышает 5%.
Таблица 1.1
|
|
|
|
|
|
|
|
|||
|
|
|||
|
|
|
||
|
|
|||
|
|
|||
|
|
|||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
ЗАДАНИЕ 2
РАСЧЁТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
С ЗАВИСИМЫМИ ИСТОЧНИКАМИ
2.1 В соответствии с номером варианта (N – порядковый номер, под которым записана фамилия студента в групповом журнале), выбрать схему(таблица 2.1) и рассчитать параметры её элементов
m = a = 2 R = R1 ; g = 1 / R2 ; R1 = R2 = ( 2 N + 10 ), Ом; E = M, B ;
I = M, мА; Rг = Rн = ( 3
N + 20 ), Ом ; R0 = ( N + 10 ), Ом,
где М - две последние цифры номера группы.
2.2. С помощью метода узловых напряжений определить выходное напряжение цепи U2 или ток I2
Таблица 2.1
Расчетные схемы задания 2
|
1 R0
|
2
|
||
|
3 Rг R0
R2 E U1 R1 I2 |
4 R0
R2
R1 mU1 U1 Rн Rг |
||
|
5 I1 R1 R2 RI1 U2
E R0
|
6 I1 R1 R2 RI1
J Rг R0
|
||
|
7 R1 R0 R2 U2
E Rн I1 RI1 |
8 R1 R0 R2
E
RI1 I1 I2 |
||
|
9 Rг R1 R2 mU1
U2 E R0 Rн |
10 R1 R2 mU1
J Rг R0 U0
|
||
|
11 R0
U2 Rн
|
12 Rг R0
gU1
|
||
|
13 gU1
J R2 I2
|
14 gU1
|
||
|
15 gU1 R1
R2 Rг R0 I2 |
16 R0
R2 Rн E R1 aI1 U2 |
||
|
17 R0
R1 R1 U2 aI1 R2 Rн
I1 E |
18 R0
R1 U2 R2 Rн J aI1 I1 |
||
|
R1 R2
Ii U2 E R0 Rн |
20 aI1 R1
I1 U2 R0 Rн J |
||
|
R1
Ii J Rг R0
I2 |
22 aI1
I1 R1
E
|
||
|
R1 R2
J
Rг I1 RI1 I2 |
24
R1 R2 U2 J
Rг RI1 Rн I1 |
Пример выполнения задания 2
2.1. Исходные данные для расчета
R1 = 30 Ом; R2 = 30 Ом;
R0 = 20 Ом; a = 3; E = 1 В.
I2 R2
 |
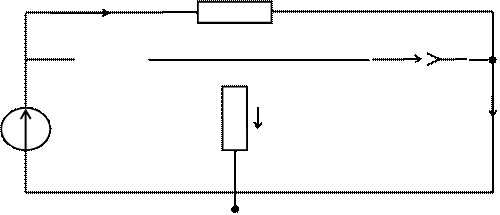U2 aI1 R1
U4 U1 I1
I3 R0 I0
E
Рис 2.1
2.2. С помощью метода узловых напряжений (МУН) определим ток I3
Данная цепь имеет 4 узла , но узловые напряжения 3 и 4 узлов равны между собой ,т.к. соединены ветвью без сопротивлений. Исходя из этого при составлении уравнений рассматриваются три неустранимых узла 1,2,3.
Примем в качестве базисного узел 3, тогда U3=U4=0 и узловое напряжение узла 1 равно U1 = E.
Составим уравнение по МУН для узла 2
(1/R1 + 1/R0 )U2 - U1/R1 = - a I1 (2.1)
По закону Ома ток I1 равен
I1 = (U 1 – U2)/R1= E /R1 – U2 / R1 . (2.2)
Подставив выражение для тока I1 в уравнение (2.1) и получим
(1/R1 + 1/R0 )U2 - E1/R1 = - a E /R1 + aU2 / R1;
(1/R1+1/R0-a/R1)U2 = (E/R1)(1-a). (2.3)
Из выражения (2.3) определяем узловое напряжение узла 2.
U2 = (( E / R1) ( 1 - a ) ) / (( 1 / R1)(1- a) + 1 / R0) =
= ( E / R1)/(( 1 / R1)+ 1 / ((1- a) R0) =
= E/(1+ R1/ ((1- a) R0))) =
=1 / (1+30/((1-3)20)) =1/(1-3/4) =1/ 0,25 = 4 B.
По закону Ома определим токи в ветвях (кроме тока I3)
I1= (U1- U2)/R1=(1- 4)/30 = -3/30 = - 0,1 A;
aI1=3(- 0,1)= - 0,3 A;
I2 = ( U1 - U4 ) / R2 = ( 1 – 0 ) / 30 = 1 / 30 = 0,03333 A;
I0 = ( U2 - U3_) / R0 = 4 / 20 = 0,2 A.
Ток I3 определяется по первому закону Кирхгофа для узла 4
I3 = I2 + aI1 = 0.03333 - 0.3 = - 0,26667 A.
ЗАДАНИЕ 3
РАСЧЁТ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
СИМВОЛИЧЕСКИМ МЕТОДОМ
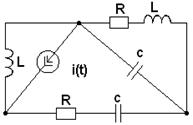
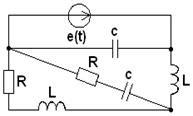
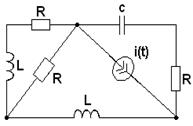
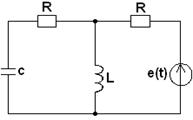
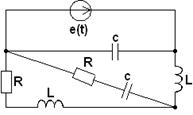
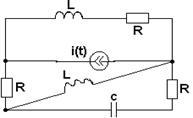
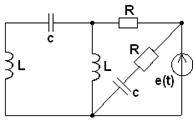
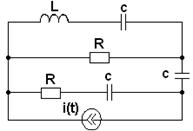
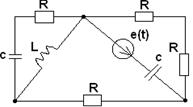
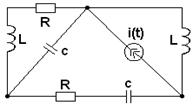
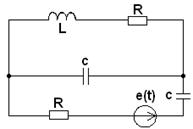
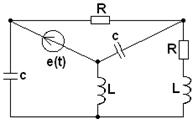
3.1. В соответствии с номером варианта (N – порядковый номер, под которым записана фамилия студента в групповом журнале), выбрать схему (табл. 3.1) и рассчитать значения её элементов
R=M+N,
Ом; wL=N+10,
Ом; 
=N+20,
Ом;
e(t) = 10
M Sin(wt+900), В;
i(t) =M Sin(wt+900), мА,
где М – последние две цифры номера группы.
3.2. Составить уравнения по законам Кирхгофа, МКТ и МУН в комплексной форме.
3.3. Рассчитать комплексные токи ветвей любым из методов расчёта.
3.4. Выполнить проверку правильности расчёта с помощью уравнения баланса комплексных мощностей.
3.5. Записать мгновенные значения токов ветвей.
Дополнительное задание
Определить эквивалентное сопротивление части цепи, подключённой к источнику;
a) на основе предыдущего расчёта;
б) путём эквивалентного преобразования цепи.
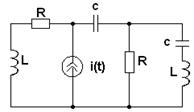
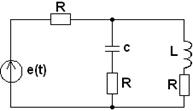
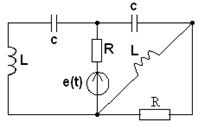
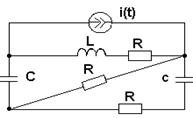
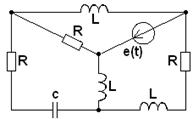
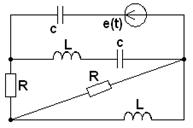
Таблица 3.1
|
1
|
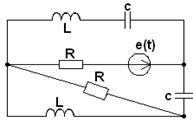
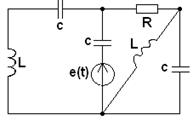
2
|
||
|
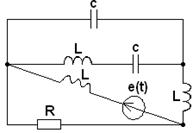
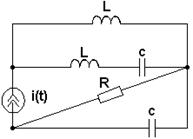
3
|
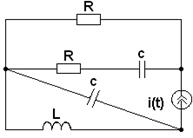
4
|
||
|
5
|
6
|
||
|
7
|
8
|
||
|
9
|
10 |
||
|
11
|
12
|
||
|
13
|
|
|
15
|
16
|
||||||
|
17
|
18
|
||||||
|
19
|
|
||||||
|
|
|
||||||
|
23
|
24
|
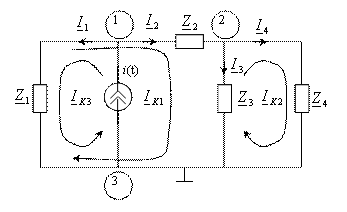
ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАНИЯ №3
3.1. Исходные данные для расчёта
N = 20, гр.Т-320, М = 20;
R =
40 Ом; wL=30 Ом;
=40 Ом;
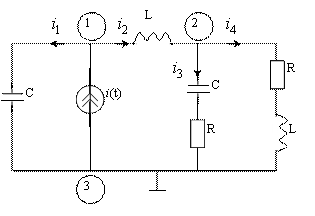i(t)=I Sin(wt+yi)=20Sin(wt+900) мА.
|
|
Рис. 3.1. Расчётная схема
|
3.2. Для составления уравнений в символической форме построем эквивалентную комплексную схему (рис. 3.2.) и определим значения её элементов
|
|
|
(3.1) |
|
|
|
|
|
|
||
|
|
||
|
Рис. 3.2. Эквивалентная комплексная схема замещения
|
||
3.2.1. Составим систему уравнений по законам Кирхгофа. Количество уравнений равно
|
|
(3.2) |
3.2.2. Составим систему уравнений по МКТ. Количество уравнений по МКТ равно
|
|
(3.3) |
3.2.3. Система уравнений по МУН. Количество уравнений по МУН равно
.
Принимаем за опорный (базисный) 3-ий узел, т.е. 
.
|
|
(3.4) |
3.3. Произведём расчёт комплексных токов ветвей. Как видно из систем уравнений, целесообразно воспользоваться МКТ или МУН, т.к. по этим методам необходимо решать системы из двух уравнений, а по законам Кирхгофа – из четырёх уравнений.
Выберем для дальнейшего расчёта МКТ.
Подставим в (3.3) числовые значения, получим систему уравнений
|
|
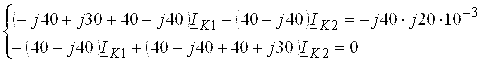
(3.5) |
Решим систему (3.5) с помощью метода подстановки. Из второго уравнения системы (3.5) имеем
.
Подставим значение 
в первое уравнение
системы (3.5)
;
;
Рассчитаем токи ветвей
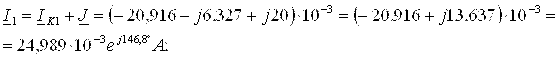
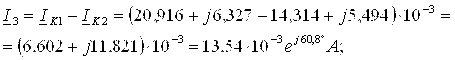
Расчёт контурных токов и токов ветвей целесообразно выполнить на ПЭВМ с помощью программы Mathcad 2001 (см. приложение П3).
3.4. Выполним проверку правильности расчёта токов с помощью уравнения баланса комплексных мощностей.
;
.
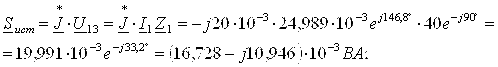
Так как комплексная мощность источника и приёмника равны, то расчёт токов выполнен правильно.
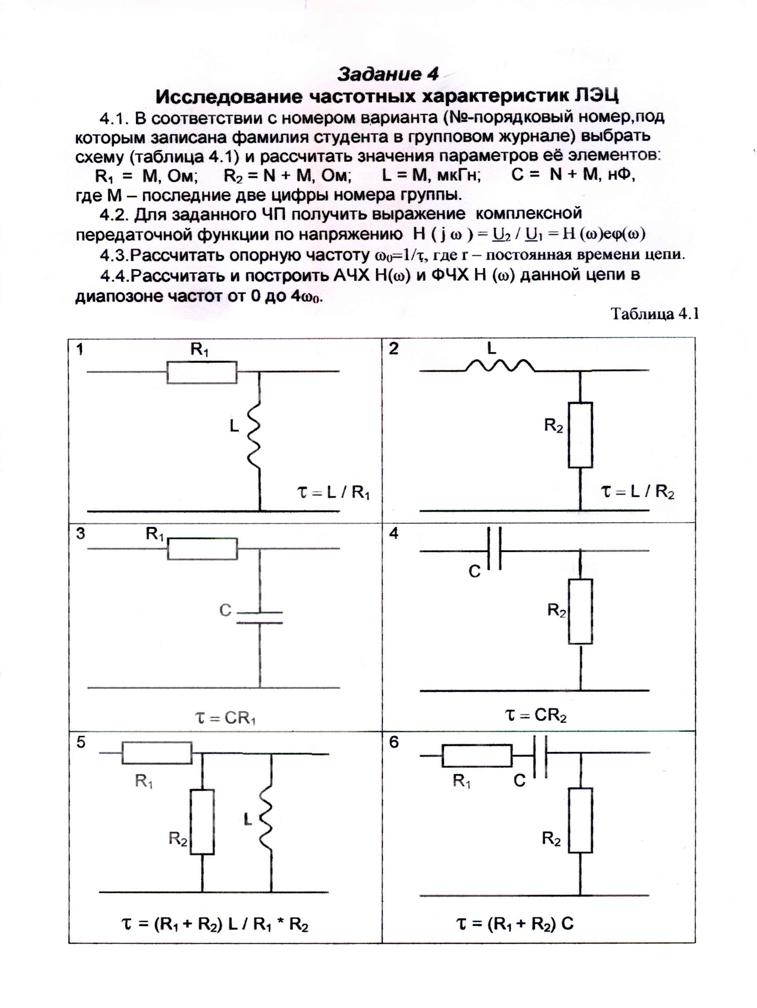
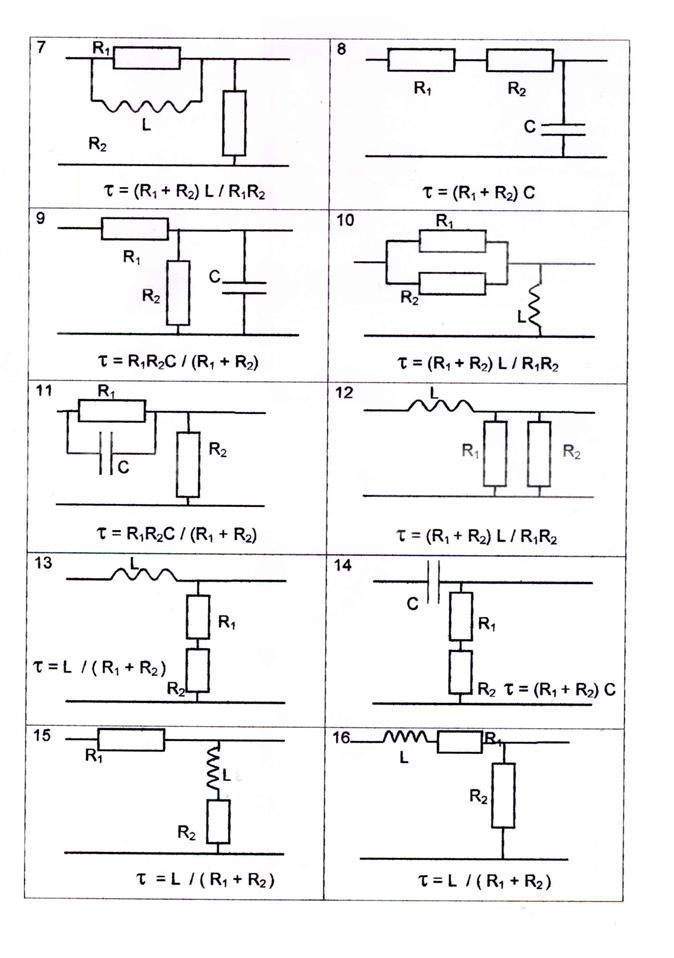
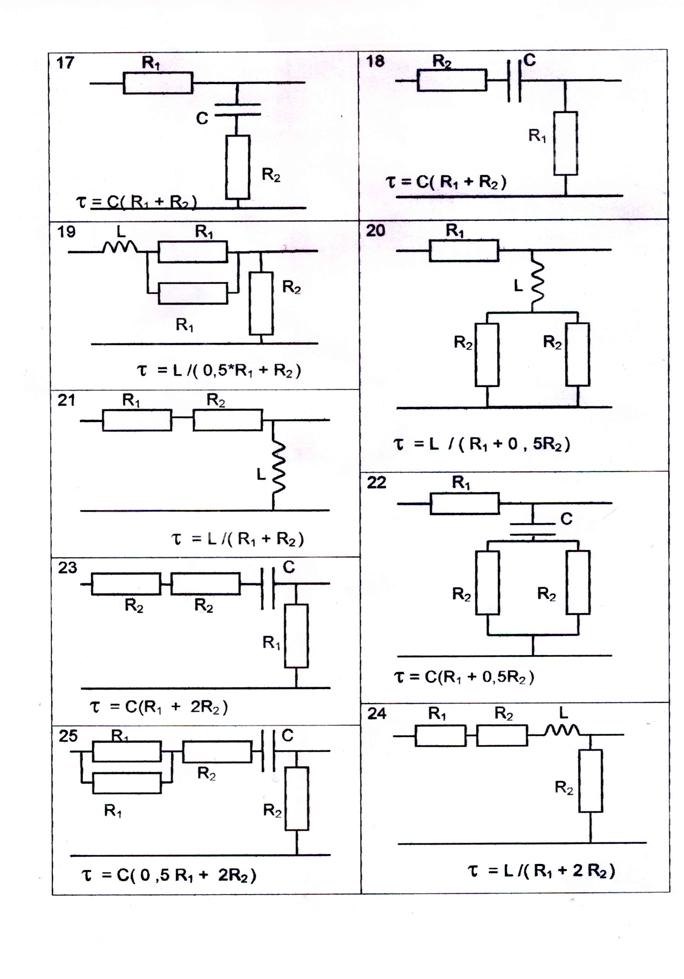
Пример выполнения задания № 4
4.1. Исходные данные :
N = 10 ; M = 20; R1 = 20 Ом; R2 = 30 Ом; L = 20 ×10 – 6 Гн;
Рис. 4.1. Расчетная схема.
4.2. Получим выражение комплексной передаточной функции по напряжению: H (iw)
H ( j w) = U2 / U1 = Z 2 / (Z 1 + Z2). (4.1)
После подстановки в (4.1.) выражений для комплексных сопротивлений
Z1 = R1 j w L / (R1+jwL) ; Z2 = R2,
получим
=
H(jw)
=
=
R2
R2 ( R1 + j w L )
|
= |
|
H(jw) |
|
= |
|
= |
+ R2
R1 j
w L R1 · R2
+ j wL ( R1 + R2 )
|
+ R2 |
R1 + j w L
|
(4.2) H(w)eiφ(w). = =
R1 R2
+ j wLR2 600 + j w·20·10 –6·30
R1 R2 + j w L ( R1 + R2 ) 600 + j w·20·10 –6·50
4.3. Рассчитаем опорную частоту
= 6· 105
c-1. = = w 0 =
1 R1R2
20·30
t L ( R1 + R2 ) 20·10-6
( 20 + 30 )
4.4. Рассчитаем и построим АЧХ и ФЧХ цепи в диапазоне частот от 0 до 4 w0..
Из (4.2) получим выражение АЧХ
H (ω)= |H (jω)|=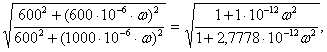 
(4.3)
Из (4.2) получим выражение ФЧХ цепи
φ(ω) = arg H (iω) = arctg (600·10-6w / 600 ) - arctg (1000۰10-6w / 600 ) =
= arctg(10-6w) - arctg(1,6667·10-6). (4.4)
Задаваясь значениями частоты w, рассчитаем АЧХ H (w) по формуле (4.3) и ФЧХ j (w) по формуле (4.4). Результаты расчета сведем в таблицу 4.2.
Таблица 4.2
|
w |
0 |
0,5w |
w |
2w |
3w |
4w |
|
wc-1 |
0 |
3 ·105 |
6 ·105 |
12 ·105 |
18 ·105 |
24 ·105 |
|
10-5w |
0 |
3 |
6 |
12 |
18 |
24 |
|
H(w) |
1 |
0,894 |
0,707 |
0,447 |
0,316 |
0,243 |
|
j(w), град |
0 |
-25 |
- 42,7 |
- 61 |
- 67,5 |
-75,4 |
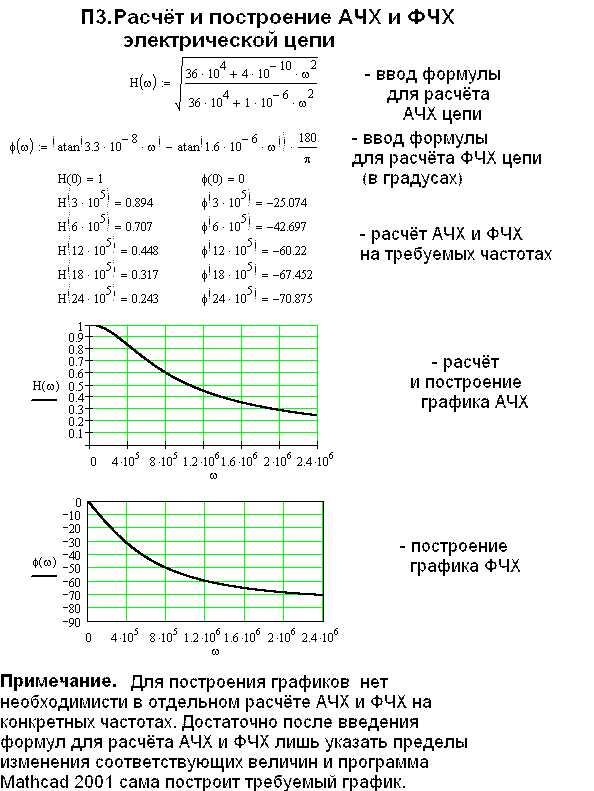
По данным таблицы 4.2 построены графики АЧХ H(w) и ФЧХ j(w) , приведенные на рис. 4.2 и рис. 4.3.
Расчет и построение АЧХ и ФЧХ удобно выполнить на ПЭВМ с помощью математической программы Mathcad 2001. (см. приложение П3).
 |
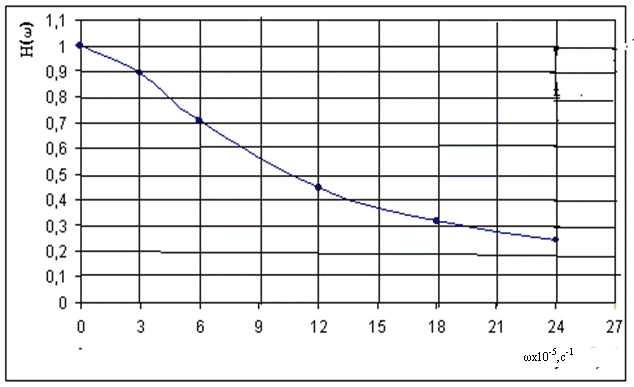Рис.4.2. Амплитудно-частотная характеристика
 |
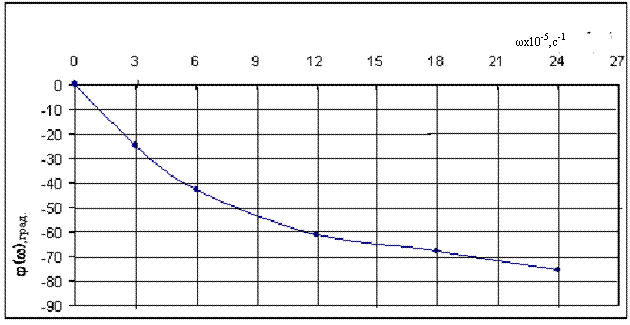Рис.4.3. Фазо-частотная характеристика цепи.
ЗАДАНИЕ 5
РАСЧЁТ ЛЭЦ ПРИ ПЕРИОДИЧЕСКОМ
НЕСИНУСОИДАЛЬНОМ ВОЗДЕЙСТВИИ
Задана периодическая последовательность
прямоугольных импульсов 
(рис 5.1) с амплитудой U=10 В и
длительностью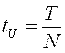 
(рис 5.1), где N – порядковый номер,
под которым записана фамилия студента в журнале;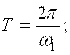 
(значение 
берётся
из задания №4).
|
|
|
Рис.5.1. График напряжения на входе цепи
|
5.1. С помощью
тригонометрического ряда Фурье представить напряжение 
в виде суммы
гармонических составляющих
.
Постоянную
составляющую входного напряжения определить по формул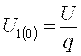е 
; где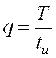 
-
скважность импульсов.
Амплитуды гармоник
входного напряжения вычисляются по формул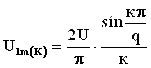е 
, где 
-
номер гармоники.
Построить
график амплитудно-частотного спектра входного напряжения в диапазоне частот 
.
5.2. Определить и построить амплитудно-частотный U2(w) и фазо-частотный спектры y2(w) выходного сигнала u2(t).
Схема цепи и численные значения параметров её элементов берутся из задания №4.
5.3.
Записать
выражение для мгновенного значения выходного напряжения 
.
Дополнительное задание
Определить действующие значения входного и выходного напряжений.
Пример выполнения задания №5
Исходные данные: N=10; M=20; R1=20 Ом; R2=20 Ом; L=20 мкГн.
|
|
|
|
Рис 5.1. Расчётная схема |
|
|
w1=w0=6*105 c-1 |
(значение берётся из п.4.3 задания №4) |
Период импульсов 
.
Длительность импульсов 
.
5.1. Представим 
в
виде тригонометрического ряда Фурье.
.
Постоянная составляющая входного напряжения
U1(0)=
1 В.
Рассчитаем
амплитуды напряжений гармоник в ручную или на ПЭВМ с помощью программы Mathcad 2001 (см.
приложение П4) по формуле 
.Результаты расчёта сведём в таблицу 5.1.
Таблица 5.1
|
к |
0 |
1 |
2 |
3 |
4 |
|
|
0 |
|
|
|
|
|
|
1 |
1,98 |
1,88 |
1,72 |
1,52 |
|
|
|||||
|
Рис. 5.2. Амплитудно-частотный спектр входного напряжения |
|||||
Мгновенное значение входного напряжения
.
5.2. Рассчитаем частотный спектр амплитуд и начальных фаз выходного напряжения исследуемой цепи.
Комплексная передаточная функция цепи
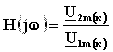, откуда
Численные
значения 
берём из таблицы 4.2.
Результаты расчёта сведём в таблицу 5.2.
Таблица 5.2
|
к |
0 |
1 |
2 |
3 |
4 |
|||
|
|
0 |
|
|
|
|
|||
|
|
1 |
0,707 |
0,447 |
0,316 |
0,243 |
|||
|
|
0 |
- 42,7 |
- 61 |
- 67,5 |
-75,4 |
|||
|
|
1 |
1,4 |
0,84 |
0,54 |
0,37 |
|||
|
|
0 |
-42,7 |
-61 |
-67,5 |
-75,4 |
|||
|
|
||||||||
|
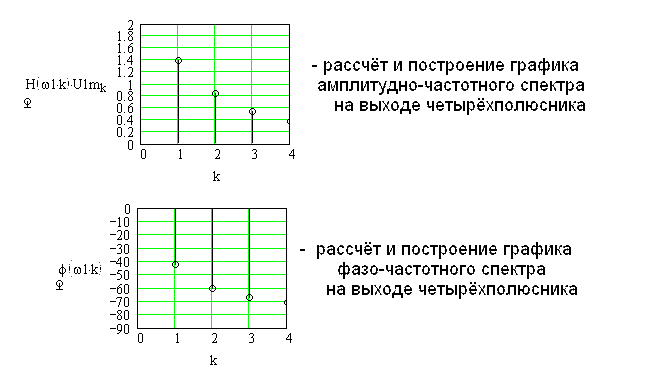
Рис. 5.3. Амплитудно-частотный спектр выходного напряжения |
||||||||
|
Рис. 5.4. Фазо-частотный спектр выходного напряжения
|
||||||||
5.3. Мгновенное значение выходного напряжения
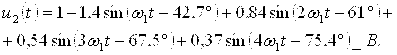
ЗАДАНИЕ 6
РАСЧЁТ ОДИНОЧНОГО ПОСЛЕДОВАТЕЛЬНОГО
КОЛЕБАТЕЛЬНОГО КОНТУРА
6.1 В соответствии с номером варианта № из таблицы 6.1 выбрать четырехзначный код. Цифры кода указывают номера четырёх заданных параметров ,значения которых определяются на основании выражений таблицы 6.2, где М - последние две цифры номера группы, K = N + M.
R L
 |
E C
Рис. 6.1. Последовательный колебательный контур
Таблица 6.1
|
№ |
Код |
№ |
Код |
№ |
Код |
№ |
Код |
|
1 |
1348 |
9 |
3458 |
17 |
3459 |
25 |
1589 |
|
2 |
2579 |
10 |
0276 |
18 |
0134 |
26 |
0345 |
|
3 |
0349 |
11 |
0136 |
19 |
1368 |
27 |
2489 |
|
4 |
4578 |
12 |
0457 |
20 |
2349 |
28 |
0257 |
|
5 |
1349 |
13 |
2589 |
21 |
0124 |
29 |
1489 |
|
6 |
2348 |
14 |
4579 |
22 |
2368 |
30 |
2360 |
|
7 |
3589 |
15 |
0137 |
23 |
0234 |
31 |
1379 |
|
8 |
1369 |
16 |
2578 |
24 |
0279 |
32 |
|
Таблица 6.2
|
0 |
I0 = 0,1 ( K + 10)/(K + 12), A |
5 |
Rс = 600(K + 10)/(K + 12), Ом |
|
1 |
L=10 ( K + 10 ), мкГн |
6 |
Q = 600 / (K + 10) |
|
2 |
C = 25 (K + 10 ), пФ |
7 |
SA = 15 (K + 10) / (K + 12), кГц |
|
3 |
¦0 =10 ( K + 10 ), МГц |
8 |
E = 0,1 ( K + 10), B |
|
4 |
R = K + 10 , Ом |
9 |
Uc0 = 600 (K + 10) / (K + 12), B |
6.2. Рассчитать 6 неизвестных параметров из таблицы 6.2 .
6.3. Рассчитать добротность и полосу пропускания резонансной цепи при подключении резистора Rн = 50 Rc (Ом) параллельно конденсатору С .
6.4. Рассчитать резонансные кривые I / I0 при добротностях Q и Qн .
Расчет осуществляется по уравнению резонансной кривой
I(Δ¦)
1
I0 √1+
(2QΔ¦/¦0)2
Построить график в функции абсолютной расстройки Δ¦ в кГц, причем максимальную расстройку взять равной двум полосам пропускания. Шаг изменения переменной взять так, чтобы справа и слева от ¦0 было не менее десяти расчетных точек.
Пример выполнения задания № 6
Вариант N = 30 , M = 10 , K = M + N = 40.
Из таблицы 6.1. для N = 30 находим код 2360.
6.1. По таблице 6.2. в соответствии с заданным кодом определяем 4 исходных параметра колебательного контура
C = 25(K + 10 ) = 25·50 = 1250 пФ =1,25 нФ ;
¦0 =10( K + 10 ) = 10 / 50 = 0,2 МГц ;
Q = 600 / (K + 10) = 600 / 50 = 12 ;
I0 = 0,1( K + 10) / (K + 12) = 0,1 * 50 / 52 = 0,961 А .
6.2. Рассчитаем оставшиеся 6 параметров , используя известные из теории соотношения.
Индуктивность контура
= L = = =
1 1 1
w02 C
(2π¦0)2 C (2π)2 0,04*1012 *1,25*10-9
= 0,507*10-3 Гн = 0,507 мГн .
Характеристическое сопротивление колебательного контура
= 636,9 Ом. Rc = =
L 0,507
* 10-3
C 1,25 * 10-9
Собственное активное сопротивление потерь колебательного контура
R = Rc / Q = 636,9 / 12 = 53,07 Ом .
Действующее значение ЭДС на входе
E = I0*R = 0,0961 * 53,07 = 5,1 В .
Напряжение на емкости при резонансе
Uco = QE = 5,1*12 = 61,2 В .
Полоса пропускания колебательного контура
SA = ¦2 - ¦1 = ¦0 / Q = 0,2*106/12 = 0,0166*106 Гц = 16,6 кГц .
6.3. Рассчитаем добротность Qн и полосу пропускания резонансной цепи при подключении сопротивления нагрузки
Rн = 50*Rc = 50*636,9 = 31845 Ом = 31,845 кОм.
=
Добротность Qн нагруженного
контура определим по формуле
Qn = 9,67. =
Q
12
1 + Rc2/R*Rн 1+ 405,64*103 /53,07*31,845*103
Полоса пропускания нагруженного колебательного контура
SAн = (¦2 - ¦1)н = ¦0 / Qн = 0,2*106 / 9,67= 0,02068*106 Гц = 20,68 кГц .
6.4. Расчет резонансной кривой колебательного контура выполним по формуле
I(Δ¦)
1
I0 √1+
(2QΔ ¦/¦0)2
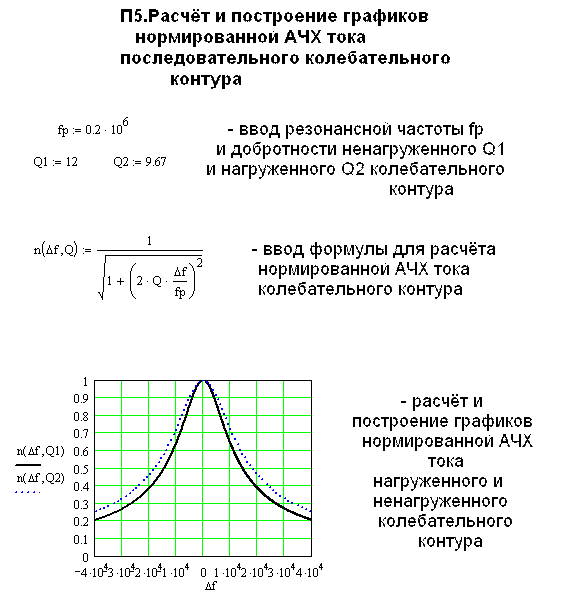
или на ПЭВМ с помощью программы Mathcad 2001 (см. приложение П5).
Результаты расчета сведем в табл. 6.3.
Таблица 6.3
|
Δ ¦, кГц |
0 |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
|
I/ I0,не нагр |
1 |
0,857 |
0,64 |
0,485 |
0,384 |
0,316 |
0,267 |
0,231 |
0,203 |
|
I/ I0, нагр |
1 |
0,90 |
0,718 |
0,567 |
0,459 |
0,38 |
0,325 |
0,283 |
0,25 |
 |
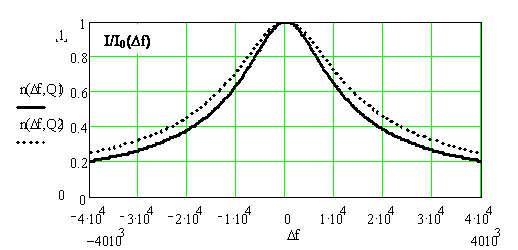График полученных зависимостей представлен на рис.6.2.
Рис.6.2. Резонансные кривые тока последовательного колебательного контура : 1 - ненагруженный контур; 2 - нагруженный контур.
 |
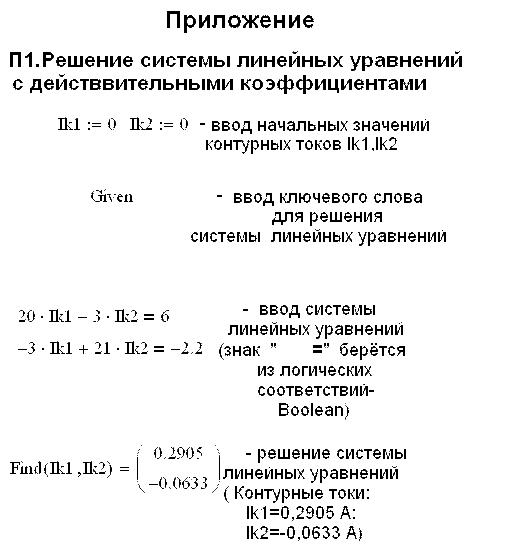П6. Программа решения системы линейных уравнений
с комплексными коэффициентами на Turbo Pascal
uses crt; {Метод Гаусса с выбором главного элемента при
комплексных коэффициентах}
const nmax=10;
var n,pr:byte;st:string;err:integer;LABEL PRINT;
type complex=record
re,im:real
end;
procedure sum(x,y:complex;var z:complex);
begin z.re:=x.re+y.re;
z.im:=x.im+y.im
end;
procedure raz(x,y:complex;var z:complex);
begin z.re:=x.re-y.re;
z.im:=x.im-y.im
end;
procedure umn(x,y:complex;var z:complex);
begin z.re:=x.re*y.re-x.im*y.im;
z.im:=x.re*y.im+x.im*y.re
end;
procedure delen(x,y:complex;var z:complex);
var zz:real;
begin zz:=sqr(y.re)+sqr(y.im);
z.re:=x.re*y.re+x.im*y.im)/zz;
z.im:=(y.re*x.im-y.im*x.re)/zz
end;
type masA=array[1..nmax,1..nmax]of complex;
type masB=array[1..nmax]of complex;
var i,j,k,m,k1:byte;A:masA;B:masB;
x:array[1..nmax]of complex;z,s,v:complex;
g:array[1..nmax]of complex;
c:array[1..nmax,1..nmax]of complex;
procedure vvodA(k:byte;var A:masA);
var i,j:byte;st:string;er:integer;
begin for i:=1 to k do
for j:=1 to k do
begin textcolor(15);
writeln(‘Введите значение коэффициента A’,i,j);
repeat textxolor(2);
if pr=1 then write(‘действительная часть=’);
readln(st);val(st,a[i,j].re,er) until er=0;
if pr=1 then
repeat textcolor(14);
write(‘мнимая часть=’);readln(st);val(st,a[i,j].im,er)until er=0
else a[i,j].im:=0;
end
end;
procedure vvodB(k:byte;var b:masB);
var i,j:byte;st:string;er:integer;
begin for i:=1 to k do
begin textcolor(15);
writeln(‘Введите значение свободного коэффициента B’,i);
repeat textcolor(2);
if pr=1 then write (‘действительная часть=’);readln(st);val(st,b[i].re,er)
until er=0;
if pr=1 then
repeat textcolor(14);
write(‘мнимая часть=’);repeat(st);val(st,b[i].im,er)
until er=0 else b[i].im:=0;
end
end;
procedure writsys0(var b:masb;n:byte);
var i,j:byte;
begin
for i:=1 to n do begin
for j:=1 to n-1 do begin textcolor(2);
write(a[i,j].re:0:2);
textcolor(15);write(‘*X’,j,’+’);
end;textcolor(2);
write(a[i,j+1].re:0:2);
textcolor(15);write(‘*X’,j+1,’=’);textcolor(2);writeln(b[i].re:0:2);
end;
end;
procedure writsys1(var a:masa;var b:masb;n:byte);
var i,j:byte;
begin
for i:=1 to n do begin
for j:=1 to n-1 do begin textcolor(2);
write(‘(‘,a[i,j].re:0:2)textcolor(14);write(‘+’,a[i,j].im:0:2,’i)’);
textcolor(15);write(‘*X’,j,’+’);
end;textcolor(2);
write(‘(‘,a[i,j+1].re:0:2);textcolor(14);write(‘+’,a[i,j+1].im:0:2,’i)’);
textcolor(15);write(‘*X’,j+1,’=(‘);textcolor(2);write(b[i].re:0:2);
textcolor(14);writeln(‘+’,b[i].im:0:2,’i)’)
end;
end;
BEGIN CLRSCR;
repeat textcolor(15);
WRITELN(‘Решение системы линейных уравнений с комплексными коэффициентами’:70);
writeln(‘методом Гаусса с выбором главного элемента’:55);
repeat
writeln(‘Введите количество переменных(<=10)=’);
readln(st);val(st,n,err)
until err=0;
WRITELN(‘Содержат ли исходные данные мнимую часть? Y/N’) ;READLN(ST);
IF (ST=’y’)OR (ST=’Y’) then pr:=1 else pr:=0;
vvodA(n,A);vvodB(n,B);
PRINT : textcolor(15);writeln(‘Итак, дана система линейных уравнений’);
if pr=1 then writsys1(a,b,n) else writsys0(a,b,n);
textcolor(15);
writeln(‘хотите внести исправления? Y/N’);readln(st);
if(st=’y’)or (st=’Y’) then begin
writeln(‘это коэффициент A? Y/N’);readln(st);
IF (st=’y’) or (st=’Y’) then begin
repeat write(‘номер строки=’);readln(st);val(st,i,err)
until (err=0)and(i>=0)and (i<=n);
repeat write(‘номер столбца=’);readln(st);val(st,j,err)
until (err=0)and (j>=0) and (j<=n);
textcolor(15);
writeln(‘Введите новое значение коэффициента A’,i,j);
repeat
textcolor(2);if pr=1 then write (‘действительная часть=’);
readln(st);val(st,a[i,j].re,err)
until
err=0;
if pr=1 then
repeat
textcolor(14);
write(‘мнимая часть=’);readln(st);val(st,a[i,j].im,err) until err=o;
end
else begin
repeat
writeln(‘Это свободный коэффициент B,введите его номер =’);
readln(st);val(st,i,err)until (err=0)and(i<=n) and (i>=0);
textcolor(15);
writeln(‘Введите новое значение коэффициента B’,i);repeat
textcolor(2);if pr=1 then write (‘действительная часть =’);
readln(st);val(st,b[i].re,err) until err=0;
if pr=1 then
repeat textcolor(14);
write(‘мнимая часть=’);readln(st);val(st,b[i].im,err) until err=0;end;
goto PRINT;
end;
for k:=1 to n-1 do begin
if abs(a[k,k].re)<=0 then begin
k1:=k+1;
for m:=k+1 to n do
if abs(a[m,k].re)>0 then
for j:=1 to n do begin v:=a[k,j];a[k,j]:=a[m,j];a[m,j]:=v;end
else continue;
v:=b[k];b[k]:=b[m];b[m]:=v;end;
delen (b[k],a[k,k],g[k]);
k1:=k+1;
for i:=k1 to n do begin umn(a[i,k],g[k],z);
raz(b[i],z,b[i]);
for m:=k to n do begin
j:=n-m+k;
delen (a[k,j],a[k,k],c[k,j]);
umn(a[i,k],c[k,j],z);
raz(a[i,j],z,a[i,j]);
end end end;
m:=n;
delen (b[n],a[n,n],x[n]);
for m:=n-1 downto 1 do begin s.re:=0;s.im:=0;
for k:=m to n-1 do
begin umn(c[m,k+1],x[k+1],z);
sum(s,z,s);end;
raz(g[m],s,x[m]);
end;
textcolor(12);
writeln (‘Результат решения системы линейных уравнений’);writeln;
for i:=1 to n do
begin textcolor(15);
write(‘x’,i,’=’);
textcolor(2);write(x[i].re:0:10);
if pr=1 then begin
textcolor(14);writeln(‘+’,x[i].im:0:10,’i’) end else writeln;
end;
textcolor(15);
writeln(‘Будете решать другую систему? Y/N’);
readln(st);
until (st=’n’)or (st=’N’);
end.
ПРОГРАММА РЕШЕНИЯ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ С ВЕЩЕСТВЕННЫМИ КОЭФФИЦИЕНТАМИ
НА BASIC
CLS
PRINT “ П7.Решение системы из n линейных алгебраических уравнений”
PRINT “с вещественными коэффициентами вида”
PRINT “a(1,1)*x(1)+a(1,2)*x(2)+...+a(1,n)*x(n)=b(1)”
PRINT “a(2,1)*x(1)+a(2,2)*x(2)+...+a(2,n)*x(n)=b(2)”
PRINT “.......................................................................”
PRINT “a(n,1)*x(1)+a(n,2)*x(2)+...+a(n,n)*x(n)=b(n)”
PRINT “методом последовательного исключения неизвестных Гаусса”
PRINT “Составил Козлов В.А. 12.09.04”
INPUT “ n=”;n
DIM a(n,n), b(n), x(n)
PRINT “ Введите коэффициенты системы уравнений a(i,j)”
FOR i=1 to n: FOR j=1 to n
PRINT “a(“;i;”,”;j;”)=”:INPUT a(i,j):NEXT j:NEXT i
PRINT “ Введите свободные члены системы уравнений b(i)”
FOR i=1 to n : PRINT “b(“;i;”)=”:INPUT b(i)
NEXT i
FOR i=1 to n-1: FOR j=i+1 to n
a(j,i)= -a(j,i)/a(i,i): FOR k=i+1 TO n
a(j,k)= a(j,k)+a(j,i)*a(i,k):NEXT k
b(j)=b(j)+a(j,i)*b(i):NEXT j:NEXT i
x(n) = b(n)/a(n,n)
FOR i = n-1 TO 1 STEP -1:h=b(i)
FOR j = i+1 TO n: h=h- x(j)*a(i,j):NEXT j
x(i) = h/a(i,i):NEXT i
PRINT “Корни системы уравнений: ”
FOR i=1 TO n: PRINT “x(“;i;”)=”; x(i)
NEXT i
PRINT “Расчёт закончен”
PRINT “_____________________________” END
ЛИТЕРАТУРА
1. Атабеков Т.И. Основы теории цепей. Учебник для вузов.М., «Энергия», 1969.- 424 с.
2. Бакалов В.Г. и др. Основы теории электрических цепей и электроники. – М.; Радио и связь, 1989.
3. Белецкий А.Ф. Теория линейных электрических цепей: Учебник для вузов.–М.: Радио и связь, 1986.-544 с.
4. Шебес М.Р., Каблукова М.В. Задачник по теории линейных электрических цепей. Учебное пособие для электротехнич., радиотехнич. спец. вузов.-4-е изд., перераб. и доп. –М.: Высшая школа, 1990.-544 с..
5. Ушаков В.Н. Электротехника и электроника: Учеб. Пособие для вузов.-М.: Радио и связь, 1997. – 328 с.
6. Кирьянов Д.В. Самоучитель MathCAD 2001.СПб.: БХВ-Петербург, 2001.-544 с.
СОДЕРЖАНИЕ
ПРЕДИСЛОВИЕ.………………………………………………...……………3
Задание 1. Расчет цепей постоянного тока с независимыми
источниками ………………………………………………………………………5
Задание 2. Расчет цепей постоянного тока с зависимыми источниками ...11
Задание 3. Расчет цепей синусоидального тока
символическим тодом…………………………………………………………...16
Задание 4. Исследование частотных характеристик ЛЭЦ……………..…..22
Задание 5. Расчет ЛЭЦ периодическом несинусоидальном воздействии……………………………………………………………………....28
Задание 6. Расчет одиночного последовательного колебательного
контура …………………………………………………………………………...32
ПРИЛОЖЕНИЕ .……………………………………………………………..36
П1. Решение системы линейных уравнений с действительными коэффициентами…………………………………………………………………36
П2. Решение системы линейных уравнений с комплексными коэффициентами…………….………………………………………..…………37
П3. Расчет и построение АЧХ и ФЧХ электрической цепи..…………….38
П4. Расчет и построение амплитудно-частотного и фаза-частотного
спектров напряжений на входе и выходе четырёхполюсника……………….39
П5. Расчет и построение графиков нормированный АЧХ
тока последовательного колебательного контура ……….. ………………….41
П6. Программа решения системы линейных уравнений с комплексными коэффициентами на Turbo Pascal……………………………………………….42
ЛИТЕРАТУРА …………………………………………………..…………..….50
СОДЕРЖАНИЕ……………………………………………...…………………..51
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К ВЫПОЛНЕНИЮ ИНДИВИДУАЛЬНОЙ РАБОТЫ
ПО ТЭЦ, ЧАСТЬ 1
Методические указания рассмотрены и рекомендованы
к печати на заседании кафедры ТЭЦ
протокол № 18 от 3 апреля 2006 г.
Составители Козлов В.А.
Белова Л.Н.
Мухаммедова З.С.
Ответственный редактор д.ф-м.н. профессор Арипов Х.К.
Корректор Олимская Т.В.