МИНИСТЕРСТВО ПО РАЗВИТИЮ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ И КОММУНИКАЦИЙ РЕСПУБЛИКИ УЗБЕКИСТАН

ТАШКЕНТСКИЙ УНИВЕРСИТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ

Кафедра ВОЛ и СИ

 

 

 

Методические указания к практическим занятиям по дисциплине "Метрология, стандартизация и сертификация" для студентов 1 – курса

всех направлений образования

 

Ташкент  2016

 

 

ВВЕДЕНИЕ

 

Мир вокруг нас – это, прежде всего, мир физических величин,реально существующих в широчайшем диапазоне их значений от микромирадо макромира в масштабе Вселенной. Физические величины являются характеристиками объектов материального мира и процессов, характеризующих различные взаимодействия этих объектов между собой или их изменения во времени. Вся история человеческой цивилизации – это история становления и развития измерительной культуры, это процесс непрерывного совершенствования методов и средств измерения и систем обеспечения единства измерений на основе повышения их необходимой точности, единообразия мер, постоянного укрепления положения служб образцовых измерений как необходимого базиса не только экономики, но и государственной власти. Оценка роли метрологии как науки об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности в научно-техническом прогрессе современного общества раскрывает широкую панораму ее возможностей и проблем.

Измерения являются одним из основных способов познания природы, ее явлений и законов. Каждому новому открытию в области естественных и технических наук предшествует большое число измерений.

Измерения служат как получению научных знаний, так и получению информации в общем смысле. Если в исследовательском процессе путем измерений могут обнаруживаться совершенно новые физические и математические зависимости, то, например, измерение характеристик продукции и технологических процессов дают измерительную информацию, необходимую для управления этими процессами, качеством продукции, обеспечения надежности процессов и организации производства. Обширная область работ в области измерений свидетельствует об их значительной роли в науке и технике, в жизни современного общества.

По состоянию измерительной службы и ее метрологического обеспечения можно судить об общем уровне развития общества. Однако весь тот огромный массив измерительной информации, который мы получаем в результате измерений, будет общественно значимым и полезным только при обязательном условии обеспечения их единства и требуемой точности независимо от места, времени и условий, в которых они проведены. Обеспечение единства измерений является одной из важнейших задач метрологии.

Задания включают в себя базовый комплект задач и некоторые примеры их решения по основополагающим разделам курса: обеспечения единства измерений, элементам теории погрешностей; нормированию погрешностей средств измерений; определению параметров переменных напряжений и показаний вольтметров различных типов; осциллографическим измерениям параметров сигналов. Задания расположены в порядке возрастания сложности. Задания содержат необходимые алгоритмы решения задач.

 

 

1.ТЕОРИЯ ВОСПРОИЗВЕДЕНИЯ ЕДИНИЦ ИЗМЕРЕНИЯ.

ЕДИНИЦЫ ИЗМЕРЕНИЯ В МЕЖДУНАРОДНОЙ СИСТЕМЕ СИ

 

В Республике Узбекистан в установленном порядке допускаются к применению единицы физических величин Международной системы единиц СИ (SI).В основу системы СИ положены семь основных физических единиц: метр, килограмм, секунда, ампер, кельвин, моль и кандела. До 1995 г. имели место еще дополнительные единицы – единицы плоского и телесного угла, радиан и стерадиан, – но с целью упрощения системы эти единицы ХХ ГКМВ были переведены в категорию безразмерны хпроизводныхединиц СИ.

 

1.1. Метр

 

Метр (обозначение: м, m; от др.– греч. Μέτρον – мера, измеритель) – единица измерения длины и расстояния в системе СИ. Метр равен расстоянию, которое проходит свет в вакууме за промежуток времени, равный 1/299 792 458 секунды.

 

 

 

 

 

 

Рис.1.1. Международный эталон метра,

использовавшийся с 1889 по 1960 годы

Метр был впервые введён во Франции в XVIII веке и имел первоначально два конкурирующих определения:

-                    как длина маятника с полупериодом качания на широте 45°, равным 1 c (в современных единицах эта длина равна примерно 0,981 м).

-                    как одна сорокамиллионная часть Парижского меридиана (то есть одна десятимиллионная часть расстояния от северного полюса до экватора по поверхности земного эллипсоида на долготе Парижа).

Первоначально за основу было принято первое определение (8 мая 1790, Французское Национальное собрание). Однако, поскольку ускорение свободного падения зависит от широты и, следовательно, маятниковый эталон недостаточно воспроизводим, Французская Академия наук в 1791 предложила Национальному собранию определить метр через длину меридиана. 30 марта 1791 это предложение было принято. 7 апреля 1795 Национальный Конвент принял закон о введении метрической системы во Франции и поручил комиссарам, в число которых входили Кулон, Лагранж, Лавуазье, Лаплас и другие учёные, выполнить работы по экспериментальному определению единиц длины и массы. Первый прототип эталона метра был изготовлен из латуни в 1795 году. Следует отметить, что единица массы (килограмм, определение которого было основано на массе 1 дм³ воды) также была привязана к определению метра.

В 1799 из сплава 90 % платины и 10 % иридия, был изготовлен эталон метра, длина которого соответствовала одной сорокамиллионной части Парижского меридиана. Впоследствии, однако, выяснилось, что из-за неправильного учёта полюсного сжатия Земли эталон оказался короче на 0,2 мм; таким образом, длина меридиана лишь приблизительно равна 40 000 км.

Во время правления Наполеона метрическая система распространилась по всей Европе. Только в Великобритании, которая не была завоёвана Наполеоном, остались традиционные меры длины: дюйм, фут и ярд.

В 1889 был изготовлен более точный международный эталон метра. Этот эталон также изготовлен из сплава платины и иридия и имеет поперечное сечение в виде буквы «X». Его копии были переданы на хранение в страны, в которых метр был признан в качестве стандартной единицы длины. Этот эталон всё ещё хранится в Международном бюро мер и весов, хотя больше по своему первоначальному назначению не используется.

С 1960 было решено отказаться от использования изготовленного людьми предмета в качестве эталона метра, и с этого времени по 1983 метр определялся как число 1 650 763,73, умноженное на длину волны оранжевой линии (6 056 Å) спектра, излучаемого изотопом криптона-86 в вакууме.

Современное определение метра в терминах времени и скорости света было введено в 1983 году:

Метр – это длина пути, проходимого светом в вакууме за (1 / 299 792 458) секунды.

         Из этого определения следует, что в системе СИ скорость света в вакууме принята равной в точности 299 792 458 м/с. Таким образом, определение метра, как и два столетия назад, вновь привязано к секунде, но на этот раз с помощью универсальной мировой константы.

         Метр – это длина пути, проходимого светом в вакууме за (1 / 299 792 458) секунды.

Из этого определения следует, что в системе СИ скорость света в вакууме принята равной в точности 299 792 458 м/с. Таким образом, определение метра, как и два столетия назад, вновь привязано к секунде, но на этот раз с помощью универсальной мировой константы.

1.2. Кратные и дольные единицы

 

Десятичные кратные и дольные единицы образуются с помощью стандартных приставок СИ. Существуют также внесистемные единицы измерения: микрон, равный 1 мкм, и ангстрем (Å), равный 0,1 нм, но их применение не рекомендуется.

Таблица 1.1

1.3. Килограмм

 

Килогра́мм (кг, kg) – единица измерения массы, одна из основных единиц СИ. Килограмм определяется как масса международного эталона килограмма, хранящегося в Международном бюро мер и весов (расположено в г. Севр близ Парижа) и представляющего собой цилиндр из платино-иридиевого сплава (90% платины, 10% иридия). Первоначально килограмм определялся как масса одного литра чистой воды при температуре 4°С и стандартном атмосферном давлении.

 

Рис.1.2. Международный эталон килограмма

1.4. Кратные и дольные единицы

 

По историческим причинам, название «килограмм» уже содержит десятичную приставку «кило», поэтому кратные и дольные единицы образуют, присоединяя стандартные приставки СИ к названию или обозначению единицы измерения «грамм» (которая, в системе СИ, сама является дольной: 1 г = 10⁻³ кг).

Таблица 1.2

1.5. Эталон килограмма

 

На данный момент килограмм – единственная единица СИ, которая определена при помощи предмета, изготовленного людьми – платиново-иридиевого эталона. Все остальные единицы теперь определяются с помощью фундаментальных физических свойств и законов.

Эталон был изготовлен в 1880-х гг. и с тех пор хранится в Международном бюро мер и весов. Были изготовлены также точные официальные копии международного эталона, которые используются как национальные эталоны килограмма. Примерно раз в 10 лет национальные эталоны сравниваются с международным. Эти сравнения показывают, что точность национальных эталонов составляет примерно 2 мкг. Так как они хранятся в тех же условиях, нет никаких оснований считать, что международный эталон точнее. Однако, по определению, масса международного эталона в точности равна одному килограмму.

Поэтому любые изменения действительной массы эталона приводят к изменению величины килограмма. Для устранения этих неточностей в настоящее время рассматриваются различные варианты переопределения килограмма на основе фундаментальных физических законов.

1.6. Грамм

 

Грамм (фр. gramme; обозначения: г, g) – единица измерения массы, одна из основных единиц системы СГС.

Её кратная единица, килограмм (1000 грамм), с точностью до 0,2% равная массе 1 дм³ химически чистой воды при температуре её наибольшей плотности (около 4°C), является основной единицей массы в системе СИ.

Наиболее часто используемые дольные единицы:миллиграмм– 10⁻³ грамма, микрограмм– 10⁻⁶ грамма, нанограмм– 10⁻⁹ грамма, пикограмм– 10⁻¹² грамма

1.7. Килограмм-сила

 

Килограмм-сила (кгс, kgf) – единица измерения силы. Определяется как сила, действующая на тело массой в 1 килограмм под воздействием стандартного ускорения свободного падения. В системе МКГСС входила в число основных единиц.

Килограмм-сила удобна тем, что вес получается численно равным массе, поэтому человеку легко представить, например, что такое сила 5 кгс.

1 кгс = 9,80665 ньютонов точно

1 Н ≈ 0,10197162 кгс

Реже применяются кратные единицы:тонна-сила: 1 тс = 10³ кгс = 9806,65 Н, грамм-сила: 1 гс = 10⁻³ кгс = 9,80665×10⁻³ Н

1.8. Секунда

 

Секунда (обозначение: s, с) – единица измерения времени, одна из основных единиц СИ.

Одна секунда – это интервал времени, равный 9 192 631 770 периодам излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133 при отсутствии возмущения внешними полями.

1.9. Кратные и дольные единицы

 

С единицей измерения «секунда», как правило, используются только дольные приставки СИ (кроме деци- и санти-). Для измерения больших интервалов времени используются единицы минута, час, сутки, и т. д.

Таблица 1.3

1.10. Ампер

 

Ампе́р (обозначение: А) – единица измерения силы электрического тока в системе СИ.

Ампер равен силе такого постоянного тока, который, будучи пущен по двум прямым параллельным проводникам бесконечной длины и незначительным поперечным сечением, помещёнными на расстоянии в 1 метр друг от друга в вакууме, создавал бы между этими проводниками силу, равную 2·10⁻⁷ ньютонов на метр длины.

Ампер назван в честь французского физика Андре Ампера.

1.11. Кратные и дольные единицы

Десятичные кратные и дольные единицы образуют с помощью стандартных приставок СИ.

Таблица 1.4

Кратные				Дольные
величина	название	обозначение		величина	название	обозначение
101 А	декаампер	даА	daA	10−1 А	дециампер	дА	dA
102 А	гектоампер	гА	hA	10−2 А	сантиампер	сА	cA
103 А	килоампер	кА	kA	10−3 А	миллиампер	мА	mA
106 А	мегаампер	МА	MA	10−6 А	микроампер	мкА	µA
109 А	Гигаампер	ГА	GA	10−9 А	наноампер	нА	nA
1012 А	Тераампер	ТА	TA	10−12 А	пикоампер	пА	pA
1015 А	петаампер	ПА	PA	10−15 А	фемтоампер	фА	fA
1018 А	Эксаампер	ЭА	EA	10−18 А	аттоампер	аА	aA
1021 А	зеттаампер	ЗА	ZA	10−21 А	зептоампер	зА	zA
1024 А	йоттаампер	ИА	YA	10−24 А	йоктоампер	иА	yA
██ применять не рекомендуется

 

1.12. Кельвин

 

Ке́львин (обозначение: K) – единица измерения температуры Международной системы единиц, предложена в 1848 году.

Один кельвин равен 1/273,16 термодинамической температуры тройной точки воды. Начало шкалы (0 К) совпадает с абсолютным нулём. Кельвин по размеру совпадает с градусом Цельсия.

Единица названа в честь английского физика Уильяма Томсона, которому было пожаловано звание барона Кельвина Ларгского из Айршира. В свою очередь это звание пошло от реки Кельвин, протекающей через университет в Глазго.

До 1968 года кельвин официально именовался градусом Кельвина.

 

1.13. Кратные и дольные единицы

 

Десятичные кратные и дольные единицы образуют с помощью стандартных приставок СИ.

Таблица 1.5

Кратные				Дольные
величина	название	обозначение		величина	название	обозначение
101 К	Декакельвин	даК	daK	10−1 К	децикельвин	дК	dK
102 К	Гектокельвин	гК	hK	10−2 К	сантикельвин	сК	cK
103 К	Килокельвин	кК	kK	10−3 К	милликельвин	мК	mK
106 К	Мегакельвин	МК	MK	10−6 К	микрокельвин	мкК	µK
109 К	Гигакельвин	ГК	GK	10−9 К	нанокельвин	нК	nK
1012 К	Теракельвин	ТК	TK	10−12 К	пикокельвин	пК	pK
1015 К	Петакельвин	ПК	PK	10−15 К	фемтокельвин	фК	fK
1018 К	Эксакельвин	ЭК	EK	10−18 К	аттокельвин	аК	aK
1021 К	Зеттакельвин	ЗК	ZK	10−21 К	зептокельвин	зК	zK
1024 К	йоттакельвин	ИК	YK	10−24 К	йоктокельвин	иК	yK
██ применять не рекомендуется

 

1.14. Кандела

 

Канде́ла (обозначение: кд, cd) – одна из семи основных единиц измерения системы СИ, равна силе света, испускаемого в заданном направлении источником монохроматического излучения частотой 540•1012 герц, энергетическая сила света которого в этом направлении составляет (1/683) Вт/ср.

Выбранная частота соответствует зелёному цвету. Человеческий глаз обладает наибольшей чувствительностью в этой области спектра. Если излучение имеет другую частоту, то для достижения той же силы света требуется бо́льшая энергетическая интенсивность.

Ранее кандела определялась как сила света, излучаемого чёрным телом перпендикулярно поверхности площадью 1/60 см² при температуре плавления платины (2042,5 К). В современном определении коэффициент 1/683 выбран таким образом, чтобы новое определение соответствовало старому.

Таблица 1.6

Сила света типовых источников

Источник	Мощность, Вт	Примерная сила света, кд
Свеча		1
Современная (2006 г) лампа накаливания	100	100
Обычный светодиод	0.015	0.001
Сверхяркийсветодиод	0.090	3
Современная (2006 г) флуоресцентная лампа	20	100

1.15. Кратные и дольные единицы

 

Десятичные кратные и дольные единицы образуют с помощью стандартных приставок СИ.

Таблица 1.7

1.16. Моль

 

Моль (обозначение – моль, mol) – единица измерения количества вещества в СИ. Соответствует количеству вещества, содержащему столько структурных единиц (атомов, молекул, ионов, электронов или любых других частиц), сколько содержится атомов в 0,012 кг изотопа 12C.

Количество частиц в одном моле любого вещества постоянно и носит название числа Авогадро (NA).

NA = 6,0221367×1023 моль⁻¹

1.17. Кратные и дольные единицы

Десятичные кратные и дольные единицы образуют с помощью стандартных приставок СИ.

 

Таблица 1.8

1.18. Задачи для самостоятельного решения

1.1.  Как выразится единица электрического напряжения (вольт, В) через основные единицы системы СИ?

Решение. Воспользуемся следующим уравнением для напряжения 

,

гдеР– мощность, выделяющаяся на участке цепи при протекании в ней тока I. Следовательно, 1 В – это электрическое напряжение, вызывающее в электрической цепи постоянный ток силой в 1 А при мощности в 1 Вт.

Дальнейшие преобразования:

 

Таким образом, получим соотношение, в котором все величины выражаются через основные единицы системы СИ. Следовательно,

1.2. Как выражается единица электрической емкости (фарад, Ф) через основные единицы системы СИ?

Ответ:                   ,

1.3. Как выражается единица электрической проводимости (сименс, См) через основные единицы системы СИ?

Ответ:                  ,

1.4. Как выражается единица измерения удельного электрического сопротивления (Ом·м) через основные единицы системы СИ?

Ответ:                  ,

1.5. Как выражается единица измерения электрической индуктивности (генри, Гн) через основные единицы системы СИ?

Ответ:                   ,

1.6. Как выражается единица магнитной индукции (тесла, Тл) через основные единицы системы СИ?

Ответ:                  ,

1.7. Размерность физической величиныХзаписана в виде формулы размерности через прописные буквыl, m,t, Iсогласно международного стандарта. Запишите выражение единиц этой величины через основные единицы системы СИ, укажите ее наименование и физическую величину, которая в ней измеряется.

Решение:

Следовательно, данная физическая величина является давлением, единица измерения которой паскаль (Па).

1.8. Решите задачу, аналогичную 1.7, если.

Ответ: работа, энергия, джоуль (Дж).

1.9. Решите задачу, аналогичную 1.7, если

Ответ: электрическое сопротивление, Ом.

1.10. Решите задачу, аналогичную 1.7, если

Ответ: магнитный поток, вебер (Вб).

1.11. Решите задачу, аналогичную 1.7, если

Ответ: напряженность электрического поля, вольт на метр (В/м).

1.12. Для измерения электрического сопротивления используется единица -

Ом, для электрической проводимости – См (сименс). Определите формулу дляперевода единицы измерения кОм в кСм.

1.13. Скорость тела может быть выражена двумя единицами измерения:м/с и км/ч. Во сколько раз будут различаться численные значения одной итой же скорости, выраженные в этих единицах?

1.14. Одна английская миля, выраженная в метрических единицах, равна1609,315 м. Верхний предел скорости автомобиля составляет 180 км/ч. Чему

равна максимальная скорость, выраженная в английских единицах – миль/ч?

1.15. В некоторых отраслях промышленности используется единицаизмерения силы – килограмм-сила (кгс). Сила величиной 1 кгс сообщает телу

массой 1 кг ускорение свободного падения (9,81 м/с). Выведите формулуперевода значения физической величины из единицы измерения ньютон вединицу килограмм-сила.

1.16. В гидравлике употребляется единица измерения кгс/см². Выведитеуравнение, связывающее эту единицу с системной единицей МПа.

1.17. Известно, что в международной системе единиц (СИ) расстояние водин метр определяется как 1/2999792458 часть пути, проходимого светом ввакууме за одну секунду. Установите связь двух единиц измерения: световой

год и метр.

1.18. Шкала Фаренгейта является шкалой интервалов, на которой:

- температура таяния льда соответствует t₀ = 32 F;

- температура кипения воды соответствует t₁ = 212 F.

Шкала Цельсия, так же являясь шкалой интервалов, определяется изследующего условия:

-температура таяния льда t₀= 0°С

- температура кипения воды t₁= 100°С.

Определите формулу для перевода численных значений шкалы Фаренгейта

в численные значения шкалы Цельсия.

1.19. Известный ученый Исаак Ньютон в 1701 году предложил свою шкалу

температур, в которой:

- температура таяния льда соответствует t₀ = 0,

- температура крови здорового человека соответствует t₁ = 12.

Определите формулу перевода численных значений этой шкалы вчисленные значения шкалы Цельсия.

1.20. Определите соответствие между базовой и исходнқми величинами, представленными в табл. 1.9.

Таблица 1.9.

 

 

 

2. ЛОГАРИФМИЧЕСКИЕ ЕДИНИЦЫ. УРОВНИ ПЕРЕДАЧИ

 

2.1. Понятие о децибелах

 

В телекоммуникациях используется большое число различных физических величин, характеризующих, например, сигнал. Это частота, длина волны, напряжение, мощность и др.

Особенность этих физических величин состоит в их большом диапазоне значений; так, длина электромагнитной волны может меняться от сотен километров до сотен нанометров (оптический диапазон), мощность - от мегаватт до нановатт, а частота -  от единиц герц до терагерц.

Очень важной величиной, которая используется как в волоконной оптике, так и в электронике для выражения усиления или затухания в системе в целом или в ее компонентах, является децибел (дБ). Эту величину ввел Александр Грэхем Белл. Единица стала называться «бел». Одна десятичная бела называется децибел (дБ). Он ввел ее для измерения силы звука.

Децибел – специфическая единица измерений, не схожая ни с одной из тех, с которыми приходится встречаться в повседневной практике. Децибел не является официальной единицей в системе единиц СИ, хотя, по решению Генеральной конференции по мерам и весам, допускается его применение без ограничений совместно с СИ, а Международная палата мер и весов рекомендовала включить его в эту систему.

Децибел – не физическая величина, а математическое понятие.

Человеческое ухо воспринимает силу звука логарифмически. Так, уровень в 100 ватт по сравнению с уровнем в 10 ватт для человеческого уха слышится громче в два раза (но не в 10 раз). Возрастание силы звука на один децибел является примерно наименьшим приростом, которое способно различить человеческое ухо.

Эта единица измерения используется в настоящее время в качестве основы для измерений относительных уровней мощностей, напряжений и других физических величин. Транзистор, например, может усиливать сигнал, увеличивая амплитуду его напряжения, тока или мощности. Это увеличение называется усилением. Аналогично, затухание - это уменьшение напряжения, тока или мощности при распространении сигнала по линии связи.

Основные уравнения, определяющие децибел, следующие:

дБ_U=20lg(U₁/U₂); дБ_I=20lg(I₁/I₂); дБ=10lg(W₁/W₂).

где U - напряжение, I - ток и W - мощность. Децибел, таким образом, характеризует отношение двух напряжений, токов или мощностей. Необходимо отметить, что в случае напряжения и тока отношение логарифмов умножается на 20, а в случае мощности на 10.

Разобраться в децибелах поможет одно общее правило. При измерении мощности потери в 3 дБ означают уменьшение мощности на 50%, т.е. если была мощность 1 мВт, то будет 0,5 мВт. Аналогично увеличение на 3 дБ означает удвоение мощности: 1мВт превращается в 2 мВт. Для напряжения или тока удвоение или уменьшение вдвое будет происходить при изменении на 6 дБ, поскольку, как видно из приведенных выше уравнений, для тока и напряжения коэффициент равен не 10, а 20. При прокладке кабелей практически всегда приходится иметь дело с мощностью.

В случае мощности правило децибел выглядит так:

Увеличение:

-          20 дБ = 100-кратное возрастание мощности;

-          10 дБ = 10-кратное возрастание мощности;

-          3 дБ = двукратное возрастание мощности.

Уменьшение:

-        -3 дБ = двукратная потеря мощности;

-        -6 дБ = 75%-ная потеря мощности (остается 25%);

-        -10 дБ = 90%-ная потеря мощности (остается 10%);

-        -20 дБ = 99%-ная потеря мощности (остается 1%);

-        -30 дБ = 99,9%-ная потеря мощности (остается 0,1%);

-        -40 дБ = 99,99%-ная потеря мощности (остается 0,01%).

При всего лишь -20 дБ теряется 99% мощности. Если исходный сигнал имеет мощность 1 мВт, то при -20 дБ остается только 0,01 мВт (10 микроватт). Мощность падает на два порядка, т.е. в 100 раз.

В волоконной оптике, как правило, имеют дело с затуханием оптической мощности. По мере перемещения по волокну свет теряет свою мощность. Эти потери выражаются в децибелах. Затухание, выраженное в децибелах, имеет отрицательную величину.

Иногда в соотношении, используемом для определения затухания или усиления, используется постоянное значение W₀. В волоконной оптике обычно используется величина в 1 милливатт (мВт).

дБ_м=10lg(W_x/1 мВт)

дБ_м (dB_m) означает «децибел, соотнесенный к милливатту». Единицы дБ_м часто используются инженерами и техниками.

                       Соотношение мощности и единиц дБ_м

 

В практических расчетах дробную часть численного значения децибел часто округляют до целого числа, однако при этом в результаты расчетов вносится дополнительная погрешность.

2.2. Уровни передачи

 

Уровни передачи принято оценивать в неперах (Нп) или децибелах (дБ). Для неперов используется натуральная система логарифмов, а для децибелов – десятичная.

Между неперами и децибелами существует следующее соотношение: 1Нп = 8,686 дБ, или 1дБ = 0,115 Нп.

По международному соглашению с 1971 года используются только десятичные логарифмы, и результаты измерений определяются в децибелах.

Уровнем передачи называется логарифмическое отношение мощности, напряжения или тока в данной точке цепи к мощности, напряжению или току, которые приняты за исходные. Количественное значение уровней передачи по мощности, напряжению или току определяется соответственно из следующих выражений:

; ; ,

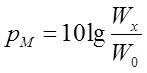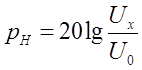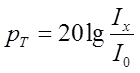гдеW_X, U_X, I_X – соответственно средняя мощность, эффективное значение напряжения сигнала и ток в рассматриваемой точке «x», уровень которых определяется;

W₀, U₀, I₀ - величина мощности, напряжения и тока, принятые за исходные при определении уровней передачи.

В общем случае уровни передачи по мощности, напряжению и току не равны между собой. Однако, на основании известного соотношения:

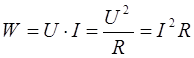
между уровнями передачи можно установить взаимозависимость, если известны сопротивления R_X и R₀, на которых выделяется соответствующая мощность W_X и W₀.

  Или :

Очевидно, что при R_X = R₀ уровни P_M =P_H = P_T. При R_X≠ R₀ – P_M≠P_H≠P_T

Исходя из приведённых определений уровней передачи, нетрудно решить обратную задачу. Определить мощность, напряжение и ток сигнала по известным уровням:

 

W_X = W₀10^0,1Pм, мВт;U_X = U₀10₀^,05Pн, Мв;I_X = I₀1^0,05Pт, мА.

 

В зависимости от значений мощности, напряжения или тока, которые приняты за исходные, различают абсолютный, измерительный и относительный уровни передачи.

Если за исходные величины мощности, напряжения и тока приняты соответственно W₀=1мВт, U₀=775 мВ, I₀=1,29 мА, определённые при сопротивлении R₀=600 Ом, то вычисленные уровни называются абсолютными и обозначаются дБ_м, дБ_н, дБ_т.

Номинал сопротивления 600 Ом исторически появился в технике связи как среднее значение модуля волнового сопротивления воздушной медной линии.

Мощность 1мВт (10^-3Вт) – средняя мощность на выходе микрофона. Чувствительность телефона 1 мкВт (10^-6Вт).

Величины U₀ и I₀ выбраны из условия, что мощность W₀ = 1 мВт рассеивается на сопротивление R₀= 600 Ом

.

Другие значения нулевых уровней напряжения и тока для симметричных и коаксиальных кабелей можно называть абсолютными только с обязательным указанием сопротивления, к которому они относятся.

Коаксиальные кабели R₀=75 Ом

Если величины мощности, напряжения и тока в рассматриваемой точке равны исходным, т.е. W_Х=1мВт, U_X=775мВ, I_X=1,29 мА, то уровни называются нулевыми абсолютными.

Абсолютный уровень мощности, напряжения или тока, в какой – либо точке системы, рекомендованный для измерения трактов или каналов, называется измерительным уровнем.

Относительный уровень передачи определяется путём сравнения мощности, напряжения или тока в данной точке тракта с мощностью, напряжением или током в точке на входе тракта, принятой за точку сравнения (отсчёта).

Обычно, в качестве точки отсчёта при определении относительных уровней используют двухпроводной вход канала тональной частоты, входное сопротивление которого равно 600 Ом. Эту характерную точку канала называют точкой нулевого относительного уровня (ТНОУ), поскольку относительный уровень сигнала в этой точке равен нулю.

Для того чтобы подчеркнуть, что уровень мощности, напряжения, тока сигнала или помехи оцениваются именно в ТНОУ, его обозначают дБм0,  дБн0, дБт0.

Относительный уровень сигнала в некоторой точке тракта может быть выражен через абсолютные уровни в этой точке и ТНОУ

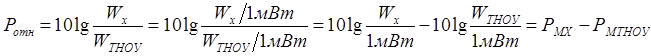
Относительные уровни равны разности абсолютных уровней в точках измерения и начальной (ТНОУ).

Введение понятия ТНОУ позволяет сравнивать мощности или уровни различных сигналов между собой, а также сопоставлять мощность сигналов и помех в тракте, приводя все эти величины к одной и той же точке тракта – ТНОУ.

Эти уровни широко используются при измерении передаточных характеристик трактов, поскольку их значения численно равны усилению по мощности, напряжению или току участка от начала цепи до данной точки.

Если р_Х>р_ТНОУ или р_отн>0, то это соответствует усилению  сигнала, т.е. S = p_X-p_ТНОУ.

Отрицательные значения уровней при этом будут соответствовать затуханию данного участка тракта.

Если p_X<p_ВХ или р_ОТН<0, то это соответствует затуханию сигнала, поэтому α=p_ТНОУ-р_Х.

Мгновенные значения мощности, напряжения или тока сигналов могут изменяться в довольно широких пределах. Для количественной оценки пределов изменения мгновенной мощности, напряжения или тока вводят понятие динамического диапазона или пик фактора сигнала.

Динамический диапазон сигнала представляет собой выраженное в децибелах отношение максимальной мощности в данной точке тракта, превышение которой может вызвать значительные нелинейные искажения вследствие перегрузки узлов аппаратуры, главным образом усилителей, к минимально допустимому значению мощности сигнала в той же точке тракта, при котором, еще обеспечивается допустимое отношение сигнал/шум

 

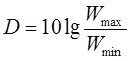, дБ                                           (2.1)

Пикфактор сигнала характеризует превышение максимальной мощности сигнал над её средним значением.

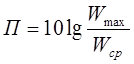, дБ                                          (2.2)

 

 

2.3. Текст задания и условие задачи

 

Для сигнала на нагрузке R_X, Ом были определены – среднее эффективное напряжение сигнала U_СР, мВ, пикфактор– П, дБ и динамический диапазон – D, дБ.

Определить в соответствии с вариантом задания (табл.2.1):

1. Максимальные и минимальные эффективные значения напряжениясигнала –U_max,,U_min,

2. Максимальные,средние и минимальные эффективные значения напряжениясигнала –I_max, I_ср, I_min.

3. Максимальные,средние и минимальные уровни тока, напряжения и мощности сигнала на нагрузке – p_Тmax, p_Тmin,p_Тср, p_Нmax, p_Нmin, p_Нср, p_Мmax, p_Мmin, p_Мср.

Таблица 2.1

Варианты задания

 

Продолжение таблицы 2.1

вариант	RX, Ом	UCР, мВ	П, дБ	D, дБ	вариант	RX, Ом	UCР, мВ	П, дБ	D, дБ
21	371	213	18	37	61	310	10,9	28	57
22	388	209	19	39	62	327	7,2	29	58
23	405	205	20	41	63	344	3,5	30	59
24	422	201	21	43	64	60	710	11	20
25	439	197	22	45	65	79	692	12	23
26	456	192,9	23	47	66	108	674	13	25
27	473	188,8	24	79	67	137	656	14	27
28	490	184,7	25	51	68	170	638	15	29
29	715	180,6	26	53	69	879	133	29	57
30	732	176,6	27	55	70	908	94	30	58
31	749	172,7	28	57	71	937	54	11	21
32	766	168,8	29	59	72	972	122,4	20	42
33	783	164,9	30	60	73	989	118,6	21	43
34	800	161	10	22	74	1006	114,8	22	45
35	1040	107,2	24	49	75	1023	111	23	48
36	1057	103,4	25	51	76	887	141,5	15	31
37	1074	99,7	26	53	77	904	137,4	16	33
38	1091	96	27	54	78	921	133,8	17	35
39	1102	92,3	28	58	79	938	130	18	38
40	1119	88,6	29	59	80	955	126,2	19	40
41	1136	84,9	30	59	81	836	153,2	12	26
42	1153	81,2	10	21	82	853	149,3	13	28
43	1170	77,5	20	42	83	870	145,4	14	3
44	1187	73,8	30	60	84	819	157,1	11	24
45	1999	70,1	11	22	85	966	16	12	22
46	55	66,4	12	24	86	995	671	13	27
47	72	62,7	13	26	87	1024	653	14	28
48	89	59	14	28	88	493	288	25	49
49	106	55,3	15	30	89	792	251	26	51
50	123	51,6	16	32	90	821	211	27	53
51	140	47,9	17	34	91	850	172	28	55
52	157	44,2	18	36	92	348	488	20	39
53	174	40,5	19	38	93	377	450	21	41
54	191	36,8	21	42	94	406	412	22	43
55	208	33,1	22	45	95	435	364	23	45
56	225	29,4	23	47	96	464	326	24	47
57	242	25,7	24	49	97	227	602	17	33
58	259	22	25	51	98	261	564	18	35
59	276	18,3	26	53	99	290	526	19	37
60	293	14,6	27	55	100	198	620	16	31

 

Дополнительныезадачи для самостоятельного решения

2.1. Для мощностей, равных 10 мВТ и 2000 мВТ, определить абсолютный уровень мощности.

2.2. Найти абсолютный уровень мощности для резистора сопротивлением1000 Ом, выделяющего мощность в1 пВт.

2.3.Определить абсолютный уровень тока для мощности 1 Вт, Если сопротивление в измеряемых точках  ,.

2.4.Для мощности 1пВт, выделяемой резистором с сопротивлением равным 150 Ом,найти абсолютный уровень напряжения.

2.5. Определить нулевой уровень мощности и тока для сопротивления

2.6.Найти абсолютный уровень напряжения для мощности 1 Вт, выделяемой резистором сопротивлением 600 Ом.

2.7. Найти абсолютный уровень мощности для мощностей 1 пВт и 1 Вт.

2.8. Определить во сколько раз увеличится напряжение на выходе четырёхполюсника если относительный уровень напряжения по мощности равен 160 дБ.

 

3.ПОГРЕШНОСТИ ИЗМЕРЕНИЙ И ИХ КЛАССИФИКАЦИЯ

 

Погрешностью результата измерения называется отклонение найденного значения от истинного (действительного) значения измеряемой физической величины.

Погрешности измерений классифицируют по ряду признаков.

По форме количественного выражения погрешности делятся на абсолютные, относительные и приведенные.

Абсолютной погрешностью, выражаемой в единицах измеряемой величины, называют отклонение результата измерения  от истинного (действительного) значения измеряемой величины х₀:

                                               (3.1)

Относительной погрешностью называют отношение абсолютной погрешности измерения к истинному (действительному)значению измеряемойвеличины:

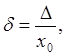                                                 (3.2)

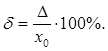
Поскольку обычно , то вместо х₀ с достаточной степенью точности можно использовать значение , т.е. относительная погрешность может быть определена как

или                                  (3.3)

Приведенной погрешностью называют отношение абсолютной погрешности  к некоторому нормирующему значению   (например, к конечному значению шкалы или сумме значений шкал при двусторонней шкале):

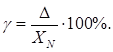                                            (3.4)

По характеру (закономерности) проявления погрешности делят на систематические, случайные и грубые (промахи).

Систематические погрешности  – это составляющие погрешности измерения, которые остаются постоянными или закономерно изменяются при повторных измерениях одной и той же величины в одних и тех же условиях.

Случайные погрешности  –составляющие погрешности, изменяющиеся случайным образом по значению и знаку при повторных измерениях одной и той же физической величины в одних и тех же условиях.

Грубые погрешности – погрешности, существенно превышающие ожидаемые при данных условиях измерения.

По причинам возникновения (по виду источника) – погрешности принято делить на методические, инструментальные, внешние и субъективные (личные).

Методические погрешности возникают вследствие несовершенства метода измерений и теоретических допущений, принимаемых при описании метода измерений.

Инструментальные (аппаратурные) погрешности возникают из-за несовершенства средств измерения, их схемы, конструкции, состояния в процессе эксплуатации.

Внешние погрешности связаны с отклонением одной или нескольких влияющих величин от нормальных значений или выходом их за пределы нормальной области.

Субъективными (личными) называют погрешности, возникающие вследствие несовершенства органов чувств экспериментатора, а также его небрежности или невнимания в процессе измерений и фиксации их результатов.

По характеру поведения измеряемой величины в процессе измерения различают статические и динамические погрешности.

Статические погрешности возникают при измерении установившегося во времени значения измеряемой величины.

Динамическиепогрешности имеют место при динамических измерениях, когда измеряемая физическая величина изменяется во времени.

По условиям эксплуатации средств измерений различают основную и дополнительную погрешности.

Основная погрешность средств измерений имеет место при нормальных условиях эксплуатации, оговоренных в регламентирующих документах.

Дополнительная погрешность средств измерений возникает из-за выхода какой-либо из влияющих величин за пределы нормальной области значений.

3.1. Задачи для самостоятельного решения

3.1. Истинное значение тока в цепи 5,23 А, измеренные значения тока, полученные с помощью двух амперметров, составили 5,3 и 5,2 А. Чему равны относительные и абсолютные погрешности измерения?

3.2. Какова основная приведенная погрешность прибора с верхним пределом измерения 5 А, если наибольшая погрешность при измерении составила 0,12 А?

3.3.Ток резистора, сопротивление которого 8 Ом, равен 2,4А. При измерении напряжения на этом резисторе вольтметр показал напряжение 19,3В. Определитьабсолютную и относительную погрешности измерения сопротивления в данном случае.

3.4.Основная приведенная погрешность показаний магнитоэлектрического прибора составляет 0,5%. Какова наибольшая возможная относительная погрешность измерения при отклонении стрелки на 75; 50; 25 % его шкалы?

3.5.При измерении напряжения потребителя, включенного в электрическую цепь, вольтметр показал 13,5 В. Найти абсолютную и относительную погрешности измерения, если сопротивление потребителя 7 Ом, ЭДС источника электрической энергии 14,2 В, его внутреннее сопротивление 0,1 Ом.

3.6. Определить класс точности амперметра с пределом измерения 10 А, если точкам шкалы 2, 4, 6, 8, 10 А соответствуют значения токов 2,041; 3,973; 6,015; 8,026; 9,976 А.

3.7. При пятикратном измерении одного и того же напряжения с помощью вольтметра были получены следующие результаты:

6,35; 6,4; 6,3; 6,45; 6,25 В. Считая среднее арифметическое значение измеряемого напряжения действительным его значением, определить границы абсолютной и относительной погрешности.

3.8.Определитьпоказание электродинамического А1 и электромагнитного А2 амперметров, включенных последовательно в RC-цепь, если напряжение на входе цепи изменяется по закону u(t)= 100 + 200sinωt, В. Параметры цепи R = 10 Ом, Хс = 10 Ом.

3.9.Определить показания электродинамического А1 и электромагнитного А2 амперметров, включенных последовательно в цепь катушки с параметрами R = 10 Ом, ХL = 10 Ом, если напряжение на входе изменяется по закону u(t)= 25 + 50sinωt В.

3.10. Класс точности амперметров А1 и А2 одинаков, а верхний предел прибора А2 больше. Какой амперметр позволяет производить более точные измерения?

3.11. Приборы каких систем –электрической, электромагнитной или электродинамической – можно использовать в цепях постоянного и переменного тока?

3.12.Чему равна наибольшая возможная абсолютная погрешность амперметра класса точности 1,0, если верхний предел его измерения равен 10 А?

3.13.Классы точности двух вольтметров одинаковы и равны 1, а верхние пределы измерения различны: у первого – 50 В, а у второго – 10 В. В каком соотношении будут находиться наибольшие абсолютные погрешности измерения вольтметров в процессе эксплуатации?

3.14. Определить класс точности магнитоэлектрического миллиамперметра с пределом измерения шкалы Ιн = 0,5 мА для измерения тока 0,1ч0,5 мА, если относительная погрешность измерения тока не превышает 1 %.

3.15. При поверке милливольтметра класса точности 1,0 с пределом измерения 300 мВ максимальные погрешности измерения напряжения от 50 до 300 мВ с шагом 50 мВ составили 1,5; 1,0; 0,5; 3,0; 2,5 мВ. Соответствует ли милливольтметр своему классу точности?

3.16. При изменении измеряемого тока от 5 до 10 мА указатель одного миллиамперметра переместился на четыре деления, а другого – на десять делений. Определить соотношения между чувствительностями и постоянными шкал приборов.

3.17. Миллиамперметр рассчитан на ток 200 мА и имеет чувствительность 0,5 дел/мА. Чему равны число делений шкалы, цена деления и измеренный ток, если указатель миллиамперметра отклонился на 30 делений?

3.18. Определить относительную погрешность косвенного изменения тока Ι, если этот ток равен: а) сумме токов Ι₁ = 4 А и Ι₂= 3 А; б) разности токов Ι₁ = 4 А и Ι₂= 3 А. Измерение производилось амперметрами класса точности 1,0 с номинальным током 5 А.

3.19. В приборе с квадратичной шкалой отклонение стрелки пропорционально квадрату измеряемого тока. Каким значениям тока соответствует отклонение указателя прибора на: а) половину шкалы; б) две трети шкалы; в) четверть шкалы, если верхний предел измерения составляет 10 А.

3.20. В приборе с логарифмической шкалой отклонение указателя пропорционально логарифму измеряемого напряжения. Каким напряжениям соответствует отклонение указателя на: а) половину шкалы; б) четверть шкалы; в) три четверти шкалы, если верхний предел измерения составляет 10 кВ.

3.21. Универсальный многопредельный прибор (тестер) имеет девять пределов измерения по напряжению 0,3; 1,5; 7,5; 30; 60; 150; 300; 600; 900 и восемь пределов измерения по току 1,5; 6; 15; 60 мА и 0,15; 0,6; 1,5 и 6 А. Определить цену деления шкалы на всех поддиапазонах измерения напряжения и тока, если длина шкалы 30 делений.

3.22. Цена деления шкалы электроизмерительного прибора изменяется в зависимости от угла поворота указателя в соответствии с выражениями: а) Сх=Сo б) Сх=Сoα; в) Сх=Сo/α. Определить характер шкалы измерительного прибора.

3.23. После ремонта щитового амперметра с классом точности 1,5 и пределом измерения 5 А произвели поверку его основной приведенной погрешности. Наибольшая абсолютная погрешность прибора составляла 30 мА. Сохранил ли амперметр свой класс точности после ремонта?

3.24. Наибольшие абсолютные погрешности измерения двух миллиамперметров одинаковы, но верхний предел измерения второго прибора больше. В каком отношении находятся классы точности приборов?

3.25. При поверке электроизмерительных приборов установлено, что основные приведенные погрешности их были равны 0,45; 1,2 и 1,8%. Какой класс точности имеет каждый из приборов? Чему может быть равна их наибольшая абсолютная погрешность при пределе измерения 100 В?

4.ИЗМЕРЕНИЕ НАПРЯЖЕНИЯ И СИЛЫ ТОКА

4.1. Краткие теоретические сведения

Измерение напряжения и силы тока в электрических цепях относится к наиболее распространенным видам измерений. Задача измерения постоянных напряжения и силы тока заключается в нахождении их значения и полярности. Целью измерения переменных напряжения и силы тока является определение, какого – либо их параметра.

Так как напряжение и сила тока связаны, согласно закону Ома, линейной зависимостью, чаще проводят измерение напряжения и по его значению аналитически вычисляют силу тока.

Современные методы и средства измерений позволяют измерять напряжения в диапазоне 10^־10...10⁶ В и силу тока в диапазоне 10^־18...10⁵ А. Вместе с тем данные измерения должны осуществляться в очень широкой полосе частот – от постоянного тока до сверхвысоких частот. Такие крайние значения величин требуют уникальных методов измерения.

Воздействие переменного напряжения на электрическую цепь можно определить по амплитудному, среднему квадратическому, среднему (постоянной составляющей) или средневыпрямленному значениям.

Мгновенное значение напряжения  - это значение напряжения в определенный момент времени.

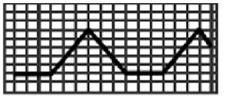
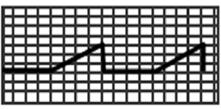
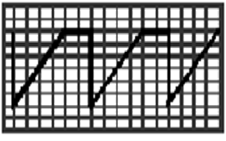
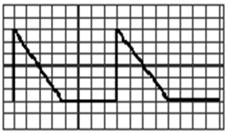
Амплитуда (пиковое значение) U_m - это наибольшее мгновенное значение напряжения (относительно оси времени) за период (рис.4.1).

 

 

 

 

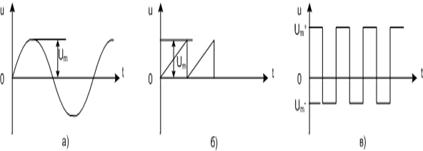
Рис. 4.1. Иллюстрации к понятию амплитуда напряжения:

На рис. 4.1 изображены: синусоидальное напряжение (рис.4.1,а);пилообразное напряжение положительной полярности (рис.4.1, б); разнополярные прямоугольные импульсы(рис.4.1, в)

Среднее квадратическое значение напряжения – это корень квадратный из среднего квадрата его мгновенного значения за период:

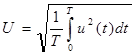                                         (4.1)

Среднее значение (постоянная составляющая) напряжения – это среднее арифметическое всех его мгновенных значений за время измерения:

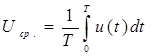                                      (4.2)

Средневыпрямленное значение напряжения – это среднее арифметическое его абсолютных мгновенных значений за время измерения:

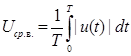                                        (4.3)

Связь между рассмотренными параметрами описывается тремя коэффициентами: амплитуды , формы  и усреднения

.

Для каждой формы физически реализуемого сигнала все три коэффициента определены, и их значения не зависят от параметров сигнала.

Так для сигнала синусоидальной формы с любой амплитудой, частотой и начальной фазой: ;; .

Для сигнала пилообразной формы вида  (рис. 4.1.б): ; ; .

Чаще измеряют среднее квадратическое значение напряжения, так как этот параметр характеризует энергетические свойства сигнала. Однако проще измерить амплитудное или средневыпрямленное значения напряжения и произвести пересчёт с применением, указанных выше коэффициентов.

Примеры

1.Имеется резистор сопротивлением 5,1 МОм, через который протекает ток, равный 200 мкА. Максимальное значение мощности рассеяния P для резистора P_max = 250 мВт. Рассчитать значение P для данного тока и сравнить с P_max, а также рассчитать с точностью до единиц микроампер максимально возможное значение тока I_max, соответствующее P_max.

Решение:

P = I ²R = 0,204 Вт = 204 мВт <P_max;

I_max =  = 221мкА.

2.Имеется конденсатор емкостью 100 пФ. В начальный момент опыта конденсатор разряжен, затем его в течение 20 мкс заряжают постоянным током, значение которого требуется определить. После этого измеряют напряжение на конденсаторе, которое оказывается равным 1 мВ. Определите выраженное в наноамперах значение тока.

Решение:

I = UC / t = 5 нА.

Примеры

3.Ток, измеренный амперметром класса точности 2 и диапазоном измерения 15А, составлял 11,5А. Определить диапазон возможного действительного значения измеряемого тока.

Решение.

Наибольшая и возможная относительная погрешность связана с приведенной погрешностью следующим соотношением:

Вместе с тем относительная погрешность определяется по выражению (4.3).

Используя эти выражения дляотносительной погрешности, можно найти расчетное соотношение для действительного значения тока

Подставляя числовые значения параметров, находим

А_D=11,5 ± 0,3 А.

4.Вольтметр класса точности 1,0 с пределом измерения 300В, имеющий максимальное число делений 150, проверен на отсчетах 30, 60, 100,120 и 150 делений, при этом абсолютная погрешность в этих точках составила 1,8; 0,7; 2,5; 1,2 и 0,8 В. Определить, соответствует ли прибор указанному классу точности, и относительные погрешности на каждой отметке.

Решение.

Вольтметр класса точности 1,0 с пределом измерения 300Вимеет наибольшую абсолютную погрешность 3 В. Так как значение абсолютной погрешности на всех поверяемых отметках менее 3 В, то прибор соответствует классу точности 1,0.

Относительные погрешности:

 

,

 

,

 

,

 

,

 

,

 

.

 

4.2. Задачи для самостоятельного решения

 

4.1. Определить наибольшую разницу в показаниях двух последовательно включенных амперметров с пределом измерения шкалы на 10 А и классами точности 0,5 и 1.

4.2. Мгновенные значения токов в двух параллельных ветвях цепи переменного тока записываются в виде: а) i₁ = 14sin314t А; i₂= 28,2 sin(314t + 45°) А; б) i₁ = 21,1sin314tА; i₂= 14,1 sin(314t + 60°) А. Что покажет электромагнитный амперметр в обоих случаях, если он включен в неразветвленную цепь?

4.3. Для измерения тока в цепи с потребителем сопротивлением 10 Ом включен амперметр с внутренним сопротивлением 0,1 Ом. Чему равно относительное изменение тока, вызванное включением амперметра?

4.4.Определить показания миллиамперметра с внутренним сопротивлением 500 Ом в цепи, состоящей из последовательно соединенных резисторов сопротивлением 17,5 кОм и конденсатора емкостью 0,5 мкФ, если цепь подключена к промышленной сети переменного напряжения 220 В. Найти относительную и абсолютную погрешности, вызванные включение миллиамперметра в цепь.

4.5. Найти относительную погрешность при определении постоянного тока во второй параллельной ветви, если токи первой параллельной цепи и неразветвленной части цепи соответственно равны: Ι₁ = 2 А и Ι₂ =5 А. Указанные значения получены в результате измерений с погрешностями 20 и 50 мА.

4.6. Ток в диагонали мостовой схемы необходимо измерять с погрешностью не выше ±1 мкА. С каким классом точности нужно выбрать микроамперметры с пределами измерения 50 и 100 мкА?

4.7. Цифровой измерительный прибор имеет следующие поддиапазоны измерения по току: 10 и 100 мА; 1 и 10 А. Определить, с какой относительной погрешностью могут быть измерены токи 5 и 40 мА; 0,3 и 1 А, если постоянные коэффициенты С и В для указанных поддиапазонов равны 1 и 0,25%.

4.8. Цифровой амперметр имеет восемь поддиапазонов измерения, причем предел измерения каждого последующего поддиапазона в 10 раз больше предыдущего, а предел измерения первого поддиапазона 10 мкА. Определить максимальный ток, который можно измерять с помощью этого амперметра. На каких поддиапазонах следует измерять токи 50 мА; 2 и 15 А?

4.9. Определить показания магнитоэлектрического, электромагнитного и электродинамического амперметров, включенных последовательно в электрическую цепь, если ток в цепи изменяется по закону i(t) = 6+8√2 sinωt.

4.10. Амперметром с внутренним сопротивлением R_A = 1 Ом следует измерить ток в 10, 100 и 1000 раз больше его номинального значения. Найти соотношение между сопротивлениями амперметра и шунтов, подобранных для выполнения указанных измерений.

4.11. Амперметр, имеющий внутреннее сопротивление 0,2 Ом и предел измерения 10А, необходимо использовать для измерения тока до 500 А. Определить сопротивление шунта прибора и падение напряжения на амперметре и шунте.

4.12. Номинальный ток амперметра Ι = 1А, сопротивление шунта Rш = 0,5 Ом (рис. 4.2, а). Определить сопротивление амперметра, если номинальное значение тока в нем было при общем токе цепи 5 А.

4.13. Номинальный ток амперметра 1 А, его внутреннее сопротивление 0,08 Ом. Какой ток проходит в электрической цепи, если амперметр с шунтом сопротивлением 0,03 Ом показывает ток 0,9 А?

4.14. Образцовые резисторы R₁ и R₂ (рис. 4.2.б) позволяют расширить пределы измерения амперметра. Определить показание амперметра с внутренним сопротивлением 0,5 Ом, если ток источника Iизм = 2,2 А, а сопротивления резисторов R₁ = 4,5 Ом и R₂=0,5 Ом.

 

 

 

 

а)                      б)

Рис. 4.2: а) к задаче 4.12, б) к задаче 4.14

 

4.15. К трансформатору тока 400/5 присоединен амперметр. Определить его показания при токе в первичной измерительной цепи, равном: а) номинальному току трансформатора; б) 300 А; в) 100 А. Какова относительная погрешность измерения, если действительный коэффициент трансформации 82?

4.16. Необходимо измерить напряжение в пределах 30-40 В. Какой из вольтметров позволяет произвести измерение с большей точностью: 1) с верхним пределом 50 В и классом точности 2,5; 2) с верхним пределом 100 В и классом точности 1,5; 3) с верхним пределом 300 В и классом точности 0,5; 4) с верхним пределом 150 В и классом точности 1?

4.17. Мгновенные значения напряжений двух последовательно соединенных резисторов записываются в виде: а) u₁ = 155sin314t В и u₂ = 51sin314t В; б) u₁ = 106sin314t В и u₂ = 155sin314t В. Что покажет электромагнитный вольтметр в обоих случаях, если он включен к источнику питания всей цепи?

4.18. Для измерения напряжения потребителя сопротивлением 1 кОм подключен вольтметр с внутренним сопротивлением 33 кОм. Определить относительное изменение потребляемого тока, вызванное включением вольтметра, если напряжение на приборе поддерживается постоянным.

4.19. Определить показание вольтметра с внутренним сопротивлением 50 кОм, подключенного к цепи, состоящей из параллельно соединенных резистора сопротивлением 2 кОм и конденсатора емкостью 0,5 мкФ. Рассчитать абсолютную и относительную погрешности измерения, вносимые внутренним сопротивлением вольтметра, если общий ток 10 мА, частота 100 Гц.

4.20. С какими внутренними сопротивлениями должен быть выбран вольтметр для измерения напряжения с относительной погрешностью не более 1 % на последовательно соединенных катушках индуктивности L = 0,1 Гн и конденсаторе С=5 мкФ? Цепь подключена к источнику напряжением 36 В и частотой 10 кГц.

4.21. Определить напряжение цепи, схема которой приведена на рис. 4.4, а, если вольтметр показал напряжение 180 В. Сопротивление R₁ = 80 Ом, полное сопротивление переменного резистора R = 240 Ом, а внутреннее сопротивление вольтметра Rv = 5 кОм.

4.22. Для измерения напряжения на обмотке реле сопротивлением Rк = 100 Ом, включенного последовательно с добавочным резистором Rдоб= 400 Ом, был использован вольтметр с Rv= 10 кОм (рис. 4.5). Определить относительную погрешность измерения вносимую внутренним сопротивлением вольтметра.

4.23. К электростатическому вольтметру, внутренняя емкость которого 200 пФ, последовательно подсоединен конденсатор емкостью 40 пФ. Какое максимальное напряжение можно измерить вольтметром теперь, если шкала его имеет 100 делений, а цена одного деления 0,5 В/дел?

4.24. Цифровой вольтметр имеет следующие поддиапазоны измерения: 100 мВ; 1; 10 и 100 В. С какой относительной погрешностью могут быть измерены напряжения 70 мВ; 0,6; 3 и 75 В, если постоянные коэффициенты В и С для всех поддиапазонов равны соответственно 0,6 и 0,25%?

 

5. ИЗМЕРЕНИЕ МОЩНОСТИ

5.1. Краткие теоретические сведения

 

Мощность цепи постоянного тока определятся с помощью амперметра и вольтметра. Определяется формулой:

,                                                 (5.1)

гдеU–показание вольтметра, включенного на участке, где определяется мощность, В;– показание амперметра на том же участке цепи, А.

Для измерения той же мощности может быть использован электродинамический ваттметр. Угол поворота подвижной части этого прибора, включенного в цепь, пропорционален мощности, значения которого нанесены на шкалу прибора.

Активную мощность в цепях переменного тока измеряют так же ваттметрами. Для расширения пределов измерения применяются измерительные трансформаторы тока и напряжения.

В трехфазной трехпроводной цепи при симметричной нагрузке для измерения активной мощности применяют один ваттметр, включенный в одну из фаз. Для определения мощности всей трехфазной цепи надо показание ваттметра умножить на три, т. е.

                                (5.2)

В трехфазной цепи при симметричной и несимметричной нагрузке активную мощность всей цепи измеряют с помощью двух ваттметров (рис. 4)

                                            (5.3)

где– показания второго и первого ваттметров, Вт

где– фазовый сдвиг между векторамии;– фазовый сдвиг между векторами

Рис. 5.1. Схема измерения активной мощности двумя ваттметрами

Для симметричной нагрузки:

,

,                                  (5.4)

где–фазовый сдвиг между напряжением и током в фазе.

В трехфазной цепи при соединении нагрузки «звездой» и наличием нулевого провода (провода нейтрали) для измерения активной мощности применяют метод трех ваттметров. Активная мощность всей цепи равна сумме показаний всех ваттметров:

                                         (5.5)

где– показания каждого ваттметра, Вт.

Показания ваттметра определяются по отсчету (в делениях шкалы), умноженному на цену деления ваттметра.

Цена деления ваттметра

                                        (5.6)

где– номинальное значение напряжения, В;– номинальное значение тока, А;– максимальное число делений ваттметра.

5.2. Рассчитать мощность, выделяемую в обмотке измерительного механизма вольтметра электромагнитной системы с пределом измерения 100 В, если активное сопротивление обмотки 1 кОм, ее индуктивность 0,3 Гн. Прибор рассчитан на измерение в цепях постоянного и переменного тока частотой 50 Гц.

Решение.Для нахождения мощности определяем измерительный ток обмотки. В цепи постоянного тока:

= 0,1 АиР= 10 Вт.

В цепи переменного тока

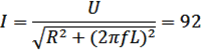
Мощность в этом случае имеет вид:

Как следует из решения, мощность, выделяемая в обмотке измерительного механизма электромагнитной системы, достаточно велика, что является недостатком этой системы.

 

5.2. Задачи для самостоятельного решения

 

5.1. Ваттметр для измерения мощности в электрической цепи имеет линейную шкалу измерения. Каков ток в приборе при мощности 30 Вт, если при мощности 10 Вт ток его равен 2 А? Напряжение параллельной цепи ваттметра считать неизменным.

5.2. Для измерения мощности потребителя в цепи постоянного тока с номинальным напряжением 110 В использовался электродинамический ваттметр (рис. 5.2, а) со следующими параметрами: Uн = 150 В; Ιн = 5 А, сопротивление последовательной обмотки 0,2 Ом. Определить номинальную мощность потребителя.

5.3. Для измерения мощности потребителя постоянного тока номинальным напряжением 110 В использовался электродинамический ваттметр (рис. 5.2, б) со следующими параметрами: Uн = 150 В;  Ιн = 5 А, ток параллельной цепи ваттметра 50 мА.  Определить номинальную мощность потребителя.

5.4. При измерении мощности методом амперметра и вольтметра (рис. 5.2, в) показания приборов при положении переключателя 1 были соответственно равны 1 А и 60 В. Определить выделяемую в резисторе мощность, если сопротивление последовательной цепи RА – 0,5 Ом.

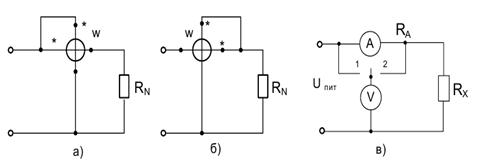
Рис.5.2. Схема измерения мощности:

а) с подключением источника;б) с подключением ваттметра

5.5. При измерении мощности методом амперметра и вольтметра (рис. 5.2, в) показания приборов при положении переключателя 2 были соответственно равны 2 А и 110 В. Определить выделяемую в резисторе мощность, если сопротивление параллельной цепи Rv = 5 кОм.

5.6. Фазные токи и напряжения в четырехпроводной трехфазной цепи (рис.5.3) с симметричной активной нагрузкой равны 5 А и 220 В. Определить показание ваттметра и активную Мощность потребителя.

Рис.5.3.Схема к задаче 5.6

 

5.7. Для измерения реактивной мощности в трехфазной цепи при симметричной нагрузке фаз с R = 5 Ом и ХL= 1 Ом используется схема включения ваттметра на рис.5.4. Определить показание ваттметра, если линейные напряжения цепи равны 220 В.

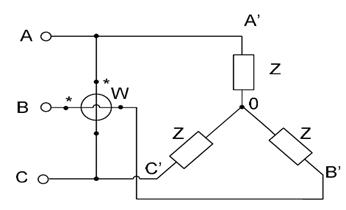
Рис. 5.4.Схема к задаче 5.7

 

5.8. Активная мощность в трехфазной цепи определяется с помощью искусственной нулевой точки (рис. 5.5). Определить показания ваттметра при симметричной активной нагрузке, если фазные токи и напряжения равны 20 А и 220 В. Чему равны напряжения на резисторах RB и RC?

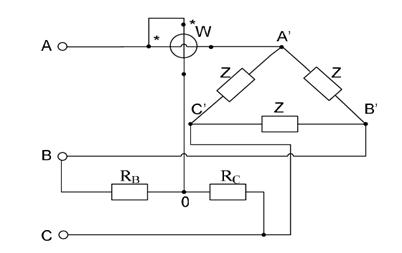
Рис.5.5. Трехфазная цепь

 

5.9. Для измерения мощности ваттметр включен через трансформаторы тока 150/5 и напряжения 6000/100. Классточности ваттметра 1,5. Найти мощность потребителя, если показание ваттметра равно 280 Вт. Чему равна наибольшая возможная абсолютная погрешность измерения?

5.10. В однофазной цепи переменного тока через трансформатор тока 300/5 и трансформатор напряжения 10000/100 включены амперметр, вольтметр и ваттметр. Начертить схему измерения и определить ток, напряжение и мощность потребителя, если показания приборов 2 А; 80 В и 250 Вт.

5.11 Мощность в цепи постоянного тока измеряется методом амперметра и вольтметра, причем показания приборов соответственно равны 9 А и 150 В. В каком диапазоне может находиться действительное значение мощности, если погрешность измерения напряжения ±3 В, а тока ±0,5 А?

5.12. Для измерения коэффициента мощности в цепи переменного тока используется схема (рис.5.6). Определить соsφ и погрешность его определения, если показания приборов равны 100 Вт ±2%; 2 А±2,5% и 60 В±1 %.

Рис. 5.6. Схема к задаче 5.12.

 

5.13. Мощность электротехнического устройства составляет 2кВт. Какое время работал счетчик, если он сделал 40 оборотов, а постоянная счетчика 1400 Вт∙с/об? Какая энергия регистрируется счетчиком за 20 оборотов?

 

 

6. ОСЦИЛЛОГРАФИЧЕСКИЕ МЕТОДЫ ИЗМЕРЕНИЯ АМПЛИТУДЫ И ИНТЕРВАЛОВ ВРЕМЕНИ ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ

 

Основным и наиболее широко применяемым прибором для исследования формы напряжения служит электронный осциллограф – прибор для визуального наблюдения электрических сигналов, а также измерения их параметров с использованием средства отображения формы сигналов. Он отличается высокой чувствительностью, большим входным сопротивлением, пренебрежимо малой инерционностью и универсальностью.

Электронно-лучевые осциллографы (универсальные) классифицируют по следующим признакам: количеству одновременно исследуемых сигналов – для исследования одного и нескольких сигналов; ширине полосы пропускания канала сигнала, определяемой нижней и верхней граничными частотами; точности воспроизведения формы напряжения сигнала, точности измерения интервалов времени и амплитудных значений напряжений; условиям эксплуатации.

Для получения осциллограммы исследуемого сигнала необходимо управлять движением электронного пучка на экране электронно – лучевой трубки (ЭЛТ) в горизонтальном и вертикальном направлениях. Под действием сигнала, который подается на канал вертикального отклонения "Y", электронный луч движется в вертикальном направлении. При линейной развертке горизонтального отклонения генератор развертки вырабатывает пилообразное напряжение. Под действием генератора линейной развертки луч движется в горизонтальном направлении.

При одновременном действии сигнала на " Y'' пластины и генера­тора развертки на "X" пластины луч движется по сложной траектории, описывая на экране ЭЛТ форму сигнала. Для того чтобы изображение сигнала на экране было неподвижным, необходимо, чтобы соблюда­лось равенство:

                                                 (6.1)

где Т_р - период пилообразного напряжения генератора развертки;

Т_с - период сигнала;

k- число, показывающее сколько периодов сигнала укладывается в периоде развертки.

При линейной развертке на экране ЭЛТ получаем изображение сигнала как функцию времени. При определении различных параметров сигнала (частоты, фазы) употребляется синусоидальная развертка. Для ее получения в осциллографе нужно отключить генератор развертки и на вход "X" подать синусоидальное напряжение. На экране получим фигуру Лиссажу.

Если известна частота сигнала, поданного на вход "Y", то можно оп­ределить частоту сигнала, поданного на вход "X", и наоборот, по формуле:

                                            (6.2)

где f_x, f_y- частоты сигналов, поданных соответственно на входы "X" и"Y", n_y, n_x- количество точек пересечения фигуры Лиссажу осями X и Y.

Если на входы "X" и "Y" подать сигналы равных частот, то в зависи­мости от сдвига фаз между сигналами на экране ЭЛТ получим частный случай фигуры Лиссажу: эллипс, круг, наклонная прямая. При равных частотах и сдвиге фаз, равном 70°, на экране будет круг. Круговую раз­вертку часто используют для измерения частоты сигнала. Меньшую по величине частоту f_xподают на вход "Y" и со сдвигом в 70° на вход "X'' Большую по величине частоту подают на вход "Z" (модулятор яркости). На экране получится круг с яркостными метками. Измеряемую частоту можно рассчитать по формуле:

                                                  (6.3)

где N - количество яркостных меток.

 

6.1 Измерение напряжения

 

Измерение напряжения производится в первом основном режиме работы осциллографа – в режиме линейной калиброванной развертки.

Измеряемое напряжение u_c(t) подается на вход Y осциллографа. На пластины X ЭЛТ поступает сигнал генератора развертки пилообразной формы и_гр(t).

 

(6.4)

  ,                                            

.

 

В этом случае на экране наблюдается осциллограмма в виде зависимости поданного на вход Yсигнала от времени. Пример осцилло­граммы для синусоидального сигнала приведен на рис. 6.1.

Рис. 6.1 Пример осциллограммы для синусоидального сигнала

 

При симметричном двухполярном сигнале его амплитуда определяется из соотношения

                                             (6.5)

где   Н_у – геометрический размер по вертикали, соответствующий"размаху" осциллограммы (разности максимального и минимального отклонения луча) [дел];

m_y - коэффициент отклонения по шкале Y(цена деления по вертикали) [В/дел].

При несимметричном однополярном сигнале его амплитуда опре­деляется по формуле:

                                         (6.6)

6.2. Измерение частоты

 

6.2.1 Измерение частоты методом линейной калиброванной развертки

 

Измерение частоты методом линейной калиброванной развертки производится в первом основном режиме работы осциллографа – в режиме линейной развертки.

При измерении частоты методом линейной калиброванной раз­вертки осциллографа измеряемый сигнал u_c(t) подается на вход Y осциллографа. На пластины X ЭЛТ поступает сигнал генератора разверт­ки пилообразной формы u_rp(t).

Пример осциллограммы для синусоидального сигнала приведен на рис. 6.2.

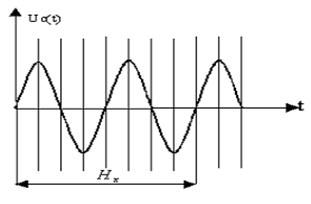
Рис. 6.2.Пример осциллограммы для синусоидального сигнала

 

Период и частота иссследуемого сигнала определяется из соотношения:

                                           (6.7)

 ,                                         (6.8)

где    n –  целое число периодов сигнала;

H_х – геометрический размер по горизонтали, соответствующий целому числу периодов сигнала [дел];

m_x – коэффициент отклонения (развертки) по шкале Х (цена деления по горизонтали) [Время/деление].

 

6.3. Измерение частоты методом синусоидальной развертки

 

Измерение частоты методом синусоидальной развертки произво­дится во втором основном режиме работы осциллографа - режиме уси­ления (сравнения, фигур Лиссажу). Гармонические сигналы подаются на входы Y и X осциллографа одним из двух указанных способов:

1)

                   (6.9)

2)

 

На экране наблюдается фигура Лиссажу, вид которой зависит от частотных и фазовых соотношений поданных сигналов.

 

 

 

 

 

 

 

Рис.6.3. Пример фигуры Лиссажу

 

Полученная фигура мысленно пересекается двумя взаимно перпен­дикулярными осями (оси не должны проходить через узлы фигуры). Подсчитывается количество точек пересечения с осью X - n_x и осью Y – n_y (рис. 6.3).

 

В этом случае выполняется соотношение

 ,                                  (6.10)

Частота напряжения, подаваемого на вход Yосциллографа, опре­деляется из соотношения (6.10)

 ,                                        (6.11)

где f_x- частота напряжения, подаваемого на вход Х осциллографа.

В зависимости от способа подачи (6.7) напряжений измеряемой Uc(t) и образцовой частот u_обр(t) неизвестная частота fбудет опреде­ляться соотношениями:

 

Первый способ

(6.12)

                                     

Второй способ

(6.13)

                                           

 

 

6.4. Текст задания и условие задачи

 

При выполнении задания выбор варианта задач определя­ется двумя последними цифрами номера зачетной книжки ML, где M- предпоследняя цифра, L- последняя цифра.

При выполнении задания в разделе необходимо решить пять задач:

Четыре задачи в соответствии с таблицами вариантов 6.1, 6.2. Тексты задач приведены в таблице 6.3. Примеры решения задач даны в разделе 6.5.

Одну задачу, приведенную в разделе 6.4.2

 

 

 

Таблица 6.1

 

Таблица 6.2

 

Таблица6.3

 

Продолжение таблицы 6.3

 

1	2
5. Определить амплитуду и период сигнала, если коэффициенты отклонения осциллографа равны 0,2 мс/ дел и 1 В/ дел
6. Определить амплитуду и период двухполярного сигнала, если коэффицитенты отклонения осциллографа равны 1 мс/ дел и 2 В/дел
7. Определить амплитуду и период сигнала, если коэффициенты отклонения осциллографа равны 5 мс/ дел и 2 В/ дел
8. Определить амплитуду и частоту сигнала,если коэффициенты отклонения осциллографа равны 0,5 мс/ дел 0,5 В/ дел
9. Определить амплитуду и период сигнала,если коэффициенты отклонения осциллографа равны 5 мкс/ дел и 10 В/ дел
10. Определить амплитуду и период сигнала,если коэффициенты отклонения осциллографа равны 1 мс/ дел и 5 В/ дел

 

 

 

 

Продолжение таблицы 6.3

 

1	2
1	2
11. Определить амплитуду и период сигнала, если коэффициенты отклонения осциллографа равны 20 мкс/ дел и 2 В/ дел
12. Определить амплитуду и период сигнала, если коэффициенты отклонения осциллографа равны 5 мс/ дел и 10 В/ дел
13. Определить амплитуду и период сигнала, если коэффициенты отклонения осциллографа равны 2 мс/ дел и 8 В/ дел
14. Определить амплитуду и период двухполярного сигнала, если коэффициенты отклонения осциллографа равны 5 мс/ дел и 10 В/дел
15. Определить частоту сигнала на входе Х, если частота сигнала на входе Y равна 600 Гц
16. Определить частоту сигнала на входе Y У, если частота сигнала на входе X равна 800 Гц
17. Определить частоту сигнала на входе Y, если частота сигнала на входе X равна 700 Гц

 

 

Продолжение таблицы 6.3

 

1	2
18. Определить частоту сигнала на входе Х, если частота сигнала на входе Y равна 500 Гц
19. Определить частоту сигнала на входе Х, если частота сигнала на входе Y равна 1600 Гц
20. Определить частоту сигнала на входе Х, если частота сигнала на входе Y равна 1500 Гц
21.  Определить частоту сигнала на входе Y, если частота сигнала на входе X равна 200 Гц
22. Определить частоту сигнала на входе Х, если частота сигнала на входе Y равна 400 Гц
23. Определить частоту сигнала на входе Y, если частота сигнала на входе X равна 1600 Гц
24. Определить частоту сигнала на входе Y, если частота сигнала на входе X равна 1400 Гц

 

Окончание таблицы 6.3

 

1	2
25. Определить частоту сигнала на входе Y, если частота сигнала на входе X равна 1800 Гц
26. Определить частоту сигнала на входе Х, если частота сигнала на входе Y равна 300 Гц
27.Определить частоту сигнала на входе Y, если частота сигнала на входе X равна 1600 Гц
28. Определить частоту сигнала на входе X, если частота сигнала на входе Y равна 400 Гц

 

Построить графически осциллограммы, если известно, что к осциллографу с одинаковой чувствительностью к отклонению по вертикали и горизонтали приложены напряжения

а) при линейной развертке

 

кпластинам"Y"

 

к пластинам"Х"

 

 

Временем обратного хода луча можно пренебречь. Значения А, В, φ, kберутся из таблиц 7.4 и 7.5.

 

Таблица 6.4

 

Таблица 6.5

 

б) при синусоидальной развертке к пластинам "Y"

 

К пластинкам "X"                                                                             

Исходные данные взять из таблиц 6.4, 6.5 и 6.6

Таблица 6.6

L	0	1	2	3	4	5	6	7	8	7
i	1	2	4	3	1	3	2	1	2	3
j	2	3	1	2	4	1	3	3	1	2

 

Примеры решения задач

Задача 1

Определить амплитуду и период сигнала, если коэффициенты от­клонения осциллографа равны 0,2 мс/дел и 1 В/дел для осциллограммы

 

Решение

Данная осциллограмма получена в первом основном режиме рабо­ты осциллографа - в режиме линейной развертки. Измерение частоты в этом режиме производится методом линейной калиброванной разверт­ки.

Сигнал на осциллограмме является однополярным, поэтому ампли­туда сигнала рассчитывается по формуле (12.6)

= 5 дел· 1 В/дел = 5 В

Измерение периода сигнала производится методом линейной ка­либрованной развертки, поэтому период сигнала рассчитывается по формуле (12.7)

 

Задача 2

Определить частоту сигнала на входе Y, если частота сигнала на вхо­де

X равна 100 Гц для осциллограммы

Решение

Данная осциллограмма в виде фигуры Лиссажу получена во втором режиме работы осциллографа - в режиме сравнения. Измерение частоты в этом режиме производится методом синусоидальной развертки.

По условию задачи напряжение измеряемой u_с(t) подается на вход Y, образцовой частоты u_обр(t) – вход Х , что соответствует первому спо­собу подачи напряжений (6.7). Тогда неизвестная частота f_сбудет определяться соотношениями (6.12):

 

отсюда

 

Задача 3

Построить осциллограмму при линейной развертке для следующих исходных данных:

 

.

 

Решение

При построении осциллограмм выполняются следующие действия.

Поле чертежа разбивается на 4 квадранта. В первом изображается сигнал U_с(t), поданный на пластины вертикального отклонения "Y", в третьем - сигнал U_p(t), поданный на пластины горизонтального откло­нения ''X", во втором квадранте строится изображение, формируемое на экране осциллографа. При этом масштабы по осям времени и ампли­туд в первом и третьем квадратах должны быть одинаковыми.

Решение задачи выполняется в следующей последовательности:

1)выбрать произвольно масштаб и построить напряжения разверт­ки Up(t);

2)построить Uc(t), учитывая, что в том же масштабе должно уложиться 2 периода (К=2) напряжения сигнала;

3)графически построить осциллограмму (рис 6.4)

 

Правило построения осциллограммы. Отложите на осях времени для U_p(t) и u_p(t) равные отрезки, разбейте их на одинаковое количество интервалов,иобозначьтеиходинаковымицифрами.Точки,обозначенныеодинаковыми цифрами и соответствующие u_p иu_p,сносите пунктирными линиями до тех пор, пока они не пересекутся.

Точки пересечения обозначьте теми же цифрами. Изображение на экране осциллографа получится путем последовательного соединения точек пересечения.

Построение осциллограммы при синусоидальной развертке производится аналогично при условии, что на пластины X и Yподается система гармонических напряжений согласно варианту МL.

 

Рис. 6.4.Графическое построение осциллограммы

 

 

 

 

 

 

7. МОСТОВЫЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ДВУХПОЛЮСНИКОВ

 

7.1. Измерение сопротивления

 

Наиболее распространенный метод – метод амперметра и вольтметра, основанный на применении закона Ома для участка цепи

                                              (7.1)

где – измеряемое сопротивление, Ом;U– падение напряжения на измеряемом сопротивлении, В; I– ток, проходящий через это сопротивление, А.

Измерение сопротивлений этим методом можно производить по двум схемам (рис. 7.1).

 

 

Рис. 7.1. Измерение сопротивления методом амперметра

и вольтметра: а) малых сопротивлений; б) больших сопротивлений

 

Если не требуется большая точность измерений, то можно воспользоваться показанием амперметра и вольтметра и рассчитать сопротивление по формуле (7.1). Для измерения малых сопротивлений с большей точностью с учетом схемы включения можно использовать схему рис. 7.1,а, для которой

                                               (7.2)

где U – напряжение, измеряемое вольтметром, В; I– ток, измеряемый амперметром, А; – сопротивление вольтметра, Ом.

Схему рис. 7.1, б можно использовать для определения действительного значения больших сопротивлений с учетом схемы включения приборов и определить его по формуле

,                                              (7.3)

где U– напряжение, измеряемое вольтметром, В;I– ток, измеряемый амперметром, А;– сопротивление амперметра, Ом.

Для выбора схемы включения амперметра и вольтметра необходимо воспользоваться критерием, что если  , то выбираем cхему на рис. 7.1, а, а если , то схему рис. 7.1, б.

Значительно точнее сопротивления могут быть измерены с помощью мостов постоянного тока. Простейшая схема моста представлена на рис. 7.2.

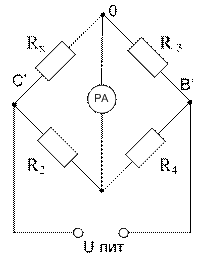
Рис. 7.2. Мостовая схема измерения сопротивления

 

В одно из плеч моста включают измеряемое сопротивление и, изменяя сопротивление любого плеча, добиваемся отсутствия тока в измерительной диагонали – индикатор нуля должен показывать ноль.

 

Примеры решения задач

1. Необходимо измерить ток потребителя в пределах 20–25 А. Имеется микроамперметр с пределом измерения 200 мкА, внутренним сопротивлением 300 Ом и максимальным числом делений 100. Определить сопротивление шунта для расширения пределов измерения до 30А и относительную погрешность измерения на отметке 85 делений, если класс точности прибора 1,0.

Решение. Необходимо вначале определить коэффициент шунтирования

.

Тогда,

.

Определяем показание амперметра, соответствующее 85 делениям, для чего цену деления 0,3 А/дел умножим на число делений 85, тогда прибор покажет

Относительная погрешность в этой точке

где A.

2.В сеть переменного тока через измерительный трансформатор тока 100/2,5 А и измерительный трансформатор напряжения 600/150 В включены амперметр, вольтметр и ваттметр, которые показали соответственно 100, 120 и 88 делений. Пределы измерения приборов следующие: амперметр – 3 А, вольтметр – 150 В, ваттметр – 2,5 А по току, 150 В – по напряжению. Все приборы класса точности = 0,5 имеют максимальное число делений 150. Определить полную потребляемую мощность, ее полное сопротивление и коэффициент мощности, наибольшую абсолютную и относительные погрешности измерения полного сопротивления, учитывая класс точности прибора.

Решение. Определяем цену деления каждого прибора как отношение измерения к максимальному числу делений. Для амперметра цена деления 0,02 А/дел, для вольтметра – 1 В/дел, для ваттметра – 2,5 Вт/дел. Тогда показания приборов:

;

Коэффициенты трансформации:

Ток, напряжение и активная мощность сети

Полную мощность, потребляемую сетью, определяем через ток и напряжение

Коэффициент мощности

Полное сопротивление сети

Ом

Наибольшее значение полного сопротивления

Ом,

 

где

 ,B;

 

 

 ,A;

 

 

Отсюда абсолютная погрешность

Относительная погрешность измерения

3.Амперметр включен в неразветвленную часть электрической цепи (рис. 8.3), причем сопротивления резисторовR₁= 2 Ом;R₂=Rз = 4 Ом, полное сопротивление переменного резистораR₄= 10 Ом.ЭДС источника питания цепи 15 В, его внутреннее сопротивлениеR_в= 0,5 Ом. Найти показания амперметра в двух крайних положениях резистора и выбрать сопротивлениеR_Aчтобы вносимая им погрешность измерения не превышала 1 %.

Рис. 7.3. Схема к задаче 3

 

Решение. Эквивалентное сопротивление цепи относительно выводов» источника определяется из выражения

R_экв=R₁+R₄+R_A+R₂Rз /(R₂+Rз).

Чтобы выбрать внутреннее сопротивление амперметра, необходимо воспользоваться формулой

 

Входное сопротивление цепи относительно выводов амперметра

R_вх=R₁+R₄+R_В+R₂Rз/(R₂+Rз).

Очевидно, что наименьшее сопротивление цепи будет при выведенном резистореR₄, т. е. для расчета необходимо выбрать

R_вх=R₁+R_В+R₂Rз/(R₂+Rз)4,5 Ом,

получаем

R_A«R_вх/100= 0,045 Ом

Эквивалентное сопротивление цепи в двух крайних положениях резистораR₄равноR_эmin= 4,5 Ом иR_эmax= 14,5 Ом. Показания амперметра соответствуют токам цепиI₁=3,3 А иI₂=1,03 А. Следовательно, верхний предел измерения амперметра должен быть не менее 5 А.

4.Методом амперметра и вольтметра измеряется сопротивление по схеме рис. 2, а. Показания амперметра и вольтметра следующие:

U=4.8 В,I=0.15 А. Приборы имеют класс точности=1,0 и пределы измерения мА,  В

Определить измеряемое сопротивление, наибольшую абсолютную и относительную погрешности измерения.

 Решение.Измеряемое сопротивление

Ом.

Наибольшая абсолютная погрешность вольтметра и амперметра соответственно с указанными пределами и классом точности

В,

мА=0,0025 А,

Наибольшее значение измеряемого сопротивления с учетом класса точности применяемых приборов

Ом.

Тогда относительная погрешность измерения

 

 

7.2. Задачи для самостоятельного решения

 

7.1. Цифровой омметр имеет следующие поддиапазоны измерения: 10 и 100 Ом; 1 и 100 кОм; 1 МОм. С какой относительной погрешностью могут быть измерены сопротивления 5, 70 и 300 Ом; 1 и 400 кОм, если постоянные коэффициенты для всех поддиапазонов равны соответственно С = 0,3 % и В = 0,1 %?

7.2. В четырехпредельном омметре, выполненном по схеме логометра, предел измерения каждого поддиапазона в 10 раз больше предыдущего, предел измерения первого – 100 Ом. Определить значения коэффициента шкалы к для каждого поддиапазона, если полный угол поворота указателя равен 90°, а соотношение между сопротивлениями рамок R_Р1 = R_Р2+ Rогр = 100 Ом. Определить максимально возможное измеряемое сопротивление в данном приборе.

7.3. Ток диагонали уравновешенного моста равен нулю при сопротивлении его плеч соответственно R₂= 100 Ом; Rз = 200 Ом; R₄ = 50 Ом. Определить сопротивление резистора RX.

7.4. Сопротивления плеч мостовой схемы (рис. 7.4): R₂ = 200 Ом; R₃ = 100 Ом; R₄ = 300 Ом и R_X = 100 Ом. Чему равно напряжение диагонали моста при холостом ходе, если напряжение питания моста 15 В?

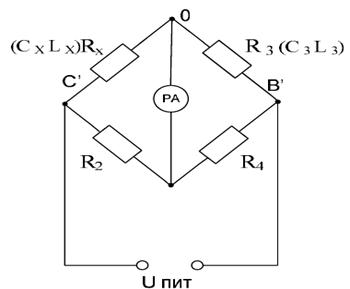
Рис. 7.4 Мостовая схема

 

7.5. Для подбора резисторов используется мостовая схема (см. рис. 7.4) с микроамперметром РА, шкала которого имеет отметки, соответствующие допуску на номинал сопротивления резисторов. Сопротивление резистора R₃ выбирается равным номинальному сопротивлению резистора Rх= 100 Ом, сопротивление плеч моста R₂ = R₄ =15 кОм. Определить значения тока, при которых на шкале можно будет поставить отметки ±1; ±2,5 и ±5%, если напряжение источника U_пит=1,5 В. Внутренними сопротивлениями микроамперметра и источника пренебречь.

7.6. Для точного измерения сопротивлений используется измерительный мост, схема которого приведена на рис. 7.5, Определить сопротивление Rх, если сопротивления плеч R₁=1 кОм; R₂ = 0,5 кОм и R₄ = 1,8 кОм, а полное сопротивление временного резистора R = 2 кОм. Равновесие моста наступает при положении подвижного контакта посередине переменного резистора.

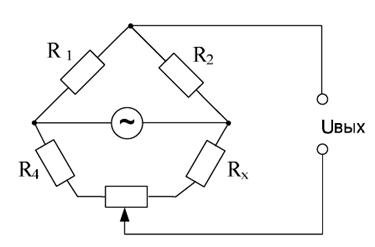
Рис. 7.5Измерительный мост

 

7.7.С помощью мостовой схемы приведенной на рис. 7.6, определяется место короткого замыкания в соединительных проводах. На каком расстоянии от измерительного прибора находится неисправность, R₃ =10 Ом и мост был уравновешен при сопротивлении R₁= 25 Ом? Соединительная линия выполнена из медного провода сечением 1,5

Рис. 7.6Мостовая схема

7.8. При измерении сопротивления резистора Rх с помощью уравновешенного моста (рис. 8.4) в смежное плечо моста включен резистор сопротивлением Rз= 1кОм, а в два других плеча поставлены два переменных резистора, сопротивления которых меняются от 0,5 до 2 кОм. В каком диапазоне могут быть изменены сопротивления в данном случае?

7.9. При измерении сопротивления резистора методом амперметра и вольтметра показания их были равны 2 А и 50 В при положении ключа 1 (всхеме на рис. 7.8). Определить сопротивление резистора, если внутреннее сопротивление амперметра R_A = 0,5 Ом.

7.10. При измерении сопротивления резистора методом амперметра и вольтметра показания их были равны 11 мА и 10 В при положении ключа 2 в схеме на рис. 7.7. Определить сопротивление резистора, если внутреннее сопротивление вольтметра RV = 100 кОм.

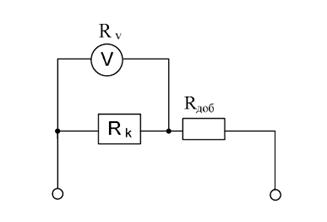
Рис. 7.7 Схема измерительного моста

7.11. При измерении сопротивления якоря двигателя переменного тока методом амперметра и вольтметра (рис 7.8) показания приборов были равны 10 А и 30 В. Амперметр имеет внутреннее сопротивление R_A = 0,1 Ом, внутреннее сопротивление вольтметра R_V=5кОм. Чему равна дополнительная относительная погрешность, вносимая внутренними сопротивлениями приборов в обоих случаях, т. е. при положениях 1 и 2 ключа?

7.12. Определить сопротивление резистора, если при положении ключа 1 (в схеме на рис. 7.8), амперметр с внутренним сопротивлением RA = 10 Ом показал 10 мА. Показание вольтметра 1В. Чему равна абсолютная погрешность измерения, если ток измерялся с точностью 1 %, а напряжение – с точностью 2 %?

7.13. Определить сопротивление резистора, если при положении ключа 2 (в схеме на рис. 7.8), вольтметр с внутренним сопротивлением RV = 10 кОм показал 1 В. Показание амперметра 10 мА.Чему равна абсолютная погрешность измерения, если ток измерялся с точностью 1,5%, а напряжение – с точностью 2,5%?

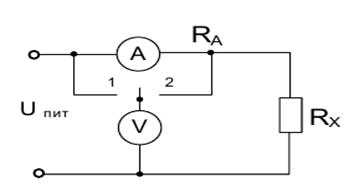
Рис.7.8Схема измерительного моста

7.14. При измерении сопротивления нелинейного элемента методом амперметра и вольтметра напряжение на нем было 6 В, а ток 2 мА. При изменении напряжения на 0,5 В ток изменился на 50 мкА.  Найти статическое и дифференциальное сопротивления элемента.

7.15. Определить сопротивление Rх в схеме на рис. 7.9, а, если при включении вольтметра с внутренним сопротивлением R_V = 40 кОм непосредственно к источнику его показание было равно 110 В, а при подключении последовательно с сопротивлением Rх стало равным 75 В.

7.16. Сопротивление измеряется с помощьюизмерительной схемы на рис. 7.9 б. Когда ключ находился в положении 2, ток амперметра был равен 0,5А, а при переводе ключа в положение 1 его показание соответствовало 0,2 А. Найти искомое сопротивление, если внутреннее сопротивление RA = 0,1 Ом, а образцовое сопротивление R0 = 50 Ом.

Рис.7.9 Схема измерительного моста

 

 

8. СТАНДАРТИЗАЦИЯ МАРКИРОВОЧНЫХ ЗНАКОВ НА ПРОДУКЦИИ

 

8.1. Краткие теоретические сведения

 

Информация, наносимая изготовителем на конкретные товары должна содержать следующие сведения:

1) наименование товара;

2) наименование страны – производителя;

3) наименование фирмы – изготовителя (эта информация может быть дополнительно обозначена буквами латинского алфавита);

4) основное или функциональное назначение или область применения;

5) правила и условия безопасного хранения, транспортирования, использования, утилизации (при необходимости);

6) основные потребительские свойства и характеристики;

7) информацию об обязательной сертификации;

8) товарный знак (марку) изготовителя (при наличии);

9) дату изготовления;

10) штриховой код товара;

11) юридический адрес изготовителя и (или) продавца;

12) массу нетто, основные размеры, объем или количество;

13) комплектность (состав);

14) срок годности (или службы);

15) обозначение нормативного или технического документа, в соответствии с которым изготавливается товар (для товаров отечественного производства);

16) информацию о добровольной сертификации (при наличии);

17) информацию о знаке соответствия товара национальным стандартам (на добровольной основе);

18) специфическую информацию для потребителя (при необходимости).

         Пункты 1 – 10 являются обязательными для указания изготовителями и (или) продавцами. В зависимости от вида технической сложности товара изготовитель может применить все или часть пунктов 11 – 18.

         Существует понятие «маркировка продукции знаком соответствия», которая представляет собой только изображение знака соответствия, нанесенного на продукцию, тару (упаковку), сопроводительную техническую документацию. Также существует понятие «знак обращения на рынке», который указывает на соответствие товара техническому регламенту. При маркировке применяют следующие технологические приемы:

1) клеймение готового изделия, упаковочной единицы;

2) оформление сопроводительной документации знаком соответствия ( и /или знаком обращения на рынке);

3) применение комплектующих изделий, упаковочных материалов и бланков сопроводительной документации с нанесением на них изображения знак соответствия;

4) прикрепление специально изготовленных носителей знака соответствия (ярлыков, этикеток, самоклеящихся лент и т.д.)

         Ответственность за соблюдение правил маркировки возложена на предприятия – изготовители, организации – импортеры, торговые организации, а также на индивидуальных предпринимателей.

         В данной практической работе рассмотрим наиболее распространенные маркировочные знаки мониторов персональных компьютеров (ПК).

 

8.2. Задание

 

         Произвести подробную расшифровку знаков, указанных на этикетке ПК

         Варианты для самостоятельного рассмотрения представленыв табл. 8.1.

Таблица 8.1

Вариант	Обозначение на мониторе ПК
1	2
1
2
3
4

Продолжение таблицы 8.1

 

Продолжение таблицы 8.1

1	2
9
10
11
12

Продолжение таблицы 8.1

1	2
13
14
15
16

Продолжение таблицы 8.1

1	2
17
18
19
20

Окончание таблицы 8.1

1	2
21
22
23
24

                                                                                                           

9. ШТРИХОВОЕ КОДИРОВАНИЕ ТОВАРОВ

 

9.1. Краткие теоретические сведения

 

         В последнее время наблюдается тенденция внедрения разновидности информационных технологий, основанных на использовании штрихового кодирования. Товары массового спроса снабжаются этикетками и ярлыками, на которые нанесен штрих – код, позволяющий однозначно идентифицировать товар и производителя. Места приема и продажи товаров снабжены техническими средствами, которые обеспечивают автоматическое считывание кодов и введение полученной информации в ЭВМ для дальнейшей обработки, проведения кассовых расчетов.

         Штриховым называется код, состоящий из знаков набора параллельных чередующихся темных (штрих) и светлых (пробел) полос различной ширины. Размеры полос стандартизированы. Самый узкий штрих принят за единицу. Каждая цифра складывается из двух штрихов и двух пробелов. Наличие штрих – кода позволяет полностью автоматизировать процесс управления движением товаров, бухгалтерскую деятельность, обеспечить контроль динамики продажи товаров, оперативно удовлетворять нужды потребителей.

         Информация в штриховом коде определяется соотношением ширины штрихов и пробелов. Высота не несет информационной нагрузки и выбирается из соображений удобства считывания.

         Штриховые коды условно можно разделить на два типа:

1)    товарные (имеют два ряда – штриховой и цифровой);

2)    технологические (имеют один штриховой ряд)

         На сегодняшний день разработано большое количество товарных штрихкодов. К ним относятся код UPC (UniformProductCode), применяемый в США и Канаде, и код EAN(EuropeanArticleNumbering), применяемый практически на всех континентах.

         Код UPC бывает 10–, 12–, 14 – разрядным. Штрихкод, состоящий из 14 цифр и обведенный в жирную темную рамку, предназначен для упаковки.

         ШтрихкодыEAN – 8 применяют для товаров небольших размеров.

 Таблица 9.1

Структура кода EAN – 8

 

Таблица 9.2

Структура кода EAN – 13

 

Таблица 9.3

Структура кода UPC – 10

 

Таблица 9.4

Структура кода UPC – 12

 

Таблица 9.4

Структура кода UPC – 14

 

         Первые три цифры кодов называются префиксом (флагом страны) национальной организации. Его присваивает EAN. Код предприятия – производителя составляется каждой стране соответствующим национальным органом.

         Контроль штрихкода необходим для исключения ошибок при вводе в компьютерные системы.

9.2. Алгоритм расчета контрольной цифры

 

         Для расчета контрольной цифры следует:

1) пронумеровать все разряды цифрового ряда справа налево, начиная с позиции контрольного разряда (первый);

2) начиная со второго, сложить цифры всех четных разрядов и полученную сумму умножить на 3;

3) начиная с третьего, сложить цифры всех нечетных разрядов;

4) сложить обе полученные суммы;

5) значение контрольного разряда является наименьшим числом, которое в сумме с величиной, полученной в пункте 4, даст число кратное 10.

 Пример

13	12	11	10	9	8	7	6	5	4	3	2	1
4	2	7	6	2	2	1	3	5	7	4	6	9

 

1) 6+7+3+2+6+2=26;

2) 26·3=78;

3) 4+5+1+2+7+4=23;

4) 78+23=101;

5) 101+9=110.

         При совпадении контрольной цифры с добавляемой для кратности цифрой – штрихкод верен.

 

9.3. Задание

 

         Проанализировать реальный штриховой код, проверить подлинность первого и третьего штрихкодов,рассчитать контрольную цифру второго штрихкода. Результаты изучения штрихкодов представить в виде табл. 9.5.

Таблтца 9.5

Информация о заданных штрихкодах

Вид штрихкода	Полный штрихкод	Цифровой код
		страны	изотовителя	товара	контрольного разряда
EAN – 8
EAN – 13
UPC – 10
UPC – 13
UPC – 14

 

Варианты задания представлены в табл. 9.6.

Таблица 9.6

Вариант	Штрихкод
1	2
1
2
3

Продолжение таблицы 9.6

1	2
4
5
6
7
8
9
10
11

 

Продолжение таблицы 9.6

1	2
12
13
14
15
16
17
18
19

 

Продолжение таблицы 9.6

1	2
20
21
22
23
24
25
26
27

Окончание таблицы 9.6

1	2
28
29
30

 

ЛИТЕРАТУРА

 

1. Метрология и электрорадиоизмерения в телекоммуникационных системах: Учебное пособие/ С.И. Боридько. Н.В. Дементьев, Б.Н. Тихонов, И.А. Ходжаев.; Под ред. Б.Н. Тихонова - М.: Горячая линия - Телеком,2007

2. Метрология и измерения в телекоммуникационных системах (Том 1): Учебник для вузов / Б.П. Хромой - М.: ИРИАС, 2007

3. Метрология и электрорадиоизмерения в телекоммуникационных системах: Учебник для вузов / В.И. Нефедов, В.И. Хахин, Е.В. Федорова и др.; Под ред. В.И. Нефедова. - М.: Высш. шк., 2005

4. Метрология и электрорадиоизмерения в телекоммуникационных системах: Учебник для вузов / В.И. Нефедов, В.И. Хахин, Е.В. Фе­дорова и др.; Под ред. В.И. Нефедова. - М.: Высш. шк., 2001

5. Метрология, стандартизация и измерения в технике связи. Учебное пособие для вузов/ Б.П. Хромой, А.В. Кандинов, А.Л. Сенявский и др.; Под ред. проф. Б.П. Хромого - М.: Радио и связь, 1986-424с.

6.Сергеев А.Г., Крохин В.В. Метрология. Учебное пособие для вузов. - М.: ЛОГОС, 2001-408с.

7. Крылова Г.Д. Основы стандартизации, сертификации, метрологии: Учебник для вузов.- 2-е изд., перераб. и доп. - М.: ЮНИТИ - ДАНА, 2000-711с.

8. Мирский Г.Я. Электронные измерения. -М.: Радио и связь, 1786- 440с.

13.Шишкин И.Ф. Метрология, стандартизация и управление качеством.-М.: Издательство стандартов, 1070.

14.GOOGLE.ru

Содержание

 

 

	Введение		3
1		Теория воспроизведения единиц измерения.Единицы измерения в международной системе СИ...............................	5
	1.1	Метр.............................................................................................	5
	1.2	Кратные и дольные единицы....................................................	7
	1.3	Килограмм…………………………………………………......	8
	1.4	Кратные и дольные единицы....................................................	9
	1.5	Эталон килограмма....................................................................	9
	1.6	Грамм..........................................................................................	10
	1.7	Килограмм-сила.........................................................................	10
	1.8	Секунда.......................................................................................	11
	1.7	Кратные и дольные единицы....................................................	11
	1.10	Ампер..........................................................................................	12
	1.11	Кратные и дольные единицы...................................................	12
	1.12	Кельвин.......................................................................................	13
	1.13	Кратные и дольные единицы....................................................	13
	1.1	Кандела.......................................................................................	14
	1.15	Кратные и дольные единицы....................................................	14
	1.16	Моль............................................................................................	15
	1.17	Кратные и дольные единицы....................................................	15
	1.18	Задачи для самостоятельного решения....................................	16
2		Логарифмические единицы. Уровни передачи……….…......	19
	2.1	Понятие о децибелах………………………………………….	19
	2.2	Уровни передачи………………………………………………	22
	2.3	Текст задания и условие задачи………………………………	26
3		Погрешности измерений и их классификация........................	29
4		Измерение напряжения и силы тока........................................	35
	4.1	Краткие теоретические сведения…………………………….	35
	4.2.	Задачи для самостоятельного решения………………………	39
5		Измерение мощности.................................................................	43
	5.1	Краткие теоретические сведения…………………………….	43
	5.2	Задачи для самостоятельного решения………………………	45
6		Осциллографические методы измерения амплитуды и интервалов времени электрических сигналов........................	49
	6.1	Измерение напряжения ………………………………………	50
	6.2	Измерение частоты……………………………………………	52
	6.3	Измерение частоты методом синусоидальной развертки….	54
	6.4	Текст задания и условие задачи……………………………...	54
7		Мостовые методы измерения параметров двухполюсников	63
	7.1	Измерение сопротивления……………………………………	63
	7.2	Задачи для самостоятельного решения……………………...	70
8		Стандартизация маркировочных знаков на продукции.........	74
	8.1	Краткие теоретические сведения..........................................	74
	8.2	Задание..................................................................................	76
9		Штриховое кодирование товаров……………………………	83
	9.1	Краткие теоретические сведения…………………………….	83
	9.2	Алгоритм расчета контрольной цифры...............................	85
	9.3	Задание…………………………………....................................	86
Список использованной литературы....................................................			91

 

 

Методические указания к практическим занятиям по дисциплине "Метрология стандартизация и сертификация" для студентов 1 – курса

всех направлений образования

 

Методические указания рассмотрены на заседании кафедры ВОЛ и СИ

(протокол № ___ от ___ апреля 2016 г.)

 

Методические указания рекомендованы к изданию учебно – методическим советом факультета Телекоммуникационные технологии (протокол № ___ от ___ мая 2016 г)

Общее руководство и ответственный редактор:

к.т.н., доцент Парпиев М.П.

Составитель:

ассистент кафедры ВОЛ и СИ Нуштаева О.Х.

Рецензент:

Профессор кафедры ТИ Исаев Р.И.

Корректор:

завкафедрой  Абдуллаева С.Х.