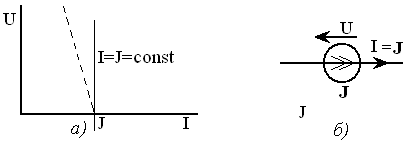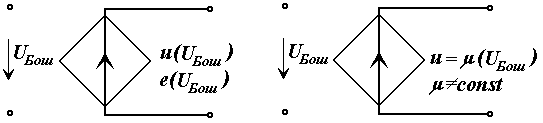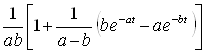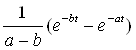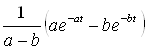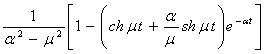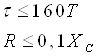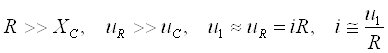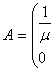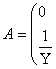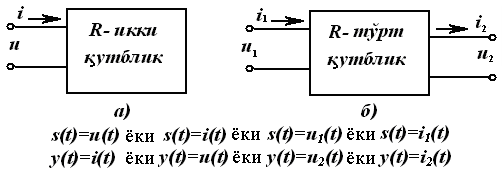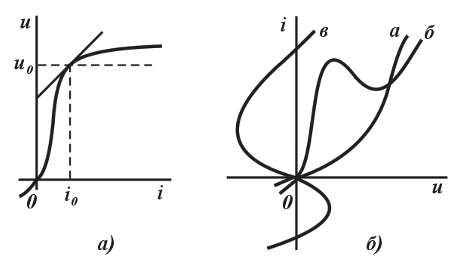К.Т.Олимхўжаев, В.А.Тўлаганова
ЭЛЕКТР ЗАНЖИРЛАР НАЗАРИЯСИ
Маърузалар матни
Ахборот технологиялари олий ўқув юртларининг 5140900 – Техник таълим педагогикаси (Телекоммуникация), 5211700 – Кино-телеоператорлик, 5211800 – Махсус ёритиш технологиялари, 5522000 – Радиотехника, 5522100 – Телевидение, радиоалоқа ва радиоэшиттириш, 5522200 –Телекоммуникация, 5525500 – Аудио-видео технологиялари, 5525600 – Компьютер графикаси, 5525700 – Овоз ёзиш технологиялари йўналишлари учун мўлжалланган
Тошкент 2011
УДК 621.3.01
Ушбу маърузалар матни Тошкени Ахборот технологиялари университетининг ўқув-услубий Кенгаши томонидан тавсия этилган.
Тақризчилар:
электромагнит майдони ва унинг ажралмас ташкил этувчилари бўлган электр ва магнит майдонлари назарияларини батафсил баён этиш билан
Ушбу маърузалар матнида ахборот технологиялари тизимларининг юқори ва ўта юқори частотали муҳитларида алоҳида аҳамиятли бўлган ўтказувчанлик, силжиш ва кўчиш токларининг физик хусусиятлари, уларнинг амалиётдаги ўринлари тасвирланиб, ўзгармас ва гармоник токли занжирларнинг асосий қонунлари, резонанс ҳодисалари, уларни ҳисоблаш ва таҳлил қилиш усуллари тушуниш учун осон ва батафсил келтирилган. Ўткинчи жараёнларни ҳисоблашнинг классик, оператор, вақт ва частотавий усуллари, улар орасидаги тафовут ва боғланишлари кўрсатилган. Тўрт қутбликлар, тарқоқ параметрли ва ночизиқли занжирлар, оддий ва рақамли фильтрларни таҳлил ва синтез қилиш, ҳисоблаш масалалари тўлиқ келтирилган.
Маърузалар матни ахборот технологиялари олий ўқув юртларининг бакалавриатура талабалари учун мўлжалланган.
ЭЛЕКТР ЗАНЖИРЛАР НАЗАРИЯСИ
Олий ўқув юртлари талабалари учун маърузалар матни.
МУНДАРИЖА
|
Кириш . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
9 |
|
1-маъруза. Зарядланган зарачалар, электромагнит майдон ва электр токи турлари. Ток узлуксизлиги . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
12 |
|
1.1. Зарядланган заррачалар ва электромагнит майдон . . . . . . . . . |
12 |
|
1.2. Ўтказувчанлик, кўчириш ва силжиш токлари. Токнинг узлуксизлиги . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
14 |
|
2-маъруза. Кучланиш, потенциаллар фарқи. Электр юритувчи куч . |
22 |
|
2.1. Кучланиш . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
22 |
|
2.2. Электр потенциали ва потенциаллари фарқи . . . . . . . . . . . . . . . . |
23 |
|
2.3. Электр юритувчи куч . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
27 |
|
3-маъруза. Электр занжири. Элементлари . . . . . . . . . . . . . . . . . . . . . . |
31 |
|
3.1. Электр занжири. Актив элементлар . . . . . . . . . . . . . . . . . . . . . . . . |
31 |
|
3.2. Пассив элементлар . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
32 |
|
3.3. Реал элементларни идеаллаштириб алмаштириш . . . . . . . . . |
35 |
|
4-маъруза. Электр занжирлари назарияси асосий қонунлари . . . . . . . |
40 |
|
4.1. Кирхгоф қонунлари . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
40 |
|
4.2. Ом қонуни . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
44 |
|
5-маъруза. Электр занжирларини ҳисоблаш усуллари . . . . . . . . . . . |
46 |
|
5.1. Эквивалент алмаштириш усули . . . . . . . . . . . . . . . . . . . . . . . . . . . |
46 |
|
5.2. Кирхгоф қонунларини татбиқ этиш . . . . . . . . . . . . . . . . . . . . . . |
48 |
|
5.3. Кирхгоф қонунлари асосида тузилган тенгламалар тўлиқлиги |
50 |
|
6-маъруза. Суперпозиция, контур токлар ва тугун потенциаллари усуллари . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
53 |
|
6.1. Суперпозиция (устлаш ёки жамлаш) усули . . . . . . . . . . . . . . . . . |
53 |
|
6.2. Контур токлар усули . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
55 |
|
6.3. Тугун потенциаллари усули . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
58 |
|
7-маъруза. Ўзгарувчан ток занжирлари . . . . . . . . . . . . . . . . . . . . . . . . |
61 |
|
7.1. Гармоник ток занжирларининг умумий тавсифлари |
61 |
|
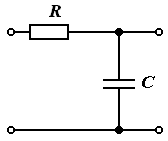
7.2. Таркибида R ,C бўлган занжирдан гармоник ток . . . . . . . . . . . . . |
63 |
|
7.3. Даврий миқдор таъсир этувчи (ўртача квадратик) қиймат . . . . |
66 |
|
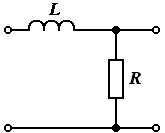
7.4. L ва r занжирда гармоник ток . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
66 |
|
7.5. Комплекс қувват. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
67 |
|
8-маъруза. Ҳисоблашнинг символик (комплекс) усули |
70 |
|
8.1. Оддий гармоник функциялар устида математик амалларни бажариш . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
70 |
|
8.2. Геометрик усул . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
70 |
|
8.3. Комплекс усул . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
71 |
|
9-маъруза. Гармоник ток занжирида қувват . . . . . . . . . . . . . . . . . . . . . |
78 |
|
9.1. Тўла қувват . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
78 |
|
9.2. Реактив қувват . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
79 |
|
9.3. Комплекс қувват . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
80 |
|
9.4. Қувват баланси (мувозанати) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
82 |
|
9.5. Максимал қувватни узатиш шартлари . . . . . . . . . . . . . . . . . . . . . . |
84 |
|
10-Маъруза. Индуктив боғланган занжирлар . . . . . . . . . . . . . . . . . . . . |
88 |
|
11-Маъруза. Комплекс узатиш функцияси . . . . . . . . . . . . . . . . . . . . . . |
97 |
|
12-Маъруза. Даврий носинусоидал таъсир ва унинг параметрлари . . |
100 |
|
12.1. Носинусоидал токли чизиқли занжирларни ҳисоблаш. . . . . . . . |
104 |
|
12.2. Мураккаб гармоник функциялари тавсифлари . . . . . . . . . . . . . . |
105 |
|
12.3. Қувват . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
107 |
|
13-Маъруза. Кетма-кет тебраниш контури. Кучланишлар резонанси |
110 |
|
14-Маъруза. Параллел тебраниш контури. Токлар резонанси. Тебраниш контурининг частота тавсифлари . . . . . . . . . . . . . . . . . . . . |
118 |
|
14.1 Частотавий тавсифлар. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
120 |
|
15-Маъруза. Чизиқли электр занжирларидаги ўтиш жараёнлари, классик усулда ҳисоблаш . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
126 |
|
15.1. Дифференциал тенгламалар. Коммутация қонунлари |
127 |
|
15.2. L, r, C контури . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
132 |
|
16-Маъруза. 1-тартибли чизиқли электр занжирларини ўзгармас кучланиш манбаига улаш ва электр занжиридан ўтиш жараёнлари |
134 |
|
16.1 L, r ли занжирга ўзгармас кучланиш манбасини улаш. . . . . . |
138 |
|
16.2. Ўзгарувчан кучланишли манбага r, С ли занжирни улаш . . . . . |
140 |
|
17-Маъруза. Ўтиш жараёнларини оператор усулда ҳисоблаш босқичлари . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
142 |
|
17.1 Оператор усули . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
142 |
|
17.2. Оддий функциялар тасвири . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
144 |
|
17.3 Оператор усули билан дифференциал тенгламаларни ечиш . . . |
147 |
|
17.4. Тасвирлар F(p) ва уларнинг оригиналлари ƒ(t) жадвали . . . . . . |
149 |
|
18-Маъруза. Оператор узатиш функцияси, унинг ноллари ва қутблари, уларнинг комплекс текисликд жойлашишлари . . . . . . . . . |
151 |
|
18.1 Нолли бошланғич шартлари бўлган ўткинчи жараённи ҳисоблаш . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
157 |
|
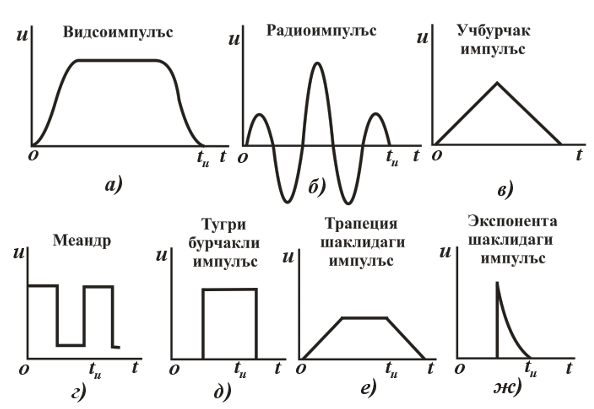
19-маъруза. Электр занжирларининг ўтиш ва импульс тавсифлари |
161 |
|
19.1. Электр занжирларига импульслар таъсирлари . . . . . . . . . . . . . |
161 |
|
19.2. Электр занжирларининг ўткинчи ва импульс тавсифлари. . . . |
164 |
|
20-маъруза. Дюамель ва жамлаш интеграллари 1-тартибли чизиқли электр занжирлар орқали тўғри бурчакли импульснинг ўтиши . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
169 |
|
20.1 Устлаш интеграли . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
171 |
|
21- маъруза. Дифференциалловчи ва интегралловчи занжирлар. . . . |
177 |
|
22-маъруза. Чизикли электр занжирини частотавий усулда таҳлил қилиш . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
183 |
|
22.1. Тебранишлар частотавий таркибининг таҳлили . . . . . . . . . . . . . |
183 |
|
22.2. Фурье интеграли . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
184 |
|
23-маъруза. Турткутбликларнинг узатиш тенгламалари параметрлари ва турлари . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
191 |
|
23.1 Тўртқутбликларнинг турлари . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
192 |
|
23.2 Тўртқутбликларнинг узатиш тенгламалари . . . . . . . . . . . . . . . . . |
192 |
|
23.3. Тўртқутбликларнинг параметрлари ва уларнинг ўзаро боғлиқлиги . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
194 |
|
24-маъруза. Тўртқутблик тавсифий параметрлари . . . . . . . . . . . . . . . |
199 |
|
24.1. Тўртқутбликларнинг каскадли боғланиши . . . . . . . . . . . . . . . . . |
202 |
|
24.2 Тўртқутбликларнинг ташқи тавсифлари . . . . . . . . . . . . . . . . . . . . |
203 |
|
24.3 Тўртқутбликнинг параметрлари. . . . . . . . . . . . . . . . . . . . . . . . . . . |
204 |
|
24.4 Тавсифий узатиш доимийси ва ишчи кучсизланиш. . . . . . . . . . . |
206 |
|
25-маъруза. Параметрлари тақсимланган электр занжирлар. . . . . . . . |
208 |
|
25.1 Умумий тушунчалар. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
208 |
|
25.2 Узун линиялар телеграф тенгламалари. . . . . . . . . . . . . . . . . . . . . |
211 |
|
25.3 Тўлқин тенгламаси ва унинг физик талқини. . . . . . . . . . . . . . . . . |
212 |
|
26-маъруза. Узун линияларда гармоник тўлқинлар. . . . . . . . . . . . . . . |
216 |
|
26. Узун линияларда импульс жараёнлар таҳлили. . . . . . . . . . . . . . . . |
222 |
|
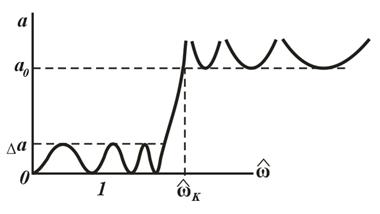
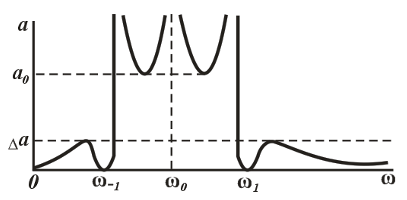
27-маъруза. Электр фильтрлари. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
229 |
|
27.1 Электр фильтрлари турлари ва тавсифлари. . . . . . . . . . . . . . . . . . |
229 |
|
27.2 Баттерворт тавсифига эга бўлган қуйи частотали полиномиал фильтри. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
231 |
|
27.3 Чебышев тавсифига эга бўлган қуйи частотали полиномиал фильтрлар. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
234 |
|
28-маъруза. Реактив электр фильтрни жадвал усулида ҳисоблаш . . |
237 |
|
28.1 Золотарев тавсифли қуйи частота фильтрлари. . . . . . . . . . . . . . |
237 |
|
28.2 Юқори частота фильтрлари. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
239 |
|
28.3 Йўлак ва рефлектор фильтрлари . . . . . . . . . . . . . . . . . . . . . . . . . . |
241 |
|
28.4 Фильтрларнинг фаза тавсифлари. . . . . . . . . . . . . . . . . . . . . . . . . . |
243 |
|
29-маъруза.Аналогли, дискретли ва ракамли фильтрлар. . . . . . . . . . . |
247 |
|
30-маъруза. Рақамли фильтрлар. Асосий тавсифлари. . . . . . . . . . . . . |
252 |
|
30.1. Дискрет сигналлар ва занжирлар. . . . . . . . . . . . . . . . . . . . . . . . . . |
252 |
|
30.2. Айирма тенгламаларни ечиш билан ЧРФни таҳлил қилиш. . . . |
255 |
|
30.3. ЧРФнинг импульс тавсифи. Ихтиёрий кириш кетма-кетлиги учун реакцияни ҳисоблаш. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
256 |
|
31-маъруза. Тескари боғланишли электр занжирлар. Турғунлик мезонлари . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
258 |
|
31.1 Барқарорлик мезони ҳақида тушунча . . . . . . . . . . . . . . . . . . . . . . |
260 |
|
31.2 Амплитудалар ва фазалар тенглик шарти . . . . . . . . . . . . . . . . . . . |
261 |
|
31.3 Ўз - ўзини қўзғатиш тебранишлари . . . . . . . . . . . . . . . . . . . . . . . |
262 |
|
32-маъруза. Автотебранишли занжирлар . . . . . . . . . . . . . . . . . . . . . . . |
265 |
|
32.1. Ташқи тескари боғланишли автогенератор. . . . . . . . . . . . . . . . . |
265 |
|
32.2. RC – генератор . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
267 |
|
32.3. Автогенератор дифференциал тенгламалари . . . . . . . . . . . . . . . . |
268 |
|
33-маъруза. Ночизиқли занжирларни таҳлил қилиш . . . . . . . . . . . . . . |
273 |
|
33.1. Инерциясиз элементли занжирларнинг таҳлили. . . . . . . . . . . . . |
276 |
|
33.2 Ночизиқли занжирларда сигнал спектрини ўзгартириш ва унинг амалиётда қўлланилиши . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
276 |
|
34-маъруза. Гармоник ток занжири. Диод ва транзисторнинг ночизиқли моделлари. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
282 |
|
34.1. Ночизиқли резистив икки қутбликлар статик тавсифлари . . . . |
282 |
|
35-маъруза. Ночизиқли занжирларни таҳлил қилиш. . . . . . . .. . . . . . . |
288 |
|
35.1. Амплитуда модулятори. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
288 |
Асосий белгилашлар
|
a - |
кучсизланиш, ишчи кучсизланиш |
|
b - |
фазавий тавсиф |
|
B - |
ўтказувчанликнинг реактив ташкил этувчиси |
|
C - |
сиғим |
|
E - |
электр юритувчи куч (эюк), таъсир этувчи қиймати |
|
Ė - |
комплекс эюк |
|
Em - |
гармоник эюк амплитудаси |
|
Ėm - |
гармоник эюкнинг комплекс амплитудаси |
|
f- |
тебраниш частотаси |
|
G - |
резистив ўтказувчанлик |
|
g - |
резистив ўтказувчанликнинг реактив ташкил этувчиси |
|
g(t) - |
занжирнинг импульс тавсифи |
|
H(jω) - |
комплекс узатиш функцияси |
|
H(p) - |
оператор узатиш функцияси |
|
I - |
токнинг таъсир этувчи қиймати, ўзгармас ток қиймати |
|
İ - |
комплекс токи |
|
Im - |
гармоник токнинг амплитудаси |
|
İm - |
токнинг комплекс амплитудаси |
|
i,i(t)- |
токнинг оний қиймати Im(a + jb) = c |
|
j - |
мавҳум бирлик |
|
k - |
алоқа коэффициенти, кучайтириш коэффициенти |
|
h(t) - |
занжирнинг ўткинчи тавсифи |
|
L - |
индуктивлик |
|
l - |
линия узунлиги |
|
M - |
ўзаро индуктивлик |
|
P - |
актив (ўртача) қувват |
|
p - |
комплекс ўзгарувчи, оний қувват, оператор белгиси |
|
Q - |
асиллик |
|
q - |
заряд |
|
R - |
резистив (Омик) қаршилик |
|
r - |
актив қаршилик |
|
T - |
тебраниш даври |
|
t - |
вақтнинг оний қиймати |
|
U - |
кучланишнинг таъсир этувчи қиймати |
|
Ů - |
комплекс кучланиш |
|
Um - |
гармоник кучланиш амплитудаси |
|
u,u(t) - |
кучланишнинг оний қийматлари |
|
X - |
қаршиликнинг реактив ташкил этувчиси |
|
Y(p) - |
икки қутбликнинг оператор ўтказувчанлиги |
|
Y(jω) - |
икки қутбликнинг комплекс ўтказувчанлиги |
|
Z(p) - |
икки қутбликнинг оператор қаршилиги |
|
Z(jω) - |
икки қутбликнинг комплекс қаршилиги |
|
ZB - |
линиянинг тўлқин қаршилиги |
|
α - |
линиянинг кучсизланиш коэффициенти |
|
β - |
линиянинг фаза коэффициенти |
|
γ - |
линиянинг тарқалиш коэффициенти |
|
∆a - |
фильтр ўтказиш оралиғи кучсизланиш тавсифининг коэффициенти |
|
δ(t) - |
бирлик импульс функцияси |
|
θ(t) - |
фаза-частотавий тавсиф |
|
ρ - |
линия (контур) тўлқин қаршилиги |
|
τ - |
ягона реактив элементли занжирнинг вақт доимийси |
|
Ψ - |
гармоник тебранишнинг бошланғич фазаси |
|
Ф - |
Магнит оқими |
|
φ - |
тебранишлар фазалари фарқи |
|
φB - |
линия тўлқин қаршилигининг аргументи |
|
φГ - |
Гурвиц комплекс полиномининг аргументи |
|
φр - |
қайтиш қуввати аргументи |
|
φY - |
икки қутблик комплекс ўтказувчанлиги аргументи |
|
φZ - |
икки қутблик комплекс қаршилиги аргументи |
|
ω - |
тебранишлар (айланма) частотаси
|
Кириш
Электр занжирларининг ривожланиши ва жамият ҳаётининг барча соҳаларига (саноат, транспорт, ахборот тизимлари, тиббиёт, маиший хизмат) жадал кириб бориши, унинг турли хил воситалар билан сигнал турини ўзгартириш, узоқ мософаларга етказиш, сигналлар ва ахборотни ўзгартириш ва узатиш муаммоларини ечишга имкон бериши билан изоҳлаш мумкин. Электрон ҳисоблаш машиналарининг жуда катта тезликда мураккаб математик амалларни, тенгламалар ва масалаларни ечишида, мураккаб ишлаб чиқариш жараёнларини автоматик бошқаришда сигналлар, тасвир ва ахборотнинг бошқа ҳар хил турларини (телеграф, радио, телевидение, мобиль, интернет алоқалари) қайта ишлаш, узатиш жараёнларида электр сигналлардан фойдаланилади.
Ҳозирги замон ахборотни етказиш, қайта ишлаш тизимлари шундай мураккаб техник қурилмалар бўлиб, электр занжирлари назарияси, радиотехника, электроника ва ҳисоблаш техникасининг энг охирги илмий техник ютуқларини ўз ичида мужассамлантиргандир. Охирги йилларда дунёнинг бир қанча давлатларида, шулар қаторида бизнинг давлатимизда ҳам, рақамли автоматик коммутацион станциялар, узатишнинг рақамли, толали-оптик тизимлари, спутник алоқа тизимлари билан жиҳозланган ҳар хил харқаро телекоммуникацион тармоқлар ишлаб чиқилмоқда ва эксплуатация қилинмоқда.
XIX аср бошларида магнетизм ва электр соҳаларидаги бажарилган илмий тадқиқотлар электр ва магнит ҳодисаларининг муҳим хусусиятларини, яъни электр зарядланган заррачаларнинг ҳаракати доимо магнит ходисалари билан бирга содир бўлишини ва уларнинг мутлоқ боғлиқлигини очиб берди. Бу билан 1600 йилда Гильберт томонидан таъкидланган электр ва магнит ҳодисаларининг ҳар бири мустақил ва ўзаро боғлиқ бўлмаган жараёнлар эканлиги ҳақидаги тушунча мутлақо ноўрин эканлиги исботлаб, 1831 йилда Фарадей электромагнит индукцияси ҳодисасини очди. У магнит майдони ёки токли контурга нисбатан ҳаракат қилаётган бошқа контурда ток ҳосил бўлишини аниқлади. Шундай қилиб, электр ҳодисалари ҳам магнит ҳодисалари жараёнининг натижасида ҳосил қилиниши мумкинлиги кўрсатиб берилди.
Бундан кейинги тадқиқотларда, жуда кичик узунликдаги электромагнит тўлқинлар ҳосил қилиниши ва тарқалиши, радио ихтиро қилиниши, радиоалоқанинг амалга оширилиши, амалий ва назарий радиотехниканинг шу каби кейинги ютуқлари Максвеллнинг электромагнит майдони назариясини экспериментал тасдиқлади.
Барча қилинган ихтиролар электр ва магнетизм ҳодисалари орасида чуқур боғлиқликлар мавжудлигини кўрсатади. Электромагнит ҳодисалар соҳасига тааллуқли бўлган назарий тушунчаларнинг умумий мажмуасида электр ва магнит занжирлари назарияси кўпроқ ривожланишга эришмоқда. Электр занжирлар назариясининг пойдеворида Ом (1827 й.), Жоуль (1841 й.), Ленц (1842 й.) ва Кирхгоф (1847 й.) асос солган қонунлар ётади. Унинг кейинги ривожланишида кўпгина олимлар ўз ҳиссаларини қўшганлар.
Телекоммуникация ва электр ўлчаш техникаси, электроэнергетик тизимлари, тезкор электрон ҳисоблаш машиналари, ахборот технологиялари, автоматик бошқарув ва назорат тизимларининг мисилсиз мураккабланиши ва ривожланиши натижасида уларни таҳлил қилиш учун умумлаштирилган услубларни ишлаб чиқиш зарурати туғилмоқда. Улар воситасида шу мураккаб тизимларнинг алоҳида қисмлари бўлган ва маълум вазифани бажарувчи электр занжирларининг бир қанча элементлари ўзларининг умумлаштирилган параметрлари орқали қаралади. Занжирнинг бундай элементлари комлекси сифатида, масалан, симли алоқа тизимларидаги, радио, телеузатишлардаги, электр ўлчашлар, автоматик бошқариш ва назоратидаги сигналлар генераторлари, кучайтиргичлари, энергия манбалари, электрон ҳисоблаш машиналаридаги мантиқий вазифаларни бажарувчи блоклари, дискрет рақамли ўзгарткичлари ва ҳ.к.бўлиши мумкин.
Бундай алоҳида комплекслар таркибига параметрлари токка боғлиқ бўлмаган занжирнинг чизиқли элементлари, масалан резисторлар, индуктивликлар, конденсаторлар ҳамда параметрлари ток ёки кучланишга боғлиқ бўлган занжирнинг ночизиқли элементлари, масалан электрон лампалар, транзисторлар, ферромагнит ўзакли индуктив ғалтаклар кириши мумкин. Занжирнинг бундай элементлари ўзаро турлича схемаларда уланган бўлади ва шу комплексларнинг таркибида етарли даражада мураккаб схемаларни ҳосил қилади. Комплекслар эса, ўз навбатида, у ёки бу усулда ўзаро уланиб, мураккаб тизимларни ҳосил қилади.
Мураккаб тизимларни таҳлил қилишнинг умумлаштирилган услублари, тизимнинг бир қисми бўлган ушбу алоҳида комплексларнинг ўзаро таъсирини тадқиқот қилиш имконини беради. Бундай умумлаштирилган услубларни қуришнинг бошланғич асослари сифатида, нисбатан мураккаб бўлмаган электр занжирларини ҳисоблашда қўлланилган, электр занжирларининг физик қонуниятлари ишлатилади.
Шунингдек, космик радиоалоқа ва радиоастрономия ҳамда янги электрофизик ва электротехнологик қурилмаларда электр, магнит майдонларини ва электромагнит нурланишларини янада тезкорлик ва кенг қўлланилиши натижасида электромагнит майдонлари ва электр занжирлар назарияларининг келгусидаги янада ривожланиши кутилмоқда.
Баён қилинган фикрлар ҳамма вақт, айниқса ҳозирги кунда, олий электротехник таълимнинг ниҳоятда юқори илмий даражада ташкил этилиши заруратини тақозо этади. Бу йўналишда ХХ асрда ЎФАнинг академиги Ғофур Раҳимович Раҳимов асос солган ва ҳозирги кунда унинг шогирдлари ва давомчилари томонидан ривожлантирилаётган «Электротехника назарий асослари» ва «Электр занжирлар назарияси» фанларининг ўқитилиши катта аҳамиятлидир.
Электр занжирлари назарияси (ЭЗН) фани, бир томондан, физика (электр ва магнетизм) ва математика (тушунтириш усуллари) фанлари асосида ташкил топган бўлса, иккинчи томондан, шу фанларнинг ривожи учун ҳам ўз ҳиссасини қўшди, яъни физиканинг электромагнит ҳодисаларини таҳлил қилиш қисмларига асос солди, ҳамда математика фанида тасвирлаш усулини ривожлантирди. Шу билан бирга, электр занжирлар назариясининг ривожланиши бир қатор янги физик тушунчалар, физик қонунларнинг янгича талқини, махсус математик усулларнинг ривожланиши, айнан электр занжирларида ва ускуналарда содир бўладиган типик ҳодисаларни таҳлил қилиш ва таърифлашда янги физик-техник масалаларнинг қайта қўрилишига олиб келди.
Компьютергача бўлган даврда муҳандис минимал ҳисоблашлардан фойдаланиб, нисбатан содда бўлган занжирларни синтез қила олар эди. Бунда занжирнинг макети тузилиб, ўлчовлар бажарилиб, созлаш, синов ишлари ўтказилар ва натижавий вариант ҳосил қилинар эди. Интеграл микросхемалар ва нисбатан арзон ЭҲМнинг пайдо бўлиши электр занжирларини ЭҲМлар ёрдамида таҳлил қилиш имкониятини туғдирди. Электр занжирларини машинада моделлаштириш дастурлари тузилди.
1-маъруза. Зарядланган зарачалар, электромагнит
майдон ва электр токи турлари. Ток узлуксизлиги
1.1 Зарядланган заррачалар ва электромагнит майдон
Электромагнит ҳодисалари соҳасидаги тадқиқотлар модда тузилиши ҳақидаги ҳозирги замон тасаввурини ҳосил қилиш учун асосий ғоя ва воситаларни берди. Ушбу тадқиқотларда асосий ва муҳим ўринни зарядланган элементар заррачалар – мусбат элементар зарядли (масалан, протон ва позитрон) ва манфий элементар зарядли (масалан, электрон) заррачалар ташкил этади. Зарядланган элементар заррачалар модданинг атомлари ва молекулалари таркибига кириши, шунингдек, эркин ҳолатда бўлиши мумкин. Улар узлуксиз ҳаракатда бўлиб, шу ҳаракатнинг характерига кўра электр майдони ёки магнит майдони (электромагнит майдони) сифатида бўлиши мумкин. Электр зарядига эга бўлган заррачалар ва уларнинг электромагнит майдонлари материянинг алоҳида турини ташкил этади. Чунки материя ҳаракатининг бошқа шаклларида, масалан, механик ҳаракат шаклида эътиборга олинмаган ҳусусиятлар, электр зарядли заррачаларда мавжуд.
Бундай заррачаларнинг электр заряди уларнинг муҳим физик ҳусусиятидир. Бу ҳусусият заррача ва унинг электромагнит майдони орасидаги ўзаро боғлиқликни ҳамда ташқи электромагнит майдон билан ўзаро таъсирини характерлайди. Электр зарядлари – шу материя заррачаларининг асосий фарқлантирувчи ҳусусиятларидир, улар яна материянинг бошқа, масалан, механикада ўрганиладиган ҳаракатнинг шаклларига хос бўлган ҳусусиятларга ҳам эга: масса, энергия ва ҳ.к.
Механика фанида моддий жисмнинг ҳаракатини масса, узунлик ва вақт орқали ифодаланса, электромагнит ҳодисаларини тасвирлашда, электромагнит ҳодисаларининг моҳиятини ифодаловчи тўртинчи асосий қийматни киритиш зарур. Бу қиймат ихтиёрий электромагнит миқдор, масалан заряднинг қиймати бўлиши мумкин. Қиймат жиҳатдан материя ёки жисм заррачасининг электр заряди фақат бошқа электр зарядланган заррача ёки бошқа зарядланган жисм билан ёки уларнинг ташқи электр майдони билан ўзаро таъсири орқали аниқланиши мумкин.
Шунга ўхшаш, электромагнит майдони тушунчасини аниқлашда зарядланган заррача тушунчасини ишлатмасдан ҳам бирор натижага эришиб бўлмайди. Чунки бошқа турдаги материяларга нисбатан электромагнит майдонининг фарқли ҳусусияти - унинг зарядланган заррачаларга бўлган таъсиридир. Электромагнит майдонининг зарядланган заррачаларга бўлган куч таъсири вектор характерига эга ва заррачанинг ҳаракат тезлигига ва улар электр зарядлари миқдорига боғлиқ. Юқорида келтирилган фикрлар асосида қуйидаги таърифларни келтириш мумкин.
Электромагнит майдон деб зарядланган заррачаларга уларнинг тезлиги ва қийматига боғлиқ равишда куч таъсирини ўтказадиган, унинг барча нуқталарида «электр майдони» ва «магнит майдони» деб номланган икки томонини характерловчи икки вектор қийматлари билан аниқланадиган материянинг турига айтилади. Элементар электр заряди деб электрон ёки протоннинг шундай хусусиятига айтиладики, унда хусусий электр майдони ва ташқи электр майдони билан уларнинг ўзаро таъсирини сон қиймати жиҳатидан абсолют миқдорга тенг, ишораси тескари (бунда электронга шартли равишда манфий ишора, протонга – мусбат ишора берилади) бўлгандаги хусусиятини аниқлайди.
Ушбу таърифлар асосида бир ёки бирнеча элементар электр зарядларидан иборат бўлган ихтиёрий зарядланган заррача - заряд ташувчи бўлади. Масалан, электрон, протон, ион, шунингдек ярим ўтказгичлардаги шартли «тешик» заряд ташувчи ҳисобланади.
Аслида, зарядланган элементар заррачалар ва уларнинг электромагнит майдонлари бир бутундир. Иккинчи томондан, электр зарядланган заррача ва унинг электромагнит майдони орасидаги аниқ чегарани кўрсатиб бўлмайди. Шу билан бирга, шундай фараз қилиш мумкин-ки, заррача ва унинг электр заряди, масалан электрон, протон ва ҳ.к. заряди, фазонинг жуда кичик соҳасида мужассамланган. Фазонинг айнан шу жуда кичик соҳаси учун материянинг шундай ҳаракат шакли характерлики, у билан электр зарядланган заррача тушунчасини боғланган. Модданинг заррачалари билан боғланмаган эркин ҳолатидаги электромагнит майдони жуда кучли гравитация майдонлари мавжуд бўлмаган вазиятда бўшлиқда с=2,998∙10 8 м/с ≈ 3∙10 8 м/с тезликда тарқалади.
Электромагнит қийматлар учун халқаро бирликлар тизимидан (ХТ ёки СИ) фодаланилади. Бу тизим етти асосий бирликлардан ташкил топган: метр – узунлик бирлиги, килограмм – масса бирлиги, секунд - вақт бирлиги, ампер – электр токи кучи бирлиги, кельвин – термодинамик ҳарорат бирлиги, моль – модда миқдори бирлиги, кандела – ёруғлик кучи бирлиги.
Электромагнит қийматларни ҳисоблаш учун, юқорида келтирилганлардан тўртта асосий бирликларни олиш зарур ва кифоялидир. Қолган электромагнит қийматлар, уларга мос равишда, уларнинг бирликлари олинган тўртта асосий бирликлардан келиб чиқади, яъни у ёки бу қонуниятлар асосида аниқланиши мумкин. ХТ бирликлар тизимида электромагнит қиймат учун тўртинчи асосий бирлик сифатида электр токи кучининг бирлиги - Ампер қабул қилинган.
Бирлик тизими МКСА (метр, килограмм, секунд, ампер) ХТ тизимининг бўлагидар. МКСА бирлик тизими электромагнит майдони рационал тизими тенгламалари билан боғланган бўлиб, унда 4р кўпайтма тенгламаларда тушунишга осон бўлган ҳолатларда учрайди, яъни сферик симметриялар билан характерланувчи боғланишлар такибига киради.
Электр зарядининг бирлиги (электр миқдори) кулон (Кл).
Ҳар қандай умумлаштирилган электромагнит ҳодисаси икки томонлама характерланади – электр ҳодисаси ва магнит ҳодисаси ҳамда улар орасида узвий алоқа мавжудлиги. Хусусан, электромагнит майдони икки ўзаро боғланган майдонлардан иборат - электр майдони ва магнит майдони.
Электр майдони - электр зарядлари ва ўзгараётган магнит майдони ёрдамида ҳосил бўлади. Магнит майдони эса ҳаракатланаётган зарядланган заррачалар ва ўзгараётган электр майдони ёрдамида ҳосил бўлади.
Электр майдони деб, электр зарядланган заррачага бўлган таъсири заррачанинг зарядига пропорционал ва унинг тезлигига боғлиқ бўлмаган куч билан характерланадиган электромагнит майдонининг икки ҳолатларидан бирига айтилади.
Электр майдони фазода узлуксиз тақсимланганлиги сабабли, фазонинг ҳар бир нуқтасида ва вақтнинг ҳар бир онида зарядланган синов жисм маълум қийматга эга ва маълум йўналишда бўлган механик куч таъсирида бўлади. Бундан фойдаланиб, электр майдонини унинг ҳар бир нуқтасида характерловчи электр майдонининг кучланганлиги деб номланган асосий физик қийматнинг таърифини аниқлаш мумкин.
Электр майдони кучланганлиги деб электр майдонини характерловчи ва электр майдони томонидан зарядланган заррачага таъсир этаётган кучни характерловчи вектор қийматга айтилади.
(Қуйида учрайдиган барча вектор қийматларни ифодаловчи ҳарфлар қуюқ шрифт билан белгиланади).
Йўналиши бўйича мусбат зарядли синов жисмга таъсир этувчи механик куч f билан мос келувчи электр майдон кучланганлиги E қуйидагича ифодаланади
E = f / q0 .
Ўрганилаётган майдон тақсимланишига q0 заряднинг таъсирини буткул йўқотиш учун q0 нинг нолга интилиши зарур. Шу сабабли, қуйидаги таърифни келтириш мумкин.
Электр майдони кучланганлиги деб, электр майдонининг кўрилаётган нуқтасига киритилган зарядланган қўзғолмас нуқтавий жисмга таъсир этаётган куч миқдорини шу заряд нолга интилгандаги миқдорига нисбатининг, нуқтавий жисмга таъсир этаётган мусбат куч йўналиши билан мос бўлган вектор миқдорига айтилади:
E
= f / q0
.
f / q0
.
1.2 Ўтказувчанлик, кўчириш ва силжиш токлари.
Токнинг узлуксизлиги
Эркин зарядларнинг йўналтирилган ҳаракат жараёни ва/ёки магнит майдони мавжудлигида электр силжиши векторининг вақт бўйича ўзгариши, тўла электр токи дейилади.
«Электр токи» атамаси на фақат ҳодисани тавсифлаш учун, балки шу ҳодисанинг жадаллигини аниқлаш учун ҳам «электр токи кучи» атамасининг синоними сифатида ишлатилади.
«Электр токи» атамасини икки хил таърифлашга бархам бериш учун «Электр» атамасини фақат ҳодисани ифодалаш учун ишлатилади.
Тўла электр токини қуйидаги асосий турларга ажратиш қабул қилинган: ўтказувчанлик токи, кўчириш токи ва силжиш токи.
Ўтказувчанлик электр токи, бирор V ҳажмда Уqi·vi ≠0 бўлгандаги электр заряди эркин ташувчиларининг йўналтирилган ҳаракати ҳодисасидир. Бунда qi ва vi – жисм V ҳажмининг N эркин зарядлар тўпламига кирувчи i-зарядининг қиймати ва ҳаракат тезлиги.
Баъзи моддалар электр ўтказувчанлик, деб номланган, вақт бўйича ўзгармайдиган электр майдон таъсирида вақт бўйича ўзгармайдиган ток ўтказиш хусусиятига эга бўладилар. Демак, бундай хусусиятга эга бўлган моддалар ўтказгичлар ёки ўтказгич моддалари, деб номланганлар. Улар учун асосий электрик хусусият - электр ўтказувчанликдир. Бир қатор моддалар мавжудки, улар учун электр ўтказувчанликнинг ташқи омилларга (масалан, ҳарорат, ёруғлик, электр ва магнит майдонлар ва ҳ.к.) боғлиқлиги характерлидир.
Ўтказувчанлик токи миқдори бирор юза s отқали вақт бирлигида ўтаётган заряд миқдори q билан ўлчанади. Вақтнинг ихтиёрий онида ўтказувчанлик токи кўрилаётган s юзадан заряд ташувчилар билан кўчирилаётган электр зарядининг вақт бўйича ҳосиласига тенг, яъни
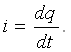
Электр токи скаляр қийматдир. Юза s нинг ҳар хил элементларида зарядланган заррачаларнинг ҳаракатланиш йўналишлари ҳар хил бўлиши мумкин. Бироқ, кўрилаётган юзанинг жуда кичик элементи Дs нинг барча нуқталарида зарядланган заррачалар йўналиши бир хил деб ҳисоблаш мумкин. Бу ҳолат Дs миқдорнинг камайиши билан, яъни Дs→ 0, янада қатъийлашади. Шу сабабли, текшириш жараёнига вектор қиймат киритилади – зарядланган заррачалар ҳаракати йўналишига нормал бўлган Дs юза элементи орқали оқаётган Дi токнинг шу элемент нолга интилаётгандаги нисбатининг лимитига, йўналиши заррачалар мусбат йўналиши билан мос келган ёки, мос равишда, манфий зарядланган заррачалар йўналиши билан мос келмаган
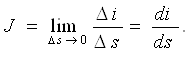
Агар J вектори юзага мусбат нормаль билан в бурчак ҳосил қилса, у ҳолда қуйидаги ифода мавжуд бўлади:
![]()
Ток чекли ўлчовлардаги s юзадан ўтганлиги учун
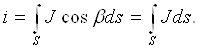
Фақат юзанинг барча нуқталарида ток зичлигининг қийматлари бир хил бўлиб, шу юзага нормаль билан бир хил бурчак ҳосил қилгандагина қуйидагини ёзиш мумкин
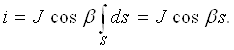
Ток бирлиги сифатида Ампер (А) ва ток зичлиги бирлиги – Ампер бўлинган квадрат метр (А/м 2 ) ишлатилади.
Ўтказгичлардаги ўтказувчанлик токининг бошқа турдаги токлардан фарқи шундаки, ўтказгич ҳарорати ўзгармас бўлганда ўтказувчанлик токи зичлиги электр майдони кучланганлигига пропорционал бўлади. Бунда изотроп муҳитда ток зичлиги вектори J йўналиши электр майдони кучланганлиги Е вектори билан мос бўлади ва ток чизиқлари электр майдони кучланганлиги чизиқлари билан мос бўлади. Шу сабабли ўтказувчанлик токи зичлиги учун ўтказгич муҳитида қуйидагини ёзиш мумкин
![]()
Бунда г катталик модданинг солиштирма ўтказувчанлиги дейилади.
Унга тескари
бўлган қиймат ![]() модданинг
солиштирма электр қаршилиги дейилади.
модданинг
солиштирма электр қаршилиги дейилади.
Демак, электр майдон кучланганлиги ва ток зичлиги орасидаги боғланишни қуйидагича ёзиш мумкин
E = сJ.
Солиштирма қаршиликнинг бирлиги Ом·метр
(Ом·м). Дарҳақиқат, ![]() боғланишдан,
унинг бирлиги учун
боғланишдан,
унинг бирлиги учун 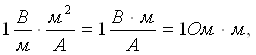 чунки 1 В/А
=1 Ом қаршилик бирлигидир. Шунингдек, солиштирма ўтказувчанликнинг
бирлиги Сименсни метрга нисбати (См/м) бўлади.
чунки 1 В/А
=1 Ом қаршилик бирлигидир. Шунингдек, солиштирма ўтказувчанликнинг
бирлиги Сименсни метрга нисбати (См/м) бўлади.
Ўтказувчи
моддаларни бирор қиймат ![]() (ёки
(ёки![]() ) билан тавсифлаш
имконияти шунинг натижасида пайдо бўлдики, ўтказувчи моддаларда берилган ҳароратда
зарядланган заррачаларнинг ўртача тезлиги, демак ток зичлиги ўзгармас магнит
майдонида ўзгармас бўлиб қолади, чунки бу заррачалар электр майдонида
тезланишидан ҳосил бўлган кинетик энергия модда атомларига узатилади ва
иссиқлик ҳаракатига айланади.
) билан тавсифлаш
имконияти шунинг натижасида пайдо бўлдики, ўтказувчи моддаларда берилган ҳароратда
зарядланган заррачаларнинг ўртача тезлиги, демак ток зичлиги ўзгармас магнит
майдонида ўзгармас бўлиб қолади, чунки бу заррачалар электр майдонида
тезланишидан ҳосил бўлган кинетик энергия модда атомларига узатилади ва
иссиқлик ҳаракатига айланади.
Металларда электр токи ўтказувчанлик электронларининг ҳаракатини тасвирлайди. Металлардан ташқари, ўтказувчи моддаларга кўмир ва электролитлар ҳам киради. Электролитларда ўтказувчанлик мусбат ва манфий ионлар билан амалга оширилади.
Ўтказувчи
моддаларда солиштирма ўтказувчанлик г ва, демак, солиштирма қаршилик![]() модда ҳароратига
боғлиқ.
модда ҳароратига
боғлиқ.
Кўчириш электр токи деганда электр зарядларини эркин фазода ҳаракатланаётган зарядланган заррачалар ёки жисмлар билан кўчириш ҳодисаси тушунилади. Кўчириш токи ўтказгичлардаги ўтказувчанлик токидан шу билан фарқланадики, унинг зичлигини J = гE боғланиш билан ифодалаб бўлмайди, ундаги солиштирма ўтказувчанлик г ток ўтказувчи муҳитни характерловчи катталик. Электр зарядли заррачалар ёки жисмларнинг электр майдонида эркин ҳаракатида уларнинг тезликлари Е майдон кучланганлигига пропорционал эмас. Дарҳақиқат, электр майдонида q зарядли заррачага таъсир этаётган куч qЕ га тенг. Бундай заррачанинг тезланиши майдон кучланганлигига пропорционал. Демак, унинг эркин фазодаги ҳаракати текис тезланувчан бўлади, чунки муҳитнинг қаршилиги бўлмайди.
Кўчириш электр токининг муҳим турларидан бири – зарядга эга бўлган элементар заррачанинг бўшлиқдаги ҳаракатидир. Кўчириш электр токининг яна бир тури – газдаги электр токидир. Кўчириш токи зичлигини v тезликда ҳаракатланаётган заррачалар ўртача ҳажм заряди с билан ифодалаймиз. Шу мақсадда фазода ҳажми dl·ds бўлган тўғри бурчакли паралеллепипед ажратамиз. Унинг dl қирраси тезлик векторига параллель бўлсин. Паралеллепипед ичидаги заряд dq=с·dl·ds. Шу заряднинг барчаси ds юзадан шундай dt вақт оралиғида ўтадики, бу вақт оралиғида зарядланган элементар заррачалар dl масофани ўтсин. Бу вақт оралиғи dl= vdt шарти орқали аниқланади. Демак, ds юза орқали оқаётган ток di=dq/dt=сv ds, ва ток зичлиги қуйидагича бўлади J=di/ds=сv. Манфий зарядли заррачалар ҳаракатида (q<0), токнинг шартли мусбат йўналиши ҳаракат йўналишига қарама-қарши бўлади, ва J билан v орасида J = -сv боғланиш мавжуд бўлади. Иккала ифода с нинг ихтиёрий ишорасида қуйидаги вектор шаклда бирлаштирилади:
J=сv.
Агар с >0 бўлса J ва v векторлар йўналишлари мос бўлади. Агар с <0 бўлса, улар қарама-қарши.
Агар бир вақтнинг ўзида зарядларнинг с+ ҳажм зичлиги, v+ тезликда мусбат зарядланган заррачалар ҳаракати ва зарядларнинг с- ҳажм зичлиги, v- тезликда манфий зарядланган заррачалар ҳаракати мавжуд бўлса, у ҳолда кўчириш токи зичлиги
JКЎЧ = с+ v+ + с-v- .
Силжиш электр токини диэлектрикларда ўзгарувчан электр майдони мавжуд бўлганда эътиборга олиш зарур бўлади.
Асосий электр ҳусусияти - электр майдони таъсирида қутбланиш (поляризация) қобилиятига эга бўлган модда диэлектрик дейилади.
Диэлектриклар
махсус гуруҳлари мавжуд, улар сегнетоэлекириклар деб номланади.
Сегнетоэлекирикларда ![]() нинг қиймати
майдон кучланганлигига кучли боғлиқликда бўлиб, майдон
кучланганлиги ва ҳароратнинг баъзи қийматларида жуда катта миқдорларга
эришиши мумкин. Коэффициент
нинг қиймати
майдон кучланганлигига кучли боғлиқликда бўлиб, майдон
кучланганлиги ва ҳароратнинг баъзи қийматларида жуда катта миқдорларга
эришиши мумкин. Коэффициент ![]() модданинг абсолют
диэлектрик таъсирчанлиги дейилади.
модданинг абсолют
диэлектрик таъсирчанлиги дейилади.
Диэлектрикнинг қутбланишини, шу жараёнини майдон таъсиридаги мусбат ва манфий зарядланган заррачаларнинг силжиши билан тушунтириш мумкин. Агар q – диполнинг мусбат заряди ва N1 – бирлик ҳажмдаги диполлар сони бўлса, у ҳолда майдоннинг s юза орқали ўтиши жараёнида E вектор йўналишида q·N1··x·s мусбат заряд силжийди ва қарама-қарши йўналишда – манфий заряд -qN1(d-x)s силжийди. Манфий заряднинг майдонига тескари йўналишда силжишига, мусбат заряднинг майдони йўналишида силжиши эквивалент бўлганлиги учун, s юзадан ўтган умумий заряд
![]()
бунда
![]() бўлганлиги
учун
бўлганлиги
учун 
Умумий ҳолатда бир жинсли бўлмаган майдон учун
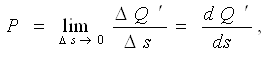 (1.1)
(1.1)
Яъни, қутбланганлик - заррачалар силжиши йўналишига нормал бўлган элемент юзаси орқали майдон ўрнатилиши жараёнида диэлектрик моддасида силжиган зарядланган заррачалар олиб ўтадиган электр зарядининг, шу элемент юзаси нолга интилгандаги нисбати лимитига тенг.
Электр майдонининг вақт бўйича ҳар қандай ўзгаришида диэлектрикнинг қутбланганлиги Р ўзгаради. Бунда диэлектрик моддасида атомлари ва молекулалари таркибига кирувчи электр зарядли элементар заррачалар ҳаракатланадилар. Диэлектрикдаги электр токининг бу тури қутбланганлик (поляризация) электр токи дейилади. Диэлектрикда зарядланган заррачалар эркин бўлмаганлиги ва электр майдони таъсирида силжиши мумкин бўлганлиги учун, қутбланганлик токини силжиш электр токи ҳам деб аталади, аниқроғи, у силжиш токининг бир ташкил этувчисидир. Бу токнинг силжишини J' модда қутбланишининг ўзгариши P билан боғлаш қийин эмас.
Агар бирор юза элементи ds зарядланган заррачалар силжиш йўналишида ихтиёрий ўрнатилган бўлса, у ҳолда Pn = dQ'/ds, бунда Pn – юқоридаги Р векторининг ds юза элементига нормаль ўтказилган ташкил этувчиси.
Р вектори вақт бўйича ўзгаришида ds юза элементидан қуйидаги ток ўтади
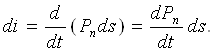
Иккинчи
томондан, ![]() бунда
бунда
![]() - ток
зичлиги J' векторининг ds элементига нормаль ташкил этувчиси. Шундай қилиб,
- ток
зичлиги J' векторининг ds элементига нормаль ташкил этувчиси. Шундай қилиб,

Юза элементи ![]() нинг вазиятини
ихтиёрий олиш мумкин бўлганлиги учун, ток зичлиги вектори J' нинг
ташкил этувчиси бирор йўналишда модда қутбланганлиги Р
векторининг вақт бўйича хосиласига тенг бўлади, деган ҳулосага
келамиз. Хусусан, J' нинг OX, OY, OZ ўқларига
проекциялари қуйидагича:
нинг вазиятини
ихтиёрий олиш мумкин бўлганлиги учун, ток зичлиги вектори J' нинг
ташкил этувчиси бирор йўналишда модда қутбланганлиги Р
векторининг вақт бўйича хосиласига тенг бўлади, деган ҳулосага
келамиз. Хусусан, J' нинг OX, OY, OZ ўқларига
проекциялари қуйидагича:
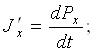
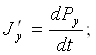
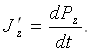
Ток зичлиги вектори
J'=i![]() +j
+j 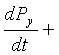 k
k ![]() =
=![]() (i Px
+j Py + k Pz
),
(i Px
+j Py + k Pz
),
бунда i, j, k – координата OX, OY, OZ ўқлари бўйлаб йўналган векторлар.
iPx + jPy + kPz = P, бўлганлиги учун
J' = dP/dt.
Демак, силжиш электр токи векторининг кўрилаётган қисми модда қутбланганлиги векторининг вақт бўйича ҳосиласига тенг экан.
Юқорида таъкидланганидек, модда қутбланганлигининг ўзгариши сабабли ҳосил бўлган силжиш токи ва, демак, силжиш токи зичлиги J', диэлектрикдаги тўла силжиш токи ва, демак, тўла силжиш токи зичлигининг бир қисмини ташкил этади. Дарҳақиқат, диэлектриклардаги электр силжиш вектори D икки D0 ва P ташкил этувчилардан иборат:
D = D0 + P,
бунда D0 = е0E. Электр майдони ўзгарганда иккала ташкил этувчилар ҳам ўзгаради. Шундай қилиб,
dD/dt = dD0/dt + dP/dt.
Кейинги ифоданинг иккинчи ташкил этувчиси, юқорида ҳозиргина аниқланганидек, диэлектрик моддасида зарядланган элементар заррачалар ҳаракати натижасида ҳосил бўлган силжиш электр токи зичлиги векторидир. Ифоданинг биринчи ташкил этувчиси ҳам ток зичлиги бирлигига эга. У электр майдони вақт бўйича ўзгаргандаги физик жараённи характерлайди. Юқорида, материянинг майдон сифатида мавжудлик шаклини ифодалайдиган фазони, яъни бизга маълум бўлган материя зарралари бўлмаган соҳани бўшлиқ, деб атасак, унда биринчи ташкил этувчини бўшлиқдаги силжиш токининг зичлиги, деб номлаш мумкин. Унинг белгиланиши қуйидагича бўлади
dD0 / dt.
Шундай қилиб, диэлектрикдаги тўла силжиш токи зичлигининг Jсж вектори:
Jсж = dD / dt = J0 + J' = dD0 / dt + dP / dt .
Электр силжиши D векторининг вақт бўйича ҳосиласини вектор тушунча сифатида кўриш шарт.
Силжиш токи зичлиги векторининг ташкил этувчилари учун барча ҳолатларда
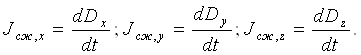
Ўзгарувчан ток бўлганда, айниқса, ахборот тизимларида учрайдиган юқори ва ўта юқори частоталарда силжиш токи, на фақат диэлектрикларда мавжуд бўлади, балки ярим ўтказгич ва ўтказгич моддаларда ҳам пайдо бўлади. Дарҳақиқат, ташқи майдон таъсирида ушбу моддалар молекулалари, диэлектриклардагидек қутбланиши зарур. Бундан ташқари, бўшлиқдаги силжиш ҳам пайдо бўлиши шарт. Ярим ўтказгич моддаларда силжиш токларини юқори частота билан ўзгарадиган майдонларда эътиборга олиш зарур. Ўтказгич моддаларда эса, катта частоталарда силжиш токлари ўтказувчанлик токларига нисбатан сезиларли бўлади, бироқ уларни, аксарият, эътиборга оллинмайди.
Юқоридаги фикрлар асосида қуйидагини таъкидлаш мумкин: электр токининг энг муҳим хусусияти – у билан боғлиқ бўлган магнит майдонининг ҳосил бўлишини – токнинг барча ташкил этувчилари учун ҳам бир хил татбиқ этиш мумкин. Бу фикрлар тажрибада тўлалигича тасдиқланди.
Юқорида келтирилган мулоҳазалар асосида тўла электр токи, ёки тўла ток скаляр қиймат бўлиб, кўрилаётган юза орқали ўтаётган ўтказувчанлик токи ва силжиш токи йиғиндиларига тенг, яъни
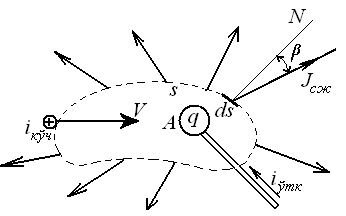
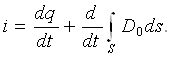
Ушбу ифодада q нинг таркибига эркин ташувчиларнинг зарядлари ҳам, модда қутбланганидаги юзадан ўтаётган йиғинди боғланган зарядлар ҳам киради.
Диэлектрикда бирор s берк юзани тасаввур қилайлик (1.1-расм) ва шу юза ичида жойлашган А жисм
1.1-расм
зарядланаяпти, деб фараз қилайлик. Жисмнинг заряди q ортганда уни ўраб турган электр майдони кучаяди ва диэлектрикда электр силжи-
ши ортади. Шунинг
учун s юза орқали ичкаридан таш-
қарига томон силжиш токи оқади. Юза s орқали сил-жиш векторининг оқими юза ичида жойлашган q эркин зарядга тенг
![]() (dD/ds)dt=q.
(dD/ds)dt=q.
Шу тенгликдан вақт
бўйича ҳосила оламиз 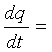 iсж
iсж
![]() Jсжds = iсж,
бунда тенгликнинг ўнг қисми юза s ичкарисидан
ташқарига томон оқаётган силжиш токидир.
Jсжds = iсж,
бунда тенгликнинг ўнг қисми юза s ичкарисидан
ташқарига томон оқаётган силжиш токидир.
Қиймат dq/dt юза s ичида жойлашган эркин заряднинг тезлиги. Юза s билан чекланган фазо ҳажмидаги мусбат эркин заряднинг ортиши фақат ташқи фазодан ҳажм ичига мусбат зарядларнинг киритилиши ёки манфий зарядларнинг тескари йўналишда узатилиши билан бажарилиши мумкин. Бу узатиш ёки s юзани кесиб ўтувчи ўтказгичлардаги ўтказувчанлик токи iўтк ёрдамида, ёки юза орқали зарядланган жисмларда ёки фазода ҳаракатланаётган зарядланган заррачалар ёрдамида кўчириш токлари iкўч билан амалга ошириш мумкин. Агар dq/dt > 0 бўлса, мусбат зарядлар ташқи фазодан s юза билан чегараланган ҳажм ичига олиб кирилади, демак, (iўтк + iкўч) токлар йиғиндиси манфий ишорали бўлади, чунки мусбат ишорали деб ташқи нормаль қабул қилинган эди. Шундай қилиб,
dq/dt = - (iўтк + iкўч).
Тенглик ![]() (dD/ds)dt
(dD/ds)dt
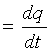 қуйидагича
қайта ёзилиши мумкин
қуйидагича
қайта ёзилиши мумкин
i = - (iўтк + iкўч) ёки i + iўтк + iкўч = 0.
Демак, ихтиёрий берк юза орқали барча турдаги токлар йиғиндиси (ўтказувчанлик, кўчириш ва силжиш токлари) нолга тенг экан.
Агар д орқали тўла ток зичлигини (д = J + Jcж) ҳамда i билан юзадан ўтаётган барча токни белгиласак, у ҳолда ихтиёрий берк юза учун қуйидаги қиймат
i = ![]() дds = 0
дds = 0
электр токи узлуксизлик принципининг умумий ифодаси дейилади. Ушбу муҳим принцип қуйидагича таърифланади: ихтиёрий муҳитда олинган берк юза орқали ўтган тўла электр токи нолга тенг. Бунда юзадан чиқаётган ток мусбат, кираётган – манфий ҳисобланади.
Шундай қилиб, ток чизиқларининг ҳач қаерида на бошланиши ва на охири бўлмайдиган, принципиал равишда берк чизиқлардир. Электр токи ҳар доим берк йўлдан оқади.
Барча келтирилган фикрлардан шуаён бўладики, токнинг узлуксизлик принципи, ёки берклик принципи фақатгина диэлектриклардаги силжиш токи ва айнан бўшлиқдаги силжиш токи тушунчасини киритиш билан умумтатбиқ аҳамиятини эгаллайди.
Мисол сифатида сигналларни узатиш линиясини кўрайлик (1.2-расм). Ўзгарувчан кучланиш бўлганда ўтказгичлар орасидаги диэлектрикда силжиш токлари бўлади. Берк юза s ни шундай ўтказамизки, у линиянинг
битта ўтказгичини қамраб олсин. Ўтказгичдаги токлар – s юзага
кирувчи (i + iсж) ва ундан чиқувчи (i )
–
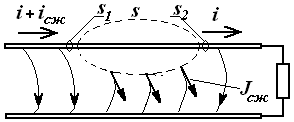 s юза орқали
диэлектрикдаги силжиш
s юза орқали
диэлектрикдаги силжиш
– токи миқдори билан ўзаро фарқланадилар.
– Шу сабабли ўтказгичдаги ўзгарувчан ток 1.2-расм
ўтказгичнинг ҳар хил кесим юзаларларида [масалан, s1 юзадаги ток (i + iсж), s2 юзадаги ток (i )] вақтнинг бир онида ҳар хил бўлади. Ушбу физик жараённи ўтказгичлар орасидаги кучланиш тез ўзгарадиган (катта частотали) занжирларда ва узун линияларда эътиборга олинади.
2-маъруза. Кучланиш, потенциаллар фарқи. Электр юритувчи куч
2.1. Кучланиш
Электр занжирлари ва электр майдони билан боғлиқ бўлган энг муҳим қийматлардан бўлган электр кучланиши, электр потенциаллари фарқи ва электр юритувчи кучларни ўрганишга ўтамиз.
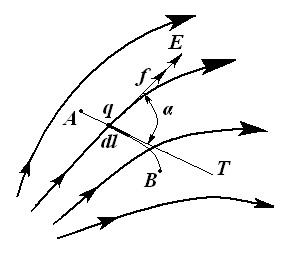 Агар q зарядли заррача электр майдонида
бирор масофа бўйлаб кўчирилса, у ҳолда унга таъсир этувчи кучлар иш
бажаради. Бу ишнинг кўчирилаётган зарядга нисбати электр кучланиши деб
аталмиш, физик қийматга тенг бўлади. Заррача q нинг dl
масофага (2.1-расм) кўчирили-шини кўрайлик, бунда майдон
кучлари қуйидаги ишни бажаради:
Агар q зарядли заррача электр майдонида
бирор масофа бўйлаб кўчирилса, у ҳолда унга таъсир этувчи кучлар иш
бажаради. Бу ишнинг кўчирилаётган зарядга нисбати электр кучланиши деб
аталмиш, физик қийматга тенг бўлади. Заррача q нинг dl
масофага (2.1-расм) кўчирили-шини кўрайлик, бунда майдон
кучлари қуйидаги ишни бажаради:
![]()
![]() qEdl.
qEdl.
Йўналиши Т уринмага мос, узунлиги dl йўл элементига тенг бўлган миқдор dl вектори билан белгиланган. Бунда б векторлар Е ва dl орасидаги бурчакдир.
А нуқтадан (2.1-расм) В нуқта-гача масофа бўйлаб заррачани кўчи-ришда майдон кучлари бажараётган иш 2.1-расм
қуйидагига тенг:
 Edl.
Edl.
Бу иш берилган масофа бўйлаб
майдон кучланганлигининг чизиқли интеграл 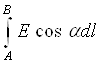 га пропорционал.
Бу чизиқли интеграл А дан В гача масофа бўйлаб электр
кучланишига тенг. Кучланишни u ҳарфи билан белгилаш қабул қилинган.
Шундай қилиб, икки нуқталар орасидаги электр кучланиш тенг:
га пропорционал.
Бу чизиқли интеграл А дан В гача масофа бўйлаб электр
кучланишига тенг. Кучланишни u ҳарфи билан белгилаш қабул қилинган.
Шундай қилиб, икки нуқталар орасидаги электр кучланиш тенг:
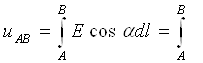 Edl.
Edl.
Демак,
A = q·u AB.
Умумий холда кўрилаётган масофа ихтиёрий муҳитдан ўтиши мумкин, хусусан, у бутунлай ўтказгичдан ўтиши мумкин, бутунлай ярим ўтказгичдан ва қисман ўтказгичдан, қисман ярим ўтказгичдан ўтиши мумкин.
Баён этилганларга мувофиқ, электр кучланиши - кўрилаётган масофа бўйлаб электр майдонини характерловчи ва қиймати жиҳатидан электр майдони кучланганлигининг шу масофа бўйлаб чизиқли интегралига тенг бўлган физик катталикка айтиладики.
Аксарият, бирор
масофа соҳаси бўйлаб электр кучланиши ҳақида гапирганда, соҳа
бўйлаб кучланишлар пасаюви атамасини ишлатадилар. Шу асосда, бирор берк
контур бўйлаб электр майдони кучланганлигининг чизиқли интеграли ![]() Edl шу
контур бўйлаб барча бўлаклар элементи кучланишлар пасаювининг йиғиндисига
тенг бўлади.
Edl шу
контур бўйлаб барча бўлаклар элементи кучланишлар пасаювининг йиғиндисига
тенг бўлади.
Кучланишнинг бирлиги Вольт [В].
Келтирилган фикрлардан шу келиб чиқадики, электр майдонининг кучланганлиги - кучланишлар пасаювининг майдон кучланганлиги чизиғининг узунлик бирлигига нисбатига тенг. Дарҳақиқат, агар масофа йўналиши майдон кучланганлиги бирлиги билан мос келса, dl масофадаги кучланишлар пасаюви du = E dl, демак E = du/dl. Шунинг учун, электр майдони кучланганлигининг ўлчов бирлиги вольт бўлинган метр (1 В/м).
2.2. Электр потенциали ва потенциаллари фарқи
 Юқорида таъкидланганидек, ўтказгич муҳитида
электр майдон кучланганлиги Е ток зичлиги J
билан қуйидаги боғланишда Е = сJ
бўлади, бунда с – муҳитнинг солиштирма қаршилиги. Оддий ҳолатда,
ўзгармас токли i тўғри чизиқли l узунликдаги ва
кесим юзаси s бўлган ўтказгичда кучланишлар пасаюви u=El бўлади,
ток эса i=Js га тенг. Шундай қилиб, u=сJl=сli /s = ri. Қиймат
r = u/ i кўрилаётган ўтказгич бўлагининг электр қаршилигидир.
Электр қаршилик Омда (Ом) ўлчанади. Ифода u= ri кўрилаётган
ўтказгич бўлаги учун Ом қонуни дейилади. Ўтказгичда вақт бирлигида
иссиқлик сифатида ажралиб чиқаётган энергия миқдорини
ифодалайдиган
Юқорида таъкидланганидек, ўтказгич муҳитида
электр майдон кучланганлиги Е ток зичлиги J
билан қуйидаги боғланишда Е = сJ
бўлади, бунда с – муҳитнинг солиштирма қаршилиги. Оддий ҳолатда,
ўзгармас токли i тўғри чизиқли l узунликдаги ва
кесим юзаси s бўлган ўтказгичда кучланишлар пасаюви u=El бўлади,
ток эса i=Js га тенг. Шундай қилиб, u=сJl=сli /s = ri. Қиймат
r = u/ i кўрилаётган ўтказгич бўлагининг электр қаршилигидир.
Электр қаршилик Омда (Ом) ўлчанади. Ифода u= ri кўрилаётган
ўтказгич бўлаги учун Ом қонуни дейилади. Ўтказгичда вақт бирлигида
иссиқлик сифатида ажралиб чиқаётган энергия миқдорини
ифодалайдиган
қувват қуйи- 2.2-расм
дагича ифодаланади p=A/t=uq/t=ui=r2i. Бў боғланиш Жоуль-Ленц қонунини ифодалайди. Қувватнинг бирлиги Ватт (Вт).
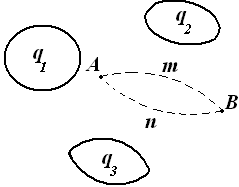
Электростатик майдон, яъни зарядланган ҳаракатсиз заррачалар майдони (2.2-расм) мавжуд бўлсин.
Электростатик майдонда ихтиёрий
берк контур бўйича майдон
кучланганлигининг чизиқли интеграли нолга тенг: ![]() Edl=0. Электростатик майдоннинг
бу муҳим хусусияти энергия сақланиш қонуни принципидан келиб
чиқади. Заряди q га тенг бўлган нуқтавий жисм AmBnA
(2.2-расм) берк контури бўйлаб кўчмоқда, деб фараз қилайлик. Берк
контурнинг бир қисмида ҳаракат майдон кучлари йўналишида бўлади ва
майдон кучлари ҳосил қилаётган иш мусбат бўлади. Берк контурнинг қолган
қисмида ҳаракат майдон кучлари йўналишига тескари бўлади ва майдон
кучлари ҳосил қилаётган иш манфий бўлади. Майдон кучлари q
зарядли жисмни бутун берк контур бўйлаб кўчириш учун ҳосил бажарган иш
нолга тенг бўлиши шарт:
Edl=0. Электростатик майдоннинг
бу муҳим хусусияти энергия сақланиш қонуни принципидан келиб
чиқади. Заряди q га тенг бўлган нуқтавий жисм AmBnA
(2.2-расм) берк контури бўйлаб кўчмоқда, деб фараз қилайлик. Берк
контурнинг бир қисмида ҳаракат майдон кучлари йўналишида бўлади ва
майдон кучлари ҳосил қилаётган иш мусбат бўлади. Берк контурнинг қолган
қисмида ҳаракат майдон кучлари йўналишига тескари бўлади ва майдон
кучлари ҳосил қилаётган иш манфий бўлади. Майдон кучлари q
зарядли жисмни бутун берк контур бўйлаб кўчириш учун ҳосил бажарган иш
нолга тенг бўлиши шарт:
q![]() Edl=0, яъни
Edl=0, яъни ![]() Edl=0.
Edl=0.
Дарҳақиқат, агар шу шарт бўлмаганда эди, AmBnA контурни айланиб ўтиш йўналишини шундай танлаб олиш мумкин бўлардики, унда бажарилган иш мусбат бўлар эди. Бироқ, берк контур бўйича айланиб ўтилгандан сўнг, тизим ва q зарядли жисм юқори аниқликда бошланғич ҳолатга қайтади, демак, q зарядли жисм контурни бирнеча (ихтиёрий) марта қайта айланиши мумкин ва ҳар бир айланишда мусбат ишни ҳосил қилиши мумкин бўлади. Бундай чексиз энергия манбасини ҳосил қилиш имкониятининг мавжудлиги энергия сақланиш қонунига зид бўлади. Шундай қилиб, электростатик майдонда ихтиёрий контур бўйлаб кучланганликнинг чизиқли интеграли нолга тенг бўлиши шарт. Бундан, бевосита берилган бошланич ва кейинги А ва В нуқталар танланишидан майдон кучланганлиги чизиқли интегралининг боғлиқ эмаслиги келиб чиқади. Дарҳақиқат,
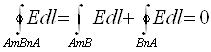 ,
,
Бундан
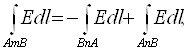
интеграллашдаги m ва п йўллар ихтиёрий танлан, демак электростатик
майдонда интеграл ![]() Edl итеграллаш
йўлини танлашга боғлиқ бўлмайди ва фақат А ва В
координаталар танланишига боғлиқ.
Edl итеграллаш
йўлини танлашга боғлиқ бўлмайди ва фақат А ва В
координаталар танланишига боғлиқ.
Шу интегралга
тенг бўлган қийматни А ва В нуқталар потенциалларининг фарқи
дейилади ва UA – UB каби белгиланади. Демак UA – UB = ![]() Edl келиб чиқади.
Edl келиб чиқади.
Иккинчи томондан, ушбу интеграл А нуқтадан В нуқтагача бирор йўл бўйлаб аниқланган кучланишга тенг. Демак, электростатик майдон учун қўллаганда «кучланиш» ва «потенциаллар фарқи» атамалари бир ҳил қийматга эга.
Бундан буён потенциаллар фарқини, кучланишга ўхшаш u ҳарфи билан белгилаймиз, шу сабабли UA – UB = uAB белгилашни қабул қиламиз.
Юқоридагилардан шу маълум бўладики, электростатик майдоннинг икки нуқтаси потенциаллари фарқи, қиймати бирга тенг бўлган мусбат ишорали зарядли нуқтавий жисмни бир нуқтадан иккинчи нуқтага кўчиргандаги майдон кучлари бажарган ишга тенг.
Кейинги нуқта
сифатида фазодаги Р нуқтани оламиз. У ҳолда интеграл ![]() Edl нинг қиймати
фақат А нуқтанинг x, y, z
координаталари функцияси бўлади. Бу функцияни UA ёки U (x,
y, z) белгиласак, қуйидагича ёзиш мумкин:
Edl нинг қиймати
фақат А нуқтанинг x, y, z
координаталари функцияси бўлади. Бу функцияни UA ёки U (x,
y, z) белгиласак, қуйидагича ёзиш мумкин:
![]() Edl = UA
= U (x, y, z).
Edl = UA
= U (x, y, z).
U қийматни
кўрилаётган майдон нуқтасининг электр потенциали дейилади. Берилган нуқта
Р потенциали нолга тенг, чунки UA=![]() Edl= 0.
Edl= 0.
Берилган майдонни характерловчи электр потенциалини, потенциали нолга тенг деб қабул қилинадиган ихтиёрий Р нуқтанинг фақат ихтиёрий ўзгармас қийматигача аниқликда ҳисоблаш мумкин. Электр потенциали деб номланган, ҳар бир нуқтасида скаляр қиймат бўлган ихтиёрий катталик билан характерланувчи электр майдонига потенциал электр майдони дейилади. Уларга электростатик майдон, электр юритувчи куч манбалари таъсирида бўлмаган ва қўзғолмас ўтказгичлардан ўтган ўзгармас ток электр майдони киради. Дарҳақиқат, бу ҳолда ўтказгичларда заряднинг тақсимланиши, электростатикадагидек, вақт бўйича ўзгармас бўлади. Ўзгармас токли қўзғолмас ўтказгичлар атрофидаги ва улар ичидаги электр майдони стационар электр майдони (Естац) деб аталади.
Электростатиканинг реал масалаларини ечишда, аксарият ернинг сатҳи потенциали нолга тенг деб қабул қилинади. Фазонинг чекланган соҳаларида жойлашган ва чексиз диэлектрик муҳит билан ўралган зарядланган жисмлар масалаларининг назарий тадқиқотларида, аксарият зарядланган заррачалардан чексиз узоқликда бўлган нуқталарнинг потенциаллари нолга тенг деб қабул қилинади, яъни потенциални қуйидаги интеграл каби аниқланади:
U =![]() Edl .
Edl .
Электр майдони
кучланганлиги чизиқларини тўғри бурчак остида кесиб ўтувчи юзалар тенг
электр потенциалли юзалар дейилади. Дарҳақиқат, бу
юзадаги ихтиёрий чизиқ бўйлаб 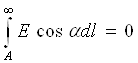 га эга бўламиз, чунки
га эга бўламиз, чунки
![]() . Демак, ушбу
юзада жойлашган икки ихтиёрий А ва В нуқталари
потенциаллари фарқи нолга тенг. U (x, y, z)=const тенглама тенг
потенциалли юзада жойлашган нуқталар мажмуасини аниқлайди, яъни шу
юза тенгамасидир. Тенг электр потенциалли юзаларнинг чизма текислигидаги изи тенг
потенциаллар чизиғи дейилади. Аёнки, тенг потенциаллар чизиқлари
майдон кучланганлиги чизиқлари билан ҳар қаерда тўғри
бурчак остида кесишади.
. Демак, ушбу
юзада жойлашган икки ихтиёрий А ва В нуқталари
потенциаллари фарқи нолга тенг. U (x, y, z)=const тенглама тенг
потенциалли юзада жойлашган нуқталар мажмуасини аниқлайди, яъни шу
юза тенгамасидир. Тенг электр потенциалли юзаларнинг чизма текислигидаги изи тенг
потенциаллар чизиғи дейилади. Аёнки, тенг потенциаллар чизиқлари
майдон кучланганлиги чизиқлари билан ҳар қаерда тўғри
бурчак остида кесишади.
Зарядларнинг статик ҳолатида ўтказгичлар ичидаги электр майдон кучланганлиги нолга тенг бўлиши керак, чунки токнинг (J =0) йўқлигида Е=сJ =0 бўлади. Шу сабабли, электростатик ҳолатда ҳар бир ўтказгич жисм ўзининг барча ҳажмида бир хил потенциалга эга бўлади: бу жисмлар юзалари - тенг электр потенциалли юзалардир ва диэлектриклардаги кучланганлик линиялари уларга нормаль бўлади.
Агар зарядланган ўтказгич жисмни ўраб олган изоляцияловчи муҳитнинг диэлектрик сингдирувчанлиги электр майдони кучланганлигига боғлиқ бўлмаса, у ҳолда диэлектрикнинг ҳамма жойида Е қиймат, демак жисмнинг U потенциали ҳам жисмнинг q зарядига пропорционал бўлади. Заряд q нинг U га нисбати жисмнинг электр сиғими дейилади:
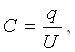
бунда потенциал чексиз катта бўлганда С=0 бўлади. Алоҳида жисмнинг электр сиғими жисмни аниқловчи g геометрик параметрларига ва уни ўраб турган муҳитнинг абсолют диэлектрик е сингдирувчанлигига боғлиқ: С=Ғ(g, е). Агар диэлектрик бир жинсли бўлса, у ҳолда С = е∙f(g). Диэлектрик сингдирувчанлик е қиймати Е га боғлиқ бўлмаса, С нинг қиймати q ва U га боғлиқ бўлмайди.
Диэлектрик билан изоляцияланган, зарядлари тенг ва қарама-қарши ишорали q1 = - q2 бўлган икки ўтказгич потенциаллари фарқи зарядлардан бирининг қийматига пропорционал бўлади. Бунда қуйидаги миқдор
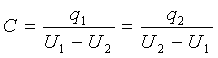
2.3-расм
шу жисмлар орасидаги электр сиғими дейилади. С жисмнинг шакли, ўлчовлари ва ўзаро жойлашганлигини ифодаловчи g геометрик параметрларга, шунингдек диэлектрикнинг абсолют диэлектрик е сингдирувчанлигига боғлиқ. Бир жинсли диэлектрик учун
С = е f(g).
Электр сиғимларида ишлатиш учун махсус таёрланган бундай икки жисмлар тизими конденсатор дейилади.
Икки жисм орасидаги сиғимнинг аналитик ифодаси учун потенциаллар фарқи ҳисобланишидаги қисмининг заряди олинади. Бунда доимо С > 0.
Сиғимнмнг ўлчов бирлиги сифатида Фарада (Ф) қабул қилинган.
Ифода е = D /
E дан е қийматнинг бирлиги

2.3. Электр юритувчи куч
Энди электр юритувчи куч катталигини ўрганайлик.
Ҳар қандай потенциал электр майдонининг, хусусан, электростатик майдонининг характерли ҳусусияти, айнан, майдон кучланганлигининг ихтиёрий берк контур бўйлаб чизиқли интеграли нолга тенглиги, электр юритувчи куч (ЭЮК) деб номланган манбаси бўлмаган фазо соҳасига тааллуқлидир.
ЭЮК тушунчасининг пайдо бўлиши ноэлектрик ва нопотенциал 2.3-расм
характердаги электр майдонларининг
мавжудлигидан келиб чиқади.
Умумий ҳолда қуйидагича талқин қиламиз: агар берк контур бўйлаб электр майдон кучланганлигининг чизиқли интеграли нолга тенг бўлмаса, берк контурда е электр юритувчи куч таъсир этаётган бўлади, қуйида кўрсатишимиздек, бу чизиқли интеграл контурда таъсир этаётган ЭЮКга тенг бўлади:
![]() Ed l= е ≠ 0.
Ed l= е ≠ 0.
ЭЮК манбалари сифатида, масалан, электр генераторлари, гальваник элементлар, аккумуля-торлар, термоэлементлар ишлати-лиши мумкин. «Электр юритувчи куч» тушунчаси тааллуқли бўлган миқдорнинг қандай эканлигини аниқлаш учун, мисол тариқасида гальваник элементни кўрамиз (2.3-расм). Гальваник элемент клеммаларига уланган А ва В жисмлар ЭЮК таъсирида зарядланади. Диэлектрикда А ва В жисмлар орасидаги ихтиёрий йўл бўйлаб Е вектордан олинган интеграл улар потенциаллари фарқига тенг:
![]() Edl = UA –
UB = uAB .
Edl = UA –
UB = uAB .
А дан В жисмгача
интеграллаш йўлини икки ҳил йўналишда бажариш мумкин: биринчиси
кўрсатилаётган АmВ йўлни олсак – А жисмдан уланиш
ўтказгичи – элементнинг мусбат электроди – электролит – манфий электрод -
уланиш ўтказгичи – В жисм, ушбу йўл бўйлаб интеграл нолга тенг бўлади: ![]() Edl = 0. Дарҳақиқат,
бу йўл тўлалигича ўтказгич муҳитидан ўтади. Металлда ўтказувчанлик
жараёни электрон ўтказувчанлиги билан таъминланади, электролитда – мусбат ва
манфий ионлар билан таъминланади. J=0 бўлганлиги учун E = сJ
= 0.
Edl = 0. Дарҳақиқат,
бу йўл тўлалигича ўтказгич муҳитидан ўтади. Металлда ўтказувчанлик
жараёни электрон ўтказувчанлиги билан таъминланади, электролитда – мусбат ва
манфий ионлар билан таъминланади. J=0 бўлганлиги учун E = сJ
= 0.
Электродларнинг юзаларидаги юпқа қатламда электрод ва электролит зарядлари кучланганлиги
Естат бўлган электр майдони ва куч-
ланганлиги Еқаршга тенг ва унга қарши йўналган ташқи электр майдони ҳосил бўлади. Улар йиғиндиси
Е = Естат + Еқарш = 0 ёки Естат = - Еқарш .
Бундан
![]() Eстат
dl = -
Eстат
dl = - ![]() Eқарш
dl =
Eқарш
dl =![]() Eқарш
dl.
Eқарш
dl.
Қиймат
![]() Eқарш
dl = e
Eқарш
dl = e
гальваник элементнинг ЭЮК ни ифодалайди. Бу ЭЮК элемент ичидаги зарядли заррачаларни электростатик майдон Естат кучларига қарама-қарши йўналишда ҳаракатга келтиришни амалга оширади.
Эътиборни шунга қаратиш зарурки, агар манбанинг ичида интеграллаш йўли унинг манфий клеммасидан мусбати томон бўлса, ЭЮК мусбат бўлади.
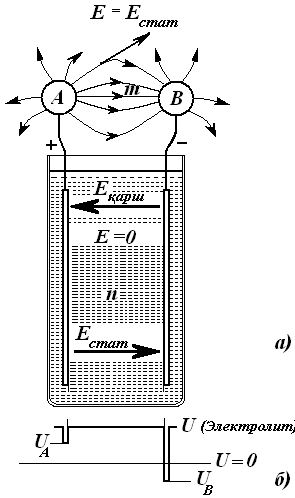
Ушбу электр юритувчи кучнинг пайдо бўлиш табиати шундаки, эриш босими остида мусбат ионлар (ўтказувчанлик электронларисиз қолган металл атомлари) электроддан электролитга ўтишга интилади. Бу ўтишга электролитдаги металл атомларининг мусбат ионлари осмотик босим билан қаршилик кўрсатади. Бу икки босимларнинг фарқи таъсирида мусбат ионларнинг электроддан электролитга ўтиши ёки шу босимдан қай бири каттароқлиги сабабли, тескари йўналишда ўтиши (электролиз жараёни) содир бўлади. Натижада, биринчи ҳолатда - электрод манфий зарядланади (металлда ортиқча ўтказгич электронлари билан), иккинчи ҳолатда – мусбат зарядланади, электролит эса қарама-қарши заряд олади. Электрод ва электролит орасида потенциаллар фарқи ўрнатилади ва ионларнинг ўтишига қаршилик кўрсатувчи электростатик майдон Естат ҳосил бўлади. Ионлар ўтиши электростатик майдон кучлари таъсирида босимлар фарқи мувозанатланганда якунланади.
Босимлар фарқи натижасида ҳосил бўлган механик f кучнинг ионга таъсири, кучланганлиги Естат = f / q га тенг бўлган электростатик майдон мавжудлигига эквивалентдир; бунда q – ионлар заряди. Шундай қилиб, мувозанат ҳолати қуйидаги шартлар бажарилганда ҳосил бўлади:
Естат + Еқарш = Е = 0.
2.3,а-расмда Еқарш ва Естат векторлар шартли равишда электролит жойлашган, электродлар орасидаги фазода ўрнатилган, аслида, юқоридаги фикрларга кўра, улар фақатгина электролит ва электродлар орасидаги юпқа қатламларда нолдан фарқли бўладилар. Бу фикрлар 2.3,б-расмдаги потенциаллар тақсимланиши графигида ўз аксини топган.
Ўзининг бир қисми билан ЭЮК манбаси ичидан ўтган берк контур AmBnA бўйлаб Е векторининг чизиқли интегралини тузамиз ва қуйидагини ҳосил қиламиз:
![]() E dl =
E dl = ![]() E dl +
E dl +![]() E d l= UA –UB
, чунки
E d l= UA –UB
, чунки ![]() E dl=0.
E dl=0.
Иккинчи томондан,
![]() E dl =
E dl = ![]() E статdl +
E статdl +![]() Еқарш
d l = е ,
Еқарш
d l = е ,
чунки
![]() E статdl = 0,
E статdl = 0,
![]() Еқарш
d l =
Еқарш
d l = ![]() Еқарш
d l = е.
Еқарш
d l = е.
Демак
e = UA - UB ,
яъни элементнинг электр юритувчи кучи потенциаллар фарқига тенг ёки, ушбу мисолда бир ҳил, ташқи занжир узилгандаги клеммалардаги (занжирда ток бўлмаганда) кучланишга тенг.
Бу фикрлардан
кўрамизки, ![]() Edl = 0 шарт фақат
ЭЮК манбасидан ташқарида бўлган фазо учун тааллуқлидир.
Edl = 0 шарт фақат
ЭЮК манбасидан ташқарида бўлган фазо учун тааллуқлидир.
Гальваник элементидан ташқари, ЭЮКни ҳосил қилишнинг бирнеча усуллари мавжуд. Булардан бири – контакт ЭЮКларидир. Бунда турли жинсли металлар контакти мавжуд бўлганда бир металлдан иккинчи металлга ўтказувчанлик электронлари ўтиши ва, шу туфайли, бир металлда ортиқча мусбат, иккинчи металлда ортиқча манфий электр зарядлари пайдо бўлади. Электронларнинг бундай ўтиши контакт жойидаги ноэлектрик характердаги ташқи электр майдонининг таъсири сифатида кўрилиши мумкин. Туташган металларда ҳар хил ишорали зарядларнинг пайдо бўлиши натижасида контактлар потенциаллари фарқи бўлишига, токнинг йўқлигида эса контакт ЭЮК деб номланган ЭЮКнинг ҳисил бўлишига олиб келади. Контакт ЭЮК туташувчи металлар турларига ва ҳароратига боғлиқ.
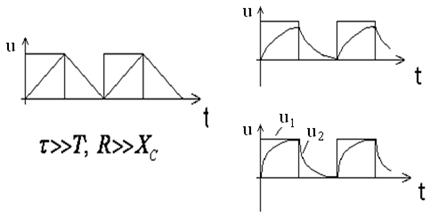
Ушбу ҳолат термоэлементларда ишлатилади. Агар икки турли жинсли ўтказгичлардан берк контур ҳосил қилсак, икки пайвандланган ўтказгичлар контактларидаги ҳар хил t ва t0 ҳароратда уланган жойлардаги контакт ЭЮКлари ҳар хил бўлади ва контур бўйлаб ўзаро компенсацияланмайди. Шу сабабли, берк контурда термоэлектрик юритувчи куч деб номланган натижавий ЭЮК ҳосил бўлади. Термоэлектрик юритувчи кучнинг умумий қиймати таркибига унинг қўшимча ЭЮКлари ҳам киради. Қўшимча ЭЮКлар икки бир жинсли ўтказгичлар бўйлаб, уларнинг бир учи иккинчи учига қараганда юқорироқ ҳароратли муҳитда бўлганлиги сабабли ҳосил бўлади. Бу қўшимча ЭЮКлар бир ҳароратли металлдаги электронларнинг иссиқлик ҳаракати бошқа ҳароратдагидан жадалроқ бўлганлигидан ўтказгич электронларининг ўтиши сабабли ҳосил бўлади. Термоэлементда токнинг оқиши натижасида ЭЮКнинг таъсири иссиқлик энергиясининг электр энергиясига айланиши билан боғлиқ. Аксарият қўлланиладиган термопараларда совуқ ва иссиқ қатламнинг ҳароратлари, мос равишда, 0 ва 100оС бўлганда, ЭЮК қиймати тахминан бирнеча милливольт ёки бирнеча ўн милливольт бўлади. Кейинги бўлимларда магнит майдонининг вақт бўйича ўзгарганидаги индуктивланадиган ЭЮК ни ўрганганимизда, «электр юритувчи куч» тушунчаси кенгайтирилади, шунда бу муҳим ҳодисанинг умумий таърифи келтирилади.
Эътиборни шунга қаратиш
зарурки, ЭЮКни таърифлаганда, юқорида келтирилганидек, интеграллаш
йўли энергия манбасининг ичида манфий клеммадан мусбат клеммага томон
ўтказилади (е=![]() Eташқdl), унинг А
ва В клеммаларидаги кучланишни аниқлаганда эса, интеграллаш ташқаридаги
йўлдан мусбат клеммадан манфий клеммага томон ўтказилади:
Eташқdl), унинг А
ва В клеммаларидаги кучланишни аниқлаганда эса, интеграллаш ташқаридаги
йўлдан мусбат клеммадан манфий клеммага томон ўтказилади:
uA = UA - UB =![]() Ed
Ed
3-маъруза. Электр занжири. Элементлари
3.1. Электр занжири. Актив элементлар
Электр занжирлари деб электромагнит жараёнларини ифодаланишда электр юритувчи куч, ток ва кучланиш тушунчаларидан фойдаланиш мумкин бўлган, электр токи оқиши учун йўлларни ҳосил қилувчи қурилмалар ва объектлар мажмуаларига айтилади.
Электр занжирларининг асосий элементларига электромагнит энергияси манбалари (қисқалик учун электр манбалари), электромагнит энергияни узатиш, қайта ишлаш ва қабул қилувчи қурилмалар киради.
Электромагнит энергиясининг манбаларига энергиянинг у ёки бу туридан – иссиқлик, кимъёвий, ядро, қуёш, шамол, механик ҳаракат энергияси ва ҳ.к. – электромагнит энергиясига айлантирувчи генератор қурилмалари киради. Буларга, масалан, айланувчи электр генераторлари, гальваник элементлар, аккумуляторлар, термоэлементлар ва ҳ.к. киради. Ҳозирги кунда иссиқлик, ядро, кимъёвий энергияларни электромагнит энергиясига айлантирувчи янги ускуналар яратилмоқда, масалан, магнитогидродинамик генераторлар, иссиқлик элементлари, қуёш батареялар ва ҳ.к.
Электромагнит энергияни узатиш элементларига алоқа линиялари, электр узатиш линиялари, электр тармоқлари киради.
Электромагнит энергияни қайта ишлашга ток ва кучланишни ўзгартирувчи трансформаторлар, частота ўзгарткичлари, кучайтиргичлар, шунингдек, ўзгармас токни ўзгарувчан токка айлантирувчи ионли ва ярим ўтказгичли инверторлар, ўзгарувчан токни ўзгармас токка айлантирувчи тўғрилагичлар ва ҳ.к.лар киради.
Электр занжирларидаги истеъмолчилар ёки юкламалар қаторига электр энергиясини бошқа турдаги энергияга айлантирувчи қурилмалар киради, масалан, радио ва телевизион жиҳозлар, электрон ҳисоблаш машиналари, электр моторлар, электролиз ускуналари, аккумуляторлар, иситкич жиҳозлари ва ҳ.к.
Доимо, у ёки бу қурилманинг – электр занжири элементининг – асосий вазифаси электромагнит энергиянинг генерацияси, уни узатиш, қайта ишлаш ёки истеъмол қилиш сифатида тайинланган бўлса, биринчи ўринга унинг фойдали иш коэффициенти юқори бўлиши талаби қўйилади.
Кўпгина ҳолларда электр занжиридаги у ёки бу элементнинг асосий вазифаси қилиб - электр сигналларини узатиш ёки қайта ишлаш, шунингдек у ёки бу катталикларни ўлчаш операциясини бажариш, у ёки бу жараёнларнинг сифатини бошқариш белгиланади. Бу элементлар қаторига телекоммуникация тизимлари, телефон ва телеграф алоқа линиялари ва уларнинг учларидаги қурилмалар, автоматика қурилмаларининг ҳар турдаги элементлари, электр ўлчаш қурилмалари, электрон ҳисоблаш машиналарининг ҳисоблаш ва бошқариш қурилмалари, ҳар турдаги радиотехник қурилмалар ва ҳ.к.лар киради. Уларнинг барчаси учун энг муҳим талаб – узатилаётган ва қайта ишланаётган сигналларнинг маълум сифатда бўлишидир. Табиийки, бу ҳолатлар учун ҳам электромагнит энергиясининг узатилиши ва қайта ишланиши амалга оширилади ва асосий бўлмаса ҳам, имкон қадар юқори фойдали иш коэффициентига эришиш мақсади қўйилади.
Келтирилган талаблар билан биргаликда, электр занжири элементлари бир қатор талабларни қониқтириши зарур – ишлашининг ишончлилиги, кўпга чидамлилиги, зарур бўлса – тез ишловчанлиги, ишдаги барқарорлиги, амалдаги аниқлиги ва ҳ.к.
Шунга мувофиқ, ҳозирги замон электротехник қурилмаларининг электр занжирлари жуда мураккабдир. Шу сабабли ҳам электр занжирлар назарияси доимий ривожланишда ва унга янада умумлаштирилган усуллар хос бўлмоқда. Ушбу фанни ўрганишда энг содда электр занжирларининг тадқиқотидан бошлаб, аста - секин мураккаб занжирларни ҳисоблаш (таҳлил ва синтез)нинг умумий усулларига ўтамиз.
Электр занжирининг электромагнит энергияси манбалари таъсир этаётган қисмини занжирнинг актив қисми (қисқача актив занжир) деб номлаймиз. Аксарият, уни ўртасида А ҳарфи бўлган тўғри тўртбурчак шаклида ва занжирнинг қолган қисмига улаш учун зарур бўлган сондаги клеммалар (ўтказгичлар) билан чизилади (3.1-расм).
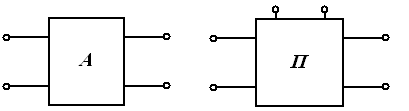 Электр занжири электромагнит энергия-си манбалари
бўлмаган қисмини занжирнинг пассив қисми, ёки қисқача
- пассив занжир деб атаймиз. Уни эса
ўр-
3.1-расм
3.2-расм
Электр занжири электромагнит энергия-си манбалари
бўлмаган қисмини занжирнинг пассив қисми, ёки қисқача
- пассив занжир деб атаймиз. Уни эса
ўр-
3.1-расм
3.2-расм
тасида П ҳарфи бўлган
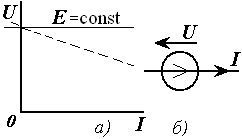 тўғри тўртбурчак шаклида ва занжирнинг қолган
қисмига улаш учун зарур бўлган сондаги клеммалар билан белгилаймиз
(3.2-расм). Бу тўғри тўртбурчаклар ичида занжир кўрилаётган қисмининг
барча элементлари, ўзаро уланишлари билан жойлаштирилади.
тўғри тўртбурчак шаклида ва занжирнинг қолган
қисмига улаш учун зарур бўлган сондаги клеммалар билан белгилаймиз
(3.2-расм). Бу тўғри тўртбурчаклар ичида занжир кўрилаётган қисмининг
барча элементлари, ўзаро уланишлари билан жойлаштирилади.
3.2. Пассив элементлар
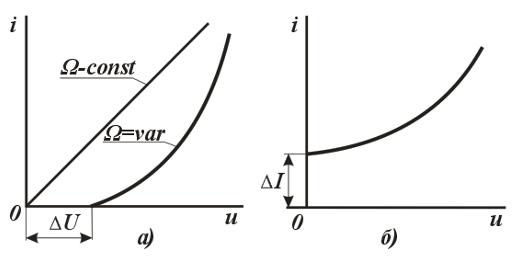
Шунга ўхшаш, занжирнинг манбаларини актив элементлар, қолганларини эса пассив элементлар деб атаймиз.
Электр занжирининг манбалари икки турга 3.3-расм
бўлинади: кучланиш ва ток манбалари. Манбалар ток ва кучланишининг ташқи таъсир натижасида ўзгаришига кўра, уларни мустақил ва номустақил манбаларга ажратилади. Манбанинг чиқиш клеммаларидаги кучланиш (ток) миқдори манбанинг юкидаги ток (кучланиш) қийматига боғлиқ бўлмаса мустақил кучланиш (ток) манбаси дейилади. 3.3-расмда мустақил кучланиш манбасининг ташқи тавсиф (а) ва (б) кўрсатилган. 3.4-расмда мустақил ток манбасининг ташқи тавсифи (а) ва схемада белгиланиши (б) кўрсатилган. Бундай манбалар қуйида келтирилган реал манбаларни идеаллаштириш билан ҳосил қилинади. Аксинча, манбанинг чиқиш клеммаларидаги кучланиш (ток) миқдори оқаётган ток (кучланиш) қийматига боғлиқ бўлса, яъни кучланиш манбасининг юкланиш токи ўзгарганда унинг кучланиши ҳам ўзгарса, ёки ток манбаси занжиридаги кучланиш ўзгариши натижасида унинг токи ҳам ўзгарса, уларни номустақил кучланиш (ток) манбалари дейилади. Реал манбаларда айнан шундай бўлади ва уларнинг ташқи тавсифлари пасаювчан (3.3 ва 3.4-расмларда пунктир чизиқ) бўлади.
|
|
3.4-расм
Манбалар бошқарилмас ва бошқарилувчи гуруҳларга ажратилади. Бошқарилувчи ток ва кучланиш манбаларининг ҳар бири уларнинг кириш қисмига келтирилган ток ва кучланиш билан бошқарилиши мумкин. Улар учун схемаларда қуйидаги белгиланишлар қабул қилинган:
|
|
а) Кучланиш билан
бошқарилувчи кучланиш манбаси КБКМ, яъни кириш қисмида UБош
бошқарувчи кучланиш, чиқишидаги кучланиш эса унга боғлиқ
u(UБош) бўлган кучланиш манбаси. Бунда боғлиқлик
пропорционал бўлса чизиқли ва, аксинча, ночизиқли бўлиши мумкин;
чизиқли КБКМ ночизиқли КБКМ
3.5-расм
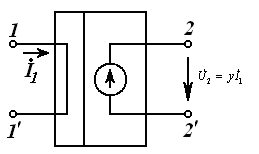
б) Ток билан бошқарилувчи кучланиш манбаси ТБКМ, яъни кириш қисмида iБош бошқарувчи ток, чиқишидаги кучланиш эса унга боғлиқ u(iБош) бўлган кучланиш манбаси. Бунда боғлиқлик пропорционал бўлса чизиқли ва, аксинча, ночизиқли бўлиши мумкин;
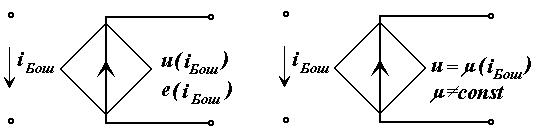
чизиқли КБТМ ночизиқли КБТМ
3.6-расм
в) Кучланиш билан бошқарилувчи ток манбаси КБКТ, яъни кириш қисмида UБош бошқарувчи кучланиш, чиқишидаги ток эса унга боғлиқ i(UБош) бўлган ток манбаси. Бунда боғлиқлик пропорционал бўлса чизиқли ва, аксинча, ночизиқли бўлиши мумкин;
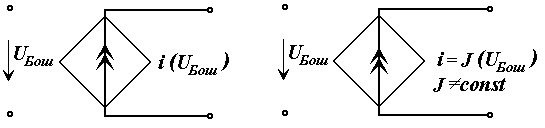
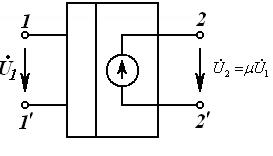
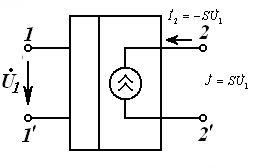
чизиқли КБТМ ночизиқли КБТМ
3.7-расм
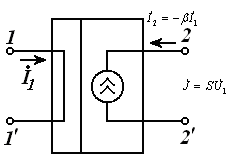
г) Ток билан бошқарилувчи ток манбаси ТБКМ, яъни кириш қисмида iБош бошқарувчи ток, чиқишидаги ток эса унга боғлиқ i(iБош) бўлган ток манбаси. Бунда боғлиқлик пропорционал бўлса чизиқли ва, аксинча, ночизиқли бўлиши мумкин.
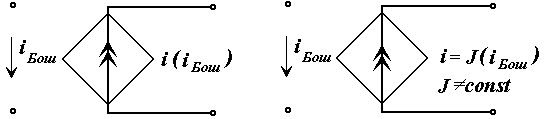
чизиқли ТБТМ ночизиқли ТБТМ
3.8-расм
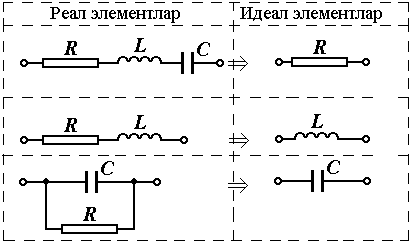
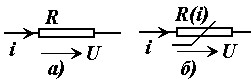 Занжирнинг пассив элементлари қаторига
резисторлар, конденсаторлар ва индуктивликлар киради.
Занжирнинг пассив элементлари қаторига
резисторлар, конденсаторлар ва индуктивликлар киради.
Резистор (баъзан резистив элемент, резистив қаршилик, Омик қаршилик деган номлари ҳам учрайди) деб, 3.9-расм
электр энергияси сарфланиб, унинг ҳусусиятлари U=R·i ёки i=G·U боғланишлар билан ифодаланган элементга айтилади. Бунда, R ва G қаршилик ва ўтказувчанлик деб номланган пропорционаллик коэффициентлари. 3.9-расмда уларнинг схемаларда белгиланиши келтирилган. R ва G ўзгармас бўлганда (а-расм) чизиқли ва, аксинча, R ва G лар ток ёки кучланишга боғлиқ ўзгарганда ночизиқли (б) қаршилик ёки ночизиқли ўтказувчанлик дейилади.
Электромагнит энергияни заҳиралаш хоссасига эга бўлган, физик хусусиятлари Ш=L·i тенглама билан ифодаланувчи индуктив ғалтакнинг идеаллаштирилган элементи индуктивлик элементи (ёки индуктивлик) дейилади. L пропорционаллик коэффициенти индуктивлик дейилади ва Генри [Нп] ўлчов бирлигига эга. 3.10-расмда чизиқли (а), ночизиқли (б) индуктивликнинг белгиланиши ҳамда Ш=L·i боғланишлар келтирилган.
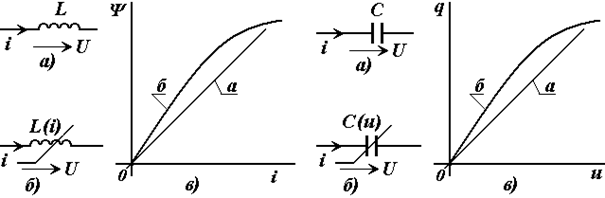
Электр
энергиясини заҳиралаш хоссасига эга бўлган, физик хусусиятлари q=C·u
тенглама билан ифодаланувчи конденсаторнинг идеаллаштирилган элементи сиғим
элементи дейилади. С пропорционаллик коэффициенти сиғим дейилади
ва Фарада [F] ўлчов бирлигига эга. 3.11-расмда чизиқли (а),
ночизиқли (б) сиғимнинг белгиланиши ҳамда q=C·u
боғланишлар келтирилган.
3.10-расм 3.11-расм
3.3. Реал элементларни идеаллаштириб алмаштириш
Кўрилган реал элементлар (резистор, сиғим, индуктивлик)нинг ҳар бири фақатгина ўзига ҳос бўлган хусусиятли бўлмасдан, балки ўзидан бошқа ҳар бир элементларнинг ҳам хусусиятларига эга. Масалан, солиштирма қаршилиги катта бўлган қотишмадан спиралсимон ўрамлар сифатида ясалган резистор хоссасини кўрайлик. Унинг асосий хусусияти бўлмиш омик қаршилигадан ташқари, ёнма-ён ўрамларининг орасида бироз сиғим ҳосил бўлади; шу ўрамлардан оқаётган ток эса резистор ўтказгичи атрофида бироз магнит майдони ва, демак, индуктивлик ҳосил қилади. Шу сабабли реал резисторда ҳам омик қаршилиги R, ҳам сиғими C, ҳам индуктивлиги L мавжуд экан.
Реал индуктивлик ғалтаги ўзининг L индуктивлик ҳусулиятидан ташқари, ғалтак ўрамлари ўтказгичида бироз R қаршилик ва ҳар бир ўрамлари орасида бироз С сиғимга эга.
|
|
Шунга
ўхшаш, реал конденсаторнинг қопламалари орасидаги
3.12-расм
диэлектрикдан силжиш токлари оқишига бироз R қаршилик таъсир кўрсатади. Буни реал конденсаторнинг қисқа муддат ишлагандаги қизишидан билиш мумкин.
Ушбу реал элементларда оқаётган токнинг ўзгариш тезлиги ёки частотаси жуда катта бўлмаган вазиятларда улар ўрнига иделлаштирилган резистор, сиғим, индуктивлик қабул қилиш мумкин. Ушбу иделлаштириш схемаси 3.12-расмда келтирилган.
 Демак, кетма-кет (3.13-расм) уланган резистор (а-b
oралиқ), конденсатор (c-d оралиқ) ва индуктивлик ғалтагидан
(h-j оралиқ)дан иборат бўлган занжир тузилган бўлсин. Фараз қилайлик,
электромагнит энергияси иссиқлик энергиясига фақат а-b соҳадаги
резистордагина ўтаяпти, яъни бу оралиқда занжирнинг барча қаршилиги
r миқдорида мужассамланган; электр силжиш
токлари фақат c-d оралиқда
конденсатор
3.13-расм
Демак, кетма-кет (3.13-расм) уланган резистор (а-b
oралиқ), конденсатор (c-d оралиқ) ва индуктивлик ғалтагидан
(h-j оралиқ)дан иборат бўлган занжир тузилган бўлсин. Фараз қилайлик,
электромагнит энергияси иссиқлик энергиясига фақат а-b соҳадаги
резистордагина ўтаяпти, яъни бу оралиқда занжирнинг барча қаршилиги
r миқдорида мужассамланган; электр силжиш
токлари фақат c-d оралиқда
конденсатор
3.13-расм
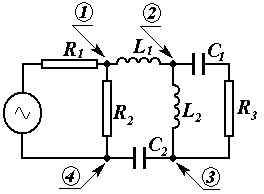 қопламалари орасида мавжуд, яъни бу соҳада
занжир-
қопламалари орасида мавжуд, яъни бу соҳада
занжир-
нинг барча С сиғими мужассамланган; ниҳоят, ўзгарувчан магнит майдон ЭЮКни фақат h-j оралиқда мужассам-ланган ғалтакда индуктивлайди, яъни ушбу соҳада занжирнинг барча L индук-тивлиги йиғилган. Умумий ҳолда анча мураккаброқ кўринишга эга бўлган ва ҳар хил элементлардан ташкил топган шун-
га ўхшаш электр занжирлари, мужас- 3.14-расм
самланган параметрли электр занжирлари дейилади.
Электр занжирлари ва, демак, улар схемалари умумий холда шохобчалар ва тугунлардан иборат.
Электр занжири схемасининг шохобчаси деб занжирнинг шундай қисмига айтиладики, унинг ихтиёрий бўлагида токнинг миқдори доимо бир хил бўлади.
Шохобча таркибида ихтиёрий миқдордаги кетма-кет уланган қаршилик, конденсатор, индуктивлик элементлари, ЭЮК манбалари бўлиши мумкин. Бунга мисол сифатида 3.15-расмни келтириш мумкин. Унда схеманинг d нуқтасидан c нуқтасига L1, r1 , e ва r2 элементлари бўйлаб юрсак, шу элементларнинг ҳар биридан бир хил ток оқишини кўрамиз. Демак, схеманинг d - L1 - r1 - e - r2 - с бўлаги шохобча экан. Шу dс оралиқни с – C – r3 – d бўйлаб юрсак, яни бир шохобчани кўрамиз. Ушбу схемада яна c – r4 – f, f -r6 - h, q - L2 - r7 – h ва d - r5 – h шохобчалар ҳам мавжуд. Демак, ҳар бир шохобчадаги элементлар ўзаро кетма-кет уланган экан.
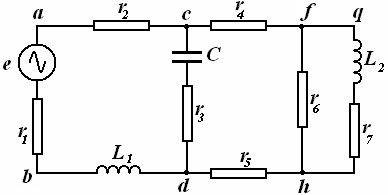
3.15-расм
Бунда электр занжири қисмларининг кетма-кет улангани деб шундай уланишига айтиладики, унда занжир шу бўлагининг ҳар бир қисмидан оқаётган ток бир бирига тенг бўлади.
Кетма-кет уланган элементларга мисол сифатида 3.16-расмда келтирилган схемаларни кўриб чиқайлик. Унда a – b оралиқда r1, C ва r2 элементлари кетма-кет уланган (3.16,а-расм); бунда уччала элементнинг токлари ir1 = iC = ir2 ўзаро тенг. Иккинчи шохобчада эса c ва d нуқталари орасида r ва L элементлари кетма-кет уланган ва ir = iL (3.16,б-расм).
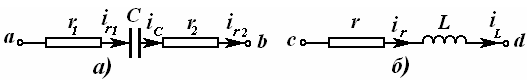
3.16-расм
Электр занжирининг тугунлари деб шохобчаларнинг уланган нуқталарига айтилади. Тугун электр схемасида нуқта билан белгиланади. Мисол сифатида 3.15-расмдаги схемани кўриш мумкин. Ундаги c, d, f, ва h нуқталар тугун дейилади.
Электр занжири (элементлари) шоходчаларининг параллел уланиши деб шундай уланишга айтиладики, унда барча (элементлар) шохобчалар занжирнинг бир жуфт тугунларига уланади ва барча (элементлар) шохобчалардаги кучланишлар бир хил бўлади. Параллел уланган шохобчаларга 3.15-расм схемасида f–h ва q-h қисмлари мисол бўлаолади.
Шохобчалари (элементлари) аралаш уланган электр занжирида кетма-кет ва параллел уланишлар биргаликда бажарилади, яъни схеманинг бир қисми параллел, бошқа қисми кетма-кет уланади.
Аралаш уланган занжир учун 3.15-расмдаги схема мисол бўла олади. Унда кетма-кет уланган r7 қаршилик ва L2 индуктивлик f ва h нуқталарда r6 қаршиликка параллел уланади. Улар, ўз навбатида, қўшилиб, натижавий қаршилик ҳосил қилади ва r4 ва r5 қаршиликларга кетма-кет уланади. Ўз навбатида, улар натижавий қаршиликни ҳосил қилиб, r4 ва r5 қаршиликларга қўшилиб, кетма-кет уланган С ва r3 шохобчага с ва d нуқталарда параллел уланади.
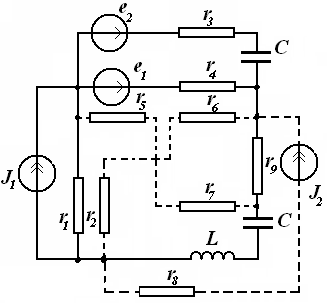 Электр занжирини текисликда схема шаклида
кесишмайдиган шохобчалар ёрдамида тасвирлаш мумкин бўлса, унда ясси (планар)
электр занжири дейилади. Бунга мисол сифатида 3.17-расмда тасвирланган
электр занжири схемасини келтириш мумкин. Бу схеманинг штрихли қисмини
расмдан олиб ташласак, планар занжири ҳосил бўлади. Схема кесишган
шохобчалар ёрдамида тасвирланса, унда ясси бўлмаган (нопланар) электр
занжири дейилади. Унга мисол бўлиб шу расмдаги схема штрихли элементлари
билан хизмат қилаолади.
Электр занжирини текисликда схема шаклида
кесишмайдиган шохобчалар ёрдамида тасвирлаш мумкин бўлса, унда ясси (планар)
электр занжири дейилади. Бунга мисол сифатида 3.17-расмда тасвирланган
электр занжири схемасини келтириш мумкин. Бу схеманинг штрихли қисмини
расмдан олиб ташласак, планар занжири ҳосил бўлади. Схема кесишган
шохобчалар ёрдамида тасвирланса, унда ясси бўлмаган (нопланар) электр
занжири дейилади. Унга мисол бўлиб шу расмдаги схема штрихли элементлари
билан хизмат қилаолади.
Электр занжири конту-
ри деб, бирнеча шохобчалар-дан ўтган ихтиёрий берк йўлга
айтилади. Бунга мисол қилиб 3.15-расмдаги abdcа, cdhfс ва fqhf контурларни олишимиз мумкин.
Икки клемма (қутб)га
эга бўлган электр занжири
икки қутблик деб аталади.
3.17-расмда икки қутблик шартли равишда тўғри тўртбурчак шаклида тасвирланган.
Занжир бутун қисмини битта икки қутблик 3.17-расм
деб қараш, занжир шу қисмининг
умумий хусусиятларини аниқлашда фойдалидир. Икки қутблик актив (3.17,а-расм) ва пассив (3.17,б-расм) турларга бўлинади.
Таркибида электр энергия манбасига эга бўлса, актив икки қутблик дейилади. Чизиқли актив икки қутблик учун яна унинг узилган клеммаларида икки қутблик ичидаги манба сабабли кучланишнинг мавжудлиги - қўшимча шарти қўйилади, яъни ушбу манбаларнинг таъсирлари икки қутблик ичида компенсацияланмаслиги зарур. Пассив икки қутблик деб таркибида электр энергия манбалари бўлмаган икки қутбликка айтилади. Манбалари ўзаро компенсацияланиб, икки қутбликнинг икки узилган клеммаларида кучланиш бўлмаса, чизиқли икки қутблик таркибида электр энергия манбалари мавжудлиги жоиз бўлади.
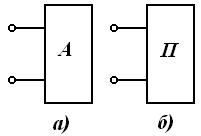 Пассив икки қутблик бўла туриб, унинг таркибида
ўзаро компенсацияланувчи манбалар мавжуд бўлишининг мумкинлиги ҳақидаги
шарт – бу заруратдир. Чунки занжирнинг бир бутун қисмини икки қутблик
билан алмаштириш ғояси, шу қисмнинг умумий ҳусусиятларини
унинг фақат ташқи клеммаларига нисбатан ўрганилишини
назарда
3.18-расм
Пассив икки қутблик бўла туриб, унинг таркибида
ўзаро компенсацияланувчи манбалар мавжуд бўлишининг мумкинлиги ҳақидаги
шарт – бу заруратдир. Чунки занжирнинг бир бутун қисмини икки қутблик
билан алмаштириш ғояси, шу қисмнинг умумий ҳусусиятларини
унинг фақат ташқи клеммаларига нисбатан ўрганилишини
назарда
3.18-расм
тутади. Ушбу шарт фақат чизиқли занжирларгагина тааллуқлидир, чунки ночизиқли занжирларда бундай компенсация фақат битта ёки фақат бирнеча ражим учун олиниши мумкин ва бошқа режимлар учун олиниши мумкин бўлмайди.
4-маъруза. Электр занжирлари назарияси асосий қонунлари
4.1. Кирхгоф қонунлари
Электр занжирларини ҳисоблаганда Кирхгофнинг икки қонуни, Ом қонуни, алмаштириш теоремаси қўлланилади. Уларни мужассамланган параметрли занжирларни ҳисоблашда кўриб чиқамиз.
Кирхгофнинг биринчи қонуни чет тиллардаги адабиётларда ҳар хил номларда учрайди, шулардан иккинчи номи Кирхгофнинг токлар қонуни, учинчиси Кирхгофнинг тугунлар учун қонуни – электр занжирининг тугунлари учун қўлланилади ва электр токининг узлуксизлиги принципига асосланади. Кирхгофнинг токлар қонуни - электр (заряд) миқдори сақланиш қонунидан келиб чиқувчи натижадир; унданда кўра аҳамиятлироқ қилиб айтганда - бу энергия сақланиш қонунининг электр занжирлари «тилидаги» ифодасидир: занжирнинг бир тугунига шохобчалардан келувчи барча токлар йиғиндиси, ушбу тугундан чиқиб кетаётган барча токлар йиғиндисига тенг.
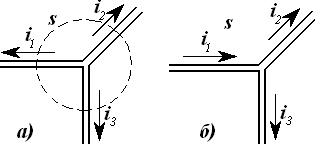 Занжирнинг тугунини берк юза s билан
ўраб оламиз (4.1,а-расм). Қабул қилинган фаразларга мувофиқ,
мужассамланган параметрли занжирлардаги барча сиғимлар занжирдаги мавжуд
конденсаторларда мужассам бўл-ган. Бу уланган
ўтказгичлардан
Занжирнинг тугунини берк юза s билан
ўраб оламиз (4.1,а-расм). Қабул қилинган фаразларга мувофиқ,
мужассамланган параметрли занжирлардаги барча сиғимлар занжирдаги мавжуд
конденсаторларда мужассам бўл-ган. Бу уланган
ўтказгичлардан
занжирнинг бошқа қисмларига электр силжиш токларининг ўти- 4.1-расм
шини эътиборга олмасликка мос келади. Шундай қилиб, берк юза s орқали шу юзани кесиб ўтаётган ўтказгичлардаги фақат ўтказувчанлик токлари оқиб ўтади.
Токнинг узлуксизлиги принципи асосида, бу ҳолат учун қуйидаги ифодага эга бўламиз:
![]() Jds = i1
+ i2 + i3 =
0.
Jds = i1
+ i2 + i3 =
0.
Занжирнинг тугунига уланган ихтиёрий п шохобча учун
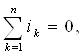 (4.1)
(4.1)
яъни, электр занжирининг тугунидаги токлар алгебраик йиғиндиси нолга тенг, мана шу Кирхгоф биринчи қонунининг таърифидир.
Кирхгоф биринчи қонунининг ҳар хил номлари ичида, унинг моҳиятини аниқроқ ифодалайдигани - Кирхгофнинг токлар қонуни (КТҚ) номидир. Келгусида бу қонунни мана шу номда ишлатамиз.
КТҚ асосида тенгламалар тузишни барча шохобчаларда токларнинг шартли-мусбат йўналишини аниқлаш ва уларни схемада стрелкалар билан белгилашдан бошлаш зарур. Токларнинг мусбат йўналиши тугундан бошланса, (4.1) тенгламанинг чап томонидаги токларнинг ҳарфли белгиларига «плюс» ишорасини, мусбат йўналиши тугун томон йўналган бўлса, токларнинг ҳарфли белгиларига «минус» ишорасини қўйилади. 4.1,а-расмдаги ҳолат учун тенгламанинг барча токлари учун «плюс» ишора, 4.1,б-расмдаги ҳолат учун эса қуйидагича ёзиш керак:
-i1 + i2 + i3 = 0. (4.1,а)
Агар ҳисоблашлар натижасида бирор ток вақтнинг бирор они учун мусбат ишорали (i k >0) бўлса, демак шу онда токнинг йўналиши стрелка кўрсатишига мос бўлади. Агар натижа i k < 0 бўлса, демак бу токнинг йўналиши аслида стрелкага тескари йўналишда бўлади.
Кирхгофнинг иккинчи қонуни, ёки бошқа номлардаги Кирхгофнинг контурлар учун қонуни, ёки Кирхгофнинг кучланишлар қонуни электр занжирларининг берк контурлари учун қўлланилади
![]() E dl =
E dl =![]() Eинд dl +
Eинд dl +![]() Eташқ
dl
.
(4.2)
Eташқ
dl
.
(4.2)
![]() Eташқdl қиймат
контурга таъсир этаётган ташқи манбалар ЭЮКларининг Уеташқ
йиғиндисидир. Тенгламанинг
Eташқdl қиймат
контурга таъсир этаётган ташқи манбалар ЭЮКларининг Уеташқ
йиғиндисидир. Тенгламанинг ![]() Eинд dl ташкил
этувчиси таркибига контурдаги барча индуктивланаётган ЭЮКлар – ҳам
электромагнит индукцияси, ҳам ўзиндукция, ҳам ўзаро индкция
асосидаги ЭЮКлар киради. Масалан, ғалтакдаги eL
= L di / dt ни олайлик. Агар (4.2) нинг биринчи
ташкил этувчисига энергия манбаси сифатида фақат генераторлардаги ЭЮКларининг
йиғиндиси Уеинд ни киритсак, у ҳолда ғалтаклардаги
индуктивланаётган ўзиндукция ва ўзаро индукция ЭЮКларини тенгламанинг чап
томонига ўтказилиши ва
Eинд dl ташкил
этувчиси таркибига контурдаги барча индуктивланаётган ЭЮКлар – ҳам
электромагнит индукцияси, ҳам ўзиндукция, ҳам ўзаро индкция
асосидаги ЭЮКлар киради. Масалан, ғалтакдаги eL
= L di / dt ни олайлик. Агар (4.2) нинг биринчи
ташкил этувчисига энергия манбаси сифатида фақат генераторлардаги ЭЮКларининг
йиғиндиси Уеинд ни киритсак, у ҳолда ғалтаклардаги
индуктивланаётган ўзиндукция ва ўзаро индукция ЭЮКларини тенгламанинг чап
томонига ўтказилиши ва ![]() E dl нинг таркибига
киритилиб, ғалтак клеммаларидаги кучланишлар пасаюви сифатида эътиборга
олиниши шарт. Масалан, ғалтак учун тенгламанинг чап томонида иL
= +L di / dt пайдо бўлади. Чап томондаги
E dl нинг таркибига
киритилиб, ғалтак клеммаларидаги кучланишлар пасаюви сифатида эътиборга
олиниши шарт. Масалан, ғалтак учун тенгламанинг чап томонида иL
= +L di / dt пайдо бўлади. Чап томондаги ![]() E dl таркибига,
яна контурга кирувчи реостатдаги кучланишлар пасаюви ri ҳам,
конденсатордаги uC = q/C кучланишлар пасаюви ҳам
киради. Контурнинг барча п шохобчаларидаги энергия манбалари ЭЮКларининг
йиғиндисини қуйидагича белгилаймиз
E dl таркибига,
яна контурга кирувчи реостатдаги кучланишлар пасаюви ri ҳам,
конденсатордаги uC = q/C кучланишлар пасаюви ҳам
киради. Контурнинг барча п шохобчаларидаги энергия манбалари ЭЮКларининг
йиғиндисини қуйидагича белгилаймиз
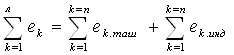
ундан
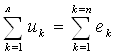 .
(4.3)
.
(4.3)
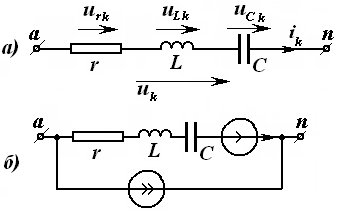 Шундай қилиб, Кирхгофнинг иккинчи қонуни қуйидагича
талқин этилади: электр занжирининг ихтиёрий берк контурдаги барча
шохобчалари кучланишлар пасаювининг йиғиндиси шу контурга таъсир этаётган
энергия манбалари ЭЮКларининг йиғиндсига тенг.
Шундай қилиб, Кирхгофнинг иккинчи қонуни қуйидагича
талқин этилади: электр занжирининг ихтиёрий берк контурдаги барча
шохобчалари кучланишлар пасаювининг йиғиндиси шу контурга таъсир этаётган
энергия манбалари ЭЮКларининг йиғиндсига тенг.
Агар k – шохобчада, умумий ҳолда, актив қаршилик ik қаршилиги, iL индуктивлик ғалтаги С сиғимли конденсатори (4.2,а-расм) бўлса, у ҳолда ушбу шохобча бўйлаб кучланишлар пасаюви
шу элементларнинг улар кучланишлари пасаювлари йиғиндисига uk = urk + uLk + uCk тенг. 4.2-расм
Унда
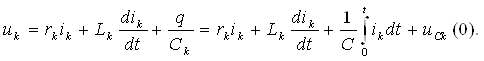
Кирхгофнинг
иккинчи қонуни асосида тенгламалар тузиш учун барча шохобчаларнинг ik
токлари ва энергия манбалари ЭЮКлари еk нинг
мусбат йўналишлари берилган бўлиши шарт. Кучланишлар пасаюви uk мусбат
йўналишлари ik токларнинг мусбат йўналишларига мос деб ҳисоблаймиз.
Шундан сўнг контурни айланиб чиқишнинг бирор йўналишини танлаб,
кучланишлар пасаюви 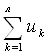 йиғиндиси
ва ЭЮКлар
йиғиндиси
ва ЭЮКлар 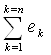 йиғиндисини
тузишда uk ва еk нинг ҳарфли
белгилари олдига «плюс» ёки «минус» ишораларини қўйиш лозим. Агар uk
ва еk қийматлар мусбат йўналишари айланиш
йўналиши билан мос келса «плюс», акси бўлса «минус» ишораси қўйилади.
йиғиндисини
тузишда uk ва еk нинг ҳарфли
белгилари олдига «плюс» ёки «минус» ишораларини қўйиш лозим. Агар uk
ва еk қийматлар мусбат йўналишари айланиш
йўналиши билан мос келса «плюс», акси бўлса «минус» ишораси қўйилади.
Мужассамланган параметрли электр занжирларида Кирхгофнинг иккинчи қонуни электр занжирини қуршаб олган фазо орқали бир тугундан иккинчи тугунга ўтадиган контур учун ҳам ёзилиши мумкин. Мужассамланган параметрли электр занжирлари назариясини қуришда қабул қилинган илмий абстракциялар асосида шуни эътиборга олишимиз зарурки, бу занжирни қуршаб олган фазода магнит ва ташқи майдонлар бўлмаслиги зарур, демак, еташқ ва еинд ЭЮКлар нолга тенг бўлиши шарт. Контурни бундай айланиш йўналишини танлаганда қуйидагини ёзиш мумкин
![]() E dl =
E dl = ![]() (4.4)
(4.4)
бунда ![]() - m ва n тугунлар орасидаги кучланишлар.
- m ва n тугунлар орасидаги кучланишлар.
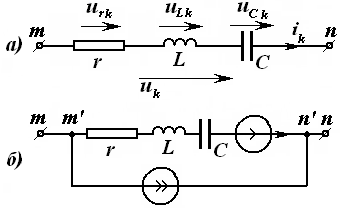 Шунга эътибор берайликки, мужассамланган параметрли
занжирнинг ташқи фазосида ҳам электр майдони мавжуд деб ҳисобланса,
интеграл айрим маънога эга бўлади. Аммо бундай майдон энергияси ва силжиш
токлари жуда кичик ва эътиборга олмаса ҳам бўлади, деб ҳисобланади.
Шунга эътибор берайликки, мужассамланган параметрли
занжирнинг ташқи фазосида ҳам электр майдони мавжуд деб ҳисобланса,
интеграл айрим маънога эга бўлади. Аммо бундай майдон энергияси ва силжиш
токлари жуда кичик ва эътиборга олмаса ҳам бўлади, деб ҳисобланади.
Шохобча k
да (4.2,б-расм) энергия манбаларининг мавжудлиги шу шохобчанинг
графигига (4.2,в-расм) ҳеч қандай таъсир этмайди. Шохобча
графидаги ток ва кучланишларни ![]() ва
ва ![]() каби
каби
белгилаймиз. Ток ![]() ва
кучла-
4.3-расм
ва
кучла-
4.3-расм
ниш ![]() , ток манбаси ва ЭЮК
(4.2,б-расм) манбасига эга бўлган, бирор умумлаштирилган шохобчага
тааллуқлидир. КТҚга асосан, 4.2,б-расмдаги
, ток манбаси ва ЭЮК
(4.2,б-расм) манбасига эга бўлган, бирор умумлаштирилган шохобчага
тааллуқлидир. КТҚга асосан, 4.2,б-расмдаги ![]() (ёки
(ёки ![]() ) тугунига
нисбатан қуйидагиларни ёзиш мумкин бўлади
) тугунига
нисбатан қуйидагиларни ёзиш мумкин бўлади
![]()
Кирхгофнинг иккинчи қонунига мувофиқ, k шохобча ўтказгичларидан m тугундан n тугунга ўтаётган ва ташқи фазодан – n тугундан m тугунга ўтаётган контур учун қуйидагини ҳосил қиламиз
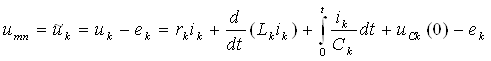 .
.
Кейинги ифода берилган схемада мавжуд бўлган ва схема графида шохобчалар токлари ва кучланишлари, ток ва ЭЮК манбалари кесмалар билан тасвирланган бўлса, графнинг умумлаштирилган шохобчаларидаги ток ва кучланишларни боғлайди.
Кирхгоф қонунлари бўйича схема графи учун тенгламалар ёзилганда шуни кўзда тутамизки, бу тенгламалар таркибига схеманинг умумлаштирилган шохобчаларидаги ток ва кучланишлар киради. Демак, схема графи учун қуйидагини ёзиш мумкин:
 ва
ва  ёки
ёки
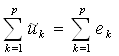 .
(4.5)
.
(4.5)
Кирхгоф иккинчи қонунининг ҳар хил номлари ичида, унинг моҳиятини аниқроқ ифодалайдигани - Кирхгофнинг кучланишлар қонуни (ККҚ) номидир. Келгусида бу қонунни мана шу номда ишлатамиз.
Ушбу маърузада
умумий ҳол учун таркибида реактив элементлари С сиғим ва L
индуктивлик ҳамда R қаршилиги бўлган занжирларнинг барқарорлик
жараёнларини кўрдик. Ўзгармас ток занжирларида d/dt=0
бўлганлиги учун ва, демак, шохобчага конденсатор уланиши – шу шохобчанинг
узилишини i=Cduc/dt=0 англатиши, индуктивликнинг мавжудлиги
эса ундаги кучланиш U![]() =Ldi/dt= 0
сезиларсиз деб ҳисобланганлиги учун: КТҚ 4.1-расмдаги схемада қуйидагича
ёзиш керак:
=Ldi/dt= 0
сезиларсиз деб ҳисобланганлиги учун: КТҚ 4.1-расмдаги схемада қуйидагича
ёзиш керак:
-I1 + I2 + I3 = 0.
ККҚ эса (4.3) ўрнига қуйидагича ёзиш керак:
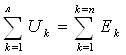 .
(4.5,а)
.
(4.5,а)
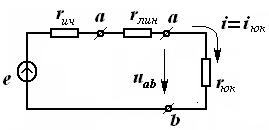
 4.2. Ом қонуни
4.2. Ом қонуни
Резистив қаршиликлари бўлган занжирлар учун силжиш ва кўчиш токлари нолга тенг деб фараз қиламиз. Натижада, 4.3-расмдаги занжирнинг фақат ўтказувчанлик токлари учун келтирилган (4.5,а) математик ифода манбанинг е ЭЮК билан ундаги i ток орасидаги боғланишни кетма-кет уланган ихтиёрик қаршиликлар
Уr = rич + rл
учун қуйидагича аниқланади:
4.4-расм
uab = rюк ·i
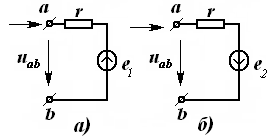 бунда rл – манбадан юкламагача
бўлган
бунда rл – манбадан юкламагача
бўлган
ихтиёрий узунликдаги линия ўтказгичи-
нинг қаршилиги. Буларни (4.5)га қўйсак юклама кучланишининг бошқача кўри-нишини оламиз:
uab = e – Уr · i (4.6)
Бундан токни аниқласак, 4.5-расм
i = (е - uаb) /Уr (4.7)
Кейинги тенглама Омнинг умумлаштирилган қонуни деб аталади. Танланган мусбат йўналишлар ўзгартирилганда, (4.7) даги барча ҳадларнинг ёки баъзи ҳадларининг ишоралари ўзгариши мумкин; масалан, 4.4,а,б-расмларда тасвирланган занжирларда, мазкур тенгламалар қуйидагича ёзилади:
uab = е1 + ir ёки i = (uab – е1)/r; (4.8)
uab = - е2 + ir ёки i=(uab+ е2)/r; (4.9)
Ўзгарувчиларнинг харфли белгиланишида мусбат ёки манфий қийматларини ифодаланиши хам мумкинлигини эслатиб ўтамиз.
Кучланиш uab ни a ва b нуқталари орасидаги потенциаллар фарқи эканлигини эътиборга олинса, яъни уни цa ва цb орқали ифодаласак, унда умумлаштирилган Ом қонуни бошқа кўриниш, масалан (4.9) учун қуйидаги кўриниш олади:
i=( цa - цb + е2)/r.
Электр занжири элементидаги ток ва кучланиш орасидаги боғланиш
uab = r · i
занжирнинг бир қисми учун Ом қонуни дейилади.
Бир контурли занжир учун Ом қонуни
i=Уе/У r, ёки Уr·i=Уе (4.9,а)
бунда Уе – контурдаги ЭЮКлар йиғиндиси; Уr – контурдаги қаршиликлар йиғиндиси.
Масалан, 4.5-расмдаги ташқи контур учун уни соат мили йўналиши бўйлаб ўтилганда (4.9) тенглама қуйидагича ёзилади:
r1 i1 - r3 i3 - r2 i2 = е1 - е2 .
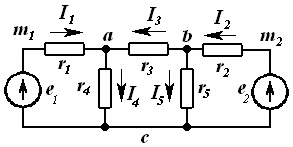 Харфлар билан белгиланаётган қийматлар, ўз
ўрнида, мусбат ёки манфий бўлиши ҳам мумкин.
Харфлар билан белгиланаётган қийматлар, ўз
ўрнида, мусбат ёки манфий бўлиши ҳам мумкин.
Кирхгофнинг иккинчи қонуни ифодасидаги Уr·i ва Уе йиғиндилар контурнинг бир қисми учун ҳам, яъни а ва b нуқталар орасида узилиш пайдо бўлганда ҳам қўлланилиши мумкин. Бундай ҳолда тенгламанинг чап томонидаги узилган нуқталар орасидаги потенциаллар фарқи кири- 4.6-расм
тилади:
Уr·i+Uab= Уе, (4.10)
бунда юқорида кўрилган ишоралаш қоидасидага амал қилинади.
Кейинги ифодани ташқи контур (4.5-расм) учун қўллаб, соат мили йўналиши билан ўтилганда, а нуқтасида ўтишни узиб b нуқтасида ўтишни давом эттириб, қуйидагини аниқлаймиз:
r1i1 - r2i2 + Uab = е1 - е2 .
5-маъруза. Электр занжирларини ҳисоблаш усуллари
5.1. Эквивалент алмаштириш усули
Кирхгоф, Ом ва Жоуль-Ленц қонунларини оддий электр занжирларига қўллаш ҳеч қандай қийинчилик уйғотмайди. Аммо кетма-кет ва параллел уланишлардаги, ҳамда оддий параллел кетма-кет уланишлардаги ток ва потенциалларнинг тақсимланишини тўғри идрок этишни алифбе ёки кўпайтириш жадвалини билгандек пухта ўзлаштириш зарур.
Кетма-кет улаш. Кучланиш манбаси билан икки қаршилик кетма-кет уланганда (5.1,а-расм) улардан фақат биргина ток оқиб ўтади
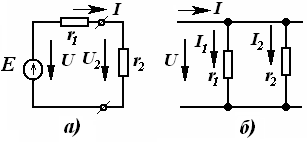 i = I = Е / (r1 + r2).
(5.1)
i = I = Е / (r1 + r2).
(5.1)
Бир қатор резисторлар кетма-кет уланган бўлса уларни битта эквивалент қаршилик билан алмаштириш мумкин:
rэ = r1 + r2 + r3 + … (5.2) 5.1-расм
Уларнинг хар бири орқали оқаётган ток I = U / rЭ, бунда
U = Е = r1I + r2I2 + r3I3 + …
кучланишлар йиғиндиси.
[Бундан сўнг, ўзгармас ток занжирлари учун (барқарорлик режимида) ток ва кучланишлар лотинча бош харфлар I ва U билан белгиланади].
Параллел улаш. Хар бири ўзаро параллел бўлган шохобчаларда кучланиш U бир хилдир, яъни тенгдир (5.1,б-расм). Агар U берилган бўлса, у холда хар бир шоҳобча учун ток қийматини Ом қонуни асосида аниқланади:
I1 = g1U; I2 = g2U; … (5.3)
бунда gk = 1/rk - қиймат k - чи шохобчанинг ўтказувчанлиги.
Кирхгофнинг биринчи қонунига асосан, умумий ток барча шохобчалар токларининг йиғиндисига тенг:
I = I1 + I2 +…= (g1 + g2 + …)U .
Параллел уланганда барча шохобчаларни бир эквивалент ўтказувчанликка эга бўлган бир шохобча билан алмаштириш мумкин:
gэ = g1 + g2+… (5.4)
Бунда ток I ва кучланиш U орасидаги боғланиш берилган занжирдагидек қийматга эга бўлади:
I = gЭU .
Занжирда икки параллел шохобчалар мавжудлиги сабабли (5.1,а-расм) U2 =U3 бўлгани учун ток қуйидагича аниқланади:
I1 = I2 + I3 = (g2 + g3)U2 = gЭ·U2 = U2/rЭ ,
бунда
 .
(5.5)
.
(5.5)
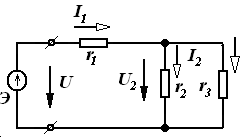 Оддий
кетма-кет-параллел занжир. Бундай
занжирни (5.2-расм) ҳисоблаш бирмунча мураккаброқ. Икки параллел шохобчани эквивалент (rЭ) қаршилик билан алмаштириб
Оддий
кетма-кет-параллел занжир. Бундай
занжирни (5.2-расм) ҳисоблаш бирмунча мураккаброқ. Икки параллел шохобчани эквивалент (rЭ) қаршилик билан алмаштириб
rЭ = r2 r3 / (r2 + r3) (5.6)
умумий токни
I1 = Е /( r1 + rЭ), (5.7)
ҳамда икки параллел шохобчада кучланишни аниқлаймиз:
5.2-расм
U2 = U3 = rЭ ·I1 , (5.8)
ундан сўнг токларни аниқлаймиз:
I2 = U2 /r2; I3 = U3 /r3 (5.9)
Кейинги ифодаларга (5.7)дан U2=U3 ни қўйиб, сўнгра I1 ва rЭ ни (5.6) ва (5.5)дан аниқлаб, барча токлар учун ифодаларни қулай ҳолатга келтириш мумкин:
![]()
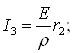
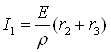 ,
(5.10)
,
(5.10)
бунда ![]() қуйидаги
уч шохобчанинг барча қаршиликларидан ҳар иккиси
кўпайтмалари йиғиндиси
қуйидаги
уч шохобчанинг барча қаршиликларидан ҳар иккиси
кўпайтмалари йиғиндиси
![]() = r1
r2 + r2 r3 + r3 r1.
(5.11)
= r1
r2 + r2 r3 + r3 r1.
(5.11)
Ушбу умумлаштирилган таъриф I2, I3 токларни ва улар йиғиндисига тенг бўлган I1 токни аниқлаш учун зарурдир.
(5.10) ифодалардан токлар орасидаги боғланишлар хам яққол кўзга ташланади:
![]()
![]()
![]() (5.12)
(5.12)
(5.10)-(5.12) боғланишлар занжирларни ҳисоблашда кўп учраб туради. Уларни қайтадан келтириб чиқармасдан эслаб қолиш зарур.
Параллел кетма-кет шохобчали занжир. Мураккаб электр занжирини кўпинча бир қатор кетма-кет ва параллел уланган қаршиликлар сифатида тасаввур қилиш мумкин. Масалан, қаршиликлари rю1; rю2;... бўлган бирнечта юкламалар, алоҳида бўлакларининг қаршиликлари rл,1; rл,2;...га тенг бўлган битта линияга уланган бўлсин (5.3-расм). 5.3-расм
Бир ўтказгичдан оқаётган барча ток, иккинчи ўтказгичдан қайтиб келадиган икки ўтказгичли
линия кўрилаётган ҳолат учун унинг ихтиёрий бўлаги қаршилиги (масалан, rл,1) тўғри ва тескари (иккала) ўтказгичлар қаршиликларини (айтайлик, rл1/2 ва rл1/2) қўйилиб, бир линияга уланган деб ҳисоблаш мумкин. Қаршиликларнинг бўндай ўрин алмашинуви натижасида линиянинг бўлагидаги кучланишлар пасаюви ўзгармайди.
5.3-расмда келтирилган схемани ўрганиш натижасида, rю,4+rл,4 қаршиликли шохобча (охирги юкланиш охирги линия бўлаги билан бирга) rю,3 (охиридан олдинги бўлак юкланиши шохобчаси) билан параллел эканлигини кўриш мумкин. Ушбу икки шохобчаларни битта эквивалент қаршилик билан алмаштириш мумкин. Бу қаршилик эса, ўз навбатида rл,3 (охиридан олдинги линия) қаршилигига кетма-кет уланган бўлади.
Шу таъриқа, барча занжир қаршиликларини «йиғиш» ва, натижада мураккаб занжирни соддалаштирилган (5.1,а-расм) холатга келтириш мумкин. Соддалаштирилган занжир учун манба токи Iл,1 ни аниқлаш қийин эмас. Бундан сўнг биринчи юкланишдаги кучланишни
Uю1 = Е - rл1·Iл1 (5.13)
ва унинг токини аниқлаш мумкин:
Iю1 =Uю1/rю1 ,
сўнгра иккинчи бўлакдаги линия токи Iл2 = Iл1 - Iю1 ни аниқланади ва ҳ.к.
5.2. Кирхгоф қонунларини татбиқ этиш
Кирхгоф қонунларидан фойдаланиб, мураккаб чизиқли занжирда, берилган қийматлар мавжудлигида, шохобчалар токлари ва тугунлар потенциалларни аниқлаш имконини берувчи тенгламалар тизимини ҳосил қилиш мумкин. Масалан, барча кучланиш манбаларининг э.ю.к.лари, барча ток манбалартнинг токлари ва барча қаршиликлар қийматлари мавжуд бўлса, барча шохобчалар токларини ҳисоблаш мумкин.
Занжирда ток ва потенциалларнинг қийматларини (қийматларни қандай усулда - ҳисоблаш усуллари ёки ўлчаш усуллари ёрдамида аниқланишидан қатьий назар) текширишда ҳам Кирхгоф қонунларини қўллаш муҳим аҳамиятлидир; чунки берилган тенгламалар тизимининг тахмин қилинган ечимини текшириш, тенгламалар тизимини қайта ечишдан кўра енгилроқдир.
Дарҳақиқат, Кирхгоф қонунларининг татбиқ этилиши орасида энг муҳим ўрин тутганлари - тенгламалар тизимини ечмасдан туриб, чизиқли электр занжирининг баъзи умумий хусусиятларини аниқлаш имконини берувчи, «принциплар» деб аталувчи усуллардир (масалан, суперпозиция принципи, ўзаролик принципи).
Кирхгоф тенгламалари тизими. Берилган занжир шохобчалари сони “Ш” га тенг бўлсин; бу сонга ток J манбасига эга бўлган шохобчалар кирмайди; ушбу J ток ва кучланиш Е қийматлари берилган бўлсин. Шохобчаларнинг чегараси бўлган тугунлар сони Т га тенг бўлсин.
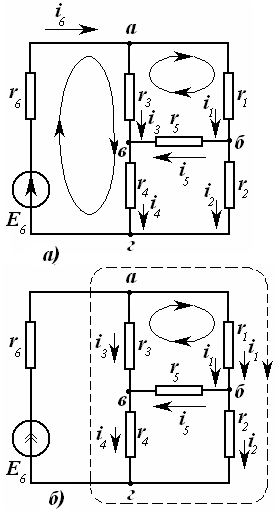 У холда КТҚга асосан мустақил тенгламалар
сони
У холда КТҚга асосан мустақил тенгламалар
сони
К1 = Т - 1 (5.14)
тугунлар сонидан 1 га кичик бўлади.
ККҚга асосан, яна К2та мустақил тенгламалар қуриш мумкин:
К2 = Ш - К1 = Ш + 1 - Т (5.15)
Бу тенгламалар берк контурлар учун тузилади. Контур тенгламаларининг ўзаро мустақиллиги аёндир, чунки хар бир контур таркибида хеч бўлмаганда битта шохобча бошқа контурлар таркибига кирмайди (бу зарурий бўлмаган, бироқ етарли бўлган шартдир).
Мустақил тенгламалар тўла сони шохобчалар сонига тенг
Ш = К1 + К2 (5.16)
Охирги тенглик (5.14) ва (5.15) дан келиб чиқади, чунки ихтиёрий К1 тугун тенгламалари ихтиёрий К2 контур тенгламалари сонига боғлиқ эмас; дарҳа-
қиқат, контур тенгламалари таркибига 5.4-расм
киритиш шарт бўлган шохобчалар қаршилиқлари тугун тенгламалари таркибига кирмайди.
Шундай қилиб, агар барча шохобчалар қаршиликлари, ҳамда манбаларнинг токлари ва кучланишлари берилган бўлса, у холда тенгламалар тизимидан барча Ш та шохобчаларнинг Ш дона номаълум токларини аниқлаш мумкин. Ш шохобчалар сонига манбали шохобчалар кирмаслиги алохида таькидланади.
Агар у ёки бу э.ю.к. (ёки қаршиликлар) номаълум бўлганда хам тенгламалар тизимининг ечимини аниқлаш мумкин. Аммо, бунда тенгламадаги бошқа қийматлар (масалан, айрим шохобчалар токи) маълум бўлиши шарт, чунки номаълумлар умумий сони шохобчалар (тенгламалар) сони Ш дан ортмаслиги шарт.
5.3. Кирхгоф қонунлари асосида тузилган
тенгламалар тўлиқлиги
 Мустақил
тугун тенгламалари сони.
Аввал ток манбаси бўлмаган занжирни кўрайлик. Занжирда (5.5,а-расм)
тўрт тугун бўлиб, уларнинг хар бири қолган тугунлар билан биргина шохобча орқали
уланган бўлсин.
Мустақил
тугун тенгламалари сони.
Аввал ток манбаси бўлмаган занжирни кўрайлик. Занжирда (5.5,а-расм)
тўрт тугун бўлиб, уларнинг хар бири қолган тугунлар билан биргина шохобча орқали
уланган бўлсин.
Ушбу тугунлар учун тенгламалар қўйидагича бўлади: 5.5-расм
I12 + I13 + I14 = 0; I21 + I23 + I24 = 0;
I31 + I32 + I34 = 0; I41 + I42 + I43 = 0,
бунда Imn - m ва n тугунларни боғловчи шохобчанинг m тугундан n тугунга йўналган токи.
Биринчи учта тенгламалар йиғин-дисини ҳисобласак (бунда I21 + I12 = 0; I13 + I31 = 0) шу маълум бўладики, ҳосил I14 + I24 + I34 = 0 бўлган йиғинди таркибида фақат тўртинчи тугунча келаётган токлар бўлар экан. Бу йиғинди тўртинчи тугун тенгламасидан фақатгина барча хадларнинг ишораси билан фарқланади, демак, охирги тугун учун ёзилган тенглама ундан олдингиларнинг натижаси экан.
Биринчи учта тенгламаларнинг мустақил эканлиги аниқ, чунки уларнинг хар бирида, хеч бўлмаганда, битта янги ток мавжуд: m тугун учун - бу m тугунни кейинги тугун (масалан 4-тугун) билан боғловчи Im4 токидир.
Агар, икки тугун, масалан 1 ва 2 тугунлар орасида бирнеча I'12,I”12,... токли параллел шохобчалар мавжуд бўлса, у ҳолда биринчи тенглама таркибида I'12 +I”12 +…, иккинчисида I'21+I”21+…, токлар қатнашган бўлар эди; юқоридаги исботлашнинг тартибида хеч ўзгариш бўлмас эди, чунки I'12 + I'21 = 0; I”12 + I”21 = 0;… .
Ушбу мулохазани ихтиёрий сонли тугунга эга бўлган занжирлар учун татбиқ этиш мумкин. Бунда, доимо мустақил тенгламалар сони тугунларнинг Т сонидан биттага кичик бўлади. Шундай қилиб (5.2) ифоданинг тўғри эканлиги исботланган бўлади.
Мустақил контур тенгламалари сони. Т тугунлари мавжуд бўлган хар қандай занжирда шундай шохобчаларни ажратиб кўрсатиш мумкин бўлсинки, бу шохобчалар бирорта берк контур ҳосил қилмасдан барча тугунларни ўзаро бирлаштирсин. Буни қуйидагича бажарамиз: икки тугунни бир шохобча билан бирлаштирайлик ва тугунларни 1 ва 2 билан белгилайлик (5.5,б-расм); сўнгра, 2 тугунни янги тугун билан боғлайлик, уни 3 билан белгилайлик, ва ҳ.к. Шу тариқа охирги тугун n=T гача олиб борайлик. Бундай боғланиш 5.2-расмдаги схемада илгари келтирилган тўрт тугунли занжир учун келтирилган. Охирги тугунни 1 тугун билан бирлаштириб бўлмайди, чунки унда берк контур ҳосил бўлади.
Агар хар бир тугун бошқа барча тугунлар билан шохобчалар орқали уланса, тугунлар олдиндан ихтиёрий равишда номерланиб, сўнгра тугунлар кетма-кет уланиши мумкин (1 ва 2, 2 ва 3, ...,Т-1 ва Т).
Аниқки, бундай уланишда шохобчалар сони тугунлар сонидан албатта биттага кам бўлади; бу барча шохобчалар кетма-кет уланган, занжир берк бўлмайди. Бироқ, ихтиёрий бир жуфт тугунларга янги шохобчалар уланса, контур хосил бўлади, чунки шартга кўра барча тугунлар қандайдир шохобча билан улангандир.
Контур ҳосил қилмасдан шу йўсинда киритиш мумкин бўлган шохобчалар-дарахт шохобчалари дейилади, улар ҳосил қилган структура дарахт деб аталади.
Таърифга кўра, дарахтга киритилган хар қандай шохобча контурни ҳосил қилади (акс холда, бундай шохобча дарахт шохобчалари қаторига кирар эди). Ана шундай берк контур ҳосил қилувчи шохобчалар ватарлар (ёки кўприклар) деб аталади. Ватарлар 5.5,б-расмда пунктир чизиқлар билан кўрсатилган.
Дарахтга битта ватарни қўшиб, илгари қурилган бошқа бир шохобчани ташлаб юбориб, ҳосил бўлган берк контурни узиш мумкин. Бунда янги дарахт, яъни берк контурсиз занжир пайдо бўлади. Бироқ, ихтиёрий янги дарахтнинг шохобчалари сони ўзгаришсиз қолади, чунки хар гал янги бир ватар қўшилганда, айнан битта бошқа шохобчани ташлаб юбориш лозим.
Шохобча-ватарлар сони Х, шахобчалар сони Ш билан дарахтга кирувчи шахобчалар (Т-1) айирмасига тенг:
X = Ш - (T - 1).
Хар қандай шохобча-ватар киритилишидан ҳосил бўлган контур учун, Кирхгофнинг иккинчи қонунига асосан тенглама тузиш мумкин. Бунда, хар бир шунга ўхшаш тенглама бошқаларидан мустақилдир, чунки уларнинг хар бирига янги номаълум берк контури хосил қилувчи янги шохобча токи киради.
Демак, мустақил контур тенгламалари сони ватарлар сонига, яъни (3.3)га биноан Ш-(Т-1)га тенг. Шуни исбот қилиш зарур эди.
Кирхгоф тенгламалари тузилган контур, бошқа оддий контурлардан фарқланиши мумкин, чунки уларнинг хар бирида фақат биттадан ватарлар мавжуд. Бу қуйидаги мулоҳазадан аёнлиги кўринади: икки мустақил тенгламаларни ўзаро қўшиб, янги тенглама ҳосил қиламиз. Бу, ўз навбатида, қолган икки асосий тенгламалардан биринчиси ёки иккинчиси билан хамкорликда икки мустақил тенгламаларни ҳосил қилади. Мустақил тенгламаларнинг умумий сони ўзгармасдан қолади.
Эслатма. Тарқоқ бўлмаган занжирни чегараловчи икки тугунлари битта тугунга қўшилувчи (Т=1) бир шохобчали (Ш=1) занжир деб қараш мумкин. Бундай занжирлар учун ҳам K1=T-1= 0 ва K2 = Ш - (T - 1) = 1 ифодалашни қўллаш мумкин. Дарҳақиқат, бундай занжир учун фақат битта контур тенгламасини тузиш мумкин. Ушбу фикрлар тугуннинг шохобча чегараси эканлиги ҳақидаги таърифга тўла мос келади.
Барча тугун тенгламаларининг хар бир контур тенгламаларига боғлик бўлмаслиги (улардан мустақиллиги) аёндир, чунки контур тенгламалари таркибида шохобчалар қаршиликлари ва э.ю.к.лари мавжуд бўлиб, тугун тенгламаларида улар қатнашмайди. Демак, тугун тенгламаларининг хар қандай чизиқли комбинациясидан контур тенгламаларини ҳосил қилиб бўлмайди. Бу эса, занжирнинг тўла мустақил тенгламалари сони шохобчалар сонига тенг эканлигини исботлайди. Демак агар қолган барча параметрлар берилган бўлса аниқланган тенгламалар тизими барча токларни аниқлаш учун етарлидир; ушбу ҳолат тенгламалар тизимининг тўлиқлигини таъкидлайди.
Юқорида келтирилган мустақил тенгламалар сони ҳақидаги барча мулоҳазалар, ток манбаси бор бўлганда ҳам ўз кучига эга, чунки ток манбаси эквивалент кучланиш манбаси билан алмаштирилиши мумкин. Бироқ, тугун тенгламаларининг ўнг томонида Кирхгофнинг биринчи қонуни таърифидагидек ток манбаларнинг токлари қатнашаяпти деб ҳисоблаб, юқоридаги мулоҳазаларни давом эттириш мумки
6-маъруза. Суперпозиция, контур токлар
ва тугун потенциаллари усуллари
6.1. Суперпозиция (устлаш ёки жамлаш) усули
Ушбу принцип чизиқли занжирлар учун қўлланганда шундай таърифланади: занжирнинг ихтиёрий шохобчасидаги токнинг миқдори, хар бир манбанинг алоҳида таъсири натижасида (бир манба таъсири кўрилаётганда қолгаларини йўқ деб ҳисоб) ушбу шохобчада ҳосил қилган токларнинг йиғиндисига тенг. Келтирилган таърифдан шуни кўриш мумкинки, кўрилаётган усулни мустақил амал қилувчи усул (ёки устлаш ёки жамлаш) усули деб аташ мумкин.
Э.ю.к. манбаларидан фақат биттаси таъсир этаётганда, барча бошқа манбаларнинг э.ю.к. лари ва ток манбаларининг токлари нолга тенг деб фараз қилинади. Кучланиш манбаларининг қисқичларида кучланишнинг йўқлиги улар клеммалари қисқа туташганлигига мос келади: ток манбалари бўлган шохобчаларда токнинг йўқлиги, ушбу шохобча узилганидан дарак беради.
Агар манба ички қаршилик ва э.ю.к. эга бўлса, у ҳолда э.ю.к. нолга тенг деб фараз қилиб, унинг шохобчасида ички қаршиликни қолдириш зарур. Шунга ўхшаш, манба - ток манбаси ва унга уланган параллел ички қаршилиги бўлган шохобча сифатида берилган бўлса, ток манбаси шохобчасини узиб (яъни, J = 0 деб ҳисоблаб), ички қаршиликли параллел шохобчани қолдириш зарур.
Суперпозиция
принципига асосан икки (ёки бир неча) режим учун ҳисобни олиб бориш
мумкин; бунда бир марта параметрлари ![]() бўлган; манбалар таъсир этади;
иккинчи марта эса
бўлган; манбалар таъсир этади;
иккинчи марта эса ![]() параметрли
манбалар таъсир этади.
параметрли
манбалар таъсир этади.
Агар ![]() ва
ва ![]() ;
; ![]() ва
ва ![]() - токлар шу икки
режимнинг токлари бўлса, у холда хақиқий режимнинг токларини аниқлаш
учун ушбу икки режим токларини
- токлар шу икки
режимнинг токлари бўлса, у холда хақиқий режимнинг токларини аниқлаш
учун ушбу икки режим токларини
![]() ;
; ![]() ; . .
.
(6.1)
; . .
.
(6.1)
устлаш (жамлаш) ёрдамида аниқлаш мумкин (агар қуйидагиларни қабул қилиш мумкин бўлса):
![]() ;
; ![]() .
(6.2)
.
(6.2)
Бунда штрихсиз қийматлар манбаларнинг хақиқий параметрларига мос келади.
Ҳисоблаш ва таҳлил қилишнинг қулайлигига эришиш учун хар хил режимларда занжирнинг ихтиёрий қисмига, аслида мавжуд бўлмаган, шартли (сохта) манбаларни киритиш мумкин, бунда, фақат устлаш натижасида шартли манбаларнинг ЭЮК йиғиндиси ва токлар йиғиндиси нолга тенг бўлиши зарур.
Умумий ҳолда суперпозиция усулини қувватлар учун татбиқ этиб бўлмайди
![]() (6.3)
(6.3)
чунки қувватлар токларнинг квадратик (ночизиқли) функцияларидир.
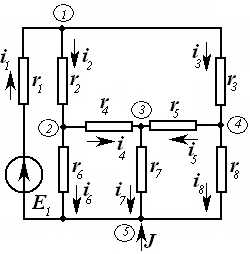 Аввалги маърузада
пропорционал қийматлар усули кўрилган эди. Суперпозиция усули билан
биргаликда ушбу усул мураккаб занжирлар учун қўлланилиши мумкин. Занжирда ягона
манба бўлса, хеч бўлмаганда битта тугунга учтадан кўп бўлмаган шохобча уланган,
ҳамда иккитагина шохобча берилиб, улар ёрдамида барча тугунлар
потенциалларини ва барча шохобчалар токини аниқлаш мумкин бўлган ҳолатларда
ушбу усулни қўллаш қулайликка олиб келади. Бу талабларни, масалан,
6.1-расмдаги занжир J =0 бўлганда қониқтиради. Аввал, икки
шохобча токларини ихтиёрий танлаб
6.1-расм
Аввалги маърузада
пропорционал қийматлар усули кўрилган эди. Суперпозиция усули билан
биргаликда ушбу усул мураккаб занжирлар учун қўлланилиши мумкин. Занжирда ягона
манба бўлса, хеч бўлмаганда битта тугунга учтадан кўп бўлмаган шохобча уланган,
ҳамда иккитагина шохобча берилиб, улар ёрдамида барча тугунлар
потенциалларини ва барча шохобчалар токини аниқлаш мумкин бўлган ҳолатларда
ушбу усулни қўллаш қулайликка олиб келади. Бу талабларни, масалан,
6.1-расмдаги занжир J =0 бўлганда қониқтиради. Аввал, икки
шохобча токларини ихтиёрий танлаб
6.1-расм
(масалан, 6.1-расмда r2 ва r6 шоҳобча-
лар токларини), 2-тугуннинг учинчи токини енгил аниқлаш, сўнгра Ом қонунига биноан бошқа ихтиёрий шохобча (масалан 6.1-расмдаги r4 ва ҳ.к.) учун потенциаллар фарқини ҳисоблаш мумкин.
Барча ҳисоблашларни
бажариш жуда осон, бироқ улар тезда бир-бирига зид натижаларга олиб
келиши ҳам мумкин. Кирхгофнинг қонунларига зидликни (шартли)
кучланиш манбаси ![]() (ёки шартли
(ёки шартли
![]() ток
манбаси)ни киритиб бартараф этиш мумкин. Бунда, ҳисоблаш натижасида барча
изланаётган токлар ва э.ю.к. лар аниқланади.
ток
манбаси)ни киритиб бартараф этиш мумкин. Бунда, ҳисоблаш натижасида барча
изланаётган токлар ва э.ю.к. лар аниқланади.
Натижада m-шохобчадаги токни аниқлаш мумкин;
![]() (6.4)
(6.4)
бунда «1» индекс билан ҳақиқатдан хам манбаси бўлган шохобча қийматлари ва «Ш» билан Кирхгоф қонунларига зидликни бартараф этиш учун киритилган «шартли» манба қийматлари белгиланган.
Сўнгра, қайта ҳисоблаш бажарилади, бунда мазкур шоҳобчаларнинг ихтиёрий танланган токларига янги қийматлар берилади. Натижада манбаларнинг янги қийматлари билан янги режим токлари аниқланади;
![]() .
(6.5)
.
(6.5)
Токнинг икки қийматларидан бирини, айтайлик иккинчисини, в коэффициентига кўпайтириб ва уларни қўшиб, қўйидагини ҳосил қиламиз;
![]() (6.6)
(6.6)
Шунга эътиборни қаратиш зарурки, барча тенгликларда ym1 ва ymШ коэффициентлар қийматлари номаълум бўлса ҳам улар бир хилдир.
Агар кўпайтувчи в нинг қиймати шундай
танланган бўлсаки, унда
![]()
![]() (6.7)
(6.7)
яъни в
= ![]() бўлса,
ундан аввалги тенглама
бўлса,
ундан аввалги тенглама
![]() (6.8)
(6.8)
шаклга келади.
Кейинги тенгликдан ym1ни аниқлаймиз, сўнгра m шохобчанинг берилган Е1 э.ю.к.ли ягон кучланиш манбаси бўлгандаги изланаётган токини аниқлаймиз;
Im = ym1· Э1 . (6.9)
Ушбу ҳисоблаш усулини ўрганиш, юзаки қараганда, бироз мушкул бўлиб кўринса ҳам, у аслида жуда ҳам осон ва рақамли натижаларни тезкорлик билан олиш имконини беришига эьтибор қаратишни зарур деб ҳисоблаймиз.
6.2. Êîíòóð òîêëàð óñóëè
Агар электр занжирларида ток ва кучланишнинг тақсимланишини ҳисоблашда Кирхгоф қонунларининг фақат биттасидан фойдаланилса, яъни тенгламалар фақат тугунлар учун (КТҚ) ёки фақат контурлар учун (ККҚ) тузилса, у холда умумий тенгламалар сони камайиши мумкин.
Тенгламалар шундай тузилиши лозимки, унда бошқа қонунлар бажарилиши таъминлансин. Бундай тенгламаларни тузишнинг икки усули Максвелл томонидан таклиф этилган; улардан бири контур токлар усули бўлса, иккинчиси - тугун потенциаллари усули деб номланган.
Электр занжирининг ихтиёрий шохобчасидаги токни, хар бири ўзининг берк контурида оқувчи, шу шохобча бўйлаб ўзгармайдиган бир неча токлар йиғиндиси деб қараш мумкин. Ҳақиқий токларнинг бундай ташкил этувчилари контур токлари деб аталади. Фақат бир контурга тааллуқли ихтиёрий шохобчанинг токи контур токи билан мос бўлади. Икки ёки бир неча контурларга тааллуқли шохобчалардаги токлар, мазкур контур токларининг алгебраик йиғиндисига тенг. Контур токлари тугунлардан ўтганда узлуксиз бўладилар: демак, токларни шундай таърифлаганда, КТҚ сўзсиз бажарилади.
Шохобча токларини контур токларига ажратиш занжирнинг таҳлилидан келиб чиқади. Контур токларини шохобча-ватар токларига ўхшатиш мумкин, бундай вазиятда мустақил контур токлари тенгламаларининг сони
К = Ш + 1 - Т (6.10)
номаълумлар сони билан тенг бўлади; барча бошқа шохобчаларнинг токлари контур токлари орқали ифодаланган бўлади.
3.13,а-расмда икки контур токлари I1 ва I2 бўлган оддий электр занжири келтирилган. Занжирнинг а ва b шохобчаларидаги токлар контур токларига тенг:
Iа= I1; Ib= I2 .
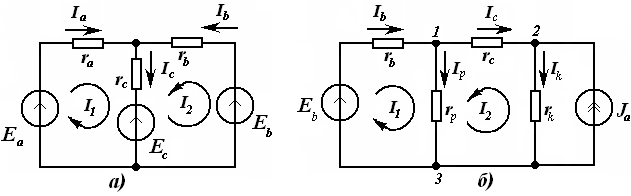
Занжирнинг с шоҳобчасидаги ток икки бошқа шохобчалар токларининг алгебраик йиғиндисига тенг: у иккала контур учун умумий бўлган шу шохобчадан оқиб ўтаётган контур токларнинг ҳам йиғиндисига тенг:
Iс = I1 + I2 .
Кирхгофнинг иккинчи қонунига биноан занжирнинг биринчи контури учун (6.2,а-расм)
raIa + rcIc = Еa - Еc
ёки
(ra + rc) I1 + rcI2 = Ea - Ec
янги белгилашлар қабул қилинса:
r11·I1 + r12I2 = Е1,
бунда r11 = ra + rc - биринчи контур таркибига кирган барча шохобчалар қаршиликларининг йиғиндиси: r12 = rc - биринчи ва иккинчи контурлар учун умумий бўлган шохобча қаршилиги: Е1=Еa - Еc - биринчи контур таркибига кирган барча ЭЮК лар алгебраик йиғиндиси: мусбат ишора билан йўналиши контур токи йўналишига мос бўлган ЭЮК белгиланган.
Шунга ўхшаш, иккинчи контурда (6.2,а -расм):
r21·I1 + r22I2 = E2
бунда
r21 = rc; r22 = rb + rc; Е2 = Еb - Еc .
Таърифланишига кўра, икки контур учун умумий бўлган шохобчанинг қаршилиги r12 = r21.
Юқорида кўрилганларни ихтиёрий контурлар сони учун умумлаштирсак, таркибида ток манбаси бўлмаган занжир учун контур токлари тенгламалари тизими қуйидаги андозада ёзилади:
![]() r11·I1+
r12·I2+ r13·I3+…
= E1 ;
r11·I1+
r12·I2+ r13·I3+…
= E1 ;
(6.11,a)
r21·I1+ r22·I2+ r23·I3+… = E2 ;
. . . . . . . . . . . . . . . .
Ушбу тенгламалар тизимини матрица шаклида қисқартириб ёзиш ҳам мумкин:
rln In = Еl . 6.11,б)
Контур токлар тенгламалар тизимидаги бир хил индексли қаршиликлар rln, L-контурдаги барча шохобчалар қаршиликлари йиғиндисига тенг: хар қандай хар хил индексли (l≠n) rln қаршилик иккала қўшни l ва n контурлар учун умумий бўлган шохобча қаршилигига тенг: агар l ва n контурларнинг умумий шохобчасидаги токлар мусбат ишоралари хар хил йўналган бўлса, у ҳолда rln қаршилиги олдида минус ишораси қуйилади.
Таъриф бўйича
rln= rnl . (6.12)
Тенгламалар тизими (6.11)нинг контур токларига нисбатан ечимини хам матрица шаклида ёзиш қулайликларга олиб келади:
In = Gnl Еl . (6.13)
Ўтказувчанлик Gnl нинг матрицаси барча элементлари бу ифодада Крамернинг D детерминанти ва мазкур қаршилик матрицаси rln нинг алгебраик қўшимчаси Aln орқали келтирилган:
Gnl = Anl / D. (6.14)
Кейинги тенглик берилган rln=rnl қаршилик тизими матрицасининг симметрик бўлганидагина хақиқийдир.
Қаршилик матрицаси (rln=rnl) симметриялигидан алгебраик қўшимчаларнинг (Anl=Aln) симметриялиги келиб чиқади ва, демак, ўтказувчанлик элементлари матрицаси ҳам симметрик бўлиши зарур:
Gnl=Gln. (6.15)
бунда Gnl коэффициентлар, умумий холда, контур ўтказувчанликлари деб аталади.
Ихтиёрий икки тугунга уланган ток Jа манбасининг занжирда мавжудлиги, контур токлари усулини қўллашга тўсқин бўла олмайди.
Шундай қилиб, (6.11,б) тенгламалар тизимининг чап томонида rla Ja ҳади қўшилади, яъни
rln In + rla Ja =El. (6.16)
Бунда, тенгламалар сони ![]() га тенглигича қолади, чунки ноъмалум контур
токлар сони ортгани
йўқ.
га тенглигича қолади, чунки ноъмалум контур
токлар сони ортгани
йўқ.
Қўшимча ҳадни тенгламаларнинг ўнг томонига ўтказиб, (6.16) тенгламалар тизимини қуйидаги шаклга келтирамиз:
rln In = El - rla Ja = З l. (6.17)
Зl қийматни
![]() контурнинг
келтирилган ЭЮКи деб номлаш мумкин.
контурнинг
келтирилган ЭЮКи деб номлаш мумкин.
![]() Мисол таъриқасида 6.2,б-расмдаги занжирни кўрамиз; унинг ўнг шохобчасида
ток манбаси мавжуд. Занжир схемасида кўрсатилган икки
контурнинг тенгламаларини тузиш етарлидир. Уларни тузишда Jа токи қаршиликда
ҳосил қилган кучланишлар
пасаювини киритиш зарур:
Мисол таъриқасида 6.2,б-расмдаги занжирни кўрамиз; унинг ўнг шохобчасида
ток манбаси мавжуд. Занжир схемасида кўрсатилган икки
контурнинг тенгламаларини тузиш етарлидир. Уларни тузишда Jа токи қаршиликда
ҳосил қилган кучланишлар
пасаювини киритиш зарур:
r11I1 + r12I2 + r1a Jа = Е1 = Еb
r21I1 + r22 I2 + r2a Jа = Е2 = 0 (6.18)
Агар Jа
токи k шохобча орқали оқиб ўтади, деб фараз қилсак, у ҳолда
![]() = 0, чунки Jа
токи биринчи контурнинг бирорта шохобчаси орқали ўтмайди, лекин
= 0, чунки Jа
токи биринчи контурнинг бирорта шохобчаси орқали ўтмайди, лекин ![]() =
= ![]() , чунки Jа
иккинчи контурнинг k шохобчаси орқали ўтиб, йўналиши иккинчи
контур токи йўналиши билан мос бўлади. Шунга эътиборни қаратиш муҳимки,
Jа токи учун бошқа йўл масалан, с ва р
шохобчалари орқали оқиб ўтишини ҳам таҳмин қилиш
мумкин эди. Бу ҳолатда (6.18) ифодада қуйидагича ўзгартириш
киритилади:
, чунки Jа
иккинчи контурнинг k шохобчаси орқали ўтиб, йўналиши иккинчи
контур токи йўналиши билан мос бўлади. Шунга эътиборни қаратиш муҳимки,
Jа токи учун бошқа йўл масалан, с ва р
шохобчалари орқали оқиб ўтишини ҳам таҳмин қилиш
мумкин эди. Бу ҳолатда (6.18) ифодада қуйидагича ўзгартириш
киритилади:
r1a = rp ва r2a = - rc - rp. (6.19)
Демак, контур токлари қийматлари хар хил бўлади, шохобчаларнинг токлари эса (контурларни ихтиёрий танлашга боғлиқ бўлмайди) контур токлари орқали хар ҳил ифодаланган бўладилар. Масалан, биринчи вазиятда
Ip = I1 - I2 (6.20)
бўлса, иккинчи ҳолатда
Ip = I1 - I2 + Jа (6.21)
бўлади.
Албатта, бу икки тенгламаларда контур токлари қийматлари хар хил, Ip эса бир хил бўлади.
6.3. Тугун потенциаллари усули
Ушбу усулнинг номидан келиб чиқилса, токлар тенгламаларини тугунлар учун тузиш кифоядир.
Фараз қилайлик,
l ва k тугунлари (6.3-расм) бирорта шохобча билан боғланган
бўлсин: ![]() - тугун l
дан k тугунга йўналган шу шохобча токи;
- тугун l
дан k тугунга йўналган шу шохобча токи; ![]() - тугун l
дан k тугун томон йўналган шу шохобча ЭЮКи;
- тугун l
дан k тугун томон йўналган шу шохобча ЭЮКи; ![]() - ушбу
шохобчанинг қаршилиги. Унда (3.7)га кўра l ва k тугунлар
орасидаги потенциаллар фарқи қуйидагича ёзилади:
- ушбу
шохобчанинг қаршилиги. Унда (3.7)га кўра l ва k тугунлар
орасидаги потенциаллар фарқи қуйидагича ёзилади:
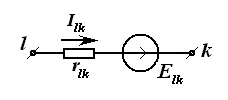
![]() . (6.22)
. (6.22)
ККҚ - берк контурнинг барча шохобчалари учун шунга ўхшаш тенгламаларни қўллаш ва сўнгра уларнинг алгебрик йиғиндиси ҳосил қилиш
натижасидир. Шунинг учун шохобчалардаги 6.3-расм
токлар айнан (6.22) тенглама бўйича ёзилса
![]() ,
(6.23)
,
(6.23)
Кирхгофнинг иккинчи қонуни
ўз-ўзидан бажарилади; бунда ![]() ; ушбу (6.23)
тенгликни Омнинг умумлаштирилган қонуни ифодаси деб қараш мумкин.
; ушбу (6.23)
тенгликни Омнинг умумлаштирилган қонуни ифодаси деб қараш мумкин.
Ушбу
белгилашларда ![]() ,
, ![]() ;
;
бироқ
![]() (6.24)
(6.24)
Занжирнинг T
= n + 1 тугуни бўлган барча шохобчаларининг қаршиликлари (ёки
ўтказувчанликлари), кучланиш манбаларининг ЭЮК ![]() лари ва ток
манбаларининг ток
лари ва ток
манбаларининг ток ![]() лари берилган деб
фараз қилиб, тугун тенгламаларини тузишга ўтамиз.
лари берилган деб
фараз қилиб, тугун тенгламаларини тузишга ўтамиз.
Агар 1-тугунга ташқаридан (ток манбасидан) J1 токи оқиб келаётган бўлса, у холда Кирхгоф қонунига мувофиқ 1-тугун учун токлар тенгламаси қуйидагича бўлади:
I12 + I13 +… + I1, n+1 = J1 ;
иккинчи тугун учун: I21 + I23 +… + I2, n+1= I2
ихтиёрий k тугун учун Ik1 + Ik2 +… + Ik, n+1 = Jk .
Хар бир ток ифодаларини (6.23)га кўра ёйиб чиқсак, k-тугун учун қуйидагини ҳосил қиламиз:
![]()
![]()
![]() (6.25)
(6.25)
Ноъмалум
потенциаллар олдидаги кўпайтувчиларни гуруҳлаб, охирги тугуннинг
потенциалини нолга тенг деб ![]() фараз қилиб,
барча маълум қийматларни тенглик аломатининг ўнг томонига ўтказиб, k-тугун
учун тенгламани қуйидаги кўринишга келтирамиз:
фараз қилиб,
барча маълум қийматларни тенглик аломатининг ўнг томонига ўтказиб, k-тугун
учун тенгламани қуйидаги кўринишга келтирамиз:
![]() (6.26)
(6.26)
Ушбу боғланишдаги
ёзувларни қисқартириш учун қуйидаги белгилашларни киритилди:
![]() (6.27)
(6.27)
бу k тугунга уланувчи
барча шохобчаларнинг ўтказувчанликлари йиғиндисидир:
![]() (6.28)
(6.28)
Бу
белгилашлардаги қатнашаётган қийматларнинг икки индекс белгиланган
тартиби ўзгариши билан ЭЮКлар олдидаги ишоралар ўзгартирилди. Эътибор
берсак, қўшилувчи ҳадлар орасида ![]() келтирилмаган.
(6.28) йиғиндининг мазмунини оддий талқин қилиш
мумкин:
келтирилмаган.
(6.28) йиғиндининг мазмунини оддий талқин қилиш
мумкин: ![]() - бу барча ҳақиқий
ва эквивалент манбалардан k тугунга келувчи тўла токдир. Унинг қийматини
тугун токининг
- бу барча ҳақиқий
ва эквивалент манбалардан k тугунга келувчи тўла токдир. Унинг қийматини
тугун токининг![]() келтирилган
қиймати деб аташ мумкин.
келтирилган
қиймати деб аташ мумкин.
(6.26) га ўлшаш
тенгламаларни охиргисидан ташқари барча тугунлар учун тизиш мумкин -
охирги тугун учун эса тугун тенгламаси барча қолган тенгламалардан келиб
чиқади. “Охирги” тугун сифатида, албатта, тугунларнинг хаммасидан
биттасини ихтиёрий танлаб олиниши мумкин; уни баъзан таянч тугун деб ҳам қабул
қилиш мумкин, чунки унинг потенциали ![]() .
.
Таркибида n
мустақил тенгламаси (n=1 тугунларнинг тўла сони) ва шунча ноъмалум
потенциаллари бўлган тенгламалар тизимини тузиш мумкин:
![]()
![]()
![]()
![]() (6.29,а)
(6.29,а)
![]()
Тенгламалар тизими (6.29) нинг потенциалларга нисбатан ечими аниқлангандан сўнг Ом қонунига биноан шохобчалар токлари ва элементлар кучланишлари ҳисобланади.
7-маъруза. Ўзгарувчан ток занжирлари
7.1. Гармоник ток занжирларининг умумий тавсифлари
Ўгарувчан ток,
яъни вақтга боғлиқ равишда ўзгарадиган ток i(t)
хақида гапирганда, у билан боғлиқ бўлган ва электр занжирини
тасвирловчи: кучланиш u(t), заряд q(t), магнит оқими Ф(t)
ва бошқа қийматларнинг ҳам вақт бўйича шундай
ўзгариши назарда тутилади. Улар ўзгаручан бўлганлиги учун (df/dt![]() 0, яъни ҳосилалари
нолга тенг бўлмаганлиги сабабли) индуктивликларда кучланишлар ҳосил
бўлади, конденсаторли шохобчалардан эса токлар оқиб ўтади (ўзгармас
токлардаги билан солиштиринг).
0, яъни ҳосилалари
нолга тенг бўлмаганлиги сабабли) индуктивликларда кучланишлар ҳосил
бўлади, конденсаторли шохобчалардан эса токлар оқиб ўтади (ўзгармас
токлардаги билан солиштиринг).
Нодаврий ва даврий ўзгарувчан қийматлар. Агар 7.1,а-расмдаги схемада r-L занжирни кучланиши Е бўлган ўзгармас ЭЮК манбасига «К» калит билан уланса, ундаги ток қиймати i=const бўлгунга қадар i(t) ўзгарувчан (7.1,б-расм) апериодик ўсувчи нодаврий бўлади. Агар шу занжир калитини (7.1,в-расм) Т давр билан t1 вақт оралиғида улаб, t2 вақт оралиғида узиб турилса, даврий носинусоидан i(t) токи (7.1,г-расм) ҳосил бўлади. Бундай мисолларни кўплаб келтириш мумкин. Ушбу ўткинчи жараёнларнинг биринчиси дарсликнинг учинчи қисмида ўрганилади. Дарсликнинг иккинчи қисмида эса иккинчи мисолдаги каби, қуйидаги
![]() (7.1)
(7.1)
Т=const шартни бажарувчи даврий ўзгарадиган қийматларни кўриш билан чекланамиз.
Бу (7.1) тенглик шуни англатадики, кўрилаётган қийматнинг даврий ўзгариши ҳар T вақт оралиғида (7.1,г, 7.2-расмлар) такрорланиб туради; бунда T- давр деб аталади. Давр Т га тескари қиймат, яни вақт бирлиги (1 секунд)даги даврлар сони эса
![]() (7.2)
(7.2)
частота деб аталади. Частота Герц (Гц) бирлигида ўлчанади. Электр тармоғи
кучланишининг стандарт частотаси ![]() 50 Гц.га шу
кучланишнинг
50 Гц.га шу
кучланишнинг
ҳар Т=0,02с.да
бир марта ўзгариши мос келади. Бунда оддий гармоник тебранишлар – синусоидал
(ёки косинусоидал) ўзгарувчи қийматларни кўрамиз (7.2-расм)
![]() ,
(7.3)
,
(7.3)
бунда ![]() - оний қиймат;
- оний қиймат;
![]() -амплитуда;
-амплитуда; ![]() - бурчак
(айланавий) частота;
- бурчак
(айланавий) частота; ![]() - радиан ёки
градусда ифодаланган фазалар фарқи;
- радиан ёки
градусда ифодаланган фазалар фарқи; ![]() - бошланғич
фаза.
- бошланғич
фаза.
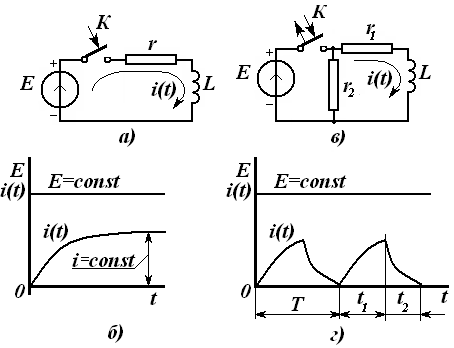
7.1-расм
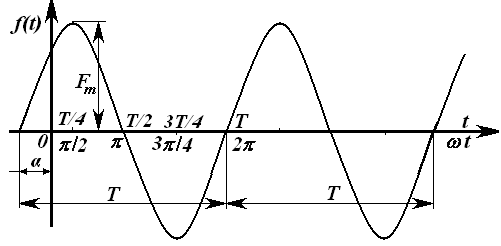
7.2-расм
Частоталари тенг бўлган гармоник функциялар йиғиндиси, зарур бўлганда, шу частотали гармоник функция шаклида ифодаланиши мумкин; унинг амплитуда ва фазалари, хеч бўлмаганда, оддий тригонометрик ўзгаришлар ёрдамида ифодаланиши мумкин:
![]()
Бунда
![]()
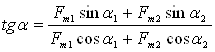 (7.4)
(7.4)
7.2. Таркибида R ,C бўлган занжирдан гармоник ток
Конденсаторда зарядланиш ва разрядланиш жараёни. Ўзгарувчан кучланиш манбаси u конденсатор С га уланиб (7.3,а-расм), берк контур ҳосил қилса, занжирдан ўзгарувчан ток i оқиб ўтади. Мисол учун, ўзгарувчан кучланиш генераторга кабель тармоғи уланганини кўрайлик (7.3,б-расм). Тармоқнинг изоляцияланган ўтказгичлари орасида электр майдони ҳосил бўлади, ўтказгичларда эса ортиқча зарядлар тўплами пайдо бўлади: потенциали юқорироқ бўлган ўтказгичда мусбат зарядли q ва пастроғида - манфий зарядли –q. Бунда заряднинг қиймати сиғим ва кучланишнинг қўлайтмаларига тенг q =Cuс = Сu. Заряднинг ўзгариши эса токнинг қуйидаги ўзгариши билан мос бўлади:
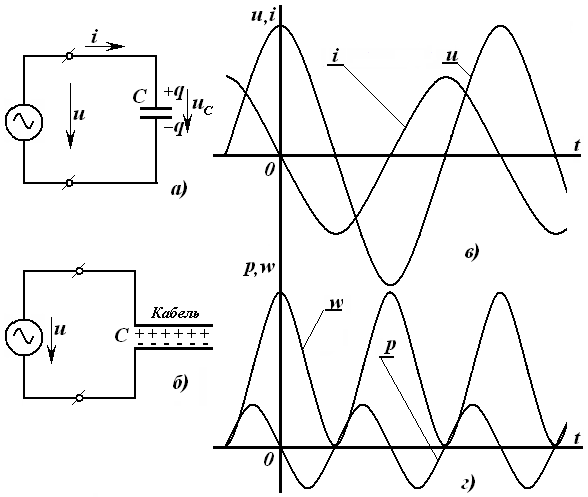
![]()
7.3-
7.3-расм
Манбанинг кучланиши берилган, деб фараз қилиб
![]() (7.5)
(7.5)
ва дифференциаллаб, ток қийматни аниқлаймиз:
![]() (7.6)
(7.6)
Кучланишнинг частотаси билан ифодаланган гармоник токнинг
аплитудаси
![]() (7.7)
(7.7)
га тенг бўлиб, фазаси бўйича
кучланишдан ![]() бурчакка
илгарилаб кетади.
бурчакка
илгарилаб кетади.
Шунга эътибор бериш зарурки, ушбу ифодани конденсатор кучланишининг хар қандай бошланғич фазаси учун ҳам қўллаш мумкин.
Кабель тормоғининг узунлиги катта бўлганда, сиғим
токининг қиймати сезиларли даражада бўлади. Мисол учун, кабель тармоғи
сиғими С=10-5 Ф. (кабель умумий узунлиги 25 км), кучланиши ![]() ва частота f = 50 Гц бўлганда, токнинг амплитудаси Iм=29,8
А. бўлади.
ва частота f = 50 Гц бўлганда, токнинг амплитудаси Iм=29,8
А. бўлади.
Агар (7.7)да сиғим токи амплитудасининг қиймати частатага пропорционал эканини эътиборга олсак, юқори частотали ва ўта юқори частатали кучланишларни узатишнинг қанчалар катта муаммолари бор эканлигини биламиз.
7.3,в-расмда кучланиш ва токлар оний қийматларининг графиги келтирилган. Бунда, кучланишнинг мусбат қиймати, 7.3,а-расмдаги белгиланганига мувофиқ, конденсаторнинг юқоридаги электроди потенциали пастдаги электроди потенциалидан баландроқ бўлган вақт оралиғига мос келади. Токнинг 7.3,а-расмдаги мусбат ишораси конденсаторнинг юқоридаги электродига мусбат заряднинг оқиб келишига мос келади.
Бирор
функция ва унинг ҳосиласи орасидаги боғланиш хақидаги оддий
мулоҳазалар шуни кўрсатадики, кондесатордаги кучланишлар экстремал
бўлган онда токнинг оний қиймати нолга тенг бўлади; кучланишлар қийматлари
нолга тенг бўлсада, улар ўзгариш тезлиги катта бўлганлигидан, шу ондаги токнинг
қийматлари экстремал (±![]() m) даражага эришади.
m) даражага эришади.
Конденсатор электр майдони энергиясининг ўзгариши
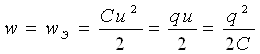 (7.8)
(7.8)
генератор ва зарядланаётган конденсатор орасидаги энергия алмашуви билан боғлиқ. Генератордан ҳар онда узатилаётган қувват, яъни унинг оний қиймати ток ва кучланишлар оний қийматларининг кўпайтмасига тенг:
![]() .
(7.9.)
.
(7.9.)
Қувватнинг
юқорида келтирилган ихтиёрий боғланишларидан шуни кўриш мумкинки, у
кучланиш частотасидан икки марта катта бўлган частата билан ўзгарар экан:
 (7.10)
(7.10)
Қувват (р) ва энергиянинг (wЭ) графиги 7.3,г-расмда келтирилган. Шунга эътибор бериш зарурки, кучланиш ва токнинг ишоралари бир хил бўлганда, қувват мусбат, ток ва кучланиш ишоралари хар хил бўлганда-манфий ва ток ёки кучланишнинг қийматлари нолга тенг бўлганда, қувват ҳам нолга тенгдир. Бир Т давр ўтиши билан конденсатор энергияси илгариги қийматига тенг бўлади. Шу сабабдан, генератордан конденсаторга бир давр ичида узатилаётган ўртача қувват нолга тенг:
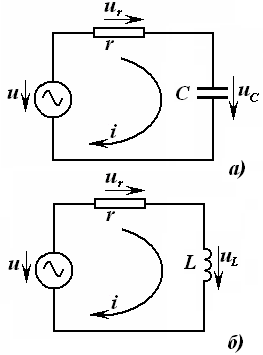
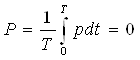 . (7.11)
. (7.11)
Бунда, ўзгарувчан токлар назариясида қабул қилинган белгилашларга мувофиқ, ўртача (бир давр ичидаги) қувват бош харф «Р» билан белгиланди. Ўртача қувватнинг нолга тенглиги, унинг айнан синусоидал функция эканлигидан келиб чиқади.
С конденсаторга кетма-кет уланган ![]() резисторни кўрайлик. Бундай занжир-лар, аксарият,
электрон схемаларда кўп учрайди (7.5-расм).
резисторни кўрайлик. Бундай занжир-лар, аксарият,
электрон схемаларда кўп учрайди (7.5-расм).
Фараз қилайлик,
конденсатордаги ўзгарувчан кучланиш
![]() (7.12)
(7.12)
Бундай вазиятда кўрилаётган занжирдан 7.4-расм
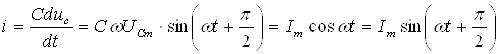 (7.13)
(7.13)
ток оқиб ўтади. Токнинг
қиймати маълум бўлгани учун резистор ![]() даги
кучланишни Ом қонуни асосида аниқлаш мумкин
даги
кучланишни Ом қонуни асосида аниқлаш мумкин
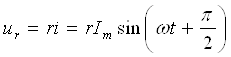 . (7.14)
. (7.14)
С, r-ли занжирнинг киришидаги кучланиш
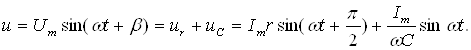 (7.15.)
(7.15.)
Бу ерда кондесатордаги кучланиш амплитудаси (7.7.) тенгликдаги токнинг амплитудаси орқали ифодаланган.
Тригонометрик (7.7.) ўзгартиришлар ёрдамида қуйидагича ёзиш мумкин.
![]() (7.16)
(7.16)
![]() (7.17)
(7.17)
Қаршилик ![]() даги қувват
исрофи. Ўзгарувчан ток i = Im Sin
даги қувват
исрофи. Ўзгарувчан ток i = Im Sin![]() t қаршлик
t қаршлик ![]() орқали
оқиб ўтганда, унда Жоуль-Лекц қонунига биноан қувват ажралиб
чиқади:
орқали
оқиб ўтганда, унда Жоуль-Лекц қонунига биноан қувват ажралиб
чиқади:
![]() . (7.18)
. (7.18)
Бир даврдаги ўртача қувват токнинг ўртача квадратик қиймати орқали ифодаланади.
Р=I2 r, (7.19)
бунда ![]() ва
ва ![]() (харф
устидаги чизиқ ўрта қиймат эканини кўрсатади).
(харф
устидаги чизиқ ўрта қиймат эканини кўрсатади).
Гармоник ток учун
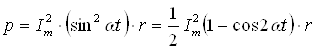 (7.20)
(7.20)
Бироқ,
гармоник функция cos2![]() t нинг бир давр
мобайнида ўртача қиймати нолга тенг.
t нинг бир давр
мобайнида ўртача қиймати нолга тенг.
Шунинг учун ![]() даги ўртача
қувват
даги ўртача
қувват
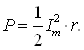 (7.21)
(7.21)
7. 3. Даврий миқдор таъсир этувчи (ўртача квадратик) қиймат
Ўртача квадратик қийматни таъсир этувчи ёки эффектив қиймат дейилади. Бу номлашни қуйидагича тушунтириш мумкун. Жоуль-Ленц қонунидаги каби, ҳар қандай катталик оний қиматларининг квадратига пропорциционал бўлганда у хар доим ўрта ҳисобда таъсир этувчи (эффектив) қийматнинг квадратига пропорционалдир. Ўрта квадратик қиймат бош харф билан хеч қандай қўшимча белгиларсиз белгиланади.
Токнинг ўрчача квадратик қиймати:
 (7.22)
(7.22)
кучланишнинг ўрчача квадратик қиймати:
 (7.23)
(7.23)
ва ҳ.к.
(7.19)ва (7.21)
дан кўринадики, гармоник функциялар учун ўртача квадратик қийматлар
амплитудани ![]() га
бўлинганига тенг, яъни
га
бўлинганига тенг, яъни
![]()
![]() (7.27)
(7.27)
Шундай
қилиб, (7.21) ўрнига қуйидаги ёзиш мумкин:
![]() (7.25)
(7.25)
Ўзгармас ток r
қаршилик орқали оқиб ўтганда, амплитудаси Im=I![]() га тенг
бўлган гармоник ток оқиб ўтгандаги каби таъсир бир хил бўлади.
га тенг
бўлган гармоник ток оқиб ўтгандаги каби таъсир бир хил бўлади.
7. 4. L ва r занжирда гармоник ток
Икки ўтказгичли l узунликдаги, узунлик бирлигининг қаршилиги r0 ва индуктивлиги L0 бўлган ҳаво линиясини кўрайлик. Линия бошида генератор уланган, кетида эса қисқа туташган бўлсин. Бундай линия қаршилиги r = r0 ·l , индуктивлиги L = L0 ·l га тенг бўлган кетма-кет r ва L занжирнинг ўзгарувчан ток генераторига уланган схемасини (7.4,б-расм) англатади.
Агар линиядан i = Imsinwt токи оқиб ўтаётган бўлса, унда генераторнинг кучланиши қуйидагича
![]() (7.26)
(7.26)
ёки
![]() (7.27)
бўлади.
(7.27)
бўлади.
Икки гармоник функциянинг йиғиндиси учун (7.3)да келтирилган тригонометрик ўзгартишларни қўллаб, генератор кучланиши
![]() ,
,
ва амплитудаси
![]() (7.28)
бўлади.
(7.28)
бўлади.
Кучланишнинг
фазаси токдан ![]() бурчакка
илгарилаб кетади, бунда
бурчакка
илгарилаб кетади, бунда
tg![]()
![]() .
(7.29)
.
(7.29)
7.5. Комплекс қувват
Генератордан
занжирга узатилаётган қувватнинг оний қиймати ток ва кучланишлар
оний қийматларининг кўпайтмасига тенг:
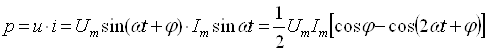 .
(7.30)
.
(7.30)
Бу тенгликнинг ўнг томонидан шу маълум бўладики, қувватнинг таркибида ўзгармас ташкил этувчиси мавжуд экан. Унинг қиймати эса ўртача қувватга тенг:
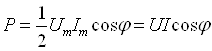 .
(7.31)
.
(7.31)
Бу боғланишни кучланиш ва токлари орасидаги фазалар фарқи ц га тенг бўлган барча занжир қувватлари учун қўллаш мумкин.
Икки марта катта частота билан пульсланувчи қувват ![]() га пропоционал бўлиб, унинг ўртача қиймати нолга
тенг. Унинг мавжудлигини яна шу билан тушунтириш мумкинки, қаршиликда исроф бўлувчи қувват (ri2)
ўзгармас бўлмайди, шу билан бирга, магнит майдон
энергияси (Li2/2) узлуксиз ўзгариб туради.
га пропоционал бўлиб, унинг ўртача қиймати нолга
тенг. Унинг мавжудлигини яна шу билан тушунтириш мумкинки, қаршиликда исроф бўлувчи қувват (ri2)
ўзгармас бўлмайди, шу билан бирга, магнит майдон
энергияси (Li2/2) узлуксиз ўзгариб туради.
Исботланган (7.30) боғланишга энергетик нуқтаи назардан хам қараш мумкин. Бунда 7.1,а-расмдаги қувват исрофининг оний қиймати
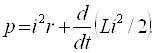 (7.32)
(7.32)
бўлади.
Токнинг қиймати i = Im sinщt бўлганда (7.32) тенгликнинг ўнг томони оддий ўзгартирилиши натижасида (7.30)га ёки шунга ўхшаш боғланишга келиш мумкин
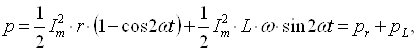 (7.33)
(7.33)
бунда ![]()
![]()
7.5-расмда ток, кучланиш, қувватнинг оний қийматлари, қувватнинг икки ташкил этувчилари ва магнит майдон энергиясининг графиги келтирилган. Пунктир чизиқлар билан қувватнинг ўртача қийматлари (Р) ва магнит майдон энергиясининг ўртача қийматлари кўрсатилган:
![]() (7.34)
(7.34)
Графикларни таҳлил қилиб қуйидаги хусусиятларга эътиборни қаратиш мумкин:
1) кучланишнинг оний қиймати нолга тенг бўлганда ҳам, токнинг оний қиймати нолга тенг бўлганда ҳам, қувватнинг шу ондаги қиймати нолга айланади. Генераторнинг узатаётган қуввати ушбу дақиқаларда (u=0, i ≠ 0 ёки i = 0, u ≠ 0) нолга тенг бўлганда ҳам, актив қаршиликдаги ажралаётган қувват (pr=i2r) нолга тенг эмас. Бу, юзаки қарагандаги номувофиқлик, фақат электромагнит майдон энергиясининг алмашинуви ҳисобига шундай бўлади: шу онларда pL манфий ва у абсолют қиймати бўйича қувват pr нинг мусбат қийматига тенг;
2) PL нинг ўртача қиймати нолга тенг бўлгани учун, хамма қувватнинг ўртача қиймати актив қаршиликда сарфланаётган қувватнинг ўртага қийматига тенг;
3) ўзгарувчан магнит майдони узатаётган қувват (яъни -pL) резистор қаршилигида сарфланаётган кувватдан (pr) катта бўлган вақт оралиғида, ўзгарувчан ток генератори бераётган қувват манфий (p<0) бўлади.
Шунга ўхшаш таҳлилни r-C занжири учун мустақил бажарилса, ўқувчи учун катта фойдали бўлади.
7.5-расм
8-маъруза. Ҳисоблашнинг символик (комплекс) усули
8.1. Оддий гармоник функцияларустида математик амалларни бажариш
Чизиқли электр занжирларини ҳисоблашда кўп марталаб уларни қўшиш, айириш, у ёки бу ўзгармас қийматларга кўпайтириб интеграллаш ва дифференциалаш амалларини бажаришга тўғри келади.
Энг оддий холатларда, берилган функциялар бир ҳил частотага эга бўлса, юқорида кўрсатилган ҳамма чизиқли операциялар натижасида шу частотали гармоник функция ҳосил бўлади. Демак, функциянинг фақат амплитудаси ва бошланғич фазалари аниқланса кифоя.
Икки гамоник функцияни қўшиш (ёки айириш) учун тригонометрик ўзгартиришнинг аналитик ифодалари ёрдамида бажариш мумкин. Бироқ, бундай ўзгартиришларнинг геометрик талқини ҳар доим амалларнинг кўргазмали, хар хил қийматларни келтириб чиқариш хулосаларининг содда бўлишини, таъминлайди, ҳамда вужудга келиши мумкин бўлган хатоларнинг олдини олишга имкон беради. Геометрик усулдан кейин кўриладиган комплекс усули эса янада каттароқ имкониятлар борлигини кўрсатади.
8.2. Геометрик усул
Тексликдаги А векторни унинг узунлиги РАР ва бошланғич ҳисоб учун танланган ихтиёрий ўқ билан шу вектор орасидаги j бурчаги орқали ифодалаш мумкин (8.1,а-расм). Бу бурчакнинг мусбат ишорасига шу векторнинг соат милига тескари йўналишдаги бурилиши мос келади. Бунда векторнинг
А = А ![]() j,
(8.1)
j,
(8.1)
белгиланиши қулай ҳисобланади, бунда А ва j унинг қутб координаталари ёки модули ва аргументи дейилади.
Босма нашрларда
(китоб ёки мақола) векторларни қалин шрифт билан [А], қўлёзма матнларда эса
ушбу харфлар юқорисидаги горизантал чизиқлар ёрдамида белгилаш қабул
қилинган [![]() ]
]
Агар аргумент вақтнинг чизиқли функцияси бўлса,
![]() ,
(8.2)
,
(8.2)
у холда бошланғич ўққа векторнинг проекцияси косинусоида сифатида берилган гармоник функциянинг оний қийматини кўрсатади:
![]() .
(8.2,а)
.
(8.2,а)
Унга перпендикуляр бўлган ўққа векторнинг проекцияси эса синусоида билан кўрсатилган гармоник функциянинг оний қийматига тенг
![]() .
(8.2,б)
.
(8.2,б)
Синусоидал ёки косинусоидал айланувчи вектор орқали ифодалаш ана шунга асосланган (8.1,б-расм).
 8.1-расм
8.1-расм
Вектор ![]() ни гармоник функция «а»нинг тасвири деб
аташ мумкин. Агар щ берилган частота бўлса,
ни гармоник функция «а»нинг тасвири деб
аташ мумкин. Агар щ берилган частота бўлса, ![]() вектори ўзи тўғрисидаги барча керакли ахборотни
ўз ичига олаган бўлади: унинг модули –
амплитудани, аргументи - бошланғич фазани аниқлайди.
вектори ўзи тўғрисидаги барча керакли ахборотни
ўз ичига олаган бўлади: унинг модули –
амплитудани, аргументи - бошланғич фазани аниқлайди.
Гармоник функциялар оний қийматларининг йиғиндисини векторлар тасвирларининг йиғиндиси орқали алмаштириш мумкин. Чунки векторлар йиғиндисининг проекцияси векторлар проекцияларининг йиғиндисига тенг.
Гармоник функцияларини тасвирловчи векторни геометрик қуришни, ҳамда векторларни график қўшишни вектор диаграммаси дейилади. Бундай диаграммалар ечимнинг йўлларини кўргазмали қилиб тушунтиради. Векторларни аниқлик билан қурилишлар натижасида изланаётган (аниқланиши зарур бўлган) амплитуда ва фазани топиш мумкин. Тахминий вектор диаграммаларини қуриш аналитик ҳисоблашнинг ишончли текшируви бўлиши мумкин ва векторларнинг қайси квадрантда бўлиши лозимлигини осон йўл билан аниқланади
8.3. Комплекс усул
 Юқорида
баён этилган ечимларни аниқлашдаги геометрик усул, аксарият ҳолларда
сермеҳнат эканлиги кўриниб турибди; муҳими, ундан фойдаланиш
натижасисида занжирнинг тенгламаларини умумий ҳолда ёзиб олиш ва уни
ташлил қилиш кўп қийинчиликларга сабаб бўлади.
Юқорида
баён этилган ечимларни аниқлашдаги геометрик усул, аксарият ҳолларда
сермеҳнат эканлиги кўриниб турибди; муҳими, ундан фойдаланиш
натижасисида занжирнинг тенгламаларини умумий ҳолда ёзиб олиш ва уни
ташлил қилиш кўп қийинчиликларга сабаб бўлади.
![]() Шунинг учун
америкалик олим Штейнметц томонидан мукаммал қилиб
ишлаб чиқилган комплекс усулини барча электротехниклар қабул қилганлар.
Бу усулни символик усул деб
Шунинг учун
америкалик олим Штейнметц томонидан мукаммал қилиб
ишлаб чиқилган комплекс усулини барча электротехниклар қабул қилганлар.
Бу усулни символик усул деб ![]()
![]() хам
аталади.
хам
аталади.
Усулнинг асосланиши. Берилган гармоник функциясини
а=Аmsin(щt+a) (8.3)
комплекс сон сифатида тасвирлаш имконини кўрайлик. Бунинг учун вақтнинг комплекс гармоник функция тушунчасини киритамиз:
![]() (8.4)
(8.4)
бунда экспонента Эйлернинг тригонометрик функцияси сифатида келтирилган.
Комплекс функция «![]() »нинг мавҳум
қисми, яъни Im
»нинг мавҳум
қисми, яъни Im![]() вақтнинг
қуйидаги гармоник функциясига айнан ўхшашдир
вақтнинг
қуйидаги гармоник функциясига айнан ўхшашдир
а=Im![]() =Im
=Im![]() (8.5)
(8.5)
Кўрсаткичли
функцияни ![]() деб қабул қилиб, янада соддароқ қилиб
ёзиш мумкин:
деб қабул қилиб, янада соддароқ қилиб
ёзиш мумкин: ![]() .
. ![]() қиймати
«
қиймати
«![]() » гармоник
функцияни тасвирловчи комплекс дейилади. Тасвирловчи комплекс қуйидаги
эффектив қиймат орқали ифодаланиши хам мумкин:
» гармоник
функцияни тасвирловчи комплекс дейилади. Тасвирловчи комплекс қуйидаги
эффектив қиймат орқали ифодаланиши хам мумкин:
![]() (8.6)
(8.6)
(охирги ҳолатда бош харф кетига «m» индекси қўйилмайди).
Агарда ![]() частота қиймати
маълум бўлса, у холда комплекс
частота қиймати
маълум бўлса, у холда комплекс ![]() ёки
ёки ![]() унга айнан
ўхшаш гармоник функция хақида тўлиқ ахборот бера олади. Функция «
унга айнан
ўхшаш гармоник функция хақида тўлиқ ахборот бера олади. Функция «![]() » нинг оний қийматини
топиш учун
» нинг оний қийматини
топиш учун ![]() комплексни
комплексни ![]() ва
ва ![]() га кўпайтириш ва
шундан сўнг олинган натижанинг
га кўпайтириш ва
шундан сўнг олинган натижанинг
![]() (8.7)
(8.7)
мавҳум қисмини аниқлаш зарур.
Гармоник
функцияни комплекс тасвирга тенглаштириб бўлмайди; фақат уларнинг
ўхшашлиги тўғрисида гапириш мумкин ва қуйидагича ёзиш мумкин: ![]() ~
~![]() бунда « ~ » ўхшашлик
белгисидир.
бунда « ~ » ўхшашлик
белгисидир.
Гармоник функцияларни қўшиш. Икки гармоник функция «a» ва «b» ларнинг йиғиндиси «c» аниқлаш лозим бўлсин:
![]() ,
(8.8)
,
(8.8)
бунда
![]() ,
, ![]() ва
ва ![]() –мос равишда комплекс функциялар.
–мос равишда комплекс функциялар.
Бироқ, икки комплекс сонлар мавҳум қисмларининг йиғиндиси комплекслар йиғиндисининг мавҳум қисмига тенг, шунинг учун
![]() (8.9)
(8.9)
ёки, агар қўшилувчиларнинг частоталари тенг бўлса
![]() .
(8.10)
.
(8.10)
(8.9) ва (8.8) ни солиштирсак, қуйидаги аниқланади:
![]()
ёки ![]() ,
(8.11)
,
(8.11)
яъни
бир хил чостотали гармоник функциялар йиғиндисини ифодаловчи комплекс қўшилувчиларни
ифодаловчи комплексларнинг йиғиндисига тенг; шундай қилиб, оний
қийматларни қўшиш амалларини комплекс тасвирларни қўшиш билан алмаштириш мумкин. Тенглик
(8.11)ни ![]() га бўлиш билан қуйидаги йиғиндининг тўғри эканлигини исботлаш мумкин:
га бўлиш билан қуйидаги йиғиндининг тўғри эканлигини исботлаш мумкин:
![]() .
(8.12)
.
(8.12)
Комплекс текислик. Хар қандай
ихтиёрий олинган комплекс ![]() ,
, ![]() сонлар учун
икки ортогонал координата ўқларидан бирига хақиқий қийматлар,
иккинчисига мавҳум қийматлар қўйилган
текисликда (8.11,а-расм) конкрет нуқталар мос
келади. Бунда комплекс
сонлар учун
икки ортогонал координата ўқларидан бирига хақиқий қийматлар,
иккинчисига мавҳум қийматлар қўйилган
текисликда (8.11,а-расм) конкрет нуқталар мос
келади. Бунда комплекс ![]() ,
, ![]() сонлар
текисликдаги комплекс координата бошидан шу нуқталарга ўтказилган
векторлар сифатида тақдим этиладилар:
сонлар
текисликдаги комплекс координата бошидан шу нуқталарга ўтказилган
векторлар сифатида тақдим этиладилар:
![]()
![]()
![]() (8.13)
(8.13)
унинг хақиқий ва мавҳум ташкил этувчилари икки координата ўқларига шу векторнинг проекцияси сифатида аниқланади.
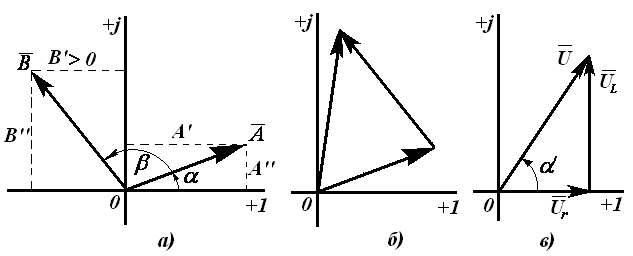
8.2-расм
Келтирилган
комплекслар қутб координатларида ҳам ифодаланиши мумкин:
![]()
![]()
![]() (8.14)
бунда
(8.14)
бунда ![]() А ва В комплекс модули (векторлар узунлиги); a,
А ва В комплекс модули (векторлар узунлиги); a, ![]() - аргумент (хақиқий
ўқга нисбатан векторларнинг бурилганлик бурчаги).
- аргумент (хақиқий
ўқга нисбатан векторларнинг бурилганлик бурчаги).
Икки комплекс йиғиндисини аниқлашда хар доим алгебрик икки хадлик шаклига ўтиш мақсадга мувофиқдир:
![]()
![]() ,
,
сўнгра алоҳида хақиқий ва алохида мавҳум ҳадлар йиғиндилари аниқланади:
![]()
![]() (8.15)
(8.15)
Шундай қилиб, гармоник функцияларни қўшиш амали бажарилишида комплекс усулни қўллаш (8.2,б-расм), геометрик усулдан фарқ қилмас экан. Бунда (8.13) ва (8.15) тенгликлардан узвий равишда (8.4) тригонометрик боғланишлар ҳам келиб чиқади.
Комплекс усулдан фойдаланганда вектор диаграммаларини қуриш тавсия этилади. Бу холда илгари кўрилганлардан фарқи шу бўладики, координата ўқларидан бири мавҳум қийматлар ўқи деб қаралади.
Шуни кўриш
мумкинки, қўшиш амалини бажариш доирасида, комплекс усулнинг геометрик
усулга нисбатан афзаллиги сезиларли эмас. Фарқни фақатгина мавҳум
қийматни хақиқий қийматдан яққол ажратиб
турувчи j = ![]() кўпайтманинг
мавжудлигида кўриш мумкин.
кўпайтманинг
мавжудлигида кўриш мумкин.
Гармоник функцияларни дифференциаллаш. Гармоник функцияни дифференциаллаганда униг тасвири j![]() га кўпайтирилади. Бошқача қилиб айтганда, агар комплек қиймат
га кўпайтирилади. Бошқача қилиб айтганда, агар комплек қиймат
![]() дифференциалланувчи гармоник функцияни
ифодаласа, у холда шу функциянинг хосиласи j
дифференциалланувчи гармоник функцияни
ифодаласа, у холда шу функциянинг хосиласи j![]() А комплекс билан тасвирланади.
А комплекс билан тасвирланади.
Дарҳақиқат, агар ![]() ~
~ ![]() бўлса, унда
бўлса, унда
![]() ~
~![]() . (8.15)
. (8.15)
Чунки ![]() ва мавҳум
қисмнинг ҳосиласи, ҳосиланинг мавҳум қисмига
тенг.
ва мавҳум
қисмнинг ҳосиласи, ҳосиланинг мавҳум қисмига
тенг.
L, r занжири учун (8.5,б-расм), кучланиш қуйидаги йиғинди сифатида ёзилиши мумкин:
![]()
Aгар занжирдан ![]() ~
~![]() токи оқаяётган,
деб фараз қилинса, бунда, аниқки, i ва
токи оқаяётган,
деб фараз қилинса, бунда, аниқки, i ва ![]() ўзаро
мос деб кўрилади.
ўзаро
мос деб кўрилади.
Дифференциаллашни
(![]() ) га
кўпайтириш билан алмаштириб қўшиш қоидаларини эътиборга олсак,
кучланишни тасвирловчи комплекс учун қуйидаги боғланишни ёзиш
мумкун:
) га
кўпайтириш билан алмаштириб қўшиш қоидаларини эътиборга олсак,
кучланишни тасвирловчи комплекс учун қуйидаги боғланишни ёзиш
мумкун:
![]() (8.16)
(8.16)
L, r занжирнинг кемплекс қаршилиги. (8.16) боғланиш ўнг томонининг биринчи кўпайтмаси (қавс ичидаги қиймат) L, r занжирининг комплекс қарашилиги дейилади.
Комплекс қаршлик хар доим бош харф Z билан белгимланади ва кўрсаткичли ёки икки хад шаклида келтирилади
Z=zе
j![]() =Z
=Z![]()
![]() (8.17)
(8.17)
Бунда модуль z=![]() - тўла қаршилик;
- тўла қаршилик;
![]() аргумент; хL=
аргумент; хL=![]() - индуктив қаршилик.
Комплекс қаршиликдан фойдаланиб, (8.16) комплекс тенгликни Ом қонуни
шаклида ёзиш мумкин:
- индуктив қаршилик.
Комплекс қаршиликдан фойдаланиб, (8.16) комплекс тенгликни Ом қонуни
шаклида ёзиш мумкин:
U=ZI (8.18)
ва уни қуйидагича таърифлаш мумкин: агар хамма қийматларни комплекс шаклда тасвирласак, занжирдаги кучланиш қиймати ток ва қаршликлар кўпайтмаларига тенг. (8.18) даги комплексларни қуйидагича ёзиш мумкин:
![]() .
.
Икки комплекс
сонлар кўпайтмасида улар аргументлари алгебрик йиғиндиси олинади; бу эса
кўрсаткичли шаклдан фойдаланиб ёзилганда кўзга кўпроқ ташланади: ![]() . Декмак
. Декмак ![]() , яъни (8.18)даги
кучланишнинг бошланғич фазаси комплекс қаршлик Z нинг
аргументи
, яъни (8.18)даги
кучланишнинг бошланғич фазаси комплекс қаршлик Z нинг
аргументи ![]() билан ток I
нинг бошланғич фазаси
билан ток I
нинг бошланғич фазаси ![]() йиғиндиларига
тенг
йиғиндиларига
тенг
![]() .
(8.19)
.
(8.19)
Бунда кучланиш амплитудаси қиймати ток ампилитудаси ва қаршилик модулининг кўпайтмасига тенг:
![]() (8.20)
(8.20)
Гармоник функцияларни интеграллаш. Гармоник
функцияни интеграллаганда унинг тасвири ![]() га бўлинади. Бошқача қилиб
айтганда, агар комплекс қиймат
га бўлинади. Бошқача қилиб
айтганда, агар комплекс қиймат ![]() интегралланувчи функцияни
тасвирласа, унда унинг интеграли
интегралланувчи функцияни
тасвирласа, унда унинг интеграли ![]() комплекс билан тасвирланади.
комплекс билан тасвирланади.
Комплекслик
белгиси j га бўлиш, аргументни ![]() бурчакка
ўзгартиради (ёки векторни шу бурчакка буради). Буларни қуйидаги боғланишлар
орқали кўрсатиш мумкин:
бурчакка
ўзгартиради (ёки векторни шу бурчакка буради). Буларни қуйидаги боғланишлар
орқали кўрсатиш мумкин:
![]() ~
~ ![]()
 ~
~ ![]() (8.21)
(8.21)![]()
Бу ерда яна қайта эслатмоқ зарурки, ушбу интегралдан чиққан функциянинг фақат гармоник ташкил этувчисини эътиборга олаяпмиз, яъни фақат барқарорлик режимни кўраяпмиз. Ўзгармас ташкил этувчиси, нолдан фарқли бўлса хам, уни ташлаб юборамиз.
Юқорида келтирилган қоидани, диффенекциаллашда қабул қилинган таҳлилга ўхшаш йўл билан текшириш мумкин. Лекин, интегралаш-диффернциаллашга тескари бўлган амал эканини эслатиш билан чекланса ҳам бўлади.
Кетма-кет уланган r ва С ли занжир кучланиши шохобча токи i билан қуйидаги тенглама орқали боғланган:
![]() (8.22)
(8.22)
бунга комплекс шаклдаги куйидаги тенглама мос келади:
![]() (8.23)
(8.23)
C, r - занжирнинг комплекс каршилиги. (8.23а қавс ичидаги купайтмани r, Cли занжирнинг комплекс каршилиги деб аташ мумкин:
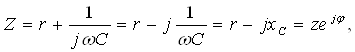 (8.24)
(8.24)
бунда
![]() - тўла қаршилик,
- тўла қаршилик, ![]() - унинг аргументи;
- унинг аргументи; ![]() сиғим қаршилиги дейилади.
сиғим қаршилиги дейилади.
Бурчак ![]() нинг манфий ишорали бўлишининг сабаби, мавҳум ташкил
этувчининг ишораси минус бўлганлигтдир
нинг манфий ишорали бўлишининг сабаби, мавҳум ташкил
этувчининг ишораси минус бўлганлигтдир
![]() .
.
Комплекс ва дифференцал тенгламаларнинг мослиги. Келтирилган қоидалар асосида электр занжирининг гармоник функциялари учун Кирхгоф қонунлари бўйича қурилган дифференциал тенгламаларга мос келувчи комплекс алгебраик тенгламаларини тузиш мумкин. Яна бир марта таъкидлаш зарурки, бунда биз фақат барқарорлашган режимни назарда тутамиз. Бу режимда барча ток ва кучланишлар гармоник фунциялардан иборат. Масалан, кетма-кет уланган r , L, C ли занжирнинг тенгламалари
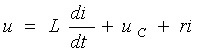 ёки
ёки ![]() (8.25)
(8.25)
бунга қуйидаги алгебрик комплекс тенглама мос келади:
![]() (8.26)
(8.26)
Оддий кетма-кет параллел уланган
занжирдаги (8.3-расм) жараённи ифодалаш учун
КТҚ асасида бир тенглама ![]() ва ККҚ асосида иккита тенглама тузиш мумкин
ва ККҚ асосида иккита тенглама тузиш мумкин
 ,
,
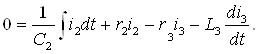
Шундай қилиб, нисбатан оғир бўлган дифференциал тенгламалар
тизимини ечиш ўрнига, енгилроқ бўлган алгебрик тенгламалар тизими ечиш таклиф этилмоқда.
Комплекс усулнинг кенг қўлланишини таъминлайдиган унинг асосий хусусияти хам мана шундадир.
Комплексларни қўшганда икки ҳадлик (алгебрик) шаклдан фойдаланган мақсадга мувофиқ, аксинча, кўпайтириш ёки бўлиш амалларини бажаришда эса қутубли (ёки кўрсаткичли) шаклдан фойдаланганлик дурустдир. Шунинг учун комплекслар билан амаллар бажарилишида алгебрик шаклдан қутб шаклга ва, аксинча, қутб шаклдан алгебраик шаклга, яъни биридан бошқасига тез-тез ўтиб туришга тўғри келади.
Комплекс шаклдаги Кирхгоф қонунлари. Юқоридагиларни умум-
лаштириб, Кирхгорнинг қонунларини қуйидаги шаклда ёзиш мумкин:
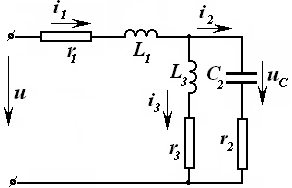
![]()
![]()
Юқоридаги мисолардан фойдаланиб келтирилган боғланишларнинг мазмунини тушуниш осон. Комплекслардан фойданилганда, қийматларнинг мусбат йўналишларини танлаш
ва елгилаш, аввалгидек, аҳаммиятлидир.
Келтириб чиқарилган барча боғланишларни ўзгарувчан ток
учун хам ёзиш мушкул иш эмас.
Масалан, кентур токлари ва 8.3-расм
тугун потенциалари тенгламалари матрица шаклида қуйидагича ёзилади:
Zkl ·Il = Ek ; B kl ·ц kl =Jkl , (8.27)
бунда матрицанинг барча элементлари комплекс шаклда ёзилган,
лекин илгаригдек ![]() - тугунлар “k”
ва
- тугунлар “k”
ва ![]() орасидаги
орасидаги ![]() бўлгандаги
ытказувчанлик ва
бўлгандаги
ытказувчанлик ва ![]() ва х.к.
ва х.к.
![]() Чизиқли боғланган тенгламалар
Чизиқли боғланган тенгламалар
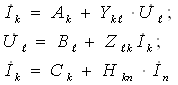 ва х.к.
(8.28)
ва х.к.
(8.28)
ҳам кучга эгадир.
Бу боғланишларда
узатиш ўтказувчанлиги ![]() узатиш қаршилиги
узатиш қаршилиги
![]() узатиш
коэффиценти
узатиш
коэффиценти ![]() илгариги
мохиятларига эга, лекин комплекс шаклда ёки комплекс холидаги матрица шаклида
ёзилган. ўзгармас қийматлар
илгариги
мохиятларига эга, лекин комплекс шаклда ёки комплекс холидаги матрица шаклида
ёзилган. ўзгармас қийматлар ![]() хам умумий
холда комплексдир.
хам умумий
холда комплексдир.
9-маъруза. Гармоник ток занжирида қувват
Қувватнинг оний қиймати ![]() ва ўртача қувват
ва ўртача қувват ![]() тушунчалари қўшимча изоҳлар талаб
этмайди. Оддий гармоник ток бўлганда актив қувват қуйидагича аниқланади:
тушунчалари қўшимча изоҳлар талаб
этмайди. Оддий гармоник ток бўлганда актив қувват қуйидагича аниқланади:
![]() ,
(9.1)
,
(9.1)
бунда j =(![]() -
-![]() )-ток ва кучланиш орасидаги фазалар фарқи; соsj - қувват коэффиценти деб аталади.
)-ток ва кучланиш орасидаги фазалар фарқи; соsj - қувват коэффиценти деб аталади.
Занжирларни таҳлил қилганда, қувватга тааллуқли бўлган бошқа тушунчалар ҳам аҳамиятлидир - булар тўла, реактив ҳамда комплекс қувватлардир.
9.1 Тўла қувват
У кучланиш ва токнинг эффектив (таъсир этувчи) қийматлари кўпайтмасига тенг:
![]() . (9.2)
. (9.2)
Фараз қийматлик, ўзгарувчан ток генератори (Г) истеъмолчи И билан кабель линияси (қалин чизиқ) орқали боғланган (9.1,а-расм).
Кабель линияси ва генератор учун чекланган (энг катта) кучланиш изоляциянинг даражаси билан чегараланади: тармоқ тизимнинг электрик мустаҳкамлиги нуқтаи назаридан кучланишни номинал қиймати Uн дан юқорироқ ошириш рухсат этилмайди. Тармоқ тизимидаги токнинг энг катта қиймати, генератор чулғамлари, тармоқ симлари, кабель симлари қизиб кетишининг олдини олиш учун токнинг номинал Iн қиймати билан чегараланади. Ушбу таъқиқловчи чекланишлар кучланиш ҳамда ток учун алоҳида киритилади ва, албатта, ток ва кучланиш фазалар бурчагига боғлиқ эмас. Номинал (рухсат этилган) кучланиш ва токлар кўпайтмаси – номинал тўла қувватни ҳосил қилади:
![]() (9.3)
(9.3)
9.1-расм
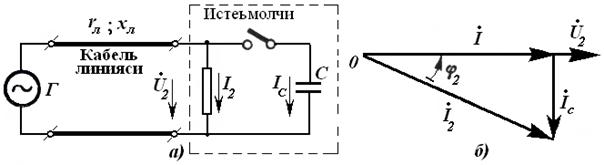
Тўла қувватнинг ![]() (номиналдан) ортиқроқ бўлиши
тақиқланган вазиятда, кабель (тармоқ)
орқали қандай ўртача қувват узатилиши мумкин? Бу қиймат
ток ва кучланиш фазалари билан аниқланади. Ўз навбатида, фаза
фарқи эса, токнинг характерига боғлиқ. Масалан, ток индуктив характерда бўлса, истеъмолчи токи I2 кучланиш U2 дан фазаси
бўйича j2 бурчакка кечикади. Бу ҳолат учун истеьмол қилинаётган қувват (фойдали қувват)
(номиналдан) ортиқроқ бўлиши
тақиқланган вазиятда, кабель (тармоқ)
орқали қандай ўртача қувват узатилиши мумкин? Бу қиймат
ток ва кучланиш фазалари билан аниқланади. Ўз навбатида, фаза
фарқи эса, токнинг характерига боғлиқ. Масалан, ток индуктив характерда бўлса, истеъмолчи токи I2 кучланиш U2 дан фазаси
бўйича j2 бурчакка кечикади. Бу ҳолат учун истеьмол қилинаётган қувват (фойдали қувват)
![]() (9.4)
(9.4)
Масалан, линиянинг охирида ток ва кучланишнинг номинал қийматлари![]() кВ;
кВ; ![]() А ва
А ва ![]() бўлсин. Бундай холатда истеьмол қилинаётган қувват
бўлсин. Бундай холатда истеьмол қилинаётган қувват
![]() МВт.дан ортиқ бўлмаслиги
шарт.
МВт.дан ортиқ бўлмаслиги
шарт.
Соsj2 миқдори қанчалар кичик бўлса, истеьмол қилинаётган қувват шунчалар кам бўлади, чунки жоиз тўла қувват ўзгармайди.
Фаза
силжишини компенсациялаш. Келтирилган 9.1,б– расмда истеъмолчига параллел
шундай қийматдаги сиғимга эга бўлган конденсатор улайликки, унда кабелнинг
ток ва кучланиши орасидаги фаза j2 нолга тенг
бўлсин, яъни қувват коэффициенти cosj 2 =1 бўлсин. Унда тармоқ орқали ![]() тўла қувват
оқиб ўтади.
тўла қувват
оқиб ўтади.
Бунда истеъмолчининг ўзидаги ток I2 номиналдан ортиқ бўлиши мумкин, бироқ линиянинг охиридаги ток I номинал қийматидан ошиб кетмайди.
Баён қилинган фикрларни 9.1,б–расмдаги вектор диаграммасида тушунтиришни давом этиш
мумкин. Кўрилаётган шароитда конденсатор шоҳобчаси токи Ic=I2sinj 2, тармоқ (кабель) охиридаги ток эса I=I2cosj 2 га тенг.
![]() бўлгани учун, ихтиёрий берилган шартлар учун зарур
бўлган қийматдаги конденсаторни аниқлаш осон.
бўлгани учун, ихтиёрий берилган шартлар учун зарур
бўлган қийматдаги конденсаторни аниқлаш осон.
9.2. Реактив қувват
Бу катталик ток ва кучланиш таъсир этувчи (эффектив) қийматлари кўпайтмаларини улар орасидаги фаза бурчагининг синусига кўпайтирилганига тенг:
![]() (9.6)
(9.6)
Эслатамиз, шартга кўра ![]() - индуктив токнинг кучланишга нисбатан фаза силжиши (кечикиши)дир.
- индуктив токнинг кучланишга нисбатан фаза силжиши (кечикиши)дир.
Кўчланиш ![]() ва
ва ![]() бўлганилиги учун индуктивликнинг истеъмол қилинаётган реактив қуввати қуйидагича аниқланади:
бўлганилиги учун индуктивликнинг истеъмол қилинаётган реактив қуввати қуйидагича аниқланади:
![]() (9.7)
(9.7)
Сиғимдаги ток ![]() кучланишдан
кучланишдан ![]() бурчакка илгарилаши сабабли ҳамда
бурчакка илгарилаши сабабли ҳамда ![]() бўлгани учун, сиғимнинг реактив қуввати қуйидагича аниқланади:
бўлгани учун, сиғимнинг реактив қуввати қуйидагича аниқланади:
![]() (9.8)
(9.8)
Реактив қувватларнинг
иккала (9.7) ва (9.8) қийматлари маълум физик мазмунга эга; уларнинг қийматлари мазкур элемент (L ва С)ларнинг максимал майдон энергияларини бурчак
частотасига кўпайтирилганига тенг. Шундай қилиб, ![]() мазкур элемент истеьмол қилаётган реактив қувватнинг максимал
оний қийматига тенг. Масалан, индуктив элиментнинг магнит майдони учун:
мазкур элемент истеьмол қилаётган реактив қувватнинг максимал
оний қийматига тенг. Масалан, индуктив элиментнинг магнит майдони учун:
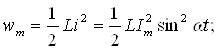
![]()
яъни ![]() .
.
Реактив қувватларнинг (9.7) ва (9.8) даги ишоралари ҳар хиллиги ҳам физик мазмунга эга. Буни фақат оддий L ва С ли
кетма-кет (ёки параллел) уланган занжирларда кўриш мумкин. Иккала холда ҳам, бирор элементнинг
максимал реактив қуввати истеъмол қилиш они иккинчисининг
максимал реактив қуввати қайтариш онига мос келади: L ва С лардаги реактив қувват пульсациясининг бўрчак
силижиши ![]() га тенг.
га тенг.
Юқорида келтирилган фаза силжишини компенсациялаш усули айнан индуктив юкдаги реактив қувват сиғимнинг реактив қуввати билан компленциялашга асосланган.
Реактив қувватларнинг қай бирини мусбат, қай бирини манфий ишора билан
белгилаш тўғрисидаги савол, мутлақо шартлидир. Масалан,
АҚШ да ![]() нинг ишорасини биздагига
(Евразиядагига) нисбатан тескари белгилаш қабул қилинган.
нинг ишорасини биздагига
(Евразиядагига) нисбатан тескари белгилаш қабул қилинган.
Келтирилган таърифлашлардан
шу маълум бўладики, тўла қувват – актив Р ва
реактив ![]() қувватлар квадратлари йиғиндисидан квадрат илдиз чиқарилганига тенг:
қувватлар квадратлари йиғиндисидан квадрат илдиз чиқарилганига тенг:
![]() (9.9)
(9.9)
ёки
![]()
9.3. Комплекс қувват
Бу қиймат комплекс кучланишнинг ва туташ комплекс токнинг кўпайтмалари билан аниқланади:
![]() (9.10)
(9.10)
Бундаги ҳақиқий қисм, яъни биринчи ҳад ўртача (актив) қувватга,
иккинчи ҳад - мавҳум қисм эса реактив қувватга тенг. Комплекслар
кўпайтмаларини ёйиб чиқиш орқали буни исботлаш мумкин. Агар ![]() ва
ва ![]() бўлса, бунда
бўлса, бунда
![]() (9.11)
(9.11)
бунда ![]() –ток ва кучланиш фаза бурчаги.
–ток ва кучланиш фаза бурчаги.
Маълумки, қувватнинг оний ва ўртача қийматлари Ваттларда (Вт) ёки унга каррали [киловатт (кВт), меговатт (МВт)], ёки ваттнинг улуши [милливатт (мВт), микроватт (мкВт) ва ҳ.к.] бирликларда ўлчанади; қувватнинг бошқа турлари шартли бирликларда ўлчанади: тўла қувват - волтампер (В·А), реактив қувват – вольтампер реактив (вар) ёки унга каррали (кВ·А; МВ·А; кВАр; МВАр).
Электр ўзатиш линиялари ва генераторларининг юкланганлиги на фақат актив қувват билан, балки тўла қувват билан ҳам аниқланганлиги учун, корхоналар электр таъминоти тизимларида на фақат истемолчининг қабул қилиб олган энергия миқдори (кВт·соат; МВТ·соат)
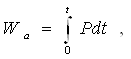 (9.12)
(9.12)
қизиқтиради, балки реактив қувват билан юкланганлиги янада эьтиборли ҳисобланади:
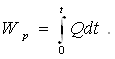 (9.13)
(9.13)
У «реактив энергияси» деб аталади ва реактив киловольтамперсоат (кВАр·с) ёки меговолтамперсоат (МВАр·с) бирликларда ўлчанади.
Қувватни кучланиш ва токнинг актив ва реактив ташкил этувчилари орқали ифодалаш. Комплекс тенглик (9.10) ҳамда актив ва реактив ташкил этувчилар тарифларини ҳисобга олган ҳолда қуйидагича ифодалаш мумкин:
![]()
![]() ва
ва ![]() (9.14)
(9.14)
Бир тоифадаги ташкил
этувчиларнинг кўпайтмалари, масалан ![]() физик мазмунга эга эмас, бироқ улар йиғиндилари
тўла қувватни ифодалайди:
физик мазмунга эга эмас, бироқ улар йиғиндилари
тўла қувватни ифодалайди:
![]() (9.15)
(9.15)
Қабул
қилинаётган ва узатилаётган қувват. Ихтиёрий икки қутблик бўлганда
(9.2-расм) ундаги қабул қилинаётган (рқаб) ва узатилаётган (рузат) қувватлар хақида гапириш мумкин. Бунда доимо рқаб = рузат шарти бажарилади. 9.2,а-расмда ![]() - узатиладиган ва
- узатиладиган ва ![]() - қабул қилинадиган қувват; 9.2,б-расмда
- қабул қилинадиган қувват; 9.2,б-расмда ![]() - қабул қилинадиган ва
- қабул қилинадиган ва ![]() - узатиладиган қувват.
- узатиладиган қувват.
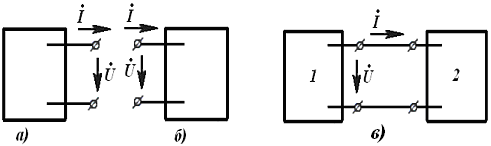
9.2-расм
Бу тушунчалар оний, комплекс, актив ва реактив қувватларга хосдир. Тўла қувватга қолганда, тарифга кўра у хар доим мусбат ишора билан белгиланади.
Реактив қувватнинг ишораси на фақат қувват узатилаётган ёки қабул қилинаётганига боғлиқ, балки мусбат реактив (индуктив) қувват ёки манфий реактив (сиғим) қуввати эканлигига ҳам боғлиқ.
Шунинг учун икки қутблик манфий реактив қувватни истеъмол қилаётган бўлса, у мусбат реактив қувватни узатаяпди дейиш мумкин.
9.4. Қувват баланси (мувозанати)
Энергиянинг сақланиш қонунига биноан, хар қандай занжир учун ихтиёрий онда қувват баланси сақланади, яъни шу занжирга узатилаётган барча қувватнинг оний қиймати занжирда истеьмол қилинаётган барча қувватлар оний қиймати (р) га тенг. Бундан эса қуйидаги хулоса келиб чиқади: занжирга хар хил манбалардан (генераторлардан) келаётган барча ўртача қувват, занжирда истеьмол қилинаётган барча ўртача қувватга тенг.
Чизиқли занжирда шундай баланс реактив қувват учун ҳам бажарилади: занжирнинг айрим элементларидан узатилаётган реактив қувватлар йиғиндиси, занжирдаги бошқа элементларнинг истеъмол қилаётган реактив қувватлари йиғиндисига тенг.
Ушбу хулоса энергиянинг сақланиш қонунига
асосланмаган бўлса ҳам, уни қуйидагича исботлаш
мумкин. Фараз қилайлик, кўрилаётган тизимда
генератор сифатида фақат ток манбалари хизмат қилаяпти; бу фаразни етарли даражада умумий дейиш мумкин,
чунки ҳар қандай кучланиш манбасини эквивалент ток манбаси деб қараш мумкин. Илгаригидек, манбанинг ![]() токи
токи ![]() потенциалга эга бўлган
потенциалга эга бўлган ![]() тугунга оқади, деб фараз қиламиз.
тугунга оқади, деб фараз қиламиз.
Кирхгофнинг биринчи қонунига асосланиб занжирнинг барча тугунлари учун
тенгламалар тизимини ёзамиз, бунда ![]() тугундан бирор п тугунга келаётган токни «
тугундан бирор п тугунга келаётган токни «![]() » индекс билан белгилаймиз:
» индекс билан белгилаймиз:

Барча токларни уларнинг туташ қийматлари орқали алмаштириб ҳамда тенгликнинг ҳар бирини ушбу тугун патенциалига кўпайтириб, қуйидаги тенгламалар тизимига келамиз:

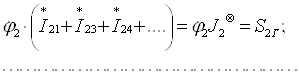
Ушбу тенгликларнинг ўнг томонида биринчи ![]() , иккинчи
, иккинчи ![]() ва ҳ.к
генераторлардан узатилаётган қувватлар комплекси
мавжуд. Бу тенгликларни қўшиб, ҳамда
ва ҳ.к
генераторлардан узатилаётган қувватлар комплекси
мавжуд. Бу тенгликларни қўшиб, ҳамда ![]() эканини эътиборга олиб, қуйидаги тенгламани ҳосил қиламиз;
эканини эътиборга олиб, қуйидаги тенгламани ҳосил қиламиз;
![]()
![]()
![]()
![]() (9.16)
(9.16)
Тенглама чап томонидаги ҳар бир ҳад, мазкур 12,13,... шохобчалар истемол қилаётган қувватга тенг:
![]()
![]()
![]() , ўнг томони эса ҳар бир генератордан
келтирилаётган қувватлар йиғиндисига, яъни
занжирга ташқаридан келаётган барча қувватлар йиғиндисига тенг:
, ўнг томони эса ҳар бир генератордан
келтирилаётган қувватлар йиғиндисига, яъни
занжирга ташқаридан келаётган барча қувватлар йиғиндисига тенг:
![]() ,
,
(5.43) тенглама комплекс қувватнинг балансини ифодалайди: занжирдаги барча истеъмол қилинаётган қувватлар йиғиндиси ![]() унга барча келтирилаётган қувватлар йиғиндиси
унга барча келтирилаётган қувватлар йиғиндиси ![]() га тенг, демак реактив қувватлар баланси ҳам:
га тенг, демак реактив қувватлар баланси ҳам:
![]() .
(9.17)
.
(9.17)
Таркибида Z қаршилиги бўлган шоҳобчанинг истемол қилаётган комплекс қувватини Жоуль-Ленц қонунига ўхшаш шаклда ёзиш мумкин:
![]()
Шунинг учун комплекс қувватлар баланси, агар ихтиёрий манбада токнинг мусбат
йўналишини э.ю.к. йўналиши билан мос келади деб ҳисобланса, қуйидаги тенглик
билан алмаштириш мумкин бўлади:
![]()
![]() (9.18)
(9.18)
Ўзгарувчан ток машиналарида ![]() кўпайтмасининг ҳақиқий қисми манфий ишорали бўлиши мумкин
(ток ва э.ю.к. нинг бир ҳил мусбат йўналишда бўлганда). Бундан хулоса шуки, олинган
манба генератор режимида эмас, мотор режимида ишламоқда. Агар аввалдан машина мотор режимида ишлаётган экани аниқ бўлса, у холда
токнинг мусбат йўналишини ўзгартириш мумкин. Бундай машина учун
кўпайтмасининг ҳақиқий қисми манфий ишорали бўлиши мумкин
(ток ва э.ю.к. нинг бир ҳил мусбат йўналишда бўлганда). Бундан хулоса шуки, олинган
манба генератор режимида эмас, мотор режимида ишламоқда. Агар аввалдан машина мотор режимида ишлаётган экани аниқ бўлса, у холда
токнинг мусбат йўналишини ўзгартириш мумкин. Бундай машина учун ![]() кўпайтмаси истемол қилинаётган қувватни кўрсатади.
Бунда (9.16) тенгликдаги мазкур ҳад тенгламанинг ўнг томонига ўтказилиши зарур (ЭЮКнинг
мусбат йўналиши, токнинг манфий йўналиши қилиб олингандан сўнг).
кўпайтмаси истемол қилинаётган қувватни кўрсатади.
Бунда (9.16) тенгликдаги мазкур ҳад тенгламанинг ўнг томонига ўтказилиши зарур (ЭЮКнинг
мусбат йўналиши, токнинг манфий йўналиши қилиб олингандан сўнг).
9.5. Максимал қувватни узатиш шартлари
Энергиянинг узатилишига қўйиладиган талаблар - сигналларни узатиш билан боғлиқ бўлган телекоммуникация тизимларида ва энергия узатишга мўлжалланган энергетик тизимларида - бир биридан тубдан фарқ қилади. Биринчисида сигнал манбадан, унинг фойдали иш коэфициентига (ф.и.к.) эътибор бермаган холда, имкон қадар максимал қувват олишга харакат қилинади. Ундан ташқари, агар сигналнинг частотаси ўзгарувчан бўлса, ёки узатилаётган сигнал таркибида ҳар хил частоталар бўлса, у ҳолда тизимнинг таҳлилида уларнинг частотавий тавсифлари масаласи кўрилади.
Икки симли линияда энергия узатишни, актив икки қутбликдан пассив икки қутбликка (9.3,а-расм) энергия узатишга ўхшатиб кўриш мумкин. Бунда
актив икки қутблик бирор ЭЮК манбаси Е ва ![]() ички қаршилигига эга
бўлган эквивалент генератор сифатида, пассив икки қутблик эса қаршилиги
ички қаршилигига эга
бўлган эквивалент генератор сифатида, пассив икки қутблик эса қаршилиги ![]() га тенг шоҳобча сифатида
кўрилиши мумкин (9.3,б-расм).
га тенг шоҳобча сифатида
кўрилиши мумкин (9.3,б-расм).
Истеъмолчи олинаётган қувват Жоуль-Ленц қонунига биноан,
![]() (9.19)
(9.19)
га тенг, бунда 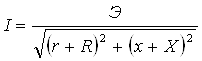 .
(9.20)
.
(9.20)
Сигнални узатиш тизимларида, қабул қилувчи имкон қадар максимал актив қувватни олиши учун, манбанинг берилган (Е = const, Zi = const) параметрларида қабул қилувчининг қаршилиги қандай бўлиши керак, деган муаммо туради, яъни Р=Рмах бўлгандаги r ва x ларнинг қийматлари аниқланиши талаб этилади. (9.19) ва (9.20) тенгликлардан яққол кўринадики, r = const бўлганда токнинг ортиши натижасида қувват қиймати ортади ва
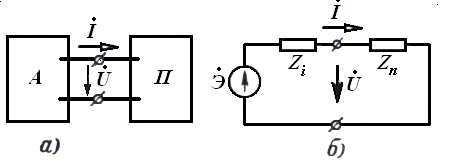
9.3-расм
х = -Х (9.21)
бўлганда максимал қийматига эришади.
Натижада ўзгармас ток электр занжирлари назариясида келтирилганидек, Р = Рмах учун қуйидаги тенгликни ҳосил қиламиз:
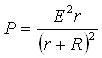 .
(9.22)
.
(9.22)
Бунда эса
r = R (9.23)
бўлиши зарур.
Икки (9.20) ва (9.21) шартларни комплекс шаклда бир боғланиш ёрдамида ифодалайми:
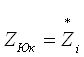 (9.24)
(9.24)
Ушбу шарт бажарилганда истеъмолчи қабул қилаётган қувват максимал бўлади:
![]() (9.25)
(9.25)
Қиймати шунга тенг бўлган қувват манбанинг ички қаришилигида сарф бўлади (чунки r= R). Шунинг учун тизимнинг ф.и.к. 50% бўлади. Албатта, бундай кичик ф.и.к. энергетика тизимларини мутлақо қониқтирмайди.
Уларда, аксарият, r нинг қиймати R га нисбаттан анча кичик бўлади.
Манба билан истеъмолчини мувофиқлаш. Истеъмолчининг кириш қаршилиги ва манбанинг ички қаршилиги тенглиги шартига мувофиқлаш шарти дейлади.
Агар максимал қувват узатиш шарти қўйилган,
ҳамда қаршиликлар характери комплекс тарзда бўлса,
уларниг тенглиги (9.24) боғланиши билан
алмаштирилади. Баъзан, физик ва конструктив сабабларга кўра, истеъмолчининг
актив қаршилигини манба ички актив қаршилиги тенг қилиб
олишнинг имконияти булмайди. Бундай ҳолларда, қўшимча
реактив элементлар киритиб, ҳосил бўлган
икки
қутибликнинг ички қаришиликларини ![]() мувофиқлаш имконияти туғилиши
мумкин экан. Мувофиқлаштириш - манба билан истеъмолчи орасига
трансфарматор киритиш билан амалга оширилиши мумкин.
мувофиқлаш имконияти туғилиши
мумкин экан. Мувофиқлаштириш - манба билан истеъмолчи орасига
трансфарматор киритиш билан амалга оширилиши мумкин.
Қуйида қўшимча реактив элиментини киритиб (9.4-расм) мувофиқлаш йўлини кўрсатамиз. Икки ректив элементлар параметрлари (х1 ва х2 ), ҳамда танланган схемага қараб, rкир нинг қийматини r га нисбатан ёки ортиқ ёки кам олиш мумкин.
Масалан, максимал қувват ҳосил қилиш шартини қуйидагича ёзиб,
![]() (9.26)
(9.26)
унда икки мустақил тенглама борлигини кўрами:
![]() ва
ва ![]()
Табийки, агар ечимлар хақиқий қийматлар бўлишига олиб келинса, юқоридаги шартларни х1 ва х2 параметрларни тегишли равишда танлаш йўли билан таъминлаш мумкин.
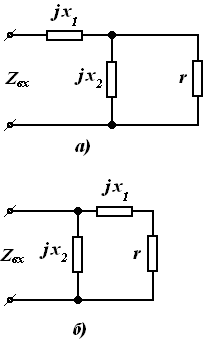 R, Х ва r қийматлари берилган деб фараз қилиб, 9.4-расмда келтирилган икки схема учун изланган х1 ва х2 қийматларни аниқлаймиз. 9.4,а-расмдаги схема учун кириш қаршилиги:
R, Х ва r қийматлари берилган деб фараз қилиб, 9.4-расмда келтирилган икки схема учун изланган х1 ва х2 қийматларни аниқлаймиз. 9.4,а-расмдаги схема учун кириш қаршилиги:
![]()
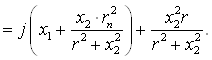
Ечим хақиқий қисмини манбанинг берилган қаршилигига тенглаштириб
![]() (9.27)
(9.27)
қуйидагини аниқлаймиз:
![]() (9.28)
(9.28)
Изланаётган ечим фақат r>R бўлган-дагина мавжуддир. Бунда 2 индексли шохоб- 9.4-расм
чага ёки индуктивлик (агар ечим илдизи олдида плюс ишора бўлса (х2>0), ёки сиғим (агар ечим илдизи олдида минус ишора олинса х2<0 ) киритилади.
Кириш қаршилигининг мавҳум қисми ишорасини манба индуктив қаршилиги (-х )нинг тескари ишорасига тенглаштириб, қуйидагини ҳосил қиламиз:
 .
.
Бунга (9.28) дан х2 ни қўйиб, оддий ўзгартиришлардан сўнг қуйидагини ҳосил қиламиз:
![]() (9.29)
(9.29)
Бу боғланишда илдиз олди юқорисидаги ишора танланган х2 нинг мусбат ишорасига мос келади.
Шунга эътибор бериш лозимки, фақат r > R бўлгандагина х1 хақиқий (мусбат ёки манфий) сон бўлади.
9.4,б-расмдаги схема учун ҳам боғланишлар шу усулда келтириб чиқарилади:
![]() (9.30)
(9.30)
![]() (9.31)
(9.31)
Бу боғланишлардан кўрамизки, 9.4,б-расмдаги схема учун фақатгина
r < R + Х2 / R (9.32)
ечим мавжуд экан.
Кучланиш частотаси ўзгариши билан мувофиқлаштириш учун киритилаётган L ва С қийматлари ҳам ўзгаради.
10-Маъруза. Индуктив боғланган занжирлар
Юқорида кўрганимиздек, бирор электр занжирининг икки контури: 1 рақамли биринчи контури (10.1,а-расм) ва 2 рақамли иккинчи контури етарли даражада яқин жойлашганда, бир контурнинг магнит майдони иккинчи контурга таъсир этади. Натижада, фақат биринчи контурдан оқаётган токка (i1≠0; i2=0) пропорционал бўлган қийматли магнит оқимига иккинчи контур илашади:
Ш21 = М21·i1 (10.1)
Бунда, биринчи контур билан улашган магнит оқим Ш11 шу контур токи ва чулғам индуктивлиги L1 нинг кўпайтмасига тенг:
Ш11=L1·i1. (10.2)
Шунга ўхшаш, ток фақат иккинчи контурда мавжуд бўлса, биринчи контур билан илашган оқим
Ш12 = М12·i2 (10.3)
га тенг бўлади.
Иккинчи контурнинг оқим илашуви
Ш22 = L2·i2. (10.4)
Магнит оқимининг барча ташкил этувчилари схематик кўриниши 1.26,б-расмда келтирилган.
Ушбу мавзу икки контурнинг «етарли даражада яқин жойлашганлиги» хақида эслатиш билан бошлаган эди; буни қандай тушунмоқ керак? Икки контурнинг бир биридан узоқлашиши натижасида уларнинг магнит боғланганлиги камайиб, занжирнинг таҳлилида M21·i1 ва M12·i2 ташкил этувчиларни эътиборга олмаса ҳам бўлади; агар бу ташкил этувчиларни эътиборга олмаслик мумкин бўлмаса, демак контурлар етарлик даражада яқин жойлашган бўлади.
Агар фақат биринчи контурда ток ўзгараётган бўлса, иккинчи контурда э.ю.к. индуктивланади:
е2 = -dШ21/dt =-M21di1/dt. (10.5)
Шунга ўхшаш, агар ток фақат иккинчи контурда ўзгарса, биринчисида э.ю.к. индуктивланади:
е1 =- dШ12/dt =- M12di2/dt. (10.6)
Юқорида мана шу ходисани ўзаро индукция ҳодисаси дейилган эди, бунда пропорционаллик коэффициенти
М12=М21=М . (10.7)
ўзаро индукция ёки ўзаро индуктивлик коэффициенти дейилади. (10.7)даги ўзаро таъсир, физика курсидан маълум бўлиб, индуктив боғланган контурларнинг энергиялари боғланишидан келиб чиқади. Ўзаро индуктивлик М хусусий индуктивлик L га ўхшаб генри (Гн) да ўлчанади.
Агар ток биринчи контурда ҳам, иккинчи контурларда ҳам (чулғамларда, шохобчаларда, ғалтакларда) оқаётган бўлса, тўла магнит илашуви ҳусусий индуктивлик ва ўзаро индуктивлик ҳосил қилган магнит илашувларининг алгебрик йиғиндисига тенг бўлади (1.26,б-расм):
![]() Ш1 = Ш11 + Ш12 = L1i1 + M12
i2;
Ш1 = Ш11 + Ш12 = L1i1 + M12
i2;
Ш2 = Ш22 + Ш21 = L2·i2 + M21·i1, (10.8)
бунда Ш1 ҳамда Ш2 - биринчи ва иккинчи контурларнинг тўла магнит илашувлари.
Ушбу (10.8) боғланишлар ёзилишида қуйидаги фаразлар қабул қилинган: ҳар бир контур мусбат токидан ҳосил бўлган магнит илашувлари иккинчи контурдаги мусбат ток ортганда ортар. Ушбу фикрлар токлар мусбат йўналишини танлашда маълум талаблар қўйилишига сабаб бўлади.
Юқорида бир неча марта таъкидланганидек, радиотехник ва электротехник тизимни электр занжири деб тан олиш учун, унинг тугунлари орасидаги кучланишлар улар орасидаги потенциаллар фарқига тенг бўлиши зарур. Шунинг учун ўзаро индукцияли занжирларда э.ю.к. нинг ҳосил бўлиши ушбу шартни мутлақо бузмайди деб ҳисоблашимиз
зарур; э.ю.к. занжирнинг бирор элементида масалан, индуктивлик ғалтагида (10.1-расм) локаллашлашади, холос.
Таркибида шундай тугунлари бўлган занжирлар мавжудки, келтирилган фикирлар улар учун мутлоқо ноўриндир. Бундай тугунлар бизнинг эътиборимизни қаратмайди.
Индуктив боғланган элементлар учларини белгилаш. Ўзиндукция магнит илашуви L1·i1 (ёки L2·i2)га ўзаро индуктивлик М·i2 (ёки М·i1) магнит илашувининг алгебраик қўшилиши ишорасини аниқлаш учун, индуктив боғланган элементларнинг қисқичлари (боши ва кети)ни белгилаш зарур. Бунда L1, L2 ва М коэффициентлари мусбат ишорали, деб ҳисобланади.
Одатда, ўзаро индуктив боғланган элементлардан бирининг бир қисқичи ихтиёрий равишда «боши» деб қабул қилинади ва схемада унинг олдига у ёки бу белгини, кўпинча нуқтани қўйилади (10.1-расмлар). Иккинчи белги шундай жойлаштириладики, i1 ва i2 токлар ушбу белгиланган қисқичларга нисбатан бир ҳил йўналтирилганда, ўзаро индукция натижасида ҳар бир индуктив боғланган элементнинг магнит илашуви ортсин (10.3,а,в,г-расмлар).
Бундай белгилашларни ҳисобга олиб, магнит илашуви қуйидагича аниқланади:
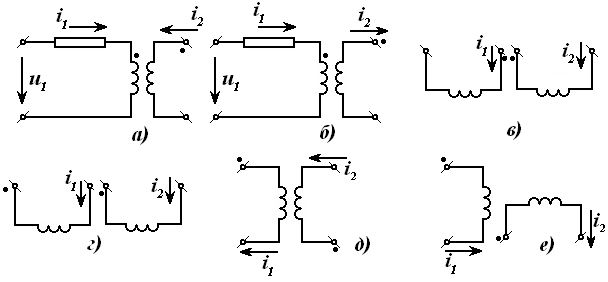 Ш1=L1·i1+M·i2; Ш2=L2·i2+M·i1
(10.9)
Ш1=L1·i1+M·i2; Ш2=L2·i2+M·i1
(10.9)
10.1-расм
Агар икки шохобчалардаги токлар ҳар хил йўналишда белгиланган бўлса (10.1,б,д,е-расмлар)да, ҳар бир элементнинг магнит илашуви қуйидагича аниқланади:
10.1-расмда келтирилган бир ўқда жойлашган, ҳамда маълум йўналишда ўралган ғалтаклар ёки икки линия учун учун белгини қандай қўйиш масаласи аниқ. Магнит майдонларнинг йўналишлари ҳақидаги маълумот бўлмаган ҳолда, белгилашни индуктивланган кучланишларни ўлчаш йўли билан аниқлаш мумкин: белгиларга нисбатан токлар йўналишлари бир хил бўлганда, ўзиндукция кучланиши
uL1=L di1/dt
ёки ![]() (10.10)
(10.10)
ўзаро индукция кучланиши Мdi2/dt ёки Mdi1/dt билан қўшилиши зарур:
![]()
![]()
![]() u(L,M)1=L1di1/dt+Mdi2/dt;
u(L,M)1=L1di1/dt+Mdi2/dt;
u(L,M)2=Mdi1/dt+L2di2/dt,
(10.11)
![]() ва шунга ўхшаш
ва шунга ўхшаш
![]()
![]() (10.12)
(10.12)
Юқорида келтирилган фикрлар (10.10) боғланишдан келиб чиқади, чунки токларнинг мувофиқ равишда йўналтирилишида магнит илашувлар L1di1/dt ва Mdi2/dt ўзгариши натижасида бир хил йўналган э.ю.к. лар ҳосил бўлади.
Аксинча, i1 ва i2 токларнинг берилган қисқичларига нисбатан йўналишлари хар хил бўлса, у холда кучланишлар қуйидагича аниқланади:
![]() u(L,M)1=L1di1/dt-Mdi2/dt;
u(L,M)1=L1di1/dt-Mdi2/dt;
u(L,M)2=Mdi1/dt+L2 di2/dt. (10.13)
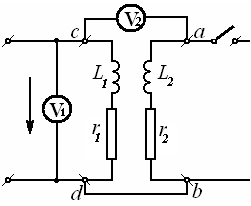 10.1,а ва б-расмлардаги индуктив боғланган
контурларнинг биринчи шохобчасида актив қаршилик ҳам келтирилган.
Шунинг учун, 10.1,а-расм кучланишлари қуйидагича аниқланади:
10.1,а ва б-расмлардаги индуктив боғланган
контурларнинг биринчи шохобчасида актив қаршилик ҳам келтирилган.
Шунинг учун, 10.1,а-расм кучланишлари қуйидагича аниқланади:
u1=i1r +L1di1/dt+Mdi2/dt , (10.14)
10.1,б-расмда эса:
u1=i1r1 +L1di1/dt-Mdi2/dt. (10.15)
1-мисол. 10.2-расмда икки индуктив
боғланган шоҳобча келтирилган.
Уларнинг биринчисида Э1 токи оқади,
иккинчисидаги ток нолга тенг (Э2=0).
10.2-расм
Биринчи элементнинг қисқичлари орасидаги кучланиш V1 вольтметр билан ўлчанади ва унинг кўрсаткичи 120В га тенг. Иккинчи элементнинг қисқичларидан бири (b) ўтказгич ёрдамида биринчи элементнинг d қисқичи билан уланган. Иккала элементнинг қолган қисқичлари (а ва с) орасига вольтметр V2 уланган ва 175В қийматни кўрсатмоқда. Биринчи элементнинг с қисқичига «боши» белгиси (нуқта) қўйилган.
Иккинчи элементнинг қайси қисқичига «боши» белгиси (нуқта)ни қўйиш зарур.
Эслатма: Барча r, L, M параметрлар мусбат ишорали деб ҳисобланади.
Ечиш. Белги (нуқта)
«b» қисқичга қўйиш керак, чунки, сdba контурга
«кўз юритиб» чиққанимизда шуни кўрамизки, ![]() с потенциал
с потенциал ![]() а потенциалидан қуйидаги
қийматга юқалироқдир:
а потенциалидан қуйидаги
қийматга юқалироқдир:
![]()
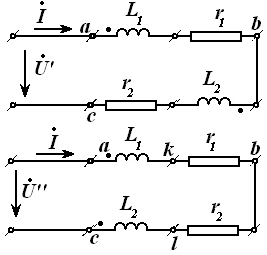 Биринчи элементдаги кучланишлар пасаюви
Биринчи элементдаги кучланишлар пасаюви ![]() нинг
ишораси иккинчи элементдаги
нинг
ишораси иккинчи элементдаги ![]() кучланишлар
пасаюви ишораси билан бир хил, чунки иккала ҳолатда ҳам «кўз
юритуви» белгидан бошланган, шунинг учун магнит илашуви L1Э1
ва МЭ1, ҳамда уларнинг ҳосилалари, бир ҳил
ишорага эга бўладилар. Бошқача фикр юритиш ҳам мумкин, масалан: U2>U1
бўлгани учун L1+M>L1
бўлади.
кучланишлар
пасаюви ишораси билан бир хил, чунки иккала ҳолатда ҳам «кўз
юритуви» белгидан бошланган, шунинг учун магнит илашуви L1Э1
ва МЭ1, ҳамда уларнинг ҳосилалари, бир ҳил
ишорага эга бўладилар. Бошқача фикр юритиш ҳам мумкин, масалан: U2>U1
бўлгани учун L1+M>L1
бўлади.
10.3-расм
Икки индуктив боғланган занжирларни кетма-кет улаш. Бу холда индуктив элементларни «мос» (10.2,а-расм) ёки «қарама-қарши» (10.2,б- уланганликларининг фарқини кўриш зарур.
Мос уланиш кўрилаётган ток иккала индуктив элементда белгиланган қис-қичларга нисбатан бир хил йўналти-рилган (10.2,а-расмдаги) иккала элемент-нинг белгиланган қисқичига ток киради; «қарама-қарши» уланганда иккала элемент белгиланган қисқичларига нис-батан ток хар хил йўналтирилган. Шу-нинг учун, контурга «кўз югурти-рилган»да шу маълум бўладики, мос уланганда тенглама қуйидагича улан-ганда тенглама қуйидагича ёзилади:
![]() (10.16)
(10.16)
Бу тенгликда ҳадлар
атайлаб шундай ажратилганки, унда: токнинг биринчи квадрат қавсдаги қийматга
кўпайтмаси биринчи элементдаги кучланиш ![]() га тенг;
кейинги ҳад - иккинчи элементдаги кучланиш
га тенг;
кейинги ҳад - иккинчи элементдаги кучланиш ![]() га тенг бўлсин.
га тенг бўлсин.
Қарама-қарши уланган контурлар учун тенглама бошқача ёзилади:
![]() (10.17)
(10.17)
Охирги тенгламада ҳам юқорида қайд қилинган ҳадларга ажратиш услуби қўлланилган. Занжирнинг параметрлари (щLk , щM, rk) ва кириш кучланиши берилган вазият учун токни аниқлаш зарур бўлганда, табиийки, токнинг барча кўпайтувчилари бирга гуруҳланган бўлиши зарур:
![]() (10.18)
(10.18)
ва
![]() (10.19)
(10.19)
Квадрат қавслар ичида занжирнинг кириш қаршиликлари жойлашган.
Кириш қаршиликларининг (ишоралари) ҳар хил эканлиги белгилаш учун асос бўлиши мумкин.
10.2-мисол. 10.2,б-расм схемаси учун а, k, b; l, с тугунларнинг потенциалларига мос келадиган нуқталарни комплекс майдонда кўрсатиб, топографик диаграммасини қуринг.
Берилган: щL1=20 Ом; щL2=60 Ом; щМ=30 Ом; r1=10 Ом; r2=20 Ом.
Ечиш: Мисолнинг
шартларида на кучланиш ва на токнинг қийматлари кўрсатилган эмас. Бироқ,
бу топографик диаграмма қуриш учун тўсиқ бўла олмайди. Агар ![]() ва Э
қийматлари берилган бўлса, диаграмманинг фақат масштаблари ўзгаради
холос.
ва Э
қийматлари берилган бўлса, диаграмманинг фақат масштаблари ўзгаради
холос.
Юқорида
эслатилганлардан шу маълум бўладики, диаграммани охиридан бошлаб қуриш мақсадга
мувофиқ. Токнинг ихтиёрий қийматини
I = 1 A. ва (С нуқта)
потенциали ![]() с=0ни
танлаб, ℓ нуқтанинг потенциалини аниқлаймиз:
с=0ни
танлаб, ℓ нуқтанинг потенциалини аниқлаймиз:
![]() B;
B;
сўнгра b нуқтанинг потенциалини аниқлаймиз:
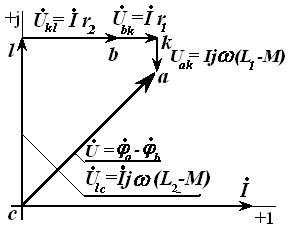
![]() B.
B.
Шу усулни қўллаб, 10.3-расмда келтирилган
диаграммани қурамиз (маштабга риоя қилинмаган).
Икки параллел индуктив боғланган
шохобчалар. Бу холатда хам шохоб-чаларнинг мос (10.4,а-расм) ва қарама- қарши (10.4,b-расм) уланишларининг фарқларини 10.4-расм
эътиборга олиш зарур; мос уланганда икки
шохобчадаги токлар бир хил белгиланган қисқичларга кирадилар; қарама-қарши уланганда эса, бир шохобчага ток белгиланган қисқичга киради, иккинчи шохобчада эса белгиланган қисқичдан чиқади. Соддалаштирилган холда уччала токнинг қийматларини аниқлаш учун учта тенглама тузилади:
![]() ;
;
![]() (10.20)
(10.20)
![]() ,
,
бунда ![]() ва
ва ![]() тенгламалар
тизимининг кейинги иккитаси индуктив боғланиши бўлмаган
шохобчалар параллел уланганидан шу билан фарқ қиладики, уларнинг
хар бирида иккитадан токлар қатнашмоқда.
тенгламалар
тизимининг кейинги иккитаси индуктив боғланиши бўлмаган
шохобчалар параллел уланганидан шу билан фарқ қиладики, уларнинг
хар бирида иккитадан токлар қатнашмоқда.
Бу тенгламаларни ечиб, қуйидагиларни
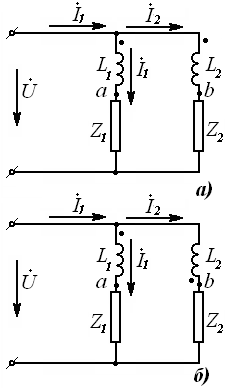 аниқлаймиз:
аниқлаймиз:
![]()
![]() (10.21)
(10.21)
![]() бунда
бунда ![]() (10.22)
(10.22)
Икки мос параллел уланган шохобчаларнинг кириш қаршилиги
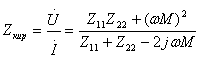 .
(10.23)
.
(10.23)
Контурлар орасида индуктив боғланиш мавжуд бўлмаса, илгари маълум бўлган тенглик келиб чиқади.
10.5-расм
Қарама-қарши уланганда (10.5,б-расм) фақат М олдидаги ишора ўзгартирилади, натижада кириш қаршилигининг реактив ташкил этувчиси камаяди.
10.5-расмда мос (а) ва қарама-қарши (б) параллел уланган шохобчалар келтирилган; бунда тугунларнинг белгилари аниқ ҳолатда келтирилмаган. 10.5-расмдан шуни тушунса бўладики, қарама-қарши йўналган (уланган) токлар умумий магнит майдони (Ф) ни камайтиради.
Икки элементли оддий параллел-кетма-кет занжирлар. Бундай занжирлар 10.5,в-расмда
келтирилган. Киргофнинг қонунларига мувофиқ тенгламалар қуриб,
кучланишлар ![]() ва
ва ![]() берилган деб ҳисоблаб, икки контур токлари учун икки тенгламалар
тизимни тузамиз:
берилган деб ҳисоблаб, икки контур токлари учун икки тенгламалар
тизимни тузамиз:
![]()
![]() (10.24)
(10.24)
бунда ![]()
![]()
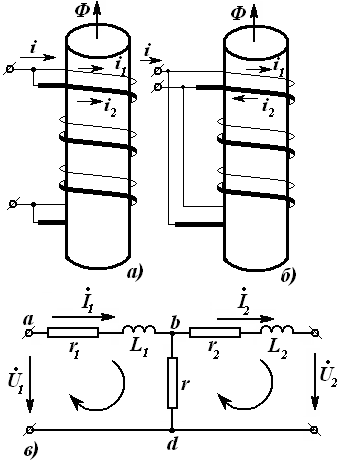 Умумий шохобча қаршилигининг ишораси (
Умумий шохобча қаршилигининг ишораси (![]() ) манфий
танланишининг саба-би, унда оқиб ўтаётган контур токлари мусбат йўналишлар-ининг
қарама-қарши эканлиги-дир; ўзаро индуктивлик қар-шилигининг
ишораси манфий (
) манфий
танланишининг саба-би, унда оқиб ўтаётган контур токлари мусбат йўналишлар-ининг
қарама-қарши эканлиги-дир; ўзаро индуктивлик қар-шилигининг
ишораси манфий (![]() ) олинганлигининг
сабаби эса, I1 ва I2 токларнинг белгили (нуқта
билан белгиланган) қисқичларга нисбатан ҳар хил йўналганликларидир.
) олинганлигининг
сабаби эса, I1 ва I2 токларнинг белгили (нуқта
билан белгиланган) қисқичларга нисбатан ҳар хил йўналганликларидир.
10.3-мисол.10.5,в-расмдаги
занжирда ![]() ва
ва ![]() шохобча-лар
ўринларини алмаштиринг; бунда b тугундаги ҳар бир алмашинаётган
шохобчалар-нинг уланишлари илгаригидек қолдирилсин; кирувчи ток I1
илгаригидек а нуқтага киради деб ҳисоблансин;
танланган
10.6-расм
шохобча-лар
ўринларини алмаштиринг; бунда b тугундаги ҳар бир алмашинаётган
шохобчалар-нинг уланишлари илгаригидек қолдирилсин; кирувчи ток I1
илгаригидек а нуқтага киради деб ҳисоблансин;
танланган
10.6-расм
контурлар (ўзаро индуктив боғлаган) илгаригидек қолдирилсин (а, b, d ва d, b, с). (10.24) тенгламадаги Z11, Z22, Z12 қаршиликларнинг янги қийматлари аниқлансин.
Ечиш. Z11 қаршилик ўзгармайди. Контурларнинг ўзаро қаршилиги Z12 энди янги қиймат қабул қилади:
![]()
Бундан ташқари иккала индуктив боғланган элементлардан ҳар хил йўналишда оқаётган I2 токли иккинчи контурнинг ўзаро қаршилиги ҳам янги қиймат қабул қилади:
![]()
Икки индуктив боғланган контурлар
магнит майдони энергияси.
Икки индуктив боғланган контурлар (шохобчалар) нинг i1 ва i2 токлари ҳосил
қилган энергияни аниқлаш учун бошланғич шарт бажариладиган ҳолатда (яъни ![]() да)
да) ![]() манбадан олинаётган энергияни ҳисоблаймиз.
манбадан олинаётган энергияни ҳисоблаймиз.
Бошланғич шартда (![]() бўлганда) манба токи фақат биринчи контур орқали
ўтади, иккинчи контур узилган ва ток ўтмайди (
бўлганда) манба токи фақат биринчи контур орқали
ўтади, иккинчи контур узилган ва ток ўтмайди (![]() ) деб фараз қиламиз. Бу ҳолатда, токнинг нолдан
) деб фараз қиламиз. Бу ҳолатда, токнинг нолдан ![]() гача бўлган
гача бўлган ![]() вақт оралиғида ўзгаришида биринчи
манбадан қуйидаги миқдорда энергия узатилади:
вақт оралиғида ўзгаришида биринчи
манбадан қуйидаги миқдорда энергия узатилади:
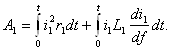 (10.25)
(10.25)
А1 дан ![]() қаршиликда исроф бўлаётган энергияни ажратиб
олсак (биринчи ҳад), биринчи манба магнит
майдонига сарфланган энергияни аниқлаймиз:
қаршиликда исроф бўлаётган энергияни ажратиб
олсак (биринчи ҳад), биринчи манба магнит
майдонига сарфланган энергияни аниқлаймиз:
![]()
Яна фараз қилайлик: ![]() онда янги манба иккинчи шохобчага уланади ва
онда янги манба иккинчи шохобчага уланади ва ![]() вақтгача бўлган оралиқда ундаги ток
нолдан
вақтгача бўлган оралиқда ундаги ток
нолдан ![]() гача ортади. Бунда агар
гача ортади. Бунда агар ![]() ток ўзгармасдан қолса, у холда иккинчи манба
магнит майдони учун қуйидаги энергияни узатиши зарур:
ток ўзгармасдан қолса, у холда иккинчи манба
магнит майдони учун қуйидаги энергияни узатиши зарур:
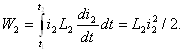
Аммо, биринчи
шохобчада ![]() ортиш жараёнида э.ю.к. индуктивланади; биринчи шохобчадаги ток ўзгармай қолиши (
ортиш жараёнида э.ю.к. индуктивланади; биринчи шохобчадаги ток ўзгармай қолиши (![]() ) учун, на фақат биринчи шохобчадаги кучланишлар пасаюви (i1r1)ни, балки ундаги
индуктивланаётган э.ю.к. ни ҳам
мувозанатловчи биринчи манба U1 кучланишини сақлаб туриши зарур:
) учун, на фақат биринчи шохобчадаги кучланишлар пасаюви (i1r1)ни, балки ундаги
индуктивланаётган э.ю.к. ни ҳам
мувозанатловчи биринчи манба U1 кучланишини сақлаб туриши зарур:
![]()
Шунинг учун ![]() токи ортиши оралиғида
биринчи манбанинг магнит майдони учун узатаётган энергияси қуйидаги
тенглик билан ифодаланади:
токи ортиши оралиғида
биринчи манбанинг магнит майдони учун узатаётган энергияси қуйидаги
тенглик билан ифодаланади:
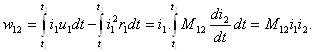 (10.26)
(10.26)
Натижада икки
индуктив боғланган шохобчаларда ![]() ва
ва ![]() токлари
бўлгандаги магнит майдонининг тўла энергияси
токлари
бўлгандаги магнит майдонининг тўла энергияси
![]() (10.27)
(10.27)
га тенг бўлади.
Юқорида келтирилган усулни қўллаб, фақат, аввал иккинчи шохобчани манбага улаб, сўнгра биринчисини манбага улаб, қуйидаги
![]() (10.28)
(10.28)
боғланишни олишимиз
мумкин. (10.27) ва (10.28) тенгликларнинг ягона фарқи шундай иборат
бўладики, биринчиси таркибида М12 коэффициенти (иккинчи
элементда бирлик токи бўлгандаги биринчи элементданинг магнит илашуви
коэффициентига тенг) бўлса, иккинчиси таркибида М21 (биринчи
элементда бирлик токи бўлгандаги иккинчи элементнинг магнит илашуви
коэффициентига тенг) мавжуд. Иккала вазиятда хам занжирнинг натижавий холати
бир хил бўлади: ![]() ва
ва ![]() токли
тизимда магнит майдони мавжуд бўлади; унинг қиймати фақат
берилган ўтказгичларнинг тузилиши билан аниқланади.
токли
тизимда магнит майдони мавжуд бўлади; унинг қиймати фақат
берилган ўтказгичларнинг тузилиши билан аниқланади.
Ушбу мулоҳазалар натижасида
![]() (10.29)
(10.29)
эканлигига иқрор бўлиш мумкин.
11-Маъруза. Комплекс узатиш функцияси
Юқорида келтирилган L, r, C кетма-кет контур, L, r, C параллел контур ва реактив икки қутбликлар учун қурилган частотавий тавсифлар электр занжири у ёки бу хусусиятларининг частотага боғлиқ эканлигини кўрсатади. Шунга ўхшаш тавсифлар, на фақат занжир таҳлили учун, балки электр занжирини синтез қилиш масалаларини ечишда ҳам қўлланилади.
Умумий холда
занжирнинг частотавий хусусиятлари ҳақида занжирнинг узатиш
функцияси деб (узатиш коэффициенти амплитуда-фаза тавсифи) номланган тавсифи
ёрдамида фикр юритилади. Узатиш функцияси ![]() дейилганда,
занжир учун чиқувчи қиймат деб қабул қилинган катталик
масалан, занжир токи, бирор қисм кучланишларидан бирининг, берилган кириш
қийматига нисбати тушунилади.
дейилганда,
занжир учун чиқувчи қиймат деб қабул қилинган катталик
масалан, занжир токи, бирор қисм кучланишларидан бирининг, берилган кириш
қийматига нисбати тушунилади.
Узатиш функцияси модулининг частотага боғлиқлиги,
яъни Н(![]() )ни
амплитуда-частота тавсифи; аргументининг частотага боғлиқлиги Y(
)ни
амплитуда-частота тавсифи; аргументининг частотага боғлиқлиги Y(![]() )ни
фаза-частота тавсифи дейилади. Масалан, 10.1-расмдаги ҳар бир резонанс эгри чизиғини кетма-кет
контурнинг берилган Q параметри
ва берилган кириш қиймати, яъни резонанс
токи Iмахнинг
маълум қиймати учун амплитуда-частота тавсифи Н(
)ни
фаза-частота тавсифи дейилади. Масалан, 10.1-расмдаги ҳар бир резонанс эгри чизиғини кетма-кет
контурнинг берилган Q параметри
ва берилган кириш қиймати, яъни резонанс
токи Iмахнинг
маълум қиймати учун амплитуда-частота тавсифи Н(![]() ) деб қараш
мумкин.
) деб қараш
мумкин.
Ушбу контур (6.1,а-расм) учун токнинг комплекс шаклда ёзилиши қуйидагича бўлади:
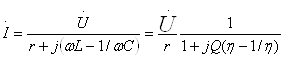 (11.1)
(11.1)
ва резонанс (![]() ) бўлгандаги қиймати
) бўлгандаги қиймати
![]()
яъни, узатиш функцияси
 .
(11.2)
.
(11.2)
Бунда ![]() нинг мавҳум
ташкил этувчисини ҳақиқий ташкил этувчисига нисбати, яъни
нинг мавҳум
ташкил этувчисини ҳақиқий ташкил этувчисига нисбати, яъни
![]() (11.3)
(11.3)
олинади.
Частотавий
тавсифларни, аксарият, ![]() вектори
учининг комплекс майдонидаги геометрик ўрни - годограф деб қабул қилинади,
вектори
учининг комплекс майдонидаги геометрик ўрни - годограф деб қабул қилинади,
бунда ![]() қийматни
боғлиқ бўлмаган ўзгарувчи деб ҳисобланади. Кетма-кет
контурнинг гадографи (унинг амплитуда-фаза тавсифи)11.1,б-расмда
келтирилган.
қийматни
боғлиқ бўлмаган ўзгарувчи деб ҳисобланади. Кетма-кет
контурнинг гадографи (унинг амплитуда-фаза тавсифи)11.1,б-расмда
келтирилган.
 11.1-расм
11.1-расм
Занжирнинг кириш қаршилиги ёки кириш ўтказувчанлиги, узатиш функцияларининг хусусий холларидан бири сифатида кўрилиши мумкин. Масалан, 11.1,в-расмдаги алмаштириш схемаси учун ғалтакнинг кириш қаршилиги
![]()
га тенг.
Амплитуда-частота тавсифи z![]() фаза-частота тавсифи
фаза-частота тавсифи ![]() ва годографи 11.1,в - д-расмларда келтирилган.
ва годографи 11.1,в - д-расмларда келтирилган.
Агар узатиш
функцияси ўлчовсиз (масалан, ![]() ) бўлса, у холда
логарифмик амплитуда-частота тавсифини (ЛАТ) аниқлаш мумкин:
) бўлса, у холда
логарифмик амплитуда-частота тавсифини (ЛАТ) аниқлаш мумкин:
![]() .
(11.4)
.
(11.4)
Непер ва децибел. Икки қийматлар
нисбати х=у/у0 ни улар логорифми ![]() ёрдамида
ўлчаш қулайдир; бу узатиш функцияси модули
ёрдамида
ўлчаш қулайдир; бу узатиш функцияси модули ![]() га ва бошқа
ўлчовсиз қийматларга тааллуқлидир. Натурал логарифм N га
тенг (масалан,
га ва бошқа
ўлчовсиз қийматларга тааллуқлидир. Натурал логарифм N га
тенг (масалан, ![]() ) бўлса,
кўрилаётган қиймат (ёки нисбат) N неперга тенг деб ҳисобланади.
Агар H нинг қиймати е = 2,72 га тенг бўлса, унинг қиймати 1
непер (Hп)га тенг деб қабул қилинади. Баъзан
) бўлса,
кўрилаётган қиймат (ёки нисбат) N неперга тенг деб ҳисобланади.
Агар H нинг қиймати е = 2,72 га тенг бўлса, унинг қиймати 1
непер (Hп)га тенг деб қабул қилинади. Баъзан ![]() ўрнига бошқа
логарифм ўлчовини, 20lgH ни киритилади. Бу қийматнинг бирлиги
децибел (дБ). Агар lgH=1/20 бўлса Н нинг қиймати 1
дБ.га тенг бўлади. 1дБ=0,115 Нп; 1Нn=8,7дБ.
ўрнига бошқа
логарифм ўлчовини, 20lgH ни киритилади. Бу қийматнинг бирлиги
децибел (дБ). Агар lgH=1/20 бўлса Н нинг қиймати 1
дБ.га тенг бўлади. 1дБ=0,115 Нп; 1Нn=8,7дБ.
Частоталар шкаласи. Уни, аксарият, логарифмик масштабда қурилади.
Частота икки марта ортишига тўғри келувчи частота интервали – октава дейилади,
ўн марта ортишга эса декада дейилади. Частотанинг ![]() дан
дан ![]() гача ўзгариш интервали учун октавалар сони
гача ўзгариш интервали учун октавалар сони
![]() (11.4)
(11.4)
ва декадалар сони
nд=lg(![]() /
/![]() )
(11.5)
)
(11.5)
яъни 1 декада = 3,32 октавага
12-Маъруза.Даврий носинусоидал таъсир ва унинг параметрлари.
Электр занжирлари
назарияси фани ўрганилиши жараёнида бир неча гармоник ташкил этувчилар ва
ўзгармас ташкил этувчи йиғиндиларидан иборат бўлган ўзгарувчан ток (ёки
кучланиш)ларни тез-тез учратиш мумкин, масалан ![]() (12.1,а
ва б-расмлар).
(12.1,а
ва б-расмлар).
Ахборот маълумотларида «гармоник ташкил этувчи» ибораси ўрнига қисқалик учун «гармоника» атамаси ишлатилади.
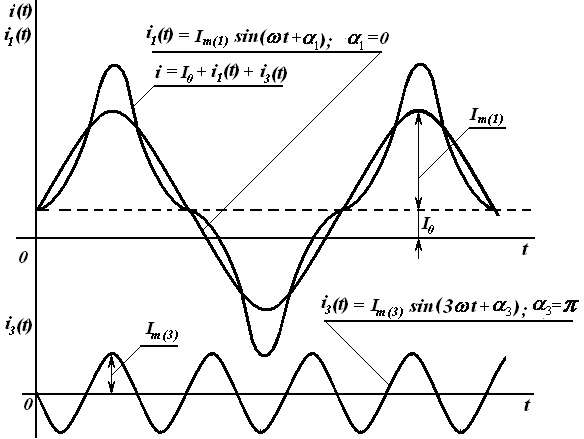
12.1,а-расм
Ҳар хил гармоникаларнинг амплитудалари ва бошланғич фазалари - мураккаб гармоник функцияларнинг спектрал таркибини ташкил қилади. Амплитуда буйича бир хил спектрал таркиби бўлиб, бошланғич фазалари эса мос келмаса, функциялар ҳар хил бўлишига 12.1,а ва б-расмларни таққослаб иқрор бўлиш мумкин.
Баъзи электротехник ва радиотехник қурилмаларда даврий функциянинг кўриниши аҳамиятли бўлса, баъзан фақат амплитуда бўйича спектрал таркиби катта эътиборга эга. Масалан, телефон мембранасидаги ҳаво босими вақт бўйича 12.1,а ва б-расмда тасвирланганидек ўзгарса, товушни сезиш ҳусусияти ўзгармайди.
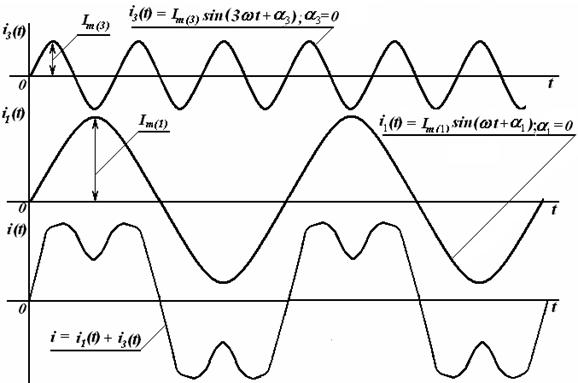
12.1,б-расм
Мураккаб гармоник
функциянинг ![]() тенглик
билан тасвирланган боғланиши барча ташкил этувчиларнинг энг кичик
умумий каррали
тенглик
билан тасвирланган боғланиши барча ташкил этувчиларнинг энг кичик
умумий каррали ![]() даврларини
ифодалайди. Масалан, даврлари
даврларини
ифодалайди. Масалан, даврлари ![]() ва
ва ![]() бўлган икки
гармоник функциялар йиғиндиси учун (8.1-расм)
бўлган икки
гармоник функциялар йиғиндиси учун (8.1-расм)
![]() (12.1)
(12.1)
бунда ![]() ва
ва ![]() энг кичик
бутун сонлар [акс ҳолда даврий функциялар йиғиндиси даврий
бўлмайди, чунки (11.1) шартни бажарувчи
энг кичик
бутун сонлар [акс ҳолда даврий функциялар йиғиндиси даврий
бўлмайди, чунки (11.1) шартни бажарувчи ![]() ва
ва ![]() сонлар
бўлмайди]. Оддий гармоникаларнинг ихтиёрий йиғиндиси бутун (ёки рационал)
сонлар n учун даврий функциядир:
сонлар
бўлмайди]. Оддий гармоникаларнинг ихтиёрий йиғиндиси бутун (ёки рационал)
сонлар n учун даврий функциядир:
![]() (12.2)
(12.2)
12.1-расмда
горизонтал ўқ бўйлаб вақтни ҳар бир гармоника учун бир хил
масштабда қўйилган, шунинг учун унинг аргументи (градусда ёки даврнинг
улушида) ҳар хил масштабга эга бўлади: биринчи гармоникаси учун ![]() (ёки 900)
радиан мос келса,
(ёки 900)
радиан мос келса, ![]() -гармоника учун
-гармоника учун ![]() радиан (ёки
радиан (ёки
![]() ) мос келади.
Гармоникаларни бир графикка қурганда шуларга эътиборни кучайтириш зарур.
) мос келади.
Гармоникаларни бир графикка қурганда шуларга эътиборни кучайтириш зарур.
Гармоник функцияларнинг ажойиб хусусиятларидан бири шундан иборатки, ихтиёрий даврий функцияни амплитудалари ва бошлангич фазалари маълум тартибда танланган оддий гармоник функциялар (синус ёки косинус)нинг чекли ёки чексиз қатор йиғиндиси деб ифодалаш мумкин (Фурье қатори). Даврий функцияларни гармоник ташкил этувчиларга ажратиш §8.6да ўрганилади.
Аксарият,
кучланиш ва токларнинг мураккаб спектрал таркиби сигналлар (ахборот)ни узатиш
ва қайта ишлашда учрайди. Энергетика тузимларида эса айниқса, уч
фазали электр узатиш линияларида, кучланишни фақат синусоидал, яъни
таркибида фақатгина биринчи (бошқача номи «асосий») гармоникаси
бўлиши таъминланади. Шу билан бирга, таркибида жуда кичик миқдорда (![]() ва ҳ.к
частотали) юқори гармоникаларнинг мавжуд бўлишига жоизлик -рухсат этувчи қатъий
қоидалар мавжуд. Бу тизимларда юқори гармоникалар, асосан,
электротехник ускуналар реал элементларининг ночизиқли тавсифлари туфайли
вужудга келади; бу фикр, айникса чала юкланган трансформатор занжирларининг
токларига таалуқлидир.
ва ҳ.к
частотали) юқори гармоникаларнинг мавжуд бўлишига жоизлик -рухсат этувчи қатъий
қоидалар мавжуд. Бу тизимларда юқори гармоникалар, асосан,
электротехник ускуналар реал элементларининг ночизиқли тавсифлари туфайли
вужудга келади; бу фикр, айникса чала юкланган трансформатор занжирларининг
токларига таалуқлидир.
Бироқ, барча электротехник қурилмаларда бўлганидек, телекоммуникация тизимларида ҳам ўзгарувчан токни ўзгармас токка айлантирувчи ярим ўтказгичли (транзисторли, вентилли) қурилмалар кенг қўлланилади. Бундай ўзгарткичнинг чиқиш қисмидаги кучланиш таркиби, ўзининг доминанти (асосий қисми) бўлмиш ўзгармас ташкил этувчиси билан бирга юқори гармоникларни ҳам ўз ичига олади.
Ярим ўтказгичли, электрон асбобларнинг электромагнит жараёнларни автоматик бошқаришдаги муҳим хусусиятлари-мослашувчанлиги, ишлаб чиқариш ва эксплуатациядаги соддалиги, инерциясизлиги уларнинг ахборотни узатиш ва қатта ишлаш тизимларида, автоматика, энергетикада кенг қўлланишига сабаб бўлди. Масалан, кучланиш ярим даврининг ихтиёрий онида токнинг «йўлини очиш» мумкин (12.2,а-расм), натижада даврий токнинг шаклини ўзгартириш билан, тармоқдан олинаётган қувватнинг қийматини бошқариш мумкин.
Автоматикада,
радиотехникада ва алоқа соҳаларида мураккаб мантиқий (логик)
функцияларни бажарувчи ҳисоблаш машиналари элементларида,
аксарият юқори частотали сигналларни қисқа Т1
вақт ичида узатиш зарур бўлади; бундай сигналлар узатишни Т даврда
такрорлаш зарур бўлади (![]() нисбат сигналнинг
кенглигини тавсифловчи қиймат). Бунинг
учун махсус генератор даврий равишда такрорланувчи тўғри бурчакли
импульсларни (12.2,в-расм)
узатади. Ушбу импульсларни юқори частотали генераторга берилса, импульс
давомийлигида ишлашга, импульс бўлмаганда эса паузада бўлишга мажбур этиб, унинг ишини
бошқаради.
нисбат сигналнинг
кенглигини тавсифловчи қиймат). Бунинг
учун махсус генератор даврий равишда такрорланувчи тўғри бурчакли
импульсларни (12.2,в-расм)
узатади. Ушбу импульсларни юқори частотали генераторга берилса, импульс
давомийлигида ишлашга, импульс бўлмаганда эса паузада бўлишга мажбур этиб, унинг ишини
бошқаради.
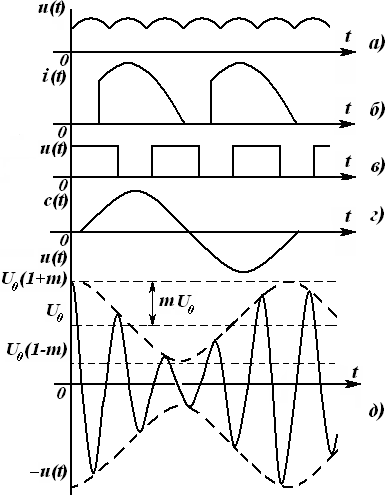
12.2-расм
Мураккаб гармоник
функциянинг жуда муҳим турларидан бири - амплитудаси гармоник қонуниятда
модуляцияланадиган гармоник тебранишлардир, масалан ![]() бунда m-модуляция
кенглиги (кўпинча, m<1);
бунда m-модуляция
кенглиги (кўпинча, m<1); ![]() - асосий ёки
узатувчи частота,
- асосий ёки
узатувчи частота, ![]() - модуляция
частотаси. Модуляцияланаётган тебранишлар амплитудаси ўзгаришининг қонуни
модуляцияланаётган сигнал турига боғлиқ. Оддий гармоник
модуляцияланаётган (12.2,г-расм) сигнал
- модуляция
частотаси. Модуляцияланаётган тебранишлар амплитудаси ўзгаришининг қонуни
модуляцияланаётган сигнал турига боғлиқ. Оддий гармоник
модуляцияланаётган (12.2,г-расм) сигнал
![]() (12.3)
(12.3)
боғланишдаги ва 12.2,д-расмда тасвирланган модуляцияланган тебраниш ҳосил бўлади.
Юқори частотали модуляцияланган сигналларнинг аҳамияти бебаҳодир, чунки улар тўғрилангандан (детекторлангандан) сўнг айнан модуляцияланган сигнал ҳосил қилинади (12.2,г-расм). Радио ва телевидение алоқаларининг ҳаммаси модуляцияланган юқори частотали сигналларни узатишга асосланган.
Шуниси эътиборга лойиқки, амплитудалари гармоник
модуляцияланган оддий тебранишлар (12.3)
бўлганда, барча гармоник ташкил этувчиларни аниқлаш жуда осондир. Дарҳақиқат, ![]() тенгликдан фойдаланиб (12.3)ни қуйидаги ҳолга келтирамиз:
тенгликдан фойдаланиб (12.3)ни қуйидаги ҳолга келтирамиз:
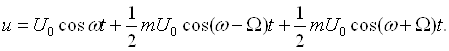 (12.4)
(12.4)
Шундай қилиб,
гармоник модуляцияланган амплитудали гармоник тебранишлар таркибида учта
гармоник ташкил этувчилари мавжуд экан, яъни ![]() асосий (ёки
узатувчи) частотали ва икки чегаравий (
асосий (ёки
узатувчи) частотали ва икки чегаравий (![]() ) ва
) ва ![]() частотали.
частотали.
Ушбу бобда қўйилаётган мақсад мураккаб гармоник (ёки носинусоидал) токлари бўлган чизиқли занжирларни ҳисоблаш ва таҳлил қилиш усулларини баён қилишдир; бунда, албатта даврий токларнинг барқарорлик жараёни кўзда тутилади. Ушбу токларнинг пайдо бўлиши ва уларнинг шаклларини ўзгартириш усуллари дарсликнинг «Ночизикли занжирлар» бўлимида кўрилади.
12.1. Носинусоидал токли чизиқли занжирларни ҳисоблаш
Ҳисоблашнинг асосий усуллари. Фақат чизиқли занжирларнигина ҳисоблаш учун мўлжалланган суперпозиция (устлаш) усулидан фойдаланиб ҳар бир гармоника учун алоҳида ҳисобларни олиб бориб, сўнгра натижаларни қўшиш мумкин.
Мураккаб гармоник таъсирга занжир реакциясининг спектрал ташкил этувчиларини аниқлаш зарур бўлган ҳолатларда ҳисоблашнинг бундай усули кенг тарқалган. Даврий таъсир юқори гармоникаларнинг катта спектрига эга бўлса (тубдан носинусоидал таъсир) ва ҳисоблаш ҳамда таҳлилда, нафақат таъсирнинг спектрал таркибини аниқлаш зарур бўлса, балки унинг вақтга нисбатан функционал боғланишини ҳам аниқлаш зарур бўлган ҳолатларда, тубдан носинусоидал таъсир тенгламаларини ечишга мўлжалланган ҳисоблаш усуллари қўлланилади. Бу бобда суперпозиция усулини қўллашга асосланган ечимлар кўрилади.
Айтайлик, кучланишнинг оний қиймати
![]() (12.5)
(12.5)
ёки комплекс шаклдаги унинг спектрал таркиби маълум бўлсин:
![]() (12.6)
(12.6)
яъни ҳар
бир частотаси ![]() бўлган n-гармониканинг
комплекс кучланишлари маълум бўлсин.
бўлган n-гармониканинг
комплекс кучланишлари маълум бўлсин.
Фараз қилайлик,
кўрилаётган кучланиш, комплекс қаршиликлари исталган частота ![]() учун
аввалдан маълум бўлган
учун
аввалдан маълум бўлган
![]() (12.7)
(12.7)
шохобчага узатилаётган бўлсин.
Ундай ҳолат учун токнинг барча гармоник ташкил этувчиларини аниқлаш мумкин:
![]() (12.8)
(12.8)
Барча гармоникаларнинг оний қийматларини қўшиш натижасида ахтарилаётган токнинг оний қийматини аниқлаш мумкин:
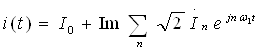 (12.9)
(12.9)
ёки
![]() (12.10)
(12.10)
бунда I0 - қиймати ![]() га мос келадиган ўзгармас ташкил этувчи.
га мос келадиган ўзгармас ташкил этувчи.
Агар қаршилик частотага боғлиқ бўлса, токнинг спектрал таркиби ва уни характерловчи эгри чизиқ i(t) кучланишнинг спектрал таркиби ва уни характерловчи u(t) эгри чизиғидан тубдан фарқланиши мумкин.
Носинусоидал токли занжирда индуктивлик ва сиғим. Индуктив реактив қаршилиги частотага (гармоника рақамига) пропорционал равишда ортади:
![]() (12.11)
(12.11)
Шунинг учун,
токдаги юқори гармоникалар нисбий таркиби уланган кучланишникидан камроқдир.
Сиғимнинг реактив қаршилиги
эса, аксинча, частотага (гармоника рақамига) тескари пропорционал:
![]() (12.12)
(12.12)
Конденсатордаги ўтказувчанлик гармоника рақамига про-порционал ортади. Агар конденсатордаги кучланиш юқори гармоникаларга эга бўлса, уларнинг ток таркибидаги таъсири каттароқ бўлади.
Агар L, C,
M мураккаб боғланишда бўлса, носинусоидал токни
аниқлаш учун, на фақат қаршиликнинг ҳақиқий ва мавҳум қисмларини ёки унинг модулини, айтайлик,
асосий частота учун билиш зарур, балки албатта 12.2) да кўрсатилганидек, бу қаршиликнинг частотага боғлиқлигининг тўлиқ ифодасини, яъни ![]() ни билиш зарур.
ни билиш зарур.
12.2 Мураккаб гармоник функциялари тавсифлари
Таъсир этувчи (эффектив) қийматни юқорида бир даврдаги ўртача квадратик қиймат деб қабул қилган эдик, ҳамда бундай таърифнинг мазмуни ҳақида тўхталган эдик. Бу таъриф ихтиёрий даврий функция учун, шу жумладан, бир неча гармоник функциялар билан ифодаланган ҳолат учун ҳам тааллуқлидир.
Берилган ![]() функциясининг
таъсир этувчи қиймати оний қийматлар квадратини (аналитик ёки
график усулда) интеграллаш натижасида аниқланиши мумкин:
функциясининг
таъсир этувчи қиймати оний қийматлар квадратини (аналитик ёки
график усулда) интеграллаш натижасида аниқланиши мумкин:
![]() (12.13)
(12.13)
Агар даврий функциянинг спектрал таркиби маълум бўлса, таъсир этувчи қиймат ҳар бир гармоника амплитудаси орқали бевосита аниқланиши мумкин.
Фараз қилайлик, даврий функциянинг (ток, кучланиш ва ҳ.к) қуйидаги таркиби маълум бўлсин:
![]()
![]() , (12.14)
, (12.14)
у ҳолда унинг ўртага квадратик қиймати
![]() (12.15)
(12.15)
бўлади; бунда ![]() -мазкур гармоникаларнинг таъсир этувчи қийматлари.
-мазкур гармоникаларнинг таъсир этувчи қийматлари.
Ушбу (12.15) тенгликни исботлаш осон. Функция (12.14) нинг квадрати таркибида ҳар бир ташкил этувчининг квадратлари йиғиндиси, ҳамда ҳар хил частотали синус функциялари кўпайтмаларининг йиғиндисини ўз ичига олади:
![]() (12.16)
(12.16)
бунда ![]() .
.
Булар қаторида ўзгармас ташкил этувчи (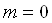 )нинг ихтиёрий гармоникага
кўпайтмаси ҳам мавжуд.
)нинг ихтиёрий гармоникага
кўпайтмаси ҳам мавжуд.
Бироқ, (12.16) турдаги кўпайтманинг интеграли нолга айланиши аниқ. Шунинг учун, нолдан фарқ килувчи ҳадларда фақат синусоидалар квадратлари йиғиндилари мавжуд бўлади; ҳар бир интеграл эса мазкур гармоник ташкил этувчининг таъсир этувчи эффектив қийматига тенг.
Ўртача қийматнинг ҳар хил турлари. Аксарият, даврий функцияларнинг уч хил ўртача қийматлари, уларнинг муҳим тавсифларини намоён қилади; бир даврдаги ўртача арифметик қиймат ёки ўзгармас ташкил этувчиси;
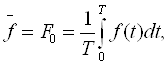 (12.17)
(12.17)
модуль буйича ўртача қиймат:
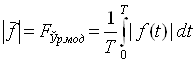 (12.18)
(12.18)
ва ниҳоят, ярим даврдаги ўртача максимал қиймат:
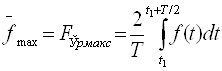 (12.19)
(12.19)
Ярим даврдаги
ўртача қиймат танлаб олинган интервалга (вақт оралиғига),
яъни танланган ![]() қийматга
боғлиқ. Таърифга кўра
қийматга
боғлиқ. Таърифга кўра ![]() ни шундай танлаш зарурки, унда интеграл максимал
бўлсин.
ни шундай танлаш зарурки, унда интеграл максимал
бўлсин.
Қуйидаги симметрия шартларидан бирини қониқтирган даврий функцияларда (12.19) таъриф қўлланилади;
![]() ёки
ёки
![]()
Ушбу шартлар бажарилганда носинусоидал функция ўзгармас ташкил этувчиси бўлмайди.
12.3. Қувват
Бир даврдаги ўртача қувват қийматининг
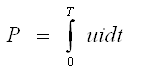 (12.20)
(12.20)
таърифи ихтиёрий даврий функциялар u(t) ва i(t) учун тааллуқлидир. Агар кучланиш ва ток гармоник қаторлардан иборат бўлса, у ҳолда интеграл белгиси остида бир ҳил гармоник частоталар кўпайтмаларининг йиғиндиси
![]()
ва ҳар хил
частотали гармоникалар кўпайтманлари (![]() ) йиғиндиси
бўлади
) йиғиндиси
бўлади
![]() .
.
Маълумки, биринчи кўпайтмаларнинг хар бири интеграл остидан чиққандан сўнг мазкур гармоникаларнинг ўртага қувватига тенг бўлади
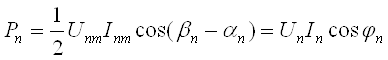 .
(12.21)
.
(12.21)
Иккинчи кўпайтмалар ҳар бирининг тўлиқ Т давр оралиғидаги интеграли нолга айланиши аниқ. Шундай қилиб биз жуда муҳим натижага эришдик: гармоник қатордан ташкил этилган даврий функциянинг ўртaча қуввати ҳар бир гармоника ўртага қувватларининг йиғиндисига тенг
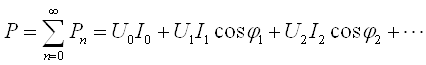 .
(12.22)
.
(12.22)
Бунда ўзгармас
ташкил этувчилар ![]() частотаси
нолга тенг бўлган гармоник ташкил этувчилар деб қаралади ҳамда ушбу
гармоник ёйилишлар ортогонал деб ҳисобланади.
частотаси
нолга тенг бўлган гармоник ташкил этувчилар деб қаралади ҳамда ушбу
гармоник ёйилишлар ортогонал деб ҳисобланади.
Оддий ўзгарувчан
ток занжири (яъни биргина гармоник ташкил этувчиси бўлгани) учун келтириб чиқарилган
тушунчаларга ўхшаш равишда, мураккаб гармоник функцияларда ҳам ўртача қувват
![]() ни актив қувват
деб аталади ва реактив қувват тушунчасини
ни актив қувват
деб аталади ва реактив қувват тушунчасини
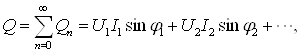 (12.23)
(12.23)
ҳамда тўла қувват тушунчалари киритилади
![]() (12.24)
(12.24)
бунда
U = ![]() ва
ва
![]()
Кейинги (8.33) боғланиш кучланиш ва токларнинг кўпайтмалари сифатида аниқланади. Ифодалар (8.31) ва (8.33)ни таққослаш натижасида қуйидагини аниқлаш табийдир
![]() (12.25)
(12.25)
Тўла қувватнинг
квадрати актив ва реактив кувватлар квадратларининг йиғиндисига тенг
бўлиши фақатгина i(t) токнинг эгри чизиғи u(t)
кучланишнинг эгри чизиғига мос бўлгандагина эришилади. Амалда бу шарт
занжирда фақат актив қаршилик бўлиб, барча гармоникалар учун бир
хил ![]() бўлганда
бажарилади.
бўлганда
бажарилади.
Шунга эътиборни қаратиш зарурки, энергиянинг соқланиш қонуни актив ва реактив қувватлар учун тааллуқлидир (реактив қувват учун сақланиш қонуни фақат чизиқли занжирлар учун таалуқли); барча манбаларнинг мазкур қувватлари йиғиндиси истеъмолчиларнинг мазкур қувватлари йиғиндисига тенг. Ушбу қонун S тўла қувват учун ҳам таалуқлидир.
S ва P
ифодаларини таққослаш натижасида, гармоник токли занжирларга қиёс
қилиб, қувват коэффициенти (![]() ) тушунчасини
келтириш мумкин;
) тушунчасини
келтириш мумкин;
![]() (12.26)
(12.26)
Кейиги ифодага
мураккаб гармоник функцияларни синусоидал функцияларга эквивалент ифодалаш мос
келади; бунда синусоидал функциялар таъсир этувчи қийматлари носинусоидал
![]() кучланиш ва
кучланиш ва
![]() токлар
таъсир этувчи қийматларига тенг ва фазалари силжиши j га тенг деб (12.26) дан
олинади.
токлар
таъсир этувчи қийматларига тенг ва фазалари силжиши j га тенг деб (12.26) дан
олинади.
Агар шундай эквивалент синусоидалар учун эквивалент реактив қувватни аниқласак
![]() ,
(12.27)
,
(12.27)
у холда биз яна бир қувват тушунчасига келамиз ва уни эквивалент реактив қувват деб номлаш мумкин.
Кейинги уч тенгликларни таққослаш натижасида қуйидагини аниқлаймиз;
![]() (12.28)
(12.28)
Мураккаб гармоник токлари мавжуд бўлган занжирларда реактив қувватни тўла компенсациялаш имкони йўқдир.
Энергетика тизимларида юқори гармоник ташкил этувчилар ҳар хил турдаги зарарли оқибатларга олиб келиши мумкин. Улар амплитуда коэффициентини оширадилар, бу эса юқори кучланишли қурилмаларда аҳамиятлидир; кўпинча юқори гармоника частоталарида резонанс пайдо бўлиши хавфи мавжуд: юқори гармоникалар телекомуникация тизимлари ва сигналлар линияларига ҳалақит берувчи таъсир кўрсатиши мумкин.
13-Маъруза. Кетма-кет тебраниш контури. Кучланишлар
резонанси
Резонанс ходисаси бир неча хил таърифланиши мумкин.
Улардан бири бўйича С ва L
элементларга эга бўлган берилган пассив икки қутбликнинг кириш қисмида
кучланиш фазаси ![]() ва ток фазаси
ва ток фазаси ![]() мос келса, яъни
мос келса, яъни ![]() бўлса, резонанс ҳодисаси мавжуд бўлади; бунда мазкур икки
қутблик ташқаридан реактив қувват олмайди (
бўлса, резонанс ҳодисаси мавжуд бўлади; бунда мазкур икки
қутблик ташқаридан реактив қувват олмайди (![]() ). Бундай резананс энергетик ёки фазали резонанс
дейилди. Резонанснинг бундай таърифи электротехникада кенг қўлланилади.
). Бундай резананс энергетик ёки фазали резонанс
дейилди. Резонанснинг бундай таърифи электротехникада кенг қўлланилади.
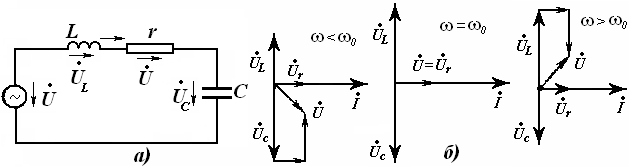 Иккинчи
таъриф ахборот технологиялари соҳаларига
кўпроқ мос келади. Унга кўра, резонанс ходисаси С ва L пассив элементлари бўлган занжирга ташқаридан
берилаётган кучланиш ёки токнинг бурчак частотаси
Иккинчи
таъриф ахборот технологиялари соҳаларига
кўпроқ мос келади. Унга кўра, резонанс ходисаси С ва L пассив элементлари бўлган занжирга ташқаридан
берилаётган кучланиш ёки токнинг бурчак частотаси ![]() занжирнинг хусусий (резонанс) частотаси
занжирнинг хусусий (резонанс) частотаси ![]() га
тенг бўлганда кузатилади. Бундай резонанс радиотехник (тўлқин) резонанс
деб аталади. Ушбу икки хил таърифланаётган ҳодиса аслида ягона холатдир, яъни
га
тенг бўлганда кузатилади. Бундай резонанс радиотехник (тўлқин) резонанс
деб аталади. Ушбу икки хил таърифланаётган ҳодиса аслида ягона холатдир, яъни
13.1-расм
![]() бўлганда
бўлганда ![]() ни кўриш
мумкин.
ни кўриш
мумкин.
Кучланиш резонанси. Занжирда L, r, C элементлар кетма-кет (13.1,а-расм) улангандаги резонанс шундай номланади.
Ушбу кетма-кет уланган занжирдаги ток қуйидагича аниқланади:
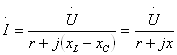 ,
(13.1,а)
,
(13.1,а)
ёки
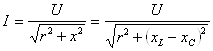 ,
(13.1,б)
,
(13.1,б)
бунда
![]() .
.
Резонанс бўлганда манба кучланишининг бурчак частотаси
хусусий бурчак частотасига тенг бўлади:![]()
![]() ,
(13.2)
,
(13.2)
пассив элементларнинг токи ўзининг максимал қийматига эришади
Imax=U/r (13.3)
ва
х = 0 бўлганлиги учун киришдаги кучланиш ![]() ва ток
ва ток ![]() фазалари мос бўлади. Бу холат 6.1,б-расмдаги вектор диаграммаларда тасвирланган.
Тенглик (13.3) дан шуни англаш мумкинки,
резанансга эришиш учун ёки манба кучланишининг частотаси
фазалари мос бўлади. Бу холат 6.1,б-расмдаги вектор диаграммаларда тасвирланган.
Тенглик (13.3) дан шуни англаш мумкинки,
резанансга эришиш учун ёки манба кучланишининг частотаси ![]() ни, ёки контурнинг L ва С (яъни xL ва xC) реактив параметрлари (ёки хусусий частотаси
ни, ёки контурнинг L ва С (яъни xL ва xC) реактив параметрлари (ёки хусусий частотаси ![]() o) қийматларини ўзгартириб эришиш мумкин
экан.
o) қийматларини ўзгартириб эришиш мумкин
экан.
Ток I, кучланиш
(UL ёки UC)ларнинг
![]() га боғлиқлиги
L ёки С ларнинг резонанс функциялари (эгри
чиқиқлари) дейилади. Ушбу функцияларнинг нисбий частота орқали
ифодалари кўпроқ қўлланилади:
га боғлиқлиги
L ёки С ларнинг резонанс функциялари (эгри
чиқиқлари) дейилади. Ушбу функцияларнинг нисбий частота орқали
ифодалари кўпроқ қўлланилади:
![]() .
(13.4)
.
(13.4)
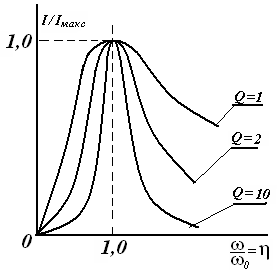
 Резонанс
контурнинг муҳим параметрларидан бир – асллик (Q)дир. Асллик деб элементлардан бири реактив қаршилиги
(яъни
Резонанс
контурнинг муҳим параметрларидан бир – асллик (Q)дир. Асллик деб элементлардан бири реактив қаршилиги
(яъни ![]() ёки 1
ёки 1![]() )нинг унга кетма-кет уланган актив қаршиликка
нисбатига айтилади:
)нинг унга кетма-кет уланган актив қаршиликка
нисбатига айтилади:
![]() . (13.5)
. (13.5)
Ушбу тенгликнинг суратида контурнинг
характеристик қаршилиги ![]() келтирилган. Унинг қиймати
келтирилган. Унинг қиймати
![]() .
(13.6)
.
(13.6)
Берилган контур резонанс функ-цияларининг нисбий бирликдаги кўрини- 13.2-расм
шлари унинг асллигига боғлиқдир (13.2
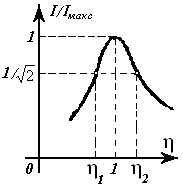 расм).
Бироқ бу боғланишлар масаланинг моҳиятини (
расм).
Бироқ бу боғланишлар масаланинг моҳиятини (![]() бўлганда токнинг максимум Iмах
га эришишини) кўрсатгани билан, Iмах
нинг абсолют қиймати қандай ўзгаришини аниқламайди. Шунинг
учун, I(
бўлганда токнинг максимум Iмах
га эришишини) кўрсатгани билан, Iмах
нинг абсолют қиймати қандай ўзгаришини аниқламайди. Шунинг
учун, I(![]() ) боғланишда токни абсолют қийматда
оладиган бўлсак, Q нинг катта қийматларида
ва
) боғланишда токни абсолют қийматда
оладиган бўлсак, Q нинг катта қийматларида
ва ![]() ≠
≠![]() 0 да I нинг қиймати бирнеча амперни ташкил этса ҳам,
0 да I нинг қиймати бирнеча амперни ташкил этса ҳам, ![]() =
=![]() 0 бўлгандаги Iмах нинг қиймати ўнлаб, баъзан эса юзлаб ампергача
етиши мумкин.
0 бўлгандаги Iмах нинг қиймати ўнлаб, баъзан эса юзлаб ампергача
етиши мумкин.
Тенглик (13.1,б)
га ўзгарувчан ![]() ва параметр Q ни киритсак, токнинг умумлаштирилган
резонанс функциясини аниқлаймиз:
ва параметр Q ни киритсак, токнинг умумлаштирилган
резонанс функциясини аниқлаймиз:
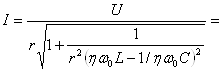
13.3-расм
 (13.7)
(13.7)
Ҳосил бўлган тенглик, ҳамда 13.2,а ва 13.2,б-расмларда келтирилган боғланишлардан шуни англаш мукинки, контурнинг асллиги қанчалар катта бўлса, токнинг резонанас эгри чизиғи шунчалар тик бўлади ва Iмах шунчалар катта бўлади.
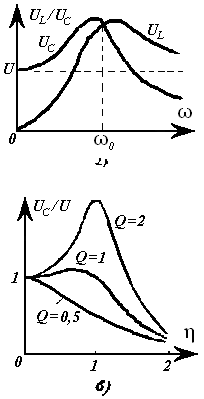
![]() Контурнинг яна
бир муҳим қийматларидан бири, резонанс функцияси кенглиги ёки контурнинг
узатиш кенглиги деб номланган
Контурнинг яна
бир муҳим қийматларидан бири, резонанс функцияси кенглиги ёки контурнинг
узатиш кенглиги деб номланган ![]()
катталикдир. У токнинг қиймати Iмах/![]() бўлгандаги
бўлгандаги ![]() ва
ва ![]() частоталар фарқига тенг (12.3-расм). Бунда контурнинг комплекс қаршилиги
резонансдаги Zmin = r минимал қаршиликка нисбатан
частоталар фарқига тенг (12.3-расм). Бунда контурнинг комплекс қаршилиги
резонансдаги Zmin = r минимал қаршиликка нисбатан ![]() марта катта бўлади.
марта катта бўлади.
Тенглик (6. 7) дан Iмах
/ I =![]() деб ҳисоблаб
деб ҳисоблаб
![]() ва
ва ![]() ларнинг қийматларини
аниқлаймиз
ларнинг қийматларини
аниқлаймиз
![]() ёки
ёки
![]() (13.8)
(13.8)
бундаги мусбат
ишора ![]() нинг қийматига,
манфий ишора эса
нинг қийматига,
манфий ишора эса ![]() қийматига
мос келади.
қийматига
мос келади.
Шундай қилиб, 13.4-расм
![]() ва
ва
![]()
![]() (13.9)
(13.9)
Бу қийматларнинг йиғиндисини ҳисоблаб, қуйидагини аниқлаймиз:
![]()
ундан
![]() ёки
ёки ![]()
![]() (13.10)
(13.10)
эканлиги маълум бўлади. Демак резонанс частотаси ![]() узатиш кенглиги чегаравий частоталарининг ўртача
геометрик қийматига тенг.
узатиш кенглиги чегаравий частоталарининг ўртача
геометрик қийматига тенг.
Резонанс частотаси ![]() ни тажриба усули билан ҳам аниқлаш мумкин. Бунинг учун
ни тажриба усули билан ҳам аниқлаш мумкин. Бунинг учун ![]() нинг қийматини ўзгартириб, токнинг
максимал қийматига мос келган
нинг қийматини ўзгартириб, токнинг
максимал қийматига мос келган ![]() ни аниқлаш кифоядир. Бироқ
тажрибалар шуни кўрсатадики, аввал
ни аниқлаш кифоядир. Бироқ
тажрибалар шуни кўрсатадики, аввал ![]() ва
ва ![]() (
(![]() ва
ва ![]() ) чегаравий частоталарни ўлчаб (бу қийматлар орқали
токнинг кескин ўзгаришини кузатиш мумкин), сўнгра (13.10) даги ўртача геометрик қиймат орқали ҳисоблаш аниқроқ натижа беради.
) чегаравий частоталарни ўлчаб (бу қийматлар орқали
токнинг кескин ўзгаришини кузатиш мумкин), сўнгра (13.10) даги ўртача геометрик қиймат орқали ҳисоблаш аниқроқ натижа беради.
Юқоридаги (13.9) тенгликларнинг иккинчисини биринчисидан айирсак, қуйидагиларни аниқлаш мумкин:
![]()
ёки
![]() .
(13.11)
.
(13.11)
Бундан шундай хулосага келамиз: резонанс функциясининг кенглиги контур асллигига тескари қийматга тенг экан; демак, резонанс функцияси шакли орқали унинг асллигини аниқлаш мумкин экан.
Индуктивлик ва сиғимдаги кучланишнинг частотага боғлиқлиги қуйидагича ифодаланади:
 (13.12)
(13.12)
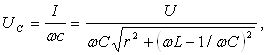 (13.13)
(13.13)
ёки нисбий частота ![]() ни киритиб ҳамда (7.5)ни
эътиборга олиб, қуйидагиларни аниқлаймиз:
ни киритиб ҳамда (7.5)ни
эътиборга олиб, қуйидагиларни аниқлаймиз:
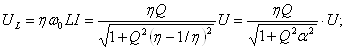 (13.14)
(13.14)
![]() (13.15)
(13.15)
бунда ![]() контурда
резонансдан узоқлашиш даражасини кўрсатувчи параметр. Уни бошқача
ифодалаш ҳам мумкин:
контурда
резонансдан узоқлашиш даражасини кўрсатувчи параметр. Уни бошқача
ифодалаш ҳам мумкин:
![]()
Резонас функциялари ![]() ва
ва ![]() 13.2,а-расмда
келтирилган. Биринчиси (агар Q>1/
13.2,а-расмда
келтирилган. Биринчиси (агар Q>1/![]() бўлса)
бўлса) ![]() га
нисбатан юқорироқ частотада максимумга эришади, чунки
га
нисбатан юқорироқ частотада максимумга эришади, чунки ![]() (13.12.) ифоданинг
суратида жойлашган, иккинчиси -
(13.12.) ифоданинг
суратида жойлашган, иккинчиси - ![]() дан қуйироқ
частотада максимумга эришади, чунки
дан қуйироқ
частотада максимумга эришади, чунки ![]() (13.13)
ифоданинг махражида жойлашган. Ушбу частоталарнинг қийматларини мазкур
функциялар максимумлари орқали аниқлаш мумкин:
(13.13)
ифоданинг махражида жойлашган. Ушбу частоталарнинг қийматларини мазкур
функциялар максимумлари орқали аниқлаш мумкин:
![]() (13.16)
(13.16)
бунда ![]() ва
ва ![]() (12.14) ва
(12.15) қийматлар максимумига мос келувчи нисбий частоталар.
(12.14) ва
(12.15) қийматлар максимумига мос келувчи нисбий частоталар.
Бу кучланишларнинг максимал қийматлари бир хил ва қуйидагича аниқланади:
 (13.17)
(13.17)
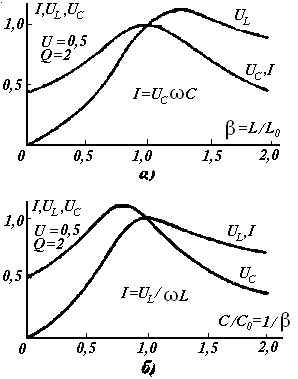 Ушбу (13.16) ва (13.17) тенгликлардан қуйидагилар
маълум бўлади. Асилликнинг қиймати Q>5 бўлганда резонанс
частоталар (
Ушбу (13.16) ва (13.17) тенгликлардан қуйидагилар
маълум бўлади. Асилликнинг қиймати Q>5 бўлганда резонанс
частоталар (![]() )да UL
ва UC функциялар максимумларини 1% аниқлик билан
)да UL
ва UC функциялар максимумларини 1% аниқлик билан ![]() га тенг деб
қабул
га тенг деб
қабул
қилиш мумкин.
13.2,б-расмда сиғим
кучланиши-нинг ![]() частота билан боғланиши умумлаштирилган
коор-динаталарда келтирилган. Асил-ликнинг қиймати
частота билан боғланиши умумлаштирилган
коор-динаталарда келтирилган. Асил-ликнинг қиймати ![]() бўлганда
частота ортиш билан аввалига
бўлганда
частота ортиш билан аввалига ![]() ортар экан;
кичик аслликларда эса частота ортиши билан
ортар экан;
кичик аслликларда эса частота ортиши билан ![]() доимо
камайиб борар экан.
доимо
камайиб борар экан.
Бунда келтирилган таҳлил ва, хусусан, (13.10), (13.11) шаклдаги тенгламалар таркибида L, r, C бўлган эквивалент контурларни ҳисоблаш учун қўлланилиши мумкин, бироқ улардаги энергия тебраниши ва сарфланиши бошқа физик жараёнлар сифатида
кўрилиши мумкин. 13.5–расм
Резонансда ўлчашлари. Юқорида кўрсатилганидан, кетма-кет уланган контурнинг сиғими ёки индуктивлиги қийматларини ўзгартириб резонанс жараёнига созлаш мумкин. Бундай созлаш натижасида ULmax ёки UCmax холатлари чапга ёки ўнгга сурилиши мумкин. Чунки L ва С қийматлар (13.12) ва (13.13) боғланишларнинг таркибида мавжуд.
13.3,а–расмда (13.7), (13.12) ва (13.13) тенгликлар ёрдамида қурилган - индуктивлик ўзгаргандаги (яъни L=var бўлганда)ги ҳамда 13.3,б-расмда конденсаторнинг сиғими ўзгарганда (яъни С=var бўлганда)ги I, Uc , UL нинг ўзгаришлари келтирилган; бунда қолган параметрлар ўзгармас.
Функциялар
максимумларининг сезиларли силжиши фақат аслликнинг кичик қийматларидагина
кўрилада, масалан 13.3,а ва б-расмлар Q=2 учун қурилган;
бундан ташқари, резонанс жараёнининг ўзи ҳам суст эканлиги кўзга
ташланади. Q нинг катта қийматларида, масалан Q>10
бўлганда UL ва ![]() ларнинг
силжишлари 1% га ҳам етмайди.
ларнинг
силжишлари 1% га ҳам етмайди.
Параллел ва кетма-кет алмаштириш схемаларининг ўзаро эквивалентлиги. Соддалаштирилган холатда реал индуктивликдаги энергиянинг сўниши ғалтак ўтказгичларидаги актив қаришилик rL нинг мавжудлиги билан тушунтирилади. Шу сабабли индуктив ғалтак ўрнига кетма-кет уланган икки элементлар L ва rL қабул қилинади. Конденсатордаги энергиянинг сўниши эса, пластинкалар орасидаги изоляция такомил эмаслиги натижасида ўтказувчанлик мавжудлиги билан тушунтирилади. Бунда, ушбу gc ўтказувчанлик сиғим С билан паралел уланган деб ҳисобланади. Қувват исрофи мавжуд бўлган ғалтак ва конденсаторлар кетма-кет уланганда (13.6,а-расм) схемасини эквивалент кетма-кет алмаштирилган схема сифатида (13.6,б-расм) келтириш қулайдир,
13.6–расм
унда rкет= gc / (g2c + щ2С2) (13.18)
ва Скет =(g2c + щ2С2)/ щ2С (13.19)
Кейинги ифодаларда С ва gc конденсаторнинг параллел уланган алмаштириш схемасига (13.6,а-расм) мос келади. Скет ва rкет - кетма-кет алмаштириш схемасига мос келади (13.6,б-расм). Эътибор берсак, gc қанчалар кичик бўлса, rкет шунчалар кичик бўлиши кўзга ташланади.
Индуктивлик ғалтаги параметрларини ҳам ихтиёрий кетма-кет уланган (L ва rL) ёки параллел уланган деб фараз қилиб олишимиз мумкин; кейинги холатда
Rпар=(щ2 L2 + r2L)/ rL (13.20)
ва Lпар=(щ2 L2 + r2L)/ щ2L. (13.21)
Шунга эътибор бериш зарурки, rL қаранчалар кичик бўлса, Rпар шунчалар катта бўлади. ғалтак параметрининг айнан шундай эквивалент алмаштириш схемаси уни сиғимлар билан параллел улаганда қўллашга қулай ҳисобланади (13.7,а ва б-расмлар).
13.7-расм
Индуктивлик ва
конденсаторлар аслликлари. Келтирилган 13.7,а ва
13.7,б-расмлардаги схемаларни таққослаб, асиллик
камайишининг сабаби ғалтак ![]() ва
конденсатордаги
ва
конденсатордаги ![]() энергия
исрофи натижаси эканлигини кўриш мумкин.
энергия
исрофи натижаси эканлигини кўриш мумкин.
Дарҳақиқат, аслликнинг ифодаси (13.21) ни таҳлил қилиб уни қуйидаги шаклга келтирсак
1/Q=r/щL = rL/щL + rкет /щL,
ҳар бир
элементнинг унга таъсирини осонликча баҳолаш мумкин. Аммо резонансда ![]() бўлгани
учун, кейинги тенгликни қуйидагича ёзиш мумкин:
бўлгани
учун, кейинги тенгликни қуйидагича ёзиш мумкин:
![]() ,
(13.22)
,
(13.22)
бунда
![]() ва
ва
![]() .
(13.23)
.
(13.23)
Аниқланган QL ва Qc (сон қийматлари) ғалтак ва конденсаторнинг асилликлари дейилади. Аёнки, асилликлар алмаштириш схемасининг бошқа параметрлари орқали ҳам ифодаланиши мумкин:
QL = Rпар /щLпар ; 1/QC = gc /щСкет ; (13.24)
уларни аниқлашда (13.23) тенгликка (13.18)–(13.21) ларни қўйиш орқали эришилди.
Частотага боғлиқ бўлган L, r, C параметрли занжирда резонанс. Бундай занжирларда резонанс параллел ва кетма-кет уланган контурларда бўлиши мумкин. Бироқ, контур асосий параметрларининг частотага боғлиқлиги, юқорида кўрилган параметрлари ўзгармас занжирлардаги резонансни ифодаловчи асосий боғланишларни тубдан ўзгариб юборади. Уларга ўхшаш, занжирнинг барча янги хусусиятлари частотавий тавсифлар бевосита киритилган тенгламаларни таҳлил қилиш натижасида осонгина келтириб чиқаради.
Аввало, шуни маълум қилиш керакки, ток ва
кучланишнинг частотага боғлиқлиги учун юқорида келтириб чиқарилган
баъзи ифодаларни ушбу ҳолат
учун мутлақо қўллаб бўлмайди;
масалан, резонанс частотаси ва асилликни резонанс тавсифининг кенглиги бўйича
аниқлашни қўллаб бўлмайди. Аксинча, частотани ўзгаришсиз қолдириб
ва сиғимнинг берилган қийматини ўзгартириш билан аввал келтириб чиқарилган
ифодалардан фойдаланиб, ўлчанган Uc/UСмах қийматлар
ёрдамида асилликни ҳам, контурнинг
индуктивлигини L(![]() ) ҳам аниқлаш мумкин. Частотанинг ҳар хил қийматлари учун шундай ўлчовларни амалга
ошириб Q ва L ёки r ва L қийматларнинг частотага боғлиқлигини аниқлаш
мумкин. Шунга ўхшаш ўлчовларни С(
) ҳам аниқлаш мумкин. Частотанинг ҳар хил қийматлари учун шундай ўлчовларни амалга
ошириб Q ва L ёки r ва L қийматларнинг частотага боғлиқлигини аниқлаш
мумкин. Шунга ўхшаш ўлчовларни С(![]() )ли
конденсатор учун ҳам бажариш мумкин.
)ли
конденсатор учун ҳам бажариш мумкин.
Якуний хулосалар. 1. Реал элементларнинг частотавий тавсифларини таҳлил қилишда, биз улар таркибида ўзгармас L, r,
C бўлган икки қутбликлар мавжуд деб тасаввур қилдик. Кўпгина ҳолатларда ушбу услуб частотанинг маълум диапазонида
реал икки қутбликнинг тавсифлари билан мос келади. Бироқ, барча ҳолатларда ҳам
бундай ўхшатишларни фақат Y(j![]() )
функциясини чекланган кўп ҳадлик
билан шартли алмаштириш деб қараш мумкин. Баъзан Y(j
)
функциясини чекланган кўп ҳадлик
билан шартли алмаштириш деб қараш мумкин. Баъзан Y(j![]() ) тавсифларни
трансцендент функциялар деб қабул қилинади. Бундай функцияни даражали қаторга ёйиб, бир неча биринчи ҳадлари билан қаноатланиб, чекланган сонли L, r,
C га эга бўлган электр занжирини аниқлаш мумкин; бунда, албатта, занжир частотавий тавсифлари чекланган диапазонда ушбу қатор
ҳадларига мос келади, деб қралади.
) тавсифларни
трансцендент функциялар деб қабул қилинади. Бундай функцияни даражали қаторга ёйиб, бир неча биринчи ҳадлари билан қаноатланиб, чекланган сонли L, r,
C га эга бўлган электр занжирини аниқлаш мумкин; бунда, албатта, занжир частотавий тавсифлари чекланган диапазонда ушбу қатор
ҳадларига мос келади, деб қралади.
2. Умумий ҳолатда, берилган частотавий тавсифларга эга бўлган икки қутблик (ёки тўрт қутублик)ни ҳосил қилиш учун L, r, C элементли схемани тузиш ва унинг параметрларини аниқлаш, электр занжирларини синтез қилишнинг асосий муаммоларини ташкил этади.
3. Кучланиш U нинг қиймати, на фақат ток I нинг қийматига боғлиқ бўлади, балки
ҳар хил ҳосилаларга,
баъзан эса, ўзининг функцияси интегралига, яъни ![]() га ҳам
боғлиқ бўлиши мумкин
дейилган эди. Хусусан j
га ҳам
боғлиқ бўлиши мумкин
дейилган эди. Хусусан j![]() ҳосилани, 1/
ҳосилани, 1/![]() эса интегрални ифодалашини эсга олсак, (13.25) дан қуйидагини аниқлаш мумкин бўлади:
эса интегрални ифодалашини эсга олсак, (13.25) дан қуйидагини аниқлаш мумкин бўлади:
![]() ёки
ёки
![]() .
.
Охирги тенгликка оний қийматлар учун ёзилган қуйидаги тенглама мос келади:
![]() (13.26)
(13.26)
14-Маъруза. Параллел тебраниш контури.Токлар
резонанси. Тебраниш контурининг частота
тавсифлари
Токлар резонанси. L, r, С ларни параллел улаш билан ҳосил қилинган резонанс ҳодисаси шундай номланган. Ушбу уч элиментлар уланишининг соддалаштирилган шакли 14.1,а-расмда келтирилган. Бу ҳолда:
![]()
![]() (14.1)
(14.1)
ёки
![]()
![]() (14.2)
(14.2)
бунда ![]() (6.27)
(6.27)
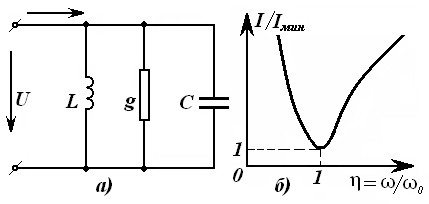
14.1-расм
Резонанс ҳолатида
![]() ва
ва ![]() бўлгани
учун токнинг фазаси кучланишнинг фазаси билан мос келади ва 14.1,а-расмдаги
соддалаштирилган занжирда токнинг қиймати I=gU минимал бўлади.
U=const бўлгандаги резонанс функцияси
бўлгани
учун токнинг фазаси кучланишнинг фазаси билан мос келади ва 14.1,а-расмдаги
соддалаштирилган занжирда токнинг қиймати I=gU минимал бўлади.
U=const бўлгандаги резонанс функцияси ![]() 14.1,б-расмда
келтирилган.
14.1,б-расмда
келтирилган.
Таҳлил қилинаётган параллел уланган L, r, С занжирнинг комплекс қаршилигини айнан шу элиментларни кетма-кет улаб уларнинг комплекс ўтказувчанлиги билан солиштирилса, улар орасида тўла ўхшашлик борлигини кўриш қийин эмас - дуаллик принципи (14.1-жадвалга қаранг).
Реактив ва актив қаршиликлари бўлган шахобчаларни параллел улаш. Бундай занжирлардаги резонансни таҳлил қилиш бирмунча мураккаброқдир. 14.1,а-расмдаги конденсаторга параллел уланган (L-rL) индуктивлик ва актив қаршилик 14.1,а-расмдаги занжирга нисбатан ўзининг чатотавий хусусиятлари билан хақиқатга яқинроқдир. Биринчи схемадаги (14.1,а-расм) занжирнинг резонанс шартлари қуйидагича ифодаланади:
Ушбу шарт 14.1-жадвалда 14.1,а-расм занжири учун келтирилган шартдан фарқлидир.
щ2р = 1/ LC – r2L/L2 . (14.3)
14.1.-жадвал
|
Кетма-кет улангандаги (14.1,а-расм)
|
Параллел улангандаги (14.1,а-расм) |
|
|
|
|
Икала ҳолатда хам
|
|
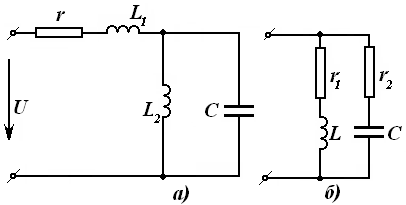
14.2.-расм
Умумий токнинг минимал қиймати резонанс частотаси щр га мос келмасдан, ундан бироз каттароқ частотага мос эканини кўриш мумкин:
![]() (14.4)
(14.4)
Мураккаб контурлардаги резонанс. Агар икки қутубликнинг реактив элиментлари сони иккитадан ортиқ бўлса (14.2-расм), унинг кириш қаршилиги частотанинг бир неча қийматларида соф актив (резонанс) бўлиши мумкин; шунга ўхшаш, ток ҳам частотанинг мазкур бир неча қийматларида ўзининг экстремал қийматларига эришиши мумкин. Баён қилинган ҳодиса реактив элементлардан бирининг ўзгаришида ҳам кўриниши мумкин.
Масалан,
14.2,а-расмдаги занжир учун биринчи токлар резонансини 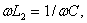 яъни кириш ўтказувчанлиги Y нолга тенг бўлганда кўриш
мумкин; бу параллел шохобчалар учун қабул қилинган
идеаллаштириш шартига мос келади, яъни шохобчаларда қувват исрофи
бўлмайди. Иккинчи резонанс:
яъни кириш ўтказувчанлиги Y нолга тенг бўлганда кўриш
мумкин; бу параллел шохобчалар учун қабул қилинган
идеаллаштириш шартига мос келади, яъни шохобчаларда қувват исрофи
бўлмайди. Иккинчи резонанс:
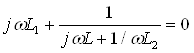 (14.5)
(14.5)
тенглик
бажарилганда ҳосил бўлади. Кейинги шарт частотанинг қиймати ![]() яъни Y=1/r
бўлганда кўрилади.
яъни Y=1/r
бўлганда кўрилади.
Кириш ўтказувчанлиги модулининг экстремаллик шартлари, ушбу ўтказувчанлик реактив ташкил этувчисининг нолга тенг бўлиши билан мос келмаслиги мумкин. Қаршилик актив ташкил этувчиларининг катта қийматларида шунга ўхшаш резонанс умуман йўқолиши ҳам мумкин.
Қизиқарли
жараённи 14.2,б-расмдаги занжирда кузатиш мумкин; агар параллел контурда r1
= r2= ![]() бўлса, у ҳолда
частотанинг ихтиёрий қийматларида ҳам кириш ўтказувчанлиги соф
актив бўлиб, қиймати
бўлса, у ҳолда
частотанинг ихтиёрий қийматларида ҳам кириш ўтказувчанлиги соф
актив бўлиб, қиймати ![]() га тенг бўлади,
яъни частотанинг ихтиёрий қийматларида резонанс сақланади.
га тенг бўлади,
яъни частотанинг ихтиёрий қийматларида резонанс сақланади.
14.1 Частотавий тавсифлар
![]() Икки қутбликлар. Чиқиқли
икки қутблик ҳақидаги тўлиқ ахборотни, ҳусусан,
келтирилган ихтиёрий кучланишга нисбатан унинг (акс) таъсирини частотавий
тавсифдан, яъни кириш қаршилиги ёки ўтказувчанлиги ҳақиқий
ва мавҳум қисмларининг частотага боғлиқлигидан қуриб
олиш мумкин:
Икки қутбликлар. Чиқиқли
икки қутблик ҳақидаги тўлиқ ахборотни, ҳусусан,
келтирилган ихтиёрий кучланишга нисбатан унинг (акс) таъсирини частотавий
тавсифдан, яъни кириш қаршилиги ёки ўтказувчанлиги ҳақиқий
ва мавҳум қисмларининг частотага боғлиқлигидан қуриб
олиш мумкин:
![]()
![]() (14.6)
(14.6)
Келтирилган кучланиш таркибида бир неча гармоник ташкил этувчилар бўлганда ҳам, частотавий тавсиф ёрдамида унинг кириш токини аниқлаш мумкин; частотавий тавсиф ёрдамида ўткинчи жараёндаги токни ҳам аниқлаш мумкин.
Шуни эътиборга олиш зарурки, чизиқли пассив икки қутблик бўлганда, комплекс ўтказувчанлик (қаршлик)нинг ҳақиқий ва мавҳум қисмлари частотавий тавсифлари ёки унинг модули ва аргументлари частотавий тавсифлари орасида маълум боғланиш мавжуддир.
Умумий холда, частотанинг комплекс функциясини қуйидагича белгилаш қабул қилинган:
![]()
бунда F1(![]() ) ва F2(
) ва F2(![]() ) ёки
соддалаштириб ёзганда F1 ва F2-
частотанинг ҳақиқий функциялари.
) ёки
соддалаштириб ёзганда F1 ва F2-
частотанинг ҳақиқий функциялари.
F1 билан F2 орасидаги маълум боғланишни умумий ҳолда қуйидаги интеграллар билан ифодалаш мумкин:
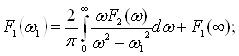
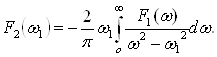 (14.7)
(14.7)
Ушбу тенгликларни
келтириб чиқариш адабиётда келтирилган бўлиб, физикада 1927 йилдан
Крамерс ва Крониг формулалари номи билан маълум; таҳминан 20 йилдан сўнг
чизиқли электр занжирлар назариясига киритилди. (14.7) ифодалар
частотанинг ![]() дан
дан ![]() гача бўлган оралиғида
ўзгаришида бир ташкил этувчи чексиз қийматга эга бўлмаса, иккинчи ташкил
этувчисининг частотавий боғланишини ушбу оралиқда аниқлаш
мумкин эканлигини кўрсатади.
гача бўлган оралиғида
ўзгаришида бир ташкил этувчи чексиз қийматга эга бўлмаса, иккинчи ташкил
этувчисининг частотавий боғланишини ушбу оралиқда аниқлаш
мумкин эканлигини кўрсатади.
Икки қутбликнинг частотавий тавсифларини эксперимент натижалари ёрдамида ҳам қуриш мумкин. Бу усул билан қурилган частотавий тавсифлар занжирларнинг алмаштириш схемаларидаги берилган параметрлар асосида ҳисобланган частотавий тавсифларга нисбатан икки қутубликнинг ҳусусиятларини тўлароқ ифодалайди, чунки кўп холларда, айниқса катта частоталарда L, r, C қийматларининг ўзи ҳам частотага боғлиқ. Ундан ташқари, занжир элементлари боғланиш схемасини чизиш жараёнида, биз уни, аксарият, соддалаштирамиз; мавжуд кичик индуктивлик, сиғим, қаршиликларни эътиборга олмаймиз.
Агар икки қутбликнинг частотавий тавсифлари маълум бўлса, ушбу икки қутблик иштирок этган занжирнинг барча ҳисоблашлари учун икки қутблик ичидаги ҳар хил элементлар уланишларини ва уларнинг параметрларини билиш шарт эмас.
Бундан ташқари, икки қутубликнинг ички қисмида
электр занжирлари назарияси ва унинг элементлари доирасига кирмайдиган
жараёнлар мавжуд бўлса, масалан
механик тебранишли ультра товуш генераторининг (МТГ) кириш қисмига
келаётган электромагнит энергияси ультра қисқа тўлқиндаги
механик энергияга айлантираётган бўлса, мазкур икки қутбликнинг
частотавий тавсифлари электр занжирлари атамаларида, аниқ ифодаланиши
мумкин ![]() .
.
Бундай механик тўлқинларнинг қуввати жуда катта бўлиши мумкин. МТГ нинг манбаси бунда
электр занжири
сифатида қаралиб, аниқ частотавий тавсифга ![]() эга бўлган
икки қутблик деб кўрилади; ушбу тавсиф резонанс характерига ҳам эга
бўлиши мумкин. Шунга ўхшаш, радио тўлқинларини тарқатувчи
аннтеннани ҳам, таъминловчи кабелга нисбатан икки қутблик деб қараш
мумкин.
эга бўлган
икки қутблик деб кўрилади; ушбу тавсиф резонанс характерига ҳам эга
бўлиши мумкин. Шунга ўхшаш, радио тўлқинларини тарқатувчи
аннтеннани ҳам, таъминловчи кабелга нисбатан икки қутблик деб қараш
мумкин.
Бир неча икки қутбликлар
параллел уланганда, уларнинг ўтказувчанлигининг йиғиндиси олинади. Шунинг
учун, бундай уланишлар натижасида ҳосил бўлган натижавий ўтказувчанлик,
хар бир икки қутбликларнинг ўтказувчанликлари йиғиндисига тенг ![]() Кетма-кет
уланганда эса улар қаршиликлари йиғиндиси олинади. Бундай вазиятда,
айрим икки қутбликлар учун тавсифлари ўтказувчанлик орқали
ифодаланган бўлса, уларни тескарисига айлантириб, қаршиликлар билан
ифодалаш зарур.
Кетма-кет
уланганда эса улар қаршиликлари йиғиндиси олинади. Бундай вазиятда,
айрим икки қутбликлар учун тавсифлари ўтказувчанлик орқали
ифодаланган бўлса, уларни тескарисига айлантириб, қаршиликлар билан
ифодалаш зарур.
Реактив икки қутбликларнинг частотавий тавсифлари. Ин-дуктивлик ғалтаги L ва конденсатори C бўлган электр занжирларини лойиҳалаш жараёнида (масалан LC-фильтрлар, фаза ўзгартирувчи контурлар) улар частотавий тавсифларининг алоҳида ҳусусиятларини ажратиб олиб ўрганиш учун, аксарият, қийматлари кичик бўлган актив қаршиликларни эътиборга олмаса ҳам бўлади, яъни икки қутбликни соф реактив деб қараш мумкин.
Бундай реактив икки қутбликларнинг частотавий тавсифлари уларни берилган тавсифлар асосида синтез қилиш имкониятини тақдим этувчи маълум қонуниятларга бўйсунади.
Оддий реактив икки қутблик деб комплекс қаршиликлари ![]() ва
ва ![]() бўлган индуктивлик L ва сиғим С га айтилади.
бўлган индуктивлик L ва сиғим С га айтилади.
Уларнинг частотавий тавсифлари 14.2,а-расмда келтирилган. L1 ва С1 лар кетма-кет улангандаги комплекс қаршиликлари қуйидаги ифодадан аниқланади:
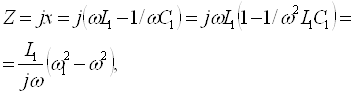 (14.8)
(14.8)
бунда ![]() кетма-кет
резонанснинг ёки кучланиш резонансининг икки қутбликнинг реактив қаршилиги
нолга тенг бўлгандаги «нол» частотаси (14.3,б-расм). L1
ва C1 лар
параллел улаганганда уларнинг комплекс қаршиликлари қуйидагича
бўлади:
кетма-кет
резонанснинг ёки кучланиш резонансининг икки қутбликнинг реактив қаршилиги
нолга тенг бўлгандаги «нол» частотаси (14.3,б-расм). L1
ва C1 лар
параллел улаганганда уларнинг комплекс қаршиликлари қуйидагича
бўлади:

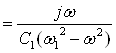 ,
(14.9)
,
(14.9)
бунда ![]() параллел
резонанс, ёки ток резонанси реактив икки қутбликнинг
қаршилиги чексизга тенг бўлгандаги-«қутб» частотаси (14.3,в-расм).
параллел
резонанс, ёки ток резонанси реактив икки қутбликнинг
қаршилиги чексизга тенг бўлгандаги-«қутб» частотаси (14.3,в-расм).
Хар қандай
реактив икки қутблик учун бўлганидаги каби,
барча қурилган тавсифлар учун ![]() шарти
бажарилади. Масалан, 14.3-расмда келтирилган икки қутбликнинг частотавий
тавсифини улар алоҳида шохобчалари тавсифларининг йиғиндиси деб қараймиз;
бунинг учун 14.3,г-расмдаги параллел контурнинг х1 ва
14.3,а-расмдаги хґ тавсифларини қўшамиз, чунки контур ва L
индуктивликлар кетма-кет уланган. Ҳосил
бўлган частотавий тавсиф dх/dщ>0
шартини қаноатлантиради, параллел резонанси частотаси
шарти
бажарилади. Масалан, 14.3-расмда келтирилган икки қутбликнинг частотавий
тавсифини улар алоҳида шохобчалари тавсифларининг йиғиндиси деб қараймиз;
бунинг учун 14.3,г-расмдаги параллел контурнинг х1 ва
14.3,а-расмдаги хґ тавсифларини қўшамиз, чунки контур ва L
индуктивликлар кетма-кет уланган. Ҳосил
бўлган частотавий тавсиф dх/dщ>0
шартини қаноатлантиради, параллел резонанси частотаси ![]() да «қутб»га эга ва кетма-кет резонанс частотаси
да «қутб»га эга ва кетма-кет резонанс частотаси ![]() да «ноль»га эга.
да «ноль»га эга.
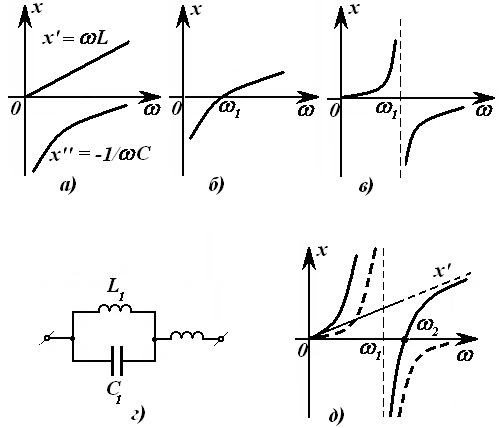
14.3-расм
Кетма-кет (14.8)
ва параллел (14.9) контурларидаги каби, икки қутбликнинг комплекс қаршилиги
Zни ![]() ва
ва ![]() резонанс
частоталари орқали
резонанс
частоталари орқали ![]() нинг каср
рационал функцияси сифатида кўрсатиш мумкин:
нинг каср
рационал функцияси сифатида кўрсатиш мумкин:
![]() (14.10.)
(14.10.)
Қаршилик Z
ифодаси ![]() частотасида
«қутб» бўлишини таъминлаш учун махражида (
частотасида
«қутб» бўлишини таъминлаш учун махражида (![]() ) икки ҳадлик
бўлиши лозим, частотаси
) икки ҳадлик
бўлиши лозим, частотаси ![]() бўлганда
«нол» бўлишини таъминлаш учун Z суратида
бўлганда
«нол» бўлишини таъминлаш учун Z суратида ![]() икки ҳадлик
мавжуд бўлиши зарур. Ундан ташқари,
жуда катта частоталарда С1 сиғимнинг қаршилиги L1 ва L индуктивликлар қаршиликларидан анчагина кичик.
Шунинг учун, 14.3,г-расмда
икки қутбликнинг қаршилиги индуктивлик L қиймати
билан аниқланади (чунки С1 сиғимнинг жуда кичик қаршилиги
L индуктивни «қисқа
туташтиради») ва
икки ҳадлик
мавжуд бўлиши зарур. Ундан ташқари,
жуда катта частоталарда С1 сиғимнинг қаршилиги L1 ва L индуктивликлар қаршиликларидан анчагина кичик.
Шунинг учун, 14.3,г-расмда
икки қутбликнинг қаршилиги индуктивлик L қиймати
билан аниқланади (чунки С1 сиғимнинг жуда кичик қаршилиги
L индуктивни «қисқа
туташтиради») ва ![]() қийматга интилади. Юқорида
келтирилган Z қаршилик
қийматга интилади. Юқорида
келтирилган Z қаршилик ![]() ва
ва ![]() бўлганда 1 га интилади, яъни ушбу боғланишда
бўлганда 1 га интилади, яъни ушбу боғланишда ![]() бўлмайди ва Z нинг қиймати
бўлмайди ва Z нинг қиймати
![]()
га яқинлашади.
Реактив қаршилик хақида теорема. Хар қандай
реактив икки қутблик учун ![]() тенгсизлиги бажарилади.
тенгсизлиги бажарилади.
Дарҳақиқат,
ҳар қандай икки қутблик m шохобчадан иборат бўлиб, ҳар
бир k-нчи шохобчалар кетма-кет уланган Lk индуктивлиги
ва Сk сиғимидан иборатдир (бир неча индуктивлик ва сиғим
кетма-кет уланган бўлса, уларни кетма-кет уланган эквивалент Lк ва
Ск билан алмаштириш мумкин). Ихтиёрий k-нчи шохобча учун ![]() шарти
бажарилади (14.3-расм).
шарти
бажарилади (14.3-расм).
Икки қутбликнинг умумий қаршилиги x барча k шохобчалар қаршиликларининг функциясидир, шунинг учун бир неча ўзгарувчилари бўлган функцияларни дифференциаллаш қоидасига мувофиқ
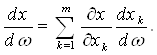 (14.11)
(14.11)
Демак, ҳар қандай
контур учун ҳосила ![]() тўғри
эканлигини исботлаш кифоядир.
тўғри
эканлигини исботлаш кифоядир.
Бунинг учун икки қутбликнинг
кириш қисмига ![]() э.ю.к.
манбасини улаймиз, k-нчи шохобчани (14.3,а-расм) ажратамиз, ҳамда
э.ю.к.
манбасини улаймиз, k-нчи шохобчани (14.3,а-расм) ажратамиз, ҳамда
![]() қаршиликни
компенциялаш принципига асосан э.ю.к.
қаршиликни
компенциялаш принципига асосан э.ю.к. ![]() билан
алмаштирамиз; бунда ифоданинг манфий ишораси
билан
алмаштирамиз; бунда ифоданинг манфий ишораси ![]() мусбат
йўналишига
мусбат
йўналишига ![]() нинг мусбат
йўналиши мослиги учун қўйилган. Суперпозиция усулидан фойдаланиб
нинг мусбат
йўналиши мослиги учун қўйилган. Суперпозиция усулидан фойдаланиб ![]() ва
ва ![]() токларни қуйидагича
ифодалаймиз:
токларни қуйидагича
ифодалаймиз:
![]()
![]() (14.12)
(14.12)
бунда ![]() ўтказувчанлик
ўтказувчанлик
![]() қаршиликка
боғлиқ эмас, яъни у ўзгаришида
қаршиликка
боғлиқ эмас, яъни у ўзгаришида ![]() ўзгаришсиз қолади.
ўзгаришсиз қолади.
![]() нинг ўрнига
унинг
нинг ўрнига
унинг ![]() қийматини
қўйсак, сўнгра иккала тенглама таркибидан ток
қийматини
қўйсак, сўнгра иккала тенглама таркибидан ток ![]() ни ажратиб
олсак,
ни ажратиб
олсак, ![]() боғланишни
аниқлаймиз:
боғланишни
аниқлаймиз:
 (14.13)
(14.13)
бундан
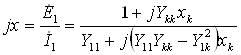 (14.14)
(14.14)
ва хосилани аниқлаймиз:
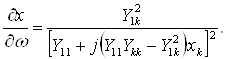
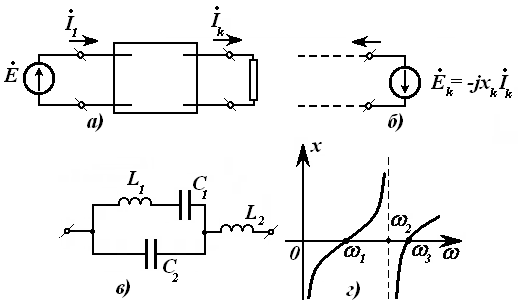
14.4-расм
15-Маъруза. Чизиқли электр занжирларидаги ўтиш
жараёнлари, классик усулда ҳисоблаш
Бундан аввалги қисмларда электр занжирларининг барқарорлик режимларида, яъни занжирдаги ток ва кучланиш ёки вақтга боғлиқ бўлмаган, ёки даврий ўзгарувчан таъсирда ишлаши ўрганилган эди. Барқарорлик режими, параметрлари ўзгармас бўлган занжирларда ўзгармас ёки ўзгарувчан кучланишли манбанинг нисбатан узоқ вақт таъсирида содир бўлади. Ўткинчи жараён занжирда коммутация (юк ёки манбанинг уланиши ёки ўчирилиши) содир бўлганидан, то барқарорлик режими бошлангунгача бўлган вақт оралиғида мавжуд бўлади. Шунинг учун занжир таҳлилининг юқорида кўрилган усуллари ўткинчи жараённи ўз ичига олмаган. Бироқ мухандислик амалиётида на фақат барқарорлик жараёни, балки у ёки бу ҳилдаги коммутация ҳамда параметрларнинг ўзгариши натижасида содир бўлувчи ўткинчи жараёнлар ҳам муҳимдир. Кучланишлари (токлари) апериодик ўзгарувчи манбалари бўлган занжирларда барқарорлик жараёни умуман учрамайди.
Электротехника, телекоммуникация ускуналари аксарият, узлуксиз ўткинчи жараёнларда ишлайдилар. Шаҳар электр транспортини бошқаришда, йўл ҳаракати талабларини бажариш мақсадида, тортувчи электр моторининг барқарорлик жараёнигача тезлигини оширишга улгурмасдан, унинг тезлигини яна щзгартиришга ёки моторни тўхтатишга тўғри келади. Телекоммуникация линияларидан бирин-кетин ҳар хил узунликдаги сигналлар ўтади: агар линиянинг кириш қисмидаги сигналга бир онда содир бўлувчи ўзгармас ток мос келса ва сигналлар бўлмаган оралиқда кучланиш нолга тенг бўлса, у ҳолда линиянинг чиқиш қисмида, яъни қабул қилиш қурилмасида муқаррар, ўткинчи жараённинг мавжудлиги (ток аста секин кўпайиб, астасекин камайиб боради) туфайли сигналлар ёйилган бўлади.
Электр тизимлар занжиридаги қисқа туташув аянчли шикасланишга олиб келиши мумкин; ушбу авария ҳолатида тизимнинг маълум қисмлари автоматик равишда ўчирилса ҳам, қисқа туташув токининг максимал қиймати қанча бўлишини лойиҳачи-мухандисларга маълум бўлиши зарур; оддий ҳолатда ўзгарувган ток занжирларида қисқа туташув содир бўлган ондан бошлаб ярим давр мобайнида токнинг ортиши билан аниқланади. Мана шу ўткинчи жараёндир. Ўткинчи жараённи ҳисоблашда автоматика тизимлари, импульс ва ўлчов техникасидаги ўткинчи жараёнлар ўта муҳимдир.
Кўпгина алоқа қурилмалари ва тизимларида ўткинчи жараёнлар улар ишлаш режимларининг «нормал» таркибий қисмига киради. Шу билан бирга, кўпгина ҳолатларда ўткинчи жараёнлар ўта кучланишга, ўта токлар пайдо бўлишига ва ноҳуш вазиятларга олиб келиши мумкин.
Ўткинчи жараёнларни ўрганиш барқарорлик жараёнидаги электр занжирлари назариясини аниқ билишни талаб этади.
Ўткинчи жараёнларни ҳисоблашда манба билан қабул қилувчи (юк)нинг орасидаги ўтказгичлар бўйлаб электромагнит сигналлари тарқалишининг чекланган тезлигини ҳисобга олиш талаб қилинади. Бундай тизимлар дарсликнинг «Тарқоқ параметри электр занжирлари назарияси» қисмида кўрилади. Ҳозирча биз ўтказгичлар бўйлаб сигналларнинг тарқалиш тезлиги, кўрилаётган қийматлар (кучланиш ёки ток)нинг сезиларли ўзгариши содир бўладиган вақт оралиғига нисбатан жуда кичик деб фараз қиламиз. Бундай занжирлардаги ўткинчи жараёнларни ўрганишга ушбу қисм бағишланган. Бироқ, айрим ҳолларда у ёки бу қийматларнинг ўзгариши бир онда содир бўлади деб қабул қиламиз. Масалан, ўзгармас ток манбасини занжирга уланишида ушбу уланиш бир онда бажарилади ва мазкур қутбларга кучланишнинг узатилиши бир онда содир бўлади, ҳамда кучланиш бир онда ортади деб фараз қиламиз. Аслида эса, коммутация қанчалар тез содир бўлмасин, у вақт бўйича чўзилиш билан давом этади. Кўпгина ҳолларда ушбу вақт чўзилишини ҳисобга олмай, кучланишнинг бир онда ортиши ҳақидаги идеаллаштирилган тассуротни қабул қилинади.
Чизиқли электр занжирлари ўткинчи жараёнларини ҳисоблашда классик усул
15.1. Дифференциал тенгламалар. Коммутация қонунлари
Ўткинчи жараёнларни ҳисоблаганда занжирнинг асосий дифференциал тенгламаларини асос қилиб олиш зарур. Уларни ечишда эса фақатгина барқарорлик жараёни учун ҳос бўлган тенгламаларнинг ҳусусий ечимлари билан чекланмасдан, уларнинг тўлиқ ечимларини аниқлаш зарур. Масалан L, r, C элементлари кетма-кет уланган занжирни u(t) кучланишли манбага уланганда қуйидаги тенгламани ечиш зарур:
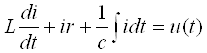 .
(15.1)
.
(15.1)
Тармоқланган занжирларни ҳисоблашда тугун ва контурлар учун Кирхгоф қонунлари асосида тузилган бирнеча тенгламалар тизимини ҳисоблаш зарур бўлади. Шуни таъкидлаш керакки, чизиқли занжир бўлганда занжирнинг барча дифференциал тенгламалари чизиқли бўлади.
Дифференциал тенгламаларни ечишда у ёки бу ҳолатда берилган бошланғич шартлардан фойдаланиш зарурдир. Бошланғич шартлар ҳақидаги батафсил ахборотни билиш дифференциал тенгламаларни аниқлашда жуда муҳим бўлган заруратдир. Дарҳақиқат, бир занжирни бир хил коммутацияда, аммо ҳар хил бошланғич шартли ишлатиш натижасида ўткинчи жараёнлар ҳар хил бўлиши аниқдир.
Масалан,
занжирдаги ўткинчи жараённинг бошланишига сабаб бўлган коммутация t=0 вақтда
бир онда занжирни ўзгартирди деб қабул қиламиз. Бу ҳолда у
ёки бу функция f(t) нинг коммутациядан олдинги f(-0) ва
коммутациядан кейинги f(+0) онларидаги қийматлари ҳақида
фикрлаш мумкин. Бу қийматларни фарқлаш учун аргумент t![]() да биринчи ҳолатда
0- деб, иккинчи холатда эса 0+ деб белгиланади. Бу белгилаш қуйидагича
талқинланади:
да биринчи ҳолатда
0- деб, иккинчи холатда эса 0+ деб белгиланади. Бу белгилаш қуйидагича
талқинланади:
![]() (15.2)
(15.2)
Бошқача
қилиб айтганда, ![]() - бу f(t)
функциянинг а нуқтадан ўнгроқдаги киймати,
- бу f(t)
функциянинг а нуқтадан ўнгроқдаги киймати, ![]() - бу f(t)
функциянинг а нуқтадан чапроқдаги қиймати бўлади.
- бу f(t)
функциянинг а нуқтадан чапроқдаги қиймати бўлади.
Функциянинг узилишлари бўлмаса, ёки масалан, «фақат t>а (≥а эмас, айнан >а) бўлгандаги f(t) функцияси ҳақида бормоқда» деган қўшимча талаб қўйилмаганда f(а) ёки а=0+ бўлганда f(0) деб ёзиш мумкин.
Коммутация онида баъзи қийматлар сакраб (кескин) ўзгариши мумкин, бундай холатда
![]()
![]()
![]() (15.3)
(15.3)
бўлади.
Бошқа қийматлар, аксинча, фақат узлуксиз ўзгариши мумкин, унда қуйидагича ёзилади:
![]() (15.4)
(15.4)
Агар занжирнинг баъзи элементлари орасида қувват алмашинуви чекланган (яъни u∙i кўпайтма чекли) бўлса, унда занжир элементларидаги энергияни аниқлайдиган барча қийматлар узлуксиз ўзгарадилар.
Масалан, ўзгармас С сиғимли конденсатор электр майдони энергиясининг қийматини унинг кучланиши аниқласа:
![]() ,
,
унда узатилаётган
қувват ![]() бўлади.
Шунинг учун қувват чекли бўлиб, uс∙i чекли
бўлганда, конденсатор кучланиши узлуксиз ўзгаради (
бўлади.
Шунинг учун қувват чекли бўлиб, uс∙i чекли
бўлганда, конденсатор кучланиши узлуксиз ўзгаради (![]() чекли) ва,
демак
чекли) ва,
демак
![]() .
(15.5)
.
(15.5)
Шунга ўхшаш, L индуктивлик элементи бўлган электр занжирининг магнит майдони энергияси индуктивликдан оқиб ўтаётган ток билан аниқланади:
![]() .
.
Шунинг учун қувватнинг қиймати чекли бўлганда индуктивликдаги ток узлуксиз оқиб ўтади:
![]() (15.6)
(15.6)
(15.5) ва (15.6) тенгликлар чекланган қувватли электр занжирлари коммутация қонунларини ифодалаб, коммутациягача аниқланган барча индуктивликлардан оқаётган токлар ва барча сиғимлардаги аниқланган кучланишлар ёрдамида зарур бўлган барча бошланғич шартларни излаб топиш учун етарлидир.
Чизиқли дифференциал тенгламаларни, масалан (15.1)ни, аксарият, икки функция йиғиндиси сифатида тасаввур қилиш қулайдир (суперпозиция усули):
![]() (15.7)
(15.7)
улардан биринчи функция ![]() – берилган дифференциал тенгламанинг хусусий ечимини
ифодалайди:
– берилган дифференциал тенгламанинг хусусий ечимини
ифодалайди:
![]() (15.8)
(15.8)
иккинчиси
![]() эса ушбу
тенгламанинг ўнг томонини нолга тенглаштириб, ҳосил бўлган характеристик
тенглама:
эса ушбу
тенгламанинг ўнг томонини нолга тенглаштириб, ҳосил бўлган характеристик
тенглама:
 (15.9)
(15.9)
нинг (умумий) ечимини ифодалайди.
Тенгламалар чизиқли бўлганлиги учун (15.8) ва (15.9) ни ҳадма-ҳад қўшиб (15.10) тенгламани хосил қиламиз ва (15.7) ечимнинг тўғрилигини тасдиқлаймиз.
Коммутация қонунларини дифференциал тенгламанинг тўла ечими қониқтириши зарур. Буни биринчи галда ўзлаштириб олиш даркор.
Электр занжирлари тенгламаларининг ўнг томони, аксарият, манбанинг кучланиши ёки токини ифодалайди, ёки умумлаштириб айтганда, ташқи таъсир кучидир. Характеристик тенглама, масалан (15.9), занжирнинг ташқи таъсир кучи бўлмаган ёки эркин режимини тасвирлайди; шунинг учун характеристик тенгламани қониқтирувчи ток ва кучланишлар эркин деб аталади.
Ўнг томони ўзгармас ёки даврий функциядан иборат бўлган тенгламанинг хусусий ечимини занжирнинг барқарорлашган режими билан ўхшатиш мумкин; уни яна мажбурланган режимнинг ечими, мазкур ток ёки кучланишларни эса мажбурланган ток ёки кучланиш дейилади.
Тенглама (15.10) нинг ҳақиқий (тўла) ечими бунда мажбурланган ва эркин ташкил этувчиларнинг йиғиндисидан иборат деб фараз қилинади:
![]()
![]() (15.10)
(15.10)
Гармоник кучланиш манбасини улаш. Фараз қилайлик,
![]() (15.11)
(15.11)
кучланишли
занжир кетма-кет уланган r қаршилик ва L индуктивликка
улансин (15.1,в-расм). (15.11) ифодадаги бошланғич фаза ![]() калит
уланиш t=0 онидаги u=Sin
калит
уланиш t=0 онидаги u=Sin![]() манба
кучланишини ифодалайди.
манба
кучланишини ифодалайди.
Ўткинчи жараённинг токини аниқлаш зарур бўлсин.
Занжирнинг дифференциал тенгламасини
![]() (15.12)
(15.12)
ечиш
учун, умумий усулга амал қилиб, аввал ўзгарувчан ток назариясида кўрилган
(![]() барқарорлик
токи) хусусий ечимни аниқлаймиз:
барқарорлик
токи) хусусий ечимни аниқлаймиз:
![]() (15.13)
(15.13)
бунда
Сўнгра, бизга маълум бўлган усул билан, таркибида интеграллаш доимийси бўлган характеристик тенглама ечими аниқлаймиз:
![]() (15.14)
(15.14)
бунда
![]()
Шундай қилиб:
![]() .
(15.15)
.
(15.15)
Ўзгармас А қийматини индуктив ток учун бошланғич шартлардан аниқлаймиз. Уланаётган шохобча коммутациягача манбадан узилган бўлганлиги учун, нолли бошланғич шартлар мавжуддир:
![]() ,
,
демак, t=0 бўлганда (9.40) бўйича
![]() (15.16)
(15.16)
бўлади.
Ҳақиқий ток (тўла ечим) қуйидагича бўлади:
![]() (15.17)
(15.17)
унинг графиги эса 15.1-расмда келтирилган.
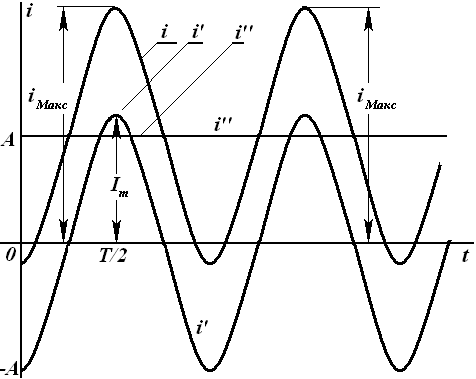
15.1-расм
Нисбатан катта вақт доимийси ![]() (кичик r
ва катта L, яъни
(кичик r
ва катта L, яъни ![]() ) бўлган занжирда
токнинг эркин ташкил этувчиси T/2 ярим даврда деярли кўп ўзгара олмайди,
аммо (15.17) нинг биринчи ташкил этувчиси ярим давр ичида ўзининг ишорасини
ўзгартиришга улгуради. Шунинг учун улашнинг энг номаъқул шароитида
(
) бўлган занжирда
токнинг эркин ташкил этувчиси T/2 ярим даврда деярли кўп ўзгара олмайди,
аммо (15.17) нинг биринчи ташкил этувчиси ярим давр ичида ўзининг ишорасини
ўзгартиришга улгуради. Шунинг учун улашнинг энг номаъқул шароитида
(![]() бўлганда) ўткинчи
жараён токининг максимал
бўлганда) ўткинчи
жараён токининг максимал ![]() қиймати барқарорлик
режими токи
қиймати барқарорлик
режими токи ![]() нинг
амплитудасидан тахминан 2 марта катта бўлиши мумкин.
нинг
амплитудасидан тахминан 2 марта катта бўлиши мумкин.
Кучланиш импульси. Агар ![]() вақт
доимийсидан кичик бўлган
вақт
доимийсидан кичик бўлган ![]() оралиқда кучланиш u
нолдан фарқ қилса, у ҳолда
оралиқда кучланиш u
нолдан фарқ қилса, у ҳолда ![]() бўлганда
занжирдаги режим фақат кучланиш импульси, яъни
бўлганда
занжирдаги режим фақат кучланиш импульси, яъни 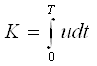 катталик билан аниқланади.
Дарҳақиқат, занжирнинг асосий тенгламаси (15.17)дан қуйидагини
аниқлаймиз:
катталик билан аниқланади.
Дарҳақиқат, занжирнинг асосий тенгламаси (15.17)дан қуйидагини
аниқлаймиз:
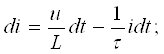
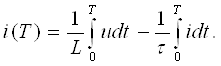 (15.18)
(15.18)
Бироқ, ўртача қийматлар назариясидан
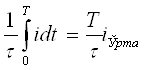 .
.
Тенглик
(15.18)даги биринчи интегралга нисбатан иккинчиси жуда кичик қиймат
бўлиб, уни ҳисобга олмаса ҳам бўлади, чунки таҳминга кўра ![]() .
.
Шундай қилиб, кучланиш эгри чизиғи шаклининг қандай бўлишидан қатъий назар унинг таъсир этиш оралиғи (ўткинчи жараён)нинг охирида занжирдаги ток қуйидагича бўлади:
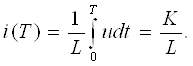 (15.19)
(15.19)
Агар t>T бўлганда кириш кучланиши нол бўлса, ток қўйидагича ифодаланади:
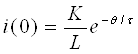 ,
,
бунда
![]() .
.
15.1. L, r, C контури
Эркин ташкил этувчилар учун тенгламалар. Уч элемент L, r, C дан ташкил топган электр занжири (контури) юқорида кўрилганлардан мураккаброқ ва иккинчи даражали дифференциал тенглама билан ифодаланади. Бироқ, унга хам юқорида баён этилган усулларни қўллаш мумкин.
Кетма-кет уланган L, r, C (15.2,а-расм) элементларни u(t) кучланишли занжирга уланишини тахлил қилайлик.
Занжирнинг (15.19)даги дифференциал тенгламасида номаълум қиймат сифатида конденсатордаги кучланиш uC ни қабул қилиш мақсадга мувофиқ; у орқали эса токни аникланади:
![]() .
.
Бунда контурнинг тенгламаси (15.20) қуйидагича ёзилади:
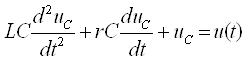 ,
(15.20)
,
(15.20)
тенгламанинг чап томонидаги биринчи ҳад ![]() индуктивликдаги, иккинчиси – актив қаршиликдаги
индуктивликдаги, иккинчиси – актив қаршиликдаги
![]() кучланишлар пасаювидир.
кучланишлар пасаювидир.
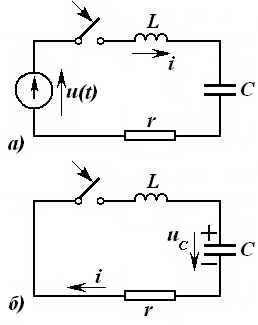 Кучланиш u(t)=0 деб ҳисоблаб
эркин ташкил этувчи учун (манба кучланиши нолга тенг) тенгламани аниқлаймиз:
Кучланиш u(t)=0 деб ҳисоблаб
эркин ташкил этувчи учун (манба кучланиши нолга тенг) тенгламани аниқлаймиз:
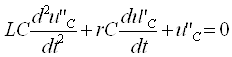 , (15.21)
, (15.21)
унга қуйидаги характеристик тенглама мос келади:
![]() ,
(15.22)
,
(15.22)
унинг илдизлари
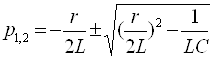
![]() (15.23)
(15.23)
15.2-расм
Бундан шундай хулоса чиқадики, сиғимдаги эркин кучланиш икки экспонента йиғиндисидан иборат бўлар экан:
![]() (15.24)
(15.24)
бунда А ва В-икки интеграллаш доимийси. Эркин ток эса қуйидагича аниқланади:
![]() (15.25)
(15.25)
Хусусий
![]() ва
ва ![]() ечимлар u(t)
функциянинг шаклига боғлиқ.
ечимлар u(t)
функциянинг шаклига боғлиқ.
16-Маъруза. 1-тартибли чизиқли электр занжирларини
ўзгармас кучланиш манбаига ўлчаш ва электр
занжиридан ўтиш жараёнлари
![]() Ўзгармас кучланиш u(t) = U манбасига r қаршилик
орқали С сиғимли конденсатор уланган бўлсин (15.1,а-расм).
Барқарорлашган режимда бундай занжирда ток бўлмайди i=0 (берк
контур йўқ). Конденсатордаги кучланиш uC = U, унинг
заряди q=CU, захираланган энергияси (электр майдони энергияси) WЭ=СU2/2
га тенг
бўлади.
Ўзгармас кучланиш u(t) = U манбасига r қаршилик
орқали С сиғимли конденсатор уланган бўлсин (15.1,а-расм).
Барқарорлашган режимда бундай занжирда ток бўлмайди i=0 (берк
контур йўқ). Конденсатордаги кучланиш uC = U, унинг
заряди q=CU, захираланган энергияси (электр майдони энергияси) WЭ=СU2/2
га тенг
бўлади.
Фараз қилайлик, «К» калитнинг уланиш онигача бўлган вақтда
конденсатор кучланиши Uдан фарқли бўлсин, масалан, у умуман
зарядланмаган ва унинг электр майдони кучланиши нолга тенг
бўлсин (U=0; Wэ=0). Бу ҳолатда,
занжирда ўткинчи жараён содир бўлиб, унинг вақт давомийлигида
ўтказгичлардан ток оқиб конденсаторларни зарядлайди. Фараз қилайлик,
занжирдаги токнинг қиймати конденсатор электродларидаги зарядлар ортиши
тезлигига тенг бўлсин:
![]()
Кирхгофнинг қонунини қўллаб
![]()
кўрилаётган занжирнинг дифференциал тенгламасини тузиш мумкин:
![]()
ёки
![]() (16.1)
(16.1)
бунда ![]()
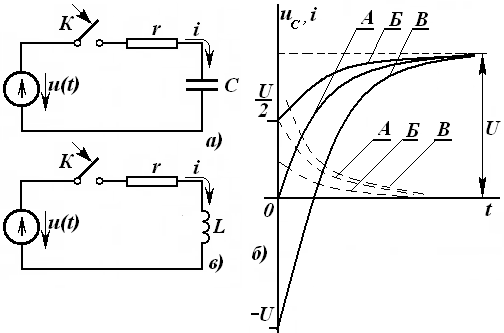
16.1-расм
Ушбу содда тенгламанинг ечими аниқлаш
осон:
![]() (16.2)
(16.2)
Биринчи
ҳади ![]() дифференциал
тенглама (16.2) нинг хусусий ечимидир - мажбурий ташкил этувчиси (барқарорлик
режимидаги) қийматидир. Иккинчи ташкил этувчиси
дифференциал
тенглама (16.2) нинг хусусий ечимидир - мажбурий ташкил этувчиси (барқарорлик
режимидаги) қийматидир. Иккинчи ташкил этувчиси ![]() , бу характеристик тенглама, яъни (16.3) нинг ўнг
томонини нолга тенглаштирилгандаги:
, бу характеристик тенглама, яъни (16.3) нинг ўнг
томонини нолга тенглаштирилгандаги:
![]() (16.3)
(16.3)
нинг ечимидир.
Характеристик
тенгламанинг ечимида интеграллаш доимийси А мавжуд. Унинг қийматини
(16.3) дан аниқлаш мумкин. Дарҳақиқат, аниқланган ечим ![]() нинг қийматини ихтиёрий ўзгармас сонга
кўпайтирганда ҳам бу тенгламани қониқтиради.
Шундай қилиб, изланаётган физик жараённи узил-кесил тасвирловчи ечимни
аниқлаш учун фақатгина дифференциал тенгламага асосланиб бўлмайди.
нинг қийматини ихтиёрий ўзгармас сонга
кўпайтирганда ҳам бу тенгламани қониқтиради.
Шундай қилиб, изланаётган физик жараённи узил-кесил тасвирловчи ечимни
аниқлаш учун фақатгина дифференциал тенгламага асосланиб бўлмайди.
Сиғимдаги кучланишнинг эркин ташкил этувчиси
![]() (16.4)
(16.4)
экспонента билан тасвирланиб, унинг камайиш тезлиги вақт доимийси
![]() (16.5)
(16.5)
орқали
ифодаланади; у фақат кўрилаётган занжир параметрлари билан аниқланади
(![]() нинг қиймати
бошлангич шартларга хам, манба кучланишига хам боғлиқ эмас). Вақт
доимийси вақт ўлчов бирлигига эга, чунки
нинг қиймати
бошлангич шартларга хам, манба кучланишига хам боғлиқ эмас). Вақт
доимийси вақт ўлчов бирлигига эга, чунки ![]() кўрсаткич
ўлчамсиз бўлиши зарур (r ва С ўрнига вольт, ампер ва
секундлар билан ўлчанадиган қийматларни қўйганда бу ўз
исботини топади).
кўрсаткич
ўлчамсиз бўлиши зарур (r ва С ўрнига вольт, ампер ва
секундлар билан ўлчанадиган қийматларни қўйганда бу ўз
исботини топади).
Вақтнинг қиймати ![]() га етганда эркин ташкил этувчининг абсолют қиймати
е марта камаяди.
га етганда эркин ташкил этувчининг абсолют қиймати
е марта камаяди.
Доимий
коэффициент ![]() нинг физик мазмунини ҳам билиш осон: берилган токнинг қийматида сиғимнинг
қиймати қанчалар катта бўлса, ундаги кучланиш шунчалар секин
ўзгаради; манба билан сиғим кучланишлари берилган фарқида
занжирдаги қаршилик қанчалар катта бўлса, ундан оқаётган ток қиймати
шунчалар кичик бўлади. Масалан, сиғим 30 мкф ва қаршилик 1 Мом
бўлса, вақт доимийси
нинг физик мазмунини ҳам билиш осон: берилган токнинг қийматида сиғимнинг
қиймати қанчалар катта бўлса, ундаги кучланиш шунчалар секин
ўзгаради; манба билан сиғим кучланишлари берилган фарқида
занжирдаги қаршилик қанчалар катта бўлса, ундан оқаётган ток қиймати
шунчалар кичик бўлади. Масалан, сиғим 30 мкф ва қаршилик 1 Мом
бўлса, вақт доимийси ![]() c. бўлади;
демак, эркин ташкил этувчининг е марта камайишига 5 минутдан сўнг
эришилади. Агар С=0,01 мкФ ва r=1 Ом бўлса,
у ҳолда эркин ташкил этуви е марта камайишига 0,01
мкс дан сўнг эришилади.
c. бўлади;
демак, эркин ташкил этувчининг е марта камайишига 5 минутдан сўнг
эришилади. Агар С=0,01 мкФ ва r=1 Ом бўлса,
у ҳолда эркин ташкил этуви е марта камайишига 0,01
мкс дан сўнг эришилади.
Дифференциал
тенгламанинг тўлиқ ечими (16.5)ни таҳлил қилганда
шу аён бўладики, у t >>![]() бўлганда барқарорлик жараёнини UC=Uни тўла
ифодалайди. Аммо t>0 ва t=0+ бўлгандаги UC(t) қиймат ўзгармас қиймат «А»га боғлик
бўлаяпти. Масалан, t=0+ бўлганда (15.2)дан
қуйидагини аниқлаймиз:
бўлганда барқарорлик жараёнини UC=Uни тўла
ифодалайди. Аммо t>0 ва t=0+ бўлгандаги UC(t) қиймат ўзгармас қиймат «А»га боғлик
бўлаяпти. Масалан, t=0+ бўлганда (15.2)дан
қуйидагини аниқлаймиз:
![]() .
(16.6)
.
(16.6)
Кейинги ифода аниқ физик талқинга эга: ўзгармас қиймат А ва, демак, занжирдаги физик жараён бошланғич шарт - конденсатордаги бошланғич кучланиш UC(0+) га боғлиқ экан.
Аммо, сиғимдаги кучланиш кўрилаётган вазиятда бир онда сакраб ўзгара олмайди, яъни UC(0+)=UC(0-) ва шунинг учун
![]() (16.7)
(16.7)
Шундай қилиб, интеграллаш доимийсини аниқлаш учун коммутациядан олдинги конденсатордаги кучланиш UC(0-) ни билиш етарлидир. Мана шу С, r ли занжир дифференциал тенгламасини тўла ечиш учун зарур ва етарли бошланғич шартдир.
Ҳар хил бошланғич шартлари бўлган С, r занжир ўткинчи жараёнини кўриб чиқайлик.
А). Зарядланмаган С конденсатори r қаршилик орқали ўзгармас кучланиш U манбасига (нолга тенг бўлган бошланғич шарт) улансин. Бу ҳолда, UC(0-)=0 демак, (16.7) дан A = - U ва
![]() (16.8)
(16.8)
Занжирдаги ток
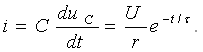 (16.9)
(16.9)
Б). Юқоридаги занжирдаги
конденсатор коммутация онигача ![]() кучланишгача зарядланган (нолга тенг бўлмаган бошланғич
шартлар). Бу холда A = - U/2 ва,
демак;
кучланишгача зарядланган (нолга тенг бўлмаган бошланғич
шартлар). Бу холда A = - U/2 ва,
демак;
![]()
В). Яна шу
занжирдаги конденсатор коммутациягача абсолют қиймати U га тенг кучланишгача зарядланган; зарядланишнинг
ишораси барқарорлик жараёнидаги ишорага тескари, яъни ![]() Бу ҳолда
Бу ҳолда
![]()
Охирги мисолда сиғимдаги электр майдони энергияси бошланғич пайтда ва барқарорлик режимида бир хил бўлса ҳам, занжирда ўткинчи жараён мавжуд бўлади, чунки манба кучланиши билан конденсатордаги кучланишлар ишоралари мослаштирилмаган.
Ушбу уч бошланғич шартлар учун конденсатордаги кучланишнинг ўзгариш графиги 16.1,б-расмда келтирилган. Шу расмда токлар ўзгаришининг графиги ҳам келтирилган.
С, r занжирдаги ток сакраб ўзгариши мумкин, чунки занжирда
индуктивлик йўқ. Шунга эътиборни қаратайликки, ҳар қандай занжирда ҳам ҳеч
бўлмаганда жуда кичик индуктивлик мавжуддир. ![]() қиймати жуда катта бўлганда С, r ли занжирдаги жараёнга унинг таъсири жуда кичикдир.
Лекин
қиймати жуда катта бўлганда С, r ли занжирдаги жараёнга унинг таъсири жуда кичикдир.
Лекин ![]() нинг қиймати бир неча микросекундда ёки
микросекунднинг кичик улишида бўлганда, ўткинчи жараённинг тўлиқ даврида
токнинг ўзгариш тезлиги шунчалар катта бўладики, индуктивликни эътиборга олмаса
бўлмайди.
нинг қиймати бир неча микросекундда ёки
микросекунднинг кичик улишида бўлганда, ўткинчи жараённинг тўлиқ даврида
токнинг ўзгариш тезлиги шунчалар катта бўладики, индуктивликни эътиборга олмаса
бўлмайди.
Г). Пировардида, u(t)=U=0, uc(0-)=U0 >0 ҳолни кўрайлик. Бунда (16.9)га кўра A=U0. Бу ҳол конденсаторнинг разрядланишидир. Шартимизга кўра, ечимда фақат эркин ташкил этувчи мавжуд бўлади:
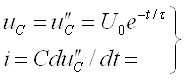
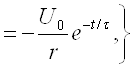 (16.10)
(16.10)
яъни
разряд токи 16.1,а-расмда кўрсатилган ток йўналишига тескари оқади.
Ўткинчи
жараён конденсаторда захира сифатида қолган энергия билан таъминланади.
Энергия балансини тузиш осон: сиғим энергиясининг камайиш тезлиги ![]() Жоуль-Ленц қонунига
асосан қаршиликдаги энергия ажралишига тенг бўлиши зарур:
Жоуль-Ленц қонунига
асосан қаршиликдаги энергия ажралишига тенг бўлиши зарур:
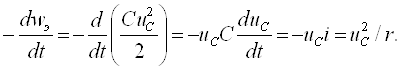 (16.11)
(16.11)
Юқорида
аниқланган ![]() ва
ва ![]() қийматлар
охириги ифодаларга мос келади, бунга қийматларни ўрнига қўйиш билан
иқрор бўлиш мумкин.
қийматлар
охириги ифодаларга мос келади, бунга қийматларни ўрнига қўйиш билан
иқрор бўлиш мумкин.
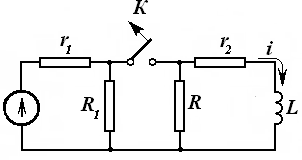 16.1 L, r ли занжирга ўзгармас кучланиш манбасини улаш
16.1 L, r ли занжирга ўзгармас кучланиш манбасини улаш
Кетма-кет уланган индуктивлик L ва қаршилик r дан иборат занжирни (16.1,в-расм) ўзгармас кучланиш u(t)=U манбасига улашжараёнини кўрайлик. Ўзгарувган токлар назариясида кўп учраган занжирнинг тенгламасини тузамиз: 16.2-расм
![]() (16.12)
(16.12)
Математик жиҳатдан унинг (16.11) тенгламадан фарқи йўқ ва унинг ечими аниқланган деб ҳисоблаш мумкин:
![]()
![]() (16.13)
(16.13)
бунда
![]() .
.
Юқорида келтирилган мисолдагидек, бир ва икки штрихлар билан хусусий ечим ёки мажбурланган (барқарорлик) режими ва характеристик тенглама ечими (эркин ташкил этувчи)лар белгиланган. Эркин ташкил этувчи r, С ли занжирларидек, бу гал ҳам экспонента сифатида ифодаланган.
Тенгламанинг тўлиқ ечимида яна ўзгармас қиймат А мавжуд. Унинг қиймати индуктивликдаги бошланғич ток i(0+) билан аниқланади. Агар коммутациягача ток мавжуд бўлмаса (нолли бошланғич шартлар), у холда:
![]() (16.14)
(16.14)
Бунда (15.13) дан қуйидагини
аниқлаймиз:
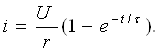 (16.15)
(16.15)
Индуктивликдаги кучланиш
![]() (16.16)
(16.16)
ва ток учун графикларни аввалги мисол ёрдамида мустақил чизишни ўқувчига тавсия этиш мумкин.
Занжирдаги
ток (16.15) нолдан бошланади. Шунинг учун жараён бошланишида манба кучланиши
тўлалигича индуктивликка тўғри келади ![]() . Дарҳақиқат,
бошланғич онда i(0+)=i(0-) бўлгани учун, қаршилик r
да кучланиш пасаюви нолга тенг.
. Дарҳақиқат,
бошланғич онда i(0+)=i(0-) бўлгани учун, қаршилик r
да кучланиш пасаюви нолга тенг.
Энди
16.2-расмда келтирилган занжирда ўзгармас кучланиш манбасига уланган
индуктивлик коммутациядан сўнг (калитни узиш) манбадан узилишини кўрайлик ![]() . Манбасиз қолган
занжирнинг бир қисмида қуйидаги тенгламани қониқтирадиган
фақат
. Манбасиз қолган
занжирнинг бир қисмида қуйидаги тенгламани қониқтирадиган
фақат
![]()
i2 эркин токи
мавжуд бўлади; бунда ![]() . Унда (i2(0)=i2(0-)
бўлгандаги i2 нинг қийматини осон аниқлаш мумкин:
. Унда (i2(0)=i2(0-)
бўлгандаги i2 нинг қийматини осон аниқлаш мумкин:
![]() (16.17)
(16.17)
Токнинг
оқиши индуктивлик захирасидаги энергия билан таъминланади: энергиянинг
сўниш тезлиги ![]() қаршиликдаги
қувват сарфига тенг бўлиши зарур;
қаршиликдаги
қувват сарфига тенг бўлиши зарур;
 (16.18)
(16.18)
Индуктивлик
![]() қанчалар
катта бўлса, бирламчи захира энергия ҳам катта бўлади, бироқ қаршилик
r қанчалак катта бўлса, захираланган энергиянинг сўниши шунчалар
жадаллашади. Шунинг учун, табийки, қаршиликнинг ортиши ток ўзгаришини
тезлаштиради, индуктивликнинг ортиши эса уни секинлаштиради; айнан шунга вақт
доимийси ифодаси
қанчалар
катта бўлса, бирламчи захира энергия ҳам катта бўлади, бироқ қаршилик
r қанчалак катта бўлса, захираланган энергиянинг сўниши шунчалар
жадаллашади. Шунинг учун, табийки, қаршиликнинг ортиши ток ўзгаришини
тезлаштиради, индуктивликнинг ортиши эса уни секинлаштиради; айнан шунга вақт
доимийси ифодаси ![]() мос келади.
мос келади.
Аниқланган натижа ва (16.18) тенгламани шунга ўхшаш конденсатор зарядсизланиши тенгламаси (16.11) билан (эркин режим) таққосланса қизиқарли хулосага келиш мумкин.
16.2. Ўзгарувчан кучланишли манбага r, С ли занжирни улаш
Занжирни (16.1,а-расм) кучланиши ўзгармас бўлмаган, мазкур хусусий ечимни аниқлаш осон бўлган бирор оддий ўзгарувчан функция u(t) ёрдамида ифодаланган бўлса, ўткинчи жараённи ҳисоблаш деярли оғирлашмайди.
Кучланиш чизиқли ортувчи бўлса. Манбанинг кучланиши қуйидаги қонуният билан ўзгарсин деб фараз қилайлик:
u(t) = 0, агар t < 0;
u(t) = U0 t/T, агар t ³ 0.
Конденсатордаги кучланишни аниқлаш учун (16.11)га ўхшаш бўлган тенглама
![]()
учун, аввало ![]() хусусий ечимни аниқлаш зарур.
хусусий ечимни аниқлаш зарур.
Шунга эътиборни қаратиш зарурки, баъзан хусусий ечимни мос келувчи функцияни танлаш йўли билан ахтарилади. Бизнинг мисолимизда қуйидагича тахмин қилиш табиийдир:
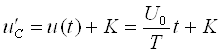 ,
,
бунда
K=cоnst; сўнгра
ўзгармас K ни шундай танлаш керакки, берилган тенглама қаноатлансин, яъни
дифференциалаш натижасида ҳосил бўлган ўзгармас ечим ![]() таркибидан
йўқолсин.
таркибидан
йўқолсин.
Аёнки, бу талабни ![]() ифода қаноатлантиради.
ифода қаноатлантиради.
Шундай қилиб, хусусий ечим қуйидагича ифодаланади:
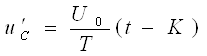
Характеристик (бир жинсли) тенгламанинг ечими тенглама ўнг томонининг шаклига боғлиқ эмас; у юқорида кўрилганидан маълум:
![]() ,
,
бунда ![]() .
.
Шундай
қилиб
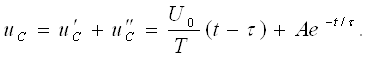
Интеграллаш доимийси А нинг қиймати аниқлаш қолди, холос.
Агар сиғим аввалдан зарядланмаган бўлса (етарли бошланғич шарт), у холда t=0 бўлганда
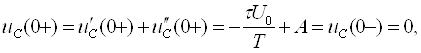
бунда ![]() .
.
Натижавий ечим қуйидагича
кўринишда бўлади:
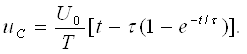 (16.19)
(16.19)
Кўрилаётган занжирдаги ток қуйидагича ифодаланади:
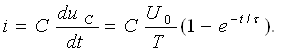 (16.20)
(16.20)
Занжир
улангандан сўнг вақт ўтиши билан занжирда (t >>![]() бўлганда) CU0/T
ўзгармас токи барқарорлашади, сиғимдаги кучланиш эса чизиқли
ортувчи бўлади; унинг қиймати манба кучланишига нисбатан r қаршиликдаги
ўзгармас кучланиш пасаюви r∙CU0/T га фарқ қилиб
камроқ бўлади.
бўлганда) CU0/T
ўзгармас токи барқарорлашади, сиғимдаги кучланиш эса чизиқли
ортувчи бўлади; унинг қиймати манба кучланишига нисбатан r қаршиликдаги
ўзгармас кучланиш пасаюви r∙CU0/T га фарқ қилиб
камроқ бўлади.
Занжирни даврий кучланишли манбага
улаш. Ечимни бизга маълум бўлган қолипда
бажариш мумкин: хусусий ечим ![]() аниқланади - бу ўзгарувчан токлар
назариясидан маълум бўлган барқарорлашган режимдир; сўнгра унга қўшимча
қилиб таркибида интеграллаш доимийси бўлган эркин ташкил этувчи
аниқланади - бу ўзгарувчан токлар
назариясидан маълум бўлган барқарорлашган режимдир; сўнгра унга қўшимча
қилиб таркибида интеграллаш доимийси бўлган эркин ташкил этувчи ![]() киритилади;
сўнгра, тўла ечим
киритилади;
сўнгра, тўла ечим ![]() ни аниқловчи бошланғич шартлар киритилади.
ни аниқловчи бошланғич шартлар киритилади.
Кўп холларда ечимни аниқлашда
суперпозиция усулини қўллаш қулайдир. Масалан, t=0 дақиқада
занжирга ![]() кучланишли
манба улансин. Бундай занжирда i токни аниқлаш талаб қилинсин.
кучланишли
манба улансин. Бундай занжирда i токни аниқлаш талаб қилинсин.
Берилган
кучланишни икки ташкил этувчига ажратиш мумкин ![]() ва
ва ![]() . Суперпозиция
усулини қўллаб, алоҳида биринчи (u1) кучланиш
уланишига занжирнинг реакциясини, сўнгра алоҳида иккинчи (u2)
кучланиш учун реакцияни аниқланади. Барча аниқланган тенгламалар
чизиқли бўлгани учун ҳақиқий кучланишга занжирнинг
реакцияси аниқланган функциялар йиғиндисига тенг (i=i1+i2).
Бунда шуни назарда тутиш зарурки,
коммутация конунлари фақат тўла ечимга нисбатан қўлланилад
. Суперпозиция
усулини қўллаб, алоҳида биринчи (u1) кучланиш
уланишига занжирнинг реакциясини, сўнгра алоҳида иккинчи (u2)
кучланиш учун реакцияни аниқланади. Барча аниқланган тенгламалар
чизиқли бўлгани учун ҳақиқий кучланишга занжирнинг
реакцияси аниқланган функциялар йиғиндисига тенг (i=i1+i2).
Бунда шуни назарда тутиш зарурки,
коммутация конунлари фақат тўла ечимга нисбатан қўлланилад
17-Маъруза. Ўтиш жараёнларини оператор усулда ҳисоблаш
босқичлари
Инглиз олими Хевисайд томонидан киритилган оператор усули занжирлардаги ўткинчи жараёнларнинг мураккаб ҳисобларини соддалаштирди. Ушбу усулнинг аҳамиятини ўзгарувчан токлар назариясидаги комплекс усули киритилишининг аҳамияти билан солиштириш мумкин, чунки ўткинчи жараёнлар киритилган «р» оператори кўп жиҳатдан ўзгарувчан токлар назарияси комплекс усули «jщ» операторига ўхшашдир.
Ҳозирги замон техник адабиётида оператор усулининг асосланишида, аксарият, Карсон ва Лапласнинг интеграл ўзгартишлари усули билан ўхшашлиги қайд этилади.
Интеграл ўзгартиришлар усулини чизиқли тўпланган параметрли занжирлар назариясининг оддий масалаларига қўллаганда Хевисайднинг оператор усулини қўллаш натижасида ҳосил бўлган ечимларга мураккаб йўллар билан эришилади. Шу пайтгача интеграл ўзгартиришлар усули мураккаб масалалар учун ишлатилганда жуда қўл келиши ва умумийлиги тан олинган эди. Бироқ, оператор усулининг кейинги ривожланишлари (Микусинский ва бошқаларнинг изланишлари) натижасида ундан ҳам умумий, таҳлил ва ҳисоблашнинг кучли усули эканлиги маълум бўлди. Хевисайд усулининг муҳим афзаллиги шундан иборатки, бу усул қўлланишида ўқувчидан комплекс ўзгарувчи функциялар назариясини билишни ҳам ва мураккаб математик келтириб чиқаришлар бўлишини ҳам талаб этмайди.
Математика фанида оператор усули ва Лаплас ўзгартишларини ўрганган ўқувчилар, тўғридан-тўғри ушбу усулнинг ўтишлари ҳамда мазкур бўлимлардаги мисолларни кўришга ўтишлари мумкин. Бунда, албатта улар ечимини аниқлашда фақат тавсия этилган умумийликлар мажмуасидан фойдаланиб қолмай балки комплекс ўзгартришлар функциясида тавсия этилган бошқа усуллар (чигирма ўрам интеграли, Бромвич интеграли усуллари)дан фойдаланишлари ҳам мумкин: бу математик усуллар ушбу дарсликда ёритилмайди.
Шунга эътиборни қаратиш
лозимки, баъзан адабиётларда ![]() ва
ва ![]() белгилаш
билан Лаплас ўзгартишларини фарқлашади. Ушбу баёнда
белгилаш
билан Лаплас ўзгартишларини фарқлашади. Ушбу баёнда ![]() белгилаш
тизимини қабул қилинади, чунки унинг бир қатор афзалликлари
мавжуд (17.1 мисолдан сўнгги эътирозга қаранг).
белгилаш
тизимини қабул қилинади, чунки унинг бир қатор афзалликлари
мавжуд (17.1 мисолдан сўнгги эътирозга қаранг).
17.1 Оператор усули
Ван-дер-Поль ғояси билан боғлиқ бўлган оператор усулининг хозирги замон талқинининг моҳияти шундан иборатки, оригинал (асл) деб аталмиш ѓ(f) функцияга F(p) тасвир қиёсланади: бунда « p » оператори вақт t дан фарқли бўлган бирор ўзгарувчи, функция ѓ(f) эса t> 0 ёки t>0 бўлганда аниқланган ва t>o да узлуксиздир.
Оригинал ва тасвирларнинг мослигини « ~ » белги билан ифодалаймиз, яъни
![]() ~
~ ![]() ёки
ёки
![]() ~
~![]() (17.1)
(17.1)
Ушбу мослик ўзаро ягона маъноликда бўлиши зарур: ихтиёрий ѓ функцияга биргина F тасвир мос бўлиши, ихтиёрий F тасвир учун ягона ѓ функция, яъни оригинал мос бўлиши шарт.
Чизиқли тизимларни кўраётганимиз сабабли, тузилаётган тасвирлар тизими чизиқлилик принципини қаноатлантириши зарур: уни бундай таърифлаш мумкин:
![]() ~
~![]() (17.2)
(17.2)
Агар ѓ1~F1 ва ѓ2~F2 , (17.3)
бунда ![]() ва
ва ![]() -ўзгармас кўпайтувчилар.
-ўзгармас кўпайтувчилар.
Кейинги ифодадан кўринадики, оригинални бирор ўзгармас қийматга кўпайтириш, тасвирни шу қийматга кўпайтиришга мос келади: оригиналга қўшиш эса тасвирни қўшишга мос.
Умумий ҳолда оригинал устидаги математик аммаларга тасвир устидаги ушбу математик амаллар мос келади. Агар шундай амаллар натижасида ѓ1 функция ѓ2 га айланса, F1 эса F2 айланса, у ҳолда натижалар учун ҳам мослик тўғри келади:
ѓ1~F1, ѓ2~ F2
Оператор усули дифференциал тенгламаларни ечиш учун киритилган, шунинг учун тасвирлаш тизими шундай қуриладики, натижада дифференциаллаш амали тасвир устида соддароқ бўлган алгебраик амал билан алмаштирилади. Бундай ҳолатда, оригинал учун ёзилган дифференциал тенглама тасвир учун ёзилган алгебраик тенглама билан алмаштирилади.
Шунга ўхшаш оригиналдан тасвирга ўтиб амалларни алмаштириб
бажариш барча учун яхши маълум. Масалан, сонларнинг логарифмларини оригиналнинг
тасвири деб қаралиши мумкин: ![]() ~
~ ![]() , бунда оригиналнинг кўпайтмаси улар тасвирининг йиғиндиси
, бунда оригиналнинг кўпайтмаси улар тасвирининг йиғиндиси
![]() ~
~![]() деб қаралади. Аниқланган тасвирлар
йиғиндиси
деб қаралади. Аниқланган тасвирлар
йиғиндиси ![]() орқали оригиналлар кўпайтмаси
орқали оригиналлар кўпайтмаси ![]() аниқланади. Гармоник функция (оригинал)ни
комплекс орқали тасвирлаш бунга яна бир яққол
мисолдир. Бунда оригинални дифференциаллаш - тасвирни jщ га
кўпайтиришга мос келади.
аниқланади. Гармоник функция (оригинал)ни
комплекс орқали тасвирлаш бунга яна бир яққол
мисолдир. Бунда оригинални дифференциаллаш - тасвирни jщ га
кўпайтиришга мос келади.
Бундан ташқари, оператор усулини қўллаш барча функцияларнинг бошланғич қийматларини аниқлашдан озод этади - улар оддий ўткинчи жараёнлар учун ҳам, худди шундан ножўя коммутация масалалари учун ҳам ўз-ўзидан келиб чиқади.
Функция ![]() ни дифференциаллаш чизиқли амал бўлганлиги учун
ни дифференциаллаш чизиқли амал бўлганлиги учун
![]() (17.4)
(17.4)
тасвир учун бажариладиган алгебраик амаллар ҳам чизиқли бўлиши шарт.
Оддий чизиқли амал - бу р операторга кўпайтиришдир: у оператор усулида дифференциаллашга хос бўлган амал, деб қабул қилинган:
агар ![]() ~
~ ![]() бўлса
бўлса ![]() ~
~![]() . (17.5)
. (17.5)
Бунда ![]() 10.1,а-расмда кўрсатилгандек
t>0 бўлганда узлуксиз
10.1,а-расмда кўрсатилгандек
t>0 бўлганда узлуксиз
t<0
17.1-расм
бўлганда нолга тенг бўлган функция ѓ(t)дан олинган умумлаштирилган ҳосилани аниқлайди, деб қабул қилинади.
17.2. Оддий функцияллар тасвири
Оригинал билан унинг оператор тасвири орасида мосликни киритиб, биз чизиқлилик талабини (17.2) ифодаладик, шу билан бирга тасвирда умумлаштирилган ҳосила бўлишига (17.5) шартлашдик.
Муайян берилган функциянинг тасвирини аниқлаш учун бирор aниқ оригинални тасвирлаш шаклини танлашимиз зарур. Бу билан умуман барча тасвирлаш тизими учун жорий этилувчи тасвирлар ва оригиналлар орасидаги боғланиш шаклини тадбиқ этилади: оригинал ѓ(f) ва тасвир F(p) орасида ўтиш калити (ёки коди) ўрнатилади, шундан сўнг барча тасвирлаш тизими ўзаро ва узил-кесил аниқланган бўлади.
Хевисайднинг оператор усулида энг содда боғланиш бўлмиш
1 ~1 (17.6)
бир сонини бир сони тасвирлайди.
Кейинги бобда келтириладиган сабабларга кўра, Хевисайд тизими баъзи афзалликларга эга бўлса ҳам, аксарият, Лапласнинг интеграл ўзгартишига мос келган боғланиш қўлланилади:
1 ~1 /p, (17.7)
-бир рақами бир бўлинган оператор р шаклида ёзилади.
Юқоридаги (17.6) ва (17.7)
ифодалар чап томонидаги функция фақат t>0
бўлганда 1 га тенг ва t<0 бўлганда нолга тенг, яъни (17.6) а (17.7)ларнинг
чап томонидаги функция-Хевисайд функциясидир.
![]() функциянинг тасвири. (17.7) ифодани (17.5) га тадбиқ этиб, ҳамда Хевисайд функциясининг ҳосиласи
функциянинг тасвири. (17.7) ифодани (17.5) га тадбиқ этиб, ҳамда Хевисайд функциясининг ҳосиласи ![]() функция эканини эътиборга олсак қуйидагини аниқлаймиз:
функция эканини эътиборга олсак қуйидагини аниқлаймиз:
![]() ~1.
(17.8)
~1.
(17.8)
Аниқ интеграл. Юқоридаги мулоҳазалардан қуйидаги хулосани чиқариш мумкин: 0 дан t гача бўлган оралиқда оригинални интеграллаш тасвирни оператор р га бўлишга мос келади:
 ~
~![]() агар ѓ~F
бўлса,
(17.9)
агар ѓ~F
бўлса,
(17.9)
чунки ҳосил бўлган функция:
 ~X
(17.10)
~X
(17.10)
t=0 бўлганда нолга тенг, яъни х (0-)=0.
Дарҳақиқат, унинг ҳосиласига (17.5) ни тадбиқ этиб, аниқлаймиз
![]() ~
~ ![]() (17.11)
(17.11)
Демак, интегралнинг тасвири Х=F/p экани исботланди.
Даража t нинг тасвири. Агар ![]() ~ F ва t<0
бўлганда ѓ=0 бўлса, унда:
~ F ва t<0
бўлганда ѓ=0 бўлса, унда:
![]() ~ pF=1/p.
~ pF=1/p.
Охирги боғланишнинг ўнг томонидан қуйидагини аниқлаймиз:
![]() ~ t
(17.12)
~ t
(17.12)
Шунга ўхшаш,
![]() ~
~![]() (17.13)
(17.13)
эканлигини топамиз.
Экспонентанинг тасвири. Фараз қилайлиқ:
![]() ~ F,
(17.14)
~ F,
(17.14)
ва t<0 бўлганда ѓ=0 бўлсин, яъни
![]() (17.15)
(17.15)
бўлсин. Бундай холатда (17.6), (17.5) ва (17.8) дан t < 0- учун
![]() ~
~ ![]() (17.16)
(17.16)
экани аниқланади.
Тенглик (17.16) нинг ўнг томонини F га нисбатан ечсак ва таърифга кўра (17.17) оригиналнинг тасвири экспонента бўлишини ёддан чиқармай туриб, қуйидагини аниқлашимиз мумкин:
![]() ~
~![]() .
(17.17)
.
(17.17)
Унга интеграллаш (10.9)ни тадбиқ этиб, қуйидагини аниқлаймиз:
![]() ~
~ ![]() .
(17.18)
.
(17.18)
«Операторлар мослиги» билан ишлашнинг оддий воситасини тушиниш учун шуни эътиборга олиш зарурки, келтириб чиқарилган ифодаларни чизиқлилик қоидаси (17.4), (17.7) ва (17.17) ифодалардан фойдаланиш йўли билан ҳам аниқлаш мумкин:
![]() ~
~ ![]() (17.19)
(17.19)
Ифоданинг ўнг
томонида умумий махражга келтириш амали бажарилди. Шу йўл билан экспоненталар (![]()
![]()
![]() ва х.к.)
билан ифодаланган турли ҳилдаги функцияларнинг тасвирини аниқлаш
мумкин.
ва х.к.)
билан ифодаланган турли ҳилдаги функцияларнинг тасвирини аниқлаш
мумкин.
[ѓ(0-) ≠ 0] бўлгандаги ҳосила тасвири. Функциялар ва тасвирлар билан амалларни бажарганда биз ѓ(0-) = 0 деб фараз қилган эдик. Агар
ѓ(0-)≠0 бўлса, у ҳолда умамлаштирилган ҳосилага қуйидаги ҳад қўшилади:
![]() ~
~ ![]() (17.20)
(17.20)
чунки бу (17.20) ифодадан келиб чиқади.
(17.20) да ўнг
томонидаги ифода чап томон тасвиридир, чунки (17.8)га кўра ![]() ~ 1 . Бу эса, ҳосиланинг тасвири эканини кўрсатади
~ 1 . Бу эса, ҳосиланинг тасвири эканини кўрсатади
![]() ~
~ ![]() (17.21)
(17.21)
Демак, охирги ифода ҳар доим қўлланилиши мумкин, чунки
ѓ(0-) =0 бўлганда ўз-ўзидан (17.21)дан хусусий ҳол (17.5) келиб чиқади.
Ифода (17.21) L- ўзгартишга мос келади; L+ ўзгартишда эса қуйидагича:
![]() ~
~ ![]() (17.21,а)
(17.21,а)
деб ёзилади.
Ушбу икки
ифодалаш коммутация қонунини ![]() амал қиладиган
бўлган барча оддий масалаларга мос келади.
амал қиладиган
бўлган барча оддий масалаларга мос келади.
Юқори ҳосилаларни (17.21) дан ҳосил қилиш осон: бунинг учун келтириб чиқарилган ифодани ц(f)=df/dt функцияга қўлланилса кифоя.
Интеграл билан ифодаланган, лекин (t=0-)да нолдан фарқли функциялар. Бундай функциялар турига, масалан сиғимдаги кучланиш ![]() киради; бунда
киради; бунда ![]() бўлган ва
бўлган ва ![]() нинг кейинги ўзгариши токнинг интеграли
ва сиғимга бўлингани билан ифодаланади:
нинг кейинги ўзгариши токнинг интеграли
ва сиғимга бўлингани билан ифодаланади:
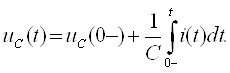 (17.22)
(17.22)
Чизиқлилик принципи (17.22) дан ҳамда ўзгармас қийматнинг (17.7) ва интегралнинг тасвирларидан (17.9) равшанки,
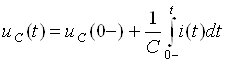 ~
~
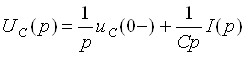
ёки
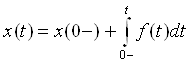 ~
~ 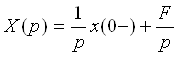 (17.23)
(17.23)
бунда ![]() ~
~![]() .
.
Охирги ифода
(17.9) ва (17.10) ни ![]() хусусий хол сифатида ўз ичига
олади.
хусусий хол сифатида ўз ичига
олади.
17.3 Оператор усули билан дифференциал
тенгламаларни ечиш
Қуйидаги тенгламани ечиш керак бўлсин:
![]() (17.24)
(17.24)
бунда бошланғич
шарт ![]() берилган бўлсин.
берилган бўлсин.
Хосилалар тасвири қоидасидан (17.21) фойдаланиб, берилган (17.24) дифференциал тенгламага мос келган оператор тенгламасини тузамиз:
![]() (17.25)
(17.25)
бунда F ~ ѓ ва Ф ~ ц.
Аниқланган (17.25) тенгламада бошланғич шарт эътиборга олиниб биринчи кўпайтма таркибига киритилди. (17.26)ни F га нисбатан ечиб, қуйидагини аниқлаймиз:
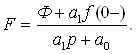 (17.26)
(17.26)
Изланаётган вақт функцияси ѓ(t) ни аниқлаш учун, унга мос келган F(p) оригинални топиш керак.
17.1-мисол. Занжир r, C ўзгармас u=U0 (17.1,б-расм)
кучланишли манбага уланганидаги токни аниқланг. Коммутациягача сиғим
![]() кучланишгача
зарядланган.
кучланишгача
зарядланган.
Ечиш. Сиғимдаги кучланиш қуйидаги тенглик билан ифодаланади:
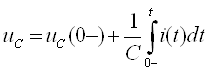
ва занжирнинг тенгламаси қуйидагича бўлади:
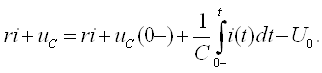
![]()
Оператор тенгламаси қуйидагига ифодаланади:
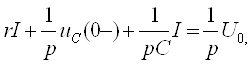
бундан изланаётган токнинг қиймати аниқланади:
 ,
,
бунда a=1/rС.
Ечимдан ўзининг ўзгармас кўпайтмаси билан фарқли бўлган тасвирнинг оригинали (17.27) бизга маълум. Ундан ташқари, ѓ ~ F бўлса aѓ=aF (17.28) эканлиги ҳам бизга маълум. Шунинг учун изланувчи функцияни аниқлаймиз:
![]() .
.
17.2-мисол. L,r занжирнинг (17.2,а-расм, бунда r2+R=r; коммутациягача ток i2=i берилган) коммутациядан кейинги токни аниқланг.
Ечиш. Оригинал ri+Ldi/dt=0 тенгламасидан унинг оператор шаклидаги ёзувчига ўтиб ва хосилани ифодалаш учун (17.21) дан фойдаланиб, қуйидагини аниқлаймиз:
rI+LpI-Li(0-)=0,
ундан I=Li(0-)/(r+Lp).
Ушбу тенгламани аввал кўрилган (17.27)га мос келган шаклга келтириб, қуйидагини аниқлаймиз:
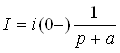 ~
~ ![]()
бунда ![]() .
.
Оператор усулида бошланғич шарт масаласи
кўрилмайди, чунки ўз-ўзидан тенглама оператор шаклида ёзилиши жараёнида ҳисобга олинади. Фақат
тенглама (17.21) ва (17.23)ни ҳисобга олиб тўғри ёзилишига эътибор
бериш зарур; бунда коммутация жўяликми [индуктивлиги бўлган занжир учун ![]() ёки ножўя
ёки ножўя ![]() коммутациями - фарқи йўқ. Ушбу
афзаллик айнан L- тизимлар учун хосдир.
коммутациями - фарқи йўқ. Ушбу
афзаллик айнан L- тизимлар учун хосдир.
17.3-мисол. Ножўя коммутация вазиятини кўрайлик (17.9,а-расм). Занжирнинг калит узилгандан сўнгги оператор тенгламаси қуйидаги шаклда ёзилган:
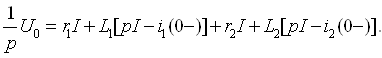
Ушбу тенглама I~i ток иккала индуктивлик учун умумий бўлган ток учун ёзилган: бироқ i (0-) токнинг қиймати L1 ва L2 учун ҳар хилдир.
Ечиш. Кейинги тенгликдан I ни аниқлаймиз:
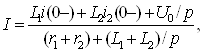 (а)
(а)
ва касрнинг тасвирига ўтамиз:
![]() (б)
(б)
бунда a=(r1+r2)/(L1+L2).
Биринчи касрнинг кўпайтувчиси, ўз-ўзидан маълумки, токнинг бошланғич шарти (қиймати), у аввал аниқланган (17.26) билан мос келади.
Иккала каср маълум бўлган вақт функцияси тасвири. Дарҳақиқат, (17.27) ва (17.28)дан қуйидагини аниқлаймиз:
I ~ i(f) = i(0+)e-бt+![]() (1- e-бt).
(в)
(1- e-бt).
(в)
Дифференциал тенгламалар юқори тартибли бўлганда ҳам тасвир тенгламаси шу тарзда тузилади. Бироқ, бунда оператор ифода F(p) дан изланаётган оригинал ѓ(t) га ўтишда мураккаброқ бўлган функциялар учун мослик мавжудлигини билиш зарур. Ҳар хил турдаги масалаларни ечишда ѓ~F мослик жадвали қурилади. Юзлаб хар ҳил функциялар тасвирларининг жадваллари кенг тарқалган. Мураккаб масалаларни ечишда ушбу жадвалларга мурожаат этиш зарур. Келтирилган қисқа 17.1-жадвалдан ҳам керакли бўлган мосликлар мажмуасини ҳосил қилиб, чизиқли занжирларнинг ҳар турдаги масалаларини ечиш мумкин.
Жадвал ёрдамида ушбу масалаларни ечиш жараёнида қуйидаги зарур бўлган амалий қадамга эътиборни қаратамиз. Аниқланган F(p) ифодада шундай алгебраик ўзгартишлар амалга оширилиши керакки, уни 17.1-жадвалдаги мавжуд ифодалардан бирига ўхшатишга имкон берсин.
17.4. Тасвирлар F(p) ва уларнинг оригиналлари ѓ(t) жадвали
17.1-жадвалнинг биринчи беш ифодадаги аввал аниқланган (17.7), (17.8), (17.12), (17.17) ва (17.18) ифодалардир. (6) ва (7) тенгликлар чизиқлилик принципи асосида авалгилари ёрдамида аниқланади.
Экспоненталар кўрсаткичлари ва махраж илдизлари тасвири. Агар тасвир каср шаклида бўлса:
![]() ~
~ ![]() ,
(17.28)
,
(17.28)
Тасвирланаётган ѓ(t) функция эса экспоненталар йиғиндиси бўлса, у ҳолда шу экспоненталар кўрсаткичлари t олдидаги коэффициентлар қуйидаги тенглама илдизига тенг:
![]()
17.1-жадвал
|
Ифодалар № |
F(p) |
t≥0 бўлгандаги ѓ(t) |
|
(1) |
1/р |
1(или 1) |
|
(2) |
1 |
|
|
(3) |
1/р2 |
t |
|
(4) |
1/(р+а) |
e-at |
|
(5) |
а/р(р+а) |
1-e-at |
|
(6) |
а2/р2(р+а) |
at-(1-e-at) |
|
(7) |
F7қ[р (р+а)(р+b)]-1 |
|
|
(8) |
pF7 |
|
|
(9) |
p2 F7 |
|
|
(10) |
F10қ{p[(p+б)2-м2]}-1 |
|
|
(11)
|
pF10 |
|
|
17.2-расм жадвал давоми |
||
|
Ифодалар№ |
F(p) |
t≥0 бўлгандаги ѓ(t) |
|
(12) |
p2 F10 |
|
|
(13) |
(p2+pб) F10 |
|
|
(14) |
F14қ{p[(p+б)2+в2]}-1 |
|
|
(15) |
pF14 |
|
|
(16) |
p2 F14 |
|
|
(17) |
(p2+pб) F14 |
e- б t сos вt=Re e-yt |
|
(18) |
1/(p2+ в2) |
1/в sin Bt |
|
(19) |
p/(p2+ в2) |
cos Bt |
|
(20) |
1/[p(p+a)2] |
|
|
(21) |
p/[p(p+a)2] |
te-бt |
|
(22) |
P2/[p(p+a)2] |
(1-at) e-бt |
18-Маъруза. Оператор узатиш функцияси, унинг ноллари
ва қутблари, уларнинг комплекс текисликд
жойлашишлари
Коммутациядан аввалги холат ѓ(0) ни эътиборга олган оператор тенгламаларининг умумий усули. Дифференциал шаклдаги Кирхгоф тенгламаларини тузиб, уларнинг оператор шаклига ўтиб, ечимлари изланаётган функциянинг тасвирини аниқлашга имкон берувчи дифференциал тенгламалар тизимини ҳосил қиламиз. Бунда, агар (17.2-жадвалга мувофиқ) интеграллар ва дифференциалларнинг тасвирлари тўғри ёзилган бўлса, барча бошланғич шартлар ўз-ўзидан ҳисобга олинган бўлади. Мисол тариқасида дифференциал тенгламаларни, уларни ечишдан олдин, оператор тенгламаларига ўтказишни кўрсатиш мумкин.
Бироз тажрибага эга бўлгандан сўнг, оператор тенгламаларни, улар ечимидан аввал, тўғридан-тўғри ёзиш мумкин.
Ушбу фикрлар қуйида кўриладиган мисоллардан сўнг аниқ ва равшан бўлади.
18.1.-мисол. Занжирнинг (18.1,а-расм) индуктивлиги бўлган шохобчасидаги ўткинчи жараён токини манбанинг узилганидан сўнг аниқланг. Коммутациягача (t=0- барқарорлик режими мавжуд бўлиб, ток ва кучланишнинг қийматлари маълум бўлган.
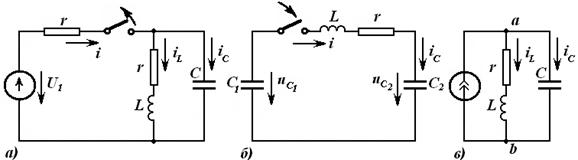 18.1-расм
18.1-расм
Ечим. Расмдаги мусбат йўналишларни
танлаб, тенгламаларни тузамиз. Биринчидан,
![]()
эканлиги аниқ, иккинчидан, манба узилганидан сўнг ундаги ток - сиғим разрядланишининг токидир (танланган мусбат йўналишни эътиборга олиб), яъни:
![]() .
.
Кейинги икки тенгламалар оператор шаклида 16.1-жадвал қоидаларига мувофиқ қуйидагича ифодаланади:
![]()
![]()
![]()
Ҳосил бўлган тенгламалар тизимини ечиб, қуйидагини аниқлаймиз:
![]()
Кейинги тенгламани 16.1-жадвалда келтирилган ифодаларга ўхшаш ҳолатга келтириш зарур. Махражнинг илдизларини аниқлаб
![]() ,
,
бунда, ![]() бўлганда ечимга қуйидаги шаклни берамиз:
бўлганда ечимга қуйидаги шаклни берамиз:
![]()
Биринчи ҳад 16.1-жадвалнинг (15) ифодасига, иккинчиси эса (16)га мос келади. Шунинг учун:
![]()
бунда ![]() ва
ва ![]()
Эслатма: Мисолни ечишда 18.1,а-расмдаги занжир учун биргина номаьлумли иккинчи даражали тенгламасидан фойдаланиш мумкин эди:
![]() .
.
Бироқ, бу ечимни енгиллаштирмайди, балки бироз мураккаблаштиради эди.
18.2-мисол. С1
сиғим кетма-кет уланган r ва L орқали бошқа С2 сиғимда
разрядланаяпти (18.2,б-расм).
Коммутация онигача ![]() B;
B; ![]() . Занжирнинг
параметрлари: r=100 Oм; L=0,01 Гн; C1=30 ва С2=15мкФ.
Кучланиш
. Занжирнинг
параметрлари: r=100 Oм; L=0,01 Гн; C1=30 ва С2=15мкФ.
Кучланиш ![]() ни аниқланг.
ни аниқланг.
Ечим. Занжирнинг тенгламаси, қуйидагича бўлади:
![]()
![]() ,
,
(бунда токнинг мусбат йўналиши биринчи сиғим разрядланишига ва иккинчи сиғимнинг разрядланишига мос келади).
Бу тенгламалар uc2(0-)=0 ва i(0-)=0 бўлганда оператор шаклда қуйидагича ёзилади:
![]()
![]() .
.
Уларнинг ![]() га нисбатан ечими қуйидагича бўлади:
га нисбатан ечими қуйидагича бўлади:
![]()
бунда
махражнинг икки ҳақиқий
илдизлари ![]() бунда
бунда ![]()
![]() (
(![]() бўлгани
учун илдизлар ҳақиқий
сонлардир).
бўлгани
учун илдизлар ҳақиқий
сонлардир).
Мисолнинг сон қийматлари қуйидагича бўлади
![]() б = 5000c-1;
б = 5000c-1; ![]() .
.
Бундай ҳолат учун 10.1-жадвалнинг (10) ифодасидан фойдаланиб, қуйидагини аниқлаймиз:
![]()
бунда t миллисекундда ўлчанади.
18.3-мисол. 17.1,б-расмдаги занжирда манба J токининг қиймати 0,5А дан 1,5А гача бир онда ўзгарди. Бунчага занжирда барқарорлик вазияти мавжуд эди. Занжирнинг параметрлари: С=10-8 Ф; r=20 Ом; L=0,1 Гн.
Талаб қилинади: сиғимдаги кучланишни оператор шаклига келтириш ва
10.1-жадвалдан бунга мос келган ѓ(t) функцияни аниқлаш.
![]() Ечиш. Занжирнинг тенгламаси куйидагича
бўлиши аён:
Ечиш. Занжирнинг тенгламаси куйидагича
бўлиши аён:
![]() (а)
(а)
![]()
шу тенгламалар оператор шаклида қуйидагича бўлади:
![]() (б)
(б)
![]() (в)
(в)
Бунда (б) тенгликда (а) даги икки тенглама бирлаштирилади: бошланғич шарт аниқланади: iL(0-)=0,5 A; Uc(0-)=10 B.
Кейинги (б) ва (в) тенгламаларнинг биргаликдаги ечими Uc нинг ифодасини қуйидаги шаклда ёзишга имкон беради:
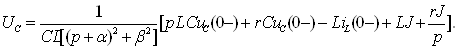
Бу тенглик ташкил этувчиларига мос келган ѓ(t) функциялар 17.1-жадвалнинг (14), (15) ва (16) ифодаларида келтирилган.
Суперпозиция усули. Ҳар қандай ўткинчи жараённи ушбу занжирнинг илгариги ҳолатидан кейинги ҳолатига, яъни биринчи барқарорлик режимидан иккинчи барқарорлик режимига ўтиш деб қараш мумкин. Занжирлардаги бундай доимий режим ўзгаришлари - янги манбаларнинг уланиши ёки занжирнинг параметрлари ўзгариши, масалан, янги шохобчанинг уланиши ёки узилиши билан боғлиқ.
Фараз қилайлик, илгариги режим бир u1 манба билан янгиси эса иккинчи u2 нинг қўшилиши билан боғлиқ бўлсин.
Занжирнинг натижавий режимини - унинг илгариги ҳолатига кейинги қўшимча таъсир, яъни u2 манбанинг қўшилиши билан ҳосил бўлган режимни устлаш деб қараш мумкин. Бу қўшимча таъсир, занжирнинг чизиқлилиги сабабли занжирнинг аввалги ҳолатига боғлиқ бўлмайди (суперпозиция принципи). Шунинг учун янги манба u2 нинг пайдо бўлиши билан ҳосил бўлган жараённи ҳисоблаш нолли бошланғич шартларда бажарилади ва, албатта, биринчи манба йўқ деб фараз қилиб амалга оширилади.
Ҳақиқий режимни аниқлаш учун, янги кучланиш уланиши сабабли ҳосил бўлган режим учун аниқланган барча ток ва кучланишларни аввалги, яъни биринчи u1 манбанинг таъсиридаги режимнинг ток ва кучланишлари билан алгебраик йиғиндиси олиниши керак.
Қандайдир шохобча ёки занжир бўлаги уланиши ёки узилиши сабабли ҳосил бўлган ўткинчи жараёнларни қўшимча эквивалент манбанинг қўшилиши деб қараш мумкин.
Мисол тариқасида 18.2,а-расмда келтирилган
занжирда бирор шохобча узулиши натижасида содир бўладиган коммутацияни
кўрайлик. Бундай узилишнинг физик жараёнини илгариги режимга унинг узилиш нуқтасида
қўшимча ток манбаси J(t) уланган (18.2,а-расм) режим қўшилаётган
(устланаётган) лиги билан тенглаштириш мумкин. Бу янги манба
токининг қиймати илгариги режимнинг шу шахобчадаги токи билан тенг ![]() бўлиб, унга тескари йўналтирилган бўлади.
бўлиб, унга тескари йўналтирилган бўлади.
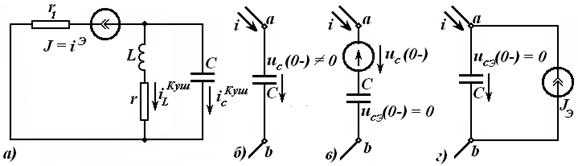 18.2-расм
18.2-расм
Илгариги ![]() ва қўшимча
ва қўшимча ![]() токларни алгебраик қўшиб (устлаш,
суперпозиция), хақиқий режимнинг токи (ёки кучланиш)ини аниқлаймиз.
токларни алгебраик қўшиб (устлаш,
суперпозиция), хақиқий режимнинг токи (ёки кучланиш)ини аниқлаймиз.
Илгариги ![]() ва J(f)
манба қўшилиши сабабли хосил бўлган қўшимча
ва J(f)
манба қўшилиши сабабли хосил бўлган қўшимча ![]() токларни алгебраик йиғиндисини
олиб, бирламги занжир узилишидан кейинги хосил бўлувган ток (ёки кучланишни),
масалан индуктивликдаги
токларни алгебраик йиғиндисини
олиб, бирламги занжир узилишидан кейинги хосил бўлувган ток (ёки кучланишни),
масалан индуктивликдаги ![]() токни аниқлаймиз.
токни аниқлаймиз.
Эквивалент манбалар усули. Занжирни ҳисоблашнинг нол бўлмаган бошланғич шартларидаги усулини нолли бошланғич шарти бўлган усул билан алмаштириш мумкин: бунда занжирга шундай қўшимча манбалар киритилиши тахмин қилинадики, унда киритилаётган манбалар берилган токларга (индуктивликда) ва кучланишларга (сиғимда) эквивалент бўлсин. Бу усул ўзининг яққоллиги билан ажралиб туради ва қўшимча (эквивалент) манбаси бўлган занжирларни нолли бошланғич шарти бўлган занжир сифатида ҳисоблаш имконини беради. Қўшимча манбалари бўлган занжирлар оператор схемалари дейилади.
Нолли бошланғич кучланиши бўлган сиғим учун эквивалент иккиқутблик. Бундай сиғим токи ва кучланиши орасидаги боғланиш (18.2,а-расм) қуйидаги тенглама билан ифодаланади:
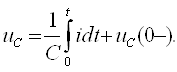 (18.1)
(18.1)
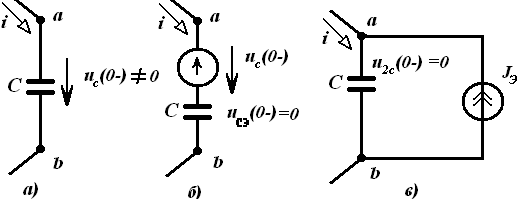
18.3-расм
Шунга ўхшаш
тенглама билан икки қутбликнинг токи ва кучланиши ифодаланади: иккиқутбликнинг таркибида кетма-кет уланган ![]() ўзгармас кучланишли манба ва қиймати нолга тенг
бўлган
ўзгармас кучланишли манба ва қиймати нолга тенг
бўлган ![]() бошланғич кучланишли сиғим (18.3,б-расм) мавжуд: бунда
бошланғич кучланишли сиғим (18.3,б-расм) мавжуд: бунда ![]() -эквивалент схема сиғимининг кучланиши.
-эквивалент схема сиғимининг кучланиши.
Демак, нолдан фарқ қилувчи бошланғич кучланиши
бўлган хар қандай сиғим, ўзига ўхшаш, лекин бошланғич кучланиши
нолга тенг [![]() ] бўлган сиғим ва унга кетма-кет уланган
] бўлган сиғим ва унга кетма-кет уланган ![]() кучланишли ўзгармас ток манбаси билан алмаштирилиши мумкин; бундай манбанинг кучланиши оператор шаклда
кучланишли ўзгармас ток манбаси билан алмаштирилиши мумкин; бундай манбанинг кучланиши оператор шаклда ![]() га тенг бўлади.
га тенг бўлади.
Кучланиш манбаси (18.3,б-расм) умумий қоидага кўра эквивалент ток манбаси Jэ (18.3,в-расм) алмаштирилиши мумкин. Манбанинг токи оператор шаклида қуйидагича ёзилади:
![]() ; (18.2)
; (18.2)
18.3,в-расмдаги манба токи 18.3,б-расмдаги манба кучланишини [яъни ![]() ]ни шахобча ўтказувчанлиги
]ни шахобча ўтказувчанлиги ![]() га кўпайтирилганига тенг.
га кўпайтирилганига тенг.
![]() Нол
бўлмаган бошланғич токли индуктивликка эквивалент бўлган иккиқутблик. Бундай индуктивлик (18.3,а-расм) учун ток ва кучланиш
Нол
бўлмаган бошланғич токли индуктивликка эквивалент бўлган иккиқутблик. Бундай индуктивлик (18.3,а-расм) учун ток ва кучланиш
боғланиши қуйидаги тенглама билан ифодаланади:
 (18.3)
(18.3)
Таркибида нолли бошланғич токи iэ(0-)
бўлган индуктивликка параллел уланган i(0-) ток манбасидан иборат эквивалент
схема иккиқутблик (18.3,б-расм)нинг токи ва кучланиши орасидаги боғланиш
хам шунга ўхшаш тенглама билан ифодаланади. Манба токининг оператор шаклидаги
ёзуви:
![]() ~
~ ![]() (18.4)
(18.4)
Ток манбасини кучланиш манбаси (18.3,в-расм) билан алмаштириш мумкин. Эквивалент манбанинг кучланиши оператор шаклидаги ёзуви қуйидагича бўлади:
![]() (18.5)
(18.5)
бунда ![]() индуктивликнинг оператор қаршилиги.
индуктивликнинг оператор қаршилиги.
Бу манба ўзида бошланғич токи бўлмаган индуктивлик L билан кетма-кет уланган (17.3,в-расм). Бироқ, индуктивликда кучланиш
![]() ~
~ ![]() (18.6)
(18.6)
таъсирида ундаги ток бир онда хосил бўлади.
Берилган нолга тенг бўлмаган бошланғич шартли занжирда барча зарядланган сиғим ва индуктивликларни эквивалент иккиқутблик билан алмаштириб, нолли бошланғич шарти бўлган хамда қўшимча эквивалент манбали янги занжирга келамиз.
Ток ва кучланишларнинг коммутациядан сўнгги биринчи онда ва барқарорлик режимида тақсимланиши.
1. Кўрилаётган функция ѓ(t) нинг коммутациядан сўнг биринчи ондаги қийматини, яъни ѓ(0+) ни, хамда унинг барқарорлик режимидаги (агар бу режим бўлса) қийматини, яъни ѓ(∞) қийматини уларнинг тасвир билан оддий боғланишидан F(p)~ f(t) аниқлаш мумкин. Бундай боғланишнинг мавжудлигини оддий функциялар тасвирлари (17.1-жадвал)дан аниқлаш мумкин.
Оригиналнинг ![]() t→ (0+) бўлгандаги қиймати тасвирнинг p→∞ бўлгандаги р қийматга
кўпайтирилганига тенг:
t→ (0+) бўлгандаги қиймати тасвирнинг p→∞ бўлгандаги р қийматга
кўпайтирилганига тенг:
![]() (18.7)
(18.7)
2. Оригиналнинг t→∞ бўлгандаги қиймати тасвирни p→0 даги р га кўпайтмасига тенг:
![]() ,
(18.8)
,
(18.8)
агар фақат t→∞ бўлганда f(t) функция чекли лимитга эга бўлса [баъзи холатларда фақат f(t)/t қиймат чекли лимитга эга бўлиши зарур].
Қилинган қўшимча шартнинг зарурлигига
осонлик билан иқрор бўлиш мумкин: (18.8) тенгликни 17.1-жадвалдаги (4)
ифодага қўллаб бўлмаслиги аниқ: чунки ![]() шунингдек, a=jщ бўлса
шунингдек, a=jщ бўлса
![]()
3. Индуктивликдаги ток ва сиғимдаги кучланиш
ўзгармасдан қолишидек жўяли коммутация бўлганида, f(0+) ни ҳисоблаш
учун занжирнинг коммутациядан сўнгги кўриш мумкин; унда коммутациядан сўнг реал
мавжуд бўлган реал манбалар билан бирга, индуктивликлар ўрнига берилган токга
тенг бўлган ток манбаси ![]() ва сиғимлар ўрнига берилган
кучланишга тенг бўлган кучланиш манбаси
ва сиғимлар ўрнига берилган
кучланишга тенг бўлган кучланиш манбаси ![]() киритилади. Нолли бошланғич қийматлар
киритилади. Нолли бошланғич қийматлар
![]() ва
ва ![]() бўлганда индуктивлиги бўлган шохобчалар
узилган (ток манбаси J=0 ), сиғимли клеммалари эса қисқа
туташган (кучланиш манбаси U=0) бўлади.17.4,а-расмда занжирнинг
уланиши қўрсатилган:
бўлганда индуктивлиги бўлган шохобчалар
узилган (ток манбаси J=0 ), сиғимли клеммалари эса қисқа
туташган (кучланиш манбаси U=0) бўлади.17.4,а-расмда занжирнинг
уланиши қўрсатилган:
18.4-расм
18.4,б-расмда ![]() бўлгандаги ток ва кучланишларнинг бошланғич
тақсимланишини аниқлаш схемаси: 18.4,в-расмда
бўлгандаги ток ва кучланишларнинг бошланғич
тақсимланишини аниқлаш схемаси: 18.4,в-расмда ![]() ва
ва ![]() бўлгандаги юқоридагига ўхшаш схема
келтирилган: албатта, охирги схема
бўлгандаги юқоридагига ўхшаш схема
келтирилган: албатта, охирги схема ![]() бўлса ундан аввалги холат учун хам қўлланилиши
мумкин.
бўлса ундан аввалги холат учун хам қўлланилиши
мумкин.
18.1 Нолли бошланғич шартлари бўлган
ўткинчи жараённи ҳисоблаш
Кўрилаётган тенглама n-тартибли бўлсин. Агар тенгламанинг (n-1)- тартибидан бошлаб барча хосилалари ўткинчи жараён бошланиш онида нолга тенг бўлса, унга мос келувчи оператор тенгламанинг ёзилиши кескин соддалашади:
![]() .
(18.9)
.
(18.9)
Бу ифодаланган шартлар нолли бошланғич
шартлар дейилади. Бундай шартларда ![]() -тартибдаги ихтиёрий хосила оператор
тенгламасида оддий m-даржадаги р нинг кўпайтмаси сифатида
тасвирланади:
-тартибдаги ихтиёрий хосила оператор
тенгламасида оддий m-даржадаги р нинг кўпайтмаси сифатида
тасвирланади:
![]() ~
~ ![]() (18.10)
(18.10)
Ушбу фикрлар таркибида интеграли бўлган тенгламаларга хам хосдир: бунда интегрални манфий ишорали хосила деб қабул қилиш мумкин. Масалан, «э» э.ю.к га уланаётган сиғимли C, r занжирдаги токнинг ифодаси қуйидагича
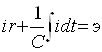 .
(18.11)
.
(18.11)
бўлади.
Бунда хосиланинг энг юқори тартиби нолга
тенг - бу ![]() функциянинг ўзидир. Бундан шундай хулоса
келадики, t=0 бўлганда минус 1-тартибли хосила нолга тенг бўлса, ёки,
бошқача қилиб айтганда, коммутациягача сиғим зарядланмаган
бўлса:
функциянинг ўзидир. Бундан шундай хулоса
келадики, t=0 бўлганда минус 1-тартибли хосила нолга тенг бўлса, ёки,
бошқача қилиб айтганда, коммутациягача сиғим зарядланмаган
бўлса:
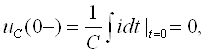 (18.12)
(18.12)
(18.9) билан ифодаланган нолли бошланғич шарт
мавжуд бўлади. Функция ![]() нинг ўзи эса бошланғич онда нолдан фарқли
бўлиши мумкин [i(0+)≠o], чунки у (18.11) тенгламада
учрайдиган хосилаларнинг энг юқорисидир (n=0).
нинг ўзи эса бошланғич онда нолдан фарқли
бўлиши мумкин [i(0+)≠o], чунки у (18.11) тенгламада
учрайдиган хосилаларнинг энг юқорисидир (n=0).
Оператор қаршилиги ва оператор узатиш функцияси. Юқоридаги барча фикрлардан шу малум бўладики, нолли бошланғич шартларда барча хосилалар р кўпайтувчи билан оддий алмаштирилади, барча интеграллар эса р га оддий бўлиш билан алмаштирилар экан: бунда занжирнинг оператор шаклида ёзилган тенгламалари, занжирнинг синусоидал токлардаги комплекс шаклда ёзилган тенгламаларига ўхшаш бўлади. Агар улардаги барча ўзгарувчиларнинг комплекс тасвирларини уларга хос оператор тасвирлар билан алмаштирилса:
![]() (18.13)
(18.13)
ва барча ![]() кўпайтувчиларни p га алмаштирилса:
кўпайтувчиларни p га алмаштирилса:
![]() (18.14)
(18.14)
у холда занжирнинг синусоидал токлардаги комплекс шаклда ёзилган тенгламалари занжирнинг оператор шаклида ёзилган тенгламаларига айланади.
Масалан, кетма-кет уланган L, r, C занжирнинг (18.4,а-расм) дифференциал тенгламаси:
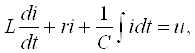 (18.15)
(18.15)
бўлса, барқарорлик режими учун гармоник ток тенгламаси
![]() ,
(18.16)
,
(18.16)
бўлса, ўткинчи жараён (нолли бошланғич шарт) учун оператор тенгламаси эса:
![]() (18.17)
(18.17)
бўлади.
Ушбу фикрни ўхшашлик билан ривожлантириб, комплекс қаршиликлар Z(jщ) га ўхшаш бўлган, оператор қаршилик Z(p) тушунчасини киритиш мумкин:
![]() (18.18)
(18.18)
Ушбу тушунчани ўтказувчаннликка
![]() ,
(18.19)
,
(18.19)
хамда узатиш функциясига тадбиқ этиш мумкин. Агар
![]() ёки
ёки ![]() (18.20)
(18.20)
бўлса, у холда юқоридагидек ўхшатиш билан:
![]() (18.21)
(18.21)
ёки
![]() (18.22)
(18.22)
Юқоридагиларга тўлиқ ишонч хосил қилиш учун қуйидагиларни ёдга олиш кифоядир. Маълумки, ўзгарувчан токлар назариясида барча ўзгаришлар ва хулосалар занжир учун дифференциал шаклдаги Кирхгофнинг икки қонунини қўллашга асосланган. Гармоник тебранишларнинг барқарорлик режимини кўра туриб, тенгламалардаги барча хосилалар ва интеграллар jщ ва 1/jщ билан алмаштирилади: ушбу масалаларни оператор усули ёрдамида ечишда хам Кирхгофнинг қонунларини қўллашга асосланган: тенгламаларни оператор шаклига ўтказиш учун (нолли бошланғич шартлар бўлганда) хосила ва интеграллни р ва 1/р га кўпайтириш зарур.
18.4-мисол. 18.4,а-расмда келтирилган занжир учун r2 қаршиликдаги ток қиймати аниқлансин.
Ечиш. Юқоридаги баён қилинганлардан
![]()
бунда ![]() ,
,
![]()
Ўзгармас ва ўзгарувчан ток занжирлари ҳисоблашдан
фойдаланиб, куйидагини аниқлаймиз:
 бунда
бунда ![]() бунда
бунда ![]() .
.
Токлар учун i2 ~ I2
натижавий ифодалар уланаётган э.ю.к. ( ![]() ~
~ ![]() )нинг турига боғлик.
)нинг турига боғлик.
18.5-мисол. Икки индуктив боғланган контурлар (трансформатор) ўзгармас кучланиш U манбасига уланаяпти. Биринчи контурнинг параметрлари r1, L1; иккинчисиники r2, L2. Ўзгаро индуктивлик М. Иккинчи контурдаги ўткинчи жараён токини аниқланг.
Ечиш. Илгаридан маълум бўлган тенгламаларни қўллаб, уларни тўғрида-туғри (I2 токнинг мусбат йўналишини ўзгартириб) оператор шаклида ёзамиз:
![]()
![]()
бунда
![]()
Бу тенгламалардан:
![]() ,
,
ёки оддий алгебраик ўзгартиришлардан сўнг қуйидагиларни аниқлаймиз:
![]()
бунда ![]() боғланиш коэффициенти: аксарият
холларда, (айтайлик, яхши трансформаторларда)
боғланиш коэффициенти: аксарият
холларда, (айтайлик, яхши трансформаторларда) ![]() ҳисоблаш мумкин, шундан сўнг
тенгламалар тартиби кескин камаяди.
ҳисоблаш мумкин, шундан сўнг
тенгламалар тартиби кескин камаяди.
I2 махражининг илдизлари:
![]() бунда
бунда ![]() ва
ва ![]()
Илдизлар аниқлангандан сўнг I2 ни қуйидагича ёзиш мумкин:
![]()
бунга 17.1-жадвалнинг (11) ифодаси мос келади:
![]()
Кутилганидек, i2 ток қиймати нолга тенг ва коммутация бошланишида tқo бўлганда (![]() ) ва охирида t→∞.
) ва охирида t→∞.
19-маъруза. Электр занжирларининг ўтиш ва импульс
тавсифлари
Ўткинчи жараёнларни ҳисоблашнинг
классик ва оператор усулларини ташқи таъсирнинг шакли содда бўлганда қўллаш
қулайдир; аммо ташқи таъсир вақт бўйича мураккаб қонун
билан ўзгарганда бу усулларни амалда қўллаш мумкин бўлмайди.
Мураккаб шаклга эга бўлган ташқи
таъсирли электр занжирларининг ўткинчи жараёнларини таҳлил қилишда
суперпозиция (устлаш) усулини қўллаш қулайликларга олиб келади.
Бундай усул фақат нолли бошланғич шарти бўлган чизиқли
занжирларда қўлланиши мумкин.
Масалан, мураккаб шаклдаги
сигнални элементар сигналларнинг йиғиндиси сифатида тасвирлаш мумкин
бўлган ҳолларда, ҳамда занжир киришидаги бу элементар сигналлар
таъсирининг занжир чиқишидаги реакцияси (акс таъсирини) қандайдир
бир йўл билан аниқлаш мумкин бўлган ҳолларда, қўйилган
масаланинг ечими шундай реакцияларнинг оддий йиғиндисини аниқлаш
билан бажарилади.
19.1. Электр занжирларига импульслар таъсирлари
Чекланган вақт оралиғида кучланиш ёки токнинг бирламчи қийматидан оғиши электр импульси дейилади (19.1-расм).
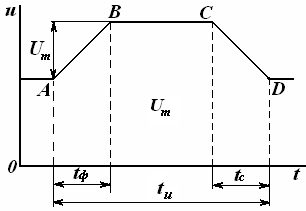 Кучланишнинг берилган қийматидан
оғиши кўриладиган АВ қисми-имульснинг фронти
дейилади. Кучланишнинг берилган қийматига қайтиши кузатиладиган СD
қисми-имульснинг қирқими дейилади. Импульснинг ВС
қисми-импульс чўққисси дейилади; АD қисми-импульс
асоси;
Кучланишнинг берилган қийматидан
оғиши кўриладиган АВ қисми-имульснинг фронти
дейилади. Кучланишнинг берилган қийматига қайтиши кузатиладиган СD
қисми-имульснинг қирқими дейилади. Импульснинг ВС
қисми-импульс чўққисси дейилади; АD қисми-импульс
асоси; ![]() импульс
амплитудаси;
импульс
амплитудаси; ![]() импульс
кенглиги;
импульс
кенглиги; ![]() фронт
кенглиги; tқ-қирқим
кенглиги
19.1-расм
фронт
кенглиги; tқ-қирқим
кенглиги
19.1-расм
дейилади.
Кетма-кет тарқалувчи
импульслар, импульслар кетма-кетлигини ташкил этади (19.1-расм).
Оний қийматлари бир хил вақт ![]() оралиғида
такрорланувчи импульслар кетма-кетлиги импульсларнинг даврий кетма -
кетлиги дейилади. Бунда
оралиғида
такрорланувчи импульслар кетма-кетлиги импульсларнинг даврий кетма -
кетлиги дейилади. Бунда ![]() импульсларнинг
такрорланиш даври дейилади;
импульсларнинг
такрорланиш даври дейилади; ![]() импульслар
такрорланиш частотаси;
импульслар
такрорланиш частотаси; ![]() импульсларнинг
зичлиги дейилади.
импульсларнинг
зичлиги дейилади.
Телекоммуникация тизимларида учрайдиган импульсларнинг шакллари 19.1-расмда келтирилган.
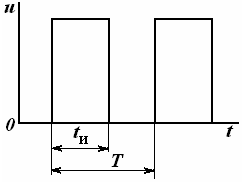 «Тасвир импульси» атамасининг ишлатилишига сабаб шу
бўлдики, бундай импульс биринчи марта телевидение техникасида қўлланилади.
«Тасвир импульси» атамасининг ишлатилишига сабаб шу
бўлдики, бундай импульс биринчи марта телевидение техникасида қўлланилади.
Суперпозиция усулини элементар қўллаганда сигналнинг стандарт шакли сифатида одатда бирлик сигнали ёки уланиш сигнали (бирлик поғона сигнали, бирлик поғона) ишлатилади.
|
|
19.2-расм
19.3-расм
Бирлик поғона сигнали деб шундай кучланиш ток сигналига айтиладики, ихтиёрий t<0 бўлганда сигналнинг қиймати нолга тенг, t≥0 бўлганда эса 1 га тенг бўлади.
|
|
t<0 бўлганда 1(t)=0
1(t)= t≥0 бўлганда 1(t)=1
Бирлик поғона сигнали
ёрдамида электр занжирига таъсири вақтнинг бирор онидан бошланадиган
ихтиёрий сигналларни тасвирлаш мумкин. Масалан, агар ![]() бўлса,
у ҳолда
бўлса,
у ҳолда ![]() кўпайтма
уланиш кучланиши (19.3,а ва б-расмлар)
дейилади.
кўпайтма
уланиш кучланиши (19.3,а ва б-расмлар)
дейилади.
![]() t<0
бўлганда, 0,
t<0
бўлганда, 0,
U1(t)= t≥0 бўлганда, U.
бунда ![]() поғонанинг
баландлиги.
поғонанинг
баландлиги.
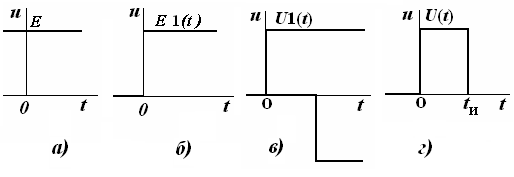
19.4-расм
Электр занжирларига таъсир этувчи
барча сигналлар вақтнинг аниқ бир онида содир бўлишини эътиборга
олсак, бу сигналларни тасвир этувчи математик ифодаларнинг барчасида, аниқлик
учун, ![]() кўпайтмани
киритишимиз шарт. Бироқ, ифоданинг ёзилишини соддалаштириш мақсадида
бирлик функцияни тушириб қолдирилади.
кўпайтмани
киритишимиз шарт. Бироқ, ифоданинг ёзилишини соддалаштириш мақсадида
бирлик функцияни тушириб қолдирилади.
Икки поғонасимон функцияни қўшиш
ёрдамида давомийлиги ![]() га
тенг бўлган тўғри бурчакли импульсни ҳосил қилиш мумкин
(19.4, в ва г-расмлар)
га
тенг бўлган тўғри бурчакли импульсни ҳосил қилиш мумкин
(19.4, в ва г-расмлар)
 U(t)=U·1(t)-U(1(t-tu).
U(t)=U·1(t)-U(1(t-tu).
Бирлик импульс функцияси. (Дирак функцияси). Уни баъзан ![]() функция
ҳам деб атайдилар.
функция
ҳам деб атайдилар.
Дирак функцияси физик амалга
ошириб бўлмайдиган математмик ҳаёлий функиця бўлиб, қизи-қарли
ҳусусиятга эга ва назарий тадқиқотларда муҳим
19.5-расм
аҳамиятлидир.
Аргументнинг нолдан фарқли
бўлган барча қийматларида ![]() функция
нолга тенг ва
функция
нолга тенг ва ![]() нкқтада
чексиз катта қийматга тенг (19.5-расм).
нкқтада
чексиз катта қийматга тенг (19.5-расм).
Электр занжирлари назариясида бу
функция қуйидаги тенглама билан ифодаланади:
![]() t<0 бўлганда, 0,
t<0 бўлганда, 0,
д (t)= t=0
бўлганда, ∞,
(19.1)
t>0
бўлганда, 0.
?Шундай
қилиб, ![]() функция
ёки
функция
ёки ![]() импульс
деб шундай сигналга айтиладики, унинг амплитудаси чексиз катта, давомийлиги
чексиз кичик ва унинг юзаси бирга тенг:
импульс
деб шундай сигналга айтиладики, унинг амплитудаси чексиз катта, давомийлиги
чексиз кичик ва унинг юзаси бирга тенг:
![]() функция
аргументнинг жуфт функциясидир
функция
аргументнинг жуфт функциясидир ![]()
![]() функциянинг
қизиқарлилиги шундаки, у фильтирловчилик хусусиятга эга:
функциянинг
қизиқарлилиги шундаки, у фильтирловчилик хусусиятга эга:
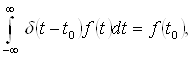 (19.2)
(19.2)
бунда![]()
![]() узлуксиз функция.
узлуксиз функция.
![]() функция
бирлик функциясидан вақт бўйича ҳосиласига тенг:
функция
бирлик функциясидан вақт бўйича ҳосиласига тенг:
![]()
19.2. Электр занжирларининг
ўткинчи ва импульс тавсифлари
Ўткинчи жараёнларни ҳисоблашнинг
вақт усули асосида занжирнинг ўткинчи ва импульс тавсифлари ётади.
Ўткинчи тавсиф деб занжир киришига бирлик функция (11.1) шаклидаги таъсирга
нисбатан занжирнинг реакциясига айтилади. Занжирнинг ўткинчи таъсири ![]() билан
белгиланади.
билан
белгиланади.
Импульс тавсифи деб занжир
киришига бирлик импульс функцияси (![]() функция)
шаклидаги (19.2) таъсирга нисбатан занжирнинг реакциясига айтилади. Импульс
тавсиф
функция)
шаклидаги (19.2) таъсирга нисбатан занжирнинг реакциясига айтилади. Импульс
тавсиф ![]() билан
белгиланади. Бунда,
билан
белгиланади. Бунда, ![]() ва
ва
![]() занжирдаги
нолли бошланғич шартларда аниқланади. Реакциянинг тури ва
таъсирнинг турига кўра (ток ёки кучланиш) ўткинчи ва импульс тавсифлари
ўлчамсиз (агар таъсир ва реакция фақат кучланиш ёки фақат токдан
иборат бўлса) ёки
занжирдаги
нолли бошланғич шартларда аниқланади. Реакциянинг тури ва
таъсирнинг турига кўра (ток ёки кучланиш) ўткинчи ва импульс тавсифлари
ўлчамсиз (агар таъсир ва реакция фақат кучланиш ёки фақат токдан
иборат бўлса) ёки ![]() (таъсир-ток,
реакция-кучланиш) ёки V/A (кучланиш ва ток) бўлиши мумкин.
(таъсир-ток,
реакция-кучланиш) ёки V/A (кучланиш ва ток) бўлиши мумкин.
Ўткинчи ва импульс тавсифлари
тушунчаларини қўллаш натижасида занжирлардаги ҳисобланиши мураккаб
бўлган ихтиёрий шаклдаги нодаврий сигналлар таъсирини бирлик ![]() ёки
импульс
ёки
импульс ![]() функцияларининг
занжирига таъсири натижасидаги занжир реакциясини аниқлаш билан
алмаштирилади; бунда берилган мураккаб таъсир
функцияларининг
занжирига таъсири натижасидаги занжир реакциясини аниқлаш билан
алмаштирилади; бунда берилган мураккаб таъсир![]() ёки
ёки ![]() билан
апроксимацияланади. Чизиқли занжирнинг натижавий таъсири (суперпозиция
усулини қўллаб) элементар
билан
апроксимацияланади. Чизиқли занжирнинг натижавий таъсири (суперпозиция
усулини қўллаб) элементар ![]() ёки
ёки
![]() таъсирларга
занжирнинг реакцияларини йиғиндиси сифатида аниқланади.
таъсирларга
занжирнинг реакцияларини йиғиндиси сифатида аниқланади.
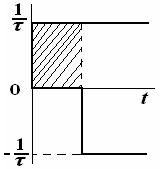 Чизиқли пассив занжирнинг
ўткинчи
Чизиқли пассив занжирнинг
ўткинчи![]() ва импульс
ва импульс ![]() тавсифлари
орасида муайян боғланиш мавжуд. Бу боғланишни аниқлаш учун
келтирилган бирлик функцияни бир-биридан
тавсифлари
орасида муайян боғланиш мавжуд. Бу боғланишни аниқлаш учун
келтирилган бирлик функцияни бир-биридан ![]() вақтга
силжитилган (19.6-расмга қаранг) бирлик функциялари айирмаларининг лимити
деб қараш лозим:
вақтга
силжитилган (19.6-расмга қаранг) бирлик функциялари айирмаларининг лимити
деб қараш лозим:
19.6-расм
![]() (19.3)
(19.3)
яъни бирлик импульс функцияси бирлик функциясининг ҳосиласига
тенг. Кўрилаётган занжир чизиқли деб фараз қилинганлиги учун,
(19.3) боғланиш занжирнинг импульс ва ўткинчи реакциялари учун ҳам
сақланиб қолади
![]() (19.4)
(19.4)
яъни импульс тавсиф ўткинчи тавсифнинг ҳосиласига
тенг бўлади.
Бу (4) тенглама ![]() (занжир
учун нолли бошланғич шартлар) вазият учун жўялидир. Агар
(занжир
учун нолли бошланғич шартлар) вазият учун жўялидир. Агар ![]() бўлса
бўлса
![]() ни
ни
![]()
![]() шаклида
ифодаланиб, ушбу ҳолат боғланиш тенгламасини аниқлаймиз:
шаклида
ифодаланиб, ушбу ҳолат боғланиш тенгламасини аниқлаймиз:
![]() (19.5)
(19.5)
Занжирнинг ўткинчи ва импульс
тавсифларини аниқлаш учун юқорида кўрилган классик ёки оператор
усулларини ҳам қўллаш мумкин. Классик усулнинг моҳияти
шундаки, унинг ёрдамида бирлик ![]() ёки
импульс
ёки
импульс ![]() функциялар
шаклидаги таъсирларнинг занжирдаги вақт бўйича реакцияси аниқланади.
функциялар
шаклидаги таъсирларнинг занжирдаги вақт бўйича реакцияси аниқланади.
Аксарият, классик усул ёрдамида
ўткинчи ![]() тавсифни
аниқлаш қулайдир; импульс тавсия
тавсифни
аниқлаш қулайдир; импульс тавсия ![]() ни
эса (19.4) ва (19.5) тенгламалар вақтнинг
ни
эса (19.4) ва (19.5) тенгламалар вақтнинг ![]() онида
кучланиш манбаи
онида
кучланиш манбаи ![]() га
уланишдаги ёки оператор усули ёрдамида аниқлаш қулайдир.
га
уланишдаги ёки оператор усули ёрдамида аниқлаш қулайдир.
Мисол. Классик усул ёрдамида
19.6-расмда келтирилган схема учун кучланиш бўйича ўткинчи тавсифини аниқланг.
Ушбу занжир учун сиғимдаги кучланиш билан мос бўлади:
![]()
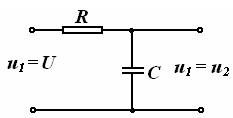 Сиғимдаги кучланишнинг
ўзгариш қонуни
Сиғимдаги кучланишнинг
ўзгариш қонуни ![]() ифодада
ифодада
![]() ни
қўйиб аниқланади:
ни
қўйиб аниқланади:
![]()
Ўткинчи ![]() ва
импульс
ва
импульс ![]() тавсифлар
оператор усул ёрдамида ҳисобланганда
тавсифлар
оператор усул ёрдамида ҳисобланганда ![]() ва
ва ![]() функциялардан
19.6-расм
функциялардан
19.6-расм
Ва ўткинчи жараёнларни ҳисоблаш (бобда
келтирилган усулдан) фойдаланилади.
Мисол. Оператор усули ёрдамида
19.6-расмда келтирилган RC-занжир учун ![]() ўткинчи
тавсифини ҳисобланг. Ушбу занжир учун оператор шаклидаги Ом қонуни
асосида қуйидагиларни ёзиш мумкин:
ўткинчи
тавсифини ҳисобланг. Ушбу занжир учун оператор шаклидаги Ом қонуни
асосида қуйидагиларни ёзиш мумкин:
![]()
![]()
![]()
![]()
![]()
бунда
![]() (19.6)
(19.6)
Шу
сабабли ![]()
Бундан
![]()
![]()
![]() (19.7)
(19.7)
яъни классик усул билан ҳисоблангандаги
натижани оламиз.
Шуни тагидлаш зарурки, (6)
тенгликдаги ![]() қиймат
сон жиҳатдан ўткинчи ўтказувчанликка тенг. Импульс тавсифининг шунга
ўхшаш тавсифи сон жиҳатдан оператор ўтказувчанлигига тенг:
қиймат
сон жиҳатдан ўткинчи ўтказувчанликка тенг. Импульс тавсифининг шунга
ўхшаш тавсифи сон жиҳатдан оператор ўтказувчанлигига тенг:
![]()
![]()
![]()

Масалан, 19.7-расмдаги RC-занжир
учун қуйидагини ҳосил қиламиз:
![]()
![]()
![]()
![]() учун
теорема разлоницияни татбиқ этиб қуйидагини ҳосил қиламиз:
учун
теорема разлоницияни татбиқ этиб қуйидагини ҳосил қиламиз:
![]() (19.8)
(19.8)
Шуни таъкидлаш зарурки, (19.8) боғланиш
бирлик импульс таъсиридаги занжир реакциясининг эркин ташкил этувчисини
ифодалайди. Умумий ҳолда, занжирнинг реакцияси таркибида, эркин режимнинг
экслоненциал ташкил этувчиларидан ташқари бирлик импульснинг ![]() даги
таъсирини акс эттирувчи импульс ташкил этувчиси ҳам мавжуд бўлади. Дарҳақиқат,
агар 18.6-расмдаги RC-занжир учун
даги
таъсирини акс эттирувчи импульс ташкил этувчиси ҳам мавжуд бўлади. Дарҳақиқат,
агар 18.6-расмдаги RC-занжир учун ![]() бўлгандаги
ток бўйича ўткинчи тавчифи га мувофиқ
бўлгандаги
ток бўйича ўткинчи тавчифи га мувофиқ
![]() (19.9)
(19.9)
эканлигини
эътиборга олсак, (18.9)ни (4)га кўра дифференциаллангандан сўнг RC-занжирнинг ![]() импульс
тавсифини қуйидаги шаклда ҳосил қиламиз:
импульс
тавсифини қуйидаги шаклда ҳосил қиламиз:
![]() (19.10)
(19.10)
яъни, ![]() реакция
икки-импульс ва экспоненциал ташкил этувчидан иборат бўлади.
реакция
икки-импульс ва экспоненциал ташкил этувчидан иборат бўлади.
(19.10)даги биринчи ташкил
этувчининг физик мазмуни шуни англатадики, занжирга ![]() онда
онда
![]() импульс
кучланишнинг таъсири натижасида зарядловчи ток бир онда ўзининг чексиз катта миқдорига
эришади, бунда вақтнинг
импульс
кучланишнинг таъсири натижасида зарядловчи ток бир онда ўзининг чексиз катта миқдорига
эришади, бунда вақтнинг ![]() онидан
онидан
![]() онигача
бўлган оралиғида сиғим элементига чекланган заряд етказилади ва
унинг кучланиши сакраб
онигача
бўлган оралиғида сиғим элементига чекланган заряд етказилади ва
унинг кучланиши сакраб ![]() гача
ўзгаради. Иккинчи ташкил этувчиси занжирда t>0 вақтдаги эркин
жараённи аниқлайди ва
гача
ўзгаради. Иккинчи ташкил этувчиси занжирда t>0 вақтдаги эркин
жараённи аниқлайди ва![]() вақт доимсмийси билан конденсаторнинг киришда қисқа
туташувидаги зарядсизланишидан ҳосил бўлади (чунки t>0 бўлганда,
вақт доимсмийси билан конденсаторнинг киришда қисқа
туташувидаги зарядсизланишидан ҳосил бўлади (чунки t>0 бўлганда,![]() бу
эса киришнинг қисқа туташувини англатади). Бундан шуни англаш
мумкинки, RC-занжирга
бу
эса киришнинг қисқа туташувини англатади). Бундан шуни англаш
мумкинки, RC-занжирга ![]() -импульс
таъсири натижасида сиғимнинг узлуксиз зарядланиши (коммутациянинг иккинчи
қонуни) бузилади. Шунга ўхшаш, индуктивлиги бўлган занжирга
-импульс
таъсири натижасида сиғимнинг узлуксиз зарядланиши (коммутациянинг иккинчи
қонуни) бузилади. Шунга ўхшаш, индуктивлиги бўлган занжирга ![]() турдаги
кучланиш берилганда индуктивликдан токнинг оқиши узлуксизлигини
(коммутациянинг иккинчи қонуни) бузилади.
турдаги
кучланиш берилганда индуктивликдан токнинг оқиши узлуксизлигини
(коммутациянинг иккинчи қонуни) бузилади.
19.1 жадвалда биринчи ва иккинчи
тартибли занжирлар учун кучланиш ва ток бўйича ўткинчи ва импульс тавифларининг
ифодалари келтирилган.
19.1 жадвал
|
Схема |
Ўткинчи тавсиф gu(t) |
Импульс тавсиф hu(t) |
|
|
ept |
д(t)+pept |
|
|
1 - ept |
-pept |
|
|
-ept |
-pept |
20-маъруза. Дюамель ва жамлаш интеграллари.
1-тартибли чизиқли электр занжирлар орқали
тўғри бурчакли импульснинг ўтиши
Агар таъсир этувчи ![]() функцияни
бир-биридан ўзаро
функцияни
бир-биридан ўзаро ![]() вақтга
силжитилган (20.1-расм) бирлик функциялари ёрдамида аппроксимация-ланса Дюамель
интегралини ҳосил қилиш мумкин. Ҳар бир поғона таъсирга
занжирнинг реакцияси қуйидагича аниқланади:
вақтга
силжитилган (20.1-расм) бирлик функциялари ёрдамида аппроксимация-ланса Дюамель
интегралини ҳосил қилиш мумкин. Ҳар бир поғона таъсирга
занжирнинг реакцияси қуйидагича аниқланади:
![]()
![]()
ѓ2(Дф)=Дѓ1g(t–Дф)
. . . . . . . . . . . . . . .
.
ѓ2(kДф)=Дѓk
g(t–kДф)
Поғонали таъсирлар тизимига
занжирнинг натижавий реакцияси супепозиция принципидан аниқланади:
![]()
 бунда
бунда ![]() таъсирнинг
таъсирнинг
![]() гача
бўлган вақт оралиғидаги аппроксимацияланувчи қисимларининг
сони йиғинди белгисининг ичидаги миқдорни
гача
бўлган вақт оралиғидаги аппроксимацияланувчи қисимларининг
сони йиғинди белгисининг ичидаги миқдорни ![]() га
алоҳида кўпайтириб ва бўлиб, сўнгра
га
алоҳида кўпайтириб ва бўлиб, сўнгра ![]() да
да
![]() эканлигини
эътиборга олиб, Дюамель интегралининг шаклларидан бирини ҳосил қилишимиз
мумкин:
эканлигини
эътиборга олиб, Дюамель интегралининг шаклларидан бирини ҳосил қилишимиз
мумкин:
![]()
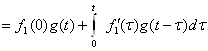 (20.1)
(20.1)
Ҳосил қилинган
тенглама берилган таъсирига занжирнинг реакциясини акс эттиради, чунки ![]() бўлганда
апроксимацияланаёт-ган функция берилган функцияга
интилади.
бўлганда
апроксимацияланаёт-ган функция берилган функцияга
интилади.
20.1 -расм
Дюамель интегралининг иккинчи
шаклини жамлаш теоремаси ёрдамида аниқланиши мумкин:
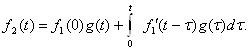 (20.2)
(20.2)
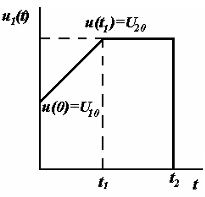 Ниҳоят, (20.1) ва (20.2)
тенгламаларнинг ифодаларининг алоҳида ташкил этувчиларини интеграллаб,
Дюамель интегралининг учинчи ва тўртинчи кўринишларини аниқлаш мумкин:
Ниҳоят, (20.1) ва (20.2)
тенгламаларнинг ифодаларининг алоҳида ташкил этувчиларини интеграллаб,
Дюамель интегралининг учинчи ва тўртинчи кўринишларини аниқлаш мумкин:
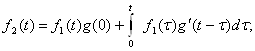 (20.3)
(20.3)
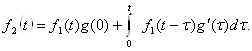 (20.4)
(20.4)
Дюамель интегралининг у ёки бу
шаклларидан бирини қўллаш интеграл остидаги ифодани ҳисоблашнинг қулайлиги
ва соддалиги билан аниқланади.
20.2-расм
Мисол. Дюамель интеграли (20.1)
ёрдамида
20.2-расмда тасвирланган кучланишга нисбатан схемаси
20.2-расмдаги занжир реакциясини аниқлаймиз. Ушбу занжирнинг ўткинчи
тавсифи қуйидагича ифодаланади:
![]()
Ўткинчи функцияни аниқлаганимиздан
сўнг, интеграллаш бўлакларининг сонини ҳисоблаймиз. Бу бўлакларда функция
узлуксиз ва дифференциалланувчи бўлиши шарт. Бу бўлаклардаги ![]() қийматларини
аниқлаймиз. Кўрилаётган таъсир учун бундай бўлаклар: 0≤t<t1
; t≤t<t2 ва t2≤t<∞.
қийматларини
аниқлаймиз. Кўрилаётган таъсир учун бундай бўлаклар: 0≤t<t1
; t≤t<t2 ва t2≤t<∞.
Учинчи бўлакни киритишнинг
зарурати шу билан тушунтириладики, занжирда ўткинчи жараёнлар туфайли кириш
таъсирининг йўқолишига қарамай, занжирда цолдир реакция мавжуд
бўлади. Ажратилган бўлакларнинг ҳар бири учун, ундан аввалги бўлак
реакциясини эътиборга олиб, (20.1) тенгламани ёзамиз:
0 ≤ t < t1 бўлакда
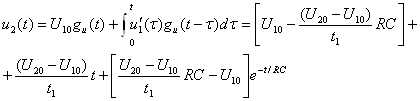
t1 ≤ t < t2
бўлакда
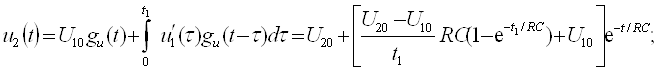
t2 ≤ t < ∞ бўлакда

|
|
20.3-расм
Агар таъсир актив занжирга
ўрнатилган бўлса (20.3,а-расм), ўткинчи
жараёнларни ҳисоблаш суперпозиция усулини қўллаб бажари мумкин.
Бунда, аввлига ҳисоблаш пассиви занжир учун (20.3,б-расм)
Дюамель интеграли ёрдамида олиб борилади. Сўнгра, классик ёки оператор усули
ёрдамида кўрилаётган шоҳобчанинг актив иккиқутубликка (20-3,в-расм)
уланишнинг реакцияси аниқланади. Натижавий реакция ҳар бир
реакцияларнинг йиғиндиси сифатида ![]() аниқланади.
аниқланади.
20.1 Устлаш интеграли
Устлаш интеграли ёрдамида
занжирнинг реакциясини аниқлашда занжирнинг импульс ![]() тавсифини
ишлатилади устлаш интегралининг умумий ифодасини аниқлаш учун
тавсифини
ишлатилади устлаш интегралининг умумий ифодасини аниқлаш учун ![]() кириш
сигналини давомийлиги
кириш
сигналини давомийлиги ![]() амплитудаси
амплитудаси
![]() ва
юзаси
ва
юзаси ![]()
![]() (20.3,г-расм)
бўлган бирлик импульслари тизими ёрдамида аппроксимациялаймиз. Ҳар бир
бирлик импульс учун занжирнинг чиқиш реакцияси
(20.3,г-расм)
бўлган бирлик импульслари тизими ёрдамида аппроксимациялаймиз. Ҳар бир
бирлик импульс учун занжирнинг чиқиш реакцияси
![]()
Устлаш принципини қўллаб,
бирлик импульслар тизимига занжирнинг натижавий реакциясини ҳисоблаш
мумкин:
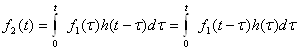
(20.4)
интеграл устлаш интеграли номини олган. Дюамель интеграли билан устлаш
интеграли орасида занжирнинг импульс ![]() ва
ўткинчи
ва
ўткинчи ![]() тавсифлари
орасида боғланишдан аниқланадиган содда боғланиш мавжуд.
Масалан, (20.4)дан
тавсифлари
орасида боғланишдан аниқланадиган содда боғланиш мавжуд.
Масалан, (20.4)дан ![]() нинг
қийматини
нинг
қийматини ![]() функциянинг
фильтрловчи ҳусусиятини (20.2) эътиборга олиб (20.4) ифодага қўйсак,
(20.3) шаклдаги Дюамель интегралини ҳосил қиламиз.
функциянинг
фильтрловчи ҳусусиятини (20.2) эътиборга олиб (20.4) ифодага қўйсак,
(20.3) шаклдаги Дюамель интегралини ҳосил қиламиз.
Мисол. RC-занжир киришига (20.2-расм)
поғонали кучланиш ![]() уланган.
Устлаш (20.4) ва Дюамель интегралларини қўллаб занжирнинг чиқишидаги
реакциясини ҳисобланг.
уланган.
Устлаш (20.4) ва Дюамель интегралларини қўллаб занжирнинг чиқишидаги
реакциясини ҳисобланг.
Ушбу занжирнинг импульс тавсифи
(20.1-жадвалга қаранг): 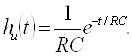 Шунинг
учун,
Шунинг
учун, 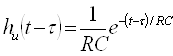 ни
(20.4) ифодага қўйсак, қуйидагини ҳосил қиламиз:
ни
(20.4) ифодага қўйсак, қуйидагини ҳосил қиламиз:
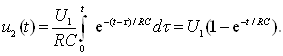
Шунга ўхшаш натижани ушбу
занжирнинг ўткинчи функцияси ва Дюамель интегралини қўллаб ҳосил қилишимиз
мумкин:
![]()
Агар таъсир этиш бошланиш они вақти
ҳисоблашнинг боши билан мос келмаса, у ҳолда (15) интеграл қуйидаги
шаклда ёзилади:
![]() (20.5)
(20.5)
(20.15) ва (20.16) устлаш
интеграллари занжирнинг кириш сигнали ва импульс тавсифининг жамланишини акс
эттиради ва электр занжирлар назарияси ва сигналларни узатиш назариясида кенг қўлланилади.
Унинг физик мазмуни-кириш сигнали ![]() нинг
нинг
![]() функцияси
ёрдамида ўзгаришини аниқлайди: вақт ўтиши билан
функцияси
ёрдамида ўзгаришини аниқлайди: вақт ўтиши билан ![]() функция
қанчалар сокин камайса, кириш таъсирининг кузатилаётган онидан шунчалар
узоқлашган қийматлари чиқиш сигналларига шунчалар қўп
таъсир кўрсатади.
функция
қанчалар сокин камайса, кириш таъсирининг кузатилаётган онидан шунчалар
узоқлашган қийматлари чиқиш сигналларига шунчалар қўп
таъсир кўрсатади.
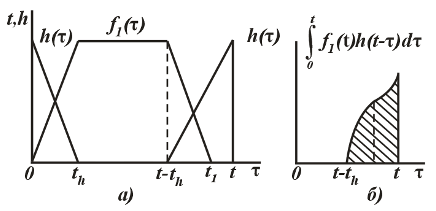
20.4-расм
20.4,а-расмда сигнал ![]() ва
ва
![]() нинг
ойнавий акси бўлган
нинг
ойнавий акси бўлган ![]()
импульс тавсифи ![]() ,
20.4,б-расмда миқдорий жиҳатдан
,
20.4,б-расмда миқдорий жиҳатдан
![]() ондаги
занжирнинг реакциясига тенг бўлган
ондаги
занжирнинг реакциясига тенг бўлган ![]() сигнал
билан
сигнал
билан ![]() функцияси
(штрихланган қисми)нинг жамланиши келтирилган.
функцияси
(штрихланган қисми)нинг жамланиши келтирилган.
20.4-расмда кўринадики,
занжирнинг чиқишдаги реакция сигнал ![]() ва
импульс тавсифининг
ва
импульс тавсифининг ![]() давомийлигидан
қисқароқ бўлмас экан. Шундай қилиб, чиқиш сигнали
шакли ўзгармасилиги учун занжирнинг импульс тавсифи
давомийлигидан
қисқароқ бўлмас экан. Шундай қилиб, чиқиш сигнали
шакли ўзгармасилиги учун занжирнинг импульс тавсифи ![]() функцияга
интилмаслиги зарур экан.
функцияга
интилмаслиги зарур экан. ![]()
Яна шу нарса аёнки, реал
занжирларнинг реакцияси таъсирга нисбатан олдинроқ ҳосил бўлмайди.
Демак, реал занжирларнинг импульс тавсифлари қуйидаги шартга жавоб бериши
шарт:
h(t)=0, агар t<0
бўлса.
Реал барқарор занжирларда
импульс тавсифларнинг абсолют интегралланувчи бўлиши ҳам шарт:
![]() |
h(t) | dt < ∞
|
h(t) | dt < ∞
Агар кириш таъсири мураккаб шаклга эга бўлса ёки график усулда берилган бўлса, занжир реакциясини ҳисоблаш учун жамлашинтеграли (20.15) ўрнига графоаналитик усул қўлланилади.
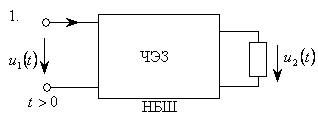
20.5-расм
Бош масала -
биртомонли таъсир ![]() га
га ![]() жавобни
топамиз.
жавобни
топамиз.
2. Таъсирни
давомлилиги ![]() бўлган тўғри
бурчакли импульсларга бўлиб чиқамиз.
бўлган тўғри
бурчакли импульсларга бўлиб чиқамиз. ![]() ҳар
бир импульсни чизиқли деб ҳисоблаш мумкин.
ҳар
бир импульсни чизиқли деб ҳисоблаш мумкин.
20.6-расм
3. Таъсирнинг интегралли кўрсатилиши.
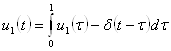
![]()
4. Жавобнинг интегралли кўрсатилиши - жамлаш интеграли.
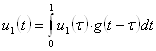
5. Жамлаш интегралини функциянинг ўралмаси деб юритилади. Функциялар ўралмаси учун қисқартирилган ёзув қўлланади:
![]()
6. Жамлаш
интегралида ![]() ва
ва ![]() функциялар
ўрин алмашиши мумкин, чунки жавобни ҳисоблашда кириш сигнали деб нимани қабул
қилишнинг фарқи йўқ. Улар ўзаро алмаштирилувчилардир.
функциялар
ўрин алмашиши мумкин, чунки жавобни ҳисоблашда кириш сигнали деб нимани қабул
қилишнинг фарқи йўқ. Улар ўзаро алмаштирилувчилардир.

20.7-расм
7. ЧЭЗ ни вақт усулида таҳлил қилиш босқичлари:
- импульс характеристикани топиш;
- жамлаш
интеграли ёрдамида жавобни ҳисоблаш.
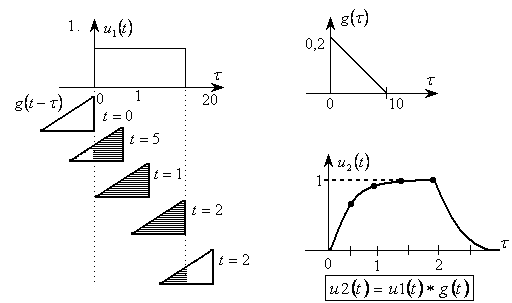
20.8-расм
«Чўзиш» усули иккита функция кўпайтмаси билан чегараланган юзани график усулда аниқлашга асосланган.
2. Агар ЧЭЗ юқоридан
(![]() частота
билан) чегараланган ўтказиш оралиғига эга бўлса, у ҳолда киришдаги
сигнални тахминан чизиқли импульслар кетма-кетлиги сифатида кўрсатиш
мумкин.
частота
билан) чегараланган ўтказиш оралиғига эга бўлса, у ҳолда киришдаги
сигнални тахминан чизиқли импульслар кетма-кетлиги сифатида кўрсатиш
мумкин.
20.9-расм
Занжирнинг жавоби
ҳар бир импульсга алоҳида жавоблар йиғиндиси каби аниқланади:
![]()
![]()
Хусусан, агар ![]() нолга тенг
бўлса, яъни
нолга тенг
бўлса, яъни ![]() давомлилиги
бўйича
давомлилиги
бўйича ![]() дан кичик бўлса,
у ҳолда киришдаги сигнал жавобига кўра чизиқли импульсга
эквивалентдир. Бунда унинг шакли эмас, юзаси
дан кичик бўлса,
у ҳолда киришдаги сигнал жавобига кўра чизиқли импульсга
эквивалентдир. Бунда унинг шакли эмас, юзаси ![]() муҳим.
муҳим.
3. Агар киришдаги
сигнал юқоридан (![]() частота
билан) чегараланган тебранишлар спектрига эга бўлса, у ҳолда импульс
характеристика тахминан чизиқли импульслар кетма-кетлиги тарзида
кўрсатилиши мумкин.
частота
билан) чегараланган тебранишлар спектрига эга бўлса, у ҳолда импульс
характеристика тахминан чизиқли импульслар кетма-кетлиги тарзида
кўрсатилиши мумкин.
20.9-расм
Агар ![]() нолга тенг
бўлса, яъни импульс характеристика жуда қисқа муддатли бўлса, у ҳолда
чиқиш сигнали кириш сигналига
нолга тенг
бўлса, яъни импульс характеристика жуда қисқа муддатли бўлса, у ҳолда
чиқиш сигнали кириш сигналига ![]() пропорционал
бўлади.
пропорционал
бўлади.
21- маъруза. Дифференциалловчи ва интегралловчи занжирлар
1. Чиқишдаги сигнали киришидаги сигналидан вақт бўйича олинган аниқмас интегралга пропорционал бўладиган занжир интегралловчи дейилади.
![]() (21.1)
(21.1)
Итегралловчи занжирнинг импульсли характеристикаси бирлик зинасимон функциядир.
2. Катта вақт доимийси ![]() га эга бўлган энг оддий RL ва RC-занжирлар интегралловчи
занжирлардир.
га эга бўлган энг оддий RL ва RC-занжирлар интегралловчи
занжирлардир.

21.1-расм
3. Тақрибий интеграллаш шарти.
Кузатиш вақти
![]() киришдаги
импульснинг давомлигига ёки киришдаги даврий сигналнинг Т даврига тенг.
киришдаги
импульснинг давомлигига ёки киришдаги даврий сигналнинг Т даврига тенг.
![]()
4. Чиқишдаги сигнали киришдаги сигналидан вақт бўйича олинган ҳосилага пропорционал бўлган занжир дифференциалловчи дейилади.
 (21.2)
(21.2)
Занжирнинг ўтиш характеристикаси чизиқли импульсдир.
5. Кичкина вақт доимийси ![]() га эга бўлган энг оддий RL- ва RC-занжирлар
дифференциалловчи занжирлардир.
га эга бўлган энг оддий RL- ва RC-занжирлар
дифференциалловчи занжирлардир.
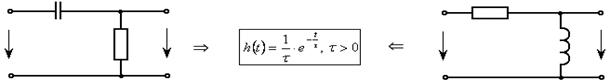
21.2-расм
![]() да,
да, ![]() функция дельта-функцияга интилади!
функция дельта-функцияга интилади!
6. Тақрибий дифференциаллаш шарти:
а) ![]() бунда
бунда ![]() олдингидек
аниқланади;
олдингидек
аниқланади;
b) 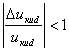 шарти
шарти ![]() дан кичик бўлган
исталган вақт оралиғида бажарилиши лозим.
дан кичик бўлган
исталган вақт оралиғида бажарилиши лозим.
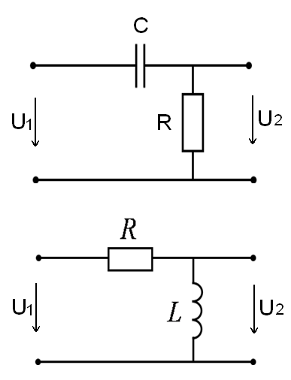 А.Содда дифференциалловчи занжирлар.
А.Содда дифференциалловчи занжирлар.
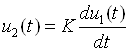
21.3-расм
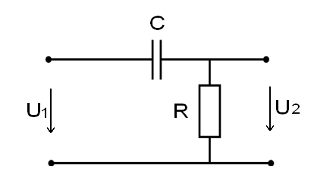 Ч нинг кичик қийматлари учун RC занжир тахминий
дифференциалловчи занжирдир.
Ч нинг кичик қийматлари учун RC занжир тахминий
дифференциалловчи занжирдир.
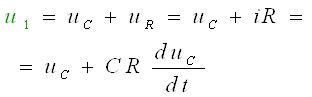
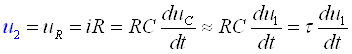 21.4-расм
21.4-расм
Вақт доимийси қанча кичик бўлса,дифференциалаш хатолиги шунча камроқ бўлади ва Ur(t) ҳам импульс функцияга шунча кўп ўхшаш бўлади.
|
|
R1L занжир кичик ![]() учун таҳминий дифференциаловчи занжирдир.
учун таҳминий дифференциаловчи занжирдир.
R1C ёки R1L занжирда ![]() қанча
кичик бўлса, дифференциалаш ҳусусияти шунча юқори бўлади,бироқ
қанча
кичик бўлса, дифференциалаш ҳусусияти шунча юқори бўлади,бироқ
![]() камайиши
билан бир вақтда чиқишдаги кучланиш Ur(t) ҳам
камаяди.(операцион кучайтиргичлардан фойдаланилади).
камайиши
билан бир вақтда чиқишдаги кучланиш Ur(t) ҳам
камаяди.(операцион кучайтиргичлардан фойдаланилади).
Б. Содда интегралловчи занжирлар.
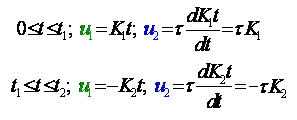
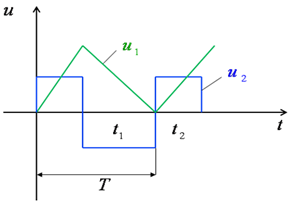
21.5-расм
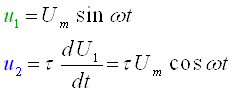
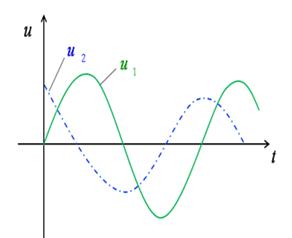
21.6-расм
RC занжир катта ![]() учун тахминий интегралловчи занжирдир.
учун тахминий интегралловчи занжирдир.
![]()
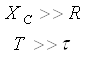
21.7-расм
![]() каттароқ
бўлса,занжирнинг интеграллаш хусусияти яхшироқ бўлади.
каттароқ
бўлса,занжирнинг интеграллаш хусусияти яхшироқ бўлади.
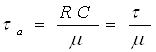
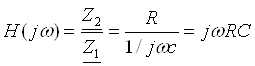
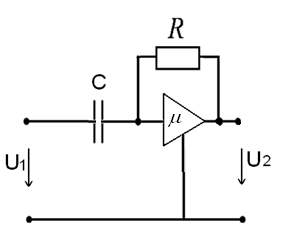
21.8-расм
L1R занжир катта ![]() учун тахминий интегралловчи занжирдир.Агар
учун тахминий интегралловчи занжирдир.Агар ![]() каттароқ бўлса, занжирнинг
интеграллаш хусусияти яхшиланади, чунки чиқишдаги кучланиш камаяди.
каттароқ бўлса, занжирнинг
интеграллаш хусусияти яхшиланади, чунки чиқишдаги кучланиш камаяди.
(кучайтиргич керак бўлади).
![]() шарт
қанча яхшироқ бажарилса,дифференциаллаш сифати шунча яхшироқ
бўлади,сиқатли интеграллаш шарти эса
шарт
қанча яхшироқ бажарилса,дифференциаллаш сифати шунча яхшироқ
бўлади,сиқатли интеграллаш шарти эса
ф щ >> 1
tu давомийликка эга бўлган импульсли таъсирлар учун сифатли дифференциаллаш шарти қуйидаги тенгсизликка эквивалент.
фщ<< tu
сифатли интеграллаш шарти эса
фщ >> tu
тенгсизликка эквивалент:
Бу шартларни қаноатлантиришмайдиган занжирлар ўтувчи (ажратувчи) деб аталади.
|
|
|||||
|
|
|||||
|
|
|||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
21.9-расм
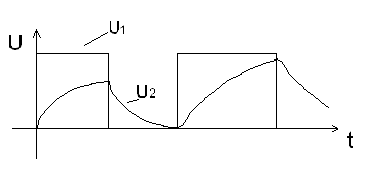
21.10-расм
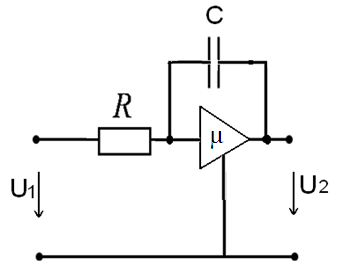
21.11-расм
22-маъруза. Чизикли электр занжирини частотавий усулда таҳлил қилиш
Электр занжирларига ихтиёрий шаклдаги сигналлар таъсири натижасида содир бўладиган ўткинчи жараёнларни таҳлил қилиш учун вақт ва оператор усулларидан ташқари, сигналларни спектрлар ёрдамида тақдим этувчи частотавий усул ҳам кенг қўлланилади.
22.1. Тебранишлар частотавий таркибининг таҳлили
Агар ҳар
хил: частотали - 0, щ1, 2щ1, 3щ1;
амплитудали ![]() ,
, ![]()
![]() ва бошланғич
фазалари
ва бошланғич
фазалари ![]() бўлган
кучланиш манбаларини кетма-кет уланса (22.1,а-расм), у ҳолда шу
занжирнинг кучланиши ва токи носинусоидал бўлади. Бундай ҳолда занжирга
битта носинусоидал даврий
бўлган
кучланиш манбаларини кетма-кет уланса (22.1,а-расм), у ҳолда шу
занжирнинг кучланиши ва токи носинусоидал бўлади. Бундай ҳолда занжирга
битта носинусоидал даврий ![]() таъсир
этаяпти, деб қараш (22.1,б-расм) мумкин. Унинг кучланиши қуйидагича
ёзиш мумкин.
таъсир
этаяпти, деб қараш (22.1,б-расм) мумкин. Унинг кучланиши қуйидагича
ёзиш мумкин.
![]()
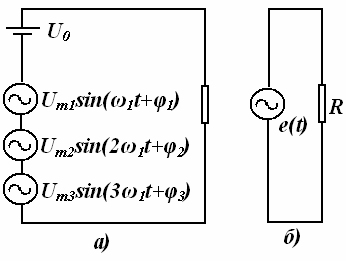
22.1-расм
Ушбу қаторнинг
биринчи ҳади ![]() ўзгармас ташкил
этувчиси ёки нолли гармоникаси деб аталади.
ўзгармас ташкил
этувчиси ёки нолли гармоникаси деб аталади. ![]() биринчи ёки асосий
гармоникаси, қолган ташкил эътувчилар юқори гармоникалар деб
аталади, ёки иккинчи ва учинчи ташкил этувчилар деб уларнинг тартиб рақами
қуйидагича қўйилади:
биринчи ёки асосий
гармоникаси, қолган ташкил эътувчилар юқори гармоникалар деб
аталади, ёки иккинчи ва учинчи ташкил этувчилар деб уларнинг тартиб рақами
қуйидагича қўйилади:
![]() иккинчи
гармоника;
иккинчи
гармоника;
![]() учинчи гармоника,
учинчи гармоника,
бунда ![]()
![]() асосий
гармониканинг бурчак частотаси;
асосий
гармониканинг бурчак частотаси; ![]() биринчи
гармоника тебранишларининг даври,
биринчи
гармоника тебранишларининг даври, ![]() унинг частотаси,
унинг частотаси,
![]()
![]()
![]() асосий ва юқори
гармоникаларнинг амплитудалари;
асосий ва юқори
гармоникаларнинг амплитудалари; ![]()
![]()
![]() - асосий ва юқори
гармониаларнинг бошланғич фазалари.
- асосий ва юқори
гармониаларнинг бошланғич фазалари.
Синусоидал ва косинусоидал функциялардан фарқли бўлган барча сигналлар носинусоидал дейилади.
Эътибор берайлик: синусоидал (гармоник) функциялар юқори гармоникаларнинг амплитудалари ва ўзгармас ташкил этувчи нолга тенг бўлган даврий носинусоидал функцияларнинг ҳусусий ҳолидир.
 Амалиётда носинусоидал кучланишларни ҳосил қилиш
учун ярим ўтказгичли схемалардан фойдаланилади. Хусусан, 22.2-расмда кучланиш
жамлагичи (сумматор) деб номланган операцион кучайтиргич (ОК) схемаси
келтирилган.
Амалиётда носинусоидал кучланишларни ҳосил қилиш
учун ярим ўтказгичли схемалардан фойдаланилади. Хусусан, 22.2-расмда кучланиш
жамлагичи (сумматор) деб номланган операцион кучайтиргич (ОК) схемаси
келтирилган.
Жамлагичнинг чиқишдаги кучланиш Uчиқ (t) қиймати унинг кири- 22.2-расм
шига келтирилган кучланишлар оний
қийматлари йиғиндисига пропорционал:
Uчиқ (t)= - ![]()
Агар ![]() бўлса
тенглама соддалашади:
бўлса
тенглама соддалашади:
Uчиқ (t)=
- ![]()
22.2. Фурье интеграли
Нодаврий сигналлар учун Фурьенинг ўзгартиришларига асосланган сигналларни спектрал шаклдаги кўринишларидан (8.18) фойдаланилади. Фурьенинг ўзгартиришларига Фурье қаторидан лимитга ўтиш билан ҳосил қилиниши мумкин. Бунинг учун чексиз оралиқда абсолют интегралланувчи
шартларига жавоб
берувчи ![]() нодаврий
сигнални кўрамиз:
нодаврий
сигнални кўрамиз:
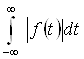 <∞.
<∞.
Физик нуқтаи назардан, ушбу шарт чекли энергияга эга бўлган, амалга
 ошириш мумкин бўлган сигнал берилишини кўрсатади.
ошириш мумкин бўлган сигнал берилишини кўрсатади.
![]() <
<![]() (22.1)
(22.1)
бу ерда ![]() мусбат ўзгармас қийматлар.(22.1)
шарт шуни
таъкидлайдики,
мусбат ўзгармас қийматлар.(22.1)
шарт шуни
таъкидлайдики,
![]() 22.3-расм
22.3-расм
модули-нинг ортиши
чеклангандир. Бусигнални ҳаёлан ![]() вақт оралиғида
даврий қайтарилувчи (22.3 - расмга қаранг) сигналга айлантирамиз.
Шу тариқа ҳосил бўлган сигналга (22.1) ёйишни татбиқ этиш
мумкин. Уни
вақт оралиғида
даврий қайтарилувчи (22.3 - расмга қаранг) сигналга айлантирамиз.
Шу тариқа ҳосил бўлган сигналга (22.1) ёйишни татбиқ этиш
мумкин. Уни ![]() вақтга
ўтилгандан сўнг қуйидагича ёзиш мумкин:
вақтга
ўтилгандан сўнг қуйидагича ёзиш мумкин:
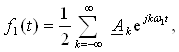 (22.2)
(22.2)
бунда
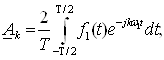
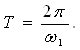 (22.3)
(22.3)
![]() нинг қийматини
(22.3)га қўйилгандан сўнг
(22.4)ни эътиборга олиб
нинг қийматини
(22.3)га қўйилгандан сўнг
(22.4)ни эътиборга олиб
 (22.4)
(22.4)
(22.4)тенгламада ![]() га ўтиб ҳамда
га ўтиб ҳамда
![]() ва
ва ![]() эканлигини
эътиборга олиб, йиғиндидан эса интегралга ўтиб, берилган сигнал учун қуйидагини
ҳосил қиламиз:
эканлигини
эътиборга олиб, йиғиндидан эса интегралга ўтиб, берилган сигнал учун қуйидагини
ҳосил қиламиз:
 (22.5)
(22.5)
Бу (22.6) тенгламадаги ички интеграл ![]() сигналнинг
спектри деб номланади:
сигналнинг
спектри деб номланади:
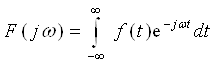 (22.6)
(22.6)
У ҳолда (22.7) ифода қуйидаги шаклга эга бўлади:
![]() (22.7)
(22.7)
(22.5) ва (22.6)
спектрал таҳлил назариясида тенгламалар ҳисобланади; бунда (22.5)
тенглама Фурьенинг тўғри ўзгартириши, (22.6) эса тескари
ўзгартириши дейилади. ![]() га ўхшашликда,
га ўхшашликда, ![]() умумий ҳолатда
частотанинг комплекс функциясидир ва алгебраик шаклда қуйидагича ёзилиши
мумкин:
умумий ҳолатда
частотанинг комплекс функциясидир ва алгебраик шаклда қуйидагича ёзилиши
мумкин:
![]() (22.8)
(22.8)
кўрсаткичли шаклда
![]() (22.9)
(22.9)
бунда
![]() dt;
dt; ![]() dt
. (22.10)
dt
. (22.10)
Унинг модули сигналнинг
![]() (22.11)
(22.11)
амплитуда спектрини, аргументи
![]() (22.12)
(22.12)
эса фаза спектрини аниқлайди.
Бунда, даврий сигналлардагидек, амплитуда спектри частотанинг жуфт функцияси,
фаза спектри-частотанинг тоқ функциясидир. Фурье ўзгартиришларининг физик
моҳияти тескари ўзгартириш (22.7)ни тригонометрик шаклда келтирилганда яққолроқ
кўринади. Агар (22.7)га ![]() нинг қийматини
(12.9)дан қўйсак, қуйидагини ҳосил қиламиз:
нинг қийматини
(12.9)дан қўйсак, қуйидагини ҳосил қиламиз:
![]()
![]()
![]() частотанинг жуфт,
синус частотанинг эса функция эканлигини эътиборга олсак, иккинчи ҳаддан
олинган интеграл нолга тенг бўлади. Шунинг учун, интеграл ости ифоданинг
биринчи ҳади жуфт эътиборга олсак, Фурьенинг тескари ўзгартириши қуйидаги
шаклда ёзилади:
частотанинг жуфт,
синус частотанинг эса функция эканлигини эътиборга олсак, иккинчи ҳаддан
олинган интеграл нолга тенг бўлади. Шунинг учун, интеграл ости ифоданинг
биринчи ҳади жуфт эътиборга олсак, Фурьенинг тескари ўзгартириши қуйидаги
шаклда ёзилади:
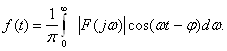 (22.13)
(22.13)
(22.13) ифодадан қуйидаги
муҳим хулосага келамиз: нодаврий сигнал амплитудалари 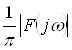 ва
ва ![]() бошланғич
фазалари бўлган чексиз катта сонли чексиз кичик гармоника тебранишларнинг йиғиндиси
(интеграли) лимити сифатида келтирилиши мумкин; қўшни гармоникалар
частоталарининг фарқи
бошланғич
фазалари бўлган чексиз катта сонли чексиз кичик гармоника тебранишларнинг йиғиндиси
(интеграли) лимити сифатида келтирилиши мумкин; қўшни гармоникалар
частоталарининг фарқи ![]() чексиз
кичик эканлигини эътиборга олсак, у ҳолда (22.13) тенгламадаги
чексиз
кичик эканлигини эътиборга олсак, у ҳолда (22.13) тенгламадаги ![]() даврий
сигналнинг спектридан фарқли равишда, узлуксиз яхлит спектрларни ташкил
этади. Шунинг учун
даврий
сигналнинг спектридан фарқли равишда, узлуксиз яхлит спектрларни ташкил
этади. Шунинг учун ![]() комплекс
спектрал зичлик дейилади,
комплекс
спектрал зичлик дейилади, ![]() эса
нодаврий сигнал амплитудаларининг спектрал зичлиги дейилади.
эса
нодаврий сигнал амплитудаларининг спектрал зичлиги дейилади.
![]() комплекс
спектрининг мазмуни даврий ва нодаврий сигналлар спектрларининг ўзаро боғлиқлигидан
келиб чиқади (22.3) ва (22.6) тенгламаларнинг таққосланиш
ушбу спектрларининг ўзаро боғлиқлигини аниқлайди:
комплекс
спектрининг мазмуни даврий ва нодаврий сигналлар спектрларининг ўзаро боғлиқлигидан
келиб чиқади (22.3) ва (22.6) тенгламаларнинг таққосланиш
ушбу спектрларининг ўзаро боғлиқлигини аниқлайди:
![]()
![]() бўлганда
бўлганда
![]() (21.14)
(21.14)
ва ![]() комплекс
амплитудалар спектри комплекс спектрал зичликка айтилади.
комплекс
амплитудалар спектри комплекс спектрал зичликка айтилади.
(22.4)дан яна бошқа муҳим 22.4-расм
хулоса келиб чиқади: нодаврий сиг-
нал спектрал зичлигининг
модули ва нодаврий сигналининг ![]() давр билан
такрорланишидан ҳосил бўлган даврий сигнал чизиқли спектрининг
ўрамаси шаклан мос келадилар ва фақат масштаблари билан фарқланадилар.
Буни тўғри бурчакли импульслар (22.4-расм) кетма-кетлигида яққол
кўрсатиш мумкин. Даврнинг ортиши натижасида спектр зичлашади (22.5,а-расм) ва
давр билан
такрорланишидан ҳосил бўлган даврий сигнал чизиқли спектрининг
ўрамаси шаклан мос келадилар ва фақат масштаблари билан фарқланадилар.
Буни тўғри бурчакли импульслар (22.4-расм) кетма-кетлигида яққол
кўрсатиш мумкин. Даврнинг ортиши натижасида спектр зичлашади (22.5,а-расм) ва ![]() қиймати
қиймати
![]() га интилганда
даврий сигнал нодаврий сигналга айланади. (22.5,б-расм), дискрет спектр
эса яхлит спектрга айланади.
га интилганда
даврий сигнал нодаврий сигналга айланади. (22.5,б-расм), дискрет спектр
эса яхлит спектрга айланади.
Фурье
ўзгартиришларининг баъзи асосий хусусиятларини кўрайлик. Агар ![]() сигнал вақтнинг
жуфт функцияси бўлса, у ҳолда унинг спектри
сигнал вақтнинг
жуфт функцияси бўлса, у ҳолда унинг спектри ![]() ҳақиқий
сондир. Дарҳақиқат, (22.6)га кўра
ҳақиқий
сондир. Дарҳақиқат, (22.6)га кўра ![]() ни қуйидагича
ёзиш мумкин:
ни қуйидагича
ёзиш мумкин:
![]() dt
dt![]() dt.
dt.
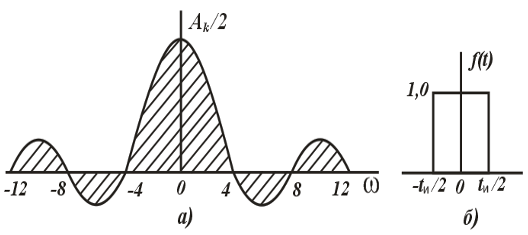
22.5-расм
Иккинчи интеграл остидаги функция тоқ бўлгани учун иккинчи ҳад нолга тенг. Шунинг учун
![]() dt
(22.14)
dt
(22.14)
Шунга ўхшаш, ![]() сигнал тоқ
бўлса,
сигнал тоқ
бўлса, ![]() мавҳум
сон.
мавҳум
сон.
Фурье
ўзгартиришнинг муҳим ҳусусиятларидан бири ![]() ва
ва ![]() ўзгарувчиларнинг
ўзаро алмашувчанлигадир. Жуфт сигнал
ўзгарувчиларнинг
ўзаро алмашувчанлигадир. Жуфт сигнал ![]() учун ва ҳақиқий
учун ва ҳақиқий
![]() учун (22.6)
ўзгартиришда
учун (22.6)
ўзгартиришда ![]() нинг олдидаги
ишораларини ўзгартиришимиз мумкин:
нинг олдидаги
ишораларини ўзгартиришимиз мумкин:
![]() (22.15)
(22.15)
Унда (22.6) ва (22.7)ни таққослаб, уларнинг ўхшаш эканлигига иқрор бўлишимиз мумкин. Фурье ўзгартиришларида ўзгарувчиларнинг ўзаро алмаштириш имкони бўлган сигналларнинг вақтга частотавий тавсифлари орасидаги боғланишни ифодалаш мумкин (22.5га қаранг).
(22.8) ва (22.9)
ифодаларга мувофиқ, сигнал ёки алгебраик шаклда ўзининг амплитуда ![]() ва фаза
спектрлари ёрдамида, ёки кўрсаткичли шаклда - ҳақиқий
ва фаза
спектрлари ёрдамида, ёки кўрсаткичли шаклда - ҳақиқий ![]() ва мавҳум
ва мавҳум ![]() спекктрлари
ёрдамида ифодаланиши мумкин. Бунда уларнинг ҳар бири (22.11)-(22.12)
ифодалар ёрдамида ўзаро боғлангандир.
спекктрлари
ёрдамида ифодаланиши мумкин. Бунда уларнинг ҳар бири (22.11)-(22.12)
ифодалар ёрдамида ўзаро боғлангандир.
Ушбу боғланиш,
айниқса, ![]() вақтнинг
мусбат ярим ўқида жойлашган сигнал учун яққол кўринади:
вақтнинг
мусбат ярим ўқида жойлашган сигнал учун яққол кўринади:
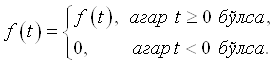 (22.16)
(22.16)
(22.13) ифодани қуйидаги шаклда ёзамиз:
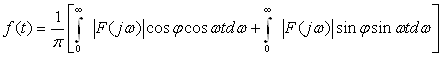
![]() Ёки
Ёки
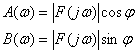 (22.17)
(22.17)
эканлигини эътиборга олсак, ![]() бўлганда қуйидагини
ҳосил қиламиз:
бўлганда қуйидагини
ҳосил қиламиз:
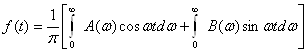 (22.18)
(22.18)
ва ![]() бўлганда
(21.17) эътиборга олиб қуйидагини ҳосил қиламиз:
бўлганда
(21.17) эътиборга олиб қуйидагини ҳосил қиламиз:
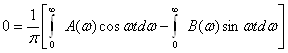 (22.19)
(22.19)
Тенгликлар (21.18) ва (21.19)ни қўшиш ва айириш натижасида қуйидагига эга бўламиз:
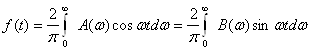 (22.20)
(22.20)
Бундан сигнал
спектрининг ҳақиқий ![]() ва мавҳум
ва мавҳум
![]() қисмлари
орасида боғланиш келиб чиқади:
қисмлари
орасида боғланиш келиб чиқади:
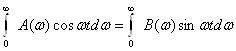 (22.21)
(22.21)
яъни, ушбу ҳолда
![]() сигнал
тўлалигига
сигнал
тўлалигига![]() комплекс
спектрининг фақат ҳақиқий
комплекс
спектрининг фақат ҳақиқий ![]() ёки мавҳум
ёки мавҳум
![]() қисмлари
билан аниқланади.
қисмлари
билан аниқланади.
Хулоса қилиб
шуни таъкидлаш мумкинки, ![]() бўлганда
(22.22) ифода қуйидаги
бўлганда
(22.22) ифода қуйидаги
![]() (22.23)
(22.23)
қийматга эга бўлади,
яъни ![]() сигнал
билан чегараланган майдонга тенг бўлади.
сигнал
билан чегараланган майдонга тенг бўлади.
Вақт ва спектр шаклида келтириш бу реал физик жараённни икки шаклллар (моделлар) билан ифодалашдир; улар электр занжирларини вақт ва частотавий усуллар билан таҳлил қилишнинг асосида ётадилар.
Пировардида
Фурье ўзгартириши ва Лаплас ўзгартириши орасидаги боғланишни аниқлаймиз.
Агар ![]() функция
(22.17) шартни бажаради, деб қабул қилинса, у ҳолда Фурьенинг
тўғри ўзгартириши қуйидаги шаклда ёзилади:
функция
(22.17) шартни бажаради, деб қабул қилинса, у ҳолда Фурьенинг
тўғри ўзгартириши қуйидаги шаклда ёзилади:
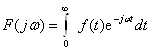 (22.24)
(22.24)
Ушбу (22.24) боғланиш
Фурьенинг биртоманлама ўзгаритириши, деб номланади. Чунки ![]() вақтнинг
мусбат ярим ўқида аниқланади. Агар, хусусий ҳол сифатида
комплекс сон
вақтнинг
мусбат ярим ўқида аниқланади. Агар, хусусий ҳол сифатида
комплекс сон ![]() да
да ![]() деб ҳисобланса,
у ҳолда
деб ҳисобланса,
у ҳолда ![]() ва
Лапласнинг тўғри ўзгартиришини
ва
Лапласнинг тўғри ўзгартиришини
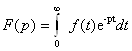 (22.25)
(22.25)
қуйидагича ёзиш мумкин
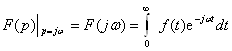 ,
(22.26)
,
(22.26)
яъни Фурьенинг бир томонлама ўзгартириши (22.27) билан тўла мос келади.
Шунга ўхшаш, Лапласнинг тескари ўзгартириши
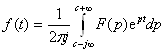
учун ҳам ![]() эканлигини
эътиборга олиб, қуйидагини олиш мумкин:
эканлигини
эътиборга олиб, қуйидагини олиш мумкин:
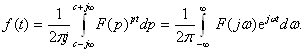 (22.27)
(22.27)
Бу эса (22.7) билан тўла мос келади.
Шундай қилиб,
Фурьенинг ўзгартириши ![]() бўлгандаги
ўзгартиришининг ҳусусий ҳоли экан. Шуни таъкидлаш зарурки, Фурьенинг
ўзгартириши Лапласнинг ўзгартиришига нисбатан анчагина торроқ соҳаларда
қўлланилади. Чунки Фурье бўйича ўзгартириладиган функцияга қўйиладиган
шартлар, Лаплас бўйича ўзгартириладиган функцияларга қўйиладиган
шартларга нисбатан қатъийроқдир. Фурье ўзгаритиришини (22.6) қўлаш
мумкин бўлган брача функциялар доимо Лаплас бўйича ўзгартирилиши мумкин, аммо
аксинча эмас. Шу сабабли,
бўлгандаги
ўзгартиришининг ҳусусий ҳоли экан. Шуни таъкидлаш зарурки, Фурьенинг
ўзгартириши Лапласнинг ўзгартиришига нисбатан анчагина торроқ соҳаларда
қўлланилади. Чунки Фурье бўйича ўзгартириладиган функцияга қўйиладиган
шартлар, Лаплас бўйича ўзгартириладиган функцияларга қўйиладиган
шартларга нисбатан қатъийроқдир. Фурье ўзгаритиришини (22.6) қўлаш
мумкин бўлган брача функциялар доимо Лаплас бўйича ўзгартирилиши мумкин, аммо
аксинча эмас. Шу сабабли, ![]() тасвирини
тасвирини ![]() сигналининг
умумлаштирилган спектри деб қараш мумкин.
сигналининг
умумлаштирилган спектри деб қараш мумкин.
23-маъруза. Турткутбликларнинг узатиш тенгламалари,
параметрлари ва турлари
Радиотехниканинг турли жабҳаларида кўпинча икки жуфт қутблари бўлган электр занжирларни тадқиқ қилиш масаласи юзага келади. Шу қутблар ёрдамида бу занжир бошқа занжир қисмлари билан боғланиши мумкин.
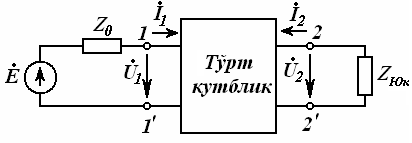 Тўртқутбликлар
назарияси икки қутбликлар назарияси ривожланишининг давоми ҳисобланади.
Исталган икки жуфт икки қутбликларга нисбатан
қуриладиган электр занжир қисми тўртқутблик деб аталади. Тўртқутбликнинг
шартли белгиланиши 23.1 – расмда келтирилган.
Тўртқутбликлар
назарияси икки қутбликлар назарияси ривожланишининг давоми ҳисобланади.
Исталган икки жуфт икки қутбликларга нисбатан
қуриладиган электр занжир қисми тўртқутблик деб аталади. Тўртқутбликнинг
шартли белгиланиши 23.1 – расмда келтирилган.
Бир жуфт
клем-малари ![]() кириш, бошқа
бир жуфти
кириш, бошқа
бир жуфти ![]() - чиқиш
клеммалари
дейилади.
23.1-расм
- чиқиш
клеммалари
дейилади.
23.1-расм
1 – қутб орқали
тўрт қутбликка кира-диган I1 ток ҳар доим ![]() қутбдан
чиқадиган токка тенг бўлади, 2 –
кутбга
қутбдан
чиқадиган токка тенг бўлади, 2 –
кутбга
кирадиган ток доимо ![]() қутбдан
чиқадиган токка тенг бўлади.
қутбдан
чиқадиган токка тенг бўлади.
Тўртқутбликларнинг умумий назариясида исталган топология учун ҳам ҳаққоний бўлган боғланишлар ўрнатилади, яъни элементларнинг боғланиш схемаларини тўртқубликнинг ўзи тузади. Бу боғланишлардан фойдаланиш мураккаб электр занжирлар таҳлилини нисбатан соддалаштиради.
Бирорта ҳолатни ҳисоблашга қадар, тўртта катталикнинг мусбат йўналишларини танлаймиз. Булар - икки кучланиш ва иккита ток йўналиш-ларидир. Йўналишлар 23.1-расмда кўрсатилганидек танланади.
Тўртқутбликнинг таҳлили масаласи қуйидагидан иборат: тўртқутбликнинг режимини аниқлайдиган тўртта катталикдан иккитаси маълум – улар таъсир орқали берилади. Қолган иккита катталикни, яъни таъсирга реакцияни аниқлаш талаб қилинади.
Мос равишда бу масалани ечиш учун иккита номаълумдан иборат иккита тенгламалар тизимини тузиш лозим. Бундай тенгламалар тўртқутбликлар назариясининг асосий тенгламалари дейилади.
Гармоник тебранишлар ҳолатида чизиқли занжирлар ҳодисасини кўриб чиқиш катта қизиқиш уйғотади.
23.1-жадвалда келтирилган комплекс параметрли тўртқутбликнинг асосий тенгламалари олтита вариантни ташкил этади.
23.1 – жадвал
|
№ |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
A (ABCD) |
Y |
H |
F (G) |
B |
23.1 Тўртқутбликларнинг турлари
Агар исталган ташқи элементлар ![]() клеммаларга
ёки
клеммаларга
ёки ![]() клеммаларга
уланса, бундай тўртқутбликлар ўтувчи деб аталади. Тўрт қутбликлар
йиғилган ёки тарқалган, элементлардан ташкил топиши мумкин. Тўртқутбликлар
чизиқли ва ночизиқли, пассив ва актив бўлиши мумкин.
клеммаларга
уланса, бундай тўртқутбликлар ўтувчи деб аталади. Тўрт қутбликлар
йиғилган ёки тарқалган, элементлардан ташкил топиши мумкин. Тўртқутбликлар
чизиқли ва ночизиқли, пассив ва актив бўлиши мумкин.
Агар тўртқутблик ичида электр энергия манбаси бўлса, бу тўртқутблик актив тўртқутблик дейилади.
Актив чизиқли тўртқутбликлар автоном ёки ноавтоном бўлиши мумкин. Автоном тўртқутбликлар автоном равишда юкда ток ва кучланиш ҳосил қилиши мумкин. Ноавтоном тўртқутбликларда юкдаги ток ва кучланиш нолга тенг.
Тўртқутбликлар симметрик ва носимметрик бўлиши мумкин. Кириш ва чиқиш учларининг ўрни алмаштирилганда ташқи занжирдаги ток ва кучланишлар ўзгармаса, бундай тўртқутбликлар симметрик тўртқутбликлар дейилади. Акс ҳолда тўртқутбликлар носимметрик дейилади.
Агар ўзаролик теоремаси бажарилса, яъни киришдаги кучланишнинг токка нисбати икки жуфт қутбларнинг қайси бири кириш ва қайси бири чиқиш учлари эканлигига боғлиқ бўлмаса, бу тўртқутблик қайтувчан дейилади. Акс ҳолда тўртқутбликлар қайтмас дейилади. Симметрик тўртқутбликлар ҳар доим қайтувчандир.
Тўртқутбликларнинг турлари 23.2 – расмда келтирилган.
Бу бобда биз гармоник таъсир остидаги элементлари йиғилган, ўтувчан пассив ва ноавтоном, чизиқли актив тўрт қутбликларни кўриб чиқамиз.
23.2 Тўртқутбликларнинг узатиш тенгламалари
Кириш учларига ![]() кучланиш қўйилган,
чиқиш учларида эса
кучланиш қўйилган,
чиқиш учларида эса ![]() кучланиш
таъсир қиладиган шартлар асосида тўртқутбликнинг ишини кўриб чиқамиз.
Ток ва кучланишларининг йўналишлари кўрсатилган тўртқутблик 23.2 – расмда келтирилган.
кучланиш
таъсир қиладиган шартлар асосида тўртқутбликнинг ишини кўриб чиқамиз.
Ток ва кучланишларининг йўналишлари кўрсатилган тўртқутблик 23.2 – расмда келтирилган.
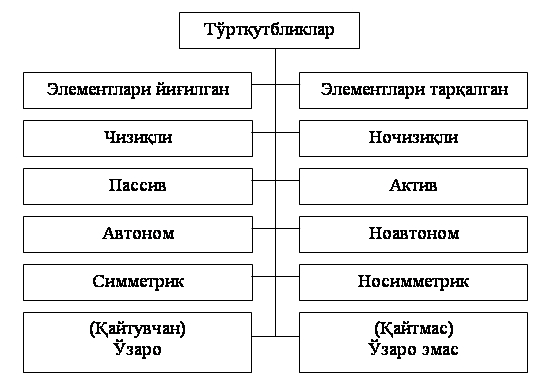
23.2 – расм
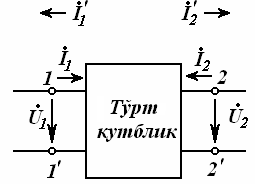
23.3 – расм.
Кучланишларнинг мусбат йўналиши деб ![]() ва
ва ![]() нинг
йўналиши, токларнинг мусбат йўналиши деб
нинг
йўналиши, токларнинг мусбат йўналиши деб ![]() ва
ва ![]() нинг йўналиши
танлаб олинса бу вариант тўғри узатиш дейилади.
нинг йўналиши
танлаб олинса бу вариант тўғри узатиш дейилади.
Агар токларнинг мусбат йўналишлари деб ![]() ва
ва ![]() ларнинг
йўналишлари қабул қилинса, бу вариант тескари узатиш дейилади.
ларнинг
йўналишлари қабул қилинса, бу вариант тескари узатиш дейилади.
Агар токларнинг мусбат йўналиши
деб ![]() ва
ва ![]() ларнинг йўналиши қабул қилинса
бу вариант қарама – қарши йўналиш дейилади.
ларнинг йўналиши қабул қилинса
бу вариант қарама – қарши йўналиш дейилади.
23.3. Тўртқутбликларнинг параметрлари ва уларнинг ўзаро
боғлиқлиги
Z - параметрлар
Т-симон тўртқутблик учун (23.4-расм) узатиш тенгламаларини тузамиз. Токларнинг қарама – қарши йўналишларини танлаб оламиз.
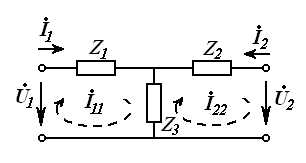
23.4–расм.
Контур токлар усулидан фойдаланиб, контур токларини ![]() ва
ва ![]() белгилаймиз
ва тенгламалар тизимини тузамиз
белгилаймиз
ва тенгламалар тизимини тузамиз
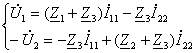 (23.1)
(23.1)
Белгилаш киритамиз ![]()
![]()
![]()
![]() ва
ва ![]() ва
ва ![]() кучланишлар ҳамда
кучланишлар ҳамда
![]() ва
ва ![]() токлардан қуйидаги
боғланишларни ҳосил қиламиз. (22.1 – жадвал, 1-бандига қаранг).
токлардан қуйидаги
боғланишларни ҳосил қиламиз. (22.1 – жадвал, 1-бандига қаранг).
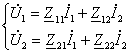 (23.2)
(23.2)
ёки матрицали кўринишда.
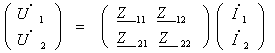
Z11, Z12, Z20, Z21 - коэффициентлар тўртқутбликнинг Z-параметрлари деб аталади. Улар комплекс катталиклар бўлиб частотага боғлиқдир. Z-параметрлар қаршилик ўлчов бирлигига эга бўлиб, улар қисқа туташув ва юксиз ишлаш режимлари ёрдамида қуйидагича аниқланади:
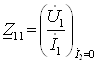 - чиқиш
учлари очиқ бўлганида кириш қутблари томонидан кириш қаршилиги;
- чиқиш
учлари очиқ бўлганида кириш қутблари томонидан кириш қаршилиги;
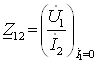 - кириш учлари очиқ
бўлганида узатиш қаршилиги;
- кириш учлари очиқ
бўлганида узатиш қаршилиги;
 - чиқиш
учлари очиқ бўлганида узатиш қаршилиги;
- чиқиш
учлари очиқ бўлганида узатиш қаршилиги;
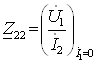 - кириш учлари очиқ
бўлганида чиқиш учлари томонидан чиқиш қаршилиги.
- кириш учлари очиқ
бўлганида чиқиш учлари томонидан чиқиш қаршилиги.
Х – параметрлар
(23.2) тенгламалар тизимидан
![]() ва
ва ![]() токларни аниқлаймиз
токларни аниқлаймиз
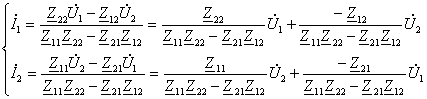
Х-параметрлар ва бу тизим аниқловчиси белгилашини киритиб
![]() ва
ва
![]()
![]()
![]()
![]()
ёки матрица кўринишда
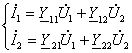 (23.3)
(23.3)
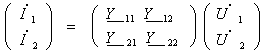
Х коэффициентлар кириш ва узатиш ўтказувчанликларини ўзида акс эттиради. Улар қуйидагича аниқланади.
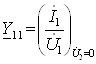 - чиқиш
учлари туташтирилганда кириш учлари томонидан кириш ўтказувчанлиги;
- чиқиш
учлари туташтирилганда кириш учлари томонидан кириш ўтказувчанлиги;
 - кириш учлари
туташтирилганда узатиш ўтказувчанлиги;
- кириш учлари
туташтирилганда узатиш ўтказувчанлиги;
 - чиқиш
учлари уланганда узатиш ўтказувчанлиги;
- чиқиш
учлари уланганда узатиш ўтказувчанлиги;
 - кириш учлари
туташтирилганда чиқиш учлари томонидан чиқиш кучланиш.
- кириш учлари
туташтирилганда чиқиш учлари томонидан чиқиш кучланиш.
А – параметрлар
(23.2) тизимнинг иккинчи
тенгламасидан биринчи токнинг ифодасини аниқлаймиз
![]()
уни (23.2) тизимнинг биринчи тенгламасига қўйиб ![]() учун ифодани ҳосил
қиламиз
учун ифодани ҳосил
қиламиз

Натижада тенгламалар тизимсини оламиз.
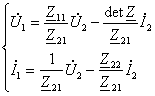
Белгилаш киритиб
![]()
![]()
![]()
![]()
![]()
А-параметрли тенгламалар тизимсини оламиз
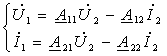 (23.4)
(23.4)
ёки матрицали кўринишида
![]() (23.5)
(23.5)
А11 ва А21 коэффициентлар
ўлчов бирлигига эга эмас, А12 - қаршилик ўлчов бирлигига
эга, А20 - ўтказувчанлик ўлчов бирлигига эга. Бу коэффициентлар қуйидагича
аниқланиши мумкин.
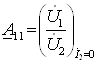 - чиқиш
учлари узилган ҳолда, кучланишлар нисбати;
- чиқиш
учлари узилган ҳолда, кучланишлар нисбати;
 - чиқиш учлари
туташтирилган ҳолда, узатиш ўтказувчанлигига тескари катталик;
- чиқиш учлари
туташтирилган ҳолда, узатиш ўтказувчанлигига тескари катталик;
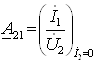 - чиқиш учлари
узилган ҳолда узатиш қаршилигига тескари катталик;
- чиқиш учлари
узилган ҳолда узатиш қаршилигига тескари катталик;
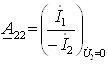 - чиқиш учлари
уланган ҳолда токлар нисбати.
- чиқиш учлари
уланган ҳолда токлар нисбати.
Н – параметрлар
(23.2) тизимнинг иккинчи тенгламасидан иккинчи токни топамиз
![]() ,
,
уни биринчи тенгламага қуйиб, қуйидагини оламиз

Натижада тенгламалар тизимини ҳосил қиламиз
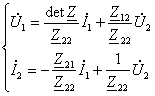 .
.
Қуйидаги белгилашларни киритиб, Н-параметрларни аниқлаймиз
![]()
![]()
![]()
![]() .
.
Н-параметрлари билан узатиш тенгламаларини ҳосил қиламиз
 .
.
ёки матрицали кўринишида
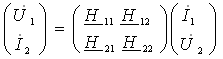 .
(23.5)
.
(23.5)
Қисқа
туташув ва юксиз ишлаш
режимларини
кўриб чиқиб, Н-параметрларнинг маъносини
аниқлаш мумкин.

![]() - қисқа
туташув ҳолатида чиқиш қутбларидаги кириш қаршилиги;
- қисқа
туташув ҳолатида чиқиш қутбларидаги кириш қаршилиги;
 - чиқиш қутблари
очиқ бўлганда кучланишнинг тескари боғланиш функцияси;
- чиқиш қутблари
очиқ бўлганда кучланишнинг тескари боғланиш функцияси;
 - чиқиш учлари қисқа
туташтирилганда токларнинг узатиш функцияси;
- чиқиш учлари қисқа
туташтирилганда токларнинг узатиш функцияси;
 - кириш учлари узилганда
чиқиш ўтказувчанлиги.
- кириш учлари узилганда
чиқиш ўтказувчанлиги.
F- параметрлар
Техник адабиётларда F белгилаш ўрнига баъзан G белгилашдан фойдаланилади.
(23.2) тизимнинг биринчи тенгламасидан биринчи токни топамиз
![]()
уни (23.2) тизимнинг иккинчи тенгламасига қўйиб, қуйидагига ифодани оламиз:
24-маъруза. Тўртқутблик тавсифий параметрлари.
Битта элементли
параллел тўртқутблик. Битта элементли параллел тўртқутбликнинг (24.1-расм) А параметрларини
аниқлаймиз. Токларнинг қарама – қарши йўналишини танлаймиз.
![]() =
=![]() эканлигини ҳисобга
оламиз. Кирхгофнинг 1-қонунини ёзамиз
эканлигини ҳисобга
оламиз. Кирхгофнинг 1-қонунини ёзамиз
![]()
Ом қонуни бўйича ![]() , мос равишда
, мос равишда ![]() . Натижада А- параметрли
тенгламалар тизимини ҳосил қиламиз
. Натижада А- параметрли
тенгламалар тизимини ҳосил қиламиз
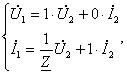
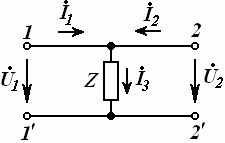
ёки матрицали кўринишда
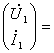
![]()
![]()
![]()
А параметрлар матрицали кўринишда қуйидагига тенг
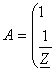
![]() 24.1 –расм.
24.1 –расм.
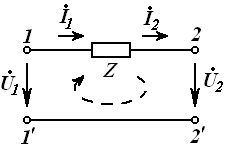 Битта элементли кетма – кет уланган тўртқутблик.
Битта элементли кетма – кет уланган тўртқутблик-нинг (24.1-расм А -параметрлари матрица-сини, аниқлаймиз.
Хилма – хиллик учун ток-ларнинг йўналишини тўғри узатишдаги каби танлаймиз.
Битта элементли кетма – кет уланган тўртқутблик.
Битта элементли кетма – кет уланган тўртқутблик-нинг (24.1-расм А -параметрлари матрица-сини, аниқлаймиз.
Хилма – хиллик учун ток-ларнинг йўналишини тўғри узатишдаги каби танлаймиз.
Кўриб ўтилган ҳолда ![]() =
=![]() Кирхгофнинг иккинчи
қонуни бўйича
Кирхгофнинг иккинчи
қонуни бўйича
![]() ва
ва ![]() .
.
Натижада токларнинг берилган 24.2–расм.
йўналишлари учун А-параметрли тенгламалар тизимини ҳосил қиламиз.
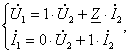
ёки матрицали кўринишда
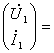
![]()
![]()
![]()
Мос равишда А-параметрларнинг матрицаси қуйидагига тенг
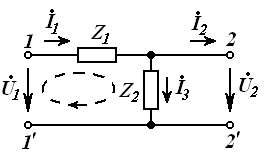
![]()
![]()
Г – симон тўртқутблик. Г-симон тўртқутбликнинг (24.3–расмдан) А-параметрлари матрицасини аниқлаймиз.
Кирхгофнинг иккинчи қонуни бўйича қуйидагиларини ёзиш мумкин.
![]() 24.3–расм.
24.3–расм.
Кирхгофнинг биринчи қонуни бўйича
![]() - бўлгани сабабли
- бўлгани сабабли ![]()
![]()
![]() бўлади.
бўлади.
24.1– жадвал.
|
|
|
|
|
|
|
|
|
|
|
|
Натижада қуйидагини оламиз.
![]()
![]() ни
ни ![]() нинг ўрнига қуйиб,
қуйидагини оламиз.
нинг ўрнига қуйиб,
қуйидагини оламиз.
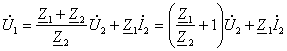
Мос равишда А-параметрли тенгламалар тизими қуйидаги кўринишига
келади
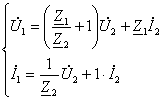
ёки матрицали кўринишда
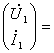
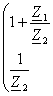
![]()
![]()
А-параметрларнинг матрицаси
қуйидагига тенг
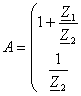
![]()
Бошқарилувчи манбалар актив чизиқли қайтувчанмас тўртқутбликлар каби қаралиши мумкин. Бу тўртқутбликларнинг А параметрлари матрицаси 24.1-жадвалда келтирилган.
24.1. Тўртқутбликларнинг каскадли боғланиши
Иккита тўртқутбликнинг каскадли боғланиш схемаси 24.4-расмда келтирилган
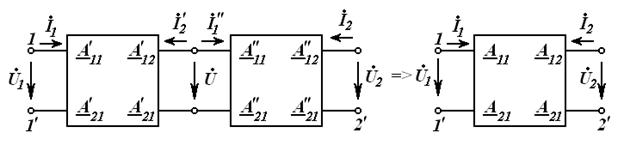 24.4 – расм.
24.4 – расм.
Биринчи тўртқутблик учун А-параметрли тенгламаларни (24.4) ёзамиз
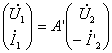 (24.1)
(24.1)
Иккинчи тўртқутблик учун А параметрли тенгламаларни ёзамиз:
![]() (24.2)
(24.2)
![]() - бўлгани сабабли
- бўлгани сабабли ![]() бўлади.
бўлади.
(24.1) ни (24.2) ифодала қуйиб қуйидагини оламиз
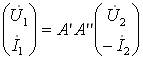 ёки
ёки 
бу ерда
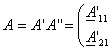
![]()
![]()
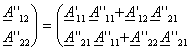
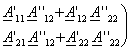
Тўртқутбликларнинг бошқа турдаги боғланишларини ҳам мавжуд. Булар: параллел, кетма – кет, кетма – кет – параллел, параллел – кетма – кет боғланишлардир. Тўртқутбликлар асосий тенгламаларининг матрицали кўринишини маълумотномалардан топиш мумкин.
Мураккаб боғланишли матрицаларни аниқлашнинг матрицали ифодалари фақат уларнинг боғланиши давомийлиги шарти бажарилгандагина ҳақиқийдир.
Агар ҳар бир тўртқутбликнинг иккита биринчи ва иккита иккинчи қутблари орқали оқадиган токлар катталиги жиҳатидан бир – бирига тенг ва йўналиши жиҳатидан қарама – қарши бўлса тўртқутбликларнинг боғланиши давомий дейилади.
24.2 Тўртқутбликларнинг ташқи тавсифлари
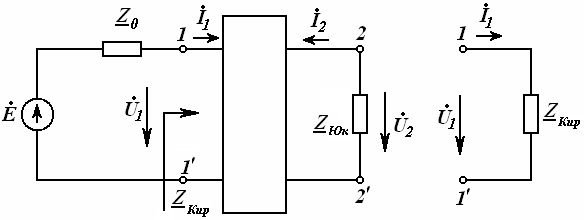 Чиқиш
клеммалари
Чиқиш
клеммалари ![]() юкланиш ZЮК қаршилигига юкланган тўртқутбликнинг
кириш қаршилиги (24.5-расм) деб, манба узилганда
юкланиш ZЮК қаршилигига юкланган тўртқутбликнинг
кириш қаршилиги (24.5-расм) деб, манба узилганда ![]() кириш клеммалари томонида ўлчанган қаршиликка
айтилади.
кириш клеммалари томонида ўлчанган қаршиликка
айтилади.
24.5–расм
Кириш қаршилиги ZКир ташқи тавсифлар сафига киради, чунки у фақат тўртқутбликнинг хусусий параметрларигагина эмас, балки ташқи юкламанинг ZЮк хоссаларига ҳам боғлиқдир.
Кириш қаршилигини (импеданс) кириш кучланишининг кириш токига нисбати
кўринишида аниқлаш мумкин:
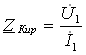
![]() ни юк қаршилиги
ZЮк ҳамда тўртқутбликнинг
А-параметрлари орқали
ифодалаймиз (2.4)
ни юк қаршилиги
ZЮк ҳамда тўртқутбликнинг
А-параметрлари орқали
ифодалаймиз (2.4)
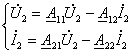
эканлигини ҳисобга олиб
![]()
ни ёзамиз.
![]()
А-параметрларни Z-, Y- ва Н-параметрлар орқали ифодалаб, бу параметрлар орқали ZКир ни аниқлаш мумкин.
Хусусий ҳолда узилган ва қисқа туташтирилган юк қаршилигида фақат тўртқутбликнинг ўзи, кириш қаршилигини характерлайди ва у фақат ўзининг коэффициентигагина боғлиқ бўлади,
масалан
![]()
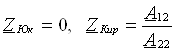
бўлганда ![]()
 (24.3)
(24.3)
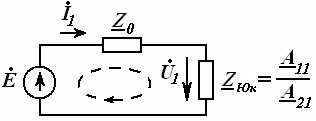
24.6 – расм.
Кирхгофнинг иккинчи қонуни бўйича қуйидагини ёзиш мумкин
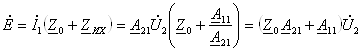
Кучланишнинг узатиш функциясини ![]() кучланишнинг
кучланишнинг ![]() га нисбати кўринишида ҳисоблаймиз,
яъни
га нисбати кўринишида ҳисоблаймиз,
яъни
![]()
24.3 Тўртқутбликнинг параметр лари
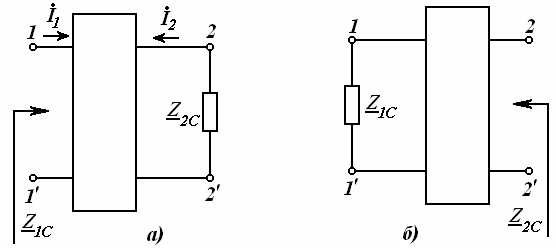
24.7– расм
Тўртқутбликлар назариясида, бирламчи параметрлардан ташқари тавсифий (иккиламчи) параметрлар ҳам қўлланилади. Булар: Z1С ва Z2С иккита қаршилик мавжудми:
1) ZЮК= Z2С бўлганда тўртқутблик кириш қаршилиги (24.7,а- расм)
ZКИР = Z1С га тенг;
2) тўртқутбликнинг кириши юкланганда (24.7,б-расм) унинг чиқиш қаршилиги ZЧиқ= Z2С га тенг.
Тавсифий қаршиликларни аниқлаш учун ZКирни аниқлаш ифодасидан фойдаланиб, ҳамда ZЮк= Z2С ва ZКир= Z1С эканлигини ҳисобга олсак, қуйидаги ифода келиб чиқади
![]() бу ерда
бу ерда ![]()
ZЧиқ= Z2С ва Z0= ZС эканлигини ҳисобга олиб қуйидагини аниқлаймиз
![]() ва мос
равишда
ва мос
равишда ![]()
А-параметрларда аниқланган ZС нинг қийматларини Z1С нинг ифодасига қўямиз.


ва квадрат тенгламани оламиз
![]()
у ҳолда
![]() ёки
ёки
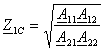
Z1С қаршилик кириш тавсифий қаршилиги дейилади. Шунга ўхшашликда чиқиш тавсифий қаршилигини аниқлаш мумкин. У қуйидагига тенг
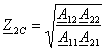
Изоҳ. Комплекс сонни квадрат
илдиздан чиқаришда иккита қийматни бери шини эсда тутиш лозим

бу ерда ![]() - арифметик илдиз.
- арифметик илдиз.
Шу сабабли топилган илдизларни физик қўлланишига текшириш лозим.
24.4 Тавсифий узатиш доимийси ва ишчи кучсизланиш
Катталик ZЮК= Z2С бўлганда тавсифий узатиш доимийси деб аталади ва қуйидагича аниқланади
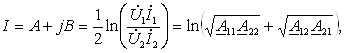
бу ерда 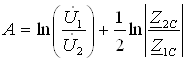 бўлиб, у тўртқутбликнинг
тавсифий кучсизланиш доимийси деб
аталади.
бўлиб, у тўртқутбликнинг
тавсифий кучсизланиш доимийси деб
аталади.
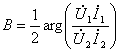 - катталик тавсифий фаза доимийси деб
аталади. Бу катталиклар ўзаро қуйидагича боғланиши мумкин
- катталик тавсифий фаза доимийси деб
аталади. Бу катталиклар ўзаро қуйидагича боғланиши мумкин
![]()
![]() ,
, ![]() ,
, ![]() .
.
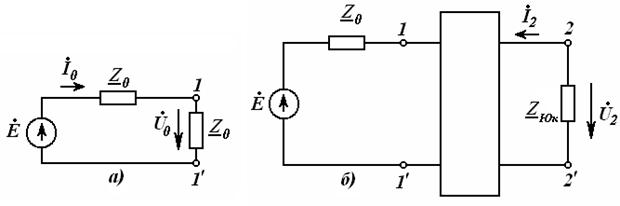
24.8 – расм
Тўртқутбликнинг ишчи кучсизланиши (децибелларда) қуйидагича аниқланади
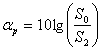 ,
, ![]() ,
, ![]()

Натижада қуйидаги тенгламалар тизимини ёзиш мумкин
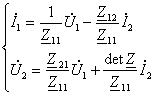
Белгилаш киритамиз
25-маъруза. Параметрлари тақсимланган электр занжирлар
25.1 Умумий тушунчалар
Шу бобгача таркибида R, L, C бўлган электр занжирлари ўрганилганда уларнинг параметрлари маълум элементларда тўпланган: индуктивлик бирор ғалтакда (ғалтакнинг магнит майдони энергияси магнит ўзакда тўпланган); сиғим эса конденсаторда мужассамланган (электр майдони конденатор қопламалари орасида тўпланган); резистив қаршилик эса резисторда тўпланган) электр энергиясини иссиқлик энергиясига айлантиришни амалга ошириш резисторнинг ток ўтказувчи қатламида амалга оширилади) деб фараз қилинган эди.
Бундай занжирларнинг геометрик ўлчамлари эътиборга олинган. Дарҳақиқат занжирлардаги жараёнларни таҳлил қилганда электромагнит майдоннинг тезлиги занжирдан сигналнинг ўтиш тезлиги ҳеч қаерда эсга олинмаган, элементлар эса фақатгина электр параметрлари билан тавсифланган, геометрик параметрлар кўрилмаган. Математика нуқтаи назаридан бундай занжирлар нул-ўлчовли объектлар деб, қаралган ва тўпланган параметрли занжирлар деб номланган.
Бироқ электр занжирларини тўпланган параметрли занжирлар сифатида тавсиф этиш ҳар доимо мумкин бўлавермайди. Масалан, алоқа линиясида, фидерда, тўлқин узаткичда ваҳоказоларда электромагнит энергиясини узатишни кўрганимизда шуни эътиборга олиш зарурки, магнит ва электр майдонлари бу қурилмаларда барча узунликлари бўйлаб тақсимланади ва электромагнит энергиясининг иссиқликка айланиши қурилмаларнинг барча узунликлари бўйлаб содир бўлади. Бундай занжирларда индуктивликлар, сиғимлар, резистив қаршиликларнинг узунлик бўйлаб тақсимланганлигини кўриш мумкин бўлади. Шунинг учун улар тақсимланган параметрли занжирлар дейилади.
Аслида, ҳар
бир элемент чекланган геометрик ўлчамларга эга; тезлиги вакуумдаги ёруғлик
тезлигидан ![]() ошмаган
занжир чиқишидаги электромагнит сигналлари киришдаги сигнал билан бир хил
вақт онида содир бўлмайди. Аммо реал занжирнинг чиқиш сигнал кириш
сигналига нисбатан кечикиши фақат шу сигнал ўзгариш вақти
сигналнинг занжирда тарқалиш вақтига яқин бўлганда, яъни
ошмаган
занжир чиқишидаги электромагнит сигналлари киришдаги сигнал билан бир хил
вақт онида содир бўлмайди. Аммо реал занжирнинг чиқиш сигнал кириш
сигналига нисбатан кечикиши фақат шу сигнал ўзгариш вақти
сигналнинг занжирда тарқалиш вақтига яқин бўлганда, яъни ![]() бўлгандагина
сезиларли бўлади. Бунда
бўлгандагина
сезиларли бўлади. Бунда ![]() сигналнинг
ўзгариш вақти;
сигналнинг
ўзгариш вақти; ![]() ёруғликнинг
тезлиги;
ёруғликнинг
тезлиги; ![]() занжирнинг
геометрик ўлчамлари. Бу импульс сигнали учун олд фронти давомийлиги (25.1,а-расм)
ёки гармоник сигнал учун чорак давр (25.1,б-расм).
занжирнинг
геометрик ўлчамлари. Бу импульс сигнали учун олд фронти давомийлиги (25.1,а-расм)
ёки гармоник сигнал учун чорак давр (25.1,б-расм).
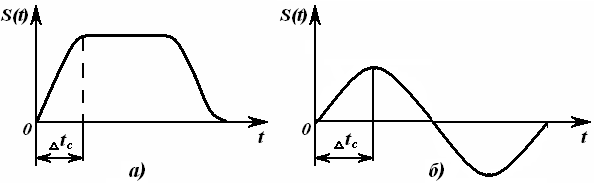
25.1-расм
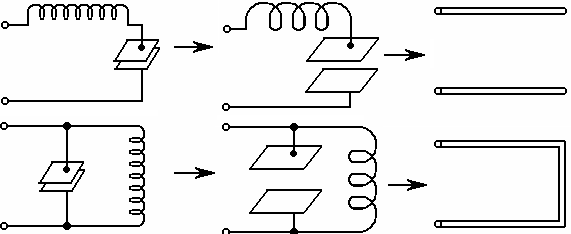 Тақсимланган параметрли занжирнинг узунлиги
бўйлаб чексиз кичик қисмининг чиқишидаги ток ва кучланиш, унинг
киришидаги, мос равишда, ток ва кучланишига тенг эмас, улар ҳам қийматлари
билан ҳам, фазалари билан фарқланадилар. Шундай қилиб,
занжирнинг ихтиёрий нуқтасидаги ток ва кучланиш, нафақат вақт
Тақсимланган параметрли занжирнинг узунлиги
бўйлаб чексиз кичик қисмининг чиқишидаги ток ва кучланиш, унинг
киришидаги, мос равишда, ток ва кучланишига тенг эмас, улар ҳам қийматлари
билан ҳам, фазалари билан фарқланадилар. Шундай қилиб,
занжирнинг ихтиёрий нуқтасидаги ток ва кучланиш, нафақат вақт
![]() нинг, балки
геометрик (фазовий) кординатларининг (масалан, занжир учларининг биригача
бўлган масофа) функциясидир. Масалан, саноат частотаси
нинг, балки
геометрик (фазовий) кординатларининг (масалан, занжир учларининг биригача
бўлган масофа) функциясидир. Масалан, саноат частотаси ![]() бўлган
ўзгарувчан ток занжири учун тарқоқ параметрли занжир моделини қўллаш
учун электр узатиш линияси узунлиги юзлаб километрни ташкил этиши зарур. Бу
катта кучланишли электр узатиш линиялари ўлчамларидандир.
бўлган
ўзгарувчан ток занжири учун тарқоқ параметрли занжир моделини қўллаш
учун электр узатиш линияси узунлиги юзлаб километрни ташкил этиши зарур. Бу
катта кучланишли электр узатиш линиялари ўлчамларидандир.
25.2-расм
Вақти ![]() бўлган ҳозирги
замон телекоммуникация тизимлари, ЭҲМ ва бошқа ахборот
технологиялари жиҳозларида, агар занжирнинг геометрик ўлчамлари
бўлган ҳозирги
замон телекоммуникация тизимлари, ЭҲМ ва бошқа ахборот
технологиялари жиҳозларида, агар занжирнинг геометрик ўлчамлари ![]() бўлса тақсимланган
параметрли занжирлар модели шлакаблок ёки платанинг ўлчамларидир.
бўлса тақсимланган
параметрли занжирлар модели шлакаблок ёки платанинг ўлчамларидир.
Тақсимланган параметрли занжир моделининг энг соддаларидан бири сифатида тебранма контурнинг (25.2-расм) “трансфорцияси”ни таҳлил қилиш жараёнида ҳосил бўладиган занжирлар узун линиялар деб номланади. Биринчи ҳолатда линия узилган, иикинчисида-қисқа туташтирилган ҳисобланади. Узун линияларга мос келадиган объектлар ҳар хил тузилишга эга (25.3-расм); бунда қуйидаги белгилашлар киритилган:
1-ўтказгич (сим); 2-диэлектрик; 3-тўқима. Ушбу линиялар
 ҳозирги замон ҳисоблаш техникаси
воситалари ва автоматик бошқариш тизимлари орасидаги улаш элементлари ҳисобланади.
ҳозирги замон ҳисоблаш техникаси
воситалари ва автоматик бошқариш тизимлари орасидаги улаш элементлари ҳисобланади.
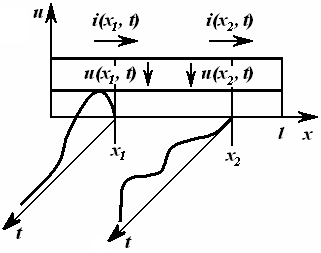 Узун линиялар узунлиги
бўйлаб: кенглиги, баландлиги (кўндаланг кесими) бўлмаган, реал физик фазодаги
бир ўлчамли объект ҳисобланади. Электр занжирлари назариясида узун
линияларни кўрсатилгандек акс
Узун линиялар узунлиги
бўйлаб: кенглиги, баландлиги (кўндаланг кесими) бўлмаган, реал физик фазодаги
бир ўлчамли объект ҳисобланади. Электр занжирлари назариясида узун
линияларни кўрсатилгандек акс
эттирилади.
Узун линиялардаги ток ва кучланиш нафақат вақтга боғлиқ,
балки координатасига ҳам боғлиқ. Шунинг учун улар икки
аргументли функцияси сифатида белгиланади: ![]()
![]() Узун
линиянинг тенгламаси ток ва кучланиш орасидаги боғланиш ихтиёрий
Узун
линиянинг тенгламаси ток ва кучланиш орасидаги боғланиш ихтиёрий ![]() нуқтада
ҳам ифодалаши шарт. Бундай тенгламалар фақат Максвелл тенгламалари
тизими ёрдамида олинади. Қуйида
физик
25.3-расм
нуқтада
ҳам ифодалаши шарт. Бундай тенгламалар фақат Максвелл тенгламалари
тизими ёрдамида олинади. Қуйида
физик
25.3-расм
Жараённинг кўргазмали эканлигига
асоссланган, соддалаштирилган
усулни келтирамиз. Бунинг учун узун линияни ![]() узунликдаги
элементар бўлакларга бўлиб чиқамиз ва ҳар бир бўлакни тўпланган
параметрли эквивалент занжир деб қараймиз. Ўтказгичларнинг индуктивлигини
ҳисобга олиш учун погон
узунликдаги
элементар бўлакларга бўлиб чиқамиз ва ҳар бир бўлакни тўпланган
параметрли эквивалент занжир деб қараймиз. Ўтказгичларнинг индуктивлигини
ҳисобга олиш учун погон ![]() индуктивлиги
(1метр узунликдаги индуктивлик)дан, ўтказгичлар орасидаги сиғим-погон сиғимлиги
индуктивлиги
(1метр узунликдаги индуктивлик)дан, ўтказгичлар орасидаги сиғим-погон сиғимлиги
![]() иссиқликка
ажралаётган қувват исрофларини-индуктивлик билан кетма-кет уланган погона
исрофлар қаршилиги
иссиқликка
ажралаётган қувват исрофларини-индуктивлик билан кетма-кет уланган погона
исрофлар қаршилиги ![]() ва сиғимга
параллел уланган кўндаланг погон ўтказувчанлик
ва сиғимга
параллел уланган кўндаланг погон ўтказувчанлик ![]() (25.5-расм)
фойдаланамиз.
(25.5-расм)
фойдаланамиз.
Ушбу L, C, r, g қийматлар занжирнинг геометрик ўлчамларига ҳамда узатиш
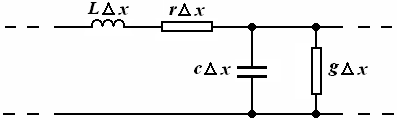
25.4-расм
линиялари ясалган материалларга боғлиқ, занжирнинг бир жинсли, яъни барча бўлаклари учун бир хил деб ҳисоблаймиз.
25.2 Узун линиялар телеграф тенгламалари
Кирхгоф ва Ом қонунлари
асосида занжирнинг бир қисми учун тенгламалар тузамиз:
![]()
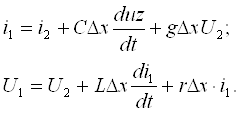
Агар ![]() деб ҳисоблаб
қуйидагиларни ҳосил қиламиз:
деб ҳисоблаб
қуйидагиларни ҳосил қиламиз:
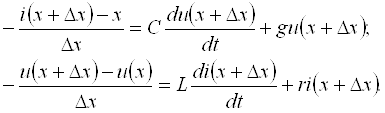
Ушбу
тенгламаларда ![]() лимитга ўтсак,
тенглик белгисининг чап томонда
лимитга ўтсак,
тенглик белгисининг чап томонда ![]() нинг хусусий ҳосилаларини,
ўнг томонда-вақт
нинг хусусий ҳосилаларини,
ўнг томонда-вақт ![]() бўйича
хусусий ҳосилаларни ҳосил қиламиз.
бўйича
хусусий ҳосилаларни ҳосил қиламиз.
![]()
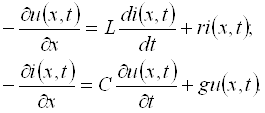 (25.1)
(25.1)
Тенгламалар тизими (25.1) узун линияларнинг телеграф тенгламалари дейилади.
Тарқоқ
параметрли занжирлар учун жараёнлар хусусий ҳосилали дифференциал
тенгламалар билан ифодаланади. Бундай тенгламалар сғимларини таҳлил
қилиш учун аввал “исрофсиз” узун линияларнинг хусусий ҳолини ![]() кўрайлик:
кўрайлик:
![]()
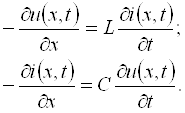 (25.2)
(25.2)
Биринчи
тенгламанинг иккала қисмини ![]() бўйича,
иккинчисини
бўйича,
иккинчисини ![]() бўйича
дифференциаллаймиз:
бўйича
дифференциаллаймиз:
![]()
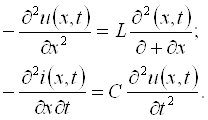 (25.3)
(25.3)
Аралаш хусусий ҳосилаларнинг
тенг эканлигини эътиборга олиб қуйидагини ҳосил қиламиз:
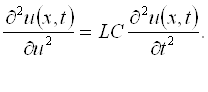
LС қийматнинг
бирлиги ![]() бўлгани
учун, қуйидагини белгилаймиз:
бўлгани
учун, қуйидагини белгилаймиз: ![]() Шунинг учун ҳосил
қилинган тенгламани қуйидагича ёзиш мумкин:
Шунинг учун ҳосил
қилинган тенгламани қуйидагича ёзиш мумкин:
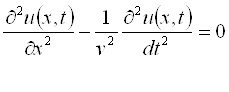 (25.4)
(25.4)
Ушбу (25.4) тенглама тўлқин тенгламаси дейилади.
25.3 Тўлқин тенгламаси ва унинг физик талқини
Тўлқин тенгламасининг умумий ечимини биринчи бўлиб Француз математиги Даламбер қуйидаги ҳолатда ҳисоблаган:
![]() (25.5)
(25.5)
бунда ![]() ва
ва ![]() тўлқин
тенгламаси учун бошланғич ва чегаравий шартлар билан аниқланадиган
ихтиёрий функциялар.
тўлқин
тенгламаси учун бошланғич ва чегаравий шартлар билан аниқланадиган
ихтиёрий функциялар.
Даламбер ечимини бевосита дифференциаллаб (25.4) тўлқин тенгламасини айниятга айлантиришга иқрор бўлишимиз мумкин.
Агар кучланиш
(25.5) шаклда бўлса, ток ![]() учун унинг
ифодасини аниқлаймиз:
учун унинг
ифодасини аниқлаймиз:![]() бўлганлиги учун, қуйидагини
ҳосил қиламиз:
бўлганлиги учун, қуйидагини
ҳосил қиламиз:
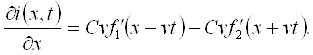
Ўзгарувчи ![]() бўйича
интеграллаб, қуйидагини аниқлаймиз:
бўйича
интеграллаб, қуйидагини аниқлаймиз:
![]()
![]()
Тенгламадаги![]() параметри
параметри ![]() ўлчов
бирлигига эга ва тўлқин қаршилиги деб номланади. Шундай қилиб,
ўлчов
бирлигига эга ва тўлқин қаршилиги деб номланади. Шундай қилиб,
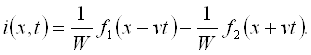 (25.5)
(25.5)
Узун линиялардаги
ток худди кучланиш каби икки ихтиёрий ![]() ва
ва ![]() функциялар
билан аниқланади. Уларнинг мазмунини батафсилроқ кўрайлик. Функция
функциялар
билан аниқланади. Уларнинг мазмунини батафсилроқ кўрайлик. Функция ![]() шарти
бажарилганда
шарти
бажарилганда ![]() бўлади.
Айтайлик,
бўлади.
Айтайлик, ![]() бўлганда
бўлганда ![]() берилган
бўлсин (24.6-расм).
берилган
бўлсин (24.6-расм).
Вақт ![]() га ўзгарганда
кучланиш
га ўзгарганда
кучланиш ![]() бўлади,
бўлади, ![]() вақтдан
сўнг эса
вақтдан
сўнг эса ![]() бўлади. Вақт
ўтиши билан
бўлади. Вақт
ўтиши билан ![]() функция
графиги
функция
графиги ![]() ўқи
бўйлаб
ўқи
бўйлаб ![]() тезлик
билан равон ўнгга сурилади. Бу ташкил этувчининг ортиши йўналишида ҳаракат
қилувчи тўғри тўлқин дейилади. Шундай қилиб,
тезлик
билан равон ўнгга сурилади. Бу ташкил этувчининг ортиши йўналишида ҳаракат
қилувчи тўғри тўлқин дейилади. Шундай қилиб, ![]() Шу тариқа,
Шу тариқа,
![]() ташкил
этувчини ҳам кўриб чиқсак, бу тескари тўлқин нинг
камайиши томонига
ташкил
этувчини ҳам кўриб чиқсак, бу тескари тўлқин нинг
камайиши томонига  тарқалар экан:
тарқалар экан:
![]()
Шундай қилиб,
узун линиянинг кучланиши бир-бирига томон ![]() тезликда тарқалувчи
тўғри
тезликда тарқалувчи
тўғри ![]() ва тескари
ва тескари ![]() тўлқинлар
йиғиндисидан иборат
экан.
тўлқинлар
йиғиндисидан иборат
экан.
25.5-расм
![]()
(25.5)дан келиб
чиққандек, линия токи ҳам икки ташкил этувчи тўлқин йиғиндисидан
иборат:
![]()
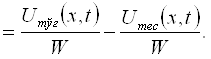 (24.6)
(24.6)
Булардан кўринадики, линиянинг
тўлқин қаршилиги ток ва кучланишлар-
нинг тўғри тўлқинини
![]() ва тескари тўлқинини
ва тескари тўлқинини
![]() боғлар
экан. Бунда линияда қувват исрофлари мавжуд бўлмайди, тўлқин қаршилиги
боғлар
экан. Бунда линияда қувват исрофлари мавжуд бўлмайди, тўлқин қаршилиги
![]() оддий қаршилик
оддий қаршилик
![]() сингари
ўлчов бирлиги
сингари
ўлчов бирлиги ![]() (Ом) бўлса ҳам,
буткул бошқа физик мазмунни акс эттиради. Бу қаршилик электр токи қувватининг
иссиқликка айланишини кўрсатмайди, балки фақат бир йўналишдаги ток
ва кучланишларнинг боғланишини ифодалайди. Тўғри ва тескари тўлқинлар
орасидаги боғланиш линиядаги чегаравий шартлардан аниқланади ва
чекли линияларни кўришдан аниқланади.
(Ом) бўлса ҳам,
буткул бошқа физик мазмунни акс эттиради. Бу қаршилик электр токи қувватининг
иссиқликка айланишини кўрсатмайди, балки фақат бир йўналишдаги ток
ва кучланишларнинг боғланишини ифодалайди. Тўғри ва тескари тўлқинлар
орасидаги боғланиш линиядаги чегаравий шартлардан аниқланади ва
чекли линияларни кўришдан аниқланади.
 Чап томонидан координата билан чекланган линияни
кўрайлик. Чекланган нуқтасида юкланиш қаршилиги RЮк
уланган (25.6-расм).
Чап томонидан координата билан чекланган линияни
кўрайлик. Чекланган нуқтасида юкланиш қаршилиги RЮк
уланган (25.6-расм).
Шубҳасиз, агар линиянинг ихтиёрий нуқтаси учун ток ва кучланишлар орасидаги боғланиш
25.6-расм
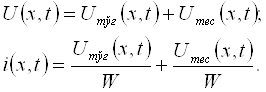
шаклида бўлса, у ҳолда ![]() нуқтада
нуқтада
![]() бўлади. Шу
шартни тўғри ва тескари тўлқинлар орқали ифодалаймиз:
бўлади. Шу
шартни тўғри ва тескари тўлқинлар орқали ифодалаймиз:
![]()
Бундан қуйидаги ифодани ҳосил қиламиз:
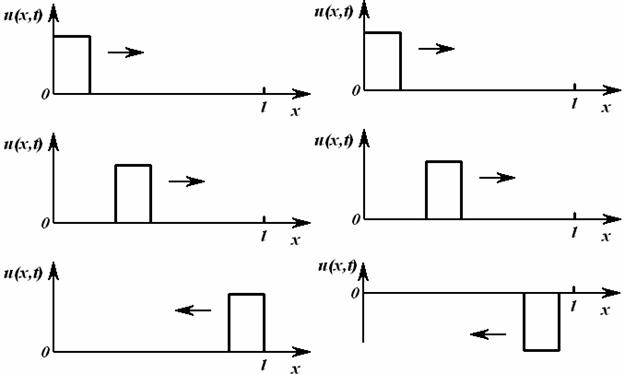 25.7-расм
25.7-расм
Коэффициент
![]()
![]() қайтариш
коэффициенти дейилади.
қайтариш
коэффициенти дейилади.
Агар ![]() бўлганда
бўлганда ![]() бўлса, у ҳолда
бўлса, у ҳолда
![]() да
да ![]() бўлар экан.
Бу жараённи электромагнит тўлқиннинг юк қаршилигидан қайтиши
дейилади. Масалан, агар
бўлар экан.
Бу жараённи электромагнит тўлқиннинг юк қаршилигидан қайтиши
дейилади. Масалан, агар ![]() бўлса, у ҳолда
тескари тўлқин пайдо бўлмайди.
бўлса, у ҳолда
тескари тўлқин пайдо бўлмайди. ![]() бўлганда
бўлганда ![]() Бу жараён тўла
қайтиш дейилади. Агар
Бу жараён тўла
қайтиш дейилади. Агар ![]() бўлса,
бўлса,
![]() Бу жараён ишорасини
ўзгартирган тўла қайтиш дейилади. 24.8-расмда шу иккала жараён
тушунтирилади.
Бу жараён ишорасини
ўзгартирган тўла қайтиш дейилади. 24.8-расмда шу иккала жараён
тушунтирилади.
26-маъруза. Узун линияларда гармоник тўлқинлар
Агар узун линияга таъсир гармоник характерга эга бўлса, у ҳолда линиянинг ихтиёрий кесимида кучланиш ва ток гармоник шаклда бўлади. Унда қуйидагиларни ёзиш мумкин:
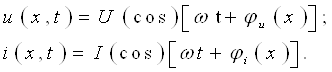 (26.1)
(26.1)
Комплекс амплитудалар усулидан фойдаланиб, қуйидаги белгилашларни киритамиз:
 (26.2)
(26.2)
Ушбу ифодаларни телеграф тенгламаларига қўйсак
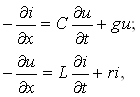 (26.3)
(26.3)
қуйидагиларни ҳосил
қиламиз:
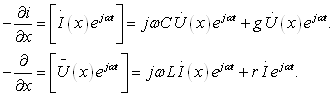 (26.4)
(26.4)
![]() га қисқартириб
ва
га қисқартириб
ва ![]() белгилаб
частотавий соҳадаги оддий дифференциал тенгламалар шаклидаги телеграф
тенгламаларини ҳосил қиламиз.
белгилаб
частотавий соҳадаги оддий дифференциал тенгламалар шаклидаги телеграф
тенгламаларини ҳосил қиламиз.
Қиймат ![]() линиянинг
комплекс кўндаланг ўтказувчанлиги,
линиянинг
комплекс кўндаланг ўтказувчанлиги, ![]() линиянинг
комплекс кўндаланг қаршилиги дейилади:
линиянинг
комплекс кўндаланг қаршилиги дейилади:
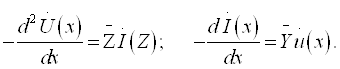 (26.5)
(26.5)
Биринчи
тенгламани ![]() бўйича
дифференциаллаб ва ҳосил бўлган тенгламани иккинчисига қўйсак, тўлқин
тенгламасининг частотавий аналагини ёки Гельмгольц тенгламасини ҳосил қиламиз:
бўйича
дифференциаллаб ва ҳосил бўлган тенгламани иккинчисига қўйсак, тўлқин
тенгламасининг частотавий аналагини ёки Гельмгольц тенгламасини ҳосил қиламиз:
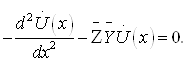 (26.6)
(26.6)
Катталик ![]() ни линияда тўлқин тарқалишининг
комплекс коэффициенти дейилади. Тенламанинг умумий ечими қуйидагича
бўлади:
ни линияда тўлқин тарқалишининг
комплекс коэффициенти дейилади. Тенламанинг умумий ечими қуйидагича
бўлади:
![]() (26.7)
(26.7)
бунда
![]() ва
ва ![]() - ихтиёрий комплекс сонлар.
- ихтиёрий комплекс сонлар.
Линиядаги токнинг комплекс амплитудаси қуйидаги
ифода ёрдамида аниқланади:
 (26.8)
(26.8)
ёки
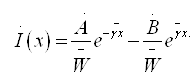 (26.9)
(26.9)
Қиймат ![]() комплекс тўлқин қаршилиги дейилади.
(26.8) ва (26.9) боғланишлар комплекс амплитудаларнинг линия бўйлаб тақсимланишини
аниқлайди.
комплекс тўлқин қаршилиги дейилади.
(26.8) ва (26.9) боғланишлар комплекс амплитудаларнинг линия бўйлаб тақсимланишини
аниқлайди.
![]() линиядаги тўғри тўлқин,
линиядаги тўғри тўлқин, ![]() тескари тўлқинга мос келишини кўрайлик. Бунинг
учун хусусий ҳол - қувват исрофсиз линиянияни кўрайлик:
тескари тўлқинга мос келишини кўрайлик. Бунинг
учун хусусий ҳол - қувват исрофсиз линиянияни кўрайлик:
![]() (26.10)
(26.10)
Бу ҳолат учун:
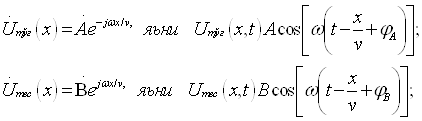 (26.11)
(26.11)
Кутганимиздек, тўғри ва тескари тўлқинлар,
шакли гармоник бўлиб, бир-бирига қарама-қарши йўналишда ![]() тезликда тарқалар экан.
тезликда тарқалар экан.
Агар ![]() ва
ва ![]() бўлса, у ҳолда тўғри тўлқин
бўлса, у ҳолда тўғри тўлқин ![]() бўлади. Унга мос бўлган
бўлади. Унга мос бўлган ![]() линия бўйлаб амплитудаси сўнувчи бўлади. Шунга
ўхшаш равишда тескари тўлқин ҳам сўнади.
линия бўйлаб амплитудаси сўнувчи бўлади. Шунга
ўхшаш равишда тескари тўлқин ҳам сўнади.
Исрофли узун линиялар ўзларининг сўнишлари билан характерланадилар.
Сўнишни, аксарият, логарифмик масштабда l масофадаги тўғри тўлқин
амплитудасининг линия бошланишидаги амплитудасига нисбатан каби аниқланади:
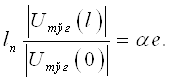 (26.12)
(26.12)
Линияниннг бирлик узунлигида сўниш ![]() га, яъни тарқалиш коэффициентининг ҳақиқий
қисмига тенг.
га, яъни тарқалиш коэффициентининг ҳақиқий
қисмига тенг.
Аксарият, амалий масалаларда нотурал логарифни эмас, ўнлик логарифми қабул қилинади. Бунда сўниш децибелда ифодаланади:
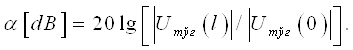 (26.13)
(26.13)
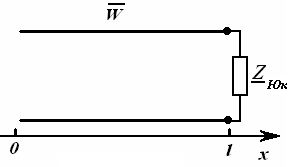 Тескари
тўлқин кучланишининг комплекс амплитудаси қуйидагича ёзалади:
Тескари
тўлқин кучланишининг комплекс амплитудаси қуйидагича ёзалади:
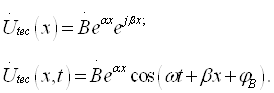
![]() ва
ва ![]() доимий қийматлар тўлқиннинг
юкдан қайтишида аниқлана-
26.1-расм
доимий қийматлар тўлқиннинг
юкдан қайтишида аниқлана-
26.1-расм
ди.
Линия охиридаги ![]() масофада юк
масофада юк ![]()
уланган
бўлсин (26.1-расм). Линиянинг ихтиёрий нуқтасида комплекс амплитудалар
(26.8) ва (26.9) ифодалар ёрдамида аниқланади. Масалан, ![]() нуқтада
нуқтада ![]() Бунда қуйидаги тенгламалар ҳақли
бўлади:
Бунда қуйидаги тенгламалар ҳақли
бўлади:
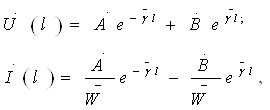 (26.14)
(26.14)
улардан
![]() ва
ва ![]() доимийларни аниқлаш мумкин:
доимийларни аниқлаш мумкин:
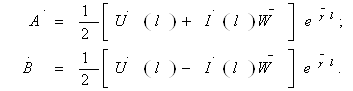 (26.15)
(26.15)
Бу ифодаларни (26.8) ва (26.9)га қўйсак, қуйидагиларни оламиз:
 (26.16)
(26.16)
Тенгламалар ҳадларини гуруҳлаб, уларни қуйидаги
шаклда қайта ёзиш мумкин:
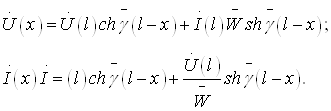 (26.17)
(26.17)
Агар 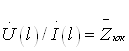 эканлигини
ва
эканлигини
ва ![]() қаршилигига
уланган
қаршилигига
уланган ![]() узунликдаги
узун линия бўлагининг кириш қаршилигини
узунликдаги
узун линия бўлагининг кириш қаршилигини ![]() деб
белгиласак, у ҳолда қуйидагича ёзиш мумкин:
деб
белгиласак, у ҳолда қуйидагича ёзиш мумкин:
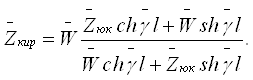 (26.18)
(26.18)
Бу линия бўлаги кириш қаршилигининг ифодасидир.
Бу қаршиликнинг қандай частотавий боғланишда эканлигини
кўрайлик. Соддалик учун линия исрофсиз деб ҳисоблаймиз: ![]() Бунда
Бунда ![]() ва кириш қаршилиги
ва кириш қаршилиги
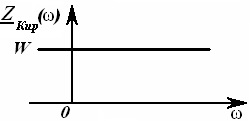
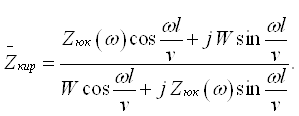
Агар ![]() яъни юк қаршилиги тўлқин қаршилигига
тенг бўлса, у ҳолда
26.2-расм
яъни юк қаршилиги тўлқин қаршилигига
тенг бўлса, у ҳолда
26.2-расм
![]()
Тўлқин қаршилигига тенг бўлган юк қаршилигига уланган линия бўлагининг кириш қаршилиги шу тўлқин қаршилигига тенг (26.2-расм).
Агар интеграллаш доимийси аниқ-ланса, унда қуйидагини ҳосил қилиш мумкин:
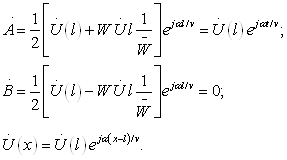 (26.19)
(26.19)
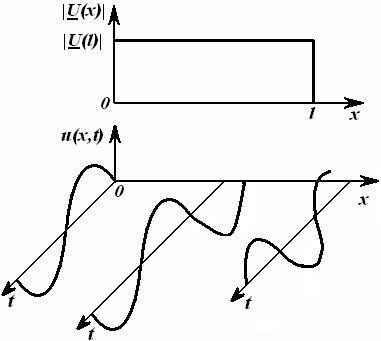
Юкланиш мувофиқланганда кучланиш ва ток амплиту-далари линиянинг узунлиги бўйлаб ўзгар-мас бўлади (26.3-расм). Линиянинг уш-бу режими юкловчи тўлқинлар режими дейилади.
Энди ![]() бўлган қисқа туташув режимини
(26.3-расм) кўрайлик:
бўлган қисқа туташув режимини
(26.3-расм) кўрайлик: ![]()
26.3-расмда бундай боғланиш-
нинг графиги кўрсатилган.
26.3-расм
Интеграллаш домийларини аниқлаб,
қуйидагиларни ҳосил қиламиз:
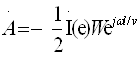 ;
; 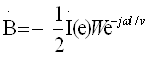
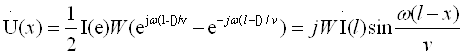 .
(26.20)
.
(26.20)
Амплитудаларнинг максимумлари координаталари кучланишлар боғламлари (лучность напряжений), ноллари эса - кучланишлар тугунлари дейилдади.
Узун линия бўлагининг кети узилган (26.3-расм) режим
учун кириш қаршилиги ![]() бўлади. Бундай боғланишнинг графиги
26.4-расмда тасвирланган. Шуни кўриш мумкинки, кети узилган линия бўлаги учун
кучланиш амплитудаси тақсимланишининг графиги 26.6-расмдагидек бўлади.
бўлади. Бундай боғланишнинг графиги
26.4-расмда тасвирланган. Шуни кўриш мумкинки, кети узилган линия бўлаги учун
кучланиш амплитудаси тақсимланишининг графиги 26.6-расмдагидек бўлади.
26.4-расм 26.5-расм
26.6-расм 26.7-расм
26.7-расмда кучланиш амплитудасининг шундай тақсимланиш графиги тасвирланган.

26.8-расм 26.9-расм
Юқорида кўрилган икки вазият тўлқинлар ҳолати
режимига таалулуқлидир. Бу режимда тўлқинлар юк қаршилигига
«югурадилар» ва қайтиш коэффициенти ![]() билан ундан тўлалигича қайтадилар. Баъзи
нуқталарда қайтувчи тўлқинлар тушувчилар билан бир хил
фазада бўлиб, кучаядилар. Бошқа нуқталарда тўғри ва тескари
тўлқинлар тескари фазада бўлиб, сусаядилар. Бунда линия бўйлаб энерги
узатилади.
билан ундан тўлалигича қайтадилар. Баъзи
нуқталарда қайтувчи тўлқинлар тушувчилар билан бир хил
фазада бўлиб, кучаядилар. Бошқа нуқталарда тўғри ва тескари
тўлқинлар тескари фазада бўлиб, сусаядилар. Бунда линия бўйлаб энерги
узатилади.
Агар 0<![]() <∞
бўлса, тўлқинлар қисман сусайиб (26.8-расм) аралаш тўлқинлар
режими ҳосил бўлади:
<∞
бўлса, тўлқинлар қисман сусайиб (26.8-расм) аралаш тўлқинлар
режими ҳосил бўлади: ![]() Линиянинг юк билан мувофиқлашиш даражаси
амплитуданинг максимал қиймати (кучланишлар боғламалари)нинг
минимал қийматига (кучланишлар тушунчаларига) нисбати билан аниқланиши
мумкин. Агар ушбу нисбат бирга тенг бўлса - бу югурувчи тўлқинлар режимига
мос бўлади, агар у чексиз бўлса - бу турғун тўлқинлар режими
дейилади
Линиянинг юк билан мувофиқлашиш даражаси
амплитуданинг максимал қиймати (кучланишлар боғламалари)нинг
минимал қийматига (кучланишлар тушунчаларига) нисбати билан аниқланиши
мумкин. Агар ушбу нисбат бирга тенг бўлса - бу югурувчи тўлқинлар режимига
мос бўлади, агар у чексиз бўлса - бу турғун тўлқинлар режими
дейилади
|
|
(26.21)
26.1 Узун линияларда импульс жараёнлар таҳлили
Ушбу қисмда
қуйидаги масалани кўрамиз: узунлиги ![]() ва тўлқин
қаршилиги
ва тўлқин
қаршилиги ![]() бўлган
исрофсиз узун линия бўлаги мустақил кучланиш манбаси
бўлган
исрофсиз узун линия бўлаги мустақил кучланиш манбаси ![]() га генератор ички
қаршилиги
га генератор ички
қаршилиги ![]() орқали
улунган. Линия бўлагининг кети
орқали
улунган. Линия бўлагининг кети ![]() элементларидан
иборат бўлган занжирга уланган. Линиянинг ихтиёрий нуқтасидаги
элементларидан
иборат бўлган занжирга уланган. Линиянинг ихтиёрий нуқтасидаги ![]() кучланишни
аниқлаш зарур. Шунга ўхшаш масалалар алоқа линиялари,
телекоммуникацион ва радиотехник жиҳозлар, ЭҲМ ва АБТнинг ишлаш
жараёнларини таҳлил қилишда катта қизиқиш уйғотади.
кучланишни
аниқлаш зарур. Шунга ўхшаш масалалар алоқа линиялари,
телекоммуникацион ва радиотехник жиҳозлар, ЭҲМ ва АБТнинг ишлаш
жараёнларини таҳлил қилишда катта қизиқиш уйғотади.
Бу масалани ечишни телеграф тенгламалари тузишни юкланиш занжири оддий
дифференциал тенгламалари билан биргаликда тўгридан-тўғри
интеграллаш йўли билан амалга ошириш мумкин. Аммо бу жараён қўпол ва
тушуниш учун кўргазмали эмас. Лаплас узгартиришлари эса самаралидир.
Лаплас ўзгартиришларини ![]() кучланиш
тўлқинига татбиқ этамиз, бунда қуйидаги белгилашлар
киритамиз.
кучланиш
тўлқинига татбиқ этамиз, бунда қуйидаги белгилашлар
киритамиз.
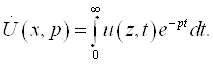 (26.22)
(26.22)
Линиянинг
бошланишида кучланишнинг тўғри ташкил этувчиси ![]() ва унинг
Лаппас бўйича ўзгартириши қуйидагича бўлади
ва унинг
Лаппас бўйича ўзгартириши қуйидагича бўлади
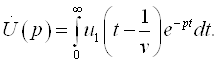 (26.23)
(26.23)
Кучланишнинг
ихтиёрий ![]() нуқтасидаги
қиймати вақт бўйича
нуқтасидаги
қиймати вақт бўйича ![]() қийматга
силжиган
қийматга
силжиган ![]() тўлқинни
тасвир этади. Унда
тўлқинни
тасвир этади. Унда
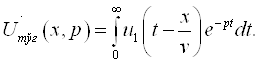 (26.24)
(26.24)
Янги ўзгарувчи ![]() киритиб, қуйидагини
ҳосил қиламиз:
киритиб, қуйидагини
ҳосил қиламиз:
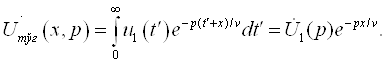 (26.25)
(26.25)
Бу ифода, агар
линия бошланишида тўғри тўлқин кучланиши ![]() тасвирга
эга бўлгандаги линиянинг ихтиёрий
тасвирга
эга бўлгандаги линиянинг ихтиёрий ![]() нуқтасидаги
сигналнинг Лаплас ўзгартириши (тасвири)дир. Шундай қилиб, юкка кучланиш
тўлқини тарқалади ва
нуқтасидаги
сигналнинг Лаплас ўзгартириши (тасвири)дир. Шундай қилиб, юкка кучланиш
тўлқини тарқалади ва ![]() нуқтадаги
унинг тасвири қуйидагича бўлади:
нуқтадаги
унинг тасвири қуйидагича бўлади:
![]() (26.26)
(26.26)
Токнинг тўғри
тўлқинига қуйидагини тўғридан-тўғри ёзиш мумкин
бўлганлиги учун
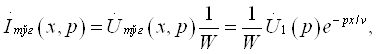 (26.27)
(26.27)
![]() нуқтадаги
қайтувчи тўлқинни билган ҳолда, қайтувчи тўлқиннинг
тасвирини шундай ёзиш мумкин. Айтайлик, унинг тасвири
нуқтадаги
қайтувчи тўлқинни билган ҳолда, қайтувчи тўлқиннинг
тасвирини шундай ёзиш мумкин. Айтайлик, унинг тасвири ![]() бўлсин.
бўлсин. ![]() бўлганлиги учун
бўлганлиги учун
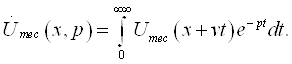 (26.28)
(26.28)
Линиянинг ![]() нуқтасида
қайтувчи тўлқин оқимида
нуқтасида
қайтувчи тўлқин оқимида ![]() шунинг учун
шунинг учун
![]() (26.29)
(26.29)
Маълумки, тескари тўлқин токининг тасвири
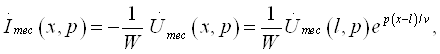 (26.30)
(26.30)
![]() нуктада
нуктада ![]() Бу ифодага
кучланиш ва токнинг тўғри ва тескари тўлқинлари учун ифодаларини
киритсак қуйидагини ҳосил қиламиз:
Бу ифодага
кучланиш ва токнинг тўғри ва тескари тўлқинлари учун ифодаларини
киритсак қуйидагини ҳосил қиламиз:
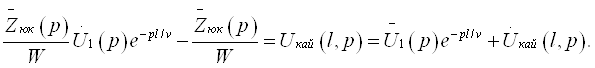
(26.31)
Бундан
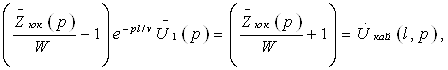 (26.32)
(26.32)
ёки 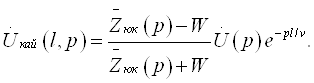
Шундай қилиб
оператор коэффициенти 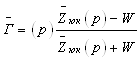 ни ҳисоблаш
ва линия бошидаги тўғри тўлқин тасвири
ни ҳисоблаш
ва линия бошидаги тўғри тўлқин тасвири ![]() ни
ни ![]() га
кўпайтириб кечикиш
га
кўпайтириб кечикиш ![]() ни эътиборга
олиб аниқлаш мумкин экан.
ни эътиборга
олиб аниқлаш мумкин экан.
Қайтувчи
тўлқинни аниқлаш. Агар ихтиёрий нуқтада қайтувчи
тўлқин кучланишини аниқлаш зарур бўлса, ![]() ни кўпайтмага
кўпайтириш кифоядир. Унда
ни кўпайтмага
кўпайтириш кифоядир. Унда
![]() (26.33)
(26.33)
Ниҳоят
юкланишдан бир марта қайтишдан сўнг, ихтиёрий нуқтадаги тўла
кучланишни тушувчи ва қайтувчи кучланишлар йиғиндиси каби аниқлаш
мумкин:
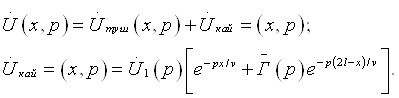 (26.34)
(26.34)
2l/v<t<3l/v вақтнинг
онлари учун ![]() ифодасини тўлқинларнинг
линия киришидаги такрорий қайтишини эътиборга олиш зарур.
Ифода (26.34) оператор қаршилиги
ифодасини тўлқинларнинг
линия киришидаги такрорий қайтишини эътиборга олиш зарур.
Ифода (26.34) оператор қаршилиги ![]() бўлган
юкланиш билан Лаплас ўзгартиришидаги
бўлган
юкланиш билан Лаплас ўзгартиришидаги ![]() кучланиши
бўлган генератор орасида
кучланиши
бўлган генератор орасида ![]() узун линия
бўладиган сигнал тасвирини ҳисоблаш имконини беради (26.9-расм).
узун линия
бўладиган сигнал тасвирини ҳисоблаш имконини беради (26.9-расм).
(26.34) ифодадан қуйидаги
муҳим хусусий хулоса келиб чиқади: линия бошланишидаги ![]() кучланиш
кучланиш
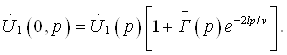 (26.35)
(26.35)
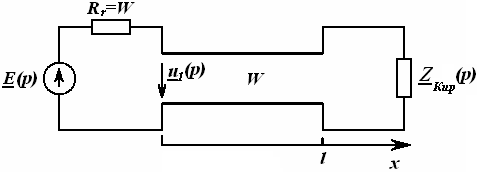 Бу ифода
линия бошидаги тўла кучланишни ифодалайди. У икки ташкил этувчилар йиғиндисидан
иборат: биринчиси-мустақил манбаадан келувчи сигнал шаклидан
Бу ифода
линия бошидаги тўла кучланишни ифодалайди. У икки ташкил этувчилар йиғиндисидан
иборат: биринчиси-мустақил манбаадан келувчи сигнал шаклидан ![]() аниқланади, иккинчиси-юкланишдан қайтган
сигнал билан аниқланади:
аниқланади, иккинчиси-юкланишдан қайтган
сигнал билан аниқланади:
26.10-расм
Вақт соҳасида қуйидагини ёзиш мумкин:
![]()
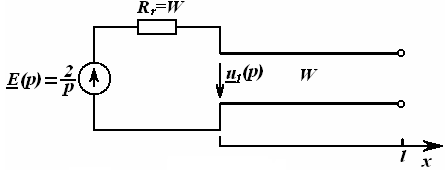
26.11-расм
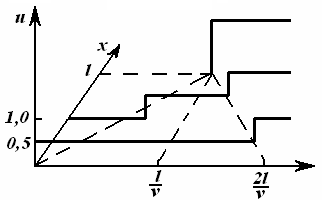
26.12-расм
![]()
бунда
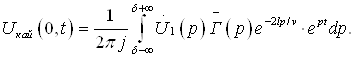
Ҳар хил юкларга уланган узатиш линияси сигналларни ҳисоблаш бўйича мисоллар кўрамиз.
Мисол 26.1. Линия бўлагининг кети узилганда (26.11-расм) сигналларни ҳисобланг.
Тушувчи тўлқин кучланишнинг Лаплас бўйича
тасвирини аниқлаймиз:
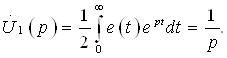
Қайтиш коэффициентининг оператор шаклидаги
кўринишини:
![]()
Ифода (26.11)га кўра линия тўла кучланишининг тасвири қуйидагича
бўлади:
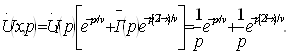
Вақт соҳасида
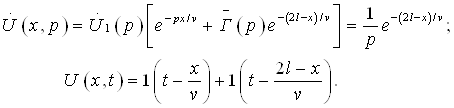
26.12-расмда линия бўлагида поғонасимон тўлқиннинг тақсимланиши кўрсатилган. 26.13-расмда эса тўлқиннинг алоҳида кесимлари келтирилган.
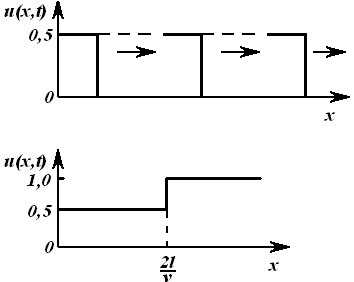
26.13-расм
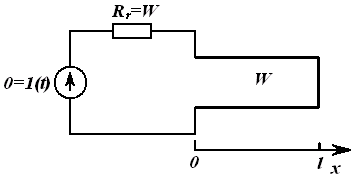
26.14-расм
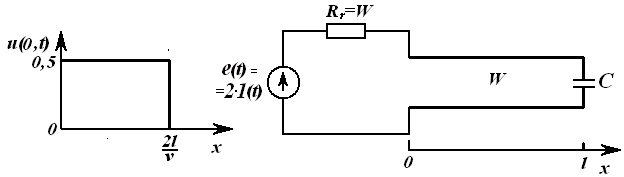
26.15-расм 26.16-расм
Мисол 26.2. Линия бўлагининг кети қисқа туташгандаги сигналларни ҳисобланг (26.16-расм).
Қайтиш коэффициентининг оператор кўриниши
![]()
Кучланиш
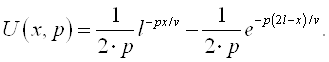
Вақт соҳасида бу тасвирга қуйидаги
функция мос:
![]()
Линия бошидаги кучланиш графиги 26.16-расмда тасвирланган. Унинг физик мазмуни қуйидагича:
![]() вақт онига қадар линия кетида қайтарувчи
юклама борлиги “номаълум” эди. Тўлқин
вақт онига қадар линия кетида қайтарувчи
юклама борлиги “номаълум” эди. Тўлқин ![]() вақт онида линия кетига “юриб” боради, қайтарилади
ва ортга қайтади, вақтнинг
вақт онида линия кетига “юриб” боради, қайтарилади
ва ортга қайтади, вақтнинг ![]() онида линия бошига келади. Тўғри тўлқин
онида линия бошига келади. Тўғри тўлқин
![]() билан қўшилиб, тескари тўлқин
билан қўшилиб, тескари тўлқин ![]() нолга тенг бўлади.
нолга тенг бўлади.
Мисол 26.3. сиғимга юкланган линия сигналларини ҳисоблаш (26.16-расм).
Ушбу ҳолда, бундан аввалгига ўхшаш, 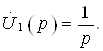 Бунда асосий тафовут қайтиш коэффициенти
оператор тавсифи бошқача
эканлигида.
Бунда асосий тафовут қайтиш коэффициенти
оператор тавсифи бошқача
эканлигида.
![]() ни аниқлаймиз:
ни аниқлаймиз: ![]()
Қайтиш коэффициенти қуйидаги шаклда
бўлади.
![]()
Бунда ![]() (26.11)дан аниқлаймиз:
(26.11)дан аниқлаймиз:
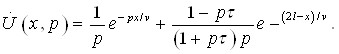
Вақт соҳасида биринчи ташкил этувчи ![]()
Иккинчи ташкил этувчи 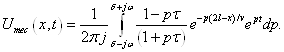
Лапласнинг тескари ўзгартиришини аниқлаш учун
чигирма теоремасидан фойдаланамиз.
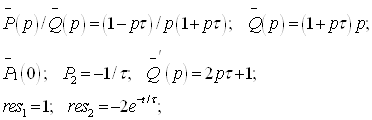
Линия бошида ![]() кучланиш
кучланиш
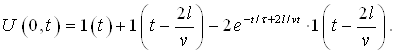
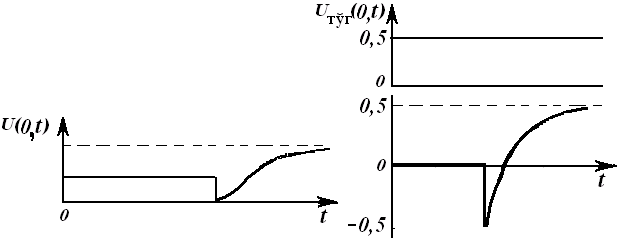
26.17-расм 26.18-расм
26.17-расмда шу кучла-нишнинг графиги келтирилган. Олинган графикнинг физик мазмунини кўргазмалироқ кўрсатиш учун, тўғри ва тескари тўлқинлар кучланиш-ларининг ташкил этувчилари-ни алоҳида кўриш зарур.
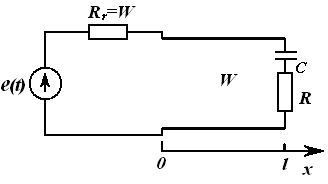
26.19-расм
Тўғри тўлқин поғона шаклида линия
бўйлаб тарқалади ва ![]() вақт онида юкланиш сиғимига етиб
боради. Бу онда сиғимдаги кучланиш нолга тенг. Бунда
вақт онида юкланиш сиғимига етиб
боради. Бу онда сиғимдаги кучланиш нолга тенг. Бунда ![]() бўлади ва тўлқин тўлалигича қарама-қарши
ишора билан қайтади. Сўнгра сиғим бошлайди. У орқали оқаётган
ток секин-аста камайиб нолга тенг бўлади ва
бўлади ва тўлқин тўлалигича қарама-қарши
ишора билан қайтади. Сўнгра сиғим бошлайди. У орқали оқаётган
ток секин-аста камайиб нолга тенг бўлади ва ![]() бўлади. Тўлқиннинг тўла қайтиши
бўлади. Тўлқиннинг тўла қайтиши ![]() да кузатилади.
да кузатилади.
27-маъруза. Электр фильтрлари
27.1 Электр фильтрлари турлари ва тавсифлари
Кейинги йилларда чоп этилаётган адабиётларда электр фильтри деб сигналларнинг зарурий ўзгартиришлари амалга оширилишини таъминлайдиган частотавий тавсифларга эга бўлган чизиқли тўртқутбликларга айтиладиган таърифлар кенг тарқалмоқда. Бу таъриф, нафақат фильтрлар учун, балки бошқа турдаги тўртқутбликлар учун ҳам таълуқлидир. Шунинг учун электр фильтрларига бериладиган таърифни аниқроқ қўйиш зарурати туғилмоқда.
Электр фильтри (қисқалик учун «фильтр») частотанинг маълум оралиғида жойлашган тебранишларини ажратиб олади. Шунинг учун, электр фильтри деб, занжир киришига келтирилган мураккаб тебранувчи электр сигнали таркибидан, берилган частоталар оралиғидаги частотавий ташкил этувчиларни ажратиб олиш ва бошқа берилган частоталар оралиғидаги частотавий ташкил этувчиларни сўндириш учун хизмат қилувчи чизиқли тўртқутбликка айтилади. Фильтрларнинг ушбу частота оралиқлари мос равишда ўтказиш йўлаги ва тўсиш йўлаги дейилади.
Ўтказиш ва тўсиш йўлакларининг ўзаро жойлашганлиги
бўйича фильтрлар қуйидаги турларга бўлинади: қуйи частота
фильтрлари (ҚЧФ) - частотани ўтказиш йўлаги ![]() дан бошлаб, бирор
дан бошлаб, бирор ![]() -қирқиш частотасигача оралиқда
жойлашган; юқори частота фильтрлари (ЮЧФ) - частотани ўтказиш йўлаги
-қирқиш частотасигача оралиқда
жойлашган; юқори частота фильтрлари (ЮЧФ) - частотани ўтказиш йўлаги
![]() дан
дан ![]() гача жойлашган; йўлак фильтрлари (ЙФ) частотани
ўтказиш йўлаги
гача жойлашган; йўлак фильтрлари (ЙФ) частотани
ўтказиш йўлаги ![]() дан
дан ![]() гача ва режекторли (тўсувчи) фильтрлар (РФ)
- частотани ўтказиш йўлаги
гача ва режекторли (тўсувчи) фильтрлар (РФ)
- частотани ўтказиш йўлаги ![]() дан
дан ![]() гача жойлашган.
гача жойлашган.
Фильтрлар тузилиши таркибида кучайтиргич элементлари мавжудлиги билан улар икки гуруҳга бўлинадилар: пассив фильтрлар - резистор, конденсатор ва индуктивликдан иборат бўлиб, кучайтиргичи йўқ; актив фильтрлар - бундай схема таркибида кучайтиргич ва пассив фильтр мавжуд. Ўз навбатида пассив фильтрлар таркибидаги элементлар турига қараб қуйидагиларга ажратилади: реактив LC-фильтрлар, инерцияли (ёки RC-) фильтрлар, пьезоэлектрик (ёки кварцли) фильтрлар.
Аввалги бобларда электр занжирлари ишини таҳлил қилиш усуллари келтирлиган эди. Электр занжирлар назариясининг муаммоларидан яна бири - берилган хусусиятларига жавоб бера оладиган электр занжирларини яратиш - синтез қилишдир.
27.1-расмда юқорида келтирилган идеал фильтрлар турларининг амплитуда-частотавий тавсифлари (АЧТ) кўрсатилган. Фильтрларни синтез қилишда уларнинг асосий талаблари қондирилиши берилган АЧТнинг шаклига боғлиқ. Айнан шу АЧТни электр занжирларининг частотавий тавсифларини ифодаловчи функциялар билан аппроксимациялаш (АЧТларга яқин бўлган математик ифодалар билан алмаштириш) зарур бўлади.
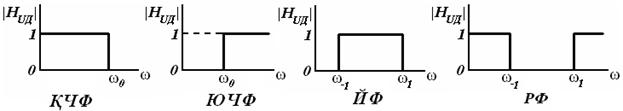
27.1-расм
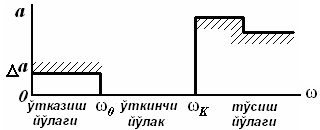 Фильтрларнинг
ўтказиш йўлаги ва тўсиш йўлаги орасида ўткинчи йўлак мавжуд бўлиб, бу
йўлакда кучсизланишга талаб қўйилмайди. Фильтрлар зарур бўлган частота
йўлагида сигнални ажратади. Масалан, ҳар бир радио станция ўзининг
частота йўлагида ишлайди ва станциялар фаолияти натижасида антенналарда
сигналлар йиғиндиси мавжуд бўлади. Радио қабул қилувчи
аппаратлари эса фильтр ёрдамида эшитувчи хоҳлаган частота бўлагидаги
тебранишларни ажратиб олади. Бошқа станциялар тўлқинларини қабул
қилиш имкони бўлиши учун фильтрни ростлаш зарур бўлади, демак бунда
ўтказиш йўлаги ва тўсиш йўлаги силжитилади.
Фильтрларнинг
ўтказиш йўлаги ва тўсиш йўлаги орасида ўткинчи йўлак мавжуд бўлиб, бу
йўлакда кучсизланишга талаб қўйилмайди. Фильтрлар зарур бўлган частота
йўлагида сигнални ажратади. Масалан, ҳар бир радио станция ўзининг
частота йўлагида ишлайди ва станциялар фаолияти натижасида антенналарда
сигналлар йиғиндиси мавжуд бўлади. Радио қабул қилувчи
аппаратлари эса фильтр ёрдамида эшитувчи хоҳлаган частота бўлагидаги
тебранишларни ажратиб олади. Бошқа станциялар тўлқинларини қабул
қилиш имкони бўлиши учун фильтрни ростлаш зарур бўлади, демак бунда
ўтказиш йўлаги ва тўсиш йўлаги силжитилади.
Фильтрлар телефон алоқасининг кўпканалли аналог тизимидаги телефон каналларида ҳам қўл- ланилади ва шовқинларни камай-тиришда ишлатилади.
Фильтр АЧТсига қўйила-диган талаблар, аксарият, кучсизла-нишнинг частотага боғлиқлигига қўйиладиган талаб сифатида шакл-ланади. Кучсизланишнинг частота- 27.2-расм
га боғлиқлиги шундай меъёрлашти-
риладики, бунда ўтказиш йўлаги ичидаги минимал кучсизланиш нолга тенг бўлсин. У ҳолда ўтказиш йўлагидаги фильтрнинг кучсизланиши бирор берилган фильтр кучсизланиши тавсифининг нотекислиги деб номланган Да қийматдан ортмасилиги, фильтрнинг тўсиш йўлагида эса фильтрнинг техник талабларида келтирилган қийматдан кичик бўлмаслиги шарт. Мисол сифатида 27.2-расмда қуйи частота фильтри кучсизланиш тавсифига қўйиладиган талаблар график шаклда келтирилган. Шу расмда ўткинчи йўлак тушунчаси тасвирланган. Ўткинчи йўлакда фильтр кучсизланиши меъёрланмаган ва унинг қиймати фильтр ўтиш йўлагидаги жойиз минимал қийматдан тўсиш йўлагида талаб этиладиган миқдоригача ортади.
Фильтр кучсизланишининг частотавий боғланишига қўйиладиган талаблар асосий ҳисобланиб, ундан ташқари фильтрнинг электр ва тузилиш параметларига ҳам қўшимча талаблар қўйилади. Хусусан, унинг ўтказиш йўлагидан сигналнинг шакли бузилмасдан ўтишини таъминлаш учун фаза-частота тавсифининг тўғри чизиқликдан фарқланишининг жоиз талаблари берилиши мумкин. Бундай ҳолатларда ёки мазкур аппроксимацияланувчи вазифа шаклланади ва масала ечилади, ёки фақат кучсизланиш талаблари билан ҳисобланган фильтрнинг фаза-частотавий тавсифи номинимал-фазавий занжирлар ёрдамида коррекцияланади.
Аналогли узатиш тизимларига хос бўлган алоҳида ҳолатларда, фильтрларда темир ўзакли ғалтак ёки транзистор мавжудлиги сабабли ҳосил бўладиган ночизиқли бузилишларга, ҳамда фильтрлардаги хос шовқинларга махсус талаблар қўйилади.
Радио узатиш қурилмалари каскадларининг охирги чиқишларида жойлашган ва импульсдаги оний қувват бир неча юз киловатни ташкил қиладиган фильтрларга, улар натижавий аслликлари ҳақида талаб қўйилиши мумкин.
Табиий, фильтр ўрнатилган аппаратнинг хусусиятларига боғлиқ равишда фильтрнинг масса-габарий кўрсаткичларига, ностабиллик туғдирувчи таъсирларга турғунлиги, ишончлилиги ва бошқа кўрсаткичларига у ёки бу талаблар қўйилади ва уларни лойиҳалаш жараёнида эътиборга олиш зарур.
Фильтрларни ҳисоблашнинг ҳар хил усулларини асослашга бағишланган жуда кўп адабиётлар мавжуд. Барча усуллардан аввал реактив тўртқутблик сифатида LC-фильтрнинг тавсифий параметрларини кўришга асосланган усуллар таклиф этилган. Ҳозирги пайтда улар ўзларининг амалий аҳамиятларини йўқотган ва электр фильтрларини синтез қилишнинг ҳозирги замон усуллари аппроксимациялаш масалаларининг оптимал ечимларини аниқлашга ва тадбиқ этишга бағишланган. Айнан шунинг учун фильтрлар турларининг ранг-баранглигидан қатъий назар, фильтрларда фойдаланиладиган тавсифлари турларининг сони чекланган.
Фильтрларнинг синтезида берилган меъёрий қаршилик
![]() ва частота
ва частота ![]() ёрдамида қаршиликлар ва частотани меъёрлаш
кенг қўлланилади, яъни:
ёрдамида қаршиликлар ва частотани меъёрлаш
кенг қўлланилади, яъни:
![]()
![]() (27.1)
(27.1)
Меъёрловчи қаршилик сифатида, аксарият, фильтр юкламаларидан бирининг қаршилиги, меъёрловчи частота сифатида ҚЧФ (ЮЧФ)нинг ўтказиш йўлаги чегаравий частотаси ёки ЙФнинг чегаравий частоталари геометрик ўртача қиймати ишлатилади. Аксарият, фильтрнинг комплекс узатиш функцияси ҳам модулининг максимал қийматига нисбатан меъёрлаштирилади.
27.2 Баттерворт тавсифига эга бўлган қуйи
частотали полиномиал фильтри
Узатиш функцияси қуйидaги полиномдан иборат бўлган фильтрлар
 (27.2)
(27.2)
полиномиал
фильтрлар дейилади. Бундай фильтрлар ўта юқори частотали (ЎЮЧ) қурилмаларида,
радиоалоқа техникаси ва техниканинг бошқа соҳаларида кўплаб қўлланилади.
Амплитуда частотавий тавсифлар ва кучсизланишнинг частотавий боғланишларини
аниқлайдиган ифодалар ![]() бўлганда қуйидагича ёзилади:
бўлганда қуйидагича ёзилади:
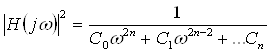 (27.2,a)
(27.2,a)
ва
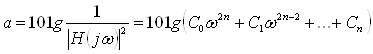 (27.2,б)
(27.2,б)
бунда
![]() - меъёрланган частота.
- меъёрланган частота.
Қуйи частотали полиномиал фильтрларнинг синтези
масаласини ечишда, аввалига идеал фильтрнинг амплитуда-частотавий тавсифини
Тейлор бўйича ![]() нуқтада аппроксимациялашни қўллаймиз.
нуқтада аппроксимациялашни қўллаймиз.
Аппроксимацияланаётган функция ![]() қиймати
қиймати ![]() бўлганда бирга тенг, унинг барча ҳосилалари
эса нольга тенг. Бунда идеал фильтрнинг АЧТ, ҳар қандай реал электр
занжириники каби ўзгарувчининг жуфт функцияси эканлигини эътиборга оламиз. Агар
(27.2,а)
бўлганда бирга тенг, унинг барча ҳосилалари
эса нольга тенг. Бунда идеал фильтрнинг АЧТ, ҳар қандай реал электр
занжириники каби ўзгарувчининг жуфт функцияси эканлигини эътиборга оламиз. Агар
(27.2,а) ![]() бўлса,
бўлса, ![]() да аппроксимацияланаётган функция
да аппроксимацияланаётган функция ![]() бўлади. Агар (27.2,а) нинг махражидаги
полиномнинг коэффициентлари (унинг энг юқори ва эркин ташкил
этувчиларидан ташқари) нольга тенг деб ҳисобланганда,
аппроксимацияланаётган функциясининг кичик тартибларининг ҳосилалари
максимал сони нолга тенг бўлади, яъни:
бўлади. Агар (27.2,а) нинг махражидаги
полиномнинг коэффициентлари (унинг энг юқори ва эркин ташкил
этувчиларидан ташқари) нольга тенг деб ҳисобланганда,
аппроксимацияланаётган функциясининг кичик тартибларининг ҳосилалари
максимал сони нолга тенг бўлади, яъни:
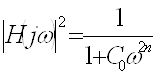 (27.3)
(27.3)
Дарҳақиқат, ![]() полиномнинг барча кичик ҳосилалари
полиномнинг барча кичик ҳосилалари ![]() нуқтада нолга тенг. У ҳолда шу нуқтада
нуқтада нолга тенг. У ҳолда шу нуқтада
![]() полиномнинг ҳамда
полиномнинг ҳамда ![]() функциянинг ҳам барча кичик ҳосилалари
нольга тенг бўлади.
функциянинг ҳам барча кичик ҳосилалари
нольга тенг бўлади.
Агар ![]() бўлса, (27.3) функция уни амалга ошириш учун
талаб қилинаётган барча шартлари қониқлантиради. Аксарият,
бўлса, (27.3) функция уни амалга ошириш учун
талаб қилинаётган барча шартлари қониқлантиради. Аксарият, ![]() унда
унда
![]() (27.4,а)
(27.4,а)
ва
![]() (27.4,б)
(27.4,б)
Кўрилган фильтларнинг амплитуда-частотавий тавсифлари графиклари
27.3,а-расмда келтирилган. 27.4,б-расмда эса фильтр реактив
элементлари сонини аниқлайдиган ![]() даражанинг кўрсаткичлари учун кучсизланишнинг
частотавий боғланишлари графиги тасвифланган.
даражанинг кўрсаткичлари учун кучсизланишнинг
частотавий боғланишлари графиги тасвифланган.
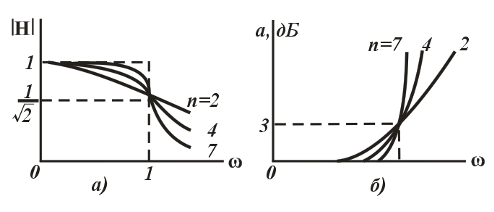
27.3-расм
Кўрилаётган фильтрларнинг кучсизланиши частота ошиши
билан текис ортади ва ![]() да, яъни
да, яъни ![]() да
да ![]() ни ташкил этади. Частота
ни ташкил этади. Частота ![]() ни фильтр ўтказиш йўлагининг чегаравий
частотаси деб аталади. Шу билан бирга фильтрнинг ўтказиш йўлаги
чегаравий частотасидан қуйида, тўсиш йўлаги эса юқорида
жойлашган деб қабул қилинган. Аёнки,
ни фильтр ўтказиш йўлагининг чегаравий
частотаси деб аталади. Шу билан бирга фильтрнинг ўтказиш йўлаги
чегаравий частотасидан қуйида, тўсиш йўлаги эса юқорида
жойлашган деб қабул қилинган. Аёнки, ![]() қанчалар катта бўлса, фильтр мураккаброқ
бўлади, амплитуда-частотавий тавсифи идеал фильтрникига шунчалар аниқликда
аппроксимацияланади, яъни тўсиш йўлагининг ихтиёрий частотасида фильтр
кучсизланиши шунчалар катта бўлади.
қанчалар катта бўлса, фильтр мураккаброқ
бўлади, амплитуда-частотавий тавсифи идеал фильтрникига шунчалар аниқликда
аппроксимацияланади, яъни тўсиш йўлагининг ихтиёрий частотасида фильтр
кучсизланиши шунчалар катта бўлади.
Меъёрий частотаси ![]() бўлганда
бўлганда ![]() функциянинг максимал сонли кичик тартибли ҳосиласи
нольга айланадиган ҳадлари бўлган қуйи частотали полиномиал
фильтрлар, яъни кучсизланишнинг частотавий боғланиши (27.4) билан аниқланадиган
фильтрлар кучсизланиш тавсифлари максимал текис фильтрлар ёки Баттерворт
тавсифли фильтрлар деб аталади. Баттерворт қуйи частотали полиномиал
фильртларни синтез қилиш масалаларига биринчи бўлиб Тейлор бўйича
аппроксимацияни киритган.
функциянинг максимал сонли кичик тартибли ҳосиласи
нольга айланадиган ҳадлари бўлган қуйи частотали полиномиал
фильтрлар, яъни кучсизланишнинг частотавий боғланиши (27.4) билан аниқланадиган
фильтрлар кучсизланиш тавсифлари максимал текис фильтрлар ёки Баттерворт
тавсифли фильтрлар деб аталади. Баттерворт қуйи частотали полиномиал
фильртларни синтез қилиш масалаларига биринчи бўлиб Тейлор бўйича
аппроксимацияни киритган.
Фильтрнинг ![]() узатиш функциясини аниқлаймиз. Бунинг учун
(27.4,а) ифоданинг махражини нольга тенглаштириб,
узатиш функциясини аниқлаймиз. Бунинг учун
(27.4,а) ифоданинг махражини нольга тенглаштириб, ![]() ўзгарувчини
ўзгарувчини ![]() га алмаштириб, ҳосил бўлган
га алмаштириб, ҳосил бўлган ![]() тенгламанинг ечимини аниқлаймиз. Унинг
илдизлари аналитик усулда аниқланади ва
тенгламанинг ечимини аниқлаймиз. Унинг
илдизлари аналитик усулда аниқланади ва
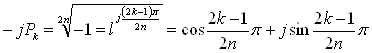
бўлганли учун
![]()
![]() (27.5)
(27.5)
Чап яримтекисликда ![]() дан
дан ![]() гача бўлган илдизлар жойлашган. Улар аниқланиши
зарур бўлган узатиш функциясининг қутблари бўлади. Бунда ҳар бир
комплекс туташ қутблар жуфтлиги
гача бўлган илдизлар жойлашган. Улар аниқланиши
зарур бўлган узатиш функциясининг қутблари бўлади. Бунда ҳар бир
комплекс туташ қутблар жуфтлиги
![]() (27.6)
(27.6)
фильтр узатиш функцияси махражи полиномининг кўпайтирувчисини ташкил этади.
Умумий ҳолда, Баттерворт тавсифлари бўлган қуйи
частота фильтрининг ўтказиш йўлагидаги ![]() жоиз кучсизланиш
жоиз кучсизланиш ![]() бўлса, унинг кучсизланиш частотавий боғланиши
қуйидагича ифодаланади:
бўлса, унинг кучсизланиш частотавий боғланиши
қуйидагича ифодаланади:
![]() (27.7)
(27.7)
Ифодалар (27.4) ёки (27.7)даги фильтр тўсиш ![]() да кучсизланиш частотавий боғланишига берилган
талабларни қаноатлантиручи полиномнинг тартиби
да кучсизланиш частотавий боғланишига берилган
талабларни қаноатлантиручи полиномнинг тартиби ![]() тенгсизлик
тенгсизлик ![]() бажарилувчи энг яқин бутун сон сифатида
аниқланади.
бажарилувчи энг яқин бутун сон сифатида
аниқланади.
27.3 Чебышев тавсифига эга бўлган қуйи
частотали полиномиал фильтрлар
Қўйилган масаланинг шартига мувофиқ, қуйи
частотали полиномиал фильтрнинг сўниш частотавий тавсифининг нотекислиги
ўтказиш йўлаги ![]() да
да ![]() дан ортмасин, яъни ўтказиш йўлагида
дан ортмасин, яъни ўтказиш йўлагида ![]() бўлсин деб фараз қилайлик. Қуйи
частотали идеал фильтрнинг тавсифи аппроксимацияси масаласининг шундай ечимини
аниқлайликки, унда синтез қилинаётган полиномиал фильтрнинг тўсиш
йўлагида кучсизланиш, узатиш функциячининг берилган тартиби
бўлсин деб фараз қилайлик. Қуйи
частотали идеал фильтрнинг тавсифи аппроксимацияси масаласининг шундай ечимини
аниқлайликки, унда синтез қилинаётган полиномиал фильтрнинг тўсиш
йўлагида кучсизланиш, узатиш функциячининг берилган тартиби ![]() имкон даражасида катта бўлсин.
имкон даражасида катта бўлсин.
Бу қўйилган вазифа (26.2) ифодаларнинг шундай
жуфт полиномини ![]() аниқлашни тақазо этадики, унинг қийматлари
аниқлашни тақазо этадики, унинг қийматлари
![]() оралиғида қуйидаги чеклашлар
шартларини бажарсин:
оралиғида қуйидаги чеклашлар
шартларини бажарсин:
![]() (27.8)
(27.8)
![]() >1 бўлганда эса, мазкур даражада ва мазкур чеклаш
талабларини бажарадиган барча бошқа жуфт полиномникидан катта бўлсин.
>1 бўлганда эса, мазкур даражада ва мазкур чеклаш
талабларини бажарадиган барча бошқа жуфт полиномникидан катта бўлсин.
Бу масаланинг ечими Чебышев полиномининг экстремал
хусусиятларини қўллашга асосланади. Дарҳақиқат, агар
ечимлари ![]() оралиқда абсольют қийматлари бўйича
1 дан катта бўлмаса,
оралиқда абсольют қийматлари бўйича
1 дан катта бўлмаса, ![]() ўзгарувчининг барча
ўзгарувчининг барча ![]() >1 тартиби жуфт полиномларидан энг катта қийматга
Чебышевнинг
>1 тартиби жуфт полиномларидан энг катта қийматга
Чебышевнинг
![]()
полиноми
эга бўлади; унда ўзгарувчи ўрнига [(Чебышев
полиноми шартларига мувофиқ)

га
мувофиқ] ![]() билан алмаштирилган. Агар бу полиномни
билан алмаштирилган. Агар бу полиномни ![]() доимийга кўпайтирсак ва бошқа
доимийга кўпайтирсак ва бошқа ![]() доимийни қўшсак, у ҳолда
доимийни қўшсак, у ҳолда ![]() ва
ва ![]() шарти билан
шарти билан ![]() масаланинг изланаётган ечими бўлади. Ҳосил
бўлган полином талаб этилаётган экстремал хусусиятларга эга,
масаланинг изланаётган ечими бўлади. Ҳосил
бўлган полином талаб этилаётган экстремал хусусиятларга эга, ![]() ўзгарувчининг
ўзгарувчининг ![]() тартиби жуфт полиноми (27.8) чеклашларга жавоб
беради ва физик тадбиқ этиш шартларига мос бўлади.
тартиби жуфт полиноми (27.8) чеклашларга жавоб
беради ва физик тадбиқ этиш шартларига мос бўлади.
Аниқланган ечимни комплекс ва таҳлил қилишга қулай шаклда ёзиш учун оддий тригонометрик боғланишлардан фойдаланамиз. Уларга кўра
![]() ва
ва ![]() .
.
У ҳолда
![]() ва
ва ![]() ва
ва ![]() бўлганлиги учун,
бўлганлиги учун,
![]() .
.
Шунинг учун
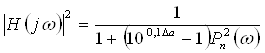 (27.9,а)
(27.9,а)
ва
![]() (27.9,б)
(27.9,б)
бунда
![]() - Чебышевнинг
- Чебышевнинг ![]() -тартибли полиноми.
-тартибли полиноми.
Аниқланган частотавий тавсифига эга бўлган қуйи частотали полиномиал фильтрлар Чебышев тавсифли фильтрлар номини олди.
Чебышев полиноми хусусиятларига мувофиқ
кўрилаётган фильтрларнинг ![]() амплитуда-частотавий тавсифлари ўтказиш йўлагида
кетма-кет
амплитуда-частотавий тавсифлари ўтказиш йўлагида
кетма-кет ![]() марта ўзларининг
марта ўзларининг ![]() минимал ва максимал (1) қийматларини
қабул қилади,
минимал ва максимал (1) қийматларини
қабул қилади,
-биринчиси, бунда![]() , яъни
, яъни ![]()
-иккинчиси, бунда![]() , яъни
, яъни ![]()
Бу фильтрларнинг тўсиш йўлларига эса частота ортиши
билан ![]() равон пасайиб боради.
равон пасайиб боради.
Уларни намойиш этиш учун 27.4-расмда ![]() учун (27.4,а-расм) ва
учун (27.4,а-расм) ва ![]() учун (27.4,б-расм)
учун (27.4,б-расм) ![]() бўлганда амплитуда-частотавий тавсифларнинг
графиклари келтирилган.
бўлганда амплитуда-частотавий тавсифларнинг
графиклари келтирилган.
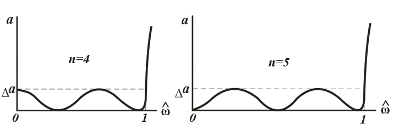
27.4-расм
Чебышев тавсифига эга бўлган фильтрлар равон тўлқинли
кучланиш тавсифларга киради. Уларнинг
кучсизланиш частотавий тавсифлари ўтказиш йўлагида кетма-кет ![]() марта ўзининг энг катта
марта ўзининг энг катта ![]() ва энг кичик
ва энг кичик ![]() қийматларини қабул қилади. Бу билан
қийматларини қабул қилади. Бу билан ![]() нинг ортиши билан “даври” камаювчи тўлқинларни
ташкил этади.
нинг ортиши билан “даври” камаювчи тўлқинларни
ташкил этади.
Чебышев тавсифларига эга бўлган фильтр узатиш
функциясининг қутблари
![]()
тенгламанинг
илдизлари бўлиб, аналитик ечим сифатида аниқланади. Улар қуйидагиларга
тенг бўладилар:

бунда

Чебышев полиноми катта ҳадининг коэффициентига
тенг бўлгани учун
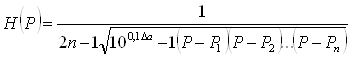 (27.10)
(27.10)
Бу ерда фильтр узатиш функциясининг ҳар бир
комплекс туташ қутблари жуфтлиги учун кўпайтирувчи мос келади.
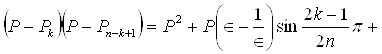
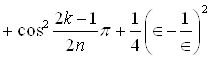 (27.11)
(27.11)
Тўсиш йўлаги ![]() да фильтр кучсизланишининг минимал жоизлигига қўйиладиган
талаблар бажарилишини таъминлайдиган фильтр узатиш функциясининг зарурий
тартиби
да фильтр кучсизланишининг минимал жоизлигига қўйиладиган
талаблар бажарилишини таъминлайдиган фильтр узатиш функциясининг зарурий
тартиби ![]() , энг яқин катта бутун сон сифатида аниқланади.
, энг яқин катта бутун сон сифатида аниқланади.

28-маъруза. Реактив электр фильтрни жадвал
усулида ҳисоблаш
28.1 Золотарев тавсифли қуйи частота фильтрлари
Агар шартларига кўра ўтиш йўлаги жуда тор бўлган фильтрни синтез қилиш зарур бўлса, полиномиал фильтрларни қабул қилиш ҳақсиз равишда катта сонли элементлар бўлишига олиб келади. Бу эса полиномиал фильтрлар тўсиқ йўлагида кучсизланиш частотавий боғланишининг равон ортувчи характери зарур бўлмаган заҳираси мавжудлигига олиб келади.
Бундай ҳолатларда тўсиқ йўлагининг чекка
частоталарида ечимлари бўлган узатиш функцияларига эга бўлган фильтрларни қабул
қилиш мақсадга мувофиқ бўлади.
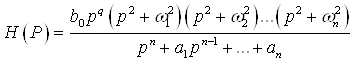 (28.1)
(28.1)
Бундай фильтрлар кучланишининг частотавий боғланиши.
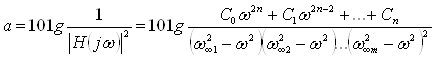 (28.2)
(28.2)
Кучланишнинг “сакрашлари” деб номланган ўзгаришлари
мавжудлиги ҳосдир. Ҳар бирида частота миқдори кучланишнинг
“сакраш” частотасига яқинлашганда у чексизликка интилади. Сакрашлар, қийматлари
фильтр функцияси ечимларига яқин бўлган чекли ва нольга тенг бўлмаган
частоталар ![]() да бўлади. Айнан кучсизланишларнинг сакрашларини
киритиш чекланаган элементли тор ўтказиш йўлакли фильтрларни синтез қилиш
имконини беради.
да бўлади. Айнан кучсизланишларнинг сакрашларини
киритиш чекланаган элементли тор ўтказиш йўлакли фильтрларни синтез қилиш
имконини беради.
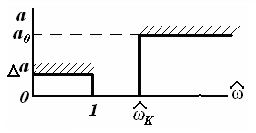 Сакрашли
кучсизланиши бўлган фильтрлар, аксарият
Сакрашли
кучсизланиши бўлган фильтрлар, аксарият ![]() берилган частотадан бошлаб фильтр
кучсизланиши частотага боғлиқ бўлмаган бирор берилган
берилган частотадан бошлаб фильтр
кучсизланиши частотага боғлиқ бўлмаган бирор берилган ![]() қийматдан кам бўлмаган, ўтказиш йўлагида
эса, илгаригидек, бошқа
қийматдан кам бўлмаган, ўтказиш йўлагида
эса, илгаригидек, бошқа ![]() миқдордан ва 28.1-расмдагидан ошмаган ҳолатларда
ишлатилади. Бунда фильтр узатиш функциясининг тартиби имкон қадар минимал
бўлиши зарур.
миқдордан ва 28.1-расмдагидан ошмаган ҳолатларда
ишлатилади. Бунда фильтр узатиш функциясининг тартиби имкон қадар минимал
бўлиши зарур.
Келтирилган масалани Петербург университети профессори Е.И. Золотарев (1821-1884) таклиф этган “нольдан фарқланувчи функциялар ҳақида қўйилган қатор муаммолар ва ечимлардан фойдала- 28.1-расм
нилса
ҳал қилиш мумкин. Булар шундай масалаки, унда берилган n-тартибли
рационал каср функциясининг ![]() оралиқдаги қийматининг абсольют қиймати
бирдан катта бўлмасин,
оралиқдаги қийматининг абсольют қиймати
бирдан катта бўлмасин, ![]() оралиқда эса
оралиқда эса ![]() унинг абсольют қиймати бўйича энг кичик миқдори
имкон қадар максимал кўп бўлсин.
унинг абсольют қиймати бўйича энг кичик миқдори
имкон қадар максимал кўп бўлсин.
Ушбу рационал каср функция Золотарев касри деб
номланиши мумкин. У ![]() - тартибнинг жуфтлигига қараб жуфт ёки тоқ
функция бўлиши мумкин. Унинг барча ноллари (қутблари)
- тартибнинг жуфтлигига қараб жуфт ёки тоқ
функция бўлиши мумкин. Унинг барча ноллари (қутблари) ![]() оралиқда жойлашади, шу оралиқда,
Чебышев полиноми сингари
оралиқда жойлашади, шу оралиқда,
Чебышев полиноми сингари ![]() марта ишораларини алмаштириб 1 ва -1 қийматларига
эга бўлади. Золотарев касрининг барча қутблари
марта ишораларини алмаштириб 1 ва -1 қийматларига
эга бўлади. Золотарев касрининг барча қутблари ![]() да жойлашган. Бу оралиқда унинг
хусусиятини унга тескари функция билан тасвирлаш қулай бўлади. Қутблари
да жойлашган. Бу оралиқда унинг
хусусиятини унга тескари функция билан тасвирлаш қулай бўлади. Қутблари
![]() бўлганда тенг тўлқинли характерга эга,
чунки масаланинг шартига кўра у абсольют қийматининг нолдан оғиши
имкон қадар минимал бўлиши зарур. Буни тасвирлаш учун 28.2,а-расмда
еттинчи тартибли Золотарев касрининг
бўлганда тенг тўлқинли характерга эга,
чунки масаланинг шартига кўра у абсольют қийматининг нолдан оғиши
имкон қадар минимал бўлиши зарур. Буни тасвирлаш учун 28.2,а-расмда
еттинчи тартибли Золотарев касрининг ![]() бўлганда ва 27.2,б-расмда
бўлганда ва 27.2,б-расмда ![]() унга тескари каср келтирилган.
унга тескари каср келтирилган.
|
|
Агар ![]() бўлса, Золотарев касрининг абсольют қийматлари
бўйича барча минималлари бир хил (тенг) бўлади. Улар касрнинг тартиби
бўлса, Золотарев касрининг абсольют қийматлари
бўйича барча минималлари бир хил (тенг) бўлади. Улар касрнинг тартиби ![]() нинг қиймати билан аниқланадилар ва
нинг қиймати билан аниқланадилар ва ![]() нинг ҳам,
нинг ҳам, ![]() нинг ҳам кўпайиши билан ортадилар. Золотарев касри
нинг ҳам кўпайиши билан ортадилар. Золотарев касри ![]() ўзгарувчини
ўзгарувчини
![]() ўзгарувчи
билан алмаштирилгандан сўнг (27.9) ечимга Чебышев
полиноми ўрнига киритилади.
ўзгарувчи
билан алмаштирилгандан сўнг (27.9) ечимга Чебышев
полиноми ўрнига киритилади.
Демак, Золотарев тавсифига эга бўлган қуйи частотали фильтрлар қуйидаги график функциялар билан аниқланади:
28.2-расм
Золотарев
касрининг хусусиятларидан келиб чиққан ҳолда, фильтрнинг
ўтказиш йўлагида кучсизланиш тенг тўлқинли характерда бўлади, тўсиш
йўлагида эса, ![]() частотадан
бошлаб,
частотадан
бошлаб, ![]() ва
ва ![]() қийматлари
бир хил бўлган барча фильтрларга нисбатан, кучсизланишнинг энг кичик қиймати
сони имкон қадар максимал бўлади. Золотарев тавсифига эга бўлган бундай
фильтрнинг
қийматлари
бир хил бўлган барча фильтрларга нисбатан, кучсизланишнинг энг кичик қиймати
сони имкон қадар максимал бўлади. Золотарев тавсифига эга бўлган бундай
фильтрнинг ![]() учун
частотавий боғланиши 28.8-расмда келтирилган. Унинг бошқа
фильтрлардан фарқли хусусиятлари шундаки, кучсизланиш тавсифининг
минимумлари тўсиш йўлагида тенг эканликларидир; ушбу минимумларнинг қийматлари
фильтр тўсиқ йўлаги чегарасидаги кучланиш қийматларига тенгдир.
учун
частотавий боғланиши 28.8-расмда келтирилган. Унинг бошқа
фильтрлардан фарқли хусусиятлари шундаки, кучсизланиш тавсифининг
минимумлари тўсиш йўлагида тенг эканликларидир; ушбу минимумларнинг қийматлари
фильтр тўсиқ йўлаги чегарасидаги кучланиш қийматларига тенгдир.
Золотарев тавсифига эга бўлган фильтрлар эллиптик фильтрлар деб аталади. Бунга сабаб, Золотарев касрининг ноллари ва қутбларининг қийматлари, улар узатиш функциялари қутблари сингари, эллиптик функциялар орқали ифодаланади; баъзан Кауэро
|
|
28.3-расм
|
|
тавсифларига эга бўлган фильтрлар деб аталади,
чунки у Золотарев ечимларидан биринчи бўлиб фильтрларнинг синтезида фойдаланган.
Пировардида шуни таъкидлаш керакки, а га ![]() жуфт сон бўлса, Золотарев касрининг сурати ва
махражидаги полиномлар бир хил тартибли бўлади. Натижада, қуйи частотали
фильтрлар кучсизланиши
жуфт сон бўлса, Золотарев касрининг сурати ва
махражидаги полиномлар бир хил тартибли бўлади. Натижада, қуйи частотали
фильтрлар кучсизланиши ![]() бўлгандагина чекли бўлади. Бунинг учун берилган
Золотарев касрида жуфт
бўлгандагина чекли бўлади. Бунинг учун берилган
Золотарев касрида жуфт ![]() учун
учун ![]() ўрнига
ўрнига ![]() билан алмаштириш етарли бўлади, бу ерда
билан алмаштириш етарли бўлади, бу ерда ![]() мавжуд
мавжуд ![]() частоталарнинг энг каттаси.
частоталарнинг энг каттаси.
28.2 Юқори частота фильтрлари
Юқори частота фильтрлари (ЮЧФ) синтезининг усулларини танлашнинг асосланиши учун, хусусан уларнинг узатиш функцияларини аниқлаш учун, юқорида кўрилган ҚЧФга таалуқли фикрларни такрорлаш мумкин. Бироқ юқорида олинган натижалардан фойдаланиб, ўзгарувчиларни шундай ўзгартириайликки, унда қуйи частоталар оралиғи юқори частоталар оралиғи билан ва аксинча, ўзгартириш мақсадга мувофиқ бўлсин. Бунинг учун қуйи частота фильтрининг узатиш функциясига кирувчи р комплекс ўзгарувчини р1 ўзгарувчи билан алмаштирамиз. Унда р билан р1 қуйидаги боғланишда бўлади:
![]() (28.3,а)
(28.3,а)
LC -
фильтрларга (27.3,а) ўзгаришларга мавжуд қуйи частота
фильтрларидаги индуктивлик ўрнига сиғим, сиғим ўрнига - индуктивлик
қабул қилиш мос келади. Дарҳақиқат, агар
ўзгартирилгунга қадар фильтрнинг бирор шохобчаси қаршилиги ![]() бўлса, у ҳолда ўзгартирилгандан сўнг шу
шохобча қаршилиги
бўлса, у ҳолда ўзгартирилгандан сўнг шу
шохобча қаршилиги ![]() бўлган икки қутблик, яъни
бўлган икки қутблик, яъни ![]() сиғим киритилиши лозим бўлади. Шунга
ўхшаш, ўтказувчанлиги
сиғим киритилиши лозим бўлади. Шунга
ўхшаш, ўтказувчанлиги ![]() бўлган шохобча, ўтказувчанлиги
бўлган шохобча, ўтказувчанлиги ![]() бўлган шохобчага, яъни
бўлган шохобчага, яъни ![]() индуктивлик билан алмаштирилади. Демак, берилган
занжир амалда қўллаш мумкин бўлган бошқа занжир билан алмаштирилар
экан.
индуктивлик билан алмаштирилади. Демак, берилган
занжир амалда қўллаш мумкин бўлган бошқа занжир билан алмаштирилар
экан.
Агар (28.3,а) ифодада р ўрнига ![]() ва
ва ![]() ўрнига
ўрнига ![]() қабул қилинса, ўзгартирилган
фильтрнинг частотавий тавсифларини аниқлаш мумкин бўлади. Унда:
қабул қилинса, ўзгартирилган
фильтрнинг частотавий тавсифларини аниқлаш мумкин бўлади. Унда:
![]() (28.4)
(28.4)
ўзгартирилган
фильтрнинг ![]() ва
ва ![]() қийматлари, мос равишда, ўзгарувчи
қийматлари, мос равишда, ўзгарувчи ![]() нинг манфий қийматларида
нинг манфий қийматларида ![]() ва
ва ![]() қийматларига тенг бўладилар.
қийматларига тенг бўладилар.
Қуйи частота фильтрларида ![]() бўлгани учун, штрих белгисини ташлаб юборсак, юқори
частота фильтрининг меъёрий комплекс ўзгарувчи ва мъёрий частотанинг қуйидаги
ифодасини ҳосил қиламиз:
бўлгани учун, штрих белгисини ташлаб юборсак, юқори
частота фильтрининг меъёрий комплекс ўзгарувчи ва мъёрий частотанинг қуйидаги
ифодасини ҳосил қиламиз:
![]() (28.5)
(28.5)
Демак, қуйи частота фильтрлари учун олинган ифодалар, частоталар учун (28.5) ни қабул қилсак, (27.4) - (27.7) лар юқори частота фильтрлари учун ҳам таалуқли бўлар экан.
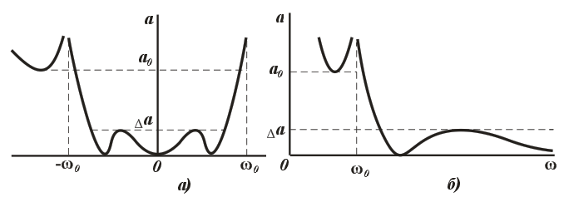
28.4-расм
Қуйи частота фильтрлари тавсифларини юқори частота фильтрлари тавсифларига айлантиришнинг ушбу усули (28.5) частотавий ўзгартиришларни қўллаш билан боғлиқ.
Частотани ўзгартириш - электр занжирининг тавсифларини мақсадли ўзгартириш усули сифатида электр фильтрларининг синтези масалаларида кенг қўлланилади. Тавсифи ўзгартирилаётган фильтр прототип фильтр деб номланади. Уларда, аксарият қуйи частота фильтрлари қўлланилади. Частотанинг энг оддий ўзгартирилиши - унинг меъёрланишидир. Айнан шу меъёрланган частота, Баттерворт, Чебышев, Золотарев ёки сакрашлари ихтиёрий жойлашган тавсифларга эга бўлган ЮЧФни ҳисоблашда қуйи частота прототип фильтрлари учун келтириб чиқарилган барча усуллар, ифодалар, номограммалар ва жадвалларни қўллаш имконини беради.
28.3 Йўлак ва рефлектор фильтрлари
Симметрик тавсифга эга бўлган йўлак фильтрлари. Йўлак фильтрларининг (ЙФ) ўткинчи функцияларини ҳам
қуйи частота прототип-фильтрлари ўткинчи функцияларига частота
ўзгартиришини киритиш йўли билан аниқлаш мумкин. Қуйи частоталар
оралиғида юқори частота фильтри комплекс ўзгартирувчи каби
ўзгариши, яъни агар ![]() бўлса
бўлса ![]() шарт, юқори частота оралиғида эса қуйи
частота фильтри комплекс ўзгарувчиси каби ўзгариши, яъни
шарт, юқори частота оралиғида эса қуйи
частота фильтри комплекс ўзгарувчиси каби ўзгариши, яъни ![]() бўлса, у ҳолда
бўлса, у ҳолда ![]() бўлиши зарур. Ўзгартирилган фильтр ўтказиш
йўлаги чегараларида комплекс ўтказувчи р, қуйи частота прототип
фильтрининг ўтказиш йўлагидаги ўзгарувчи каби ўзгариши лозим.
бўлиши зарур. Ўзгартирилган фильтр ўтказиш
йўлаги чегараларида комплекс ўтказувчи р, қуйи частота прототип
фильтрининг ўтказиш йўлагидаги ўзгарувчи каби ўзгариши лозим.
Бу талабларни қондирувчи энг оддий ўзгарувчи
функция - қуйи ва юқори частота фильтрлари комплекс
ўзгарувчиларининг йиғиндиси сифатида тасвирланади:
![]() (28.6)
(28.6)
Ўзгартирилган фильтрнинг частотаси ![]() оралиқда ўзгариши билан
оралиқда ўзгариши билан
![]() (28.6,б)
(28.6,б)
![]() бўлганда частота
бўлганда частота ![]() гача ва
гача ва ![]() бўлганда
бўлганда ![]() гача ўзгаради. Ушбу боғланишнинг
графиги 28.5,а-расмда келтирилган. ҚЧФнинг ўтказиш йўлаги юқоридан
гача ўзгаради. Ушбу боғланишнинг
графиги 28.5,а-расмда келтирилган. ҚЧФнинг ўтказиш йўлаги юқоридан
![]() частота билан чегараланганлиги ва
частота билан чегараланганлиги ва ![]() бўлганлиги учун, ушбу оралиқда
бўлганлиги учун, ушбу оралиқда ![]() нинг ортиши билан
нинг ортиши билан ![]() қийматига ўзгартирилган фильтрнинг
қийматига ўзгартирилган фильтрнинг ![]() частотаси мос келади; частотанинг
частотаси мос келади; частотанинг ![]() қийматига -
қийматига -![]() частота, ўзгартирилган фильтр ўтказиш йўлагининг
юқори чегаравий частотаси
частота, ўзгартирилган фильтр ўтказиш йўлагининг
юқори чегаравий частотаси ![]() мос келади.
мос келади.
Кўрилаётган фильтр частотавий тавсифларининг
хусусиятлари уларни кучсизланиш тавсифлари (геометрик) симметрик бўлган
фильтрлар, деган ном олишларига сабаб бўлди. Тавсифларнинг симметрик бўлиши
шартидан шуни кўрамизки, ![]() частотаси фильтр ўтказиш йўлагининг чегаравий
частоталари
частотаси фильтр ўтказиш йўлагининг чегаравий
частоталари ![]() ва
ва ![]() нинг геометрик ўртача қиймати экан, яъни:
нинг геометрик ўртача қиймати экан, яъни:
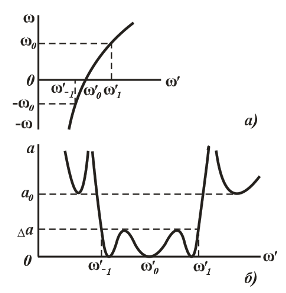
![]() (28.7)
(28.7)
Частоталар ![]() бўлганда (28.10,а-расм қаранг)
бўлганда (28.10,а-расм қаранг) ![]() лиги учун (28.5,б) ифодага мувофиқ
лиги учун (28.5,б) ифодага мувофиқ ![]() . Агар иккинчи ҳадда, (28.7) ни эътиборга олиб,
. Агар иккинчи ҳадда, (28.7) ни эътиборга олиб, ![]() ни унинг қиймати
ни унинг қиймати ![]() билан алмаштирсак, унда
билан алмаштирсак, унда
![]() (28.8)
(28.8)
бўлади, яъни ЙФ да ўтказиш йўлагининг кенглиги ўзгартирилган
28.5-расмган ҚЧФнинг ўтказиш йўлаги кенглигига тенг бўлади.
Қуйи частота прототип-фильтрларида ![]() бўлганлиги учун, (28.6) ва (28.8) ифодаларда
йўлак фильтрининг меъёрланган комлекс ўзгартирувчи ва мъёрланган частотаси учун
қуйидаги ифодаларни ҳосил қиламиз:
бўлганлиги учун, (28.6) ва (28.8) ифодаларда
йўлак фильтрининг меъёрланган комлекс ўзгартирувчи ва мъёрланган частотаси учун
қуйидаги ифодаларни ҳосил қиламиз:
![]() (28.9,а)
(28.9,а)
![]() (28.9,б)
(28.9,б)
буларда штрих тушириб қолдирилган.
Уларда агар берилган ҚЧФнинг ифодаларида ушбу ўзгартиришларни қўлланса, йўлак фильтрлари учун вақт ва частотавий тавсифларининг ифодаларини аниқлашга ёрдам беради.
Симметрик тавсифли режектор фильтрлари. Симметрик (геометрик) тавсифли режектор фильтрлари қуйи частота прототип-фильтрлардан қуйидаги ифода ёрдамида ўзгартирилиб олиниши мумкин:
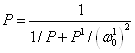 (28.10,а)
(28.10,а)
Бунга ўзгартирилаётган фильтр ўзгарувчиси ![]() билан режектор фильтри частотаси
билан режектор фильтри частотаси ![]() орасида қуйидаги боғланиш мос
келади:
орасида қуйидаги боғланиш мос
келади:
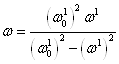
|
|
Юқоридагиларга ўхшаш, бундай ҳолатда
берилган қуйи частота LC - фильтрларининг ҳар бир индуктив
элементи резо-нанс частотаси ![]() бўлган параллел тебранма кон-турга, ҳар
бир сиғим - шу резонанс частотаси
кетма-
бўлган параллел тебранма кон-турга, ҳар
бир сиғим - шу резонанс частотаси
кетма-
кет тебраниш контурига айланишига ишонч ҳосил қилиш осон.
28.6-расм
28.4 Фильтрларнинг фаза тавсифлари
Тўртқутбликларнинг фаза тавсифлари деб, занжир
киришига келтирилган гармоник таъсир билан унинг чиқишидаги гармоник
реакция орасидаги фазалар фарқининг частотага ![]() боғлиқлигига айтилади. Фаза тавсифи
тўртқутбликнинг фаза-частотавий тавсифидан фақат ўзининг ишораси
билан фарқ қилади, яъни
боғлиқлигига айтилади. Фаза тавсифи
тўртқутбликнинг фаза-частотавий тавсифидан фақат ўзининг ишораси
билан фарқ қилади, яъни ![]() .
.
Кўпгина ҳолатларда фильтрларнинг фаза тавсифлари ўрнига ёки улар билан биргаликда, фаза фарқлари ҳосиласининг частотага боғлиқлигини ишлатиш қулайроқ
![]() (28.11)
(28.11)
Частотанинг функция ![]() ни (фильтрнинг) гуруҳ ўтиш вақти деб
аталади. Бу билан элементлари тақсимланган занжирга, ёки тўлқинларнинг
у ёки бу муҳитда тарқалиш жараёнларигагина татбиқ этиш мумкин
бўлган маълум физик маънодаги (мантиқдаги) жараёнларни мужассам параметрли
занжирларга тадбиқ этамиз. Бунда шу нарса аёнки, фаза-частотавий
номосликдан холи бўлган чизиқли фаза тавсиф
ни (фильтрнинг) гуруҳ ўтиш вақти деб
аталади. Бу билан элементлари тақсимланган занжирга, ёки тўлқинларнинг
у ёки бу муҳитда тарқалиш жараёнларигагина татбиқ этиш мумкин
бўлган маълум физик маънодаги (мантиқдаги) жараёнларни мужассам параметрли
занжирларга тадбиқ этамиз. Бунда шу нарса аёнки, фаза-частотавий
номосликдан холи бўлган чизиқли фаза тавсиф ![]() га гуруҳ вақтининг ўзгармас қиймати
га гуруҳ вақтининг ўзгармас қиймати
![]() мос келади.
мос келади.
Фильтрлар фаза тавсифларининг хусусиятларини таҳлил
қилишни узатиш функцияларининг ![]() махражида Гурвица полиноми суратида - ҳақиқий,
аксарият мусбат ўзгармас қатнашадиган полиномиал фильтрлар тавсифларидан
бошлаш қулайдир. Гурвица полиномини
махражида Гурвица полиноми суратида - ҳақиқий,
аксарият мусбат ўзгармас қатнашадиган полиномиал фильтрлар тавсифларидан
бошлаш қулайдир. Гурвица полиномини ![]() бўлганда кўрсаткичли функция шаклда
бўлганда кўрсаткичли функция шаклда ![]() ёзиб, полиномиал фильтрлар фаза тавсифлари
ёзиб, полиномиал фильтрлар фаза тавсифлари ![]() ва
ва ![]() бўлгандаги Гурвица полиноми аргументининг
частотавий боғланиши билан мос бўлишини аниқлаймиз, яъни:
бўлгандаги Гурвица полиноми аргументининг
частотавий боғланиши билан мос бўлишини аниқлаймиз, яъни:
![]() (28.12)
(28.12)
Демак, полиномиал фильтрлар фаза тавсифлари
частотанинг бир текисда ортувчи функция экан. Бунда у частотанинг 0 дан ![]() гача ўзгаришида
гача ўзгаришида ![]() радианга ортади.
радианга ортади.
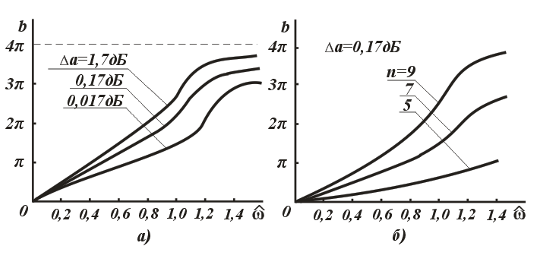
28.7-расм
Боғланишларнинг таҳлили қуйидаги
хулосаларга олиб келади. Чебышев
туридаги полиномиал фильрларнинг фаза тавсифлари ўтиш йўлининг фақат қуйи
қисмида чизиқли боғланишга яқин бўлади ![]() ва n қанчалар
кичик бўлса чизиқлилик шунчалар кенг бўлади. Частотанинг ортиши билан фильтрлар фаза тавсифлари
тиклиги
(гуруҳ ўтиш вақти) ортади; унинг қиймати
ўтиш йўлаги чегаравий частотаси яқинида энг катта бўлиб, сўнгра кескин пасаяди.
ва n қанчалар
кичик бўлса чизиқлилик шунчалар кенг бўлади. Частотанинг ортиши билан фильтрлар фаза тавсифлари
тиклиги
(гуруҳ ўтиш вақти) ортади; унинг қиймати
ўтиш йўлаги чегаравий частотаси яқинида энг катта бўлиб, сўнгра кескин пасаяди.
Бунда фильтр ўтиш йўлагида унинг фаза тавсифи
пасаювининг асосий қисми тўпланган. Нотекислик ![]() нинг қийматлари 0,3 . . 0,5
нинг қийматлари 0,3 . . 0,5 ![]() дан ортганда фильтрлар ўтказиш йўлагида гуруҳ
ўтиш вақти бир қатор экстремумларга эга бўлади; бу эса тавсифида бир максимуми бўлган
дан ортганда фильтрлар ўтказиш йўлагида гуруҳ
ўтиш вақти бир қатор экстремумларга эга бўлади; бу эса тавсифида бир максимуми бўлган
тавсифларга нисбатан фаза коррекциясини кескин
мушкуллаштиради.
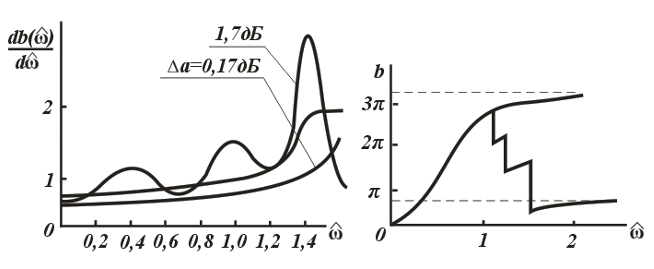
28.8-расм 288.9-расм
Бошқа тенг шартларда ҚЧФ ўтказиш йўлаги қанчалар
тор бўлса вақти гуруҳ ўтказиш вақти
![]()
шунчалар катта бўлади.
Кучланиш тавсифлари максимал тенг бўлган полиномиал
фильтрларнинг фаза тавсифлари юқорида кўрилган фильтрларга ўхшаш бўлади.
Бироқ уларнинг гуруҳ ўтиш вақти
тавсифлари ![]() бўлганда
бўлганда ![]() оралиқда фақат битта максимумга эга.
оралиқда фақат битта максимумга эга.
Полиномиал фильтрлардаги каби, кучланиш чеклашлари
бўлган қуйи частота фильтрларида ўтказиш йўлигидаги фаза тавсифлари, фақатгина
уларнинг узатиш функцияси махражида қатнашувчи Гурвица полиномининг
аргументи билан аниқланади. Дарҳақиқат, фильтр
кучсизланишининг сакрашини ҳосил қилувчи ![]()
![]() полином фақат ҳаққий қийматларни
қабул қилади. Шунинг учун унинг аргументи ёки 0 га ёки
полином фақат ҳаққий қийматларни
қабул қилади. Шунинг учун унинг аргументи ёки 0 га ёки ![]() га тенг бўлади ва полином ишораси ўзгариши билан
га тенг бўлади ва полином ишораси ўзгариши билан
![]() га ўзгариши мумкин; бу эса агар полином тоқ
карра 0 га эга бўлса, фақатгина фильтрнинг тўсиш йўлагида бўлиши мумкин.
га ўзгариши мумкин; бу эса агар полином тоқ
карра 0 га эга бўлса, фақатгина фильтрнинг тўсиш йўлагида бўлиши мумкин.
Кейинги ифодаларнинг таҳлили шуни кўрсатадики, юқори
частота фильтрларининг гуруҳ вақти юқори ташкил этувчилари
учун частота ортиши билан қўпаяди ва ![]() да нолга интилади. Симметрик тавсифли йўлак
фильтрларида эса ўтказиш йўлаги қанчалар тор бўлса, ўтказиш йўлагидаги
гуруҳ кучсизланиш тавсифлари турдош бўлган берилган қуйи частотали
прототип-фильтрлардаги каби, юқори частота фильтрлари ва йўлак фильтрлари
фаза тавсифлари чизиқли боғланишдан фарқ қиладилар;
уларнинг гуруҳ ўтиш вақтларининг частотавий боғланишлари
мусбат ҳақиқий ўзгармасдан фарқ қиладилар. Бу
эса, ўзнавбатида, фильтрларнинг дискрет ахборот узатиш каналларида қўлланилишида
коррекция зарурлигини тақозо этади. Аксарият, бу мақсадда номинимал-фаза
занжири қўлланилади. Фаза тавсифларини минимал-фаза турдаги
фильтрлар билан чизиқлилаштириш, уларнинг селектив хусусиятини
сусайтиради. Шу сабабли, фильтрлар синтез қилишнинг бу усули кенг қўлланилмайди.
да нолга интилади. Симметрик тавсифли йўлак
фильтрларида эса ўтказиш йўлаги қанчалар тор бўлса, ўтказиш йўлагидаги
гуруҳ кучсизланиш тавсифлари турдош бўлган берилган қуйи частотали
прототип-фильтрлардаги каби, юқори частота фильтрлари ва йўлак фильтрлари
фаза тавсифлари чизиқли боғланишдан фарқ қиладилар;
уларнинг гуруҳ ўтиш вақтларининг частотавий боғланишлари
мусбат ҳақиқий ўзгармасдан фарқ қиладилар. Бу
эса, ўзнавбатида, фильтрларнинг дискрет ахборот узатиш каналларида қўлланилишида
коррекция зарурлигини тақозо этади. Аксарият, бу мақсадда номинимал-фаза
занжири қўлланилади. Фаза тавсифларини минимал-фаза турдаги
фильтрлар билан чизиқлилаштириш, уларнинг селектив хусусиятини
сусайтиради. Шу сабабли, фильтрлар синтез қилишнинг бу усули кенг қўлланилмайди.
29-маъруза. Аналогли, дискретли ва ракамли фильтрлар
Аналог занжирларидаги каби, тартиби юқори бўлган фильтрли дискрет занжирларни ҳам вақт оралиғида аналитик ҳисоблаш мураккаб бўлади.
Дискрет занжирлар учун Лаплас ўзгартириши усулининг аналоги Z-ўзгартиришидир. Дискрет кетма-кетлигини қуйидагича ёзиш мумкин:
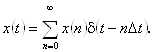
Ифоданинг чап ва ўнг томонларидан Лаплас ўзгартиришини аниқлаймиз:
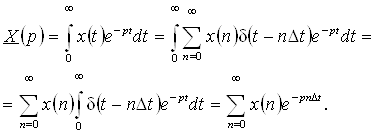
Комплекс ўзгарувчи ![]() ни қуйидагича белгилаймиз:
ни қуйидагича белгилаймиз:
![]() (29.1)
(29.1)
Ушбу ![]() ўзгартириш (29.1)
ўзгартириш (29.1) ![]() -текислигидаги бирлик айланада p ярим текисликни
ички сатҳга, ўнг ярим текисликни - ташқи сатҳга акс эттиради.
Мавҳум ўқ
-текислигидаги бирлик айланада p ярим текисликни
ички сатҳга, ўнг ярим текисликни - ташқи сатҳга акс эттиради.
Мавҳум ўқ ![]() бирлик радиусга эга бўлган айлана билан акс
эттирилади (29.1 -расм).
бирлик радиусга эга бўлган айлана билан акс
эттирилади (29.1 -расм).
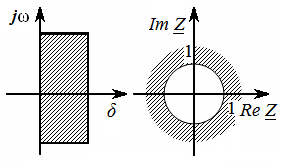 Шундай қилиб,
Шундай қилиб,
![]() кетма-кетлик комплекс ўзгарувчининг функциясига мувофиқ
қуйидагича ёзилиши мумкин:
кетма-кетлик комплекс ўзгарувчининг функциясига мувофиқ
қуйидагича ёзилиши мумкин:
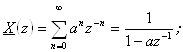 (29.2)
(29.2)
29.1-расм
Ушбу (29.6) ўзгартириш ![]() кетма-кетликнинг Z-ўзгартириши
дейилади.
кетма-кетликнинг Z-ўзгартириши
дейилади.
Ихтиёрий ![]() шаклдаги кетма-кетлик учун Z-ўзгартиришни аниқлаймиз.
Геометрик прогрессия ифодасидан
шаклдаги кетма-кетлик учун Z-ўзгартиришни аниқлаймиз.
Геометрик прогрессия ифодасидан
![]()
Ихтиёрий кетма-кетликнинг Z-ўзгартиришини ![]() функциясини Лоран қаторига ёзиш деб қараш
мумкин:
функциясини Лоран қаторига ёзиш деб қараш
мумкин:
![]()
У ҳолда берилган кетма-кетликнинг қийматлари
ушбу қатор коэффициентлари бўлади. Шундай қилиб, тескари масалани
ечиш мумкин: бирор кетма-кетликнинг Z-ўзгартириши ёрдамида шу кетма-кетликни
аниқлаш.
![]() функциясининг Лорен қатори
коэффициентларини аниқлаш ифодасидан фойдаланиб:
функциясининг Лорен қатори
коэффициентларини аниқлаш ифодасидан фойдаланиб:
![]() (29.3)
(29.3)
Мисол. Берилган ![]() бўлсин. Шундай кетма-кетликни аниқлайликки,
унинг учун
бўлсин. Шундай кетма-кетликни аниқлайликки,
унинг учун ![]() кетма-кетлик Z-ўзгартириши бўлсин.
кетма-кетлик Z-ўзгартириши бўлсин.
![]()
Бу ҳолат учун ![]()
![]() Қутб
Қутб ![]()
![]() демак,
демак,![]() . Бундан
. Бундан ![]() .
.
![]() ўзгартириш хусусиятлари Лаплас ўзгартиришларининг
ўхшаш.
ўзгартириш хусусиятлари Лаплас ўзгартиришларининг
ўхшаш.
1. Чизиқлилик. Агар
![]()
![]() берилган бўлса, у ҳолда чизиқлилик
шартлари асоси
берилган бўлса, у ҳолда чизиқлилик
шартлари асоси 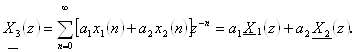 .
.
2. Силжиш
теоремаси. Агар ![]() бўлса, у ҳолда
бўлса, у ҳолда
![]()
Бу
![]() ифодага
ифодага ![]() қўйсак, қуйидагини ҳосил қиламиз:
қўйсак, қуйидагини ҳосил қиламиз:
![]()
![]() бўлгани учун,
бўлгани учун,
![]()
бунинг ниҳоясида
![]()
ҳосил бўлади.
3. Жамлаш теоремаси. Икки кетма-кетлик дискрет жамлашнинг Z-ўзгартириши ҳар бир кетма-кетлик Z-ўзгартиришларининг кўпайтмасига тенг:
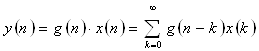
Жамлшни қуйидаги кетма-кетлик шаклига келтирамиз:
![]()
![]()
![]()
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
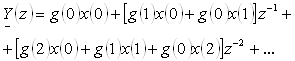
Бундан шуни кўриш мумкинки, бу ифода ![]() кетма-кетликларнинг Z-ўзгартиришлари кўпайтмаси
бўлади. Дарҳақиқат,
кетма-кетликларнинг Z-ўзгартиришлари кўпайтмаси
бўлади. Дарҳақиқат,
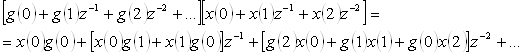
Пировардида бу ифодани қуйидагича ёзиш мумкин бўлади:
![]() (29.3)
(29.3)
Ушбу (29.35) дан кўринадики, кетма-кетликлар дискрет жамлашига улар Z-ўзгартиришларининг кўпайтмалари мос келар экан.
Z-ўзгартиришнинг келтирилган ҳусусиятлари
ЧРФларни таҳлил қилиш қоидаларини ифодалаш имкониятини
беради; аксарият, бу усуллар аввалги усулларга нисбатан қамроқ
ресерс сарфлашга олиб келади. Демак, бизга маълум бўлгани, чиқиш
кетма-кетлиги ![]() кириш кетма-кетлиги
кириш кетма-кетлиги ![]() билан ёки айирма тенгламаси
билан ёки айирма тенгламаси
![]()
ёки жамлаш тенгламаси
![]()
билан боғланишда экан.
Иккинчи томондан, ![]() .
.
Импульс тавсифининг Z-ўзгартириши ЧРФнинг узатиш функцияси дейилади. Демак, жамлашни ҳисоблашнинг ўрнига қуйидагиларни аниқлаш мумкин:
кириш кетма-кетлигининг Z-ўзгартиришини
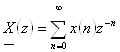 ;
;
![]() узатиш функциясини;
узатиш функциясини;
чиқиш кетма- кетлигининг Z-ўзгартиришини
![]() ;
;
чиқиш кетма- кетлигини
Вычет теоремаси ёрдамида чиқиш кетма-кетлигининг
![]() ўзгартиришини
ўзгартиришини
![]()
Узатиш функцияси ![]() ни импульс тавсифининг
ни импульс тавсифининг ![]() ўзгартириши сифатида ҳам
ўзгартириши сифатида ҳам
![]()
айирма тенгламаси сифатида ҳам аниқлаш мумкин.
Занжирнинг узатиш функциясини айирма тенгламаси
сифатида аниқлаймиз:
![]()
Тенгликнинг ўнг ва чап томонлари учун ![]() ўзгартиришни татбиқ этамиз:
ўзгартиришни татбиқ этамиз:
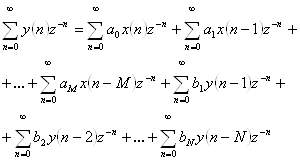
Бу ифодага кирувчи ҳар бир йиғинди қуйидаги
шаклда ўзгартирилиши мумкин:

Шунга ўхшаш
![]()
У ҳолда қуйидагиларни ҳосил қиламиз:
![]()
ёки
![]()
Демак,
![]() (29.4)
(29.4)
Ушбу (29.9) боғланиш занжирнинг функцияси ва айирма тенгламасини ўзаро боғлайди. Унинг ёрдамида ЧРФнинг айирма тенгламаси орқали унинг узатиш функциясини аниқлаш мумкин.
Баъзан бунга тескари бўлган масалани ечишга тўғри келади: узатиш функциясидан айирма тенгламасини аниқланади ва у ёрдамида ЧРФ схемаси таркибий тузилмасини қурилади. Бундай масала ЧРФ тузилишини амалга ошириш масаласи дейилади. Бунинг учун узатиш функциясини (29.9) шаклига келтириш лозим. Аниқланган коэффициентлар айнан айирма тенгламасини ташкил этади.
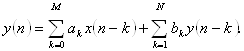
Масалан, узатиш функцияси ![]() бўлган ЧРФни тузишни амалга ошириш талаб
этилсин.
бўлган ЧРФни тузишни амалга ошириш талаб
этилсин. ![]() ни қуйидаги кўринишга келтирамиз:
ни қуйидаги кўринишга келтирамиз:
![]()
Бундан
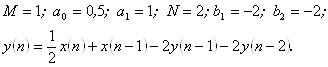
Ушбу тенгламага мос келган дискрет схеманинг тузилиши 29.6-расмда келтирилган.
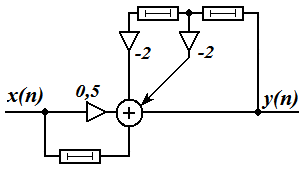 Мисол
учун тузилган ЧРФнинг киришига
Мисол
учун тузилган ЧРФнинг киришига ![]() кетма-кетлик уланганда, унинг чиқишидаги
сигнални аниқлашни кўрайлик.
кетма-кетлик уланганда, унинг чиқишидаги
сигнални аниқлашни кўрайлик.
Кириш кетма-кетлигининг Z-ўзгартиришини аниқлаймиз:
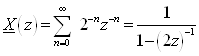
29.2-расм
30-маъруза. Рақамли фильтрлар. Асосий тавсифлари
30.1. Дискрет сигналлар ва занжирлар
Узлуксиз
ўзгарувчи функциялар-кучланиш ![]() , ток
, ток ![]() ва бошқа
миқдорларнинг узлуксиз ўзгарувчи вақт
ва бошқа
миқдорларнинг узлуксиз ўзгарувчи вақт ![]() га бўлган
боғланишлари - узлуксиз ҳақиқий ўзгарувчи
га бўлган
боғланишлари - узлуксиз ҳақиқий ўзгарувчи ![]() нинг
функциялари, Фурье спектрлари ва Лапласнинг ўзгартиришлари сифатида ифодаланган
эди. RLC – элементлардан, бошқарувчи кучланиш ва ток манбаларидан
ташкил топган электр занжирлар аналог тизимлари дейилади. Уларнинг математик моделлари дифференциал тенгламалар,
комплекс частотавий тавсифлар, узатиш функциялардан иборат.
нинг
функциялари, Фурье спектрлари ва Лапласнинг ўзгартиришлари сифатида ифодаланган
эди. RLC – элементлардан, бошқарувчи кучланиш ва ток манбаларидан
ташкил топган электр занжирлар аналог тизимлари дейилади. Уларнинг математик моделлари дифференциал тенгламалар,
комплекс частотавий тавсифлар, узатиш функциялардан иборат.
Сигналларни қайта ишлаш мақсадида аналог занжирлари ўрнида рақамли техника воситаларини қўллаш, узлуксиз аналог сигналларни дискрет сигналлар билан алмаштиришни тақозо этади. Сигнал рақамлар кетма-кетлиги сифатида берилган бўлса, у ЭҲМ дастури ёки махсус процессорлар ёрдамида қайта ишланиши мумкин.
Маълумки, Котельников теоремасига мувофиқ
частота ![]() билан чекланган спектрдаги сигналлар, ўзларининг
билан чекланган спектрдаги сигналлар, ўзларининг
![]() вақт оралиғида олинган дискрет қийматлари
кетма-кетлиги ёрдамида кўрсатилиши мумкин. Узлуксиз
вақт оралиғида олинган дискрет қийматлари
кетма-кетлиги ёрдамида кўрсатилиши мумкин. Узлуксиз ![]() сигнал учун
сигнал учун ![]() оралиқни яққол кўрсатилмасдан
оралиқни яққол кўрсатилмасдан ![]() деб белгилаймиз. Унда
деб белгилаймиз. Унда ![]() тўплам кетма-кетлик деб, яъни натурал
аргумент
тўплам кетма-кетлик деб, яъни натурал
аргумент ![]() нинг функцияси деб аталади.
нинг функцияси деб аталади.
Агар кириш кетма-кетлигини ![]() деб,
чиқиш кетма-кетлигини эса
деб,
чиқиш кетма-кетлигини эса ![]() деб белгиланса, у ҳолда дискрет занжир деб
кириш
деб белгиланса, у ҳолда дискрет занжир деб
кириш ![]() кетма-кетлик тўпламини чиқиш
кетма-кетлик тўпламини чиқиш
![]() кетма-кетлик тўпламига айлантирувчи
объектга айтилади.
кетма-кетлик тўпламига айлантирувчи
объектга айтилади.
Агар ихтиёрий кириш кетма-кетлиги ![]() га чиқиш
га чиқиш ![]() кетма-кетлигини аниқлаш мумкин бўлса,
занжир берилган деб ҳисобланади. Баъзан
кетма-кетлигини аниқлаш мумкин бўлса,
занжир берилган деб ҳисобланади. Баъзан ![]() аргументи вақт дискрети деб ҳам
аталади. Мавжуд ҳар хил дискрет занжирлар орасида кўпроқ қизиқиш
уйғотадиган занжирлар - бу уч асосий элементлардан иборат бўлган қуйидаги
уч композициялардир:
аргументи вақт дискрети деб ҳам
аталади. Мавжуд ҳар хил дискрет занжирлар орасида кўпроқ қизиқиш
уйғотадиган занжирлар - бу уч асосий элементлардан иборат бўлган қуйидаги
уч композициялардир:
1)
жамлагичлар кетма-кетлиги
![]() ;
;
2)
ўзгармас коэффициентга кўпайтиргич
![]() ;
;
3) кечиктиргич элементи
![]()
бунда
![]() - берилган бошланғич шарт.
- берилган бошланғич шарт.
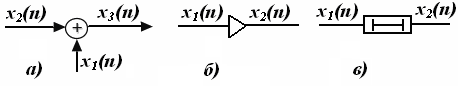
29.1-расм

30.2-расм
Бундай элементлардан ташкил топган занжирлар чизиқли дискрет занжирлар ёки чизиқли рақамли фильтрлар (ЧРФ)
деб аталади.
Дискрет сигнал қуйидаги
![]()
ифода ёрдамида берилган бўлсин.
30.2,а-расмда бундай кетма-кетлик графиги кўрсатилган.
Чизиқли дискрет занжир 30.2,б-расмда келтирилгандек элементлардан уланган бўлсин. Ушбу занжирнинг математик модели қуйидаги шаклга эга:
![]() (30.1)
(30.1)
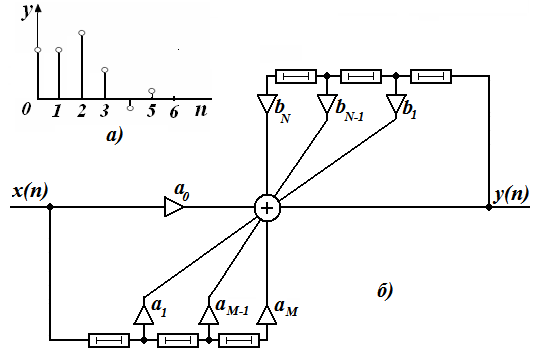
30.3-расм
(30.1) тенглама биринчи тартибли айирмали тенглама дейилади. Ушбу айирмали тенглама чиқиш кетма-кетлигини кириш кетма-кетлиги орқали аниқлаш имконини беради.
Бизнинг мисолда, ![]() бўлсин. Кириш кетма-кетлиги сифатида 30.3,а-расмдаги
графикни оламиз. Натижада
бўлсин. Кириш кетма-кетлиги сифатида 30.3,а-расмдаги
графикни оламиз. Натижада ![]() чиқиш кетма-кетлигини аниқлаймиз.
Таърифга кўра
чиқиш кетма-кетлигини аниқлаймиз.
Таърифга кўра ![]()
![]() Унда қуйидагича ёзиш мумкин:
Унда қуйидагича ёзиш мумкин:
![]() бўлганда
бўлганда ![]()
![]() бўлганда
бўлганда ![]()
![]() бўлганда
бўлганда ![]()
![]() бўлганда
бўлганда ![]()
![]() бўлганда
бўлганда ![]()
![]() бўлганда
бўлганда ![]()
30.3,а-расмда ушбу рақамли фильтрлар чиқиш
кетма-кетлигининг графиги кўрсатилган. Умумий ҳолда чизиқли рақамли
фильтрнинг математик модели қуйидаги шаклдаги ![]() тартибли айирма тенламадан иборат бўлади:
тартибли айирма тенламадан иборат бўлади:
![]()
![]() (30.2)
(30.2)
бунда
![]() ,
, ![]() ва
ва ![]() коэффициентлар - ҳақиқий
сонлар.
коэффициентлар - ҳақиқий
сонлар.
Фильтрнинг чиқиш (30.2) кетма-кетлигини ҳисоблаш
учун кириш кетма-кетлигини ![]() ва бошланғич шартларни
ва бошланғич шартларни ![]() билиш зарур. Ушбу математик модель билан
ифодаланган ЧРФ бир неча ҳар хил, аммо ўзгартиришлари бўйича эквивалент
бўлган кириш-чиқиш тизимларига эга бўлиши мумкин. Шулардан энг соддаси
30.3,б-расмда келтирилган.
билиш зарур. Ушбу математик модель билан
ифодаланган ЧРФ бир неча ҳар хил, аммо ўзгартиришлари бўйича эквивалент
бўлган кириш-чиқиш тизимларига эга бўлиши мумкин. Шулардан энг соддаси
30.3,б-расмда келтирилган.
ЧРФни таҳлил қилишда чизиқли аналог занжирларни таҳлил қилишда ишлатилган усулларни қўллаш мумкин. Уларга қуйидагилар киради:
1) айирма тенгламаларни ечиш (дифференциал тенгламаларни ечишнинг аналоги);
2) импульс тавсиф билан йиғиш;
3) Z-ўзгартиришни қўллаш (Лаплас ўзгартишининг аналоги).
30.2. Айирма тенгламаларни ечиш билан ЧРФни таҳлил қилиш
Айирма теоремаси
ёрдамида ЧРФ чиқиш сигналларини ҳисоблашнинг энг содда усули -
фильтр тенгламасига ![]() ни қўйиб,
ни қўйиб,
![]() ни қуйидаги
ифода ёрдамида ҳисоблашдир.
ни қуйидаги
ифода ёрдамида ҳисоблашдир.

Бу мақсадда, боғланиш ўнг томонидаги ифодани дастурланади. Масалан, қуйидаги шаклдаги айирма тенглама
![]() (30.3)
(30.3)
бошланғич
шартлари ![]() билан тўғридан-тўғри ўрнига қўйиш
усули билан ечиш мумкин:
билан тўғридан-тўғри ўрнига қўйиш
усули билан ечиш мумкин:
![]()
![]()
![]()
![]()
![]() .
.
ЭҲМни қўллаш натижасида юқори
тартибли айирма тенгламаларини ечиш ҳам имкониятли бўлади. Бироқ,
чизиқли дифференциал тенгламалардаги каби, чизиқли айирма
тенгламалар учун ҳам аналитик ечимни аниқ ҳолда олиш мумкин.
Бунда асосий ғоя - айирма тенгламанинг икки ечимини аниқлашни
назарда тутади: бир жинсли тенгламанинг умумий ечимини ва бир жинсли бўлмаган
тенгламанинг хусусий ечимини аниқлаш. Бир жинсли тенгламанинг умумий
ечимини ![]() нинг ўрнига нолларни қўйиб ҳосил қилганда
ва ноллли кириш кетма-кетлиги бўлгандаги нол бўлмаган бошланғич шартларга
бўлган реакцияси аниқланади. Хусусий ечим эса берилган
нинг ўрнига нолларни қўйиб ҳосил қилганда
ва ноллли кириш кетма-кетлиги бўлгандаги нол бўлмаган бошланғич шартларга
бўлган реакцияси аниқланади. Хусусий ечим эса берилган ![]() учун
учун ![]() кетма-кетликни танлаш билан аниқланади.
кетма-кетликни танлаш билан аниқланади.
Бир жинсли тенглама қуйидаги кўринишга эга:
![]() (30.4)
(30.4)
Маълумки, бир жинсли айирма тенгламалар тавсифий
ечимлари ![]() (аналог занжирлардаги
(аналог занжирлардаги ![]() га ўхшаш) бўлади. Шунинг учун, (30.4)
тенгламадаги
га ўхшаш) бўлади. Шунинг учун, (30.4)
тенгламадаги ![]() ўрнига
ўрнига ![]() қўйсак, қуйидагини ҳосил қиламиз:
қўйсак, қуйидагини ҳосил қиламиз:
![]()
![]()
![]()
![]()
Кириш кетма-кетлиги ![]() га мос келувчи хусусий ечимни
га мос келувчи хусусий ечимни ![]() шаклида аниқлашга ҳаракат қиламиз.
шаклида аниқлашга ҳаракат қиламиз.
Бунга тенгламани қўйсак қуйидагини ҳосил қиламиз:
![]()
Даража ![]() нинг тенг қийматли ҳадлари
коэффициентларини тенглаштириб, қуйидагиларни аниқлаймиз:
нинг тенг қийматли ҳадлари
коэффициентларини тенглаштириб, қуйидагиларни аниқлаймиз:
![]()
Шундай қилиб, умумий ечим қуйидаги
![]()
шаклда бўлади.
Коэффициент А бошланғич шартлардан ![]() аниқланади, унга кўра
аниқланади, унга кўра ![]() ва
ва ![]() .
.
Ушбу ифодани ![]() учун текшириш шуни кўрсатадики, у бевосита ҳисобланган
ечим билан тўла мос келади.
учун текшириш шуни кўрсатадики, у бевосита ҳисобланган
ечим билан тўла мос келади.
30.3. ЧРФнинг импульс тавсифи. Ихтиёрий кириш кетма-кетлиги
учун реакцияни ҳисоблаш
ЧРФнинг импульс
тавсифи ![]() деб, нолли
бошланғич шартлар бўлганда
деб, нолли
бошланғич шартлар бўлганда ![]() кириш
кетма-кетликка нисбатан схеманинг жавобига айтилади.
кириш
кетма-кетликка нисбатан схеманинг жавобига айтилади.
Биринчи тартибли ЧРФнинг импульс тавсифини аниқлаймиз:
![]()
![]()
![]()
![]()
![]()
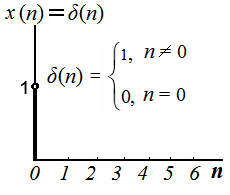 .
. . . . .
. . . .
.
. . . . .
. . . .
![]()
Бунда, агар ![]() яъни
яъни ![]() деб белгиласак, у ҳолда ихтиёрий кириш
кетма-кетлиги учун қуйидаги ёзув ҳақли бўлади:
деб белгиласак, у ҳолда ихтиёрий кириш
кетма-кетлиги учун қуйидаги ёзув ҳақли бўлади:
![]()
ёки буни қисқартирилган ҳолда 30.4-расм
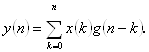
Ушбу ифода ![]() ва
ва ![]() кетма-кетликларнинг дискрет йиғмаси
деб аталади.
кетма-кетликларнинг дискрет йиғмаси
деб аталади.
ЧРФнинг ихтиёрий кетма-кетликка реакцияси кириш
кетма-кетлиги ва импульс тавсифининг йиғмаси сифатида аниқланиши
мумкин. Ушбу таъриф барча тартибдаги
ЧРФга тааллуқлидир. Шундай қилиб, дискрет занжирда кириш сигналини ҳисоблашнинг
иккинчи усули - ЧРФ импульс тавсифини аниқлаб, уни кириш кетма-кетлиги
билан йиғмаси бажарилади. Бу фикр аналог занжирлари учун 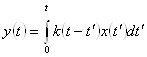 йиғмаси билан ўхшашдир.
йиғмаси билан ўхшашдир.
31-маъруза. Тескари боғлинишли электр занжирлар.
Турғунлик мезонлари
Чиқишидаги сигнал қайтадан киришига узатиладиган занжир тескари боғланишли (ТБ) занжир деб аталади. (31.1-расм).

31.1- расм
Занжирга тескари боғланишни киритиш занжирнинг ишчи тавсифларини ўзгартиради. Масалан чиқишидаги сигналнинг бир қисми ТБ орқали киришга узатилса ҳамда у киришдаги сигналдан айириб ташланса бундай ТБ манфий тескари боғланиш деб аталади. (манфий ТБ).
Агар чиқишдаги сигналнинг бир қисми киришга узатилса ҳамда у киришдаги сигналга қўшилса бундай тескари боғланиш мусбат тескари боғланиш (Мусбат ТБ) ёки регенератив тескари боғланиш дейилади.
Манфий тескари боғланиш кучайтириш коэффициентини камайтиради ва текислайди, унинг ўтказиш оралиғини кенгайтиради, шовқин ва бўзилишларни камайтиради. Кучайтиргичларда кўпроқ манфий ТБ қўлланади.
Мусбат тескари боғланиш кучайтириш коэффициентини орттиради, ўтказиш оралиғини кичрайтиради ва кучайтириш барқарорлигини камайтиради. Мусбат ТБ кўпинча генераторларда қўлланади.
Актив ночизиқли элементлардан ташкил топган электр занжирларда электр тебранишлар даврий таъсирсиз ўз ичидан ҳосил бўлиши мумкин.
Ўзгармас манбалар энергиясининг тебранишлар энергиясига алмашиш жараёни занжирдаги автотебранишлар бед аталади.
Автотебранишлар ҳосил бўладиган занжир тескари боғланишли занжирдир.
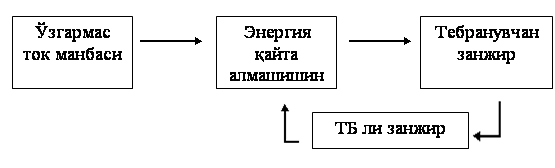
31.2-расм
Одатда бошқарувчи қайта алмашиш сифатида актив ночизиқли элементлар: транзисторлар, диодлар, элеатрон лампалардан фойдаланилади. ТБ ли занжир ва тебранувчан занжир - бу чизиқли занжирдир.
Тизимли нуқтаи назардан тескари боғланишли занжир муаммосини қўриб чиқамиз. Оператор узатиш функцияларини К(Р) ва в (Р) бўлган иккита тизим 31.2- расмда кўрсатилганидай боғланган бўлсин.
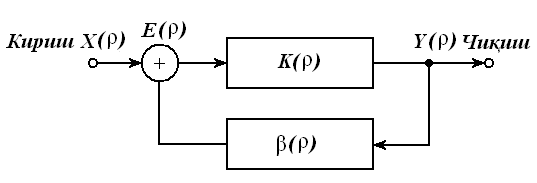 Асосий
тизим
Асосий
тизим
Тескари боғланиш тизими
31.3 – расм
Бундай тизим тескари боғланишли тизим дейилади. Х (Р) ва Y (Р) мос равишда киришдаги ва чиқишдаги оператор
сигналлар бўлсин. Бу тизимнинг узатиш функцияси Н (Р)ни аниқлаймиз.
![]()
![]() ва
ва ![]()
эканлигини ҳисобга олсак
келиб чиқади 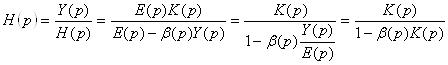
Р = jщ
бўлганда бу ифодани кўриб чиқамиз.
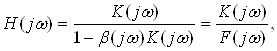
бу ерда F (jщ)=1-в (jщ)·K (jщ) – тескари боғланишнинг фактор комплекс чуқурлиги.
Агар |1-в (jщ)·K (jщ)|>1 бўлса, тизимнинг узатиш коэффициенти модули ва унга мос равишда чиқишдаги сигнал амплитудаси камайгани сабабли тескари боғланиш манфий ТБ бўлади.
Агар |1-в (jщ)·K (jщ)|<1 бўлса, тескари боғланиш мусбат ТБ бўлади.
Масалан, Кучайтириш коэффициенти K (jщ)=1000 бўлса, темкари боғланишнинг узатиш
коэффициенти в (jщ)=-0,099 бўлса, у ҳолда тескари боғланишни ўз ичига
олган кучайтиргичнинг умумий кучайтириш коэффициенти қуйидагига тенг
бўлади.
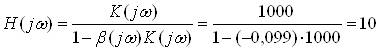
Агар Re [в (jщ) K(jщ)]»1, шарт бажарилса,
махраждаги бирликни ҳисобга олмаса ҳам бўлади.

яъни Н(jщ) узатиш функцияси Н(jщ) тескари боғланиш параметри в (jщ) орқали аниқланади ва асосий система К(jщ) нинг хоссаларига боғлиқ бўлмайди.
31.1 Барқарорлик меъзони ҳақида тушунча
К(Р) оператор узатиш функцияси ҳамда актив элементлари бўлган, асосий занжир ва в (Р) оператор узатиш функциясига эга бўлган тескари боғланиш занжири орқали кириши билан чиқиши ўзаро боғланган автоном чизиқли тизимни кўриб чиқамиз
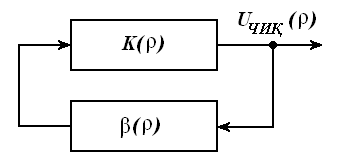
31.4 – расм
Чиқишдаги
оператор кучланиш қуйидагига тенг деб ёзиш мумкин.
![]()
Ҳаммасини чап томонга ўтказиб қуйидагини оламиз
![]()
Чиқишдаги кучланиш тождественно нольга тенг бўлиши мумкин эмас: Uчиқ(Р)≠0, акс ҳолда тизим қўзголмаган (уйғонмаган) бўларди, мос равишда қуйидаги тавсифий тенгламани оламиз
1-К(р) · в (p)=0
Бу тенгламани ечиб, унинг илдизлари р1, р2, …
ларни аниқлаймиз. Кўрилаётган тизим чизиқли бўлгани сабабли, умумий
ҳолда чиқишдаги сигнал қуйидаги кўринишга эга бўлади
![]()
Бу сигнал чегараланган бўлиши учун тавсифий тенгламанинг илдизлари манфий ҳақиқий қисмга эга бўлиши лозим, яъни улар Р
ўзгарувчининг чап ярим текислигида жойлашиши керак. Агар занжир шу хоссаларга эга бўлса, бу занжир мутлақо барқарор занжир ҳисобланади.
Агар К(Р) ва в (Р) ни Р даражали кўпҳадларнинг нисбати кўринишида ифодаланса, бу нисбатларни Гурвиц полиномига келтириш мумкин.
31.2 Амплитудалар ва фазалар тенглик шарти
Электрон аппаратурада ўзгарувчан кучланишнинг турли генераторлари кенг қўлланади. «Генератор» сўзи «ишлаб чиқарувчи» маъносини билдиради.
Генератор озиқланиш энергиясини тебранишлар энергиясига алмаштирувчи қурилма ҳисобланади.
Кучланиш бўйича комплекс узатиш коэффициенти
![]()
бўлган
кучатиргич базасида яратилган генераторни кўриб чиқамиз (31.4 – расм).
Унинг кучланиш бўйича комплекс узатиш коэффициенти
![]()
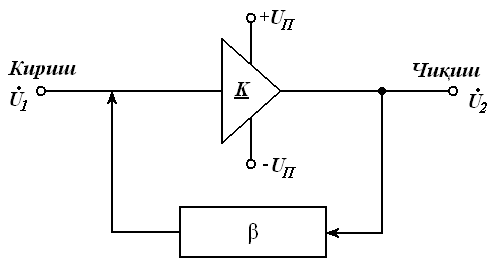 га тенг, ҳамда мусбат тескари боғланишга эга.
га тенг, ҳамда мусбат тескари боғланишга эга.
31.5 – расм
![]() или
или ![]()
Кучайтиргич киришида щ0 бурчакий частотага ва Um амплитудага эга бўлган гармоник тебранишлар таъсир қилаётган бўлсин. Бу тебранишларни сақлаб туриш учун бутун занжирни айланиб чиқгандан сўнг (К ва в) киришга худди шундай частотали, фазали ва амплитудали тебранишларни бериш лозим.
Кучайтиргич киришига берилаётган ўзгарувчан кучланиш қўзғолиш
сигнали дейилади. Бу ситуацияга қуйидаги
шарт мос келади. Қуйидагини ҳисобга олсак:
![]()
мос равишда в К=1.
Бу
тенгламани кўрсаткичли кўринишда ёзамиз
![]() или
или![]() и
и ![]()
бу ерда k=0, 1, 2, …..
Кучайтиргич ночизиқли актив элементга эга эканлигини ҳисобга олсак,
у ҳолда узатиш коэффициенти амплитуда Um га боғлиқ
бўлади, яъни
![]()
Бу шарт амплитудалар тенглик шарти деб аталади.
Резонанс контури мавжуд бўлганда фазанинг силжиши частотага қаттиқ
боғлиқ
![]()
бу ерда k=0, 1, 2, ….- фазалар тенглик шарти.
Амалга генераторнинг фазалар фарқи 3600 бўлиши керак, чунки кучайтиргич одатда сигнални инвертлайди бу ҳолда фазалар фарқи 1800 бўлади, мусбат ТБ ли частотавий – сайловчан занжир эса керакли частотада 1800 га тенг бўлган қўшимча фазалар фарқини ҳосил қилади.
Тебранишларнинг текис амплитудасида бутун системанинг умумий коэффициенти.
Кв<1 бўлганда тебранишлар амплитудаси камаяди, Кв >1 бўлганда эса тебранишлар амплитудаси Um ортади.
Фазалар тенглик шартидан генерация частотаси аниқланади.
31.3 Ўз-ўзини қўзғатиш тебранишлари
Генераторларда тескари боғланишнинг мусбат дейилишига сабаб, у киришдаги сигнал ўзгаришини ушлаб туради ва уни кучайтиради. Агар кучайтиргичнинг кириш занжирига тебраниш контури уланган бўлса, ўзгарувчан кучланиш бу контурда қўзғатувчи сигнал бўлиб хизмат қилади. Агар контурда сўнмайдиган тебранишлар ҳосил бўлса, у ҳолда кучайтиргич генераторга айланади. Юкда барқарор ўзгарувчан кучланиш ҳосил бўлади.
Бундай иш ҳолати ўз-ўзини қўзғатиш деб аталади. Контурда сўнмайдиган тебранишларни ушлаб турувчи, қўзгатувчи тебранишларни ўзининг киришига киритиши юқоридаги иш ҳолатининг ҳосил бўлишига сабаб бўлади.
Ўз-ўзини қўзғатиш учун, амплитудалар ва фазалар тенглик шарти бажарилиши лозим.
Биполяр транзисторли кучайтириш каскади.
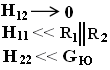
Кучайтиргичнинг
ўзгармас ва ўзгарувчан ток бўйича силжиш занжирлари бир биридан кескин фарқ
қилади. ![]() параметр
кўпинча в деб белгиланади ва ток
бўйича кучайтириш коэфициенти деб номланади.
параметр
кўпинча в деб белгиланади ва ток
бўйича кучайтириш коэфициенти деб номланади.
Майдонли транзисторда кучайтириш каскади.
![]() параметр
кўпинча S ҳарфи билан белгиланади ва кучайтириш тиклиги деб номланади.
параметр
кўпинча S ҳарфи билан белгиланади ва кучайтириш тиклиги деб номланади.
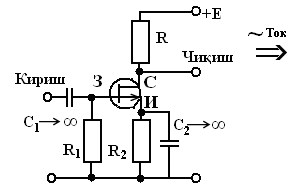
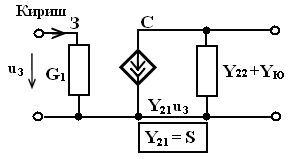
Операцион кучайтиргичли каскад.

![]() параметр кўпинча µ ҳарфи билан белгиланади ва кучланиш бўйича
кучайтириш коэффиценти деб номланади.
параметр кўпинча µ ҳарфи билан белгиланади ва кучланиш бўйича
кучайтириш коэффиценти деб номланади.
Кучайтириш асбоблари параметрлари учун каттагина нотурғунлик хосдир. Шунинг учун улар шундай танланадики, унда:
- уларни таёрлаш технологиясида ҳосил бўлувчи қийматлар тарқалиши минимумга келсин:
- уларни таёрлаш технологиясида ҳосил бўлувчи қийматлар тарқалиши минимумга келсин:
- ишлатилиш шароитлари ўзгаришларига (температура, таминловчи кучланиш ва ҳ.к.) сезгирлиги минимумга келсин
Кучайтиргичнинг чиқишидан киришига сигналнинг қисман узатилиши тескари богланиш (ТБ) дейилади.
Ўз ичига кучайтириш асбобини ва нассив тўртқутубликни олган берк иккисимлик халқа ТБ халқаси дейилади.
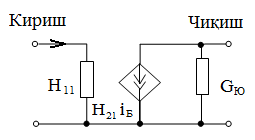
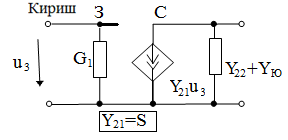
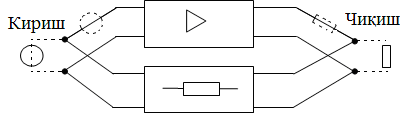
Халқа бўйлаб узатиш коэффициентлар кўпайтмаси (киришдан чиқишга ва чиқишдан киришга) халқали кучайтириш Т дейилади.
Халқали кучайтириш Т мусбат (манфий) ишорага ега бўлса, ТБ мусбат (манфий) дейилади.
Манфий ТБ (МаТБ) алоқанинг чуқурлиги (1-Т) билан характерланади.
Реал манба ТБ халқасига нисбатан узунасига ёки кўндалангига уланган шахобчадек уланиш мумкин. Биринчи ҳолда ТБ параллел, иккингисига эса – кетма-кет дейилади.
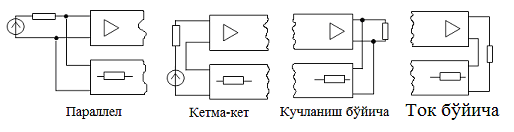
![]() Юк қаршилиги ҳам ТБ хақасига
нисбатан кўндаланг ёки кетма-кет уланган шахобчадек уланиши мумкин. Биринчи
холда ТБ кучланиш бўйича ТБ (чиқишига кўра параллел), иккинчи холда эса
ток бўйича ТБ (чиқишига кўра кетма-кет) дейилади.
Юк қаршилиги ҳам ТБ хақасига
нисбатан кўндаланг ёки кетма-кет уланган шахобчадек уланиши мумкин. Биринчи
холда ТБ кучланиш бўйича ТБ (чиқишига кўра параллел), иккинчи холда эса
ток бўйича ТБ (чиқишига кўра кетма-кет) дейилади.
32-маъруза. Автотебранишли занжирлар
Автотебранишларнинг диссипатив занжирлардаги бошқа тебранувчан жараёнлардан асосий фарқи шундаки, уларни сақлаб туриш учун ташқаридан даврий таъсир талаб қилинмайди.
Юқорида айтиб ўтилганидай автогенераторларда сўнувчан тебраниш тизимини ажратиб олиш мумкин. Одатда тебраниш контури, кучайтиргич ва тескари боғланиш занжиридир.
Генераторда автотебранишлар қуйидагича ўрнатилади. RLC контур озиқланиш блокига уланганда тасодифан кичик амплитудали тебранишлар ҳосил бўлади, кучайтиргичдаги ночизиқли элемент тескари боғланиш занжири орқали контурдаги кучайишини бошқаради. Контурда йўқотишлар контурга киритиладиган энергияга нисбатан камроқ бўлганда контурдаги тебранишлар амплитудаси ортиб боради. Тебраниш амплитудаси ортиши билан актив элементнинг ночизиқлилиги туфайли контурга келадиган энергия камаяди ва тебранишнинг қайсидир амплитудасида йўқотишлар билан тенглашади.
Натижада турғун даврий тебранишлар ҳолати ўрнатилади ва бу ҳолатда ўзгармас кучланиш манбаи ҳамма энергия йўқотишларининг ўрнини тўлдиради.
Шундай қилиб автотебранишларни ўрнатиш учун ночизиқлик зарур бўлиб, у озиқланиш манбаидан келадиган ва ўрнини тўлдирадиган энергия йўқотишларини бошқаради.
Автотебранишлар хусусий ва мажбурий тебранишлардан амплитудаси ва частотаси тизимнинг параметрлари орқали аниқланиши ва бошланғич шартларга боғлиқ эмаслиги билан фарқ қилади.
Ҳақиқатан ҳам хусусий тебранишлар частотаси тизимнинг параметрлари орқали аниқланади, мажбурий тебранишларнинг амплитудаси, частотаси ва фазаси эса ташқи таъсирлар орқали аниқланади.
32.1. Ташқи тескари боғланишли автогенератор
Ишчи частотаси 500 МГц гача бўлган генераторларда одатда LC боғланишли ТБ қўлланади.
Бундай LC генераторларнинг асосини параллел резонанс LC генератор ташкил қилади. Резонанс частотада контур резистив қаршиликни ташкил қилади. Резонансдан фарқли частоталарда контурнинг қаршилиги сиғимий ёки индуктив характерга эга.
Генераторларда қўлланадиган контурларнинг баъзи схемаларига мисоллар келтирамиз.
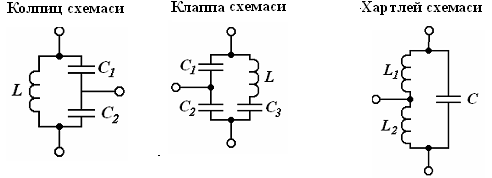
32.1-расм
Сиғимий боғланишли генератор схемасини кўриб чиқамиз – «сиғимли уч нуқта», 32.1 – расмда кўрсатилган бўлиб, бу ерда RЭ – эмиттер қаршилиги; RК – кейинги каскаднинг қаршилиги; СФ- фильтрнинг конденсатори; Са – ажратувчи конденсатор; R1 ва R2 – ажратувчининг қаршилиги.
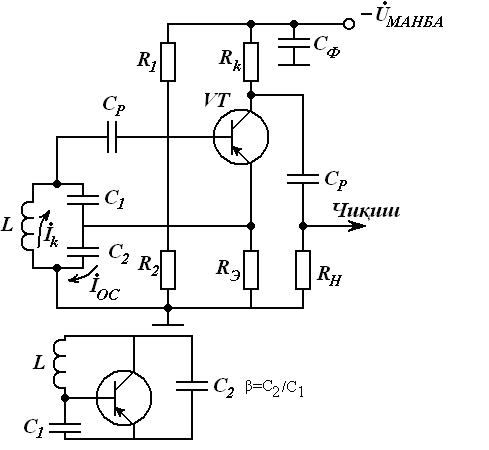
32.2 расм
Тескари боғланиш кучланиши сиғим С1 дан ўлчанади. Тескари боғланиш кучланиши тўғридан – тўғри контурга берилади. Бу ерда сиғимда қаршилик С1 қанча катта бўлса тескари боғланиш шунча кучли бўлади. Конденсаторнинг сиғимий қаршилиги С2 қанча катта бўлса коллектор юкламаси ҳам шунча катта бўлади. Конденсаторнинг сиғимий қаршилиги унинг сиғимига тескари пропорционал, шу сабабли С1 ортиши билан тескари боғланиш сусаяди, С2 сиғим ортиши билан эса коллектор юкламасининг қаршилиги камаяди. Индуктив боғланишли автогенераторнинг индуктивликли уч нуқта схемасини кўриб чиқамиз (32.2 - расм).
Аввалги схемадаги симлари транзистор контурга ўзгарувчан ток бўйича учта нуқта уланган бўлиб, булар: эмиттер, база ва коллектордир. Тескари боғланиш кучланиши L1 дан ўлчанади.
Амплитудалар тенглик шартининг бажарилиши контур индуктивлигининг қанча қисми база – эмиттер қисмига уланганига боғлиқдир.
Индуктивлик L1 нинг қанчалик кўп қисми база ва эмиттер орасига уланган бўлса, транзисторнинг чиқишига унинг киришидан шунча кўп энергия узатилади. Бу схемада бутун контур эмас, балки унинг бир қисми L2 юклама ўисобланади. (L2 нинг юқори учи эмиттерга уланган, пастки учи эса фильтрнинг конденсатори СФ орқали коллекторга уланган).
32.2 RC – генератор
Кичик частоталарда индуктивликнинг ҳажми кескин катталашиб кетгани сабабли улар микроминиатюризацияга бўйсуниши қийин. Шу сабабдан уларни қўлламасликка интилишади. 19 кГц дан кичик частоталарда генераторлар RC элементларда яратилади.
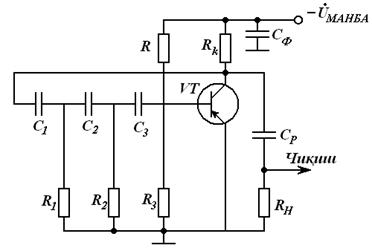
32.3 – расм.
32.3-расмдан кўринадики RC генератор схемасида тебраниш контури йўқ бўлиб R ва C элементлар шундай танланганки RC элементлардан иборат тизим фазани 1800 га буради, лекин бундай бурилиш фақат битта частотада амалга ошади, бошқа частоталарда эса фазалар фарқи 1800 дан катта ёки кичик бўлади.
Генерация (ишлаб чиқариш) жараёни қуйидагича амалга ошади. Базадаги шовқинли кучланиш транзистор ёрдамида, тескари боғланиш занжири билан, RC занжир орқали кучайтирилади ва қайтадан базага тушади. Шовқинлар спектри жуда кенг бўлиб, унда ҳамма ташкил этувчиларнинг частоталари қатнашади. Базага ноқулай фаза билан келадиган частотавий ташкил этувчилар сусаяди ва фақат биттагина ташкил этувчи, бу ташкил этувчи учун RC занжир фазалар фарқини 1800 га тенг қилганида кучайтира бошлайди.
Кучланиш унинг коллектор озиқланиши чегаралагунича ортиб боради коллектор ва база кучланиши ўз – ўзидан актив элемент ўисобига 1800 га сурилади ва RC занжирнинг қўшимча 1800 га бурилиши умумий фазалар фарқини 3600 га етказади.
32.3. Атогенератор дифференциал тенгламалари
32.4 – расмда келтирилган.
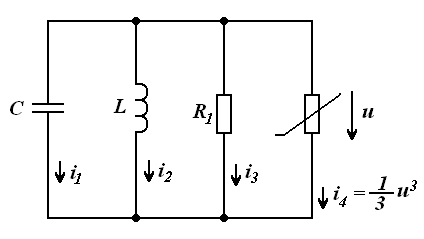
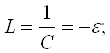
![]()
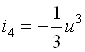 (32.1)
(32.1)
32.4 – расм.
U кучланишга нисбатан дифференциал тенгламани тузамиз. Кирхгофнинг биринчи қонуни бўйича.
i1+i2+i3+i4=0 (32.2)
бу ерда
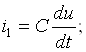
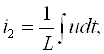
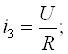
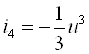 (32.3)
(32.3)
(323) ни (32.2) га қўямиз
![]()
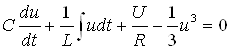 (32.4)
(32.4)
(32.4)
ни вақт бўйича дифференциаллаб қуйидагини оламиз.

ёки
 (32.5)
(32.5)
(32.1) ни (32.5) га қўйиб Ван – дер – Польнинг ночизиқли дифференциал тенгламасини оламиз.
![]() (32.6)
(32.6)
Тебраниш контури бўлган автогенераторларнинг кўплаб тенгламалари Ван – дер – Поль тенгламаларига келтирилади. Ван – дер – Поль автогенератори тенгламаларини текширишнинг осон усули бу сонли усулдир. Масалан тўртинчи тартибли Рунге – Кутт усули (CИГМА 2 дастурлар пакети) бўлиб, у о=0 да тизим чизиқли бўлишини кўрсатади.
 Ҳисоб натижасида сўнмайдиган гармоник тебранишлар ҳосил бўлади
Ҳисоб натижасида сўнмайдиган гармоник тебранишлар ҳосил бўлади
(32.5 - расм).
о<<1 бўлганда (кичик чизиқлилик) барқарор тебранишлар гармоник тебранишлардан кам фарқ қилади. (32.5 - расм)
![]() <<1
<<1
![]() >>1
>>1
32.6 – расм 32.7 – расм
о>>1 бўлганда (кучли чизиқлилик) тебранишлар релаксацион бўлади (32.6 - расм).
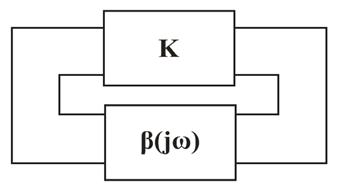
Ташқи таъсирсиз тебранишлар пайдо булувчи электр занжири автогенератор дейилади.
Автогенераторнинг умумий схемасига кучайтиргич ва ТБ тўртқутблиги киради; уларнинг узатиш коэффициентлари шартини қаноатлантирадиган килиб танланади.
Одатдаги тебраниш контури таъсир бўлмаган холда фақат сўнувчи тебранишлар беради.
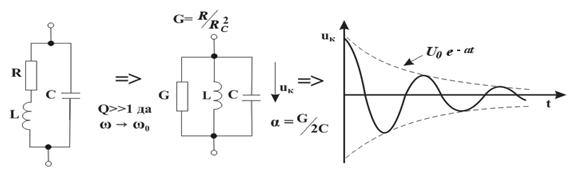
Агар контурга КБТМ (узатиш ўтказувчанлиги GBI, катта бўлган) уланса, у холда тебранишлар ўсувчи бўлиб қолади.
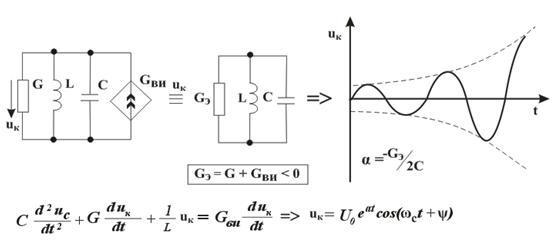
Манфий ишорали ўтказувчанлик GBН ни мусбат ТБ ли кучайтиргич ёрдамида олиш мумкин.
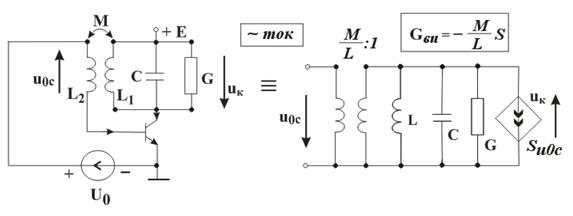
Транзистор ва трансформатор сигнал фазасини 180°га айлантиради.
Транзисторга берилувчи ўзгармас ток ва кучланиш силжиш токи ва кучланиши дейилади.
Силжиш токи ва кучланиши транзисторнинг ўтиш вольт-ампер ха-рактеристикасидан ишчи нуқтанинг координаталарини белгилайди.
Ишчи нуқтани танлаш автогенераторнинг уйғониш режимини аниқлайди.
Юмшоқ режимли уйғониш амплитудасииииг текис ўсиши билан белгиланади (М ошиши билан). Бу унинг ижобий жиҳатидир.
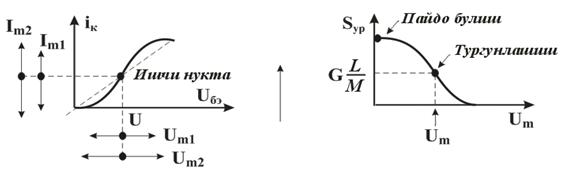
Юмшоқ режим ишчи нуқтани фаол бўлакнинг ўртасида танлаш билан белгиланади.
Каттиқ режимли уйғониш тебранишлар амплитудасининг кескин, сакраб ўсиши билан белгиланади. Унинг ижобий жиҳати - юқори Ф.И.К. идир.
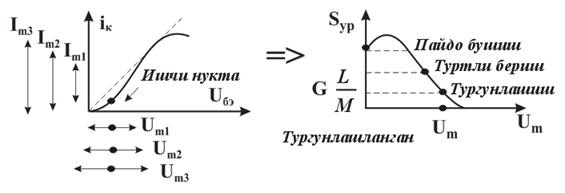
Қаттиқ режимда ишчи нуқта қирқилиш бўлаги яқинида танланади.
Иккала режимларнинг ижобий жиҳатлари автогенератор схемасига ишчи нуқтани автоматик тарзда силжитиш занжирчаси СБ, RБ ни киритиш орқали бирлаштирилади.
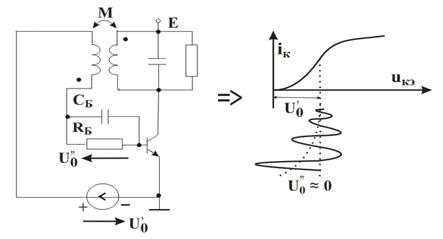
Индуктивли учнуқталик.
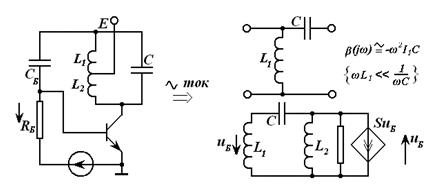
Автотрансформаторли алоқадаги схемани бошқариш осонроқ, шунинг учун трансформаторли алоқадаги схемага қараганда кўпроқ ишлатилади.
Қуйи частоталар ишлаб берувчи RС-генератор схемаси.
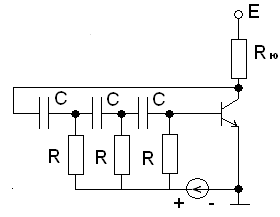
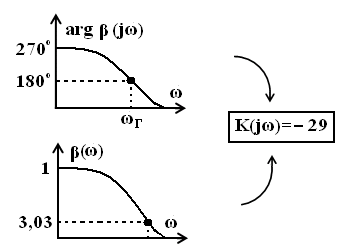
LC-генераторлар (қуйи частоталар учун) индуктивлик ғалтакларининг қийматлари (ва ўлчамлари) жуда катта бўлгани учун ишлатилмайди.
Юқори ва ўта юқори частоталар ишлаб чиқарувчи туннелли диодли генератор схемаси.
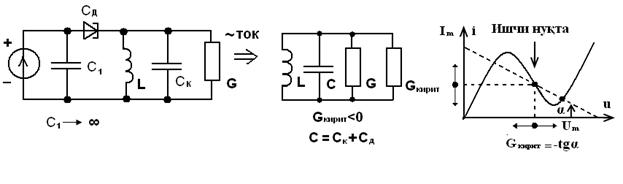
Туннели диодларнинг қайта уланиш вақти жуда қисқа: 10-12 – 1014 с. Шу сабабли улар ўта юқори частоталарда яхши ишлайди
33-маъруза. Ночизиқли занжирларни таҳлил қилиш
33.1 Инерциясиз элементли занжирларнинг таҳлили
Таркибида сиғим ва индуктивликлари, яъни энергияни заҳираловчи реактив элементлари бўлмаган электр занжирлари резистив занжирлар дейилади. Уларнинг математик моделлари ночизиқли тенгламалар тизимидан иборат бўлади. Умумий ҳолда бу тенгламалар аналитик ечимга эга бўлмайдилар. Уларни ечиш учун график, графоаналитик ва рақамли усуллардан фойдаланилади.
Аксарият, ночизиқли резистив занжирларни таҳлил қилганда масала қуйидаги кетма-кетликда ечилади.
Берилган: маълум
тавсифларга эга бўлган ночизиқли элемент ва чизиқли қаршилик,
ўзгармас ток ва кучланиш манбалари ҳамда занжир киришида таъсир этаётган
ўзгарувчи ![]() сигнал
манбаси.
сигнал
манбаси.
Аниқлаш керак: занжирнинг y(t) реакциясини; занжирнинг киришидаги ёки чиқишидаги ток (кучланиш)ни.
|
|
33.1-расм
Биринчи ҳолатда
занжирни икки қутблик (16.1,а-расм), иикинчисида-тўртқутблик
(32.1,б-расм) сифатида тасаввур қилиш мумкин. Резистив икки қутбликнинг
кириш тавсифи деб кириш сигнали ![]() оний қийматининг
чиқишдаги реакция
оний қийматининг
чиқишдаги реакция ![]() оний қийматига
боғланишига, яъни
оний қийматига
боғланишига, яъни ![]() ифодасига
айтилади. Резистив тўртқутбликнинг узатиш функцияси деб кириш
сигнали
ифодасига
айтилади. Резистив тўртқутбликнинг узатиш функцияси деб кириш
сигнали ![]() оний қийматининг
чиқишидаги реакция
оний қийматининг
чиқишидаги реакция ![]() оний қиймати
таъсирига, яъни
оний қиймати
таъсирига, яъни ![]() ифодага
айтилади. Ушбу тавсифларни тажриба усулида олиш мумкин. Бунинг учун
ифодага
айтилади. Ушбу тавсифларни тажриба усулида олиш мумкин. Бунинг учун ![]() сифатида
бошқарилувчи кучланиш ёки (ток) манбасини олиб, кириш қийматни
ўзгариши билан чиқиш қийматининг ўзгариши аниқланади.
сифатида
бошқарилувчи кучланиш ёки (ток) манбасини олиб, кириш қийматни
ўзгариши билан чиқиш қийматининг ўзгариши аниқланади.
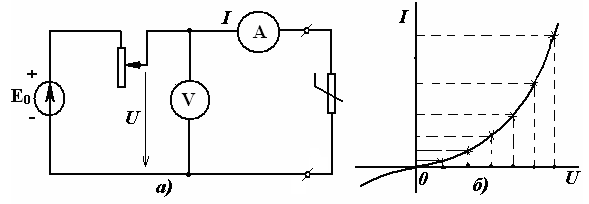 33.2-расм
33.2-расм
33.2-расмда тажриба ёрдамида кириш тавсифини олиш схемаси ва олинган тавсиф графиги келтирилган. Агар ночизиқли элемент кириш тавсифи ёки узатиш функцияси берилган бўлса, у ҳолда ҳар қандай ихтиёрий кириш сигналига унинг реакциясини аниқлаш мумкин.
Ушбу фикрларни ВАТ 33.2-расмда берилган диод учун унга гармоник кучланиш таъсир этаётганда ундан оқаётган токнинг таҳлили ёрдамида оддий график усулни қўллашни ўрганайлик.
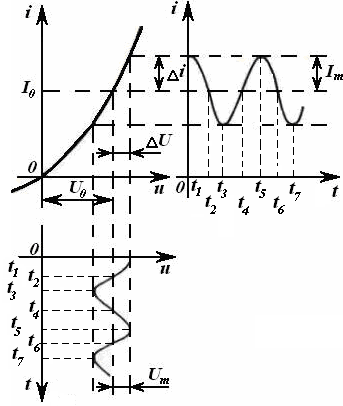 Ечимни ночизиқли элементнинг тавсифини кириш-чиқиш
координата тизимида қуришдан бошланади. Берилган мисолда ушбу тавсиф
сифатида икки қутбликнинг ВАТ олинган, кириш қиймат икки қутбликдаги
кучланиш, чиқиш эса ундан оқаётган ток. Ундан сўнг қийматнинг
(ушбу мисолда кучланиш) вақтга боғлиқлиги графигини чизамиз
ва координата ўқларини кириш қиймати ўқи билан мос
жойлаштирамиз. Бунда вақт t нинг ўқи пастга йўналган бўлади;
кириш қиймат ва ВАТнинг бир ҳил координаталари (бу мисолда
кучланиш) ёнма-ён жойланади. Сўнгра ўнг томонда чиқиш қиймат
графигини олиш учун координата тизимлари қурилади. Чиқиш қиймат
ток
Ечимни ночизиқли элементнинг тавсифини кириш-чиқиш
координата тизимида қуришдан бошланади. Берилган мисолда ушбу тавсиф
сифатида икки қутбликнинг ВАТ олинган, кириш қиймат икки қутбликдаги
кучланиш, чиқиш эса ундан оқаётган ток. Ундан сўнг қийматнинг
(ушбу мисолда кучланиш) вақтга боғлиқлиги графигини чизамиз
ва координата ўқларини кириш қиймати ўқи билан мос
жойлаштирамиз. Бунда вақт t нинг ўқи пастга йўналган бўлади;
кириш қиймат ва ВАТнинг бир ҳил координаталари (бу мисолда
кучланиш) ёнма-ён жойланади. Сўнгра ўнг томонда чиқиш қиймат
графигини олиш учун координата тизимлари қурилади. Чиқиш қиймат
ток ![]() 33.3-расм
33.3-расм
ва ВАТларнинг ўқлари ҳам муво-
фиқлаштирилиб, параллел координата боши эса бир тўғри чизиқда жойлаштирилади.
Ихтиёрий ![]() вақтни
танлаймиз ва унга мос бўлган масштабда кириш ва чиқиш қийматларининг
вақтни
танлаймиз ва унга мос бўлган масштабда кириш ва чиқиш қийматларининг
![]() ўқларига
жойлаштирамиз. Ушбу вақт онига мос келган кириш қиймати u ни
ВАТ графигида проекциясини олиб, ундан ток i ни аниқлаб,
горизонтал кесма ўтказиб, чиқиш қийматининг
ўқларига
жойлаштирамиз. Ушбу вақт онига мос келган кириш қиймати u ни
ВАТ графигида проекциясини олиб, ундан ток i ни аниқлаб,
горизонтал кесма ўтказиб, чиқиш қийматининг ![]() нуқтасига
перпендикуляр билан кесишгунча давом эттирамиз (33.2-расмга қаранг). Бу
нуқтасига
перпендикуляр билан кесишгунча давом эттирамиз (33.2-расмга қаранг). Бу ![]() вақтга
мос келган чиқиш токининг графигида аниқловчи биринчи нуқта
бўлади. Шунга ўхшаш, кейинги
вақтга
мос келган чиқиш токининг графигида аниқловчи биринчи нуқта
бўлади. Шунга ўхшаш, кейинги ![]() нуқтани
танлаб, кучланиш оний қийматини аниқлаб, ВАТдан унга мос токнинг
оний қийматини аниқлаб, чиқиш қийматнинг координата
тизимидаги графигининг иккинчи нуқтасини аниқланади. Шу тариқа,
кириш кучланишини бошқа нуқталарига мос келган чиқиш токининг
тўлиқ графигини ҳосил қилиш мумкин.
нуқтани
танлаб, кучланиш оний қийматини аниқлаб, ВАТдан унга мос токнинг
оний қийматини аниқлаб, чиқиш қийматнинг координата
тизимидаги графигининг иккинчи нуқтасини аниқланади. Шу тариқа,
кириш кучланишини бошқа нуқталарига мос келган чиқиш токининг
тўлиқ графигини ҳосил қилиш мумкин.
График усул содда ва кўргазмали, бироқ аниқ миқдорларни олишга қийинчилик ҳосил қилади. Аммо, бу усул ҳисобларни ЭҲМ ёрдамида дастурлаб ечишга энг қулай, осон ва кўргазмали йўл ҳисобланади.
ЭҲМлари пайдо бўлгунга қадар, ушбу масалаларни ечиш учун ҳар хил усуллардан фойдаланилган. Улардан бири ва кенг қўлланиладигани-кўпҳадлар ёрдамида аппроксимациялаш усулидир:
![]()
Агар ИНТ тавсифи учун аппроксимацияловчи кўпҳаднинг коэффициентлари аниқланса, у ҳолда чиқиш қийматини оддий ўрнига қўйиш усули билан аниқлаш мумкин:
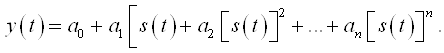
Масалан, 33.2-расмдаги ВАТ ![]() кўпҳад ёрадмида аппроксимацияланиши мумкин
бўлса, у ҳолда
кўпҳад ёрадмида аппроксимацияланиши мумкин
бўлса, у ҳолда ![]() кириш кучланиши учун диод орқали оқаётган
ток қуйидагича ёзилиши мумкин:
кириш кучланиши учун диод орқали оқаётган
ток қуйидагича ёзилиши мумкин:
![]()
Агар ИНТ учун кириш ёки узатиш тавсифини аниқлаш мумкин бўлмаса ёки жуда қийин бўлса, у ҳолда график ва графо-аналитик усуллар қўлланилиши мумкин бўлмайди. Бундай ҳолатларда Кирхгоф ва Ом қонунлари ёрдамида занжирнинг тўла тенгламаларини тузиб, сонли ечими аниқланади.
Ушбу усулни мисол кўрсатиб тушунтирамиз. Схемаси 33.3-расмда келтирилган резистив занжир берилган бўлсин. Занжирнинг тенгламасини тузамиз:
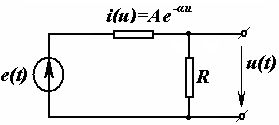
![]()
![]()
![]()
Ушбу тенгламани ихтиёрий ![]() қийматлари учун
қийматлари учун ![]() га
нисбатан
33.3-расм
га
нисбатан
33.3-расм
оддий итерация усули, Нютон усули ёки ихтиёрий бошқа рақамли усуллар ёрдамида ечиш мумкин.
33.2 Ночизиқли занжирларда сигнал спектрини
ўзгартириш ва унинг амалиётда қўлланилиши
Ночизиқли занжирларнинг муҳим хусусиятларидан бири кириш сигналлари спектрини ўзгартиришдир. Бу хусусият шундан иборатки, занжирнинг киришида гармоник ёки ҳар хил частотали бир неча гармоник функцияларнинг йиғиндисидан иборат бўлган даврий сигнал таъсир этаётганда, реакция (ихтиёрий шохобчадаги ток ёки кучланиш) нафақат кириш таъсирининг гармоникалари, балки кириш сигнал таркибида бўлмаган бошқа янги гармониклардан ҳам иборат бўлади.
Спектрни ўзгартиришнинг бундай хусусияти ўзгармас параметрли (RLC) чизиқли занжирларда мутлақо мумкин эмас. Уларда ихтиёрий шохобчадаги ток ва кучланиш таркибида фақат кириш сигнал таркибида мавжуд бўлган гармоникалар бўлади холос.
Агар узатиш (ёки кириш) тавсифи кўрсаткичли полином шаклида берилган ночизиқли резистив занжир бўлса, уни ечишни ВАТ мисолида кўрсак бўлади
![]() (33.1)
(33.1)
Аввал, киришда гармоник сигнал бўлгандаги ҳолатни кўрамиз
![]() (33.2)
(33.2)
Кейинги
(33.2) ифодани (33.1)га қўйсак, қуйидагини ҳосил қиламиз
![]()
Тригонометрик ўзгартиришлардан сўнг қуйидагиларни ҳосил қиламиз
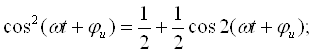
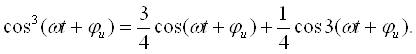 (33.3)
(33.3)
Бундан кўринадики, ![]() даражаси гармоник функция карра частотали
гармоник функциялар йиғиндисига эквивалент экан, бунда жуфт даражали ҳад
фақат жуфт гармоникалардан, тоқлари - фақат тоқ
гармоникалардан ташкил топган бўлади. Гармоникаларнинг энг катта
даражаси гармоник функция карра частотали
гармоник функциялар йиғиндисига эквивалент экан, бунда жуфт даражали ҳад
фақат жуфт гармоникалардан, тоқлари - фақат тоқ
гармоникалардан ташкил топган бўлади. Гармоникаларнинг энг катта ![]() даражаси занжир тавсифининг юқори даражаси
билан аниқланади:
даражаси занжир тавсифининг юқори даражаси
билан аниқланади:
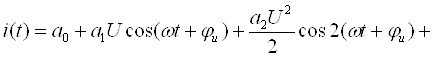
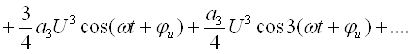
Умумий ҳолда қуйидагича ёзиш мумкин
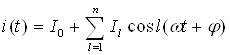 .
(33.4)
.
(33.4)
33.4-расмда умумий шаклдаги ночизиқлик учун (а), жуфт (б) ва тоқ (в) i=i(u) функцияси кириш ва чиқиш сигналларнинг дискрет спектрлари келтирилган.
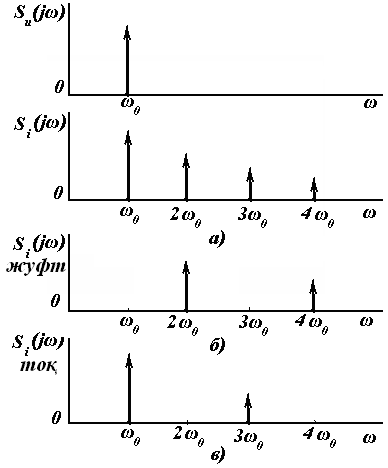
33.4-расм
Частоталари ![]() ва
ва ![]() бўлган икки гармоник функциялар йиғиндисидан
ташкил топган сигнал таъсирини кўрайлик:
бўлган икки гармоник функциялар йиғиндисидан
ташкил топган сигнал таъсирини кўрайлик:
![]() (33.5)
(33.5)
Занжирнинг реакцияси икки ҳадликларнинг йиғиндисидан иборат бўлади
![]() (33.6)
(33.6)
Агар икки ҳадлик кўрсаткичи n = 2 ёки 3 бўлса, (33.5) қуйидагича бўлади:
![]() ёки
ёки
![]()
Бир сигнал таъсири бўлгандаги ҳолатдан фарқли
равишда, икки функциялар йиғиндисидан иборат сигнал таъсир этганда,
даражаларнинг кўпайтмалари ![]() шаклидаги қўшимча ҳадлар ҳосил
бўлади.
шаклидаги қўшимча ҳадлар ҳосил
бўлади.
Юқорида кўрганимиздек, гармоник функцияларнинг
даражалари карра частотали синусоидал йиғиндиларни беради. Икки гармоник
функциялар кўпайтмалари - частоталари кўпайтирувчиларининг частоталари фарқи
ва йиғиндисига тенг бўлган частотали функцияларни беради. Шуларни
эътиборга олиб, қуйидагиларни ёзиш мумкин:
![]()
![]()
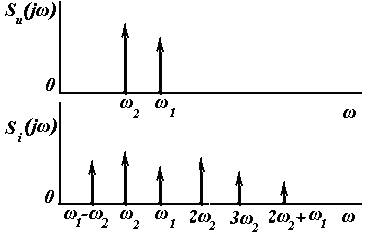 Шундай қилиб,
тартибларнинг
Шундай қилиб,
тартибларнинг ![]()
![]()
![]() кўпайтмаларида ёки умумий ҳол учун
кўпайтмаларида ёки умумий ҳол учун ![]() mn=1,2,
…, n
mn=1,2,
…, n![]() частоталарга эга бўламиз. Частотаси
частоталарга эга бўламиз. Частотаси ![]() га тенг бўлган тебранишлар комбинацияланган
тебраниш,
га тенг бўлган тебранишлар комбинацияланган
тебраниш,
33.5-расм
![]() йиғинди эса комбинацияланган тебраниш
тартиби дейилади. Киришида икки гармоник функциялар йиғиндисидан
иборат бўлган сигнал таъсиридаги ИНТ чиқишидаги сигналлар спектри
33.5-расмда келтирилган.
йиғинди эса комбинацияланган тебраниш
тартиби дейилади. Киришида икки гармоник функциялар йиғиндисидан
иборат бўлган сигнал таъсиридаги ИНТ чиқишидаги сигналлар спектри
33.5-расмда келтирилган.
Умумий ҳолда икки гармоник сигналлар йиғиндиси
таъсир этганда
![]() (33.3)
(33.3)
ИНТнинг кириш сигнали таркибида бўлмаган сигналларнинг унинг чиқиш сигнали таркибида пайдо бўлишидан техникада кенг фойданилади.
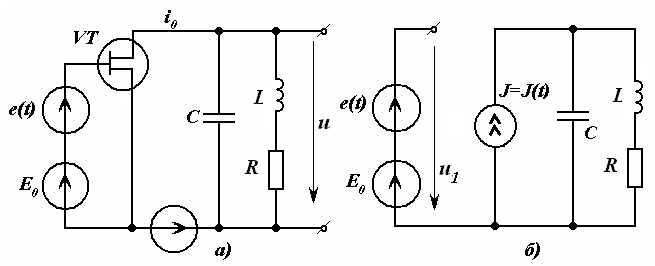 Частота
кўпайтиргичи деб, берилган
Частота
кўпайтиргичи деб, берилган
![]() шаклдаги сигнални
шаклдаги сигнални ![]() шаклига ўзгартирувчи электр занжирига айтилади.
Бу қурилма ночизиқли элемент ва зарур бўлган гармоника
частотасининг резонансига созланган йўлак фильтрининг уланишидан ҳосил қилинади.
33.6,а-расмда ушбу қурилманинг принципиал схемаси, 33.6,б-расмда
эквивалент схемаси келтирилган.
шаклига ўзгартирувчи электр занжирига айтилади.
Бу қурилма ночизиқли элемент ва зарур бўлган гармоника
частотасининг резонансига созланган йўлак фильтрининг уланишидан ҳосил қилинади.
33.6,а-расмда ушбу қурилманинг принципиал схемаси, 33.6,б-расмда
эквивалент схемаси келтирилган.
 33.6-расм
33.6-расм
Масалан, ![]() берилган бўлса, аввал ток
берилган бўлса, аввал ток ![]() ни аниқлаймиз. Фараз қилайлик
транзисторнинг ночизиқли тавсифи квадратик полином
ни аниқлаймиз. Фараз қилайлик
транзисторнинг ночизиқли тавсифи квадратик полином ![]() билан ифодалансин, унда
билан ифодалансин, унда
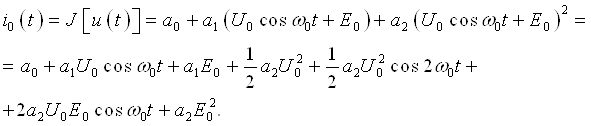
![]() ни шундай танлайликки, унда
ни шундай танлайликки, унда 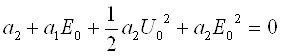 бўлсин. Унда ток
бўлсин. Унда ток
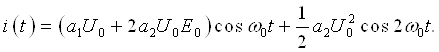
33.7-расмда кириш кучланиши ![]() спектри ва ток
спектри ва ток ![]() келтирилган. Контурдаги кучланиш, ихтиёрий икки қутбликдаги
сингари, частота оралиғида аниқланиши мумкин:
келтирилган. Контурдаги кучланиш, ихтиёрий икки қутбликдаги
сингари, частота оралиғида аниқланиши мумкин:
![]()
![]()
RLC-контур
учун (16.6-расм) қуйидагига эга бўламиз

Нисбатан R/Lнинг кичик қийматлари учун,
яъни катта аслллик ![]() ва
ва ![]() учун
учун ![]() боғланиши 33.7-расмда келтирилган.
боғланиши 33.7-расмда келтирилган.
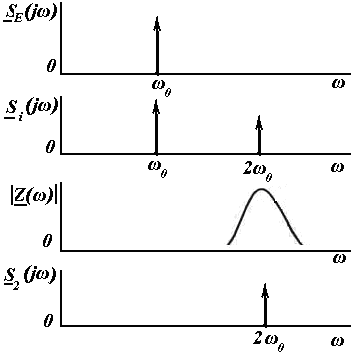
33.7-расм
Унда ![]() частота учун
частота учун ![]() ва
ва ![]() бўлади. Резонанс
бўлади. Резонанс ![]() частотага созланганда
частотага созланганда
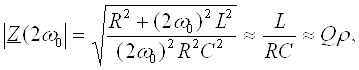
бунда
с=(L/C)1/2
- контурнинг тавсифий қаршилиги;
![]()
Шундай қилиб, ![]() бўлганда частота кўпайтиргичининг чиқиш
кучланиши (33.8-расм) қуйидагича ифодаланади.
бўлганда частота кўпайтиргичининг чиқиш
кучланиши (33.8-расм) қуйидагича ифодаланади.
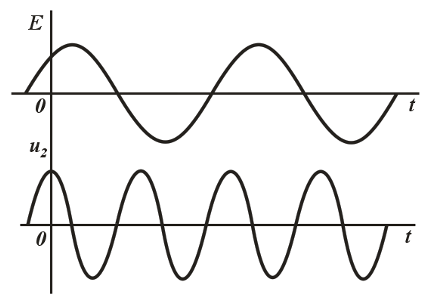
33.8-расм
Агар ![]() бўлса, J(u)нинг ночизиқлигини камида 3-тартибли кўпҳад
сифатида олиниши ва RLC – контурни
бўлса, J(u)нинг ночизиқлигини камида 3-тартибли кўпҳад
сифатида олиниши ва RLC – контурни ![]() частотага созлаш зарур бўлади. Шунга ўхшаш,
частотани
частотага созлаш зарур бўлади. Шунга ўхшаш,
частотани ![]() марта кўпайтириш учун ночизиқлилик тартиби
марта кўпайтириш учун ночизиқлилик тартиби ![]() дан кам бўлмаслиги зарур.
дан кам бўлмаслиги зарур.
34-маъруза Гармоник ток занжири. Диод ва
транзисторнинг ночизиқли моделлари
34.1 Ночизиқли резистив икки қутбликлар статик тавсифлари
Юқорида ўрганилган занжирлар чизиқли занжирлар турларига киради. Бундай занжирларнинг параметрлари, яъни қаршиликлари, индуктивликлари, бошқарувчи манбаларнинг сиғимлари - уларга келтириб уланган кучланишлар ёки улардан оқиб ўтаётган токларнинг қийматларига боғлиқ эмас эди. Масалан, элементнинг қаршилиги 10 Щ дейилганда - шу резистор қутбларидаги кучланиш U нинг миқдори (10kV, 1V, 100mV, 10мV), шу қаршиликдан оқиб ўтаётган ток I нинг (1kА, 10А, 1mА, 1мА) миқдори қандайлигидан қатъий назар, унга нисбати доимо 10 Щ га тенг бўлади, яъни қаршиликнинг кучланиши ва токи орасидаги боғланиш U(I)=Щ·I=const доимо ўзгармас деб ҳисобланган эди.
Аслида эса, ихтиёрий реал элемент Щ нинг бундай кенг диапазонида ўзгармас бўла олмайди, электр занжирларининг чизиқлилик назарияси токнинг ёки кучланишнинг бирор кичик оралиғидагина кучга эга. Шундай муҳим элеменлар ва жиҳозлар туркумлари мавжудки, уларнинг параметрлари улар орқали оқиб ўтаётган ток ёки кучланиш миқдорарларига тубдан боғлиқ бўлади. Бундай элементлар ночизиқли деб аталади. Таркибида ҳеч бўлмаса битта шундай ночизиқли (НЧ) элементи бўлган занжир ночизиқли электр занжири (НЧЭЗ) дейилади.
Ночизиқли қаршилик ![]() ёки
ёки ![]() ночизиқли сиғим
ночизиқли сиғим ![]() ёки
ёки ![]() ночизиқли индуктивликларнинг
ночизиқли индуктивликларнинг ![]() ёки
ёки ![]() схемаларда шартли белгиланишлари 33.1-расмда
кўрсатилган.
схемаларда шартли белгиланишлари 33.1-расмда
кўрсатилган.
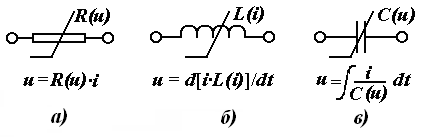
34.1-расм
НЧ занжирларнинг бундай хусусиятлари ночизиқли элементларнинг табиатидан келиб чиқиб, кучланиш ва ток орасидаги боғланишнинг пропорционаллигини бузади ва занжирлар тенгламаларининг ночизиқли бўлишига олиб келади.
НЧ тенгламаларни ечишнинг умумий усуллари йўқ. Фақат бир қатор ҳолатлардагина аниқ ечимларни ҳисоблаш мумкин. НЧ занжирларни таҳлил қилишнинг қийинчиликлари ҳам мана шу сабаблидир. Чунки НЧ тенгламаларга ва демак НЧ занжирларга суперпозиция усулини қўллаш мумкин эмас.
НЧ икки қутбликлар хусусиятлари, аксарият,
статик тавсифлар ёрдамида ифодаланади. Ночизиқли икки қутбликнинг
кенг тарқалган ифодаси Вольт-Ампер тавсифидир (ВАТ), яъни барқарорлик
режимидаги ночизиқли икки қутбликдан оқиб ўтаётган ток ![]() нинг миқдори унга уланган кучланиш қийматига
боғлиқдир.
нинг миқдори унга уланган кучланиш қийматига
боғлиқдир.
|
|
Эслаб кўрайлик, чизиқли икки қутблик
учун ВАТ тўғри чизиқдан иборат эди (34.2,а-расм). НЧ
элементларнинг ВАТ эса шу расмда эгри чизиқ сифатида келтирилган.
Ночизиқли икки қутбликлар ВАТнинг сон-саноқсиз шакллари
мавжуд ва уларни 6 турга ажратиш мумкин: улардан бирнечаси 34.3-расмда
келтирилган.
Баъзи ҳолатларда ВАТ носезгирлик оралиғига
ҳам эга бўлиши ҳам мумкин. Масалан, 34.2,а-расмда ![]() кучланиш бўйича ва 34.2,б-расмда
кучланиш бўйича ва 34.2,б-расмда ![]() ток бўйича носезгирлик оралиғи келтирилган.
ток бўйича носезгирлик оралиғи келтирилган.
34.2-расм
Ночизиқли резистив элемент. Таркибида сиғим ва индуктивликлари, яъни энергияни заҳираловчи реактив элементлари бўлмаган электр занжирлари резистив занжирлар дейилади. Резистив элементнинг схемадаги шартли белгиси 34.1,а-расмда келтирилган. НЧ резистив элементнинг ВАТларидан яна бири 34.3,а-расмда кўрсатилган.
НЧ резистив элементни аниқлашда албатта унинг
Вольт-Ампер тавсифи берилган бўлиши шарт. Шу тавсифнинг ҳар бир ![]()
![]() нуқтасидаги статик қаршилик
нуқтасидаги статик қаршилик
![]()
ва қиймати ушбу нуқтадан ВАТга ўтказилган уринма бурчагининг тангенсига тенг бўлган динамик (дифференциал) қаршилик деб номланган тушунчани киритиш мумкин:
34.3,а-расмдаги график ушбу қаршиликлар
геометрик маъноларини тушунишга ёрдам беради. НЧ резистив элементлар ВАТ
шаклларининг умумийлашган турлари график координата ![]() текислигининг қайси квадрантида жойлашган
эканлигига боғлиқ. Агар график фақат биринчи ва учинчи квадрантда
жойлашган бўлса, у ҳолда ВАТ пассив элементга таалуқли бўлади;
бунда пассив элементнинг манбадан исътеъмол қилаётган қуввати p
= u·i ≥ 0 га тенг бўлади. Агар графикнинг бир қисми иккинчи
ёки тўртинчи квадрантга кирса, у ҳолда ВАТ актив элементга мос бўлади.
Бундан шундай хулоса қилиш мумкинки - НЧ элемент таркибида манба ёки бошқа
турдаги энергияни электр энергиясига айлантирувчи элемент ҳам қатнашиши
мумкин экан.
текислигининг қайси квадрантида жойлашган
эканлигига боғлиқ. Агар график фақат биринчи ва учинчи квадрантда
жойлашган бўлса, у ҳолда ВАТ пассив элементга таалуқли бўлади;
бунда пассив элементнинг манбадан исътеъмол қилаётган қуввати p
= u·i ≥ 0 га тенг бўлади. Агар графикнинг бир қисми иккинчи
ёки тўртинчи квадрантга кирса, у ҳолда ВАТ актив элементга мос бўлади.
Бундан шундай хулоса қилиш мумкинки - НЧ элемент таркибида манба ёки бошқа
турдаги энергияни электр энергиясига айлантирувчи элемент ҳам қатнашиши
мумкин экан.
НЧ резистив элементларнинг яна бошқа умумийлаштирувчи хусусиятлари - ВАТнинг равон ёки норавонлигидир.
Норавон ўзгарувчи ВАТнинг шундай бўлаги мавжуд бўладики, унда ВАТ ҳосиласининг ишораси бошқа бўлаклардаги ҳосила ишорасидан фарқли бўлади. 33.3,б-расмда ВАТнинг равонлиги бўйича уч тури келтирилган:
|
|
а -
равон ВАТ; б - норавон (ёки N-симон) ВАТ; б - норавон (ёки
S-симон) ВАТ.
34.3-расм
Занжирларни таҳлил қилганда ВАТнинг
равонлиги алоҳида аҳамиятлидир, чунки тенгламаларни тузишда ![]() , ҳисоблаганда унга тескари боғланишлардан
фойдаланилади. Равон тавсифга тескари бўлган тавсиф ҳам равон бўлади.
Норавон боғланишлар бўлганда кўп қийматли функциялари мавжуд бўлган
тенгламаларни ечишга тўғри келади.
, ҳисоблаганда унга тескари боғланишлардан
фойдаланилади. Равон тавсифга тескари бўлган тавсиф ҳам равон бўлади.
Норавон боғланишлар бўлганда кўп қийматли функциялари мавжуд бўлган
тенгламаларни ечишга тўғри келади.
Реал элементларнинг НЧ резистив элементлар моделлари шаклидаги тавсифланишига диодлар (34.4,а-расм), тиристорлар (34.4,в-расм), динисторлар (34.4,г-расм) мисол бўла олади.
Амалиётда ишлаш принципини ночизиқли элемент ВАТ ташкил этадиган мисоллар қўплаб учрайди.
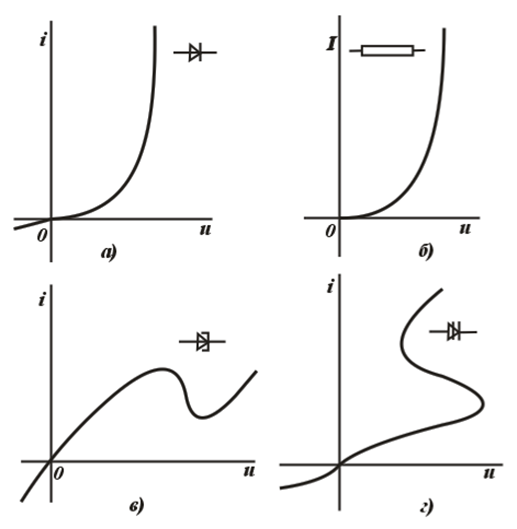 Инерциясиз
ночизиқли тўртқутбликлар. Қутбларидаги ток ва
кучланишларининг оний қийматлари орасидаги боғланишлари бошқа
қутбларидаги ток ва кучланишлар оний қийматларини тўла-тўкис акс
эттирувчи икки ўзгарувчили x1 ва x2
Инерциясиз
ночизиқли тўртқутбликлар. Қутбларидаги ток ва
кучланишларининг оний қийматлари орасидаги боғланишлари бошқа
қутбларидаги ток ва кучланишлар оний қийматларини тўла-тўкис акс
эттирувчи икки ўзгарувчили x1 ва x2
![]() ва
ва![]() функциялар билан берилган тўртқутбликлар инерциясиз
ночизиқли тўртқутбликлар (ИНТ) дейилади (34.4-расм).
функциялар билан берилган тўртқутбликлар инерциясиз
ночизиқли тўртқутбликлар (ИНТ) дейилади (34.4-расм).
34.4-расм
ИНТлар ўз қутбларидаги ток ва кучланишларни акс эттирувчи тенгламалар ёрдами-да ифодаланиши мумкин:
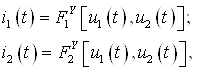
 ёки
кучланиш ва токларини
ёки
кучланиш ва токларини
34.5-расм
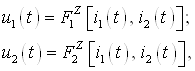
ифодаловчи тенгламалар ёрдамида ёки аралаш енгламалар ёрдамида ифодаланиши мумкин.
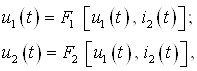
ИНТ сифатида тасвирланиши мумкин бўлган реал элементлардан тавсифлари 34.6-расмда кўрсатилган транзисторларни келтириш мумкин.
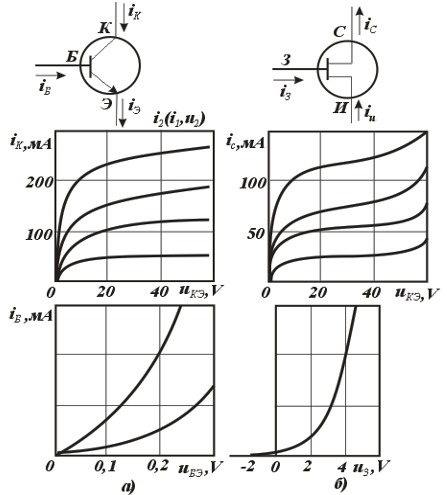
34.6-расм
Ночизиқли сиғим. Ночизиқли сиғимнинг схемадаги шартли белгиланиши 33.1,в-расмда келтирилган. Ундаги заҳираланган заряд
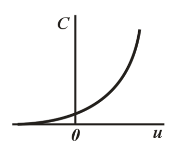 кучланишга
кучланишга
![]() ночизиқли боғланишда бўлади. Агар
ночизиқли сиғимдаги
ночизиқли боғланишда бўлади. Агар
ночизиқли сиғимдаги ![]() кучланиш таъсирида ундан оқаётган токнинг
кучланиш таъсирида ундан оқаётган токнинг ![]() вақтга боғлиқлиги аниқланса,
у ҳолда
вақтга боғлиқлиги аниқланса,
у ҳолда ![]() бўлганлиги
бўлганлиги
учун,
мураккаб функцияни дифференциаллаб
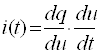 34.7-расм
34.7-расм
 ни ҳосил
қиламиз. Функция
ни ҳосил
қиламиз. Функция 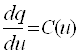 ни Вольт-Фарада тавсифи дейилади
(34.7-расм), ундан ночизиқли сиғимнинг математик моделини қуйидаги
кўринишда ҳосил қилиш
мумкин:
ни Вольт-Фарада тавсифи дейилади
(34.7-расм), ундан ночизиқли сиғимнинг математик моделини қуйидаги
кўринишда ҳосил қилиш
мумкин:
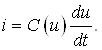 34.8-расм
34.8-расм
Шартли белгиси 33.8-расмда келтирилган ночизиқли сиғимнинг модели сифатида ишлатиладиган реал элементлардан бири варикап - ярим ўтказгичли асбобдир.
Ночизиқли индуктивликнинг электр
схемадаги шартли белгиси 34.1,б-расмда келтирилган. У магнит илашув ![]() нинг ток
нинг ток ![]() га ночизиқли боғланганлигини ифодалайди
га ночизиқли боғланганлигини ифодалайди ![]() Магнит майдони ўзгариши на-тижасида индуктивлик ғалтагида
индуктивланаётган э.ю.к. (кучланиш) магнит илашувнинг ҳосиласига пропорционал
Магнит майдони ўзгариши на-тижасида индуктивлик ғалтагида
индуктивланаётган э.ю.к. (кучланиш) магнит илашувнинг ҳосиласига пропорционал
![]() бўлганлиги учун,
бўлганлиги учун, ![]() ни мураккаб функция сифатида дифференциаллаб қуйидагини
ҳосил қиламиз:
ни мураккаб функция сифатида дифференциаллаб қуйидагини
ҳосил қиламиз:
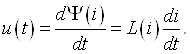
![]() қиймат ночизиқли индуктивлик дейилади.
Ночизиқли индуктивликлар билан ферромагнит ўзакли ғалтаклар боғланишлари
ифодаланади.
қиймат ночизиқли индуктивлик дейилади.
Ночизиқли индуктивликлар билан ферромагнит ўзакли ғалтаклар боғланишлари
ифодаланади.
35-маъруза. Ночизиқли занжирларни таҳлил қилиш
35.1 Амплитуда модулятори
Амплитуда модулятори деб ![]() шаклидаги сигнални
шаклидаги сигнални ![]() шаклига сигналга ўзгартирувчи элементга
айтилади. Амплитуда модуляциясини ҳосил қилиш жараёни
модуляцияланувчи деб номланган «оҳиста» ўзгарувчи
шаклига сигналга ўзгартирувчи элементга
айтилади. Амплитуда модуляциясини ҳосил қилиш жараёни
модуляцияланувчи деб номланган «оҳиста» ўзгарувчи ![]() сигнални амплитудаси
сигнални амплитудаси ![]() қонунияти бўйича ўзгарадиган «тез»
тебранувчи сигналга ўзгартиришдан иборат:
қонунияти бўйича ўзгарадиган «тез»
тебранувчи сигналга ўзгартиришдан иборат:
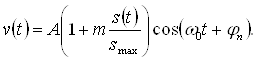 (35.1)
(35.1)
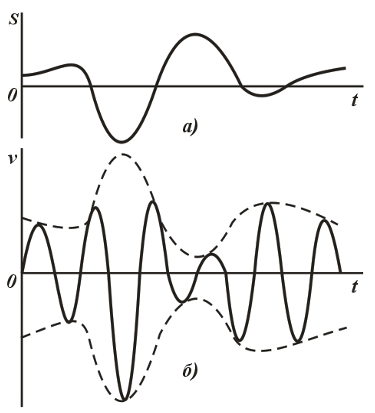 Бунда
Бунда ![]() кўтарувчи тебраниш
деб номланган функция;
кўтарувчи тебраниш
деб номланган функция; ![]() -модуляциялаш коэффици-енти (
-модуляциялаш коэффици-енти (![]() );
); ![]()
![]() . Масалан, агар
. Масалан, агар ![]() сигнал графиги 35.1,а-расмда келтирилган
сигнал бўлса, у ҳолда унга мос келган модуля-цияланган амплитудали сигнал
(МА-сигнал)нинг графиги 35.1,б-расмдагидек бўлади. МА-тебраниш спектри
хусусиятларидан келтириб чиқариш мумкин. Маса-лан,
сигнал графиги 35.1,а-расмда келтирилган
сигнал бўлса, у ҳолда унга мос келган модуля-цияланган амплитудали сигнал
(МА-сигнал)нинг графиги 35.1,б-расмдагидек бўлади. МА-тебраниш спектри
хусусиятларидан келтириб чиқариш мумкин. Маса-лан, ![]() функ-ция учун қуйидаги спектр-га эга
бўламиз:
функ-ция учун қуйидаги спектр-га эга
бўламиз:
35.1-расм
![]()
бунда
![]() қиймат
қиймат ![]() функциянинг спектри:
функциянинг спектри:
![]()

Бизнинг ҳолатда ![]() , унда
, унда
![]() .
.
Демак,
МА – тебраниш спектри ![]() модуляцияловчи сигнал спектри орқали
қуйидагича ёзилади:
модуляцияловчи сигнал спектри орқали
қуйидагича ёзилади:
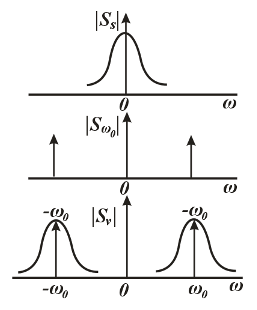
![]()
![]()
35.2-расмда модуляцияловчи сигнал ва кўтарувчи сигнал МА – тебраниш спектрлари келтирилган.
Амплитуда модуляцияси жараёни ![]() сигнали спектрининг оддий ўзгартирилишларидан
бири ҳисобланади ва ночизиқли элементи бўлган занжирда амалга
оширилиши мумкин. МА – тебранишларни ҳосил қилиш икки сигналлар:
модуляция-ловчи
сигнали спектрининг оддий ўзгартирилишларидан
бири ҳисобланади ва ночизиқли элементи бўлган занжирда амалга
оширилиши мумкин. МА – тебранишларни ҳосил қилиш икки сигналлар:
модуляция-ловчи ![]() ва кўтарувчи
ва кўтарувчи ![]() бўлишини тақозо этганлиги учун, ночизиқли
элементга
35.2-расм
бўлишини тақозо этганлиги учун, ночизиқли
элементга
35.2-расм
шу сигналларнинг йиғиндиси таъсир этиши керак.
Ночизиқли резистив тўртқутблик билан кетма-кет уланган чизиқли йўлак фильтри (ЙФ) – кўтарувчи частотага созланган контур – МА- тебранишга мос бўлган частота оралиғини ажратиб олади (35.3-расм).
ИНТ нинг ВАТ иккинчи тартибли ![]() кўпхад ёрдамида ифодаланган бўлсин.
кўпхад ёрдамида ифодаланган бўлсин.
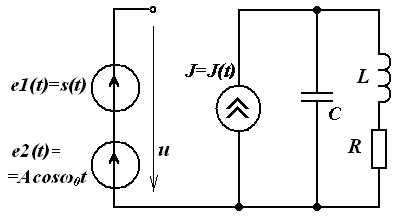
35.3-расм
Йўлак фильтрининг киришидаги токни аниқлаймиз:
![]()
![]()
![]()
![]()
Резонанс частотаси ![]() спектридаги максимал частотага нисбатан жуда
катта
спектридаги максимал частотага нисбатан жуда
катта ![]() деб ҳисоблаб, токнинг спектрал ташкил
этувчиларини аниқлаймиз. 35.4-расмдаги S1 спектрни
ўзгармас ташкил этувчи ва S(t), S2(t) қатнашган ҳадлари,
S2, S3 спектрларни эса
деб ҳисоблаб, токнинг спектрал ташкил
этувчиларини аниқлаймиз. 35.4-расмдаги S1 спектрни
ўзгармас ташкил этувчи ва S(t), S2(t) қатнашган ҳадлари,
S2, S3 спектрларни эса ![]()
![]() қатнашган сигналлар ҳосил қилади.
Агар йўлак фильтрининг ўтказиш йўлаги
қатнашган сигналлар ҳосил қилади.
Агар йўлак фильтрининг ўтказиш йўлаги ![]() га яқин жойлашган бўлса (графикда пунктир
чизиқ), у ҳолда фильтр
га яқин жойлашган бўлса (графикда пунктир
чизиқ), у ҳолда фильтр ![]() тебранишларни ажратади. Айнан
тебранишларни ажратади. Айнан ![]() МА-тебранишини ифодалайди.
МА-тебранишини ифодалайди.
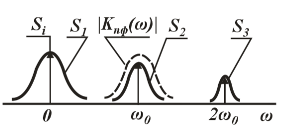 35.5-расмда
35.5-расмда
![]() сигналнинг модуляцияси, кўтарувчи ва чиқиш
кучланишининг осциллограммалари келтирилган.
сигналнинг модуляцияси, кўтарувчи ва чиқиш
кучланишининг осциллограммалари келтирилган.
МА-модуляция жараёнини амалга оширишда кенг қўлланилади-ган схема 35.6-расмда келтирилган 35.4-расм
майдон транзисторли схема бўлиб,
унда аввалига модуляция ва кўтарувчи тебранишлар қўшилади.
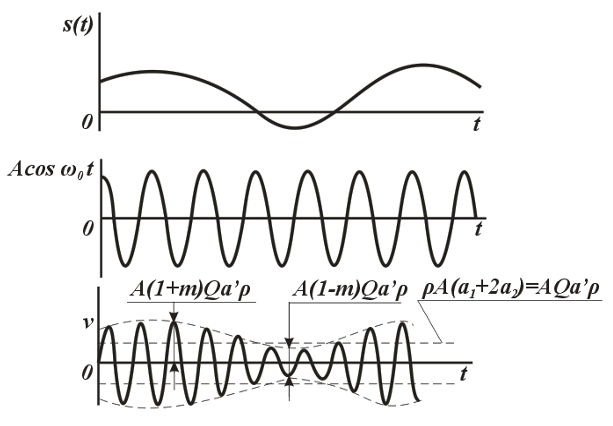
35.5-расм
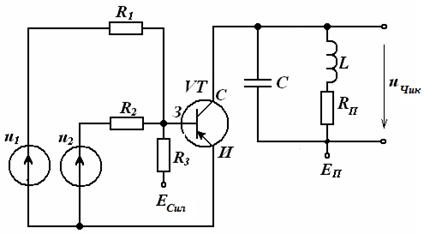
35.6-расм
Затвор ва оқим
боши (исток) орасидаги ![]() кучланишни қуйидаги
ифода ёрдамида ҳисобланади: апапа
кучланишни қуйидаги
ифода ёрдамида ҳисобланади: апапа
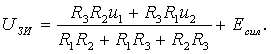
Қаршиликлар ![]() ва силжиш кучланиши
ва силжиш кучланиши ![]() қийматларини танлаш йўли билан
транзистор узатиш тавсифидаги ишчи нуқтасини
(35.7,а-расм) танлаш амалга оширилади.
қийматларини танлаш йўли билан
транзистор узатиш тавсифидаги ишчи нуқтасини
(35.7,а-расм) танлаш амалга оширилади.
35.7-расм
Ишчи нуқтанинг тавсифдаги энг яхши жой шундай ҳисобланадики, унда ВАТни ёйиш коэффициентлари чиқиш токи биринчи гармоникасининг модуляция коэффициентини максимал қийматда бўлишини таъминласин.
Модуляцияланган сигнал RLC-контурдаги кучланиш
сифатида аниқланади; контурнинг параметрлари эса ![]() частотани таъминлаши шарт. Исрофлар қаршилиги
шундай катталикда бўлиши керакки, унда занжир асллиги
частотани таъминлаши шарт. Исрофлар қаршилиги
шундай катталикда бўлиши керакки, унда занжир асллиги ![]() етарли даражада катта бўлсин, яъни ўтказиш
йўлаги
етарли даражада катта бўлсин, яъни ўтказиш
йўлаги ![]() бўлсин. Иккинчи томондан, модуляцияланган сигнал
спектри шакли бузилмаслиги, демак
бўлсин. Иккинчи томондан, модуляцияланган сигнал
спектри шакли бузилмаслиги, демак ![]() тенгсизлик бажарилиши зарур. Тенглик
тенгсизлик бажарилиши зарур. Тенглик ![]() дан фойдаланиб,
дан фойдаланиб, ![]() параметрларни ҳисоблаш учун тенгсизликларни
келтириб чиқарамиз:
параметрларни ҳисоблаш учун тенгсизликларни
келтириб чиқарамиз:
![]()
Транзисторнинг ночизиқли тавсифининг шаклини аниқловчи
коэффициентлар ![]() қийматлари берилган қаршиликлар
қийматлари берилган қаршиликлар ![]() дан затвордаги силжишни танлашга боғлиқ.
Шу силжиш ўзгарганда чиқиш кучланиши
дан затвордаги силжишни танлашга боғлиқ.
Шу силжиш ўзгарганда чиқиш кучланиши ![]() нинг амплитудаси
нинг амплитудаси ![]() ўзгаради. Ночизиқли элемент чиқишидаги
биринчи гармоник амплитудасининг ўзгармас силжиш кучланишига боғлиқлиги
статик модуляцион тавсиф (35.7,б-расм) дейилади. Модулятор иши
учун оптимал
ўзгаради. Ночизиқли элемент чиқишидаги
биринчи гармоник амплитудасининг ўзгармас силжиш кучланишига боғлиқлиги
статик модуляцион тавсиф (35.7,б-расм) дейилади. Модулятор иши
учун оптимал ![]() қийматни статик модуляцион тавсиф чизиқли
қисмининг ўртасида бўлиши танланади. Сигнал максимуми
қийматни статик модуляцион тавсиф чизиқли
қисмининг ўртасида бўлиши танланади. Сигнал максимуми ![]() модуляцион тавсиф чизиқли қисми
чегарасидан чиқмаслиги шарт.
модуляцион тавсиф чизиқли қисми
чегарасидан чиқмаслиги шарт.
Модуляцияга тескари бўлган жараён демодуляция ёки детекторлаш дейилади.
Тебраниш ![]() бўйича детекторланганда
бўйича детекторланганда ![]() сигнални тиклаш зарур. Ушбу жараённи амалган оширувчи қурилма
амплитуда демодулятори ёки детектори деб аталади.
Детекторланганда
сигнални тиклаш зарур. Ушбу жараённи амалган оширувчи қурилма
амплитуда демодулятори ёки детектори деб аталади.
Детекторланганда ![]() сигнални шундай ўзгартириш керакки, кейин
сигнални шундай ўзгартириш керакки, кейин ![]() сигнални ажратиб олиш мумкин бўлсин. Бундай
ўзгартиришни ИНТга қуйи частотали фильтр
сигнални ажратиб олиш мумкин бўлсин. Бундай
ўзгартиришни ИНТга қуйи частотали фильтр
35.8-расм
улаш ёрдамида бажариш мумкин.
Айтайлик, НТнинг ВАТ квадратик парабора ![]() ёрдамида ифодалансин. Унда
ёрдамида ифодалансин. Унда
![]()
![]()
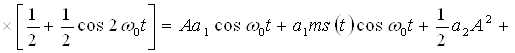
![]()
Токнинг спектрида фойдали ташкил этувчиси ![]() мавжуд; у қуйи частота фильтри ёрдамида
ажратиб олиниши мумкин. 35.9-расмда
мавжуд; у қуйи частота фильтри ёрдамида
ажратиб олиниши мумкин. 35.9-расмда ![]() сигнали спектрида максимал частота
сигнали спектрида максимал частота ![]() бўлиш шарти бажарилгандаги токнинг спектрал
ташкил этувчилари келтирилган. ҚЧФнинг ўтказиш йўлагига
бўлиш шарти бажарилгандаги токнинг спектрал
ташкил этувчилари келтирилган. ҚЧФнинг ўтказиш йўлагига ![]() га пропорционал бўлган ташкил этувчилар кириб қолиши
мумкин (16.26-расмдаги пунктир чизиқ). Бироқ модуляция
коэффициентлари кичик бўлганда уларни эътиборга олмаса ҳам бўлади.
га пропорционал бўлган ташкил этувчилар кириб қолиши
мумкин (16.26-расмдаги пунктир чизиқ). Бироқ модуляция
коэффициентлари кичик бўлганда уларни эътиборга олмаса ҳам бўлади.
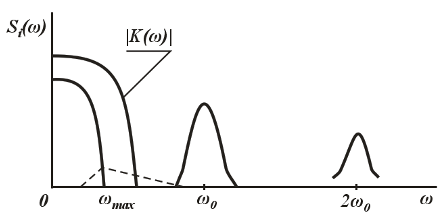
35.9-расм
ҚЧФ ток спектридаги барча юқори
гармоникаларни фильтрлайди ва унинг чиқишида ![]() га пропорционал бўлган ўзгармас ташкил этувчиси аниқлигида
сигнал мавжуд бўлади (35.10,а-расм). Ўзгармас ташкил этувчи эса ҚЧФнинг
чиқишига сиғим уланиши билан осонгина фильтрланиши мумкин.
га пропорционал бўлган ўзгармас ташкил этувчиси аниқлигида
сигнал мавжуд бўлади (35.10,а-расм). Ўзгармас ташкил этувчи эса ҚЧФнинг
чиқишига сиғим уланиши билан осонгина фильтрланиши мумкин.
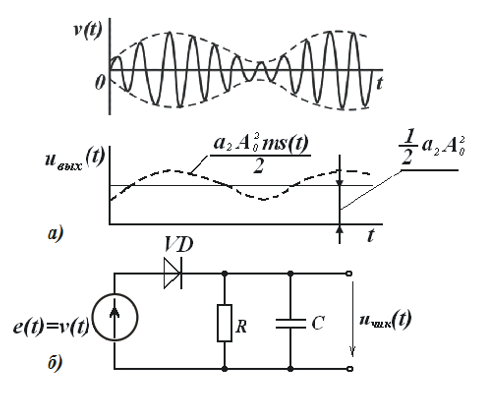
35.10-расм
Амалиётда кенг тарқалган демодулятор сифатида
диод детектори схемаси хизмат қилади (35.10,б-расм). Бунда ҚЧФ
сифатида RC-занжир ишлатилади; барча юқори гармоника токлари
кучланишлар пасаюви ҳосил қилмасдан сиғим орқали оқиб
ўтади ва, шунинг учун ![]() кучланиши
кучланиши ![]() га пропорционал бўлади (35.11-расм).
га пропорционал бўлади (35.11-расм).
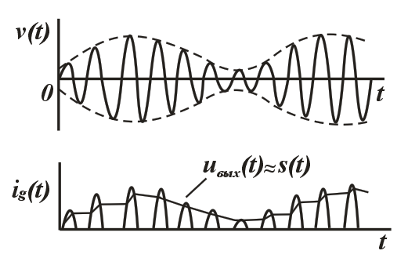
35.11-расм
Шуни таъкидлаш зарурки, детекторлаш учун ҳар қандай ночизиқли элемент ҳам мос бўлавермайди, масалан, тоқ ночизиқлиликни ишлатиб бўлмайди.