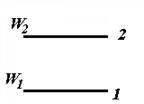УЗБЕКСКОЕ АГЕНТСВО СВЯЗИ   И  ИНФОРМАТИЗАЦИИ

ТАШКЕНТСКИЙ  УНИВЕСИТЕТ ИНФОРМАЦИОННЫХ  ТЕХНОЛОГИЙ

Х.К. Арипов, Г.Н. Кузьмина, А.М. Абдуллаев, А.М. Афанасьева

Кафедра электронных и квантовых приборов

МИКРОВОЛНОВЫЕ ПОЛУПРОВОДНИКОВЫЕ ПРИБОРЫ

Конспект лекций

для высшего образования отрасли по направлению:

В 522500

В 523600

Ташкент - 2003

Х.К. Арипов, Г.Н. Кузьмина, А.М. Абдуллаев, А.М. Афанасьева. Микроволновые полупроводниковые приборы. Конспект лекций - Ташкент: ТУИТ 2003.

В данном конспекте лекций обобщен материал по дисциплине " Микроволновые полупроводниковые приборы". Отличительной особенностью конспекта является наличие концептуальных диаграмм, соответствующих содержанию изучаемых тем. Они должны помочь студентам при самостоятельном изучении курса.

Конспект лекций предназначен для бакалавров факультета РРТ  по направлению В 522500, В 523600.

Ответственный редактор:

                            д.ф-м.н., проф.                                                        Арипов Х.К.

Рецензент:

                 д.ф-м.н., проф.                                                        Баходирханов М.С.

Ó Издание Ташкентского университета информационных технологий, 2003

СОДЕРЖАНИЕ

									стр.
ЛЕКЦИЯ № 1. Особенности микроволнового диапазона и динамического принципа управления преобразованием энергии................................................................									5
1.1.		Концептуальная диаграмма.............................................................................................							5
1.2.		Диапазоны волн, используемые в телекоммуникации, необходимость использования микроволнового диапазона..................................................................							5
1.3.		Достоинства и недостатки использования микроволнового диапазона.....................							7
1.4.		Статический и динамический принципы   управления   преобразованием энергии..............................................................................................................................							8
1.5.		Особенности динамического принципа управлении преобразованием.......................							9
1.6.		Классификация приборов микроволнового диапазона................................................							11
1.7.		Контрольные вопросы.....................................................................................................							13
ЛЕКЦИЯ № 2. Электрофизические свойства однородных и неоднородных полупроводников........................................................................................................................									14
2.1.		Концептуальная диаграмма............................................................................................							14
2.2.		Зонная структура состояний электронов в твердом теле.............................................							14
2.3.		Свободные носители зарядов в полупроводниках.......................................................							15
2.4.		Равновесная концентрация СНЗ в примесных и беспримесных полупроводниках.....							18
2.4.1				Равновесная концентрация зарядов в собственном полупроводнике...................					18
2.4.2.				Равновесная концентрация зарядов в примесном полупроводнике.........................					19
2.4.2.1.								Полупроводник с донорной примесью...............................................................	19
2.4.2.2.								Полупроводник с акцепторной примесью.........................................................	20
2.5.		Движение  СНЗ в электрическом поле...........................................................................							20
2.6.		Дрейфовая скорость, подвижность.................................................................................							21
2.7.		Контрольные вопросы.....................................................................................................							22
ЛЕКЦИЯ № 3. p-n переход в равновесном и неравновесном состоянии..........................									23
3.1.		Концептуальная диаграмма............................................................................................							23
3.2.		Электрические переходы...............................................................................................							23
3.3.		Условие  равновесия электрического перехода. Перенос заряда в  электрическом переходе, ток диффузии, ток дрейфа, ток рекомбинации................							24
3.4.		Электрические и геометрические параметры p-n перехода........................................							27
3.4.1.				Высота потенциального барьера и контактная разность потенциалов.................					27
3.4.2.				Соотношение между концентрациями......................................................................					27
3.4.3.				Ширина запирающего слоя........................................................................................					27
3.4.4.				Вольтамперная характеристика p-n-перехода..........................................................					28
3.4.5.				Статическое и дифференциальное сопротивления..................................................					28
3.4.6.				Барьерная емкость......................................................................................................					29
3.4.7.				Диффузионная емкость.................................................................................................					30
3.5.		Способы нарушения равновесия....................................................................................							30
3.6.		Уравнение тока через p-n переход..................................................................................							31
3.7.		Контрольные вопросы....................................................................................................							33
ЛЕКЦИЯ № 4. Свойства p-n перехода на микроволновом диапазоне...............................									34
4.1.		Концептуальная диаграмма.............................................................................................							34
4.2.		Эффект накопления заряда.............................................................................................							34
4.3.		Диоды с накоплением заряда..........................................................................................							35
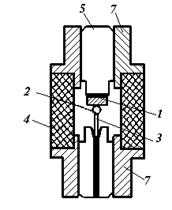
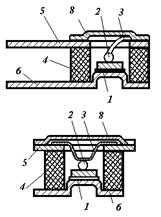
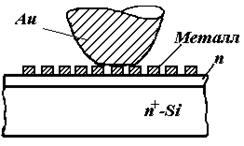
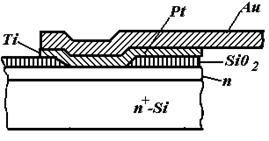
4.4.		Технологические особенности изготовления диодов СВЧ диапазона.......................							36
4.5.		Контрольные вопросы.......................................................................................................							40
ЛЕКЦИЯ № 5. Туннельный диод..............................................................................................									41
5.1.		Концептуальная диаграмма............................................................................................							41
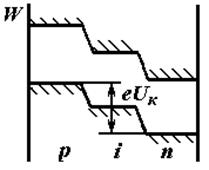
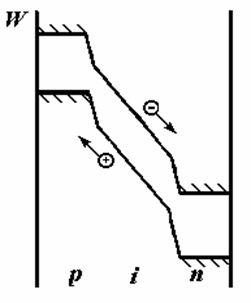
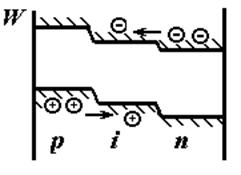
5.2.		Процессы, происходящие в полупроводнике в случае туннельного эффекта...........							41
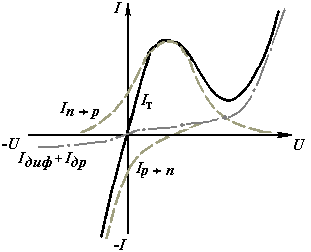
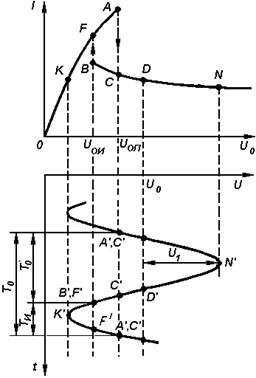
5.3.		Вольт-амперная характеристика туннельного диода...................................................							42
5.4.		Параметры, применение..................................................................................................							45
5.5.		Контрольные вопросы.....................................................................................................							48
ЛЕКЦИЯ № 6. Диод Шоттки, p-i-n диод....................................................................................									49
6.1.		Концептуальная диаграмма.............................................................................................							49
6.2.		Принцип действия, параметры и характеристики диода Шоттки и р-i-n диода.........							49
6.2.1.					Диод  Шоттки.............................................................................................................				49
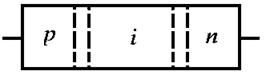
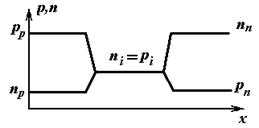
6.2.2.					p-i-n диод.....................................................................................................................				53
6.3.		Контрольные вопросы.....................................................................................................							56
ЛЕКЦИЯ № 7. Лавинно-пролетный диод................................................................................									57
7.1.		Концептуальная диаграмма.............................................................................................							57
7.2.		Лавинное умножение носителей....................................................................................							57
7.3.		Пролетный режим работы ЛПД.....................................................................................							59
7.4.		Параметры и характеристики, особенности устройства и применения ЛПД...........							61
7.5.		Контрольные вопросы.....................................................................................................							63
ЛЕКЦИЯ № 8. Диод Ганна...........................................................................................................									64
8.1.		Концептуальная диаграмма. .........................................................................................							64
8.2.		Междолинный переход электронов................................................................................							64
8.3.		Объемное отрицательное сопротивление.......................................................................							68
8.4.		Режимы работы. Характеристики и параметры диода Ганна.......................................							69
8.4.1.					Доменные режимы работы.......................................................................................				69
8.4.1.1.						Пролетный режим генератора..............................................................................			69
8.4.1.2.						Режим с задержкой образования домена.............................................................			70
8.4.1.3.						Режим с подавлением домена...............................................................................			71
8.4.2.				Режим ограниченного накопления объемного заряда (ОНОЗ)...............................					72
8.4.3.				Гибридный режим........................................................................................................					74
8.4.4.				Параметры диода Ганна..............................................................................................					74
8.5.		Контрольные вопросы.....................................................................................................							74
ЛЕКЦИЯ№ 9. СВЧ транзисторы..............................................................................................									76
9.1.		Концептуальная диаграмма...............................................................................................							76
9.2.		Биполярные микроволновые транзисторы. Геометрия, характеристики и параметры......................................................................................................................							76
9.2.1.			Геометрия биполярного транзистора СВЧ................................................................						77
9.2.2.			Основные характеристики и параметры СВЧ-транзисторов...................................						78
9.2.2.1.							Граничная частота................................................................................................		79
9.2.2.2.							Коэффициент усиления и максимальная частота генерации...........................		79
9.2.2.3.							Коэффициент шума...............................................................................................		80
9.3.		Высокочастотные полевые транзисторы.  Характеристики и параметры.................							81
9.4.		Контрольные вопросы.....................................................................................................							84
ЛЕКЦИЯ №10. Полупроводниковые приборы оптического диапазона...........................									85
10.1.	Концептуальная диаграмма.............................................................................................								85
10.2.	Физические основы работы квантовых приборов оптического диапазона................								85
10.2.1.				Квантовые переходы...................................................................................................					86
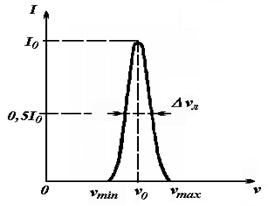
10.2.2.				Ширина спектральной линии....................................................................................					89
10.2.3.				Возможность усиления электромагнитного поля в квантовых системах................					90
10.3.	Особенности создания инверсной населенности..........................................................								93
10.4.	Полупроводниковый инжекционный лазер, устройство, применение.......................								94
10.5.	Лазеры на гетеропереходах, устройство, применение..................................................								97
10.6.	Контрольные вопросы.....................................................................................................								98
Основные обозначения.........................................................................................................									99
Литература.............................................................................................................................									102

ЛЕКЦИЯ № 1

Особенности микроволнового диапазона и динамического принципа управления преобразованием энергии

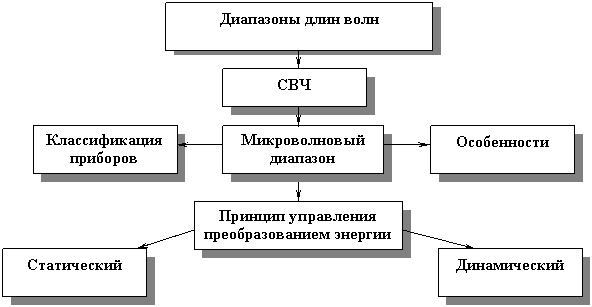
1. Концептуальная диаграмма.

2. Диапазоны волн, используемые в телекоммуникации, необходимость использования микроволнового диапазона.

3. Достоинства и недостатки использования микроволнового диапазона.

4. Статический и динамический принципы управления преобразованием энергии.

5. Особенности динамического принципа управлении преобразованием.

6. Классификация приборов микроволнового диапазона.

7. Контрольные вопросы.

1.1.Концептуальная диаграмма

1.2.Диапазоны волн, используемые в телекоммуникации, необходимость использования микроволнового диапазона.

 Характер распространения электромагнитных сигналов в различных средах и линиях связи в первую очередь зависит от частоты сигнала. В соответствии с этим различают следующие типовые диапазоны применяемых частот, приведенных в табл.1.1:

               Таблица 1.1

Название	Сокращение	Длина волны	Частоты
Сверхдлинные волны	СДВ	100 ... 10 км	3 ... 30 кГц
Длинные волны	ДВ	10 ... 1 км	30 ... 300 кГц
Средние волны	СВ	1,0 ... 0,1 км	0,3 ... 3 МГц
Короткие волны	КВ	100 ... 10м	3 ... 30 МГц
Ультракороткие волны	УКВ	10.... 1 м	30 ... 300 МГц
Дециметровые волны	ДЦМ	1 ... 0,1 м	300 ... 3000 МГц или 0,3 ... 3 ГГц
Сантиметровые волны	СМ	10 ... 1 см	3 ... 30 ГГц
Миллиметровые волны	ММ	10 ... 1 мм	30 ... 300 ГГц
Оптический диапазон	ОД	10 ... 0,1 мкм	3^.10^11…3^.10^16 Гц

К диапазону СВЧ обычно относят область частот от 300 МГц до 300 ГГц. Этот диапазон частот, ширина которого в 10⁵ раз превышает сумму всех диапазонов, используемых «обычной» радиотехникой и электротехникой, принято условно делить на несколько более узких диапазонов длин волн: дециметровый, сантиметровый и миллиметровый.

Оптический диапазон (3∙10¹¹—3∙10¹⁶ Гц) включает субмиллиметровые и инфракрасные волны, волны видимого и ультрафиолетового излучений. Видимое излучение занимает относительно узкую область спектра оптического излучения и ограничено длинами волн от 0,78 до 0,38 мкм.

На рис. 1.1 показано, как используются СВЧ и оптический диапазоны в современных системах связи:

1 — телевизионное вещание;

2 — радиорелейная связь;

3 — тропосферная радиосвязь;

4 — космическая радиосвязь;

5 — метеорная радиосвязь;

6 — дальняя космическая связь;

7— волноводные линии связи;

8— волоконно-оптические линии связи;

9— лазерная связь для космоса.

Рис. 1.1.Системы связи использующие микроволновый диапазон

Линии радиорелейной и космической связи работают в сантиметровом и дециметровом диапазонах волн. Системы связи с использованием искусственных спутников Земли (ИСЗ), как ретрансляторов, становятся одним из важнейших средств связи на большие расстояния, обеспечивающих передачу большого числа телефонных разговоров и программ телевидения.

Телевизионное вещание ведется в настоящее время в метровом и дециметровом диапазонах волн. Дециметровый диапазон позволяет разместить большое число каналов, уменьшить взаимное влияние близко расположенных передатчиков вследствие повышенного затухания дециметровых волн и получить высокое качество принимаемого изображения за счет незначительного влияния индустриальных помех.

Диапазон миллиметровых волн позволяет создавать многоканальные волноводные линии связи с очень широкой полосой частот, в которой можно разместить несколько сотен тысяч телефонных каналов. Миллиметровые волны нашли применение в новой области космической связи — передаче сигналов со спутника на спутник в линии международной связи, содержащей несколько спутников.

На базе оптических квантовых генераторов разрабатываются эффективные системы лазерной связи. Передавать лазерное излучение в атмосфере целесообразно на коротких линиях связи или в космосе между спутниками. Для передачи света на большие расстояния с малыми потерями необходима специальная направляющая система. Наиболее перспективными для лазерных систем связи оказались оптические волноводы — исключительно тонкие диэлектрические стержни (3—80 мкм в диаметре), которые из-за малых поперечных размеров называются волокнами. В настоящее время разработаны волоконно-оптические кабели с затуханием 1—3 дБ/км. Во многих странах мира ведутся разработки волоконно-оптических линий связи (ВОЛС), которые обладают целым рядом преимуществ по сравнению с обычными кабельными: высокая помехоустойчивость, значительно большая широкополосность, малая масса и небольшие габариты, потенциально низкая стоимость.

Роль диапазона СВЧ непрерывно возрастает в связи с бурным развитием самых разнообразных областей науки и техники — радиолокации, радиоуправления, связи, телевидения, телефонии, промышленной электроники и компьютерных информационных сетей. Сверхвысокочастотные приборы широко используются в ряде областей народного хозяйства и медицине, технике телекоммуникаций и компьютерных технологиях. В будущем потребуется еще более широкое применение техники и приборов сверхвысоких частот.

1.3. Достоинства и недостатки использования микроволнового диапазона.

Электромагнитные колебания микроволнового и оптического диапазонов обладают целым рядом специфических особенностей и свойств, отличающими их от смежных участков спектра.

 На сверхвысоких частотах длина волны соизмерима с линейными размерами физических тел. Геометрические размеры схемотехнических элементов аппаратуры, в том числе и антенн, также оказываются соизмеримыми с длиной волны и могут значительно превышать ее. Поэтому волны диапазона СВЧ обладают квазиоптическими свойствами, т. е. по характеру распространения приближаются к световым волнам. Наряду с этим принципы работы СВЧ устройств в значительной мере определяются явлениями дифракции и не могут непосредственно использовать законы геометрической оптики, а также законы обычных электрических цепей.

Квазиоптические свойства волн СВЧ диапазона особенно ценны для направленной передачи сигналов, а также для определения координат объектов.

Еще большей направленностью обладает лазерное излучение. Высокая направленность излучения позволяет во много раз повысить помехоустойчивость систем передачи информации и снизить мощность передающих устройств.

 В отличие от более длинных радиоволн (до 10-15м.) и инфракрасных излучений, волны СВЧ, особенно на участке между 100 Мгц и 10 ГГц, почти беспрепятственно проникают сквозь ионизированные слои, окружающие Землю, а также сквозь атмосферу. Существование в атмосфере Земли широкого окна прозрачности в диапазоне сверхвысоких частот дает возможность, с одной стороны, исследовать космическое пространство радиоастрономическими методами, СВЧ излучение Солнца, звезд и других космических тел. Диапазон СВЧ незаменимым для развития космических систем связи для обмена инфор-мацией между наземными пунктами связи и космическими ретрансляционными спутниками.

Недостатком спутниковых систем связи является действие космических шумов на наземные радиоприемные устройства.

 Величина кванта энергии, соответствующая диапазону СВЧ, соизмерима с разностью энергий близко расположенных энергетических уровней атомов и молекул атмосферы Земли. Поэтому СВЧ электромагнитные колебания, в особенности колебания, лежащие в сантиметровом, миллиметровом и субмиллиметровом диапазонах, обладают способностью резонансного энергетического взаимодействия с веществом. Это обстоятельство широко используется при анализе строения вещества методами СВЧ радиоспектроскопии. Помимо решения специфических научных проблем, это направление, в свою очередь, оказывает сильное влияние на развитие техники СВЧ связи, использование этих частот невозможно для линий космической радиосвязи ввиду большого резонансного поглощения радиоволн на этих частотах. Использование резонансного взаимодействия СВЧ колебаний с атомами и молекулами привело к разработке принципиально новых устройств — квантовых молекулярных усилителей и генераторов и к развитию квантовой электроники.

Основным достоинством СВЧ диапазона является то, что в этом диапазоне можно разместить значительно большее число каналов связи, чем на более низких частотах. Например, нетрудно видеть, что даже узкая полоса частот в 1 % при средней частоте 10 ГГц (длина волны 3 см) позволяет разместить столько же независимых каналов, сколько их имеется во всем диапазоне от сверхдлинных до ультракоротких волн. Большая информационная емкость СВЧ диапазона позволяет осуществлять многоканальную телефонную и телевизионную связь, в особенности на сантиметровых, миллиметровых и субмиллиметровых волнах. Создание квантовых генераторов и усилителей оптического диапазона (лазеров) дает возможность еще более повысить информационную емкость каналов связи с непосредственным использованием методов и аппаратуры СВЧ диапазона.

1.4.Статический и динамический принципы управления преобразованием энергии

 Любой электронный прибор с конструктивной точки зрения представляет определенную систему электродов, размещенных в вакууме или твердом теле (полупроводнике). Можно утверждать, что в приборе способном усиливать мощность, есть два главных межэлектродных промежутка (рис. 1.2), один из которых (управляемый) ответственен за преобразование энергии источника питания в энергию полезного сигнала, а второй промежуток является управляющим и регламентирует процессы, протекающие в управляемом промежутке (соответственно преобразователе), согласно команде входного сигнала[M1] .

Рис 1.2. Блок-схема активного электронного преобразователя

Таким образом, чтобы создать активный электронный преобразователь необходимо прежде всего отыскать способ воздействия на интенсивность электронных процессов, протекающих в одном межэлектродном промежутке, с помощью другого межэлектродного промежутка, напряжение на котором задается входным сигналом.

Интенсивность процессов, протекающих в межэлектродном промежутке, а значит и в той цепи, в которую входит этот промежуток, определяется двумя факторами - количеством электронов участвующих в процессе, и эффективностью их взаимодействия с полем этого промежутка. Из этого следует, что возможны два пути поиска способа управления преобразованием - это либо способ управления количеством электронов, движущихся в управляемом межэлектродном промежутке, либо способ управления эффективностью взаимодействия электронов с полем управляемого промежутка. Последний способ управления электронным потоком состоит в модуляции электронов по скорости, превращении модуляции по скорости в модуляцию по плотности и в передаче энергии колебаний от модулированного по плотности потока колебательной системе. При этом время пролета имеет решающее значение, так как только в процессе движения электронов происходит их группирование.

Развитие электроники показало, что практически реализуемы оба эти способа, или, лучше сказать, принципа управления преобразованием энергии вспомогательного источника в энергию полезного сигнала. Первый принцип назван статическим принципом управления, второй принцип назван динамическим принципом управления.

В табл. 1.2 приведены данные о приборах использующих принципы статического и динамического управления.

                                                               Таблица 1.2

Наименование принципа управления	Содержание принципа	Типы приборов	Диапазон рабочих частот (ГГц)
Статический принцип управления.	Управление преобразованием энергии вспомогательного источника в энергию электрического тока в выходной цепи прибора осуществляется путем изменения статической проводимости соответствующего междуэлектродного промежутка в электронном приборе.	СВЧ-триоды, маячковые лампы, полупроводниковые биполярные и полевые транзисторы, интегральные микросхемы.	3 ×10^-4 - 10 (1 км - 3 см)
Динамический принцип управления.	Управление преобразованием энергии осуществляется путем изменения динамики взаимодействия электронного потока с электромагнитным полем, в результате чего изменяется доля энергии пучка, преобразуемая в энергию поля.	Клистроны, приборы с бегущей волной, магнетроны, диоды Ганна, параметрические диоды, лавинно-пролетные диоды (ЛПД).	0, 3 - 300 ( 1 м - 1 мм)

Определяющим в статическом принципе управления является управление количеством электронов (или вообще свободных носителей заряда (СНЗ)), движущихся в управляемом межэлектродном промежутке. Статическая проводимость промежутка, т. е. ток переноса в этом промежутке при постоянном напряжении на промежутке – определяется количеством СНЗ в этом промежутке. Таким образом, статический принцип управления —это управление статической (т. е. установившейся) проводимостью межэлектродного промежутка, включенного последовательно с источником питания и той цепью, в которой реализуется преобразованный (выходной) сигнал.

Статический принцип управления основан на предположении о существовании однозначной связи между током в управляемом промежутке и напряжением или током в управляющем промежутке. Эта связь действительно однозначна если токи (напряжения) являются постоянными во времени. При переменных напряжениях (токах) однозначность связей уже отсутствует.

1.5. Особенности динамического принципа управления преобразованием

Идея динамического управления процессом преобразования энергии предполагает возможность управления эффективностью энергообмена между электронным потоком, пронизывающем область локализации выходного электромагнитного поля и этим полем. При этом управление производится путем воздействия на электронный поток со стороны входного электромагнитного поля, локализованное в другом или том же самом межэлектродном промежутке.

Значит носителем первичной энергии, за счет, которой формируется выходной сигнал, является сам электронный поток. Источник питания служит лишь для сообщения электронному потоку необходимой энергии. Во-вторых, предполагается, что как управляющее (входное), так и управляемое (выходное) электромагнитное поле могут быть локализованы в элементах объема электронного прибора. Отсюда следует, что динамический принцип управления может быть реализован только на сверхвысоких частотах (длина волны не более 1м).

Так же электронный поток рассматривается не как простая совокупность движущихся электронов, а как некий целостный ансамбль, и именно энергообмен этого ансамбля с полем имеет решающее значение.

Возможность управления энергообменом ансамбля с электромагнитным полем заключается в зависимости как знака энергообмена, так и его величины от состояния ансамбля. Если ансамбль находится в равновесном состоянии, то при его взаимодействии с электромагнитным полем энергообмена происходить практически не будет. Энергии как ансамбля электронов, так и поля будут оставаться неизменными. Если же с полем взаимодействует ансамбль, находящийся в неравновесном состоянии, то происходит энергообмен, причем тем более интенсивный, чем в большей степени состояние ансамбля отличается от равновесного. Эта особенность, является общей для взаимодействия с электромагнитных полем любых ансамблей.

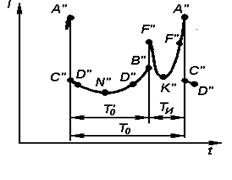
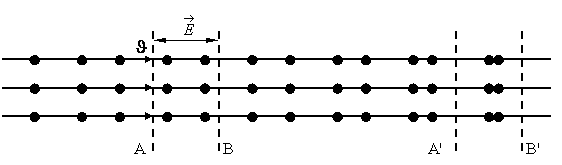
Рис.1.3. Распределение плотности электронного пучка при динамическом

управлении

Равновесным состоянием потока электронов является такое состояние, при котором скорости всех электронов будут одинаковыми, а плотность электронов вдоль потока постоянной.

Предположим, что такой поток пронизывает область между электродами АВ (рис.1.3.), в которой локализовано электромагнитное поле типа стоячей волны.

Допустим, что скорость электронов в потоке настолько велика, что время пролета электронов через промежуток АВ ничтожно мало по сравнению с периодом изменения напряжения на этом промежутке. Тогда за время пролета электрона через промежуток напряжение на промежутке практически не изменится, и электрон будет двигаться так, как двигался бы в постоянном поле с напряженностью, равной мгновенному значению напряженности переменного поля в момент пролета электрона. Электроны, пролетевшие промежуток за положительный полупериод, ускоряются (каждый по-своему), а электроны, пролетевшие промежуток за отрицательный полупериод, замедляются (опять каждый по-своему). Поскольку, однако, плотность электронов в пучке всюду одинакова, то количества электронов, проходящих промежуток АВ за положительный и отрицательный полупериоды, будут одинаковы. Половина электронов ансамбля ускоряется и увеличивает свою энергию за счет энергии поля, половина электронов ансамбля замедляется и уменьшает свою энергию, отдавая ее полю. Ни энергия ансамбля, ни энергия поля не изменяются. Энергообмен незначителен по величине и практически равен нулю.

При прохождении пучка через область электромагнитного поля происходит изменение скорости электронов - одни электроны ускоряется, другие - замедляются. Но как только скорости электронов станут неодинаковыми возникнет причина, приводящая к нарушению равномерного их пространственного распределения вдоль пучка. Начнут образовываться сгустки и разрежения, периодически расположенные вдоль пучка.

Электронный поток пронизывает промежуток АВ, в котором электромагнитное поле связано с входным сигналом и которое требуется, например, усилить. Это поле, воздействуя на поток электронов, модулирует электроны пучка по скоростям, выводя, тем самым, ансамбль электронов из равновесия. Далее этот, уже неравновесный поток электронов, пронизывает второй промежуток а'В', в котором локализовано поле индуцированное этим неравновесным потоком, поддерживая его на некотором уровне путем непрерывной передачи части своей энергии. Чем больше амплитуда поля в промежутке АВ (амплитуда входного сигнала) тем большей будет амплитуда модуляции скорости электронов в пучке, а значит тем большей будет доля энергии, передаваемой от электронного пучка электромагнитному полю в промежутке А'В', тем большей будет амплитуда установившегося поля в этом промежутке.

Таким образом, особенности динамического управления электронным потоком состоят в модуляции электронов по скорости, превращении модуляции по скорости в модуляцию по плотности и передаче энергии колебаний от модулированного по плотности потока колебательной системе. При этом время пролета имеет решающее значение, так как только в процессе движения электронов происходит их группирование.

Динамическое управление преобразованием энергии электронного пучка в энергию СВЧ поля обязательно включает в себя, три процесса:

-модуляцию электронов по скорости полем входного сигнала;

-пространственную группировку электронов в пучке, обеспечивающую положительный энергообмен с СВЧ полем выходного сигнала;

-отбор энергии от неоднородного по плотности пучка и формирование СВЧ поля выходного сигнала.

Эти три процесса могут протекать в раздельных элементах объема прибора и в указанной временной последовательности (клистрон), или в одном к том же элементе объема и налагаясь друг на друга во времени (лампы бегущей волны).

1.6. Классификация приборов микроволнового диапазона

В настоящее время разработано много приборов, отличающихся как принципом действия, так и областью применения. На рис. 1.4. приведена классификация электронных приборов СВЧ, а на рис. 1.5. — квантовых приборов. Данная классификация не претендует на полноту и не является единственно возможной.

Электровакуумные приборы СВЧ диапазона могут быть по характеру энергообмена разделены на приборы типов О и М. В приборах типа О происходит преобразование кинетической энергии электронов в энергию СВЧ поля в результате торможения электронов этим полем. Магнитное поле или не используется совсем, или применяется только для фокусировки электронного потока и принципиального значения для процесса энергообмена не имеет. В приборах типа М, которые еще также называются приборами со скрещенными полями (потому что постоянное магнитное поле перпендикулярно постоянному электрическому полю, ускоряющему электроны) в энергию СВЧ поля переходит потенциальная энергия электронов.

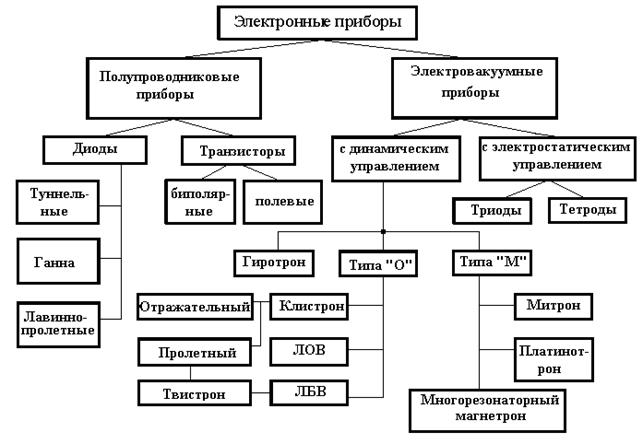
Рис. 1.4. Классификация электронных приборов СВЧ

По продолжительности взаимодействия с СВЧ полем приборы разделяются на приборы с кратковременным (прерывным) и длительным (непрерывным) взаимодействием. В первом случае используется взаимодействие электронов с СВЧ полем резонаторов, а во втором — с бегущей электромагнитной волной.

Приборы с кратковременным взаимодействием одновременно являются приборами типов О (пролетные и отражательные клистроны). Приборы с длительным взаимодействием могут быть как типа О — ЛБВ, ЛОВ, так и типа М — ЛБВМ, ЛОВМ, магнетрон, платинотрон. По типу управления электронным потоком приборы подразделяются на приборы с электростатическим и динамическим управлениями.

В полупроводниковых приборах СВЧ выделяются группа диодов с отрицательным сопротивлением и группа СВЧ транзисторов.

Квантовые приборы (рис. 1.5) обычно разделяются на два класса в зависимости от диапазона рабочих частот. В СВЧ диапазоне это мазеры и квантовые стандарты частоты, а в оптическом — лазеры. Затем лазеры подразделяются в зависимости от агрегатного состояния активного вещества на газовые, твердотельные, жидкостные, полупроводниковые. Хотя используемые в квантовой электронике полупроводники являются твердыми телами, полупроводниковые лазеры выделены в отдельную группу связи с тем, что характер генерации в полупроводниках существенно отличается от генерации в обычных твердотельных квантовых генераторах.

Рис. 1.5. Классификация квантовых приборов

В зависимости от режима работы различают лазеры, работающие в непрерывном режиме, в импульсном режиме с длительностью импульсов 10^-3—10^-6 с, режиме гигантских импульсов длительностью 10^-7— 10^-9 с и режиме синхронизации мод, при котором длительность импульса может быть 10^-10—10^-12 с.

1.7. Контрольные вопросы:

1. В каких областях телекоммуникации используют СВЧ и оптический диапазоны?

2. Поясните основные достоинства и недостатки микроволнового диапазона.

3. В чем заключаются статический и динамический принципы управления преобразованием энергии?

4. Какое состояние потока электронов называют равновесным?

5. В чем заключается возможность управления энергообменом ансамбля электронов с электромагнитным полем?

6. По каким признакам производится классификации приборов СВЧ диапазона?

ЛЕКЦИЯ № 2

Электрофизические свойства однородных и неоднородных полупроводников

1. Концептуальная диаграмма.

2. Зонная структура состояний электронов в твердом теле.

3. Свободные носители зарядов в полупроводниках.

4. Равновесная концентрация СНЗ в примесных и беспримесных полупроводниках.

5. Движение СНЗ в электрическом поле.

6. Дрейфовая скорость, подвижность.

7. Контрольные вопросы.

2.1. Концептуальная диаграмма

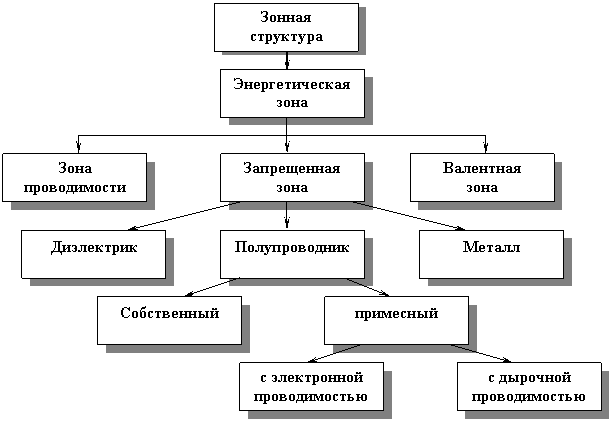2.2. Зонная структура состояний электронов в твердом теле

Твердые тела делятся на аморфные и кристаллические. Большинство применяемых в настоящее время полупроводников относятся к кристаллическим телам, атомы которых, расположенные в определенном порядке, образуют пространственную решетку. Почти все они обладают ковалентной связью, при которой взаимное притяжение двух атомов осуществляется благодаря общей паре валентных электронов, вращающихся по орбите вокруг этих атомов.

Согласно принципу Паули в атоме не может быть более двух электронов, находящихся в одном и том же энергетическом состоянии, причем эти электроны должны обладать взаимно противоположными спинами. Общее количество электронов, окружающих ядро атома данного элемента в невозбужденном состоянии, определяется его порядковым номером.

При сближении атомов (для образования кристалла) их взаимодействие усиливается и на некотором расстоянии становится настолько значительным, что вызывает расщепление каждого энергетического уровня изолированного атома в энергетическую зону — область значений полной энергии электронов в кристалле, характеризуемую максимальным и минимальным значениями энергии. Число энергетических уровней в каждой зоне равно числу объединяющихся атомов. В 1 см³ твердого тела число атомов составляет около 10²³, следовательно, и число уровней в каждой разрешенной зоне должно иметь тот же порядок. Ширина верхней из заполненных зон — валентной— максимальна; по мере приближения к атомному ядру расщепление энергетического уровня атома создает все более узкие зоны. Все внутренние зоны целиком заполнены электронами. Так как эти электроны сильно связаны с ядром, они не влияют на проводимость кристалла, и в дальнейшем внутренние зоны рассматриваться не будут. Между зонами, разрешенными для электронов, располагаются запрещенные зоны — области значений энергии, которыми не может обладать электрон в идеальном кристалле (кристалле без примесей и дефектов решетки). В полупроводниках обычно рассматривается лишь запрещенная зона, отделяющая валентную зону от зоны проводимости (свободной зоны при Т=0К), на уровнях которой при возбуждении атома могут находиться электроны.

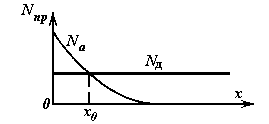
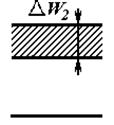
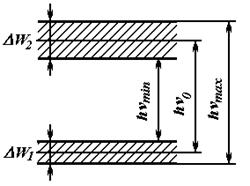
На рис.2.1 представлена схема энергетических зон, где заштрихованы разрешенные зоны; между ними расположены запрещенные зоны шириной ΔW, ΔW₁... По оси ординат отложены величины энергии электронов W, а по оси абсцисс — расстояния х в направлении толщины кристалла. Ширина верхней запрещенной зоны ΔW равна разности энергий между нижним уровнем («дном») зоны проводимости W_np и верхним уровнем («потолком») валентной зоны W_B.

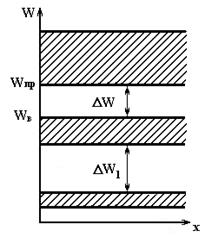
Рис. 2.1 Схема энергетических зон полупроводника

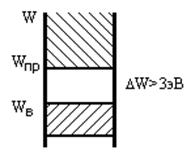
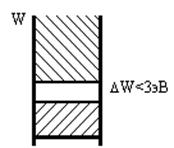
В металлах, где все валентные электроны являются электронами проводимости; запрещенная зона отсутствует, и валентная зона частично перекрывается с зоной проводимости (рис. 2.2а). При ΔW<3 эВ твердое тело условно принято считать полупроводником (рис. 2.2в), при ΔW>3 эВ — диэлектриком (рис. 2.2б).

а)	б)	в)

Рис.2.2 Распределение энергетических зон:

а) в металле; б) в диэлектрике; в) в полупроводнике

2.3. Свободные носители зарядов в полупроводниках

Полупроводники представляют собой вещества, которые по своей удельной электрической проводимости (10^-6—10^-8 Ом^-1см^-1) являются промежуточными между проводниками и диэлектриками. Их удельная проводимость сильно зависит от температуры и концентрации примесей, а во многих случаях — и от различных внешних воздействий (света, электрического поля и др.). По своему составу полупроводники можно разделить на простые, если они образованы атомами одного химического элемента (например, германия Ge, кремния Si, селена Se), и сложные, если они являются химическим соединением или сплавом двух или нескольких химических элементов (например, антимонид индия InSb, арсенид галлия GaAS и др.).

Полупроводник приобретает электропроводность в том случае, если электронам, находящимся на энергетических уровнях внутри валентной зоны, внешним воздействием (нагреванием, освещением и т. д.) сообщается энергия (равная или большая ΔW), достаточная для перехода электронов из валентной зоны в зону проводимости. Электрон, находящийся в зоне проводимости и являющийся подвижным носителем заряда, называется электроном проводимости. Одновременно в валентной зоне из-за ухода электронов появляются свободные уровни и, следовательно, валентные электроны также получают возможность переходить с одних уровней на другие (свободные) и тем самым изменять свою энергию. Это означает, что валентные электроны, так же как и электроны проводимости, могут создавать ток через полупроводник.

При уходе валентного электрона образуется положительный заряд, равный по абсолютной величине заряду электрона; этот положительный заряд следует относить к валентной связи между двумя атомами, нарушенной уходом валентного электрона.

Незанятое электроном энергетическое состояние в валентной зоне, обладающее положительным зарядом, принято называть дыркой. При создании электрического поля в полупроводнике валентные электроны переходят из заполненных связей в соседние незанятые связи в направлении увеличения потенциала поля, что эквивалентно перемещению дырок в обратном направлении.

Итак, в полупроводниках возможны два вида электропроводности - электронная - в результате перемещения электронов проводимости и дырочная -в результате перемещения дырок.

По типу электропроводности при любом способе возбуждения различают:

1. собственные полупроводники (полупроводники i-типа, индекс «i» означает «intrinsic» — собственный или беспримесный), если их электропроводность обусловлена генерацией пар электрон—дырка;

2. примесные полупроводники с электронной проводимостью (полупроводники n-типа), если их электропроводность обусловлена в основном перемещением электронов, появившихся в результате ионизации атомов донорной примеси (отдающей электроны),

3. примесные полупроводники с дырочной проводимостью (полупроводники p-типа), если их проводимость обусловлена в основном перемещением дырок, возникших в результате ионизации атомов акцепторной примеси (связывающей электроны).

Если в собственный четырехвалентный кремний (или германий) ввести атом пятивалентного элемента, например фосфора (Р), сурьмы (Sb) или мышьяка (As), то четыре из пяти валентных электронов введенного атома примеси вступят в связь с четырьмя соседними атомами Si (или Ge) и образуют устойчивую оболочку из восьми электронов, а пятый электрон оказывается слабо связанным с ядром атома примеси. Этот «лишний» (условно «примесный») электрон движется по орбите значительно большего размера и легко (при небольшой затрате энергии) отрывается от примесного атома, т.е. становится свободным. При этом неподвижный атом превращается в положительный ион. Свободные электроны «примесного» происхождения добавляются к свободным электронам исходного собственного полупроводника, поэтому электрическая проводимость полупроводника при большой концентрации примеси становится преимущественно электронной. Такие примес-ные полупроводники называются электронными или n-типа (от слова negative - отрица-тельный). Примеси, обусловливающие электронную проводимость, называют донорными.

Если в собственный полупроводник, например кремний, ввести примесный атом трехвалентного элемента, например бора (В), галлия (Ga) или алюминия (Al), то все валентные электроны атома примеси включатся в ковалентные связи с тремя из четырех соседних атомов собственного полупроводника. Для образования устойчивой восьми-электронной оболочки (четыре парные связи) примесному атому не хватает одного электрона. Им может оказаться один из валентных электронов, который переходит от ближайших атомов кремния. В результате у такого атома кремния появится «вакансия», т.е. дырка, а неподвижный атом примеси превратится в ион с единичным отрицательным зарядом. Дырки примесного происхождения добавляются к собственным дыркам, так что при большой концентрации примеси проводимость полупроводника становится преимущественно дырочной. Такие примесные полупроводники называют дырочными или p-типа (от слова positive - положительный). Примеси, обеспечивающие получение большой концентрации дырок, называют акцепторными («захватывающие» электроны).

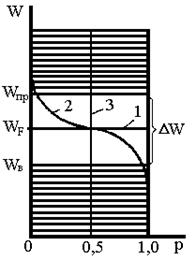
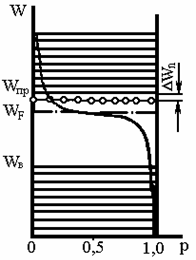
На рис.2.3 а показана зонная модель собственного полупроводника. Между валентной зоной и зоной проводимости находится запрещенная зона. Посередине запрещенной зоны располагается уровень Ферми W_f — энергетический уровень, функция Ферми для которого учитывает вероятность заполнения, равную 0,5 при температурах, отличных от 0К.

На оси абсцисс (рис.2.3а) отложена вероятность p заполнения электронами соответст-вующих энергетических уровней. Эта вероятность определяется законом Ферми—Дирака.

При температуре 0 К, все валентные уровни заполнены с вероятностью, равной единице, а вероятность заполнения любого уровня зоны проводимости равна нулю, что свидетельствует об отсутствии проводимости кристалла (рис.2.3 а, прямая 1).

При комнатной температуре (300 К) происходит термогенерация носителей. Часть валентных электронов переходит в зону проводимости, и вероятность заполнения уровня валентной зоны оказывается меньше единицы (рис.2.3 а, кривая 2). Кривая распределения Ферми-Дирака всегда симметрична относительно уровня Ферми W_F.

При высокой температуре (Т®¥) вероятность заполнения любого разрешенного уровня Р (W) ®0,5 (рис. 2.3 а, прямая 3).

а)	б)	в)

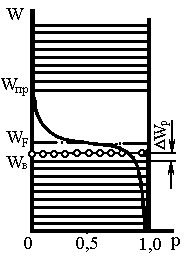
Рис. 2.3. Зонная модель и функция вероятности заполнения электронами энергетических уровней:

а) в собственном полупроводнике;

б) в полупроводнике n-типа;

в) в полупроводнике p-типа.

На рис.2.3 б показана зонная модель примесного полупроводника с электропровод-ностью n-типа. По этой модели валентные электроны атомов донорной примеси располагаются на так называемых примесных уровнях, которые находятся ниже дна зоны проводимости на величину энергии DW_n. При комнатной температуре почти все электроны с примесного уровня переходят в зону проводимости. В результате заполнения зоны проводимости электронами примесных уровней кривая распределения Ферми—Дирака, а также уровень Ферми W_F смещаются вверх.

На рис.2.3 в показана зонная модель примесного полупроводника с электропровод-ностью p-типа. У этого полупроводника на расстоянии DW_p от валентной зоны появляется примесный уровень, который заполняют валентные электроны, захватываемые трехвалентными атомами. При комнатной температуре многие валентные электроны переходят на примесный уровень, что приводит к появлению большого количества дырок в валентной зоне. В результате кривая распределения Ферми—Дирака и уровень Ферми смещаются вниз. Расположение уровня Ферми относительно примесного уровня зависит от концентрации акцепторной примеси.

В собственном полупроводнике концентрации электронов и дырок одинаковы. В примесных полупроводниках они отличаются на много порядков, поэтому носители заряда с большей концентрацией называют основными, а с меньшей - неосновными. В полупроводнике n-типа основные носители - электроны, а в полупроводнике p-типа -дырки.

Значения концентраций свободных электронов и дырок устанавливаются (состояние равновесия) в результате действия двух противоположных процессов: процесса генерации носителей (прямой процесс) и процесса рекомбинации электронов и дырок (обратный процесс).

Рекомбинация означает, что свободный электрон восстанавливает ковалентную связь (устраняет вакансию). Этот процесс можно представить на энергетической диаграмме как переход электрона из зоны проводимости на свободный энергетический уровень валентной зоны. Результатом восстановления связи является одновременное исчезновение свободного носителя отрицательного заряда и свободной положительно заряженной дырки, т.е. исчезновение пары свободных носителей с противоположным знаком заряда, каждый из которых до этого мог участвовать в создании электрического тока. В состоянии равновесия скорость генерации носителей заряда равна скорости рекомбинации.

2.4. Равновесная концентрация СНЗ в примесных и беспримесных полупроводниках

2.4.1. Равновесная концентрация зарядов в собственном полупроводнике

Вероятность p нахождения свободного электрона в энергетическом состоянии W определяется статистической функцией Ферми— Дирака:

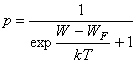                                                                                                      (2.1)

где W_F — уровень Ферми; kT— средняя энергия теплового движения микрочастицы при температуре Т К; k=1,38×10^-23 Дж/К — постоянная Больцмана.

В интервале значений энергий от W до W+dW число энергетических уровней, на которых могут находиться электроны проводимости, равно

                                                                                   (2.2)

где m_n- эффективная масса электрона проводимости (в германии и кремнии, например, она составляет 0,22-0,33 от массы покоя электрона соответственно), h = 6,62×10^-34 Дж×с - постоянная Планка.

 Из соотношений (2.1), (2.2) можно определить концентрацию электронов проводимости для собственного полупроводника:

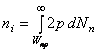                                                                                                               (2.3)

При умеренных температурах, когда , концентрация электронов проводимости для собственного полупроводника

                                                                           (2.4)

где n_пр — эффективная плотность состояний в зоне проводимости (N_пр=5×10¹⁹ см^-3 для германия, N_пр=2×10²⁰ см^-3 для кремния), ΔW - ширина запрещенной зоны (ΔW =0,66 эВ для германия, ΔW=1,12 эВ для кремния).

Число дырок в идеальной кристаллической решетке собственного полупроводника равно числу свободных электронов:

p_i = n_i.                                                                                                                             (2.5)

На основании приведенного соотношения можно сосчитать, что при комнатной температуре, т. е. при T=300 К, число свободных электронов в германии n_i = 2,5×10¹³ см ^-3.

Поскольку в кристаллической решетке германия в каждом 1 см³ объема находится 4,4×10²² атомов, один свободный электрон приходится на 1 млрд. атомов вещества. В кремнии при той же температуре число свободных электронов на три порядка меньше вследствие более высокой энергии ионизации: n_i = 1,4×10¹⁰ см^-3.

Полученные величины концентраций электронов и дырок представляют собой результат динамического равновесия двух процессов — генерации и рекомбинации подвижных носителей заряда.

Скорость рекомбинации, т. е. число исчезающих в единицу времени электронно-дырочных пар, определяется свойствами полупроводника; кроме того, она пропорциональна концентрации электронов и дырок, так как чем больше число носителей заряда, тем вероятнее их встреча, завершающаяся рекомбинацией. Таким образом, скорость рекомбинации

_рек = γ_i × n_i × p_i = γ_i × n²_i

где γ_i — коэффициент рекомбинации, определяемый свойствами полупроводника.

Скорость генерации — число освобождающихся в единицу времени электронно-дырочных пар — зависит от температуры полупроводника и ширины его запрещенной зоны.

В стационарном режиме должно существовать динамическое равновесие — скорость генерации должна равняться скорости рекомбинации:

_ген = γ× n_i².

Отсюда

n_i² = _ген /γ.

2.4.2. Равновесная концентрация зарядов в примесном полупроводнике

2.4.2.1. Полупроводник с донорной примесью

 Обозначим концентрацию донорной примеси N_д. Так как ее энергия ионизации DW_n очень невелика (DW_n » 0,01 эВ), то при комнатной и даже более низкой температуре практически все примесные атомы оказываются ионизированными; кроме того, согласно соотношению (2.4), ионизируется некоторая часть атомов основного вещества n*_i. Таким образом, концентрация электронов проводимости в полупроводнике с донорной примесью

n_n = N_д + n*_i,                                                                                                                  (2.6)

т.е. она больше, чем в беспримесном полупроводнике. Обычно концентрация донорной примеси N ³ n*_i и

n_n » N_д                                                                                                                             (2.7)

Поскольку скорость рекомбинации носителей заряда в полупроводнике пропорциональна концентрации электронов и дырок:

ν_реκ = γ×n_n ×p_n,

а скорость генерации при малых концентрациях примеси остается той же, что и в собственном полупроводнике:

_гeн = γ×n_i²,

то при динамическом равновесии, когда _гeн =_рeк,

_гeн = n_i²

Отсюда равновесная концентрация дырок в примесном полупроводнике:

p_n =n_i²/n_n =n_i²/N_д.                                                                                                                                               (2.8)

т. е. она значительно ниже, чем в беспримесном полупроводнике.

Положение уровня Ферми W_F в полупроводнике n-типа можно определить с помощью соотношений (2.1) и (2.4). Для частичной ионизации примесей получаем

                                                                                     (2.9)

При Т=0 К уровень Ферми находится посередине между дном зоны проводимости W_пр и уровнем доноров W_n, а с повышением температуры он постепенно смещается к середине запрещенной зоны.

2.4.2.2.Полупроводник с акцепторной примесью

Пусть концентрация акцепторов равна N_a. Так как акцепторные атомы при комнатной температуре практически все ионизированы, то концентрация дырок

p_p= N_a+ p_i*,                                                                                                                    (2.10)

где p_i* — концентрация дырок, обусловленная ионизацией атомов основного вещества.

Концентрация электронов определяется соотношением, аналогичным (2.8):

pi* £ N_a и p_p » N_a (2.11)

Положение уровня Ферми W_Fp в полупроводнике p-типа определяется соотношением, аналогичным (2.9):

                                                                                        (2.12)

При Т=0 К уровень Ферми находится между потолком валентной зоны W_в и уровнем акцепторов W_p, с повышением температуры он смещается к середине запрещенной зоны.

2.5. Движение СНЗ в электрическом поле

В собственном полупроводнике при Т=0К электроны и дырки отсутствуют и внешнее напряжение не вызывает в нем ток. При Т>0К в отсутствии электрического поля электроны и дырки движутся хаотически. Если же к полупроводнику приложить внешнее напряжение, то внутри него возникает упорядоченное движение электронов в направлении положительного градиента потенциала du/dx, а дырок — в обратном направлении.

В полупроводнике под влиянием различных энергетических воздействий может возникнуть неравновесная концентрация зарядов. После прекращения воздействия избыточные носители постепенно рекомбинируют и концентрация вновь становится равновесной.

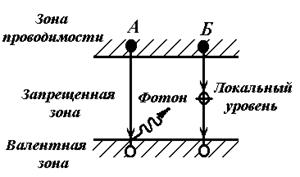
В полупроводниковых диодах и транзисторах неравновесные носители заряда образуются при прохождении электрического тока. Процесс рекомбинации электронов и дырок может происходить либо прямым путем — из зоны в зону (рис. 2.4, случай А), либо через локальные энергетические уровни в запрещенной зоне, называемые центрами рекомбинации или ловушками (рис. 2.4, случай Б). Второй механизм рекомбинации является более вероятным, чем первый, так как здесь движется лишь один носитель заряда, а другой неподвижен, и вероятность сближения их на расстояние, при котором возможна рекомбинация (~0,1 нм), значительно выше, чем в случае, когда оба носителя заряда перемещаются по кристаллической решетке.

Рис.2.4. Процесс рекомбинации электронов и дырок

Центры рекомбинации создаются примесями, имеющими энергетические уровни вблизи середины запрещенной зоны полупроводника. К таким примесям относятся медь, никель, кобальт, золото. Дефекты решетки, донорные и акцепторные примеси также могут создавать центры рекомбинации.

Рекомбинация может происходить не только в объеме, но и на поверхности полупроводника, а скорость ее протекания может быть различной даже в одном и том же типе полупроводника. Время жизни неравновесных носителей заряда в германии и кремнии может составлять широкий диапазон значений (от долей микросекунды до тысяч микросекунд) в зависимости от количества и типа примеси, а также от состояния и чистоты поверхности. Последнее объясняется тем, что на поверхности полупроводника всегда имеются различные дефекты структуры, а также пленки окислов и молекулы адсорбированных газов, которые могут образовывать большое число локальных уровней, вызывающих интенсивный процесс рекомбинации электронно-дырочных пар. Роль поверхностной рекомбинации тем выше, чем больше отношение площади поверхности образца к объему, т. е. чем меньше размеры образца. Условимся считать в дальнейшем, что представляет собой эффективное время жизни, определяемое как объемной, так и поверхностной рекомбинацией носителей заряда, а для неоднородного полупроводника — также скоростью и направлением движения носителей заряда.

2.6. Дрейфовая скорость, подвижность

 Электроны и дырки в кристалле находятся в состоянии хаотического теплового движения. При возникновении электрического поля на хаотическое движение накладывается компонента направленного движения, обусловленного действием этого поля. В результате электроны и дырки начинают перемещаться вдоль кристалла — возникает электрический ток, который называют дрейфовым током.

При движении в полупроводнике электроны периодически сталкиваются с колеблющимися атомами кристаллической решетки. Обозначив среднее время свободного пробега электронов  и полагая, что движение электронов в промежутке между столкновениями является равноускоренным, а при столкновении с решеткой они теряют приобретенную под действием поля скорость, получим выражение для средней направленной скорости электронов в полупроводнике, называемой скоростью дрейфа:

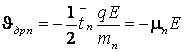,                                                                                         (2.15)

где q=1,6^.10^-19 Кл — заряд электрона.

Величина

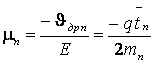                                                                                                (2.16)

называется подвижностью электрона проводимости.

Тому же значению (2.15) будет равно и среднее по всему коллективу значение направленного движения. Таким образом, скорость дрейфа пропорциональна напряженности поля.

Аналогичные рассуждения приводят к следующим выражениям для скорости дрейфа и подвижности дырок:

                                                                                            (2.17)

и

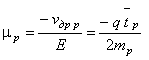
Подвижность дырок в полупроводнике определяется средней направленной скоростью дырок ν_ρ , приобретаемой под действием электрического поля Е.

 Подвижность электронов зависит от свойств кристаллической решетки, наличия примесей и температуры. При комнатной температуре подвижность электронов в германии, как показывают измерения, равна 3900 см²/(В^.с), а в кремнии — 1350 см²/(В^.с). С ростом температуры вследствие усиления тепловых колебаний решетки подвижность электронов уменьшается. Примеси не оказывают существенного влияния на величину подвижности при невысоких концентрациях (до 10¹⁵-10¹⁶ см^-3). При более высоких концентрациях подвижность носителей заряда начинает снижаться вследствие рассеяния электронов на ионах примеси. При слабых полях (до 100 В/см в германии) подвижность не зависит от напряженности электрического поля. При значительном увеличении напряженности поля и соответственно дрейфовой скорости электронов эффективность их взаимодействия с решеткой возрастает, электроны теряют во время столкновений относительно большую энергию и их подвижность начинает снижаться. В германии при напряженности поля порядка 8 кВ/см подвижность уменьшается пропорционально 1/E и с повышением напряженности поля дрейфовая скорость электронов более не возрастает, достигнув максимального значения _max = 6^.10⁶ см/с. При напряженности поля порядка 100 кВ/см возникает лавинная ионизация атомов решетки, число носителей заряда и ток резко возрастают, наступает пробой полупроводника.

В кремнии максимальное значение дрейфовой скорости _max = 8,5^.10⁶ см/с.

Подвижность дырок, по данным измерений, значительно ниже подвижности электронов. С ростом температуры подвижность дырок снижается несколько быстрее, чем подвижность электронов.

2.7. Контрольные вопросы:

1. Что называют энергетической зоной?

2. Какие зоны называют валентными, зонами проводимости, запрещенными зонами?

3. Какой электрон называют электроном проводимости? Что такое дырка?

4. Какие типы электропроводности полупроводников вы знаете? Охарактеризуйте их.

5. Что такое дрейфовая скорость?

6. Что называют подвижностью электрона (дырки)?

ЛЕКЦИЯ № 3

p-n переход в равновесном и неравновесном состоянии

1. Концептуальная диаграмма.

2. Электрические переходы.

3. Условие равновесия электрического перехода. Перенос заряда в электрическом переходе, ток диффузии, ток дрейфа, ток рекомбинации.

4. Электрические и геометрические параметры p-n перехода.

5. Способы нарушения равновесия.

6. Уравнение тока через p-n переход.

7. Контрольные вопросы.

3.1. Концептуальная диаграмма

3.2. Электрические переходы

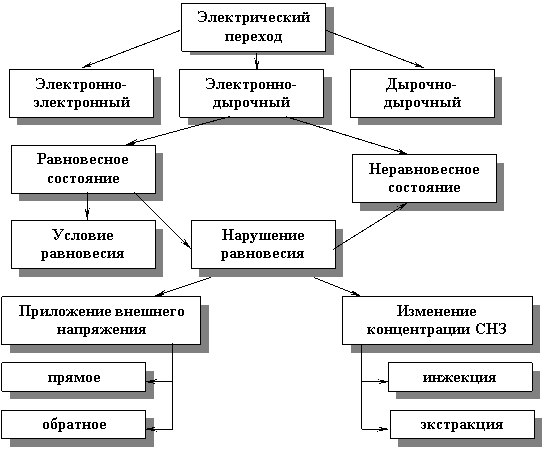
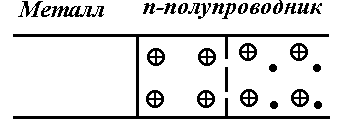
Электрическим переходом называется слой в полупроводнике между двумя областями с различными типами электропроводности (n-полупроводник, p-полупроводник, металл, диэлектрик) или разными величинами удельной электрической проводимости. Если переход создается между двумя областями полупроводника, одна из которых имеет электропроводность n-типа, а другая p-типа, то такой переход называется электронно-дырочным или p-n-переходом.

Переход между двумя областями полупроводника n-типа, обладающими различной удельной проводимостью, называется электронно-электронным или n-n⁺-переходом, причем знак «+»относится к области с более высокой удельной электрической проводимостью; аналогично переход между двумя областями полупроводника p-типа с различной удельной электрической проводимостью называется p-p+-переходом. Широкое применение получили переходы металл - полупроводник.

Электрические переходы могут создаваться как на основе полупроводников с оди-наковой шириной запрещенной зоны, т.е. одинаковых материалов (гомопереходы), так и с различными значениями ширины (гетеропереходы). Заметим, что предельным случаем ге-тероперехода является контакт металл - полупроводник (у металла нет запрещенной зоны).

Если линейные размеры перехода, определяющие площадь последнего, значительно больше его толщины, то такой переход называется плоскостным; если же линейные размеры меньше, чем длина, определяющая физические процессы в переходе (например, диффузионная длина), то переход называют точечным.

3.3. Условие равновесия электрического перехода. Перенос заряда в электрическом переходе, ток диффузии, ток дрейфа, ток рекомбинации

Равновесное состояние имеет место при отсутствии внешнего напряжения (U = 0). Примем, что в рассматриваемой p-n-структуре концентрация дырок в дырочной области выше, чем в электронной (p_p>>р_п), а концентрация электронов в электронной области выше, чем в дырочной (п_п>>п_р), на границе электронной и дырочной областей существует градиент концентрации носителей заряда. В этом случае возникает диффузия основных носителей — электронов из n-области в p-область. Подобным же образом дырки — основные носители p-области — диффундируют во встречном направлении из p-области в n-область, ибо р_р>>р_п. В результате этих процессов нарушается электрическая нейтральность областей полупроводника по обе стороны от контакта. Носители заряда, перешедшие через контакт, становятся неосновными и рекомбинируют с основными носителями той области, куда они перешли, что приводит к образованию по обе стороны от контакта слоев с малой концентрацией подвижных носителей и, следовательно, с большим сопротивлением.

Слой полупроводника, в котором концентрация основных носителей оказывается уменьшенной, называется обедненным или запирающим. В пределах обедненного слоя по одну сторону от контакта в p-области образуется нескомпенсированный отрицательный пространственный заряд ионизованных акцепторов, в то время как по другую сторону контакта в n-области возникает положительный пространственный заряд ионизованных доноров. На рис. 3.1, а для упрощения носители и атомы примесей показаны только в области перехода.

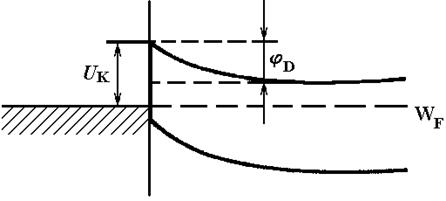
 Это приводит к появлению контактной разности потенциалов и_к = j_n - j_р в пределах p-n-перехода (рис.3.1,г). и электрического поля (вектор напряженности Е_к) (рис.3.1,д). Причем возникшее контактное поле будет противодействовать дальнейшему диффузионному перемещению основных носителей обеих областей через p-n-переход. Как видно, в п — p-переходе возникает потенциальный барьер, препятствующий диффузионному переходу носителей. На рис. 3.1,г изображен барьер для электронов, стремящихся за счет диффузии перемещаться слева направо (из области п в область р). Если бы мы отложили вверх положительный потенциал, то получили бы изображение такого же потенциального барьера для дырок, которые стремятся диффундировать справа налево (из области p в область n). Высота барьера равна контактной разности потенциалов и обычно составляет десятые доли вольта.

На рис. 3.1,в показано распределение концентрации носителей в p-n-переходе.

Вместе с тем под действием поля E_K возникает дрейфовое движение через границу неосновных носителей зарядов: дырок из n-области в p-область и электронов в обратном направлении. На рис. 3.1,а такое перемещение неосновных носителей (дрейф) показано также стрелками. При постоянной температуре p-n-переход находится в состоянии динамического равновесия. Каждую секунду через границу в противоположных направлениях диффундирует определенное число электронов и дырок, а под действием поля столько же их дрейфует в обратном направлении.

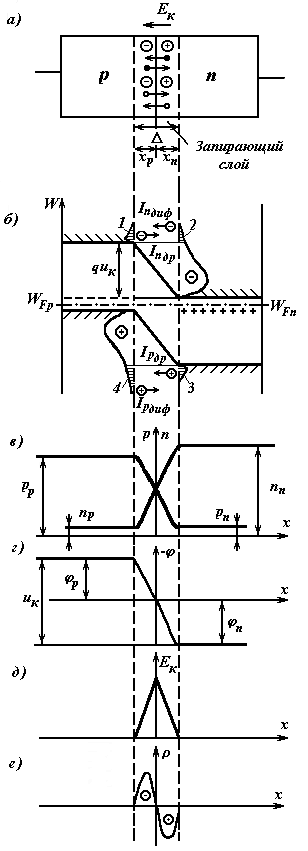
Рис. 3.1. Равновесный p-п переход:

а) схема перехода; б) энергетическая диаграмма перехода;

в) концентрация подвижных зарядов; г) распределение потенциала;

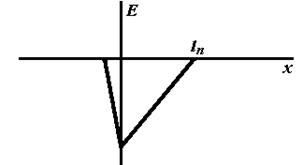
д) напряженность поля; е) концентрация неподвижных зарядов

Взаимная рекомбинация подвижных носителей в p-n-переходе происходит с такой интенсивностью , что в любой точке слоя, обедненного подвижными носителями , будет примерное равенство: pn » n_i². Данное состояние полупроводника называется равновесным.

Условие равновесия в полупроводнике выглядит следующим образом:

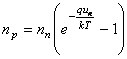                                                                                                    (3.1)

Перемещение носителей за счет диффузии — это диффузионный ток (I_диф), а движение носителей под действием поля — ток дрейфа (I_др).

Каждый из токов I_диф и I_др имеет электронную и дырочную составляющие

                                                                                                  (3.2)

                                                                                                       (3.3)

 Значения этих составляющих различны, так как зависят от концентрации и подвижности носителей.

Электронный дрейфовый ток I_{n др} создается неосновными носителями p-области — электронами зоны проводимости (рис.3.1.б 1), которые под действием ускоряющего электрического поля напряженностью Е_к, образованного контактной разностью потенциалов U_K, выводятся в n-область. Переход для электронов p-области является неограниченным стоком, который вытягивает все электроны, поступающие к его поверхности из толщи p-области в результате их диффузии из объема глубиной, равной диффузионной длине L_n электронов в p-области. Одновременно внутри p-области в результате генерации пар образуются новые электроны.

Определим плотность дрейфового электронного тока, как j_ηдр =r_{n n} = —qn_pL_n/τ_n, где _п — средняя скорость электронов; r_n — объемная плотность заряда электронов; — диффузионная длина электронов в p-области; τ_n — среднее время жизни электронов, D_n- коэффициент диффузии электронов; следовательно,

                                                                                                      (3.4)

Электронный диффузионный ток I_{n диф} создается основными носителями n-области — электронами зоны проводимости, которые вводятся через p-n-переход в p-область полупроводника (2, рис. 3.1., б). Ток возникает благодаря тому, что концентрация электронов в n-области п_п значительно больше п_р и поэтому можно определить плотность этого тока в переходе как обусловленного диффузией:

(3.5)

Ток I_{n диф} создается лишь теми электронами, которые располагаются в зоне проводимости n-области на сравнительно высоких уровнях и обладают достаточно большой энергией, чтобы преодолеть энергетический барьер в p-n-переходе (заштрихованы на рис. 3.1., б). В p-области эти электроны становятся неосновными носителями заряда.

Электронные токи I_{n др} и I_{n диф} в состоянии равновесия равны между собой и плотность результирующего электронного тока через переход равна нулю.

 Дырочный дрейфовый ток I_{р др} создается неосновными носителями — дырками валентной зоны n-области (3, рис. 3.1., б), которые, подойдя в результате диффузионного движения к переходу, под действием ускоряющего контактного поля в нем переходят в p-область, где становятся основными носителями. Плотность дырочного дрейфового тока

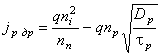(3.6)

Дырочный диффузионный ток I _{р диф} возникает в результате прохождения основных носителей p-области — дырок валентной зоны через переход в n-область, где они становятся неосновными носителями (4, рис. 3.1., б). Необходимо отметить, что дырки обладают более высокой энергией, если они занимают более низкий энергетический уровень в валентной зоне; чем ниже этот уровень, тем меньшее число дырок его занимает.

Плотность дырочного диффузионного тока

(3.7)

Высота потенциального барьера всегда устанавливается именно такой, чтобы наступило равновесие, т. е. диффузионный ток и ток дрейфа компенсируют друг друга. В установившемся режиме, т. е. при динамическом равновесии перехода, эти токи равны и противоположны по направлению. Поэтому полный ток через переход равен нулю, что и должно быть при отсутствии внешнего напряжения.

 (3.8)

 Поскольку суммарный ток равен нулю, система должна характеризоваться единым уровнем Ферми W_F (рис. 3.1, б).

В запирающем слое могут протекать процессы генерации подвижных зарядов и их рекомбинации. Процесс рекомбинации частиц обусловлен тем, что частицы с энергией недостаточной для преодоления потенциального барьера, проникая на некоторую глубину в запирающий слой, теряют свою скорость в поле перехода и выносятся этим полем обратно. В результате значительного времени пребывания таких частиц в запирающем слое увеличивается вероятность их рекомбинации через ловушки и другие дефекты структуры и появляется ток рекомбинации I_рек.

В состоянии динамического равновесия (U=0) встречные потоки носителей компенсируются, так что ток генерации равен току рекомбинации.

3.4. Электрические и геометрические параметры p-n перехода

3.4.1. Высота потенциального барьера и контактная разность потенциалов

Высота потенциального барьера на переходе равна контактной разности потенциалов qи_к.

                                                                                                 (3.9)

Последняя формула имеет наглядный физический смысл, так как показывает, что контактная разность потенциалов определяется отношением концентрации носителей с одним знаком заряда: основных в одной области структуры и неосновных - в другой. Результат не зависит от выбора знака заряда (электронов или дырок).

3.4.2. Соотношение между концентрациями

Соотношение между концентрациями по обе стороны перехода легко получить, потенцируя выражение (3.9):

                                                                                                               (3.10)

                                                                                                                (3.11)

3.4.3. Ширина запирающего слоя

Обозначим (рис. 3.1) ширину обедненного слоя D, а его части в p- и n-полу-проводнике х_p и х_n.

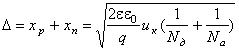.                                                                        (3.12)

где ε₀ — диэлектрическая постоянная; ε — относительная диэлектрическая проницаемость кристалла; N_д»n_n и N_a»р_p — концентрация ионизированных атомов донорной и акцепторной примесей

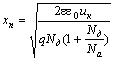_,                                                                                                                                                (3.13)

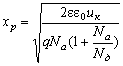(3.14)

Ширина запирающего слоя, к которому приложено внешнее напряжение U

(3.15)

3.4.4. Вольт-амперная характеристика p-n-перехода

Вольт-амперная характеристика p-n-перехода является нелинейной и имеет асимметричный характер.

Уравнение вольт-амперной характеристики выводится при следующих допущениях:

— рассматривается p-n-переход настолько тонкий, что внутри него можно было бы пренебречь процессами генерации и рекомбинации носителей;

— однородные p- и n-области считаются настолько длинными, что инжектированные в них носители полностью рекомбинируют, и через контакты выводов протекает исключительно ток основных носителей; ,

— движение носителей считается одномерным — вдоль оси х;

— все внешнее напряжение приложено к p-n-переходу.

В общем виде выражение для полного тока можно записать следующим образом:

                                                                                                          (3.16)

где I₀ — обратный ток, называемый тепловым током или током насыщения (так как он не меняется с изменением U).

Выражение (3.16) описывает вольт-амперную характеристику идеализированного p-n-перехода.

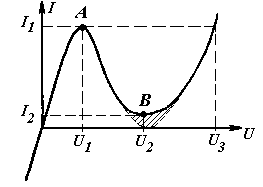
На рис. 3.2 приведена вольт-амперная характеристика идеализированного p-n-перехода I=f(U), построенная в соответствии с полученной формулой (3.16).

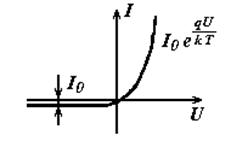
Рис. 3.2. Вольт-амперная характеристика электронно-дырочного перехода

При прямом напряжении можно пренебречь единицей по сравнению с экспоненциальной составляющей:

                                                                                                               (3.17)

При обратном напряжении порядка 0,1-0,2 В экспоненциальный член в формуле полного тока намного меньше единицы и им можно пренебречь. Тогда I»I₀.

3.4.5. Статическое и дифференциальное сопротивления

Дифференциальное сопротивление определяется выражением R_диф = dU/dI и характеризует крутизну ВАХ в рассматриваемой точке. Для идеализированного перехода по формуле (3.16) можно получить аналитическое выражение:

                                                                                                       (3.18)

Для прямой ветви ВАХ, где I>>I₀,

                                                                                                                  (3.17а)

При комнатной температуре . Выразив I в миллиамперах, получим широко используемую для оценок формулу:

                                                                                                     (3.19)

Статическое сопротивление определяется выражением R_ст = U/I.

Зависимость R_диф и статического сопротивления R_ст от напряжения показана на рис.3.3. При прямом напряжении R_диф мало и убывает с ростом напряжения, а при обратном очень велико. Дифференциальное сопротивление называют также сопротивлением переменному току.

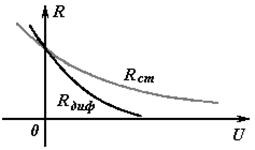
Рис. 3.3. Зависимость динамического R_диф и статического сопротивления R_ст от напряжения

3.4.6. Барьерная емкость

Обедненный слой перехода подобен конденсатору, так как в нем «связаны» равные по величине, но противоположные по знаку заряды ионов акцепторов Q_a и доноров Q_д (|Q_a|=Q_д). Так как эти заряды определяют потенциальный барьер, то и емкость называется дифференциальной барьерной.

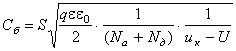                                                                         (3.20)

Зависимость С_б от напряжения (вольт-фарадная характеристика) показана на рис.3.4. Значение барьерной емкости при U= 0.

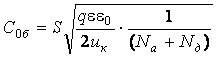                                                                              (3.21)

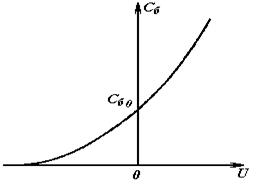
Рис.3.4. Вольт-фарадная характеристика p-n-перехода

Используя (3.21), можно переписать (3.20) в более простом виде:

.                                                                                                   (3.22)

3.4.7. Диффузионная емкость

Эта емкость связана с наличием в р- и n-областях избыточных носителей.

Процесс накопления избыточных зарядов - инерционный процесс, связанный с временем жизни неосновных носителей. Это накопление принято характеризовать дифференциальной диффузионной емкостью, которая учитывает изменение избыточных носителей (дырок и электронов) в обеих областях при изменении напряжения:

(3.23)

Для идеализированного p-n-перехода -дифференциальное сопротивление R_диф (3.17 а), поэтому

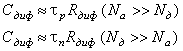(3.24)

Диффузионная емкость растет с увеличением времени жизни неосновных носителей (t_р, t_n) или диффузионной длины (,), так как при этом происходит увеличение числа накопленных избыточных носителей в областях. В отличие от барьерной емкости диффузионная емкость зависит от частоты приложенного переменного напряжения. На высоких частотах, когда период напряжения становится меньше времени жизни, инжектируемые носители не успевают накапливаться в областях.

Следует отметить еще одно важное отличие С_диф от барьерной емкости. Через барьерную емкость протекают токи смещения, в то время как через диффузионную емкость - ток носителей. Диффузионная емкость отражает инерционность процесса накопления и рассасывания избыточных носителей в областях р-n-структуры. Поэтому диффузионную емкость называют иногда «фиктивной» емкостью, формально позволяющей описать инерционные свойства p-n-перехода. При этом также говорят о зарядке и разрядке этой емкости, как для обычного конденсатора.

3.5. Способы нарушения равновесия

Равновесие в переходе может быть нарушено либо путем изменения напряженности поля в переходе, либо путем изменения концентрации СНЗ.

Концентрация СНЗ как в переходе, так и прилегающих к нему областях полупроводника, может быть изменена, например, путем облучения полупроводника светом подходящей длины волны или путем любого другого воздействия, изменяющего скорость генерации (рекомбинации) свободных носителей заряда в этих областях. Она может быть изменена также путем принудительного введения (инжекции) в переход или, наоборот, путем принудительного извлечения (экстракции) из перехода СНЗ.

Напряженность поля в переходе может быть изменена путем приложения к переходу внешнего напряжения. Разность потенциалов на границах p-n перехода при этом или уменьшается, или возрастает, в зависимости от полярности приложенного напряжения. Если разность потенциалов на границах перехода уменьшается, то включение перехода называется прямым, если же она увеличивается, то включение называют обратным.

Поскольку концентрация СНЗ и напряженность поля величины, связанные между собой, поэтому, независимо от того на какую из них воздействует внешний фактор, изменяться будут обе эти величины. Напряженность поля и разность потенциалов на переходе становятся отличными от своих равновесных значений и в переходе, как и в прилегающих к нему областях, появляются избыточные или неравновесные СНЗ.

Независимо от причины, вызывающей нарушение равновесия в переходе силы действующие на каждый из носителей зарядов, оказываются не скомпенсированными, и электроны и дырки приходят в движение. Если внешняя цепь перехода замкнута, то в переходе возникает электрический ток, если же эта цепь разомкнута - на внешних выводах контактирующих полупроводников устанавливается некоторое напряжение (термоЭДС, фотоЭДС и т.д.).

 Действие большой группы электропреобразовательных полупроводниковых приборов основано на инициировании электрического тока в p-n переходах путем приложения к ним внешнего напряжения.

Действие фотоэлектрических полупроводниковых приборов основано на инициировании в переходе электрического тока (фотоЭДС) электромагнитным излучением (световым потоком).

3.6. Уравнение тока через p-n переход

Рассмотрим значение тока при приложении к p-n переходу обратного и прямого напряжения.

Внешнее напряжение U приложенное к p-n переходу называется обратным, если плюс источника питания подается к n-области, а минус — к p-области (рис. 3.6). Это напряжение оказывается той же полярности, что и контактная разность потенциалов u_к.

В этом случае поля складываются, потенциальный барьер между p- и n-областями возрастает и становится равным сумме u_к+U. Количество основных носителей, способных преодолеть отталкивающее действие результирующего поля, уменьшается. Соответственно уменьшается и ток диффузии. Под влиянием электрического поля, создаваемого источником напряжения U, основные носители будут оттягиваться от приконтактных слоев вглубь полупроводника. В результате ширина запирающего слоя увеличивается по сравнению с шириной в равновесном состоянии.

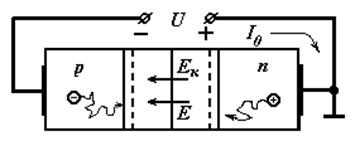
Рис. 3.6. Электронно-дырочный переход при подключении внешнего напряжения в обратном направлении

По мере увеличения внешнего напряжения остается все меньше подвижных носителей, способных преодолеть возрастающее тормозящее электрическое поле, и поэтому диффузионный ток через переход с увеличением обратного напряжения стремится к нулю. Эта зависимость имеет экспоненциальный характер:

                                                                                                         (3.25)

                                                                                                        (3.26)

где 1_по и I_р0 — диффузионный ток электронов из n-области и дырок из р-области при U=0.

При комнатной температуре q/kT = 39 В^-1 поэтому экспоненциальная зависимость очень сильная.

Согласно (3.2) и с учетом (3.25)и (3.26) получаем, что общий диффузионный ток

                                                                                 (3.27)

где I_диф0 = 1_р0 + I_n0.

Полный ток через переход равен разности диффузионного и теплового токов, поскольку они направлены в разные стороны. Практически все неосновные носители, подходящие к p-n-переходу, перемещаются в соседнюю область. Поэтому тепловой ток зависит от концентрации неосновных носителей в n-, p-областях и не зависит от напряжения, приложенного к p-n-переходу. Полный ток через p-n-переход

                                                                                                        (3.28)

При внешнем напряжении, равном нулю, I_диф0 = I₀. поэтому зависимость тока от обратного напряжения принимает вид :

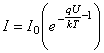                                                                                                           (3.29)

В случае приложения к p-n-переходу прямого напряжения U плюс источника подается к p-области, а минус — к n-области полупроводника. (рис. 3.7). В этом случае потенциальный барьер между p-n-областями уменьшается. Диффузия основных носителей через p-n-переход облегчается и во внешней цепи возникает ток, примерно равный току диффузии.

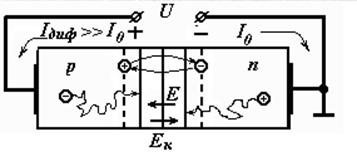
Рис. 3.7. Электронно-дырочный переход при подключении внешнего напряжения в прямом направлении

Так как прямое напряжение вызывает встречное движение дырок и электронов, то их концентрация в приконтактных областях возрастает, что приводит к уменьшению ширины запирающего слоя. Зависимость тока диффузии от прямого напряжения имеет вид

                                                                                                        (3.30)

Так же как и для обратного включения, тепловой ток не будет зависеть от напряжения. Полный ток через p-n-переход равен разности диффузионного и теплового:

                                                                       (3.31)

Формулу (3.31) можно считать универсальной, если принять, что внешнее напряжение в нее входит со своим знаком (прямое направление положительное, обратное — отрицательное).

При прямом смещении на р-n-переходе экспоненциальный член быстро возрастает и единицей в фигурных скобках можно пренебречь, поэтому I=I_диф. При обратном смещении на р-n-переходе экспоненциальный член стремится к нулю и ток через p-n-переход равен тепловому току I₀.

Зависимость тока I от внешнего напряжения, т. е. теоретическая вольт-амперная характеристика p-n-перехода, соответствующая формуле (3.31), показана на рис. 3.2.

На вольт-амперную характеристику сильно влияет температура. С изменением температуры смещается как обратная, так и прямая ветвь характеристики. Зависимость от температуры обратной ветви вольт-амперной характеристики определяется температурной зависимостью тока I₀.

При повышении температуры увеличивается число пар электрон — дырка, возникающих в p- и n-областях вследствие теплового движения атомов. Это приводит к увеличению теплового тока I₀   p-n-перехода.

Зависимость от температуры прямой ветви вольт-амперной характеристики при малых прямых напряжениях согласно выражению (3.31) определяется изменениями тока I₀ и показателя экспоненты. Прямой ток через p-n-переход возрастает с увеличением температуры вследствие увеличения тока I₀ . Но при больших прямых токах основную роль начинает играть проводимость полупроводникового кристалла, которая уменьшается с увеличением температуры, что приводит к снижению прямого тока.

3.7. Контрольные вопросы:

1. Какие электрические переходы вы знаете? Дайте им определения.

2. Какие процессы происходят в равновесном p-n-переходе. Запишите условие равновесия перехода.

3. Перечислите основные параметры электронно-дырочного перехода.

4. Каким образом можно нарушить равновесие в p-n-переходе?

5. Запишите выражения для тока при подключении к переходу внешнего напряжения.

ЛЕКЦИЯ № 4

Свойства p-n перехода В микроволновом диапазоне

4.1.Концептуальная диаграмма.

4.2.Эффект накопления заряда.

4.3.Диоды с накоплением заряда.

4.4.Технологические особенности изготовления диодов СВЧ диапазона.

4.5.Контрольные вопросы.

4.1. Концептуальная диаграмма

4.2. Эффект накопления заряда

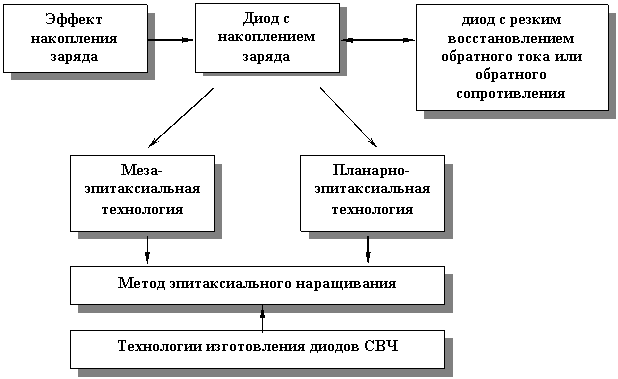Частотные свойства p-n-перехода определяются инерционностью процессов накапливания и рассасывания неосновных носителей заряда. Длительность этих процессов зависит от времени жизни неосновных носителей t_р, и при уменьшении этого времени частотные свойства диодов улучшаются.

Уменьшение времени жизни неосновных носителей достигается введением специальных примесей, энергетические уровни которых расположены вблизи середины запрещенной зоны («глубокие уровни») и увеличивают вероятность рекомбинации. Например, введение золота в кремний n-типа снижает время жизни дырок до (1—5)^.10^-9 с.

Быстродействие диодов с р-n-переходом зависит также от закона распределения примесей (доноров и акцепторов) по структуре. Исследование этого вопроса привело к созданию диодов с накоплением заряда (ДНЗ).

Рассмотрим в чем заключается эффект накопления заряда.

В случае подачи на диод коротких импульсов напряжения длительностью порядка единиц или долей микросекунды необходимо учитывать инерционность его включения и выключения, обусловленную переходными процессами. При протекании прямого тока через диод в его базе из-за инжекции накапливаются неосновные неравновесные носители заряда. Если изменить полярность приложенного к диоду напряжения с прямой на обратную, этот заряд рассасывается постепенно, и возникающий обратный ток вследствие высокой концентрации неосновных неравновесных носителей в базе окажется вначале значительно больше статического тока насыщения; величина его будет ограничиваться лишь внешней нагрузкой. Следовательно, при быстром переключении с прямого напряжения на обратное диод запирается не сразу. Это явление связано со спецификой работы p-n-перехода и обусловлено так называемым эффектом накопления заряда.

4.3. Диоды с накоплением заряда

Распределение концентрации примесей в диодах с накопление заряда показано на рис.4.1 а. Переход создается в результате диффузии акцепторной примеси в полупроводник n-типа с равномерной концентрацией донорной примеси N_д. Концентрация акцепторов N_a убывает по экспоненциальному закону и p-n-переход образуется вблизи сечения х₀ , где N_а=N_д. Концентрация дырок в р-области (рис. 4.1 б) определяется разностью N_a — N_д , а электронов в n-области — разностью N_д—N_a. Появление градиентов дырок и электронов вызовет диффузию. В n-области электроны (основные носители) начнут перемещаться из мест с большей концентрацией в места с меньшей концентрацией и вызовут нарушение электрической нейтральности. В правой части n-области, откуда ушли электроны, проявится положительный заряд донорных ионов, а в левой части — отрицательный заряд пришедших сюда электронов. Таким образом, в n-области возникает электрическое поле Е_n (см. рис.4.1б). Это поле вызовет в n-области дрейфовый ток электронов, направление которого противоположно диффузионному току. Когда дрейфовый ток станет равен диффузионному, наступает состояние равновесия, характеризуемое определенным значением напряженности электрического поля Е_п в n-области. Такие же процессы происходят в р-области, в которой появится поле с напряженностью Е_р. При подаче на диод прямого напряжения происходит инжекция дырок в n-область и электронов в p-область. Однако в ДНЗ электрическое поле Е_п препятствует диффузии инжектированных дырок вглубь n-области, поэтому они концентрируются (накапливаются) вблизи перехода. Аналогично инжектированные электроны накапливаются в р-области вблизи границы перехода. В отличие от диодов с равномерным распределением акцепторов и доноров, в ДНЗ инжектированные электроны и дырки оказываются «сгруппированными» около границ перехода.

а)
б)

Рис. 4.1 Распределение концентрации:

а) примесей; б) дырок в р-области

При скачкообразном изменении напряжения с прямого на обратное в момент t=0 на рис. 4.2 концентрация ранее инжектированных неосновных носителей на границах перехода должна уменьшиться. Появление градиента концентрации носителей вызовет диффузионное движение этих носителей, которые потом перейдут в другую область, так как электрическое поле в переходе является для неосновных носителей областей р-n-перехода ускоряющим. Появляется большой обратный ток перехода, который ограничивается сопротивлением цепи (горизонтальный участок на рис. 4.2). Для ДНЗ характерно то, что импульс обратного тока резко обрывается в некоторый момент времени t₁, когда хорошо «сгруппированные» около границ перехода неосновные носители заканчивают прохождение перехода. При надлежащем выборе закона распределения примесей в ДНЗ интервал времени от t₁ до t₂, при котором обратный ток достигнет значения 1,2I₀ (I₀ — обратный ток в статическом режиме), может составлять сотни или десятки пикосекунд. Поэтому ДНЗ называют также диодами с резким восстановлением обратного тока или обратного сопротивления.

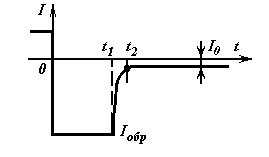
Рис.4.2. Переходная характеристика диода с накоплением заряда

При воздействии на ДНЗ синусоидального напряжения, вызывающего как прямой, так и обратный токи, форма импульсов обратного тока оказывается резко несинусоидальной. Несинусоидальная форма обратного тока обусловливает появление гармонических составляющих высокого порядка с большой амплитудой и возможность эффективного умножения частоты, т.е. спектр периодических импульсов тока содержит много гармоник, поэтому ДНЗ применяются вместо других типов диодов в схемах умножения частоты и позволяют получить бóльший коэффициент умножения. Пример параметров схемы умножения на ДНЗ: частота входного сигнала 2 ГГц, выходного — 10 ГГц, входная мощность 2 Вт, выходная — 0,15 Вт. На более низких частотах можно получить бóльшую выходную мощность.

Основными требованиями, предъявляемые к диодам с накоплением заряда является малая емкость перехода и минимальное сопротивление базы, для чего площадь перехода и толщину базы выполняют малыми. В диодах с накоплением заряда t_р должно быть достаточно велико, чтобы «удержать» накопленный заряд. Для уменьшения площади перехода до 10^-5 см² в случае работы в наносекундном диапазоне используют меза- или планарно-эпитаксиальную технологию. Следует указать, что эффект резкого восстановления обратного сопротивления в той или иной степени присущ любому полупроводниковому диоду с диффузионным р-n-переходом.

4.4. Технологические особенности изготовления диодов СВЧ диапазона

Характерной особенностью p-n-переходов диодов и транзисторов СВЧ-диапазона является их малая емкость, что достигается уменьшением площади перехода. Конструкция приборов на основе р-n-переходов и технология их изготовления должны обеспечивать точное и воспроизводимое выполнение как поперечных размеров перехода, так и толщины слоев полупроводниковых материалов, а также требуемый уровень и профиль легирования.

Первые СВЧ-диоды были изготовлены точечно-контактным методом. Для этого к предварительно отполированной и протравленной пластине Si или Ge прижималась игла из вольфрама или фосфористой бронзы (часто в виде пружины) с диаметром острия от нескольких микрометров до 20 — 30 мкм. При электроформовке, заключающейся в разогреве области контакта при пропускании мощных коротких импульсов тока, образовывался контакт типа барьера Шоттки.

Диффузионный метод создания переходов основан на диффузии в полупроводник примеси, находящейся в газообразной, жидкой или твердой фазе (рис. 4.3). В зависимости от глубины залегания перехода х₀ он может быть плавным или резким. При малой толщине р-области переход можно считать резким со ступенчатым изменением концентрации примеси.

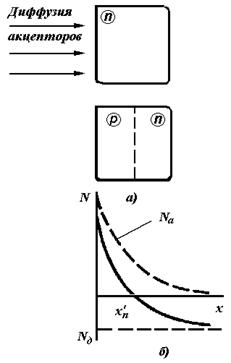
Рис. 4.3 Формирование диффузионного p-n-перехода (а) и распределение примесей в переходе (б)

Для уменьшения последовательного сопротивления объема полупроводника при изготовлении переходов часто используют эпитаксиальные слои. Метод эпитаксиального наращивания позволяет получать пленки полупроводникового материала с требуемой концентрацией примеси на поверхности исходного монокристалла (подложки). Структура кристаллической решетки эпитаксиального слоя при этом идентична структуре подложки. Для получения эпитаксиального слоя на поверхности монокристалла разлагают химические соединения полупроводникового материала с примесью веществ, необходимых для легирования слоя. Можно получать эпитаксиальные слои как с тем же типом элект-ропроводности, что и исходный материал подложки, но с другим удельным сопротивлением, так и с противоположным типом электропроводности. В первом случае, например, на поверхности сильнолегированной низкоомной подложки формируют слаболегированный высокоомный слой нужной толщины. Во втором — эпитаксиальный р-n-переход.

Πо конструкции переходы делятся на планарные и мезаструктуры. На рис. 4.4 приведена схема технологического процесса изготовления планарного перехода на эпитаксиальной подложке. Исходная подложка с нанесенным на нее эпитаксиальным слоем (рис. 4.4 а) имеет толщину порядка долей миллиметра, толщина высокоомной пленки I_эп, являющейся базой перехода, может составлять от долей до нескольких десятков микрометров. Малые площади переходов получают за счет использования прецизионной фотолитографии. Для этого эпитаксиальную пленку окисляют, в результате чего на ее поверхности образуется слой двуокиси кремния толщиной порядка 1 мкм. Далее наносят слой фоточувствительного материала — фоторезиста (ФР) (рис. 4.4 б). При освещении фоторезиста ультрафиолетовым светом через маску (фотошаблон) экспонированные участки полимеризуются. После растворения неэкспонированных участков фоторезиста в пленке окисла протравливают окна заданной конфигурации и размеров (рис. 4.4 в). Диаметр окна (или его ширина) при изготовлении приборов СВЧ равен обычно нескольким микрометрам — десятым долям миллиметра. Через полученные окна проводят локальную диффузию акцепторной примеси, например бора, для формирования р-области в эпитаксиальном слое n-Si (рис. 4.4 г). При малых размерах окна следует учитывать, что примесь проникает не только в глубь подложки, но и под края окон, образуя краевые области, имеющие обычно сферическую или цилиндрическую форму.

Эпитаксиальная технология позволяет получать переходы с малой толщиной базы. Отметим, что при малой толщине высокоомного эпитаксиального слоя I_эп область, обедненная основными носителями, может перекрыть весь эпитаксиальный слой и достигнуть сильнолегированной подложки (эффект смыкания).

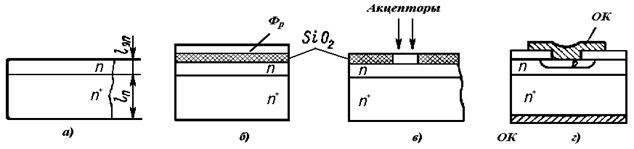
Рис. 4.4 Схема технологического процесса изготовления диффузионного планарного р-n-перехода на эпитаксиальной подложке

Важное место в изготовлении приборов занимают процессы формирования невыпрямляющих (омических) контактов (ОК на рис. 4.4 г), служащих выводами прибора. Такие контакты должны иметь малое сопротивление, не зависящее от полярности приложенного напряжения. Омические контакты выполняются чаще всего в виде соединения металла с сильнолегированным полупроводником. В простейшем случае сильнолегированный слой полупроводника образуется при сплавлении металла с полупроводником (при этом металл является донором или акцептором). Омические контакты могут быть многослойными, т. е. состоять из различных металлов. Например, омические контакты в приборах из GaAs получают, напыляя вольфрам и никель с последующим осаждением золота.

На одной исходной подложке обычно получают несколько десятков и даже сотен переходов. При производстве многослойных приборов, например транзисторов, процессы фотолитографии и локальной диффузии повторяют несколько раз.

Планарную технологию применяют также при создании приборов из Ge и GaAs. Пленку SiO₂ в этом случае осаждают на поверхности полупроводника при термическом разложении кремнийорганических соединений.

Устройство диода с мезаструктурой показано на рис. 4.5 На подложке полупроводника n-типа формируют область p-типа и омические контакты (рис. 4.5 а). Затем верхний контакт защищают фоторезистом и через маску формируют вывод р-области требуемого диаметра. После вытравливания металла и полупроводника остается участок диаметром а и высотой А, возвышающийся над подложкой в виде столбика (рис. 4.5 б). Подложка может быть выполнена по эпитаксиальной технологии, что позволяет изготовлять переходы с толщиной базы, составляющей единицы микрометров. Диаметр мезаструктуры а (рис. 4.5 б) определяется емкостью перехода и составляет обычно десятки — сотни микрометров; высота зависит от назначения прибора и, как правило, равна единицам — десяткам микрометров. Боковая поверхность мезаструктуры может быть защищена слоем SiO₂ для уменьшения токов утечки и увеличения пробивного напряжения.

В последние годы для создания переходов с малой толщиной полупроводниковых слоев применяют метод ионного легирования (ионной имплантации), при котором поверхность полупроводника бомбардируют пучком ионов (акцепторов или доноров), сфокусированных и ускоренных до высоких энергий. Глубина проникновения ионов определяется их энергией, а степень легирования — продолжительностью облучения мишени. При энергия частиц 100 кэВ глубина имплантированного слоя обычно около 1 мкм.

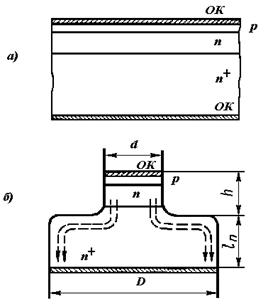
Рис. 4.5 Эпитаксиальная мезаструктура:

а ) исходная пластина с p-n-переходом и омическими контактами; б)устройство диода

Приборы с выпрямляющим контактом типа барьера Шоттки могут иметь планарную конструкцию (рис. 4.6) или выполняться в виде мезаструктуры. При их создании используется полупроводниковый материал с одним типом электропроводности, поэтому в технологическом процессе отсутствуют операции диффузии (или ионного легирования). Основным методом получения выпрямляющего контакта является вакуумное напыление металлических слоев на монокристалл полупроводника. Большое значение для получения качественного контакта с барьером Шоттки имеют состояние поверхности полупроводника и выбор материала металлического электрода. Металлическую пленку обычно напыляют на полупроводник, после чего ее толщину увеличивают электролитическим осаждением или повторным напылением. Контакты чаще всего бывают многослойными и состоят из различных металлов. Металл для внешнего покрытия выбирают с учетом последующих паек при монтаже прибора.

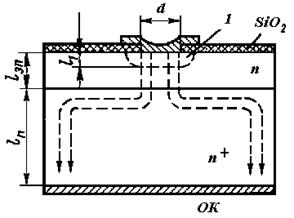
Рис. 4.6. Структура диода с барьером Шоттки, изготовленного методами планарной технологии

Уменьшить сопротивление объема полупроводника и улучшить отвод теплоты от перехода в планарных и мезаструктурах можно путем уменьшения толщины полупроводниковой подложки и замены ее материалом с большей теплопроводностью, например медью или золотом. Конструкции таких структур, называемых приборами с интегральным теплоотводом, показаны на рис. 4.7 Толщина полупроводниковой структуры l_стр может быть доведена до 10 — 20 мкм. Толщина медной подложки l_м обычно составляет несколько десятков — сотни микрометров.

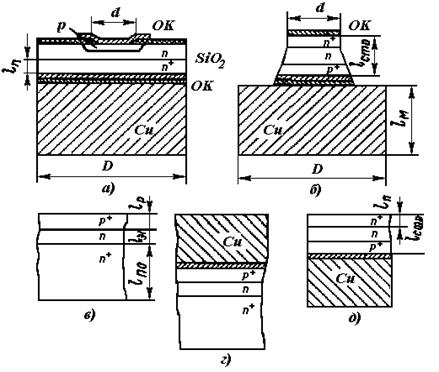
Рис. 4.7. Планарная (а) и мезаструктура (б) с интегральным теплоотводом; в, г, д — последовательности технологических операций при изготовлении структуры

При изготовлении таких структур на исходной (например, из низкоомного полупроводника n⁺-типа) подложке толщиной l_п0 эпитаксиальным наращиванием получают пленку n-материала толщиной l_эп, а затем полупроводника p⁺-типа с образованием р⁺-n-перехода (рис. 4.7 в). После выполнения на p⁺-материале омического контакта на структуре с этой же стороны гальваническим методом осаждают слой меди большой толщины (рис.4.7г). С противоположной стороны шлифовкой и селективным травлением уменьшают толщину исходной подложки до l_п так, что толщина всей полупроводниковой структуры становится небольшой (рис. 4.7 д). Далее методом фотолитографии формируют мезаструктуру (рис. 4.7 б), При монтаже структуры в корпус медное основание припаивают к массивному держателю, поэтому такие переходы могут рассеивать мощность в десятки ватт.

4.5. Контрольные вопросы:

1. В чем заключается эффект накопления заряда?

2. Почему ДНЗ называют диодами с резким восстановлением обратного тока или обратного сопротивления?

3. Перечислите основные требования к ДНЗ.

4. Перечислите методы изготовления диодов СВЧ. Кратко опишите каждый из них.

ЛЕКЦИЯ № 5

ТуннельныЙ диод

1. Концептуальная диаграмма.

2. Процессы, происходящие в полупроводнике в случае туннельного эффекта.

3. Вольт-амперная характеристика туннельного диода.

4. Параметры, применение.

5. Контрольные вопросы.

5.1. Концептуальная диаграмма

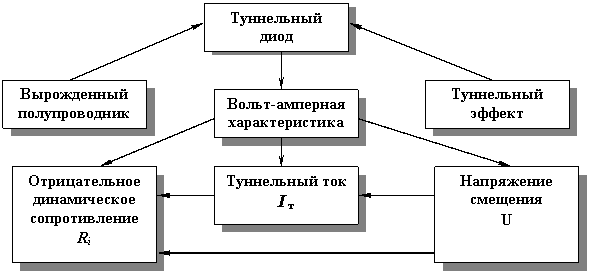5.2. Процессы, происходящие в полупроводнике в случае туннельного эффекта

Туннельный диод относится к группе полупроводниковых приборов, вольт-амперные характеристики которых имеют участок, соответствующий отрицательному дифференциальному сопротивлению прибора. Туннельный диод применяется как многофункциональный прибор (усиление, генерация, переключение и др.) для работы преимущественно в области СВЧ. Он может работать и на более низких частотах, однако его эффективность в этом случае значительно ниже, чем, например, транзистора.

Туннельный диод создается на основе вырожденного полупроводника. При этом высокая доза примеси в высоколегированном полупроводниковом материале вызывает смещение уровня Ферми настолько, что он располагается у электронного полупроводника в зоне проводимости, а у дырочного — в валентной зоне (рис. 5.2, а). Таким образом, при изготовлении туннельного диода как в p-область, так и в n-область вводят легирующие примеси в очень большой концентрации (примерно 10¹⁹¸10²⁰ см^-3, что на 2—3 порядка выше, чем в обычных диодах). Вследствие этого ширина перехода весьма мала — порядка 0,01мкм. Внутри перехода возникает электрическое поле напряженностью Е=10⁵¸10⁶ В/см.

В основе работы туннельного диода лежит туннельный эффект, сущность которого заключается в том, что электрон, обладающий энергией, меньшей, чем высота потенциального барьера, может проникнуть с некоторой вероятностью сквозь этот тонкий потенциальный барьер. Электрон как бы пользуется своеобразным туннелем, чтобы пройти сквозь барьер, не поднимаясь над его уровнем. Этот процесс происходит очень быстро (со скоростью света).

При образовании p-n-перехода происходит смещение энергетических зон полупроводников с различным типом проводимости в такой мере, что уровень Ферми для них становится прямой горизонтальной линией. При этом в случае вырожденных полупроводников нижняя граница зоны проводимости n-области становится ниже верхней границы валентной зоны р-области. Для простоты рассуждений будем считать, что все разрешенные уровни, расположенные ниже уровня Ферми, заняты, а расположенные выше него — свободны.

В очень узких p-n-переходах возникают условия для относительно свободного туннельного прохождения электронов через потенциальный барьер. Однако для этого необходимо, чтобы напротив занятого электроном уровня по одну сторону барьера имелся свободный уровень за барьером.

5.3. Вольт-амперная характеристика туннельного диода

            На рис. 5.1 а приведена вольт-амперная характеристика туннельного диода. Особенность этой характеристики заключается в следующем. В области обратных напряжений обратный ток растет очень быстро с повышением напряжения, т. е. туннельный диод обладает весьма малым обратным дифференциальным сопротивлением. В области прямых напряжений с увеличением напряжения прямой ток сначала растет до пикового значения I₁ при напряжении U₁ в несколько десятков милливольт, а затем начинает уменьшаться (участок АВ, в пределах которого туннельный диод обладает отрицательной проводимостью G (рис.5.1 б). Ток спадает до минимального значения I₂ при напряжении U₂ порядка нескольких сотен миливольт, в дальнейшем прямой ток вновь начинает увеличиваться с ростом напряжения.

Заштрихованная область вольт-амперной характеристики (рис.5.1 а) соответствует так называемому избыточному току туннельного диода. На этом участке ток туннельного диода определяется суммой двух токов: прямым туннельным током и током диффузии. Однако многочисленные экспериментальные исследования показали, что ток I₂ реального туннельного диода существенно больше тока I₂ идеализированного туннельного диода. Разность этих токов называют избыточным током. Установлено, что он в основном зависит от концентрации технологически неконтролируемых примесей и степени легирования исходного материала, но окончательно природа избыточного тока неясна.

Дифференциальная проводимость G при изменении смещения от 0 до U₃ дважды (в точках, соответствующих напряжениям U₁ и U₂) обращается в нуль, т. е. туннельный диод способен дважды разорвать внешнюю электрическую цепь, превращаясь из пассивного элемента в активный и наоборот. Это обстоятельство привело к широкому применению туннельных диодов в импульсной технике.

Ток, протекающий через туннельный диод, содержит пять составляющих:

 — туннельный ток , обусловленный туннельным переходом электронов из валентной зоны p-области в зону проводимости n-области;

 — туннельный ток , обусловленный туннельным переходом электронов из зоны проводимости n-области в валентную зону р-области;

 — дрейфовый ток неосновных носителей обеих областей через р-п переход I_др;

 — диффузионный ток основных носителей обеих областей через р-n переход I_диф;

 — так называемый избыточный ток, который можно рассматривать как частный случай тока — туннельного перехода носителей с использованием разрешенных (примесных или дислокационных) уровней в запрещенной зоне.

Таким образом, результирующий ток через переход

                                                                            (5.1)

а)
б)
в)

Рис. 5.1. Характеристики туннельного диода:

а), в) вольт-амперные;

б) зависимость проводимости диода от напряжения

            Подчеркнем различие между туннельными токами сквозь барьер и дрейфовым и диффузионным токами через барьер; в первом случае электроны переходят из валентной зоны одной области в зону проводимости другой области или в обратном направлении; во втором случае электроны (или дырки) переходят из зоны проводимости (валентной) одной области в ту же самую зону другой области. На рис. 5.1 в вольт-амперная характеристика туннельного диода представлена как зависимость суммы токов I_nр, I_pn и обычного диодного (диффузионного и дрейфового) тока от приложенного напряжения.

Теперь рассмотрим более подробно вольт-амперную характеристику туннельного диода по выделенным на ней отдельным точкам (а, б, в, г, д, е, ж, рис. 5.2):

а) при нулевом смещении электронам проводимости n-области противостоят валентные электроны р-области (рис. 5.2, а). Если все указанные уровни заполнены, то туннельные переходы невозможны. В действительности при комнатной температуре некоторая часть этих уровней освобождается за счет электронов, переброшенных на уровни, расположенные выше уровня Ферми. Поэтому существует определенная вероятность, что валентный электрон р-области, не меняя своей энергии, совершит туннельный переход и займет соответствующий уровень в зоне проводимости n-области. Существует точно такая же вероятность туннельного перехода электрона проводимости n-области в валентную зону p-области. Так как эти вероятности одинаковы, то встречные потоки электронов, совершающих туннельные переходы, взаимно компенсируются и суммарный туннельный ток оказывается равным нулю (I_Т=0, рис. 5.2, а). При дальнейших рассуждениях эти составляющие учитываться не будут;

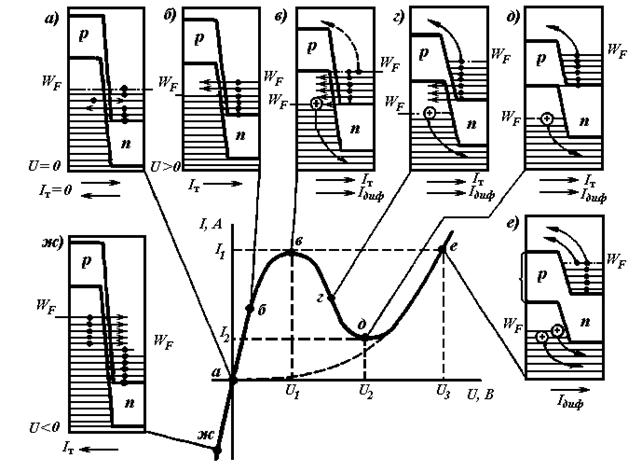
Рис. 5.2. Энергетические диаграммы туннельного диода при различных напряжениях смещения и его вольт-амперная характеристика

б) если к p-n-переходу приложить небольшое прямое напряжение, то энергетические уровни р-области понизятся относительно энергетических уровней n-области (рис. 5.2, б). В этом случае уровни некоторых электронов проводимости n-области расположатся против свободных уровней, находящихся в валентной зоне р-области, что создает благоприятные условия для их туннельного перехода. Поэтому в р-n-переходе появится туннельный ток, величина которого будет зависеть от смещения энергетических зон, т. е. от приложенного прямого смещения (туннельный ток протекает от р-области к n-области в направлении, противоположном движению электронов);

в) при увеличении прямого смещения туннельный ток будет увеличиваться до тех пор, пока не произойдет совмещение уровня Ферми n-области с верхним уровнем валентной зоны р-области. В этом случае туннельный ток достигает максимума, так как против уровней электронов проводимости n-области располагаются все свободные уровни валентной зоны р-области, превышающие уровень Ферми (рис. 5.2, в);

г) при дальнейшем увеличении прямого смещения некоторые уровни электронов проводимости n-области располагаются против запрещенной зоны р-области и туннельный ток уменьшается (рис. 5.2, г). В результате на вольт-амперной характеристике получается участок с отрицательным сопротивлением;

д) при некотором значении прямого напряжения зона проводимости n-области и валентная зона р-области начинают расходиться и туннельный ток прекращается (рис.5.2,д,е);

е) при прямом напряжении в р-n-переходе наряду с туннельным током появляется диффузионный ток, как у обычного диода (на вольт-амперной характеристике он показан штриховой линией). При расхождении зоны проводимости n-области с валентной зоной р-области (начиная с точки д) существует только диффузионный ток и туннельный диод при таком условии подобен обычному диоду, включенному в прямом направлении (рис.5.2, д, е);

ж) при обратном смещении р-n-перехода туннельного диода валентная зона р-области перекрывается с разрешенными и незаполненными уровнями зоны проводимости n-области. При этом возникают условия для относительно свободного туннельного прохождения валентных электронов р-области в зону проводимости n-области. В результате этого появляется значительный туннельный ток обратного направления, величина которого очень сильно зависит от смещения зон, т. е. от величины обратного напряжения (рис. 5.2, ж).

На рис. 5.3 приведены для сравнения вольт-амперные характеристики туннельных диодов из различных полупроводниковых материалов. Из рисунка видно, что диоды из арсенида галлия обладают наибольшим отношением I₁/I₂и напряжением переключения ΔU_n .

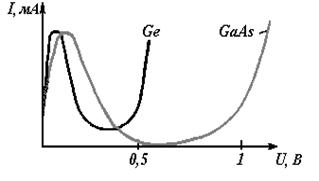
Рис. 5.3. Вольт-амперные характеристики германиевых и арсенидгаллиевых туннельных диодов

5.4. Параметры, применение

Из вышесказанного следует, что туннельный диод не имеет запирающего направления. Рабочим участком вольт-амперной характеристики туннельного диода является участок в—д (рис.5.2), на котором он обладает отрицательным динамическим (дифференциальным) сопротивлением:

R_i=dU/dI < 0                                                                                                                            (5.2)

Минимальное абсолютное значение этого сопротивления является одним из основных параметров туннельного диода. Для различных типов диода оно имеет значение от единиц до десятков Ом.

Другими основными параметрами туннельных диодов являются (рис. 5.1 а):

— максимальный прямой ток I₁ в точке максимума вольт-амперной характеристики;

— минимальный прямой ток I₂ в точке минимума вольт-амперной характеристики;

— отношение токов в максимуме и в минимуме вольт-амперной характеристики I₁/I₂;

— отрицательная дифференциальная проводимость G на участке АВ в точке максимума производной;

— напряжение переключения ΔU_n = U₃—U₁, которое определяет возможный скачок напряжения на нагрузке при работе туннельного диода в схеме переключения;

— барьерная емкость C(U₂) диода, которая обычно измеряется при минимуме тока.

— емкость в максимуме тока равна C(U₁) 0,8C(U₂).

— напряжения, соответствующие максимальному и минимальному значениям тока U₁ и U₂.

— напряжение раствора U₃, соответствующее максимальному току на второй восходящей ветви вольт-амперной характеристики.

Рис. 5.4. Эквивалентная схема туннельного диода

На рис. 5.4 приведена эквивалентная схема туннельного диода по переменному току. Она состоит из барьерной емкости p-n-перехода С_б; динамического (отрицательного) сопротивления R_i - величины обратной крутизне ВАХ; сопротивления кристалла полу-проводника, контактов и подводящих проводов r_s;  индуктивности выводов диода L-полной последовательности индуктивности диода при заданных условиях и емкости корпуса С_кор. Емкость между выводами диода :

С=С_б+С_кор (5.3)

Основным преимуществом туннельных диодов является сохранение ими отрицательного сопротивления вплоть до сотен гигагерц. Дело в том, что туннельный ток не связан с медленными процессами диффузии или дрейфа носителей, а распространяется как обычный ток в проводнике со скоростью света.

Емкость перехода при толщине последнего порядка 10^-2 мкм составляет С=0,1¸0,5пФ. Так как от величины емкости зависят частотные свойства туннельного диода, ее стремятся сделать минимальной. Индуктивность L (порядка 10^-10Гн) является паразитным параметром, так как ограничивает собственную резонансную частоту ω_о. Для уменьшения L контакты осуществляют мембраной, прижимом массивного электрода и т. п. Величина r_s измеряется десятыми долями Ом и единицами Ом.

Полное сопротивление схемы при данной частоте ω:

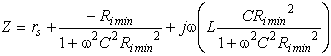,                                                              (5.4)

где R_{i min2}= 1/С.

            Приравнивая к нулю действительную часть полного сопротивления, находим предельную частоту, на которой туннельный диод способен генерировать колебания:

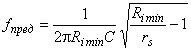                                                                                               (5.5)

Максимальное значение предельной частоты получается при R_imin=2r_s. Следовательно, частотные свойства туннельного диода определяются постоянной времени r_sС.

Уменьшать емкость С путем уменьшения площади перехода нецелесообразно, так как при этом уменьшается и пиковый ток I₁, что увеличит отрицательное сопротивление, и, следовательно, предельная частота останется без изменения. Таким образом, при уменьшении С ток I₁ должен оставаться неизменным, поэтому качество туннельного диода удобно характеризовать отношением .

Для изготовления туннельных диодов применяются различные полупроводниковые материалы: германий, кремний, арсенид галлия, фосфат индия, арсенид индия, антимонид индия и антимонид галлия. Выбор материала в значительной степени определяется требуемыми параметрами прибора. Наиболее перспективным материалом является арсенид галлия, обладающий наилучшими параметрами. Для германиевых диодов в качестве доноров используют фосфор или мышьяк, а в качестве акцепторов — галлий или алюминий. Для арсенид-галлиевых - олово, свинец, серу, селен, теллур (доноры), цинк, кадмий (акцепторы). Для получения узкого p-n-перехода применяется метод вплавления или диффузии примесей.

Основными достоинствами туннельного диода являются:

— высокие рабочие частоты — до 40 ГГц и весьма малое время переключения, которые определяются преимущественно конструктивными особенностями, а не временем прохождения электронами р-n перехода, составляющим около 10^-13сек;

— высокая температуростойкость; у арсенид-галлиевых туннельных диодов рабочая тем-пература достигает +600°С, у германиевых - до +200°С. Возможность работы туннельных диодов при более высоких температурах по сравнению с обычными диодами объясняется тем, что в них используется вырожденный полупроводник с большой концентрацией примесей. При большой концентрации примесей концентрация электронов велика и влияние собственной электропроводности сказывается при более высоких температурах;

— низкий уровень шума;

— большая плотность тока, свойственная туннельному эффекту, достигающая 10^3.10⁴А/см².

Как недостаток, следует отметить малую мощность туннельных диодов из-за низких рабочих напряжений и малых площадей перехода. К их недостаткам следует отнести так же то, что они являются двухполюсниками. Поэтому в ряде схем, созданных на туннельных диодах, возникают определенные сложности с разделением цепей входа и выхода. Кроме того, туннельные диоды нуждаются в высокостабильных источниках питающих напряжений.

Для обеспечения возможности работы туннельных диодов на высоких частотах выбирают такие конструктивные формы, которые обеспечивают малые величины r_s и L. Сопротивление r_s понижают уменьшением размеров элементов. У туннельных диодов из гер-мания это сопротивление составляет 0,1¸0,5 Ом, а у диодов из арсенида галлия — 1¸10Ом.

Для образования контакта к кристаллу присоединяют мембранный массивный электрод и ленточный лепесток или припаивают плоскую пластину. При этом индуктивность составляет величину 10^-10 Гн. Тонкая проволока неприемлема, так как подобные выводы имеют индуктивность не меньше, чем 3^.10^-9 Гн.

Германиевые туннельные диоды оформляются в металло-стеклянном корпусе с гибкими выводами, а арсенид-галлиевые туннельные диоды — в металлокерамическом корпусе.

В качестве примера можно привести следующие туннельные диоды:

1И302А —германиевый диод;

I₁ = 1,7¸ 2,3 мА; I₁/I₂== 4,5; U₁ = 60 мВ; C = 80 пФ.

3И301А—арсенид-галлиевый диод;

I₁ = 1,5¸2,4 мА; I₁/I₂= 8; U₁ =180 мВ; U₃ ≥ 0,65 В; С=12 пф.

Различные конструкции туннельных диодов представлены схематически на рис. 5.5

а)	б)
в)

Рис. 5.5 Конструкции туннельных диодов:

а) патронного типа; б) таблеточного типа: в) с ленточными выводами;

1— полупроводниковый кристалл; 2 — p-n-переход; 3 — соединительный электрод; 4— корпус; 5, 6—выводы; 7—втулка корпуса; 8 — крышка

Туннельные диоды используются в схемах генераторов и усилителей диапазона СВЧ, в быстродействующих ключевых и импульсных устройствах, в преобразователях частоты, детекторах, умножителях частоты, в логических устройствах и других схемах. В табл.5.1 показано применение туннельных диодов в зависимости от величины I₁ :

Таблица 5.1

I1, мА	Применение туннельного диода
0,03¸0,3	Смеситель, видеодетектор(обращенный туннельный диод)
0,5¸3	Усилитель, смеситель с усилением
5¸100	Генератор

5.5. Контрольные вопросы:

1. Какой полупроводник называется вырожденным?

2. Какова сущность туннельного эффекта?

3. Начертите вольт-амперную характеристику туннельного диода.

4. Какими факторами ограничивается предельная частота туннельного диода?

5. Достоинства и недостатки туннельного диода.

ЛЕКЦИЯ № 6

Диод Шоттки, p-i-n диод

1. Концептуальная диаграмма.

2. Принцип действия, параметры и характеристики диода Шоттки и р-i-n диода.

3. Контрольные вопросы.

6.1. Концептуальная диаграмма

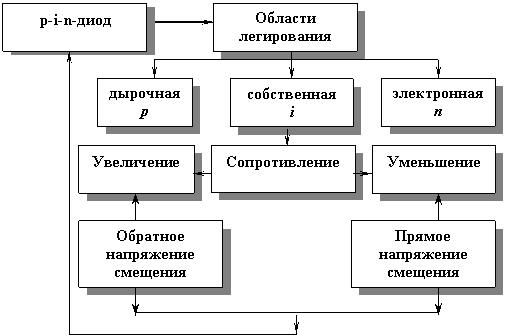6.2. Принцип действия, параметры и характеристики диода Шоттки и р-i-n диода

6.2.1. Диод Шоттки

Физические исследования контакта металл — полупроводник стимулировались прогрессом в области точечно-контактных полупроводниковых выпрямителей. В предвоенные годы немецкий ученый Шоттки получил основные математические соотношения, описывающие электрические характеристики этого контакта, вследствие чего подобную структуру стали называть барьером Шоттки. Однако многие замечательные свойства, предсказываемые теорией для барьера Шоттки, практически наблюдать не удалось из-за очень резкого отличия точечных диодов от идеализированной модели (значительные механические напряжения в приконтактной области, наличие промежуточных окисных слоев, мультиконтактность и т. п.). Этим, а также большими успехами приборов с p-n-переходами и объясняется тот ограниченный интерес в отношении исследований контакта металл — полупроводник и создания приборов на его основе.

а)
б)
в)
г)
д)

Рис. 6.1. Схема контакта металл — полупроводник (а) и его энергетическая диаграмма при нулевом (б), прямом (г) и обратном (д) смещении

Лишь в последние годы в связи с небывалыми успехами полупроводниковой технологии стало возможным получение структур, близких к идеальному барьеру Шоттки, и практическое конструирование на этой основе различных приборов. Это обусловливает тот огромный интерес, который проявляют к барьеру Шоттки специалисты в области физики, технологии и применения полупроводниковых приборов.

Рассмотрим особенности работы диода с барьером Шоттки на основе контакта металла с полупроводником n-типа для случая, когда работа выхода металла φ_0м больше, чем работа выхода φ_0п полупроводника (рис. 6.1 а). При образовании контакта электроны переходят из материала с меньшей работой выхода в материал с большей работой выхода, в результате чего уровни Ферми металла и полупроводника выравниваются. При этом полупроводник оказывается заряженным положительно, а возникающее внутреннее электрическое поле препятствует переходу электронов в металл. Между металлом и полупроводником возникает контактная разность потенциалов U_к = φ_0м — φ_0п.

Благодаря разности работ выхода металла и полупроводника между ними происходит обмен электронами. Электроны из полупроводника, имеющего меньшую работу выхода, переходят в металл с большей работой выхода. В равновесном состоянии (рис. 6.1 а) металл заряжается отрицательно, в результате чего возникает электрическое поле, прекращающее однородный переход электронов.

Из-за резкого различия концентраций свободных электронов по обе стороны от контакта практически все падение напряжения приходится на приконтактную область полупроводника. Приложенное внешнее напряжение изменяет высоту барьера лишь со стороны полупроводника. Электроны зоны проводимости отталкиваются возникшим контактным нолем. Создается обедненный слой с пониженной концентрацией подвижных носителей. Около контакта вследствие изгиба границ зон полупроводник n-типа переходит в полупроводник p-типа.

Распределение электрического поля (рис. 6.1 в) и объемного заряда в этом случае описывается теми же уравнениями, что и для резкого p-n-перехода. В полупроводнике возникает область, обедненная основными носителями заряда с пониженной проводимостью, ширина которой l_п зависит от уровня легирования полупроводника. В состоянии равновесия поток электронов (основных носителей полупроводника) в металл уравновешивается потоком электронов из металла в полупроводник.

При прямом смещении (рис. 6.1 г) потенциальный барьер со стороны полупроводника понижается и число переходов электронов в металл увеличивается. При обратном смещении (рис. 6.1 д), напротив, ток из полупроводника уменьшается, стремясь с ростом напряжения к нулю. Ток электронов из металла все время остается неизменным: роль его незначительна при прохождении прямого тока, им же обусловлен ток утечки при обратном смещении. Величина этого обратного тока в приборах с барьером Шоттки порядка единиц микроампер.

В реальных контактах линейная зависимость высоты барьера от работы выхода металла наблюдается редко ввиду того, что на поверхности полупроводника из-за ее неидеальности имеются поверхностные заряды. При нанесении металла такой поверхностный заряд экранирует влияние металла, вследствие чего высота потенциального барьера в основном определяется состоянием поверхности полупроводника. Кроме того, на свойства контакта металл — полупроводник влияют токи утечки, токи генерации — рекомбинации носителей заряда в обедненной области и возможность туннельного перехода электронов в случае сильнолегированного полупроводника. В целом вольт-амперная характеристика контакта с барьером Шоттки в широких пределах изменения тока соответствует характеристике типа:

                                                                                              (6.1)

где a — коэффициент «неидеальности». При обратном смещении ток через контакт обычно увеличивается с ростом напряжения. Особенностью выпрямляющих контактов металл — полупроводник, отличающих их от p-n-переходов, является отсутствие инжекции неосновных носителей в полупроводник при прямых напряжениях.

Таким образом, в диоде Шоттки отсутствуют накопление неосновных носителей заряда в областях диода при прямом напряжении и рассасывание этого заряда при изменении знака напряжения. Это улучшает быстродействие диода, т. е. частотные и импульсные свойства. Время восстановления обратного сопротивления с диодом Шоттки при использовании кремния и золота — примерно 10 нс и меньше.

Достоинством диода Шоттки при современном уровне технологии является также то, что его вольт-амперная характеристика оказывается очень близкой к характеристике идеализированного p-n-перехода. В формуле (6.1) коэффициент n близок к единице (a ≈1,04), в то время как у обычных диодов a =1,5-2,5. Это означает, что прямая ветвь характеристики диода Шоттки идет круче, чем у обычных диодов.

Шумы диода Шоттки определяются дробовым шумом и тепловым шумом последовательного сопротивления областей и контактов. Вследствие малого влияния неосновных носителей на процессы в диоде Шоттки вклад генерационно-рекомбинационных шумов в дробовый шум оказывается незначительным. Кроме того, уменьшается последовательное сопротивление областей диода, так как одна из областей является металлом. Поэтому уровень шумов диода Шоттки оказывается меньше, чем в аналогичных по применению точечных диодах на p-n-переходах.

Применяются диоды Шоттки в качестве детекторных и смесительных диодов вплоть до миллиметрового и субмиллиметрового диапазонов волн. Изготавливаются они из арсенида галлия. Для уменьшения емкости диаметр контакта уменьшается до 1 мкм и менее. Смесители на диодах Шоттки используются до 300 ГГц. На частоте 170 ГГц коэффициент шума диода Шоттки К_ш = 4,8-5,5 дБ, а охлаждение до 20 К снижает его примерно вдвое.

Диоды с барьером Шоттки могут быть использованы для умножения и преобразования частот. Умножение может быть основано как на нелинейной зависимости сопротивления диода от напряжения (нелинейное сопротивление), так и на нелинейной зависимости емкости от напряжения (нелинейная емкость). Эффективность умножения при использовании диода Шоттки на основе арсенида галлия примерно в 3 раза выше, чем у кремниевых диодов с прижимным контактом при одинаковых с ним входной частоте (3 — 4 ГГц) и кратности умножения (три). Особенно существенны преимущества диода Шоттки при преобразовании слабых сигналов. Эти диоды используются также и как быстродействующие переключательные диоды.

Варианты разновидностей диодов Шоттки приведены на рис. 6.2.

а)	б)
в)	г)

Рис.6. 2. Разновидности выпрямляющих структур диодов Шоттки:

а) меза-диод; б) планарный диод; в) мультиконтактная структура;

г) планарный диод с балочным выводом

Диоды с барьером Шоттки широко используются в качестве детекторных и смесительных СВЧ диодов, вытесняя традиционные точечные диоды. При этом наилучшее сочетание параметров удается достигнуть при использовании арсенида галлия – материала, характеризующегося большей подвижностью основных носителей заряда по сравнению с кремнием. На рис. 6.3. показана структура СВЧ-диода Шоттки из арсенида галлия. Диоды Шоттки позволяют значительно уменьшить коэффициент шума. В них использован выпрямляющий контакт между полупроводником и металлом, в котором ток переносится основными носителями. Эти диоды обладают наименьшей способностью накопления неравновесных носителей заряда. Серийные образцы диодов Шоттки на частоте 50 ГГц, имеют уровень шумов и потерь менее 5 и 3,5 dB соответственно. Кроме того диоды Шоттки значительно более стойки к выгоранию, чем точечные приборы.

Успехи гибридной технологии (сочетание барьера Шоттки с p-n переходом ) позволили создавать мощные высокочастотные выпрямители, которые широко применяются в малогабаритных и интегральных “бестрансформаторных” источниках питания и солнечных батареях.

Предельная частота СВЧ-диодов Шоттки доведена до 500 ГГц.

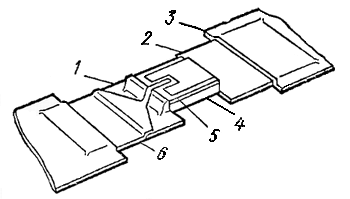
Рис. 6.3. СВЧ-диод с переходом Шоттки на арсениде галлия:

1— SiO₂; 2 —омический контакт; 3 — полосковая линия из золота; 4 — n⁺GaAs;

5 — nGaAs; 6 —контакт перехода Шоттки

Подытоживая сказанное выше, перечислим основные преимущества барьера Шоттки по сравнению с р-п переходом:

1. Относительная простота варьирования высоты потенциального барьера без изменения свойств полупроводника за счет выбора соответствующего металла.

2. Высокая крутизна вольт-амперной характеристики (a≈1, тогда как для p-n переходов на кремнии типично a≈1,5), обусловливающая лучшие детектирующие свойства.

3. Малая инерционность как в детекторном режиме, так и в режиме переключения (на 1—2 порядка меньше, чем у самых «быстрых» легированных золотом кремниевых диодов с p-n переходом).

4. Малый уровень шумов (справедливо вплоть до f ≈∙10¹² Гц, тогда как в случае p-n перехода частотная зависимость дробового шума определяется механизмом диффузии и рекомбинации неосновных носителей заряда).

5. Принципиальная возможность получения меньших (по сравнению с приборами с p-n переходами) значений последовательного электрического сопротивления и теплового сопротивления, так как металлический слой по этим свойствам превосходит любой сильно легированный слой полупроводника.

6. Резкое различие оптических свойств металла и полупроводника (значительно более резкое, чем в случае полупроводников n- и p-типов проводимости), позволяющее создавать ряд оригинальных фотоэлектрических приборов.

7. Технологическая простота, сочетающаяся с широтой возможностей (изготовление в однотипных процессах различных — выпрямляющих и омических — контактов).

8. Принципиальная совместимость методов изготовления контактов металл — полупроводник с технологией интегральных схем.

6.2.2. p-i-n диод

p-i-n-диод (рис. 6.4. а) состоит из трех чередующихся областей: с дырочной, собственной и электронной проводимостью. Между сильно легированными областями с дырочной и электронной электропроводностью находится i-область с концентрацией носителей, близкой к концентрации p_i и n_i в собственном полупроводнике (рис. 6.4. б). Концентрации носителей в р-области р_р и п_р , а в n-области n_n и р_п∙

При подаче прямого напряжения в i-область одновременно инжектируются дырки из р-области и электроны из n-области. Сопротивление i-области и всего диода становится малым, его значение определяется постоянным током, протекающим через диод.. При обратном напряжении дырки и электроны экстрагируются из i-области в p- и n-области соответственно. Уменьшение концентрации носителей в i-области приводит к увеличению сопротивления i-об-ласти и всего диода. Такая зависимость сопротивления p-i-n-диода от напряжения объясняет эффективность его применения в качестве мощного выпрямительного диода, у которого должны быть малое прямое и большое обратное, сопротивления. Разработка p-i-n-диодов с малой емкостью позволила использовать их в СВЧ диапазоне.

Дифференциальное сопротивление p-i-n-диода при изменении знака напряжения изменяется на несколько порядков, в то время как емкость диода, определяемая в основном шириной i-области, изменяется незначительно. Слабая зависимость емкости от напряжения расширяет возможности использования p-i-n-диодов в СВЧ схемах с колебательными системами.

а)	б)

Рис. 6.4. Структура и области легирования p-i-n диода

На рис. 6.5 показано расположение энергетических зон в диоде типа p-i-n. На границе между соседними областями образуются запирающие слои. Контактная разность потенциалов между областями p и n в диоде в этом случае такая же, как и в отсутствие области i. При приложении обратного напряжения сопротивление i-области увеличивается, так как электрическое поле отсасывает из нее носители, что ведет к увеличению падения напря-жения, создаваемого в ней обратным током. При приложении прямого напряжения, наобо-рот, сопротивление i-области уменьшается из-за инжекции в нее электронов из n-области и дырок из р-области, поэтому падение напряжения в i-области уменьшается.

Диод типа p-i-n предназначен для схем мощных выпрямителей и СВЧ переключателей. Для получения большого выпрямленного напряжения нужно обеспечить высокое допустимое обратное напряжение U_обр, а для получения большого выпрямленного тока — малое прямое сопротивление диода. Эти два требования взаимно противоречивы. Высокое U_обр можно получить путем увеличения толщины p-n-перехода, для чего следует уменьшить примесную проводимость p- и n-областей. Но при этом увеличивается сопротивление материала полупроводника, что имеет существенное значение в случае работы диода при больших прямых токах. Указанное противоречие можно устранить, если между p- и n-областями) расположить область из высокоомного материала с очень малой концентрацией примесей, близкой к собственному полупроводнику, что обеспечит высокое значение U_обр. В то же время области р и п выполняют с большой концентрацией акцепторных и донорных примесей, благодаря чему сопротивление этих областей диода может быть малым. На границе между областями концентрация примесей должна резко изменяться.

а)		б)
в)

Рис. 6.5. Диаграмма энергетических зон диода типа p-i-n:

                                        а) в состоянии равновесия;

                                        б) при обратном напряжении;

                                        в) при прямом напряжении

На рис. 6.6 показана p-i-n-структура одного из наиболее широко применяемых в промышленности переключающих СВЧ-диодов.

Диод типа p-i-n изготовляется путем диффузии акцепторной и донорной примесей с противоположных сторон пластины кремния с собственной электропроводностью, который имеет высокое сопротивление.

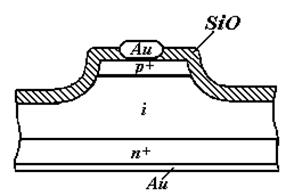
Рис. 6.6. Структура p-i-n-диода

При низких частотах диод типа р-i-п обнаруживает выпрямительные свойства, аналогичные обычному p-n-переходу. Однако при более высоких частотах накопление заряда в области i препятствует выпрямлению. Таким образом, когда к диоду прикладывается прямое напряжение смещения, он работает как переменное сопротивление, зависящее от величины напряжения. Когда к диоду прикладывается обратное напряжение, то наблюдается постепенное уменьшение последовательного сопротивления ввиду увеличения ширины обедненного слоя. Это увеличение ширины продолжается до тех пор, пока не произойдет пробой и проводимость быстро увеличится.

В СВЧ диапазоне p-i-n-диоды используются для создания переключающих цепей (СВЧ мультиплексоров), переменных и ступенчатых аттенюаторов, амплитудных модуляторов, плавных и ступенчатых фазовращателей. Например, для создания ступенчатого фазовращателя (широко применяемых в фазированных антенных решетках) p-i-n-диоды включаются с определенным интервалом в линию передачи. Переключатели на p-i-n-диодах устойчивы в работе и имеют малые потери на СВЧ. Недостатками p-i-n-диодов является меньшее, чем у диодов Шоттки, быстродействие и отсутствие усиления.

Выпускаются р-i-n-диоды с разными толщиной i-слоя, площадью структуры, рассеиваемой мощностью и быстродействием. Емкость полупроводниковых структур обычно лежит в интервале от 0,1 до 3 пФ.

В мощных p-i-n-диодах для СВЧ диапазона ширина i-области делается большой (0,1—0,5 мм), чтобы они могли работать при больших амплитудах напряжения (свыше 1 кВ) и импульсной мощности 10 кВт и более. Большая ширина i-области позволяет также увеличить площадь сечения диода без существенного возрастания емкости, улучшить теплоотвод и поднять среднюю рабочую мощность. Диоды с большой толщиной i слоя на частотах СВЧ-диапазона не являются выпрямителями, но могут быть использованы для управления СВЧ- мощностью в качестве переключательных диодов. Их сопротивление изменяется под действием внешнего низкочастотного напряжения.

 Следует заметить, что p-i-n-диоды применяются как при малых уровнях мощности, так и на больших мощностях, достигающих сотен ватт в непрерывном режиме и сотен киловатт в импульсе.

6.3. Контрольные вопросы:

1. Особенности работы диода Шоттки.

2. Основные преимущества барьера Шоттки.

3. Каково расположение энергетических зон в p-i-n диоде в состоянии равновесия, при прямом и обратном смещении? Поясните.

4. Где применяются p-i-n диоды?

ЛЕКЦИЯ № 7

Лавинно-пролетный диод

1. Концептуальная диаграмма.

2. Лавинное умножение носителей.

3. Пролетный режим работы ЛПД.

4. Параметры и характеристики, особенности устройства и применения ЛПД.

5. Контрольные вопросы.

7.1. Концептуальная диаграмма

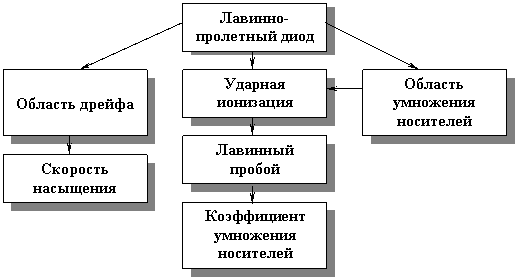7.2. Лавинное умножение носителей

Лавинно-пролетный диод (ЛПД)— это полупроводниковый СВЧ-диод, в котором для получения носителей заряда используется лавинное умножение (ударная ионизация) в области электрического перехода и взаимодействие этих носителей с переменным полем в переходе в течение времени пролета. Лавинно-пролетные диоды относятся к классу двух-полюсников, обладающих отрицательным сопротивлением на зажимах, что позволяет испо-льзовать ЛПД для создания генераторов и усилителей. Отрицательное сопротивление ЛПД проявляется только на достаточно высоких частотах и не проявляется в статическом режи-ме. Причиной этого является наличие фазового сдвига между током и напряжением на ЛПД.

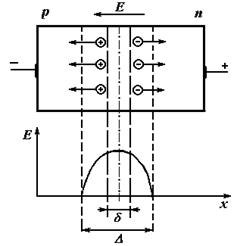
Рис. 7.1. Схема ЛПД и распределение напряженности электрического поля:

D — ширина запирающего слоя; d— ширина слоя умножения

В иностранной литературе такие диоды часто называют диодами Рида по фамилии ученого, предложившего в 1958 г. структуру типа р—п—i—р и принципы работы устройства, однако эта структура была реализована только в 1965 г. Первый ЛПД создан в СССР А. С. Тагером с сотрудниками на основе обнаруженного в 1959 г. эффекта генерации СВЧ-колебаний при лавинном пробое германиевых диодов.

На рис. 7.1 показана схема плавного p-n-перехода ЛПД и распределение электрического поля в переходе. На диод подается обратное напряжение такой величины, что рабочая точка смещается в область лавинного умножения (рис.7.2). В p-n-переходе начинается процесс ударной ионизации атомов кристаллической решетки подвижными носителями заряда и образование новых пар электронов и дырок. С этим явлением связан резкий рост обратного тока перехода, называемый лавинным пробоем. Для количественной характеристики процесса ударной ионизации вводят коэффициенты ионизации α_n и α_p для электронов и дырок — число электронно-дырочных пар, создаваемых на единице пути (1 см) электроном и дыркой соответственно.

Лавинный пробой возникает, в результате ударной ионизации нейтральных атомов в р-n-переходе быстрыми электронами или дырками. В результате генерируются новые пары носителей заряда, которые, двигаясь в электрическом поле перехода, вновь при столкновении с атомами образуют новые пары носителей и т. д., т. е. носители в переходе лавинообразно размножаются. Параметром этого процесса является коэффициент умножения М, определяемый как отношение числа носителей, выходящих из p-n-перехода, к числу носителей того же типа, входящих в переход. Коэффициент М можно рассчитать по следующей эмпирической формуле:

                                                                                                    (7.1)

где U_пр - напряжение пробоя.

Показатель степени для кремния и германия n-типа b = 3; для германия p-типа b=5,5. Величина пробивного напряжения не зависит от типа носителей и растет с увеличением удельного сопротивления полупроводника; у кремния это напряжение выше, чем у германия при тех же значениях удельного сопротивления.

Принято считать, что лавинный пробой наступает при таком обратном напряжении на переходе, когда коэффициент лавинного умножения обращается в бесконечность. Если начало лавинного умножения вызвано дырками (I_P0>>I_n0), то условие лавинного пробоя будет выглядеть следующим образом:

                                                                                                                    (7.2)

Условие (7.2) имеет простой физический смысл; для возникновения лавинного пробоя необходимо, чтобы каждый электрон и каждая дырка, вошедшие в переход и возникающие в переходе, создавали в среднем до одной электронно-дырочной паре. Если α_п¹α_р, то носители, имеющие больший коэффициент ионизации, должны создавать при прохождении перехода в среднем более одной пары, чтобы скомпенсировать уменьшение коэффициента ионизации носителей другого типа.

Напряженность электрического поля максимальна на границе между р- и n-областями. Поэтому ударная ионизация происходит лишь в узком слое умножения δ, прилежащем к плоскости границы. Вновь созданные электроны и дырки под действием сильного поля дрейфуют через p- и n- пролетные участки запирающего слоя, расположенные по обе стороны от слоя умножения. Дырки дрейфуют через p-слой, а электроны через n-слой. При возрастании электрического поля скорость носителей заряда растет линейно. Но уже при напряженности поля, вызывающей лавинное умножение носителей (Е >> 10⁵ В/м), скорость носителей заряда становится практически постоянной.

Пролетное время носителей заряда пропорционально ширине области пролета D и это объясняет запаздывание лавинного тока от напряжения в ЛПД. Сдвиг фазы между изменением напряженности поля и изменением тока при определенной частоте составит π/2. Дрейфуя через пролетные участки, электроны и дырки частично компенсируют объемный заряд ионов примеси и снижают напряженность поля в слое умножения.

7.3. Пролетный режим работы ЛПД

Пролетный режим (IМРАТТ -Avalanche Transit Time — ударная ионизация и пролетное время) работы диода основан на использовании лавинного пробоя и эффекта времени пролета носителей в обедненной области различных полупроводниковых структур. Распределение поля в этой области, определяющее физические процессы в диоде, зависит от типа структуры и закона распределения концентрации примесей в областях структуры. Ниже будет рассмотрена структура типа n+—р—i—p+ (диод Рида) (рис. 7.2, a), в которой области лавинного умножения и дрейфа носителей пространственно разделены. Распределение концентрации примесей в областях структуры показано на рис. 7.2,б. Концентрация примеси в крайних областях p⁺, n⁺ много больше, чем в р-области, по концентрации носителей i-область близка к собственному полупроводнику.

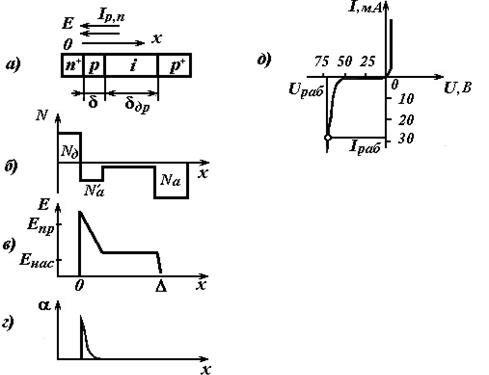
Рис. 7.2 Структура лавинно-пролетного диода (a) и распределение в нем концентрации примеси (6), электрического поля (в), коэффициента ударной ионизации (г), а также вoльт-aмпepнaя характеристика ЛПД (д)

Максимальная напряженность электрического поля имеет место в области р⁺-n-пepexoдa (рис. 7.2. в). Электрическое поле резко убывает в n-области и остается практически постоянным в i-cлoe, который полностью обеднен при больших обратных напряжениях. Если обратное напряжение увеличивать, то электрическое поле в переходе превысит значение пробивной напряженности E_пp, при которой коэффициент ударной ионизации α достигает больших значений (порядка 10⁵ cм^-1). поскольку α сильно зависит от E, то протяженность области ударной ионизации невелика (рис. 7.2, г). В ней происходит лавиннообpaзнoe нарастание количества свободных носителей заряда. Эту область называют областью лавинного умножения. Образующиеся дырки увлекаются внутренним электрическим полем перехода в p⁺-область, а электроны, попадая в i-cлoй, движутся к n-⁺области в постоянном электрическом поле. Если напряженность электрического поля в слаболегированной области велика и превышает несколько кB/cм, то скорость электронов остается почти постоянной и равной υ_нac = 10⁵ м/с. Происходит так называемое насыщение дрейфовой скорости носителей. Следовательно, носители заряда дрейфуют с конечной скоростью за конечный промежуток времени. Это предельное значение дрейфовой скорости называют скоростью насыщения. Обедненную область, в которой происходит движение электронов с постоянной скоростью, называют областью дрейфа. Поскольку при этом дифференциальная подвижность электронов близка к нулю, при движении электронов не происходит уменьшения объемной плотности заряда.

Принцип работы ЛПД поясним с помощью пространственно-временной диаграммы, показанной на рис. 7.3.

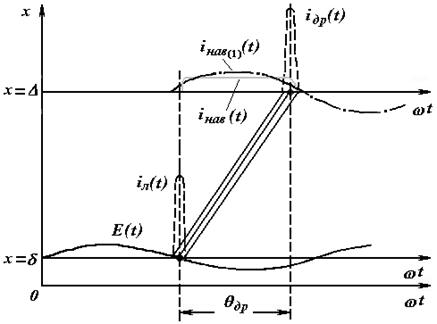
Рис. 7.3. Пространственно-временная диаграмма

Предположим, что в слое умножения и дрейфа имеется одинаковая и достаточно большая напряженность электрического поля, изменяющаяся во времени по синусоидальному закону E(t). При большой амплитуде поля лавинный процесс приводит к образованию короткого сгустка носителей, запаздывающего на четверть периода от максимума поля. Этому сгустку соответствует короткий импульс лавинного тока i_л(t) на границе x=d между слоями умножения и дрейфа. Далее носители сгустка двигаются в электрическом поле слоя дрейфа, пока не достигнут его границы (х—D) при угле пролета θ_дp. Пространственно-временная диаграмма для слоя дрейфа изображена на рис. 7.3 прямыми линиями, так как дрейфовая скорость носителей постоянна.

Угол пролета при выбранной ширине слоя D зависит от частоты. Если θ_дp<π, то носители все время пролета находятся в тормозящем полупериоде поля и отдают свою энергию полю, вызывая увеличение этого поля. При θ_дp>π последнюю часть пути в области дрейфа носители летят в ускоряющем полупериоде поля, что ослабляет эффект предыдущего взаимодействия и приводит в целом к снижению энергии, передаваемой носителями полю за все время пролета. Если θ_дp—2π, то эффект взаимодействия носителей и поля исчезает.

На рис. 7.3. при х—D показана зависимость дрейфового тока от времени i_др(t) в виде узкого импульса, повторяющего импульс i_л(t). Одновременно изображена кривая наведенного тока i_нaв(t). созданного движением короткого сгустка на пути от x=d до χ=D. В случае короткого сгустка форма кривой наведенного тока близка к прямоугольной. Разложением в ряд Фурье может быть определена первая гармоника i_нaв(1) этого тока. В идеальном случае она совпадает по фазе с полем, если θ_дp=π.

7.4. Параметры их характеристики, особенности устройства и применения ЛПД

Основными параметрами ЛПД являются:

а) выходная мощность P_вых—мощность генератора на ЛПД в заданном диапазоне частот и напряжения питания. Это важнейший параметр ЛПД. Максимальная полезная мощность генератора при заданном сопротивлении нагрузки зависит от добротности диода и от амплитуды переменного тока и напряжения. Максимальное значение выходной мощности различных типов ЛПД колеблется в пределах 10—100 мВт на частоте 7-50 ГГц;

б) пробивное напряжение U_пр — величина напряжения лавинного пробоя перехода. Этот параметр необходим для задания режима работы. Величина напряжения лавинного пробоя ЛПД обычно не превышает 30 В. Но имеются приборы с U_np, достигающим 160 В. СВЧ-генератор на ЛПД обычно работает при напряжении на  0,5—1,5В, превышающем пробивное;

в) номинальный рабочий ток I_ном—величина обратного тока ЛПД, при котором обеспечивается выходная мощность генератора. Величина I_ном составляет 54-15 мА для различных классов приборов;

г) максимальная емкость p-n-перехода С_mах—максимальное значение емкости ЛПД при напряжении, близком к пробивному;

д) сопротивление растекания r_s— максимальное последовательное сопротивление ЛПД в режиме генерации при заданном токе и напряжении. Отечественные приборы имеют r_s не более 10 Ом;

е) коэффициент полезного действия лавинно-пролетных диодов (сравнительно низок и составляет несколько процентов);

ж) температурный коэффициент мощности ТКМ и частоты ТКЧ — параметры, показывающие изменения мощности и частоты при изменении температуры окружающей среды на 1°С;

з) максимально-допустимый ток I_max— максимальная величина тока, при которой ЛПД работает в течение гарантированного срока с заданным уровнем надежности. Величина I_max обычно ограничивается максимальной температурой перехода T_{п mах}.

Для изготовления ЛПД используют кремний, германий и арсенид галлия. Требуемую структуру получают методами эпитаксиального наращивания, диффузии и ионного легирования. При их изготовлении стремятся по возможности снизить активные потери: утечку тока по поверхности p-n-перехода и сопротивление объема кристалла. Необходимо обеспечить однородность p-n-перехода, в противном случае возможно возникновение локальных пробоев и т. д.

На рис.7.4 приведена одна из структур ЛПД диода, изготовленного по планарной технологии. Для устранения пробоя по поверхности создано охранное кольцо n-типа.

Преимуществом ЛПД перед другими генераторами СВЧ-мощности является незначительная суммарная толщина структуры (один переход). Это очень важно, так как ЛПД работает в режиме лавинного пробоя и плотность мощности на переходе достигает больших величин до 10⁵ Вт/см². Тонкие структуры облегчают отвод тепла от перехода. Кроме того, для лучшего отвода тепла в ЛПД применяют так называемую обратную сборку, кристалл присоединяют к теплоотводу той стороной, где переход расположен на небольшой глубине от поверхности кристалла.

Мощность и КПД генераторов на ЛПД сравнительно невелики, зависят от рабочей частоты и от теплоотвода. Для улучшения теплоотвода в мощных ЛПД в качестве подложки используют алмаз.

ЛПД, работающие в пролетном режиме, используют также для усиления колебаний, однако из-за большого коэффициента шума (20—40 дБ) они не пригодны для входных устройств. Диод является активным двухполюсником, т. е. двухполюсником с отрицательным дифференциальным (динамическим) сопротивлением. Поэтому в усилителе применяется циркулятор, обеспечивающий разделение входного и выходного сигналов. Коэффициент усиления при каскадном включении достаточно велик (до 30 дБ и более).

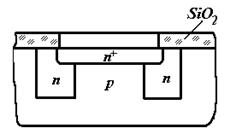
Рис. 7.4. Структура кристалла ЛПД

 Недостатком ЛПД является очень низкий КПД. Это объясняется тем, что амплитуда колебательного напряжения на диоде намного меньше величины постоянного напряжения, приложенного к диоду для обеспечения режима лавинного умножения. Низкий КПД ЛПД, кроме того, объясняется зависимостью вольт-амперной характеристики ЛПД от частоты колебаний. На частоте, на которой отрицательное сопротивление имеет наибольший модуль, амплитуда переменного напряжения значительна, но амплитуда тока мала. В результате получается, что отдаваемая мощность мала.

В настоящее время на частоте 1 ГГц получен КПД до 60% в Si-диодах и до 45% на частоте 2—3 ГГц в Ge-диодах. Однако большие плотности тока, требуемые для возникновения аномального режима, не позволяют осуществить непрерывную генерацию.

ЛПД с рабочей частотой выше 50 ГГц трудно изготовлять из-за очень малых размеров, а ЛПД с частотой ниже 1 ГГц имеют большие размеры, поэтому трудно отводить тепло от перехода.

На рис. 7.5 приведены два вида конструкций лавинно-пролетных диодов в коаксиальном исполнении. Для интегральных полосковых схем разрабатываются бескорпусные ЛПД с полосковыми выводами.

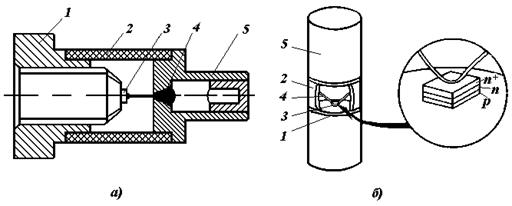
Рис. 7.5. Конструкция ЛПД: а — германиевого; б — кремниевого; 1— метал-лическое основание; 2 — керамическая втулка; 3— кристалл; 4 — соединительный электрод; 5—ниппель

В пролетном режиме ЛПД отрицательное сопротивление существует в широкой области рабочих частот. Поэтому частоту генерации в генераторах на ЛПД можно изменять в пределах более октавы механической перестройкой колебательной системы. Широко исполь-зуют также электрическую перестройку частоты, включая в колебательную систему СВЧ варикап или ферритовые элементы. В первом случае диапазон перестройки обычно невелик, а во втором — достигает 10%. Температурный коэффициент частоты генератора зависит от изменения как параметров диода, так и колебательной системы. Для одноконтурного генератора ТКЧ= ± 10^-41/°C, но может быть снижен в результате принятия специальных мер.

Высокий уровень шума ЛПД позволяет использовать их для создания генераторов шума СВЧ диапазона. Эти генераторы очень просты, имеют большую спектральную плотность мощности шума, низкую потребляемую мощность, малые массу и габариты, т. е. выгодно отличаются от электровакуумных генераторов шума.

Усилители на ЛПД вследствие значительного коэффициента шума (20— 30 дБ) не используются во входных усилителях. По коэффициенту преобразования амплитудной модуляции в фазовую (АМ/ФМ) усилители на ЛПД сравнимы с лампами бегущей волны.

В заключение следует отметить существование аномального режима ЛПД— режима с захваченной плазмой или ТRАРРАТ — режима (сокращение от слов ТРАрреd Plasma Avalanche Triggered Transit — захваченная плазма, пробег области лавинного умножения). В электронно-дырочном переходе в этом режиме создаются условия для движения фронта ла-винного умножения со скоростью, в несколько раз большей максимальной скорости носите-лей (скорости насыщения). Поэтому в переходе очень быстро образуется электронно-дыроч-ная плазма, что приводит к резкому снижению напряжения на переходе, а следовательно, к уменьшению скорости электронов и дырок в плазме (захваченная плазма). Увеличение вре-мени пролета носителей в переходе вызывает снижение частоты генерации в несколько раз по сравнению с пролетным режимом работы ЛПД. Однако достоинством ЛПД с захваченной плазмой является снижение потребляемой мощности, вследствие понижения  напряжения

Сведения о мощности и КПД в перечисленных режимах работы приведены в табл.7.1 Преимущества режима с захваченной плазмой проявляются на более низких частотах.

Таблица 7.1

Режим работы	Частота, ГГц	Выходная мощность. Вт		КПД, %	Материал
		в непрерывном режиме	в импульсном режиме
Пролетный	2—4	—	40	20	Si
	8,2—12,4	2,7	10	10—11	Si
	100	0,16	—	7	Si
	4—8	4	10	5—17	GaAs
	8,2—12,4	4	—	5—17	GаАs
	1—2	10	500	60	Si
С захваченной плазмой	12,4—18	—	30	5	Si

В пролетном режиме работы ЛПД отрицательное сопротивление существует в широкой полосе рабочих частот. Следовательно, можно изменять частоту генерации в больших пределах механической перестройкой колебательной системы. Широко применяют также электрические способы перестройки частоты. Один из способов состоит в изменении собственной частоты колебательной системы (резонатора) с помощью варакторного СВЧ-диода. Диапазон перестройки в зависимости от схемы включения варакторного диода доходит до 3—5%. Применяют для перестройки также ферритовые элементы, помещенные в резонатор ГЛПД, при этом диапазон перестройки может достигать 10%. Для перестройки частоты в небольших пределах используют зависимость частоты от постоянного тока (электронное смещение частоты). Крутизна электронного смещения частоты в сантиметровом диапазоне — несколько мегагерц на миллиампер, а диапазон перестройки — несколько десятых долей процента.

5. Контрольные вопросы:

1. Условие лавинного пробоя и его физический смысл.

2. Какую область называют областью лавинного умножения, областью дрейфа?

3. Какие режимы работы ЛПД вы знаете? Опишите каждый из них.

4. Основные параметры ЛПД.

5. Перечислите преимущества и недостатки ЛПД.

ЛЕКЦИЯ № 8

Диод Ганна

8.1. Концептуальная диаграмма.

8.2. Междолинный переход электронов.

8.3. Объемное отрицательное сопротивление.

8.4. Режимы работы. Характеристики и параметры диода Ганна.

8.5. Контрольные вопросы.

8.1. Концептуальная диаграмма.

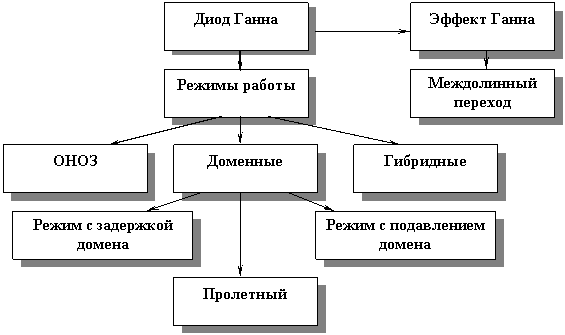8.2. Междолинный переход электронов

Для ycилeния и гeнepaции кoлeбaний CBЧ-диaпaзoнa мoжeт быть иcпoльзoвaнa aнoмaльнaя зaвиcимocть cкopocти элeктpoнoв oт нaпряжeннocти элeктpичecкoгo пoля в нeкoтopыx пoлyпpoвoдникoвыx coeдинeнияx, пpeжде вceгo в apcенидe гaллия. Пpи этoм ocнoвнyю poль игpaют пpoцeccы, пpoиcxoдящиe в oбъeмe пoлyпpoвoдникa, a нe в p-n-пepexoдe. В 1961 -1962гг. Ридли, Уоткинс и Хилсум теоретически показали, что однородные образцы из некоторых полупроводниковых материалов могут иметь отрицательную дифференциальную проводимость. В 1963 г. Дж.Ганн экспериментально обнаружил токовую неустойчивость (высокочастотные периодические импульсы тока) в однородных образцах из GaAs и InP с электронной проводимостью (пoэтoмy тaкиe пpибopы нaзывaют диoдaми Гaннa). В oтeчecтвeннoй литepaтype иx нaзывaют тaкжe прибopaми c oбъeмнoй нeycmoйчивocmью или c мeждoлинным пepeнocoм элeкmpoнoв, пocкoлькy aктивныe cвoйcтвa диoдoв oбycлoвлeны пepexoдoм элeктpoнoв из «цeнтpaльнoй» энepгетичecкoй дoлины в «бoкoвyю», гдe oни xapaктepизyютcя бoльшoй эффeктивнoй мaccoй и мaлoй пoдвижнocтью. В инocтpaннoй литepaтype пocлeднeмy нaзвaнию cooтвeтcтвyeт тepмин TED (Traпsferred Electroп Device).

Рассмотрим физическую природу эффекта Ганна. Внутри любого кристаллического полупроводника существует пространственно-периодическое электрическое поле. При ионной связи оно создается разноименно заряженными ионами в соседних узлах кристаллической решетки, при ковалентной - положительно заряженными атомными «остатками» и электронами связи. Влияние этого поля чрезвычайно усложняет задачу описания движения электронов под действием внешнего электрического поля. Однако квантовая теория показывает, что усредненные по периоду внутри-кристаллического поля параметры движения можно описать уравнениями классической физики при замене в них массы электрона т на некоторую эффективную массу т_n. Так, усредненная скорость электрона при его движении во внешнем поле E может быть найдена с помощью классического уравнения Ньютона:

                                                                                                         (8.1)

Подобным же образом вводится эффективная масса дырки, но мы не будем ею интересоваться, так как в ДГ применяются электронные полупроводники. Величина эффективной массы зависит от материала и структуры кристалла, а также энергии носителя заряда.

Соотношение между энергией электрона проводимости и его импульсом р (или волновым числом k = р/; ħ = h/2π, где h - постоянная Планка) также можно записать в приближении эффективной массы:

 (8.2)

Дважды дифференцируя это выражение по k, получаем

                                                                                                     (8.3)

Эту формулу используют для определения m_n по зависимости W(k). Как правило, такая зависимость немонотонна. Рассмотрим упрощенную зависимость W(k), описывающую поведение электронов в зоне проводимости такого материала (рис. 8.1). Ее особенностью является наличие двух минимумов, называемых энергетическими долинами. Полупроводники, описываемые подобной зависимостью W(k), называют двухдолинными. Минимальная энергия электронов, имеющая место при k=0, соответствует дну зоны проводимости; верхняя долина 2 отделена от нижней 1 энергетическим зазором ΔW', который значительно меньше ширины запрещенной зоны ΔW (для GaAs ΔW = 0,36 эВ, а ΔW'= 1,42эВ). Зависимость W(k) в окрестности обоих минимумов хорошо аппроксимируется параболами (штриховые линии на рис. 8.1), поэтому в соответствии с формулой (8.3) эффективные массы электронов, находящихся в нижней и верхней долинах, почти постоянны, но различаются по значению из-за разной ширины долин. Так, для GaAs, часто используемого в диодах Ганна, т_n1 = 0,072 т, m_n2 = 1,2m. Подвижность электронов μ = q·τ_с/m_n, где τ_с - среднее время между столкновениями с решеткой. Для GaAs μ₁ = 8·10³ см/В·с,μ₂ = 10² см/В· с. Это означает, что дрейфовая скорость «легких» электронов нижней долины ν_др1 = μ₁·Е почти на два порядка больше скорости «тяжелых» электронов верхней долины ν_др2 = μ₂·Е.

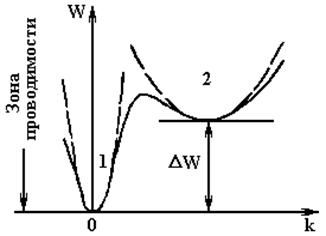
Рис. 8.1. Энергетические долины в зоне проводимости полупроводника

При комнатной температуре средняя энергия свободных электронов мала и почти все они находятся в нижней долине. Увеличение температуры кристалла приводит к росту средней энергии («разогреву») электронов, и все большее число их приобретает энергию, достаточную для преодоления потенциального барьера, разделяющего долины. В результате нижняя долина опустошается, а верхняя - заполняется. Этот процесс называют междолинным переходом.

Однако разогрев (т.е. увеличение энергии) электронного газа можно осуществить не только повышением температуры кристалла, но и с помощью внешнего электрического поля Е, изменяя напряженность которого можно управлять междолинным переходом электронов. Значение Е, при котором начинается интенсивный междолинный переход, называют пороговым и обозначают Е_п. Для GaAs Е_п » 3,2 кВ/см.

Исследования показывают, что пороговое значение напряженности Е_п, при котором начинается междолинный переход электронов, достигается лишь в узкой области образца, где имеется неоднородность концентрации примеси или флуктуация электрического поля.

Предположим, что на некотором небольшом участке с протяженностью d концент-рация донорной примеси несколько меньше, чем в остальной части образца (рис.8.2 а). Увеличение электрического сопротивления приведет к росту падения напряжения на участке d по сравнению с другими участками такой же длины и к росту напряженности поля Е в нем (рис. 8.2 б). Пусть напряженность поля на участке d несколько выше, а вне его несколько ниже пороговой напряженности Е_п. Тогда на участке d начнется переход электронов из нижней долины в верхнюю, сопровождающийся понижением дрейфовой скорости электронов.

Оказавшиеся в верхней долине электроны начинают отставать от неперешедших электронов, так что в левой части участка наблюдается избыток электронов (отрицательный объемный заряд), а в правой — недостаток электронов, т. е. объемный положительный заряд донорных ионов, который теперь не компенсируется зарядом электронов. Образующийся двойной электрический слой объемного заряда (рис. 8.2 в) называется электрическим доменом. В целом домен должен быть электрически нейтральным. Так как электроны в образце двигаются, то и домен перемещается в том же направлении (на рис. 8.2 в вправо), уходя от участка с неоднородностью. На рис. 8.2 в изображены положения домена в моменты времени t₁ и t₂.

Образование домена означает увеличение напряженности поля в нем (рис. 8.2 г) и разности потенциалов на участке, занимаемом доменом (рис. 8.2 д). При постоянном внешнем напряжении U₀ на образце это должно приводить к уменьшению падения напряжения на остальной части образца и напряженности поля вне домена. Поле на участке неоднородности становится значительно меньше порогового, что препятствует возникновению нового домена. Затем электроны из домена уходят во внешнюю цепь, домен начинает исчезать (рассасываться), напряженность поля в нем из-за уменьшения числа электронов падает, а напряженность поля в остальной части образца возрастает. Поэтому в процессе исчезновения домена электроны в образце увеличивают дрейфовую скорость. В момент исчезновения домена поле в образце восстановится и на участке неоднородности превысит пороговое значение. После этого начнется образование нового домена и т. д.

Таким образом, в образце движется только один домен, место возникновения которого определяется неоднородностью.

Найдем плотность дрейфового тока, протекающего через двухдолинный полупроводник n-типа. Учитывая, что ток образуется как «легкими», так и «тяжелыми» электронами, можем записать

.                                                           (8.4)

Здесь n₁(E) и n₂(E) - концентрации электронов в нижней и верхней долинах, зависящие от напряженности внешнего поля Е. Отметим, что полная концентрация электронов n₀=n₁(Е) + n₂(Е) не зависит от Е, так как она определяется только концентрацией доноров.

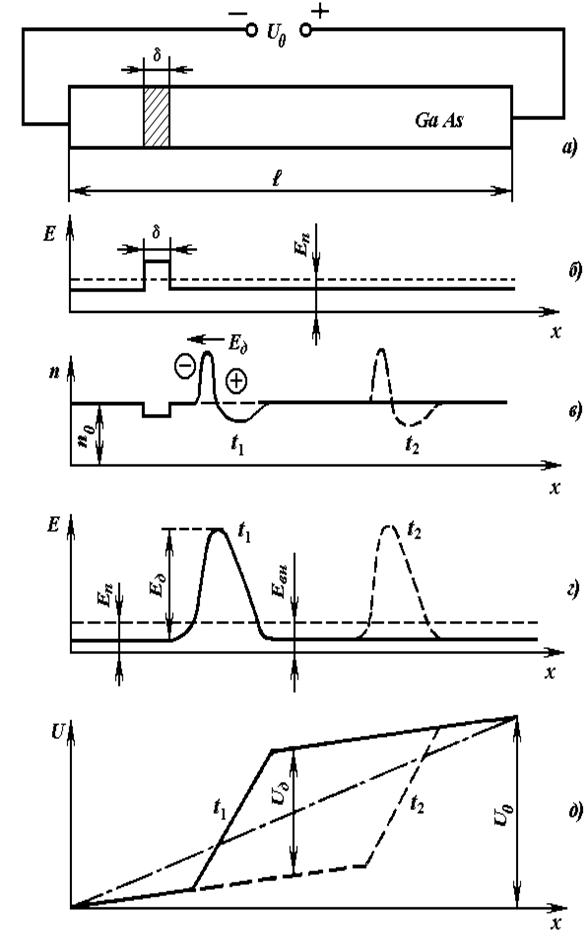
Рис. 8.2. Графики образования и движения доменов в полупроводнике

 Перепишем (8.4), умножив и разделив правую часть на n₀:

,                                                                                (8.5)

где

                                                                  (8.6)

-усредненная по двум долинам (по «легким» и «тяжелым» электронам) подвижность.

                  Учитывая это, вместо (8.5) можно записать

;                                                                                  (8.7)

n_др(Е) = m_ср(Е)Е -усредненная по двум долинам дрейфовая скорость.

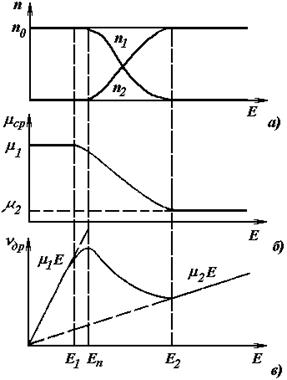
Рис. 8.3. Зависимость концентраций электронов в верхней и нижней долинах (а),подвижности электронов (б) и скорости _др (в) от напряженности

Таким образом, поле-скоростная характеристика _др(E) полностью определяет зависимость j(Е). Рассмотрим ее, считая m₁>>m₂. На рис. 8.3 а показан примерный вид зависимостей n₁(E) и n₂(Е). В слабых полях (при Е < Е₁) почти все электроны находятся в нижней энергетической долине, т.е. n₁» n₀, n₂» 0 и в соответствии с (8.6) m_ср >> m₁. При Е>E₁ в результате «разогрева» электронов полем начинается интенсивный междолинный переход, вследствие чего в диапазоне E₁ < E < Е₂ n₁, уменьшается, а n₂ растет.

При Е » E₂ переход завершается; при Е> Е₂ нижняя долина практически опустошена, а верхняя заполнена, т.е. п₁ » 0, n₂ » n₀, m_сp » m₂. Соответствующие сказанному зависимости m_сp(Е) и _др(E) = m_сp(E)E показаны на рис. 8.3 б, в. Важной особенностью характеристики _др(E) является падающий участок с отрицательной дифференциальной проводимостью, начинающийся при напряженности поля Е_п, которая была названа пороговой.

8.3. Объемное отрицательное сопротивление

Общим условием усиления или генерации колебаний является наличие отрицательного дифференциального сопротивления, или дифференциальной проводимости. Найдем условие, при котором возможно существование отрицательной дифференциальной проводимости в однородных полупроводниках.

Плотность тока через полупроводник в общем виде определяется зависимостью (8.4). Условием возникновения отрицательной проводимости является dj/dE<0. Дифференцируя (8.4), с учетом dп₁/dE = —dп₂/dE и μ₁>>μ₂ (пренебрегаем членами с μ₂) условие возникновения отрицательной проводимости получим в виде

d n₂ / dE > n₁ / E.                                                                                      (8.8)

Это означает, что на участке отрицательной проводимости переход электронов из одного минимума в другой должен быть достаточно интенсивным при небольших изменениях E.

По выражению (8.7) плотность тока зависит от напряженности поля так же, как и дрейфовая скорость. Так как ток диода I=jS, где S - площадь его поперечного сечения, а напряжение на диоде U=Eℓ, где ℓ - расстояние между контактами (длина диода), то

(8.9)

Это выражение определяет вольт-амперную характеристику диода Ганна при однородном распределении электрического поля по продольной координате. Дифференциальная проводимость ДГ

в диапазоне напряжений питания от U_п=E_nℓ до U₂=E₂ℓ отрицательна и может компенсировать потери в подсоединенной к диоду пассивной цепи, что открывает возможность использовать его для генерации или усиления колебаний.

Изложенный физический механизм образования отрицательного сопротивления в арсениде галлия был убедительно подтвержден экспериментами по влиянию давления на характеристики диодов Ганна.

8.4. Режимы работы. Характеристики и параметры диода Ганна

В зaвиcимocти oт пapaмeтpoв диoдa (cтeпeни и пpoфиля лeгиpoвaния мaтepиaлa, длины и плoщaди ceчeния oбpaзцa и eгo тeмпepaтypы), a тaкжe oт нaпpяжeния питaния и cвoйcтв нaгpyзки диoд Гaннa, кaк гeнepaтop и ycилитeль CBЧ-диaпaзoнa, мoжeт paбoтaть в paзличныx peжимax: дoмeнном, oгpaничeния нaкoплeния oбъeмнoro зapядa (OHOЗ), гибpиднoм, бeryщиx вoлн oбъeмнoro зapядa, oтpицaтeльнoй пpoвoдимocти

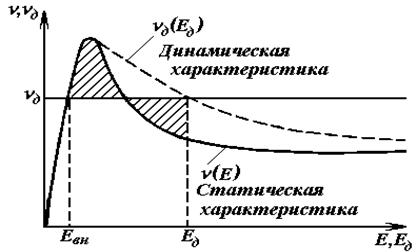
Pиc. 8.4. Зависимость скорости домена от напряженности

8.4.1. Доменные режимы работы

Рассмотрим следующие разновидности доменных режимов:

- пролетный;

- режим с задержкой домена;

- режим с подавлением (гашением) домена.

Для дoмeнныx peжимoв paбoты диoдa Гaннa xapaктepнo нaличиe в oбpaзцe cфopмиpoвaвшeгocя дипoльнoгo дoмeнa в тeчeниe знaчитeльнoй чacти пepиoдa кoлeбaний.

Скopocть дoмeнa _д и мaкcимaльнaя нaпpяжeннocть пoля в нeм E_д cвязaны пpaвилoм paвныx плoшaдей

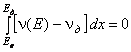                                                                                 (8.10)

В cooтвeтcтвии c (8.10) плoщaди, зaштpиxoвaнныe нa риc. 8.4 и oгpaничeнныe линиями (E), _д = const, E_д = const, являютcя oдинaкoвыми. Kaк виднo из pиc. 8.4, мaкcимaльнaя нaпpяжeннocть пoля E_д в дoмeнe знaчитeльнo пpeвышaeт пoлe E_вн внe дoмeнa и мoжeт дocтигaть дecяткoв кB/cм.

8.4.1.1. Пролетный режим генератора.

Обычно так называют режим работы, в котором колебательная система, связанная с прибором Ганна, имеет низкую добротность. В этом случае переменное напряжение на колебательной системе мало по сравнению с постоянным напряжением и не оказывает обратного влияния на процессы в образце из GaAs. Если постоянное напряжение превышает пороговое значение, то в образце возникнут импульсы тока, частота следования которых определяется временем пролета. Этот режим уже рассмотрен как эффект Ганна.

Частота генерации в пролетном режиме определяется формулой :

,

где Т_о — время пролета домена.

Условие пролетного режима определяется неравенством

                                                                                    (8.11)

Теоретический анализ показывает, что КПД в пролетном режиме максимален, когда n₀ℓ составляет от одной до нескольких единиц на 10¹²см^-2, домен занимает примерно половину длины образца, а форма тока почти синусоидальная. Обычно . Мощность колебаний в пролетном режиме можно оценить по формуле

P=ηP₀,                                                                                                      (8.12)

 где P₀— потребляемая от источника мощность

                                 Р₀=I₀U₀.                                                                                                   (8.13)

Необходимое напряжение источника U₀=E_nℓ, а ток I₀=qn_0дрS. Тогда P₀ пропорциональна ℓS. Однако площадь влияет на сопротивление образца в слабом поле R₀:

 (8.14)

Для получения необходимой выходной мощности и КПД следует выбирать определенное отношение активного сопротивления нагрузки R_н и образца R₀. Таким образом, нельзя выбирать любую площадь образца: ее величина оказывается обратно пропорциональной сопротивлению R_a. На основании соотношений (8.12) — (8.14) можно получить произведение мощности на сопротивление

                                                                                   (8.15)

Таким образом,

                                                                                     (8.16)

т. е. произведение мощности на сопротивление обратно пропорционально квадрату частоты. Действительно, для увеличения пролетной частоты необходимо уменьшить длину образца, что приводит к уменьшению сопротивления образца R₀ и необходимости снижения напряжения питания U₀. При постоянстве отношения R_н/R₀ требуется уменьшить сопротивление нагрузки. Следовательно, уменьшение как U₀, так и R_H вызовет снижение полезной мощности.

Длина образца ℓ определяется выбранной рабочей частотой, а концентрация п₀ — условием (8.11), поэтому сопротивление образца R₀ можно изменять только выбором площади образца S. При этом можно обеспечить значение R_н/R₀, необходимое для получения заданной мощности и КПД. Из-за сильной зависимости мощности и КПД от частоты пролетный режим приборов с объемной неустойчивостью не нашел применения в СВЧ-генераторах.

8.4.1.2. Режим с задержкой образования домена.

Этот режим наблюдается, когда резонатор имеет высокую добротность, постоянное напряжение больше порогового значения (U₀>U_0n), а время пролета домена Т₀ меньше периода колебаний Т.

На рис. 8.5 показаны вольт-амперная характеристика прибора, изменение во времени напряжения на приборе в режиме генерации с амплитудой U₁ и изменение во времени тока.

Когда напряжение на образце

U =U₀ +U₁ sinωt = U₀+U₁ sin(2πt/T)                                                     (8.17)

достигает порогового значения U_оп, возникает домен, ток уменьшается в соответствии с участком АС вольт-амперной характеристики. Далее зависимость тока от напряжения должна изображаться участком CDN, а после прохождения через амплитудное значение напряжения — обратным движением по ветви NDCB. Однако если время пролета Т₀<Т настолько, что когда домен подойдет к аноду, напряжение станет меньше порогового (точка М), домен исчезнет, а ток возрастет. Следующий домен возникнет только с задержкой на время Т-Т₀, когда U достигнет порогового значения. В интервале времени Т_И=Т-Т₀ (пассивная часть периода) образец является омическим сопротивлением и изменения тока и напряжения соответствуют на вольт-амперной характеристике сначала участку FK, а затем KFA. После этого возникает новый домен и весь процесс повторяется.

Период колебаний Т определяется настройкой резонатора. При заданном времени пролета домена T₀ возможна механическая перестройка частоты в некотором интервале, зависящем от выбора величин U₀ и U_0n, которые определяют отношение Т/Т₀. Очевидно, T/T₀→2 при U₀→U_0n. Таким образом, при U₀ » U_0п частота генератора может изменяться настройкой резонатора в пределах от пролетной частоты f_пр=1/T₀ до вдвое меньшей величины: f_np > f > f_пр /2. Если U₀>U_0п, диапазон перестройки уменьшается.

Уточним условия существования режима с задержкой образования домена. Кроме условия T₀<T необходимо, чтобы амплитуда переменного напряжения не была настолько велика, что во время пролета домена напряжение упадет ниже значения напряжения исчезновения U_0и. В случае U₀=U_0и необходимо, чтобы U₁<(U_0п-U_0и).

В энергетическом отношении режим с задержкой образования домена более выгоден, чем пролетный режим. Длительность импульса тока Т_К=Т—Т₀ может превышать сумму времени нарастания и рассасывания домена, которая определяет длительность импульса в пролетном режиме. КПД возрастает с увеличением длительности импульса T_И и достигает максимального значения примерно при T_И=T/2=T₀, т. е. на рабочей частоте, вдвое меньшей пролетной.

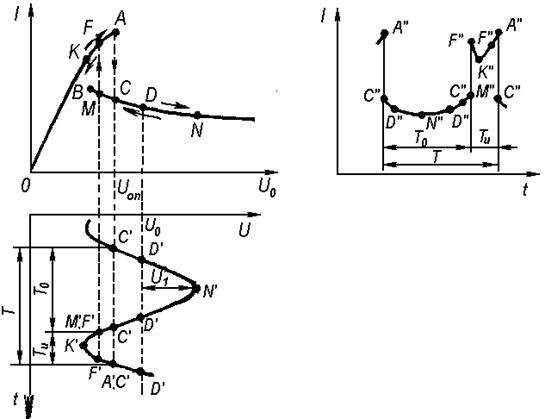
Рис. 8.5. Вольт-амперная характеристика в режиме задержки образования домена

В режиме с задержкой образования домена КПД теоретически достигает 25%, а экспериментально получено 20% при отдаваемой импульсной мощности 100 Вт.

8.4.1.3. Режим с подавлением домена.

В этом режиме домен исчезает (подавляется) раньше, чем он дойдет до анода, т. е. в момент времени, когда напряжение на образце становится меньше U_0и.

На рис. 8.6 этот момент смещен относительно момента возникновения домена на время Т'₀, которое можно было бы назвать временем жизни домена или временем его существования, в отличие от времени пролета Т₀ в пролетном режиме, когда он проходит через весь образец (T₀=ℓ/ν_д, T'₀=ℓ'/ν_д , ℓ'<ℓ). Следующий домен возникает лишь спустя время Т₀—Т'₀, когда напряжение достигнет порогового значения. Пользуясь вольт-амперной характеристикой, нетрудно определить изменение тока во времени. В интервале времени t_n=T₀—Т'₀ образец ведет себя как омическое сопротивление. Время жизни домена в режиме с подавлением домена меньше периода колебаний генератора (Т'₀<Т). Частоту колебаний удобно сравнивать с возможной пролетной частотой, которая определяется временем пролета Т₀ через образец. В нашем случае, очевидно, Т'₀<Т₀ (домен гибнет, не доходя до конца образца). Само же время пролета может быть и больше периода колебаний, так как оно никак далее не влияет на процессы в образце. Таким образом, возможны два случая:

                     Т'₀ < Т₀ < Т;                                                                                             (8.18)

                     Т'₀ < Т < Т₀.                                                                                             (8.19)

Рис. 8.6. Вольт-амперная характеристика в режиме с подавлением домена

Неравенству (8.18) соответствует частота генерируемых колебаний меньше пролетной частоты образца, при U₀=U_0п она составляет примерно 0,75f_пр. Неравенство (8.19) означает возможность получения частоты больше пролетной. Ограничение по частоте сверху реально связано с тем, что период колебания не может быть меньше суммы времени формирования и исчезновения домена. Верхняя частота может в несколько раз превышать f_пр. Следовательно, диапазон механической перестройки частоты в режиме с подавлением домена оказывается достаточно широким.

При заданном напряжении питания U₀ постоянная составляющая тока I₀, амплитуда первой гармоники I₁ выходная мощность Р, электронный КПД η и сопротивление нагрузки R_н зависят от амплитуды напряжения U₁. При определенных значениях U₁, соответствующих согласованной нагрузке генератора, КПД будет максимальным. Достоинством режима работы с подавлением домена, как показывает анализ, является то, что в широком диапазоне рабочих частот мощность в нагрузке и КПД генератора при неизменных напряжении питания и величине нагрузки остаются постоянными.

8.4.2. Режим ограниченного накопления объемного заряда (ОНОЗ).

Название режима связано с тем, что и в нем домены не успевают сформироваться и объемный заряд в каждой неустойчивости оказывается ограниченным, т. е. меньшим заряда в полностью сформированном домене. Для получения такого режима период колебаний должен быть много меньше времени формирования домена (T<<t_Ф).

Предположим, что к образцу приложено постоянное напряжение U₀, больше порогового значения (U₀>U_0п), и переменное напряжение с амплитудой U₁>(U₀—U_0п), как показано на рис. 8.7. Когда результирующее напряжение превысит U_0п, начинает образовываться домен. Если в ту часть периода, пока U₀>U_0п. домен не успевает сформироваться (условие режима ОНОЗ), то зависимость тока от поля не совпадает с вольт-амперной характеристикой прибора с доменной неустойчивостью, как в прежних режимах, а повторяет вольт-амперную характеристику образца без домена, т. е. зависимость дрейфовой скорости от поля. При этом ток сначала уменьшается, а затем растет до значения I_маx при U₀=U_0п. В эту часть периода t' образец ведет себя как отрицательное сопротивление и происходит передача мощности в СВЧ - цепь. В оставшуюся часть периода t' = T - t'_и U < U_on по определению режима объемный заряд должен рассасываться. Если он не успевает исчезнуть, то за несколько периодов накопится такой заряд, что прибор выйдет из режима ОНОЗ. В интервале t" прибор ведет себя как положительное сопротивление (поглощение мощности), а ток изменяется в соответствии с начальной ветвью вольт-амперной характеристики. Таким образом, изменение тока имеет сложный вид, определяемый характеристикой  (E).

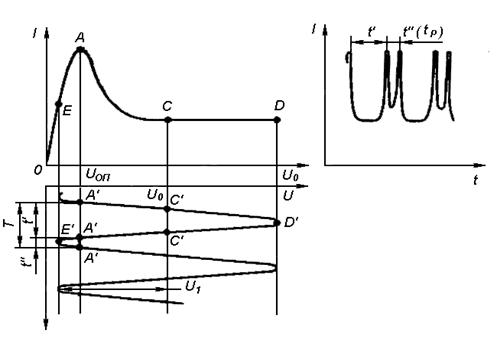
Рис. 8.7. Вольт-амперная характеристика в режиме ограниченного накопления объемного заряда

СВЧ - мощность, создаваемая в единице объема при амплитуде первой гармоники тока I₁ и напряжении U₁=E₁ℓ (E₁ — амплитуда напряженности поля), равна Р=U₁I₁/2. Отрицательное дифференциальное сопротивление образца

                                                                      (8.20)

Используя формулу (8.20), получаем

.                                                                                       (8.21)

т. е. в режиме ОНОЗ произведение мощности на сопротивление не зависит от частоты и определяется амплитудой переменной составляющей поля в домене Е₁ и длиной образца ℓ.

            Режим ОНОЗ особенно эффективен на высоких частотах (f ³ 3^.10 ГГц), так как в нем, в отличие от других режимов, нет ограничения на время пролета и время формирования домена. Однако имеется принципиальное ограничение для частоты, связанное с тем, что, как уже отмечалось, на частотах более 20 ГГц зависимость дрейфовой скорости от поля заметно отличается от статической зависимости. Расчеты показывают, что максимальная частота генерации не может превысить 200 ГГц. Наибольшая достигнутая частота в режиме ОНОЗ составляет 160 ГГц. Отмеченное принципиальное ограничение приводит к падению КПД с ростом частоты. Максимальное значение КПД на частоте около 20 ГГц составляет 20—25%. Значение КПД можно несколько увеличить (до 30%), если обеспечить получение несинусоидальной формы напряжения на приборе. Подобное влияние гармоник на КПД проявляется и в других приборах. Для создания несинусоидальной формы напряжения необходимо, чтобы резонатор возбуждался колебаниями тока как на рабочей частоте, так и на ее гармониках.

Режим ОНОЗ характеризуется большой амплитудой колебаний. Однако ввод в этот режим представляет значительные трудности.

В режиме ОНОЗ частота колебаний определяется внешней цепью (резонатором), при этом применяют как механическую, так и электрическую перестройку последнего с помощью варакторного диода.

8.4.3. Гибридный режим

Этот режим является промежуточным между режимами ОНОЗ и с подавлением домена. Отличие от режима ОНОЗ состоит в том, что время формирования домена составляет бóльшую часть периода, а от режима подавления — в том, что домен рассасывается, не успев полностью сформироваться.

При понижении рабочей частоты наблюдается плавный переход из режима ОНОЗ в гибридный режим, а далее из гибридного режима — в режим с подавлением домена. Таким образом, возможно изменение частоты в очень широком диапазоне, перекрывающем диапазоны отдельных режимов работы.

Режим OHOЗ и гибридные режимы работы диода Ганна относят к режимам с «жестким» самовозбуждением, для которых характерна зависимость отрицательной электронной проводимости от амплитуды высокочастотного напряжения. Ввод генератора в гибридный режим (как и в режим OHOЗ) представляет сложную задачу и обычно осуществляется последовательным переходом диода из пролетного режима в гибридные.

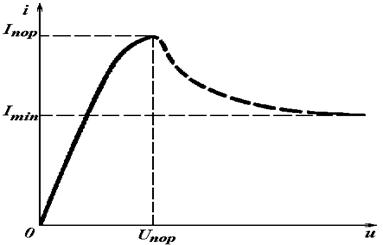
Рис. 8.8. Статическая вольт-амперная характеристика диода Ганна

8.4.4 Параметры диода Ганна

Подытоживая сказанное выше, перечислим основные параметры диода Ганна:

- концентрация примесей в активной области п₀, подвижность электроновm_n в слабом электрическом поле (т. е. при напряжениях на диоде, меньших порогового);

- длина активной области ℓ, площадь контакта S;

- пороговое напряжение U_пор, пороговый ток I_пор, сопротивление в слабом поле R₀=U_пор /I_пор, статическая емкость диода C₀ = εS/ℓ.

Электрические параметры ДГ U_пор, I_пор, R₀ определяются по статической вольт-амперной характеристике (рис. 8.8).

8.5. Контрольные вопросы:

1. Какой процесс называют междолинным переходом?

2. Что такое домен?

3. Условия возникновения отрицательной проводимости.

4. Какие режимы работы диода Ганна вы знаете? Охарактеризуйте каждый из них.

5. Основные параметры диода Ганна.

ЛЕКЦИЯ № 9

СВЧ транзисторы

1. Концептуальная диаграмма.

2. Биполярные микроволновые транзисторы. Геометрия, характеристики и параметры.

3. Высокочастотные полевые транзисторы. Характеристики и параметры.

4. Контрольные вопросы

9.1. Концептуальная диаграмма

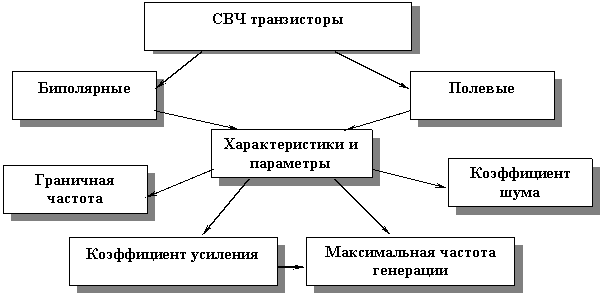9.2. Биполярные микроволновые транзисторы. Геометрия, характеристики и параметры

Транзистором называют электропреобразовательный полупроводниковый прибор с одним или несколькими электрическими переходами, имеющий три и более выводов. Термин "транзистор" происходит от английских слов transfer of resistor (преобразователь сопротивления).

В отличие от вакуумных СВЧ приборов, не имеющих, с точки зрения механизма работы, аналогов в низкочастотном диапазоне, в основе работы полупроводниковых СВЧ-транзисторов лежат те же физические процессы, которые определяют работу транзисторов на низких частотах.

Рассмотрим факторы, которые, с одной стороны, ограничивают возможность использования низкочастотных транзисторов в СВЧ-диапазоне и которые приводят, с другой стороны, к конструктивным особенностям СВЧ-транзисторов, являясь основанием для выделения их в самостоятельную группу транзисторных приборов.

Bо-первых, следует отметить, что частотный диапазон транзистора ограничивается временем переноса носителей заряда через транзистор. Применяемые в настоящее время СВЧ-транзисторы работают с малым временем пролета. Bо-вторых, существуют частотные ограничения, которые обусловлены скоростью изменения заряда, накопленного в транзисторе: введение носителей заряда в обедненные области p-n-переходов сопровождается накоплением заряда, и напряжение на переходах устанавливается равным входному спустя лишь некоторое время, определяемое постоянными зарядки емкостей p-n-переходов. В третьих, конструкции выводов электродов транзистора и соответствующие им паразитные емкости и индуктивности влияют на частотные характеристики транзистора.

Группа транзисторов объединяет ряд разновидностей этих приборов, среди которых следует выделить два типа наиболее распространенных транзисторов, отличающихся друг от друга принципом действия, основными характеристиками и параметрами. Это биполярные (БT) и полевые транзисторы (ПТ).

Биполярным называют транзистор, в котором используются заряды носителей обеих полярностей. Биполярный транзистор имеет три области: эмиттер, базу и коллектор.

9.2.1.Геометрия биполярного транзистора СВЧ

Рассмотрим на примере биполярного транзистора(рис. 9.1), какие конструктивно-технологические решения позволяют создать транзисторы, работающие в СВЧ-диапазоне.

Исходным материалом для изготовления планарного транзистора служит пленка 6 высокоомного кремния с проводимостью n-типа, создаваемая методом эпитаксиального наращивания на подложке 7, на которой формируют вывод коллектора прибора. Методом ступенчатой фотолитографии в изолирующей пленке создают окна, через которые в несколько стадий вводят легирующие примеси и формируют область базы 4 с проводимостью p-типа, низкоомную приконтактную область базы 5 р⁺-типа, а в дальнейшем эмиттерную область 3 с проводимостью n⁺-типа. Металлическая пленка 1 и 2 обеспечивает подачу управляющих напряжений соответственно к базе и эмиттеру транзистора. Hа границе эмиттер — база создается обедненный подвижными носителями заряда эмиттерный p-n-переход 9, на границе база—коллектор коллекторный p-n-переход 8.

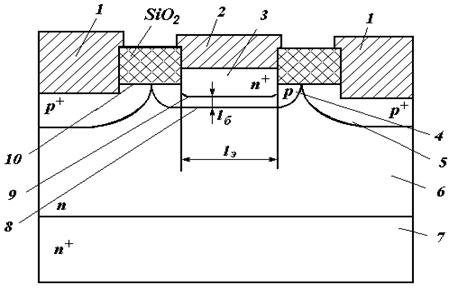
Рис. 9.1 Устройство биполярного СВЧ-транзистора

СВЧ-БТ отличаются от низкочастотных прежде всего размерами активных областей, которые характеризуются шириной эмиттерной полоски l_э и толщиной базы l_б (рис. 9.1). Существенное уменьшение этих размеров, необходимое для создания СВЧ-транзисторов, стало возможным благодаря совершенствованию технологии изготовления приборов. В частности, уменьшение вертикальных размеров обязано в основном развитию диффузионных процессов и ионной имплантации, а Уменьшение горизонтальных размеров связано с успехами литографии. Современная технология позволяет получить эмиттерные полоски шириной l_э меньше 0,1 мкм и толщину базы l_б несколько десятков нанометров. Наличие сверхтонкой базы является одной из особенностей транзисторов СВЧ.

Конфигурация эмиттера и базы важна для нахождения верхней частотной границы СВЧ-транзистора. Транзистор должен иметь максимальный периметр эмиттера при минимальной площади. Первое требование определяется необходимостью обеспечить равномерное распределение тока эмиттера, второе — необходимостью уменьшения емкости эмиттера, шунтирующей эмиттерный p-n-переход и снижающей уровень инжекции.

В гребенчаmой структуре (рис. 9.2, а) маломощных малошумящих СВЧ-транзисторов в настоящее время создают эмиттерные полоски шириной до 0,1 мкм, что близко к предельным возможностям современной технологии изготовления полупроводниковых структур.

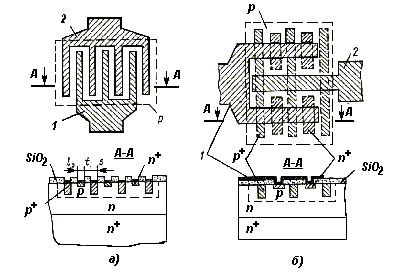
Рис. 9.2. Структуры СВЧ-транзисторов: а — гребенчатая; б — многоэмиттерная; 1 — вывод эмиттера; 2 — вывод базы

Для более мощных СВЧ-транзисторов используется объединение в одном кристалле большого числа единичных структур (до 150) с сохранением большого отношения периметр/площадь. Так, в многоэмиттерной структуре (рис. 9.2,6) в теле кристалла могут быть созданы полоски из низкоомного p⁺-слоя. Внутри каждой ячейки расположен “прямоугольник” эмиттера. Вывод эмиттера изолирован от базовой сетки слоем оксида SiO₂.

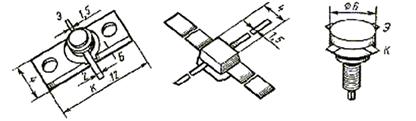
Рис. 9.3. СВЧ-транзисторы с ленточными выводами в металлокерамических корпусах

Особенности СВЧ-транзисторов с точки зрения конструкции выводов эмиттера, коллектора и базы состоят в том, что выводы делают в виде коротких полосок, удобных для сочленения с микро полосковыми линиями передачи. Такая геометрия выводов наиболее полно отвечает требованиям уменьшения их «паразитных» емкостей и индуктивностей. По этой же причине СВЧ транзисторы, как правило, выполняют без внешнего металлического корпуса (рис. 9.3).

9.2.2. Основные характеристики и параметры СВЧ-транзисторов

Получить характеристики транзистора можно путем решения системы дифферен-циальных уравнений переноса, непрерывности и Пуассона при соответствующих начальных условиях. Ввиду сложности задачи такой подход, по существу, не находит применения.

Hа практике широко используют представление СВЧ-транзистора эквивалентными схемами (схемами замещения). Эквивалентные схемы составляют таким образом, чтобы токи и напряжения, протекающие в них, в достаточной мере отвечали процессам в транзисторе.

Отметим, что расчеты по эквивалентным схемам считаются вполне удовлетворительными, если они обеспечивают ≈30% расхождение с экспериментом. Практически это реализуется до частот ~ l÷2 ГГц. Hа более высоких частотах продуктивнее оказывается подход, основанный на непосредственном измерении S-параметров транзистора. Эквивалентные схемы на сосредоточенных элементах при этом используют только для качественных прогнозов хода характеристик или приводят для установления соответствия с экспериментом методами оптимизации с помощью ЭBM.

Основными параметрами являются рабочая частота, коэффициент усиления по мощности, выходная мощность, КПД и коэффициент шума. При этом коэффициент шума важен только для маломощных (малошумящих) транзисторов, а КПД — для мощных СВЧ транзисторов.

9.2.2.1. Граничная частота

Частотные свойства транзисторов обычно характеризуются граничной частотой (частотой отсечки) f_гр, которая связана с временем задержки сигнала, распространяющегося от эмиттера к коллектору τ_эк:

,                                                                                                              (9.1)

где

                                                                                            (9.2)

где τ_э — время зарядки барьерной емкости эмиттерного перехода С_э; τ_б — время пролета носителей заряда через базовую область; τ_кп — время задержки в коллекторном переходе, связанное с временем пролета; τ_к — время зарядки емкости коллекторного перехода.

Время перезарядки емкости эмиттерного перехода определяется как:

,                                                                                             (9.3)

где r_э - дифференциальное сопротивление эмиттерного перехода; φ_т - температурный потенциал, I_э- рабочий ток.

Задержка τ_кn связана с пролетом электронов через коллекторный переход. Благодаря сильному полю электроны движутся в нем с предельной скоростью, называемой скоростью насыщения _нас. При оценках τ_кп обычно принимается равным половине времени пролета электронов через обедненный слой коллекторного перехода t_кпр:

                                                                                             (9.4)

где l_к - ширина коллекторного перехода, а скорость дрейфа принята равной скорости насыщения _нас.

Компонента задержки τ_к в (9.2) обусловлена временем перезарядки барьерной емкости коллекторного перехода С_K через сопротивления базовой r_б и коллекторной r_к областей:

                                                                                                        (9.5)

Уменьшение ширины базовой области примерно до 0,1 мкм снижает τ_б до единиц пикосекунд. В этом случае граничная частота в основном будет определяться τ_эп и τ_кп, которые примерно равны 10 пс. Поэтому для увеличения f_гp необходимо выдвигать дополнительные требования: уменьшение емкости эмиттерного перехода C_э, ширины коллекторного перехода l_к и сопротивления коллекторной области r_к, влияющего на значение τ_к.

Однако требования, предъявляемые к СВЧ транзисторам, противоречивы. Например, повышение концентрации примеси, необходимое для уменьшения ширины коллекторного перехода (уменьшения l_к), приводит к росту емкости этого перехода. Уменьшение площади перехода для снижения его емкости будет сопровождаться падением мощности транзистора. Необходимого уменьшения величин r_к и l_к можно добиться повышением концентрации примеси, но при этом произойдет сужение коллекторного перехода, увеличится емкость, а кроме того, снизится напряжение пробоя и выходная мощность. Таким образом, повышение граничной частоты биполярного транзистора сопровождается падением мощности и важнейшим ограничением является напряжение пробоя коллекторного перехода, которое зависит и от выбора полупроводникового материала.

9.2.2.2. Коэффициент усиления и максимальная частота генерации.

Для характеристики усилительных свойств СВЧ БТ вводится коэффициент однонаправленного усиления К_р. Он характеризует прямое усиление транзистора по мощности при условиях его согласования с источником сигнала и нагрузкой и компенсации обратной связи внешней цепью без потерь. Этот коэффициент является общей характеристикой БТ. Он не зависит от схемы включения транзистора. Пользуясь эквивалентной схемой БТ при включении с общей базой, можно получить при условии (ω/ω_гp)² <<1 следующее выражение для коэффициента усиления по мощности К_р.

                                                                                               (9.6)

где r_б — объемное сопротивление базы; C_К — емкость коллекторного перехода; α₀ — коэф-фициент передачи тока эмиттера (h_21б).

Частота, на которой коэффициент усиления по мощности К_р равен единице при условии компенсации действия внутренней обратной связи (без внесения потерь) и согласования на входе и выходе, является максимальной частотой генерации f_mаx. Это важный параметр СВЧ-транзисторов. Из (9.6) следует, что:

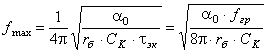                                                                 (9.7)

Если ширины эмиттерных, базовых полосок и промежутков между ними одинаковы и равны l, длина L а удельные (на единицу площади) сопротивление базы r₀ и емкость коллектора С₀, то Поэтому (9.7) приводится к виду

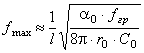                                                                                                (9.8)

Из (9.8) следует, что f_max возрастает с уменьшением размера l. Это подтверждает необходимость уменьшения ширины полосок и зазоров в транзисторных структурах. Поэтому l, будучи характерной наименьшей величиной для горизонтальных размеров транзистора, определяет верхнюю границу для f_max.

Hа частотах, превышающих f_mах, транзистор перестает быть активным элементом, т.е. только поглощает входной сигнал. Генерация или усиление в этом случае невозможны ни при каких схемах включения. Таким образом, для того чтобы БT можно было использовать для работы в коротковолновой части диапазона СВЧ, необходимо принимать меры, обеспечивающие снижение r_б и C_К а также увеличивающие f_гр. Kак было показано ранее, такие требования к конструкции транзистора и его электрическим параметрам оказываются противоречивыми и не могут быть улучшены одновременно.

Современные БT работают на частотах до 15 ГГц, их максимальная выходная мощность в непрерывном режиме достигает 300 Bт на частоте 1 ГГц, 20 Bт ~ на 3 ГГц, 1Bт на 10 ГГц и 0,1 Bт на 14 ГTц. Hа частотах 1 — 3 ГГц КПД превышает 50%, на верхней частотной границе КПД около 20%. Минимальный коэффициент шума 2,5—3 дБ на 24 ГГц и ~ 7 дБ на частотах более 10 ГГц.

9.2.2.3. Коэффициент шума

Важным параметром для маломощных транзисторов является шум-фактор или коэффициент шума K_ш. Он представляет собой отношение мощности шумов на выходе реального транзистора к мощности шумов, возникающих на выходе нешумящего транзистора в результате усиления теплового шума сопротивления r_г, подключенного ко входу транзистора. Следовательно,

                                                                                                     (9.9)

где P_ш — мощность теплового шума в сопротивлении r_г , P_шc — мощность собственных шумов транзистора.

На средних и высоких частотах основными источниками шума в транзисторе являются дробовые шумы в эмиттерном и коллекторном переходах, тепловой шум сопротивления базы и шумы токо-распределения, связанные со случайным характером распределения эмиттерного тока между коллектором и базой.

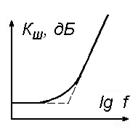
Рис. 9.4. Зависимость коэффициента шума от частоты

Зависимость коэффициента шума от частоты показана рис.9.4, горизонтальный участок кривой объясняется в основном тепловыми шумами объемного сопротивления базы r_б. Чем выше граничная частота транзистора f_гр, тем протяженней участок кривой с наименьшим коэффициентом шума. Коэффициент шума зависит также от сопротивления источника сигнала, при этом существует оптимальное сопротивление, при котором К_ш достигает минимального качения. Существует также оптимальное значение тока эмиттера. Следует отметить, что условия, при которых коэффициент шума имеет минимальное зна-чение, могут не совпадать с условиями получения максимального коэффициента усиления.

9.3. Высокочастотные полевые транзисторы. Характеристики и параметры

Полевым транзистором называется полупроводниковый прибор, усилительные свойства которого обусловлены потоком основных носителей, протекающим через проводящий канал, управляемый электрическим полем.

Полевые транзисторы были запатентованы в Англии в 1939 г., задолго до появления БT. Kонструктивно-технологические отличия ПT, вытекающие из их принципа действия, позволяют повысить частотную границу СВЧ-транзисторных устройств по сравнению с устройствами на основе БT.

Принцип действия ПT заключается в том, что при изменении напряжения на затворе меняются эффективная ширина пролетного канала и соответственно ток в цепи исток — сток. Полевые транзисторы различаются по методу управления потоком основных носителей заряда, движущихся в полупроводниковом канале. Они могут иметь изолированный затвор, затвор на основе p-n-перехода или затвор на основе барьера Шоттки. Полевые транзисторы с p-n-переходом не позволяют существенно увеличивать уровень мощности вследствие низких допустимых напряжений и малой площади поверхности, отводящий теплоту.

Наиболее широкое применение на СВЧ находят ПТ с барьером Шоттки (рис. 9.5). В таких транзисторах в высокоомной подложке 1, выполненной из GаAs, создан эпитаксиальный проводящий канал 2 n-типа. Через невыпрямляющие контакты, образованные n⁺- областями 3 и металлическими пленками 4 и 6, канал 2 подсоединен к выводам истока И и стока C. Между истоком и стоком расположен затвор 5, у которого на границе с n-каналом образован барьер Шоттки. При подаче напряжения между стоком и истоком через n-канал протекает электронный ток. Отметим, что подвижные носители заряда в ПT вводятся в n-канал и выводятся из него через невыпрямляющие контакты. Поэтому ПT относят к однополярным (униполярным) полупроводниковым приборам.

Затвор 5 используется в ПT для управления током транзистора с помощью внешнего сигнала. При протекании тока через канал возникает падение напряжения на распределенном сопротивлении канала вдоль его длины. Поэтому часть барьера Шоттки, расположенная ближе к стоку, оказывается сильнее смещенной в обратном направлении, чем остальная часть транзистора. Это приводит к несимметричному расширению слоя обедненного заряда 7 под затвором (на рис. 9.5 область 7 заштрихована). Область обедненного слоя может расширяться до высокоомной подложки 1 и перекрывать проводящий канал. При этом ток транзистора в цепи исток — сток практически перестает зависеть от напряжения стока; наступает режим насыщения тока исток — сток на рабочем участке характеристики транзистора. Характерные размеры БТ: ширина затвора 0,2—2 мм, длина затвора 0,5—2 мкм толщина эпитаксиальной пленки 0,15—0,5 мкм.

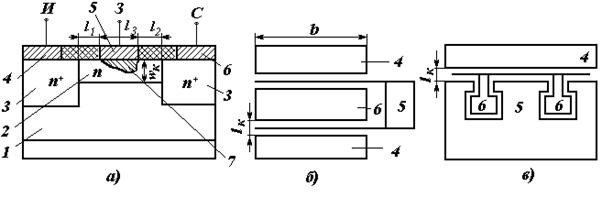
Рис. 9.5. Структура полевого СВЧ-транзистора с затвором Шоттки (а), топологическая схема транзистора гребенчатого типа (б) и транзистора с двумя выводами затвора (в):

1-подложка; 2 - канал; 3 - области n⁺ - вывода истока и стока;

4 - исток; 5 - затвор; 6 - сток; 7 -обедненная область

Повышение обратного смещения на электроде затвора вызывает увеличение ширины обедненной области и тем самым сужение n–канала. При этом возрастает сопротивление n-канала и уменьшается ток стока. Таким образом осуществляется модуляция электронного потока в n-канале с помощью внешнего управляющего напряжения.

В соответствии с общим определением граничной частоты транзистора f_гp как частоты, на которой коэффициент передачи входного тока равен единице. Тогда

                                                                                                                (9.10)

где t_пр - время пролета электронов через канал.

Таким образом, граничная частота определяется временем пролета электронов в канале t_np, минимальное значение которого достигается при движении электронов со скоростью насыщения _нас и равно

t_пр = L/_{нас .} (9.11)

где L — длина канала; L = l₁ + l₂ +l₃ ;

Очевидно, что для получения высокочастотных приборов необходимо обеспечить малую длину канала и большую дрейфовую скорость насыщения. Из этих условий вытекает ряд требований к материалу транзистора и к размерам его электродов. В качестве материала канала в ПT используют преимущественно арсенид галлия GаAs. Это объясняется тем, что подвижность электронов в этом материале примерно в 6 раз выше, чем в кремнии.

Однако сокращая L, нужно одновременно уменьшать и глубину канала w_к (рис. 9.5) так, чтобы выполнялось условие L/w_к> 1, в противном случае затвор транзистора не сможет эффективно контролировать движение электронов в канале. Для уменьшения w_к используют более высокий уровень легирования канала, не превышающий, однако, 5·10¹⁷см^-3 (во избежание пробоя). При таком уровне легирования минимальная длина затвора ограничена значением около 0,1 мкм, что соответствует граничной частоте f_гр=100 ГГц.

Имеются данные о создании ПT на основе фосфида индия InP, в котором дрейфовая скорость носителей в 1,5 раза выше, чем в арсениде галлия.

Усилительные свойства ПТ на СВЧ, как и в случае БТ, характеризуют коэффициентом однонаправленного усиления К_р и максимальной частотой генерации f_max.

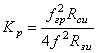                                                                                                            (9.12)

где R_cи - дифференциальное выходное сопротивление, R_зи - сопротивление части канала между истоком и затвором, неперекрытой обедненным слоем барьера Шоттки

Определяем частоту f_тax из условия К_р (f_mах) = 1:

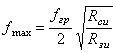(9.13)

Из (9.13) следует, что для повышения f_max нужно оптимизировать отношение сопротивлений R_си/R_зи и, главное, увеличивать граничную частоту f_гp, т.е. уменьшать время пролета электронов в канале t_пp.

Важнейшим преимуществом ПТ перед БТ, определившим их широкое применение в приемных устройствах, является малый уровень шумов. Важным направлением в разработке маломощных полевых транзисторов с барьером Шоттки на арсениде галлия является снижение коэффициента шума. Основные источники шума в этом транзисторе — тепловой шум в канале, индуцированный шум затвора и шум паразитных (пассивных) элементов. Тепловой шум в канале — это тепловой шум сопротивления проводящей части канала. Индуцированный шум затвора является следствием шума в канале, так как любая флуктуация потенциала в канале вызывает флуктуацию напряжения между затвором и каналом. Эти шумы при коротких каналах сильно коррелированы (коэффициент корреляции близок к единице). Шумы пассивных элементов связаны с сопротивлением затвора и истока и по своей природе тепловые. Так как шумы в активной области полевых транзисторов с барьером Шоттки очень малы, то шумы пассивных элементов дают больший относительный вклад в общий шум, чем в биполярных транзисторах.

Минимальный коэффициент шума ПТ, реализуемый при оптимальной настройке входной цепи и оптимальной проводимости источника сигнала, определяется выражением

                                                                                 (9.14)

где S - крутизна транзистора, r_з—сопротивление металлизации затвора, R_и- сопротивление части эпитаксиального n-слоя на участках И-3, которые включает в себя сопротивления контактов И.

Из (9.14) следует, что для улучшения шумовых характеристик ПТ нужно уменьшать длину затвора и снижать паразитные сопротивления затвора r_з и истока r_и.

Поскольку в ПТ преобладают шумы теплового происхождения, то особенно эффективным способом снижения шумов оказывается охлаждение. Одновременно оно позволяет поднять усиление ПТ, так как в GаАs в отличие от кремния и германия при уменьшении температуры возрастают подвижность электронов и их дрейфовая скорость.

Особенностью полевых транзисторов является большое различие сопротивлений источника сигнала, необходимых для получения максимального коэффициента усиления и минимального коэффициента шума. Это приводит к тому, что при минимальном коэффициенте шума коэффициент усиления примерно в 2 раза меньше максимально возможного. Однако в этом случае коэффициент усиления еще достаточно велик (8-15дБ). Необходимо отметить, что существует также трудность согласования полевого транзистора со стандартным СВЧ трактом, особенно на частотах ниже 1—2 ГГц. В связи с этим приходится увеличивать ширину затвора, хотя последнее и приводит к увеличению емкости и сопротивления металлизации затвора.

Для мощных полевых транзисторов требование низкого уровня шума не существенно. Применение арсенида галлия с большой шириной запрещенной зоны (1,4эВ) позволяет повысить рабочую температуру вплоть до 350°C.

В мощных полевых транзисторах необходимо обеспечить высокое напряжение пробоя затвора, низкоомные контакты истока и стока, а также возможно большее значение периметра истока.

Наибольшее применение полевые транзисторы на GаАs с барьером Шоттки нашли в малошумящих СВЧ усилителях. В диапазоне 4—20 ГГц они являются лучшими по шумовым и усилительным характеристикам, чем другие приборы того же назначения. Большой динамический диапазон и хорошие шумовые характеристик» позволяют использовать их в смесителях. В последнее время наметилась тенденция к широкому внедрению полевых транзисторов с барьером Шоттки в усилителях, предназначенных для замены ламп бегущей волны и в параметрических усилителях.

В последнее время значительный интерес проявляется к охлаждаемым усилителям на полевых транзисторах из GаАs с барьером Шоттки. Так как шумы в этих приборах в основном имеют тепловую природу, то охлаждение приводит к существенному, уменьшению коэффициента шума. При этом, в отличие от биполярных транзисторов, коэффициент усиления увеличивается. Трехкаскадный усилитель для спутниковой связи США в диапазоне 11,7—12,2 ГГц имеет при комнатной температуре коэффициент шума 5,3 дБ, а коэффициент усиления 18 дБ. Охлаждение усилителя до 40 К снижает K_ш до 1,6дБ и увеличивает коэффициент усиления до 31 дБ, что сравнимо с параметрами неохлаждаемых параметрических усилителей.

Малошумящие усилители на полевых транзисторах из GаАs с барьером Шоттки по сравнению с параметрическими усилителями характеризуются простотой настройки, высоким постоянством усиления, большой мощностью насыщения.

Преимущества ПT, как уже отмечалось, заметно проявляются с повышением рабочей частоты. Так, на частоте 6 ГГц выходная мощность ПT достигает 25 Bт при КПД около 50% и коэффициенте шума 3 дБ. Hа частоте 15 ГГц мощность остается значительной — около 2 Bт, КПД—в пределах 20-25% и коэффициент шума 3 — 6 дБ. Hа частоты выше 15 ГГц БT промышленного выпуска отсутствуют, тогда как ПT, например на частоте 18 ГГц, имеют мощность более 1 Bт при КПД около 10 — 20% и коэффициенте шума, равном 5 — 8 дБ. Малошумящие ПT имеют коэффициент шума 0,7 дБ на частоте 4ГГц; 1,7 дБ на 12 ГГц и менее 3 дБ на частоте 18 ГГц. Малошумящие ПT имеют меньший коэффициент усиления (около 5 дБ). В ближайшее время возможно появление ПT, работающих на частоте до 30 ГГц с выходной мощностью около 1 Bт и коэффициентом шума 3 дБ.

В настоящее время конструктивные параметры и высокочастотные характеристики биполярных и полевых микроволновых транзисторов рассчитываются с применением широко доступных компьютерных программ, позволяющих определить оптимальные режимы по коэффициенту усиления и шума, а также цепям согласования по входу и выходу транзисторов. Компьютерная разработка транзисторных структур позволяет обеспечить их высокую надежность при эксплуатации, улучшить высокочастотные свойства, совершенствовать методы отвода тепла от полупроводникового кристалла, значительно сократить время разработки и ее стоимость.

9.4. Контрольные вопросы:

1. Какой транзистор называют биполярным? Его устройство?

2. С чем связана граничная частота биполярного транзистора?

3. Что называют максимальной частотой генерации? Приведите формулу.

4. Какой транзистор называют полярным? Его устройство?

5. Перечислите основные характеристики полярного транзистора.

6. Преимущества полевого транзистора.

ЛЕКЦИЯ №10

Полупроводниковые приборы оптического диапазона

1. Концептуальная диаграмма.

2. Физические основы работы квантовых приборов оптического диапазона.

3. Особенности создания инверсной населенности,

4. Полупроводниковый инжекционный лазер на гомопереходе, устройство, применение..

5. Лазеры на гетеропереходах, устройство, применение.

6. Контрольные вопросы

10.1.Концептуальная диаграмма

10.2.  Физические основы работы квантовых приборов оптического диапазона

В отличие от электронных приборов, в которых для усиления или генерации электромагнитного поля используется энергия свободных носителей зарядов, в квантовых приборах используется, как правило, внутренняя энергия микрочастиц (энергия атомов, ионов, молекул). При этом сами микрочастицы могут находиться в движении. Исключением является полупроводниковый лазер, в котором используются потоки свободных носителей заряда, однако излучение света связано с квантовыми эффектами (излучательная рекомбинация).Электроны, входящие в состав микрочастиц, называются связанными.

Как известно, энергия свободной частицы может принимать любые значения. Квантовая система, состоящая из микрочастиц, электронов, ядер, атомов и т. д., отличается тем, что ее внутренняя энергия, т. е. энергия, не связанная с движением системы как целого, может принимать только дискретные значения. Возможные дискретные значения энергии называют энергетическими уровнями.

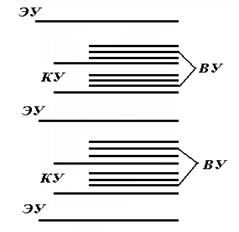
Рис. 10.1. Система уровней энергии

В свободных атомах квантуется энергия электронов и имеется система энергетических уровней электронов, или система электронных уровней атома. Наблюдаются следующие движения частиц: движение электронов в атоме, колебания атомов в молекуле, вращение и поступательное движение молекул. Энергия трех видов движения, кроме поступательного, квантуется. Квантование энергии приводит к образованию сложной системы энергетических уровней, показанной на рис. 10.1. Основой системы являются электронные уровни ЭУ, отстоящие друг от друга на 1—10 эВ. Между электронными уровнями располагаются колебательные уровни КУ с расстоянием примерно 0,1 эВ, а между колебательными уровнями находятся вращательные уровни ВУ с интервалом 10^-3 эВ и менее. Переходы между электронными уровнями соответствуют излучению в видимом и ультрафиолетовом диапазонах, между колебательными уровнями — инфракрасному, а между вращательными — СВЧ диапазону.

10.2.1. Квантовые переходы

В твердых телах взаимодействие частиц становится настолько сильным, что образуются зоны с очень близко расположенными уровнями, между этими зонами имеются зоны запрещенных значений энергии (запрещенные зоны). Уровень, соответствующий наименьшей допустимой энергии микрочастицы, называется основным, а остальные – возбужденными.

В атомах осуществляются только те переходы между энергетическими уровнями, которые удовлетворяют правилам отбора, устанавливающим допустимые различия квантовых чисел. Переходы, удовлетворяющие правилам отбора, называются разрешенными, а остальные — запрещенными.

Изменение внутренней энергии называется переходом с уровня на уровень. При переходе с более высокого энергетического уровня W₂ на низкий W₁ выделяется энергия DW₂₁=W₂ - W₁. Переходы с излучением или поглощением квантов электромагнитной энергии (фотонов) называют излучательными, а переходы, в которых квант энергии выделяется в виде тепла в среде, — безызлучательными. Состояние, из которого запрещены все излучательные переходы в более низкие энергетические состояния, называется метастабильным. Эти состояния играют важную роль в квантовых приборах.

Переходы, которые совершаются в системах микрочастиц, классифицируются по различным признакам. Основными видами переходов являются спонтанные, вынужденные и релаксационные.

Спонтанные переходы - самопроизвольные излучательные квантовые переходы из верхнего энергетического состояния в нижнее. Электромагнитное поле спонтанного излучения характеризуется тремя параметрами: центральной частотой спектральной линии ν_π, спектральной плотностью излучения S(v) и мощностью излучения. Центральная частота излучения называется также частотой квантового перехода и частотой спектральной линии и определяется постулатом Бора:

,                                                                                                  (10.1)

где W₂ и W₁ - энергии верхнего и нижнего уровней соответственно; h -постоянная Планка.

Определим теперь мощность спонтанного излучения.

Пусть в рассматриваемом объеме содержится N₂ частиц с энергией W₂ и N₁ частиц с энергией W₁. Число частиц в единице объема с данной энергией называется населенностью уровня. Спонтанные переходы носят случайный характер и оцениваются вероятностью перехода в единицу времени A₂₁, которая называется коэффициентом Эйнштейна для спон-танных переходов. Если населенность уровня Ν₂ остается неизменной во времени(или изме-няется незначительно), то число переходов в единицу времени с уровня W₂ на уровень W₁ составит

n₂₁ = Ν₂×Α₂₁.                                                                                                                 (10.2)

При каждом переходе выделяется энергия W₂-W₁₌ hv₂₁ поэтому мощность излучения

Р₂₁ = n₂₁×(W₂ -W₁) = N₂×A₂₁×h×v₂₁.                                                                                (10.3)

 Между коэффициентом Эйнштейна и средним временем жизни частицы на уровне (время, за которое при отсутствии внешнего возбуждения населенность уровня падает в е раз) существует простая связь:

A₂₁=1/t₂.                                                                                                                      (10.4)

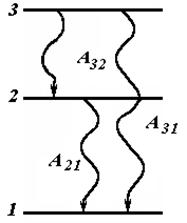
Рис. 10.2 Спонтанные переходы частиц с одного уровня на другой

В системе частиц, имеющих несколько энергетических уровней, возможны спонтанные переходы частиц с данного уровня на нижние (рис. 10.2). Полная вероятность a_j спонтанного перехода с уровня j на все нижние уровни i равна сумме вероятностей отдельных спонтанных переходов А_ji:

.                                                                        (10.5)

Уровни, для которых вероятность спонтанных переходов очень мала, называют метастабильными.

Время жизни на уровне j в многоуровневой системе определяется аналогично (10.4) с учетом (10.5):

                                                                                                                     (10.6)

Среднее время жизни на уровне составляет величину в пределах от единицы до сотен наносекунд. На метастабильных уровнях время жизни составляет миллисекунды.

Вынужденные переходы - это квантовые переходы частиц под действием внешнего электромагнитного поля, частота которого совпадает или близка к частоте перехода. При этом возможны переходы с верхнего уровня 2 на нижний 1 и с нижнего на верхний. В первом случае под действием внешнего электромагнитного поля с частотой v₂₁ происходит вынужденное испускание кванта энергии. Особенность вынужденного испускания состоит в том, что появившийся фотон полностью идентичен фотону внешнего поля. Вынужденное излучение имеет такие же частоту, фазу, направление распространения и поляризацию, как и вынуждающее излучение. Поэтому вынужденное излучение увеличивает энергию электромагнитного поля с частотой перехода v₂₁. Это служит предпосылкой для создания квантовых усилителей и генераторов.

При каждом вынужденном переходе снизу вверх затрачивается квант энергии внешнего поля hv₂₁.

Вынужденные переходы (как и спонтанные) имеют статистический характер. Поэтому вводятся вероятностные коэффициенты: W₂₁ - вероятность вынужденного перехода сверху вниз и W₁₂ - снизу вверх в 1с. Эти вероятности пропорциональны объемной плотности энергии внешнего поля u_v в единичном спектральном интервале на частоте перехода и определяются соотношениями

W₂₁=B₂₁ × u_{v ,}

W₁₂=B₁₂× u_{v ,}                                                                                                                 (10.7)

где B₂₁ и B₁₂ - коэффициенты Эйнштейна для вынужденных переходов с излучением и поглощением энергии соответственно.

Коэффициенты B₂₁ и Β₁₂ имеют смысл вероятностей вынужденных переходов в 1 с при единичной объемной плотности энергии внешнего поля (u_v = 1 Дж см ^-3c ^-1).

Число вынужденных переходов сверху вниз с излучением энергии в единицу времени в единице объема пропорционально вероятности W₂₁ и населенности верхнего уровня n₂, т.е. с учетом (10.7)

n₂₁=W₂₁ ×N₂=B₂₁ × u_v ×N_{2 .}                                                                                              (10.8)

Аналогично при тех же условиях число вынужденных переходов снизу вверх с поглощением энергии

n₁₂=W₁₂ ×N₁=B₁₂ × u_v ×N_{2 .}                                                                                              (10.9)

В приборах СВЧ-диапазона, работающих на «низкой» частоте, вероятность спонтанных переходов по сравнению вынужденными мала и их роль невелика. В лазерах же, работающих на оптических частотах, пренебрегать спонтанными переходами нельзя.

Релаксационные переходы. Переход системы частиц в состояние термодинамического равновесия называется процессом релаксации, а квантовые переходы, которые способствуют установлению и поддержанию термодинамического равновесия, называются релаксационными переходами.

Релаксационные процессы происходят как в газах, так и в твердых телах и носят статистический характер.. Переход кинетической энергии одной частицы во внутреннюю энергию другой при неупругих столкновениях молекул газа является примером релаксационных переходов. Вероятности релаксационных переходов между уровнями W₁ и W₂ будем обозначать w₁₂, а обратных переходов w₂₁. В большинстве случаев, имеющих место в квантовых приборах, релаксационные переходы являются безызлучательными.

В состоянии термодинамического равновесия населенности уровней не изменяются во времени, поэтому число безызлучательных переходов с уровня 1 на уровень 2 в 1 с равно числу обратных безызлучательных переходов с уровня 2 на уровень 1:

Ν_1Б ×w₁₂ = Ν_2Б ×w₂₁                                                                                                     (1.10)

В состоянии термодинамического равновесия распределение населенностей определяется законом Больцмана. С учетом (10.10) получаем

w₂₁ / w₁₂ = ехр(hv₂₁ / kT)                                                                                          (10.11)

Из (10.11) следует, что вероятность безызлучательных переходов сверху вниз больше, чем снизу вверх (w₂₁ > w₂₁) в отличие от вероятностей вынужденных переходов, которые одинаковы. Если hv₂₁ << kT, что обычно справедливо для квантовых приборов СВЧ-диапазона, то (10.11) можно заменить приближенным выражением

w₂₁/w₁₂ = 1 + hν₂₁/kΤ                                                                                               (10.12)

10.2. 2. Ширина спектральной линии

До сих пор мы рассматривали ансамбли одинаковых частиц имеющих, например, энергетические уровни W₂ и W₁ между которыми совершаются переходы. При излучательных переходах между уровнями W₂ и W₁ различных частиц частота излучения всех частиц по формуле (10.1) должна быть одинаковой. Однако в соответствии с принципом Паули в системе частиц не может быть больше двух частиц, имеющих одинаковую энергию.

а)	б)

Рис. 10.3. Уровни энергии : простейший случай (а), с учетом принципа Паули (б)

Поэтому при образовании ансамбля одинаковых частиц их энергетические уровни несколько расщепляются. Степень размытия уровней определяется соотношением Гайзенберга, которое можно записать в форме

ΔWΔt ³ h,                                                                                                                  (10.13)

где ΔW и Δt- неопределенности энергии и времени.

Предположим, что необходимо определить частоту излучения при переходе с уровня 2 на основной уровень 1 (рис. 10.3,а). Время жизни частиц в возбужденном состоянии определяется (10.4): τ₂ = 1/A₂₁. Следует считать, что неопределенность времени равна времени жизни частицы, т.е. Δt=τ₂. Подставляя Δt (10.13), получаем неопределенность энергии уровня 2: ΔW₂ ³ h/τ₂ (рис. 10.3,б). Наиболее широкими оказываются уровни с малым временем жизни. Неопределенность частоты перехода между «размытыми» уровнями 2 и 1 с ширинами ΔW₂ и ΔW₁ (рис. 10.4,а) находится из соотношения

v_max - v_min = (ΔW₂ + ΔW₁)/h                                                                                       (10.14)

и определяется суммой неопределенностей энергии обоих уровней. Ширина спектральной линии, определяемая только временем жизни частиц по спонтанному излучению, минимальна и называется естественной шириной спектральной линии.

Ширину контура спектральной линии принято определять как разность частот, на которых интенсивность I равна половине максимального значения I₀ (Δν_л на рис. 10.4,б). Частотой перехода (центральной частотой перехода) называют частоту, соответствующую максимуму спектральной линии. Форма спектральной линии может быть представлена так называемой лоренцевой кривой:

I/Iо =Δν²/[(ν-ν₀)² +Δν²],                                                                                          (10.15)

совпадающей с резонансной кривой колебательного контура. Реальные наблюдаемые спектральные линии имеют ширину больше естественной.

Причиной уширения спектральной линии может служит столкновений молекул в газах. Доплеровское уширение спектральной линии связано с эффектом Доплера, т.е. с зависимостью наблюдаемой частоты излучения от скорости движения излучателя.

а)	б)

Рис. 10.4. Частота излучения с учетом «размытости» энергетических

 уровней (а) и спектр излучения (б)

В квантовых приборах широко используются твердые вещества с примесными ионами, квантовые переходы которых являются рабочими. Колебания кристаллической решетки создают переменное электрическое поле, которое влияет на ионы решетки и изменяет их энергию, а это приводит к размытию энергетических уровней и уширению спектральной линии. Кроме того, ширина линии увеличивается вследствие тепловых колебаний самих ионов. Причиной уширения спектральной линии твердого тела может быть также пространственная неоднородность физических параметров среды или неоднородности электрического и магнитного полей. Причиной уширения спектральной линии может быть также электромагнитное излучение, вызывающее вынужденные переходы между рассматриваемыми уровнями и приводящее к изменению времени жизни частицы. Поэтому, например, процесс генерации излучения в квантовых приборах будет приводить к изменению ширины линии.

10.2.3. Возможность усиления электромагнитного поля в квантовых системах

То обстоятельство, что вынужденное излучение возбужденных микрочастиц при переходах с верхнего энергетического уровня на нижний когерентно (совпадает по частоте, фазе, поляризации и направлению распространения) с вынуждающим, наталкивает на мысль о возможности использования вынужденных переходов для усиления электромагнитного поля. Чтобы оценить возможность такого усиления, рассмотрим обмен энергии между полем и веществом. Будем предполагать, что вещество имеет два энергетических уровня W₁ и W₂ с населенностями N₁ и Ν₂ (рис. 10.6),а частота внешнего поля равна частоте квантового перехода ν₂₁.

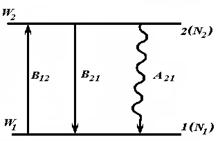
Рис. 10.6. Энергетические уровни и их населенности

При объемной плотности энергии u_v число вынужденных переходов в единицу времени в единице объема с выделением энергии

n₂₁= B × u_v × N₂                                                                                                            (10.16)

а выделяемая при этих переходах энергия в единице объема в единицу времени, т.е. мощность,

 Р_выд = n₂₁ ×h ×v₂₁ = B ×u_v ×N₂ ×h ×v₂₁                                                                                (10.17)

Аналогично число вынужденных переходов с поглощением энергии и поглощаемая от внешнего поля мощность в единице объема соответственно

n₁₂= B × u_v × N₁                                                                                                            (10.18)

P_пoгл= B×u_v×N₁×h×v₂₁.                                                                                                    (10.19)

 С учетом (10.17) и (10.19) изменение мощности электромагнитного поля

P= P_выд-P_пoгл= B×h×v₂₁(N₂ -N₁ ).                                                                                 (10.20)

Назовем эту величину мощностью взаимодействия.

Если Ρ>0, т.е. выделяемая мощность превышает поглощаемую, то в системе происходит увеличение энергии поля или усиление электромагнитного поля. При Ρ<0 преобладает поглощение энергии и энергия внешнего поля убывает.

Таким образом, условием усиления (Р>0) из (10.20) будет

N₂-N₁>0 или N₂/N₁>1                                                                                              (10.21)

В состоянии термодинамического равновесия населенность верхнего уровня меньше, чем нижнего (N_2Б < N_1Б) в соответствии с законом Больцмана. Поэтому вещество в этом состоянии поглощает энергию внешнего поля (Р<0), так как число квантовых переходов п₁₂ снизу вверх (1®2) с поглощением энергии больше числа квантовых переходов сверху вниз (2®1) п₂₁ c выделением энергии.

Соотношение N₂>Ν₁ является обратным (инверсным) по отношению к состоянию термодинамического равновесия, когда N_2Б<N_1Б. Поэтому состояние, при котором N₂>N₁, т.е. возможно усиление, называют состоянием с инверсией населенностей уровней.

Закон Больцмана, справедливый для термодинамического равновесия:

                                                                         (10.22)

Величину Т_п называют температурой перехода. Формально при состоянии с инверсией населенностей эта температура отрицательна (T_п < 0).

Среда, в которой имеется состояние с инверсией населенностей, называется также активной средой, так как в ней возможно усиление электромагнитного поля.

В состоянии термодинамического равновесия N_1Б>N_2Б, поэтому при воздействии электромагнитного поля число вынужденных переходов снизу вверх (1®2) больше числа вынужденных переходов сверху вниз (2®1): населенность нижнего уровня убывает, а верхнего - растет. При достаточно большой объемной плотности энергии поля u_v может произойти выравнивание населенностей уровней (N₂=N₁), когда числа вынужденных переходов 1®2 и 2®1 равны, т.е. наступает динамическое равновесие. Явление выравнивания населенностей уровней называют насыщением перехода. Таким образом, при воздействии электромагнитного поля на двухуровневую систему можно добиться насыщения перехода, но не инверсии населенностей.

Населенности уровней при любом значении объемной плотности энергии поля находятся из решения скоростных (кинетических) уравнений. Для двухуровневой системы скорости изменения населенностей уровней

dN₁/dt = -N₁ B u_ν – N₁w₁₂ + N₂Bu_v + W₂A₂₁ + N₂w₂₁,                                              (10.23)

dN₂/dt = Ν₁Β u_ν + N₁ w₁₂ - N₂B u_v - Ν₂A₂₁ - N₂w₂₁;                                                  (10.24)

N₁+N₂ = Ν,                                                                                                               (10.25)

где Ν - полное число частиц.

Стационарные величины N₁ и Ν₂, их разность и отношение определяются следующим образом:

;                                                                    (10.26)

;                                                                              (10.27)

;                                                                      (10.28)

;                                                                                             (10.29)

.                                                                                                 (10.30)

На рис. 10.7,a показаны зависимости N₁ и Ν₂ от объемной плотности энергии u_ν для случая, когда система до воздействия электромагнитного поля находилась в термодинамическом равновесии с населенностями N_1Б и N_2Б, определяемыми законом Больцмана. Из (10.26) и (10.27) следует, что при малых значениях u_v населенность нижнего уровня N₁ убывает, а верхнего N₂ растет по линейному закону. При очень больших значениях плотности энергии (u_v®¥) N₁ и N₂ стремятся к среднему значению N/2 = (N_1Б + N_2Б)/2,соответствующему насыщению переходов.

На рис. 10.7,б показаны зависимости Ν₁ и N₂ от u_v при воздействии электромагнитного поля на систему с инверсией населенностей уровней. При отсутствии поля (u_v=0) населенности уровней равны  и , причем . С ростом u_v N₂ убывает, а N₁ растет от значений  и  по линейному закону, но при больших υ_ν асимптотически они приближаются к среднему значению , соответствующему насыщению перехода. Разность населенностей уровней N₂-N₁ (10.28) определяет мощность взаимодействия Р, введенную формулой (10.20). Подставив (10.28) в (10.20), получим

                                                              (10.31)

Эта формула позволяет найти зависимость мощности взаимодействия от объемной плотности энергии u_ν электромагнитного поля, взаимодействующего с веществом. Зависимость P(u_v), представленная на рис. 10.8, определяется в (10.31) отношением u_v/(1 + δ₁₂u_v). При увеличении u_ν мощность сначала (когда δ₁₂u_v<<1) линейно растет, а затем стремится к предельному значению Р_пред, которое определяется путем раскрытия неопределенности в (10.31) при u_v®¥, т.е. в состоянии насыщения перехода:

                                                                    (10.32)

а)	б)

Рис.10.7. Зависимости N₁ и Ν₂ от объемной плотности энергии u_ν:

а)в состоянии термодинамического равновесия; б) при воздействии электромагнитного поля

Используя соотношение (10.11) и учитывая, что обычно вероятность релаксационных переходов много больше вероятности спонтанных, выражению (10.31) можно придать более простой и наглядный вид:

(10.33)

где t_рел- время релаксации.

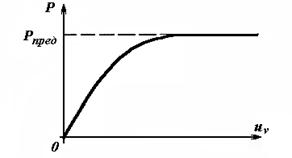
Рис. 10.8. Зависимость мощности взаимодействия от объемной плотности энергии электромагнитного поля

В состоянии насыщения при u_v ® ¥ (N₁=N₂), когда мощность, выделяемая при вынужденных переходах 2 ® 1, равна мощности, поглощаемой при вынужденных переходах 1 ® 2, от электромагнитного поля отбирается мощность Р_пред. Эта мощность необходима для поддержания равенства населенностей уровней, которое постоянно стремится нарушаться из-за наличия спонтанных и безызлучательных переходов с вероятностями А₂₁> w₂₁ и w₁₂. Число этих переходов непосредственно от плотности энергии не зависит и определяется только населенностью уровней. Получаемая от электромагнитного поля энергия рассеивается в веществе, например в кристаллической решетке, в виде теплоты.

10.3. Особенности создания инверсной населенности уровней

В полупроводниковых лазерах используется инверсия населенностей, получаемая в полупроводниках с одним или с различными типами проводимости (p-n-переход).

Идеальным было бы состояние (рис. 10.9), когда верхние уровни в области 2 полностью заполнены электронами проводимости а нижние в области 1 полностью свободны от валентных электронов, т. е. полностью заполнены дырками. В этом случае инверсия населенности была бы наибольшей.

Формально полупроводник, в котором большинство уровней в области 2 зоны проводимости занято электронами, а в области 1 валентной зоны — дырками, можно назвать вырожденным одновременно для электронов и дырок, в то время как обычно удается создать либо электронные, либо дырочные вырожденные полупроводники. Предположим, что в такой полупроводник попадает фотон с энергией hv, большей ширины запрещенной зоны ΔW₀, но меньшей ΔW— величины, соответствующей границам областей 2 и 1, заполненных электронами и дырками:

                                                                                                       (10.34)

При этом условии будут происходить вынужденные переходы из области 2 в область 1 с испусканием новых фотонов. Если энергия падающего фотона hv>ΔW, то начнется поглощение квантов и возникнут переходы из области 3 валентной зоны, где есть валентные электроны, на свободные уровни области 4 зоны проводимости.

В вырожденном электронном полупроводнике верхняя граница заполненной электронами области 2 в зоне проводимости приблизительно совпадает с уровнем Ферми для электронов W_Fn, а в вырожденном дырочном нижняя граница заполненной дырками области 1 в валентной зоне — с уровнем Ферми для дырок W_Fp. Поэтому

                                                                                                     (10.35)

и условие (10.34) для получения вынужденного излучения запишем в виде

.                                                                                        (10.36)

Вынужденное излучение будет появляться при воздействии фотонов с энергией, заключенной в пределах от h×v_max=DW₀ до h×v_max = DW₀ = W_Fn - W_Fp. Такие фотоны всегда есть в полупроводнике вследствие процесса рекомбинации электронов и дырок. Рекомбинационное излучение имеет спонтанный характер, т. е. фотоны распределены хаотически, по времени, направлению и поляризации. «Спонтанные» фотоны вызывают вынужденное излучение, однако для получения самовозбуждения необходимо обеспечить многократное прохождение излучения через среду с инверсией населенности. Достигается это созданием отражающих поверхностей на торцах полупроводникового образца.

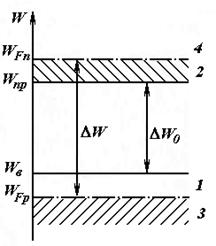
Рис. 10.9. Состояние энергетических уровней

В полупроводниковых лазерах можно получить очень большую инверсию населенностей и высокое усиление на единицу длины вследствие высокой концентрации частиц в твердом теле. Поэтому длину образца полупроводника можно уменьшить до долей миллиметра, а требования к величине коэффициента отражения зеркал снизить.

В полупроводниках возможны следующие методы получения инверсии населенностей: инжекция носителей через р—n-переход (инжекционные лазеры), электронная накачка и оптическая накачка. Наибольшее распространение получил метод инжекции носителей.

10.4.Полупроводниковый инжекционный лазер на гомопереходе, устройство, применение

Лазером называют квантовый генератор или усилитель электромагнитного излучения оптического диапазона, основанный на использовании вынужденного излучения. Процесс генерации в лазере происходит благодаря усилению в активной среде (веществе с инверсией населенностей уровней) и наличию положительной обратной связи.

а)	б)

Рис. 10.10 Энергетическая диаграмма

В инжекционных лазерах используется p-n-переход, образованный вырожденными полупроводниками с разным типом электропроводности. На рис. 10.10,а показана энергетическая диаграмма такого p-n-перехода в состоянии равновесия, т.е. при отсутствии внешнего напряжения, а следовательно, и тока через переход. Уровни Ферми W_Fn и W_Fp в обеих областях совпадают. Приближенно можно считать, что в n-области электроны проводимости располагаются на уровнях между «дном» зоны проводимости W_пр и уровнем Ферми W_Fn, а в р-области дырки - между «потолком» валентной зоны W_в и уровнем Ферми W_Fр.

Энергетическая диаграмма для случая, когда к p-n-переходу приложено прямое напряжение u₀, показана на рис. 10.10,б. Понижение потенциального барьера на величину U₀ увеличивает поток электронов из n-области и поток дырок из р-области через переход. Через p-n-переход потечет ток, и вблизи перехода установится некоторое распределение концентрации неравновесных носителей заряда.

Известно, что при неравновесном состоянии теряет смысл понятие уровня Ферми. Однако для определения полной концентрации носителей в неравновесном состоянии можно воспользоваться прежними формулами, если вместо уровней Ферми ввести квазиуровни Ферми для электронов и дырок. Вдали от перехода (см. рис. 10.10,6), где сохраняется равновесное состояние, применимы обычные уровни Ферми W_Fn и W_Fp. В области перехода, где имеются неравновесные носители, существуют два квазиуровня Ферми -для электронов W'_Fn и для дырок W'_Fр. Обычно предполагают, что в пределах перехода до пересечения линии W_Fn с границей зоны проводимости величины W_Fn и W'_Fn мало отличаются. Аналогичное предположение делают и для уровней W_Fp и W'_Fp. Далее кривая квазиуровня электронов W'_Fn опускается и сливается с уровнем Ферми W_Fp. Соответственно кривая квазиуровня для дырок W'_Fр поднимается и сливается с уровнем Ферми W_Fn.

В некоторой области перехода с шириной δ одновременно велико число электронов проводимости в группе уровней ΔW_пр и дырок в группе уровней ΔW_в. Поэтому в области δ распределение носителей зарядов подобно распределению их на рис. 10.10, и в ней можно получить инверсную населенность. В этой области перехода наблюдается наиболее интен-сивная излучательная рекомбинация электронов и дырок, так как скорость рекомбинации пропорциональна произведению концентраций электронов и дырок, а они в рассматриваемой области велики. Рекомбинация электронов и дырок в переходе сопровождается спонтанным излучением с энергией, большей ширины запрещенной зоны hv > δ W₀.

С увеличением внешнего напряжения u₀ растут концентрации электронов и дырок в области δ перехода и, следовательно, увеличивается инверсия населенностей. При некотором пороговом напряжении (пороговом токе), когда вынужденное излучение, вызванное спонтанным излучением, достаточно для компенсации потерь света в материале полупроводника и в отражающих поверхностях, наступит генерация. Таким образом, p-n-переход при малых токах является источником спонтанного (рекомбинационного) излучения (светодиод), а при токах более порогового - источником когерентного излучения (лазер).

Пороговое значение тока сильно зависит от температуры и концентрации примесей. Понижение температуры облегчает вырождение полупроводника и, следовательно, уменьшает пороговый ток. Лазеры на арсениде галлия на гомопереходе обычно работают при температуре жидкого гелия 4,2 К или жидкого азота 77 К. В настоящее время появились инжекционные лазеры, работающие при комнатной температуре. Экспериментально установлено, что изменение температуры от 4,2 К до комнатной может привести к увеличению плотности порогового тока до 100 раз. При комнатной температуре необходима плотность порогового тока до 10⁵ А/см².

Широкое распространение получил инжекционный лазер на основе вырожденного арсенида галлия (GaAs), конструкция которого показана на рис. 10.11. Две грани полупроводника перпендикулярны плоскости p-n-перехода и образуют после полировки зеркала резонатора. Две другие грани наклонены к плоскости р-n-перехода, чтобы не создавать в этом направлении условий для самовозбуждения. Размеры сторон полупроводника порядка нескольких десятых долей миллиметра. Излучение выходит из узкой области p-n-перехода перпендикулярно параллельным граням полупроводника.

Излучение инжекционного лазера имеет большую угловую расходимость вследствие дифракционных явлений в резонаторе. Пусть толщина области p-n-перехода, в которой происходит генерация, δ = 1 мкм, а расстояние между зеркалами L = 0,1 мм. Оценки показывают, что для этого примера угловая расходимость составляет 5. . .6°. Однако в другой плоскости (в плоскости p-n-перехода) угловая расходимость значительно меньше (примерно 1°) из-за большего размера области излучения.

Спектр излучения инжекционного лазера зависит от выходной мощности, которая, в свою очередь, определяется плотностью тока через p-n-переход. Когда плотность тока незначительно превышает пороговую плотность тока, имеется только одна мода с шириной линии излучения около 0,05 нм и длиной волны λ = 0,84 мкм, соответствующей ИК-диапазону. С ростом плотности тока число мод увеличивается. Частота генерируемых мод зависит от температуры, так как последняя влияет на коэффициент преломления кристалла и ширину запрещенной зоны. При изменении температуры возможен «перескок» от одной моды к другой. Поэтому долговременная стабильность частоты оказывается гораздо меньше, чем у газовых лазеров. Следует отметить, что излучение инжекционных лазеров поляризовано.

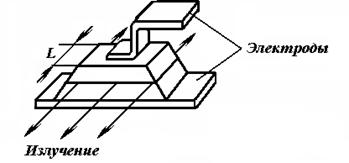
Рис. 10.11. Конструкция инжекционного лазера на основе вырожденного арсенида галлия

Обычно инжекционные лазеры на гомопереходе работают в импульсном режиме, при этом максимальная мощность в импульсе ограничивается перегревом кристалла и зависит от рабочей температуры и длительности импульса. Наибольшая импульсная мощность при температуре жидкого азота в лазерах на GaAs составила 100 Вт при длительности импульсов примерно несколько микросекунд и частоте следования до 10 кГц. Основным достоинством инжекционных лазеров является возможность модуляции излучения изменением напряжения на р-n-переходе.

Коэффициент полезного действия полупроводникового лазера η, определяемый как отношение мощности генерируемого излучения к мощности накачки, в первом приближении может быть определен формулой

где η_внутр - внутренний квантовый выход рекомбинационного излучения. Он учитывает то, что не все электроны рекомбинируют с излучением кванта света (излучательная рекомбинация), а часть электронов рекомбинирует без излучения кванта света (безызлучательная рекомбинация). Отношение ΔW₀/qU₀ учитывает то обстоятельство, что энергия полученного кванта света приблизительно равна ширине запрещенной зоны ΔW₀, а энергия, которую нужно затратить, чтобы ввести из внешней цепи электрон и дырки, равна qU₀. Правильный выбор степени легирования и использование чистых материалов позволяет получить η_внутр близким к единице, поэтому КПД инжекционных лазеров теоретически должен быть также близким к единице. У реальных лазеров он меньше. Это объясняется следующими причинами. Во-первых, часть электронов, двигающихся в р-n-переходе, вследствие большой длины свободного пробега проходит активную область, не участвуя в создании вынужденного излучения. Во-вторых, генерируемое световое излучение распространяется не только в активной области, но и рядом с ней, где отсутствует инверсия населенностей, и, следовательно, происходит поглощение излучения. Кроме этих причин имеется потеря мощности источника питания, связанная с прохождением тока через области и контакты. Тем не менее у лазеров, изготовленных из арсенида галлия, при охлаждении жидким азотом получен КПД 70...80 %.

Особенностью полупроводниковых лазеров является сильная зависимость от температуры КПД и мощности. Это объясняется рядом причин. Во-первых, с ростом температуры растет доля безызлучательной рекомбинации, что приводит к снижению η_внутр, во-вторых, снижается разность населенностей уровней.

Полупроводниковые лазеры имеют высокий КПД, малые размеры, возможность легкой модуляции до очень высоких частот. Однако они, как правило, требуют охлаждения, имеют широкий спектр излучения и большой угол расходимости.

Особое место занимают лазеры в области связи. Инжекционные лазеры находят применение в "коротких" открытых линиях связи и в волоконно-оптических линиях.

10.5. Лазеры на гетеропереходах, устройство, применение

Ж.И.Алферовым предложены инжекционные лазеры на основе гетеропереходов (гетеролазеры), имеющие высокий КПД. В этих лазерах для создания переходов используются полупроводниковые материалы с различной шириной запрещенной зоны.

Полупроводниковая структура гетеролазеров (рис. 10.12,a) состоит из области GaAs n-типа, узкой области GaAs p-типа и области тройного соединения Al_xGа_1-xAs p-типа. Активной является средняя область, где создается инверсия населенностей. На границе средней и правой областей образуется потенциальный барьер, который ограничивает длину свободного пробега электронов, инжектированных из левой области, и тем самым повышает эффективность образования вынужденного излучения. Кроме того, одновременно уменьшается поглощение света в правой неактивной области, так как из-за различия в коэффициентах преломления в средней и правой областях (рис. 10.12,б) наблюдается полное внутреннее отражение света на их границе (волноводный эффект) В результате этих процессов удалось при T=300 К понизить плотность порогового тока от 20—100 кА/см² до 7— 10 кА/см² и увеличить КПД до 10%.. В нашей стране были разработаны также гетеролазеры с полным внутренним отражением света с обеих сторон от активного слоя, лазеры с двойной гетероструктурой, или ДГС-лазеры. В этих лазерах удалось существенно понизить плотность порогового тока и получить большой КПД, что позволило при комнатной температуре осуществить режим непрерывного излучения, который был ранее возможен только при температуре жидкого азота. В ДГС-лазерах на основе GaAs-GaAlAs при комнатной температуре получена плотность порогового тока менее 1 кА/см².

Отличительной особенностью гетеролазеров является возможность изготовления лазеров с различной длиной волны излучения изменением концентрации примесного алюминия. Например, изменение последней в пределах от 0 до 30% вызывает изменение длины волны от 0,9 до 0,68 мкм. Другими особенностями гетеролазеров являются высокий КПД, удобство возбуждения, малые габариты.

Крупным достижением лазерной техники последних лет явилось создание гетеролазера с распределенной обратной связью. В таком полупроводниковом лазере торцевые зеркальные поверхности, образующие оптический резонатор, заменены дифракционной решеткой, которая, как известно, на определенных частотах полностью отражает падающее на нее излучение.

Повышения мощности излучения инжекционных лазеров добиваются изготовлением набора (решеток) лазерных диодов. Например, при комнатной температуре получена импульсная мощность от 10 до 1000 Вт при частоте следования импульсов до 1 кГц и длительности импульсов 70...200 нс. При этом число лазерных диодов в решетке колеблется от 10 до 60.

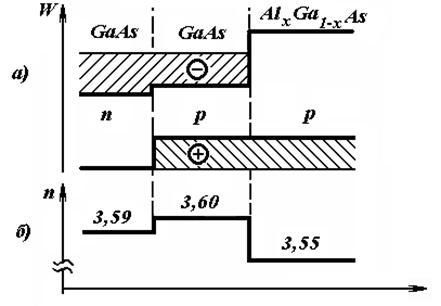
Рис. 10.12. Полупроводниковая структура гетеролазеров

Недостатки полупроводниковых лазеров - невысокая степень когерентности излучения, плохая температурная и радиационная устойчивость и пока еще низкая долговечность. Так, в лабораторных условиях получена долговечность 10⁴ ч, однако в промышленных образцах она на один-два порядка ниже.

Одной из  областей применения полупроводниковых лазеров является система оптической связи и обработки информации. Для применения в волоконно-оптических линиях связи разрабатываются полупроводниковые лазеры специальной конструкции для эффективного согласования лазера с волоконной линией. В открытых линиях связи используются обычные полупроводниковые лазеры на гетеропереходах в тройных (GaAlAs) и четверных (GaInAsP) системах. Лазеры работают при комнатной температуре в интервале длин волн от 0,65 до 1,6 мкм.

Необходимо отметить использование лазеров в научных исследованиях. Лазеры применяют в медицине. Применение лазеров в логических элементах позволило создать быстродействующие ЭВМ.

10.6. Контрольные вопросы:

1. Что называют энергетическими уровнями?

2. Какие виды квантовых переходов вы знаете? Охарактеризуйте их.

3. Что может служить причиной уширения спектральной линии?

4. В чем заключается возможность усиления электромагнитного поля в квантовых системах?

5. Какое состояние называют состоянием с инверсией населенностей?

6. Что называют лазером?

7. Поясните энергетическую диаграмму p-n-перехода, образованного вырожденными полупроводниками с разными типами электропроводности.

8. Из чего состоит полупроводниковая структура гетеролазера?

9. Каковы достоинства и недостатки полупроводниковых лазеров?

Основные обозначения

A21 -	коэффициент Эйнштейна для спонтанных переходов
aj -	полная вероятность спонтанного переходя с уровня i на все нижние
a -	коэффициент неидеальности
B21 , B12 -	коэффициенты Эйнштейна для вынужденных переходов с излучением и поглощением энергии соответственно
C0 -	статическая емкость диода, удельная емкость коллектора
C0б -	барьерная емкость при U=0
Cmах -	максимальная емкость p-n-перехода
СK -	емкость коллекторного перехода
Cб -	барьерная емкость
Cдиф -	дифференциальная диффузионная емкость
Cкор -	емкость корпуса
Dn , Dp -	коэффициенты диффузии электронов и дырок
E -	напряженность поля
Eп -	пороговая напряженность поля
f -	частота
fmаx -	максимальная частота генерации
fгр -	граничная частота
fпред -	предельная частота
G -	отрицательная дифференциальная проводимость
h -	постоянная Планка
I -	интенсивность излучения
I0 -	обратный ток, ток насыщения, тепловой ток
I1 -	максимальный прямой ток
I2 -	минимальный прямой ток
Imax -	максимально-допустимый ток
In дp -	электронная составляющая тока дрейфа
In диф -	электронная составляющая диффузионного тока
Ip диф -	дырочная составляющая диффузионного тока
Ip др -	дырочная составляющая тока дрейфа
Iдиф -	диффузионный ток
Iдр -	ток дрейфа
Iном -	номинальный рабочий ток
Iпор-	пороговый ток
Iрек -	ток рекомбинации
Iт -	суммарный туннельный ток
iл(t) -	импульс лавинного тока
iнав -	наведенный ток
jдр -	плотность дрейфового тока
Kш -	коэффициент шума
Кр -	коэффициент усиления по мощности
k -	постоянная Больцмана, волновое число
L -	индуктивность, длина канала
Ln , Lp -	диффузионная длина электронов и дырок
lб -	толщина базы
lк -	толщина коллекторного перехода
lм -	толщина медной подложки
lп -	толщина подложки
lстр -	толщина полупроводниковой структуры
lэ -	ширина эмиттерной полоски
M -	коэффициент умножения
mn ,mp -	эффективные массы электрона и дырки
Ν -	полное число частиц
Na -	концентрация ионизированных атомов акцепторной примеси
Ni -	населенность уровня i
Nд -	концентрация ионизированных атомов донорной примеси
Nпр -	эффективная плотность состояний в зоне проводимости
n0 -	полная концентрация электронов
n21 -	число переходов с уровня 2 на уровень 1
ni -	концентрация электронов в собственном полупроводнике
P0 -	мощность потребляемая от источника
Р21 -	мощность излучения
Рвыд -	выделяемая мощность
Pвых -	выходная мощность
Рпред -	предельное значение мощности
Pпoгл -	поглощаемая мощность
Pш -	мощность теплового шума
Pшc -	мощность собственных шумов транзистора
p -	вероятность
pi -	концентрация дырок в собственном полупроводнике
pn ,nn -	концентрация носителей в n-области
pp ,np -	концентрация носителей в p-области
q -	заряд электрона
R0 -	сопротивление образца; сопротивление в слабом поле
Rcи -	дифференциальное выходное сопротивление
Ri -	динамическое (отрицательное) сопротивление
Rдиф -	дифференциальное сопротивление
rз -	сопротивление металлизации затвора
Rзи -	сопротивление части канала между истоком и затвором
Rи-	сопротивление части эпитаксиального n-слоя на участках исток - затвор
Rн -	сопротивление нагрузки
Rст -	статическое сопротивление
r0 -	удельное сопротивление базы
rs -	сопротивление растекания;сопротивление контактов, подводящих проводов
rб -	сопротивление базовой области
rк -	сопротивление коллекторной области
rэ -	дифференциальное сопротивление эмиттерного перехода
S -	площадь, крутизна
S(v) -	спектральная плотность излучения
T -	температура
T0 -	время пролета домена
Тп -	температура перехода
Tпmax -	максимальная температура перехода
t -	время
-	среднее время свободного пробега электрона и дырки
tпр -	время пролета электронов через канал
tф -	время формирования домена
u0 -	прямое напряжение
U1 ,U2 -	напряжения, соответствующие I1 и I2
U3 -	напряжение раствора
uv -	объемная плотность энергии внешнего поля
Uк -	контактная разность потенциалов
Uобр -	обратное напряжение
Uпр -	напряжение пробоя
-	скорость электрона
vmax -	максимальная скорость дрейфа
vд -	скорость домена
vдр -	скорость дрейфа
νπ -	центральная частота спектральной линии
vнас -	скорость насыщения
vрек -	скорость рекомбинации
W12 -	вероятность вынужденного перехода снизу вверх в 1с
Wi -	энергия уровня i
W21 -	вероятность вынужденного перехода сверху вниз в 1с
WF -	уровень Ферми
Wв -	"потолок" валентной зоны
Wпр -	"дно" зоны проводимости
w12 -	вероятность релаксационных переходов между уровнями W1 и W2
w21 -	вероятность релаксационных переходов между уровнями W2 и W1
wк -	глубина канала
xn -	части ширины запирающего слоя n-полупроводнике
xp -	части ширины запирающего слоя p-полупроводнике
Z -	полное сопротивление
α0 -	коэффициент передачи тока эмиттера
an ,ap -	коэффициенты ионизации электронов и дырок
D -	ширина запирающего слоя
Δt -	неопределенность времени.
DW -	ширина запрещенной зоны, неопределенность энергии
d -	слой умножения
e -	относительная диэлектрическая проницаемость
e0 -	диэлектрическая постоянная
g -	коэффициент рекомбинации
h -	коэффициент полезного действия (КПД)
hвнутр -	внутренний квантовый выход рекомбинационного излучения
jт -	температурный потенциал
l -	длина волны
m -	подвижность
mср -	средняя подвижность
qдр -	угол пролета
rn -	объемная плотность заряда электронов
t -	время жизни
t2 -	средне временя жизни
tj -	временя жизни на уровне j
tб -	время пролета носителей заряда через базовую область;
tк -	время зарядки емкости коллекторного перехода
tкп -	время задержки в коллекторном переходе,
tрел-	время релаксации
tэ -	время зарядки барьерной емкости эмиттерного перехода
tэк -	временя задержки сигнала, распространяющегося от эмиттера к коллектору
w0 -	собственная резонансная частота
ℓ -	расстояние между контактами

Литература

1. Основная литература:

1. Андрушко Л.М., Федоров Н.Д. Электронные м квантовые приборы СВЧ.: Учебник, М.: Радио и связь, 1981г.

2. Федоров Н.Д. Электронные приборы.: учебник, М.: Атомиздат, 1979г.

3. Лебедев И.В. Техника и приборы сверхвысоких частот. М.: Высшая школа,1972г.

4. Андреев И.С., Арипов Х.К., Кузьмина Г.Н. Электронные и квантовые приборы, часть 1, Ташкент, ТЭИС, 1998г.

5. Бобровский Ю.Л., Корнилов С.А., Кратиров И.А., Овчинников К.Д., Пышкина Н.И., Федоров Н.Д. Электронные, квантовые приборы и микроэлектроника.: Учебное пособие для вузов / Под ред. проф.Н.Д. Федорова -М.Радио и связь,1998г.

2. Дополнительная литература:

1. Батушев В.А. Электронные приборы: Учебник для вузов. - М.: Высш. школа,1980г.

2. Овечкин Ю.А. Полупроводниковые приборы; Учебник для техникумов. -М.: Высш. школа,1979г.

3. В.В. Воскресенский, А.М. Иваницкий Применение туннельных диодов в импульсной технике. М.:"Связь", 1974г.

4. Дулин В.Н. Электронные приборы. Учебник для студентов вузов, обучающихся по спец."Радиотехника"-М.:"Энергия",1977г.

5. Березин В.М., Буряк В.С., Гутцайт Э.М., Марин В.П. Электронные приборы СВЧ: Учеб. Пособие для вузов по спец." Электронные приборы". -М.: Высш. школа,1985г.

---

[M1]