Лекция 6. Начальные сведения о полупроводниках.

6.1. Концептуальная диаграмма.

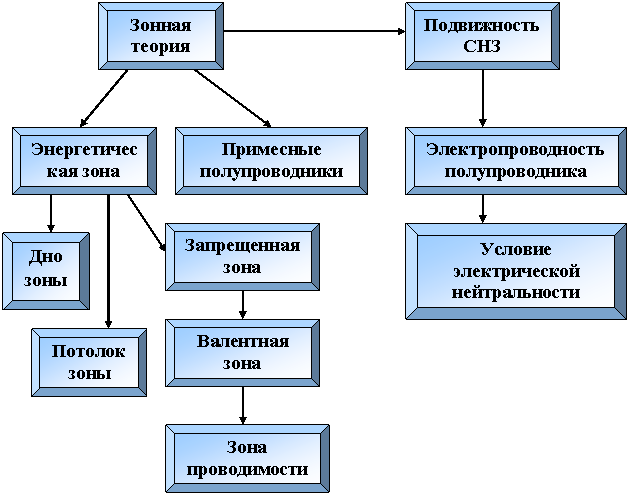6.2. Зонная теория

Та форма материи, которая в физике называется веществом, представляет систему, состоящую из атомных ядер и электронов в той или иной мере связанных с ядрами. Физико-химические свойства вещества определяются характерными особенностями тех состояний, в которых находится система. Так как ядра и электроны являются квантовыми частицами, то их состояние, как и состояние образуемых ими систем, описывается законами квантовой механики, основным из которых является уравнение Шредингера:

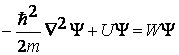(6.1)

где ħ = h/2p, m - масса частицы, U - потенциальная энергия взаимодействия частицы с остальными частицами и внешним полем, Ñ²-оператор Лапласа, т.е. сумма вторых частных производных по координатам пространства, Y - волновая функция, квадрат которой имеет смысл вероятности обнаружения частицы в заданной точке пространства в состоянии, характеризуемом энергией W.

Зонная теория основывается на следующих основных предположениях, определяющих модель идеального кристалла.

1. Атомные ядра (или атомные остовы) являются неподвижными центрами силового поля, действующего на электроны. Это предположение вытекает из того, что масса ядра много больше массы электрона и поэтому можно думать, что положение ядер будет изменяться пренебрежимо мало с изменением положения электронов. Атомным остовом называется система, включающая ядро и все электроны, кроме валентных. Атомные остовы вместо атомных ядер рассматриваются в тех случаях, когда интерес представляют механические, тепловые, электрические, оптические свойства кристаллов, целиком зависящие от состояния движения валентных электронов.

2. Взаимодействие электронов друг с другом заменяется некоторым эффективным полем, порождаемым всеми электронами и действующим на каждый электрон. Другими словами, вместо того, чтобы рассматривать движение электрона под действием кулоновских сил взаимодействия с ядрами (атомными остовами) и друг с другом, рассматривается задача движения электрона в стационарном поле, слагающимся из поля неподвижных ядер (остовов) и «фонового» поля всей системы электронов. Задача многих тел, таким образом, сводится к одноэлектронной задаче.

Состояние электрона в твердом теле (всюду далее будет иметься в виду только кристаллические твердые тела) определяется значением проекции спина и значением квазиимпульса.

Квазиимпульс – квантовомеханический параметр состояния электрона, имеющий размерность импульса. Для тех состояний электронов, которые особенно существенны в практической физике полупроводников, квазиимпульс можно воспринимать как импульс электрона p=mv, лишь под m нужно понимать не истинную массу электрона, а так называемую эффективную массу.

Периодичность потенциальной энергии обусловливает дискретность значений квазиимпульса электрона в твердом теле. Эти значения определяются выражениями:

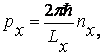
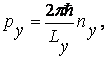
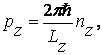(6.2)

где n_x, n_y, n_z – целые положительные или отрицательные числа, включая нули, ограниченные условиями:

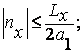
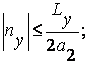
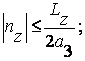(6.3)

где L_x_,_y_,_z- величины порядка линейных размеров кристалла, а_1,2,3- периоды решетки в направлении осей x, y, z, соответственно.

Совокупность всех физически неэквивалентных значений квазиимпульса называется зоной Бриллюэна. Условия (6.3) определяют границы первой зоны Бриллюэна. Разности между соседними значениями квазиимпульса (2pħ/L) весьма малы, поэтому дискретность квазиимпульса не проявляется в электрических и оптических свойствах кристаллов и его можно рассматривать как квазинепрерывную величину.

Связь энергии свободного электрона с импульсом является, как известно параболической: W_k= mv²/2 = p²/2m. Связь энергии электрона в твердом теле с квазиимпульсом более сложная. Во-первых, эта связь неоднозначна в том смысле, что заданным значениям p_x, p_y, p_z соответствует множество различных

значений энергии W. Иначе говоря, существует ряд функций W = W_l(p), удовлетворяющих уравнению Шредингера при заданных условиях. Число l-номер соответствующей функции, если эти функции выстроить в ряд так, чтобы W₁(p) =< W₂(p) =< W₃(p)… Во-вторых, каждая из зависимостей W_l(p) не является, вообще говоря, параболической.

Компоненты квазиимпульса (6.2) лежат в интервалах (6.3). Соответственно, энергия будет иметь квазинепрерывный ряд значений, заключенных в некотором интервале от до . Интервал энергий в пределах которого значения изменяются непрерывно называется разрешенной энергетической зоной. Значение называется дном зоны номера , – потолком этой зоны.

Если наугад взятое значение энергии W не попадает ни на одну из разрешенных энергетических зон, то это означает, что в данном теле нет электронов с такой энергией. Если в твердом теле имеется электрон с некоторым значением энергии W, то говорят, что соответствующий уровень занят электроном.

В зависимости от типа и параметров решетки, а также номера зоны возможны следующие три случая:

См. рис. 6.1

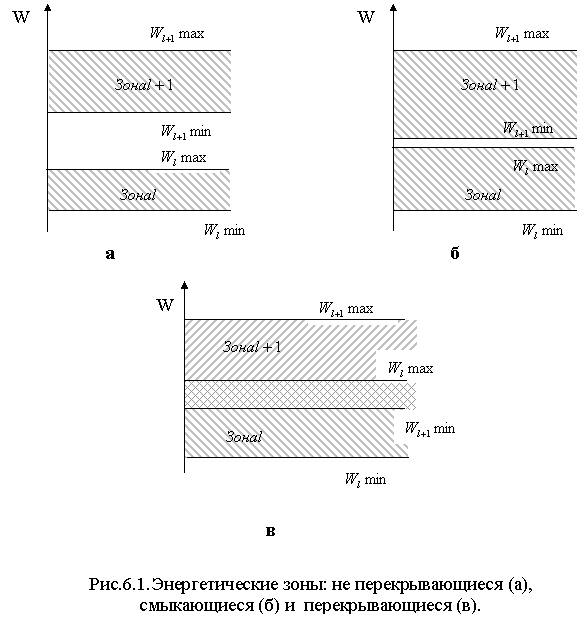
В первом случае, соседние зоны разделены запрещенной зоной, ширина которой

Во втором случае, говорят о смыкающихся зонах, а в третьем случае – о перекрывающихся зонах.

Электрические свойства твердого тела однозначно определяются характером распределения валентных электронов по энергетическим зонам. При температуре абсолютного нуля возможны только две ситуации:

1. Все зоны, включая номер , полностью заполнены электронами, во все верхние зоны, начиная с , полностью свободны;

2. Самая верхняя из заполненных зон, заполнена лишь частично.

Электрический ток заключается в переносе электрического заряда системой заряженных частиц. Если заряженные частицы, как в твердом теле, представляют термодинамическую систему, то перенос заряда имеет место только тогда, когда нарушается термодинамическое равновесие в системе и суммарный импульс частиц становится отличным от нуля. Следовательно, электрическое поле может вызвать появление тока в твердом теле только в том случае, если оно способно изменить состояние движения системы электронов.

Нетрудно заметить, что в первой из упомянутых ситуаций, электрический ток невозможен. Все состояния в нижних зонах заняты, и изменить состояние системы, не нарушая принципа Паули, с помощью электрического поля не слишком большой напряженности невозможно. Твердые тела, у которых нижние энергетические зоны до номера при T=0 K полностью заняты, а вышележащие зоны полностью свободны, являются диэлектриками.

Если ширина запрещенной зоны, разделяющей верхнюю полностью занятую зону, не превышает примерно 2,5 эВ, то при комнатной температуре некоторые из электронов, вследствие теплового возбуждения, переходят из нижней зоны в верхнюю. Теперь уже состояние системы электронов может быть изменено сколь угодно малым электрическим полем (уровни в зонах квазинепрерывны) и тело обладает электропроводностью. Такие тела называются полупроводниками. У классических полупроводников германия и кремния, например, ширина запрещенной зоны при Т=0 К равны 0,744 эВ и 1,15 эВ, соответственно. При комнатной температуре те же величины имеют значения 0,67 эВ и 1,12 эВ.

Верхнюю полностью заполненную при Т=0 К энергетическую зону полупроводников и диэлектриков принято называть валентной зоной. Вышележащую незаполненную зону называют зоной проводимости.

Во второй, из упоминавшихся ранее ситуаций, уже при Т=0 К верхняя зона заполнена лишь частично. Вследствие наличия незанятых состояний в зоне, тело обладает электропроводностью при Т=0 К. Такие тела относят к классу проводников.

Характер распределения электронов по зонам при Т=0 К определяется соотношением между числом электронов и числом состояний в зонах. Рассмотрим это на конкретных примерах.

Возьмем любой из элементов первой группы, допустим, натрий. Атом натрия содержит 11 электронов, один из них –валентный. В изолированном атоме этот электрон находится в состоянии 3s (главное квантовое число n=3, орбитальное квантовое число l=0, что шифруется буквой s). Соседним будет являться состояние 3p (l=1). Состояние 3s дуплетно, так как возможны две ориентации спина: +1/2 и –1/2. Состояние 3p представляет, фактически, 6 различных состояний (три различных значения магнитного квантового числа m_s=-1,0,+1 и по два, в каждом случае, значения проекции спина: +1/2 и –1/2). При образовании твердого тела, каждое из состояний электрона в изолированном атоме расщепляется на N состояний, соответственно числу атомов в теле. Следовательно, в s-зоне натрия будет содержаться N-дуплетных состояний, а число валентных электронов всего N. Зона будет заполнена лишь наполовину. Так как, кроме того, в натрии зона s перекрывается зоной p, то фактически занятость в этой составной группе будет еще меньше. Натрий, как и все элементы первой группы, – типичные проводники. Такими же являются элементы второй и третьей группы, вследствие перекрытия s и p зон.

Перейдем к элементам четвертой группы. У этих элементов 4 валентных электрона: 2 в состоянии s и 2 в состоянии p. В объединенной s-p зоне будет содержаться, таким образом, 4N дуплетных состояний. Так как число валентных электронов равно 4N, то составная зона должна быть заполнена только на ½ и элементы четвертой группы должны были бы быть проводниками. Так оно и есть для углерода в кристаллической модификации графита, имеющего гексагональную решетку с довольно рыхлой упаковкой вдоль гексагональной оси. В более плотных решетках типа алмаза (алмаз, германий, кремний) расстояние между ядрами атомов t₀ настолько мало, что объединенная s-p зона вновь разделяется на две подзоны, но теперь уже с 2N дуплетными состояниями в каждой подзоне (см. рис.6.2).

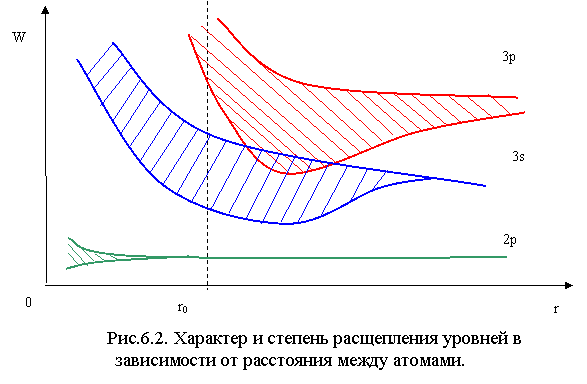
В результате все 4N валентных электронов полностью заполняют нижнюю подзону, а верхняя подзона остается свободной. При Т=0 К вещества этого типа являются диэлектриками. Ширина запрещенной зоны, разделяющей две s-p подзоны, возрастает с уменьшением расстояния между ядрами атомов. Так, минимальное расстояние между атомами в алмазе, кремнии и германии равно: 0,154 нм, 0,235 нм и 0,244 нм. Соответственно, ширина запрещенной зоны этих материалов равна: 5,47 эВ; 1,12 эВ; 0,67 эВ. Алмаз остается диэлектриком вплоть до высоких температур, кремний и германий становятся полупроводниками при Т = 200 К.

6.3. Электрофизические свойства однородных твердотельных полупроводников и пассивные приборы на их основе

К полупроводникам относится большая группа химических элементов, расположенных главным образом в IV-VI группах периодической системы элементов Д.И.Менделеева (C, Si, Ge, As, P, Se, Te и др.), а также обширная группа бинарных и тройных соединений элементов I-VIII групп: A^IB^VII, A^IB^VI, A^IB^V и др. Однако далеко не все вещества используются при производстве полупроводниковых приборов. Основными материалами в промышленности полупроводниковых приборов служат германий (Ge), кремний (Si) и арсенид галлия (GaAs). Основные электрофизические параметры этих веществ приведены в табл. 1.1

Полупроводниковые резисторы являются простейшими полупроводниковыми приборами. В радиоэлектронике находят применение терморезисторы, варисторы, фоторезисторы и линейные полупроводниковые резисторы (используются в качестве пассивных элементов в интегральных микросхемах).

Терморезисторы - это приборы, проводимость которых очень сильно зависит от температуры. Для их изготовления обычно используется мелкозернистый порошок смеси окислов металлов: двуокиси титана и окиси магния, окиси марганца и никеля и некоторые другие соединения, обладающие полупроводниковыми свойствами с относительно большой собственной проводимостью.

Порошку, смоченному связующей жидкостью, прессовкой придается нужная форма и объем, при этом одновременно в изделие запрессовывается два ввода. После термической обработки, связующее вещество испаряется, и зерна спекаются.

Основными параметрами терморезистора являются:

Начальное (исходное) сопротивление R₂₀⁰C - это сопротивление при температуре t⁰=20⁰C.

Температурный коэффициент сопротивления

a_Rt=ΔR/(R_tΔT)=-0.024¸0.06 K^-1

Он характеризует собой относительное изменение сопротивления терморезистора. Этот коэффициент отрицателен и по модулю на один-два порядка больше, чем у металлов.

Терморезисторы применяют для дистанционного измерения температуры, для измерения мощности электромагнитных излучений, в цепях и устройствах температурной компенсации, термостатах и др.

Таблица 6.1

Параметр	Германий	Кремний	Арсенид галлия
Заряд ядра	32	14	-
Валентность, s	4	4	-
Диэлектрическая проницаемость, e (отн.ед.)	16	12	11
Температура плавления, Т_пл, ⁰С	940	1420	1280
Эффективная масса электронов, m_n	0,22	0,33	0,07
Эффективная масса дырок, m_p	0,39	0,55	0,5
Ширина запрещенной зоны, ΔЕ_з, эВ *	0,67	1,11	1,4
Подвижность электронов, m_n, см²/(В^.с)	3800	1400	8500
Подвижность дырок, m_р, см²/(В^.с)	1800	500	450
Собственное удельное сопротивление, r_i, Ом^.см	50	2^.10⁵	4^.10⁸
Собственная концентрация, n_i, см^-3	2,5^.10¹³	2^.10¹⁰	1,5^.10⁶
Коэффициент диффузии электронов, D_n, см²/с	100	36	290
Коэффициент диффузии дырок, D_р, см²/с	45	13	12

Эффективная масса дана в единицах относительно массы покоя электрона m » 9,1^.10^-31кг.

*Значение всех последующих параметров даны для комнатной температуры (Т = 300 К).

Варисторы - это полупроводниковые нелинейные приборы, сопротивление которых зависит от приложенного напряжения. В качестве полупроводникового вещества используется карбид кремния с примесями алюминия, кальция и магния. Этот полупроводник имеет дырочную проводимость. Мелкие зерна карбида кремния смешиваются с огнеупорной глиной или жидким стеклом. После прессовки и термической обработки связующая масса затвердевает, при этом зерна основного материала на некоторой небольшой части своей поверхности соприкасаются тонкими пленками кварцевого стекла, которые образуются в процессе термической обработки. После изготовления варистор подвергают высоковольтной импульсной формовке. Формирующие высоковольтные импульсы пробивают изолирующие прослойки между зернами, расширяют поры и микротрещины в связующей массе.

6.4. Примесные полупроводники

Совершенная кристаллическая решетка – это определенная идеализация. В действительности кристалл содержит целый ряд самых различных дефектов. Первым таким дефектом является граница кристалла. Здесь порядок упаковки атомов нарушается, что приводит не только к искажению энергетических зон, но и к появлению целой системы дискретных уровней, лежащих в пределах запрещенной зоны. Это, так называемые поверхностные уровни или поверхностные состояния.

Из объемных дефектов следует отметить точечные и линейные нарушения периодичности (дислокации), пустые узлы решетки, атомные остовы смещенные в междуузлия и, наконец, чужеродные атомы, расположенные как в узлах, так и в междуузлиях.

Свободные носители заряда (СНЗ) так или иначе, взаимодействуют с дефектами решетки, так что роль последних в физических свойствах кристалла может быть весьма существенной. Помимо существенного рассеяния СНЗ на дефектах может происходить также захват носителей некоторыми дефектами. Такие дефекты получили название центров захвата или ловушек. Некоторые дефекты способны аккумулировать энергию и затем отдавать ее в виде кванта электромагнитного излучения. Такие дефекты получили название центров люминесценции. Ряд дефектов способен стимулировать исчезновение СНЗ противоположных знаков. Такие дефекты называются центрами рекомбинации. Наконец, некоторые дефекты инициируют генерацию СНЗ того или иного типа.

Введение понятий различного рода центров есть тот шаг к усложнению физической модели твердого тела, который необходим для более полного охвата процессов в реальных объектах. Ограничимся учетом примесей, инициирующих генерацию СНЗ, так как этого будет достаточно для понимания всех основных свойств полупроводника.

К примесям указанного рода относятся элементы, валентность которых на единицу больше или на единицу меньше валентности основного вещества. По отношению к германию и кремнию, как основным веществам, такими являются элементы 5 и 3 групп. На рис.6.3 представлена энергетическая диаграмма примесных германия и кремния с указанием значений энергии (в эВ) некоторых примесных состояний электронов, отсчитанных от краев соответствующих зон. Электроны, с уровней близко расположенных от дна зоны проводимости, легко переходят в эту зону при термическом возбуждении. В результате образуется электрон проводимости и положительно заряженный ион примеси. Примесь, отдающая электрон в зону проводимости и, тем самым, увеличивающая концентрацию электронов проводимости, называется донорной примесью. Примесь, захватывающая электрон из валентной зоны при его термическом возбуждении, называется акцепторной примесью. При захвате электрона акцептор превращается в отрицательно заряженный ион, а в валентной зоне появляется незанятое (вакантное) состояние. Акцепторная примесь инициирует генерацию СНЗ, называемых дырками.

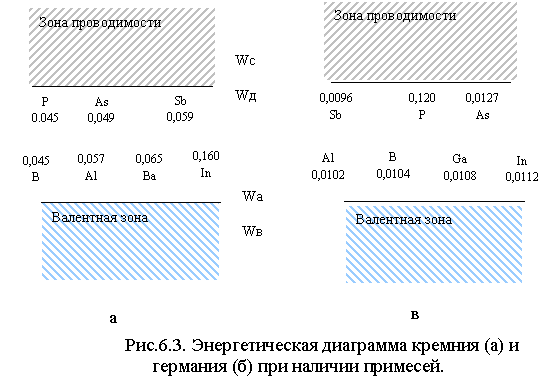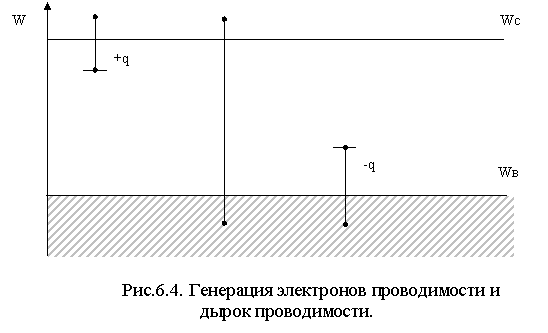
Как говорилось, при Т ¹ 0 К имеется определенная вероятность термического возбуждения электрона и перехода его из состояния, соответствующего валентной зоне, в одно из состояний, соответствующих зоне проводимости (см. рис.6.4). Точно также возможен переход электрона в зону проводимости с донорного уровня или переход электрона из валентной зоны на уровень акцептора.

Электрон, находящийся в одном из состояний соответствующих зоне проводимости, проявляет себя как СНЗ, поскольку его состояние может быть изменено сколь угодно малым электрическим полем. Такие электроны принято называть электронами проводимости. Однако проводимость полупроводников обусловливается не только электронами проводимости.

Система электронов валентной зоны, когда из этой системы удален один электрон (например, в зону проводимости) проявляет себя как один свободный носитель заряда, причем довольно своеобразный. Так проявляет себя не один какой-то электрон валентной зоны, а именно вся система электронов этой зоны. Своеобразие этого СНЗ заключается, прежде всего, в том, что число таких зарядов тем больше, чем больше электронов удалено из валентной зоны. Получается, что удаление электрона не уменьшает способности оставшейся совокупности электронов переносить электрические заряды, а, напротив, увеличивает ее.

Действительно, если все состояния в валентной зоне заняты, то поле ничего не может изменить, и электроны вообще не проявляют себя как СНЗ. Последних просто нет. Электропроводность равна нулю. Но если в валентной зоне имеется незанятое состояние, то электрическое поле уже будет изменять состояние оставшейся системы электронов. Появится электропроводность. Второе своеобразие заключается в том, что этот свободный носитель имеет заряд, знак которого противоположен знаку электрона.

6.5. Подвижность СНЗ

Все величины, относящиеся к электронам проводимости, обозначаются индексом n, а величины, относящиеся к дыркам, индексом p. Рассмотрим движение совокупности электронов в поле напряженностью Е.

В отсутствии поля электрон проводимости движется хаотически, испытывая непрерывные столкновения с теми или иными неоднородностями в решетке. Обозначим через t_n время между двумя последовательными столкновениями для какого-либо электрона на каком-то этапе его движения. Как величина случайная, t_nбудет конечно различной у разных электронов в фиксированный промежуток времени и у одного и того же электрона в разные промежутки времени. Но среднее значение этой величины, как по всему коллективу, так и у одного электрона, за достаточно большой промежуток времени будет вполне определенным и постоянным.

Электрическое поле будет ускорять электрон и на его хаотическое движение наложится направленное движение. Средняя скорость смещения электронов вдоль сил поля за промежуток времени будет, в соответствии с законом Ньютона, равна:

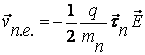(6.4)

Будем предполагать, что при каждом столкновении электрон полностью передает решетке накопленную за счет работы энергию, так что v_n_e обращается в ноль в момент каждого столкновения. Тогда, следовательно, скорость направленного движения со временем возрастать не будет, а будет испытывать случайные колебания вместе с колебанием значения t_n. Среднее за большой промежуток времени значение скорости направленного движения электрона, которое называют скоростью дрейфа, будет равно:

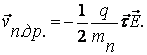(6.5)

Тому же значению будет равно и среднее по всему коллективу значение скорости направленного движения. Таким образом, скорость дрейфа пропорциональна напряженности поля. Величина

(6.6)

называется подвижностью электрона проводимости.

Аналогичные рассуждения приводят к следующим выражениям для скорости дрейфа и подвижности дырок:

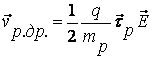(6.7)

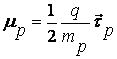(6.8)

В таблице 6.2 даны значения эффективных масс и подвижностей электронов и дырок в германии и кремнии. За единицу эффективной массы принята истинная масса электрона m₀=9.11*10^-28г.

Таблица 6.2

Тип полупроводника	Эффективная масса электронов			Эффективная масса дырок			Подвижность см²В^-1с^-1
	M_n_^	m_n11	M_n_рез	M_p1	m_p2	m_p_рез	m_n	m_p
Германий	0,0815	1,588	0,12	0,31	0,044	0,25	3900	1900
Кремний	0,1905	0,9163	0,26	0,49	0,16	0,38	1500	600

Выражения (1.6) и (1.8) являются справедливыми для полей ≤10⁴В см^-1. В более сильных полях подвижность убывает с возрастанием напряженности поля.

6.6. Электропроводность полупроводника

В полупроводнике заряды переносятся электронами и дырками. Если концентрации электронов и дырок обозначить через n и p, соответственно, то плотность тока выразится следующим образом:

(6.9)

Сопоставляя это выражение с законом Ома в дифференциальной форме, , приходим к заключению, что удельная электропроводность полупроводника равна:

(6.10)

Для электронного полупроводника при n>>p:

(6.11)

Для дырочного полупроводника при p>>n:

(6.12)

Носители заряда, которые в основном определяют электропроводность данного полупроводника, называются основными. Носители заряда противоположного знака называются неосновными.

6.7. Условие электрической нейтральности

Полупроводник содержит электрические заряды 4 видов: подвижные заряды в виде электронов и дырок и неподвижные заряды в виде ионизированных атомов донорной и акцепторной примеси. Дырки и ионы доноров имеют положительный заряд, равный заряду электрона, электроны и ионы акцептора имеют отрицательный заряд. В силу закона сохранения количества электричества, суммарный заряд кристалла всегда равен нулю. Это означает, что общее количество дырок и ионов доноров в полупроводнике всегда равно общему количеству электронов и ионов акцептора.

Это правило будет справедливым не только для всего кристалла, но и для любого его как угодно малого элемента объема, если распределение примесей в кристалле будет равномерным. Полупроводники с равномерным распределением примесей называются однородными. Условие электрической нейтральности для однородного полупроводника запишется в виде:

(6.13)

где N_d⁺ и N_a^- - концентрации ионизированных атомов донорной и акцепторной примеси соответственно.

Если примесь распределена в кристалле неравномерно, то (6.13) уже не будет выполняться для некоторых областей кристалла. В этих областях плотность пространственного заряда не будет равна нулю и в них всегда будет существовать электрическое поле. Такие области получили название электрических переходов в полупроводнике.

Контрольные вопросы:

1. Какие предположения определяют модель идеального кристалла?

2. Что такое зона Бриллюэна?

3. Какие зоны называют валентными, зонами проводимости, запрещенными зонами?

4. Какие пассивные приборы изготавляют на основе твердотельных полупроводников?

5. Что такое примесные полупроводники?

6. Запишите уравнение электропроводности.

7. Напишите и объясните условие электрической нейтральности.

Лекция 7. Неоднородные полупроводники. Электрические переходы.

7.1. Концептуальная диаграмма

7.2. Виды неоднородностей полупроводников

Распределение неоднородностей в полупроводниках, т.е. элементах объема, отличающихся физическими свойствами, может носить нерегулярный, случайный характер или регулярный характер, подчиненный определенной закономерности. Первый случай нас интересовать не будет, второй же имеет большое практическое значение. Регулярную неоднородность в полупроводнике принято называть электрическим переходом, поскольку такая неоднородность порождает электрическое поле.

Электрический переход – это область пространственного заряда, обусловленного наличием переходного слоя, заключенного между двумя областями полупроводника, отличающимися типом электропроводности или значением удельной электропроводности. Так как тип электропроводности и значение удельной электропроводности определяются шириной запрещенной зоны, составом и концентрацией примесей, то существуют электрические переходы двух основных видов.

Переходы первого вида представляют собой слои переменного химического состава, заключенные между областями разной химической природы и с неодинаковой шириной запрещенной зоны, имеющие вместе с тем единую кристаллическую решетку. Такие переходы называются гетеропереходами.

Переходы второго вида представляют собой слои с переменной концентрацией донорной и акцепторной примеси, заключенные между областями одинаковой химической природы, но содержащие разные по типу или концентрации примеси. Такие переходы называются гомогенными переходами или гомопереходами.

Современное электронное приборостроение основывается, главным образом, на использовании гомопереходов. Однако гетеропереходы обладают целым рядом замечательных свойств, и по мере совершенствования технологии приготовления удельный вес использования этих переходов в приборостроении будет, безусловно, возрастать. Особенно перспективно применение гетеропереходов в системах волоконно-оптической связи.

7.3. Электрический переход

Концентрация СНЗ в примесном полупроводнике определяется концентрацией донорной и акцепторной примесей, точнее их разностью. Поскольку эта величина в переходе непостоянна, то и концентрация СНЗ в переходе будет также непостоянной. Это приводит к нарушению локальной электрической нейтральности полупроводника, образованию пространственного заряда и внутреннего электрического поля.

Для лучшего уяснения процесса образования электрического поля в переходе допустим, что примеси в области неоднородности распределены плоскими слоями так, что величина N_d-N_a является функцией только одной координаты пространства – x, отсчитываемой в направлении, перпендикулярном к этим слоям (рис.7.1). Это предположение является не только модельно упрощением. Оно фактически наилучшим образом соответствует характеру распределения примесей в активных элементах полупроводниковых приборов, изготовляемых по наиболее современной планарной и планарно-эпитаксиальной технологии. Сущность планарной технологии заключается в том, что примеси вводятся через плоскую поверхность кристаллической пластинки методом диффузии или методом бомбардировки соответствующими ионами (ионная имплантация). Сущность планарно-эпитаксиальной технологии заключается в том, что перед процессом диффузии на кристаллической подложке наращивается из газовой среды или жидкого раствора тонкий плоский кристаллический слой с заданным составом примесей.

На рис.7.1. дано сечение некоторого кристалла плоскостью перпендикулярной к плоскостям равных концентраций примесей в переходе. Штриховкой показаны области I и II с _{равномерным} распределением примесей. Между ними лежит более или менее протяженная область перехода с неравномерным распределением примесей. Ось х направлена перпендикулярно к плоскостям равных концентраций. Начало координат выбрано в глубине одной из однородных областей.

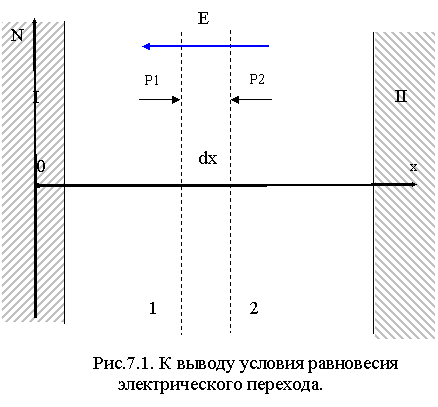Допустим, для определенности, что N_d-N_a=ƒ(x) является возрастающей функцией х. Тогда, в неоднородной по концентрации примесей области, концентрация электронов должна являться возрастающей функцией х, а концентрация дырок, наоборот, убывающей функцией х. Иначе говоря, плотность электронного газа и его давление будут возрастать в направлении оси х. Плотность и давление дырочного газа будут убывать в направлении оси х. Но тогда, если на эти газы не действуют никакие другие силы, они должны смещаться как целое под действием существующего перепада давлений. Дырочный газ потечет в направлении оси х, электронный газ потечет в противоположном направлении. Если бы "молекулы" рассматриваемых газов были нейтральны, то перемещение происходило бы до тех пор, пока плотность и парциальное давление каждого из газов не стали бы одинаковыми по всему объему кристалла.

Но в нашем случае "молекулы" заряжены и, поэтому, смещение газов приводит к немедленному возникновению электрического поля, которое будет препятствовать их дальнейшему смещению. Равновесие наступит раньше, чем выровняется парциальное давление. Действительно, допустим на мгновение, что плотность электронного газа, т.е. концентрация электронов стала одинаковой по всему объему. Ясно, что эта величина будет иметь некоторое промежуточное значение между минимальным ее значением, соответствующим области I, и максимальным значением, соответствующим области II. Значит, концентрация электронов в левой части неоднородной области станет больше того значения, которое соответствует электрической нейтральности, а в правой части, наоборот, концентрация электронов станет меньше значения, соответствующего электрической нейтральности. Правая половина приобретает положительный заряд, а левая - отрицательный. Легко проследить, что к тому же последствию приводит и смещение дырочного газа. Совместно эти два эффекта обусловливают возникновение в полупроводнике поля, направленного так, как показано на рис.7.1. Смещение газов прекратится и в полупроводнике наступит динамическое равновесие, когда сила, действующая на любой элемент объема электронного (дырочного) газа, обусловленная перепадом давлений, будет уравновешена силой электрического поля, действующей на тот же элемент.

Таким образом, образование пространственного заряда в электрическом переходе, есть своеобразная поляризация полупроводника, обусловленная неоднородностью распределения примесей в нем и, возникающая как необходимое условие равновесия системы подвижных (СНЗ) и неподвижных (ионы доноров и акцепторов) электрических зарядов в полупроводнике.

7.4. Распределение потенциала и концентрации СНЗ в равновесном электрическом переходе

Выделим мысленно бесконечно тонкий слой dx электронного газа, заключенный между плоскостями I и II с координатами х и x+dx. Этот слой будет испытывать со стороны окружающего электронного газа давление Р₁ слева и Р₂ справа. Давление газа, как известно, равно nkT, где n- концентрация частиц этого газа. Обозначим концентрацию электронов в плоскости 1 через n₁ а в плоскости II через n₂. Тогда разность давлений ∆Р на рассматриваемый слой будет равна:

(7.1)

Сила перепада давлений, действующая на слой dx, будет равна:

(7.2)

где s- площадь границ слоя. Знак " - " показывает, что эта сила противоположна направлению вектора градиента концентрации электронов.

Определим силу электрического поля, действующую на тот же слой. Электрический заряд слоя ∆Q равен:

(7.3)

Электрическая сила , действующая на слой, будет равна:

(7.4)

В состоянии равновесия сумма сил, действующих на слой, равна нулю. Следовательно:

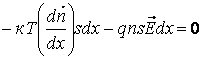
или

(7.5)

Так как, то

(7.6)

Решая это дифференциальное уравнение, получим:

(7.7)

Рассуждая аналогично в отношении дырочного газа, найдем, что

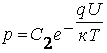(7.8)

Константы интегрирования С1 и С2 определяются как всегда из граничных условий. Начало координат мы поместили в глубине однородной области I полупроводника. Здесь выполняется условие локальной электрической нейтральности и поле отсутствует. Примем потенциал этой области в окрестности начала координат равным нулю. Тогда, подставляя в (7.7) и (7.8) значения x = 0; U = 0; n = n₁; p = p₁, получим С1= n₁, С2 = р₁. Следовательно:

(7.9)

(7.10)

Таким образом, концентрация СНЗ и потенциал в электрическом переходе связаны между собой экспоненциальной зависимостью.

Распределение потенциала в переходе определим, решив уравнение Пуассона. Плотность пространственного заряда в любом слое равна:

(7.11)

или, учитывая (7.9) и (7.10):

(7.12)

Следовательно, уравнение Пуассона будет иметь вид:

(7.13)

Поскольку распределение примесей, т.е. (N_d-N_a) = ƒ(х) известно, то, решая (7.13), найдем U = U(x).

Так как соотношения (7.9) и (7.10) должны быть справедливы для любого элемента объема полупроводника, то, применяя их для второй однородной области, где концентрации электронов и дырок соответственно равны n₂ и p₂ получим, что потенциал этой области U₂ равен:

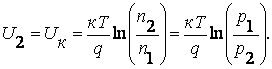(7.14)

Разность потенциалов на концах электрического перехода пропорциональна логарифму отношения концентраций однотипных СНЗ в однородных областях полупроводника, разделенных переходом. Эта разность называется контактной разностью потенциалов перехода.

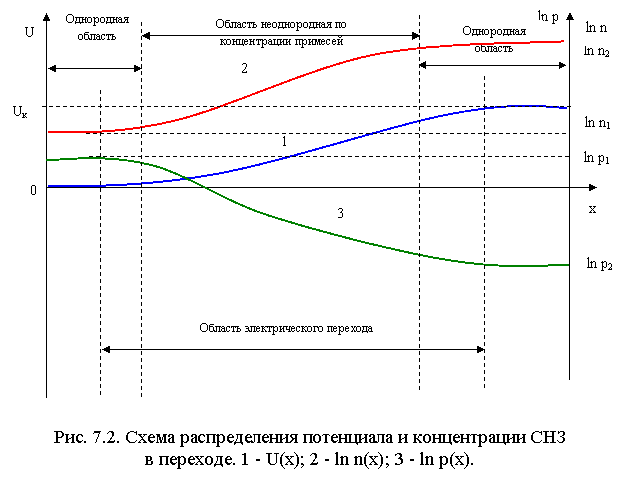
Подводя итог, можно заключить, что в области электрического перехода потенциал возрастает в направлении возрастания разности между концентрацией акцепторных атомов. Соответственно в том же направлении в экспоненциальной зависимости от U возрастает концентрация электронов, а концентрация дырок уменьшается обратно пропорционально концентрации электронов (рис.7.2.)

Ширина электрического перехода всегда превышает ширину области в полупроводнике с неоднородной концентрацией примесей так, что переход частично захватывает области однородного полупроводника.Если ширина неоднородной, по концентрации примесий, области настолько велика, что ее можно считать сравнимой с шириной перехода, то переход называют плавным. Если ширина локализации неоднородности существенно меньше ширины перехода, то переход называют резким.

7.5. Диффузионное уравнение

При инжекции или экстракции неосновных носителей их распределение в объеме соответствующих областей полупроводника будет неравномерным. Хаотическое тепловое движение приведет в этом случае к возникновению макроскопического процесса переноса частиц, называемого диффузией. Как известно, количество частиц, переносимых при диффузии за единицу времени через плоскость площадью s и перпендикулярную к направлению вектора градиента концентрации частиц, равно:

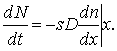(7.15)

В этом уравнении: D - коэффициент диффузии, -значение градиента концентрации в рассматриваемой плоскости х. Знак "-" показывает, что диффузионный перенос совершается в направлении противоположном направлению градиента концентрации(dn/dx). Рассмотрим бесконечно тонкий слой dx, n-полупроводника, параллельный плоскости p-n перехода и ограниченный плоскостями x и x+dx (рис.7.3).

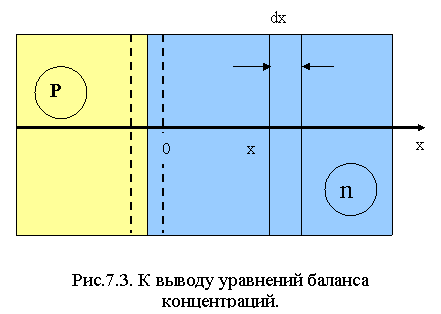Через границы х и х+dx этого слоя за единицу времени продиффундирует, соответственно

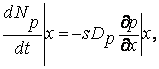(7.16)

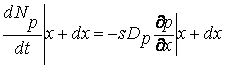(7.17)

дырок. Так как внутри слоя распределение дырок можно считать равномерным, то изменение количества дырок в слое за единицу времени можно представить как произведение объема слоя на скорость изменения концентрации дырок. С другой стороны, эта величина должна равняться разности (7.16) и (7.17). Следовательно:

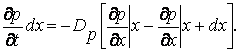(7.18)

Градиент концентрации является непрерывной функцией х, поэтому:

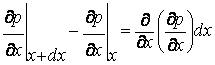(7.19)

Учитывая (7.19), уравнение баланса (7.18) можно записать в виде:

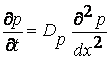(7.20)

Уравнение (7.20) носит название второго уравнения Фика.

Если в полупроводнике не происходит никаких других процессов кроме диффузии, то концентрация неосновных носителей в любом элементе объема изменяется со скоростью, пропорциональной значению второй производной от концентрации этих носителей по координате в этом элементе объема. Заметим, что коэффициенты диффузии электронных и дырочных газов, соответственно, равны:

(7.21)

где l_n и l_р - длины свободного пробега соответствующих носителей заряда.

7.6. Уравнение непрерывности

Нарушение равновесия в полупроводнике сопровождается протеканием одновременно всех трех рассмотренных кинетических процессов. Если считать эти процессы взаимно независимыми, что определенно имеет место при не очень высоких значениях градиента концентрации неосновных носителей и напряженности поля, то результирующая скорость изменения концентрации неосновных носителей будет равна сумме парциальных скоростей, т.е.:

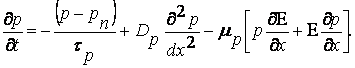(7.22)

Такое же уравнение можно написать и для электронов в р-полупроводнике.

Уравнение (7.22) называют уравнением непрерывности. Это уравнение отражает в математической форме то естественное утверждение, что изменение концентрации носителей заряда в любом элементе объема полупроводника может произойти либо в результате генерации (рекомбинации) этих частиц, либо в результате прихода (ухода) их в процессе диффузии или электрического переноса, либо, наконец, в результате того, другого и третьего одновременно.

Уравнение непрерывности является основным уравнением кинетики процессов в полупроводнике и позволяет определить концентрацию носителей заряда в любой точке полупроводника, в любой момент времени, при любом внешнем воздействии, нарушающем равновесие полупроводника. Определив концентрацию носителей, нетрудно будет определить пространственную и временную зависимость других физических величин, например, силы тока, протекающего как в однородном, так и в неоднородном полупроводнике любой структуры.

7.7. P-n переход

Одной из важных в практическом отношении разновидностей электрического перехода является так называемый электронно-дырочный, или p-n переход, имеющий место, когда величина (N_d-N_a) в области неоднородности полупроводника изменяет знак с отрицательного на положительный или наоборот. Иначе говоря, электронно-дырочным или p-n переходом называется переход между двумя областями полупроводника, одна из которых имеет электропроводность p-типа, а другая n-типа.

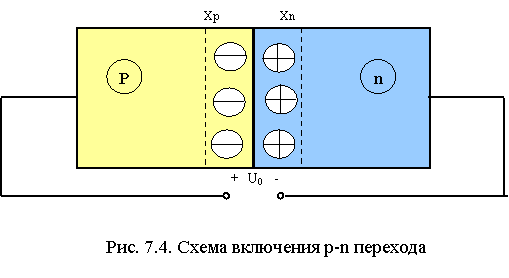
Схема включения p-n перехода во внешнюю цепь представлена на рис. 7.4.

Распределение концентрации примесей в идеализированном резком p-n переходе можно представить ступенчатой кривой (рис.7.5.)

При х ≤ 0, N_a(x) = N_a= const, N_d= 0. При x ≥ 0, N_a= 0, N_d(x) = N_d= const. Плоскость х = 0 называется технологической границей перехода.

В соответствии с ранее полученными выражениями распределение концентрации электронов и дырок в p-n переходе определяется функциями:

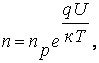
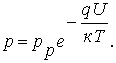(7.23)

Контактная разность потенциалов равна:

(7.24)

Здесь n_p и p_p - равновесные концентрации электронов и дырок в р-области полупроводника, n_n и р_n - равновесные концентрации тех же частиц в n-области полупроводника. W_1._n и W_1._p - энергии уровня Ферми в отдельно взятых n- и р- полупроводниках при той же концентрации примесей, что и в контактирующих областях.

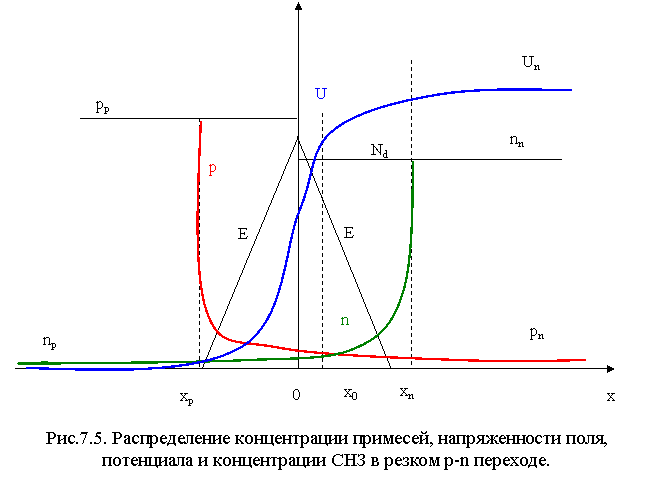
Уравнение Пуассона будет выглядеть следующим образом:

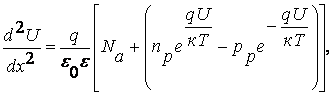(7.25)

справедливое при х ≤ 0 и

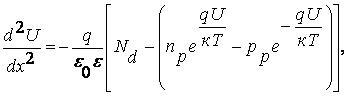(7.26)

справедливое при х ≥ 0.

Обозначим через (-х_р) координату границы пространственного заряда в р-области, а через (+х_n) координату границы пространственного заряда в n-области (рис.7.5). Величина р_ре^-^qU^/кТ очень быстро уменьшается при возрастании х, т.е. при удалении от границы (-х_р) в сторону границы (+х_n). Поэтому, почти во всем переходе эта величина пренебрежимо мала по сравнению как с N_a , так и с N_d. То же самое справедливо и в отношении величины n_pe^qU^/кТ. Пренебрегая этими величинами, придем к уравнениям:

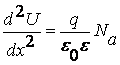(7.25`)

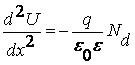(7.26`)

Решение уравнений (7.25`) и (7.26`) должны удовлетворять следующим граничным условиям:

U = 0 при х ≤ -х_р;

U = U_к при х ≥ х_n;

при х ≤ х_р и х ≥ х_n.

Интегрируя уравнение (7.25`) в пределах от х = -х_р до х = 0, а уравнение (7.26`) в пределах от х = 0 до х = х_n, получим:

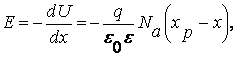(7.27)

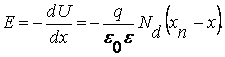(7.28)

Поскольку в плоскости х = 0 оба решения должны тождественно совпадать, то, приравнивая их, приходим к важному выводу:

(7.29)

Ширина участков резкого p-n перехода, лежащих в каждой из контактирующих областей полупроводника, обратно пропорциональна концентрации примесей в этих областях.

Напряженность поля в резком p-n переходе изменяется по линейному закону в каждой из областей, достигая максимума, равного на технологической границе перехода (рис.7.5).

Интегрируя (7.27) и (7.28) в тех же пределах, получим:

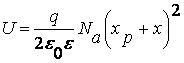(для х ≤ 0) (7.29)

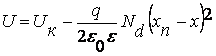(для х ≥ 0) (7.30)

Потенциал изменяется по квадратичному закону в зависимости от расстояния выбранной плоскости от каждой из границ пространственного заряда (рис.7.5).

Так как (7.29) и (7.30) должны тождественно совпадать при х = 0, то из этого следует:

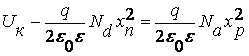(7.31)

Соотношение (7.31) позволяет определить положение границ пространственного заряда и полную ширину p-n перехода Δ₀ в состоянии равновесия.

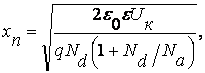
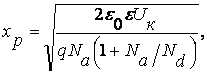(7.32)

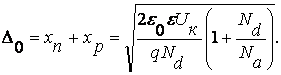(7.33)

Если учесть (7.24), то

(7.34)

Ширина равновесного p-n перехода увеличивается при увеличении температуры и уменьшении концентрации примесей.

Подставив (7.29) и (7.30) в (7.23), получим функции распределения концентрации СНЗ в явном виде (рис.7.5). Заметим, что если N_d¹ N_a, то плоскость в которой n = p, т.е. плоскость инверсии типа проводимости (х₀ на рис.7.5) не совпадает с технологической границей перехода. Такой переход называют несимметричным переходом.

Контрольные вопросы:

1. Что такое электрический переход? Какие переходы называют гомогенными, гетерогенными?

2. От чего зависит контактная разность потенциалов?

3. Объясните понятие «диффузия». Чему равны коэффициенты диффузии электронных и дырочных газов?

4. Как влияют на ширину равновесного p-n-перехода внешние факторы?

5. Напишите и объясните уравнение непрерывности.

6. Нарисуйте схему включения p-n-перехода во внешнюю цепь. Поясните ее.

Лекция 8. Нарушение равновесия в p-n-переходе.

8.1. Концептуальная диаграмма.

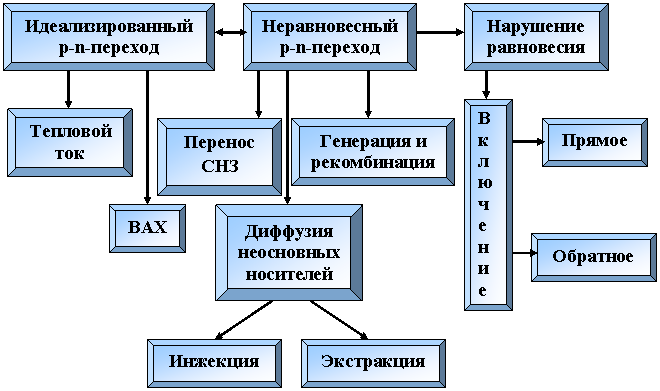
8.2. Условия нарушения равновесия в переходе

Равновесие в переходе основано на численном равенстве силы внутреннего электрического поля, действующей на любые элементы объемов электронного и дырочного газов и, силы, обусловленной перепадом парциальных давлений этих газов. Отсюда следует, что равновесие в переходе может быть нарушено либо путем изменения напряженности поля в переходе, либо путем изменения концентрации СНЗ, значению которой пропорциональны парциальные давления.

Концентрация СНЗ как в переходе, так и в прилегающих к нему областях полупроводника, может быть изменена, например, путем облучения полупроводника светом подходящей длины волны или путем любого другого воздействия, изменяющего скорость генерации (рекомбинации) свободных носителей заряда в этих областях. Она может быть изменена также путем принудительного введения (инжекции) в переход или, наоборот, путем принудительного извлечения (экстракции) из перехода СНЗ.

Напряженность поля в переходе может быть изменена путем приложения к переходу внешнего напряжения. Разность потенциалов на границах p-n перехода при этом или уменьшается, или возрастает, в зависимости от полярности приложенного напряжения. Если разность потенциалов на границах перехода уменьшается, то включение перехода называется прямым, если же она увеличивается, то включение называют обратным.

Концентрация СНЗ и напряженность поля - величины, связанные между собой и, поэтому, независимо от того на какую из них непосредственно воздействует внешний фактор, изменяться будут обе эти величины. Напряженность поля и разность потенциалов на переходе становятся отличными от своих равновесных значений, и в переходе, как и в прилегающих к нему областях, появляются избыточные или неравновесные СНЗ.

Независимо от причины, вызывающей нарушение равновесия в переходе, силы, действующие на каждый из газов, оказываются не скомпенсированными, и газы приходят в движение. В переходе возникает электрический ток, если внешняя цепь перехода замкнута, или на внешних выводах контактирующих полупроводников устанавливается некоторое напряжение, если эта цепь разомкнута (термоЭДС, фотоЭДС и т.д.).

Действие большой группы электропреобразовательных полупроводниковых приборов основано на инициировании электрического тока в p-n переходах путем приложения к ним внешнего напряжения.

Действие фотоэлектрических полупроводниковых приборов основано на инициировании в переходе электрического тока (фотоЭДС) электромагнитным излучением (световым потоком).

8.3. Процессы в объеме полупроводника при нарушении равновесия

Когда к p-n переходу приложено внешнее напряжение, то равновесие нарушается не только в переходе, но и в прилегающих к нему областях полупроводника. Во-первых, в этих областях устанавливается хотя и слабое, но не равное нулю поле. Во-вторых, и это наиболее существенно, в эти области происходит инжекция (или экстракция) неосновных носителей заряда, в результате чего их концентрация становится заметно отличной от равновесного значения. Нарушение равновесия в объеме полупроводника приводит к возникновению в нем следующих трех процессов, каждый из которых протекает в таком направлении, чтобы вернуть полупроводник в состояние равновесия.

Первым из этих процессов является так называемый генерационно - рекомбинационный процесс, заключающийся в том, что при концентрации СНЗ отличной от равновесного значения становятся неравными скорости рекомбинации и генерации. В результате концентрация СНЗ начинает либо убывать, либо возрастать, стремясь к значению, соответствующему интенсивности воздействия внешнего фактора, нарушающего равновесие.

Второй процесс связан с неравномерностью распределения СНЗ в объеме полупроводника и заключается в диффузии неравновесных носителей заряда в направлении убывания их концентрации.

Третий процесс заключается в переносе свободных носителей заряда электрическим полем.

Заметим, что первые два из перечисленных процессов особенно существенны для неосновных носителей, так как вследствие малой концентрации этих частиц достаточно сравнительно слабых внешних воздействий, чтобы вызвать весьма значительное ее относительное изменение. Третий процесс, напротив, наиболее существенен для основных носителей заряда. Концентрация основных носителей заряда настолько велика, что даже в слабых электрических полях перенос полем превалирует над другими процессами, протекающими в системе этих частиц.

Установление поля в переходе, т.е. процесс поляризации полупроводника, является процессом практически безинерционным. Время этого развития составляет величину порядка 10^-12…10^-13 секунды. Однако, установление тока в переходе происходит значительно медленнее и лимитируется процессами в объеме полупроводника. Действительно, перенос заряда в областях, прилегающих к переходу, осуществляется в значительной мере инжектируемыми или экстрагируемыми неосновными носителями. Скорость этого переноса и время его установления определяются скоростью протекания и временем установления перечисленных кинетических процессов.

8.4. Электронно-дырочный переход в неравновесном состоянии

Если к p-n переходу подключить источник напряжения, то равновесное состояние нарушается – в цепи потечет ток. Так как сопротивление обедненного слоя значительно превышает сопротивление нейтральных областей, то при малом токе внешнее напряжение U практически полностью прикладывается к обедненному слою. Под действием этого напряжения изменяется высота потенциального барьера.

Если плюс источника питания подключен к р-области, а минус к n-области, то напряжение на переходе называют прямым (U > 0). При прямом напряжении потенциальный барьер понижается, поскольку внешнее поле направлено навстречу внутреннему полю перехода. При обратном напряжении на переходе (минус источника подключается к р-области) потенциальный барьер повышается, так как внешнее поле складывается с внутренним.

Вместе с высотой потенциального барьера изменяется и его толщина. При обратном напряжении L_об увеличивается, что можно объяснить смещением основных носителей от перехода под действием электрического поля. При этом обнажаются дополнительные ионы примесей у границ перехода, что приводит к росту толщины обедненного слоя и высоты барьера. Этот процесс происходит за время, близкое времени диэлектрической релаксации. При прямом напряжении L_об уменьшается вследствие смещения основных носителей в сторону обедненного слоя. Проникая в обедненный слой, они компенсируют часть его объемного заряда, что приводит к снижению толщины слоя. Для несимметричного ступенчатого p-n перехода:

(8.1)

где - контактная разность потенциалов при Т=0 К.

На энергетических диаграммах перехода (рис.8.1.) при прямом (а) и обратном (б) смещении уровни Ферми в областях р- и n- типа в отличие от равновесной диаграммы располагаются на разной высоте, а разность между ними равна q/U/.

При прямом смещении напряженность поля в переходе уменьшается, условие равновесия диффузионного и дрейфового токов нарушается – диффузия электронов из n-области и встречная диффузия дырок преобладают по сравнению с их дрейфовым движением. Вследствие диффузии увеличивается концентрация неосновных носителей в нейтральных областях, граничащих с переходом. Этот процесс называется инжекцией неосновных носителей.

Инжекции присущи резкая зависимость концентрации неосновных носителей от напряжения: при повышении напряжения всего лишь на 2,3 j_Т (60 мВ при Т = 300 К) концентрация возрастает на порядок.

Избыточные неосновные носители могут возникать у границ перехода не только за счет приложения внешнего напряжения, но и вследствие воздействия других факторов, например света. В результате на переходе появляется напряжение (ЭДС), которое может быть выражено через концентрации неосновных носителей по (8.2) , (8.3), если их разрешить относительно напряжения.

(8.2)

(8.3)

где - контактная разность потенциалов при температуре Т.

Таким образом, независимо от причины, вызывающей появление избыточных концентраций неосновных носителей, связь их с напряжением определяется выражениями (8.2) , (8.3).

При высоком напряжении толщина перехода (8.1) возрастает не пропорционально напряжению, в результате напряженность электрического перехода увеличивается и в нем преобладает дрейфовое движение носителей по сравнению с диффузионным: дырки в n-области и электроны в р-области вследствие теплового хаотического движения могут пересечь границы перехода, где они попадают в ускоряющее поле, переносящее их в соседнюю область. В результате уменьшаются концентрации неосновных носителей у границ перехода; это явление называют экстракцией неосновных носителей. Выражения (8.2) , (8.3) справедливы и для экстракции, при U < 0 из них следует ∆n_р< 0, ∆р_n< 0, что соответствует уменьшению концентраций неосновных носителей по сравнению с равновесными концентрациями.

8.5. Идеализированное уравнение тока через p-n переход

Идеализированный р-n-переход представляет собой упрощенную модель реального р-n-перехода, в которой приняты следующие основные допущения: в обедненном слое нет генерации, рекомбинации и рассеяния носителей; носители проходят через обедненный слой мгновенно, т.е. токи носителей одного знака на обеих границах одинаковы;

вне обедненного слоя нет электрического поля, здесь носители движутся только вследствие диффузии; сопротивление нейтральных областей в сравнении с сопротивлением обедненного слоя считаются пренебрежимо малыми; уровень инжекции низкий;

границы р-n-перехода являются плоскими, носители движутся только в направлении, перпендикулярном этим границам, краевые эффекты не учитываются.

В рассматриваемой модели р-n-перехода предполагается, что изменение концентрации неосновных носителей в областях за границами перехода при небольшом прямом напряжении не нарушает электрическую нейтральность этих областей. Это объясняется быстрой (за время диэлектрической релаксации) нейтрализацией заряда инжектированных неосновных носителей основными носителями, поступающими из внешней цепи. Предположим, что толщины нейтральных областей много больше диффузионной длины неосновных носителей в этих областях. Физические процессы при прямом напряжении р-n-перехода поясняет рис.8.2. На рис.8.2 (а) показаны направления движения основных носителей, создающих прямой ток.

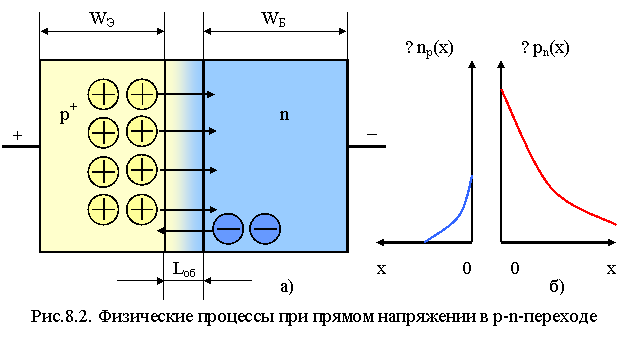Перемещение этих носителей через р-n-переход приводит к инжекции избыточных неосновных носителей – электронов в нейтральную р-область, а дырок в n-область. В нейтральных областях около р-n-перехода неосновные носители движутся от его границ вследствие диффузии, вызванной возникшим градиентом этих носителей. Стационарные распределения концентраций избыточных неосновных носителей в этих областях ∆n_p(х) и ∆р_n(х) определяются из уравнений диффузии при условиях, что на границах перехода, принятых за начало отсчета, концентрации определяются по (8.2) и (8.3), а в глубине нейтральных областей они стремятся к нулю вследствие рекомбинации. Решение уравнений диффузии имеет вид:

(8.4)

где L_p, L_n – диффузионные длины дырок в n-области и электронов в р-области соответственно.

Распределение концентраций показаны на рис.8.2(б), где приняты разные начала и направления отсчета координаты х – от соответствующей границы p-n перехода. Определим выражение вольт-амперной характеристики (ВАХ) p-n перехода. Ток через p-n-переход состоит из электронного и дырочного токов, которые на его границах равны:

(8.5)

где S – площадь перехода; коэффициенты диффузии электронов в р-области и дырок в n-области. Подставляя в (8.5) избыточные концентрации электронов на границе р-области (8.2) и дырок на границе n-области (8.3), получим ВАХ идеализированного p-n-перехода:

(8.6)

где I₀ – тепловой ток, который является единственным параметром и имеет смысл обратного тока, так как при и

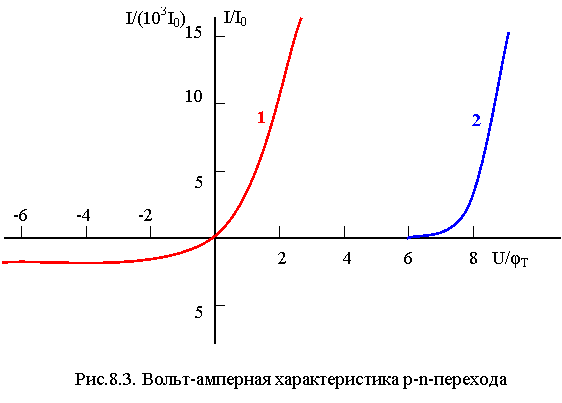Вольт-амперная характеристика для малых прямых напряжений показана на рис.8.3 (кривая 1, правая шкала отсчета). При прямом напряжении ток резко возрастает: изменению тока на порядок соответствует изменение напряжения на (60 мВ при Т = 300 К). При обратном напряжении, превышающем по модулю , обратный ток идеализированного p-n-перехода не зависит от напряжения и равен I₀. Для прямых токов порядка (10³¸10⁴)I₀ ВАХ (кривая 2) соответствует левая шкала отсчета токов, для которой обратная ветвь и начальный участок прямой ветви не видны на графике. Поэтому для прямой и обратной ветвей ВАХ, если их необходимо изобразить на одном графике, используют разные масштабы.

Контрольные вопросы:

1. Каким образом можно изменить концентрацию СНЗ в области перехода полупроводника?

2. Какие процессы происходят в полупроводнике при нарушении равновесия?

3. Прямое и обратное напряжение на переходе. Инжекция и экстракция неосновных носителей.

4. Чем отличается идеализированный p-n-переход от реального?

5. Объясните вывод ВАХ идеализированного p-n-перехода.

Лекция 9. Полупроводниковые диоды.

9.1. Концептуальная диаграмма

9.2. Полупроводниковые диоды

Диодом называют электропреобразовательный прибор, который, как правило, содержит один или несколько электрических переходов и два вывода для подключения к внешней цепи. Принцип работы большинства диодов основан на использовании физических явлений в электрическом переходе. Наиболее часто в диодах применяются электронно-дырочный переход, контакт металл – полупроводник, гетеропереход. Однако существуют диоды, структура которых не содержит выпрямляющих электрических переходов (например, диоды Ганна) либо содержит несколько переходов (например, p-i-n-диод, динистор), а также диоды с более сложной структурой переходов (например, МДМ- и МДП-диоды и др.). Полупроводниковый диод как элемент цепи является нелинейным двухполюсником, т.е. электронным прибором, с двумя внешними выводами и нелинейной вольт-амперной характеристикой (ВАХ). Он выполняет функцию преобразования сигналов (выпрямление, детектирование, умножение частоты, преобразование световой энергии в электрическую и др.).

В основу классификации диодов можно положить различные признаки – вид электрического перехода (точечный и плоскостный диоды), физические процессы в переходе (туннельный, лавинно-пролетный диоды и др.), характер преобразования энергии сигнала (светодиод, фотодиод и др.), метод изготовления электрического перехода (сплавные, диффузионные, эпитаксиальные диоды и др.) и т.п. В справочниках по полупроводниковым приборам обычно приводится классификация диодов по применению в радиэлектронной аппаратуре (РЭА) или по назначению. При этом классификация отражает принцип использования преобразующих и нелинейных свойств электрического перехода (выпрямительные и импульсные диоды, преобразовательные, переключательные, варикапы, стабилитроны и др.), диапазон рабочих частот (низкочастотные, высокочастотные, СВЧ-диоды, диоды оптического диапазона и т.п.), исходный материал для изготовления диодных структур (кремниевые, селеновые, германиевые, арсенид-галлиевые диоды и др.)

В системе условных обозначений современных полупроводниковых диодов находят отражение их назначение, физические свойства, основные электрические параметры, конструктивно-технологические признаки, исходный полупроводниковый материал. Все эти данные о приборе связаны со структурой его электрического перехода.

Структура реального диода содержит один или несколько электрических переходов. По конструктивно-технологическим особенностям электрических переходов различают точечные, микросплавные, сплавные, диффузионные, эпитаксиальные, с барьером Шоттки, поликристаллические и другие типы диодов.

У точечных диодов электронно-дырочный переход образован контактом заостренной металлической иглы, например из сплава вольфрама с молибденом, полупроводниковым кристаллом кремния, германия, арсенида галлия и других материалов. Структура перехода изображена на рис.9.1.а. Свойства окружающей среды, чистота поверхности кристалла и механические условия контактирования определяют в значительной мере электрические параметры диода и его ВАХ. Слой р-типа образуется в кристалле полупроводника в результате термодиффузии акцепторных примесей (например, индия или алюминия в германий n-типа) с конца металлической иглы, возникающей под воздействием больших импульсов тока, пропускаемых через контакт. Линейные размеры перехода точечного диода соизмеримы с толщиной его обедненной области. Площадь контакта менее 50 мкм², поэтому емкость перехода мала, а прямые токи через переход не превышают десятков миллиампер. Область р-типа под контактом геометрически неоднородна, и обычно в ней сосредоточено наибольшее количество дефектов кристаллической структуры. Сильное электрическое поле в области контакта способствует появлению значительных токов утечки и генерации.

Структура электронно-дырочного перехода сплавных диодов образуется вплавлением в кристалл полупроводника n-типа сплава с акцепторной примесью, например индия в германий, алюминия в кремний и т.п. В кристалле полупроводника n-типа подвижность электронов в 2-2,5 раза больше, чем дырок в р-полупроводнике. Поэтому при одинаковой электропроводности полупроводников р- и n-типа концентрацию доноров в кристалле – базе диода можно уменьшить и тем самым повысить пробивное напряжение перехода. Этими соображениями обусловлен выбор в диодах в качестве базы кристалла полупроводника с электронной проводимостью.

При изготовлении кремниевых сплавных диодов, структура перехода которых приведена на рис.9.1.б, в кремний вплавляется тонкая алюминиевая проволока при температуре 600-700 ⁰С. В месте сплава формируется тонкий обогащенный алюминием рекристаллизованный слой кремния с той же кристаллической структурой, что и исходный полупроводник, но проводимостью р-типа. Между рекристаллизованным слоем (толщиной в несколько микрометров) и монокристаллом возникает р-n-переход, граница которого указана на рисунке штриховой линией.

Электронно-дырочные переходы сплавных диодов – резкие или ступенчатые. Они пропускают прямые токи до десятков ампер. Из-за большой площади переходов их емкости относительно велики. У микросплавных диодов несколько больший по площади р-n-переход, чем у точечных. Электрический переход микросплавных диодов с золотой связкой (рис.9.1.в) формируется методом микровплавления в кристалл германия тонкой золотой проволочки с присадкой галлия на конце. Под контактом образуется рекристаллизованный слой германия р-типа. Граница р-n-перехода показана на рисунке штриховой линией.

У диффузионных диодов электрический переход изготавливается методом общей или локальной диффузии донорных или акцепторных примесей в кристалл полупроводника. Диффузию можно проводить однократно и многократно. Например, структура электрического перехода кремниевого диода (рис.9.1.г) p⁺-p-n-n⁺типа изготавливается методом общей многократной диффузии. Область р-типа формируется диффузией акцепторной примеси – алюминия в кремниевую пластину n-типа, а область n⁺типа – диффузией в эту же пластину фосфора – донорной примеси. Для образования р⁺ - области проводится вторая диффузия бора в р-область. Омические контакты с р⁺- и n⁺-

областью изготавливают химическим осаждением никеля и последующим гальваническим золочением.

При изготовлении германиевых диффузионных диодов выбирается пластина германия р-типа, так как донорные примеси по сравнению с акцепторными лучше диффундируют в германий. В качестве диффузанта используется сурьма. Для формирования омического контакта с n-областью диффузионной структуры применяется оловянный припой с присадкой сурьмы. Омический контакт с р-областью германия образует вплавленный в эту область индий.

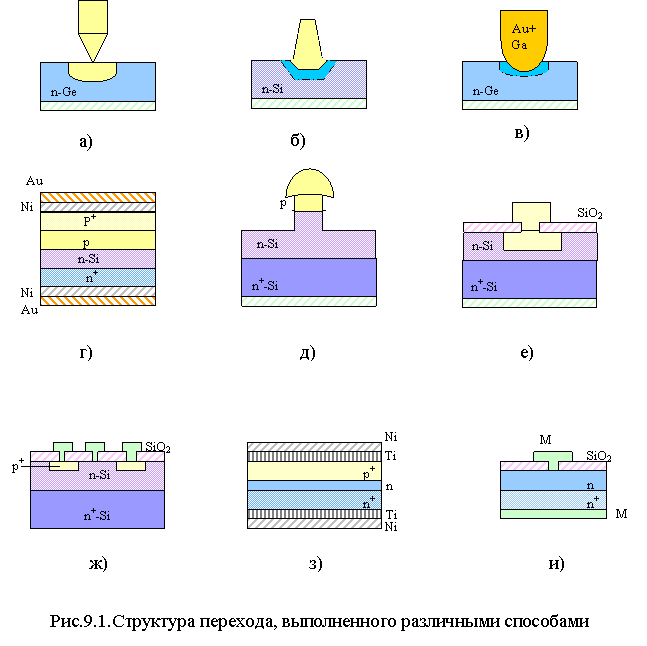
Для уменьшения емкости p-n перехода в высокочастотных диффузионных диодах используется мезаструктура (рис.9.1.д), получаемая методом глубоко химического травления. В результате первой общей диффузии создается n⁺-Si-слой в кристалле n-типа. После второй общей диффузии, формирующей р-слой в кристалле кремния, образования омического контакта и защиты отдельных участков кристалла через маску осуществляется травление поверхности его незащищенных участков. В результате р-n-переход остается только на небольших участках кристалла под омическим контактом. Участки возвышаются над поверхностью кристалла в виде стола (меза – по-испански). Диаметр р-n-перехода после травления уменьшается до нескольких десятков микрометров.

При диффузии получается неравномерное распределение примесей вдоль координаты, перпендикулярной поверхности кристалла. Концентрация диффузанта с глубиной падает, поэтому у диффузионных диодов с плоскостным и плавным р-n-переходом в базе появляется тормозящее электрическое поле.

Эпитаксиальные (планарные, эпитаксиально-планарные) диоды изготавливаются с использованием процесса эпитаксии и локальной диффузии.

Эпитаксией называется процесс наращивания монокристаллических слоев на подложку, используемую как несущая конструкция структуры. В наращиваемом слое сохраняется кристаллическая ориентация подложки. Эпитаксия позволяет наращивать слои любого типа проводимости и удельного сопротивления толщиной в несколько микрометров. Однако р-n-переход создается в большинстве случаев диффузией примесных атомов в эпитаксиальный слой через окно в маске (например, из оксида кремния на рис.9.1.е). Омические контакты с р⁺- и n⁺- областями кристалла создаются операциями металлизации. В кремниевых диодах для создания омических контактов широко используется алюминий.

Планарные или планарно-эпитаксиальные диоды имеют «поверхностную» структуру, а выводы контактирующих областей электрического перехода расположены в одной плоскости. Электрический переход создан в поверхностном слое кристалла толщиной порядка единиц и десятков микрометров от его поверхности (рис.9.1.ж). При изготовлении структуры на подложку кремния n⁺-типа наращивается эпитаксиальный слой n-типа. Затем через окна защитной маски из оксида кремния в нем формируется несколько р⁺-областей диффузией бора, после чего осуществляется металлизация выводов от общей базовой и эмиттерных областей. Таким образом изготовляется диодная матричная планарно-эпитаксиальная структура.

Широкое распространение получают ионно-лучевые методы изготовления электрического перехода диода. При ионной имплантации легирование пластины полупроводника осуществляется бомбардировкой примесными ионами, ускоренными до высоких энергий. Концентрация примесей в имплантированном слое зависит от плотности тока в ионном луче и времени экспозиции. Высокая контролируемость процесса и низкая температура позволяют проводить ионную имплантацию на любой стадии процесса изготовления диода. Глубина проникновения ионов в полупроводник зависит от их энергии. Изменяя энергию ионов, можно обеспечить сложный закон распределения примесей по глубине. Структура электрического перехода диода, созданная ионно-лучевым методом, приведена на рис.9.1.з. На подложке кремния n⁺-типа выращен эпитаксиальный n-слой, в котором ионной имплантацией создана р⁺-область. Омические контакты получены химическим осаждением сначала титана, а затем никеля на полупроводниковую пластину с обеих сторон.

Диоды с барьером Шоттки (рис.9.1.и) в большинстве случаев изготавливаются напылением металла на очищенную поверхность кристалла в вакуумной среде, химическим осаждением металла на полупроводник или с помощью высокочастотного ионного распыления металла. В качестве подложки используются кремний, арсенид галлия. Электрические свойства перехода зависят от подобранной пары металл-полупроводник. В качестве контактирующего металла выпрямляющего перехода применяют алюминий, золото, молибден и др.

Кроме рассмотренных структур плоскостных диодов широко используются комбинированные структуры (эпитаксиально-диффузионные, диффузионно-сплавные, мезасплавные и др.).

Особую группу диодов составляют селеновые и титановые диоды. Электронно-дырочный гетеропереход селеновых выпрямителей образован селеном с проводимостью р-типа и селенидом кадмия с проводимостью n-типа, а гетеропереход титановых выпрямителей диоксида – слоем титана n-типа с напыленной в вакууме металлической пленкой (золото, серебро, висмут). Образование электрического перехода в селеновых выпрямителях происходит в процессе химической реакции при нанесении кадмия на селен.

Диоды выпускаются в различном конструктивном исполнении: металлокерамическом, стеклянном, керамическом, металлостеклянном, металлопластмассовом, пластмассовом корпусе с гибкими и жесткими выводами, а также на керамических микроплатах в бескорпусном исполнении с защитным покрытием и гибкими выводами. Корпус защищает электрический переход диода от вредных факторов окружающей среды.

9.3. Генерационно-рекомбинационные процессы в переходе, роль уровня инжекции, роль объемного сопротивления базы

При выводе ВАХ идеализированного p-n перехода учитывались лишь самые главные физические эффекты: инжекция и экстракция неосновных носителей и их диффузия в нейтральных областях, прилегающих к p-n переходу. В реальных p-n-переходах наблюдаются различные физические эффекты, влияющие на вид ВАХ. Это ток рекомбинации, сопротивление базы, ток генерации. Рассмотрим их влияние.

Прямая ветвь ВАХ. Ток рекомбинации. В области p-n перехода, как и в нейтральных областях полупроводника, происходит рекомбинация носителей. Электроны n-области, обладающие достаточной энергией, могут попасть в обедненный слой и рекомбинировать там с дырками, приходящими из р-области. При этом электроны уходят из n-области, а дырки - из р-области. Вследствие такого движения носителей возникает дополнительный прямой ток, называемый током рекомбинации. Полный прямой ток p-n перехода складывается из тока инжекции I_инж и тока рекомбинации I_рек. Следовательно, в реальном p-n переходе прямой ток больше, чем в идеализированном.

Ток рекомбинации:

(9.1)

Это выражение справедливо при Здесь L_об(U) – толщина обедненного слоя; τ – время жизни носителей в p-n переходе.

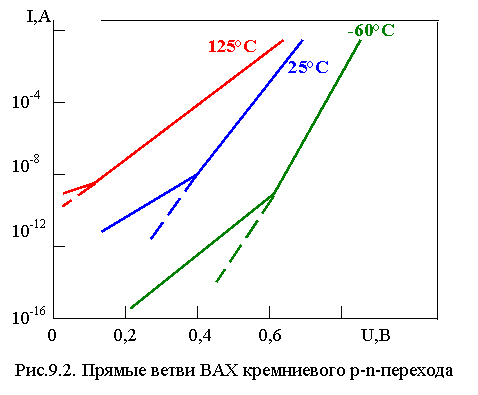На рис.9.2. Приведены прямые ветви ВАХ кремниевого p-n перехода в широком диапазоне токов (в полулогарифмическом масштабе), рассчитанные для трех значений температуры. При малых напряжениях (например, для кремния при U < 0,4 В, Т = 25°С) преобладает ток рекомбинации, характеристика изображается прямой линией, для которой увеличение тока на порядок соответствует приращению напряжения на 4,6φ_Т. при больших напряжениях основную часть тока составляет ток инжекции; эта область также изображается прямой линией, но с углом наклона вдвое большим. Граничное значение тока, разделяющее два участка, слабо зависит от температуры.

Влияние сопротивления базы. При выводе ВАХ идеализированного p-n перехода сопротивление базы r_Б полагается равным нулю. В реальных p-n переходах оно составляет десятки и сотни Ом. При этом внешнее напряжение распределяется между обедненным слоем и базовой областью. Тогда уравнение ВАХ будет выглядеть следующим образом:

(9.2)

или

(9.3)

При малых прямых токах второе слагаемое можно не учитывать. Однако с ростом тока падение напряжения на базе может превысить падение напряжения на p-n переходе, при этом на ВАХ появится почти линейный участок.

При высоком уровне инжекции наблюдается эффект модуляции сопротивления базы – уменьшение с ростом тока из-за увеличения концентрации носителей в базе. В этом случае , где r_б0 – немодулированное сопротивление; При I = 10 мА, W_б= 50 мкм, L_р= 10 мкм получим r_б= 18 Ом, тогда как r_б0 = 50 Ом. На практике прямую ветвь ВАХ реального p-n перехода аппроксимируют формулой где и (фактор неидеальности) – это параметры аппроксимации, подбираемые из условия наилучшего совпадения данной формулы с экспериментальной ВАХ.

Обратная ветвь ВАХ. Ток генерации. В реальном p-n переходе при обратном напряжении электроны и дырки, образующиеся в обедненном слое вследствие термогенерации, движутся в электрическом поле в противоположных направлениях: электроны – в сторону n-области, а дырки в сторону р-области. Дрейфовое движение этих носителей образует ток генерации. Число носителей, генерируемых в единице объема за единицу времени (скорость генерации), равно , где время жизни носителей в обедненном слое. Умножая эту величину на объем обедненного слоя получим полное число носителей, генерируемых в p-n переходе за единицу времени. Все они выбрасываются электрическим полем из обедненного слоя, поэтому ток генерации

(9.4)

Следовательно, обратный ток реального p-n перехода больше, чем идеального, поскольку кроме теплового тока I₀ течет ток генерации. Последний увеличивается с ростом обратного напряжения из-за расширения обедненного слоя. Т.е. доля тока генерации в полном обратном токе тем выше, чем больше ширина запрещенной зоны и ниже температура. Например, для кремниевого p-n перехода при Т = 25°С и U = -1 В имеем I_r = 10^-9А, а I₀ = 10^-14А.

9.4. Вольт-амперная характеристика идеализированного полупроводникового диода

Будем считать, что удельная проводимость контактирующих полупроводников настолько велика, что падением напряжения вне перехода можно пренебречь и считать U₀ равным приложенному к электродам диода внешнему напряжению. Кроме того, будем считать, что в p-n переходе не происходит ни размножения, ни потерь СНЗ и температура в переходе равна температуре всего кристалла.

Определим число электронов, пересекающих в единицу времени при своем хаотическом движении границу (-х_р) слева направо. Согласно уравнениям газокинетической теории, число частиц, пересекающих в единицу времени произвольно ориентированную площадку s, равно , где n- концентрация частиц; - средняя скорость теплового движения этих частиц. Следовательно, искомая нами величина равна:

(9.5)

где s- площадь p-n перехода. Стрелка указывает направление движения. В направлении справа налево границу (-х_р) в единицу времени пересекут те из электронов, пересекших в том же направлении границу (х_n), у которых кинетическая энергия не меньше q(U_к-U₀).

(9.6)

Таким образом, результирующий поток электронов через границу (-х_р) будет равен:

(9.7)

В статическом режиме поток электронов должен быть одинаковым через любую плоскость, параллельную плоскости (-х_р). Выражение (9.7) можно переписать в виде:

(9.8)

Электронную компоненту тока получим, умножив (9.8) на заряд электрона (-q).

(9.9)

Дырочная компонента тока определяется путем аналогичных рассуждений.

(9.10)

Полный ток p-n перехода равен:

(9.11)

Заметим, что все полученные выражения справедливы как для прямого, так и для обратного включения, достаточно лишь величину U₀ считать, соответственно, положительной или отрицательной.

Выражениям (9.9)-(9.11) можно придать вид более часто употребляемый и, вместе с тем, более универсальный, если ввести понятие времени жизни носителя и его длины диффузии.

Молекулы электронного и дырочного газов отличаются от молекул обычных газов не только наличием электрического заряда, но и тем, что они существуют сравнительно короткое время. При заданной температуре концентрация СНЗ имеет определенное и достаточно устойчивое значение. Но это значение есть статически средняя величина, устанавливающаяся при динамическом равновесии процессов генерации и рекомбинации СНЗ. О каждом же из свободных носителей заряда, если бы его можно было как-то пометить, можно было бы сказать, что он возникает в некоторый момент времени, когда происходит возбуждение какого-либо валентного электрона твердого тела и спустя какой-то срок прекращает свое существование, когда происходит девозбуждение этого электрона. Время существования СНЗ или время его жизни величина, естественно, случайная. Если мысленно взять достаточно большое число N₀ СНЗ, возникших в один и тот же момент времени t=0, то изменение их числа N(t) с течением времени будет описываться выражением:

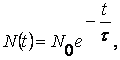(9.12)

где параметр носит название среднего времени жизни свободного носителя заряда. Как видим, среднее время жизни носителя равно тому промежутку времени, в течение которого первоначальное количество одновременно возникших носителей уменьшается в раз.

Если электроны и дырки движутся хаотически со средними по величине скоростями и , соответственно. Длина пути, проходимого частицей в заданном физически выделенном, но не нарушающим распределения, направлении, за время, равное среднему времени жизни этой частицы, называется длиной диффузии. Таким образом, длины диффузии электронов и дырок равны:

(9.13)

Учитывая (9.13), придадим уравнениям (9.9)-(9.11) вид:

(9.9.1)

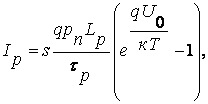(9.10.1)

(9.11.1)

График зависимости (9.11.1), т.е. вольт-амперной характеристики идеализированного диода приведен на рис. 8.1. В области значений можно ограничиться первыми членами разложения в ряд величины 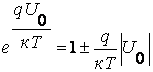и представить (9.11.1) в виде:

Иначе говоря, начальный участок характеристики диода линеен, как при прямом, так и при обратном включении. Поскольку величина линейно связана с концентрацией неосновных носителей в контактирующих полупроводниках, а последняя при прочих равных условиях в кремнии примерно на два порядка ниже, чем в германии, то начальные участки характеристик кремниевого диода идут соответственно более полого, чем начальные участки характеристик германиевых диодов.

В области значений U₀>> кТ/q единицей в (9.11.1) можно пренебречь и считать ток экспоненциально зависящим от приложенного прямого напряжения. При обратном включении диода и /U₀/ >> кТ/q, напротив, можно пренебречь величиной по сравнению с единицей. Следовательно, обратный ток диода в области напряжений, превышающих примерно 0, 1 В не зависит от напряжения и равен I₀. По этой причине величину I₀ называют током насыщения обратно включенного диода.

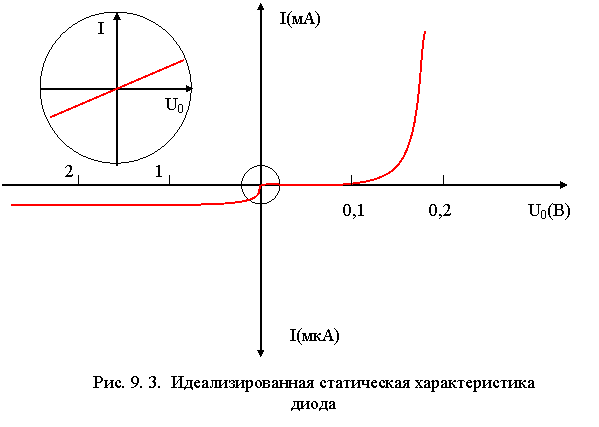Опираясь на выражения (9.9.1) - (9.11.1), величине I₀ можно дать следующую трактовку. Величина есть вероятность рекомбинации электрона за единицу времени в единице объема. Следовательно, - есть число рекомбинаций электронов за единицу времени в единице объема в р-полупроводнике. В равновесных условиях число рекомбинаций равно числу генераций. Отсюда, величина - есть число электронов, генерируемых за единицу времени в слое р-полупроводника толщиной L_n, прилегающем к p-n переходу. Соответственно, величина - есть число дырок, генерируемых за единицу времени в слое n-полупроводника толщиной L_p. Ток насыщения J₀ равен суммарному заряду неосновных носителей, генерируемых за единицу времени в прилегающих к переходу слоях, толщина которых равна длине диффузии соответствующих носителей. Так как границы перехода может достичь, в среднем, только тот носитель, который выходит из плоскости, удаленной от границы не более чем на длину диффузии, то при обратном включении перехода неосновные носители будут экстрагироваться только из слоев толщиной L_n и L_p , соответственно. Понятно, что тот экстракции не может превышать значение J₀ равное заряду, генерируемому в указанных слоях за единицу времени.

9.5. Дифференциальное сопротивление

идеализированного р-n-перехода

Дифференциальное сопротивление идеализированного р-n-перехода определяется:

(9.14)

При прямом смещении r_диф уменьшается с ростом тока. Для Т = 300 К и I = 1мА получаем r_диф= 26 Ом, а для I = 10 мА – r_диф= 2,6 Ом. При обратном напряжении дифференциальное сопротивление резко увеличивается, при . При прямом токе I >> I₀ дифференциальное сопротивление линейно возрастает с повышением температуры.

Дифференциальное сопротивление используется для описания работы р-n-перехода на малом переменном сигнале. Пусть к р-n-переходу приложено напряжение где постоянное напряжение, определяющее положение рабочей точки на ВАХ, а напряжение малого переменного сигнала, например причем f – низкая частота, а U_m удовлетворяет условию малого сигнала U_m<<φ_T. Тогда полный ток через р-n-переход .

Таким образом, для малого низкочастотного сигнала р-n-переход представляется линейным резистором, сопротивление которого зависит от режима, т.е. от положения рабочей точки на ВАХ.

Контрольные вопросы:

1. Что такое полупроводниковый диод? По каким признакам классифицируются диоды?

2. Как влияет на ВАХ ток рекомбинации?

3. Влияние сопротивления базы.

4. Обратная ветвь ВАХ. Ток генерации.

5. Объясните понятие «ток насыщения».

6. Как определяется дифференциальное сопротивление идеализированного p-n-перехода?

Лекция 10. Пробой p-n-перехода. Стабилитрон.

10.1. Концептуальная диаграмма.

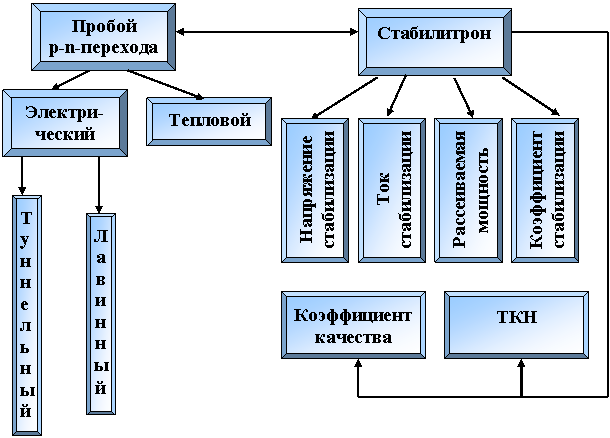10.2. Электрический пробой p-n перехода

При больших значениях приложенного к p-n переходу обратного напряжения напряженность поля в переходе достигает величины, при которой в переходе возникают процессы дополнительной генерации СНЗ, вызванные самим электрическим полем. Обратный ток перехода резко возрастает при сравнительно небольшом возрастании обратного напряжения сверх некоторого порогового значения (рис. 10.1, кривые 1, 2). Такое состояние перехода названо электрическим пробоем.

Механизм электрического пробоя может иметь двоякую природу. В первом случае, стимулированная полем генерация СНЗ, происходит в результате ударной ионизации атомов основного вещества электронами и дырками, движущимися через переход и ускоренными полем перехода до энергий, превышающих ширину запрещенной зоны. Так как, при достаточной ширине p-n перехода, в процессе ударной ионизации могут принять участие и те электроны и дырки, которые сами образовались в процессе ударной ионизации, то процесс размножения носителей в переходе носит лавинный характер. По этой причине данный вид пробоя получил название лавинного пробоя.

Во втором случае генерация СНЗ происходит в результате туннельного перехода электронов из валентной зоны полупроводника в зону проводимости. Соответственно, этот вид пробоя получил название туннельного пробоя.

Остановимся детальнее на каждом из упомянутых видов пробоя.

Лавинный пробой. Для того, чтобы электрон или дырка при столкновении с атомом основного вещества могли ионизировать этот атом, т.е. перевести валентный электрон из состояния, соответствующего валентной зоне, в состояние, соответствующее зоне проводимости, необходимо, чтобы они перед столкновением обладали энергией, не меньшей ширины запрещенной зоны (W_c-W_v).

Энергию, избыточную над средней энергией теплового движения, СНЗ может набрать за счет работы электрического поля на участке пути, равном длине свободного пробега. Если среднее значение напряженности поля в переходе равно Е и длина свободного пробега соответствующего носителя равна l, то указанная работа приближенно равна

(10.1)

Так как среднее значение напряженности поля в переходе равно Е=U_обр/∆, то

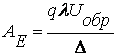(10.2)

Ударная ионизация станет возможной, если

(10.3)

В рассматриваемой области значений обратного напряжения U_обр>>U_к, поэтому ширина резкого p-n перехода ∆, будет равна:

(10.4)

На основании (10.3) и (10.4) приходим к следующему приближенно- ориентировочному значению напряжения пробоя:

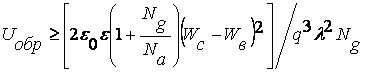(10.5)

Напряжение лавинного пробоя возрастает с ростом ширины запрещенной зоны и с уменьшением концентрации примесей в полупроводнике.

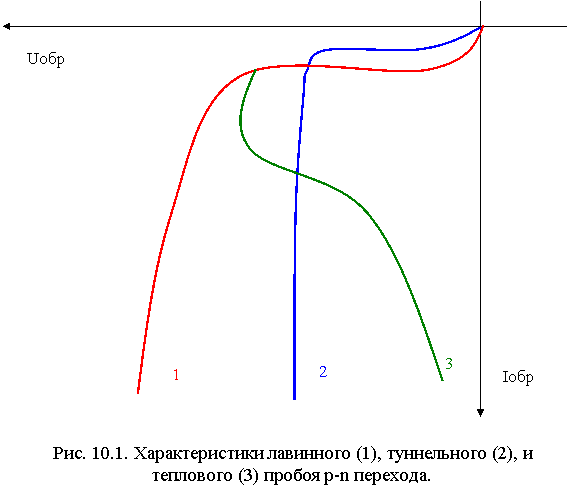Зависимость тока лавинного пробоя от приложенного обратного напряжения может быть получена на основании следующих соображений. Введем понятие коэффициента ударной ионизации a(Е), определив его как величину, равную среднему числу электронно-дырочных пар, образуемых электроном или дыркой на единице пути при заданной напряженности поля Е. Будем считать a(Е) одинаковым для электронов и дырок. Рассмотрим случай несимметричного перехода, в котором n_n>>p_p. Это предположение не ограничивает общности метода и лишь упрощает математические выкладки. Поскольку n_n>>p_p, то ток экстракции будет, практически, представляться только током электронов образующихся при ударной ионизации в бесконечно тонком слое dx, с координатой х. Допустим, что число экстрагируемых из р-области электронов равно N₀, а число электронов, образовавшихся на участке х_р…х в результате ударной ионизации, равно N_x. Тогда плоскость х пересечет N₀+N_x электронов и они в слое dx образуют (N₀+N_x)a(E)dx электронно-дырочных пар. Кроме того, в слой dx через его правую границу x+dx входят дырки, образованные в процессе ударной ионизации в промежутке от плоскости x+dx до правой границы p-n перехода x_n. Пусть количество этих дырок равно N_x^'. Тогда в слое dx дырки произведут N_x^'a(E)dx электронно-дырочных пар. Таким образом, всего в слое dx в результате ударной ионизации образуется dN электронов, причем

(10.6)

Полное количество электронов, образующихся в объеме p-n перехода в результате ударной ионизации, определится выражением:

(10.7)

Так как при ударной ионизации электроны и дырки возникают одновременно и в равных количествах, то число дырок, образовавшихся в промежутке x…x_n, будет равно числу электронов, образовавшихся в том же промежутке. Следовательно, величина N_x+N_x^'=N есть искомое количество электронов, образующихся в системе p-n перехода в результате ударной ионизации. Так как эта величина от координаты x не зависит, то ее можно вынести за знак интеграла и тогда получим:

(10.8)

Или

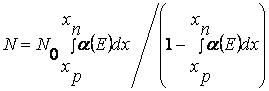(10.9)

Правую границу перехода x_n пересечет N+N₀ электронов, в то время как левую границу x_p, по предположению, пересекло только N₀ электронов. Коэффициент умножения электронов в переходе M_n будет равен:

(10.10)

А ток перехода:

(10.11)

Где I₀ - ток экстракции при заданном значении приложенного к переходу напряжения.

Значение интеграла определяется свойствами полупроводника, шириной перехода и величиной приложенного обратного напряжения U_обр. Определим напряжение пробоя, как такое значение обратного напряжения, при котором коэффициент умножения электронов , т.е. при котором интеграл равен единице. Тогда выражение (10.11) можно переписать в виде:

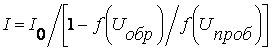(10.11*)

В виду сложности аналитического представления функции ƒ(U_обр), на практике вместо (10.11*) используют следующую эмпирическую зависимость обратного тока диода от обратного напряжения в режиме пробоя:

(10.12)

Показатель степени b может иметь значения от 2 до 6 для различных полупроводниковых материалов.

Туннельный пробой. Если приложенное к переходу обратное напряжение удовлетворяет неравенству U_обр>(W_c-W_b)/q, то на потенциальной диаграмме перехода дно зоны проводимости n-полупроводника окажется ниже потолка валентной зоны p-полупроводника (рис. 10.3)

При этом становится возможным туннельный переход валентных электронов р-полупроводника в зону проводимости n-полупроводника. Рассмотрим особенности этого процесса.

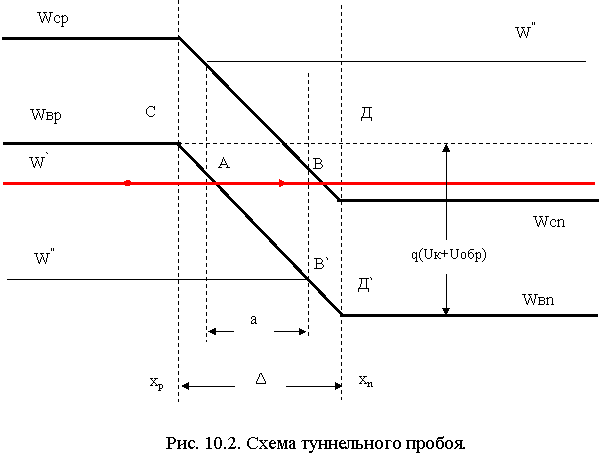Эффективная масса электрона верхней половины валентной зоны отрицательна. Следовательно, если такой электрон окажется в пределах p-n перехода, то на него будет действовать сила, выталкивающая его обратно в область р, а не в область n, как это имеет место по отношению к электронам проводимости р-области. Высоту потенциального барьера, который требуется преодолеть валентному электрону, чтобы перейти в n-область, нетрудно определить.

Рассмотрим произвольный электрон валентной зоны р-полупроводника с энергией W^' большей, чем энергия дна зоны проводимости n-полупроводника (рис. 10.3). Пройдя границу перехода x_p, этот электрон будет затормаживаться и в плоскости А, значение его кинетической энергии станет равным нулю (потенциальная энергия равна полной энергии W^`). С другой стороны, электрон зоны проводимости, обладающий такой же энергией W^', проникнет в область p-n перехода только до плоскости В. Слой, заключенный между плоскостями А и В, с точки зрения законов классической физики, недоступен для электронов с энергией W^'. До плоскости В, однако, дойдут электроны валентной зоны, обладающие энергией W^", равно как до плоскости А дойдут электроны проводимости, энергия которых равна W^{" '}. Следовательно, электронам с энергией W^' для преодоления промежутка АВ требуется дополнительная энергия в количестве (W^'-W^")=(W^'
"-W^')=(W_c-W_в). Это количество и есть искомая высота потенциального барьера, отделяющего состояние электрона валентной зоны с энергией W_вр≥W^'≥W_cn от состояния электрона в зоне проводимости с такой же энергией. Высота барьера равна, таким образом, ширине запрещенной зоны.

Ширина потенциального барьера, т.е. ширина промежутка АВ, определяется из подобия треугольников АВВ^' и СДД^'. Учитывая, что U_обр>>U_к, получим:

(10.13)

Число туннельных переходов за единицу времени определяется формой потенциального барьера, его высотой и шириной. Для прямоугольного барьера это число, с учетом сделанных выводов, пропорционально величине:

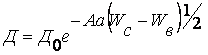(10.14)

Где Д₀ и А некоторые константы.

Ширина перехода Δ при U_обр>>U_к, согласно (10.4), равна В(U_обр)^1/2. Следовательно

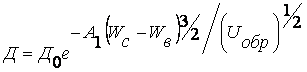(10.15)

Заметим, что электрон валентной зоны р-полупроводника не проявляет себя как свободный носитель заряда. Когда же он туннельно переходит в зону проводимости n-полупроводника, то уже проявляет себя как электрон проводимости. Одновременно в валентной зоне р-полупроводника возникает вакантное состояние, т.е. число дырок в р-полупроводнике увеличивается на единицу. Таким образом, туннельный переход валентных электронов из р в n-полупроводник внешне проявляется как своеобразный, квантомеханический, процесс генерации электронно-дырочных пар с одновременным их разделением электрическим полем перехода.

Естественно, существует и обратный процесс туннельного перехода электронов проводимости n-полупроводника на вакантные уровни валентной зоны р-полупроводника, что эквивалентно рекомбинации электронно-дырочных пар. Однако, поскольку концентрация незанятых состояний в валентной зоне р-полупроводника несравнимо меньше концентрации занятых состояний, то скорость туннельной генерации будет существенно выше скорости рекомбинации. Формула (10.15) дает приближенное представление о зависимости тока туннельного пробоя (который пропорционален Д) от величины обратного напряжения U_обр. Эта формула показывает, что туннельный пробой играет особо существенную роль в переходах малой ширины Δ, т.е. в переходах, образованных сильно легированным полупроводником. Вид характеристики туннельного пробоя схематически представлен кривой 2 на рис. 10.2. Напряжение пробоя определяется эмпирическими зависимостями:

U_проб=99r_n+48r_p для германия, и

(10.16)

U_проб=39r_n+8r_p для кремния.

Здесь r_n_,_p- удельные сопротивления соответствующих областей полупроводника, выраженные в Ом^.см.

То обстоятельство, что в режиме лавинного или туннельного пробоя напряжение на переходе мало изменяется при значительном изменении тока через переход, позволяет применять соответствующие диоды для стабилизации напряжения.

10.3. Тепловой пробой р-n перехода

Сопротивление обратно включенного p-n перехода значительно и, поэтому, даже при малых значениях обратного тока в переходе выделяется заметное количество тепла. Если скорость отвода тепла будет недостаточной, то температура в переходе будет возрастать. Возрастание температуры приведет к возрастанию концентрации неосновных носителей, а значит и величины обратного тока. Но это вызовет еще большее возрастание температуры, приводящее к еще большему увеличению концентрации неосновных носителей. Так развивается тепловой пробой. Поскольку между изменением температуры и изменением обратного тока перехода имеет место, как видно, положительная обратная связь, то вольтамперная характеристика теплового пробоя (рис.10.2) имеет участок отрицательного дифференциального сопротивления, т.е. участок, на котором увеличение тока диода сопровождается уменьшением падения напряжения на переходе.

Условие развития теплового пробоя можно получить следующим образом. Температурная зависимость обратного тока I_обр может быть представлена выражением:

(10.17)

Следовательно, температурная зависимость превращающейся в тепло электрической мощности в p-n переходе представится как:

(10.18)

Отводимая от p-n перехода тепловая мощность, согласно формуле Ньютона, равна:

(10.19)

Где Т_кор - температура корпуса, R_{пер-кор} - так называемое внутренне тепловое сопротивление диода (1/R_{пер-кор} - внутренняя тепловая проводимость, равная количеству тепла, отводимого от перехода за единицу времени при перепаде температур между переходом и корпусом равном 1К). Величина R_{пер-кор} определяется конструкцией диода.

Описанный выше процесс будет развиваться, если скорость нарастания с температурой электрической мощности, т.е. , будет превышать скорость нарастания с температурой отводимой мощности, т.е. . На основании (10.18) и (10.19) получим математическое выражение условия развития теплового пробоя:

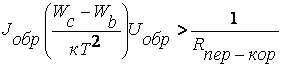(10.20)

Формула (10.20) показывает, что при равных значениях тепловых сопротивлений R_{пер-кор} кремниевого и германиевого диодов, тепловой пробой кремниевого диода наступит при заметно большем значении обратного напряжения, поскольку ток насыщения этого диода во много раз меньше тока насыщения германиевого диода. Если цепь диода не содержит ограничивающего величину тока сопротивления, или оно недостаточно велико, то тепловой пробой может привести к разрушению p-n перехода.

Согласно (10.19), для снижения рабочей температуры перехода Т при заданном значении рассеиваемой диодом мощности Р_э=Р_т, или для увеличения максимально допустимой рассеиваемой мощности при заданном значении рабочей температуры, требуется обеспечить достаточно высокую тепловую проводимость, и возможно более низкую температуру корпуса. Первое достигается специальной конструкцией кристаллодержателя, второе - путем использования, при необходимости, радиаторов, механически скрепляемых с корпусом.

10.4. Стабилитроны

Напряжение на диоде в области электрического пробоя слабо зависит от протекающего через диод обратного тока. Эта особенность может быть использована для стабилизации напряжения. Полупроводниковые диоды, предназначенные для стабилизации напряжения на основе эффекта слабой зависимости напряжения от тока в области электрического пробоя, называют стабилитронами.

Одним из параметров стабилитрона является напряжение стабилизации U_ст, т.е. напряжение на стабилитроне при протекании заданного тока стабилизации. Током стабилизации называется значение обратного тока диода в режиме электрического пробоя, ограниченное значениями I_ст.мин. и I_{ст.макс.} (рис.10.4). Первое из этих предельных значений, I_ст.мин, т.е. минимальное значение тока стабилизации, при котором обеспечивается заданная надежность, определяется условиями наступления и развития электрического пробоя. Второе значение - I_{ст.макс}, определяется значением максимально допустимой рассеиваемой мощности стабилитрона Р_макс.

Промышленность выпускает стабилитроны с напряжением стабилизации от 3 до 200 В. Поскольку напряжение пробоя определяется шириной p-n перехода, а последняя связана с концентрацией примесей в базе диода, низкие значения U_ст (»7В) характерны для узких p-n переходов, в которых определяющую роль играет туннельный пробой. Более высокие значения U_ст характерны для широких p-n переходов, в которых определяющую роль играет лавинный пробой.

При необходимости стабилизировать высокие напряжения применяется последовательное соединение стабилитронов.

Напряжение стабилизации зависит от температуры (рис.10.4), причем по-разному для стабилитронов с туннельным и лавинным пробоями.

Напряжение лавинного пробоя обратно пропорционально квадрату длины свободного пробега СНЗ. Так как при сравнительно малой концентрации примесей в базе диода (что характерно для лавинных стабилитронов) рассеяние СНЗ происходит главным образом на тепловых флуктуациях плотности атомов основного вещества, то с ростом температуры длина свободного пробега будет уменьшаться. Соответственно, напряжение стабилизации с ростом температуры возрастает.

В стабилитронах с туннельным пробоем одним из определяющих факторов развития пробоя является, согласно (10.15), высота потенциального барьера, т.е. ширина запрещенной зоны. Поскольку ширина запрещенной зоны германия и кремния уменьшается с ростом температуры, то соответственно уменьшается напряжение стабилизации.

Температурная зависимость напряжения стабилизации характеризуется температурным коэффициентом напряжения стабилизации (ТКН) a_ст. ТКН определяется как частное от деления относительного изменения напряжения стабилизации к вызвавшему его изменению температуры

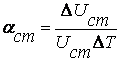(10.21)

и выражается, чаще всего, в %/⁰С. Использование в качестве стабилитронов систем из встречновключенных p-n переходов с ТКН противоположных знаков, позволяет снизить результирующий ТКН до очень малых значений (тысячные доли процента на ⁰С).

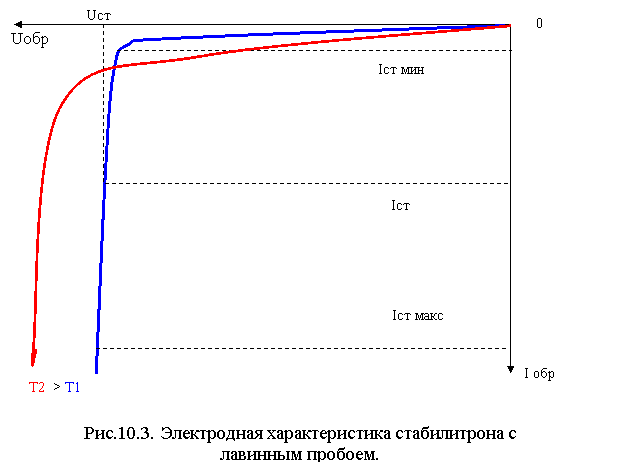Стабилизирующие свойства стабилитронов характеризуются так называемым коэффициентом качества Q_ст, который определяется как отношение дифференциального сопротивления стабилитрона r_ст к его статическому сопротивлению R_стат.

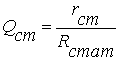
Коэффициент качества можно рассматривать как отношение относительного изменения напряжения стабилизации к относительному изменению тока стабилизации. Действительно,

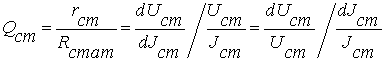
Стабилизирующие свойства тем лучше, чем меньше значение Q_ст. Численное значение дифференциального сопротивления стабилитронов различных типов лежит в пределах от нескольких Ом, до нескольких десятков Ом. Значения статического сопротивления заключены, соответственно, в пределах от одного, до нескольких десятков кОм. Таким образом, коэффициент качества имеет величину порядка 10^-3…10^-2.

Кроме параметров, отмеченных выше, для стабилитронов существенны еще следующие параметры:

ü Максимально допустимое постоянное обратное напряжение U_{обр.макс};

ü Максимально допустимое импульсное обратное напряжение U_{обр(и)макс};

ü Максимально допустимый импульсный ток стабилизации I_{ст(и)макс};

ü Полная емкость стабилитрона С и эквивалентная индуктивность L;

ü Временная нестабильность напряжения стабилизации dU_ст за заданный промежуток времени;

ü Максимально допустимая импульсная мощность стабилитрона Р_и.макс, которая определяется при заданных скважности и длительности импульса;

ü Спектральная плотность шума стабилитрона s_ш.ст, определяемая как эффективное значение напряжения шума, отнесенное к полосе 1 Гц в оговоренном диапазоне частот при заданном токе стабилизации.

По конструкции и технологии изготовления стабилитроны подобны выпрямительным диодам и могут использоваться вместо последних.

На рис. 10.5 приведена схема простейшего стабилизатора напряжения.

Сопротивление балластного резистора R_бал подбирается таким образом, чтобы при заданном номинальном значении входного напряжения U_вх, ток стабилизации диода примерно равнялся среднему значению между I_ст.мин и I_{ст.макс}. Обозначив это значение тока стабилизации как I_ст.0, на основании правил Кирхгофа, получим:

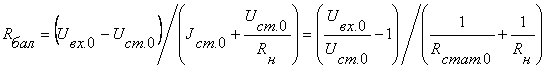(10.22)

Где U_вх.0 - номинальное напряжение входного напряжения, U_ст.0 - напряжение стабилизации при токе стабилизации I_ст.0, R_стат.0 - статическое сопротивление стабилитрона при том же токе.

Отклонение входного напряжения от номинального напряжения на величину ΔU_вх, вызовет изменение тока стабилизации на величину ΔI_ст и напряжения стабилизации на величину ΔU_ст. В режиме медленно изменяющегося напряжения, стабилитрон может быть представлен резистором с сопротивлением равным дифференциальному сопротивлению стабилитрона r_ст, так как влиянием емкости в этом случае можно пренебречь. Тогда, на основании тех же правил Кирхгофа, получим:

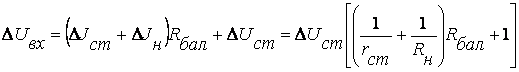(10.23)

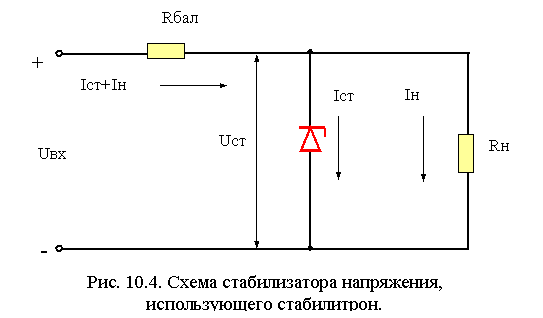Учитывая, что обычно R_н>> r_ст и R_н >> r, получим приближенное равенство:

(10.24)

Коэффициентом стабилизации К_ст называют величину, равную частному от деления относительного изменения входного напряжения на относительное изменение выходного напряжения, т.е. напряжения стабилизации. Учитывая (10.22) и (10.24), найдем

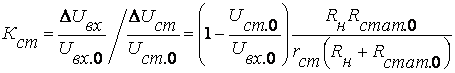(10.25)

Коэффициент стабилизации возрастает с ростом сопротивления нагрузки, ростом входного напряжения и в предельном случае равен обратному значению коэффициента качества стабилитрона. Увеличение входного напряжения приводит к увеличению потерь мощности источника питания на балластном сопротивлении, поэтому входное напряжение выбирают так, чтобы оно превышало U_ст не более чем в два, три раза.

Малая величина коэффициента стабилизации при малом значении сопротивления нагрузки и сильная его зависимость от сопротивления нагрузки являются причиной того, что описанные стабилизаторы используются преимущественно как датчики высокостабильного опорного напряжения, работающие на высокоомную нагрузку в более сложных транзисторных стабилизаторах напряжения.

Контрольные вопросы:

1. Какое состояние перехода называется пробоем?

2. Нарисуйте и объясните характеристики лавинного, туннельного и теплового пробоя.

3. Что такое стабилитрон? Нарисуйте ВАХ стабилитрона и объясните ее.

4. Назовите основные параметры стабилитрона.

5. Изобразите простейшую схему стабилизатора напряжения и поясните принцип ее работы.

Лекция 11. Типы диодов.

11.1. Концептуальная диаграмма.

11.2. Инжекционные высокочастотные и импульсные диоды.

Инерционность диодов обусловлена барьерной емкостью С_б и накоплением в базе инжектированных неосновных носителей заряда, что формально выражается как наличие у диода диффузионной емкости С_диф. Поскольку каждая из этих величин пропорциональна площади p-n перехода, то одним из обязательных методов повышения быстродействия диодов является уменьшение площади перехода, хотя это и сопряжено со снижением преобразуемой мощности.

Однако уменьшение площади перехода не может изменить соотношения между активной и реактивной составляющими тока диода и, поэтому, улучшение, например, выпрямительных свойств диода на высоких частотах можно получить только системой мер, приводящих либо к сокращению времени рассасывания инжектированных в базу носителей, либо исключающих сам процесс инжекции таких носителей.

Начнем с совокупности мер, обеспечивающих высокую скорость рассасывания неосновных носителей. Прежде всего, эта скорость определяется временем жизни неосновных носителей. Время жизни неравновесных носителей уменьшается при введении в базу примеси, образующей рекомбинационные ловушки для СНЗ. Такой примесью является, например, золото. Далее, если ширину базы сделать меньше длины диффузии и одновременно обеспечить высокую скорость рекомбинации неосновных носителей на электроде базы, то количество накапливающихся в базе за полупериод или импульс прямого напряжения неравновесных носителей уменьшится, и, соответственно, уменьшится диффузионная емкость.

Наконец, время рассасывания неосновных носителей можно уменьшить, создав в базе внутреннее электрическое поле, способствующее их экстракции. Такое поле можно создать путем неравномерного распределения донорной (или акцепторной) примеси в базе.

Перечисленные пути уменьшения инерционности, в той или иной степени, реализуются в разработанных ныне технологических методах изготовления высокочастотных и импульсных диодов. Таких методов четыре.

Исторически первым был разработан метод изготовления точечных диодов с прижимным контактом (рис.11.1.а). Пружинящая игла из сплава вольфрама с молибденом, покрытая тонким слоем индия (германиевые диоды) или алюминия (кремниевые диоды), прижимается к поверхности кристалла полупроводника n-типа, напаянного на кристаллодержатель. В результате электроформовки, заключающейся в пропускании через контакт серии мощных импульсов тока, вызывающих локальный разогрев области полупроводника под контактом, происходит диффузия акцепторной примеси (индия, алюминия) в кристалл. Образуется p-n переход, граничная поверхность которого имеет вид полусферы, с радиусом 5…40 мкм.

Второй метод (рис.11.1.б) использует микросплавную технологию. Игла из золота, покрытого тонким слоем индия или алюминия, при пропускании импульсов тока, вплавляется в кристалл n-типа. Происходящая при этом диффузия акцепторной примеси и золота формирует p-n переход и обогащает базу дефектами, способствующими уменьшению времени жизни неравновесных носителей заряда.

Третий метод основан на создании мезаструктуры (рис.11.1.в). После проведения диффузии акцепторной примеси в поверхностный слой n-полупроводника (или, наоборот, донорной примеси в р-полупроводник) и вплавления электрода производится химическое травление диффузионного слоя по всей поверхности кристалла за исключением малой области, расположенной под вплавленным электродом. В результате образуется столообразное возвышение на поверхности кристалла, содержащее p-n переход, площадь которого может быть меньше площади электрода.

Четвертый метод использует планарную технологию (рис.11.1.г). Диффузия акцепторной примеси и золота производится через окно малой площади в защитном покрытии из двуокиси кремния, являющейся, к тому же, хорошим диэлектриком. Электрод изготавливается методом напыления алюминия, вывод - методом термокомпрессии.

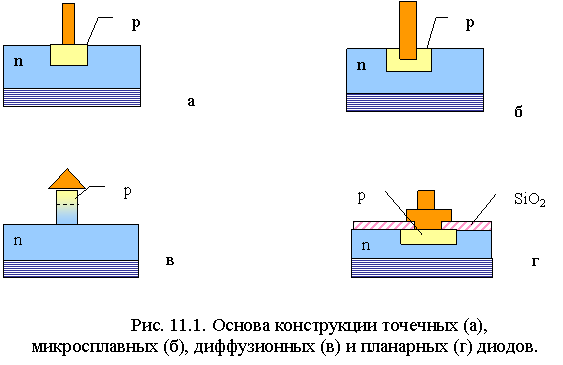Достоинство двух последних технологических методов заключается в высокой степени контролируемости процесса изготовления диодов на всех его стадиях.

Корпус высокочастотных и импульсных диодов изготавливается из стекла или керамики. Форма выводов предусматривает максимальное снижение паразитных емкостей и индуктивностей, а также удобство сочленения с коаксиальными линиями.

По функциональному назначению высокочастотные диоды подразделяются на детекторные, смесительные, умножительные и модуляторные. Каждый из этих видов диодов имеет конструктивно-технологические особенности. Например, для детекторных диодов важна высокая степень реакции на переменное напряжение малой амплитуды, поэтому использование германия здесь более предпочтительно. Сопротивление базы этих диодов должно быть малым, а это значит, что степень ее легирования должна быть довольно высокой. Но последнее обусловливает малую ширину p-n перехода и низкое значение максимально допустимого обратного напряжения. Следовательно, для детектирования сигналов большой амплитуды требуются диоды других типов, например, кремниевые диоды или диоды Шоттки. Обращенный диод хорошо удовлетворяет условиям детектирования сигналов малой амплитуды.

Помимо упоминавшихся ранее параметров, общих для всех типов полупроводниковых диодов, для детекторных диодов важны значания таких параметров как чувствительность по току и чувствительность по напряжению, определяемые, соответственно, как отношения приращения выпрямленного тока или приращения выходного напряжения к мощности высокочастотного сигнала Р_вч.

Для смесительных диодов важно значение параметра, характеризующего эффективность преобразования энергии высокочастотного сигнала в энергию сигнала промежуточной частоты. Этот параметр носит название потерь преобразования и определяется выражением:

(11.1)

Где Р_вч – мощность высокочастотного сигнала; Р_пр – мощность принимаемого сигнала.

Эффективность преобразования зависит от степени нелинейности электродной характеристики диода. Поскольку нелинейность возрастает с ростом тока диода, то потери преобразования уменьшаются с ростом тока, протекающего через диод. Для различных типов диодов значения L_преоб лежат в пределах от 5 до 10 дБ.

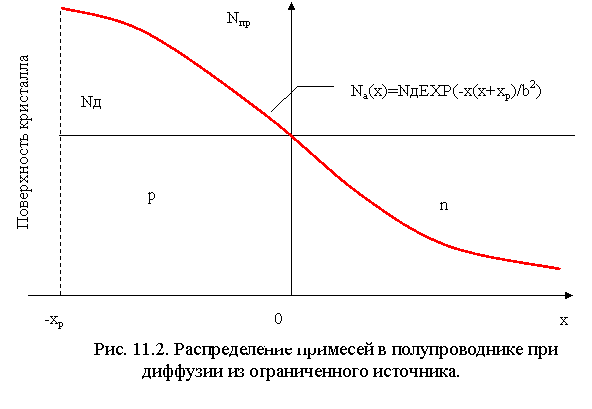Для преобразовательных диодов всех типов имеет важное значение уровень собственных шумов, характеризуемых относительной температурой шума t. Значение этой величины лежит обычно в пределах 2…3.

В классе импульсных диодов можно выделить диоды с накоплением заряда, которые используются для преобразования и формирования импульсных сигналов. В технологии изготовления этих диодов обращается особое внимание на меры, приводящие к уменьшению продолжительности участка t₁- t₂ процесса восстановления обратного сопротивления диода. В результате импульс обратного тока таких диодов имеет очень крутые фронты.

Достигается сказанное тем, что, проводя диффузию акцепторной примеси в n-полупроводник из ограниченного источника, добивается плавного спада ее концентрации в толще n-полупроводника (рис.11.2).

Технологическая граница p-n перехода (х=0) будет соответствовать плоскости, в которой N_a-N_d. В базе, т.е. в области x>0 разность между концентрацией доноров и концентрацией акцепторов N_d-N_a(x) будет нарастать с ростом х. В соответствии с условиями электрического и термодинамического равновесия, в базе возникнет поле, направленное в сторону р-полупроводника. Это поле, "прижимая" инжектируемые дырки к границам p-n перехода, будет способствовать их экстракции при переключении диода с прямого на обратное. Кроме того, уменьшение глубины проникновения неравновесных носителей (дырок) в базу приводит к увеличению их концентрации. Вследствие этого увеличивается скорость рекомбинации.

11.3. Варикапы.

Полупроводниковый диод, в котором используется зависимость емкости от величины обратного напряжения, и, который предназначен для применения в качестве электрически управляемой емкости, называется варикапом. Помимо систем автоматического управления частоты (АРЧ) гетеродинов, варикапы применяются в качестве умножителей частоты (варакторы) и параметрических усилителей в СВЧ диапазоне (параметрические диоды).

В общем случае зависимость емкости варикапа от величины обратного напряжения может быть представлена выражением:

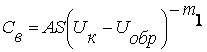(11.2)

в котором А - константа, определяемая значением удельной емкости равновесного p-n перехода и значением контактной разности потенциалов U_к. Значение показателя степени m1 зависит от характера распределения примесей в переходе. Для резкого перехода m1=1/2. Величины А и m1, при необходимости, могут быть определены по значению номинальной емкости (при заданном номинальном значении обратного напряжения) и значению так называемого коэффициента перекрытия по емкости К_с. Коэффициент перекрытия по емкости равен отношению емкостей варикапа при двух заданных значениях обратного напряжения.

Следующим важным параметром варикапа является температурный коэффициент емкости (ТКЕ) a_св, характеризующий зависимость С_В от температуры. Эта зависимость обусловлена температурной зависимостью контактной разности потенциалов U_к. ТКЕ равен отношению относительного изменения емкости варикапа к вызывающему его изменению температуры.

Качество варикапа характеризуется его добротностью Q_В. Добротность варикапа - есть отношение реактивного сопротивления варикапа на заданной частоте переменного напряжения к сопротивлению потерь при заданном значении емкости или постоянного обратного напряжения.

Полное сопротивление варикапа равно:

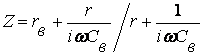
где r - результирующее сопротивление параллельно соединенных сопротивлений утечки r_у и дифференциального сопротивления r_диф. Разделяя активную и реактивную компоненты, получим:

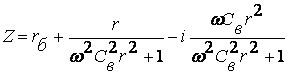(11.3)

Отсюда, учитывая, что , найдем

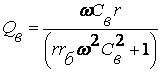(11.4)

Найденная зависимость добротности от частоты приведена на рис. 11.3 (д). В области низких частот wСв<<1/(rr_б)^1/2, и

(11.5)

В области высоких частот, напротив wСв >> 1/(rr_б)^1/2 и

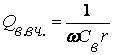(11.6)

Приравнивая нулю производную Q_В (11.4) по частоте, найдем, что на частоте

(11.7)

добротность варикапа максимальна и равна:

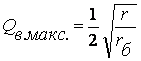(11.8)

Отношение r_диф /r_б порядка 10⁷. Отношение r/r_б, из-за наличия сопротивления утечки r_у, несколько меньше. Однако, несмотря на это, добротность варикапов может достигать нескольких тысяч единиц.

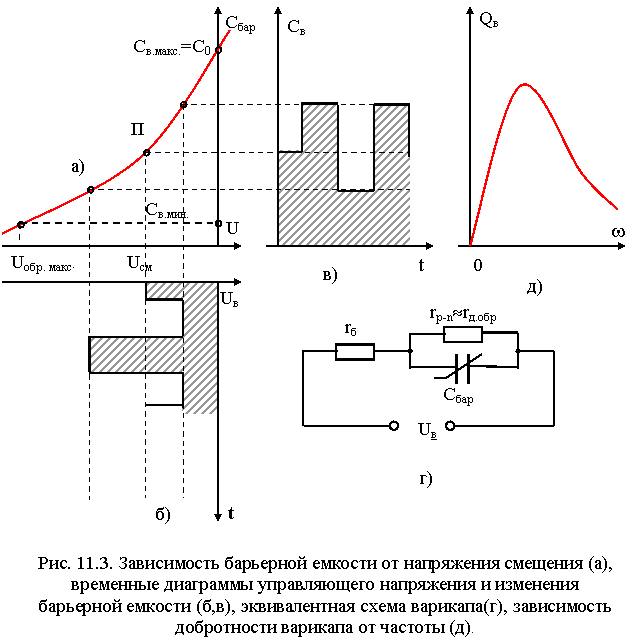
Таким образом, повышение добротности на низких частотах, как и повышение добротности на оптимальной частоте, требует увеличения дифференциального сопротивления обратно смещенного p-n перехода. Рассмотрим как это может быть реализовано.

Дифференциальное сопротивление r_диф определяется по формуле:

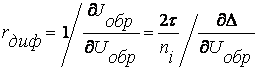(11.9)

Зависимость ширины перехода Δ от величины приложенного обратного напряжения в случае резкого перехода определяется выражением:

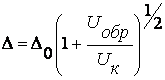(11.10)

Где Δ₀ - ширина невозмущенного (равновесного) перехода. В общем случае, охватывающем плавные переходы, указанную зависимость можно представить в виде:

(11.11)

Где m2 ≥ 2. Отсюда

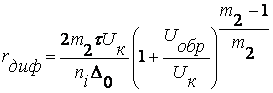(11.12)

Если U_{обр.мин.}>>U_к, то

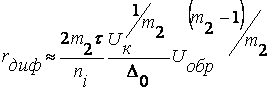(11.13)

Таким образом, требуемое увеличение дифференциального сопротивления может быть получено путем использования полупроводника с широкой запрещенной зоной (малое значение n_i) и сравнительно узких p-n переходов.

На высоких частотах требуемое значение добротности может быть получено путем снижения сопротивления базы. Это достигается либо повышением степени легирования базы, либо применением структур типа p⁺-n-n⁺. Слой слабо легированного полупроводника n-типа заключен между сильно легированными слоями p⁺ и n⁺ типов. Слой n-типа берется малой ширины, так что уже при сравнительно небольших обратных напряжениях граница p-n перехода х_n достигает границы n⁺- области. База оказывается расположенной в весьма низкоомной n⁺- области. Достоинством этого метода является то, что наряду с обеспечением малого сопротивления базы, сохраняется большая величина максимально допустимого обратного напряжения. Кроме того, в таких структурах существенно возрастает степень нелинейности зависимости барьерной емкости от обратного напряжения, что очень важно для варакторов, т.е. варикапов, используемых для умножения частоты сигнала.

11.4. Диод Шоттки, туннельный и обращенный диоды, диоды с накоплением заряда (диод Ганна).

Диодами Шоттки называются диоды, выпрямляющие свойства которых обусловлены образованием электрического перехода в n-полупроводнике контактирующем с металлом, работа выхода которого превышает работу выхода полупроводника (рис. 11.4а). Поскольку А_m>А_n, то при образовании контакта в металл будет переходить вначале больше электронов, чем их переходит из металла в полупроводник. Приконтактный слой полупроводника обедняется электронами, в нем образуется положительный пространственный заряд и края зон смещаются, как в любом другом электрическом переходе.

Так как концентрация электронов в металле на несколько порядков выше концентрации электронов в полупроводнике, то переход будет лежать целиком в n-полупроводнике. Проникновение поля в металл будет ничтожно малым.

Контактная разность потенциалов, определяющая высоту потенциального барьера для электронов n-полупроводника в равновесном состоянии, будет, очевидно, равна разности работ выхода, выраженных в электроновольтах

(11.14)

Работа перехода электронов из металла в полупроводник равна разности работы выхода металла А_m и электронного сродства c_n электронов полупроводника (рис. 11.3.б)

(11.15)

Поскольку поле в металл не проникает, то эта работа от величины приложенного к диоду внешнего напряжения не зависит, в то время как высота потенциального барьера для электронов полупроводника, при их переходе в металл, будет изменяться с изменением приложенного напряжения как и во всяком электрическом переходе. На этом основано выпрямляющее действие диода Шоттки.

Переход электронов из металла в полупроводник можно рассматривать как своеобразную термоэлектронную эмиссию через барьер, высота которого определяется (11.15). Следовательно, число электронов переходящих из металла в полупроводник за единицу времени, будет равно

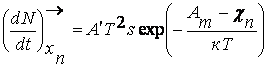(11.16)

Результирующий поток электронов будет равен:

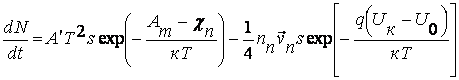(11.17)

Учитывая, что при равновесии (U₀=0) имеет место равенство

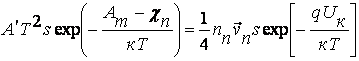
и умножая (11.17) на заряд электрона q, получим уравнение идеализированной электродной характеристики диода Шоттки

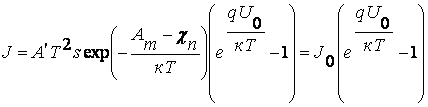(11.18)

В котором А = А^`q - константа Зоммерфельда. Как видим, формально статическая характеристика диода Шоттки имеет такой же вид, как и у диодов на p-n переходе, хотя значение тока насыщения J₀ иное.

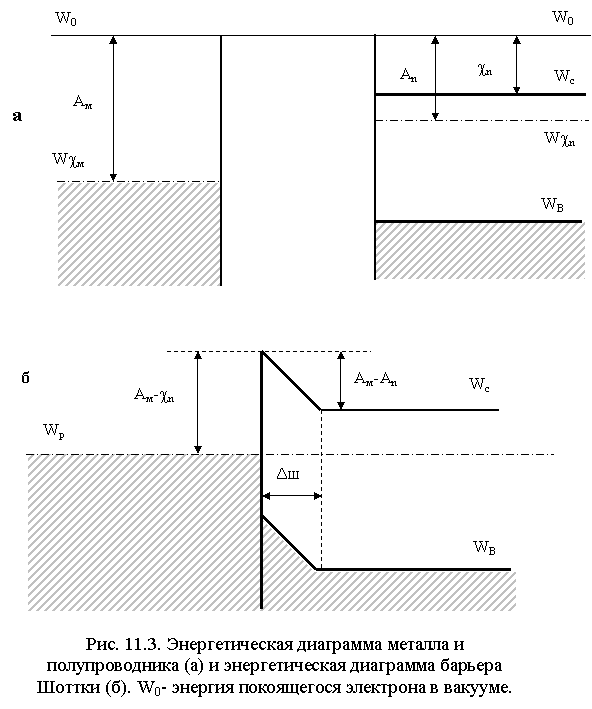По существу же, диод Шоттки обладает целым рядом достоинств, по сравнению с обычными диодами. Важнейшим из этих достоинств является исключительно малая инерционность. Диоды Шоттки могут работать на частотах в несколько десятков гигагерц. Связано это с тем, что в диодах Шоттки, как видно из приведенных энергетических диаграмм, роль "базы", в которую происходит инжекция электронов при прямом включении, выполняет металл, где эти "горячие" электроны практически мгновенно (за 10^-13…10^-12 сек) рассеивают избыточную энергию и становятся термодинамически равновесными электронами. Никакого накопления заряда в "базе" не происходит. Диффузионная емкость равна нулю. Таким же естественным образом решается проблема сопротивления базы, так как оно определяется сопротивлением металла. Что касается барьерной емкости, то она также может быть сделана достаточно малой, как путем уменьшения площади перехода, так и путем увеличения его ширины при использовании структуры металл-n-n⁺полупроводник.

Технология изготовления диодов Шоттки довольно сложна из-за трудностей устранения различного рода поверхностных дефектов полупроводника.

Туннельным диодом называется диод на основе вырожденных полупроводников, в котором из-за перекрытия зон туннельный эффект приводит к появлению на электродной характеристике при прямом включении участка с отрицательным дифференциальным сопротивлением.

Энергетическая диаграмма p-n перехода в вырожденных полупроводниках и электродная характеристика приведены на рис. 11.4. Степень вырождения полупроводников такова, что уровни Ферми лежат в разрешенных зонах и в состоянии термодинамического равновесия дно зоны проводимости n-полупроводника лежит ниже потолка валентной зоны р-полупроводника. Так как ширина перехода очень мала, то обмен электронами в состоянии равновесия происходит главным образом за счет их туннелирования сквозь потенциальный барьер. При малых значениях прямого напряжения, когда дно зоны проводимости n-полупроводника смещается вверх, число туннельных переходов электронов из n-полупроводника в р-полупроводник возрастает и становится больше числа таких же переходов в состоянии равновесия. Число обратных туннельных переходов при этом, напротив, уменьшается. В результате возникает прямой туннельный ток диода, возрастающий с ростом приложенного напряжения. Это возрастание, однако, имеет место лишь до тех пор, пока квазиуровень Ферми n-полупроводника не поднимется до уровня потолка валентной зоны р-полупроводника. Дальнейшее увеличение прямого напряжения приведет к тому, что все большая часть заполненных уровней зоны проводимости n-полупроводника будет приходиться против запрещенной зоны р-полупроводника, куда туннелирование невозможно. Прямой туннельный ток станет уменьшаться. Так как ток надбарьерной инжекции электронов при этих напряжениях еще мал, то уменьшение туннельного тока буде означать и уменьшение полного тока. Когда прямое напряжение достигает значений, при которых становится существенной надбарьерная инжекция, полный ток вновь начинает возрастать.

При обратном включении диода превалируют туннельные переходы электронов из р-полупроводника в n-полупроводник (образование электронно-дырочных пар). Ток непрерывно нарастает с ростом обратного напряжения.

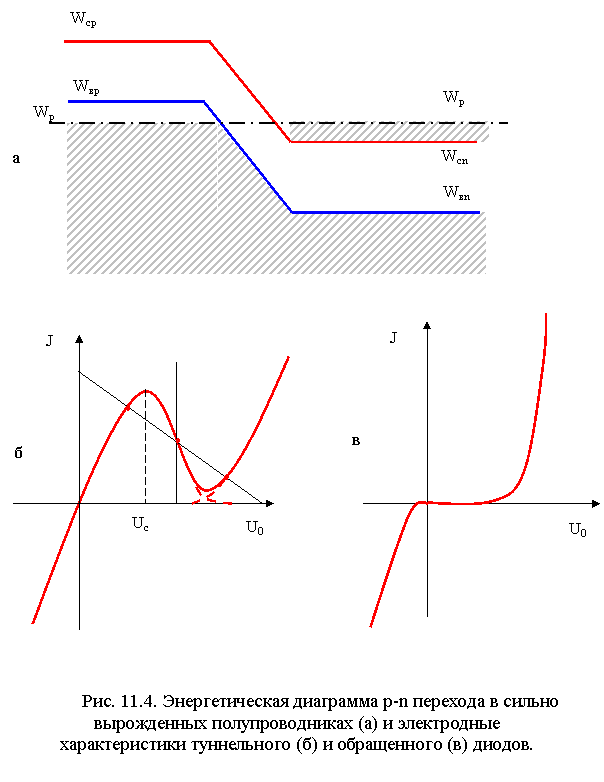Наличие участка характеристики с отрицательным дифференциальным сопротивлением является той особенностью туннельных диодов, которая позволяет использовать их в качестве усилителей и генераторов электрических колебаний высоких и сверхвысоких частот, а также в схемах сверхвысокоскоростного переключения (цифровые или логические схемы). Изготавливаются туннельные диоды из германия или арсенида галлия. Германиевые диоды имеют меньший уровень собственных шумов, что важно при их использовании в качестве усилителей. Диоды из арсенида галлия обладают большим значением напряжения U_с, соответствующего максимуму туннельного тока (~1В, вместо ~0,4В для германия), поэтому им отдается предпочтение при использовании в цифровых схемах и генераторах.

Высокое быстродействие туннельных диодов обусловлено тем, что сам туннельный эффект безинерционен и развитие процесса определяется временем релаксации электрического поля в полупроводнике t=re₀e, которое составляет величину порядка 10^-12…10^-13с. Таким образом, реально, инерционность диода будет обусловливаться только наличием барьерной емкости и индуктивности выводов L, которая становится существенной на сверхвысоких частотах.

Предельную частоту можно определить, опираясь на эквивалентную схему туннельного диода, представленную на рис.11.5.На этой схеме R-сопротивление потерь в полупроводнике.

Полное сопротивление диода в режиме отрицательного дифференциального сопротивления равно

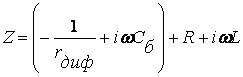(11.19)

Отсюда, активная составляющая полного сопротивления

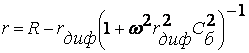(11.20)

Диод представляет активный элемент, пока величина r меньше нуля. Предельной частотой w_п называют частоту, на которой r становится равным нулю. Из (11.20) получаем

(11.21)

Обращенным диодом называется диод на основе вырожденных полупроводников, у которых степень вырождения подобрана так, что уровень Ферми совпадает с краями соответствующих разрешенных зон. В таких диодах проводимость при обратном напряжении значительно больше проводимости при прямом напряжении.

Если обратиться к рис. 11.4 и представить, что уровень Ферми совпадает с потолком валентной зоны р-полупроводника и дном зоны проводимости n-полупроводника, то можно усмотреть, что при прямом смещении туннельные переходы будут невозможны. При обратном же смещении они будут иметь такую же интенсивность как и в туннельных диодах. Следовательно, прямая проводимость будет обусловлена только надбарьерной инжекцией, а обратная проводимость туннельным эффектом. Крутизна нарастания тока инжекции при малых напряжениях очень мала и, во всяком случае, значительно меньше крутизны нарастания обратного туннельного тока. Таким образом, пропускным направлением для такого диода является направление обратного включения, запирающим - прямое включение. Отсюда и название - обращенный диод. Достоинством обращенного диода является исключительно малое падение напряжения в пропускном направлении и сохранение сверхвысокочастотных свойств туннельного диода. Это позволяет использовать его в качестве детектора, смесителя и т. д. на сверхвысоких частотах при условии малой амплитуды сигнала (когда токи прямого включения еще малы).

Диоды Ганна используются в основном для генерирования колебаний ВЧ и СВЧ. В основе принципа действия этих диодов лежит эффект Ганна, проявляющийся наиболее сильно в кристаллах арсенида галлия электронного типа. Этот эффект связан с особой зависимостью подвижности электронов проводимости от напряженности электрического поля. Далее все физические величины, относящиеся к слабому и более сильному полям обозначаются соответственно индексами 1 и 2. В слабых электрических полях подвижность электронов относительно велика и постоянна m_n₁=const. Плотность дрейфового тока прямо пропорциональна Е, т.е. , где n_n – концентрация электронов проводимости в полупроводнике, – проводимость полупроводника, величина, прямо пропорциональная тангенсу угла наклона характеристики на участке ОА (рис. 11.6 (а)).

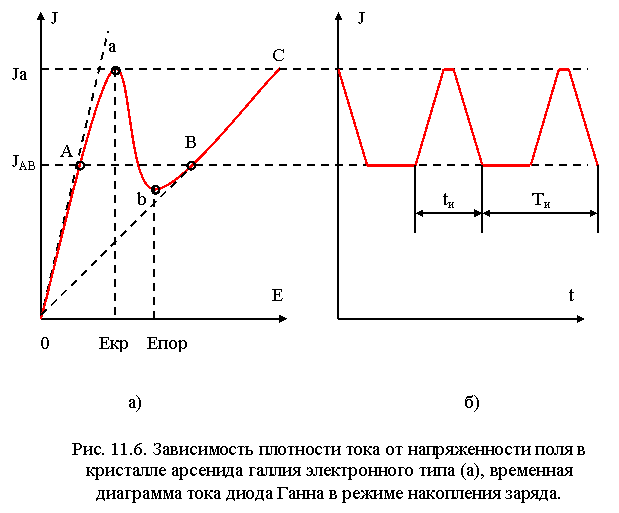При увеличении напряженности электрического поля вследствие увеличения скорости электронов между соударениями и повышения частоты этих соударений происходит уменьшение подвижности электронов, называемых «горячими». При некотором пороговом значении все электроны становятся «горячими», поэтому, где - подвижность «горячих» электронов, - проводимость полупроводника при , величина, прямо пропорциональная тангенсу угла наклона характеристики на участке ВС.

Переход из одного состояния к другому изображается на характеристике (рис. 11.6 (а)), падающим участком ab, в пределах которого диод обладает отрицательным дифференциальным сопротивлением.

В работающем диоде к пластине кристалла с хорошими омическими контактами прикладывается напряжение (плюс к аноду, минус к катоду – рис. 11.7(а)), создающее напряженность электрического поля чуть меньше критической. Поэтому в начальный момент в кристалле возникает ток с плотностью, чуть меньшей j_a (рис.11.6 (а)), определяемый электронами с большой подвижностью m_n1.

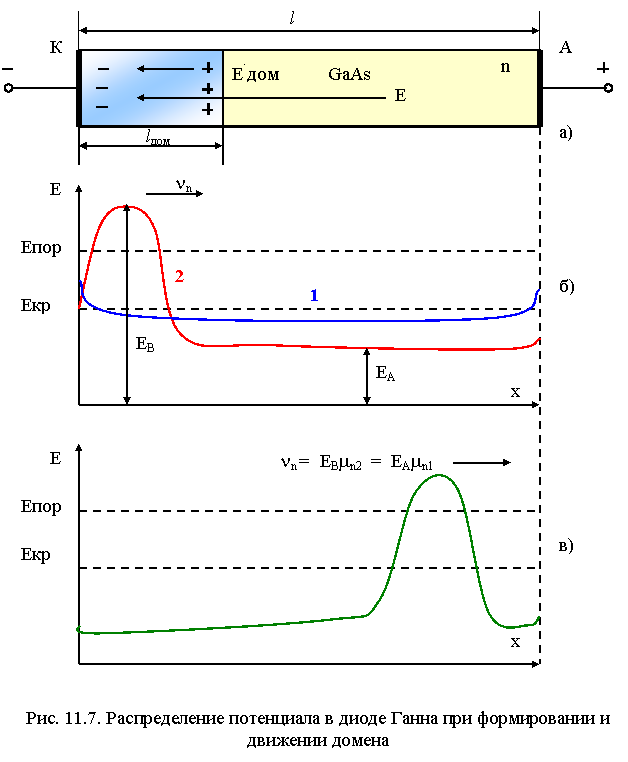Из-за неоднородности структур (контакт-кристалл) напряженность поля в области контактов оказывается больше критической (рис.11.7.(б), кривая 1). Около катода при появляются электроны, обладающие меньшей подвижностью m_n₂. Отставание этих электронов () приводит к образованию возле катода так называемого домена – двойного электрического слоя, в котором слева находится заряд замедленных электронов, а справа – некомпенсированный заряд доноров, проявившийся в связи с отставанием электронов от общего потока. В этом домене возникает дополнительная напряженность поля , усиливающая начавшийся процесс. Кроме того, рост напряженности поля в домене при неизменном внешнем напряжении должен приводить к снижению напряженности поля до за пределами домена (рис.11.7(б), кривая 2). Значения поля в домене Е_В и вне его Е_А можно найти из условия, что все электроны на участке домена и за его пределами должны двигаться к аноду с одинаковыми скоростями , создавая ток с плотностью (рис. 11.6 (б)). С такой же скоростью движется к аноду и сам домен (рис. 11.7 (в)). Достигнув анода, доме исчезает, в результате чего восстанавливается исходное значение напряженности поля и возникают условия для зарождения возле катода нового домена и т.д.

Таким образом, работающий диод Ганна формирует импульсный ток с длительностью импульсов (равной сумме времени зарождения и исчезновения домена) с периодом следования, равным времени прохождения домена через кристалл где длина кристалла; скорость движения домена. Нетрудно заметить, что в этом режиме диод Ганна генерирует колебания с постоянным периодом, определяемым длиной кристалла . В предельном случае, когда домен занимает весь кристалл, колебания приобретают почти гармоническую форму с частотой .

Если к диоду Ганна вместе с постоянным напряжением, создающим напряженность электрического поля в пределах , приложить быстропеременное напряжение с частотой , то домен не будет успевать полностью формироваться. При увеличивающемся внешнем напряжении напряженность поля в кристалле будет увеличиваться, а проводимость и ток – уменьшаться. При уменьшающемся внешнем напряжении напряженность поля уменьшается, а проводимость и ток – увеличиваются. Следовательно, диод Ганна в этом режиме, получившем название режима с ограниченным накоплением объемного заряда, ведет себя как отрицательное динамическое сопротивление и может использоваться как источник СВЧ колебаний, рабочая частота которого (до 300 ГГц) определяется не диодом, а резонансной системой, подключенной к диоду.

Контрольные вопросы:

_1.Расскажите об основных методах изготовления полупроводниковых диодов.

2. Какие полупроводниковые диоды называются варикапами? Назовите основные параметры варикапов.

3. Дайте определение диоду Шоттки. Выведите уравнение идеализированной электродной характеристики диода Шоттки.

4. Что такое туннельный диод? Нарисуйте эквивалентную схему туннельного диода и поясните ее.

5. Расскажите об особенностях работы обращенных и лавинно-пролетных диодов.

Литература:

1. Андреев И.С., Арипов Х.К., Атаметов Р.К., Рахматов Ш.Б. Методическое руководство по экспериментальному определению параметров диодов и расчету устройств на их основе с помощью ПЭВМ. – Т.: ТЭИС, 1991.

2. Бочаров Л.Н. Электронные приборы: Учебник для техникумов. - М.: Энергия, 1979.

3. Викулин И.М., Стафеев В.И. Физика полупроводниковых приборов. – М.: Сов. радио, 1980.

4. Кушманов И.В., Васильев Н.И., Леонтьев А.Г. Электронные приборы. - М.: Связь, 1973.

5. Электронные, квантовые приборы и микроэлектроника: Учебное пособие для ВУЗов / Ю.Л. Бобровский, С.А. Корнилов, И.А. Кратиров и др. Под ред. Проф. Н.Д.Федорова. - М.: Радио и связь, 1998.

6. Электронные приборы: Учебник для ВУЗов / В.Н. Дулин, Н.А. Аваев, В.П. Демин и др.; Под ред. Г.Г. Шишкина. – 4-е изд., перераб. и доп.- М.: Энергоатомиздат, 1989.- 496 с.: ил.

Р а з д е л

Лекция 7. Неоднородные полупроводники. Электрические переходы.

7.5. Диффузионное уравнение

Контрольные вопросы:

8.4. Электронно-дырочный переход в неравновесном состоянии

Контрольные вопросы:

Ударная ионизация станет возможной, если

Контрольные вопросы:

11.3. Варикапы.

Ахмед Маллаевич Абдуллаев