При программировании на Delphi или Паскале иногда попадаются задачи, которые трудно "втиснуть" в стандартные конструкции языка. А решение лежит совсем рядом - в теории конечных автоматов. Мы не будем залезать в дебри, а просто покажем как это делается.
|
Автор заранее просит у читателя прощения за то,
что в тексте статьи используются блок-схемы. Это не модно сейчас,
однако есть случаи, когда все-таки стоит их использовать. Рассуждения об алгоритмах - как раз такой особый случай. |
Однажды, еще в школе, на уроке алгебры, я в первый раз услышал о существовании формальных преобразований. Помнится это были (a+b) 2.
Это было нечто! Меня поразила сама возможность выполнять ряд простых шагов и гарантированно получать правильный результат.
Ну а уж потом были примеры из тригонометрии: четырехэтажные дроби с ужасным количеством синусов, косинусов и бесконечно длинными аргументами, которые путем небольшой игры ума сворачивались в робкое 1+sin(x), а то и просто в неприметную 1.
С тех самых пор я весьма неравнодушен к формальным преобразованиям и стараюсь найти им применение в программировании. И, вы знаете, иногда получается! :-)
Почему я говорю то Паскаль, то Дельфи? Просто потому, что лингвистическая основа Delphi - это Object Pascal, сильно выросший из детских штанишек, но все же узнаваемый. И новые объектно-ориентированные возможности и замечательные библиотеки классов в совокупности с CASE-средствами так и не скрыли полностью длинные уши структурного языка (и это замечательно!). Они вылезают то здесь, то там, в отдельных процедурах, в обработчиках событий... :-)
Так вот, в те давние времена возникла следующая ситуация:
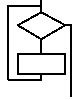
| Итак, структурное программирование учит нас, что есть 5 основных конструкций, из которых как из кубиков строится любая процедура: | ||||
 |
 |
 |
 |
 |
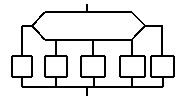| SEQUENCE | IF-THEN-ELSE | WHILE-DO | REPEAT-UNTIL | CASE |
|
По этому поводу тоже было немало дебатов: сколько же структур действительно основных, а какие следует считать производными. Левые радикалы даже дошли до того, что основных структур только две: SEQUENCE и WHILE, а все остальные можно построить из них. Самое смешное, что это действительно так. Правда, размер текста программы при этом распухает неимоверно, но это уже детали... :-) | ||||
В нашем запутанном алгоритме наверняка не все так ужасно, как кажется. Скорее всего, там можно найти несколько фрагментов, подходящих под определение чисто структурных конструкций. Вопрос лишь в том, как эти конструкции соединить между собой.
А вот в этом как раз может помочь наша рабочая лошадка - непотопляемая конструкция REPEAT-CASE. При умелом применении эта нехитрая пара команд может "переварить" алгоритм любой сложности и запутанности. Главное, чтобы ВЫ четко представляли что делаете.
Предположим, у нас есть алгоритм следующего вида:
|
Хитрый ли он? Да нет, конечно! Если приглядеться, он легко разбивается на 3 вложенные стандартные структуры: 
|
Так что мы с легкой душой можем воплотить его в программе вроде такой:
repeat
while C1 do B1;
if C2 then B2
else B3;
until C3;
И все! Очень красиво и компактно, спасибо большое дедушке Вирту.Как было бы хорошо, если бы в жизни нам попадались только такие алгоритмы. Однако в таком случае, вам незачем было бы читать эту статью! :-) | |
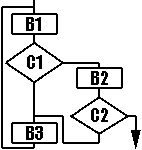
А что вы скажете на это:
|
Выглядит вроде просто, это мы мигом! Гмм.. да.. пробуем и так и эдак - в стандартный Паскаль это явно не укладывается. Можно, конечно, попытаться "расшить" процедурные блоки B1 и B3 или применить GOTO или EXIT из цикла. Но все это, согласитесь, выглядит как-то жалко и самодеятельно. Опять же надо каждый раз думать где разомкнуть цикл... И вот тут-то появляемся мы, (на белом коне !-) с нашей универсальной отмычкой по имени REPEAT-CASE.
|
var State:integer;
begin
State:=1; {для любого алгоритма}
repeat
case State of
...
end;
until State=0; {тоже для любого алгоритма}
end;
case State of
1: begin B1; if C1 then State:=2 else State:=3 end;
2: begin B2; if C2 then State:=0 else State:=3 end;
3: begin B3; State:=1 end;
end;
Проводя указанные действия несколько раз для разных алгоритмов, можно заметить, что на самом деле наши произвольно расставленные точки-состояния не такие уж случайные и произвольные. Как правило, при более глубоком рассмотрении вашего конкретного алгоритма можно найти каждому из этих состояний свое название. Это название может быть гораздо более выразительным, чем просто 1-2-3, поскольку это действительно состояния вашей программы.
О чем я говорю? Пусть ваш алгоритм занимается, скажем, синтаксическим разбором HTML-файла. Тогда одно из состояний может звучать как "Обнаружен тэг BODY" или "Найден конец документа".
Паскаль предлагает нам замечательное средство для работы с такими обозначениями в символическом виде и об этом средстве сейчас часто забывают. Программа из нашего примера может выглядеть так:
var State:(START, EOF_found, Line_Added, DONE);
begin
State:=START; {для любого алгоритма}
repeat
case State of
START: begin B1; if C1 then State:=EOF_Found else State:=Line_Added end;
EOF_Found: begin B2; if C2 then State:=DONE else State:=Line_Added end;
Line_Added: begin B3; State:=START end;
end;
until State=DONE; {тоже для любого алгоритма}
end;
Замечательно, что Delphi все еще поддерживает эту спецификацию и даже показывает при отладке символьное представление состояния! Это очень удобно на практике.
Спасибо, Borland!
Возможно вы, как и я, проделав подряд несколько таких преобразований и войдя во вкус, заметите, что стали мыслить при программировании чуть-чуть иначе. Иногда, особенно когда задача несколько запутана, хочется сразу выделить несколько важных состояний и строить обработчик уже вокруг них. Это правильное желание, ему стоит потакать. :-)
Кстати, сейчас тема конечных автоматов вновь стала актуальной и то и дело мелькает на страницах компьютерных журналов.
Как сказал один мудрый человек, "Идея, доведенная до абсурда, часто превращается в свою противоположность". Давайте попробуем довести наш метод до крайней степени.
В нашем случае это означает добавление еще двух состояний - 4 и 5. Тогда программа примет вид:
case State of
1: begin B1; State:=4 end;
2: begin B2; State:=5 end;
3: begin B3; State:=1 end;
4: if C1 then State:=2 else State:=3;
5: if C2 then State:=0 else State:=3;
end;
Хорошо это или плохо?
Хорошо, в том смысле, что даже при таком издевательстве программа не перестает работать правильно. С другой стороны, посмотрите на исходный код: где прозрачность, где легкость и ясность? Суть алгоритма растворена в сплошных переходах состояний и из-за этого теряется.
Нет, пожалуй этот вариант нам не подходит.
А что, если пойти в другую сторону и уменьшить число выделенных состояний?
В нашем примере реально только исключить состояние 2.
После "приведения подобных" программа будет иметь следующий вид:
case State of
1: begin
B1; State:=3;
if C1 then begin
B2; if C2 then State:=0
end
end;
3: begin B3; State:=1 end;
end;
(Если непонятно, то здесь формально получаются две ветки ELSE, ведущие обе к третьему состоянию. Если состояние вынести вверх, до условия, то программа получается короче. Впрочем, это - дело вкуса :)
Как вам этот вариант? Мне кажется он тоже имеет право на жизнь, хотя лично мне вариант с четырьмя состояниями нравится больше. Как-то он нагляднее показывает что куда переходит и при каких условиях. А вам?
А если серьезно, то устойчивость работы преобразованных таким образом программ прямо и недвусмысленно показывает, насколько удачно вы проработали исходную блок-схему и насколько аккуратно ее преобразовали. Поскольку на то оно и инвариантное преобразование, чтобы ничего не менять в смысле и логике программы, а затрагивать лишь ее внешнее представление.
|
Возможно кто-нибудь захочет поручить и само это преобразование программе, это мог бы быть компонент Delphi или отдельная утилита, этакий Diagram Automation Wizard. Если такое случится, мне бы очень хотелось посмотреть на результат.
|
Я ни в коей мере не претендую на авторство в данном формальном подходе, более того, все проблемы и решения, изложенные в этой статье, известны уже довольно давно. Моя цель была просто напомнить вам об одном красивом, но, боюсь, забытом подходе к программированию на Паскале и Delphi.
Пишите, если надумаете чем поделиться,
George Columbow