Часть 1. Элементы нейрологики с позиции аппаратной реализации

Основные нейросетевые парадигмы разработаны несколько десятилетий назад, по их исследованию опубликовано огромное число работ с обзорами которым можно познакомиться в [1-4]. Мы лишь, для лучшего понимания в дальнейшей архитектурно-схемотехнический решений нейровычислительных систем остановимся на наиболее важных элементах нейрологики с позиции аппаратной реализации.

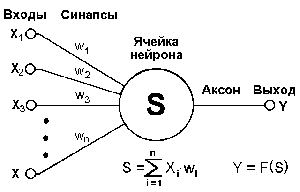
Одним из основных достоинств нейровычислителя является то, что его основу составляют относительно простые, чаще всего - однотипные, элементы (ячейки), имитирующие работу нейронов мозга - "нейроны". Каждый нейрон характеризуется своим текущим состоянием по аналогии с нервными клетками головного мозга, которые могут быть возбуждены или заторможены. Он обладает группой синапсов - однонаправленных входных связей, соединенных с выходами других нейронов, а также имеет аксон - выходную связь данного нейрона, с которой сигнал (возбуждения или торможения) поступает на синапсы следующих нейронов. Общий вид нейрона приведен на рисунке 2.

Рис.2. Общий вид нейрона.

Каждый синапс характеризуется величиной синаптической связи или ее весом w_i, который по физическому смыслу эквивалентен электрической проводимости. Текущее состояние нейрона определяется, как взвешенная сумма его входов:

Выход нейрона есть функция его состояния: y = f(s) (2), которая называется активационной и может иметь различный вид (некоторые из типовых активационных функций представлены на рисунке 3). Одной из наиболее распространенных - является нелинейная функция с насыщением, так называемая логистическая функция или сигмоид (т.е. функция S-образного вида):

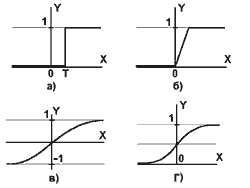
Рис2.5
а) единичная пороговая функция;
б) линейный порог (гистерезис);
в) сигмоид - гиперболический тангенс;
г) логистический сигмоид.

При уменьшении сигмоид становится более пологим, в пределе при =0 вырождаясь в горизонтальную линию на уровне 0.5, при увеличении сигмоид приближается по внешнему виду к функции единичного скачка с порогом T в точке x=0. Из выражения для сигмоида очевидно, что выходное значение нейрона лежит в диапазоне [0,1]. Одно из ценных свойств сигмоидной функции - простое выражение для ее производной.

Параллелизм обработки достигается путем объединения большого числа нейронов в слои и соединения определенным образом различных нейронов между собой. В качестве примера простейшей НС приведем трех нейронный персептрон (рис.3), нейроны которого имеют активационную функцию в виде единичной пороговой функции, работа которого подробно рассмотрена в литературе [2-4]. На n входов поступают некие сигналы, проходящие по синапсам на 3 нейрона, образующие единственный слой этой НС и выдающие три выходных сигнала:

Очевидно, что все весовые коэффициенты синапсов одного слоя нейронов можно свести в матрицу W, в которой каждый элемент w_ij задает величину i-ой синаптической связи j-ого нейрона. Таким образом, процесс, происходящий в НС, может быть записан в матричной форме: Y=F(XW), где X и Y - соответственно входной и выходной сигнальные векторы, F( V) - активационная функция, применяемая поэлементно к компонентам вектора V. Теоретически число слоев и число нейронов в каждом слое может быть произвольным.

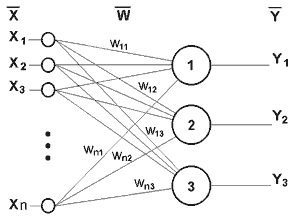
Рис.3 Однослойный персептрон.

Для того чтобы нейронная сеть работала - ее надо обучить. От качества обучения зависит способность сети решать поставленные перед ней проблемы. На этапе обучения кроме параметра качества подбора весовых коэффициентов важную роль играет время обучения. Как правило, эти два параметра связаны обратной зависимостью и их приходится выбирать на основе компромисса. Обучение НС может вестись с учителем или без него. В первом случае сети предъявляются значения как входных, так и желательных выходных сигналов, и она по некоторому внутреннему алгоритму подстраивает веса своих синаптических связей. Во втором случае выходы НС формируются самостоятельно, а веса изменяются по алгоритму, учитывающему только входные и производные от них сигналы.

Рассматривая классификацию НС можно выделить: бинарных (цифровые) и аналоговых НС, предварительно обученные (неадаптивные) и самообучающиеся (адаптивные) нейронные сети, что крайне важно при их аппаратной реализации. Бинарные оперируют с двоичными сигналами, и выход каждого нейрона может принимать только два значения: логический ноль ("заторможенное" состояние) и логическая единица ("возбужденное" состояние). К этому классу сетей относится и рассмотренный выше трех нейронный персептрон, так как выходы его нейронов, формируемые функцией единичного скачка, равны либо 0, либо 1. В аналоговых сетях выходные значения нейронов могут принимать непрерывные значения, что могло бы иметь место после замены активационной функции нейронов персептрона на сигмоид.

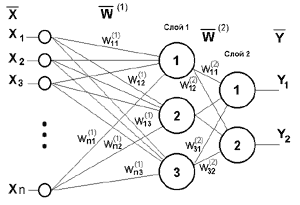
Рис. 4. Двухслойный персептрон

Сети также можно классифицировать по топологии (числу слоев и связей между ними). На рисунке 4 представлен двухслойный персептрон, полученный из персептрона рисунка 3 путем добавления второго слоя, состоящего из двух нейронов. При этом нелинейность активационной функции имеет конкретный смысл: так как, если бы она не обладала данным свойством или не входила в алгоритм работы каждого нейрона, результат функционирования любой p-слойной НС с весовыми матрицами W⁽ⁱ⁾, i=1,2,...p для каждого слоя i сводился бы к перемножению входного вектора сигналов X на матрицу W⁽⁾=W⁽¹⁾..W⁽²⁾ Ч...ЧW(p) , то есть фактически такая p-слойная НС эквивалентна однослойной НС с весовой матрицей единственного слоя W(): Y=XW() .

Существует великое множество различных алгоритмов обучения, которые делятся на два больших класса: детерминированные и стохастические. В первом из них подстройка весов представляет собой жесткую последовательность действий, во втором - она производится на основе действий, подчиняющихся некоторому случайному процессу.

Практически 80% реализованных на сегодня нейрочипов, ориентированных на задачи цифровой обработки сигналов, используют при обучении НС алгоритм обратного распространения ошибки, кроме всего прочего он стал неким эталоном для измерения производительности нейровычислителей (например, как БПФ на 1024 отсчета для сигнальных процессоров), поэтому на нем стоит остановиться подробнее.

Рассмотрим этот алгоритм в традиционной постановке [1-4]. Он представляет распространение сигналов ошибки от выходов НС к ее входам, в направлении, обратном прямому распространению сигналов в обычном режиме работы. Этот алгоритм обучения НС получил название процедуры обратного распространения (Back Propagation). Согласно методу наименьших квадратов, минимизируемой целевой функцией ошибки НС является сигнал ошибки обучения:

где - реальное выходное состояние нейрона j выходного слоя N нейронной сети при подаче на ее входы p-го образа; d_jp - идеальное (желаемое) выходное состояние этого нейрона. Суммирование ведется по всем нейронам выходного слоя и по всем обрабатываемым сетью образам. Минимизация ведется методом градиентного спуска, что означает подстройку весовых коэффициентов следующим образом:

Здесь w_ij - весовой коэффициент синаптической связи, соединяющей i-ый нейрон слоя n-1 с j-ым нейроном слоя n, - коэффициент скорости обучения, 0<<1.

Здесь под y_j, как и раньше, подразумевается выход нейрона j, а под s_j - взвешенная сумма его входных сигналов, то есть аргумент активационной функции. Так как множитель dy_j/ds_j является производной этой функции по ее аргументу, из этого следует, что производная активационной функция должна быть определена на всей оси абсцисс, т.е. в них применяются такие гладкие функции, как гиперболический тангенс или классический сигмоид с экспонентой. В случае гиперболического тангенса

Третий множитель s_j/w_ij, очевидно, равен выходу нейрона предыдущего слоя yi^(n-1), для выражения производной сигнала ошибки по выходному сигналу имеем:

Здесь суммирование по k выполняется среди нейронов слоя n+1.

Введя новую переменную

мы получим рекурсивную формулу для расчетов величин j⁽ⁿ⁾ слоя n из величин k⁽ⁿ⁺¹⁾ более старшего слоя n+1.

Для выходного же слоя

Теперь мы можем записать основное выражение для весовых коэффициентов в обобщенном виде:

Иногда для придания процессу коррекции весов некоторой инерционности, сглаживающей резкие скачки при перемещении по поверхности целевой функции, дополняется значением изменения веса на предыдущей итерации (т.е. мы уже вплотную подошли к хорошо известному адаптивному LMS алгоритму).

где - коэффициент инерционности, t - номер текущей итерации.

Диаграмма сигналов в сети при обучении по алгоритму обратного распространения представлена на рис.5. Она структурно отражает все нейросетевые операции и наглядно иллюстрирует те структурно-функциональные элементы, которые должны быть реализованы в элементарной ячейке нейровычислителя.

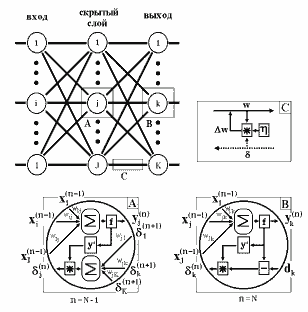
Рис.5. Диаграмма сигналов в сети при обучении по алгоритму обратного распространения [3]

Рассмотренная НС имеет целый ряд недостатков [1-4]: Во-первых, в процессе обучения может возникнуть ситуация, когда большие положительные или отрицательные значения весовых коэффициентов сместят рабочую точку на сигмоидах многих нейронов в область насыщения. Малые величины производной от логистической функции приведут к остановке обучения, что парализует НС. Во-вторых, применение метода градиентного спуска не гарантирует, что будет найден глобальный, а не локальный минимум целевой функции. Эта проблема связана еще с одной, а именно - с выбором величины скорости обучения. Доказательство сходимости обучения в процессе обратного распространения основано на производных, то есть приращения весов и, следовательно, скорость обучения должны быть бесконечно малыми, однако в этом случае обучение будет происходить неприемлемо медленно. С другой стороны, слишком большие коррекции весов могут привести к постоянной неустойчивости процесса обучения. Поэтому в качестве обычно выбирается число меньше 1, но не очень маленькое, например, 0.1, и оно, вообще говоря, может постепенно уменьшаться в процессе обучения. Кроме того, для исключения случайных попаданий в локальные минимумы иногда, после того как значения весовых коэффициентов застабилизируются, кратковременно сильно увеличивают, чтобы начать градиентный спуск из новой точки. Если повторение этой процедуры несколько раз приведет алгоритм в одно и то же состояние НС, можно более или менее уверенно сказать, что найден глобальный максимум, а не какой-то другой.

Другим простым примером является построение нейроадаптивной системы управления на линиях задержки. При этом нейровычислитель может быть реализован на базе адаптивных сумматоров (трансверсальных фильтров, например на базе ИМС А100), при этом наличие нелинейности на выходе нейронов не требуется. Структурная схема такой нейросистемы для одномерного случая и обработкой во временной области, представленная на рис.6, состоит из пяти слоёв, входные сигналы нейронов 2-4 слоёв формируют сдвиговые регистры RG, длина которых определяет порядок системы управления. Нейроны слоев 1 и 5 производят только суммирование входных сигналов. Нейроны второго слоя осуществляют учет изменения характеристик объекта управления на участке от измерителя до регулятора, для чего в состав схемы введен генератор, некоррелированный с входным сигналом. Третий слой нейросети осуществляет формирование сигнала управления, а четвертый осуществляет учет влияния регулятора на первичные измерители. Такое построение одномерной сиситемы управления позволяет организовать пятиуровневый конвейер, причем предложенный подход к корректировке весовых коэффициентов позволяет отказаться от классической процедуры обратного распространения для обучения нейросети и использовать нейроны без нелинейных элементов на выходах.

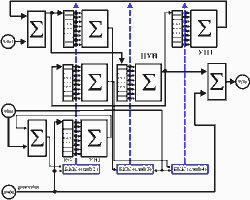
Рис.6. Структурная схема одномерной нейроадаптивной системы управления на линиях задержки.

Алгоритм работы нейроадаптивной системы управления такой структуры следующий

Первый слой:    g(n)=x(n)-q(n-1),e1(n)=e(n)-v(n-1).
Второй слой:    c2(n)i=c2(n-1)i - 2 gen(n-i) e1(n),

Третий слой:    h(n)i=h(n-1)i - m(n-i) e(n), 
Четвертый слой: c1(n)i=c1(n-1)i - 1 s(n-i) e(n), .
Пятый слой:     y(n)=w(n)+gen(n).

Где x(n) - последовательность входных сигналов, y(n) - последовательность сигналов компенсации, e(n) - сигнал ошибки компенсации, w(n), e₁(n), s(n), g(n), q(n), v(n) - промежуточные сигналы, gen(n) - последовательность сигналов генератора, h(n), c₁(n), c₂(n) - весовые коэффициенты. Переход к системе управления более высокой пространственной размерности может быть осуществлено путем каскадного соединения однотипных нейромодулей, аналогичных представленному на рис.6. В этом случае нейроны первого слоя также будут наделены свойствами взвешенного суммирования входных сигналов от датчиков, а значения весовых коэффициентов будут учитывать взаимную корреляцию между датчиками.

Аппаратно данная система может быть реализована на основе 32 разрядного DSP фирмы Texas Instruments TMS320C32-60 с 24 разрядной адресной шиной и производительностью до 60 мл. операций с плавающей точкой в секунду (время выполнения комплексного преобразования Фурье для кадра в 1024 отсчета составляет около 1.6 мс). Данный процессор имеет неймановскую архитектуру (общее адресное пространство для исполняемого кода и данных) и обеспечивает выполнение двух операций с плавающей точкой за один машинный цикл и имеет возможность одновременно с обработкой информации проводить операции ввода/вывода. Высокое быстродействие обеспечивается за счет параллельной обработки и большой внутренней памяти (два банка внутреннего ОЗУ 256х32 + Cache команд 64х32). Все команды процессора имеют фиксированную длину в 32 бита при этом имеется возможность выполнения параллельных команд за один машинный цикл, что позволяет реализовывать нейросетевые алгоритмы (однако выигрыш в производительности от использования нейроалгоритмов меньше, чем при мультипроцессорной архитектуре). Для данной реализации участок листинга программы нахождения вектора весовых коэффициентов центрального узла настройки системы управления приведен в таблице 2.

Табл.3. Участок листинга алгоритма обучения.

Участок листинга алгоритма обучения

....
; AR0 - адрес регистра с имп. хар. h(N-1),
 AR1 - адрес регистра со значениями x(n-N+1), RC регистр счетчика
; со значением равным N-2, BK - регистр циклической адресации со значением равным N.

MPYF3    *AR0++(1),*AR1++(1)%,R1 ;перемножаем два плав. числа и результат заносим
                                 ;в регистр повышенной точности R1 (float -40 бит).
LDF 0.0, R0                      ;загружаем плав. число 0.0 в рег. R0 - инициализация
RPTS     RC                      ;Начало цикла (RC - 32 битный регистр счетчика)
MPYF3    *AR0++(1),*AR1++(1)%,R1||ADDF3 R1,R0,R0
                                 ;параллельно за один машинный цикл осуществляем
                                 ;умножение и сложение чисел. (выполняем N-1 раз)
ADDF     R1,R0,R1                ;производим последнее суммирование в цикле
........
RETS     ; Выход

Данный участок листинга программы работы нейроадаптивной системы управления занимает шесть 32-битовых слов с временем выполнения TЦУН = 32*(11+(N-1)) (нс), для узла настройки с N=160 это займет: TЦУН = 32*(11+(N-1)) = 32*(11 + 159) = 5440 нс.

Выигрыш при использовании нейросетевого подхода, по сравнению с традиционным, заключается в том, что возможно проводить вычисления параллельно, а это в свою очередь дает возможность реализовать системы управления более высокого порядка при приемлемых показателях сходимости и, следовательно, добиться более высокого качества управления. Нейросетевой подход к реализации многомерных пространственных систем управления во многом снимает проблемы стоявшие перед разработчиками по необходимости выполнения векторно-матричных операций высокой размерности в реальном времени.

Кроме многослойных нейронных сетей обратного распространения, основной недостаток которых - это невозможность гарантировать наилучшее обучение за конкретный временной интервал, на сегодня известно достаточно большое количество других вариантов построения нейронных сетей с использованием разнообразных нейросетевых алгоритмов, однако и они имеют как определенные преимущества, так и специфические недостатки. Всё это делает актуальным решение конкретных теоретических и практических задач применения нейросетевых технологий для различных областей, чему, мы надеемся, будут способствовать материалы данного и последующих обзоров.

В общем случае проектирование нейросистем сложный и трудоемкий процесс, в котором выбор конкретного алгоритма - это только один из нескольких шагов процесса проектирования. Он, как правило, включает: исследование предметной области, структурно-функциональное проектирование, топологическое проектирование и т.д. В качестве примера на рис.7. приведена часть алгоритма проектирования нейросетевого блока управления микропроцессорной системы активного управления волновыми полями (в данном случае акустическим [8]).

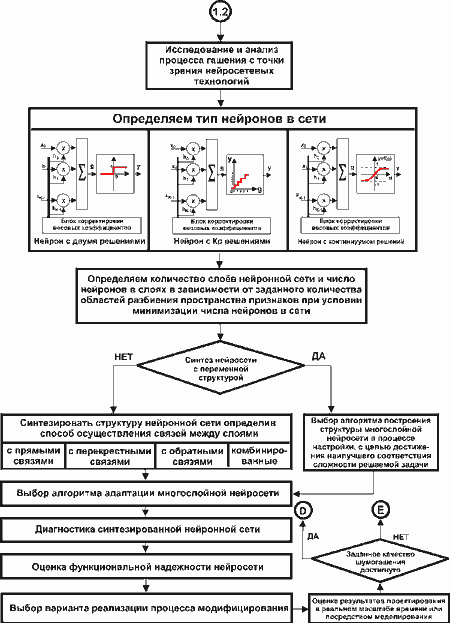
Рис.7. Алгоритм проектирования нейроадаптивной системы активного управления акустическим полем.

Вопросы, стоящие перед разработчиками нейросетевой элементной базы и нейровычислителей, во многом сложны и требуют дополнительных исследований: как целесообразней реализовать нейрочип - со встроенными нелинейными преобразованиями (пусть и фиксированного набора, но реализованных аппаратно) или позволить программисту - разработчику нейронной сети, самому формировать активационную функцию программно (размещая соответствующий код в ПЗУ). Стоит ли гнаться за универсальностью нейрочипа, которая позволила бы реализовывать любые топологии и парадигмы, или следует ориентироваться на выпуск специализированных предметно ориентированных нейрочипов, использовать ли базовые матричные кристаллы (БМК) и ПЛИС: все эти вопросы требуют ответа (по крайней мере обсуждения). Мы предлагаем всем заинтересованным лицам продолжить данное обсуждение в on-line форуме на сервере "Новости с Российского рынка нейрокомпьютеров" (http://neurnews.iu4.bmstu.ru).

В заключении подчеркнем, что эффективное применение нейрокомпьютеров характерно для случаев, требующих резкого сокращения времени обработки при решении пространственных задач повышенной размерности, которых можно найти множество практически в любой области деятельности. В следующих разделам мы подробнее остановимся на элементной базе нейровычислителей и архитектуре их построения.

Литература:

1. Проблемы построения и обучения нейронных сетей / под ред. А.И.Галушкина и В.А.Шахнова. - М. Изд-во Машиностроение. Библиотечка журнала Информационные технологии №1. 1999. 105 с.
2. А.И.Галушкин Некоторые исторические аспекты развития элементной базы вычислительных систем с массовым параллелизмом (80- и 90- годы) // Нейрокомпьютер, №1. 2000. - С.68-82
3. А.Н.Горбань, Д.А.Россиев Нейронные сети на персональном компьютере. - Новосибирск: Наука. Сибирская издательская фирма РАН, 1996. - 276 с.
4. Э.Ю. Кирсанов Цифровые нейрокомпьютеры: Архитектура и схемотехника / Под ред. А.И.Галушкина. - Казань: Казанский Гос. У-т. 1995. 131 с.
5. А.И. Власов. Аппаратная реализация нейровычислительных управляющих систем //Приборы и системы управления - 1999, №2, С.61-65.
6. В. Степанов ФОНДОВЫЙ РЫНОК И НЕЙРОСЕТИ // МИР ПК. 1998. № 12. - C.40-46
7. Роберт Хехт-Нильсен Нейрокомпьютинг: история, состояние, перспективы // Открытые системы. N4. 1998.
8. А.И. Власов Нейросетевая реализация микропроцессорных систем активной акусто- и виброзащиты// Нейрокомпьютеры:разработка и применение, №1, 2000. С.40-44.
9. http://neurnews.iu4.bmstu.ru
10. http://www.module.ru