Уважаемые читатели!
Я продолжаю знакомить Вас с серией статей Кристофера Дейта, посвященной 30-летию реляционной модели данных. Во второй статье Дейт продолжает обсуждение мало известной статьи Эдгара Кодда, опубликованной в виде технического отчета компании IBM. По моему мнению, знакомство со статьями Дейта полезно потому, что позволяет взглянуть на важные исторические вехи реляционных систем с современной точки зрения. Интересно также сравнить академический и местами трудно понятный стиль доктора Кодда с легким для чтения и понимания изложением Дейта. Лично мне было также очень любопытно познакомиться с новым для меня подходом к написанию современных статей на основе толкования темных мест классики. Что Дейт не сделает, все к лучшему :).
С уважением, Сергей Кузнецов
Volume 1, Number 2, November 1998
C.J. Date
Оригинал статьи можно найти по адресу http://www.intelligententerprise.com/9811/online2.html
В прошлом месяце я начал свой ретроспективный обзор двух первых статей Кодда, посвященных реляционному подходу, -- "Derivability, Redundancy, and Consistency of Relations Stored in Large Data Banks" (IBM Research Report RJ599, August 19, 1969) and "A Relational Model of Data for Large Shared Data Banks" (CACM 13, June 1970). В частности, я детально рассмотрел первый раздел первой статьи. Напомню Вам, что статья состояла из шести разделов:
Кодд начинает этот раздел со следующего решающего наблюдения: "Применение реляционного представления данных ... делает возможной разработку универсального подъязыка выборки, основанного на логике предикатов второго порядка". (Обратите внимание на слова "второго порядка"; в статье 1969 г. явно допускалась возможность определения отношений на доменах, содержащих в качестве элементов отношения. Я вернусь к этому моменту при подробном обсуждении статьи 1970 года.)
Величайшая интуиция Кодда подсказала ему, что можно представлять базу данных как набор отношений, которые, в свою очередь, могут представляться в виде наборов высказываний (по договоренности считающихся истинными), и следовательно, языки и понятия логики могут быть прямо применены к проблеме доступа данных и связным проблемам. В этом разделе статьи он обрисовал основные черты языка доступа, основанного на этих понятиях. Эти черты включают следующее: Язык должен быть ориентирован на работу с множествами, основное внимание должно быть сосредоточено на выборке данных (хотя должен также включать и операции обновления). Кроме того, язык не должен быть вычислительно полным; это означало, что речь идет о "подъязыке", "[встраиваемом] в разнообразные включающие языки ... Любые требуемые [вычислительные] функции могут определяться во [включающем языке] и вызываться [из подъязыка]". Лично я никогда не был полностью убежден в том, что выделение средств доступа к данным в отдельный подъязык было хорошей идеей, но он пребывает с нами в течение довольно долгого времени (в обличии встраиваемого SQL). Между прочим, в связи с этим интересно заметить, что с добавлением к стандарту SQL в 1996 г. возможности PSM (Persistent Stored Modules) SQL сам по себе теперь стал вычислительно полным языком, что означает отсутствие потребности во включающем языке (включающем SQL).
Кодд также писал: "Выполнение некоторых операций удаления может вызываться другими такими операциями, если объявлены зависимости по удалениям." Другими словами, уже в 1969 г. Кодд допускал возможность автоматически вызываемых "ссылочных действий", таких как CASCADE DELETE (и в статье 1970-го года он расширил это поняти, введя и ссылочные действия UPDATE. Кроме того, язык должен обеспечивать симметричное использование. Т.е. пользователь должен иметь возможность доступа к данному отношению с использованием любой комбинации его атрибутов, как известных, так и оставшихся неизвестными. "Эта возможность отсутствует в большинстве современных информационных систем." Совершенно верно. Ны мы принимаем это теперь как sine qua non (обязательное условие), по крайней мере, в реляционном мире. (По некоторым причинам в объектном мире эту возможность не считают настолько важной.)
В этом разделе статьи приводятся определения некоторых реляционных операций; другими словами, в нем описывается то, что позже стали называть манипуляционной частью реляционной модели. Прежде, чем вдаваться в определения, Дейт утверждает: "Эти операции не будут напрямую интересовать большинство пользователей. Однако проектировщики информационных и люди, отвечающими за управление банками данных, должны быть досконально знакомы [с ними]" (Курсив К.Дейта.) Как это верно! По моему опыту, к сожалению, люди, которым следует быть досконально знакомыми с этими операциями, слишком часто не обладают соответствующими знаниями.
В число определенных Коддом операций входят перестановка (permutation), проекция (projection), соединение (join), связывание (tie) и композиция (composition) (в статье 1970-го г. добавлена операция ограничения (restriction), которую я описываю здесь для удобства). Интересно заметить, что определения ограничения и соединения отличаются от тех, которые используются сегодня, а операции связывания и композиции теперь редко принимаются во внимание. В том, что следует ниже, символы X, Y, ... (и т.д.) по мере необходимости обозначают либо индивидуальные атрибуты, либо комбинации атрибутов. Кроме того, по причинам, которые скоро будут понятны, определение соединения откладывается до конца раздела.
Перестановка. Переупорядочение атрибутов отношения слева направо. (Как я отмечал в прошлом месяце, в статье 1969-го года предполагалась упорядоченность атрибутов отношения слева направо. В отличие от этого, в статье 1970-го года утверждается, что перестановка рассчитана исключительно на внутреннее использование, поскольку упорядоченность атрибутов слева направо не является -- или не должна являться -- существенной для пользователей.)
Проекция. Понималась более или менее так же, как и сегодня (хотя синтаксис был другим; далее я буду использовать синтаксис R{X} для обозначения проекции R на X). Замечание: название "проекция" происходит из того факта, что отношение степени n можно рассматривать как представление точек в n-мерном пространстве, и к проекции этого отношения на m его атрибутов (m<=n) можно относиться как к проекции этих точек на соответствующие m осей.
Связывание. Для данного отношения A{X1,X2,...,Xn} связывание A - это ограничение A до тех строк, в которых A.Xn = A.X1 (если использовать термин "ограничение" в его современном смысле, а не в специальном смысле, определяемом ниже.)
Композиция. Для данных отношений A{X,Y} и B{Y,Z} композицией A c B называется проекция на X и Z соединения (a join) A с B (причина, по которой я говорю "a join", а не "the join", объясняется ниже). Замечание: естественная композиция - это проекция на X и Z естественного соединения.
Ограничение. Для данных отношений A{X,Y} и B{Y} ограничение A по B определяется как максимальное подмножество A такое, что A{Y} является подмножеством -- не обязательно точным -- B.
Кодд также говорит, что "весь обычный набор операций [также] применим ... [но] результат может не являться отношением". Другими словами, когда Кодд писал свою статью 1969-го года, он оставил на будущее определения специализированных реляционных вариантов декартова произведения, объединения, пересечения и вычитания.
Приступим теперь к определению соединения. Для данных отношений A{X,Y} и B{Y,Z} соединение A с B в статье определяется как любое отношение C{X,Y,Z} такое, что C{X,Y} = A и C{Y,Z} = B. Заметим, что следовательно A и B можно соединить (или они "соединяемы"), только если их проекции на Y идентичны -- т.е. только если A{Y} = B{Y}, условие, которое вряд ли удовлетворяется на практике. Также заметим, что если A и B соединяемы, то могут существовать различные соединения (в общем случае). Хорошо известное естественное соединение -- называемое в статье линейным естественным соединением, чтобы отличить его от другого вида, именуемого циклическим соединением -- это важный частный случай, но не единственно возможный.
Однако странно то, что приводимое в статье определение естественного соединения не требует соединяемости A и B в приведенном специальном смысле! На самом деле, это определение почти такое же, как то, которое мы используем сегодня.
Постараюсь объяснить, откуда берется это довольно ограничительное понятие "соединимости". Кодд начинает свое обсуждение соединений с важного вопроса: При каких условиях соединение двух отношений сохраняет всю информацию, содержащуюся в этих двух отношениях? И он показывает, что свойство "соединяемости" является достаточным для обеспечения сохранения всей информации (поскольку в результате соединения не теряется ни одна строка ни одного операнда). Далее он также показывает, что если A и B соединяемы, и либо A.X функционально зависит от A.Y либо B.Z функционально зависит от B.Y, то естественное соединение является единственным возможным соединением (хотя реально он не использует терминологию функциональных зависимостей -- это также оставлено на будущее). Другими словами, Кодд здесь закладывает фундамент важнейшей теории декомпозиции без потерь (которую он, конечно, развил в последующих статьях).
Замечательно, что Кодд также приводит пример, показывающий, что уже в 1969 г. он осознавал тот факт, что некоторые отношения не могут быть декомпозированы без потерь в две проекции, но могут быть декомпозированы без потерь в три проекции! Этот пример был, очевидно, не замечен большинством первоначальных читателей статьи; во всяком случае для исследовательского сообщества оказалось неожиданностью повторное открытие этого факта несколькими годами позже. Именно это повторное открытие привело к изобретению Рональдом Фейджином окончательной нормальной формы 5NF, называемой также нормальной формы проекции-соединения (PJNF).
В соответствии с Коддом с банком данных ассоциируются три набора отношений: выражаемые, именованные и хранимые. Выражаемое отношение может быть определено через выражение языка доступа к данным (предполагается, что в этом языке поддерживаются операции, описанные в предыдущем разделе); у именованного отношения имеется известное пользователям имя; и хранимое отношение каким-то образом непосредственно представляется в физической памяти.
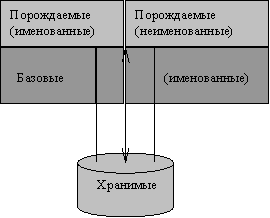
По этому поводу у меня имеется небольшое недовольство (если снова следовать правилу 20/20 для взгляда в прошлое). Кажется слегка неудачным способ использования Коддом термина хранимое отношение. Лично я предпочел бы разбить выражаемые отношения на два вида - базовые и производные отношения; я определил бы производное отношение как такое выражаемое отношение, значение которого в каждый момент времени производится из других выражаемых отношений в соответствии с некоторым реляционным выражением, а базовое отношение - как выражаемое отношение, не являющееся базовым в этом смысле. Другими словами, базовые отношения - "заданные"; порождаемые отношения - все остальные выражаемые отношения. И затем я бы четко прояснил, что базовые и хранимые отношения - это не обязательно одно и то же (см. рис. 1). Тем не менее, в статье фактически считается, что базовые и хранимые отношения являются одним и тем же (в основном потому, что в ней в ней вообще не упоминаются базовые отношения в качестве отдельной категории).

Рис. 1. Виды отношений
Верно, что базовые отношения представляют, по существу, то же самое, что и хранимые отношения в большинстве сегодняшних SQL-ориентированных продуктов. Другими словами, большинство людей считает, что в этих продуктах базовые отношения отображаются совершенно напрямую в физическую память. Но отсутствуют логические требования для такого простого отображения; на самом деле, различие между моделью и реализацией диктует то, что мы вообще ничего не говорим в модели о физической памяти. Более конкретно, степень различия между базовыми и хранимыми отношениями должна быть по крайней мере такой, как для представлений и базовых отношений; единственным логическим требованием является то, должна иметься возможность получения базовых отношений из тех, которые хранятся физически (а тогда могут быть получены и порождаемые отношения).
Однако, как я уже отмечал, в большинстве сегодняшних продуктов обеспечивается очень незначительная поддержка этой идеи; т.е. большинство сегодняшних продуктов обеспечивает намного меньшую независимость данных, чем теоретически возможно для реляционной модели. И именно поэтому мы впадаем в рассуждения о пресловутой денормализации. Конечно, иногда денормализация необходима (по соображениям эффективности), но ее следует производить на уровне физической памяти, а не на логическом уровне и не на уровне базовых отношений. Однако, поскольку в большинстве сегодняшних систем хранимые и базовые отношения воспринимаются, по существу, как одно и то же, этот простой вопрос приводит к большой путанице; кроме того, денормализация обычно обладает побочным эффектом порчи чистого во всех остальных отношениях логического проекта, с хорошо известными нежелательными последствиями.
Достаточно по поводу этих огорчений. Кодд продолжает: "Если интенсивность доступа к некоторому неименованному, но выражаемому отношению возрастает до значительного показателя, следует дать ему имя и тем самым включить в именованный набор." Другими словами, сделайте его представлением! Так что уже в 1969 г. Кодд говорил об идее представлений как "законсервированных запросов".
"Решения, связанные с тем, какие отношения принадлежат к именованному набору, основываются ... на логических нуждах сообщества пользователей, и, в частности, в потребности возрастающих инвестиций в программы, использующие именованные отношения, по причине предыдущего членства ... в именованном наборе." Здесь Кодд говорит о том, что представления являются механизмом для обеспечения логической независимости данных -- механизмом, который, в частности, гарантирует продолжение возможности выполнять программы при развитии базы данных. И он продолжает: "С другой стороны, решения, связанные с тем, какие отношения принадлежат хранимому набору, основываются ... на ... требованиях к производительности ... и изменениях, возникающих в этих [требованиях]." Здесь Кодд проводит очень четкую грань между логическим и физическим уровнями.
В этом разделе Кодд начинает обсуждать некоторые вопросы, которые позже вошли в целостную часть реляционной модели. Отношение называется порождаемым, если и только если оно является выражаемым в смысле предыдущего раздела. (Заметим, что это определение порождаемости не является точно тем же, которое я защищал выше, поскольку -- по крайней мере, неявно -- под него подпадают и базовые отношения.) Набор отношений называется строго избыточным, если включает по крайней мере одно отношение, порождаемое (в смысле Кодда) из других отношений этого набора.
В статье 1970-го г. это определение слегка улучшено: Набор отношений называется строго избыточным, если включает по крайней мере одно отношение, некоторая проекция которого -- возможно, тождественная проекция, т.е. проекция на все атрибуты -- порождаема из других отношений этого набора. (Я взял на себя смелость несколько упростить определение Кодда, хотя, конечно, старался сохранить его исходный смысл.)
Затем Кодд приводит наблюдение, что именованные отношения, вероятно, будут строго избыточны в этом смысле, потому что они, вероятно, будут включать как базовые отношения, так и представления, порождаемые из этих базовых отношений. (На самом деле, в статье говорится, что "[такая избыточность] может служить для улучшения доступности определенных видов информации, для которой существует большой спрос"; это один из способов сказать, что представления обеспечивают полезную сокращенную запись.)
Однако хранимые отношения обычно не будут строго избыточны. Кодд развивает эту мысль в статье 1970-го г.: "Если ... строгая избыточность в именованном наборе прямо отражается ... на хранимом наборе ... то, вообще говоря, расходуются дополнительные пространство памяти и время обновления, [хотя может также достигаться] сокращение времени выполнения некоторых запросов и загрузки центральных процессоров."
Лично я сказал бы, что базовые отношения определенно не должны быть строго избыточными, но хранимые отношения могут быть таковыми (в зависимости -- как всегда на уровне хранения -- от соображений эффективности).
Кодд говорит, что система должна иметь информацию о любой избыточности в данном наборе отношений, чтобы она могла обеспечивать согласованность; набор будет согласованным, если он соответствует установленным избыточностям. Однако я должен заметить, что в этом определении согласованности не учитываются все аспекты целостности, а концепция строгой избыточности не охватывает все возможные виды избыточности. В качестве простого контрпримера рассмотрим базу данных, содержащую всего одно отношение EMP {EMP#, DEMP#, BUDGET}, в котором удовлетворяются следующие функциональные зависимости:
EMP# -> DEPT# DEPT# -> BUDGET
В этой базе данных определенно присутствует некоторая избыточность, хотя она не является "строго" избыточной в соответствии с определением.
Я должен объяснить, почему Кодд использует термин строгая избыточность. Он делает это для того, чтобы отличить ее от избыточности другого рода, также определенной в статье и называемой слабой избыточностью. Однако я опускаю детали, потому что в отличие от любого другого понятия, введенного в первых двух статьях, это конкретное понятие, как кажется, не привело к чему-либо значительному. (Во всяком случае, приведенный в статье пример не соответствует даже собственному определению Кодда.) За конкретными деталями читатель отсылается к оригиналу статьи.
В этом завершающем разделе статьи 1969-го года содержится несколько замечаний по поводу протоколов, определяющих требуемые действия при обнаружении рассогласованности." Возникновение рассогласованности ... может журнализоваться внутренним образом, чтобы в том случае, если она не устраняется в течении некоторого разумного времени ... система могла оповестить сотрудника безопасности [sic]. Или же система могла бы [информировать] пользователя, что такие-то и такие-то отношения нуждаются в изменении для восстановления согласованности ... В идеале должны быть возможны [разные действия системы] ... для разных поднаборов отношений."
Это завершает мое обсуждение статьи 1969-го года. В следующий раз внимание будет посвящена более знаменитой статье 1970-го года.