Глава 3.  Основные типы антенн УКВ

 

3.1  Симметричный вибратор

Распределение тока и заряда по вибратору

Изучение симметричного электрического вибратора представляет большой интерес, так как, во-первых, этот вибратор применяется как само­стоятельная антенна и, во-вторых, он является составным элементом ряда сложных антенн. Симметричные вибраторы начали широко применять в первой половине двадцатых годов в связи с возникновением и развитием ра­диосвязи на коротких волнах. В настоящее время симметричный вибратор как самостоятельная антенна применяется на коротких, метровых и деци­метровых волнах. В этих же диапазонах широко используются сложные ан­тенны, состоящие из ряда симметричных вибраторов. Симметричные вибра­торы используются также в сантиметровом диапазоне волн в качестве эле­ментов сложных систем (например, облучатели зеркальных антенн).

Симметричный вибратор состоит из двух одинаковых по размерам и форме проводников, между которыми включается генератор высокой часто­ты (часто эти проводники называются плечами). Рассмотрим симметричный вибратор, представляющий собой тонкий цилиндрический проводник дли­ной 2ℓ и радиусом а (Рис.3.1), находящийся в свободном пространстве.

 

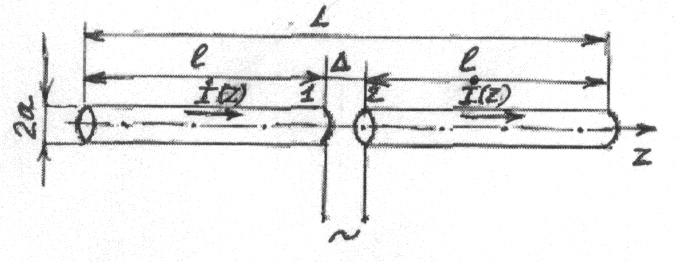
Рис. 3.1. Симметричный вибратор

 

Существует приближенный метод расчета поля, создаваемого симметричным вибратором в дальней зоне. В основе этого ме­тода лежит предположение о синусоидальном распределении тока по вибра­тору, основанное на некоторой внешней аналогии между симметричным вибратором и двухпроводной разомкнутой на конце линией без потерь. Дей­ствительно, от двухпроводной линии (Рис.3.2.а) можно перейти к симмет­ричному вибратору, если провода линии развернуть под углом 180° друг к другу (Рис.3.2.б). Можно полагать, что при переходе от двухпроводной ли­нии к симметричному  вибратору  закон  распределения  тока  не  нарушается,  т.е. I_z = I_пsink(ℓ-|z|)  , где I_п - амплитуда тока в пучности тока вибратора (в общем случае, это величина комплексная) İ_п = I_пexp(iΨ); ℓ- длина одного плеча вибратора; z - расстояние от начала вибратора (точки питания) до про­извольной точки на вибраторе (текущая координата); k = 2π/λ, - волновое число (коэффициент фазы тока в вибраторе).

Полагают, что длина волны в виб­раторе λ, равна длине волны в свободном пространстве. В действительности данная аналогия весьма приближённа. Обе системы - линия и вибратор – являются колебательными системами с распределенными параметрами, однако они существенно различаются.  Во-первых, распределенные параметры  линии (L_i,C_i) не изменяются по ее длине, распределенные параметры вибра­тора непостоянны по его длине (Рис.3.2.б).

 

 

 

 

 

 

 

 

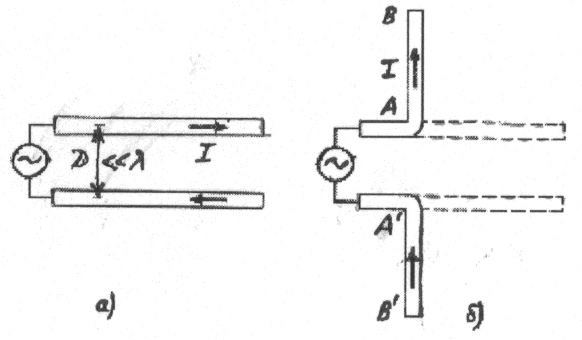
Рис.3.2. Преобразование двухпроводной линии в симметричный вибратор (а – линия, б – вибратор)

 

Во-вторых, линия служит для ка­нализации электромагнитных волн и является практически неизлучающей системой; вибратор же излучает волны. В разомкнутой на конце линии ток изменяется по закону стоячей волны только в том случае, если линия выпол­нена из идеального проводника, т.е. в ней нет потерь энергии.

В вибраторе, выполненном даже из идеального проводника, обязатель­но есть потери (полезные) на излучение. Очевидно, поэтому ток в вибраторе, строго говоря, не может быть распределен по закону стоячей волны. Однако расчет поля симметричного вибратора по формулам, основанным на сину­соидальном распределении тока, дает хорошее совпадение с эксперимен­тальными данными для дальней зоны и тонких вибраторов. Поэтому для ин­женерного расчета это приближение в ряде случаев вполне допустимо. Стро­гая теория симметричного вибратора подтверждает, что в тонких вибраторах ток распределен по закону, весьма близкому к синусоидальному. Задавшись законом распределения тока по вибратору, легко установить приближенный закон распределения заряда τ_z=τ_Пcosk(ℓ-|z|), где τ_П амплитуда заряда в его пучности. Этот закон распределения заряда вдоль симметричного вибратора совпадает с законом распределения потенциала (напряжения) в разомкнутой на конце длинной линии без потерь. В теории антенн понятием напряжения следует пользоваться с большой осторожностью, так как поле антенны не яв­ляется потенциальным. Понятием напряжения применительно к антенне можно пользоваться, если расстояние между точками измерения мало по сравнению с длиной волны. Это справедливо при измерении напряжения между зажимами антенны (точки присоединения генератора), а также для длинноволновых антенн. На Рис.3.3 приведены кривые распределения ам­плитуд тока и заряда на вибраторах разной длины. По аналогии с волновым сопротивлением длинной линии вводится понятие волнового сопротивления симметричного вибратора. Как известно, из теории длинных линий, волно­вое сопротивление двухпроводной   линии    без потерь определяется вы­ражением W =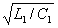, где L₁-распределенная индуктивность линии (индуктивность, приходящаяся на единицу длины ли­нии), Г/м; C₁ -, распределенная емкость линии, Ф/м. 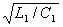Так как 1/= с, где с - скорость света, м/с, то

 

                                          W=l/cC₁, Ом.                                                       (3.1)

 

Волновое сопротивление двухпроводной линии связано с ее геометри­ческими размерами соотношением

       W=2761g (D/a),                                                              (3.2)

 

где D - расстояние между центрами про­водов линии; а - радиус провода.

                             

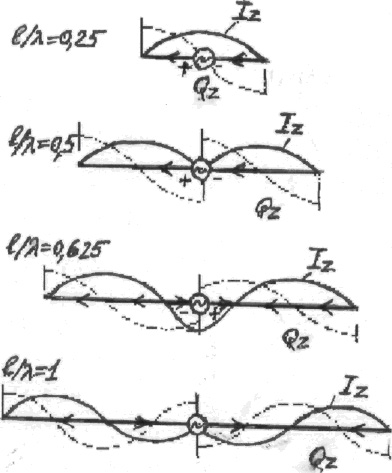
          Рис. 3.3.  Распределение амплитуд тока и заряда на вибраторах разной длины

 

Волновое   сопротивление   симмет­ричного вибратора (а также других ли­нейных антенн, т.е. антенн, длина кото­рых   значительно   превосходит   размеры поперечного  сечения)  рассчитывают  по формуле   (3.1).   Однако   распределенная емкость по длине вибратора непостоянна. Поэтому в данном случае под C₁ подра­зумевается усредненная величина, равная отношению полной статической емкости антенны (С_А) к ее длине (2l). Одним из наиболее распространенных приближен­ных методов расчета полной статической емкости является метод Хоу или метод усредненных потенциалов. Волновое со­противление  симметричного  вибратора из провода цилиндрической формы, оп­ределенное по методу Хоу:

 

W_A=120(ln l/a-1), Oм,                                                  (3.3)

 

где   l-длина плеча вибратора; а - радиус провода.

 

Расчет волнового сопротивления вибратора методом Хоу дает приемлемую точность для вибраторов, коротких по сравнению с длиной волны. Точность этого метода снижается по мере удлинения вибратора.

 

 

 

Направленные свойства симметричного вибратора

 

Рассмотрим симметричный вибратор произвольной длины (Рис.3.4). Задаемся синусоидальным законом распределения тока вдоль вибратора I_z = (I₀/sinkl)sink(l -|z|), где I₀ - ток в точках питания вибратора (I₀=I_пsinkl). Мысленно разобьем вибратор на бесконечно большое число элементов dz. Так как длина каждого элемента бесконечно мала, то можно полагать, что в пределах его ток не изменяется ни по амплитуде, ни по фазе. Таким образом, весь симметричный вибратор можно рассматривать как совокупность элементарных электрических вибраторов dz и поле симметричного вибрато­ра рассматривать как результат сложения (интерференции) полей, излучае­мых элементарными вибраторами. Ввиду малости воздушного промежутка (зазора) между плечами вибратора можно пренебречь влиянием электриче­ского поля (магнитного тока), существующего в нем на излучение, и считать, что электрический ток течет по сплошному проводнику длиной 2l. Выделим на вибраторе (Рис.3.4) элементы 1 и 2, каждый длиной dz, симметричные относительно центра вибратора 0, и определим поле, создаваемое этими эле­ментами в произвольной точке наблюдения М, находящейся в зоне излуче­ния. Проведем от элементов 1 и 2 и от центра вибратора линии в точку на­блюдения r₁, r₀, r₂. Поскольку расстояние до точки наблюдения очень велико по сравнению с длиной вибратора, то направления от всех точек вибратора на точку М можно считать параллельными. Напряженность поля, излучаемо­го первым элементом в точке М

                                  

                                                                   dE₁ = i [60πI_zdz/ (r₁ λ)] sinθexp (-ikr₁)                                                (3.4.a)

 

Напряженность   поля, излучаемого вторым элементом в той же точке М

 

                                                                   dE₂ = i [60πI_zdz/ (r₂  λ)] sinθexp (-ikr₂)                                                           (3.4.б)

 

Здесь I_z - амплитуда тока в эле­менте, находящемся на расстоянии z от центра вибратора;  r₁ -расстояние от первого эле­мента до точки М; г₂ - расстояние от второго эле­мента до точки М; θ- угол между осью вибратора  и направлением на точку наблюде­ния.

 

Найдем суммарное поле, создаваемое в точке наблюдения элемента­ми 1 и 2. Так как векторы напряженности полей, создаваемых всеми элемен­тами вибратора в точке наблюдения, направлены вдоль одной прямой (пер­пендикулярной направлению от данного элемента в точку наблюдения), то поля, создаваемые отдельными элементами, можно складывать алгебраиче­ски. Поэтому

         

                                    dE = dE₁+dE₂=i (60πI_zdz/λ) sin θ[(exp (-ikr₁)/r₁+exp (-ikr₂)/r₂)]                           (3.5)

 

 

 

                                                                                   

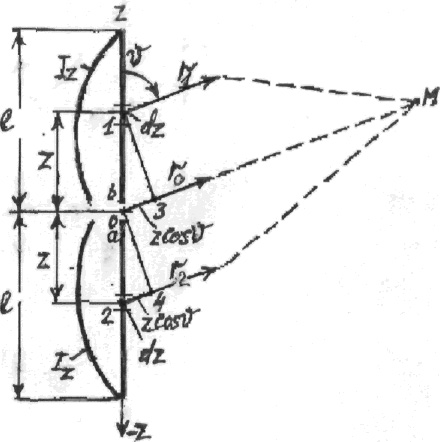
                                                    Рис.3.4.  К определению поля излучения симметричного вибратора

 

 

Выразим расстояния r₁ и r₂ через расстояние r₀. Для этого из точки 1 (Рис.3.4) опустим перпендикуляр на направление r₀ и из точки 0 опустим перпендикуляр на направление r₂. Из прямоугольных треугольников 1-0-3 и 2-0-4 находим, что разность расстояний от данных элементов и центра виб­ратора до точки наблюдения равна Δr = |z|cosθ.

 

Следовательно,       r₁ = r₀ - |z|cosθ       и        r₂ = r₀ + |z|cosθ.                                       (3.6)

 

Величину Δr часто называют разностью хода лучей. Так как точка на­блюдения находится в дальней зоне, то величина Δr мала по сравнению с r₀ и расстояния r₁ и r₂ мало отличаются друг от друга. Поэтому можно считать, что амплитуды напряженности полей, создаваемых элементами 1 и 2 в точке наблюдения М, одинаковы. Однако пренебрегать разностью хода в фа­зовых множителях (exp(-ikr₁) и exp(-ikr₂)) ни в коем случае нельзя, так как пространственный сдвиг фаз между полями элементов 1 и 2           kΔr = 2k|z|cosν = 4 π (|z|/λ)cosθ определяется отношением разности хода лучей к длине волны. На основании формул (3.6) получаем следующие выражения для фазовых множителей:

 

                                                               exp (-ikr₁) = exp (-ikr₀) exp (ik|z|) cosθ;

 

                                                                               exp (-ikr₂) =   exp (-ikr_o) exp (-ik|z|) cosθ.

 

Подставляя эти выражения в формулу (3.5), вынося за скобки общие множители и полагая, что в знаменателях r₁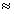r₂ 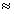r₀, получаем

 

                                               dE=i[60πI₀sink(l-|z|)dz/(r₀ λsinkl)]sinθexp(-ikr₀)[(exp(ik|z|)cosθ+exp (-ik|z|) cosθ)].

 

Воспользовавшись известной формулой exp(iα) + exp(-iα) = 2cosα, по­лучаем следующее выражение

 

                                                   dE = i[120πI₀/( r₀ λsinkl)] sinθ exp(-ikr₀)sink(l-|z|)cos(k|z|cosθ)dz.

 

 

Для определения напряженности поля, создаваемого в точке наблюде­ния всем симметричным вибратором, необходимо это выражение проинтег­рировать по длине одного плеча вибратора

                                        Е=i[120πI₀/(r₀ λsinkl)] sinθ exp(-ikr₀)∫ sink(l-|z|)cos(k|z|cosθ)dz.

В результате интегрирования получается формула для расчета напряженности поля симметричного   электрического   вибратора   в   дальней  зоне

                                                 E=i [60I₀/ (r₀sinkl)] [(cos (klcosθ) - coskl) / sinθ] exp (-ikr₀).               (3.7)

 

Как и в случае элементарного электрического вибратора, эта формула состоит из трех множителей: множителя, определяющего только величину напряженности поля и не зависящего от направления в данную точку [60I₀/(r₀sinkl)], множителя, определяющего направленные свойства (характе­ристика направленности) и фазового множителя Ψ = iexp(-ikr₀) из выражения (3.7) видно, что симметричный вибратор обладает направленными свойствами только в ме­ридиональной плоскости (плоскость электрического вектора). Напряжен­ность электрического поля симметричного вибратора в его экваториальной плоскости (плоскость магнитного вектора ν= π/2) - определяется выражени­ем

 

                                                         E = i [60I₀/ (r₀sinkl)] (l-coskl) exp (-ikr_o),                                 (3.8)

 

т.е. не зависит от азимутального угла φ. Поэтому диаграмма   направленности симметричного вибратора в его экваториальной плоскости, как и в случае элементарного вибратора,  представляет в полярной системе координат окружность.

                                                                

 

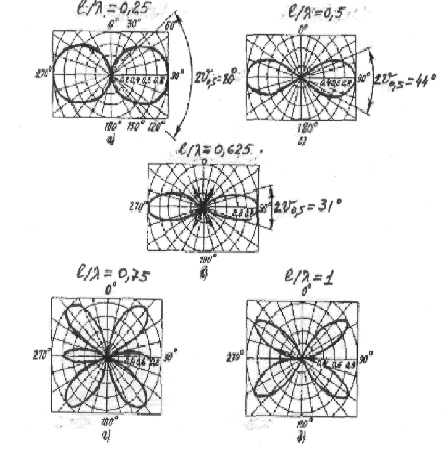
                                                                    Рис.3.5. Диаграммы направленности симметричного вибратора

 

Как видно из формулы (3.7), направленные свойства симметрич­ного вибратора определяются только отношением длины плеча вибратора к длине волны l/λ.В случае полуволнового вибратора (l/λ=0,25) формула (3.7) при­нимает вид

 

                                                                           Е= iA{cos[(π/2)cosθ]/(sinθ)}exp (-ikr₀).

 

Амплитудные диаграммы направленности, рассчитанные по форму­ле (3.7), для вибраторов с различной относительной длиной l/λ показаны на  Рис.3.5. Анализ формулы (3.7) и рассмотрение этих кривых показывают, что при любой величине отношения l/λ симметричный  вибратор  не  излучает  вдоль  своей оси. Если длина плеча симметричного вибратора l ≤ 0,5λ,  то  в  направлении, перпендикулярном   его   оси 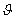  (= 90°, θ= 270°),   т.е.   в   экватори­альной плоскости, поля всех  элементарных вибраторов  максимальны,  синфазны  и складываются   арифметически.   Поэтому поле   в    данном    направле­нии является максимальным. Диаграмма направленности при l/λ ≤ 0,5 со­стоит из двух (главных) лепестков (Рис. 3.5.а, 3.5.б).  Увеличение  длины  виб­ратора  до l=0,5λ сопровождается ростом  излучения  в  направлении,  перпен­дикулярном  оси вибратора (главное направление излучения), за счет уменьшения излучения в других направлениях. При этом диаграмма направленности становится уже. При увеличении l/λ до 0,625 излучение в главном направлении продолжает возрастать, но характеристика направ­ленности проходит через нуль не только при θ=0° и θ=180°, но и при неко­торых других значениях углаθ. Главные лепестки диаграммы становятся уже, но появляются боковые лепестки (Рис.3.5.в). При дальнейшем увеличе­нии l/λ  излучение в главном направлении уменьшается, и возрастают боко­вые лепестки. Уменьшение излучения в главном направлении объясняется следующим. Результирующий сдвиг фаз полей, излучаемых элементарными вибраторами в данном направлении, определяется пространственным сдви­гом фаз и сдвигом фаз токов, возбуждающих эти вибраторы. При l/λ >0,5 на вибраторе появляются участки с противофазными токами (Рис.3.3), длина которых растет по мере увеличения l/λ. Поэтому в данном случае, хотя в главном направлении пространственные сдвиги фаз равны нулю, по­ля, излучаемые отдельными элементами вибратора, складываются несинфазно, т.е. геометрически. При l/λ= 1 (или при l/λ = п, где п = 1, 2, ..,) излу­чение в главном направлении отсутствует, так как противофазные участ­ки вибратора имеют одинаковую длину. Рост l/λ сопровождается также ростом боковых лепестков. Уже при l/λ=0,75 напряженность поля в на­правлении максимума бокового лепестка превосходит напряженность поля в главном направлении (Рис.3.3.г).

 

Нормированная характеристика направленности симметричного виб­ратора, определяемая как F(θ) = f(θ)/f(90°), равна

 

                                                                      F (θ) = [cos (klcosθ) - coskl]/ [(l – coskl) sinθ].                        (3.9)

           

У Диполя Герца 2θ_0,5= 90°. Полуволновый симметричный вибратор имеет ширину диаграммы направленности по половинной мощности 2θ_0,5= 80°, волновой симметричный вибратор - 2θ_0,5= 44°, симметричный вибратор, у которого l/λ=0,625, имеет 2θ_0,5= 31°. Последний вибратор обладает наи­лучшими направленными свойствами, так как при дальнейшем увеличении l/λ, сильно возрастают боковые лепестки, хотя главный лепесток диаграммы направленности становится уже. На практике применяются симметричные вибраторы, у которых l/λ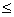 0,7. Фаза напряженности поля, создаваемого симметричным вибратором в соответствии с выражением (3.7), в пределах одного лепестка диаграммы направленности не зависит от координатного углаθ. Она изменяется скачком на обратную при переходе напряжённости поля через нуль. Симметричный вибратор излучает сферические волны, о  чем   свидетельствует   множитель              exp(-ikr)/r. Эти волны как бы исходят из од­ной точки, совпадающей с центром вибратора.

 

 

 

Мощность излучения, сопротивление излучения и КНД симметричного вибратора

Мощность электромагнитной волны, излучаемой симметричным виб­ратором, можно определить, как и для элементарного вибратора, методом вектора Пойнтинга. В соответствии с данным методом симметричный вибра­тор окружается сферой, радиус которой r »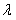, вследствие чего поверхность сферы находится в дальней зоне поля вибратора. Центр вибратора совпадает с центром сферы, ось вибратора лежит на оси z прямоугольной системы ко­ординат. На поверхности сферы выделяется бесконечно малый элемент dS, площадь которого в сферической системе координат                         dS = r²sinνdθdφ.                                                                          

Излучаемая мощность, приходящаяся на данный элемент поверхности

                                                                      dP_Σ = П_срdS= (E²/2W_c) dS.                     (3.10)

 

Здесь Е - амплитуда (модуль)  напряженности  электрического  поля  в  любой точке элемента dS определяемая выражением

                                                            E = (60I_п/r) |[cos (kl cosθ) - cos kl] / sinθ|                        (3.11)

 

В общем виде выражение для сопротивления излучения имеет вид

                                                         R_Σп = [r²Е² _макс/ (Wc I_п²)] 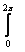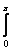F²(θ,φ) sinθ dνdφ                           (3.12)

                                                                                                   P_Σ = I_п²R_Σп/2.

 

Величина R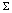_п определяется характером распределения электромагнит­ного поля в дальней зоне, т.е. диаграммой направленности рассматриваемой антенны. Интегрирование дает следующую формулу, впервые полученную Баллантайном в 1924г.

 

           R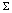_п  = 30 [2 (τ+ln2kl - Ci 2kl) + cos 2kl (τ+lnkl+ Ci 4kl - 2Ci 2kl) +sin2kl (Si 4kl- 2Si 2kl)].                                                                                 (3.13)

 

Здесь τ = 0,5772... - постоянная Эйлера; Si x =   (sin u/u)du – интегральный

синус; Ci x = 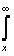(cos u/u)du - интегральный косинус.

 

Как видно из формулы (3.13), сопротивление излучения симметрично­го вибратора зависит только от величины отношения l/λ. Формула (3.13) яв­ляется приближенной, поскольку при ее выводе исходили из синусоидально­го распределения тока по вибратору, что справедливо только для тонких вибраторов. Однако результаты расчетов по формуле (3.13) хорошо совпа­дают с экспериментальными данными. Это объясняется тем, что сопротив­ление излучения определяется полем в дальней зоне, которое мало зависит от толщины вибратора. Следует также иметь в виду, что изложенный здесь метод расчета дает только активную составляющую сопротивления излуче­ния, так как учитывается только излученная активная мощность.

 

                                                                                             

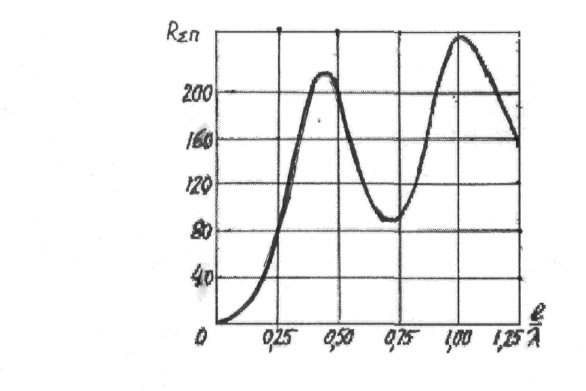
                                                                                        Рис 3.6. Зависимость R_{Σ п}  от величины l/λ

 

В литературе имеются таблицы и графики R_Σп как функции отношения (Рис.3.6), рассчитанные по формуле (3.13). Осциллирующий характер зави­симости объясняется тем, что интерференционная картина поля в дальней зоне меняется при изменении l/λ.

 

КНД симметричного вибратора можно определить по формуле

 

                     D = (120 / R_Σп) (1 -coskl)².                     (3.14)

 

При l/λ=0,25   R_Σп = 73,1 Ом и D= 1,64 ;

     l/λ= 0,5    R_Σп =199 Ом и D = 2,4;

    l/λ=0,625 R_Σп =110 Ом и D = 3,l.

 

Для сравнения КНД элементарного электрического вибратора имеет D = 1,5. 

 

КНД любой вибраторной антенны можно рассчитать по формуле

 

                D = (120/ R_Σп) f²_max (ν,θ).                     (3.15)

 

В этой формуле R_Σп  - полное сопротивление излучения  антенны.  Дей­ствующая  длина   симметричного   вибратора    определяется    по     формуле

 

                                                                                                 l_д = λ(1 - coskl) / (πsinkl).                     (3.16)

Входное сопротивление симметричного вибратора. Инженерный метод расчета входного сопротивления

 

Часть мощности, подводимой от генератора к симметричному вибрато­ру, излучается. Другая часть мощности теряется в самом вибраторе (нагрева­ние проводов), в изоляторах и в окружающих вибратор предметах. Излучен­ной мощности соответствует активное сопротивление излучения. Мощности потерь соответствует активное сопротивление потерь. Кроме излученного, есть колеблющееся вблизи антенны связанное с ней электромагнитное поле, которому соответствует реактивная мощность. Эта мощность то отдается ге­нератором, переходя в ближнее поле, то возвращается к нему обратно. Реактивной мощности в большинстве случаев соответствует реактивное сопро­тивление антенны.

Таким образом, включенный в антенну генератор нагружен на комплексное сопротивление, которое называется входным сопротивлением антенны и равно отношению напряжения на зажимах вибратора (точки питания) к току в точках питания Z_BX=U₀/I₀=R_BX+i X_BX.

                                                                                               

    

 

 

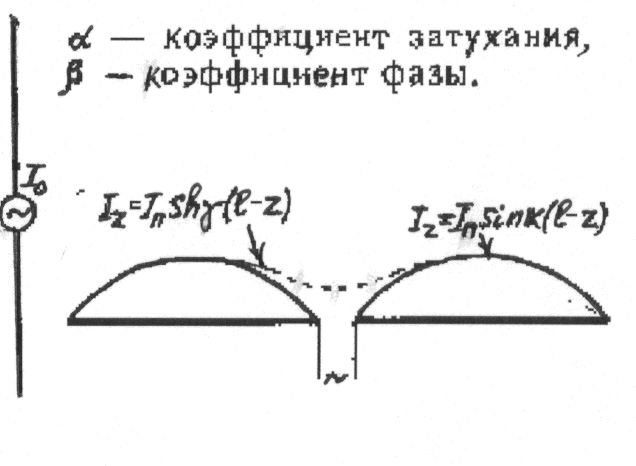
                                                             Рис.3.7. Распределение тока по “коротким” и “длинным” вибраторам

 

Величина и характер входного сопротивления определяют режим работы включенного в антенну гене­ратора. Обычно в симметричных виб­раторах потери малы, поэтому будем полагать, что R_BX 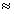 R_Σo, где R_Σo - со­противление излучения вибратора, отнесенное к току в точках питания. Для точного определения входного сопротивления необходимо знать за­кон распределения тока вдоль вибра­тора. Часто с достаточной для инженерных целей точностью входное сопротивление рассчитывается, исходя из приближенных законов распределения тока по вибратору. Рассмотрим такой приближенный (инженерный) метод расчета входного сопротивления. Предположив, что ток вдоль вибратора распределен по закону синуса, найдем входное сопротивление симметричного вибратора, у которого l/λ=0,5 (Рис.3.7). В этом случае ток в точках питания оказывается равным нулю и очевидно, что Z_BX = U₀/I₀=∞ . В действительности же ток в точках пита­ния никогда не бывает равен нулю (его величина обязательно конечна), а, следовательно, входное сопротивление симметричного вибратора никогда не бывает бесконечно велико. Физически это совершенно ясно. Ведь закон си­нуса (стоячая волна) справедлив в линиях только при отсутствии потерь. Вибратор же в принципе является системой с потерями на излучение. Следо­вательно, при расчете входного сопротивления лучше проводить аналогию между симметричным вибратором и разомкнутой на конце линией с потеря­ми. Известно, что ток в такой линии распределен по закону гиперболическо­го синуса (Рис.3.7) I_z = I_пshγ (z - l),                      где γ = α + iβ - коэффициент распро­странения, α- коэффициент затухания,  β- коэффициент фазы.

 

Из Рис.3.7 видно, что существенная разница в распределении тока по законам кругового и гиперболического синусов получается только на сравнительно близких расстояниях от узла тока. Поэтому при расчете входных сопротивлений "коротких" вибраторов  (l/λ) ≤0,35...0,4; (0,6...0,65) ≤l/λ ≤ (0,85...0,9), т.е. таких, у которых узел тока находится от точек питания вибратора не ближе, чем на расстоянии (0,1...0,15)λ, исходят из синусоидального распределения тока. При расчете входного сопротивления "длинных" вибраторов (0,35≤ l/λ ≤0,65) следует исходить из распределения тока по закону гиперболического синуса. Найдем  формулы для расчета активной и реактивной составляющих входного сопротивления "короткого" вибратора. Выразив мощность, излучаемую вибратором, через амплитуды тока в пучно­сти (I_П) и в точках питания (I₀), получим

 

 P_Σ = (I_п²R_Σп)/2   и  P_Σ = (I₀² R_Σ0)/2.                                                                     (3.17)

 

Так как левые части этих выражений равны между собой, то I²_п R_Σп = I₀² R_Σ0. Решая это равенство относительно R_Σ0, получаем R_Σ0= R_Σп (I_п²/ I₀²).

Подставляя вместо I₀ выражение I₀=I_пsinkl, получаем формулу для рас­чета активной составляющей входного сопротивления вибратора (без учета потерь в вибраторе)

 

                                                                                        R_Σ0 = R_Σп /sin²kl.                                                                                                                                                 (3.18)

 

 

Величину R_Σп  для вибратора заданной длины легко найти из таблиц или графиков. При расчете реактивной составляющей входного сопротивле­ния короткого симметричного вибратора пользуются формулой входного со­противления разомкнутой на конце двухпроводной линии без потерь, заме­няя в ней волновое сопротивление линии волновым сопротивлением антен­ны

 

                                                                                        X_вх= -i W_Actg kl.                                                                                                                                                 (3.19)

 

 

Таким образом, полное входное сопротивление короткого вибратора можно определить по формуле

 

                                                                           Z_вх= (R_Σп/sin²kl) – i W_Actg kl.                                               (3.20)

 

Точность расчетов по формуле (3.20) повышается при уменьшении размеров поперечного сечения вибратора. В случаях длинных вибраторов входное сопротивление рассчитывается аналогично входному сопротивле­нию двухпроводной разомкнутой на конце линии, обладающей потерями

 

Z_вх = W_A [(sh2αl- (α/β) sin 2βl) / (ch2αl - cos 2βl)] – i W_A [(α/β) sh 2αl+

+ sin 2βl) / (ch2αl - cos 2βl)].                                         (3.21)

 

Здесь W_A - волновое сопротивление вибратора; l- длина плеча вибра­тора; β- коэффициент фазы в вибраторе; α- коэффициент затухания. По аналогии с длинными линиями, пренебрегая потерями в проводах вибратора коэффициент затухания можно рассчитать по формуле α = R_Σ1 / W_A, где R_Σ1 -активное сопротивление излучения, приходящееся на единицу длины вибра­тора. Приближенно полагая, что сопротивление излучения R_Σп распределено равномерно по всей длине вибратора, для расчета R_Σ1 получают формулу  R_Σ1= R_Σп/[l(l - (sin2kl/2kl)]. Данная формула позволяет, зная сопротивление излучения, отнесенное к пучности тока, найти распределенное сопротивле­ние излучения. Следовательно, коэффициент затухания

 

                                                                            α = R_Σ1/ W_A = R_Σп/ [lW_A (1- (sin2kl/2kl))]

 

                                                                                                                        

                 

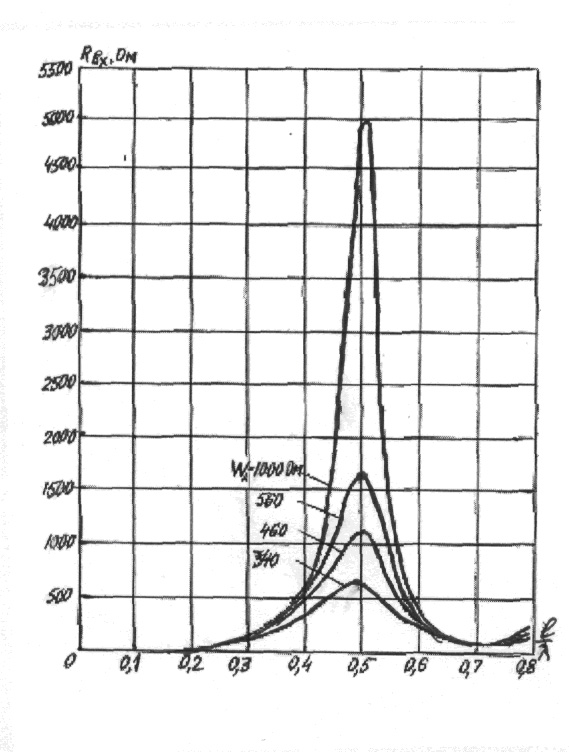
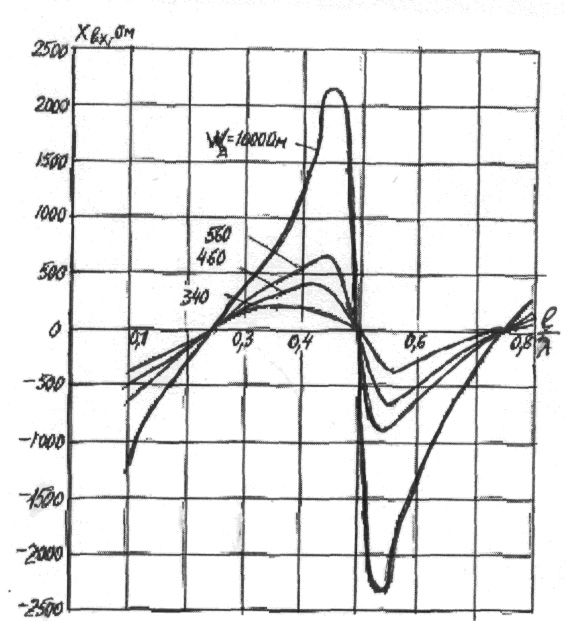
                                    Рис. 3.8. Зависимость R _вх  от величины   l/λ

                                                           Рис. 3.9. Зависимость    X _вх   от    величины   l/λ

 

Зависимость входного сопротивления сим­метричного вибратора от величины отношения l/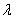 и от вол­нового сопротивления W_A по­казана на Рис.3.8 и 3.9.

Кривые рассчитаны по формуле (3.21). При расчете полагалось, что β= k. Из кривых видно, что при увеличении l/λ активная со­ставляющая входного сопро­тивления постепенно растет и достигает при l/λ=0,5 макси­мума, величина которого тем больше, чем больше w_a, т.е. чем тоньше вибратор. При даль­нейшем увеличении l/λ r_bx по­степенно уменьшается и дос­тигает минимума при l/λ=0,75. Затем R_вх снова начинает увеличиваться и достигает основного максимума при l=λ (на рисунке этот максимум не показан). Вообще максимумы R_вх повторяются при всех отношениях l/λ, кратных 0,5. Актив­ная составляющая входного сопротивления минимальна в тех случаях, когда относительная длина вибратора становится равной нечетному числу λ/4. В случае полуволнового вибратора минимум R_вх отсутствует. Реактивная со­ставляющая входного сопротивления вибратора изменяется периодически, проходя через нуль при l/λ=0,25; 0,5;0,75; 1 и т.д. При l/λ<0,25 Х_вх имеет емкостный характер, при 0,25< l/λ<0,5 - индуктивный. Можно сказать, что вблизи значений l/λ= (2n + 1)/4, где n=0, 1, 2..., симметричный вибратор ведет себя подобно последовательному колебательному контуру (резонанс напряжения), а вблизи значений l/λ=n/2- подобно параллельному колеба­тельному контуру (резонанс токов). В первом случае вибратор питается в пучности тока, а во втором - в узле тока. Наибольшую длину волны, при ко­торой вибратор оказывается настроенным в резонанс с питающим его гене­ратором (Х_вх= 0), называют собственной длиной волны антенны. Как видно из формул (3.20) и (3.21), собственная длина волны симметричного вибратора λ₀=4l. В действительности из-за того, что фазовая скорость распростране­ния в вибраторе несколько меньше скорости света (β> k), резонансные дли­ны вибраторов оказываются несколько меньшими, чем получаемые по фор­мулам (3.20) и (3.21). При этом, чем толще вибратор, тем меньше фазовая скорость и тем короче его резонансная длина. В частности, при l/λ=0,25 и а→0     Х_вх=i42,5 Ом. Обычно стремятся к нулевой реактивной составляющей входного сопротивления вибратора на рабочей частоте. Поэтому длину плеча вибратора делают несколько короче, чем λ/4 или λ/2. Величина укорочения тем больше, чем толще вибратор. Активная составляющая входного сопро­тивления симметричного вибратора при питании вибратора в пучности тока (последовательный резонанс), как следует из формулы (3.20), равна R_вх=R_Σ0=R_Σп.. При определении входного сопротивления симметричного вибратора, питаемого вблизи узла тока, полагая, что αl<<1 (что соответству­ет действительности), можно несколько преобразовать выражение (3.21) и получить следующие формулы:

 

                        R_вх = R_Σп / [sin² kl+ (R_Σп²/W²_A)];                        (3.22)

 

                          Х_вх = - i (W_A/2) [sin2kl/ (sin² kl + (R_Σп²/W²_A))] .                  (3.23)

 

 

В случае параллельного резонанса (kl=180°) получаем

 

                           R_Σ0 = W_A² / R_Σп    и      Х_вх = 0.                       (3.24)

 

Из формулы (3.24) видно, что в случае параллельного резонанса R_Σ0   весьма велико, так как R_Σп ≈200 Ом, a W_A составляет 300 ... 1000 Ом. Фор­мулами (3.22) и (3.23) можно пользоваться наряду с формулой (3.21) для расчета входного сопротивления симметричного вибратора, если 0,35 ≤ l/λ≤0,65. Отметим, что при увеличении волнового сопротивления вибратора за­кон распределения тока по нему становится ближе к синусоидальному.

Поэтому в случае тонких вибраторов (W_A=700...1000 Ом) пределы приме­нимости формулы (3.20) расширяются. Как видно из кривых Рис. 3.8 и 3.9, при уменьшении волнового сопротивления вибратора уменьшается зависи­мость его активного и реактивного входного сопротивления от частоты (улучшаются диапазонные свойства).

 

По аналогии с обычным колебатель­ным контуром можно сказать, что при уменьшении W_A уменьшается доб­ротность вибратора, под которой понимается отношение связанной с виб­ратором реактивной энергии к активной (излученной и теряемой) энергии. Добротность вибратора определяется выражением

 

                                                                 Q_A= A (W_A/R_вх),                                            (3.25)

 

где А - коэффициент пропорциональности.

 

W_A уменьшают, увеличивая размеры по­перечного сечения вибратора. При этом увеличивается распределенная емкость C₁ вибрато­ра.

 

Зависимость R_вх и Х_вх от относительной длины плеча вибраторов реальной толщины приведены на Рис.3.10.

 

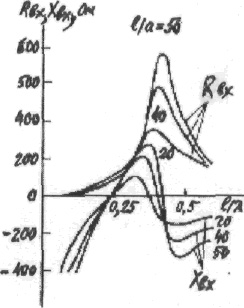
                                                                             Рис.3.10. R_вх и X_вх  реальных вибраторов от величины   l/λ

 

Основные результаты, даваемые строгой теорией симметричного

вибратора

Задача об излучении тонкого симметричного вибратора (электриче­ский радиус вибратора ka < 0,1) в строгой электродинамической постановке была решена Халленом и независимо от него российскими учеными М.А.Леонтовичем и М.Л.Левиным методом интегро-дифференциального уравнения. Как показали расчеты, даже в случае сравнительно тонких вибраторов (ka ≈ 0,05) распределение тока уже несколько отличается от си­нусоидального. Таким образом, метод интегро-дифференциального уравне­ния подтверждает правильность выбора приближенного (синусоидального) закона распределения тока и позволяет найти точное распределение тока в тонких вибраторах. Однако он не позволяет найти закон распределения тока в вибраторах средней (ka= 0,1...0,5) и большой (ka > 0,5) толщины. Кроме того, в рассмотренном методе не учитывается влияние ширины возбуждаю­щего зазора на распределение тока. Входное сопротивление полуволнового вибратора, рассчитанное этим методом, при а→0 оказывается комплексным и равным     Z_вх = 73,1 + i42,5 Ом. Как видно, активная составляющая входно­го сопротивления (R_Σ0) получается такой же, как и по методу вектора Пойнтинга. Реактивная составляющая входного сопротивления имеет индуктив­ный характер. Укорочение ∆l, необходимое для того, чтобы сделать вибра­тор резонансным, определяется по формуле

 

                          ∆l/l = - 0,225/ ln (l/a).                    (3.26)

 

Расчет входного сопротивления полуволнового вибратора с учетом только первого приближения показал, что даже в случае тонких вибраторов величина радиуса заметно, влияет на входное сопротивление.

 

Задача об излучении толстого вибратора (ka>0,5) в строгой постановке была решена Е. Н. Васильевым в 1958-1959 гг. В отличие от методов Халлена или Леонтовича-Левина, где использовались граничные условия для век­торов электрического поля на поверхности вибратора, в методе Васильева используется граничное условие для векторов магнитного поля. Полученное из этого условия интегральное уравнение относительно текущего по вибра­тору тока решается численно при помощи ЭВМ. Решение тем более точно, чем толще вибратор. В дальнейшем Е.Н. Васильевым и Г.Д. Малушковым был разработан более общий метод решения задачи возбуждения осесимметричного тела вращения, позволяющий рассчитать распределение тока на вибра­торах среднего электрического радиуса (ka = 0,1...0,5), что особенно важно для анализа работы вибраторов, применяемых в метровом и особенно в де­циметровом диапазонах волн. Проведенные расчеты показали, что распреде­ление тока в вибраторах средней и большой толщины значительно отличает­ся от синусоидального. Ток на кромке торца имеет конечную величину. В центре торца ток равен нулю. Расчеты показали также, что: 1) с увеличением радиуса цилиндра существенно уменьшается коэффициент отражения от его концов и распределение тока по вибратору приобретает характер бегущей волны: амплитуда тока постепенно уменьшается по мере удаления от точек питания вибратора, фаза тока изменяется примерно по линейному закону; 2) ширина зазора между плечами вибратора значительно влияет на распреде­ление тока вблизи точек питания вибратора. Зависимость распределения то­ка от толщины вибратора влияет на диаграмму направленности последнего. С увеличением толщины вибратора направления нулевого излучения заме­няются направлениями минимального излучения. При этом, чем толще виб­ратор, тем менее глубоки минимумы.

Действительные диаграммы направленности заметно отличаются от рассчитанных приближенным методом при l/а, равном нескольким десяткам.

 

 

 

3.2  Связанные вибраторы

 

 

Направленные свойства системы из двух связанных вибраторов

Одиночные вибраторы применяют только тогда, когда требуется нена­правленное или почти ненаправленное излучение. В тех же случаях, когда необходимо получить однонаправленное излучение или узкие диаграммы направленности применяют антенны, состоящие из двух или нескольких вибраторов, расположенных на небольшом расстоянии (меньше λ) друг от друга. Такие вибраторы заметно влияют друг на друга, поэтому их называют связанными. Взаимодействие связанных вибраторов аналогично взаимодей­ствию связанных колебательных контуров с сосредоточенными постоянны­ми. Поле одного вибратора наводит в другом вибраторе некоторую ЭДС, что эквивалентно изменению сопротивления излучения или входного сопротив­ления вибратора. Поле, создаваемое системой вибраторов, является резуль­татом сложения полей, - создаваемых отдельными вибраторами, с учетом фаз этих полей, определяемых как разностью хода лучей, так и разностью фаз токов в излучателях. Ниже рассматривается работа двух связанных сим­метричных вибраторов. Получаемые при этом результаты нетрудно распро­странить на случай нескольких связанных вибраторов. Выведем формулу для расчета характеристики направленности двух параллельных вибраторов 1 и 2, находящихся на расстоянии d друг от друга (Рис. 3.11), питаемых токами .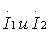

Обозначим 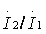                                                                     =q exp(iΨ),                                                                 (3.27)

где q - отношение модулей токов 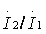;Ψ - сдвиг фазы тока I₂ по отношению к току I₁.

 

                                                                                           

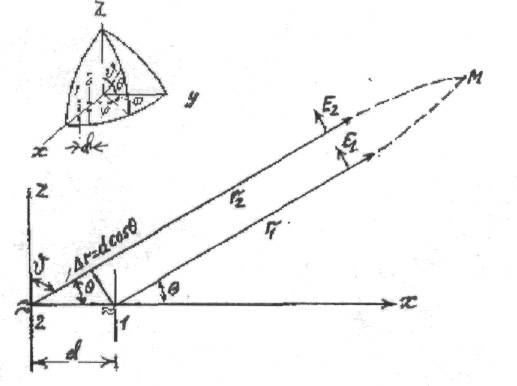
                                                                Рис. 3.11. К определению поля излучения связанных вибраторов

 

Рассмотрим поле в мери­дианальной плоскости вибраторов xoz. Так как расстояние между вибраторами d несоизмеримо мало по сравнению с расстояниями до точки наблюдения (r₁ и r₂), на­правления в точку М можно счи­тать параллельными. Опустив из центра первого вибратора перпен­дикуляр на направление r₂, найдем разность расстояний от 44 вибрато­ров до точки наблюдения,    равную ∆r = d cosθ, где         θ- угол между нормалью к оси вибратора и направлением на точку наблюдения. Обозначим напряженность поля, создаваемого в точке наблюдения первым вибратором, через E₁. Выразим напряженность поля второго вибратора в точке наблюдения М через напряженность поля первого вибратора, приняв ее фазу в точке наблюдения за нулевую. Так как напряженность, создаваемо­го вибратором, поля пропорциональна току в вибраторе и влиянием разности расстояний от вибратора до точки наблюдения на амплитуду напряженности поля можно пренебречь, то 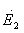= E₁q exp(-ikdcosθ) exp(iΨ), где kd cosθ- сдвиг фаз полей из-за разности хода лучей (пространственный сдвиг фаз). Найдем суммарное поле, создаваемое обоими вибраторами в данной точке

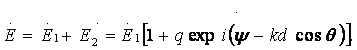                                 (3.28)

 

На основании формулы (3.7) и с учетом того, что угол 0 является дополнительным по отношению к углу 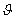, запишем

 

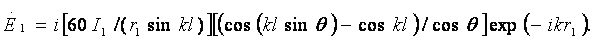
Обычно интересуются величиной напряженности суммарного поля, а не ее фазой. Поэтому, переходя к модулю выражения (3.28), получаем

 

     E = (60I_П1 / r) [(cos (klsinθ) - coskl) / cosθ] 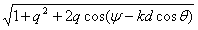       (3.29)

 

 

                                  

                                                                           

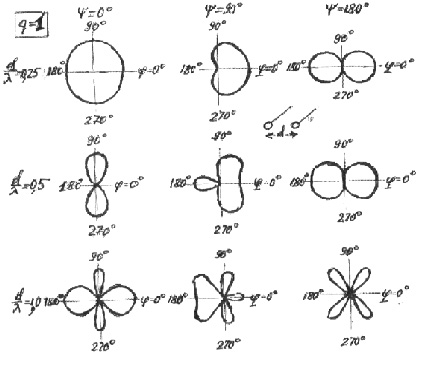
Рис. 3.12. ДН связанных вибраторов для разных значений Ψ и d/λ, при q=1

Как видно из формулы (3.29), амплитудная характеристика направленности системы из двух связанных вибраторов определяется двумя множителями. Первый множитель f₁(θ) представляет собой характеристику направленности симметричного вибратора, находящегося в свободном пространстве. Второй множитель f_c(θ) учитывает наличие второго вибратора; он зависит от рас­стояния d между вибраторами, от отношения амплитуд токов в вибраторах q и от сдвига фаз токов в вибраторах Ψ. Этот множитель называют множителем системы. В экваториальной плоскости направленные свойства данной системы определяются только множителем системы, так как одиночный симметричный вибратор в этой плоскости (θ= 0°) не обладает на­правленными свойствами. Напряженность суммарного поля в экваториаль­ной плоскости определяется выражением

                                               Е = А (1- coskl) .                               (3.30)

В зависимости от величин d/λ, q и Ψ диаграммы направленности могут иметь различную форму (Рис.3.12), При увеличении расстояния между вибраторами (начиная от d/λ = 0,5) диаграмма направленности приобретает многолепестковый характер; чем больше d/λ, тем больше лепестков. Особенно важен случай однонаправленного излучения. Пусть токи в вибраторах одинаковы по величине       (q = 1). Тогда формулу (3.30), воспользо­вавшись формулой для косинуса двойного угла, можно привести к виду

                                                                        Е = 2А (1 - cos kl) cos [Ψ/2 - (kd/2) cosφ]                                       (3.31)

Положим теперь, что Ψ=± 90° и расстояние между вибраторами d =λ/4. При этом формула (4.5) принимает вид  Е = 2А (1 - cos kl) cos (±45° - 45°cosφ).

Множитель f(φ) = cos(±45°- 45°cosφ) описывает кардиоиду.  ПриΨ= + 90° и φ= 0° этот множитель обращается в единицу; при φ=180° он обращается в нуль. Таким образом, в направлении φ= 0° напряженность по­ля удваивается (по сравнению с полем одиночного вибратора, возбуждаемо­го током, одинаковым с текущим по одному из связанных вибраторов). Это увеличение в одном направлении происходит за счет уменьшения поля в других направлениях. При Ψ = - 90° напряженность поля удваивается в об­ратном направлении (φ=180°); поле равно нулю в направлении φ=0°.

Поясним эти результаты. Если ток во втором вибраторе опережает по фазе ток в первом вибраторе, то в точке наблюдения, находящейся в направ­лении φ= 0°, поля от обоих вибраторов складываются в фазе, так как сдвиг фаз за счет несинфазности возбуждающих токов (Ψ= 90°) компенсируется пространственным сдвигом фаз (Ψ_р= kd = (2π/λ)(λ /4)= 90°). Этот сдвиг фаз берется со знаком минус, так как второй вибратор находится дальше от точ­ки наблюдения, чем первый. В обратном направлении (φ= 180°) множитель f(φ) обращается в нуль, потому что в этом направлении поля от первого и второго вибраторов складываются в противофазе и компенсируют друг дру­га, так как Ψ_рез=Ψ+ Ψ_р=180°. Если ток во втором вибраторе отстает по фазе на 90° от тока в первом вибраторе (Ψ= - 90°), то получается обратная карти­на. В первом случае (Ψ= 90°) второй вибратор усиливает излучение в на­правлении на первый вибратор. Во втором случае (Ψ= -90°) он усиливает излучение в обратном направлении и ослабляет излучение в направлении первого вибратора. Вибратор, усиливающий излучение в направлении на другой вибратор и ослабляющий излучение в обратном направлении, называется рефлектором (отражате­лем). Чтобы рефлектирующее действие вибратора было полным (в одном на­правлении поле увеличивается, а в противоположном - равно нулю), в рас­сматриваемом случае (d =λ/4) токи в обоих вибраторах должны быть равны по величине (q = 1), а ток в рефлекторе должен опережать ток во втором свя­занном вибраторе на 90°. Вибратор, ослабляющий излучение в на­правлении на другой вибратор и усиливающий излучение в противополож­ном направлении, называется директором (направителем). В идеальном слу­чае директор должен работать в режиме: q=l; Ψ= -π/2  (при d = λ/4). Отметим, что в обоих случаях напряженность поля увеличивается в направлении отставания фазы возбуждающего тока. Получить однонаправ­ленное излучение можно и при расстояниях между вибраторами, отличных от  λ/4. Как видно из формулы (3.31), условие отсутствия излучения в направ­лении φ = 180° можно записать в виде Ψ +kd = 180°. Для выполнения этого условия при d < λ/4 угол сдвига фаз у должен быть больше 90°. Хотя диа­грамма направленности при этом оказывается однонаправленной, и макси­мум излучения лежит в направлении φ = 0°, однако напряженность поля в этом направлении не удваивается. Чем ближе друг к другу расположены виб­раторы, тем меньшая напряженность поля получается в направлении макси­мального излучения (считая, что при изменении d величина тока в вибрато­рах постоянна).

 

Возбуждение каждого из двух связанных вибраторов токами, сдвину­тыми по фазе, усложняет систему питания. Поэтому в большинстве случаев вибраторы, выполняющие роль рефлекторов или директоров, не содержат источников питания (генераторов), т.е. являются пассивными. Они возбуж­даются электромагнитным полем активного (питаемого) вибратора. В случае пассивных вибраторов не удается осуществить режим, обеспечивающий пол­ное рефлекторное или директорное действие, так как не удается получить со­вместно q = 1 и Ψ = 90°. Поэтому не получается полного удвоения поля в главном направлении и нуля поля - в обратном.

 

 

Расчет сопротивления излучения и входного сопротивления связанных вибраторов методом наведенных ЭДС

Сущность метода наведенных ЭДС

Полное сопротивление излучения одного из связанных вибраторов Z_Σ1 состоит из двух частей: собственного сопротивления Z_Σ11, т.е. сопротивле­ния, которым обладает данный вибратор в свободном простран­стве, и сопротивления, наведенного электромагнитным полем второго вибратора Z_Σ12^нав. Таким образом, Z_Σ1= Z_Σ11 + Z_Σ12^нав и                                Z_Σ2= Z_Σ22 + Z_Σ21^нав.

Полное сопротивление излучения связанного вибратора можно найти методом наведенных ЭДС. Идея этого метода была предложена незави­симо друг от друга в 1922 г. российским ученым Д.А.Рожанским и францу­зом Бриллюэном. Непосредственно к расчету антенн этот метод применен И.Г.Кляцкиным, А.А.Пистолькорсом и В.В.Татариновым.

 

Метод наведен­ных ЭДС позволяет находить наведенные и собственные сопротивления вибраторов, а также амплитуды и фазы токов в пассив­ных вибраторах. Сущность данного метода такова. Рассмотрим    два      связанных      произвольно ориентирован­ных друг относительно друга симметричных вибратора. Поле второго вибратора может создать у по­верхности бесконечно малого элемента dz первого виб­ратора составляющую, параллельную оси этого вибра­тора (тангенциальную составляющую), E_z12, вследствие чего в элементе dz возникает (наводится) ЭДС                 dЭ₁₂ = E_z12dz.

Однако при этом нарушаются граничные условия, согласно которым на поверхности идеального проводника тангенциальная составляющая на­пряженности электрического поля равна нулю. Для выполнения граничных условий в элементе dz должна появиться ЭДС –dЭ₁₂, компенсирующая ЭДС dЭ₁₂. Вблизи поверхности элемента dz появляется тангенциальная состав­ляющая напряженности электрического поля -E_z12, равная по величине и противоположная по фазе тангенциальной составляющей наведенного поля E_z12. Вследствие этого тангенциальная составляющая напряженности суммарного электрического поля у поверхности элемента dz обращается в нуль и граничное условие выполняется. Появление тангенциальной состав­ляющей напряженности поля - E_z12 говорит о том, что под влиянием поля второго вибратора происходит перераспределение поля первого вибратора. ЭДС –dЭ₁₂ создается генератором, включенным в первый вибратор. Энергия, затрачиваемая генератором для создания этой ЭДС в элементе dz, переходит в энергию электромагнитного поля. Если известны ЭДС, возникающая на поверхности элемента dz, и ток в этом элементе I_z1 можно определить мощность dP_Σ12, затрачиваемую генератором первого вибратора (под действием поля второго вибратора), на создание поля, компенсирующе­го тангенциальную составляющую напряженности электрического поля вто­рого вибратора на поверхности данного элемента. При этом ток в элементе dz и составляющая E_z12 на поверхности этого элемента могут иметь различ­ные фазы. Считается, что закон распределения тока по одному из связанных вибраторов в результате действия поля другого вибратора не изменяется и является синусоидальным.

Полная мощность, расходуемая генератором первого вибратора на соз­дание в окружающем пространстве электромагнитного поля, тангенциальная составляющая напряженности электрического поля которого компенсирует на всей поверхности вибратора тангенциальную составляющую напряженно­сти электрического поля, создаваемого током второго вибратора

 

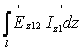                         P_Σ12 = - (1/2).                        (3.32)

Итак, мощность, отдаваемая генератором первого вибратора под дей­ствием поля второго вибратора, определяется током, текущим по первому вибратору, и тангенциальной составляющей напряженности электрического поля, создаваемого вторым вибратором вблизи первого. Ее активная часть представляет собой излученную мощность. Реактивная часть характеризует электромагнитное поле, колеблющееся вблизи вибратора. Выражение (3.32) математически формулирует метод наведенных ЭДС.

Расчет взаимных и собственных сопротивлений связанных  вибраторов

Для того чтобы определить сопротивление, наведенное на первый виб­ратор вторым, нужно знать закон распределения тока в первом вибраторе, его комплексную амплитуду в пучности и тангенциальную составляющую напряженности электрического поля, создаваемого вторым вибратором у по­верхности первого. Активная составляющая наведенного сопротивления R_Σ12^нав характеризует активную мощность, излучаемую первым вибратором под действием поля второго. Реактивная составляющая наведенного сопротивления X_Σ12^нав характеризует мощность электромагнитного поля, связан­ного с вибратором, возникающего также под действием поля второго вибра­тора.

Наведенное сопротивление рассчитать значительно проще в частном случае, когда связанные вибраторы имеют одинаковую длину, оси их парал­лельны и токи в них имеют одинаковую величину и фазу. Очевидно, что в этом случае сопротивление, наведенное первым вибратором на второй, равно сопротивлению, наведенному вторым вибратором на первый.

В этом частном случае наведенное сопротивление называется взаимным (Z₁₂). При известном взаимном сопротивлении двух вибраторов весьма про­сто рассчитать наведенное сопротивление, если задано соотношение токов в вибраторах. Вза­имное сопротивление является функцией вели­чин l/λ, d/λ и h/λ, т.е. определяется исключи­тельно геометрическими размерами системы. Оно аналогично сопротивлению связи двух ко­лебательных контуров c сосредоточенными па­раметрами и определяется по таблицам и гра­фикам. Таблицы для определений активной составляющей (R₁₂) взаимного сопротивления полуволновых вибраторов рассчитаны А.А.Пистолькорсом в 1928 г., а для реактивной составляющей (Х₁₂) - В.В.Татариновым в 1936 г.

   

                                                                                               

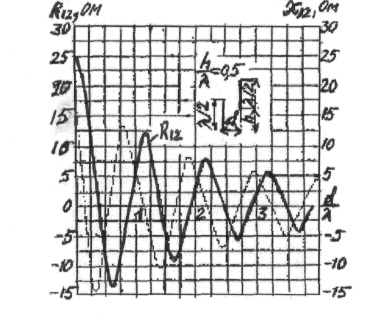
                                                                                            Рис.3.13. Графики взаимных сопротивлений

Графики, изображающие зависимости R₁₂ = f(d/λ) и X₁₂ = f (d/λ) при h/λ= const, представлены на Рис.3.13. Имеются также графики, позволяющие оп­ределять взаимные сопротивления вибраторов, длина которых отличается от полуволны. Как видно из Рис.3.13, активная и реактивная составляющие вза­имного сопротивления в зависимости от относительного расстояния между вибраторами d/λ принимают как положительные, так и отрицательные значе­ния и при некоторых значениях d/λ проходят через нуль. Такой ход кривых взаимных сопротивлений объясняется изменением фазы наведенной ЭДС при изменении расстояния между вибраторами. Если фаза наведенной ЭДС равна или противоположна фазе текущего по вибратору тока, то взаимное сопротивление является чисто активным. Если фаза наведенной ЭДС отлича­ется от фазы текущего по вибратору тока на π/2, то взаимное сопротивление является чисто реактивным. Активная составляющая взаимного сопротивле­ния может быть положительной или отрицательной; R₁₂ отрицательно в тех случаях, когда под действием поля второго вибратора мощность поля, излу­чаемого первым вибратором, уменьшается (при неизменном токе в первом вибраторе).

Метод наведенных ЭДС может быть применен также для определения собственного сопротивления излучения вибратора. Формула для расчета R_Σ11 совпадает с формулой (3.13) для расчета R_Σп, полученной методом вектора Пойнтинга, т.е. R_Σ11 = R_Σп .Это понятно, так как при расчете сопротивления излучения методом вектора Пойнтинга также, как и в данном случае, исходят из синусоидального распределения тока.

Формула для расчета X_Σ11 имеет вид

 

                                           X_Σ11 = X_Σп = 30[2Si 2kl + sin 2kl (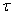+ lnkl +Ci 4kl - 2Ci 2kl -2ln (l/a)) +
                                                                          + cos 2kl (- Si 4kl + 2Si 2kl)].                                          (3.33)

 

Результаты, полученные по методу наведенных ЭДС, тем более точны, чем тоньше вибратор.

                     

Расчет наведенного и полного сопротивлений излучения

Пусть имеются два активных связанных вибратора, токи, в которых не равны ни по амплитуде, ни по фазе. Требуется найти полное сопротивление излучения каждого вибратора. Заменим связанные вибраторы эквивалентной схемой, состоящей из двух связанных колебательных контуров с сосредото­ченными параметрами (Рис.4.7). Каждый контур содержит генератор высо­кой частоты, сопротивления Z₁₁ или Z₂₂, равные собственным сопротивлени­ям вибраторов, и наведенные сопротивления Z_Σ12^нав и Z_Σ21^нав  которые   неизвестны. Напряжение генератора, включенного в связанный контур, компен­сирует падение напряжения на собственном сопротивлении контура и на со­противлении связи. Учитывая это, запишем уравнения Кирхгофа для данной эквивалентной схемы, считая, что сопротивления связи (взаимные сопротив­ления) известны. Эти уравнения имеют вид:

 

                                             U_п1= I_п1Z_Σ11 + I_п2Z₁₂;                   (3.34)

                              U_п2=I_п2 Z_Σ22+I_п1Z₂₁.              (3.35)

 

Здесь U_п1 и U_п2 - напряжения первого и второго генераторов, пересчи­танные к точкам пучности тока в вибраторах. Данные уравнения позволяют при заданных напряжениях U_п1 и U_п2 и известных собственных и взаимных сопротивлениях определить токи в вибраторах. Полагая, что токи в вибрато­рах найдены, определим наведенные сопротивления. Пусть I_п1 / I_п2 =qexp(iΨ). Перепишем уравнения (3.34) и (3.35), вынося за скобки в уравнении (3.34) вели­чину I_п1, а в уравнении (3.35) величину I_п2 и учитывая, что Z₁₂ = Z₂₁

                              U_п1= I_п1 [Z_Σ11 + q exp (iΨ) Z_I2];               (3.36)

                              U_п2= I_п2 [Z_Σ22+ (l/ q) exp (-iΨ) Z₁₂].       (3.37)

 

Разделив уравнение (3.36) на I_п1, а уравнение (3.37) на I_п2, получим вы­ражения для полных сопротивлений контуров (вибраторов):

 

                U_пl/ I_п1= Z_Σ1 = R_Σ1 + i X_Σ1= Z_Σ11+ q exp (iΨ) Z₁₂ ;         (3.38)

            U_п2/ I_п2 = Z_Σ2 = R_Σ2+ i X_Σ2= Z_Σ22 + (1/q) exp (-iΨ) Z₁₂.     (3.39)

 

Так как полное сопротивление излучения вибратора равно сумме соб­ственного и наведенного сопротивлений излучения, то наведенные сопро­тивления вибраторов равны:

              Z_Σ12^нав = R_Σ12^нав + i X_Σ12^нав = q exp (iΨ) (R₁₂ + i X₁₂);            (3.40)

                    Z_Σ21^нав  = R_Σ21^нав + i X_Σ21^нав = (1/q) exp (-iΨ) (R₁₂ + i X₁₂).          (3.41)

 

 

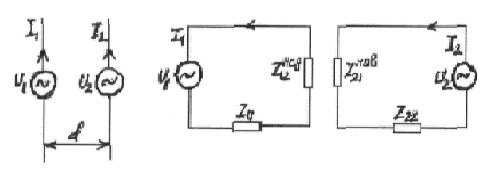
  Рис.3.14. Эквивалентная схема связанных вибраторов

 

Таким   образом,   если известно  взаимное сопротивление вибраторов (оно зависит только от  относительных  геометрических размеров системы     l/λ,      d/λ,     h/λ, и определяется по  таблицам или по графикам) и известны    отношения амплитуд  токов q и сдвиг  фаз токов в вибраторах Ψ, то наведенное сопротивление определяется весьма просто. Полная мощность, излучаемая двумя связанными вибраторами, равна              .

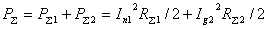Входные сопротивления связанных вибраторов могут быть рассчитаны по формулам, применяемым при инженерном расчете входного сопротивления. В случае коротких вибраторов (расстояние от точек питания до узла тока не менее 0,15λ) входное сопротивление связанного вибратора можно определить по формуле

 

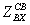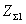                                                          =/sin²k/ или 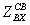=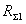/sin²kl+i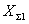/sin²k l,                       (3.42)

 

где 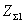- полное сопротивление излучения связанного вибратора.

 

В случае длинных вибраторов (расстояние от точек питания до минимума тока меньше 0,15λ) входное сопротивление связанного вибратора рассчитывается по формуле, аналогичной (3.21)

                      

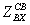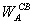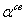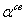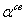                                                              = [(sh2 l - (/k) sin2k l) / (ch2 l - cos2k l)] -

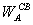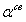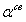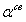                                                                                                                                      - i  [((/k) sh2l + sin2kl) / (ch2l - cos2kl)].                           (3.43)

 

В данной формуле учтено влияние одного вибратора на волновое сопротивление другого вибратора и на его коэффициент затухания.

Здесь 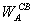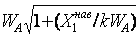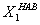₌, -реактивное наведенное сопротивление, приходящееся на единицу длины вибратора, определяемое по формуле                  

                                                     

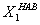                                                                                                                       = 2 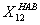/[l(1- (sin2kl / 2kl))];

                                         

 

Расчет тока в пассивных вибраторах

Пассивные вибраторы широко применяются для создания однонаправленного излучения в качестве рефлекторов и директоров. Чтобы вибратор играл роль рефлектора или директора, ток в нем должен иметь определенную величину и фазу по отношению к току в активном вибраторе (в идеальном случае при расстоянии между вибраторами d= λ/4 должны выполняться условия q = 1 и Ψ = ±90°). Величины q и ψ для пассивного вибратора зависят от расстояния между пассивным и активным вибраторами и от величин активного и реактивного сопротивлений пассивного вибратора. Эти величины можно регулировать, изменяя реактивное сопротивление пассивного вибратора.

 

 

 

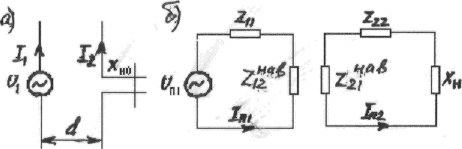
Рис. 3.15. Эквивалентная схема связанных вибраторов, один из которых пассивный

 

 

Рассчитаем вели­чины q и Ψ. Заменим два связан­ных  симметричных вибратора, из
которых один пассивный с вклю­ченным в его середину сопротив­лением настройки Х_н0 (Рис.3.15.а), эквивалентной схемой (Рис.3.15.б).

 

Уравнения Кирхгофа для этой системы имеют вид:

                                               

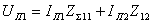                                                                                                                                               (3.44)

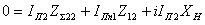                                                                                                   .                                                      (3.45)

 

где 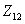 - взаимное сопротивление вибраторов; Х_н - реактивное сопротивле­ние настройки, включенное в пассивный вибратор и отнесенное к пучности тока.

 

Можно считать известными ток в активном вибраторе 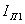, а также соб­ственные 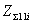,  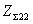и взаимное 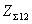сопротивления, поскольку относительная длина вибраторов l/λ и относительное расстояние между вибраторами d/λ заданы. Задано также сопротивление настройки. Таким образом, в уравнени­ях (3.44) и (3.45) неизвестен только ток во втором вибраторе (I₂), который определяется из уравнения (3.45) I_п2 = -I_П1[(Z₁₂/(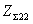 + iX_H)).

Ранее было обозначено .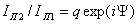

 

Поэтому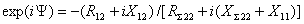. Отсюда модуль отношения токов

                                                                                                            

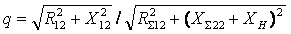                                                                                .                                         (3.46)

 

Относительная фаза тока в пассивном вибраторе

                                

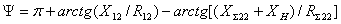                                                                                                .                                                (3.47)

 

Входящие в формулы (3.46) и (3.47) сопротивления 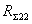, , 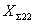R₁₂ и Х₁₂ отнесены к пучности тока. Сопротивление X_но пересчитывается к пучности тока в случае короткого вибратора по формуле .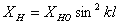

В случае длинного вибратора такой пересчет можно сделать по форму­ле, учитывающей распределение тока по закону гиперболического синуса 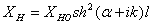, где α- коэффициент затухания, без учета влияния активно­го вибратора.

 

В случае пассивного вибратора величины q и Ψ взаимозависимы. При изменении Х_н меняются одновременно обе эти величины. Поэтому добиться одновременно нужных значений q и Ψ для пассивного вибратора невозмож­но. Пассивный вибратор обычно настраивают так, чтобы получить макси­мальный коэффициент защитного действия. Получаемые при этом величины q и Ψ отличаются от соответствующих величин в идеальном случае (q = 1, Ψ = 90°), и поэтому максимальное защитное действие обычно получается не больше 10...20. Ток в пассивном рефлекторе должен опережать  по   фазе   ток   в   активном вибраторе. Анализ формулы (3.47) показывает, что пассивный вибратор будет играть роль рефлектора в том случае, когда его полное реактивное сопротивление (собственное плюс сопротивление настройки)  имеет индуктивный характер. Этот вывод справедлив, если 0,1λ ≤ d ≤ 0,25λ.

 

Для получения оптимального рефлекторного действия расстояние между рефлектором и активным вибра­тором следует брать примерно (0,15...0,25)λ, а реактивное положительное сопротивление - приблизительно 10...50 Ом. Ток в пассивном директоре должен отставать по фазе от тока в активном вибраторе. Из анализа формулы (3.47) следует, что для работы пассивного вибратора в режиме директора при 0,1λ ≤ d ≤ 0,25λ его полное реактивное сопротивление должно быть отрица­тельным, т.е. должно иметь емкостный характер. В коротковолновом диапа­зоне пассивные вибраторы обычно настраивают, включая в середине вибра­тора настроечное реактивное сопротивление в виде отрезка короткозамкнутой двухпроводной линии, длину которой можно регулировать передвижным короткозамыкателем. В диапазонах метровых и дециметровых волн настро­ечное сопротивление обычно не применяется. Пассивный вибратор настраи­вается изменением его длины. Чтобы пассивный вибратор работал в качестве рефлектора, его полная длина должна быть несколько больше λ/2 (входное сопротивление разомкнутой на конце двухпроводной линии, длина которой больше λ/4, имеет индуктивный характер). Чтобы пассивный вибратор рабо­тал в качестве директора, его полная длина должна быть несколько меньше λ/2. Величина необходимого удлинения или укорочения определяется рас­стоянием между вибраторами и их толщиной.

 

 

 

 

3.3  Антенные решетки с поперечным излучением

Плоская антенная решетка. Равномерная линейная антенная решетка

Пусть имеется ряд из n симметричных вибраторов, одинаковым обра­зом ориентированных в пространстве. Расстояние между центра­ми соседних вибраторов равно d₁. Линейной решеткой называется система идентичных излучателей, центры излучения которых расположены на пря­мой, называемой осью решетки. Будем считать, что токи во всех элементах решетки имеют одинаковую величину (I₁=I₂=…I_n = I), фаза же тока в каж­дом последующем вибраторе данного ряда отстает от фазы тока в предыду­щем на величину Ψ. Таким образом, I₂ = Iexp(-iΨ)...I_n = Iexp [-i (n-l)Ψ]. Следо­вательно, вдоль каждого ряда вибраторов фаза возбуждающего тока изменя­ется по линейному закону.

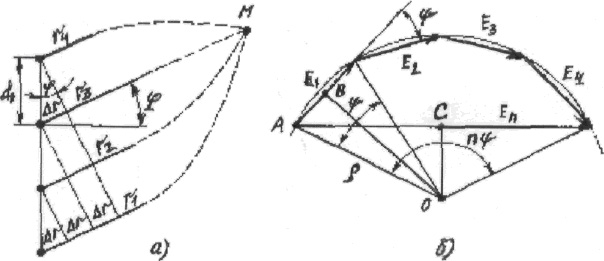
Рис.3.16. К определению множителя решетки поперечного излучения

Рассмотрим вначале линейную систему из n ненаправленных излуча­телей, расположенных на равных расстояниях друг от друга, возбужденных токами, равными по амплитуде. Такая система вибраторов называется экви­дистантной равноамплитудной решеткой. Пусть фаза тока в каждом после­дующем вибраторе отстает на угол Ψ по отношению к току предыдущего. На большом удалении от антенны в точке М, когда d₁<<r, лучи от отдельных вибраторов можно считать параллельными. Поле в точке М (Рис.3.16.а), соз­данное вибратором 1, обозначим через E₁. В равноамплитудной решетке ам­плитуды поля, созданные различными вибраторами на большом удалении, можно принять равными амплитуде поля первого вибратора, но фазы этих полей будут различными. Поле Е₂ вибратора 2 за счет разности хода лучей r будет опережать поле вибратора 1 по фазе на угол k∆r = kd₁sinφ и отставать на угол Ψ за счет питания. Результирующий сдвиг по фазе между полями, созданными вибраторами 1 и 2 равен Ф = kd₁sin(φ-Ψ). Этот сдвиг по фазе будет и для полей, созданных любыми соседними вибраторами. На Рис.3.16.б приведено графическое сложение полей отдельных вибраторов, сдвинутых по фазе друг относительно друга на угол Ф.

 

Векторы полей образуют часть правильного многоугольника, замыкающая сторона которого Е_n равна результирующей напряженности поля, созданной всеми вибраторами в точке М. Перпендикуляры, восстановленные из сере­дин сторон (векторов Е) правильного многоугольника, пересекутся в одной точке 0, являющейся центром описанной окружности радиуса ρ. Для тре­угольников ОАВ и ОАС можно записать

                        

                                                                sin (Ф/2) = АВ/ρ = Е₁/2ρ и sin (nФ/2) = АС/ρ = Е_n/2ρ.

 

Поделив одно уравнение на другое, получим

 

                                                        Е_n/Е₁= sin (0,5 nФ)/sin(0,5Ф) или Е_n = Е₁f_с (φ),

где Ф = kd₁sinφ-Ψ;

f_c(φ) = sin (0,5 nФ)/sin(0,5Ф) = sin[0,5 n(kd₁sinφ -Ψ)]/ sin[0,5(kd₁sinφ -Ψ)]                      (3.48)

 

Здесь рассматривалась решетка, состоящая из ненаправленных излуча­телей. Если линейную решетку составить из направленных излучателей, на­пример, симметричных вибраторов, то поле Е₁ созданное каждым вибрато­ром, определится его направленными свойствами f₁(φ) и результирующая характеристика направленности будет равна

 

                                           f (φ) = f₁ (φ) f_c (φ).                       (3.49)

 

На основании выражения (3.49) может быть сформулирован общий принцип умножения характеристик направленности: характеристика на­правленности системы (антенной решетки) однотипных излучателей пред­ставляет собой произведение характеристики направленности одного эле­мента данной системы на множитель системы.

При большом числе вибраторов n множитель системы при изменении угла φ изменяется, значительно быстрее, чем множитель f₁(φ). Это объясня­ется тем, что величина nkd₁/2 значительно больше величины kl. Поэтому ха­рактеристика направленности решетки, в основном, определяется множите­лем системы. Поскольку множитель системы sin(nu)/sin(u) является перио­дической функцией, то при изменении угла φ этот множитель может обра­щаться в нуль, затем он возрастает, достигая максимального значения, далее уменьшается, снова становится равным нулю и т.д. Поэтому можно утвер­ждать, что диаграмма направленности решетки имеет многолепестковый ха­рактер.

 

Синфазная решетка

Широкое практическое применение находят антенные решетки с оди­наковыми по амплитуде и фазе токами в вибраторах (равноамплитудные синфаз­ные решетки). Полагая в формуле (3.48) Ψ=0⁰, получим формулу для характе­ристики направленности, такой решетки из т рядов в плоскости E

 

                                                                      E= (m60I_п/r) [(cos (klsinφ) -coskl)/ соsφ] *

*sin [(n/2) (kd₁sinφ)]/sin [(l/2) (kd₁sinφ)].                              (3.50)

 

Напряженность, излучаемого антенной, поля максимальна в направле­нии φ=0° (главный максимум), т.е. в экваториальной плоскости антенны. Каждый из вибраторов в этом направлении излучает с максимальной интен­сивностью, если l/λ≤0,7; множитель f₁(φ) в этом случае равен 1 - coskl. Поля от отдельных вибраторов в направлении φ=0⁰ синфазны и складываются арифметически, так как в направлении нормали к осям вибраторов разность расстояний до точки наблюдения равна нулю. Выражение множителя сис­темы в этом случае представляет собой неопределенность вида 0/0 , при рас­крытии которой по правилу Лопиталя оказывается, что множитель системы максимален и равен n. Таким образом, в данном случае выражение (3.50) принимает вид Е_mах= nЕ_1mах. Здесь n - число симметричных вибраторов в решет­ке. Такой же вид принимает выражение (3.50) и при φ=180⁰. Как следует из формулы (3.50), нормированная характеристика направленности определяется выражением

 

                                                F (φ) = (Е/Е_макс) = [(cos (klsinφ) - coskl) / соsφ (1- coskl)] *
                                                          *sin [(n/2) (kd₁sinφ)]/ {[nsin (l/2) kd₁sinφ)]}.              (3.51)

 

При некоторых значениях угла φ сдвиг фаз между полями соседних вибраторов, равный kd₁sinφ, становится таким, что в результате интерферен­ции полей от всех вибраторов суммарное поле обращается в нуль. Направле­ния, в которых отсутствует излучение, определяются из условия равенства нулю числителя множителя системы, т.е. (nkd₁/2)sinφ₀ = N, откуда sin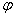₀ = Nλ/(nd₁), N = 1, 2, 3, ... . Так как синус всегда меньше единицы, то чем больше знаменатель, тем больше направлений нулевого излучения (N) имеет диаграмма направленности. Следовательно, чем больше число вибра­торов п (точнее, чем больше относительный размер nd₁/λ решетки), тем больше лепестков в диаграмме направленности. Направления нулевого из­лучения рассчитываются по формуле

 

                     φ₀=arcsin [Nλ/ (nd₁)], где N= 1, 2, 3, ...                    (3.52)

 

Направления максимумов боковых лепестков приближенно можно найти из условия максимума числителя множителя системы, так как знаме­натель этого множителя при kd₁<<nkd₁ (т.е. при большом числе вибраторов) с изменением угла φ изменяется значительно медленнее числителя. Это ус­ловие записывается в виде sin[(nkd₁/2)sinφ_max] = ±1, откуда   nu=(nkd₁/2)sinφ_max = (2N+l)π /2,   N= 1,2,3,...

 

Направления максимумов боковых лепестков рассчитываются по формуле

 

                φ_max = arcsin [(2N+l)λ / (2nd₁)], где N= 1,2,3, ...        (3.53)

 

На Рис.3.17 приведены диаграммы направленности синфазной решетки (в плоскости Е) для разного количества симметричных полуволновых вибраторов и расстояния между ними. Ближайшее к главному максимуму направление нулевого излучения определяют по формуле sinφ₀ = λ/(nd₁).

Следовательно, главный лепесток диаграммы направленности заключен в угле, равном 2φ₀. Как видно из формулы главный лепесток диаграммы на­правленности тем уже, чем больше вибраторов в одном ряду, или чем боль­ше относительная длина антенны nd₁/=L/λ.

                                                                                          

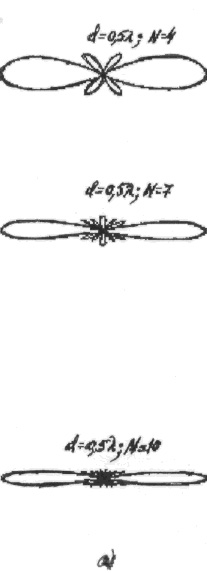
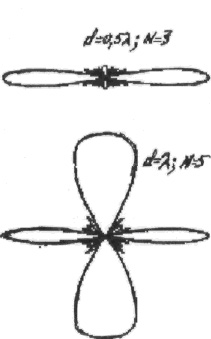
                                                                                            Рис. 3.17. ДН синфазных антенных решёток

                                                                                                                     2φ₀ = 2(λ/nd₁), рад    или    2φ₀ ≈115°λ/nd₁.                     (3.54)

 

В случае равномерной синфазной решетки ширину диаграммы направ­ленности по половинной мощности можно определить по приближенной формуле

 

                                                                 2φ_{0,5 ≈}0,89(λ/nd₁), рад    или    2φ_0,5≈ 51⁰ λ/nd_1.                 (3.55)

 

Симметричный вибратор с относительной длиной l/λ = 0,5 имеет ширину диаграммы направленности шириной по половинной мощности 44°. Для того чтобы сузить диаграмму направленности до 6,4°, т.е. примерно в 7 раз, надо приме­нить 8 синфазных симметричных вибраторов, т.е. увеличить размер антенны примерно в 8 раз.

 

Направленные свойства антенны характеризуются не только шириной главного лепестка диаграммы направленности, но и уровнем боковых лепе­стков

 

                                                  ζ_N= l/nsin {[(2N+l)/n)] (π/2)}.                                                 (3.56)

 

При большом значении n (аргумент синуса мал) можно перейти к сле­дующей приближенной формуле для расчета первых двух боковых лепестков ζ_N= 2/[(2N+l)π]. В этом случае уровень первого бокового лепестка ζ₁=2/3π ≈ 0,21. Уровень второго бокового лепестка составляет примерно 0,13. Уровень первого бокового лепестка в децибелах составляет примерно -13,3 дБ. Отметим, что два главных максимума        (при φ=0° и φ=180°) или два главных лепестка в диаграмме направленности получаются только при d₁<λ. При d₁ ≥λ возможно одновременное обращение в нуль числителя и знамена­теля множителя системы при некоторых значениях углов φ, не равных 0° и 180°. Это происходит при выполнении условия (kd₁sinφ)/2 = Nπ или kd₁sinφ = 2Nπ, т.е. в том случае, когда сдвиг фаз между полями соседних вибраторов равен или кратен 2π. При этом множитель системы, как и в случаях φ=0° и φ=180°, имеет наибольший максимум, равный n. Это приводит к появлению в диаграмме направленности антенны, кроме боковых лепестков дополни­тельных (вторичных) боковых лепестков. Уровень этих лепестков тем боль­ше, чем шире диаграмма направленности одного элемента решетки. Он ра­вен единице, если элементы не обладают направленными свойствами.

 

Так как симметричный вибратор не обладает направленными свойст­вами в экваториальной плоскости, то характеристика направленности син­фазной решетки в плоскости H определяется только мно­жителем системы, который совершенно аналогичен этому множителю для плоскости E. Ширину диаграммы направленности, на­правления максимумов боковых лепестков и их уровень определяют по фор­мулам, полученным для плоскости вектора Е решетки, заменяя в них угол 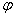  углом 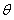. Чем больше рядов m в синфазной решетке, тем уже ее диаграмма направленности в плоскости H. КНД синфазной решетки в направлении максимального излучения может быть рассчитан по формуле

            

                                D = (120/ R_Σполн) (mn)² (1-coskl)²,                 (3.57)

 

где R_Σполн - полное сопротивление излучения антенны.

 

Заметим, что при d₁=>0, d₂=>0, n=>∞, m=>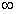 но при nd₁= const = b и md₂ = const = а, где а и b – разме­ры излучающей системы в плоскостях Н и Е соответственно, с помощью предельного перехода можно перейти от формул характеристик направлен­ности антенных решеток к формулам характеристик направленности систем с непрерывным распределением возбуждающих источников (излучающих поверхностей). При а >>λ,    b >>λ и небольших расстояниях между излучате­лями (d₁ < 0,07λ) характеристики направленности обеих систем практически совпадают.

 

 

 

 

 

Управление диаграммой направленности равномерной

линейной  решетки

Выясним направленные свойства линейной равномерной решетки. Как видно из выражений (3.48) и (3.51), множители системы равноамплитудной эквивалентной линейной и равноамплитудной эквидистантной синфазной решеток идентичны и отличаются только аргумен­тами синусов. Однако в случае равноамплитудной эквидистантной линейной решетки множитель системы максимален и равен п при условии u = 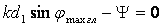. При этом поля от всех элементов антенны в точке наблюдения, характеризуются углом 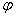_mах, имеют одинаковую фазу, так как сдвиг фаз из-за несинфазности возбуждения Ψ компенсируется пространственным сдвигом фаз  Ψ_p = kd₁ sinφ. Из множителя системы, получаем

 

                                  sinφ _maxгл = Ψλ / (2π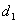).                           (3.58)

 

Таким образом, линейный закон изменения фазы возбуждающего поля приводит к изменению направления максимального излучения. Это направ­ление отклоняется от перпендикуляра к оси решетки на угол φ_maxгл. Так как излучение максимально в том направлении, в котором происходит взаимная компенсация сдвигов фаз Ψ и Ψ_р, то диаграмма направленности поворачива­ется обязательно в сторону отставания фазы возбуждающего тока. Поворот диаграммы направленности, т.е. управление ею путем изменения величины сдвига фаз Ψ, находит широкое применение на практике.

 

Направление нулевых излучений можно определить по формуле                                   

 

                                                 sinφ₀ = Nλ/ (nd₁cosφ_maxгл).

 

При узких диаграммах направленности значение 2φ₀ равно

 

                                                      2φ₀ = 2λ/ (n d₁cos φ_maxгл).

 

Таким образом, ширина диаграммы направленности растет по мере от­клонения направления максимального излучения от перпендикуляра к оси решетки. Уровень боковых лепестков, близких к главному, приближенно может быть найден тем же методом, что и в случае синфазной решетки. На­правления максимумов боковых лепестков при этом определяются из фор­мулы sin φ_maxгл, = (2N+l)λ/(2nd₁cos φ_maxгл).

 

Так как при отклонении направления максимального излучения от нормали к оси решетки диаграмма направленности расширяется, а уровень боковых лепестков не изменяется, то, казалось бы, что КНД решетки должен уменьшаться. Однако при этом пространственная диаграмма направленности приобретает коническую форму и телесный угол, в пределах которого за­ключено излученное поле (главный лепесток), уменьшается, что компенси­рует расширение диаграммы направленности в плоскости вектора Е. В ре­зультате оказывается, что КНД линейной равномерной решетки не зависит от угла φ_maxгл. КНД линейной равномерной решетки, можно рассчитать по формуле D = 101,5/2φ_0,5, где 2φ_0,5 - ширина диаграммы направленности по половинной мощности, рад. Рассмотренные антенные решетки излучают с максимальной интенсивностью либо в направлении нормали к своей оси (φ = 0⁰ - синфазная решетка), либо под некоторым углом к нормали (равно­мерная линейная решетка). Вдоль оси решетки (ось у) излучение равно нулю, так как элементы решетки в этом направлении не излучают, это - решетки с поперечным излучением.

 

Вывод. Ширина ДН синфазной решетки сужается с уменьшением длины волны, увеличением числа вибраторов и увеличением расстояния ме­жду ними. Если в синфазной решетке уменьшить число вибраторов и увели­чить расстояния между ними так, чтобы сохранить неизменным произве­дение nd₁, т.е. линейные размеры антенны, то ширина главного лепестка останется неизменной, но возрастут уровни боковых лепестков. При d₁< 0,5 λ, уровни боковых лепестков практически остаются неизменными, но возрастает число вибраторов и усложняется система питания. Поэтому расстояния d₁ между центрами ненаправленных или полуволновых вибрато­ров обычно выбирают равными 0,5λ, а одноволновых - λ. Для уменьшения уровня боковых лепестков применяют эквидистантные решетки, в которых центральные вибраторы имеют большие токи, а периферийные — меньшие или равноамплитудные решетки, в которых расстояния между вибратора­ми по мере удаления от центра антенны увеличиваются. Подбирая закон распределения амплитуд или размещения вибраторов, можно снижать уровни боковых лепестков до необходимых значений.

При заданных линейных размерах антенны наибольшим КНД обладают равноамплитудные эквиди­стантные решетки. Следовательно, снижение уровня боковых лепестков достигается уменьшением КНД или увеличением размеров антенны.

Диаграмма направленности системы ненаправленных (изотропных) синфазных излучателей, расположенных вдоль прямой линии есть ДН линей­ной решетки, являющейся фигурой вращения, ось которой совпадает с ли­нией расположения вибраторов в решетке. В плоскости, перпендикулярной линии расположения вибраторов и проходящей через ее центр, синфазная линейная решетка имеет круговую (ненаправленную) ДН. Для получения уз­ких ДН в двух плоскостях, например в горизонтальной и вертикальной, син­фазная решетка должна быть двухмерной.

При линейном законе изменения фаз токов в вибраторах ДН поворачи­вается в сторону отставания фаз.

 

 

 

 

 

 

 

 

 

 

3.4  Антенные решетки с осевым излучением (антенны бегущей волны)

 

Излучение равномерного линейного ряда вибраторов, перпендикулярных оси решетки

 

Рассмотрим равномерную линейную решетку, состоящую из ряда вибраторов, оси которых параллельны и каждый вибратор излучает с максимальной интенсивностью вдоль оси решетки (оси Х). Необходимый сдвиг фаз токов, в элементах антенны (ψ) можно создать с помощью соот­ветствующих фазовращателей. Однако схема питания антенны при этом по­лучается весьма сложной. Проще последовательно возбуждать элементы ан­тенны с помощью бегущей электромагнитной волны, распространяющейся от начала антенны (первый вибратор) к ее концу с определенной фазовой скоростью.

 

При этом ток в последующем вибраторе отстает по фазе от тока в предыдущем на величину ψ = β d₁, где d₁ -  расстояние между вибраторами, β = ω/v = kc/v - коэффициент фазы, c/v - коэффициент замедления. Таким об­разом, если считать, что токи в вибраторах равны по амплитуде, то

 

      

 

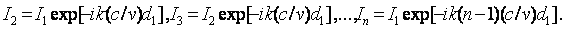
Так как последующий вибратор возбуждается позже предыдущего, но находится ближе к точке наблюдения, то сдвиг фаз между полями соседних вибраторов в этой точке (фаза поля первого вибратора принимается за нуле­вую) равен

 

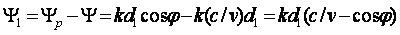                      (3.59)

Сдвиг фаз между полями крайних вибраторов

                    Ψ_n = (n - l) k^d₁  (cosφ - c/v).                   (3.60)

 

Учитывая сказанное, а также то, что имеется только один ряд вибрато­ров (m=1), можно от формулы (3.50) перейти к формуле (плоскость Е)

 

                                                                         Е = (60I_п/ r) [(cos (klsinφ) - coskl) / cosφ] *

                                                     * sin [(knd₁/2) (c/v - cosφ)]/sin [(k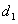/2) (c/v - cosφ)].                   (3.61)

 

Так как в плоскости Н элемент антенны не обладает направленными свойствами (φ=0°), то напряженность поля в этой плоскости определяется по формуле

 

                                                     Е = (60I_п/r)(l- cosk^l) sin[(kn d₁/2)(c/v - cosθ)]/sin[(k d₁/2)(c/v - cosθ)].      (3.62)

 

Как видно из формул (3.61) и (3.62) характеристика направленности в плоскости Н определяется только множителем системы; в плоскости Е характеристика направленности зависит также и от направленных свойств од­ного элемента решетки, но, в основном, определяется также множителем системы F_с (φ) или F_c (θ). Поэтому далее при анализе направленных свойств антенны бегущей волны (АБВ) будем рассматривать только этот множитель.

Видно, что направленные свойства АБВ зависят от числа элементов решетки n, расстояния между ними d₁ и от фазовой скорости питающей волны v. Оп­ределим направления нулевого излучения и максимумов боковых лепестков. Для определения направлений нулевого излучения приравняем числитель множителя системы нулю или его аргумент (kn^d₁/2)(c/v - cosθ) = Nπ, где N = 1,2, ... .

 

Отсюда:      

                                                            n^d₁ (c/v - cosθ) = Nλ     и       θ_ON = arccos (c/v - Nλ / n^d1).                      (3.63)

 

Для определения направлений максимумов боковых лепестков при­равняем числитель множителя системы единице или его аргумент

                                                                      (kn^d1/2) > (c/v - cosθ) = (2N+1) (π/2),    где N = 1,2, ....

 

Отсюда:

      n^d1 (c/v - cosθ) = (2N+1) [λ/ (2n^d1)]   и   θ_maxN = arcos{c/v - (2N+1) (λ/ (2n^d1)}        (3.64)

 

Рассмотрим три режима работы антенны бегущей волны: 1) v = с; c/v = 1 (волна свободного пространства); 2) v > с; c/v < 1 (быстрая волна) и 3) v < с; c/v >1 (медленная волна).

 

1)   c/v = l. В этом случае при φ=0° множитель системы максимален и равен n. Нормированный множитель системы:

            

                                                    F_c (θ) = (1/n) sin [(kn^d1/2) (l - cosθ)]/sin [(k^d1/2) (l - cosθ)].                  (3.65)

 

Результирующее поле максимально в направлении θ = 0° вследствие того, что поля от всех элементов антенны в точке наблюдения складываются синфазно, так как сдвиг фаз из-за несинфазности возбуждения Ψ полностью компенсируется пространственным сдвигом фаз Ψ_р. При увеличении или уменьшении угла φ (это же относится и к углу θ) Ψ ≠Ψ_р. Вследствие этого напряженность результирующего поля в точке наблюдения, характеризуемой некоторым углом θ ≠ 0⁰, будет мень­ше, чем в точке, лежащей на продол­жении оси антенны. Если cosθ отрица­телен (90°<θ<270°), то фазовые сдвиги Ψ и Ψр при d₁< λ/2 имеют одинаковые знаки. В этом случае вибратор, возбу­ждающийся раньше, находится ближе к точке наблюдения, чем вибратор, возбуждающийся позже  (пространст­венный сдвиг фаз отрицателен).

 

 

                                                                                           

                                              

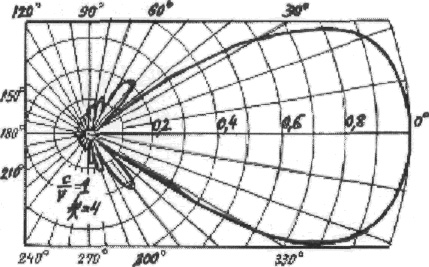
                                                                                                     Рис.3.18. ДН АБВ при c/v=1

 

 

Сдвиг фаз ψ1 между полями соседних вибраторов при малых d1 велик и результирующее поле в точке наблюдения мало. Следовательно, антенна бегущей волны обладает преимущественно однонаправленными свойствами и излучает с максимальной интенсивностью вдоль своей оси (антенна с осе­вым излучением) (Рис.3.18). На практике встречаются антенны бегущей волны, которые можно рассматривать как непрерывное линейное распределение слабонаправленных излучателей (например, диэлектрическая антенна). Без учета затухания возбуждающего тока по длине антенны множитель системы может быть получен из  выражения  (3.65) путем предель­ного перехода. Полагая n =>∞, d=>0, n^d1=>L, получаем

 

                                                          F_c (θ) = sin [(kL/2) (l- cosθ)]/ [(kL/2) (l- cosθ)].                         (3.66)

 

Уровень первого бокового лепестка ξ₁ =F(θ_1mах)=2/3π ≈ 0,21 такой же, как у синфазной решетки вибраторов. Ширину диаграммы направленности по направлениям нулевого излучения найдем из условия (kL/2)(l-cosφ₀) = π.

 

 

При малых значениях λ/L (L - длина антенной решётки)
                                      

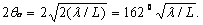                                                                                                                                         (3.67)

 

Ширина диаграммы направленности по половинной мощности может быть определена по приближенной формуле

                2θ _0,5 ≈ 10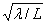8°.                              (3.68)

 

Сравнивая данную антенну с равномерной синфазной решеткой, следу­ет отметить, что хотя диаграмма направленности АБВ получается шире, чем у синфазной решетки такой же длины, но зато один ряд вибраторов, возбуж­даемых бегущей волной тока, обладает направленными свойствами в любой плоскости, проходящей через ось антенны, в то время как один ряд синфаз­ной решетки обладает направленными свойствами только в одной плоскости. Если элементы АБВ не обладают направленным действием или оно невели­ко, то диаграмму направленности антенны можно считать осесимметричной. При этом КНД антенны бегущей волны можно определить по общей форму­ле

                                     

                                                                      D₀= kL/ [Si2kL - (l - cos2kL)/ (2kL)].                                               (3.69)

 

При 2kL » I (практически при L/λ > 1) D₀≈ 4L /λ.

 

2)      c/v < 1. На основании формулы (3.62), имея в виду, что при условии
cosθ = c/v, множитель системы максимален и равен n (при этом условии
множитель системы обращается в неопределенность вида 0/0), и, используя
предельный переход (d₁=>0, n=>∞, n^d1>L), получаем нормированную характеристику направленности

 

                                                         F (θ) = sin [(kL/2) (c/v - cosθ)]/ [(kL/2) (c/v - cosθ)].                  (3.70)

 

Условие cosθ = c/v может выполняться при двух значениях угла θ = ± θ _mах, следовательно, имеются два направления максимального излуче­ния, не совпадающие с осью антенны. Данный режим работы является невы­годным, так как направленные свойства антенны ухудшаются. Однако антен­ны быстрых волн находят применение для создания диаграмм направленно­сти специальной формы для качания (сканирования) диаграммы направлен­ности. Основой большинства антенн быстрых волн являются волноводные структуры с неоднородностями (например, волновод со щелями).

 

 

3)   c/v > 1. Как видно из выражений (3.59) и (3.60), в данном случае отсут­ствует направление, в котором поля отдельных элементов антенны склады­ваются синфазно, так как ни при каком значении θ отношение c/v не может стать равным cosθ и сдвиг фаз не может обратиться в нуль.

Наименьший   фазовый   сдвиг   между   полями   отдельных   вибраторов                      Ψ₁^min = kd₁(c/v -1) получается в направлении θ =0⁰, т.е. вдоль оси антенны. Поля отдельных вибраторов в точке наблюдения, лежащей в направлении θ =0⁰, в данном случае складываются геометрически, как показано на вре­менной векторной диаграмме (Рис.3.19). Расчеты по формулам (3.62) и (3.70) показывают, что уменьшение фазовой скорости, начиная от v = c, сопровожда­ется постепенным сужением основного лепестка диаграммы направленности и ростом боковых лепестков. Излучение в главном направлении θ =0⁰, снача­ла растет, достигая максимума при некоторой определенной (для данного значения L =nd₁) величине c/v, а затем начинает уменьшаться и обращает­ся в нуль при критической величине c/v

 

                          (c/v)_кр = 1+(λ/nd₁).                 (3.71)

 

                                                

 

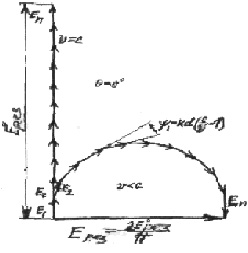
                                                                                         Рис.3.19. Векторное сложение полей АБВ

 

Сужение главного лепестка диаграммы направленности приводит к росту КНД антенны, а увеличение уровня боковых лепестков - к его умень­шению. При увеличении c/v, начиная от c/v = 1, сначала увеличивается КНД из-за сужения диаграммы направленности. После достижения некоторой определенной величины c/v дальнейший ее рост приводит к уменьшению КНД из-за увеличения уровня боковых лепестков. Сле­довательно, имеется оптимальная величина c/v (при заданной длине антенны L), при которой КНД достигает максимального значения. В случае не­направленных элементов антенны формула для КНД оказывается весьма громоздкой. Ее анализ показывает, что КНД антенны бегущей волны при заданной длине антенны зависит от величины ре­зультирующего сдвига фаз между полями, созда­ваемыми крайними (первым и последним) элемен­тами антенны в точке наблюдения, лежащей на продолжении ее оси (θ = 0°). КНД получается максимальным, если сдвиг фаз ψ_n, определяемый по формуле (3.60), равен 180°, т.е. если поля, создаваемые крайними элементами антенны бегущей волны в точке, лежащей на продолжении оси антенны, находятся в противофазе (см. Рис.3.19). Таким образом, на основании формулы (3.60) условием по­лучения максимального КНД является

 

                           ψ_{n опт.} = kL(c/v - 1) =π.                     (3.72)

 

Воспользовавшись этой формулой, можно определить оптимальную величину c/v при заданной длине антенны L или определить оптимальную длину антенны при заданной фазовой скорости. Очевидно, что:

 

                                  (c/v)_опт. =1+(λ/2L),                    (3.73)

                             (L/ λ)_опт. = 1/[2(c/v - 1)].               (3.74)

 

Как видно из формулы (3.72), оптимальная длина антенны увеличивается при увеличении фазовой скорости. В случае выполнения условия (3.72) КНД оп­ределяется по формуле

 

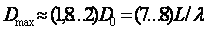                                                    (3.75)

где D₀ - КНД антенны бегущей волны данной длины при с/v =1.

На Рис.3.20 приведены графики зависимости отношения D/D₀ от сдвига фаз меж­ду полями крайних элементов антенны ψ_n, где D - КНД антенны опреде­ленной длины, работающей в режиме замедления (v < с) или ускорения (v >c).

 

                                                                                           

 

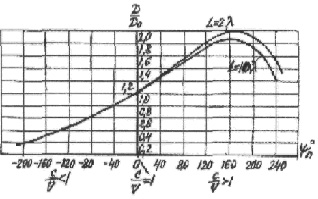
                                                                                            Рис.3.20. Зависимость D/D₀  от величины ψ_n   

 

Как видно из векторной времен­ной диаграммы (Рис.3.19), в опти­мальном случае               (ψ_n = 180°) век­тор напряженности результи­рующего поля в π/2 раз меньше, чем в случае АБВ, работающей в первом режиме (приближенно можно считать, что вектор на­пряженности результирующего поля в оптимальном случае равен диаметру окружности, половина длины которой равна вектору напря­женности результирующего поля при c/v = 1). Казалось бы, что КНД первой антенны должен быть меньше, чем второй. Увеличение КНД антенны, рабо­тающей в режиме, близком к оптимальному, объясняется тем, что при опти­мальном и близких к нему отношениях c/v токи в элементах антенны из-за взаимного влияния возрастают. В частности, при оптимальном отношении c/v ток в элементах антенны увеличивается примерно в (π/2)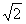раз по срав­нению с током в элементах антенны, работающей в режиме c/v = 1 (при не­изменной излучаемой мощности). Это приводит к увеличению напряженно­сти поля, излучаемого каждым элементом антенны. Приведенные здесь соот­ношения, характеризующие оптимальный режим работы АБВ, справедливы только для ненаправленных или слабонаправленных элементов антенны. При наличии у элементов антенны значительных направленных свойств эти соот­ношения изменяются. Ширина диаграммы направленности по нулевому излучению антенны, работающей в оптимальном режиме, на основании формулы (3.70) находится из условия (kL/2)(c/v - cosθ₀)= π. Подставляя вме­сто c/v выражение (3.73) и проводя рассуждения, аналогичные случаю   c/v = 1, получаем sinθ₀ =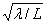. При малых отношениях λ/L синус можно заменить аргументом. Тогда

       

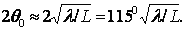
                                                                                                                        (3.76)

 

и, как видно из сравнения формул (3.67) и (3.76), в этом случае АБВ с пони­женной фазовой скоростью (оптимальной) имеет диаграмму направленности в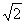раз уже, чем антенна той же длины с c/v = 1. Ширина диаграммы на­правленности по половинной мощности может  быть  приближенно  определена  (для антенны, у которой L/λ »1) по формуле

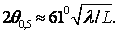                                                                                                                        (3.77)

 

 

Диаграмма направленности АБВ с пониженной фазовой скоростью, имеющей оптимальную длину, изображена на Рис.3.21. Сужение диаграммы направленности антенны оптимальной длины по сравнению с диаграммой направленности антенны такой же длины, но работающей в первом режиме (c/v =1), объясняется тем, что при увеличении угла φ напряженность результирующего поля в случае c/v >1 убывает значительно быстрее, чем в случае c/v = 1. Это происходит потому, что в случае антенны оптимальной длины сдвиги фаз между полями соседних вибраторов в точке наблюдения, определяемой углом θ₁ [при этом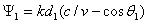], больше, чем в случае антенны с c/v = 1 [при этом].

                                                                             

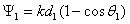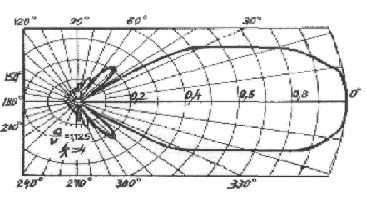
                                                                                                    Рис.3.21. ДН АБВ при c/v>1

 

Определим уровень первого бокового лепестка диаграммы направленно­сти оптимальной антенны. Максимальная величина нормированной характе­ристики направленности оптимальной антенны, определяемая по формуле (3.70), при  θ = 0⁰ и   c/v = 1+λ/2L равна 2π. Значение F(θ) в направлении мак­симума первого бокового лепестка можно определить, положив аргумент си­нуса в формуле (3.70) равным 3π /2 и найдя из этого равенства cos θ_1max. Под­ставляя в формулу (3.70) найденное значение cosθ_1max и заменяя c/v его вы­ражением (6.15), получаем   F(θ_lmax) = 2π/3. Отсюда уровень первого бокового лепестка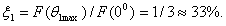

 

При увеличении длины антенны по сравнению с оптимальной излуче­ние в главном направлении уменьшается, и растут боковые лепестки. При L = 2L_ОПТ излучение в главном направлении совершенно исчезает. При уменьшении длины антенны по сравнению с оптимальной главный лепесток диаграммы направленности расширяется, уровень боковых лепестков уменьшается. Для того чтобы диаграмма направленности становилась уже, надо увеличивать длину антенны. Вместе с тем, чтобы при удлинении антен­ны бегущей волны ее длина оставалась оптимальной, необходимо в соответ­ствии с соотношением (3.72) увеличивать фазовую скорость волны в антенне.

 

В антеннах бегущей волны, применяющихся на практике, амплитуда возбуждающего тока уменьшается вдоль оси решетки по экспоненциальному закону, т.е.                                            I₂ =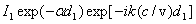. Это имеет место вследствие потерь энергии в антенне или вследствие постепенного излучения энергии элемен­тами антенны. Степень убывания бывает разной и в некоторых случаях, при расчетах этим уменьшением пренебрегают. Убывание амплитуды тока при­водит к расширению основного лепестка диаграммы направленности, к уве­личению уровня боковых лепестков и к исчезновению направлений нулевого излучения, которые заменяются направлениями минимального излучения.                                                                                                                     

 

Практическим примером выполнения антенны бегущей волны в виде ряда вибраторов является директорная антенна, широко применяемая в УКВ диапазоне (особенно на метровых и дециметровых волнах). Эта антенна со­стоит из одного питаемого (активного) и нескольких пассивных вибраторов, один из которых работает в режиме рефлектора, а остальные - в режиме ди­ректора. Оси всех вибраторов параллельны. Пассивные вибраторы возбуж­даются электромагнитным полем активного вибратора. Длина активного вибратора (2l) обычно берется несколько меньше λ/2 с тем, чтобы он был ре­зонансным. Для того чтобы пассивный вибратор работал в режиме рефлекто­ра, его входное сопротивление должно иметь индуктивный характер, что достигается некоторым удлинением этого вибратора по сравнению с актив­ным. Пассивный вибратор, работающий в режиме директора, должен обла­дать реактивным сопротивлением емкостного характера, для чего он должен быть несколько короче активного вибратора. Так как рефлектор усиливает поле в направлении активного вибратора (вперед) и ослабляет поле в обрат­ном направлении, то применение нескольких рефлекторов не имеет смысла, так как все рефлекторы, следующие за первым, будут очень слабо возбуж­даться. Первый директор усиливает поле в направлении следующего дирек­тора и поэтому, если установить несколько директоров, то все они будут воз­буждаться достаточно интенсивно. Длины директоров и расстояния между ними подбирают так, чтобы в каждом последующем вибраторе ток отставал по фазе от тока в предыдущем на величину βd₁, несколько большую величи­ны k^d1. Такую антенну можно рассматривать как АБВ с пониженной фазовой скоростью (c/v > 1). Максимум излучения совпадает с осью антенны (θ=0⁰).

 

 

Излучение провода, ток в котором изменяется по закону

бегущей волны

Рассмотрим провод длиной L, ток в котором изменяется по закону бе­гущей волны. Пренебрегая затуханием, I_z = I₀exp[-ik(c/v)z], где I₀ - ампли­туда тока в начале провода;  z - текущая координата. Из формулы (3.70) известен множитель системы в случае непрерывного распределения источ­ников поля. На основании правила перемножения характеристик направлен­ности нормированная характеристика направленности провода

                                                                                                                                                 

 

                                                                                                                                                                                                      (3.78)

 

 

где sinυ - характеристика направленности элемента провода.

 

Множитель системы выражения (3.78) максимален при θ = 0⁰ (если     v = c). Однако результирующее поле провода в направлении его оси θ =0^.) равно нулю, так как sinθ в формуле (3.78) обращается в нуль. Физически это объясняется тем, что элементарный вибратор не излучает вдоль своей оси. Так как множитель системы максимален в направлении оси провода (это на­правление наиболее благоприятно для сложения полей отдельных элементов провода), а характеристика направленности элемента провода максимальна в направлении, перпендикулярном оси провода (θ= 90°), то результирующее поле оказывается максимальным в некотором промежуточном направлении, составляющем угол υ_max (меньший 90°) с осью провода. Очевидно, что таких направлений имеется два (в первом и в четвертом квадрантах). При большой относительной длине провода L/λ характеристика направленности приблизи­тельно становится максимальной, когда максимален числитель множителя системы (первый максимум). Поэтому угол максимального излучения можно приближенно найти из выражения

                                                                                                   cos υ_max= (2L - λ)/2L.                                               (3.79)

                                                                                                                                                                   

                                                                                         Рис.3.22. ДН провода с бегущей волной тока

Чем больше относительная длина провода L/λ, тем меньше угол θ_mах, т.е. тем сильнее излучаемое поле прижато к оси провода. Чем больше L/λ, тем уже глав­ный лепесток диаграммы направленности, но тем боль­ше количество и уровень боковых лепестков. Главные ле­пестки диаграммы направленности наклонены в сторону движения волны в проводе (Рис.6.5), т.е. пространст­венная диаграмма направленности имеет вид конуса. Вследствие наличия двух направлений максимального излучения (в одной плоскости) нецелесообразно применять одиночный провод с бегущей волной тока в качестве антенны. Однако в антенной технике с успехом применяются различные   комбинации из таких проводов, обладающие достаточно хорошими направленными свой­ствами (например, ромбическая антенна).

 

 

 

 

 

 

 

 

3.5 Апертурные антенны

 

Рупорные антенны

 

Антенны в виде открытого конца волновода

В качестве слабонаправленных антенн УКВ широко используются антенны в виде открытого конца волноводов прямоугольного или круглого сечений. Электромагнитная волна, распространяющаяся по волноводу, дойдя до его открытого конца, частично излучается и частично отражается. Физическими источниками излучения являются электрические токи, возбуждаемые главным образом, на внутренних стенках волновода.

 

В инженерном решении приближенно полагают, что структура электромагнитного поля в плоскости открытого конца волновода такая же, как в поперечном сечении бесконечно длинного волновода, т. е. пренебрегают волнами высших типов, излучением токов, затекающих на наружные поверхности стенок волноводов, и не учитывают волны, отраженные от открытого конца волновода. В случае волновода прямоугольного сечения (Рис.3.23), возбуждаемого основной волной Н₁₀, на его открытом конце существуют взаимно перпендикулярные тангенциальные составляющие поля Е_y и H_х, зависимость которых от координат известна.

                                               

                                                                                                     

 

 

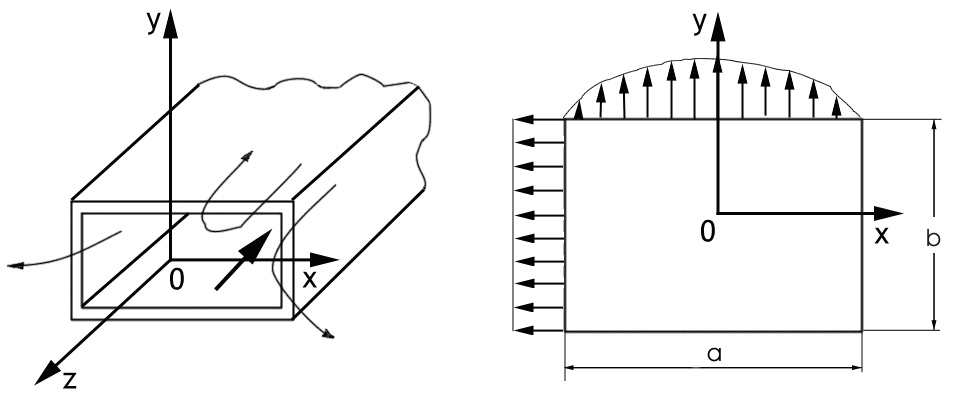
Рис.3.23. Открытый конец прямоугольного волновода

 

Таким образом, характеристику направленности открытого конца волновода прямоугольного сечения в плоскости Е, параллельной размеру b поперечного сечения, можно представить в виде произведения множителя системы плоского   раскрыва на характеристику направленности элемента Гюйгенса в этой плоскости.

В плоскости Н характеристика направленности открытого конца волновода прямоугольного сечения представляет собой произведение множителя системы синфазного раскрыва с косинусоидальным распределением амплитуды возбуждающего поля на характеристику направленности элемента Гюйгенса в плоскости Н.

Поскольку поперечные размеры прямоугольного волновода а и b невелики и соизмеримы с длиной волны λ (обычно для стандартных волноводов  а = 0,7λ , b = 0,35λ) и поверхностные токи затекают на внешние стенки волновода, то ДН антенны в виде открытого конца волновода имеет один широкий лепесток, т.е. антенна является слабонаправленной.

Следует отметить, что точность расчетов по апертурным формулам является удовлетворительной только в переднем полупространстве.

 

Характеристики направленности открытого конца волновода круглого сечения радиусом а в плоскостях Е и Н можно рассчитать по приближенным формулам, полученным при тех же допущениях, что и для прямоугольного волновода. При этом множитель системы выражается цилиндрическими функциями.

 

Антенны в виде открытого конца волновода применяются в сантиметровом диапазоне волн в тех случаях, когда требуется широкая ДН. Их часто используют в качестве облучателей зеркальных антенн.

Антенна в виде открытого конца волновода оказывается плохо согласованной со свободным пространством из-за резкого изменения условий распространения при переходе от волновода к свободному пространству. Коэффициент отражения от открытого конца прямоугольного волновода достигает значения 0,25...0,3, коэффициент отражения от открытого конца круглого волновода несколько меньше и составляет 0,1...0,25. Применяя подстроечные элементы, можно значительно снизить коэффициент отражения от открытого конца волновода.

 

Принцип действия, основные свойства рупорных антенн

 

Концентрация излучения в пределах более узкого телесного угла достигается увеличением размеров синфазно возбужденной поверхности. Если размеры сечения волновода выбираются таким образом, чтобы обеспечить формирование необходимой структуры поля, то, плавно увеличивая сечение волновода, эту структуру можно сохранить, а размеры излучаемой поверхности увеличить. В месте перехода от волновода

 

 

к рупору возникают высшие типы волн, но при достаточно плавном расширении волновода   (малый   угол   раствора рупора)  интенсивность этих волн невелика.

          

                                                                                                                  

 

 

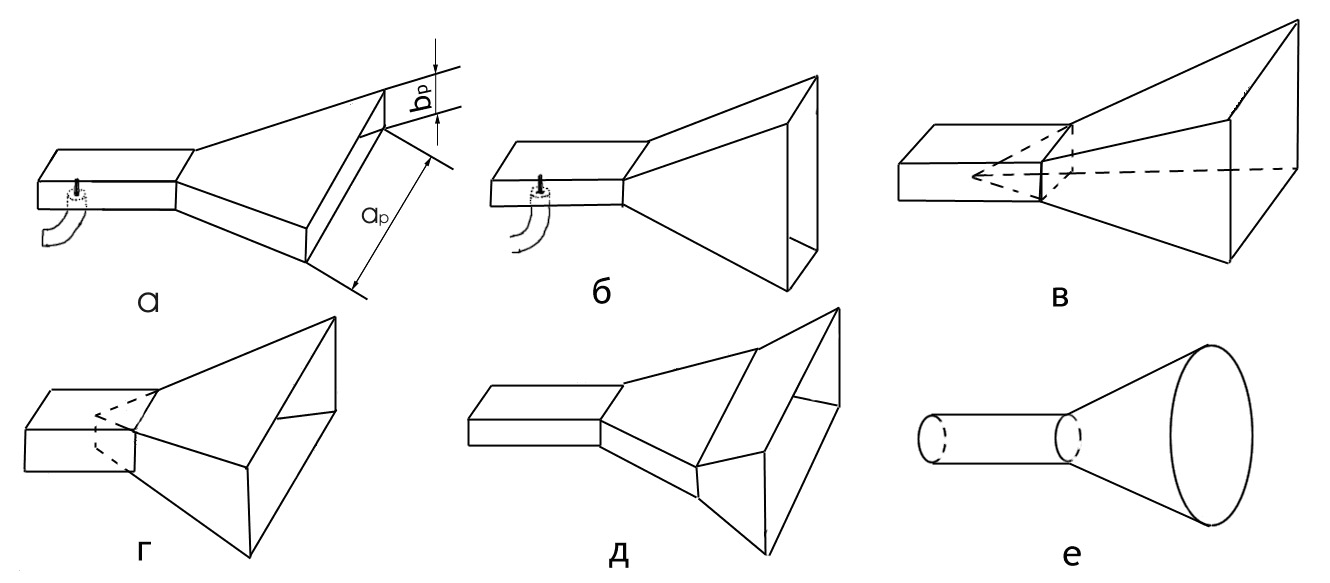
Рис.3.24. Типы рупорных антенн

 

Существуют различные типы   рупоров.   Рупор, образованный увеличением размера        а       волновода, параллельного  вектор Н, называется  секториальным Н-плоскостным (Рис.3.24.а). Рупор, образованный увеличением размера b волновода, параллельного вектору Е, называется секториальным Е-плоскостным (Рис.3.24.б). Рупор, образованный   одновременным   увеличением   размеров   a  u  b   поперечного сечения волновода, называется пирамидальным (см. Рис.3.24.в,г), а увеличением поперечного сечения круглого волновода - коническим (Рис.3.24.е). При плавном переходе от волновода к рупору структура поля в последнем напоминает структуру поля в волноводе.

Векторы электромагнитного поля при переходе из волновода в рупор несколько изменяют свою форму, чтобы обеспечить выполнение граничных условий на стенках рупора.

Направленные свойства рупорной антенны приближенно можно анализировать, как и в случае открытого конца волновода, пользуясь принципом эквивалентности. На излучающей поверхности рупора действуют две взаимно перпендикулярные тангенциальные составляющие поля Е_у и Н_х (прямоугольный раскрыв), амплитуды которых не зависят от координаты у, а вдоль координаты х они изменяются по закону косинуса. Однако в отличие от поверхности открытого конца волновода плоская излучающая поверхность рупора не может быть синфазной, так как в раскрыве рупора имеются фазовые искажения. Найдем фазу возбуждающего поля в произвольной точке М излучающего раскрыва H-плоскостного рупора (Рис.3.25). Дуга NOP окружности с центром в точке О есть линия равных фаз. Предполагая для простоты, что в рупоре β ≈ k ≈ 2π/λ, получаем

где L_h - длина H-плоскостного рупора.

 

                                                                                                                               

 

 

 

 

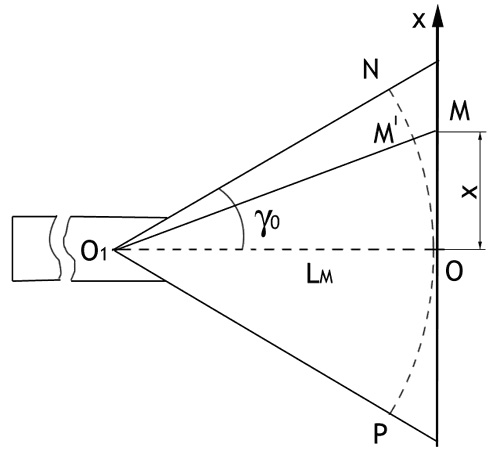
Рис.3.25. Фронт  волны в H-плоскостном  рупоре

 

 

Поскольку в рупорной антенне практически невозможно добиться полной синфазности излучающей поверхности, то обычно, задаваясь некоторым допустимым сдвигом фаз, выбирают размеры раскрыва рупора и его длину.

 

Этот сдвиг должен быть таким, чтобы ДН рупорной антенны мало отличалась от ДН синфазной излучающей поверхности, размеры которой равны размерам раскрыва рупора.

 

Допустимый максимальный сдвиг фаз определяется условием получения максимального КНД при заданной относительной длине L/λ рупора. С увеличением относительных размеров раскрыва рупора (а_р/λ или b_р /λ) при неизменной длине его ДН сначала становится уже и КНД растет, так как увеличиваются размеры излучающей поверхности, которая практически остается синфазной (сдвиг фаз ψ_мах мал). При дальнейшем увеличении размеров заметно растут фазовые искажения, вследствие чего ДН начинает расширяться и КНД уменьшается. На Рис.3.26 по оси ординат отложено произведение КНД Е-плоскостного рупора на отношение λ_b/а_р. Аналогичные кривые существуют и для H-плоскостных рупоров. При заданном отношении L/λ имеется определенное оптимальное значение а_р/λ или b_р/λ, при котором КНД антенны - максимально возможный. Оптимальному значению а_р/λ или b_р/λ соответствует допустимый сдвиг фаз. Рупор, размеры которого подобраны так, чтобы при заданной длине L/λ получить максимальный КНД, называется оптимальным.

                                                                                                                 

 

 

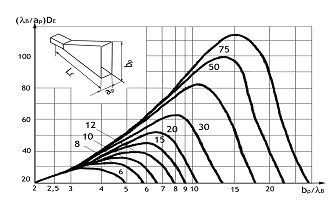
       Рис.3.26. Зависимость КНД от длины и величины раскрыва рупора

 

Из формул для ψ_max видно, что для того, чтобы при увеличении размеров раскрыва рупора максимальный сдвиг фаз не изменялся, оставаясь равным допустимому, т.е. КНД возрастал, относительная длина рупора L/λ должна увеличиваться пропорциональ­но квадрату относительных размеров раскрыва рупора.

 

Анализ кривых, приведенных на Рис.3.26, показывает, что в случае Е – плоскостного рупора   максимальный КНД получается    при    выполнении    равенства 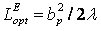 , тогда допустимый   максимальный   сдвиг фаз   для   Е   -   плоскостного   рупора  .

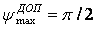Рассмотрев   аналогичные   кривые   D_Hλ /b = f(L_H /λ,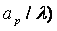,   можно найти допустимый сдвиг фаз и оптимальную длину Н - плоскостного рупора  .

Увеличение допустимого сдвига фаз в случае Н - плоскостного рупора по сравнению     с     E-плоскостным     объясняется      спаданием     амплитуды возбуждающего поля к краям раскрыва этого рупора в плоскости Н.

Коэффициент    направленного    действия    оптимального    Е -  или    Н-плоскостного рупора может быть рассчитан по формуле D=v_a4πS/λ²,  причем  КИП рупора с учетом

 

несинфазности и неравномерности возбуждения составляет 0,64 (у пирамидального рупора v_a = 0,52).

Е - плоскостной рупор сужает ДН в плоскости Е, а Н - плоскостной рупор - в плоскости Н.

 

В настоящее время находят применение рупоры, у которых сдвиги фаз поля в раскрыве значительно превосходят максимально допустимые. При больших по сравнению с λ раскрывах а_р и b_р и больших углах растворов рупора γ_o ДН становится по форме близкой к столообразной. Такие расфазированные рупоры обладают более широким рабочим диапазоном, чем синфазные ру­поры. Их ДН при ψ_max > 1,5π сравнительно мало зависят от частоты.

Рупорные антенны с круговой поляризацией

Для получения круговой (или близкой к ней) поляризации, излучаемого рупором поля, применяются фазирующие секции, устанавливаемые в волноводе, питающем рупор. В фазирующей секции происходит разложение вектора линейно поляризованного электромагнитного поля на две взаимно перпендикулярные составляющие, лежащие в плоскости, перпендикулярной направлению распространения волны, и обеспечение между ними на выходе секции сдвига фаз в 90⁰.

 

                                                                                                                      

 

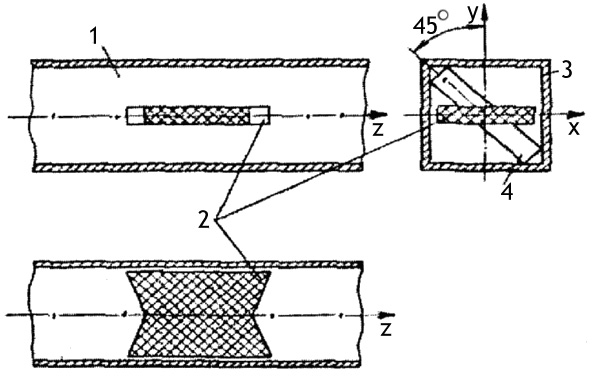
Рис.3.27. К получению круговой поляризации (1- фазирующая секция, 2- диэлектрическая пластина, 3- плоскость поперечного сечения фазирующей секции, 4- плоскость поперечного сечения волновода)

 

Существуют различные фазирующие секции. В качестве фазирующей секции можно, например, использовать отрезок волновода с квадратным поперечным сечением, возбуждаемый прямоугольным волноводом с волной  H₁₀.

 

Возбуждающий волновод соединяется с фазирующей секцией плавным пирамидальным переходом. Поперечные сечения возбуждающего волновода и фазирующей секции повернуты относительно друг друга на 45° (Рис.3.27). В результате вектор Е поля в фазирующей секции будет иметь составляющие Е_х и Е_у, параллельные взаимно перпендикулярным стенкам. Таким образом, поле в секции можно рассматривать как суперпозицию волн Н₁₀  и  H₀₁.

Для создания необходимого сдвига фаз между составляющими Е_х и Е_у в фазирующую секцию (1) устанавливают тонкую диэлектрическую пластинку (2), причем так, чтобы большой размер ее поперечного сечения был параллелен либо составляющей Е_х, либо Е_у. Такая пластинка влияет, в основном, на фазовую скорость той волны, линии вектора Е которой параллельны поверхности пластины. Толщина пластинки выбирается достаточно малой по сравнению с рабочей длиной волны. Тем самым она не оказывает заметного влияния на фазовую скорость волны, вектор Е которой перпендикулярен поверхности пластины.

При квадратном раскрыве пирамидального рупора ширина главного лепестка ДН в двух взаимно перпендикулярных плоскостях получается неодинаковой из-за различных амплитудных распределений возбуждающего поля в Е - и Н-плоскостях. В H-плоскости ДН (по нулевому излучению) примерно в 1,5 раза шире, чем в E-плоскости. Между тем в ряде случаев желательно иметь одинаковые ДН в обеих плоскостях. Это особенно важно при круговой поля­ризации излучаемого поля.

Один из способов получения одинаковых ДН состоит в том, что в квадратном раскрыве устанавливаются металлические ребра высотой Δ на расстоянии с < λ/2 друг от друга (Рис.3.28). Если вектор Е поляризован вдоль оси x, то такая волна не может распространяться между пластинами, параллельными оси x, из-за того, что размер с < λ/2. Для нее размер раскрыва а_р как бы уменьшается и становится равным а – 2Δ. Если            Δ= 0,17/а_р, то размер  апертуры  α_p,  параллельный оси х, в 1,5 раза будет меньше размера b_р, параллельного оси у. Так как на составляющую Е_y данные ребра не воздействуют, то ДН для обеих поляризаций поля в плоскости xoz будут примерно одинаковы. Аналогичным образом (с помощью ребер, прикрепленных к другим стенкам рупора) можно выровнять ДН в плоскости yoz.

Можно реализовать свойства фазирующей секции и без размещения диэлектрической пластины. Для этого вместо волноводной секции квадратного сечения следует взять волновод, несколько отличающийся от квадратного сечения.

                                                                                         

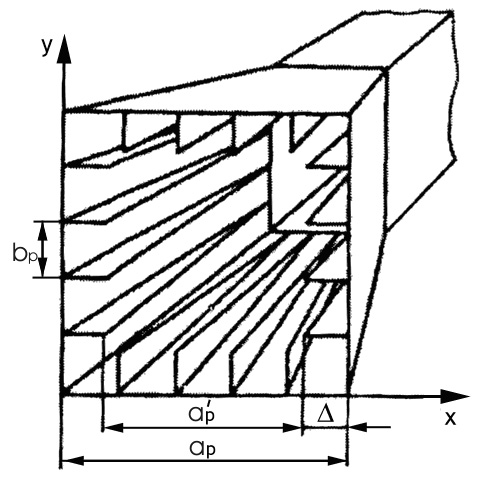
Рис.3.28. Рупор с квадратным раскрывом и одинаковыми ДН

                                    

Зеркальные параболические антенны

Зеркальная осесимметричная параболическая антенна состоит из отражающей поверхности, выполненной в виде параболоида вращения, и небольшой слабонаправленной антенны - облучателя, установленной в фокусе параболоида, и облучающей внутреннюю поверхность последнего. На базе такой классической зеркальной антенны разработаны различные модификации, многообразие которых приводит к целесообразности сгруппировать их, т.е. привести классификацию по основным отличительным признакам. Так, по числу отражающих зеркал различают одно- и многозеркальные антенны. Последние, как правило, содержат два зеркала. Часто эту группу называют двухзеркальными антеннами.

По взаимной ориентации зеркал и облучателей антенны могут быть симметричными и осенесимметричными. В симметричных антеннах отражающее зеркало обладает осевой симметрией и поле, отраженное от вершины такого зеркала, попадает в облучатель. Если не принять специальных мер, то согласование антенны будет невысоким. В осенесимметричных схемах антенн волны, отраженные от зеркала, проходят мимо облучателя. Такие схемы называют еще антеннами с вынесенным облучателем (АВО). Их отличает высокое согласование с трактом питания, но в то же время они обладают повышенным уровнем кроссполяризации, что при одновременной работе на ортогональных поляризациях является источником дополнительных помех.

По числу основных лучей, создаваемых зеркальной антенной, различают одно- и многолучевые антенны. Число лучей определяется числом облучателей. Многолучевые антенны могут создаваться как в симметричном, так и в осенесимметричном варианте. По типу кривизны основного зеркала используются параболические и сферические отражающие зеркала, зеркала с классическим и модифицированным профилями, обеспечивающими высокий результирующий КИП в условиях компромисса между апертурным КИП и потерями за счет «перелива» энергии за края зеркала. Это так называемые оптимизированные антенны.

При фиксированном положении отражающего зеркала направление максимального излучения (приема) может быть либо фиксированным, либо антенна может работать в режиме сканирования. Особое место занимают зеркальные антенны с пониженным УБЛ.

 

 

Геометрические свойства  и  принцип  действия  параболической антенны

В прямоугольной системе координат (начало в вершине параболоида) параболическая поверхность (Рис.3.29) описывается уравнением х² + у² = 4f₀z,  где  f₀ - фокусное расстояние.

 

В сферической системе координат (начало в фокусе) эта поверхность описывается уравнением r'=2f₀/(1+ cosγ), где r' - расстояние от фокуса до любой точки на внутренней поверхности параболоида; γ - угол между направлением на данную точку и фокальной осью зеркала (полярный угол).

 

В случае параболоида вращения (Рис.3.29) плоскость раскрыва (плоскость, проходящая через крайние точки поверхности зеркала и перпендикулярная его фокальной оси) имеет круглую форму; радиус этой плоскости называется радиусом раскрыва зеркала (R₀).

 

 

                            

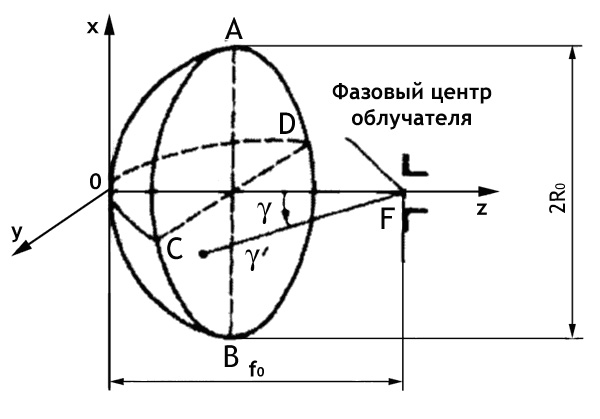
Рис.3.29. К принципу работы параболической антенны

 

                                                

 

                                                                                                    

 

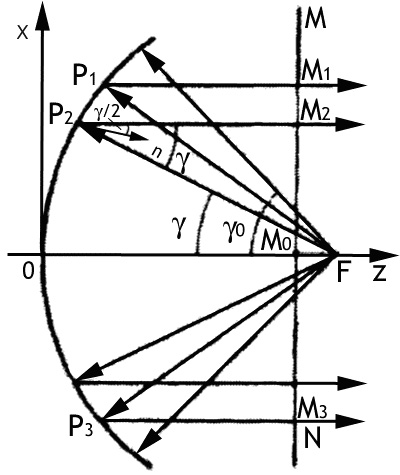
                                                                                Рис.3.30. К получению плоского фронта волны

 

 

Радиус раскрыва и угол раскрыва зеркала (угол γ₀ между фокальной осью и прямой, проведенной из фокуса к кромке па­раболоида) связаны соотношением R₀=2f₀tg(γ_o/2).

Форма зеркала характеризуется отношением R₀/2f₀ или углом раскрыва γ₀. Зеркало называется длиннофокусным (мелким), если R₀/2f₀<1 либо 2γ₀<π или короткофокусным (глубоким), если R₀/2f₀>1 либо 2γ₀ >π.

 

Принцип действия зеркальной антенны следующий. При падении, излучаемой облучателем, электромагнитной волны на зеркало на последнем возникают электрические поверхностные токи (вторичные источники электромагнитного поля). Эти токи существуют не только на внутренней, обращенной к облучателю поверхности зеркала, но также из-за явления дифракции электро­магнитных волн и на его внешней поверхности. Электромагнитное поле, создаваемое зеркальной антенной в любой точке окружающего  пространства, есть результат сложения (интерференции)  полей:   вторичного,   создаваемого поверхностными        токами,     и     первичного,    создаваемого   облучателем.

 

Рассмотрим сечение параболоида в плоскости xoz (Рис.3.30).   Образованная  этим   сечением   парабола обладает тем свойством, что расстояния  от  ее  фокуса   F   до   любой    точки,    лежащей   на   линии   MN, перпендикулярной  оси параболы и параллельной ее директрисе, по ломаным путям, (FP₁M₁, FP₂M₂ и др.) одинаковы. Следовательно, получается плоский фронт волны. Установленный в точке F облучатель излучает волны, близкие к сферическим. При этом расходящиеся лучи совпадают с линиями FP₁, FP₂ и т.д. Если бы длина волны первичного источника была бесконечно мала, то лучи, падающие на внутреннюю поверхность параболоида, отражались бы от нее по законам геометрической оптики. При этом вследствие параболической формы зеркала, все отраженные лучи были бы параллельны оси z и, таким образом, сферическая волна преобразовывалась бы параболоидом в плоскую. В действительности длина волны облучателя не бесконечно мала, и поэтому отраженные лучи идут не параллельно, а несколько расходятся. Однако расходимостью отраженных от зеркала лучей на небольшом участке пути от зеркала до поверхности раскрыва можно пренебречь, и эту поверхность можно считать синфазно возбужденной.

 

                     Приближенные методы расчета ДН зеркальной параболической антенны

Имеется два приближенных метода определения направленных свойств параболической антенны: апертурный и токовый.

 

Апертурный метод состоит в определении электромагнитного поля излучения по известному распределению возбуждающего поля на поверхности зеркала - на основе принципа эквивалентности. Пренебрегая влиянием ряда факторов, считают, что излучающей поверхностью зеркала является только поверхность его раскрыва.

 

Амплитудное распределение в раскрыве зеркала и, следовательно, ДН антенны определяются ДН облучателя и формой зеркала (отношением R₀/f₀). При расчете амплитудного распределения полагают, что зеркало относи­тельно облучателя находится в дальней зоне. Это допустимо, так как обычно расстояние от фокуса до поверхности зеркала составляет десятки длин волн. В этом случае относительная амплитуда напряженности поля, создаваемого облучателем в любой точке поверхности зеркала (Рис.3.31.а), могла быть найдена из следующих соображений. Поле облучателя, являясь обычно сферической волной, убывает обратно пропорционально пройденному расстоянию r'. С учетом этого амплитуда напряженности поля в произвольной точке поверхности зеркала E₃/E₀=F₀(γ)f/r'; F₀(γ) -нормированная ДН облучателя; Е₀ - амплитуда напряженности поля у вершины зеркала. Пренебрегая затуханием поля при его распространении до плоского раскрыва зеркала, принимаем, что амплитуда напряженности поля  в произвольной   точке   раскрыва   E_S  =  Е₃.   В   нормированном   представлении

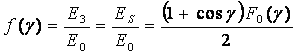                                                                                                              (3.80)

Отношение Е_S/Е₀ - амплитудное распределение поля в апертуре - удобно изображать в виде графика и рассматривать как функцию относительного переменного радиуса раскрыва ρ/R₀ (Рис.3.31..б). Отметим, что представление амплитудного распределения в виде точной аналитической функции f₁(ρ/R₀) либо невозможно, либо приводит к громоздким вычислениям при расчете ДН.

В случае осесимметричной ДН облучателя хорошие результаты дает аппроксимация функции f₁(ρ/R₀) степенным рядом

                       

                                                                  f (ρ/R₀) =1 + a²(ρ/R₀)² + a⁴(ρ/R₀)⁴ +….                              (3.81)

 

При этом для практических, расчетов можно ограничиться только первыми тремя членами ряда. Характеристика направленности излучающего раскрыва (без учета направленных свойств элемента Гюйгенса) будет иметь вид   

 

                                                              f(θ)=(1+а₂+а₄)Λ₁(и) - (а₂/2+а₄)Λ₂(и) + (а₄/3)Λ₃(и),                            (3.82)

 

где и = kR₀ sinθ; Λ₁(u), Λ₂(u), Λ₃(u)-лямбда-функции.

 

                                                                                                                                       

 

             

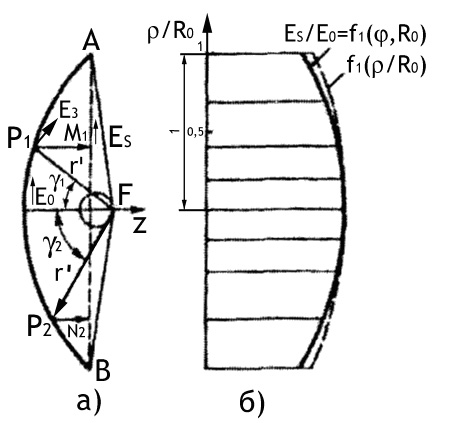
Рис.3.31. К получению амплитудного распределения в раскрыве зеркала

 

                                                                                                                            

 

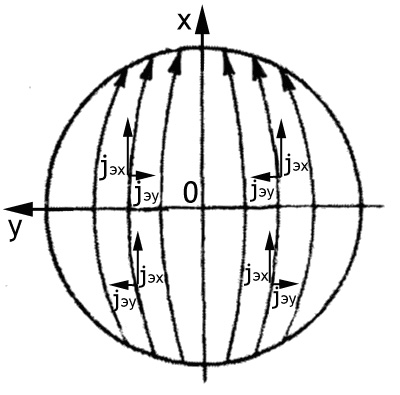
Рис.3.32. Распределение поверхностного тока

 

 

Для  расчета ДН необходимо предварительно определить постоянные коэффициенты а₂ и а₄. Для этого по известной ДН облучателя строится график амплитудного распределения f₁(ρ/R₀) (см. Рис.3.31.б). Аппроксимирование этого амплитудного рас­пределения функций (3.81) сводится к такому подбору коэффициентов а₂ и а₄, чтобы аппроксимирующая функция f(ρ/R₀) совпадала с функцией (амплитудного распределения f₁(ρ/R₀) в двух точках, например, при ρ/R₀=1 и ρ/R₀=0,5 (в точке ρ/R₀=0 совпадение функции f₁(ρ/R₀) с функцией (ρ/R₀) выполняется автоматически).

 

 

Пусть при ρ/R₀=1  f₁(ρ/R₀)=Δ₁   и при ρ/R₀=0,5 f₁(р/R₀) = Δ₂. Тогда получаем

 

                                                                                 1 + a₂+а₄=Δ_1;    1 + a₂(0,5)²+а₄(0,5)⁴=Δ₂.                                                    (3.83)

 

В результате решения этих уравнений определяются  неизвестные коэффициенты а₂ и а₄.

 

Токовый    метод   определения   направленных   свойств    параболической антенны базируется на известном распределении поверхностных токов на внутренней поверхности зеркала. Полагая, что эти токи существуют только на внутренней поверхности зеркала, можно вектор плотности тока в данной точке поверхности зеркала определить с учетом ориентации векторов Н в падающей и отраженной волнах по формуле J_э = 2[пН₁ ], где п - единичный вектор внешней нормали к данной точке поверхности зеркала; Н₁ - вектор напряженности магнитного поля, создаваемого падающей волной облучателя в данной точке на поверхности зеркала.

На Рис.3.32 изображено распределение поверхностного тока, спроекти­рованное на плоскость хоу. Облучателем является элементарный электрический вибратор (ось вибратора параллельна оси х) с контррефлектором, обеспечивающим однонаправленное излучение в сторону зеркала. Зная закон распределения тока на поверхности зеркала, можно рассчитать его ДН. Для этого необходимо проинтегрировать по всей поверхности зеркала выражение для напряженности поля, которое создает элемент поверхности зеркала, рассматриваемый как элементарный электрический вибратор.

 

Как видно из Рис.3.32, поле в направлении оси z зеркала в случае вертикальной поляризации создается только составляющими вектора J_э, параллельными оси х, которые во всех квадрантах имеют одинаковые направления. Поля Е_х, излучаемые ими в направлении оси z, складываются синфазно, т.е. это направление является направлением

 

 

максимального излучения. Составляющие плотности поверхностного тока J_эy в различных квадрантах имеют взаимно противоположные направления; поля Е_у, обусловленные ими в направлении оси z, попарно противофазны, следовательно, J_эy не создают излучения в главном направлении. В других (боковых) направлениях из-за появляющейся разности хода между полями от составляющих J_эу тока возникает поле с поляризацией, перпендикулярной по отношению к основной составляющей Е_х.

 

Составляющие J_эz также не создают излучения вдоль оси z (вибратор вдоль своей оси не излучает). Составляющие J_эу  и J_эz не создают излучения в обеих главных плоскостях (плоскости xoz и yoz). Поляризация излучаемого поля в главных плоскостях является линейной (Е_х). В других плоскостях, проходящих через ось z, имеет место также излучение за счет составляющих J_эу и J_эz, вследствие чего появляется поперечная (относительно основной) поляризация поля. Суммарное поле оказывается эллиптически поляризованным. Поперечная поляризация (кроссполяризация) является паразитной; она несколько уменьшает КНД антенны.  Уровень  кроссполяризации  тем  ниже,  чем   меньше  отношение R₀/f₀, т.е. чем более длиннофокусным является зеркало. Таким образом, токовый метод позволяет учесть поляризационные эффекты в зеркальной антенне.

 

Расчет ДН зеркальной антенны, основанный на приближенном определении токов на ее рабочей поверхности, обеспечивает достаточно точные результаты в пределах главного лепестка и прилегающих к нему одного - трех боковых лепестков.

 

Оба метода (апертурный и токовый) тем более точны, чем больше относительные размеры зеркала R₀/λ и его радиус кривизны (т.е. чем меньше отношение R₀/f₀).

 

 

 

Коэффициенты  усиления  и  направленного  действия параболической антенны

Как было показано выше, коэффициент усиления G антенны связан с ее коэффициентами направленного действия D и полезного действия η простым соотношением G = Dη.

 

Коэффициент полезного действия η зеркальной антенны учитывает тепловые потери энергии в облучателе, элементах крепления облучателя, краске, покрывающей внутреннюю поверхность зеркала, и т.д. Обычно принимают η = 1. Поэтому рассмотрим подробно определение КНД.

 

Коэффициент направленного действия зеркальной антенны можно рассчитать по формуле для КНД, заменив в ней апертурный КИП (ν_a) множителем ν_рез (результирующий или полный КИП), учитывающим уменьшение КНД из-за действия ряда факторов: переливания части, излученной облучателем, энергии через края зеркала, вызывающего увеличение УБЛ ДН зеркальной антенны в задних квадрантах (дальние боковые лепестки); ошибки в фазовом распределении на раскрыве; затенения части поверхности раскрыва облучателем и элементами его крепления; кроссполяризации излучаемого поля и др. Таким образом, D = v _рез 4πS /λ², где S - πR₀² - площадь раскрыва; ν_рез = ν_aν₁ν₂ν₃ν₄ν₅... . Здесь v_а—апертурный КИП раскрыва зеркала; ν₁ - множитель, определяемый переливанием части энергии через края зеркала; ν₂ - множитель, определяемый затенением; v₃ -множитель, определяемый фазовыми ошибками; ν₄ - множитель, учитывающий явление кроссполяризации; ν₅ - множитель, учитывающий дифракцию поля на кромке зеркала.

 

Множитель ν₁, называемый коэффициентом перехвата, - есть отношение мощности, излученной облучателем и перехватываемой зеркалом, к полной мощности, излученной облучателем, при этом потери в зеркале не учитываются.

 

Если при заданной форме зеркала (R₀/f₀=const) расширять ДН облучателя (кривая 1 на Рис. 3.33), то амплитудное распределение в раскрыве зеркала становится более равномерным (v_a растет). Однако вместе с тем увеличивается доля энергии, проходящей мимо зеркала, приводящая к росту боковых лепестков (уменьшается v₁). При сужении ДН облучателя наоборот: уменьшается v_а и увеличивается v₁. Два противоположно действующих на результирующие КИП и КНД фактора при постоянной величине отношения R₀/f₀ или угла раскрыва зеркала γ₀ и изменяемой ширине ДН облучателя определяют условие оптимального облучения зеркала с точки зрения получения максимального КНД. Условие оптимального облучения примерно обеспечивается при Δ_kр = Е_kр/Е₀ =0,316    (-10 дБ),      где Е_kр - напря­женность поля на краю зеркала. При этом  v_av₁ = 0,7...0,8.

 

С точки зрения получения максимального КНД при заданных размерах зеркала идеальной является ДН облучателя, изображенная на Рис.3.33 (кривая 2). Она должна быть осесимметричной и имеет два максимума в направлениях на края зеркала. Амплитудное распределение раскрыва зеркала в данном случае получается близким к равномерному (с учетом разных расстояний от фокуса зеркала до его вершины и краев), т.е. v_a = 1; пе­реливание энергии за края зеркала отсутствует (ДН имеет бесконечную крутизну ската), таким образом, v₁=1.

Для обеспечения высокого значения v_рез ДН облучателя должна иметь форму, по возможности приближающуюся к идеальной (например, кривая 3 на Рис.3.33). Близкие к ней ДН можно получить с помощью расфазированных рупоров и их модификаций. Кроме того, надо исключить или уменьшить влияние других факторов, снижающих результирующий КИП антенны (устранить затенение раскрыва облучателем, снизить кроссполяризацию и т.д.).

                                                           

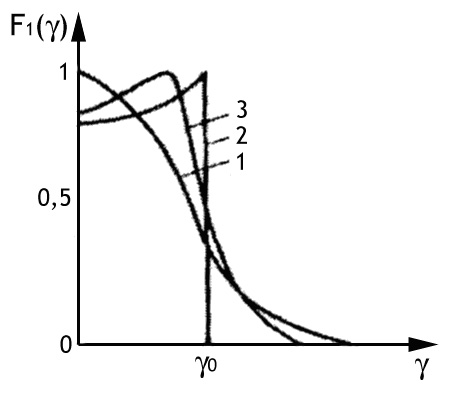
                                                                               Рис.3.33. К влиянию ДН облучателя на ДН антенны

 

 

Реализация высоких значений ν_рез, а, следовательно, КНД антенн не является единственно важной задачей в практическом приложении. В антенных системах ряда радиослужб предъявляются высокие требования к УБЛ. Например, в системах спутни­ковой связи, использующих геостационарную орбиту, от уровня первых боковых лепестков, примыкающих к главному, во многом зависят помехозащищенность и электромагнитная             совместимость, поэтому он должен быть ниже главного минимум на 25...30 дБ.  В  ряде  случаев,  в  частности,  в  радиорелейной   связи,  важное  значение  имеет  УБЛ  в  задних квадрантах в направлениях, близких к 180°. В этих направлениях излучение (коэффициент защитного действия) должно составлять не более -(60...70) дБ. Для параболических антенн с углами раскрыва 2γ₀ =120...180° КЗД составляет - (50...60)дБ.

 

 

Влияние точности выполнения зеркальной антенны на ее направленные свойства

Неточности, неизбежные при создании конструкции антенны (например, при выполнении поверхности зеркала, установке облучателя), вызывают отклонение распределения поля на излучающей поверхности от расчетного и соответствующие искажения ДН. Ошибки в распределении поля по раскрыву могут быть систе­матическими и случайными.

 

К систематическим ошибкам относятся такие, которые можно предусмотреть при полном и точном расчете антенны. Причинами этих ошибок могут быть смещение облучателя из фокуса, затенение раскрыва зеркала облучателем и элементами его крепления и др. Случайные ошибки обусловлены незакономерными и обычно небольшими отклонениями параметров антенны от их расчетных значений. Причинами таких ошибок являются недостаточная точность обработки поверхности зеркала, случайные деформации поверхности антенны вследствие изменения температуры или ветровых нагрузок и др.

 

Статистический анализ влияния случайных ошибок на направленные свойства зеркальной антенны позволяет сделать следующие выводы:

 

1.Случайные ошибки в распределении возбуждающего поля в раскрыве антенны увеличивают УБЛ и уменьшают КНД.

 

2.Уровень боковых лепестков параболической антенны пропорционален среднеквадратической    фазовой    ошибке    Δψ²    и    квадрату    интервала корреляции, измеренного в длинах волн.

 

3.Участки   зеркала,   на  которых   реальная   поверхность   отклоняется  от расчетной, должны быть небольшими, т.е. при одном и том же допуске на точность обработки поверхности зеркало с меньшим интервалом корреляции (более шероховатая поверхность) обеспечит более низкий УБЛ.

 

4. При повышении частоты увеличиваются как фазовые ошибки (Δρ2π/λ, где Δρ - неточность изготовления зеркала), так и интервал корреляции, выраженный в длинах волн. Поэтому КНД антенны с неизменной площадью раскрыва увеличивается не пропорционально квадрату частоты, а медленнее. При данной точности выполнения поверхности зеркала и данном интервале корреляции существует предельный КНД, который нельзя превзойти уменьшением λ, или увеличением диаметра зеркала.

 

5. Характер ДН в области боковых лепестков определяется в большей степени точностью изготовления антенны, а не способом ее облучения.

Влияние отражений от зеркала на входное сопротивление антенны (реакция зеркала на облучатель)

Часть, отраженных от зеркала, лучей, на пути которых находится облучатель, перехватывается последним (реакция зеркала). По отношению к отраженным от зеркала волнам облучатель ведет себя как приемная антенна. В основном, на облучатель воздействуют волны, отраженные вблизи вершины зеркала. Очевидно, что чем больше КНД облучателя, тем большую мощность он перехватывает. Перехваченная мощность создает в линии пита­ния волну, идущую от облучателя к генератору, аналогичную по действию обычной отраженной волне, возникающей в линии вследствие ее рассогласования с нагрузкой. Появление в тракте отраженной от зеркала волны ухудшает согласование антенны, так как эквивалентно изменению входного сопротивления антенны.

 

                                                                                                                                             

 

                       

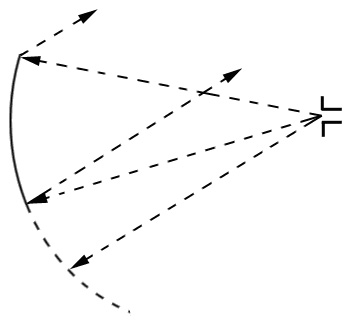
Рис.3.34. Способ уменьшения влияния зеркала на облучатель

 

 

Отраженную волну можно скомпенсировать с помощью какого-либо  согласующего    устройства,   устанавливаемого     у вершины зеркала (вспомогательное зеркало), либо в питающей линии вблизи облучателя (ферритовый вентиль). Однако действие такого устройства будет эффективным только на фиксированной частоте, поскольку с изменением частоты (из-за изменения разности хода лучей) вновь появится отраженная волна.

Если антенна излучает поле вращающейся поляризации, то реакция зеркала на облучатель будет практически отсутствовать. Дело в том, что при отражении от зеркала, излучаемой облучателем, волны направление вращения плоскости поляризации изменяется на обратное, вследствие чего она не принимается облучателем. Это антенна с поляризационной развязкой.

Удачным  способом устранения реакции зеркала на облучатель    в    широкой    полосе    частот    является применение невзаимных устройств,     например ферритовых вентилей и циркуляторов. Они устанавливаются в волноводном тракте   перед облучателем и, внося сравнительно малые потери для прямой волны, на 20...25 дБ ослабляют отраженную волну. Наиболее радикальный способ уменьшения реакции зеркала состоит в выносе облучателя из поля отраженных от зеркала лучей. Для этого облучатель устанавливают в фокусе зеркала (разворачивают) так, чтобы направление  его  максимального   излучения  составило  некоторый  угол   с фокальной осью зеркала (Рис.3.34). При этом облучается только часть зеркала, расположенная выше его оси, и отраженные от нее лучи проходят мимо облучателя. Необлучаемая часть зеркала удаляется (осенесимметричная антенна).

 

 

 

Управление ДН параболической антенны

 

Если фазовый центр облучателя сместить из фокуса в направлении, перпендикулярном оси зеркала (Рис.3.35.a), то поверхность раскрыва зеркала перестанет быть синфазной. Лучи 1 и 1’,2 и 2’, отраженные от поверхности зеркала, достигают поверхности раскрыва неодновременно. Можно показать, что при небольшом смещении облучателя Δx и достаточно длиннофокусном зеркале фазовое распределение поверхности раскрыва близко к линейному (3). Поэтому вынос облучателя из фокуса в направлении, перпендикулярном оси зеркала, приводит к повороту ДН в сторону, противоположную смещению облучателя.

 

 

 

 

                                                                                                                              

                                             

 

 

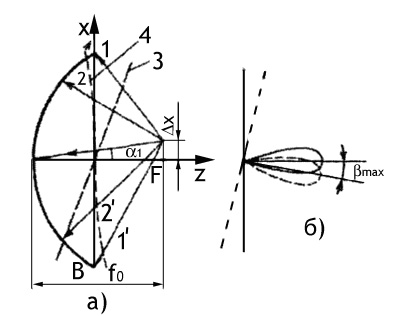
Рис.3.35. К управлению ДН

 

Угол поворота ДН θ_mах (Рис.3.35.б) при малых смещениях облучателя примерно равен углу смещения облучателя α₁, определяемому по формуле tgα₁=Δx/f₀. Синфазный фронт волны в раскрыве зеркала поворачивается на угол α₁. С увеличением Δх кроме линейного изменения фазы появляются заметные фазовые ошибки более высоких порядков, из которых наибольшую роль играют кубические (4). Знаки кубического и линейного фазового распределений противоположны (Рис.3.35.а). В этом случае ДН поворачивается на угол, меньший, чем α₁, главный лепесток становится несимметричным относительно своего максимума и УБЛ со стороны, противоположной смещению ДН, возрастает.

 

Смещение облучателя из фокуса используется в антеннах систем спутниковой связи и в радиолокации для сопровождения цели (ИСЗ, самолет и т.д.). Во избежание значительных искажений ДН из-за появления кубической фазовой ошибки угол поворота ДН должен быть невелик и обычно не может превышать нескольких значений ширины главного лепестка ДН (по половинной мощности).

При смещении облучателя из фокуса вдоль оси зеркала на поверхности раскрыва возникают квадратичные фазовые искажения, симметричные относительно вершины зеркала, что расширяет главный лепесток и увеличивает УБЛ ДН. При больших смещениях излучение в главном направлении уменьшается и главный лепесток раздваивается. Чтобы фазовая  ошибка   из-за  смещения  облучателя  не  превышала  допустимого значения π/4, должно выполняться условие Δz_дon < λ /[8(1 - cos γ₀)].                                                                          

 

 

 

Двухзеркальные антенны

Рассмотренные зеркальные параболические антенны по сравнению с другими типами антенн обладают хорошими электрическими характеристиками, технологичны в изготовлении и имеют сравнительно простую конструкцию. Наряду с этими достоинствами они обладают недостатками, которые в ряде случаев не позволяют удовлетворять комплексу требований, предъявляемых к современным антеннам. Такими недостатками являются: большая длина фидерного тракта от антенны до приемопередающей аппаратуры и его размещение в поле излучения антенны; сложность обеспечения амплитудного распределения поля в раскрыве, близкого к равномерному, с сохранением высокого значения результирующего КИП (v_peз); неприемлемые в ряде случаев продольные габаритные размеры антенны и др. Поэтому наряду с однозеркальными схемами антенн были разработаны, так называемые, двухзеркальные антенны, в которых перечисленные недостатки проявляются в меньшей степени либо полностью устраняются.

 

Среди многообразия типов двухзеркальных антенн есть две классические: это двухзеркальные антенны Кассегрена (Рис.3.36.а) и Грегори (Рис.3.36.б).

 

В этих антеннах используются две отражающие поверхности: основная - большое (обычно параболическое) зеркало и вспомогательная - малое зеркало, выполненное либо в виде части гиперболоида вращения (Рис.3.36.а), либо в виде части эллипсоида вращения (Рис.3.36.б).

 

                                                                                                                

 

 

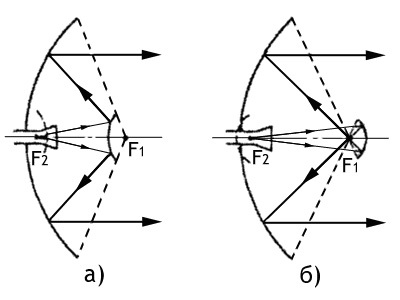
                                                           Рис.3.36. Двухзеркальные антенны (а – Кассегрена, б – Грегори)

 

Пусть облучатель с фазовым центром, находящимся в точке F₂, излучает в направлении малого зеркала сферическую волну. В каждой точке поверхности зеркала соблюдается правило: угол отражения равен углу падения. При этом вследствие геометрических свойств гиперболы (или эллипса) отражаемая малым зеркалом волна, снова оказываясь сферической, как бы исходит из одной точки - фокуса гиперболы (или эллипса) F₁, совмещенного с фокусом, большого зеркала - параболы. Эта волна трансформируется большим зеркалом в плоскую. Второй  фокус  малого  зеркала F₂  совмещается с фазовым центром облучателя (обычно рупора).

Геометрия двухзеркальной антенны определяется следующими параметрами (Рис.3.37): R₀ и R_м - соответственно радиусы раскрывов большого и малого зеркал, обычно R_м=(0,1...0,2)R₀; 2γ₀ - угол раскрыва большого параболоида; 2α₀ - угол облучения источником (облучателем) краев малого зеркала; f₀ - фокусное расстояние большого зеркала; f_м - фокусное расстояние малого зеркала; 2с - расстояние между фокусами малого зеркала; е - эксцентриситет малого зеркала. Из перечисленных параметров неза­висимыми являются четыре параметра, остальные могут быть определены через них. Обычно в качестве независимых переменных берутся R₀, R_м, γ₀, α₀.

                                                                                                                  

 

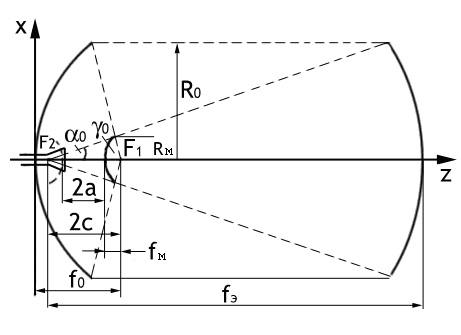
Рис.3.37. Геометрия двухзеркальной антенны

В антенне Кассегрена угол γ₀ может быть больше 90^o . В антенне Грегори угол γ₀ может быть взят лишь меньше 90° (если γ₀>90°, то отраженные от одной половины малого зеркала лучи на пути к большому встретят вторую половину малого зеркала, т.е. будут им затенены). Поэтому антенны Грегори  могут  быть только длиннофокусными.

 

Для расчета ДН двухзеркальной антенны необходимо знать   амплитудное распределение в раскрыве большого зеркала, которое можно найти методом геометрической оптики. Для этого следует заменить двухзеркальную систему эквивалентным параболоидом и найти амплитудное распределение в его раскрыве.

 

Такой прием позволяет при расчете амплитудного распределения исключить из рассмотрения вспомогательное зеркало. Поверхность эквивалентного параболоида представляет собой геометрическое место точек пересечения лучей, создаваемых облучателем, находящимся в фокусе малого зеркала F₂, с лучами, отраженными от основного зеркала (см. Рис.3.37).

 

Двухзеркальная антенна по своим электрическим свойствам эквивалентна однозеркальной антенне с параболическим зеркалом с фокусным расстоянием f_э рассчитываемым по формулам, полученным методом геометрической оптики: f_э = (е +1)f₀/(е -1) (вспомогательное зеркало   -   гиперболоид);   f_э =(е + 1)f₀/(1-е) (вспомогательное   зеркало   - эллипсоид); е - эксцентриситет малого зеркала.

 

Радиус раскрыва эквивалентного  параболоида равен  радиусу  раскрыва большого зеркала  двухзеркальнои  антенны  R₀.  Величины   f₀    и   f_э  связаны соотношением

 

 

 

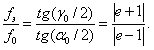
Амплитудные распределения в раскрывах эквивалентного параболоида и основного зеркала одинаковы и рассчитываются так же, как в случае однозеркальной антенны. Для получения близкого к равномерному амплитудного распределения (максимального КИП) ДН облучателя должна быть похожа на идеализированную диаграмму, изображенную на Рис.3.33 (кривая 2).

 

Фокусное расстояние эквивалентного параболоида больше фокусного расстояния основного зеркала. Следовательно, при данном облучателе амплитудное распределение в раскрыве двухзеркальной антенны получается более равномерным, чем у однозеркальной антенны с таким же отношением R₀/f_0.

 

Двухзеркалъная антенна обладает рядом преимуществ по сравнению с однозеркальной. Вспомогательное зеркало облегчает подбор наиболее благоприятного амплитудного распределения в раскрыве параболоида (подробный анализ показывает, что трансформация амплитуд поля источника происходит только на малом зеркале; большое зеркало лишь выравнивает фазовое распределение) и тем самым обеспечивает сравнительно высокий результирующий КИП зеркала. Так как в двухзеркальной антенне облучатель можно расположить близко к основному зеркалу, то упрощается подводка питания к облучателю, укорачивается длина линии питания и облегчается крепление этой линии и облучателя. Укорочение линии питания ведет к уменьшению потерь в ней и снижению шумовой температуры тракта питания, что важно при использовании антенн в спутниковой и космической радиосвязи.

 

Применяя в двухзеркальной системе поверхности, несколько отличные от правильных параболоидов, эллипсоидов и гиперболоидов (квазипараболические или оптимизированные антенны), можно добиться более равномерного амплитудного распределения поля в раскрыве основного зеркала при меньшем переливании энергии через его края, чем это имеет место в обычной двухзеркальной антенне. Более равномерное амплитудное распределение в раскрыве большого зеркала при большом коэффициенте перехвата (v₁) обеспечивается малым зеркалом благодаря модификации формы его поверхности. При этом модифицированная форма поверхности большого зеркала восстанавливает синфазность возбуждения его раскрыва.

Оптимизация двухзеркальной антенны состоит в подборе профилей зеркал в соответствии с заданной формой ДН облучателя. Основными требованиями, предъявляемыми к форме ДН облучателя оптимизируемой антенны, являются ее осевая симметрия и минимальная утечка энергии вне сектора облучения малого зеркала (крутые скаты ДН).

 

Антенны Кассегрена маркируются АДГ (антенна двухзеркальная с малым гиперболическим зеркалом), а антенны Грегори - АДЭ (антенна двухзеркальная с малым эллиптическим зеркалом). Цифра, следующая за АДГ или АДЭ, обозначает диаметр зеркала в метрах.

 

 

 

3.6 Антенны поверхностных волн

Диэлектрические стержневые антенны

Диэлектрические стержневые антенны, относящиеся к антеннам осевого излучения, наиболее широко применяются в диапазоне сантиметровых волн. Антенны представляют собой диэлектрический стержень, выполненный из высокочастотного диэлектрика с малыми  потерями (полистирол, тефлон и др.). Возбуждение обычно осуществляется отрезком волновода прямоугольного или круглого сечения          (Рис. 3.38). Структура поля в волноводе соответствует волне основного типа - H₁₀ (прямоугольный волновод) или H₁₁ (круглый волновод).

 

                                                                                                                               

 

                           

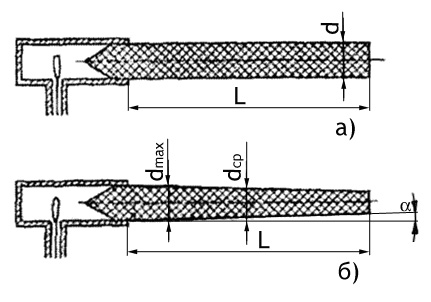
Рис.3.38. Диэлектрическая стержневая антенна

 

                                                                                                                

 

     

                                                                       Рис.3.39. Структура поля волны HE11

 

При бесконечной длине стержня указанный способ возбуждения приводит к возникновению в стержне как в диэлектрическом волноводе бегущей волны гибридного типа НЕ₁₁, имеющей продольные составляющие как магнитного, так и электрического поля. Структура поля    этой    волны изображена на Рис.3.39.

Волна НЕ₁₁ относится к, так называемым, поверхностным волнам, поле которых при удалении от поверхности стержня в радиальном направлении убывает по закону, близкому к экспоненциальному. Физически возникновение поверхностной волны объ­ясняется эффектом полного внутреннего отражения на границе раздела диэлектрик - воздух. Фазовая скорость волны υ зависит от материала стержня. Чем больше диаметр стержня, тем ближе υ к скорости света в неограниченном диэлектрике, т.е. к величине 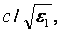 где ε₁ - относительная диэлектрическая проницаемость материала стержня. С уменьшением d величина υ → с, при этом волна слабо связана со стержнем. Зависимость υ/c от ε₁ и отношения d/λ приведена на Рис.3.40. Особенностью волны НЕ₁₁ в диэлектрическом  волноводе  является  отсутствие  критической длины волны (λ_kp=∞), т.е. волна может распространяться в стержне при любом его диаметре. Однако при большом диаметре в стержне могут возбудиться волны высших типов, что нежела­тельно, т.к. они искажают ДН.

Отметим, что поверхностной волной НЕ₁₁ передается только часть мощности (P₁), подведенной к возбуждающему волноводу. Остальная часть мощности (Р₂) непосредственно излучается возбудителем в окружающее пространство. Соотношение между этими мощностями определяет эффективность возбудителя β = Р₁ /(Р₁ + Р₂) .

 

При конечной длине диэлектрического стержня можно приближенно полагать, что структура поля остается такой же, как в бесконечном волноводе, однако обрыв стержня приводит к возникновению излучения.

                                                                                                                     

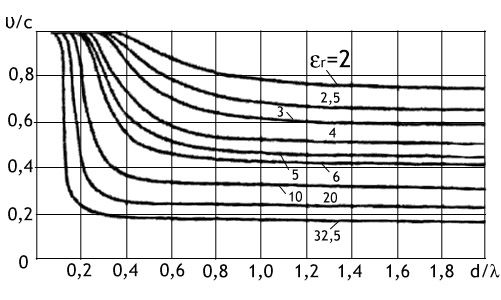
                                                                                              Рис.3.40. Зависимость υ/С = f(ε,d/λ)

 

 

Результирующая ДН антенны определяется взаимодействием излучения,
формируемого за счет конечности стержня, и непосредственного излучения возбудителя. Сложный характер формирования ДН затрудняет оценку точного положения фазового центра. В первом приближении считают, что он находится в средней точке по длине стержня.

 

Приближенно можно считать, что по направленным  свойствам диэлектрическая антенна соответствует непрерывной системе излучателей, возбуждаемых с равной амплитудой и линейным изменением фазы, характерным для антенны бегущей волны. Роль излучателей   играют, так называемые, токи поляризации, плотность которых определяется разностью диэлектрической проницаемости стержня и диэлектрической проницаемости окружающей среды.

Как видно из Рис.3.39, токи поляризации, соответствующие волне НЕ₁₁, имеют преимущественное направление, параллельное оси х, и формируют линейно поляризованное поле излучения. Направленные свойства каждого элементарного излучателя могут не учитываться в приближенных расчетах основного лепестка результирующей ДН. Однако в области первых боковых лепестков ДН излучающего элемента может оказать сильное влияние.

Отраженная волна от конца стержня приводит к появлению в ДН дополнительных боковых лепестков, соответствующих излучению антенны в обратную сторону. Коэффициент отражения зависит от скорости υ волны в стержне. Для уменьшения отраженной волны стержню придают коническую форму (Рис.3.38.б); что приводит к постепенному росту фазовой скорости υ и приближению ее к скорости света с у конца стержня. Уровень боковых лепестков у конической антенны получается меньше. На Рис.3.41 приведены результаты точного расчета ДН двух антенн длиной L = 3,Зλ: конического стержня с максимальным диаметром  d_max = 0,627λ  и  углом  α = 4° (сплошная линия) и цилиндрического стержня с диаметром, равным среднему диаметру конического стержня (штриховая линия). Диэлектрическая проницаемость в обоих случаях ε_r =2,5.

Диэлектрические     антенны     являются сравнительно   широкополосными.   Диапазон рабочих частот определяется, в основном, свойствами возбуждающего волновода. Ширина ДН по уровню половинной мощности одиночной диэлектрической антенны составляет обычно не менее 20...25°. Применяются диэлектрические антенны как самостоятельные излучатели, облучатели зеркал и элементы различных антенных решеток поперечного излучения.

 

                                                                       

 

 

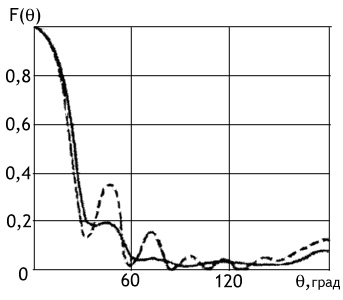
Рис.3.41. ДН диэлектрической антенны (сплошная линия – конической формы, пунктирная – цилиндрической формы)

 

 

Используются также ребристо-стержневые антенны, аналогичные по своим свойствам диэлектрическим стержневым антеннам (Рис.3.42.a). Для получения вращающейся поляризации возбуждение ребристо-стержневых антенн осуществляется спиральным излучателем (Рис.3.42.б).

                                                                                                                              

                                 

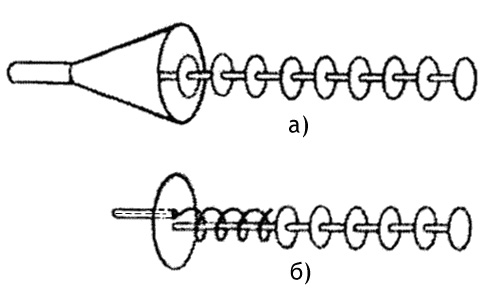
        Рис.3.42. Ребристо-стержневые антенны

 

 

Плоские антенны поверхностных волн

Наряду с диэлектрическими стержневыми антеннами применяют плоские диэлектрические и ребристые (гофрированные) антенны, получившие также название импедансных. Антенны состоят из возбудителя, например, рупорного типа и структуры, направляющей волну, в виде слоя диэлектрика на металле или ребристой поверхности (Рис.3.43). Ребристые структуры обычно применяются в сантиметровом диапазоне волн.

 

Диэлектрические структуры, имеющие несколько большие потери, предпочтительны в дециметровом диапазоне из-за конструктивных преимуществ. Антенны могут быть также снабжены экраном, выступающим перед направляющей структурой. Роль экрана может играть поверхность корпуса объекта, на котором расположена антенна.

 

При соответствующем выборе параметров направляющей структуры поле над ней имеет характер поверхностной волны типа Е, не обладающей критической   длиной   волны    (λ_kp= ∞),   причем    при    указанном   способе возбуждения вектор магнитного поля параллелен оси у, а электрическое поле кроме Ė_Z имеет составляющую Ė_X. Направляющую структуру принято характеризовать поверхностным сопротивлением (импедансом), равным отношению   касательных   к  поверхности  составляющих  векторов  Ė   и   H:      Z_S =.

 

Величина Z_S для ребристой структуры зависит от глубины канавок, для диэлектрического слоя - от диэлектрической проницаемости ε_r и толщины слоя. Для поддержания поверхностной волны сопротивление Z_S = iX_S должно иметь индуктивный характер. Для ребристой поверхности это достигается, если глубина канавок не превосходит 0,25λ.

 

                                                                                                                                 

 

 

 

Рис.3.43. Плоские антенны поверхностных волн (а – ребристые, б – диэлектрические)

 

Направленные свойства плоской АПВ, как и диэлектрической стержневой антенны, определяются, в основном, взаимодействием излучения, вызываемого ограниченными размерами направляющей поверхности, и непосредственного излучения возбуждающего устройства. Приближенно ДН может быть вычислена так же, как для антенны бегущей волны длиной L с замедленной фазовой скоростью. На форму ДН в Е-плоскости влияют также токи, возбуждаемые на экране. Конечность экрана приводит к отклонению максимума излучения от продольной оси антенны на некоторый угол. Отметим, что точный расчет оптимальной длины антенны затруднен ввиду сложной зависимости ее от эффективности работы возбудителя.

 

Преимуществом плоских АПВ является малая высота. Подобные антенны практически не выступают над поверхностью объекта, на котором они установлены, поэтому их особенно целесообразно использовать на самолетах и других передвижных объектах.

 

 

Синтез плоских АПВ

Направленные свойства АПВ можно существенно улучшить, если применить структуру с переменными по длине параметрами (модулированные антенны). Такими параметрами могут быть глубина канавок в ребристой структуре или толщина слоя диэлектрика и форма направляющей поверхности. С помощью модулированных антенн можно достичь повышения КПД или получить ДН специальной формы, например секторной, косекансной или с малым УБЛ.

 

Рассмотрим задачу синтеза антенн с высокой направленностью излучения. В обычных АПВ, излучение которых определяется длиной антенны и коэффициентом замедления волны, получение узких ДН не может быть реализовано по следующим причинам. В случае малых 2θ_0,5 необхо­дима большая длина антенны, что требует малого значения γ, т.е. малого замедления  поверхностной  волны.  При γ_opt≈1 амплитуда  поверхностной волны медленно спадает при удалении от направляющей поверхности. Подобную волну трудно возбудить, в результате чего мощность, подведённая    к антенне, в основном, тратится на непосредственное излучение из возбудителя и почти не переходит мощность поверхностной антенны.

                                                                                                        

 

 

Рис.3.44. Формирование поверхностной волны АПВ

 

 

Представим теперь  антенну,  в которой с помощью рупорного возбудителя  (Рис.3.44) формируется поверхностная волна с большим замедлением. Поверхностная волна с большим замедлением (волна питания) используется в дальнейшем только для подведения энергии к участкам, вызывающим излучения энергии.

Поле, формирующее ДН антенны (волну излучения), представим в виде поверхностной     волны с малым замедлением,   распространяющейся в общем случае под некоторым углом α к оси z (см. Рис.3.44). Естественно, что направление максимума излучения при этом будет совпадать с осью z'. Амплитуду  поля  излучения  следует выбирать из условия энергетического баланса, т.е. из равенства мощностей волны питания, возбуждаемой рупором, и волны излучения.

Задача синтеза заключается в отыскании параметров антенны, при которых волна питания преобразуется за счет неоднородностей импедансной структуры в волну излучения. Искомыми параметрами при решении данной задачи являются глубина канавок и огибающая рёбер (профиль антенн Рис.3.45).

                                                                                                                  

 

 

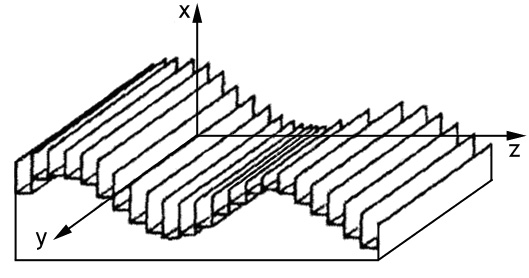
Рис.3.45. Модулированная структура АПВ

 

Эти параметры находятся исходя из следующих соображений. Поскольку направляющая    поверхность антенны чисто реактивна, т.е. отсутствует как поглощение, так и излучение энергии в целом по поверхности и в каждой ее точке, то вектор Пойнтинга (точнее, его среднее значение П_ср = Re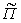) в каждой точке на­правлен по касательной к поверхности. 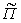Так как согласно постановке задачи структура полного поля является заданной, то профиль антенны может быть найден в виде кривой, касательная к  которой в каждой точке совпадает с направлением вектора Re, определяемого по полному полю (т.е. сумме волн питания и излучения). Глубина канавок находится по значению поверхностного импеданса Z_S, под которым следует понимать отношение электрического и магнитного полей, касательных к поверхности антенны в данной точке.

 

Выполнение условия энергетического баланса, в соответствии с которым выбирается амплитуда поля излучения, обеспечивает полный переход энергии питающей волны в энергию волны излучения. Этому соответствует профиль антенны, конечная точка которого (точка В) лежит на линии, где интенсивность волны питания пренебрежимо мала (линия 1-1', Рис.3.44). Поэтому направленные свойства подобных антенн могут быть рассчитаны с учетом эквивалентных электрических и магнитных токов в апертуре, соответствующих только волне излучения.

 

Возможно также представление поля, формирующего заданную ДН, в виде группы поверхностных волн с разным замедлением, распространяющихся под различными углами к продольной оси антенн, или в виде поля, соответствующего излучению решетки из элементов с заданным соотношением амплитуд и фаз токов. Подобное представление волны излучения позволяет реализовывать широкий класс ДН, т.е. существенно расширяет возможности схемы по сравнению с обычными конструкциями АПВ.