КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

 

2.1. Плоская электромагнитная волна, падая из среды с параметрами eа1 и mа1 на плоскую границу со средой, параметры которой eа2 и mа2 (eа и mа – абсолютные диэлектрическая и магнитная проницаемость среды, соответственно), в общем случае частично отражается от границы, а частично проходит во вторую среду, меняя направление распространения. Совместим плоскость xoy (рис.2.1) с границей раздела.

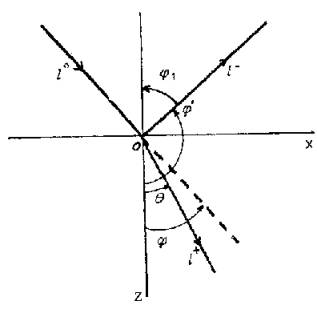
              Рис.2.1. Геометрия отражения и прохождения волны

 

Плоскость xoz, проходящая через нормаль (ось z) к границе раздела и направлениe распространения падающей волны , называется плоскостью падения волны.

Отраженная и прошедшая  (преломленная) волны также будут плоскими, а направления их распространения  и   будут лежать в плоскости падения волны.

Угол j между направлением распространения падающей волны и нормалью к границе раздела (угол отсчитывается от положительного направления оси z) называется углом падения волны.

Угол j¢ между направлением распространения отраженной волны и нормалью к границе раздела определяет в общем угол отражения. Однако в геометрической оптике, которой мы следуем, углом отражения j1 называют угол дополняющий j¢ до 1800.

Угол q между направлением распространения прошедшей (преломленной) волны и нормалью к границе раздела называется  углом преломления.

Связь между величинами углов j, j¢ и q выражается законами Снеллиуса:

 

                                          j¢ = p - j ,                                              (2.1)

 

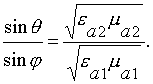                                           (2.2)

 

2.2. Вектор  напряженности  электрического  поля  падающей  волны , перпендикулярный направлению распространения, в общем случае может быть расположен по-разному относительно плоскости падения. Но, так как он всегда может быть представлен в виде суммы двух взаимно перпендикулярных векторов, то достаточно рассмотреть два случая: вектор  лежит в плоскости падения волны и вектор   перпендикулярен плоскости падения волны.

В первом случае поляризация волны называется параллельной. При этом вектор   имеет две проекции на оси координат  и , а вектор  - одну   (рис.2.2.а). Векторы и  отраженной и преломленной волн также лежат в плоскости падения волны.

Во втором случае поляризация волны называется  нормальной. При этом вектор   имеет одну проекцию , а вектор  - две,  и . Векторы  и отраженной и преломленной волн также перпендикулярны плоскости падения волны.

2.3. Коэффициентом отражения R называется отношение комплексных амплитуд напряженностей электрического поля отраженной волны и  падающей волны   , т.е.

                                           .                                                         (2.3)

 

    

 

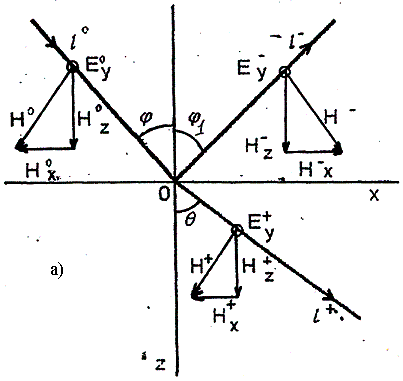
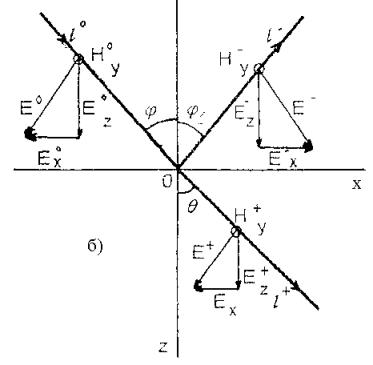
Рис.2.2. К пояснению нормальной и параллельной поляризаций

 

Коэффициентом прохождения c называется отношение комплексных амплитуд напряженностей электрического поля преломления волны  и  падающей волны, т.е.

                                          .                                              (2.4)

 

Отметим, что R и c  являются в общем случае комплексными величинами. Их модули характеризуют отношение амплитуд соответствующих волн, а аргументы – сдвиг фаз между этими полями на границе раздела.

В случае параллельной поляризации (рис.2.2.а):

 

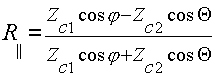                                 ,                               (2.5)

 

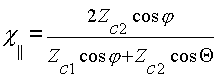                                 ,                                 (2.6)

 

а в случае нормальной поляризации (рис.2.2.б):

 

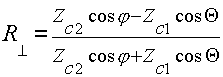                                   ,                               (2.7)

 

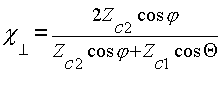,                                      (2.8)

где Zc1 = , Zc2  =  - волновые сопротивления первой и второй среды, соответственно.

Выражения (2.5)…(2.8) часто называют формулами Френеля.

 

2.4. В случае падения плоской электромагнитной волны на плоскую поверхность проводника волна отражается. В проводниках волновое сопротивление определяется выражением

 

                                          ,

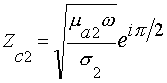где w = 2pf  - круговая частота,

 s - удельная проводимость среды.

Для идеального проводника волновое сопротивление равно нулю. Поэтому при падении плоской волны из диэлектрика на поверхность идеального проводника независимо от угла падения из формул (2.5)…(2.8) следует:

 

                          R|| = 1,      R^ = -1,      c|| = c^ = 0                            (2.9)

 

и, следовательно, волна полностью отражается, а поле внутри идеального проводника отсутствует.

Реальные металлы имеют конечную проводимость, но ввиду того, что проводимость металлов велика, во всем диапазоне радиочастот волновое сопротивление металлов близко к нулю. Следовательно, при любых углах падения волны, модуль коэффициента отражения незначительно отличается от единицы.

2.5. В случае падения плоской электромагнитной волны на плоский слой диэлектрика толщиной d, расположенный в воздухе (рис.2.3) падающая на верхнюю границу слоя волна частично отражается, а частично проходит в слой. При достижении нижней границы слоя волна опять частично отражается, а частично выходит  из слоя. Отраженная от нижней границы слоя волна падает на верхнюю границу, где опять частично отражается, а частично выходит из слоя и т.д. Очевидно, что волна, отраженная от слоя, представляет собой наложение бесконечного числа волн, распространяющихся в одинаковом направлении (под углом к оси z). Эти волны отличаются друг от друга амплитудами и фазами, которые зависят от числа отражений волны внутри слоя. Аналогичный вывод можно сделать относительно волны, прошедшей через слой диэлектрика.

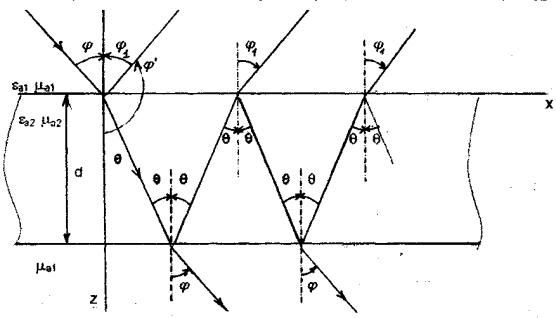
              Рис. 2.3. Падение плоской волны на слой диэлектрика

 

Заметим, что направление распространения прошедшей через слой диэлектрика волны совпадает с направлением распространения падающей волны.

Суммируя комплексные амплитуды всех волн, составляющих отраженную волну, для коэффициентов отражения волн от слоя Rсл и прохождения волны cсл через слой можно получить выражения:

 

Rсл  = ,

 

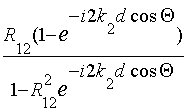cсл = ,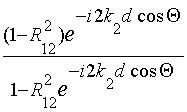

 

где R12 – коэффициент отражения при падении волны на границу слоя из воздуха, определяемый в случае параллельной поляризации по формуле (2.5), а при перпендикулярной поляризации по формуле (2.7).

k2=, а угол  определяется из второго закона Снеллиуса (2.2).

Модули коэффициентов отражения и прохождения равны:

 

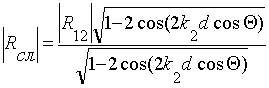,                                (2.10)

 

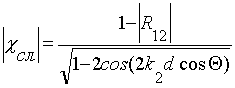     .                      (2.11)

 

 

2.6.Если обе среды являются диэлектриками, и, следовательно, mа1=mа2=m0, то коэффициент отражения нормально - поляризованной волны не может быть равен нулю ни при каком угле падения. При параллельной поляризации существует угол падения

                                    ,                               (2.12)

называемый углом Брюстера, при котором коэффициент отражения равен нулю, и волна полностью проходит во вторую среду.

При падении параллельно - поляризованной плоской волны под углом Брюстера на плоский слой диэлектрика также наблюдается полное прохождение волны через слой. Это видно из выражений (2.10) и (2.11). Так как при данных условиях коэффициент отражения R12=0, то модули коэффициентов отражения от слоя диэлектрика и прохождения через этот слой соответственной равны 0 и 1.