2. КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

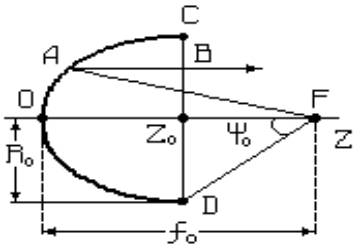
Параболическая антенна состоит из облучателя и зеркала, которое, преобразуя сферическую волну облучателя в плоскую, формирует остронаправленное излучение. На рис.2.1 приведен эскиз параболического зеркала с указанием лучей, идущих из фокуса зеркала F, где находится точечный источник сферических волн. Отрезок OF называется фокусным расстоянием и обозначается ƒ_о. Часть плоскости (при Z = Z₀), ограниченная кромкой параболоида, называется раскрывом зеркала. Линия CD представляет собой сечение плоскости раскрыва параболоида.

Рис.2.1. Эскиз параболической антенны

Ломаная линия FAB обозначает путь произвольного луча электромагнитной волны облучателя. Из аналитической геометрии известно, что длина этого пути не зависит от положения точки на поверхности параболоида. Поэтому все, отраженные от зеркала, лучи в плоскости раскрыва и плоскостях, параллельных ей, оказываются в фазе. Таким образом, параболическая антенна преобразует сферическую волну точечного источника в плоскую. Реальные облучатели не являются точечными. Однако, если фазовый центр облучателя совпадает с фокусом параболоида, можно считать, что облучатель является точечным источником, расположенным в фокусе параболы.

Если фазовый центр облучателя смещен относительно фокуса в направлении перпендикуляра к оси зеркала (рис.2.2.а), то лучи, отраженные в соответствующих точках зеркала, достигают поверхности раскрыва не одновременно. Так, луч 2 достигает поверхность раскрыва позже чем луч 1, а луч 3 позже, чем луч 2, то есть поверхности раскрыва зеркала перестает быть синфазной. На рис.2.2.б показаны соответствующие законы распределения фаз в раскрыве параболы при разных значениях величин смещения ΔX облучателя. При небольшой величине смещения ΔX облучателя и достаточно длиннофокусном зеркале, фазовое распределение на поверхности раскрыва близко к линейному. Поэтому, в этом случае, вынос облучателя из фокуса в направлении перпендикуляра к оси зеркала, приводит к повороту диаграммы направленности в сторону противоположную смещению облучателя, как показано на рис.2.1.в. Угол поворота диаграммы направленности υ₂ при малых смещениях облучателя примерно равен углу смещения облучателя υ₁ .

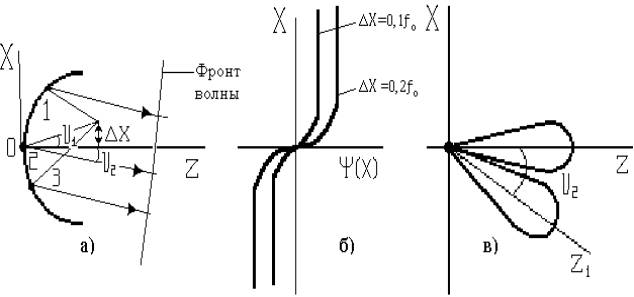
Рис.2.2. К формированию диаграммы направленности антенны

Увеличение смещения ΔX приводит к появлению фазовых искажений (преимущественно кубических) в раскрыве антенны. Чтобы величина фазовых искажений не превышала допустимой (45⁰), должно выполняться условие

Δх £ 0,6 λ/sinΨ₀, (2.1)

где λ – длина волны,

Ψ₀ – угол раскрыва зеркала.

Смещение облучателя из фокуса в направлении перпендикуляра к оси параболы широко используется в практике для управления диаграммой направленности параболической антенны. При этом обычно облучатель перемещается не перпендикулярно оси Z, а по дуге, радиус которой равен фокусному расстоянию.

При смещении облучателя вдоль фокальной оси (вдоль оси Z) также возникают нелинейные (преимущественно квадратичные) фазовые искажения поля в раскрыве антенны, которые приводят к расширению диаграммы направленности параболической антенны и исчезновению нулей на ней.

Диаграммы направленности реальных облучателей таковы, что не вся, излученная облучателем, энергия попадает на зеркало. Часть энергии облучателя проходит мимо зеркала, что увеличивает уровни боковых лепестков диаграммы направленности зеркальной антенны.

Коэффициент направленного действия (КНД) параболической антенны можно рассчитать по формуле (2.2).

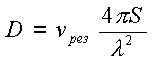, (2.2)

где S – площадь поверхности раскрыва;

ν_рез = νη₁ – результирующий КИП (коэффициент использования поверхности раскрыва) зеркальной антенны;

ν – КИП раскрыва зеркала (апертурный КИП), определяемый только амплитудным распределением в раскрыве (если раскрыв возбуждается синфазно);

η₁ = Р_Σ/ Р_ОБЛ- отношение мощности, излученной зеркалом, к мощности излученной облучателем (потери в зеркале здесь не учитываются).

Коэффициент усиления (КУ) G можно определить по формуле

G = η₂*D, (2.3)

где η₂ = Р_Σ / Р_ОБЛ;

Р _ОБЛ – мощность подведенная к облучателю.

Коэффициент η₂, который можно назвать КПД зеркальной антенны, учитывает тепловые потери энергии в облучателе, в элементах крепления облучателя, в краске, покрывающей внутреннюю поверхность зеркала и т.д.

Если при заданной форме зеркала (R₀/ƒ₀ = const) расширять диаграмму направленности облучателя, то облучение зеркала становиться более равномерным (апертурный КИП растет), что ведет к росту ν рез и КНД. Однако вместе с тем увеличивается доля энергии, проходящей мимо зеркала (уменьшается η₁), что уменьшает ν_рез и КНД.

При сужении диаграммы направленности облучателя возрастает неравномерность амплитудного распределения (уменьшается ν), при этом уменьшается ν_рез и КНД, но одновременно уменьшается переливание энергии через края зеркала (растет η₁), что вызывает увеличение ν_рез и КНД.

Два, противоположно действующих на КНД антенны, фактора при постоянной величине R₀/ƒ₀ или угла раскрыва зеркала (2Ψ₀) и при изменяемой ширине диаграммы направленности облучателя, определяют условия оптимального облучения зеркала, при котором КНД становится максимальным.

Для большинства, применяющихся на практике, облучателей оптимальное условие облучения зеркала выполняется, если диаграмма направленности облучателя обеспечивает уменьшение напряженности поля на краях зеркала (Е_КР) относительно напряженности поля у его вершины (Е₀) на 10 дБ, т.е. 20lg(Е_КР /Е₀) = -10 дБ или Е_КР /Е₀ = 0,316.

Диаграмма направленности параболической антенны определяется диаграммой направленности облучателя и формой зеркала (R₀ /f₀)