| На главную | Содержание учебника | Предыдущая <<<<<глава | Следующая глава>>>>> | Контрольные вопросы |
Звуковым полем называется пространство, в котором происходит распространение звуковых колебаний.
Представим излучатель звуковых колебаний в виде жесткого поршня, который помещен в отверстие бесконечно большой жесткой стены (рис .2.1).

Рассмотрим процесс возникновения звуковых колебаний в воздушной среде в правом полупространстве. Предположим, что поршень совершает периодические колебания вдоль некоторой оси Х. При движении поршня вправо он приводит в движение прилегающий к его поверхности слой частиц воздуха, уплотняя его. Давление в этом слое становится больше атмосферного и частицы перемещаются вправо, отклоняясь от своего положения равновесия и создавая уплотнение в следующем слое и т.д. Таким образом, фаза сжатия частиц распространяется в пространстве, удаляясь от излучателя, передаваясь от одного слоя к другому.
При достижении поршнем своего крайнего положения он начнет двигаться влево. При этом перед ним образуется разрежение частиц воздуха, давление в этой области станет меньше атмосферного и сюда устремятся частицы из прилегающего слоя. На том месте, где они перед этим находились, в свою очередь образуется область разрежения, куда устремятся частицы из соседнего слоя, образуя следующую область разрежения и т.д. В результате от поршня в пространстве будет распространяться фаза разрежения. Таким образом, колебания поршня вызывают во внешней среде возмущения в виде сгущения и разрежения частиц. При этом частицы, как и поршень, совершают периодические колебания относительно своего положения равновесия. Очевидно, что одному периоду колебаний (движения поршня вперед и назад) соответствует одно сгущение и одно разрежение.
Поскольку частицы совершают колебания вдоль некоторого направления их колебания называют продольными. Эти колебания распространяются от одних частиц воздуха к другим с определенной скоростью, называемой скоростью звука.
Скорость звука в воздухе при температуре 20°С и нормальном атмосферном давлении приблизительно равна 340 м/с .
Описанное выше волнообразное изменение плотности среды, вызванное звуковыми колебаниями называется звуковой волной. Направление, в котором распространяются звуковые колебания, называется звуковым лучом.
Поверхность, на которой расположены частицы среды, колеблющиеся с одинаковой фазой называется фронтом волны. Фронт всюду перпендикулярен направлению распространения волны , т.е. звуковым лучам .
Расстояние между соседними фронтами, находящимися в одинаковой фазе называется длиной волны.
Если период колебаний Т, скорость звука с и частота f , то длина волны
|
|
(2.1) |
Частоты звуковых колебаний, используемые в технике связи и вещания, лежат в пределах 20 - 20000 Гц. Соответственно длины звуковых волн имеют величину от 17 м до 1,7 см.
В физике давлением называется сила, приходящаяся на единицу поверхности тела. Она измеряется в Н/м2. Обозначим эту величину " p".
|
|
(2.2) |
где F–сила, действующая на тело;
S–поверхность, на которую действует сила.
Единица 1 Н/м2 названа паскалем – [ Па ].
Звуковым давлением называется разность между суммарным мгновенным значением давления в некоторой точке поля и атмосферным давлением.
|
p(t)=pS(t)-p0 |
(2.3) |
здесь P(t) –величина звукового давления;
pS(t)–суммарное мгновенное значение давления в некоторой точке поля;
p0 –атмосферное давление.
В области сжатия (сгущения) частиц среды pS(t) больше атмосферного и звуковое давление положительно. В области разрежения–отрицательно.
Измеряется звуковое давление также в Паскалях (система СИ). В прежней системе CGS звуковое давление имело размерность дина/см2, и называлась "бар" (1 Па=10 бар).
В акустике приходится иметь дело с величинами звукового давления, не превышающими по амплитуде 100 Па. Если учесть, что нормальное атмосферное давление составляет 1,01 ·105 Па, то становится ясным насколько малы значения звукового давления по сравнению с атмосферным.
В технических расчетах принято измерять звуковое давление не в амплитудных, а в эффективных значениях.
Колебательная скорость – это мгновенное значение скорости колебательного движения частиц среды при распространении в ней звуковой волны.
Нельзя путать эту величину со скоростью звука. Скорость звука–это скорость, с которой возбуждение передается от ближних к источнику частиц среды ко все более и более удаленным. Здесь же речь идет о скорости колебаний частиц относительно своей точки покоя.
Если смещение частицы среды относительно своей точки покоя x=xmejwt, то колебательная скорость
|
|
(2.4) |
В технических расчетах принято измерять колебательную скорость, как и давление, в эффективных значениях.
Звуковая мощность–это энергия, переносимая звуковой волной в единицу времени в направлении распространения звуковых волн через всю площадь фронта волны. Звуковая мощность по своей физической сущности является механической мощностью. Мощность, как известно, есть работа, произведенная за единицу времени. В электроакустике имеется в виду работа, которую совершает излучатель против силы, действующей на него со стороны среды.
|
|
(2.5) |
где P–звуковая мощность;
А–работа;
F–сила, действующая на излучатель со стороны среды;
x–смещение излучателя;
p–звуковое давление.
Интенсивность или сила звука–это поток звуковой энергии, проходящей в единицу времени через единицу поверхности фронта волны.
|
|
(2.6) |
где I–сила звука;
S–площадь фронта волны.
Плотность звуковой энергии–это среднее количество звуковой энергии, приходящееся на единицу объема. Обычно обозначается буквой e, ее размерность– [Дж/м3].
|
|
(2.7) |
де с–скорость звука.
Из предыдущего материала видно, что приведенные зависимости определяются соотношением двух величин: звукового давления p и колебательной скорости V. Определим, как они связаны между собой.
Выделим элементарный слой воздуха, ограниченный площадками dS (рис.2.2). Толщину слоя обозначим dx, предполагая, что звуковая волна распространяется вдоль некоторой оси x.
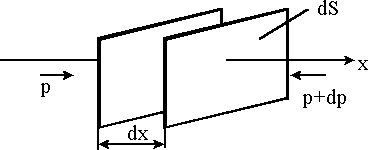
Предположим, что на выделенный слой воздуха слева действует давление p, справа p+dp. Соответственно силы, действующие на слой с обеих сторон, будут: F1=pdS; F2=(p+dp)dS.
Результирующая сила, которая сообщит слою ускорение, будет равна разности сил:
dF=F2-F1=dpdS
Согласно закону инерции эта сила должна быть равна силе инерции с обратным знаком: Fин=-am,
здесь  –ускорение;
–ускорение;
m=rdSdx – масса слоя воздуха;
r–плотность воздушной среды.
Таким образом, dF=Fин или 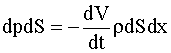
После сокращения на dS получаем:
|
|
(2.8) |
Таким образом, градиент давления, взятый с обратным знаком, равен произведению плотности среды на ускорение.
Эта зависимость позволяет установить связь между звуковым давлением и колебательной скоростью для волны любой формы.
По конфигурации фронта волны различают в частности волны плоские и шаровые, свойства которых необходимо рассмотреть подробно.
Плоской называется такая звуковая волна, фронт которой представляет собой плоскость, перпендикулярную направлению распространения волны. Звуковые лучи, которые должны быть перпендикулярны фронту волны, будут направлены в этом случае параллельно друг другу. Это указывает на то, что звуковая энергия не расходится в пространстве, а распространяется пучком, т.е. мы имеем случай направленного излучения.
Плоская волна может возникнуть в том случае, если размеры излучателя больше длины излучаемой волны. Это условие выполняется при работе громкоговорителя на верхних звуковых частотах. Плоскую волну можно создать искусственно, нагрузив громкоговоритель на трубу с жесткими стенками. Стенки трубы не дадут волне расходится даже, если размеры излучателя будут меньше длины волны.
Для установления свойств плоской волны определим связь между давлением и колебательной скоростью в ней. Представим излучатель в виде жесткого поршня, колеблющегося вдоль некоторой оси х и излучающего плоскую волну.
Звуковое поле в точке у поверхности источника, излучающего гармоническое колебание, определится как: p=pmejwt.
В точке на некотором удалении от излучателя давление запоздает по фазе на время
![]() (2.9) и станет
равным p=pmejw(t-t).
(2.9) и станет
равным p=pmejw(t-t).
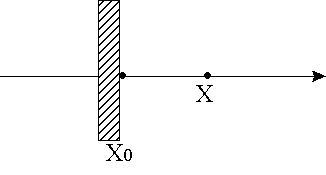
Х0–координата точки звукового поля у поверхности излучателя;
Х–координата точки на некотором удалении от излучателя.
Введем понятие волнового числа.
|
|
(2.10) |
Физический смысл волнового числа – изменение фазы колебаний на единицу расстояния при распространении звуковой волны.
Чтобы определить, как изменится фаза колебания при прохождении волной некоторого
расстояния Х, необходимо умножить волновое число на расстояние: j=kx.
Так, если волна прошла путь x=0.5l,
то фаза колебания изменится на угол ![]() .
.
Так как ![]() , то согласно (2.9)
и (2.10) получим wt=kx
, то согласно (2.9)
и (2.10) получим wt=kx
Выражение для звукового давления в точке с произвольной координатой Х теперь можно записать в более удобной форме:
|
p=pmej(wt-kx). |
(2.11) |
Для получения выражения колебательной скорости используем
уравнение движения (2.8.), в соответствие с которым 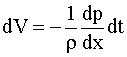 .
.
Так как p=pmej(wt-kx), то
|
|
Таким образом:
|
|
|
|
|
Поскольку p=pmej(wt-kx)
и 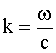 , то
, то 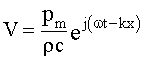 или
или
|
|
(2.12) |
Полученная зависимость между давлением и колебательной скоростью определяет свойства плоской волны.
Величина ![]() в знаменателе формулы колебательной скорости называется удельным акустическим
сопротивлением.
в знаменателе формулы колебательной скорости называется удельным акустическим
сопротивлением.
Обозначим эту величину как ![]() .
.
Для технических расчетов принято
считать 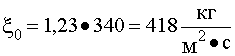
Физически x0–это то сопротивление, которое оказывает среда единице поверхности излучателя.
Если эту величину умножить на всю поверхность излучателя, то получим полное сопротивление реакции среды, иначе говоря, сопротивление излучения.
|
|
(2.13) |
Так как в плоской волне отсутствует сдвиг по фазе между давлением и колебательной скоростью, то сопротивление излучения является активной величиной.
Запишем в несколько ином виде выражение для силы звука (2.6)
|
|
(2.14) |
Если перейти к амплитудным значениям получим
|
|
(2.15) |
Излучаемая источником акустическая мощность активна:
|
P=IS=V2x0S=V2xR |
(2.16) |
Волна называется шаровой, если энергия от источника распространяется равномерно во всех направлениях и фронт волны имеет сферическую форму. Идеальным источником шаровых волн является пульсирующий шар–сфера с радиусом R, поверхность которой совершает малые радиальные колебания синфазные и одинаковые по амплитуде (рис. 2.4).
Как видно из рисунка звуковые лучи в шаровой волне совпадают с радиусами сферы.
Если P–излучаемая мощность; S1–площадь фронта волны на расстоянии r1 от излучателя, то сила звука I1 на поверхности фронта волны:
|
|
На расстоянии r2 сила звука будет:
|
|
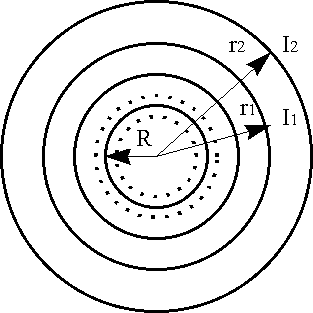
Так как r2 > r1 , то и I2<I1
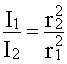
Из этих выражений видно, что сила звука в шаровой волне убывает обратно пропорционально квадрату расстояния от излучателя.
Поскольку энергия расходится во всех направлениях, положение некоторой точки
в пространстве придется теперь определять тремя координатами в декартовой системе
X,Y,Z и выражения для давления получается при этом достаточно громоздким.
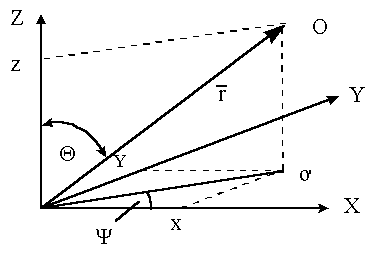
Этого можно избежать, если перейти к полярной системе координат. В этой системе положение точки в пространстве определяется тремя величинами: величиной радиуса-вектора r, азимутом Y и углом Q, дополнительным до широты.
Поскольку фронт волны представляет собой сферу, то при любых значениях Y и Q все точки, лежащие на поверхности такого фронта с радиусом r будут колебаться синфазно с одинаковыми амплитудами. Следовательно, амплитуда и фаза колебаний частиц в шаровой волне будут зависеть только от расстояния до источника звука.
В таком случае выражение для звукового давления будет аналогично выражению для плоской волны
|
p=pmej(wt-kr) |
(2.16) |
Определим амплитуду давления в сферической волне. Интенсивность звука :
|
|
где S–площадь фронта волны, то есть сферы.
С другой стороны, согласно (2.15) 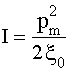 . Приравнивая
эти выражения для силы звука, получим
. Приравнивая
эти выражения для силы звука, получим 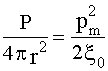 , откуда
, откуда
|
|
Обозначим 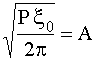 , тогда
, тогда
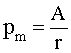 , откуда
следует, что в шаровой волне звуковое давление убывает обратно пропорционально
расстоянию.
, откуда
следует, что в шаровой волне звуковое давление убывает обратно пропорционально
расстоянию.
Таким образом, значение давления в произвольно взятой точке пространства в шаровой волне на расстоянии r от излучателя определяется как:
|
|
(2.17) |
Определим выражение для колебательной скорости, используя уравнение
движения (2.8) т.е. ![]() , откуда
, откуда
![]()
|
|
После упрощения получаем
|
|
|
|
|
|
|
|
Учитывая, что 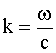 , получаем
, получаем
|
|
|
|
|
(2.18) |
|
|
Выразим комплексное число ![]() в показательной
форме. Напомним , что
в показательной
форме. Напомним , что ![]() .
.
В нашем случае ![]() .
.
Таким образом, ![]() (2.19)
(2.19)
Выражение же для колебательной скорости примет вид:
|
|
(2.20) |
Последний множитель показывает, что колебательная скорость отстает от давления на угол a.
Полученные соотношения для звукового давления и колебательной скорости определяют свойства шаровой волны.
1. Амплитуда давления и колебательной скорости убывают с расстоянием от излучателя. Чем больше расстояние, тем больше площадь фронта волны, тем меньше приходится звуковой энергии на единицу площади. Характер изменения давления и колебательной скорости с расстоянием показан на рис.2.6.
Из рисунка видно, что окружающее источник звука пространство можно условно разделить на две характерные зоны. Ближняя зона–пространство непосредственно примыкающее к излучателю и заключенное в